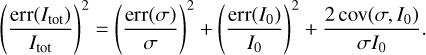Emission line variability of young 10–30 MJup companions

D. Demars; M. Bonnefoy; C. Dougados; Y. Aoyama; T. Thanathibodee; G.-D. Marleau; P. Tremblin; P. Delorme; P. Palma-Bifani; S. Petrus; B. P. Bowler; G. Chauvin; A.-M. Lagrange

doi:10.1051/0004-6361/202346221

Home

All issues

Volume 676 (August 2023)

A&A, 676 (2023) A123

Full HTML

Open Access

Issue		A&A Volume 676, August 2023


Article Number		A123
Number of page(s)		22
Section		Planets and planetary systems
DOI		https://doi.org/10.1051/0004-6361/202346221
Published online		21 August 2023

A&A 676, A123 (2023)

Emission line variability of young 10–30 M_Jup companions

I. The case of GQ Lup b and GSC 06214-00210 b^★,^★★

D. Demars¹, M. Bonnefoy¹, C. Dougados¹, Y. Aoyama²^,3^,4, T. Thanathibodee⁵^,6, G.-D. Marleau⁷^,8^,9^,10, P. Tremblin¹¹, P. Delorme¹, P. Palma-Bifani¹², S. Petrus¹³^,14, B. P. Bowler¹⁵, G. Chauvin¹²^,1 and A.-M. Lagrange¹⁶^,1

¹ Univ. Grenoble Alpes, CNRS, IPAG, 38000 Grenoble, France
e-mail: dorian.demars@univ-grenoble-alpes.fr
² Institute for Advanced Study, Tsinghua University, Beijing 100084, PR China
³ Department of Astronomy, Tsinghua University, Beijing 100084, PR China
⁴ Department of Earth and Planetary Science, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-0033, Japan
⁵ Department of Astronomy, University of Michigan, 1085 S. University Ave., Ann Arbor, MI 48109, USA
⁶ Institute for Astrophysical Research and Department of Astronomy, Boston University, 725 Commonwealth Ave., Boston, MA 02215, USA
⁷ Fakultät für Physik, Universität Duisburg-Essen, Lotharstraße 1, 47057 Duisburg, Germany
⁸ Institut für Astronomie und Astrophysik, Universität Tübingen, Auf der Morgenstelle 10, 72076 Tübingen, Germany
⁹ Physikalisches Institut, Universität Bern, Gesellschaftsstr. 6, 3012 Bern, Switzerland
¹⁰ Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
¹¹ Maison de la Simulation, CEA, CNRS, Univ. Paris-Sud, UVSQ, Université Paris-Saclay, 91191 Gif-sur-Yvette, France
¹² Université Côte d’Azur, OCA, Lagrange CNRS, 06304 Nice, France
¹³ Instituto de Física y Astronomía, Facultad de Ciencias, Universidad de Valparaíso, Av. Gran Bretaña 1111, Valparaíso, Chile
¹⁴ Núcleo Milenio Formación Planetaria – NPF, Universidad de Valparaíso, Av. Gran Bretaña 1111, Valparaíso, Chile
¹⁵ Department of Astronomy, The University of Texas at Austin, 2515 Speedway, Stop C1400, Austin, TX 78712, USA
¹⁶ LESIA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, UPMC Univ. Paris 06, Univ. Paris Diderot, Sorbonne Paris Cité, 5 place Jules Janssen, 92195 Meudon, France

Received: 22 February 2023
Accepted: 26 April 2023

Abstract

Context. Emission lines that are indicative of active accretion have been observed for a number of low-mass companions (M < 30 M_Jup) to stars. Line variability is ubiquitous on stellar accretors, but it has never been characterized in detail for low-mass companions. Such characterizations can offer insights into the accretion mechanism at play.

Aims. We aim to characterize the short-to-long-term H I Paschen β emission line variability of two 10 to 30 M_Jup companions on wide orbits: GQ Lup b and GSC 06214-00210 b. We also aim to clarify their accretion mechanisms.

Methods. We used J-band observations at R = 1800–2360, obtained with VLT/SINFONI in 2017, to record time-series investigations of the hours-to-weeks variability of the H I Paschen β emission line (1.282 µm). Contrary to H_∝, it should be less affected by chromospheric activity contamination. The photospheric emission was analyzed at each epoch and removed with the ForMoSA forward-modeling tool, using new grids of ATMO models exploring different C/O and [M/H] values. The time series of line profiles and intensities were compared to those of more massive accretors and to predictions from the latest magnetospheric accretion and shock models. To complement these results, we also re-investigated archival spectroscopic observations at near-infrared wavelengths of each target to increase the time frame up to a decade and to build a more comprehensive understanding of the variability processes at play.

Results. For GQ Lup b, we find line variability on timescales of several months to decades, whereas it is within the acceptable noise levels on shorter timescales. For GSC 06214-00210 b, we find line variability on timescales of tens of minutes all the way up to a decade. The line profiles of GSC 06214-00210 b are partially resolved in at least one epoch. Both objects show H I Paschen β flux variability that is moderate (<50%), on timescales that are below their rotation period, and that is more significant on longer timescales (up to ~1000% on decade-long timescales). This behavior resembles that of classical T Tauri stars. The line profiles of GQ Lup b are blue-shifted and can only be reproduced by magnetospheric accretion models, while those of GSC 06214-00210 b are fairly well reproduced by both magnetospheric accretion and shock models, except for one epoch for which the shock model is highly favored. The companions have C/O values broadly consistent with solar values.

Conclusions. While magnetospheric accretion is favored for GQ Lup b, higher resolution (R > 10 000) observations are required to disentangle the two (non-exclusive) emitting mechanisms. The similar variability behavior observed in these low mass companions and in classical T Tauri stars may support similar accretion mechanisms. The high amplitude of variability on timescales of over a month and longer that is found for both objects could be key to explaining the low yield of H_∝ imaging campaigns.

Key words: planets and satellites: formation / planets and satellites: individual: GQ Lup b / planets and satellites: individual: GSC 06214-00210 b / accretion, accretion disks

^★

Individual spectra are only available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/676/A123

^★★

Based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere under ESO program 099.C-0760.

© The Authors 2023

Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Gas accretion on giant planets and brown-dwarf companions undergoing formation processes is a critical step in determining their early physical evolution and internal structure (e.g., Marley et al. 2007; Baraffe et al. 2009; Cumming et al. 2018), as well as the dissipation of their angular momentum (e.g., Bryan et al. 2018; Batygin 2018). It may also drive disk-planet migration (e.g., Pierens & Raymond 2016) as well as the formation and water content of exo-moons (e.g., Heller & Pudritz 2015), which can potentially harbor life.

The theoretical understanding of the accretion processes is still in its infancy. Companions are expected to accrete part of their mass from circumplanetary disks (hereafter CPDs, Miki 1982) that form around them. A boundary-layer accretion is assumed to develop if the CPD hits the planet surface (e.g., Dong et al. 2021; Fu et al. 2023, and ref. therein), producing a shock within a thin boundary at the disk-planet interface. The most recent radiative-hydrodynamic (RHD) simulations of planets embedded in CPDs predict that part of the mass should fall onto the planet embryo from the circumstellar disk via high-altitude flows and producing an accretion shock at the CPD surface or directly on the planet surface (e.g., Szulágyi et al. 2014, or Fig. 1 in Szulágyi & Ercolano 2020 for a representation).

The picture of accretion may not, in fact, be fully captured by the RHD approach. The strength of the dipole component of Jupiter’s current magnetic field is only about 4 G (Smith et al. 1974), but the interiors of young exoplanets and low-mass brown dwarfs are predicted to be strongly convective and ionized, and so, they should be able to fuel ~kG magnetic fields (Reiners & Christensen 2010) that are sufficient to affect the gas flow (Cridland 2018) and truncate the CPD (Fendt 2003). It thus remains to be seen to what extent the magnetospheric accretion framework applies in the planetary-mass regime.

The heated gas, either at the accretion shock or within the funnels, produces a set of emission lines from the UV to the NIR whose intensity and spectral profiles can start to be predicted by accretion models (e.g., Thanathibodee et al. 2019; Szulágyi & Ercolano 2020; Aoyama et al. 2020; Marleau & Aoyama 2022). These lines have now been found on a handful of young directly-imaged young companions with mass below ~30 M_Jup (TWA 5 B, GQ Lup B, CT Cha B, USco CTIO 108 B, DH Tau B, GSC 06214-00210 B, SR 12 C, PDS 70 b and c, 2M0249c, Delorme 1(AB)b, HIP 77900B, HIP 78530B, USco 161031.9-16191305B, and YSES 1b; Neuhäuser et al. 2000; Seifahrt et al. 2007; Schmidt et al. 2008; Béjar et al. 2008; Bonnefoy et al. 2014; Bowler et al. 2011; Santamaría-Miranda et al. 2018, 2019; Wagner et al. 2018; Zhou et al. 2014; Haffert et al. 2019; Chinchilla et al. 2021; Petrus et al. 2020; Zhang et al. 2021) and are estimated to be frequent (~50% frequency, Bowler et al. 2017) below 15 Myr. These companions are found in systems spanning a wide range of ages (1–40 Myr) and with diverse architectures – within the cavity of circumstellar disks, in hierarchical systems, or orbiting single or binary stars of various masses.

All the line detections have also been fortuitous and follow up-studies are starting to improve the understanding of their origin and to constrain the accretion models. Zhou et al. (2014) and Zhou et al. (2021) recorded measurements of the shock emission of four companions in the UV (GQ Lup b, GSC 0621400210 b, DH Tau b and PDS 70 b, all within 10–30 M_Jup and < 15 Myr). They were able to measure accretion rates in the range 10⁻⁹–10⁻¹¹ M_⊙ yr⁻¹. They also argued that a significant fraction of the energy released at the accretion shock is reprocessed at H_∝. Line ratio measurements on Delorme 1 (AB)b (~14 M_Jup , ~40 Myr, Delorme et al. 2013) at near-infrared wavelengths (Betti et al. 2022b,a) were found to be compatible with non-LTE accretion-shock models for planets (Aoyama et al. 2018). Highresolution observations of the Balmer lines of Delorme 1 (AB)b in the UV show line profiles suggestive of magnetospheric accretion operating on that 40 Myr old companion (Ringqvist et al. 2023). Constraints on the H_α/H_β line-ratio of PDS 70 b indicate significant extinction in the line-of-sight due to surrounding dust or a CPD (Hashimoto et al. 2020).

Variability among the emission lines is observed across a wide stellar mass spectrum (for a review, see Fischer et al. 2022) and it traces episodic variability in the accretion and ejection over the course of the stars evolution. Non-steady accretion is predicted to occur on low-mass companions and has a significant impact on their early physical evolution (Baraffe et al. 2009; Cumming et al. 2018) as well as our ability to detect them (Brittain et al. 2020). Global hydrodynamic and magneto-hydrodynamic simulations of protoplanets embedded in a circumstellar disk indicate modulations on decades-long timescales (see Gressel et al. 2013; Szulágyi & Ercolano 2020). Instabilities or dead zones developing through the CPD (Lubow & Martin 2012; Zhu et al. 2016) are expected to modulate the accretion flow on Keplerian timescales (from months to years). If magnetospheric accretion is in operation, then hot spots and funnel flows should produce variability of the emission lines along the object rotation period as it does for to stars (e.g., Sicilia-Aguilar et al. 2015). A variable extinction in the line of sight should modulate the line emission further (Szulágyi & Ercolano 2020; Marleau et al. 2022).

The study of the emission line variability timescales and amplitude thus offers an opportunity to probe both the accretion mechanism and the effect of the local environment of young companions. Line variability has been detected on a timescale of about 1 yr on GQ Lup b and GSC 06214-00210 b (see below). Wolff et al. (2017) found the Pa_β line of DH Tau b (a ~1Myr old ~15 M_Jup companion, Itoh et al. 2005) to disappear within ~5 weeks. Eriksson et al. (2020) found the H_α line of Delorme 1(AB)b (a 30–40 Myr old, ~ 14 M_Jup companion Delorme et al. 2013) to vary over a few hours. Zhou et al. (2021) reported several measurements of the H_α line of PDS 70 b over timescales of days to months, and an upper limit of 30% for the variability.

In this paper, we focus on the spectroscopic monitoring ofthe Paβ emission line of two low-mass companions, GQ Lup b and GSC 06214-00210 b, with previously reported line variability over the course of a semester (Lavigne et al. 2009). We combine these observations with archival data to probe line variability for timescales ranging from several minutes to decades. The Pa_β line is well adapted to a monitoring with standard adaptive-optics fed instruments from the ground and is more intense above the continuum than the Br_γ line in young accreting late-type objects (Natta et al. 2004; Betti et al. 2022b). Moreover, it is known to be less affected by chromospheric activity than H_α in the stellar and sub-stellar mass regimes (Natta et al. 2004; Antoniucci et al. 2011; Rigliaco et al. 2012; Manara et al. 2013).

We present a compendium of the presently known properties of the two objects in Sect. 2. The observations of GQ Lup b and GSC 06214-00210 b are detailed in Sect. 3, followed by the data extraction strategy in Sect. 4. The photospheric parameters, and emission line variability (timescale, intensity, profiles) are presented in Sect. 5 and compared to models. We analyze how the Paβ line behavior relates to other accretors, contextualize possible line profile variations, and discuss the implication of line variability for the detectability of protoplanets in Sect. 6. Our results are summarized in Sect. 7.

2 Information on targets

2.1 GQ Lup system

GQ Lup b is a 10–40 M_Jup companion resolved by Neuhäuser et al. (2005) at ~0.7″ (~108 au at 154.10 ± 0.69 pc; Gaia Collaboration 2022) from a 2–5 Myr old K7Ve-type T Tauri star (M_★ = 1.02 ± 0.05 M_⊙; MacGregor et al. 2017; Gaia Collaboration 2022) that is a member of the Lupus I cloud (Herbig 1977). The star is surrounded by a circumstellar disk inclined at 60° showing spiral structures (e.g., van Holstein et al. 2021) in scattered light up to 0.84” (129 au), while the disk shows smaller extension at millimeter and sub-millimeter wavelengths both in the continuum and ¹²CO (20–46 au; MacGregor et al. 2017; Wu et al. 2017b; Long et al. 2020). Long et al. (2020) report a gap at 10 au in the dust component of the disk at millimeter wavelengths, which might be carved by a planet at this separation. It is unclear whether this possible planet could explain the significant radial-velocity variation of GQ Lup A noticed by Donati et al. (2012) over a 2-yr time span. The star has a reported spin axis inclination of ~30^° misaligned with the disk and is experiencing dominantly pole-ward magnetospheric accretion that produces a set of emission lines, including Pa_β (Broeg et al. 2007; Donati et al. 2012; Frasca et al. 2017; Seifahrt et al. 2007).

GQ Lup b is also known to display a bright H_α emission line found at four epochs spanning two decades: 1) on April 10, 1999 HST/WFPC2 wide-field imaging data (F606W filter; λ_cen = 605.4, FWHM = 220.5 nm; Marois et al. 2007); 2) in HST/WFC3-UVIS2 data (Zhou et al. 2014) acquired on February 25, 2012 with a narrower filter (F656N, λ_cen = 656.2 nm, FWHM = 187.1 nm); 3) on ground-based Magellan/MagAO imaging (Wu et al. 2017b) with a custom H_α filter on April 16, 2015 (λ_cen = 656.0 nm, FWHM = 6.3 nm); and 4) with VLT/MUSE medium-resolution (R = 2516) optical spectroscopy on April 19, 2019 (Stolker et al. 2021). Wu et al. (2017b) has argued that the line could be showing variability, but the different instrumental setup stands in the way of a robust homogeneous comparison of the reported H_α fluxes. The MUSE spectrum shows the Ca II triplet in emission (λ8498, 8542, 8662 Å), but no H_β line.

The companion displays a Pa_β emission line first seen on September 18, 2006 (EW = -3.83 ± 0.12 Å) from data acquired with VLT/SINFONI (Seifahrt et al. 2007) at R = 2360. The line is also detected in Gemini/NIFS data (R ~ 5000) collected on May 30, 2017, but at a significantly weaker flux level (EW = -0.46 ± 0.08 Å), supporting the observed variability at H_α. The No Br_γ emission line is reported in K-band spectra obtained at four epochs (Neuhäuser et al. 2005; McElwain et al. 2007; Seifahrt et al. 2007; Lavigne et al. 2009).

The set of available near-infrared spectra revealed an inconsistency in the spectral slope of the SINFONI spectrum of Seifahrt et al. (2007), which we re-investigate in Sect. 4. The compendium of 0.6–5 µm spectro-photometry on the companion allowed Stolker et al. (2021) to derive T_eff of 2700 K consistent with the optical spectral type of M9 (e.g., Luhman et al. 2003) and the luminosity-based “hot-start” mass of 30 M_Jup. The analysis also confirms a significant in-line extinction (Av = 2.3 mag) and an excess emission long-wards of 2.5 µm that could be caused by infalling material from the circumplanetary disk or a CPD. ALMA observations have failed to detect this CPD thus far (MacGregor et al. 2017; Wu et al. 2017b) and no intrinsic linear polarization is detected at the location of the companion (van Holstein et al. 2021). High-resolution spectroscopy (VLT/CRIRES, R ~ 100 000) of GQ Lup b centered on the ¹²CO overtone at K-band allowed for the measurement of a projected rotational velocity (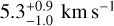 ${5.3}_{- 1.0}^{+ 0.9} km s^{- 1}$ $5.3_{ - 1.0}^{ + 0.9}\,{\rm{km}}\,{{\rm{s}}^{ - 1}}$ ; Schwarz et al. 2016), which is in the lower range of values measured on young 10–50 M_Jup objects (Kurosawa et al. 2006; Bryan et al. 2018, 2020), setting an upper limit on the rotation period of 82 h.

GQ Lup b’s orbital motion has been monitored since its original discovery (Ginski et al. 2014; Schwarz et al. 2016) and now it covers ~1% of its estimated orbit. Tentative constraints on the mutual inclination with the circumstellar disk indicate the companion might be on a polar orbit (Stolker et al. 2021) with a semi-major axis of 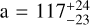$a = 117_{- 23}^{+ 24}$ ${\rm{a}} = 117_{ - 23}^{ + 24}$ au and low eccentricity possibly crossing the circumstellar disk.

A second accreting low-mass stellar companion (2MASS 15491331-3539118; projected separation ~2400 au; M ~ 0.15 M_⊙, GQ Lup C) was recently found to be bound to the star. GQ Lup c bears its own detached disk that is roughly aligned with the one of the primary star and with the large-scale dust filament of Lupus I containing GQ Lup (Alcalá et al. 2020; Lazzoni et al. 2020).

In summary, this system shows companions of different masses and offers a unique means to better understand the early formation and dynamical evolution of planetary systems.

2.2 GSC 06214-00210 system

GSC 06214-00210 b (hereafter, GSC06214b) is a 14.5 ± 2 Mj_up co-moving companion (Kraus et al. 2008; Ireland et al. 2011; Pearce et al. 2019) resolved on a wide orbit (2.2″ separation, corresponding to a projected physical separation of 240 au at 108 . 8 ± 0. 3 pc; Gaia Collaboration 2022) from the weak-line T Tauri star GSC 06214-00210 (K5 ± 1; M_★ = 0.80 ± 0.11 M_⊙; Bowler et al. 2014; Pearce et al. 2019).

The star is reported to be a member of the Upper Scorpius sub-group of the Scorpius-Centaurus (Sco-Cen) OB association (Preibisch et al. 1998), with a median age of ~10 Myr (Pecaut et al. 2012; Feiden 2016). We notice that the kinematic analysis tool BANYAN Σ (Gagné et al. 2018b) now suggests a possible alternative membership (58.8% probability) to the older Upper-Scorpius Centaurus (UCL) sub-group of Sco-Cen (16 Myr; Pecaut et al. 2012) based on the Gaia-DR3 astrometry. This possible membership to UCL is better consistent with the revised isochronal age of 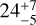$24_{- 5}^{+ 7}$ $24_{ - 5}^{ + 7}$ Myr reported in Pearce et al. (2019) and based on the Baraffe et al. (2015) evolutionary tracks and their 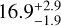${16.9}_{- 1.9}^{+ 2.9}$ $16.9_{ - 1.9}^{ + 2.9}$ Myr age inferred using the magnetized evolutionary models of Feiden (2016) and a prior on the age of Sco-Cen. We adopted this latter value in our study.

The star is known to have no reported excess emission, a weak H_α emission line, and no Pa_β emission (Preibisch et al. 1998; Bowler et al. 2011). Conversely, medium-resolution 1.17–1.83 µm spectroscopy (R = 3800) of the system with OSIRIS at Keck in 2010 (Bowler et al. 2011) revealed a bright Pa_β emission line (EW= –11.4 ± 0.3 Å) on GSC06214b. The HST/WFC3 photometry also reveals the companion to emit at H_α (Zhou et al. 2014). The companion has a continuum excess emission noticeable at K- and L′- bands (1.8–4.2 µm; Bowler et al. 2011; van Holstein et al. 2021), which indicates it is likely to bear a CPD. The CPD has remained elusive at sub-millimeter wavelengths (Bowler et al. 2015; Wu et al. 2017a) indicative of a compact detached disk. However, a likely intrinsic polarization signal (van Holstein et al. 2021) was detected with VLT/SPHERE. van Holstein et al. (2021) argued that the CPD must have an inclination of ~48º to explain the measured degree of polarization. They used the possible constraints on the CPD inclination and the measured rotational velocity of 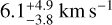${6.1}_{- 3.8}^{+ 4.9} km s^{- 1}$ $6.1_{ - 3.8}^{ + 4.9}\,{\rm{km}}\,{{\rm{s}}^{ - 1}}$ of GSC06214b (Bryan et al. 2018) to narrow down the companion rotation period to 22–77 h.

An additional 0.9–2.5 µm spectrum of GSC06214b was obtained with GNIRS on June 23, 2011 by Lachapelle et al. (2015), with a resolution that is lower than that of OSIRIS (R ~ 1000). It shows a weaker Paβ emission (EW = -4.4 ± 0.5 Å) than in Bowler et al. (2011) and a Br_γ emission line (EW = −0.24 ± 0.05 Å), making GSC06214b the third companion with mass below 20 M_Jup to display this line (Zhang et al. 2021; Betti et al. 2022b). K-band (1.965–2.381 µm) OSIRIS spectra obtained on June 26, 2012 at R = 3800 do not show the reported Br_γ line. Bryan et al. (2018) do not mention the detection of this line in their R = 25 000 Keck/NIRSPEC spectrum (2.03–2.38 µm) of the target obtained on June 3, 2015 either. But this line was detected again in archival VLT/SINFONI spectra (R ~ 5000) obtained on May 28, 2014 and July 07, 2014 (Palma-Bifani et al., in prep.), further hinting at a significant year-to-year variability for the accretion lines on that companion. All sets of near-infrared spectra allow for this companion to be classified as an M9-M9.5 low-gravity object (Lavigne et al. 2009; Bowler et al. 2014). GSC06214b offers the opportunity to probe the accretion processes at the Deuterium-burning boundary in a more evolved system, thus complementing the analysis of GQ Lup b.

3 Observations and data reduction

3.1 Monitoring sequences with VLT/SINFONI

We monitored GQ Lup b and GSC06214b with the Integral Field Spectrograph (IFS) SINFONI. SINFONI is a now decommissioned instrument previously installed at VLT/UT4 Cassegrain focus and composed of a custom adaptive optics module (MACAO) feeding an IFS (SPIFFI). SPIFFI splits the field-of-view into 32 horizontal slices (slitlets) and re-arranges them to form a pseudo-slit that is dispersed by a grating on a 2k × 2k HAWAII-2RG detector (Eisenhauer et al. 2003; Bonnet et al. 2004). The instrument was operated with pre-optics and gratings in the J-band (1.1–1.35 µm). For GQ Lup b, the setup provided a 0.8” square field of view (FoV) composed of 12.5 × 25 mas spaxels, with a resolving power of 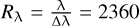$R_{λ} = \frac{λ}{Δλ} = 2360$ ${R_{\rm{\lambda }}} = {{\rm{\lambda }} \over {{\rm{\Delta \lambda }}}} = 2360$ . For GSC06214b, the setup provided a 3.2” square field of view (FoV) composed of 50 × l00 mas spaxels, with a resolving power of $R_{λ} = \frac{λ}{Δλ} = 1800$ ${R_{\rm{\lambda }}} = {{\rm{\lambda }} \over {{\rm{\Delta \lambda }}}} = 1800$ . They translate into line spread function (LSF) widths of 127 and 167 km s⁻¹ for GQ Lup b and GSC06214b, respectively.

MACAO used the host stars for wavefront sensing. The derotator at the Cassegrain focus was used to align the star and companions horizontally in the FoV at acquisition. A telescope offset was then applied to place the host stars PSF cores outside of the FoV and allow for deeper exposures. Small additional dithering were applied along the vertical direction of the FoV in-between each exposure to ensure that the companion signal did not fall all the time on bad pixels. A blank-sky exposure (with identical DIT) was performed at the end of the dithering sequence to ensure a proper removal of the OH- emission lines and thermal background. We then moved the star back in the FoV and recorded an additional short-exposure to record a PSF, to be used for calibration purposes.

GSC06214b was observed on April 25, May 4, June 1, and August 18, 2017 as part of our program (099.C-0760). GQ Lup b was observed on April 25, 30, 2017 and June 1, 2017 as part of the same program (UT dates). We also decided to re-process SINFONI data of GQ Lup b obtained on 2006-09-18 (program 077.C-0264) and presented in Seifahrt et al. (2007) for consistency and given that the published SINFONI spectrum has been shown to be discrepant with respect to other studies (McElwain et al. 2007; Lavigne et al. 2009). These observations used the same setup and followed an identical data-extraction strategy as for the 2017 observations. The log of observations is detailed in Table 1.

3.2 SINFONI cube reconstruction and calibration

SINFONI records bi-dimensional raw frames of the 32 dispersed slitlets. We used the Toolkit for Exoplanet deTection and chaRacterization with IfS (hereafter TExTRIS; Petrus et al. 2021, Bonnefoy et al., in prep.) to correct them for any static noise caused by the detector electronics (Bonnefoy et al. 2014).

The SINFONI data handling pipeline v3.0.0 (Abuter et al. 2006) was then used to reconstruct calibrated data cubes encoding the spatial and spectral dimensions (X, Y, λ) from these raw data. The pipeline uses calibration frames obtained at day time to apply basic cosmetic steps on the raw frames and correct them from the distortion introduced by optical elements and the detector. It identifies the position of slitlets on the raw frames and builds a reference 2D map associating the pixels to given wavelengths. The sky emission was evaluated and removed through the field subtracting cubes of reconstructed exposures on sky. Sky OH- emission lines residuals were then evaluated and subtracted using the method of Davies (2007). Because residuals hot/cosmics pixels were found in the cubes, they were corrected for by using the LACOSMIC Python package on each individual wavelength frame (van Dokkum 2001).

The wavelength solution relies on day-time calibration frames obtained with an Argon lamp and that has proven to be inaccurate on other datasets (Petrus et al. 2021; Zhang et al. 2021). We therefore improved the pipeline wavelength calibration with routines from TExTRIS, comparing the many telluric absorption lines contained in each spaxel to a model generated for the observing conditions using the ESO Skycalc tool (Noll et al. 2012; Jones et al. 2013). The method is applicable whenever the spaxels contain enough stellar light to infer the telluric absorptions. We evaluated the shifts in the wavelength interval 1.1–1.3 µm using cross-correlations of spaxels with a signal-to-noise ratio (S/N) above 10 at Pa_β. A master median-combined map of wavelength shift was then created and each individual cube was corrected from the median of the shifts of individual spaxels meeting the S/N criterion. The corrected wavelength shifts at each epochs are reported in Table 1, for an average wavelength calibration uncertainty of ~0.2 Å and ~0.3 Å for GQ Lup b and GSC06214b, respectively. Because of the relatively low S/N in the science target cubes, we used the wavelength solution found with the telluric standard stars (relying on the same original calibration as the science target) as the solution for the whole sequence.

3.3 New investigation of Keck/OSIRIS data

In the analysis, we also included the individual spectra of GSC06214b obtained on July 9, 2010 with the OH-Suppressing Infrared Imaging Spectrograph (OSIRIS; Larkin et al. 2006) mounted on Keck II. OSIRIS is a lenslet-based IFS operated with the Keck adaptive optics system. The instrument produced data cubes sampling a rectangular FoV (0.8 × 3.2″) with 0.05 × 0.05″ spaxels. The Jbb band grating provided 1.18–1.416 µm spectra at R ~ 3800. Eight 5-min long exposures were recorded. The stacked data cubes are presented in Bowler et al. (2011) and the companion is sufficiently separated from the star to directly extract its spectrum within a circular aperture. The data analysis is described in more detail in Bowler et al. (2011). Here, we re-analyzed the individual data cubes in an attempt to detect the Paβ variability from one exposure to the next.

4 Spectral extraction

4.1 Halo removal

Both GQ Lup b and GSC06214b spectra are contaminated by the PSF wings of the primary stars located outside of the FoV. The data cubes obtained at the end of each sequence of observations with the host stars in the FoV do not probe the extended wings of the PSF and therefore do not allow for a direct subtraction of the contamination. Therefore, we had to develop a specific procedure (described below) that was applied to each individual SINFONI data cube on both targets.

Prior to the halo removal, the cube rectangular spaxels were linearly interpolated to produce a regular spatial sampling of 12.5 mas in the horizontal and vertical directions. The contamination was then evaluated and corrected in each individual frame of the data cubes, with a CLEAN-like algorithm (Högbom 1974). The algorithm fits a two-component flux model made up of: (i) a third-order bi-dimensional gradient, approximating the primary star PSF wings and (ii) a PSF model placed at the companion location and scaled to the companion’s flux. The latter step requires the definition of a PSF model. We used the primary star data cubes (normalized to 1) for that purpose in the 2017 data. Data cubes of the primary star were not available in the 2006 data and we chose to use those corresponding to the telluric standard star instead. The two flux components were successively fitted and subtracted from the original frames, for a total of four iterations, which is a trade-off between 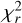$χ_{r}^{2}$ $\chi _r^2$ and S/N optimization. See Fig. 1 for a visual representation and Fig. A.1 for residuals.

The host star gradient subtraction allows us to subtract the large-scale structures but cannot remove more complex features such as the diffraction pattern caused by the telescope spiders. This component is most important on GQ Lup b and was then approximated as a 1-day Gaussian profile in the direction perpendicular to the spider axis and subtracted in the gradient-subtracted cubes.

SINFONI shows a static dark horizontal area in the lower half part of all data cubes (see Fig. 1) likely caused by some persistence appearing in the lamp flat-fields taken in the day time. This was discovered during data reduction and affected the spectra profiles when the companion was located in this region. We decided to exclude the corresponding cubes and spectra from the analysis.

Table 1

Log of SINFONI observations.

Fig. 1

Illustration of the halo subtraction, for the first data cube of the GQ Lup b 2017-04-30 epoch (median along the wavelength axis). We also report the location of the diffraction pattern of the telescope spiders, along with the identified area with improperly calibrated instrument transmission that affects the lower half of the images.

4.2 Extraction and flux calibration

The PSF model estimated from the primary (or telluric standard) star was not a good enough match to the companion PSF to extract spectra from profile fitting. Therefore, the companions spectra were extracted within a circular aperture on the contamination-corrected data cubes of constant radius with wavelengths. The size of the aperture was chosen to conserve the spectral slope and to avoid integrating noise due to the imperfect removal of the stellar halo in the background-limited area. This procedure is similar as the one adopted in Bonnefoy et al. (20 4) and proven to provide a robust extraction of the spectral features and slope on J-band SINFONI data. The adopted radii were ranging from 50 to 75 mas. We retrieve spectra of various S/N depending on the observing conditions. For GQ Lup b, the S/N ranges from 20 to 30 in the 2006-09-8 and 20 7-06-0 epochs, while it ranges from 35 to 50 in the 20 7-04-25 and 20 7-04-30 epochs. For GSC062 4b, the S/N is relatively stable, within the 5–30 range for all epochs.

The atmospheric transmission was evaluated computing the ratio between the extracted spectra of telluric standard stars and their synthetic spectra: black-bodies scaled to the 2MASS JHK, and WISE W and W2 photometry of the objects (Cutri et al. 2003; Cutri & et al. 20 2) collected with the VOSA¹ tool (Bayo et al. 2008). The Pa_β absorption line of the standards were evaluated and removed beforehand as follows. The telluric standard star spectrum was corrected from telluric absorptions by a model created with the SkyCalc tool (Noll et al. 2012; Jones et al. 2013). The line profile was then fitted in the by a Voigt profile function, then subtracted from the spectrum. The spectrum was then applied the same telluric absorption model. This ensures that the line shape evaluation is not impacted by weak telluric features in the line wings and that it does not bias the companion emissions at these wavelengths.

We performed an absolute flux calibration of the individual spectra using the telluric standard star as a spectro-photometric reference (2MASS J-band photometry). The use of the telluric standard stars was favored over the use of the host stars because of their potential photometric variability. This is the case for GQ Lup A which is a known high-amplitude variable star (∆J = 0.87, Batalha et al. 2001; Broeg et al. 2007). The remaining J-band magnitudes inferred from the individual epochs were averaged to remove part of the uncertainty on the photometric calibration due to variation in observing conditions and AO performance between the telluric standard stars and the companion observations. We decided to exclude the 2006 epoch on GQ Lup b from this process because the companion and the telluric standard were observed under poor and variable adaptive-optics conditions.

We find a magnitude of 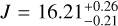$J = {16.21}_{- 0.21}^{+ 0.26}$ $J = 16.21_{ - 0.21}^{ + 0.26}$ on GSC06214b. The value is well consistent with the one measured by Lachapelle et al. (2015) and Bowler et al. (2011) (J = 16.19 ± 0.04 and J = 16.25 ± 0.04, respectively) derived from the contrast between the primary and the companion and the tabulated 2MASS J-band magnitude of the system. We decided to use the latter value.

We find 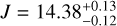$J = {14.38}_{- 0.12}^{+ 0.13}$ $J = 14.38_{ - 0.12}^{ + 0.13}$ for GQ Lup b. Lavigne et al. (2009) found J = 15.13 ± 0.44 but the measurement accuracy was limited by the partial saturation of the host star in their data and the photometry relies on the 2MASS magnitude of the host star, which is known to be variable (as previously mentioned). McElwain et al. (2007) found J = 14.90 ± 0.11 using a similar procedure as ours and this photometry was used in all contemporaneous studies on the system (e.g., Stolker et al. 2021). However, this measurement was performed on OSIRIS data at a high airmass with a narrower wavelength range and at a lower signal-to-noise ratio. Given the amplitude of variability of the primary star (∆J = 0.87, Broeg et al. 2007), the discrepancy between published values and ours is not surprising. The SINFONI photometry makes the J-K color of GQ Lup b (1.0 ± 0.2 mag, assuming the K-band magnitude of GQ Lup bre-evaluated by Neuhäuser et al. 2008) in better agreement with that of other companions of the same luminosity, spectral type, and age range (e.g., Fig. 4 of Gagné et al. 2018a). Furthermore, our value is also consistent with the magnitude correction (0.30–0.66 mag) found by Stolker et al. (2021) to use a single atmospheric model to adjust the J-band scaled to the McElwain et al. (2007) photometry with the rest of the companion spectral energy distribution. We therefore chose to adopt the J-band magnitude inferred from the SINFONI data later on (see Sect. 6.3 for a discussion on possible photometric variations).

The spectra were also corrected for the Barycentric Earth Radial Velocity (BERV), the primary radial velocities, and the companion keplerian motions. The BERV is computed following Piskunov & Valenti (2002) for each individual data cube. The GQ Lup b radial velocity is −0.8 ± 0.4 km s⁻¹ (Schwarz et al. 2016). The GSC06214b radial velocity is −3.98 ± 0.88 km s⁻¹, computed from a combination of its orbital velocity (0.61 ± 0.09 km s⁻¹, Pearce et al. 2019) and the radial velocity of the primary star (−4.59 ± 0.88 km s⁻¹, Gaia DR2). Radial velocities are given in the heliocentric system.

For the remainder of this analysis, error bars were computed from the dispersion around Pa_β , on the residual photosphere-subtracted and baseline-corrected (polynomial approximation of residual baselines, see Sect. 5.3) spectra. For velocity conversion (e.g., right panels of Fig. 2), we used the Paβ rest-frame wavelength gathered on NIST (Kramida et al. 2022), λ₀ = 1.2821578 µm (vacuum, Chang & Deming 1996).

Fig. 2

Companion spectra. Top row: GQ Lup b spectra. Bottom row: GSC 06214-00210 b spectra. Left column: full spectra. Right column: Zoom on the Pa_β line. In both cases, the spectra continuum are normalized to 1 as the mean value on the 1.27–1.28 µm and 1.29–1.30 µm ranges. The 2010-07-09 (OSIRIS) epoch of GSC06214b was degraded to SINFONI resolution (R = 1800) in the left column, but is shown at full resolution (R = 3800) in the right column. The spectral slopes differences are the results of different Strehl Ratios between epochs, despite the AO correction. Our re-extraction of GQ Lup b spectrum initially presented in Seifahrt et al. (2007) produces a pseudo-continuum short-wards of 1.24 µm that is in better agreement with the more recent SINFONI epochs and observations produced by NIFS.

4.3 Photospheric contribution

Both GQ Lup b and GSC06214b exhibit a rich spectrum of molecular absorption lines and shallow KI doublets at 1.169/1.177 µm and 1.243/1.253 µm that are characteristic of young M-L transition objects (e.g., Bonnefoy et al. 2014). Molecular absorption lines overlap with the Paβ line, affecting the emission line profiles. The spectra were therefore corrected for the photospheric features using our forward modeling tool ForMoSA (Petrus et al. 2020, 2023).

This tool compares pre-computed grids of atmospheric models with observations using the Nested Sampling Bayesian inference algorithm (Skilling 2004). As input, we used the ATMO models (Tremblin et al. 2015, 2016), which explore effective temperature and surface gravity in the expected range of values for the late-M companions. The grids, described in more details in Table C.1 of Petrus et al. (2023), allowed us to explore non-solar C/O and [M/H] values, as well as the adiabatic index γ. ForMoSA also allows for fitting of the radial velocity (RV), rotational broadening (vsin(i)), limb-darkening coefficient (ϵ), and interstellar extinction (Av). We did not fit the photospheric contribution on each individual spectrum, but rather on the averaged spectrum at each epoch and we used the RV shift to compensate for residual wavelength shifts from one epoch to another, which may have arised from imperfect wavelength re-calibrations.

The resulting parameter corner plots are presented in Sect. 5.2. The 1D histograms were used to find the resulting best values for each parameter’s bi-modal Gaussian fitting (different σ for the upper and lower halves). The free parameters are the peak location µ₀ and the two sigmas, σ₁ and σ₂. The retained value is µ₀ with the corresponding error bars. The dispersion of values between epochs makes it clear that the Bayesian process on individual epochs provides posterior distributions whose extents are not representative of the true error bars on the values. We therefore estimated the adopted value as the mean of all epochs and the error bars from the dispersion of the ensemble of posteriors of the different epochs. Values at the edge of the grid (upper or lower limits) were ignored when computing the adopted value. The results are presented in Table 2 and discussed in the following section.

Fig. 3

Pa_ß profiles, corrected from the atmospheric contribution and baseline subtracted (see Sects. 5.2 and 5.3). Each spectrum is labeled with the corresponding UT time at the start of the integration. First row: GQ Lup b lines for each epoch. Second and third rows: Same but for GSC06214b, with the addition of the individual OSIRIS lines from Bowler et al. (2011) (2010-07-09 epoch).

5 Results

In this section, we present the resulting spectra and atmospheric parameters, along with their line properties (profiles and variability) and modeling.

5.1 Companion J-band spectra

The mean spectra for each epoch are presented in Fig. 2, along with a zoom on the Pa_ß lines. Pa_ß lines of individual data cubes are presented in Fig. 3. The spectra all have a relatively similar spectral slope, with a discrepancy for the 2017-06-01 epoch for both objects. We argue that this is due to the lower Strehl ratios for that night, with the AO performance being significantly worse than for other epochs, affecting mostly the blue part of the spectrum, leading to larger flux loss at smaller wavelengths. Overall, our spectral slope is in agreement with the already published spectra (Lavigne et al. 2009; Bowler et al. 2011), but the GQ Lup b spectra differ from the Seifahrt et al. (2007), which has already been pointed out by Lavigne et al. (2009). This may be explained by residual primary flux in their spectrum, which is in line with the wider Paβ line profile (see Fig. 2, top-right panel). We observed spectroscopic features typical of late-M/early-L dwarfs for both objects at all epochs: the two KI doublets (1.17 and 1.25 µm), the FeH absorption band (1.17– 1.22 µm), and the numerous H₂O absorption lines (1.13–1.16 µm and >1.32 µm, see Fig. 2). The spectra are also composed of numerous less prominent molecular features all over the band, which are best described by photosphere models (see Sect. 5.2).

Table 2

Atmospheric parameters retrieved with ForMoSA.

Fig. 4

ForMoSA resulting photosphere parameters. Left: GQ Lup b results. Right: GSC06214b results. The Radius, Av, radial velocity (RV), and limb-darkening coefficients are omitted from these plots for the sake of clarity.

5.2 Atmospheric and physical parameters

Here, we present the results from atmospheric modeling of the J-Band spectra with ForMoSA (Sect. 4.3). The best fits for both sources can be found in Table 2. A comparison of the various atmospheric parameters can be found in Fig. 4, as corner plots. A visual comparison of data and fitted spectra can be found in Fig. 5. Some parameters have converged at the edge of the parameter range, such as the adiabatic index γ, either consistently or occasionally. The spectral slopes of both companions on June 1, 2017 are discrepant with regard to the other epochs and the retrieved atmospheric parameters (at the very least T_eff and Av) are likely to be non-representative.

Fig. 5

Visual comparison of the photosphere fitting with ForMoSA, for each epoch of both objects, with a zoom on Pa_ß in the right column. Grayed-out wavelength ranges were excluded from fitting as the model either did not include corresponding species (FeH absorption band, Pa_ß) or the data were too noisy (>1.34 µm).

5.2.1 Inferred values and correlations

Correlations have been observed between T_eff and log g. The behavior is similar to that observed on the spectral analysis of the young late-M companion HIP 78530B with ForMoSA in Petrus et al. (2020) (although these authors used BT-SETTL atmospheric models). The correlation might be caused by the increase in strength of the K I and FeH absorptions with both decreasing T_eff and increasing surface gravities at the M-L transition (Rice et al. 2010; Bonnefoy et al. 2014).

On the other hand, the log g and C/O are anti-correlated. This is due to the sensitivity to these two parameters of the numerous FeH and H₂O absorptions at J-band. Finally, both sources show either no correlations between [M/H] and C/O, or a positive one. We do not notice strong degeneracies between γ and the others parameters, which suggests that the limited exploration of that parameter does not bias the estimate of the other parameters.

For GQ Lup b, atmospheric parameters are consistent for all epochs: log g ~ 4.2, 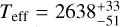$T_{eff} = 2638_{- 51}^{+ 33}$ ${T_{{\rm{eff}}}} = 2638_{ - 51}^{ + 33}$ K (we caution that error bars do not include systematics of the model) and γ > 1.05. The log g and T_eff are both well consistent with the values found in Stolker et al. (2021) adjusting the VLT/MUSE optical spectrum of the companion with BT-SETTL models. We however find with ForMoSA a higher radius than the estimates of Stolker et al. (2021) (found by adjusting a synthetic spectra on the companion s spectro-photometry). This might be due to the increased J-band apparent flux that we measure in Sect. 4.2. Part of the difference could also be caused by the use of different atmospheric models (see more below).

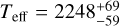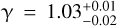For GSC06214b, we find log g ~ 4.24, $T_{eff} = 2248_{- 59}^{+ 69}$ ${T_{{\rm{eff}}}} = 2248_{ - 59}^{ + 69}$ K and $γ = {1.03}_{- 0.02}^{+ 0.01}$ $\gamma = 1.03_{ - 0.02}^{ + 0.01}$ . Lachapelle et al. (2015) found T_eff = 2300 ± 200 K and log g = 3.0−1.0 using different models (BT-SETTL and DRIFT-PHOENIX, Allard et al. 2011; Helling et al. 2008; Witte et al. 2009, 2011) and spectra, but which remain broadly consistent with our values.

We present the first estimates of C/O and [M/H] for both companions. Both objects have C/O values that are compatible with solar value (C/O_⊙ = 0 55) within 1σ. However, they exhibit different kinds of behavior in terms of metallicity: GSC06214b has a solar metallicity (within 1σ), while that of GQ Lup b appears slightly super-solar (>3σ). We interpret these abundances in Sect. 6.1.

The extinction of GQ Lup b is consistent with the value found by (Av ~ 2.3 mag, Stolker et al. 2021). It is above the values reported on GQ Lup A and C (Av ~ 1 .0 mag, McElwain et al. 2007; Alcalá et al. 2020). The extinction of GSC06214b is within the range of values measured on the primary star (Av = 0.7 ± 0.5 mag, Barenfeld et al. 2016; Anders et al. 2022).

5.2.2 Use of evolutionary tracks

Using our estimated T_eff from ForMoSA, recent “hot-start” evolution models (Phillips et al. 2020) predict a mass of 15.5 ± 0.5 M_Jup at the age of the system (Sect. 2.2) for GSC06214b, which is consistent with previous estimates based on the bollometric luminosity. Our estimated surface gravity is also broadly consistent with expectations at the age of UCL (log g = 4.07 ± 0.01) and Upper Scorpius (log g = 4.04 ± 0.02) and does not allow for discrimination between the two possible system memberships. Predicted radii range from 1.8 to 2.0 R_Jup, e.g. ~20% larger than the value found with atmospheric models alone. The mismatch amplitude is consistent with the predictions of the same atmospheric models for VHS1256b, a cooler (T_eff ~ 1400 K) companion of the same mass range as GSC06214b and might point to a systematic overestimation of the absolute near-infrared fluxes by the ATMO models across a broad T_eff range (Petrus et al. 2023). This is not, however, an issue with respect to removing the photospheric contribution, since the radii are only used to scale the synthetic spectrum to the companion’s continuum emission level.

The use of GQ Lup b’s T_eff from ForMoSA as input for the ATMO evolutionary tracks predict a mass of 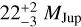$22_{- 3}^{+ 2} M_{Jup}$ $22_{ - 3}^{ + 2}\,{M_{{\rm{Jup}}}}$ , a radius in the range of 2.65 −= 3.3 R_Jup and with log g ~ 3.8−3.9 dex at the system age (Sect. 2.1). Both the predicted radius and log g are inconsistent with those inferred from ForMoSA and the deviation is at odds with that observed for GSC06214b. The use of the older AMES-DUSTY tracks (Chabrier et al. 2000) do not change the conclusions. This could arise from uncertainties in the evolutionary tracks not capturing the physics of the interior of this more massive companion (e.g., deuterium burning). However, the radius is degenerate with the extinction in our fit and higher extinction than estimated would naturally lead to a better agreement between ForMoSA and evolutionary model predictions. Stolker et al. (2021) found radii of 3.55–4.13 R_Jup and a higher extinction (2.3–2.7 mag), which remain slightly inconsistent with the Phillips et al. (2020) evolutionary models. The large radii and inconsistent log g derived from atmospheric models could also be produced because of additional flux contribution such as veiling increasing the flux and requiring a larger dilution factor (Sect. 6.3). A similar mismatch has also been observed on other companions of the same T_eff range in

Upper Scorpius (Petrus et al. 2020) and an unresolved binarity has been proposed as an explanation. If GQ Lup b were to be an equal-luminosity equal-T_eff binary, the apparent J-band flux would be deviant, namely, overestimated by a factor two with respect to a single object. In such a case, the corresponding radius of individual components found with ForMoSA (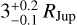 $3_{- 0.1}^{+ 0.2} R_{Jup}$ $3_{ - 0.1}^{ + 0.2}\,{R_{{\rm{Jup}}}}$ ) would match the evolutionary model predictions for the fitted T_eff well.

Fig. 6

Gaussian-fitting resulting parameters for the Pa_β line of GSC06214b. Left: correlations between intrinsic FWHM and the line peak location µ₀, arrows represent an upper limit on the intrinsic FWHM. Right: correlations between the Pa_β line flux and the line peak location µ₀. The intrinsic FWHM is computed as the square root of the quadratic difference between the measured line FWHM and the LSF FWHM. The µ₀ parameter is relative to the line expected wavelength in vacuum (1.2821578 µm).

5.3 Analysis of Pa_β time series

Pa_β emission line profiles for individual data cubes are presented in Fig. 3. We performed a Gaussian fitting of the lines to infer their width, position, and flux (see Table A.2).

We find the Pa_β line profiles to be partly resolved in the 2006 epoch of GQ Lup b (1–1.5 times the LSF width, 1–3 σ) and mostly unresolved in the 2017 epochs of GSC06214b (1–1.2 times the LSF width, 1–2 σ). However, we do find the line to be partly resolved in the 2010-07-09 epoch (OSIRIS) (1.2–1.9 the LSF width, 4–8 σ). We refer to Table A.2 for details. We also find the peak of the Pa_β emission lines in GQ Lup b to be slightly blue-shifted. For GSC06214b, they are mostly centered at zero velocity and show no significant asymmetries (with respect to the line center), except for the 2017-06-01 epoch of GSC06214b, for which the line has a wider red-wing in comparison to the blue wing. This is reminiscent of emission lines formed in mag-netospheric accretion columns in T Tauri stars, which show prominent blue-red asymmetry (Edwards et al. 1994). Shock-induced accretion lines also produce lines with a red-shifted peak, hence a wider red wing. These will be explored in more detail in Sect. 6.2.

We studied the variability for both the line profiles and fluxes. We note that studying integrated fluxes is equivalent to studying EWs, as they were all computed on a similar continuum baseline. Integrated fluxes were computed by Gaussian fitting of the line profiles after local baseline correction (polynomial, n = 2), for which the main results are reported in Table A.2 and shown in Fig. 6.

As illustrated in Fig. 6, we find, for GSC06214b, possible correlations between the line intrinsic width and its peak velocity (FWHM_in–µ₀, left panel) and between the line flux and its peak velocity (F(Pa_β)-µ₀, right panel). We computed Pearson’s correlations coefficients and p-values using an MCMC approach almost equal to the pymccorrelation tool (Curran 2015; Privon et al. 2020), with the added constraint that the intrinsic FWHM distributions cannot be negative. For the first correlation, ignoring upper limits we find 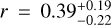$r = {0.39}_{- 0.22}^{+ 0.19}$ $r = 0.39_{ - 0.22}^{ + 0.19}$ and log 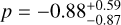$p = - {0.88}_{- 0.87}^{+ 0.59}$ $p = - 0.88_{ - 0.87}^{ + 0.59}$ . We note that while they were excluded, upper limits still appear in the correct region for the trend. For the second correlation (excluding the 2010-07-09 epoch), we find 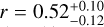$r = {0.52}_{- 0.12}^{+ 0.10}$ $r = 0.52_{ - 0.12}^{ + 0.10}$ and log 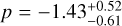$p - {1.43}_{- 0.61}^{+ 0.52}$ $p - 1.43_{ - 0.61}^{ + 0.52}$ . The FWHM_in–µ₀ correlation, if true, could be the sign of either (i) red-shifted absorption within the line (as absorption increases, the line centroid will be moved to the blue) or (ii) increasing red-wing contribution as the line flux increases. The F(Pa_β)–µ₀ correlation, if true could be explained in the same way as the second explanation for the peak-velocity-and-FWHM correlation. The possible implications are discussed in Sect. 6.2.

From Fig. 3, we see unambiguous EW variability from an epoch to another for both sources. There is no clear sign of line profile variability within the SINFONI sequences – with the exception of a possible red-wing variability on the GSC06214b 2017-06-01 epoch. However, we do see line flux variability within multiple sequences of GSC06214b, in particular the 2010-07-09 one.

Figure 7 shows the relative Pa_β flux variation, computed as (Fmax-Fmin)/Fmin for each individual pair of lines, as a function of their time difference. The marker’s color reports the significance of the measurement, namely, the σ-distance between the two lines used to compute this value. While a small and noisy denominator may artificially increase the relative variation, the measurement will appear gray as the two values would not be statistically far apart. In other words, gray measurements are compatible with no relative flux variation (given our uncertainties), while colored points highlight an actual variation (given the σ level). GQ Lup b shows overall close to no flux variability (3 σ confidence level, <50%) on timescales of an hour or more. However, we do see significant variability (>100%) on timescales of about a month and longer. We note that the ~year timescale corresponds to the variation between the 2006-09-18 and the Lavigne et al. (2009) (2007-05-30) epochs. GSC06214b, on the other hand, shows definitive flux variability around the 30-min and ~hour time scales (>5σ significance). We also do see clear (>5σ) line variability on time scales of weeks, months, and years. The line flux variability at the ~hour time scale appears within multiple datasets: the OSIRIS epoch (2010-07-09), the 2017-05-04 epoch and between the two sets of the 2017-04-25 epochs. In both objects, the amplitude of variability stays below 50–60% for timescales that are shorter than their estimated rotation periods, while stronger variability amplitude (up to a factor 10) is observed on longer timescales. We discuss these findings in the more general context of variable young stars in Sect. 6.2.

Fig. 7

Pa_β flux variability for both sources, as a function of the timescale, with respect to the lowest-flux point of the pair. For GQ Lup b, are included data points from this study as well as the spectrum from Lavigne et al. (2009). For GSC06214b, are included data points from this study as well as those from the individual Bowler data cubes (Bowler et al. 2011) and the mean spectrum from Lachapelle et al. (2015). The color of the points represents the significance of the measurement, i.e., the σ-distance between the two lines used to compute this value. The horizontal and vertical bars correspond respectively to the bin size, and the spread (weighted by significance) within that bin. The red-shaded regions mark the average observed continuum variability among the SINFONI sequences (see Table ). The orange shaded regions represent the expected rotational period of the objects (see Sect. 2).

5.4 Comparison to protoplanet accretion models

Pa_β emission in the spectra of low-mass free-floating brown dwarfs of the same mass, age, and spectral-type range as the two companions studied here have been investigated by Natta et al. (2004) and Manara et al. (2013). The Pa_β line intensity is shown to be strongly correlated with the accretion luminosity, while the chromospheric activity does not contribute significantly to the line intensity for accretion rates above 10⁻¹¹ – 10⁻¹² M_⊙yr⁻¹ at ages 3–10 Myr. Furthermore, none of the non-accreting sources display Pa_β emission lines. We therefore assume that most, if not all, of the Pa_β emission is produced by accretion. In this section, we explore two accretion models in the planetary mass regime predicting Pa_β line flux and profiles, and compare their predictions to our time-series observations, in order to infer the corresponding physical parameters.

Fig. 8

Comparison of the best-fit models for both GQ Lup b (first row) and GSC06214b (2nd and 3rd rows). Colorbars represent the reduced χ² ( $χ_{r}^{2}$ $\chi _r^2$ ) of the Shock (blue) and Mag Acc (red) models. For each epoch, all best models (within the $χ_{r}^{2}$ $\chi _r^2$ range given in the colorbar) are over-plotted with a color scaling with the reduced χ² color. The fitting limits and number of parameters of each model yield a number of degrees of freedom equal to 14 for the Shock model and 9 for the MagAcc model.

Fig. 9

$χ_{r}^{2}$ $\chi _r^2$ maps illustrating the accretion models degeneracies when fitting the Pa_β lines. Left panel: T_max vs Ṁ degeneracy for the MagAcc model (GQ Lup b, epoch: 2006-09-18). Right panel: n₀ vs υ₀ degeneracy for the Shock model (GSC06214b, epoch: 2010-07-09 – OSIRIS).

5.4.1 Description of accretion models

Thanathibodee et al. (2019) proposed a version of the magneto-spheric accretion models developed for Classical T Tauri Stars (CTTS, see the review of Hartmann et al. 2016, and ref. therein) extended to the planetary mass range. It assumes that the central object’s dipolar magnetic field is intense enough at young ages to truncate the inner CPD, lift material from the CPD, and channel it towards the central object. Material then falls down to the planetary surface at free fall velocity along accretion funnels. In these funnels, the material is heated to temperatures high enough (~10⁴ K) to trigger atomic Hydrogen line emission (H_α, Pa_β, Br_γ, …). The free-falling material then creates a shock at the base of the funnel flows when it hits the planetary surface, which triggers hot continuum emission that can be absorbed by the infalling gas, leading to red-shifted absorption features within the emission line profiles. Red-shifted absorption also occurs when the accretion flow absorbs the photosphere emission itself. Blue-shifted absorption may also be present due to jets or outflows, but these are not accounted for by these models. The magnetospheric accretion model from Thanathibodee et al. (2019) is described by: the accretion column launching radius R_in, its width, its maximum temperature T_max, the accretion rate Ṁ, the inclination, the planet mass M, the planet radius R_p, and the planet effective temperature T_eff. The model is axis-symmetric and assumes that the large scale dipolar magnetic field is aligned with the central object rotation axis. The model neglects line emission contribution from the shock at the base of the accretion funnels. This model will be referred to as the MagAcc model hereafter.

Conversely, Aoyama et al. (2018) proposed that accretion lines, rather than being triggered within accretion funnels, would be triggered within an accretion shock either at the planet or the CPD surface. In such a scenario, material flows from the circumstellar disk down to the planetary or CPD surface. This may happen for planet embedded within the circumstellar disk of their host star, through polar-inflow (Marleau et al. 2022) or, as was proposed for GQ Lup b, if material from the circumstellar disk channels up to the planet immediate environment (Stolker et al. 2021). Alternatively, this model could also describe line emission formed in the shock at the base of magnetospheric accretion columns. This model considers two parameters: the infall velocity υ₀ and the pre-shock density n₀. We add an additional flux scaling parameter, S_eff, the effective shock surface (i.e., 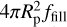$4 π R_{p}^{2} f_{fill}$ $4\pi R_{\rm{p}}^2{f_{{\rm{fill}}}}$ if it takes place at the planetary surface). We provide more details in the next section. We note that this model is referred to as the Shock model, hereafter.

5.4.2 Model fitting

We used both aforementioned models (MagAcc and Shock, Thanathibodee et al. 2019; Aoyama et al. 2018) to try to retrieve the physical parameters of the accretion mechanisms by fitting the Pa_β line of both GQ Lup b and GSC06214b.

Both models were scaled to the distance of the objects (Sect. 2). For the MagAcc model, this was performed by applying a factor (R_p/D)², with D the distance and R_p the planet radius. For the Shock model, we applied a factor S_eff/(4πD²). The fits were performed on photosphere-subtracted and baseline-corrected Pa_β emission line profiles, with continuum-subtracted models. This allows accretion models fitting not to be biased by continuum discrepancies, and allows us to focus solely on the line profile. The models are then convolved to the instruments resolution (R = 2360 and R = 1800 for GQ Lup b and GSC06214b SINFONI data respectively, R = 3800 for OSIRIS).

The fits were performed on the mean emission line of each epoch, computing the 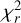$χ_{r}^{2}$ $\chi _r^2$ on the whole grid of models. Fiducial results are presented in Fig. 8. The GQ Lup b lines are only reproduced by the MagAcc models: this is because the Shock models cannot reproduce a blue shifted emission line peak, as is clearly apparent from the first row of Fig. 8. Note that the red-shifted absorption in the 2017 epochs of GQ Lup b and fitted by the models is mostly likely caused by noise in the data. However, GSC06214b lines are well reproduced by both models. Maps of the best 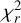$χ_{r}^{2}$ $\chi _r^2$ are shown in Fig. 9. We only represent the T_eff–Ṁ axis in the figure for the MagAcc model, because others parameters are mostly unconstrained.

In the case of the MagAcc scenario, there is a clear degeneracy between the accretion column temperature and the accretion rate. This behavior was already seen in the context of magnetospheric accretion on T Tauri stars (Muzerolle et al. 2001) and the degeneracy could be lifted with very high resolution observations and/or fitting multiple accretion lines simultaneously. This shows that in the magnetospheric accretion framework, we cannot derive an accurate measurement of the accretion rate, but only a lower limit. For GQ Lup b, this leads to Ṁ ≳ 10⁻¹¹ M_⊙ yr⁻¹ for the (bright) 2006-09-18 epoch and Ṁ ≳ 10^−11.5M_⊙ yr⁻¹ for the other epochs. For GSC06214b, this leads to a lower limit of Ṁ ≳ 10⁻¹²M_⊙ yr⁻¹ for all epochs. Zhou et al. (2014) derived values of 10^−10.8 M_⊙yr⁻¹ and 10^−9.3 M_⊙yr⁻¹ from fitting the UV-optical excess emission for GSC06214b and GQ Lup b, respectively, which are consistent with our lower limits.

GSC06214b lines are also well reproduced with the Shock model. In this scenario, fits are mostly degenerated over the parameter space, except for the 2010-07-09 (OSIRIS) epoch, for which high velocity models are strongly favored, as shown in Fig. 9. The high shock velocity models correspond to infall velocities υ_ff > 150 km s⁻¹, which imply a shock location at R < 2.4 R_Jup, consistent with the estimated radius of the object (Sect. 5.2). These solutions would indicate that the shock is located at the planetary surface. However, lower infall velocities in the range of 30–170 km s⁻¹ cannot be fully excluded. They are consistent with a shock located anywhere within 60 R_Jup, so either at the protoplanet surface or on the CPD at larger scales. In the 2010-07-09 (OSIRIS) epoch, our best-fit values of S_eff, υ₀, and n₀ (1.5 × 10⁻² S_jup, 180 km s⁻¹ and 10²⁰ m⁻³) yield a mass accretion rate of Ṁ ~ 10⁻⁹ M_⊙ yr⁻¹. Assuming a shock at the planetary surface, the accretion rate can be given as Ṁ = Sµv₀υ₀, with µ the mean molecular weight (3.84 × 10⁻²⁷ kg as per Aoyama et al. 2018). Inverting the equation, we find the shock surface given as a fraction of the planetary surface (with an estimated radius of 1.8–2.0 R_Jup), this corresponds to a filling factor of 0.38–0.47%. This is of the same order (0.3%) as reported for the older analogue companion Delorme 1 (AB)b and using similar models on Balmer lines (Ringqvist et al. 2023).

6 Discussion

In this section, we first interpret the derived atmospheric abundances of both objects. We then discuss the implications brought by our results for the origin of the H I line emission in planetary-mass objects and the possible impact of variable veiling. Finally, we extrapolate how emission line variability, as seen here, could impact protoplanet detection surveys.

6.1 Atmospheric abundances as formation tracers

The star forming regions Sco-Cen and Lupus I are expected to have nearly solar metallicity (e.g., Bubar et al. 2011; Biazzo et al. 2017; Murphy et al. 2021, and ref. therein) and it has been shown that nearby solar-type stars with [M/H] = 0 have C/O distributed around the solar value (Suárez-Andrés et al. 2018; Tautvaišienė et al. 2022). We note, however, that there is a spectroscopic determination of [M/H] = −0.06 ± 0.01 and −0.35 ± 0.01 dex for GSC06214A and GQ Lup A, respectively (Swastik et al. 2021). The value found for GQ Lup A is at odd with expectations and implies that GQ Lup b is significantly enriched in metals ( $Δ [M / H] = {0.61}_{- 0.10}^{+ 0.05}$ $\Delta [{{\rm{M}} \mathord{\left/ {\vphantom {{\rm{M}} {\rm{H}}}} \right. \kern-\nulldelimiterspace} {\rm{H}}}] = 0.61_{ - 0.10}^{ + 0.05}$ ) with respect to its host star, while GSC06214b metallicity remains compatible within 1σ with that of GSC06214A. Swastik et al. (2021) accounted for veiling affecting the depth of stellar absorption lines of GQ Lup A in their inversion of the high-resolution optical spectra of the source. They chose, in particular, the less-contaminated and emission-free region of 5900–5965 Å for the analysis. However, the H_α line of GQ Lup A appears as the most intense of their sample and remaining effects of veiling at considered wavelengths might lead to an underestimation of the [M/H] value for that particular star.

The metallicity of GSC06214b and GQ Lup b are both compatible with the envelope of values predicted for planet population synthesis models based on the core-accretion framework assuming a pristine solar-composition (see Fig. 9 of Petrus et al. 2021). Disk-instability models predict a wide range of metallicity values, including solar (Boley et al. 2011). If the companions formed inside the circumstellar disks surrounding their host stars, the nearly-solar C/O implies they should have accreted a substantial fraction of solids. In summary, the derived abundances based on our J-band data do not permit us to firmly conclude on the formation scenario of either objects, but an in-situ formation via turbulent fragmentation remains plausible (i.e., fragmentation of the solar nebula into the primary and its companion, Padoan & Nordlund 1999, 2004).

6.2 Constraints on accretion processes in planetary mass objects

We show in Sect. 5.4.2 that the GQ Lup b lines are only reproduced by the MagAcc model, while the GSC06214b lines are well reproduced by both MagAcc and Shock models.

6.2.1 MagAcc and Shock models’ relative contributions

Although we studied the MagAcc and the Shock scenarios independently, they are not mutually exclusive. The magnetospheric accretion scenario also involves a shock at the base of the accretion columns on the planetary surface, while the Shock model makes no assumptions as to where the accretion shock takes place. Therefore, the Shock model could very well explain the line emission at the base of a magnetospherically induced funnel.

The relative contributions of the accretion funnels and the accretion shock to the Pa_β emission line may vary over time. The MagAcc induced lines are usually asymmetric with a larger blue wing, whereas Shock-induced lines tend to be more symmetric with a slightly stronger red wing. A time modulation of the MagAcc-Shock contributions could then be the key to explaining the correlations observed between the line centroid, as well as its width and flux (Fig. 6).

Figure 2 of Aoyama et al. (2021) shows the relative contributions of the funnel flows and the planetary shock H_α emission, assuming a filling factor of 1–10% and planet mass of 6 M_Jup (corresponding to PDS 70 b) depending on the accretion rate. Our higher mass range and different line may quantitatively change the accretion rate threshold at which both emissions become comparable, but this will hardly change the qualitative picture. For the mass accretion rate of GSC06214b (10^−10.8 M_⊙yr⁻¹, Zhou et al. 2014), both MagAcc and Shock contributions are about the same order of magnitude. For the mass accretion rate of GQ Lup b (10^−9.3 M_⊙yr⁻¹, Zhou et al. 2014), the contribution from the accretion funnels largely dominates, which could explain why it is only the MagAcc model that is able to reproduce the blue-shifted lines of GQ Lup b.

6.2.2 Others explanations for line variability

While we focused the MagAcc and Shock scenarios, other physical mechanisms have been proposed to modulate the accretion lines properties. Marleau et al. (2022) studied the effects of gas and dust extinction on the H_α line intensity profile. According to their Fig. 5, for the gas extinction to alter significantly the H_α flux (A_R > 1) for an object of ~15 M_Jup, the accretion rate must be at least 10⁻⁵ M_Jup/yr, which is far above the accretion rates of GQ Lup b or GSC06214b. Figures 6, 7, and 8 in Marleau et al. (2022) show intrinsic H_α line profiles for the same Shock model, as in this work, both with and without gas extinction, for various accretion flow geometries, planet masses, and accretion rates. Some of these H_α lines show significant asymmetries (in their intrinsic profile), including an absorption of the red-wing of the line. If the behavior in the Pa_β line is similar, the correlations observed in Fig. 6 could be explained by such gas self-absorption effects. As for dust extinction, they find that it should be negligible for masses above a few M_Jup.

Szulágyi & Ercolano (2020) performed 3D simulations of an accreting protoplanet embedded in a circumstellar disk and studied the lines variation due to the variable shock-front (as the planet orbits around the star) and density variations in the protoplanet vicinity. They find the Pa_β line amplitude variability to be about ~8–41% (depending on the modeling hypothesis) for a 10 M_Jup planet, on Keplerian timescales. The different environments of GSC06214b and GQ Lup b (non-embedded) make this scenario implausible for these two objects and the proposed timescales do not match our observations.

6.2.3 Line variability on similar objects

Variability of PMCs has already been seen on various timescales. In the Pa_β study of DH Tau b by Wolff et al. (2017), the authors reported four epochs separated by a number of days and weeks. According to their Table 1, they find the Pa_β line to disappear within ~5 weeks (3.8σ) and a tentative variability within a week (80 ± 50%, 1.7σ). Eriksson et al. (2020) conducted a multi-epoch H_α study of Delorme 1 (AB)b. Applying the same methods as in Fig. 7 to their Table B.1 data, we find H_α EW variability spanning ~30 ± 20% along the ~2 h sequence, with no difference between the <1 h and >1 h timescales. In comparison, we find the variability amplitude to be ~7 ± 7% and ~20 ± 17% for GQ Lup b and GSC06214b, respectively, for timescales of <2 h (noting that error bars represent the spread of the variability, and not an uncertainty), compatible with Delorme 1 (AB)b.

6.2.4 Similarities with CTTS

Both GQ Lup b and GSC06214b show maximum variability for timescales above their estimated rotation periods (see Fig. 7). This behavior is also seen in CTTS (Costigan et al. 2014; Zsidi et al. 2022). The Pa_β line profiles of both companions also show strong similarities with the centrally peaked line profiles observed in solar mass accreting young stars (CTTS, see Folha & Emerson 2001). The line profile of GSC06214b on May 04, 2017 and August 19, 2017 matches that of DG Tau surprisingly well, which was observed at October 10, 1994 and December 15, 1995 by Folha & Emerson (2001). The blue-shifted Pa_β line of GQ Lup b is also well reproduced by their observations of DD Tau. Both objects are sub-solar-mass CTTS. Magnetospheric accretion models have been very successful at reproducing these line profiles (Muzerolle et al. 2001). These similarities suggest that the mechanisms proposed for the formation of the H I emission lines in CTTS (i.e., magnetospheric accretion) are at play down to the planetary mass regime. The estimates of mass accretion rates for GSC06214b and GQ Lup b are also in line with the global decrease of mass accretion rates with object mass, which extends down to isolated ~15 M_Jup objects (e.g., Muzerolle et al. 2005; Joergens et al. 2013).

Ringqvist et al. (2023) reported recent high-resolution UV spectra (2 epochs taken within 1h) of the 13 ± 5 M_Jup companion Delorme 1 (AB)b where they find line blue-shifted profiles indicative of magnetospheric accretion. While the profiles of these lines cannot be directly compared to those of Pa_β, this further suggests this mechanism could be universal for young 10–30 M_Jup companions with ages from 3 to 40 Myr. Both Delorme 1 (AB)b and GSC06214b have estimated filling factors of the accretion shock of the order ~1%. These values are consistent with those found in CTTS (e.g., Alencar & Batalha 2002; Batalha et al. 2002; Pittman et al. 2022), although the methodologies used to derive these factors on stars can be different.

Magnetospheric accretion holds only if the objects interior can generate powerful magnetic fields. Following Eq. (1) from Hartmann et al. (2016) with the values found from evolutionary tracks (Sect. 5.2, GQ Lup b: M = 22 M_Jup, R = 3 R_Jup, Ṁ = 10^−9.3 M_⊙yr⁻¹; GSC06214b: M = 15 M_Jup, R = 2 R_Jup, Ṁ = 10^−10.8 M_⊙yr⁻¹), the lower limits on their rotational period (5h for GQ Lup b, 20h for GSC06214b) and ξ = 0.7, they would require a minimum dipolar magnetic field of ~70 G and ~150 G, respectively. These increase to ~750 G and 1.7 kG for the rotational period upper limits (80h). Magnetic field strengths on young companions are just starting to be investigated (Katarzyński et al. 2016; Cendes et al. 2022) but no measurement exists yet. Recent radio and H_α observations of low-mass brown dwarfs and planetary-mass objects in the same mass range as our companions suggest that the magnetic field strength could reach several k-Gauss at early ages (Kao et al. 2018). Time-series of line profiles at higher resolutions (R > 10 000) should further help to place constraints on the MagAcc and Shock models (Marleau et al. 2022). More direct measurements of the magnetic fields strength on accreting free-floating planets or companions on wider-orbits with spectro-polarimeters (e.g., SPIRou) might be possible and would also help to confirm the MagAcc scenario.

6.3 Evidence for continuum variability?

In our analysis of the Pa_β line variability, we have assumed that the continuum emission remained constant. Photospheric emission of young dwarfs at the M-L transition is not expected to show high-amplitude modulation due to non-homogeneous cloud coverage (e.g., Artigau 2018; Vos et al. 2022). It remains possible that variable veiling or extinction due to accretion and the circum-“planetary” environment or magnetic spots affect the J-band and could change the contrast between the lines and their surrounding continua, thus producing at least a portion the observed variability. Carpenter et al. (2002) find a 0.15mag variability at J-band of the faintest members of Chameleon whose colors (J–K ~ 0.8−1.0) are close to the one of GQ Lup b and correspond to spectral type in the mid- to late-M range (Cao et al. 2022).

Zhou et al. (2014) measured the shock contribution from 1D slab models (continuum excess produced by the accretion shock) and the H_α luminosity of both companions using HST data. Their model indicate a negligible contribution of the slab for GSC06214b beyond 1 µm and a contamination at the percent level for GQ Lup b at J-band. However, the shock contribution is expected to be linked to the line intensity, this could work as a variable continuum component at J band that could explain observed Pa_β equivalent width variations. Photometric variability of GQ Lup b is known to be negligible at K-band (σ_K = 0.073 mag, Neuhäuser et al. 2008), but no monitoring has been conducted at the J-band where the effect of veiling could be more important.

Veiling would both decrease the prominent K I doublets and the Pa_β emission lines. Figure 10 shows the EW of Pa_β and the KI absorption lines (corresponding values are given in Table A.1). A variation along a line with slope -1 is expected if the observed EW variability is only due to a variation in the continuum level. GQ Lup b lines show no clear correlations in 2017, although there might be a slight trend in 2006. Because the 2006 epoch and the 2017 epochs are not following the same slope, their EW difference cannot be explained only by continuum variability. To explain the EW variation observed within the 2006 epoch, a variation of the continuum level of ~30–50% within 2 h would be required, corresponding to changes of J-band magnitudes of 0.3–0.4 mag, compatible with the dispersion of values reported in Table 1.

For GSC06214b, the trend appears between all epochs except 2017-08-19 and 2010-07-09. The Pa_β EW variability between those might therefore be explained by continuum variability. Although, in a similar fashion as for GQ Lup b, the Pa_β EW variation between the 2017-08-19/2010-07-09 and other 2017 epochs cannot be explained only based on continuum variability.

Given the current constraints, we assume that both objects have EW variability that is driven by intrinsic line flux variability. Accurate photometric monitoring of both companions at J-band simultaneous to Pa_β emission line variability campaign would be required to fully confirm this hypothesis.

6.4 Implications for protoplanet detection

Several surveys have been conducted to detect accreting planets nested in circumstellar disks using narrow-band imaging at H_α (Mendigutía et al. 2018; Wagner et al. 2018; Cugno et al. 2019; Uyama et al. 2020; Zurlo et al. 2020; Huélamo et al. 2022; Follette et al. 2023), or integral field spectroscopy targeting H_α (Haffert et al. 2019; Xie et al. 2020) and Pa_β emissions (Uyama et al. 2017, 2021). Thus far, H_α point source detections have been claimed in four systems (LkCa15, AB Aur, PDS70, CS Cha; Sallum et al. 2015; Huélamo et al. 2018; Currie et al. 2022; Zhou et al. 2021; Follette et al. 2023). The nature of the detection remains unclear in two of these systems (LkCa15, AB Aur; Whelan et al. 2015; Follette et al. 2023; Zhou et al. 2022). With the exception of Delorme 1 (AB)b, which does not seem to be in a protoplanetary-disk, no detection has ever been achieved at Pa_β.

PDS 70 b and c are known to be affected by significant inline extinction (Hashimoto et al. 2020; Wang et al. 2021) caused by surrounding material, while they are otherwise found within a large cavity. Extinction is therefore a good candidate to explain the poor yield of H_α and Pa_β deep imaging searches, especially in disks with significant amount of gas and dust. However, most are single-epoch observations and emission line variability might also provide an additional explanation for the low yield of these observations.

Xie et al. (2020) report in their Fig. 11, the H_α detection limit achieved for 30min of effective VLT/MUSE observations of PDS 70. Their observations of PDS 70 are the deepest presented in the paper and probe deeper apparent line fluxes than all the narrow-band observations presented in Cugno et al. (2019) and Huélamo et al. (2022). They also report the measured apparent H_α emission line flux of the two accreting planets.

Both PDS 70 b & c, unlike GQ Lup b and GSC06214b, are embedded and interacting with the circumstellar disk. It is therefore reasonable to assume that the majority of variability happens on Keplerian timescales. Given the variety of ages and environments of known accreting objects, our Pa_β variability analysis might only serve as a first order approximation of the general H_α variability. Should our observed Pa_β variations still be representative of H_α variability of others companions, the 100 to 400% variability amplitude at year to decades-long timescales measured for GSC06214b and GQ Lup b would imply that at other epochs, both PDS 70 planets might have been emitting below the VLT/MUSE detection threshold. The various H_α flux measurements of PDS70 b shown in Zhou et al. (2021) tend to indicate that such amplitude of variability is plausible for the companion on a timescale of years. Our findings clearly advocate new visits of these young systems to maximize the detection probability. Similarly, variability might have also helped in detection surveys.

Fig. 10

Correlations between equivalent widths (EW) of both potassium absorption doublets and the Pa_β line. The equivalent width is positive for absorption lines and negative for emission lines. Gray lines correspond to a slope equal to -1, where the EW variability can be explained by sole continuum variability.

7 Conclusions

We present the results of a J-band spectroscopic monitoring campaign of GQ Lup b and GSC06214b at a medium resolving power (R = 1800–2360) with VLT/SINFONI. We also re-detect the Pa_β emission line at each epoch. We report our main conclusions below:

We confirm that GQ Lup b is a ~2640 K, 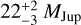$22_{- 3}^{+ 2} M_{Jup}$ $22_{ - 3}^{ + 2}\,{M_{{\rm{Jup}}}}$ companion, and GSC06214b is a ~2250 K, 15.5 ± 0.5 M_Jup companion, given photosphere fitting and evolutionary tracks. We note that error bars may not be representative of systematic uncertainties of the models;
We measure C/O values on both objects compatible with solar value (GQ Lup b: 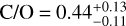$C / O = {0.44}_{- 0.11}^{+ 0.13}$ ${{\rm{C}} \mathord{\left/ {\vphantom {{\rm{C}} {\rm{O}}}} \right. \kern-\nulldelimiterspace} {\rm{O}}} = 0.44_{ - 0.11}^{ + 0.13}$ , GSC06214b: $C / O = {0.48}_{- 0.12}^{+ 0.16}$ ${{\rm{C}} \mathord{\left/ {\vphantom {{\rm{C}} {\rm{O}}}} \right. \kern-\nulldelimiterspace} {\rm{O}}} = 0.48_{ - 0.12}^{ + 0.16}$ , C/O_⊙ = 0.55). We find GSC06214b’s [M/H] to be compatible with solar value (−0.16 ± 0.17), while GQ Lup b’s is slightly super-solar (0.23 ± 0.06). The uncertainties on the atmospheric parameters are driven by small systematic errors in the data revealed by our multi-epoch observations, while Bayesian inference at single epoch provides overly optimistic estimates of the error bars;
For both objects, the Pa_β intensity variability is found to be moderate (<50%) on timescales below their rotation period, and more important on longer timescales (up to ~1000% for a decade), a behavior similar to that of CTTS. We studied whether variable veiling could change the contrast of the line above the continuum. We find that such flux component does not explain the long-term variability of either object, but we cannot exclude it might explain the shorter term evolution of the lines;
Both companions had their maximum recorded line brightness at first (historical) epochs. Their variability amplitude can be up to ~1000% on a decades-long timescale. Should that amplitude extend to H_α, this might explain the low yield of H_α and Pa_β (spectro)-imaging campaigns for protoplanet detection.
The blue-shifted Pa_β lines of GQ Lup b are reproduced only by the protoplanet magnetospheric accretion models. Those of GSC06214b are well reproduced by both magnetospheric accretion and shock models at quiescence, while the shock model is favored when the line is more intense (2010 epoch). We find filling factors of the accretion shock below 1% at that epoch and compatible with the value found on the older companion Delorme 1 (AB)b;
We identify a tentative correlation between GSC06214b’s emission line center and its width, which could be explained either by asymmetries in magnetospheric accretion-induced lines or by gas extinction in shock-induced lines.

Our study presents the first monitoring of emission lines of young accreting companions at the edge of the deuterium-burning boundary. It illustrates how variability timescales could be used to investigate whether the phenomena at play are a downsizing of those happening on protostars or more specific ones. Our results advocate multiple visits of young systems on a year-span at least to maximize the detection probability of young protoplanets. Observations at higher resolution (R > 10000, e.g., ERIS) would now be required to better constrain the line profiles and emitting mechanism.

Acknowledgements

We thank the ESO staff for the help during the preparation of the observations and their execution. We are grateful to B. Tessore and J. Bouvier for useful discussions on their magnetospheric accretion models. We acknowledge support in France from the French National Research Agency (ANR) through project grant ANR-20-CE31-0012 and the Programmes Nationaux de Planetologie et de Physique Stellaire (PNP and PNPS). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (COBREX; grant agreement 885 593). G.-D.M. acknowledges the support of the DFG priority program SPP 1992 “Exploring the Diversity of Extrasolar Planets” (MA 9185/1), and from the Swiss National Science Foundation under grant 200021_204847 “PlanetsInTime”. Parts of this work have been carried out within the framework of the NCCR PlanetS supported by the Swiss National Science Foundation. This publication makes use of VOSA, developed under the Spanish Virtual Observatory (https://svo.cab.inta-csic.es) project funded by MCIN/AEI/10.13039/501100011033/through grant PID2020-112949GB-I00. VOSA has been partially updated by using funding from the European Union’s Horizon 2020 Research and Innovation Programme, under Grant Agreement nr. 776403 (EXOPLANETS-A).

Appendix A Supplementary material

Figure A.1 contains a visual representation of the extraction process for both objects, along with residuals. Table A.1 contains the measured equivalent widths of the two KI doublets and the Pa_β line of each individual cube. Table A.2 contains the resulting fitted Gaussian parameters of the Pa_β line. The Pa_β integrated fluxes used for Fig. 7 were computed from these parameters as 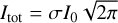$I_{tot} = σ I_{0} \sqrt{2 π}$ ${I_{{\rm{tot}}}} = \sigma {I_0}\sqrt {2\pi }$ . The error bar on the integrated flux accounts for correlations between parameters:

${(\frac{err (I_{tot})}{I_{tot}})}^{2} = {(\frac{err (σ)}{σ})}^{2} + {(\frac{err (I_{0})}{I_{0}})}^{2} + \frac{2 cov (σ, I_{0})}{σ I_{0}} .$ ${\left( {{{{\rm{err}}\left( {{I_{{\rm{tot}}}}} \right)} \over {{I_{{\rm{tot}}}}}}} \right)^2} = {\left( {{{{\rm{err}}\left( \sigma \right)} \over \sigma }} \right)^2} + {\left( {{{{\rm{err}}\left( {{I_0}} \right)} \over {{I_0}}}} \right)^2} + {{2{\mathop{\rm cov}} \left( {\sigma ,{I_0}} \right)} \over {\sigma {I_0}}}$ (A.1)

Fig. A.1

Visual representation of the last iteration of the extraction for both GQ Lup b and GSC06214b, on epochs 2017-04-30 and 2017-08-19 respectively. As mentioned in Sect. 4, the horizontal spider is subtracted for GQ Lup b, but not for GSC06214b as it does not extend below the companion. Are also marked the spiders locations for both targets and some persistence effects in the GSC06214b data.

Table A.1

Equivalent widths

Table A.2

Gaussian fitting results

References

Abuter, R., Schreiber, J., Eisenhauer, F., et al. 2006, New A Rev., 50, 398 [Google Scholar]
Alcalá, J. M., Majidi, F. Z., Desidera, S., et al. 2020, A&A, 635, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Alencar, S. H. P., & Batalha, C. 2002, ApJ, 571, 378 [Google Scholar]
Allard, F., Homeier, D., & Freytag, B. 2011, in Astronomical Society of the Pacific Conference Series, 448, 16th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, eds. C. Johns-Krull, M.K. Browning, & A.A. West, 91 [Google Scholar]
Anders, F., Khalatyan, A., Queiroz, A. B. A., et al. 2022, A&A, 658, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Antoniucci, S., García López, R., Nisini, B., et al. 2011, A&A, 534, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Aoyama, Y., Ikoma, M., & Tanigawa, T. 2018, ApJ, 866, 84 [NASA ADS] [CrossRef] [Google Scholar]
Aoyama, Y., Marleau, G.-D., Mordasini, C., & Ikoma, M. 2020, arXiv e-prints, [arXiv:2011.06608] [Google Scholar]
Aoyama, Y., Marleau, G.-D., Ikoma, M., & Mordasini, C. 2021, ApJ, 917, L30 [CrossRef] [Google Scholar]
Artigau, É. 2018, in Handbook of Exoplanets, eds. H.J. Deeg, & J.A. Belmonte, 94 [Google Scholar]
Baraffe, I., Chabrier, G., & Gallardo, J. 2009, ApJ, 702, L27 [NASA ADS] [CrossRef] [Google Scholar]
Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Barenfeld, S. A., Carpenter, J. M., Ricci, L., & Isella, A. 2016, ApJ, 827, 142 [Google Scholar]
Batalha, C., Lopes, D. F., & Batalha, N. M. 2001, ApJ, 548, 377 [CrossRef] [Google Scholar]
Batalha, C., Batalha, N. M., Alencar, S. H. P., Lopes, D. F., & Duarte, E. S. 2002, ApJ, 580, 343 [NASA ADS] [CrossRef] [Google Scholar]
Batygin, K. 2018, AJ, 155, 178 [NASA ADS] [CrossRef] [Google Scholar]
Bayo, A., Rodrigo, C., Barrado Y., Navascués, D., et al. 2008, A&A, 492, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Béjar, V. J. S., Zapatero Osorio, M. R., Pérez-Garrido, A., et al. 2008, ApJ, 673, L185 [CrossRef] [Google Scholar]
Betti, S. K., Follette, K. B., Ward-Duong, K., et al. 2022a, ApJ, 941, L20 [NASA ADS] [CrossRef] [Google Scholar]
Betti, S. K., Follette, K. B., Ward-Duong, K., et al. 2022b, ApJ, 935, L18 [NASA ADS] [CrossRef] [Google Scholar]
Biazzo, K., Frasca, A., Alcalá, J. M., et al. 2017, A&A, 605, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Boley, A. C., Helled, R., & Payne, M. J. 2011, ApJ, 735, 30 [Google Scholar]
Bonnefoy, M., Chauvin, G., Lagrange, A. M., et al. 2014, A&A, 562, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bonnet, H., Conzelmann, R., Delabre, B., et al. 2004, SPIE Conf. Ser., 5490, 130 [Google Scholar]
Bowler, B. P., Liu, M. C., Kraus, A. L., Mann, A. W., & Ireland, M. J. 2011, ApJ, 743, 148 [Google Scholar]
Bowler, B. P., Liu, M. C., Kraus, A. L., & Mann, A. W. 2014, ApJ, 784, 65 [NASA ADS] [CrossRef] [Google Scholar]
Bowler, B. P., Andrews, S. M., Kraus, A. L., et al. 2015, ApJ, 805, L17 [Google Scholar]
Bowler, B. P., Kraus, A. L., Bryan, M. L., et al. 2017, AJ, 154, 165 [Google Scholar]
Brittain, S. D., Najita, J. R., Dong, R., & Zhu, Z. 2020, ApJ, 895, 48 [CrossRef] [Google Scholar]
Broeg, C., Schmidt, T. O. B., Guenther, E., et al. 2007, A&A, 468, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bryan, M. L., Benneke, B., Knutson, H. A., Batygin, K., & Bowler, B. P. 2018, Nat. Astron., 2, 138 [Google Scholar]
Bryan, M. L., Ginzburg, S., Chiang, E., et al. 2020, ApJ, 905, 37 [NASA ADS] [CrossRef] [Google Scholar]
Bubar, E. J., Schaeuble, M., King, J. R., Mamajek, E. E., & Stauffer, J. R. 2011, AJ, 142, 180 [Google Scholar]
Cao, L., Pinsonneault, M. H., Hillenbrand, L. A., & Kuhn, M. A. 2022, ApJ, 924, 84 [NASA ADS] [CrossRef] [Google Scholar]
Carpenter, J. M., Hillenbrand, L. A., Skrutskie, M. F., & Meyer, M. R. 2002, AJ, 124, 1001 [Google Scholar]
Cendes, Y., Williams, P. K. G., & Berger, E. 2022, AJ, 163, 15 [CrossRef] [Google Scholar]
Chabrier, G., Baraffe, I., Allard, F., & Hauschildt, P. 2000, ApJ, 542, 464 [Google Scholar]
Chang, E. S., & Deming, D. 1996, Sol. Phys., 165, 257 [CrossRef] [Google Scholar]
Chinchilla, P., Béjar, V. J. S., Lodieu, N., Zapatero Osorio, M. R., & Gauza, B. 2021, A&A, 645, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Costigan, G., Vink, J. S., Scholz, A., Ray, T., & Testi, L. 2014, MNRAS, 440, 3444 [NASA ADS] [CrossRef] [Google Scholar]
Cridland, A. J. 2018, A&A, 619, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cugno, G., Quanz, S. P., Hunziker, S., et al. 2019, A&A, 622, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cumming, A., Helled, R., & Venturini, J. 2018, MNRAS, 477, 4817 [Google Scholar]
Curran, P. A. 2015, Astrophysics Source Code Library, [record ascl:1504.008] [Google Scholar]
Currie, T., Lawson, K., Schneider, G., et al. 2022, Nat. Astron., 6, 751 [NASA ADS] [CrossRef] [Google Scholar]
Cushing, M. C., Rayner, J. T., & Vacca, W. D. 2005, ApJ, 623, 1115 [Google Scholar]
Cutri, R. M., et al. 2012, VizieR Online Data Catalog: II/311 [Google Scholar]
Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
Davies, R. I. 2007, MNRAS, 375, 1099 [Google Scholar]
Delorme, P., Gagné, J., Girard, J. H., et al. 2013, A&A, 553, A5 [Google Scholar]
Donati, J. F., Gregory, S. G., Alencar, S. H. P., et al. 2012, MNRAS, 425, 2948 [Google Scholar]
Dong, J., Jiang, Y.-F., & Armitage, P. J. 2021, ApJ, 921, 54 [NASA ADS] [CrossRef] [Google Scholar]
Edwards, S., Hartigan, P., Ghandour, L., & Andrulis, C. 1994, AJ, 108, 1056 [Google Scholar]
Eisenhauer, F., Abuter, R., Bickert, K., et al. 2003, Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, 4841, 1548 [CrossRef] [Google Scholar]
Eriksson, S. C., Asensio Torres, R., Janson, M., et al. 2020, A&A, 638, A6 [Google Scholar]
Feiden, G. A. 2016, A&A, 593, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Fendt, C. 2003, A&A, 411, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Fischer, W. J., Hillenbrand, L. A., Herczeg, G. J., et al. 2022, arXiv e-prints, [arXiv:2203.11257] [Google Scholar]
Folha, D. F. M., & Emerson, J. P. 2001, A&A, 365, 90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Follette, K. B., Close, L. M., Males, J. R., et al. 2023, AJ, 165, 225 [NASA ADS] [CrossRef] [Google Scholar]
Frasca, A., Biazzo, K., Alcalá, J. M., et al. 2017, A&A, 602, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Fu, Z., Huang, S., & Yu, C. 2023, ApJ, 945, 165 [NASA ADS] [CrossRef] [Google Scholar]
Gagné, J., Allers, K. N., Theissen, C. A., et al. 2018a, ApJ, 854, L27 [CrossRef] [Google Scholar]
Gagné, J., Mamajek, E. E., Malo, L., et al. 2018b, ApJ, 856, 23 [Google Scholar]
Gaia Collaboration 2022, VizieR Online Data Catalog: I/355 [Google Scholar]
Ginski, C., Schmidt, T. O. B., Mugrauer, M., et al. 2014, MNRAS, 444, 2280 [Google Scholar]
Gressel, O., Nelson, R. P., Turner, N. J., & Ziegler, U. 2013, ApJ, 779, 59 [NASA ADS] [CrossRef] [Google Scholar]
Haffert, S. Y., Bohn, A. J., de Boer, J., et al. 2019, Nat. Astron., 3, 749 [Google Scholar]
Hartmann, L., Herczeg, G., & Calvet, N. 2016, ARA&A, 54, 135 [Google Scholar]
Hashimoto, J., Aoyama, Y., Konishi, M., et al. 2020, AJ, 159, 222 [Google Scholar]
Heller, R., & Pudritz, R. 2015, ApJ, 806, 181 [NASA ADS] [CrossRef] [Google Scholar]
Helling, C., Ackerman, A., Allard, F., et al. 2008, MNRAS, 391, 1854 [Google Scholar]
Herbig, G. H. 1977, ApJ, 214, 747 [Google Scholar]
Högbom, J. A. 1974, A&AS, 15, 417 [Google Scholar]
Huélamo, N., Chauvin, G., Schmid, H. M., et al. 2018, A&A, 613, A5 [Google Scholar]
Huélamo, N., Chauvin, G., Mendigutía, I., et al. 2022, A&A, 668, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Ireland, M. J., Kraus, A., Martinache, F., Law, N., & Hillenbrand, L. A. 2011, ApJ, 726, 113 [Google Scholar]
Itoh, Y., Hayashi, M., Tamura, M., et al. 2005, ApJ, 620, 984 [NASA ADS] [CrossRef] [Google Scholar]
Joergens, V., Bonnefoy, M., Liu, Y., et al. 2013, A&A, 558, A7 [Google Scholar]
Jones, A., Noll, S., Kausch, W., Szyszka, C., & Kimeswenger, S. 2013, A&A, 560, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Kao, M. M., Hallinan, G., Pineda, J. S., Stevenson, D., & Burgasser, A. 2018, ApJS, 237, 25 [NASA ADS] [CrossRef] [Google Scholar]
Katarzyński, K., Gawroński, M., & Goździewski, K. 2016, MNRAS, 461, 929 [CrossRef] [Google Scholar]
Kramida, A.Yu, Ralchenko, Reader, J., & NIST ASD Team 2022, NIST Atomic Spectra Database (ver. 5.10), [Ońlińe]. Available: https://physics.nist. gov/asd (Gaithersburg, MD: National Institute of Standards and Technology) [Google Scholar]
Kraus, A. L., Irelańd, M. J., Martinache, F., & Lloyd, J. P. 2008, ApJ, 679, 762 [NASA ADS] [CrossRef] [Google Scholar]
Kurosawa, R., Harries, T. J., & Littlefair, S. P. 2006, MNRAS, 372, 1879 [NASA ADS] [CrossRef] [Google Scholar]
Lachapelle, F.-R., Lafrenière, D., Gagné, J., et al. 2015, ApJ, 802, 61 [Google Scholar]
Larkin, J., Barczys, M., Krabbe, A., et al. 2006, SPIE Conf. Ser., 6269, 62691A [NASA ADS] [Google Scholar]
Lavigne, J.-F., Doyon, R., Lafrenière, D., Marois, C., & Barman, T. 2009, ApJ, 704, 1098 [Google Scholar]
Lazzoni, C., Gratton, R., Alcalá, J. M., et al. 2020, A&A, 635, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Long, D. E., Zhang, K., Teague, R., & Bergin, E. A. 2020, ApJ, 895, L46 [NASA ADS] [CrossRef] [Google Scholar]
Lubow, S. H., & Martin, R. G. 2012, ApJ, 749, L37 [NASA ADS] [CrossRef] [Google Scholar]
Luhman, K. L., Stauffer, J. R., Muench, A. A., et al. 2003, ApJ, 593, 1093 [Google Scholar]
MacGregor, M. A., Wilner, D. J., Czekala, I., et al. 2017, ApJ, 835, 17 [Google Scholar]
Manara, C. F., Testi, L., Rigliaco, E., et al. 2013, A&A, 551, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Marleau, G.-D., & Aoyama, Y. 2022, RNAAS, 6, 262 [NASA ADS] [Google Scholar]
Marleau, G. D., Aoyama, Y., Kuiper, R., et al. 2022, A&A, 657, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Marley, M. S., Fortney, J. J., Hubickyj, O., Bodenheimer, P., & Lissauer, J. J. 2007, ApJ, 655, 541 [Google Scholar]
Marois, C., Macintosh, B., & Barman, T. 2007, ApJ, 654, L151 [NASA ADS] [CrossRef] [Google Scholar]
McElwain, M. W., Metchev, S. A., Larkin, J. E., et al. 2007, ApJ, 656, 505 [Google Scholar]
Mendigutía, I., Oudmaijer, R. D., Schneider, P. C., et al. 2018, A&A, 618, L9 [CrossRef] [EDP Sciences] [Google Scholar]
Miki, S. 1982, Progr. Theor. Phys., 67, 1053 [NASA ADS] [CrossRef] [Google Scholar]
Murphy, S. J., Joyce, M., Bedding, T. R., White, T. R., & Kama, M. 2021, MNRAS, 502, 1633 [NASA ADS] [CrossRef] [Google Scholar]
Muzerolle, J., Calvet, N., & Hartmann, L. 2001, ApJ, 550, 944 [Google Scholar]
Muzerolle, J., Luhman, K. L., Briceño, C., Hartmann, L., & Calvet, N. 2005, ApJ, 625, 906 [NASA ADS] [CrossRef] [Google Scholar]
Natta, A., Testi, L., Muzerolle, J., et al. 2004, A&A, 424, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Neuhäuser, R., Guenther, E. W., Petr, M. G., et al. 2000, A&A, 360, L39 [NASA ADS] [Google Scholar]
Neuhäuser, R., Guenther, E. W., Wuchterl, G., et al. 2005, A&A, 435, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Neuhäuser, R., Mugrauer, M., Seifahrt, A., Schmidt, T. O. B., & Vogt, N. 2008, A&A, 484, 281 [CrossRef] [EDP Sciences] [Google Scholar]
Noll, S., Kausch, W., Barden, M., et al. 2012, A&A, 543, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Padoan, P., & Nordlund, Å. 1999, ApJ, 526, 279 [CrossRef] [Google Scholar]
Padoan, P., & Nordlund, Å. 2004, ApJ, 617, 559 [NASA ADS] [CrossRef] [Google Scholar]
Pearce, L. A., Kraus, A. L., Dupuy, T. J., et al. 2019, AJ, 157, 71 [NASA ADS] [CrossRef] [Google Scholar]
Pecaut, M. J., Mamajek, E. E., & Bubar, E. J. 2012, ApJ, 746, 154 [Google Scholar]
Petrus, S., Bonnefoy, M., Chauvin, G., et al. 2020, A&A, 633, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Petrus, S., Bonnefoy, M., Chauvin, G., et al. 2021, A&A, 648, A59 [EDP Sciences] [Google Scholar]
Petrus, S., Chauvin, G., Bonnefoy, M., et al. 2023, A&A, 670, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Phillips, M. W., Tremblin, P., Baraffe, I., et al. 2020, A&A, 637, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Pierens, A., & Raymond, S. N. 2016, MNRAS, 462, 4130 [NASA ADS] [CrossRef] [Google Scholar]
Piskunov, N. E., & Valenti, J. A. 2002, A&A, 385, 1095 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Pittman, C. V., Espaillat, C. C., Robinson, C. E., et al. 2022, AJ, 164, 201 [NASA ADS] [CrossRef] [Google Scholar]
Preibisch, T., Guenther, E., Zinnecker, H., et al. 1998, A&A, 333, 619 [NASA ADS] [Google Scholar]
Privon, G. C., Ricci, C., Aalto, S., et al. 2020, ApJ, 893, 149 [NASA ADS] [CrossRef] [Google Scholar]
Reiners, A., & Christensen, U. R. 2010, A&A, 522, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Rice, E. L., Barman, T., Mclean, I. S., Prato, L., & Kirkpatrick, J. D. 2010, ApJS, 186, 63 [NASA ADS] [CrossRef] [Google Scholar]
Rigliaco, E., Natta, A., Testi, L., et al. 2012, A&A, 548, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Ringqvist, S. C., Viswanath, G., Aoyama, Y., et al. 2023, A&A, 669, A12 [Google Scholar]
Sallum, S., Follette, K. B., Eisner, J. A., et al. 2015, Nature, 527, 342 [Google Scholar]
Santamaría-Miranda, A., Cáceres, C., Schreiber, M. R., et al. 2018, MNRAS, 475, 2994 [Google Scholar]
Santamaría-Miranda, A., Cáceres, C., Schreiber, M. R., et al. 2019, MNRAS, 488, 5852 [CrossRef] [Google Scholar]
Schmidt, T. O. B., Neuhäuser, R., Seifahrt, A., et al. 2008, A&A, 491, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Schwarz, H., Ginski, C., de Kok, R. J., et al. 2016, A&A, 593, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Seifahrt, A., Neuhäuser, R., & Hauschildt, P. H. 2007, A&A, 463, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Sembach, K. R., & Savage, B. D. 1992, ApJS, 83, 147 [NASA ADS] [CrossRef] [Google Scholar]
Sicilia-Aguilar, A., Fang, M., Roccatagliata, V., et al. 2015, A&A, 580, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Skilling, J. 2004, in American Institute of Physics Conference Series, 735, Bayesian Inference and Maximum Entropy Methods in Science and Engineering: 24th International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering, eds. R. Fischer, R. Preuss, & U.V. Toussaint, 395 [Google Scholar]
Smith, E. J., Davis, L.J., Jones, D.E., et al. 1974, Science, 183, 305 [NASA ADS] [CrossRef] [Google Scholar]
Stolker, T., Haffert, S. Y., Kesseli, A. Y., et al. 2021, AJ, 162, 286 [NASA ADS] [CrossRef] [Google Scholar]
Suárez-Andrés, L., Israelian, G., González Hernández, J. I., et al. 2018, A&A, 614, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Swastik, C., Banyal, R. K., Narang, M., et al. 2021, AJ, 161, 114 [Google Scholar]
Szulágyi, J., & Ercolano, B. 2020, ApJ, 902, 126 [CrossRef] [Google Scholar]
Szulágyi, J., Morbidelli, A., Crida, A., & Masset, F. 2014, ApJ, 782, 65 [CrossRef] [Google Scholar]
Tautvaišienė, G., Mikolaitis, Š., Drazdauskas, A., et al. 2022, ApJS, 259, 45 [CrossRef] [Google Scholar]
Thanathibodee, T., Calvet, N., Bae, J., Muzerolle, J., & Hernández, R. F. 2019, ApJ, 885, 94 [NASA ADS] [CrossRef] [Google Scholar]
Tremblin, P., Amundsen, D. S., Mourier, P., et al. 2015, ApJ, 804, L17 [CrossRef] [Google Scholar]
Tremblin, P., Amundsen, D. S., Chabrier, G., et al. 2016, ApJ, 817, L19 [NASA ADS] [CrossRef] [Google Scholar]
Uyama, T., Tanigawa, T., Hashimoto, J., et al. 2017, AJ, 154, 90 [NASA ADS] [CrossRef] [Google Scholar]
Uyama, T., Norris, B., Jovanovic, N., et al. 2020, J. Astron. Telescopes Instrum. Syst., 6, 045004 [NASA ADS] [Google Scholar]
Uyama, T., Xie, C., Aoyama, Y., et al. 2021, AJ, 162, 214 [NASA ADS] [CrossRef] [Google Scholar]
van Dokkum, P. G. 2001, PASP, 113, 1420 [Google Scholar]
van Holstein, R. G., Stolker, T., Jensen-Clem, R., et al. 2021, A&A, 647, A21 [EDP Sciences] [Google Scholar]
Vos, J. M., Faherty, J. K., Gagné, J., et al. 2022, ApJ, 924, 68 [NASA ADS] [CrossRef] [Google Scholar]
Wagner, K., Follete, K. B., Close, L. M., et al. 2018, ApJ, 863, L8 [Google Scholar]
Wang, J. J., Vigan, A., Lacour, S., et al. 2021, AJ, 161, 148 [Google Scholar]
Whelan, E. T., Huélamo, N., Alcalá, J. M., et al. 2015, A&A, 579, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Witte, S., Helling, C., & Hauschildt, P. H. 2009, A&A, 506, 1367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Witte, S., Helling, C., Barman, T., Heidrich, N., & Hauschildt, P. H. 2011, A&A, 529, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Wolff, S. G., Ménard, F., Caceres, C., et al. 2017, AJ, 154, 26 [Google Scholar]
Wu, Y.-L., Close, L. M., Eisner, J. A., & Sheehan, P. D. 2017a, AJ, 154, 234 [Google Scholar]
Wu, Y.-L., Sheehan, P. D., Males, J. R., et al. 2017b, ApJ, 836, 223 [CrossRef] [Google Scholar]
Xie, C., Haffert, S. Y., de Boer, J., et al. 2020, A&A, 644, A149 [EDP Sciences] [Google Scholar]
Zhang, Y., Snellen, I. A. G., Bohn, A. J., et al. 2021, Nature, 595, 370 [NASA ADS] [CrossRef] [Google Scholar]
Zhou, Y., Herczeg, G. J., Kraus, A. L., Metchev, S., & Cruz, K. L. 2014, ApJ, 783, L17 [Google Scholar]
Zhou, Y., Bowler, B. P., Wagner, K. R., et al. 2021, AJ, 161, 244 [NASA ADS] [CrossRef] [Google Scholar]
Zhou, Y., Sanghi, A., Bowler, B. P., et al. 2022, ApJ, 934, L13 [NASA ADS] [CrossRef] [Google Scholar]
Zhu, Z., Ju, W., & Stone, J. M. 2016, ApJ, 832, 193 [CrossRef] [Google Scholar]
Zsidi, G., Manara, C. F., Kóspál, Á., et al. 2022, A&A, 660, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Zurlo, A., Cugno, G., Montesinos, M., et al. 2020, A&A, 633, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

^{http://svo2.cab.inta-csic.es/theory/vosa/}

Based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere under ESO program 099.C-0760.

All Tables

Table 1

Log of SINFONI observations.

In the text

Table 2

Atmospheric parameters retrieved with ForMoSA.

Equivalent widths

Gaussian fitting results

In the text

All Figures

	Fig. 1 Illustration of the halo subtraction, for the first data cube of the GQ Lup b 2017-04-30 epoch (median along the wavelength axis). We also report the location of the diffraction pattern of the telescope spiders, along with the identified area with improperly calibrated instrument transmission that affects the lower half of the images.
In the text

Fig. 2

Companion spectra. Top row: GQ Lup b spectra. Bottom row: GSC 06214-00210 b spectra. Left column: full spectra. Right column: Zoom on the Pa_β line. In both cases, the spectra continuum are normalized to 1 as the mean value on the 1.27–1.28 µm and 1.29–1.30 µm ranges. The 2010-07-09 (OSIRIS) epoch of GSC06214b was degraded to SINFONI resolution (R = 1800) in the left column, but is shown at full resolution (R = 3800) in the right column. The spectral slopes differences are the results of different Strehl Ratios between epochs, despite the AO correction. Our re-extraction of GQ Lup b spectrum initially presented in Seifahrt et al. (2007) produces a pseudo-continuum short-wards of 1.24 µm that is in better agreement with the more recent SINFONI epochs and observations produced by NIFS.

In the text

	Fig. 3 Pa_ß profiles, corrected from the atmospheric contribution and baseline subtracted (see Sects. 5.2 and 5.3). Each spectrum is labeled with the corresponding UT time at the start of the integration. First row: GQ Lup b lines for each epoch. Second and third rows: Same but for GSC06214b, with the addition of the individual OSIRIS lines from Bowler et al. (2011) (2010-07-09 epoch).
In the text

	Fig. 4 `ForMoSA` resulting photosphere parameters. Left: GQ Lup b results. Right: GSC06214b results. The Radius, Av, radial velocity (RV), and limb-darkening coefficients are omitted from these plots for the sake of clarity.
In the text

	Fig. 5 Visual comparison of the photosphere fitting with `ForMoSA`, for each epoch of both objects, with a zoom on Pa_ß in the right column. Grayed-out wavelength ranges were excluded from fitting as the model either did not include corresponding species (FeH absorption band, Pa_ß) or the data were too noisy (>1.34 µm).
In the text

Fig. 6

Gaussian-fitting resulting parameters for the Pa_β line of GSC06214b. Left: correlations between intrinsic FWHM and the line peak location µ₀, arrows represent an upper limit on the intrinsic FWHM. Right: correlations between the Pa_β line flux and the line peak location µ₀. The intrinsic FWHM is computed as the square root of the quadratic difference between the measured line FWHM and the LSF FWHM. The µ₀ parameter is relative to the line expected wavelength in vacuum (1.2821578 µm).

In the text

Fig. 7

Pa_β flux variability for both sources, as a function of the timescale, with respect to the lowest-flux point of the pair. For GQ Lup b, are included data points from this study as well as the spectrum from Lavigne et al. (2009). For GSC06214b, are included data points from this study as well as those from the individual Bowler data cubes (Bowler et al. 2011) and the mean spectrum from Lachapelle et al. (2015). The color of the points represents the significance of the measurement, i.e., the σ-distance between the two lines used to compute this value. The horizontal and vertical bars correspond respectively to the bin size, and the spread (weighted by significance) within that bin. The red-shaded regions mark the average observed continuum variability among the SINFONI sequences (see Table ). The orange shaded regions represent the expected rotational period of the objects (see Sect. 2).

In the text

Fig. 8

Comparison of the best-fit models for both GQ Lup b (first row) and GSC06214b (2nd and 3rd rows). Colorbars represent the reduced χ² ( $χ_{r}^{2}$ $\chi _r^2$ ) of the Shock (blue) and Mag Acc (red) models. For each epoch, all best models (within the $χ_{r}^{2}$ $\chi _r^2$ range given in the colorbar) are over-plotted with a color scaling with the reduced χ² color. The fitting limits and number of parameters of each model yield a number of degrees of freedom equal to 14 for the Shock model and 9 for the MagAcc model.

In the text

	Fig. 9 $χ_{r}^{2}$ $\chi _r^2$ maps illustrating the accretion models degeneracies when fitting the Pa_β lines. Left panel: T_max vs Ṁ degeneracy for the MagAcc model (GQ Lup b, epoch: 2006-09-18). Right panel: n₀ vs υ₀ degeneracy for the Shock model (GSC06214b, epoch: 2010-07-09 – OSIRIS).
In the text

	Fig. 10 Correlations between equivalent widths (EW) of both potassium absorption doublets and the Pa_β line. The equivalent width is positive for absorption lines and negative for emission lines. Gray lines correspond to a slope equal to -1, where the EW variability can be explained by sole continuum variability.
In the text

Fig. A.1

Visual representation of the last iteration of the extraction for both GQ Lup b and GSC06214b, on epochs 2017-04-30 and 2017-08-19 respectively. As mentioned in Sect. 4, the horizontal spider is subtracted for GQ Lup b, but not for GSC06214b as it does not extend below the companion. Are also marked the spiders locations for both targets and some persistence effects in the GSC06214b data.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Abuter, R., Schreiber, J., Eisenhauer, F., et al. 2006, New A Rev., 50, 398 [Google Scholar]

[2] Alcalá, J. M., Majidi, F. Z., Desidera, S., et al. 2020, A&A, 635, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[3] Alencar, S. H. P., & Batalha, C. 2002, ApJ, 571, 378 [Google Scholar]

[4] Allard, F., Homeier, D., & Freytag, B. 2011, in Astronomical Society of the Pacific Conference Series, 448, 16th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, eds. C. Johns-Krull, M.K. Browning, & A.A. West, 91 [Google Scholar]

[5] Anders, F., Khalatyan, A., Queiroz, A. B. A., et al. 2022, A&A, 658, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[6] Antoniucci, S., García López, R., Nisini, B., et al. 2011, A&A, 534, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[7] Aoyama, Y., Ikoma, M., & Tanigawa, T. 2018, ApJ, 866, 84 [NASA ADS] [CrossRef] [Google Scholar]

[8] Aoyama, Y., Marleau, G.-D., Mordasini, C., & Ikoma, M. 2020, arXiv e-prints, [arXiv:2011.06608] [Google Scholar]

[9] Aoyama, Y., Marleau, G.-D., Ikoma, M., & Mordasini, C. 2021, ApJ, 917, L30 [CrossRef] [Google Scholar]

[10] Artigau, É. 2018, in Handbook of Exoplanets, eds. H.J. Deeg, & J.A. Belmonte, 94 [Google Scholar]

[11] Baraffe, I., Chabrier, G., & Gallardo, J. 2009, ApJ, 702, L27 [NASA ADS] [CrossRef] [Google Scholar]

[12] Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[13] Barenfeld, S. A., Carpenter, J. M., Ricci, L., & Isella, A. 2016, ApJ, 827, 142 [Google Scholar]

[14] Batalha, C., Lopes, D. F., & Batalha, N. M. 2001, ApJ, 548, 377 [CrossRef] [Google Scholar]

[15] Batalha, C., Batalha, N. M., Alencar, S. H. P., Lopes, D. F., & Duarte, E. S. 2002, ApJ, 580, 343 [NASA ADS] [CrossRef] [Google Scholar]

[16] Batygin, K. 2018, AJ, 155, 178 [NASA ADS] [CrossRef] [Google Scholar]

[17] Bayo, A., Rodrigo, C., Barrado Y., Navascués, D., et al. 2008, A&A, 492, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[18] Béjar, V. J. S., Zapatero Osorio, M. R., Pérez-Garrido, A., et al. 2008, ApJ, 673, L185 [CrossRef] [Google Scholar]

[19] Betti, S. K., Follette, K. B., Ward-Duong, K., et al. 2022a, ApJ, 941, L20 [NASA ADS] [CrossRef] [Google Scholar]

[20] Betti, S. K., Follette, K. B., Ward-Duong, K., et al. 2022b, ApJ, 935, L18 [NASA ADS] [CrossRef] [Google Scholar]

[21] Biazzo, K., Frasca, A., Alcalá, J. M., et al. 2017, A&A, 605, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[22] Boley, A. C., Helled, R., & Payne, M. J. 2011, ApJ, 735, 30 [Google Scholar]

[23] Bonnefoy, M., Chauvin, G., Lagrange, A. M., et al. 2014, A&A, 562, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[24] Bonnet, H., Conzelmann, R., Delabre, B., et al. 2004, SPIE Conf. Ser., 5490, 130 [Google Scholar]

[25] Bowler, B. P., Liu, M. C., Kraus, A. L., Mann, A. W., & Ireland, M. J. 2011, ApJ, 743, 148 [Google Scholar]

[26] Bowler, B. P., Liu, M. C., Kraus, A. L., & Mann, A. W. 2014, ApJ, 784, 65 [NASA ADS] [CrossRef] [Google Scholar]

[27] Bowler, B. P., Andrews, S. M., Kraus, A. L., et al. 2015, ApJ, 805, L17 [Google Scholar]

[28] Bowler, B. P., Kraus, A. L., Bryan, M. L., et al. 2017, AJ, 154, 165 [Google Scholar]

[29] Brittain, S. D., Najita, J. R., Dong, R., & Zhu, Z. 2020, ApJ, 895, 48 [CrossRef] [Google Scholar]

[30] Broeg, C., Schmidt, T. O. B., Guenther, E., et al. 2007, A&A, 468, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[31] Bryan, M. L., Benneke, B., Knutson, H. A., Batygin, K., & Bowler, B. P. 2018, Nat. Astron., 2, 138 [Google Scholar]

[32] Bryan, M. L., Ginzburg, S., Chiang, E., et al. 2020, ApJ, 905, 37 [NASA ADS] [CrossRef] [Google Scholar]

[33] Bubar, E. J., Schaeuble, M., King, J. R., Mamajek, E. E., & Stauffer, J. R. 2011, AJ, 142, 180 [Google Scholar]

[34] Cao, L., Pinsonneault, M. H., Hillenbrand, L. A., & Kuhn, M. A. 2022, ApJ, 924, 84 [NASA ADS] [CrossRef] [Google Scholar]

[35] Carpenter, J. M., Hillenbrand, L. A., Skrutskie, M. F., & Meyer, M. R. 2002, AJ, 124, 1001 [Google Scholar]

[36] Cendes, Y., Williams, P. K. G., & Berger, E. 2022, AJ, 163, 15 [CrossRef] [Google Scholar]

[37] Chabrier, G., Baraffe, I., Allard, F., & Hauschildt, P. 2000, ApJ, 542, 464 [Google Scholar]

[38] Chang, E. S., & Deming, D. 1996, Sol. Phys., 165, 257 [CrossRef] [Google Scholar]

[39] Chinchilla, P., Béjar, V. J. S., Lodieu, N., Zapatero Osorio, M. R., & Gauza, B. 2021, A&A, 645, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[40] Costigan, G., Vink, J. S., Scholz, A., Ray, T., & Testi, L. 2014, MNRAS, 440, 3444 [NASA ADS] [CrossRef] [Google Scholar]

[41] Cridland, A. J. 2018, A&A, 619, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[42] Cugno, G., Quanz, S. P., Hunziker, S., et al. 2019, A&A, 622, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[43] Cumming, A., Helled, R., & Venturini, J. 2018, MNRAS, 477, 4817 [Google Scholar]

[44] Curran, P. A. 2015, Astrophysics Source Code Library, [record ascl:1504.008] [Google Scholar]

[45] Currie, T., Lawson, K., Schneider, G., et al. 2022, Nat. Astron., 6, 751 [NASA ADS] [CrossRef] [Google Scholar]

[46] Cushing, M. C., Rayner, J. T., & Vacca, W. D. 2005, ApJ, 623, 1115 [Google Scholar]

[47] Cutri, R. M., et al. 2012, VizieR Online Data Catalog: II/311 [Google Scholar]

[48] Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]

[49] Davies, R. I. 2007, MNRAS, 375, 1099 [Google Scholar]

[50] Delorme, P., Gagné, J., Girard, J. H., et al. 2013, A&A, 553, A5 [Google Scholar]

[51] Donati, J. F., Gregory, S. G., Alencar, S. H. P., et al. 2012, MNRAS, 425, 2948 [Google Scholar]

[52] Dong, J., Jiang, Y.-F., & Armitage, P. J. 2021, ApJ, 921, 54 [NASA ADS] [CrossRef] [Google Scholar]

[53] Edwards, S., Hartigan, P., Ghandour, L., & Andrulis, C. 1994, AJ, 108, 1056 [Google Scholar]

[54] Eisenhauer, F., Abuter, R., Bickert, K., et al. 2003, Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, 4841, 1548 [CrossRef] [Google Scholar]

[55] Eriksson, S. C., Asensio Torres, R., Janson, M., et al. 2020, A&A, 638, A6 [Google Scholar]

[56] Feiden, G. A. 2016, A&A, 593, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[57] Fendt, C. 2003, A&A, 411, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[58] Fischer, W. J., Hillenbrand, L. A., Herczeg, G. J., et al. 2022, arXiv e-prints, [arXiv:2203.11257] [Google Scholar]

[59] Folha, D. F. M., & Emerson, J. P. 2001, A&A, 365, 90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[60] Follette, K. B., Close, L. M., Males, J. R., et al. 2023, AJ, 165, 225 [NASA ADS] [CrossRef] [Google Scholar]

[61] Frasca, A., Biazzo, K., Alcalá, J. M., et al. 2017, A&A, 602, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[62] Fu, Z., Huang, S., & Yu, C. 2023, ApJ, 945, 165 [NASA ADS] [CrossRef] [Google Scholar]

[63] Gagné, J., Allers, K. N., Theissen, C. A., et al. 2018a, ApJ, 854, L27 [CrossRef] [Google Scholar]

[64] Gagné, J., Mamajek, E. E., Malo, L., et al. 2018b, ApJ, 856, 23 [Google Scholar]

[65] Gaia Collaboration 2022, VizieR Online Data Catalog: I/355 [Google Scholar]

[66] Ginski, C., Schmidt, T. O. B., Mugrauer, M., et al. 2014, MNRAS, 444, 2280 [Google Scholar]

[67] Gressel, O., Nelson, R. P., Turner, N. J., & Ziegler, U. 2013, ApJ, 779, 59 [NASA ADS] [CrossRef] [Google Scholar]

[68] Haffert, S. Y., Bohn, A. J., de Boer, J., et al. 2019, Nat. Astron., 3, 749 [Google Scholar]

[69] Hartmann, L., Herczeg, G., & Calvet, N. 2016, ARA&A, 54, 135 [Google Scholar]

[70] Hashimoto, J., Aoyama, Y., Konishi, M., et al. 2020, AJ, 159, 222 [Google Scholar]

[71] Heller, R., & Pudritz, R. 2015, ApJ, 806, 181 [NASA ADS] [CrossRef] [Google Scholar]

[72] Helling, C., Ackerman, A., Allard, F., et al. 2008, MNRAS, 391, 1854 [Google Scholar]

[73] Herbig, G. H. 1977, ApJ, 214, 747 [Google Scholar]

[74] Högbom, J. A. 1974, A&AS, 15, 417 [Google Scholar]

[75] Huélamo, N., Chauvin, G., Schmid, H. M., et al. 2018, A&A, 613, A5 [Google Scholar]

[76] Huélamo, N., Chauvin, G., Mendigutía, I., et al. 2022, A&A, 668, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[77] Ireland, M. J., Kraus, A., Martinache, F., Law, N., & Hillenbrand, L. A. 2011, ApJ, 726, 113 [Google Scholar]

[78] Itoh, Y., Hayashi, M., Tamura, M., et al. 2005, ApJ, 620, 984 [NASA ADS] [CrossRef] [Google Scholar]

[79] Joergens, V., Bonnefoy, M., Liu, Y., et al. 2013, A&A, 558, A7 [Google Scholar]

[80] Jones, A., Noll, S., Kausch, W., Szyszka, C., & Kimeswenger, S. 2013, A&A, 560, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[81] Kao, M. M., Hallinan, G., Pineda, J. S., Stevenson, D., & Burgasser, A. 2018, ApJS, 237, 25 [NASA ADS] [CrossRef] [Google Scholar]

[82] Katarzyński, K., Gawroński, M., & Goździewski, K. 2016, MNRAS, 461, 929 [CrossRef] [Google Scholar]

[83] Kramida, A.Yu, Ralchenko, Reader, J., & NIST ASD Team 2022, NIST Atomic Spectra Database (ver. 5.10), [Ońlińe]. Available: https://physics.nist. gov/asd (Gaithersburg, MD: National Institute of Standards and Technology) [Google Scholar]

[84] Kraus, A. L., Irelańd, M. J., Martinache, F., & Lloyd, J. P. 2008, ApJ, 679, 762 [NASA ADS] [CrossRef] [Google Scholar]

[85] Kurosawa, R., Harries, T. J., & Littlefair, S. P. 2006, MNRAS, 372, 1879 [NASA ADS] [CrossRef] [Google Scholar]

[86] Lachapelle, F.-R., Lafrenière, D., Gagné, J., et al. 2015, ApJ, 802, 61 [Google Scholar]

[87] Larkin, J., Barczys, M., Krabbe, A., et al. 2006, SPIE Conf. Ser., 6269, 62691A [NASA ADS] [Google Scholar]

[88] Lavigne, J.-F., Doyon, R., Lafrenière, D., Marois, C., & Barman, T. 2009, ApJ, 704, 1098 [Google Scholar]

[89] Lazzoni, C., Gratton, R., Alcalá, J. M., et al. 2020, A&A, 635, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[90] Long, D. E., Zhang, K., Teague, R., & Bergin, E. A. 2020, ApJ, 895, L46 [NASA ADS] [CrossRef] [Google Scholar]

[91] Lubow, S. H., & Martin, R. G. 2012, ApJ, 749, L37 [NASA ADS] [CrossRef] [Google Scholar]

[92] Luhman, K. L., Stauffer, J. R., Muench, A. A., et al. 2003, ApJ, 593, 1093 [Google Scholar]

[93] MacGregor, M. A., Wilner, D. J., Czekala, I., et al. 2017, ApJ, 835, 17 [Google Scholar]

[94] Manara, C. F., Testi, L., Rigliaco, E., et al. 2013, A&A, 551, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[95] Marleau, G.-D., & Aoyama, Y. 2022, RNAAS, 6, 262 [NASA ADS] [Google Scholar]

[96] Marleau, G. D., Aoyama, Y., Kuiper, R., et al. 2022, A&A, 657, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[97] Marley, M. S., Fortney, J. J., Hubickyj, O., Bodenheimer, P., & Lissauer, J. J. 2007, ApJ, 655, 541 [Google Scholar]

[98] Marois, C., Macintosh, B., & Barman, T. 2007, ApJ, 654, L151 [NASA ADS] [CrossRef] [Google Scholar]

[99] McElwain, M. W., Metchev, S. A., Larkin, J. E., et al. 2007, ApJ, 656, 505 [Google Scholar]

[100] Mendigutía, I., Oudmaijer, R. D., Schneider, P. C., et al. 2018, A&A, 618, L9 [CrossRef] [EDP Sciences] [Google Scholar]

[101] Miki, S. 1982, Progr. Theor. Phys., 67, 1053 [NASA ADS] [CrossRef] [Google Scholar]

[102] Murphy, S. J., Joyce, M., Bedding, T. R., White, T. R., & Kama, M. 2021, MNRAS, 502, 1633 [NASA ADS] [CrossRef] [Google Scholar]

[103] Muzerolle, J., Calvet, N., & Hartmann, L. 2001, ApJ, 550, 944 [Google Scholar]

[104] Muzerolle, J., Luhman, K. L., Briceño, C., Hartmann, L., & Calvet, N. 2005, ApJ, 625, 906 [NASA ADS] [CrossRef] [Google Scholar]

[105] Natta, A., Testi, L., Muzerolle, J., et al. 2004, A&A, 424, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[106] Neuhäuser, R., Guenther, E. W., Petr, M. G., et al. 2000, A&A, 360, L39 [NASA ADS] [Google Scholar]

[107] Neuhäuser, R., Guenther, E. W., Wuchterl, G., et al. 2005, A&A, 435, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[108] Neuhäuser, R., Mugrauer, M., Seifahrt, A., Schmidt, T. O. B., & Vogt, N. 2008, A&A, 484, 281 [CrossRef] [EDP Sciences] [Google Scholar]

[109] Noll, S., Kausch, W., Barden, M., et al. 2012, A&A, 543, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[110] Padoan, P., & Nordlund, Å. 1999, ApJ, 526, 279 [CrossRef] [Google Scholar]

[111] Padoan, P., & Nordlund, Å. 2004, ApJ, 617, 559 [NASA ADS] [CrossRef] [Google Scholar]

[112] Pearce, L. A., Kraus, A. L., Dupuy, T. J., et al. 2019, AJ, 157, 71 [NASA ADS] [CrossRef] [Google Scholar]

[113] Pecaut, M. J., Mamajek, E. E., & Bubar, E. J. 2012, ApJ, 746, 154 [Google Scholar]

[114] Petrus, S., Bonnefoy, M., Chauvin, G., et al. 2020, A&A, 633, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[115] Petrus, S., Bonnefoy, M., Chauvin, G., et al. 2021, A&A, 648, A59 [EDP Sciences] [Google Scholar]

[116] Petrus, S., Chauvin, G., Bonnefoy, M., et al. 2023, A&A, 670, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[117] Phillips, M. W., Tremblin, P., Baraffe, I., et al. 2020, A&A, 637, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[118] Pierens, A., & Raymond, S. N. 2016, MNRAS, 462, 4130 [NASA ADS] [CrossRef] [Google Scholar]

[119] Piskunov, N. E., & Valenti, J. A. 2002, A&A, 385, 1095 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[120] Pittman, C. V., Espaillat, C. C., Robinson, C. E., et al. 2022, AJ, 164, 201 [NASA ADS] [CrossRef] [Google Scholar]

[121] Preibisch, T., Guenther, E., Zinnecker, H., et al. 1998, A&A, 333, 619 [NASA ADS] [Google Scholar]

[122] Privon, G. C., Ricci, C., Aalto, S., et al. 2020, ApJ, 893, 149 [NASA ADS] [CrossRef] [Google Scholar]

[123] Reiners, A., & Christensen, U. R. 2010, A&A, 522, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[124] Rice, E. L., Barman, T., Mclean, I. S., Prato, L., & Kirkpatrick, J. D. 2010, ApJS, 186, 63 [NASA ADS] [CrossRef] [Google Scholar]

[125] Rigliaco, E., Natta, A., Testi, L., et al. 2012, A&A, 548, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[126] Ringqvist, S. C., Viswanath, G., Aoyama, Y., et al. 2023, A&A, 669, A12 [Google Scholar]

[127] Sallum, S., Follette, K. B., Eisner, J. A., et al. 2015, Nature, 527, 342 [Google Scholar]

[128] Santamaría-Miranda, A., Cáceres, C., Schreiber, M. R., et al. 2018, MNRAS, 475, 2994 [Google Scholar]

[129] Santamaría-Miranda, A., Cáceres, C., Schreiber, M. R., et al. 2019, MNRAS, 488, 5852 [CrossRef] [Google Scholar]

[130] Schmidt, T. O. B., Neuhäuser, R., Seifahrt, A., et al. 2008, A&A, 491, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[131] Schwarz, H., Ginski, C., de Kok, R. J., et al. 2016, A&A, 593, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[132] Seifahrt, A., Neuhäuser, R., & Hauschildt, P. H. 2007, A&A, 463, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[133] Sembach, K. R., & Savage, B. D. 1992, ApJS, 83, 147 [NASA ADS] [CrossRef] [Google Scholar]

[134] Sicilia-Aguilar, A., Fang, M., Roccatagliata, V., et al. 2015, A&A, 580, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[135] Skilling, J. 2004, in American Institute of Physics Conference Series, 735, Bayesian Inference and Maximum Entropy Methods in Science and Engineering: 24th International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering, eds. R. Fischer, R. Preuss, & U.V. Toussaint, 395 [Google Scholar]

[136] Smith, E. J., Davis, L.J., Jones, D.E., et al. 1974, Science, 183, 305 [NASA ADS] [CrossRef] [Google Scholar]

[137] Stolker, T., Haffert, S. Y., Kesseli, A. Y., et al. 2021, AJ, 162, 286 [NASA ADS] [CrossRef] [Google Scholar]

[138] Suárez-Andrés, L., Israelian, G., González Hernández, J. I., et al. 2018, A&A, 614, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[139] Swastik, C., Banyal, R. K., Narang, M., et al. 2021, AJ, 161, 114 [Google Scholar]

[140] Szulágyi, J., & Ercolano, B. 2020, ApJ, 902, 126 [CrossRef] [Google Scholar]

[141] Szulágyi, J., Morbidelli, A., Crida, A., & Masset, F. 2014, ApJ, 782, 65 [CrossRef] [Google Scholar]

[142] Tautvaišienė, G., Mikolaitis, Š., Drazdauskas, A., et al. 2022, ApJS, 259, 45 [CrossRef] [Google Scholar]

[143] Thanathibodee, T., Calvet, N., Bae, J., Muzerolle, J., & Hernández, R. F. 2019, ApJ, 885, 94 [NASA ADS] [CrossRef] [Google Scholar]

[144] Tremblin, P., Amundsen, D. S., Mourier, P., et al. 2015, ApJ, 804, L17 [CrossRef] [Google Scholar]

[145] Tremblin, P., Amundsen, D. S., Chabrier, G., et al. 2016, ApJ, 817, L19 [NASA ADS] [CrossRef] [Google Scholar]

[146] Uyama, T., Tanigawa, T., Hashimoto, J., et al. 2017, AJ, 154, 90 [NASA ADS] [CrossRef] [Google Scholar]

[147] Uyama, T., Norris, B., Jovanovic, N., et al. 2020, J. Astron. Telescopes Instrum. Syst., 6, 045004 [NASA ADS] [Google Scholar]

[148] Uyama, T., Xie, C., Aoyama, Y., et al. 2021, AJ, 162, 214 [NASA ADS] [CrossRef] [Google Scholar]

[149] van Dokkum, P. G. 2001, PASP, 113, 1420 [Google Scholar]

[150] van Holstein, R. G., Stolker, T., Jensen-Clem, R., et al. 2021, A&A, 647, A21 [EDP Sciences] [Google Scholar]

[151] Vos, J. M., Faherty, J. K., Gagné, J., et al. 2022, ApJ, 924, 68 [NASA ADS] [CrossRef] [Google Scholar]

[152] Wagner, K., Follete, K. B., Close, L. M., et al. 2018, ApJ, 863, L8 [Google Scholar]

[153] Wang, J. J., Vigan, A., Lacour, S., et al. 2021, AJ, 161, 148 [Google Scholar]

[154] Whelan, E. T., Huélamo, N., Alcalá, J. M., et al. 2015, A&A, 579, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[155] Witte, S., Helling, C., & Hauschildt, P. H. 2009, A&A, 506, 1367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[156] Witte, S., Helling, C., Barman, T., Heidrich, N., & Hauschildt, P. H. 2011, A&A, 529, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[157] Wolff, S. G., Ménard, F., Caceres, C., et al. 2017, AJ, 154, 26 [Google Scholar]

[158] Wu, Y.-L., Close, L. M., Eisner, J. A., & Sheehan, P. D. 2017a, AJ, 154, 234 [Google Scholar]

[159] Wu, Y.-L., Sheehan, P. D., Males, J. R., et al. 2017b, ApJ, 836, 223 [CrossRef] [Google Scholar]

[160] Xie, C., Haffert, S. Y., de Boer, J., et al. 2020, A&A, 644, A149 [EDP Sciences] [Google Scholar]

[161] Zhang, Y., Snellen, I. A. G., Bohn, A. J., et al. 2021, Nature, 595, 370 [NASA ADS] [CrossRef] [Google Scholar]

[162] Zhou, Y., Herczeg, G. J., Kraus, A. L., Metchev, S., & Cruz, K. L. 2014, ApJ, 783, L17 [Google Scholar]

[163] Zhou, Y., Bowler, B. P., Wagner, K. R., et al. 2021, AJ, 161, 244 [NASA ADS] [CrossRef] [Google Scholar]

[164] Zhou, Y., Sanghi, A., Bowler, B. P., et al. 2022, ApJ, 934, L13 [NASA ADS] [CrossRef] [Google Scholar]

[165] Zhu, Z., Ju, W., & Stone, J. M. 2016, ApJ, 832, 193 [CrossRef] [Google Scholar]

[166] Zsidi, G., Manara, C. F., Kóspál, Á., et al. 2022, A&A, 660, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[167] Zurlo, A., Cugno, G., Montesinos, M., et al. 2020, A&A, 633, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

I. The case of GQ Lup b and GSC 06214-00210 b★,★★

1 Introduction

2 Information on targets

2.1 GQ Lup system

2.2 GSC 06214-00210 system

3 Observations and data reduction

3.1 Monitoring sequences with VLT/SINFONI

3.2 SINFONI cube reconstruction and calibration

3.3 New investigation of Keck/OSIRIS data

4 Spectral extraction

4.1 Halo removal

4.2 Extraction and flux calibration

4.3 Photospheric contribution

5 Results

5.1 Companion J-band spectra

5.2 Atmospheric and physical parameters

5.2.1 Inferred values and correlations

5.2.2 Use of evolutionary tracks

5.3 Analysis of Paβ time series

5.4 Comparison to protoplanet accretion models

5.4.1 Description of accretion models

5.4.2 Model fitting

6 Discussion

6.1 Atmospheric abundances as formation tracers

6.2 Constraints on accretion processes in planetary mass objects

6.2.1 MagAcc and Shock models’ relative contributions

6.2.2 Others explanations for line variability

6.2.3 Line variability on similar objects

6.2.4 Similarities with CTTS

6.3 Evidence for continuum variability?

6.4 Implications for protoplanet detection

7 Conclusions

Acknowledgements

Appendix A Supplementary material

References

All Tables

All Figures

Emission line variability of young 10–30 M_Jup companions

I. The case of GQ Lup b and GSC 06214-00210 b^★,^★★

5.3 Analysis of Pa_β time series