EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 675 (July 2023) A&A, 675 (2023) A33 Full HTML
Open Access
Issue
A&A
Volume 675, July 2023
Article Number A33
Number of page(s) 13
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202345969
Published online 29 June 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Mass loss is a ubiquitous phenomenon that affects all massive stars. While it is generally weak during the main sequence, stellar wind mass loss rises as the star evolves and becomes more luminous. In a single star of 15 M⊙ initially, it leads to a cumulative mass reduction of ~10%, but this fraction may rise to 90% for the highest mass stars by the time they reach core collapse (Maeder & Meynet 1987; Langer et al. 1994). Mass transfer in interacting binaries leads to short-lived, but stronger mass-loss episodes, often causing the loss of the H-rich envelope and leading to H-deficient progenitors at core collapse (Podsiadlowski et al. 1992; Wellstein & Langer 1999; Eldridge et al. 2008; Langer 2012). In such binaries, stellar wind mass loss is also at play and may influence the frequency of Type Ib versus Type Ic SNe (Yoon 2017; Aguilera-Dena et al. 2022; see Filippenko 1997 for a review of SN classification). Instead of constraining mass loss through the observation of the atmospheres and environments of stars at various stages of their lives, we might monitor core-collapse supernovae (SNe) for years and decades after explosion when the ejecta expand into and interact with the material lost by the star during the last hundreds or thousands of years before collapse. For a SN shock ramming at velocity Vsh into a steady-state wind with mass-loss rate Ṁ and velocity V∞, the instantaneous power released by the interaction is 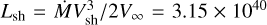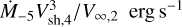Lsh=M˙Vsh3/2V∞=3.15×1040${L_{{\rm{sh}}}} = {{{\dot MV_{{\rm{sh}}}^3} \mathord{\left/ {\vphantom {{\dot MV_{{\rm{sh}}}^3} {2V}}} \right. \kern-\nulldelimiterspace} {2V}}_\infty } = 3.15 \times {10^{40}}$ M˙−5 Vsh,43/V∞,2 erg s−1${{\dot M}_{ - 5}}\,{{V_{{\rm{sh},4}}^3} \mathord{\left/ {\vphantom {{V_{{\rm{sh}}}^3} {{V_{\infty ,2}}}}} \right. \kern-\nulldelimiterspace} {{V_{\infty ,2}}}}\,{\rm{erg}}\,{{\rm{s}}^{ - 1}}$, where Ṁ−5 ≡ Ṁ/10−5M⊙ yr−1, Vsh,4 ≡ Vsh/10,000 km s−1, and V∞,2 ≡ V∞/100 km s−1. As a result, even modest wind strengths rival with radioactive decay power at late times (Dessart & Hillier 2022)1. Unfortunately, such late-time observations of SNe are relatively rare (see, e.g., Milisavljevic et al. 2012, or more recently Rizzo Smith et al. 2023) and most SN observations (even today) remain focused on the earlier, brighter phase of the SN evolution.

The observational signatures suggestive of ejecta interaction with circumstellar material (CSM) are diverse. The interaction may produce radio and X-ray emission, as observed over a yearlong scale in the luminous fast-declining Type II SN 1979C (Chevalier 1982a,b; Weiler et al. 1991). In some objects, this emission is observed with a delay, as in SN2014C (Margutti et al. 2017), suggesting interaction with material not directly at the progenitor surface but far away from it, at 1016–1017 cm. Strong ultraviolet (UV) emission is also identified, in particular in strongly interacting events like the Type IIn SN2010jl (Fransson et al. 2014) or the Type Ibn SN2006jc (Immler et al. 2008), but UV emission is typically expected for all ejecta-CSM interactions (Fransson 1984). Because of an observational bias, spectroscopic signatures of interaction are mostly confined to the optical range. Early-time emission profiles with narrow cores and symmetric broad wings are the defining signature of Type IIn SNe. This profile morphology may persist for many days (e.g., SN 1998S; Leonard et al. 2000, or SN2020tlf; Jacobson-Galán et al. 2022) or only for hours (e.g., SN2013fs; Yaron et al. 2017), corresponding to different extent and mass of the CSM. In some Type II SNe, a high-velocity absorption feature is observed in some lines, in particular, in Hα, which suggests the presence of a dense shell at the interface between ejecta and CSM (Chugai et al. 2007; Gutiérrez et al. 2017; Dessart & Hillier 2022). Ejecta-CSM interactions may also boost the emissivity of the outer ejecta. One such manifestation is observed in the optical spectra of the Type IIb SN 1993J, which revealed broad boxy emission profiles throughout the nebular phase and detectable for years after explosion (Matheson et al. 2000a,b). Since SN 1993J, other SNe have shown broad, sometimes boxy emission, although generally limited to Hα, and with a turn-on occurring at different times: at ~200d in SNe 2007od, 2017ivv, and 2014G (Andrews et al. 2010; Gutiérrez et al. 2020; Terreran et al. 2016), at ~450 d in SN2013by (Black et al. 2017), or at ~600 d in SNe 2007it and 2017eaw (Andrews et al. 2011; Weil et al. 2020).

On the theoretical and modeling side, most works have been focused on early-time signatures of interaction and superluminous SNe – that is, interaction with massive CSM corresponding to very large mass-loss rates of order 10−1 M⊙ yr−1, as inferred for SN2010jl. However, theory predicts that massive stars may undergo episodes of intense mass loss, especially in interacting binaries, producing intermediate states between mass-loss rates of 10−6 M⊙ yr−1 that are typical of the red-supergiant (RSG) star Betelgeuse today (Dolan et al. 2016) and the most extreme events like SN 2010jl (Fransson et al. 2014; Dessart et al. 2015). In most cases, such pre-SN mass-loss rates would be too small to produce an optically thick CSM, hence, the transient would never show (or at best very briefly after shock breakout) the narrow spectral signatures that flag the event as Type IIn (Dessart & Hillier 2022). Yet, the power from interaction could be substantial, rivaling and even superseding the contribution from decay power at late times (see, e.g., indications for this based on the Hα line strength in Chugai 1990). Signatures of interaction should be present at some level and with much diversity in essentially all core-collapse SNe, as this should be the norm, rather than the exception.

The impact of ejecta-CSM interaction in a standard RSG star explosion model was recently explored by Dessart & Hillier (2022). To mimic a range in steady-state pre-SN wind mass-loss rate from a value vanishingly small up to about 10−3 M⊙ yr−1 (which is still a factor of a hundred smaller than inferred for SN2010jl), shock power was introduced in the outer ejecta in a dense shell of 0.1 M⊙ located at ~11 000 km s−1 and with a constant rate between zero and 1043 erg s−1. The simulations were evolved from 15 d until 350 d, thus covering the photospheric and the nebular phase. In the model without shock power, a high-velocity absorption feature developed at the recombination epoch in numerous lines, including Hα, Hβ, Na ID, O I 7774 Å, or the Ca II near-infrared (IR) triplet. However, with shock power, the models exhibited a weak boost in continuum optical flux, a broad boxy Hα emission component, and a boost to the UV flux which strengthened with time, the more so for greater shock power. All these properties are compatible with the observations, but the models suggest that the current sample of observations is capturing only weakly the full breadth of interaction signatures and these signatures should also be more frequently detected. The spectacular evolution captured for SN 1993J over a decade after discovery was made possible in part because of its proximity, but the pre-SN mass loss was inferred to be modest, with a value of only a few times 10−5 M⊙ yr−1 (e.g., Fransson & Björnsson 1998; Tatischeff 2009). Current 8-m-class telescopes and future facilities such as the Vera Rubin Observatory should be able to capture signatures of interaction in all core-collapse SNe (albeit depending on the SN distance) and help constrain the pre-SN mass-loss rate of massive stars, whether it is compatible with single-star or binary-star evolution, and so on.

In this paper, we extend the study of Dessart & Hillier (2022), which covered epochs prior to 350 d, and focus on the evolution from 350 to 1000 d of a Type II SN model with and without shock power. The qualitative evolution is similar for a wide range of interaction powers, so we focus on only one case with an injected shock power of 1040 erg s−1 – this power, associated with a RSG progenitor wind mass-loss rate as low as 10−6 M⊙ yr−1, is comparable to the decay power absorbed in the ejecta at about 350 d (Dessart & Hillier 2022). In other words, any RSG star explosion should be subject to that power level and thus our results are representative, default expectations for a standard SN II. Lower values would suggest even weaker mass-loss rates, which would imply a negligible impact of wind mass loss on the progenitor evolution. In the next section, we start by emphasizing how the exponential decline of radioactive decay should eventually be swamped by ejecta-CSM interaction at late times. In Sect. 3, we describe the models and setup for the present calculations. Section 4 discusses the results for the photometric and spectroscopic evolution for the models with and without shock power, covering a timeframe from 350 until 1000d. In Sect. 5, we compare these results to a few well-observed events exhibiting signatures of interaction. The implications as well as the limitations of our results are discussed in Sect. 6. We present our conclusions in Sect. 7.

2 All core-collapse SNe should eventually be powered by interaction

Figure 1 illustrates the evolution of the decay power emitted by the most abundant unstable isotopes produced in the explosion of a star of 15.2 M⊙ initially (Sukhbold et al. 2016), presented in order of increasing atomic mass: 44Ti, 48Cr, 49Cr, 51Mn, 52Fe, 55Co, 56Ni, and 57Ni. The associated yields are listed in Table 1 together with other ejecta properties. These parent isotopes are part of a two-step decay chain. In this model, which is representative of a standard core-collapse SN in terms of explosive yields, 56Ni is the main source of decay power up until ~1000 d, followed by an intermediate phase during which the decay of 57Ni dominates, until the decay of 44Ti takes over after about 3000 d. During the first 100 d after explosion, the power released from 56Ni is of order 1042 erg s−1 and thus comparable to a Type II SN luminosity. When 57Ni takes over, the total decay power emitted is only 1037 erg s−1, after which the slow-decaying 44Ti isotope (which has a half-life of 21,915 d) delivers a near-constant power of about 1036 erg s−1 (a maximum time of 7000 d is used in Fig. 1).

Such powers can easily be matched at late times by ejecta interaction with CSM. A standard secular steady-state mass-loss rate of 10−6 M⊙ yr−1 in an RSG should deliver a power of about 1040 erg s−1, which is, thus, greater than the total decay power in Fig. 1 at all times > 600 d. The major uncertainty here involves how much of that power is thermalized in the outer ejecta to escape as lower energy photons and what fraction of these come out in the UV and in the optical (a further aspect is whether the radiation emerges in the continuum or in lines; Dessart & Hillier 2022). This will depend on the previous history of the ejecta, namely, the presence or absence of a dense shell in the outer ejecta, which will form through the continuous pile-up of wind material (Chugai et al. 2007), but also directly at shock breakout (Dessart et al. 2017) and the magnitude of the RSG wind mass-loss rate. If the shock power is not thermalized, the SN should be X-ray luminous. Somehow, this power has to come out, and we note that it is not negligible, even for a modest wind-mass loss.

However, SN 1987A is one example that demonstrates that it may take a very long time before the interaction with CSM becomes the dominant power source. Indeed, modeling the nebular-phase spectrum of SN 1987A suggests that its ejecta were powered primarily by the decay of 44Ti at 8 yr after explosion (Jerkstrand et al. 2011). The low late-time power inferred from optical and near-IR radiation suggests that the CSM density is low, which may in part be due to the large wind velocity of the blue-supergiant progenitor relative to the RSG case.

thumbnail Fig. 1

Emitted decay power as a function of time since explosion in model s15p2 (see Table 1 for the yields). We show the individual contributions from the dominant unstable isotopes (the label refers to the parent isotope of the two-step decay chains) as colored curves, with the total given by the black dashed curve. Because of γ-ray escape, the power effectively absorbed by the ejecta is only a fraction of the power emitted (about 25% at 1000 d in this model). The dominant source of power is 56Ni in the first 1000 d, while 44Ti takes over beyond about 3000 d. Evidently, ejecta interaction with a standard RSG wind, which delivers a power of about 1040 erg s−1 would dominate over radioactive decay after about 600 d.
Table 1

Summary of ejecta properties for model s15p2 (Sukhbold et al. 2016; Dessart et al. 2021).

3 Numerical setup

Simulations carried out with the time-dependent nonlocal thermodynamic equilibrium radiative transfer code CMFGEN (Hillier & Dessart 2012) presented by Dessart & Hillier (2022) were focused on the earlier-time evolution of Type II SN ejecta under the influence of shock power. In that case, the issue of chemical mixing is not critical and so, a simple boxcar mixing was used, which introduces both macroscopic and microscopic mixing. Here, we focus on the late time evolution when the treatment of mixing is critical. We thus used the shuffling method of Dessart & Hillier (2020b)3 and employed the detailed 15.2 M⊙ model of Sukhbold et al. (2016), with the numerical setup presented by Dessart et al. (2021, the model is named s15p2). To avoid repetition – and since the focus in this paper is on the influence of interaction power on the SN radiation rather than the impact of chemical mixing – we refer to Dessart et al. (2021, in particular Sect. 2) for additional details.

In our study, we evolved this model s15p2 from the initial time of 350 d until 1000 d after explosion accounting for the radioactive decay from 56Ni and 56Co. A first model, named s15p2NoPwr, neglects any contribution from shock power. Because energy deposition from radioactive decay occurs within the inner ejecta, this model s15p2NoPwr was truncated at 6000 km s−1 (the decay power absorbed at that velocity is 10 000 times smaller than in the inner ejecta; see details in Fig. 2). A second model, named s15p2Pwr1e40, was evolved with an extra power of 1040 erg s−1 injected at 8000 km s−1 within a dense shell of 0.1 M⊙ – both models have (at all times) the same density, velocity, and composition profiles below 6000 km s−1. This power corresponds to the thermalized part of the shock power arising from interaction with CSM, which (for this value) could arise from a pre-SN wind of about 10−6 M⊙ yr−1 in the case of efficient thermalization. To mimic the potential breakup of the shell in three dimensions, we spread the dense shell over a thickness of about 10% of the shell radius and introduce clumping to maintain a high gas density within the shell. The clumping profile follows a Gaussian with a minimum volume filling factor of 1% at the shell center. Initial ejecta properties at 350 d are shown for this model in Fig. A.1. Ultimately, the exact structure of this dense shell requires three-dimensional (3D) radiation-hydrodynamics simulations of the ejecta-CSM interaction and such simulations are currently unavailable.

We performed a few additional simulations for model s15p2 at 350 d by varying the injected shock power from 1 × 1040 to 7 × 1040 erg s−1. These simulations are analogous to model s15p2Pwr1e40 at 350 d. They are used for comparison to observations in Sect. 5 and shown in Fig. A.2.

In the models with shock power, 70 extra grid points were needed to resolve the dense, clumped shell. Models with (without) shock power used 420 (350) grid points and each model in the sequence took about a week to reach convergence (this is aggravated by the need for a small turbulent velocity of 10 km s−1 in the CMFGEN calculation; Dessart & Hillier 2020a). Because of this cost, it is not practical to run many simulations. At earlier times, the simpler mixing can be used and only 100 grid points are needed (Dessart & Hillier 2022). At times later than 1000d (or earlier in Type IIb, Ib, or Ic SN ejecta), it might be more efficient to focus only on the outer dense shell, which would require only about 70 points. At intermediate nebular epochs of 1–3 yr, which are the focus of the present study, an accurate calculation requires a high resolution for both the inner ejecta mixed with the shuffling technique and the narrow outer dense shell where the shock power is deposited.

4 Results

4.1 Ejecta properties

Figure 2 shows the evolution of some ejecta properties from 350d until 1000d after explosion in the model s15p2Pwr1e40 (i.e., the model that includes a shock power of 1040 erg s−1). In the top panel, we show the total power absorbed in the ejecta due to both radioactive decay (which is biased toward the inner, denser, ejecta layers where 56Ni is present) and shock power (which by design is deposited exclusively within the outer dense shell at 8000 km s−1). The curves are scaled by the quantity (tn/t0)3 to counter the effect of expansion, where t0 = 350 d is the initial time in the sequence and tn corresponds to one of the n epochs spanning from t0 until 1000 d. The offset between the curves arises from the drop in decay power and the increasing γ-ray escape with time: 87% of the emitted decay power is trapped at 350 d and this drops to only 26% at 1000 d. The shock power is chosen constant so all curves overlap in the outer region. Evidently, the shock power reaches a maximum value in the outer regions that rivals the maximum decay power absorbed in the inner regions. As time progresses, because of the exponential decline of radioactive decay, the shock power becomes the dominant power source.

This is also seen in the middle panel showing the gas temperature, which systematically decreases with time in the inner ejecta layers, while it remains roughly constant in some parts of the dense shell centered at 8000 km s−1. In the intermediate regions between 4000 and 8000 km s−1, the gas temperature is boosted by the absorption of UV radiation emitted from the dense shell. In the absence of shock power, the temperature beyond a few 1000 km s−1 drops to around 1000 K (not shown); however, with shock power, it reaches a few 1000 K in these intermediate regions and peaks at 15 000 K in the dense shell. In the inner ejecta regions, the evolution follows what was described for earlier times by Dessart & Hillier (2020b) and Dessart et al. (2021) in similar shuffled-shell models of the explosion of a 15 M⊙ star. In the inner ejecta, the temperature and ionization (bottom panel of Fig. 2) exhibit rapid variations because of the strong chemical stratification (this is in contrast to the smooth profile of the decay power absorbed). In the outer ejecta, the hydrogen ionization is relatively high except in the central, clumped part of the dense shell where the recombination rates are boosted (see, for example, discussion for the effect of clumping in Type II SN ejecta by Dessart et al. 2018). The oxygen ionization exhibits a similar profile (hence not shown), being low in the O-rich zones, and with O+ dominating within the dense shell.

thumbnail Fig. 2

Evolution of ejecta properties for model s15p2Pwr1e40 from t0 = 350 to 1000 d. From top to bottom, we show the profile of the total power absorbed (scaled to counter the effect of expansion; see text), of the gas temperature, and of the hydrogen ionization. In the bottom panel, we overplot the hydrogen mass fraction (dashed line).
thumbnail Fig. 3

Evolution of photometric properties at late times for models s15p2Pwr1e40 (solid) and s15p2NoPwr (dashed). From top to bottom, we show the bolometric luminosity, the fractional power emerging in the far-UV (δLFUV; 1000 < λ/Å < 2000), the near-UV (δLNUV; 2000 < λ/Å < 3500), the optical (δLopt; 3500 < λ/Å < 9500), and the IR (δLIR; λ/Å > 9500), followed by the R-, U-, and UV W2-band magnitudes and the U - V color.

4.2 Photometric properties

Figure 3 illustrates the photometric evolution of model s15p2 with and without shock power. As discussed by Dessart & Hillier (2022), the impact of a shock power of 1040 erg s−1 at 350 d is modest in the optical, in the IR, and in the bolometric luminosity, but it is clearly visible in the U band and even more so in the UV. As time progresses beyond 350 d, the contribution from radioactive decay decreases and the contribution from shock power grows, dominating totally at 1000 d. In the optical (e.g., the R band; 6th panel from top), this switch from decay-powered to shock-powered appears as a knee in the light curve at ~600–700d, about 100–200 d later than it does in Lbol. This knee appears in spite of the constancy of the shock power that is introduced. In other words, the knee results from the changing contrast between shock power and decay power, driven here by the intrinsic, exponential decline of radioactive decay. In the model without shock power, the bulk of the flux emerges in the optical (about 70%) and in the IR (about 25%) at 350 d. However, in the model with shock power, the flux emerges primarily in the UV. As time passes, the model without (with) shock power becomes even more biased in favor of the IR (UV). As previously predicted for earlier times, the UV range is the spectral region to investigate to capture the most obvious signatures of interaction, where the model with shock power remains 3–5 mag brighter than its counterpart without shock power. As advocated by Dessart et al. (2022) and confirmed here for SNe II 1–3 yr after explosion, the U-band survey of the Vera Rubin Observatory is expected to detect SNe II with an “anomalously” high U-band brightness. We note that for the present, mainly conceptual study, the discussion holds for filters having a similar passband, such as the u-band SDSS filter and the U-band Johnson filter.

4.3 Spectroscopic properties

The spectral evolution of models s15p2NoPwr and s15p2Pwr1e40 is shown in Fig. 4, for both the optical (left column) and the full UV, optical, and near-IR ranges (right column; contributions in the optical range from individual species are illustrated in Fig. A.3). This figure offers some clues about the photometric properties shown in Fig. 3. In the optical, the main feature introduced by the shock power at 8000 km s−1 is the excess Hα, optically thin emission, producing a broad boxy profile that contrasts with the narrower Hα component powered by radioactive decay and associated with hydrogen advected inward in the inner, slow-moving, ejecta. As a result, apart from this weak broad boxy Hα emission, the entire optical spectrum is powered by radioactive decay (this is not the case for the UV – see below). As time passes, the model powered exclusively by radioactive decay becomes increasingly faint. In contrast, in the model with shock power, we see the morphing of the ejecta from being radioactively powered and dominated by narrower lines forming in the inner ejecta to becoming shock powered and dominated by broader lines forming in the outermost layers of the ejecta (in the dense shell). At intermediate epochs (e.g., ~700 d), numerous lines show a hybrid morphology with both a narrow and a broad component (e.g., Hα and [O I] λλ 6300, 6364), while others exhibit only a narrow component (e.g., Mg I] λ 4571 and [Ca II] λλ 7291, 7323). Here, the identification of the contribution from the outer dense shell powered by the shock is obvious because we assume spherical symmetry. If the dense shell were asymmetric, or if it were spherical but rammed into an asymmetric CSM, the emission would no longer produce broad, boxy, symmetric line profiles but instead narrower, or skewed, or spiky line profiles. The example of SN 1993J with its broad, boxy, symmetric line profiles at 976 d (Matheson et al. 2000a) suggests that in some cases, the outer dense shell and the CSM are probably roughly spherical on large scales.

At the latest epoch in model s15p2Pwr1e40, when the shock power dominates, the entire spectrum forms in the outer dense shell, whose temperature is in the range 5000–15000 K and with a sizeable ionization (H and O are partially ionized in the dense shell). The spectrum shows strong Hα (with a contribution from [N II] λλ 6548, 6583), multiple lines of Fe II below 5500 Å, strong [N II] λ 5755 (which overlaps with weak and narrow Na I D emission), and broad, boxy [O I] λλ 6300, 6364 which overlaps with and causes a blue hump on Hα. Further to the red, [O II] λλ 7319, 7320 overlaps with the narrow [Ca II] λλ 7291, 7323 arising from the inner ejecta and produces a broad, boxy, symmetric profile with a narrow central bump. A similar profile is obtained for He 110 830 Å. The model predicts a strong broad Mg II λλ 9218, 9244 line flux, although the line appears with slanted wings (in part because it overlaps with some background Fe II emission).

Interestingly, the top part of this Mg II λλ 9218, 9244 doublet is slightly slanted rather than flat – there is a small excess flux in the blue part. A similar slant is also present in [N II] λ 5755 or [O II] λλ 7319, 7320, and in fact in all reasonably isolated and strong lines (this feature is best seen in spectra computed for individual ions; see Fig. A.3)3. This slant arises from a relativistic effect and the associated enhancement or reduction of the emissivity received in the observer's frame from the approaching or receding parts of the ejecta (see, e.g., Mihalas 1980 or Sect. 11.2 of Hillier & Dessart 2012). If we recompute the spectrum without the relativistic terms (forcing the emissivity to be the same in the comoving frame and the observer’s frame; see Eq. (41) of Hillier & Dessart 2012), these broad boxy lines exhibit a slant in the opposite direction; that is to say, the flux rises toward the red. This red excess is then caused by electron scattering. It is only when we switch off the relativistic terms and artificially quench the electron-scattering opacity in the computation of the spectrum that the top part of these lines appears flat (not shown).

The right panel in Fig. 4 shows the full spectrum from 0.09 to 2.5 µm. To accommodate the large variation from short to long wavelengths and between models s15p2NoPwr and s15p2Pwr1e40, the flux density is shown on a logarithmic scale. This confirms that the offset between the two models is initially confined to regions below 3000 Å (with thus a rough agreement in the U band at 350 d), but that the offset grows with time and becomes ever more pronounced at later times. More importantly, the spectrum formation regions become more and more distinct, with model s15p2NoPwr becoming increasingly faint with a spectrum forming in the inner radiatioctive-decay powered layers, while model s15p2Pwr1e40 remains luminous with a spectrum dominated by broad lines forming in the outer ejecta. While Lyα and Mg II λλ 2796, 2803 are the two strongest lines in the UV range, they eventually also dominate over the UV continuum flux, especially Lyα, which itself contains ~65% of the bolometric flux at 1000 d.

thumbnail Fig. 4

Comparison of multiepoch, normalized spectra from 350 d to 1000 d between models s15p2NoPwr (red) and s15p2Pwr1e40 (black) over the optical range (left) and over the UV, optical, and near-IR ranges (right; flux density is shown on a log scale). The same normalization factor is applied to both models at each epoch in order to preserve the relative offset between the spectra.
Table 2

SN sample including references to spectroscopic and photometric data and some SN characteristics.

thumbnail Fig. 5

R-band light curves for model s15p2NoPwr and s15p2Pwr1e40 compared with a set of observations (for a few objects, we show the r-band magnitude instead; see Table 2). All light curves are shifted so that the magnitude is zero at the onset of the nebular phase (when the fall from the plateau stops and the SN initially follows the rate of 56Co decay).

5 Comparison with observations

In this section, we compare our model results with observed Type II SNe. The sample was selected based on observed properties reminiscent of the interaction features we obtain in this work as well as on the association with ejecta-CSM interaction made in previous work. Our search was focused on objects with late-time spectra exhibiting peculiar spectral properties such as broad boxy line profiles, an anomalously strong Hα line, and so on. The sample consists of seven objects with spectra ranging between 269 and 1145 d from explosion, and specifically SNe 2004et, 2007od, 2013by, 2013ej, 2014G, 2017eaw, and 2017ivv. Basic information on each object and relevant references are presented in Table 2.

Figure 5 compares the R-band light curve of the sample of observations with the models presented in Sect. 4. To facilitate the comparison, the light curves have been shifted so that the magnitude is zero at the onset of the nebular phase (i.e., when the magnitude falls on a slow linear decline after the abrupt drop at the end of the high-brightness, plateau phase). This corrects for differences in distance, reddening, and 56Ni mass. The element of interest is to identify if the R-band magnitude follows continuously a roughly linear decline4 as in model s15p2NoPwr or if a kink appears in the light curve – as in the case of model s15p2Pwr1e40. SNe 2013by, 2013ej, and 2014G do not exhibit any R-band light-curve kink. Their light curves may not extend sufficiently late to make a strong case, but it implies nonetheless that interaction is at most a weak component to the flux in the R band. In contrast, SNe 2004et, 2017eaw, and 2017ivv exhibit an R-band kink at 600–1000 d, 700–900 d, and 350–500 d, respectively. The exact timing is unclear because of the coarse photometric monitoring. The model s15p2Pwr1e40 with its shock power of 1040 erg s−1 yields a qualitative agreement with the R-band light curves of SNe 2004et, 2017eaw, and 2017ivv. Compared to the model, the kink occurs about 200 d earlier in SN 2017ivv and at about the same time in SN 2017eaw. An earlier kink implies a stronger interaction or a stronger thermalization of the shock power, or both. Photometrically, SN 2007od is an outlier in our sample with the sharp drop in brightness between 100 and 200 d followed by a flattening, suggestive of a very low 56Ni mass (Andrews et al. 2010). In the context of the present work, the very early kink in R-band magnitude at about 200 d suggests that interaction power dominates the optical radiation (and thus even more so in the UV, which is unobserved) as early as 200 d. This is confirmed by its spectral evolution.

Figure 6 shows a comparison of optical spectra for the models of Sect. 4 and the sample of observations at about 350 d, 450 d, and at very late times of 800 d to ~1200 d. In each panel, we order the models and the observations such that signs of interaction appear stronger as we progress downward. In all cases, the most obvious sign of interaction in the optical range is found in the Hα profile, with the presence of a broad but not always boxy profile on top of a narrower emission component. When the extent of this Hα line is large, it may overlap with [O I] λλ 6300, 6364, causing a ledge between Hα and [O I] λλ 6300, 6364 (i.e., the flux does not go down to zero between the two lines as it typically does in the nebular-phase spectra of Type II SNe; see, e.g., Leonard et al. 2002). At around 350 d (top panel of Fig. 6), SNe 2004et, 2013by, 2013ej, and 2017eaw show no obvious spectroscopic sign of interaction in the optical. In contrast, SNe 2014G and 2017ivv exhibit a broad Hα component, which also boosts the red component of [O I] λλ 6300, 6364. The model with a power of 7 × 1040 erg s−1 gives a good match to these last two SNe although the broad Hα emission appears to be more boxy than in the observations.

At about 450 d (middle panel of Fig. 6), obvious signs of interaction are still absent in SNe 2004et, 2013ej, and 2017eaw, but SN 2013by now shows a broad Hα profile, which overlaps with [O I] λλ 6300, 6364, as observed with SN 2014G at 350 d (top panel). Surprisingly, SN 2013by exhibits narrow Hα emission as well, probably powered by radioactive decay, but the equivalent narrow emission in [Ca II] λλ 7291, 7323 has essentially disappeared. Finally, SN 2017ivv continues to show signs of interaction, with an Hα line that now looks triangular, suggesting a boost to the Hα emissivity over a range of velocities in the outer ejecta, together with emission from the inner ejecta where [O I] λλ 6300, 6364 and [Ca II] λλ 7291, 7323 also form.

At times greater than 800 d, the contribution from the inner ejecta powered by radioactive decay is becoming very small and ejecta-CSM interaction is the reason for the detection of these SNe at such late times. This explains the more boxy and broad Hα profiles in SNe 2004et, 2007od, 2013ej, and 2017eaw. The spectra are quite noisy at those late times, but we tentatively identify broad [O I] λλ 6300, 6364 (except in SN 2007od), whose overlap with Hα causes a blue hump in that line. A similar overlap may be at the origin of the skewed and slanted feature at 7300 Å in SN 2013ej at 806 d. This line may be a composite of [Ca II] λλ 7291, 7323 and [O II] λλ 73I9, 7320, and is seen as a broad boxy profile in SN 2004et at 933 d. In the blue part of the spectrum, Hβ as well as multiple Fe II lines (all broad) are likely present, as in model s15p2Pwr1e40. The narrow features that appear in numerous line profiles are unlikely to arise from unshocked CSM or from the inner ejecta. They probably arise instead from the small overlap between broad lines or from the clumpy structure of the interaction region (see, e.g., a discussion of SN 1993J by Matheson et al. 2000b).

The model s15p2Pwr1e40 gives a satisfactory match to the observations of SNe 2004et and 2017eaw at the latest time (bottom panel of Fig. 6), although the Hα line profile exhibits a central depression that is not present in our sample of observations. This dip is likely caused by an optical depth effect arising from the adoption of a narrow dense shell, causing enhanced absorption at the limb (this effect is similar to limb darkening). Breaking the lateral coherence of the shell would enhance photon escape for regions moving perpendicular to the line of sight, and would thus likely erase this central dip (see discussion of a similar effect in the context of clumping in Wolf-Rayet winds by Flores et al. 2023). A central dip is observed in some emission lines of SNe 1998S and 1993J. In addition, Fransson et al. (2005) also explained this feature through an optical-depth effect associated with the narrow, optically thick, emitting dense shell.

Some emission features, both in the models and in the observations, are clearly not boxy but triangular. For example, in the model, a myriad of Fe II lines overlap in the 4340 Å region and produce a triangular emission feature that is much broader than the Hα profile (Fig. 4). Emission over a range of velocities would also tend to produce a more triangular profile shape, as observed throughout the nebular phase in SN 2017ivv (Figs. 6 and 7). In contrast, our models tend to emit exclusively from within the narrow dense shell at very late times so that all emission lines are intrinsically boxy and of the same width.

thumbnail Fig. 6

Spectral comparison between models and the selected sample of observations (see Table 2) at ~350 d (top panel), ~450 d (middle panel), and 800–1000 d (lower two panels). In each panel, we stacked models and observations in strengthening signs of interaction as we progress downwards. A distinct color is used for each SN while black is used for the models (see labels; light (dark) colors correspond to the original (smoothed) spectra). The galaxy lines were removed from the observed spectra, and the data were binned to reduce the noise.
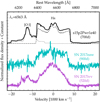thumbnail Fig. 7

Illustration of some profile morphologies in model s15p2Pwr1e40 at 700 d together with the observations of SNe 2017eaw at 900 d and 2017ivv at 520 d. The spectral region shown is centered on the rest wavelength of Hα. At the top, the flux contributions associated with O I (dotted line; primarily associated with [O I] λλ 6300, 6364) and H I (dashed line; primarily associated with Hα) are shown. The residual flux offset in this spectral region is primarily due to a forest of Fe I and Fe II lines.

6 Discussion

The main uncertainty in this work is the treatment of shock power in CMFGEN. As discussed by Dessart & Hillier (2022), performing one-dimensional radiation hydrodynamics of the interaction at late times is superfluous since conditions are optically thin and the dynamical effects are vanishingly small, while the treatment of the gas in LTE is inappropriate (see discussion in Dessart et al. 2015). Since the power released by the shock between ejecta and CSM is known analytically, one may directly model the nonLTE problem within a radiative transfer code like CMFGEN, as done by Dessart & Hillier (2022). The benefits are enormous, as shown with the simulations presented here, but there are numerous uncertainties that impact the results quantitatively. While the shock is originally released in the form of high-energy radiation and particles, we focus here on the fraction that is absorbed by the outer ejecta. Ultimately, this fraction of thermalized X-rays requires detailed 3D multigroup radiation hydrodynamics simulations of the interaction. The thermalization also depends on the structure of the outer ejecta, and in particular whether there is a dense shell at the interface between ejecta and CSM. This dense shell may form directly at the time of shock breakout and accumulate mass as the ejecta sweeps up progressively more CSM. This shell should break up, be turbulent, and form clumps. The transfer of radiation within this structured medium is very complex. All these aspects impact the results presented here. Multiwavelength observations covering from the X-rays to the UV and optical would help constrain these structural properties.

In this and previous works, the shock power is deposited in a narrow, clumped, dense shell in the outer ejecta (here at 8000km s−1). The high density in the shell leads to efficient reprocessing at the site of deposition, which ultimately leads to a boost in line emissivity within the shell, causing a broad boxy profile with vertical edges in numerous emission lines like Hα. That is to say, all the emission comes from this narrow shell at late times. In practice, if the dense shell were less dense and massive, some of the shock power deposited would be reprocessed deeper in the ejecta and would boost the line emissivity over a range of velocities (i.e., ejecta depth), which would produce flattop profiles with extended slanted wings (rather than a profile with a sharp, vertical edge).

This “distributed” emission is likely to hold in SN 2017ivv, where it is not possible to distinguish the broad from the narrow emission component at very late times since the Hα profile is smooth, triangular with no sharp jump. At earlier times, the Hα profile is dominated by a narrow component, which requires the presence of hydrogen at low velocity in the ejecta. This is in tension with the Type IIb classification proposed by Gutiérrez et al. (2020), who also suggested a peculiar formation process of [O I] λλ 6300, 6364 to explain the near equal intensity in each component of the doublet. The peculiar intensity ratio is explained here as the overlap of the red component of [O I] λλ 6300, 6364 with the blue wing of the broad Hα component. Finally, it is intriguing that SN 2017ivv exploded in one of the lowest luminosity host galaxies, suggestive of a low metallicity. Such conditions are unfavorable for a high RSG mass-loss rate. One possibility is that the progenitor of SN 2017ivv was in an interacting binary that was undergoing mass transfer in the final decades or centuries prior to core collapse.

For simplicity, all simulations in this work assume spherical symmetry. This is a sensible first step since spherical symmetry is more uniquely defined than asymmetry, which can take an infinite number of forms. Nonetheless, the interaction between ejecta and CSM should be clumped on small scales and could even exhibit asymmetries on large scales because of the asymmetry of the ejecta, the CSM, or both. Small-scale clumping would lead to small-scale variations within line profiles (as observed in SN 1993J; Matheson et al. 2000b). Large-scale asymmetry would produce asymmetric, skewed rather than boxy symmetric line profiles. For example, emission from a hollow shell produces a flat-topped profile but emission from a disk-like structure would yield a double-horned profile (see, e.g., Jerkstrand 2017). Such boxy symmetric profiles are seen, for instance, in SN 1993J, which clearly demonstrate that asymmetry is not universal in core-collapse SNe and may, in fact, be mostly present deeper in the ejecta (the radio emission from SN 1993J two years after explosion is also largely spherical; see, e.g., Marcaide et al. 1995).

A related issue is the prediction by the models at late times of an Hα emission profile that exhibits a central dip and two horns rather than a flat top. This effect arises because the line optical depth is large, causing an enhanced attenuation of the photons emitted from the ejecta regions moving perpendicular to the line of sight. The lack of such a dip in the observations argues for the break-up of the dense shell at the ejecta-CSM interface, as advocated in the context of clumpy Wolf-Rayet winds (Flores et al. 2023). We also refer to the discussion in Fransson et al. (2005) for more details. Similar simulations in the context of SNe are straightforward and will be explored in the near future. One specific ramification of this feature is that in some cases where the dense shell would retain a full lateral coherence without breaking up (if it retained a spherical geometry), the Hα emission profile should exhibit two peaks. Interestingly, double-peaked profile are sometimes observed in SNe II at late times (e.g., iPTF14hls; Andrews & Smith 2018) and generally attributed to disk-like geometries. An interesting alternative is that the double-peaked profile could stem from an optical-depth effect, similar to limb darkening, in an emitting narrow dense shell.

The possibility for late-time interaction in core-collapse SNe has implications for the post-explosion photometry at the SN site. This is generally used to argue for the disappearance of the progenitor, but often a source of emission is found and it is not clear whether the source being observed is, in fact, a binary companion, a cluster of stars (Maund et al. 2015; Sun et al. 2021), or even a light echo (e.g., Schmidt et al. 1994). It may instead be the case that the emitting source arises from an ejecta-CSM interaction (see, e.g., Rizzo Smith et al. 2023 or Van Dyk et al. 2023). Observing core-collapse SNe at late times in the U band together with the optical would help determine the properties of the progenitor site and whether there is an ongoing ejecta-CSM interaction. This could be performed in part with the Vera Rubin Observatory, which will collect deep photometric data for a huge number of core-collapse SNe. However, much more compelling evidence for interaction would be given by UV observations, for example, with the Hubble Space Telescope or possibly in the more distant future with UVEX (Kulkarni et al. 2021).

7 Conclusions

In this work, we present a set of simulations for Type II SN ejecta from 350 d until 1000 d after explosion. Chemical mixing in the metal-rich regions was handled with the shuffled-shell approach of Dessart & Hillier (2020b) to enforce macroscopic mixing without introducing microscopic mixing. This allows for the deposition of decay power throughout the inner ejecta, powering the metal lines observed in SNe II at nebular phases. One model (named s15p2NoPwr) was evolved until 1000 d with the time-dependent solver, a time step set to 10% of the current time, and under the influence of radioactive-decay heating from 56Ni and 56Co (its ejecta was truncated at 6000 km s−1 since the decay power absorbed at larger velocity is negligible – no external dense shell was included either). In another model (named s15p2Pwr1e40), we injected in addition a constant power of 1040 erg s−1 in a narrow dense shell of 0.1 M⊙ located at 8000 km s−1. Both models have the same structure and composition below 6000 km s−1. Molecule formation and dust formation in the ejecta were ignored. The results are qualitatively analogous to a similar model presented by Dessart & Hillier (2022) but are quantitatively widely different.

From 350 to 1000 d, model s15p2Pwr40 morphed from being decay powered to being interaction powered, while exhibiting hybrid properties in between. In the optical, the evidence for this transformation is most apparent in the line profiles of Hα or [O I] λλ 6300, 6364. Originally forming in the slow, decay-powered layers of the ejecta, a broad component appears, which eventually dominates at late times. In our spherical model, this broad component is boxy and flat topped, and can give rise to overlap with other lines (e.g., the blue edge of Hα overlapping with the red component of [O I] λλ 6300, 6364). At late times, all lines are broad and boxy and can lead to strong overlap. We note that there is one exception to this: the strong broad triangular feature around 4300 Å, which is a blend of Fe II transitions. In the UV, the impact of interaction is large since the bulk of the emission is channeled in that UV region, and most strongly in Lyα and Mg II λλ 2796, 2803. Both lines are strong, optically thick, and skewed. The rest of the UV flux is primarily associated with emission from a forest of Fe II transitions, including the strong feature around 1800 Å.

Compared with the observations, our model s15p2Pwr1e40 yields a good match to a sample of SNe II with broad and strong Hα emission at late times, namely SNe 2004et, 2007od, 2013by, 2013ej, 2014J, 2017eaw, and 2017ivv. All of them display a similar behavior, but the strengthening of the Hα line turns on at distinct post-explosion times, namely, around 200 d in SN 2017ivv, but only after 600 d in SN2017eaw. This strengthening of the Hα line is in part responsible for the kink observed in the R band, which is also predicted by model s15p2Pwr1e40. Although the exact level of thermalization of shock power in the outer ejecta is unknown, our results suggest that these SNe II are ramming into a wind of modest density, probably standard for an RSG progenitor (see also Rizzo Smith et al. 2023). Ultraviolet observations are needed to firmly establish this conclusion.

Acknowledgements

This work was supported by the “Programme National de Physique Stellaire” of CNRS/INSU co-funded by CEA and CNES. H.K. was funded by the Academy of Finland projects 324504 and 328898. A.V.F. is grateful for the support of the Christopher R. Redlich Fund and numerous individual donors. This work was granted access to the HPC resources of TGCC under the 2021 and 2022 allocations A0110410554 and A0130410554 made by GENCI, France. This research has made use of NASA's Astrophysics Data System Bibliographic Services.

Appendix A Additional figures

thumbnail Fig. A.1

Summary of ejecta properties for model s15p2Pwr1e40 at 350 d after explosion. From top to bottom, we show the mass density (scaled by the volume filling factor fvol), the electron density (also scaled by fvol), the volume filling factor fvol, and a set of composition profiles and the (normalized) shock power. All quantities are shown versus ejecta velocity. The model without shock power has initially the same ejecta structure below 6000 km s−1.
thumbnail Fig. A.2

Spectral montage of the Hα region for model s15p2 at 350 d with shock power increasing upward from zero (label NoPwr) to 7 × 1040 erg s−1 (label Pwr7e40). Some of these models are used for comparison with observations in Section 5. A broader range of shock powers covering up to 1043 erg s−1 is used in Dessart & Hillier (2022). The flux offset between models is modest in the optical and greatest in the UV range, as discussed in Dessart & Hillier (2022).
thumbnail Fig. A.3

Line contributions to the full spectrum for model s15p2Pwr1e40 at 350 (top row), 600 (middle row), and 800 d (bottom row). In each row, we show the total normalized flux density as a black line together with the flux from individual ions (the same normalization is applied to all spectra) including H I, He I, N II, O I, O II, Na I, Mg I, Mg II, Ca II, Fe I, Fe II, and Ni II. For better visibility, we split the species into two groups and as many panels (at left and at right in each row).

References

  1. Aguilera-Dena, D. R., Langer, N., Antoniadis, J., et al. 2022, A&A, 661, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Andrews, J. E., & Smith, N. 2018, MNRAS, 477, 74 [Google Scholar]
  3. Andrews, J. E., Gallagher, J. S., Clayton, G. C., et al. 2010, ApJ, 715, 541 [Google Scholar]
  4. Andrews, J. E., Sugerman, B. E. K., Clayton, G. C., et al. 2011, ApJ, 731, 47 [NASA ADS] [CrossRef] [Google Scholar]
  5. Black, C. S., Milisavljevic, D., Margutti, R., et al. 2017, ApJ, 848, 5 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bose, S., Sutaria, F., Kumar, B., et al. 2015, ApJ, 806, 160 [Google Scholar]
  7. Buta, R. J., & Keel, W. C. 2019, MNRAS, 487, 832 [NASA ADS] [CrossRef] [Google Scholar]
  8. Chevalier, R. A. 1982a, ApJ, 258, 790 [NASA ADS] [CrossRef] [Google Scholar]
  9. Chevalier, R. A. 1982b, ApJ, 259, 302 [Google Scholar]
  10. Chugai, N. N. 1990, Soviet Astron. Lett., 16, 457 [Google Scholar]
  11. Chugai, N. N., Chevalier, R. A., & Utrobin, V. P. 2007, ApJ, 662, 1136 [NASA ADS] [CrossRef] [Google Scholar]
  12. de Jaeger, T., Zheng, W., Stahl, B. E., et al. 2019, MNRAS, 490, 2799 [NASA ADS] [CrossRef] [Google Scholar]
  13. Dessart, L., & Hillier, D. J. 2020a, A&A, 642, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Dessart, L., & Hillier, D. J. 2020b, A&A, 643, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Dessart, L., & Hillier, D. J. 2022, A&A, 660, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Dessart, L., Audit, E., & Hillier, D. J. 2015, MNRAS, 449, 4304 [Google Scholar]
  17. Dessart, L., Hillier, D. J., & Audit, E. 2017, A&A, 605, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Dessart, L., Hillier, D. J., & Wilk, K. D. 2018, A&A, 619, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Dessart, L., John Hillier, D., Sukhbold, T., Woosley, S. E., & Janka, H. T. 2021, A&A, 652, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Dessart, L., Prieto, J. L., Hillier, D. J., Kuncarayakti, H., & Hueichapan, E. D. 2022, A&A, 666, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Dolan, M. M., Mathews, G. J., Lam, D. D., et al. 2016, ApJ, 819, 7 [Google Scholar]
  22. Eldridge, J. J., Izzard, R. G., & Tout, C. A. 2008, MNRAS, 384, 1109 [Google Scholar]
  23. Faran, T., Poznanski, D., Filippenko, A. V., et al. 2014, MNRAS, 445, 554 [NASA ADS] [CrossRef] [Google Scholar]
  24. Filippenko, A. V. 1997, ARA&A, 35, 309 [NASA ADS] [CrossRef] [Google Scholar]
  25. Flores, B. L., Hillier, D. J., & Dessart, L. 2023, MNRAS, 518, 5001 [Google Scholar]
  26. Fransson, C. 1984, A&A, 133, 264 [NASA ADS] [Google Scholar]
  27. Fransson, C., & Björnsson, C.-I. 1998, ApJ, 509, 861 [NASA ADS] [CrossRef] [Google Scholar]
  28. Fransson, C., Challis, P. M., Chevalier, R. A., et al. 2005, ApJ, 622, 991 [NASA ADS] [CrossRef] [Google Scholar]
  29. Fransson, C., Ergon, M., Challis, P. J., et al. 2014, ApJ, 797, 118 [Google Scholar]
  30. Gutiérrez, C. P., Anderson, J. P., Hamuy, M., et al. 2017, ApJ, 850, 89 [CrossRef] [Google Scholar]
  31. Gutiérrez, C. P., Pastorello, A., Jerkstrand, A., et al. 2020, MNRAS, 499, 974 [CrossRef] [Google Scholar]
  32. Hillier, D. J., & Dessart, L. 2012, MNRAS, 424, 252 [CrossRef] [Google Scholar]
  33. Immler, S., Modjaz, M., Landsman, W., et al. 2008, ApJ, 674, L85 [Google Scholar]
  34. Inserra, C., Turatto, M., Pastorello, A., et al. 2011, MNRAS, 417, 261 [Google Scholar]
  35. Jacobson-Galán, W. V., Dessart, L., Jones, D. O., et al. 2022, ApJ, 924, 15 [CrossRef] [Google Scholar]
  36. Jerkstrand, A. 2017, Spectra of Supernovae in the Nebular Phase (Berlin: Springer International Publishing AG), 795 [Google Scholar]
  37. Jerkstrand, A., Fransson, C., & Kozma, C. 2011, A&A, 530, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Kulkarni, S. R., Harrison, F. A., Grefenstette, B. W., et al. 2021, ArXiv e-prints [arXiv:2111.15608] [Google Scholar]
  39. Langer, N. 2012, ARA&A, 50, 107 [CrossRef] [Google Scholar]
  40. Langer, N., Hamann, W. R., Lennon, M., et al. 1994, A&A, 290, 819 [NASA ADS] [Google Scholar]
  41. Leonard, D. C., Filippenko, A. V., Barth, A. J., & Matheson, T. 2000, ApJ, 536, 239 [Google Scholar]
  42. Leonard, D. C., Filippenko, A. V., Gates, E. L., et al. 2002, PASP, 114, 35 [Google Scholar]
  43. Maeder, A., & Meynet, G. 1987, A&A, 182, 243 [NASA ADS] [Google Scholar]
  44. Maguire, K., Di Carlo, E., Smartt, S. J., et al. 2010, MNRAS, 404, 981 [NASA ADS] [CrossRef] [Google Scholar]
  45. Marcaide, J. M., Alberdi, A., Ros, E., et al. 1995, Science, 270, 1475 [CrossRef] [Google Scholar]
  46. Margutti, R., Kamble, A., Milisavljevic, D., et al. 2017, ApJ, 835, 140 [NASA ADS] [CrossRef] [Google Scholar]
  47. Matheson, T., Filippenko, A. V., Barth, A. J., et al. 2000a, AJ, 120, 1487 [NASA ADS] [CrossRef] [Google Scholar]
  48. Matheson, T., Filippenko, A. V., Ho, L. C., Barth, A. J., & Leonard, D. C. 2000b, AJ, 120, 1499 [NASA ADS] [CrossRef] [Google Scholar]
  49. Maund, J. R., Fraser, M., Reilly, E., Ergon, M., & Mattila, S. 2015, MNRAS, 447, 3207 [CrossRef] [Google Scholar]
  50. Mihalas, D. 1980, ApJ, 237, 574 [NASA ADS] [CrossRef] [Google Scholar]
  51. Milisavljevic, D., Fesen, R. A., Chevalier, R. A., et al. 2012, ApJ, 751, 25 [NASA ADS] [CrossRef] [Google Scholar]
  52. Misra, K., Pooley, D., Chandra, P., et al. 2007, MNRAS, 381, 280 [NASA ADS] [CrossRef] [Google Scholar]
  53. Podsiadlowski, P., Joss, P. C., & Hsu, J. J. L. 1992, ApJ, 391, 246 [Google Scholar]
  54. Richmond, M. W. 2014, J. Am. Assoc. Variab. Star Observ., 42, 333 [NASA ADS] [Google Scholar]
  55. Rizzo Smith, M., Kochanek, C. S., & Neustadt, J. M. M. 2023, MNRAS, 523, 1474 [NASA ADS] [CrossRef] [Google Scholar]
  56. Sahu, D. K., Anupama, G. C., Srividya, S., & Muneer, S. 2006, MNRAS, 372, 1315 [Google Scholar]
  57. Schmidt, B. P., Kirshner, R. P., Leibundgut, B., et al. 1994, ApJ, 434, L19 [NASA ADS] [CrossRef] [Google Scholar]
  58. Silverman, J. M., Foley, R. J., Filippenko, A. V., et al. 2012, MNRAS, 425, 1789 [Google Scholar]
  59. Sukhbold, T., Ertl, T., Woosley, S. E., Brown, J. M., & Janka, H.-T. 2016, ApJ, 821, 38 [Google Scholar]
  60. Sun, N.-C., Maund, J. R., Crowther, P. A., Fang, X., & Zapartas, E. 2021, MNRAS, 504, 2253 [NASA ADS] [CrossRef] [Google Scholar]
  61. Tatischeff, V. 2009, A&A, 499, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Terreran, G., Jerkstrand, A., Benetti, S., et al. 2016, MNRAS, 462, 137 [Google Scholar]
  63. Valenti, S., Sand, D., Pastorello, A., et al. 2014, MNRAS, 438, L101 [Google Scholar]
  64. Valenti, S., Sand, D., Stritzinger, M., et al. 2015, MNRAS, 448, 2608 [NASA ADS] [CrossRef] [Google Scholar]
  65. Van Dyk, S. D., Zheng, W., Maund, J. R., et al. 2019, ApJ, 875, 136 [Google Scholar]
  66. Van Dyk, S. D., de Graw, A., Baer-Way, R., et al. 2023, MNRAS, 519, 471 [Google Scholar]
  67. Weil, K. E., Fesen, R. A., Patnaude, D. J., & Milisavljevic, D. 2020, ApJ, 900, 11 [Google Scholar]
  68. Weiler, K. W., van Dyk, S. D., Discenna, J. L., Panagia, N., & Sramek, R. A. 1991, ApJ, 380, 161 [NASA ADS] [CrossRef] [Google Scholar]
  69. Wellstein, S., & Langer, N. 1999, A&A, 350, 148 [NASA ADS] [Google Scholar]
  70. Yaron, O., & Gal-Yam, A. 2012, PASP, 124, 668 [Google Scholar]
  71. Yaron, O., Perley, D. A., Gal-Yam, A., et al. 2017, Nat. Phys., 13, 510 [NASA ADS] [CrossRef] [Google Scholar]
  72. Yoon, S.-C. 2017, MNRAS, 470, 3970 [NASA ADS] [CrossRef] [Google Scholar]
  73. Yuan, F., Jerkstrand, A., Valenti, S., et al. 2016, MNRAS, 461, 2003 [Google Scholar]
1

This also implies that extraordinary mass-loss rates reaching up to 0.1 M⊙ yr−1 are not necessary to produce an interaction-powered SN at late times – such huge mass-loss rates are invoked to explain the superluminous and extremely rare Type IIn SNe like 2010jl that peak at 1044 erg s−1 (Fransson et al. 2014; Dessart et al. 2015). Such extreme mass-loss rates, often associated with the most extreme luminous blue variables, are thus not considered in this work.

2

The shuffling method of Dessart & Hillier (2020b) operates a rearrangement of shells of distinct composition within a Lagrangian mass Msh. In practice, the main shells Fe/He, Si/S, O/Si, O/Ne/Mg, O/C, He/C, He/N, and H/He are split into subshells and rearranged in mass space within Msh – we choose Msh to be about 1 M⊙ above the base of the H/He shell in the original, unmixed ejecta. This shuffling in mass space is equivalent to a shuffling in velocity space and captures the essence of macroscopic mixing in core-collapse SNe. This shuffling introduces no microscopic mixing and thus preserves the original composition mixture of all shells. For example, the relative fraction of O, Ne, and Mg in the material belonging to the O/Ne/Mg shell is the same before and after the shuffling. Full details about the method are provided in Dessart & Hillier (2020b).

3

Such a slant is also predicted at nebular times for lines forming in the outer ejecta of Type Ia SNe (Blondin et al., in prep.).

4

The decline may not be exactly linear, but should be close, if the R-band magnitude is only affected by a progressive and weak color shift and enhanced γ-ray escape.

All Tables

Table 1

Summary of ejecta properties for model s15p2 (Sukhbold et al. 2016; Dessart et al. 2021).

In the text
Table 2

SN sample including references to spectroscopic and photometric data and some SN characteristics.

In the text

All Figures

thumbnail Fig. 1

Emitted decay power as a function of time since explosion in model s15p2 (see Table 1 for the yields). We show the individual contributions from the dominant unstable isotopes (the label refers to the parent isotope of the two-step decay chains) as colored curves, with the total given by the black dashed curve. Because of γ-ray escape, the power effectively absorbed by the ejecta is only a fraction of the power emitted (about 25% at 1000 d in this model). The dominant source of power is 56Ni in the first 1000 d, while 44Ti takes over beyond about 3000 d. Evidently, ejecta interaction with a standard RSG wind, which delivers a power of about 1040 erg s−1 would dominate over radioactive decay after about 600 d.
In the text
thumbnail Fig. 2

Evolution of ejecta properties for model s15p2Pwr1e40 from t0 = 350 to 1000 d. From top to bottom, we show the profile of the total power absorbed (scaled to counter the effect of expansion; see text), of the gas temperature, and of the hydrogen ionization. In the bottom panel, we overplot the hydrogen mass fraction (dashed line).
In the text
thumbnail Fig. 3

Evolution of photometric properties at late times for models s15p2Pwr1e40 (solid) and s15p2NoPwr (dashed). From top to bottom, we show the bolometric luminosity, the fractional power emerging in the far-UV (δLFUV; 1000 < λ/Å < 2000), the near-UV (δLNUV; 2000 < λ/Å < 3500), the optical (δLopt; 3500 < λ/Å < 9500), and the IR (δLIR; λ/Å > 9500), followed by the R-, U-, and UV W2-band magnitudes and the U - V color.
In the text
thumbnail Fig. 4

Comparison of multiepoch, normalized spectra from 350 d to 1000 d between models s15p2NoPwr (red) and s15p2Pwr1e40 (black) over the optical range (left) and over the UV, optical, and near-IR ranges (right; flux density is shown on a log scale). The same normalization factor is applied to both models at each epoch in order to preserve the relative offset between the spectra.
In the text
thumbnail Fig. 5

R-band light curves for model s15p2NoPwr and s15p2Pwr1e40 compared with a set of observations (for a few objects, we show the r-band magnitude instead; see Table 2). All light curves are shifted so that the magnitude is zero at the onset of the nebular phase (when the fall from the plateau stops and the SN initially follows the rate of 56Co decay).
In the text
thumbnail Fig. 6

Spectral comparison between models and the selected sample of observations (see Table 2) at ~350 d (top panel), ~450 d (middle panel), and 800–1000 d (lower two panels). In each panel, we stacked models and observations in strengthening signs of interaction as we progress downwards. A distinct color is used for each SN while black is used for the models (see labels; light (dark) colors correspond to the original (smoothed) spectra). The galaxy lines were removed from the observed spectra, and the data were binned to reduce the noise.
In the text
thumbnail Fig. 7

Illustration of some profile morphologies in model s15p2Pwr1e40 at 700 d together with the observations of SNe 2017eaw at 900 d and 2017ivv at 520 d. The spectral region shown is centered on the rest wavelength of Hα. At the top, the flux contributions associated with O I (dotted line; primarily associated with [O I] λλ 6300, 6364) and H I (dashed line; primarily associated with Hα) are shown. The residual flux offset in this spectral region is primarily due to a forest of Fe I and Fe II lines.
In the text
thumbnail Fig. A.1

Summary of ejecta properties for model s15p2Pwr1e40 at 350 d after explosion. From top to bottom, we show the mass density (scaled by the volume filling factor fvol), the electron density (also scaled by fvol), the volume filling factor fvol, and a set of composition profiles and the (normalized) shock power. All quantities are shown versus ejecta velocity. The model without shock power has initially the same ejecta structure below 6000 km s−1.
In the text
thumbnail Fig. A.2

Spectral montage of the Hα region for model s15p2 at 350 d with shock power increasing upward from zero (label NoPwr) to 7 × 1040 erg s−1 (label Pwr7e40). Some of these models are used for comparison with observations in Section 5. A broader range of shock powers covering up to 1043 erg s−1 is used in Dessart & Hillier (2022). The flux offset between models is modest in the optical and greatest in the UV range, as discussed in Dessart & Hillier (2022).
In the text
thumbnail Fig. A.3

Line contributions to the full spectrum for model s15p2Pwr1e40 at 350 (top row), 600 (middle row), and 800 d (bottom row). In each row, we show the total normalized flux density as a black line together with the flux from individual ions (the same normalization is applied to all spectra) including H I, He I, N II, O I, O II, Na I, Mg I, Mg II, Ca II, Fe I, Fe II, and Ni II. For better visibility, we split the species into two groups and as many panels (at left and at right in each row).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.