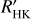| Issue |
A&A
Volume 675, July 2023
|
|
|---|---|---|
| Article Number | A183 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202245774 | |
| Published online | 19 July 2023 | |
The planetary system around HD 190622 (TOI-1054)
Measuring the gas content of low-mass planets orbiting F-stars★,★★,★★★
1
Institute of Planetary Research, German Aerospace Center (DLR),
Rutherfordstrasse 2,
12489
Berlin, Germany
e-mail: juan.cabrera@dlr.de
2
Dipartimento di Fisica, Universita degli Studi di Torino,
via Pietro Giuria 1,
10125
Torino, Italy
3
Physikalisches Institut, University of Bern,
Sidlerstrasse 5,
3012
Bern, Switzerland
4
Space Research Institute, Austrian Academy of Sciences,
Schmiedl-strasse 6,
8042
Graz, Austria
5
Center for Space and Habitability, University of Bern,
Gesellschaftsstrasse 6,
3012
Bern, Switzerland
6
Observatoire Astronomique de l’Université de Genève,
Chemin Pegasi 51,
1290
Versoix, Switzerland
7
Department of Astronomy, Stockholm University, AlbaNova University Center,
10691
Stockholm, Sweden
8
Centre for Exoplanet Science, SUPA School of Physics and Astronomy, University of St Andrews,
North Haugh,
St Andrews
KY16 9SS, UK
9
Instituto de Astrofísica e Ciencias do Espaço, Universidade do Porto, CAUP,
Rua das Estrelas,
4150-762
Porto, Portugal
10
Astrobiology Research Unit, Université de Liège,
Allée du 6-Août 19C,
4000
Liège, Belgium
11
Space sciences, Technologies and Astrophysics Research (STAR) Institute, Université de Liège,
Allée du 6-Août 19C,
4000
Liège, Belgium
12
Rheinisches Institut für Umweltforschung,
Abt. Planetenforschung, an der Universität zu Köln,
50931
Cologne, Germany
13
Aix-Marseille Univ., CNRS, CNES, LAM,
38 rue Frédéric Joliot-Curie,
13388
Marseille, France
14
European Southern Observatory,
Alonso de Cordova
3107,
Vitacura, Santiago de Chile, Chile
15
Instituto de Astrofísica de Canarias,
c/Vía Láctea, s/n
38205
La Laguna, Tenerife, Spain
16
Departamento de Astrofísica, Universidad de La Laguna, Avenida Astrofísico Francisco Sánchez,
s/n. Facultad de Ciencias, Sección de Física, Apartado 456,
38200
San Cristóbal de La Laguna, S/C de Tenerife, Spain
17
Institut de Ciències de l’Espai (ICE, CSIC),
Campus UAB, Can Magrans s/n,
08193
Bellaterra, Spain
18
Institut d’Estudis Espacials de Catalunya (IEEC),
Gran Capità, 2-4 Edifici Nexus, Desp. 201
08034
Barcelona, Spain
19
Admatis,
5. Kandó Kálmán Street,
3534
Miskolc, Hungary
20
Sub-department of Astrophysics, Department of Physics, Clarendon Laboratory, Parks Road, University of Oxford,
Oxford
OX1 3PU, UK
21
Depto. de Astrofísica, Centro de Astrobiología (CSIC-INTA),
ESAC campus,
28692
Villanueva de la Cañada (Madrid), Spain
22
Departamento de Física e Astronomia, Faculdade de Ciencias, Universidade do Porto,
Rua do Campo Alegre,
4169-007
Porto, Portugal
23
Université Grenoble Alpes, CNRS, IPAG,
38000
Grenoble, France
24
INAF, Osservatorio Astronomico di Padova,
Vicolo dell’Osservatorio 5,
35122
Padova, Italy
25
Zentrum für Astronomie und Astrophysik, Technische Universität Berlin,
Hardenbergstr. 36,
10623
Berlin, Germany
26
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université Paris Cité,
5 place Jules Janssen,
92195
Meudon, France
27
Université de Paris, Institut de physique du globe de Paris, CNRS,
1 Rue Jussieu,
75005
Paris, France
28
Caltech/IPAC-NASA Exoplanet Science Institute
Pasadena, CA, USA
29
Center for Planetary Systems Habitability and McDonald Observatory, The University of Texas at Austin,
2305 Speedway Stop C116,
Austin Texas
78712-1692, USA
30
Center for Astrophysics, Harvard & Smithsonian,
60 Garden St,
Cambridge, MA
02138, USA
31
Department of Physics and Astronomy, George Mason University,
4400 University Dr.
Fairfax, VA
22030, USA
32
American Association of Variable Star Observers,
185 Alewife Brook Parkway, Suite 410,
Cambridge, MA
02138,
USA
33
Centre for Mathematical Sciences, Lund University,
Box 118,
221 00
Lund, Sweden
34
Centre Vie dans l’Univers, Faculté des sciences, Université de Genève,
Quai Ernest-Ansermet 30,
CH-1211
Genève 4, Switzerland
35
Thüringer Landessternwarte Tautenburg,
Sternwarte 5,
07778
Tautenburg, Germany
36
Leiden Observatory, University of Leiden,
PO Box 9513,
2300 RA
Leiden, The Netherlands
37
Department of Space, Earth and Environment, Chalmers University of Technology, Onsala Space Observatory,
439 92
Onsala, Sweden
38
University of Vienna, Department of Astrophysics,
Türkenschanzs-trasse 17,
1180
Vienna, Austria
39
Department of Physics, University of Warwick,
Gibbet Hill Road,
Coventry
CV4 7AL, UK
40
Cavendish Laboratory,
JJ Thomson Avenue,
Cambridge
CB3 0HE, UK
41
Science and Operations Department - Science Division (SCI-SC), Directorate of Science, European Space Agency (ESA), European Space Research and Technology Centre (ESTEC),
Keplerlaan 1,
2201-AZ
Noordwijk, The Netherlands
42
NASA Ames Research Center,
Moffett Field, CA
94035, USA
43
Konkoly Observatory, Research Centre for Astronomy and Earth Sciences,
1121
Budapest,
Konkoly Thege Miklós út 15-17, Hungary
44
ELTE Eötvös Loránd University, Institute of Physics,
Pázmány Péter sétány 1/A,
1117
Budapest, Hungary
45
Stellar Astrophysics Centre, Department of Physics and Astronomy, Aarhus University,
Ny Munkegade 120,
8000
Aarhus C, Denmark
46
IMCCE, UMR8028 CNRS, Observatoire de Paris, PSL Univ., Sorbonne Univ.,
77 av. Denfert-Rochereau,
75014
Paris, France
47
Institut d’Astrophysique de Paris, UMR7095 CNRS, Université Pierre & Marie Curie,
98bis bld. Arago,
75014
Paris, France
48
Department of Astronomy & Astrophysics, University of Chicago,
Eckhardt, 5640 S Ellis Ave,
Chicago IL
60637, USA
49
Astrophysics Group, Keele University,
Staffordshire,
ST5 5BG,
UK
50
Department of Physics and Kavli Institute for Astrophysics and Space Research, Massachusetts Institute of Technology,
70 Vassar St,
Cambridge MA
02139, USA
51
Mullard Space Science Laboratory, University College London,
Holmbury St Mary, Dorking,
Surrey
RH5 6NT, UK
52
INAF, Osservatorio Astrofisico di Catania,
Via S. Sofia 78,
95123
Catania, Italy
53
Institute of Optical Sensor Systems, German Aerospace Center (DLR),
Rutherfordstrasse 2,
12489
Berlin, Germany
54
Dipartimento di Fisica e Astronomia “Galileo Galilei”, Universita degli Studi di Padova,
Vicolo dell’Osservatorio 3,
35122
Padova, Italy
55
ETH Zürich, Department of Physics,
Wolfgang-Pauli-Strasse 2,
8093
Zürich, Switzerland
56
ESTEC, European Space Agency,
2201AZ
Noordwijk, NL, The Netherlands
57
Institut für Geologische Wissenschaften, Freie Universität Berlin,
Malteserstraße 74-100,
12249
Berlin, Germany
58
Astronomy Department and Van Vleck Observatory, Wesleyan University,
96 Foss Hill,
Middletown, CT
06459, USA
59
Department of Earth, Atmospheric, and Planetary Sciences, Massachusetts Institute of Technology,
77 Massachusetts Ave Bldg 54,
Cambridge MA
02139, USA
60
Department of Aeronautics and Astronautics, Massachusetts Institute of Technology,
77 Massachusetts Ave Bldg 54,
Cambridge, MA
02139, USA
61
ELTE Eötvös Loránd University, Gothard Astrophysical Observatory,
9700
Szombathely,
Szent Imre h. u. 112, Hungary
62
MTA-ELTE Exoplanet Research Group,
9700
Szombathely,
Szent Imre h. u. 112, Hungary
63
SETI Institute,
339 N Bernardo Ave Suite 200,
Mountain View, CA
94043, USA
64
Institute of Astronomy, University of Cambridge,
Madingley Road,
Cambridge,
CB3 0HA, UK
65
Department of Astrophysical Sciences, Princeton University,
4 Ivy Lane,
Princeton, NJ
08544, USA
Received:
23
December
2022
Accepted:
25
April
2023
Context. Giant planets are known to dominate the long-term stability of planetary systems due to their prevailing gravitational interactions, but they are also thought to play an important role in planet formation. Observational constraints improve our understanding of planetary formation processes such as the delivery of volatile-rich planetesimals from beyond the ice line into the inner planetary system. Additional constraints may come from studies of the atmosphere, but almost all such studies of the atmosphere investigate the detection of certain species, and abundances are not routinely quantitatively measured.
Aims. Accurate measurements of planetary bulk parameters – that is, mass and density – provide constraints on the inner structure and chemical composition of transiting planets. This information provides insight into properties such as the amounts of volatile species, which in turn can be related to formation and evolution processes.
Methods. The Transiting Exoplanet Survey Satellite (TESS) reported a planetary candidate around HD 190622 (TOI-1054), which was subsequently validated and found to merit further characterization with photometric and spectroscopic facilities. The KESPRINT collaboration used data from the High Accuracy Radial Velocity Planet Searcher (HARPS) to independently confirm the planetary candidate, securing its mass, and revealing the presence of an outer giant planet in the system. The CHEOPS consortium invested telescope time in the transiting target in order to reduce the uncertainty on the radius, improving the characterization of the planet.
Results. We present the discovery and characterization of the planetary system around HD 190622 (TOI-1054). This system hosts one transiting planet, which is smaller than Neptune (3.087-0.053+0.058REarth, 7.7 ± 1.0 MEarth) but has a similar bulk density (1.43 ± 0.21 g cm−3) and an orbital period of 16 days; and a giant planet, not known to be transiting, with a minimum mass of 227.0 ± 6.7 MEarth in an orbit with a period of 315 days.
Conclusions. Our measurements constrain the structure and composition of the transiting planet. HD 190622b has singular properties among the known population of transiting planets, which we discuss in detail. Among the sub-Neptune-sized planets known today, this planet stands out because of its large gas content.
Key words: planetary systems / planets and satellites: detection
Radial velocity and photometry data of HD 190622 are only available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/675/A183
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The precise characterization of the bulk density of planets provides meaningful evidence for theories of planet formation. In this paper, we characterize, for the first time, the planetary system around the F star HD 190622, which consists of an inner transiting sub-Neptune planet with an orbital period of 15.5 days and an outer giant planet with a semi-major axis of 0.92 au. The architecture of this system – with an inner low-mass planet and an outer giant – has motivated theoretical studies, as it has been found that a large majority of stars with giant planets in about 1 au orbits also host inner lower-mass planets (see Zhu & Wu 2018; Bryan et al. 2019; Herman et al. 2019; Schlecker et al. 2021; Zhu & Dong 2021; Rosenthal et al. 2022; Zhu 2022, and references therein).
The typical mechanisms that occur in planet formation processes (migration, accretion of planetesimals, outgassing, atmospheric erosion etc.) are sensitive to the density of the planet-forming material present in the disk. Information linked to these mechanisms is partially preserved in the final composition and architecture of the resulting planetary systems. However, low-mass planets for which measurements of mass and radius are available are so diverse in composition that their inner structure is highly degenerate;, and it is therefore not straightforward to infer the abundances of their main constituents. Some seminal studies can be cited here (Valencia et al. 2007; Wagner et al. 2012; Dorn et al. 2015) and we refer interested readers to recent review papers, such as Grenfell et al. (2020) or Wordsworth & Kreidberg (2022). To first order, our understanding of compositional degeneracies can be aided by the precise measurement of the mass and radius of transiting planets. Nevertheless, the theoretical studies mentioned above base their conclusions on radial velocity surveys or on data from the Kepler mission (Borucki et al. 2010), which means that in most cases either the radius or the mass of the planet are not well characterized and our understanding of the inner composition of the planet is limited.
The Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2015) has found transiting planets around stars brighter than its predecessors, CoRoT (Baglin et al. 2006) and Kepler. These are planetary systems that are amenable to spectro-scopic characterization with ground-based surveys. However, the TESS observing strategy results in most of the sky being observed with 27 day sectors (which can be reobserved a few years later) and consequently the detectability and precise characterization of long-period planets is partially limited (see e.g., Kunimoto et al. 2022). The TESS primary mission goals are focussed on low-mass stars. The short baseline of TESS combined with larger stellar radii make the detection of small planets around hot stars less likely (but see Zhou et al. 2019).
Recently, accurate bulk density measurements of a few of these systems – which host inner low-mass planets and outer massive planets – were obtained. However, these planets orbit K stars, such as Kepler-167 (Chachan et al. 2022), or G stars, such as π Men (Gandolfi et al. 2018; Huang et al. 2018), HD 137496 (Azevedo Silva et al. 2022), HD 191939 (Lubin et al. 2022), and HD 86226 (Teske et al. 2020).
There are other examples that have not yet been fully characterized, either because the inner planet is not transiting – e.g., BD-11 4672 (Barbato et al. 2020) and HD 164922 (Benatti et al. 2020) –, or because the star is too faint for acquisition of precise radial velocities – e.g., TOI-1670 (Tran et al. 2022) and Kepler-1514 (Dalba et al. 2021), the latter being the only other F star among these systems.
For these reasons, HD 190622 (also known as TOI-1054) is a very interesting target for detailed characterization. The inner planet was statistically validated by Giacalone et al. (2021). However, the solution provided by these authors for the planetary radius is 20% larger than the value that we present in this paper. This is probably due to the fact that our spectroscopic observations allow us to characterize the stellar properties with better accuracy and precision (see also Reiners & Zechmeister 2020, whose stellar characterization is consistent with our results). Prior to the discovery of the planetary companion, the system attracted the attention of Cruzalèbes et al. (2019), who included the star in their catalog of mid-infrared stellar diameters and fluxes (MDF), and of Heller et al. (2017), who considered optimized trajectories for interstellar travel. Kervella et al. (2019) found an anomaly in the proper motion of the star and presented a solution for a possible planetary companion. However, as we discuss below, our discovered planet c currently escapes the detection threshold of Gaia, and so the proper motion anomaly found by these authors probably has a different origin that remains to be determined.
The KESPRINT collaboration1 selected TOI-1054b as one of its primary targets for mass characterization with ground-based facilities. In parallel, the CHEOPS Science Team also selected this same planet as a target for detailed radius characterization in a Guaranteed Time Observing program designed to study low-mass planets with potentially extended atmospheres. Here we present the analysis of the TESS discovery of the inner planetary candidate, a detailed characterization of the planetary radius with CHEOPS, confirmation of the planetary nature of the candidate, and the discovery of the outer planet with observations gathered by the KESPRINT consortium.
2 Observations
2.1 TESS discovery light curves
HD 190622 (TIC 366989877) was observed by TESS in Sectors 13 (June 2019) and 27 (July 2020) with a two-minute cadence. The data were processed by the TESS Science Processing Operations Center (SPOC, Jenkins et al. 2016), which included aperture photometry, flagging of low-quality data, removal of trends related to systematic sources (pre-search data conditioning), and finally a search for transiting planets (Jenkins 2002; Jenkins et al. 2020; Twicken et al. 2018; Li et al. 2019). The Sector 13 processing resulted in the identification of a planet candidate that satisfied all of the validation criteria and was subsequently ranked as TESS object of interest (TOI) 1054.01(Guerrero et al. 2021). The vetting procedure included the acquisition of speckle data on the Southern Astrophysical Research telescope (SOAR; Tokovinin 2018) and photometric observations from Las Cumbres Observatory Global Telescope (LCOGT; Brown et al. 2013), which confirmed that the candidate was on target with the expected ephemeris. The TESS pre-search data conditioning simple aperture photometry (PDCSAP Stumpe et al. 2014, 2012; Smith et al. 2012) light curve of this target does not show any strong signs of residuals of systematic features or stellar activity.
The TESS pixel scale is ~21″ pixel−1, and photometric apertures typically extend out to roughly 1 arcminute, which generally results in multiple stars blending in the TESS aperture. We acquired ground-based time-series follow-up photometry of TOI-1054as part of the TESS follow-up observing program sub-group 1 (TFOP SG1; Collins 2019)2 to attempt to rule out or identify nearby eclipsing binaries (NEBs) as potential sources of the detection in the TESS data and detect the transit-like event on target.
We observed full predicted transit windows of TOI-1054.01 in Pan-STARRS z-short band using the LCOGT 1.0 m network node at Siding Spring Observatory on UTC 2019 August 31 and UTC 2020 July 06. We used the TESS Transit Finder, which is a customized version of the Tapir software package (Jensen 2013), to schedule our transit observations. The 1 m telescopes are equipped with 4096 × 4096 SINISTRO cameras with an image scale of 0″/389 per pixel, resulting in a 26′ × 26′ field of view. The images were calibrated by the standard LCOGT BANZAI pipeline (McCully et al. 2018). Differential photometric data were extracted using AstroImageJ (Collins et al. 2017).
The first observation intentionally saturated TOI-1054 to check for deep NEB events in the fainter Gaia DR3 stars within 2’5 that are sufficiently bright in the TESS band to cause the TOI-1054.01 event. We find that the root-mean-square of each of the 19 possible contaminating stars is at least a factor of 5 smaller than the expected NEB depth in the respective star. We then visually inspected the light curve of each neighboring star in order to rule out any obvious eclipse-like signal. All of our follow-up light curves and supporting results are available on the EXOFOP-TESS website3.
The second observation was intentionally defocused to improve photometric precision in an attempt to detect the shallow transit-like event in TOI-1054. We used a circular photometric aperture with radius 11″.7, which excluded all flux from the potentially contaminating Gaia DR3 stars. We measured an event with a depth of 620 ± 110 ppm and a transit center time of 2459037.16 ± 0.01 BJD, which are consistent to within ~1σ with the depth and ephemeris derived from the joint model of this work. The ground-based light-curve data and best-fit model are shown in Fig. 1.
 |
Fig. 1 LCOGT observations of the TOI-1054 candidate confirming the TESS ephemeris. |
2.2 CHEOPS characterization
The ESA mission CHEOPS is a 30 cm space telescope in low Earth orbit launched in 2019 whose main goal is to improve radius measurements of planets in known systems (Benz et al. 2021). We observed TOI-1054b with the Guaranteed Time Observing Program number 24 Gas content of low-mass planets in order to precisely characterize the radius of the planet. We acquired three transit observations with CHEOPS (see reference data in Table 1).
The data were processed with the CHEOPS Data Reduction Pipeline (DRP, Hoyer et al. 2020, version 13.1.0), which automatically performs standard calibration (bias and dark correction, linearization and color-dependent flat fielding of stars, etc.) and correction (cosmic rays, background, and smear corrections) of the CHEOPS data. Finally, the DRP automatically extracts and delivers the photometry on four standard apertures. In this work, we used the DEFAULT aperture (with a radius of 25 pixels), which provides the best performance, increasing the signal-to-noise ratio (S/N), and allowing an unbiased measurement of the transit fit. Our analysis of the results of the first visit (file key CH_PR100024_TG012201) revealed an issue with the cosmic-ray correction module of the pipeline. We reprocessed the data with a custom configuration of the cosmic-ray module, which improved the S/N in this visit. In the present article, we provide the customized reduction. Upcoming releases of the CHEOPS DRP (beyond version 13.1.0) will correct this problem. For consistency, we compared the DRP results with the independent PSF imagette photometric extraction package4 (PIPE Brandeker et al. 2022) and we found no significant difference.
Reference data for the CHEOPS observations of TOI-1054.
2.3 HARPS radial velocity follow-up
We acquired 117 useful high-resolution (R ≈ 115000) spectra of HD 190622 using the High Accuracy Radial Velocity Planet Searcher (HARPS; Mayor et al. 2003) spectrograph mounted at the ESO-3.6m telescope at La Silla Observatory. The observations span more than 3 yr between 18 September 2019 and 24 November 2022 (UT); they were performed as part of the high-precision Doppler follow-up program of TESS small planets carried out by the KESPRINT consortium using the HARPS spectrograph (IDs: 1102.C-0923 and 106.21TJ.001; PI: Gandolfi). We set the exposure time to 1200-2100 s depending on the sky conditions and schedule constraints, leading to a median (S/N) of about 120 per pixel at 550 nm. The spectra were reduced and extracted using the dedicated HARPS data reduction software (DRS; Pepe et al. 2002; Lovis & Pepe 2007) immediately after acquisition. The DRS provides the user with absolute radial velocity (RV) measurements by cross-correlating the observed Échelle spectra against a G2 numerical mask (Baranne et al. 1996). It also computes the full width at half maximum (FWHM) and the bisector inverse slope (BIS) of the cross-correlation function (CCF), along with the CaII H & K line activity indicator5 log 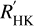 . The log
. The log 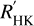 value of −4.952 ± 0.011 (see Table 2) is roughly in the middle of the old star population in the solar neighborhood. Applying the relation between this activity indicator and age (Mamajek & Hillenbrand 2008), we obtain an age of 5.1 Gyr with uncertainty of 1 Gyr, which is consistent with the stellar evolutionary models discussed in the analysis below (see Sect. 3).
value of −4.952 ± 0.011 (see Table 2) is roughly in the middle of the old star population in the solar neighborhood. Applying the relation between this activity indicator and age (Mamajek & Hillenbrand 2008), we obtain an age of 5.1 Gyr with uncertainty of 1 Gyr, which is consistent with the stellar evolutionary models discussed in the analysis below (see Sect. 3).
As a sanity check, we also extracted relative RV measurements using the Template Enhanced Radial velocity Re-analysis Application (TERRA; Anglada-Escudé & Butler 2012). The DRS and TERRA RVs are listed in Table 3 along with the FWHM and BIS of the CCF, and log 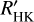 . While the model parameters retrieved from the DRS and TERRA Doppler measurements are consistent well within their nominal 1σ uncertainty, we find that the TERRA data set provides a lower root-mean-square deviation. We therefore used it for the subsequent analyses presented in this work.
. While the model parameters retrieved from the DRS and TERRA Doppler measurements are consistent well within their nominal 1σ uncertainty, we find that the TERRA data set provides a lower root-mean-square deviation. We therefore used it for the subsequent analyses presented in this work.
The generalized Lomb-Scargle (GLS) periodogram of the HARPS TERRA RVs (Fig. 2) shows a significant peak at ƒc = 0.00316 d−1 (Pc = 316.8 d) with a semi-amplitude of ~21ms−1. We estimated its false-alarm probability (FAP) following the bootstrap method described in Kuerster et al. (1997). Briefly, we computed the GLS periodogram of 106 mock time series obtained by randomly shuffling the Doppler measurements and their uncertainties, while keeping the time-stamps fixed. The FAP was defined as the fraction of randomised time-series whose highest GLS power exceeds that of the original data set at any frequency. We considered a peak to be significant if its FAP is lower than 0.001. For the peak at fc, we find no false positives out of the 106 trials, implying a FAP < 10−6. We note that this peak is undetected in the FWHM, BIS, and log 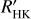 (Fig. 2), which provides compelling evidence that this signal is due the presence of a long-period companion with a minimum mass consistent with a giant planet. Hereafter, we refer to this object as HD 190622c (TOI-1054c). Given the solution provided by the RV analysis, we can estimate the time of inferior conjunction. None of the existing ground- or space-based observations used in this paper took place within reasonable periods of time around the possible transit of the planet. As of today, TOI-1054c is not known to transit. If the planet was transiting in a nongrazing orbit, it should be possible to detect it from space with the photometric precision that TESS or CHEOPS missions provide.
(Fig. 2), which provides compelling evidence that this signal is due the presence of a long-period companion with a minimum mass consistent with a giant planet. Hereafter, we refer to this object as HD 190622c (TOI-1054c). Given the solution provided by the RV analysis, we can estimate the time of inferior conjunction. None of the existing ground- or space-based observations used in this paper took place within reasonable periods of time around the possible transit of the planet. As of today, TOI-1054c is not known to transit. If the planet was transiting in a nongrazing orbit, it should be possible to detect it from space with the photometric precision that TESS or CHEOPS missions provide.
The GLS periodogram of the RV residuals following the subtraction of the signal at ƒc (Fig. 2) shows a significant peak (FAP ≈ 10−5) at the transit frequency ƒb = 0.06448 d−1 (P = 15.5076 d). This peak has no counterpart in the peri-odograms of the FWHM, BIS, and log 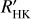 , spectrescopically, confirming the planetary nature of the transit signal detected in TESS data. We further searched the RV residuals for additional signals but find no other peaks with FAP < 0.001 (Fig. 2).
, spectrescopically, confirming the planetary nature of the transit signal detected in TESS data. We further searched the RV residuals for additional signals but find no other peaks with FAP < 0.001 (Fig. 2).
Kervella et al. (2019) found an anomaly in the proper motion of the star and presented a solution for a possible planetary companion. However, the mass that these authors determined for the companion has an uncertainty of 100% (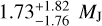 , and so it is not a significant astrometric detection. With the parameters that we find for planet с in the present study, the reflex motion of the host star has an amplitude of less than 10 µas, which is well below the detection threshold of Gaia at this magnitude.
, and so it is not a significant astrometric detection. With the parameters that we find for planet с in the present study, the reflex motion of the host star has an amplitude of less than 10 µas, which is well below the detection threshold of Gaia at this magnitude.
Stellar properties of HD 190622 (TOI-1054).
 |
Fig. 2 Generalized Lomb-Scargle periodogram of: the HARPS TERRA RV measurements (first panel); the RV residuals following the subtraction of the Doppler signal of HD 190622c (second panel); the RV residuals following the subtraction of the Doppler signals of HD 190622b and c (third panel); the FWHM and BIS of the CCF (fourth and fifth panels); and the CaIIH&K line activity indicator log |
3 Characterization of the star
The stellar parameters of HD 190622 are presented in Table 2. The analysis of the co-added HARPS stellar spectra was done following the same methodology described in Sousa (2014); Santos et al. (2013); and Sousa et al. (2021) in order to derive the stellar atmospheric parameters (Teff, log ɡ, microturbulence, [Fe/H]), and its respective uncertainties using ARES+MOOG. We used the list of iron lines presented in Sousa et al. (2008). The equivalent widths (EWs) for these lines were measured using the ARES code6 (Sousa et al. 2007, 2015; Santos et al. 2013). We used a minimization process to find ionization and excitation equilibrium and converge to the best set of spectroscopic parameters. This process makes use of a grid of Kurucz model atmospheres (Kurucz 1993) and the radiative transfer code MOOG (Sneden 1973). We obtained a temperature of 6088 + 62 K, a log g of 4.40 + 0.10 dex, a [Fe/H] of −0.185 + 0.042, and a microturbulence of 1.27 + 0.03 m/s. We also derived the trigonometric surface gravity using Gaia data following the same methodology as described in Sousa et al. (2021), and obtained a value of 4.32 + 0.02 dex, which is the value reported in Table 2.
To determine the stellar radius of HD 190622, we used a modified infrared flux method (IRFM) in a Markov chain Monte Carlo (MCMC) approach (Blackwell & Shallis 1977; Schanche et al. 2020). First, we compute the apparent bolometric flux by building SEDs from stellar atmospheric models defined using the stellar parameters derived from our spectral analysis and comparing derived synthetic photometry with broadband fluxes and uncertainties from the most recent data releases for the following bandpasses: Gaia G, GBP, and GRP, 2MASS J, H, and K, and WISE Wl and W2 (Skrutskie et al. 2006; Wright et al. 2010; Gaia Collaboration 2023). We then converted the bolometric flux into stellar effective temperature and angular diameter; this latter is translated into the stellar radius using the offset-corrected Gaia parallax (Lindegren et al. 2021). Finally, we used Bayesian model averaging of the ATLAS (Kurucz 1993; Castelli & Kurucz 2003) and PHOENIX (Allard 2014) catalogs in order to account for uncertainties in stellar atmospheric modeling, and we determine R⋆+ = 1.205 + 0.008 R⊙.
Using the aforementioned stellar atmospheric parameters, we determined the abundances of Mg ([Mg/H] = −0.14 + 0.05 dex) and Si ([Si/H] = −0.17 + 0.03 dex) closely following the classical curve-of-growth analysis method described, for example, by Adibekyan et al. (2018, Adibekyan et al. 2015). As for the stellar parameter determination, we used ARES to measure the EWs of the spectral lines of these elements, and used a grid of Kurucz model atmospheres (Kurucz 1993) and MOOG (Sneden 1973) to convert the EWs into abundances under the assumption of local thermodynamic equilibrium. The low [Mg/Fe] and [Si/Fe] abundances of the star (see Fig. 3) suggest that the star belongs to the Galactic thin-disk population. Following the procedure of Wilson et al. in prep., we computed the UVW Galactic space velocities (Johnson & Soderblom 1987), which are compared to sets of velocity dispersion standards (Bensby et al. 2003, 2014; Reddy et al. 2006; Chen et al. 2021) of the Milky Way thin disk, thick disk, and halo in a Monte Carlo fashion. This analysis yields a 99% probability that HD 190622 belongs to the thin disk.
Finally, we used the input set made of Teff, [Fe/H], and R⋆ to derive the isochronal mass M⋆ and age t⋆ using two different stellar evolutionary models. A first pair of mass and age values (M⋆,1; t⋆,1) was computed by the isochrone placement algorithm (Bonfanti et al. 2015, 2016), which interpolates the input parameters within precomputed grids of PARSEC7 vl.2S (Marigo et al. 2017) isochrones and tracks. Finally, we determined the second pair (M⋆,2; t⋆,2) using CLES (Code Liégeois d’Évolution Stellaire; Scuflaire et al. 2008), which computes the best-fit evolutionary track according to the stellar input parameters and following the Levenberg-Marquadt minimization scheme (see e.g., Salmon et al. 2021). After that, we checked the mutual consistency of the two respective pairs of outcomes through the χ2 -based criterion presented in Bonfanti et al. (2021a) and we merged the results so as to obtain more robust estimates, which are 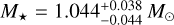 and
and 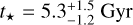 .
.
 |
Fig. 3 [Mg/Fe] and [Si/Fe] abundance ratios as a function of [Fe/H] for HD 190622 (large blue circle) and the HARPS GTO sample stars (gray dots) from Adibekyan et al. (2012). The blue horizontal and vertical lines indicate the solar values. |
4 Transit photometry and RV joint analysis
We performed a global analysis of the observational data using different tools simultaneously in order to check the robustness of the results. We used the PyCHEOPS code (Maxted et al. 2022), the TLCM code (Csizmadia 2020), and pyaneti (Barragán et al. 2019, 2022) for a combined solution of the photometry and the RV amplitude. The results of the three joint analyses are consistent with each other and we present as baseline those of pyaneti in Table 3.
We performed the joint analysis of the TESS and CHEOPS transit photometry, and the HARPS TERRA Doppler measurements using the software suite pyaneti, which combines a Bayesian approach with MCMC sampling in order to determine the planetary system parameters. We fitted the TESS and CHEOPS transit light curves of HD 190622b using the limb-darkened quadratic law of Mandel & Agol (2002). TheRV model includes two Keplerian orbits to account for the Doppler reflex motions induced by HD 190622b and c. For the eccentricity and argument of periastron, we adopted the parametrization proposed by Anderson et al. (2011) as implemented in pyaneti. We accounted for any instrumental noise not included in the nominal uncertainties by fitting for three “jitter” terms for the HARPS TERRA, TESS, and CHEOPS time series.
We performed a preliminary analysis setting uniform uninformative priors for all the fitted parameters. We find the mean stellar density 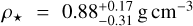 , as derived from the transit modelling, to be consistent with the mean density ρ⋆ = 0.841 ± 0.037 g cm−3 derived from the stellar mass and radius (Table 2), further confirming the planetary nature of the transit signal (Tingley et al. 2011). However, the transit light curve poorly constrains the scaled semi-major axis (a/R⋆). We therefore adopted a Gaussian prior on (a/R⋆) using Kepler’s third law, the orbital period, and the stellar mass and radius.
, as derived from the transit modelling, to be consistent with the mean density ρ⋆ = 0.841 ± 0.037 g cm−3 derived from the stellar mass and radius (Table 2), further confirming the planetary nature of the transit signal (Tingley et al. 2011). However, the transit light curve poorly constrains the scaled semi-major axis (a/R⋆). We therefore adopted a Gaussian prior on (a/R⋆) using Kepler’s third law, the orbital period, and the stellar mass and radius.
Details of the modeled parameters and prior ranges are given in Table 3. We used 500 independent Markov chains initialized randomly inside the prior ranges. Once all chains converged, we used the last 5000 iterations and saved the chain states every 10 iterations. This approach generates a posterior distribution of 25 000 000 points for each model parameter. Table 3 lists the inferred planetary parameters; they are defined as the median and 68% region of the credible interval of the posterior distributions for each fitted parameter. The TESS and CHEOPS phase-folded transit light curves are displayed in Fig. 4 along with the best-fitting transit models for the two band passes. The HARPS TERRA RV time series, the phase-folded RV curves of HD 190622b and c, and the best-fitting models are shown in Fig. 5.
As a final sanity check, we fitted two independent planet-to-star radius ratios (Rp/R⋆) for the TESS and CHEOPS transit light curves, while modeling all the remaining parameters jointly. We find that TESS and CHEOPS data provide consistent values of the planetary radius of HD 190622b that are well within the nominal error bars.
Fitted and derived parameter values for TOI-1054 b and c based on the joint fit to the photometric light curves and RV data detailed in this section.
 |
Fig. 4 TESS and CHEOPS transit light curve of HD 190622b and best-fitting model for the two band passes. The TESS and CHEOPS data in bins of 15 min each are displayed with green and red circles, respectively. |
5 Discussion
5.1 Planetary interior
The precise characterization of the bulk parameters (radius: 2%, mass: 13%) of planet b allows us to put constraints on its planetary interior and possible atmospheric evolution. The internal composition of planets depends on the composition of the initial nebula where the planet formed and the evolution conditions experienced over time. For the analysis of the internal structure of planet b, we apply a Bayesian inference model that uses the mass and radius values and the stellar properties derived in Sect. 4. The details of the method we used can be found in Leleu et al. (2021a), but we briefly summarize the main aspects in the following.
The input parameters of the Bayesian model are the radius, mass, effective temperature, and age of the star, the stellar abundances and metallicity (stellar observables), and then the mass of the planet relative to its host star, the transit depth, and the period of the planet (planetary observables). The Bayesian inference scheme then uses a forward model to calculate the radius of a planetary structure with a given mass and composition. This forward model assumes that the planet consists of four perfectly spherically symmetric, fully distinct layers: an inner iron core (following the equation of state from Hakim et al. 2018), a silicate mantle (Sotin et al. 2007), a water layer (Haldemann et al. 2020), and a H/He atmosphere, which is modeled according to Lopez & Fortney (2014). However, we note that the gas layer is modeled fully independently from the rest of the planet in the current version of our model, which means that any pressure or temperature effects of the atmosphere on the rest of the planet are neglected. In particular, we use a fixed temperature (300 K) and pressure (1 bar) as the outer boundary conditions for modeling the water layer, while the atmosphere is modeled separately on top of this solid core. We further assume that the Si/Mg/Fe ratios of the planet are identical to the ratios of its host star (Thiabaud et al. 2015). However, we note that the recent work of Adibekyan et al. (2021) suggests that the stellar and planetary abundances may not be always correlated in a one-to-one relation.
As output, the model provides posteriors of various internal structure parameters, namely the mass fractions of the iron core, the silicate mantle, and the water layer with respect to the solid planet without the H/He layer, the gas mass, and the molar mass fractions of Fe and S in the inner core and Si, Mg, and Fe in the silicate mantle. However, these depend to a certain extent on the chosen priors for these internal-structure parameters. We chose a prior that is uniform for the mass fractions of the inner core, the silicate mantle, and the water layer under the condition that they need to add up to 1 and that the water mass fraction has a maximal value of 0.5 (Thiabaud et al. 2014; Marboeuf et al. 2014). For the gas mass, we chose a prior that is uniform on a logarithmic scale.
The results of the internal structure modeling are presented in Fig. 6. The gas mass is constrained reasonably well and with a value of 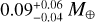 it qualifies as being relatively large compared to other known planets. This corresponds to a thickness of
it qualifies as being relatively large compared to other known planets. This corresponds to a thickness of 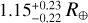 (37% of the radius). Meanwhile, the water mass fraction is mostly unconstrained.
(37% of the radius). Meanwhile, the water mass fraction is mostly unconstrained.
The approach described above for the internal modeling is not unique. We can challenge the robustness of these results using models based on different assumptions. Our motivation is to understand the impact of different assumptions on the uncertainties of the results of the interior structure modeling. We chose to follow the approach of Baumeister et al. (2020), who use machine-learning techniques (ML) based on mixture density neural networks to infer the interior characterization of low-mass exoplanets. Significant differences with the model of Leleu et al. (2021a) are: (i) the water mass layer is not constrained to 50% in mass, (ii) we do not constrain the silicon, iron, and magnesium abundances relative to the measured stellar abundances (see comment about the relevance of this approach above), and (iii) we couple the atmospheric layer to the water layer below (we solve the interior structure with the atmosphere fully integrated into the interior structure model, so that pressure and temperature at the bottom of the atmosphere set the boundary conditions for the water layer below). The atmosphere is isothermal at the equilibrium temperature of 917 K. The water layer is adiabatic with a top temperature that is consistent with the assumptions on the atmospheric layer (917 K). This approach has the following limitations: (i) There is a large coupling between the water and atmospheric layers; this implies that we can extend the amount of atmosphere at the expense of reducing the water layer, as the observations available are not precise enough to remove this degeneracy. (ii) We use the silicon and magnesium abundances representative for Earth; as the abundances of these two elements in exoplanetary bodies are not constrained observationally, it is difficult to establish whether this approach is more meaningful than using the stellar abundances. (iii) Finally, our atmospheric model uses an isothermal profile at the equilibrium temperature of the planet, which means that for a gas layer of a given size, we tend to overestimate the gas mass fraction. Figure 7 shows the results of this alternative approach, which can be compared with Fig. 6. Caution must be taken when comparing the two figures, because of the differences in the definitions of the mass (or radius) fractions. The Bayesian model uses the iron core mass fraction with respect to the solid planet without the gas part, while the ML model provides the iron core mass fraction with respect to the entire planet. The ML results are consistent with the Bayesian approach above, but they have larger uncertainties. We believe that this is due to the relaxation of the constraints on the abundances in the mantle and in the core and because of the coupling between atmosphere and water (ice) layer. The ML approach is consistent with a larger mass fraction in the atmosphere, as expected, but still consistent with the Bayesian study. It is well known that degeneracies in interiorcompositions remain a challenge to the modeling of the interior structure of planets, even in our Solar System (e.g., Helled & Fortney 2020; Mollière et al. 2022).
Possible approaches to remove these degeneracies would be the study of multiplanet systems (e.g., Leleu et al. 2021a), where the constraints on Si or Mg should be consistent for all planets, or the observation of additional measurable quantities, such as the k2 Love number (see Baumeister et al. 2020).
 |
Fig. 5 Radial velocity analysis of the planetary system. Upper panel: HARPS TERRA RV time series of HD 190622. Lower panels: phase-folded RV curves of HD 190622b (left) and HD 190622c (right). The best-fitting Keplerian models are overplotted with thick black lines. The vertical light-blue lines mark the error bars including the RV jitter. |
5.2 Atmospheric evolution
We considered the stellar and planetary parameters derived in Sects. 3 and 4 and the present-day planetary atmospheric mass fraction presented in Sect. 5.1 of planet b in order to reconstruct the evolution of the stellar rotation rate and of the planetary atmosphere. In particular, we constrain the evolution of the stellar rotation period, which we use as a proxy for the evolution of the stellar high-energy emission affecting atmospheric escape, and the predicted initial atmospheric mass fraction of the detected planets 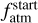 , which is the mass of the planetary atmosphere at the time of the dispersal of the protoplanetary disk; we assume this to be at 5 Myr.
, which is the mass of the planetary atmosphere at the time of the dispersal of the protoplanetary disk; we assume this to be at 5 Myr.
We reach these results using the Planetary Atmospheres and Stellar RoTation rAtes (PASTA; Bonfanti et al. 2021b) code, which is an updated version of the original code presented by Kubyshkina et al. (2019a,b). Briefly, PASTA constrains the evolution of planetary atmospheres and of the stellar rotation rate by combining a model predicting planetary atmospheric escape rates based on hydrodynamic simulations (this has the advantage over other commonly used analytical estimates in that it accounts for both extreme ultraviolet(XUV)-driven and core-powered mass loss; Kubyshkina et al. 2018), a model of the stellar high-energy (X-ray plus XUV) flux evolution (Bonfanti et al. 2021b), a model relating planetary parameters and atmospheric mass (Johnstone et al. 2015), and stellar evolutionary tracks (Choi et al. 2016). PASTA works under two main assumptions: (1) planet migration did not occur after the dispersal of the protoplanetary disk; and (2) the planets hosted at some point in the past or still host a hydrogen-dominated atmosphere. PASTA returns realistic uncertainties on the free parameters (i.e., the planetary initial atmospheric mass fractions at the time of the dispersal of the protoplanetary disk, and the indexes of the power law controlling the stellar rotation period that is used as a proxy for the stellar XUV emission) by implementing the atmospheric evolution algorithm in a Bayesian framework (Cubillos et al. 2017), using the system parameters with their uncertainties as input priors. All details of the algorithm can be found in Bonfanti et al. (2021b). The only difference with respect to the analysis of the systems considered by Bonfanti et al. (2021b) is that here we fit the planetary atmospheric mass fraction given in Sect. 5.1 instead of the planetary radius. This enables the code to be more accurate by avoiding the continuous conversion of the atmospheric mass fraction into planetary radius, given the other system parameters (see e.g., Delrez et al. 2021).
As a proxy for the evolution of the stellar rotation period, Fig. 8 displays the posterior distribution (including the high posterior density, HPD) of the stellar rotation period at an age of 150 Myr (Prot,150), where it is compared to that of star members of young open clusters that are of comparable mass extracted from Johnstone et al. (2015). The stellar rotation history of the star is poorly constrained as only one planet is available as an observational constraint. However, PASTA does exclude a very slow rotator. The gyro-relation build into PASTA estimated a present-day rotation rate of 17.9 + 2.6 days. Given the stellar radius from Table 2, the expected rotation velocity would be υexp = 3.4 + 0.5 km s−1·. The υ sin i⋆ as derived from spectroscopy is significantly higher, υ sin i⋆ = 5.2 + 0.9 km s−1. To explain this tension at the 2 sigma level, one might consider that the rotational period may be overestimated and the star should rotate faster. Gyro relations are calibrated on open clusters (generally younger than a couple of gigayears) and there are several papers in the literature discussing the reliability of gyro relations applied to field stars, which can also be older than a couple of gigayears (as in our target). Alternatively, υ sin i⋆ may be overestimated and the star should rotate slower. There is a certain degeneracy on the computed solution for υ sin i⋆ with the macro-turbulence velocity. In any case, the impact of this difference on our interpretation of the results is minor.
Figure 9 shows the posterior distribution of the initial atmospheric mass fraction for planet b in comparison to the present-day atmospheric mass fraction. For a given set of system parameters, the amount of mass loss is mainly determined by the evolution of the stellar rotation period. The more rapidly rotating the star, the more XUV energy is emitted, resulting in higher escape rates (Sanz-Forcada et al. 2011). As the stellar rotation history of TOI-1054 is only poorly constrained by PASTA, we also find a certain ambiguity in the resulting mass-loss rates. PASTA clearly prefers evolutionary scenarios with only very little atmospheric mass loss happening. Although present, this would suggest that the mass-loss did not play a significant role in the evolution of the planet. However, PASTA cannot exclude the possibility that the star is a very fast rotator, which in turn would result in significant mass loss. In Fig. 9, these rapid rotator scenarios are represented by a nonzero posterior distribution at higher mass-loss rates.
 |
Fig. 6 Distributions resulting from the internal structure modeling following Leleu et al. (2021a). The values above the histograms are the median and the 5th and 95th percentiles of the posterior distribution (same as the dashed lines). The plotted internal structure parameters are: the iron core and water mass fractions of the solid planet (without gas); the molar mass fractions of Si and Mg in the mantle and of Fe in the core; and the decimal logarithm of the absolute gas mass expressed in Earth masses. |
 |
Fig. 7 Distributions resulting from the internal structure modeling following Baumeister et al. (2020). The values above the histograms are the median and the 16th and 84th percentiles of the posterior distribution (same as the dashed lines). The plotted internal structure parameters are: the radius fraction of the core, mantle, ice (of water), and gas layers. |
5.3 The planetary system in the context of planet population analyses
Figure 10 shows the position of TOI-1054b in the mass–radius diagram of known extrasolar planets with precise mass measurements (uncertainty on the mass of less than 15%; see also Otegi et al. 2020). Among the sub-Neptune-sized planets known today, TOI-1054b stands out because of its large gas content. The known planet with closest properties to TOI-1054b would be HIP 41378b (Santerne et al. 2019), displaying a slightly shorter radius (2.595 + 0.036 REarth) and a similar orbital period (15.6 days). The system is also bright (V = 8.92) and most of the attention in the literature has been directed toward planet f in the system, which has an orbital period of 542 days. However, its properties are challenging to characterize (Bryant et al. 2021; Alam et al. 2022; Belkovski et al. 2022). The next closest planets orbiting F stars are the pair around Kepler-1705 (Leleu et al. 2021b) with orbital periods of 9 and 11 days. These are slightly smaller (2.03 ± 0.12 REarth and 2.05 ± 0.014 REarth respectively) and more difficult to characterize, as the host star is fainter (V = 15.8). Finally, HD 80653b is an ultrashort-period planet (Frustagli et al. 2020) with a rocky composition (0.72 days period, 1.613 ± 0.071 REarth) around a V = 9.5 magnitude star. As discussed in the previous section, the fact that TOI-1054b has not experienced significant atmospheric escape explains why it lies in the upper part of the mass-radius distribution. Therefore, this planet can be used to define the upper edge of this distribution, which in turn can be used to better understand how planets form and evolve (Kubyshkina & Fossati 2022).
It is also interesting to look at the distribution of the density-versus-mass plot (see, e.g., Hatzes & Rauer 2015). Figure 10 highlights the planets orbiting F stars, which are defined here as dwarf stars with an effective temperature of over 6000 and below 7500 K. In the core accretion formalism, one of the fundamental parameters is the maximum size that a planetary core must reach before accreting a significant amount of volatiles, subsequently becoming a gas-rich planet. There is an insufficient number of known planets to provide a conclusive observational constraint on this parameter. Answering this question will be work for future missions such as PLATO (Rauer et al. 2014), while constraints on the chemical composition of the atmospheres will also certainly help to improve our understanding of planetary formation processes (Tinetti et al. 2018). For example, the C/O ratio is considered to be a signature of where the planet has formed. Recently, it has been proposed that other elements might also be needed to constrain the full picture (Öberg et al. 2011; Eistrup et al. 2022). Given the architecture of this system, large-scale migration seems unlikely. A Jupiter-like planet would migrate faster than a smaller one and thus would have overtaken the smaller one had these planets undergone a significant migration process. Consequently, we can assume that these planets must have formed where they are now, as in our Solar System. If this is the case, the inner one should have the C/O ratio of a planet that formed in the inner part of the planetary system, which could serve as a reference as to the expected C/O abundance of such planets. The transmission spectroscopy metric (TSM) for TOI-1054b is 81 (Kempton et al. 2018), so it should be pretty favourable for JWST transmission spectroscopy.
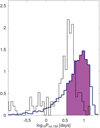 |
Fig. 8 Posterior distribution (dark blue) of the stellar rotation rate of HD 190622 after 150 Myr derived by PASTA. The purple area represents the HPD interval of the distribution. The black line represents the distribution of the stellar rotation rate of young open cluster stars with masses comparable to that of HD 190622 based on the collection of data provided by Johnstone et al. (2015). See main text for details. |
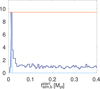 |
Fig. 9 Posterior distribution (dark blue) for the mass of the planetary atmosphere of planet b at the time of the dispersal of the protoplanetary disk derived by PASTA. The light-blue line represents the distribution of the estimated present-day atmospheric mass fraction. The orange horizontal line indicate the uninformative prior distribution. See main text for details. |
 |
Fig. 10 Mass vs. radius (top) and mass vs density (bottom) plots for planets with mass uncertainty below 15%. The planets known to orbit F stars are highlighted with blue circles, while TOI-1054b is shown with a diamond. |
6 Summary
With this paper, we present the discovery and characterization of the planetary system around HD 190622, also known as TOI-1054. The system consists of a short-period gas-rich subNeptune transiting planet and an outer Jupiter-mass companion in an orbit of 0.92 au. We provide a precise characterization of the inner planet in terms of mass and radius. Its properties are unique among the current population of precisely characterized planets orbiting F stars and it provides useful constraints for planetary formation theories.
Unfortunately, the nontransiting planet c is not likely to be detected with direct imaging with forthcoming facilities such as the Nancy Grace Roman Space Telescope (Spergel et al. 2013), LUVOIR (Bolcar et al. 2016), or HabEx (Mennesson et al. 2016). At a distance of 88 pc (Gaia Collaboration 2023; for a description of the Gaia mission see Gaia Collaboration 2016), the expected angular separation between the planet and the star is 10 mas, while for example the inner working angle of LUVOIR-A is about 25 mas. As the orbit is only slightly eccentric, there is little chance that the outer planet will be characterized with direct imaging in the near future (see methodology in Carrión-González et al. 2021). Future facilities like LIFE (Quanz et al. 2022) could be more successful in characterizing the outer planet in the system. We used LIFESim (Dannert et al. 2022) to estimate the detectability prospects, concluding that a S/N of 8.6 for detection is possible with 10h integration (in the intermediate configuration, which is not optimistic nor pessimistic). Atmospheric characterization will be more challenging. Although it is expected that LIFE will concentrate on nearby planetary systems (about 20 pc), the prospects of obtaining a more complete characterization of the system are encouraging.
Acknowledgements
We would like to thank the anonymous referee for the careful reading and comments that improved the quality of the manuscript. CHEOPS is an ESA mission in partnership with Switzerland with important contributions to the payload and the ground segment from Austria, Belgium, France, Germany, Hungary, Italy, Portugal, Spain, Sweden, and the United Kingdom. The CHEOPS Consortium would like to gratefully acknowledge the support received by all the agencies, offices, universities, and industries involved. Their flexibility and willingness to explore new approaches were essential to the success of this mission. CHEOPS data analysed in this article will be made available in the CHEOPS mission archive (https://cheops.unige.ch/archive_browser/) K.G.I. is the ESA CHEOPS Project Scientist and is responsible for the ESA CHEOPS Guest Observers Programme. She does not participate in, or contribute to, the definition of the Guaranteed Time Programme of the CHEOPS mission through which observations described in this paper have been taken, nor to any aspect of target selection for the programme. This work was supported by the KESPRINT collaboration, an international consortium devoted to the characterization and research of exoplanets discovered with space-based missions (http://www.kesprint.science). This paper includes data collected with the TESS mission, obtained from the MAST data archive at the Space Telescope Science Institute (STScI). Funding for the TESS mission was provided by the NASA Explorer Program. STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5–26555. We acknowledge the use of public TESS data from pipelines at the TESS Science Office and at the TESS Science Processing Operations center. Resources supporting this work were provided by the NASA High-End Computing (HEC) Program through the NASAAdvanced Supercomputing (NAS) Division atAmes Research centre for the production of the SPOC data products. D.G. and L.M.S. gratefully acknowledge financial support from the CRT foundation under Grant No. 2018.2323 “Gaseous or rocky? Unveiling the nature of small worlds”. Ph. B. and N.T. acknowledge support by the DFG Schwerpunkt SPP 1992 “Exploring the Diversity of Extrasolar Planets” (grant TO 704/3-1) and by the DFG Research Unit FOR 2440 “Matter under planetary interior conditions” (grant PA 3689/1-1). A.C.C. and T.G.W. acknowledge support from STFC consolidated grant numbers ST/R000824/1 and ST/V000861/1, and UKSA grant number ST/R003203/1. This work was supported by FCT - Fundação para a Ciência e a Tecnologia through national funds and by FEDER through COMPETE2020 -Programa Operacional Competitividade e Internacionalização by these grants: UID/FIS/04434/2019; UIDB/04434/2020; UIDP/04434/2020; PTDC/FIS-AST/32113/2017 & POCI-01-0145-FEDER-032113; PTDC/FIS-AST/28953/2017 and POCI-01-0145-FEDER-028953; PTDC/FIS-AST/28987/2017 and POCI-01-0145-FEDER-028987, 2022.06962.PTDC. Y.A., M.J.H. and J.A.E. acknowledge the support of the Swiss National Fund under grant 200020_172746. A.B. was supported by the SNSA. L.D. is an F.R.S.-FNRS Postdoctoral Researcher. The Belgian participation to CHEOPS has been supported by the Belgian Federal Science Policy Office (BELSPO) in the framework of the PRODEX Program, and by the University of Liège through an ARC grant for Concerted Research Actions financed by the Wallonia-Brussels Federation. E.G. gratefully acknowledges the support by the Thüringer Ministerium für Wirtschaft, Wissenschaft und Digitale Gesellschaft. S.H. gratefully acknowledges CNES funding through the grant 837319. S.G.S. acknowledges support from FCT through FCT contract nr. CEECIND/00826/2018 and POPH/FSE (EC). We acknowledge support from the Spanish Ministry of Science and Innovation and the European Regional Development Fund through grants ESP2016-80435-C2-1-R, ESP2016-80435-C2-2-R, PGC2018-098153-B-C33, PGC2018-098153-B-C31, ESP2017-87676-C5-1-R, MDM-2017-0737 Unidad de Excelencia “María de Maeztu”- Centro de Astrobiolog’ia (INTA-CSIC), as well as the support of the Generalitat de Catalunya/CERCA programme. S.C.C.B. acknowledges support from FCT through FCT contracts nr. IF/01312/2014/CP1215/CT0004. X.B., S.C.C.B., D.G., M.F. and J.L. acknowledge their role as ESA-appointed CHEOPS science team members. This work makes use of observations from the LCOGT network. Part of the LCOGT telescope time was granted by NOIRLab through the Mid-Scale Innovations Program (MSIP). MSIP is funded by NSF. H.J.D. acknowledges support from the Spanish Research Agency of the Ministry of Science and Innovation (AEI-MICINN) under grant PID2019-107061GB-C66, DOI: 10.13039/501100011033. This project was supported by the CNES. O.D.S.D. is supported in the form of work contract (DL 57/2016/CP1364/CT0004) funded by national funds through FCT. B.-O.D. acknowledges support from the Swiss National Science Foundation (PP00P2-190080). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (project FOUR ACES; grant agreement No 724427). It has also been carried out in the frame of the National Centre for Competence in Research PlanetS supported by the Swiss National Science Foundation (SNSF). DE acknowledges financial support from the Swiss National Science Foundation for project 200021_200726. A.De. acknowledges the financial support of the National Centre of Competence in Research PlanetS supported by the Swiss National Science Foundation under grants 51NF40_182901 and 51NF40_205606. M.F. and C.M.P. gratefully acknowledge the support of the Swedish National Space Agency (DNR 65/19, 174/19, 174/18). M.G. is an F.R.S.-FNRS Senior Research Associate. K.W.F.L. acknowledges support by DFG grants RA714/14-1 within the DFG Schwerpunkt SPP 1992, “Exploring the Diversity of Extrasolar Planets”. This work was granted access to the HPC resources of MesoPSL financed by the Region Ile de France and the project Equip@Meso (reference ANR-10-EQPX-29-01) of the programme Investissements d’Avenir supervised by the Agence Nationale pour la Recherche. M.L. acknowledges support of the Swiss National Science Foundation under grant number PCEFP2_194576. R.L. acknowledges funding from University of La Laguna through the Margarita Salas Fellowship from the Spanish Ministry of Universities ref. UNI/551/2021-May 26, and under the EU Next Generation funds. P.M. acknowledges support from STFC research grant number ST/M001040/1. G.P., I.P., V.N. and R.R. acknowledge the funding support from Italian Space Agency (ASI) regulated by “Accordo ASI-INAF n. 2013-016-R.0 del 9 luglio 2013 e integrazione del 9 luglio 2015 CHEOPS Fasi A/B/C”. This work was also partially supported by a grant from the Simons Foundation (PI: Queloz, grant number 327127). I.R. acknowledges support from the Spanish Ministry of Science and Innovation and the European Regional Development Fund through grant PGC2018-098153-B- C33, as well as the support of the Generalitat de Catalunya/CERCA programme. N.C.S. acknowledges support from the European Research Council through the grant agreement 101052347 (FIERCE). Gy.M.Sz. acknowledges the support of the Hungarian National Research, Development and Innovation Office (NKFIH) grant K-125015, a PRODEX Institute Agreement between the ELTE Eötvös Loránd University and the European Space Agency (ESA-D/SCI-LE-2021-0025), the Lendület LP2018-7/2021 grant of the Hungarian Academy of Science and the support of the city of Szombathely. V.V.G. is an F.R.S-FNRS Research Associate. S.S. has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 833925, project STAREX). N.A.W. acknowledges UKSA grant ST/R004838/1. The MOC activities have been supported by the ESA contract No. 4000124370. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.
References
- Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012, A & A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V., Figueira, P., Santos, N. C., et al. 2015, A & A, 583, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V., de Laverny, P., Recio-Blanco, A., et al. 2018, A & A, 619, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V., Dorn, C., Sousa, S. G., et al. 2021, Science, 374, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Alam, M. K., Kirk, J., Dressing, C. D., et al. 2022, ApJ, 927, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Allard, F. 2014, IAU Symp., 299, 271 [Google Scholar]
- Anderson, D. R., Collier Cameron, A., Hellier, C., et al. 2011, ApJ, 726, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Anglada-Escudé, G., & Butler, R. P. 2012, ApJS, 200, 15 [Google Scholar]
- Azevedo Silva, T., Demangeon, O. D. S., Barros, S. C. C., et al. 2022, A & A, 657, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baglin, A., Auvergne, M., Boisnard, L., et al. 2006, COSPAR Scientific Assembly, 36, 3749 [NASA ADS] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A & AS, 119, 373 [NASA ADS] [Google Scholar]
- Barbato, D., Pinamonti, M., Sozzetti, A., et al. 2020, A & A, 641, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barragán, O., Gandolfi, D., & Antoniciello, G. 2019, MNRAS, 482, 1017 [Google Scholar]
- Barragán, O., Aigrain, S., Rajpaul, V. M., & Zicher, N. 2022, MNRAS, 509, 866 [Google Scholar]
- Baumeister, P., Padovan, S., Tosi, N., et al. 2020, ApJ, 889, 42 [Google Scholar]
- Belkovski, M., Becker, J., Howe, A., Malsky, I., & Batygin, K. 2022, AJ, 163, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Benatti, S., Damasso, M., Desidera, S., et al. 2020, A & A, 639, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., & Lundström, I. 2003, A & A, 410, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., & Oey, M. S. 2014, A & A, 562, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benz, W., Broeg, C., Fortier, A., et al. 2021, Exp. Astron., 51, 109 [Google Scholar]
- Blackwell, D. E., & Shallis, M. J. 1977, MNRAS, 180, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Bolcar, M. R., Feinberg, L., France, K., et al. 2016, SPIE Conf. Ser., 9904, 99040J [NASA ADS] [Google Scholar]
- Bonfanti, A., Ortolani, S., Piotto, G., & Nascimbeni, V. 2015, A & A, 575, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfanti, A., Ortolani, S., & Nascimbeni, V. 2016, A & A, 585, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfanti, A., Delrez, L., Hooton, M. J., et al. 2021a, A & A, 646, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfanti, A., Fossati, L., Kubyshkina, D., & Cubillos, P. E. 2021b, A & A, 656, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
- Brandeker, A., Heng, K., Lendl, M., et al. 2022, A & A, 659, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, T. M., Baliber, N., Bianco, F. B., et al. 2013, PASP, 125, 1031 [Google Scholar]
- Bryan, M. L., Knutson, H. A., Lee, E. J., et al. 2019, AJ, 157, 52 [Google Scholar]
- Bryant, E. M., Bayliss, D., Santerne, A., et al. 2021, MNRAS, 504, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Carrión-González, Ó., García Muñoz, A., Santos, N. C., et al. 2021, A & A, 651, A7 [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2003, IAU Symp., 210, A20 [Google Scholar]
- Chachan, Y., Dalba, P. A., Knutson, H. A., et al. 2022, ApJ, 926, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, D.-C., Xie, J.-W., Zhou, J.-L., et al. 2021, ApJ, 909, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, J., Dotter, A., Conroy, C., et al. 2016, ApJ, 823, 102 [Google Scholar]
- Collins, K. 2019, AAS Meeting Abstracts, 233, 140.05 [NASA ADS] [Google Scholar]
- Collins, K. A., Kielkopf, J. F., Stassun, K. G., & Hessman, F. V. 2017, AJ, 153, 77 [Google Scholar]
- Cruzalèbes, P., Petrov, R. G., Robbe-Dubois, S., et al. 2019, MNRAS, 490, 3158 [Google Scholar]
- Csizmadia, S. 2020, MNRAS, 496, 4442 [Google Scholar]
- Cubillos, P., Harrington, J., Loredo, T. J., et al. 2017, AJ, 153, 3 [Google Scholar]
- Dalba, P. A., Kane, S. R., Isaacson, H., et al. 2021, AJ, 161, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Dannert, F. A., Ottiger, M., Quanz, S. P., et al. 2022, A & A, 664, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delrez, L., Ehrenreich, D., Alibert, Y., et al. 2021, Nat. Astron., 5, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Dorn, C., Khan, A., Heng, K., et al. 2015, A & A, 577, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eistrup, C., Cleeves, L. I., & Krijt, S. 2022, A & A, 667, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frustagli, G., Poretti, E., Milbourne, T., et al. 2020, A & A, 633, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A & A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A & A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A & A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gandolfi, D., Barragán, O., Livingston, J. H., et al. 2018, A & A, 619, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giacalone, S., Dressing, C. D., Jensen, E. L. N., et al. 2021, AJ, 161, 24 [Google Scholar]
- Grenfell, J. L., Leconte, J., Forget, F., et al. 2020, Space Sci. Rev., 216, 98 [CrossRef] [Google Scholar]
- Guerrero, N. M., Seager, S., Huang, C. X., et al. 2021, ApJS, 254, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Hakim, K., Rivoldini, A., Van Hoolst, T., et al. 2018, Icarus, 313, 61 [Google Scholar]
- Haldemann, J., Alibert, Y., Mordasini, C., & Benz, W. 2020, A & A, 643, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hatzes, A. P., & Rauer, H. 2015, ApJ, 810, L25 [Google Scholar]
- Helled, R., & Fortney, J. J. 2020, Philos. Trans. R. Soc. London Ser. A, 378, 20190474 [NASA ADS] [Google Scholar]
- Heller, R., Hippke, M., & Kervella, P. 2017, AJ, 154, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Herman, M. K., Zhu, W., & Wu, Y. 2019, AJ, 157, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A & A, 355, L27 [Google Scholar]
- Hoyer, S., Guterman, P., Demangeon, O., et al. 2020, A & A, 635, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huang, C. X., Burt, J., Vanderburg, A., et al. 2018, ApJ, 868, L39 [Google Scholar]
- Jenkins, J. M. 2002, ApJ, 575, 493 [Google Scholar]
- Jenkins, J. M., Twicken, J. D., McCauliff, S., et al. 2016, SPIE, 9913, 99133E [NASA ADS] [Google Scholar]
- Jenkins, J. M., Tenenbaum, P., Seader, S., et al. 2020, Kepler Data Processing Handbook: Transiting Planet Search, Kepler Science Document KSCI-19081-003 [Google Scholar]
- Jensen, E. 2013, Astrophysics Source Code Library [record ascl:1386.887] [Google Scholar]
- Johnson, D. R. H., & Soderblom, D. R. 1987, AJ, 93, 864 [Google Scholar]
- Johnstone, C. P., Güdel, M., Stökl, A., et al. 2015, ApJ, 815, L12 [Google Scholar]
- Kempton, E. M. R., Bean, J. L., Louie, D. R., et al. 2018, PASP, 130, 114401 [Google Scholar]
- Kervella, P., Arenou, F., Mignard, F., & Thévenin, F. 2019, A & A, 623, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kubyshkina, D., & Fossati, L. 2022, A & A, 668, A178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kubyshkina, D., Fossati, L., Erkaev, N. V., et al. 2018, A & A, 619, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kubyshkina, D., Cubillos, P. E., Fossati, L., et al. 2019a, ApJ, 879, 26 [Google Scholar]
- Kubyshkina, D., Fossati, L., Mustill, A. J., et al. 2019b, A & A, 632, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuerster, M., Schmitt, J. H. M. M., Cutispoto, G., & Dennerl, K. 1997, A & A, 320, 831 [NASA ADS] [Google Scholar]
- Kunimoto, M., Winn, J., Ricker, G. R., & Vanderspek, R. K. 2022, AJ, 163, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 1993, SYNTHE Spectrum Synthesis Programs and Line Data (Cambridge, Mass.: Smithsonian Astrophysical Observatory) [Google Scholar]
- Leleu, A., Alibert, Y., Hara, N. C., et al. 2021a, A & A, 649, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leleu, A., Chatel, G., Udry, S., et al. 2021b, A & A, 655, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, J., Tenenbaum, P., Twicken, J. D., et al. 2019, PASP, 131, 024506 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Bastian, U., Biermann, M., et al. 2021, A & A, 649, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lopez, E. D., & Fortney, J. J. 2014, ApJ, 792, 1 [Google Scholar]
- Lovis, C., & Pepe, F. 2007, A & A, 468, 1115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lubin, J., Van Zandt, J., Holcomb, R., et al. 2022, AJ, 163, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [Google Scholar]
- Mamajek, E. E., Prsa, A., Torres, G., et al. 2015, ArXiv e-prints [arXiv: 151S.S7674] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [Google Scholar]
- Marboeuf, U., Thiabaud, A., Alibert, Y., Cabral, N., & Benz, W. 2014, A & A, 570, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2017, ApJ, 835, 77 [Google Scholar]
- Maxted, P. F. L., Ehrenreich, D., Wilson, T. G., et al. 2022, MNRAS, 514, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- McCully, C., Volgenau, N. H., Harbeck, D.-R., et al. 2018, SPIE Conf. Ser., 10707, 107070K [Google Scholar]
- Mennesson, B., Gaudi, S., Seager, S., et al. 2016, SPIE Conf. Ser., 9904, 99040L [Google Scholar]
- Mollière, P., Molyarova, T., Bitsch, B., et al. 2022, ApJ, 934, 74 [CrossRef] [Google Scholar]
- Öberg, K. I., Murray-Clay, R., & Bergin, E. A. 2011, ApJ, 743, L16 [Google Scholar]
- Otegi, J. F., Bouchy, F., & Helled, R. 2020, A & A, 634, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F., Mayor, M., Galland, F., et al. 2002, A & A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quanz, S. P., Ottiger, M., Fontanet, E., et al. 2022, A & A, 664, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [Google Scholar]
- Reddy, B. E., Lambert, D. L., & Allende Prieto, C. 2006, MNRAS, 367, 1329 [Google Scholar]
- Reiners, A., & Zechmeister, M. 2020, ApJS, 247, 11 [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Rosenthal, L. J., Knutson, H. A., Chachan, Y., et al. 2022, ApJS, 262, 1 [Google Scholar]
- Salmon, S. J. A. J., Van Grootel, V., Buldgen, G., Dupret, M. A., & Eggenberger, P. 2021, A & A, 646, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santerne, A., Malavolta, L., Kosiarek, M. R., et al. 2019, ArXiv e-prints [arXiv:1911.07355] [Google Scholar]
- Santos, N. C., Sousa, S. G., Mortier, A., et al. 2013, A & A, 556, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanz-Forcada, J., Micela, G., Ribas, I., et al. 2011, A & A, 532, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schanche, N., Hébrard, G., Collier Cameron, A., et al. 2020, MNRAS, 499, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Schlecker, M., Mordasini, C., Emsenhuber, A., et al. 2021, A & A, 656, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scuflaire, R., Théado, S., Montalbán, J., et al. 2008, Ap & SS, 316, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. C., Stumpe, M. C., Van Cleve, J. E., et al. 2012, PASP, 124, 1000 [Google Scholar]
- Sneden, C. A. 1973, PhD thesis, University of Texas, Austin, USA [Google Scholar]
- Sotin, C., Grasset, O., & Mocquet, A. 2007, Icarus, 191, 337 [Google Scholar]
- Sousa, S. G. 2014, in Determination of Atmospheric Parameters of B (Berlin: Springer), 297 [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Monteiro, M. J. P. F. G. 2007, A & A, 469, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A & A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Adibekyan, V., Delgado-Mena, E., & Israelian, G. 2015, A & A, 577, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Adibekyan, V., Delgado-Mena, E., et al. 2021, A & A, 656, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spergel, D., Gehrels, N., Breckinridge, J., et al. 2013, ArXiv e-prints [arXiv:1305.5422] [Google Scholar]
- Stumpe, M. C., Smith, J. C., Van Cleve, J. E., et al. 2012, PASP, 124, 985 [Google Scholar]
- Stumpe, M. C., Smith, J. C., Catanzarite, J. H., et al. 2014, PASP, 126, 100 [Google Scholar]
- Teske, J., Díaz, M. R., Luque, R., et al. 2020, AJ, 160, 96 [Google Scholar]
- Thiabaud, A., Marboeuf, U., Alibert, Y., et al. 2014, A & A, 562, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thiabaud, A., Marboeuf, U., Alibert, Y., Leya, I., & Mezger, K. 2015, A & A, 580, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tinetti, G., Drossart, P., Eccleston, P., et al. 2018, Exp. Astron., 46, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Tingley, B., Bonomo, A. S., & Deeg, H. J. 2011, ApJ, 726, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Tokovinin, A. 2018, PASP, 130, 035002 [Google Scholar]
- Tran, Q. H., Bowler, B. P., Endl, M., et al. 2022, AJ, 163, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Twicken, J. D., Catanzarite, J. H., Clarke, B. D., et al. 2018, PASP, 130, 064502 [Google Scholar]
- Valencia, D., Sasselov, D. D., & O’Connell, R. J. 2007, ApJ, 665, 1413 [Google Scholar]
- Wagner, F. W., Tosi, N., Sohl, F., Rauer, H., & Spohn, T. 2012, A & A, 541, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wordsworth, R., & Kreidberg, L. 2022, ARA & A, 60, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]
- Zhou, G., Huang, C. X., Bakos, G. Á., et al. 2019, AJ, 158, 141 [Google Scholar]
- Zhu, W. 2022, AJ, 164, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, W., & Dong, S. 2021, ARA & A, 59, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, W., & Wu, Y. 2018, AJ, 156, 92 [Google Scholar]
The last version of ARES code (ARES v2) can be downloaded at https://github.com/sousasag/ARES
PAdova and TRieste Stellar Evolutionary Code: http://stev.oapd.inaf.it/cgi-bin/cmd
All Tables
Fitted and derived parameter values for TOI-1054 b and c based on the joint fit to the photometric light curves and RV data detailed in this section.
All Figures
 |
Fig. 1 LCOGT observations of the TOI-1054 candidate confirming the TESS ephemeris. |
| In the text | |
 |
Fig. 2 Generalized Lomb-Scargle periodogram of: the HARPS TERRA RV measurements (first panel); the RV residuals following the subtraction of the Doppler signal of HD 190622c (second panel); the RV residuals following the subtraction of the Doppler signals of HD 190622b and c (third panel); the FWHM and BIS of the CCF (fourth and fifth panels); and the CaIIH&K line activity indicator log |
| In the text | |
 |
Fig. 3 [Mg/Fe] and [Si/Fe] abundance ratios as a function of [Fe/H] for HD 190622 (large blue circle) and the HARPS GTO sample stars (gray dots) from Adibekyan et al. (2012). The blue horizontal and vertical lines indicate the solar values. |
| In the text | |
 |
Fig. 4 TESS and CHEOPS transit light curve of HD 190622b and best-fitting model for the two band passes. The TESS and CHEOPS data in bins of 15 min each are displayed with green and red circles, respectively. |
| In the text | |
 |
Fig. 5 Radial velocity analysis of the planetary system. Upper panel: HARPS TERRA RV time series of HD 190622. Lower panels: phase-folded RV curves of HD 190622b (left) and HD 190622c (right). The best-fitting Keplerian models are overplotted with thick black lines. The vertical light-blue lines mark the error bars including the RV jitter. |
| In the text | |
 |
Fig. 6 Distributions resulting from the internal structure modeling following Leleu et al. (2021a). The values above the histograms are the median and the 5th and 95th percentiles of the posterior distribution (same as the dashed lines). The plotted internal structure parameters are: the iron core and water mass fractions of the solid planet (without gas); the molar mass fractions of Si and Mg in the mantle and of Fe in the core; and the decimal logarithm of the absolute gas mass expressed in Earth masses. |
| In the text | |
 |
Fig. 7 Distributions resulting from the internal structure modeling following Baumeister et al. (2020). The values above the histograms are the median and the 16th and 84th percentiles of the posterior distribution (same as the dashed lines). The plotted internal structure parameters are: the radius fraction of the core, mantle, ice (of water), and gas layers. |
| In the text | |
 |
Fig. 8 Posterior distribution (dark blue) of the stellar rotation rate of HD 190622 after 150 Myr derived by PASTA. The purple area represents the HPD interval of the distribution. The black line represents the distribution of the stellar rotation rate of young open cluster stars with masses comparable to that of HD 190622 based on the collection of data provided by Johnstone et al. (2015). See main text for details. |
| In the text | |
 |
Fig. 9 Posterior distribution (dark blue) for the mass of the planetary atmosphere of planet b at the time of the dispersal of the protoplanetary disk derived by PASTA. The light-blue line represents the distribution of the estimated present-day atmospheric mass fraction. The orange horizontal line indicate the uninformative prior distribution. See main text for details. |
| In the text | |
 |
Fig. 10 Mass vs. radius (top) and mass vs density (bottom) plots for planets with mass uncertainty below 15%. The planets known to orbit F stars are highlighted with blue circles, while TOI-1054b is shown with a diamond. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.