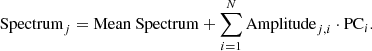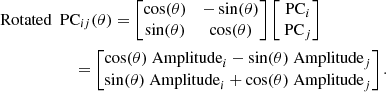| Issue |
A&A
Volume 675, July 2023
|
|
|---|---|---|
| Article Number | A83 | |
| Number of page(s) | 29 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202245334 | |
| Published online | 04 July 2023 | |
The Carnegie Supernova Project I
Spectroscopic analysis of stripped-envelope supernovae
1
Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
e-mail: max@phys.au.dk
2
Observatories of the Carnegie Institution for Science, 813 Santa Barbara St., Pasadena, CA 91101, USA
3
Carnegie Observatories, Las Campanas Observatory, Casilla 601, La Serena, Chile
4
Department of Physics, Virginia Tech, Blacksburg, VA 24061, USA
5
Department of Physics, Florida State University, 77 Chieftain Way, Tallahassee, FL 32306, USA
6
Institute of Space Sciences (ICE, CSIC), Campus UAB, Carrer de Can Magrans, s/n, 08193 Barcelona, Spain
7
Institut d’Estudis Espacials de Catalunya (IEEC), 08034 Barcelona, Spain
8
Instituto de Astrofísica de La Plata (IALP), CONICET, Paseo del Bosque s/n, 1900 La Plata, Argentina
9
Facultad de Ciencias Astronómicas y Geofísicas (FCAG), Universidad Nacional de La Plata (UNLP), Paseo del Bosque s/n, 1900 La Plata, Argentina
10
Department of Physics and Astronomy, University of Oklahoma, 440 W. Brooks, Rm 100, Norman, OK 73019, USA
11
Finnish Centre for Astronomy with ESO (FINCA), 20014 University of Turku, Finland
12
Tuorla Observatory, Department of Physics and Astronomy, 20014 University of Turku, Finland
13
DTU Space, National Space Institute, Technical University of Denmark, Elektrovej 327, 2800 Kgs. Lyngby, Denmark
14
George P. and Cynthia Woods Mitchell Institute for Fundamental Physics and Astronomy, Department of Physics and Astronomy, Texas A&M University, College Station, TX 77843, USA
Received:
31
October
2022
Accepted:
13
March
2023
An analysis leveraging 170 optical spectra of 35 stripped-envelope (SE) core-collapse supernovae (SNe) observed by the Carnegie Supernova Project I and published in a companion paper is presented. Mean template spectra were constructed for the SNe IIb, Ib, and Ic subtypes, and parent ions associated with designated spectral features are identified with the aid of the spectral synthesis code SYNAPPS. Our modeled mean spectra suggest the ∼6150 Å feature in SNe IIb may have an underlying contribution due to silicon, while the same feature in some SNe Ib may have an underlying contribution due to hydrogen. Standard spectral line diagnostics consisting of pseudo-equivalent widths (pEWs) and blue-shifted Doppler velocity were measured for each of the spectral features. Correlation matrices and rolling mean values of both spectral diagnostics were constructed. A principle component analysis (PCA) was applied to various wavelength ranges of the entire dataset and suggests clear separation among the different SE SN subtypes, which follows from trends previously identified in the literature. In addition, our findings reveal the presence of two SNe IIb subtypes, a select number of SNe Ib displaying signatures of weak, high-velocity hydrogen, and a single SN Ic with evidence of weak helium features. Our PCA results can be leveraged to obtain robust subtyping of SE SNe based on a single spectrum taken during the so-called photospheric phase, separating SNe IIb from SNe Ib with ∼80% completion.
Key words: supernovae: general
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Between 2004 and 2009, the Carnegie Supernova Project I (hereafter CSP-I; Hamuy et al. 2006) obtained optical and near-infrared light curves (Stritzinger et al. 2018a, hereafter Paper I) and visual-wavelength spectroscopy (Stritzinger et al. 2023, hereafter Paper IV) of nearly three dozen stripped envelope (SE) core-collapse supernovae (SNe). SE SNe are associated with the deaths of massive stars that have lost the majority of their hydrogen (and helium) envelopes prior to explosion. Within this context, stars with increasing amounts of mass stripping lead to characteristic spectra of different subtypes being either hydrogen (H) poor and helium (He) rich (SNe IIb), hydrogen deficient with He features (SNe Ib), or objects that are deficient of both H and He features (SNe Ic).
In a series of papers focusing on the CSP-I SE SN sample, we summarize key facets of our contemporary knowledge of SE SNe. This includes the topics of light curves and possible progenitor systems in Paper I, which also presents the broadband photometry of three dozen SE SNe. In Paper II (Stritzinger et al. 2018b), the photometry is used to devise improved methods to estimate host-galaxy reddening, while Paper III (Taddia et al. 2018) presents a detailed analysis of the light curves and inferred explosion parameters. In Paper IV a summary of the visual-wavelength spectroscopic properties and spectral classification of SE SNe is presented, along with the CSP-I SE SN spectroscopic sample consisting of 170 low-redshift (i.e., z < 0.1) spectra of 35 SE SNe (see Paper IV).
In a classic paper on the spectroscopic studies of SE SNe, Matheson et al. (2001) studied 84 low-dispersion visual-wavelength spectra of 28 SE SNe extending from early to late phases, and in doing so were the first to characterize the heterogeneous nature of the different SE SN subtypes. Over the years, numerous single object case studies have been published (for a review see Branch & Wheeler 2017, Chapters 15-17), while spectroscopic samples and associated analysis papers have been published by the Center for Astrophysics SN group (Modjaz et al. 2014; Liu et al. 2016; Williamson et al. 2019), as well as the Palomar Transient Factory (PTF) and intermediate PTF surveys (Fremling et al. 2018). The methods used in our analysis of the CSP-I SE SN spectroscopy dataset were inspired by these previous sample studies, as well as in part by a select number of papers analyzing the spectroscopic datasets of thermonuclear SNe (e.g., Hsiao et al. 2007; Blondin et al. 2012; Silverman et al. 2012; Folatelli et al. 2013).
The organization of this paper is as follows. First in Sect. 2, we focus on spectral line identification, including the construction of mean template spectra in Sect. 2.1, the calculation of synthetic spectra in Sect. 2.2, and the association of spectral line features with parent ion(s) in Sect. 2.3. We then turn to line diagnostics measurements and correlation matrices for the line measurements of pseudo-equivalent widths (pEWs) in Sect. 3 and Doppler velocity line measurements in Sect. 4. A principle component analysis (PCA) of the dataset is presented in Sect. 5, which is then followed by the discussion in Sect. 6 and a summary of our key findings in Sect. 7.
2. Spectral line identification
2.1. Construction of SE SN mean spectra
Close inspection of the CSP-I SE SN spectral sequences presented in Paper IV reveals the presence of numerous spectral features superposed on a pseudo-continuum with the shapes and strengths of the features being significantly time dependent. Before we make direct measurements of the various spectral features, we first set out to identify the key spectral features and determine their commonality among the different subtypes. Once the locations of key spectral features are identified we construct mean template spectra which are compared with synthetic spectra computed using SYNAPPS1 (Thomas et al. 2011), which enables us to link the observed spectral features to parent ions (see Sect. 2.2). Then, spectral line diagnostic measurements are made for the entire suite of identified features.
As a first step, a single median spectrum is constructed for each SE SN subtype using all of the spectra listed in Table 1, except those of SNe 2004qv, 2009bb, and 2009ca. The resulting median spectrum of each SE SN subtype are plotted in Fig. 1, along with the individual input spectra. In the middle panel, the spectra of the Type Ib SN 2004gq that exhibit high-velocity features are plotted in green, while in the bottom panel the spectra of the broad-lined Type Ic SNe 2009bb and 2009ca are plotted in red. These spectra are not included in construction of the mean spectrum plotted in the figure of these two subtypes. A comparison between the three median spectra reveals a number of common features as well as a handful of features that are typically only present in SN IIb and/or SN Ib spectra. As indicated in Fig. 1, 10 different complexes of spectral features are assigned a specific number (running from Feature 1 to Feature 10) and in some cases a feature may be attributed to multiple ions. Key characteristics of these features are highly dependent on the phase of the spectrum. An accurate study of the spectroscopic. properties of our sample requires a larger grid of mean template spectra. We therefore produce a coarse time-series of mean template spectra for each subtype to be modeled with SYNAPPS.
 |
Fig. 1. Median spectrum for each SE SN subtype (black line) constructed from all of the spectra plotted in gray and listed in Table 1. The vertical dashed lines indicate 10 regions of interest. Regions 1–5, 9 and 10 are typically present in each SE SN subtype, while regions 6–8 are typically found in SNe IIb and SNe Ib and are usually most prevalent in the weeks after maximum light. Green lines in the middle panel are spectra of the high-velocity Type Ib SN 2004gq, and red lines plotted in the bottom panel correspond to the spectra of the Type Ic-BL SN 2009bb (dotted) and the unusual Type Ic SN 2009ca (dashed). These spectra were excluded in making the median spectra. Finally, the number of spectra used to create each median spectrum plotted in each panel is indicated within parenthesis located just below the given spectral subtypes. |
Spectroscopic sample of CSP-I SE SNe.
Mean spectra were constructed for the SN IIb and SN Ib subtypes for the epochs: −7 d, +0 d, +7 d, +14 d and +21 d. Due to a dearth of early data we did not construct a −7 d mean spectrum for SNe Ic. The steps required to construct a mean spectrum are several fold. First we identified an input set of spectra that met the criteria of being obtained within ±3.5 d of the epoch under consideration. The spectra of each subsample were then corrected for Milky Way and host reddening using values estimated by Stritzinger et al. (2018b). Next the spectra were smoothed using a Fourier Transform (FT) technique (see Marion et al. 2009), re-sampled, and then combined yielding a mean spectrum. An associated error spectrum was also computed using a semi-automated line fitting program written in PYTHON named Measure Intricate Spectral Features In Transient Spectra (hereafter misfits)2. misfits enables robust measurements of standard line diagnostics, and in doing so estimates a realistic error snake. This is done by computing 10 000 realizations of each spectrum following a Monte Carlo approach. The resultant 1σ standard deviation of the Monte Carlo distribution for each spectrum then serves as the error snake.
The resulting series of mean spectra and their 1-σ error snakes of each SE SN subtype are plotted in Figs. 2–4. Within Fig. 2 and Fig. 3 features 1–10 are identified and labeled with their parent ion(s) as implied from SYNAPPS modeling (see Sect. 2.2), while in Fig. 4 the features associated with He I are excluded. Furthermore, a line is drawn connecting the red and blue edges of each feature to define a pseudo-continuum.
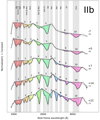 |
Fig. 2. Mean template spectra for the Type IIb SE SN subtype at epochs of −7 d, 0 d, +7 d, +14 d, and +21 d. The number of spectra used to construct each template is indicated within parenthesis below the corresponding epoch. Each numerically indicated spectral feature is labeled with its parent ion(s) as determined from SYNAPPS fits. Thin gray lines indicate the 1-σ error spectrum. |
 |
Fig. 3. Mean template spectra for the Type Ib SE SN subtype at epochs of −7 d, 0 d, +7 d, +14 d, and +21 d. The number of spectra used to construct each template is indicated within parenthesis below the corresponding epoch. Each numerically indicated spectral feature is labeled with its parent ion(s) as determined from SYNAPPS fits. Thin gray lines indicate the 1-σ error spectrum. |
 |
Fig. 4. Mean template spectra for the Type Ic SE SN subtype at epochs of 0 d, +7 d, +14 d, and +21 d. The number of spectra used to construct each template is indicated within parenthesis below the corresponding epoch. Each numerically indicated spectral feature is labeled with its parent ion(s) as determined from SYNAPPS fits. Thin gray lines indicate the 1-σ error spectrum. The vertical dashed line corresponds to the rest wavelength of C IIλ6580. |
Refined spectral feature IDs and line diagnostic fitting parameters.
2.2. Computing synthetic spectra with SYNAPPS
Synthetic spectra were computed with SYNAPPS (Thomas et al. 2011) which is an automated implementation of the highly parameterized spectral synthesis code SYNOW (SYnthesis NOW; Fisher 2000). SYNOW is a synthetic spectrum code based on a number of underlying assumptions, including spherical symmetry (see Thomas et al. 2011). Despite these shortcomings, SYNOW and SYNAPPS have proven to be effective tools to aid in spectroscopic studies of various flavors of stripped core-collapse and thermonuclear supernovae (e.g., Deng et al. 2000; Folatelli et al. 2006; Branch et al. 2007; Thomas et al. 2011; Hsiao et al. 2015; Parrent et al. 2016). Holmbo (2018) discusses in detail our SYNAPPS analysis, which is summarized in Appendix A for the interested reader.
2.3. Line identification
2.3.1. SNe IIb
-
Feature 1 is characterized by a W-shape line profile (see Fig. 1, panel a). SYNAPPS fits suggest this feature is produced from a blend of Hγ (forming the bluer of the two dips in the W), a forest of Fe lines including that of Fe IIλ4550, a contribution from Ti IIλλ4395, 4444, 4469, and also He Iλ4471 which mostly produces the red dip of the W-shape profile.
-
Feature 2 is produced by a blend of lines. At early phases the feature is primarily formed by Hβ with a contribution from Fe IIλλ4924, 5018, while at later phases a contribution due to He Iλ4922 emerges (see the +21 d mean SN IIb spectrum in Fig. 2).
-
Feature 3 is largely produced by the third member of the Fe II multiplet 42, λ5169. This feature is well defined in each of the SE SN subtypes, and is used as a proxy for the bulk velocity of the SN ejecta.
-
Feature 4 is produced by Na Iλλ5890, 5896 and He Iλ5876.
-
Feature 5 is ubiquitous to SNe IIb and is formed by Hα. The absorption profile of the feature in the mean spectra show an extended blue wing, which as indicated by the SYNAPPS fits shown in Fig. A.1a, could be due to a contribution from the Si IIλ6355 doublet. Indeed, the velocity would match that of Fe II, as we show for SNe Ib and Ic below. If Feature 5 was purely hydrogen, the pEW of this line would be expected to decrease with time. However, as can be seen in Fig. 5, the pEW is constant with time. This is likely due to both the contribution from the blue feature (which is most likely Si II).
-
Features 6, 7, 8 are attributed to He Iλ6678, He Iλ7065 and He Iλ7281, respectively. In general, the strength of these features grows over time becoming most prominent several weeks past maximum.
-
Feature 9 is attributed to O Iλ7774. This line is often contaminated by the telluric O2 A-band absorption feature. As demonstrated in Paper IV, we were able to successfully correct for telluric absorption for many spectra in the sample, particularly those obtained with the du Pont telescope equipped with the Wide Field re-imaging CCD (WFCCD) camera.
-
Feature 10 is attributed to the Ca II NIR triplet λλ8498, 8542, 8662. In some objects, for example, the SNe Ib/c (flat-velocity SNe IIb) 2005bf and SN 2007Y, their early spectra exhibit a distinct high-velocity component that promptly vanishes over several days of evolution, while a photospheric component emerges and grows in strength (Folatelli et al. 2006; Stritzinger et al. 2009).
 |
Fig. 5. Pseudo-equivalent width values for Features 1–10 plotted vs. days relative to the epoch of T(B)max. The measurement symbols are encoded by SN subtype with SNe IIb appearing as blue triangles, SNe Ib as yellow squares, and SNe Ic as magenta squares. Filled shaded regions correspond to the mean ±1-σ standard deviation of a rolling window characterized with a size of ten days. The rolling windows are evaluated on epochs containing at least three distinct pEW measurements and two pEW measurements in the preceding and subsequent epochs. |
2.3.2. SNe Ib and SNe Ic
-
Feature 1 is produced (similar to SNe IIb) by a forest of Fe II and Ti II lines, with an additional contribution from He Iλ4471 in SNe Ib, which turns the characteristic SNe IIb W-shape profile to a Y-shape profile. As SNe Ic lack both Hγ and He I the feature takes on a U-shape profile (see Fig. 1).
-
Feature 2 is formed by Fe IIλλ4924, 5018, with SNe Ib having an additional contribution from He Iλ4921.
-
Feature 3 is largely produced by Fe IIλ5169. In the case of SNe Ic this feature may also contain a contribution from Co IIλ5526, which increases in strength during the post-maximum evolution.
-
Feature 4 is attributed to the Na Iλλ5890,5896 doublet in SNe Ic, while in in SNe Ib a significant contribution comes from He Iλ5876.
-
Feature 5, unlike in Type IIb SNe, is not hydrogen by the traditional spectral classification system. Although in the past it has been linked to the Si IIλ6355 doublet (e.g., Harkness et al. 1987; Branch et al. 2002), various different ions have been proposed for this feature. Other than Si II, these include high-velocity Hα (Liu et al. 2016; Williamson et al. 2019), as well as Fe II, Co II, C II, and Ne I (see Gal-Yam 2017, and references therein). Close inspection of the template spectra reveals evidence of a blend of at least two features contained within Feature 5, which we refer to as the red and blue portions. The red portion is stronger than the blue portion, especially up to +14 days in both SN subtypes. It is unlikely that the red portion, which is stronger, is produced by Si II, as its position of maximum absorption would imply a red-shifted Doppler velocity. However, assuming the blue portion is due to Si II brings the velocities in line with other ions, which is demonstrated in Fig. 6. With the blue portion attributed to Si II, the synthetic spectra suggest that the red portion of the feature could be formed by a residual amount of H detached from the photosphere. In fact, it has been identified as H in so-called transitional SNe Ib/c (e.g., SN 1999ex, Hamuy et al. 2002), which Folatelli et al. (2014) refer to as flat-velocity SNe IIb. However, identifying Feature 5 as H possibly contradicts theoretical and observational evidence showing SNe Ic to be deficient in H and He (Taddia et al. 2018; Hachinger et al. 2012). As previously mentioned, the red portion could instead be one of the other proposed lines (Fe II, Co II, C II, and Ne I), or a blend. Shahbandeh et al. (2022) found evidence of strong C I features in NIR spectra of SNe Ic, indicating the optical feature could at least partially be due to C II. In our analysis and figures, we assume the blue portion to be Si II for SNe Ib and Ic when it can be reliably measured, while the red portion is not used.

Fig. 6. Time evolution of the Doppler velocity at maximum absorption (−vabs) for Features 1–10 and color-coded by SE SN subtype. Shaded regions correspond to the standard deviation of the rolling mean computed using a window size of ten days and color-coded by spectroscopic subtype as indicated. The rolling windows are evaluated on epochs having a minimum of three measurements and at least two measurements before and after. We note that the peculiar SNe Ic 2009bb and 2009ca are excluded.
-
Features 6, 7, 8 are, as in the case of SNe IIb, attributed to He Iλ6678, He Iλ7065, and He Iλ7281, respectively. By definition SNe Ic contain no He features, but see Sect. 5.3.2.
-
Feature 9 is attributed to O Iλ7774.
-
Feature 10 is attributed to the Ca II NIR triplet.
3. Analysis of pseudo-equivalent width measurements
In this section pEW measurements for Features 1–10 for the entire sample of spectra are computed and used to construct correlation matrices for various pairs of Features 1–10. The strength and evolution of pEWs (and Doppler velocities, see below) provides a wealth of information related to the progenitor stars (Branch & Wheeler 2017). For example, the spectral features themselves provide a window to the ionizaton state and chemical content of the ejecta above the photosphere. As the SN ejecta expand and cool, the photosphere recedes into the inner ejecta enabling a direct view to the otherwise opaque inner regions of the progenitor stars. In addition, the presence (or lack thereof), strength and time-evolution of features produced from certain ions (e.g., H and/or He) provides information on the spectral type of the progenitors, their mass-loss history and even their explosion physics, while the expansion velocities provides a measure of the explosion energy (see Paper III, and references therein).
3.1. Measuring pseudo-equivalent widths
Armed with the spectral line identifications of Features 1–10, we conduct a quantitative analysis of the line strength and evolution of the various features via pEW measurements. This is a common line diagnostic having been utilized to study large spectroscopic samples of thermonuclear supernovae (e.g., Branch et al. 2006; Garavini et al. 2007; Blondin et al. 2012; Silverman et al. 2012; Folatelli et al. 2013). Liu et al. (2016) and Fremling et al. (2018) have also followed suit, using both pEW and Doppler velocity measurements in their analysis of the CfA and PTF SE SN spectroscopic datasets, respectively. The use of pEW measurements serves as a flexible and accurate line diagnostic, particularly compared to fitting a Gaussian function, which is often not appropriate given the asymmetric and time-dependent spectral features inherent to SE SNe.
The term pseudo in pEW highlights the difficulties faced when attempting to separate continuum flux from absorption and emission flux of time-dependent spectral features that also suffer significant Doppler broadening. Following Folatelli (2004), we define the pseudo-continuum to be a straight line connecting two maxima defining a spectral absorption feature:
Here λi corresponds to the wavelength of each pixel contained within the spectral range located between the blue and red edges of a specific feature. Furthermore, N is the number of pixels contained between the red and blue edges, the parameter Δλi represents the width of pixel i, f(λi) corresponds to the observed flux at λi, fc(λi) is the pseudo-continuum at λi, and Δλi is the sum over the defined wavelength interval.
Given the number of spectra in the CSP-I sample and having up to 10 features, it quickly becomes cumbersome to measure the pEWs by hand. We therefore developed the misfits spectral analysis package, and in doing so, created a resource that minimizes user bias while enabling efficient measurements in a standard manner. To make pEW measurements of Features 1–10 for a given spectrum we adopted the following steps. First misfits smooths an observed spectrum following the use of a Fourier Transform (FT) smoothing technique (Marion et al. 2009) and then identifies the highest peak located between the defined boundaries at the blue and red end of Features 1–10. The wavelength ranges for each blue/red boundary of each of the Features measured are listed in Table 2. With boundary end points identified, a pseudo-continuum is defined by connecting the boundary points with a straight line. This is demonstrated in Fig. 2 where the spectral regions of each feature are identified. These regions are used to infer pEW values using Eq. (1).
Each pEW measurement also has an associated 1-σ uncertainty estimated via the following recipe. The error spectrum is first multiplied by a random number taken from a normal distribution and the resulting product is added to the FT smoothed observed spectrum. pEW measurements are computed from the altered spectrum, and following a Monte Carlo approach, this is done for 10 000 realizations. The 1-σ value of the resulting pEW distribution then serves as the pEW 1-σ measurement uncertainty. This method accounts for the uncertainty associated with the ability of the algorithms to accurately determine the heights of the blue/red boundaries of the spectral line features.
3.2. pEW measurement results for Features 1–10
The definitive pEW measurements of Features 1–10 computed for all of the photospheric phase spectra are plotted in Fig. 5 versus phase relative to the epoch of B-band maximum. Over-plotted in each of the panels are filled shaded regions color-coded by spectral subtype representing the mean 1-σ standard deviation computed using a rolling window with a size of ten days. The rolling windows were evaluated only on epochs containing a minimum of three measurements and have at least two preceding and subsequent measurements.
Inspection of Fig. 5 reveals that the pEWs for most of the features generally increase in strength over the week prior to maximum. Depending on the particular feature, this behavior continues, or they at least remain constant over the duration of ≈3 − 6 weeks past maximum. The pEW values are found to range from as little as ∼10 Å (e.g., He I features at early times) all the way up to ≳600 Å in the case of the Ca II NIR triplet. We now briefly summarize the nature of the pEW measurement of Features 1–10 and in passing compare and contrast the results amongst the different subtypes.
-
Feature 1 (Fe II, Ti II in each subtype with additional contributions from Hγ and He Iλ4471 in SNe IIb and He I in SNe Ib). The pEW values typically increase within a few weeks from maximum and then remain relatively constant over the duration of our observations. pEW values range from ∼100 Å up to ∼250 Å. At early times SNe Ic tend to exhibit smaller values as compared to SNe IIb and SNe Ib.
-
Feature 2 (Fe II in each subtype with an additional contribution from Hβ and He I in SNe IIb and only He I in SNe Ib) The pEW values generally increase over time for the SNe IIb while the increase in SNe Ib exhibits a shallower slope. pEW values typically reach peak values in excess of 100 Å within 2 to 3 weeks past maximum and then remain constant and/or slowly decrease. The feature is less prevalent in SNe Ic with pEW values reaching around 50 Å at all epochs.
-
Feature 3 (Fe II and Co II in SNe Ic) consists of a forest of Fe II lines, often displaying a prominent P-Cygni Fe II emission profile, making it a somewhat troublesome feature for misfits to accurately identify the red boundary point automatically (see Fig. 2). This can lead misfits to compute negative values at early phases for some of the objects. Nevertheless within a week past maximum the majority of objects exhibit pEW values between ∼20 Å to 70 Å, and these continue to increase reaching ∼50 to 150 Å by a month and half past maximum. In SNe Ic there may be at later times a contribution from Co II, however, the mean pEW values are consistent with those inferred from the SNe IIb and SNe Ib, indicating this feature is largely dominated by Fe II.
-
Feature 4 (Na I and/or He I) in the majority of objects exhibits pEW values that increase with time. In the week leading to maximum the SNe IIb and SNe Ib exhibit very different pEW values with the former below 50 Å, while the later are in excess of 75 Å (indicated by a dashed line) with the rolling mean values around ∼100 Å. In the SNe Ib at early times, the feature appears to slightly decrease and at around +10 d begins to increase and thereafter follow the same trend as the SNe IIb. Over time the pEW values for both SNe IIb and SNe Ib continue to increase reaching similar values out to +50 d. On the other hand, the SNe Ic exhibit an average pEW value of ∼40 ± 30 Å at maximum and generally exhibit lower pEW values as time goes on relative to both SNe IIb and SNe Ib. Given the significant difference between the premaximum pEW measurements of this feature in SNe Ib relative to the both SNe IIb, the pEW value of this feature could serve as a useful aid in spectral classification (see Sect. 6.2.1).
-
Feature 5 (Hα and/or Si II) pEW values show diversity dependent on spectral subtype and the phase of the spectrum. The majority of SNe IIb exhibit pEW values in excess to those characterizing SNe Ib and SNe Ic and this trend appears to increase over time. As indicated by the dashed line in the Feature 5 panel of Fig. 5 there is a clear separation at pEW of ≈140 Å between the pEW values measured in SNe IIb compared to the values measured in SNe Ib and SNe Ic. Quantitatively, the pEW values of SNe IIb take on high values (pEW ∼ 140 − 200 Å) from early phases and onward. On the other hand, the SNe Ib and SNe Ic exhibit smaller pEW values ranging between ≈60 − 100 Å. In the earliest observations of SNe Ib, Feature 5 shows higher values and this is likely due to absorption associated with a small shell of hydrogen material retained by their progenitor stars. As the photosphere recedes the pEW value in these cases drops to values similar to the SNe Ic, indicating that the feature becomes dominated by Si II and has little to no contribution from Hα. In other words, the fact that SNe Ib and SNe Ic exhibit similar pEW values around maximum light and beyond, provides an argument that at these phases the red component of Feature 5 in SNe Ib is largely produced by Si II. We quantify this separation in a PCA analysis presented below. The finding that SNe IIb exhibit larger pEW values of Feature 5 at early times as compared to SNe Ib is consistent with the idea that their progenitor stars retain higher amounts of hydrogen relative to the progenitors of SNe Ib.
-
Features 6-8 (He I) increase in strength from early phases out to weeks past maximum. As expected by the atomic data of He I, Feature 7 is significantly more prominent than Features 6 and 8 at all epochs. Quantitatively, Feature 7 reaches pEW values in excess of 100 Å while Features 6 and 8 extend between 10–80 Å.
-
Feature 9 (O I) in the SNe IIb and SNe Ib exhibits pEW values that generally increase from ≤50 Å around maximum to in excess of 100 Å a month past maximum. SNe Ic show more premaximum diversity with pEW values ranging from ∼25 Å up to ∼100 Å. The rolling means indicate that beyond +30 d the pEW values level off or even decrease to values < 100 Å. During the same phases, SNe IIb and SNe Ib exhibit mean pEW values ≳100 Å.
-
Feature 10 (Ca II) overall exhibits an increase in the pEW value for each SE SN subtype. Prior to maximum the SNe IIb and SNe Ib exhibit pEW values of around 160 ± 50 Å that evolve up to ∼400 Å by +40 d. Around maximum, SNe Ic tend to reach somewhat larger pEW values compared to SNe IIb and SNe Ib, while by a month past maximum the three SE SN subtypes show similar values.
4. Analysis of Doppler velocity measurements
The wavelength of maximum absorption for a given spectral feature provides an estimate on the bulk velocity of the line-forming material. Although prominent features may be produced from the blending of numerous lines, in general, the Doppler velocity at maximum absorption (−vabs) provides a useful measure of the kinematics of the line-forming region, and depending on the spectral features used, a constraint on the explosion energy of the supernova (see, e.g., Branch et al. 2002; Fremling et al. 2018; Taddia et al. 2018).
4.1. Measuring Doppler velocity
Determining a value of −vabs based on a spectral feature in a 1D supernova spectrum is done using the relativistic Doppler approximation (see Blondin et al. 2006, their Eq. (6)). Measuring the observed wavelength (λobs) of a feature from a 1D spectrum is relatively straightforward, however, the use of an automatic detection of the exact position of a feature’s minimum becomes increasingly difficult in low signal-to-noise spectra due to an accompanying increase in the number of local minima. To overcome this problem an algorithm was developed to detect groupings of minima within a certain threshold and treat each of the groupings as a single minimum.
4.2. Doppler velocities and evolution
Plotted in Fig. 6 are the −vabs values measured for Features 1–10 using all of our spectra obtained prior to +100 days relative to the epoch of B-band maximum. We note that in SNe IIb Feature 1 and Feature 2 have an additional absorption component attributed to Hγ and Hβ, respectively. We therefore separate each feature into two features denoted as Feature (a) and Feature (b). We now summarize the overall trends for Features 1–10, and then examine the correlation matrices computed for the various pairs of the −vabs.
-
Feature 1a (mostly Hγ in SNe IIb) can be problematic to measure given the spectral range of this feature is often noisy. Feature 1a plotted in the top left panel of Fig. 6 exhibits, as do the majority of other features, −vabs values that decrease over the first two weeks of evolution. The feature exhibits −vabs ∼ 10 000 − 14 000 km s−1 in the week prior to maximum, and by +21 d decreases to ∼8000 − 10 000 km s−1.
-
Feature 1b (Fe II, Ti II & He I) is similar in SNe IIb and SNe Ib with −vabs values between 3000–6000 km s−1 from −10 d to +10 d. Upon reaching a minima −vabs at around +10 d, it experiences an upturn, reaching within three weeks, similar (in SNe IIb) or even higher values (SNe Ib) compared to those inferred from spectra in the week leading up to maximum. By +40 d the velocity evolution decreases in SNe Ib leveling off to mean −vabs values of ∼6000 km s−1, which is similar to the SNe IIb mean value of ∼4000 km s−1. Coverage of the SNe Ic begins a week after the SNe IIb/Ib with a mean −vabs value between +0 d to +10 d of ∼7000 km s−1. Between +10 d to +25 d the mean −vabs value drops to ∼2500 km s−1, similar to the mean values exhibited by the SNe IIb and SNe Ib when they reached their initial minima occurring 10–15 days earlier. The (delayed) upturn in the SNe Ic extends through +30 d, and then again, turns over declining to values around a factor of 2 or more less than inferred from the SNe IIb and SNe Ib at similar epochs (i.e., around +45 d).
-
Feature 2a (Hβ) rolling mean −vabs values extend between ∼11 000 ± 2000 km s−1 down to ∼9000 ± 1000 km s−1 from −10 d to +50 d. The velocities and evolution of this feature are quite consistent with that of Feature 1a.
-
Feature 2b (Fe IIλ5018 & He I) in SNe Ib exhibits rolling mean −vabs values that are ∼2000 km s−1 higher than the SNe IIb. At the earliest phases covered, SNe Ib reach rolling mean −vabs values of ∼13 000 km s−1, while SNe IIb never exceed 12 000 km s−1. SNe Ic mean values lie between the SNe IIb/Ib until +20 d, and then subsequently drop to ∼6000 km s−1, slightly below the SNe Ib mean values. Close inspection of panel F2b also reveals an SN Ib at early times exhibiting a −vabs value ∼17 000 km s−1. This object is SN 2004gv and also exhibits high −vabs values in its other Features, particularly those attributed to He I (see F3, F4, F6, F7). SN 2004gv is not included in the computation of the various rolling mean −vabs values plotted in the figure.
-
Feature 3 (Fe II & possibly Co II in SNe Ic) exhibits at most epochs similar rolling mean −vabs values in both SNe Ib and SNe IIb. At the earliest phases of coverage SNe Ib show −vabs values extending ≳4000 km s−1 higher than that of the SNe Ib rolling mean 1-σ dispersion. Quantitatively, in the week leading to maximum, SNe Ib exhibit mean −vabs ∼ 13 000 ± 2000 km s−1 while SNe IIb exhibit mean −vabs ∼ 10 000 ± 2000 km s−1. Between ∼ + 0 d to +10 d the SNe Ic exhibit mean −vabs values fully consistent with the SNe IIb, while beyond +10 d their values are typically a few 1000 km s−1 higher than the mean values of both SNe IIb and SNe Ib.
-
Feature 4 (Na I & He I in SNe IIb and SN Ib) exhibits at all phases similar mean −vabs values and 1-σ error snakes. At early phases a large range of velocities are measured extending from ∼6000 km s−1 up to and in excess of ∼14 000 km s−1, with SNe Ib exhibiting somewhat more dispersion than SNe IIb. Turning to SNe Ic, the rolling mean −vabs values are consistent with the SNe IIb/Ib though their error snake is characterized by larger dispersion.
-
Feature 5a (Si II in SNe Ib and SNe Ic) −vabs values were measured for the objects in the sample having a clear feature likely produced by Si II. Between maximum and +14 d the rolling mean −vabs values of the SNe Ib decrease from ∼13 000 ± 1000 km s−1 to ∼9000 km s−1, whereupon they slow to just above 8000 km s−1 out to +45 d. Our temporal coverage of this feature is limited in the SNe Ic sample, with mean −vabs values ranging between 13 000 km s−1 to 9000 km s−1 between +0 d to +21 d.
-
Feature 5b (Hα) exhibits a smoothly evolving rolling mean −vabs values in the SNe IIb sample ranging from ∼16 000 ± 2000 km s−1 down to a value of ∼10 000 ± 1000 km s−1 at +30 d. Subsequently, the feature remains constant for weeks, consistent with the idea H gas is not mixed with the heavier, lower velocity elements. The purported Hα feature measured in our sample of SNe Ib has rolling mean values and evolution similar to that of SNe IIb, though its 1-σ error snake is larger and our sample does not extend in phase as far. The feature vanishes from the majority of the SNe Ib by +21 d (see Fig. 3). This accounts for the rolling mean of the SNe Ib ending around +30 d, while that of the SNe IIb extends to later phases, and is consistent with the idea that the former retain smaller amounts of hydrogen compared with the latter.
-
Features 6, 7 and 8 (He I) slowly evolve over time. The −vabs values and evolution of Features 6 and 7 are completely consistent with one another. In the case of SNe Ib both features exhibit rolling mean −vabs values that extend from ∼8000 ± 3000 km s−1 a week before maximum to ∼6000 ± 1000 km s−1 by +40 d. We note that the rolling mean −vabs values for the SNe IIb sample begin several days post maximum. Feature 8 consistently shows lower −vabs values compared to Features 6 and 7 with both subtypes exhibiting rolling mean −vabs values of ∼6000 ± 2000 km s−1 between +0 d to +40 d.
-
Feature 9 (O I) in general emerges first in SNe Ic followed soon after by SNe Ib, while for at least our small sample, this feature typically emerges in SNe IIb more than a week past maximum. SNe Ic exhibit high rolling mean −vabs values with significant dispersion at all epochs. Around maximum the SNe Ic mean values are around ∼9500 ± 2000 km s−1 and then subsequent slowly evolve over a period of a month. Rolling mean −vabs values of SNe IIb are consistently ∼2000 km s−1 less than the SNe Ic mean values, and typically ∼2000 km s−1 higher compared with the SNe IIb.
-
Feature 10 (Ca II) shows an exponentially declining rolling mean −vabs evolution for each SE SN subtype. Already by −7 d the SNe IIb and SNe Ib exhibit a high degree of similarity with rolling mean values of ∼14 000 ± 1000 km s−1. SNe Ic exhibit higher rolling mean −vabs values compared to the He-rich subtypes at all phases though the associated mean error snake is large at early phases mostly due to SN 2009dp. This is a noteworthy object as it is as bright as SN 2009bb and shows high −vabs values yet no broad-line features.
4.3. Doppler velocity correlation coefficients
Spearman’s rank correlation coefficients were computed for different pairs of −vabs values for Features 1-10, and examined and shown in the Appendix B. SNe Ic and SNe Ib are found to only have a handful of pairs that are correlated, and those that are correlated typically show a low-to-moderate degree of correlation. In the case of the SNe Ib, the He I features only show correlations of low statistical significance as their −vabs values evolve very little, and do not monotonically change as required to produce a statistically significant correlation. On the other hand, SNe IIb show a larger number of moderately to highly correlated pairs, particularly for the photospheric phase subset of the data. This is due to the spectral features appearing more prominent at earlier phases compared to in the SNe Ib and SNe Ic, and as a result of the rapid early evolution, a number of moderately to highly correlated pairs were computed.
5. Principal component analysis
Principal Component Analysis (PCA; Pearson 1901) provides a means to reconstruct the multidimensional information contained within the CSP-I SE SN spectral library using just a few variables. This can be achieved through the use of the Singular Value Decomposition (SVD) of a data matrix (see Hsiao et al. 2007; Cormier & Davis 2011 and Holmbo 2018; Williamson et al. 2019; Shahbandeh et al. 2022 for the applications of PCA to SNe Ia and SE SN spectral datasets, respectively). PCA is applied to summarize the large amount of information contained within an extended dataset by reducing its dimensionality while using only the most informative explanatory variables that can be derived from the dataset.
PCA is essentially a linear decomposition of a collection of data by a change of basis defined by the principal components (PCs; also known as eigenvectors) of the covariance matrix and the amplitudes (also known as projections) defined by the inner product between the data and the new basis. PCs are sorted/ranked by the degree to which they contribute to the variance within the data. This effectively means that the first basis vector, that is PC1, accounts for the largest variation within the dataset, PC2 the second largest, and so on and so forth as the dimensionality increases. Since PCA requires little human intervention and is algorithmically performed by a computer in a matter of seconds, it provides a means to explore data in a much less labor intensive manner as compared to the line diagnostics visited in the previous sections.
In the following we examine the PCs contributing to the largest variations within various segments of our spectral data library. Our analysis makes use of the scikit-learn PCA decomposition toolbox (Pedregosa et al. 2011) and adheres to standard procedures as described in detail by Holmbo (2018, 2020). First, each observed spectrum is normalized to a common scale such that its mean flux is equal to zero, and a common spectral range is used. A mean spectrum is then determined for these input spectra, from which PCs and the amount of variance they account for are calculated using SVD. In practice this means that, for each input spectrumj used to estimate the mean spectrum, a set of PCi are obtained, along with their corresponding Amplitudesji that reflect the degree to which PCi contributes to the variations of the data used to determine the mean spectrum. This is represented by the formalism:
We now examine our PCA results obtained using a large subset of the CSP-I SE SN spectral library before turning our focus toward more nuanced aspects of the data by inspecting sets of PCs determined from particular phase and spectral wavelengths ranges that effectively trace the strength and temporal evolution of the spectral features associated with H I and He I.
5.1. PCs associated with color and spectral line strength
Plotted in the top of Fig. 7 is the mean spectrum (solid black line) computed using all CSP-I SE SNe spectra, which was used for this portion of our PCA. This includes 111 spectra covering the temporal phase out to +40 d and over the spectral wavelength range 3950–8700 Å3. Over-plotted on the mean spectrum with shaded red and blue coloring is the full range of Amplitudei ⋅ PCi covered by the input data, with PC1 shown in the upper half-panel and PC2 in the lower half-panel. Here the blue shading indicates a negative while the red indicates a positive contribution. PC1 accounts for 61% of the total spectral variations of the data, PC2 accounts for 11%, and PC3 (not shown) accounts for 7%. The significant amount of variation associated with PC1, particularly at the blue end of the spectral wavelength range, is consistent with the observed broadband photometric colors of SE SNe (see Paper II), while the positions and amplitudes of PC2 suggests a connection to the depth/height of the spectral features. As shown in Paper IV, the spectral colors are directly correlated to the photometric colors, with a typical rms uncertainty of ≲0.1 mag.
 |
Fig. 7. Results from PCA. Top: solid black line is the mean spectrum computed using all observed (i.e., 111) spectra obtained out to +40 d and over the spectral range of 3950–8700 Å. The shaded regions correspond to Mean spectrum + Amplitudei ⋅ PCi, yielding the range of amplitudes shown in the panel below. Here the blue shaded regions correspond to negative values, and the red regions correspond to positive values. Bottom: amplitude1 versus Amplitude2, color-coded by spectral subtype and with the intensity of colors corresponding to the phase of the observed spectra following the multicolumn colorbar located to the right. |
Turning to the bottom of Fig. 7, we plot the values of Amplitude1 and Amplitude2 as determined from our application of PCA. Each point in the figure is computed from a single spectrum with the color-coding of the points differentiating the subtype, and with the intensity of the coloring providing an indication of its temporal phase relative to the epoch of B-band maximum. Here, negative Amplitude1 values correspond to a subtraction from the mean spectrum and are coded blue. On the other hand, points with positive Amplitude1 values correspond to adding a larger contribution of PC1, and are coded red. This explains why the cluster of SNe IIb and SNe Ib points located within the left-half of the plot are associated with early phase spectra when the spectral energy distributions of their associated SNe are hot and bluer. Subsequently, as the SN ejecta expands and cools, their broadband colors evolve to longer (red) wavelengths. This therefore explains why the right-half side of the plot is populated predominately with points associated with post-maximum phase spectra. Unfortunately, there is a dearth of SNe Ic spectra in the days leading up to maximum light, preventing a more rigorous comparison between their early phase spectra with those of the He-rich SE SNe.
Further inspection of the distribution of points indicates significant diversity among the Amplitude2 values inferred from the post-maximum phase spectra of the different SE SN subtypes. Interestingly, the vast majority of post-maximum phase SNe IIb are found to preferentially cluster within the upper-right quadrant of the figure contained within the parameter space of Amplitude1 > 0 and Amplitude2 ≳ 1. This is fully consistent with the temporal evolution of the pEWs of SNe IIb previously documented in Sect. 3.2, which indicated a strengthening of most spectral features (e.g., those associated with He I) over time. On the other hand, the SNe Ib (and to a lesser extent the SNe Ic) exhibit a range of Amplitude2 values that produces the triangular distribution of points within the bottom of Fig. 7. For example, some maximum and post-maximum spectra of both subtypes exhibit little change in their Amplitude2 relative to premaximum epochs. However, other points associated with SN Ib exhibit Amplitude2 values ranging between −6 all the way up to 9, while in the case of SNe Ic the Amplitude2 parameter space ranges between ∼ − 9 up to 2. In short, the wide diversity among the Amplitude2 parameter space is largely inherent to the difference in the suite of lines present in the various SE SN subtypes and the phase of the spectra. In order to assess the level of variations within the PCs that are largely associated with the various Balmer and He I features, we now turn to PCA results obtained by examining more limited spectral wavelength regions.
5.2. PCs associated with H I and He I
5.2.1. PC2 versus PC3
Figure 8 presents the PCA results obtained using all (128) of the spectra contained within the CSP-I SE SN library extending up to +70 d and over the spectral wavelength range of 3950–7350 Å. The temporal range ensures that the line strength evolution of the features are well sampled, while the spectral wavelength range excludes features associated with O Iλ7773, Ca II H&K and the Ca II NIR triplet4. By using a more limited wavelength range that excludes these common SE SN lines, the top PCs will contain more of the variance in H and He features, thereby avoiding diluting our results. As in Fig. 7, the black solid line in the top of Fig. 8 corresponds to the mean spectrum and the over-plotted blue/red (negative/positive) shaded regions display the full range of Amplitudei⋅ PCi covered by the data, where i = 2 is shown in the upper panel and i = 3 in the lower panel. PC1 (not plotted) accounts for 65% of the spectral variations and is linked to color, as previously discussed. Meanwhile, PC2 and PC3 account for 9% and 6% of the overall spectral variations, respectively. The majority of the blue/red shaded regions of PC2 are located bluewards of the He I rest-wavelengths (i.e., F1b, F2b, F4, F6, F7, F8). Similarly, PC3 exhibits clear variations from the mean spectra at locations just bluewards of the rest wavelengths of Balmer features (i.e., F1a, F2a, F5b). However, both PCs also likely have contamination from other (non-He or non-H) features (interested readers are referred to Sect. 2.3.2).
 |
Fig. 8. Results from PCA. Top: solid black line is the mean PCA spectrum computing using all observed spectra obtained out to +70 d and covering the wavelength region 3950–7350 Å. Blue and red shaded regions correspond to the full range of Amplitudei with blue (red) corresponding to negative (positive) values. Vertical gray regions correspond to He I (PC2 panel) and H I (PC3 panel) related features (same as in Fig. 2), indicating that variation in PC2 corresponds strongly to Helium and in PC3 to Hydrogen. Bottom: amplitude2 versus Amplitude3, color-coded by spectral subtype with the intensity of colors corresponding to the phase of the observed spectra following the multicolumn colorbar located to the right. |
We first consider the comparison between Amplitude2 versus Amplitude3, which is presented in the bottom of Fig. 8. As before, the points are color-coded based on SE SN subtype with the intensity of the color corresponding to the temporal phase. Interestingly, the comparison of PC2 and PC3 exhibits groupings separating SNe IIb from SNe Ib and SNe Ic, and also SNe Ib from SNe Ic, although the latter is less well differentiated. We now examine some specifics of the groupings.
Relative to the coordinate origin (0,0) located at the center of the plot, the SNe IIb points overwhelmingly populate the Amplitude3 ≳ 0 parameter space, that is, they essentially cover the entire top-half region of the figure. On the other hand, the points associated with SNe Ib and SNe Ic tend to populate the entire bottom-half region (i.e., Amplitude3 ≲ 0) with SNe Ib mostly located in the bottom-right quadrant (i.e., Amplitude2 ≳ 0) and the SNe Ic in the bottom-left quadrant (i.e., Amplitude2 ≲ 0). These groupings are essentially dictated by the presence (or lack thereof), strength and time-dependence of the Balmer and He I features, as traced by PC2 and PC3. The temporal dependence of the Balmer features explains why the SNe IIb points associated with premaximum and around maximum spectra generally exhibit high Amplitudes3 values as this is when the Balmer features are most prevalent. Similarly, the points associated with the post-maximum SNe IIb points (when Balmer lines typically weaken as the photosphere recedes into deeper layers of the ejecta devoid of H) are found to group among the SNe Ib with much lower Amplitudes3 values and higher Amplitude2 values.
Turning to SNe Ic, its main grouping is generally located within the bottom-left quadrant of the Amplitude2 versus Amplitude3 diagram, reflecting the traditional SE SN spectroscopic taxonomy where SNe Ic lack both H I and He I features. However, both the SN Ic and SN Ib subtypes do have several members that are mixed together along the Amplitude2 (primarily He I) axis. In addition, to the mixture between the SN Ib and SN Ic subtypes in Amplitude2, there are two early points located in the top-left quadrant among the peripheral grouping of young SNe IIb spectra with positive Amplitude3 values (i.e, ∼2) that are associated with SN 2009ca. SN 2009ca is a superluminous SN Ic that is more than 2 mag brighter than the rest of the sample (Taddia et al. 2018). Therefore, due to the expected spectral differences between SLSN-Ic and normal SNe Ic, its position separated from the rest of the SNe Ic is not surprising.
Figure 8 suggests that the SN IIb, SN Ib and SN Ic subtypes can be differentiated based solely on PC2, PC3, and phase. The strongest dichotomy appears to exist among SNe IIb and the SNe Ibc, which is investigated more deeply in the next section. The difference in SNe IIb is primarily from Amplitude3 with a smaller contribution from Amplitude2 and the phase, although at late times they do evolve toward lower Amplitude3 and more closely resemble SNe Ib. As discussed below, these findings are consistent with pEW measurements of Hα post maximum (see, e.g., Liu et al. 2016, and our F5 panel in Fig. 5).
5.2.2. Linear combinations of PC2 and PC3
In order to explore whether PCA can be used to differentiate SNe Ibc from SNe IIb, we use the fact that PCs are orthogonal, linear combinations of the input variables. A linear combination of a linear combination is another linear combination. Therefore, we search for a rotation of PC2 and PC3 (a rotation is just a linear combination) that creates a large separation between SNe IIb and the SNe Ibc. As demonstrated below, by introducing linear combinations as a change of basis we achieve greater separation between the subtypes. This aids both in the visualizations and the interpretability of the PCA results. This is performed by applying the 2D rotation matrix to the basis defined by PC2 and PC3 following:
We reiterate that the resulting Rotated PCs are orthogonal, linear combinations of the original PCs. Instead of giving them new names, for clarity, we explicitly refer to them by their linear combination expressions.
Figure 9 presents the PCA results obtained for the first Rotated PC, (0.87 ⋅ Amplitude3 − 0.50 ⋅ Amplitude2), corresponding to a Rotation of θ = 30°. As SNe IIb and SNe Ib generally evolve toward each other at late times (see Fig. 8), here PCA was restricted to data obtained to ∼ + 40 d and the spectral range was limited to 3950–7000 Å. Plotted in the top panel of Fig. 9 is the mean SE SN spectrum with the full range of the first rotated PC (0.87 ⋅ Amplitude3 − 0.50 ⋅ Amplitude2) over-plotted and indicated by shaded regions, while the bottom panel contains the linear combination of Amplitude2 and Amplitude3 versus phase. Inspection of the bottom panel reveals that with a Rotation of θ = 30°, we obtain good separation between the SNe IIb and SNe Ibc. This is attributed to the larger contribution of Amplitude3, particularly during the post-maximum phases. This is also fully consistent with the results of Fig. 8 where PC3 was identified as primarily (but not entirely) associated with H Balmer features. Meanwhile Amplitude2, which is primarily made up of He features, contributes less. Clearly, a linear combination of PC2 and PC3 can reliably identify SNe IIb and differentiate them from SNe Ib between ∼ + 20 to +40 d. There is only a single interloping point that breaks this dichotomy, and we subsuquently return to the question of classifying and differentiating SNe IIb from SNe Ib (see Sect. 6.2). Such interloping points also suggest that the differences among groupings are not just due to uncertainties (see Sect. 5.3.2).
 |
Fig. 9. Results from PCA. Top: full range of the linear combination of Amplitude2 and Amplitude3 determined after applying a θ = 30° rotation following Eq. (3). Over-plotted the mean spectrum (black line) determined from all spectra extending to +45 d and covering the wavelength range of 3950–7000 Å. Blue and red shaded regions correspond to the full range of the first rotated PC (0.87 ⋅ Amplitude3 − 0.50 ⋅ Amplitude2) with the blue corresponding negative values and red to positive. Balmer series features are indicated with gray regions as in Fig. 2. Bottom: the corresponding linear combination of Amplitude2 and Amplitude3, plotted versus phase. This particular linear combination separates particularly well between +20 d to +40 d the SNe IIb from the SNe Ib and SNe Ic. |
5.3. PCA between 6000–7000 Å
As the rotated PCs in Sect. 5.2.2 are able to separate SNe IIb from the SNe Ib and SNe Ic, we now search for a manner to better separate the groupings of all three subtypes using a similar methodology. Previously, the biggest uncertainty when attempting to do this with PC2 and PC3 was contamination from spurious spectral features associated with ions other than H and He, which tautologically should be the defining distinction between the SE SN subtypes. In order to ascertain whether the mixture among groupings of SNe IIb, SNe Ib and SNe Ic as seen in Fig. 8 are an effect of the spectral wavelength range adopted in the PCA, we apply PCA to the even more restricted spectral range of 6000–7000 Å. This spectral wavelength range should primarily contain Hα, and if present, features associated with He I λ6678 and possibly He I λ7065. In addition, the narrow wavelength range ensures that the amplitude of any PCs primarily corresponding to the shape of the SED (like PC1 encountered in Sect. 5.1) are limited.
Following Sect. 5.2, we identified the linear combinations of PCs (i.e., PC1 and PC2) that represent a rotation creating separation among the different SE SN subtypes. Following Eq. (3), we once again identified a rotation angle of θ = 30° to be ideal. The results of this portion of our analysis are presented in Fig. 10. The mean spectrum is plotted in the two upper panels as a black line, while the left panel shows the first rotated PC 0.87 ⋅ Amplitude1 − 0.50 ⋅ Amplitude2 and the right panel displays the (orthogonal) second rotated PC 0.50 ⋅ Amplitude1 + 0.87 ⋅ Amplitude2. The two rotated PCs are compared in the bottom panel of Fig. 10, with each point color-coded by spectral subtype and with the intensity of the shading indicating the temporal phase.
 |
Fig. 10. Results from PCA. Top: linear combinations of the first two PCs determined from PCA applied to the spectra extending to +70 d and between 6000–7000 Å. Bottom: a linear combination of Amplitude1 and Amplitude2 plotted versus its orthogonal (30°) rotation. In addition to the CSP-I SE SN sample, PCA resutls are shown for the normal Type Ia SN 2013gy (Holmbo et al. 2019) and unpublished CSP-II spectra of the Type Ic superluminous SN 2015bn (Phillips et al. 2019). Solid curved lines highlight subtypes of He I-rich SE SNe (see Sect. 5.3). GMM clusters are indicated with one and two sigma contours for each cluster using dashed and dot-dashed lines (see Sect. 5.3.1 and Table 3), respectively. To guide the eye, curved arrows are over-plotted highlighting the temporal evolution of SNe IIb and SNe Ib. |
Figure 10 reveals a separation between the groupings (similar to Fig. 8). SNe IIb clearly occupy the right half side of the figure with rotated PC 0.87 ⋅ Amplitude1 − 0.50 ⋅ Amplitude2 ≳ 1, while the SNe Ib and Ic occupy the left-half of the panel, with the SNe Ib in the upper-quadrant and the SNe Ic in the lower-quadrant. Between the right and left sides a clear separation appears within the plotted parameter space devoid of objects and which is highlighted in gray. This region suggests that, at least for this sample, there is not a clear continuum over the parameter space covered by these PCs.
Considering the evolution of SE SN subtypes with phase, we first notice in Fig. 10 that the young SNe IIb located toward the lower/middle right of the figure evolve in time toward the right side of the quadrant reflected by increasing values of the second rotated PC 0.50 ⋅ Amplitude1 + 0.87 ⋅ Amplitude2. Beginning around maximum and extending over a month, the SNe IIb then follow one of two distinct tracks, which are highlighted in Fig. 10 with blue-curved arrows. One track is populated with objects exhibiting PC 0.87 ⋅ Amplitude1 − 0.50 ⋅ Amplitude2 ≳ 2.1–3.0 and the other track exhibits values ≲2.1. However, after a month past maximum the two tracks begin to overlap, and as the SNe IIb continue to evolve with decreasing values of the rotated PCs they are found to populate the same region of parameter space as old SNe Ib. On the other hand, the SNe Ib located on the left quadrant of the figure (except for a few interlopers) first appear with 0.50 ⋅ Amplitude1 + 0.87 ⋅ Amplitude2 ≲0.5. As time evolves through maximum and beyond, these objects migrate upward with ever increasing 0.50 ⋅ Amplitude1 + 0.87 ⋅ Amplitude2 of ≳1.6, and then later exhibit lower PCs values. Turning to the SNe Ic, they occupy the lower left quadrant of Fig. 10, and evolve further left with phase (although there are a handful of SNe Ib mixed in at early and late times).
Based on the groupings reflected in Fig. 10, in the case of the SNe IIb and SNe Ib, the first rotated PC 0.87 ⋅ Amplitude1 − 0.50 ⋅ Amplitude2 mainly traces H, while the second rotated PC 0.50 ⋅ Amplitude1 + 0.87 ⋅ Amplitude2 mainly traces He. As SNe Ic by definition lack both H and He features, they occupy a relatively narrow region of the parameter space, especially among the second rotated PC (He). The evolution along the first rotated PC, tracing mainly H, can be explained by contamination from an additional feature. The origin of this feature in SNe Ic spectra remains under debate (see discussion in Sect. 2.3.2).
5.3.1. Clustering analysis
In order to explore the inherent clustering in our PCA data and to statistically test our qualitative identification of the three main groupings, we used unsupervised learning making use of the scikit-learn package (Pedregosa et al. 2011) to perform clustering analysis using K-means and Gaussian Mixture Modeling (GMM). In other words, rather than adopting a by-eye approach, we wish to quantitatively assess how well PCA can distinguish between the SE SN subtypes using the original (single template) PCs.
Using three component models and as described with some detail at the end of Appendix C, both K-means and GMM readily identified three clusters centered at the qualitatively identified location of each grouping from the previous section. We tabulate the completeness of each algorithmically derived cluster compared to the known labels (i.e., IIb, Ib, Ic) in Table 3, and which are IIb ∼80%, Ib ∼50%, and Ic ∼95%, respectively. Results from this analysis consisting of the one and two sigma contours for each Gaussian component of the GMM fit are included in Fig. 10.
Results of K-means and GMM clustering analysis.
5.3.2. Interlopers among SNe Ib, IIb, and Ic groupings
Upon examination of interlopers appearing among the groupings revealed in the bottom panel of Fig. 10, we notice some interesting patterns. Most noticeably, a handful of SNe Ib at early times intrude within the SNe IIb grouping and have rotated PC 0.87 ⋅ Amplitude1 − 0.50 ⋅ Amplitude2 ≳ 1. These are SN 2004ew (single spectrum at +26 d) and SN 2007kj (spectra at +9 d and +14 d). Two more SNe Ib including SN 2005bf and SN 2007Y also appear close, but do not violate our arbitrary limit. With the exception of SN 2004ew, the rest of these objects are part of a sub-group of SNe Ib that exhibit a flat-velocity evolution of the He Iλ6678 line, as illustrated in Fig 11. This sub-group appears to show evidence of a weak feature at around 6250 Å, which could be high-velocity Hα (see, e.g., Folatelli et al. 2014). Although SN 2004ew does not belong to this flat-velocity SN Ib sub-group, it also initially shows the same absorption feature at ∼6250 Å. By the second spectrum at +40 d, this feature disappears and SN 2004ew returns to being firmly among the other SNe Ib in Fig. 10. The absorption related to this feature seems to drive the positive evolution along the x-axis (first rotated PC) in Fig. 10. As can be seen in the top left panel of the Fig. 10, there is a deep red trough at around this position, which is positively correlated with the first rotated principal component 0.87 ⋅ Amplitude1 − 0.50 ⋅ Amplitude2 and explains the interlopers. It is important to point out that, where we do have spectral coverage, they are found to evolve back over time toward the SNe Ib grouping, and do not remain among the SNe IIb.
 |
Fig. 11. Time-evolution of the Doppler velocity measured from the minimum of the He Iλ5876 feature. Each object is plotted with a unique combination of symbol and color where the color indicate subtype, with SN Ib plotted in blue and SN Ib in green. The three SN Ib plotted with filled symbols are SNe 2005bf, 2007Y, and 2007kj, and are identified as ‘flat-velocity’ SNe IIb by Folatelli et al. (2014), while others have referred to such objects as transitional SNe Ib/c (e.g., Hamuy et al. 2002; Stritzinger et al. 2009). Using classification criteria based on the pEW of Features 4 and 5 as discussed in this paper these objects are consistent with a Type Ib classification (see also Liu et al. 2016 and Prentice & Mazzali 2017 for additional discussion). |
Looking at the interlopers belonging to the SNe Ic subtype, the most noticeable are SN 2005aw and SN 2009ca having, respectively, the highest and most negative values of the second rotated PC, corresponding to He I. As discussed previously, the origin of the features in this region is under debate, but an association with H and He is not expected, especially a strong one. Nevertheless, as can be seen in Fig. 12, SN 2005aw shows evidence of early He features. Therefore, it is not surprising to find it as an interloper among the SNe Ib and having a high value of the second rotated PC. In the case of the other interloper, SN 2009ca, it is known to be an unusually bright SN Ic with peculiar features (see Taddia et al. 2018, Paper III). Hence, its separation from the rest of the grouping is not surprising.
 |
Fig. 12. Spectroscopic time-series from +7 d to +23.2 d of the Type Ic SN 2005aw. The spectra are plotted in velocity space with the segments of data containing the He Iλλ5876, 6678, and 7065 features plotted on top of each other. As revealed from the PCA results and consistent the data, SN 2005aw exhibits discernible features likely formed by He I with −vabs ∼ 8500 km s−1. |
Looking at the interlopers belonging to SNe IIb, we primarily see a few early phase points near the early SNe Ib and SNe Ic groupings, which all belong to the type IIb SN 2009K. The earliest spectrum of SN 2009K taken on −18.4 d actually lacks Balmer features, however they do emerge by −13.5 d, which explains the early divergence.
Switching gears, we note that the two very late-phase SNe IIb points appearing in the same region as the SNe Ib are in fact expected as the former evolve to resemble the latter during the post-maximum epochs as the H features dissipate in SNe IIb. A similar convergence between SNe IIb and SNe Ib was seen in the late-time pEW evolution of the Feature 5. For this reason, spectral epochs later than +40 d were not included in Fig. 9. On the whole, SNe IIb seem to be the most well separated, which we subsuquently return to in the discussion.
The fact that distinguishing spectral features can explain the interlopers suggests that the differences are real, and not merely driven by uncertainty of the spectra or PCA analysis. Therefore, we have not considered the uncertainties of the PC amplitudes in the discussion, which is a nontrivial undertaking.
6. Discussion
6.1. Comparison with literature findings
Here we examine our line diagnostic results presented in Sect. 3 and Sect. 4 to average behavior of key features reported in the literature by the Berkeley SN group (Matheson et al. 2001; Shivvers et al. 2019), the CfA SN group (Modjaz et al. 2014; Liu & Modjaz 2014), the (i)PTF survey (Fremling et al. 2018), and also Prentice & Mazzali (2017) who compiled a (mostly) literature-based sample. Considering features studied in common by the literature, we find broadly consistent results which we now summarize.
6.1.1. Fe II and C0 II: Feature 3
Mean −vabs velocities of Feature 3 reported by Liu et al. (2016) are systematically higher in SNe Ib than in SNe IIb. We find for the CSP-I sample a similar trend up to maximum (see Fig. 6), however during post maximum phases, the sample shows no bifurcation between the two subtypes. Turning to SNe Ic, we find that around maximum they exhibit similar mean −vabs values as the SNe IIb, while SNe Ib mean values are ≳2000 km s−1 higher. Due to the lack of early SN Ic spectra in the CSP-I sample, we are unable to comment on premaximum phases. However beginning around a week past maximum, the average values in our SNe Ic tend to be larger than in SNe Ib. We remind the reader that Feature 3 in SNe Ic may have a nonnegligible contribution from Co II, and therefore this comparison should be approached with caution. Finally, to our knowledge, no measurements on the pEW of Feature 3 are available in the literature for us to compare.
6.1.2. He I: Features 4, 6, 7
He I lines corresponding to Features 4, 6, and 7 are the most commonly studied SE SN spectral features, with broad consensus in the literature on their characterization. In general, and as demonstrated in Fig. 5, the He I features emerge earlier in SNe Ib and consistently exhibit higher pEW mean values. As highlighted in the Feature 4 panel of the figure with a horizontal dashed line, the differences between the pEW values of the two subtypes prior to maximum is significant, while mean pEW values for Features 6, 7 (and 8) reveal somewhat less significant differences. In the weeks following maximum brightness and as the photospheres of the SNe IIb recede into deeper He-rich layers of ejecta, prominent He I features emerge with mean pEW values fully consistent with those of the SNe Ib. Again, this is in agreement with findings in the literature (see Liu et al. 2016; Prentice & Mazzali 2017; Fremling et al. 2018; Shivvers et al. 2019).
Turning to Doppler velocity, work by Liu et al. (2016), Prentice & Mazzali (2017) and Fremling et al. (2018) indicated SNe Ib tend to exhibit higher values prior to maximum than SNe IIb, while during post-maximum phases their mean values are similar. Similarly, and as demonstrated in Fig. 6, we also find agreement between their mean values beginning from maximum and beyond. Unfortunately, do to a dearth of data, we are unable to comment on premaximum phases.
6.1.3. Feature 5: Si II and/or Hα
Liu et al. (2016) and Prentice & Mazzali (2017) report distinct pEW values between the SNe IIb and SNe Ib at all phases. As shown in Fig. 5 and highlighted by a horizontal dashed line, the SNe IIb in the CSP-I sample do exhibit consistently higher pEW values than the SNe Ib, however, given the large dispersion of values measured for the SNe Ib there is some overlap between −5 d to +15 d. In the case of SNe Ic, we computed mean pEW values significantly less than those of the SNe IIb at all phases, while between +0 d to +10 d they appear somewhat less than SNe Ib, and then between +10 d to +30 d they are found to overlap.
Liu et al. (2016) and Prentice & Mazzali (2017) report higher −vabs values in their SNe Ib samples relative to SNe IIb. This is contrary to the results of Feature 5 presented in Fig. 6, which indicates quite consistent rolling mean values between the two subtypes. In fact, at the earliest days of our coverage, the SNe IIb exhibit somewhat higher mean values, though we note this is based on smaller sample size than that considered by Liu et al. and Prentice & Mazzali. Beyond maximum, the SNe IIb and SNe Ib exhibit similar rolling mean −vabs values for around a month.
6.1.4. Feature 9: O I
Between maximum and ∼two weeks post maximum, Fig. 5 reveals that the mean pEW values of Feature 9 are ≳ 50 Å higher in the SNe Ic, followed by SNe Ib and then SNe IIb. Similarly, Fig. 6 indicates Feature 9 systematically exhibits higher mean −vabs values in SNe Ic by a few thousand km s−1, followed by SNe Ib and then SNe IIb. These results are in line with findings presented in the literature (cf. Matheson et al. 2001; Liu et al. 2016; Fremling et al. 2018; Shivvers et al. 2019).
6.1.5. Feature 10: Ca II
Previous sample studies of SE SN spectra do not consider the Ca II NIR triplet. Only Matheson et al. (2001), who previously reported (based on a handful of spectra taken at different, mostly post-maximum phases) a mean velocity in SNe Ic of 10 800 ± 800 km s−1, which is significantly less than what we find for CSP-I SNe Ic. Even upon removal of a single object in our sample with very high velocities, we find mean −vabs around maximum light on the order of ≳14 000 km s−1.
6.2. Classification
6.2.1. Line diagnostics
Here we consider a few rules of thumb to follow that others may find useful in their quest to subtype SE SN based on either premaximum and/or post-maximum phase spectra based on a few of the key findings presented in Sect. 3.2. Considering the pEW trends of the CSP-I SE SN shown in Fig. 5, we suggest that the pEW values of Features 4 and 5 in premaximum spectra can reliably differentiate between SNe IIb and SNe Ib. As indicated by the dashed line in the panel of Feature 4, SNe Ib consistently exhibit pEW values in excess of ≳75 Å, while the other subtypes typically exhibit pEW values below this cutoff. The panel of Feature 5 shows a clear bifurcation at all phases between SNe IIb and SNe Ic with the latter consistently exhibiting pEW values below 100 Å, while the former exhibit values in excess of 120 Å. We suggest Feature 5 can serve as a reliable indicator to differentiate SNe IIb from SNe Ib, beginning from +20 d onward. This is contrary to the advice of Liu et al. (2016) who advocated that Feature 5 provides a clear indication between SNe IIb and SNe Ib at all phases, and this is due to those SNe Ib that do exhibit (modest) Hα at early times. These objects are responsible for the significant variance of the premaximum rolling mean pEW values. Feature 5 being a robust discriminator during post-maximum phases is in agreement with our PCA analysis (see below). Finally, we note that Feature 9 (O I) also provides some indication of the SE SN subtype as discussed in Sect. 6.1.4. In particular, the velocity of Feature 9 in SNe Ic is consistently higher than exhibited in the SNe Ib and IIb, and at early times, SNe Ic show larger pEW values as compared with the other subtypes.
6.2.2. PCA
The PCA analysis presented in Sect. 5.2 and the results obtained in Fig. 9 demonstrate we are able to reliably classify SNe IIb distinctly from SNe Ib using a combination of phase, PC2, and PC3, with results being strongest at phases between +20 d to +40 d. This result mirrors previous findings of Liu et al. (2016) and Prentice & Mazzali (2017) whom pointed out that the pEW value of Hα is a suitable diagnostic to distinguish between SNe IIb and Ib. Appendix C contains a practical guide on how to leverage PCA for those wishing to distinguish between SNe IIb and Ib using one or more spectra taken at any phase. Whether SNe Ib discovered during these post-maximum epoch are SNe Ib, or are simply SNe IIb that evolved to become SNe Ib has been questioned previously (e.g., Milisavljevic et al. 2013). We note that all but one SN Ib in our sample (SN 2004ew) have early spectra indicating they are not traditional SNe IIb with strong H features. This suggests there is a clear separation of these observables between the two subtypes. Indeed, as estimated in Sect. 5.3.1, interlopers from the SNe IIb into SNe Ib subtype can be found with ∼80% completeness.
Contrary to Modjaz et al. (2014) and Liu et al. (2016) who report a similar separation, we did not re-classify any of our SNe, nor did we exclude transitional or peculiar SNe from our PCA as was done by Williamson et al. (2019). Nevertheless, we obtain a similar result and find a clear separation between SNe IIb and SNe Ib, indicating that the re-classification in these papers can not account for the observed differences.
As discussed in Sect. 5.3.2 and depicted in Fig. 10, we naturally find more scatter and some outliers within group properties such as PCs, pEWs, and −vabs values, even though they are accountable by peculiar outlier SNe. Specifically, for separating between SNe IIb and SNe Ib, the main exceptions to the PCA based classification, which were transitory outliers are: 1) SNe Ib with early and weak high-velocity H features all but one of which exhibit He I lines that slowly evolve over time, and 2) SNe IIb with H features that are stronger than SNe Ib, but relatively weak compared to the rest of the SNe IIb. Aside from these two interloping sub-subtypes, our results indicate that SNe Ib, IIb, and Ic are distinct. It can be argued that these interlopers represent a continuum from SN IIb with weak H to SN Ib with weak H, or they can be interpreted as distinct subtypes themselves. Future PCA results from larger datasets and detailed study of these interlopers are required to disentangle the two possibilities.
To serve as a comparison, rotated PCs of the normal Type Ia SN 2013gy relative to the SE SN mean spectrum are also plotted in Fig. 10 (gray stars). The PCs of this normal SN Ia are clearly separated from the SE SNe, and therefore, such objects are not expected to serve as a source of confusion. However, PCs of superluminous SNe Ic (gold stars), as exemplified by SN 2015bn, do appear within the same region as less luminous SNe Ic.
Shahbandeh et al. (2022) showed that PCA of NIR SE SN spectra can differentiate SNe Ib from Ic. While a good degree of differentiation was also seen in our un-tuned optical results (Sect. 5.3), the difference between SNe Ib and Ic was not as robust as in the NIR, nor as the difference between SNe IIb and Ibc (although we specifically delved deeper on the latter). One reason for this could be that in the optical, variance among SNe Ib and Ic is not as high as variance among SNe IIb and Ibc. Since we did not consider higher order PCs, we may have missed PCs which better differentiate SNe Ib from SNe Ic. As Shahbandeh et al. (2022) notes, NIR PCA is very good at this task due to features at 1 and 2 micron produced by He and/or C, while the optical is better for H. Similar to our investigation of H and He when aiming to classify SNe IIb, our results could be extended to focusing on optical regions containing He and C, and extending to higher order PCs. This may tease out to search for an optical counterpart to the NIR results of Shahbandeh et al. (2022).
The significance of our PCA based result is that it is not reliant upon the particular methodology used to construct pEWs measurements or infer velocities. As noted by Fremling et al. (2018), the choice of how to make these measurements can be the most significant uncertainty in the analysis. Our PCA methodology is fully reproducible and agnostically applicable to any past or future SE SN samples. Unlike spectral template matching methods widely used in the literature, the groupings can be entirely re-constructed from a given sample of SE SNe without relying on external data. Thus, it can be used as an independent verification for classification of SE SNe, particularly for SNe IIb and Ib, and especially if the initial classification is done via another method such as spectral template matching.
Future efforts related to PCA and SE SNe spectroscopic samples could focus on applying a similar analysis using an expanded sample. A guide to using PCA for this purpose, including a discussion of the practical considerations, is provided in Appendix C.
7. Summary
We presented a detailed analysis of the CSP-I SE SN optical spectroscopic sample. Key completed tasks and highlights of the analysis include:
-
The construction of mean spectra for each SE SN subtype at distinct phases. Prevalent spectral line features were then identified in the mean spectra of each SE SN subtype. Spectral synthesis modeling using SYNAPPS enabled the identification of the parent ions associated with the designated features. This includes the potential inclusion of: Si IIλ6355 in some SNe IIb, Hα in some SNe Ib, and a contribution to the ∼6150 Å feature in SNe Ic by an unknown species.
-
Pseudo-equivalent width (pEW) width and Doppler absorption velocity (−vabs) measurements were measured for the spectral features in all photospheric phase spectra. With these measurements rolling mean values for both spectral indicators were determined and Spearman’s rank correlation coefficient matrices constructed.
-
Adopting a PCA formalism, we devise a method to reliably classify SE SNe using a single spectrum taken during the photospheric phase. Using linear combinations of key principle components, we identify distinct groupings between the different SE SN subtypes. Moreover, based on a single post maximum spectrum we demonstrate the ability of PCA to provide a robust means to disentangle SNe IIb and Ib. This finding reflects results already in the literature suggesting the pEW of Hα can be used as a proxy to distinguish between SNe IIb and Ib (see Liu et al. 2016).
-
Outliers among the distinct SE SN groupings are identified and considered in detail. In summary we find: (i) two SNe IIb subtypes, (ii) two SNe Ib subtypes and (iii) a single SN Ic with He I features all exhibiting similar −vabs values. The difference between the two SNe IIb subtypes is the strength of the Hα feature. In the case of the SNe Ib, along with those objects that fall within the traditional classification, our PCA analysis indicates the existence of a second type of SNe Ib exhibiting weak, high-velocity Hα along with He I features characterized by a flat-velocity evolution. However, as indicated by our PCA results those SNe Ib that exhibit Hα eventually evolve to appear as a normal SNe Ib weeks after maximum.
In this paper, we demonstrated PCA provides a avenue to gain deeper insights into the different SE SN subtypes and a means to classify SE SNe free of human bias. Further efforts should aim to study the full public SE SN sample and include NIR spectroscopy.
While +40 d was used in Sect. 5.1, we now extend it to cover line evolution, since the PCA analysis worked well and the mean epoch of the template is slightly after peak. However, the trade-off is that the number of SNe Ic spectra from late epochs included in the template is minimal.
Acknowledgments
The Aarhus supernova group is funded by the Independent Research Fund Denmark (IRFD, grant numbers 8021-00170B and 10.46540/2032-00022B), and by the VILLUM FONDEN (grant number 28021). L.G. acknowledges financial support from the Spanish Ministerio de Ciencia e Innovación (MCIN), the Agencia Estatal de Investigación (AEI) 10.13039/501100011033, and the European Social Fund (ESF) “Investing in your future” under the 2019 Ramón y Cajal program RYC2019-027683-I and the PID2020-115253GA-I00 HOSTFLOWS project, from Centro Superior de Investigaciones Científicas (CSIC) under the project PIE 20215AT016 and LINKA20409, and the program Unidad de Excelencia María de Maeztu CEX2020-001058-M. The CSP has received support from the National Science Foundation (USA) under grants AST–0306969, AST–0607438, AST–1008343, AST–1613426, AST–1613455, and AST-1613472. This research used resources from the National Energy Research Scientific Computing Center (NERSC), which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. This research has made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. Lead authors contribution statement: Maximilian Stritzinger (MS) wrote the abstract, the majority of Sects. 1–4, significant portions of Sect. 5, all of Sect. 6.1, portions of 6.2, and all of Sect. 7. Emir Karamehmetoglu (EK) performed the clustering analysis, co-wrote Sect. 5 (PCA analysis) and the discussion in Sect. 6.2, and the entirety of Appendix C. The rest of the paper, including data preparation, data analysis, SYNAPPS calculations and the initial figures, were created by Simon Holmbo (SH). SH had input on the text and wrote several paragraphs. SH led all aspects of the paper during his PhD thesis, while iteratively working through data analysis, figures, and discussion in each section with MS and EK. EK and MS made changes to and re-plotted Figs. 3, 5–9, as well as revising the draft following co-author comments.
References
- Blondin, S., Dessart, L., Leibundgut, B., et al. 2006, AJ, 131, 1648 [NASA ADS] [CrossRef] [Google Scholar]
- Blondin, S., Matheson, T., Kirshner, R. P., et al. 2012, AJ, 143, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Branch, D., & Wheeler, J. C. 2017, Supernova Explosions (Springer-Verlag GmbH Germany) [CrossRef] [Google Scholar]
- Branch, D., Benetti, S., Kasen, D., et al. 2002, ApJ, 566, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Branch, D., Dang, L. C., Hall, N., et al. 2006, PASP, 118, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Branch, D., Troxel, M. A., Jeffery, D. J., et al. 2007, PASP, 119, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Cormier, D., & Davis, T. M. 2011, MNRAS, 410, 2137 [NASA ADS] [CrossRef] [Google Scholar]
- Deng, J. S., Qiu, Y. L., Hu, J. Y., Hatano, K., & Branch, D. 2000, ApJ, 540, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, A. K. 2000, PhD Thesis, The University of Oklahoma, USA [Google Scholar]
- Folatelli, G. 2004, New A Rev., 48, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Folatelli, G., Contreras, C., Phillips, M. M., et al. 2006, ApJ, 641, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Folatelli, G., Morrell, N., Phillips, M. M., et al. 2013, ApJ, 773, 53 [Google Scholar]
- Folatelli, G., Bersten, M. C., Kuncarayakti, H., et al. 2014, ApJ, 792, 7 [Google Scholar]
- Fremling, C., Sollerman, J., Kasliwal, M. M., et al. 2018, A&A, 618, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gal-Yam, A. 2017, in Observational and Physical Classification of Supernovae, eds. A. W. Alsabti, & P. Murdin, 195 [Google Scholar]
- Garavini, G., Folatelli, G., Nobili, S., et al. 2007, A&A, 470, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hachinger, S., Mazzali, P. A., Taubenberger, S., et al. 2012, MNRAS, 422, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Maza, J., Pinto, P. A., et al. 2002, AJ, 124, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Folatelli, G., Morrell, N. I., et al. 2006, PASP, 118, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Harkness, R. P., Wheeler, J. C., Margon, B., et al. 1987, ApJ, 317, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Holmbo, S. 2018, Master Thesis, Aarhus University, Denmark [Google Scholar]
- Holmbo, S. 2020, PhD Thesis, Aarhus University, Denmark [Google Scholar]
- Holmbo, S., Stritzinger, M. D., Shappee, B. J., et al. 2019, A&A, 627, A174 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hsiao, E. Y., Conley, A., Howell, D. A., et al. 2007, ApJ, 663, 1187 [Google Scholar]
- Hsiao, E. Y., Burns, C. R., Contreras, C., et al. 2015, A&A, 578, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, Y., & Modjaz, M. 2014, ArXiv e-prints [arXiv:1405.1437] [Google Scholar]
- Liu, Y.-Q., Modjaz, M., Bianco, F. B., & Graur, O. 2016, ApJ, 827, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Marion, G. H., Höflich, P., Gerardy, C. L., et al. 2009, AJ, 138, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Matheson, T., Filippenko, A. V., Li, W., Leonard, D. C., & Shields, J. C. 2001, AJ, 121, 1648 [NASA ADS] [CrossRef] [Google Scholar]
- Milisavljevic, D., Margutti, R., Soderberg, A. M., et al. 2013, ApJ, 767, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Modjaz, M., Blondin, S., Kirshner, R. P., et al. 2014, AJ, 147, 99 [Google Scholar]
- Parrent, J. T., Milisavljevic, D., Soderberg, A. M., & Parthasarathy, M. 2016, ApJ, 820, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, K. 1901, London Edinburgh Dublin Philos. Mag. J. Sci., 2, 559 [CrossRef] [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
- Phillips, M. M., Contreras, C., Hsiao, E. Y., et al. 2019, PASP, 131, 014001 [Google Scholar]
- Prentice, S. J., & Mazzali, P. A. 2017, MNRAS, 469, 2672 [Google Scholar]
- Shahbandeh, M., Hsiao, E. Y., Ashall, C., et al. 2022, ApJ, 925, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Shivvers, I., Filippenko, A. V., Silverman, J. M., et al. 2019, MNRAS, 482, 1545 [Google Scholar]
- Silverman, J. M., Kong, J. J., & Filippenko, A. V. 2012, MNRAS, 425, 1819 [NASA ADS] [CrossRef] [Google Scholar]
- Stritzinger, M., Mazzali, P., Phillips, M. M., et al. 2009, ApJ, 696, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Stritzinger, M. D., Anderson, J. P., Contreras, C., et al. 2018a, A&A, 609, A134 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stritzinger, M. D., Taddia, F., Burns, C. R., et al. 2018b, A&A, 609, A135 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stritzinger, M. D., Holmbo, S., Morrell, N., et al. 2023, A&A, 675, A82 (Paper IV) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taddia, F., Stritzinger, M. D., Bersten, M., et al. 2018, A&A, 609, A136 (Paper III) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thomas, R. C., Nugent, P. E., & Meza, J. C. 2011, PASP, 123, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Williamson, M., Modjaz, M., & Bianco, F. B. 2019, ApJ, 880, L22 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Spectral line identification with SYNAPPS
Here we summarize the results presented by Holmbo (2018), who computed SYNAPPS synthetic spectra to match the mean spectra discussed in Sect. 2.1, in order to obtain plausible line identifications. Following the standard protocols (see Thomas et al. 2011), SYNAPPS requires a number of basic input parameters including: a velocity range encompassing the outer and lower bounds of the photosphere (vph), a black-body temperature (TBB), and an input list of ions each with their own set of input parameters. The input list of ions include: H I, He I, C II, O I, Na I, Mg II, Si II, S II, Ca II, Ti II, Fe II, Co II and Ni II. All but S II and C II are found to most likely contribute to the formation of at least one or more of Features 1–10 (see Fig. 1) for at least one of the SE SN subtypes (see below). We note that there is also evidence for C II appearing as a notch in the mean SN Ic spectra. This is highlighted with a vertical dashed line in Fig. 4, though the line identification in our opinion is not significant enough to warrant a Feature designation in the present analysis.
As for an initial vph value we adopted the Doppler velocity at maximum absorption (−vabs) measured from the Fe IIλ5169 (i.e., Feature 3) in the maximum light mean spectra, while the lower bound was taken to be 5,000 km s−1 and the upper bound was set to 30,000 km s−1. Fe IIλ5169 provides a reasonable proxy for the velocity of the bulk of the SN ejecta (see Paper 3, and references therein). SYNAPPS tunes the vph value in the fitting process and overall found values between 7,000–10,000 km s−1 for all of the mean spectra, except the +14 d SN Ic mean spectrum, which has a best-fit spectrum characterized by vph ≈ 12, 600 km s−1. TBB was initially set to 7,000 K and then it was fine tuned by SYNAPPS to values between 6,000 K to 8,000 K for all of the best-fit mean spectra, except the +21 d SN Ic spectrum, which best-fit model has TBB ≈ 5,000 K.
Each input ion also has an accompanying set of input parameters. These include the line opacity (τ) at a specified reference velocity (vref), upper and lower velocity limits (vmax and vmin), a value for the parameterization of the opacity profile (here with an exponential e-folding length ve), and an excitation temperature (Texc). Values of these parameters can vary significantly between the various ions within a single synthetic spectrum, as well as significant variation of any given ion over the range of the spectral evolution covered by our set of mean spectra. SYNOW was used to obtain initial values for the input parameter set used in our SYNAPPS calculations.
We found the most efficient manner to perform the calculations was to initially begin with the +21 d mean spectrum of each subtype and then work backwards to the earlier phases, where for each successive spectrum the results from the previous spectrum were used to guide the range of the various input parameters. Once the SNe IIb spectra were modeled we continued with the SNe Ib mean spectra, which were modeled including all of the same ions as in the case of the SNe IIb. This was followed by modeling of the mean SNe Ic spectra omitting both H I and He I.
The SYNAPPS spectra for each of the SE SN subtypes are plotted in Figs. A.1–A.3. This includes the SYNAPPS fit to each of the template spectra, as well as the model spectrum of each of the individual ions. Comparison of the templates to the synthetic spectra reveals reasonable matches for the majority of Features 1–10, though in some cases there is some ambiguity. The ions identified contributing in whole or partially to Features 1–10 are listed in Table A.1.
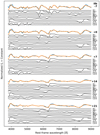 |
Fig. A.1. SYNAPPS fits (red lines) computed for mean template spectra (black lines) representing epochs of −7 d, +0 d, +7 d, +14 d and +21d. Each mean template spectrum was computed using data obtained within ±3.5 days relative to its specific epoch. Spectral features attributed to each ion are also plotted in black. |
 |
Fig. A.2. SYNAPPS fits (red lines) computed for SE SN template spectra (black lines) representing epochs of −7 d, +0 d, +7 d, +14 d and +21d. Each mean template spectrum was computed using data obtained within ±3.5 days relative to its specific epoch. Spectral features attributed to each ion are also plotted in black. |
 |
Fig. A.3. SYNAPPS fits (red lines) computed for SE SN template spectra (black lines) representing epochs of +0 d, +7d, +14 d and +21 d. Each mean template spectrum was computed using data obtained within ±3.5 days relative to its specific epoch. Spectral features attributed to each ion are also plotted in black. |
Spectral features 1 through 10.
Appendix B: Spearman’s rank pEW and Doppler velocity correlation coefficients
With our pEW measurements in hand, we examined the extent of the correlations between different pairs of Features 1–10. To visualize the large amount of information encoded within the pEW measurements and to obtain quantitative measurements of the strength of correlation among various pairs of pEW parameters, Spearman’s rank correlation coefficients (ρ) were computed. The results of this analysis are summarized in Fig. B.1. In this case, each SE SN subtype has its own panel. Within the off-diagonal triangle containing the ρ values determined from spectra obtained up to the first three weeks relative to the epoch of B-band maximum. Color-coding provides an indication of the degree of correlation with lighter colors indicating higher degrees of correlation or anticorrelation. Quantitatively, pairs with ρ values greater than 0.4 are considered to be moderately to highly correlated, while those with ρ values less than −0.4 are considered to be moderately to highly anticorrelated. Furthermore, pairs with ρ values between −0.4 to 0.4 are of low correlation, while pairs with ρ values characterized by p-values below 0.1 are considered to be of low statistical significance and are shown in Fig. B.1 by gray.
 |
Fig. B.1. Spearman’s rank correlation coefficients (ρ) between pairs of pEW measurements. The colors of the boxes is associated with the correlation coefficient with numeric values indicated by the colorbar at the top of the figure. The lighter the color, the stronger the correlation. Contained within the triangle of each panel are the correlation coefficients between pairs of pEW measurements computed using spectra obtained up to three weeks post the epoch of B-band maximum. The relative significance of ρ for each pair is indicated through the use of white lines. Here white-dotted, white-dashed and white-solid lines correspond to pEW pairs having low (0.4< |ρ| ≤0.6), moderate (0.6< |ρ| ≤0.8), or high (0.8< |ρ|) correlation coefficients, respectively. Colored boxes with no white lines exhibit minimal correlation. Gray squares have low statistical significance and are characterized by probability (p) values p > 0.1. |
Examination of the three panels indicates that a handful of the features are correlated, however determining whether or not any correlation is due to a particular physical relationship between a given pair of features is difficult. We note the following findings:
-
In SNe Ic the pair of features that are most correlated are Features 1 (Fe II, Ti II) and Feature 2 (Fe II), in SNe Ib they are Feature 7 (He I) and Feature 8 (He I), and in SNe IIb, Feature 1 (Fe II, Hγ, Ti II, He I) and Feature 3 (Fe II) display the highest correlation.
-
The diagonal of the SNe IIb correlation coefficients panel indicates that the Feature 6 (He I) presents a high degree of correlation with Features 7 and 8. A similar trend is also seen in the SNe Ib, but to a lesser degree, while as mentioned previously, Features 7 and 8 are highly correlated.
-
Feature 4 (He Iλ5876 and Na Iλλ5890, 5896) and Feature 7 (He Iλ7065) are highly correlated with high statistical significance in SNe IIb at all phases, while SNe Ib exhibit moderate to low correlation. The high degree of correlation between these two features therefore suggests He I is a significant contributor to Feature 4 rather than Na I in SNe IIb, since Na I does not, at all, contribute to Feature 7.
-
The pEW measurements of Feature 4 versus those of Feature 5 (Hα, Si II) at early times show a positive (though low) correlation for the SNe Ic and no correlation among the SNe IIb and SNe Ib. This could indicate that the correlation in the SNe Ic is driven by Na I and Si II, where both features become somewhat more prevalent over time (see Fig. 5). The lack of correlation in the SNe IIb and SNe Ib may be due to He I and Hα being susceptible to nonthermal affects, and Na I contributing less to the formation of Feature 4.
-
SNe Ic show only a handful of correlations with statistical significance. Most notable are Feature 1 and Feature 2 which are moderately correlated at early phases in all 3 subtypes.
-
There is little evidence of anticorrelations among the various pEW pairs. However, the diagonal in the SNe IIb panel of Fig. B.1 does reveal some anticorrelation between Feature 5 and Feature 9 in SNe IIb. The physical causes for this anticorrelation could be related to the fact that SNe IIb are less stripped than the other SE SN subtypes, which may then result in low pEW values inferred for Feature 9 from spectra obtained around maximum light.
In the spirit of completeness, the Spearman’s rank correlation coefficients (ρ) between pairs of velocity (−vabs) measurements for the different SE SN subtypes are given in Fig. B.2.
 |
Fig. B.2. Spearman’s rank correlation coefficients (ρ) between pairs of velocity (−vabs) measurements. The color indicates the correlation coefficients with numeric values connected to colors as indicated by the mapping of the colorbar at the top of the figure. The lighter the color, the stronger the correlation. Contained within the triangle of each panel are the correlation coefficients between −vabs pairs computed from spectra obtained within the first three weeks relative to the time of B-band maximum. To highlight the relative significance of the Spearman’s rank correlation coefficient each of the squares are marked with a different white line where the white dotted, white dashed and white solid lines indicate −vabs pairs of low (0.4< |ρ| ≤0.6), moderate (0.6< |ρ| ≤0.8), and high (0.8< |ρ|) correlation coefficients, respectively. Gray squares are correlations of low statistical significance characterized by probability values (p-values) > 0.1. |
Appendix C: Classification and distinguishing SNe IIb and Ib several weeks past maximum
As seen in Fig. 10 and discussed in Sect. 6.2, our results indicate that it is possible to distinguish between SNe IIb and SNe Ib, even if the spectra are obtained a few weeks after maximum light. Previously, in the literature and in practice, there has been an appreciation that SNe Ib classified with spectra taken after maximum could be SNe IIb in disguise. Essentially, if the prevalent H features have disappeared, it is difficult to tell whether the objects in question are SNe IIb or SNe Ib. This is an important consideration for population level studies of SE SNe, or their progenitors, since many SNe Ib may either be excluded or contribute significantly to the final error budget.
Our PCA results provide a blueprint for overcoming this practical difficulty. Therefore, we outline an algorithm for applying our PCA results to past and future SE SN samples. Fundamentally, there are two different approaches. The first is seemingly harder one of creating and using a new template spectrum from a new or expanded sample, and determining appropriate PCs to use in the PCA. Second, using an established template from a literature sample (such as the template in this work), adding the new SNe only during the PCA phase (not into the template), and using the previously determined PCs of importance. Although the latter seems simpler, care must be taken to verify and keep the same PCs by not “overloading” the template sample, but also not washing out the new spectra. The simplest way to achieve this is by calculating the PCs for each new spectrum or SN, or small sets of spectra/SNe (a good rule of thumb is ≲10% of the template sample), and by verifying that the PCs can appropriately recreate the new input spectrum when added onto the template. Since both approaches have parts of the same basic steps, we now provide practical guidance on each step.
Create a template (mean) spectrum. Using spectra of similar wavelength range and not too dissimilar resolving power (i.e., not mixing high-, medium-, and low-resolution spectra), a common template for all SE SNe should be created. SNe with uncertain classification should be excluded if contamination by SNe Ia or SLSNe is possible, or if they make balancing the classes difficult. The template is a mean spectrum, defined by time and wavelength bins. We show that the wavelength range between 6000 to 7000 Å is an appropriate choice, and the limited range has the benefit of significantly aiding in including the maximum number of SNe for consideration, while excluding PCs borne of the SED shape instead of spectral features. Under ideal conditions, the time bins would be small, but our results show that even binning the entire sample together, from −20 to +40 days, is adequate.
Most importantly, care should be taken to not over-represent individual SNe with dense spectral coverage by ensuring that one or two SNe do not dominate the template at any time or wavelength bin. Similarly, bin sizes should be chosen to provide a relatively even mix of SN subtypes and a relatively uniform distribution in time, if a large time bin is chosen. The most appropriate choice of bin size is an investigation we leave to future work, but our results can be replicated using the previously mentioned 6000 to 7000 Å bin in the optical with a time bin covering the typical bell shaped light curves of SE SN up to 5-6 weeks past maximum. All spectra must be normalized to a common scale, where we have chosen this to be such that the mean flux is zero, which is a mathematically advantageous choice. We note that well sampled, diverse, high N literature template(s) could be constructed and used in the future.
Perform PCA on all of the spectra. The spectra to perform PCA on can be included in the template sample, or an appropriately robust literature template could be used. Our analysis in Sect. 5 already contains a detailed practical guide and software recommendation. The main point is that for each spectrum, a set of PCs is obtained, where the top few PCs correspond to the majority of the observed variation in the input spectrum compared to the template. A good check of having used enough PCs, and the appropriateness of PCA, is if the input spectrum can be approximately recreated by summing the PCs and adding them to the template spectrum. This verification gains increased importance if the input spectrum is not a part of the sample used to make the template. As discussed, it can be desirable to leave out the new input spectrum from the template sample to avoid the next step of selecting appropriate PCs.
It is important to highlight that, even when using a previously calculated template, all spectra, including the ones that went into the template, should be included in the PCA! Otherwise, the outcome will live in an entirely different PC space each time. However, this is not a requirement if the new spectra are numerous enough, and contain many secure classifications. Moreover, the most appropriate PCs will have to be re-derived, and systematic differences which make this more difficult are possible.
Select the strongest PCs corresponding to spectral features. Because the variability among SE SN subtypes is not random, the top PCs likely represent independent orthogonal processes. In our work, we found that in the limited range between 6000 Å to 7000 Å, the top PCs roughly corresponded to H and He features, while in the wider wavelength range the top PC represented SED color. However, the correlated nature of SN spectra might mean that the PCs constructed from a different template or sample can correspond to another feature, a mix of characteristics, or something even more difficult to interpret physically. To replicate our results and differentiate SNe IIb from SNe Ib, care should be taken to exclude the PC, if any, that corresponds to the overall SED shape/color, and focus on PCs which seem to correspond to spectral line features, even if the precise line cannot be identified. A plot like the top panels of our PCA Figs. 9 and 10 can be helpful, showing the contribution of each PC to the observed variability about the template.
In theory, the number of PCs can be anywhere from two to N. However, we show that two are enough for this task and allow a visually verifiable PC space to investigate. Multidimensional clustering and classification is difficult to visually interpret, but if employed, should be able to boost these results.
Optionally, using the strongest PCs corresponding to spectral features, the PC space which creates the greatest variation among known (template) SNe IIb, Ib, and Ic groupings should be created. One way of doing this is using rotated PCs as we have shown in Fig. 10. However, simple relations between the strongest PCs, or between PCs and epoch as in Fig. 9 can also work, as long as the separation between subtypes in observed.
Classification with clustering. Using the newly created or existing PC space, SNe Ib with spectra only at late time should be compared to the SN IIb and SN Ib groupings. In our work presented in Sect. 5.3.1, interlopers from the SNe IIb into SNe Ib class can be found with more than 80% completeness. The essential task is to create a decision boundary for classification in the PC space. This can be performed either by eye, or by using clustering analysis. Ultimately, this step will improve with increasing data size, allowing for more robust decision boundaries which take into account not just clustering, but the paths that various subtypes and sub-groups among the SN subtypes take in the PC space as they evolve. If using our template, a reasonable decision boundary is > 1 in the first rotated PC space represented by the x-axis of Fig. 9.
Technical details related to the clustering analysis. The K-means fitting was done robustly using 50 random restarts, and identifies the three most tightly bound clusters in the dataset without assuming any distribution. Following standard procedure by using the K-means results to initialize our GMM, we used the Expectation Maximization algorithm to find the best fit maximum log-likelihood for our GMM model. Unlike K-means which forces a single label on every item, GMM is a soft clustering algorithm which assigns a probability for each item being inside a cluster or not based on well known properties of Gaussian distributions. Therefore, the results in Table 3 assumes the label with the highest probability to be the correct one for calculating completeness of our GMM. While the means (centers) of our clusters are well separated, there is significant overlap at the two-sigma level for every cluster. This can be due to noise from the relatively low number of points or it could represent the fact that there is a continuum of classification between SE SN subtypes. However, the center of each cluster is well separated from the other. Only a minority of objects overlap between groupings or are interlopers. We note that our findings should be regarded with caution as (i) the sample is limited in size and wavelength range (∼1000 Å), and (ii) assumes no time-dependency among the sample, which is incorrect given the time-dependent nature of the spectral energy distributions of SE SNe.
All Tables
All Figures
 |
Fig. 1. Median spectrum for each SE SN subtype (black line) constructed from all of the spectra plotted in gray and listed in Table 1. The vertical dashed lines indicate 10 regions of interest. Regions 1–5, 9 and 10 are typically present in each SE SN subtype, while regions 6–8 are typically found in SNe IIb and SNe Ib and are usually most prevalent in the weeks after maximum light. Green lines in the middle panel are spectra of the high-velocity Type Ib SN 2004gq, and red lines plotted in the bottom panel correspond to the spectra of the Type Ic-BL SN 2009bb (dotted) and the unusual Type Ic SN 2009ca (dashed). These spectra were excluded in making the median spectra. Finally, the number of spectra used to create each median spectrum plotted in each panel is indicated within parenthesis located just below the given spectral subtypes. |
| In the text | |
 |
Fig. 2. Mean template spectra for the Type IIb SE SN subtype at epochs of −7 d, 0 d, +7 d, +14 d, and +21 d. The number of spectra used to construct each template is indicated within parenthesis below the corresponding epoch. Each numerically indicated spectral feature is labeled with its parent ion(s) as determined from SYNAPPS fits. Thin gray lines indicate the 1-σ error spectrum. |
| In the text | |
 |
Fig. 3. Mean template spectra for the Type Ib SE SN subtype at epochs of −7 d, 0 d, +7 d, +14 d, and +21 d. The number of spectra used to construct each template is indicated within parenthesis below the corresponding epoch. Each numerically indicated spectral feature is labeled with its parent ion(s) as determined from SYNAPPS fits. Thin gray lines indicate the 1-σ error spectrum. |
| In the text | |
 |
Fig. 4. Mean template spectra for the Type Ic SE SN subtype at epochs of 0 d, +7 d, +14 d, and +21 d. The number of spectra used to construct each template is indicated within parenthesis below the corresponding epoch. Each numerically indicated spectral feature is labeled with its parent ion(s) as determined from SYNAPPS fits. Thin gray lines indicate the 1-σ error spectrum. The vertical dashed line corresponds to the rest wavelength of C IIλ6580. |
| In the text | |
 |
Fig. 5. Pseudo-equivalent width values for Features 1–10 plotted vs. days relative to the epoch of T(B)max. The measurement symbols are encoded by SN subtype with SNe IIb appearing as blue triangles, SNe Ib as yellow squares, and SNe Ic as magenta squares. Filled shaded regions correspond to the mean ±1-σ standard deviation of a rolling window characterized with a size of ten days. The rolling windows are evaluated on epochs containing at least three distinct pEW measurements and two pEW measurements in the preceding and subsequent epochs. |
| In the text | |
 |
Fig. 6. Time evolution of the Doppler velocity at maximum absorption (−vabs) for Features 1–10 and color-coded by SE SN subtype. Shaded regions correspond to the standard deviation of the rolling mean computed using a window size of ten days and color-coded by spectroscopic subtype as indicated. The rolling windows are evaluated on epochs having a minimum of three measurements and at least two measurements before and after. We note that the peculiar SNe Ic 2009bb and 2009ca are excluded. |
| In the text | |
 |
Fig. 7. Results from PCA. Top: solid black line is the mean spectrum computed using all observed (i.e., 111) spectra obtained out to +40 d and over the spectral range of 3950–8700 Å. The shaded regions correspond to Mean spectrum + Amplitudei ⋅ PCi, yielding the range of amplitudes shown in the panel below. Here the blue shaded regions correspond to negative values, and the red regions correspond to positive values. Bottom: amplitude1 versus Amplitude2, color-coded by spectral subtype and with the intensity of colors corresponding to the phase of the observed spectra following the multicolumn colorbar located to the right. |
| In the text | |
 |
Fig. 8. Results from PCA. Top: solid black line is the mean PCA spectrum computing using all observed spectra obtained out to +70 d and covering the wavelength region 3950–7350 Å. Blue and red shaded regions correspond to the full range of Amplitudei with blue (red) corresponding to negative (positive) values. Vertical gray regions correspond to He I (PC2 panel) and H I (PC3 panel) related features (same as in Fig. 2), indicating that variation in PC2 corresponds strongly to Helium and in PC3 to Hydrogen. Bottom: amplitude2 versus Amplitude3, color-coded by spectral subtype with the intensity of colors corresponding to the phase of the observed spectra following the multicolumn colorbar located to the right. |
| In the text | |
 |
Fig. 9. Results from PCA. Top: full range of the linear combination of Amplitude2 and Amplitude3 determined after applying a θ = 30° rotation following Eq. (3). Over-plotted the mean spectrum (black line) determined from all spectra extending to +45 d and covering the wavelength range of 3950–7000 Å. Blue and red shaded regions correspond to the full range of the first rotated PC (0.87 ⋅ Amplitude3 − 0.50 ⋅ Amplitude2) with the blue corresponding negative values and red to positive. Balmer series features are indicated with gray regions as in Fig. 2. Bottom: the corresponding linear combination of Amplitude2 and Amplitude3, plotted versus phase. This particular linear combination separates particularly well between +20 d to +40 d the SNe IIb from the SNe Ib and SNe Ic. |
| In the text | |
 |
Fig. 10. Results from PCA. Top: linear combinations of the first two PCs determined from PCA applied to the spectra extending to +70 d and between 6000–7000 Å. Bottom: a linear combination of Amplitude1 and Amplitude2 plotted versus its orthogonal (30°) rotation. In addition to the CSP-I SE SN sample, PCA resutls are shown for the normal Type Ia SN 2013gy (Holmbo et al. 2019) and unpublished CSP-II spectra of the Type Ic superluminous SN 2015bn (Phillips et al. 2019). Solid curved lines highlight subtypes of He I-rich SE SNe (see Sect. 5.3). GMM clusters are indicated with one and two sigma contours for each cluster using dashed and dot-dashed lines (see Sect. 5.3.1 and Table 3), respectively. To guide the eye, curved arrows are over-plotted highlighting the temporal evolution of SNe IIb and SNe Ib. |
| In the text | |
 |
Fig. 11. Time-evolution of the Doppler velocity measured from the minimum of the He Iλ5876 feature. Each object is plotted with a unique combination of symbol and color where the color indicate subtype, with SN Ib plotted in blue and SN Ib in green. The three SN Ib plotted with filled symbols are SNe 2005bf, 2007Y, and 2007kj, and are identified as ‘flat-velocity’ SNe IIb by Folatelli et al. (2014), while others have referred to such objects as transitional SNe Ib/c (e.g., Hamuy et al. 2002; Stritzinger et al. 2009). Using classification criteria based on the pEW of Features 4 and 5 as discussed in this paper these objects are consistent with a Type Ib classification (see also Liu et al. 2016 and Prentice & Mazzali 2017 for additional discussion). |
| In the text | |
 |
Fig. 12. Spectroscopic time-series from +7 d to +23.2 d of the Type Ic SN 2005aw. The spectra are plotted in velocity space with the segments of data containing the He Iλλ5876, 6678, and 7065 features plotted on top of each other. As revealed from the PCA results and consistent the data, SN 2005aw exhibits discernible features likely formed by He I with −vabs ∼ 8500 km s−1. |
| In the text | |
 |
Fig. A.1. SYNAPPS fits (red lines) computed for mean template spectra (black lines) representing epochs of −7 d, +0 d, +7 d, +14 d and +21d. Each mean template spectrum was computed using data obtained within ±3.5 days relative to its specific epoch. Spectral features attributed to each ion are also plotted in black. |
| In the text | |
 |
Fig. A.2. SYNAPPS fits (red lines) computed for SE SN template spectra (black lines) representing epochs of −7 d, +0 d, +7 d, +14 d and +21d. Each mean template spectrum was computed using data obtained within ±3.5 days relative to its specific epoch. Spectral features attributed to each ion are also plotted in black. |
| In the text | |
 |
Fig. A.3. SYNAPPS fits (red lines) computed for SE SN template spectra (black lines) representing epochs of +0 d, +7d, +14 d and +21 d. Each mean template spectrum was computed using data obtained within ±3.5 days relative to its specific epoch. Spectral features attributed to each ion are also plotted in black. |
| In the text | |
 |
Fig. B.1. Spearman’s rank correlation coefficients (ρ) between pairs of pEW measurements. The colors of the boxes is associated with the correlation coefficient with numeric values indicated by the colorbar at the top of the figure. The lighter the color, the stronger the correlation. Contained within the triangle of each panel are the correlation coefficients between pairs of pEW measurements computed using spectra obtained up to three weeks post the epoch of B-band maximum. The relative significance of ρ for each pair is indicated through the use of white lines. Here white-dotted, white-dashed and white-solid lines correspond to pEW pairs having low (0.4< |ρ| ≤0.6), moderate (0.6< |ρ| ≤0.8), or high (0.8< |ρ|) correlation coefficients, respectively. Colored boxes with no white lines exhibit minimal correlation. Gray squares have low statistical significance and are characterized by probability (p) values p > 0.1. |
| In the text | |
 |
Fig. B.2. Spearman’s rank correlation coefficients (ρ) between pairs of velocity (−vabs) measurements. The color indicates the correlation coefficients with numeric values connected to colors as indicated by the mapping of the colorbar at the top of the figure. The lighter the color, the stronger the correlation. Contained within the triangle of each panel are the correlation coefficients between −vabs pairs computed from spectra obtained within the first three weeks relative to the time of B-band maximum. To highlight the relative significance of the Spearman’s rank correlation coefficient each of the squares are marked with a different white line where the white dotted, white dashed and white solid lines indicate −vabs pairs of low (0.4< |ρ| ≤0.6), moderate (0.6< |ρ| ≤0.8), and high (0.8< |ρ|) correlation coefficients, respectively. Gray squares are correlations of low statistical significance characterized by probability values (p-values) > 0.1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.