| Issue |
A&A
Volume 673, May 2023
|
|
|---|---|---|
| Article Number | A86 | |
| Number of page(s) | 33 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202245128 | |
| Published online | 10 May 2023 | |
The distribution of globular clusters in kinematic spaces does not trace the accretion history of the host galaxy
1
GEPI, Observatoire de Paris, PSL Research University, CNRS, Place Jules Janssen, 92195 Meudon, France
e-mail: giulia.pagnini@obspm.fr
2
Leibniz-Institut für Astrophysik Potsdam (AIP), 14482 Potsdam, Germany
3
Lund Observatory, Department of Astronomy and Theoretical Physics, Box 43, 221 00 Lund, Sweden
4
Observatoire de Paris, LERMA, CNRS, Sorbonne University, PSL Research University, 75014 Paris, France
5
Collège de France, 11 place Marcelin Berthelot, 75231 Paris, France
Received:
4
October
2022
Accepted:
24
February
2023
Context. Reconstructing how all the stellar components of the Galaxy formed and assembled over time by studying the properties of the stars that form it is the aim of Galactic archaeology. Thanks to the launch of the ESA Gaia astrometric mission and the development of many spectroscopic surveys in recent years, we are for the first time in the position to delve into the layers of the past of the Galaxy. Globular clusters play a fundamental role in this research field since they are among the oldest stellar systems in the MW and thus bear witness to its entire past.
Aims. As a natural result of galaxy formation, globular clusters did not necessarily all form in the Galaxy itself. Indeed, a fraction of them could have been formed in satellite galaxies accreted by the Milky Way over time. In recent years, there have been several attempts to constrain the nature of clusters (accreted or formed in the Milky Way itself) through the analysis of kinematic spaces, such as the E − Lz, Lperp − Lz, eccentricity − Lz, and the action space, as well as attempts to reconstruct the properties of the accretion events experienced by the Milky Way through time from this kind of analysis. This work aims to test a widely used assumption about the clustering of the accreted populations of globular clusters in the integrals of motions space.
Methods. In this paper we analyse a set of dissipationless N-body simulations that reproduce the accretion of one or two satellites with their globular cluster population on a Milky Way-type galaxy.
Results. Our results demonstrate that a significant overlap between accreted and ‘kinematically heated’ in situ globular clusters is expected in kinematic spaces for mergers with mass ratios of 1:10. In contrast with the standard assumptions made in the literature so far, we find that accreted globular clusters do not show dynamical coherence, that is, they do not cluster in kinematic spaces. In addition, we show that globular clusters can also be found in regions dominated by stars that have a different origin (i.e. a different progenitor). This casts doubt on the association between clusters and field stars that is generally made in the literature and is used to assign them to a common origin. By means of Gaussian mixture models, we demonstrate that the overlap of clusters is not only a projection effect on specific planes but is also found when the whole set of kinematic properties (i.e. E, Lz, Lperp, eccentricity, radial, and vertical actions) is taken into account. Overall, our findings severely question the recovered accretion history of the Milky Way based on the phase-space clustering of the globular cluster population.
Key words: Galaxy: formation / Galaxy: evolution / Galaxy: kinematics and dynamics / methods: numerical
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Our Galaxy, the Milky Way (MW), is a collection of hundreds of billions of stars mostly distributed in a disc that extends over distances of at least 20 kiloparsecs from the Galactic centre. The disc is surrounded by a diffuse stellar, oblate-shaped halo, which contains only a few percent of the total stellar mass of the Galaxy (Hartwick 1987; Deason et al. 2011, 2019; Belokurov et al. 2018). A stellar bulge-bar sits at the centre of the Galaxy and dominates the mass and light distribution in the inner kiloparsecs (e.g., Wegg & Gerhard 2013; Ness & Lang 2016). All these components are made of stars that have, on average, different properties in terms of ages, chemical abundances, and kinematics, thus suggesting different scenarios for their formation. Reconstructing how all these stellar components formed and assembled over time by studying the properties of the stars that compose them is the aim of Galactic archaeology.
In these last years, this field of research has seen a succession of fascinating new discoveries thanks to the launch of the ESA Gaia astrometric mission1 and the delivery of its catalogues comprising full 6D positions and motions for millions of stars (33 million stars have full 6D phase-space information in the Gaia Data Release 3; see Gaia Collaboration 2022). In addition, many spectroscopic surveys, such as the APOGEE survey with SDSS (Prieto et al. 2008) and the soon operational WEAVE@WHT (Dalton et al. 2012), MOONS@VLT (Cirasuolo et al. 2014, 2020), and 4MOST (de Jong et al. 2012) surveys, are aimed at complementing Gaia by providing detailed chemical abundances for millions of stars. We are, for the first time, in the position to delve into the layers of the far and recent past of our Galaxy, bringing to light the timeline of events that helped make the MW the galaxy that we observe today. Having survived billions of years through the MW’s changes, globular clusters (hereafter, ‘GCs’) observed today in the Galaxy bear witness to this entire past. In general, GCs are dense, gravitationally bound stellar systems distributed from the Galactic centre to the most remote regions of the Galaxy (up to 150 kpc from the Galactic centre; see Harris & Racine 1979; Harris 1996; Meylan & Heggie 1997). They are very luminous objects with typical masses of 105 M⊙ and are very compact, having sizes of only a few parsec (Harris et al. 2013; Baumgardt & Hilker 2018; Gratton et al. 2019). Being very old, typically older than 10 Gyr (Marín-Franch et al. 2009; Carretta et al. 2010; VandenBerg et al. 2013), GCs can serve as tracers of the early epochs of the Galaxy, as they contain precious information about its formation and evolution. At present, more than 160 GCs are known in the MW (see, for example, Baumgardt & Vasiliev 2021, for a recent derivation of their distances).
According to the ΛCDM cosmological paradigm, galaxy formation proceeds in a bottom-up scenario where small structures merge together to build up larger galaxies, such as those we observe today (White & Rees 1978). The MW is a prime example of this formation mechanism. For example, the discovery of the Sagittarius dwarf spheroidal galaxy, which is in the process of being accreted by our Galaxy and disrupted by its gravitational tidal field, has demonstrated this process (Ibata et al. 1994; Newberg et al. 2002; Majewski et al. 2003). Within this scenario, not only field stars but also GCs may be accreted (Penarrubia et al. 2009). Indeed, a fraction of the Galactic GCs may have been formed in satellite galaxies accreted by the MW over time, while the remaining fraction would have formed in situ, that is, in the Galaxy itself. This double nature of the Galactic GC system is now fully accepted, and evidence of this duality has come from analyses of observational data (Marín-Franch et al. 2009; Forbes & Bridges 2010; Dotter et al. 2010; Leaman et al. 2013; VandenBerg et al. 2013) as well as of models (Renaud et al. 2017; Kruijssen et al. 2019, 2020; Pfeffer et al. 2020; Chen & Gnedin 2022).
In recent years, there have been several attempts to constrain the origin of clusters (accreted or formed in the MW itself) and to reconstruct the properties (e.g., mass, numbers) of the accretion events experienced by the MW through time. Concerning GCs originally belonging to satellite galaxies that are still being accreted (e.g., the Sagittarius dwarf galaxy), it is possible to reconstruct their origin from the similarity between their positions, velocities, and orbits and those of stars belonging to the tidal stream tracing the ongoing accretion (Bellazzini et al. 2020). However, for GCs that were accreted in the past, such an approach is not feasible since the systems accreted long ago are expected to be spatially mixed with the in situ population of GCs, and as a consequence, these systems should have lost all spatial coherence. Since the publication of the Gaia DR2 catalogue (Gaia Collaboration 2018a) and the access to phase-space information for almost the entire cluster population (Gaia Collaboration 2018b; Vasiliev 2019b), different works have tried to establish the accreted or in situ nature of Galactic GCs using kinematic spaces, such as the energy-angular momentum space (hereafter, E − Lz, where E is the total orbital energy and Lz is the z component of the angular momentum space in a reference frame with the Galactic disc in the xy plane). Under the hypothesis that accreted clusters conserve a dynamical coherence even several billion years after their accretion onto the Galaxy (i.e. they cluster in kinematic spaces) and that different groups are related to different accretion events (Helmi & de Zeeuw 2000), Galactic GCs located in different regions of the E − Lz space have been associated to different progenitors (see for example Massari et al. 2019). Since the models in Helmi & de Zeeuw (2000) assume an analytic and static Galactic potential and no dynamical friction is taken into account, the energies and angular momenta of the accreted satellites are conserved overall by definition. Thus, the fact that accreted GCs stand out as clumps in the E − Lz space corresponding to different satellites is generally a direct consequence of the assumptions made in a model rather than an intrinsic feature of the accretion event.
In addition to the E − Lz space, the Lperp − Lz space (where Lperp is the projection of the total angular momentum onto the Galactic plane) has been used several times as a natural space to search for the presence of stellar currents ever since the initial work of Helmi & de Zeeuw (2000). This approach has been carried out by assuming that Lperp, though not strictly conserved, varies only marginally during a merging process. In particular, the Helmi stream has been identified in the Lperp − Lz space as a localised overdensity in the prograde region (Lz > 0) with a high orbital inclination (high Lperp; see, for example, Helmi et al. 1999; Kepley et al. 2007; Koppelman et al. 2019). Consequently in the literature, this space has also been applied in order to retrieve the origin of GCs together with the E − Lz space (see for instance Massari et al. 2019). Eccentricity is another important parameter in describing an orbit that has been used, for instance, to separate the Gaia-Sausage-Enceladus debris from the rest of the stellar halo (e.g., Belokurov et al. 2018; Mackereth et al. 2019; Naidu et al. 2020). In particular, the eccentricity − Lz plane has been suggested by Lane et al. (2022) as another tool to identify accreted systems (see also Cordoni et al. 2021). Another kinematic space that has been considered in the literature is the action space where the horizontal axis is the (normalised) azimuthal action (Jϕ/Jtot ≡ Lz/Jtot, where 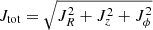 ), while the vertical axis is the (normalised) difference between the vertical and radial actions ((Jz − JR)/Jtot). The action space has been suggested as the ideal plane to identify and study possible substructures and debris from accretion events (e.g., Myeong et al. 2018, 2019; Vasiliev 2019b; Lane et al. 2022) since actions are nearly conserved under the hypothesis that the potential is slowly evolving (Binney & Spergel 1982).
), while the vertical axis is the (normalised) difference between the vertical and radial actions ((Jz − JR)/Jtot). The action space has been suggested as the ideal plane to identify and study possible substructures and debris from accretion events (e.g., Myeong et al. 2018, 2019; Vasiliev 2019b; Lane et al. 2022) since actions are nearly conserved under the hypothesis that the potential is slowly evolving (Binney & Spergel 1982).
Dynamical coherence is the common thread that has guided the interpretation of the kinematic spaces just listed, leading to several tentative reconstructions of the merger history of the MW. For instance, by making use of the GC classification proposed by Massari et al. (2019), Kruijssen et al. (2020) inferred the stellar masses and accretion redshifts of five satellite galaxies accreted by our Galaxy over time, namely, Kraken (Kruijssen et al. 2019), the Helmi stream (Helmi et al. 1999), Gaia-Sausage Enceladus (Nissen & Schuster 2010; Belokurov et al. 2018; Haywood et al. 2018; Helmi et al. 2018), Sequoia (Myeong et al. 2019), and the still accreting Sagittarius galaxy (Ibata et al. 1994). Malhan et al. (2022) recovered other past mergers such as Cetus (Newberg et al. 2009), Arjuna/Sequoia/I’itoi (Naidu et al. 2020), and LMS-1/Wukong (Yuan et al. 2020) and discovered a possible new merger called Pontus (see also Malhan 2022). The classification by Massari et al. (2019), slightly revised, has been also used by Forbes (2020), who combined it with ages, metallicities, and [α/Fe] abundances of GCs to reconstruct the properties of their progenitor galaxies, while the classifications by Kruijssen et al. (2019) and Malhan et al. (2022) have been used by Hammer et al. (2023) to estimate their infall time.
However, the assumptions used in the previous cited works, namely, the hypothesis that accreted clusters should show a dynamical coherence, has not been proven, even as several works have started doubting it. For example, various simulations have shown that even a single merger debris span over the large range in the E − Lz space (Jean-Baptiste et al. 2017; Grand et al. 2019; Simpson et al. 2019; Koppelman et al. 2020), where, for instance, chaotic mixing may further affect the coherence of the tidal debris (Vogelsberger et al. 2008; Price-Whelan et al. 2016). Moreover, a single merger could result in a number of features or overdensities in the E − Lz space (Jean-Baptiste et al. 2017; Grand et al. 2019; Koppelman et al. 2020). Finally, neither E nor Lz are conserved quantities in the case of an evolving and non-axisymmetric galaxy due to the substantial mass growth of the galaxy over time (Panithanpaisal et al. 2021) and the pericentric passages of massive satellites (Erkal et al. 2021; Conroy et al. 2021) perturbing both accreted and in situ components of the halo.
In this paper, we thus wish to test the hypothesis of dynamical coherence in the E − Lz space as well as the other above-cited spaces by analysing N-body simulations of the accretion of satellite galaxies and their GC systems onto a MW-type galaxy containing its own system of clusters. We focus on mergers with mass ratios of about 1:10 because MW-type galaxies are expected to have experienced mergers of similar mass (i.e. relative to the MW at the time of the accretion; see for example Deason et al. 2016; Renaud et al. 2021; Khoperskov et al. 2022a) and also because this is roughly the mass ratio estimated for the Gaia-Sausage-Enceladus accretion event (see Helmi et al. 2018, but also Kruijssen et al. (2020) for a lower estimate). It is worth mentioning that some studies have considered even higher Gaia-Sausage-Enceladus masses (e.g., a 1:5 mass ratio in Naidu et al. 2020). As detailed in the next sections, our analysis demonstrates that for such mass ratios, accreted GCs do not show the claimed grouping in energy-angular momentum space nor in other kinematic spaces, which is in agreement with the results of numerical simulations modelling the population of field stars (see Jean-Baptiste et al. 2017; Amarante et al. 2022; Khoperskov et al. 2022a,b). This finding has strong implications for the reconstruction of GCs kinematic-based galaxy membership and questions the accretion history of our Galaxy, as traced so far in the literature (Massari et al. 2019; Myeong et al. 2019; Forbes 2020; Kruijssen et al. 2020; Malhan et al. 2022).
This paper is organised as follows: In Sect. 2, we present the numerical method and the characteristics of the simulations. In Sect. 3, we present the results of this study. We focus our analysis firstly on the spatial distribution of accreted and in situ GCs (Sect. 3.1) and secondly on their distribution in the E − Lz plane (Sect. 3.2), and we generalise our results, showing also how GCs redistribute in other kinematic spaces, such as the Lperp − Lz and the eccentricity − Lz planes as well as the action space (see Sect. 3.3). Finally, we apply a Gaussian mixture model (GMM) to the outcomes to check whether such a procedure is able to retrieve the real accretion history of the simulated galaxies (Sect. 3.4). Motivated by our findings, we reconsider the classification of Galactic GCs made on the basis of their distribution in the E − Lz plane (Massari et al. 2019), showing that this classification cannot be supported by the age-metallicity relation (AMR) described by these clusters (see Sect. 4). Last, we present our conclusions (Sect. 5).
2. Numerical method
2.1. Main simulations
In this paper, we analyse 14 dissipationless, high-resolution N-body simulations of a MW-type galaxy accreting one or two satellites. These simulations are similar to those presented in Jean-Baptiste et al. (2017). As comprehensively explained in that paper, in the simulations both the satellite(s) and the MW-type galaxy can react to the interaction and experience kinematical heating, tidal effects, and dynamical friction. Each satellite has a mass that is 1:10 of the mass of the MW-like galaxy, and this choice is motivated by the fact that mergers with these mass ratios are inevitable for MW-type galaxies in ΛCDM simulations (Read et al. 2008; Stewart et al. 2008; De Lucia & Helmi 2008; Deason et al. 2016). Both the main galaxy and the satellite(s) are embedded in a dark matter halo and contain a thin, an intermediate, and a thick stellar disc - mimicking the Galactic thin disc, the young thick disc, and the old thick disc, respectively (see Haywood et al. 2013; Di Matteo 2016). A population of GCs initially redistributed in a disc is also taken into account, and this population is represented as point masses.2 The total number of particles used in these simulations is Ntot = 27 500 110 for the case of a single accretion and Ntot = 30 000 120 when two accretions are modelled. The total number of stellar particles (i.e. thin, intermediate, and thick disc) in the main galaxy is 20 000 000, the number of GC particles is 100, and the number of dark matter particles is 5 000 000. The satellite galaxies are re-scaled versions of the main galaxy with masses and a total number of particles ten times smaller and sizes reduced by a factor . All these values are listed in Table 1. The discs were modelled with Miyamoto-Nagai density distributions (Miyamoto & Nagai 1975) of the form:
. All these values are listed in Table 1. The discs were modelled with Miyamoto-Nagai density distributions (Miyamoto & Nagai 1975) of the form:
Masses, characteristic scale lengths and heights, number, and mean masses of particles for the different components of the MW-type galaxy and the satellite(s).
where masses (M*), characteristic lengths (a*), and heights (h*) vary for the thin, intermediate, and thick disc populations (see Table 1). The system of disc GCs has a scale length and scale height equal to those of the thick disc. The dark matter halo was modelled as a Plummer sphere:
The characteristic mass (Mdm) and radius (adm) are listed in Table 1. The choice of using a core dark matter halo for both the MW-type galaxy and the satellite(s) comes from various observational evidence that seems to be more consistent with a dark halo profile with a nearly flat density core (Flores & Primack 1994; De Blok et al. 2001; Marchesini et al. 2002; Gentile et al. 2005; De Naray et al. 2008). The final N-body models of the main disc galaxy and of the satellite were built by using the iterative method described in Rodionov et al. (2009). We note that we do not include any significant spheroidal bulge in our model, since the contribution of a classical bulge to the total stellar mass of the MW has been shown to be limited to a few percentage points (see, for example, Shen et al. 2010; Kunder et al. 2012; Di Matteo et al. 2015; Gómez et al. 2018), nor any population of halo clusters before the interaction(s); as previously stated, the GCs are all initially confined in the disc. The inner regions of the Galaxy are indeed dominated by a stellar bar whose impact on the kinematics and distribution of GCs has recently started to be explored (see for instance Pérez-Villegas et al. 2020).
Once the N-body systems, which represent the main galaxy and the satellite, were generated, we translated the barycentre of the satellite galaxy to the (xsat, ysat, zsat) positions and assigned it velocities (vx, sat, vy, sat, vz, sat) in order to have a parabolic orbit where the satellite is initially at a distance of 100 kpc from the MW-type galaxy. For each 1 × (1:10) interaction, we also varied the initial orientation of the satellite orbital plane (Φorb) by rotating it about the y-axis in such a way that it spanned a range of possible orientations, including prograde orbits (Φorb = 0° ,30° ,60°, with Φorb = 0° being the planar, prograde orbit), a polar orbit (Φorb = 90°), and retrograde orbits (Φorb = 120° ,150° ,180°, with Φorb = 180° being the planar, retrograde orbit). For the 2 × (1:10) interactions, we used a combination of the initial orbital conditions adopted for the single 1 × (1:10) mergers as the initial orbital conditions of the two satellites. All these initial values for the 14 simulations (seven 1 × (1:10) and seven 2 × (1:10)) are reported in Table 2. In this table, each simulation has been given an identifier in the form ‘MWsat_nN_Φα1(−α2)’, with N being the number of satellites in the simulation and α1 (α2) as the angles of the satellite(s) orbital plane(s) relative to the x − y plane. As for the initial inclination of the satellite disc, each satellite has an internal angular momentum whose initial orientation was assigned as being parallel to the z-axis of the host.
Initial positions and velocities of the barycentres of the simulated satellite galaxies.
2.2. Additional simulations
A couple of simulations with mass ratio 1:10 (namely, the simulations with ID MWsat_n1_Φ60 and MWsat_n2_Φ30-150) were rerun in a static Galactic mass distribution, artificially imposing that the latter simulation was not influenced by the accretion of the satellite(s). This experiment allowed us to study how the results of the present work would change if dynamical friction exerted by the MW-like galaxy on the satellite and on the clusters was neglected (see Appendix A).
Finally, the 1:10 mass ratio simulations were complemented through a set of seven simulations with mass ratio 1:100 and whose initial conditions and analyses are presented in Appendix B. The aim of these simulations was to show the distribution of clusters from low-mass galaxies in kinematic spaces.
All simulations were run by making use of the TreeSPH code described in Semelin & Combes (2002). Gravitational forces were calculated using a tolerance parameter3θ = 0.7 and include terms up to the quadruple order in the multiple expansion. A Plummer potential was used to soften gravitational forces, with constant softening lengths for different species of particles. In all the simulations described, we adopted ϵ = 50 pc. The equations of motion were integrated using a leapfrog algorithm with a fixed time step of Δt = 2.5 × 105 yr.
In this work, we make use of the following sets of units: Distances are given in kiloparsec, masses in units of 2.3 × 109 M⊙, velocities in units of 100 km s−1, and G = 1. Energies are thus given in units of 104 km2 s−2 and time is in a unit of 107 years. With this choice of units, the stellar mass of the MW-type galaxy at the beginning of the simulation is 8.4 × 1010 M⊙.
3. Results
In this section, we present and discuss the effect of one or two 1:10 mass ratio accretions on the MW-type galaxy, focusing our attention on the resulting GC system. We concentrate our analysis on understanding how accreted and in situ clusters distribute themselves spatially in the final galaxy, what information about the in situ or accreted nature of clusters can be extracted from the so-called integrals-of-motion spaces, and whether we can use the kinematic information contained in the Galactic GC system today to trace the accretion history of the Galaxy.
We show and discuss first the spatial distribution of accreted and in situ GCs (Sect. 3.1); second, we discuss their distribution in the E − Lz plane (Sect. 3.2); and finally, we generalise our results by showing how GCs also redistribute in other kinematic spaces and applying a GMM to the outcomes to check whether such an approach is able to provide robust information about the accretion history experienced by the remnant galaxy (Sect. 3.3).
In the following analysis, all quantities are evaluated in a reference frame whose origin is at the centre of the MW-type galaxy with the spin of the MW-type galaxy oriented as the z-axis and positive. The centre is evaluated at each snapshot of the simulations as the density centre following the method described in Casertano & Hut (1985).
3.1. Spatial distribution of accreted and in situ clusters
Figure 1 shows the GC projections in the x − y and x − z planes from one of the seven single-accretion simulations (Φorb = 60°; i.e. simulation ID = MWsat_n1_Φ60) at different times: the initial time (T = 0 Gyr), two intermediate times (T = 1 Gyr, 2.5 Gyr), and at the final time (T = 5 Gyr). The distribution of field (in situ and accreted) stars is also shown in the background.
 |
Fig. 1. Time evolution of the simulated merging process. Left, middle columns: projections of the simulated GC positions on the x − y and x − z planes for different times of the single-accretion simulation with Φorb = 60° (MWsat_n1_Φ60). (See Table 2 for the initial parameters.) The times increase from top to bottom. The in situ clusters are represented by grey circles and the accreted clusters by magenta circles. In the background, the surface density of the totality of the stars of the simulation is also shown. Right column: distributions of accreted GCs and field stars of the same satellite in the E − Lz space for different times of the single-accretion simulation MWsat_n1_Φ60. The times increase from top to bottom. Each GC is colour-coded according to its escape time from the progenitor satellite, which is also specified by the number on the top right and increases from 0.42 Gyr for GC1 to 5 Gyr for GC10 (see Sect. 3.2 for the definition of tesc). |
At the beginning of the simulation, the Galactic and satellite GC systems as well as the corresponding field stellar particles all had an axisymmetric disc distribution. This initial axisymmetric configuration of the clusters and field stars was rapidly disturbed by the first satellite passage (occurring at T ≃ 0.3 Gyr; see Fig. 2) at time T = 1.0 Gyr. The satellite disturbed the outer parts of the disc of the MW-type galaxy, which had developed an extended spiral-like structure. In the meantime, the outer parts of the satellite were tidally disrupted by the main galaxy, and one of the clusters originally associated with the satellite escaped to join the outer parts of the massive galaxy. The vertical structure of the disc of the massive galaxy and the corresponding cluster system also started to be kinematically ‘heated’ at this time. As seen from the edge, the disc had thickened, and it showed tidal plumes in the outer parts. The plumes were partly caused by tidal pulls of the satellite and partly by in situ stars disturbed by the interaction. This kinematic heating was the result of the redistribution of a fraction of the orbital energy of the satellite into internal energy of the stars in the merger remnant (see, for example, Quinn et al. 1993; Walker et al. 1996; Villalobos & Helmi 2008; Zolotov et al. 2009; Purcell et al. 2010; Di Matteo et al. 2011; Qu et al. 2011; McCarthy et al. 2012; Cooper et al. 2015; Jean-Baptiste et al. 2017). At T = 2.5 Gyr the merging process was towards the end, and this stage of the accretion is also visible in Fig. 1, as the stellar distribution of the satellite is no longer clearly separated from that of the main galaxy and most of its GCs are now part of the bulk of the MW population. However, a series of tidal plumes and two GCs originating from the satellite that have not yet been trapped by the MW-type galaxy can still be seen in the x − y and x − z maps in the third row of Fig. 1. At the final time of the simulation (T = 5 Gyr), the majority of the clusters (in situ and accreted) were located in the inner densest regions of the final galaxy – if it were not for the different colours in the figure, they would not be distinguishable from each other.
 |
Fig. 2. Time evolution of accreted and in situ GCs distances from the MW-type galaxy. Top panel: time evolution of the distances of the satellite (black line) and its GCs (coloured lines) from the MW-type galaxy for the simulation MWsat_n1_Φ60. Each GC is colour-coded according to its escape time from the progenitor satellite. Bottom panel: time evolution of the apocentres of the orbits of all in situ clusters in the MW-type galaxy for the simulation MWsat_n1_Φ60. Thick and coloured lines indicate clusters whose orbital apocentres at the final time of the simulation are at least 1.5 times larger than their corresponding initial values. The lines are colour-coded according to the ratio of the final apocentre over the initial apocentre. |
The decay of part of the accreted clusters in the innermost regions of the remnant can be understood because these are the clusters that remain gravitationally bound to the satellite until the final phases of the merger. It is primarily the dynamical friction experienced by the satellite to which these clusters belong that makes them decay towards the centre of the main galaxy. It is only when these clusters become gravitationally unbound from the satellite that their motions decouple from their progenitor galaxy. This can be appreciated in Fig. 2 where we show, for the case of the simulation MWsat_n1_Φ60, the temporal evolution of the distance of the satellite to the main galaxy along with the corresponding evolution of all the clusters initially bound to the satellite. Soon after the first pericentre passage, the satellite can be seen to lose one of its clusters, which becomes trapped on an orbit with apocentre at about 40 kpc, while the satellite itself moves to its first apocentre, at about a distance of 95 kpc from the main galaxy centre. A second cluster is lost by the satellite at its next pericentre passage (T = 2 Gyr). The cluster lost at this time is ejected onto a high-energy orbit that has an apocentre at more than 140 kpc from the centre of the MW-type galaxy. Over the entire duration of the merging process, this loss of the satellite clusters from their progenitor leads to their redistribution over a large range of distances (pericentres and apocentres) from the merger remnant at the final time. While clusters associated to the satellite galaxy are lost at different times of the interaction, and hence contribute to populating both the outer and inner regions of the remnant galaxy, clusters initially in the MW-type galaxy, which we highlight were initially distributed in a disc-like configuration, have their orbits perturbed by the interaction. In the bottom panel of Fig. 2, we show the evolution with time of the orbital apocentres, computed as the maxima of the 3D distance, of all the 100 clusters in the MW-type galaxy. The GCs whose orbital apocentres at the end of the simulation are at least 1.5 times larger than their corresponding initial values are shown as thick and colour-coded lines. As shown in the figure, the orbital apocentre of 14% of the clusters increased by a factor of 1.5 at least, and for some of the clusters, this kind of kinematical heating coincides with the last phases of accretion of the satellite (around T = 2 Gyr). The number of kinematically heated clusters increased to 27% when we considered GCs that had their final orbital apocentre increased by at least a factor of 1.2.
3.2. Energy-angular momentum space
All the results presented in this section concern the distribution of GCs in the energy-angular momentum space (E − Lz) in the case of a MW-type galaxy accreting one or two satellites. This space has been proposed as the natural place for one to look for the signatures of past accretion events (Helmi & de Zeeuw 2000).
3.2.1. Accreted clusters
We start our analysis with the case of a single accretion. In Fig. 1 (right column), we show the distribution in the E − Lz space of the accreted clusters in the case of the Φorb = 60° simulation (ID=MWsat_n1_Φ60), at different times (T = 0, 1, 2.5, 5 Gyr). (These times correspond to those for which the x − y and x − z maps are shown in the left and middle columns of the same figure.) In these E − Lz plots, we also report, for each cluster, the escape time from its progenitor satellite. This escape time has been estimated by means of a simple spatial criterion, that is, it is defined as the time when the distance between the GC and the centre of mass of the parent satellite is larger than 15 kpc. For comparison, the distribution in the E − Lz space of field stars of the satellite is also plotted in the background. At the beginning of the interaction, the distribution of satellite stars and GCs is clumped in the E − Lz space and characterised by high energy. This is understandable because the satellite is, at the beginning of the simulation, a gravitationally bound system. At T = 1 Gyr, the satellite is close to an apocentre passage (see Fig. 2), resulting in a broad extent in Lz4. Globally, as an effect of dynamical friction, the energy and the absolute value of the angular momentum decrease, and the satellite penetrates deeper and deeper into the potential well of the main galaxy. This results in a distribution with a funnel-like shape, as the satellite’s stars and GCs tend to be spread in energy but converge in angular momentum. Table 3 lists the mean and standard deviation of the initial and final Lz and E of the accreted GCs, and it quantifies this trend well. In fact, the final Lz results are on average closer to zero and less spread, while the energy is on average lower and more dispersed. In general, clusters lost in late phases of the interaction have low orbital energies, that is, they tend to be found in the potential well of the merger remnant, while clusters lost in the early phases of the satellite accretion tend to be positioned in the upper part of the E − Lz plane (i.e. at high energies). (We refer the reader to Appendix A to see how this behaviour changes when considering a static MW-type potential where the satellite does not experience dynamical friction). This tendency is clear in Fig. 3 where the final energy of all the accreted clusters in all the 1 × (1:10) simulations is shown as a function of the escape time from their satellites (tesc), as clusters lost in the early phases of the interaction (low tesc) tend to have higher energies than clusters lost at more advanced stages of the merging process. In Fig. 3 three main groups can also be identified: the first consists of GCs with tesc < 1 Gyr, the second is of GCs with 1.8 Gyr < tesc < 3.6 Gyr, and the last is of GCs with tesc = 5 Gyr. The first two groups are associated with GCs lost either at the first or subsequent pericentric passages. The GCs with tesc = 5 Gyr are those that did not escape from the satellite before the end of the merging process. From the colour coding of GCs in Fig. 3, it is possible to also notice that the clusters that escaped from the progenitor satellite the earliest are those that were initially less bound to their progenitor. They are indeed the clusters with the highest values of Eint, where Eint is the sum of the kinetic energy of clusters in the satellite and of their potential energies, both estimated relative to the satellite centre. As expected, GCs that are more tightly bound to the satellite tend to escape later and have a lower final energy relative to the MW-type galaxy reference system. However, Fig. 1 (bottom-right panel) illustrates that this trend has a number of exceptions. For instance, at the end of the simulation, the cluster lost at ≃2.59 Gyr has lower energy (E ≈ −9.5) than the clusters lost later at ≃3.05 Gyr (E ≈ −8.0). Additionally, the GC lost at 0.58 Gyr has a higher energy than the cluster lost at 0.42 Gyr by the end of the simulation. This happens because after leaving their parent satellite, the energy and angular momentum of the GCs may change due to changes in the gravitational potential induced by the final phases of accretion of the same satellite.
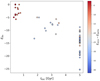 |
Fig. 3. Final energy of all the accreted clusters in the single-accretion simulations as a function of their escape time from their satellites (tesc). The colour coding indicates the clusters’ initial energy in the reference frame of their progenitor satellite. |
Mean and standard deviation of the initial and final Lz and E for the populations of accreted GCs within the different single-accretion simulations.
When two satellites are accreted, the interpretation of the energy-angular momentum space becomes even more complex (see also Trelles et al. 2022). Figure 4 (left-middle panel) shows the distribution in the E − Lz space of the GCs originally belonging to the two satellites for the accretion simulation MWsat_n2_Φ30 − 150. The background density maps show the fractional contribution of stars from satellite 1 (left panel) and satellite 2 (middle panel) relative to the totality of stars. As shown in the figures, the GC populations of the two satellites mix and overlap with each other. Furthermore, the cluster distribution does not necessarily coincide with the distribution of the stars of the same satellite. For example, nearly half of the GC population belonging to satellite 1 is redistributed in a region of the E − Lz space dominated by stars of satellite 2 (see middle panel). The contribution of the stars belonging to satellite 1 is still significant in this region, but not exclusive. Therefore, the stellar halo substructures and accreted GCs located in the same E − Lz regions can not be directly associated with the same dwarf galaxy progenitor accreted in the past, as regions of the E − Lz space dominated by stellar populations of a given progenitor can indeed contain a significant number of clusters (and stars) originating from a different progenitor.
 |
Fig. 4. Accretion of two satellites on the MW-type galaxy (MWsat_n2_Φ30-150). Left-middle panel: distribution in the E − Lz space of GCs originally belonging to the two satellites (magenta and white colours, respectively). The density maps show the fractional contribution of stars from satellite 1 (left panel) and satellite 2 (middle panel) relative to the totality of the stars. Right panel: distribution in the E − Lz space of GCs originally belonging to the two satellites (magenta and white colours, respectively) and to the MW-type galaxy (grey circles). The density map shows the fractional contribution of stars from the two satellites relative to the totality of the stars. |
3.2.2. In situ clusters
The right panel of Fig. 4 shows the distribution in the E − Lz space of GCs originally belonging to the two satellites (distribution equal to that in the left and middle panels) with the addition of GCs belonging to the MW-type galaxy. The density map illustrates the fractional contribution of the stars from the two satellites relative to the totality of stars. This panel also allows us to show an additional result: Part of the in situ cluster population overlaps with the accreted clusters in the E − Lz space. This in situ population is made of disc clusters that have been perturbed enough by the interaction to be ‘pushed’ into the halo (see also Fig. 2, bottom panel), following the same dynamical mechanism extensively discussed for in situ field stars (see, for example, Zolotov et al. 2009; Purcell et al. 2010; Qu et al. 2011; Jean-Baptiste et al. 2017; Khoperskov et al. 2022b). We emphasise that, by construction, our modelled MW-type galaxy does not contain any population of halo clusters before the interaction(s), as they are all initially confined in the disc. This implies that the overlap of in situ GCs with satellite GCs could be even more significant if part of the in situ population already had halo-like kinematics before the accretion(s). We further address this issue in Sect. 3.5. Interestingly, when comparing the distribution of GCs with the distribution of stars in the right panel of Fig. 4, we noticed that a part of the in situ GC population is found in regions of the E − Lz space dominated by stars accreted from the two satellites. All this consequently affects the interpretation of the E − Lz space, as the stars and clusters cannot be associated to the same origin (i.e. the same progenitor galaxy) simply because they are found at similar values of E and Lz. Specifically, clusters from a satellite can be found in regions where the stellar density distribution is dominated by another satellite (middle panel, Fig. 4), and clusters originally in the main galaxy can be found in regions of the E − Lz space dominated by accreted stars (right panel Fig. 4).
Regarding the possibility of separating in situ clusters from accreted clusters, it is of interest to cite the numerical work by Callingham et al. (2022), who constructed mock catalogues of accreted and in situ clusters from the AURIGA simulations, reporting that ‘the total in situ population is, in general, well recovered with very high purity. Rarely does the methodology misidentify an accreted GC as an in situ one in our mock tests, with a median purity of 98%.’ This conclusion clearly contradicts our results, but it can be explained by the fact that though the accreted GC populations in the work of Callingham et al. (2022) are drawn from the AURIGA simulations, the in situ GCs were added a posteriori (that is, they were not extracted self-consistently from the AURIGA simulations, as it was done for the accreted population). In their work, the in situ GCs are constructed to be either in the bulge or in the disc, and they did not allow the possibility for part of the in situ GC population to have halo-like kinematics (which is indeed the case, as we have shown, when part of a pre-existing disc GC population is heated by a merger). The reason they could separate the in situ disc GCs from accreted GCs in kinematic spaces so well (see for example the E − Lz diagram shown in their Fig. 3) is due to the way they constructed the in situ GC population, and it is not a result of a self-consistent evolution of the in situ population itself during the merger(s). It would have been interesting, and more realistic, to also draw the in situ GC population from the AURIGA simulations by randomly extracting stars formed in the AURIGA MW-like progenitors. If this was the case, we argue that the separation of in situ components from accreted components would have been more challenging in their models.
3.2.3. Overlap in the E − Lz space
Figure 5 shows the final GC distribution in the E − Lz space for the whole set of 1 × (1:10) accretion simulations. The distribution of the in situ GCs from all the simulations at T = 5 Gyr has been stacked in the figure. This figure summarises the results presented so far. Regardless of the initial inclination of the satellite orbital plane, the overlap between the accreted and in situ GCs is clear and becomes critical in the most gravitationally bound regions. This may be partly caused by the narrowing of the Lz range at high binding energies, but it may also reflect the tendency of high-mass ratio mergers to radialise their orbits (e.g., Amorisco 2017; Naidu et al. 2020; Vasiliev et al. 2022). The figure also shows that, in the case of a single accretion, the angular momenta of clusters at high energies (E ≳ −10 in our units) correlate with the inclination of the orbital plane of the infalling satellite at early times. Therefore, the higher the orbital inclination Φorb of the parent satellite, the less prograde (lower Lz) the orbits of the clusters are. In the following paragraph, we show that this trend is less prominent in the case of two accretions.
 |
Fig. 5. E − Lz distribution for the whole set of 1 × (1:10) merger simulations at T = 5 Gyr. The distribution of the in situ population of GCs has been stacked and is shown by the grey circles. The colour coding of accreted GCs is according to the initial inclination of the satellite orbital plane with respect to the MW-like reference frame, Φorb. |
Figure 6 shows the distribution in the energy-angular momentum plane of the whole set of GCs in the 2 × (1:10) accretion simulations. In the figure, the distribution of the in situ population of the GCs has been stacked. As we show in Fig. 6, the in situ and accreted GCs overlap almost everywhere in the E − Lz space. Only for E ≳ −6, and/or Lz ≲ −3 in principle, can the two groups be distinguished. Even in that case, however, it is not possible to identify from which of the two satellites the clusters originate because, as mentioned above, these clusters appear mixed, that is, the clusters originating from different satellites can have similar energies and angular momenta by the end of the simulation. Moreover, the trend between Φorb and the final Lz found for high-energy clusters in the case of a single accretion is no longer evident in the case of the two mergers. Looking, for example, at the case of satellites accreted with an initial orbital inclination of Φorb = 180° (such as for the simulations MWsat_n2_Φ0-180 and MWsat_n2_Φ180-90), the final distribution of their clusters in the E − Lz plane is different for the two 2 × (1:10) simulations (compare the top-left and top-right panels of Fig. 6). This distribution also appears different from the one generated by clusters whose progenitor is on a Φorb = 180° inclination orbit, in the case of a single accretion (Fig. 5). This indicates that unless there are strong reasons to think that the Galaxy experienced only one main massive accretion (and not several), we cannot infer the inclination of the progenitor satellite based on the current distribution of its accreted GC population.
 |
Fig. 6. E − Lz distribution for the whole set of 2 × (1:10) merger simulations at T = 5 Gyr. The distribution of the in situ population of GCs has been stacked and is shown by the grey circles. The colour coding of the satellite GCs (satellite 1: left panel; satellite 2: right panel) is according to the initial inclination of the satellite orbital plane with respect to the MW-like reference frame, Φorb. |
From this analysis, we conclude that the only merger events that in principle could be distinguished in the E − Lz plane are: (1) those that are still occurring and for which the population of GCs that the satellite itself is bringing populates a rather delimited region at very high energies (as is the case for the Sagittarius dwarf galaxy and its GC system; see Bellazzini et al. 2020); (2) those that occurred in the past and are characterised by a smaller mass ratio, typically 1:100 and lower (as discussed in Jean-Baptiste et al. 2017). In this case, stellar debris tend to be distributed in the high-energy regions of the E − Lz plane (see Sect. 4.4 in Jean-Baptiste et al. 2017, and also Pfeffer et al. 2020), and a similar behaviour is found for the associated GC population. We refer the reader to Appendix B for the distribution in the E − Lz space obtained when considering the MW accreting four 1:100 mass ratio satellites.
3.3. Other kinematic spaces: Lperp − Lz, eccentricity − Lz, and the action space
Next, we examine how the populations of GCs in our simulations redistribute in other kinematic spaces. In addition to the E − Lz space, we analysed the Lperp − Lz space where Lperp is the projection of the total angular momentum onto the Galactic plane and is defined as: 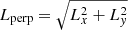 (with Lx and Ly as the x and y component, respectively, of the angular momentum space in a reference frame with the Galactic disc in the x − y plane). Eccentricity (e), defined as
(with Lx and Ly as the x and y component, respectively, of the angular momentum space in a reference frame with the Galactic disc in the x − y plane). Eccentricity (e), defined as 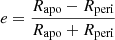 (with Rapo and Rperi respectively as the apocentre and the pericentre of the orbit), is another important parameter in describing an orbit. In this work, we used the eccentricity parameter by combining it with Lz, as suggested in Lane et al. (2022; see also Cordoni et al. 2021). The last kinematic space we analysed is the action space where the horizontal axis is the (normalised) azimuthal action (Jϕ/Jtot ≡ Lz/Jtot, where
(with Rapo and Rperi respectively as the apocentre and the pericentre of the orbit), is another important parameter in describing an orbit. In this work, we used the eccentricity parameter by combining it with Lz, as suggested in Lane et al. (2022; see also Cordoni et al. 2021). The last kinematic space we analysed is the action space where the horizontal axis is the (normalised) azimuthal action (Jϕ/Jtot ≡ Lz/Jtot, where 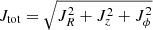 ) and the vertical axis is the (normalised) difference between the vertical and radial actions ((Jz − JR)/Jtot). The right and left points of the space (|Lz|=Jtot, see bottom-right panel in Fig. 7) are in-plane prograde and in-plane retrograde orbits, respectively. The top point (Jz = Jtot) is a circular polar orbit, and the bottom point (JR = Jtot) is a radial orbit. The bottom-right and bottom-left edges are prograde and retrograde in-plane orbits, respectively. The top-right and top-left edges are prograde and retrograde circular orbits, respectively.
) and the vertical axis is the (normalised) difference between the vertical and radial actions ((Jz − JR)/Jtot). The right and left points of the space (|Lz|=Jtot, see bottom-right panel in Fig. 7) are in-plane prograde and in-plane retrograde orbits, respectively. The top point (Jz = Jtot) is a circular polar orbit, and the bottom point (JR = Jtot) is a radial orbit. The bottom-right and bottom-left edges are prograde and retrograde in-plane orbits, respectively. The top-right and top-left edges are prograde and retrograde circular orbits, respectively.
 |
Fig. 7. Final GC distributions in the kinematic spaces E − Lz, Lperp − Lz, eccentricity − Lz, and the action space for the simulation MWsat_n1_Φ60. The in situ population of GCs is represented by grey circles, while the accreted population is indicated with magenta circles. |
Figures 7 and 8 show the final GC distributions in the four kinematic spaces, E − Lz, Lperp − Lz, eccentricity − Lz, and the action space for the two previously examined simulations MWsat_n1_Φ60 and MWsat_n2_Φ30-150 with one or two accretions, respectively. The actions represented in the figures were computed using the Stäckel fudge approach (Binney 2012), as implemented in the AGAMA code (Vasiliev 2019a). The addition of Lperp (see top-right panel in Fig. 7) to the previous analysis of the E − Lz space confirmed the previously drawn conclusions that at the end of the simulation, the overall superposition between the in situ and accreted population is considerable everywhere. Only the GCs lost by the satellite at the first pericentric passage (tesc ≃ 0.5), which are therefore at high energies (E ≳ −5), are in principle distinguishable from the rest. Furthermore, the accretion event generated a population of in situ halo clusters (consisting of disc GCs heated by the interaction) whose distribution extended towards high Lperp. From the eccentricity − Lz and action spaces (see bottom panels in Fig. 7), it is not possible to make any difference between the accreted and in situ GCs. In the action space, we noticed a higher density in the right-hand corner related to the more prograde orbits where the in situ and accreted GCs definitely overlap. Overall, as shown in the bottom-right panel of Fig. 7, the clusters from the satellite are preferentially located towards prograde in-plane orbits but do not form groups that are distinct from in situ clusters. The strength of the action space should lie in the fact that distinct types of orbits occupy different loci in the space (see Lane et al. 2022), but this is not sufficient to reconstruct the origin of the GCs (i.e. accreted or in situ) since they are scattered and mixed over most of the space during the merger process.
 |
Fig. 8. Final GC distributions in the kinematic spaces E − Lz, Lperp − Lz, eccentricity − Lz, and the action space for the simulation MWsat_n2_Φ30-150. The in situ population of GCs is represented by grey circles, while the accreted populations are indicated with magenta for satellite 1 and orange for satellite 2. |
As we have already mentioned, when we consider the merging with two satellites (see Fig. 8), the interpretation of kinematic spaces does not improve. We can confirm that, overall, the GCs that end with a higher energy in the E − Lz plane are accreted. In the MWsat_n2_Φ30-150 simulation, they also stand out as the most retrograde (see top-left and bottom-left panels of Fig. 8). Despite this characteristic, distinguishing between the clusters coming from the first or second satellite is hardly feasible, and it is evident that also in situ clusters originally in the disc can be found with retrograde orbits at these energy levels (−12 < E < −5). If the points in the figure were not colour coded, it would not be possible to identify which galactic progenitor they belong to on the basis of their location in the E − Lz space. Other kinematic spaces added in the analysis did not seem provide any relevant information for the purpose of retrieving the original galactic membership of GCs. In the Lperp − Lz and eccentricity − Lz spaces, in fact, the only clusters that were detached from the rest of the mixed population of accreted and in situ clusters were those with a more retrograde orbit comprising two MW GCs, two clusters originating from satellite 2, and one GC from satellite 1. In the action space, again, the clusters were scattered and mixed over most of the plane; the accreted clusters were predominantly in the region characterised by radial in-plane orbits, but we could not identify groups with the same galactic membership. The small clumps detectable by eye in the bottom-right panel of Fig. 8 are all composed of GCs of different origins. In this respect, it is worth recalling the work by Lane et al. (2022), which extensively investigates the best kinematic spaces to separate radially anisotropic halo populations from isotropic halo populations. To this aim, the authors concluded that the ‘action diamond’ space is superior to other spaces used in the literature. The problem with their conclusion is that clusters of different natures (accreted or in situ and/or belonging to different satellite progenitors) can end up having similar orbital anisotropy (see, for example, Figs. 7 and 8). Thus, a kinematic space can be very good for separating stars (or clusters) with specific orbital properties. However, the space does not allow for assessment of their origin. Therefore, the analysis presented in the literature is limited by the fact that it associates a specific region of a kinematic space, and hence specific orbital characteristics, with a specific accretion origin.
In Figs. 9 and 10 we stacked together the GC distributions in Lperp − Lz, eccentricity − Lz, and the action space for the whole set of 1 × (1:10) and 2 × (1:10) simulations, respectively, as done in Figs. 5 and 6. These figures allowed us to generalise the conclusions we drew for the two examples of single and double accretion, the most important of which concerns the fact that the kinematic spaces considered in addition to the E − Lz space did not add any useful insight for discriminating between GCs originating from satellites accreted over time by the MW or formed in the MW itself. Regarding the Lperp − Lz plane, we note that in the case of a single accretion, if we selected the region with Lperp ≥ 20 and Lz ≲ 30, we would certainly find satellite clusters. However, this argument no longer holds true if we analyse simulations with double accretion. Indeed, in cases of double accretion we discovered several in situ clusters that were so kinematically heated that at the end of the simulation were found to have Lperp > 20. When looking at the eccentricity − Lz plane, the only noteworthy point we observed was the fact that with both one and two accreted satellites at fixed |Lz|> 0, we found the accreted GCs to have more eccentric orbits (e ≥ 0.8) than those of the in situ GCs, while for |Lz|≃0, the accreted and in situ clusters shared the same more extended range of eccentricities. As far as action space is concerned, we can say that, in general, the accreted clusters tend to have in-plane prograde or radial orbits. The distribution of in situ GCs is denser in regions that correspond to prograde in-plane orbits, and this makes sense since, by hypothesis, the clusters formed in the MW-type galaxy initially have disc orbits. Despite this general feature, we also find in situ GCs at the opposite extreme, that is, with strongly retrograde orbits, and indeed, the most retrograde clusters are actually in situ in all cases. If we had also considered in situ GCs with halo-like orbits, this feature would have been even more evident (see Sect. 3.5).
 |
Fig. 9. Distribution in Lperp − Lz, eccentricity − Lz, and the action space for the whole set of 1 × (1:10) merger simulations at T = 5 Gyr. The distribution of the in situ population of GCs has been stacked and is shown by the grey circles. The colour coding of the satellite GCs is according to the initial inclination of the satellite orbital plane with respect to the MW-like reference frame Φorb. |
 |
Fig. 10. Distribution in Lperp − Lz, eccentricity − Lz, and the action space for the whole set of 2 × (1:10) merger simulations at T = 5 Gyr. The distribution of the in situ population of GCs has been stacked and is shown by the grey circles. The colour coding of the satellite GCs (satellite 1: left column; satellite 2: right column) is according to the initial inclination of the satellite orbital plane with respect to the MW-like reference frame Φorb. |
3.4. Does a clustering analysis allow for the recovery of the accretion history?
To make our analysis more quantitative, we exploited a GMM for its function as a clustering algorithm but also mainly for its fundamental purpose: modelling the overall distribution of input data. The purpose of this analysis was to investigate whether the algorithm can grasp any properties of the final distributions of GCs in kinematic spaces not visible to the eye and in a more quantitative manner. Recently, several works have used this type of tool to both distinguish between accreted and in situ stars and/or GCs and to retrieve the number of accretions undergone by the MW (see for instance Donlon & Newberg 2023; Callingham et al. 2022). We proceeded as follows. For each simulation, we considered a six-dimensional space consisting of the GCs’ kinematic quantities previously examined, namely, the z component of the angular momentum Lz, the total orbital energy E, the projection of the angular momentum onto the galactic plane Lperp, the eccentricity e, the normalised azimuthal action Lz/Jtot, and the difference between the vertical and radial actions (Jz − JR)/Jtot. We tried to fit the GCs’ kinematic quantities with a two or three-component GMM (depending on the number of accreted satellites considered in addition to the in situ component) viewed as a clustering model, but the results were not particularly useful, as the real memberships were not retrieved. Therefore, we fitted several models with an increasing number of components and determined the optimal number of components for our dataset by minimising the Bayesian information criterion (BIC; Schwarz 1978). Figures 11 and 12 respectively show the GC distributions in the four kinematic spaces for the simulations MWsat_n1_Φ60 and MWsat_n2_Φ30-150. The clusters are colour-coded according to the groups retrieved by the minimum BIC criterion in the GMM and are bordered according to the true label given by our simulation. The bottom panels of Figs. 11 and 12 show the confusion matrix. Interestingly, there is a predicted class that includes both the majority of accreted and in situ clusters for both the single and the double accretion simulations. This class (group five in Fig. 7 and group eight in Fig. 8) covers the region of the E − Lz space where there is the largest overlap between GCs from different galactic progenitors, namely, the region with −17 ≲ E ≲ −12. Overall, the groups that did not contain accreted clusters were those that traced highly prograde disc orbits in the E − Lz space, while the rest of the groups into which the MW is divided also contained a high fraction of satellite(s) clusters. The GMM, as it is designed, practically cuts the different kinematic spaces (with the exception of the action space) into separate slices that overlap only slightly. This behaviour therefore tends to support the interpretation suggested so far based on grouping in kinematic spaces but fails in grasping the underlying physical process. We acknowledge the good prospects in using this type of tool to describe, in a quantitative manner, the distribution of stars and clusters in kinematic spaces, but also suggest caution in interpreting the results, as the components retrieved by the algorithm are not directly related to the accretion events experienced by our Galaxy: the number of groups does not trace the number of satellites accreted over time, and groups are in general made of a mixture of in situ and accreted populations.
 |
Fig. 11. GMM applied to the GCs’ kinematic quantities obtained in the single accretion simulation. Top-middle row: Final GC distributions in the kinematic spaces E − Lz, Lperp − Lz, eccentricity − Lz, and the action space for the simulation MWsat_n1_Φ60. The colour coding of the GCs is related to the different components retrieved when applying the minimum BIC criterion in the GMM. Truly accreted GCs (i.e. those given the ‘true’ label by our simulation) are bordered by magenta circles. Bottom panel: Confusion matrix obtained by the GMM. Each row represents the true labels given by the simulations (MW, satellite), while each column represents the predicted group identified by the model. Values are normalised to the total number of GCs in each true class. |
 |
Fig. 12. GMM applied to the GCs’ kinematic quantities obtained in the double accretion simulation. Top-middle row: final GC distributions in the kinematic spaces E − Lz, Lperp − Lz, eccentricity − Lz, and the action space for the simulation MWsat_n2_Φ30-150. The colour coding of the GCs is related to the different components retrieved when applying the minimum BIC criterion in the GMM. Truly accreted GCs (i.e. those given the ‘true’ label by our simulation) are bordered by magenta and orange circles respectively for satellite 1 and satellite 2. Bottom panel: Confusion matrix obtained by the GMM. Each row represents the true labels given by the simulations (MW, satellite 1, satellite 2), while each column represents the predicted group identified by the model. Values are normalised to the total number of GCs in each true class. |
3.5. Adding an in situ halo population
As we have stressed several times in previous sections, by construction, our modelled MW-type galaxy does not contain any population of halo clusters before the interaction(s) since the in situ GCs are all initially confined in a Miyamoto-Nagai disc (see Sect. 2). In the literature, the presence of an in situ halo is still being debated. For instance, the only in situ population Haywood et al. (2018), Di Matteo et al. (2019) report finding in great proportions in Gaia DR2 and APOGEE data is the thick disc (i.e. the early disc of the Galaxy heated to hot kinematics). On the other hand, Belokurov & Kravtsov (2022) support a period of chaotic pre-disc evolution where stars are born in dense clumps scattered on all kinds of orbits and populate a hot halo. If the latter scenario were the case (both for stars and GCs), this would imply that the overlap between in situ and satellite GCs in kinematic spaces could be even more significant. To test this claim with our simulations, we randomly selected a group of 20 particles from the dark matter halo of the MW-type galaxy, initially modelled with a Plummer distribution, and we assumed these particles to be GCs formed in situ, originally with halo kinematics. This was feasible since, as shown in Table 1, the mass of dark matter particles in our simulations is ≃7.4 × 104 M⊙ and therefore consistent with the mass range of MW GCs (see, for example, Baumgardt et al. 2019).
Figure 13 shows the final GC distributions in the four kinematic spaces analysed, the E − Lz, Lperp − Lz, eccentricity − Lz, and the action space, for the simulation MWsat_n1_Φ60 with the addition of the mock halo in situ GCs. As expected, the population of in situ GCs that initially has halo kinematics maintains the same type of kinematics. In E − Lz space, they end up in a rather high-energy region since the dynamical friction on the individual clusters is not strong enough to allow them to lose energy, and we also find many GCs with negative Lz. As a result, the different kinematic spaces, in particular the E − Lz space, become even more indecipherable, and at this point, we are no longer sure whether even high-energy or highly retrograde clusters are accreted. In this scenario, therefore, with only kinematic information, not even GCs coming from less massive satellites, for instance satellites with a 1:100 mass ratio (see Appendix B), would be distinguishable from in situ GCs.
 |
Fig. 13. Same as in Fig. 7 but with the addition of in situ GCs with halo kinematics at the beginning of the simulation. The added in situ GCs are represented as empty circles. |
4. Discussion: A new look at Galactic globular clusters
The results presented in the previous section show that we do not expect GCs accreted with their own parent satellite to clump in specific regions of the E − Lz plane nor in the other analysed kinematic spaces, unless there are reasons to assume that the Galaxy has not experienced any significant (i.e. mass ratio ∼1 : 10) merger, an assumption which would contradict the current estimates of the mass ratio of the Gaia-Sausage-Enceladus merger (see, for example, Helmi et al. 2018). Moreover, if the Galaxy has experienced more than one significant merger during its evolution (see, for example, Kruijssen et al. 2020), clusters associated to these mergers could overlap and mix in the E − Lz space, particularly in the most gravitationally bound regions of the diagram (i.e. regions with low energies). A suite of mergers would also muddle the traces left by previous accretion events in this space. Finally, a region of the E − Lz space dominated by stars associated to a progenitor satellite is not necessarily dominated by clusters associated to the same accretion event.
The current reconstruction of the merger tree of the Galaxy is based exactly on the following assumptions: (1) dynamical coherence of GCs in the kinematic spaces, (2) negligible overlap of clusters originating in different satellite galaxies in all the kinematic spaces, (3) no kinematic heating of the in situ population, and (4) straightforward correspondence between field stars and clusters in the E − Lz space, meaning that the regions of this space where field stars associated to Sequoia, Gaia-Sausage-Enceladus, the Helmi stream, and other possible accretions have been identified are also the regions used as boundaries to assign clusters to each of these progenitors.
Our results show that there is no physical reason to proceed in this way. If we want to look for the remnants of these accretion events, we cannot require that the associated clusters satisfy any dynamical coherence in kinematic spaces. In this respect, we recall the results by Kruijssen et al. (2019), who identified traces of an ancient accretion event in the Galaxy called Kraken when studying the system of Galactic GCs. More specifically, Kruijssen et al. (2019) based their conclusions on the study of the AMR of these clusters, which were compared to that of a suite of cosmological zoom-in simulations of MW-mass galaxies from the E-MOSAICS project. This association of the possible clusters linked to Kraken was then questioned by Massari et al. (2019), who noted that most of the clusters reported in Kruijssen et al. (2019) as possible members of Kraken were not dynamically coherent5 since they were associated to different regions of the E − Lz diagram. The authors thus reconsidered the initial suggestion of Kraken-like GCs made by Kruijssen et al. (2019), proposing a new classification where Kraken-like clusters are a group of dynamically coherent clusters found in the low-energy part of the E − Lz plane and concluded that ‘... taking into account the dynamical properties is fundamental to establishing the origin of the different GCs of our Galaxy.’ We note that it is with this new classification that Kruijssen et al. (2020) subsequently made their reconstruction of the merger tree of the MW (see also Forbes 2020). Our work urges reconsideration of this overall approach since it demonstrates that the remnants of massive accretion events are not expected to show any global clustering in this space, which has already been shown to be the case also for field stars (Jean-Baptiste et al. 2017; Amarante et al. 2022; Khoperskov et al. 2022a). Moreover, it is not because of a lack of dynamical coherence in the E − Lz space that a subset of Galactic GCs cannot be associated to the same progenitor.
Returning to the classification of the Galactic GCs made by Massari et al. (2019) on the basis of their kinematics (energies and angular momenta), we take a new look at the AMRs of clusters which in their study are associated to different progenitors. It is important to briefly re-discuss the AMRs here because they have been used in the literature to further justify kinematically based classifications. For example, Massari et al. (2019) concluded that, quite remarkably, ‘the dynamical identification of associations of GCs results in AMRs that are all well-defined and that depict different shapes or amplitudes’. However, in their work, no actual fit to the data was done (as acknowledged by the authors themselves). It is thus worth reconsidering whether the kinematic classification by Massari et al. (2019) effectively leads to groups whose AMRs have different shapes and amplitudes, especially considering that all age estimates come with associated errors; whether each sample has a finite and limited number of clusters for which ages are available (typically less than ten); and whether different ages and metallicity estimates exist in literature. Since the apparent difference between AMRs of groups of clusters identified on the basis of their kinematics has been used as an additional probe of the robustness of the classification itself, the fundamental questions to investigate are: Do kinematically based classifications effectively lead to select clusters with different enrichment histories? And how dependent are the retrieved enrichment histories on the chosen set of ages and metallicities? To re-discuss this issue, we made use of the ages and metallicities from the literature data reported by Marín-Franch et al. (2009) and VandenBerg et al. (2013). We recall some main differences and similarities amongst these studies. Marín-Franch et al. (2009) measured the relative ages of a sample of 64 Galactic GCs observed in the framework of the HST/ACS Survey of Galactic GCs. The corresponding ages and errors are reported in Table 4 of their paper for a set of different theoretical isochrones and metallicities for two abundance scales. We adopt in the following analysis the ages corresponding to the theoretical isochrones of Dotter et al. (2007) using the Zinn & West (1984) abundance scale. VandenBerg et al. (2013) analysed 55 clusters, many of which are also in the work of Marín-Franch et al. (2009), and the ages and metallicities are reported in Table 2 of their paper. The resulting AMRs are shown in Fig. 14, and the different galaxy progenitors to which Massari et al. (2019) associated the clusters include Gaia-Sausage-Enceladus, Sagittarius, Helmi stream, and Sequoia along with two additional groups, the low-energy clusters and high-energy clusters (see Table C.1). Despite the differences in the shape and extension of the AMRs resulting from these two datasets, we noticed that:
-
Some of the clusters classified as accreted clusters associated to either the low-energy group or to the Helmi stream, namely, E3, NGC 6441, and NGC 6121, have ages and metallicities compatible with being in situ disc clusters heated to halo kinematics (see also Forbes 2020; Horta et al. 2020, for similar conclusions). They are indeed on the old, metal-rich branch of the AMR (see for example the left panel of Fig. 14) where most of the disc-bulge clusters lie but have hotter kinematics than what is expected from disc-bulge systems (and this is the reason why they have not been classified by Massari et al. (2019) as in situ clusters).6
-
The young branch at [M/H] ≳ −1.4 (see left panel of Fig. 14) or [Fe/H] ≳ −1.4 (see right panel) is made of clusters that have been associated to different progenitors but have age and metallicities that are indistinguishable from one another. When looking at the left panel of Fig. 14, between the group of clusters associated to Gaia-Sausage-Enceladus (such as NGC 5286, NGC 6205, NGC 7089, NGC 2808, NGC 288, NGC 362, NGC 1261, NGC 1851, red colours in Fig. 14, and possibly NGC 5139, red empty circle in the same figure) we find a cluster identified as a disc cluster (NGC 6752, blue point), two clusters that have been associated to the Helmi stream (NGC 5272, NGC 6981, orange points, and possibly NGC 5904, orange empty circle), two high-energy clusters (NGC 6584 and NGC 6934, cyan points), one cluster associated to Sagittarius (NGC 6715, green point), and one possibly associated to Sequoia (NGC 3201, brown empty circle). At higher [M/H] > −0.8, the Pal 1 cluster, which is classified as a disc cluster, lies in between two clusters associated to the Sagittarius galaxy, Palomar 12, and Terzan 7. The only three clusters in this region that seem to slightly separate from the bulk of the distribution are NGC 4147, Arp 2, and NGC 6535 (which have relative ages lower than 1.0 and −1.6 < [M/H] ≤ −1.5), but they are still compatible within 2σ with the other clusters.
-
At [M/H] < −1.4, no distinction can be made on the basis of the AMR among the clusters that have been classified as Sequoia, Gaia-Sausage-Enceladus, bulge-disc, or Sagittarius clusters.
 |
Fig. 14. Age-metallicity relations of Galactic GCs from the literature. Left panels: sample of ages and metallicities from Marín-Franch et al. (2009). Right panel: sample of ages and metallicities from VandenBerg et al. (2013). Following the classification given by Massari et al. (2019), the different colours and symbols in each plot indicate the different galaxy progenitors of the clusters. The clusters of Gaia-Sausage Enceladus (G-E), Sequoia (Seq), Helmi stream (H99), Sagittarius (Sag), low-energy (L-E), and high-energy (H-E) are shown by solid circles, while tentative associations are shown by empty circles. Clusters classified as in situ by Massari et al. (2019; M-D and M-B groups) are shown with blue dots. Errors on ages are also reported. Bottom panels: Fits to the AMRs of accreted GCs in the G-E, H99, Sag, and L-E groups. For each group, the mean fit to the data as a function of metallicity is shown together with the corresponding standard deviation. Metallicities and ages are as provided by Marín-Franch et al. (2009) and were used for the fits shown in the left panel. In the right panel, we made use of the ages and metallicities reported by VandenBerg et al. (2013). The in situ clusters are also shown for comparison (blue points). The two clusters identified by a purple cross in the bottom-left panel are NGC 6441 and NGC 6121, which have been excluded from the fit, as motivated in the text. Error bars are not reported in these two panels to avoid having overly complex figures, but they have been taken into account in the fitting procedure (see text). |
To further probe that the accreted groups in the Massari et al. (2019) classification, which we again highlight constitutes the backbone of many other classifications that have been published afterwards in the literature (see also Forbes 2020; Pfeffer et al. 2020; Callingham et al. 2022), do not depict specific AMRs in terms of shapes or amplitude, in the bottom panels of Fig. 14, we report a fit to the AMR of each of the groups Massari et al. (2019) identified. We note that we restricted this analysis only to the groups for which the association was considered robust (i.e. Sag, H99, G-E, and L-E but not such groups as H99/G-E, H99?, G-E?, etc). We excluded Sequoia (Seq) and the high-energy group (H-E) since, for them, the number of clusters for which ages are provided by Marín-Franch et al. (2009) or VandenBerg et al. (2013) is less than three, making any fit meaningless. In the case of the AMRs from Marín-Franch et al. (2009) data, we also excluded two clusters that were assigned by Massari et al. (2019) to the L-E group (NGC 6121 and NGC 6441) since, as discussed previously, their ages, metallicities, and chemical abundances are more compatible with them being in situ clusters. To perform the fit, we first bootstrapped the data, and for each bootstrapped sample, we drew ages from Gaussian distributions with means and dispersions that were the same as those reported in Marín-Franch et al. (2009; bottom-left panel of Fig. 14) and VandenBerg et al. (2013; bottom-right panel). When repeating this procedure a hundred times, both the limited statistics and the uncertainties on ages were taken into account in the analysis. The functional form of the curve fitted to the data is consistent with a leaky-box evolution of the systems, and it takes the form:
where p is the effective yield, t is the look-back time, and tf is the time in the past when the chemical enrichment started.
The results of this analysis are shown in the bottom panels of Fig. 14 and in Fig. 15. If we use the AMRs by Marín-Franch et al. (2009), we find that the chemical evolutions of the Sag and H99 groups have similar yields (respectively, p = 0.72 ± 0.14 and p = 0.79 ± 0.15) and formation times (respectively, tf = 1.06 ± 0.07 and tf = 1.10 ± 0.06). The L-E and G-E groups have slightly higher p and tf (respectively, p = 0.80 ± 0.01 and p = 0.83 ± 0.06, tf = 1.20 ± 0.01, and tf = 1.18 ± 0.03); however, the evolution of G-E is still compatible, within 1σ, with what is found for the Sag and H99 groups. If we use the AMRs by VandenBerg et al. (2013), the retrieved chemical enrichment histories are all indistinguishable within 1σ (H99: p = 0.71 ± 0.12, tf = 12.94 ± 0.40; Sag: p = 0.68 ± 0.09, tf = 13.20 ± 0.34; L-E: p = 0.64 ± 0.06, tf = 13.40 ± 0.27; and G-E: p = 0.75 ± 0.04, tf = 13.48 ± 0.19). Thus, the conclusion that kinematically based classifications lead to groups of clusters with different chemical enrichment histories is not supported by a robust analysis of the data. This conclusion proved to be valid for two independent datasets of ages and metallicities.
 |
Fig. 15. Time, tf, when the chemical enrichment started as a function of the effective yield p for the four different groups reported in Fig. 14. Top panel: the p and tf values are obtained from fitting the AMR of Marín-Franch et al. (2009). Bottom panel: the p and tf values are obtained from fitting the AMR of VandenBerg et al. (2013). |
To summarise, we have demonstrated that the assumption of ‘dynamical coherence’ for the interpretation of GCs in kinematic spaces is not supported by physical arguments (unless a very specific merger history for our Galaxy is assumed), and indeed we do not find in the observational data any confirmation that merger histories based on this assumption identify clusters with specific AMRs and hence neither the star formation histories of their progenitor systems. There is room for a new interpretation of AMR and/or chemical abundance spaces. Dynamical coherence should not be the a priori assumption to analyse GC data, which has essentially been done by all studies published in the literature so far (see, for example, Forbes 2020; Callingham et al. 2022), with the exception of Kruijssen et al. (2019) and Horta et al. (2020). Even if uncertainties on ages are still significant and even if possible overlaps among different evolutionary sequences can be challenging,7 it is by finding the features in the AMRs or in abundance spaces, which are conserved quantities through time, that we can hope to solve the question of the accretion history of the Galaxy.
5. Conclusions
In this paper, we analysed dissipationless N-body simulations of a MW-type galaxy accreting one or two satellites with mass ratios of 1:10, as well as some with ratios of 1:100. Each galactic system in our simulations has a population of disc GCs represented by point masses. We analysed this set of simulations to investigate the possibility of using kinematic information to find accreted GCs in the Galaxy as remnants of past accretion events that have lost their spatial coherence. In particular, we have examined the energy-angular momentum (E − Lz) space and found that:
-
Clusters originating from the same progenitor generally do not group together in the E − Lz space, and thus GCs populating a large range of energy and/or angular momentum could have a common origin.
-
If several satellites are accreted, their GC populations can overlap, particularly in the E − Lz plane region where the most gravitationally bound clusters are found (i.e. low energies).
-
The cluster distributions do not necessarily match that of the field stars of the same progenitor galaxy. In several cases we find regions of the E − Lz space populated by clusters originating from one satellite but dominated by field stars from another satellite. This implies that the correspondence between field stars and associated clusters in the E − Lz diagram is not necessarily trivial. If a certain region of this space is dominated by the stellar debris of a satellite, this does not imply that clusters found in the same region all originate from the same satellite.
-
The in situ population of GCs (i.e. in our models, the GCs initially confined onto a disc) can be heated up by accretion, and a fraction of the population acquires halo-like kinematics, thus becoming indistinguishable – on the basis of the kinematics alone – from the accreted populations.
We find that accreted clusters are confined in a tight range of energies only when they originate from low-mass progenitors (mass ratio of 1:100). For such mass ratios, the distribution of angular momenta is still very extended, and these clusters tend to all be in the high-energy part of the E − Lz diagram since dynamical friction is not able to bring them to the inner regions of the MW-type galaxy before their parent satellite is severely affected by the gravitational tides exerted by the main galaxy. Because clusters associated with low-mass progenitors are all found at high energies in our simulations, a significant overlap is also found for these systems. We note that apart from the effects studied in this paper (i.e. dynamical friction, perturbations induced by the other ongoing accretions; see also Garrow et al. 2020), other processes can contribute to the non-conservation of energy and angular momenta of GCs, including the mass growth of the Galaxy with time, which is expected to be significant especially in the first 4 − 5 Gyr of its evolution (Snaith et al. 2014). Notably, simulations run in a cosmological context (Khoperskov et al. 2022a,b) have recently confirmed the results of tailored N-body simulations (Jean-Baptiste et al. 2017; Amarante et al. 2022) regarding the large spread of accreted stars in the E − Lz plane. For these reasons, we are confident that these results are robust and would also find confirmation in a cosmological framework.
We also exploited other kinematic spaces suggested in the literature to reconstruct the accretion history of our Galaxy, namely, Lperp − Lz, eccentricity − Lz, and the action space. This additional analysis only confirmed the problems encountered in disentangling GCs in the E − Lz space, as clusters with different origins also appear scattered and mixed together in those spaces. By means of GMMs, we have demonstrated that the overlap of clusters is not only a projection effect on specific planes but that the effect is also found when the whole set of kinematic properties (i.e. E, Lz, Lperp, eccentricity, radial, and vertical actions) is taken into account. Consequently, applying algorithms, such as GMMs – a method lately used to identify groups of Galactic GCs in kinematic spaces – is conceptually wrong if the results of such methods are used to infer the merger tree of the Galaxy, and the interpretation of the results of these models tends to support the classification based on dynamical coherence.
Together, these findings question the history of accretions experienced by the Galaxy, as it has so far been reconstructed by analysing its GC system (see Massari et al. 2019; Kruijssen et al. 2020; Malhan et al. 2022). Indeed, this reconstruction usually assumes a dynamical coherence for clusters originating in the same accreted galaxy – an assumption theoretically motivated by the work of Helmi & de Zeeuw (2000), which was based on a number of oversimplifications, as extensively discussed in Jean-Baptiste et al. (2017). When more realistic simulations are analysed, indeed, the dynamical coherence of the accreted stars and GCs is no longer guaranteed. When we tested one of the merger histories (specifically, the first one proposed by Massari et al. 2019), we found no confirmation for the association made so far in the literature between clusters and their progenitor galaxies through analysis of the AMRs of Galactic GCs.
To understand the origin of the GC population in the MW, we need to exploit the information from other dimensions, such as detailed chemical abundances and ages coming from the spectroscopic APOGEE survey and the soon operational WEAVE@WHT and MOONS@VLT surveys. The kinematic information could potentially still be useful, for example, in retrieving the paths traced in kinematic planes by GCs with the same origin and putting constraints on the orbital history of the progenitor satellites. However, this can be done only at the point when the distinction between accreted and in situ GCs and the association with different satellites has already been made.
Resolving both the simulated galaxies and the GCs as N-body systems is currently not possible due to a large range of spatial scales that should be modelled – from sub-parsec resolution to hundreds of kiloparsec. In Renaud & Gieles (2015), a numerical method to describe the dynamical evolution of clusters in tidal fields is carried out. We report to future works that employ the more generic method described in Renaud et al. (2011), which is particularly adapted to study the dynamics of some of our clusters – modelled as N-body systems – in the evolving tidal field generated by some of these accretion events.
Before the end of the merging process, a fraction of satellite stars and GCs are still gravitationally bound to the system. For this reason, along with the motion of the centre of mass of the satellite relative to the MW centre, one needs to also take into account the motion of satellite stars and GCs relative to the satellite centre. Since the angular momentum Lz depends on the distance from the centre of the main galaxy, the effect of the peculiar velocities is particularly evident at large distances from the MW centre (i.e. at the apocentre), and it is reduced when the satellite is at its pericentre.
We note, however, the caution expressed by Kruijssen et al. (2019) themselves on this association.
We note that these clusters are either absent from the analysis of the AMR done in Massari et al. (2019; see their Appendix A.2 for a discussion about the metal-rich clusters analysed in their study) or, as it is the case for NGC 6121, only the age by VandenBerg et al. (2013) has been taken into account. This age brings this cluster halfway between the young and old branches (see right panel of Fig. 14), while the estimates by Marín-Franch et al. (2009) suggest an older age.
Acknowledgments
We are grateful to the referee for their report, which much improved the presentation of the results. We also wish to thank J. Pfeffer for his comments to a first version of this manuscript. GP and PDM thank P. Boldrini and D. Valls-Gabaud, for their comments on this work. This work has made use of the computational resources obtained through the DARI grant A0120410154. AMB acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 895174. FR acknowledges support from the Knut and Alice Wallenberg Foundation.
References
- Amarante, J. A. S., Debattista, V. P., Beraldo e Silva, L., Laporte, C. F. P., & Deg, N. 2022, ApJ, 937, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Amorisco, N. 2017, MNRAS, 464, 2882 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., & Hilker, M. 2018, MNRAS, 478, 1520 [Google Scholar]
- Baumgardt, H., & Vasiliev, E. 2021, MNRAS, 505, 5957 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., Hilker, M., Sollima, A., & Bellini, A. 2019, MNRAS, 482, 5138 [Google Scholar]
- Bellazzini, M., Ibata, R., Malhan, K., et al. 2020, A&A, 636, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belokurov, V., & Kravtsov, A. 2022, MNRAS, 514, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Belokurov, V., Erkal, D., Evans, N., Koposov, S., & Deason, A. 2018, MNRAS, 478, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J. 2012, MNRAS, 426, 1324 [Google Scholar]
- Binney, J., & Spergel, D. 1982, ApJ, 252, 308 [Google Scholar]
- Callingham, T. M., Cautun, M., Deason, A. J., et al. 2022, MNRAS, 513, 4107 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2010, A&A, 516, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casertano, S., & Hut, P. 1985, ApJ, 298, 80 [Google Scholar]
- Chen, Y., & Gnedin, O. Y. 2022, MNRAS, 514, 4736 [NASA ADS] [CrossRef] [Google Scholar]
- Cirasuolo, M., Afonso, J., Carollo, M., et al. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, Int. Soc. Opt. Photonics, 9147, 91470N [NASA ADS] [Google Scholar]
- Cirasuolo, M., Fairley, A., Rees, P., et al. 2020, The Messenger, 180, 10 [NASA ADS] [Google Scholar]
- Conroy, C., Naidu, R. P., Garavito-Camargo, N., et al. 2021, Nature, 592, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, A. P., Parry, O. H., Lowing, B., Cole, S., & Frenk, C. 2015, MNRAS, 454, 3185 [Google Scholar]
- Cordoni, G., Da Costa, G., Yong, D., et al. 2021, MNRAS, 503, 2539 [NASA ADS] [CrossRef] [Google Scholar]
- Dalton, G., Trager, S. C., Abrams, D. C., et al. 2012, in Ground-based and Airborne Instrumentation for Astronomy IV, SPIE, 8446, 220 [Google Scholar]
- Deason, A. J., Belokurov, V., & Evans, N. W. 2011, MNRAS, 416, 2903 [NASA ADS] [CrossRef] [Google Scholar]
- Deason, A. J., Mao, Y.-Y., & Wechsler, R. H. 2016, ApJ, 821, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Deason, A. J., Belokurov, V., & Sanders, J. L. 2019, MNRAS, 490, 3426 [NASA ADS] [CrossRef] [Google Scholar]
- De Blok, W., McGaugh, S. S., Bosma, A., & Rubin, V. C. 2001, ApJ, 552, L23 [CrossRef] [Google Scholar]
- de Jong, R. S., Chiappini, C., & Schnurr, O. 2012, EPJ Web of Conferences, 19, (EDP Sciences) 09004 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Lucia, G., & Helmi, A. 2008, MNRAS, 391, 14 [NASA ADS] [CrossRef] [Google Scholar]
- De Naray, R. K., McGaugh, S. S., & De Blok, W. 2008, ApJ, 676, 920 [CrossRef] [Google Scholar]
- Di Matteo, P. 2016, PASA, 33 [Google Scholar]
- Di Matteo, P., Lehnert, M. D., Qu, Y., & van Driel, W. 2011, A&A, 525, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Matteo, P., Gómez, A., Haywood, M., et al. 2015, A&A, 577, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Matteo, P., Haywood, M., Lehnert, M., et al. 2019, A&A, 632, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donlon, T., & Newberg, H. J. 2023, ApJ, 944, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A., Chaboyer, B., Jevremović, D., et al. 2007, AJ, 134, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A., Sarajedini, A., Anderson, J., et al. 2010, ApJ, 708, 698 [Google Scholar]
- Erkal, D., Deason, A. J., Belokurov, V., et al. 2021, MNRAS, 506, 2677 [NASA ADS] [CrossRef] [Google Scholar]
- Flores, R. A., & Primack, J. R. 1994, ApJ, 427, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, D. A. 2020, MNRAS, 493, 847 [Google Scholar]
- Forbes, D. A., & Bridges, T. 2010, MNRAS, 404, 1203 [NASA ADS] [Google Scholar]
- Gaia Collaboration 2022, VizieR Online Data Catalog, I/355 [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018a, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Helmi, A., et al.) 2018b, A&A, 616, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrow, T., Webb, J. J., & Bovy, J. 2020, MNRAS, 499, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Gentile, G., Burkert, A., Salucci, P., Klein, U., & Walter, F. 2005, ApJ, 634, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez, A., Di Matteo, P., Schultheis, M., et al. 2018, A&A, 615, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grand, R. J., Deason, A. J., White, S. D., et al. 2019, MNRAS, 487, L72 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R., Bragaglia, A., Carretta, E., et al. 2019, A&A Rev., 27, 1 [CrossRef] [Google Scholar]
- Hammer, F., Li, H., Mamon, G. A., et al. 2023, MNRAS, 519, 5059 [CrossRef] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [Google Scholar]
- Harris, W. E., & Racine, R. 1979, ARA&A, 17, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E., Harris, G. L., & Alessi, M. 2013, ApJ, 772, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Hartwick, F. 1987, The Galaxy (Springer), 281 [CrossRef] [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M. D., Katz, D., & Gómez, A. 2013, A&A, 560, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M. D., et al. 2018, ApJ, 863, 113 [Google Scholar]
- Helmi, A., & de Zeeuw, P. T. 2000, MNRAS, 319, 657 [Google Scholar]
- Helmi, A., White, S. D. M., de Zeeuw, P. T., & Zhao, H. 1999, Nature, 402, 53 [Google Scholar]
- Helmi, A., Babusiaux, C., Koppelman, H. H., et al. 2018, Nature, 563, 85 [Google Scholar]
- Horta, D., Schiavon, R. P., Mackereth, J. T., et al. 2020, MNRAS, 493, 3363 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R., Gilmore, G., & Irwin, M. 1994, Nature, 370, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Jean-Baptiste, I., Di Matteo, P., Haywood, M., et al. 2017, A&A, 604, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kepley, A. A., Morrison, H. L., Helmi, A., et al. 2007, AJ, 134, 1579 [NASA ADS] [CrossRef] [Google Scholar]
- Khoperskov, S., Minchev, I., Libeskind, N., et al. 2022a, A&A, submitted [arXiv:2206.04521] [Google Scholar]
- Khoperskov, S., Minchev, I., Libeskind, N., et al. 2022b, A&A, submittted [arXiv:2206.04522] [Google Scholar]
- Koppelman, H. H., Helmi, A., Massari, D., Roelenga, S., & Bastian, U. 2019, A&A, 625, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koppelman, H. H., Bos, R. O., & Helmi, A. 2020, A&A, 642, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kruijssen, J. D., Pfeffer, J. L., Reina-Campos, M., Crain, R. A., & Bastian, N. 2019, MNRAS, 486, 3180 [NASA ADS] [CrossRef] [Google Scholar]
- Kruijssen, J. D., Pfeffer, J. L., Chevance, M., et al. 2020, MNRAS, 498, 2472 [NASA ADS] [CrossRef] [Google Scholar]
- Kunder, A., Koch, A., Rich, R. M., et al. 2012, AJ, 143, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Lane, J. M., Bovy, J., & Mackereth, J. T. 2022, MNRAS, 510, 5119 [NASA ADS] [CrossRef] [Google Scholar]
- Leaman, R., VandenBerg, D. A., & Mendel, J. T. 2013, MNRAS, 436, 122 [Google Scholar]
- Mackereth, J. T., Schiavon, R. P., Pfeffer, J., et al. 2019, MNRAS, 482, 3426 [Google Scholar]
- Majewski, S. R., Skrutskie, M. F., Weinberg, M. D., & Ostheimer, J. C. 2003, ApJ, 599, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Malhan, K. 2022, ApJ, 930, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Malhan, K., Ibata, R. A., Sharma, S., et al. 2022, ApJ, 926, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Marchesini, D., D’Onghia, E., Chincarini, G., et al. 2002, ApJ, 575, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Marín-Franch, A., Aparicio, A., Piotto, G., et al. 2009, ApJ, 694, 1498 [Google Scholar]
- Massari, D., Koppelman, H. H., & Helmi, A. 2019, A&A, 630, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCarthy, I. G., Font, A. S., Crain, R. A., et al. 2012, MNRAS, 420, 2245 [NASA ADS] [CrossRef] [Google Scholar]
- Meylan, G., & Heggie, D. C. 1997, A&A Rev., 8, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Miyamoto, M., & Nagai, R. 1975, PASJ, 27, 533 [NASA ADS] [Google Scholar]
- Myeong, G., Evans, N., Belokurov, V., Sanders, J., & Koposov, S. 2018, ApJ, 856, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Myeong, G. C., Vasiliev, E., Iorio, G., Evans, N. W., & Belokurov, V. 2019, MNRAS, 488, 1235 [Google Scholar]
- Naidu, R. P., Conroy, C., Bonaca, A., et al. 2020, ApJ, 901, 48 [Google Scholar]
- Ness, M., & Lang, D. 2016, AJ, 152, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Newberg, H. J., Yanny, B., Rockosi, C., et al. 2002, ApJ, 569, 245 [Google Scholar]
- Newberg, H. J., Yanny, B., & Willett, B. A. 2009, ApJ, 700, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Nissen, P. E., & Schuster, W. J. 2010, A&A, 511, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Panithanpaisal, N., Sanderson, R. E., Wetzel, A., et al. 2021, ApJ, 920, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Penarrubia, J., Walker, M. G., & Gilmore, G. 2009, MNRAS, 399, 1275 [CrossRef] [Google Scholar]
- Pérez-Villegas, A., Barbuy, B., Kerber, L. O., et al. 2020, MNRAS, 491, 3251 [Google Scholar]
- Pfeffer, J. L., Trujillo-Gomez, S., Kruijssen, J. M. D., et al. 2020, MNRAS, 499, 4863 [CrossRef] [Google Scholar]
- Price-Whelan, A. M., Johnston, K. V., Valluri, M., et al. 2016, MNRAS, 455, 1079 [NASA ADS] [CrossRef] [Google Scholar]
- Prieto, C. A., Majewski, S., Schiavon, R., et al. 2008, Astron. Nachr.: Astron. Notes, 329, 1018 [NASA ADS] [CrossRef] [Google Scholar]
- Purcell, C. W., Bullock, J. S., & Kazantzidis, S. 2010, MNRAS, 404, 1711 [NASA ADS] [Google Scholar]
- Qu, Y., Di Matteo, P., Lehnert, M. D., & van Driel, W. 2011, A&A, 530, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quinn, P. J., Hernquist, L., & Fullagar, D. P. 1993, ApJ, 403, 74 [Google Scholar]
- Read, J., Lake, G., Agertz, O., & Debattista, V. P. 2008, MNRAS, 389, 1041 [CrossRef] [Google Scholar]
- Renaud, F., & Gieles, M. 2015, MNRAS, 448, 3416 [NASA ADS] [CrossRef] [Google Scholar]
- Renaud, F., Gieles, M., & Boily, C. M. 2011, MNRAS, 418, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Renaud, F., Agertz, O., & Gieles, M. 2017, MNRAS, 465, 3622 [NASA ADS] [CrossRef] [Google Scholar]
- Renaud, F., Agertz, O., Read, J. I., et al. 2021, MNRAS, 503, 5846 [NASA ADS] [CrossRef] [Google Scholar]
- Rodionov, S., Athanassoula, E., & Sotnikova, N. Y. 2009, MNRAS, 392, 904 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, G. 1978, Ann. Stat., 461 [Google Scholar]
- Semelin, B., & Combes, F. 2002, A&A, 388, 826 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shen, J., Rich, R. M., Kormendy, J., et al. 2010, ApJ, 720, L72 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, C. M., Gargiulo, I., Gómez, F. A., et al. 2019, MNRAS, 490, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Snaith, O. N., Haywood, M., Di Matteo, P., et al. 2014, ApJ, 781, L31 [CrossRef] [Google Scholar]
- Stewart, K. R., Bullock, J. S., Wechsler, R. H., Maller, A. H., & Zentner, A. R. 2008, ApJ, 683, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Trelles, A., Valenzuela, O., Roca-Fábrega, S., & Velázquez, H. 2022, A&A, 668, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- VandenBerg, D. A., Brogaard, K., Leaman, R., & Casagrande, L. 2013, ApJ, 775, 134 [Google Scholar]
- Vasiliev, E. 2019a, MNRAS, 484, 2832 [Google Scholar]
- Vasiliev, E. 2019b, MNRAS, 482, 1525 [Google Scholar]
- Vasiliev, E., Belokurov, V., & Evans, N. W. 2022, ApJ, 926, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Villalobos, Á., & Helmi, A. 2008, MNRAS, 391, 1806 [Google Scholar]
- Vogelsberger, M., White, S. D., Helmi, A., & Springel, V. 2008, MNRAS, 385, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, I. R., Mihos, J. C., & Hernquist, L. 1996, ApJ, 460, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Wegg, C., & Gerhard, O. 2013, The Messenger, 154, 54 [NASA ADS] [Google Scholar]
- White, S. D., & Rees, M. J. 1978, MNRAS, 183, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, Z., Chang, J., Beers, T. C., & Huang, Y. 2020, ApJ, 898, L37 [Google Scholar]
- Zinn, R., & West, M. J. 1984, ApJS, 55, 45 [Google Scholar]
- Zolotov, A., Willman, B., Brooks, A. M., et al. 2009, ApJ, 702, 1058 [Google Scholar]
Appendix A: Static Milky Way potential
To illustrate how the distribution in the E − Lz plane changes when the dynamical friction experienced by the satellite during the interaction with the MW is not taken into account, we show the results obtained by considering a static potential for the MW-type galaxy. To this aim, we have run the same simulations with either one or two accreted satellites but in this case while keeping the positions of the MW particles fixed at the initial values.
Figure A.1 is the analogue of Fig. 1. Thus, it shows the GC projections in the x − y and x − z planes for the single-accretion simulation with Φorb = 60° (i.e. simulation MWsat_n1_Φ60) at different times: the initial (T = 0 Gyr), two intermediate times (T = 1 Gyr and T = 2.5 Gyr), and at the final time (T= 5 Gyr). In all the plots, the in situ GC system is represented. The distribution of field (in situ and accreted) stars is also shown in the background. Fig. A.2 shows the temporal evolution of the distance of the satellite to the main galaxy along with the corresponding evolution of all the clusters initially bound to the satellite. Due to its quasi-parabolic orbit in this scenario, we can see the satellite approaching the fixed MW-type galaxy at T≃0.4 Gyr and then moving away again. During the approach, the satellite loses a GC that is trapped by the MW on an orbit with an apocentre at about 35 kpc, and as a result of the satellite’s consequent departure, it retains the rest of its GCs. This can also be seen in Fig. A.1 (left- middle columns) where indeed at T = 1 Gyr the satellite is shown to be receding (at T = 2.5, 5 Gyr it is no longer visible within the 100 kpc) after having deposited its GCs and part of its stars in the MW, which at the end of the simulation (T = 5 Gyr) constitute the halo of the MW.
 |
Fig. A.1. Time evolution of the simulated merging process. Left and middle columns: Projections of the simulated GC positions on the x − y and x − z planes for different times (increasing from top to bottom, same as Fig. 1) of the single-accretion simulation with Φorb = 60° (MWsat_n1_Φ60, see Tab. 2 for the initial parameters). The in situ clusters are represented by grey circles and the accreted clusters by magenta circles. In the background, the surface density of the totality of the stars of the simulation is also shown. Right column: Distributions of accreted GCs and field stars of the same satellite in the E − Lz space for different times (increasing from top to bottom) of the single-accretion simulation with Φorb = 60°. |
The corresponding evolution of the distributions in the E − Lz space (right column of Fig. A.1) of the GCs and field stars of the accreted satellite are very different from the full N-body case (see Fig. 1, right column). At the beginning of the simulation, the satellite, which is still a bound system, appears to be clumped. With the passing of time, however, since in this case the positions of the MW particles are fixed and energy redistribution is not possible (i.e. there is no dynamical friction), the orbital energy of the satellite does not decrease, as the satellite does not penetrate deeper into the potential well of the main galaxy. As a consequence, at the end of the simulation, we did not see a distribution of satellite stars and GCs in the E − Lz space with a funnel-like shape elongated towards low energies as we had seen in the full N-body scenario. The energy fluctuates instead of decreasing, as can be seen in Fig. A.2 (bottom panel), showing the temporal evolution of the orbital energy of the ten satellite GCs. In fact the mean energy of the GCs remains equal to -3.3 which is the same as the initial mean energy. Angular momentum is not conserved since the mass distribution of the system is not axisymmetric and changes over time. Moreover, as we observed, the satellite does not merge with the MW, and this implies a drift in time of the Lz for the stars and clusters that remain attached to it. This trend is clearly visible in Fig. A.2 (middle panel) where (except for the GC trapped by the MW for which Lz fluctuates) for nearly all the satellite’s clusters, the Lz increases over time as it moves away. The mean Lz in fact goes from being equal to 34.5 at the beginning of the simulation to being equal to 203.1 at the end, and the spread in Lz also rises, as the standard deviation increases from 27.0 to 92.7.
 |
Fig. A.2. Time evolution of distances, angular momenta and orbital energies of satellite GCs. Top panel: Time evolution of the distances of the satellite (black line) and its GCs (coloured lines) from the MW-type galaxy for the simulation with a fixed MW potential MWsat_n1_Φ60. Middle panel: Time evolution of the angular momenta of the satellite GCs. Bottom panel: Time evolution of the orbital energies of the satellite GCs. |
As a simulation with two accretions, we re-ran the simulation with ID = MWsat_n2_Φ30 - 150 with a fixed MW potential. Figure A.3 shows the final distribution in the E − Lz space of the MW and satellite(s) GCs for the single and double accretion simulations with fixed galactic potential. The plots in the figure summarise the arguments presented in the previous paragraph, as the satellites’ GCs are generally positioned at high energies and drift towards large angular momenta. We did not find well-defined groups of clusters at different E − Lz levels resembling the regions populated by different galactic progenitors in Fig. 4 of Helmi & de Zeeuw (2000). Furthermore, in this scenario, MW clusters end up in a typical disc-like distribution since they are not heated up to halo-type kinematics by the redistribution of the energy, and this prevents us from accounting for a more realistic overlap between the accreted and in situ GCs.
 |
Fig. A.3. Distribution of GCs in the E − Lz space at the end of the simulations. Top panel: Distribution from the single-accretion simulation (MWsat_n1_Φ60). Bottom panel: Distribution from the double accretion simulation (MWsat_n2_Φ30-150). The MW’s GCs are identified as grey circles, while satellite(s) GCs are represented as magenta and orange circles. |
Appendix B: 4x(1:100) mergers
In this section, we show how GCs distribute in the E − Lz space in the full N-body case when the MW-type galaxy accretes four satellites with relative mass ratios of 1:100 with respect to the MW. In these simulations, the MW-type galaxy has the same properties (in terms of masses and sizes of its components and the number of particles adopted) as those of the main simulations described in Sect. 2. As for the satellites, each is made of 25, 000 particles and contains a population of five GCs. We explored seven different inclinations for the initial orbital plane of the satellite relative to the MW disc. In this appendix, we present the results of two such simulations following the accretion over a period of 5 Gyrs that differ, as before, in the initial inclination of the various satellites, Φorb, and the simulations are thus referred to as MWsat_n4_Φ150-60-0-30 and MWsat_n4_Φ180-90-30-120.
Figures B.1 and B.2 both show the initial and final distributions of GCs and stars belonging to each accreted satellite for the two simulations. All the satellites in both the simulations are shown as starting with a clumpy distribution of stars and clusters. However, the final stellar distributions of the satellites are different, as three types of shapes can be identified. There are high-energy and angular-momentum spread distributions (see satellites 1 and 2 in Fig. B.1 and satellites 1 and 3 in Fig. B.2), which correspond to the satellites that do not end up merging but instead move away from the MW after an initial approach. There are more clumped distributions in energy-angular momentum (see satellites 2 and 4 in Fig. B.2), which correspond to satellites that are at the beginning of the merging process. Lastly, there are more elongated distributions in energy (see satellites 3 and 4 in Fig. B.1), which correspond to satellites that have orbited the MW for a while and are towards the end of the merging process. For some satellites (see for example satellite 2, 3, and 4 in Fig. B.2), there are also structures that start from the main distribution and elongate towards higher and lower energies that correspond to the trailing and leading tails, respectively. When looking at how the clusters are distributed, it be can seen that in all the accreted systems, most of the clusters are positioned at the lower extremes in energy of the corresponding stellar distributions.
 |
Fig. B.1. Distributions of accreted GCs and stars in the E − Lz space for the four accreted satellites (simulation with ID = MWsat_n4_Φ150-60-0-30). Left panel: Initial distributions. Right panel: Final distributions. We note that the ranges on the x− and y−axes are the same for all panels. |
Fig. B.3 shows the final E − Lz distributions of GCs belonging to all the four accreted satellites and to the MW-type galaxy respectively for the MWsat_n4_Φ150-60-0-30 and MWsat_n4_Φ180-90-30-120 simulations. As a general trend, the accreted GCs remain at high energies compared to the cases involving mergers with satellites with a 1:10 mass ratio. This happens because the progenitors to which they belong, being less massive, cannot penetrate deep enough into the MW-type galaxy potential. The only satellites that are able to lose more energy and carry a part of their clusters at energies lower than -5 (see satellites 3 and 4 in Fig. B.1) also deposit some GCs at high energies, thus resulting in a final distribution that is not clustered as expected. In fact, even in this case, we cannot identify clumps of clusters belonging to the same progenitor, as they are generally mixed and spread over an extended range of angular momentum.
 |
Fig. B.3. Final E − Lz distribution of GCs for the two simulations MWsat_n4_Φ150-60-0-30 (left panel) and MWsat_n4_Φ180-90-30-120 (right panel). GCs originating from the MW-type galaxy are identified as grey circles while accreted GCs are identified by colour-coded circles related to the different satellite of origin. |
Appendix C: Literature age-metallicities
Metallicities, ages, and errors on ages (when available) for all Galactic GCs studied in Massari et al. (2019). Ages and metallicities are taken from (1) Marín-Franch et al. (2009) and (2) VandenBerg et al. (2013). We note that in the case of (1), ages are relative, while for (2) they are expressed in units of Gyr. For each cluster, its progenitor galaxy as reported by Massari et al. (2019) is also given.
All Tables
Masses, characteristic scale lengths and heights, number, and mean masses of particles for the different components of the MW-type galaxy and the satellite(s).
Initial positions and velocities of the barycentres of the simulated satellite galaxies.
Mean and standard deviation of the initial and final Lz and E for the populations of accreted GCs within the different single-accretion simulations.
Metallicities, ages, and errors on ages (when available) for all Galactic GCs studied in Massari et al. (2019). Ages and metallicities are taken from (1) Marín-Franch et al. (2009) and (2) VandenBerg et al. (2013). We note that in the case of (1), ages are relative, while for (2) they are expressed in units of Gyr. For each cluster, its progenitor galaxy as reported by Massari et al. (2019) is also given.
All Figures
 |
Fig. 1. Time evolution of the simulated merging process. Left, middle columns: projections of the simulated GC positions on the x − y and x − z planes for different times of the single-accretion simulation with Φorb = 60° (MWsat_n1_Φ60). (See Table 2 for the initial parameters.) The times increase from top to bottom. The in situ clusters are represented by grey circles and the accreted clusters by magenta circles. In the background, the surface density of the totality of the stars of the simulation is also shown. Right column: distributions of accreted GCs and field stars of the same satellite in the E − Lz space for different times of the single-accretion simulation MWsat_n1_Φ60. The times increase from top to bottom. Each GC is colour-coded according to its escape time from the progenitor satellite, which is also specified by the number on the top right and increases from 0.42 Gyr for GC1 to 5 Gyr for GC10 (see Sect. 3.2 for the definition of tesc). |
| In the text | |
 |
Fig. 2. Time evolution of accreted and in situ GCs distances from the MW-type galaxy. Top panel: time evolution of the distances of the satellite (black line) and its GCs (coloured lines) from the MW-type galaxy for the simulation MWsat_n1_Φ60. Each GC is colour-coded according to its escape time from the progenitor satellite. Bottom panel: time evolution of the apocentres of the orbits of all in situ clusters in the MW-type galaxy for the simulation MWsat_n1_Φ60. Thick and coloured lines indicate clusters whose orbital apocentres at the final time of the simulation are at least 1.5 times larger than their corresponding initial values. The lines are colour-coded according to the ratio of the final apocentre over the initial apocentre. |
| In the text | |
 |
Fig. 3. Final energy of all the accreted clusters in the single-accretion simulations as a function of their escape time from their satellites (tesc). The colour coding indicates the clusters’ initial energy in the reference frame of their progenitor satellite. |
| In the text | |
 |
Fig. 4. Accretion of two satellites on the MW-type galaxy (MWsat_n2_Φ30-150). Left-middle panel: distribution in the E − Lz space of GCs originally belonging to the two satellites (magenta and white colours, respectively). The density maps show the fractional contribution of stars from satellite 1 (left panel) and satellite 2 (middle panel) relative to the totality of the stars. Right panel: distribution in the E − Lz space of GCs originally belonging to the two satellites (magenta and white colours, respectively) and to the MW-type galaxy (grey circles). The density map shows the fractional contribution of stars from the two satellites relative to the totality of the stars. |
| In the text | |
 |
Fig. 5. E − Lz distribution for the whole set of 1 × (1:10) merger simulations at T = 5 Gyr. The distribution of the in situ population of GCs has been stacked and is shown by the grey circles. The colour coding of accreted GCs is according to the initial inclination of the satellite orbital plane with respect to the MW-like reference frame, Φorb. |
| In the text | |
 |
Fig. 6. E − Lz distribution for the whole set of 2 × (1:10) merger simulations at T = 5 Gyr. The distribution of the in situ population of GCs has been stacked and is shown by the grey circles. The colour coding of the satellite GCs (satellite 1: left panel; satellite 2: right panel) is according to the initial inclination of the satellite orbital plane with respect to the MW-like reference frame, Φorb. |
| In the text | |
 |
Fig. 7. Final GC distributions in the kinematic spaces E − Lz, Lperp − Lz, eccentricity − Lz, and the action space for the simulation MWsat_n1_Φ60. The in situ population of GCs is represented by grey circles, while the accreted population is indicated with magenta circles. |
| In the text | |
 |
Fig. 8. Final GC distributions in the kinematic spaces E − Lz, Lperp − Lz, eccentricity − Lz, and the action space for the simulation MWsat_n2_Φ30-150. The in situ population of GCs is represented by grey circles, while the accreted populations are indicated with magenta for satellite 1 and orange for satellite 2. |
| In the text | |
 |
Fig. 9. Distribution in Lperp − Lz, eccentricity − Lz, and the action space for the whole set of 1 × (1:10) merger simulations at T = 5 Gyr. The distribution of the in situ population of GCs has been stacked and is shown by the grey circles. The colour coding of the satellite GCs is according to the initial inclination of the satellite orbital plane with respect to the MW-like reference frame Φorb. |
| In the text | |
 |
Fig. 10. Distribution in Lperp − Lz, eccentricity − Lz, and the action space for the whole set of 2 × (1:10) merger simulations at T = 5 Gyr. The distribution of the in situ population of GCs has been stacked and is shown by the grey circles. The colour coding of the satellite GCs (satellite 1: left column; satellite 2: right column) is according to the initial inclination of the satellite orbital plane with respect to the MW-like reference frame Φorb. |
| In the text | |
 |
Fig. 11. GMM applied to the GCs’ kinematic quantities obtained in the single accretion simulation. Top-middle row: Final GC distributions in the kinematic spaces E − Lz, Lperp − Lz, eccentricity − Lz, and the action space for the simulation MWsat_n1_Φ60. The colour coding of the GCs is related to the different components retrieved when applying the minimum BIC criterion in the GMM. Truly accreted GCs (i.e. those given the ‘true’ label by our simulation) are bordered by magenta circles. Bottom panel: Confusion matrix obtained by the GMM. Each row represents the true labels given by the simulations (MW, satellite), while each column represents the predicted group identified by the model. Values are normalised to the total number of GCs in each true class. |
| In the text | |
 |
Fig. 12. GMM applied to the GCs’ kinematic quantities obtained in the double accretion simulation. Top-middle row: final GC distributions in the kinematic spaces E − Lz, Lperp − Lz, eccentricity − Lz, and the action space for the simulation MWsat_n2_Φ30-150. The colour coding of the GCs is related to the different components retrieved when applying the minimum BIC criterion in the GMM. Truly accreted GCs (i.e. those given the ‘true’ label by our simulation) are bordered by magenta and orange circles respectively for satellite 1 and satellite 2. Bottom panel: Confusion matrix obtained by the GMM. Each row represents the true labels given by the simulations (MW, satellite 1, satellite 2), while each column represents the predicted group identified by the model. Values are normalised to the total number of GCs in each true class. |
| In the text | |
 |
Fig. 13. Same as in Fig. 7 but with the addition of in situ GCs with halo kinematics at the beginning of the simulation. The added in situ GCs are represented as empty circles. |
| In the text | |
 |
Fig. 14. Age-metallicity relations of Galactic GCs from the literature. Left panels: sample of ages and metallicities from Marín-Franch et al. (2009). Right panel: sample of ages and metallicities from VandenBerg et al. (2013). Following the classification given by Massari et al. (2019), the different colours and symbols in each plot indicate the different galaxy progenitors of the clusters. The clusters of Gaia-Sausage Enceladus (G-E), Sequoia (Seq), Helmi stream (H99), Sagittarius (Sag), low-energy (L-E), and high-energy (H-E) are shown by solid circles, while tentative associations are shown by empty circles. Clusters classified as in situ by Massari et al. (2019; M-D and M-B groups) are shown with blue dots. Errors on ages are also reported. Bottom panels: Fits to the AMRs of accreted GCs in the G-E, H99, Sag, and L-E groups. For each group, the mean fit to the data as a function of metallicity is shown together with the corresponding standard deviation. Metallicities and ages are as provided by Marín-Franch et al. (2009) and were used for the fits shown in the left panel. In the right panel, we made use of the ages and metallicities reported by VandenBerg et al. (2013). The in situ clusters are also shown for comparison (blue points). The two clusters identified by a purple cross in the bottom-left panel are NGC 6441 and NGC 6121, which have been excluded from the fit, as motivated in the text. Error bars are not reported in these two panels to avoid having overly complex figures, but they have been taken into account in the fitting procedure (see text). |
| In the text | |
 |
Fig. 15. Time, tf, when the chemical enrichment started as a function of the effective yield p for the four different groups reported in Fig. 14. Top panel: the p and tf values are obtained from fitting the AMR of Marín-Franch et al. (2009). Bottom panel: the p and tf values are obtained from fitting the AMR of VandenBerg et al. (2013). |
| In the text | |
 |
Fig. A.1. Time evolution of the simulated merging process. Left and middle columns: Projections of the simulated GC positions on the x − y and x − z planes for different times (increasing from top to bottom, same as Fig. 1) of the single-accretion simulation with Φorb = 60° (MWsat_n1_Φ60, see Tab. 2 for the initial parameters). The in situ clusters are represented by grey circles and the accreted clusters by magenta circles. In the background, the surface density of the totality of the stars of the simulation is also shown. Right column: Distributions of accreted GCs and field stars of the same satellite in the E − Lz space for different times (increasing from top to bottom) of the single-accretion simulation with Φorb = 60°. |
| In the text | |
 |
Fig. A.2. Time evolution of distances, angular momenta and orbital energies of satellite GCs. Top panel: Time evolution of the distances of the satellite (black line) and its GCs (coloured lines) from the MW-type galaxy for the simulation with a fixed MW potential MWsat_n1_Φ60. Middle panel: Time evolution of the angular momenta of the satellite GCs. Bottom panel: Time evolution of the orbital energies of the satellite GCs. |
| In the text | |
 |
Fig. A.3. Distribution of GCs in the E − Lz space at the end of the simulations. Top panel: Distribution from the single-accretion simulation (MWsat_n1_Φ60). Bottom panel: Distribution from the double accretion simulation (MWsat_n2_Φ30-150). The MW’s GCs are identified as grey circles, while satellite(s) GCs are represented as magenta and orange circles. |
| In the text | |
 |
Fig. B.1. Distributions of accreted GCs and stars in the E − Lz space for the four accreted satellites (simulation with ID = MWsat_n4_Φ150-60-0-30). Left panel: Initial distributions. Right panel: Final distributions. We note that the ranges on the x− and y−axes are the same for all panels. |
| In the text | |
 |
Fig. B.2. Same as in Fig. B.1 but for the simulation with ID = MWsat_n4_Φ180-90-30-120. |
| In the text | |
 |
Fig. B.3. Final E − Lz distribution of GCs for the two simulations MWsat_n4_Φ150-60-0-30 (left panel) and MWsat_n4_Φ180-90-30-120 (right panel). GCs originating from the MW-type galaxy are identified as grey circles while accreted GCs are identified by colour-coded circles related to the different satellite of origin. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \rho _{*}(R,z) = \Bigg (\frac{h_{*}^2M_{*}}{4\pi }\Bigg )\frac{a_{*}R^2 + (a_{*} + 3\sqrt{z^2 + h_{*}^2})(a_{*} + \sqrt{z^2 + h_{*}^2})^2}{\Big [a_{*}^2 + \Big (a_{*} + \sqrt{z^2 + h_{*}^2}\Big )^2\Big ]^{5/2} (z^2 + h_{*}^2)^{3/2}} ,\end{aligned} $$](/articles/aa/full_html/2023/05/aa45128-22/aa45128-22-eq3.gif)
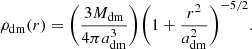
![$$ \begin{aligned} \mathrm{[Fe/H]} = p \times \ln \left( \frac{t_f-t}{t_f} \right) ,\end{aligned} $$](/articles/aa/full_html/2023/05/aa45128-22/aa45128-22-eq13.gif)