| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A136 | |
| Number of page(s) | 22 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202449291 | |
| Published online | 04 October 2024 | |
Metallicity distributions of halo stars: do they trace the Galactic accretion history?
1
Dipartimento di Fisica e Astronomia, Università di Firenze, Via G. Sansone 1, 50019 Sesto Fiorentino, Firenze, Italy
2
GEPI, Observatoire de Paris, PSL Research University, CNRS, Place Jules Janssen, 92195 Meudon, France
3
INAF – Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5, 50125 Firenze, Italy
4
Leibniz-Institut für Astrophysik Potsdam (AIP), 14482 Potsdam, Germany
Received:
19
January
2024
Accepted:
15
May
2024
Context. The standard cosmological scenario predicts a hierarchical formation for galaxies. Many substructures have been found in the Galactic halo, usually identified as clumps in kinematic spaces, like the energy-angular momentum space (E − Lz), under the hypothesis that these quantities should be conserved during the interaction. If these clumps also feature different chemical abundances, such as the metallicity distribution function (MDF), these two arguments together (different kinematic and chemical properties) are often used to motivate their association with distinct and independent merger debris.
Aims. The aim of this study is to explore to what extent we can couple kinematic characteristics and metallicities of stars in the Galactic halo to reconstruct the accretion history of the Milky Way (MW). In particular, we want to understand whether different clumps in the E − Lz space with different MDFs should be associated with distinct merger debris.
Methods. We analysed dissipationless, self-consistent, high-resolution N-body simulations of a MW-type galaxy accreting a satellite with a mass ratio of 1:10, with different orbital parameters and different metallicity gradients, which were assigned a posteriori.
Results. We confirm that accreted stars from a ∼1:10 mass ratio merger event redistribute in a wide range of E and Lz, due to the dynamical friction process, and are thus not associated with a single region. Because satellite stars with different metallicities can be deposited in different regions of the E − Lz space (on average the more metal-rich ones end up more gravitationally bound to the MW), this implies that a single accretion of ∼1:10 can manifest with different MDFs, in different regions of the E − Lz space.
Conclusions. Groups of stars with different E, Lz, and metallicities may be interpreted as originating from different satellite galaxies, but our analysis shows that these interpretations are not physically motivated. In fact, as we show, the coupling of kinematic information with MDFs to reconstruct the accretion history of the MW can bias the reconstructed merger tree towards increasing the number of past accretions and decreasing the masses of the progenitor galaxies.
Key words: methods: numerical / Galaxy: abundances / Galaxy: evolution / Galaxy: formation / galaxies: interactions / Galaxy: kinematics and dynamics
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
According to the standard cosmological model (i.e. Λ cold dark matter, ΛCDM), galaxies are supposed to grow hierarchically from small sub-units that gradually merge to make up the galaxies that we observe (e.g. White & Rees 1978). The study of a galaxy’s merging history is thus crucial to understanding how galaxies form and evolve. In this paper, we aim to find methods to reconstruct the hierarchical build-up of galaxies by focusing on our own Milky Way (MW), for several reasons. First, the total stellar mass of the MW is M* = 6 ± 1 × 1010 M⊙ (Bland-Hawthorn & Gerhard 2016), which places it at the peak of the distribution of galaxy masses in the local Universe (i.e. at redshifts ≤0.1, see van Dokkum et al. 2013; Papovich et al. 2015). Thus, the merging history of a large fraction of galaxies can be understood through that of a MW-type galaxy. Second, the MW is the only massive galaxy for which we are able to resolve single stars of different masses, ages, and compositions, and to study their distances, motions, chemical abundances, and ages. Therefore, it is the benchmark for the study of galaxy formation and evolution. Finally, we can now rely on an unprecedented amount of data for MW stars thanks to the ESA astrometric mission Gaia and its complementary spectroscopic surveys. Indeed, the third Gaia data release (Gaia Collaboration 2016, 2023) delivered parallaxes and proper motions for over a billion MW stars, along with full 6D phase-space information for 33 million stars (Katz et al. 2023). On the other hand, spectroscopic surveys like APOGEE (Majewski et al. 2017), GALAH (De Silva et al. 2015; Buder et al. 2021), Gaia-ESO Survey (Gilmore et al. 2012; Randich et al. 2013), H3 (Conroy et al. 2019), LAMOST (Zhao et al. 2012) and soon 4MOST (de Jong et al. 2019), WEAVE (Jin et al. 2023), and MOONS (Cirasuolo et al. 2020) are providing chemical abundances and radial velocities for several million stars in the Galaxy up to several kiloparsecs from the Sun. Understanding how to interpret these new data is key to shedding light on the properties of the building blocks that made up our Galaxy.
Galaxies grow their stellar mass both by forming new stars, which represent the in situ population, and by accreting nearby satellite galaxies, which bring their own stars that form the so-called ex situ populations (Tacconi et al. 2010; Scoville et al. 2014). These ex situ stellar populations provide information on the number and mass of accreted satellites, and thus on the build-up of the MW. Stars belonging to satellite galaxies in the process of being accreted are still observable in the Galactic halo, since these satellites are not totally disrupted yet, but rather form stellar streams that are identifiable in the plane of the sky. The most famous example is the Sagittarius dwarf spheroidal galaxy, which is the closest MW companion, located at ≈24 kpc from the Sun (Ibata et al. 1994), forming a stellar stream on a polar-like orbit (Newberg et al. 2002; Majewski et al. 2003; Antoja et al. 2020).
The reconstruction of the past accretion1 events of our Galaxy is not trivial, since nowadays the accreted stars associated with those events are completely mixed with the ones formed in situ. The accreted stars, indeed, lose their spatial coherence and after a few Gyr they cannot be detected anymore as spatial over-densities in specific regions of the sky due to mixing timescales in the inner Galaxy (dynamical timescale at a solar radius of ∼250 Myr). Nevertheless, several studies have shown that stars accreted a long time ago, in the first billion years after the formation of our Galaxy, could still be detected as coherent structures in kinematics-related spaces of integral of motions, which are supposed to be conserved during the merger events (Helmi et al. 1999, 2006; Helmi & de Zeeuw 2000; Knebe et al. 2005; Brown et al. 2005; Font et al. 2006; Choi et al. 2007; Morrison et al. 2009; Gómez et al. 2010; Re Fiorentin et al. 2015). The most used kinematics-related space is the energy-angular momentum space (E − Lz), where E is the total energy and Lz is the z component of the angular momentum in a reference system with the x − y plane set on the Galactic disc and the z axis oriented as its spin.
Helmi & de Zeeuw (2000) showed that the stellar clumps in several of these kinematics-related spaces (E − Lz, E − L and L − Lz) are still present after 12 Gyr of evolution, when the system has phase-mixed completely. Thus, the authors concluded that the space of motion integrals are the natural spaces to look for the substructures produced by accreted satellites and to infer the total number of accretion events. The Helmi Stream was the first substructure found in the MW by applying this method. Helmi et al. (1999) showed that ≈10% of the metal-poor stars ([Fe/H] ≤ −1.6 dex) in the Galactic halo come from a single coherent structure.
These results, however, have been based on a number of assumptions, as is discussed in Jean-Baptiste et al. (2017). When these assumptions are removed, accreted stars do not generally conserve their initial clumping in the so-called ‘integral (or pseudo-integral)-of-motion’ spaces (hereafter simply kinematic spaces), since none of the quantity of interest is conserved: neither the energy, nor the z component of the angular momentum, nor the actions (these actions are also often used to discriminate ex situ populations (see, for example, Malhan et al. 2022). The limitations of this approach have been shown to affect both field stars (Jean-Baptiste et al. 2017) and the globular cluster population (Pagnini et al. 2023), and have been confirmed by a number of numerical works since the early results of Jean-Baptiste et al. (2017) (see Koppelman et al. 2020; Amarante et al. 2022 for idealised simulations and Khoperskov et al. 2023b,c for simulations in a cosmological context). Not only can accreted stars from the same progenitor redistribute over a large portion of the above-cited spaces, provided that the merger mass ratio is high enough (≥1 : 10), but in situ stars can also occupy regions of the kinematic spaces where accreted stars (or globular clusters) are deposited (Jean-Baptiste et al. 2017; Pagnini et al. 2023; Khoperskov et al. 2023b,c), making the use of these spaces alone to reconstruct the merger history of our Galaxy questionable.
A potential way to overcome the problem and still use kinematic information to reconstruct the accretion history of the Galaxy is to make use of the metallicity distribution function (hereafter MDF) of stars located in different regions of kinematic spaces: groups of stars that are characterised by different kinematic properties and that also have different MDFs can be indicative of independent accretion events. The discovery of the Sequoia merger event (M* ∼ 5 × 107 M⊙) is an example of this procedure. Sequoia (Myeong et al. 2019) was proposed to have provided the bulk of the high-energy retrograde stars in the stellar halo (already known, see Myeong et al. 2018; Koppelman et al. 2018), while only the null component (Lz ∼ 0) would be related to the Gaia-Sausage Enceladus (hereafter GSE, M* ∼ 6 × 108 M⊙) event (Nissen & Schuster 2010; Belokurov et al. 2018; Haywood et al. 2018a; Helmi et al. 2018). This distinction was motivated by the fact that these two structures have different MDFs: while the GSE MDF peaks at [Fe/H] = −1.3, the Sequoia MDF peaks at [Fe/H] = −1.6, being more metal-poor (Myeong et al. 2019). A difference in [Na/Fe], [Mg/Fe] and [Ca/Fe] has also been pointed out by Matsuno et al. (2019), but these abundances differ even within the various definitions of Sequoia (see Horta et al. 2023). The general difficulty of reconstructing clean samples for GSE and Sequoia has been rigorously addressed by Feuillet et al. (2020, 2021). The latter study, in particular, recognises how the abundance properties of Sequoia change with its kinematic definition. This kind of study has been applied to other regions of kinematic spaces (see, for example, Naidu et al. 2020; Ruiz-Lara et al. 2022), making use of the same overall approach: once different MDFs have been identified, the average metallicity value for each identified region of the kinematic spaces is calculated and these different average metallicities are associated with different stellar masses of the progenitor satellites by making use of mass-metallicity relations.
Finding different average metallicities for different regions of kinematic spaces may at first glance seem proof that the general approach is correct; if different regions of kinematic spaces also have different average metallicities, the straightforward explanation is that they are populated by stellar populations of different origins. But the question is whether this approach is globally valid or whether we are using a somewhat circular argument, by making use of the results (different MDFs) to support the hypothesis (different kinematic properties identify different progenitors). It is therefore necessary to reverse the problem and ask ourselves how the fact that kinematic quantities, such as energy, angular momentum, and actions, are not generally conserved during a merger (if it is sufficiently massive) is reflected in the MDFs of stars located in different regions of kinematic spaces. It is also necessary to ask how this depends on the initial (pre-accretion) metallicity gradients of the satellite galaxies. These questions constitute the motivations of the present work, in which we analyse N-body simulations of galaxy mergers complemented by chemical information to verify the extent to which the above described approach is robust.
This paper is organised as follows. In Section 2, we describe the simulations that we use for the analysis, together with the orbital parameters and different chemical abundances gradients that we have considered. In Section 3, we report the results in the kinematic spaces complemented by chemical information, studying in the first place the metallicity patterns in these spaces (Section 3.1). Then we analyse MDFs in different regions of the kinematic spaces and report the results in Section 3.2, varying both the volume of the simulations considered (Section 3.3) and the orbital parameters (see also Appendix B). Furthermore, we make a tentative reconstruction of the accretion history of the Galaxy by means of these MDFs in Section 3.3 and analyse the relation between the metallicity gradient in the satellite and the one in the kinematic space in Section 3.4. Finally, all the conclusions of the analysis are summarised in Section 4.
2. Numerical methods
In this study, we analyse seven dissipationless, high-resolution N-body simulations of the accretion of a satellite onto a MW-type galaxy with different orbital parameters. The mass ratio is 1:10 since MW-type galaxies have likely experienced such accretions during their evolution (see Fattahi et al. 2018; Fragkoudi et al. 2020). These simulations are fully self-consistent, since both the satellites and the main galaxy are modelled as a collection of particles that reacts to the interaction, experiencing tidal effects and dynamical friction. The interaction is simulated for 5 Gyr, which is sufficient time to complete the merger and have a dynamical relaxation, at least in the inner regions of the remnant galaxy. These simulations are the same 1:10 single accretion (MWsat_n1_Φ) analysed in Pagnini et al. (2023), which we refer to for further details. We focus on single accretion events since we show that they already generate complex patterns that are not easily interpretable.
All the parameters are reported in Table 1. The total number of particles (MW and satellite) is NTOT = 27 500 110, of which NMW = 25 000 100 represent MW-type (stellar and dark matter) particles. Both galaxies consist of a thin, an intermediate, and a thick disc, mimicking the galactic thin disc, the young thick disc, and the old thick disc (Haywood et al. 2013; Di Matteo 2016). The thin disc is as massive as the sum of the thick and intermediate ones (Snaith et al. 2014). The discs have different scale heights (a) and lengths (h). The modelled galaxies also comprise a hundred globular clusters and they are embedded in a dark matter halo. The discs were modelled with Miyamoto-Nagai density distributions (Miyamoto & Nagai 1975):
Scale lengths (a) and heights (h), mass (M), number of particles (N), and particle mass (m) for the disc components of the MW and the satellite, considering a cut-off in radius at ten times the scale length.
with M*, a*, and h* masses and characteristic lengths and heights. The dark halo was modelled as a Plummer sphere:
with Mhalo and ahalo, a characteristic mass and radius, respectively.
The number of stellar particles in the MW-like galaxy is 20 × 106 with a total mass of M* ∼ 9 × 1010 M⊙; thus, it has an average particle mass of m* ∼ 4 × 103 M⊙. The number of dark matter particles is 5 × 106 and the total mass is MDM ∼ 3.7 × 1011 M⊙; hence, it has a particle mass of mDM ∼ 7 × 104.
The mass and total number of particles in each disc component in the satellite is ten times smaller, while their sizes are reduced by a factor of 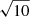 (see Fernández Lorenzo et al. 2013, for the mass–size relation), which is reported in Table 1. The total mass of the satellite has been assumed to be Mhalo = 4.6 × 1010 M⊙ and the visible mass M* = 9 × 109 M⊙, which is compatible with the typical dwarf galaxies in the Local Group. The total mass is smaller than the one estimated for GSE (∼1011); thus, the results found in this case would be even more evident in a GSE-like case. The choice to use a core dark matter halo comes from a number of pieces of observational evidence that are more consistent with a nearly flat density core profile (de Blok 2010).
(see Fernández Lorenzo et al. 2013, for the mass–size relation), which is reported in Table 1. The total mass of the satellite has been assumed to be Mhalo = 4.6 × 1010 M⊙ and the visible mass M* = 9 × 109 M⊙, which is compatible with the typical dwarf galaxies in the Local Group. The total mass is smaller than the one estimated for GSE (∼1011); thus, the results found in this case would be even more evident in a GSE-like case. The choice to use a core dark matter halo comes from a number of pieces of observational evidence that are more consistent with a nearly flat density core profile (de Blok 2010).
In a reference frame with the x − y plane initially set on the MW disc and the z axis oriented as its spin, initial satellite positions and 3D velocities relative to the main galaxy are reported in Table 2. Their orbital planes are inclined of ϕorb with respect to the MW-type galaxy disc.
Initial positions and velocities of the satellite.
The distance of the satellite from the MW centre is initially Dsat = 100 kpc. Initial orbital velocities of the satellite correspond to that of a parabolic orbit for a 1:10 mass ratio with a MW-type galaxy mass of 200 (in units of this mass). The choice of exploring parabolic orbits is in agreement with cosmological predictions (Khochfar & Burkert 2006). The seven simulations differ in the initial orientation of the satellite orbital plane, which could have the following values: ϕorb = 0 ° ,30 ° ,60 ° ,90 ° ,120 ° ,150 ° ,180°, ϕorb = 0 ° ,30 ° ,60° corresponding to direct orbits, ϕorb = 90° to a polar orbit, and ϕorb = 120 ° ,150 ° ,180° to retrograde orbits.
Initial conditions were generated by adopting the iterative method described in Rodionov et al. (2009). All simulations were run by making use of the TreeSPH code described in Semelin & Combes (2002). Gravitational forces were calculated using a tolerance parameter of θ = 0.7 and include terms up to the quadrupole order in the multiple expansion. A Plummer potential was used to soften gravitational forces, with constant softening lengths for different particle species. In all of the simulations described here, ϵ = 50 pc was adopted. The equations of motion were integrated using a leapfrog algorithm with a fixed time step of Δt = 2.5 × 105 yr. In this work, the following set of units is used: distances are given in kiloparsecs, angular momenta in 102 kpc km/s, energies in 104 km2/s2, and time in 107 yr.
As was stated in the previous section, the simulations analysed in this paper are dissipationless, which implies that no star formation or chemical enrichment was modelled. However, following an approach already used in a number of works (see, for example, Di Matteo et al. 2013; Martinez-Valpuesta & Gerhard 2013; Fragkoudi et al. 2017, 2018; Khoperskov et al. 2018), we have assigned, a posteriori, chemical abundances to the stellar particles of the MW-type galaxy and the satellite based on their kinematic properties and the current observational constraints, as is detailed below.
The case of initial vertical abundance gradients. In this first case, the mean metallicity of disc particles is independent of radius; that is, no radial metallicity gradient is initially present in either the disc of the MW-type galaxy or in the satellite. However, a vertical abundance gradient has been taken into account on the basis of observational evidence in the MW. In our Galaxy, indeed, the thick disc is on average more metal-poor and more α-enhanced with respect to the thin disc (Fuhrmann 1998; Haywood et al. 2013; Bensby et al. 2014; Bovy et al. 2012). In particular, in the inner regions of the Galaxy, where all the disc components are present, the metallicity and the α abundance can be described by different Gaussian distributions (Hayden et al. 2015).
For the MW-type galaxy, then, the [Fe/H] and the [Mg/Fe] values were assigned to the particles with normal distributions, with three different mean (μ) and standard deviation (σ) values for the thin, intermediate, and thick discs, with decreasing mean values for the mean metallicity and increasing ones for the α abundances (see Table 3).
Mean and standard deviation values of the normal distributions that define the [Fe/H] and [Mg/Fe] values for the particles of the thin, intermediate, and thick discs of the MW-type galaxy.
As for the satellite galaxy, uniform distributions between different minimum and maximum values were used to assign metallicities to its thin, intermediate, and thick discs (Table 4), to which a dispersion of 0.05 dex was added. In the first place, we assumed a uniform distribution for the sake of simplicity. This simple hypothesis, indeed, already generates a great complexity in the final metallicity patterns in the E − Lz space, and thus is enough for the point we wanted to make out. The choice to assign different metallicity intervals to the satellite disc components simply mimics the case in which satellite stars with hotter kinematics also have lower mean metallicities. On average, the mean metallicity of the satellite is lower than that of the MW-type galaxy, as was found in observational studies (Kirby et al. 2013). As for the [Mg/Fe] abundances of the satellite galaxy, we assigned them in such a way to reproduce qualitatively the behaviour of α-elements with [Fe/H], as was observed in a number of dwarf galaxies of the Local group (see, for example, Matteucci 2007; Tolstoy et al. 2009). These low-mass systems tend to show a nearly flat dependence of α elements with [Fe/H] until a characteristic value of [Fe/H] (the so-called “knee”) at which the [α/Fe] ratio shows an inflection. For metallicities larger than the value at the knee (hereafter [Fe/H]knee), the [α/Fe] ratios show a decrease with increasing [Fe/H]. The value of [Fe/H] at the knee of the [α/Fe]–[Fe/H] relation is in general not the same for all dwarf galaxies (see, for example, Fig. 11 in Tolstoy et al. 2009) but changes from galaxy to galaxy, reflecting their different star formation histories. To mimic this behaviour, we assigned [Mg/Fe] ratios to the satellite stellar particles in the following way:
Minimum and maximum values of the uniform distributions used to assign a metallicity value to the satellite particles.
with [Mg/Fe]knee = 0.22, [Fe/H]knee = −1.3, m = −0.4, and q = −0.3. With such a choice of values, the distribution of in situ and accreted stars in the [Mg/Fe]–[Fe/H] plane is qualitatively similar2 to that found for stars in the solar vicinity (Nissen & Schuster 2010) or in a volume a few kiloparsecs from the Sun (Hayes et al. 2018) (see Fig. 1, top panel). In particular, the choice of [Fe/H]knee = −1.3 was made to be in agreement with the value of metallicity at which Nissen & Schuster (2010) have reported the appearence of the low-α, accreted, halo sequence.
 |
Fig. 1. The [Mg/Fe]–[Fe/H] space and its normalised marginal distributions, in the case of a vertical metallicity gradient only (upper panel) and in the case of an additional radial metallicity gradient (lower panel). |
Adding an initial radial metallicity gradient. In this second case, we have explored the possibility that both the thin discs of the MW-type galaxy and the satellite initially show a negative radial metallicity gradient that co-exists with the vertical gradients discussed before.
In the thin disc of the MW, indeed, it is known that the inner regions have [Fe/H] ∼ 0.3, while the outer regions (beyond 10 kpc) have [Fe/H] ∼ −0.7 (e.g. Hayden et al. 2015). A metallicity gradient is currently absent in the thick disc (Cheng et al. 2012; Hayden et al. 2015), a fact that could be due to its formation during a more turbulent phase, which would have led to an efficient mixing of metals (Haywood et al. 2013, 2015; Lehnert et al. 2014). The assignment of the radial metallicity gradient to the stellar particles was done on the basis of their initial (t = 0) positions. In particular, the metallicity of the thin disc particles of the MW-type galaxy was assigned as follows:
where R is the distance of the particle from the MW-type galaxy centre, projected in the disc plane, ![$ \mathrm{[Fe/H]}_{\mathrm{MW,thin}}^{\mathrm{max}} $](/articles/aa/full_html/2024/10/aa49291-24/aa49291-24-eq6.gif) is the maximum metallicity at the centre of the thin disc (R = 0), which we assigned to be equal to 0.3 dex, and Rmax, MWthin is the maximum distance from the galaxy centre at which stellar particles of the thin disc of the MW-type galaxy are found. With Rmax, MWthin being equal to 50 kpc, this implies that Eq. (4) can be rewritten as
is the maximum metallicity at the centre of the thin disc (R = 0), which we assigned to be equal to 0.3 dex, and Rmax, MWthin is the maximum distance from the galaxy centre at which stellar particles of the thin disc of the MW-type galaxy are found. With Rmax, MWthin being equal to 50 kpc, this implies that Eq. (4) can be rewritten as
with fMW, thin = 0.02 dex/kpc. We caution the reader that the metallicity gradient of the MW disc is known to be more complex than what we have used, with a steeper slope a few kiloparsecs from the Sun (see Haywood et al. 2024, for a recent study). While the adopted values of the gradient can change the mean metallicities of stellar populations and the shapes of the MDFs, the bottom line of the results that we present below does not change.
Similarly, for the thin disc of the satellite galaxy,
where R is now the distance of a stellar particle of the satellite from the satellite centre, ![$ \mathrm{[Fe/H]}_{\mathrm{sat,thin}}^{\mathrm{max}} $](/articles/aa/full_html/2024/10/aa49291-24/aa49291-24-eq9.gif) is the maximum metallicity at the centre of the satellite thin disc (which we assigned to be equal to −0.8 dex), and fsat, thin = 0.05 dex/kpc, in such a way that the satellite thin disc has a metallicity of −1.5 dex at its edge. This gradient is consistent with the ones observed in Local Group dwarf galaxies (e.g., see Taibi et al. 2022). In cosmological simulations, similar gradients are also observed (e.g., Khoperskov et al. 2023a).
is the maximum metallicity at the centre of the satellite thin disc (which we assigned to be equal to −0.8 dex), and fsat, thin = 0.05 dex/kpc, in such a way that the satellite thin disc has a metallicity of −1.5 dex at its edge. This gradient is consistent with the ones observed in Local Group dwarf galaxies (e.g., see Taibi et al. 2022). In cosmological simulations, similar gradients are also observed (e.g., Khoperskov et al. 2023a).
The bottom panel of Figure 1 shows the distribution of stars (accreted and in situ) in the [Mg/Fe]–[Fe/H] space when an initial radial metallicity gradient is added. The main trends are those observed already in the case of a vertical gradient only: the flatness of the [Mg/Fe] ratio for [Fe/H] ≲ −1.3 dex, the appearance of a low-α sequence at higher metallicities, and the redistribution of stars into an α-enhanced thick disc and a low-α thin disc counterpart. To these general features, the inclusion of a radial metallicity gradient has the effect of introducing a certain amount of complexity: the low-α thin disc sequence and the low-α accreted sequence are no longer uniformly populated, but show prominent metal-rich peaks that clearly appear in the total MDF, as well as in the MDFs of the satellite and of the MW-type galaxy, taken separately. The α-DFs, instead, stay the same, since in this second scenario no hypothesis about an α-gradient with radius was taken into account. In particular, in both cases (with or without a radial metallicity gradient) the α-DF of the MW-type galaxies is bimodal, as has been found for stars in the MW disc (Haywood et al. 2018b).
In the following, we refer to the two different initial conditions for the metallicity gradients with the suffix ‘nograd’, to indicate the case in which no radial metallicity gradient is initially present in the main and satellite discs, and with the suffix ‘grad’, to indicate the case in which radial metallicity gradients are initially present. This suffix was added to the identificator of the simulation, which was defined in the previous section. For example, the simulation named MWsat_n1_Φ0_grad refers to a single 1:10 merger, in which the satellite is initially on a planar prograde orbit and in which the thin discs of both the MW-type galaxy and the satellite are initially characterised by a radial metallicity gradient.
3. Results
As far as the kinematics-related spaces are concerned, we confirm earlier results (Jean-Baptiste et al. 2017; Koppelman et al. 2020; Panithanpaisal et al. 2021; Amarante et al. 2022; Khoperskov et al. 2023c); that is, energy and angular momentum are not generally conserved quantities for such a significantly massive satellite, and this is independent of the specific orbital inclination of the satellite galaxy relative to the main galaxy disc. Therefore, a single accretion event can redistribute stars over a large extent of the E − Lz space and these stars are not smoothly redistributed in this space. They form clumps whose number and density depend on the number of passages the satellite has experienced around the MW-type galaxy before complete coalescence and on the mass loss it has experienced at each passage. The stars lost by the satellite in the early phases of its accretion onto the Galaxy tend to redistribute in the upper part of the E − Lz space; that is, at high energies. These stars also span a wide range of Lz values. Hence, one accreted satellite gives rise to several overdensities in the E − Lz space. On the other hand, stars which were in the disc of the main galaxy before the accretion are kinematically heated during the interaction, acquiring halo-like kinematics, and thus contributing to the formation of a stellar halo together with the accreted stars (Zolotov et al. 2009; Purcell et al. 2010; Di Matteo et al. 2019, and references therein). As a consequence, they redistribute in E − Lz space in a region that partially overlaps with that of accreted stars.
3.1. Metallicity patterns in kinematic spaces
After assigning the metallicity to the star particles of the simulation, the first step we took was to study the kinematics-related spaces with this additional information, in order to see where stars with different metallicities would redistribute and to check for a dependence on differences in the initial conditions of the metallicity gradients. We started by discussing the simulation with ϕorb = 150° to show the general trends in the kinematics-related spaces, then we considered different volumes of the simulation to verify the feasibility of this kind of analysis with local observational data. Finally, we compared it with the outcomes of the other simulations with different orbital parameters.
In Figure 2, we show the distributions in the E − Lz space, since among the different kinematics-related spaces it is the one most used in the literature. They are colour-coded at each point by the mean metallicity of all the overlapping star particles. The different columns of Figure 2 correspond to MW-type galaxy (first column), satellite (second one), and total (third one) stellar particles of the simulation. The first row shows the distributions in the E − Lz space of all the star particles of the simulation in the ‘nograd’ case, resulting in both thin discs being more metal-rich than the thick ones on average. The second row shows the E − Lz of the stars in the case of an additional initial radial metallicity gradient. The scales of the colour bars are different depending on which galaxy is considered, in order to make their specific metallicity patterns emerge in a more evident way. For the same purpose, the metallicity colour bar does not cover the whole metallicity range of the metallicity distribution of the star particles of the galaxies of the simulation, but we have considered the percentiles of the distribution and restricted the range of the colour bar to 98% of the metallicity distribution, as is done in the rest of this analysis.
 |
Fig. 2. E − Lz space of in situ (first column), satellite (second column), and total (third column) star particles in the simulation, colour-coded at each point with the mean metallicity. The first and second rows show the E − Lz space in the case of an initial vertical gradient only and in the case of an additional initial radial metallicity gradient, respectively. The scales of the colour bars are different depending on which galaxy is considered, in order to make their specific metallicity patterns more evident. We also recall that in these plots stars on prograde orbits (which rotate as the disc) have negative Lz, while stars on retrograde orbits have positive Lz. |
As far as the in situ star distribution in the E − Lz space is concerned (top left plot), we can observe where the different disc components of the MW-type galaxy, characterised by different mean metallicities, dominate in the E − Lz space. We can see that the most metal-rich stars (in orange-red) redistribute in the region of prograde circular orbits of the thin disc, while the most metal-poor stars (violet-blue) are mainly found in the E − Lz region dominated by the thick disc (see Appendix A for the distributions of the thin, intermediate, and thick disc stars in the E − Lz space separately).
Regarding the satellite stars’ distribution (top middle plot), instead we can notice that there is a region in the upper part of the E − Lz space where the mean metallicity is higher on average. This region is characterised by very high values of energy, and thus is the region populated by the first stars that escape from the satellite during its interaction with the main galaxy, getting bound to the MW-type galaxy potential (Figure 3). These stars are those on the outskirts of the satellite thin disc; indeed, since they are at larger (radial) distances from the satellite baricenter, they are less bound by its potential, and thus more inclined to leave it. In the case we are considering now of no radial gradient in the thin disc, but only a negative vertical metallicity gradient, the thin disc stars are the most metal-rich, which explains the mean metallicity pattern of the satellite distribution in the E − Lz space.
 |
Fig. 3. Final distribution of the satellite stars in the E − Lz space as in the middle column of Figure 2, but colour-coded by their escape time from the satellite potential. The dots represent the mean values of energy and z component of the angular momentum of bound satellite stars, defined by being less than 15 kpc from its barycentre. There are five hundred dots (one for each snapshot of the simulation) and they are colour-coded with the same colour-bar scale but for the time of the simulation (every 10 Myr to cover the 5 Gyr time interval). |
Thus, the existence of an initial metallicity gradient inside the satellite has a consequence in the E − Lz space: different regions show different mean metallicities. We check in the following Section 3.2 how this fact is reflected in the MDFs of the different regions, too, in order to see if in addition to a change in the mean value of the distribution, its shape also changes. Finally, as far as the total star distribution is concerned (top right plot), we can observe a strong metallicity gradient in the E − Lz space, which reflects the regions where the more metal-rich in situ stars dominate on more prograde orbits and have lower energy values and the regions where instead most of the more metal-poor satellite stars lie on more retrograde orbits and have higher energy values. In addition to the fact that on average in situ stars are more metal-rich than satellite ones, we can still observe that inside the distribution of these two galaxies there are metallicity gradients, as was described above.
In order to verify whether these results would be dependent on differences in the initial conditions for the metallicity gradients, we have also studied the case of an additional radial negative gradient in the thin discs of both the satellite and the MW-type galaxy, and the outskirts of the discs thus being more metal-poor than the inner parts. We report the corresponding results in the second row of Figure 2: the MW-type galaxy distribution (left plot) overall resembles the one seen previously in the case of the vertical metallicity gradient only. However, we can notice the effect of having introduced a negative radial gradient too: the region of the E − Lz space populated by the thin disc (towards the edge of the E − Lz distribution, for negative values of Lz) is not homogeneously coloured anymore, as it was in the case of the vertical metallicity gradient only, but exhibits a gradient. We can see that the upper regions are more metal-poor than in the previous case. These regions at high energies are indeed populated by stars that initially are less gravitationally bound (i.e. high energies and large distances from the main galaxy centre). On the other hand, the low-energy regions are more metal-rich than before, because the populations that are initially more gravitationally bound (and more metal-rich) are also closer to the galaxy centres. As far as the satellite distribution is concerned (middle plot), we can again observe the consequence of the choice made for the initial metallicity gradient: the upper region that was populated before by the most metal-rich stars is now on the contrary populated by the most metal-poor ones. This is clearly a consequence of assigning a radial metallicity gradient to satellite disc stars. Finally, regarding the total distribution (right plot), we can observe an overall metallicity gradient again, which is even stronger than before (see Section 3.4), and we can still see the gradients inside the two galaxies.
3.1.1. Solar-like volume
Once the previous results for the total distributions of star particles in the E − Lz space were obtained, we were interested in understanding what it was actually possible to obtain with the data we had in a limited volume observed. Thus, in order to check the feasibility of detecting accreted structures in this space in local volumes, we restricted our analysis to a ‘solar-vicinity’ or a ‘solar-like volume’. It was defined as a spherical volume that is centred at 8 kpc from the MW-type galaxy centre and that has a radius of 5 kpc, which is the typical size around the Sun for which we currently have accurate-enough parallaxes, proper motions, and line-of-sight velocities. In order to take into account the fact that accreted stars do not necessarily redistribute uniformly, we considered several different volumes homogeneously distributed in the azimuth position of the centre: ϕ⊙ = 0 ° ,90 ° ,180 ° ,270° (in cylindrical coordinates). In the following analysis, we show the results for the first solar volume (with ϕ⊙ = 0°), which are also valid for all the other volumes examined. Figure 4 shows the final distributions in the E − Lz space when the solar-like volume is considered, colour-coded at each point with the mean metallicity.
 |
Fig. 4. E − Lz space of in situ (first column), satellite (second column), and total (third column) star particles in the simulation, colour-coded at each point with the mean metallicity, when the analysis is restricted to a solar-like volume. The first row shows the E − Lz space in the case of an initial vertical metallicity gradient only. Likewise, the second row shows it, but in the case of an additional initial radial metallicity gradient. The scales of the colour bars are different depending on which galaxy is considered, in order to make their specific metallicity patterns emerge in a more evident way. We recall that in these plots stars on prograde orbits (which rotate as the disc) have negative Lz, while stars on retrograde orbits have positive Lz. |
We can see in the right-most panels of Figure 4 that the same overall trends observed for the whole volume are found: a metal-poor population with retrograde or null Lz, and a more metal-rich one as the orbits become more prograde (negative Lz), in both the metallicity gradient cases. Furthermore, it is interesting to notice how a retrograde single-merger event can produce a Sequoia-like debris, which corresponds to the outer parts of its GSE-like progenitor. However, when the analysis is restricted to 5 kpc around the Sun, we can no longer capture the very metal-rich (metal-poor) satellite stars found at very high energies (see, for example, the orange (blue) color in the middle panel of the top (bottom) row of Figure 2).
This implies that the MDF of the GSE may still exhibit biases, particularly in the absence of observations for the most metal-rich (metal-poor) stars (consistently with the results of Carrillo et al. 2024). This limitation could potentially be addressed more comprehensively with upcoming surveys such as SDSSV/4MOST (allowing us to get a more complete sample of the accreted stars now bound to the MW, but outside the solar-like volume we defined) or, more promisingly, with MOONS. MOONS will survey the bulge of the Galaxy (Gonzalez et al. 2020), allowing us to explore the eventual accreted populations in the innermost regions of the MW and check for differences in the metallicity distributions with respect to those in the solar neighbourhood.
3.1.2. Exploring different orbital inclinations
In order to check the dependence of our results on the satellite orbital parameters, we analysed the star distributions in all the previous spaces (colour-coded at each point with the mean metallicity) for all the other simulations with a different initial inclination of the satellite orbital plane with respect to the MW-type galaxy, ϕorb = 0 ° ,30 ° ,60 ° ,90 ° ,120 ° ,150 ° ,180°. To seek a synthesis, in the following we only report the results for the E − Lz space for ϕorb = 0 ° ,90 ° ,180°. In Figure 5, we show the final distributions in the E − Lz space colour-coded at each point with the mean metallicity for the total volume of the simulations, with ϕorb = 0 ° ,90 ° ,180° in different rows, for the in situ (first column), satellite (second column), and total (third column) star particles.
 |
Fig. 5. E − Lz spaces of the in situ (first column), satellite (second column), and total (third column) star particles in the simulation, colour-coded at each point with the mean metallicity. Each row shows a simulation with a different value of the initial inclination of the satellite orbital plane: ϕorb = 0 ° ,90 ° ,180°. The upper (lower) panel is for nograd (grad) case. |
The top panel of Figure 5 shows the distributions in the case of an initial vertical metallicity gradient only. The in situ distributions are all very similar. The satellite distributions, instead, show a dependence on the orbital parameter, ϕorb, with: (i) more metal-poor stars on prograde orbits (negative values of Lz) at high energies for initial prograde orbits of the satellite, and (ii) more on retrograde orbits at high energies for initial retrograde orbits of the satellite. In any case, the most metal-rich stars are those of the thin disc, lost early and at high values of energy. These two features can be observed in the total distribution, which shows different regions dominated by metal-poor stars, depending on the initial satellite orbital properties.
In the bottom panel of Figure 5, we show the same distributions in the case of an additional initial radial metallicity gradient. The in situ distributions are all very similar, this time showing the radial metallicity gradient in the region of the circular prograde orbits (thin disc). As far as the satellite distributions are concerned, unlike before, the most metal-poor stars are the ones of the thin disc, lost at low values of time and high values of energy. The distributions of satellite stars still show a dependence on the orbital parameter, ϕorb, with more metal-poor stars on prograde orbits (negative values of Lz) at high energies for initial prograde orbits of the satellite and more on retrograde orbits at high energies for initial retrograde orbits of the satellite. Again, this can be appreciated in the total distribution, which shows different regions dominated by metal-poor stars, depending on the initial satellite orbital properties.
This dependence could be useful to characterise the orbital parameters of the accretion events experienced by the MW. However, this can be challenging if the analysis is restricted to a volume of a few kiloparsecs in radius around the Sun (as is the case with many spectroscopic surveys). When we restrict the analysis to the solar-like volume, indeed, the final distributions in the E − Lz space all become very similar to one another, losing the dependence of the metallicity pattern on the ϕorb parameter, since the differences in the final distribution considering the whole volume are due to satellite stars deposited at high energy values, which do not reach the solar vicinity.
As was mentioned above, the mean metallicity throughout the E − Lz space for bound regions does not depend strongly on the orbital parameters of the accretion event. More quantitatively, we show in the upper row of Figure 6 the mean metallicity (and standard deviation) in the energy interval −5 < E < 0 as a function of the angular momentum for all the possible initial values of the inclination of the satellite orbital plane (different colours) and for both the nograd case (left panels) and the grad case (right).
 |
Fig. 6. Mean metallicity and standard deviation as a function of the angular momentum interval of the E − Lz space (in every column of Figures 7, B.1) for all the simulations with Φ = 0 ° ,30 ° ,60 ° ,90 ° ,120 ° ,150 ° ,180°, in the energy range −5 < E < 0. The left panel shows the case with the initial vertical metallicity gradient only, while the right panel shows the one with the additional radial metallicity gradient. |
 |
Fig. 7. Total star distribution in the E − Lz space in the case of an initial vertical metallicity gradient only (upper panel) and an additional initial radial metallicity gradient (lower panel), colour-coded at each point with the mean metallicity. The superimposed grid shows the splitting of the space used to analyse the MDFs in different regions. |
We can see a dependence on the initial conditions assumed for the metallicity distribution of the satellite. In fact, both the left and right panels show a knee at approximately null angular momentum and then a plateau at low metallicity at more retrograde Lz values (more positive). However, the nograd case also features a plateau at high metallicity and at prograde angular momentum values (negative Lz), whereas the grad case shows a decreasing mean metallicity value the more prograde the orbit. In the lower row of Figure 6, we also show the same plots in the energy interval −10 < E < −5 for a comparison.
3.2. Metallicity distribution functions in different regions of the E − Lz space
After discussing the variation in the mean metallicity across the E − Lz space, the next step was to analyse the variation in the MDFs. The interest in looking at the MDF is due to the fact that all of the previous plots show the average metallicity in a given region of the E − Lz plane, while the MDF can provide more insight into the population(s) which contribute(s) to a given average value. As before, to start off, we show the results for the simulation with an initial inclination of the satellite orbital plane with respect to the MW-type galaxy disc, ϕorb, equal to 150°. The results concerning the simulations with direct, polar, and retrograde orbits (ϕorb = 0 ° ,90 ° ,180°) are reported in Appendix B.
In order to analyse the MDFs in different regions of the E − Lz space, we divided this space into rectangles 20 × 102 kpc km/s wide in angular momentum and 5 × 104 km2 s−2 high in energy, so as to reproduce the average dimensions of the substructures found so far in the E − Lz space. The splitting is shown in Figure 7. In Figure 8, we show the resulting MDFs for different regions of the E − Lz space contained in the large red rectangle of Figure 7. In this way, different rows show the MDFs for a fixed value of energy (increasing in the bottom-up direction), while different columns show the MDFs for a fixed value of angular momentum (increasing in the left-right direction). The angular momentum and energy intervals are reported in every cell, together with the number of in situ and accreted stars, in red and blue, respectively. Every plot then shows the MDF considering all the stars in the region (in black), the MDF of the MW-type stars only (in red), and the MDF of the satellite stars only (in blue), all normalised in order to compare means, peaks, and shapes. The solid lines show the mean of the distribution, while the dotted ones show its peak(s). The values of the fraction of satellite stars in the different E − Lz regions, as well as the mean values of the total MDFs, in the two cases (nograd and grad) explored in this paper, are reported in Tables 5, 6 and 7, respectively.
 |
Fig. 8. MDFs of different regions of the E − Lz, in the nograd case (top panel) and in the grad one (bottom panel). The red, blue, and black histograms show the MW-type galaxy, satellite, and total MDF, respectively, all normalised. The solid lines show the mean of the distribution. Energy intervals row by row (top to bottom): (i) 0 < E < 5, (ii) −5 < E < 0, (iii) −10 < E < −5, (iv) −15 < E < −10, (v) −20 < E < −15. Angular momentum intervals column by column (left to right): (i) −50 < Lz < −30, (ii) −30 < Lz < −10, (iii) −10 < Lz < 10, (iv) 10 < Lz < 30, (v) 30 < Lz < 50, (vi) 50 < Lz < 70. The red (blue) number shows the amount of in situ (accreted) stars in every cell. |
We start with the case of the vertical metallicity gradient only. The E − Lz space has been divided, as was described above and as is shown in the top panel of Figure 7. Starting from the bottom row of Figure 8, the lowest energy interval considered (−10 ≤ Lz ≤ 10, −20 ≤ E ≤ −15), the global MDF in black of both accreted and in situ stars almost coincides with that of in situ stars only, since they dominate this region (see Figure 1). The central rectangle of the following row (−15 ≤ E ≤ −10) is still dominated by in situ stars, but now the total MDF shows a bump at low metallicity ([Fe/H] ∼ −1.2) due to satellite stars. So far, satellite MDFs are all very similar one to each other, resembling the total satellite MDF (see Figure 1): there is a single-peaked distribution (at [Fe/H] ∼ −1.2), with a bump at higher metallicities. The following row (−10 ≤ E ≤ −5) instead shows some differences. The satellite MDF starts to peak at higher metallicities (at [Fe/H] ∼ −1) in the central region with Lz ∼ 0, due to the fact that a larger fraction of satellite metal-rich stars are found at higher energies as they escape the satellite at earlier times. Moreover, we observe a broader distribution in the region with −10 ≤ Lz ≤ 10 and a region in which the MDF is double-peaked (10 ≤ Lz ≤ 30), even if the initial total MDF of the satellite was not. We also see that the total MDF in regions with stars on more retrograde orbits has significant contributions from the satellite stars at low metallicities. As a consequence, its mean is shifted towards lower metallicities while moving towards more retrograde orbits (more positive values of Lz), but also towards higher energies, where satellite stars represent a higher fraction of the total (see Table 5). We can observe all these features in the least bound row (−5 ≤ E ≤ 0), where the distributions are broader and peaked at lower metallicities as we move towards more retrograde star orbits (positive Lz). In particular, the right-most plot of the figure, which contains the stars with the highest energies and most retrograde orbits, is the one where the MDF peaks at the lowest metallicities; that is, at [Fe/H] ∼ −1.5. For completeness, we also report the unbound energy interval 0 < E < 5, even if these stars end up several hundreds kiloparsecs away from the main galaxy centre. We can also appreciate in this region the same trend; namely, the mean of the total MDF decreases for more retrograde orbits (see Tables 6 and 7).
We now discuss the results in the case of an additional initial radial metallicity gradient, both in the satellite and in the MW-type galaxy. We recall that the introduction of the radial gradient makes the MDFs of both the MW-type galaxy and the satellite double-peaked (see Figure 1). The highest peak is due to the thin disc component and the second to the intermediate and thick disc components together (see the top panel of Figure 9, where we show the MDFs of the various disc components in different colours). The in situ MDF peaks are at [Fe/H] ∼ 0.2 and at [Fe/H] ∼ −0.2, while the satellite MDFs are at [Fe/H] ∼ −0.9 and [Fe/H] ∼ −1.2. We were interested, then, in checking if we recover these features in the MDF restricted to different regions of the E − Lz space. We proceeded in the same way as the previous case, so the E − Lz space was divided as before and as is shown in the lower panel of Figure 7. In the bottom row of Figure 8, we show the MDFs in the E − Lz space with E ≤ −15. We can see that the MDF of the single galaxies, the MW-type galaxy (in red) and the satellite (in blue), are usually quite representative of the total initial ones, being bimodal and peaked at the initial positions in metallicities. Nevertheless, considering higher energy intervals (−15 ≤ E ≤ −10 and −10 ≤ E ≤ −5), the total MDF (in black) already starts to change, reflecting the increasing relative importance of the satellite contribution, and thus beginning to show bumps at lower metallicities and means more shifted towards lower metallicities too. This trend is hence independent of the choice of initial conditions for the metallicity gradient, but is mostly due to the fact that regions of higher energies and more retrograde angular momentum are more dominated by satellite stars (see Table 5), which are on average more metal-poor. In the regions with the highest energies (bound and not, −5 ≤ E ≤ 0 and 0 ≤ E ≤ 5), we can see that the satellite MDFs change a lot in shape and mean, becoming broader, losing bimodality, and being on average at lower metallicities. Once again, the total MDF always coincides more with the satellite one, moving towards higher energies and more retrograde orbits, and thus changing a lot in mean towards lower metallicities.
 |
Fig. 9. Top panels: MDF of the satellite stars (in filled blue) and the same MDF restricted to the satellite stars that reach a solar-like volume by the end of the simulation (in patterned blue). The solid lines are the means of the distributions (broader for the total distribution, thinner for the solar one). The dashed (dash-dotted) lines are the peak(s) of the total (solar) distribution. The satellite MDF divided into disc components is shown by the red, green, and blue curves for the thin, intermediate, and thick discs, respectively. Bottom panel: Difference between the two normalised distributions in the top panel (Δ), i.e. the total distribution minus the solar-like restricted one. The left column shows the case with the vertical metallicity gradient only, and the right column the one with the additional radial metallicity gradient. |
We can conclude that, independently of the initial choice of metallicity gradient for the satellite, its MDFs in different regions of the E − Lz space can be significantly different one from each other in shape, mean, and peak values, even if they all result from the same accretion event. Therefore, different regions of the E − Lz space showing different kinematic and MDFs can actually be associated with the same single original accreted satellite, making the E − Lz very hard to interpret. Nevertheless, we have found trends in the MDFs’ varying energy and angular momentum values. In particular, we have shown that the mean and the peak(s) of the global MDF of both accreted and in situ stars move towards lower metallicities for higher values of energy and angular momentum (i.e. for more retrograde orbits). This is a consequence of the increasing importance of the more metal-poor satellite contribution in stellar density.
Global versus local metallicity distribution functions. So far, we have shown MDFs estimated over the full galactic extent, in the ideal case – as in a simulation – in which all stars (or stellar particles) in the galaxy can be observed. In reality, spectroscopic surveys provide chemical abundances over a limited volume around the Sun. It is thus interesting to understand to what extent ‘local’ MDF can be representative of the global one; in particular, if we were able to select a pure accreted sample of stars (that is, with null or very limited pollution of in situ stars) a few kiloparsecs from the Sun, the extent to which its MDF would be representative of that of the whole satellite.
We recall that we defined the ‘solar-vicinity’ as a spherical volume centred at 8 kpc from the MW-type galaxy centre and with a radius of 5 kpc. The top panels of Figure 9 show the MDF of all satellite stars (in filled gray) and its local counterpart, in which only the contribution of stars that at the end of the simulation are found in a solar-like volume are shown (in patterned gray). Both the cases with and without an initial radial metallicity gradient in the satellite are shown (right and left panels, respectively). We can notice that in both cases the global shape of the MDF is conserved, as the metallicity range featured is also.
The bottom panels show Δ, the difference between the two normalised distributions. We can see that in the nograd case there is an under-representation of high-metallicity stars (i.e. stars with [Fe/H] ≥ −1.1), while in the grad case there is a deeper drop at [Fe/H] ∼ −1.0.
By way of a comparison with the MDFs of the single disc components (thick, intermediate, and thin ones in red, green, and blue, respectively, in the top panel), we can associate the under-representation with missing thin disc stars; that is, with stars initially on the outskirts of the satellite that are lost in the early phases of the accretion, and that are deposited at energies too high to be sampled in the solar vicinity. Depending on the metallicity that these stars initially have, this will give rise to an under-representation of these metallicities in local MDFs.
3.3. Reconstructing a possible (but wrong) accretion history from kinematic spaces and metallicity distribution functions
The results discussed in the previous section can lead one to reconstruct accretion histories that may look realistic, but that are in fact very far from true. An example of the difficulty of using these spaces to reconstruct the merger tree of a MW-type galaxy is given below.
Suppose we have a dataset of halo stars, distributed over an extended range of energies and angular momenta. We might be led to interpret different regions of this space as being dominated by stars of different origins, and to infer the properties of the galaxies in which these stars formed by studying the characteristics of their MDFs. For example, by making use of a mass-metallicity relation given by Kirby et al. (2013),
we may in principle reconstruct the stellar mass of the progenitor galaxies, given the mean metallicity of stars in a given E − Lz region (Tables 6 and 7). If we apply this reasoning to our simulations, we would get the following:
-
Unbound stars (0 < E < 5) found in the nograd simulation (upper panel of Figure 7) are dominated at null angular momentum (−10 < Lz < 10) by stars of a galaxy whose stellar mass was ∼108.4 M⊙, since the mean metallicity of stars in this region is ⟨[Fe/H]⟩ ∼ −1.0, while stars of the same energy but more retrograde angular momenta (50 < Lz < 70) would be associated with a satellite galaxy with a stellar mass equal to 107 M⊙, given that the mean stellar metallicity in this region is ⟨[Fe/H]⟩ ∼ −1.4.
-
At lower energies (−10 < E < −5), the problem would persist. In particular, in the region around null angular momentum (−10 < Lz < 10), the mean metallicity being ⟨[Fe/H]⟩ ∼ −0.7, this may be interpreted as a signature of a massive accretion, M* ∼ 109.4 M⊙.
-
Similar conclusions would hold for the grad case, in which, depending on the region we look at, we may end up finding traces of low-mass accretions (M* ∼ 107.4 M⊙ at −5 < E < 0 and 50 < Lz < 70, corresponding to a mean of ⟨[Fe/H]⟩ ∼ −1.3) and also more massive ones (M* ∼ 108.4 M⊙ at −10 < E < −5 and 10 < Lz < 30, corresponding to a mean of ⟨[Fe/H]⟩ ∼ −1.0).
An even more complex situation would arise if we tried to interpret the multiple peaks present in the MDFs of some specific regions of the E − Lz space as being due to distinct accretion events.
Regardless of the details of the average metallicity values, and thus the masses of the progenitors, the common feature of this type of analysis is to overestimate the number of accretions and underestimate the associated masses.
3.4. Metallicity gradient in the satellite versus in the E − Lz space
Once it had been established that analysing separately the metallicity distribution of limited regions inside the kinematic spaces is not necessarily informative about the initial conditions of the original satellite, we tried to consider the global picture in order to characterise the accretion event. To this end, we set the initial conditions for both the galaxies to the grad case, but while for the MW-type galaxy it was fixed as is described in Section 2, for the satellite we let the steepness of the radial metallicity gradient vary in the range: fsat, thin ∈ [ − 0.06, 0.02]. In this way, we could evaluate the dependence on this parameter of the metallicity patterns in the E − Lz space, without pre-selecting a certain group of accreted stars on the basis of kinematic arguments.
For every fsat, thin value, we considered the final distribution of both satellite and MW-type thin disc stars in the E − Lz space and we computed the mean metallicity as a function of the energy. We generally found a monotonic decreasing function as the energy increases, and thus we fit it with a line (more details about the method can be found in Appendix C) and analysed the relation between the slope of this linear fitting (d⟨[Fe/H]⟩/dE) and fsat, thin itself. The relation is shown by the solid lines in Figure 10, in different colours for the different orbital parameter values (see captions). We can see that it is a linear relation, which is independent of the initial inclination of the satellite orbital plane, and thus from the metallicity gradient in the kinematic space as a function of energy one can obtain information about the initial conditions of the metallicity gradient in the original satellite.
 |
Fig. 10. Relation between the slope of the initial radial metallicity gradient in the satellite thin disc (fsat, thin) and the slope of the metallicity gradient in the final distribution of all the thin disc stars in the E − Lz space as a function of energy (d⟨[Fe/H]⟩/dE), in the total volume of the simulation (solid lines), and in the restricted solar-like volume (dashed line). The case of ϕorb = 0° also features the dash-dotted curve described in Section 3.4. |
There is only one exception, which is the case of ϕorb = 0° and which is shown by the dash-dotted line in Figure 10. This is due to the fact that for this planar orbit satellite stars reach very bound orbits, and thus are redistributed at very low energy values in the E − Lz space. As a consequence, they dump the mean metallicity at low energy, which then becomes an increasing function of energy in the lowest interval, −25 < E < −22, and starts to decrease as before after this value. If we then fit the relation with a cut in energy to include only the decreasing range, we obtain the solid blue line that is consistent with all the other curves for the different inclinations.
As a final step, we performed the same analysis considering the final distribution in the E − Lz space of the thin disc stars that reach the solar vicinity. The relations for every ϕorb value are shown by the dashed lines in Figure 10. We obtain the same relation, yet shifted to more negative values of the slope of the metallicity gradient in the final distribution in the E − Lz space as a function of energy (d⟨[Fe/H]⟩/dE).
We have shown that merger debris is not clustered, making it challenging to derive merger parameters due to variations in the MDF across different regions of E − Lz. This limitation may seem to render the IOM space less useful. However, there is a positive aspect to consider. Thanks to the energy differentiation of the debris, we gain insights into the structure of the galaxy-progenitors, as is demonstrated through the gradient relation in this analysis (see also Khoperskov et al. 2023d). Moreover, this would not be achievable if mergers were viewed as E − Lz clumps.
4. Conclusions
In this paper, we have analysed N-body simulations of the accretion of a satellite galaxy onto a MW-type galaxy (an accretion with a mass ratio of 1:10), to explore the extent to which we can couple kinematic characteristics and metallicities of stars in the halo to reconstruct the accretion history of our Galaxy. The main conclusions of our work are the following:
-
We confirm earlier results that accreted stars from ∼1:10 mass ratio satellites are redistributed in a wide range of energies and angular momenta (Jean-Baptiste et al. 2017; Koppelman et al. 2020; Amarante et al. 2022; Khoperskov et al. 2023c) and that in particular stars deposited at higher energies have on average different metallicities than those of stars that at the end of the accretion process end up being more gravitationally bound to the MW (Amarante et al. 2022; Khoperskov et al. 2023a,d).
-
Because satellite stars with different metallicities can be deposited in different regions of the E − Lz space, this implies that a single accretion of ∼1:10 can manifest with different MDFs, in different regions of the E − Lz space.
-
Groups of stars with different E, Lz, and metallicities may be interpreted as originating from different satellite galaxies, but our analysis shows that these interpretations are not physically motivated.
-
When the analysis is restricted to a solar-like volume, we can no longer capture the very metal-rich (or metal-poor, depending on the initial conditions in the satellite) accreted stars found at very high energies. This implies that the MDF of the GSE may still exhibit biases.
-
Reconstructing the Galactic accretion history through mass-metallicity relations using the MDF mean values of single clumps can be very misleading. For example, a single merger of a galaxy with a mass of 5 × 1010 can be erroneously interpreted as three with masses of ∼107, ∼108.4, and ∼109.4. As we show, coupling kinematic information with the MDFs to reconstruct the accretion history of the MW can bias the reconstructed merger tree towards increasing the number of past accretions and decreasing the masses of the progenitor galaxies.
-
From the metallicity gradient in the E − Lz space as a function of energy, one can retrieve information about the initial conditions of the radial metallicity gradient in the original satellite.
A number of possible accretion events have been proposed in the literature by making use of this approach, and our analysis reinforces previous suggestions that at least some of these accretion events are disputable. Indeed, we have shown how a single massive accretion can produce MDFs whose characteristics change across the E − Lz plane. In a scenario in which the MW may have experienced more than a single significant accretion in its past, it is clear that the interpretation of these spaces, and related MDFs, becomes even more challenging. In this respect, we recall that even the GSE merger initially discovered in a solar vicinity volume (Nissen & Schuster 2010) was already suspected to have been made by more than one galaxy at the time of its local discovery (see discussion in Nissen & Schuster 2010). New evidence has recently been published on the possibility that this accretion event indeed hides multiple ones (Donlon & Newberg 2023; Nissen et al. 2023).
Ultimately, overall the merger tree of the MW is still far from being robustly established, and – even more importantly – we still need to establish sound methods of discriminating between accretion scenarios. Although various abundance ratios have already been used to characterise different accretion events (e.g., Matsuno et al. 2019, 2022a,b; Monty et al. 2020; Horta et al. 2023; Ceccarelli et al. 2024), our study emphasises the importance of going not only beyond [Fe/H] but also a revision of the kinematic identification of merger debris. This will be vital for a more realistic reconstruction of the MW merger history in light of coming data from WEAVE, 4MOST, SDSSV, and other spectroscopic surveys.
Acknowledgments
AM and SS acknowledge support from the ERC Starting Grant NEFERTITI H2020/808240. This work has made use of the computational resources obtained through the DARI grant A0120410154 (PI: P. Di Matteo). The authors thank P. Bonifacio for insightful discussion.
References
- Amarante, J. A. S., Debattista, V. P., Beraldo e Silva, L., Laporte, C. F. P., & Deg, N. 2022, ApJ, 937, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Antoja, T., Ramos, P., Mateu, C., et al. 2020, XIV.0 Scientific Meeting (virtual) of the Spanish Astronomical Society, 117 [Google Scholar]
- Belokurov, V., Erkal, D., Evans, N. W., Koposov, S. E., & Deason, A. J. 2018, MNRAS, 478, 611 [Google Scholar]
- Bensby, T., Feltzing, S., & Oey, M. S. 2014, A&A, 562, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bland-Hawthorn, J., & Gerhard, O. 2016, ARA&A, 54, 529 [Google Scholar]
- Bovy, J., Rix, H.-W., & Hogg, D. W. 2012, ApJ, 751, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, A. G. A., Velázquez, H. M., & Aguilar, L. A. 2005, MNRAS, 359, 1287 [NASA ADS] [CrossRef] [Google Scholar]
- Buder, S., Sharma, S., Kos, J., et al. 2021, MNRAS, 506, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Carrillo, A., Deason, A. J., Fattahi, A., Callingham, T. M., & Grand, R. J. J. 2024, MNRAS, 527, 2165 [Google Scholar]
- Ceccarelli, E., Massari, D., Mucciarelli, A., et al. 2024, A&A, 684, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cheng, J. Y., Rockosi, C. M., Morrison, H. L., et al. 2012, ApJ, 746, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, J.-H., Weinberg, M. D., & Katz, N. 2007, MNRAS, 381, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Cirasuolo, M., Fairley, A., Rees, P., et al. 2020, The Messenger, 180, 10 [NASA ADS] [Google Scholar]
- Conroy, C., Bonaca, A., Cargile, P., et al. 2019, ApJ, 883, 107 [NASA ADS] [CrossRef] [Google Scholar]
- de Blok, W. J. G. 2010, Adv. Astron., 2010, 789293 [CrossRef] [Google Scholar]
- de Jong, R. S., Agertz, O., Berbel, A. A., et al. 2019, The Messenger, 175, 3 [NASA ADS] [Google Scholar]
- De Silva, G. M., Freeman, K. C., Bland-Hawthorn, J., et al. 2015, MNRAS, 449, 2604 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, P. 2016, PASA, 33, e027 [CrossRef] [Google Scholar]
- Di Matteo, P., Haywood, M., Combes, F., Semelin, B., & Snaith, O. N. 2013, A&A, 553, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Matteo, P., Haywood, M., Lehnert, M. D., et al. 2019, A&A, 632, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donlon, T., & Newberg, H. J. 2023, ApJ, 944, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Fattahi, A., Navarro, J. F., Frenk, C. S., et al. 2018, MNRAS, 476, 3816 [Google Scholar]
- Fernández Lorenzo, M., Sulentic, J., Verdes-Montenegro, L., & Argudo-Fernández, M. 2013, MNRAS, 434, 325 [Google Scholar]
- Feuillet, D. K., Feltzing, S., Sahlholdt, C. L., & Casagrande, L. 2020, MNRAS, 497, 109 [Google Scholar]
- Feuillet, D. K., Sahlholdt, C. L., Feltzing, S., & Casagrande, L. 2021, MNRAS, 508, 1489 [NASA ADS] [CrossRef] [Google Scholar]
- Font, A. S., Johnston, K. V., Bullock, J. S., & Robertson, B. E. 2006, ApJ, 646, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Fragkoudi, F., Di Matteo, P., Haywood, M., et al. 2017, A&A, 607, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fragkoudi, F., Di Matteo, P., Haywood, M., et al. 2018, A&A, 616, A180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fragkoudi, F., Grand, R. J. J., Pakmor, R., et al. 2020, MNRAS, 494, 5936 [Google Scholar]
- Fuhrmann, K. 1998, A&A, 338, 161 [NASA ADS] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Gómez, F. A., Helmi, A., Brown, A. G. A., & Li, Y.-S. 2010, MNRAS, 408, 935 [Google Scholar]
- Gonzalez, O. A., Mucciarelli, A., Origlia, L., et al. 2020, The Messenger, 180, 18 [NASA ADS] [Google Scholar]
- Hayden, M. R., Bovy, J., Holtzman, J. A., et al. 2015, ApJ, 808, 132 [Google Scholar]
- Hayes, C. R., Majewski, S. R., Shetrone, M., et al. 2018, ApJ, 852, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M. D., Katz, D., & Gómez, A. 2013, A&A, 560, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M., Di Matteo, P., Snaith, O., & Lehnert, M. D. 2015, A&A, 579, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M. D., et al. 2018a, ApJ, 863, 113 [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M., et al. 2018b, A&A, 618, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M., Khoperskov, S., Cerqui, V., et al. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202348767 [Google Scholar]
- Helmi, A., & de Zeeuw, P. T. 2000, MNRAS, 319, 657 [Google Scholar]
- Helmi, A., White, S. D. M., de Zeeuw, P. T., & Zhao, H. 1999, Nature, 402, 53 [Google Scholar]
- Helmi, A., Navarro, J. F., Nordström, B., et al. 2006, MNRAS, 365, 1309 [Google Scholar]
- Helmi, A., Babusiaux, C., Koppelman, H. H., et al. 2018, Nature, 563, 85 [Google Scholar]
- Horta, D., Schiavon, R. P., Mackereth, J. T., et al. 2023, MNRAS, 520, 5671 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Gilmore, G., & Irwin, M. J. 1994, Nature, 370, 194 [Google Scholar]
- Jean-Baptiste, I., Di Matteo, P., Haywood, M., et al. 2017, A&A, 604, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jin, S., Trager, S. C., Dalton, G. B., et al. 2023, MNRAS, 530, 2688 [Google Scholar]
- Katz, D., Sartoretti, P., Guerrier, A., et al. 2023, A&A, 674, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khochfar, S., & Burkert, A. 2006, A&A, 445, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khoperskov, S., Di Matteo, P., Haywood, M., & Combes, F. 2018, A&A, 611, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khoperskov, S., Minchev, I., Libeskind, N., et al. 2023a, A&A, 677, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khoperskov, S., Minchev, I., Libeskind, N., et al. 2023b, A&A, 677, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khoperskov, S., Minchev, I., Libeskind, N., et al. 2023c, A&A, 677, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khoperskov, S., Minchev, I., Steinmetz, M., et al. 2023d, A&A, in press, https://doi.org/0.1051/0004-6361/202348767 [Google Scholar]
- Kirby, E. N., Cohen, J. G., Guhathakurta, P., et al. 2013, ApJ, 779, 102 [Google Scholar]
- Knebe, A., Gill, S. P. D., Kawata, D., & Gibson, B. K. 2005, MNRAS, 357, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Koppelman, H., Helmi, A., & Veljanoski, J. 2018, ApJ, 860, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Koppelman, H. H., Bos, R. O. Y., & Helmi, A. 2020, A&A, 642, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lehnert, M. D., Di Matteo, P., Haywood, M., & Snaith, O. N. 2014, ApJ, 789, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Majewski, S. R., Skrutskie, M. F., Weinberg, M. D., & Ostheimer, J. C. 2003, ApJ, 599, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Malhan, K., Ibata, R. A., Sharma, S., et al. 2022, ApJ, 926, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez-Valpuesta, I., & Gerhard, O. 2013, ApJ, 766, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuno, T., Aoki, W., & Suda, T. 2019, ApJ, 874, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuno, T., Dodd, E., Koppelman, H. H., et al. 2022a, A&A, 665, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsuno, T., Koppelman, H. H., Helmi, A., et al. 2022b, A&A, 661, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matteucci, F. 2007, ASP Conf. Ser., 374, 89 [NASA ADS] [Google Scholar]
- Miyamoto, M., & Nagai, R. 1975, PASJ, 27, 533 [NASA ADS] [Google Scholar]
- Monty, S., Venn, K. A., Lane, J. M. M., Lokhorst, D., & Yong, D. 2020, MNRAS, 497, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Morrison, H. L., Helmi, A., Sun, J., et al. 2009, ApJ, 694, 130 [CrossRef] [Google Scholar]
- Myeong, G. C., Evans, N. W., Belokurov, V., Sanders, J. L., & Koposov, S. E. 2018, ApJ, 856, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Myeong, G. C., Vasiliev, E., Iorio, G., Evans, N. W., & Belokurov, V. 2019, MNRAS, 488, 1235 [Google Scholar]
- Naidu, R. P., Conroy, C., Bonaca, A., et al. 2020, ApJ, 901, 48 [Google Scholar]
- Newberg, H. J., Yanny, B., Rockosi, C., et al. 2002, ApJ, 569, 245 [Google Scholar]
- Nissen, P. E., & Schuster, W. J. 2010, A&A, 511, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nissen, P. E., Amarsi, A. M., Skúladóttir, Á., & Schuster, W. J. 2023, A&A, 682, A116 [Google Scholar]
- Pagnini, G., Di Matteo, P., Khoperskov, S., et al. 2023, A&A, 673, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Panithanpaisal, N., Sanderson, R. E., Wetzel, A., et al. 2021, ApJ, 920, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Papovich, C., Labbé, I., Quadri, R., et al. 2015, ApJ, 803, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Purcell, C. W., Bullock, J. S., & Kazantzidis, S. 2010, MNRAS, 404, 1711 [NASA ADS] [Google Scholar]
- Randich, S., Gilmore, G., & Gaia-ESO Consortium 2013, The Messenger, 154, 47 [NASA ADS] [Google Scholar]
- Re Fiorentin, P., Lattanzi, M. G., Spagna, A., & Curir, A. 2015, AJ, 150, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Rodionov, S. A., Athanassoula, E., & Sotnikova, N. Y. 2009, MNRAS, 392, 904 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiz-Lara, T., Matsuno, T., Lövdal, S. S., et al. 2022, A&A, 665, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scoville, N., Aussel, H., Sheth, K., et al. 2014, ApJ, 783, 84 [CrossRef] [Google Scholar]
- Semelin, B., & Combes, F. 2002, A&A, 388, 826 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snaith, O. N., Haywood, M., Di Matteo, P., et al. 2014, ApJ, 781, L31 [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., Neri, R., et al. 2010, Nature, 463, 781 [Google Scholar]
- Taibi, S., Battaglia, G., Leaman, R., et al. 2022, A&A, 665, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tolstoy, E., Hill, V., & Tosi, M. 2009, ARA&A, 47, 371 [Google Scholar]
- van Dokkum, P. G., Leja, J., Nelson, E. J., et al. 2013, ApJ, 771, L35 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., & Rees, M. J. 1978, MNRAS, 183, 341 [Google Scholar]
- Zhao, G., Zhao, Y.-H., Chu, Y.-Q., Jing, Y.-P., & Deng, L.-C. 2012, RAA, 12, 723 [Google Scholar]
- Zolotov, A., Willman, B., Brooks, A. M., et al. 2009, ApJ, 702, 1058 [Google Scholar]
Appendix A: Distributions in E − Lz space for different disc components
In Figure A.1, we report – for the simulation with the initial inclination of the satellite orbital plane of ϕorb = 150° analysed in the paper – the final distribution in the E − Lz space of the satellite (top row) and in situ (bottom row) stars, divided into their disc components: thin, intermediate, and thick disc stars in the first, second, and third columns, respectively.
Since the different disc components have been assigned different metallicity values, these distributions are crucial to interpreting the metallicity patterns and gradients that we observe at the end in the E − Lz space.
 |
Fig. A.1. Final distributions in the E − Lz space for different disc components (thin, intermediate, and disc components in the first, second, and third columns, respectively), for satellite stars in the first row and in situ stars in the second one. |
Appendix B: Metallicity distribution function in different regions of the E − Lz space for different ϕorb
We wanted to check the dependence of the results concerning the MDF analysis on the orbital parameter, ϕorb; that is, the initial inclination of the satellite orbital plane. We considered three more cases for a planar, polar, and retrograde orbit, ϕorb = 0 ° ,90 ° ,180°, and we performed the same analysis made in the ϕorb = 150° case (described in Section 3.2).
 |
Fig. B.1. Same as Figure 7, but for the case of ϕorb = 0 ° ,90 ° ,180° in the first, second, and third columns, respectively. The first row shows the case of an initial vertical metallicity gradient only and the second row that with an additional initial radial metallicity gradient. |
In Figure B.1, we show the final total distribution in the E − Lz plane colour-coded by the mean metallicity at each point (described in Section 3.1), in which the different columns correspond to ϕorb = 0 ° ,90 ° ,180° and the two different rows correspond to the nograd and grad cases, respectively. The grid shows the splitting of the E − Lz regions in which we analysed the MDFs, and the red rectangles indicate the ones reported in the following Figures B.2, B.3, and B.4.
Every panel of Figures B.2, B.3, and B.4 then shows the MDF, considering all the stars in the region (in black), the MDF of the MW-type stars only (in red), and the MDF for the satellite stars only (in blue), all normalised in order to compare means, peaks, and shapes. The solid lines show the mean of the distribution. In all these figures, different rows show the MDFs for a fixed interval of energy, which from top to bottom are: i) 0 < E < 5, ii) −5 < E < 0, iii) −10 < E < −5, iv) −15 < E < −10, and v) −20 < E < −15. The different columns, on the other hand, show the MDFs for a fixed interval of angular momentum (increasing from left to right). The angular momentum intervals, column by column, are, from left to right: for Figure B.2, i) −130 < Lz < −110, ii) −110 < Lz < −90, iii) −90 < Lz < −70, iv) −70 < Lz < −50, v) −50 < Lz < −30, vi) −30 < Lz < −10, vii) −10 < Lz < 10, and viii) 10 < Lz < 30; for Figure B.3, i) −70 < Lz < −50, ii) −50 < Lz < −30, iii) −30 < Lz < −10, iv) −10 < Lz < 10, and v) 10 < Lz < 30, vi) 30 < Lz < 50; and for Figure B.4, i) −70 < Lz < −50, ii) −50 < Lz < −30, iii) −30 < Lz < −10, iv) −10 < Lz < 10, v) 10 < Lz < 30, vi) 30 < Lz < 50, vii) 50 < Lz < 70, and viii) 70 < Lz < 90.
The aim is to analyse the MDF in different regions of the E − Lz space, in order to find any trend in their means, peaks, and overall shape as a function of the region considered; for instance, fixing the value of the energy and varying the one of the angular momentum, and vice versa. All the simulations show a lower value of mean metallicity the higher the energy.
 |
Fig. B.2. Same as Figure 8, but for the case of ϕorb = 0°. The upper panel shows the case of an initial vertical metallicity gradient only and the lower panel the one with an additional initial radial metallicity gradient. |
 |
Fig. B.3. Same as Figure 8, but for the case of ϕorb = 90°. The upper panel shows the case of an initial vertical metallicity gradient only and the lower panel the one with an additional initial radial metallicity gradient. |
 |
Fig. B.4. Same as Figure 8, but for the case of ϕorb = 180°. The upper panel shows the case of an initial vertical metallicity gradient only and the lower panel the one with an additional initial radial metallicity gradient. |
Appendix C: Fitting the metallicity gradient in the E − Lz space as a function of energy
As far as the relation mentioned in Section 3.4 between the metallicity gradient in the satellite and in the E − Lz space is concerned, we proceeded in the following way. In Figure C.1, we report an example of the analysis we performed for every value of the slope of the radial metallicity gradient in the satellite thin disc before the interaction (fsatthin ∈ [ − 0.06, 0.02] dex/kpc), in the case of fsatthin = 0.05 dex/kpc and fMWthin = 0.02 dex/kpc, which is also analysed in the rest of the paper. The first column shows the distribution in the [Mg/Fe]-[Fe/H] space and the MDF for every satellite disc component, with their means (peaks) in solid (dashed) lines. The second column shows instead the final distributions in the E − Lz space of the satellite (and in situ) thin disc stars in the top (bottom) panel, in the case of the initial inclination of the satellite orbital plane of ϕorb = 150° also analysed in previous sections.
We computed the mean metallicity (< [Fe/H]> ) as a function of energy (E), reported in the third column of Figure C.1 for only satellite thin disc stars in the top panel and for satellite and in situ thin disc stars in the bottom one. We then performed a linear fit considering four different cases. The cases we considered differ in the first place in taking into account stars either with all values of angular momentum (Lz) or only in the interval −10 ≤ Lz ≤ 10 (Lz ∼ 0), and secondly in taking into account stars either with all values of energy (E) or performing a cut at low energy values (E ≥ −15 for satellite stars only, E ≥ −18 for satellite stars together with in situ ones), in order to avoid a plateau of the bulk of very bound stars having almost the same iron abundance. From the fits, we derived the slopes (d< [Fe/H]> /dE) that we report in Tables C.1 and C.2.
We then selected the case of all Lz values, together with the cut in energy, in order to restrict the analysis to the monotonic behaviour, and related its slope to fsatthin in Section 3.4.
Slopes (d< [Fe/H]> /dE) of the linear fit of the mean metallicity of satellite thin disc stars as a function of energy, in the four cases described in Appendix C.
Same as Table C.1, but for the cases of satellite and in situ thin disc stars.
 |
Fig. C.1. Description of the method for fitting the metallicity gradient in the E − Lz space as a function of energy. The first column shows the distribution in the [Mg/Fe]-[Fe/H] space and the MDF for every satellite disc component, with their means (peaks) in solid (dashed) lines. The second column shows instead the final distributions in the E − Lz space of the satellite (and in situ) thin disc stars in the top (bottom) panel, colour-coded at each point with the mean metallicity. Finally, the third column shows the mean metallicity (< [Fe/H]> ) as a function of energy (E) of the satellite (and in situ) thin disc stars in the top (bottom) panel. |
All Tables
Scale lengths (a) and heights (h), mass (M), number of particles (N), and particle mass (m) for the disc components of the MW and the satellite, considering a cut-off in radius at ten times the scale length.
Mean and standard deviation values of the normal distributions that define the [Fe/H] and [Mg/Fe] values for the particles of the thin, intermediate, and thick discs of the MW-type galaxy.
Minimum and maximum values of the uniform distributions used to assign a metallicity value to the satellite particles.
Slopes (d< [Fe/H]> /dE) of the linear fit of the mean metallicity of satellite thin disc stars as a function of energy, in the four cases described in Appendix C.
Same as Table C.1, but for the cases of satellite and in situ thin disc stars.
All Figures
 |
Fig. 1. The [Mg/Fe]–[Fe/H] space and its normalised marginal distributions, in the case of a vertical metallicity gradient only (upper panel) and in the case of an additional radial metallicity gradient (lower panel). |
| In the text | |
 |
Fig. 2. E − Lz space of in situ (first column), satellite (second column), and total (third column) star particles in the simulation, colour-coded at each point with the mean metallicity. The first and second rows show the E − Lz space in the case of an initial vertical gradient only and in the case of an additional initial radial metallicity gradient, respectively. The scales of the colour bars are different depending on which galaxy is considered, in order to make their specific metallicity patterns more evident. We also recall that in these plots stars on prograde orbits (which rotate as the disc) have negative Lz, while stars on retrograde orbits have positive Lz. |
| In the text | |
 |
Fig. 3. Final distribution of the satellite stars in the E − Lz space as in the middle column of Figure 2, but colour-coded by their escape time from the satellite potential. The dots represent the mean values of energy and z component of the angular momentum of bound satellite stars, defined by being less than 15 kpc from its barycentre. There are five hundred dots (one for each snapshot of the simulation) and they are colour-coded with the same colour-bar scale but for the time of the simulation (every 10 Myr to cover the 5 Gyr time interval). |
| In the text | |
 |
Fig. 4. E − Lz space of in situ (first column), satellite (second column), and total (third column) star particles in the simulation, colour-coded at each point with the mean metallicity, when the analysis is restricted to a solar-like volume. The first row shows the E − Lz space in the case of an initial vertical metallicity gradient only. Likewise, the second row shows it, but in the case of an additional initial radial metallicity gradient. The scales of the colour bars are different depending on which galaxy is considered, in order to make their specific metallicity patterns emerge in a more evident way. We recall that in these plots stars on prograde orbits (which rotate as the disc) have negative Lz, while stars on retrograde orbits have positive Lz. |
| In the text | |
 |
Fig. 5. E − Lz spaces of the in situ (first column), satellite (second column), and total (third column) star particles in the simulation, colour-coded at each point with the mean metallicity. Each row shows a simulation with a different value of the initial inclination of the satellite orbital plane: ϕorb = 0 ° ,90 ° ,180°. The upper (lower) panel is for nograd (grad) case. |
| In the text | |
 |
Fig. 6. Mean metallicity and standard deviation as a function of the angular momentum interval of the E − Lz space (in every column of Figures 7, B.1) for all the simulations with Φ = 0 ° ,30 ° ,60 ° ,90 ° ,120 ° ,150 ° ,180°, in the energy range −5 < E < 0. The left panel shows the case with the initial vertical metallicity gradient only, while the right panel shows the one with the additional radial metallicity gradient. |
| In the text | |
 |
Fig. 7. Total star distribution in the E − Lz space in the case of an initial vertical metallicity gradient only (upper panel) and an additional initial radial metallicity gradient (lower panel), colour-coded at each point with the mean metallicity. The superimposed grid shows the splitting of the space used to analyse the MDFs in different regions. |
| In the text | |
 |
Fig. 8. MDFs of different regions of the E − Lz, in the nograd case (top panel) and in the grad one (bottom panel). The red, blue, and black histograms show the MW-type galaxy, satellite, and total MDF, respectively, all normalised. The solid lines show the mean of the distribution. Energy intervals row by row (top to bottom): (i) 0 < E < 5, (ii) −5 < E < 0, (iii) −10 < E < −5, (iv) −15 < E < −10, (v) −20 < E < −15. Angular momentum intervals column by column (left to right): (i) −50 < Lz < −30, (ii) −30 < Lz < −10, (iii) −10 < Lz < 10, (iv) 10 < Lz < 30, (v) 30 < Lz < 50, (vi) 50 < Lz < 70. The red (blue) number shows the amount of in situ (accreted) stars in every cell. |
| In the text | |
 |
Fig. 9. Top panels: MDF of the satellite stars (in filled blue) and the same MDF restricted to the satellite stars that reach a solar-like volume by the end of the simulation (in patterned blue). The solid lines are the means of the distributions (broader for the total distribution, thinner for the solar one). The dashed (dash-dotted) lines are the peak(s) of the total (solar) distribution. The satellite MDF divided into disc components is shown by the red, green, and blue curves for the thin, intermediate, and thick discs, respectively. Bottom panel: Difference between the two normalised distributions in the top panel (Δ), i.e. the total distribution minus the solar-like restricted one. The left column shows the case with the vertical metallicity gradient only, and the right column the one with the additional radial metallicity gradient. |
| In the text | |
 |
Fig. 10. Relation between the slope of the initial radial metallicity gradient in the satellite thin disc (fsat, thin) and the slope of the metallicity gradient in the final distribution of all the thin disc stars in the E − Lz space as a function of energy (d⟨[Fe/H]⟩/dE), in the total volume of the simulation (solid lines), and in the restricted solar-like volume (dashed line). The case of ϕorb = 0° also features the dash-dotted curve described in Section 3.4. |
| In the text | |
 |
Fig. A.1. Final distributions in the E − Lz space for different disc components (thin, intermediate, and disc components in the first, second, and third columns, respectively), for satellite stars in the first row and in situ stars in the second one. |
| In the text | |
 |
Fig. B.1. Same as Figure 7, but for the case of ϕorb = 0 ° ,90 ° ,180° in the first, second, and third columns, respectively. The first row shows the case of an initial vertical metallicity gradient only and the second row that with an additional initial radial metallicity gradient. |
| In the text | |
 |
Fig. B.2. Same as Figure 8, but for the case of ϕorb = 0°. The upper panel shows the case of an initial vertical metallicity gradient only and the lower panel the one with an additional initial radial metallicity gradient. |
| In the text | |
 |
Fig. B.3. Same as Figure 8, but for the case of ϕorb = 90°. The upper panel shows the case of an initial vertical metallicity gradient only and the lower panel the one with an additional initial radial metallicity gradient. |
| In the text | |
 |
Fig. B.4. Same as Figure 8, but for the case of ϕorb = 180°. The upper panel shows the case of an initial vertical metallicity gradient only and the lower panel the one with an additional initial radial metallicity gradient. |
| In the text | |
 |
Fig. C.1. Description of the method for fitting the metallicity gradient in the E − Lz space as a function of energy. The first column shows the distribution in the [Mg/Fe]-[Fe/H] space and the MDF for every satellite disc component, with their means (peaks) in solid (dashed) lines. The second column shows instead the final distributions in the E − Lz space of the satellite (and in situ) thin disc stars in the top (bottom) panel, colour-coded at each point with the mean metallicity. Finally, the third column shows the mean metallicity (< [Fe/H]> ) as a function of energy (E) of the satellite (and in situ) thin disc stars in the top (bottom) panel. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \rho _{*}(R,z)=\left(\frac{h_{*}^2 M_{*}}{4\pi }\right) \frac{a_* R^2 + \left(a_* + 3\sqrt{z^2 + h_*^2}\right)\left(a_* + \sqrt{z^2 + h_*^2}\right)^2}{\left[a^2 + \left(a_* + \sqrt{z^2 + h_*^2}\right)^2 \right]^{5/2}(z^2 + h_*^2)^{3/2}}, \end{aligned} $$](/articles/aa/full_html/2024/10/aa49291-24/aa49291-24-eq1.gif)
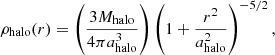
![$$ \begin{aligned} \mathrm{[Mg/Fe]}_{\rm sat}&= {\left\{ \begin{array}{ll} \mathrm{[Mg/Fe]}_{\rm knee}&\mathrm{if}\; \mathrm{[Fe/H]}_{\rm sat}< \mathrm{[Fe/H]}_{\rm knee},\\ \mathrm{[Fe/H]}_{\rm sat}*m +q&\mathrm{if}\; \mathrm{[Fe/H]}_{\rm sat}\ge \mathrm{[Fe/H]}_{\rm knee} \end{array}\right.} \end{aligned} $$](/articles/aa/full_html/2024/10/aa49291-24/aa49291-24-eq4.gif)
![$$ \begin{aligned} \mathrm{[Fe/H]}_{\rm MW,thin} = \mathrm{[Fe/H]}_{\rm MW,thin}^\mathrm{max} - \frac{R}{R_{\rm max,MWthin}}, \end{aligned} $$](/articles/aa/full_html/2024/10/aa49291-24/aa49291-24-eq5.gif)
![$$ \begin{aligned} \mathrm{[Fe/H]}_{\rm MW,thin} = \mathrm{[Fe/H]}_{\rm MW,thin}^\mathrm{max} - f_{\rm MW,thin}*R, \end{aligned} $$](/articles/aa/full_html/2024/10/aa49291-24/aa49291-24-eq7.gif)
![$$ \begin{aligned} \mathrm{[Fe/H]}_{\rm sat,thin} = \mathrm{[Fe/H]}_{\rm sat,thin}^\mathrm{max} - f_{\rm sat,thin}*R, \end{aligned} $$](/articles/aa/full_html/2024/10/aa49291-24/aa49291-24-eq8.gif)
![$$ \begin{aligned} \langle \mathrm{[Fe/H]}\rangle = (-1.69 \pm 0.04) + (0.30 \pm 0.02) \log \left(\frac{M_*}{10^6\,M_{\odot }}\right), \end{aligned} $$](/articles/aa/full_html/2024/10/aa49291-24/aa49291-24-eq10.gif)