| Issue |
A&A
Volume 673, May 2023
|
|
|---|---|---|
| Article Number | A49 | |
| Number of page(s) | 19 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202245103 | |
| Published online | 04 May 2023 | |
Glitches in solar-like oscillating F-type stars
Theoretical signature of the base of the convective envelope on the ratios r010
1
LUPM, Université de Montpellier, CNRS, Place Eugène Bataillon, 34095 Montpellier, France
e-mail: morgan.deal@umontpellier.fr
2
Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas, 4150-762 Porto, Portugal
3
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université de Paris, 5 place Jules Janssen, 92195 Meudon, France
4
Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto, Rua do Campo Alegre, 4169-007 Porto, Portugal
5
Université de Rennes, CNRS, IPR (Institut de Physique de Rennes) – UMR 6251, 35000 Rennes, France
6
Sternberg Astronomical Institute, Lomonosov Moscow State University, 119234 Moscow, Russia
7
Département d’Astronomie, Université de Genève, Chemin Pegasi 51, 1290 Versoix, Switzerland
Received:
30
September
2022
Accepted:
21
March
2023
Context. The transition between convective and radiative stellar regions is still not fully understood. This currently leads to a poor modelling of the transport of energy and chemical elements in the vicinity of these regions. The sharp variations in sound speed located in these transition regions give rise to a signature in specific seismic indicators, opening the possibility to constrain the physics of convection to radiation transition. Among those seismic indicators, the ratios of the small to large frequency separation for l = 0 and 1 modes (r010) were shown to be particularly efficient to probe these transition regions. Interestingly, in the Kepler Legacy F-type stars, the oscillatory signatures left in the r010 ratios by the sharp sound-speed variation have unexpected large amplitudes that still need to be explained.
Aims. We analyse the r010 ratios of stellar models of solar-like oscillating F-type stars in order to investigate the origin of the observed large amplitude signatures of the r010 ratios.
Methods. We tested different possibilities that may be at the origin of the large amplitude signatures using internal structures of stellar models. We then derived an analytical expression of the signature, in particular, of the amplitude of variation, that we tested against stellar models.
Results. We show that the signature of the bottom of the convective envelope is amplified in the ratios r010 by the frequency dependence of the amplitude compared to the signal seen in the frequencies themselves or the second differences. We also find that with precise enough data, a smoother transition between the adiabatic and radiative temperature gradients could be distinguished from a fully adiabatic region. Furthermore, we find that among the different options of physical input investigated here, large amplitude signatures can only be obtained when convective penetration of the surface convective zone into the underlying radiative region is taken into account. In this case and even for amplitudes as large as those observed in F-type stars, the oscillating signature in the r01 ratios can only be detected when the convective envelope is deep enough (i.e. at the end of the main sequence). Assuming that the origin of the large amplitude glitch signal is due to penetrative convection (PC), we find that the PC must extend downward the convective to radiative transition significantly (about 1 − 2Hp) in order to reproduce the large amplitudes observed for the ratios of F-type stars. This deep extension of the convective envelope causes doubt that the origin of the large amplitudes is due to PC as it is modelled here or implies that current stellar modelling (without PC) leads to an underestimation of the size of convective envelopes. In any case, studying the glitch signatures of a large number of oscillating F-type stars opens the possibility to constrain the physics of the stellar interior in these regions.
Key words: stars: oscillations / stars: evolution / convection
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Asteroseismology is a powerful tool for probing stellar interiors. This is done through the interpretation of stellar intrinsic oscillation frequencies (e.g., Cox 1980; Unno et al. 1989; Gough 1993; Cunha et al. 2007; Chaplin & Miglio 2013; García & Ballot 2019, and references therein). The properties of the oscillation modes and their frequencies are determined by the structure in the regions in which they are trapped. In solar-like oscillating stars such as the Sun, the turbulent convection in the outer layers excites the normal modes of the star in a frequency domain in which they are almost purely acoustic, and their frequencies follow a nearly regular pattern (asymptotic regime). Deviations from this regularity arise when the structure varies more rapidly locally than the wavelength of the excited modes (so-called glitch). This generates an oscillatory component (so-called glitch signature) to the frequencies and the frequency differences in addition to the smooth component (Gough 1990; Roxburgh & Vorontsov 2001). The study of the signatures of acoustic glitches has been proven to successfully unveil internal stellar characteristics such as the location of the base of the surface convective zone (BSCZ) and the helium second-ionisation (HeII) zone for the Sun (Monteiro et al. 1994; Roxburgh & Vorontsov 1994; Christensen-Dalsgaard et al. 1995, 2011; Ballot et al. 2004; Monteiro & Thompson 2005; Houdek & Gough 2007; Roxburgh 2009) and distant stars (Monteiro et al. 2000; Gough 2002; Mazumdar et al. 2012; Verma et al. 2017, 2019; Farnir et al. 2019).
Here we focus on the determination of the location of the base of the convection zone and its properties. The determination of the location of the BSCZ allows us to characterise the convection process at the transition with the underlying radiative interior. This is crucial to improve our current understanding of stellar convection, and especially to constrain its modelling in stellar evolution models. The current modelling of convection in stellar evolution models is based on the mixing length theory (hereafter MLT; Böhm-Vitense 1958; Canuto et al. 1996). This theory assumes that the fluid acceleration vanishes at the boundary of the convective zone, defined either by the Schwarzschild or Ledoux criteria. However, due to their inertia, convective cells penetrate the sub-adiabatic region below the convective envelope. These motions are able to impact the local temperature gradient and mix the chemical elements to an extent that is not yet known. Three types of processes can occur in this situation (e.g., Zahn 1991; Anders et al. 2022a). Convective overshoot corresponds to turbulent motions from the convective region which penetrate in the neighbouring radiative region but not altering the radiative gradient. Convective entrainment refers to turbulent motions which do alter the radiative gradient or erode the gradient of chemical composition. The third process, the penetrative convection, changes the radiative temperature to the adiabatic one in a region that is stable by the Schwarzschild criterion (see Anders et al. 2022b, for a more detailed description of the three processes). Penetrative convection is the focus of this work. Zahn (1991) predicted a penetrative convection region (i.e. with a fully adiabatic temperature gradient) at the base of the convective envelope of the order of one pressure scale height. The extension of the penetrative region was measured for the Sun to be about 0.2–0.3 pressure scale height (Hp). In addition, a smooth and mostly subadiabatic transition from the adiabatic to a radiative temperature gradient was favoured by the data (e.g., Christensen-Dalsgaard et al. 2011; Zhang et al. 2019).
Different seismic indicators can provide information on the location of the BSCZ: the frequency variations can be inspected directly (e.g., Monteiro et al. 1994), or alternatively, quantities such as the phase shift variation (Roxburgh & Vorontsov 1994; Roxburgh 2009), the second differences (e.g., Gough 1990), the fourth differences (Basu 1997), and the ratios of small to large separation (Roxburgh 2009; Mazumdar et al. 2014). Because the amplitude of the signature of the acoustic glitches is a few orders of magnitude lower than the actual frequencies, all these methods require high-precision data. This precision was achieved for distant stars with the space missions CoRoT (Baglin 2006; Baglin et al. 2013) with uncertainties of about 0.50 μHz, and with Kepler (Borucki et al. 2009; Koch et al. 2010) with an uncertainty of about 0.05 μHz for the best targets. With the exception of the ratios of the small to large separations, in all seismic indicators mentioned above, the signature of the helium second-ionisation region dominates the signature left by the BSCZ. This issue can be critical when the uncertainties on the individual frequencies are large, especially for F-type stars. Monteiro et al. (1994) developed a method, using the frequency variation, that allows filtering the HeII signature out. This method was successful in determining the location of the BSCZ of the Sun and other Kepler stars (Pereira et al. 2017). Later, Roxburgh (2009) showed that the signature of the BSCZ dominates in the ratios of small to large separations of l = 0, 1 p-modes (hereafter r010) of the Sun, while the signature of HeII is found to be residual. The frequency ratios can be described by a smooth variation in frequency (hereafter a smooth component), on which is superimposed a periodic variation with frequency (oscillating component). The smooth component is an efficient indicator of the convective core extension (Deheuvels et al. 2016).
Similarly to the Sun, the oscillatory component found in the r010 ratios of the CoRoT star HD52265 was proposed to be the signature of envelope penetrative convection, hereafter PC (Lebreton & Goupil 2012, 2014). This was the first detection of this signature in another star than the Sun. Moreover, the amplitude of the signature was found to be larger than in the Sun, even though the stars have similar properties. Mazumdar et al. (2014) used the oscillatory signature in the r010 ratios to determine the acoustic radius of the BSCZ of 12 Kepler stars. The use of the r010 ratios to probe PC was extended to 19 Kepler Legacy stars by Christophe (2019). The amplitude of the signature for some stars was found to be much larger than the one found for the Sun, allowing us to characterise the location of the BSCZ for distant stars, despite the larger uncertainties in the frequencies.
In the present work, we focus on the ratios of small to large separations r01 and r10 (r010), and more precisely, on the oscillating part of these ratios. Our goal is to investigate whether the origin of the large-amplitude signature in the oscillations of these ratios in F-type stars is PC. Then, we investigate to what extent constraints may be placed on the temperature gradient immediately below the convective envelope and on the extension of the PC region if this process caused the signature. Our study is based on stellar models and on an analytical (nearly independent of the stellar model) study of this signature in the sharply varying region (adapted from Monteiro et al. 1994).
In Sect. 2 we describe the seismic indicators used to characterise the location of the BSCZ and the observations. In Sect. 3 we investigate the origin of the large amplitude signature in solar-like oscillating F-type stars. In Sect. 4 we define an expression of the signature of the glitch in the ratios according to the structure of the star in the sharply varying region. Then, we compare theoretical predictions of the amplitude and period of the signal to those of stellar models in Sect. 5. We determine the detectability of this signature in Sect. 6. In Sect. 7 we compare the results obtained with the frequency ratios to those obtained with other seismic indicators, namely the frequencies themselves and the second differences. The impact of some specific changes in the structure below the BSCZ is addressed in Sect. 8. We finally discuss the results and conclude in Sect. 9.
2. Large-amplitude signature in the ratios r010 of solar-like oscillating F-type main-sequence stars
2.1. Definition
The five-point small separations between modes (with frequencies νn, l) of angular degree l = 0 and 1 and radial order n are defined by (Roxburgh & Vorontsov 2003)
The ratios of small to large separation are defined by
where Δl(n) = νn, l − νn − 1, l is the large separation. We hereafter refer to r010 as the function representative of r01 and r10 with frequency. These ratios of small to large separations are only weakly sensitive to surface layers (Roxburgh & Vorontsov 2003), which means that surface effects do not need to be considered when observations are compared to models. Magnetic activity may nevertheless have a slight impact on the ratios (Thomas et al. 2021). For stars similar to the Sun, these specific ratios are dominated by the signature of the BSCZ and convective core, and they are less sensitive to the helium second-ionisation glitches. On the other hand, these frequency differences have larger uncertainties than the frequencies alone, and care must be taken when the observed ratios are interpreted.
2.2. Observations
Figure 1 shows the r010 ratios according to the ratio of the frequency ν and the frequency at maximum power νmax for the Sun, computed from the BISON frequencies (Broomhall et al. 2009; Hale et al. 2016) and for three Kepler Legacy stars (KIC 10162436, KIC 6679371 and KIC 1435467) using the ratios provided by Lund et al. (2017a,b). Two main characteristics can be seen: a long-term smooth trend, and an oscillatory component. The long-term trend of the ratios decreases with increasing frequencies. It has been shown that the slope and mean value of r010 ratios are good indicators of the extension of convective cores (when present) and of the amount of hydrogen in the core (Popielski & Dziembowski 2005; Cunha & Metcalfe 2007; Deheuvels et al. 2010, 2016; Silva Aguirre et al. 2011; Cunha & Brandão 2011; Brandão et al. 2014).
 |
Fig. 1. r010 ratios according to the frequency scaled to νmax. Left: for the Sun (computed from the BISON frequencies; Broomhall et al. 2009; Hale et al. 2016) and KIC 10162436. Right: for KIC 1435467 and KIC 6679371 (data from Lund et al. 2017a). |
The oscillatory component is visible in the ratios of all stars presented in Fig. 1. For the Sun, Roxburgh (2009) showed that this signature is related to the BSCZ and that the period of the signal is related to its acoustic radius 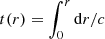 (its counterpart, the acoustic depth τ, is defined by
(its counterpart, the acoustic depth τ, is defined by 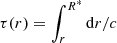 , with R* being the radius of the star). Christophe (2019)1 showed that these oscillations are also present in some Kepler Legacy stars (at least 19 stars with amplitudes larger than the uncertainties on the ratios). He identified the signal to be the signature of a glitch below the second helium-ionisation zone and associated it with the BSCZ. He also showed that for stars in which the signature can be measured, the amplitude of the signal is larger for F-type than for G-type stars. In the following sections, we assess the origin of these large signals compared to the Sun and determine the link between the shape of the signal and the physical properties of the sharply varying region.
, with R* being the radius of the star). Christophe (2019)1 showed that these oscillations are also present in some Kepler Legacy stars (at least 19 stars with amplitudes larger than the uncertainties on the ratios). He identified the signal to be the signature of a glitch below the second helium-ionisation zone and associated it with the BSCZ. He also showed that for stars in which the signature can be measured, the amplitude of the signal is larger for F-type than for G-type stars. In the following sections, we assess the origin of these large signals compared to the Sun and determine the link between the shape of the signal and the physical properties of the sharply varying region.
3. Origin of the large-amplitude signals
3.1. Possible causes
The oscillatory component of the ratios r010 or the signature of the acoustic glitch is induced by a sharp variation in the adiabatic sound speed,
where Γ1 is the first adiabatic exponent, P is the pressure, ρ is the density, T is the temperature, μ is the mean molecular weight at a given level within the star, kB is the Boltzmann constant, and mH is the proton mass. The rapid variation in the sound speed can arise from sharp variations in Γ1, the temperature, and/or in the mean molecular weight μ, or from a variation of all these parameters.
However, as we show in Sect. 3.2, standard stellar models do not predict an oscillatory component with large amplitudes. Hence the origin of the large magnitude of the oscillation amplitude is not yet identified. Three cases are then possible:
First adiabatic exponent (Γ1). A sharp variation in Γ1 may be induced by an ionisation region that is not well taken into account in stellar models, such as the region of heavy elements, which is located below the helium region. Brito & Lopes (2017, 2018, 2019) showed that these ionisation regions create a signal in the derivative of the frequency phase shift. This signature is not well reproduced by the models, and the authors suggested that a process such as radiative accelerations (e.g., Michaud et al. 2015) could maintain enough metals in the surface convective zone to reconcile models and observations. These authors also suggested that an equation of state based on the chemical approach, such as SAHA-S (Gryaznov et al. 2004, 2006; Ayukov et al. 2004; Baturin et al. 2013, 2017), may induce this type of signature in stellar models.
Mean molecular weight (μ). Sharp variations in μ occur at the transition between fully mixed and stable regions (i.e. at the transition between convective and radiative regions) and are usually neglected in standard models.
Temperature (T). Sharp variations in the temperature gradient are due to the transition between different processes of energy transport inside the star due to the presence of convection. They are known to induce glitches, especially in presence of penetrative convection or overshooting. Because the amplitude of the oscillatory component in the r010 ratios is larger for F-type stars, the signal may also come from the iron-nickel convective zone induced by the accumulation of these elements by the effect of radiative accelerations around T ≈ 200 000 K (Richard et al. 2001; Théado et al. 2009; Deal et al. 2016). This iron/nickel convective zone appears deeper than the hydrogen/helium zones.
Frequency ratios r010 have little sensitivity to the surface layers, and some of the above possibilities can therefore be discarded. The impact of radiative accelerations is mostly noted at the very surface of stars, and we tested that the impact of the accumulation of heavy elements and the formation of an iron convective zone cannot be detected by the ratios (see Sect. 6 for more details). Competition between microscopic and macroscopic transport processes is also likely to reduce the formation of a strong mean molecular weight gradient.
3.2. Stellar models
In order to identify the origin of the large-amplitude oscillatory component of the r010 ratios, we computed stellar models with the Cesam2k20 stellar evolution code (the new version of the Code d’Evolution Stellaire Adaptatif et Modulaire, previously called CESTAM; Morel & Lebreton 2008; Marques et al. 2013; Deal et al. 2018) with the aim of testing different scenarios according to the possible causes mentioned above. The input physics of the reference standard model A0 is presented in Table 1. The other models are presented in Table 2.
Inputs physics of the A0 model.
Stellar models with changes in the input physics with respect to model A0.
3.2.1. Input physics
All stellar models were computed with a mass of 1.40 M⊙, typical of the F-type stars at solar metallicity, and Xc < 0.3, which is representative of the three F-type stars shown in Fig. 1 (see Silva Aguirre et al. 2017). The effect of mass is addressed in Sect. 6. We used the OPAL2005 (Rogers & Nayfonov 2002) or SAHA-S (Baturin et al. 2017) equations of state and the OP opacity tables (Seaton 2005). Nuclear reaction rates were taken from the NACRE compilation (Angulo 1999), except for the 14N(p, γ)15O reaction, for which we used the LUNA rate (Imbriani et al. 2004). We adopted an Eddington grey atmosphere for surface boundary conditions. Convection was computed according to the Canuto et al. (1996) formalism with a solar-calibrated mixing length parameter, αCGM = 0.6838. We chose the AGSS09 metal mixture (Asplund et al. 2009) with meteoritic abundances for refractory elements from Serenelli (2010) and adopted calibrated solar values for the initial composition. All stellar models, except when specified otherwise, include the effect of atomic diffusion without radiative accelerations following the Michaud & Proffitt (1993) formalism.
Convective-core step overshoot was included with an extension of 0.15Hp except when specified otherwise. Anticipating the results of later sections, we draw specific attention to the impact on the ratios of the temperature gradient profiles below the convective envelope that is induced by convective penetration.
3.2.2. Temperature gradient profiles in the PC region
We considered two types of temperature gradients in the penetrative convective region below the convective border defined by the Schwarzschild criterion. Models A3, A4, and A5 include a PC region with a fully adiabatic temperature gradient following the Zahn (1991) formalism, whereas models A6, A7, B3, and B4 were built assuming a smoother transition between the adiabatic and the radiative temperature gradients, following Eq. (6) (qualitatively similar to the temperature gradient shown in Fig. 2 of Anders et al. 2022a). In all these models, the PC region is assumed to be fully mixed with a uniform chemical composition.
Fully adiabatic temperature gradient. The Zahn (1991) formalism is based on two main hypotheses. Firstly, the temperature gradient is considered fully adiabatic in the PC region. Secondly, the convective flux is assumed to be proportional to ρ3W, where W is the root mean square of the velocities directed downward. This leads to an extent of the penetrative convective region (Lp) defined by
where Hp is the pressure scale height, χp is the conductivity gradient, and ξPC is the ratio of the convective efficiency in the unstable region to that of the stable region. This last parameter cannot be determined from first principles and needs to be calibrated. Zahn (1991) determined that ξPC should have a value of the order of unity (see also Berthomieu et al. 1993, for the Sun). The higher its value, the deeper the PC region. Models A3, A4, and A5 were computed with ξPC = 0.2, 1.0, and 2.0, respectively. This represents 3.9, 19, and 39% of the size of the surface convective zones of the models at Xc = 0.10, respectively. For a 1.0 M⊙, assuming the same input physics as model A4 (ξPC = 1.0), we find an increase of 21 and 22% of the depth of the convective envelope at the age of the Sun and at Xc = 0.10, respectively. However, for the Sun, the increase is found to be about ten times smaller from helioseismology (e.g., Christensen-Dalsgaard et al. 2011; Zhang et al. 2019).
We stress that ξPC ≈ 1.0 found for the Sun in the early 1990s came for the use of an equation of state that was less accurate than the current ones. This affects the value of χP, hence the value of ξPC. All this tends to indicate that the value of ξPC depends on the input physics of the models and therefore probably on the type of stars. Hence, the same calibration value should not be expected for ξPC for an F-type and a G-type star.
Smoother temperature gradient in the PC region. For the Sun, Baturin & Mironova (2010) proposed that the temperature gradient in the PC region undergoes a smooth transition between the adiabatic and radiative gradient. Later, Christensen-Dalsgaard et al. (2011) confirmed this with helioseismology. Anders et al. (2022a) showed with 3D simulations that the penetrative convective regions were adiabatic over almost 90% of the region, with a smoother rather than a steep transition close to the bottom of the region. They also predicted a PC region extension of 20–30% of a mixing length, which is larger than the depth seismically characterised for the Sun.
When the large amplitude of the glitch signatures in F stars is assumed to be due to the presence of a PC region below the CZ, PC extensions larger than that of the Sun must be considered. Accordingly, we cannot use the expression of the temperature gradient from Christensen-Dalsgaard et al. (2011). This expression assumes that the radiative gradient decreases monotonically below the Schwarzschild boundary, which is not the case for the stellar envelopes in F-type stars. Following the shape of the transition predicted by Anders et al. (2022a; see their Fig. 2), we rather define an empirical ad hoc expression for the temperature gradient in the PC region,
where ζ(r) = r − rcz, with rcz being the radius where ∇ad = ∇rad, αPC is the extension of the PC region in units of pressure scale height, Hp(rcz) is the pressure scale height at rcz, and β is the parameter controlling the steepness of the transition (higher values of β lead to smoother transitions). Models A6 and B3 were computed with β = 0.5 and αOV = 1.0Hp, and models A7 and B4 were computed with β = 2.0 and αOV = 1.0Hp.
3.2.3. Cause of the signal
All stellar models presented in this section are compared at the same evolutionary status, that is, at the moment at which their hydrogen content in the core is Xc = 0.10. Figure 2 shows the r010 ratios for models A0 to A5. The ratios exhibit a smooth component that is qualitatively similar to that of KIC 10162436. The standard A0 model shows no large oscillatory component. The changes in the input physics affecting Γ1 and μ have no significant impact on the ratios (models A1 and A2 in Fig. 2). The only scenario inducing a large oscillatory component (i.e. that could be detected despite the larger uncertainties on the frequencies of F-type stars) of those we tested is the addition of a large region of PC (model A5). This conclusion is consistent with that of Lebreton & Goupil (2012) and Christophe (2019). We therefore theoretically explore the possibility of large PC regions. The observed F-type stars will be analysed in a future work.
 |
Fig. 2. r010 ratios for the 1.4M⊙ models A0 to A5 all at Xc = 0.10. All curves have a mean of about 0.07, and all but A0 are gradually shifted by 0.01 for clarity. |
Assuming the large-amplitude signature seen in the ratios r010 of F-type stars is linked to large PC regions, the period of the signal is related to tcz, the acoustic radius of the base of the PC region, and the amplitude is larger when the PC region is larger. This aspect is analytically demonstrated in Sects. 4.2 and 6.
4. Theoretical BSCZ glitch signature
In this section, we determine the analytical expression of the amplitude of the signal in the r010 ratios according to the structural quantities, similarly to what Monteiro et al. (1994) and Roxburgh & Vorontsov (1994) reported for the frequency and phase shift variations, respectively. This expression is useful to extract valuable information about the convection to radiation transition in stars for which the amplitude of the glitch signature is larger in the r010 ratios than in the frequency variations. We considered the expression for the frequency variation as given by Monteiro et al. (1994) and propagated it into Eq. (3), assuming a fully adiabatic PC region (Zahn 1991). For convenience, specific models without atomic diffusion (B1 and B2) were computed and used only in this section in order to satisfy the assumption on dμ/dτ (see below). Their input physics are presented at the bottom of Table 2.
4.1. Signal in the frequency variations
The frequency variations induced by the sharp change in temperature gradient from adiabatic to radiative at the BSCZ is described by (Monteiro et al. 1994; Roxburgh & Vorontsov 1994)
where 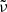 is a reference frequency, τd is the acoustic depth of the BSCZ, and ϕ is some constant phase. The above expression can be rewritten as
is a reference frequency, τd is the acoustic depth of the BSCZ, and ϕ is some constant phase. The above expression can be rewritten as
with
The amplitudes a1 and a2 (expressed in Hz) are related to the structure of the star at τd by
with
Here, U and Vg are defined as (Unno et al. 1989, Eq. (18.18))
𝒯 = t(R*) is the total acoustic radius of the star, g is the local gravity, γ is the ratio of specific heats and is equal to Γ1 = 5/3 in the perfect gas approximation, r is the local radius, G is the gravitational constant, and ∇ad and ∇rad are the adiabatic and radiative temperature gradients, respectively. The total amplitude of the signal at  is defined by
is defined by
These expressions are obtained under the following assumptions for the region around the BSCZ:
-
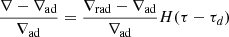 , with H(τ) the Heaviside function. For a fully adiabatic penetrative convection region, this assumption is verified close to the transition region, as shown in Fig. 3.
, with H(τ) the Heaviside function. For a fully adiabatic penetrative convection region, this assumption is verified close to the transition region, as shown in Fig. 3. -
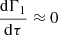 (see right panel of Fig. 3 for the validity of this assumption, i.e. dΓ1/dτ < 1.5 × 10−5 s−1)
(see right panel of Fig. 3 for the validity of this assumption, i.e. dΓ1/dτ < 1.5 × 10−5 s−1) -
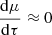 ,
, -
The region is fully ionised, and the pressure in the fully ionised region is approximated by ideal gas plus radiative pressure.
 |
Fig. 3. Internal structure profiles with and without penetrative convection. Left: temperature gradients as function of acoustic radius for the B1 and B2 models with M = 1.4 M⊙ and Xc = 0.15. The grey lines represent the adiabatic and radiative gradients of model B2 (which are very similar to those of B1). The vertical dashed black line on the right represents the position of the Schwarzschild limit for both models. The line on the left represents the bottom of the penetrative convective region of model B2. The downward arrow shows the middle of the acoustic cavity (tcz/𝒯 ≈ 4180 s). Right: dΓ1/dτ as a function of the acoustic radius for models B1 and B2. |
In the context of a fully adiabatic PC region, all these assumptions are reasonable, except for the neglect of a possible gradient in the mean molecular weight that can arise because of the effect of atomic diffusion (see Fig. 4 and model A2 in Fig. 2). Accordingly, in this section, our stellar models are computed assuming no atomic diffusion in order to avoid any potential contamination of the signal from any sharp variations in μ in the relevant region. The variation in the amplitude induced by atomic diffusion (i.e. the μ gradient) has already been discussed for the Sun (Basu & Antia 1994). The impact of this specific assumption for F-type stars will be estimated in a future work.
 |
Fig. 4. μ gradient as a function of the acoustic radius for models A0, A5, and A5 with the turbulent mixing calibrated by Verma & Silva Aguirre (2019). |
Figure 5 shows a1, a2, and Amax for models B1 and B2 (see Tables 1 and 2 for the input physics). Below the Schwarzschild convective zone limit ((rcz − r)/Hp > 0.1), a1 decreases and a2 increases. a1 is only slightly affected by the inclusion of a PC (model B2) region, whereas a2 becomes significantly larger (by about a factor of 2) than in absence of convective penetration, and it therefore dominates the a1 contribution in the presence of PC. Moreover, the deeper the PC region, the higher the a2 value because the difference between the adiabatic and radiative temperature gradients increases.
 |
Fig. 5. Glitch parameters and signature with and without penetrative convection. Top: amplitudes a1 (dotted lines), a2 (dashed lines), and Amax (solid lines) (Eq. (11), (12), and (15)) as functions of the extent of the PC region in pressure scale height for models B1 (left panel) and B2 (right panel) at Xc = 0.15. The dot-dashed lines represent the BSCZ. Bottom: ratios r010 according to the frequency for the same models. The error bar represents the typical mean uncertainty on the ratios, such as the one obtained for KIC 10162436. |
4.2. Signal in the r010 ratios
We now use the expression of the frequency variation (Eq. (7)) and inject it in Eq. (3). We obtain the following expression for the ratio of small to large separations of l = 0, 1 models (see Appendix A for the detailed calculation):
with
where 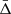 is the mean large separation assumed to be the same for the l = 0 and l = 1 mode degrees.
is the mean large separation assumed to be the same for the l = 0 and l = 1 mode degrees.
Because the period of the signature of the BSCZ in the r010 ratios is the acoustic radius of the BSCZ rather than its acoustic depth (Roxburgh 2009), we converted the expressions so that they are written in terms of td instead of τd.
Because 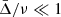 ,
,
where 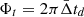 . We then recover the same frequency dependence as for δν in Eq. (7), except for an amplification factor
. We then recover the same frequency dependence as for δν in Eq. (7), except for an amplification factor 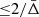 . For model B2 at Xc = 0.15, the amplitude of δν is ≤0.2 μHz and that of r010, glitch is ≤0.0067. This is to be compared with the uncertainties around νmax of KIC 10162436, for instance (Fig. 1), which are 0.17 μHz and 0.0030 for the frequencies and the ratios, respectively. Whereas the maximum amplitude of δν is very close to the uncertainty, the amplitude of the signature in the ratios is amplified up to more than a factor of 2, facilitating the signature detection with the ratios.
. For model B2 at Xc = 0.15, the amplitude of δν is ≤0.2 μHz and that of r010, glitch is ≤0.0067. This is to be compared with the uncertainties around νmax of KIC 10162436, for instance (Fig. 1), which are 0.17 μHz and 0.0030 for the frequencies and the ratios, respectively. Whereas the maximum amplitude of δν is very close to the uncertainty, the amplitude of the signature in the ratios is amplified up to more than a factor of 2, facilitating the signature detection with the ratios.
For 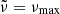 and for frequencies ν around νmax, the expression can be written
and for frequencies ν around νmax, the expression can be written
where f12/21(νmax)≈f12(νmax)≈f21(νmax). In this case, the ratios approximately depend on a constant amplitude.
5. Validation
5.1. Validation of the fitting procedure
In this section, we test the analytical expression of the r010 ratios defined in Sect. 4.2 using stellar models. Oscillation frequencies were computed with the code ADIPLS (Christensen-Dalsgaard 2008). The ratios can be divided into two components (smooth and oscillatory) following an expression of the form
Deheuvels et al. (2016, hereafter D16) developed a method for characterising the signal of the smooth component with a second-order polynomial fitting and constrained the extension of convective cores for eight Kepler stars. The second-order polynomial expression of the frequency is defined by
where β, γ1, and γ2 should be adapted so that c0, c1, and c2 are uncorrelated (see Appendix B of D16). For the purpose of this work, the c coefficients do not necessary need to be uncorrelated. We then characterise the smooth component with a simpler form of the second-order polynomial such as
This expression is used to characterise the smooth component of the ratios in the following sections. The ratios are then fitted using the following expression:
where a1, a2, td, and ϕ are the parameters fitted simultaneously with the coefficients c0, c1, and c2 of the smooth component P(ν). The reference frequency is defined as 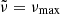 . We also tested a second approximated expression,
. We also tested a second approximated expression,
because a2 dominates a1 in presence of PC. We used model B2 as an illustration.
We assessed three scenarios:
-
One scenario using precise frequencies with a mean uncertainty of σfreq = 0.10 μHz and a frequency range of [0.6; 1.4] νmax (representative of the total frequency range of KIC 10162436),
-
A second scenario considering a mean uncertainty of 0.17 μHz (representative of KIC 10162436) and a frequency range of [0.7; 1.2] νmax (more centred around νmax),
-
Finally, a third scenario considering a mean uncertainty of 0.30 μHz and a frequency range of [0.7; 1.2] νmax.
We finally selected seven test cases. Cases 1 and 2 represent model B2 at Xc = 0.25 and 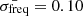 and 0.17 μHz, respectively. Cases 3, 4, and 5 represent model B2 at Xc = 0.15 and
and 0.17 μHz, respectively. Cases 3, 4, and 5 represent model B2 at Xc = 0.15 and 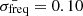 , 0.17, and 0.30 μHz, respectively. Finally, cases 6 and 7 represent model B2 at Xc = 0.05 and
, 0.17, and 0.30 μHz, respectively. Finally, cases 6 and 7 represent model B2 at Xc = 0.05 and 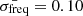 and 0.17 μHz, respectively. All the cases are presented in Table 3. The uncertainties were generated randomly with a Gaussian distribution around the mean value using a standard deviation of 20% of the mean value.
and 0.17 μHz, respectively. All the cases are presented in Table 3. The uncertainties were generated randomly with a Gaussian distribution around the mean value using a standard deviation of 20% of the mean value.
Cases considered to validate the fitting procedure with model B2.
The fitting procedure is based on the EMCEE Python package (Foreman-Mackey et al. 2013). We used 5000 burning steps and 500 production steps for the Markov chain Monte Carlo method (MCMC). Uniform uninformative priors were chosen for a1, a2 ([0.0; 0.4]), tcz ([500; 8500] s) and ϕ ([−2π; 4π]) to keep the parameters in the range expected for stellar interiors. Similarly to D16, the covariance matrix 𝒞 was estimated with a Monte Carlo simulation using the frequencies of the model and the random uncertainties described above for all cases. Because the covariance matrix is nearly non-invertible, we truncated it using the singular value decomposition (SVD) approach. The likelihood function ℒ is then
where D and Θ represent the target and the model parameters, respectively. The quantity r010, target represents the ratios of the target models and in later section those of a real star. The quantity r010, mod represents the ratios obtained with Eqs. (24) and (25). The results of the fit for each case are presented in Table 3.
5.2. Validation of the results
For the validation, we considered the numerical frequencies of model B2 as our data and fit their r010 ratios using Eqs. (24) and (25). In the fit, the functions 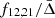 were assumed to be known and were computed according to Eqs. (17) and (18). We now compare the amplitudes and acoustic radius resulting from the fit with the theoretical predictions computed according to Eqs. (11) and (12). An example of posterior distributions for the fitted parameters is shown in Appendix B. The amplitudes Amax and the acoustic radius td = tcz are well retrieved by the fitting procedure within the 1σ interval for most cases (and 2σ for all cases). Similarly to the results of Monteiro et al. (1994), we find a degeneracy between a1 and a2, as shown in Fig. C.1. The two fitting functions perform similarly for all cases, indicating that the function with the fewest parameters (Eq. (25)) may be sufficient to analyse stars other than the Sun. Figure 6 shows the predicted glitch signature from Eq. (16) for model B1 and B2.
were assumed to be known and were computed according to Eqs. (17) and (18). We now compare the amplitudes and acoustic radius resulting from the fit with the theoretical predictions computed according to Eqs. (11) and (12). An example of posterior distributions for the fitted parameters is shown in Appendix B. The amplitudes Amax and the acoustic radius td = tcz are well retrieved by the fitting procedure within the 1σ interval for most cases (and 2σ for all cases). Similarly to the results of Monteiro et al. (1994), we find a degeneracy between a1 and a2, as shown in Fig. C.1. The two fitting functions perform similarly for all cases, indicating that the function with the fewest parameters (Eq. (25)) may be sufficient to analyse stars other than the Sun. Figure 6 shows the predicted glitch signature from Eq. (16) for model B1 and B2.
For case 5, we considered a larger mean uncertainty of 0.30 μHz. The uncertainties are of the same order of magnitude as the amplitude, and the fitting of the glitch signature is more dependent on the prior imposed on tcz. In this case, we therefore adopted a two-step procedure. Firstly, we fit the signature without any informative prior. The distribution of tcz is presented in Fig. 7 for model B2 at Xc = 0.15. Two peaks are clearly seen. One peak at large tcz (close to the surface) is representative of a small-amplitude oscillation made possible by the large uncertainties and a second peak at the value extracted from the structure of the model. The strength of the latter depends on the ratio of the amplitude and the uncertainties. Secondly, we again performed the fit with informative priors ([3000; 4500] s) around the significant peak. In this case, and when the second peak can be detected, the amplitude is retrieved much more clearly.
 |
Fig. 7. Probability density of tcz when no prior is imposed for the model B2 at Xc = 0.15 with a mean uncertainty of 0.30 μHz. The vertical dashed blue lines represent the theoretical value given by the stellar model from which the frequencies were computed. The downward arrow shows the middle of the acoustic cavity (tcz ≈ 4180 s). |
The reliability of the fit depends on the contrast between the amplitude of the signature and the uncertainties on the ratios. For ξPC < 1.0, the amplitude is often not large enough to be detected for uncertainties typical of F-type stars (e.g., 0.17 μHz for KIC 10162436, which represents 0.0030 for the ratios; see bottom panels of Fig. 5) with the input physics we considered in the models. An analysis of the detectability of the signature is deferred to Sect. 6. We first consider the case of the Sun as representative of a small PC region, but with highly precise frequencies in the following section.
5.3. Sun as a test case
We first tested our procedure on a solar-calibrated model with the same physics as model A0. The results are of the same quality level sd the cases presented in Sect. 5.2.
We next applied the one-step procedure to the BISON data of the Sun (Broomhall et al. 2009; Hale et al. 2016). We considered a prior on tcz of [500; 2000] s because the position of the BSCZ of the Sun is expected to be about tcz/𝒯 < 0.5 (with 𝒯 = 3701 s obtained with ΔνSun = 135.1 μHz). The results of the fits are presented in Table 4. When compared to the results of Monteiro et al. (1994), Ballot et al. (2004), and Christensen-Dalsgaard et al. (2011), the fitted value of tcz lies between the values found in the three papers. The total amplitudes determined from the fits are similar for both fitting equations and similar to those found in previous studies. The differences found for the acoustic radius between the three determinations may come from the use of different solar frequency data sets (the Libbrecht et al. 1990 data set was used in Monteiro et al. 1994, the six-year GOLF data set is used in Ballot et al. 2004; the Schou 1999 data set is used in Christensen-Dalsgaard et al. 2011, and the BISON data set is used in this work). Moreover, the value of the total acoustic radius of the Sun used to determine tcz from τcz was obtained here using ΔνSun = 135.1 μHz, which may not be the same values as for the large separations used in the other studies. For example, a change of a few μHz would reconcile the value of acoustic radii of the BSCZ. We checked that the two-step approach does not improve the agreement of tcz. The frequencies of the Sun are so precisely known that the approximations made in Appendix A maybe be too crude to analyse the solar signature of the glitch. The approach was also restricted to the use of l = 0 and 1 (because we used r010 ratios) to mimic the conditions for stars other than the Sun, while the frequency variation method (see Monteiro et al. 1994) used as a comparison was applied with many more degrees (l up to 20). All this may explain the difference in tcz. We also stress that when compared to the results of Roxburgh (2009), which were also obtained with r010 ratios, tcz is very similar.
Fitted parameters of the ratios for the Sun.
6. Detectability of the signal in the r010 ratios
Because the r010 ratios are not expected to be sensitive to surface layers, the signature of the BSCZ is only detectable if the surface convective zone extends deep enough downward. The top left panel of Fig. 8 shows the evolution of the ratio of the acoustic radius of the BSCZ (tcz) over the acoustic radius of the star (𝒯) for stellar models with masses between 1.2 and 1.5 M⊙, with a solar initial chemical composition and a PC region of ξPC = 2.0 (same input physics as model A5). In order to determine whether the signature of the glitch is detectable, we compared the total amplitude at ν = νmax (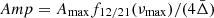 ) presented in Eq. (20) with typical uncertainties of 0.0015 and 0.0030. The first uncertainty is the mean uncertainty of the ratios around νmax of 16 Cyg A, and the second uncertainty is the mean uncertainty of the ratios for frequencies between 0.85 and 1.15 νmax of KIC 10162436. The detection threshold was set to Amp/σratio = 1. This criterion is a convenient indication of detectability, it is sufficient but not necessary, as it does not mean that a detection cannot be made with a lower amplitude to the uncertainty ratios. Using this criterion, we remain on the conservative side. For the smallest ratio uncertainty, the signature of the BSCZ is detectable in the r010 ratios according to the selected threshold if the BSCZ is deeper than tcz/𝒯 ≈ 0.55. It extends below tcz/𝒯 ≈ 0.45 for the largest uncertainty, which is representative of KIC 10162436. This implies that in stars with a deep surface convective zone (M ≲ 1.3 M⊙ at solar metallicity or for Xc < 0.3 − 0.2 for more massive stars), the signature is more likely detectable. When the input physics is set, the detectability is directly linked to the effective temperature of the star (Teff < 6500 K and Teff < 6183 K for uncertainties of 0.0015 and 0.0030, respectively, for the models presented in Fig. 8). This can be explained by the fact that the size of the surface convective zone is directly correlated with Teff. The detection of a high amplitude glitch signature like this then provides strong constraints on the input physics of the models that control the lifetime of a star on the main sequence (e.g., overshoot or chemical transport close to the core).
) presented in Eq. (20) with typical uncertainties of 0.0015 and 0.0030. The first uncertainty is the mean uncertainty of the ratios around νmax of 16 Cyg A, and the second uncertainty is the mean uncertainty of the ratios for frequencies between 0.85 and 1.15 νmax of KIC 10162436. The detection threshold was set to Amp/σratio = 1. This criterion is a convenient indication of detectability, it is sufficient but not necessary, as it does not mean that a detection cannot be made with a lower amplitude to the uncertainty ratios. Using this criterion, we remain on the conservative side. For the smallest ratio uncertainty, the signature of the BSCZ is detectable in the r010 ratios according to the selected threshold if the BSCZ is deeper than tcz/𝒯 ≈ 0.55. It extends below tcz/𝒯 ≈ 0.45 for the largest uncertainty, which is representative of KIC 10162436. This implies that in stars with a deep surface convective zone (M ≲ 1.3 M⊙ at solar metallicity or for Xc < 0.3 − 0.2 for more massive stars), the signature is more likely detectable. When the input physics is set, the detectability is directly linked to the effective temperature of the star (Teff < 6500 K and Teff < 6183 K for uncertainties of 0.0015 and 0.0030, respectively, for the models presented in Fig. 8). This can be explained by the fact that the size of the surface convective zone is directly correlated with Teff. The detection of a high amplitude glitch signature like this then provides strong constraints on the input physics of the models that control the lifetime of a star on the main sequence (e.g., overshoot or chemical transport close to the core).
 |
Fig. 8. Detectability of the signature in the r010 ratios for different quantities. The open and black circles show that the signature of the BSCZ glitch has an amplitude, |
Equation (20) shows that the amplitude of the signal mainly depends on the product of Amax/(4Δν) and the functions f12/21. The contributions to the amplitude of these terms are presented in the middle panels and in the bottom panel of Fig. 8. For the signal to be detectable, the amplitude Amax needs to be larger than about 0.1 μHz, but the contribution of f12/21 also plays an important role. f12/21 are five times larger at tcz/𝒯 = 0.3 than at 0.6. In other words, the deeper the convection to radiation transition, the more likely the detection, almost independently of the value of Amax, as shown in the bottom panel of Fig. 8. This point also strengthens the constraining potential of this signal on the modelling of the stellar interior of these stars.
We also found that the changes in Γ1 induced by the SAHA-S equation of state, or the sharp temperature gradient induced by an iron-nickel convective zone (see the dashed line in the top left panel of Fig. 8) appears too close to the surface to be detected. This explains the fact these changes do not lead to any signal in the r010 ratios.
The top right panel of Fig. 8 shows the position of 3 Kepler F-type stars in a Kiel diagram. The input physics of the models of the theoretical evolutionary tracks place KIC 10162436 in the detectable region (considering uncertainties on the ratios of 0.003), while the two other stars are placed in the detectable region considering uncertainties of the ratios of 0.0015. These three stars will be analysed in a forthcoming paper.
7. Comparison with other seismic indicators
In this section, we analyse the same models as in the previous section (cases 1, 3, and 6) using other seismic indicators, namely the frequency variation (Monteiro et al. 1994) and the second differences (e.g., Gough 1990; Monteiro et al. 1993; Verma et al. 2019). The fit of the signal was performed with the code called seismic inferences for glitches in stars (SIGS) presented in Pereira et al. (2017).
The version of the code2 for fitting the frequencies implements an automatic procedure for extracting the signal in νn, ℓ through an iterative approach for removing the smooth component for each set of frequencies of degree ℓ and as a function of mode order n. This implementation uses the method described by Monteiro et al. (1994) in Appendix C, with the simplification done for low-degree data as used by Monteiro et al. (2000). The smooth component of the frequencies of the oscillations (what these would be in a star without a glitch) was iterated until it converged, and the final residuals were used to fit with the predicted expression for the signal. Pereira et al. (2017) added an automatic and fairly robust approach to accomodate the need to have an initial guess and when the data are sparse and contain significant observational uncertainties.
The version of the code3 for fitting the second differences uses the approach from Monteiro et al. (1993). For low-degree data, a simplification was introduced by replacing the spline fits with the use of Eq. (27), which is similar to what was reported by Gough (1990) and also used by several other authors (e.g., Mazumdar et al. 2014, and references therein). The approach removes a smooth component once from the second differences of the frequencies, defined as
and then fits the predicted expression of the signal to the residuals.
The details for both implementations and for the building of the automatic procedure are given in Pereira et al. (2017). The method reported by Pereira et al. (2017) can use any variation in the expression for the signature in the frequencies and second differences. In their application, the lowest-amplitude case was considered by assuming no PC (a1 is the only term used). This choice does not have a significant impact on the determination of the reference amplitude Amax, calculated at νmax. Because we here test the effect of a PC, the frequency dependence of the amplitude of the signature is better represented, as shown by Monteiro et al. (1994), by including the a2 term because a2 ≫ a1 in the presence of PC. The fitting functions (see Appendix C for the details on the signal for the second differences) are then
Both procedures in SIGS include the additional component, with an amplitude AHeII that takes the glitch due to the second He ionisation into account.
In order to make the comparison of amplitudes meaningful, the amplitude of δΔ2ν associated with the BSCZ (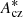 ) is expressed according to a2 following the same approach as in Appendix A. It can then be written
) is expressed according to a2 following the same approach as in Appendix A. It can then be written
where ϕ′=ϕ − π/4. Amax ≈ a2 in the considered cases because the models include PC. Amax can then be retrieved from 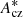 using the amplitude of Eq. (29).
using the amplitude of Eq. (29).
The results of the fit of the signals for the three cases are presented in Table 5. For cases 1 and 3, the position of the glitch is well retrieved by both seismic indicators. The amplitude is also well recovered with the fit of the frequency variation. Nevertheless, the deeper the glitch (i.e. the more evolved the star), the less efficiently retrieve these two indicators the glitch properties because the amplitude of the signature is smaller (see Fig. 8 for the variation of Amax with depth), especially for the frequency fit. For the second differences, the amplification of the amplitude by the frequency dependence is maximum for BSCZ at tcz/𝒯 = 0.5 and decreases when the BSCZ deepens (see Fig. C.1), which is consistent with the results of Ballot et al. (2004). This explains why the position and amplitude of the glitch signature for case 6 are not well retrieved by the second differences either.
Results of the fit for cases 1, 3, and 6 of the frequency variation (freq.) and the second differences (diff.).
Accordingly, for G-type stars with highly precise frequencies (e.g., the Sun), the three methods ought to perform equivalently to retrieve the properties of the glitch signature induced by the BSCZ. For stars with lower frequency precision, the second differences and the ratios r010 are expected to perform better than the frequency variation. The efficiency of these last two methods depends on the position of the glitch. Deeper glitches (tcz/𝒯 < 0.4) should be better retrieved by the ratios, and the second differences should perform better for tcz/𝒯 > 0.4. For F-type stars, the conclusions are the same.
8. Impact of a smoother transition and a μ gradient
The top panels of Fig. 9 show the comparisons of the temperature gradients and r010 ratios for models B2, B3, and B4 at Xc = 0.10. The smoother transition of models B3 and B4 occurs at the same location as the bottom of the PC region of model B2. The fitted amplitudes (with a mean uncertainty on the frequency of 0.10 μHz and using Eq. (24)) are 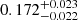 ,
, 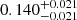 and
and 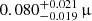 Hz for models B2, B3, and B4, respectively. The distinction between the two types of temperature gradients may be possible with precise frequencies (σfreq ≈ 0.10 μHz), but would be more difficult for larger uncertainties (e.g., typical error for F-type stars).
Hz for models B2, B3, and B4, respectively. The distinction between the two types of temperature gradients may be possible with precise frequencies (σfreq ≈ 0.10 μHz), but would be more difficult for larger uncertainties (e.g., typical error for F-type stars).
 |
Fig. 9. Impact of the μ-gradient and of the smoothness of the temperature gradient on the r010 ratios. Left: temperature gradients of model B2 (orange), B3 (blue), and B4 (green) for the top panel, and A5 (orange), A6 (blue), and A7 (green) for the bottom panel as a function of the acoustic radius at Xc = 0.10. Right: corresponding r010 ratios as a function of the frequency. |
When atomic diffusion is taken into account, a μ gradient is built at the bottom of the PC region. We assumed here that the mixing in the PC region was the same as in the convective zone down to the position at which the temperature gradient is radiative (below the transition, around 2600 s). The bottom panels of Fig. 9 show the comparisons of the temperature gradients and r010 ratios for models A5, A6, and A7 at Xc = 0.10. The smoother transition of models A6 and A7 occurs at the same location as the bottom of the PC region of model A5. The fitted amplitudes (with a mean uncertainty on the frequency of 0.10 μHz) are 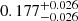 ,
, 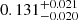 and
and 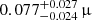 Hz for models A5, A6, and A7, respectively.
Hz for models A5, A6, and A7, respectively.
For model A5, the amplitude appears to be amplified (see the discussion in Sect. 4.1 about the impact of a μ gradient). We note that in addition to the BSCZ glitch signature, a second signature seems to distort the signal for the models with atomic diffusion (i.e. models A6 and A7 with a μ gradient at a different position than the BSCZ). This might indicate that the signal is composed of the signature of the BSCZ and a deeper μ gradient. This needs confirmation, however.
9. Discussion and conclusion
We have theoretically studied the diagnostic power of the ratios r010 to probe the depth of the surface convective zone of F-type stars. The oscillations of these ratios indeed present very large amplitudes that are not observed in G-type stars, that is, stars with lower mass, and especially, cooler stars with deeper convective envelopes.
Our numerical and analytical investigations confirm that convective penetration below the convective envelope is able to produce the large-amplitude variations of the glitch signature that are observed in the frequency ratios of solar-like F-type stars. Stellar models including a large extension of the convective penetration indeed produce large-amplitude BSCZ glitch signatures as observed and the r010 ratios. These signatures provide the location for the base of the extended convective region in the models. No other physical effect investigated here is able to explain these observations. For the F-type star models and the input physics we considered in this study, the large amplitudes can indeed only be achieved when the extent is sufficiently deep (1 − 2Hp) so as not to be filtered by the ratios of frequencies. The frequency dependence of the amplitude also amplifies the detectability of the signature according to the depth of the transition between the convective envelope and the radiative zone below. However, the depth of the PC region exceeds that measured for the Sun. For models with other input physics (e.g., initial chemical composition or transport processes), the extent of the PC region needed to explain the signature may be different. Hence, this high value may be an indication that the input physics of the models is still incomplete, which leads to an underestimation of the size of convective envelopes, or it might indicate that another mechanism causes the signature. This should be assessed by modelling of the F-type stars of the Kepler Legacy sample, with additional physics that may affect the BSCZ.
Although convective penetration is also expected in lower-mass, cooler stars such as the Sun, no such large amplitudes are observed. Assuming then that PC causes the large-amplitude signature of the r010 ratios, we find that the transition between the convective envelope to the radiative interior is smoother and shallower for less massive stars. For the Sun, we also found that the free extension parameter ξ in the Zahn (1991) formalism is no longer unity when updated microphysics is used, but is rather a factor of ten lower. This tends to indicate that this parameter depends on the physics of the models and that the Zahn (1991) formalism needs to be developed further.
The analysis of the signature of the BSCZ in ratios r010 was performed (similarly to previous works) without the contribution of the μ gradient. We nevertheless found that it may impact the oscillatory signature of the ratios, hence the characterisation of the glitch properties. The second paper of this series will indeed be devoted to investigate the contribution of the μ gradient for a deeper understanding of the glitch signatures seen in the ratios r010.
Finally, our study emphasised that the ratios of small to large separations can be used for stars other than the Sun to determine valuable constraints on stellar interiors, despite larger uncertainties on the frequencies. We also showed that in some specific cases, the ratios r010 allow us to better recover the position of the BSCZ than the second differences or the frequencies themselves. Much can be done with the l = 0 and 1 modes alone, which can be easily accessible for a large number of solar-like oscillating main-sequence stars. This opens new interesting possibilities to test 3D simulation predictions of temperature gradients in the penetration convection regions outside of the solar parameter space (e.g., Anders et al. 2022a; Breton et al. 2022) and to place constraints on the physical conditions of these regions.
See chapter II of https://tel.archives-ouvertes.fr/tel-02883979/document
SIGS for frequencies: https://github.com/Fill4/sigs_freq
SIGS for second differences: https://github.com/Fill4/sigs_diff
Acknowledgments
We gratefully thank our anonymous referee whose comprehensive readings and remarks helped to improve the content of the manuscript. We also thank Jérôme Ballot for an interesting discussion related to this work. This work was supported by CNES, focused on PLATO. This work was supported by FCT/MCTES through the research grants UIDB/04434/2020, UIDP/04434/2020 and PTDC/FIS-AST/30389/2017. MD and MSC (CEECIND/02619/2017) are supported by national funds through FCT in the form of a work contract. GB acknowledges fundings from the SNF AMBIZIONE grant No 185805 (Seismic inversions and modelling of transport processes in stars). MD thanks Gaëtan Sary for fruitful mathematical discussions.
References
- Anders, E. H., Jermyn, A. S., Lecoanet, D., & Brown, B. P. 2022a, ApJ, 926, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E. H., Jermyn, A. S., Lecoanet, D., et al. 2022b, Res. Notes Am. Astron. Soc., 6, 41 [Google Scholar]
- Angulo, C. 1999, Am. Inst. Phys. Conf. Ser., 495, 365 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Ayukov, S. V., Baturin, V. A., Gryaznov, V. K., Iosilevsky, I. L., & Starostin, A. N. 2004, in Equation-of-State and Phase-Transition in Models of Ordinary Astrophysical Matter, eds. V. Celebonovic, D. Gough, & W. Däppen, Am. Inst. Phys. Conf. Ser., 731, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Baglin, A. 2006, in The CoRoT Mission Pre-Launch Status– Stellar Seismology and Planet Finding, eds. M. Fridlund, A. Baglin, J. Lochard, & L. Conroy, ESA Spec. Pub., 1306, 111 [Google Scholar]
- Baglin, A., Michel, E., & Noels, A. 2013, in Progress in Physics of the Sun and Stars: A New Era in Helio- and Asteroseismology, eds. H. Shibahashi, & A. E. Lynas-Gray, ASP Conf. Ser., 479, 461 [NASA ADS] [Google Scholar]
- Ballot, J., Turck-Chièze, S., & García, R. A. 2004, A&A, 423, 1051 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Basu, S. 1997, MNRAS, 288, 572 [NASA ADS] [Google Scholar]
- Basu, S., & Antia, H. M. 1994, MNRAS, 269, 1137 [NASA ADS] [Google Scholar]
- Baturin, V. A., & Mironova, I. V. 2010, Ap&SS, 328, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Baturin, V. A., Ayukov, S. V., Gryaznov, V. K., et al. 2013, in Progress in Physics of the Sun and Stars: A New Era in Helio- and Asteroseismology, eds. H. Shibahashi, & A. E. Lynas-Gray, ASP Conf. Ser., 479, 11 [Google Scholar]
- Baturin, V. A., Däppen, W., Morel, P., et al. 2017, A&A, 606, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berthomieu, G., Morel, P., Provost, J., & Zahn, J. P. 1993, in IAU Colloq. 137: Inside the Stars, eds. W. W. Weiss, & A. Baglin, ASP Conf. Ser., 40, 60 [NASA ADS] [Google Scholar]
- Böhm-Vitense, E. 1958, ZAp, 46, 108 [NASA ADS] [Google Scholar]
- Borucki, W., Koch, D., Batalha, N., et al. 2009, in Transiting Planets, eds. F. Pont, D. Sasselov, & M. J. Holman, 253, 289 [NASA ADS] [Google Scholar]
- Brandão, I. M., Cunha, M. S., & Christensen-Dalsgaard, J. 2014, MNRAS, 438, 1751 [CrossRef] [Google Scholar]
- Breton, S. N., Brun, A. S., & García, R. A. 2022, A&A, 667, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brito, A., & Lopes, I. 2017, MNRAS, 466, 2123 [NASA ADS] [CrossRef] [Google Scholar]
- Brito, A., & Lopes, I. 2018, ApJ, 853, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Brito, A., & Lopes, I. 2019, MNRAS, 488, 1558 [NASA ADS] [CrossRef] [Google Scholar]
- Broomhall, A.-M., Chaplin, W. J., Davies, G. R., et al. 2009, MNRAS, 396, L100 [NASA ADS] [CrossRef] [Google Scholar]
- Canuto, V. M., Goldman, I., & Mazzitelli, I. 1996, ApJ, 473, 550 [NASA ADS] [CrossRef] [Google Scholar]
- Chaplin, W. J., & Miglio, A. 2013, ARA&A, 51, 353 [Google Scholar]
- Christensen-Dalsgaard, J. 2008, Ap&SS, 316, 113 [Google Scholar]
- Christensen-Dalsgaard, J., Monteiro, M. J. P. F. G., Rempel, M., & Thompson, M. J. 2011, MNRAS, 414, 1158 [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J., Monteiro, M. J. P. F. G., & Thompson, M. J. 1995, MNRAS, 276, 283 [NASA ADS] [Google Scholar]
- Christophe, S. 2019, PhD Thesis, Université PSL, https://tel.archives-ouvertes.fr/tel-02883979/document [Google Scholar]
- Cox, J. P. 1980, Theory of Stellar Pulsation [Google Scholar]
- Cunha, M. S., & Brandão, I. M. 2011, A&A, 529, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cunha, M. S., & Metcalfe, T. S. 2007, ApJ, 666, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha, M. S., Aerts, C., Christensen-Dalsgaard, J., et al. 2007, A&ARv, 14, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Deal, M., Richard, O., & Vauclair, S. 2016, A&A, 589, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deal, M., Alecian, G., Lebreton, Y., et al. 2018, A&A, 618, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deheuvels, S., Michel, E., Goupil, M. J., et al. 2010, A&A, 514, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deheuvels, S., Brandão, I., Silva Aguirre, V., et al. 2016, A&A, 589, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farnir, M., Dupret, M. A., Salmon, S. J. A. J., Noels, A., & Buldgen, G. 2019, A&A, 622, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- García, R. A., & Ballot, J. 2019, Liv. Rev. Sol. Phys., 16, 4 [Google Scholar]
- Gough, D. O. 1990, in Comments on Helioseismic Inference, eds. Y. Osaki, & H. Shibahashi, 367, 283 [Google Scholar]
- Gough, D. O. 1993, Astrophysical Fluid Dynamics– Les Houches, 1987, 399 [Google Scholar]
- Gough, D. O. 2002, in Stellar Structure and Habitable Planet Finding, eds. B. Battrick, F. Favata, I. W. Roxburgh, & D. Galadi, ESA Spec. Pub., 485, 65 [NASA ADS] [Google Scholar]
- Gryaznov, V. K., Ayukov, S. V., Baturin, V. A., et al. 2004, in Equation-of-State and Phase-Transition in Models of Ordinary Astrophysical Matter, eds. V. Celebonovic, D. Gough, & W. Däppen, Am. Inst. Phys. Conf. Ser., 731, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Gryaznov, V. K., Ayukov, S. V., Baturin, V. A., et al. 2006, J. Phys. A Math. Gen., 39, 4459 [NASA ADS] [CrossRef] [Google Scholar]
- Hale, S. J., Howe, R., Chaplin, W. J., Davies, G. R., & Elsworth, Y. P. 2016, Sol. Phys., 291, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Houdek, G., & Gough, D. O. 2007, MNRAS, 375, 861 [CrossRef] [Google Scholar]
- Huber, D., Bedding, T. R., Stello, D., et al. 2011, ApJ, 743, 143 [Google Scholar]
- Imbriani, G., Costantini, H., Formicola, A., et al. 2004, A&A, 420, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koch, D. G., Borucki, W. J., Basri, G., et al. 2010, ApJ, 713, L79 [Google Scholar]
- Lebreton, Y., & Goupil, M. J. 2012, A&A, 544, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lebreton, Y., & Goupil, M. J. 2014, A&A, 569, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Libbrecht, K. G., Woodard, M. F., & Kaufman, J. M. 1990, ApJS, 74, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Lund, M. N., Silva Aguirre, V., Davies, G. R., et al. 2017a, ApJ, 850, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Lund, M. N., Silva Aguirre, V., Davies, G. R., et al. 2017b, ApJ, 835, 172 [Google Scholar]
- Marques, J. P., Goupil, M. J., Lebreton, Y., et al. 2013, A&A, 549, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mazumdar, A., Monteiro, M. J. P. F. G., Ballot, J., et al. 2012, Astron. Nachr., 333, 1040 [NASA ADS] [Google Scholar]
- Mazumdar, A., Monteiro, M. J. P. F. G., Ballot, J., et al. 2014, ApJ, 782, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Michaud, G., & Proffitt, C. R. 1993, in IAU Colloq. 137: Inside the Stars, eds. W. W. Weiss, & A. Baglin, ASP Conf. Ser., 40, 246 [NASA ADS] [Google Scholar]
- Michaud, G., Alecian, G., & Richer, J. 2015, Atomic Diffusion in Stars (Springer International Publishing Switzerland) [Google Scholar]
- Monteiro, M. J. P. F. G., & Thompson, M. J. 2005, MNRAS, 361, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Monteiro, M. J. P. F. G., Christensen-Dalsgaard, J., & Thompson, M. J. 1993, in Inside the Stars, eds. W. W. Weiss, & A. Baglin, IAU Colloq. 137, ASP Conf. Ser., 40, 557 [NASA ADS] [Google Scholar]
- Monteiro, M. J. P. F. G., Christensen-Dalsgaard, J., & Thompson, M. J. 1994, A&A, 283, 247 [NASA ADS] [Google Scholar]
- Monteiro, M. J. P. F. G., Christensen-Dalsgaard, J., & Thompson, M. J. 2000, MNRAS, 316, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Morel, P., & Lebreton, Y. 2008, Ap&SS, 316, 61 [Google Scholar]
- Pereira, L. F. R., Faria, J. P. S., & Monteiro, M. J. P. F. G. 2017, Eur. Phys. J. Web Conf., 160, 01015 [CrossRef] [EDP Sciences] [Google Scholar]
- Popielski, B. L., & Dziembowski, W. A. 2005, Acta Astron., 55, 177 [NASA ADS] [Google Scholar]
- Richard, O., Michaud, G., & Richer, J. 2001, ApJ, 558, 377 [Google Scholar]
- Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [Google Scholar]
- Roxburgh, I. W. 2009, A&A, 493, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roxburgh, I. W., & Vorontsov, S. V. 1994, MNRAS, 268, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Roxburgh, I. W., & Vorontsov, S. V. 2001, MNRAS, 322, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Roxburgh, I. W., & Vorontsov, S. V. 2003, A&A, 411, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schou, J. 1999, ApJ, 523, L181 [NASA ADS] [CrossRef] [Google Scholar]
- Seaton, M. J. 2005, MNRAS, 362, L1 [Google Scholar]
- Serenelli, A. M. 2010, Ap&SS, 328, 13 [Google Scholar]
- Silva Aguirre, V., Ballot, J., Serenelli, A. M., & Weiss, A. 2011, A&A, 529, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Silva Aguirre, V., Lund, M. N., Antia, H. M., et al. 2017, ApJ, 835, 173 [Google Scholar]
- Théado, S., Vauclair, S., Alecian, G., & LeBlanc, F. 2009, ApJ, 704, 1262 [Google Scholar]
- Thomas, A. E. L., Chaplin, W. J., Basu, S., et al. 2021, MNRAS, 502, 5808 [NASA ADS] [CrossRef] [Google Scholar]
- Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial Oscillations of Stars (Tokyo: University of Tokyo Press) [Google Scholar]
- Verma, K., & Silva Aguirre, V. 2019, MNRAS, 489, 1850 [NASA ADS] [CrossRef] [Google Scholar]
- Verma, K., Raodeo, K., Antia, H. M., et al. 2017, ApJ, 837, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Verma, K., Raodeo, K., Basu, S., et al. 2019, MNRAS, 483, 4678 [Google Scholar]
- Zahn, J. P. 1991, A&A, 252, 179 [Google Scholar]
- Zhang, Q.-S., Li, Y., & Christensen-Dalsgaard, J. 2019, ApJ, 881, 103 [Google Scholar]
Appendix A: Expression of the r010 ratios
We first write all the frequencies needed to calculate d01 and d10 with a constant frequency (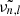 ) plus a small variation,
) plus a small variation,
and assuming a mean large separation over 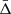 for angular degree 0 and 1, we obtain
for angular degree 0 and 1, we obtain
The frequencies needed to calculate the small separations are then defined for l = 0, 1 by
Using the asymptotic expression of the frequency
we can define the relation between l = 0 and l = 1 modes by
We can then express the five frequencies required to estimate the r01 ratios according to the frequency νn, 0,
When this is injected in Eq. 3, we obtain
We now assume that the small frequency departure is due to the BSCZ glitch and use Eq. 7 for δν. In the following, we replace νn, 0 by ν for sake of clarity,
When we insert Eq. A.9 and A.10 into Eq. A.8, the r01 ratios then become
Similarly, centring the expression around the νn, 1 and replacing it by ν for sake of clarity, we obtain the same expression for r01(ν). In the following, we then refer to r010(ν) as the combination of r10(ν) and r01(ν).
Because the period of the signature in the r010 ratios is the acoustic radius rather than the acoustic depth (Roxburgh 2009), we convert the previous expression in terms of td = 𝒯 − τd instead of τd (using 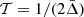 ). The r010 ratios are then given by
). The r010 ratios are then given by
with
For the excited solar-like oscillation modes, the ratio
This is confirmed in Table 3, which lists ℛ ∼ 0.05 << 1, which is roughly the same for the considered stellar models. Then at first order,
where 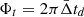 and
and 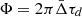 .
.
We consider the ratios
Table 3 shows that Δtd ∼ 1/4. This means 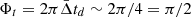 . On the other hand,
. On the other hand, 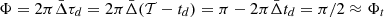 , then
, then
This indicates that f11, f22 are negligible compared to f12, f21, respectively. This is illustrated in Fig. A.1, which shows the fij coefficients.
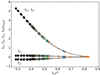 |
Fig. A.1. Value of the f functions at |
Appendix B: Fitting of a1, a2, Amax, and td
Figure B.1 shows the resulting parameters of the fit of the r010 signature of model B2 using Eq. 24.
Appendix C: Expression of Δ2ν according to a1 and a2
The second differences are defined by
Following the same approach as in Appendix A, the signature of the BSCZ in the second differences is expressed as
with
Similarly to the ratios r010, the frequency-dependent terms ff11, ff22 are negligible compared to ff12, ff21, respectively. This is illustrated in Fig. C.1, which shows the ffij coefficients.
 |
Fig. C.1. Value of the ff functions at |
Again here as in Appendix A, we consider Δ/ν < < 1 and Φ = 2πΔτd, then
Moreover, for 2Φ ≠ 0 (when ff11 = ff22 = 0), then
Furthermore, |ff11/ff12|< < 1.
Again taking Φt = Φ ≈ π/2, then
These types of approximated behaviour are shown in Fig. C.1.
At ν ∼ νmax, we obtain
All Tables
Results of the fit for cases 1, 3, and 6 of the frequency variation (freq.) and the second differences (diff.).
All Figures
 |
Fig. 1. r010 ratios according to the frequency scaled to νmax. Left: for the Sun (computed from the BISON frequencies; Broomhall et al. 2009; Hale et al. 2016) and KIC 10162436. Right: for KIC 1435467 and KIC 6679371 (data from Lund et al. 2017a). |
| In the text | |
 |
Fig. 2. r010 ratios for the 1.4M⊙ models A0 to A5 all at Xc = 0.10. All curves have a mean of about 0.07, and all but A0 are gradually shifted by 0.01 for clarity. |
| In the text | |
 |
Fig. 3. Internal structure profiles with and without penetrative convection. Left: temperature gradients as function of acoustic radius for the B1 and B2 models with M = 1.4 M⊙ and Xc = 0.15. The grey lines represent the adiabatic and radiative gradients of model B2 (which are very similar to those of B1). The vertical dashed black line on the right represents the position of the Schwarzschild limit for both models. The line on the left represents the bottom of the penetrative convective region of model B2. The downward arrow shows the middle of the acoustic cavity (tcz/𝒯 ≈ 4180 s). Right: dΓ1/dτ as a function of the acoustic radius for models B1 and B2. |
| In the text | |
 |
Fig. 4. μ gradient as a function of the acoustic radius for models A0, A5, and A5 with the turbulent mixing calibrated by Verma & Silva Aguirre (2019). |
| In the text | |
 |
Fig. 5. Glitch parameters and signature with and without penetrative convection. Top: amplitudes a1 (dotted lines), a2 (dashed lines), and Amax (solid lines) (Eq. (11), (12), and (15)) as functions of the extent of the PC region in pressure scale height for models B1 (left panel) and B2 (right panel) at Xc = 0.15. The dot-dashed lines represent the BSCZ. Bottom: ratios r010 according to the frequency for the same models. The error bar represents the typical mean uncertainty on the ratios, such as the one obtained for KIC 10162436. |
| In the text | |
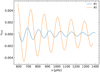 |
Fig. 6. Predicted glitch signature from Eq. (16) for model B1 and B2 at Xc = 0.15. |
| In the text | |
 |
Fig. 7. Probability density of tcz when no prior is imposed for the model B2 at Xc = 0.15 with a mean uncertainty of 0.30 μHz. The vertical dashed blue lines represent the theoretical value given by the stellar model from which the frequencies were computed. The downward arrow shows the middle of the acoustic cavity (tcz ≈ 4180 s). |
| In the text | |
 |
Fig. 8. Detectability of the signature in the r010 ratios for different quantities. The open and black circles show that the signature of the BSCZ glitch has an amplitude, |
| In the text | |
 |
Fig. 9. Impact of the μ-gradient and of the smoothness of the temperature gradient on the r010 ratios. Left: temperature gradients of model B2 (orange), B3 (blue), and B4 (green) for the top panel, and A5 (orange), A6 (blue), and A7 (green) for the bottom panel as a function of the acoustic radius at Xc = 0.10. Right: corresponding r010 ratios as a function of the frequency. |
| In the text | |
 |
Fig. A.1. Value of the f functions at |
| In the text | |
 |
Fig. C.1. Value of the ff functions at |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



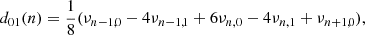
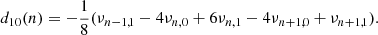
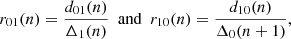
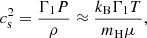
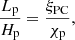
![$$ \begin{aligned} \nabla = \nabla _\mathrm{ad} - \frac{\nabla _\mathrm{ad} - \nabla _\mathrm{rad} }{2}\left[1 - \frac{2}{\pi }\arctan \left(\frac{\zeta (r)-\alpha _{\rm PC}H_{\rm p}(r_\mathrm{cz} )}{\beta (\nabla _\mathrm{ad} -\nabla _\mathrm{rad} )^4}\right)\right], \end{aligned} $$](/articles/aa/full_html/2023/05/aa45103-22/aa45103-22-eq8.gif)
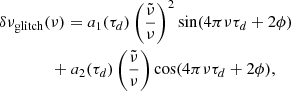
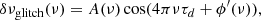
![$$ \begin{aligned}&A(\nu )=\left[a_1(\tau _d)^2\left(\frac{\tilde{\nu }}{\nu }\right)^4+a_2(\tau _d)^2\left(\frac{\tilde{\nu }}{\nu }\right)^2\right]^{1/2},\end{aligned} $$](/articles/aa/full_html/2023/05/aa45103-22/aa45103-22-eq12.gif)
![$$ \begin{aligned}&\phi ^{\prime }(\nu )=2\phi -\arctan \left[\frac{a_1(\tau _d)}{a_2(\tau _d)}\left(\frac{\tilde{\nu }}{\nu }\right)\right]. \end{aligned} $$](/articles/aa/full_html/2023/05/aa45103-22/aa45103-22-eq13.gif)
![$$ \begin{aligned}&a_1(\tau )=\frac{g}{32\pi ^3\tilde{\nu }^2\mathcal{T} }\left[h_1(\tau )h_2(\tau )-\frac{1}{4}\left(\frac{\gamma -1}{\nabla _\mathrm{ad} }\frac{\mathrm{d} \nabla _\mathrm{rad} }{\mathrm{d} \tau }\right)\right],\end{aligned} $$](/articles/aa/full_html/2023/05/aa45103-22/aa45103-22-eq14.gif)
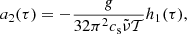
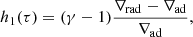
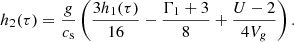
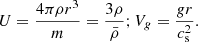
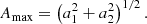
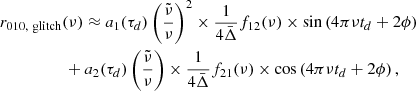
![$$ \begin{aligned}&f_{12}(\nu )=3+\left[\frac{\nu ^2(\nu ^2+\bar{\Delta }^2)}{(\nu ^2-\bar{\Delta }^2)^2}\right]\cos \left(4\pi \bar{\Delta }t_d\right)\nonumber \\&\qquad \qquad + \left[\frac{4\nu ^2(\nu ^2+\bar{\Delta }^2/4)}{(\nu ^2-\bar{\Delta }^2/4)^2}\right]\cos \left(2\pi \bar{\Delta }t_d\right), \end{aligned} $$](/articles/aa/full_html/2023/05/aa45103-22/aa45103-22-eq25.gif)
![$$ \begin{aligned}&f_{21}(\nu )=3+ \left[\frac{\nu ^2}{\nu ^2 - \bar{\Delta }^2}\right]\cos \left(4\pi \bar{\Delta }t_d\right) \nonumber \\&\qquad \qquad + \left[\frac{4\nu ^2}{\nu ^2-\bar{\Delta }^2/4}\right]\cos \left(2\pi \bar{\Delta }t_d\right), \end{aligned} $$](/articles/aa/full_html/2023/05/aa45103-22/aa45103-22-eq26.gif)
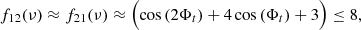
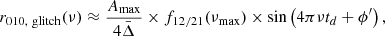
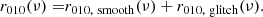
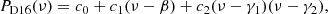
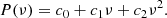
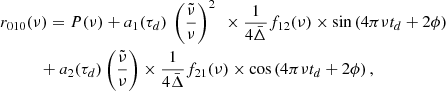
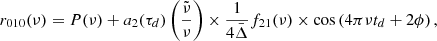
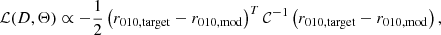
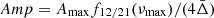
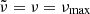
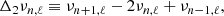
![$$ \begin{aligned}&\delta \nu = a_2 \left(\frac{\tilde{\nu }}{\nu }\right) \cos (4\pi \nu \tau _\mathrm{cz} +2\phi )\nonumber \\&\qquad + A_\mathrm{HeII} \left(\frac{\tilde{\nu }}{\nu }\right)\sin ^2(2\pi \beta _\mathrm{HeII} \nu )\cos (4\pi \nu \tau _\mathrm{HeII} +2\phi _\mathrm{HeII} ),\nonumber \\&\delta \Delta _2\nu = A_\mathrm{cz} ^*\left(\frac{\tilde{\nu }}{\nu }\right) \sin (4\pi \nu \tau _\mathrm{cz} +2\phi )\nonumber \\&\qquad + A_\mathrm{HeII} ^*\left(\frac{\nu }{\tilde{\nu }}\right)\exp \left[-\beta _\mathrm{HeII} \left(\frac{\tilde{\nu }}{\nu }\right)^2\right]\sin (4\pi \nu \tau _\mathrm{HeII} +2\phi _\mathrm{HeII} ). \end{aligned} $$](/articles/aa/full_html/2023/05/aa45103-22/aa45103-22-eq127.gif)
![$$ \begin{aligned}&\delta \Delta _2\nu _\mathrm{cz} \approx a_2(\tau )\left(\frac{\tilde{\nu }}{\nu }\right)\left[\frac{2\nu ^2}{\nu ^2-\bar{\Delta }^2}\cos \left(4\pi \bar{\Delta }\tau _d\right)- 2\right]\cos \left(4\pi \nu \tau _\mathrm{cz} +2\phi \right)\nonumber \\&\qquad \ \ \approx a_2(\tau )\left(\frac{\tilde{\nu }}{\nu }\right)\left[2-\frac{2\nu ^2}{\nu ^2-\bar{\Delta }^2}\cos \left(4\pi \bar{\Delta }\tau _d\right)\right]\sin \left(4\pi \nu \tau _\mathrm{cz} +2\phi ^{\prime }\right), \end{aligned} $$](/articles/aa/full_html/2023/05/aa45103-22/aa45103-22-eq129.gif)
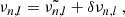
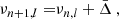
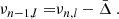
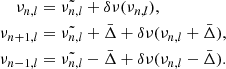
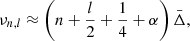
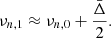
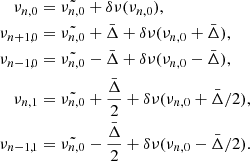
![$$ \begin{aligned} \begin{aligned} r_{01}(n)=&\frac{1}{8\bar{\Delta }}\left[\delta \nu (\nu _{n,0}-\bar{\Delta })-4\delta \nu (\nu _{n,0}-\frac{\bar{\Delta }}{2})+6\delta \nu (\nu _{n,0})\right. \\&\left.-4\delta \nu (\nu _{n,0}+\frac{\bar{\Delta }}{2})+\delta \nu (\nu _{n,0}+\bar{\Delta })\right].\\ \end{aligned} \end{aligned} $$](/articles/aa/full_html/2023/05/aa45103-22/aa45103-22-eq161.gif)
![$$ \begin{aligned} \begin{aligned} \delta \nu (\nu \pm \bar{\Delta })=&a_2(\tau _d)\left(\frac{\tilde{\nu }}{\nu \mp \bar{\Delta }}\right)\left[\cos \left(4\pi \nu \tau _d+2\phi \right)\cos \left(4\pi \bar{\Delta }\tau _d\right)\right.\\&\left.\mp \sin \left(4\pi \nu \tau _d+2\phi \right)\sin \left(4\pi \bar{\Delta }\tau _d\right)\right]\\&+a_1(\tau _d)\left(\frac{\tilde{\nu }}{\nu \pm \bar{\Delta }}\right)^2\left[\sin \left(4\pi \nu \tau _d+2\phi \right)\cos \left(4\pi \bar{\Delta }\tau _d\right)\right.\\&\left.\pm \cos \left(4\pi \nu \tau _d+2\phi \right)\sin \left(4\pi \bar{\Delta }\tau _d\right)\right], \end{aligned} \end{aligned} $$](/articles/aa/full_html/2023/05/aa45103-22/aa45103-22-eq162.gif)
![$$ \begin{aligned} \begin{aligned} \delta \nu (\nu \pm \frac{\bar{\Delta }}{2})=&a_2(\tau _d)\left(\frac{\tilde{\nu }}{\nu \pm \frac{\bar{\Delta }}{2}}\right)\left[\cos \left(4\pi \nu \tau _d+2\phi \right)\cos \left(2\pi \bar{\Delta }\tau _d\right)\right.\\&\left.\mp \sin \left(4\pi \nu \tau _d+2\phi \right)\sin \left(2\pi \bar{\Delta }\tau _d\right)\right]\\&+a_1(\tau _d)\left(\frac{\tilde{\nu }}{\nu \pm \frac{\bar{\Delta }}{2}}\right)^2\left[\sin \left(4\pi \nu \tau _d+2\phi \right)\cos \left(2\pi \bar{\Delta }\tau _d\right)\right.\\&\left.\pm \cos \left(4\pi \nu \tau _d+2\phi \right)\sin \left(2\pi \bar{\Delta }\tau _d\right)\right]. \end{aligned} \end{aligned} $$](/articles/aa/full_html/2023/05/aa45103-22/aa45103-22-eq163.gif)
![$$ \begin{aligned} \begin{aligned} r_{01}(\nu )=&\frac{a_2(\tau _d)}{4\bar{\Delta }}\left[\left(\frac{\tilde{\nu }\nu }{\nu ^2-\bar{\Delta }^2}\right)\cos \left(4\pi \bar{\Delta }\tau _d\right)-\left(\frac{4\tilde{\nu }\nu }{\nu ^2-\bar{\Delta }^2/4}\right)\cos \left(2\pi \bar{\Delta }\tau _d\right)\right. \\&\left.+3\left(\frac{\tilde{\nu }}{\nu }\right)\right]\times \cos \left(4\pi \nu \tau _d+2\phi \right)\\ +&\frac{a_2(\tau _d)}{4\bar{\Delta }}\left[\left(\frac{\tilde{\nu }\bar{\Delta }}{\nu ^2-\bar{\Delta }^2}\right)\sin \left(4\pi \bar{\Delta }\tau _d\right)-\left(\frac{2\tilde{\nu }\bar{\Delta }}{\nu ^2-\bar{\Delta }^2/4}\right)\sin \left(2\pi \bar{\Delta }\tau _d\right)\right] \\&\times \sin \left(4\pi \nu \tau _d+2\phi \right)\\ +&\frac{a_1(\tau _d)}{2\bar{\Delta }}\left[-\left(\frac{\tilde{\nu }^2\nu \bar{\Delta }}{(\nu ^2-\bar{\Delta }^2)^2}\right)\sin \left(4\pi \bar{\Delta }\tau _d\right)\right.\\&\left.+\left(\frac{2\tilde{\nu }^2\nu \bar{\Delta }}{(\nu ^2-\bar{\Delta }^2/4)^2}\right)\sin \left(2\pi \bar{\Delta }\tau _d\right)\right]\times \cos \left(4\pi \nu \tau _d+2\phi \right)\\ +&\frac{a_1(\tau _d)}{4\bar{\Delta }}\left[\left(\frac{\tilde{\nu }^2(\nu ^2+\bar{\Delta }^2)}{(\nu ^2-\bar{\Delta }^2)^2}\right)\cos \left(4\pi \bar{\Delta }\tau _d\right)\right.\\&\left.-\left(\frac{4\tilde{\nu }^2(\nu ^2+\bar{\Delta }^2/4)}{(\nu ^2-\bar{\Delta }^2/4)^2}\right)\cos \left(2\pi \bar{\Delta }\tau _d\right)+3\left(\frac{\tilde{\nu }}{\nu }\right)^2\right]\\&\times \sin \left(4\pi \nu \tau _d+2\phi \right). \end{aligned} \end{aligned} $$](/articles/aa/full_html/2023/05/aa45103-22/aa45103-22-eq164.gif)
![$$ \begin{aligned} \begin{aligned} r_{010}(\nu )=&\frac{a_1(\tau _d)}{4\bar{\Delta }}\left(\frac{\tilde{\nu }}{\nu }\right)^2\left[f_{11}(\nu )\times \cos \left(4\pi \nu t_d+2\phi \right)+\right.\\&\left.+f_{12}(\nu )\times \sin \left(4\pi \nu t_d+2\phi \right)\right]\\ +&\frac{a_2(\tau _d)}{4\bar{\Delta }}\left(\frac{\tilde{\nu }}{\nu }\right)\left[ f_{21}(\nu )\times \cos \left(4\pi \nu t_d+2\phi \right)\right.\\&\left.+f_{22}(\nu )\times \sin \left(4\pi \nu t_d+2\phi \right)\right], \end{aligned} \end{aligned} $$](/articles/aa/full_html/2023/05/aa45103-22/aa45103-22-eq166.gif)
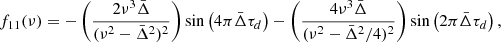
![$$ \begin{aligned} \begin{aligned} f_{12}(\nu )=&\left[\frac{\nu ^2(\nu ^2+\bar{\Delta }^2)}{(\nu ^2-\bar{\Delta }^2)^2}\right]\cos \left(4\pi \bar{\Delta }t_d\right)\\ +&\left[\frac{4\nu ^2(\nu ^2+\bar{\Delta }^2/4)}{(\nu ^2-\bar{\Delta }^2/4)^2}\right]\cos \left(2\pi \bar{\Delta }t_d\right) +3, \end{aligned} \end{aligned} $$](/articles/aa/full_html/2023/05/aa45103-22/aa45103-22-eq168.gif)
![$$ \begin{aligned} \begin{aligned} f_{21}(\nu )=&\left[\frac{\nu ^2}{\nu ^2 - \bar{\Delta }^2}\right]\cos \left(4\pi \bar{\Delta }t_d\right)\\ +&\left[\frac{4\nu ^2}{\nu ^2-\bar{\Delta }^2/4}\right]\cos \left(2\pi \bar{\Delta }t_d\right)+3, \end{aligned} \end{aligned} $$](/articles/aa/full_html/2023/05/aa45103-22/aa45103-22-eq169.gif)
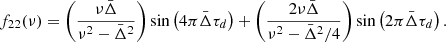
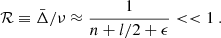
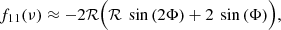
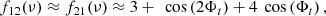
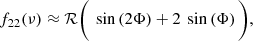

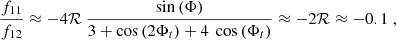
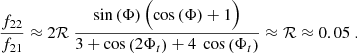
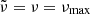

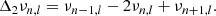
![$$ \begin{aligned} \begin{aligned} \Delta _2\nu _{n,l,cz}=&a_1(\tau )\left(\frac{\tilde{\nu }}{\nu }\right)^2[ff_{11}(\nu )\cos \left(4\pi \nu \tau _d+2\phi \right)\\&+ff_{12}(\nu )\sin \left(4\pi \nu \tau _d+2\phi \right)]\\&+a_2(\tau )\left(\frac{\tilde{\nu }}{\nu }\right)[ff_{21}(\nu )\cos \left(4\pi \nu \tau _d+2\phi \right)\\&+ff_{22}(\nu )\sin \left(4\pi \nu \tau _d+2\phi \right)]\\ \end{aligned} \end{aligned} $$](/articles/aa/full_html/2023/05/aa45103-22/aa45103-22-eq184.gif)
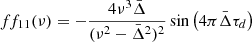
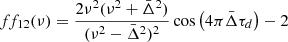
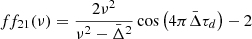
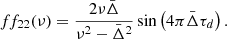
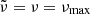
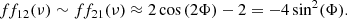
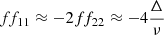
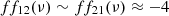
![$$ \begin{aligned} \begin{aligned} \Delta _2\nu _{n,l,cz}&\approx a_1(\tau ) [ ff_{12}(\nu )\sin \left(4\pi \nu \tau _d+2\phi \right)]\\&+a_2(\tau ) [ff_{21}(\nu )\cos \left(4\pi \nu \tau _d+2\phi \right) ]\\&\approx -4 [ a_1(\tau ) \sin \left(4\pi \nu \tau _d+2\phi \right)]\\&+a_2(\tau ) \cos \left(4\pi \nu \tau _d+2\phi \right) ]\\ \end{aligned} .\end{aligned} $$](/articles/aa/full_html/2023/05/aa45103-22/aa45103-22-eq193.gif)