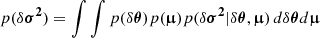| Issue |
A&A
Volume 663, July 2022
|
|
|---|---|---|
| Article Number | A60 | |
| Number of page(s) | 15 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202243298 | |
| Published online | 12 July 2022 | |
Properties of the ionisation glitch
II. Seismic signature of the structural perturbation
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université de Paris, 5 Place Jules Janssen, 92195 Meudon, France
e-mail: pierre.houdayer@obspm.fr
Received:
9
February
2022
Accepted:
13
May
2022
Aims. In the present paper, we aim to constrain the properties of the ionisation region of a star from the oscillation frequency variation (a so-called glitch) caused by rapid structural variations in this very region. In particular, we seek tof avoid the use of calibration based on stellar models, thus providing a truly independent estimate of these properties. These include both the helium abundance and other physical quantities that can have a significant impact on the oscillation frequencies, such as the electronic degeneracy parameter or the extent of the ionisation region.
Methods. Building on previous findings, we applied structural perturbations of the ionisation zone to the wave equation for radial oscillations in an isentropic region. The resulting glitch model is thus able to exploit the information contained in the fast frequency oscillation caused by the helium ionisation but also that in the slow trend accompanying the ionisation of hydrogen. This information can be directly expressed in terms of parameters related to the helium abundance, electronic degeneracy, and the extent of the ionisation region, respectively.
Results. Using Bayesian inference, we show that substantial recovery of the properties at the origin of the glitch is possible. We find a degeneracy between the helium abundance and the electronic degeneracy, which particularly affects the helium estimate. Extending the method to cases where the glitch is subject to contamination (e.g., surface effects), we note the importance of the slow glitch trend associated with hydrogen ionisation. We propose the use of a Gaussian process to disentangle the frequency glitch from surface effects.
Key words: asteroseismology / stars: oscillations / stars: interiors / stars: abundances
© P. S. Houdayer et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
When a star is subject to various forms of excitation, certain resonances may emerge that depend on its geometry and internal structure. When the star is spherically symmetric, each of these sustained oscillations can be described by quantum numbers such as its radial order n and degree ℓ, which reflect the geometric properties of the oscillations. The overall way in which the pulsation frequencies νn, ℓ vary with radial order has been described with asymptotic developments (Vandakurov 1967; Tassoul 1980). These approximations have been very successful in describing solar-like oscillations, especially for large radial orders.
In addition to this asymptotic trend, the advent of high-precision photometry with CoRoT (Baglin et al. 2006), Kepler (Gilliland et al. 2010; Lund et al. 2017), and now TESS (Ricker et al. 2015; Stassun et al. 2019) has enabled the identification of more subtle contributions, including a particularly remarkable component, namely the ionisation glitch. Initially observed for the Sun, this deviation from the global trend manifests itself as an oscillatory component whose period, amplitude, and damping reflects local properties of the ionisation region (Gough 1990, 2002; Christensen-Dalsgaard & Perez Hernandez 1992). Numerous studies have then exploited this particular signature in solar-like stars in order to determine the position of their ionisation region (e.g., Verma et al. 2014, 2017; Broomhall et al. 2014) or the amount of helium contained in this latter (e.g., Vorontsov et al. 1992; Perez Hernandez & Christensen-Dalsgaard 1994; Lopes et al. 1997; Verma et al. 2014, 2019). Most of the recent approaches are based on empirical models of the perturbation caused by the ionisation of helium (e.g., Monteiro & Thompson 2005; Houdek & Gough 2007) and relate their parameters to actual physical quantities via calibration on realistic models (Houdek & Gough 2011; Verma et al. 2014, 2019). In our first article (Houdayer et al. 2021, hereafter Paper I), we made various comments on this procedure and presented an alternative approach to modelling the ionisation region as well as the perturbation caused by a change in its properties. The derived structure is found to depend on three parameters that correspond respectively to the surface helium abundance, the electron degeneracy in the convective zone, and the extent of the ionisation region. Characterising the glitch based on such a model would thus allow us to extract physical quantities, such as the helium abundance, without the need for calibration, as well as other interesting constraints, such as the electronic degeneracy in the star’s convection zone.
In order to reach this objective, we establish, in the present paper, the relation between the properties of the ionisation region and the resulting glitch. After providing some details on the glitch modelling in Sect. 2, we present the corresponding formalism (and the underlying assumptions) in Sect. 3. We subsequently present the tests that we carried out in order to assess how well the properties of the ionisation region may be recovered from a glitch. The results are described in Sect. 4 for an ideal case and Sect. 5 when a contamination is included. The closing Sect. 6 is dedicated to our conclusions.
2. Creating an ionisation glitch model
2.1. Modelling the ionisation region
In Paper I, we presented a thermodynamically derived model of the structure inside the ionisation region. This is done by means of an analytical approximation of the first adiabatic exponent Γ1(ρ, T, Xi > 1) inside an adiabatic region; the Xi > 1 refer here to the abundances of all elements except hydrogen. When applied to a hydrogen-helium mixture (of respective abundances 1 − Y and Y), solving the hydrostatic equilibrium as well as Poisson’s equation defines the entirety of the associated structure (i.e., the density ρ, pressure P, sound speed c, and so on) at any location t (we often refer to the position in the star by its normalised acoustic depth 0 ≤ t ≤ 1 in this paper). The resulting structural model, 𝒮(t), is therefore able to account for the impact of different amounts of helium in the ionisation region. More specifically, this model is fully determined by three parameters: (1) Ys, the surface helium abundance, (2) ψCZ, the value of the electron degeneracy parameter inside the convective zone, and (3) ε, a small parameter defining the position and extent of the ionisation region. For a more compact notation, this parameterisation is hereafter designated by the vector θ = [Ys, ψCZ, ε]T (and thus the associated structural model 𝒮θ(t)).
In the same paper, we proposed the use of a difference of these models δ𝒮θ, δθ(t) = 𝒮θ + δθ(t)−𝒮θ(t) instead of an ad hoc profile in order to model the structural perturbation causing the ionisation glitch. Indeed, in exchange for an increased numerical cost (i.e., the time needed to compute the model 𝒮θ + δθ(t) for each δθ), this approach has many advantages, such as the possibility to account for more complex and realistic perturbations; the ability to model the perturbation of any structural profile and not only that of the first adiabatic exponent Γ1; the way it relates these perturbations to actual physical properties of the region; and the fact that it is not limited to the impact of a pure helium change, and this for a limited number of parameters (3). In addition to the structural aspects raised here, we show that the method also leads to benefits regarding the exploitation of glitches.
2.2. Modelling the ionisation glitch using an ad hoc perturbation profile
Many approaches to obtaining an expression for the seismic glitch rely on formulae derived from the variational principle, which relate changes in oscillation frequencies to internal structure perturbations (Dziembowski et al. 1990; Gough & Thompson 1991; Antia & Basu 1994). Subsequently, the general aim would be to eliminate certain contributions to obtain a final expression that depends only on perturbations that can be described analytically. Therefore, a starting point to many derivations of theoretical forms of the frequency shift is the neglect of the contributions of slowly varying perturbations, such as differences in pressure δxP/P or density δxρ/ρ compared to δxΓ1/Γ1 (e.g., Monteiro & Thompson 2005; Houdek & Gough 2007, 2011) where δx designates a perturbation taken at fixed normalised radius x = r/R. As an example, the approximation used in Appendix A of Houdek & Gough (2007) gives the resulting (quadratic) frequency difference with respect to a given reference:
where ω = 2πν is the angular oscillation frequency, V designates the volume of the star, and ξ is the Lagrangian displacement caused by the oscillation. Such an expression can be highly useful; indeed, having an analytical expression for the single perturbation involved δxΓ1 is sufficient to provide a parametric form of the glitch. If it is also possible to approximate the eigenfunction (e.g. with the WKB formalism, cf. Bender & Orszag 1978), then a fully analytical expression for the frequency shift can be derived (Monteiro et al. 1994, 1998; Houdek & Gough 2007), although the many assumptions needed to achieve this may affect the reliability of the approximation. The main drawback of this analytical development lies in its primary interest: it eliminates the need to use a complete model of the structure. From then on, it is no longer possible to fit frequency differences from a reference model (δν). Instead, the frequencies (ν) must be fitted directly. Although the frequency shift can be approximated by Eq. (1), the reference frequencies, νref, are not explicitly defined in this case. Rather than trying to model them roughly (e.g., via an asymptotic relationship), it is preferable to consider second differences in order to limit the error introduced (Gough 1990):
Applied to Eq. (1), the use of the second differences leads to
where Δν corresponds to the asymptotic large separation and ℱ(ν) is an analytical approximation of
This way, the d2νref component is generally assumed to be smooth, in the sense that it can be the result of a second derivative applied to the oscillation frequencies of a ‘glitch-free’ model. It is therefore usually eliminated from d2ν by fitting a slowly varying function. We note that a significant assumption made here is the persistence of the linear perturbation regime, and thus that the perturbed model differs only slightly from the glitch-free model.
2.3. Modelling the ionisation glitch using a structural perturbation model
In contrast, the structural perturbation model δ𝒮θ, δθ(t) on which we rely allows us to express the perturbation of each structural quantity, so that we are no longer limited to a formula that depends only on δxΓ1. It is therefore possible to rely on a more comprehensive form than Eq. (1), in which some of the contributions to the glitch are neglected. Also, it is possible to numerically compute the reference frequencies ωref as well as the eigenfunctions ξ based on 𝒮θ(t). With this in mind, we tried to construct a glitch model that makes the link explicit between a change in physical properties, δθ, and frequency perturbations 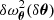 . The link between δθ and the structural perturbation δ𝒮θ, δθ(t) having been established in our first paper, it is now a matter of deriving an expression analogous to Eq. (1) in order to express the relation between this structural perturbation and the glitch. A schematic representation of our approach is shown in Fig. 1.
. The link between δθ and the structural perturbation δ𝒮θ, δθ(t) having been established in our first paper, it is now a matter of deriving an expression analogous to Eq. (1) in order to express the relation between this structural perturbation and the glitch. A schematic representation of our approach is shown in Fig. 1.
 |
Fig. 1. Schematic diagram of the method adopted here to derive a glitch model. The aim of Sect. 3 is represented by the rightmost arrow, i.e., how to derive the glitch from a given structural difference. |
3. Impact of structural perturbations on oscillation frequencies
Here, we aim to describe the behaviour of the oscillation frequencies when disturbed by a perturbation of the equilibrium quantities in the ionisation region. We rely on the following two assumptions: (1) the perturbation is localised in a convective zone, meaning that we consider the region to be strictly isentropic, and (2) the perturbation is close enough to the surface so that we can assume the displacement (at least for low degree pulsation modes) to be purely radial.
These approximations lead to the following simplifications in the calculations:
and therefore the exact cancellation of both Lamb Sℓ and Brunt–Väisälä 𝒩 frequencies. Within this framework, the remaining constraints on the wave propagation (which are needed in order to define a cavity for a standing wave) are grouped under the term cut-off frequency and denoted ωc.
3.1. The wave equation
Under the assumption of adiabatic and radial pulsations, the wave equation relating the oscillation frequency ω to the displacement amplitude ξ can be reduced to a Schrödinger equation expressed on the acoustic depth 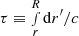 (Roxburgh & Vorontsov 1994a,b):
(Roxburgh & Vorontsov 1994a,b):
with,
and the rescaling variable λ defined as
In order to relate all the quantities that are homogeneous to a frequency in Eq. (8), it is useful to introduce
the frequency scale of any structural quantity s. In this formalism, the cut-off frequency can be written as a quadratic form over a few frequency scales:
by making use of the following properties:
From Eq. (11), we observe that the constraints to the wave propagation can be both of a geometrical (involving the terms in Fr, Fg ∼ c/r which dominate near the star’s centre) and structural nature (composed of the terms in Fρ, Fc, or Fdc/dr ∼ g/c, dominating in the upper layers). A representation of the ratio between the resulting cut-off and oscillation frequencies 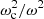 with respect to the normalised acoustic depth t = τ/τ0 (
with respect to the normalised acoustic depth t = τ/τ0 (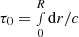 being the star’s acoustic radius) is given in Fig. 2. From Eq. (7), we see that this ratio contains all the information about the propagation: as long as its value remains below 1 (blue area), the wave will adopt an oscillatory behaviour, whereas the wave will be evanescent if the ratio exceeds this limit (red area). The variations close to the surface, which break the symmetry between the centre and surface of the star, constitute a typical signature of the ionisation region.
being the star’s acoustic radius) is given in Fig. 2. From Eq. (7), we see that this ratio contains all the information about the propagation: as long as its value remains below 1 (blue area), the wave will adopt an oscillatory behaviour, whereas the wave will be evanescent if the ratio exceeds this limit (red area). The variations close to the surface, which break the symmetry between the centre and surface of the star, constitute a typical signature of the ionisation region.
 |
Fig. 2. Example of the ratio |
Before going further, let us reiterate that we are interested here in describing the behaviour of the glitch and not of the frequencies that appear in Eq. (7). To this end, it is more convenient to normalise this relation by introducing quantities that can be compared from one structure to another. Accordingly, we rewrite the above Eq. (7) in terms of the following normalised variables: σ = ωτ0, σc = ωcτ0, t = τ/τ0, and η = λξ/∥λξ∥ with the notation:
The wave equation verified by the normalised eigenfunction η(t, σ) can now be rewritten as follows:
3.2. Obtaining a glitch model
Taking the product of Eq. (13) and η, and integrating the result from t = 0 to 1, we can naively write (after integrating by parts):
remembering that η is normalised and therefore 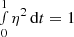 . It is possible to show that the part in brackets can be considered to be null as long as it is possible to find a thin layer in both the surface and centre where the variations of Γ1 are negligible. As this layer can be as thin as desired, we consider hereafter the following approximation:
. It is possible to show that the part in brackets can be considered to be null as long as it is possible to find a thin layer in both the surface and centre where the variations of Γ1 are negligible. As this layer can be as thin as desired, we consider hereafter the following approximation:
It is clear that the actual oscillation frequencies (σ) can significantly differ from the modelled expression of oscillation frequencies (σmod) provided above. Indeed, if the assumptions of isentropy and radial oscillations appear to be coherent for pulsations located in a surface convective zone (and a fortiori in the ionisation region), these have been implicitly extended to the whole star during the integration. The resulting difference is accounted for by the function ℛ, such that:
In this form, Eq. (16) is particularly well-suited to studying the frequency difference δσ = σB − σA between two models A and B. Using the variational principle (Chandrasekhar 1964) in order to perturb Eq. (16) merely provides, at first order:
where δt designates a difference in profile at identical t (where δ stands for a simple difference in quantity) between the two models (Paper I; Christensen-Dalsgaard & Thompson 1997). The advantage of using normalised variables becomes apparent: while no problem arises with the difference in profile at a fixed value of t, it would have been different at fixed τ if ever 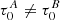 .
.
Equation (17) satisfies the objective set at the end of Sect. 2: it provides an explicit link between the perturbation of the oscillation frequencies δσ2 and the perturbation of the structure through 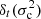 . In this equation, δℛ characterises how closely the actual glitch δσ2 is approximated by our modelled glitch expression
. In this equation, δℛ characterises how closely the actual glitch δσ2 is approximated by our modelled glitch expression 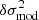 . We note that it is not necessary for
. We note that it is not necessary for 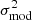 to be a good approximation of σ2 for δℛ to be small. Indeed, it is only necessary for the assumptions to be verified in the regions where the structure differs between the models (as
to be a good approximation of σ2 for δℛ to be small. Indeed, it is only necessary for the assumptions to be verified in the regions where the structure differs between the models (as 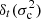 ) would be strictly null in the other regions in any case).
) would be strictly null in the other regions in any case).
3.3. Comparison of glitch models with a numerically derived glitch
Although Eq. (17) does meet the criteria we set ourselves, it does not constitute the only possible approximation of the glitch. In particular, we propose to compare Eq. (17) (to which we refer with the index I) with the approximation of the glitch proposed by Eq. (1) (index II):
In order to compare these two formulae, it is necessary to define the structural models A and B from which the glitch results. It may be noted that neither Eq. (19) nor Eq. (18) imposes a particular choice for model A or B as long as it is possible to derive the required structural perturbations. Here we choose two instances of the structural models defined in Paper I, 𝒮θ⊙(t) and 𝒮θ⊙ + δθ(t), respectively parameterised by ![$ \boldsymbol{\theta}^\odot = [Y_{\rm s}^\odot = 0.255, \psi_\mathrm{CZ}^\odot = -5, \varepsilon^\odot = 0.015]^\mathsf{T} $](/articles/aa/full_html/2022/07/aa43298-22/aa43298-22-eq32.gif) and θ⊙ + δθ. Such a situation can be seen as ideal, in the sense that the assumptions used to derive both glitch expressions I and II are verified by design (in particular, the two models differ only in the ionisation region). Expressions I and II should therefore be satisfactory approximations of δσ2 (at first order) and this assertion is tested in Fig. 3. The reference for our comparison, the ‘true’ glitch, is merely the difference in oscillation frequency between the structures 𝒮θ⊙(t) and 𝒮θ⊙ + δθ(t). The frequencies of each structure have been calculated numerically using InversionKit (Reese et al. 2016) and appear in black symbols. This comparison is made for low degree modes ℓ ≤ 2 and a wide range of radial orders to show the asymptotic behaviour. Three glitches are considered (respectively in panels a, b, and c), corresponding to a difference in each parameter, the amplitude of which was chosen to cause a similar impact on the frequencies in terms of amplitude: δθ = {[0.05,0,0]T,[0,0.2,0]T,[0,0,0.001]T}. Finally, in order to better account for the departures, we have chosen to compare δσ/σ with
and θ⊙ + δθ. Such a situation can be seen as ideal, in the sense that the assumptions used to derive both glitch expressions I and II are verified by design (in particular, the two models differ only in the ionisation region). Expressions I and II should therefore be satisfactory approximations of δσ2 (at first order) and this assertion is tested in Fig. 3. The reference for our comparison, the ‘true’ glitch, is merely the difference in oscillation frequency between the structures 𝒮θ⊙(t) and 𝒮θ⊙ + δθ(t). The frequencies of each structure have been calculated numerically using InversionKit (Reese et al. 2016) and appear in black symbols. This comparison is made for low degree modes ℓ ≤ 2 and a wide range of radial orders to show the asymptotic behaviour. Three glitches are considered (respectively in panels a, b, and c), corresponding to a difference in each parameter, the amplitude of which was chosen to cause a similar impact on the frequencies in terms of amplitude: δθ = {[0.05,0,0]T,[0,0.2,0]T,[0,0,0.001]T}. Finally, in order to better account for the departures, we have chosen to compare δσ/σ with 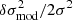 rather than δσ2 with
rather than δσ2 with 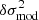 directly.
directly.
 |
Fig. 3. Comparison of numerically derived glitches δσ/σ (black symbols, 0 ≤ ℓ ≤ 2, 5 ≤ n ≤ 70) with both modelled expressions |
A first thing to note about the glitches calculated numerically is that they seem to share a unique relationship regardless of their degree, which is in line with our hypothesis, which states that the displacement resulting from these low degree modes is almost radial in the perturbed region. Also, in addition to the clearly visible oscillation caused by the ionisation of helium, which gradually fades away at high frequencies, a slowly varying component is apparent. This component, which is visible in every panel, persists for longer than the component of helium and also oscillates much more slowly. A standard interpretation in terms of glitch tends to suggest an origin that is both more localised and superficial than that of helium. We believe that this is the signature of hydrogen ionisation, which has an impact on 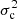 as can be seen in Fig. 2 at t ∼ 0.02 (this is to be compared with the impact of helium ionisation at 0.1 < t < 0.2).
as can be seen in Fig. 2 at t ∼ 0.02 (this is to be compared with the impact of helium ionisation at 0.1 < t < 0.2).
Regarding the modelled expressions, the glitch evaluated using Eq. (18) (darker curves) provides a near perfect recovery of the ‘true’ glitch in each situation. Considering the residual function 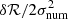 , a subtle undershoot is visible which is to be expected from a first-order approximation. In comparison, Eq. (19) (lighter curves) provides poorer approximations, even though it can account for part of the oscillation (we note that
, a subtle undershoot is visible which is to be expected from a first-order approximation. In comparison, Eq. (19) (lighter curves) provides poorer approximations, even though it can account for part of the oscillation (we note that 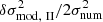 was corrected by an offset to better account for the asymptotic behaviour). However, by looking at the residuals, we see that by neglecting the pressure and inertia perturbations, Eq. (19) has not only discarded the slowly varying component but also some of the quickly oscillating part of the glitch.
was corrected by an offset to better account for the asymptotic behaviour). However, by looking at the residuals, we see that by neglecting the pressure and inertia perturbations, Eq. (19) has not only discarded the slowly varying component but also some of the quickly oscillating part of the glitch.
4. Estimating the properties of the ionisation region from the glitch
As stated above, it is worth noting that we do not assume a specific shape for the structural perturbations up to Eqs. (18) and (19). For instance, we consider the structural perturbations 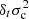 and δxΓ1/Γ1 as given to perform the comparisons in Fig. 3. As suggested in Sect. 2 (and in Fig. 1), our objective is now to combine the structural perturbation model δ𝒮θ, δθ(t) with Eq. (18) to obtain a parameterised model of the ionisation glitch. With such a model, we investigate in this section how to infer the properties of the ionisation region δθ from the glitch δσ2.
and δxΓ1/Γ1 as given to perform the comparisons in Fig. 3. As suggested in Sect. 2 (and in Fig. 1), our objective is now to combine the structural perturbation model δ𝒮θ, δθ(t) with Eq. (18) to obtain a parameterised model of the ionisation glitch. With such a model, we investigate in this section how to infer the properties of the ionisation region δθ from the glitch δσ2.
4.1. Constructing a glitch model from a structural perturbation model
Used in its present form, Eq. (17) could allow us to find, knowing the shape of the glitch, the profile of 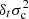 by inversion. However, it seems likely in practice that this recovery would be patchy, especially given the number of frequencies available and the complexity of the cut-off frequency profile. As pointed out in Sect. 2, we instead prefer to consider the shape of the perturbation as constrained by a parametric structural perturbation model δ𝒮θ, δθ(t). This implies the following assumption:
by inversion. However, it seems likely in practice that this recovery would be patchy, especially given the number of frequencies available and the complexity of the cut-off frequency profile. As pointed out in Sect. 2, we instead prefer to consider the shape of the perturbation as constrained by a parametric structural perturbation model δ𝒮θ, δθ(t). This implies the following assumption: 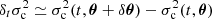 . The resulting perturbation
. The resulting perturbation 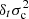 can therefore be fully described using the pair (θ, δθ). In practice, the quantity θ designates the value of the parameters in our reference model and is therefore known by design. In contrast, δθ accounts for the parameter differences that best explain the structural difference and must be inferred from the available data. For brevity, our glitch model is therefore written as a function of δθ only, although it depends on the chosen reference:
can therefore be fully described using the pair (θ, δθ). In practice, the quantity θ designates the value of the parameters in our reference model and is therefore known by design. In contrast, δθ accounts for the parameter differences that best explain the structural difference and must be inferred from the available data. For brevity, our glitch model is therefore written as a function of δθ only, although it depends on the chosen reference:
The quantity 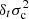 being perfectly defined as a function of δθ, this expression can be used in its present form to estimate the variation in parameters responsible for the glitch. However, in the following, we mainly focus on the linearised form of this expression:
being perfectly defined as a function of δθ, this expression can be used in its present form to estimate the variation in parameters responsible for the glitch. However, in the following, we mainly focus on the linearised form of this expression:
with
As discussed in Sect. 2, the main trade-off between the use of this model and the fully analytical forms of the glitch is in numerical cost. Whatever the value of δθ, it is necessary to compute the model 𝒮θ + δθ(t) in order to find the profile 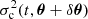 required to calculate Eq. (20). Equation (21) completely eliminates this constraint because it is only necessary to estimate
required to calculate Eq. (20). Equation (21) completely eliminates this constraint because it is only necessary to estimate 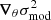 once and for all, thus introducing an error in 𝒪(δθTδθ) in the process. We note that this linearisation assumes that the gradient
once and for all, thus introducing an error in 𝒪(δθTδθ) in the process. We note that this linearisation assumes that the gradient 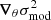 only depends slightly on the parameters of the reference model, which means that our expression (20) only depends on δθ and is locally insensitive to θ (which justifies its omission in the glitch model).
only depends slightly on the parameters of the reference model, which means that our expression (20) only depends on δθ and is locally insensitive to θ (which justifies its omission in the glitch model).
4.2. The fitting method
We now quantify the overall error on the recovery of δθ from a glitch δσ2 using Eq. (21). For this purpose, we consider the example of a glitch caused by the change of parameters δθtrue = [0.05, 0.2, 0.001]T. Regarding Fig. 3, this implies studying the glitch that results from combining the perturbation in each panel. This example offers two insights: firstly, it can reveal potential non-linearities as it is a non-negligible perturbation (each impact is of the order of the helium change δYs = 0.05, and therefore their combination constitutes a significant departure from the reference). Secondly, closer inspection of Fig. 3 leads us to expect a certain degree of degeneracy between the effects of δYs and δψCZ. Although the helium glitch is fairly similar in all panels (comparable amplitudes, periods, and damping), these two parameters, that is, δYs and δψCZ, also cause a comparable hydrogen glitch but with opposite sign. As we can expect a near cancellation by combining these two contributions, it is interesting to see how much information can be recovered about the parameter differences from Eq. (21).
Hereafter, δσ2 denotes the vector of frequency shifts forming the glitch at all radial orders. The recovery is achieved by means of a probabilistic approach, that is assuming that our parameter vector δθ is a random variable, and we try to estimate its distribution given the observation of a certain glitch δσ2. This random variable is referred to here as δθ|δσ2 and its probability density function is referred to as the posterior distribution. Such an approach may excessively complicated for a linear problem like this one, but it is nevertheless essential to account for the potential degeneracies of this problem as well as the uncertainties on our estimate.
The distribution p(δθ|δσ2) is estimated with the help of the Python library emcee1, which implements MCMC methods for sampling distributions. Further details about this procedure and the underlying assumptions can be found in Appendix A.1. The synthetic data, δσ2, generated for this purpose result from the oscillation frequency differences between the structures 𝒮θ⊙(t) and 𝒮θ⊙ + δθ(t) as was done in the previous section. The parameter recovery can therefore be seen as an ‘inverse crime’, in the sense that the assumed ionisation region structure in Eq. (21) actually corresponds to the one used to calculate the synthetic glitch. It constitutes therefore an ideal framework that tests the derivation of Eq. (17) and the subsequent linearisation Eq. (21) rather than the relevance of the structural model itself. In contrast to Sect. 3, we consider here only purely radial modes with orders ranging from 11 to 27, in accordance with the modes we expect to observe. The standard deviation on the frequencies was set to sn = 5 × 10−3, which would result in a ∼0.2 μHz dispersion for frequencies typical of a solar-like star. Although optimistic, this value is not unrealistic either: it is typically of the order of the mean uncertainty on the radial and dipolar modes in the Kepler LEGACY sample (Lund et al. 2017).
4.3. The resulting posterior distribution
The resulting posterior distribution after applying the above procedure is shown in Fig. 4 and summaries of this same distribution can be found in Table 1. The corner plot shows the univariate (two times marginalised) distributions on the diagonal as well as each bivariate (one time marginalised) distributions below, which means that the figure, as a whole, is fairly representative of the underlying (3D) distribution.
 |
Fig. 4. MCMC estimate of the distribution p(δθ|δσ2). The dashed lines indicate the value of the true δθtrue = [0.05, 0.2, 1 × 10−3]T used to generate δσ2 (the PDF gives at this point: lnp(δθtrue|δσ2) = 15.72). The mode of this distribution is δθMAP = [0.036, 0.178, 0.951 × 10−3]T. This plot was made with the Python package ChainConsumer (https://samreay.github.io/ChainConsumer). |
Comparison of the exact and fitted change in parameters.
Compared to the actual value of δθ (shown with dashed lines), the most plausible value according to the PDF, δθMAP, is somewhat underestimated (∼30% on δYs, ∼10% on δψCZ and ∼5% on δε) albeit fairly close. The extent of the PDF is directly related to the noise level surrounding the oscillation frequencies sn. Nevertheless, it is possible to draw some conclusions independently of a specific sn value: the estimate of the helium abundance seems to be the most volatile, followed by that of the electronic degeneracy, while the estimate of δε is the most stable. The reasons behind this statement are clearly apparent from Fig. 4. As expected, a strong degeneracy appears between δYs and δψCZ (the two parameters share a correlation coefficient of 0.98) as they produce relatively similar effects on the glitch (cf. Fig. 3). It should be noted that this degeneracy was already expected from the structure itself because both parameters impact the depth of the helium wells in the Γ1 profile (Paper I). This degeneracy especially increases the uncertainties on the helium abundance, making extreme values like δYs = 0 still relatively credible. It can also be noted that these two parameters also show a certain degree of correlation with δε. This, unlike the previous degeneracy, which is of physical origin, can be imputed to a lack of information in the data and in particular on the hydrogen component of the glitch. This particular point is investigated in Appendix B, where a recovery of the parameters with additional low-order frequencies is presented.
Finally, it is tempting to judge the quality of the fit based on a distance such as ∥θtrue − θMAP∥ for instance, eventually defining a metric accounting for the distribution spread in each direction. However, it would be complicated for such a distance to account for strong correlations or degeneracies in the distribution, in which case the parameter space admits preferential directions. A very natural way to proceed is to consider the value of the PDF at θtrue, lnp(δθtrue|δσ2), which at the same time penalises estimates that are too distant or too vague (because of the normalisation of the distribution) while taking into account the degeneracies2. In the present case, this metric gives the value lnp(δθtrue|δσ2) = 15.72. This value on its own has only limited meaning (although it is clear that it should be as high as possible). It is nonetheless interesting to compare it with other parameter recoveries, as we show in the following section.
To visualise the posterior distribution in terms of frequency shifts, we show in Fig. 5 a comparison between the numerical glitch and our glitch model. Here, we compare the model for the true value of the parameters, δθtrue, the model for the most probable value of the parameters given the data, δθMAP, and more than 300 curves drawn according to the posterior distribution on the parameters. These curves give an idea of how the spread of the distribution effectively propagates through the glitch models.
 |
Fig. 5. Comparison of the numerical glitch δσ2/2σ2 (circular symbols, ℓ = 0 and 11 ≤ n ≤ 27) with the modelled glitch expression ( |
Regarding the appearance of the curves, it is not surprising to see that the synthetic glitch is fairly similar to the one shown in panel c of Fig. 3 (in the corresponding frequency range) because the helium and electronic degeneracy contributions to the glitch approximately cancel out. A first thing to note is that the model, even in this linear version, accurately reproduces the actual glitch for the true value of δθ and thus justifies the linearisation in Eq. (21). This curve is noticeably close to that of the maximum a posteriori (MAP) estimate, δθMAP, which confirms the relevance of the retrieved solution. Also, the models drawn a posteriori account well for the uncertainties on the glitch based on the lighter curves. This illustrates the importance of the degeneracy on the helium abundance: glitch models that differ by more than 0.05 in δYs may sometimes barely be distinguished.
5. Preliminary applications to seismic data
The results presented in the previous section suggest our method is able to recover most of the information on the ionisation region properties contained in the glitch, and this without needing any calibration on realistic models. Therefore, despite the degeneracy affecting the reliability of our helium estimate, the procedure introduced seems to provide reasonable predictions for the parameters (as an indication, the MAP estimate on the total parameters would give θMAP = [0.291, −4.82, 1.60 × 10−2]T to be compared with θtrue = [0.305, −4.80, 1.60 × 10−2]T). However, at this point, it is important to bear in mind that the recovery of parameters in Sect. 4 is carried out in an ideal framework. Although we have only considered an observable range of radial modes with an acceptable noise level, the difference between the two models under consideration is a perturbation of the ionisation region. By design, this implies that the synthetic frequency differences only reflect the presence of the ionisation glitch.
It is fairly easy to draw the limits of this case when confronted with actual seismic data3: (1) by assuming γ = Γ1, we neglected contributions of the Brunt–Väisälä frequency δ𝒩2 to the frequency shift δσ2. Although they are indeed zero in the ionisation region, such differences could very well occur in a radiative region because of the μ-gradient for instance (Deheuvels & Michel 2010; Noll et al. 2021). Thus, the unexpected presence of a convective core in the observed star or a deficient modelling of the chemical composition in this region can impact the differences in the oscillation frequencies. However, it should be noted that the glitch model can easily be extended to the case δ𝒩2 ≠ 0 by simply replacing the cut-off frequency perturbation 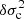 by the total acoustic potential perturbation δ𝒱 (Roxburgh & Vorontsov 1994b).
by the total acoustic potential perturbation δ𝒱 (Roxburgh & Vorontsov 1994b).
(2) By restricting ourselves to the ionisation region, we have neglected many of the perturbations to the cut-off frequency occurring elsewhere. Other well-known contributions are the signature of the transition between the convective and radiative regions, and surface effects. The first signature results from a much deeper layer than the ionisation region for the stars we are interested in and thus manifests itself as a higher frequency (and lower amplitude) oscillation in the glitch (e.g., Monteiro et al. 1994; Houdek & Gough 2007). By far the most important in terms of amplitude, surface effects are at the origin of much slower components. They can be considered as the main source of ‘contamination’ to the ionisation glitch fit and are one of the reasons for using second differences (cf. Eq. (2)) instead of frequencies directly.
These effects, if not treated properly, are likely to have a severe impact on our estimate of the properties of the ionisation region. In the remainder of this section, we explore two approaches for applying our method despite the presence of interfering components in the data. The first is very common and seeks to reduce these components by combining frequencies and the second attempts to fit the frequencies directly using Gaussian processes.
5.1. Using frequency combinations as a diagnostic
Considering a diagnostic, y, expressed as a linear combination of the squared frequencies, σ2, we write:
where C is a matrix for which we can assume a general form at this point. We note here that the diagnostic introduced above differs slightly from those that are used habitually, which are written as a combination of the frequencies directly. Using squared frequencies brings a more intuitive understanding in the formalism introduced so far, while giving identical results, as confirmed by supplementary numerical tests. The general idea, and a fortiori the elimination of the most superficial components when C is the discrete derivative operator, remains very similar.
Subsequently, from Eqs. (21) and (22), it follows immediately from Eq. (23) that
with
where η2 is the vector composed of all the normalised eigenfunctions η2. We note that in this vector form (accounting for all frequencies at once) ∇θymod designates a matrix, which is very similar to
the vector form of Eq. (22). In fact, ∇θymod refers to the decomposition of the same function, 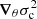 , but on different kernels, namely Cη2 instead of η2. While η2 designates oscillating functions of constant amplitude in the major part of the star, the combinations Cη2 can take more general envelopes. In the specific case where C = Dk, with Dk being the discrete derivative operator to a given power k, this envelope varies as sink(πt) independently of the frequency σ (Ballot et al. 2004). This combination can therefore be seen as enhancing the signal of
, but on different kernels, namely Cη2 instead of η2. While η2 designates oscillating functions of constant amplitude in the major part of the star, the combinations Cη2 can take more general envelopes. In the specific case where C = Dk, with Dk being the discrete derivative operator to a given power k, this envelope varies as sink(πt) independently of the frequency σ (Ballot et al. 2004). This combination can therefore be seen as enhancing the signal of 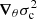 at t = t1 compared to t = t2 by a factor of (sin(πt1)/sin(πt2))k. With regard to the concerns raised above, the main advantage of this method clearly appears when it comes to getting rid of the surface effects. Taking the example of a ‘contamination’ at tsurf ∼ 0.01 and a helium glitch at tHe ∼ 0.15, the signal of the latter is comparatively amplified by a factor of more than 200 for k = 2 (corresponding to a second derivative). However, the same reasoning holds for the hydrogen component – for which tH ∼ 0.02 – which is thereby completely removed. It is therefore important to assess the impact of this loss of information in our fit, especially as we expect this component to be essential when recovering the different parameters.
at t = t1 compared to t = t2 by a factor of (sin(πt1)/sin(πt2))k. With regard to the concerns raised above, the main advantage of this method clearly appears when it comes to getting rid of the surface effects. Taking the example of a ‘contamination’ at tsurf ∼ 0.01 and a helium glitch at tHe ∼ 0.15, the signal of the latter is comparatively amplified by a factor of more than 200 for k = 2 (corresponding to a second derivative). However, the same reasoning holds for the hydrogen component – for which tH ∼ 0.02 – which is thereby completely removed. It is therefore important to assess the impact of this loss of information in our fit, especially as we expect this component to be essential when recovering the different parameters.
To this end, we performed a similar analysis to that conducted in Sect. 4, this time aiming to fit the perturbation of the second differences δy = δ(D2σ2) instead of that of the frequencies δσ2 directly. The method is completely analogous to that described above, and some details can be found in Appendix A.2. For the exact same value of δθtrue = [0.05, 0.2, 1 × 10−3]T, Fig. 6 gives a MCMC sampling of the posterior distribution p(δθ|δy) using the diagnostic δy. Compared to the reference distribution p(δθ|δσ2) found in Fig. 4 and shown in grey-scale here, this new PDF is notably more spread out. This is not surprising, because the elimination of the slowly varying component can only result in a loss of information; nevertheless it is worth quantifying this loss. We see that an important loss of information concerns the parameter δε, which can be seen in the spreading of its marginal distribution. As mentioned in Sect. 4, with the compensation of the contributions of δYs and δψCZ, it is expected that the hydrogen component mainly constrains δε. Thus, its absence here is most clearly manifested by this last parameter.
 |
Fig. 6. MCMC estimate of the distribution p(δθ|δy) in the case y = D2σ2 (in blue) compared to the case y = σ2 shown in Fig. 4. The dashed lines indicate the true value of δθtrue = [0.05, 0.2, 1 × 10−3]T used to generate δy (the PDF gives at this point: lnp(δθtrue|δy) = 12.17). The mode of this distribution is δθMAP = [0.026, 0.195, 0.888 × 10−3]T. |
In addition, the shape of the distribution significantly changes on the δYs vs. δψCZ panel, with the clear degeneracy between the two parameters now being more diffuse. Without the reference distribution for comparison, we might have concluded that the degeneracy was removed. However, the comparison makes it apparent that it is rather the presence of the helium oscillation alone (i.e. without the contribution of hydrogen) that allows more pairs (δYs, δψCZ) to be credible. Thus, the physically based degeneracy between δYs and δψCZ seems to be ‘resolved’ when sufficient information is available, while being hidden in the uncertainty when knowledge on the slowly varying component is lacking.
Finally, the mode of distribution, δθMAP = [0.026, 0.195,0.888 × 10−3]T, has changed compared to the previous case, although not drastically regarding the extent of the distribution (however, we may note that the most plausible value of δYs is underestimated by ∼50% compared to the true value). However, as mentioned earlier, a more appropriate way to judge the quality of the fit is through the value of the distribution in δθtrue, which gives lnp(δθtrue|δy) = 12.17. This metric notably tells us that p(δθtrue|δy) is about 35 times lower than p(δθtrue|δσ2) and thus quantifies the deterioration of the fit by using the second differences as a diagnostic.
We once more compared our model provided by Eq. (24) and the diagnostic obtained from numerical frequency deviations in Fig. 7. This time a single oscillatory component, that of helium, appears as expected. A first observation stands out, namely the considerable amplification of the uncertainty due to the linear combination. The errors shown in the figure are given by the square root of the diagonal coefficients of Σy, the covariance matrix, for lack of a better representation. Therefore, while being visually dominant, these error bars are not necessarily representative of the uncertainties on the diagnostic y as they do not account for the correlated part of the noise (which helps to reduce some of the overall uncertainty). We may also note the proximity of the curves given by (∇θymod)Tδθ and (∇θymod)TδθMAP despite their difference in terms of the parameters. More generally, many curves drawn from p(δθ|δy) are of comparable amplitude, whereas some of them differ by more than 0.1 in δYs for instance.
Overall, we can see that the use of a diagnostic, while mitigating contamination of the ionisation glitch, such as that caused by surface effects, might hinder our ability to recover the solution. Even in the ideal case presented here (in the absence of contamination), finding a way to preserve the hydrogen component appears essential. Therefore, in the following section we present an approach to fit the ionisation glitch directly even in the presence of additional components.
5.2. Using frequencies directly
In this section, we take the explicit example of a contamination by surface effects and therefore consider a direct approximation of δσ2 by relying on the following model:
where 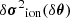 is given by Eq. (21) and
is given by Eq. (21) and 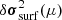 designates a parameterised model of the surface effects. Expressing such a model explicitly is by no means straightforward, especially because what we refer to as ‘surface effects’ depend more on what is included (or not) in our reference structural model than on a well-defined physical phenomenon. It is therefore clear that the model describing the corresponding frequency shifts must be somewhat flexible. Meanwhile, this model must satisfy constraints, which are that the frequency shifts must (1) vary on sufficiently large scales – by definition, these effects include the most superficial deviations from the structure; and (2) be much weaker at low than at high frequencies. Indeed, the acoustic modes are becoming more and more sensitive to the surface effects with increasing radial orders.
designates a parameterised model of the surface effects. Expressing such a model explicitly is by no means straightforward, especially because what we refer to as ‘surface effects’ depend more on what is included (or not) in our reference structural model than on a well-defined physical phenomenon. It is therefore clear that the model describing the corresponding frequency shifts must be somewhat flexible. Meanwhile, this model must satisfy constraints, which are that the frequency shifts must (1) vary on sufficiently large scales – by definition, these effects include the most superficial deviations from the structure; and (2) be much weaker at low than at high frequencies. Indeed, the acoustic modes are becoming more and more sensitive to the surface effects with increasing radial orders.
To satisfy these conditions, here we have chosen to model these surface effects by a Gaussian process (GP) whose parameterisation by μ is specified in Appendix A.3. To illustrate the possibilities offered by this GP, Fig. 8 shows 200 realisations of the process given by Eqs. (A.10) and (A.11) for a fixed set of values for μ. As desired, the generated functions are indeed of low amplitude at low frequencies and exhibit a polynomial envelope. They also show a certain flexibility and generally end up deviating from a simple power law at higher frequencies, which allows them to mimic a more comprehensive behaviour. It is also clear that many of the functions in this sample do not correspond to a plausible observation of surface effects. Without observational constraints, this sample only provides us with an a priori view of the functions that the process generates.
 |
Fig. 8. Example of 200 realisations of the Gaussian process |
On a practical level, the use of GPs is implemented via the Python library george4 while the distribution sampling is carried out as in Sect. 4. Naturally, we need to synthetically generate surface effects this time in order to test the method in a controlled framework. We followed the prescription of Sonoi et al. (2015) to generate ad hoc surface effects that we would expect to find from a solar-like star. Based on their scaling relations and taking into account our non-dimensionalisation, we obtained the following expression:
This artificial frequency shift was added to the glitch studied in Sect. 4 in order to generate the ‘observed’ frequency deviation δσ2. The probability distribution of the parameters given this data realisation, p(δθ, μ|δσ2), is shown in Fig. 9 (in blue scale) and compared with the one obtained in Fig. 4 in the absence of contamination (in grey-scale). As is the case in the previous section, the distribution has expanded, because of the uncertainty caused by surface effects on the one hand and the fixed amount of information that is now shared by five parameters on the other. The marginalised distribution over μ, visible in the six upper panels, shows many similarities with p(δθ|δy) in Fig. 6. In particular, we observe the more diffuse degeneracy between δYs and δψCZ as well as the expansion of the distribution on the previously best-constrained parameter, δε. However, these effects occur to a lesser degree as indicated by the value of lnp(δθtrue|δσ2) = 12.67 being larger than lnp(δθtrue|δy). In some ways, the fact that this method provides a better parameter recovery in the presence of synthetic surface effects than using second differences without any contamination emphasises the benefits of the procedure. Also, as was done with the contamination-free fit, we investigate the improvement of this recovery with the use of additional frequencies in Appendix B.
 |
Fig. 9. MCMC estimate of the distribution p(δθ, μ|δσ2) (in blue) compared to the reference without any contamination found in Fig. 4 (in grey). The dashed lines indicate the value of δθtrue = [0.05, 0.2, 1 × 10−3]T used to generate δσ2 (the marginalised PDF over μ gives at this point: lnp(δθtrue|δσ2) = 12.67). The mode of this distribution is given by δθMAP = [0.027, 0.178, 1.051 × 10−3]T and μMAP = [42.8, 7.63]T. |
Once again, a more visual representation of this distribution is available in Fig. 10 through realisations of the models 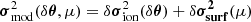 ,
, 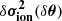 and
and 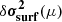 according to the distribution p(δθ, μ|δσ2) (light curves). Figure 10 also allows us to assess the magnitude of the surface effects (red symbols) compared to the glitch. In particular, their amplitude is three times higher at high frequencies, largely impacting the resulting frequency shift (black symbols) when compared to the ionisation glitch (blue symbols). Despite this, it is not surprising that the model in its entirety (black curves) manages to adequately reproduce this frequency shift considering the added flexibility it is given. Having said this, it is far more interesting to see what the model assumes about
according to the distribution p(δθ, μ|δσ2) (light curves). Figure 10 also allows us to assess the magnitude of the surface effects (red symbols) compared to the glitch. In particular, their amplitude is three times higher at high frequencies, largely impacting the resulting frequency shift (black symbols) when compared to the ionisation glitch (blue symbols). Despite this, it is not surprising that the model in its entirety (black curves) manages to adequately reproduce this frequency shift considering the added flexibility it is given. Having said this, it is far more interesting to see what the model assumes about 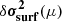 and especially
and especially 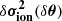 (red and blue curves respectively) based solely on the observation of δσ2. Concerning the surface effects model, we can see in particular that the mean of the GP has clearly changed in comparison with the a priori process (cf. Fig. 8). All these curves do appear to be plausible realisations of surface effects (at least when compared to those we artificially imposed) and overall only slightly underestimate their amplitude. The shape of the glitch is also fairly well guessed, although the most likely model gradually deviates from that shape at high frequencies. We note that we obtain constraints not only on the fast oscillation but also on the slower trend of the glitch. Thus, some of the information on the hydrogen component is recovered and more can be retrieved if it is possible to obtain even lower radial orders (cf. Appendix B). The envelope formed by the sampling is naturally larger than in Fig. 5 and thus reflects the uncertainty introduced by the added contamination.
(red and blue curves respectively) based solely on the observation of δσ2. Concerning the surface effects model, we can see in particular that the mean of the GP has clearly changed in comparison with the a priori process (cf. Fig. 8). All these curves do appear to be plausible realisations of surface effects (at least when compared to those we artificially imposed) and overall only slightly underestimate their amplitude. The shape of the glitch is also fairly well guessed, although the most likely model gradually deviates from that shape at high frequencies. We note that we obtain constraints not only on the fast oscillation but also on the slower trend of the glitch. Thus, some of the information on the hydrogen component is recovered and more can be retrieved if it is possible to obtain even lower radial orders (cf. Appendix B). The envelope formed by the sampling is naturally larger than in Fig. 5 and thus reflects the uncertainty introduced by the added contamination.
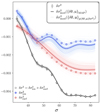 |
Fig. 10. Comparison of the synthetic frequency shift δσ2 (black symbols) resulting from the ionisation glitch |
6. Conclusion
In the present paper, we develop a method for estimating the properties of the ionisation region from the glitch caused by rapid structural variations in this very region. In particular, the method presented here is designed to overcome the dependence on realistic stellar models caused by calibration in order to provide a truly independent estimate of these properties. These include both the helium abundance and other physical quantities that can have a significant impact on the oscillation frequencies such as the electronic degeneracy parameter or the extent of the ionisation region.
This paper takes Paper I as a starting point and combines the structural perturbations of the ionisation zone presented there with the perturbation of a wave equation. To this end, we consider a framework suited to the ionisation region (purely radial oscillations in an isentropic region) and verify that the resulting formula is able to correctly reproduce glitches produced by various structural perturbations. Although it only involves the perturbation of the (normalised) cut-off frequency 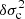 , this formulation is more accurate than common glitch expressions that only consider the perturbation of the first adiabatic exponent δΓ1. This gain in accuracy is especially useful for us: the resulting glitch model is thus able to exploit the information contained in the fast oscillation caused by the helium ionisation but also in the slow trend accompanying the ionisation of hydrogen. By using the work conducted in Paper I, this information can be directly expressed in terms of parameters δθ = [δYs, δψCZ, δε]T, which represent a difference in helium abundance, the electronic degeneracy, and the extent of the ionisation region (from a fixed reference), respectively.
, this formulation is more accurate than common glitch expressions that only consider the perturbation of the first adiabatic exponent δΓ1. This gain in accuracy is especially useful for us: the resulting glitch model is thus able to exploit the information contained in the fast oscillation caused by the helium ionisation but also in the slow trend accompanying the ionisation of hydrogen. By using the work conducted in Paper I, this information can be directly expressed in terms of parameters δθ = [δYs, δψCZ, δε]T, which represent a difference in helium abundance, the electronic degeneracy, and the extent of the ionisation region (from a fixed reference), respectively.
We quantify this parameter recovery through Bayesian inference in the context of limited (observable radial modes) and noisy synthetic data. By design, the ‘observed’ glitch is generated based only on structural differences localised in the ionisation region, and therefore constitutes a robust reference for evaluating the performance of the procedure in an ideal case (without any external contamination). We thus verified that the properties at the origin of the glitch can mostly be recovered. Specifically, the best constrained parameter is the extent of the region, followed by electronic degeneracy, while the most variable estimate concerns the helium abundance. At the origin of this uncertainty is a degeneracy between δYs and δψCZ which was already expected in Paper I and which particularly extends over the helium abundance. Unlike the correlations between the other parameters which disappear when more data are available (see Appendix B), this degeneracy has a physical origin and does not seem to be specifically inherent to this approach. Indeed, both parameters have (locally) similar impacts within the structure of the star itself, which fundamentally makes it difficult to disentangle them. Therefore, an increase in the number of observed frequencies or even a decrease in the considered noise level does not make this degeneracy disappear but limits its extent.
We then considered how to extend the procedure to the non-ideal (but more realistic) case of a contamination of the observed glitch by an additional component, typically surface effects. A first possibility is to extend the formalism to other diagnostics such as frequency combinations. While this adaptation does not raise any fundamental problems, a strong degradation of the parameter recovery is already observed in the ideal case. We attribute this deterioration to the loss of information on the slow trend of the glitch. Indeed, while frequency combinations allow the amplitude of a slowly varying contamination to be mitigated, they also remove all trace of the glitch component resulting from the ionisation of hydrogen. We therefore considered a second possibility in order to preserve this component despite the contamination by exploiting Gaussian processes. The latter allows us to introduce an additional degree of flexibility in the model and takes into account additional components not explicitly defined while introducing a limited number of additional parameters (two in our case). A deterioration appears compared to the ideal case, but is mainly due to the impact of the surface effects (the amplitude of which is a few times higher than that of the glitch at high frequencies) and the fact that a fixed amount of information in the data is now used to constrain additional parameters. It was thus possible to graphically verify that the slowly varying component was partially recovered and the estimate of surface effects was plausible. We note that this fit provides better results (in the sense of cross-entropy with the target distribution) than a second differences fit in the absence of contamination.
This work now needs to be extended to the analysis of actual data and account for the accuracy and uncertainty on a retrieval of the ionisation region properties. To this end, we point out the benefit of combining a glitch model with a Gaussian process. The number of options offered by GPs is immense and the results presented here show only one particular attempt based on weak assumptions. It is clear that this procedure can be adapted to cases where the contamination is more significantly constrained based on physical grounds and can provide results accordingly. Therefore, although it remains a prospect for now, we would like to emphasise the information that this method can provide by focusing on the slow glitch trend and directly dealing with the frequencies rather than their combination.
Acknowledgments
The authors would like to thank the referee for his or her constructive report and willingness to improve and clarify the content of this article.
References
- Aigrain, S., Hodgkin, S. T., Irwin, M. J., Lewis, J. R., & Roberts, S. J. 2015, MNRAS, 447, 2880 [NASA ADS] [CrossRef] [Google Scholar]
- Aigrain, S., Parviainen, H., & Pope, B. J. S. 2016, MNRAS, 459, 2408 [NASA ADS] [Google Scholar]
- Angus, R., Morton, T., Aigrain, S., Foreman-Mackey, D., & Rajpaul, V. 2018, MNRAS, 474, 2094 [Google Scholar]
- Antia, H. M., & Basu, S. 1994, A&AS, 107, 421 [NASA ADS] [Google Scholar]
- Baglin, A., Auvergne, M., Barge, P., et al. 2006, in The CoRoT Mission Pre-Launch Status– Stellar Seismology and Planet Finding, eds. M. Fridlund, A. Baglin, J. Lochard, & L. Conroy, ESA Spec. Publ., 1306, 33 [Google Scholar]
- Ballot, J., Turck-Chièze, S., & García, R. A. 2004, A&A, 423, 1051 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bender, C. M., & Orszag, S. A. 1978, Advanced Mathematical Methods for Scientists and Engineers (New York: McGraw Hill) [Google Scholar]
- Broomhall, A. M., Miglio, A., Montalbán, J., et al. 2014, MNRAS, 440, 1828 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1964, A&A, 139, 664 [Google Scholar]
- Christensen-Dalsgaard, J., & Perez Hernandez, F. 1992, MNRAS, 257, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J., & Thompson, M. J. 1997, MNRAS, 284, 527 [NASA ADS] [Google Scholar]
- Deheuvels, S., & Michel, E. 2010, Astron. Nachr., 331, 929 [Google Scholar]
- Dziembowski, W. A., Pamyatnykh, A. A., & Sienkiewicz, R. 1990, MNRAS, 244, 542 [NASA ADS] [Google Scholar]
- Gilliland, R. L., Brown, T. M., Christensen-Dalsgaard, J., et al. 2010, PASP, 122, 131 [Google Scholar]
- Gough, D. O. 1990, in Comments on Helioseismic Inference, eds. Y. Osaki, & H. Shibahashi, 367, 283 [Google Scholar]
- Gough, D. O. 2002, in Stellar Structure and Habitable Planet Finding, eds. B. Battrick, F. Favata, I. W. Roxburgh, & D. Galadi, ESA Spec. Publ., 485, 65 [NASA ADS] [Google Scholar]
- Gough, D. O., & Thompson, M. J. 1991, The Inversion Problem, 519 [Google Scholar]
- Houdayer, P. S., Reese, D. R., Goupil, M.-J., & Lebreton, Y. 2021, A&A, 655, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Houdek, G., & Gough, D. O. 2007, MNRAS, 375, 861 [CrossRef] [Google Scholar]
- Houdek, G., & Gough, D. O. 2011, MNRAS, 418, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Kjeldsen, H., Bedding, T. R., & Christensen-Dalsgaard, J. 2008, ApJ, 683, L175 [Google Scholar]
- Lopes, I., Turck-Chieze, S., Michel, E., & Goupil, M.-J. 1997, ApJ, 480, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Lund, M. N., Silva Aguirre, V., Davies, G. R., et al. 2017, ApJ, 835, 172 [Google Scholar]
- Monteiro, M. J. P. F. G., & Thompson, M. J. 1998, in New Eyes to See Inside the Sun and Stars, eds. F. L. Deubner, J. Christensen-Dalsgaard, & D. Kurtz, IAU Symp., 185, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Monteiro, M. J. P. F. G., & Thompson, M. J. 2005, MNRAS, 361, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Monteiro, M. J. P. F. G., Christensen-Dalsgaard, J., & Thompson, M. J. 1994, A&A, 283, 247 [NASA ADS] [Google Scholar]
- Noll, A., Deheuvels, S., & Ballot, J. 2021, A&A, 647, A187 [EDP Sciences] [Google Scholar]
- Perez Hernandez, F., & Christensen-Dalsgaard, J. 1994, MNRAS, 269, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Rasmussen, C. E., & Williams, C. K. I. 2006, Gaussian Processes for Machine Learning (MIT Press) [Google Scholar]
- Reese, D., Buldgen, G., & Zharkov, S. 2016, InversionKit: Linear Inversions from Frequency Data [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Sys., 1, 014003 [Google Scholar]
- Roxburgh, I. W., & Vorontsov, S. V. 1994a, MNRAS, 268, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Roxburgh, I. W., & Vorontsov, S. V. 1994b, MNRAS, 268, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Sonoi, T., Samadi, R., Belkacem, K., et al. 2015, A&A, 583, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stassun, K. G., Oelkers, R. J., Paegert, M., et al. 2019, AJ, 158, 138 [Google Scholar]
- Tassoul, M. 1980, ApJS, 43, 469 [Google Scholar]
- Vandakurov, Y. V. 1967, AZh, 44, 786 [NASA ADS] [Google Scholar]
- Verma, K., Faria, J. P., Antia, H. M., et al. 2014, ApJ, 790, 138 [Google Scholar]
- Verma, K., Raodeo, K., Antia, H. M., et al. 2017, ApJ, 837, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Verma, K., Raodeo, K., Basu, S., et al. 2019, MNRAS, 483, 4678 [Google Scholar]
- Vorontsov, S. V., Baturin, V. A., & Pamiatnykh, A. A. 1992, MNRAS, 257, 32 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Details about the recovery of the posterior distributions
Here, we provide details about the Bayesian inference on which Sections 4 and 5 rely.
A.1. Fitting the frequencies using δσ2mod(δθ)
We first provide a prior distribution on θ by decomposing it on each parameter (assumed to be a priori independent):
with p(X) designating the probability density function (PDF) of the random variable X. Specifically, we use the following distribution laws
The natural parameters (α, β) of these two laws can easily be determined from our parameterisation via the mean, μ, and standard deviation, s:
with v± = μ(1 ± μ)/s2. We chose the above distributions because they are defined on appropriate domains and have advantageous properties: 0 ≤ Ys ≤ 1, ψCZ < 0 (the convective region in solar-like pulsators cannot be degenerate), ε > 0 (by design). The means given correspond more or less to solar values but with sufficient variability so as to remain rather uninformative. The prior distribution on δθ trivially follows from:
with θ⊙ = [0.255, −5, 0.015]T being our (fixed) reference. We assume that the observed glitch distribution differs from the model only by an unbiased multivariate Gaussian, that is:
with 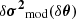 denoting the vector composed of all modelled (quadratic) frequency deviations from the reference given by Eq. (21). Our modelling of the noise n remains very rudimentary: we assume a frequency-independent and uncorrelated error distribution on δσ, that is,
denoting the vector composed of all modelled (quadratic) frequency deviations from the reference given by Eq. (21). Our modelling of the noise n remains very rudimentary: we assume a frequency-independent and uncorrelated error distribution on δσ, that is, 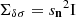 . From there, the noise distribution is easily propagated from δσ to δσ2:
. From there, the noise distribution is easily propagated from δσ to δσ2:
with diag(σ) being the diagonal matrix composed of σ. From Bayes’ theorem, the most plausible values of δθ|δσ2 minimise the following function (explicitly written in terms of the distributions introduced above):
with
the marginal likelihood that can be treated as a normalising constant in this case.
A.2. Fitting the frequencies using δymod(δθ)
In the presence of a contamination by surface effects, the observed frequency differences will be broken down into two components (in addition to the noise n):
where 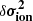 designates the ionisation glitch and
designates the ionisation glitch and 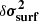 the deviation caused by surface effects. The method presented in Section 5.1 consists in introducing the combination:
the deviation caused by surface effects. The method presented in Section 5.1 consists in introducing the combination:
in the hope that C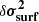 ≪ C
≪ C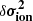 . In such a case, it is possible to approximate δy using the ionisation diagnostic model C
. In such a case, it is possible to approximate δy using the ionisation diagnostic model C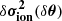 (given by Eq. (24)) together with Cn. In the case considered in the main text where C = D2, the noise covariance matrix is given by:
(given by Eq. (24)) together with Cn. In the case considered in the main text where C = D2, the noise covariance matrix is given by:
A.3. Fitting the frequencies using δσ2mod(δθ,μ)
A comprehensive introduction to the theory of GPs is given in Rasmussen & Williams (2006) and most of the notation appearing in this Appendix is based on that paper. For instance, we write:
to designate a model of the surface effects following the GP with mean function msurf(σ) = 0 and covariance function ksurf(σ, σ′). Although it may seem surprising, the choice of a zero mean a priori is rather common and enables us to avoid expressing a parametric form of msurf(σ) explicitly. Constrained by the observations 𝒟 = {σ,δσ2}, it is clear that this mean will no longer be zero but will instead be expressed in terms of ksurf( ⋅ , σ) and δσ2. The explicit definition of the process in Eq. (A.10) then boils down to expressing the covariance function, ksurf(σ, σ′), which gives the covariance between any choice of two frequencies (σ, σ′). Many astrophysical applications of GPs such as corrections of systematics and detrending of K2 light curves or estimates of stellar rotation periods (e.g. Aigrain et al. 2015, 2016; Angus et al. 2018) already make use of the ‘squared exponential’ (SE) and ‘quasi-periodic’ (QP) covariance functions. In this paper, in order to satisfy the constraints described above, we choose ksurf to be the product of a sixth order ‘homogeneous polynomial’ (HP) and a SE covariance function:
In this function, each part acts as follows:
-
The HP covariance function reduces the variance of the frequency, σ, when its value diminishes. Thus the process will take on values close to its mean (in this case 0) at low frequencies and allow a larger dispersion at higher frequencies. The ‘envelope’ of the process (in the sense of equally likely values as a function of frequency) is polynomial and varies as σ6/β. The choice of the exponent (6) is due to the observation that the surface effects vary approximately as δσsurf ∝ σ5 in the solar case (Kjeldsen et al. 2008), thus making
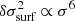 . This choice is somewhat arbitrary although we see that the process can widely deviate from this envelope.
. This choice is somewhat arbitrary although we see that the process can widely deviate from this envelope. -
The SE covariance function reduces the covariance between two frequencies, σ and σ′, that are distant in value. This introduces a characteristic scale of variation that behaves as
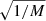 and allows for a progressive departure from a strict polynomial relationship. This covariance function therefore adds flexibility to the process.
and allows for a progressive departure from a strict polynomial relationship. This covariance function therefore adds flexibility to the process.
The process 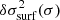 can then be seen as parameterised by the two values β2 and M (strictly speaking, they are hyperparameters), which influence the probability distribution of finding the value
can then be seen as parameterised by the two values β2 and M (strictly speaking, they are hyperparameters), which influence the probability distribution of finding the value 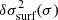 at frequency σ. Both of these parameters being positive (and potentially very large), we refer to this parameterisation as μ = [log β2, log M]T (and to the corresponding GP as
at frequency σ. Both of these parameters being positive (and potentially very large), we refer to this parameterisation as μ = [log β2, log M]T (and to the corresponding GP as 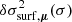 ). Based on this GP, our parameterised model of surface effects in Eq. (27) directly follows from the estimate of the mean process on σ for a fixed value of μ:
). Based on this GP, our parameterised model of surface effects in Eq. (27) directly follows from the estimate of the mean process on σ for a fixed value of μ:
We also adopt the notation
to designate the covariance matrix resulting from applying ksurf, μ to any pair of frequencies in σ.
Given an observation of surface effects, it would then be fairly easy to deduce the process a posteriori from the GP prior (given in Eq. (A.10)). However, such a case never appears in practice. As highlighted by Eq. (A.7), the observation of a surface effect will never occur independently of that of the glitch and of a stochastic component. Even if the ionisation glitch component is purely deterministic (unlike the other two), it is useful to write the entire sum as a GP itself to exploit its properties. Thus, the process representing the entirety of the observed frequency shift can be written as:
with 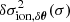 the prediction of the model given by Eq. (21) at σ, kn(σ, σ′) the (non-stationary) white noise covariance function defined as
the prediction of the model given by Eq. (21) at σ, kn(σ, σ′) the (non-stationary) white noise covariance function defined as
and associated with the covariance matrix Σδσ2, δ(x) being the Dirac function. Indeed, it is clear from Eqs. (A.4) and (A.15) that we have kn(σ, σ) = Σδσ2. We note that the deterministic aspect of the ionisation glitch component results in the addition of a mean value to the process only without any additional covariance compared to Eq. (A.10). Also, as for μ, δθ can be considered here as a hyperparameter in the sense that it designates a parameter of the underlying process (its mean function) and not of a particular realisation δσ2.
By noticing that δσ2|δθ, μ simply follows the normal law 𝒩(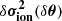 ,Ksurf(μ)+Σδσ2) from Eq. (A.14), the resulting marginalised likelihood is given by:
,Ksurf(μ)+Σδσ2) from Eq. (A.14), the resulting marginalised likelihood is given by:
with N denoting the number of radial orders considered. Here, the designation ‘marginal’ may seem obscure when compared to Eq. (A.6), where it referred to an integration over any possible δθ. In Eq. (A.16), we refer instead to a marginalisation over the realisations of the GP for fixed values of δθ and μ (hence their designation as hyperparameters). We note that this expression is analytically tractable only because we assume our frequency shift model to be a GP. Subsequently, accounting for the prior distributions, we sample the following hyperparameter posterior:
with p(δθ) resulting from Eq. (A.1), p(μ) being taken as an improper (in the sense of Bayesian inference) uniform prior, p(δσ2|δθ, μ) being given by Eq. (A.16) and
being the normalising constant.
Appendix B: Parameter recovery with additional frequencies
Considering all the distribution sampling performed so far, it may be interesting to try to quantify the impact of the various nuisances on the parameter recovery. In our case, besides potential imperfections of the model we presented, a clearly identifiable source of error lies in the absence of very low degree frequencies. Indeed, these frequencies contain the most information on the slowly varying component of the glitch, which we expect to be essential for a complete retrieval of the parameters. To this end, we present in Figs. B.1 and B.2 the sampling of the distributions shown in Figs. 4 and 9 with additional frequencies corresponding to 7 ≤ n ≤ 10 (the noise level on the oscillation frequencies, sn, remains the same).
 |
Fig. B.1. MCMC estimate of the distribution p(δθ|δσ2) with the additional low order frequencies 7 ≤ n ≤ 10 (in blue) in comparison with the reference shown in Fig. 4 (in grey). The dashed lines indicate the value of the true δθtrue = [0.05, 0.2, 1 × 10−3]T used to generate δσ2 (the PDF gives at this point: lnp(δθtrue|δσ2) = 16.91). The mode of this distribution is δθMAP = [0.047, 0.200, 0.989 × 10−3]T. |
 |
Fig. B.2. MCMC estimate of the distribution p(δθ, μ|δσ2) with the additional low order frequencies 7 ≤ n ≤ 10 (in blue) in comparison with the reference shown in Fig. 9 (in grey). The dashed lines indicate the value of δθtrue = [0.05, 0.2, 1 × 10−3]T used to generate δσ2 (the marginalised PDF over μ gives at this point: lnp(δθtrue|δσ2) = 14.37). The mode of this distribution is given by δθMAP = [0.046, 0.214, 1.083 × 10−3]T and μMAP = [43.2, 7.57]T. |
Figure B.1 shows the significant improvement in the parameter recovery when fitting the frequencies δσ2 in the ideal case (to be compared with the distribution found in Fig. 4, shown in grey). The mode, δθMAP = [0.047, 0.200, 0.989 × 10−3]T, is now much closer to the true value δθtrue and the extent of the distribution in general has considerably narrowed, now giving lnp(δθtrue|δσ2) = 16.91. We also note the clearly distinct nature of the δYs − δψCZ degeneracy with its physical origin and the correlation of these two parameters with δε. The first one, although shortened, conserves the same shape while the second one completely disappears to give fully uncorrelated parameters. Therefore, if the latter is indeed the result of a lack of information on the slow component associated with hydrogen (cf. Sections 4 and 5), we witness here the fundamentally different nature of the δYs − δψCZ degeneracy. If its extent can be reduced as is done here (a decrease in the noise level sn also diminishes its size), any glitch estimate of the helium abundance will be confronted with this elongated shape, which results from an ambivalence within the structure of the star itself.
Figure B.2 shows a similar test for the case of a contamination by surface effects. We therefore choose the distribution p(δθ, μ|δσ2) as a reference, shown in Fig. 9 and appearing here in grey. Interestingly, the additional frequencies do not have any impact on the distribution marginalised over δYs and δψCZ (6 rightmost panels) where the new distribution perfectly overlaps with the reference. This new information only effectively constrains the distribution on δYs and δψCZ (visible in the uppermost bivariate distribution) and the latter is largely improved. The MAP estimate, δθMAP = [0.046, 0.214, 1.083 × 10−3]T, has moved closer to δθtrue and the distribution extent has narrowed, resulting in a value of lnp(δθtrue|δσ2) = 14.37.
We therefore emphasis the importance of these very low radial orders, in particular when constraining the physical quantities, especially the helium abundance and the electronic degeneracy parameter. Let us note that adding high radial orders (> 27), on the other hand, hardly changes the retrieved distributions.
All Tables
All Figures
 |
Fig. 1. Schematic diagram of the method adopted here to derive a glitch model. The aim of Sect. 3 is represented by the rightmost arrow, i.e., how to derive the glitch from a given structural difference. |
| In the text | |
 |
Fig. 2. Example of the ratio |
| In the text | |
 |
Fig. 3. Comparison of numerically derived glitches δσ/σ (black symbols, 0 ≤ ℓ ≤ 2, 5 ≤ n ≤ 70) with both modelled expressions |
| In the text | |
 |
Fig. 4. MCMC estimate of the distribution p(δθ|δσ2). The dashed lines indicate the value of the true δθtrue = [0.05, 0.2, 1 × 10−3]T used to generate δσ2 (the PDF gives at this point: lnp(δθtrue|δσ2) = 15.72). The mode of this distribution is δθMAP = [0.036, 0.178, 0.951 × 10−3]T. This plot was made with the Python package ChainConsumer (https://samreay.github.io/ChainConsumer). |
| In the text | |
 |
Fig. 5. Comparison of the numerical glitch δσ2/2σ2 (circular symbols, ℓ = 0 and 11 ≤ n ≤ 27) with the modelled glitch expression ( |
| In the text | |
 |
Fig. 6. MCMC estimate of the distribution p(δθ|δy) in the case y = D2σ2 (in blue) compared to the case y = σ2 shown in Fig. 4. The dashed lines indicate the true value of δθtrue = [0.05, 0.2, 1 × 10−3]T used to generate δy (the PDF gives at this point: lnp(δθtrue|δy) = 12.17). The mode of this distribution is δθMAP = [0.026, 0.195, 0.888 × 10−3]T. |
| In the text | |
 |
Fig. 7. Same as Fig. 5 but for the synthetic diagnostic δy and the modelled expression (∇θymod)Tδθ. |
| In the text | |
 |
Fig. 8. Example of 200 realisations of the Gaussian process |
| In the text | |
 |
Fig. 9. MCMC estimate of the distribution p(δθ, μ|δσ2) (in blue) compared to the reference without any contamination found in Fig. 4 (in grey). The dashed lines indicate the value of δθtrue = [0.05, 0.2, 1 × 10−3]T used to generate δσ2 (the marginalised PDF over μ gives at this point: lnp(δθtrue|δσ2) = 12.67). The mode of this distribution is given by δθMAP = [0.027, 0.178, 1.051 × 10−3]T and μMAP = [42.8, 7.63]T. |
| In the text | |
 |
Fig. 10. Comparison of the synthetic frequency shift δσ2 (black symbols) resulting from the ionisation glitch |
| In the text | |
 |
Fig. B.1. MCMC estimate of the distribution p(δθ|δσ2) with the additional low order frequencies 7 ≤ n ≤ 10 (in blue) in comparison with the reference shown in Fig. 4 (in grey). The dashed lines indicate the value of the true δθtrue = [0.05, 0.2, 1 × 10−3]T used to generate δσ2 (the PDF gives at this point: lnp(δθtrue|δσ2) = 16.91). The mode of this distribution is δθMAP = [0.047, 0.200, 0.989 × 10−3]T. |
| In the text | |
 |
Fig. B.2. MCMC estimate of the distribution p(δθ, μ|δσ2) with the additional low order frequencies 7 ≤ n ≤ 10 (in blue) in comparison with the reference shown in Fig. 9 (in grey). The dashed lines indicate the value of δθtrue = [0.05, 0.2, 1 × 10−3]T used to generate δσ2 (the marginalised PDF over μ gives at this point: lnp(δθtrue|δσ2) = 14.37). The mode of this distribution is given by δθMAP = [0.046, 0.214, 1.083 × 10−3]T and μMAP = [43.2, 7.57]T. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



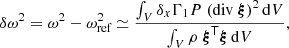
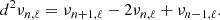
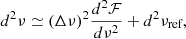
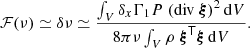
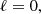

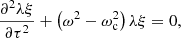
![$$ \begin{aligned} \omega _{\rm c}^2 = \frac{1}{4}\left(\frac{2c}{r}-\frac{g}{c}-\frac{\mathrm{d} c}{\mathrm{d} r}\right)^{2}-\frac{c}{2} \frac{ \mathrm{d} }{ \mathrm{d} r}\left[\frac{2c}{r}-\frac{g}{c}-\frac{\mathrm{d} c}{\mathrm{d} r}\right] -4 \pi G \rho , \end{aligned} $$](/articles/aa/full_html/2022/07/aa43298-22/aa43298-22-eq10.gif)
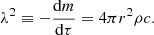
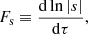
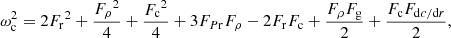
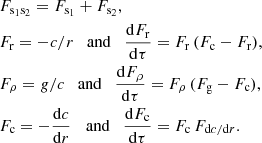
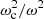
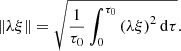
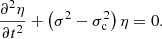
![$$ \begin{aligned} \sigma ^2_\mathrm{mod} = \int _0^1 \left(\sigma _{\rm c}^2\,\eta ^2+{\left(\frac{\partial \eta }{\partial t}\right)}^2\right)\mathrm{d}t-\left[\eta \frac{\partial \eta }{\partial t}\right]_0^1, \end{aligned} $$](/articles/aa/full_html/2022/07/aa43298-22/aa43298-22-eq20.gif)
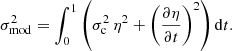
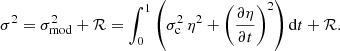
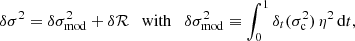
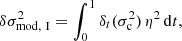
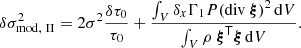
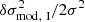
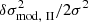
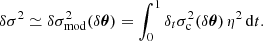
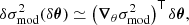
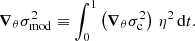
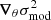
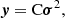
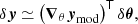
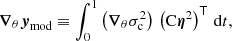
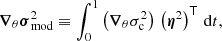
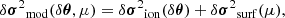
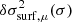
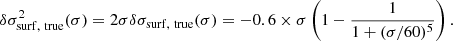
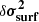
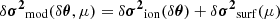
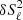
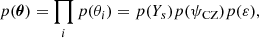
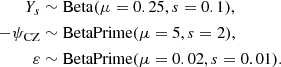
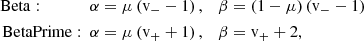
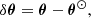
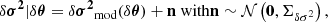
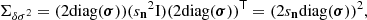
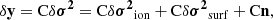
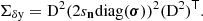
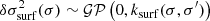
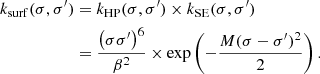
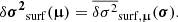
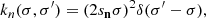
![$$ \begin{aligned}&\ln p(\delta \boldsymbol{\sigma ^2}|\delta \boldsymbol{\theta },\boldsymbol{\upmu }) = \nonumber \\&-\frac{1}{2}\left(\delta \boldsymbol{\sigma ^2} - \delta \boldsymbol{\sigma ^2}_\mathrm{ion} (\delta \boldsymbol{\theta })\right)^\mathsf T {\left[\mathrm{K} _\mathrm{surf} (\boldsymbol{\upmu })+\Sigma _{\delta \sigma ^2}\right]}^{-1}\left(\delta \boldsymbol{\sigma ^2}- \delta \boldsymbol{\sigma ^2}_\mathrm{ion} (\delta \boldsymbol{\theta })\right) \\&-\frac{1}{2}\ln \left|\mathrm{K} _\mathrm{surf} (\boldsymbol{\upmu })+\Sigma _{\delta \sigma ^2}\right| -\frac{N}{2}\ln 2\pi ,\nonumber \end{aligned} $$](/articles/aa/full_html/2022/07/aa43298-22/aa43298-22-eq107.gif)