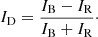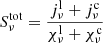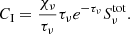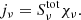| Issue |
A&A
Volume 672, April 2023
|
|
|---|---|---|
| Article Number | A47 | |
| Number of page(s) | 15 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202245390 | |
| Published online | 27 March 2023 | |
Small-scale loops heated to transition region temperatures and their chromospheric signatures in the simulated solar atmosphere⋆
1
Institute for Solar Physics, Department of Astronomy, Stockholm University, Roslagstullsbacken 21, Stockholm, Sweden
e-mail: moa.skan@astro.su.se
2
High Altitude Observatory, National Center for Atmospheric Research, PO Box 3000 Boulder, CO 80307, USA
Received:
7
November
2022
Accepted:
13
December
2022
Context. Recent observations have revealed loop-like structures at very small scales visible in observables that sample the transition region (TR) and even coronal temperatures. These structures are referred to as either ‘unresolved fine structures’, ‘dynamic cool loops’, ‘miniature hot loops’ or ‘campfires’ depending on the observables in which they are detected. Their formation remains unclear.
Aims. Realistic magnetohydrodynamic simulations and forward synthesis of spectral lines are used to investigate how these features occur.
Methods. Computations were carried out using the MURaM code to generate model atmospheres. The synthetic Hα and Si IV spectra are calculated at two angles (μ = 1, μ = 0.66) using the Multi3D code. We traced magnetic field lines in the model and examined the evolution of the underlying field topology.
Results. The synthetic Hα Dopplergrams reveal loops that evolve dramatically within a few minutes. The synthetic Hα line profiles show observed asymmetries and Doppler shifts in the line core. However, they also show strong emission peaks in the line wings, even at the slanted view. The synthetic Si IV emission features partly coincide with structures visible in Hα Dopplergrams and partly follow separate magnetic field threads. Some are even visible in the emission measure maps for the lg(T/K) = [5.8, 6.2] temperature interval. The emission areas trace out the magnetic field lines rooted in opposite polarities in a bipolar region.
Conclusions. The model shows that a loop-like structure in a bipolar system with footpoints undergoing rapid movement and shuffling can produce many small-scale recurrent events heated to high temperatures. It demonstrates that heating to different temperatures occurs and can be confined to a small part of the loop, at the location where resistive and viscous heating increases. The model largely reproduces the observed features in terms of size, lifetime and morphology in chromospheric, TR and coronal observables. The morphology and evolution of the resulting observable features can vary depending on the viewing angle.
Key words: Sun: atmosphere / Sun: chromosphere / Sun: transition region / magnetohydrodynamics (MHD) / radiative transfer
Movie associated to Fig. 16 is only available at https://www.aanda.org
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The coronal heating problem has been widely discussed since it was discovered roughly eight decades ago when Grotrian (1939) saw emission lines in the corona that suggested that the coronal plasma is at very high temperatures. It is widely accepted that the motions of the plasma in the convective zone is a significant source of the energy injected into the corona, but how the energy is transported and dissipated remains an open question. The two main theories that have been accepted by the community are direct current (DC) and alternating current (AC) heating (Klimchuk 2006), which differ in the relevant timescales on which convective motions affect the footpoints of magnetic field lines. The mechanism behind DC heating is the slow gradual buildup of stresses due to the displacement of the footpoints of magnetic field lines. As a consequence, the magnetic field higher up in the atmosphere is being contracted, expanded, or twisted to some degree and pushed together which results in the creation of current sheets. The current sheets dissipate gently through Ohmic heating and nanojets (Parker 1988), or violently by magnetic reconnection. Several numerical experiments have been carried out to explore this subject; see e.g. (Gudiksen & Nordlund 2005; Bingert & Peter 2013; Hansteen et al. 2015; Rempel 2017). In these models, heating is highly intermittent in both space and time. The heating structures are loop-like as they follow the magnetic field lines. Their lifetimes vary from less than a minute to an hour, depending on their size and the unsigned magnetic flux in the model.
Over the last decade, the theoretical models has been further challenged by the new instrumentation that provides observations of the solar atmosphere in increasingly fine detail. The High-resolution Coronal Imager (Hi-C, Rachmeler et al. 2019) revealed features as small as 1 − 5 Mm in length apparently heated to coronal temperatures (> 1 MK, Peter et al. 2013). A further study (Barczynski et al. 2017) considered different scenarios to explain the appearance of these latter features and settled on the conclusion that they might be miniature loops. It remains unclear as to what drives them to reach these extreme temperatures.
Interface Region Imaging Spectrograph (IRIS, De Pontieu et al. 2014) allowed us to resolve transition region (TR) heights where the ‘unresolved fine structure’ (UFS) loops resided as suggested by Feldman (1983). Hansteen et al. (2014) confirmed that these are indeed shaped out of loop-like structures disconnected from the corona. These features are very bright with respect to their background with sizes that go from 10 to a few Mm in height. They are very dynamic, heated to transition region temperatures (4 × 104 − 2.2 × 105 K), and have lifetimes of a few minutes. Subsequently, Brooks et al. (2016) examined 109 cases of these small features and concluded that they might well be individual structures and not made up of multiple magnetic threads. Pereira et al. (2018) found that some of these features have counterparts in chromospheric observables sampled with the 1m Swedish Solar Telescope (SST, Scharmer et al. 2003). The appearance of inverse Y-shaped structures in Hα line wings visible above the Si IV loops suggests that magnetic reconnection is taking place in these cases. As stated by these latter authors, this is also confirmed by the apparent opposite flows, visible in Hα Dopplergrams, which seem to trace the magnetic field lines. However, these authors were puzzled by several facts. If magnetic reconnection is taking place, the question remains as to why they find no indication of heating in chromospheric observables. Also, in some cases, they find Si IV below or at lower heights than Hα signatures, which contradicts the scenario in which cool chromospheric plasma is being pushed into higher layers where reconnection with the overlying field occurs. The questions also remains as to their role in the heating of the solar atmosphere given how infrequent their appearance is Judge (2021). As suggested, they might be a consequence of less frequent flux emergence, which may not be the cause of heating for typical loops in the solar atmosphere.
Finally, the Extreme Ultraviolet Imager (EUI, Rochus et al. 2020) on board the Solar Orbiter (Müller et al. 2020) revealed many features with lengths between 400 km and 4000 km heated to apparent temperatures of ≈1 MK (Berghmans et al. 2021). These localised brightenings visible in the 17.4 nm passband are named ‘campfires’. They appear close to the chromospheric network and last for between 10 s and 200 s. Using the triangulation with an assumption that these features are semi-circular loops, it is estimated that their formation height is between 1000 and 5000 km above the photosphere. Kahil et al. (2022) compared the location of these features with photospheric magnetograms obtained with the Polarimetric and Helioseismic Imager (PHI, Solanki et al. 2020), finding that a large majority of campfires can be projected onto a bipolar system. The authors interpret the appearance of campfires as a sign of magnetic reconnection.
In this paper, we examine the evolution of similar features in realistic magnetohydrodynamics (MHD) simulations. Many localised heating events similar to the observed small-scale structures at TR and coronal temperatures are produced in one of the bipolar systems. We focus on synthetic observables Hα and Si IV line profiles as observed by SST and IRIS, respectively. We study their formation and how the motions of the footpoints affect their morphology and evolution. We use this to illustrate how a combination of complex magnetic topology and realistic footpoint driving can lead to the appearance of small compact features such as those recently observed. The sections of the article are organised as follows: Sect. 2 describes the theoretical model and the computation of synthetic observables. Section 3 first presents synthetic observables at two viewing angles. We show line profiles and formation heights. We then present the result of tracing magnetic field lines and their evolution. Section 4 includes a discussion of similarities and differences to observed cases. In Sect. 5, we present our conclusions.
2. Modelling
2.1. Model atmospheres
The MURaM code (Vögler et al. 2005; Rempel 2017) is used to generate the numerical 3D models of the solar atmosphere. The model includes the near-surface layers of the convection zone and self-consistently considers mass transport between subsurface layers, photosphere, chromosphere, and corona. The model is built in phases starting from the non-magnetic convection simulation to which a uniform bipolar field of 200 G is added. After the field configuration has evolved generating magnetic structures on mesogranular and larger scales, the potential field extrapolations are used to extend the computational domain and include the upper atmosphere. After the initialisation procedure we ran the model for a few solar hours before we increased the resolution and then ran it for an additional half an hour. The final extent of the simulation domain is 40 × 40 × 22 Mm, spanning vertically from −8 Mm to 14 Mm above the average τ500 = 1 height. The grid spacing of the simulation used in this paper is 39 km and 22.5 km in the horizontal and vertical directions, respectively. The same model is used to study properties and dynamics of chromospheric fibrils (Danilovic 2023; Danilovic et al. 2022). It contains only the most basic physics to be called ‘comprehensive’: 3D grey local thermodynamic equilibrium (LTE) radiative transfer, a tabulated LTE equation of state, Spitzer heat conduction, and optically thin radiative losses in the corona based on CHIANTI (Landi et al. 2012). The numerical diffusive and resistive terms in this run are set so that an effective magnetic Prandtl number Pm > 1. This makes viscous heating the largest contributor. The time t = 0 s is arbitrarily chosen and marks the time when the model reached the relaxed state and the snapshots are outputted every 2.5 s. Figure 1 displays the photospheric vertical component of the magnetic field in black and white, the magnetic field lines of the full computational domain in blue, and the magnetic field lines of the region of interest (ROI) in red. The red field lines are traced from regions with a high current density in the area.
 |
Fig. 1. Overview of the full computational domain (40 × 40 × 22 Mm) and magnetic field configuration. The plane shows the vertical photospheric magnetic field in μ = 1 at t = 102 s. Red field lines show traced magnetic field lines in the region of the loop-like structure, sampled at high current density. Blue field lines show the magnetic field in the full FOV. This figure was produced using VAPOR (Li et al. 2019; www.vapor.ucar.edu). |
2.2. Radiative transfer computations
Multi3D (Leenaarts & Carlsson 2009) is a 3D non-local thermodynamic equilibrium (NLTE) radiative transfer code that treats the radiative transfer computations using the accelerated lambda iteration (ALI) method developed by Rybicki & Hummer (1992). We computed the radiation field in full 3D where, for each grid point, angle integration for rays in 24 directions (three angles in each octant) were carried out using the A4 ray set provided by Carlson (1963). In order to increase the stability of the runs, the patch by Bjørgen et al. (2019) was used. The electron densities were calculated assuming the LTE and using the opacity package included in the Multi3D code.
Every fourth snapshot is used as input for the computations of the emergent spectrum. To reduce computation time, we crop the model in two ways. The vertical span of the input model is limited to 360 points, which includes the range of temperatures at which the spectral lines that we generate are formed. In the horizontal direction, we use every second grid point to make computations faster. Tests show that this does not affect the appearance of synthetic features.
2.3. Model atoms
We used two model atoms for our computations; hydrogen and silicon.
Hα was calculated using a three-level plus continuum H model atom. The model was used by Leenaarts et al. (2012), and modified by Bjørgen et al. (2019) who removed the n = 4 and n = 5 levels to increase numerical stability and ensure convergence of the multilevel accelerated lambda iterations (M-ALI) in Multi3D. Processes included in the model are excitation from electron collisions with positive ions, and ionisation by electron collisions.
The Si IV model atom includes three ionisation levels (Si III, Si IV and Si V) in order to synthesise the 1394 Å and 1403 Å lines that originate in the 2p63s2S1/2 − 2p63p2P3/2 and 2p63s2S1/2 − 2p63p2P1/2 transitions, respectively. All oscillator strengths fij and energy levels were taken from the NIST database (Kramida et al. 2021). The abundance of Si with respect to hydrogen was set constant as ASi = 7.51, as per Asplund et al. (2009). We used the photospheric abundance as it has been shown that low first ionisation potential (FIP) elements can have photospheric composition in the upper atmosphere during impulsive heating events (Warren et al. 2016). In the Si IV model, we include excitation from electron collisions with positive ions, collisional ionisation, collision auto-ionisation, charge transfer with neutral hydrogen atoms, electron impact ionisation of complex ions, and radiative recombination. In the computations, the dielectronic recombination rate is suppressed (using a subroutine in Multi3D which follows the work of Summers 1974) as it is an effect that takes place for high electron densities in the ranges in which our results lie. Density-sensitive dielectronic recombination can lead to an elevated Si IV fraction. The effect of including dielectronic auto-ionisation and secondary auto-ionisation corrections is clearly visible for Si I to V (see Fig. 14 in Appendix B of Kerr et al. 2019). The coefficients for all the processes that are included were taken from the Si IV model atom used in Vissers et al. (2019).
The Multi3D computations are done assuming statistical equilibrium (SE) and complete frequency redistribution (CRD, Leenaarts et al. 2012). In Fig. 2 we present the full field of view (FOV) in (a) Hα blue wing at 53 km s−1, (b) Hα line core intensity, and (c) intensity of Si IV 1394 Å line summed over all frequencies 1393.755 ± 0.79 Å. The white box indicates the ROI.
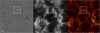 |
Fig. 2. Synthetic observables over the full FOV at μ = 1, t = 102 s. The box shows the selected subfield in Fig. 3. In panel a we plot the blue wing of Hα, (b) the Hα line core intensity, and (c) Si IV summed over all frequencies ±0.79 Å around the line centre. |
3. Results
Further on, we focus on ROI and show synthetic observables at two viewing angles μ = 1 and μ = 0.66. We show what the features look like in two observables and how projection effects matter. We discuss in detail how the Hα and Si IV lines form for the first viewing angle. In the final subsection, we study the field evolution and demonstrate how these features are formed.
3.1. Synthetic structure at μ = 1
3.1.1. Evolution of synthetic structure at μ = 1
In Fig. 3, the time evolution of the resulting synthetic structure is shown at μ = 1. The upper row of the figure shows the blue wing of the Hα line. In the second row, we constructed a Dopplergram in order to showcase the strong Doppler shifts in the Hα wings. The Dopplergrams were created by subtracting the red wing from the blue and dividing it by the sum of the two, as follows:
 |
Fig. 3. Time evolution of the synthetic loop at μ = 1. From the top to the bottom: normalised Hα blue wing intensity at vD = 53 km s−1, Hα Dopplergram at velocities ±53 km s−1 (black and white represent red and blue wings, respectively), Si IV 1393 Å summed over frequencies ±0.79 Å around line centre, composite image of the Hα Dopplergram (black and white) and frequency-summed Si IV (orange), Hα line core, composite image of Hα line core and frequency-summed Si IV and vertical magnetic field (black and white represent downward and upward magnetic field, respectively). |
We chose to sample wavelengths that correspond to Doppler shifts of vD = 53 km s−1, as in Pereira et al. (2018).
The third row from the top displays the Si IV emission summed over frequency. The fourth row is a composite of the Dopplergram and the Si IV emission. The fifth row shows the Hα line core and the sixth is a composite of the summed Si IV intensity and the Hα line core. The bottom row displays the vertical magnetic field Bz at a photospheric level, where black and white indicate negative and positive directions of the field, respectively.
The figure shows a time period of 155 s during which we see the appearance and disappearance of one complex feature visible in Hα Dopplergrams. Throughout the entire evolution, this loop-like structure has a predominantly positive ID. In the first two snapshots, a jet-like feature is visible emanating from the positive-polarity region. No structure can be seen in the Hα blue wing at t = 0 s. Over 20 s, a loop-like structure appears in the blue wing which increases in brightness and grows to about 2 Mm in length. At 39 s, the loop-like structure forms a fork with a smaller branch staying visible until t = 83 s. Up until this point, the loop has mainly positive ID, but at t = 83 s the ID at the top of the loop becomes negative. The entire structure grows in complexity, that is, multiple strands of red- and blueshifts are created and disappear at a fast rate up until t = 122 s. During the same time period, the width of the loop-like structure grows until 102 s and then shrinks. At the very end of the run, at t = 155 s, the loop-like structure is almost completely gone. Instead, slightly shifted and in a different direction, a long loop with predominantly negative ID appears.
The Si IV evolution is different from that in Hα. Increased emission is visible in almost the whole ROI. The bright points are distributed in the regions with a strong vertical magnetic field. In parts where the magnetic field is more horizontal, the Si IV emission is concentrated in stripes that largely follow the fibrils visible in the Hα line core. Very bright, randomly distributed spots form and disappear. Some of them overlap with the loop-like shape visible in the Hα Dopplergrams. At t = 102 s, some overlapping bright points remain, but a straight shape forms in a different spatial plane from the loop. For 20 s, this feature grows by approximately 1 Mm in length diagonally over the Hα loop-like structure. In the last snapshot, the same feature has shrunk in thickness, length, and brightness. A new, smaller elongated feature appears parallel to the loop-like structure visible in Hα. The Si IV-Hα line-core composite image shows a behaviour where the Si IV emission seemingly follows the hydrogen line core structure between 83 and 155 s.
In Fig. 4, we chose to highlight the snapshot at t = 102 s. In the top row, the synthetic Hα blue wing intensity is presented. The middle row shows a Hα Dopplergram created in the same manner as in Fig. 3, but with the difference that ID > 0 and ID < 0 are represented with by blue and red colours, respectively. The Dopplergram is over-plotted over the photospheric vertical magnetic field. In the bottom row, the Si IV frequency-summed intensity is plotted over the same field map. The white, green, and red circles that appear in all subplots mark three pixels of interest, which we analyse using four panel diagrams in Figs. 5–7 as well as using the Si IV emissivity j in Figs. 8–11, including the pixel marked with the blue circle. Three of the four chosen pixels are in regions where the Hα loop-like structure and Si IV emission overlap. In the middle row of Fig. 4, we see a complex structure in red to the left of the loop at the positive pole of the bipolar region, as well as the feature below the loops where Doppler shifts of both sign are present. The Hα loop like-structure is stretched between the two magnetic poles with a slight curvature, making it bulge out from the region directly between the two. The footpoints do not reach the poles in this Dopplergram at ±53 km s−1. However, Dopplershifts at ±39 km s−1 do indeed show a loop-like structure with footpoints overlapping with the magnetic poles. In the case of Si IV, the elongated structure in emission is spanning between the poles in an approximately straight line. The straight structure crosses the Hα Dopplergram loop-like structure but is not parallel to it; it is located in a different spatial plane.
 |
Fig. 4. Hα blue wing intensity (top row), Hα Dopplergram (middle row) and Si IV frequency-integrated intensity (bottom row) in the snapshot at t = 102 s. Four pixels of interest are highlighted using red, green, white, and blue circles. The dotted line marks the position of the vertical cut shown in Fig. 14. |
 |
Fig. 5. Hαμ = 1 four-panel diagram at t = 102 s in the pixel indicated with a white circle in Fig. 4. The quantities, plotted as functions of frequency and altitude, are indicated in the upper left corner of each subplot and are plotted in grayscale. z = 0 Mm marks the photosphere. In all panels, the vertical velocity is shown as a function of altitude (white dotted line), where upwards velocity is positive and downwards is negative. In the upper left panel, vz = 0 is indicated by a vertical solid white line. Additionally, the altitude where τ = 1 is also plotted in all subplots (orange dotted line). The different quantities are as follows. Upper left: opacity χν over optical depth τν. Upper right: total source function Sν (Eq. (2)), temperature (green line) and source function (blue line). Lower left: attenuation factor τνexp(−τν). Lower right: contribution function CI (Eq. (3)), and emergent intensity (solid white line). |
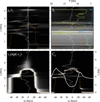 |
Fig. 6. Hαμ = 1 four-panel diagram at t = 102 s in the pixel indicated by the green circle in Fig. 4. The format of the diagram is the same as in Fig. 5. |
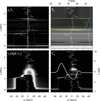 |
Fig. 7. Hαμ = 1 four-panel diagram at t = 102 s in the pixel indicated by the red circle in Fig. 4. The format of the diagram is the same as in Fig. 5. |
In summary, in this subsection we show that both synthetic Hα Dopplergrams and Si IV slitjaw-like images reveal the formation of several loop-like structures over a course of a few minutes. The brightest feature in Si IV is not aligned with the loops in the Hα Dopplergrams, but crosses them. Some smaller Si IV bright points partly overlap Hα features.
3.1.2. Hα line formation
In Figs. 5–7 we analyse the three pixels indicated by circles in Fig. 4 in more detail using four-panel schematic Hα line formation diagrams (as introduced by Carlsson & Stein 1997). The chosen pixels are associated with ID of opposite sign. The red and white pixels mark locations where the signatures in Hα and Si IV overlap. Each of the Figs. 5–7 is divided into four subplots. In all of the subplots, the dotted orange line represents τ = 1, and the dotted white line is the line-of-sight velocity vz. Positive Δv marks an upwards flow of the plasma. In the upper left subplot we show how the opacity divided by optical depth, χν/τν, is changing with Dopplershift Δv and altitude z. Regions with high opacity and low optical depth are visible as bright areas in the plot; these indicate that the density of Hα-emitting particles at that specific height and Dopplershift is higher than in the surrounding areas. The straight solid line indicates where Δv = 0 km s−1. The upper right subplot displays the source function 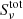 as greyscale.
as greyscale. 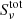 is the total source function which combines the line source function
is the total source function which combines the line source function 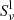 and the continuum source function
and the continuum source function 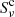 ;
;
where 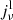 and
and 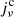 are the line and continuum emission coefficients, and
are the line and continuum emission coefficients, and 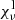 and
and 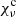 are the line and continuum extinction coefficients (see Rutten 2003). Additionally, line source function
are the line and continuum extinction coefficients (see Rutten 2003). Additionally, line source function 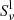 expressed as excitation temperature and the gas temperature are plotted as a blue and green line, respectively. The lower left subplot shows the attenuation factor τνe−τν. Finally, the lower right subplot shows the contribution function CI = dIν/dz, that is, the contribution to the Hα emergent intensity. CI is calculated here as
expressed as excitation temperature and the gas temperature are plotted as a blue and green line, respectively. The lower left subplot shows the attenuation factor τνe−τν. Finally, the lower right subplot shows the contribution function CI = dIν/dz, that is, the contribution to the Hα emergent intensity. CI is calculated here as
The intensity profile is over-plotted as a white solid line.
Figure 5 is created from a strongly Dopplershifted pixel in the region marked by a white circle in Fig. 4. In the upper left panel, we see that χν/τν is higher in regions that experience strong gradients in up- and downflows where τ = 1. In the regions around 1.7 and 2.5 Mm there is an increased χν/τν that is broadened in both blue and red line wings as a consequence of the strong velocity gradients. At about 3 Mm, there is emission that is almost constant for all considered frequencies. This area is exposed to a downflow from above. The red wing is formed at an altitude of 1.7 Mm where the plasma has a downward velocity. The blue wing is formed in a region located higher up at an altitude of about 2.4 Mm in material that is travelling upwards. The line core is formed at 3 Mm, slightly below a strong downflow and a hot cell in the upper chromosphere. In the upper right panel, the line source function is constant for all frequencies as we assume CRD. We see that two hot pockets are formed in the atmosphere at altitudes of 1.7 − 2 Mm and 3.1 − 3.6 Mm, and that the TR is located slightly below 5.1 Mm. 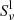 follows the temperature fairly well from the photosphere up to 1.7 Mm, where it then decouples from the Planck function in the lower hot chromospheric pocket. Some spikes in the source function appear in this region as a result of the high density of hot plasma in the area. Between the two hot pockets,
follows the temperature fairly well from the photosphere up to 1.7 Mm, where it then decouples from the Planck function in the lower hot chromospheric pocket. Some spikes in the source function appear in this region as a result of the high density of hot plasma in the area. Between the two hot pockets, 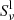 globally declines in strength, with the exception of a peak at 2.4 Mm, which coincides with an upflow of the local material. In the upper hot pocket, the source function experiences three additional peaks. The lower left plot displays the area where τ is close to 1. The strongest values of τνe−τν are obviously centred around the orange dotted τ = 1 curve, but there is a broad bright area between 3 and 4.2 Mm centered around zero Dopplershift. Additionally, there is a symmetrical and strong broadening in the wing-forming region and below. From the contribution function plot in the lower right, we can see that the line core is formed at 3 Mm, the blue wing at 2.5 Mm, and the red wing around 1.7 Mm. Both of the wings are in emission and the core in absorption. There is an asymmetry in the wings where the red part has a higher intensity than its blue counterpart. The line core is approximately symmetric. The wing asymmetry originates from the peak in the line source function at 1.7 Mm, which is higher than the peak at altitude in which the blue wing is formed. Both of the wings display a ‘knee’, which is formed in regions that experience a strong velocity gradient.
globally declines in strength, with the exception of a peak at 2.4 Mm, which coincides with an upflow of the local material. In the upper hot pocket, the source function experiences three additional peaks. The lower left plot displays the area where τ is close to 1. The strongest values of τνe−τν are obviously centred around the orange dotted τ = 1 curve, but there is a broad bright area between 3 and 4.2 Mm centered around zero Dopplershift. Additionally, there is a symmetrical and strong broadening in the wing-forming region and below. From the contribution function plot in the lower right, we can see that the line core is formed at 3 Mm, the blue wing at 2.5 Mm, and the red wing around 1.7 Mm. Both of the wings are in emission and the core in absorption. There is an asymmetry in the wings where the red part has a higher intensity than its blue counterpart. The line core is approximately symmetric. The wing asymmetry originates from the peak in the line source function at 1.7 Mm, which is higher than the peak at altitude in which the blue wing is formed. Both of the wings display a ‘knee’, which is formed in regions that experience a strong velocity gradient.
The four-panel diagram created in the pixel indicated by a green circle in Fig. 4 is presented in Fig. 6. This pixel experiences a much more complex opacity field than in the case of Fig. 5. Here, we see numerous bright spots in the upper left panel at a variety of altitudes and frequencies in contrast to the previous case where broad profiles are centred in a few regions with strong velocity gradients. A feature seen in both four-panel diagrams is that both have emission at the upper chromosphere-lower TR. There are two hot pockets along the column that are overlapping with the peaks in upflowing vertical velocity and peaks in the line-source function. 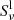 follows the temperature curve in the lower chromosphere up until it reaches the lower hot pocket at an altitude of 1.9 Mm where NLTE decoupling occurs. We can, as in Fig. 5, see broadening in τνe−τν, which in this case mainly occurs between 2.1 and 2.5 Mm where the plasma experiences strong upflow. Line-wing and core intensities are all receiving contributions from more than one altitude. In the line core, the lower line formation region at an altitude just above 3 Mm is blueshifted, causing the line core to become slightly asymmetric as it is absorbing some of the photons emitted by the blue wing formed below the core. Similar to the profile in Fig. 5, both of the wings in the line profile are in emission. This pixel also displays a knee, but here only in its blue wing.
follows the temperature curve in the lower chromosphere up until it reaches the lower hot pocket at an altitude of 1.9 Mm where NLTE decoupling occurs. We can, as in Fig. 5, see broadening in τνe−τν, which in this case mainly occurs between 2.1 and 2.5 Mm where the plasma experiences strong upflow. Line-wing and core intensities are all receiving contributions from more than one altitude. In the line core, the lower line formation region at an altitude just above 3 Mm is blueshifted, causing the line core to become slightly asymmetric as it is absorbing some of the photons emitted by the blue wing formed below the core. Similar to the profile in Fig. 5, both of the wings in the line profile are in emission. This pixel also displays a knee, but here only in its blue wing.
Finally, in Fig. 7 we show the four-panel diagram of the pixel indicated by a red circle in Fig. 4. The pixel is located where the loop-like shape in the Hα blue wing is overlapping with the larger Si IV structure that stretches across the area. In contrary to the two other pixels, there is no significant broadening of τνe−τν due to the fact that the velocity does not have as complex a profile as that seen in Figs. 5 and 6. There is a peak in upwards velocity around 2 Mm and a peak in downflow slightly below 3 Mm. In the lower right panel we see that the line profile of Hα is strong in its blue wing and that the line core is slightly asymmetric. When investigating the contribution function CI, it is clear that the strong blue wing has its origin at ≈2.2 − 2.5 Mm in an area with a peak in temperature, just above an upflowing region. The red wing is hardly in emission, and it receives contributions from a range of altitudes. The line core is slightly redshifted, causing it to absorb some of the red wing photons that are emitted at a lower altitude. There is contribution to the line core between ≈2.5 − 5 Mm, with its largest contribution coming from a range between 3 and 4.2 Mm. The line profile does not display a knee in any of its wings as is the case in the two preceding four-panel diagrams, which is due to the lack of harsh velocity gradients.
In summary, in this subsection we illustrate that the Hα line formation is rather complex. The wing asymmetry comes from high LOS velocities of the order of 50 km s−1 that also coincide with a slight increase in temperature. The three main layers that contribute to the observed spectral features are located at heights of 1.7, 2, and 2.4 Mm. The upper layers show upflows and the velocity at 1.7 Mm switches its direction along the feature.
3.1.3. Si IV line formation
The Si IV lines are considered to be optically thin, in which case the approximate formation height of the line is where the emissivity is at its maximum. The emissivity can be calculated as
Each of the Figs. 8–10 is composed of four panels with quantities from the pixels marked by circles in Fig. 4. In panel a, the line profiles of Si IV 1394 Å (solid black line) and Si IV 1403 Å (dashed black line) are plotted together and panel b shows their ratio. Panel c shows the emissivity jν of the Si IV 1394 Å and the vertical velocity vz (blue solid line) as they vary with Dopplershift and altitude. The orange solid line marks the height at which τ = 1. The grey dashed line indicates where Δv = 0 km s−1. The emissivity of 1403 Å line is very similar in all cases, and so we omit it here. In panel d, the gas temperature T (red) and electron density ne (black) are plotted as functions of height. The grey dashed lines indicates the interval in which LTE Si IV formation occurs (104.2 − 104.6 K), and the dotted vertical line represents the interval of coronal equilibrium Si IV formation (104.7 − 105.1 K; see e.g. Fig. 4 in Rutten 2016).
 |
Fig. 8. Si IV formation diagram in the pixel marked by a white circle in Fig. 4. The panels show (a) Line profiles of Si IV 1394 Å (solid black) and Si IV 1403 Å (dashed black). (b) Intensity ratio of Si IV 1394 Å and Si IV 1403 Å lines. (c) Emissivity j of the 1394 Å line (Eq. (4), j0.6) and vertical velocity vz (blue). The vertical dashed line indicates where Δv = 0 km s−1. The orange line marks the height at which τ = 1 is reached. (d) Gas temperature T (red) and electron density ne (black) of Si IV. The dashed vertical lines represents the LTE Si IV formation temperature interval and the dotted vertical lines represent the coronal equilibrium formation temperature interval. Positive Δν indicates an upwards velocity. |
In Fig. 8, the two line profiles are approximately symmetrical around their respective line cores in panel a. We see a high emissivity at z = 2 Mm and slightly below, appearing in one thicker band at 1.9 Mm and two thinner bands at 2 and 1.8 Mm. These three bands in the emissivity coincide with locations where temperature is around 104.8 K. The symmetrical shape of the line profiles is due to the presence of symmetric moderate flows in both directions, both up- and downflows of 10 − 20 km s−1 in the area. The emissivities are very similar in both 1394 Å and 1403 Å and the lines are formed in the same regions. This is also true for Figs. 9 and 10.
Figure 9 shows a broad peak in jν at 2.3 Mm that is overlapping with a high temperature and the electron density of 1012 cm−3. In the region where the emissivity is peaking, the velocity gradient is steep with the maximum upflow velocity of ≈50 km s−1. A smaller peak jν at ≈2.2 Mm overlaps with a small downflow of −10 km s−1. As a result, the line profiles are asymmetric and largely blueshifted, with a slightly extended red wing.
Figures 10 and 11 show the properties of the pixels located on the larger structure in Si IV. In Fig. 10, the line profiles are highly asymmetric with two peaks. The smaller peak is located around Δv = 0 km s−1 and the larger is redshifted to a velocity of −34 km s−1. In the emissivity diagram, we see an emission peak centred at around 3 Mm that coincides with a peak in temperature and the electron density of less than 1011 cm−3. Most of the emission occurs in a downflowing region, giving rise to the almost completely redshifted line profiles. The smaller peak in the line profiles comes from the region slightly above, where the vertical plasma velocity is close to Δv = 0 km s−1. Figure 11 corresponds to the pixel that is further down the straight Si IV feature visible in Fig. 4. Temperature peak is at the same height as in Fig. 10, but now the corresponding electron density is 60% higher. The emission peak is located in the region at a temperature of ≈104.7 K where the velocity jumps from a downflow of ≈50 km s−1 to the ≈20 km s−1 upflow. This gives a relatively symmetric line profiles. The secondary emission peak in line profiles comes from variations in the electron density.
To check whether the optically thin assumption holds, we overplot the height at which optical depth unity is reached and calculate the ratio of the intensities of the two lines. These are shown in panels b and c of Figs. 8–11. In the optically thin regime, the ratio of the intensity profiles of Si IV is equal to the rate of their oscillator strengths, which is exactly f1394/f1403 = 2. Also, the optical depth unity level in that case should be far from the locations of strong emission. In all chosen pixels, the line ratio shows wavelength dependence with values going larger than two in the line wings. However, when we look at the τ = 1 level, the wavelength range where its location is close to the emission peak is very narrow and corresponds to the location where the line ratio is 1.6. Only in the case shown in Fig. 10 does the Si IV lines seems to be formed in optically thin regime. If we calculate the wavelength integrated ratio of the two lines
we get values of between 1.6 and 1.8, which means R < 2 in all four cases.
In summary, in this subsection we show that some of the Si IV emission comes from the same layers as the Hα emission peaks. The resulting Si IV line profiles can be symmetric if they sample locations of bi-directional flows. In at least some parts of the feature, the opacity effects become considerable and the lines optically thick.
3.2. Synthetic structure at μ = 0.66
Figure 12 shows the temporal evolution of ROI at μ = 0.66. The figure outline is the same as in Fig. 3, without the rows that show the vertical magnetic field and the Hα line centre. Hα Dopplergrams show not one, but two loop-like structures in this slanted view. The upper loop is the same one that is visible at μ = 1, but the structure has a more defined loop shape consisting of thin strands relative to the case of μ = 1. The half-length of the loop-like structure is roughly 2.4 Mm. At t = 0 s, there are some thin strands with opposite ID values that over time form a loop of complex red- and blueshifts. At t = 83 s, a substructure of negative ID at the right footpoint starts to form and travels up and towards the apex of the loop; it eventually starts to fade and loses its shape at t = 155 s. At the same time instance, there are two more loop structures visible with the same Doppler-shifted patterns, negative ID on the left and positive ID on the right. One of these features appears already at t = 19 s with predominantly positive ID, until t = 102 s when a negative layer of ID connects. The same feature is almost invisible at μ = 1. Only a small point reveals its position, where the Hα Doppler shifts of opposite sign meet at t = 102 s and t = 108 s (Fig. 3). The second loop-like feature that appears at μ = 1 is also visible in the same snapshot at μ = 0.66 as the highest and largest loop emanating from the left footpoint; at this angle, at time instance t = 155 s, it is the faintest loop-looking structure in the Dopplergrams.
 |
Fig. 12. Time evolution of the synthetic loop at μ = 0.66. The rows show the same quantities as in Fig. 3, but without the vertical magnetic field and the Hα line centre. |
The Si IV emission at both footpoints is much more visible at μ = 0.66 than in the μ = 1 case. There is a string of small bright points forming in the same region as the loop-like structure in the Dopplergram. The bright points form at first on the left and then to the right, until t = 83 s when a large emission feature becomes clearly visible to the right of the apex. The structure grows in size and intensity, forming an arch above the Hα loop. At t = 155 s, the Si IV emission is slightly faded but some traces of it remain.
Hα spectra of three pixels on the loop-like structure at t = 102 s in μ = 0.66 are displayed in the right panel of Fig. 13. The Hα spectra in the pixel marked with a blue circle in the left panel are represented by the blue curve in the plot to the right, and so on. All three line profiles are asymmetric, similarly to the ones that appear in the case of μ = 1. The emission peaks in line wings are still there also at the slanted view. The difference between this and the μ = 1 case is the most pronounces closest to the line centres, where there is an indication of knees. The green and blue pixels that are on the opposite sides of one of the loop-like structures show the line core shifted in opposite directions.
 |
Fig. 13. Diagram showing the line profiles of Hα at μ = 0.66. Left: loop in synthetic Hα at μ = 0.66 at t = 102 s, where three chosen pixels are indicated by circles in green, orange, and blue. Right: normalised Hα intensity for the pixels indicated with the respective colour in the left panel. |
In summary, in this subsection we show that some Hα features are visible in Dopplergrams at μ = 0.66 that were not there at μ = 1. At μ = 0.66, the Si IV emission appears to be on top of the Hα loop, close to its apex. The Hα line cores at the slanted view show shifts in opposite directions in different parts of the feature.
3.3. Formation of the synthetic feature
Figure 14 shows a vertical cut along the dotted line marked in Fig. 4. The cut covers the bright feature visible in the Hα blue wing and crosses the Si IV emission feature. Figure 14 shows various atmospheric parameters as a function of height, together with the emissivity j1394 in the bottom right panel. Formation heights of both the Hα blue wing and line core are plotted over all 2D cuts of different quantities. In the temperature map (upper left panel), two hot pockets are visible, of which the lower one lies at a height of 1.5 − 2 Mm. This hot region generates the peaks visible in the source functions in Figs. 5 and 6. This is exactly where the Hα blue wing forms, but also bright points visible in Si IV images. The same region shows a magnetic field of opposite orientation (middle left), an increase in the heating rate (bottom left), and strong upflows (middle right). At the apex of the upflowing feature, we can see a shape that resembles the inclined Y. All this coincides with a slight decrease in density. The density drop in the second hot pocket formed higher up at ∼3 Mm is greater. This region overlaps with strong downflows, adjacent upflows and increased heating rates. The Hα line core is formed below this hot pocket which is also visible in the fourth row in Fig. 3. There, the line-core intensity noticeably drops along a thin line where Si IV emission increases (t = 102 s) and space forms between Hα line core filaments. The resulting Si IV line profiles formed in this region are shown in Figs. 10 and 11.
 |
Fig. 14. Vertical cut along the dotted line plotted in Fig. 4. From top to bottom, left to right: temperature, density, vertical components of magnetic field and velocity, sum of resistive and viscous heating terms and total line emissivity for 1394 Å. The red line marks the formation height of Hα line core. The green line marks the formation height of the Hα blue wing at vD = −53 km s−1. Black vertical lines, from left to right, mark the positions of the red, green, and white pixels in Fig. 4, respectively. |
Figure 15 shows again the same snapshot at t = 102 s, but now visualised in 3D. The magnetic field lines are traced in the regions where the Hα blue wing and Si IV 1394 Å lines are formed. Isosurfaces in yellow correspond to the largest values of 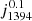 visible in Fig. 14. The green isosurface represents the formation height of the Hα blue wing at −53 km s−1. The vertical component of the photospheric magnetic field is displayed as a surface in black and white. The magnetic field lines are colour-coded so that the blue and red colours indicate the up- and downflowing plasma, respectively, clipped at ±122 km s−1. Figure is divided into three panels, where the right panel shows the feature at μ = 1 and the other two show the feature from two slightly different side angles. The figures show two groups of yellow surfaces. The lower, smaller group lies just at the edge of the green isosurface, which is where the Hα blue wing is formed. The magnetic field lines traced from this region show the same upflowing Y-shape visible in Fig. 14. The footpoints of these lines spread over a large area where negative polarity resides. The other footpoint is connected to the outer edge of the positive polarity. The field lines that are traced from the higher yellow region naturally rise further up. Their footpoints are shifted towards the centres of magnetic features. Their direction outlines the direction of the Si IV emission feature in Fig. 4. These field lines show upflows at the apex and strong downflows all the way down to the photosphere. A local twist is visible in both sets of magnetic field lines.
visible in Fig. 14. The green isosurface represents the formation height of the Hα blue wing at −53 km s−1. The vertical component of the photospheric magnetic field is displayed as a surface in black and white. The magnetic field lines are colour-coded so that the blue and red colours indicate the up- and downflowing plasma, respectively, clipped at ±122 km s−1. Figure is divided into three panels, where the right panel shows the feature at μ = 1 and the other two show the feature from two slightly different side angles. The figures show two groups of yellow surfaces. The lower, smaller group lies just at the edge of the green isosurface, which is where the Hα blue wing is formed. The magnetic field lines traced from this region show the same upflowing Y-shape visible in Fig. 14. The footpoints of these lines spread over a large area where negative polarity resides. The other footpoint is connected to the outer edge of the positive polarity. The field lines that are traced from the higher yellow region naturally rise further up. Their footpoints are shifted towards the centres of magnetic features. Their direction outlines the direction of the Si IV emission feature in Fig. 4. These field lines show upflows at the apex and strong downflows all the way down to the photosphere. A local twist is visible in both sets of magnetic field lines.
 |
Fig. 15. Three-dimensional rendering of the area of interest over the photospheric vertical component of the magnetic field at t = 102 s. Here, we choose to plot the formation height of the Hα blue wing at −53 km s−1 (green isosurface), the formation height of the Si IV 1394 Å line (yellow isosurface) and magnetic field lines of the structure in blue and red, corresponding to up- and downflowing material with vz = ±122 km s−1 respectively. This figure was produced using VAPOR. |
To learn what drives the formation of these twists, we trace the magnetic field lines as curvatures in 3D space (Leenaarts et al. 2015). The time cadence between snapshots used for the field tracing is around 2.5 s. The starting seeds are planted across and not along the Hα blue-wing emission feature visible in Fig. 4; they are placed equidistantly at the height range from 2 to 4 Mm. Figure 16 shows 60 field lines at three time instances. The field topology at t = 102 s is almost the same as in Fig. 15 which confirms that the starting seeds are well spread. Figure 16 shows that the two opposite polarities connect in a complex way. Most of the field lines sampled with these seeds are connected to the outer edge of the positive polarity. Lying under them, a few loops extend in a different direction, forming an angle with the rest of the loops above. One of the footpoints of these low-lying loops ends in the extended branch of negative polarity that undergoes a rapid movement downwards. As these footpoints move, the field lines rise and touch those higher up. An upward zip-like motion is visible in the accompanying movie, especially in the range at x = 20 − 22 Mm, exactly where the Hα features appear for the same time instances. The sampled field lines are most concentrated at t = 102 s, which is expected, as this is the time instance that is used to start line tracing. After that, the field lines unwind and spread out, some rising higher, close to 4 Mm.
 |
Fig. 16. Evolution of traced magnetic field lines. On the left, traced magnetic field lines are plotted over the vertical component of the photospheric magnetic field. In the middle, the position of the corresponding footpoints is marked over the sum of resistive and viscous heating terms integrated over the height range [0.6 − 3.8] Mm (second column) and [2.7 − 7] Mm (third column). On the right, we show the projection of the traced field lines to the z-axis. The background shows density along the horizontal cut at y = 28 Mm. The movie is available online. |
The middle panels of Fig. 16 show a sum of resistive and viscous heating terms integrated over two different height ranges, namely [0.6 − 3.8] Mm and [2.7 − 7] Mm, showcasing features formed lower and higher up. The heating pattern in the form of stripes that connect two polarities is visible in both middle columns. The highest heating rates appear where the stripes seem to cross. The heating happens on different temporal scales. There are very short, transient events on one side and long-lasting patterns on the other. The events in the latter group seem to outline the features visible in the Hα line exactly. The heating in the higher layers outlines the Si IV emission feature starting with a long fibrillar structure at t = 61 s, visible also in the corresponding image in the third row of Fig. 3.
Figure 17 zooms into two main footpoints and the corresponding paths they cross during these few minutes. The figure shows footpoints of only fairly stable magnetic field lines. The positive footpoints are very unstable, displaying frequent jumps from one side to the other of the magnetic concentration. The side-projected field lines in Fig. 16 also show a relatively high level of dynamics close to the positive end. The negative polarity shows a more linear behaviour, with all footpoints undergoing the motion in the same direction, counterclockwise. The shape of the feature suggests that there might be an onset of a vortex flow, but the time interval is too short to be certain. As a result of both types of movement, the field lines become wound up and then unwind all within a matter of minutes.
In summary, in this subsection we demonstrate that footpoint motion leads to entanglement of magnetic field lines, as a result of which an increase in resistive and viscous heating takes place. This happens in many locations over the wide range of heights starting from 1.5 Mm. The Hα spectral line reveals traces of features situated lower down. The Si IV emission better captures the ones situated higher up. In the cuts, we identified two hot pockets that are mainly responsible for features analysed in the previous subsections.
4. Discussion
We study an example of a bipolar system in radiative MHD (rMHD) simulations that shows the formation of several small-scale loop-like structures in synthetic Hα and Si IV 1394 and 1403 Å lines. These structures appear in several places between the two opposite polarities ≈8 Mm apart over the few minutes we consider in this study. In the synthetic Hα Dopplergrams, we see a complex mixture of strands of plasma with negative and positive values extending to both of the magnetic polarities. At the same time, we see signatures in synthetic Si IV spectral lines that do not extend all the way down to the magnetic concentrations at the footpoints of the underlying field lines. We find that our results are consistent with observations in terms of the geometry, lifetime, dynamics, and morphology of the features visible in Si IV and the Hα wings (Pereira et al. 2018; Brooks et al. 2016; Hansteen et al. 2014). Although the length of the magnetic loops connecting the two polarities is greater, the part that show emission in Si IV lines is ≈2 Mm, which is what is found in observations. The lifetimes of these loop-like features are also consistent with observations, where the distribution with an average of 107 s is found (Brooks et al. 2016). One of the modelled loop-like structures first appears in the Hα wings and then a minute later in Si IV. This indicates that after approximately 1 min, the material is heated to TR temperatures and the fraction of Si IV becomes significant. Other loop-like structures display different development depending on the viewing angle.
Pereira et al. (2018) reported a spatial overlap of Hα and Si IV, which is only partly true in our case. There is some overlap of the loop-like structure in the Hα wings with small bright points in Si IV, but the more pronounced Si IV emission loop is forming in a different spatial plane. Due to projection effects, the Si IV emission appears to sit on top of the structure in Hα, although in reality the two features form more than 1 Mm apart. We also find a case where signatures in Hα are situated above the Si IV emission in side-angle view. However, detailed examination reveal that two types of signatures correspond to different magnetic field strands. This suggests caution should be taken when interpreting observations.
Nevertheless, there are locations where Hα and Si IV signatures coincide. The model therefore supports interpretations from observational studies (Tian et al. 2016), which state that in some cases the hot pockets can produce signatures in both observables co-spatially. The model shows similarities with features such as Ellerman bombs, UV bursts, and explosive events (Young et al. 2018). These latter features, as interpreted by Huang et al. (2017), can have different morphologies and undergo dissimilar evolution. We find events in our model that reproduce these observations rather well.
Hα profiles produced by the model are asymmetric with pronounced emission in the line wings, which is typical of Elleman bombs and is reminiscent of what has been described as ‘moustache’-type spectra (Bello González et al. 2013; Rutten 2016). There features are formed when the increase in temperature and density is accompanied by high velocities (Danilovic 2017). The emission peak intensity in the line wings does not correlate with the formation height but more with the summit in the source function, as the four-panel diagrams illustrate. Also, the asymmetry in the emission peaks does not necessarily seem to be correlated with the velocity in the regions where the line core forms, as first suggested by Kitai (1983).
However, several discrepancies can be found if we compare the synthetic Hα profiles with observations by Pereira et al. (2018). First, observations do not show any Hα profiles with wings in emission. It is possible that some wing emission occurs outside the observed wavelength range and is therefore not observed. It is also clear from our analysis that higher velocities would shift the emission peaks further away from the nominal line centre. It is also likely that our model underestimates the velocities and overestimates the size of the region heated to the temperatures that Hα is formed at. Second, we do not see inverted Y-shape in the synthetic Dopplergrams; although the shape is visible in the model in the field configuration as demonstrated in Fig. 14, and is not a product of emerging flux reconnecting with the overlying field. It may be that we do not sample the event from an angle that would allow this feature to be imprinted on Hα spectra. Third, only one observed example resembles the pattern we see in our synthetic Dopplergrams, namely the Doppler shifts with opposite signs on opposite parts of the loop; these are visible only in case A in Pereira et al. (2018). Cases B and C in this latter paper show only one sign Doppler shift, and these latter authors do not clarify which case of the two is more frequent and why this might happen. Our findings, especially the long loop visible at t = 155 s, suggest the Doppler pattern depends very much on the viewing angle.
To synthesise Si IV lines, we used the full 3D NLTE calculation instead of the coronal approximation. As shown by Rathore & Carlsson (2015), who use the C II line as an example, this treatment leads to lower formation temperatures and higher intensities (Fig. 9 in that paper). The synthetic Si IV emission is concentrated above and around magnetic features. The increased Si IV intensity is even more visible from the slanted view, and resembles facular brightening. The same is reported observationally (Rathore et al. 2015; Ayres et al. 2021).
The intensity of the synthetic Si IV 1394 Å and 1403 Å emission lines is comparable to that observed in local heating events, such as UV bursts (Young et al. 2018), but not as strong as what is expected in flare ribbons (Kerr et al. 2019). We find a range of synthetic emission profiles, both symmetric and asymmetric, and blue- and redshifted. The Dopplershifts are of the order of 50 km s−1. As shown in Figs. 8–11, the bulk of Si IV emission comes from small hot pockets with temperatures of 104.9 K. In at least some parts of the features, the opacity effects become considerable and the lines optically thick. In these cases we find that the peak ratio of Si IV 1394 Å and 1403 Å drops to ≈1.6. This is in agreement with other studies, where authors find that the intensity ratio reflects the ratio of the source functions instead (Rathore & Carlsson 2015; Kerr et al. 2019) and can have any value in the optically thick regime. The wavelength-integrated ratio in these cases is between 1.6 and 1.8. Tripathi et al. (2020) found the same ratio in the quiet Sun areas as well as in the periphery of emerging regions. As the event studied here is smaller in size and energy, it shows quantitative agreement with these latter observations.
In this paper, we do not consider effects from non-equilibrium ionisation (NEQ). These effects are important for both species H and Si (Leenaarts et al. 2007; Olluri et al. 2015) when the timescales of the dynamics are shorter than the typical ionisation and recombination times of the emitting atoms and ions. Based on the tests performed by Leenaarts et al. (2007) and the fact that these features appear in dense and rather hot parts of the chromosphere, the ionisation timescale should be short, and therefore SE is a good approximation for H. Regarding Si, Olluri et al. (2015) show that Si IV can originate at temperatures as low as 104 K and the resulting intensity can be from 10% to 40% higher depending on the region when NEQ effects are taken into account. Given that the process is slow and the feature that we study here is relatively long lived, we do not think that the difference coming from NEQ would lead to qualitatively different results. However, using the generalised Ohm’s law, including the effects of ambipolar and Hall drift (Cheung & Cameron 2012; Martínez-Sykora et al. 2012), might potentially change the area of interest. This is also not certain given the recent study that shows that differences including both effects are not fundamental (Nóbrega-Siverio et al. 2020).
Tracing the field lines shows that there are three types of footpoint drivers that lead to the observable dynamics. The main observational features are the product of a reconnection that takes place as the footpoints of low-lying field lines move fast towards the main bipolar system. At the same time, the two opposite polarities where the main bipolar system is rooted undergo different types of dynamics. The positive polarity shows a complex flux concentration where field lines constantly reconnect and as a result the Hα Dopplergrams show faster and more frequent flows. The negative footpoint shows indications of a vortex flow formation. All these types of motions lead to stresses in the magnetic field of structures connecting opposite polarities. The injected stresses lead to gradients in the field that cause current sheets to form, leading to heating and the occuring of dissipation at multiple places over the period of a few minutes. This is agreement with observations that show recurrence and reappearance of the loop-like structures visible in Si IV slit-jaw movies (Hansteen et al. 2014). We expect that these features are sustained by complex footpoint motions similar to the ones seen in our model.
Evolution maps of averaged resistive and viscous heating terms show many places where heating signatures have a morphology that is visible in observables. The synthetic Si IV loops show no twisted structures, which is in agreement with Peter et al. (2022), but the field-line tracking reveals a twist in the apex of the loop-like shape where the Si IV is being formed, which is in agreement with Hansteen et al. (2015).
Figures 18 and 19 show emission measures for the lg(T/K) = [5.8, 6.2] and the lg(T/K) = [5.0, 5.5], respectively. The former covers the temperature-response function peaks for AIA 171 and AIA 193 channels (Boerner et al. 2012) and is also comparable to EUI 173 and the HI-C 193 passbands. The latter samples the low-T contribution to these channels. Figure 19 shows several features that are also partly visible in the Si IV lines: a loop at t = 61 s in the lower part of the ROI, and the two counterparts of the Si IV emission features in between opposite polarities at t = 102 s and t = 153 s. Features of the same or a slightly shorter length can be seen in Fig. 18 at all three time steps as well. The loops observed in Peter et al. (2013) and Barczynski et al. (2017) have similar properties to the one that we see in our results in terms of geometry and lifetime and even temperature, as illustrated in Fig. 18.
 |
Fig. 18. Emission measure for the lg(T/K) = [5.8, 6.2] temperature interval. Bottom row shows a zoom onto the area marked with the white rectangle. The area size and time steps are the same as in Fig. 16. |
The field configuration in the model is similar to one of the four possible scenarios of the campfire configurations listed in Berghmans et al. (2021). This is also what Chen et al. (2021) find in their rMHD model. The model presented here and that presented by Chen et al. (2021) differ in the modelled mean field strength, meaning that the former represents more active regions on the Sun and models the network, as opposed to the latter, which contains only a weak network. The chromosphere is lifted higher up in our model than it is in the model of Chen et al. (2021), which may simply be a result of the increased flux. As a result, the relevant features form at similar heights in our model to those in Chen et al. (2021), but we simply see them at 1 dex higher electron densities.
A study of adjacent photospheric magnetic features and their evolution by Kahil et al. (2022), indicates that a large majority of campfires appear within a bipolar system. These authors do state that there is no significant movement of the two opposite polarities in half of the cases, but still, the authors interpret the appearance of the campfire as a sign of reconnection. They also find that a quarter of all analysed campfires occur within a region containing small, randomly scattered magnetic features in very close vicinity. Closer inspection of the representative example of this category of campfires reveals that there are larger magnetic elements a few Mm away from the feature identified as the campfire. This scenario resembles the ROI from our model. The observational facts related to the campfires do not exclude that the appearance of these features is a product of the evolution similar to the magnetic system in our model where features appear in one of the heated regions at various heights as a result of rapid and complex footpoint motion.
5. Conclusion
Our model largely reproduces the properties of loop-like features simultaneously observed in Hα and Si IV. It also shows that coronal temperatures can be reached. Although the model has some limitations, we draw the following conclusions:
-
Two magnetic concentrations of opposite polarity and ≈8 Mm away from each other are connected by numerous thread-like structures in the viscous and resistive heating, the majority of which are situated in the chromosphere, with some in the transition region and corona.
-
Convective motions and the complexity of magnetic concentration combined lead to the generation of many localised recurrent heating events at different heights and temperature regimes, including in the relatively dense chromosphere.
-
Magnetic reconnection in the simulated loop system can take place without flux emergence.
-
The features observed in Hα and Si IV highlight the location of the current sheets.
-
Localised heating can result in coronal temperatures, lighting up a few Mm of the ≈10 Mm loops.
-
The appearance of the Hα Dopplergrams depends very much on the viewing angle.
-
Projection effects make Hα and Si IV features appear co-spatial, even if they are occurring at different locations in the atmosphere.
The model is not necessarily perfectly representative, but rather provides guidance and insight for interpreting the observation and for improving our understanding of these small-scale phenomena and their place in the solar atmosphere. Further, the model shows that features called either ‘unresolved fine structures’, ‘dynamic cool loops’, ‘miniature hot loops’, or ‘campfires’ can be produced without flux emergence. In our case, they appear low in the atmosphere, in dense layers where heat conduction plays no role. This allows the length of the observed emission structures to be much smaller than the actual length of the underlying magnetic loop and explains the miniature hot loops discussed in Peter et al. (2013) and Barczynski et al. (2017).
Although we confirm that the bright loops visible in Si IV are supplied by the upward-directed mechanical energy, we do not claim that this scenario explains the total TR emission. Indeed, Fig. 2b shows a large fraction of Si IV emission coming from the regions that outline the magnetic field concentrations in the photosphere. These connect to high-lying loops, reflecting the scenario described by Judge (2021).
Movies
Movie 1 associated with Fig. 12 (fig12) Access here
Movie 2 associated with Fig. 16 (fig16_4p) Access here
Acknowledgments
This project has received funding from Swedish Research Council (2021-05613), Swedish National Space Agency (2021-00116) and the Knut and Alice Wallenberg Foundation. This research data leading to the results obtained has been supported by SOLARNET project that has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement no. 824135. This material is based upon work supported by the National Center for Atmospheric Research, which is a major facility sponsored by the National Science Foundation under Cooperative Agreement No. 1852977. The calculations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Centre (NSC) at Linköping University and the PDC Centre for High Performance Computing (PDC-HPC) at the Royal Institute of Technology in Stockholm.
References
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Ayres, T., De Pontieu, B., & Testa, P. 2021, ApJ, 916, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Barczynski, K., Peter, H., & Savage, S. L. 2017, A&A, 599, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bello González, N., Danilovic, S., & Kneer, F. 2013, A&A, 557, A102 [Google Scholar]
- Berghmans, D., Auchère, F., Long, D. M., et al. 2021, A&A, 656, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bingert, S., & Peter, H. 2013, A&A, 550, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bjørgen, J. P., Leenaarts, J., Rempel, M., et al. 2019, A&A, 631, A33 [Google Scholar]
- Boerner, P., Edwards, C., Lemen, J., et al. 2012, Sol. Phys., 275, 41 [Google Scholar]
- Brooks, D. H., Reep, J. W., & Warren, H. P. 2016, ApJ, 826, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Carlson, B. 1963, Special Functions of Applied Mathematics (New York: Academic Press) [Google Scholar]
- Carlsson, M., & Stein, R. F. 1997, ApJ, 481, 500 [Google Scholar]
- Chen, Y., Przybylski, D., Peter, H., et al. 2021, A&A, 656, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cheung, M. C. M., & Cameron, R. H. 2012, ApJ, 750, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Danilovic, S. 2017, A&A, 601, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovic, S. 2023, Adv. Space Res., 71, 1939 [NASA ADS] [CrossRef] [Google Scholar]
- Danilovic, S., Bjørgen, J. P., Leenaarts, J., & Rempel, M. 2022, A&A, 670, A50 [Google Scholar]
- De Pontieu, B., Title, A. M., Lemen, J. R., et al. 2014, Sol. Phys., 289, 2733 [Google Scholar]
- Feldman, U. 1983, ApJ, 275, 367 [CrossRef] [Google Scholar]
- Grotrian, W. 1939, Naturwissenschaften, 27, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Gudiksen, B. V., & Nordlund, Å. 2005, ApJ, 618, 1020 [Google Scholar]
- Hansteen, V., De Pontieu, B., Carlsson, M., et al. 2014, Science, 346, 1255757 [Google Scholar]
- Hansteen, V., Guerreiro, N., De Pontieu, B., & Carlsson, M. 2015, ApJ, 811, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, Z., Madjarska, M. S., Scullion, E. M., et al. 2017, MNRAS, 464, 1753 [NASA ADS] [CrossRef] [Google Scholar]
- Judge, P. 2021, ApJ, 914, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Kahil, F., Hirzberger, J., Solanki, S. K., et al. 2022, A&A, 660, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kerr, G. S., Carlsson, M., Allred, J. C., Young, P. R., & Daw, A. N. 2019, ApJ, 871, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Kitai, R. 1983, Sol. Phys., 87, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Klimchuk, J. A. 2006, Sol. Phys., 234, 41 [Google Scholar]
- Kramida, A., Ralchenko, Yu., Reader, J., & NIST ASD Team 2021, NIST Atomic Spectra Database (ver. 5.9) (Gaithersburg, MD: National Institute of Standards and Technology) https://physics.nist.gov/asd [Google Scholar]
- Landi, E., Del Zanna, G., Young, P. R., Dere, K. P., & Mason, H. E. 2012, ApJ, 744, 99 [Google Scholar]
- Leenaarts, J., & Carlsson, M. 2009, in The Second Hinode Science Meeting: Beyond Discovery-Toward Understanding, eds. B. Lites, M. Cheung, T. Magara, J. Mariska, & K. Reeves, ASP Conf. Ser., 415, 87 [Google Scholar]
- Leenaarts, J., Carlsson, M., Hansteen, V., & Rutten, R. J. 2007, A&A, 473, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leenaarts, J., Carlsson, M., & Rouppe van der Voort, L. 2012, ApJ, 749, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Leenaarts, J., Carlsson, M., & Rouppe van der Voort, L. 2015, ApJ, 802, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Li, S., Jaroszynski, S., Pearse, S., Orf, L., & Clyne, J. 2019, Atmosphere, 10, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Sykora, J., De Pontieu, B., & Hansteen, V. 2012, ApJ, 753, 161 [CrossRef] [Google Scholar]
- Müller, D., St. Cyr, O. C., Zouganelis, I., et al. 2020, A&A, 642, A1 [Google Scholar]
- Nóbrega-Siverio, D., Moreno-Insertis, F., Martínez-Sykora, J., Carlsson, M., & Szydlarski, M. 2020, A&A, 633, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olluri, K., Gudiksen, B. V., Hansteen, V. H., & De Pontieu, B. 2015, ApJ, 802, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1988, ApJ, 330, 474 [Google Scholar]
- Pereira, T. M. D., Rouppe van der Voort, L., Hansteen, V., & De Pointeu, B. 2018, A&A, 611, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peter, H., Bingert, S., Klimchuk, J. A., et al. 2013, A&A, 556, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peter, H., Chitta, L. P., Chen, F., et al. 2022, ApJ, 933, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Rachmeler, L. A., Winebarger, A. R., Savage, S. L., et al. 2019, Sol. Phys., 294, 174 [Google Scholar]
- Rathore, B., & Carlsson, M. 2015, ApJ, 811, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Rathore, B., Pereira, T. M. D., Carlsson, M., & De Pontieu, B. 2015, ApJ, 814, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M. 2017, ApJ, 834, 10 [Google Scholar]
- Rochus, P., Auchère, F., Berghmans, D., et al. 2020, A&A, 642, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rutten, R. J. 2003, Radiative Transfer in Stellar Atmospheres, 255 [Google Scholar]
- Rutten, R. J. 2016, A&A, 590, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rybicki, G. B., & Hummer, D. G. 1992, A&A, 262, 209 [NASA ADS] [Google Scholar]
- Scharmer, G. B., Bjelksjo, K., Korhonen, T. K., Lindberg, B., & Petterson, B. 2003, in Innovative Telescopes and Instrumentation for Solar Astrophysics, eds. S. L. Keil, & S. V. Avakyan, SPIE Conf. Ser., 4853, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K., del Toro Iniesta, J. C., Woch, J., et al. 2020, A&A, 642, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Summers, H. P. 1974, MNRAS, 169, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, H., Xu, Z., He, J., & Madsen, C. 2016, ApJ, 824, 96 [CrossRef] [Google Scholar]
- Tripathi, D., Nived, V. N., Isobe, H., & Doyle, G. G. 2020, ApJ, 894, 128 [CrossRef] [Google Scholar]
- Vissers, G. J. M., de la Cruz Rodríguez, J., Libbrecht, T., et al. 2019, A&A, 627, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [Google Scholar]
- Warren, H. P., Brooks, D. H., Doschek, G. A., & Feldman, U. 2016, ApJ, 824, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Young, P. R., Tian, H., Peter, H., et al. 2018, Space Sci. Rev., 214, 120 [Google Scholar]
All Figures
 |
Fig. 1. Overview of the full computational domain (40 × 40 × 22 Mm) and magnetic field configuration. The plane shows the vertical photospheric magnetic field in μ = 1 at t = 102 s. Red field lines show traced magnetic field lines in the region of the loop-like structure, sampled at high current density. Blue field lines show the magnetic field in the full FOV. This figure was produced using VAPOR (Li et al. 2019; www.vapor.ucar.edu). |
| In the text | |
 |
Fig. 2. Synthetic observables over the full FOV at μ = 1, t = 102 s. The box shows the selected subfield in Fig. 3. In panel a we plot the blue wing of Hα, (b) the Hα line core intensity, and (c) Si IV summed over all frequencies ±0.79 Å around the line centre. |
| In the text | |
 |
Fig. 3. Time evolution of the synthetic loop at μ = 1. From the top to the bottom: normalised Hα blue wing intensity at vD = 53 km s−1, Hα Dopplergram at velocities ±53 km s−1 (black and white represent red and blue wings, respectively), Si IV 1393 Å summed over frequencies ±0.79 Å around line centre, composite image of the Hα Dopplergram (black and white) and frequency-summed Si IV (orange), Hα line core, composite image of Hα line core and frequency-summed Si IV and vertical magnetic field (black and white represent downward and upward magnetic field, respectively). |
| In the text | |
 |
Fig. 4. Hα blue wing intensity (top row), Hα Dopplergram (middle row) and Si IV frequency-integrated intensity (bottom row) in the snapshot at t = 102 s. Four pixels of interest are highlighted using red, green, white, and blue circles. The dotted line marks the position of the vertical cut shown in Fig. 14. |
| In the text | |
 |
Fig. 5. Hαμ = 1 four-panel diagram at t = 102 s in the pixel indicated with a white circle in Fig. 4. The quantities, plotted as functions of frequency and altitude, are indicated in the upper left corner of each subplot and are plotted in grayscale. z = 0 Mm marks the photosphere. In all panels, the vertical velocity is shown as a function of altitude (white dotted line), where upwards velocity is positive and downwards is negative. In the upper left panel, vz = 0 is indicated by a vertical solid white line. Additionally, the altitude where τ = 1 is also plotted in all subplots (orange dotted line). The different quantities are as follows. Upper left: opacity χν over optical depth τν. Upper right: total source function Sν (Eq. (2)), temperature (green line) and source function (blue line). Lower left: attenuation factor τνexp(−τν). Lower right: contribution function CI (Eq. (3)), and emergent intensity (solid white line). |
| In the text | |
 |
Fig. 6. Hαμ = 1 four-panel diagram at t = 102 s in the pixel indicated by the green circle in Fig. 4. The format of the diagram is the same as in Fig. 5. |
| In the text | |
 |
Fig. 7. Hαμ = 1 four-panel diagram at t = 102 s in the pixel indicated by the red circle in Fig. 4. The format of the diagram is the same as in Fig. 5. |
| In the text | |
 |
Fig. 8. Si IV formation diagram in the pixel marked by a white circle in Fig. 4. The panels show (a) Line profiles of Si IV 1394 Å (solid black) and Si IV 1403 Å (dashed black). (b) Intensity ratio of Si IV 1394 Å and Si IV 1403 Å lines. (c) Emissivity j of the 1394 Å line (Eq. (4), j0.6) and vertical velocity vz (blue). The vertical dashed line indicates where Δv = 0 km s−1. The orange line marks the height at which τ = 1 is reached. (d) Gas temperature T (red) and electron density ne (black) of Si IV. The dashed vertical lines represents the LTE Si IV formation temperature interval and the dotted vertical lines represent the coronal equilibrium formation temperature interval. Positive Δν indicates an upwards velocity. |
| In the text | |
 |
Fig. 9. Same layout as in Fig. 8, but for the pixel marked by a green circle in Fig. 4. |
| In the text | |
 |
Fig. 10. Same layout as in Fig. 8, but for the pixel marked by a red circle in Fig. 4. |
| In the text | |
 |
Fig. 11. Same layout as in Fig. 8, but for the pixel marked by a blue circle in Fig. 4. |
| In the text | |
 |
Fig. 12. Time evolution of the synthetic loop at μ = 0.66. The rows show the same quantities as in Fig. 3, but without the vertical magnetic field and the Hα line centre. |
| In the text | |
 |
Fig. 13. Diagram showing the line profiles of Hα at μ = 0.66. Left: loop in synthetic Hα at μ = 0.66 at t = 102 s, where three chosen pixels are indicated by circles in green, orange, and blue. Right: normalised Hα intensity for the pixels indicated with the respective colour in the left panel. |
| In the text | |
 |
Fig. 14. Vertical cut along the dotted line plotted in Fig. 4. From top to bottom, left to right: temperature, density, vertical components of magnetic field and velocity, sum of resistive and viscous heating terms and total line emissivity for 1394 Å. The red line marks the formation height of Hα line core. The green line marks the formation height of the Hα blue wing at vD = −53 km s−1. Black vertical lines, from left to right, mark the positions of the red, green, and white pixels in Fig. 4, respectively. |
| In the text | |
 |
Fig. 15. Three-dimensional rendering of the area of interest over the photospheric vertical component of the magnetic field at t = 102 s. Here, we choose to plot the formation height of the Hα blue wing at −53 km s−1 (green isosurface), the formation height of the Si IV 1394 Å line (yellow isosurface) and magnetic field lines of the structure in blue and red, corresponding to up- and downflowing material with vz = ±122 km s−1 respectively. This figure was produced using VAPOR. |
| In the text | |
 |
Fig. 16. Evolution of traced magnetic field lines. On the left, traced magnetic field lines are plotted over the vertical component of the photospheric magnetic field. In the middle, the position of the corresponding footpoints is marked over the sum of resistive and viscous heating terms integrated over the height range [0.6 − 3.8] Mm (second column) and [2.7 − 7] Mm (third column). On the right, we show the projection of the traced field lines to the z-axis. The background shows density along the horizontal cut at y = 28 Mm. The movie is available online. |
| In the text | |
 |
Fig. 17. Footpoints of the chosen traced field lines. The colours are the same as in Fig. 16. |
| In the text | |
 |
Fig. 18. Emission measure for the lg(T/K) = [5.8, 6.2] temperature interval. Bottom row shows a zoom onto the area marked with the white rectangle. The area size and time steps are the same as in Fig. 16. |
| In the text | |
 |
Fig. 19. Same format as in Fig. 18 but for the lg(T/K) = [5.0, 5.5] temperature interval. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.