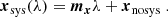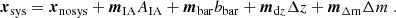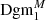| Issue |
A&A
Volume 667, November 2022
|
|
|---|---|---|
| Article Number | A125 | |
| Number of page(s) | 22 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202243868 | |
| Published online | 16 November 2022 | |
Persistent homology in cosmic shear
II. A tomographic analysis of DES-Y1
1
Argelander-Institut für Astronomie, Auf dem Hügel 71, 53121 Bonn, Germany
e-mail: sven@astro.uni-bonn.de
2
ETH Zürich, Department of Mathematical Sciences, Rämistrasse 101, 8092 Zürich, Switzerland
3
School of Mathematics, Statistics and Physics, Newcastle University, Herschel Building, NE1 7RU Newcastle-upon-Tyne, UK
4
Astrophysics Research Institute, Liverpool John Moores University, 146 Brownlow Hill, Liverpool L3 5RF, UK
5
Ruhr University Bochum, Faculty of Physics and Astronomy, Astronomical Institute (AIRUB), German Centre for Cosmological Lensing, 44780 Bochum, Germany
6
Osservatorio Astronomico di Trieste, via Tiepolo 11, 34131 Trieste, Italy
7
Institute for Fundamental Physics of the Universe, via Beirut 2, 34151 Trieste, Italy
8
INFN – Sezione di Trieste, 34100 Trieste, Italy
9
Universitäts-Sternwarte, Fakultät für Physik, Ludwig-Maximilians-Universität München, Scheinerstr.1, 81679 München, Germany
10
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Straße 1, 85741 Garching, Germany
11
Aix-Marseille Univ, CNRS, CNES, LAM, Marseille, France
Received:
26
April
2022
Accepted:
11
August
2022
We demonstrate how to use persistent homology for cosmological parameter inference in a tomographic cosmic shear survey. We obtain the first cosmological parameter constraints from persistent homology by applying our method to the first-year data of the Dark Energy Survey. To obtain these constraints, we analyse the topological structure of the matter distribution by extracting persistence diagrams from signal-to-noise maps of aperture masses. This presents a natural extension to the widely used peak count statistics. Extracting the persistence diagrams from the cosmo-SLICS, a suite of N-body simulations with variable cosmological parameters, we interpolate the signal using Gaussian processes and marginalise over the most relevant systematic effects, including intrinsic alignments and baryonic effects. For the structure growth parameter, we find S8 = 0.747−0.031+0.025, which is in full agreement with other late-time probes. We also constrain the intrinsic alignment parameter to A = 1.54 ± 0.52, which constitutes a detection of the intrinsic alignment effect at almost 3σ.
Key words: gravitational lensing: weak / methods: data analysis / cosmological parameters / dark energy
© S. Heydenreich et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
In the past decades, weak gravitational lensing has emerged as an indispensable tool for studying the large-scale structure (LSS) of the Universe. Weak lensing primarily relies on accurate shape and distance measurements of galaxies. Ongoing and recently completed surveys have provided the community with a sizeable amount of high-quality data; for example, the Kilo Degree Survey (KiDS, de Jong et al. 2013), the Dark Energy Survey (DES, Flaugher 2005), and the Hyper Suprime-Cam Subaru Strategic Program (HSC, Aihara et al. 2018). Further surveys are scheduled to start observing in the next years; they will probe deeper and larger areas enabling measurements of cosmological parameters with sub-per cent accuracy; for example, the Vera Rubin Observatory’s Legacy Survey of Space and Time (LSST, Ivezic et al. 2008), the Euclid survey (Laureijs et al. 2011), and the Nancy Grace Roman Space Telescope (RST) survey (Spergel et al. 2013). These upcoming surveys are of special relevance for solving tensions related to measurements of the structure growth parameter 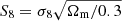 (Hildebrandt et al. 2017; Planck Collaboration VI 2020; Joudaki et al. 2020; Heymans et al. 2021; Abbott et al. 2022), which is defined along the main degeneracy direction in conventional weak lensing studies. Here, Ωm is the dimensionless matter density parameter and σ8 parametrises the amplitude of the matter power spectrum. Improved data and independent analysis choices are crucial to determine whether this tension is due to new physics, a statistical fluctuation, or the manifestation of unknown systematics. For example, Joudaki et al. (2017) showed that the current tension in S8 between the CMB and the local Universe could be lifted when allowing for a dynamical dark energy model, meaning that measuring the equation of state of dark energy is of the utmost importance in the next decades.
(Hildebrandt et al. 2017; Planck Collaboration VI 2020; Joudaki et al. 2020; Heymans et al. 2021; Abbott et al. 2022), which is defined along the main degeneracy direction in conventional weak lensing studies. Here, Ωm is the dimensionless matter density parameter and σ8 parametrises the amplitude of the matter power spectrum. Improved data and independent analysis choices are crucial to determine whether this tension is due to new physics, a statistical fluctuation, or the manifestation of unknown systematics. For example, Joudaki et al. (2017) showed that the current tension in S8 between the CMB and the local Universe could be lifted when allowing for a dynamical dark energy model, meaning that measuring the equation of state of dark energy is of the utmost importance in the next decades.
Shear two-point statistics have emerged as the prime analysis choice for cosmic shear as they present a number of key advantages (e.g., Secco et al. 2022; Hikage et al. 2019; Asgari et al. 2021). Such statistics are physically motivated by the fact that they describe the early Universe almost perfectly. The late Universe, however, contains a considerable amount of non-Gaussian information that is not captured by two-point statistics, such that jointly investigating second- and higher-order statistics increases the constraining power on cosmological parameters (see, e.g., Bergé et al. 2010; Pyne & Joachimi 2021). This additional information is currently explored with a variety of analysis tools, which either use analytical models (e.g., Halder et al. 2021; Gatti et al. 2021; Burger et al. 2022) or rely on large suites of numerical simulations. For this work, the most relevant examples for a simulation-based analysis are peak statistics (Martinet et al. 2021b, and references therein, hereafter M+21) and Minkowski functionals (e.g., Shirasaki & Yoshida 2014; Petri et al. 2015; Parroni et al. 2020), which are both based on aperture mass maps constructed from shear fields. M+21 also showed that a joint analysis of peaks and two-point correlation functions (2PCF) improves cosmological constraints on S8, Ωm, and the dark energy equation-of-state parameter w0 by 46%, 57%, and 68%, respectively. Zürcher et al. (2021) showed that a joint analysis using 2PCF with Minkowski functionals, a topological summary statistic, on aperture mass maps increases the figure of merit in the Ωm–σ8 plane by a factor of 2. We note that there exist many other promising simulation-based methods such as bayesian hierarchical forward modelling (Porqueres et al. 2021, 2022), likelihood-free inference (Jeffrey et al. 2021), or the scattering transform (Cheng et al. 2020).
In this paper, we focus on persistent homology, a topological method that combines the advantages of peak statistics and Minkowski functionals but also captures information about the environment of topological features. Persistent homology specialises in recognising persistent topological structures in data and we refer the interested reader to a recent review written by Wasserman (2018), who highlights its diverse applications in various fields. Following early concepts about persistent homology and Betti numbers in cosmology (van de Weygaert et al. 2013), several groups have formalised the approach (Sousbie 2011; Pranav et al. 2017; Feldbrugge et al. 2019; Pranav 2021). In particular, Kimura & Imai (2017) were the first to show that the hierarchical topological structure of the galaxy distribution decreases with increasing redshift using small patches of Sloan Digital Sky Survey (SDSS). More recently, Xu et al. (2019) developed an effective cosmic void finder based on persistent homology, while Kono et al. (2020) detected baryonic acoustic oscillations in the quasar sample from the extended Baryon Oscillation Spectroscopic Survey in SDSS. Moreover, Biagetti et al. (2020, 2022) showed with simulations that persistent homology is able to identify primordial non-Gaussian features. Heydenreich et al. (2021, hereafter H+21) performed a mock analysis using persistent homology on cosmic shear simulations, highlighting its potential to break the degeneracy between S8 and w0.
Persistent homology summarises the topological structure of data in so-called persistence diagrams. There are different methods for performing statistical analyses on such diagrams (see Sect. 3.2). In H+21, we worked with persistent Betti numbers. In this work, we opted for ‘heatmaps’, which constitute a more robust statistic for persistence diagrams. We extract heatmaps from a series of mock data that match the DES-Y1 survey properties (Flaugher 2005; Harnois-Déraps et al. 2021, hereafter HD+21), including a Cosmology Training Set, a Covariance Training Set, and a suite of Systematics Training Set, constructed from the SLICS (Harnois-Déraps & van Waerbeke 2015), the cosmo-SLICS simulations (Harnois-Déraps et al. 2019) and the Magneticum hydrodynamical simulations (Biffi et al. 2013; Saro et al. 2014; Steinborn et al. 2015, 2016; Dolag 2015; Teklu et al. 2015; Bocquet et al. 2016; Remus et al. 2017; Castro et al. 2018, 2021). Following HD+21, we then train a Gaussian process regression (GPR) emulator, which is fed to a Markov chain Monte Carlo (MCMC) sampler to obtain cosmological parameter estimates. We significantly expand on the results from H+21 by including the main systematic effects related to cosmic shear analyses, namely photometric redshift uncertainty, shear calibration, intrinsic alignment of galaxies, baryon feedback and masking. These systematics, particularly baryon feedback and intrinsic alignments, account for 25% of our reported final error budget. Furthermore, as introduced in M+21, our results are obtained for a tomographic topological data analysis where we include the cross-redshift bins analyses. This leads to the first cosmological parameter constraints obtained from persistent homology based on analysing cosmic shear data, here provided by the DES year-1 survey (Abbott et al. 2018).
The paper is organised as follows: In Sect. 2 we describe the data and simulations; the theoretical background on persistent homology, a description of our data compression methods, the formalism for the two-point statistics and the cosmological parameter estimation are presented in Sect. 3. In Sect 4 we discuss our mitigation strategies for systematic effects and show the validation of our pipeline in Sect. 5. We finalise our work with the results shown in Sect. 6 and our discussion in Sect. 7.
2. Data and simulations
2.1. DES-Y1 data
We use in this work the public1 Year-1 data released by DES presented in Abbott et al. (2018, DES-Y1 hereafter). The primary weak lensing data consist of a galaxy catalogue in which positions and ellipticities are recorded for tens of millions of objects, based on observations from DECam mounted at the Blanco telescope at the Cerro Tololo Inter-American Observatory (Flaugher et al. 2015). The galaxies selected in this work match those of Troxel et al. (2018, hereafter T+18) and HD+21, applying the FLAGS SELECT, METACAL, and the REDMAGIC filters to the public catalogues, yielding a total unmasked area of 1321 deg2 and 26 million galaxies.
The shear signal γ1/2 is inferred from the METACALIBRATION technique (Sheldon & Huff 2017), which further provides each galaxy with a METACAL response function Si that must be included in the measurement. As explained in T+18, this method requires a prior on an overall multiplicative shear correction of m ± σm = 0.012 ± 0.023, which we then use to calibrate the measured galaxy ellipticities as ϵ1/2 → ϵ1/2(1 + m). We then assume that these ellipticities are an unbiased estimator for the shear γ.
Following T+18, the galaxy sample is further split into four tomographic bins based on their individual estimated photometric redshift ZB, which is measured with the BPZ method (Benítez 2000). At this point, the redshift distribution of the four tomographic populations are estimated with the ‘DIR’2 method, following Joudaki et al. (2020) and HD+21. As argued in these two references, the DIR approach is more robust to potential residual selection effects in their training sample than the DES-Y1 BPZ stacking method presented in Hoyle et al. (2018). Although it could also be affected by incomplete spectroscopy and colour pre-selection (Gruen & Brimioulle 2017), bootstrap resampling of the spectroscopic samples points towards a significantly smaller uncertainty in the mean redshift of the populations, achieving σz = 0.008, 0.014, 0.011 and 0.009 for tomographic bins 1..4, respectively (Joudaki et al. 2020). Despite these important differences, the DIR n(z) is consistent with the fiducial estimate presented by the DES collaboration. It brings in excellent agreement the DES-Y1 and the KV-450 cosmic shear data (Hildebrandt et al. 2020, also based on the DIR method). Asgari et al. (2020) showed that the inferred S8 value is affected by less than 1σ, which is certainly a considerable effect but causes no internal tension between the two methods of redshift estimation.
2.2. Mock galaxy catalogues
The analysis presented in this work largely follows the simulation-based inference methods of HD+21, which completely relies on numerical weak lensing simulations for the cosmology inference, the estimation of the uncertainty and the mitigation of systematics and secondary effects. Most of the mock data used in this work has been presented in HD+21, which we review in this section.
2.2.1. Cosmology Training Set
This set of simulations is used to model the dependence of the signal on cosmology. Based on the cosmo-SLICS (Harnois-Déraps et al. 2019), it consists of weak lensing light cones sampling 26 points in a wCDM cosmological model (i.e. cold dark matter with dark energy beyond the cosmological constant Λ), where 25 points are distributed on a Latin Hypercube, covering the ranges Ωm ∈ [0.10, 0.55], S8 ∈ [0.60, 0.90], h ∈ [0.6, 0.82] and w0 ∈ [ − 2.0, −0.5], where h is the reduced Hubble parameter. The last point is set manually to a fiducial, ΛCDM cosmology. Each node consists of two independent N-body simulations produced by CUBEP3M (Harnois-Déraps et al. 2013), with initial conditions designed such as to suppress the sampling variance. The code follows the non-linear evolution of 15363 particles in a 505 h−1 Mpc box, producing between 15 and 28 mass sheets of co-moving thickness equivalent to half the box size, filling up a 10 × 10 deg2 light cone to z = 3.0. Random orientations and shifting are introduced in this process such that a total of 25 pseudo-independent light cones are generated per N-body run. Five of these are used in the current paper, out of 25, which is sufficient to model the statistics within the DES-Y1 precision (as in HD+21). Validation tests revealed that the third line of sight from the first N-body seed is a statistical outlier: for example, the standard deviation of the convergence σκ differs from the mean of the full cosmo-SLICS light cones by more than 4σ. Due to the limited size of our training sample, this particular line of sight could bias our cosmological model. We thus skipped over it and verified afterwards that the results are not strongly affected by this choice, although it slightly improves the accuracy on S8 during the validation test. In total, the Cosmology Training Set consists of 26 × 9 = 234 survey realisations.
2.2.2. Covariance Training Set
This suite is mainly used to estimate the sampling covariance in the data vector. Based on the SLICS (Harnois-Déraps & van Waerbeke 2015), it is produced from 124 fully independent N-body realisations, with the same mass resolution and simulation volume as the cosmo-SLICS. All carried out at the same cosmology, these light cones started from different noise realisations of the initial conditions, thereby sampling the statistical variance in the data. The mean over all measurements from the Covariance Training Set is also independent of the Cosmology Training Set and well converged towards the ensemble average, making this an ideal data set with which we validate our cosmology inference pipeline later on.
2.2.3. Systematics Training Set – Mass resolution
The force resolution of N-body simulations is limited by the number of particles, the choice of softening length and the force accuracy setting. This inevitably translates into a decrease in the clustering of dark matter in the highly non-linear scales, which in turn affects the statistics under study. The SLICS-HR are a suite of high-resolution simulations introduced in Harnois-Déraps & van Waerbeke (2015), in which the force accuracy of CUBEP3M has been significantly increased, yielding 5 light cones with more accurate mass densities. As detailed in Sect. 4, we verify that our training data are not strongly affected by this known limitation.
2.2.4. Systematics Training Set – Baryons
Baryonic feedback processes from sustained stellar winds, supernovae and active galactic nuclei are known to redistribute the matter around over-dense regions of the Universe in a manner that directly affects the weak lensing measurements (Semboloni et al. 2011). If left unmodelled, these processes will significantly bias the inferred cosmology in analyses based on 2PCF or non-Gaussian statistics (e.g., Coulton et al. 2020; Zürcher et al. 2021; Martinet et al. 2021a). In this work, our approach consists of measuring our statistics in hydrodynamical simulations in which the baryon feedback can be turned on and off. The relative impact on the data vector is then used to model the effect of baryons on our statistics. As in HD+21, we use the Magneticum simulations3 to achieve this, more precisely the Magneticum Run-2 and Run-2b (Castro et al. 2021), in which stellar formation, radiative cooling, supernovae and AGN feedback are implemented in cosmological volumes of 352 and 640 h−1 Mpc, respectively, with a spatial resolution that is high enough to capture the baryonic effects at scales relevant to our study. The adopted cosmology is consistent with the SLICS cosmology, with Ωm = 0.272, h = 0.704, Ωb = 0.0451, ns = 0.963, and σ8 = 0.809. These simulations reproduce a number of key observations, including many statistical properties of the large-scale, intergalactic, and intercluster medium (see Hirschmann et al. 2014; Teklu et al. 2015; Castro et al. 2018, for more details). Moreover, the resulting overall feedback is consistent with that of the BAHAMAS simulations (McCarthy et al. 2017), which are based on a completely independent sub-grid calibration method. The Baryons Training Set and their dark-matter-only counterpart are used to inspect the impact of baryonic physics on the data vector, from which we extract a correction factor used to forward-model the effect on dark-matter-only simulations. Full details on the treatment of the systematics are presented in Sect. 4.
2.2.5. Systematics Training Set – Photometric redshifts
The redshift distribution of the data is known to a high precision within the DIR method however, the residual uncertainty must be accounted for in the analysis. For this, we use the mocks described in HD+21 in which the n(z) has been shifted by a small amount in order to study the impact on the signal. These sample at ten points the posterior of the expected shifts in the mean redshifts of the DIR method itself (Joudaki et al. 2020), and in each case, we construct 10 full survey realisations at the cosmo-SLICS fiducial cosmology, from which we extract our statistics. This approach allows us to measure the derivative of the persistent homology statistics with respect to shifts in dz. The priors on dz are listed in Table 1.
Prior ranges of cosmological and nuisance parameters in the likelihood analysis.
2.2.6. Systematics Training Set – Intrinsic Alignments
The assumption that the observed shapes of galaxies are randomly aligned in absence of foreground lensing matter fails to account for their intrinsic alignment (IA), an important contribution that arises from a coupling between their shapes and the large-scale structure they are part of (for a review see Joachimi et al. 2015). This important secondary signal tends to counteract the cosmic shear signal, which can therefore interfere with the cosmological inference. Although there exist analytical models to describe this effect for two-point functions, higher-order statistics must rely on IA-infused simulations to account for this important effect. In this work, we use the infusion method presented in Harnois-Déraps et al. (2022), where intrinsic galaxy shapes are linearly coupled with the projected tidal field, consistent with the non-linear alignment model of Bridle & King (2007). Although the redshift distribution of these mocks exactly follows that of the data, their construction requires that the galaxy ellipticities linearly trace the simulation density fields, whose positions therefore no longer replicate that of the DES-Y1 data. These mocks have no masking, nor METACALIBRATION responses included and are therefore used to estimate the relative impact of IA on our persistent homology measurements. They have an IA amplitude that is allowed to vary, as controlled by the AIA parameter. We measure the persistent homology statistics from 50 cosmo-SLICS light cones at the fiducial cosmology, for values of AIA ∈ [ − 5.0, 5.0], and use these to construct a derivative, similar to the way we handle the photometric redshift uncertainty.
2.2.7. Creating the galaxy catalogues
The output of each simulation is a series of 100 deg2 lensing planes that serve to assign convergence (κ) and shear (γ1/2) to copies of the DES-Y1 data. As described in HD+21, the survey footprint is segmented into 19 regions, or tiles, which all fit inside our simulated maps. The summary statistics are computed individually on each tile and combined afterwards to construct the data vector. In this construct, the galaxy positions, ellipticities ϵ1/2 and METACALIBRATION weights Si in the mock data exactly match that of the real data, avoiding possible biases arising in non-Gaussian statistics when these differ (see e.g., Kacprzak et al. 2016, Appendix D of H+21). Mock ellipticities are obtained by rotating the observed ellipticities by a random angle and combining the resulting randomised signal ϵn with the simulated (noise-free) reduced shear g via:
where bold symbols denote complex numbers (for example, g = g1 + ig2). We calculate the reduced shear as g = γ/(1−κ). In total, we compute 10 shape-noise realisations for every simulated survey realisation, each using a different random seed in the rotation. This procedure allows us to average out a large part of the fluctuations introduced by the shape noise, improving both our predictions and our estimate of the sample covariance while preserving the data noise levels. Redshifts are assigned to every simulated galaxy by sampling from the DIR redshift distribution corresponding to the tomographic bin they belong to.
2.3. Calculating maps of aperture masses
As in H+21, we perform our computations on signal-to-noise maps of aperture masses (Schneider 1996; Bartelmann & Schneider 2001), computing the signal ℳap(θ) and noise σ(ℳap(θ)) on a grid as:
where the wi are optional weights assigned to measured galaxy ellipticities (set to 1.0 in this work), Si are the respective responses calculated by the METACALIBRATION shear estimator (T+18), and the tangential component of the shear ϵt(θi; θ) is calculated via
We then compute the signal-to-noise map (S/N map) of aperture masses as the ratio between the two quantities. As before, we use the following Q-filter function (Schirmer et al. 2007; Martinet et al. 2018, hereafter M+18):
with a concentration index of xc = 0.15 (Hetterscheidt et al. 2005), which was chosen to optimally select the mass profiles of dark matter halos (Navarro et al. 1997). For the filter radius we choose θap = 12.5′. As in H+21, we compute the S/N maps by distributing both galaxy ellipticities ϵi and their squared moduli |ϵi|2 for each tile on a (600 × 600) pixel grid, and perform the convolutions in Eqs. (2) and (3) via a Fast Fourier-Transform. Contrary to previous work, we use a cloud-in-cell algorithm to distribute the galaxy ellipticities on a grid, yielding more accurate results for small scales when dealing with high-quality data.
As shown in M+21, the traditional approach of computing the aperture mass statistics for individual tomographic bins only (hereafter auto-bins) does not yield optimal results. Instead, we perform the computation for all combinations of tomographic bins by concatenating the respective galaxy catalogues (cross-bins). This approach allows us to extract additional information about correlated structures along the line of sight. For example, a massive, nearby galaxy cluster can be detected as a peak in the S/N maps for tomographic bins 1 and 2. However, if we were only to analyse persistence heatmaps of the two respective bins, both would register the cluster as a peak, but the information that the peak is at the same position in both maps would be lost. To utilise this information, we also need to analyse the S/N map of a combination of both bins. Based on the four fiducial DES-Y1 redshift bins, this optimised method leads to 15 bin combinations (1, 2, 3, 4, 1∪2, ..., 3∪4, ..., 1∪2∪3∪4) from which we extract heatmaps.
As the galaxies in our mock data follow the exact positions of the real galaxy catalogue, they are subject to the overall survey footprint and internal masked regions. We only want to consider the parts of our S/N maps where we have sufficient information from surrounding galaxies, therefore we construct our own mask in the following way: we combine the galaxy catalogues of all four tomographic bins and distribute these galaxies on a grid. Then we mask all pixels of the tile where the effective area containing galaxies within the aperture radius θap is less than 50%. In particular, we mask the boundary of each tile to ensure that neighbouring tiles are treated as independent in the persistence calculations (compare H+21). This mask is then applied to every combination of tomographic bins of the respective survey tile.
With this method, we compute the S/N maps for each of the 19 tiles of the DES-Y1 survey footprint, for each of the 15 tomographic bins and for each of the 10 shape noise realisations. The next section describes how cosmological information is extracted from these maps with statistics based on persistent homology.
3. Methods
We use methods from persistent homology to quantify the statistical properties of S/N maps of aperture masses and analyse their dependence on the underlying cosmological parameters. The main idea can be described as follows.
We take a S/N map of aperture masses and apply a threshold to that map. We then cut off all parts where the value of the S/N map exceeds that threshold (compare Fig. 1). This gives rise to two types of topological features. The first types are connected components, that is regions of low S/N that are surrounded by a region of higher S/N, which is above the cut-off threshold. These connected components correspond to local minima in the S/N map, which in turn correspond to an under-density in the matter distribution. The second type of topological features are holes, that is regions of high S/N that are above the cut-off threshold, with an environment of S/N that surrounds them and is lower than the cut-off threshold. These holes correspond to the local maxima of the S/N map, which indicate an overdensity in the underlying matter distribution.
 |
Fig. 1. Example signal-to-noise map of aperture masses for a 5 × 5 deg2 sub-patch of one of the Covariance Training Set catalogue (left), and the same map when a threshold of 0.5 is applied (right). The white ‘holes’ in the right map correspond to local maxima of the map and give rise to the topological ‘features’ that are summarised in Dgm1. |
When the cut-off threshold is gradually increased, these features change. Connected components start to show up (are born) once the threshold is higher than their minimum S/N value. At some higher threshold, the connected component will merge with a different connected component (or die)4. Similarly, an overdensity starts to form a hole once the cut-off threshold exceeds the S/N value of its environment. This hole is completely filled in once the threshold exceeds the maximal S/N value of the overdensity.
For each such topological feature, we write b for its birth (the threshold at which it is born) and d for its death (the threshold at which it dies). We plot the collection of all points (b, d) as a scatter plot, called the persistence diagram Dgm; we write Dgm0 for the persistence diagram of connected components and Dgm1 for the one of the holes (see Fig. 2). In particular, it is straightforward to recover the peak count statistics from this: The death of a hole corresponds to the maximal S/N value of an overdensity, so the set of deaths is the collection of all peaks in the S/N map. However, persistent homology offers one crucial advantage: the persistence of a feature, defined by d − b, yields information about how much a peak protrudes from its surrounding environment. In particular, features with a very small persistence are more likely to be caused by noise fluctuations, which can be taken into account in the following statistical analysis. Persistent homology offers a natural way to account for masked regions, which we describe in the next subsection. We denote the persistence diagrams that account for the presence of masked regions by 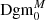 and
and 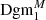 .
.
 |
Fig. 2. Two persistence diagrams for the simulation shown in Fig. 1. The blue crosses represent features of Dgm0, the orange crosses represent features of Dgm1. For visibility, only every 500th feature is shown. We note that all points in this diagram lie above the diagonal. |
From the persistence diagrams 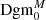 and
and 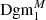 we then create so-called heatmaps by smoothing the diagrams with a Gaussian. Every point of the heatmap can now be used for statistical analysis of the persistent topological structure of the S/N maps of aperture mass. In the next two subsections, we give a slightly more formal introduction into these statistics derived from persistent homology and describe their application.
we then create so-called heatmaps by smoothing the diagrams with a Gaussian. Every point of the heatmap can now be used for statistical analysis of the persistent topological structure of the S/N maps of aperture mass. In the next two subsections, we give a slightly more formal introduction into these statistics derived from persistent homology and describe their application.
3.1. Persistent homology
In this section, we give a short overview of the aspects of persistent homology that we use in the present paper. More detailed explanations can be found in Sect. 2.3 of H+21. For a general introduction to the topic that is geared towards its applications in data science, see Chazal & Michel (2021) or Otter et al. (2017); further information about the mathematical background can be found in Oudot (2015).
Persistent homology is a technique from topological data analysis that allows summarising the topological features of a sequence of spaces. This is a versatile tool that can be applied in many different settings. However, the application that is relevant for the present article is that persistent homology gives a summary of the topological features of a map f : X → ℝ ∪ { ± ∞}, where X is in principle any (topological) space. (Here, the sequence of spaces is given by taking subsets of X that consist of points where the value of f lies below a certain threshold.) In our setting, X is a (10 × 10 deg2) tile of the sky (which we interpret as a subset of ℝ2 and represent by a (600 × 600) pixel grid) and f is the function that assigns to every point its S/N value as defined in Sect. 2.3. An example of this can be found in Fig. 1.
The persistent homology of each such map f can be summarised by two persistence diagrams Dgm0 = Dgm0(f) and Dgm1 = Dgm1(f). Each of these persistence diagrams is a collection of intervals [b, d), where b, d ∈ ℝ ∪ { ± ∞}. As each such interval is determined by the two values b < d, one can equivalently see a persistence diagram as a collection of points (b, d) in (ℝ ∪ { ± ∞})2 that lie above the diagonal. We call such a point (b, d) a feature of the persistence diagram; b is commonly called the birth and d is its death. Roughly speaking, the points in Dgm0 correspond to the local minima of the function f, whereas the points in Dgm1 correspond to the local maxima. In both cases, the difference d − b of such a feature (b, d) is called its persistence and describes how much the corresponding extremum protrudes from its surroundings.
The actual computation of the Dgm0 or Dgm1 associated with an S/N map f is done as follows: as explained in Sect. 2.3, the S/N maps we compute are defined on a (600 × 600) pixel grid, and a subset of these pixels are masked. We set the value of every masked pixel to be −∞ and compute the persistence diagrams Dgm0 and Dgm1 associated to this map5 (see Fig. 2). As explained in H+21 (Sect. 2.3.3), relative homology offers a natural way to work with persistent homology in the presence of masks. The idea here is that a feature in Dgmi that is of the form ( − ∞, d) corresponds to a minimum or maximum of f that originates from a masked area as these are the only points where f takes the value −∞. This is why we do not actually work with Dgm0 or Dgm1 but instead define ‘masked’ persistence diagrams 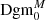 and
and 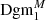 as follows: the persistence diagram
as follows: the persistence diagram 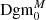 is obtained from Dgm0 by simply removing all features coming from the masks, meaning all points of the form ( − ∞, d). To get
is obtained from Dgm0 by simply removing all features coming from the masks, meaning all points of the form ( − ∞, d). To get 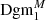 from Dgm1, we again start by removing all points of the form ( − ∞, d′), but then for every feature of the form ( − ∞, d) in Dgm0 (so those that got removed when transforming Dgm0 into
from Dgm1, we again start by removing all points of the form ( − ∞, d′), but then for every feature of the form ( − ∞, d) in Dgm0 (so those that got removed when transforming Dgm0 into 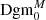 ), we add a new feature (d, ∞) to
), we add a new feature (d, ∞) to 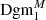 6.
6.
3.2. Persistence statistics
From the calculations described in the previous section, we obtain for each S/N map two persistence diagrams 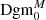 and
and 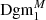 . In order to carry out a statistical analysis of these persistence diagrams, one needs to be able to compute expected values and covariances. A priori, a persistence diagram is a particular collection of points in (ℝ ∪ { ± ∞})2, and there is no canonical way of computing distances, sums and averages of such collections. There are different approaches to overcoming these difficulties. Most of them proceed by converting persistence diagrams into elements of a suitable vector space and then using tools for statistics and data analysis in this space. An overview of different options to perform statistics on persistence diagrams can be found in Chazal & Michel (2021), in particular Sect. 5.9 and in Pun et al. (2018). For this work, we tested three different approaches to the problem: persistent Betti numbers, persistence landscapes and heatmaps. All of these convert persistence diagrams into elements of certain function spaces.
. In order to carry out a statistical analysis of these persistence diagrams, one needs to be able to compute expected values and covariances. A priori, a persistence diagram is a particular collection of points in (ℝ ∪ { ± ∞})2, and there is no canonical way of computing distances, sums and averages of such collections. There are different approaches to overcoming these difficulties. Most of them proceed by converting persistence diagrams into elements of a suitable vector space and then using tools for statistics and data analysis in this space. An overview of different options to perform statistics on persistence diagrams can be found in Chazal & Michel (2021), in particular Sect. 5.9 and in Pun et al. (2018). For this work, we tested three different approaches to the problem: persistent Betti numbers, persistence landscapes and heatmaps. All of these convert persistence diagrams into elements of certain function spaces.
Persistent Betti numbers are probably the most direct approach and were used in H+21. They represent a persistence diagram Dgmi by the function βi : (ℝ ∪ { ± ∞})2 → ℝ, where βi(x, y) is the number of points (b, d) in Dgmi that lie to the ‘upper left’ of (x, y), meaning that x ≤ b and d ≤ y. For more explanations about persistent Betti numbers, see H+21, Sect. 2.2.3 and Appendix B.
Persistent landscapes are a more elaborate alternative, introduced in Bubenik (2015) and already successfully used in applications, for example in Chittajallu et al. (2018) and Kovacev-Nikolic et al. (2016). However, we were not able to set them up in a way that led to competitive results. We suspect that the reason for this was the great number of features (around 500 000 per line of sight) in our persistence diagrams. The problem we were facing was that because of this number of features, we obtained a very large and noisy data vector. We reduced its dimension using a principal component analysis, similar to Kovacev-Nikolic et al. (2016), but unfortunately, the quality of the resulting data was not good enough to obtain sufficiently tight bounds on the cosmological parameters. This might change when the principal component analysis can be applied to a less noisy data vector that is extracted from a larger training sample.
Heatmaps are the method that worked best for us in the present setting. These are defined in the spirit of the multi-scale kernel introduced in Reininghaus et al. (2015). The idea is to replace each point in a persistence diagram with a Gaussian. More precisely, one considers the diagram as a discrete measure (i.e. a sum of Dirac delta distributions) on D ⊂ ℝ2, where D = {(x, y)∈ℝ2|x < y} and convolves this with a two-dimensional isotropic Gaussian distribution. The result is for every value t > 0 a continuous function ut(x, y):D → ℝ that can be seen as a smoothed version of the persistence diagram. The value t is called the scaling parameter and determines how much smoothing is applied to the initial diagram. For an example of such a heatmap, see Fig. 3.
 |
Fig. 3. Heatmap of the persistence diagram in Fig. 2 with a scaling parameter of t = 0.2 (for the computation of the Heatmaps, all features are taken into account, not just every 500th as in Fig. 2). The red points correspond to the evaluation points that were chosen by the χ2-maximiser outlined in Sect. 3.3. The extracted data vector can be seen in Fig. 4. |
We compute the heatmaps in the following way: we first compute the persistence diagram DgmM for the S/N maps of each tiled realisation of the DES-Y1 footprint and for each tomographic bin. For each of these, we create a two-dimensional histogram of the persistence diagram with 100 × 100 bins. For Dgm0 our bins cover the S/N range [ − 3, 2]2, for Dgm1 the bins cover the S/N range [ − 1, 4]2. The upper limit of 4 in the S/N maps avoids issues with source-lens coupling as elaborated in Martinet et al. (2018). All persistence features that lie outside of this range are projected to the edge of the respective bin ranges. Afterwards, we convolve these histograms with a Gaussian kernel of scaling parameter t = 0.2 using two-dimensional FFTs7.
3.3. Data compression
To perform a Bayesian cosmological parameter inference, we compress the data provided by the persistence heatmaps. We explored several compression methods, which are discussed in Appendix A. In the end, we opted for an adaptation of our method developed in H+21; we iteratively build a data vector in the following way: As a first step, for each pixel x of a heatmap, we compute the mean squared difference between the single cosmologies of cosmo-SLICS and their mean, weighted by the inverse variance within the SLICS
This Δxweighted describes the cosmological information content of a pixel from the heatmap, as it quantifies how much its value varies between different cosmologies with respect to the expected standard deviation. As the first point of our data vector, we choose the one with the highest cosmological information content. Then we proceed to add more points in the following way: assuming we already have n entries in our data vector, we determine the next entry from the mean squared difference, weighted by the inverse sub-covariance matrix estimated from the SLICS. In other words: Let Δxi ≡ xcosmoSLICS, i − ⟨xcosmoSLICS⟩ be the difference between the data vector of the ith cosmology of cosmo-SLICS and the mean data vector of all cosmo-SLICS. For each pixel in the heatmap that is not already part of the data vector x, we create a new data vector x′ that contains this pixel, and then we compute
The pixel yielding the highest 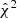 is then added to the data vector, and the procedure is repeated until we have reached the desired amount of data points. Again, this serves to maximise the cosmological information content of our data vector with respect to the expected covariance. To ensure that our data vector follows a Gaussian distribution, we only consider elements of the heatmaps that count at least 100 features (compare Fig. A.2). We found that 12 data points per tomographic bin combination yield good results, but the dependence on the number of data points is weak. An example of such a resulting data vector can be seen in Fig. 4.
is then added to the data vector, and the procedure is repeated until we have reached the desired amount of data points. Again, this serves to maximise the cosmological information content of our data vector with respect to the expected covariance. To ensure that our data vector follows a Gaussian distribution, we only consider elements of the heatmaps that count at least 100 features (compare Fig. A.2). We found that 12 data points per tomographic bin combination yield good results, but the dependence on the number of data points is weak. An example of such a resulting data vector can be seen in Fig. 4.
 |
Fig. 4. Data vector for the individual cosmologies from our Cosmology Training Set, colour-coded by their respective value of S8 (dotted lines) and the measured values in the DES-Y1 survey (black). For better visibility, the bottom panel shows the same data vector where all values are divided by the mean of our Covariance Training Set. |
While this method certainly does not capture all of the information residing in the heatmaps, this ‘χ2-maximiser’ manages to capture most information and is therefore competitive with the other data compression methods. A comparison is given in Appendix A.
3.4. Two-point statistics
The established methods to infer statistical properties of the matter and galaxy distribution concentrate on the second-order statistics such as the 2PCFs, their Fourier counterparts, the power spectra, or derived measures such as COSEBIs (Schneider et al. 2010; Asgari et al. 2020). The key advantage of these statistics over others is that, although they capture only the Gaussian information of the large-scale structure, they can be calculated analytically from the well-understood matter power spectrum P(k, z). Indeed, the lensing power spectrum between galaxies of tomographic bin i with redshift distribution ni(z) and those of tomographic bin j with nj(z) is modelled in the Limber approximation as
where χH is the co-moving distance to the horizon and W(χ) is the lensing efficiency defined as
Here, ![$ q(\chi)=n(z[\chi])\frac{{\text{d}}z[\chi]}{{\text{d}}\chi} $](/articles/aa/full_html/2022/11/aa43868-22/aa43868-22-eq25.gif) is the line of sight probability density of the galaxies, H0 the Hubble parameter and c the speed of light. From the projected lensing power spectrum, the cosmic shear correlation functions
is the line of sight probability density of the galaxies, H0 the Hubble parameter and c the speed of light. From the projected lensing power spectrum, the cosmic shear correlation functions 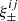 are computed as
are computed as
where J0, 4 are the Bessel functions of the first kind. To compute the theoretical two-point correlation functions we calculate the power spectrum P(k) using the public HALOFIT model (Takahashi et al. 2012).
We use the software TREECORR (Jarvis et al. 2004) to estimate the 2PCF 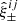 (ϑ) from the simulations and the DES-Y1 lensing data, computed as
(ϑ) from the simulations and the DES-Y1 lensing data, computed as
where the sums are over all galaxy pairs (a, b) in tomographic bins (i, j) that are inside the corresponding ϑ-bin. As in HD+21, we used 32 logarithmically spaced ϑ-bins in the range [0.5′,475′.5], although not all angular scales are used in the parameter estimation (see the following section).
3.5. Cosmological parameter estimation
As in H+21, we train a GPR emulator using data extracted from the 26 different cosmo-SLICS models to interpolate our data vector at arbitrary cosmological parameters within the training range. We refer the reader to H+21 and HD+21 for more details on the emulator. We assess its accuracy by performing a leave-one-out cross-validation: we remove one cosmology of the cosmo-SLICS from our training sample and let the GPR-emulator predict this cosmology, training on the other 25. We repeat this procedure for all 26 cosmologies and use the mean squared difference between predictions and truth as an estimate for the error of the emulator, which is typically well below the statistical error (compare Fig. 5). We then add this to the diagonal of our sample covariance matrix to account for uncertainties in the modelling.
 |
Fig. 5. Accuracy of the GPR emulator evaluated by a leave-one-out cross-validation, shown here for the case where the aperture mass maps are constructed from the concatenation of all four tomographic redshift bins (i.e. no tomography). The x axis depicts the data vector entry, and the y axis the relative difference between predicted and measured value. The 26 individual dotted lines correspond to one cosmology that is left out of the training set and then predicted, the solid black line is the mean of all dotted lines. The black dashed lines depict the standard deviation from the Covariance Training Set. |
An alternative method to estimate the uncertainty of the predictions is to use the error provided by the GPR emulator itself. We also tested this method and found that, while this method is a bit slower (since the inverse covariance matrix needs to be re-computed in every step of the MCMC), it provides comparable, albeit slightly tighter constraints than the first method. In the end, we opted for the more conservative choice of estimating the modelling uncertainties via cross-validation.
As in HD+21, we then integrate our GPR emulator into the COSMOSIS analysis pipeline (Zuntz et al. 2015) and infer the cosmological parameters by sampling the likelihood using the polychord sampling method (Handley et al. 2015), which constitutes a good compromise between speed and accuracy (Lemos et al. 2022). A few relatively minor changes to the COSMOSIS likelihood module allow for an easy and fast joint analysis of both persistent homology statistics and shear two-point correlation functions.
Finally, we estimate our sample covariance matrix from the 124 survey realisations of the Covariance Training Set. Specifically, we compute a matrix for each of the 10 different realisations of the shape noise and use the average over those 10 covariance matrices as our best estimate. Here, we randomly distribute the 124 lines of sight for the 19 regions to avoid over-estimating the sample variance (compare HD+21). Further, since the inverse of a simulation-based covariance matrix is generally biased (Hartlap et al. 2007), we mitigate this effect by adopting a multivariate t-distribution likelihood (Sellentin & Heavens 2016). The extracted covariance matrix can be seen in Fig. 6, the priors used for cosmological parameter estimation are listed in Table 1.
 |
Fig. 6. Correlation matrix for a joint analysis with both persistent homology and two-point correlation functions. |
4. Mitigating systematic effects
Our cosmological parameter analysis needs to account for systematic effects that are known to affect cosmic shear data. The most important ones for this work are intrinsic alignments of source galaxies, baryonic physics, multiplicative shear bias and uncertainties in the redshift estimation of galaxies (Mandelbaum 2018). On top of these, limits in the force resolution of the cosmo-SLICS might introduce a bias into our modelling, plus source clustering can produce systematic differences between the data and the simulations, in which the latter is absent. While we investigate the former, the latter has been shown in HD+21 to be largely subdominant in the aperture mass statistics measured in the DES-Y1 data and is therefore neglected here. In this section, we explain how these systematic effects affect our 2PCFs and persistent homology measurements and detail the mitigation strategies we chose to account for their impact.
4.1. 2PCF
We use the public modules in COSMOSIS to marginalise over the impact of intrinsic alignments. Following T+18, we model IA with the non-linear alignment model (Bridle & King 2007, hereafter referred to as the NLA model), which adds a contribution to the matter power spectrum that propagates into the lensing signal following Eqs. (8) and (10). More sophisticated IA models, including tidal torque terms (notably the Tidal Alignment and Tidal Torque model, or TATT Blazek et al. 2019) have been used recently in cosmic shear analyses, but there is no clear evidence that the data prefer such a model over the NLA (T+18, Secco et al. 2022). The NLA model can have multiple parameters (amplitude, redshift dependence, luminosity dependence, pivot scales, colour); however, we follow HD+21 and vary only the amplitude (AIA) and luminosity (α) parameters, considering no other dependencies. This is justified by the weak constraints that exist on them in the DES-Y1 data (compare T+18). The parameters AIA and α are allowed to vary in the range [−5.0, 5.0].
Following the fiducial DES-Y1 choices, the impact of baryon feedback is minimised by cutting out angular scales in the ξ± statistics where unmodelled baryonic physics with a strong AGN model8 could shift the data by more than 2%. We, therefore, exclude from our analysis the same small scales as those of T+18, which are different for ξ+ and ξ−, and further vary with redshift.
The shear inference is obtained with the METACALIBRATION method in this work, which has a small uncertainty that can be captured by a shape calibration factor Δm, which multiplies the observed ellipticities as ϵ1/2 → ϵ1/2(1 + Δm). As described in T+18, Δm is a nuisance parameter that we sample by a Gaussian distribution with a width of 0.023, centred on 0.012 when analysing the data and on zero when analysing simulations. COSMOSIS includes this nuisance on the two-point function model directly, namely 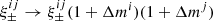 . The priors on m are listed in Table 1.
. The priors on m are listed in Table 1.
Photometric errors in the 2PCFs are mitigated by using the generic module within COSMOSIS, which shifts the ni(z) by small bias parameters Δzi and updates accordingly the lensing predictions. These bias parameters are sampled from Gaussian distributions with widths corresponding to the posterior DIR estimates of the mean redshift per tomographic bin ‘i’, also tabulated in Table 1.
4.2. Persistent homology
As mentioned in Sect. 2.2, we assess the impact of systematics on the topology of aperture mass maps by using the Systematics Training Set, which are numerical simulations specifically tailored for this exercise. Following HD+21, we neglect the cosmology scaling of these systematics and only evaluate their relative impact at the fiducial cosmology. We find that the overall impact of systematic effects is sufficiently well captured by a linear modelling strategy: for each systematic effect with respective nuisance parameter λ (i.e. AIA for intrinsic alignments, Δz for redshift uncertainties, Δm for multiplicative bias and bbar for baryons), we measure the impact xsys(λ) on the measured data vector from the associated Systematics Training Set and fit each point of the data vector with a straight line:
In particular, x(0)≡xnosys is the data vector which is not impacted by any systematic effects. For a given set of values of the nuisance parameters, we combine these different sources of uncertainty to model our systematics-infused data vector as:
While this certainly constitutes a simplified approach that does not capture potential cross-correlations between different systematic effects nor any cosmology dependence, we consider it sufficient at the current level of uncertainties (compare Fig. 7). To compute mIAAIA, the Intrinsic Alignments mocks are infused with AIA values of [−5.0, −2.0, −1.0, 0.5, 0.0, 0.5, 1.0, 2.0 and 5.0], however we set the redshift dependence to zero, given the weakness of the constraints on this parameter in the DES-Y1 data (see T+18). In the upper left panel of Fig. 7 we report the fractional effect on the signal and observe that positive IA suppresses the elements of the data vector. This is caused by the partial cancellation of the lensing signal by IA, which attenuates the contrasts in the aperture mass maps, which translates into a topological structure with fewer features. The figure also presents the results as modelled by the linear interpolation, which reproduces the nodes on which the training was performed to sufficient accuracy, indicating that our approach is adequate to model IA, at least for the range of AIA values tested here.
 |
Fig. 7. Impact of the main systematic effects on the data vector. For each systematic, we show the measured (solid line) and interpolated (dotted line) ratio of the systematic-infused data vector over a reference data vector. For simplicity, we only show the results for the combination of all four tomographic redshift bins. The black dashed lines correspond to the 1σ standard deviation estimated from the Covariance Training Set. |
The impact of shear calibration uncertainty is modelled by measuring the statistics for ellipticities modified with four values of Δm, namely −0.025, −0.0125, 0.0125, and 0.025, and once again fitting a straight line through each element of the homology data vector as a function of Δm. The results are presented in the upper right panel of Fig. 7, showing that within this range, shear calibration affects the statistics by less than one per cent except for two elements, which are affected by up to 4%.
Photometric uncertainties are modelled from the dedicated Systematics Training Set in which the n(z) in each tomographic bin has been shifted by 10 values Δzi, from which we are once again able to fit a linear response for each element of the data vector. In the case of cross-redshifts, the mean of all shifts is used to compute the derivative, as in HD+21. The lower right panel of Fig. 7 shows the impact on the data vector, which is sub-dominant compared to the IA. This is largely due to the tight priors on Δzi that we are able to achieve with the DIR method, as derived in Joudaki et al. (2020) and reported in Table 1.
The Magneticum simulations are used in a similar way to test the impact of baryonic feedback, with the main difference that we can only fit mbar on two points: the simulations with and without baryons (bbar = 1 and 0, respectively). We nevertheless apply the same methodology here, which allows us to interpolate between these two cases to mimic milder models (e.g., bbar = 0.5) and even to extrapolate and explore stronger feedback models (bbar > 1.0). The lower right panel of Fig. 7 shows that baryonic feedback with bbar = 1.0 has almost as much importance as an IA model with AIA = 1.0 and should therefore not be neglected in this analysis.
The last systematic effect that we include in this analysis is the impact of the force accuracy in the N-body simulations that are used in the modelling. We inspect the difference between the data vector measured from the high-accuracy mocks to that of the main Cosmology Training Sample at the fiducial cosmology and find that the overall impact of this effect is sub-dominant to the sample variance of the SLICS. Nevertheless, we measure the ratio of the high-resolution data vector over the fiducial one and apply it as a correction factor to re-calibrate our model in the analysis of observed data.
4.3. Mitigation strategy
We further estimate the impact of the different systematic effects on the cosmology inference by running likelihood analyses for data vectors that have been infused with one systematic effect while keeping these unmodelled. The results of these tests can be seen in Fig. 8. We observe that the baryons have a small impact on the inferred Ωm and can bias S8 by 1σ, assuming bbar = 1.0. Unmodelled IA (with AIA = 1.0) tend to bias both Ωm and S8 towards lower values; both photometric redshift uncertainties and multiplicative shear bias have a minor impact on the posterior constraints, given the tight priors available on Δz and Δm.
 |
Fig. 8. Impact of unmodelled systematic biases on the posterior of a likelihood analysis with heatmaps. In all cases, we do not marginalise over any systematic effects. The target data vector is then infused with one systematic bias, and we run a likelihood analysis for this infused data vector. For comparison, we show the constraints on a data vector that is not infused by systematics (grey). Note that the values of the dz shifts are given in units of the standard deviation of the dz prior (compare Table 1). |
We finally investigate how marginalisation over the different systematic biases changes the posterior contours in our likelihood analysis in Fig. 9. We find that marginalisation over baryonic effects and intrinsic alignments both decrease the constraining power on Ωm and S8 by about 25%, whereas the marginalisation over multiplicative shear biases and photometric redshift uncertainties have a negligible impact. Both analyses suggest that the impact of systematic effects on persistent homology statistics is noticeable but not severe and that our marginalisation strategies work as expected.
 |
Fig. 9. Effects of marginalising over different systematic effects. In all cases, we perform a likelihood analysis on mock data, marginalising over one systematic effect. For comparison, we show the constraints we achieve when we do not marginalise over any systematics (grey). The case where we marginalise over all systematics corresponds to the blue contours in Fig. 10. |
5. Validation
In this work, we want to investigate whether a likelihood analysis of tomographic cosmic shear data with persistent homology is feasible and whether a joint analysis with two-point statistics yields more information than an analysis that solely utilises two-point statistics. For this purpose, we perform three likelihood analyses of the same mock data extracted from the Covariance Training Set: one solely with two-point correlation functions that we model within the COSMOSIS pipeline, one solely with our persistent homology method, and finally the combined analysis.
As can be seen in Fig. 10 and Table 2, the persistent homology analysis is already able to constrain S8 better than the two-point analysis (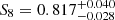 for persistent homology versus S8 = 0.772 ± 0.043 for two-point statistics). However, a joint analysis offers several additional benefits. While two-point statistics are able to constrain the parameter to
for persistent homology versus S8 = 0.772 ± 0.043 for two-point statistics). However, a joint analysis offers several additional benefits. While two-point statistics are able to constrain the parameter to 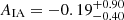 , persistent homology yields
, persistent homology yields 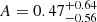 and a joint analysis is able to reduce the error bars to AIA = 0.29 ± 0.36. Apart from tighter constraints on S8 (
and a joint analysis is able to reduce the error bars to AIA = 0.29 ± 0.36. Apart from tighter constraints on S8 (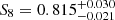 for a joint analysis), a joint analysis also yields competitive lower limits on the equation-of-state parameter of dark energy (w0 > −1.14 at 68% confidence), while two-point statistics are unable to place any constraints on this parameter, with our choice of sampling method. Most importantly, all cosmological and nuisance parameters are recovered within 1σ. We thus conclude that our analysis pipeline has been validated and move on towards a cosmological parameter analysis of real data.
for a joint analysis), a joint analysis also yields competitive lower limits on the equation-of-state parameter of dark energy (w0 > −1.14 at 68% confidence), while two-point statistics are unable to place any constraints on this parameter, with our choice of sampling method. Most importantly, all cosmological and nuisance parameters are recovered within 1σ. We thus conclude that our analysis pipeline has been validated and move on towards a cosmological parameter analysis of real data.
 |
Fig. 10. Results of likelihood analyses for DES-Y1 mock data. We show the results for two-point statistics (red), persistent homology (blue), and for the joint analysis (grey, filled). The dotted lines show the prior ranges, the solid black lines visualise the true value of each parameter, and the black crosses denote the nodes of our Cosmology Training Set. The complete results can be seen in Fig. C.2, the marginalised posterior constraints can be seen in Table 2. |
6. Results
Having validated our analysis pipeline, we now use it to perform our cosmological parameter analyses using the DES-Y1 data. In order to do that, we split the source galaxy catalogue into the same 19 tiles as our mock data and compute the persistence statistics as well as the two-point correlation functions for each tile individually.
The results can be seen in Fig. 11. We observe that neither persistent homology nor two-point correlation functions are able to place meaningful constraints on the equation of state parameter for dark energy, w0. For the matter clustering parameter S8, the constraints from persistent homology (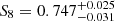 ) are tighter than, but fully consistent with, the constraints from two-point correlation functions (
) are tighter than, but fully consistent with, the constraints from two-point correlation functions (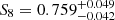 ). The same goes for the amplitude of galaxy intrinsic alignments (A = 1.54 ± 0.52 for persistent homology and
). The same goes for the amplitude of galaxy intrinsic alignments (A = 1.54 ± 0.52 for persistent homology and 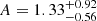 for two-point correlation functions). In particular, this implies that persistent homology detects the intrinsic alignment effect roughly at the 3σ level. Interestingly, the constraints for the matter density parameters are not consistent (
for two-point correlation functions). In particular, this implies that persistent homology detects the intrinsic alignment effect roughly at the 3σ level. Interestingly, the constraints for the matter density parameters are not consistent (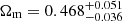 for persistent homology and
for persistent homology and 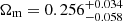 for two-point correlation functions). Hamana et al. (2020) observed a similar trend when observing data from the HSC: While a real- and Fourier-space analysis yield perfectly consistent values for S8, a slight tension between the Ωm constraints can be observed in their Fig. 15. We observe a much larger tension that prevents us from performing a joint parameter analysis, which would tighten the S8-constraints considerably. We discuss this in more detail in Appendix B, where we show that such a tension arises in about 0.5% of all cases due to a mere statistical fluctuation. A visual inspection of the data vector suggests that this tension might be caused by the highest signal-to-noise peaks (see Appendix B), but when excluding these in a parameter analysis, we find only a marginal improvement of the tension that is likely just due to the loss of constraining power. We note that the upper limit in the constraints for Ωm from persistent homology barely passes our criterion not to be dominated by the prior (compare Table 2). This means that a wider prior for Ωm would likely lead to a higher upper limit in the constraints. The lower limit should not be strongly affected by the prior, as the likelihood of Ωm already started falling for Ωm > 0.5.
for two-point correlation functions). Hamana et al. (2020) observed a similar trend when observing data from the HSC: While a real- and Fourier-space analysis yield perfectly consistent values for S8, a slight tension between the Ωm constraints can be observed in their Fig. 15. We observe a much larger tension that prevents us from performing a joint parameter analysis, which would tighten the S8-constraints considerably. We discuss this in more detail in Appendix B, where we show that such a tension arises in about 0.5% of all cases due to a mere statistical fluctuation. A visual inspection of the data vector suggests that this tension might be caused by the highest signal-to-noise peaks (see Appendix B), but when excluding these in a parameter analysis, we find only a marginal improvement of the tension that is likely just due to the loss of constraining power. We note that the upper limit in the constraints for Ωm from persistent homology barely passes our criterion not to be dominated by the prior (compare Table 2). This means that a wider prior for Ωm would likely lead to a higher upper limit in the constraints. The lower limit should not be strongly affected by the prior, as the likelihood of Ωm already started falling for Ωm > 0.5.
 |
Fig. 11. Results of our likelihood analyses for the DES-Y1 survey. We show the results for two-point statistics (red), persistent homology (blue) and report as well the constraints achieved by HD+21 with peak count statistics (black). The dotted lines denote the prior ranges, the black crosses denote the nodes of our Cosmology Training Set. The complete results including nuisance parameters can be seen in Fig. C.3, while the marginalised posterior constraints can be seen in Table 2. |
Comparing our results with the ones from peak count statistics, where HD+21 measured 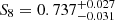 on the same data set, we observe remarkably consistent results (compare Fig. 11). The trend towards high values of Ωm can also be observed in HD+21 (see in particular Fig. 17 and 18 in HD+21). This is particularly interesting since their constraints have been achieved using a pipeline that is fully independent of ours, utilising a different statistic on signal-to-noise maps of aperture masses constructed with an independent code, albeit based on the same set of N-body simulations. Furthermore, we can see that the constraints achieved from persistent homology outperform the ones from peak statistics, albeit not by much. This improvement is still significant since, contrary to HD+21, we include an error estimate for the emulator and a marginalisation over intrinsic alignments and baryonic effects, which decrease the constraining power of our analysis pipeline.
on the same data set, we observe remarkably consistent results (compare Fig. 11). The trend towards high values of Ωm can also be observed in HD+21 (see in particular Fig. 17 and 18 in HD+21). This is particularly interesting since their constraints have been achieved using a pipeline that is fully independent of ours, utilising a different statistic on signal-to-noise maps of aperture masses constructed with an independent code, albeit based on the same set of N-body simulations. Furthermore, we can see that the constraints achieved from persistent homology outperform the ones from peak statistics, albeit not by much. This improvement is still significant since, contrary to HD+21, we include an error estimate for the emulator and a marginalisation over intrinsic alignments and baryonic effects, which decrease the constraining power of our analysis pipeline.
Comparing our results to T+18, we see that our results from two-point statistics are a bit different (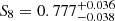 in T+18 and
in T+18 and 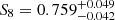 here), which is driven mainly by the different redshift distribution estimates (as shown in Joudaki et al. 2020). Considering the intrinsic alignment effect, we achieve consistent, but tighter constraints (compare the NLA case of Fig. 16 in T+18). Regarding the tension we measure for Ωm, T+18 report
here), which is driven mainly by the different redshift distribution estimates (as shown in Joudaki et al. 2020). Considering the intrinsic alignment effect, we achieve consistent, but tighter constraints (compare the NLA case of Fig. 16 in T+18). Regarding the tension we measure for Ωm, T+18 report 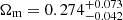 , which is fully consistent with our results from two-point correlation functions and also disagrees with our constraints from persistent homology.
, which is fully consistent with our results from two-point correlation functions and also disagrees with our constraints from persistent homology.
7. Discussion
In this work, we carried out a likelihood analysis on tomographic cosmic shear data using persistent homology, including the marginalisation over systematic effects, and have shown from simulated data that the posterior constraints can be significantly improved in a joint analysis. While this holds true especially for the intrinsic alignment parameter AIA and the equation of state of dark energy w0, the constraints on the matter clustering parameter S8 also improve substantially.
For our analysis, we had to make a number of choices, including which persistence statistic to use, which smoothing scale to apply to the heatmaps, and which data compression method to utilise. We have noticed that the posterior constraints achieved by a likelihood analysis do not strongly depend on any of these choices, as can be seen for example in Fig. C.1. While further fine-tuning could probably slightly improve the constraining power of our analysis, we believe that this overall stability with respect to different analysis choices provides strong evidence that we have reached the true sensitivity of persistence statistics to cosmology.
When applying our analysis pipeline to real data, we find that high values of the matter density parameter Ωm are preferred, as observed in HD+21, where a fully independent pipeline and a different summary statistic were utilised. The remarkable similarity between these results suggests that peak count statistics and persistent homology quantify similar aspects of the large-scale structure distribution. The fact that both methods favour larger values of Ωm may point to a statistical fluctuation in the DES-Y1 data or an unknown effect modifying the topological structure of the matter distribution. We investigate this in Appendix B and show that the chance of such a tension arising due to a statistical fluctuation in the data is about 0.5%. We also note that our underlying training data, the shear catalogues of the Cosmology Training Sets, are the same as the ones used in HD+21, so this bias might also point towards a statistical fluctuation in this training set. A larger simulation suite would be able to shine a light on this, even though this seems unlikely given the fact that the tension does not exist when validating on simulated data (see Fig. 10). Our analysis of the tension in Appendix B, a visual inspection of the data suggests that the tension might be at least partly driven by the high signal-to-noise peaks in the aperture mass maps, which carry both the most cosmological signal and are most affected by systematics. However, excluding those peaks did not remove the tension, which means that it can certainly not be fully explained by these high signal-to-noise peaks.
We performed several consistency checks to investigate whether the tension is artificially created by our analysis setup: We tried a parameter inference with two-point correlation functions by measuring them in the Cosmology Training Set and emulating them via the same pipeline that we used for persistent homology. Furthermore, we tried removing some nodes from the Cosmology Training Set and applying different methods of data compression. The results were stable under all these tests, suggesting that the simulation-based inference is not the driver of the tension we measure for Ωm.
Another possible explanation is that the DES-Y1 data include an effect that we have not accounted for. This might be an unknown systematic or a sign of new physics. For example, 2PCF are not sensitive to primordial non-Gaussianities, whereas persistent homology is (Biagetti et al. 2022).
Overall our constraints on S8 are consistent with previous works (see Fig. 12); the largest discrepancy is between our analysis and the one from T+18, which is mainly driven by a different method of estimating the source redshift distribution. When comparing our results to similar works with peak count statistics, the constraining power of persistent homology appears to be slightly better. In addition, there are a few key differences between our work and HD+21. Firstly, while HD+21 apply a boost factor to account for baryons, we marginalise over continuous baryonic effects (and intrinsic alignments) with a wide prior, which is inflating our constraints. Secondly, we account for the emulator uncertainty as described in Sect. 3.5; this is not done in HD+21. Comparing with H+21, we see that this emulator uncertainty also inflates cosmological parameter constraints, indicating that the contours reported in HD+21 may be slightly too small. This effect is amplified by the fact that we were only able to train our emulator on 9 lines of sight per cosmology, compared to the 50 lines of sight in H+21. Lastly, and most importantly, we have shown in H+21 that persistent homology excels in a high signal-to-noise range, which is not accessible in a tomographic analysis of current-generation surveys. We thus expect this method to out-perform several other higher-order statistics in next-generation surveys.
 |
Fig. 12. Comparison of the constraints on the matter clustering parameter S8 from DES-Y1 survey data in a wCDM cosmology with fixed neutrino mass. |
DES-Y1 catalogues: des.ncsa.illinois.edu/releases/dr1.
This method relies on the direct calibration of the n(z) from a sub-sample of DES-Y1 galaxies for which external spectroscopic data are available. See Lima et al. (2008) for more details.
We use the Cubical Complexes module of the public software GUDHI (Dlotko 2020).
The power spectrum of the OWLS AGN model (van Daalen et al. 2014) is used for this assessment.
Acknowledgments
S.H acknowledges support from the German Research Foundation (DFG SCHN 342/13), the International Max-Planck Research School (IMPRS) and the German Academic Scholarship Foundation. S.U. acknowledges support from the Max Planck Society and the Alexander von Humboldt Foundation in the framework of the Max Planck-Humboldt Research Award endowed by the Federal Ministry of Education and Research. Joachim Harnois-Déraps acknowledges support from an STFC Ernest Rutherford Fellowship (project reference ST/S004858/1). Computations for the N-body simulations were enabled by Compute Ontario (www.computeontario.ca), Digital Research Alliance of Canada (alliancecan.ca). The SLICS numerical simulations can be found at http://slics.roe.ac.uk/, while the cosmo-SLICS can be made available upon request. T.C. is supported by the INFN INDARK PD51 grant and by the fare Miur grant ‘ClustersXEuclid’ R165SBKTMA. K.D. acknowledges support by the COMPLEX project from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program grant agreement ERC-2019-AdG 882679 the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2094 – 390783311 and by the DFG project nr. 490702358. The Magneticum Simulations were carried out at the Leibniz Supercomputer Center (LRZ) under the project pr86re and pr83li. We thank the anonymous referee for insightful comments given on a previous version of this article. Author contributions: All authors contributed to the development and writing of this paper. After the lead author, they are separated into two groups, both listed alphabetically. In the first group, B.B. developed the necessary mathematical background, P.B. oversaw the measurement and validation of two-point statistics, J.H.D. provided the suites of numerical simulation tailored to the measurement and S.U. developed the integration into COSMOSIS. In the second group, T.C., K.D. and N.M. were responsible for running and post-processing the Magneticum simulations, extracting the mass maps and computing the lensing statistics.
References
- Abbott, T. M. C., Abdalla, F. B., Allam, S., et al. 2018, ApJS, 239, 18 [Google Scholar]
- Abbott, T. M. C., Aguena, M., Alarcon, A., et al. 2022, Phys. Rev. D, 105, 023520 [CrossRef] [Google Scholar]
- Aihara, H., Arimoto, N., Armstrong, R., et al. 2018, PASJ, 70, S4 [NASA ADS] [Google Scholar]
- Asgari, M., & Schneider, P. 2015, A&A, 578, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asgari, M., Tröster, T., Heymans, C., et al. 2020, A&A, 634, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asgari, M., Lin, C.-A., Joachimi, B., et al. 2021, A&A, 645, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bartelmann, M., & Schneider, P. 2001, Phys. Rep., 340, 291 [Google Scholar]
- Benítez, N. 2000, ApJ, 536, 571 [Google Scholar]
- Bergé, J., Amara, A., & Réfrégier, A. 2010, ApJ, 712, 992 [CrossRef] [Google Scholar]
- Biagetti, M., Cole, A., & Shiu, G. 2021, JCAP, 04, 061 [CrossRef] [Google Scholar]
- Biagetti, M., Calles, J., Castiblanco, L., Cole, A., & Noreña, J. 2022, JCAP, 10, 002 [CrossRef] [Google Scholar]
- Biffi, V., Dolag, K., & Böhringer, H. 2013, MNRAS, 428, 1395 [Google Scholar]
- Blazek, J. A., MacCrann, N., Troxel, M. A., & Fang, X. 2019, Phys. Rev. D, 100, 103506 [NASA ADS] [CrossRef] [Google Scholar]
- Bocquet, S., Saro, A., Dolag, K., & Mohr, J. J. 2016, MNRAS, 456, 2361 [Google Scholar]
- Bridle, S., & King, L. 2007, New J. Phys., 9, 444 [Google Scholar]
- Bubenik, P. 2015, J. Mach. Learn. Res., 16, 77 [Google Scholar]
- Burger, P., Friedrich, O., Harnois-Déraps, J., & Schneider, P. 2022, A&A, 661, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castro, T., Quartin, M., Giocoli, C., Borgani, S., & Dolag, K. 2018, MNRAS, 478, 1305 [Google Scholar]
- Castro, T., Borgani, S., Dolag, K., et al. 2021, MNRAS, 500, 2316 [Google Scholar]
- Chazal, F., & Michel, B. 2021, Front. Artif. Intell., 4, 108 [Google Scholar]
- Cheng, S., Ting, Y.-S., Ménard, B., & Bruna, J. 2020, MNRAS, 499, 5902 [Google Scholar]
- Chittajallu, D. R., Siekierski, N., Lee, S., et al. 2018, in IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), IEEE, 232 [Google Scholar]
- Coulton, W. R., Liu, J., McCarthy, I. G., & Osato, K. 2020, MNRAS, 495, 2531 [Google Scholar]
- D’Agostino, R. B. 1971, Biometrika, 58, 341 [CrossRef] [Google Scholar]
- D’Agostino, R., & Pearson, E. S. 1973, Biometrika, 60, 613 [Google Scholar]
- de Jong, J. T. A., Verdoes Kleijn, G. A., Kuijken, K. H., & Valentijn, E. A. 2013, Exp. Astron., 35, 25 [Google Scholar]
- Dlotko, P. 2020, GUDHI User and Reference Manual, 3.1.1 edn (GUDHI Editorial Board) [Google Scholar]
- Dolag, K. 2015, in IAU General Assembly, 29, 2250156 [Google Scholar]
- Feldbrugge, J., van Engelen, M., van de Weygaert, R., Pranav, P., & Vegter, G. 2019, JCAP, 2019, 052 [CrossRef] [Google Scholar]
- Ferreira, T., Zhang, T., Chen, N., Dodelson, S., Dark Energy Science, L. S. S. T., & Collaboration., 2021, Phys. Rev. D, 103, 103535 [NASA ADS] [CrossRef] [Google Scholar]
- Flaugher, B. 2005, Int. J. Mod. Phys. A, 20, 3121 [Google Scholar]
- Flaugher, B., Diehl, H. T., Honscheid, K., et al. 2015, AJ, 150, 150 [Google Scholar]
- Gatti, M., Jain, B., Chang, C., et al. 2021, PRD, accepted [arXiv:2110.10141] [Google Scholar]
- Gruen, D., & Brimioulle, F. 2017, MNRAS, 468, 769 [Google Scholar]
- Halder, A., Friedrich, O., Seitz, S., & Varga, T. N. 2021, MNRAS, 506, 2780 [CrossRef] [Google Scholar]
- Hamana, T., Shirasaki, M., Miyazaki, S., et al. 2020, PASJ, 72, 16 [Google Scholar]
- Handley, W. J., Hobson, M. P., & Lasenby, A. N. 2015, MNRAS, 453, 4384 [Google Scholar]
- Harnois-Déraps, J., Pen, U.-L., Iliev, I. T., et al. 2013, MNRAS, 436, 540 [Google Scholar]
- Harnois-Déraps, J., & van Waerbeke, L. 2015, MNRAS, 450, 2857 [Google Scholar]
- Harnois-Déraps, J., Giblin, B., & Joachimi, B. 2019, A&A, 631, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harnois-Déraps, J., Martinet, N., Castro, T., et al. 2021, MNRAS, 506, 1623 [CrossRef] [Google Scholar]
- Harnois-Déraps, J., Martinet, N., & Reischke, R. 2022, MNRAS, 509, 3868 [Google Scholar]
- Hartlap, J., Simon, P., & Schneider, P. 2007, A&A, 464, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heavens, A. F., Jimenez, R., & Lahav, O. 2000, MNRAS, 317, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Heavens, A. F., Sellentin, E., de Mijolla, D., & Vianello, A. 2017, MNRAS, 472, 4244 [NASA ADS] [CrossRef] [Google Scholar]
- Hetterscheidt, M., Erben, T., Schneider, P., et al. 2005, A&A, 442, 43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heydenreich, S., Brück, B., & Harnois-Déraps, J. 2021, A&A, 648, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heymans, C., Tröster, T., Asgari, M., et al. 2021, A&A, 646, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hikage, C., Oguri, M., Hamana, T., et al. 2019, PASJ, 71, 43 [Google Scholar]
- Hildebrandt, H., Viola, M., Heymans, C., et al. 2017, MNRAS, 465, 1454 [Google Scholar]
- Hildebrandt, H., Köhlinger, F., van den Busch, J. L., et al. 2020, A&A, 633, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirschmann, M., Dolag, K., Saro, A., et al. 2014, MNRAS, 442, 2304 [Google Scholar]
- Hoyle, B., Gruen, D., Bernstein, G. M., et al. 2018, MNRAS, 478, 592 [Google Scholar]
- Ivezic, Z., Axelrod, T., Brandt, W. N., et al. 2008, Serb. Astron. J., 176, 1 [Google Scholar]
- Jarvis, M., Bernstein, G., & Jain, B. 2004, MNRAS, 352, 338 [Google Scholar]
- Jeffrey, N., Alsing, J., & Lanusse, F. 2021, MNRAS, 501, 954 [Google Scholar]
- Joachimi, B., Cacciato, M., Kitching, T. D., et al. 2015, Space Sci. Rev., 193, 1 [Google Scholar]
- Joudaki, S., Mead, A., Blake, C., et al. 2017, MNRAS, 471, 1259 [NASA ADS] [CrossRef] [Google Scholar]
- Joudaki, S., Hildebrandt, H., Traykova, D., et al. 2020, A&A, 638, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kacprzak, T., Kirk, D., Friedrich, O., et al. 2016, MNRAS, 463, 3653 [Google Scholar]
- Kimura, Y., & Imai, K. 2017, Adv. Space Res., 60, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Kono, K. T., Takeuchi, T. T., Cooray, S., Nishizawa, A. J., & Murakami, K. 2020, ArXiv e-prints [arXiv:2006.02905] [Google Scholar]
- Kovacev-Nikolic, V., Bubenik, P., Nikolić, D., & Heo, G. 2016, Stat. Appl. Genet. Mol. Biol., 15, 19 [CrossRef] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Lemos, P., Weaverdyck, N., Rollins, R. P., et al. 2022, ArXiv e-prints [arXiv:2202.08233] [Google Scholar]
- Lima, M., Cunha, C. E., Oyaizu, H., et al. 2008, MNRAS, 390, 118 [Google Scholar]
- Mandelbaum, R. 2018, ARA&A, 56, 393 [Google Scholar]
- Martinet, N., Schneider, P., Hildebrandt, H., et al. 2018, MNRAS, 474, 712 [Google Scholar]
- Martinet, N., Harnois-Déraps, J., Jullo, E., & Schneider, P. 2021a, A&A, 646, A62 [EDP Sciences] [Google Scholar]
- Martinet, N., Castro, T., Harnois-Déraps, J., et al. 2021b, A&A, 648, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCarthy, I. G., Schaye, J., Bird, S., & Le Brun, A. M. C. 2017, MNRAS, 465, 2936 [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [Google Scholar]
- Otter, N., Porter, M. A., Tillmann, U., Grindrod, P., & Harrington, H. A. 2017, EPJ Date Science, 6, 17 [CrossRef] [Google Scholar]
- Oudot, S. Y. 2015, in Persistence Theory: from Quiver Representations to Data Analysis, (Providence, RI: American Mathematical Society), Math. Surv. Monogr., 209 [CrossRef] [Google Scholar]
- Parroni, C., Cardone, V. F., Maoli, R., & Scaramella, R. 2020, A&A, 633, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petri, A., Liu, J., Haiman, Z., et al. 2015, Phys. Rev. D, 91, 103511a [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Porqueres, N., Heavens, A., Mortlock, D., & Lavaux, G. 2021, MNRAS, 502, 3035 [NASA ADS] [CrossRef] [Google Scholar]
- Porqueres, N., Heavens, A., Mortlock, D., & Lavaux, G. 2022, MNRAS, 509, 3194 [Google Scholar]
- Pranav, P. 2021, ArXiv e-prints [arXiv:2109.08721] [Google Scholar]
- Pranav, P., Edelsbrunner, H., van de Weygaert, R., et al. 2017, MNRAS, 465, 4281 [Google Scholar]
- Pun, C. S., Xia, K., & Lee, S. X. 2018, ArXiv e-prints [arXiv:1811.00252v1] [Google Scholar]
- Pyne, S., & Joachimi, B. 2021, MNRAS, 503, 2300 [NASA ADS] [CrossRef] [Google Scholar]
- Reininghaus, J., Huber, S., Bauer, U., & Kwitt, R. 2015, in Proceedings of the IEEE conference on computer vision and pattern recognition, 4741 [Google Scholar]
- Remus, R.-S., Dolag, K., & Hoffmann, T. 2017, Galaxies, 5, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Saro, A., Liu, J., Mohr, J. J., et al. 2014, MNRAS, 440, 2610 [Google Scholar]
- Schirmer, M., Erben, T., Hetterscheidt, M., & Schneider, P. 2007, A&A, 462, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, P. 1996, MNRAS, 283, 837 [Google Scholar]
- Schneider, P., Eifler, T., & Krause, E. 2010, A&A, 520, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Secco, L. F., Samuroff, S., Krause, E., et al. 2022, Phys. Rev. D, 105, 023515 [NASA ADS] [CrossRef] [Google Scholar]
- Sellentin, E., & Heavens, A. F. 2016, MNRAS, 456, L132 [Google Scholar]
- Semboloni, E., Hoekstra, H., Schaye, J., van Daalen, M. P., & McCarthy, I. G. 2011, MNRAS, 417, 2020 [Google Scholar]
- Sheldon, E. S., & Huff, E. M. 2017, ApJ, 841, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Shirasaki, M., & Yoshida, N. 2014, ApJ, 786, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Sousbie, T. 2011, MNRAS, 414, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D., Gehrels, N., Breckinridge, J., et al. 2013, ArXiv e-prints [arXiv:1305.5422] [Google Scholar]
- Steinborn, L. K., Dolag, K., Hirschmann, M., Prieto, M. A., & Remus, R.-S. 2015, MNRAS, 448, 1504 [Google Scholar]
- Steinborn, L. K., Dolag, K., Comerford, J. M., et al. 2016, MNRAS, 458, 1013 [Google Scholar]
- Takahashi, R., Sato, M., Nishimichi, T., Taruya, A., & Oguri, M. 2012, ApJ, 761, 152 [Google Scholar]
- Teklu, A. F., Remus, R.-S., Dolag, K., et al. 2015, ApJ, 812, 29 [Google Scholar]
- Troxel, M. A., MacCrann, N., Zuntz, J., et al. 2018, Phys. Rev. D, 98, 043528 [Google Scholar]
- Uzeirbegovic, E., Geach, J. E., & Kaviraj, S. 2020, MNRAS, 498, 4021 [CrossRef] [Google Scholar]
- van Daalen, M. P., Schaye, J., McCarthy, I. G., Booth, C. M., & Dalla Vecchia, C. 2014, MNRAS, 440, 2997 [NASA ADS] [CrossRef] [Google Scholar]
- van de Weygaert, R., Vegter, G., Edelsbrunner, H., et al. 2013, ArXiv e-prints [arXiv:1306.3640] [Google Scholar]
- Wasserman, L. 2018, Ann. Rev. Stat. Appl., 5, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, X., Cisewski-Kehe, J., Green, S. B., & Nagai, D. 2019, Astron. Comput., 27, 34 [Google Scholar]
- Zuntz, J., Paterno, M., Jennings, E., et al. 2015, Astron. Comput., 12, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Zürcher, D., Fluri, J., Sgier, R., Kacprzak, T., & Refregier, A. 2021, JCAP, 2021, 028 [Google Scholar]
Appendix A: Data compression of heatmaps
As the raw heatmaps contain 10100 entries per combination of tomographic redshift bins, a direct cosmological parameter analysis with these maps is currently impossible. We, therefore, need to explore different methods of compressing the raw data.
Our first approach to data compression is a principal component analysis (PCA). This rather simple method is highly efficient at reducing complex data to only a few manageable dimensions (see e.g. Uzeirbegovic et al. 2020). For each combination of tomographic redshift bins, we apply a PCA to the heatmap extracted from all 19 regions. We see that the PCA correctly identifies that the differences between the S/N maps of the different cosmo-SLICS are driven by the changes of the cosmological parameters Ωm and S8.
A PCA is still an incredibly useful tool to not only extract cosmological information from a data vector but also to understand the behaviour of the data itself better. For example, Fig. A.1 shows that the first principal component is almost exactly antiproportional to S8, whereas the second principal component is proportional to Ωm. Comparing these findings with Fig. A.3, we see that a high value of Ωm leads to a large number of features in Dgm1 (peaks) being born and dying between signal-to-noise values of 1 and 2, whereas a low value of Ωm leads to more features in Dgm1 being born and dying between S/N values of −0.5 and 0.5. A similar analysis for the first principal components yields the expected conclusion that a higher value of S8 leads to more peaks being born and dying at higher S/N values and more voids being born and dying at lower S/N values. One disadvantage of PCA is the fact that it is not straightforward to include the internal covariance of the data vector: While the PCA might detect huge differences between two different cosmo-SLICS simulations, these might just be caused by the fact that this specific part of the data vector is particularly noisy, and not by differences in the cosmological signal.
 |
Fig. A.1. Cosmology dependence of the first four principal components. Each point in the scatter plot represents one of the 26 cosmologies of the cosmo-SLICS. In the top row, the x and y coordinates correspond to the value of the first two principal components; in the bottom row, they correspond to the values of the third and fourth principal components. In the left column, the colours represent the value of Ωm of the respective cosmo-SLICS simulation; in the right column, they denote the value of S8. |
 |
Fig. A.2. Test results for the final data-vector’s Gaussianity. For each of the 180 data vector entries, we take the set of 10 × 124 measurements in the Covariance Training Sample and test the null hypothesis that this sample was drawn from a normal distribution using the measured skewness and kurtosis (D’Agostino 1971; D’Agostino & Pearson 1973). We then plot a histogram of the corresponding p-values (blue). If each entry of the data vector is Gaussian, then the distribution of p-values is uniform. For comparison, we show the results of the same test with a data vector that contains only points with about 10 features (orange). While the blue histogram may show small deviations from a uniform distribution (there appears to be a downward slope towards higher p-values), we believe that the assumption of a normal distribution is reasonable. |
 |
Fig. A.3. First four (normalised) principal components of the heatmaps in a principal component analysis. |
A more sophisticated method of data compression is the Massively Optimized Parameter Estimation and Data compression (MOPED, Heavens et al. 2000, 2017; Ferreira et al. 2021). Assuming a Gaussian likelihood, Gaussian posterior distributions and a constant covariance matrix C, this compression method preserves the entirety of the Fisher information to Nparam dimensions, where Nparam is the number of cosmological (and nuisance) parameters present in the inference. However, this method uses the Fisher formalism, and thus knowledge of the inverse covariance matrix C−1 is required. As our uncompressed data vector contains 151 500 entries and we can only estimate C with about 103 sets of simulations, the matrix is singular and thus not invertible (Hartlap et al. 2007). We, therefore, opted for sub-sampling our data vector and performing a MOPED compression for each individual combination of tomographic redshift bins, but doing this we neglected the information contained in the cross-correlation between different combinations of redshift bins, yielding parameter constraints that were not competitive with the ones from other data compression methods.
While MOPED is an elegant method to compress a data vector to the absolute minimum of required dimensions, this also means that all additional information that was not part of this data compression gets lost. In particular, imperfect knowledge of the covariance matrix and noisy derivatives heavily affect the constraining power of MOPED. Asgari & Schneider (2015) analysed this loss of information and developed a method that is more stable with respect to changes in the covariance matrix and derivatives and offers more constraining power in the case of non-linear parameter degeneracies (like the one between Ωm and σ8).
All things considered, all data compression methods manage to extract a comparable amount of information out of the raw data vector (see Fig. C.1). We thus opt for the χ2-maximiser method as the data vector obtained from this method is easiest to interpret.
Appendix B: On the observed Ωm tension in the analysis of DES-Y1
When analysing DES-Y1 data, we observe a 3.2σ tension between the values of Ωm estimated from 2PCF and persistent homology. In principle, there are several possible scenarios that can cause this tension. Our validation tests show that this is unlikely to be caused by a bug in the pipeline. A second possibility is that this is caused by a statistical fluctuation in the data. The third and most interesting scenario would be the presence of something unknown (and thus unaccounted for) in the DES-Y1 data. This could either be a systematic effect that we have not properly taken into account or a sign of deviations from the wCDM cosmological model that affects the topological structure of the data, but not its two-point statistics. For example, we know that persistent homology is very sensitive to primordial non-Gaussianities in the large-scale structure (Biagetti et al. 2022), which can not be detected by two-point statistics.
B.1. Investigating the severity of the tension
The fact that we achieve extraordinarily consistent results with HD+21 using a fully independent measurement and inference pipeline points to the conclusion that this tension is not caused by a bug in the pipeline. To investigate the probability of a statistical fluctuation causing this effect, we run our inference pipeline for both 2PCF and persistent homology on 100 individual lines of sight of the Covariance Training Sample. For each individual line of sight, we then estimate the tension between 2PCF and persistent homology on each cosmological parameter. The results are shown in Fig. B.1. We observe that persistent homology seems to favour higher values of Ωm and lower values of σ8 than 2PCF, while S8 remains relatively unbiased. We assume that these tensions follow a normal distribution and compute its mean and variance, constructing a Gaussian fit to the values. According to this analysis, the chance that the observed bias in Ωm is due to a statistical fluctuation is at 0.5% (2.6% for σ8), which is still unlikely, but not as unlikely as the initial 3.2σ tension we observed suggests. Recall that no tension is observed when running our pipeline on the mock data vector constructed from all simulations of the Covariance Training Set, which is about 12× larger, suggesting that the observed tension results from statistical fluctuations that are averaged down in our validation test.
 |
Fig. B.1. Histogram of the tensions in cosmological parameters between 2PCF and persistent homology measured on 100 individual lines of sight in the Covariance Training Set (blue) and a Gaussian fit to these values (orange). The actual tension we measured in DES-Y1 is shown by the dashed black line. No tension is observed when running our pipeline on the mock data vector constructed from all simulations of the Covariance Training Set, which is about 12× larger. |
This effect certainly warrants further investigation. If something similar shows up in an analysis of KiDS-1000 (Harnois-Déraps et al. in prep., Heydenreich et al. in prep.), an investigation into potential causes for a bias in Ωm becomes highly warranted. If, however, that analysis does not show any bias in Ωm, we can assume that this tension is likely to be a mere statistical fluctuation in the data.
B.2. Investigating the cause of the tension
When investigating Fig. B.2, we see that an increase in Ωm by 80% and a simultaneous decrease in S8 by 10% almost cancels out, except for the very first point of the data vector. This one corresponds to the point in the heatmap that measures the very high, very persistent peaks (see Fig. 3). We observe this behaviour consistently throughout all combinations of redshift bins. However, when we remove the first entry (corresponding to the high persistent peaks) from every tomographic bin combination, the tension between the two-point correlation function and persistent homology is reduced (see Fig. B.3) but does not vanish, and most likely, the decrease in the tension is just due to the lower constraining power. We can conclude that potentially a part of the reason for the Ωm-tension is that we measure significantly fewer high signal-to-noise peaks in the DES-Y1 data than in the simulations, however, the tension is not caused by those peaks. The most important unmodelled systematic effect that would affect these peaks would be source-lens coupling (Martinet et al. 2018), but that one would increase the number of peaks in the simulations, not decrease it.
 |
Fig. B.2. Same as Fig. 4, but we show the data vector for the individual cosmologies from our Cosmology Training Set, colour-coded by their respective value of S8 (dotted lines) and the measured values in the DES-Y1 survey (black). For a better visibility, all values are divided by the mean of our Covariance Training Set. In addition, we predict with the GPR Emulator a data vector where Ωm is increased by 80% with respect to the cosmology of the Covariance Training Set (dashed line), one where S8 is increased by 10% (dash-dotted line), and one where Ωm is increased by 80% and simultaneously S8 is decreased by 10% (solid line). |
 |
Fig. B.3. Results of our likelihood analyses for the DES-Y1 survey. We show the results for two-point statistics (red), persistent homology (blue) and report as well the constraints achieved by removing the first data point for each tomographic bin (black). The dotted lines denote the prior ranges, the black crosses denote the nodes of our Cosmology Training Set. |
Although the exclusion of the high signal-to-noise peaks would reduce the Ωm-tension without significantly affecting our constraining power on S8, we keep our fiducial analysis choices, as switching to this analysis would constitute a major post-unblinding change.
Appendix C: Complete parameter constraints of the MCMC
 |
Fig. C.1. Comparison of the constraining power of different data compression methods. Our chosen method, the χ2-maximiser is shown in grey, two alternative methods (PCA and Asgari & Schneider 2015, in red and blue, respectively). |
 |
Fig. C.2. Same as Fig.10, but with all cosmological and nuisance parameters. We note that the constraints on the shear measurement bias parameters (m1 - m4) and the photometric redshift errors (bias 1 - bias 4) are dominated by the (Gaussian) prior (compare Tab. 1). |
 |
Fig. C.3. Same as Fig.11, but with all cosmological and nuisance parameters. We note that the constraints on the shear measurement bias parameters (m1 - m4) and the photometric redshift errors (bias 1 - bias 4) are dominated by the (Gaussian) prior (compare Tab. 1). |
All Tables
Prior ranges of cosmological and nuisance parameters in the likelihood analysis.
All Figures
 |
Fig. 1. Example signal-to-noise map of aperture masses for a 5 × 5 deg2 sub-patch of one of the Covariance Training Set catalogue (left), and the same map when a threshold of 0.5 is applied (right). The white ‘holes’ in the right map correspond to local maxima of the map and give rise to the topological ‘features’ that are summarised in Dgm1. |
| In the text | |
 |
Fig. 2. Two persistence diagrams for the simulation shown in Fig. 1. The blue crosses represent features of Dgm0, the orange crosses represent features of Dgm1. For visibility, only every 500th feature is shown. We note that all points in this diagram lie above the diagonal. |
| In the text | |
 |
Fig. 3. Heatmap of the persistence diagram in Fig. 2 with a scaling parameter of t = 0.2 (for the computation of the Heatmaps, all features are taken into account, not just every 500th as in Fig. 2). The red points correspond to the evaluation points that were chosen by the χ2-maximiser outlined in Sect. 3.3. The extracted data vector can be seen in Fig. 4. |
| In the text | |
 |
Fig. 4. Data vector for the individual cosmologies from our Cosmology Training Set, colour-coded by their respective value of S8 (dotted lines) and the measured values in the DES-Y1 survey (black). For better visibility, the bottom panel shows the same data vector where all values are divided by the mean of our Covariance Training Set. |
| In the text | |
 |
Fig. 5. Accuracy of the GPR emulator evaluated by a leave-one-out cross-validation, shown here for the case where the aperture mass maps are constructed from the concatenation of all four tomographic redshift bins (i.e. no tomography). The x axis depicts the data vector entry, and the y axis the relative difference between predicted and measured value. The 26 individual dotted lines correspond to one cosmology that is left out of the training set and then predicted, the solid black line is the mean of all dotted lines. The black dashed lines depict the standard deviation from the Covariance Training Set. |
| In the text | |
 |
Fig. 6. Correlation matrix for a joint analysis with both persistent homology and two-point correlation functions. |
| In the text | |
 |
Fig. 7. Impact of the main systematic effects on the data vector. For each systematic, we show the measured (solid line) and interpolated (dotted line) ratio of the systematic-infused data vector over a reference data vector. For simplicity, we only show the results for the combination of all four tomographic redshift bins. The black dashed lines correspond to the 1σ standard deviation estimated from the Covariance Training Set. |
| In the text | |
 |
Fig. 8. Impact of unmodelled systematic biases on the posterior of a likelihood analysis with heatmaps. In all cases, we do not marginalise over any systematic effects. The target data vector is then infused with one systematic bias, and we run a likelihood analysis for this infused data vector. For comparison, we show the constraints on a data vector that is not infused by systematics (grey). Note that the values of the dz shifts are given in units of the standard deviation of the dz prior (compare Table 1). |
| In the text | |
 |
Fig. 9. Effects of marginalising over different systematic effects. In all cases, we perform a likelihood analysis on mock data, marginalising over one systematic effect. For comparison, we show the constraints we achieve when we do not marginalise over any systematics (grey). The case where we marginalise over all systematics corresponds to the blue contours in Fig. 10. |
| In the text | |
 |
Fig. 10. Results of likelihood analyses for DES-Y1 mock data. We show the results for two-point statistics (red), persistent homology (blue), and for the joint analysis (grey, filled). The dotted lines show the prior ranges, the solid black lines visualise the true value of each parameter, and the black crosses denote the nodes of our Cosmology Training Set. The complete results can be seen in Fig. C.2, the marginalised posterior constraints can be seen in Table 2. |
| In the text | |
 |
Fig. 11. Results of our likelihood analyses for the DES-Y1 survey. We show the results for two-point statistics (red), persistent homology (blue) and report as well the constraints achieved by HD+21 with peak count statistics (black). The dotted lines denote the prior ranges, the black crosses denote the nodes of our Cosmology Training Set. The complete results including nuisance parameters can be seen in Fig. C.3, while the marginalised posterior constraints can be seen in Table 2. |
| In the text | |
 |
Fig. 12. Comparison of the constraints on the matter clustering parameter S8 from DES-Y1 survey data in a wCDM cosmology with fixed neutrino mass. |
| In the text | |
 |
Fig. A.1. Cosmology dependence of the first four principal components. Each point in the scatter plot represents one of the 26 cosmologies of the cosmo-SLICS. In the top row, the x and y coordinates correspond to the value of the first two principal components; in the bottom row, they correspond to the values of the third and fourth principal components. In the left column, the colours represent the value of Ωm of the respective cosmo-SLICS simulation; in the right column, they denote the value of S8. |
| In the text | |
 |
Fig. A.2. Test results for the final data-vector’s Gaussianity. For each of the 180 data vector entries, we take the set of 10 × 124 measurements in the Covariance Training Sample and test the null hypothesis that this sample was drawn from a normal distribution using the measured skewness and kurtosis (D’Agostino 1971; D’Agostino & Pearson 1973). We then plot a histogram of the corresponding p-values (blue). If each entry of the data vector is Gaussian, then the distribution of p-values is uniform. For comparison, we show the results of the same test with a data vector that contains only points with about 10 features (orange). While the blue histogram may show small deviations from a uniform distribution (there appears to be a downward slope towards higher p-values), we believe that the assumption of a normal distribution is reasonable. |
| In the text | |
 |
Fig. A.3. First four (normalised) principal components of the heatmaps in a principal component analysis. |
| In the text | |
 |
Fig. B.1. Histogram of the tensions in cosmological parameters between 2PCF and persistent homology measured on 100 individual lines of sight in the Covariance Training Set (blue) and a Gaussian fit to these values (orange). The actual tension we measured in DES-Y1 is shown by the dashed black line. No tension is observed when running our pipeline on the mock data vector constructed from all simulations of the Covariance Training Set, which is about 12× larger. |
| In the text | |
 |
Fig. B.2. Same as Fig. 4, but we show the data vector for the individual cosmologies from our Cosmology Training Set, colour-coded by their respective value of S8 (dotted lines) and the measured values in the DES-Y1 survey (black). For a better visibility, all values are divided by the mean of our Covariance Training Set. In addition, we predict with the GPR Emulator a data vector where Ωm is increased by 80% with respect to the cosmology of the Covariance Training Set (dashed line), one where S8 is increased by 10% (dash-dotted line), and one where Ωm is increased by 80% and simultaneously S8 is decreased by 10% (solid line). |
| In the text | |
 |
Fig. B.3. Results of our likelihood analyses for the DES-Y1 survey. We show the results for two-point statistics (red), persistent homology (blue) and report as well the constraints achieved by removing the first data point for each tomographic bin (black). The dotted lines denote the prior ranges, the black crosses denote the nodes of our Cosmology Training Set. |
| In the text | |
 |
Fig. C.1. Comparison of the constraining power of different data compression methods. Our chosen method, the χ2-maximiser is shown in grey, two alternative methods (PCA and Asgari & Schneider 2015, in red and blue, respectively). |
| In the text | |
 |
Fig. C.2. Same as Fig.10, but with all cosmological and nuisance parameters. We note that the constraints on the shear measurement bias parameters (m1 - m4) and the photometric redshift errors (bias 1 - bias 4) are dominated by the (Gaussian) prior (compare Tab. 1). |
| In the text | |
 |
Fig. C.3. Same as Fig.11, but with all cosmological and nuisance parameters. We note that the constraints on the shear measurement bias parameters (m1 - m4) and the photometric redshift errors (bias 1 - bias 4) are dominated by the (Gaussian) prior (compare Tab. 1). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



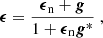
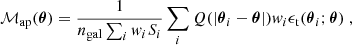
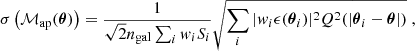
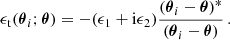
![$$ \begin{aligned}&Q(\theta ) = \left[1 + \exp \left(6 -150 \frac{\theta }{\theta _{\rm ap}}\right) + \exp \left(-47 +50 \frac{\theta }{\theta _{\rm ap}}\right)\right]^{-1} \nonumber \\&\qquad \quad \times \left(\frac{\theta }{x_{\rm c}\theta _{\rm ap}}\right)^{-1} \tanh \left(\frac{\theta }{x_{\rm c}\theta _{\rm ap}}\right)\, , \end{aligned} $$](/articles/aa/full_html/2022/11/aa43868-22/aa43868-22-eq7.gif)
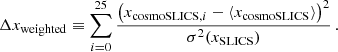
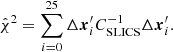
![$$ \begin{aligned} C_\ell ^{ij} = \int _0^{\chi _\mathrm{H} } \frac{W^i(\chi )W^j(\chi )}{\chi ^2}P\left(\frac{\ell +1/2}{\chi },z[\chi ]\right) \mathrm{d}\chi \,, \end{aligned} $$](/articles/aa/full_html/2022/11/aa43868-22/aa43868-22-eq23.gif)
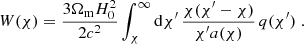
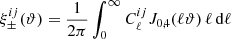
![$$ \begin{aligned} {{\xi }}_{\pm }^{ij}( \vartheta ) = \frac{ \sum _{a,b } { w}_a { w}_b\left[\epsilon ^i_\mathrm{t} (\boldsymbol{\theta }_a)\epsilon ^j_\mathrm{t} (\boldsymbol{\theta }_b) \pm \epsilon ^i_\times (\boldsymbol{\theta }_a)\epsilon ^j_\times (\boldsymbol{\theta }_b)\right]}{\sum _{a,b} { w}_a { w}_b S_a S_b} \, , \end{aligned} $$](/articles/aa/full_html/2022/11/aa43868-22/aa43868-22-eq29.gif)