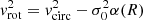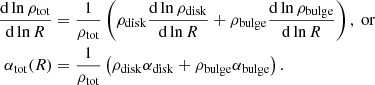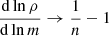| Issue |
A&A
Volume 665, September 2022
|
|
|---|---|---|
| Article Number | A159 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202244143 | |
| Published online | 23 September 2022 | |
Kinematics and mass distributions for non-spherical deprojected Sérsic density profiles and applications to multi-component galactic systems
1
Max-Planck-Institut für extraterrestrische Physik (MPE), Giessenbachstr. 1, 85748 Garching, Germany
e-mail: sedona@mpe.mpg.de
2
Cavendish Laboratory, University of Cambridge, 19 J.J. Thomson Avenue, Cambridge CB3 0HE, UK
3
Kavli Institute for Cosmology, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
4
Sterrewacht Leiden, Leiden University, Postbus 9513, 2300 RA Leiden, The Netherlands
5
Universitäts-Sternwarte Ludwig-Maximilians-Universität (USM), Scheinerstr. 1, 81679 München, Germany
6
Departments of Physics and Astronomy, University of California, Berkeley, CA 94720, USA
7
Physics Department, University of Alaska, Fairbanks, AK 99775, USA
8
University of the Western Cape, Bellville, Cape Town 7535, South Africa
Received:
30
May
2022
Accepted:
12
July
2022
Using kinematics to decompose the mass profiles of galaxies, including the dark matter contribution, often requires parameterization of the baryonic mass distribution based on ancillary information. One such model choice is a deprojected Sérsic profile with an assumed intrinsic geometry. The case of flattened, deprojected Sérsic models has previously been applied to flattened bulges in local star-forming galaxies (SFGs), but can also be used to describe the thick, turbulent disks in distant SFGs. Here, we extend this previous work that derived density (ρ) and circular velocity (vcirc) curves by additionally calculating the spherically-enclosed 3D mass profiles (Msph). Using these profiles, we compared the projected and 3D mass distributions, quantified the differences between the projected and 3D half-mass radii (Re; r1/2, mass, 3D), and compiled virial coefficients relating vcirc(R) and Msph(< r = R) or Mtot. We quantified the differences between mass fraction estimators for multi-component systems, particularly for dark matter fractions (ratio of squared circular velocities versus ratio of spherically enclosed masses), and we considered the compound effects of measuring dark matter fractions at the projected versus 3D half-mass radii. While the fraction estimators produce only minor differences, using different aperture radius definitions can strongly impact the inferred dark matter fraction. As pressure support is important in analyses of gas kinematics (particularly, at high redshifts), we also calculated the self-consistent pressure support correction profiles, which generally predict less pressure support than for the self-gravitating disk case. These results have implications for comparisons between simulation and observational measurements, as well as for the interpretation of SFG kinematics at high redshifts. We have made a set of precomputed tables and the code to calculate the profiles publicly available.
Key words: galaxies: luminosity function, mass function / galaxies: kinematics and dynamics
© S. H. Price et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model.
This Open access funding provided by Max Planck Society.
1. Introduction
Galaxy kinematics, such as rotation curves, are a powerful tool to measure the mass of all components in a galaxy (e.g., van der Kruit & Allen 1978; Courteau et al. 2014). Notably, this technique has been used to study the dark matter content of galaxies at a wide range of epochs, including constraints on the halo profile shapes (e.g., Sofue & Rubin 2001; de Blok 2010; Genzel et al. 2020, among many others). Furthermore, by using kinematics to probe the mass and angular momentum distribution within galaxies, it is possible to constrain the processes regulating galaxy growth and evolution over time (van der Kruit & Freeman 2011; Förster Schreiber & Wuyts 2020; see also, e.g., Mo et al. 1998; Sofue & Rubin 2001; Romanowsky & Fall 2012). It is especially informative to study the kinematics of star-forming galaxies (SFGs), which tend to lie on a tight “star-forming main sequence” where much of cosmic star formation occurs (Speagle et al. 2014; Rodighiero et al. 2011; Whitaker et al. 2014; Tomczak et al. 2016). However, there are challenges to recovering the intrinsic mass properties of galaxies from their observed kinematics.
One such challenge is that in order to overcome degeneracies in kinematic mass decomposition (particularly when including an unseen dark component; e.g., van Albada et al. 1985), separate constraints on the baryonic (gas and stellar) component are needed, either through empirical measurements or with a choice of parameterization (e.g., Persic et al. 1996; de Blok & McGaugh 1997; Palunas & Williams 2000; Dutton et al. 2005; de Blok et al. 2008; Courteau et al. 2014). Multi-wavelength imaging and spectroscopy (in emission or absorption) can constrain the distribution of gas and stars in galaxies. Such observations of individual galaxies provide projected information and not the 3D quantities needed for kinematic modeling. Consequently, it is often necessary to first parameterize the projected distributions and then make reasonable assumptions about the galaxies’ intrinsic geometries in order to deproject the surface distributions into 3D mass profiles.
Observationally, the light distributions of galaxies are often described by Sérsic (1968) profiles (e.g., Peng et al. 2002, 2010; Simard et al. 2002, 2011; Blanton et al. 2003; Wuyts et al. 2011; van der Wel et al. 2012; Conselice 2014, and numerous others). In some cases, there are distinct components within galaxies, but these are also frequently described by Sérsic profiles with distinct indices, n, and effective radii, Re, (e.g., a disk and bulge for star-forming galaxies; Courteau et al. 1996; Bruce et al. 2012; Lang et al. 2014). Thus, Sérsic profiles are a natural choice for the projected parameterization.
Deprojections of Sérsic profiles have been studied in numerous previous works, for spherical (e.g., Ciotti 1991; Ciotti & Lanzoni 1997; Baes & Ciotti 2019a,b), triaxial (e.g., Stark 1977; Trujillo et al. 2002), and axisymmetric geometries (e.g., Noordermeer 2008). Additionally, the dynamics for exponential surface profiles have been derived for both razor-thin (Freeman 1970) and finitely thick (Casertano 1983) geometries (although these are generalizable to arbitrary Sérsic index; e.g., see Binney & Tremaine 2008). These intrinsic geometries have applications for various galaxies or galaxy components, depending on the galaxy properties and epoch.
In particular, the mass distribution geometry of SFGs changes over time. Nearby SFGs often have thin disks, particularly in the gas components (van der Kruit & Freeman 2011), while distant (massive) SFGs tend to have thick, turbulent disks (Glazebrook 2013; Förster Schreiber & Wuyts 2020, and references therein). While more observations are needed to better constrain the vertical disk structure of distant, massive SFGs, flattened (oblate) distributions are more appropriate models (as adopted by, e.g., Wuyts et al. 2016; Genzel et al. 2017, 2020), using the same geometric deprojection used by Noordermeer (2008) to describe the flattening of nearby bulges.
A second challenge is that the observed rotation must be corrected for pressure support. This correction is important for gas kinematic measurements, especially at high redshifts where disks have high gas turbulence. A number of works have considered different analytic prescriptions for correcting for the pressure support in gas kinematics (e.g., Weijmans et al. 2008; Burkert et al. 2010; Dalcanton & Stilp 2010; Kretschmer et al. 2021). In general, such corrections require measurements of the gas turbulence σ from spatially resolved spectroscopy (i.e., slit along the major axis or kinematic maps) as well as constraints on or parameterizations of the gas density profile. If deprojected Sérsic distributions are used to model the mass and vcirc profiles for the gas and stellar components of galaxies, then a pressure support prescription derived using the density slope can be adopted for a self-consistent kinematic analysis (as in, e.g., Weijmans et al. 2008; Burkert et al. 2010; Dalcanton & Stilp 2010). If galaxies exhibit non-constant dispersion, support from dispersion gradients or anisotropy can also be included (e.g., Weijmans et al. 2008; Dalcanton & Stilp 2010).
In order to further consider implications for the interpretation of the kinematics of high-redshift SFGs modeled using deprojected, flattened Sérsic profiles, in this paper we revisit and extend the framework first presented by Noordermeer (2008, hereafter N08). We first present various profile derivations for deprojected, flattened Sérsic profiles, including the density and circular velocity profiles determined by N08 as well as the spherically-enclosed 3D mass profiles (Sect. 2). Using the calculated profiles, we examine the relationship between projected 2D and 3D mass distributions, including differences between the 2D Re and 3D r1/2, mass, 3D (Sect. 2.4). The circular velocity and 3D mass distributions are also used to calculate virial coefficients (Sect. 3). Next, we examine the circular velocity and enclosed mass profiles for multi-component systems for a range of realistic z ∼ 2 galaxy properties (Sect. 4). We find the composite baryonic 3D half-mass radius r1/2, 3D, baryons is often smaller than the projected disk effective radius Re, disk. While different dark matter fraction estimators  (the ratio of the dark matter to total circular velocities squared) and
(the ratio of the dark matter to total circular velocities squared) and 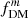 (the ratio of the dark matter to total mass enclosed within a sphere) are similar when calculated at the same radius, large differences in fDM can result from the use of different aperture radii (r1/2, 3D, baryons vs. Re, disk). We then determine the self-consistent turbulent pressure support correction, assuming a constant σ0, which is typically only half the amount predicted for a self-gravitating disk, and demonstrate the correction for a range of realistic z ∼ 2 galaxy properties (Sect. 5). Finally, we discuss these results and their implications, in particular, for comparisons between simulations and observations and for studies of disk galaxy kinematics at z ∼ 1 − 3 (Sect. 6). We highlight how typical observational and simulation “half-mass” radius estimates can lead to differences of up to ∼0.15 in measured fDM, and how the lower pressure support correction derived for these mass distributions (compared to the self-gravitating disk prescription) would imply a typically lower inferred fDM from the observations.
(the ratio of the dark matter to total mass enclosed within a sphere) are similar when calculated at the same radius, large differences in fDM can result from the use of different aperture radii (r1/2, 3D, baryons vs. Re, disk). We then determine the self-consistent turbulent pressure support correction, assuming a constant σ0, which is typically only half the amount predicted for a self-gravitating disk, and demonstrate the correction for a range of realistic z ∼ 2 galaxy properties (Sect. 5). Finally, we discuss these results and their implications, in particular, for comparisons between simulations and observations and for studies of disk galaxy kinematics at z ∼ 1 − 3 (Sect. 6). We highlight how typical observational and simulation “half-mass” radius estimates can lead to differences of up to ∼0.15 in measured fDM, and how the lower pressure support correction derived for these mass distributions (compared to the self-gravitating disk prescription) would imply a typically lower inferred fDM from the observations.
A set of tables containing precomputed profiles and values – including vcirc(R) (Eq. (5)), Msph(< r = R) (Eq. (8)), Mspheroid(< m = R) (Eq. (6)), ρ(r = R) (Eq. (2)), dlnρ/dlnR (derived from Eq. (17)), r1/2, mass, 3D, ktot(Re, disk) (Eq. (10)), and k3D(Re, disk) (Eq. (9)) – for a range of intrinsic axis ratios q0 and Sérsic indices, and the code used to compute the profiles, are made available1. For reference, key variables and their definitions are listed in Table 1. We assume a flat ΛCDM cosmology with Ωm = 0.3, ΩΛ = 0.7, and H0 = 70 km s−1 Mpc−1.
Definitions of key variables.
2. Derivation of mass profiles and rotation curves
In this section, we present the formulae for the mass profiles and rotation curves for models whose projected intensity distributions follow Sérsic profiles, but that have oblate (flattened) or prolate axisymmetric 3D density distributions (i.e., the isodensity contours follow oblate or prolate spheroids), following the deprojection derivation of N08.
2.1. Deprojected Sérsic density profile
We assume that the mass density of the 3D spheroid can be written as ρ(x, y, z) = ρ(m), where (m/a)2 = (x/b)2 + (y/a)2 + (z/c)2 specifies the isodensity surfaces for a given set of semi-axis lengths a, b, c. For an axisymmetric system, this is simplified to 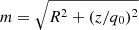 , where
, where 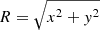 is the distance in the plane of axisymmetry, z is the distance from the midplane, the semi-axes a = b, and q0 = c/a is the intrinsic axis ratio of the spheroid. To project the intrinsic galaxy coordinates to the observer’s frame, we adopt the transformation from (x, y, z) to (ζ, κ, ξ) from Eq. (1) of N08, where ζ lies along the line of sight, κ, and ξ lie along the galaxy major and minor axes (as viewed in the sky plane, for oblate geometries2; i.e., κ = a), respectively, and i is the inclination of the system relative to the observer (see also Fig. 1 of N08). The observed axis ratio of the ellipsoid is then
is the distance in the plane of axisymmetry, z is the distance from the midplane, the semi-axes a = b, and q0 = c/a is the intrinsic axis ratio of the spheroid. To project the intrinsic galaxy coordinates to the observer’s frame, we adopt the transformation from (x, y, z) to (ζ, κ, ξ) from Eq. (1) of N08, where ζ lies along the line of sight, κ, and ξ lie along the galaxy major and minor axes (as viewed in the sky plane, for oblate geometries2; i.e., κ = a), respectively, and i is the inclination of the system relative to the observer (see also Fig. 1 of N08). The observed axis ratio of the ellipsoid is then 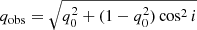 .
.
Within the observer’s coordinate frame, the relationship between the 3D mass density profile and the projected light intensity along the major axis of the galaxy is (ξ = 0; from Eq. (8) of N083):
where Υ(m) is the mass-to-light ratio of the galaxy and 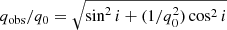 . For simplicity, we assume a constant mass-to-light ratio, Υ(m)≡Υ.
. For simplicity, we assume a constant mass-to-light ratio, Υ(m)≡Υ.
The deprojected density profile is found by inverting this Abel integral, with (c.f. Eq. (9), N08):
We express the Sérsic profile as (c.f. Eq. (11), N08):
where Re is the effective radius, n is the Sérsic index, Ie is the surface brightness at Re, and bn satisfies 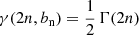 , where Γ(a) and γ(a, x) are the regular and lower incomplete gamma functions, respectively (e.g., Graham & Driver 2005). The derivative is then:
, where Γ(a) and γ(a, x) are the regular and lower incomplete gamma functions, respectively (e.g., Graham & Driver 2005). The derivative is then:
By inserting Eq. (4) into Eq. (2), we can numerically integrate these equations to obtain the deprojected density profile ρ(m). For the adopted convention here, where the projected κ lies along a in the midplane (so this is the usual projected major axis for oblate cases but is the projected minor axis for prolate cases), we have Re = a as the projected effective radius.
2.2. Rotation curves
Next, we determine the circular rotation curve for this class of density profiles, following the derivation of Binney & Tremaine (2008, Eq. (2.132); also Eq. (10), N08). The circular rotation curve at the midplane of the galaxy is thus:
As noted by N08, this equation is valid for any observed intensity profile I(κ). Here, we combine Eqs. (2) and (5), which can be numerically integrated to yield vcirc(R).
2.3. Enclosed 3D mass
We next derive the enclosed mass for models with the density profiles given above. Given the modified coordinate m, the mass enclosed within a spheroid with intrinsic axis ratio, q0, can be expressed as:
Integrated to infinity, this is equivalent to the total luminosity of the Sérsic profile times the constant assumed mass-to-light ratio, or Mtot = ΥLtot, so the intensity normalization for a flattened Sérsic profile with observed axis ratio, qobs, is:
However, there may be situations where we wish to compute the mass enclosed within a sphere of radius 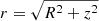 instead of within a flattened (or prolate) spheroid. We thus use a change of coordinates to calculate the spherical enclosed mass:
instead of within a flattened (or prolate) spheroid. We thus use a change of coordinates to calculate the spherical enclosed mass:
using ρ(m) from Eq. (2), with 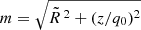 . This integral can be numerically evaluated to find the 3D spherical enclosed mass profile corresponding to the deprojected, axisymmetric Sérsic profile. We note that when q0 ≠ 1, then
. This integral can be numerically evaluated to find the 3D spherical enclosed mass profile corresponding to the deprojected, axisymmetric Sérsic profile. We note that when q0 ≠ 1, then 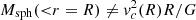 (with
(with 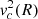 from Eq. (5)); however, the enclosed mass and circular velocity can be related through the introduction of a non-unity, radially varying virial coefficient (see Sect. 3).
from Eq. (5)); however, the enclosed mass and circular velocity can be related through the introduction of a non-unity, radially varying virial coefficient (see Sect. 3).
Finally, we note that the mass enclosed within an ellipsoidal cylinder of axis ratio qobs (and infinite length) is equivalent to the enclosed luminosity for the 2D projected Sérsic profile times the mass-to-light ratio, 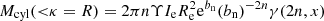 , with x = bn(R/Re)1/n (e.g., Graham & Driver 2005).
, with x = bn(R/Re)1/n (e.g., Graham & Driver 2005).
2.4. Properties of enclosed mass and circular velocity curves for non-spherical deprojected Sérsic profiles
The 3D spherical enclosed mass profiles for models with a range of Sérsic indices (n = 0.5, 1, …, 8) and different intrinsic axis ratios q0 = 1, 0.4, 0.2) are shown in Fig. 1. The 3D spherical half-mass radius (where r1/2, mass, 3D satisfies Msph(< r1/2, mass, 3D) = Mtot/2) is r1/2, mass, 3D ∼ 1.3Re when q0 = 1 (as shown by Ciotti 1991). However, from the q0 = 0.2, 0.4 enclosed mass profiles, we see that the ratio r1/2, mass, 3D/Re varies with the model intrinsic axis ratio.
 |
Fig. 1. Fractional mass enclosed within a sphere of radius r = R for deprojected Sérsic models of different intrinsic axis ratios. From left to right: enclosed Msph is plotted as a function of log radius (relative to the projected 2D effective radius, Re), assuming intrinsic axis ratios of q0 = 1, 0.4, 0.2, respectively. The colored curves denote the enclosed mass profiles for Sérsic indices from n = 0.5 to n = 8 (yellow to purple). The vertical lines denote R = Re (grey dashed) and R = 1.3Re (≈r1/2, mass, 3D for q0 = 1; grey dash-dotted), and the horizontal colored lines denote the fraction of the mass enclosed within r = Re for n = 1, 4 (lime, teal dashed, respectively) and 50% of the total mass (grey dashed dotted). For q0 = 1, the half-mass 3D spherical radius is indeed r1/2, mass, 3D ≈ 1.3Re regardless of n, as in Ciotti (1991). For flattened (i.e., oblate) systems, the half-mass 3D spherical radius is smaller, and approaches Re as q0 decreases. See also Fig. 2. |
We quantify the dependence of the ratio between the 3D spherical half-mass radius and the projected effective radius, r1/2, mass, 3D/Re, in Fig. 2, as a function of Sérsic index, n, and intrinsic axis ratio, q04. van de Ven & van der Wel (2021) make a similar comparison for both axisymmetric and triaxial systems using an approximation for ρ, but show r1/2, mass, 3D relative to the projected major axis, so for the axisymmetric, prolate systems our ratio differs from theirs. The 3D spherical half-mass radius is larger than the 2D projected effective radius enclosing half of the total light (and half of the total mass, assuming constant M/L and an optically thin medium). There is a larger dependence of the ratio r1/2, mass, 3D/Re on q0 than on n, where r1/2, mass, 3D/Re ∼ 1.3 − 1.36 when q0 = 1 for all n = 0.5 − 8, but as q0 decreases the ratio decreases towards r1/2, mass, 3D/Re ∼ 1 for all n.
 |
Fig. 2. Comparison between the 3D spherical half-mass radius, r1/2, mass, 3D, and the projected 2D effective radius, Re, for a range of Sérsic indices n and intrinsic axis ratios q0 (left, colored by q0; right, colored by n). For oblate cases, Re is the projected major axis, while for prolate cases Re is the projected minor axis. For all cases, r1/2, mass, 3D > Re. However, as q0 decreases (i.e., flatter Sérsic distributions), the 3D half-mass radius approaches the value of Re. Overall, the systematic difference between r1/2, mass, 3D and Re highlights that while half of the model mass is enclosed within a projected 2D ellipse of major axis Re (e.g., an infinite ellipsoidal cylinder), less than half the total mass is enclosed within a sphere of radius Re (ignoring any M/L gradients or optically thick regions, which would change Re, light/Re, mass). |
Next, we examine how the relation between the mass and circular velocity profiles deviates from the relation that holds for spherical symmetry, where 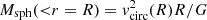 . In Fig. 3 we show computed fractional enclosed mass (top) and circular velocity profiles (bottom) for n = 1, 4 (top and bottom rows, respectively), and for q0 = 1, 0.4, 0.2 (left, center, and right columns, respectively).
. In Fig. 3 we show computed fractional enclosed mass (top) and circular velocity profiles (bottom) for n = 1, 4 (top and bottom rows, respectively), and for q0 = 1, 0.4, 0.2 (left, center, and right columns, respectively).
 |
Fig. 3. Example fractional enclosed mass (top) and circular velocity (bottom) profiles computed or inferred under different assumptions. The top and bottom rows show the profiles for Sérsic indices n = 1, 4, respectively, while the columns show intrinsic axis ratios q0 = 1, 0.4, 0.2 (from left to right). For the top panels, we show the edge-on 2D projected mass enclosed within ellipses of axis ratio q0 (orange solid line), the 3D mass profile enclosed within a sphere (red dashed line), the 3D mass profile enclosed within ellipsoids of intrinsic axis ratio q0 (purple dash-dotted line), and the mass profile inferred from the flattened deprojected Sérsic model circular velocity under the simplifying assumption of spherical symmetry (i.e., q0 = 1; black dotted line). In the bottom panels, we then compare the flattened deprojected Sérsic model circular velocity (black dotted line) to the inferred velocity profiles computed from the 3D spherical (red solid line) and the 3D ellipsoidal (purple dash-dotted) mass profiles under the simple assumption of spherical symmetry. The same total mass Mtot = 5 × 1010 M⊙ is used for all cases. The vertical lines denote R = Re (grey dashed) and R = 1.3Re (≈r1/2, mass, 3D for q0 = 1; grey dash-dotted). These enclosed mass and velocity profiles demonstrate that when q0 ≠ 1, Msph(< r = R)≠vcirc(R)2R/G. The non-spherical potentials for q0 < 1 even result in (vcirc(R)2R/G)/Mtot > 1 between R ∼ 1 − 10Re (i.e., potentially leading to ≳15% overestimates in the system mass). We also see that as q0 decreases, Msph approaches the 2D projected mass profile, as the mass enclosed in a sphere versus an infinite ellipsoidal cylinder are equivalent for infinitely thin mass distributions. |
For the spherically symmetric (q0 = 1) cases, the numerical evaluation of Msph(< r = R) (red dashed line; Eq. (8)) and vcirc(R) (black dotted line; Eq. (5)) follow the expected relation (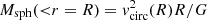 ), and the isodensity spheroids are spherical, so there is no difference between the enclosed spherical and spheroidal profiles. Echoing the previous figures, we also see that the enclosed 3D mass profile increases more slowly as a function of R than the 2D projected profile (solid orange line; Eq. (3)).
), and the isodensity spheroids are spherical, so there is no difference between the enclosed spherical and spheroidal profiles. Echoing the previous figures, we also see that the enclosed 3D mass profile increases more slowly as a function of R than the 2D projected profile (solid orange line; Eq. (3)).
In contrast, for flattened deprojected models with q0 < 1, the deviation of the Msph(< r = R) and vcirc(R) profiles from the spherical relation become more pronounced for lower intrinsic axis ratios. Also, 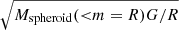 (purple dashed-dotted line; Eq. (6)) does not match the correct vcirc(R) curve. As q0 decreases, Msph(< r = R) approaches the projected 2D ellipse curve, because for flatter deprojected models there is less additional mass outside the sphere along the remaining line-of-sight collapse.
(purple dashed-dotted line; Eq. (6)) does not match the correct vcirc(R) curve. As q0 decreases, Msph(< r = R) approaches the projected 2D ellipse curve, because for flatter deprojected models there is less additional mass outside the sphere along the remaining line-of-sight collapse.
3. Virial coefficients for enclosed 3D and total masses
We now quantify the relationship between mass- and velocity-derived quantities for different Sérsic indices and intrinsic axis ratios. By including a “virial” coefficient k3D(R) which depends on the geometry and mass distribution (Binney & Tremaine 2008), the spherical enclosed mass and circular velocity can be related via:
This virial coefficient is evaluated by combining Eqs. (5) and (8).
For comparison with integrated galaxy quantities, it is also useful to define a “total” virial coefficient ktot(R) which relates the total system mass to the circular velocity at a given radius:
Figure 4 shows ktot(R = Re) and k3D(R = Re) versus Sérsic index n for a range of q0. For the spherical case (q0 = 1), k3D(R = Re) = 1, as expected by spherical symmetry. However, as Re < r1/2, mass, 3D for spherical deprojected Sérsic models, ktot(R = Re, q0 = 1)≠2, instead it exceeds 2 for all n (i.e., 2.933 when n = 1). For oblate flattened Sérsic deprojected models (i.e., q0 < 1), the value for ktot(R = Re) is lower than the q0 = 1 case for all n, while prolate cases (q0 > 1) have larger ktot(R = Re). For k3D(R = Re), the trends are more complex, but for n ≳ 2, the oblate (prolate) models all have k3D(R = Re) < 1 (> 1). For reference, we also present values of ktot(R) and k3D(R) for a range of R, n, and q0 in Table 2. These total virial coefficients, in particular, allow for a more precise comparison between the dynamical Mtot and projection-derived quantities, such as M* or Mgas, particularly when full dynamical modeling is not possible (e.g., the approach used in Erb et al. 2006; Miller et al. 2011; Price et al. 2016, 2020, and numerous other studies).
 |
Fig. 4. Total ktot(Re) (left) and 3D enclosed k3D(Re) (right) virial coefficients as a function of Sérsic index, n, and intrinsic axis ratio q0. The solid lines denote q0 = 0.2 (orange) to q0 = 1 (black) and two prolate cases are shown with dashed lines (q0 = 1.5, 2 in dark, light grey, respectively). |
Virial coefficients for select profiles and radii.
4. Mass distributions of multi-component galactic systems
4.1. Mass and velocity distributions of systems including both flattened and spherical components
While the virial coefficients derived in the previous section allow for the conversion from circular velocities to enclosed masses for a single non-spherical mass component, observed galaxies tend to have multiple mass components of varying intrinsic shapes and profiles. Here, we explore the enclosed mass and circular velocity distributions for galaxies with multiple mass components, focusing on how the non-spherical components impact the mass fraction distributions inferred from velocity profile ratios.
We calculated profiles for a “typical” z = 2 main-sequence star-forming galaxy of stellar mass log10(M*/M⊙) = 10.5 consisting of a bulge, disk, and halo, over a range of bulge-to-total ratios, B/T. We thus adopted a total Mbar = 6.6 × 1010 M⊙ (using the gas fraction scaling relation of Tacconi et al. 2020). We assumed a thick, flattened disk modeled as a deprojected Sérsic distribution with q0, disk = 0.25, and adopt ndisk = 1, Re, disk = 3.4 kpc (from observed trends and scaling relations; Wuyts et al. 2011; van der Wel et al. 2014). The bulge is modeled as a deprojected Sérsic component with nbulge = 4, Re, bulge = 1 kpc, and q0, bulge = 1. We also included a NFW halo without adiabatic contraction, assuming conchalo = 4.2 and Mhalo = 8.9 × 1011 M⊙ (following observed halo concentration and stellar mass to halo mass relations, e.g., Dutton & Macciò 2014; Moster et al. 2018)5. In Fig. 5, for each of the B/T ratios (left to right), we show the enclosed mass (top row) and circular velocity profiles (middle row) as a function of radius. The impact of shifting the baryonic mass from entirely in the disk (the only oblate, non-spherical mass component; B/T = 0) to entirely in the bulge (only spherical mass components; B/T = 1) can be seen in both the Msph and vcirc profiles. The lower Sérsic index and larger Re of the disk (blue dashed line) relative to the bulge (red dash-dotted) result in more slowly rising mass and vcirc curves for the baryonic component (green dash-dot-dot) at low B/T, with the curves rising more quickly as the bulge contribution increases. The total galaxy mass and vcirc curves (solid black) are dominated by the baryonic components in the inner regions, but at large radii (R ≳ 10 kpc) where the halo begins dominating the mass and vcirc profiles, the curves are similar for all B/T.
 |
Fig. 5. Enclosed mass (3D spherical, top), circular velocity (middle), and dark matter (bottom) profiles for different components of an example galaxy as a function of projected major axis radius, for bulge-to-total ratios of B/T = 0, 0.25, 0.5, 0.75, 1 (left to right). For all cases, we compute the mass components assuming values for a typical z = 2 massive main-sequence galaxy with log10(M*/M⊙) = 10.5: Mbar = 6.6 × 1010 M⊙, Re, disk = 3.4 kpc, ndisk = 1, q0, disk = 0.25, Re, bulge = 1 kpc, nbulge = 4, q0, bulge = 1, and a NFW halo with Mhalo = 8.9 × 1011 M⊙ and c = 4.2. Shown are the Msph(< r = R) and vcirc(R) profiles for the disk (dashed blue), bulge (dash-dotted red), total baryons (disk+bulge; dash-dot-dot green), halo (dotted purple), and composite total system (solid black). Vertical lines mark R = Re, disk (solid grey) and the 3D spherical half-mass radii r1/2, mass, 3D for the disk (dashed blue), bulge (dash-dotted red), and total baryons (dash-dot-dot green). Two dark matter fraction definitions are shown in the bottom panels, |
We also show the radial variation of the 3D enclosed halo to total mass ratio MDM, sph/Mtot, sph (long light-grey dashed line) and the squared halo to total circular velocity ratio 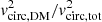 (dark-grey dashed-triple dotted line) in the bottom row (and the Msph and vcirc panels, respectively). As expected when B/T < 1, these two ratios are not equivalent, although they get closer as B/T → 1 and more of the total galaxy mass is found in spherical components. For B/T = 1, the galaxy is spherically symmetric, so the two ratios are equal.
(dark-grey dashed-triple dotted line) in the bottom row (and the Msph and vcirc panels, respectively). As expected when B/T < 1, these two ratios are not equivalent, although they get closer as B/T → 1 and more of the total galaxy mass is found in spherical components. For B/T = 1, the galaxy is spherically symmetric, so the two ratios are equal.
4.2. Defining dark matter fractions
As illustrated in Fig. 5, the approximation 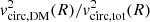 deviates from the enclosed spherical mass fraction MDM, sph(< r = R)/Mtot, sph(< r = R) for galaxies with a non-spherical disk component, particularly when the B/T ratio is ≲0.5. This deviation thus leads to differences in inferred dark matter fractions, depending on how the fraction is defined.
deviates from the enclosed spherical mass fraction MDM, sph(< r = R)/Mtot, sph(< r = R) for galaxies with a non-spherical disk component, particularly when the B/T ratio is ≲0.5. This deviation thus leads to differences in inferred dark matter fractions, depending on how the fraction is defined.
If the dark matter fraction is defined as the ratio of the dark matter to total mass enclosed within a sphere of a given radius, we have 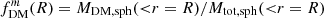 . This approach is often adopted for simulations, where it is easy to determine mass within a given radius. However, observations cannot directly probe the mass distributions, so generally the fraction is defined based on the circular velocity ratio,
. This approach is often adopted for simulations, where it is easy to determine mass within a given radius. However, observations cannot directly probe the mass distributions, so generally the fraction is defined based on the circular velocity ratio, 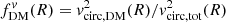 . If a galaxy has only spherically symmetric components, these two definitions are equivalent (as seen in the right column of Fig. 5); however, as noted in Fig. 5, the two definitions are no longer equivalent with non-spherical components, where
. If a galaxy has only spherically symmetric components, these two definitions are equivalent (as seen in the right column of Fig. 5); however, as noted in Fig. 5, the two definitions are no longer equivalent with non-spherical components, where 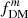 is generally larger than
is generally larger than 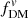 .
.
To further quantify how much these definitions can vary, we compare the value of the ratio between 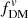 and
and 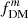 at Re, disk over a range of B/T ratios and intrinsic disk thicknesses q0, disk in Fig. 6. For this example case (using a massive galaxy with Mbar = 6.6 × 1010 M⊙ at z = 2, as in Fig. 5), we see that
at Re, disk over a range of B/T ratios and intrinsic disk thicknesses q0, disk in Fig. 6. For this example case (using a massive galaxy with Mbar = 6.6 × 1010 M⊙ at z = 2, as in Fig. 5), we see that 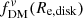 can be as low as ∼85% of
can be as low as ∼85% of 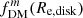 – in the extreme case with q0, disk = 0.01. For more typical expected disk thicknesses for galaxies at z ∼ 1 − 3, q0, disk ∼ 0.2 − 0.25, we find a minimum of
– in the extreme case with q0, disk = 0.01. For more typical expected disk thicknesses for galaxies at z ∼ 1 − 3, q0, disk ∼ 0.2 − 0.25, we find a minimum of 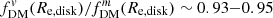 (for B/T = 0). While this deviation is fairly small in this example, using consistent definitions of fDM when comparing simulations and observations would avoid introducing systematic shifts between the values.
(for B/T = 0). While this deviation is fairly small in this example, using consistent definitions of fDM when comparing simulations and observations would avoid introducing systematic shifts between the values.
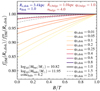 |
Fig. 6. Ratio between the dark matter fraction at Re, disk calculated from the circular velocity and from the 3D spherical enclosed mass, |
4.3. Impact of aperture effects on dark matter fractions
While the fractional differences between the 3D half mass radii r1/2, mass, 3D and the projected 2D effective radii Re for a single component and between the 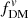 and
and 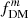 definitions are generally small for expected galaxy thicknesses, measuring fDM (of either indicator) at different radii – such as the easily measurable r1/2, mass, 3D for simulations versus Re for observations – can lead to very large discrepancies in the fDM values. We demonstrate this issue in Fig. 7.
definitions are generally small for expected galaxy thicknesses, measuring fDM (of either indicator) at different radii – such as the easily measurable r1/2, mass, 3D for simulations versus Re for observations – can lead to very large discrepancies in the fDM values. We demonstrate this issue in Fig. 7.
 |
Fig. 7. Ratio between the composite disk+bulge 3D half-mass radius and the 2D projected disk effective radius (r1/2, 3D, baryons/Re, disk; left) and the difference between the dark matter fraction estimators at these radii ( |
First, while we show the ratio of r1/2, mass, 3D/Re for a single component in Fig. 2, the ratio for a multi-component system is not self-similar, but depends also on the ratio of effective radii for the components. For a disk + bulge system, a number of observational studies use the disk effective radius as the dark matter fraction aperture. We thus determine the 3D half-mass radius for the composite disk+bulge system, and plot the ratio r1/2, 3D, baryons/Re, disk as a function of B/T in the left panel of Fig. 7, for a range of ratios Re, bulge/Re, disk (line style) and disk intrinsic thicknesses (q0, disk, assuming a spherical bulge). Depending on the Re, bulge/Re, disk and q0, disk values, this ratio can range from ∼0.3 − 1.3 (for oblate or spherical disk geometries, or up to ∼1.7 for prolate disks), with the lowest values arising from the combination of a low Re, bulge/Re, disk and a high B/T.
We then demonstrate the effects of measuring fDM at these different aperture radii in the right panel of Fig. 7. Here we plot the absolute difference 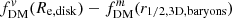 as a function of B/T, calculated for the same Re, bulge/Re, disk and q0, disk values. For consistency, the fDM estimators for each are chosen to reflect the typical definitions from observations and simulations, respectively, in line with the “half-mass” radii choices (although, as seen in Fig. 6, using
as a function of B/T, calculated for the same Re, bulge/Re, disk and q0, disk values. For consistency, the fDM estimators for each are chosen to reflect the typical definitions from observations and simulations, respectively, in line with the “half-mass” radii choices (although, as seen in Fig. 6, using 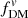 versus
versus 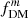 contributes very little to the differences seen in this figure). For very low B/T, most cases produce
contributes very little to the differences seen in this figure). For very low B/T, most cases produce 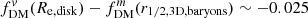 (e.g., larger
(e.g., larger 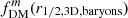 ). For most practical cases with a larger disk than bulge (Re, bulge/Re, disk < 1), the difference increases towards larger B/T, with
). For most practical cases with a larger disk than bulge (Re, bulge/Re, disk < 1), the difference increases towards larger B/T, with 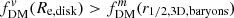 by B/T ∼ 0.2 − 0.5 (for Re, bulge/Re, disk = 0.2, 0.5, respectively). This difference can be very large, up to ∼0.2 for large B/T and low Re, bulge/Re, disk, as might be expected for massive galaxies that simultaneously have massive bulges (i.e., high B/T) but also large effective radii for the disk (i.e., low Re, bulge/Re, disk).
by B/T ∼ 0.2 − 0.5 (for Re, bulge/Re, disk = 0.2, 0.5, respectively). This difference can be very large, up to ∼0.2 for large B/T and low Re, bulge/Re, disk, as might be expected for massive galaxies that simultaneously have massive bulges (i.e., high B/T) but also large effective radii for the disk (i.e., low Re, bulge/Re, disk).
We extended these test cases to consider how fDM for the different definitions and apertures change with redshift and stellar mass for a “typical” star-forming galaxy, as shown in Fig. 8. We used empirical scaling relations or other estimates to determine Re, disk, q0, disk, fgas, B/T, log10(Mhalo/M⊙), and chalo for a range of z and log10(M*/M⊙) (assuming the disk and bulge follow deprojected Sérsic models, with fixed ndisk = 1, nbulge = 4, and Re, bulge = 1 kpc; top panels). These toy models predict 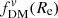 (Fig. 8, center left) to increase over time at fixed stellar mass (in part because of the increasing chalo and Re, disk over time) and that lower M* galaxies have higher
(Fig. 8, center left) to increase over time at fixed stellar mass (in part because of the increasing chalo and Re, disk over time) and that lower M* galaxies have higher 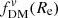 at fixed redshift, with relatively low
at fixed redshift, with relatively low 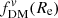 for the most massive galaxies (∼20%) at z ∼ 1 − 3. This is qualitatively in agreement with recent observations (e.g., Genzel et al. 2020; Price et al. 2021; Bouché et al. 2022), although these recent studies also provide evidence for non-NFW halo profiles (in particular, cored profiles), which would produce lower
for the most massive galaxies (∼20%) at z ∼ 1 − 3. This is qualitatively in agreement with recent observations (e.g., Genzel et al. 2020; Price et al. 2021; Bouché et al. 2022), although these recent studies also provide evidence for non-NFW halo profiles (in particular, cored profiles), which would produce lower 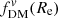 for the same Mhalo than our toy models. As a further example, we consider how the predictions would change over time for a Milky Way and M31-mass progenitor. In both cases, the predicted
for the same Mhalo than our toy models. As a further example, we consider how the predictions would change over time for a Milky Way and M31-mass progenitor. In both cases, the predicted 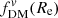 decrease from z = 3 to a minimum at z ∼ 1.5, and then increase until the present day. For these toy values, the difference in dark matter fraction definitions measured (specifically) at the same radius (Re, disk; Fig. 8, center right) typically differ by only ∼ − 0.005 to ∼ − 0.025 (typically ∼4 − 6% of the measured values), with a larger typical offset at lower redshifts and for lower masses.
decrease from z = 3 to a minimum at z ∼ 1.5, and then increase until the present day. For these toy values, the difference in dark matter fraction definitions measured (specifically) at the same radius (Re, disk; Fig. 8, center right) typically differ by only ∼ − 0.005 to ∼ − 0.025 (typically ∼4 − 6% of the measured values), with a larger typical offset at lower redshifts and for lower masses.
 |
Fig. 8. Toy model of how |
We find the ratio of the 3D baryonic half mass radius to the disk effective radius (r1/2, 3D, baryons/Re, disk; Fig. 8, bottom left) for these models decreases towards lower redshifts and with increasing stellar mass, from ∼1 at z ∼ 2 − 3 to ∼0.94 at z = 0 for the lowest M*, and from ∼0.8 at z = 3 down to ∼0.6 at z = 0 for the highest M*. For the MW and M31 progenitors, this ratio decreases from ∼1, 0.96 at z = 3 down to ∼0.72, 0.59 at z = 0, respectively. The difference between the two dark matter fraction definitions measured at these different radii apertures (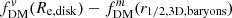 ; Fig. 8, bottom right) for these toy models is typically much larger than the difference for the definitions alone, and tends to increase towards lower redshifts and with stellar mass. The difference changes from ∼ − 0.015, 0.,0.025 at z = 3 to ∼ − 0.01, 0.015, 0.14 at z = 0 for log10(M*/M⊙) = 9, 10, 11, respectively. The MW and M31 progenitors have offsets increasing from ∼ − 0.013, −0.003 at z = 3 to ∼0.065, 0.14 at z = 0, respectively.
; Fig. 8, bottom right) for these toy models is typically much larger than the difference for the definitions alone, and tends to increase towards lower redshifts and with stellar mass. The difference changes from ∼ − 0.015, 0.,0.025 at z = 3 to ∼ − 0.01, 0.015, 0.14 at z = 0 for log10(M*/M⊙) = 9, 10, 11, respectively. The MW and M31 progenitors have offsets increasing from ∼ − 0.013, −0.003 at z = 3 to ∼0.065, 0.14 at z = 0, respectively.
Given the very modest offsets for the fDM definition differences alone, these offsets are nearly entirely driven by the differences between the aperture radii. Indeed, although the differences for these toy calculations – driven almost entirely by the aperture mismatches – do not reach the extreme differences of 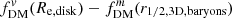 seen in Fig. 7 for parts of the parameter space (in part because the maximum toy model B/T is ∼0.4), we still predict absolute differences up to almost ∼0.15 at z = 0, and ∼0.03 − 0.07 at z ∼ 1 − 2. This offset is on par with the current observational uncertainties at z ≳ 1 (∼0.1 − 0.2; e.g., Genzel et al. 2020). To ensure the most direct comparison between observations and simulations – particularly as observational constraints on fDM at higher redshifts continue to improve – it will be important to account for such aperture differences (either by measuring in equivalent apertures, or by applying an appropriate correction factor) in order to better determine if, and how, observation and simulation predictions differ.
seen in Fig. 7 for parts of the parameter space (in part because the maximum toy model B/T is ∼0.4), we still predict absolute differences up to almost ∼0.15 at z = 0, and ∼0.03 − 0.07 at z ∼ 1 − 2. This offset is on par with the current observational uncertainties at z ≳ 1 (∼0.1 − 0.2; e.g., Genzel et al. 2020). To ensure the most direct comparison between observations and simulations – particularly as observational constraints on fDM at higher redshifts continue to improve – it will be important to account for such aperture differences (either by measuring in equivalent apertures, or by applying an appropriate correction factor) in order to better determine if, and how, observation and simulation predictions differ.
5. Turbulent pressure support effects on rotation curves
5.1. Derivation of pressure support for a single component
As many dynamical studies of high-redshift, turbulent disk galaxies use gas motions as the dynamical tracer, here, we consider how turbulent pressure support will modify the rotation curves if the gas is described by a deprojected Sérsic model. We followed the derivation of Burkert et al. (2010) and also assumed the pressure support is due only to the turbulent gas motions (i.e., the thermal contribution is negligible).
We thus begin from Eq. (2) of Burkert et al. (2010), where the pressure-corrected gas rotation velocity is:
where vcirc is the circular velocity in the midplane of the galaxy determined from the total system potential (including all mass components: stars, gas, and halo; i.e., the rotational velocity if there is no pressure support), ρg is the gas density, and σ is the (one-dimensional) gas velocity dispersion. While the gas has the same circular velocity as the total system, the pressure support correction term from the turbulent gas motions only applies to the gas rotation and only depends on the gas density distribution and the gas velocity dispersion.
This relation can be generally rewritten as:
where 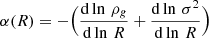 . If we assume the velocity dispersion σ = σ0 is constant, then this can be simplified to:
. If we assume the velocity dispersion σ = σ0 is constant, then this can be simplified to:
For a self-gravitating exponential disk, as assumed in Burkert et al. (2010), 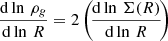 , which yields:
, which yields:
Burkert et al. (2016) generalized this result to a self-gravitating disk with an arbitrary Sérsic index, where αself − grav, n(R) = 2bn(R/Re)1/n.
Alternatively, as derived by Dalcanton & Stilp (2010) (their Eqs. (16) and (17)), for a disk with turbulent pressure Pturb ∝ Σ0.92, where the authors infer the exponent using results from hydrodynamical simulations of turbulence in stratified gas by Joung et al. (2009) combined with a Schmidt law of slope N = 1.4 (Kennicutt 1998), the pressure support is described by:
for arbitrary σR(R) (not only constant σ0 as considered here). Further forms of the pressure support have also been explored, as compared and discussed by Bouché et al. (2022), including the case for constant disk thickness (Meurer et al. 1996; Bouché et al. 2022), or when accounting for the full Jeans equation (Weijmans et al. 2008).
For gas following a deprojected Sérsic model, we find α(R) = α(R, n) by differentiating ρg = ρ(m = R, n)6. After combining Eqs. (2) and (4), performing a change of variable, and applying the Leibniz rule, we have:
This expression for dρ(m)/dm can be evaluated numerically, and together with the numerical evaluation of ρ(m), we have dlnρ/dlnm = (m/ρ)(dρ/dm)7. Alternatively, the log density can be differentiated numerically. (A similar derivation of the pressure support for spherical deprojected Sérsic profiles is presented in Sect. 2.2.3 of Kretschmer et al. 2021, who also showed α(n) versus n at select radii in their Fig. 6, and gave an approximate equation for α(n) at select radii in Sect. 3.5)8.
Figure 9 (left panel) shows the α(R, n) derived for the deprojected Sérsic models as a function of radius for a range of Sérsic index n (colored lines). For comparison, we also show the self-gravitating disk case αself − grav(R) as presented in Burkert et al. (2010) (black dashed line), as well as α determined following Dalcanton & Stilp (2010), and as measured from simulations in Kretschmer et al. (2021). In the latter, the density is determined from the smoothed cumulative mass profile of the cold gas and Re of the cold gas is the half-mass radius measured within 0.1Rvir (c.f. Sects. 2.3 and 3.2 of Kretschmer et al. 2021). The right panel additionally shows the ratio α/αself − grav. We find that α(n) is lower than αself − grav at R ≳ 0.2 − 0.8Re for n ≳ 1. However, at small radii (R ≲ Re) we find α(n) > αself − grav for n ≳ 1 (with the cross-over radius varying with n). In contrast, we find the inverse for n = 0.5: α(n = 0.5) is lower than αself − grav up to R ∼ 2.4Re, but then α(n) exceeds αself − grav at larger radii. In comparison to the self-gravitating disk case, we find the deprojected Sérsic α(n) are in better agreement with the pressure support for an exponential distribution from Dalcanton & Stilp (2010), as well as with the simulation-derived pressure support by Kretschmer et al. (2021, and similar findings by Wellons et al. 2020), with roughly half as much pressure support as the self-gravitating case.
 |
Fig. 9. Pressure support correction, α(R), versus R/Re for a self-gravitating exponential disk and deprojected Sérsic models. The left panel directly compares αself − grav(r) = 3.36(R/Re) for the self-gravitating disk (as in Burkert et al. 2010; black dashed line) to α(R, n) = − dlnρ(R, n)/dlnR determined for a range of Sérsic indices n (colored lines). The ratio α/αself − grav(R) is shown in the right panel. For n ≥ 1, α(n) is smaller than αself − grav when R ≳ 0.2 − 0.8Re; however, α(n ≥ 1) does exceed αself − grav at the smallest radii. This implies that for most radii, there is less asymmetric drift correction (and thus higher vrot) for the deprojected Sérsic models (e.g., n = 1) than for the self-gravitating disk. However, for n = 0.5, α(n) is greater than αself − grav at R ≳ 2.4Re, so at large radii the n = 0.5 deprojected Sérsic model predicts a larger pressure support correction than for the self-gravitating disk case. The lower pressure support predicted for α(n ≳ 1) than for αself − grav is in agreement with recent predictions from simulations by Kretschmer et al. (2021) (red circles; with the vertical grey bars denoting the 1σ distribution), as well the relation by Dalcanton & Stilp (2010) for a power law relationship between the gas surface density and the turbulent pressure (orange dashed line). |
Furthermore, as demonstrated by Bouché et al. (2022) (using an example vcirc with n = 1.5 and an NFW profile), the Dalcanton & Stilp (2010) correction produces pressure support that is very similar to the constant scale height (ρ(R)∝Σ(R), Meurer et al. 1996; Bouché et al. 2022) and Weijmans et al. 2008 cases (assuming constant dispersion), which all predict lower support corrections than for the self-gravitating disk case. This difference arises because these three cases assume constant scale height or a thin disk approximation, resulting in a correction of approximately dlnΣ(R)/dlnR. In contrast, the self-gravitating disk case explicitly assumes a constant vertical dispersion, so predicts ρ(R)∝Σ(R)2, yielding a correction term that is roughly twice that of the other cases.
These differences between α predict different pressure support-corrected vrot(R) for the same circular velocity profile and intrinsic velocity dispersion. We demonstrate these differences for α for deprojected Sérsic models and a self-gravitating disk in Fig. 10, over a range of Sérsic indices (n = 0.5, 1, 2, 4; left to right) and intrinsic axis ratios (q0 = 1, 0.2; top and bottom, respectively)9. For all cases, we determine the circular velocity vcirc (solid black line) assuming the mass distribution follows a single deprojected Sérsic model of Mtot = 1010.5 M⊙ (i.e., a pure gas disk, or gas+stars where both components follow the same density distribution). We then calculate vrot using both α(n) and αself − grav (dashed and dotted lines, respectively). As implied by Fig. 9, for n ≳ 1 the rotation curves vrot computed with α(n) are higher than with αself − grav at R ≳ Re (i.e., smaller correction from vcirc). The difference between the two vrot curves becomes more pronounced towards larger radii, in line with the continued decrease of α(n)/αself − grav with increasing radius. We also see the opposite behavior in the n = 0.5 case, where vrot computed in the self-gravitating case is higher than for α(n) at R ≳ 2.4Re (but the vrot computed with α(n) is higher than with αself − grav at smaller radii).
 |
Fig. 10. Comparison between |
The amplitude of the intrinsic dispersion further impacts the vrot profiles by causing disk truncation for sufficiently high σ0 relative to vcirc, as previously discussed by Burkert et al. (2016). For the highest dispersion case (σ0 = 90 km s−1; orange), the pressure support correction predicts disk truncation (i.e., 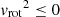 ) within R ≲ 5Re for both α(n) and αself − grav. With medium dispersion (σ0 = 60 km s−1; turquoise), we still find disk truncation at R ≲ 5Re for all n when using αself − grav, but only α(n = 0.5, 1) produce truncation within this radial range. Finally, αself − grav does not produce truncation within 5Re in any case at the lowest dispersion (σ0 = 30 km s−1; purple), and only α(n = 0.5) predicts truncation at R ∼ 5Re (for both the spherical and flattened cases).
) within R ≲ 5Re for both α(n) and αself − grav. With medium dispersion (σ0 = 60 km s−1; turquoise), we still find disk truncation at R ≲ 5Re for all n when using αself − grav, but only α(n = 0.5, 1) produce truncation within this radial range. Finally, αself − grav does not produce truncation within 5Re in any case at the lowest dispersion (σ0 = 30 km s−1; purple), and only α(n = 0.5) predicts truncation at R ∼ 5Re (for both the spherical and flattened cases).
5.2. Pressure support for multi-component systems
Generally, however, the gas in galaxies may be distributed in more than one component, which would modify the pressure support correction term10. We can then derive the composite αtot(R) using the α(R, n) of the individual gas components. For example, if the composite system includes gas in both a bulge and a disk, we have the total ρtot = ρdisk + ρbulge. As dlnρ/dlnR = (R/ρ)(dρ/dR), we have:
As discussed in Sect. 5.1, this composite gas pressure support term is applicable to the gas velocity curve regardless of the distribution of the other, non-gas mass components.
We demonstrate an example composite pressure support term for a galaxy with gas distributed in both a disk and bulge over a range of B/T and Re, bulge/Re, disk values in Fig. 11. Here, we assume ndisk = 1 and nbulge = 4, that is, an exponential disk and de Vaucouleurs spheroid bulge, as adopted for recent bulge and disk decompositions at z ∼ 1 − 3, given the current observation spatial resolution limitations (Bruce et al. 2012; Lang et al. 2014), with a range of B/T (from disk- to bulge-only; black to light red colors) and Re, bulge/Re, disk (from Re, disk = 5Re, bulge down to Re, disk = Re, bulge; solid to dotted line styles). As expected, the composite αtot is lower than αself − grav at large radii, but can be larger than αself − grav at R/Re, disk ≲ 1 when there is non-zero bulge contribution (see Fig. 9).
 |
Fig. 11. Composite pressure support correction, αtot(R), for gas distributed in a composite disk+bulge system (with ndisk = 1, nbulge = 4), for a range of B/T (colors) and Re, bulge/Re, disk ratios (dash length). For the limiting cases, we recover the profiles shown in Fig. 9: B/T = 0 has αtot = α(n = 1) (black solid line), while B/T = 1 has αtot = α(n = 4) but with different radial scaling, owing to the different adopted Re, bulge/Re, disk ratios (colored lines). For the cases with 0 < B/T < 1, the bulge contribution modifies the α(n = 1) profile at both small and large radii, leading to larger αtot in inner regions and smaller αtot in the outskirts (R/Re, disk ≲ , ≳ 1 − 2). At fixed B/T, the deviation from the disk α(n = 1) in the center (R/Re, disk ≲ 1 − 2) is larger for smaller Re, bulge/Re, disk, while at large radii the deviation is larger for larger Re, bulge/Re, disk. For reference, we mark Re, bulge/Re, disk with vertical light grey lines, and also show αself − grav (grey dash-dotted line). |
Compared to the disk-only α(n = 1) (solid black line), the inclusion of the bulge component leads to larger αtot at small radii (R/Re, disk ≲ 1 − 2) and lower αtot at large radii (R/Re, disk ≳ 1 − 2). This is the result of a steeper inner density slope together with a shallower decline at large radii for n = 4 compared to an exponential deprojected Sérsic model, so the bulge component becomes more important at very small and very large radii. When varying Re, bulge/Re, disk, we find the most pronounced changes to αtot at small radii when the Re, bulge/Re, disk ratio is smallest (solid lines). This effect is less pronounced for larger Re, bulge/Re, disk values, as the bulge density profile is more extended and the disk profile becomes important at smaller R/Re, disk. For larger radii, the opposite holds: the largest changes with B/T are found for the largest Re, bulge/Re, disk (dotted lines), as the bulge component becomes important at smaller R/Re, disk owing to the larger Re, bulge.
6. Discussion and implications
In this paper, we present properties and implications when using deprojected, axisymmetric Sérsic models to describe mass density distributions or kinematics, over a wide range of possible galaxy parameters. Some of these effects will be more important for certain galaxy populations and epochs than others (as initially hinted in Fig. 8). Here, we discuss the implications for the models presented in this work, focusing on which aspects are most important for interpreting observations and for comparing observations to simulations as a function of cosmic time and galaxy mass.
6.1. Low redshift
Nearby, present-day star-forming galaxies (that are not dwarf galaxies) typically host fairly thin disk components and some also host a bulge. The disks of such galaxies would generally be characterized by geometries with small q0 – relatively similar to the infinitely thin exponential disk case (Freeman 1970). Thus, when modeling the circular velocity curves of these disks, the choice of adopting the infinitely thin disk versus deprojected oblate Sérsic models has a relatively small impact. The thin gas disks of these local galaxies also have relatively low intrinsic velocity dispersions, with relatively little pressure support. The exact pressure support correction formulation therefore has less of an impact on the interpretation of the dynamics.
However, the low q0 and typically large disk effective radii Re, disk in z ∼ 0 star-forming galaxies, when coupled with a non-negligible bulge component, do result in ratios of r1/2, 3D, baryons/Re, disk less than 1. This deviation of the 2D and 3D half-mass radii can lead to large aperture effects when interpreting projected versus 3D quantities, such as when comparing observational or simulation quantities (e.g., fDM). This aperture mismatch would be most severe for higher mass low-z galaxies, as these will tend to have larger values of Re, disk and B/T (since a more prominent bulge will decrease r1/2, 3D, baryons relative to Re, disk). For example, aperture differences can lead to discrepancies of up to ΔfDM = fDM(Re, disk)−fDM(r1/2, 3D, baryons)∼0.15 at M* ∼ 1011 M⊙ for typical values of Re, disk and B/T (Fig. 8, lower right). In contrast, lower mass low-z galaxies are generally less impacted by aperture mismatches, owing to the lower typical B/T and smaller Re, disk of these galaxies.
Compared to the impact of aperture mismatches, definition differences in fDM (as might be measured from observations and simulations) lead to only minor discrepancies. However, for lower stellar mass low-z galaxies where the aperture mismatch is relatively minor, the typically low B/T and thus more prominent thin disk leads to a larger relative impact of fDM estimator differences, as these galaxies are overall less spherically symmetric (see Figs. 6 and 8).
Overall, for star-forming galaxies at low redshift, the most important effect to consider is to correct for – or avoid – any aperture mismatches when comparing measurements between simulations and observations of, for instance, fDM, particularly for high stellar masses. The impact of other aspects (use of infinitely thin disks vs. finite thickness, pressure support correction formulation, or fDM estimator definition) are all relatively minor and can be ignored for most purposes.
6.2. High redshift
In contrast to the local universe, at high redshift (e.g., z ∼ 1 − 3), relatively massive star-forming galaxies generally exhibit thick disks, with increasing bulge contributions towards higher masses. These thick disks would be reasonably well described by elevated q0 ∼ 0.2 − 0.25. As the derived circular velocity curve for such a geometry is fairly different from that of an infinitely thin exponential disk (e.g., N08), the choice of rotation curve parameterization (i.e., adopting vcirc based o a deprojected profile such as those presented here versus using an infinitely thin exponential disk) is important at high-z.
The thick geometries of high-z disks are coupled with relatively high intrinsic velocity dispersions, which implies that the overall amount of pressure support is expected to be much higher than for the dynamically-cold, thin disks at low-z. Thus, not only is it more important to account for pressure support, but the choice of adopted pressure support correction matters much more for interpreting kinematics at high-z than for nearby galaxies.
In this paper, we derive the log density slope-driven pressure support correction α(n) as a function of radius R for the deprojected Sérsic models, and compare this correction term to other formulations, particularly the correction for a self-gravitating exponential disk, αself − grav (as in Burkert et al. 2010, 2016). A key implication of the differences between these pressure support corrections is that, for the same vrot(R) and σ0, α(n) predicts a lower vcirc than would be inferred when applying αself − grav (i.e., the inverse of the demonstration in Fig. 10). Furthermore, the shape of the inferred vcirc profile can also differ (particularly when considering a composite disk+bulge gas distribution; Fig. 11). Both effects can impact the results of mass decomposition from modeling of galaxy kinematics, which have important implications for the measurement of dark matter fractions.
Although the smaller disk sizes of high-z galaxies help to alleviate the disk-halo degeneracy that strongly impacts kinematic fitting at z ∼ 0, there are nonetheless often degeneracies between mass components when performing kinematic modeling at z ∼ 1 − 3 (see e.g., Price et al. 2021, Sect. 6.2 and Fig. 5). The strong pressure correction from αself − grav can further complicate the reduced but still present disk-halo degeneracy at high-z. When combined with high σ0, modest variations in σ0 (allowed within the uncertainties) can extend the degeneracy between galaxy-scale dark matter fractions and total baryonic masses – in the most extreme cases, allowing the 1σ region to extend from 0% to 50+% dark matter fractions.
However, the strength of this added degeneracy effect depends not only on σ0, but also on the pressure support prescription. The large correction from αself − grav can result in a falling vrot even for a flat or rising vcirc (with a large halo contribution; Fig. 5b of Price et al. 2021). Alternatively, if α(n) were adopted, the comparable correction to vcirc would produce a less steeply dropping (or potentially flat) vrot profile. Thus, to match the observed vrot profile, the intrinsic vcirc would be limited to lower amplitudes (i.e., implying lower dynamical masses) with less shape modification than when using α(n) instead of αself − grav. This in turn implies partial breaking of the added pressure support impact to the disk-halo degeneracy, restricting the higher likelihood regions towards a lower value for fDM. While adopting α(n) would have the greatest impact on the objects with high σ0 (where the pressure support has the largest impact), the change in prescription should impact the inferred mass distribution for all objects to some extent. The choice of pressure support formulation is thus an important factor in the interpretation of dynamics of high-redshift galaxies and has direct implications for the interpretation of mass fractions. Overall, this will have the largest impact for galaxies with low vrot/σ0 (and the smallest impact for high vrot/σ0), as this will lead to the largest fractional change in vrot relative to vcirc. Since there is currently no observed trend of σ0 with M* at high-z (e.g., Übler et al. 2019; although the dynamic range of M* is currently limited), the correlation of vrot with M* would then cause this effect to generally be most important for low-mass galaxies.
On the other hand, the higher q0 and lower Re, disk of high-z disk galaxies implies that aperture effects arising from deviations of r1/2, 3D, baryons versus Re, disk are less important than for low-z galaxies, as the disk and bulge sizes are more similar. Still, there can be up to ∼20% radii aperture differences in the 2D and 3D half-mass radii (although with only ∼2.5% fDM differences), so depending on the particular measurement quantity and accuracy required, this effect could still be important. As is the case for the local limit, the aperture radii difference (and the resulting impact on inferred fDM) typically has a larger impact for higher mass objects, since these tend to have higher B/T and Re, disk than lower mass objects. Finally, as with the low-z case, the fDM estimator differences are relatively minor compared to the other effects and can be generally ignored. We note, however, that the same comments on trends with B/T and necessary comparison accuracy from the low-z discussion apply in this case.
In conclusion, for high-redshift star-forming galaxies, the most important effects to consider are:
-
Adopting circular velocity curves that account for the finite, thick-disk geometry;
-
Including a reasonable pressure support correction when interpreting rotation curves.
In this limit (higher q0, lower Re, disk, high σ0), the other aspects (2D vs. 3D half-mass radii apertures, fDM estimator definitions) have relatively small impacts and can typically be ignored.
7. Summary
We present a number of properties for 3D deprojected Sérsic models with a range of values for the intrinsic axis ratio q0 = c/a (i.e., flattened or oblate, spherical, or prolate). We followed the derivation of N08, who presented the deprojection of the 2D Sérsic profile to a 3D density distribution ρ(m), as well as the midplane circular rotation curve vcirc(R) for such a mass distribution. We then extended this work by numerically deriving spherical enclosed mass profiles Msph(< r = R) and the log density slope dlnρ/dlnR.
Using these profiles, we determined a range of properties of these mass models. Specifically, we examined the differences between the 2D projected effective radius, Re, and the 3D spherically-enclosed half-mass radius, r1/2, mass, 3D, over a range of intrinsic axis ratios q0 and Sérsic indices n, and find r1/2, mass, 3D > Re, with the ratio approaching unity as q0 → 0, in agreement with previous results. We also calculated virial coefficients that relate the circular velocity to either the total mass (ktot) or the enclosed mass within a sphere (k3D).
Furthermore, we calculated derived properties for example composite galaxy systems (consisting of both flattened deprojected Sérsic and spherical components), to consider how varying galaxy properties (i.e., B/T, Re, disk, z) impacts these properties, such as r1/2, 3D, baryons/Re, disk. We also examined the impact of different methods of inferring fDM(< R) and the compounding effects from measuring fDM within different aperture radii. We find that using different apertures, such as r1/2, 3D, baryons versus Re, disk, can lead to very large differences in the measured fDM, particularly for high B/T and low Re, bulge/Re, disk. In contrast, using different fDM definitions, such as 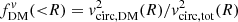 and
and 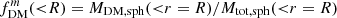 , only produces minor differences when measured at the same radius. Using toy models, we estimated how r1/2, 3D, baryons/Re, disk and the fDM estimators (measured both at Re, disk and with mismatched r1/2, 3D, baryons vs. Re, disk apertures) change as a function of redshift and stellar mass and find increasing offsets towards higher M* and lower z.
, only produces minor differences when measured at the same radius. Using toy models, we estimated how r1/2, 3D, baryons/Re, disk and the fDM estimators (measured both at Re, disk and with mismatched r1/2, 3D, baryons vs. Re, disk apertures) change as a function of redshift and stellar mass and find increasing offsets towards higher M* and lower z.
We additionally used the deprojected Sérsic models to derive self-consistent pressure support correction terms, with α(R, n) = − dlnρg(R, n)/dlnR for constant gas velocity dispersion. At R ≳ Re, we find that α(R, n) typically predict a smaller pressure support correction than is inferred for a self-gravitating disk (as in Burkert et al. 2010, 2016) and are more similar to predictions derived for thin disks with ∼constant scale heights under various assumptions (e.g., Dalcanton & Stilp 2010; Meurer et al. 1996; Bouché et al. 2022; Weijmans et al. 2008) and from simulations (e.g., Kretschmer et al. 2021; also Wellons et al. 2020). The effect of a lower pressure support with α(n) implies larger vrot for the same vcirc and σ0 (or lower vcirc for the same vrot and σ0)than if assuming αself − grav, and would predict any disk truncation (where vrot → 0, as in Burkert et al. 2016) at larger radii than for the self-gravitating case.
Finally, we discuss implications of this work for future studies of galaxy mass distributions and kinematics. Low-z star-forming disk galaxies typically have thin disks with small q0 and low intrinsic velocity dispersion, so the most important effect to consider is aperture mismatches when comparing measurements – such as measuring fDM within 2D and 3D apertures, as typically adopted for observations and simulations, respectively. In contrast, the thick disks in high-z star-forming galaxies are characterized by large q0 and high intrinsic velocity dispersion, so adopting circular velocity curves accounting for this finite thickness and accounting for the pressure support correction are the most important aspects. The high σ0 of these high-z galaxies can produce large pressure support corrections, in some cases causing greater-than-Keplerian falloff in outer rotation curves (e.g., Genzel et al. 2017). In this limit of relatively large correction amplitudes, the choice of the adopted pressure support correction is also important and can impact constraints of the disk-halo mass decomposition, as lower correction amplitudes (e.g., using α(n) versus the larger correction of αself − grav) will tend to lead to lower inferred dark matter fractions, particularly for high σ0. Furthermore, while differences in quantity estimators (e.g., 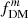 vs.
vs. 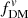 ) have only modest effects at both low and high-z, as measurements improve it would be worth correcting for, or avoiding, estimator differences to improve the accuracy of comparisons between different studies.
) have only modest effects at both low and high-z, as measurements improve it would be worth correcting for, or avoiding, estimator differences to improve the accuracy of comparisons between different studies.
The deprojected Sérsic profile models presented here can be used to aid comparisons between observations and simulations and help convert between simulation quantities that are typically determined within spherical shells and observational constraints based on 2D projected quantities. As demonstrated in this work, commonly adopted apertures for simulations (3D half-mass) versus observations (2D projected half-light or half-mass) can probe different physical scales, impacting observation-simulation comparisons, particularly for dark matter fractions. The pre-computed profiles and values (or similar calculations) can help in shifting towards more direct, apples-to-apples comparisons between the two, without resorting to the more direct but complex step of constructing and analyzing mock observations based on simulated galaxies (as in, e.g., Übler et al. 2021; but see also Genel et al. 2012; Teklu et al. 2018; Simons et al. 2019). The code used to compute these profiles, as well as precomputed profiles and other quantities for a range of Sérsic index, n, and intrinsic axis ratio, q0, have been made publicly available.
The python package deprojected_sersic_models used in this paper and the pre-computed tables are both available for download from sedonaprice.github.io/deprojected_sersic_models/downloads.html; the full code repository is publicly available at github.com/sedonaprice/deprojected_sersic_models. The code also includes functions for scaling and interpolating the profiles from the pre-computed tables to arbitrary total masses and Re as a function of radius.
For prolate geometries, the projected major axis lies parallel to the long intrinsic axis, c. Here, however, we use a geometry definition where κ is parallel to a for all cases, for a consistent convention relative to the rotation axis (z; parallel to c) – so technically κ is parallel to the major axis as usual for oblate geometry, but lies along the minor axis for prolate geometry.
In N08, ρ(m) denotes the 3D luminosity density distribution, while we define ρ(m) as the 3D mass density. Thus, we instead write the 3D luminosity density as ρ(m)/Υ(m) in the projection integral.
However, many massive SFGs at these redshifts exhibit lower fDM that suggest more cored halo profiles; see e.g., Genzel et al. (2020).
Note that the pressure correction term α(n) discussed here is the same as αρ as defined in Kretschmer et al. (2021). However, we emphasize that it is not directly comparable to the αv derived by Kretschmer et al. for their simulations. Kretschmer et al. determine circular velocities from mass enclosed within a sphere, 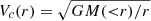 , and instead fold the effects of non-spherical potentials into the correction term ΔQ. Here we explicitly consider vcirc determined for non-spherical deprojected Sérsic profiles, so α(n) does not need such a correction. Of course, the total α considered here would be modified by terms incorporating variable σ(R) or anisotropic velocity dispersion, but these terms vanish as we assume a constant σ0.
, and instead fold the effects of non-spherical potentials into the correction term ΔQ. Here we explicitly consider vcirc determined for non-spherical deprojected Sérsic profiles, so α(n) does not need such a correction. Of course, the total α considered here would be modified by terms incorporating variable σ(R) or anisotropic velocity dispersion, but these terms vanish as we assume a constant σ0.
Only the gas density distribution that impacts α(R), regardless of other (e.g., stellar or halo) components (see Sect. 5.1).
Acknowledgments
We thank Michael Kretschmer for sharing the values of αρ derived from the simulated galaxies presented in Fig. 4 of Kretschmer et al. (2021), Taro Shimizu for helpful discussions, and Dieter Lutz for comments on the manuscript. We also thank the anonymous referee for their comments and suggestions that improved this manuscript. HÜ gratefully acknowledges support by the Isaac Newton Trust and by the Kavli Foundation through a Newton-Kavli Junior Fellowship. This work has made use of the following software: Astropy (http://www.astropy.org; Astropy Collaboration 2013, 2018), dill (McKerns et al. 2011; McKerns & Aivazis 2010), IPython (Pérez & Granger 2007), Matplotlib (Hunter 2007), Numpy (Van Der Walt et al. 2011; Harris et al. 2020), Scipy (Virtanen et al. 2020)
References
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baes, M., & Ciotti, L. 2019a, A&A, 626, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baes, M., & Ciotti, L. 2019b, A&A, 630, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics: Second Edition (Princeton, NJ USA: Princeton University Press) [Google Scholar]
- Blanton, M. R., Hogg, D. W., Bahcall, N. A., et al. 2003, ApJ, 594, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Bouché, N. F., Bera, S., Krajnović, D., et al. 2022, A&A, 658, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruce, V. A., Dunlop, J. S., Cirasuolo, M., et al. 2012, MNRAS, 427, 1666 [NASA ADS] [CrossRef] [Google Scholar]
- Burkert, A., Genzel, R., Bouché, N., et al. 2010, ApJ, 725, 2324 [Google Scholar]
- Burkert, A., Förster Schreiber, N. M., Genzel, R., et al. 2016, ApJ, 826, 214 [Google Scholar]
- Casertano, S. 1983, MNRAS, 203, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Ciotti, L. 1991, A&A, 249, 99 [NASA ADS] [Google Scholar]
- Ciotti, L., & Lanzoni, B. 1997, A&A, 321, 724 [NASA ADS] [Google Scholar]
- Conselice, C. J. 2014, ARA&A, 52, 291 [CrossRef] [Google Scholar]
- Courteau, S., de Jong, R. S., & Broeils, A. H. 1996, ApJ, 457, L73 [NASA ADS] [Google Scholar]
- Courteau, S., Cappellari, M., de Jong, R., et al. 2014, Rev. Mod. Phys., 86, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Dalcanton, J. J., & Stilp, A. M. 2010, ApJ, 721, 547 [NASA ADS] [CrossRef] [Google Scholar]
- de Blok, W. J. 2010, Adv. Astron., 2010, 789293 [CrossRef] [Google Scholar]
- de Blok, W. J. G., & McGaugh, S. S. 1997, MNRAS, 290, 533 [NASA ADS] [CrossRef] [Google Scholar]
- de Blok, W. J., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2648 [NASA ADS] [CrossRef] [Google Scholar]
- Dutton, A. A., & Macciò, A. V. 2014, MNRAS, 441, 3359 [Google Scholar]
- Dutton, A. A., Courteau, S., de Jong, R., & Carignan, C. 2005, ApJ, 619, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Erb, D. K., Steidel, C. C., Shapley, A. E., et al. 2006, ApJ, 646, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Förster Schreiber, N. M., & Wuyts, S. 2020, ARA&A, 58, 661 [Google Scholar]
- Freeman, K. C. 1970, ApJ, 160, 811 [Google Scholar]
- Genel, S., Naab, T., Genzel, R., et al. 2012, ApJ, 745, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Schreiber, N. M. F., Übler, H., et al. 2017, Nature, 543, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Price, S. H., Übler, H., et al. 2020, ApJ, 902, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Glazebrook, K. 2013, PASA, 30, e056 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A. W., & Driver, S. P. 2005, PASA, 22, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Joung, M. R., Mac Low, M. M., & Bryan, G. L. 2009, ApJ, 704, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kretschmer, M., Dekel, A., Freundlich, J., et al. 2021, MNRAS, 503, 5238 [NASA ADS] [CrossRef] [Google Scholar]
- Lang, P., Wuyts, S., Somerville, R. S., et al. 2014, ApJ, 788, 11 [NASA ADS] [CrossRef] [Google Scholar]
- McKerns, M., & Aivazis, M. 2010, pathos: a framework for heterogeneous computing. https://uqfoundation.github.io/project/pathos [Google Scholar]
- McKerns, M., Strand, L., Sullivan, T., Fang, A., & Aivazis, M. 2011, in Proceedings of the 10th Python in Science Conference, Arxiv e-prints [arxiv:1202.1056] [Google Scholar]
- Meurer, G. R., Carignan, C., Beaulieu, S. F., & Freeman, K. C. 1996, AJ, 111, 1551 [Google Scholar]
- Miller, S. H., Bundy, K., Sullivan, M., Ellis, R. S., & Treu, T. 2011, ApJ, 741, 115 [Google Scholar]
- Mo, H. J., Mao, S., & White, S. D. M. 1998, MNRAS, 295, 319 [Google Scholar]
- Moster, B. P., Naab, T., & White, S. D. 2013, MNRAS, 428, 3121 [Google Scholar]
- Moster, B. P., Naab, T., & White, S. D. 2018, MNRAS, 477, 1822 [NASA ADS] [CrossRef] [Google Scholar]
- Noordermeer, E. 2008, MNRAS, 385, 1359 [Google Scholar]
- Palunas, P., & Williams, T. B. 2000, AJ, 120, 2884 [Google Scholar]
- Papovich, C., Labbé, I., Quadri, R., et al. 2015, ApJ, 803, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2010, AJ, 139, 2097 [Google Scholar]
- Pérez, F., & Granger, B. E. 2007, Comput. Sci. Eng., 9, 21 [Google Scholar]
- Persic, M., Salucci, P., & Stel, F. 1996, MNRAS, 281, 27 [Google Scholar]
- Price, S. H., Kriek, M., Shapley, A. E., et al. 2016, ApJ, 819, 80 [Google Scholar]
- Price, S. H., Kriek, M., Barro, G., et al. 2020, ApJ, 894, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Price, S. H., Shimizu, T. T., Genzel, R., et al. 2021, ApJ, 922, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Rodighiero, G., Daddi, E., Baronchelli, I., et al. 2011, ApJ, 739, L40 [Google Scholar]
- Romanowsky, A. J., & Fall, S. M. 2012, ApJS, 203, 52 [Google Scholar]
- Sérsic, J. L. 1968, Atlas de galaxias australes (Cordoba, Argentina: Observatorio Astronomico) [Google Scholar]
- Simard, L., Mendel, J. T., Patton, D. R., Ellison, S. L., & McConnachie, A. W. 2011, ApJS, 11, 25 [Google Scholar]
- Simard, L., Willmer, C. N. A., Vogt, N. P., et al. 2002, ApJS, 142, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Simons, R. C., Kassin, S. A., Snyder, G. F., et al. 2019, ApJ, 874, 59 [Google Scholar]
- Sofue, Y., & Rubin, V. 2001, ARA&A, 39, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Speagle, J. S., Steinhardt, C. L., Capak, P. L., & Silverman, J. D. 2014, ApJS, 214, 52 [Google Scholar]
- Stark, A. 1977, ApJ, 213, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., & Sternberg, A. 2020, ARA&A, 58, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Teklu, A. F., Remus, R.-S., Dolag, K., et al. 2018, ApJ, 854, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Tomczak, A. R., Quadri, R. F., Tran, K.-V. H., et al. 2016, ApJ, 817, 118 [Google Scholar]
- Trujillo, I., Asensio Ramos, A., Rubiño-Martîn, J. A., et al. 2002, MNRAS, 333, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Übler, H., Genzel, R., Wisnioski, E., et al. 2019, ApJ, 880, 48 [Google Scholar]
- Übler, H., Genel, S., Sternberg, A., et al. 2021, MNRAS, 500, 4597 [Google Scholar]
- van Albada, T. S., Bahcall, J. N., Begeman, K., & Sancisi, R. 1985, ApJ, 295, 305 [Google Scholar]
- van de Ven, G., & van der Wel, A. 2021, ApJ, 914, 45 [NASA ADS] [CrossRef] [Google Scholar]
- van der Kruit, P., & Freeman, K. 2011, ARA&A, 49, 301 [NASA ADS] [CrossRef] [Google Scholar]
- van der Kruit, P. C., & Allen, R. J. 1978, ARA&A, 16, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Van Der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
- van der Wel, A., Bell, E. F., Häussler, B., et al. 2012, ApJS, 203, 24 [NASA ADS] [CrossRef] [Google Scholar]
- van der Wel, A., Franx, M., van Dokkum, P. G., et al. 2014, ApJ, 788, 28 [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Weijmans, A. M., Krajnović, D., Van De Ven, G., et al. 2008, MNRAS, 383, 1343 [NASA ADS] [CrossRef] [Google Scholar]
- Wellons, S., Faucher-Giguère, C. A., Anglés-Alcázar, D., et al. 2020, MNRAS, 497, 4051 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., Franx, M., Leja, J., et al. 2014, ApJ, 795, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Wuyts, S., Förster Schreiber, N. M., van der Wel, A., et al. 2011, ApJ, 742, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Wuyts, S., Förster Schreiber, N. M., Wisnioski, E., et al. 2016, ApJ, 831, 149 [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Fractional mass enclosed within a sphere of radius r = R for deprojected Sérsic models of different intrinsic axis ratios. From left to right: enclosed Msph is plotted as a function of log radius (relative to the projected 2D effective radius, Re), assuming intrinsic axis ratios of q0 = 1, 0.4, 0.2, respectively. The colored curves denote the enclosed mass profiles for Sérsic indices from n = 0.5 to n = 8 (yellow to purple). The vertical lines denote R = Re (grey dashed) and R = 1.3Re (≈r1/2, mass, 3D for q0 = 1; grey dash-dotted), and the horizontal colored lines denote the fraction of the mass enclosed within r = Re for n = 1, 4 (lime, teal dashed, respectively) and 50% of the total mass (grey dashed dotted). For q0 = 1, the half-mass 3D spherical radius is indeed r1/2, mass, 3D ≈ 1.3Re regardless of n, as in Ciotti (1991). For flattened (i.e., oblate) systems, the half-mass 3D spherical radius is smaller, and approaches Re as q0 decreases. See also Fig. 2. |
| In the text | |
 |
Fig. 2. Comparison between the 3D spherical half-mass radius, r1/2, mass, 3D, and the projected 2D effective radius, Re, for a range of Sérsic indices n and intrinsic axis ratios q0 (left, colored by q0; right, colored by n). For oblate cases, Re is the projected major axis, while for prolate cases Re is the projected minor axis. For all cases, r1/2, mass, 3D > Re. However, as q0 decreases (i.e., flatter Sérsic distributions), the 3D half-mass radius approaches the value of Re. Overall, the systematic difference between r1/2, mass, 3D and Re highlights that while half of the model mass is enclosed within a projected 2D ellipse of major axis Re (e.g., an infinite ellipsoidal cylinder), less than half the total mass is enclosed within a sphere of radius Re (ignoring any M/L gradients or optically thick regions, which would change Re, light/Re, mass). |
| In the text | |
 |
Fig. 3. Example fractional enclosed mass (top) and circular velocity (bottom) profiles computed or inferred under different assumptions. The top and bottom rows show the profiles for Sérsic indices n = 1, 4, respectively, while the columns show intrinsic axis ratios q0 = 1, 0.4, 0.2 (from left to right). For the top panels, we show the edge-on 2D projected mass enclosed within ellipses of axis ratio q0 (orange solid line), the 3D mass profile enclosed within a sphere (red dashed line), the 3D mass profile enclosed within ellipsoids of intrinsic axis ratio q0 (purple dash-dotted line), and the mass profile inferred from the flattened deprojected Sérsic model circular velocity under the simplifying assumption of spherical symmetry (i.e., q0 = 1; black dotted line). In the bottom panels, we then compare the flattened deprojected Sérsic model circular velocity (black dotted line) to the inferred velocity profiles computed from the 3D spherical (red solid line) and the 3D ellipsoidal (purple dash-dotted) mass profiles under the simple assumption of spherical symmetry. The same total mass Mtot = 5 × 1010 M⊙ is used for all cases. The vertical lines denote R = Re (grey dashed) and R = 1.3Re (≈r1/2, mass, 3D for q0 = 1; grey dash-dotted). These enclosed mass and velocity profiles demonstrate that when q0 ≠ 1, Msph(< r = R)≠vcirc(R)2R/G. The non-spherical potentials for q0 < 1 even result in (vcirc(R)2R/G)/Mtot > 1 between R ∼ 1 − 10Re (i.e., potentially leading to ≳15% overestimates in the system mass). We also see that as q0 decreases, Msph approaches the 2D projected mass profile, as the mass enclosed in a sphere versus an infinite ellipsoidal cylinder are equivalent for infinitely thin mass distributions. |
| In the text | |
 |
Fig. 4. Total ktot(Re) (left) and 3D enclosed k3D(Re) (right) virial coefficients as a function of Sérsic index, n, and intrinsic axis ratio q0. The solid lines denote q0 = 0.2 (orange) to q0 = 1 (black) and two prolate cases are shown with dashed lines (q0 = 1.5, 2 in dark, light grey, respectively). |
| In the text | |
 |
Fig. 5. Enclosed mass (3D spherical, top), circular velocity (middle), and dark matter (bottom) profiles for different components of an example galaxy as a function of projected major axis radius, for bulge-to-total ratios of B/T = 0, 0.25, 0.5, 0.75, 1 (left to right). For all cases, we compute the mass components assuming values for a typical z = 2 massive main-sequence galaxy with log10(M*/M⊙) = 10.5: Mbar = 6.6 × 1010 M⊙, Re, disk = 3.4 kpc, ndisk = 1, q0, disk = 0.25, Re, bulge = 1 kpc, nbulge = 4, q0, bulge = 1, and a NFW halo with Mhalo = 8.9 × 1011 M⊙ and c = 4.2. Shown are the Msph(< r = R) and vcirc(R) profiles for the disk (dashed blue), bulge (dash-dotted red), total baryons (disk+bulge; dash-dot-dot green), halo (dotted purple), and composite total system (solid black). Vertical lines mark R = Re, disk (solid grey) and the 3D spherical half-mass radii r1/2, mass, 3D for the disk (dashed blue), bulge (dash-dotted red), and total baryons (dash-dot-dot green). Two dark matter fraction definitions are shown in the bottom panels, |
| In the text | |
 |
Fig. 6. Ratio between the dark matter fraction at Re, disk calculated from the circular velocity and from the 3D spherical enclosed mass, |
| In the text | |
 |
Fig. 7. Ratio between the composite disk+bulge 3D half-mass radius and the 2D projected disk effective radius (r1/2, 3D, baryons/Re, disk; left) and the difference between the dark matter fraction estimators at these radii ( |
| In the text | |
 |
Fig. 8. Toy model of how |
| In the text | |
 |
Fig. 9. Pressure support correction, α(R), versus R/Re for a self-gravitating exponential disk and deprojected Sérsic models. The left panel directly compares αself − grav(r) = 3.36(R/Re) for the self-gravitating disk (as in Burkert et al. 2010; black dashed line) to α(R, n) = − dlnρ(R, n)/dlnR determined for a range of Sérsic indices n (colored lines). The ratio α/αself − grav(R) is shown in the right panel. For n ≥ 1, α(n) is smaller than αself − grav when R ≳ 0.2 − 0.8Re; however, α(n ≥ 1) does exceed αself − grav at the smallest radii. This implies that for most radii, there is less asymmetric drift correction (and thus higher vrot) for the deprojected Sérsic models (e.g., n = 1) than for the self-gravitating disk. However, for n = 0.5, α(n) is greater than αself − grav at R ≳ 2.4Re, so at large radii the n = 0.5 deprojected Sérsic model predicts a larger pressure support correction than for the self-gravitating disk case. The lower pressure support predicted for α(n ≳ 1) than for αself − grav is in agreement with recent predictions from simulations by Kretschmer et al. (2021) (red circles; with the vertical grey bars denoting the 1σ distribution), as well the relation by Dalcanton & Stilp (2010) for a power law relationship between the gas surface density and the turbulent pressure (orange dashed line). |
| In the text | |
 |
Fig. 10. Comparison between |
| In the text | |
 |
Fig. 11. Composite pressure support correction, αtot(R), for gas distributed in a composite disk+bulge system (with ndisk = 1, nbulge = 4), for a range of B/T (colors) and Re, bulge/Re, disk ratios (dash length). For the limiting cases, we recover the profiles shown in Fig. 9: B/T = 0 has αtot = α(n = 1) (black solid line), while B/T = 1 has αtot = α(n = 4) but with different radial scaling, owing to the different adopted Re, bulge/Re, disk ratios (colored lines). For the cases with 0 < B/T < 1, the bulge contribution modifies the α(n = 1) profile at both small and large radii, leading to larger αtot in inner regions and smaller αtot in the outskirts (R/Re, disk ≲ , ≳ 1 − 2). At fixed B/T, the deviation from the disk α(n = 1) in the center (R/Re, disk ≲ 1 − 2) is larger for smaller Re, bulge/Re, disk, while at large radii the deviation is larger for larger Re, bulge/Re, disk. For reference, we mark Re, bulge/Re, disk with vertical light grey lines, and also show αself − grav (grey dash-dotted line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



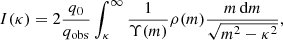
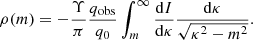
![$$ \begin{aligned} I(\kappa )=I_{\rm e}\exp \left\{ -b_{\mathrm{n} }\left[\left(\frac{\kappa }{R_{\mathrm{e} }}\right)^{1/n}-1\right]\right\} , \end{aligned} $$](/articles/aa/full_html/2022/09/aa44143-22/aa44143-22-eq12.gif)
![$$ \begin{aligned} \frac{{\mathrm{d} }I}{{\mathrm{d} }\kappa }=-\frac{I_{\rm e}\,b_{\mathrm{n} }}{n\,R_{\mathrm{e} }}\exp \left\{ -b_{\mathrm{n} }\left[\left(\frac{\kappa }{R_{\mathrm{e} }}\right)^{1/n}-1\right]\right\} \left(\frac{\kappa }{R_{\mathrm{e} }}\right)^{(1/n)-1}. \end{aligned} $$](/articles/aa/full_html/2022/09/aa44143-22/aa44143-22-eq14.gif)
![$$ \begin{aligned}&{ v}_{\mathrm{circ} }^2(R)=-4G\,q_{\mathrm{obs} }\Upsilon \nonumber \\&\qquad \qquad \times \int _{m=0}^{R}\left[\int _{\kappa =m}^{\infty }\frac{{\mathrm{d} }I}{{\mathrm{d} }\kappa }\frac{{\mathrm{d} }\kappa }{\sqrt{\kappa ^2-m^2}}\right]\frac{m^2\,\mathrm{d} m}{\sqrt{R^2-(1-q_0^2)m^2}} . \end{aligned} $$](/articles/aa/full_html/2022/09/aa44143-22/aa44143-22-eq15.gif)
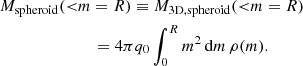
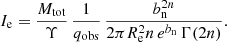
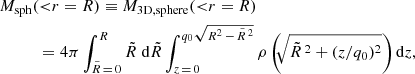
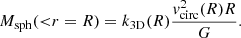
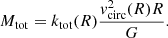
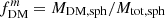
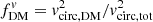
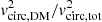
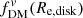
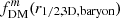
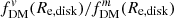
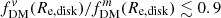
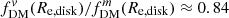
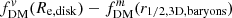
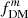
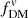
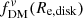
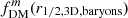
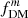
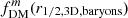
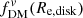
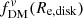
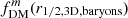
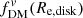
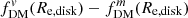
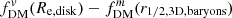
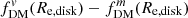
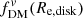
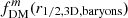
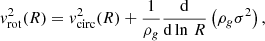
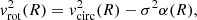
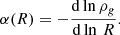
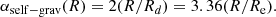
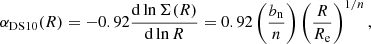
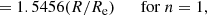
![$$ \begin{aligned}&\frac{{\mathrm{d} } \rho (m)}{{\mathrm{d} } m} = \frac{\Upsilon }{\pi } \frac{q_{\mathrm{obs} }}{q_0} \frac{I_{\rm e} b_{\mathrm{n} }}{n\,R_{\mathrm{e} }} \frac{m}{R_{\mathrm{e} }^2} \int _0^{\infty } f(m,x) \, \mathrm{d} x , \\&f(m,x) = \exp \left\{ -b_{\mathrm{n} } \left[ { v}^{1/n}-1\right]\right\} { v}^{\left(1/n -4\right)} \left[\frac{1}{n}- 2 - \frac{b_{\mathrm{n} }}{n} { v}^{1/n}\right], \nonumber \\&\qquad \quad \mathrm{for} \ { v} = \frac{1}{R_{\mathrm{e} }}\sqrt{x^2+m^2}. \nonumber \end{aligned} $$](/articles/aa/full_html/2022/09/aa44143-22/aa44143-22-eq89.gif)