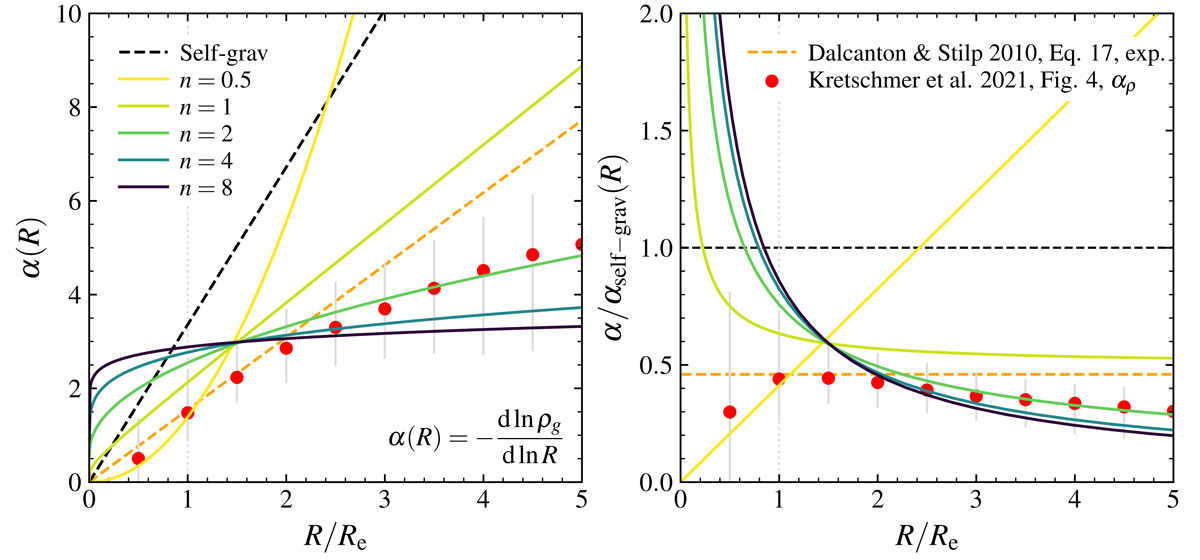
Pressure support correction, α(R), versus R/R_e for a self-gravitating exponential disk and deprojected Sérsic models. The left panel directly compares α_{self − grav}(r) = 3.36(R/R_e) for the self-gravitating disk (as in Burkert et al. 2010; black dashed line) to α(R, n) = − dlnρ(R, n)/dlnR determined for a range of Sérsic indices n (colored lines). The ratio α/α_{self − grav}(R) is shown in the right panel. For n ≥ 1, α(n) is smaller than α_{self − grav} when R ≳ 0.2 − 0.8R_e; however, α(n ≥ 1) does exceed α_{self − grav} at the smallest radii. This implies that for most radii, there is less asymmetric drift correction (and thus higher v_rot) for the deprojected Sérsic models (e.g., n = 1) than for the self-gravitating disk. However, for n = 0.5, α(n) is greater than α_{self − grav} at R ≳ 2.4R_e, so at large radii the n = 0.5 deprojected Sérsic model predicts a larger pressure support correction than for the self-gravitating disk case. The lower pressure support predicted for α(n ≳ 1) than for α_{self − grav} is in agreement with recent predictions from simulations by Kretschmer et al. (2021) (red circles; with the vertical grey bars denoting the 1σ distribution), as well the relation by Dalcanton & Stilp (2010) for a power law relationship between the gas surface density and the turbulent pressure (orange dashed line).