| Issue |
A&A
Volume 665, September 2022
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 20 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202142399 | |
| Published online | 31 August 2022 | |
Formation and heating of chromospheric fibrils in a radiation-MHD simulation⋆
1
Institute for Solar Physics, Department of Astronomy, Stockholm University, AlbaNova University Centre, 106 91 Stockholm, Sweden
e-mail: malcolm.druett@astro.su.se
2
Centre for mathematical Plasma Astrophysics, Department of Mathematics, KU Leuven, Celestijnenlaan 200B, 3001 Leuven, Belgium
3
Institute of Theoretical Astrophysics, University of Oslo, PO Box 1029 Blindern, 0315 Oslo, Norway
4
Rosseland Centre for Solar Physics, University of Oslo, PO Box 1029 Blindern, 0315 Oslo, Norway
Received:
8
October
2021
Accepted:
22
June
2022
Aims. We examine the movements of mass elements within dense fibrils using passive tracer particles (corks) in order to understand the creation and destruction processes of fibrils.
Methods. Simulated fibrils were selected at times when they were visible in a Hα image proxy. The corks were selected within fibril Hα formation regions. From this set, we selected a cork and constructed the field line passing through it. Other fibrilar corks close to this field line were also selected and pathlines were constructed, revealing the locations of the mass elements forwards and backwards in time. Finally, we analysed the forces acting on these mass elements.
Results. The main process of fibrilar loading in the simulation is different to the mass loading scenario in which waves steepen into shocks and push material upwards along the field lines from locations near their footpoints. The twisted, low-lying field lines were destabilised and then they untwisted, lifting the material trapped above their apexes via the Lorentz force. Subsequently, the majority of the mass drained down the field lines towards one or both footpoints under the influence of gravity. Material with large horizontal velocities could also be elevated in rising field lines, creating somewhat parabolic motions, but the material was not generally moving upward along a stationary magnetic field line during loading.
Conclusions. The processes observed in the simulation are additional scenarios that are plausible. The criteria for observing such events are described in this work. We note that it is desirable for our simulations to also be able to form more densely packed fibrils from material fed from the base of field footpoints. The experimental parameters required to achieve this are also discussed in this paper.
Key words: Sun: chromosphere / Sun: magnetic fields / Sun: transition region / magnetohydrodynamics (MHD) / plasmas
Movies associated to Figs. 1, 4, 9, 14 are available at https://www.aanda.org
© M. K. Druett et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Fibrils are long (500−20 000 km), narrow (∼180 km) fibre-like features, with lifetimes of around 200−400 s, that are seen in chromospheric lines (de Pontieu et al. 2007; Gafeira et al. 2017; Jafarzadeh et al. 2017). Fibrils are ubiquitously observed on the Sun, in magnetic bright points, plages, sunspots, and regions of the quiet Sun that have any significant photospheric concentrations of a magnetic field, which may act as the roots of the structures (Wiegelmann et al. 2010). They are generally narrower in active regions, and broader in the quiet Sun. They can be bright or dark in appearance, and they have been observed in Hα (Hansteen et al. 2006; Leenaarts et al. 2015; Mooroogen et al. 2017; Gopalan Priya et al. 2018), Ca II 8542 (Asensio Ramos et al. 2017), Ca II H & K (Gafeira et al. 2017; Jafarzadeh et al. 2017; Kianfar et al. 2020), He I 10830 (Schad et al. 2013), He I D3 triplet (Libbrecht et al. 2019), He II 304 (Zhang et al. 2014), and Lyα (Rutten 2017), for instance.
Dark Hα fibrils are thought to be the observational signatures of locations with high ridges of increased mass density at chromospheric temperatures. Under these conditions, the Hα line optical depth reaches unity at greater physical heights above the photosphere because the Hα line opacity is relatively insensitive to typical chromospheric temperature variations, but it does heavily depend heavily on mass density.
The combination of this opacity variation with the decrease in source function with height, and scattering-dominated 3D radiative transfer effects, produces a negative correlation of emission intensity in Hα with the increased height of the line core formation (Leenaarts et al. 2015).
Because the density of the material in fibrils is so much greater than that of the surrounding material, fibrils are essential to improving our understanding of the balance of mass throughout the solar atmosphere. Thus, it is important to get a clear picture of the sources of this mass and the forces loading it into these fibrilar structures.
Fibrils also play an important role in the transport of energy from the photosphere to the chromosphere and, possibly, the corona as well (Gafeira et al. 2017) via wave propagation (Carlsson et al. 2007; Morton et al. 2014) or small-scale reconnection (Parker 1972).
Several scenarios to explain mass loading of fibrils exist, based on observational evidence and earlier models. The standard mass loading scenario is that p-mode oscillations in the photosphere drive compressive longitudinal waves that are guided by the magnetic field and feed mass up relatively static field lines (Hansteen et al. 2006; de Pontieu et al. 2007). More recently, Rutten et al. (2019) suggested that some dark Hα fibrils are the cooling aftermaths of heating events associated with upward jets. They are also thought to form around the boundaries of active regions due to the rising horizontal field seen in areas of late stage flux emergence (Bernasconi et al. 2002; Mandrini et al. 2002; Xu et al. 2010). Some apparent motions of material in chromospheric fine structure are not so well explained by motions confined to narrow tubes of plasma. Judge et al. (2011) show that these can be better attributed to opacity effects due to the line of sight ripples in what are essentially 2D sheet structures with magnetic tangential discontinuities, comparable to the folds in a semi-transparent curtain moving in a breeze. In particular, this theory could explain observational reports (Judge et al. 2012) of the extremely high apparent velocities of features that greatly exceed local Alfvén speeds.
In this paper, we therefore address several unanswered questions regarding mass loading of fibrils using simulations, namely: the source(s) that supplies fibrils with their mass; the physical mechanisms or forces that load this mass into the fibrils; the dominant forces and energy sources that act on the plasma elements in fibrils are and what changes they bring about; the processes that have the ability to destroy fibrils; the location the mass that is contained in a fibril flows towards.
2. Experiment description
2.1. Bifrost experiment description
The simulation for this work was performed in 3D using the Bifrost code (Gudiksen et al. 2011), which solves the resistive magnetohydrodynamic (MHD) equations on a staggered Cartesian mesh. Additional modules in the simulation included optically thick radiative transfer in the photosphere and low chromosphere, parameterised radiative losses in the upper chromosphere, transition region and corona, and thermal conduction along the magnetic field lines.
The simulation was run on a re-sampled mesh based on the one used in Carlsson et al. (2016) and for two studies of fibrils in Leenaarts et al. (2012, 2015), namely 504 × 504 × 496 grid cells. In our experiment, the vertical number of grid cells increased to 512 in order to help improve the code stability. The horizontal extent of the model is of 24 × 24 Mm and the vertical extent is 16.8 Mm. The vertical grid spans from 2.4 Mm below to 14.4 Mm above average optical depth unity at 500 nm, thereby encompassing the upper convection zone, photosphere, chromosphere, and lower corona. The x- and y-axes are equidistant with a grid spacing of 48 km. The z-axis grid spacing is 20 km between −1 and 4.5 Mm, but this spacing increases toward the upper and lower boundaries reaching a maximum of 98 km, in the corona. Figure 1 shows a snapshot of the experimental setup. As in Carlsson et al. (2016), Leenaarts et al. (2012, 2015), Zacharias et al. (2018), here the magnetic field in the photosphere is a predominantly bipolar structure seen as two clusters of magnetic concentrations of opposite polarity. This field was introduced into the simulation by specifying the vertical magnetic field at the bottom boundary with an averaged signed field of zero and two patches of opposite polarity separated by 8 Mm. A potential field extrapolation then provided the magnetic field throughout the box. This simulation ran for 3000 s of solar time before the grid re-sampling and then a further 2400 s before the beginning of the experiment presented here. Hereafter, we only refer to the times of the experiment, with t = 0 s starting 5400 s after the initialisation of the box. The experiment was run for a further 1270 s giving a total time of 6670 s for the box. Figure 2 shows the height of the experiment photosphere plotted in blue against time in order to illustrate the timing and amplitude (around 100 km, peak-to-peak) of the global mode of the box oscillations throughout the experiment.
 |
Fig. 1. Simulation setup, with vertical magnetic field (a) and temperature (b) in the photosphere at z = 0 Mm, and mass density (c) and temperature (d) at z = 1.5 Mm in the chromosphere. Movies are available online. |
For a full description of the box oscillations in Bifrost experiments, we refer to Stein & Nordlund (2001), Carlsson et al. (2016). We note that there are double-peaked oscillations in the experiment, which were likely caused by the re-gridding in the z-axis; however, the inclusion of an additional mode should not effect the reality of the results. The red line in Fig. 2 shows the oscillations of the τ = 1 layer for the Hα line core, which match well with the photospheric oscillations, except for a delayed response in the event of a double-peak photospheric oscillation.
 |
Fig. 2. Box oscillations in the simulation. The blue curve shows the time evolution of the height where the average temperature is 6500 K in the photosphere, with height scale shown on the right y-axis. These oscillations are the simulation equivalent to the p-mode oscillations of the photosphere on the Sun. The red curve shows the oscillations in the mean height of the unit optical depth in the Hα spectral line core, taken across the entire x- and y- range of the experiment. The height scale is shown on the left y-axis. |
A test run was conducted that also included the effects of non-equilibrium ionisation of hydrogen as in Leenaarts et al. (2012,2015). Because of the high computational expense of this physics and the fact that it was not essential for our analysis of the MHD variables in these high-density, low-temperature fibrilar structures, the module was not included for the production run. We use Lagrangian tracer particles which flow with the mass elements present (hereafter referred to simply as ‘corks’) to analyse the simulation (Leenaarts 2018; Zacharias et al. 2018).
In particular, the corks module is accurate and versatile because the cork positions are updated on the time-steps of the MHD simulations, rather than using saved data that is stored at intervals much greater than the simulation time-steps (Shelyag et al. 2013; Nóbrega-Siverio et al. 2016). Although the positions and other data for the corks is updated with the hydrodynamic time-steps, this data is only saved to files at the same intervals as the rest of the experiment. This implies that influences acting in shorter timescales than the snapshots may not be accurately captured in our analysis, although they will be captured by the motions of the corks. Instantaneous variable values for the corks used in our analysis are re-calculated from the values saved for the experiment grid at each snapshot. These variables include the densities, magnetic flux densities (hereafter referred to as the magnetic field strength), pressures and temperatures, momenta, x-y-z force components (from the Lorentz force, numerical momentum and mass diffusion, pressure gradient, and viscous stress forces) as well as heating quantities (from energy diffusion, Joule heating, viscous heating, radiation, and Spitzer conduction).
We conducted a sandbox experiment to check the time-scales on which forces acted upon the corks, saving the output data at intervals of 0.5 s, 1 s, and 10 s. It was confirmed that spikes in the values of particular forces that act on the corks do indeed sometimes occur on timescales less than 10 s, in particular the action of the Lorentz force and viscous stress forces. However, the general dynamics of the structures we are studying can be inferred from the data saved at 10 s intervals.
Through regular injection of new corks in cork-free voids and removal of corks in regions where they pile up, this module allows tracing of velocity pathlines starting from any time and at any location in the simulation. In this experiment, the number of corks (∼2 × 108) was much greater than in the 2D experiment of Leenaarts (2018) (∼4 × 105 corks) in order to avoid unnecessary gluts of corks using up huge amounts of processing and memory and to avoid voids through which flows could not be traced, the cork injection and pruning processes were switched on, with the snapshot frequency of 10 s. If there was no cork in the cube of grid space closest to any given grid point at the time of the data snapshot, a cork was injected at the grid point. If more than two corks were in the same cube, then corks were removed until only two remained. Using 10 s snapshots, around 7% of the total number corks present are injected at each snapshot.
These benefits in terms of the memory, computational cost, and the lack of voids in the experiment come at a price: when constructing pathlines for the corks in time, some fraction of the corks will either have been injected at this point (in the case of backward-constructed timelines) or pruned (for forward-timelines). In such a case, the pathline jumped to the nearest cork that was not removed in the same snapshot. For forward pathlines (where corks disappear due to being pruned), we are guaranteed that the size of this jump is bounded to 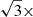 the grid cell separation. A test run produced a mean jump distance of 0.367 grid cells in 3D, with an upper bound almost exactly equal to
the grid cell separation. A test run produced a mean jump distance of 0.367 grid cells in 3D, with an upper bound almost exactly equal to 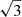 grid cells. Most importantly, we wish to discern the sources of the mass loaded onto fibrils and therefore require accurate backward constructed pathlines. The ‘removed’ corks in these pathlines will have been injected into voids in the experiment and therefore come with no guarantee that the cork does not jump a large distance. A test experiment was performed for backward constructed pathlines. The mean jump distance for these corks was 0.563 grid cells, with a positively skewed distribution and some corks experienced larger jumps. However, only one cork from over 46 000 in the test was found to experience a jump over a distance larger than two grid cells (2.10 grid cells), and this was in the high corona, well away from the fibrilar features. The majority of the larger jumps come from cells in the high corona, where a cork had recently (in hydrodynamic time-steps) exited the cell, but none had yet entered it. Therefore, we can be confident of the accuracy of the forward- and backward-traced pathlines in our experiment, in particular, to a much greater degree than experiments using post-processing particles from data that are saved as output to files.
grid cells. Most importantly, we wish to discern the sources of the mass loaded onto fibrils and therefore require accurate backward constructed pathlines. The ‘removed’ corks in these pathlines will have been injected into voids in the experiment and therefore come with no guarantee that the cork does not jump a large distance. A test experiment was performed for backward constructed pathlines. The mean jump distance for these corks was 0.563 grid cells, with a positively skewed distribution and some corks experienced larger jumps. However, only one cork from over 46 000 in the test was found to experience a jump over a distance larger than two grid cells (2.10 grid cells), and this was in the high corona, well away from the fibrilar features. The majority of the larger jumps come from cells in the high corona, where a cork had recently (in hydrodynamic time-steps) exited the cell, but none had yet entered it. Therefore, we can be confident of the accuracy of the forward- and backward-traced pathlines in our experiment, in particular, to a much greater degree than experiments using post-processing particles from data that are saved as output to files.
2.2. Selection of the corks contained in fibrils
Fundamentally, fibrils are an observed phenomenon in a number of chromospheric lines. In order to build on results from Leenaarts et al. (2012, 2015), we considered fibrils that appear in the Hα line. Due to limits on the available computing resources, this simulation was not run with non-equilibrium hydrogen ionisation and we did not compute synthetic Hα images. Instead, we created proxy Hα images based on the anti-correlation between Hα line core intensity and τ = 1 height. The column mass at which the Hα line core reaches optical depth unity is taken to be 3 × 10−5 g cm−2, as found in Fig. 12 of Leenaarts et al. (2012) and the text of Leenaarts et al. (2015).
We then proceeded to select corks in the fibrils: For each xy-pixel in our simulation, we computed the height for which the column mass is 3 × 10−5 g cm−2. The value τ = 1 height is not always representative for the actual formation height of the line core (Leenaarts et al. 2012) and the chromosphere might not be overly dense at this height. Therefore, we inspected all grid cells above this height that have a temperature below 10 kK and we selected the height with maximum density zd as a proxy for the Hα formation height.
To select the corks in a fibril, we first visually identified fibrils via the Hα intensity proxy. We then selected xy-pixels in the fibril using a local intensity threshold. All corks in a given column in the fibril whose height was less than 100 km away from zd(x, y) were considered to be located in the fibril. This intensity threshold relates to a minimum threshold of height, which was varied slightly (between z = 2.1 Mm and z = 2.3 Mm) to make sure that the visible body of each fibril was well represented. In the case shown (fibril 1) the threshold intensity was equivalent to a τ = 1 height of 2.3 Mm. For other fibrils reported later the heights where 2.3 Mm (fibril 2) and 2.1 Mm (fibril 3).
An example of the results of this selection process is shown in Fig. 3. To demonstrate that fibrilar corks are ‘draped over’ fibrilar density ridges, rather than occupying a solid structure, we also show corks located close to the vertical cut indicated in panel b. The green ‘ridge’ structure shows a height range of the fibril, which is much larger than the typical span of the line core formation region of only a few hundred kilometers (Leenaarts et al. 2015).
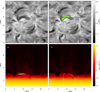 |
Fig. 3. Example of selection of corks in a fibril at t = 750 s. The Hα line intensity proxy is shown in panels a and b. Panels c and d: density in the xz-plane along the magenta line in panel b. The locations of all corks in a fibril are indicated in green, while the fibrilar corks located along the xz-cut are indicated in magenta in panel c. The white curve shows a magnetic field line passing through the fibril; fibrilar corks located on or very close to the field line are shown in blue. |
In order to analyse forces on individual corks a further subset was selected by constructing the field line through a cork that was centrally located in the fibril (see panel 3d). All corks within one grid-cell of the field line were selected and are shown in blue in panels b and d. Finally, we constructed pathlines from t = 0 s to t = 1270 s for each cork in the fibril. This allows us to trace the evolution of the mass inside the fibril both forwards and backwards in time. The reader may also be interested in the alignment of fibrilar structures with the individual fieldlines and groups of fieldlines, which has been studied in detail in Leenaarts et al. (2012, 2015).
This procedure was repeated for twenty fibrils. Representative examples of the behaviour of three fibrils and some of the corks within them are presented in the next section.
3. Results
3.1. Fibril 1
The first fibril that we present is a particularly thick, conspicuous, curved fibril near the centre of the field of view between the opposite polarity regions (Fig. 3). A close-up, more detailed view of the spatial evolution of this fibril is presented in Fig. 4. This fibril displays a formation and mass loading scenario that is common in this simulation, hereafter referred to as ‘lift and drain’.
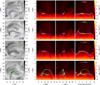 |
Fig. 4. Time evolution of fibril 1. Rows show from top to bottom the time evolution of the fibril, with the time indicated in the rightmost panels. The first column shows an image of the Hα density proxy, the locations of the corks that make up the fibril at t = 750 s, and two magnetic field lines. The field lines are initially close together, but have drifted apart at t = 1100 s as seen in the bottom row, with the cork A and B locations (and their associated field lines) shown in magenta and cyan respectively. The second column shows the density in a vertical cut in the xz-plane, with the field lines and cork locations over-plotted. The third column shows the same as the second column, but for a yz-cut. The fourth column shows a similar vertical cut, but now traced along the xy-position of one of the field lines, with the representative Hα core formation height ‘z_d’ used for the Hα proxy images over-plotted using a white line. Movies are available online. |
The fibril was very prominent at t = 750 s, so the corks were seeded into the fibril at this time as shown in Fig. 3, except we chose to add an additional constraint by showing only the closest 2000 corks to the selected field line for the ease of display (this constraint was also applied for fibril 2).
Figure 4 shows the positions of these 2000 corks in the fibril closest to the field line at the seed time (green). Two field lines that pass through our corks that we selected for presentation in this paper are shown in dark blue (fibril 1, cork A) and light blue (cork B), with the locations of the corks marked with a cross.
The top row shows the locations of the corks at t = 500 s, before the fibril formed. The corks were not located at the loop footpoints, but instead located more centrally along the field lines, and already on a ridge of plasma above a region of lower density (see Fig. 4, top right panel). At earlier times, the corks were slightly further apart over time, but there was no significant group motions away from this point (see videos of this figure). Between t = 500 s and t = 750 s the field lines rose and relaxed to become less twisted, at the same time as the global box oscillation moved upwards. Beforehand the field line apex had flattened and twisted (Fig. 4, compare first and second rows), but then the central part of the field lines rose up to form a more semicircular shape (Fig. 4, compare second and third rows). By t = 750 s, the corks had migrated towards the apex of the fibril field line (hence, their selection at the seed time).
As the field lines continued to rise, a fraction of the corks start to drain towards the footpoints of the field lines. Another fraction of the corks actually rises, and as we show below, they reach transition-region temperatures.
The t = 1100 s row in Fig. 4 shows the fates of the material after the destruction of the fibril. From the Hα proxy panels on the left, we can see that there is still a fibril in the vicinity of the one we study, but this fibril is made up from different material to the fibril at t = 750 s, as indicated by the mismatch between the cork positions and the fibril at t = 1100 s. We note that at t = 750 s, the field lines show only a general, but not a one-to-one correspondence with the shape of the fibril, and become rapidly disassociated from its position after the fibril is destroyed.
In summary, for this ‘lift and drain’ scenario, material along the central length of low-lying field lines is raised up to form high-density ridges and then subsequently drains into the footpoints, rather than being fed upwards from the footpoints of relatively static field lines. Some material does not drain, but instead moves up into the transition region.
In Sect. 3.1.2, we describe the evolution of a cork in fibril 1 (which we label cork A) that ultimately drains towards a field line footpoint. In Sect. 3.1.3, we describe the evolution of cork B, which moves into the transition region.
3.1.1. Analysing the forces acting on a cork
The fibrils are located in a low plasma-β regime, where the forces and dynamics behave differently depending on whether they are parallel or orthogonal to the magnetic field. Therefore, we use the Frenet-Serret (Serret 1851; Frenet 1852) coordinate frame to analyse the motions of corks with respect to the field lines. This frame is defined at each point along a field line by components in the directions of three orthogonal unit vectors as follows: T is a unit vector pointing in the direction of the magnetic field; N is a normal vector to T and points towards the centre of curvature of the field line; P the binormal component in the direction defined by P = T × N. This forms a natural set of axes to investigate motions with respect to the field line as longitudinal components are determined via the T component and the transverse motions are shown via the N and P components.
In Figs. 5, 7, 10, and 12, we show the position, velocity, acceleration, and forces acting on the corks. The global box oscillation in the photosphere from Fig. 2 is shown for comparison. The cork loading (or formation) period is shown shaded in a light grey and the destruction period is shown using a darker grey. There is also a plot of the magnetic tension, pressure, and their sum (i.e. the Lorentz force) is shown for the z-direction component.
 |
Fig. 5. Positions, velocities, and accelerations for representative cork A in fibril 1 as functions of time. In each panel the cork formation period, defined by the upswing of the photospheric box oscillation, is shaded a lighter grey and the fibril destruction period is shown in a darker grey. Top row, left: cork position (solid), box oscillation for comparison (dashed, on an arbitrary scale); centre: vertical components of magnetic pressure and tension, along with their sum, the Lorentz force; right: additional panel only in this figure, showing vertical force components averaged over cork A and the two corks that were closest to it at the seed time. Second row: cork velocity with a vz = 0 line over-plotted for reference. Third row: cork acceleration computed for three different assumptions. Red: computed from all forces acting on the cork; blue: computed only from the Lorentz force, gas pressure gradient, and gravity; green: computed as the time derivative of the velocity in panel b. Fourth row: acceleration owing to the gas pressure gradient, the Lorentz force, and gravity, as well as their sum (aPLG). Left column: vertical direction. Middle column: direction tangential to the field line (the T-direction in the Frenet-Serret frame). Right column: direction normal to the field line (the N-direction). |
The third row of panels shows the instantaneous acceleration in a given direction calculated from the net force that was saved for each snapshot (labelled a_forces). We also show the acceleration computed from the velocity saved in the snapshot (a_vel). This represents an ‘average’ acceleration over the snapshot interval time of 10 s. Finally, we show the instantaneous acceleration caused by the sum of the pressure gradient, Lorentz, and gravitational forces (a_PLG), which are typically the dominant forces that determine the motions of the corks. In the bottom panels, we show each of these three forces individually.
We note that the total acceleration from the force components shows spiked profiles in, for example Fig. 5, owing to the short-term variations of the individual force components. We do not resolve this variation using the 10 s time interval with which we save the simulation state (Leenaarts 2018). However, there are also many corks where this short-term variation is small (an example is shown in Fig. 10).
In Fig. 5, one additional panel is included (panel c) which shows acceleration values averaged over the actual cork and the two nearest other corks at the seed time. This is provided in order to demonstrate some smoothing out of these short-term spikes when multiple corks are used. The technique was employed again when analysing fibril 3. The disadvantage of averaging over many corks is the loss of precise physical data, which is increasingly problematic further from the seed time, when the selected corks may be much further apart. Nevertheless, comparing Fig. 5c with the single cork plots from panels g and j, it is clear that some insight can be gained, in particular regarding the Lorentz force influence at around t = 600 s, as discussed in the subsequent sections.
The viscous stress and mass and momentum diffusion also cause a force (see Sect. 2.1). We do not show these three additional forces because they clutter, rather than clarify, the motions within the fibril, but their contributions can be seen from the difference between a_Forces and a_PLG in the third row.
It turns out that the diffusion forces were negligible in almost all cases, but the stress force shows sharply spiked, short-term variations. These spikes seem to be primarily a response to the spikes in the Lorentz force, which the viscosity acts to dampen, as can be seen from the gentler variations of a_forces compared to a_PLG and its Lorentz force component, particularly during the destruction of the fibril (Fig. 5, around t = 1000 s).
3.1.2. Fibril 1, cork A: Draining
We discuss the behaviour of cork A in fibril 1, which drained to a fibril footpoint, in Figs. 5 and 6. Before the fibril formed, the cork was situated in the low chromosphere and slowly rose from z = 1.2 Mm to z = 1.8 Mm during the first 600 s (Fig. 5a). During this time the density dropped by an order of magnitude but stays relatively in line with the surrounding plasma at the same height (Fig. 6b). The temperature of the material stays relatively constant (Fig. 6c). At t = 600 s a strong p-mode oscillation passes upward. The cork received a strong upwards net Lorentz force (Figs. 5g and j) and rose to around z = 2.7 Mm over the next 100 s with a peak vertical velocity of 10 km s−1. As confirmed by Fig. 4, the Lorentz force is acting roughly perpendicular to the local field line. The vertical gas pressure gradient was reduced during this period and the sum of gravity, gas pressure, and Lorentz forces accounted well for the total acceleration. The drop in gas pressure gradient towards zero caused the gravitational deceleration of the material to its quasi ‘rest’ position in the fibril between t = 650 s and t = 700 s (Fig. 5j). In this fibril, the short-term spikes in individual force values make the influences responsible for the formation process less clear. Therefore, in panel c, the averaged forces over a few neighbouring corks are shown. This averaging attenuates the spikes in other at other times which upward influence of the Lorentz force and its contribution to the total at around t = 600 s remains clear.
 |
Fig. 6. Heating and MHD quantities of the representative cork A in fibril 1 as functions of time. In each panel the cork formation period defined by the upswing of the photospheric box oscillation is shaded a lighter grey and the fibril destruction period is shown in a darker grey. Panel a: heating rate divided by internal energy density Q/e for work done by energy diffusion (magenta), compression (cyan), Joule heating (brown), radiation (blue), viscosity (green), and their sum (red). Panel b: mass density (thick blue), as well as the average mass density at the height of the cork (thin blue). Panel c: temperature. Panel d: magnetic field strength (blue) and plasma β (red). |
A decomposition of the Lorentz force into magnetic tension and pressure (Fig. 5b) reveals that the cork experiences an upward force due to an upward magnetic pressure that is not quite balanced by magnetic tension. The motion tangential to the field line was rather consistent and gentle before and during the mass loading (Fig. 5e). The top of the field line was flattened throughout and thus there was almost zero net tangential force from gravity force over this time (Fig. 5k).
During the loading of the fibril, the density of the cork decreases, but by much less than the mean density of the surrounding atmosphere, leading to the typical over-dense fibrilar structure (Fig. 6b). Joule heating and energy diffusion from the surrounding hot plasma increased the temperature of the cork from 6 kK to 7 kK over the course of 50 s starting at t = 650 s (Figs. 6a and c). In Sect. 6.4 of Leenaarts et al. (2012), it was concluded that fibrils only form in the low plasma β regime where β < 0.1, and this relationship also holds for the simulated fibrils in the present study (see Fig. 6d).
The cork was relatively stable within the fibril from t = 800 s to t = 1000 s, rather than falling back down after the peak of the box oscillation excursion (Fig. 5a); instead, it began falling at only a few km s−1, but, critically, it continued to decrease in density by nearly an order of magnitude.
The prominent acceleration tangential to the field began just after t = 700 s (Fig. 5k), under the influence of gravity, which overcame the upward action of the gas pressure gradient when the angle of the field line became more vertical, as can be inferred from the increase of the size of the gravitational component at this time. We note that the positive direction is defined relative to the tangential orientation of the field vector – in this case, the positive direction points approximately to the left of the cork in the top-down view of the xy-plane, towards lower x-values.
By t = 1000 s, the density had dropped to 10−10 kg m−3, which then led to runaway heating that destroyed the fibril. We note that a more extensive survey was conducted for this work and it was often the case that during the destruction of dark fibrils, the disappearing ‘trails’ of the fibrils could often be mistaken for draining material. There was certainly material draining from these structures, but it was usually the runaway heating and expansion of the material that was responsible for chasing the visible trail of the fibril downwards at a speed much faster than that of the actual draining motions of the material.
It is interesting to note that the tangential Lorentz force obtains a somewhat non-negligible values between around t = 1000 s and t = 1100 s (Fig. 5i). This is surprising since the Lorentz force is usually negligible in the tangential direction to the field line because the term comes from j × B and is thus perpendicular to the magnetic field vector. It is observed that in this case and the other instances of non-zero tangential Lorentz force terms, the non-perpendicular components are linked to strong Joule heating events (strong current, j) and instances when the magnetic tension and pressure terms are changing rapidly. Non-zero tangential values can also arise from the finite precision of the calculations. For example small inaccuracies in the calculation of the Frenet-Serret vectors and the non-uniform grid mesh when using interpolation.
The first cork we followed was, however, caught in the draining material and thus avoided much of the heating. At t = 1000 s, the material element was heated over a few tens of seconds from 7 kK to 12 kK (Fig. 6). The sources of the heating event are the same as in the previous heating that occurred when the fibril was forming, again with Joule heating being the clearly dominant process due to the currents passing through this hotter, less dense material. Radiative losses kept the material from reaching temperatures where hydrogen would be completely ionised, and then cooled the plasma back down to 7 kK from t = 1100 s to t = 1200 s. When a fibril is destroyed in this manner (including all subsequent cases), the magnetic pressure upwards and magnetic tension downwards increase sharply in magnitude, but the resultant magnitude of their sum is not altered substantially. This strong increase of the magnetic pressure gradient causes the separation of nearby field lines that is linked to the destruction of the fibrilar structures. As the cork drains out of the fibril, we notice that it becomes under-dense with respect to the average for material at a similar height (Fig. 6b, t > 1000 s).
In the more horizontal of the transverse directions, fibril formation is associated with an oscillating behaviour. Neither the normal or binormal vectors were very close to purely horizontal throughout the fibril lifetime, the binormal averaged 63.8° to horizontal, while the normal vector averaged 25.0° (Figs. 5f, i, and l, shown with a restricted time range in order to focus on the oscillations during the fibril formation). The oscillations occurred as the cork was loaded to the fibrilar heights (between t = 600 s and t = 800 s). This oscillation results from the Lorentz force and are thus likely Alfvénic waves propagating along the fibril. The oscillations in this case have a period of ∼80 s and decay quickly during the first period from a velocity amplitude of 10 km s−1 to 2 km s−1 and then this amplitude perseveres for another period and a half before they are overcome by the increasing gas pressure gradient force at t = 800 s, just before the draining of the fibril.
3.1.3. Fibril 1, cork B: Runaway heating
Next we inspected a cork that does not successfully drain from the fibril, but is instead trapped at the top of the structure when the density drops towards coronal values (Figs. 7 and 8).
 |
Fig. 7. Position, velocity, and acceleration in the z, T, and N directions of representative cork B in fibril 1. Format as in Fig. 5. The time range is restricted to display only the relevant time span. |
 |
Fig. 8. Heating and MHD quantities of the representative cork B in fibril 1. Format as in Fig. 6 except the time range is restricted to display only the relevant time span. |
As in the case of cork A, cork B was not initially located at the footpoint of a loop, but more centrally on the field line loops that rose at around t = 600 s (Fig. 4). The same general values of height increase occurred due to the Lorentz force. The same pattern of oscillations caused by the Lorentz force variations then occurred in the N-direction.
However, at the location of this cork, the field line became more vertical after t = 900 s, so there was no rapid acceleration of the material in a direction tangential to the field line at t = 700 s (Figs. 7g and j). This resulted in the cork not draining down the field line as quickly as in the case of cork A. Instead, cork B continued to rise (Fig. 7a) when the next pressure mode hit, and the density of the material decreased (Fig. 8b). After t = 900 s, Joule heating increased sharply (Figs. 8a and c), which heated, expanded, and ionised the material further. This runaway effect resulted in a sharp spike in temperature shortly after t = 1000 s when the hydrogen was fully ionised, with the material reaching transition region temperatures of around 60 kK at t = 1200 s. The selection of the two corks illustrates the two main mechanisms through which material leaves the fibrils in our experiment: the majority by draining, along with a a smaller fraction leaving through Joule heating and energy diffusion to transition region temperatures.
To quantify these proportions, we estimated the fraction of mass in the fibril at t = 750 s that reaches transition region or coronal temperatures at any time during the experiment. To do so, we assigned a mass to each cork in the same manner as in Zacharias et al. (2018). That is, by taking the mass density at the seed time (t = 750 s), multiplying it by the volume of each grid cell, and then equally dividing this mass between each cork present in that grid cell. The total mass present in the fibril was 6.675 × 107 kg. We then computed the fraction of the total mass in a given temperature range as function of time by adding up the masses assigned to each cork in a given temperature range. Table 1 shows the origins and destinations of the mass elements selected in fibril 1.
Temperatures of corks prior to, during, and subsequent to being located in the fibril.
We can see that for this fibril, the mass was fed from the lower chromosphere where the temperature is lower than 10 kK. By the end of the experiment most of the fibrilar material had successfully drained down towards chromospheric temperatures, but 12% is still hotter than 10 kK. 0.036% is hotter than 50 kK, representing 24 000 kg. This hot material still appears to be draining and the mass is represented by only a few corks. The fibrils that lift and drain are not very effective suppliers of mass to the transition region or corona.
However, during the destruction of the fibril, 3% of the mass obtained temperatures over 30 kK and 1% over 50 kK (see Table 2) that could make them temporarily visible in transition region observations. This signature of the heated trail of formerly fibrilar material is a potential observable via simultaneous observations in Hα and transition region lines. This 3% mass fraction would occupy a cube with side length 600 km assuming a lower corona or transition region mass density of 10−11 kg m−3, which would make it visible in the Atmospheric Imaging Assembly’s (AIA) 304 observations. In some cases, strong upward motions also occur during the destruction of the fibril. We discuss such a case using fibril 2.
Transient heating in fibril 1.
3.2. Fibril 2
The ‘lift and drain’ fibrils are abundant throughout the experiment. However, lift and drain scenarios do not preclude behaviours such as material transiting across the apex of the field line or supplying greater proportions of fibrilar mass to the transition region. An example exhibiting both these behaviours are presented via fibril 2. For completeness, we also present another type of behaviour in Sect. 3.3: a set of corks that appeared to be loaded up from the footpoint of a static field line due to their nearly parabolic motions, but were in fact subject to strong horizontal motions at a similar time as the rising of the field line in another lift and drain scenario.
3.2.1. Fibril 2, cork A: Traversing the apex of a fibril
The spatial evolution of fibril 2 is shown in Fig. 9. The lifting events for this cork in the fibril (at t = 600 s and t = 950 s, see Figs. 10a and c) were again correlated in time with the photospheric box oscillations, although with slightly different offset compared to fibril 1. We note that the difference in timing is suggestive of the correlation being due to selection bias, although a similar pattern was found for fibrils seeded (at t = 500 s and t = 1000 s also). In the force plots, they were associated with a clear upward Lorentz force as the field lines rise and again relax into a more semicircular arc (Figs. 10f and i), the key vertical evolution seems largely unrelated to the direct influence of gas pressure forces.
 |
Fig. 10. Position, velocity, and acceleration in the z, T, and N directions of representative cork A in fibril 2. Format as in Fig. 5 except the time range is restricted to display only the relevant time span. |
This was the only event in this study where we found that the magnetic pressure gradient and the magnetic tension force both pointed upwards during formation – in contrast to all the other fibrils that we studied (including fibril 1), where these forces point in opposite directions. At t = 600 s, the magnetic pressure was the larger upward force, but at t = 900 s it was the magnetic tension. Shortly after the second lifting event, both values diverged rapidly into their more typical values (large magnetic pressure upwards and magnetic tension downwards) as the destruction of the fibril began.
The motion tangential to the field line was unaffected by the Lorentz force (Fig. 10j). Because a tangential Lorentz force is associated with Joule heating, we expect the temperature of the cork to be largely unaffected by Joule heating. This is precisely what is seen in Fig. 11, with only one small Joule heating event that did not cause a significant rise in temperature. The cork maintained a relatively constant temperature throughout its journey along the fibril. The formation of dark Hα fibrils in our simulations is not intrinsically linked with heating of the material during loading. The motion tangential to the field line during loading resulted from an excess of gas pressure over gravity (Fig. 10j), suggesting that perhaps the p-modes played a direct part in the formation of the fibril, but not noticeably in the z-direction. The draining of the cork along the field line is again caused by an excess of gravity over the pressure gradient force that began at around t = 1000 s for this cork; however, some initial motion threading the fieldline was also caused by viscous stress forces at around 900 s in this instance (hence the difference between a_PLG and the acceleration total from forces and velocity at this time that is visible in Fig. 10g). The descent of the material is halted by an upward pressure force due to meeting the denser material below (around t = 1200 s) and simultaneously the temperature of the material at the location of the cork increased in temperature by around 500 K.
 |
Fig. 11. Heating and MHD quantities for the representative cork A in fibril 2. Format as in Fig. 6, except the time range is restricted to display only the relevant time span. |
3.2.2. Fibril 2, cork B: Runaway heating
During the destruction of the fibril, the angle of the field towards the vertical increased, which resulted in material, such as cork A, achieving near “footpoint to footpoint” trajectories. However, increasing pressure force and Lorentz force spikes along some smaller section of the fibril were responsible for the raising of some material high into the atmosphere (see online video of Fig. 9). An example of this behaviour is shown via cork B (Figs. 12 and 13). Although this cork did not rise so high as many of the others, it displays the relevant behaviour. The material expanded (Fig. 13b, t = 1000−1200 s) and was then heated by incoming radiation (Fig. 13a, t = 1100 s). Finally, energy diffusion from the surrounding hot plasma and Joule heating caused a dramatic temperature increase up towards coronal values at the very end of the experiment (Figs. 13a and c, after t = 1200 s). This action of the gas pressure gradient during the destruction of the fibril meant that a much higher proportion of mass was heated to transition region temperatures than for the other simulated fibrils. Tables 3 and 4 illustrate this fact.
 |
Fig. 12. Position, velocity, and acceleration in the z, T, and P directions of representative cork B in fibril 2. Formatting as in Fig. 5, except for the right panels which show the P rather than the N component because the P component was more horizontal at the relevant times for this cork. Also the time range is restricted to display only the relevant time span. |
 |
Fig. 13. Heating and MHD quantities for the representative cork B in fibril 2. Formatting as in Fig. 6. The time range is restricted to display only the relevant time span. |
Around 97% of the material is supplied from chromospheric sources, with around 95% coming from the lower chromosphere and this figure jumps to over 99% lower chromospheric origin if you consider the start of the experiment to be around t = 300 s, so the feeding of the mass into the fibril is similar; namely, it comes almost exclusively from the lower chromosphere. However, in the destruction of the fibril, around 15% of the 8.456 × 107 kg of the mass obtains and maintains transition region temperatures and sustains them until the end of the experiment, with some half a percent obtaining coronal temperatures. Therefore, in cases such as fibril 2, where the fibril destruction happens during an upward pressure mode, it was found that the disruption to draining can be an effective supplier of mass to the transition region (Fig. 9, and Tables 3 and 4). Assuming similar densities for the transition region and low corona as for fibril 1, the destruction of this fibril supplies a mass that fills a volume the size of a cube with a side length of 1 Mm.
3.3. Fibril 3
In our study, there were also fibrilar mass elements observed to be showing more ‘parabolic’ loading paths with simultaneous horizontal and vertical motion occurring, as is generally the case in solar observations. An example of this mechanism is presented here.
The individual mass elements in fibril 3 underwent a particularly large amount of short-term spikes in the Lorentz and viscous stress terms. Therefore, we present the averaged results of 21 mass elements. These elements remained remarkably adjacent throughout the event, which aids interpretation greatly.
Figure 14 shows the spatial evolution of these 21 mass elements in the fibril, from which we can see that this was still fundamentally a ‘lift and drain’ event, but in this case, there was a large horizontal velocity present in the material as the field lines rise. There was again significant untwisting of the field line that occurs simultaneously with the lifting, this time towards the end of the fibril with lower x values.
Figure 15 shows the acceleration components in the x-, z-, and the magnetic field tangential directions. In this instance the Lorentz and gas pressure gradient forces were working in unison to raise the material at around t = 500 s to t = 600 s, despite being significantly damped by the residual forces (not shown), which were dominated by the viscous stress terms. This can be seen by comparing the totals of the Lorentz, gas pressure and gravitational force (blue line, bottom left panel of Fig. 15g) to the total acceleration from all forces (red and green lines): the upward impulse before t = 600 s seen in a_PLG is being significantly countered by the residual forces, as can be seen by its inclusion in a_forces. However, there is some resulting effect that causes the material to rise, and after t = 600 s, another upwards impulse from the pressure gradient and Lorentz forces raises the material further. Therefore, while the Lorentz force from rising field lines is the dominant process of supplying fibrilar mass to the chromosphere in Bifrost simulations, the p-modes can also have a significant direct influence.
 |
Fig. 15. Mean position, velocity, and acceleration in the z, T, and x directions for the 21 representative corks in fibril 3. Formatting as in Fig. 5, except for the right panels which show the x rather than the N component in order to discuss the horizontal plasma motions, and the time range is restricted to display the relevant time span. |
After t = 650 s, a large spike in the gas pressure gradient force acts to accelerate the material in the negative x-direction, against the influence of the Lorentz force (Fig. 15l). This is confirmed by the noticeable spike in the gas pressure gradient force tangential to the field line around the same time (Fig. 15k). The Lorentz force spike in the x- and tangential directions is again intimately linked to a strong Joule heating event (not presented here).
In this case, a mass loading scenario that appeared to be a standard solar scenario, that is, upward from near the footpoint of a static magnetic field line (due to the relatively ‘parabolic’ trajectory), transpired to result from a combination of Lorentz and gas pressure gradient forces, with lateral motions that were dominated by gas pressure gradients, combined with rising field lines of the “lift and drain” scenario. This process of mass loading could be distinguished from the general solar scenario of loading in observations with magnetic field analysis because the origin of the material is not at the footpoint of a field line rooted in the photosphere.
3.4. Mass loading and field line twist
To look more formally at the untwisting of the field lines observed in the previous examples, we examined the α parameter, which describes the twist of a field line and is defined by the relationship:
From this relationship, the twist parameter can be calculated as:
as presented in Lin et al. (2020). We calculate the total twist number of the field line for the magnetic twist by integrating the values of this parameter along the field line as presented in Berger & Prior (2006) (their Sect. 2.4.4 iii). This integral is performed over the section of the magnetic field line that passes through the low β regime,
where dl is the infinitesimal length along the field line at a given point.
We provide a twist parameter map for cork A in fibril 1 (Fig. 16). In Fig. 16, the twist parameter map is provided via the blue colour map on the left side. This is left without a colorbar as the values themselves are not particularly informative for small fractions of the fibril length. However, the total integrated twist number inside the low beta plasma regime is shown as a function of time by the cyan line in the right panel, with the axes positioned at the top of that panel. Again, we can see that the main raising event for the material in fibril 1 began just before t = 600 s (the blue over-plotted line in the right panel shows un-scaled vertical position of cork A from Fig. 5a). The field lines became destabilised at the same time as a p-mode (magenta line) swept the photosphere upwards. This (or some other agent) resulted in pulses seen as the tracks in the twist parameter that propagated upwards from near the bases of both footpoints after t = 600 s (white values in the colour maps) and a spike in the total twist number for the field line (cyan line). The change in twist was also visible in evolution of the field displayed in Fig. 4, and was accompanied by the beginning of transverse Alfvénic wave oscillations of the material, that is, two or more periods of transverse oscillation with Lorentz force as a restoring force (not shown in this paper).
 |
Fig. 16. Fibril formation map for fibril 1. Left: background image shows the twist parameter values along the field line length (x-axis. White shows positive values, black negative, and blue shows zero) for the field line that passed through cork F1A. The location of the cork along the field line is indicated by the red line. The outer green lines show the edges of the low β region, outside of which the twist parameter values are typically larger due to pressure dominating the motions (see the bands of dark and light outside of these green lines). Right: background image shows the logarithm of the plasma density, with over-plotted coloured lines that are not scaled similarly to the background image and each other in the x-direction. The magenta line shows the p-mode driven oscillations of the photosphere from Fig. 2, the blue line shows the vertical z-position of the cork chosen (see Fig. 5a). The cyan line shows the total integrated twist number along the field line, with its axis scaling shown at the top of the image. |
3.5. Material outside the fibrils
In our simulations, the dark Hα fibrils are high density ridges or bridges of chromospheric material (e.g. Fig. 4, third row, right panel). To complete our picture of fibrils it is important to briefly contrast this fibrilar material with the material outside of them. Two examples are presented. Firstly, a statistical sample of 100 000 corks with heights similar to those at the apexes of fibrils 1 and 2 at t = 750 s and with a temperature above 100 kK. This subset was taken to enable a comparison between the material in fibrils and the rest of the atmospheric material at similar heights that is certainly not considered ‘chromospheric’. Secondly, we selected the corks within 100 km of a particular field line in a region of low density with a similar apex height to fibrils 1 and 2 at t = 750 s, with only the corks above the minimum height of those corks in fibril 1 chosen. This second example is chosen close to an individual field line in order to present a more like-for-like comparison with with the subsets selected in the fibrils. Figure 17 presents the mean log10 temperature evolution of the material in the fibrils alongside the two samples described.
 |
Fig. 17. Mean temperature of sets of corks as functions of time. The blue line shows results for a random sample of 100 000 corks at similar heights as the corks in fibrils 1 and 2 and which had a temperature above 100 K at the seed time. The red line shows the results for corks near an individual field line with similar height of the apex to fibrils 1 and 2 but in a low-density region. The associated dashed lines show the 10th percentiles, to illustrate cooling due to draining of material towards the chromosphere. Values for the means of the corks in the fibrils are also shown, and their dashed lines indicate the 90th percentile to illustrate heating to transition region temperatures. |
The material in the second subset (the low density loop) stays at relatively high temperatures throughout the experiment. At t = 750 s the material in the low density loop was at around 1 MK, with the general material outside the fibrils around 500 kK. Following these corks backwards in time, we see that they were generally at lower temperatures the further back we go, around 300−400 kK (105.5 − 105.6 on the logarithmic temperature scale) at the start of the experiment. The slow increase of the mean temperature between the start of the experiment and the seed time is representative of the corks general drift over time away from the selected hot loop. This brings down the average temperature over time and shows that there is some cycling of material between layers of the atmosphere. Already at the start of the experiment (over 12 min earlier), less that 10% of the corks were at chromospheric temperatures, seen from the 10th percentiles shown as dashed lines in Fig. 17.
Moving forward from the seed time, much of the material stays at coronal temperatures but a fraction drains rather more rapidly that is seen in the 10th percentile after t = 900 s. This draining is somewhat reminiscent of much of the material in the fibrils, albeit at much higher initial temperatures. The statistical sample (blue line) follows a similar trend to the individual loop, but with somewhat lower average temperatures, indicating that we selected a hotter than average loop by selecting from an area with particularly low density. It is also noticeable that there was a larger proportion of the mass draining from the general hot atmosphere than from the low density loop, which decreases the mean temperature dramatically at around t = 1100 s.
Comparing this to material at similar heights, but contained within the fibrils, we see a very different temperature evolution, where the peak temperature occurs much later in the experiment and resulted from energy diffusion and Joule heating during the destruction of the fibrils. It is possible that material being heated at the tops of ‘spicule’ structures are the main supplies of material from the chromospheric regions to the transition region and corona. A subsequent investigation will check the flow of mass in more vertical fibrilar structures called mottles. However, material in a fibril that is being destroyed can supply a significant amount of mass if their draining is disrupted by an action such as experiencing an upward pressure mode. This is illustrated via the 90th percentile dotted line for fibril 2 in Fig. 17 at the end of the experiment.
4. Conclusions
In this study, we used Lagrangian tracer particles to study the mass loading and unloading of fibrils in order to investigate several issues:
The source that supplies the fibrils with their mass: the origin of the material loaded into the fibrils is almost entirely from the low chromosphere, with a very small proportion coming from the transition region or corona.
The physical mechanisms of forces that load this mass into the fibrils: the dominant form of mass loading in this experiment was a process involving ‘lifting and draining’, where the mass was loaded up into the fibrils from the low chromosphere, primarily under the direct action of the Lorentz force. We summarize our conclusions in the following.
-
The loaded mass mainly originated from above the apexes of flattened or twisted field loops in the low chromosphere.
-
These field lines were destabilised by actions that changed their local environment. In the instances investigated in our experiment, such as the cases of fibrils 1 and 2, a plausible and correlated destabilising influence was the box oscillations, that is, p-modes. However, any action that can perturb the local atmospheric force balance could cause a destabilisation of twisted fields on the Sun; these include processes such as alterations in the neighbouring field, granular buffeting, and p-modes (Zaqarashvili & Erdélyi 2009, see the first paragraph of Sect. 5.2 and further references therein).
-
This assumption that the p-mode was the destabilising agent for the cases of fibrils 1 and 2 is based on the temporal correlation between the upswing of the box oscillation between t = 600 s and t = 750 s, with the rise in the vertical position of the corks, the visual untwisting of the field line, the pulses in alpha twist parameter sent upwards from the edges of the low beta regime at these times and the evolution of the total twist number for the field line. However, this suggestion is also based on the causal relationship between motions of plasma near the footpoints of a field line (in this case due to the p-mode) and the resulting perturbations to the forces near the apexes of those field lines. Nevertheless, we reiterate that we could not determine a formal deductive link for this supposition and that many actions could cause the field lines to destabilise.
-
Whatever action or mechanisms are the triggers in each individual case, the magnetic pressure gradient increases and in the emerging fibrils the material rises primarily under the influence of Lorentz force to form over-dense ridges high in the chromosphere as the field relaxes into more semicircular shapes.
This relaxation of the magnetic field allows the field lines to gain a greater angle to the horizontal as they become more arched in shape and thus the fibrilar material begins to drain down towards one or both footpoints under the influence of gravity. We point out that the motions both of loading and draining studied here refer to actual mass motions, and not to the apparent observational motions of fibrilar structures that can be caused by opacity effects.
It seems that the ‘lift and drain’ mechanism was also the dominant formation process for fibrils in the simulations of Leenaarts et al. (2012, 2015), as evidenced by their Doppler shift diagrams that show blue-shifted material for nearly the entire length of fibrils simultaneously, with red-shifted material draining simultaneously from both ends. This loading process is in contrast to the standard solar picture in which material is given a positive upward velocity from acoustic shocks and guided upwards along relatively static field lines from the footpoints. The standard model of mass loading is strongly corroborated by solar observations of fibrils with visible leading edges coming from the bases of the network groups that decelerate over time and can then fall back (Hansteen et al. 2006; Kianfar et al. 2020).
There may well be solar fibrils with mass loaded via the ‘lift and drain’ scenario. Signatures of the scenario would be the observation of simultaneous approximately equal Doppler blue-shifts along the central lengths of a fibril, rather than decreasing Doppler blue-shift of the profiles observed from the footpoint towards the apex of the fibril. This is reminiscent of the rising horizontal field seen in areas of flux emergence, as in, for instance, the observations of Bernasconi et al. (2002; see their Fig. 9) with surges and rising centres and draining towards the footpoints (Mandrini et al. 2002; Xu et al. 2010).
It was found that there were some loading scenarios that looked like the standard scenario, but these are also essentially due to the ‘lift and drain’ mechanism. The false impression of loading of mass up static field lines was generated by strong horizontal or tangential impulses that happen co-temporally with the rising of a field line (e.g. Sect. 3.3). If this process of mass loading is active in the Solar atmosphere, it can be identified by the fact that the apparent footpoint will be rooted between magnetic field concentrations and if the magnetic field vector can be reliably recovered, there will also be a strong misalignment between the instantaneous vertical field vector and the motion of the head of the fibril. However, Leenaarts et al. (2015) also highlight that the vertical magnetic field vector can be misaligned with the fibril orientation for other reasons, for instance, that the fibril forms due to a large group of field lines with the apparent body of the fibril tracing out portions of different field lines that are in reality offset from each other.
What processes can destroy fibrils, and what are the dominant forces and energy sources acting on the plasma elements in fibrils? We also consider what processes are capable of destroying fibrils and what the dominant forces and energy sources are that act on the plasma elements within in them: in the lift and drain scenario observed in our simulation, the draining phase is closer to that from the classical picture. When the density of the fibril drops towards coronal values, energy diffusion from the hot coronal material surrounding the cork and Joule heating can rapidly increase the temperatures of the remaining material and, thus, the visible trail of the fibril in chromospheric lines can ‘drain’ much faster than solar gravity due to this material being heated to transition region temperatures. This heating also provides a possible explanation for transient brightenings of low lying loop sections in transition region lines without strong associated footpoint heating, as well as a lack of connectivity to the corona in these events (Hansteen et al. 2014; Pereira et al. 2018). Our simulations do not link these events with y-shaped jets above them (Pereira et al. 2018), although in some cases, strong upward motions are caused during the destruction of the fibril, as seen in the case of fibril 2.
To which locations does the mass that is contained in a fibril flow? With regard to the question of the location which the mass contained in a fibril flows to: footpoint draining constitutes the overwhelming majority of the destinations of mass in the simulated fibrils. In a typical simulated fibril, around 1% of the mass ever reaches the AIA 304 Å sensitivity peak temperature of 50 000 K and this is only a transient phase during the the process of fibril destruction, with less than 0.1% maintaining this temperature for any length of time. There are exceptions to this, for example, when a fibril is struck by a strong pressure mode during its destruction, which can increase the amount of mass supplied to the transition region to over 10% of the fibrilar mass, populating large regions of the transition region and corona.
The fibrils in Bifrost simulations replicate many of the features of solar fibrils such as the intensity contrast, Doppler shift magnitudes, and lifetimes (Leenaarts et al. 2012, 2015). However, since the dominant mechanism of mass loading in these simulations appears to be different from that from solar observations, it is important to attempt to more closely replicate this. The lack of ‘from-footpoint-static-field’ loading events could also be the reason that fibrils in Bifrost simulations are so sparsely packed when compared to the observations (Leenaarts et al. 2015). The sparsity of the packing of simulated fibrils compared to those from observations has already been noted in Leenaarts et al. (2015; Sect. 4.2). In the observations, it appears that mass loading is coming from the footpoints via dynamic fibrils (Hansteen et al. 2006; de Wijn & De Pontieu 2006; Rouppe van der Voort & de la Cruz Rodríguez 2013) or through flux emergence (Zhong et al. 2019; Verma et al. 2020). In this simulation, the magnetic field is introduced via a field extrapolation rather than emerged from the lower boundary of the experiment. The scales of the footpoint separations of the loops (8 Mm) are much smaller than those of a supergranule boundary and other larger observed footpoint separations of the order of a few tens of Mm (Zhong et al. 2019; Kianfar et al. 2020; Verma et al. 2020). Finally, we ask what the cause of this discrepancy is and how it may be addressed?
-
Many pressure gradient force events in the positive vertical direction are suppressed by the viscous stress forces in our simulation, so a reduction of the numerical viscosity terms may be important and given the strength of its contribution in this experiment, perhaps energy diffusion should be toned down too.
-
Cases with more horizontal chromospheric field lines showed somewhat more similar evolution to the classic fibril loading mechanism. Therefore, perhaps we require more horizontal field structures, which could be attained by increasing the domain size or introducing a global field over the top of the simulation to force chromospheric field lines trapped beneath to be more horizontal.
-
Simulation resolution could also play a part if a fine structure can help these features to form.
-
Comparing the previous Bifrost simulations showing fibrils with those from MURaM simulations (Bjørgen et al. 2019), it seems that strong (kG) and complex field structure are always present in regions of the simulation producing densely packed fibrils. It will be interesting to see whether increasing the field strength in our simulations creates more densely packed fibrils.
-
Perhaps some missing physics, such as generalised Ohms law or violations of MHD assumptions such as charge neutrality, will play a role in creating fibrils and modelling these effects to account for multi-fluid physics will be necessary.
It is known that mass loading from near the footpoints and up relatively static field lines occurs on the Sun even from regions with weak magnetic field, so it is important for this to be investigated further in forthcoming simulations to determine the physical mechanisms responsible for this behaviour.
Movies
Movie 1 associated with Fig. 1 (BifrostFibrils2022Atmos) Access here
Movie 2 associated with Fig. 4 (BifrostFibrils2022Fib1Spatial) Access here
Movie 3 associated with Fig. 9 (BifrostFibrils2022Fib2Spatial) Access here
Movie 4 associated with Fig. 14 (BifrostFibrils2022Fib3Spatial) Access here
Acknowledgments
This work was supported by The Swedish Research Council, grant number 2017-04099. M.D. is supported by FWO project G0B4521N. J.L. received support from the Knut and Alice Wallenberg foundation. The computations were enabled by resources provided by the Swedish National Infrastructure for Computing (SNIC) at the High Performance Computing Center North at UmeÅ University, and the PDC Centre for High Performance Computing (PDC-HPC) at the Royal Institute of Technology in Stockholm, partially funded by the Swedish Research Council through grant agreement no. 2018-05973. This research was supported by the Research Council of Norway through its Centres of Excellence scheme, project number 262622, and through grants of computing time from the Programme for Supercomputing. We also thank the anonymous referee for their detailed analysis of our manuscript, from which the final version has benefited greatly.
References
- Asensio Ramos, A., de la Cruz Rodríguez, J., Martínez González, M. J., & Socas-Navarro, H. 2017, A&A, 599, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berger, M. A., & Prior, C. 2006, J. Phys. A Math. Gen., 39, 8321 [Google Scholar]
- Bernasconi, P. N., Rust, D. M., Georgoulis, M. K., & Labonte, B. J. 2002, Sol. Phys., 209, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Bjørgen, J. P., Leenaarts, J., Rempel, M., et al. 2019, A&A, 631, A33 [Google Scholar]
- Carlsson, M., Hansteen, V. H., de Pontieu, B., et al. 2007, PASJ, 59, S663 [Google Scholar]
- Carlsson, M., Hansteen, V. H., Gudiksen, B. V., Leenaarts, J., & De Pontieu, B. 2016, A&A, 585, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Pontieu, B., McIntosh, S., Hansteen, V. H., et al. 2007, PASJ, 59, S655 [NASA ADS] [CrossRef] [Google Scholar]
- de Wijn, A. G., & De Pontieu, B. 2006, A&A, 460, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frenet, F. 1852, Journal de mathématiques pures et appliquées, 1re série, 17, 437 [Google Scholar]
- Gafeira, R., Lagg, A., Solanki, S. K., et al. 2017, ApJS, 229, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Gopalan Priya, T., Su, J.-T., Chen, J., Deng, Y.-Y., & Prasad Choudhury, D. 2018, Res. Astron. Astrophys., 18, 017 [CrossRef] [Google Scholar]
- Gudiksen, B. V., Carlsson, M., Hansteen, V. H., et al. 2011, A&A, 531, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansteen, V. H., De Pontieu, B., Rouppe van der Voort, L., van Noort, M., & Carlsson, M. 2006, ApJ, 647, L73 [Google Scholar]
- Hansteen, V., De Pontieu, B., Carlsson, M., et al. 2014, Science, 346, 1255757 [Google Scholar]
- Jafarzadeh, S., Rutten, R. J., Solanki, S. K., et al. 2017, ApJS, 229, 11 [CrossRef] [Google Scholar]
- Judge, P. G., Tritschler, A., & Chye Low, B. 2011, ApJ, 730, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Judge, P. G., Reardon, K., & Cauzzi, G. 2012, ApJ, 755, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Kianfar, S., Leenaarts, J., Danilovic, S., de la Cruz Rodríguez, J., & José Díaz Baso, C. 2020, A&A, 637, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leenaarts, J. 2018, A&A, 616, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leenaarts, J., Pereira, T., & Uitenbroek, H. 2012, A&A, 543, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leenaarts, J., Carlsson, M., & Rouppe van der Voort, L. 2015, ApJ, 802, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Libbrecht, T., de la Cruz Rodríguez, J., Danilovic, S., Leenaarts, J., & Pazira, H. 2019, A&A, 621, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, P. H., Kusano, K., Shiota, D., et al. 2020, ApJ, 894, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Mandrini, C. H., Démoulin, P., Schmieder, B., Deng, Y. Y., & Rudawy, P. 2002, A&A, 391, 317 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mooroogen, K., Morton, R. J., & Henriques, V. 2017, A&A, 607, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morton, R. J., Verth, G., Hillier, A., & Erdélyi, R. 2014, ApJ, 784, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Nóbrega-Siverio, D., Moreno-Insertis, F., & Martínez-Sykora, J. 2016, ApJ, 822, 18 [Google Scholar]
- Parker, E. N. 1972, ApJ, 174, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Pereira, T. M. D., Rouppe van der Voort, L., Hansteen, V. H., & De Pontieu, B. 2018, A&A, 611, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rouppe van der Voort, L., & de la Cruz Rodríguez, J. 2013, ApJ, 776, 56 [CrossRef] [Google Scholar]
- Rutten, R. J. 2017, A&A, 598, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rutten, R. J., Rouppe van der Voort, L. H. M., & De Pontieu, B. 2019, A&A, 632, A96 [EDP Sciences] [Google Scholar]
- Schad, T. A., Penn, M. J., & Lin, H. 2013, ApJ, 768, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Serret, J. A. 1851, Journal de mathématiques pures et appliquées, 1re série, 16, 193 [Google Scholar]
- Shelyag, S., Cally, P. S., Reid, A., & Mathioudakis, M. 2013, ApJ, 776, L4 [Google Scholar]
- Stein, R. F., & Nordlund, Å. 2001, ApJ, 546, 585 [Google Scholar]
- Verma, M., Denker, C., Diercke, A., et al. 2020, A&A, 639, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiegelmann, T., Solanki, S. K., Borrero, J. M., et al. 2010, ApJ, 723, L185 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Z., Lagg, A., & Solanki, S. K. 2010, A&A, 520, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zacharias, P., Hansteen, V. H., Leenaarts, J., Carlsson, M., & Gudiksen, B. V. 2018, A&A, 614, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zaqarashvili, T. V., & Erdélyi, R. 2009, Space Sci. Rev., 149, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Q., Liu, R., Wang, Y., et al. 2014, ApJ, 789, 133 [Google Scholar]
- Zhong, S., Hou, Y., & Zhang, J. 2019, ApJ, 876, 51 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Temperatures of corks prior to, during, and subsequent to being located in the fibril.
All Figures
 |
Fig. 1. Simulation setup, with vertical magnetic field (a) and temperature (b) in the photosphere at z = 0 Mm, and mass density (c) and temperature (d) at z = 1.5 Mm in the chromosphere. Movies are available online. |
| In the text | |
 |
Fig. 2. Box oscillations in the simulation. The blue curve shows the time evolution of the height where the average temperature is 6500 K in the photosphere, with height scale shown on the right y-axis. These oscillations are the simulation equivalent to the p-mode oscillations of the photosphere on the Sun. The red curve shows the oscillations in the mean height of the unit optical depth in the Hα spectral line core, taken across the entire x- and y- range of the experiment. The height scale is shown on the left y-axis. |
| In the text | |
 |
Fig. 3. Example of selection of corks in a fibril at t = 750 s. The Hα line intensity proxy is shown in panels a and b. Panels c and d: density in the xz-plane along the magenta line in panel b. The locations of all corks in a fibril are indicated in green, while the fibrilar corks located along the xz-cut are indicated in magenta in panel c. The white curve shows a magnetic field line passing through the fibril; fibrilar corks located on or very close to the field line are shown in blue. |
| In the text | |
 |
Fig. 4. Time evolution of fibril 1. Rows show from top to bottom the time evolution of the fibril, with the time indicated in the rightmost panels. The first column shows an image of the Hα density proxy, the locations of the corks that make up the fibril at t = 750 s, and two magnetic field lines. The field lines are initially close together, but have drifted apart at t = 1100 s as seen in the bottom row, with the cork A and B locations (and their associated field lines) shown in magenta and cyan respectively. The second column shows the density in a vertical cut in the xz-plane, with the field lines and cork locations over-plotted. The third column shows the same as the second column, but for a yz-cut. The fourth column shows a similar vertical cut, but now traced along the xy-position of one of the field lines, with the representative Hα core formation height ‘z_d’ used for the Hα proxy images over-plotted using a white line. Movies are available online. |
| In the text | |
 |
Fig. 5. Positions, velocities, and accelerations for representative cork A in fibril 1 as functions of time. In each panel the cork formation period, defined by the upswing of the photospheric box oscillation, is shaded a lighter grey and the fibril destruction period is shown in a darker grey. Top row, left: cork position (solid), box oscillation for comparison (dashed, on an arbitrary scale); centre: vertical components of magnetic pressure and tension, along with their sum, the Lorentz force; right: additional panel only in this figure, showing vertical force components averaged over cork A and the two corks that were closest to it at the seed time. Second row: cork velocity with a vz = 0 line over-plotted for reference. Third row: cork acceleration computed for three different assumptions. Red: computed from all forces acting on the cork; blue: computed only from the Lorentz force, gas pressure gradient, and gravity; green: computed as the time derivative of the velocity in panel b. Fourth row: acceleration owing to the gas pressure gradient, the Lorentz force, and gravity, as well as their sum (aPLG). Left column: vertical direction. Middle column: direction tangential to the field line (the T-direction in the Frenet-Serret frame). Right column: direction normal to the field line (the N-direction). |
| In the text | |
 |
Fig. 6. Heating and MHD quantities of the representative cork A in fibril 1 as functions of time. In each panel the cork formation period defined by the upswing of the photospheric box oscillation is shaded a lighter grey and the fibril destruction period is shown in a darker grey. Panel a: heating rate divided by internal energy density Q/e for work done by energy diffusion (magenta), compression (cyan), Joule heating (brown), radiation (blue), viscosity (green), and their sum (red). Panel b: mass density (thick blue), as well as the average mass density at the height of the cork (thin blue). Panel c: temperature. Panel d: magnetic field strength (blue) and plasma β (red). |
| In the text | |
 |
Fig. 7. Position, velocity, and acceleration in the z, T, and N directions of representative cork B in fibril 1. Format as in Fig. 5. The time range is restricted to display only the relevant time span. |
| In the text | |
 |
Fig. 8. Heating and MHD quantities of the representative cork B in fibril 1. Format as in Fig. 6 except the time range is restricted to display only the relevant time span. |
| In the text | |
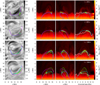 |
Fig. 9. Time evolution of fibril 2. Format as in Fig. 4. Movies are available online. |
| In the text | |
 |
Fig. 10. Position, velocity, and acceleration in the z, T, and N directions of representative cork A in fibril 2. Format as in Fig. 5 except the time range is restricted to display only the relevant time span. |
| In the text | |
 |
Fig. 11. Heating and MHD quantities for the representative cork A in fibril 2. Format as in Fig. 6, except the time range is restricted to display only the relevant time span. |
| In the text | |
 |
Fig. 12. Position, velocity, and acceleration in the z, T, and P directions of representative cork B in fibril 2. Formatting as in Fig. 5, except for the right panels which show the P rather than the N component because the P component was more horizontal at the relevant times for this cork. Also the time range is restricted to display only the relevant time span. |
| In the text | |
 |
Fig. 13. Heating and MHD quantities for the representative cork B in fibril 2. Formatting as in Fig. 6. The time range is restricted to display only the relevant time span. |
| In the text | |
 |
Fig. 14. Time evolution of fibril 3. Formatting as in Fig. 4. Movies are available online. |
| In the text | |
 |
Fig. 15. Mean position, velocity, and acceleration in the z, T, and x directions for the 21 representative corks in fibril 3. Formatting as in Fig. 5, except for the right panels which show the x rather than the N component in order to discuss the horizontal plasma motions, and the time range is restricted to display the relevant time span. |
| In the text | |
 |
Fig. 16. Fibril formation map for fibril 1. Left: background image shows the twist parameter values along the field line length (x-axis. White shows positive values, black negative, and blue shows zero) for the field line that passed through cork F1A. The location of the cork along the field line is indicated by the red line. The outer green lines show the edges of the low β region, outside of which the twist parameter values are typically larger due to pressure dominating the motions (see the bands of dark and light outside of these green lines). Right: background image shows the logarithm of the plasma density, with over-plotted coloured lines that are not scaled similarly to the background image and each other in the x-direction. The magenta line shows the p-mode driven oscillations of the photosphere from Fig. 2, the blue line shows the vertical z-position of the cork chosen (see Fig. 5a). The cyan line shows the total integrated twist number along the field line, with its axis scaling shown at the top of the image. |
| In the text | |
 |
Fig. 17. Mean temperature of sets of corks as functions of time. The blue line shows results for a random sample of 100 000 corks at similar heights as the corks in fibrils 1 and 2 and which had a temperature above 100 K at the seed time. The red line shows the results for corks near an individual field line with similar height of the apex to fibrils 1 and 2 but in a low-density region. The associated dashed lines show the 10th percentiles, to illustrate cooling due to draining of material towards the chromosphere. Values for the means of the corks in the fibrils are also shown, and their dashed lines indicate the 90th percentile to illustrate heating to transition region temperatures. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.