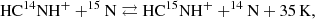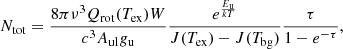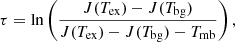EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 664 (August 2022) A&A, 664 (2022) L2 Full HTML
Open Access
Issue
A&A
Volume 664, August 2022
Article Number L2
Number of page(s) 8
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202244301
Published online 03 August 2022

© S. Spezzano et al. 2022

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe-to-Open model.

Open Access funding provided by Max Planck Society.

1. Introduction

Isotopologue abundance ratios are pivotal for tracing the origin and evolution of the molecular material in the process of star and planetary system formation. Stable isotope ratios can in fact be measured in star-forming regions as well as in the Solar System. Nitrogen has two stable isotopes, 14N and 15N. The 14N/15N ratio varies greatly across the Solar System, depending on the material and molecular tracer. This ratio is ∼440 in the solar wind and Jupiter (reflecting the composition of the protosolar nebula), ∼270 on Earth (for molecular nitrogen), ∼150 in comets (for CN, HCN, and NH2), and ∼200 in protoplanetary disks (for HCN) (Füri & Marty 2015; Guzmán et al. 2015). The origins of the different 14N/15N ratios among Solar System bodies are not yet fully understood. However, given that nitrogen is generally enriched in 15N in more pristine material such as comets, the different 14N/15N ratios that we observe are potentially inherited from the early phase in the formation of the Solar System. Furthermore, recent observations of different 14N/15N ratios in HCN and CN towards a protoplanetary disk point to the existence of multiple isotopic reservoirs of nitrogen for forming planets (Hily-Blant et al. 2019). In the dense interstellar medium (ISM), the 14N/15N ratio is inferred from N-bearing species and it is 300–500 for CN, HCN, and HNC (Hily-Blant et al. 2013a, 2013b). The 14N/15N ratio in N2H+ instead varies from 180 to 1000 (Fontani et al. 2015; Bizzocchi et al. 2013; Redaelli et al. 2018; Colzi et al. 2019). State-of-the-art reaction networks fail to reproduce the 14N/15N variation in N2H+ (Roueff et al. 2015; Wirström & Charnley 2018), although a faster recombination with electrons of the 15N isotopologues in L1544 with respect to the normal species might explain the depletion of N2H+ in 15N (Loison et al. 2019; Hily-Blant et al. 2020; Redaelli et al. 2020). The use of 13C isotopologues to derive the column densities of CN, HCN, and HNC is suggested to be done with caution by Roueff et al. (2015) because of the possible depletion of 13C with respect to the ISM 12C/13C ratio, and due to the interdependence of the 13C and 15N chemistry (Colzi et al. 2020).

Aside from local nuclear synthesis which causes an increasing excess of 15N towards the Galactic centre (Adande & Ziurys 2012), two main mechanisms are responsible for the nitrogen fractionation in the ISM: isotope exchange at low temperatures and isotope-selective photodissociation. Isotope exchange is the main chemical path to enrich molecules in deuterium towards the centre of pre-stellar cores (e.g., Caselli et al. 2003). In the case of HCN, as an example for nitrogen bearing species, the isotope exchange reaction is

H C 14 N H + + 15 N ⇄ H C 15 N H + + 14 N + 35 K , $$ \begin{aligned} \mathrm {HC}^{14}\mathrm {NH}^+ + ^{15}\mathrm {N} \rightleftarrows \mathrm {HC}^{15}\mathrm {NH}^+ + ^{14}\mathrm {N} + 35\,\mathrm {K}, \end{aligned} $$(1)

followed by the dissociative recombination of the cation with electrons. The isotope exchange reactions enrich molecules in the heavier isotope at a low temperature because of the lower zero-point energy of the heavier molecular species and the exothermicity of the reaction (Terzieva & Herbst 2000). The isotope exchange reactions involving nitrogen were later found to have barriers (Roueff et al. 2015), and hence they are not favourable to reproduce its fractionation (Wirström & Charnley 2018). Isotope-selective photodissociation favours the photodissociation of the 15N-bearing isotopologues of N2. With 14N2 being more abundant, it can self-shield better than 14N15N and is consequently less affected by photodissociation (Heays et al. 2014; Visser et al. 2018). With 14N15N being more photodissociated than 14N2, the 15N available to form molecules increases. The effect of selective isotope-photodissociation on nitrogen fractionation has already been clearly observed in protoplanetary disks (Hily-Blant et al. 2019). The effect of the local physical conditions on the fractionation of nitrogen in star-forming regions has been recently explored by Colzi et al. (2018) who found large scatter in the 14N/15N ratio in HCN towards high-mass star-forming cores. However, the spatial variation of the 14N/15N ratio towards pre-stellar cores has not been mapped yet.

Isotope-selective photodissociation is expected to be effective only at very low extinction (AV = 1−3 mag, Heays et al. 2014), and it is not considered in chemical models for the fractionation of nitrogen in dense cores. Its effects are only considered as inherited from the parent cloud (Furuya & Aikawa 2018; Furuya et al. 2018), and they still cannot reproduce the ‘anti-fractionation’ of nitrogen measured in N2H+ (Redaelli et al. 2020).

In this paper we present the first 14N/15N ratio map towards the prototypical pre-stellar core L1544, showing clear evidence that isotope-selective photodissociation is affecting the 15N fractionation in HCN. The same result is found for CN towards four offsets across the core, and qualitatively for HNC. In Sect. 2 we describe the observations, and in Sect. 3 we provide the analysis of the data. Our results are reported in Sect. 4, and finally we discuss our conclusions and outlook in Sect. 5.

2. Observations

The emission maps of the 1-0 transition of the 13C and 15N isotopologues of CN, HCN, and HNC towards L1544 were obtained using the IRAM 30 m telescope (Pico Veleta, Spain) in two different observing runs in 2013 and 2015. We performed a 2.5′ × 2.5′ on-the-fly (OTF) map centred on the source dust emission peak (α2000 = 05h04m17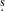 . s $ \overset{\text{s}}{.} $21, δ2000 = +25°10′42 . ″ $ \overset{\prime \prime }{.} $8). We used position switching with the reference position set at (−180″, 180″) offset with respect to the map centre. The observed transitions are summarised in Table 1. The EMIR E090 receiver was used with the Fourier transform spectrometer (FTS) backend with a spectral resolution of 50 kHz. For the HN13C 1-0 transition, we used the VESPA backend with a spectral resolution of 6 kHz. The mapping was carried out in good weather conditions (τ225 GHz ∼ 0.3) and a typical system temperature of Tsys ∼ 90–150 K. The data processing was done using the GILDAS software (Pety 2005). The emission maps have a beam size of 30.1″, and were gridded to a pixel size of 6″ with the CLASS software in the GILDAS package, which corresponds to ∼1/5 of the beam size, chosen to ensure Nyquist sampling. The integrated intensity maps of H13CN and HC15N shown in Fig. 1 have been computed in the 6.8–7.8 km s−1 velocity range, where the vLSR of the source is 7.2 km s−1. The integrated emission maps of H13CN and HC15N are shown in Fig. 1. Given the weakness of the lines, we could not produce maps for 13CN and C15N. We were nevertheless able to extract their spectra towards different regions across L1544, and they are shown in Sect. 3.

Table 1.

Spectroscopic parameters of the observed lines.

thumbnail Fig. 1.

Integrated intensity maps of the 1-0 transitions of H13CN and HC15N towards the inner 2′ × 2′ of L1544. The 30″ beam of the 30m telescope is shown at the bottom left of each map. The solid white contours are 30%, 60%, and 90% of the peak intensity of the N(H2) map of L1544 computed from Herschel/SPIRE data (Spezzano et al. 2016). The dashed black contours indicate the 10σ integrated emission with steps of 10σ for H13CN, and 5σ with steps of 5σ for HC15N (rmsH13CN = 6 mK km s−1, rmsHC15N = 7 mK km s−1).

3. Analysis

The spectrum of the 1-0 transition of H13CN observed towards the dust peak of L1544 was extracted from the centre of the map shown in Fig. 1 and fit with the HyperFine Structure (HFS) tool in CLASS using frequencies measured in the laboratory (Fuchs et al. 2004) with the assumption of the same excitation temperature of the hyperfine components. We derived Tex = 3.5 K and an optical depth of 0.4, 2, and 1.2 for the J = 1-0 F = 1-1, 2-1, and 0-1 components, respectively. We repeated the same exercise towards a sample of four other positions in the mapped area, so as to test whether we could assume a constant 3.5 K Tex across L1544, which was the case. The integrated intensity maps shown in Fig. 1 were used to compute the column density maps of H13CN and HC15N, assuming Tex = 3.5 K, and subsequently the 14N/15N ratio map shown in Fig. 2. In order to retrieve the column density of the main isotopologue, we multiplied the map of H13CN with the isotopic ratio for the local ISM, 12C/13C = 68 (Milam et al. 2005). The column density maps were computed using the formula reported in Mangum & Shirley (2015) for the optically thick emission, assuming that the source fills the beam, and with a constant Tex = 3.5 K:

N tot = 8 π ν 3 Q rot ( T ex ) W c 3 A ul g u e E u kT J ( T ex ) − J ( T bg ) τ 1 − e − τ , $$ \begin{aligned} N_{\rm tot} = \frac{8\pi \nu ^3Q_{\rm rot}(T_{\rm ex})W}{c^3A_{\rm ul}g_{\rm u}}\frac{e^{\frac{E_{\rm u}}{kT}}}{J(T_{\rm ex}) - J(T_{\rm bg})}\frac{\tau }{1-e^{-\tau }}, \end{aligned} $$(2)

thumbnail Fig. 2.

14N/15N ratio map of HCN towards L1544. The map was computed only in the pixels where the integrated emission of both H13CN and HC15N was detected with a signal-to-noise ratio larger than 5. The IRAM 30 m beam of 30″ (∼5000 au) is shown in the bottom right of the map. The solid white contours are 30%, 60%, and 90% of the peak intensity of the N(H2) map of L1544 computed from Herschel/SPIRE data (Spezzano et al. 2016). The column density of HCN was computed from the column density of H13CN assuming the 12C/13C ratio of 68 (Milam et al. 2005). The corresponding error is shown in Fig. A.3.

with

τ = ln ( J ( T ex ) − J ( T bg ) J ( T ex ) − J ( T bg ) − T mb ) , $$ \begin{aligned} \tau = \ln \left(\frac{J(T_{\rm ex}) - J(T_{\rm bg})}{J(T_{\rm ex}) - J(T_{\rm bg}) - T_{\rm mb}}\right), \end{aligned} $$(3)

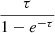where τ 1 − e − τ $ \frac{\tau}{1-e^{-\tau}} $ is the optical depth correction factor, τ is the line opacity, 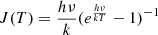J ( T ) = h ν k ( e h ν kT − 1 ) − 1 $ J(T) = {\frac{h\nu}{k}}(e^{\frac{h\nu}{kT}}-1)^{-1} $ is the equivalent Reyleigh-Jeans temperature, k is the Boltzmann constant, ν is the frequency of the line, h is the Planck constant, c is the speed of light, Aul is the Einstein coefficient of the transition, gu is the degeneracy of the upper state, Eu is the energy of the upper state, and Qrot is the partition function of the molecule at the given temperature Tex. Furthermore, Tbg, Tmb are the background (2.7 K) and the main beam temperatures, respectively. The maps shown in Fig. 2 were computed only in the pixels where the integrated emission of both molecules was detected with a signal-to-noise ratio larger than 5.

The emission maps of 13CN and C15N do not have a signal-to-noise ratio that allows for the computation of the 14N/15N ratio map. To check whether the same trend observed in HCN is also found in CN, we averaged the C15N 1-0 transition and one of the hyperfine components of the 13CN 1-0 transition towards several positions across the core. In the left panel of Fig. 3, the regions where the spectra of C15N and 13CN have been averaged are marked as black circles on the H2 column density map of L1544. The size of the areas has been optimised to have a signal-to-noise ratio of at least 3. The black crosses mark the centre of each region, and their offsets with respect to the centre of the map (i.e., the dust peak of L1544) are reported in the respective spectra shown in the right panel. The right panel of Fig. 3 shows the averaged spectra from each region.

thumbnail Fig. 3.

14N/15N ratio of CN in 4 positions across L1544. Left panel: H2 column density map of L1544 computed from Herschel/SPIRE observations (Spezzano et al. 2016). The black crosses show the centre of the areas where the spectra shown in the right panel have been extracted. The black circles show the regions where the spectra shown in the right panel have been averaged. Right panel: spectra of 13CN (N, J, F1, F = 1 3/2 2 3-0 1/2 1 2) in black and C15N (N, J, F= 1 3/2 2-0 1/2 1) in red, extracted towards the offsets marked in the left panel. The values in boldface in blue report the 14N/15N ratio in CN for each set of spectra derived using the 12CN column density directly from the spectra shown in Fig. B.1. The values in boldface in green report the 14N/15N ratio computed from the column density of 13CN using the 12C/13C ratio of 68 (Milam et al. 2005).

The hyperfine structure of the 1-0 transition of HN13C could not be resolved with the 6 kHz resolution of the VESPA spectra. The line shape that we observe deviates from previous observations towards other starless cores, for example those from van der Tak et al. (2009) and Padovani et al. (2011), suggesting that some of the hyperfine transitions might be self-absorbed. We used the four effective hyperfine transitions described in van der Tak et al. (2009) and derived the optical depth of each component using the HFS tool in CLASS. The resulting τ are 1.7, 3.1, 1.9, and 0.1 for the four lines ordered by increasing velocity. Given that the weakest hfs component, at 87090.67 MHz, is optically thin towards the dust peak, we performed a Gaussian fit with four components for all pixels in our map with PYSPECKIT (Ginsburg & Mirocha 2011), with the aim of isolating the thin component and using it to compute the column density map. Unfortunately, the resulting integrated intensity map is observed at 3σ only in the central 30″ of the map. We extracted the spectra of HN13C and H15NC towards the same positions used for the CN isotopologues in Fig. 3 (see Fig. A.1). To make a direct comparison with HCN as well, we extracted the spectra of the 13C and 15N isotopologues of HCN towards the same regions (see Fig. A.2).

4. Results and discussion

The 14N/15N ratio map of HCN in the left panel of Fig. 2 shows a clear decrease towards the south-east of L1544. The HC14N/HC15N in the north-west of the core is 367 ± 54, while in the south-east it is 187 ± 34. Towards the dust peak, the HC14N/HC15N is 437 ± 63, similar to the 14N/15N ratio reported for HC3N in Hily-Blant et al. (2018). The pre-stellar core L1544 is located at the end of a filament in the eastern edge of the Taurus Molecular Cloud. Because of its location and its structure, the southern part of L1544 is more efficiently illuminated by the interstellar radiation field (ISRF) than the northern part, and this has already been shown to have an impact on the chemical differentiation within the core (Spezzano et al. 2016). The 14N/15N ratio map of HCN towards L1544 in this work suggests that the uneven illumination from the ISRF on L1544 has an impact on the 15N fractionation. As the largest 15N fractionation is observed towards the southern part of L1544, which is the most illuminated by the ISRF, we conclude that the dominant fractionation process is the isotope-selective photodissociation of N2 (Heays et al. 2014). Guzmán et al. (2017) tentatively observed the effect of isotope-selective photodissociation towards the protoplanetary disk V4046 Sgr. This result was later confirmed by Hily-Blant et al. (2019) towards the disk orbiting the T Tauri star TW Hya. The 14N/15N ratio in HCN increases towards the dust peak of L1544 because we are looking through the densest regions of L1544, where the high density reduces the efficiency of the photodissociation, and consequently the enrichment of 15N in molecular species.

While we cannot compute the 14N/15N ratio maps for CN, the spectra extracted towards four positions across the core in Fig. 3 strongly suggest that also for CN the nitrogen fractionation is affected by the ISRF. In boldface in each spectrum, the 14N/15N ratio for CN derived in the corresponding region is reported. In green we report the C14N/C15N derived using the 12C/13C ratio of 68, as we did for HCN, and the resulting 14N/15N ratio is similar for both molecules. In blue we report the C14N/C15N derived directly using 12CN towards those positions (see Appendix B for more information). The 12C/13C ratio observed for CN ranges from 120 to 190 and the corresponding C14N/C15N ratios are as high as 1100, similar to what is observed for N2H+ in L1544 and other starless cores (Bizzocchi et al. 2013; Redaelli et al. 2018). The large 12C/13C and 14N/15N ratios that we present here for CN warrant a dedicated in-depth study of the fractionation of carbon and nitrogen in L1544. It is, however, important to note that 12CN/13CN ratios larger than 68 have already been observed towards L1544 in Hily-Blant et al. (2010), and they are predicted by the chemical models in Roueff et al. (2015) and Colzi et al. (2020), although for either early time steps or low volume densities. For the purpose of this Letter, we highlight that our conclusions as to the effect of the illumination on the C14N/C15N are not affected by the choice of 12C/13C ratio. We do not use the 12C/13C ratio derived from CN for HCN because the two molecules do not necessarily share all fractionation pathways, as shown in Figs. 6 and 7 of Colzi et al. (2020).

Figure A.1 shows the spectra of the 1-0 transitions of HN13C and H15NC extracted in the same position used for CN in Fig. 3 and for HCN in Fig. A.2. We computed the HN13C column density using the thin hyperfine component of the 1-0 transition following the description of the four effective components described in van der Tak et al. (2009), the 12C/13C ratio of 68, and Tex = 4.5 K derived from the CLASS HFS fit towards the dust peak. In boldface in each spectrum, the 14N/15N ratio for HNC derived is reported in the corresponding region using the 12C/13C ratio of 68. The resulting 14N/15N ratios are significantly different with respect to HCN and CN, and the trend across the core shows an increase in the 14N/15N ratio towards the south-east, contrary to what we observe for HCN and CN. While spatial variations of the fractionation of HCN, CN, and HNC across a core have not been explored by chemical models yet, Fig. 8 in Roueff et al. (2015) shows that their 14N/15N abundance ratio profiles can differ, especially between 105 and 106 yr. Nevertheless, the 14N/15N ratios in HCN, CN, and HNC shown in Fig. 8 of Roueff et al. (2015) only range between 390 and 450, while we observe ratios that vary from 150 to 450. Non-local thermodynamic equilibrium (non-LTE) modelling is necessary to confirm our results, in particular for the HN13C line where an isolated hyperfine component is not present.

5. Conclusions

Our 14N/15N ratio map of HCN towards L1544 shows, for the first time, that the fractionation of nitrogen presents significant variations across a pre-stellar core. The 14N/15N ratio in HCN decreases towards the south-east of the core, the region of L1544 that corresponds to a steeper drop in H2 column density and is consequently more efficiently illuminated by the ISRF. This was already shown in previous observations of carbon-chain molecules, which in fact peak towards the region L1544 which is more exposed to the ISRF, where a significant fraction of carbon is maintained in atomic form (Spezzano et al. 2016). The same trend is also observed for CN and the opposite trend is observed for HNC. Our results indicate that isotope-selective photodissociation plays an important role in the fractionation of nitrogen in L1544. We note that 14N15N photodissociates more efficiently than 14N2 because it is not abundant enough to self-shield. The photodissociation of 14N15N is expected to be more efficient towards the more illuminated southern part of the core, where more atomic 15N will be available to form cyanides such as HCN and CN. Furthermore, HNC shows the opposite behaviour with respect to HCN and CN. Further studies are necessary to understand the underlying cause.

The effect of isotope-selective photodissociation in nitrogen fractionation has already been observed towards a protoplanetary disk where the irradiation from UV photons in the inner part of the disk translates into a lower 14N/15N ratio in HCN (Hily-Blant et al. 2019). With our work we show that the uneven illumination from the ISRF onto a pre-stellar core has an effect on the 14N/15N ratio through the isotope-selective photodissociation. With the 14N/15N ratio in atomic nitrogen decreasing towards the southern part of L1544, the 14N2/14N15N ratio will have the opposite behaviour and increase towards the south of L1544 because the 14N2 is expected to be less affected by photodissociation. As a consequence, we expect the 14N/15N ratio in molecules that are formed from molecular nitrogen, such as N2H+, to show the opposite behaviour with respect to HCN and CN. This trend has already been observed towards the high-mass star-forming region IRAS 05358+3543 in Colzi et al. (2019). Future maps of 14N2H+/14N15NH+ or 14N2H+/15N14NH+ towards L1544 are needed to confirm this point for low-mass star-forming regions.

We also present here the direct measurement of the 12CN/13CN ratio across L1544, showing that it ranges between 130 and 190 in the inner 2 × 2 arcmin2 of the core. Furthermore, we show that column density ratios between the 13C and 15N isotopologues is ∼6 for HCN and CN and ∼2 for HNC towards the dust peak. A dedicated work on the chemical modelling of carbon and nitrogen fractionation towards L1544 in currently ongoing. Nevertheless, our results on CN indicate that the effect of the illumination on the nitrogen fractionation of HCN and CN across the core is not affected by the fractionation of carbon.

Pre-stellar cores provide the budget of material that will finally be inherited by forming planets. In order to assess what the 14N/15N budget is that can be inherited from pre-stellar cores, it is important to consider the illumination-induced variations across the core, which could account for different 15N reservoirs of future stellar systems, together with the 15N fractionation variation within a protoplanetary disk (Hily-Blant et al. 2017, 2019).

Acknowledgments

The authors wish to thank Laura Colzi for useful discussion, and the anonymous referee for insightful suggestions. We gratefully acknowledge the support of the Max Planck Society.

References

  1. Adande, G. R., & Ziurys, L. M. 2012, ApJ, 744, 194 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bizzocchi, L., Caselli, P., Leonardo, E., et al. 2013, A&A, 555, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Bogey, M., Demuynck, C., & Destombes, J. L. 1984, Can. J. Phys., 62, 1248 [NASA ADS] [CrossRef] [Google Scholar]
  4. Caselli, P., Walmsley, C. M., Zucconi, A., et al. 2002, ApJ, 565, 331 [NASA ADS] [CrossRef] [Google Scholar]
  5. Caselli, P., van der Tak, F. F. S., Ceccarelli, C., et al. 2003, A&A, 403, L37 [CrossRef] [EDP Sciences] [Google Scholar]
  6. Ciolek, G. E., & Basu, S. 2000, ApJ, 529, 925 [Google Scholar]
  7. Colzi, L., Fontani, F., Caselli, P., et al. 2018, A&A, 609, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Colzi, L., Fontani, F., Caselli, P., et al. 2019, MNRAS, 485, 5543 [NASA ADS] [CrossRef] [Google Scholar]
  9. Colzi, L., Sipilä, O., Roueff, E., et al. 2020, A&A, 640, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Crapsi, A., Caselli, P., Walmsley, M. C., et al. 2007, A&A, 470, 221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Creswell, R. A., Pearson, E. F., Winnewisser, M., et al. 1976, Zeitschrift Naturforschung Teil A, 31, 221 [NASA ADS] [CrossRef] [Google Scholar]
  12. Daniel, F., Gérin, M., Roueff, E., et al. 2013, A&A, 560, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Fontani, F., Caselli, P., Palau, A., et al. 2015, ApJ, 808, L46 [NASA ADS] [CrossRef] [Google Scholar]
  14. Fuchs, U., Bruenken, S., Fuchs, G. W., et al. 2004, Zeitschrift Naturforschung Teil A, 59, 861 [NASA ADS] [CrossRef] [Google Scholar]
  15. Füri, E., & Marty, B. 2015, Nat. Geosci., 8, 515 [CrossRef] [Google Scholar]
  16. Furuya, K., & Aikawa, Y. 2018, ApJ, 857, 105 [Google Scholar]
  17. Furuya, K., Watanabe, Y., Sakai, T., et al. 2018, A&A, 615, L16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Ginsburg, A., & Mirocha, J. 2011, Astrophysics Source Code Library [record ascl:1109.001] [Google Scholar]
  19. Goldsmith, P. F., & Langer, W. D. 1999, ApJ, 517, 209 [Google Scholar]
  20. Guzmán, V. V., Öberg, K. I., Loomis, R., et al. 2015, ApJ, 814, 53 [CrossRef] [Google Scholar]
  21. Guzmán, V. V., Öberg, K. I., Huang, J., et al. 2017, ApJ, 836, 30 [CrossRef] [Google Scholar]
  22. Hacar, A., Bosman, A. D., & van Dishoeck, E. F. 2020, A&A, 635, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Heays, A. N., Visser, R., Gredel, R., et al. 2014, A&A, 562, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Hily-Blant, P., Walmsley, M., Pineau Des Forêts, G., et al. 2010, A&A, 513, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Hily-Blant, P., Pineau Des Forêts, G., Faure, A., et al. 2013a, A&A, 557, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Hily-Blant, P., Bonal, L., Faure, A., et al. 2013b, Icarus, 223, 582 [NASA ADS] [CrossRef] [Google Scholar]
  27. Hily-Blant, P., Magalhaes, V., Kastner, J., et al. 2017, A&A, 603, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Hily-Blant, P., Faure, A., Vastel, C., et al. 2018, MNRAS, 480, 1174 [NASA ADS] [CrossRef] [Google Scholar]
  29. Hily-Blant, P., Magalhaes de Souza, V., Kastner, J., et al. 2019, A&A, 632, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Hily-Blant, P., Pineau Des Forêts, G., Faure, A., et al. 2020, A&A, 643, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Klisch, E., Klaus, T., Belov, S. P., et al. 1995, A&A, 304, L5 [NASA ADS] [Google Scholar]
  32. Loison, J.-C., Wakelam, V., Gratier, P., et al. 2019, MNRAS, 484, 2747 [NASA ADS] [CrossRef] [Google Scholar]
  33. Mangum, J. G., & Shirley, Y. L. 2015, PASP, 127, 266 [Google Scholar]
  34. Milam, S. N., Savage, C., Brewster, M. A., et al. 2005, ApJ, 634, 1126 [Google Scholar]
  35. Müller, H. S. P., Schlöder, F., Stutzki, J., et al. 2005, J. Mol. Struct., 742, 215 [CrossRef] [Google Scholar]
  36. Padovani, M., Walmsley, C. M., Tafalla, M., et al. 2011, A&A, 534, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Pety, J. 2005, SF2A-2005: Semaine de l’Astrophysique Francaise, 721 [Google Scholar]
  38. Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spectr. Rad. Transf., 60, 883 [Google Scholar]
  39. Redaelli, E., Bizzocchi, L., Caselli, P., et al. 2018, A&A, 617, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Redaelli, E., Bizzocchi, L., & Caselli, P. 2020, A&A, 644, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Roueff, E., Loison, J. C., & Hickson, K. M. 2015, A&A, 576, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Saleck, A. H., Simon, R., & Winnewisser, G. 1994, ApJ, 436, 176 [NASA ADS] [CrossRef] [Google Scholar]
  43. Spezzano, S., Bizzocchi, L., Caselli, P., et al. 2016, A&A, 592, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Terzieva, R., & Herbst, E. 2000, MNRAS, 317, 563 [Google Scholar]
  45. van der Tak, F. F. S., Müller, H. S. P., Harding, M. E., et al. 2009, A&A, 507, 347 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Visser, R., Bruderer, S., Cazzoletti, P., et al. 2018, A&A, 615, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Wampfler, S. F., Jørgensen, J. K., Bizzarro, M., et al. 2014, A&A, 572, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Wirström, E. S., & Charnley, S. B. 2018, MNRAS, 474, 3720 [CrossRef] [Google Scholar]

Appendix A: Observed spectra

Figures A.1 and A.2 show the spectra of the 13C and 15N isotopologues of HCN and HNC towards the positions shown in the left panel of Figure 3 (where the spectra of 13CN and C15N were extracted). A sharp decrease can be seen towards the south in the lines of the 13C isotopologues, while the intensities of the lines of the 15N isotopologues are almost constant across the core.

The spectra shown in Figures A.1 and A.2, as well as in Figure 3 show a small shift in velocity across the core. Such a shift is predicted by the model from Ciolek & Basu (2000) shown in Fig. 6 in Caselli et al. (2002), and it has already been observed in L1544 (see for example Figure B.1 in Spezzano et al. (2016)). Figure A.3 shows the error map on the HC14N/HC15N column density ratio map, and it is calculated by propagating the errors on the column density maps of H13CN and HC15N, which include the rms of the spectra as well as a 10% calibration error.

thumbnail Fig. A.1.

Spectra of HN13C (N = 1-0) in black and H15NC (N= 1-0) in red extracted in the regions shown as black circles in the left panel in Figure 3. The values in boldface report the 14N/15N ratio in HNC for each set of spectra derived using the 12C/13C ratio of 68 (Milam et al. 2005).

thumbnail Fig. A.2.

Spectra of H13CN (J, F = 1 2 - 0 1) in black and HC15N (N= 1-0) in red extracted in the regions shown as black circles in the left panel in Figure 3. The values in boldface report the 14N/15N ratio in HCN for each set of spectra derived using the 12C/13C ratio of 68 (Milam et al. 2005). We note the sharp decrease in the H13CN line towards the south, when compared to the almost constant HC15N.

thumbnail Fig. A.3.

Error map of 14N/15N ratio of HCN towards L1544. The map was computed only in the pixels where the integrated emission of both H13CN and HC15N was detected with a signal-to-noise ratio larger than 5. The IRAM 30m beam of 30″ (∼5000 au) is shown in the bottom right of the map. The solid white contours are 30%, 60%, and 90% of the peak intensity of the N(H2) map of L1544 computed from Herschel/SPIRE data (Spezzano et al. 2016).

Appendix B: Effect of the 12C/13C fractionation

We extracted the spectra of the N =1-0 J = 3/2-1/2 F1 = 2-1 F = 3-2 transition of 13CN and the N =1-0 J = 1/2-1/2 F = 1-1 of CN towards the four positions marked in the left panel in Figure 3 and derived the 12CN/13CN (see Figure B.1). We used the map of the weakest hyperfine component of the 1-0 transition of the main isotopologue, which is only slightly optically thick, with τ ranging from 1.1 to 1.4 across the map, and it does not show signs of self-absorption in our spectra with 50 kHz resolution. In contrast to the spectra shown in Figures A.2 and A.1, where the lines of the 13C and 15N isotopologues do not decrease at the same pace towards the south of L1544, the intensity variations of the lines of 12CN and 13CN do not show a substantial difference. We computed the column density for 12CN and 13CN from the spectra shown in Figure B.1, assuming optically thick emission, and Tex=4.2K. The excitation temperature and optical depth were derived by modelling the observed line of 12CN with RADEX, assuming a kinetic temperature of 8 K and a volume density of 1 × 105 cm−3, and it is consistent with the excitation temperature previously derived for 13CN and C15N in Hily-Blant et al. (2013a). Please note that the choice of volume density has an impact on the resulting excitation temperature, and consequently on the optical depth of the 12CN line and the resulting column density. For example, if we assume a volume density of 5 × 105 cm−3, the corresponding excitation temperature is 5 K, which reduces the optical depth of the 12CN line by almost a factor of two, and in turn decreases the 12CN/13CN ratios in the central and northern offset, where the 12CN line is brighter. The 12CN/13CN ratio derived in this work (193±10 towards the dust peak) is larger than the values derived in B1b, where 12CN/13CN = 50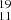 11 19 $ ^{19}_{11} $ (Daniel et al. 2013). However, the chemical models presented in Colzi et al. (2020) can reproduce values of 12CN/13CN larger than 68 (the isotopic ratio for the local ISM, Milam et al. 2005), as seen in Figure 7 of Colzi et al. (2020). The variation of the 12CN/13CN ratio with density and time in the models is mainly connected to the competition between the enrichment of carbon monoxide in 13C and the availability of 13C+. Our results for CN indicate that the effect of the illumination on the nitrogen fractionation across the core is not affected by the fractionation of carbon. Consequently, we can assume that the 14N/15N ratio map of HCN in the left panel of Figure 2 might need to be corrected by an offset (i.e. a different 12C/13C ratio), but it will not change its trend substantially because of the carbon fractionation. Chemical modelling for the combined fractionation of carbon and nitrogen is currently underway and is beyond the scope of this Letter. It is however important to note that the ratio between the 13C and 15N isotopologues for CN and HCN is the same towards the dust peak of L1544, ∼6, and it drops for both molecules to ∼3 towards the south-west of the core, strongly suggesting that both molecules undergo the same chemical paths for the fractionation of nitrogen. While the normal isotopologues trace the core and the cloud where the core is embedded, it is safe to assume that the 13C and 15N isotopologues only trace the core. Therefore, it might be more appropriate to compare the 13C and 15N isotopologue ratios instead of the ratios involving the main isotopologue, even when it is possible to derive a direct measurement.

thumbnail Fig. B.1.

Spectra of 13CN (N =1-0 J = 3/2-1/2 F1 = 2-1 F = 3-2) in black and CN ( N =1-0 J = 1/2-1/2 F = 1-1) in red extracted in the regions shown as black circles in the left panel in Figure 3. The 12CN/13CN column density ratio derived towards the four offsets is written in boldface in each spectrum.

All Tables

Table 1.

Spectroscopic parameters of the observed lines.

In the text

All Figures

thumbnail Fig. 1.

Integrated intensity maps of the 1-0 transitions of H13CN and HC15N towards the inner 2′ × 2′ of L1544. The 30″ beam of the 30m telescope is shown at the bottom left of each map. The solid white contours are 30%, 60%, and 90% of the peak intensity of the N(H2) map of L1544 computed from Herschel/SPIRE data (Spezzano et al. 2016). The dashed black contours indicate the 10σ integrated emission with steps of 10σ for H13CN, and 5σ with steps of 5σ for HC15N (rmsH13CN = 6 mK km s−1, rmsHC15N = 7 mK km s−1).
In the text
thumbnail Fig. 2.

14N/15N ratio map of HCN towards L1544. The map was computed only in the pixels where the integrated emission of both H13CN and HC15N was detected with a signal-to-noise ratio larger than 5. The IRAM 30 m beam of 30″ (∼5000 au) is shown in the bottom right of the map. The solid white contours are 30%, 60%, and 90% of the peak intensity of the N(H2) map of L1544 computed from Herschel/SPIRE data (Spezzano et al. 2016). The column density of HCN was computed from the column density of H13CN assuming the 12C/13C ratio of 68 (Milam et al. 2005). The corresponding error is shown in Fig. A.3.
In the text
thumbnail Fig. 3.

14N/15N ratio of CN in 4 positions across L1544. Left panel: H2 column density map of L1544 computed from Herschel/SPIRE observations (Spezzano et al. 2016). The black crosses show the centre of the areas where the spectra shown in the right panel have been extracted. The black circles show the regions where the spectra shown in the right panel have been averaged. Right panel: spectra of 13CN (N, J, F1, F = 1 3/2 2 3-0 1/2 1 2) in black and C15N (N, J, F= 1 3/2 2-0 1/2 1) in red, extracted towards the offsets marked in the left panel. The values in boldface in blue report the 14N/15N ratio in CN for each set of spectra derived using the 12CN column density directly from the spectra shown in Fig. B.1. The values in boldface in green report the 14N/15N ratio computed from the column density of 13CN using the 12C/13C ratio of 68 (Milam et al. 2005).
In the text
thumbnail Fig. A.1.

Spectra of HN13C (N = 1-0) in black and H15NC (N= 1-0) in red extracted in the regions shown as black circles in the left panel in Figure 3. The values in boldface report the 14N/15N ratio in HNC for each set of spectra derived using the 12C/13C ratio of 68 (Milam et al. 2005).
In the text
thumbnail Fig. A.2.

Spectra of H13CN (J, F = 1 2 - 0 1) in black and HC15N (N= 1-0) in red extracted in the regions shown as black circles in the left panel in Figure 3. The values in boldface report the 14N/15N ratio in HCN for each set of spectra derived using the 12C/13C ratio of 68 (Milam et al. 2005). We note the sharp decrease in the H13CN line towards the south, when compared to the almost constant HC15N.
In the text
thumbnail Fig. A.3.

Error map of 14N/15N ratio of HCN towards L1544. The map was computed only in the pixels where the integrated emission of both H13CN and HC15N was detected with a signal-to-noise ratio larger than 5. The IRAM 30m beam of 30″ (∼5000 au) is shown in the bottom right of the map. The solid white contours are 30%, 60%, and 90% of the peak intensity of the N(H2) map of L1544 computed from Herschel/SPIRE data (Spezzano et al. 2016).
In the text
thumbnail Fig. B.1.

Spectra of 13CN (N =1-0 J = 3/2-1/2 F1 = 2-1 F = 3-2) in black and CN ( N =1-0 J = 1/2-1/2 F = 1-1) in red extracted in the regions shown as black circles in the left panel in Figure 3. The 12CN/13CN column density ratio derived towards the four offsets is written in boldface in each spectrum.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.