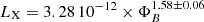EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 662 (June 2022) A&A, 662 (2022) A41 Full HTML
Free Access
Issue
A&A
Volume 662, June 2022
Article Number A41
Number of page(s) 13
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202243251
Published online 10 June 2022

© ESO 2022

1. Introduction

Sun-like and low-mass stars generate magnetic fields through a hydromagnetic dynamo operating in their interiors (Parker 1955; Charbonneau 2013). The stellar dynamo is believed to transform the kinetic energy, Ekin, of the star’s turbulent convective motion into magnetic energy, EB. In analogy to the Sun, starspots and stellar activity are believed to be a consequence of the emergence of magnetic flux at the stellar surface (e.g., Cameron & Schüssler 2015; Brun & Browning 2017). Heating in the stellar corona and chromosphere is closely related to magnetic flux (Pevtsov et al. 2003; Güdel 2004), and magnetically active regions cause most of the stellar energy output variation on timescales ranging from minutes to centuries (Fröhlich & Lean 2004).

Magnetic fields determine the variability and rotational evolution of main-sequence stars as well as the evolution of planetary systems. The relation between angular momentum loss and age yields a predictable evolution of stellar rotation and can provide estimates for stellar age from rotation measurements (Skumanich 1972), a method called gyrochronology (Barnes 2003). This spin-down mechanism acts most effectively in young stars and, over time, transforms them into old field stars with terminal rotation rates that are mass-dependent (McQuillan et al. 2014). Magnetic activity influences planetary evolution through the amount of high-energy radiation emitted during the phase when the planetary atmosphere is young because intense high-energy radiation and winds can evaporate the atmosphere of a planet in a close orbit (Sanz-Forcada et al. 2011; Johnstone et al. 2015). Magnetic fields and their variability are among the main obstacles for the radial velocity detection of low-mass planets (Reiners et al. 2013; Lisogorskyi et al. 2020; Haywood et al. 2020; Crass et al. 2021).

It is often suggested that the well-established stellar activity-rotation relation (e.g., Skumanich 1972; Noyes et al. 1984; Pizzolato et al. 2003; Wright et al. 2011, 2018; Reiners et al. 2014) is a causal consequence of a hydromagnetic dynamo generating stronger magnetic fields in more rapidly rotating stars. The influence of rotation on convective motion is often expressed in terms of the Rossby number, Ro = P/τ, the ratio between rotation period, P, and convective turnover time, τ; chromospheric and coronal emission are observed to saturate in stars rotating more rapidly than Ro ≈ 0.1. Slowly rotating stars (Ro ≳ 0.1) emit chromospheric and coronal emission in approximate proportion to the inverse of the rotational period squared, P−2, which leads to a weakening of stellar activity with age because of angular momentum loss. A mild dependence between X-ray emission and rotation is also observed in the saturated regime (Pizzolato et al. 2003; Reiners et al. 2014; Magaudda et al. 2020).

There is some direct evidence of the magnetic dynamo showing a similar dependence on rotation; the magnetic energy generated in rapidly rotating planets and stars is approximately limited by kinetic energy flux from convection (Christensen et al. 2009), and evidence for saturation in magnetic field strength exists from semi-empirical methods (Reiners et al. 2009a) and from detailed modeling in a limited sample (Shulyak et al. 2017). Furthermore, observations in very active M dwarfs reveal a relation between the field strength and rotation rate (Shulyak et al. 2017, 2019; Kochukhov 2021), and observations of large-scale surface magnetic fields from Zeeman Doppler imaging (ZDI) show a similar relation (Vidotto et al. 2014).

A major challenge in predicting stellar magnetic field strengths is the broad range of timescales and length-scales involved, rendering detailed simulations of stellar convection impractical (Kupka & Muthsam 2017). Instead, simplified models approximate the effects of turbulent convection, rotation, and Lorentz force feedback (Brun & Browning 2017). For example, a balance between Coriolis, buoyancy, and Lorentz forces (MAC balance) leads to EB ∼ Ekin/Ro. On the other hand, a balance between advection and Lorentz forces results in magnetic fields in equipartition with convective kinetic energy. Scaling relations between magnetic dynamo efficiency and luminosity or rotation rate can in principle be estimated from models (e.g., Augustson et al. 2019), but the extent to which such simplified models can be compared to physical objects remains unclear. Furthermore, direct magnetic field measurements and the range of stellar parameters covered by observations have so far not provided enough empirical evidence to guide dynamo models, especially in slowly rotating stars.

The signatures of magnetism on surfaces of Sun-like and low-mass stars are very subtle. The most direct diagnostic of stellar magnetic fields is the Zeeman effect (e.g., Landi Degl’Innocenti & Landolfi 2004; Donati & Landstreet 2009; Reiners 2012; Kochukhov 2021). In general, it can be observed in polarized or in unpolarized light. Measurements in polarized light can detect the distribution of very weak fields on the order of a few Gauss. The analysis of circularly polarized light alone is prone to cancellation effects, but the measurement of linearly polarized light is very demanding. Often, deconvolution techniques are employed to construct average line profiles with very high signal-to-noise ratios (S/N; e.g., Semel 1989; Semel et al. 1993; Rosén et al. 2015). Unpolarized light can potentially reveal the full and unbiased magnetic field including very small-scale components, but here averaging spectral lines to boost the signal is not possible, and line formation must be modeled in great detail (see Kochukhov 2021). Direct measurement of the surface-average magnetic field, ⟨B⟩, therefore requires exceptionally high S/N (at high spectral resolution) plus sophisticated radiative transfer calculations that can model polarization. In consequence, only a limited number of average field measurements based on detailed profile modeling exist, and no empirical relation is known between magnetic fields, fundamental stellar parameters, and rotation. On the theory side, ab initio predictions about stellar magnetic fields are very challenging (Brun & Browning 2017), and empirical information about magnetic fields could help identify the parameter space in which stellar dynamos can operate.

Collecting data that meet the high requirements for average magnetic field measurements in a sizeable sample of low-mass stars is a challenge that can hardly be met by programs investigating the stars or stellar activity alone. On the other hand, radial velocity surveys searching for planetary companions around low-mass stars acquire extensive data sets that can also be used for the study of the host stars. The data we present in this paper were collected during the course of the CARMENES survey for exoplanets around M dwarfs (Reiners et al. 2018; Quirrenbach et al. 2020). Average magnetic field measurements in a subsample of very active stars were already presented in Shulyak et al. (2019). Here, we investigate data from the full CARMENES sample and present average magnetic fields for active and inactive stars.

2. Data

For the CARMENES survey, we observed more than 300 M dwarfs since early 2016 with the goal to monitor radial velocities, leading to a number of exoplanet discoveries (e.g., Ribas et al. 2018; Morales et al. 2019; Zechmeister et al. 2019). The sample used here is based on the one from Reiners et al. (2018) and includes a number of stars that were added later. We excluded the multiple systems reported in Baroch et al. (2021) as well as visual binaries. CARMENES is operating at the 3.5m telescope at Calar Alto observatory, Spain, and consists of the two channels VIS and NIR that cover wavelength ranges 5200–9600 Å (VIS) and 9600–17 100 Å (NIR) at spectral resolution R = λ/Δλ of 94 600 and 80 400, respectively (Quirrenbach et al. 2016). Data from both channels were used for this work.

Data were reduced with the caracal pipeline (Caballero et al. 2016) using optimal extraction (Zechmeister et al. 2014). We computed radial velocities for each spectrum and co-added individual spectra to obtain a master spectrum for each star using the serval package (Zechmeister et al. 2018). Our master spectrum is therefore a time-average of many spectra obtained during the CARMENES survey. Before co-addition, we modeled and removed atmospheric absorption lines from the Earth’s atmosphere with the package molecfit (Smette et al. 2015) as described in Nagel (2019). The S/N of the final spectra depends on the number of observations per star and the amount of telluric contamination. Typical numbers of individual exposures per star are between 10 and 100, and typical values of S/N are in the 100–1000 range. The sample of stars used for our analysis, the number of spectra co-added for each star, and the approximate S/N around λ = 8700 Å are provided in Table B.1.

3. Analysis

We measured average magnetic field strength ⟨B⟩ from comparison of spectral absorption lines to radiative transfer calculations as explained in Shulyak et al. (2017, 2019). As demonstrated there, polarized radiative transfer calculations for atmospheres of M-type stars can reproduce observed line profiles with relatively high quality. The degeneracy between line broadening mechanisms can be overcome using lines with different Zeeman sensitivities, that is, including lines with low and high Landé-g factors simultaneously. Furthermore, several lines in the near-infrared part of the spectrum (8000–10 000 Å) are relatively strong and show potentially observable Zeeman enhancement caused by “desaturation” through the wavelength shifts of the individual absorption components in the presence of a magnetic field (Basri et al. 1992).

3.1. Line selection

The selection of spectral lines is crucial for Zeeman broadening analysis, we refer to Kochukhov (2021) for a detailed review. The set of lines should cover a range of Landé-g values to break degeneracies between different broadening mechanisms. Lines at longer wavelengths are more Zeeman sensitive and therefore preferable (Donati & Landstreet 2009; Reiners 2012). Unfortunately, the density of absorption lines in M dwarf spectra is relatively low beyond 10 000 Å, and lines are often severely contaminated by telluric absorption. Kochukhov & Lavail (2017) and Shulyak et al. (2017) showed that a group of Ti I lines around 9700 Å is very useful for Zeeman analysis, and some lines of molecular FeH that are relatively free of telluric contamination are available around 10 000 Å. We identified a set of suitable spectral lines with a range of Landé-g values to separate magnetic Zeeman broadening from other broadening effects. Spectral lines available for comparison are summarized in Table 1. The list includes atomic lines from Ti I, Fe I, K I, and a particularly useful pair of lines from molecular FeH. Except for the two K I lines, we could not use any other line beyond λ = 10 000 Å.

Table 1.

Absorption lines used for our analysis.

For radiative transfer calculations, we used stellar atmosphere models from the MARCS library (Gustafsson et al. 2008). Based on these models, we computed synthetic spectra on a grid of effective temperatures and surface gravity with step sizes of ΔTeff = 100 K in the Teff = 2500–4000 K range, and log g = 4.5, 5.0, and 5.5 dex. For each star, we linearly interpolated the specific synthetic spectra according to their value of Teff and log g from the grid (see Sect. 4.1 and Table B.1; we computed log g from mass and radius). The required data about atomic absorption lines, including Landé-g factors, were taken from VALD line lists (Piskunov et al. 1995; Kupka et al. 1999). For lines from the molecule FeH, we followed a semi-empirical approach to compute the wavelength-shifting of individual Zeeman components (Afram et al. 2008; Shulyak et al. 2010).

For each star, we selected a subset of lines from the available line list based on the temperature of the star and the quality of the observed data in the spectral range of each line. A line was selected only if the average S/N in its wavelength range exceeded a value of 50. Some lines are located in close vicinity of telluric absorption lines. Depending on the radial velocity of the star and the time of individual observations, these lines could be more or less affected by telluric contamination and could be selected in some stars but not in all. The intensity of the lines and also of line blends are strong functions of stellar temperature. We investigated the usefulness of the lines from our list as a function of stellar temperature and employed the following scheme. For stars with Teff >  3750 K, we used all the available lines from Table 1. In stars cooler than Teff = 3750 K, the lines at λ = 8355.46 and 8470.73 Å were not included in the fit, and in stars cooler than Teff = 3600 K, the line λ = 8516.41 Å was also excluded. In addition to atomic Ti I and Fe I lines, we included the K I lines at λ = 12 435.68 and 12 525.56 Å in our list. These lines carry relevant information in the presence of strong magnetic fields (B ≳ 1 kG; Fuhrmeister et al. 2022) but are less useful in weakly magnetic stars because of the strong intrinsic line broadening. We therefore included the K I lines only in very active stars with log LHα/Lbol >  −4.6. All fits were visually inspected, and we removed individual lines in cases where the spectra were obviously affected by systematics. This was necessary in cases where contamination by telluric lines removed a substantial part of the line profile while our threshold average S/N of 50 was still met. In a few stars, individual orders of our spectra were affected by systematics from template construction and/or telluric correction. The multiline approach can only reliably disentangle Zeeman broadening from rotational broadening if the lines cover a range of different Landé-g values. It is particularly important to include at least one line that shows little or no sensitivity to Zeeman broadening in order to determine vsini and disentangle rotational from Zeeman broadening. For all magnetic field strength measurements included in Table B.1, four or more spectral lines were used, of which at least one line has Landé-g = 0.0.

3.2. Fitting strategy

We observed that simultaneously fitting v sini and Zeeman broadening often leads to overestimated rotational broadening, which is visible when the model predicts profiles that are too broad in the Landé-g = 0.0 lines. Therefore, we first determined vsini using only the Landé-g = 0.0 lines. We emphasize that rotation significantly smaller than instrumental broadening (v sini≲ 1–2 km s−1) has little effect on the line profile. In a second step, we fixed v sini and determined the magnetic field distribution as described below. A comparison between observations and model spectra was carried out through computation of χ2, that is, the quadratic sum over their residuals. The fitting process was performed with the MCMC-toolkit SoBAt (Anfinogentov et al. 2021). For each star, we constructed a grid of synthetic line profiles for a predefined range of magnetic field strengths. The line profiles were modeled from this grid as the weighted sum of B-components with different field strengths; we divided the surface of the star into spatial components that each contribute to the total spectrum with a local spectrum according to the field strength chosen for that B component. The weight of each B component is defined by its filling factor. The choice of field components available to the fit procedure was made according to the predetermined v sini and the Hα emission of the star. Because the Zeeman shift of our most magnetically sensitive lines is approximately 2.5 km s−1 kG−1, we sampled the field distribution in steps of ΔB = 1 kG for stars with a projected rotational velocity v sini <  5 km s−1 and ΔB = 2 kG for stars with higher rotational broadening. This strategy should minimize degeneracies between the individual field components but capture all information from the line profiles. Our models included field components in the range 0–4 kG in inactive or moderately active stars with log LHα/Lbol <  −4.5. For more active stars, components up to 12 kG were used. We confirmed that the choice of field components in number and range did not significantly influence the results. Our fitting strategy optimized the fit for Nc + Nl − 1 free parameters, with Nc the number of magnetic field components and Nl the number of lines. The free parameters were the Nc − 1 weights (fi) for the individual field components i, with Σifi = 1, and Nl line scaling parameters, one for each line. With the scaling parameters, we made it possible to adjust each line strength according to an optical depth scaling law. The scaling effectively compensates for uncertainties in oscillator strengths and element abundance. We used uninformative priors for all free parameters in the [0, 1] range for the field components’ weights and in the [0.3, 1.3] range for the line strength scaling.

3.3. Parameter uncertainties

Estimating uncertainties from high-S/N line fits is notoriously difficult, although an MCMC method provides a convenient way to estimate and visualize uncertainties and also degeneracies between free parameters. As uncertainties of our magnetic field measurements, we report 2σ uncertainties from the MCMC distributions. The underlying assumption is that residuals between a model and observations (χ2) are caused by statistical processes but not by a systematic model mismatch. In our spectra, however, the photon noise is often far smaller than systematic uncertainties expected in our data that are caused, for example, by limited precision in normalization and co-adding and by systematic imperfections of the model. Therefore, the photon noise is often not a good estimator for the likelihood of a fit. Methods that compare likelihoods can partially overcome and reliably identify the most likely solution, but parameter uncertainties remain affected by systematic components in the residuals (see, e.g., Bonamente 2017). We therefore implemented a two-step procedure to estimate uncertainties. First, we carried out the fitting procedure with formal photon uncertainties. Then, we multiplied the photon noise of our data by the square root of χ ν 2 $ \chi^2_{\nu} $, the reduced chisquare, calculated for each spectral line, and we carried out the fit procedure again with the modified uncertainties (in other words, we assume that our best fit is also a good fit; see Press et al. 1986). We confirmed that the second step did not significantly alter the result but produces more realistic estimates of our measurement uncertainties. We treated field measurements as upper limits instead of detections if the result is consistent within an average field of ⟨B⟩=100 G within 2σ uncertainties. In these cases, we report the 2σ upper limit in our plots and Table B.1. Stars for which only upper limits could be determined were not considered in our regression curve calculations in the following.

3.4. Example and literature comparison

We show an example for our line fits in Fig. 1. Plots of all fits are available in electronic format1. The distribution of the field component posteriors shows that there is a degeneracy between components from adjacent bins, fi and fi ± 1, but there is little crosstalk between components with very different field strengths. The figures show the observed data together with the models for all lines and also the distribution of field components and their uncertainties. We measured the average magnetic field strength in 292 stars. For 36 of these, the field strength was measured before by Shulyak et al. (2017, 2019) and Kochukhov & Reiners (2020). Shulyak et al. (2019) also used CARMENES data focusing on very active stars. The other works are based on data from other sources. We compare the results of our analysis to those previously reported in Fig. 2. The comparison shows that, except for a handful of stars in which our new results are up to 50% smaller or larger than earlier field estimates, the results are typically consistent within 25%. Discrepancies between our and earlier measurements are smaller than 2σ in the majority of stars. The main differences between our and earlier measurements are the selection of lines and the setup of the model. This demonstrates that formal (statistical) fit uncertainties are often smaller than systematic uncertainties. We estimate that the accuracy of our average magnetic field measurements is better than 25%.

thumbnail Fig. 1.

Top panel: example fit for one of our stars; J05019+011 (M4.0 V). Data are shown as black line with uncertainties. The best fit solution is shown as red line, the best solution with ⟨B⟩=0 G as blue dashed line. The absorbing species are indicated together with the effective Landé-g factor for atomic lines. Bottom panel: cornerplot for posterior MCMC parameter distribution. In this example, six field components f1–f6 were used, and twelve lines were fit for which one scaling parameter (mag1–mag11) per line is shown. Corresponding lines are shown in the upper panel in the same order. The posterior distribution for ⟨B⟩=ΣBifi is included in the plot at the bottom row. Inset panel: relative distribution of filling factors fi for field components Bi. Uncertainties of individual field components are indicated as cyan lines.

thumbnail Fig. 2.

Comparison of our average field measurements to literature values. Red and blue symbols indicate slow and fast rotators, respectively (see Sect. 4.3), and gray symbols show stars with no information on rotation period. Symbol size and brightness indicate stellar mass. The dashed black line shows identity between our measurements and literature values, and the gray dotted lines mark the region where the discrepancy is within ±25%.

For many of our target stars, Moutou et al. (2017) reported average magnetic field measurements from an “indirect” method (Kochukhov 2021). We provide a comparison between their results and our values in Appendix A.

4. Results

In this section, we investigate relations between average magnetic fields, rotation, and nonthermal emission. We augment our sample with stars for which average magnetic field measurements have been reported in the literature.

4.1. Sample

Our sample on Sun-like and low-mass stars consists of our measurements of 292 M dwarfs observed with CARMENES and 22 additional stars taken from the literature. From our original sample, we excluded those that did not meet the quality criteria for the selection of lines as described in Sect. 3. From the literature, we added only magnetic field measurements from radiative transfer calculations in multiple lines and considering multiple magnetic field components; following Kochukhov (2021), we added six M dwarfs from Shulyak et al. (2017). We also included the results on 15 young Sun-like stars from Kochukhov et al. (2020) and the value for the Sun from Trujillo Bueno et al. (2004).

The parameters for all 314 stars of our sample are listed in Table B.1. For the CARMENES stars, mass, radius, and luminosity are taken from Schweitzer et al. (2019). These values are derived from PARSEC isochrones and PHOENIX-ACES model fits to the high-resolution spectra (see Passegger et al. 2018). X-ray luminosities are computed from X-ray fluxes from Voges et al. (1999) using distances from Gaia Collaboration (2021). Normalized Hα luminosities are from CARMENES data (see Schöfer et al. 2019). They are only reported for the stars with Hα in emission. Ca H&K luminosities are estimated from normalized Ca emission R HK ′ $ R^\prime_\text{HK} $ in Perdelwitz et al. (2021), we use L Ca = R HK ′ L bol $ L_\text{Ca} = R^\prime_\text{HK} L_\text{bol} $. The main sources for uncertainties in X-ray, Hα, and Ca H&K luminosities are variability of the emission and uncertainties in the stellar parameters used to compute the luminosities from line equivalent widths. Variability and uncertainties are typically on the order of a few tenths of a dex (see, e.g., Schöfer et al. 2019; Perdelwitz et al. 2021). References for rotation periods are included in Table B.1. We discarded several periods measured by Díez Alonso et al. (2019) following a reanalysis of the same photometric data as used in that work but using more conservative thresholds for significance. As discussed in the references, it cannot be excluded that a few of the periods are false positives or harmonics of the real rotation periods. Obvious suspects could potentially be identified in cases where reported periods are in strong disagreement with the average relations between rotation and other information. For the young Suns from Kochukhov et al. (2020), we collected literature values for mass and radius from Takeda et al. (2007) and Chandler et al. (2016). We estimate the Rossby number, Ro = P/τ, with τ = 12.3 d ×(Lbol/L⊙)−1/2, with rotation period, P, in days and bolometric luminosity, Lbol. The expression for τ was taken from Eq. (10) in Reiners et al. (2014), Psat = 1.6 d × (Lbol/L⊙)−1/2, and τ = Psat/Rosat. We use Rosat = 0.13 for the transition between saturated and non-saturated activity (see Wright et al. 2011, 2018; Reiners et al. 2014). We note that Wright et al. (2018) derived a relationship τ(M) from X-ray observations in partially and fully convective stars that results in a similar scaling as the one we use here, but that yields smaller values of τ particularly for very low stellar mass. We confirmed that the main results of our analysis remain valid for τ(M) as expressed in Wright et al. (2018), and we emphasize that the relations we report in the following are independent of the choice of τ.

The distribution of mass, M, rotation period, P, and Rossby number are shown in Fig. 3. The sample covers one order of magnitude in stellar mass with a concentration in the mass range M = 0.4–0.5 M⊙. The original motivation for the CARMENES survey was to search for planets around low-mass stars; our sample of magnetic field measurements therefore underrepresents stars more massive than 0.5 M⊙. Most of the stars from Kochukhov et al. (2020) have masses close to the solar value. The sample covers three orders of magnitude in P and Ro with a strong concentration around Ro = 0.6; 51 stars (16%) of the sample are in the 0.5 <  Ro <  0.8 (log g ≈ −0.2) range. Although our sample mainly consists of stars that were observed to discover exoplanets, it was not intentionally biased towards slowly rotating or inactive stars. The rotational distribution of the sample is therefore a fair, albeit certainly not unbiased, representation of the (non-binary) stars in the local Galaxy. The distribution implies systematic biases and needs to be taken into account for what follows. The same applies for potential harmonics in the rotational periods, although their impact is probably small because of the large range in periods covered by our sample.

thumbnail Fig. 3.

Distributions of our sample of stars with average magnetic field measurements. Left: stellar mass. Center: rotational period. Right: Rossby number. Rotational periods are known for 162 of the 314 sample stars, and the remaining 152 stars do not appear in the distributions of P and Ro.

4.2. Period–mass diagram

The evolution in time of stellar rotation as a function of mass can be followed in a period–mass diagram (e.g., Barnes 2003; Irwin et al. 2011; Reinhold et al. 2013; McQuillan et al. 2014). Observations of star clusters and field stars show the rotational evolution of stars from rapid rotators with very short rotational periods (P <  1 d) to slower rotators with periods of P = 10 d and longer depending on stellar mass. Stars are believed to lose angular momentum through the interaction between stellar wind and magnetic fields (e.g., Mestel 1968; Kraft 1970; Skumanich 1972; Pallavicini et al. 1981; Kawaler 1988; Reiners & Mohanty 2012; Matt et al. 2015; Gallet & Bouvier 2015; Vidotto 2021).

Observations of nonthermal energy have shown that stellar activity is intimately coupled with rotation (Noyes et al. 1984; Pizzolato et al. 2003; Wright et al. 2011, 2018), and that the timescales for angular momentum loss and activity reduction depend on stellar mass (West et al. 2008). Stellar magnetic fields are the physical connection between nonthermal emission and rotational evolution. With our large set of magnetic field observations we can investigate this relation in detail and across a large parameter range. In Fig. 4, we show the distribution of our sample stars in the period–mass diagram and indicate the magnetic field strength. We include the stars with measured rotational periods from Newton et al. (2017) to show the distribution of available field measurements in context of a larger sample. We confirm that the two samples appear very similar in the mass–period diagram, and we refer the reader to Newton et al. (2017) for a discussion of this distribution in the context of stellar activity and rotational braking.

thumbnail Fig. 4.

Period–mass diagram indicating magnetic field strength in color and symbol size. Data from this work are shown as circles, and other data are shown as squares. Literature values are from Kochukhov et al. (2020) for young Sun-like stars and for seven additional targets from Shulyak et al. (2017). The solar datum from Trujillo Bueno et al. (2004) is annotated. Gray open circles show stars with known rotation periods as reported by Newton et al. (2017). Dashed lines show values of the Rossby number Ro = 0.1 and 1.0, assuming that bolometric luminosity Lbol ∝ M4 and τ ∝ L bol − 0.5 $ \tau \propto L_\text{bol}^{-0.5} $ for dwarf stars.

Figure 4 can be compared to diagrams visualizing the basic properties of the large-scale magnetic topologies of cool stars from ZDI, for example, in Donati & Landstreet (2009, Fig. 3) and Kochukhov (2021, Fig. 14). A remarkable feature of such diagrams is a lack of stars at low masses (M ≲ 0.3 M⊙) and rotation periods around 10 d and longer (or Ro ≳ 0.1). This can partly be explained by a detection bias: small and slowly rotating stars have low Doppler broadening below the threshold values for ZDI. A low density of stars is also visible in Fig. 4 for masses below 0.3 M⊙ in the period range around 10–40 d. However, stars with rotation periods around P = 100 d do appear in this mass range. There is no obvious reason why rotation periods of several tens of days should be more difficult to detect than longer ones. Potential explanations for the low density of stars in this parameter range include enhanced braking efficiency in the relevant period range (see, e.g., Newton et al. 2016) and therefore rapid evolution of low-mass stars from a few days to about 100 d (similarly to attempts to explain the so-called Vaughan-Preston gap; Rutten 1987), as well as cancellation of contrast features caused by a transition from dark to bright surface features (see, e.g., Reinhold et al. 2019). The distribution of magnetic fields in the period-mass diagram shows no peculiar features beyond a mass-dependent weakening of average magnetic fields with slower rotation. This is discussed in the following subsection.

4.3. Rotation–magnetic field relation

The decay of average magnetic field strength with rotation coincides with the well-studied dependence of stellar activity on rotation, as observed in nonthermal emission. The distribution of magnetic fields in Fig. 4 suggests a monotonous relation between rotation and average magnetic field, which is similar to the rotation–activity relation. The latter is often expressed as a dependence between normalized chromospheric or coronal emission from active regions (Lactivity/Lbol) and the Rossby number. In Fig. 5, we show a similar relation between the average magnetic field ⟨B⟩ and Rossby number.

thumbnail Fig. 5.

Magnetic field–rotation relation for solar-like and low-mass stars. Symbols for stars rotating slower than Ro = 0.13 are colored red, while those of faster rotators are colored blue. Larger and darker symbols indicate higher stellar mass than smaller and lighter symbols. The gray dashed lines show linear fits separately for the slowly rotating stars (Ro >  0.13; ⟨B⟩=200 G ×Ro−1.25) and the fast rotators (Ro <  0.13; ⟨B⟩=2050 G ×Ro−0.11). Downward open triangles show upper limits for ⟨B⟩.

Our sample reveals a clear dependence between average magnetic field and Rossby number over more than three orders of magnitude in Ro. Similarly to the rotation–activity relation, the rotation-magnetic field relation exhibits a break between slow and rapid rotators, the saturated and the non-saturated groups of stars. The non-saturated group have Rossby numbers above Ro = 0.13 (shown as red symbols in Fig. 5 and the following figures). In this group, the average magnetic field strongly depends on Ro. In the saturated group (blue symbols), the average field strength shows a much weaker dependence on rotation. The rotation-magnetic field relation of the saturated group was already apparent in Fig. 3 of Shulyak et al. (2017) and Fig. 12 of Kochukhov (2021).

In order to quantify the relation between average magnetic field and Rossby number, we calculated linear regression curves following the ordinary least-squares (OLS) bisector method from Isobe et al. (1990) 2. We chose the bisector method because the values of Ro come with a relatively large uncertainty introduced by large systematic uncertainties in the convective turnover time, τ. Coefficients of the relation are reported in Table 2. Additionally, our data suggest the existence of two branches for very slow rotation at Ro ≈ 1. Stars rotating slower than this limit (Ro >  1) are predominantly partially convective stars (see Fig. 4). Among them, some of the more massive stars’ field strengths seem to depend less on Ro than the overall trend, but this speculation rests on very few data points only.

Table 2.

Relations between average magnetic field strength, ⟨B⟩ (in G), and Rossby number, Ro, and between magnetic flux, ΦB (in Mx) for the slow rotators (and the ratio ⟨B⟩/Bkin for the fast rotators), and rotation period, P (in d).

An alternative view on the rotation–activity relation is the scaling of chromospheric or coronal emission (non-normalized instead of normalized) with rotation period (instead of Rossby number). Such a scaling was suggested by Pallavicini et al. (1981), and Pizzolato et al. (2003) pointed out that the convective turnover time approximately scales as τ ∝ L bol − 1 / 2 $ \tau \propto L_\text{bol}^{-1/2} $. This parameterization is in general agreement with theoretical predictions (Kim & Demarque 1996), but it is not obvious to what extent this justifies conclusions about the nature of the dynamo because τ likely depends on other parameters as well. Furthermore, the relevant τ may exhibit a discontinuity at the fully convective boundary (Cranmer & Saar 2011), although so far no evidence for such a discontinuity was found (Wright et al. 2018). The scaling of τ with Lbol implies that a relation between normalized emission (Lactivity/Lbol) and Rossby number (P/τ) is equivalent to a relation between Lactivity and rotation period. Furthermore, saturation of activity at a fixed Rossby number is equivalent to saturation at a fixed value of Lactivity/Lbol (see Reiners et al. 2014).

We investigated scaling laws equivalent to the relation between average magnetic field and Rossby number (Fig. 5) and show an alternative view on the rotation-magnetic field relation in Fig. 6. In its upper panel, we show the ratio between the average magnetic field, ⟨B⟩, and the kinetic field strength limit (Reiners et al. 2009b),

thumbnail Fig. 6.

Alternative version of the rotation–magnetic field relation. Top panel: ratio of average field, ⟨B⟩, to kinetic field limit, Bkin, as function of rotation period. Stars rotating faster than the saturation period are colored blue, while other stars are shown in gray. Bottom panel: magnetic flux, ΦB. Stars rotating slower than the saturation limit are colored red, while faster rotators are shown in gray. Symbols and colors are the same as in Fig. 5. See text for details about Bkin.

B kin = 4800 G × ( M L 2 R 7 ) 1 / 6 , $$ \begin{aligned} B_\text{kin} = 4800\,\text{ G} \times \left(\frac{ML^2}{R^7}\right)^{1/6}, \end{aligned} $$(1)

with M being the stellar mass, L luminosity, and R radius, all in solar units. This expression estimates the maximum field strength under the hypothesis that energy flux determines the magnetic field strength in rapidly rotating stars (Christensen et al. 2009). We find that the observed average field strengths in the rapid rotators indeed populate a relatively narrow region with values ⟨B⟩≈Bkin. We also find that the ratio ⟨B⟩/Bkin shows a mild dependence on rotation with a power law coefficient that is significantly different from zero (see Table 2). Stars rotating slower than the saturation limit (gray symbols in the upper panel of Fig. 6) fall short of this relation. For these non-saturated stars, however, their magnetic flux, ΦB = 4πR2B, follows a relatively close relation with rotation period, as is shown in the lower panel of Fig. 6.

In the non-saturated stars of our sample, magnetic flux shows a clear dependence on rotational period. We report the relation between ΦB and P in Table 2 and indicate the relation as a dashed line in the lower panel of Fig. 6. A group of stars at P <  6 d shows a somewhat different behavior, with values of ΦB significantly below the overall trend. The group consists of relatively massive stars from the young Sun sample that may indicate an additional mass- or age-dependence, or that may be caused by a systematic offset in the literature values. We chose to not include stars with M >  0.9 M⊙ and P <  6 d in our fit (seven stars). Potential reasons for this deviation from the trend defined by the lower mass stars include underestimated radii of the young stars (note that ΦB ∝ R2), an additional dependence of ΦB on radius, age, or other parameters, and selection effects in our sample. We note that for the slow rotators, our relation between ⟨B⟩ and Ro and the one between ΦB and P are conceptually equivalent because from the equations in Table 2, we estimate ⟨B⟩∝R−2 ∝ τ1.26, and hence τ ∝ R−1.6. For main-sequence stars, this yields approximately τ ∝ L−0.4, which is consistent with the scaling we assumed between τ and L, as discussed above.

4.4. Predictive relations

Our results allow us to predict stellar magnetic fields from fundamental stellar parameters and rotational period, and therefore provide a missing link for physically consistent models of nonthermal emission (Linsky 2017), cool star mass loss (Cranmer & Saar 2011), and angular momentum evolution (Gallet & Bouvier 2015). One of our main results is that the average magnetic field of a main-sequence star with M ≲ 1 M⊙, generated by the magnetic dynamo, can be approximated from stellar parameters mass, M, radius, R, luminosity, L, (all in solar units), and rotation period, P, (in days) in the following way:

B pred = 8570 G × R − 2 × P − 1.25 ( slow rotation; P > P sat ) , $$ \begin{aligned}&B_\text{pred} = 8570\,\mathrm{G} \times R^{-2} \times P^{-1.25}\quad \quad (\text{ slow} \text{ rotation;}\, P > P_{\text{sat}}), \end{aligned} $$(2)

B pred = 5300 G × ( M L 2 R 7 ) 1 6 × P − 0.16 ( fast rotation; P < P sat ) . $$ \begin{aligned}&B_\text{pred} = 5300\,\mathrm{G} \times \left(\frac{ML^2}{R^7}\right)^{\frac{1}{6}} \times P^{-0.16}\quad (\text{ fast} \text{ rotation;}\, P < P_{\text{sat}}). \end{aligned} $$(3)

Equation (2) follows from the relations between ΦB and P for the slow rotators in Table 2 and is independent of the choice of τ. Equation (3) follows from the relation between ⟨B⟩/Bkin and P for the fast rotators together with Eq. (1). The critical period can be estimated as Psat = 1.6 d × (Lbol/L⊙)−1/2, which corresponds to Ro = 0.13. In Fig. 7, we show the measured average fields in relation to the predicted values. In the histogram, we show the distribution of the ratio ⟨B⟩/Bpred. We find that 75% of the predicted values agree with the measured values within a factor of two.

thumbnail Fig. 7.

Values for predicted value of average magnetic field calculated from Eqs. (2) and (3) valid for all masses. The dashed gray line indicates identity between ⟨B⟩ and Bpred, and the histogram shows the distribution of ⟨B⟩ around Bpred. We derive from the histogram that our relation estimates the value for ⟨B⟩ within roughly a factor of two uncertainty; this range is indicated with the two dotted lines.

4.5. Nonthermal emission

The magnetic field–rotation relation (Fig. 5) shows remarkable similarity to the activity–rotation relation from X-ray emission. Other frequently used indicators of stellar activity include the hydrogen Hα line of the Balmer series and the Ca H&K lines. X-rays are emitted at temperatures occurring in the stellar coronae, while both Hα and Ca H&K form at lower temperatures in the chromosphere (Vernazza et al. 1981). A relation between photospheric magnetic flux, ΦB, and X-ray spectral luminosity, LX, was established by Pevtsov et al. (2003) that applies to X-ray irradiance from bright stellar surface regions as well as the total stellar X-ray output. Such a relation constrains possible heating and emission models for the Sun and other stars (Fontenla et al. 2016).

Before we turn to the emission/magnetic flux relation, we investigated the dependence between normalized line luminosity (L(X, Hα, Ca)/Lbol) and average magnetic field in Fig. 8. These relations show a relatively large scatter but provide information about the typical field strengths required to generate observable chromospheric and coronal emission. We find that X-ray and Ca H&K emission are observable in stars with very low magnetic field strengths, which possibly includes a basal component that is unrelated to stellar magnetic activity (Schrijver et al. 1989). On the other hand, we find that a minimum average field strength of several hundred G is required in order to generate detectable Hα emission in a stellar chromosphere. This is consistent with chromosphere models in low-mass stars, showing that Balmer line emission is only generated in the presence of a sufficiently massive chromosphere (Cram & Mullan 1979). For Ca H&K, we observe a saturation of the normalized emission at a magnetic field strength ⟨B⟩≳800 G, that is, an increase in the average magnetic field beyond 800 G does not lead to an obvious increase in LCa/Lbol.

thumbnail Fig. 8.

Normalized coronal (X-ray, top panel) and chromospheric (Hα, middle panel; Ca H&K, bottom panel) emission as a function of average magnetic field. Symbol size and color are the same as in Fig. 5. The arrow in the bottom panel indicates the field strength at which the normalized Ca H&K emission saturates.

In Fig. 9, we show that well-defined relations exist between magnetic flux and emission luminosities in all three stellar activity indicators, that is, X-rays, hydrogen Hα, and Ca H&K. These relations show significantly less scatter than those between normalized activity and average magnetic field in Fig. 8. Ca H&K and X-ray emission are already visible at magnetic flux levels below ΦB = 1024 Mx. Hα emission requires more magnetic heating and goes together with relatively strong Ca H&K emission (Robinson et al. 1990). For the plot showing Ca H&K emission (bottom panel in Fig. 9), we applied a saturation limit of Bmax = 800 G in the calculation of magnetic flux because higher average fields show no increase in normalized emission for stronger fields (see above); for all stars with ⟨B⟩> 800 G, we set ⟨B⟩=800 G when calculating ΦB. We interpret this as saturation of chromospheric Ca H&K emission at a field strength of ∼800 G. We note that the choice of higher maximum field strengths would essentially shift the blue points (rapid rotators) in the bottom panel of Fig. 9 toward the right; a limit of 1000 G instead of 800 G already moves the blue points significantly away from the relation.

thumbnail Fig. 9.

Coronal (LX, top panel) and chromospheric (LHα, middle panel; LCa, bottom panel) emission luminosities as a function of magnetic flux, ΦB. Symbol size and color are the same as in Fig. 5. Linear power laws are reasonable approximations for X-ray, Hα, and Ca luminosities describing both rapid and slow rotators. Relations are provided in Eqs. (4)–(6). Ca H&K emission shows a saturation at magnetic flux density ⟨B⟩≈800 G (see Fig. 8). This limit is applied to the magnetic flux values in the bottom panel (Ca H&K), but no limit is applied in the other two panels.

We summarize relations between chromospheric and coronal emission and magnetic flux in Eqs. (4)–(6). The relations apply to all stars across the entire range of masses and rotation rates included in our sample (taking into account the field limit in Ca H&K). Our relations quantitatively describe the dependence of nonthermal chromospheric and coronal emission on the stellar dynamo. With luminosities, L, in erg s−1 and magnetic flux, ΦB, in Mx, we can write:

L X = 3.28 10 − 12 × Φ B 1.58 ± 0.06 $$ \begin{aligned}&L_\text{X} = 3.28\,10^{-12} \times \Phi _{B}^{1.58 \pm 0.06}\end{aligned} $$(4)

L H α = 4.80 10 − 9 × Φ B 1.43 ± 0.05 $$ \begin{aligned}&L_{\text{H}\alpha } = 4.80\,10^{-9} \times \Phi _{B}^{1.43 \pm 0.05}\end{aligned} $$(5)

L Ca = 1.22 10 − 19 × Φ B 1.88 ± 0.05 ( apply B max = 800 G ) . $$ \begin{aligned}&L_\text{Ca} = 1.22\,10^{-19} \times \Phi _\text{B}^{1.88 \pm 0.05} \qquad (\text{ apply}B_{\text{max}}= 800\,\text{ G}) .\end{aligned} $$(6)

5. Summary and discussion

We provided direct measurements of average magnetic field strengths in 292 low-mass main-sequence stars from radiative transfer calculations considering multiple magnetic field components. For 260 stars of our sample, average field values are reported here for the first time. Our new data were collected as part of the CARMENES survey for planets around M dwarfs; in total, we used 15 058 spectra for our analysis, which were corrected for telluric contamination before co-addition.

The average field strengths we measured span approximately two orders of magnitude with a lower limit around 100 G and maximum values of 8000 G. Not surprisingly, we observe a relatively large scatter in our investigations of average field strengths, but a number of clear trends appear that allow us to draw firm conclusions about the role of average magnetic fields in the framework of stellar activity. For our analysis, we included literature data for 22 stars that were obtained with similar methods.

First, we find that the saturation-type, rotation–activity relation, which is well known from nonthermal coronal emission, can be traced back to a rotation–magnetic field relation between average field strength, rotation period, and fundamental stellar parameters. Our data show that rapid and slow rotators behave differently with a break around Ro = 0.13, which is where the average surface field reaches the kinetic field strength limit. This demonstrates that a saturation effect in the magnetic dynamo is the reason for saturation of nonthermal emission instead of a limit in the available stellar surface area (filling factor equal to unity). We provided relations between magnetic flux (ΦB = 4πR2B) and rotation period valid for the non-saturated (slowly rotating) stars. From this relation, we derived a relationship between average magnetic field strength as a function of rotation period and stellar radius that is independent of the choice of the convective turnover time. As an equivalent description of the rotation–magnetic field relation, we also find a relationship between average magnetic field and Rossby number. We see some systematic deviations between our data and the predictions, which hints at additional effects that go beyond our scaling relations. Saturated (rapidly rotating) stars consistently show average field strengths close to the kinetic field strength limit; the ratio between average field strength and the kinetic limit is close to unity in the saturated stars but reveals a mild dependence on rotation.

Second, we investigated relations between nonthermal chromospheric and coronal emission from X-ray, Hα, and Ca H&K measurements. We observe that emission luminosity normalized by the stars’ bolometric luminosity is related to average field strengths. In addition, Ca H&K line emission shows saturation at an average field strength around 800 G. Taking this saturation into account provides close relations between X-ray, Hα, and Ca H&K luminosity with magnetic flux for all our sample stars. We reported relations between magnetic flux and emission luminosities for the three types of emission lines.

The universal correspondence between magnetic flux and nonthermal emission sheds some light on the proposed mechanism of centrifugal stripping, according to which that correspondence was suspected to break down in the most rapid rotators (Jeffries et al. 2011; Christian et al. 2011). Centrifugal stripping is consistent with the apparent reduction of flaring activity in very rapidly rotating M dwarfs with P ≲ 0.3 d (Günther et al. 2020; Ramsay et al. 2020). A potential mechanism is decreased effective gravity leading to distortion of magnetic field lines and cooling of the coronal plasma to chromospheric temperatures (Antiochos et al. 2011). An observational signature of this effect would be rapidly rotating stars with typical chromospheric but abnormally low coronal luminosities with respect to their magnetic flux. The observed correlation between X-ray emission and magnetic flux (Fig. 9) shows no evidence for supersaturation caused by a break in coronal heating. Instead, saturation of normalized emission with magnetic flux density is visible in the chromospheric Ca H&K lines (Fig. 8). Our results are therefore not consistent with the coronal stripping scenario.

Our data allow us to test the prediction from force balance (MAC balance) that magnetic energy grows in proportion to the ratio between kinetic energy and Rossby number, EB ∼ Ekin/Ro (e.g., Brun & Browning 2017). We show this relation for our sample stars in Fig. 10. A clear correlation is visible, but we can identify a few obvious trends that show systematic deviations from the simplified scaling law, for example, at Ekin/Ro ≈ 1039 erg; intermediate mass stars show values of EB that are about one order of magnitude larger than the highest or lowest mass stars in our sample. Our data set provides valuable input for more detailed tests of dynamo models that go beyond the scope of this paper.

thumbnail Fig. 10.

Relation between magnetic energy and the ratio between kinetic energy and Rossby number for our sample stars. Such a relation is motivated by the assumption of a balance between Coriolis, buoyancy, and Lorentz forces (MAC balance). Symbols are the same as in Fig. 5.

Looking at all observations together, we conclude that the rotation–activity relation, including its saturation effect, is a causal consequence of the characteristics of the magnetic dynamo and its dependence on rotation. We promote the notion that the magnetic dynamo generates magnetic flux proportionally to the rotation rate with a limit defined by the available kinetic energy. Coronal and chromospheric emission are generated with total nonthermal emission proportionally to magnetic flux. Therefore, nonthermal emission scales with rotation period until the magnetic field saturation limit is reached, beyond which point the emission only mildly depends on rotation (because a mild dependence between magnetic flux and rotation still exists in the saturation regime). With this background, coronal and chromospheric emission can be estimated from stellar parameters according to Eqs. (2)–(6). For example, for coronal X-ray emission in non-saturated stars, we estimate that L X ∝ Φ B 1.58 ± 0.06 $ L_{\text{X}} \propto \Phi_{{B}}^{1.58 \pm 0.06} $ and ΦB ∝ P−1.25 ± 0.07, which implies LX ∝ P−1.98 ± 0.07, which is consistent with the observed X-ray activity–rotation relation from much larger samples.

The new observations provide a direct view into magnetic dynamos of low-mass stars, and they yield a consistent picture of chromospheric and coronal emission for stars of different masses and rotation periods. The relations between fundamental stellar parameters, rotation, average magnetic fields, and nonthermal emission provide useful information for models of stellar and planetary evolution.

Acknowledgments

We thank an anomymous referee for helpful suggestions, and we thank Almudena García López for setting up the electronic data archive. CARMENES is an instrument at the Centro Astronómico Hispano-Alemán (CAHA) at Calar Alto (Almería, Spain), operated jointly by the Junta de Andalucía and the Instituto de Astrofísica de Andalucía (CSIC). The authors wish to express their sincere thanks to all members of the Calar Alto staff for their expert support of the instrument and telescope operation. CARMENES was funded by the Max-Planck-Gesellschaft (MPG), the Consejo Superior de Investigaciones Científicas (CSIC), the Ministerio de Economía y Competitividad (MINECO) and the European Regional Development Fund (ERDF) through projects FICTS-2011-02, ICTS-2017-07-CAHA-4, and CAHA16-CE-3978, and the members of the CARMENES Consortium (Max-Planck-Institut für Astronomie, Instituto de Astrofísica de Andalucía, Landessternwarte Königstuhl, Institut de Ciències de l’Espai, Institut für Astrophysik Göttingen, Universidad Complutense de Madrid, Thüringer Landessternwarte Tautenburg, Instituto de Astrofísica de Canarias, Hamburger Sternwarte, Centro de Astrobiología and Centro Astronómico Hispano-Alemán), with additional contributions by the MINECO, the Deutsche Forschungsgemeinschaft through the Major Research Instrumentation Programme and Research Unit FOR2544 “Blue Planets around Red Stars”, the Klaus Tschira Stiftung, the states of Baden-Württemberg and Niedersachsen, by the Junta de Andalucía. We acknowledge financial support from the Agencia Estatal de Investigación of the Ministerio de Ciencia e Innovación and the ERDF “A way of making Europe” through project PID2019-109522GB-C5[1:4]/AEI/10.13039/501100011033 and the Centre of Excellence “Severo Ochoa” and “María de Maeztu” awards to the Instituto de Astrofísica de Canarias (CEX2019-000920-S), Instituto de Astrofísica de Andalucía (SEV-2017-0709), and Centro de Astrobiología (MDM-2017-0737), the Deutsche Forschungsgemeinschaft Heisenberg programme (KA4825/4-1), and the Generalitat de Catalunya/CERCA programme.

References

  1. Afram, N., Berdyugina, S. V., Fluri, D. M., Solanki, S. K., & Lagg, A. 2008, A&A, 482, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Anfinogentov, S. A., Nakariakov, V. M., Pascoe, D. J., & Goddard, C. R. 2021, ApJS, 252, 11 [Google Scholar]
  3. Antiochos, S. K., Mikić, Z., Titov, V. S., Lionello, R., & Linker, J. A. 2011, ApJ, 731, 112 [Google Scholar]
  4. Augustson, K. C., Brun, A. S., & Toomre, J. 2019, ApJ, 876, 83 [Google Scholar]
  5. Barnes, S. A. 2003, ApJ, 586, 464 [Google Scholar]
  6. Baroch, D., Morales, J. C., Ribas, I., et al. 2021, A&A, 653, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Basri, G., Marcy, G. W., & Valenti, J. A. 1992, ApJ, 390, 622 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bonamente, M. 2017, Statistics and Analysis of Scientific Data (Berlin: Springer) [CrossRef] [Google Scholar]
  9. Brun, A. S., & Browning, M. K. 2017, Liv. Rev. Sol. Phys., 14, 4 [Google Scholar]
  10. Caballero, J. A., Guàrdia, J., López del Fresno, M., et al. 2016, in Observatory Operations: Strategies, Processes, and Systems VI, Proc. SPIE, 9910, 99100E [Google Scholar]
  11. Cameron, R., & Schüssler, M. 2015, Science, 347, 1333 [Google Scholar]
  12. Chandler, C. O., McDonald, I., & Kane, S. R. 2016, AJ, 151, 59 [NASA ADS] [CrossRef] [Google Scholar]
  13. Charbonneau, P. 2013, Solar and Stellar Dynamos, Saas-Fee Advanced Course [CrossRef] [Google Scholar]
  14. Christensen, U. R., Holzwarth, V., & Reiners, A. 2009, Nature, 457, 167 [Google Scholar]
  15. Christian, D. J., Mathioudakis, M., Arias, T., Jardine, M., & Jess, D. B. 2011, ApJ, 738, 164 [NASA ADS] [CrossRef] [Google Scholar]
  16. Cram, L. E., & Mullan, D. J. 1979, ApJ, 234, 579 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cranmer, S. R., & Saar, S. H. 2011, ApJ, 741, 54 [Google Scholar]
  18. Crass, J., Gaudi, B. S., Leifer, S., et al. 2021, ArXiv e-prints [arXiv:2107.14291] [Google Scholar]
  19. Díez Alonso, E., Caballero, J. A., Montes, D., et al. 2019, A&A, 621, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Donati, J.-F., & Landstreet, J. D. 2009, ARA&A, 47, 333 [NASA ADS] [CrossRef] [Google Scholar]
  21. Fontenla, J. M., Linsky, J. L., Witbrod, J., et al. 2016, ApJ, 830, 154 [Google Scholar]
  22. Fröhlich, C., & Lean, J. 2004, A&ARv, 12, 273 [Google Scholar]
  23. Fuhrmeister, B., Czesla, S., Nagel, E., et al. 2022, A&A, 657, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Gallet, F., & Bouvier, J. 2015, A&A, 577, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Güdel, M. 2004, A&ARv, 12, 71 [CrossRef] [Google Scholar]
  27. Günther, M. N., Zhan, Z., Seager, S., et al. 2020, AJ, 159, 60 [Google Scholar]
  28. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Haywood, R.D., Milbourne, T.W., Saar, S.H., et al. 2020, ApJ, submitted [arXiv:2005.13386] [Google Scholar]
  30. Irwin, J., Berta, Z. K., Burke, C. J., et al. 2011, ApJ, 727, 56 [Google Scholar]
  31. Isobe, T., Feigelson, E. D., Akritas, M. G., & Babu, G. J. 1990, ApJ, 364, 104 [Google Scholar]
  32. Jeffries, R. D., Jackson, R. J., Briggs, K. R., Evans, P. A., & Pye, J. P. 2011, MNRAS, 411, 2099 [Google Scholar]
  33. Johnstone, C. P., Güdel, M., Stökl, A., et al. 2015, ApJ, 815, L12 [Google Scholar]
  34. Kawaler, S. D. 1988, ApJ, 333, 236 [Google Scholar]
  35. Kim, Y.-C., & Demarque, P. 1996, ApJ, 457, 340 [NASA ADS] [CrossRef] [Google Scholar]
  36. Kochukhov, O. 2021, A&ARv, 29, 1 [Google Scholar]
  37. Kochukhov, O., & Lavail, A. 2017, ApJ, 835, L4 [Google Scholar]
  38. Kochukhov, O., & Reiners, A. 2020, ApJ, 902, 43 [Google Scholar]
  39. Kochukhov, O., Hackman, T., Lehtinen, J. J., & Wehrhahn, A. 2020, A&A, 635, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Kraft, R. P. 1970, Stellar Rotation (Berkeley: University of California Press), 385 [Google Scholar]
  41. Kupka, F., & Muthsam, H. J. 2017, Liv. Rev. Comput. Astrophys., 3, 1 [Google Scholar]
  42. Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Landi Degl’Innocenti, E., & Landolfi, M. 2004, Polarization in Spectral Lines, 307 [Google Scholar]
  44. Linsky, J. L. 2017, ARA&A, 55, 159 [Google Scholar]
  45. Lisogorskyi, M., Boro Saikia, S., Jeffers, S. V., et al. 2020, MNRAS, 497, 4009 [NASA ADS] [CrossRef] [Google Scholar]
  46. Magaudda, E., Stelzer, B., Covey, K. R., et al. 2020, A&A, 638, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Matt, S. P., Brun, A. S., Baraffe, I., Bouvier, J., & Chabrier, G. 2015, ApJ, 799, L23 [Google Scholar]
  48. McQuillan, A., Mazeh, T., & Aigrain, S. 2014, ApJS, 211, 24 [Google Scholar]
  49. Mestel, L. 1968, MNRAS, 138, 359 [NASA ADS] [CrossRef] [Google Scholar]
  50. Morales, J. C., Mustill, A. J., Ribas, I., et al. 2019, Science, 365, 1441 [Google Scholar]
  51. Moutou, C., Hébrard, E. M., Morin, J., et al. 2017, MNRAS, 472, 4563 [NASA ADS] [CrossRef] [Google Scholar]
  52. Nagel, E. 2019, PhD Thesis, Universität Hamburg [Google Scholar]
  53. Newton, E. R., Irwin, J., Charbonneau, D., et al. 2016, ApJ, 821, 93 [Google Scholar]
  54. Newton, E. R., Irwin, J., Charbonneau, D., et al. 2017, ApJ, 834, 85 [Google Scholar]
  55. Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [Google Scholar]
  56. Pallavicini, R., Golub, L., Rosner, R., et al. 1981, ApJ, 248, 279 [NASA ADS] [CrossRef] [Google Scholar]
  57. Parker, E. N. 1955, ApJ, 122, 293 [Google Scholar]
  58. Passegger, V. M., Reiners, A., Jeffers, S. V., et al. 2018, A&A, 615, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Perdelwitz, V., Mittag, M., Tal-Or, L., et al. 2021, A&A, 652, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Pevtsov, A. A., Fisher, G. H., Acton, L. W., et al. 2003, ApJ, 598, 1387 [Google Scholar]
  61. Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [Google Scholar]
  62. Pizzolato, N., Maggio, A., Micela, G., Sciortino, S., & Ventura, P. 2003, A&A, 397, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Press, W. H., Flannery, B. P., & Teukolsky, S. A. 1986, Numerical Recipes. The Art of Scientific Computing (Cambridge: Cambridge University Press) [Google Scholar]
  64. Quirrenbach, A., Amado, P. J., Caballero, J. A., et al. 2016, in Ground-based and Airborne Instrumentation for Astronomy VI, Proc. SPIE, 9908, 990812 [Google Scholar]
  65. Quirrenbach, A., CARMENES Consortium, Amado, P. J., et al. 2020, SPIE Conf. Ser., 11447, 114473C [Google Scholar]
  66. Ramsay, G., Doyle, J. G., & Doyle, L. 2020, MNRAS, 497, 2320 [NASA ADS] [CrossRef] [Google Scholar]
  67. Reiners, A. 2012, Liv. Rev. Sol. Phys., 9, 1 [Google Scholar]
  68. Reiners, A., & Mohanty, S. 2012, ApJ, 746, 43 [Google Scholar]
  69. Reiners, A., Basri, G., & Browning, M. 2009a, ApJ, 692, 538 [NASA ADS] [CrossRef] [Google Scholar]
  70. Reiners, A., Basri, G., & Christensen, U. R. 2009b, ApJ, 697, 373 [NASA ADS] [CrossRef] [Google Scholar]
  71. Reiners, A., Shulyak, D., Anglada-Escudé, G., et al. 2013, A&A, 552, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Reiners, A., Schüssler, M., & Passegger, V. M. 2014, ApJ, 794, 144 [Google Scholar]
  73. Reiners, A., Zechmeister, M., Caballero, J. A., et al. 2018, A&A, 612, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Reinhold, T., Reiners, A., & Basri, G. 2013, A&A, 560, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Reinhold, T., Bell, K. J., Kuszlewicz, J., Hekker, S., & Shapiro, A. I. 2019, A&A, 621, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Ribas, I., Tuomi, M., Reiners, A., et al. 2018, Nature, 563, 365 [Google Scholar]
  77. Robinson, R. D., Cram, L. E., & Giampapa, M. S. 1990, ApJS, 74, 891 [NASA ADS] [CrossRef] [Google Scholar]
  78. Rosén, L., Kochukhov, O., & Wade, G. A. 2015, ApJ, 805, 169 [Google Scholar]
  79. Rutten, R. G. M. 1987, A&A, 177, 131 [NASA ADS] [Google Scholar]
  80. Sanz-Forcada, J., Micela, G., Ribas, I., et al. 2011, A&A, 532, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Schöfer, P., Jeffers, S. V., Reiners, A., et al. 2019, A&A, 623, A44 [Google Scholar]
  82. Schrijver, C. J., Dobson, A. K., & Radick, R. R. 1989, ApJ, 341, 1035 [NASA ADS] [CrossRef] [Google Scholar]
  83. Schweitzer, A., Passegger, V. M., Cifuentes, C., et al. 2019, A&A, 625, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  84. Semel, M. 1989, A&A, 225, 456 [NASA ADS] [Google Scholar]
  85. Semel, M., Donati, J. F., & Rees, D. E. 1993, A&A, 278, 231 [Google Scholar]
  86. Shulyak, D., Reiners, A., Wende, S., et al. 2010, A&A, 523, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Shulyak, D., Reiners, A., Engeln, A., et al. 2017, Nat. Astron., 1, 0184 [NASA ADS] [CrossRef] [Google Scholar]
  88. Shulyak, D., Reiners, A., Nagel, E., et al. 2019, A&A, 626, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Skumanich, A. 1972, ApJ, 171, 565 [Google Scholar]
  90. Smette, A., Sana, H., Noll, S., et al. 2015, A&A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Takeda, G., Ford, E. B., Sills, A., et al. 2007, ApJS, 168, 297 [Google Scholar]
  92. Trujillo Bueno, J., Shchukina, N., & Asensio Ramos, A. 2004, Nature, 430, 326 [Google Scholar]
  93. Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [Google Scholar]
  94. Vidotto, A. A. 2021, Liv. Rev. Sol. Phys., 18, 3 [Google Scholar]
  95. Vidotto, A. A., Gregory, S. G., Jardine, M., et al. 2014, MNRAS, 441, 2361 [Google Scholar]
  96. Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
  97. West, A. A., Hawley, S. L., Bochanski, J. J., et al. 2008, AJ, 135, 785 [Google Scholar]
  98. Wright, N. J., Drake, J. J., Mamajek, E. E., & Henry, G. W. 2011, ApJ, 743, 48 [Google Scholar]
  99. Wright, N. J., Newton, E. R., Williams, P. K. G., Drake, J. J., & Yadav, R. K. 2018, MNRAS, 479, 2351 [Google Scholar]
  100. Zechmeister, M., Anglada-Escudé, G., & Reiners, A. 2014, A&A, 561, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  101. Zechmeister, M., Reiners, A., Amado, P. J., et al. 2018, A&A, 609, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  102. Zechmeister, M., Dreizler, S., Ribas, I., et al. 2019, A&A, 627, A49 [NASA ADS] [EDP Sciences] [Google Scholar]

Appendix A: Comparison to Moutou et al. (2017)

Similarly to our literature comparison in Fig. 2, where we considered only analyses using multi-component radiative transfer and multiple lines, Fig. A.1 shows a comparison between the results from Moutou et al. (2017) and our values, extending the comparison carried out by Kochukhov (2021, which is shown in their Fig. 11). Both sets of results show relatively little correlation. Most of the values from Moutou et al. (2017) scatter around Bf= 1–2 kG, which includes stars where we measured significantly lower field strengths. A potentially systematic effect among the slow rotators was already suspected by Moutou et al. (2017).

thumbnail Fig. A.1.

Comparison between average magnetic field measurements reported by Moutou et al. (2017) and our results. Lines, symbols and colors are the same as in Fig. 2.

All Tables

Table 1.

Absorption lines used for our analysis.

In the text
Table 2.

Relations between average magnetic field strength, ⟨B⟩ (in G), and Rossby number, Ro, and between magnetic flux, ΦB (in Mx) for the slow rotators (and the ratio ⟨B⟩/Bkin for the fast rotators), and rotation period, P (in d).

In the text

All Figures

thumbnail Fig. 1.

Top panel: example fit for one of our stars; J05019+011 (M4.0 V). Data are shown as black line with uncertainties. The best fit solution is shown as red line, the best solution with ⟨B⟩=0 G as blue dashed line. The absorbing species are indicated together with the effective Landé-g factor for atomic lines. Bottom panel: cornerplot for posterior MCMC parameter distribution. In this example, six field components f1–f6 were used, and twelve lines were fit for which one scaling parameter (mag1–mag11) per line is shown. Corresponding lines are shown in the upper panel in the same order. The posterior distribution for ⟨B⟩=ΣBifi is included in the plot at the bottom row. Inset panel: relative distribution of filling factors fi for field components Bi. Uncertainties of individual field components are indicated as cyan lines.
In the text
thumbnail Fig. 2.

Comparison of our average field measurements to literature values. Red and blue symbols indicate slow and fast rotators, respectively (see Sect. 4.3), and gray symbols show stars with no information on rotation period. Symbol size and brightness indicate stellar mass. The dashed black line shows identity between our measurements and literature values, and the gray dotted lines mark the region where the discrepancy is within ±25%.
In the text
thumbnail Fig. 3.

Distributions of our sample of stars with average magnetic field measurements. Left: stellar mass. Center: rotational period. Right: Rossby number. Rotational periods are known for 162 of the 314 sample stars, and the remaining 152 stars do not appear in the distributions of P and Ro.
In the text
thumbnail Fig. 4.

Period–mass diagram indicating magnetic field strength in color and symbol size. Data from this work are shown as circles, and other data are shown as squares. Literature values are from Kochukhov et al. (2020) for young Sun-like stars and for seven additional targets from Shulyak et al. (2017). The solar datum from Trujillo Bueno et al. (2004) is annotated. Gray open circles show stars with known rotation periods as reported by Newton et al. (2017). Dashed lines show values of the Rossby number Ro = 0.1 and 1.0, assuming that bolometric luminosity Lbol ∝ M4 and τ ∝ L bol − 0.5 $ \tau \propto L_\text{bol}^{-0.5} $ for dwarf stars.
In the text
thumbnail Fig. 5.

Magnetic field–rotation relation for solar-like and low-mass stars. Symbols for stars rotating slower than Ro = 0.13 are colored red, while those of faster rotators are colored blue. Larger and darker symbols indicate higher stellar mass than smaller and lighter symbols. The gray dashed lines show linear fits separately for the slowly rotating stars (Ro >  0.13; ⟨B⟩=200 G ×Ro−1.25) and the fast rotators (Ro <  0.13; ⟨B⟩=2050 G ×Ro−0.11). Downward open triangles show upper limits for ⟨B⟩.
In the text
thumbnail Fig. 6.

Alternative version of the rotation–magnetic field relation. Top panel: ratio of average field, ⟨B⟩, to kinetic field limit, Bkin, as function of rotation period. Stars rotating faster than the saturation period are colored blue, while other stars are shown in gray. Bottom panel: magnetic flux, ΦB. Stars rotating slower than the saturation limit are colored red, while faster rotators are shown in gray. Symbols and colors are the same as in Fig. 5. See text for details about Bkin.
In the text
thumbnail Fig. 7.

Values for predicted value of average magnetic field calculated from Eqs. (2) and (3) valid for all masses. The dashed gray line indicates identity between ⟨B⟩ and Bpred, and the histogram shows the distribution of ⟨B⟩ around Bpred. We derive from the histogram that our relation estimates the value for ⟨B⟩ within roughly a factor of two uncertainty; this range is indicated with the two dotted lines.
In the text
thumbnail Fig. 8.

Normalized coronal (X-ray, top panel) and chromospheric (Hα, middle panel; Ca H&K, bottom panel) emission as a function of average magnetic field. Symbol size and color are the same as in Fig. 5. The arrow in the bottom panel indicates the field strength at which the normalized Ca H&K emission saturates.
In the text
thumbnail Fig. 9.

Coronal (LX, top panel) and chromospheric (LHα, middle panel; LCa, bottom panel) emission luminosities as a function of magnetic flux, ΦB. Symbol size and color are the same as in Fig. 5. Linear power laws are reasonable approximations for X-ray, Hα, and Ca luminosities describing both rapid and slow rotators. Relations are provided in Eqs. (4)–(6). Ca H&K emission shows a saturation at magnetic flux density ⟨B⟩≈800 G (see Fig. 8). This limit is applied to the magnetic flux values in the bottom panel (Ca H&K), but no limit is applied in the other two panels.
In the text
thumbnail Fig. 10.

Relation between magnetic energy and the ratio between kinetic energy and Rossby number for our sample stars. Such a relation is motivated by the assumption of a balance between Coriolis, buoyancy, and Lorentz forces (MAC balance). Symbols are the same as in Fig. 5.
In the text
thumbnail Fig. A.1.

Comparison between average magnetic field measurements reported by Moutou et al. (2017) and our results. Lines, symbols and colors are the same as in Fig. 2.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.