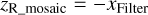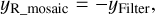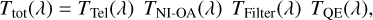| Issue |
A&A
Volume 662, June 2022
|
|
|---|---|---|
| Article Number | A92 | |
| Number of page(s) | 32 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202142897 | |
| Published online | 24 June 2022 | |
Euclid preparation
XVIII. The NISP photometric system
1
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg,
Germany
e-mail: schirmer@mpia.de
2
AIM, CEA, CNRS, Université Paris-Saclay, Université de Paris,
91191
Gif-sur-Yvette,
France
3
Max Planck Institute for Extraterrestrial Physics,
Giessenbachstr. 1,
85748
Garching,
Germany
4
Universitäts-Sternwarte München, Fakultät für Physik, Ludwig-Maximilians-Universität München,
Scheinerstrasse 1,
81679
München,
Germany
5
Carnegie Observatories,
Pasadena,
CA
91101,
USA
6
Infrared Processing and Analysis Center, California Institute of Technology,
Pasadena,
CA
91125,
USA
7
Univ Lyon, Univ Claude Bernard Lyon 1, CNRS/IN2P3, IP2I Lyon, UMR 5822,
69622
Villeurbanne,
France
8
Centro de Astrofísica da Universidade do Porto, Rua das Estrelas,
4150-762
Porto,
Portugal
9
Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas,
4150-762
Porto,
Portugal
10
Institut de Ciències del Cosmos (ICCUB), Universitat de Barcelona (IEEC-UB),
Martí i Franquès 1,
08028
Barcelona,
Spain
11
Institut d’Estudis Espacials de Catalunya (IEEC),
Carrer Gran Capitá 2-4,
08034
Barcelona,
Spain
12
Institute of Space Sciences (ICE, CSIC),
Campus UAB, Carrer de Can Magrans, s/n,
08193
Barcelona,
Spain
13
Department of Astronomy, University of Geneva,
ch. dÉcogia 16,
1290
Versoix,
Switzerland
14
Department of Mathematics and Physics E. De Giorgi, University of Salento,
Via per Arnesano, CP-I93,
73100
Lecce,
Italy
15
INFN, Sezione di Lecce,
Via per Arnesano, CP-193,
73100
Lecce,
Italy
16
Université de Paris, CNRS, Astroparticule et Cosmologie,
75013
Paris,
France
17
Institut d’Astrophysique de Paris,
98bis Boulevard Arago,
75014
Paris,
France
18
Aix-Marseille Univ, CNRS, CNES, LAM,
Marseille,
France
19
Observatoire Astronomique de Strasbourg (ObAS), Université de Strasbourg - CNRS, UMR 7550,
Strasbourg,
France
20
European Space Agency/ESTEC,
Keplerlaan 1,
2201 AZ
Noordwijk,
The Netherlands
21
INAF-Sezione di Lecce, c/o Dipartimento Matematica e Fisica,
Via per Arnesano,
73100
Lecce,
Italy
22
Institute of Cosmology and Gravitation, University of Portsmouth,
Portsmouth
PO1 3FX,
UK
23
Aix-Marseille Univ, CNRS/IN2P3, CPPM,
Marseille,
France
24
INAF-Osservatorio di Astrofisica e Scienza dello Spazio di Bologna,
Via Piero Gobetti 93/3,
40129
Bologna,
Italy
25
INAF-Osservatorio Astronomico di Padova,
Via dell’Osservatorio 5,
35122
Padova,
Italy
26
INAF-Osservatorio Astrofisico di Torino,
Via Osservatorio 20,
10025
Pino Torinese (TO),
Italy
27
Department of Mathematics and Physics, Roma Tre University,
Via della Vasca Navale 84,
00146
Rome,
Italy
28
INFN-Sezione di Roma Tre,
Via della Vasca Navale 84,
00146
Roma,
Italy
29
INAF-Osservatorio Astronomico di Capodimonte,
Via Moiariello 16,
80131
Napoli,
Italy
30
INAF-IASF Milano,
Via Alfonso Corti 12,
20133
Milano,
Italy
31
Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology,
Campus UAB,
08193
Bellaterra (Barcelona),
Spain
32
Port d’Informació Científica,
Campus UAB, C. Albareda s/n,
08193
Bellaterra (Barcelona),
Spain
33
INAF-Osservatorio Astronomico di Roma,
Via Frascati 33,
00078
Monteporzio Catone,
Italy
34
Department of Physics “E. Pancini”, University Federico II,
Via Cinthia 6,
80126
Napoli,
Italy
35
INFN section of Naples,
Via Cinthia 6,
80126
Napoli,
Italy
36
Dipartimento di Fisica e Astronomia “Augusto Righi” – Alma Mater Studiorum Universitá di Bologna,
Viale Berti Pichat 6/2,
40127
Bologna,
Italy
37
INAF-Osservatorio Astrofisico di Arcetri,
Largo E. Fermi 5,
50125
Firenze,
Italy
38
Centre National d’Etudes Spatiales,
Toulouse,
France
39
Institut national de physique nucléaire et de physique des particules,
3 rue Michel-Ange,
75794
Paris Cedex 16,
France
40
Institute for Astronomy, University of Edinburgh, Royal Observatory,
Blackford Hill,
Edinburgh
EH9 3HJ,
UK
41
Jodrell Bank Centre for Astrophysics, Department of Physics and Astronomy, University of Manchester,
Oxford Road,
Manchester
M13 9PL,
UK
42
ESAC/ESA, Camino Bajo del Castillo, s/n, Urb. Villafranca del Castillo,
28692
Villanueva de la Canada,
Madrid,
Spain
43
European Space Agency/ESRIN,
Largo Galileo Galilei 1,
00044
Frascati,
Roma,
Italy
44
Institute of Physics, Laboratory of Astrophysics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Sauverny,
1290
Versoix,
Switzerland
45
Departamento de Física, Faculdade de Ciências, Universidade de Lisboa,
Edifício C8, Campo Grande,
1749-016
Lisboa,
Portugal
46
Instituto de Astrofísica e Ciências do Espaço, Faculdade de Ciên-cias, Universidade de Lisboa,
Campo Grande,
1749-016
Lisboa,
Portugal
47
Université Paris-Saclay, CNRS, Institut d’astrophysique spatiale,
91405
Orsay,
France
48
INFN-Padova,
Via Marzolo 8,
35131
Padova,
Italy
49
INAF-Osservatorio Astronomico di Trieste,
Via G. B. Tiepolo 11,
34131
Trieste,
Italy
50
Istituto Nazionale di Astrofisica (INAF) - Osservatorio di Astrofisica e Scienza dello Spazio (OAS),
Via Gobetti 93/3,
40127
Bologna,
Italy
51
Istituto Nazionale di Fisica Nucleare, Sezione di Bologna,
Via Irnerio 46,
40126
Bologna,
Italy
52
Dipartimento di Fisica “Aldo Pontremoli”, Universitá degli Studi di Milano,
Via Celoria 16,
20133
Milano,
Italy
53
INAF-Osservatorio Astronomico di Brera,
Via Brera 28,
20122
Milano,
Italy
54
INFN-Sezione di Milano,
Via Celoria 16,
20133
Milano,
Italy
55
Institute of Theoretical Astrophysics, University of Oslo,
PO Box 1029 Blindern,
0315
Oslo,
Norway
56
Leiden Observatory, Leiden University,
Niels Bohrweg 2,
2333 CA
Leiden,
The Netherlands
57
Jet Propulsion Laboratory, California Institute of Technology,
4800 Oak Grove Drive,
Pasadena,
CA
91109,
USA
58
Technical University of Denmark,
Elektrovej 327,
2800 Kgs.
Lyngby,
Denmark
59
Mullard Space Science Laboratory, University College London,
Holmbury St Mary, Dorking,
Surrey
RH5 6NT,
UK
60
Université de Genève, Département de Physique Théorique and Centre for Astroparticle Physics,
24 quai Ernest-Ansermet,
1211
Genève 4,
Switzerland
61
Department of Physics and Helsinki Institute of Physics,
Gustaf Hällströmin katu 2,
00014
University of Helsinki,
Finland
62
NOVA optical infrared instrumentation group at ASTRON,
Oude Hoogeveensedijk 4,
7991 PD
Dwingeloo,
The Netherlands
63
Argelander-Institut für Astronomie, Universität Bonn,
Auf dem Hügel 71,
53121
Bonn,
Germany
64
Dipartimento di Fisica e Astronomia “Augusto Righi” – Alma Mater Studiorum Università di Bologna,
via Piero Gobetti 93/2,
40129
Bologna,
Italy
65
INFN-Sezione di Bologna,
Viale Berti Pichat 6/2,
40127
Bologna,
Italy
66
Institute for Computational Cosmology, Department of Physics, Durham University,
South Road,
Durham
DH1 3LE,
UK
67
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange,
Bd de l’Observatoire, CS 34229
06304
Nice Cedex 4,
France
68
CEA Saclay, DFR/IRFU, Service d’Astrophysique,
Bât. 709,
91191
Gif-sur-Yvette,
France
69
Sorbonne Universités, UPMC Univ Paris 6 et CNRS, UMR 7095, Institut d’Astrophysique de Paris,
98bis bd Arago,
75014
Paris,
France
70
Department of Physics and Astronomy, University of Aarhus,
Ny Munkegade 120,
8000
Aarhus C,
Denmark
71
Centre for Astrophysics, University of Waterloo,
Waterloo,
Ontario
N2L 3G1,
Canada
72
Department of Physics and Astronomy, University of Waterloo,
Waterloo,
Ontario
N2L 3G1,
Canada
73
Perimeter Institute for Theoretical Physics,
Waterloo,
Ontario
N2L 2Y5,
Canada
74
Institute of Space Science,
Bucharest
077125,
Romania
75
Max-Planck-Institut für Astrophysik,
Karl-Schwarzschild Str. 1,
85741
Garching,
Germany
76
IFPU, Institute for Fundamental Physics of the Universe,
via Beirut 2,
34151
Trieste,
Italy
77
INFN-Sezione di Roma,
Piazzale Aldo Moro, 2 – c/o Dipartimento di Fisica, Edificio G. Marconi,
00185
Roma,
Italy
78
Dipartimento di Fisica e Astronomia “G. Galilei”, Universitá di Padova,
Via Marzolo 8,
35131
Padova,
Italy
79
Centro de Investigaciones Energéticas, Medioambientales y Tec-nológicas (CIEMAT),
Avenida Complutense 40,
28040
Madrid,
Spain
80
Instituto de Astrofísica e Ciências do Espaço, Faculdade de Ciên-cias, Universidade de Lisboa,
Tapada da Ajuda,
1349-018
Lisboa,
Portugal
81
Universidad Politécnica de Cartagena, Departamento de Electrónica y Tecnología de Computadoras,
30202
Cartagena,
Spain
82
INAF-IASF Bologna,
Via Piero Gobetti 101,
40129
Bologna,
Italy
83
Kapteyn Astronomical Institute, University of Groningen,
PO Box 800,
9700 AV
Groningen,
The Netherlands
84
Dipartimento di Fisica, Universitá degli Studi di Torino,
Via P. Giuria 1,
10125
Torino,
Italy
85
INFN-Sezione di Torino,
Via P. Giuria 1,
10125
Torino,
Italy
86
Space Science Data Center, Italian Space Agency,
via del Politec-nico snc,
00133
Roma,
Italy
87
INFN, Sezione di Trieste,
Via Valerio 2,
34127
Trieste TS,
Italy
88
SISSA, International School for Advanced Studies,
Via Bonomea 265,
34136
Trieste TS,
Italy
89
Departamento de Astrofísica, Universidad de La Laguna,
38206
La Laguna,
Tenerife,
Spain
90
Instituto de Astrofísica de Canarias,
Calle Vía Láctea s/n,
38204
San Cristóbal de La Laguna,
Tenerife,
Spain
91
Institut de Recherche en Astrophysique et Planétologie (IRAP), Université de Toulouse, CNRS, UPS, CNES,
14 Av. Edouard Belin,
31400
Toulouse,
France
92
Dipartimento di Fisica – Sezione di Astronomia, Universitá di Trieste,
Via Tiepolo 11,
34131
Trieste,
Italy
93
Dipartimento di Fisica e Scienze della Terra, Universitá degli Studi di Ferrara,
Via Giuseppe Saragat 1,
44122
Ferrara,
Italy
94
INAF, Istituto di Radioastronomia,
Via Piero Gobetti 101,
40129
Bologna,
Italy
95
INFN-Bologna,
Via Irnerio 46,
40126
Bologna,
Italy
96
Department of Physics and Astronomy, University of California,
Davis,
CA
95616,
USA
97
University of Lyon,
UCB Lyon 1, CNRS/IN2P3, IUF, IP2I,
Lyon,
France
98
INFN-Sezione di Genova,
Via Dodecaneso 33,
16146
Genova,
Italy
99
INAF-Istituto di Astrofisica e Planetologia Spaziali,
via del Fosso del Cavaliere, 100,
00100
Roma,
Italy
100
Department of Physics, Oxford University,
Keble Road,
Oxford
OX1 3RH,
UK
101
School of Physics, HH Wills Physics Laboratory, University of Bristol,
Tyndall Avenue,
Bristol
BS8 1TL,
UK
102
Instituto de Física Teórica UAM-CSIC,
Campus de Cantoblanco,
28049
Madrid,
Spain
103
Institut de Ciencies de 1’Espai (IEEC-CSIC), Campus UAB, Carrer de Can Magrans,
s/n Cerdanyola del Vallés,
08193
Barcelona,
Spain
104
Department of Physics,
PO Box 64,
00014
University of Helsinki,
Finland
105
Department of Physics, Lancaster University,
Lancaster
LA1 4YB,
UK
106
Université PSL, Observatoire de Paris, Sorbonne Université, CNRS, LERMA,
75014
Paris,
France
107
Code 665, NASA Goddard Space Flight Center,
Greenbelt,
MD
20771 and SSAI, Lanham, MD 20770,
USA
108
Helsinki Institute of Physics, Gustaf Hällströmin katu 2, University of Helsinki
Helsinki,
Finland
109
Centre de Calcul de 1’IN2P3,
21 avenue Pierre de Coubertin,
69627
Villeurbanne Cedex,
France
110
Dipartimento di Fisica, Sapienza Università di Roma,
Piazzale Aldo Moro 2,
00185
Roma,
Italy
111
Zentrum für Astronomie, Universität Heidelberg,
Philosophenweg 12,
69120
Heidelberg,
Germany
112
Institut für Theoretische Physik, University of Heidelberg,
Philosophenweg 16,
69120
Heidelberg,
Germany
113
Ruhr University Bochum, Faculty of Physics and Astronomy, Astronomical Institute (AIRUB), German Centre for Cosmological Lensing (GCCL),
44780
Bochum,
Germany
114
Institute for Computational Science, University of Zurich,
Winterthurerstrasse 190,
8057
Zurich,
Switzerland
115
Departamento de Física, FCFM, Universidad de Chile,
Blanco Encalada,
2008
Santiago,
Chile
116
Department of Astrophysical Sciences, Peyton Hall, Princeton University,
Princeton,
NJ
08544,
USA
117
Department of Physics,
PO Box 35 (YFL),
40014
University of Jyväskylä,
Finland
Received:
13
December
2021
Accepted:
31
March
2022
Euclid will be the first space mission to survey most of the extragalactic sky in the 0.95–2.02 µm range, to a 5 σ point-source median depth of 24.4 AB mag. This unique photometric dataset will find wide use beyond Euclid’s core science. In this paper, we present accurate computations of the Euclid YE, JE, and HE passbands used by the Near-Infrared Spectrometer and Photometer (NISP), and the associated photometric system. We pay particular attention to passband variations in the field of view, accounting for, among other factors, spatially variable filter transmission and variations in the angle of incidence on the filter substrate using optical ray tracing. The response curves’ cut-on and cut-off wavelengths – and their variation in the field of view – are determined with ~0.8 nm accuracy, essential for the photometric redshift accuracy required by Euclid. After computing the photometric zero points in the AB mag system, we present linear transformations from and to common ground-based near-infrared photometric systems, for normal stars, red and brown dwarfs, and galaxies separately. A Python tool to compute accurate magnitudes for arbitrary passbands and spectral energy distributions is provided. We discuss various factors, from space weathering to material outgassing, that may slowly alter Euclid’s spectral response. At the absolute flux scale, the Euclid in-flight calibration program connects the NISP photometric system to Hubble Space Telescope spectrophotometric white dwarf standards; at the relative flux scale, the chromatic evolution of the response is tracked at the milli-mag level. In this way, we establish an accurate photometric system that is fully controlled throughout Euclid’s lifetime.
Key words: instrumentation: photometers / space vehicles: instruments
© Euclid Collaboration 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1 Introduction
The Euclid mission will observe 15 000 deg2 of extragalactic sky (Euclid Collaboration 2022) from the Sun–Earth Lagrange point L2. It will employ weak gravitational lensing and galaxy clustering – including baryonic acoustic oscillations and redshift space distortions – as cosmological probes to determine the expansion history and growth rate of cosmic structures over the last 10 billion years. The measurements will be performed in several tomographic redshift bins, covering the time when the acceleration of the Universe became important (Laureijs et al. 2011; Euclid Collaboration 2020). In this way, Euclid addresses the nature and properties of dark energy, dark matter, gravitation, and the Universe’s initial conditions. The results should be decisive for the validity of the A cold dark matter concordance model and general relativity on cosmic scales.
Euclid must determine the near-infrared (NIR) photometry of at least 1 billion galaxies to a relative accuracy of better than 1.5%. This will establish a NIR photometric reference system that will be in wide use for arguably the next few decades. To achieve this with Euclid’s 1.2 m telescope and within the planned mission duration of six years, the Near-Infrared Spectrometer and Photometer (NISP; Prieto et al. 2012; Maciaszek et al. 2016) carries a large focal plane array (FPA) of 16 Teledyne HAWAII-2RG detectors. The NISP wide-field optical system uses filters with a diameter of 130 mm, the largest NIR filters flown in a civilian spacecraft to date.
Euclid’s core cosmology science requires the 0.95–2.02 µm range to be covered in three passbands (YE, JE, and HE; see Fig. 1), with rectangular shape, equal relative spectral width Δλ/λ, and without inter-passband gaps. While overlapping with the common ground-based Y, J, and H passbands, the Euclid passbands are about twice as wide as they are not constrained by atmospheric absorption. The passbands’ flanks – that is, the transition regions from out-of-band blocking to full in-band transmission – must be defined by the filters alone. Together with complementary ground-based photometry, these pass-bands enable the calculation of the mean photometric redshifts (photo-z) of the tomographic redshift bins with an accuracy of 0.002(1 + z) (Laureijs et al. 2011; Euclid Collaboration 2021).
The photo-z accuracy required for Euclid implies that the edges of the NISP passbands must be known to better than l.Onm. In this paper we show that the passbands are blueshifted by up to 6nm when going from the centre of the focal plane towards its corners. This effect is mostly due to variations in the angle of incidence (AOI) on the filter surface, and to a lesser degree to a systematic blueshift of the filter’s transmission towards its edges. Using a careful assessment of the transmission measurements conducted by the filter coating manufacturer, as well as accurate ray tracing methods, we determine the pass-bands with sub-nanometer accuracy anywhere in the field of view; this will also serve all purposes of legacy science.
This paper is organised as follows. In Sect. 2, we introduce the filter substrates, the various transmission measurements, and their limitations. In particular, we focus on intrinsic, local variations in the filter transmission. In Sect. 3, we use optical ray tracing to quantify the AOI on the filter surface, which blueshifts the passband for non-zero AOIs. In Sect. 4, we use these results to compute the effective filter transmission and its blueshift towards the corners of the focal plane. In Sect. 5, we compute the spectral response, that is, the total system transmission, including telescope optics, filters, and detectors. We introduce the NISP photometric system in Sect. 6, together with transformations to common ground-based NIR photometric systems. We summarise the main results and data products in Sect. 7.
 |
Fig. 1 Comparison of the NISP spectral response (shaded) with typical ground-based NIR passbands, in this case VIRCAM at VISTA (Sutherland et al. 2015). Both sets of response curves account for mirrors, filters, and detector QE. The grey line displays the atmospheric transmission for a precipitable water vapour of 1 mm and at zenith, taken from the ESO VISTA instrument description. The ground-based Z and K bands lie outside the NISP wavelength range, whereas Y, J, and H cover approximately half of the corresponding NISP passbands. |
2 Filter characteristics and transmission data
2.1 Terminology
2.1.1 Beam footprint
With ‘beam footprint’ we refer to the intersection of the optical beam on the filter surface. The beam footprint is asymmetric in shape and has a de-centred obstruction. Its geometry is important for the transmission calculations. More details about the footprint can be found in Sect. 3.1.
2.1.2 Passband, transmission, and response
With ‘passband’ we refer to the YE, JE, and HE wavelength intervals transmitted by the NISP filters. These passbands are characterised by their wavelength-dependent ‘local transmission’, t(λ), which varies as a function of position on the filter substrate. The filters ‘effective transmission’, T(λ), is obtained by integrating t(λ) over the beam footprint on the filter substrate (Sect. 4). The ‘response’ – that is the total system throughput – is computed by multiplying T(λ) with the transmission of other optical elements and the detector quantum efficiency (QE; Sect. 5).
The ‘mean peak transmission’ is computed over the wavelength interval where the transmission exceeds 97% of its maximum value.
2.1.3 Wavelength-related parameters: Cut-on and cut-off
At the ‘50% cut-on wavelength’ (hereafter: cut-on), the near-rectangular transmission curve has transitioned halfway from out-of-band blocking to the mean peak transmission. The 50% cut-off is found correspondingly at the long-wavelength end of the passband; specifically, we used cubic spline interpolation to locate the cut-on and cut-off with a precision better than 0.1 nm. We refer to the transition regions as the ‘passband flanks’, which are approximately centred at the cut-on and cut-off. These quantities can be computed for both the transmission and the response curves.
We calculate the ‘passband width’ as the wavelength interval between the cut-on and cut-off. Lastly, we define the passband’s ‘central wavelength’ as
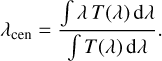 (1)
(1)
Because of the nearly rectangular transmission curve, the central wavelength computed in this way is within less than 0.5 nm of the mid-point between the cut-on and cut-off.
2.2 Filter substrate, dielectric coatings, and blocking
The 130 mm diameter NISP filter substrates were made by Heraeus (Germany) from their proprietary ‘Suprasil 3001’ type fused silica, and shaped by Winlight Optics (France). The filters have a centre thickness of 11–12 mm, depending on the specific filter, with the sky-facing side being slightly convex with a curvature radius of about 10 000 mm.
The filters carry quarterwave stacks of dielectric layers with alternating high and low refractive index, defining the passband through interference. The coatings were performed by Optics Balzers Jena (OBJ; now Materion Balzers Optics). Coating stacks of up to 200 alternating interference layers of SiO2 and Nb2O5 were deposited, to a total stack height of up to 20 µm per filter side, using a plasma-assisted magnetron sputtering process (PARMS). The coatings block photons outside the nominal passbands very efficiently (Sect. 5.2). The coating layers defining a single passband flank are deposited on both sides of the filter, which becomes relevant in Sect. 3.4. A characteristic effect of interference filters is the blueshift of the passband when the filter is tilted in a collimated beam against the surface normal vector. This is because the phase factor of an individual dielectric layer decreases with increasing AOI (Rienstra 1998; Smith 2008).
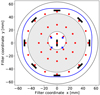 |
Fig. 2 Filter geometry and measurement points. The filters have a diameter of 130 mm (black circle). The blue line shows the baffle, blocking light paths outside without causing vignetting. The nine-point original measurement apertures are shown by the black rectangles (to scale). Our refined 37-point measurements are marked by red dots instead of black rectangles, to avoid cluttering. The grey annulus displays the 90 mm obstructed beam footprint, that is, the part of the filter seen by a source at the centre of the FPA. The obstruction is off-centred due to the telescope’s off-axis design. The response curves made available online are integrated over this grey annulus. The light of a source mapped onto any of the four corners of the FPA intersects different parts of the filter; the centres of the correspondingly shifted footprints are shown by the blue squares. |
2.3 Measurement strategy with the PE950
The transmission of all filters – one flight model and two flight spares for each band – was measured with a Perkin Elmer Lambda 950 (PE950). This is a double beam, double monochromator, intensity ratio recording spectrophotometer working in the 175–3300 nm range. In the NIR regime, the PE950 used by OBJ has a nominal wavelength reproducibility of 0.05 nm, an absolute wavelength accuracy of ≤0.32nm, and is certified periodically by Perkin Elmer Corp.
Measurements were taken at 1 nm wavelength steps at nine positions (Fig. 2). They were repeated for two AOIs, θ = 0° and θ = 7°, the latter approximating the largest AOI realised on the filters. This calibrates the blueshift of the passband for oblique AOIs. Hereafter, we refer to these data as the ‘nine-point data’.
Higher spatial sampling was achieved for the single YE band ‘engineering qualification model’ filter – not used in NISP – using a single-beam photometer with lower spectral resolution, to determine the cut-on at over 200 positions (Fig. 3).
The assumption behind this dual approach was that the coating process would be repeatable, replicating the topography of the cut-on and cut-off ‘surfaces’ for all filters. The sparsely sampled nine-point PE950 data taken over the full wavelength range would be complemented by the high spatial resolution measurements of the cut-on surface. This would be sufficient to create accurate interpolation models, to compute the effective pass-bands by integration over the 90 mm obstructed beam footprints (Fig. 2). We show in Sect. 2.4 that this assumption is invalid.
2.4 Non-repeatability of the coating process and wavelength accuracy of the PE950
The flight model filters passed all acceptance tests and were integrated in NISP. Our analysis of the local transmission data, however, showed that the topography of the cut-on and cut-off surfaces varies considerably, even between flight models and flight spares of the same passband. Consequently, the assumption of a repeatable coating process is invalid, and the high spatial resolution mapping data (Fig. 3) are not suitable to improve the interpolation models. Furthermore, we show in the following that the PE950 operated at least partially outside its wavelength specifications summarised at the beginning of Sect. 2.3.
 |
Fig. 3 Variation in the 50% cut-on wavelength of the YE-band engineering qualification filter. Measurements were done with a single-beam photometer in 213 apertures 2 × 2 mm in size (shown to scale), at AOI θ = 0°. The cut-on varies by 8 nm over the unbaffied area and is a consequence of the coating layers getting systematically thinner by about 0.4% towards the outer edge. When the grey annulus moves across this surface (different object positions in the field of view), the effective transmission changes by 0.5–1.0 nm. Lines are the same as in Fig. 2. |
2.4.1 Inconsistencies in the nine-point transmission data
During the first measurement run of the flight spare filters, not all θ = 7° data were taken for the YE and HE-band models. A complete set of the nine-point data including the θ = 0° setting was repeated at a later time. Having the same positions at θ = 0° measured twice, we could check the wavelength reproducibility and accuracy of the PE950 (Sect. 2.3). To this end, we computed the normalised wavelength difference 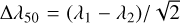 for each measurement position, where λ1 and λ2 are the cut-ons in the two measurement runs; the same was done for the cut-off. Assuming normally distributed errors, the RMS of Δλ50 is then an estimator of the PE950’s wavelength accuracy.
for each measurement position, where λ1 and λ2 are the cut-ons in the two measurement runs; the same was done for the cut-off. Assuming normally distributed errors, the RMS of Δλ50 is then an estimator of the PE950’s wavelength accuracy.
We did not detect a systematic wavelength offset between the runs. However, the long-term RMS, 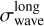 , of the Δλ50 data from the nine-point measurements exceeds the PE950’s specification; we refer to this RMS as ‘long-term’ because many months have passed between the measurements (see Sect. 2.4.2 for the short-term RMS). In particular,
, of the Δλ50 data from the nine-point measurements exceeds the PE950’s specification; we refer to this RMS as ‘long-term’ because many months have passed between the measurements (see Sect. 2.4.2 for the short-term RMS). In particular,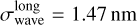 (left panel of Fig. 4) is higher than the specification of ≤0.32nm. This implies that both the PE950’s internal wavelength reproducibility of 0.05 nm as well as the wavelength accuracy were not met for the flight spare runs. Ageing effects are ruled out since the filter coatings are very durable. We do not have repeated measurements for the flight model filters, and hence assume that the same uncertainties apply to them.
(left panel of Fig. 4) is higher than the specification of ≤0.32nm. This implies that both the PE950’s internal wavelength reproducibility of 0.05 nm as well as the wavelength accuracy were not met for the flight spare runs. Ageing effects are ruled out since the filter coatings are very durable. We do not have repeated measurements for the flight model filters, and hence assume that the same uncertainties apply to them.
 |
Fig. 4 Wavelength accuracy of the PE950 spectrophotometer. Left panel: joint long-term reproducibility of the cut-on and cut-off between the nine-point measurement runs on the same substrates. The RMS is |
2.4.2 37-point transmission data on flight spare filters
To better understand these inconsistencies, we designed a refined test protocol for the second set of flight spare filters that were still accessible at that time. Transmission was measured at 37 points (red dots in Fig. 2), including the central position of the original nine-point pattern. The remaining positions were placed in three rings with diameters of 14, 28, and 48 mm, respectively. Five of the positions were measured repeatedly, to check for hysteresis, wavelength reproducibility, and systematic drifts.
We computed the short-term RMS of the Δλ50 data, 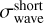 = 0.35 nm, from the repeatedly visited points (right panel in Fig. 4). This is within the PE950’s nominal wavelength reproducibility of 0.05 nm, for all three flight spares. Meaningful systematic effects were not found.
= 0.35 nm, from the repeatedly visited points (right panel in Fig. 4). This is within the PE950’s nominal wavelength reproducibility of 0.05 nm, for all three flight spares. Meaningful systematic effects were not found.
Comparing the passband flanks of the common central position between the 37-point and the nine-point measurements, we find 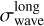 = 0.52 nm (0.16 nm) for the first (second) run of nine-point data. This is above (below) the PE950 specification of ≤0.32nm for wavelength accuracy.
= 0.52 nm (0.16 nm) for the first (second) run of nine-point data. This is above (below) the PE950 specification of ≤0.32nm for wavelength accuracy.
2.4.3 Conclusion about wavelength accuracy
The origin of these inconsistencies, in particular between the original nine-point measurements (Sect. 2.4.1), remains unclear. It could be due to temporal instabilities and uncalibrated long-term drifts of the PE950, or tolerances in the preparation and execution of the measurements. While the 37-point data show that the PE950 can deliver data with high internal consistency, it is not clear whether this applies to the flight model data, for which only a single measurement epoch is available. Therefore, we assume that the nine-point flight model data have the same uncertainties as the nine-point flight spare data.
The spatial interpolation of the local transmission is based on nine data points; in these runs, the wavelength has a statistical uncertainty of 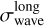 = 1.47 nm (Sect. 2.4.1). Integration over the interpolating function (Sect. 4) has an averaging effect on these uncertainties, plausibly by a factor of
= 1.47 nm (Sect. 2.4.1). Integration over the interpolating function (Sect. 4) has an averaging effect on these uncertainties, plausibly by a factor of 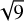 . Here, we were more conservative and set σ50 = 0.8 nm for the cut-on and cut-off wavelengths of the integrated transmission in Sect. 4. The passband’s central wavelength, when approximated as the midpoint between the cut-on and cut-off, has an uncertainty of
. Here, we were more conservative and set σ50 = 0.8 nm for the cut-on and cut-off wavelengths of the integrated transmission in Sect. 4. The passband’s central wavelength, when approximated as the midpoint between the cut-on and cut-off, has an uncertainty of 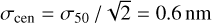 .
.
 |
Fig. 5 Ray tracing of the NI-OA. Shown are the obstructed beams for three sources located at the centre of the focal plane and at two opposing edges. The NI-OA consists of four lenses; the filter also acts as a lens, albeit only weakly. The dichroic element is located in the pupil plane of the telescope and is not part of NISP. We notice how the beam paths cover different parts of the filter surface, because – contrary to the dichroic – the filter is located outside the pupil plane. This leads to 10–23% of the passband variations in the focal plane due to local variations in the filter transmission. The AOI on the filter changes noticeably for the three sources; this is the dominant cause for passband variations. |
3 Root causes of the NISP passband variations
Passband variations, that is, changes in the cut-on and cut-off as a function of position in the focal plane, must be accurately known for Euclid to meet its requirements on photo-z accuracy. Two factors contribute to passband variations. The first is increasingly bluer transmission towards the filter edge, in combination with a moving beam footprint across the filter surface (up to 23% of the total blueshift for NISP). The second is variations in the AOI on the filter surface, in combination with the filter coating’s effective refractive index, neff (up to 90% of the total blueshift).
Euclid’s telescope is based on a Korsch design (Korsch 1977) in an off-axis configuration (Laureijs et al. 2011). This leads to a number of effects we need to account for when quantifying the two factors introduced above: (i) a de-centred central obstruction of the beam by the secondary mirror (Fig. 2); (ii) a tilted FPA, and slightly tilted NISP optics; (iii) an elliptical beam footprint shape; and (iv) AOI asymmetries on the planar and curved filter surfaces. The results of our analysis in this section are used in Sect. 4, where we compute the effective filter transmission and its variation across the field of view.
3.1 Beam footprint geometry on the filter surface
In Fig. 5, we display the optical paths for three different point sources at two edges and in the centre of the FPA. The corresponding footprints on the filter surface have an annular shape with outer and inner diameters of about 91.0mm and 27.8 mm, respectively (Fig. 6). The off-axis configuration leads to a slight ellipticity and off-centred central obstruction. A single footprint covers ~56% of the filter area, and its location on the filter surface depends on the source position in the field of view (Figs. 5, 6); the footprint can move away from the filter centre by up to 11.9 mm. In combination with the spatially variable filter transmission (Fig. 3), this causes a dependence of the effective passband on the image field.
Depending on the position on the filter, the major axis of the footprint changes between 89.8 mm and 92.9 mm. The footprint shapes are nearly circular, with differences from 0.0 to 1.3 mm between the minor and major axes. The circular obstruction has a diameter of 27.8 mm for the central footprint, and scales correspondingly for footprints at the corners. The obstruction is spatially offset in the beam by 3.7mm (Figs. 2, 3, 6, and 7).
 |
Fig. 6 Mean AOI, |
3.2 Transmission blueshift due to oblique AOI
Like all optical interference filters, the transmitted passband is blueshifted with increasing AOI, θ, due to the changing phase-difference of reflected and incident rays. The blueshift also depends on the coating’s effective refractive index, neff(λ) (e.g. Amra et al. 2021). In vacuum, and with the small angle approximation applicable here, a particular passband feature seen at wavelength λ0 for θ = 0° is blueshifted to
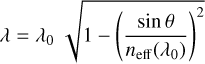 (2)
(2)
(for details, see Smith 2008; Löfdahl et al. 2011). The maximum AOI realized on the NISP filters is θ = 7.5°; polarization splitting due to polarization-dependent Fresnel reflections is ignored, as it becomes important for larger angles, only.
Thus, to compute the passband blueshift for a given footprint, we had to determine two quantities: neff from measurements and/or the filter coating design (Sect. 3.3), and the spatial dependence of θ(x, y), with x and y specifying the location where the individual rays intersect the filter’s surface (Sect. 3.4).
 |
Fig. 7 Same as Fig. 6, now showing |
Effective refractive index.
3.3 Effective refractive index, neff
While neff is known from the coating design, imperfections in the coating process cause thickness variations in the layers, and thus modulate neff. In Table 1 we list the expected and measured values of neff, obtained using Eq. (2) by comparing the cut-on and cut-off determined from the OBJ measurements at θ = 0° and θ = 7° (Sect. 2.3).
The nine-point measurements of neff for the flight model filters show a RMS of up to 6%. This can be caused by local thickness variations in the layers, and by the inherent wavelength uncertainty of the PE950 data. The 37-point measurements – having higher internal consistency – show subtler variations in neff across the flight spare substrates, de-correlating for spatial distances above 20–30 mm. Since we integrated the effective passband over a ~90mm beam footprint, the variations in neff were smoothed accordingly. We thus adopted the mean of all design values listed in Table 1, 〈neff〉 = 1.769, similar to the mean value (1.763) of the measured data. The error made by this simplification – that is, constant neff – is negligible (see Sect. 4.4).
3.4 AOI from Zemax optical ray tracing
As stated above, the sky-facing side of the NISP filters is slightly convex, with a curvature radius of 10 000 mm, and their rear side is flat; thus, the angles of incidence and exitance are different. As mentioned in Sect. 2.2, a single passband flank is defined by coatings on both surfaces, with more details undisclosed to us. Since the angles of incidence and exitance of a ray differ at most by [−0.32°; +0.25°], we simply used their mean value, 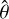 . The error made by this simplification was estimated by repeating the computation for both angles or filter surfaces (see Sect. 4).
. The error made by this simplification was estimated by repeating the computation for both angles or filter surfaces (see Sect. 4).
Using Zemax ray tracing, we determined the distribution of θ(x, y) on both filter surfaces for a grid of 9 × 9 positions in the field of view. For each position, the pupil plane of the optical system was sampled with a regular grid of 100 × 100 rays, some of which were vignetted1.
The resulting values of 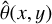 are shown in Fig. 6, where every second footprint from the 9 × 9 grid is omitted for clarity. In the computation of the effective transmission (Sect. 4), we used a 2D spline interpolation for
are shown in Fig. 6, where every second footprint from the 9 × 9 grid is omitted for clarity. In the computation of the effective transmission (Sect. 4), we used a 2D spline interpolation for 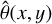 for each node in the 9 × 9 grid. Averaging
for each node in the 9 × 9 grid. Averaging 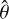 for each footprint, we find
for each footprint, we find 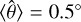 for the central position; this fairly large value is caused by a deliberate small tilt of the NISP optics to optimise the image quality in the off-axis system. For the footprints in the bottom and top corners, we find
for the central position; this fairly large value is caused by a deliberate small tilt of the NISP optics to optimise the image quality in the off-axis system. For the footprints in the bottom and top corners, we find 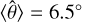 and 7.1°, respectively. Within a footprint,
and 7.1°, respectively. Within a footprint, 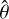 varies by about ± 0.3°; this is displayed in Fig. 7, where we plot
varies by about ± 0.3°; this is displayed in Fig. 7, where we plot 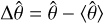 .
.
The conclusion of this section is that neff and 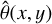 are well understood and accurately known for the computation of the effective filter transmission, T(λ), in Sect. 4.
are well understood and accurately known for the computation of the effective filter transmission, T(λ), in Sect. 4.
4 Computing the filters’ effective transmission
4.1 Numerical integration with blueshift
4.1.1 Computational principle
Let t(λ, x, y) be the local filter transmission for θ(x, y) = 0°, where x and y are the Cartesian filter coordinates defined in Fig. 2. For an oblique angle, θ, the blueshifted transmission, t′, is found by looking up the original transmission, t, at the correspondingly redshifted wavelength, λ′,
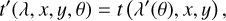 (3)
(3)
The scaling factor is just the inverse of the one in Eq. (2), used to compute the blueshift.
In general, we have t′(λ) + t(λ′), as the transmission at an oblique angle decreases with respect to normal incidence. However, for small values of θ, and for angle-tuned coating designs, this effect can be neglected: For NISP we measured a reduction in mean peak transmission of 0.03%, 0.17% and 0.04% for YE, JE, and HE, respectively, for θ = 7° with respect to θ = 0°, and thus Eq. (3) remains valid.
Now we consider a source image anywhere in the focal plane. The corresponding chief ray intersects the filter substrate at a point P. The effective transmission, T(λ), for the source is given by integrating the local blueshifted transmission, t(λ′), in the filter plane over the annular footprint A centred on P,
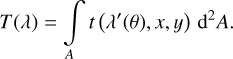 (5)
(5)
To numerically compute this integral, we constructed a spline interpolating function2 to the nine-point data that sample t(λ′(θ), x, y). The interpolation was quadratic in the two spatial dimensions and cubic in the spectral dimension. And we replaced θ(x, y) by a spline interpolation of the mean AOI,  (see Sect. 3.4).
(see Sect. 3.4).
4.1.2 Simplifications to the beam footprint geometry
To facilitate the numeric integration in Eq. (5), we simplified the footprint geometry. The outer edge of the footprint is nearly circular, with the largest ellipticity of 91.8 × 93.0 mm realised for a source in one of the corners of the FPA. We approximated the edge with a circle, taking the mean of the minor and major axes as the radius. The circle’s diameter varies between 89.8 mm and 92.4 mm, depending on position on the filter substrate.
Likewise, the de-centred obstruction was considered circular. We approximated it with a fixed diameter of 27.8 mm and a fixed spatial offset of y = +3.7 mm in the filter coordinate system, independent of footprint location. Together, these simplifications altered the cut-on and cut-off wavelengths by less than 0.01 nm, and are ignored in our error budget.
4.1.3 Simplifications in the transmission integration
In Sect. 3.4, we show that, due to the unknown coating design, we must use the mean AOI, 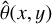 , from the curved and planar filter sides. To estimate the error made by this approximation, we re-computed Eq. (5) for the central footprint position twice, once using θ(x, y) for the curved side and once for the planar side. The resulting wavelength shifts of the passbands’ cut-on and cut-off are within [−0.014; 0.017] nm with respect to the computation for
, from the curved and planar filter sides. To estimate the error made by this approximation, we re-computed Eq. (5) for the central footprint position twice, once using θ(x, y) for the curved side and once for the planar side. The resulting wavelength shifts of the passbands’ cut-on and cut-off are within [−0.014; 0.017] nm with respect to the computation for 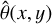 . Hence, this simplification is valid and the error small enough to be ignored in the error budget.
. Hence, this simplification is valid and the error small enough to be ignored in the error budget.
4.2 Passband variations
4.2.1 Mathematical model for the total passband shift
To determine the variation in the cut-on and cut-off across the focal plane, we evaluated T (λ) for each node of the 9 × 9 grid introduced in Sect. 3.4. The results are displayed in Fig. 8, for cold conditions and in vacuum (Sect. 4.3), in the physical R_mosaic (z, y) coordinate system in which the positions of the NISP detectors are accurately known. The transformation of the filter coordinate system used in Fig. 6 to the R_mosaic system is
meaning the panels in Fig. 8 are rotated by 180° with respect to the panels in Fig. 6.
For accurate and unbiased photo-z measurements, we need a mathematical prescription that provides the cut-on and cut-off wavelengths for any position in the focal plane. To this end, we fit 2D third degree polynomials of the following form to the cut-on and cut-off surfaces in the focal plane for each filter,
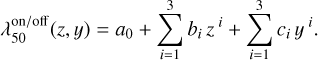 (8)
(8)
These fits have residuals with an RMS of σ = 0.011 nm, with a maximum value of 0.06 nm (Fig. 9). The coefficients are listed in Table A.1. The inclusion of crossterms did not improve the quality of thefits.
The maximum blueshift, ΔλVAR, seen by the FPA increases about linearly with wavelength, from 2.7 nm for the YE-band cut-on, to 5.8 nm for the HE-band cut-off. These values are also given in Table 3 and shown in Fig. 10.
By setting θ = 0 for all rays in the computation, we switched off the dependence on the AOI and computed the contribution of the intrinsic filter variations only. We find that they contribute between 10–23% to the total focal plane variations. The published NISP response curves (Sect. 7.2) were computed for an object at the centre of the FPA, near the location where the cut-on and cut-off have their longest wavelengths (Fig. 8).
4.2.2 Passband variations for the field corners due to uncertainties in neff
In Sect. 3.3, we reviewed the uncertainties and variations in neff. They enter T(λ) through Eq. (4), increasing or decreasing the blueshift in the field corners with respect to the field centre. For a conservative estimate, we re-computed T(λ) twice, increasing and decreasing neff by 5%, and find the following:
At the centre of the FPA, where the typical AOI is θ = 0.5°, the passbands always shift by 0.002 nm or less. The published response curves (Sect. 7.2) are computed for this footprint. At the corners of the FPA, with typical values of θ = 7°, however, significant shifts occur. If neff is larger (smaller) by 5%, the blueshift Δλneff for YE, JE, and HE increases (decreases) by 0.2, 0.3 and 0.4 nm, respectively. In relative terms, the difference of the cut-on wavelength between the centre of the FPA and its corners increases (decreases) by 7–10%; same for the cut-off.
4.2.3 Passband variations and effect on source photometry
Without correcting for passband variations, the measured flux of a source depends on its position in the field of view, for two reasons. First, the blueshifted passband selects a different part of the source’s spectral energy distribution (SED), increasing or decreasing the measured flux. Second, the cut-off experiences a larger blueshift than the cut-on when moving from the centre of the FPA to a corner. This ‘passband compression’ reduces the widths of the YE-, JE, and HE-bands by 0.7, 0.8 and 1.2 nm, respectively, resulting in a SED-dependent flux reduction.
To estimate the joint amplitude of both effects, we used the catalogues from the Euclid SC8 (‘science challenge 8’), simulating 100 deg2 of sky with realistic SEDs as they will be seen by the Euclid Wide Survey (Euclid Collaboration 2022). We randomly selected 1.8 million stars and 1.1 million redshifted galaxies from the SC8 catalogues (see Sect. 6.2.1 for details) and computed the difference in source photometry for a position at the centre of the FPA and another one in the most blueshifted corner. The results are shown in Fig. A.1 for galaxies and Fig. A.2 for stars. The effect on individual source photometry is of the order of 1–5 mmag. The differential photometry for galaxies shows a very low but also broad tail up to 0.6 mag. This tail comprises galaxies with bright emission lines that shift in – or out – of a passband as the source moves across the field of view. In principle, if such emission line galaxies were identified in the survey data, they could be used to improve the knowledge error of the passbands’ cut-on and cut-off as tabulated in Table 3.
Due to the slightly reduced transmission at oblique AOI, generic flux losses of up to 0.2% can occur in the corners of the focal plane (Sect. 4.1.1). This effect is systematic and automatically removed by the illumination correction procedure in the data processing pipeline.
 |
Fig. 8 Cut-on and cut-off wavelengths (in nm) as a function of FPA position, cold and in vacuum. The blueshift towards the field corners is evident. The black lines and coloured background show the polynomial fits introduced in Sect. 4.2; the fit parameters are listed in Table A.1, and the joint residuals are shown in Fig. 9. The fits are based on the 9×9 object positions (small dots) for which we inferred the AOI distribution on the filter surface using Zemax ray tracing. The shaded squares display the 16 NISP detectors, numbered in yellow from 11 to 44. The position of the number indicates the location of the (111) pixel of a detector. The published response curves (Sect. 7.2) were computed for the central dot marked with the white square. R_mosaic (z, y) is a physical coordinate system in the focal plane, to describe – among other factors – the detector positions. |
4.3 Temperature and vacuum wavelength shifts
The transmission measured at ambient temperature3, τ, and pressure will change in vacuum and at near cryogenic temperatures. The temperature dependence is caused by the thermal contraction of the dielectric coating layers, as well as a change in neff (e.g. Tan & Arndt 2000, for SiO2).
To quantify these effects, YE-, JE-, and HE-band coating samples were cryocycled in a vacuum chamber at Martin-Luther-University Halle-Wittenberg (Germany), while simultaneously recording their transmission. We determined the cut-on and cutoff in the same manner as for the actual filters. As expected, the passbands redshift slightly when going into vacuum, and experience a larger blueshift when cold; the combined effect on the passband flanks is shown in Fig. 10.
4.3.1 Temperature dependence
The temperature-related blueshift is normally computed with the Sellmeier equation (see Fang et al. 2019, for a review). Here, however, since the transmission was measured at two temperatures only, we linearly fit the cool-down blueshift as
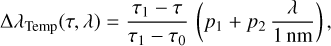 (9)
(9)
with τ1 = 295 K and τ0 = 120 K given by the setup, and p1 and p2 are the filter-dependent fit coefficients in Table 2.
The expected in-flight filter temperature is τ = 132 K. The central wavelengths of the YE-, JE-, and HE-band filters shift by −0.60 nm, −2.04 nm, and −1.13 nm, respectively. We corrected all wavelengths for their individual temperature dependence, ΔλTemp(τ,λ).
We note that τ = 132K is the temperature we used for the passbands’ characteristics reported in Table 3. It is unlikely that the passbands need to be corrected for the actual in-flight temperature that will only be known after launch; the expected temperature bracket for the NISP optics is 130–135 K. For reference, a change by +1K in filter temperature would cause a redshift by 0.004–0.012 nm, only. Furthermore, the error we made by using the linear fit in Eq. (9) instead of the nonlinear Sellmeier equation is less than 0.1 nm, and therefore neglected.
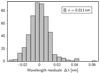 |
Fig. 9 Joint wavelength residuals of the polynomial fits to the passband variations, for all filters (their cut-on and cut-off; see also Fig. 8). The RMS is σ = 0.011 nm; 92% of the residuals are smaller than 0.02 nm. |
4.3.2 Vacuum dependence
In analogy to the temperature dependence, we computed a linear fit of the passband redshift when going into vacuum,
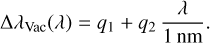 (10)
(10)
The coefficients are collected in Table 2. The corrections are minor, amounting to 0.21 nm, 0.023 nm, and 0.053 nm at the central wavelengths of the YE-, JE-, and HE-band filters, respectively. As for the temperature dependence, we corrected all wavelengths for their individual vacuum dependence.
4.4 Summary of the relevant passband uncertainties
In Sect. 3.3, we discussed the uncertainties of neff and used a constant 〈neff〉 = 1.769 for all filters. In Sect. 4.2.2, we estimated corresponding errors of the cut-on and cut-off of 0.2, 0.3, and 0.4 nm for filters YE, JE, and HE, respectively, for the corners of the FPA. This error is negligible at the centre of the FPA.
In Sect. 2.4.3, we placed a conservative measurement accuracy for the cut-on and cut-off wavelengths of 0.8 nm, applicable to all filters. Adding in quadrature the errors for neff as given in the previous paragraph, we obtained increased total uncertainties in the FPA corners of σ50 = 0.8, 0.9 and 0.9 nm, respectively, for the three bands. The estimated uncertainty for the passbands’ central wavelengths is σcen = 0.6 nm for any point in the field of view, for all bands. The uncertainties are listed in Table 3.
All other uncertainties, and errors made due to simplifications, are below 0.1 nm and neglected.
4.5 Effect on photometric redshifts
Since photo-z estimates are one of NISP’s principal purposes, we briefly describe the effect of the derived passband knowledge uncertainties on the photo-z estimates. Obviously, the effect is highly dependent on the sources’ redshifted SEDs, and on the uncertainties of complementary optical passbands used. It is beyond this paper to quantify this accurately. Nonetheless, a simple example illustrates the overall suitability of the computed NISP passbands for photo-z purposes:
We consider the 0.95−1.21 µm range of the YE-band (Table 3). The characteristic 4000 Å break falls within the YE-band for redshifts z ∈ [1.375,2.025]. If the 4000 Å break was the sole spectral feature determining the photo-z of a source, then the uncertainty in the central wavelength, σcen = 0.6 nm, would introduce a redshift bias of Δz = σcen/400nm = 0.0015, compared to the requirement of 0.002(1 + z) = 0.0048 for z = 1.375. Hence, in this example, the knowledge error of the pass-band flanks is sufficient. In practice, there are many sources of bias, which need to be quantified with realistic simulations for a wide range of redshifted SEDs, folding in complementary ground-based observations and their uncertainties (e.g. Euclid Collaboration 2021). We remark that the bias Δz can be calibrated, as well as the effects of the passband variations across the focal plane.
5 Total system response
Euclid observes simultaneously with NISP and its Visible Instrument (VIS; Cropper et al. 2012) using a dichroic beam splitter. To prepare well-defined input passbands for both instruments, Euclid relies on a finely orchestrated balance of mirror coatings, the dichroic, filters, the NISP optical assembly (NI-OA; see Sect. 5.1.2), and detector QE, as illustrated in Fig. 11, and more quantitatively in Fig. 12. While the NISP filters alone define the cut-on and cut-off wavelengths, it is only in conjunction with the other elements that excellent out-of-band blocking is achieved. The total NISP transmission is therefore given by
where TTel(λ) is the telescope contribution, accounting for the mirrors and the dichroic. Dependencies of the individual factors T on the AOI are negligible. We explain Euclid’s chromatic selection function (Figs. 11 and 12) in the following.
 |
Fig. 10 NISP passband flanks and variations. The solid red lines show the local transmission at the filter centre (Fig. 2). The solid blue lines show the combined vacuum and temperature shifts on the red curve. The thick black lines show the effective transmission after integrating over the central beam footprint (centred on the white squares in Fig. 8), cold and in vacuum. The coloured areas enclosed by dashed lines show the range of blueshifts seen by the FPA: the leftmost dashed line corresponds to the bluest FPA corners and the rightmost to the reddest passband near – but not necessarily coincident with – the FPA centre. The grey rectangles show the maximum spread, |
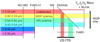 |
Fig. 11 Chromatic selection function of the Euclid optical elements. The VIS detectors have zero QE for photons with λ > 2.15 µm. The exact behaviour of the dichroic above 2.2 µm is unknown: longer wavelengths could enter NISP and would be blocked by the filters (see Sect. 5.1 and Fig. 12 for more details). |
5.1 Euclid’s chromatic selection function
5.1.1 Telescope transmission
The telescope optics common to VIS and NISP consists of – in this order – the primary mirror Ml, the secondary mirror M2, folding mirrors FoMl and FoM2, the tertiary mirror M3, and the dichroic element. Ml, M2 and M3 are coated with protective silver and provide a very broad wavelength coverage longwards of 0.34 µm. After the dichroic and in the VIS optical path only, folding mirror FoM3 is also coated with protected silver.
At wavelengths of 0.5 µm and below, VIS and NISP have considerable QE, which is undesirable for both instruments: At these wavelengths, galaxy images are increasingly dominated by intrinsic substructures, adding noise to the VIS weak lensing shape measurement; and for NISP, unflltered UV/blue photons would contaminate the NIR photometry. Therefore, folding mirrors FoM1 and FoM2 have dielectric coatings including three layers of gold, each. By means of destructive interference and absorption, these layers block light shortwards of 0.42 µm, reach maximum reflectivity at 0.50 µm, and maintain it beyond 2 µm.
The dichroic has a complex wavelength selection function (Figs. 11 and 12). It cuts out a wavelength range from 0.54–0.93 µm and reflects it to VIS. Photons within 0.93–2.15 µm are transmitted to NISP. Photons below 0.54µm are also sent to NISP, and are blocked by the filters and – partially – by the NI-OA (Sect. 5.2). Photons above 2.15 µm are mostly reflected to VIS again. This does not matter for VIS, as the CCDs do not detect photons longwards of ~11 µm. The dichroic’s reflectance was not determined nor specified beyond 2.2 µm. The NISP filters block out to 2.9 µm (Sect. 5.2), and the detectors have a QE cut-off at 2.3 µm (Sect. 5.1.3).
The combined transmission, TTel(λ), of this arrangement entering the NISP instrument is shown as the black line in Fig. 12. More details can be found in Venancio et al. (2020).
Summary of the Euclid NISP AB mag photometric system.
5.1.2 NISP optical assembly (NI-OA) transmission
NISP carries four lenses, collectively known as the NI-OA (Bodendorf et al. 2019; Grupp et al. 2019); their transmission was not measured. However, we have the transmission from witness samples that were present in the coating chamber, used by industry to demonstrate that a minimum transmission requirement has been exceeded. The joint transmission of these witness samples is shown as the pink curve in Fig. 12.
This transmission estimate varies between 0.93–0.96 over the 0.95–2.02 µm range. It is unclear whether these variations are also replicated in the flight model optics that may deviate by several percent. Steep gradients are not expected across this wavelength range, since only a few coating layers were used. The true transmission of NI-OA will be constrained further in-flight, once observations of white dwarf (WD) spectrophotometric standard stars are available (Sect. 6.3.2).
The NI-OA blocks photons below 0.58 µm, apart from a narrow transmission window between 0.46–0.52 µm that overlaps with wavelengths transmitted by the dichroic. The residual optical transmission into NISP is suppressed by the filters (Sect. 5.2).
5.1.3 NISP detector quantum efficiency
The NISP detectors have a sharp QE cut-off at 2.3 µm, controlled by the Cd concentration in the HgCdTe alloy (Rogalski 2005). This provides further rejection of long wavelengths, in addition to the dichroic sending most photons above 2.15 µm to VIS.
The QE was measured for each pixel in steps of 50 nm from 0.60 to 2.55 µm (Waczynski et al. 2016). The relative accuracy – that is, the knowledge error of the QE curve shape – across this wavelength range is 1%. The absolute scaling is uncertain to 5%, since the pure QE is difficult to disentangle from the detector gain (Secroun et al. 2018, and A. Waczynski, priv. comm.). For the computation of the out-of-band blocking, only, we linearly extrapolated the QE to zero from 0.60 µm to 0.30 µm.
The mean QE curves of the detectors are very uniform across the 0.95–2.2 µm range (Bai et al. 2018), and within just a few percent of each other. Computed for individual detectors at monochromatic wavelengths, the pixel-to-pixel RMS is 1.2–2.4% globally, and 1.0% locally. Their impact on the passband flanks is entirely negligible.
For this paper, we use the mean QE (blue line in Fig. 12) computed from all pixels of 14 out of the 16 detectors. We excluded one detector because of its slightly lower QE below 1.0 µm, and another because of its increasing QE towards 2.0 µm. The original QE values between 1.65–1.75 µm are excluded from all detectors due to a measurement artefact, and replaced by a local, linear interpolation.
5.2 NISP out-of-band blocking and flux contamination
5.2.1 Out-of-band blocking
By requirement, the NISP filters must reject light to better than 10−3 long- and shortwards of their passband; the requirement over the VIS range from 0.54–0.93 µm is relaxed to 10−2, since these photons are directed to VIS already. The blocking of the flight model filters was measured locally at the centre of the substrates, in steps of 2nm from 0.3 to 2.9 µm.
With a transmission of 10−5 to 10−7 below 0.55 µm, the filters eliminate the residual transmission from the dichroic and the NI-OA. Between 0.55 µm and the filters’ cut-on, and longwards of the filters’ cut-off, the blocking is better than 10−3−10−4.
The NISP total out-of-band blocking, including telescope, NI-OA, filters, and QE, is shown in Fig. 13. Below 0.9 µm, the blocking is 10−7 or better. Above 2.2 µm, the blocking is 10−5, improving to 10−7 at 2.4 µm, although there are uncertainties from extrapolating the telescope transmission to longer wavelengths. Between 0.9 and 2.2 µm, the blocking is at least 10−4.
 |
Fig. 12 Transmission of elements in the NISP optical path. The telescope component (black line) contains all mirrors and the dichroic; the latter redirects the 0.54–0.93 µm range to VIS and cuts off at 2.15 µm. The pink line shows the transmission of the NI-OA. The blue line shows the interpolated mean detector QE, originally measured at 50 nm intervals. The thin lines show the effective filter transmission integrated over the beam footprint, and the shaded areas the total response (accounting for the filter, telescope, NI-OA, and QE). The residual optical transmission from the dichroic and the NI-OA between 0.45 and 0.54 µm is fully suppressed by the filters’ out-of-band blocking (see Fig. 13). These curves do not include effects from particulate contamination. |
 |
Fig. 13 Joint NISP out-of-band blocking, including flight model filters, telescope, NI-OA, and QE. The curves are the same as the shaded curves in Fig. 12, with the difference that the blocking was measured at the filter centre only, in wavelength steps of 2 nm. We smoothed the data on a 20 nm baseline to reduce the noise at the lowest transmission levels. The residual optical transmission from the dichroic and the NI-OA at 0.45–0.54 µm (Fig. 12) – shortwards of the VIS bandpass – is suppressed by a factor ≥4 × 10¯7. Overall, blocking is excellent across the full wavelength range. |
5.2.2 Flux Contamination from Out-of-band Photons
To estimate the contribution from out-of-band photons to the ‘measured flux’ – that is, the total flux reaching the detector including out-of-band light – we considered sources with a power-law SED fv ∝ vα for frequency v. For α = 1 and α = −3, the sources are blue and red with JE − HE colours of −0.27 mag and +0.84 mag, respectively, in the AB mag system. We also considered α = 0, that is, sources whose AB mag colours are zero.
We then computed the ‘in-band flux’ by integrating fv T(v) within a passband’s 0.1% cut-on and cut-off wavelengths (Table 3), with T(v) as shown in Fig. 13. The predicted measured flux was obtained by integrating over the frequency range corresponding to the 0.35−2.50 µm interval.
Accordingly, the maximum relative contribution from out-of-band flux – outside the 0.1% cut-on and cut-off – to the total flux in the YE- and JE-bands is 1.4 × 10−3 and 2.3 × 10−4, respectively, for red SEDs with α = −3. For HE-band, we find a maximum contribution of 1.9 × 10−4 for the blue SED with α = 1. Out-of-band contamination of the NISP photometry is therefore at most at the level of 2mmag, and more typically 0.2mmag, negligible for virtually all practical purposes. This is not restricted to wavelengths within 0.35–2.50 µm, since there is essentially no sensitivity or response outside this range.
5.3 In-flight changes of the total transmission
The transmission of the elements presented in this section will slowly degrade with time. In practice, Eq. (11) becomes
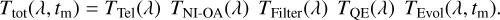 (12)
(12)
Here, TEvol(λ, tm) absorbs the combined evolution of the other four factors with progressing mission time, tm. At the end of Euclid’s life time, we expect an unrecoverable reduction of 5% in the response, or TEvol(λ) ~ 0.95. Several factors contribute:
During launch, particulates inthe spacecraft and in the rocket fairing will be redistributed because of acoustic and mechanical vibrations. This leads to an increased contamination of Euclid’ s primary mirror, and therefore increased optical scattering.
Once in orbit at L2, Euclid will be subject to space weathering from radiation damage and dust pitting that lower the system transmission. Radiation damage, for example, can darken dielectric coatings, an effect that is minimised by protective coating layers; see Sheikh et al. (2008) for the Kepler space telescope, and also Pelizzo et al. (2021).
Proton and electron radiation can degrade the QE of HgCdTe photodiodes such as in the NISP HAWAII-2RG detectors, as damage displacement in the alloy generates recombination centres. The expected total ionisation dose at L2 for the NISP detectors at the end of the mission is 2.5 krad; any reduction in QE, whether chromatic or achromatic, is expected to be minor. We note that QE degradation due to radiation damage is highly dependent on the photodiode architecture (see, e.g. Sun et al. 2020; Crouzet et al. 2020), and can thus be very different for instruments other than NISP.
Surface pitting by dust and meteoroids (Rodmann et al. 2019) as well as by electrons (Simonetto et al. 2020) increases the micro-roughness of optical surfaces, and thus the wavelength-dependent scattering. The sky-facing primary mirror, in particular, will be subject to surface erosion. The level of dust pitting at L2 is fairly well known (Grün et al. 1985; Gaia Collaboration 2016).
Material outgassing in vacuum (Green 2001; Chiggiato 2020) will contaminate Euclid’ s optical surfaces, mostly with water ice. This alters the total transmission by wavelength-dependent scattering, interference, and absorption. Contrary to radiation damage and surface erosion, this process is reversible by heating the spacecraft, restoring TEvol(λ, tm) closer to 1. We will discuss contamination effects in a forthcoming paper.
There are also indirect effects. Electron bombardment lowers the efficiency of a spacecraft’s multi-layer insulation thermal blankets (Engelhart et al. 2017), resulting in increasing internal temperatures and, thus, a – most likely negligible – redshift of the passbands (Sect. 4.3).
Apart from this temperature effect, the cut-on and cut-off wavelengths are unaffected by these processes. Primarily, the system response – in practice, TEvol(λ, tm) – will gradually reduce over time, which we track with a tight in-flight calibration program (Sects. 6.3.2 and 6.3.3).
6 The NISP photometric system
6.1 Photometric zero points
In general, the number of photo-electrons created per second in a detector in the frequency interval [vmin, vmax] is
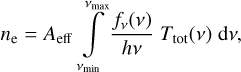 (13)
(13)
where Aeff is the effective collecting area, fv(v) the source’s spectral flux density in frequency units, h = 6.602 × 10−27 erg Hz−1 Planck’s constant, v the photon frequency, and Ttot(v) the total ‘transmission’ (i.e. the probability that a photon entering the telescope is converted to a photo-electron) as given in Sects. 4 and 5. We assume a perfect detection and extraction chain, meaning a photo-electron created in a pixel is registered by the readout electronics and caught by software processing.
Euclid’s photometric measurements will be given in the AB magnitude system (Oke & Gunn 1983), where the relation between monochromatic (i.e. per frequency interval) AB magnitude and spectral flux density is4
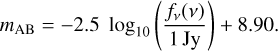 (14)
(14)
This equation is also valid for a broad-band observation in case of a frequency-flat source spectrum.
We define the photometric zero point (ZP) of a Euclid broadband observation as the magnitude of a source creating a single photo-electron per second, or nE = 1 s−1. Assuming a frequency-flat source spectrum, fv(v) = const, we solve Eq. (13) for fv, replace it in Eq. (14), and find the ZP as
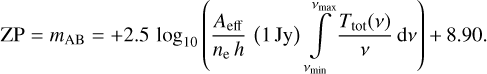 (15)
(15)
Using Aeff = 9.926 × 103 cm2 (L. Venancio, priv. comm.), for Euclid
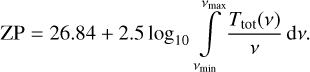 (16)
(16)
Setting vmin and vmax to the frequency interval where Ttot(v) exceeds 0.1% of the mean peak total transmission (see Table 3), we derive the following AB mag photometric ZPs,
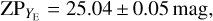 (17)
(17)
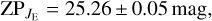 (18)
(18)
 (19)
(19)
When computed for the 50% cut-on and cut-off wavelengths, these ZPs decrease by 0.01 mag.
The uncertainty of these ZPs is dominated by the 5% uncertainty of the absolute QE measurement (Sect. 5.1.3). For comparison, the absolute accuracy of the spectrophotometers used to measure the mirror reflectances, and the NISP filter and dichroic transmissions, is 0.02–0.2%. An initial in-flight flux scaling will tie the NISP photometric system to a WD spectrophotometric standard star with known absolute flux (Sect. 6.3.2), constraining the ZPs much more accurately. Yet, throughout the mission, the ZPs will slowly evolve as explained in Sect. 5.3.
6.2 Transformations to other NIR systems
The NISP photometric system, summarised in Table 3, is geared towards photo-z measurements. It deviates considerably from common ground-based NIR systems, such as 2MASS (Carpenter 2001), Mauna Kea Observatories (MKO; Leggett et al. 2006), VISTA (González-Fernández et al. 2017), and UKIRT (Hodgkin et al. 2009), the latter being built upon MKO (see also Hewett et al. 2006). All of these are primarily dictated by the atmospheric transmission windows (Fig. 1).
6.2.1 Linear transformations for stars and galaxies
In Appendices B to E we provide linear transformations between these external photometric systems and the NISP photometric system. The transformations are based on the Euclid SC8 catalogues, containing realistic SEDs for 100 deg2 of sky as it will be seen by the Euclid Wide Survey (Euclid Collaboration 2022). We randomly selected 1.8 million stars and 1.1 million redshifted galaxies from the SC8 catalogues, and computed their colours in the NISP, 2MASS, MKO, and VISTA photometric systems.
The stellar catalogue is composed of Besançon models at the faint end, and the observed stars of Pickles & Depagne (2010) –their Table 15 in the online edition – for the bright end (1.8 million in total). Late M-type stars and L and T dwarfs (hereafter ‘MLT types’) are from Euclid Collaboration (2019) (61000 in total).
The galaxy catalogue in SC8 is built on the Euclid flagship simulation supported by CosmoHub5 (Tallada et al. 2020). The templates are based on Ilbert et al. (2009), in turn relying on the templates by Bruzual & Charlot (2003) and Polletta et al. (2007). Included are effects from two different internal extinction laws (Prevot et al. 1984; Calzetti et al. 2000).
We then fit – for the galaxies and stars separately – linear relations, including a constant offset, of the form
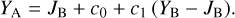 (20)
(20)
In this example, an instrument A Y-band magnitude is estimated from instrument B Y - and J-band magnitudes. Simple χ2 minimisation yields the c0 and c1 coefficients, including a 3 σ outlier rejection, and we chose the neighbouring bands that produced the best fit for each case.
Higher-order polynomial fits did not significantly reduce the fit residuals. We also find that when a constant offset c0 is included in the fit as we do here, then there is no significant benefit in using more than two bands. For the majority – but not all –of the conversions even a two-band linear fit omitting the offset produces results with errors almost as low as the ones listed in Appendices E and B.
The fits were performed for the following object classes.
Galaxies. Equations (B.1) through (B.13) convert 2MASS, MKO, and VISTA NIR magnitudes to NISP magnitudes. Equations (B.14) through (B.22) convert in the other direction, from NISP magnitudes to 2MASS, MKO, and VISTA magnitudes.
Stars without MLT types. Likewise, see Eqs. (C.1) through (C.13) and Eqs. (C.14) through (C.22).
MLT types. Likewise, see Eqs. (D.1) through (D.13), and Eqs. (D.14) through (D.22).
Stars of all spectral types. Likewise, see Eqs. (E.1) through (E.13), and Eqs. (E.14) through (E.22).
6.2.2 Limitations of the linear transformations
The colour range for which the transformations are applicable is given by the x-axes of the plots in Appendices B to E. The plots encompass 99% of the sources in the SC8 catalogues, and therefore the validity range can be considered universal for these simple parameterizations.
The transformations for galaxies have residuals of 0.04–0.06 mag, and are therefore usable for many purposes needing a simple translation between the different photometric systems. Notable exceptions are the computed Z- and Ks-band magnitudes, where residuals amount to 0.1–0.2 mag.
The transformations for stars of spectral types O to K have residuals of 0.02–0.04 mag. Notable exceptions are the computed Z-band magnitudes, with residuals as large as 0.11 mag. The transformations for MLT types have residuals of 0.04–0.12 mag. Notable exceptions are the Z-band magnitudes, with residuals up to 0.38 mag. When working with such red types, the photometry package (Sect. 6.2.3) should be used. The transformations for stars of all spectral types (O to K, MLT) have residuals of 0.03–0.08 mag. Again, notable exceptions are the Z-band magnitudes with residuals up to 0.25 mag.
As a caveat, we emphasise that the SC8 catalogues are representative for the Euclid Wide Survey area at galactic latitude |b| ≳ 30°. The stellar disk population is therefore underrepre-sented in these catalogues, as are lines of sight of appreciable dust extinction (Euclid Collaboration 2022). Our transformations must therefore be used with caution when working at low galactic latitudes. While the Euclid Wide Survey does not extend into the galactic plane, observations during a future mission extension could do so.
We emphasise that all transformations between filter systems given in this paper are computed in the AB mag system. The 2MASS magnitudes in Cutri et al. (2003) are given in the Vega system. Before they can be used in any of our transformations, they must be converted to AB magnitudes, for example using the conversions by Pons et al. (2019).
6.2.3 A Python transformation tool
The linear transformations provided in this paper should be useful for many general purposes. However, individual objects may deviate by 0.1 mag or more, in particular for galaxies and very blue or red sources (see Sect. 6.2.2, and Figs. E.1 to B.2).
For accurate photometry and filter systems other than the ones presented here, we recommend to use the external, standalone Python photometry6 package. The NISP response curves of this paper have been integrated in photometry, which includes a notebook7 showing how to re-compute magnitudes in other passbands for arbitrary stellar and non-stellar SEDs.
6.3 In-flight lifetime of the NISP photometric system
6.3.1 Validity
At the time of this writing, Euclid is still at least one year from launch. The transmission measurements presented here are not expected to change significantly until launch. The space-grade optical coatings are very durable, and all hardware is kept in clean conditions in a controlled environment up to and including launch. Only a small degree of particulate contamination is expected during this time, which is well under control, and whose additional contribution to the flux loss will be much smaller than the uncertainty of 5% for the absolute detector QE.
Therefore, the cut-on and cut-off wavelengths presented in this paper are not expected to change, neither due to the remaining time on-ground nor during flight. What will change over time is – to first order – the overall response as encoded in the ZPs of Sect. 6.1. This will be tracked using a tight calibration program outlined in Sects. 6.3.2 and 6.3.3. Hence, the AB magnitudes of sources reported in future Euclid data releases are unaffected by (i.e. corrected for) any response losses.
Second-order effects arise due to wavelength-dependent changes of the response. For example, scattering by dust and water ice on optical surfaces is larger at shorter wavelengths, making objects appear redder than they are. In Eq. (12), we have absorbed the time dependence of the response in the additional term TEvol(λ, tm). The Euclid calibration program (Sects. 6.3.2 and 6.3.3) has been specifically developed to determine and monitor TEvol(λ, tm) with great accuracy. This will eventually even enable SED-dependent corrections of source fluxes, once our understanding of the system and TEvol(λ, tm) has matured at later data releases.
Conclusively, we expect that the NISP photometric system presented in this paper will maintain its validity throughout the mission. This should also hold for the linear transformation equations in Sect. 6.2, whose uncertainties are dominated by the large diversity of the redshifted source SEDs. In the following two sections, we summarise the in-flight maintenance.
6.3.2 Absolute calibration observations
The absolute flux calibration of NISP must be known to better than 5% of established reference photometric systems; we expect to achieve about 1 –2%. To this end, Euclid will observe one of several suitable WD spectrophotometric standard stars on a 5 × 5 grid per detector and per filter, before the beginning of the routine science observations; hot, stable WDs are excellent flux calibrators (Bohlin 2014; Bohlin et al. 2020). Euclid will also take spectra of a WD on five positions per detector. Furthermore, one of the Euclid WDs is located in Euclid’s self-calibration field (Sect. 6.3.3), which is visited regularly on a monthly basis.
Our approved Hubble Space Telescope (HST) program (ID #16702) has begun obtaining NIR spectra of a total of six WDs in Euclid s survey area. These data will tightly connect the NISP photometric system to the well-known HST photometric system (Bohlin & Deustua 2019). Other spectrophotometric standards that happen to be in the survey area will be used for additional spot checks of the absolute calibration.
6.3.3 Relative calibration observations
NISP s relative photometric accuracy must be better than 1.5%. To fulfil this requirement – independently of the WD observations – Euclid will observe a self-calibration field every 25035 days (Euclid Collaboration 2022). It is located at αJ2000 = 268°.813 and δJ2000 = +65°.29 near the North Ecliptic Pole (NEP), within Euclid s continuous viewing zone, and covers an area of ~3.0 deg2. Each visit will reach a depth of about 25.4 AB mag in the NISP bands, one magnitude deeper than the Euclid Wide Survey. At each dither point, VIS and NISP images in all bands will be taken, including a NISP spectroscopic exposure. Over time, the Self-cal field will become the deepest Euclid field.
The Self-cal field contains about 40000 unsaturated stars in the J = 16.5−24.0 AB mag interval, with a signal-to-noise ratio of S /N ≳ 10. Gaia Collaboration (2019) have shown that about 9% of all Gaia stars are variable down to a precision of 5–10mmag. Even if half of all stars detected by Euclid were variable, the statistical basis for ZP monitoring is excellent, also because variability between stars is uncorrelated. We expect to detect ZP changes down to 1 –2 mmag, per NISP detector, and in two disjoint colour bins (SED bins) per filter. In case needed, we can fold in twice as many galaxies to improve the statistics.
Should the monthly sampling turn out to be insufficient, for example in the presence of faster ZP variations due to material outgassing, then we can include photometry from sources appearing in the overlap areas of adjacent survey fields. Euclid observes about 19 adjacent fields every 24 h.
The monthly visits of the Self-cal field also provide spectroscopic observations of the WD standard, and of about 2000 field stars with S /N ≳ 10 per spectral resolution element. Using statistical stacking of all spectra, we can detect chromatic changes per spectral resolution element of the order of 1 mmag, globally for the full focal plane – although not per detector as with the imaging observations.
These observations can only weakly distinguish which optical surface is losing transmission, or whether detectors degrade in QE, and due to which effects. Nonetheless, these calibrations put Euclid in an excellent position to determine the net effect on the data, as encoded in TEvol(λ, tm), maintaining the NISP photometric system throughout Euclid s lifetime.
Excerpt of the published NISP response and transmission curves (abridged, reduced numeric precision).
7 Summary and data products
7.1 Context and main results
Euclid will observe 15 000 deg2 of the darkest extragalactic sky to a median depth of 24.4 AB mag for 5 σ point sources (Euclid Collaboration 2022), establishing a photometric reference dataset with considerable legacy value. Using detailed filter transmission measurements and optical ray tracing, we have determined the edges of the spectral response curves for any position in the focal plane with a – conservatively estimated –accuracy of 0.8 nm. The out-of-band blocking of the YE, JE, and HE passbands is excellent over the 0.3–3.0 µm range, with out-of-band contributions of 0.2mmag for typical power-law SEDs. The main passband properties and the polynomial coefficients to compute the passband edges as a function of field position are given in Tables 3 and A.1, respectively.
We also derived the photometric ZPs in the AB mag system. The NISP passbands are about twice as wide as their ground-based counterparts, which are constrained by the atmospheric transmission windows. We provide linear transformations for stars and galaxies separately, to convert between the NISP and the ground-based photometric systems. A Python module is available for the computation of arbitrary transformations and magnitudes.
We strongly recommend that authors use the ‘E’ subscript –as in YE-band8 – when referring to Euclid passbands and magnitudes. This avoids any confusion with the ground-based YJH passbands that have only half the spectral width.
Overall, we designed and built a well-defined photometric system for NISP with great legacy value. Our rigorous inflight calibration program puts Euclid in an excellent position to maintain this photometric system throughout the mission.
7.2 Published data products and versioning
The YE, JE, and HE spectral responses at the centre of the NISP FPA are available online9. Included are the transmission for the filters, telescope, and NI-OA, as well as the mean detector QE, from which the total spectral response was computed; an excerpt is reproduced in Table 4. For convenience, the tables are available in both ASCII and FITS (Hanisch et al. 2001) format and can be readily displayed with TOPCAT (Taylor 2005) and processed with astropy (Astropy Collaboration 2013, 2018).
We registered a digital object identifier (DOI)10 for the electronic response tables (version v1.0) published in this paper. If updated response curves become available, a new DOI will be registered for them. The landing web page for the old DOI will inform the visitor that a new version is available. Older versions will be retained for reference.
Acknowledgements
The Euclid Consortium acknowledges the European Space Agency and a number of agencies and institutes that have supported the development of Euclid, in particular the Academy of Finland, the Agenzia Spaziale Italiana, the Belgian Science Policy, the Canadian Euclid Consortium, the French Centre National d’Etudes Spatiales, the Deutsches Zentrum für Luft- und Raumfahrt, the Danish Space Research Institute, the Fundação para a Ciência e a Tecnologia, the Ministerio de Economia y Competitividad, the National Aeronautics and Space Administration, the National Astronomical Observatory of Japan, the Netherlandse Onderzoekschool Voor Astronomie, the Norwegian Space Agency, the Romanian Space Agency, the State Secretariat for Education, Research and Innovation (SERI) at the Swiss Space Office (SSO), and the United Kingdom Space Agency. A complete and detailed list is available on the Euclid web site (http://www.euclid-ec.org). The first group of authors (up to and including M. Weiler) worked directly on this paper. The other authors made substantial, multi-year contributions totheEuclid project that enabled this paper in the first place. The authors at MPIA acknowledge funding by the German Space Agency DLR under grant numbers 50 OR 1202 and 50 QE 2003. The work by J.M. Carrasco and M. Weiler was (partially) funded by the Spanish MICIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe” by the European Union through grant RTI2018-095076-B-C21, and the Institute of Cosmos Sciences University of Barcelona (ICCUB, Unidad de Excelencia “Maria de Maeztu”) through grant CEX2019-000918-M. The authors thank Thomas Weber (OBJ; now Materion Balzers Optics) for the technical support with the transmission measurements of the NISP filter substrates, and the anonymous referee for their useful comments. The plots in this publication were prepared with TOPCAT (Taylor 2005) and Matplotlib (Hunter 2007).
Appendix A Passband variations
Coefficients for Eq. (8) to compute the blueshifted cut-on and cut-off wavelengths,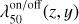 , of the filter flanks in the focal plane’s R_mosaic coordinate system (Sect. 4.2). We use the e-notation to simplify a software implementation. The last column, ‘Test’, can be used to verify computer code for z = 30, y = 50. The corresponding blueshift of the passbands is shown in Fig. 8.
, of the filter flanks in the focal plane’s R_mosaic coordinate system (Sect. 4.2). We use the e-notation to simplify a software implementation. The last column, ‘Test’, can be used to verify computer code for z = 30, y = 50. The corresponding blueshift of the passbands is shown in Fig. 8.
 |
Fig. A.1 Maximum magnitude difference for galaxies in the Euclid SC8 catalogue due to passband variations when a source moves from the centre of the FPA to the corner. We note the log-scaling of the y axis: the effect is typically of the order of a few milli-mag (see Table A.2). |
Appendix B Transformation from and to the NISP photometric system for galaxies
Equations (B.1) through (B.13) convert NISP AB magnitudes to 2MASS, MKO and VISTA AB magnitudes for galaxies. Before using these transformations, Sect. 6.2.2 should be read (see also Fig. B.1).
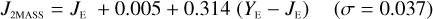 (B.1)
(B.1)
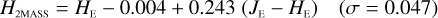 (B.2)
(B.2)
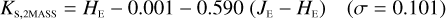 (B.3)
(B.3)
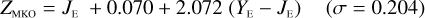 (B.4)
(B.4)
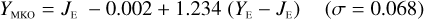 (B.5)
(B.5)
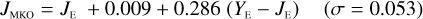 (B.6)
(B.6)
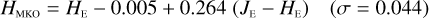 (B.7)
(B.7)
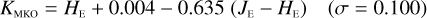 (B.8)
(B.8)
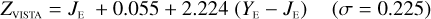 (B.9)
(B.9)
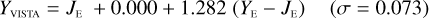 (B.10)
(B.10)
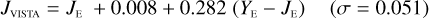 (B.11)
(B.11)
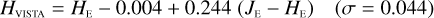 (B.12)
(B.12)
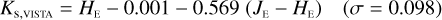 (B.13)
(B.13)
Equations (B.14) through (B.22) convert 2MASS, MKO and VISTA AB magnitudes to NISP AB magnitudes for galaxies. Before using these transformations, Sect. 6.2.2 should be read (see also Fig. B.2).
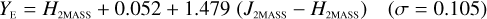 (B.14)
(B.14)
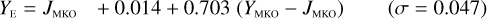 (B.15)
(B.15)
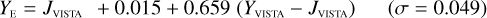 (B.16)
(B.16)
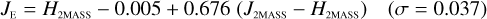 (B.17)
(B.17)
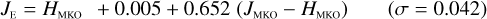 (B.18)
(B.18)
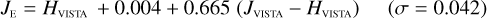 (B.19)
(B.19)
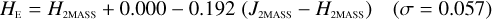 (B.20)
(B.20)
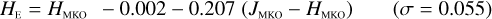 (B.21)
(B.21)
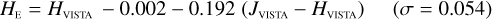 (B.22)
(B.22)
B.1 About the substructure in Figs. B.1 and B.2
Some of the colour-colour plots in Figs. B.1 and B.2 show substructure that appear artificial. We note that these are not real observations, but the SC8 synthetic SED templates, redshifted between z = 0.0 and 2.3. Some of the redshifted templates distribute fairly widely over the colour-colour space, whereas others – mostly star-forming galaxies – remain more concentrated. The latter then visually dominate the appearance of the linearly scaled colour-colour density maps. We chose a linear scaling so that the causal connection between the data and the linear fits (red lines) becomes evident. A logarithmic scaling is misleading in most cases, insinuating a poor fit quality.
As an example for substructure, we consider the bottom two rows of Fig. B.2, which show the difference in the NISP HE-band and VISTA H-band magnitudes on the y axis. Two parallel main branches are seen, mostly from star-forming galaxies. This is a consequence of the NISP HE-band being nearly twice as wide as the VISTA H-band (see Fig. 1). The two bands respond differently to spectra with specific continuum shapes and emission lines, also depending on redshift. The small bridge connecting the two branches represents starbursts with a specific metallicity and extinction evolving from redshift z = 0.25 to 0.55. The true complexity of this specific colour-colour space is shown in Fig. B.3. This also illustrates that the linear transformation equations may fail catastrophically for individual galaxies.
 |
Fig. B.1 Magnitude differences for galaxies between external systems (2MASS, MKO, and VISTA) and NISP, as a function of NISP colour. The red lines show the linear fits given in Eqs. (B.1) through (B.13). |
 |
Fig. B.2 Magnitude differences for galaxies between NISP and external systems (2MASS, MKO, and VISTA), as a function of colour in an external system. The red lines show the linear fits given in Eqs. (B.14) through (B.22). |
 |
Fig. B.3 Zoomed-in view into the lower-left panel of Fig. B.2, showing more data and details about how the redshifted Euclid SC8 galaxy SEDs populate this particular colour-colour space. The contours trace the point density with a logarithmic spacing. Template numbers 0–7 correspond to elliptical and lenticular types, templates 8–11 to Hubble types Sa and Sb, templates 12–18 to types Sc and Sd, and templates 18-30 to starbursts of various age and metallicity. |
Appendix C Transformation from and to the NISP photometric system for stars (spectral types O to K)
Equations (C.1) through (C.13) convert NISP AB magnitudes to 2MASS, MKO, and VISTA AB magnitudes for stars of spectral types O to K. The 1 σ residuals are given in parentheses. Before using these transformations, Sect. 6.2.2 should be read (see also Fig. C.1).
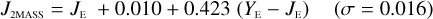 (C.1)
(C.1)
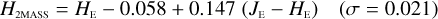 (C.2)
(C.2)
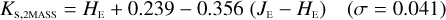 (C.3)
(C.3)
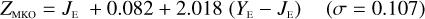 (C.4)
(C.4)
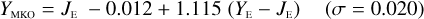 (C.5)
(C.5)
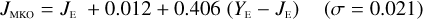 (C.6)
(C.6)
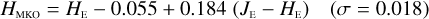 (C.7)
(C.7)
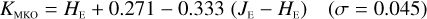 (C.8)
(C.8)
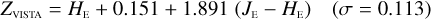 (C.9)
(C.9)
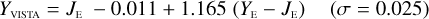 (C.10)
(C.10)
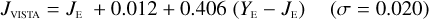 (C.11)
(C.11)
 (C.12)
(C.12)
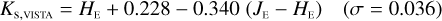 (C.13)
(C.13)
Equations (C.14) through (C.22) convert from 2MASS, MKO and VISTA AB magnitudes to NISP AB magnitudes for stars of spectral types O to K. Before using these transformations, Sect. 6.2.2 should be read (see also Fig. C.2).
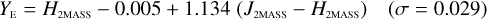 (C.14)
(C.14)
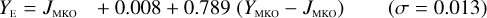 (C.15)
(C.15)
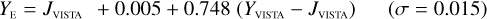 (C.16)
(C.16)
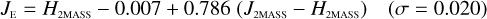 (C.17)
(C.17)
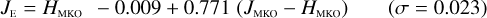 (C.18)
(C.18)
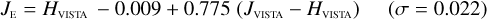 (C.19)
(C.19)
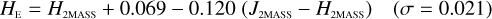 (C.20)
(C.20)
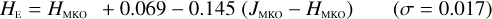 (C.21)
(C.21)
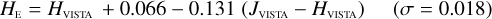 (C.22)
(C.22)
 |
Fig. C.1 Magnitude differences for stars of spectral types O to K between external systems (2MASS, MKO, and VISTA) and NISP, as a function of NISP colour. Data are taken from the Euclid SC8 simulation pilot catalogues. The red lines show the linear fits given in Eqs. (C.1) through (C.13). |
 |
Fig. C.2 Magnitude differences for stars of spectral types O to K between NISP and external systems (2MASS, MKO, and VISTA), as a function of colour in an external system. The red lines show the linear fits given in Eqs. (C.14) through (C.22). |
Appendix D Transformation from and to the NISP photometric system for stars (MLT types)
Equations (D.1) through (D.13) convert NISP AB magnitudes to 2MASS, MKO and VISTA AB magnitudes for MLT types. The 1 σ residuals are given in parentheses. Before using these transformations, Sect. 6.2.2 should be read (see also Fig. D.1).
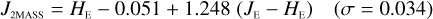 (D.1)
(D.1)
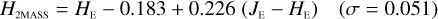 (D.2)
(D.2)
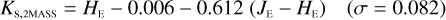 (D.3)
(D.3)
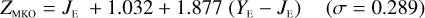 (D.4)
(D.4)
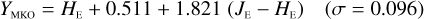 (D.5)
(D.5)
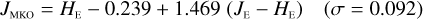 (D.6)
(D.6)
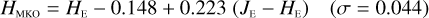 (D.7)
(D.7)
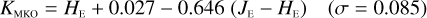 (D.8)
(D.8)
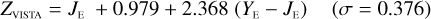 (D.9)
(D.9)
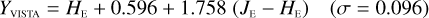 (D.10)
(D.10)
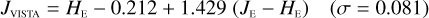 (D.11)
(D.11)
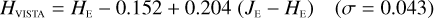 (D.12)
(D.12)
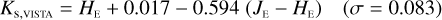 (D.13)
(D.13)
Equations (D.14) through (D.22) convert from 2MASS, MKO and VISTA AB magnitudes to NISP AB magnitudes for MLT types. Before using these transformations, Sect. 6.2.2 should be read (see also Fig. D.2).
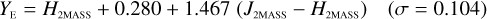 (D.14)
(D.14)
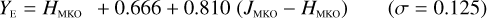 (D.15)
(D.15)
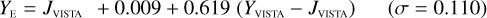 (D.16)
(D.16)
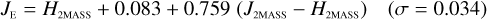 (D.17)
(D.17)
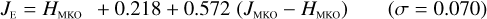 (D.18)
(D.18)
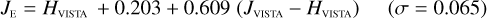 (D.19)
(D.19)
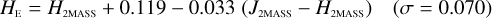 (D.20)
(D.20)
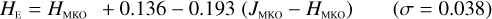 (D.21)
(D.21)
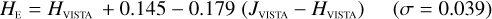 (D.22)
(D.22)
 |
Fig. D.1 Magnitude differences for MLT types between external systems (2MASS, MKO, and VISTA) and NISP, as a function of NISP colour. Data are taken from the Euclid SC8 simulation pilot catalogues. The red lines show the linear fits given in Eqs. (D.1) through (D.13). |
 |
Fig. D.2 Magnitude differences for MLT types between NISP and external systems (2MASS, MKO, and VISTA), as a function of colour in an external system. The red lines show the linear fits given in Eqs. (D.14) through (D.22). |
Appendix E Transformation from and to the NISP photometric system for stars (all spectral types)
Equations (E.1) through (E.13) convert NISP AB magnitudes to 2MASS, MKO and VISTA AB magnitudes for stars of all spectral types. The 1 σ residuals are given in parentheses. Before using these transformations, Sect. 6.2.2 should be read (see also Fig. E.1).
 (E.1)
(E.1)
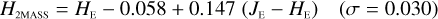 (E.2)
(E.2)
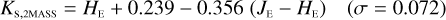 (E.3)
(E.3)
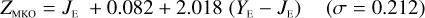 (E.4)
(E.4)
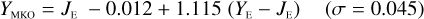 (E.5)
(E.5)
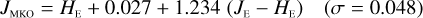 (E.6)
(E.6)
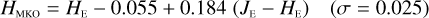 (E.7)
(E.7)
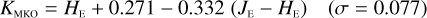 (E.8)
(E.8)
 (E.9)
(E.9)
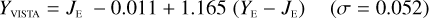 (E.10)
(E.10)
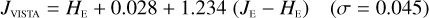 (E.11)
(E.11)
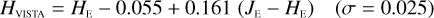 (E.12)
(E.12)
 (E.13)
(E.13)
Equations (E.14) through (E.22) convert from 2MASS, MKO, and VISTA AB magnitudes to NISP AB magnitudes for stars of all spectral types. Before using these transformations, Sect. 6.2.2 should be read (see also Fig. E.2).
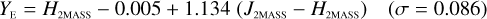 (E.14)
(E.14)
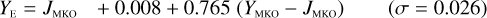 (E.15)
(E.15)
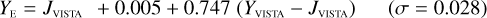 (E.16)
(E.16)
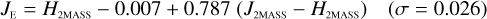 (E.17)
(E.17)
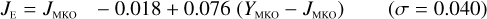 (E.18)
(E.18)
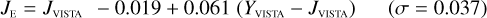 (E.19)
(E.19)
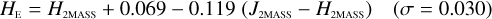 (E.20)
(E.20)
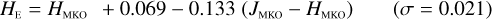 (E.21)
(E.21)
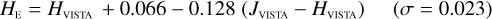 (E.22)
(E.22)
 |
Fig. E.1 Magnitude differences for stars of all spectral types between external systems (2MASS, MKO, and VISTA) and NISP, as a function of NISP colour. Data are taken from the Euclid SC8 simulation pilot catalogues. The red lines show the linear fits given in Eqs. (E.1) through (E.13). |
 |
Fig. E.2 Magnitude differences for stars of all spectral types between NISP and external systems (2MASS, MKO, and VISTA), as a function of colour in an external system. The red lines show the linear fits given in Eqs. (E.14) through (E.22). We note that the two fits displayed in the third row are skewed by a number of very red sources that are not easily visible in these linear grey scale maps. This shows that a simple, ‘one-flts-alľ model is not always an appropriate way to transform between photometric systems. |
References
- Amra, C., Lequime, M., & Zerrad, M. 2021, Electromagnetic Optics of Thin-Film Coatings: Light Scattering, Giant Field Enhancement, and Planar Microcavities (Cambridge University Press) [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Bai, Y., Farris, M., Fischer, L., et al. 2018, in High Energy, Optical, and Infrared Detectors for Astronomy VIII, eds. A. D. Holland, & J. Beletic, SPIE, 10709, 261 [Google Scholar]
- Bodendorf, C., Geis, N., Grupp, F., et al. 2019, in Astronomical Optics: Design, Manufacture, and Test of Space and Ground Systems II, eds. T. B. Hull, D. W. Kim, & P. Hallibert, SPIE, 11116, 257 [Google Scholar]
- Bohlin, R. C. 2014, AJ, 147, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., & Deustua, S. E. 2019, AJ, 157, 229 [Google Scholar]
- Bohlin, R. C., Hubeny, I., & Rauch, T. 2020, AJ, 160, 21 [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Carpenter, J. M. 2001, AJ, 121, 2851 [Google Scholar]
- Chiggiato, P. 2020, ArXiv e-prints [arXiv:2886.87124] [Google Scholar]
- Cropper, M., Cole, R., James, A., et al. 2012, SPIE Conf. Ser., 8442, 84420V [NASA ADS] [Google Scholar]
- Crouzet, P.-E., Shortt, B., Beaufort, T., et al. 2020, in X-Ray, Optical, and Infrared Detectors for Astronomy IX, eds. A. D. Holland, & J. Beletic, SPIE, 11454, 43 [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
- Engelhart, D. P., Cooper, R., Cowardin, H., et al. 2017, in Advanced Maui Optical and Space Surveillance (AMOS) Technologies Conference, ed. S. Ryan, 21 [Google Scholar]
- Euclid Collaboration (Barnett, R., et al.) 2019, A&A, 631, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Euclid Collaboration (Blanchard, A., et al.) 2020, A&A, 642, A191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Euclid Collaboration: (Ilbert, O., et al.) 2021, A&A, 647, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Euclid Collaboration (Scaramella, R., et al.) 2022, A&A, https://doi.org/10.1051/0004-6361/202141938 [Google Scholar]
- Fang, Y., Furniss, D., Jayasuriya, D., et al. 2019, Opt. Mater. X, 2, 100030 [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Eyer, L., et al.) 2019, A&A, 623, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González-Fernández, C., Hodgkin, S. T., Irwin, M. J., et al. 2017, MNRAS, 474, 5459 [Google Scholar]
- Green, D. B. 2001, Satellite Contamination and Materials Outgassing Knowledgebase - An Interactive Database Reference, NASA STI/Recon Technical Report N [Google Scholar]
- Grün, E., Zook, H., Fechtig, H., & Giese, R. 1985, Icarus, 62, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Grupp, F., Kaminski, J., Bodendorf, C., et al. 2019, SPIE Conf. Ser., 11116, 1111618 [NASA ADS] [Google Scholar]
- Hanisch, R. J., Farris, A., Greisen, E. W., et al. 2001, A&A, 376, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hewett, P. C., Warren, S. J., Leggett, S. K., & Hodgkin, S. T. 2006, MNRAS, 367, 454 [Google Scholar]
- Hodgkin, S. T., Irwin, M. J., Hewett, P. C., & Warren, S. J. 2009, MNRAS, 394, 675 [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Korsch, D. 1977, Appl. Opt., 16, 2074 [NASA ADS] [CrossRef] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Leggett, S. K., Currie, M. J., Varricatt, W. P., et al. 2006, MNRAS, 373, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Löfdahl, M. G., Henriques, V. M. J., & Kiselman, D. 2011, A&A, 533, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maciaszek, T., Ealet, A., Jahnke, K., et al. 2016, SPIE Conf. Ser., 9904, 99040T [NASA ADS] [Google Scholar]
- Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Pelizzo, M. G., Corso, A. J., Santi, G., et al. 2021, Scientific Rep., 11, 3429 [NASA ADS] [CrossRef] [Google Scholar]
- Pickles, A., & Depagne, É. 2010, PASP, 122, 1437 [NASA ADS] [CrossRef] [Google Scholar]
- Polletta, M., Tajer, M., Maraschi, L., et al. 2007, ApJ, 663, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Pons, E., McMahon, R. G., Simcoe, R. A., et al. 2019, MNRAS, 484, 5142 [NASA ADS] [CrossRef] [Google Scholar]
- Prevot, M. L., Lequeux, J., Maurice, E., Prevot, L., & Rocca-Volmerange, B. 1984, A&A, 132, 389 [Google Scholar]
- Prieto, E., Amiaux, J., Auguères, J.-L., et al. 2012, SPIE Conf. Ser., 8442, 84420W [NASA ADS] [Google Scholar]
- Rienstra, J. L. 1998, in Infrared Imaging Systems: Design, Analysis, Modeling, and Testing IX, 3377, International Society for Optics and Photonics, 267 [NASA ADS] [Google Scholar]
- Rodmann, J., Miller, A., Bunte, K. D., & Millinger, M. 2019, in First International Orbital Debris Conference, 2109, 6070 [NASA ADS] [Google Scholar]
- Rogalski, A. 2005, Rep. Progr. Phys., 68, 2267 [CrossRef] [Google Scholar]
- Secroun, A., Barbier, R., Buton, C., et al. 2018, in SPIE Conf. Ser., 10709, [Google Scholar]
- High Energy, Optical, and Infrared Detectors for Astronomy VIII, eds. A. D. Holland, & J. Beletic, 1070921 [Google Scholar]
- Sheikh, D. A., Connell, S. J., & Dummer, R. S. 2008, in Space Telescopes and Instrumentation 2008: Optical, Infrared, and Millimeter, eds. J. M.O. Jr., M. W. M. de Graauw, & H. A. MacEwen, SPIE, 7010, 1277 [Google Scholar]
- Simonetto, F., Marmonti, M., & Potenza, M. A. C. 2020, J. Astron. Telescopes Instrum. Syst., 6, 038004 [NASA ADS] [Google Scholar]
- Smith, W. 2008, Modern Optical Engineering: The Design of Optical Systems, McGraw Hill professional (McGraw-Hill Professional) [Google Scholar]
- Sun, X., Abshire, J., Lauenstein, J.-M., et al. 2020, IEEE Trans. Nuclear Sci., PP, 1 [Google Scholar]
- Sutherland, W., Emerson, J., Dalton, G., et al. 2015, A&A, 575, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tallada, P., Carretero, J., Casals, J., et al. 2020, Astron. Comput., 32, 100391 [Google Scholar]
- Tan, C., & Arndt, J. 2000, J. Phys. Chem. Solids, 61, 1315 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, M. B. 2005, in Astronomical Society of the Pacific Conference Series, 347, Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, 29 [NASA ADS] [Google Scholar]
- Venancio, L. M. G., Carminati, L., Amiaux, J., et al. 2020, in Space Telescopes and Instrumentation 2020: Optical, Infrared, and Millimeter Wave, eds. M. Lystrup, M. D. Perrin, N. Batalha, N. Siegler, & E. C. Tong, SPIE, 11443, 45 [Google Scholar]
- Waczynski, A., Barbier, R., Cagiano, S., et al. 2016, SPIE Conf. Ser., 9915, 991511 [NASA ADS] [Google Scholar]
All Tables
Excerpt of the published NISP response and transmission curves (abridged, reduced numeric precision).
Coefficients for Eq. (8) to compute the blueshifted cut-on and cut-off wavelengths,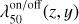 , of the filter flanks in the focal plane’s R_mosaic coordinate system (Sect. 4.2). We use the e-notation to simplify a software implementation. The last column, ‘Test’, can be used to verify computer code for z = 30, y = 50. The corresponding blueshift of the passbands is shown in Fig. 8.
, of the filter flanks in the focal plane’s R_mosaic coordinate system (Sect. 4.2). We use the e-notation to simplify a software implementation. The last column, ‘Test’, can be used to verify computer code for z = 30, y = 50. The corresponding blueshift of the passbands is shown in Fig. 8.
All Figures
 |
Fig. 1 Comparison of the NISP spectral response (shaded) with typical ground-based NIR passbands, in this case VIRCAM at VISTA (Sutherland et al. 2015). Both sets of response curves account for mirrors, filters, and detector QE. The grey line displays the atmospheric transmission for a precipitable water vapour of 1 mm and at zenith, taken from the ESO VISTA instrument description. The ground-based Z and K bands lie outside the NISP wavelength range, whereas Y, J, and H cover approximately half of the corresponding NISP passbands. |
| In the text | |
 |
Fig. 2 Filter geometry and measurement points. The filters have a diameter of 130 mm (black circle). The blue line shows the baffle, blocking light paths outside without causing vignetting. The nine-point original measurement apertures are shown by the black rectangles (to scale). Our refined 37-point measurements are marked by red dots instead of black rectangles, to avoid cluttering. The grey annulus displays the 90 mm obstructed beam footprint, that is, the part of the filter seen by a source at the centre of the FPA. The obstruction is off-centred due to the telescope’s off-axis design. The response curves made available online are integrated over this grey annulus. The light of a source mapped onto any of the four corners of the FPA intersects different parts of the filter; the centres of the correspondingly shifted footprints are shown by the blue squares. |
| In the text | |
 |
Fig. 3 Variation in the 50% cut-on wavelength of the YE-band engineering qualification filter. Measurements were done with a single-beam photometer in 213 apertures 2 × 2 mm in size (shown to scale), at AOI θ = 0°. The cut-on varies by 8 nm over the unbaffied area and is a consequence of the coating layers getting systematically thinner by about 0.4% towards the outer edge. When the grey annulus moves across this surface (different object positions in the field of view), the effective transmission changes by 0.5–1.0 nm. Lines are the same as in Fig. 2. |
| In the text | |
 |
Fig. 4 Wavelength accuracy of the PE950 spectrophotometer. Left panel: joint long-term reproducibility of the cut-on and cut-off between the nine-point measurement runs on the same substrates. The RMS is |
| In the text | |
 |
Fig. 5 Ray tracing of the NI-OA. Shown are the obstructed beams for three sources located at the centre of the focal plane and at two opposing edges. The NI-OA consists of four lenses; the filter also acts as a lens, albeit only weakly. The dichroic element is located in the pupil plane of the telescope and is not part of NISP. We notice how the beam paths cover different parts of the filter surface, because – contrary to the dichroic – the filter is located outside the pupil plane. This leads to 10–23% of the passband variations in the focal plane due to local variations in the filter transmission. The AOI on the filter changes noticeably for the three sources; this is the dominant cause for passband variations. |
| In the text | |
 |
Fig. 6 Mean AOI, |
| In the text | |
 |
Fig. 7 Same as Fig. 6, now showing |
| In the text | |
 |
Fig. 8 Cut-on and cut-off wavelengths (in nm) as a function of FPA position, cold and in vacuum. The blueshift towards the field corners is evident. The black lines and coloured background show the polynomial fits introduced in Sect. 4.2; the fit parameters are listed in Table A.1, and the joint residuals are shown in Fig. 9. The fits are based on the 9×9 object positions (small dots) for which we inferred the AOI distribution on the filter surface using Zemax ray tracing. The shaded squares display the 16 NISP detectors, numbered in yellow from 11 to 44. The position of the number indicates the location of the (111) pixel of a detector. The published response curves (Sect. 7.2) were computed for the central dot marked with the white square. R_mosaic (z, y) is a physical coordinate system in the focal plane, to describe – among other factors – the detector positions. |
| In the text | |
 |
Fig. 9 Joint wavelength residuals of the polynomial fits to the passband variations, for all filters (their cut-on and cut-off; see also Fig. 8). The RMS is σ = 0.011 nm; 92% of the residuals are smaller than 0.02 nm. |
| In the text | |
 |
Fig. 10 NISP passband flanks and variations. The solid red lines show the local transmission at the filter centre (Fig. 2). The solid blue lines show the combined vacuum and temperature shifts on the red curve. The thick black lines show the effective transmission after integrating over the central beam footprint (centred on the white squares in Fig. 8), cold and in vacuum. The coloured areas enclosed by dashed lines show the range of blueshifts seen by the FPA: the leftmost dashed line corresponds to the bluest FPA corners and the rightmost to the reddest passband near – but not necessarily coincident with – the FPA centre. The grey rectangles show the maximum spread, |
| In the text | |
 |
Fig. 11 Chromatic selection function of the Euclid optical elements. The VIS detectors have zero QE for photons with λ > 2.15 µm. The exact behaviour of the dichroic above 2.2 µm is unknown: longer wavelengths could enter NISP and would be blocked by the filters (see Sect. 5.1 and Fig. 12 for more details). |
| In the text | |
 |
Fig. 12 Transmission of elements in the NISP optical path. The telescope component (black line) contains all mirrors and the dichroic; the latter redirects the 0.54–0.93 µm range to VIS and cuts off at 2.15 µm. The pink line shows the transmission of the NI-OA. The blue line shows the interpolated mean detector QE, originally measured at 50 nm intervals. The thin lines show the effective filter transmission integrated over the beam footprint, and the shaded areas the total response (accounting for the filter, telescope, NI-OA, and QE). The residual optical transmission from the dichroic and the NI-OA between 0.45 and 0.54 µm is fully suppressed by the filters’ out-of-band blocking (see Fig. 13). These curves do not include effects from particulate contamination. |
| In the text | |
 |
Fig. 13 Joint NISP out-of-band blocking, including flight model filters, telescope, NI-OA, and QE. The curves are the same as the shaded curves in Fig. 12, with the difference that the blocking was measured at the filter centre only, in wavelength steps of 2 nm. We smoothed the data on a 20 nm baseline to reduce the noise at the lowest transmission levels. The residual optical transmission from the dichroic and the NI-OA at 0.45–0.54 µm (Fig. 12) – shortwards of the VIS bandpass – is suppressed by a factor ≥4 × 10¯7. Overall, blocking is excellent across the full wavelength range. |
| In the text | |
 |
Fig. A.1 Maximum magnitude difference for galaxies in the Euclid SC8 catalogue due to passband variations when a source moves from the centre of the FPA to the corner. We note the log-scaling of the y axis: the effect is typically of the order of a few milli-mag (see Table A.2). |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1, but for stars. |
| In the text | |
 |
Fig. B.1 Magnitude differences for galaxies between external systems (2MASS, MKO, and VISTA) and NISP, as a function of NISP colour. The red lines show the linear fits given in Eqs. (B.1) through (B.13). |
| In the text | |
 |
Fig. B.2 Magnitude differences for galaxies between NISP and external systems (2MASS, MKO, and VISTA), as a function of colour in an external system. The red lines show the linear fits given in Eqs. (B.14) through (B.22). |
| In the text | |
 |
Fig. B.3 Zoomed-in view into the lower-left panel of Fig. B.2, showing more data and details about how the redshifted Euclid SC8 galaxy SEDs populate this particular colour-colour space. The contours trace the point density with a logarithmic spacing. Template numbers 0–7 correspond to elliptical and lenticular types, templates 8–11 to Hubble types Sa and Sb, templates 12–18 to types Sc and Sd, and templates 18-30 to starbursts of various age and metallicity. |
| In the text | |
 |
Fig. C.1 Magnitude differences for stars of spectral types O to K between external systems (2MASS, MKO, and VISTA) and NISP, as a function of NISP colour. Data are taken from the Euclid SC8 simulation pilot catalogues. The red lines show the linear fits given in Eqs. (C.1) through (C.13). |
| In the text | |
 |
Fig. C.2 Magnitude differences for stars of spectral types O to K between NISP and external systems (2MASS, MKO, and VISTA), as a function of colour in an external system. The red lines show the linear fits given in Eqs. (C.14) through (C.22). |
| In the text | |
 |
Fig. D.1 Magnitude differences for MLT types between external systems (2MASS, MKO, and VISTA) and NISP, as a function of NISP colour. Data are taken from the Euclid SC8 simulation pilot catalogues. The red lines show the linear fits given in Eqs. (D.1) through (D.13). |
| In the text | |
 |
Fig. D.2 Magnitude differences for MLT types between NISP and external systems (2MASS, MKO, and VISTA), as a function of colour in an external system. The red lines show the linear fits given in Eqs. (D.14) through (D.22). |
| In the text | |
 |
Fig. E.1 Magnitude differences for stars of all spectral types between external systems (2MASS, MKO, and VISTA) and NISP, as a function of NISP colour. Data are taken from the Euclid SC8 simulation pilot catalogues. The red lines show the linear fits given in Eqs. (E.1) through (E.13). |
| In the text | |
 |
Fig. E.2 Magnitude differences for stars of all spectral types between NISP and external systems (2MASS, MKO, and VISTA), as a function of colour in an external system. The red lines show the linear fits given in Eqs. (E.14) through (E.22). We note that the two fits displayed in the third row are skewed by a number of very red sources that are not easily visible in these linear grey scale maps. This shows that a simple, ‘one-flts-alľ model is not always an appropriate way to transform between photometric systems. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



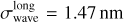
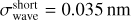
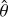
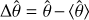
![$\lambda '\left( \theta \right) = \lambda {\left[ {1 - {{\left( {{{\sin \theta } \over {{{\rm{n}}_{{\rm{eff}}}}\left( \lambda \right)}}} \right)}^2}} \right]^{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-\nulldelimiterspace} 2}}}.$](/articles/aa/full_html/2022/06/aa42897-21/aa42897-21-eq30.png)