EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 662 (June 2022) A&A, 662 (2022) A121 Full HTML
Free Access
Issue
A&A
Volume 662, June 2022
Article Number A121
Number of page(s) 24
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202141035
Published online 30 June 2022

© ESO 2022

1 Introduction

The collapse and fragmentation of molecular cloud cores frequently leads to the formation of binary stars or higher order multiple systems (e.g. Bate 2018; Reipurth et al. 2014). In a tight multiple system, the outer parts of the individual discs in the system are affected by tidal forces from the companions, usually resulting in disc truncation. The effect of tidal disruption of discs on the ability of protoplanetary discs in multiple systems to form planets is still under investigation.

From an observational point of view, exoplanet detection surveys were initially strongly biased towards binary systems with separations of ≥200 au (Eggenberger & Udry 2010), because these searches focused on stellar environments as similar as possible to the Solar System. However, in 2003 the first exoplanet in a close binary was detected in the γ Cephei system (Hatzes et al. 2003) and exoplanets have been detected in many multiple systems (Hatzes 2016), and in close-binaries with a separation of ~20 AU. In particular, 217 exoplanets are known in binary-star systems and 51 in higher multiplicity systems (updated to Sep 2021)1.

In multiple systems, dynamical interactions experienced by circumstellar discs affect their evolution (Papaloizou & Pringle 1977; Artymowicz & Lubow 1994; Rosotti & Clarke 2018; Zagaria et al. 2021a) and may have a negative impact on the formation and evolution of planetary systems. Tidal effects due to interactions may lead the outer parts of the discs to become strongly misaligned or warped (Lodato & Facchini 2013), impacting planet migration and orbit stability and evolution (Holman & Wiegert 1999; Jensen & Akeson 2014). Moreover, disc truncation may affect the availability of the building blocks of planets (Zsom et al. 2011; Kraus et al. 2016) and may reduce the lifetimes of either or both of the discs around the primary or secondary component (Monin et al. 2007). These considerations could suggest that multiplicity reduces the probability of planet formation because there is insufficient mass to form planets or insufficient time for planetesimal formation to operate before the disc is dispersed.

The detection of planets in multiple stellar systems and in close binaries has triggered studies investigating how such planets could form and, more generally, how planet formation is affected by binarity (Thebault & Haghighipour 2015). In particular, to investigate these two aspects, the observation of circumstellar discs in multiple systems is crucial in order to study how discs evolve and how interactions between discs in multiple systems affect their evolution.

Surveys of multiple stellar systems conducted with the Submillimeter Array (SMA) and the Atacama Large Millimeter/submillimeter Array (ALMA) are providing constraints on the theory of disc evolution in multiple systems. In particular, observations of discs around multiple stars in the Taurus and ρ-Ophiucus regions (Harris et al. 2012; Akeson & Jensen 2014; Cox et al. 2017; Akeson et al. 2019; Manara et al. 2019; Long et al. 2019; Zurlo et al. 2021) show that discs in multiple systems are on average fainter in the (sub)millimetre at any given stellar mass than those in single systems. The dusty disc around the primary component, that is the more massive star, is usually brighter and more massive than the disc around the secondary component.

Manara et al. (2019) discussed a sample of ten multiple stellar systems in the Taurus star-forming region, which is composed of eight binaries and two higher order multiple systems – UZ Tau (e.g., White & Ghez 2001) and T Tau (e.g., Köhler et al. 2016). The sample was part of a high-angular-resolution (~0.″12) and high-sensitivity (~50 μJy beam−1 at 225 GHz–1.33 mm) survey of 32 protoplanetary discs around stars with spectral types earlier than M3 (Long et al. 2018, 2019) and covers a wide range of system parameters. Manara et al. (2019) showed that, in general, the dust radii of the discs around secondary or tertiary components of multiple systems are statistically smaller than the sizes of the discs around primary stars in multiple systems, which are in turn smaller than the discs around single stars and whose brightness profiles present a steeper outer edge than singles. The typical measured ratio between Rdisc,dust and the projected separation (ap) was ≲0.1. This result can be reconciled with tidal truncation models (e.g., Papaloizou & Pringle 1977; Artymowicz & Lubow 1994) only in the highly improbable case where the observed binary systems were all on highly eccentric (e > 0.7) orbits. Assuming that dust radii are smaller than gas radii by factors of ≳2–3 (e.g., Ansdell et al. 2018) – possibly due to a more effective drift of the dust probed by 1.3 mm observations – would result in values of eccentricities in agreement with the expected ones, 0 ≲ e ≲ 0.5 (e.g., Duchêne & Kraus 2013). However, the analysis above was performed using the dust disc radii estimates, because the data available did not cover the gas emission in these discs, which is nevertheless the component that we need to compare with current models of tidal truncation as this is the one that best responds to the disc dynamics. By considering the effect of dust growth and drift in truncated systems, Zagaria et al. (2021b) recently showed that the results by Manara et al. (2019) can be reconciled with tidal truncation models without the need to invoke extremely high eccentric orbits. This result must however be confirmed also observationally by measuring the sizes of the gas discs around multiple systems.

In this work, we analyse new high-resolution ALMA observations of line and continuum emission in the same sample of multiple stellar systems in the Taurus star-forming region as that used by Manara et al. (2019). Our aim is to test tidal truncation models by measuring for the first time the sizes of the gas discs in multiple stellar systems in a uniform way, with the same instrument and a similar noise level at high spatial resolution.

The paper is organised as follows. In Sect. 2 we present the sample analysed in our work. In Sect. 3 we discuss the observations, and how the data were calibrated. In Sect. 4 we analyse the new ALMA observations, deriving the geometrical properties of the discs and the disc radii. We then discuss the results in Sect. 5, comparing the measured radii to theoretical models to constrain the eccentricities of the orbits expected with our data. Finally, we draw our conclusions in Sect. 6.

2 Sample properties

The sample we analyse here comprises eight targets: seven binary systems, CIDA 9, DH Tau, DK Tau, HK Tau, HN Tau, RW Aur, V710 Tau, and one quadruple system, UZ Tau. The primary components of the CIDA 9 and UZ Tau systems are very bright, and their circumprimary discs show ring-like structures, while the other systems have smooth discs around the primary stars (Long et al. 2018).

Eleven systems were originally selected for the apparent multiplicity of their stars (ten systems from Manara et al. 2019 and GK Tau from Long et al. 2019). New ALMA observations were requested to detect CO lines in nine of the ten targets of Manara et al. (2019) (i.e. CIDA 9, DH Tau, DK Tau, HK Tau, HN Tau, T Tau, UY Aur, UZ Tau, V710 Tau) and in GK Tau. For the last target of Manara et al. (2019), RW Aur, CO observations with similar resolution and sensitivity were already available in the ALMA archive (Rodriguez et al. 2018). Three sources, GK Tau, UY Aur, and T Tau, were then excluded from the analysis performed in this work. GK Tau and GI Tau are possibly part of a bound system. However, considering the high separation of the targets (~1700 au; Hartigan et al. 1994; Herczeg & Hillenbrand 2014) the sizes of both GI Tau and GK Tau are not affected by tidal truncation (Pearce et al. 2020), and are therefore excluded from the analysis in this work. Finally, the observations of UY Aur and T Tau do not show a velocity pattern compatible with Keplerian rotation (see Sect. 3), making it difficult to determine whether or not the gas emission is reflecting the disc dynamics, and therefore to estimate the radius of individual discs. The data for these two objects will be analysed in future work.

Table 1 reports information on the eight multiple stellar systems analysed in this work. We assumed the stellar masses inferred by Manara et al. (2019). In that work, the effective temperature was used with the stellar luminosity corrected assuming the Gaia DR2 distances of the targets (Gaia Collaboration 2018), and masses were obtained assuming the evolutionary models by Baraffe et al. (2015) and the nonmagnetic models by Feiden (2016), as already done in Pascucci et al. (2016) and Long et al. (2019). Only in two cases are the stellar masses derived from orbital dynamics and not as described immediately above: UZ Tau E (Simon et al. 2000) and HN Tau A (Simon et al. 2017).

The projected separations (ap, assumed from Manara et al. 2019, and references therein) of the individual components in the systems range from ~49 au to 461 au, the mass ratios (q = M2/M1) from ~0.9 to ~0.1, and the mass parameters (μ = M1 M2/(M1 + M2)) from ~0.1 to ~0.5.

Table 1

Information on the stellar and multiplicity properties of the targets analysed in this work.

3 Observations and data reduction

The ALMA observations presented here were obtained in program 2018.1.00771.S, (PI: Manara). The observations were conducted in ALMA Band 6 with an angular resolution of 0.″15 – ~21 au at the distance of Taurus, and with an integration time of ~40 min per source. These observations present an angular resolution slightly lower and a longer integration time than the previous Band 6 observations presented by Long et al. (2018, 2019) and Manara et al. (2019), i.e. 0712 and ~4–9 min/source, respectively. The aim of the new observations was to detect different molecular emission lines with a higher signal-to-noise ratio (S/N). The spectral setup was chosen to include one continuum band (centered at 233 GHz), and the following molecular emission lines: 12CO (J = 2–1), 13CO (J = 2–1), C18O (J = 2–1), N2D (J = 3–2), DCN (υ = 0, J = 3–2), and H2CO 3(0, 3)–2(0, 2). Two configurations were requested, C43-6 and C43-3, but only observations in the former configuration were executed. Therefore, the maximum recoverable scale of the observations was only ~1.″8.

The targets were observed in two scheduling blocks (SBs), one including HN Tau, T Tau, and V710 Tau, and the other one including the remaining seven targets of the program. Each science target was observed multiple times in different execution blocks (EBs), three and six for each SB respectively. The observations of the first SB, including three science targets, were executed between August 17, 2019, and September 19, 2019, while those of the second SB, including seven targets, were carried out between September 21, 2019, and September 27, 2019. J0510+1800 was used as flux, bandpass, pointing, and atmosphere calibrator, while J0440+1437 and J0438+3004 were used as phase calibrators.

The calibrated data were retrieved using the script for PI provided by the observatory. In order to improve the S/N, the data were self-calibrated in each EB separately. This step was performed using the Common Astronomy Software Applications package (CASA, version 5.6.1, McMullin et al. 2007). To speed up the calibration, we applied a channel averaging of 125 MHz in each spectral window (spw): this led to eight channels in the continuum spw centred on 233.0 GHz with a bandwidth of 1875.00 MHz, and one channel in the other five spws, which was used for the line observations. The channel averaging was done after flagging any channel in which emission lines were found. In each EB we applied from one to four rounds of phase-only self-calibration, stopping the calibration when no significant improvement was measured in the S/N from one step to the next. We then concatenated all EBs and applied one round of amplitude self-calibration. The final improvement in S/N was always greater than 100% for all targets thanks to both a drop in the noise and an improvement in the observed flux. As a final step, we applied the phase and amplitude calibration to the spectral windows containing emission lines.

Continuum and line images were created with the CASA task tclean. Continuum images were created using both the continuum spectral window and the line-free channels of the three spws in which CO isotopologue emission was detected. The cleaning was performed with Briggs weighting and a robust parameter of +0.5 using an interactive cleaning, except for the line images of HN Tau, GK Tau, UY Aur, and T Tau which were created through the CASA auto-multithresh algorithm with Briggs weighting and a robust parameter of +0.5. The cleaning was performed with a channel width of 0.1 kms−1 for 12CO emission, except in the case of HN Tau where a 0.2 km s−1 channel width was used. The 13CO and C18O lines were cleaned with a channel width of 0.2–0.5 kms−1.

In this work, in order to estimate disc radii and test tidal truncation models, we analyse the 12CO emission. In Table 2 we report the rms of the resulting continuum image and of the zeroth moment image of the CO isotopologues and the beam sizes. Figure 1 shows the 12CO zeroth moment images of the ten systems observed in our program, of which three (GK Tau, UY Aur, and T Tau) are excluded from the analysis provided in this paper (see Sect. 2).

We detect and spatially resolve discs around all primary stars both in continuum and 12CO emission. For discs around the secondary stars, three discs (V710 Tau B, HN Tau B, DH Tau B) are not detected with either dust continuum or CO emission, CIDA 9 B disc does not show any CO emission despite hosting a dusty disc detected in the continuum, and both components are detected in the remaining sample. For each system, Table 3 shows the components that are detected in the continuum emission and in CO emission.

Figure 2 shows the velocity maps of the observed targets, including the three systems not analysed in this work. In particular, we show the ‘quadratic’ method to image the velocity maps, created with bettermoments tools (Teague & Foreman-Mackey 2018), and application of a 4-sigma clipping process. Excluding T Tau and UY Aur systems, a pattern compatible with Keplerian rotation is observed in all detected circumprimary and circumsecondary discs, a few of which are already well known from the literature (e.g. HK Tau discs, Jensen & Akeson 2014). The spectra and the first moment images of all targets in the sample are presented in Appendix A.

To this sample, we add the high-angular-resolution observation of the tidally disrupted protoplanetary discs of the RW Aurigae system analysed by Rodriguez et al. (2018). As part of ALMA Cycle 3 and 4 projects 2015.1.01506.S (PI: Rodriguez) and 2016.1.00877.S (PI: Rodriguez), RW Aur was observed in Band 6 (225 GHz) with the 12 m array for a total integration time of 311.17 min and with the 7 m array for a total additional integration time of 217.23 min. Additionally, RW Aur was observed in Band 7 (338 GHz) for a total integration time of 22.8 min. The data were calibrated by the NAASC, and two rounds of phase-only self-calibration were applied to each set of observations. The 12CO 2–1 and 3–2 lines were imaged at a velocity resolution of 0.5 kms−1 using a Briggs weighting with a robust value of 0.5, and with a uv-taper of 0.″6 × 0.″25, resulting in a synthesised beam of 0.″30 × 0.″25 and an rms of 1.5 mJy beam−1.Figure 3 shows the 12CO zeroth moment image (left), the 12CO first moment map (central), and the 12CO velocity map imaged with bettermoments quadratic method (right) for RW Aur system.

The channel maps and the spectra of the 12CO emission for all targets in the sample are reported in Appendix A and are useful to check for absorption due to foreground cloud material in the data. Signatures of partial absorption around the systemic velocity are observed in almost all discs; absorption in the red-shifted velocities is observed in the disc around CIDA 9 A, while the redshifted velocities around DH Tau A are totally absorbed by the cloud below the continuum level. These absorption features are in line with previous observations (e.g. Guilloteau et al. 2013; Akeson & Jensen 2014; Czekala et al. 2019). Table 4 summarises the absorbed velocities in the disc 12CO emission.

Table 2

Information on the cleaned images.

Table 3

Detections of continuum and CO isotopologues.

4 Data analysis

In this section, we estimate the radii of the discs. In order to measure this quantity, one needs first to determine the position angle (PA) and inclination of the discs. Once these disc parameters are derived, an analysis on the image plane is performed in order to calculate the disc radii.

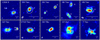thumbnail Fig. 1

12CO zeroth moment images of the discs around multiple stars in the Taurus star-forming region observed in the new ALMA observations. All bars in the bottom right of each panel are of 1″ in length, which is ~140 au at the typical distance of the Taurus region. The FWHM beam size is shown in the bottom left of each panel. In each image, the colour scale has the peak flux as the maximum, and two times the image rms as minimum. White contours show five times the rms of the continuum emission. The components of the systems are labelled. The label for any undetected secondary components in the continuum emission is not shown.
thumbnail Fig. 2

12CO velocity map images of the discs created with the bettermoments quadratic method (Teague & Foreman-Mackey 2018). A 4-sigma clipping process was applied to all images. The FWHM beam size is shown in the bottom left of each panel. Each image is scaled so that the maximum and the minimum are equal to the systemic velocity of the primary target ±2 km s−1. Green contours show five times the rms of the continuum emission. The components of the systems are labelled. The label for any undetected secondary components in the continuum emission is not shown.

4.1 Geometrical properties of discs from Keplerian modelling

The geometrical properties of interest for each disc are the disc inclination i, its PA, and the target centre (RA, Dec). To estimate these properties, we used the eddy tool (Teague 2019), which is designed to reconstruct the rotational profile of a gas emission line by fitting a Keplerian rotation pattern to the velocity map of the observations, taking into account the relative uncertainties calculated with the bettermoments tool (Teague & Foreman-Mackey 2018) and assuming a geometrically thin disc.

As there is a degeneracy between the inclination i and the stellar mass M★, the stellar mass was fixed to the values reported in Table 1. In this way, eddy would fit five free parameters (ra, dec, PA, i and the systemic velocity υLSR) given two fixed parameters (M★ and the distance d of the disc from the observer). To account for the impact of the uncertainty on M★ on the estimate of the parameters of the discs, we performed three fits for each target, one adopting the assumed value of M★, and one each for the ±1σ values of M★ given the uncertainty (see Table 1). The fit parameters are initialised using the moment zero value for the target centre, and the values by Manara et al. (2019) for inclination and PA. Flat priors for all parameters were chosen, with Gaussian priors only for the target centre. The number of walkers and steps needed to achieve the convergence of the chain was typically 200 walkers and ~1000–2000 steps, with the last ~800–1000 steps used to sample the posterior distribution.

We account for cloud absorption in discs while excluding the velocities absorbed by the cloud from the fit (see Table 4). As the disc around DH Tau A is heavily absorbed in the redshifted velocities, we only fit the 13CO velocity map of DH Tau. We did not fit the disc around the secondary star of the HK Tau system. This disc is almost edge-on, meaning that the assumption of geometrically thin disc emission cannot be applied and the vertical height of the disc must be considered. As the HK Tau system is well known in the literature, we assumed the PA and the inclination estimated in a previous work by McCabe et al. (2011) (see also Jensen & Akeson 2014): PA = (42 ± 0)° and i = (85 ± 1)°.

To avoid issues with the convergence of the eddy fit, we estimated the source centre of the circumsecondary discs fitting two elliptical Gaussian components to the 12CO image with the CASA task imfit. All other parameters of circumsecondary discs were estimated through eddy. Table 5 reports the estimated disc properties for each disc.

The agreement between the source centres obtained here with those derived by Manara et al. (2019) is good when accounting for the typical proper motion of the targets. We also compared the PA and inclination obtained fitting the gas emission with eddy with the values obtained by Manara et al. (2019) fitting the continuum data in the uv plane. This comparison is shown in Fig. 4. The values obtained with the two methods are in agreement within the (3σ) uncertainties, with the exception of the circumsecondary discs around DK Tau В, RW Aur B, and UZ Tau Wa, where the estimates with both methods are uncertain due to the small size of the targets. Another exception, probably due to some issues in the Galano fitting, is the circumprimary disc around HN Tau A. The agreement of the estimates with the two different methods within the uncertainties confirms that the assumptions on the stellar masses are reasonable, except possibly in the four cases mentioned immediately above. Indeed, Manara et al. (2019) did not need any assumption on stellar masses to fit the continuum, whereas a value of M★ was assumed in the Keplerian modelling performed here.

thumbnail Fig. 3

Maps of the RW Aur system observed by Rodriguez et al. (2018). Left: 12CO zeroth moment. The colour scale has the peak flux as the maximum, and two times the image rms as minimum. Right: 12CO first velocity maps created with bettermoments quadratic method (Teague & Foreman-Mackey 2018) and with a 4-sigma clipping process. The image scaled so that the maximum and the minimum are equal to the systemic velocity of the primary target ±2 km s−1.
Table 4

Systemic velocities (in km s−1; second column) and absorbed velocities (in km s−1; third and fourth columns) in the disc 12CO emission.

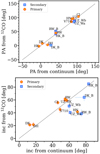thumbnail Fig. 4

PA (top) and inclination (bottom) estimated using eddy fitting on 12CO first moment maps compared with that estimate by Manara et al. (2019) using (u, υ)-plane modelling of the continuum data with Galario. Red circles refer to circumprimary discs, while blue squares refer to circumsecondary discs.

4.2 Disc radii estimate: the cumulative flux technique

To estimate the disc radii, we perform an image plane analysis using the cumulative flux technique (e.g. see Ansdell et al. 2018). For reference, this method is referred to as ‘curve of growth’ by Ansdell et al. (2018). We use it to compute aperture photometry on the zeroth moment images of the 12CO emission and on the continuum images using the CASA tool imstat. This technique is applied on the continuum emission (both on new data and on data from Manara et al. 2019) and on the 12CO zeroth moment image of each target, both primary and secondary (tertiary), when detected.

The cumulative flux technique consists of calculating the flux of the source at increasingly large radii. In particular, for each target the flux is calculated by summing over concentric annuli centred on the source centre and corrected for the projected position of the disc (PA and inclination from Table 5). The annuli are increased in steps of dr = 0.″05 (one-third of the angular resolution of the data), and the flux uncertainty in each annulus is estimated as the standard deviation of the fluxes in 100 random annuli selected well outside the disc. We consider the error on the disc parameters calculating three cumulative flux curves assuming in each of these either the maximum or minimum allowed values for the PA and inclination of the ellipses given the errors on these two quantities. In this way, both the uncertainty due to the (statistical) standard deviation of fluxes (random annuli in the field) and to the uncertainty on the stellar masses (uncertainty on PA and i) are considered.

Once the maximum flux is calculated, we estimate the disc radius Rdisc (or R95) as the radius containing 95% of the total flux and the effective disc radius Reff (or R68) as that containing 68% of the total flux. The uncertainty on the radius is calculated considering the statistical error on the maximum flux and, as the error on the radius estimate must be at least half of the resolution, we summed this error in quadrature with 0.″075.

A different procedure from the one described above was applied in the case of the HK Tau B disc. For this target, known from the literature to be an edge-on disc (e.g. McCabe et al. 2011; Jensen & Akeson 2014), the vertical structure in the gas emission is more extended than the continuum. Assuming an inclination of ~85° (McCabe et al. 2011; Jensen & Akeson 2014) would lead to a much larger estimated gas radius than the separation between the components of the HK Tau system. To correct for this effect, the disc radius is measured along the major axis, centring on the source rectangles with increasing width and fixed height (i.e. fixed to the HK Tau beam size in that direction, ~0.″25), and rotated by the PA of the disc. No significant change in the estimated disc radius was found when modifying the height of the rectangles from 0.″10 to 0.″25. The size of the dust disc is instead affected by optical depth effects. Being an almost edge-on disc, the brightness profile of HK Tau B is less peaked at small radii (near the disc centre) because of dust self-absorption (Villenave et al. 2020). The observed profile is dominated by the emission from larger radii, where the disc is colder, resulting in a larger estimate of its radius (see Sect. 5.1 for further details).

As the RW Aur system is known to experience interaction between the components (Rodriguez et al. 2018), in order to avoid considering the emission due to the interaction, the 12CO total flux of the RW Aur A and B discs was assumed to be the enclosed flux closest to that estimated through the CASA tool imfit (two-Gaussian fit), namely 3.661 ± 0.094 Jy km s−1 and 0.949 ± 0.076 Jy km s−1, respectively. As the southern part of the 12CO emission of the circumprimary disc of DH Tau is absorbed by the cloud (Fig. A.1), we applied the cumulative flux technique only on the northern part, masking the emission from the southern half of the disc. The PA of the DH Tau A disc is ~180°, and so we masked the emission observed below a line with PA = 90° centred on the source centre. We also masked the southern part of the UZ Tau Wa disc and the northern part of the UZ Tau Wb disc, both in the continuum and 12CO emission, in order to exclude emission arising from the other component of the system. As the PA of UZ Tau Wa and Wb discs is ~270°, we drew two lines with PA = 90° centred on UZ Tau Wa disc centre and UZ Tau Wb disc centre and we masked the emission observed below and above each line, respectively.

Figures 5 and 6 show the cumulative flux curves for each disc in the sample. The first columns show the cumulative sum of the fluxes measured on the continuum emission from the data by Manara et al. (2019) and the new data; the second, third, and fourth columns show the cumulative flux relative to the 12CO, 13CO, and C18O emission, respectively. The blue lines show the total fluxes (see Table 6), while the red lines show the disc radii (R95, see Table 7).

Table 7 shows the estimated radii and their error for each disc, while Fig. 7 shows the ellipses including 95% (solid) and 68% (dashed) of the total flux overlapped to the zeroth moment maps. As shown by the red solid ellipses, the radii estimated with the cumulative flux technique get the very outer extent of the discs, where little emission is detected, providing the possibility to test tidal truncation models. Table 6 shows the total fluxes we estimated for each disc with the cumulative flux technique applied on the continuum image and on the 12CO, 13CO, and C18O zeroth moment images.

The effective disc radii estimated for the RW Aur system are in very good agreement with the ones reported in Rodriguez et al. (2018), and were estimated using the CASA built-in measurement tool (McMullin et al. 2007), both for the circumprimary and the circumsecondary discs: ~58 au and ~38, respectively, at a distance of 140 pc (assumed by Rodriguez et al. 2018).

Table 5

Source centres (ra,dec), inclination i, PA, and systemic velocity υLSR for all discs in the analysed sample.

thumbnail Fig. 5

Cumulative fluxes as a function of aperture radius estimated using the cumulative flux technique. Each panel shows the fluxes for a different data set or image (the name of the target for each row is shown in the lower right corner of the first column). First column: continuum emission of the data from Manara et al. (2019) (green dots) and the continuum emission from the new data (black dots). Second, third, and fourth columns: the 12CO, 13CO, and C18O moment zero emission from the new data, respectively. The blue dashed lines show the estimated disc total fluxes; the red solid lines show the disc radii, which are defined as the radii containing 95% of the total flux (see values reported in Tables 6 and 7). In the first column, only the total fluxes and disc radii estimated from the new continuum data are shown.
thumbnail Fig. 6

Cumulative flux curves as a function of aperture radius estimated using the cumulative flux technique. Same as in Fig. 5 but for the remaining discs in the sample. The total fluxes and disc radii estimated from the continuum data from Manara et al. (2019) are shown in the case of RW Aur A and В discs (first column, last two rows). In all the other cases, the total fluxes and disc radii estimated from new continuum data are shown.
thumbnail Fig. 7

12CO zeroth moment images of the discs with overlapping ellipses including 95 (solid) and 68% (dashed) of the total flux. The ellipses are centred on the target source centre. All bars in the bottom right of each panel are of 1.″0 in length, which is ~140 au at the distance of Taurus. The beam FWHM size is shown in the bottom left of each panel. In each image, the colour scale has the peak flux as the maximum, and two times the image rms as minimum. White contours show five times the rms of the continuum emission.
Table 6

Total fluxes measured with the cumulative flux technique.

5 Discussion

5.1 Comparing dust and gas disc radii

The emission arising from the dusty component of discs, and thus the dust disc radius measurement, is regulated by several processes, such as growth, fragmentation, and transport of dust. On the contrary, the gas emission extent is regulated by chemical processes and by the dynamics of the disc, which in our case means the tidal interaction of the components of the multiple systems we are studying. Here we investigate whether the ratio between the sizes of the discs (defined as the radius containing 95% of the total flux) measured in the 12CO gas component and in the dust component (Rdisc,gas/Rdisc,dust) is different in systems where tidal truncation is at work with respect to more isolated systems.

The ratio Rdisc,gas/Rdisc,dust has been studied in a limited number of targets in Taurus (Kurtovic et al. 2021), and in a larger sample in the Lupus star-forming region first analysed by Ansdell et al. (2018), and recently revised by Sanchis et al. (2021). The ratio Rdisc,gas/Rdisc,dust in mostly isolated or wide binary systems in the Lupus star-forming region has a median and a mean value of ~2.5 and ~2.8, respectively, both when considering the radii at 68 and 95% of the total flux. In general, the larger gas sizes can be explained as a combination of the effect of radial drift of dust, and of the different opacity between the two components (e.g. Facchini et al. 2017; Trapman et al. 2020). Sanchis et al. (2021) noted that the gas disc to dust disc size ratios and the stellar masses are uncorrelated, contrary to expectations from theoretical and observational works suggesting that the radial drift is more effective in discs around low-mass stars (e.g. Pascucci et al. 2016; Pinilla et al. 2013). For the sake of this work, the lack of any correlation between these two quantities assures us that we can carry out a comparison between our results and those of Sanchis et al. (2021) with no bias due to the different stellar mass distributions.

For the following discussion, we use the values of Rdust obtained by Manara et al. (2019) by modelling the continuum data in the visibility plane using the Galario library (Tazzari et al. 2018) because this makes the results directly comparable with Sanchis et al. (2021), who performed a similar analysis. Our sample of multiple system reveals that the gas disc radii are typically about two to four times larger than the dust disc radii, for both the effective gas-to-dust radii R68,gas/R68,dust and the gas-to-dust disc radii R95,gas/R95,dust (Fig. 8). As shown by Fig. 8, the disc of HK Tau B is the biggest outlier in the gas-to-dust size ratio distribution, with R95,gas/R95,dust ~ 1. As it is an almost edge-on disc, this small ratio may be due to optical depth effects, resulting in overestimation of the dust radius and, as a consequence, underestimation of the gas-to-dust disc radius ratio. We therefore decided to exclude the HK Tau B disc from the statistical analysis discussed below.

The average value (and relative standard deviation) of R68,gas/R68,dust is 3.2 ± 1.1 (3.1 ± 1.1 and 3.4 ± 0.9 for circumprimary and circumsecondary discs, respectively), and R95,gas/R95,dust = 4.2 ± 1.6 (with average values of 3.9 ± 1.2 for circumprimary discs and 5.0 ± 1.9 for the circumsecondary). The Kolmogorov-Smirnov (K-S) two-sided test for the null hypothesis that the samples of gas-to-dust disc size ratios around primary stars and around secondary stars are drawn from the same continuous distribution leads to a p-value of ~0.06 (for both the 68 and the 95% ratios), confirming that the circumprimary and circumsecondary discs are likely to be drawn from the same distribution (see Fig. 11).

Figure 9 shows the ratio Rdisc,gas/Rdisc,dust as a function of the projected separation of the components in the systems. No evidence of a correlation between the size ratio and the projected separation is shown, suggesting that the gas-to-dust disc size ratio does not depend on the distance between the components in the system. Other features, such as the eccentricity of the orbits, need to be considered to explain the observed distribution of size ratios (see Sect. 5.2).

Figures 10 and 11 show the comparison between the 95 and the 68% gas-to-dust disc size ratios measured in our sample of multiple stellar systems in the Taurus region, and those measured by Sanchis et al. (2021) for 42 discs in the Lupus star-forming regions, which are mainly single-star systems or, in two cases, wide binary systems with separations of ~1000 au, which is large enough that the discs are not affected by tidal truncation (Pearce et al. 2020).

The effective ratio R68,gas/R68,dust estimated in Taurus multiple system is in very good agreement with the average ratio obtained in the sample of discs around single stars by Sanchis et al. (2021) (~3.2 vs. ~2.8, respectively). The K-S test performed on these two samples confirms that the gas-to-dust disc size ratios in Taurus multiples are likely to be drawn from the same distribution of Lupus single discs (p-value ~0.13). On the contrary, the R95,gas/R95,dust average ratio in Taurus multiple systems is larger than the ratio estimated by Sanchis et al. (2021), with the K-S test confirming the two samples to be statistically different (p-value ~0.012).

The difference in the values of R95,gas/R95,dust estimated in discs around binaries and in singles is possibly due to the sharp truncation of the outer dusty discs in binary systems (Manara et al. 2019). However, this difference may also be affected by the method through which the gas disc radii have been estimated. As discussed, we applied the cumulative flux technique directly to the zeroth moment image, with no parametric form to model the emission profile, while Sanchis et al. (2021) modelled the CO emission of each disc by fitting the integrated line map to a Gaussian (or a Nuker) profile in the image plane before applying the cumulative flux technique on the modelled emission profile. The latter method may lead to underestimation of the 95% disc radii, smoothing the outer emission of the discs.

In general, we conclude that the ratio between the sizes of gas and dust discs in multiple stellar systems is found to be on the higher side of the distribution of values when compared to a population of more isolated systems and considering the 95% disc radius, which is more sensitive to the full disc size.

Table 7

Radii estimated with the cumulative flux technique.

thumbnail Fig. 8

12CO estimated radii as a function of dust radii obtained with (u, υ)-plane modelling of the continuum data by Manara et al. (2019). Dust and gas radii estimated as the radii including 68 (right) and 95% (left) of the total flux. The red circles are for circumprimary discs, while blue squares for the circumsecondary.
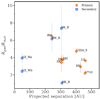thumbnail Fig. 9

Gas-to-dust disc size ratios (R95,gas/R95,dust) as a function of the projected separation. The red circles are for circumprimary discs, while blue squares show circumsecondary discs.

5.2 Comparison of gas disc radii with tidal truncation models

We now compare the observed 12CO disc radii with the theoretical expectations for tidal truncation predicted by Artymowicz & Lubow (1994). As discussed by Manara et al. (2019), and references therein, it can be analytically computed that the truncation radius for a disc in a binary system with a circular orbit inclined along the plane of the sky (eccentricity e = 0, mass ratio q =1, disc orbit misalignment = 0°) is ~0.33 a, where a is the semi-major axis of the binary orbit. The value of the truncation radius becomes larger for the circumprimary disc when the mass ratio q is smaller than 1, and smaller for the circumsecondary disc for smaller values of q. The truncation radii instead decrease with higher eccentricities both in circumprimary and circumsecondary discs. For systems with e ≳ 0.9, more violent processes than the disc–satellite interaction would occur, such as the collision between the disc and the companion star.

Let us first assume that the projected separation ap is ~a, which again is correct if the orbit has low eccentricity and the plane of the orbit is aligned close to the plane of the sky, and compare the estimated gas disc radii R95,gas with the projected separation between the components (reported in Table 1). As the UZ Tau system is a quadruple system (with UZ Tau E being a spectroscopic binary), when comparing observations with analytical models, we consider the UZ Tau system as two binaries. The first binary is composed of UZ Tau E and UZ Tau Wab (considering the sum of the masses of UZ Tau Wa and Wb), and has a projected separation of 3.″52 (assuming the position of UZ Tau Wab as the centre of mass of the two stars); the second binary is composed of UZ Tau Wa and UZ Tau Wb, and has ap = 0.″375.

Figure 12 shows that the typical observed ratio R95,gas/ap in our sample is ~0.15–0.35, and more specifically >0.1 in all targets, contrary to the typical ratio of ≲0.1 measured for the dust radii in Manara et al. (2019). This typical observed ratio is due to the fact that the gas disc radii are larger than the dust disc radii, as discussed in Sect. 5.1, and already suggested by Manara et al. (2019). However, this is the first time that this value R95,gas/ap is measured in a large sample of objects.

The observed distribution of gas disc radii points to the fact that the data do not agree with a simple description, as the ratio R95,gas/ap typically differs from the expected value of 0.33 (only 2/13 discs show a ratio of ~0.33). Therefore, a more detailed comparison is to be considered. To better quantify this result, we compare R95,gas/ap with theoretical models by Artymowicz & Lubow (1994), using the equation derived by Manara et al. (2019) under the assumption that the discs and the binary orbit are co-planar: Rtruncap=0.49⋅qi2/30.6⋅qi2/3+ln(1+qi1/3)(b⋅ec+0.88μ0.01)⋅[ 1−e21+e⋅cosv1−sin2(ω+v)sin2i ]−1,$\matrix{{{{{R_{{\rm{trunc}}}}} \over {{a_{\rm{p}}}}}} \hfill & = \hfill & {{{0.49 \cdot q_i^{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}} \over {0.6 \cdot q_i^{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}} + \ln \left({1 + q_i^{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} \right)}}\left({b \cdot {e^c} + 0.88{\mu ^{0.01}}} \right)} \hfill \cr {} \hfill & {} \hfill & {\cdot {{\left[{{{1 - {e^2}} \over {1 + e \cdot \cos v}}\sqrt {1 - {{\sin}^2}\left({\omega + v} \right){{\sin}^2}i}} \right]}^{- 1}},} \hfill \cr} $(1)

where v the true anomaly, ω the longitude of periastron, and i the inclination of the plane of the orbit with respect to the line of sight, qi is the mass ratio (either q1 = M1/M2 or q2 = q = M2/M1), and b and c are the parameters derived by Manara et al. (2019) that depend on the disc viscosity or equivalently on the Reynolds number, ℛ. Figure 13 shows this comparison in the case of zero-eccentricity orbits (e = 0) and inclination of the orbit i = 0. Excluding the discs around UZ Tau E and CIDA 9 A and the disc around RW Aur A, the measured values of the observed ratios point to disc radii that are typically smaller than expectations from tidal truncation models at zero eccentricity.

As discussed in Manara et al. (2019), at a given inclination of the orbital plane i, the truncation radius Rt in units of the projected separation ap has a minimum when the secondary star is observed at the apoastron − ap = a(1 + e) – and has a maximum at the periastron − ap = a(1 − e): 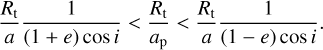Rta1(1+e)cosi<Rtap<Rta1(1−e)cosi.${{{R_{\rm{t}}}} \over a}{1 \over {\left({1 + e} \right)\cos i}} &lt; {{{R_{\rm{t}}}} \over {{a_{\rm{p}}}}} &lt; {{{R_{\rm{t}}}} \over a}{1 \over {\left({1 - e} \right)\cos i}}.$(2)

The minimum ratio is found at i = 0° and Rt/ap increases for higher orbital inclination. In Fig. 14, we plot the ratio of the truncation radius to the projected separation of the orbit as a function of eccentricity for all the targets in the sample, assuming an orbital inclination i = 0° with respect to the line of sight. The intersection between the observed Rt/ap (red bands in Fig. 14) and the theoretical model assuming that the secondary is observed at apoastron (lower black curves in the figure) represents the minimum possible value of the eccentricity for the system. This statement holds even in the case where the orbital plane of the binary is misaligned with respect to the disc (i > 0°), because the black curves in Fig. 14 will move to higher values leading to a larger minimum eccentricity. As an example, we refer to the V710 A disc (second row, last column in the figure). To be compatible with tidal truncation models, the observed ratio of disc radius to separation must lie between the bottom and the top black curves. The observed ratio is shown as a red band in the plot, from which we see that, in this case, the eccentricity must be larger than ≃0.2. For inclined orbits, the minimum eccentricity must be even larger. The dominant uncertainty on the eccentricity estimated in this way comes from the lack of information on the local Reynolds number, and hence different Reynolds numbers are assumed − ℛ = 104,105,106.

For each target, Table 8 shows the ratio between disc radii and separations predicted by the models assuming e = 0 and the observed ratio between disc radii R95,gas and projected separations. Finally, the minimum eccentricities of the orbits estimated assuming zero orbital inclination and physical separation a between the components that matches the projected separation ap are shown in the last column in Table 8 and in Fig. 15.

The tidal truncation models assuming face-on inclination of the orbit cannot explain the observed large values of Rt/ap in the CIDA 9, UZ Tau, and RW Aur systems, except assuming unrealistic parameters (e ~ 1 and targets observed at the periastron); this can be explained either by a high inclination of the orbit with respect to the plane of the sky or by the fact that the disc sizes are regulated by other additional processes (e.g. substructures and interaction between the components) – in addition to tidal truncation – that are not included in the model. Excluding these systems, the estimated minimum eccentricities show typical values of ~0.15−0.5 and an average value of ~0.3, in very good agreement with the observed distribution of eccentricities for main sequence binary systems of low mass (e.g. Duchêne & Kraus 2013). This is observational conformation of the result by Zagaria et al. (2021b) that no highly eccentric orbits need to be invoked to explain the observed small dust radii of discs in multiple stellar systems. When comparing both the circumprimary and circumsecondary disc sizes to the models, a comparison only possible in DK Tau and HK Tau systems, very good agreement with the two estimated eccentricities is found.

We finally explore whether more eccentric orbits would have an impact on the relative sizes of the gas and dust components of discs, as predicted by previous theoretical works (e.g. Clarke & Pringle 1993). Figure 16 shows that no correlation is observed between the observed gas-disc to dust-disc size ratios and the estimated eccentricity of the orbits. However, to definitively refute a dependence of the gas-disc to dust-disc size ratio on the eccentricity, it is necessary to significantly increase the sample of systems with measured size ratio and eccentricity.

thumbnail Fig. 10

Comparison between the gas-to-dust size ratio for discs in the Taurus binaries (red and blue triangles) and for single discs in Lupus (grey diamonds). Effective disc radii R68 (left) and disc radii R95 (right) are shown.
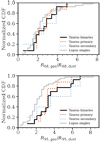thumbnail Fig. 11

Normalised cumulative distribution function for the gas-to-dust effective disc sizes R68,gas/R68,dust (top) and for the gas-to-dust disc sizes R95,gas/R95,dust (bottom) for discs around single stars in Lupus (grey, Sanchis et al. 2021) and discs around multiple stellar system in Taurus (black). Discs around primary stars in Taurus are shown in red, while circumsecondary discs in Taurus are shown in blue.
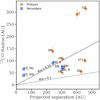thumbnail Fig. 12

Observed 12CO gas radii as a function of the projected separation. Blue squares refer to the circumsecondary discs, while red circles to the circumprimary discs.
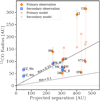thumbnail Fig. 13

12CO gas radii as a function of the projected separation. Blue squares and red circles show the observed ratio in the circumsecondary discs and the circumprimary discs, respectively. Blue plus symbols and red crosses show the expected ratio from the tidal truncation model in the case of circular orbits (e = 0) for circumsecondary discs and circumprimary discs, respectively. The longer the dashed line that links observed radii with models, the weaker the agreement with the zero-eccentricity model.

5.3 Disc misalignment

The amount of alignment of the plane of rotation of the disc in a multiple system can be used as a constraint to star formation models. In the most simplified case, disc fragmentation would tend to form close binaries with aligned angular momentum vectors, while turbulent fragmentation would produce more randomly distributed binary orientation (e.g. Bate 2000, 2018; Offner et al. 2010; Kratter et al. 2010). It is therefore instructive to explore the observed values of the relative inclinations for the discs in our sample for use in constraining disc evolution models in multiple systems.

Figure 17 shows the alignment of discs around the components of the multiple systems in which both components are detected and resolved. The PAs and inclinations used to make this comparison are those reported in Table 5. The first two letters of the system name are labelled. In the case of the UZ Tau system, we compare the UZ Tau E disc with the UZ Tau Wab discs separately (labeled as UZ_Wa and UZ_Wb), and the UZ Tau Wa disc with the UZ Tau Wb disc. The inclination of the components of the multiple systems appears to be different in most cases (top panel), with only the east and west components of UZ Tau showing some agreement. The PAs of the discs are also usually similar, with the exception of the HK Tau discs, which show different values (bottom panel).

However, the degree of alignment should be explored using the relative inclination of the discs, computed using the spherical law of cosines: cos(∆i) = cos(i1) · cos(i2) + sin(i1) sin(i2) cos(Ω1 − Ω2), with i the inclination (ambiguous in sign, so that it leads to two families of solutions) and Ω the PA. The result is shown in Fig. 18. The discs in the UZ Tau system show relative inclination differences ≲0–20°, while the RW Aur, DK Tau, and HK Tau systems show a larger relative inclination (~25°, ~40°, and ~50°, respectively). For the latter, this is in line with the earlier results of Jensen & Akeson (2014). We conclude that most of the observed binaries appear not to be coplanar, possibly a result of turbulent fragmentation, rather than disc fragmentation.

thumbnail Fig. 14

Condition on the eccentricity of the stellar orbits for which the estimated truncation radii of the discs in the sample are in agreement with theoretical predictions (see Sect. 5.2). Red bands show the estimated R95,gas/ap with their uncertainties. Black curves show the expected truncation radius in units of the projected separation for different Reynolds numbers: dashed curves for ℛ = 104, solid for ℛ = 105, and dotted for ℛ = 106. The lower black curves are obtained assuming that the secondary is observed at apoastron, while black curves at the top assuming that the secondary is located at periastron. The expected Rt/ap increases for higher orbital inclination, and thus the black curves would move to higher values in the plot if the assumption of face-on orbits is not fulfilled (see Eq. (2)).
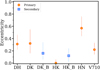thumbnail Fig. 15

Estimated minimum eccentricities for each target. Red circles refer to circumprimary discs, while blue squares refer to circumsecondary discs.
Table 8

Comparison between observed disc radii and tidal truncation models.

thumbnail Fig. 16

Gas-disc to dust-disc size ratios (R95,gas/R95,dust) as functions of the minimum eccentricities of the orbits. Red circles refer to circumprimary discs, while blue squares refer to circumsecondary discs.

6 Conclusions

Here we present new Band 6 ALMA observations of CO line and continuum emission in ten multiple stellar systems in the Taurus star-forming region. The observed sample comprises seven binaries, one triple, one quadruple, and one star that is part of a very wide binary system, and was observed at a spatial resolution of ~0.″15 and with an integration time of ~40 min/target. Three systems (GK Tau, UY Aur and T Tau) were not analysed here. One additional multiple system, RW Aur, was also included in the analysis using ALMA archival data. Of this sample, eight multiple stellar systems were analysed in this work.

We derived the disc geometrical properties using the eddy tool (Teague 2019), and then performed an image plane analysis of the data to estimate the disc total fluxes with a cumulative flux technique. Assuming as disc radii those enclosing a certain fraction of the total disc flux (68 or 95%), we compared the gas radii to the dust radii estimated by Manara et al. (2019), and derived the gas-disc-to-dust-disc size ratio to be between approximately two and four. The effective (68%) gas-disc-to-dust-disc size ratio distribution is found to be statistically compatible with the ratio estimated by Sanchis et al. (2021) in a population of single discs. On the contrary, considering the 95% disc radius, the gas-disc-to-dust-disc size ratio is found to be on the high end of the distribution of the gas-disc-to-dust-disc size ratios measured in a population of more isolated systems, which is possibly due to the sharp truncation of the outer dusty discs in binary systems (Manara et al. 2019).

We compared our estimates with analytical predictions for the tidal truncation on disc sizes in binary systems (Artymowicz & Lubow 1994). In general, the 95% gas disc radii are ~0.15–0.35 times the projected separation of the binaries, suggesting that the systems are not in circular orbits. Exceptions to this typical ratio are the discs around UZ Tau E, CIDA 9 A, and RW Aur, which show very large ratios, possibly due to projection effects or additional processes regulating disc truncation (e.g. substructure for the first two systems and interaction between the component for RW Aur). When comparing these ratios with the theoretical predictions, the minimum eccentricities of the orbits are 0 ≲ e ≲ 0.5, with an average value of ~0.3, in good agreement with expectations (e.g. Duchêne & Kraus 2013). Finally, the discs in multiple systems appear to be misaligned, possibly a result of turbulent fragmentation.

This study shows the importance of deep ALMA observations of line emission from discs in multiple stellar systems in deriving their sizes and constraining models of tidal interactions. Future studies targeting multiple systems should aim at larger samples and should cover a larger span of binary separations, in particular focusing on the shorter separations.

thumbnail Fig. 17

Comparison between the PAs (top) and inclination (bottom) for the discs around the primary and the secondary in each multiple stellar system where both discs are detected and resolved. We considered the UZ Tau system as two binaries, comparing UZ Tau E parameters with UZ Tau Wab parameters (comparison labeled as UZ_Wa and UZ_Wb for the two UZ Tau Wab discs) and UZ Tau Wa parameters with UZ Tau Wb parameters (comparison labeled as UZ_Wab). In the other cases, the first two letters of the target name are labelled.
thumbnail Fig. 18

Relative inclination of the discs in each multiple stellar system as a function of their projected separation. We considered the UZ Tau system as two binaries, comparing UZ Tau E parameters with UZ Tau Wab parameters (comparison labeled as UZ_Wa and UZ_Wb for the two UZ Tau Wab discs) and UZ Tau Wa parameters with UZ Tau Wb parameters (comparison labelled as UZ_Wab). In the other cases, the first two letters of the target name are labelled.

Acknowledgements

We thank the anonymous referee for the comments that greatly improved this paper. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2018.1.00771.S, ADS/JAO.ALMA#2016.1.00877.S, ADS/JAO.ALMA#015.1.01506.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. The authors are thankful to Joey Rodriguez for sharing the reduced CO cubes for RW Aur, to Enrique Sanchis for sharing the values of the gas disc radii prior to publication, and to Leonardo Testi for very helpful tips on the self-calibration of the data. A.A.R. thanks Cristiano Longarini for useful discussions. A.A.R. acknowledges support from ESO for a six month visit through the SSDF Funding. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 823823 (DUSTBUSTERS). This work was partly supported by the Deutsche Forschungs-Gemeinschaft (DFG, German Research Foundation) – Ref no. FOR 2634/1 TE 1024/1-1. M.T. has been supported by the UK Science and Technology research Council (STFC) via the consolidated grant ST/S000623/1, and by the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 823823 (RISE DUSTBUSTERS project). F.Me, G.v.d.P. acknowledge funding from ANR of France under contract number ANR-16-CE31-0013. H.-W.Y. acknowledges support from Ministry of Science and Technology (MOST) in Taiwan through the grant MOST 108-2112-M-001-003-MY2. P.P. acknowledges support provided by the Alexander von Humboldt Foundation in the framework of the Sofja Kovalevskaja Award endowed by the Federal Ministry of Education and Research. E.R. acknowledges financial support from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 681601 and No. 864965). F.L. acknowledges support from the Smithsonian Institution as the Submillimeter Array (SMA) Fellow. D.H. is supported by CICA through a grant and grant number 110J0353I9 from the Ministry of Education of Taiwan.

Appendix A Maps and spectra for the whole sample

In this section, we report the maps, the spectra, and the channel maps of all analysed and detected targets. Although in this work we focus on the 12CO emission, the targeted emission lines also include CO isotopologues 13CO and C18O.

The continuum and CO zeroth and first moment maps are shown with the integrated spectra for all targets in Figure A.1. The detected discs (see Table 3) show a rotation pattern that is fitted with eddy (Section 4.1). The channel maps shown in Figures A.2-A.8 were also used to identify the channels affected by absorption due to the foreground molecular cloud, which is particularly pronounced in the 12CO emission. The velocity ranges affected by cloud absorption are reported in Table 4, and excluded from the analysis with eddy.

thumbnail Fig. A.1

Images and spectra of all targets in the analysed sample. Each row refers to a system in the sample. The first columns show the continuum images with the names of the targets indicated in the top left. The second, fourth, and sixth columns show the zeroth moment images for the 12CO, the 13CO, and the C18O emission, respectively, scaled so that the maximum is equal to the peak flux and the minimum is clipped at the image rms. The third, fifth, and seventh columns show the first moment images (calculated through the bettermoments tool) for the 12CO, 13CO, and C18O emission, respectively, scaled so that the maximum and the minimum are equal to the systemic velocity of the target ±2 km/s. The FWHM beam size is shown in the bottom left of each panel. All bars in the bottom right of each panel are 0.″5 long. The last two columns show the 12CO and 13CO spectra of the circumprimary (red), circumsecondary (blue), and circumtertiary (green) discs (when applicable), with vertical black lines showing the systemic velocities fitted with the eddy tool and grey band showing the excluded absorbed velocities in eddy fitting on circumprimary disc rotation maps (see Table 4).
thumbnail Fig. A.2

Channel maps of the 12CO emission in the CIDA 9 A disc. Each panel shows the velocity of the channel in the upper left corner. The FWHM beam size is shown in the bottom left. The images are scale so that the maximum is equal to the peak flux and the minimum is clipped at the image rms. White contours show 5, 30, and 100 times the rms of the continuum emission.
thumbnail Fig. A.3

Channel maps of the 12CO emission in the DH Tau A disc. Panels and symbols are as in Figure A.2.
thumbnail Fig. A.4

Channel maps of the 12CO emission in the DK Tau discs. Panels and symbols are as in Figure A.2.
thumbnail Fig. A.5

Channel maps of the 12CO emission in the HK Tau discs. Panels and symbols are as in Figure A.2.
thumbnail Fig. A.6

Channel maps of the 12CO emission in the HN Tau A disc. Panels and symbols are as in Figure A.2.
thumbnail Fig. A.7

Channel maps of the 12CO emission in the UZ Tau discs. Panels and symbols are as in Figure A.2.
thumbnail Fig. A.8

Channel maps of the 12CO emission in the V710 Tau A disc. Panels and symbols are as in Figure A.2.

Appendix B Comparison between new continuum data and older continuum data

As described in Sect. 2, the new data analysed here have been taken for the same sample as the one presented by Manara et al. (2019) and Long et al. (2019). The main differences between these samples, in addition to the presence in the new one of the 12CO emission, are the spatial resolution and the sensitivity of the observations. The new data have slightly poorer spatial resolution (0.″15 vs 0.″12) and better sensitivity (~30 μJy rms vs ~50μJy beam−1). Whereas this work focuses on the analysis of the gas emission, we discuss here the differences between the two data sets in the continuum emission, and describe our motivation for the choices of data sets and analysis techniques used to discuss our results.

We first show in Figure B.1 that the measured flux of the continuum emission measured on the data presented by Manara et al. (2019) agrees with the total flux measured on the new data within the 10% uncertainty that is usually assumed on ALMA flux measurements. Exceptions to this good agreement are the circumsecondary discs around the stars in the UZ Tau system, whose fluxes differ by ~20 – 30%.

We then compare the measured sizes of the discs using the old and new data, accounting for the differences in resolution and method. Images of interferometric data are always the result of the convolution of the effective beam of the interferometer with the intensity profile of the science target, i.e. the disc. The size of the beam therefore has a greater effect when it is close to the physical size of the target. In order to estimate the impact of the beam on our measurements, we first neglect the fact that the beam is elliptical with beam major axis BMAJ and minor axis BMIN, and we make the assumption that the beam can be modelled as a one-dimensional Gaussian: 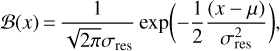ℬ(x)=12πσresexp(−12(x−μ)σres2),${\cal B}\left(x \right) = {1 \over {\sqrt {2\pi} {\sigma_{{\rm{res}}}}}}\exp \left({- {1 \over 2}{{\left({x - \mu} \right)} \over {\sigma_{{\rm{res}}}^2}}} \right),$(B.1)

where μ is the source centre and the standard deviation σres is linked to the beam size Г (FWHM beam) as 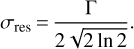σres=Γ22 ln 2.${\sigma_{{\rm{res}}}} = {{\rm{\Gamma}} \over {2\sqrt {2\,\ln \,2}}}.$(B.2)

The convolution of the beams size with the intrinsic (‘true’) intensity profile of the disc is then calculated under the corresponding assumption that the disc can be described with a one-dimensional Gaussian. Hence, the standard deviation σtrue of the Gaussian is equal to the effective disc radius R68,true (since the effective disc radius is defined as the radius containing the 68% of the total flux). The convolution between these two Gaussians is a one-dimensional Gaussian with standard deviation equal to 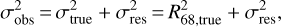σobs2=σtrue2+σres2=R68,true2+σres2$\sigma_{{\rm{obs}}}^2 = \sigma_{{\rm{true}}}^2 + \sigma_{{\rm{res}}}^2 = R_{68,{\rm{true}}}^2 + \sigma_{{\rm{res}}}^2$(B.3)

which represents the observed effective disc radius: σobs ≡ R68,obs.

Table B.1

Beam sizes of the observations by Manara et al. (2019).

The data analysed here have a spatial resolution of 0.″15, whereas the observations analysed by Manara et al. (2019) had an angular resolution of 0.″12. Tables 2 and B.1 show for each target the synthesised beams of the observations respectively for the new data and the data by Manara et al. (2019). As we are assuming a one-dimensional Gaussian intensity profile and beam, we are neglecting the PA effect both of the disc and of the beam. Hence, the minimum BMIN gives an estimate of the best beam resolution, while the maximum BMAJ gives an estimate of the worst beam resolution. In the continuum data by Manara et al. (2019), the minimum BMIN and the maximum BMAJ are respectively Γmin,old = 0.″099 and Γmax,old = 0.″142 (BMIN of CIDA 9 and BMAJ of HN Tau, respectively). In the new continuum data, the minimum BMIN and the maximum BMAJ are respectively Γmin,new = 0.″120 and Γmax,new = 0.″282 (BMIN of HN Tau and BMAJ of V710 Tau, respectively). In this way, the maximum effect on the ratio of the beam size between the data by Manara et al. (2019) and the new data is given by σobs,newσobs,old|max(σtrue)=σtrue2+[ Γmax,new/(22 ln 2) ]2σtrue2+[ Γmin,old/(22 ln 2) ]2,${\left. {{{{\sigma_{{\rm{obs}},{\rm{new}}}}} \over {{\sigma_{{\rm{obs,old}}}}}}} \right|_{\max}}\left({{\sigma_{{\rm{true}}}}} \right) = \sqrt {{{\sigma_{{\rm{true}}}^2 + {{\left[{{{{{\rm{\Gamma}}_{{\rm{max}},{\rm{new}}}}} \mathord{\left/ {\vphantom {{{{\rm{\Gamma}}_{{\rm{max}},{\rm{new}}}}} {\left({2\sqrt {2\,\ln \,2}} \right)}}} \right. \kern-\nulldelimiterspace} {\left({2\sqrt {2\,\ln \,2}} \right)}}} \right]}^2}} \over {\sigma_{{\rm{true}}}^2 + {{\left[{{{{{\rm{\Gamma}}_{{\rm{min}},{\rm{old}}}}} \mathord{\left/ {\vphantom {{{{\rm{\Gamma}}_{{\rm{min}},{\rm{old}}}}} {\left({2\sqrt {2\,\ln \,2}} \right)}}} \right. \kern-\nulldelimiterspace} {\left({2\sqrt {2\,\ln \,2}} \right)}}} \right]}^2}}}} ,$(B.4)

where σtrue is the true effective disc radius, i.e. R68,true. On the contrary, the minimum effect is given by σobs,newσobs,old|min(σtrue)=σtrue2+[ Γmin,new/(22 ln 2) ]2σtrue2+[ Γmax,old/(22 ln 2) ]2.${\left. {{{{\sigma_{{\rm{obs,new}}}}} \over {{\sigma_{{\rm{obs,old}}}}}}} \right|_{{\rm{min}}}}\left({{\sigma_{{\rm{true}}}}} \right) = \sqrt {{{\sigma_{{\rm{true}}}^2 + {{\left[{{{{{\rm{\Gamma}}_{\min ,{\rm{new}}}}} \mathord{\left/ {\vphantom {{{{\rm{\Gamma}}_{\min ,{\rm{new}}}}} {\left({2\sqrt {2\,\ln \,2}} \right)}}} \right. \kern-\nulldelimiterspace} {\left({2\sqrt {2\,\ln \,2}} \right)}}} \right]}^2}} \over {\sigma_{{\rm{true}}}^2 + {{\left[{{{{{\rm{\Gamma}}_{\max ,{\rm{old}}}}} \mathord{\left/ {\vphantom {{{{\rm{\Gamma}}_{\max ,{\rm{old}}}}} {\left({2\sqrt {2\,\ln \,2}} \right)}}} \right. \kern-\nulldelimiterspace} {\left({2\sqrt {2\,\ln \,2}} \right)}}} \right]}^2}}}} .$(B.5)

If the disc is described by a one-dimensional Gaussian intensity profile, as R95,true is defined as the radius containing 95% of the total flux, R95 ≡ 2R68. Therefore, when estimating the maximum and minimum effect of the difference in the beam size as a function of the disc radii R95 the factor two simplifies, and Equations (B.4) and (B.5) hold with σtrue expressing the dust disc radii R95.

Figure B.2 shows these maximum (black solid line) and minimum (black dashed line) effects and compares these estimates with the observed ratio between the dust effective radii (R68, left panel) and the dust radii (R95, right panel) estimated with the cumulative flux technique applied to the data by Manara et al. (2019) and the new continuum data. In general, as shown by the black lines, the smaller the disc size, the greater the beam-size effect, while, as expected, for larger discs the effect due to the different beam size tends towards 1. The general trend of the observed ratio (red circles for circumprimary discs and blue squares for circumsecondary discs) shows good agreement with the estimates (black lines). Figure B.2 also shows a systematic shift on the (y-direction of the observed ratio both between R68 and R95. Such a systematic shift in the ratio between the dust radii R95 (and not between R68) is expected given the difference in integration time between the observations by Manara et al. (2019) and the new observations: ~4 – 9 min/target versus ~40 min/target, respectively. This difference makes the new observations deeper, i.e. more sensitive, than the ones by Manara et al. (2019). However, as mentioned, Figure B.1 shows that the dust fluxes estimated using the new data are in good agreement with those using the data by Manara et al. (2019), with 10% uncertainty usually assumed on ALMA flux measurements. Therefore, in most systems, this systematic shift is probably not due to a sensitivity effect and its cause requires further investigation. In particular, the systematic shift might be due to the assumption on the intensity profile of the disc, which is not a Gaussian, but a profile with less peaked emission in the centre, meaning that 68% (and 95%) of the emission is distributed over a larger radius.

Finally, we compare the radii estimated with the analysis carried out in the (u, υ) plane (Manara et al. 2019) with those obtained with the method used in this work (Sect. 4). This is shown in Figure B.3. With the visibility plane analysis a resolution down to one-third of the beam can be achieved (e.g. Jennings et al. 2020). On the other hand, the cumulative flux technique is performed in the image plane, and therefore the convolution of the beam with the intensity profile of the disc places an intrinsic resolution limit.

The left-hand panel in Figure B.3 shows the comparison between the effective dust radii R68 estimated with the two methods. We cannot identify any particular difference between the two radii estimates, with the only exceptions being the RW Aur discs and the DK Tau B disc. We think that the fit with Galario for RW Aur and the fit with eddy for DK Tau B could have led to spurious results.

On the contrary, in the right panel showing the comparison between the dust radii R95, we can see that the dust radii estimated from the new observations are typically slightly larger than those obtained with the data by Manara et al. (2019). This is due to the cumulative flux technique, which preferentially samples the really outer extent of the discs, where little emission is detected (see Figure 7).

In the visibility plane analysis, a resolution under the beam size is achievable, and so the dust radii estimated using Galario are more reliable, especially for the more compact discs.

thumbnail Fig. B.1

Comparisons between the total disc fluxes measured from the new continuum observation with that measured from the data presented by Manara et al. (2019). The left panel shows the ratio between the total fluxes calculated using the data by Manara et al. (2019) (FManara,c.f.t.) and using the new continuum data (Fnew), both estimated through the cumulative flux technique. The right-hand panel instead reports the ratio using the fluxes calculated by Manara et al. (2019) with the uv-modelling method (FManara,Galario), and using the new continuum data with the cumulative flux technique. Red circles are used for circumprimary discs, blue squares for circumsecondary ones.
thumbnail Fig. B.2

Observed ratio between the dust radii estimated with the cumulative flux technique applied to the data by Manara et al. (2019) and the dust radii from the new continuum data (Rnew/RManara) as a function of the new dust radii (Rnew). Left: Dust radii estimated as the radii including 68% of the total flux (i.e. effective disc radii). Right: Dust radii estimated as the radii including 95% of the total flux. Black lines show the maximum (solid) and minimum (dashed) effect on the ratio of the beam size between the data by Manara et al. (2019) and the new data (see Equations (B.4) and (B.5)). Blue squares refer to the circumsecondary disc and red circles to the circumprimary discs.
thumbnail Fig. B.3

Comparison between dust disc radii estimated with the cumulative flux technique (c.f.t.) applied on the data by Manara et al. (2019) and with those estimated by Manara et al. (2019) with Galario-modelling (Rc.f.t/RGalario). Left: Dust radii estimated as the radii including the 68% of the total flux (i.e. effective disc radii). Right: Dust radii estimated as the radii including the 95% of the total flux. Red circles are used for circumprimary discs, blue square for circumsecondary discs.

References

  1. Akeson, R. L., & Jensen, E. L. N. 2014, ApJ, 784, 62 [Google Scholar]
  2. Akeson, R. L., Jensen, E. L. N., Carpenter, J., et al. 2019, ApJ, 872, 158 [Google Scholar]
  3. Ansdell, M., Williams, J. P., Trapman, L., et al. 2018, ApJ, 859, 21 [NASA ADS] [CrossRef] [Google Scholar]
  4. Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [Google Scholar]
  5. Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Bate, M. R. 2000, MNRAS, 314, 33 [Google Scholar]
  7. Bate, M. R. 2018, MNRAS, 475, 5618 [Google Scholar]
  8. Clarke, C. J., & Pringle, J. E. 1993, MNRAS, 261, 190 [Google Scholar]
  9. Cox, E. G., Harris, R. J., Looney, L. W., et al. 2017, ApJ, 851, 83 [Google Scholar]
  10. Czekala, I., Chiang, E., Andrews, S. M., et al. 2019, ApJ, 883, 22 [NASA ADS] [CrossRef] [Google Scholar]
  11. Duchêne, G., & Kraus, A. 2013, ARA&A, 51, 269 [Google Scholar]
  12. Eggenberger, A., & Udry, S. 2010, Astrophys. Space Sci. Lib., 366, 19 [NASA ADS] [CrossRef] [Google Scholar]
  13. Facchini, S., Birnstiel, T., Bruderer, S., & van Dishoeck, E. F. 2017, A&A, 605, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Feiden, G. A. 2016, IAU Symp., 314, 79 [NASA ADS] [Google Scholar]
  15. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Guilloteau, S., Di Folco, E., Dutrey, A., et al. 2013, A&A, 549, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Harris, R. J., Andrews, S. M., Wilner, D. J., & Kraus, A. L. 2012, ApJ, 751, 115 [Google Scholar]
  18. Hartigan, P., Strom, K. M., & Strom, S. E. 1994, ApJ, 427, 961 [NASA ADS] [CrossRef] [Google Scholar]
  19. Hatzes, A. P. 2016, Space Sci. Rev., 205, 267 [Google Scholar]
  20. Hatzes, A. P., Cochran, W. D., Endl, M., et al. 2003, ApJ, 599, 1383 [NASA ADS] [CrossRef] [Google Scholar]
  21. Herczeg, G. J., & Hillenbrand, L. A. 2014, ApJ, 786, 97 [Google Scholar]
  22. Holman, M. J., & Wiegert, P. A. 1999, AJ, 117, 621 [Google Scholar]
  23. Jennings, J., Booth, R. A., Tazzari, M., Rosotti, G. P., & Clarke, C. J. 2020, MNRAS, 495, 3209 [Google Scholar]
  24. Jensen, E. L. N., & Akeson, R. 2014, Nature, 511, 567 [NASA ADS] [CrossRef] [Google Scholar]
  25. Köhler, R., Kasper, M., Herbst, T. M., Ratzka, T., & Bertrang, G. H. M. 2016, A&A, 587, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Kratter, K. M., Matzner, C. D., Krumholz, M. R., & Klein, R. I. 2010, ApJ, 708, 1585 [NASA ADS] [CrossRef] [Google Scholar]
  27. Kraus, A. L., Ireland, M. J., Huber, D., Mann, A.W., & Dupuy, T. J. 2016, VizieR Online Data Catalog: J/AJ/ 152/8 [NASA ADS] [Google Scholar]
  28. Kurtovic, N. T., Pinilla, P., Long, F., et al. 2021, A&A, 645, A139 [EDP Sciences] [Google Scholar]
  29. Lodato, G., & Facchini, S. 2013, MNRAS, 433, 2157 [NASA ADS] [CrossRef] [Google Scholar]
  30. Long, F., Pinilla, P., Herczeg, G. J., et al. 2018, ApJ, 869, 17 [Google Scholar]
  31. Long, F., Herczeg, G. J., Harsono, D., et al. 2019, ApJ, 882, 49 [Google Scholar]
  32. Manara, C. F., Tazzari, M., Long, F., et al. 2019, A&A, 628, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. McCabe, C., Duchêne, G., Pinte, C., et al. 2011, ApJ, 727, 90 [NASA ADS] [CrossRef] [Google Scholar]
  34. McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, ASP Conf. Ser., 376, 127 [Google Scholar]
  35. Monin, J. L., Clarke, C. J., Prato, L., & McCabe, C. 2007, in Protostars and Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 395 [Google Scholar]
  36. Offner, S. S. R., Kratter, K. M., Matzner, C. D., Krumholz, M. R., & Klein, R. I. 2010, ApJ, 725, 1485 [Google Scholar]
  37. Papaloizou, J., & Pringle, J. E. 1977, MNRAS, 181, 441 [NASA ADS] [CrossRef] [Google Scholar]
  38. Pascucci, I., Testi, L., Herczeg, G. J., et al. 2016, ApJ, 831, 125 [Google Scholar]
  39. Pearce, L. A., Kraus, A. L., Dupuy, T. J., et al. 2020, ApJ, 894, 115 [CrossRef] [Google Scholar]
  40. Pinilla, P., Birnstiel, T., Benisty, M., et al. 2013, A&A, 554, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Reipurth, B., Clarke, C. J., Boss, A. P., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press) 267 [Google Scholar]
  42. Rodriguez, J. E., Loomis, R., Cabrit, S., et al. 2018, ApJ, 859, 150 [Google Scholar]
  43. Rosotti, G. P., & Clarke, C. J. 2018, MNRAS, 473, 5630 [Google Scholar]
  44. Sanchis, E., Testi, L., Natta, A., et al. 2021, A&A, 649, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Schwarz, R., Funk, B., Zechner, R., & Bazsó, Á. 2016, MNRAS, 460, 3598 [Google Scholar]
  46. Simon, M., Dutrey, A., & Guilloteau, S. 2000, ApJ, 545, 1034 [NASA ADS] [CrossRef] [Google Scholar]
  47. Simon, M., Guilloteau, S., Di Folco, E., et al. 2017, ApJ, 844, 158 [Google Scholar]
  48. Tazzari, M., Beaujean, F., & Testi, L. 2018, MNRAS, 476, 4527 [Google Scholar]
  49. Teague, R. 2019, J. Open Source Softw., 4, 1220 [Google Scholar]
  50. Teague, R., & Foreman-Mackey, D. 2018, Res. Notes Am. Astron. Soc., 2, 173 [Google Scholar]
  51. Thebault, P., & Haghighipour, N. 2015, Planetary Exploration and Science: Recent Advances and Applications, Planet Formation in Binaries (Berlin: Springer), 309 [Google Scholar]
  52. Trapman, L., Ansdell, M., Hogerheijde, M. R., et al. 2020, A&A, 638, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Villenave, M., Ménard, F., Dent, W. R. F., et al. 2020, A&A, 642, A164 [EDP Sciences] [Google Scholar]
  54. White, R. J., & Ghez, A. M. 2001, ApJ, 556, 265 [Google Scholar]
  55. Zagaria, F., Rosotti, G. P., & Lodato, G. 2021a, MNRAS, 504, 2235 [CrossRef] [Google Scholar]
  56. Zagaria, F., Rosotti, G. P., & Lodato, G. 2021b, MNRAS, 507, 2531 [NASA ADS] [CrossRef] [Google Scholar]
  57. Zsom, A., Sándor, Z., & Dullemond, C. P. 2011, A&A, 527, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Zurlo, A., Cieza, L. A., Ansdell, M., et al. 2021, MNRAS, 501, 2305 [NASA ADS] [CrossRef] [Google Scholar]
1

The data of all detected planets are collected in the Exoplanet catalogue maintained by J. Schneider (http://exoplanet.eu); whereas the binary and higher multiplicity systems can be found separately in the catalogue of exoplanets in binary star systems maintained by R. Schwarz (Schwarz et al. 2016; http://www.univie.ac.at/adg/schwarz/multiple.html).

All Tables

Table 1

Information on the stellar and multiplicity properties of the targets analysed in this work.

In the text
Table 2

Information on the cleaned images.

In the text
Table 3

Detections of continuum and CO isotopologues.

In the text
Table 4

Systemic velocities (in km s−1; second column) and absorbed velocities (in km s−1; third and fourth columns) in the disc 12CO emission.

In the text
Table 5

Source centres (ra,dec), inclination i, PA, and systemic velocity υLSR for all discs in the analysed sample.

In the text
Table 6

Total fluxes measured with the cumulative flux technique.

In the text
Table 7

Radii estimated with the cumulative flux technique.

In the text
Table 8

Comparison between observed disc radii and tidal truncation models.

In the text
Table B.1

Beam sizes of the observations by Manara et al. (2019).

In the text

All Figures

thumbnail Fig. 1

12CO zeroth moment images of the discs around multiple stars in the Taurus star-forming region observed in the new ALMA observations. All bars in the bottom right of each panel are of 1″ in length, which is ~140 au at the typical distance of the Taurus region. The FWHM beam size is shown in the bottom left of each panel. In each image, the colour scale has the peak flux as the maximum, and two times the image rms as minimum. White contours show five times the rms of the continuum emission. The components of the systems are labelled. The label for any undetected secondary components in the continuum emission is not shown.
In the text
thumbnail Fig. 2

12CO velocity map images of the discs created with the bettermoments quadratic method (Teague & Foreman-Mackey 2018). A 4-sigma clipping process was applied to all images. The FWHM beam size is shown in the bottom left of each panel. Each image is scaled so that the maximum and the minimum are equal to the systemic velocity of the primary target ±2 km s−1. Green contours show five times the rms of the continuum emission. The components of the systems are labelled. The label for any undetected secondary components in the continuum emission is not shown.
In the text
thumbnail Fig. 3

Maps of the RW Aur system observed by Rodriguez et al. (2018). Left: 12CO zeroth moment. The colour scale has the peak flux as the maximum, and two times the image rms as minimum. Right: 12CO first velocity maps created with bettermoments quadratic method (Teague & Foreman-Mackey 2018) and with a 4-sigma clipping process. The image scaled so that the maximum and the minimum are equal to the systemic velocity of the primary target ±2 km s−1.
In the text
thumbnail Fig. 4

PA (top) and inclination (bottom) estimated using eddy fitting on 12CO first moment maps compared with that estimate by Manara et al. (2019) using (u, υ)-plane modelling of the continuum data with Galario. Red circles refer to circumprimary discs, while blue squares refer to circumsecondary discs.
In the text
thumbnail Fig. 5

Cumulative fluxes as a function of aperture radius estimated using the cumulative flux technique. Each panel shows the fluxes for a different data set or image (the name of the target for each row is shown in the lower right corner of the first column). First column: continuum emission of the data from Manara et al. (2019) (green dots) and the continuum emission from the new data (black dots). Second, third, and fourth columns: the 12CO, 13CO, and C18O moment zero emission from the new data, respectively. The blue dashed lines show the estimated disc total fluxes; the red solid lines show the disc radii, which are defined as the radii containing 95% of the total flux (see values reported in Tables 6 and 7). In the first column, only the total fluxes and disc radii estimated from the new continuum data are shown.
In the text
thumbnail Fig. 6

Cumulative flux curves as a function of aperture radius estimated using the cumulative flux technique. Same as in Fig. 5 but for the remaining discs in the sample. The total fluxes and disc radii estimated from the continuum data from Manara et al. (2019) are shown in the case of RW Aur A and В discs (first column, last two rows). In all the other cases, the total fluxes and disc radii estimated from new continuum data are shown.
In the text
thumbnail Fig. 7

12CO zeroth moment images of the discs with overlapping ellipses including 95 (solid) and 68% (dashed) of the total flux. The ellipses are centred on the target source centre. All bars in the bottom right of each panel are of 1.″0 in length, which is ~140 au at the distance of Taurus. The beam FWHM size is shown in the bottom left of each panel. In each image, the colour scale has the peak flux as the maximum, and two times the image rms as minimum. White contours show five times the rms of the continuum emission.
In the text
thumbnail Fig. 8

12CO estimated radii as a function of dust radii obtained with (u, υ)-plane modelling of the continuum data by Manara et al. (2019). Dust and gas radii estimated as the radii including 68 (right) and 95% (left) of the total flux. The red circles are for circumprimary discs, while blue squares for the circumsecondary.
In the text
thumbnail Fig. 9

Gas-to-dust disc size ratios (R95,gas/R95,dust) as a function of the projected separation. The red circles are for circumprimary discs, while blue squares show circumsecondary discs.
In the text
thumbnail Fig. 10

Comparison between the gas-to-dust size ratio for discs in the Taurus binaries (red and blue triangles) and for single discs in Lupus (grey diamonds). Effective disc radii R68 (left) and disc radii R95 (right) are shown.
In the text
thumbnail Fig. 11

Normalised cumulative distribution function for the gas-to-dust effective disc sizes R68,gas/R68,dust (top) and for the gas-to-dust disc sizes R95,gas/R95,dust (bottom) for discs around single stars in Lupus (grey, Sanchis et al. 2021) and discs around multiple stellar system in Taurus (black). Discs around primary stars in Taurus are shown in red, while circumsecondary discs in Taurus are shown in blue.
In the text
thumbnail Fig. 12

Observed 12CO gas radii as a function of the projected separation. Blue squares refer to the circumsecondary discs, while red circles to the circumprimary discs.
In the text
thumbnail Fig. 13

12CO gas radii as a function of the projected separation. Blue squares and red circles show the observed ratio in the circumsecondary discs and the circumprimary discs, respectively. Blue plus symbols and red crosses show the expected ratio from the tidal truncation model in the case of circular orbits (e = 0) for circumsecondary discs and circumprimary discs, respectively. The longer the dashed line that links observed radii with models, the weaker the agreement with the zero-eccentricity model.
In the text
thumbnail Fig. 14

Condition on the eccentricity of the stellar orbits for which the estimated truncation radii of the discs in the sample are in agreement with theoretical predictions (see Sect. 5.2). Red bands show the estimated R95,gas/ap with their uncertainties. Black curves show the expected truncation radius in units of the projected separation for different Reynolds numbers: dashed curves for ℛ = 104, solid for ℛ = 105, and dotted for ℛ = 106. The lower black curves are obtained assuming that the secondary is observed at apoastron, while black curves at the top assuming that the secondary is located at periastron. The expected Rt/ap increases for higher orbital inclination, and thus the black curves would move to higher values in the plot if the assumption of face-on orbits is not fulfilled (see Eq. (2)).
In the text
thumbnail Fig. 15

Estimated minimum eccentricities for each target. Red circles refer to circumprimary discs, while blue squares refer to circumsecondary discs.
In the text
thumbnail Fig. 16

Gas-disc to dust-disc size ratios (R95,gas/R95,dust) as functions of the minimum eccentricities of the orbits. Red circles refer to circumprimary discs, while blue squares refer to circumsecondary discs.
In the text
thumbnail Fig. 17

Comparison between the PAs (top) and inclination (bottom) for the discs around the primary and the secondary in each multiple stellar system where both discs are detected and resolved. We considered the UZ Tau system as two binaries, comparing UZ Tau E parameters with UZ Tau Wab parameters (comparison labeled as UZ_Wa and UZ_Wb for the two UZ Tau Wab discs) and UZ Tau Wa parameters with UZ Tau Wb parameters (comparison labeled as UZ_Wab). In the other cases, the first two letters of the target name are labelled.
In the text
thumbnail Fig. 18

Relative inclination of the discs in each multiple stellar system as a function of their projected separation. We considered the UZ Tau system as two binaries, comparing UZ Tau E parameters with UZ Tau Wab parameters (comparison labeled as UZ_Wa and UZ_Wb for the two UZ Tau Wab discs) and UZ Tau Wa parameters with UZ Tau Wb parameters (comparison labelled as UZ_Wab). In the other cases, the first two letters of the target name are labelled.
In the text
thumbnail Fig. A.1

Images and spectra of all targets in the analysed sample. Each row refers to a system in the sample. The first columns show the continuum images with the names of the targets indicated in the top left. The second, fourth, and sixth columns show the zeroth moment images for the 12CO, the 13CO, and the C18O emission, respectively, scaled so that the maximum is equal to the peak flux and the minimum is clipped at the image rms. The third, fifth, and seventh columns show the first moment images (calculated through the bettermoments tool) for the 12CO, 13CO, and C18O emission, respectively, scaled so that the maximum and the minimum are equal to the systemic velocity of the target ±2 km/s. The FWHM beam size is shown in the bottom left of each panel. All bars in the bottom right of each panel are 0.″5 long. The last two columns show the 12CO and 13CO spectra of the circumprimary (red), circumsecondary (blue), and circumtertiary (green) discs (when applicable), with vertical black lines showing the systemic velocities fitted with the eddy tool and grey band showing the excluded absorbed velocities in eddy fitting on circumprimary disc rotation maps (see Table 4).
In the text
thumbnail Fig. A.2

Channel maps of the 12CO emission in the CIDA 9 A disc. Each panel shows the velocity of the channel in the upper left corner. The FWHM beam size is shown in the bottom left. The images are scale so that the maximum is equal to the peak flux and the minimum is clipped at the image rms. White contours show 5, 30, and 100 times the rms of the continuum emission.
In the text
thumbnail Fig. A.3

Channel maps of the 12CO emission in the DH Tau A disc. Panels and symbols are as in Figure A.2.
In the text
thumbnail Fig. A.4

Channel maps of the 12CO emission in the DK Tau discs. Panels and symbols are as in Figure A.2.
In the text
thumbnail Fig. A.5

Channel maps of the 12CO emission in the HK Tau discs. Panels and symbols are as in Figure A.2.
In the text
thumbnail Fig. A.6

Channel maps of the 12CO emission in the HN Tau A disc. Panels and symbols are as in Figure A.2.
In the text
thumbnail Fig. A.7

Channel maps of the 12CO emission in the UZ Tau discs. Panels and symbols are as in Figure A.2.
In the text
thumbnail Fig. A.8

Channel maps of the 12CO emission in the V710 Tau A disc. Panels and symbols are as in Figure A.2.
In the text
thumbnail Fig. B.1

Comparisons between the total disc fluxes measured from the new continuum observation with that measured from the data presented by Manara et al. (2019). The left panel shows the ratio between the total fluxes calculated using the data by Manara et al. (2019) (FManara,c.f.t.) and using the new continuum data (Fnew), both estimated through the cumulative flux technique. The right-hand panel instead reports the ratio using the fluxes calculated by Manara et al. (2019) with the uv-modelling method (FManara,Galario), and using the new continuum data with the cumulative flux technique. Red circles are used for circumprimary discs, blue squares for circumsecondary ones.
In the text
thumbnail Fig. B.2

Observed ratio between the dust radii estimated with the cumulative flux technique applied to the data by Manara et al. (2019) and the dust radii from the new continuum data (Rnew/RManara) as a function of the new dust radii (Rnew). Left: Dust radii estimated as the radii including 68% of the total flux (i.e. effective disc radii). Right: Dust radii estimated as the radii including 95% of the total flux. Black lines show the maximum (solid) and minimum (dashed) effect on the ratio of the beam size between the data by Manara et al. (2019) and the new data (see Equations (B.4) and (B.5)). Blue squares refer to the circumsecondary disc and red circles to the circumprimary discs.
In the text
thumbnail Fig. B.3

Comparison between dust disc radii estimated with the cumulative flux technique (c.f.t.) applied on the data by Manara et al. (2019) and with those estimated by Manara et al. (2019) with Galario-modelling (Rc.f.t/RGalario). Left: Dust radii estimated as the radii including the 68% of the total flux (i.e. effective disc radii). Right: Dust radii estimated as the radii including the 95% of the total flux. Red circles are used for circumprimary discs, blue square for circumsecondary discs.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.