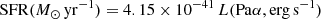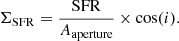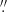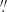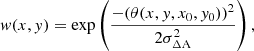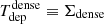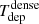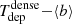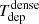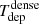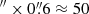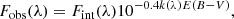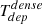| Issue |
A&A
Volume 660, April 2022
|
|
|---|---|---|
| Article Number | A83 | |
| Number of page(s) | 30 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202142396 | |
| Published online | 13 April 2022 | |
Spatially resolved star-formation relations of dense molecular gas in NGC 1068⋆
1
Centro de Astrobiología (CSIC/INTA), Ctra de Torrejón a Ajalvir, km 4, 28850 Torrejón de Ardoz, Madrid, Spain
e-mail: mariasg@cab.inta-csic.es
2
Observatorio Astronómico Nacional (OAN-IGN)-Observatorio de Madrid, Alfonso XII, 3, 28014 Madrid, Spain
3
Centro de Astrobiología (CAB, CSIC-INTA), ESAC Campus, 28692 Villanueva de la Cañada, Madrid, Spain
Received:
8
October
2021
Accepted:
12
January
2022
Context. According to the current understanding of star formation (SF), the regulation of this phenomenon in galaxy disks reflects a complex balance between processes that operate in molecular gas on local cloud scales as well as on global disk scales.
Aims. We analyse the influence of the dynamical environment on the SF relations of the dense molecular gas in the starburst (SB) ring of the Seyfert 2 galaxy NGC 1068.
Methods. We used ALMA to image the emission of the 1–0 transitions of HCN and HCO+, which trace dense molecular gas in the r ∼ 1.3 kpc SB ring of NGC 1068, with a resolution of 56 pc. We also used ancillary data of CO(1–0) as well as CO(3–2) and its underlying continuum emission at the resolutions of ∼100 pc and ∼40 pc, respectively. These observations allow us to probe a wide range of molecular gas densities (nH2 ∼ 103 − 5 cm−3). The star-formation rate (SFR) in the SB ring of NGC 1068 is derived from Paα line emission imaged by HST/NICMOS. We analyse how different formulations of SF relations change depending on the adopted aperture sizes and on the choice of molecular gas tracer.
Results. The scatter in the Kennicutt–Schmidt relation, linking the SFR density (ΣSFR) with the (dense) molecular gas surface density (Σdense), is about a factor of two to three lower for the HCN and HCO+ lines compared to that derived from CO(1–0) for a common aperture. Correlations lose statistical significance below a critical spatial scale of ≈300−400 pc for all gas tracers. The SF efficiency of the dense molecular gas, defined as SFEdense ≡ ΣSFR/Σdense, shows a scattered distribution as a function of the HCN luminosity (L′(HCN)) around a mean value of ≃0.01 Myr−1. An alternative prescription for SF relations, which includes the dependence of SFEdense on the combination of Σdense and the velocity dispersion (σ), resolves the degeneracy associated with the SFEdense − L′(HCN) plot. The SFEdense values show a positive trend with the boundedness of the gas, measured by the parameter b ≡ Σdense/σ2. We identify two branches in the SFEdense − b plot that correspond to two dynamical environments within the SB ring; they are defined by their proximity to the region where the spiral structure is connected to the stellar bar. This region corresponds to the crossing of two overlapping density wave resonances, where an increased rate of cloud-cloud collisions would favour an enhanced compression of molecular gas.
Conclusions. These results suggest that galactic dynamics plays a major role in the efficiency of the conversion of gas into stars. Our work adds supporting evidence that density-threshold SF models, which argue that the SFEdense should be roughly constant, fail to account for spatially resolved SF relations of dense gas in the SB ring of NGC 1068.
Key words: galaxies: individual: NGC 1068 / galaxies: Seyfert / galaxies: star formation
Reduced datacubes and maps are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/660/A83
© ESO 2022
1. Introduction
The study of the processes that power star formation (SF) in galaxies is paramount to understanding how galaxies form and evolve. If we assume that the gas scale-height is constant, the power law relating the gas volume density and the star-formation rate (SFR) volume density, originally proposed by Schmidt (1959), finds its equivalent in terms of the corresponding surface densities of the SFR (ΣSFR) and the gas (Σgas) in the expression
In this equation A is a normalisation constant and N is the power-law index. Under the hypothesis that the relevant timescale for SF is the local free-fall time for the gas, the theoretically predicted value for N is 1.5. This relation is known as the Kennicutt–Schmidt (KS) law (Schmidt 1959; Kennicutt 1998a). In addition to the empirical power-law relation between Σgas and ΣSFR, another key parameter in SF studies is the star-formation efficiency (SFE), defined as
which represents the inverse of the depletion time (Tdep) of the gas that is consumed by SF.
Different proxies for ΣSFR and Σgas have been chosen for observations carried out during the last few decades on different galaxy populations. First, from spatially unresolved galaxy-scale global measurements, which used CO and HI as neutral gas tracers in different galaxy samples, observers found a single law with a range of indexes ≃1.2 − 1.7 (Kennicutt 1998a; Yao et al. 2003; Bouché et al. 2007; Daddi et al. 2010; Genzel et al. 2010; Liu et al. 2015; Kennicutt & De Los Reyes 2021). However, there is mounting evidence that global KS laws show signs of bimodality or multi-modality, which tend to separate the branches of normal galaxies from that of more extreme merger systems (Daddi et al. 2010; Genzel et al. 2010; Liu et al. 2015; Kennicutt & De Los Reyes 2021).
Furthermore, high-resolution imaging of neutral gas in galaxies has allowed the analysis of the KS relation at kiloparsec and sub-kiloparsec scales in a growing number of galaxies (e.g. Kennicutt et al. 2007; Bigiel et al. 2008; Leroy et al. 2008, 2017; Blanc et al. 2009; Casasola et al. 2015). In particular, Bigiel et al. (2008) used CO(2–1) as a tracer of molecular gas in a sample of 18 nearby star forming galaxies (SFGs) and found a single linear KS relation (N ≃ 1), which holds for gas surface densities Σgas ≥ 10 M⊙ pc−2. This dividing line identifies the transition from atomic to molecular gas. Leroy et al. (2008) derived a radial dependence in N with a decreasing SFE at larger radii within individual galaxies. Moreover, Casasola et al. (2015) derived KS relations in the nuclear regions of four low luminosity active galactic nuclei (AGN) using interferometric CO images on spatial scales between 20 pc and 200 pc. The KS relations were found to be sub-linear, but also super-linear, with a wide range of slopes, ∼[0.5 − 1.3]. Leroy et al. (2017) studied the local dynamical state of molecular gas in M 51 and found that the gas with stronger self-gravity forms stars at a higher rate. The variability in resolved KS relations also suggests a higher SFE in lower mass, low metallicity galaxies (e.g. Schruba et al. 2011; Leroy et al. 2013) and in late Hubble types (e.g. Colombo et al. 2018; Ellison et al. 2021).
The high-resolution CO observations of M 33 published by Onodera et al. (2010) show that at spatial scales similar to those of giant molecular clouds (GMCs; ∼50 − 100 pc), the correlation between ΣSFR and Σgas is lost. In qualitative agreement with this picture, Schruba et al. (2010) observed a breakdown of the SF relation at scales of ≤300 pc in M 33. Moreover, the recent work of Williams et al. (2018) found significant correlations in M 33 down to scales of 100 pc, while the measured Schmidt index shows a marked dependence on the spatial scale. The breakdown of the KS relation observed below a ‘critical’ spatial scale can be attributed to the need of averaging over sufficiently large scales in order to have a statistical sampling of star forming sites at different evolutionary stages (e.g. Kruijssen & Longmore 2014).
The most recent studies of the SF relation reported above, which use low-J CO lines (sometimes in combination with HI data) as tracers of the bulk of neutral gas, cast doubts on the existence of a ‘universal’ or ‘uni-modal’ KS relation at all spatial scales. Dense molecular gas, namely gas with volume densities typically exceeding 104 − 5 cm−3, is believed to condense into GMCs and be therefore more directly related to recent and massive SF (Lada et al. 2010; André et al. 2010). In particular, observations of HCN(1–0) and HCO+(1–0) lines, which have associated critical densities of ncrit[HCN(1–0)] ∼ 1.7 × 105 cm−3 and ncrit[HCO+(1–0)] ∼ 2.9 × 104 cm−3 (Shirley 2015), are well suited for fairly tracing the dense molecular gas mass (Mdense) in galaxies. Dense gas probes have been used to study ‘galaxy-scale’ KS relations (e.g. Gao & Solomon 2004a,b; Solomon & Vanden Bout 2005; Graciá-Carpio et al. 2006, 2008; García-Burillo et al. 2012; Liu et al. 2015). As expected, the SF relations derived for the dense gas show a less scattered linear correlation (i.e. with N ≃ 1) compared to the global KS laws obtained from low-J CO lines. However, the residual but nevertheless significant scatter present in the SFR–Mdense plane has been interpreted as indicative of different average physical properties of the dense gas in normal SFGs and mergers (Graciá-Carpio et al. 2008; García-Burillo et al. 2012).
High-resolution (kiloparsec and sub-kiloparsec) single-galaxy studies of the SF relations of the dense molecular gas have started to resolve the degeneracy in the SFR–Mdense parameter space by showing how scaling laws change for different dynamical environments within a galaxy, including the Milky Way (Longmore et al. 2013; Kruijssen et al. 2014; Murphy et al. 2015; Usero et al. 2015; Bigiel et al. 2015, 2016; Chen et al. 2017; Viaene et al. 2018; Querejeta et al. 2019; Jiménez-Donaire et al. 2019; Bešlić et al. 2021). In particular, Usero et al. (2015) observed HCN(1–0) and CO(1–0) lines at several positions in the disks of 29 SFGs and found that SFEdense, derived from the IR/HCN ratio, is ∼6 − 8 times lower near galaxy centres than in the outer regions of the disks. Furthermore, Querejeta et al. (2019) found that SFEdense values measured on ∼100 pc scales from radio continuum-to-HCN ratios vary by more than 1 dex among the different dynamical environments of the disk of M 51. More recently, Bešlić et al. (2021) found significant differences in the ∼100 pc-scale SFEdense values between the galaxy centre, bar, and bar-end regions of the nearby barred galaxy NGC 3627. These results contradict models that rely on a universal gas density threshold for SF (e.g. Gao & Solomon 2004b; Wu et al. 2005; Lada et al. 2010, 2012; Evans et al. 2014) and suggest instead that the dynamical environment of the dense molecular gas in GMCs can determine its efficiency at forming stars. This is supported by models of turbulent SF (e.g. Krumholz & McKee 2005; Krumholz & Thompson 2007; Hennebelle & Falgarone 2012; Meidt et al. 2013, 2018, 2020; Federrath 2015; Meidt 2016).
In this paper we study the spatially resolved SF relations of the dense molecular gas in the starburst (SB) ring of the nearby (D ≃ 14 Mpc; Bland-Hawthorn et al. 1997) Seyfert 2 barred galaxy NGC 1068, a target considered as an archetype of the composite SB and AGN classification. Previous interferometer images have resolved the large-scale distribution of molecular gas in the disk of the galaxy (Helfer & Blitz 1995; Schinnerer et al. 2000; Krips et al. 2011; Tsai et al. 2012; García-Burillo et al. 2014, 2017, 2019; Takano et al. 2014; Viti et al. 2014; Scourfield et al. 2020). Molecular line and dust continuum emissions are detected from a r ∼ 200 pc circumnuclear disk (CND), from the ∼2.6 kpc diameter stellar bar region, and from a ring where molecular gas is accumulating and feeding a SB episode. The SB ring is formed by a tightly wound two-arm spiral structure that starts from the ends of the stellar bar and unfolds in the disk over ∼180° in azimuth, forming a pseudo-ring at r ∼ 18″(1.3 kpc).
We used new images of the distribution of dense molecular gas (nH2 ≥ 104 − 5 cm−3) obtained by the Atacama Large Millimeter Array (ALMA) in the 1−0 transitions of HCN and HCO+ with a native resolution of 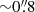 (56 pc). This spatial resolution is comparable to the typical size of GMCs. We also use high-resolution (
(56 pc). This spatial resolution is comparable to the typical size of GMCs. We also use high-resolution (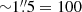 pc) CO (1–0) images of the galaxy obtained by the IRAM array (Schinnerer et al. 2000), as well as available CO(3–2) and dust continuum images obtained by ALMA at a spatial resolution of
pc) CO (1–0) images of the galaxy obtained by the IRAM array (Schinnerer et al. 2000), as well as available CO(3–2) and dust continuum images obtained by ALMA at a spatial resolution of 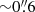 (40 pc) (García-Burillo et al. 2014). The ensemble of these observations allows us to probe a wide range of molecular gas densities (nH2 ≃ 103 − 5 cm−3) in the SB ring. To probe SF, we use Paα line images obtained by the Hubble Space Telescope (HST). We analyse how SF relations change depending on the adopted spatial resolution, on the choice of molecular gas tracer, and on the particular dynamical environment throughout the SB ring.
(40 pc) (García-Burillo et al. 2014). The ensemble of these observations allows us to probe a wide range of molecular gas densities (nH2 ≃ 103 − 5 cm−3) in the SB ring. To probe SF, we use Paα line images obtained by the Hubble Space Telescope (HST). We analyse how SF relations change depending on the adopted spatial resolution, on the choice of molecular gas tracer, and on the particular dynamical environment throughout the SB ring.
The paper is organised as follows: Sect. 2 presents the new ALMA observations and accompanying ancillary data. We describe in Sect. 3 the conversion factors adopted. Section 4 describes the molecular gas and Paα images used in this work. We study the different KS relations derived in NGC 1068 in Sect. 5. Section 6 explores a different prescription of SF relations and analyses the environmental dependence of SFEdense as a function of a set of physical parameters in the different regions of the SB ring. We describe a scenario for the SF in the SB ring in Sect. 7. The main conclusions of this work are summarised in Sect. 8.
2. Observations
In this section we present an overview of the different datasets used to probe the distribution of molecular gas (Sect. 2.1) and the recent SF (Sect. 2.2) required to derive the SF relations in the SB ring of NGC 1068.
2.1. Molecular gas tracers
2.1.1. New ALMA data
We used ALMA to map the emission of HCN(1–0) and HCO+(1–0) in the central r ∼ 2.5 kpc of the NGC 1068 disk. Observations were executed during Cycle 2 in one track in August 2015 (project-ID: # 2013.1.00055.S, PI: S. García-Burillo). We used band 3 receivers and a single pointing with a field of view (FOV) of ∼70″ (∼5 kpc), covering the CND and the SB ring of the galaxy. Observations made use of 34 antennas of the array with projected baselines ranging from 12 m to 1430 m. The phase tracking centre was set to α2000 = 02h42m40.771s, δ2000 = −00° 00′47.84″, which is the centre of the galaxy according to SIMBAD taken from the Two Micron All Sky Survey (2MASS; Skrutskie et al. 2006). The tracking centre is offset by ≤1″ relative to the AGN position: α2000 = 02h42m40.71s, δ2000 = −00° 00′47.94″ (Gallimore et al. 1996, 2016, 2004; García-Burillo et al. 2014, 2016; Imanishi et al. 2016). The galaxy has a systemic velocity of vsys(HEL) ∼ 1130 km s−1 (García-Burillo et al. 2014, 2019).
Four spectral windows were placed, two in the lower sideband and two in the upper sideband. All the sub-bands have a spectral bandwidth of 1.875 GHz. The setup allowed us to simultaneously observe HCN(J = 1 − 0) (88.632 GHz at rest) and HCO+(J = 1 − 0) (89.189 GHz at rest) in the higher frequency lower sideband, as well as H13CN(J = 1 − 0) (86.340 GHz at rest) and H13CO+(J = 1 − 0) (86.754 GHz at rest) in the lower frequency lower sideband. The two spectral windows in the upper sideband were centred around the CS(J = 2 − 1) (97.981 GHz at rest) line and the continuum emission around 100 GHz, respectively. The CS(2–1) map was published by Scourfield et al. (2020). The 86.6 GHz-continuum map of the galaxy was published by García-Burillo et al. (2017).
The data were calibrated using the ALMA reduction package CASA1. The calibrated uv-tables were exported to GILDAS2-readable format (Guilloteau & Lucas 2000) in order to perform the mapping and cleaning steps as detailed below. We estimated that the absolute flux accuracy is about 5%, which is in line with the goal of standard ALMA observations at these frequencies. The synthesised beam obtained using natural weighting is 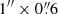 (70 pc × 42 pc) at a position angle PA = 69°. The line data cube was binned to a frequency resolution of 2.92 MHz (∼10 km s−1). We estimated a 1σ sensitivity of 0.4 mJy beam−1 per channel of 10 km s−1 using line-free emission areas in the data. The conversion factor between Jy beam−1 and K is 247.6 K Jy−1 per beam in both emission lines. The spectral line maps were obtained after subtraction of the continuum emission performed in the (u, v) plane using the GILDAS tasks uv-average and uv-subtract.
(70 pc × 42 pc) at a position angle PA = 69°. The line data cube was binned to a frequency resolution of 2.92 MHz (∼10 km s−1). We estimated a 1σ sensitivity of 0.4 mJy beam−1 per channel of 10 km s−1 using line-free emission areas in the data. The conversion factor between Jy beam−1 and K is 247.6 K Jy−1 per beam in both emission lines. The spectral line maps were obtained after subtraction of the continuum emission performed in the (u, v) plane using the GILDAS tasks uv-average and uv-subtract.
We obtained the zeroth, first and second moment maps from the line data cubes using the GILDAS task moments, adopting a velocity window |v − vsys| = 250 km s−1, which is enough to cover the span of velocities due to rotation in the disk of the galaxy (García-Burillo et al. 2014). The total uncertainty on the velocity-integrated emission maps, ΔI, was derived from
where
Here, ΔInoise is the velocity-integrated intensity error, which results from propagating the error of individual channels, σ = 0.4 mJy beam−1, of width δV = 10 km s−1, to the number of channels considered in the integration window, Nwindow = 50. Furthermore, ΔIcalib is the uncertainty due to the absolute flux calibration error, which is about ≃5%×I for ALMA band 3 observations (see ALMA Technical Handbook3). All in all, for a typical flux integrated value ≥5σ characteristic of the regions in the SB ring of NGC 1068 studied in this work, the total uncertainty on I as well as on all the related parameters, namely line luminosities and gas masses, amounts at most to ±0.09 dex in logarithmic units4.
The largest angular scale (LAS) of our observations is ∼4″ (∼280 pc). Since our observations do not contain short-spacing correction, the flux can start to be filtered out on scales larger than the LAS. The HCN emission, and very likely also the HCO+ emission, are expected to arise from a highly clumpy medium consisting of an ensemble of dense cloud cores. This particular hierarchy of the dense molecular gas probed by HCN and HCO+ helped by the velocity structure observed in the molecular disk of NGC 1068 (e.g. see García-Burillo et al. 2014) allows us to foresee that the amount of flux filtered on the spatial scales that are the most relevant for this paper is kept low in both lines.
To validate this hypothesis we estimated the maximum percentage of missing flux in the HCN image of NGC 1068 by comparing the fluxes measured by ALMA and by the IRAM 30-m telescope (Usero et al. 2021, priv. comm.) at different locations of the disk. With this aim we derived the spatially integrated fluxes using the single-dish aperture sizes ∼30″ ∼ 2 kpc (see Appendix A for details). The result of this comparison indicates that the maximum percentage of missing flux in the HCN ALMA map is about 25% on scales of 2 kpc. As the spatial scales relevant for this paper are much smaller (40−700 pc), we can conclude that 25% is a conservative upper limit on the missing flux for HCN (and very likely also for HCO+).
2.1.2. Ancillary data
We used the CO(3–2) line and 349 GHz (859 μm) continuum emission images of the galaxy obtained by García-Burillo et al. (2014) with ALMA during the Cycle 0 of the array in band 7 (project-ID: # 2011.0.00083.S, PI: S. García-Burillo). The angular resolution of these data is 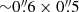 (42 pc × 35 pc) at a position angle of ∼60°. We refer to García-Burillo et al. (2014) for a detailed description of the data reduction steps. As the observations of García-Burillo et al. (2014) do not contain short-spacing correction, we expect that a non-negligible amount of flux may start to be filtered out on scales beyond the reported LAS ≥6″ (420 pc) for the continuum and CO(3–2) emission images. Based on a comparison between the fluxes measured by ALMA and different single-dish telescopes using a set of apertures, García-Burillo et al. (2014) estimated that their interferometer images may be filtering up to 20−30% and 65% of the total flux on spatial scales of about 1 kpc for the CO(3–2) and continuum emission, respectively. However, the clumpy distribution of the gas and also (in the case of the CO line) the velocity structure of the emission are expected to favour the recovery of most of the flux in the line and continuum maps on smaller apertures (≤6″ ∼ 420 pc) centred on the brightest emission spots of the SB ring.
(42 pc × 35 pc) at a position angle of ∼60°. We refer to García-Burillo et al. (2014) for a detailed description of the data reduction steps. As the observations of García-Burillo et al. (2014) do not contain short-spacing correction, we expect that a non-negligible amount of flux may start to be filtered out on scales beyond the reported LAS ≥6″ (420 pc) for the continuum and CO(3–2) emission images. Based on a comparison between the fluxes measured by ALMA and different single-dish telescopes using a set of apertures, García-Burillo et al. (2014) estimated that their interferometer images may be filtering up to 20−30% and 65% of the total flux on spatial scales of about 1 kpc for the CO(3–2) and continuum emission, respectively. However, the clumpy distribution of the gas and also (in the case of the CO line) the velocity structure of the emission are expected to favour the recovery of most of the flux in the line and continuum maps on smaller apertures (≤6″ ∼ 420 pc) centred on the brightest emission spots of the SB ring.
We also used the CO(1–0) line map of the galaxy obtained by the IRAM array on the Plateau de Bure Interferometer (PdBI), published by Schinnerer et al. (2000). The CO(1–0) line allows us to study the bulk of the molecular gas reservoir in the disk of NGC 1068. The angular resolution of these data is 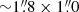 (126 pc × 70 pc) at a position angle of ∼24°. Schinnerer et al. (2000) estimated that the CO PdBI map misses about 25 − 30% of the total flux on scales ∼55″ (3.8 kpc), based on the comparison between the CO flux measured by the PdBI and the flux derived from the CO maps obtained through the combination of the Berkeley-Illinois-Maryland-Association (BIMA) array and the 12 m Kitt Peak single-dish data published by Helfer & Blitz (1995). We derived a new upper limit on the missing flux in the CO(1–0) map based on a comparison between the fluxes measured by PdBI and the IRAM 30-m telescope in Appendix A (∼40−45% on scales ∼24″ ∼ 1.7 kpc). As in this paper the relevant spatial scales used in our analysis are smaller, we can therefore expect that the missing flux factors reported above can be taken as strict upper limits.
(126 pc × 70 pc) at a position angle of ∼24°. Schinnerer et al. (2000) estimated that the CO PdBI map misses about 25 − 30% of the total flux on scales ∼55″ (3.8 kpc), based on the comparison between the CO flux measured by the PdBI and the flux derived from the CO maps obtained through the combination of the Berkeley-Illinois-Maryland-Association (BIMA) array and the 12 m Kitt Peak single-dish data published by Helfer & Blitz (1995). We derived a new upper limit on the missing flux in the CO(1–0) map based on a comparison between the fluxes measured by PdBI and the IRAM 30-m telescope in Appendix A (∼40−45% on scales ∼24″ ∼ 1.7 kpc). As in this paper the relevant spatial scales used in our analysis are smaller, we can therefore expect that the missing flux factors reported above can be taken as strict upper limits.
2.2. Star-formation tracer
We used the emission of the Paα hydrogen recombination line at 1.875 μm to image the distribution of recent SF in the disk of NGC 1068. We used the HST/NICMOS (NIC3) narrow-band (F187N, F190N) images of the galaxy retrieved from the Hubble Legacy Archive (HLA)5 to derive the continuum-subtracted Paα map, and followed the calibration and continuum subtraction steps detailed in Sect. 2.2 of García-Burillo et al. (2014). The pixel size of the HLA images is 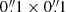 . The angular resolution (full width at half maximum) of the Paα image is
. The angular resolution (full width at half maximum) of the Paα image is 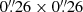 (∼18 pc × 18 pc), as determined from the estimated size of the point spread function in the observations. Uncertainties on flux calibration are at the 15−20% level (Böker et al. 1999; Alonso-Herrero et al. 2006), which implies associated uncertainties ≤ ± 0.09 − 0.10 dex for the regions of the SB ring of NGC 1068 examined in this work. The Paα line traces ionised gas produced by associations of massive (≳30 M⊙) and young (≲8 − 10 Myr) stars. The main advantage of the near-infrared (NIR) recombination line compared to its optical counterpart, namely Hα, resides in the significantly lower extinction by dust of Paα (Kennicutt 1998b; Calzetti et al. 2007). We may therefore neglect any dust-extinction correction when we derive the SFR from the Paα fluxes. The validity of this hypothesis is examined in Appendix B, where we compare the Paα fluxes measured by HST over a number of hot spots of the SB ring with those measured in Hα using the ground-based image of the galaxy published by Díaz et al. (2000). We estimate an overall low extinction correction at 1.875 μm for the SB ring knots: APaα shows a median value ∼0.03 mag, compatible with optically thin emission (see Appendix B for details). If we allow for a ∼20% uncertainty in the flux scales due to absolute calibration errors, we conclude that the Paα map of the SB ring does not require any significant correction for dust extinction.
(∼18 pc × 18 pc), as determined from the estimated size of the point spread function in the observations. Uncertainties on flux calibration are at the 15−20% level (Böker et al. 1999; Alonso-Herrero et al. 2006), which implies associated uncertainties ≤ ± 0.09 − 0.10 dex for the regions of the SB ring of NGC 1068 examined in this work. The Paα line traces ionised gas produced by associations of massive (≳30 M⊙) and young (≲8 − 10 Myr) stars. The main advantage of the near-infrared (NIR) recombination line compared to its optical counterpart, namely Hα, resides in the significantly lower extinction by dust of Paα (Kennicutt 1998b; Calzetti et al. 2007). We may therefore neglect any dust-extinction correction when we derive the SFR from the Paα fluxes. The validity of this hypothesis is examined in Appendix B, where we compare the Paα fluxes measured by HST over a number of hot spots of the SB ring with those measured in Hα using the ground-based image of the galaxy published by Díaz et al. (2000). We estimate an overall low extinction correction at 1.875 μm for the SB ring knots: APaα shows a median value ∼0.03 mag, compatible with optically thin emission (see Appendix B for details). If we allow for a ∼20% uncertainty in the flux scales due to absolute calibration errors, we conclude that the Paα map of the SB ring does not require any significant correction for dust extinction.
3. Conversion to physical parameters
3.1. Molecular gas masses
To derive the distribution of ‘local’ dense molecular gas mass (Mdense) from the HCN(1–0) velocity-integrated luminosities (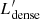 ) we assumed the standard conversion factor commonly applied for ‘global’ scales, αHCN = 10 M⊙ (K km s−1 pc2)−1 for HCN, following Gao & Solomon (2004a), for the different local scales used in this work. This factor includes a correction for helium. A canonical ‘constant’ conversion factor is usually adopted in the literature for both lines, which are considered as reliable tracers of the dense molecular gas phase above densities n ≈ 104 cm−3 (see, however, García-Burillo et al. 2012; Evans et al. 2020).
) we assumed the standard conversion factor commonly applied for ‘global’ scales, αHCN = 10 M⊙ (K km s−1 pc2)−1 for HCN, following Gao & Solomon (2004a), for the different local scales used in this work. This factor includes a correction for helium. A canonical ‘constant’ conversion factor is usually adopted in the literature for both lines, which are considered as reliable tracers of the dense molecular gas phase above densities n ≈ 104 cm−3 (see, however, García-Burillo et al. 2012; Evans et al. 2020).
This fixed conversion factor assumes that the HCN(1–0) emission is originated from gravitationally-bound ‘cores’ or clumps with volume-averaged density nH2 ∼ 3 × 104 cm−3 and a brightness temperature Tb ∼ 35 K. However, under the hypothesis that the emission of the HCN line is mostly optically thick, if the volume-averaged density of the emitting clumps is lower than 3 × 104 cm−3 or if the Tb is larger than 35 K, the αHCN could be smaller than the factor suggested by Gao & Solomon (2004a). In this context, Wu et al. (2005) estimated the value of αHCN in Galactic star-forming cores, finding a slightly lower conversion factor at smaller scales: αHCN = 7 ± 2 M⊙ (K km s−1 pc2)−1. This value differs only by 30% from the global conversion factor used by Gao & Solomon (2004a), which is the one adopted in this work. We nevertheless note that adopting a lower value of the conversion factor for HCN would result in slightly lower molecular gas surface density values, particularly in the regions of the SB ring that show comparatively higher SF activity and SFE values (see discussion in Sect. 6).
We therefore derived Mdense as
The line luminosity, L′, is defined following Solomon et al. (1997) as
where the velocity-integrated fluxes SdenseΔ V are in Jy km s−1 particularised for each line, the observed frequency νobs is in GHz and the luminosity distance DL is in Mpc units.
We obtained face-on values of the dense molecular gas surface densities (Σdense in M⊙ pc−2 units) from
where i = 40° is the inclination of the disk of NGC 1068 (Bland-Hawthorn et al. 1997; Brinks et al. 1997; García-Burillo et al. 2014) and Aaperture is the area of the aperture used in pc2.
Similarly, we transformed the measured CO(1–0) luminosities into molecular gas masses and surface densities using the conversion prescription of Bolatto et al. (2013), which assumes a standard Galactic conversion factor αCO = 4.4 M⊙ (K km s−1 pc2)−1, which already includes a correction for helium.
We used the GILDAS task gauss-smooth to convolve the initial resolution versions of the molecular line data cubes with the appropriate Gaussian kernels adapted to generate all the image versions for the common set of spatial resolutions used in this work, which range from ∼40 − 56 pc (∼100 pc for CO(1–0)) up to ∼700 pc (see Sect. 5.1).
3.2. Star-formation rates
We adopted the prescription proposed in Kennicutt & Evans (2012) regarding the conversion factor used to calculate the local SFR map from the Paα line luminosities. In particular, we assumed a Kroupa initial mass function (Kroupa 2001) as well as an intrinsic ratio for Hα/Paα ∼ 7.81 (Hummer & Storey 1987), which applies for the case B recombination at Te = 5000 K and ne = 103 cm−3. These conditions are found in starbursting galaxies (Roy et al. 2008; Rieke et al. 2009).
We obtained the SFR from the expression
We derived the corresponding SFR surface densities (ΣSFR) in units of M⊙ yr−1 pc−2 from
We estimated the SFR for the range of spatial resolutions analysed in this work following the same procedure described in Sect. 3.1, which uses the GILDAS task gauss_smooth to convolve the initial resolution images with the appropriate Gaussian kernels.
4. Dense molecular gas and SF maps
4.1. The HCN and HCO+ maps
Figure 1 shows the HCN(1–0) and HCO+(1–0) velocity-integrated intensity maps of NGC 1068 obtained by ALMA in the central r ∼ 2.5 kpc of the disk. Overall, the distribution of dense molecular gas is similar to that shown by other molecular gas tracers as seen in previous interferometer images of the galaxy (Schinnerer et al. 2000; Krips et al. 2011; Tsai et al. 2012; García-Burillo et al. 2014, 2019; Viti et al. 2014; Scourfield et al. 2020). In particular, the bulk of the HCN(1–0) and HCO+(1–0) emission stems from three main regions.
 |
Fig. 1. HCN(1–0) and HCO+(1–0) integrated intensity maps of NGC 1068. Left panel: velocity-integrated intensity map of HCN(1–0) of NGC 1068 obtained with ALMA. The map is shown in a logarithmic colour scale with contour levels of 3σ, 5σ, 7σ, 12σ, 24σ, 50σ, 120σ, and 200σ, where 1σ = 0.028 Jy beam−1 km s−1. We highlight the location of several representative regions of the emission, namely the CND, the bar, and the SB ring. Right panel: same as the left panel but for the HCO+(1–0) line map, with the same list of contour levels but here truncated at 120σ. The position of the AGN is identified by the dark grey star marker. The black bar in the top-right corner of each panel shows the spatial scale (in pc). The magenta filled ellipses at the bottom-left corners of the panels represent the ALMA beam size (1 |
The first is the CND. Described as an asymmetric elliptical ring of 6″ × 4″–size (r ∼ 200 pc), the CND shows two emission knots located ∼1″ east and ∼1.5″ west of the AGN. The CND ring is off-centred relative to the AGN locus. The two emission knots are bridged by weaker emission north and south of the AGN. The morphology of the HCN and HCO+ maps of the CND is to a large extent similar to that of the ALMA CO and CS maps (García-Burillo et al. 2014, 2019; Scourfield et al. 2020).
The second is the bar. There is HCN and HCO+ emission in the region occupied by the ∼2.6 kpc diameter stellar bar, which is oriented along PA = 46° ±2° (Scoville et al. 1988; Schinnerer et al. 2000). As shown by other molecular gas tracers, the emission in this region from both lines (especially for HCN), tends to accumulate along the leading edges of the bar. We also detect significant emission in the ‘bow-shock arc’ feature identified in the CO(3–2) and continuum dust emission maps of García-Burillo et al. (2014) on the north-east side of the disk at r ∼ 4″ − 7″ (300 pc–500 pc).
The third is the SB ring. Most of the dense molecular gas in the disk concentrates in a ring of r ∼ 18″(1.3 kpc) formed by two tightly wound spiral arms, which unfold over ∼180° in azimuth in the disk from the ends of the stellar bar. The SB ring concentrates also most of the massive star forming complexes in the disk identified in the Paα image (see Sect 4.2). The emission of HCN and HCO+ is unevenly distributed azimuthally over the SB ring: in both lines the emission is strongest around two regions, located at r ∼ 18″ and PA ∼ 15° −75° ( ± 180°), where the ring is connected to the stellar bar ends. The emission of HCN and HCO+ in the SB ring is clumpy and it appears to be organised as coming from molecular cloud associations of ≥50 pc size. The SB ring is connected at larger radii to two emission lanes located at the edge of the HCN and HCO+ maps shown in Fig. 1 along PA ∼ 50° ±180°.
Figure 2 shows the HCN-to-HCO+ line brightness ratio (Rdense) in the disk of the galaxy. The Rdense map was obtained assuming a common 3σ threshold on the integrated intensities of both lines. The Rdense ratio changes significantly across the different regions of the disk identified above. In particular, Rdense ≃ 1.5 − 3.5 in the CND and the bow-shock arc region, for which we estimated a mean value ⟨Rdense⟩≃2.2. On the other hand, Rdense ≃ 0.5 − 1.5 in the SB ring and the corresponding mean value ⟨Rdense⟩≃1.1.
 |
Fig. 2. HCN(1–0)/HCO+(1–0) brightness temperature ratio map (Rdense) derived at the common spatial resolution of ≃56 pc. The brown circle of 8″ in radius (≃560 pc) locates the inner region of the galaxy disk where the molecular outflow signature has been identified in the kinematics of molecular gas (García-Burillo et al. 2014, 2019). This region, purposely excluded from our analysis of SF relations, shows significantly higher line ratios (Rdense ≃ 1.5 − 3.5) compared to the SB ring (Rdense ≃ 0.5 − 1.5). Other symbols are the same as in Fig. 1. |
The high Rdense values measured in the CND and the bow-shock arc are related to the molecular outflow signature identified in the kinematics of molecular gas in these regions (García-Burillo et al. 2014, 2019). The outflow is thought to be driven by the interaction of the AGN wind and the radio jet with the molecular gas in the disk in a mostly coplanar geometry. Besides leaving a distinct kinematic signature in the CND and the bow-shock arc, the outflow has left its imprint on the excitation and the chemistry of molecular gas, which is under the influence of large-scale shocks and a strong UV irradiation in these regions (Viti et al. 2014; García-Burillo et al. 2017).
4.2. The Paα map
Figure 3 shows the Paα image of NGC 1068 obtained at the initial resolution of the HST/NICMOS camera: 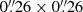 (∼18 pc × 18 pc). The central region of the image reveals strong emission stemming from an asymmetric bipolar nebula of ionised gas. Both the morphology and the kinematics of the gas in this structure have been modelled in terms of an AGN-driven wind (e.g. Crenshaw & Kraemer 2000; Cecil et al. 2002; Das et al. 2006; Müller-Sánchez et al. 2011; Barbosa et al. 2014; Miyauchi & Kishimoto 2020). The AGN wind occupies a hollow bicone that extends up to a radius r ∼ 8″ (550 pc) on its northern side. The bicone feature is oriented along PA ∼ 30°, and is characterised by a wide opening angle (∼80°). In our subsequent analysis of the SF relations we therefore screen the central r ≤ 8″ region of the galaxy, where Paα cannot be considered as a reliable tracer of SF.
(∼18 pc × 18 pc). The central region of the image reveals strong emission stemming from an asymmetric bipolar nebula of ionised gas. Both the morphology and the kinematics of the gas in this structure have been modelled in terms of an AGN-driven wind (e.g. Crenshaw & Kraemer 2000; Cecil et al. 2002; Das et al. 2006; Müller-Sánchez et al. 2011; Barbosa et al. 2014; Miyauchi & Kishimoto 2020). The AGN wind occupies a hollow bicone that extends up to a radius r ∼ 8″ (550 pc) on its northern side. The bicone feature is oriented along PA ∼ 30°, and is characterised by a wide opening angle (∼80°). In our subsequent analysis of the SF relations we therefore screen the central r ≤ 8″ region of the galaxy, where Paα cannot be considered as a reliable tracer of SF.
 |
Fig. 3. HST/NICMOS continuum-subtracted Paα image of NGC 1068. The map is shown in colour scale with contour levels of 3σ, 9σ, 15σ, 32σ, 50σ, 120σ, and 700σ, where 1σ = 0.212 × 10−16 erg s−1 cm−2 pixel−1. The colour scale range is shown in units of 10−16 erg s−1 cm−2 pixel−1. The (truncated) square region identifies the outer edge of the HST/NICMOS FOV. The angular resolution of the image is 0 |
Outside the bright AGN bicone structure, most of the Paα emission comes from the SB ring. Similar to the distribution of the dense molecular gas, SF traced by Paα is not uniformly distributed throughout the SB ring. As for HCN and HCO+, the brightest SF complexes are located at the north-east section, and most particularly, at the south-west section of the SB ring (at PA ∼ 195° −255°). In either case these are the two regions where the ring is connected to the ends of the stellar bar. Rico-Villas et al. (2021) studied the 147 GHz free-free emission associated with SF and identified a similar concentration of massive super star clusters in the bar-ring interface region.
Figure 4 shows the overlay of the HST/NICMOS Paα emission image on the HCN(1–0), HCO+(1–0), and CO(1–0) maps. For a proper comparison we degraded the Paα image to the common spatial resolution of HCN and HCO+ (∼56 pc), and to that of CO (∼100 pc). A visual inspection of this figure illustrates that the Paα maxima do not always coincide with the strongest emission peaks in HCN, HCO+ or CO throughout the SB ring.
 |
Fig. 4. Overlay of the HST/NICMOS Paα image on the molecular gas tracer maps. Left panel: overlay of the HST/NICMOS Paα image (contours) on the ALMA HCN(1–0) map (colour scale). Contours have a logarithmic spacing from 3σ to 1536σ, in steps of 0.3 dex, where 1σ = 0.180−16 erg s−1 cm−2 pixel−1. The colour scale is shown in units of Jy beam−1 km s−1. Middle panel: same as the left panel but showing the overlay of the HST/NICMOS Paα contours on the ALMA HCO+(1–0) map (colour scale). Right panel: same as the left panel but showing the overlay of the HST/NICMOS Paα contours on the PdBI CO(1–0) map of Schinnerer et al. (2000) (colour scale). Contour spacing is the same as in the left and right panels, but with 1σ = 0.162 × 10−16 erg s−1 cm−2 pixel−1. The magenta filled ellipses at the bottom-left corners in all panels represent the beam sizes of the molecular line maps: 1 |
5. Star-formation relations in NGC 1068
5.1. Kennicutt–Schmidt laws
We use in this section the images described in Sects. 2.1 and 2.2 to obtain different versions of the pixel-wise spatially resolved KS relations in the SB ring of NGC 1068 for a set of seven spatial resolutions, ranging from ∼40 − 56 pc (∼100 pc for CO(1–0)) up to ∼700 pc. To derive ΣSFR and Σgas for each spatial scale we degraded our datasets to the selected resolutions using the GILDAS task gauss-smooth. In our analysis we only consider pixels with a signal ≥3σ in ΣSFR and Σgas. Furthermore, to minimise the redundancy in the scatter plots we explore the ΣSFR − Σgas plane using a grid with Nyquist sampling adapted for each spatial resolution.
Table 1 lists the power-law indexes, as well as the Pearson correlation (ρps) and Spearman rank (ρsp) parameters obtained for the KS laws (in logarithmic space) for the different spatial resolutions and tracers used in this work. We carried out the fits of log(ΣSFR) versus log(Σgas) using the orthogonal distance regression (ODR) method. We considered that a correlation is noteworthy and statistically significant when its two-sided p-value < 1% and both ρps and ρsp are ≥0.4. Validated correlations are highlighted in boldface in Table 1. Furthermore, in order to counterbalance the dependence of the estimated p-values on the size of the sample, we derived these using a common number of randomly selected points for the different spatial scales.
Correlation parameters obtained for the KS laws derived for different tracers and spatial scales.
As an illustration of the wide variance of SF relations resulting from this analysis, we show in Fig. 5 the different versions of the KS law representing ΣSFR as a function of Σdense (here derived from HCN) for all the spatial scales explored in this work, namely from the ‘initial resolution’ (56 pc) up to 700 pc. This figure shows that the correlation becomes looser with higher resolution, and it is hardly visible in the plot with a resolution of 56 pc. The KS relation for the dense gas at the initial resolution is highly scattered: ΣSFR and Σdense span 1.5 dex each and show scarce evidence of correlation. We fit a super-linear KS relation with a power-law slope N = 3.74 ± 0.22. The correlation parameters at the initial resolution have low values (ρsp = 0.38 and ρps = 0.42) and their corresponding two-sided p-values > 1%. At scales of 100 pc we obtain a power-law slope N = 2.17 ± 0.19 with correlation parameters of ρsp = 0.35 and ρps = 0.43. In contrast, at 400 pc and 700 pc, the scatter in the KS relation is significantly reduced: ΣSFR and Σdense span 1 dex each and the derived best-fit KS relation yields a power-law index N = 1.01 ± 0.22 and N = 1.08 ± 0.12, respectively, with correlation parameters ρsp = 0.43, ρps = 0.45 and ρsp = 0.85, ρps = 0.82, with associated p-values < 1%. We represent the KS plots for all the tracers in Figs. C.1–C.4.
 |
Fig. 5. SFR surface density (ΣSFR) as a function of the dense molecular gas surface density (Σdense) derived from HCN(1–0) for the different resolutions explored in this work: 56 pc, 100 pc, 200 pc, 300 pc, 400 pc, 500 pc, 600 pc and 700 pc. The red lines show the ODR fits to the data. The dashed lines identify the correlations that are not found to be statistically significant. We only show on both axes the data points above 3σ that are considered in the fits. We indicate the Spearman’s rank correlation coefficients (ρsp) and the power-law indexes (N) of the best fits. Vertical and horizontal error bars at the lower-right corner of each panel account for the typical uncertainties, which amount to ±0.09 dex on both axes. |
Figure 6 shows how ρps and ρsp change as a function of the spatial resolution used for the different molecular gas and dust tracers used in this comparison. The grey-shaded region in Fig. 6 identifies the range of spatial scales where the correlation is judged not to be statistically significant. For spatial scales ≥300 − 400 pc the correlation improves monotonically as a function of the aperture size for all gas tracers excluding CO(1–0). The ρps and ρsp parameters for CO(1–0) show values ≤0.3 for the entire range of spatial resolutions explored. We nevertheless find that for any spatial resolution the correlation parameters derived from the high-density tracers (CO(3–2), HCN(1–0) and HCO+(1–0)) are about a factor of two to three larger than that derived from CO(1–0). Dust continuum emission shows a behaviour similar to that of the rest of high-density tracers with the important particularity that the correlation is significant already at 100 pc scales. This result confirms that continuum emission is mostly sensitive to the column densities of the dust that is being directly heated by recent SF activity in the SB ring.
 |
Fig. 6. Pearson and Spearman correlation coefficients (ρps: left panel; ρsp: right panel) of the KS laws derived for the different gas tracers used in this work as a function of the spatial resolution. Error bars represent the 67% confidence interval around the mean values. For spatial scales larger than the range identified by the grey-coloured region (≤350 pc) all the gas tracers (leaving aside CO(1–0)) show statistically significant correlations in their KS laws, defined by p-values < 1% and ρps, ρsp > 0.4. |
The reported breakdown of the KS relations observed in the SB ring below a critical spatial scale of ∼300 − 400 pc is in qualitative agreement with the findings of Onodera et al. (2010), Schruba et al. (2010) in M 33 and Kreckel et al. (2018) in NGC 628. The existence of a ‘critical scale’ for KS laws can be explained by the diverse evolutionary states of the GMC population, which can be singled out in high spatial resolution observations. The exact value of this critical scale may change from galaxy to galaxy. It may also depend on the criterion adopted to choose the data points used to generate the scatter plots: either a ‘blind’ pixel-wise Nyquist sampling or a ‘biased’ selection of apertures centred either around SF or gas emission peaks (e.g. see discussion in Williams et al. 2018). Different GMC states can reflect an ordered time sequence of SF determined by the large-scale dynamics in galaxy disks or a more stochastic pattern due to the local dispersal of molecular gas by stellar feedback.
Figure 7 shows how the power-law index N obtained from the fit to the KS relation changes as a function of the spatial resolution for the different molecular gas and dust tracers. As in Fig. 6, the grey-shaded region in Fig. 7 identifies the range of spatial scales where the correlation is not statistically significant. Overall, we find a strong scale dependence of N. The power-law index for HCN and HCO+ shows a fairly systematic decrease with the spatial resolution from N = 3.5 ± 0.3 (at the initial resolution) to N = 1.0 ± 0.1 (at 700 pc). The value of N stays around ∼1.0 ± 0.1 for the whole range of spatial scales where the correlation is significant (≥300 − 400 pc). For CO(3–2) N shows values marginally below unity in the 300 pc–500 pc range. Similarly, the value of N for the dust continuum indicates a sub-linear relation (N < 1) within the range 100 pc–600 pc. The power law becomes nevertheless linear at 700 pc as for most of the high-density tracers. The reported slightly different behaviour of CO(3–2) and dust continuum relative to HCN or HCO+ can be attributed to the fact that, although all these tracers are sensitive to the presence of dense molecular gas, CO(3–2) and dust continuum are also to a large extent mostly sensitive to the presence of comparatively hotter molecular gas, characterised by high kinetic temperatures6.
 |
Fig. 7. Power-law indexes (N) of the KS relations obtained from the ODR fit to the data for the different gas tracers used in this work as a function of the spatial resolution adopted. Symbols and colour codes are the same as in Fig. 6. |
The linear behaviour of the power law observed for all the dense gas tracers in NGC 1068 is in agreement with the results obtained in other galaxies (e.g. Gao & Solomon 2004a,b; Graciá-Carpio et al. 2008; Wu et al. 2010; García-Burillo et al. 2012; Usero et al. 2015; Liu et al. 2015; Chen et al. 2017; Williams et al. 2018; Querejeta et al. 2019). The weak correlation found between Paα and CO(1–0) at all scales indicates that the distribution of the general molecular gas traced by CO(1–0) is not strongly correlated with the current location of recent SF in the SB ring. While we do not expect to have missed a high fraction of the CO(1–0) flux in the PdBI map on scales ≤200 − 300 pc (see Sect. 2.1.2 and Appendix A), the likely increasing fraction of flux filtered on scales close to the ∼1 kpc limit could be an explanation for the poor correlation shown by CO(1–0) in Fig. 6.
5.2. The Kennicutt–Schmidt laws of NGC 1068 in context
We compare in this section the KS relations derived from HCN(1–0) in the SB ring of NGC 1068 with those obtained by previous works in different populations of galaxies. Table 2 lists the references used in this comparison. These works comprise galaxy-scale studies of SFGs and (ultra-)luminous infrared galaxies ((U)LIRGs) (e.g. see the compilation by García-Burillo et al. 2012, and references therein), as well as spatially resolved studies of individual galaxies (Usero et al. 2015; Murphy et al. 2015; Bigiel et al. 2016; Chen et al. 2017; Viaene et al. 2018; Querejeta et al. 2019). These references used the equations of Sect. 3 to convert HCN(1–0) intensities into (deprojected) surface densities of dense gas and adopted the same HCN conversion factor used in this paper. However, the SF tracers chosen in these works are different, as detailed in Table 2.
Published work on SF relations.
Figure 8 compares the different versions of the KS law derived from HCN(1–0) in NGC 1068 at three spatial resolutions (56 pc, 100 pc, and 700 pc) with those obtained in the references listed in Table 2. NGC 1068 data lie within the linear power-law branch occupied by the rest of the galaxies shown in Fig. 8. Galactic dense cores, at sub-parsec scale, align along the same relationship (Wu et al. 2005, 2010; Rosolowsky et al. 2011; Stephens et al. 2016; Shimajiri et al. 2017). Taken at face value, this suggests that the SFE (SFR per unit dense molecular mass) is nearly constant on average. As expected, the internal scatter in the distribution NGC 1068 data points is lower as we move to larger apertures. Furthermore, NGC 1068 data points shift towards lower surface densities within the power law as we move to larger apertures.
 |
Fig. 8. Comparison of the KS laws derived from HCN(1–0) in NGC 1068 with those obtained in different populations of galaxies for a range of spatial scales: global measurements (around a few kiloparsec) of the disks of SFGs and (U)LIRGs (García-Burillo et al. 2012), ≃0.3−1 kiloparsec-scale regions of the disks of nearby SFGs (Murphy et al. 2015; Usero et al. 2015; Bigiel et al. 2016), and 0.1−0.2 kpc size regions in the disk of M 51 (Chen et al. 2017; Viaene et al. 2018; Querejeta et al. 2019). For the sake of a better comparison with the reference sample, the scatter plots for NGC 1068 (magenta circles and isodensity contours) are displayed for three spatial resolutions: 56 pc (left panel), 100 pc (middle panel), and 700 pc (right panel). The scatter plot for M 51 at 100 pc resolution is displayed by the green circles and isodensity contours. The open squares stand for the median values of the distributions in NGC 1068 and M 51. |
Compared at a common scale of 100 pc, the SB ring of NGC 1068 appears as a more extreme environment relative to the SF regions of M 51 studied by Querejeta et al. (2019). As illustrated in Fig. 8, the median values of the distributions of ΣSFR and Σdense are about a factor of three to five higher in NGC 1068: ΣSFR[NGC 1068] ≃ 1.5 M⊙ Myr−1 pc−2 ≃ 3 × ΣSFR[M 51] and Σdense[NGC 1068] ≃ 174 M⊙ pc−2 ≃ 5 × Σdense[M 51]. Furthermore, when examined at scales of 700 pc, NGC 1068 occupies in the KS plot a position intermediate between that of normal galaxies and (U)LIRGs, a result that hints at the relatively extreme conditions in the SB ring.
5.3. Environmental dependence of the star-formation efficiency of the dense gas
The observed linear relation between ΣSFR and Σdense shown in Fig. 8 has been considered as evidence of the validity of density-threshold models of SF. For these models the SFE of dense molecular gas, defined as SFEdense = ΣSFR/Σdense or its inverse, which represents the depletion time of the dense gas (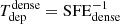 ), are about constant in different populations of galaxies and also for different dynamical environments within galaxies (Gao & Solomon 2004b; Wu et al. 2005; Lada et al. 2010, 2012; Evans et al. 2014). In this section we use the NGC 1068 data to explore the existence of an environmental dependence of SFEdense inside the SB ring.
), are about constant in different populations of galaxies and also for different dynamical environments within galaxies (Gao & Solomon 2004b; Wu et al. 2005; Lada et al. 2010, 2012; Evans et al. 2014). In this section we use the NGC 1068 data to explore the existence of an environmental dependence of SFEdense inside the SB ring.
Figure 9 (left panel) overlays the HST/NICMOS Paα image on the HCN(1–0) map of NGC 1068 obtained at the initial resolution of 56 pc. We identify the positions used to extract the fluxes of Paα and HCN(1–0) over the SB ring from the Nyquist-sampled grid7. SFEdense values span almost 1.5 dex and show a highly scattered distribution as a function of 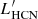 around an ‘apparently’ constant mean value of about 0.01 Myr−1, equivalent to a
around an ‘apparently’ constant mean value of about 0.01 Myr−1, equivalent to a 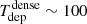 Myr (see right panel of Fig. 9). This result is similar to the findings of Gallagher et al. (2018) and Querejeta et al. (2019) obtained from their high spatial resolution images of a sample of galaxies. Notwithstanding that we might attribute part of the scatter in the SFEdense −
Myr (see right panel of Fig. 9). This result is similar to the findings of Gallagher et al. (2018) and Querejeta et al. (2019) obtained from their high spatial resolution images of a sample of galaxies. Notwithstanding that we might attribute part of the scatter in the SFEdense − 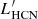 plot to possible small-scale variations in the αHCN conversion factor, any plausible range for these potential variations would nevertheless fall short of accounting for the bulk of the 1.5 dex span shown in Fig. 9.
plot to possible small-scale variations in the αHCN conversion factor, any plausible range for these potential variations would nevertheless fall short of accounting for the bulk of the 1.5 dex span shown in Fig. 9.
 |
Fig. 9. Distribution of the HCN and Paα peaks and the apertures showing the highest SFEdense in NGC 1068. Left panel: overlay of the HST/NICMOS Paα image (contours) on the HCN(1–0) map (grey scale). The contours and grey scale are the same as in Fig. 4. The set of 56 pc size circular apertures used to extract the fluxes of Paα and HCN(1–0) are colour-coded differently, depending on whether they are centred on HCN peaks (in blue), on Paα peaks (in red), or on the 10% of the apertures showing the highest values of SFEdense (in green). The black dots identify the centres of all the Nyquist-sampled 56 pc size apertures where there are reliable estimates of SFEdense across the SB ring. Right panel: distribution of SFEdense values (in Myr−1-units) as a function of LHCN (in K km s−1 pc2-units) in the SB ring of NGC 1068. Symbols are the same as in left panel. Vertical and horizontal error bars at the lower-right corner of the panel account for the typical uncertainties, which amount to ±0.13 dex and ±0.09 dex, respectively. |
Although Figs. 8 and 9 indicate that there is an overall relationship between the HCN luminosity and recent SF in the SB ring, we explore below the existence of systematic trends in SFEdense. With this aim, we selected within our initial grid a number of non-overlapping 56 pc size apertures centred on local maxima either in the HCN or the Paα maps, following the same procedure used by Querejeta et al. (2019) in their analysis of M 51 data. The local maxima were identified as the pixels with peak intensities within circular regions (‘clumps’), obtained from successive cuts in the maps. We therefore started from a high threshold (a large multiple of the noise level) and iteratively explored lower values from isolated circular regions. To collect a similar number of points selected from HCN and Paα peaks we continued to identify new clumps down to different threshold values of 12σ and 44σ, respectively. We use different colours to identify in the two panels of Fig. 9 the apertures centred on HCN peaks (blue colour), on Paα peaks (red colour), and also on the 10% of the apertures showing the highest values of SFEdense (green colour).
Figure 9 shows that the apertures showing the top 10% SFEdense values are not uniformly distributed throughout the SB ring. High SFEdense values are preferentially located at the south-west and north-east sections of the ring, namely where the ring is connected to the ends of the stellar bar. We also identify high SFEdense values further out at the north-east extreme of the SB ring. As expected, the clumps with the strongest Paα emission are also located in the regions with the highest SFEdense. Furthermore, although the overall distribution of the highest (dense) gas column density apertures also corresponds to the ends of the stellar bar, on small scales there is no one-to-one correspondence between Paα and HCN peaks. This reflects the significant variance in the evolutionary states of the dense gas clumps in these regions. In particular, the gas ridge traced by the HCN maxima tends to appear ‘upstream’ relative to the Paα maxima at the south-west section of the SB ring8.
In order to minimise the bias introduced due to the presence of HCN in the two axes of the right panel of Fig. 9, we replaced HCN by HCO+ luminosities along the x axis by selecting from our grid of points those positions satisfying 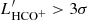 . Figure 10 shows the results obtained following the same steps leading to Fig. 9. As expected, Fig. 10 eliminates the slight anti-correlation trend identified in the SFEdense −
. Figure 10 shows the results obtained following the same steps leading to Fig. 9. As expected, Fig. 10 eliminates the slight anti-correlation trend identified in the SFEdense − 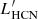 plot of Fig. 9, but the main results described above remain virtually unchanged.
plot of Fig. 9, but the main results described above remain virtually unchanged.
6. Star-formation efficiency and dense gas fraction
The overall SFE of molecular gas (SFEmol) can be expressed as the product of SFEdense and the dense gas fraction (Fdense), namely: SFEmol ≡ SFEdense × Fdense. There is mounting evidence supporting the existence of significant variations in SFEdense and Fdense as a function of the galactic environment, based on observations of molecular clouds in the centre of our Galaxy (Longmore et al. 2013; Kruijssen et al. 2014) and in nearby galaxies for a range of spatial scales (Usero et al. 2015; Bigiel et al. 2015, 2016; Gallagher et al. 2018; Querejeta et al. 2019; Jiménez-Donaire et al. 2019; Bešlić et al. 2021). In the following sections we study the trends in SFEdense and Fdense as a function of a number of physical variables with the aim of resolving the degeneracy of SF laws in the SB ring of NGC 1068. Table 3 lists the Spearman rank parameters for the different combinations of variables and spatial scales explored below.
Spearman rank parameters for different scaling relations.
6.1. Trends as a function of the boundedness of the gas
In this section we use an alternative prescription for the SF relations of the SB ring, which includes explicitly the dependence of SFEdense on a combination of Σdense and the gas velocity dispersion (σ), in an attempt to resolve the degeneracy associated with the scatter in the SFEdense − L′(HCN) plot of Fig. 9. This approach was first used by Leroy et al. (2017) in their analysis of SF relations in M 51 and also adopted by Kreckel et al. (2018) in a similar study carried out in NGC 628. Leroy et al. (2017) and Kreckel et al. (2018) used CO(1–0) and CO(2–1) to trace the bulk of the molecular gas on 40−50 pc-scales in M 51 and NGC 628, respectively. In the following analysis we use HCN(1–0) to specifically trace the dense molecular gas in the SB ring of NGC 1068 on spatial scales (∼56 pc) comparable to those explored by Leroy et al. (2017) and Kreckel et al. (2018)9.
The degree of self-gravity or boundedness of molecular gas clouds determines to a large extent their ability at forming stars. The virial parameter, defined as αvir ≈ 2KE/UE, captures the balance of gravitational potential (UE) and kinetic energy (KE) and is commonly used in turbulent models of SF as a predictor of the efficiency of SF (Krumholz & McKee 2005; Padoan et al. 2012, 2017).
We define similarly to Leroy et al. (2017) the boundedness parameter, here particularised for the dense molecular gas phase traced by HCN, as 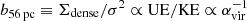 , where σ is the velocity dispersion and Σdense is the column density of dense gas measured both at the initial resolution of 56 pc. We derived intensity-weighted averages of b56 pc using two different apertures ΔA = 100 pc and 400 pc over the Nyquist sampled grid, defined as follows:
, where σ is the velocity dispersion and Σdense is the column density of dense gas measured both at the initial resolution of 56 pc. We derived intensity-weighted averages of b56 pc using two different apertures ΔA = 100 pc and 400 pc over the Nyquist sampled grid, defined as follows:
The Gaussian weight w(x, y) is defined as
where θ(x, y, x0, y0) is the angular distance from the measurement point (x0, y0), σΔA is the σ-width of the Gaussian averaging beam, and ΔA corresponds to the adopted averaging scale (100 pc and 400 pc in our case). In Eq. (10), b56 pc and I56 pc are the boundedness parameter and the HCN integrated intensity, respectively, measured at a generic position (x, y) of the grid10.
Figure 11 shows how the depletion time of the dense molecular gas estimated from HCN, 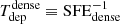 , changes as a function of the self-gravity of the gas, measured by the b parameter, at three spatial scales: 56 pc (the initial resolution), 100 pc, and 400 pc. The values of ⟨b⟩ΔA for the 100 pc and 400 pc apertures were derived from Eq. (10). Furthermore, similarly to the rest of the physical parameters analysed in Sects. 6.2–6.4, the average value of
, changes as a function of the self-gravity of the gas, measured by the b parameter, at three spatial scales: 56 pc (the initial resolution), 100 pc, and 400 pc. The values of ⟨b⟩ΔA for the 100 pc and 400 pc apertures were derived from Eq. (10). Furthermore, similarly to the rest of the physical parameters analysed in Sects. 6.2–6.4, the average value of 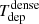 inside the two values of ΔA were derived using the Gaussian weighting function of Eq. (11).
inside the two values of ΔA were derived using the Gaussian weighting function of Eq. (11).
 |
Fig. 11. Depletion time of the dense molecular gas estimated from HCN, |
Figure 11 shows a significant monotonic decrease in 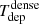 as a function of ⟨b⟩ΔA when we represent these parameters averaged over the two apertures. Specifically, we obtain (anti) correlation Spearman rank parameters ρsp = −0.43 and −0.66 for ΔA = 100 pc and 400 pc, respectively, and associated two-sided p-values < 1%. Overall, this is indicative of a higher rate of SF per unit mass of dense gas (lower
as a function of ⟨b⟩ΔA when we represent these parameters averaged over the two apertures. Specifically, we obtain (anti) correlation Spearman rank parameters ρsp = −0.43 and −0.66 for ΔA = 100 pc and 400 pc, respectively, and associated two-sided p-values < 1%. Overall, this is indicative of a higher rate of SF per unit mass of dense gas (lower 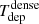 ) for regions characterised by a stronger self-gravity (higher b or lower αvir values).
) for regions characterised by a stronger self-gravity (higher b or lower αvir values).
The anti-correlation reported above is more pronounced in the intensity-weighted version of the plot derived at 400 pc scales. We identify a turnover in the Tdep − b scatter plot for ΔA = 400 pc located around log10(⟨b⟩) ≃ 0.2 M⊙ pc−2 (km s−1)−2, as shown in the right panel of Fig. 11. The observed change of tendency around this point defines two regimes in the Tdep − b parameter space. To quantify the two-regime trend and the turnover, we used the Multivariate Adaptive Regression Splines (MARS) fit routine from the Rstudio package11. We performed the MARS fit on 100 realisations of the Tdep versus b relation at ΔA = 400 pc taking into account the data uncertainties. From this Monte Carlo simulation, we obtained a turnover at log10(⟨b⟩) = 0.23 ± 0.02 M⊙ pc−2 (km s−1)−2 which is indicated in the right panel of Fig. 11. Furthermore, for ⟨b⟩ values below the turnover the trend is approximately flat (slope = 0.02 ± 0.11). In contrast, the MARS routine fits a slope = −1.59 ± 0.15 beyond the turnover. This slope is larger than the one obtained by Leroy et al. (2017) (≃ − 0.9) in their analysis of the M 51 CO(1–0) data, derived using the same averaging spatial scales (400 pc). Kreckel et al. (2018) found nevertheless no significant correlation in their analysis of the CO(2–1) data of NGC 628, which used an averaging scale of 500 pc. Compared to the shallower or nonexistent trends identified in M 51 and NGC 628, the steeper decline of 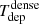 with ⟨b⟩ in the SB ring of NGC 1068 reflects the tighter link between the boundedness of dense molecular gas and SFE.
with ⟨b⟩ in the SB ring of NGC 1068 reflects the tighter link between the boundedness of dense molecular gas and SFE.
Figure 12 shows the spatial distribution of 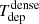 and ⟨b⟩ derived for ΔA = 400 pc in the SB ring of NGC 1068. The
and ⟨b⟩ derived for ΔA = 400 pc in the SB ring of NGC 1068. The 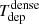 map of Fig. 12 confirms the picture drawn from the analysis of Sect. 5.3: the regions showing comparatively higher (lower) SFEdense (
map of Fig. 12 confirms the picture drawn from the analysis of Sect. 5.3: the regions showing comparatively higher (lower) SFEdense (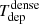 ) values are preferentially located closer to the region where the SB ring is connected to the ends of the stellar bar around PA ∼ 15° −75° ( ± 180°). We also see a similar spatial segregation in the ⟨b⟩ map, which shows higher ⟨b⟩ values closer to the bar-ring interface region. Besides the azimuthal dependence of
) values are preferentially located closer to the region where the SB ring is connected to the ends of the stellar bar around PA ∼ 15° −75° ( ± 180°). We also see a similar spatial segregation in the ⟨b⟩ map, which shows higher ⟨b⟩ values closer to the bar-ring interface region. Besides the azimuthal dependence of 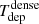 and ⟨b⟩ within the SB ring, we also identify a radial dependence for both parameters especially in the southern section of the bar-ring interface: in particular, the highest (lowest)
and ⟨b⟩ within the SB ring, we also identify a radial dependence for both parameters especially in the southern section of the bar-ring interface: in particular, the highest (lowest) 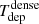 (⟨b⟩) values tend to appear upstream (smaller radii) along the gas circulation lines if we assume that the sense of rotation of the gas in the disk is counterclockwise. The two branches in the
(⟨b⟩) values tend to appear upstream (smaller radii) along the gas circulation lines if we assume that the sense of rotation of the gas in the disk is counterclockwise. The two branches in the 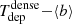 plot of Fig. 11 correspond to a large extent to the two regions of the SB ring identified in Fig. 12. Similar results are found in Appendix E when we consider the HCO+ as dense gas tracer. The trends and statistical parameters derived are practically identical to the ones obtained using HCN.
plot of Fig. 11 correspond to a large extent to the two regions of the SB ring identified in Fig. 12. Similar results are found in Appendix E when we consider the HCO+ as dense gas tracer. The trends and statistical parameters derived are practically identical to the ones obtained using HCN.
 |
Fig. 12. Maps of the depletion time and the b parameter in the SB ring of NGC 1068. Left panel: map of the depletion time of the dense molecular gas ( |
We can speculate if the reported trends of 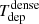 as a function of ⟨b⟩ for ΔA = 400 pc, visualised in Figs. 11 and 12, could be entirely attributed to potential variations in the αHCN conversion factor on these spatial scales. In this context it is worth noting that the range explored by
as a function of ⟨b⟩ for ΔA = 400 pc, visualised in Figs. 11 and 12, could be entirely attributed to potential variations in the αHCN conversion factor on these spatial scales. In this context it is worth noting that the range explored by 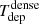 as a function of ⟨b⟩, which amounts to 0.6 dex (a factor of four), is a significant factor of three larger than the differences found between the global kiloparsec-scale and the ‘small’ parsec-scale HCN conversion factors reported by Wu et al. (2005), as mentioned in Sect. 3.1. Although we have no way of confirming or refuting the existence of significantly larger changes of αHCN based on our data, we note that adopting a lower value of the conversion factor for HCN would result in lower molecular gas surface densities, particularly in the regions of the SB ring of NGC 1068 that happen to show comparatively higher (lower) SFEdense (
as a function of ⟨b⟩, which amounts to 0.6 dex (a factor of four), is a significant factor of three larger than the differences found between the global kiloparsec-scale and the ‘small’ parsec-scale HCN conversion factors reported by Wu et al. (2005), as mentioned in Sect. 3.1. Although we have no way of confirming or refuting the existence of significantly larger changes of αHCN based on our data, we note that adopting a lower value of the conversion factor for HCN would result in lower molecular gas surface densities, particularly in the regions of the SB ring of NGC 1068 that happen to show comparatively higher (lower) SFEdense (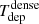 ) values. These regions very likely comprise a collection of hot core-like clouds akin to the Galactic SF cores studied by Wu et al. (2005) for which
) values. These regions very likely comprise a collection of hot core-like clouds akin to the Galactic SF cores studied by Wu et al. (2005) for which 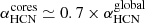 . As a direct consequence, the trends shown in Figs. 11 and 12 would be further enhanced rather than being suppressed.
. As a direct consequence, the trends shown in Figs. 11 and 12 would be further enhanced rather than being suppressed.
6.2. Trends as a function of the dense gas fraction
Observations of molecular gas in our Galaxy and in a number of nearby galaxies have found clear evidence of trends in SFEdense as a function of Fdense, which are indicative of anti-correlation (e.g. Longmore et al. 2013; Chen et al. 2015; Murphy et al. 2015; Usero et al. 2015; Bigiel et al. 2016; Gallagher et al. 2018; Querejeta et al. 2019; Jiménez-Donaire et al. 2019). In particular, Usero et al. (2015) found that SFEdense is about six to eight times lower near the galaxy centres than in the outer regions of the galaxy disks analysed in their IRAM 30-m survey. This radial trend is reversed for Fdense in their sources. Furthermore, Longmore et al. (2013) found anomalously low SFR values in a large fraction of high-density molecular clouds in the centre of the Milky Way, suggestive of an anti-correlation between SFEdense and Fdense. A similar trend has been found recently by Querejeta et al. (2019) in their study of M 51, and by Jiménez-Donaire et al. (2019) from an analysis of the data obtained by the EMPIRE survey in nine spiral galaxies. We examine in this section the existence of a trend in SFEdense as a function of Fdense in the SB ring of NGC 1068.
We define two proxies for the ‘dense gas fraction’ in the SB ring. First, the ratio of the dense molecular gas surface density derived from HCN (1–0) to the bulk molecular gas surface density derived from CO(1–0), that is, Fdense = Σdense/Σmol ∝ IHCN(1 − 0)/ICO(1 − 0). We consider that CO line traces the bulk of the molecular gas in the galaxy (nH2 ≳ 102 − 3 cm−3), while HCN traces material with nH2 ≳ 104 − 5 cm−3. We therefore use the HCN(1–0)/CO(1–0) line ratio (hereafter RHCN/CO) as a proxy for the dense gas fraction in the SB ring. Secondly, we also use the CO(3–2)/CO(1–0) ratio (hereafter R3 − 2/1 − 0) in the SB ring derived by García-Burillo et al. (2014) as an alternative proxy for Fdense.
Figures 13 and 14 show RHCN/CO and R3 − 2/1 − 0 in Tmb units. To derive the brightness temperature ratios, we degraded the HCN(1–0) and CO(3–2) maps to the spatial resolution of the CO(1–0) observations of Schinnerer et al. (2000). The RHCN/CO ratio changes significantly across the disk of NGC 1068. The highest values of RHCN/CO, > 0.4 − 1.2, correspond to the CND. Although in the SB ring RHCN/CO shows a wide range of values, this ratio is higher in the bar-ring interface region (RHCN/CO ∼ 0.2 − 0.4) than elsewhere in the ring (RHCN/CO ∼ 0.05 − 0.2). The R3 − 2/1 − 0 ratio, shown in Fig. 14, changes also significantly across the disk. The R3 − 2/1 − 0 ratio in the CND (∼2 − 6) is higher than in the SB ring, in agreement with previous estimates by Krips et al. (2011) and Tsai et al. (2012). While the average ratio is ∼1.2 ± 0.02 in the SB ring, R3 − 2/1 − 0 is higher in the bar-ring interface region (R3 − 2/1 − 0 ∼ 0.6 − 3) and comparatively lower elsewhere in the ring (R3 − 2/1 − 0 ∼ 0.1 − 0.8).
 |
Fig. 13. HCN(1–0)/CO(1–0) brightness temperature ratio map (RHCN/CO; colour scale and contours) derived at the common (lower) spatial resolution of the CO(1–0) observations of Schinnerer et al. (2000) (≃100 pc). The brown circle of 8″ in radius (≃560 pc) locates the inner region excluded from our analysis of SF relations. |
 |
Fig. 14. Same as Fig. 13 but showing the CO(3–2)/CO(1–0) brightness temperature ratio map (R3 − 2/1 − 0; colour scale and contours) derived at the common (lower) spatial resolution of the CO(1–0) observations. |
The RHCN/CO ratio is hardly sensitive to kinetic temperature (Tk), as the energy levels giving rise to both rotational transitions are similar (Ek[J = 1, CO] ∼ 5.5 K, Ek[J = 1, HCN] ∼ 4.3 K). However, as the excitation of both CO lines are sensitive to both nH2 and Tk, R3 − 2/1 − 0 is comparatively a more indirect and less straightforward tracer of Fdense relative to RHCN/CO. Leaving aside the uncertainties on the value of αHCN in SF regions, which may reflect a peculiar hot-core like chemistry, RHCN/CO is therefore the most reliable proxy for the dense gas fraction and as such is widely used in extragalactic studies, and we therefore adopt it in the following analysis. In either case, we note that both line ratios suggest a higher excitation of HCN(1–0) and CO(3–2) lines relative to CO(1–0) in the bar-ring interface region.
Figure 15 represents SFEdense as a function of Fdense estimated from RHCN/CO in the SB ring. We adopted the same approach followed in Sect. 6.1 to obtain estimates of both variables over two averaging scales: ΔA = 100 pc and 400 pc. Figure 15 shows that there is no significant trend in SFEdense as a function of Fdense for ΔA = 100 pc: we estimate a Spearman rank parameter ρsp = +0.03 with a two-sided p-value > 1%. For ΔA = 400 pc there is nevertheless a more significant positive correlation (ρsp = +0.34, with a p-value < 1%). This trend is a direct consequence of the spatial distribution of SFE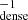 and Fdense shown, respectively, in Figs. 12 and 13. The monotonic increase shown in the right panel of Fig. 15 suggests that the comparatively denser molecular gas of the bar-ring interface region inside the SB ring forms stars at higher rate per unit dense gas mass.
and Fdense shown, respectively, in Figs. 12 and 13. The monotonic increase shown in the right panel of Fig. 15 suggests that the comparatively denser molecular gas of the bar-ring interface region inside the SB ring forms stars at higher rate per unit dense gas mass.
 |
Fig. 15. Star-formation efficiency of the dense gas (SFEdense) as a function of dense gas fraction (Fdense: estimated from the HCN(1–0)-to-CO(1–0) line ratio of Fig. 13) in NGC 1068 using two averaging scales: 100 pc (left panel) and 400 pc (right panel). Magenta circles correspond to data measurements evaluated at the Nyquist-sampled grid of points after convolution with the appropriate Gaussian for each aperture. Black circles show median SFEdense values, and error bars indicate the rms scatter in the bins. Vertical and horizontal error bars at the lower-right corner of both panels account for the typical uncertainties, which amount to ±0.13 dex. |
This result seems to be in contradiction with the anti-correlation trends found between SFEdense and Fdense in previous works in other galaxies. Specifically, Usero et al. (2015) found an index N ∼ −1.6 for the SFE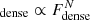 power-law fitting their data. A similar index (N ∼ −1.5) can be estimated from the data compiled by Querejeta et al. (2019).
power-law fitting their data. A similar index (N ∼ −1.5) can be estimated from the data compiled by Querejeta et al. (2019).
6.3. Trends as a function of the stellar mass surface density
Several works studying the existence of trends in SFEdense as a function of Σstar on kiloparsec scales in a number of nearby galaxies have found that SFEdense is seen to decrease in the central parts of galaxy disks, namely in regions characterised by high Σstar. These observations also showed that Fdense tends to increase systematically with Σstar (Chen et al. 2015; Usero et al. 2015; Bigiel et al. 2016; Gallagher et al. 2018; Jiménez-Donaire et al. 2019). Querejeta et al. (2019) studied different regions in the disk of M 51 and found that similar correlations are recovered at 100 pc-scales. We investigate below the trends in SFEdense and Fdense as a function of Σstar in the SB ring of NGC 1068.
Near-infrared emission is commonly used to trace the stellar mass in nearby galaxies, since light at these wavelengths mainly comes from old stars and is less affected by extinction (Quillen et al. 1994). With this aim, we used the HST NIR continuum narrow-band image of NGC 1068 at 1.9 μm, obtained with the F190N filter on the NICMOS 3 camera, to trace the distribution of the stellar mass in the disk of the galaxy. We assumed a constant mass-to-light ratio M/L1.9 μm = 0.2 M⊙/L⊙ (e.g. see Querejeta et al. 2015) to obtain the local stellar mass surface density. Figure 16 overlays the HCN(1–0) integrated intensity contours on the HST/NICMOS F190N image. The stellar bar feature is easily identified in the NIR image. Judging from the overall distribution of Σstar in the disk, it appears that the bar-ring interface is characterised by higher Σstar values compared to the regions located elsewhere in the SB ring.
 |
Fig. 16. Overlay of the ALMA HCN(1–0) map (contours) on the HST/NICMOS F190N continuum image at 1.9 μm HST (colour scale as shown in Jy). The contour spacing is 3σ, 7σ, 12σ, 24σ, 50σ, and 120σ, where 1σ = 0.028 Jy beam−1 km s−1. The white circle of r = 8″ locates the inner region of the galaxy disk, which was excluded of our analysis. The HST/NICMOS F190N image has been degraded to the spatial resolution of HCN(1–0) (1 |
Figure 17 represents SFEdense as a function of Σstar across the SB ring of NGC 1068 for the three working apertures adopted in Sect. 6.1. SFEdense does not show any significant correlation with Σstar at the initial resolution (ρsp = +0.10, with a p-value > 1%), or at the 100 pc averaging scale (ρsp = +0.15, with a p-value > 1%). On the contrary, SFEdense shows a statistically significant positive correlation with Σstar in the SB ring for ΔA = 400 pc (ρsp = +0.59, with a p-value < 1%). We compare the location of NGC 1068 in the SFEdense − Σstar parameter space with the position occupied by the galaxies studied by the references listed in Table 2 in the middle panel of Fig. 17. NGC 1068 clearly deviates from the overall anti-correlation trend followed by other galaxies. The positive correlation observed in the NGC 1068 SB ring is in stark contrast with the anti-correlation trends identified in the galaxies studied by Usero et al. (2015) (ρsp = −0.50), Querejeta et al. (2019) (ρsp = −0.57), and Gallagher et al. (2018) (ρsp = −0.66). In this context it is noteworthy that Querejeta et al. (2019) noticed that for a given value of Σstar the data points of M 51 span a significant 1 dex range of SFEdense, namely similar to the spread of values seen in the NGC 1068 SB ring. This is an indication of the wide range of dynamical environments probed in both galaxies.
 |
Fig. 17. Star-formation efficiency of the dense gas (SFEdense) as a function of the stellar mass surface density (Σstar) in the SB ring of NGC 1068 at the initial resolution of 56 pc (left panel) and at two averaging scales: 100 pc (middle panel) and 400 pc (right panel). Magenta circles and isodensity contours correspond to data measurements evaluated at the Nyquist-sampled grid of points after convolution with the appropriate Gaussian for each aperture. Black circles show median SFEdense values, and error bars indicate the rms scatter in the bins. Symbols and isodensity contours in the middle panel identify the data obtained in other galaxies. The dashed orange line represents the fit of Usero et al. (2015). Vertical and horizontal error bars at the lower-right corner of each panel account for the typical uncertainties, which amount to ±0.13 dex and ±0.09 dex, respectively. |
Figure 18 represents Fdense as a function of Σstar across the SB ring of NGC 1068 for the two averaging scales adopted in Sect. 6.1. Fdense shows already a significant correlation with Σstar at ΔA = 100 pc (ρsp = +0.40, with a p-value < 1%). The correlation is further reinforced when we use 400 pc as averaging scale (ρsp = +0.67, with a p-value < 1%). This is qualitatively and quantitatively similar to the trends identified in the data of the galaxies shown in the left panel of Fig. 18 at scales of 100 pc, for which Querejeta et al. (2019) derived a Spearman rank parameter of ρsp ∼ +0.45, and ρsp ∼ +0.7 when they added the data points from Chen et al. (2017) and Gallagher et al. (2018).
 |
Fig. 18. Fraction of dense gas (Fdense) as a function of the stellar mass surface density (Σstar) in the SB ring of NGC 1068 at the two averaging scales: 100 pc (left panel) and 400 pc (right panel). Symbols are the same as in Fig. 17. Vertical and horizontal error bars at the lower-right corner of each panel account for the typical uncertainties, which amount to ±0.13 dex and ±0.09 dex, respectively. |
6.4. Trends as a function of velocity dispersion
The role of velocity dispersion in setting the efficiency of molecular gas at forming stars is central to current models of turbulence-driven SF via their dependence on the Mach number (e.g. Krumholz & McKee 2005; Hennebelle & Falgarone 2012; Federrath 2015). From the observational point of view, and under the hypothesis that the velocity dispersion measured at a given scale reflects mainly turbulent motions in molecular gas, identifying trends in SFE as a function of local velocity dispersion may indicate whether SF tends to be either enhanced or suppressed by turbulence. The predictions of models on the expected trends of SFEdense as a function of the ‘observed’ velocity dispersion (σ) differ depending on the role of turbulence versus large-scale bulk motions (e.g. streaming motions) that are driven by the background gravitational potential. The degree of coupling to the large-scale gravitational potential implies that the critical threshold for SF is not universal and that SFEdense is therefore not constant. Specifically, the recent model published by Meidt et al. (2020) foresees that SFEdense should decrease with σ at fixed values of Fdense and Σmol.
Leroy et al. (2017) found a decreasing trend between the efficiency of the bulk molecular gas (SFEmol) and σ measured from CO(1–0) in M 51. Querejeta et al. (2019) also found a significant anti-correlation between SFEdense and σ in M 51 (ρsp = −0.62). A comparison of the observations of M 31 (Viaene et al. 2018) and M 51 (Querejeta et al. 2019) with the predictions of the Meidt et al. (2020) model shows a fair agreement for apertures of 100 pc.
Figure 19 examines the trends in SFEdense as a function of σ across the SB ring of NGC 1068 for the three apertures adopted in Sect. 6.1. We note that the value of σ derived on scales of 56 pc is not a good proxy for the ‘internal’ turbulence of the dense cores probed by HCN, which in all likelihood have sizes of around a few parsec. Instead, σ likely encapsulates a mix of the ‘macroscopic’ turbulence between the cores and the residual gradient of large-scale bulk motions within the ALMA beam. The correlation shown in Fig. 19 is not statistically significant for the two extreme values of the averaging apertures (56 pc and 400 pc). However, there is a weak yet significant trend at 100 pc scales, for which we derive a ρsp = −0.28, with a p-value = 0.3%. Overall, the results obtained in NGC 1068 show a very marginal agreement with the results of Viaene et al. (2018) and Querejeta et al. (2019) and, therefore, with the predictions of the Meidt et al. (2020) model. As illustrated in Fig. 20, a fraction of the data corresponding to the SB ring in NGC 1068 lies in the region predicted by Meidt et al. (2020) for Fdense ∼ 0.25 and a range for Σmol ∼ 500 − 5000 M⊙ pc−2. Although these values are in rough agreement with the ones estimated for a high fraction of the SB ring positions, the decreasing trend in SFEdense as a function of σ is seen to be much shallower than the one predicted by Meidt et al. (2020). However, as noted by Meidt et al. (2020), a gravitational potential linked to a strong density wave (bar or spiral) may tend to degrade the strength of the expected decreasing trend, which is estimated in their model using a purely axisymmetric disk.
 |
Fig. 19. Star-formation efficiency of the dense gas (SFEdense) as a function of the velocity dispersion of HCN (σ) in NGC 1068 for three averaging scales: 56 pc (left panel), 100 pc (middle panel), and 400 pc (right panel). Measurements at 100 pc scales are compared to literature data for other galaxies. Symbols are the same as in Fig. 17. Vertical and horizontal error bars at the lower-right corner of each panel account for the typical uncertainties, which amount to ±0.13 dex and ±0.06 dex, respectively. |
 |
Fig. 20. Same as the middle panel of Fig. 19 but adding a comparison with the trends of SFEdense as a function of the velocity dispersion of the gas (σ) predicted by the model of Meidt et al. (2020). This model foresees different locations of galaxies in the SFEdense − σ parameter space depending on the fraction of dense gas (Fdense) and, also, on the total molecular gas column densities (Σmol). Symbols are the same as in Fig. 17. Vertical and horizontal error bars at the lower-right corner account for the typical uncertainties, which amount to ±0.13 dex and ±0.06 dex, respectively. |
Figure 21 explores the trends of Fdense as a function of σ in the SB ring for the two averaging scales adopted in Sect. 6.1. In contrast with the trends identified in M 31 and M 51 by Viaene et al. (2018) and Querejeta et al. (2019) on 100 pc scales, Fdense fails to show any significant correlation with σ in the SB ring of NGC 1068 for ΔA = 100 pc (ρsp = +0.10, with a p-value > 1%), However, a significant positive trend appears when we use 400 pc as averaging scale (ρsp = +0.50, with a p-value < 1%).
 |
Fig. 21. Dense gas fraction (Fdense) as a function of velocity dispersion in the SB ring of NGC 1068 at the two averaging scales: 100 pc (left panel) and 400 pc (right panel). Measurements at 100 pc scales are compared to literature data for other galaxies. Symbols are the same as in Fig. 17. Vertical and horizontal error bars at the lower-right corner of each panel account for the typical uncertainties, which amount to ±0.13 dex and ±0.06 dex, respectively. |
6.5. Relation between the star-formation rate and the dense gas fraction
Viaene et al. (2018) observed a significant correlation (ρsp = 0.63) between the SFR and Fdense in a number of regions in the disk of M 31 observed with a spatial resolution of 100 pc. Querejeta et al. (2019) explored the correlation between ΣSFR and Fdense in M 51 after incorporating the data obtained by Chen et al. (2017) in M 51 on similar spatial scales and derived a similar positive trend: ρsp = 0.63, with a p-value < 1%. This correlation improved when Querejeta et al. (2019) included the M 31 and NGC 3627 data of Viaene et al. (2018) and Murphy et al. (2015), respectively (ρsp = 0.66).
Figure 22 shows the region occupied by the NGC 1068 data in the ΣSFR − Fdense plot for an adopted averaging scale ΔA = 100 pc. We do not find a strong correlation between ΣSFR and Fdense (ρsp = 0.22) when we consider the NGC 1068 data alone. In particular, this correlation is weaker than the one found between ΣSFR and Σdense for the same spatial scales (ρsp = 0.35; see Table 1). This result is an indication that the dense gas fraction is not a better predictor of SF than the dense gas content in the SB ring. However, if we include the data published for the galaxies displayed in Fig. 22, the overall correlation improves significantly (ρsp = 0.72). Querejeta et al. (2019) used all the available data at 100 pc scales and similarly concluded that the dense gas fraction does not seem to be a better predictor of the SFR surface density than the dense gas surface density.
 |
Fig. 22. Star formation rate surface density (ΣSFR) as a function of dense gas fraction (Fdense) in NGC 1068 measured at 100 pc scales compared to the data obtained in other galaxies (symbols as in Fig. 8). Vertical and horizontal error bars at the lower-right corner account for the typical uncertainties, which amount to ±0.09 dex and ±0.13 dex, respectively. |
7. A scenario for star formation in the SB ring
The results of our work support the relevance of dynamical environment in setting the efficiency of SF of the dense molecular gas in galaxy disks. Specifically, we find that SFEdense is comparatively boosted by up to a factor of three to four in the bar-ring interface of NGC 1068 relative to the regions located elsewhere in the ring.
The velocity dispersion of the dense gas as derived from the HCN(1–0) line at the initial resolution of ALMA shows little variations over the SB ring. For an averaging scale of 400 pc, Fig. 23 shows that σ changes from ∼14 to ∼19 km s−1 with an estimated mean value of about 16 km s−112. Specifically, σ shows only a moderate ∼30% increase in the southern region of the bar-ring interface (see Fig. 23). This is in agreement with the picture drawn from the analysis of the velocity dispersion estimated at 42 pc resolution from the CO(3–2) line, as illustrated by Fig. 10 of García-Burillo et al. (2014). Furthermore, the right panel of Fig. 21 shows that, while Fdense increases by ∼0.6 dex, the corresponding increase in σ (∼0.12 dex) is a factor of three smaller. Although Fdense and Σdense are not identical quantities, the super-linear trend of Fdense as a function σ implies that the trends in the boundedness parameter described in Sect. 6.1 are mostly driven by the observed boost in Fdense in the bar-ring interface. All in all, these results suggest that molecular gas undergoes an efficient compression likely as a result of an enhanced rate of cloud-cloud collisions in the bar-ring interface. However, the shallow trends in σ suggest that cloud-cloud collisions have not increased to any significant level the ‘macroscopic’ turbulence between the cores of dense gas probed on scales of 56 pc in this region.
 |
Fig. 23. Same as Fig. 12 but showing the map of the velocity dispersion (σ) obtained using 400 pc as an averaging scale. Contour levels for σ go from 14.0 to 19.0 in steps of 0.5 km s−1. |
The SB ring is formed by a tightly wound two-arm spiral structure. The gas accumulates in a region where two density-wave resonances are thought to be overlapping: the inner Lindblad resonance (ILR) of the ∼17 kpc size outer stellar oval and the corotation of the ∼2.6 kiloparsec-diameter stellar bar (Bland-Hawthorn et al. 1997; Schinnerer et al. 2000; Emsellem et al. 2006). The accumulation of gas at the SB ring suggests that the barrier imposed by the corotation of the (nuclear) stellar bar has been overcome13. This could reflect either the influence of the outer stellar oval, which produces gas inflow down to its ILR, or the influence of a decoupled (lower pattern speed) spiral mode, which would also induce gas inflow inside its own corotation. Based on a Fourier decomposition of streaming motions derived from CO(3–2), García-Burillo et al. (2014) found the signature of systematic gas inflow across the SB ring, an indication that the two-arm spiral constitutes an independent wave feature characterised by a lower pattern speed. The inward motions detected are particularly strong at the region connecting the bar with the spiral (see Fig. 14 of García-Burillo et al. 2014). In either case, orbital crowding and the intersection of molecular gas on the orbits of the bar and the spiral are seen to enhance SFEdense in their interface region. Rico-Villas et al. (2021) recently analysed the continuum emissions at 147 and 350 GHz observed with ALMA, together with the Paα HST/NICMOS image of NGC 1068, and identified 14 super star clusters in the SB ring. In agreement with the scenario described above, most of the super star clusters (11 out of 14) are seen to be located at the bar ends.
NGC 1068 is not by any means an isolated case that illustrates how the complex molecular gas dynamics in a bar-spiral arm interface can trigger SF activity in a galaxy disk. In particular, Beuther et al. (2012) found evidence that the particular dynamical environment of the W43 mini-SB complex in the Milky Way has likely increased cloud interactions and the subsequent SF activity in this region, which is located near the Galactic bar-spiral arm interface. Furthermore, Beuther et al. (2017), and more recently, Bešlić et al. (2021) found an increase in SF activity in the bar-spiral arm interface region of the strongly barred galaxy NGC 3627, as a result of the accumulation of gas where the two orbit families (related to the bar and the spiral) intersect, triggering cloud-cloud collisions. Specifically, the work of Bešlić et al. (2021) reveals that, compared to other regions in the disk of NGC 3627, the efficiency of the dense molecular gas derived from Hα/HCN ratios is significantly enhanced in the bar-spiral arm interface region. Similarly to the scenario described by Beuther et al. (2017) for NGC 3627, we conclude that a configuration where the bar and spiral may rotate at two different pattern speeds can explain the intense SF at the bar-ring interface of NGC 1068.
Several hydrodynamical numerical simulations have been used to investigate the role of large-scale bars in AGN fuelling and in triggering SF in galaxy disks (e.g. Renaud et al. 2013, 2015; Emsellem et al. 2015). In particular, Renaud et al. (2015) showed that the SFE and the formation of massive stellar associations are enhanced at the extremities of the bar to a level comparable to the one observed in galaxy-galaxy interactions as a result of cloud-cloud collisions. This scenario seems to account for the observed pattern of SFEdense in NGC 1068.
8. Summary and conclusions
We used ALMA to image the emission of dense molecular gas in the r ∼ 1.3 kpc SB ring of the Seyfert 2 galaxy NGC 1068 with a resolution of ∼56 pc using the 1–0 transitions of HCN and HCO+. We also used ancillary data of CO(1–0) as well as CO(3–2) and its underlying continuum emission at the resolutions of ∼100 pc and ∼40 pc, respectively. These observations allow us to probe a wide range of molecular gas densities (nH2 ∼ 103 − 5 cm−3). The SFR is derived from Paα line emission imaged by HST/NICMOS. We analysed the influence of the dynamical environment on different formulations of SF relations in the SB ring and compared our results with the general predictions of density-threshold and turbulent SF models.
The main results of this paper are summarised as follows:
-
We derived spatially resolved KS laws for a set of eight spatial resolutions, ranging from ∼40 pc up to ∼700 pc. We studied how these relations change depending on the adopted aperture sizes and on the choice of molecular gas tracer. For a given spatial resolution the correlation parameters derived from the high-density tracers (CO(3–2), HCN(1–0) and HCO+(1–0)) are about a factor of two to three larger than that derived from CO(1–0).
-
The KS correlations lose statistical significance below the critical spatial scale of ≈300-400 pc, common for all gas tracers. For spatial scales ≥300 − 400 pc the correlation improves monotonically as a function of the aperture size for all gas tracers, with the exception of CO(1–0). While dust continuum emission shows a behaviour similar to other high-density tracers, the dust-based KS correlation is significant already at 100 pc scales.
-
NGC 1068 lies within the general ΣSFR − Σdense linear KS relationship derived from a compilation of data obtained in other galaxies. In particular, the location of NGC 1068 in the KS plot is intermediate between that of normal galaxies and that of (U)LIRGs, a result that underlines the relatively extreme conditions in the SB ring.
-
The SFE of the dense molecular gas, defined as SFEdense ≡ ΣSFR/Σdense, shows a scattered distribution as a function of the HCN luminosity at the initial resolution of ALMA (∼56 pc) around a mean value of ≃0.01 Myr−1. However, we find evidence of a significant environmental dependence of SFEdense reflected in the existence of systematic trends across the different regions of the SB ring, which are inconsistent with the predictions of density-threshold models.
-
With the aim of resolving the degeneracy associated with the SFEdense − L′(HCN) plot, we explored an alternative prescription for SF relations, which includes the dependence of SFEdense on the boundedness of the gas that is measured by the parameter b defined as
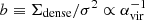 . We identified two branches in the version of the SFEdense − b plot derived for an averaging scale of 400 pc. The two branches correspond to two dynamical environments defined by their proximity to the region where the SB ring is connected to the stellar bar of NGC 1068.
. We identified two branches in the version of the SFEdense − b plot derived for an averaging scale of 400 pc. The two branches correspond to two dynamical environments defined by their proximity to the region where the SB ring is connected to the stellar bar of NGC 1068. -
We studied the trends in SFEdense as a function of the dense gas fraction (Fdense), the stellar mass surface density (Σstar), and the velocity dispersion (σ) in the SB ring using different averaging scales. We find that SFEdense correlates both with Fdense and Σstar. However, we find no significant correlation of SFEdense with σ. These results differ to a large extent from those derived from previous kiloparsec-scale studies of galaxy disks and high-resolution (∼100 pc) observations of M 51.
-
The trends in the boundedness parameter in the SB ring are mostly driven by the observed boost in Fdense in the bar-ring interface region. The results reflect a significant compression of molecular gas as a result of an enhanced rate of cloud-cloud collisions in the bar-ring interface on the one hand and an efficient dissipation of turbulence on the other.
The outcome of our work emphasises the relevance of different dynamical environments to modulating SFEdense in galaxy disks. Taken at face value, this result is inconsistent with the predictions of density-threshold models, which foresee the existence of a nearly constant canonical value for SFEdense. There is mounting observational evidence that SFEdense can show systematic trends based on studies carried out in both our Galaxy and nearby galaxies. However, the theoretical scenarios advanced to explain the variations in SFEdense reported in the literature are diverse. This diversity reflects the variety of trends observed in SFEdense as a function of key physical variables such as Fdense, Σstar, and σ in galaxy disks. Similarly to the case of the barred galaxy NGC 3627 discussed by Beuther et al. (2017), the enhanced SF activity in the bar-ring interface of NGC 1068 could be explained by a dynamical configuration in which the bar and the two-arm spiral feature are independent m = 2 modes rotating at different pattern speeds. Further studies are required to explore the frequency of this type of dynamical decoupling between bars and spirals and their role at setting the SFE of dense molecular gas in galaxy disks in general and in galactic rings in particular.
The corresponding values for ΔIcalib range respectively from ≃10%×I to ≃15%×I for the ALMA band 7 observations and the PdBI CO(1–0) data used in this paper (see Sect. 2.1.2). These values imply similar typical uncertainties on I ≤ ±0.09 − 0.10 dex in either case for the regions of the SB ring of NGC 1068 examined in this work.
Tsai et al. (2012) studied the KS law in NGC 1068 using CO(3–2) and the FIR luminosity and also found a sub-linear power law for the LCO(3 − 2)–LFIR relation with N ∼ 0.50 at scales of ∼300 pc.
The black dots in Fig. 9 single out the grid positions where the fluxes of HCN and Paα are both > 3σ.
We can assign an upstream location of HCN relative to Paα after assuming that the sense of rotation of the gas in the disk is counterclockwise (e.g. García-Burillo et al. 2014).
Querejeta et al. (2019) applied the methodology of Leroy et al. (2017) to the HCN(1–0) data of M 51, yet at a spatial resolution of ∼100 pc, that is, about a factor of two lower than the one used in our work.
Leroy et al. (2017) used a slightly different definition of the intensity-weighted average of the b parameter: ⟨b⟩≡⟨Σgas⟩/⟨σ2⟩. With this definition the averaging is performed separately for the numerator and the denominator of the b parameter. As shown in Appendix D, the trends and statistical parameters derived following this definition are virtually identical to the ones obtained in Sect. 6.1.
Acknowledgments
We thank the referee for the useful comments and suggestions. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2013.1.00055.S and #2011.0.00083.S. ALMA is a partnership of ESO (representing its member states), NSF (USA), and NINS (Japan), together with NRC (Canada) and NSC and ASIAA (Taiwan), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO, and NAOJ. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. We used observations made with the NASA/ESA Hubble Space Telescope, and obtained from the Hubble Legacy Archive, which is a collaboration between the Space Telescope Science Institute (STScI/NASA), the Space Telescope European Coordinating Facility (ST-ECF/ESA), and the Canadian Astronomy Data centre (CADC/NRC/CSA). M.S.G. acknowledges support from the Spanish Ministerio de Economía y Competitividad through the grants BES-2016-078922 and ESP2015-68964-P. S.G.B. and M.Q. acknowledge support from the research project PID2019-106027GA-C44 of the Spanish Ministerio de Ciencia e Innovación. A.F. acknowledges support from the research project PID2019-106235GB-I00. A.A.H., S.G.B. and A.U. work was funded by grant PGC2018-094671-B-I00 funded by MCIN/AEI/ 10.13039/501100011033 and by ERDF A way of making Europe. A.A.H’s work was done under project No. MDM-2017-0737 Unidad de Excelencia “María de Maeztu”- Centro de Astrobiología (INTA-CSIC). M.P.S. acknowledges support from the Comunidad de Madrid through the Atracción de Talento Investigador Grant 2018-T1/TIC-11035 and PID2019-105423GA-I00 (MCIU/AEI/FEDER,UE). L.C. and M.S.G. acknowledge support from the research project PID2019-106280GB-100.
References
- Alonso-Herrero, A., Rieke, G. H., Rieke, M. J., et al. 2006, ApJ, 650, 835 [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barbosa, F. K. B., Storchi-Bergmann, T., McGregor, P., Vale, T. B., & Rogemar Riffel, A. 2014, MNRAS, 445, 2353 [Google Scholar]
- Beuther, H., Tackenberg, J., Linz, H., et al. 2012, A&A, 538, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Meidt, S., Schinnerer, E., Paladino, R., & Leroy, A. 2017, A&A, 597, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bešlić, I., Barnes, A. T., Bigiel, F., et al. 2021, MNRAS, 506, 963 [CrossRef] [Google Scholar]
- Bigiel, F., Leroy, A., Walter, F., et al. 2008, AJ, 136, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Bigiel, F., Leroy, A. K., Blitz, L., et al. 2015, ApJ, 815, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Bigiel, F., Leroy, A. K., Jiménez-Donaire, M. J., et al. 2016, ApJ, 822, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Blanc, G. A., Heiderman, A., Gebhardt, K., Evans, N. J., II, & Adams, J. 2009, ApJ, 704, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Bland-Hawthorn, J., Gallimore, J. F., Tacconi, L. J., et al. 1997, Ap&SS, 248, 9 [Google Scholar]
- Böker, T., Calzetti, D., Sparks, W., et al. 1999, ApJS, 124, 95 [CrossRef] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [CrossRef] [Google Scholar]
- Bouché, N., Cresci, G., Davies, R., et al. 2007, ApJ, 671, 303 [Google Scholar]
- Brinks, E., Skillman, E. D., Terlevich, R. J., & Terlevich, E. 1997, Ap&SS, 248, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D. 2001, PASP, 113, 1449 [Google Scholar]
- Calzetti, D., Kinney, A. L., & Storchi-Bergmann, T. 1994, ApJ, 429, 582 [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Kennicutt, R. C., Engelbracht, C. W., et al. 2007, ApJ, 666, 870 [Google Scholar]
- Casasola, V., Hunt, L., Combes, F., & García-Burillo, S. 2015, A&A, 577, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cecil, G., Dopita, M. A., Groves, B., et al. 2002, ApJ, 568, 627 [Google Scholar]
- Chen, H., Gao, Y., Braine, J., & Gu, Q. 2015, ApJ, 810, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, H., Braine, J., Gao, Y., Koda, J., & Gu, Q. 2017, ApJ, 836, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Colombo, D., Kalinova, V., Utomo, D., et al. 2018, MNRAS, 475, 1791 [NASA ADS] [CrossRef] [Google Scholar]
- Crenshaw, D. M., & Kraemer, S. B. 2000, ApJ, 532, L101 [Google Scholar]
- Daddi, E., Elbaz, D., Walter, F., et al. 2010, ApJ, 714, L118 [NASA ADS] [CrossRef] [Google Scholar]
- Das, V., Crenshaw, D. M., Kraemer, S. B., & Deo, R. P. 2006, AJ, 132, 620 [Google Scholar]
- Díaz, A. I., Álvarez, M. Á., Terlevich, E., et al. 2000, MNRAS, 311, 120 [CrossRef] [Google Scholar]
- Ellison, S. L., Lin, L., Thorp, M. D., et al. 2021, MNRAS, 501, 4777 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Fathi, K., Wozniak, H., et al. 2006, MNRAS, 365, 367 [Google Scholar]
- Emsellem, E., Renaud, F., Bournaud, F., et al. 2015, MNRAS, 446, 2468 [Google Scholar]
- Evans, N. J., II, Heiderman, A., & Vutisalchavakul, N. 2014, ApJ, 782, 114 [CrossRef] [Google Scholar]
- Evans, N. J., II, Kim, K.-T., Wu, J., et al. 2020, ApJ, 894, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C. 2015, MNRAS, 450, 4035 [Google Scholar]
- Gallagher, M. J., Leroy, A. K., Bigiel, F., et al. 2018, ApJ, 858, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Gallimore, J. F., Baum, S. A., O’Dea, C. P., & Pedlar, A. 1996, ApJ, 458, 136 [Google Scholar]
- Gallimore, J. F., Baum, S. A., & O’Dea, C. P. 2004, ApJ, 613, 794 [Google Scholar]
- Gallimore, J. F., Elitzur, M., Maiolino, R., et al. 2016, ApJ, 829, L7 [Google Scholar]
- Gao, Y., & Solomon, P. M. 2004a, ApJS, 152, 63 [Google Scholar]
- Gao, Y., & Solomon, P. M. 2004b, ApJ, 606, 271 [NASA ADS] [CrossRef] [Google Scholar]
- García-Burillo, S., Usero, A., Alonso-Herrero, A., et al. 2012, A&A, 539, A8 [Google Scholar]
- García-Burillo, S., Combes, F., Usero, A., et al. 2014, A&A, 567, A125 [Google Scholar]
- García-Burillo, S., Combes, F., Ramos Almeida, C., et al. 2016, ApJ, 823, L12 [Google Scholar]
- García-Burillo, S., Viti, S., Combes, F., et al. 2017, A&A, 608, A56 [Google Scholar]
- García-Burillo, S., Combes, F., Ramos Almeida, C., et al. 2019, A&A, 632, A61 [Google Scholar]
- Genzel, R., Tacconi, L. J., Gracia-Carpio, J., et al. 2010, MNRAS, 407, 2091 [NASA ADS] [CrossRef] [Google Scholar]
- Graciá-Carpio, J., García-Burillo, S., Planesas, P., & Colina, L. 2006, ApJ, 640, L135 [CrossRef] [Google Scholar]
- Graciá-Carpio, J., García-Burillo, S., Planesas, P., Fuente, A., & Usero, A. 2008, A&A, 479, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guilloteau, S., & Lucas, R. 2000, in Imaging at the IRAM Plateau de Bure Interferometer, eds. J. G. Mangum, & S. J. E. Radford, ASP Conf. Ser., 217, 299 [NASA ADS] [Google Scholar]
- Helfer, T. T., & Blitz, L. 1995, ApJ, 450, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., & Falgarone, E. 2012, A&ARv, 20, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Hummer, D. G., & Storey, P. J. 1987, MNRAS, 224, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Imanishi, M., Nakanishi, K., & Izumi, T. 2016, ApJ, 822, L10 [Google Scholar]
- Jiménez-Donaire, M. J., Bigiel, F., Leroy, A. K., et al. 2019, ApJ, 880, 127 [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr. 1998a, ApJ, 498, 541 [Google Scholar]
- Kennicutt, R. C., Jr. 1998b, ARA&A, 36, 189 [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr., Calzetti, D., Walter, F., et al. 2007, ApJ, 671, 333 [Google Scholar]
- Kennicutt, R. C., Jr., & De Los Reyes, M. A. C. 2021, ApJ, 908, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Kreckel, K., Faesi, C., Kruijssen, J. M. D., et al. 2018, ApJ, 863, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Krips, M., Martín, S., Eckart, A., et al. 2011, ApJ, 736, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kruijssen, J. M. D., & Longmore, S. N. 2014, MNRAS, 439, 3239 [NASA ADS] [CrossRef] [Google Scholar]
- Kruijssen, J. M. D., Longmore, S. N., Elmegreen, B. G., et al. 2014, MNRAS, 440, 3370 [Google Scholar]
- Krumholz, M. R., & McKee, C. F. 2005, ApJ, 630, 250 [Google Scholar]
- Krumholz, M. R., & Thompson, T. A. 2007, ApJ, 669, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Lombardi, M., & Alves, J. F. 2010, ApJ, 724, 687 [Google Scholar]
- Lada, C. J., Forbrich, J., Lombardi, M., & Alves, J. F. 2012, ApJ, 745, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [Google Scholar]
- Leroy, A. K., Walter, F., Sandstrom, K., et al. 2013, AJ, 146, 19 [Google Scholar]
- Leroy, A. K., Schinnerer, E., Hughes, A., et al. 2017, ApJ, 846, 71 [Google Scholar]
- Liu, L., Gao, Y., & Greve, T. R. 2015, ApJ, 805, 31 [Google Scholar]
- Longmore, S. N., Bally, J., Testi, L., et al. 2013, MNRAS, 429, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Meidt, S. E. 2016, ApJ, 818, 69 [CrossRef] [Google Scholar]
- Meidt, S. E., Schinnerer, E., García-Burillo, S., et al. 2013, ApJ, 779, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Meidt, S. E., Leroy, A. K., Rosolowsky, E., et al. 2018, ApJ, 854, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Meidt, S. E., Glover, S. C. O., Kruijssen, J. M. D., et al. 2020, ApJ, 892, 73 [CrossRef] [Google Scholar]
- Miyauchi, R., & Kishimoto, M. 2020, ApJ, 904, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Müller-Sánchez, F., Prieto, M. A., Hicks, E. K. S., et al. 2011, ApJ, 739, 69 [Google Scholar]
- Murphy, E. J., Dong, D., Leroy, A. K., et al. 2015, ApJ, 813, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Onodera, S., Kuno, N., Tosaki, T., et al. 2010, ApJ, 722, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., Haugbølle, T., & Nordlund, Å. 2012, ApJ, 759, L27 [Google Scholar]
- Padoan, P., Haugbølle, T., Nordlund, Å., & Frimann, S. 2017, ApJ, 840, 48 [Google Scholar]
- Querejeta, M., Meidt, S. E., Schinnerer, E., et al. 2015, ApJS, 219, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Querejeta, M., Schinnerer, E., Schruba, A., et al. 2019, A&A, 625, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quillen, A. C., Frogel, J. A., & Gonzalez, R. A. 1994, ApJ, 437, 162 [Google Scholar]
- Renaud, F., Bournaud, F., Emsellem, E., et al. 2013, MNRAS, 436, 1836 [NASA ADS] [CrossRef] [Google Scholar]
- Renaud, F., Bournaud, F., Emsellem, E., et al. 2015, MNRAS, 454, 3299 [NASA ADS] [CrossRef] [Google Scholar]
- Rico-Villas, F., Martín-Pintado, J., González-Alfonso, E., et al. 2021, MNRAS, 502, 3021 [NASA ADS] [CrossRef] [Google Scholar]
- Rieke, G. H., Alonso-Herrero, A., Weiner, B. J., et al. 2009, ApJ, 692, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Rosolowsky, E., Pineda, J. E., & Gao, Y. 2011, MNRAS, 415, 1977 [NASA ADS] [CrossRef] [Google Scholar]
- Roy, A. L., Goss, W. M., & Anantharamaiah, K. R. 2008, A&A, 483, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schinnerer, E., Eckart, A., Tacconi, L. J., Genzel, R., & Downes, D. 2000, ApJ, 533, 850 [Google Scholar]
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Schruba, A., Leroy, A. K., Walter, F., Sandstrom, K., & Rosolowsky, E. 2010, ApJ, 722, 1699 [NASA ADS] [CrossRef] [Google Scholar]
- Schruba, A., Leroy, A. K., Walter, F., et al. 2011, AJ, 142, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Scourfield, M., Viti, S., García-Burillo, S., et al. 2020, MNRAS, 496, 5308 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N. Z., Matthews, K., Carico, D. P., & Sanders, D. B. 1988, ApJ, 327, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Shimajiri, Y., André, P., Braine, J., et al. 2017, A&A, 604, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shirley, Y. L. 2015, PASP, 127, 299 [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., & Vanden Bout, P. A. 2005, ARA&A, 43, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., Downes, D., Radford, S. J. E., & Barrett, J. W. 1997, ApJ, 478, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, I. W., Jackson, J. M., Whitaker, J. S., et al. 2016, ApJ, 824, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Takano, S., Nakajima, T., Kohno, K., et al. 2014, PASJ, 66, 75 [NASA ADS] [Google Scholar]
- Tsai, M., Hwang, C.-Y., Matsushita, S., Baker, A. J., & Espada, D. 2012, ApJ, 746, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Usero, A., Leroy, A. K., Walter, F., et al. 2015, AJ, 150, 115 [Google Scholar]
- Viaene, S., Forbrich, J., & Fritz, J. 2018, MNRAS, 475, 5550 [NASA ADS] [CrossRef] [Google Scholar]
- Viti, S., García-Burillo, S., Fuente, A., et al. 2014, A&A, 570, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Williams, T. G., Gear, W. K., & Smith, M. W. L. 2018, MNRAS, 479, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, J., Evans, N. J., II, Gao, Y., et al. 2005, ApJ, 635, L173 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, J., Evans, N. J., II, Shirley, Y. L., & Knez, C. 2010, ApJS, 188, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Yao, L., Seaquist, E. R., Kuno, N., & Dunne, L. 2003, ApJ, 597, 1271 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Determination of the missing flux in HCN and CO maps
We estimated the missing flux in the HCN(1–0) map obtained by ALMA and in the CO(1–0) map of the IRAM array (PdBI) (Schinnerer et al. 2000). To this aim, we measured the spatially integrated fluxes in both lines using a set of four apertures covering the region occupied by the SB ring of NGC 1068. The interferometer fluxes are compared with the corresponding single-dish fluxes measured from observations obtained by the IRAM 30-m telescope (Usero et al. 2021, priv. comm.). Figure A.1 illustrates the apertures chosen overlaid on the HCN (upper panel) and CO (lower panel) interferometer images of the galaxy. The sizes of the apertures used to derive the spatially integrated fluxes of the interferometer maps correspond to the single-dish beams of the IRAM 30-m telescope, which are ∼30″ and ∼24″ for HCN and CO, respectively.
 |
Fig. A.1. Selection of four apertures to study the missing flux in the HCN and CO maps of NGC 1068. Upper panel: Overlay of the four ∼30″ size apertures (black circles, identified by the numerical labels 1-4) selected to cover the SB ring of NGC 1068 on the ALMA HCN(1–0) map (colour scale and contours as in Fig. 1), used in Appendix A to estimate the missing flux correction. Lower panel: Same as the upper panel but showing the overlay of the four ∼12″ size apertures (black circles, identified by the numerical labels 1-4) selected to cover the SB ring of the galaxy on the PdBI CO(1–0) map of Schinnerer et al. (2000). The colour scale is given in Jy km s−1 beam−1 units and the position of the AGN is identified by the black star markers in both maps. The magenta filled ellipses at the bottom-left in the two panels represent the beam sizes. |
Figures A.2 and A.3 compare the spectra of HCN and CO obtained by integrating the emission of the lines inside the four selected regions shown in Fig. A.1 with the IRAM 30-meter spectra. Based on this comparison we estimate that on scales of ∼30″ (∼2 kpc) approximately 20 − 25% of the total flux gets filtered in the HCN ALMA map. A similar estimate for the CO map yields a flux filtering of about 40-45% on scales ∼24″ (∼1.7 kpc). This is about a factor of two larger than the value estimated by Schinnerer et al. (2000), who compared the fluxes measured with the PdBI with those measured with the combined BIMA array and Kitt Peak single-dish telescope datasets on scales ∼55″ (3.8 kpc).
 |
Fig. A.2. Comparison of the HCN(1–0) emission observed by ALMA (blue histograms) and the IRAM 30-m telescope (black histograms) inside the four selected regions identified in Fig. A.1 (labelled as 1, 2, 3, and 4 in each panel). |
 |
Fig. A.3. Same as Fig. A.2, but showing the comparison of the CO(1–0) emission observed by the IRAM-PdBI (blue histograms) and the IRAM 30-m telescope (black histograms) inside the four selected regions identified in Fig. A.1 (labelled as 1, 2, 3, and 4 in each panel). |
As in this paper we analyse spatial scales that are much smaller than the critical scales reported above (≈ 2-4 kpc), we can foresee that the missing flux factors will be significantly less than 25-45% for the scales that are relevant to our study.
Appendix B: Paα analysis as SFR tracer
To validate our working assumption, namely that the Paα image used in this work to derive the distribution of recent SF in NGC 1068 does not require a significant correction by dust extinction, we compared the Paα fluxes measured in the HST/NICMOS image of the galaxy with the Hα fluxes measured using the ground-based image of Díaz et al. (2000) over a representative number of hot spots of the SB ring. Figure B.1 shows the position of the eight regions considered in this comparison selected from Table 4 of Díaz et al. (2000). We derived the Paα spatially-integrated fluxes inside the eight selected regions using the sizes of Hα SF knots listed in Table 4 of Díaz et al. (2000) and obtained the Hα/Paα flux ratios for each aperture (listed in Table B.1). To estimate the colour excess (E(B − V)) and extinction (APaα) values we used the prescriptions of Calzetti (2001) (see also Calzetti et al. 1994, 2000) and the standard equation:
 |
Fig. B.1. HST/NICMOS Paα image of NGC 1068. The white labels identify the regions selected to estimate the extinction of Paα, according to the nomenclature used by Díaz et al. (2000). |
Observed line ratios and derived extinction parameters for the SB ring knots of NGC 1068.
where Fobs and Fint are the observed and intrinsic fluxes for the lines, respectively, and E(B − V) is the colour excess. We assumed that the differential extinction between the two lines is determined by k(Hα)−k(Paα) = 2.104 (Calzetti 2001). Table B.1 lists the Hα/Paα line ratios as well as the values estimated for E(B − V) and APaα for the eight selected regions.
The median value for the distribution of Hα/Paα ratios listed in Table B.1 is ∼6.8. This is close to the expected value corresponding to the canonical case B recombination: ∼7.8. The implied mean extinction correction at 1.875 μm is APaα = 0.03 mag, which translates into very low dust opacities for the ensemble of the studied SF knots. Although in regions 18, 19 and 20, APaα is seems to reach values ∼0.1 − 0.2, the implied opacities are still compatible with optically thin emission for Paα. Moreover, assuming that the flux scale is uncertain to ±20% due to absolute calibration errors, we can therefore conclude that Paα emission is not significantly affected by dust extinction in the SB ring of NGC 1068.
Appendix C: Kennicutt–Schmidt plots
We represent the KS plots derived from the different tracers for the range of scales used in this work (Figs. C.1, C.2, C.3 and C.4).
 |
Fig. C.1. Same as Fig. 5, but showing all the spatial scales used in this work for HCO+(1-0). Vertical and horizontal error bars at the lower-right corner of each panel account for the typical uncertainties, which amount to ±0.09 dex on both axes. |
 |
Fig. C.2. Same as Fig. 5, but showing all the spatial scales used in this work for CO(3-2). Vertical and horizontal error bars at the lower-right corner of each panel account for the typical uncertainties, which amount to ±0.09 dex on both axes. |
 |
Fig. C.3. Same as Fig. 5, but showing all the spatial scales used in this work for dust continuum emission. Vertical and horizontal error bars at the lower-right corner of each panel account for the typical uncertainties, which amount to ±0.09 dex on both axes. |
 |
Fig. C.4. Same as Fig. 5, but showing all the spatial scales used in this work for CO(1-0). Vertical and horizontal error bars at the lower-right corner of each panel account for the typical uncertainties, which amount to ±0.09 dex and ±0.10 dex, respectively. |
Appendix D: Alternative formulation of the intensity-weighted average of the b parameter
Leroy et al. (2017) used a definition of the intensity-weighted average of the b parameter different to the one used in Sect. 6.1. In particular, instead of deriving the averages of b as defined in Eq. (10), they performed the averages of Σgas and σ2 separately and defined ⟨b⟩≡⟨Σgas⟩/⟨σ2⟩. We derived a new version of Eq. (11) using the definition of Leroy et al. (2017) particularised for Σdense and our set of two apertures (100 pc and 400 pc). The results obtained with this definition, shown in Fig. D.1 are virtually identical to those shown in Fig. 11. In particular, we obtain (anti) correlation Spearman rank parameters ρsp = −0.42 and −0.60 for ΔA = 100 pc and 400 pc, respectively, and associated two-sided p-values < 1%. Furthermore, after applying the MARS routine to the 400 pc-scale scatter plot we find a turnover at log10(⟨b⟩) = 0.18 M⊙pc−2(km s−1)−2 and a slope ≃ − 1.4 for ⟨b⟩ values beyond the turnover.
 |
Fig. D.1. Same as Fig. 11 but derived using the alternative formulation of the intensity-weighted average of the b parameter used by Leroy et al. (2017). |
Appendix E: Trends as a function of the boundedness of the gas from HCO+
We have studied in Sect. 6.1 how the depletion time of the dense molecular gas estimated from HCN changes as a function of the self-gravity of the gas (b paramater). We now analyse this with the other dense gas tracer that we use in this work, HCO+. Figure E.1 represents the depletion time as a function of the b parameter at 56 pc, 100 pc and 400 pc. We observe a similar trend to Fig. 11, obtaining (anti) correlation Spearman rank parameters ρsp = -0.07 (p-value = 0.06), -0.32 (< 1%) and -0.65 (< 1%) for 56 pc, 100 pc and 400 pc, respectively. At 400 pc scales, we identify a turnover in the plot located around log10(⟨b⟩) ≃ 0.2 M⊙pc−2(km s−1)−2 and a slope ≃ -0.91 for ⟨b⟩ values beyond the turnover.
 |
Fig. E.2. Same as Fig. 12 but estimated from HCO+. Left panel: contour levels for log10( |
Figure E.1 shows the spatial distribution of 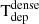 and ⟨b⟩ derived for ΔA = 400 pc in the SB ring of NGC 1068 from HCO+. We observe that higher (lower) SFEdense (
and ⟨b⟩ derived for ΔA = 400 pc in the SB ring of NGC 1068 from HCO+. We observe that higher (lower) SFEdense (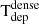 ) values are located closer to the bar-ring interface. We find that the HCN and HCO+ show similar correlations in the SB ring of NGC 1068.
) values are located closer to the bar-ring interface. We find that the HCN and HCO+ show similar correlations in the SB ring of NGC 1068.
All Tables
Correlation parameters obtained for the KS laws derived for different tracers and spatial scales.
Observed line ratios and derived extinction parameters for the SB ring knots of NGC 1068.
All Figures
 |
Fig. 1. HCN(1–0) and HCO+(1–0) integrated intensity maps of NGC 1068. Left panel: velocity-integrated intensity map of HCN(1–0) of NGC 1068 obtained with ALMA. The map is shown in a logarithmic colour scale with contour levels of 3σ, 5σ, 7σ, 12σ, 24σ, 50σ, 120σ, and 200σ, where 1σ = 0.028 Jy beam−1 km s−1. We highlight the location of several representative regions of the emission, namely the CND, the bar, and the SB ring. Right panel: same as the left panel but for the HCO+(1–0) line map, with the same list of contour levels but here truncated at 120σ. The position of the AGN is identified by the dark grey star marker. The black bar in the top-right corner of each panel shows the spatial scale (in pc). The magenta filled ellipses at the bottom-left corners of the panels represent the ALMA beam size (1 |
| In the text | |
 |
Fig. 2. HCN(1–0)/HCO+(1–0) brightness temperature ratio map (Rdense) derived at the common spatial resolution of ≃56 pc. The brown circle of 8″ in radius (≃560 pc) locates the inner region of the galaxy disk where the molecular outflow signature has been identified in the kinematics of molecular gas (García-Burillo et al. 2014, 2019). This region, purposely excluded from our analysis of SF relations, shows significantly higher line ratios (Rdense ≃ 1.5 − 3.5) compared to the SB ring (Rdense ≃ 0.5 − 1.5). Other symbols are the same as in Fig. 1. |
| In the text | |
 |
Fig. 3. HST/NICMOS continuum-subtracted Paα image of NGC 1068. The map is shown in colour scale with contour levels of 3σ, 9σ, 15σ, 32σ, 50σ, 120σ, and 700σ, where 1σ = 0.212 × 10−16 erg s−1 cm−2 pixel−1. The colour scale range is shown in units of 10−16 erg s−1 cm−2 pixel−1. The (truncated) square region identifies the outer edge of the HST/NICMOS FOV. The angular resolution of the image is 0 |
| In the text | |
 |
Fig. 4. Overlay of the HST/NICMOS Paα image on the molecular gas tracer maps. Left panel: overlay of the HST/NICMOS Paα image (contours) on the ALMA HCN(1–0) map (colour scale). Contours have a logarithmic spacing from 3σ to 1536σ, in steps of 0.3 dex, where 1σ = 0.180−16 erg s−1 cm−2 pixel−1. The colour scale is shown in units of Jy beam−1 km s−1. Middle panel: same as the left panel but showing the overlay of the HST/NICMOS Paα contours on the ALMA HCO+(1–0) map (colour scale). Right panel: same as the left panel but showing the overlay of the HST/NICMOS Paα contours on the PdBI CO(1–0) map of Schinnerer et al. (2000) (colour scale). Contour spacing is the same as in the left and right panels, but with 1σ = 0.162 × 10−16 erg s−1 cm−2 pixel−1. The magenta filled ellipses at the bottom-left corners in all panels represent the beam sizes of the molecular line maps: 1 |
| In the text | |
 |
Fig. 5. SFR surface density (ΣSFR) as a function of the dense molecular gas surface density (Σdense) derived from HCN(1–0) for the different resolutions explored in this work: 56 pc, 100 pc, 200 pc, 300 pc, 400 pc, 500 pc, 600 pc and 700 pc. The red lines show the ODR fits to the data. The dashed lines identify the correlations that are not found to be statistically significant. We only show on both axes the data points above 3σ that are considered in the fits. We indicate the Spearman’s rank correlation coefficients (ρsp) and the power-law indexes (N) of the best fits. Vertical and horizontal error bars at the lower-right corner of each panel account for the typical uncertainties, which amount to ±0.09 dex on both axes. |
| In the text | |
 |
Fig. 6. Pearson and Spearman correlation coefficients (ρps: left panel; ρsp: right panel) of the KS laws derived for the different gas tracers used in this work as a function of the spatial resolution. Error bars represent the 67% confidence interval around the mean values. For spatial scales larger than the range identified by the grey-coloured region (≤350 pc) all the gas tracers (leaving aside CO(1–0)) show statistically significant correlations in their KS laws, defined by p-values < 1% and ρps, ρsp > 0.4. |
| In the text | |
 |
Fig. 7. Power-law indexes (N) of the KS relations obtained from the ODR fit to the data for the different gas tracers used in this work as a function of the spatial resolution adopted. Symbols and colour codes are the same as in Fig. 6. |
| In the text | |
 |
Fig. 8. Comparison of the KS laws derived from HCN(1–0) in NGC 1068 with those obtained in different populations of galaxies for a range of spatial scales: global measurements (around a few kiloparsec) of the disks of SFGs and (U)LIRGs (García-Burillo et al. 2012), ≃0.3−1 kiloparsec-scale regions of the disks of nearby SFGs (Murphy et al. 2015; Usero et al. 2015; Bigiel et al. 2016), and 0.1−0.2 kpc size regions in the disk of M 51 (Chen et al. 2017; Viaene et al. 2018; Querejeta et al. 2019). For the sake of a better comparison with the reference sample, the scatter plots for NGC 1068 (magenta circles and isodensity contours) are displayed for three spatial resolutions: 56 pc (left panel), 100 pc (middle panel), and 700 pc (right panel). The scatter plot for M 51 at 100 pc resolution is displayed by the green circles and isodensity contours. The open squares stand for the median values of the distributions in NGC 1068 and M 51. |
| In the text | |
 |
Fig. 9. Distribution of the HCN and Paα peaks and the apertures showing the highest SFEdense in NGC 1068. Left panel: overlay of the HST/NICMOS Paα image (contours) on the HCN(1–0) map (grey scale). The contours and grey scale are the same as in Fig. 4. The set of 56 pc size circular apertures used to extract the fluxes of Paα and HCN(1–0) are colour-coded differently, depending on whether they are centred on HCN peaks (in blue), on Paα peaks (in red), or on the 10% of the apertures showing the highest values of SFEdense (in green). The black dots identify the centres of all the Nyquist-sampled 56 pc size apertures where there are reliable estimates of SFEdense across the SB ring. Right panel: distribution of SFEdense values (in Myr−1-units) as a function of LHCN (in K km s−1 pc2-units) in the SB ring of NGC 1068. Symbols are the same as in left panel. Vertical and horizontal error bars at the lower-right corner of the panel account for the typical uncertainties, which amount to ±0.13 dex and ±0.09 dex, respectively. |
| In the text | |
 |
Fig. 10. Same as Fig. 9 but replacing HCN(1–0) with HCO+(1–0) along the x axis of the right panel. |
| In the text | |
 |
Fig. 11. Depletion time of the dense molecular gas estimated from HCN, |
| In the text | |
 |
Fig. 12. Maps of the depletion time and the b parameter in the SB ring of NGC 1068. Left panel: map of the depletion time of the dense molecular gas ( |
| In the text | |
 |
Fig. 13. HCN(1–0)/CO(1–0) brightness temperature ratio map (RHCN/CO; colour scale and contours) derived at the common (lower) spatial resolution of the CO(1–0) observations of Schinnerer et al. (2000) (≃100 pc). The brown circle of 8″ in radius (≃560 pc) locates the inner region excluded from our analysis of SF relations. |
| In the text | |
 |
Fig. 14. Same as Fig. 13 but showing the CO(3–2)/CO(1–0) brightness temperature ratio map (R3 − 2/1 − 0; colour scale and contours) derived at the common (lower) spatial resolution of the CO(1–0) observations. |
| In the text | |
 |
Fig. 15. Star-formation efficiency of the dense gas (SFEdense) as a function of dense gas fraction (Fdense: estimated from the HCN(1–0)-to-CO(1–0) line ratio of Fig. 13) in NGC 1068 using two averaging scales: 100 pc (left panel) and 400 pc (right panel). Magenta circles correspond to data measurements evaluated at the Nyquist-sampled grid of points after convolution with the appropriate Gaussian for each aperture. Black circles show median SFEdense values, and error bars indicate the rms scatter in the bins. Vertical and horizontal error bars at the lower-right corner of both panels account for the typical uncertainties, which amount to ±0.13 dex. |
| In the text | |
 |
Fig. 16. Overlay of the ALMA HCN(1–0) map (contours) on the HST/NICMOS F190N continuum image at 1.9 μm HST (colour scale as shown in Jy). The contour spacing is 3σ, 7σ, 12σ, 24σ, 50σ, and 120σ, where 1σ = 0.028 Jy beam−1 km s−1. The white circle of r = 8″ locates the inner region of the galaxy disk, which was excluded of our analysis. The HST/NICMOS F190N image has been degraded to the spatial resolution of HCN(1–0) (1 |
| In the text | |
 |
Fig. 17. Star-formation efficiency of the dense gas (SFEdense) as a function of the stellar mass surface density (Σstar) in the SB ring of NGC 1068 at the initial resolution of 56 pc (left panel) and at two averaging scales: 100 pc (middle panel) and 400 pc (right panel). Magenta circles and isodensity contours correspond to data measurements evaluated at the Nyquist-sampled grid of points after convolution with the appropriate Gaussian for each aperture. Black circles show median SFEdense values, and error bars indicate the rms scatter in the bins. Symbols and isodensity contours in the middle panel identify the data obtained in other galaxies. The dashed orange line represents the fit of Usero et al. (2015). Vertical and horizontal error bars at the lower-right corner of each panel account for the typical uncertainties, which amount to ±0.13 dex and ±0.09 dex, respectively. |
| In the text | |
 |
Fig. 18. Fraction of dense gas (Fdense) as a function of the stellar mass surface density (Σstar) in the SB ring of NGC 1068 at the two averaging scales: 100 pc (left panel) and 400 pc (right panel). Symbols are the same as in Fig. 17. Vertical and horizontal error bars at the lower-right corner of each panel account for the typical uncertainties, which amount to ±0.13 dex and ±0.09 dex, respectively. |
| In the text | |
 |
Fig. 19. Star-formation efficiency of the dense gas (SFEdense) as a function of the velocity dispersion of HCN (σ) in NGC 1068 for three averaging scales: 56 pc (left panel), 100 pc (middle panel), and 400 pc (right panel). Measurements at 100 pc scales are compared to literature data for other galaxies. Symbols are the same as in Fig. 17. Vertical and horizontal error bars at the lower-right corner of each panel account for the typical uncertainties, which amount to ±0.13 dex and ±0.06 dex, respectively. |
| In the text | |
 |
Fig. 20. Same as the middle panel of Fig. 19 but adding a comparison with the trends of SFEdense as a function of the velocity dispersion of the gas (σ) predicted by the model of Meidt et al. (2020). This model foresees different locations of galaxies in the SFEdense − σ parameter space depending on the fraction of dense gas (Fdense) and, also, on the total molecular gas column densities (Σmol). Symbols are the same as in Fig. 17. Vertical and horizontal error bars at the lower-right corner account for the typical uncertainties, which amount to ±0.13 dex and ±0.06 dex, respectively. |
| In the text | |
 |
Fig. 21. Dense gas fraction (Fdense) as a function of velocity dispersion in the SB ring of NGC 1068 at the two averaging scales: 100 pc (left panel) and 400 pc (right panel). Measurements at 100 pc scales are compared to literature data for other galaxies. Symbols are the same as in Fig. 17. Vertical and horizontal error bars at the lower-right corner of each panel account for the typical uncertainties, which amount to ±0.13 dex and ±0.06 dex, respectively. |
| In the text | |
 |
Fig. 22. Star formation rate surface density (ΣSFR) as a function of dense gas fraction (Fdense) in NGC 1068 measured at 100 pc scales compared to the data obtained in other galaxies (symbols as in Fig. 8). Vertical and horizontal error bars at the lower-right corner account for the typical uncertainties, which amount to ±0.09 dex and ±0.13 dex, respectively. |
| In the text | |
 |
Fig. 23. Same as Fig. 12 but showing the map of the velocity dispersion (σ) obtained using 400 pc as an averaging scale. Contour levels for σ go from 14.0 to 19.0 in steps of 0.5 km s−1. |
| In the text | |
 |
Fig. A.1. Selection of four apertures to study the missing flux in the HCN and CO maps of NGC 1068. Upper panel: Overlay of the four ∼30″ size apertures (black circles, identified by the numerical labels 1-4) selected to cover the SB ring of NGC 1068 on the ALMA HCN(1–0) map (colour scale and contours as in Fig. 1), used in Appendix A to estimate the missing flux correction. Lower panel: Same as the upper panel but showing the overlay of the four ∼12″ size apertures (black circles, identified by the numerical labels 1-4) selected to cover the SB ring of the galaxy on the PdBI CO(1–0) map of Schinnerer et al. (2000). The colour scale is given in Jy km s−1 beam−1 units and the position of the AGN is identified by the black star markers in both maps. The magenta filled ellipses at the bottom-left in the two panels represent the beam sizes. |
| In the text | |
 |
Fig. A.2. Comparison of the HCN(1–0) emission observed by ALMA (blue histograms) and the IRAM 30-m telescope (black histograms) inside the four selected regions identified in Fig. A.1 (labelled as 1, 2, 3, and 4 in each panel). |
| In the text | |
 |
Fig. A.3. Same as Fig. A.2, but showing the comparison of the CO(1–0) emission observed by the IRAM-PdBI (blue histograms) and the IRAM 30-m telescope (black histograms) inside the four selected regions identified in Fig. A.1 (labelled as 1, 2, 3, and 4 in each panel). |
| In the text | |
 |
Fig. B.1. HST/NICMOS Paα image of NGC 1068. The white labels identify the regions selected to estimate the extinction of Paα, according to the nomenclature used by Díaz et al. (2000). |
| In the text | |
 |
Fig. C.1. Same as Fig. 5, but showing all the spatial scales used in this work for HCO+(1-0). Vertical and horizontal error bars at the lower-right corner of each panel account for the typical uncertainties, which amount to ±0.09 dex on both axes. |
| In the text | |
 |
Fig. C.2. Same as Fig. 5, but showing all the spatial scales used in this work for CO(3-2). Vertical and horizontal error bars at the lower-right corner of each panel account for the typical uncertainties, which amount to ±0.09 dex on both axes. |
| In the text | |
 |
Fig. C.3. Same as Fig. 5, but showing all the spatial scales used in this work for dust continuum emission. Vertical and horizontal error bars at the lower-right corner of each panel account for the typical uncertainties, which amount to ±0.09 dex on both axes. |
| In the text | |
 |
Fig. C.4. Same as Fig. 5, but showing all the spatial scales used in this work for CO(1-0). Vertical and horizontal error bars at the lower-right corner of each panel account for the typical uncertainties, which amount to ±0.09 dex and ±0.10 dex, respectively. |
| In the text | |
 |
Fig. D.1. Same as Fig. 11 but derived using the alternative formulation of the intensity-weighted average of the b parameter used by Leroy et al. (2017). |
| In the text | |
 |
Fig. E.1. Same as Fig. 11 but estimated from HCO+. |
| In the text | |
 |
Fig. E.2. Same as Fig. 12 but estimated from HCO+. Left panel: contour levels for log10( |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



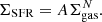
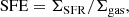

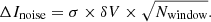
![$$ \begin{aligned} M_{\rm dense}[M_{\odot }] = \alpha _{\rm HCN}L_{\rm dense}^\prime [\mathrm{K\,km\,s^{-1}\,pc^{2}}]. \end{aligned} $$](/articles/aa/full_html/2022/04/aa42396-21/aa42396-21-eq14.gif)
![$$ \begin{aligned} L^\prime _{\rm dense}[\mathrm{K\,km\,s^{-1}\,pc^{2}}] = 3.25 \times 10^{7} \times S_{\rm dense} \Delta V \nu _{\rm obs}^{-2} D_{\rm L}^{2}(1+z)^{-3}, \end{aligned} $$](/articles/aa/full_html/2022/04/aa42396-21/aa42396-21-eq15.gif)