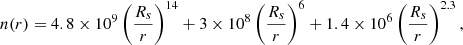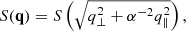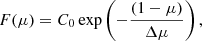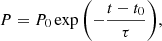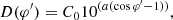EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 656 (December 2021) A&A, 656 (2021) A34 Full HTML
Issue
A&A
Volume 656, December 2021
Solar Orbiter First Results (Cruise Phase)
Article Number A34
Number of page(s) 9
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202140998
Published online 14 December 2021

© ESO 2021

1. Introduction

Solar type III radio bursts, which are produced by electron beams that are propagating along open magnetic field lines in the corona and interplanetary medium, are among the most intense radio sources in the kilometric range (Wild 1950, 1967). While the precise mechanism of their production has not yet been established, it is widely accepted that type III bursts originate via a plasma emission mechanism in which the fast electrons form a bump-on-tail instability, which then excites Langmuir waves at the local plasma frequency (Ginzburg & Zhelezniakov 1958; Melrose 1980). These Langmuir waves are then transformed into electromagnetic radiation by mechanisms which are not yet fully understood (Sturrock 1964; Zheleznyakov & Zaitsev 1970; Smith et al. 1976; Melrose 1987; Dulk 1985; Tkachenko et al. 2021).

Radio waves propagate through the solar corona and interplanetary medium, where they are both refracted and scattered by turbulent plasma processes, with radio-wave scattering on density fluctuations playing a dominant role in the propagation effects (Kontar et al. 2017; Kuznetsov et al. 2020). The observed properties of the radio sources are, therefore, a combination of their intrinsic properties at the emission site and these propagation effects. Radio-wave scattering causes both an increase in the radio source sizes and a very wide emission diagram responsible for the detection of type III radio bursts at all angles in the heliosphere (Steinberg et al. 1984, 1985; Bonnin et al. 2008), a shift of the radio source positions (Fokker 1965; Chrysaphi et al. 2018), and a widening of the intensity time profiles of the radio bursts (Krupar et al. 2018; Kontar et al. 2019).

The effect of radio-wave scattering on solar radio bursts has been studied using ray-tracing simulations (Steinberg et al. 1971; Thejappa & MacDowall 2008; Krupar et al. 2018, 2020), where isotropic scattering is assumed. However, recent observational results strongly suggest that the properties of solar radio emissions cannot be successfully explained on the basis of isotropic scattering (Kontar et al. 2019; Chen et al. 2020). Kontar et al. (2019) presented the results of ray-tracing simulations of radio-wave propagation in the heliosphere, assuming the anisotropic scattering of the radio-waves. These authors showed that scattering was at the origin of the broadening of radio source sizes and radio-burst time profiles, but also that, on average, both properties could only be simultaneously described when anisotropic radio-wave scattering was considered.

The first measurements of the directivity of type III radio bursts were performed by Caroubalos & Steinberg (1974), Caroubalos et al. (1974), using simultaneous observations from the Earth and from the probe Mars-3, at 169 MHz. At lower frequencies (100–500 kHz), Dulk (1985) and Lecacheux et al. (1989) reported that type III radio bursts were detected by instruments irrespective of the position of the radio source. The first stereoscopic directivity measurements were reported by Hoang et al. (1997), who used a combination of ground-based observations from the ARTEMIS spectrograph around 150 MHz and space observations from the radio receiver on board Ulysses (up to 1 MHz). The first stereoscopic measurements, in the same frequency range, aimed at studying the radio burst directivity were performed by Bonnin et al. (2008), using observations from the Ulysses and Wind spacecraft. Bonnin et al. (2008) used the observations of more than 2000 radio bursts, observed simultaneously by both probes, to statistically derive the directivity of the type III radio bursts between 80 and 1000 kHz. These authors confirmed the frequency dependence of the averaged radio burst directivity that was observed by Hoang et al. (1997). These studies had to rely on a statistical analysis of a large sample of bursts, as they had access to only two simultaneous observations of a single event: the directivity profile is therefore calculated using hundreds to thousands of radio flux ratios. With the launch of Solar Orbiter (Müller et al. 2020) and Parker Solar Probe (PSP, Fox et al. 2016), radio measurements at two different points in the heliosphere can be added to the already existing measurements of STEREO-A (Solar Terrestrial Relations Observatory, Kaiser 2005) and Wind (Ogilvie & Desch 1997), providing, for the first time, an opportunity to study radio emission directivity for single type III radio bursts. In this paper, we present the analysis of five events observed in the early phase of the Solar Orbiter mission (July and November 2020). These observational measurements are compared to the predictions of ray-tracing simulations of the radio-wave propagation with anisotropic radio-wave scattering on turbulent fluctuations of the ambient plasma density. The ray-tracing simulation results are presented in Sect. 2 and the observations are presented in Sect. 3. The comparison between the simulation results and the observed properties of the type III bursts, as well as the implications regarding the radio emission directivity and the properties of the ambient plasma are presented in Sect. 4.

2. Directivity of radio emission from radio-wave propagation simulations

2.1. Simulation setup

We performed simulations of radio-wave propagation in the heliosphere using the ray-tracing simulations described in Kontar et al. (2019). The ray-tracing simulations detail the propagation of photons through the interplanetary medium, where anisotropic density fluctuations (and, thus, anisotropic scattering) can be assumed. A radio source is placed at a given distance from the solar surface and the corresponding plasma frequency is deduced from the position of the source, assuming a density model. We used the density model described in Kontar et al. (2019):

n ( r ) = 4.8 × 10 9 ( R s r ) 14 + 3 × 10 8 ( R s r ) 6 + 1.4 × 10 6 ( R s r ) 2.3 , $$ \begin{aligned} n(r) = 4.8 \times 10^9 \left(\frac{R_s}{r}\right)^{14} + 3 \times 10^8 \left(\frac{R_s}{r}\right)^{6} + 1.4 \times 10^6 \left(\frac{R_s}{r}\right)^{2.3} ,\end{aligned} $$(1)

where n(r) is the plasma density in cm−3, r is the position of the source, and Rs is the solar radius.

The radio frequency is usually set to a factor of 1.1 or 1.2 (for fundamental emission), or 2 (harmonic emission) of the plasma density, and it remains constant during the radio-wave propagation.

During their propagation, radio-waves are subject to scattering due to turbulent fluctuations of the ambient plasma density. An anisotropic spectrum of density fluctuation S(q), with q being the wave-vector of electron density fluctuations, is assumed, with an axial symmetry. The spectrum is thus parameterised as:

S ( q ) = S ( q ⊥ 2 + α − 2 q ‖ 2 ) , $$ \begin{aligned} S(\mathbf q ) = S \left( \sqrt{q_{\bot }^2 + \alpha ^{-2} q_{\parallel }^2} \right) ,\end{aligned} $$(2)

where α is the anisotropy factor defined as the ratio of perpendicular to parallel correlation lengths: α = h⊥/h∥. When α < < 1, the spectrum of density fluctuations is dominated by the fluctuations in the perpendicular direction. In the case of isotropic scattering, α = 1.

The photon propagation is simulated until photons reach a distance from the Sun, where both refraction and scattering become negligible (i.e. when the photon frequency, which is kept constant in the simulations, becomes much larger than the local plasma frequency) or until they reach a distance of 1 au. For each photon, at the end of the simulation, the time, t, of arrival and its position, r, and wave-vector, k, are recorded in a Sun-centred coordinate system.

2.2. Anisotropic scattering and directivity

We summarise the geometry we used to analyse the results of the ray-tracing simulation in Fig. 1. The direction of propagation of the radio source, the z-axis, is a symmetry axis for the directivity of the radio emission. Therefore, the directivity can be described as a function of the angle θP defined in the figure, or of its cosine, μ = cos(θP). In our study, as in past studies (e.g. Hoang et al. 1997; Bonnin et al. 2008), we assume that the directivity follows an exponential shape as a function of μ:

F ( μ ) = C 0 exp ( − ( 1 − μ ) Δ μ ) , $$ \begin{aligned} F(\mu ) = C_0 \exp \left( - \frac{\left( 1-\mu \right)}{\Delta \mu } \right) ,\end{aligned} $$(3)

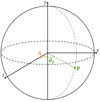thumbnail Fig. 1.

Geometry of the simulation: radio source S is emitted on the z-axis. The angle θP is the angle between the direction of the radio source S (the z-axis) and the direction of an observer at position P. In this paper, the radio source is always situated on the z-axis while the probe P has different positions in the 3D space.

where C0 is a normalization constant and Δμ is the key parameter controlling the shape of the radio emission directivity pattern. In the simulations, the parameter μ is calculated as μ = kz/|k|.

The radio emission directivity pattern depends on the anisotropy factor α. We recall here that α = 1 for isotropic scattering and that α < 1 results in a stronger scattering in the perpendicular direction. Smaller values of α should therefore lead to a more peaked directivity (Kontar et al. 2019), which translates to smaller values of the parameter Δμ in Eq. (3). We performed ray-tracing simulations of the radio-wave propagation with the following settings: (1) a radio source located at 11RS, leading to a plasma density fpe = 681 kHz, and fundamental radio emission emitted at 1.1 × fpe1; and (2) anisotropy factor α = 0.25, 0.30, 0.40, 0.50, 0.60, 0.75, 1.00.

The directivity obtained at these frequencies for photons arriving around the peak time of the corresponding lightcurve is shown in Fig. 3. To select the photons around the peak time, we generated the lightcurves for the radio emission using the propagation time of each photon resulting from the ray-tracing simulations, and selected photons arriving in the time interval where the lightcurve is above 80% of the peak time intensity. The directivity obtained with these different simulations, and normalised to the maximum intensity, is displayed in Fig. 2. Each directivity curve was fitted with the model described by Eq. (3), using the mpfitfun procedure to perform the Levenberg-Marquardt least-squares minimisation (Markwardt et al. 2009). The result of this fit is also shown in Fig. 2. As seen in the figure, in the case of isotropic scattering (α = 1), the exponential model is a good approximation of the directivity. When we increase the anisotropy of the scattering (by decreasing the ratio α), the directivity starts to deviate from an exponential shape. However, we keep this model in order to quantify the change of shape of the directivity with the anisotropy factor. As we increase the anisotropy, the directivity distribution gets thinner, as expected, leading to smaller values of the parameter Δμ of the exponential model. In the bottom panel of Fig. 2, the evolution of Δμ resulting from the fits, as a function of the anisotropy factor α, is displayed. This evolution is fitted by a model of the form Δμ ∝ e(a0α), which gives a0 = 2.2 ± 0.3.

thumbnail Fig. 2.

Effect of the anistropy of density fluctuations on the directivity of the radio emission. Top: normalised directivity as histograms calculated from the results of the simulations (described in Sect. 2.2), with anisotropy factors α = 0.25, 0.30, 0.40, 0.50, 0.60, 0.75, and 1.0. The result of the exponential fit is shown as a line for each curve and the values of the parameter Δμ resulting from this fit are displayed in the low right corner. Bottom: evolution of the parameter Δμ with the anisotropy factor α. The distribution is fitted with an exponential model: Δμ ∝ e(a0α), which gives a0 = 2.2 ± 0.3. The result of this fit is shown as a dashed line.

2.3. Evolution of directivity with frequency

The influence of frequency on the directivity of radio bursts in the radio-wave propagation simulations is examined with the following simulation settings: (1) a radio source located at 5, 8.5, 10, 13, 18, or 30RS, leading to a plasma density of fpe = 2077, 938, 765, 558, 382, or 211 kHz, respectively, and fundamental radio emission emitted at 1.2 × fpe; (2) anisotropy factor α = 0.30.

As described in Sect. 2.2, the directivity shown in Fig. 3 is obtained here for photons arriving around the peak time. As can be seen in the figure, there is small dependence of the shape of directivity on frequency, with the parameter Δμ decreasing with increasing frequency. We note that this evolution is a small and remains within the error bars for Δμ. We also note that when we select all photons (instead of the photons arriving near the peak time of the light curve), the directivity pattern no longer depends on the frequency.

thumbnail Fig. 3.

Normalised directivity as histograms calculated from the results of the simulations described in Sect. 2.3, with anisotropy factor α = 0.30 and plasma frequency of 2077, 938, 765, 558, 382, and 211 kHz in red, orange, green, light blue, dark blue, and purple, respectively. The result of the exponential fit is shown as a line for each curve, and the values of the parameter Δμ resulting from this fit are displayed in the low right corner.

2.4. Time profiles at different angles

Radio-wave scattering is responsible for delays in the propagation time and results in a broadening of the time profiles of type III radio bursts. We used the simulations presented in Sect. 2.2 to quantify the time profile broadening introduced by scattering and the effect of both the radio emission frequency and the anisotropy of the scattering process on the time profile widths (or decay times).

An example of time profiles collected in different directions in space (i.e. at different angles from the radio source direction along the z-axis) is shown in Fig. 4. As can be seen in the figure, the time profiles cannot be fully described by an exponential decay: there is a break in the slope taking place roughly when the intensity falls below 10% of the maximum intensity. This behaviour is introduced by the anisotropy in the scattering process, which is responsible for an ’echo’ in the light curve, as described using the same ray-tracing simulations, but at higher frequencies, by Kuznetsov et al. (2020).

thumbnail Fig. 4.

Example of time profiles obtained for photons collected on a sphere of radius 111RS (where propagation effects become negligible), at different angles θP, from the simulations of radio-wave propagation from an emission source at 11RS and an anisotropy factor or α = 0.30. Dashed vertical lines indicate the peak time for each time profile.

For each time profile, the peak time and the full width at half maximum (FWHM) is determined.

Then the decay part of the time profiles is fitted with an exponential model of the form:

P = P 0 exp ( − t − t 0 τ ) , $$ \begin{aligned} P = P_0 \exp { \left( - \frac{t-t_0}{\tau } \right)} ,\end{aligned} $$(4)

where τ is the decay time. This fit is performed using the mpfitfun procedure to perform a Levenberg-Marquardt least-squares minimisation (Markwardt et al. 2009). For this fit, we used only the part of the profile after the peak time, for which the flux is above 10% of the peak flux.

The evolution of the decay time with the anisotropy factor and the radio frequency is shown in Fig. 5. This analysis demonstrates that: (1) the decay time does not vary significantly from one point of view in space to another (from one angle to another); (2) the decay time varies significantly with the anisotropy factor α: as shown in the top panel of Fig. 5, the decay time increases significantly as the anistropy factor increases towards α = 1, as reported in Kontar et al. (2019); (3) the decay times vary significantly with the radio emission frequency, as shown in the bottom panel of Fig. 5, whereas the decay time decreases as the frequency increases, as also reported in Kontar et al. (2019).

thumbnail Fig. 5.

Evolution of the light curve decay times in the simulations. Top: evolution of the decay time as a function of the anisotropy factor α, for emissions at 818 kHz. Bottom: evolution of the decay time as a function of the radio emission frequency (assuming fundamental emission) for an anisotropy factor of 0.3. On each plot, the decay time is determined at different angles from the radio source.

3. Multi-spacecraft observations of type III radio bursts

In this section, we describe briefly the space-born radio instruments used in this study and the corresponding data, which have all been calibrated to radio Solar Flux Units (SFU, 1 SFU = 10−22 W m−2 Hz−1). All these instruments operate in the radio kilometric range, with corresponding frequencies spanning between a few kHz to 10–20 MHz, just below the ionospheric radio cutoff. We then go on to describe our observations and the results of our analyses.

3.1. Descriptions of the instruments

We used radio observations embarked on board the Wind (Ogilvie & Desch 1997), the STEREO-A (Kaiser 2005), the Parker Solar Probe (Fox et al. 2016), and the Solar Orbiter (Müller et al. 2020; Zouganelis et al. 2020) spacecraft.

On Wind, the Waves experiment (Bougeret et al. 1995) carries three electric dipole antennas; two of them are co-planar and orthogonal wire dipole antennas in the spin-plane, whereas the other is a rigid spin-axis dipole. We used the Wind/Waves demodulated data, derived from a so-called direction-finding method by Manning & Fainberg (1980) and calibrated using the radio galaxy background (Zaslavsky et al. 2011). This technique provides the absolute radio flux of the observed sources, as well as their polarization properties, directions, and sizes.

On STEREO-A, the S/Waves instrument (Bougeret et al. 2008) performs radio measurements using three orthogonal antenna monopoles. This time, the calibration was based on direction finding techniques specific to three-axis stabilised spacecraft (Cecconi et al. 2008; Krupar et al. 2012, 2016)).

On Parker Solar Probe, we used data recorded by the Radio Frequency Spectrometer (RFS, Pulupa et al. 2017; Bale 2020) connected to the FIELDS electric antennas (Bale et al. 2016). On PSP, the full direction finding radio data pipeline is still in development. However, for sources observed in the frequency range we use in this study (from 400 to 1000 kHz), the heliospheric locations (12–6Rs, using the Leblanc et al. 1998 density model) are such that the angles between their k-vectors and the radial direction is negligible. Under these conditions, the radio flux can be defined as the sum of the power spectral densities measured by each of the two crossed dipoles, multiplied by their respective sin(θDi)2, with θDi being the angle between the radial and the given FIELDS dipole. For the events studied here, the values of θDi range between 66 and 81°. The conversion from power spectral densities to radio fluxes in SFU is obtained using the gains as defined by Maksimovic et al. (2020a).

Finally, on Solar Orbiter, we used radio data recorder by the radio receiver part of the RPW (Radio and Plasma Waves) instrument (Maksimovic et al. 2020b). As for PSP, the full direction-finding radio data pipeline is also in development for RPW. Therefore, we made the same assumptions for the directions of the radio sources’ k-vectors. The only difference is that, contrary to PSP, the RPW antenna dipoles are always perpendicular to the radial direction. We therefore define the radio flux for SO as being two times the power spectral density as measured by one dipole (the factor of 2 comes from the fact that we assume the source to be non-polarised), multiplied by the calibration gains that have been extensively described by Vecchio et al. (2021).

3.2. Observations

For this study, we selected five type III radio bursts that were observed by four widely-separated spacecraft: the first event was observed on 11 July 2020 at about 02:30 UT, the second and third events were observed on 21 July 2020 around 03:00 and 07:00 UT, respectively, and the fourth and fifth events were observed on 18 November 2020 at about 02:00 and 22:30 UT, respectively. The positions of the probes on each day are displayed in Fig. 6. The dynamic spectra of the radio fluxes in SFU for the four spacecraft for the event on 11 July 2020 at about 02:30 UT are given in Fig. 7. As for the other events, we chose to analyse well-defined and isolated type III bursts, which are clearly visible on the four probes.

thumbnail Fig. 6.

Position of Solar Orbiter, Parker Solar Probe, STEREO-A and Wind projected in the plane of the Heliocentric Earth Ecliptic (HEE) coordinate system. Left: position on 11 July 2020 at 02:30 UT. The position of the radio source is shown as crosses near the Sun. Middle: position on 21 July 2020 at 03:00 UT. The positions of the radio sources from the two events of that day are indicated by coloured crosses near the Sun. Since both events are from the same region, they are superimposed. Right: position on 18 November 2020 at 02:00 UT. The position of the radio sources for the two events of that day are shown as coloured crosses near the Sun. On this day there is a difference between the location of the radio sources from the first event and from the second event. The determination of the radio source location is described in the text. On each plot, dotted lines are used to point the direction of the radio sources.

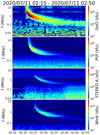thumbnail Fig. 7.

Dynamic spectrum of the radio fluxes in SFU for the four spacecraft for the event on 11 July 2020 at about 02:30 UT. Top to bottom: Solar Orbiter, Parker Solar Probe, STEREO-A, and Wind.

We selected eight frequency channels for analysing the radio emission, namely: 411, 430, 511, 635, 663, 755, 788, and 979 kHz. These particular frequencies were chosen because they correspond to clean RPW frequencies that are not polluted by the strong electromagnetic emission from the Solar Orbiter platform (Maksimovic et al. 2021)

Figure 8 displays temporal variations of the radio fluxes at 634.5 kHz for the four spacecraft and for the event on 11 July 2020 at about 02:30 UT. For each of these light curves, the median of the radio signal on an interval of 30 minutes before 2:20 UT has been removed. All remaining light curves have a classic shape, rapidly reaching a maximum and decaying exponentially. For each of the probes, the time of the peak flux is indicated by the vertical dashed lines.

thumbnail Fig. 8.

Light curves of the radio fluxes at 634.5 kHz for the event on July 11 2020, observed at Solar Orbiter, Parker Solar Probe, STEREO-A, and Wind. For each of these light curves, the median of the radio signal on an interval of 30 min before 2:20 UT has been removed. For each of the probes, the time of the peak flux is indicated by the vertical dashed lines.

3.2.1. Decay times of the type III radio fluxes

The decay time of the radio bursts was determined at each of the eight selected frequencies by fitting an exponential curve to the decaying part of the burst, using the same model as the one used to analyse the light curves from the simulations (Eq. (4)). The interval chosen to perform the fit is from the peak time to the time when the flux falls below 10 % of the peak intensity. The result of these fits is shown in Fig. 9. As expected, the decay time decreases with increasing frequency. However, there is no clear variation of the decay times between the different events. These observed decay times are aligned with previous measurements of the evolution of the decay time with frequency, such as the compilation of measurement fitted in Kontar et al. (2019), or the recent observations of 30 type III bursts by STEREO and Parker Solar Probe presented in Krupar et al. (2020).

thumbnail Fig. 9.

Decay times of the radio bursts presented as a function of the frequency of the radio emission. Different colours show different type III bursts and different symbols show the different probes. The dashed black line show the result of the fit to the data performed by Kontar et al. (2019) on several data sets. The dashed red and orange lines show the result of the fit on the distribution of decay times from 30 radio bursts observed by STEREO and Parker Solar Probe, respectively (Krupar et al. 2020)

3.2.2. Directivity fit to observations

Simultaneous observations of type III radio bursts with four different observation angles allow for a determination of the directivity of the radio emission. While the position of each instrument is well known, the position of the radio source is an unknown parameter. We therefore used the radio flux measurements at the four spacecraft to determine both the shape of the radio emission directivity pattern and the location of the radio source. The geometrical used is illustrated in Fig. 10: the positions of the probes are given in the Heliocentric Earth Ecliptic (HEE) coordinate system, where the z-axis is the solar rotation axis and the x-axis is in the plane containing the z-axis and Earth; the coordinates (ri, φi, θi) correspond to the distance to the Sun, as well as the longitude and latitude of probe i in this coordinate system.

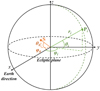thumbnail Fig. 10.

Position of the radio source and probe i in the HEE coordinate system: longitudes are noted with angle φ, latitudes with angle θ.

During our observations, the different spacecraft are at different distances from the radio source. Since the radio source remains very close to the Sun, we assume that we can correct the flux intensity of each spacecraft for their relative distance to the radio source by using the heliocentric distance of the spacecraft. The fluxes corrected for the different distances are noted as Iau since they represent the radio flux that would have been measured if the spacecraft was positioned at 1 au from the Sun.

The radio flux at 1 au depends on the position of the observation point with respect to the radio source, the intensity of the radio emission, and the directivity of the emission. Therefore, it can be described as a function of the source position (φ0, θ0), the probe position (φ, θ), and the parameter Δμ for the directivity. The directivity is modelled using Eq. (3) with μ = cos(φ − φ0)cos(θ − θ0) and C0 the maximum intensity, when φ = φ0 and θ = θ0.

In the case of multi-spacecraft observations of type III radio bursts, the position of the probes (φi, θi) is known for each probe i, while the position of the source (φ0, θ0) and the parameters Δμ and C0 are the four unknowns. Using the MPFIT procedure, we fit a directivity profile to best represent the radio fluxes measured at the different spacecraft. The result of the fit gives both a measurement of the directivity parameter Δμ and a location of the radio source (φ0, θ0), independent of other methods to locate the source (e.g. triangulation).

For the events presented in this paper, the probes are all located close to the ecliptic plane, at low latitudes; therefore, there are poor constraints on the latitude of the radio source θ0 and this parameter was thus kept fixed to 0 for the directivity fit. The directivity model is fitted using the peak intensity at each of the eight frequencies selected, resulting in eight directivity profiles for each event. An example of the directivity fit shown in the ecliptic plane is displayed in Fig. 11. The main results of these fits are the amplitude of the radio emission directivity pattern of the radio burst, characterised by the parameter Δμ, and the position of the radio source (longitude, with the assumption of a source in the ecliptic plane).

thumbnail Fig. 11.

Directivity fit on the peak fluxes measured during the 11 July 2020 event at different frequencies indicated with different colours. STEREO-A, WIND, Parker Solar Probe, and Solar Orbiter measurements are indicated by crosses and labelled as STA, WND, PSP, and SOLO respectively. The vertical lines show the position of the radio source in longitude as determined from the directivity fit.

Changes in the level of uncertainties in the measured fluxes at the different probes do not significantly affect the results of the directivity fit: while the uncertainty on the parameters is linked to the uncertainty on the measured fluxes, the parameter values themselves do not change significantly. Moreover, even if the fluxes from the RPW and FIELDS are not determined with the full direction-finding radio data pipelines in this paper, no significant change to the results presented here should be expected once the final calibration to the data is applied.

In order to determine the radio source location, we use the results of our directivity fit, which provide the longitude and latitude of the source, and estimate the radial distance of the source to the Sun using a density model. In this paper, the latitude of the source is assumed to be 0, and we used the density model described by Eq. (1), assuming that the radio emission is emitted at the fundamental frequency. The resulting source positions are displayed in each panel of Fig. 6 as coloured crosses for each event. On 21 July 2020, the radio sources positions from the two type III radio bursts overlap. On 18 November 2020, the radio sources positions from the two type III radio bursts are slightly shifted, and it is likely that these sources are emitted by electron beams originating from the same active region. For all events, the deduced locations of the radio emission sources roughly correspond to a longitude at which active regions are present in the synoptic maps of the magnetic field of the solar surface.

The amplitude of the radio burst directivity, determined from the directivity fit, is displayed as a function of frequency in Fig. 12. As seen in the figure, the values of the parameter Δμ can vary significantly from one event to another. However, no clear variation with frequency is found for the parameter Δμ. The mean values of the parameters and the standard deviation for each event are displayed in Fig. 1. For the first three events, the value of Δμ is found to be between 0.21 and 0.25, with very little deviation. For the last two events, the value of Δμ is found to be around 0.4, but with greater uncertainties.

thumbnail Fig. 12.

Parameter Δμ determined during the directivity fitting of the peak fluxes for the five radio bursts selected.

Table 1.

Δμ averaged over the different frequencies for each event, and corresponding standard deviation (The standard deviation here is calculated over the different frequencies for each individual event.).

4. Discussion

4.1. Comparison of observational and simulation results

Ray-tracing simulations were used to explore the variations of radio burst properties with respect to the variation of several parameters of the ambient plasma. As shown in Kontar et al. (2019) (and recalled in this paper) the time profile and directivity of the radio emission depends on the anisotropy factor introduced to account for anisotropic scattering of radio-waves on density fluctuations of the ambient plasma. Using the results of ray-tracing simulations with different anisotropy factor α, we established a clear relation between the shape of the radio emission directivity, characterised by the parameter Δμ and the level of anisotropy. We also show here that simulation results suggest that this parameter Δμ exhibits only a weak dependence on the radio emission frequency.

The directivity of type III radio bursts can only be determined from observations when simultaneous observations of type III radio bursts are available from several different vantage points. In this paper, we use observations at four different probes, which are all located close to the ecliptic plane: we therefore limited our analysis in this plane and made the assumption that the radio sources were emitted in the ecliptic plane. For the first three events, the averaged values of Δμ lie between 0.21 and 0.25, which corresponds to anisotropy factors α between 0.36 and 0.44 in the simulations presented in Sect. 2. For the last two events, the average value of Δμ is of 0.4, corresponding to an anisotropy factor of 0.6.

As shown in Fig. 5, with an anisotropy factor as low as α = 0.30, the decay times from the simulations are higher than the observed decay time by roughly a factor of 2. Given the uncertainties in the measurements and the approximations made in the simulations, this retains a good agreement. However, given that higher anisotropy factors lead to increased decay times, it may be more difficult to explain the observed decay times for the last two events for which the anisotropy factor is believed to be around 0.6. Thus, a further investigation of the influence of the assumptions and other parameters in the simulation are necessary to completely explain these observations. We also noted that anisotropic scattering of radio waves introduced an ‘echo’ that is manifested in the light curves as a deviation from the exponential shape of the decay part of the curve. However, this deviation is subtle and only visible after the time when the intensity drops roughly below 10% of the peak intensity. This property might therefore be challenging to discern in the observations.

4.2. Individual radio burst properties compared to statistical results

This paper reports on multi-spacecraft observations of single type III radio bursts, whose properties can be compared to the results of previous studies that have examined such parameters statistically.

As discussed in Sect. 3, the decay times of the radio bursts show similar (or slightly lower) values as the decays times reported for STEREO and Parker Solar Probe observations (Krupar et al. 2020) or as compiled in Kontar et al. (2019) based on a range of studies. The decreasing trend of the decay time with increasing frequency is also observed on a single event basis. We show here that this decay times does not vary significantly with the angle between the source and the point of observation (probe position).

On the other hand, the directivity profiles determined in this study for individual radio bursts can be compared to the directivity of radio bursts determined statistically on thousands of events, as reported by Bonnin et al. (2008), Hoang et al. (1997). In their study, the average directivity of radio burst was determined by fitting the distribution of flux ratios observed by two probes, for thousands of events. A slightly different model was then used for the directivity, taking the form:

D ( φ ′ ) = C 0 10 ( a ( cos φ ′ − 1 ) ) , $$ \begin{aligned} D(\varphi ^{\prime }) = C_0 10^{(a ( \cos \varphi ^{\prime } -1))} ,\end{aligned} $$(5)

where φ′ is the angle between the source direction and the probe position in a source-centered coordinate system. In our analysis, we consider the angles in a sun-centered system. However, since the frequency of our measurements is above 400 kHz, the radio sources remain very close to the Sun, and we consider that φ′=φ, with φ being the difference between the probe longitude and the source longitude. In that specific case, the relation between parameters a and Δμ is simple: a = (ln(10)Δμ)−1.

We used this model described by Eq. (5) to fit the data, following the same method used to calculate the Δμ parameter, but this time to calculate the values of the parameter a that is consistent with our observations, which was then compared to the values of this parameter found by the previous studies. The results are shown in Fig. 13. The values of the parameter are of the same order of magnitude as the ones calculated in the statistical studies, which could be considered to be average values, as it is expected that the values from a single event to another can vary significantly and differ from the average. We also note that the values of the parameter a found by fitting the data verify the expected relation: a = (ln(10)Δμ)−1.

thumbnail Fig. 13.

Parameter a describing the amplitude of the directivity, for the model described by Eq. (5), and determined by a fit of this model to the peak fluxes for the five radio bursts selected, shown as coloured crosses. Previous results obtained in statistical studies of flux ratios of type III radio bursts by Bonnin et al. (2008) and Hoang et al. (1997) are also shown as squared boxes.

In the frequency range studied here, there is no obvious evolution of the directivity shape with frequency. In particular, Bonnin et al. (2008) and Hoang et al. (1997) reported a variation of the directivity with frequency, which was significant at frequencies below 400 kHz. It can be noted that such a dependence is not observed in the ray-tracing simulations; however, at frequencies below 400 kHz, it is probable that we can no longer assume that the angles that are defined with respect to the centre of the Sun (as it is the case in the simulations) and those defined with respect to the source (as it is in these studies) can be considered to be similar. This change in geometry could therefore account for the frequency dependence of the directivity profiles found in these past results.

We note that the directivity profiles found for the last two events presented here are similar to the results found in the previous studies of Bonnin et al. (2008) and Hoang et al. (1997), while the directivity profile for the first three events is narrower (with higher values of the parameter a). These observations demonstrate how the directivity profile can deviate from the average values determined by past studies. It is interesting to note that it is possible that the shape of directivity (i.e. the values of Δμ or a) seems to remain consistent over time: the two events most closely related in time (on 21 July 2020) show almost identical directivity profiles. Since those events also share the same location, this can be interpreted as events for which the solar wind conditions remains the same. These results therefore demonstrate a potential for this type of analysis to probe the plasma and solar wind conditions at the sources of the radio emission in the inner heliosphere.

5. Conclusion

The launch of the Solar Orbiter and Parker Solar Probe missions, in combination with the STEREO and Wind missions, have opened the opportunity for the simultaneous observations by four widely-separated spacecraft of solar events, such as type III radio bursts. Multi-spacecraft observations of these radio emissions are used here to study the directivity of single type III radio burst. In the past, directivity measurements could only be performed by a statistical analysis of radio flux ratios from many different bursts, whereas, in the present study, we also provide an estimation of the source locations. As the data presented here were taken early in the Solar Orbiter mission, all measurements are performed close to the ecliptic plane and, therefore, no information on the latitude of the radio sources can be reliably inferred; however, as the Solar Orbiter mission continues, the satellite orbit will increase in inclination in regards to the ecliptic plane (Müller et al. 2020; Zouganelis et al. 2020), providing an opportunity to further study the directivity of the radio emissions in the 3D space for individual events.

In this study, we looked at five different radio bursts and we show that while their directivity could be consistent with the previous averaged results, it could also vary significantly from these averaged values and from one event to another. The two closest events in terms of time and space, namely, on 21 July 2020, show very similar directivity profiles, suggesting that the radio emission was emitted in similar solar wind conditions. This suggests, as we might expect, that the radio emission directivity is significantly affected by the properties of the ambient plasma and solar wind.

Ray-tracing simulations of radio-wave propagation with anisotropic scattering on density fluctuations suggest that the directivity pattern of radio emission strongly depends on the ambient plasma conditions and, in particular, on the anisotropy of the density fluctuations of the plasma. Multi-spacecraft radio emission diagnostics therefore enable us to characterise the anisotropy in the plasma density fluctuations. In the 400–1000 kHz range, we typically probe plasma in the range 5–20 solar radii from the Sun. At this distance range, it will be possible to combine the type of observations presented in this paper with in situ measurements by Parker Solar Probe at its closest approach, and also to get beyond the range explored in situ by the probe.

1

We also simulated a radio sources at a frequency of 1.2 × fpe and obtained the same directivity profiles.

Acknowledgments

Solar Orbiter is a space mission of international collaboration between ESA and NASA, operated by ESA. Parker Solar Probe was designed, built, and is now operated by the Johns Hopkins Applied Physics Laboratory as part of NASA’s Living with a Star (LWS) program (contract NNN06AA01C). Support from the LWS management and technical team has played a critical role in the success of the Parker Solar Probe mission. The Wind/WAVES investigation is a collaboration of the Observatoire de Paris, NASA/GSFC, and the University of Minnesota. S. Musset is supported by an ESA Research Fellowship. V. Krupar acknowledges the support by NASA under grants 18-2HSWO218_2-0010 and 19-HSR-19_2-0143. N. Chrysaphi thanks CNES for its financial support. Data analysis was performed using IDL (Exelis Visual Information Solutions, Boulder, Colorado).

References

  1. Bale, S. D. 2020, Parker Solar Probe, FIELDS Radio Frequency Spectrometer, RFS, High Frequency Receiver, HFR, Spectra, Level 2 (L2), 7 s and 56 s Data (NASA Space Physics Data Facility) [Google Scholar]
  2. Bale, S. D., Goetz, K., Harvey, P. R., et al. 2016, Space Sci. Rev., 204, 49 [Google Scholar]
  3. Bonnin, X., Hoang, S., & Maksimovic, M. 2008, A&A, 489, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bougeret, J. L., Kaiser, M. L., Kellogg, P. J., et al. 1995, Space Sci. Rev., 71, 231 [CrossRef] [Google Scholar]
  5. Bougeret, J. L., Goetz, K., Kaiser, M. L., et al. 2008, Space Sci. Rev., 136, 487 [CrossRef] [Google Scholar]
  6. Caroubalos, C., & Steinberg, J. L. 1974, A&A, 32, 245 [NASA ADS] [Google Scholar]
  7. Caroubalos, C., Poquerusse, M., & Steinberg, J. L. 1974, A&A, 32, 255 [NASA ADS] [Google Scholar]
  8. Cecconi, B., Bonnin, X., Hoang, S., et al. 2008, Space Sci. Rev., 136, 549 [CrossRef] [Google Scholar]
  9. Chen, X., Kontar, E. P., Chrysaphi, N., et al. 2020, ApJ, 905, 43 [NASA ADS] [CrossRef] [Google Scholar]
  10. Chrysaphi, N., Kontar, E. P., Holman, G. D., & Temmer, M. 2018, ApJ, 868, 79 [NASA ADS] [CrossRef] [Google Scholar]
  11. Dulk, G. A. 1985, ARA&A, 23, 169 [Google Scholar]
  12. Fokker, A. D. 1965, Bull. Astron. Inst. Neth., 18, 111 [Google Scholar]
  13. Fox, N. J., Velli, M. C., Bale, S. D., et al. 2016, Space Sci. Rev., 204, 7 [Google Scholar]
  14. Ginzburg, V. L., & Zhelezniakov, V. V. 1958, Sov. Astron., 2, 653 [Google Scholar]
  15. Hoang, S., Poquerusse, M., & Bougeret, J. L. 1997, Sol. Phys., 172, 307 [NASA ADS] [CrossRef] [Google Scholar]
  16. Kaiser, M. L. 2005, Adv. Space Res., 36, 1483 [NASA ADS] [CrossRef] [Google Scholar]
  17. Kontar, E. P., Yu, S., Kuznetsov, A. A., et al. 2017, Nat. Commun., 8, 1515 [NASA ADS] [CrossRef] [Google Scholar]
  18. Kontar, E. P., Chen, X., Chrysaphi, N., et al. 2019, ApJ, 884, 122 [NASA ADS] [CrossRef] [Google Scholar]
  19. Krupar, V., Santolik, O., Cecconi, B., et al. 2012, J. Geophys. Res. (Space Phys.), 117, A06101 [Google Scholar]
  20. Krupar, V., Eastwood, J. P., Kruparova, O., et al. 2016, ApJ, 823, L5 [CrossRef] [Google Scholar]
  21. Krupar, V., Maksimovic, M., Kontar, E. P., et al. 2018, ApJ, 857, 82 [NASA ADS] [CrossRef] [Google Scholar]
  22. Krupar, V., Szabo, A., Maksimovic, M., et al. 2020, ApJS, 246, 57 [Google Scholar]
  23. Kuznetsov, A. A., Chrysaphi, N., Kontar, E. P., & Motorina, G. 2020, ApJ, 898, 94 [CrossRef] [Google Scholar]
  24. Leblanc, Y., Dulk, G. A., & Bougeret, J.-L. 1998, Sol. Phys., 183, 165 [NASA ADS] [CrossRef] [Google Scholar]
  25. Lecacheux, A., Steinberg, J. L., Hoang, S., & Dulk, G. A. 1989, A&A, 217, 237 [Google Scholar]
  26. Maksimovic, M., Bale, S. D., Berčič, L., et al. 2020a, ApJS, 246, 62 [Google Scholar]
  27. Maksimovic, M., Bale, S. D., Chust, T., et al. 2020b, A&A, 642, A12 [EDP Sciences] [Google Scholar]
  28. Maksimovic, M., Souček, J., Chust, T., et al. 2021, A&A, 656, A41 (SO Cruise Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Manning, R., & Fainberg, J. 1980, Space Sci. Instrum., 5, 161 [NASA ADS] [Google Scholar]
  30. Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
  31. Melrose, D. B. 1980, Space Sci. Rev., 26, 3 [NASA ADS] [CrossRef] [Google Scholar]
  32. Melrose, D. B. 1987, Sol. Phys., 111, 89 [NASA ADS] [CrossRef] [Google Scholar]
  33. Müller, D., St. Cyr, O. C., Zouganelis, I., et al. 2020, A&A, 642, A1 [Google Scholar]
  34. Ogilvie, K. W., & Desch, M. D. 1997, Adv. Space Res., 20, 559 [Google Scholar]
  35. Pulupa, M., Bale, S. D., Bonnell, J. W., et al. 2017, J. Geophys. Res. (Space Phys.), 122, 2836 [NASA ADS] [CrossRef] [Google Scholar]
  36. Smith, R. A., Goldstein, M. L., & Papadopoulos, K. 1976, Sol. Phys., 46, 515 [NASA ADS] [CrossRef] [Google Scholar]
  37. Steinberg, J. L., Aubier-Giraud, M., Leblanc, Y., & Boischot, A. 1971, A&A, 10, 362 [NASA ADS] [Google Scholar]
  38. Steinberg, J. L., Hoang, S., Lecacheux, A., Aubier, M. G., & Dulk, G. A. 1984, A&A, 140, 39 [Google Scholar]
  39. Steinberg, J. L., Hoang, S., & Dulk, G. A. 1985, A&A, 150, 205 [NASA ADS] [Google Scholar]
  40. Sturrock, P. A. 1964, Type III Solar Radio Bursts, 50, 357 [NASA ADS] [Google Scholar]
  41. Thejappa, G., & MacDowall, R. J. 2008, ApJ, 676, 1338 [NASA ADS] [CrossRef] [Google Scholar]
  42. Tkachenko, A., Krasnoselskikh, V., & Voshchepynets, A. 2021, ApJ, 908, 126 [NASA ADS] [CrossRef] [Google Scholar]
  43. Vecchio, A., Maksimovic, M., Krupar, V., et al. 2021, A&A, 656, A33 (SO Cruise Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Wild, J. P. 1950, Aust. J. Sci. Res. Phys. Sci., 3, 541 [NASA ADS] [Google Scholar]
  45. Wild, J. P. 1967, Proc. Astron. Soc. Aust., 1, 38 [NASA ADS] [CrossRef] [Google Scholar]
  46. Zaslavsky, A., Meyer-Vernet, N., Hoang, S., Maksimovic, M., & Bale, S. D. 2011, Radio Sci., 46, RS2008 [Google Scholar]
  47. Zheleznyakov, V. V., & Zaitsev, V. V. 1970, Sov. Astron., 14, 47 [NASA ADS] [Google Scholar]
  48. Zouganelis, I., De Groof, A., Walsh, A. P., et al. 2020, A&A, 642, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1.

Δμ averaged over the different frequencies for each event, and corresponding standard deviation (The standard deviation here is calculated over the different frequencies for each individual event.).

In the text

All Figures

thumbnail Fig. 1.

Geometry of the simulation: radio source S is emitted on the z-axis. The angle θP is the angle between the direction of the radio source S (the z-axis) and the direction of an observer at position P. In this paper, the radio source is always situated on the z-axis while the probe P has different positions in the 3D space.
In the text
thumbnail Fig. 2.

Effect of the anistropy of density fluctuations on the directivity of the radio emission. Top: normalised directivity as histograms calculated from the results of the simulations (described in Sect. 2.2), with anisotropy factors α = 0.25, 0.30, 0.40, 0.50, 0.60, 0.75, and 1.0. The result of the exponential fit is shown as a line for each curve and the values of the parameter Δμ resulting from this fit are displayed in the low right corner. Bottom: evolution of the parameter Δμ with the anisotropy factor α. The distribution is fitted with an exponential model: Δμ ∝ e(a0α), which gives a0 = 2.2 ± 0.3. The result of this fit is shown as a dashed line.
In the text
thumbnail Fig. 3.

Normalised directivity as histograms calculated from the results of the simulations described in Sect. 2.3, with anisotropy factor α = 0.30 and plasma frequency of 2077, 938, 765, 558, 382, and 211 kHz in red, orange, green, light blue, dark blue, and purple, respectively. The result of the exponential fit is shown as a line for each curve, and the values of the parameter Δμ resulting from this fit are displayed in the low right corner.
In the text
thumbnail Fig. 4.

Example of time profiles obtained for photons collected on a sphere of radius 111RS (where propagation effects become negligible), at different angles θP, from the simulations of radio-wave propagation from an emission source at 11RS and an anisotropy factor or α = 0.30. Dashed vertical lines indicate the peak time for each time profile.
In the text
thumbnail Fig. 5.

Evolution of the light curve decay times in the simulations. Top: evolution of the decay time as a function of the anisotropy factor α, for emissions at 818 kHz. Bottom: evolution of the decay time as a function of the radio emission frequency (assuming fundamental emission) for an anisotropy factor of 0.3. On each plot, the decay time is determined at different angles from the radio source.
In the text
thumbnail Fig. 6.

Position of Solar Orbiter, Parker Solar Probe, STEREO-A and Wind projected in the plane of the Heliocentric Earth Ecliptic (HEE) coordinate system. Left: position on 11 July 2020 at 02:30 UT. The position of the radio source is shown as crosses near the Sun. Middle: position on 21 July 2020 at 03:00 UT. The positions of the radio sources from the two events of that day are indicated by coloured crosses near the Sun. Since both events are from the same region, they are superimposed. Right: position on 18 November 2020 at 02:00 UT. The position of the radio sources for the two events of that day are shown as coloured crosses near the Sun. On this day there is a difference between the location of the radio sources from the first event and from the second event. The determination of the radio source location is described in the text. On each plot, dotted lines are used to point the direction of the radio sources.
In the text
thumbnail Fig. 7.

Dynamic spectrum of the radio fluxes in SFU for the four spacecraft for the event on 11 July 2020 at about 02:30 UT. Top to bottom: Solar Orbiter, Parker Solar Probe, STEREO-A, and Wind.
In the text
thumbnail Fig. 8.

Light curves of the radio fluxes at 634.5 kHz for the event on July 11 2020, observed at Solar Orbiter, Parker Solar Probe, STEREO-A, and Wind. For each of these light curves, the median of the radio signal on an interval of 30 min before 2:20 UT has been removed. For each of the probes, the time of the peak flux is indicated by the vertical dashed lines.
In the text
thumbnail Fig. 9.

Decay times of the radio bursts presented as a function of the frequency of the radio emission. Different colours show different type III bursts and different symbols show the different probes. The dashed black line show the result of the fit to the data performed by Kontar et al. (2019) on several data sets. The dashed red and orange lines show the result of the fit on the distribution of decay times from 30 radio bursts observed by STEREO and Parker Solar Probe, respectively (Krupar et al. 2020)
In the text
thumbnail Fig. 10.

Position of the radio source and probe i in the HEE coordinate system: longitudes are noted with angle φ, latitudes with angle θ.
In the text
thumbnail Fig. 11.

Directivity fit on the peak fluxes measured during the 11 July 2020 event at different frequencies indicated with different colours. STEREO-A, WIND, Parker Solar Probe, and Solar Orbiter measurements are indicated by crosses and labelled as STA, WND, PSP, and SOLO respectively. The vertical lines show the position of the radio source in longitude as determined from the directivity fit.
In the text
thumbnail Fig. 12.

Parameter Δμ determined during the directivity fitting of the peak fluxes for the five radio bursts selected.
In the text
thumbnail Fig. 13.

Parameter a describing the amplitude of the directivity, for the model described by Eq. (5), and determined by a fit of this model to the peak fluxes for the five radio bursts selected, shown as coloured crosses. Previous results obtained in statistical studies of flux ratios of type III radio bursts by Bonnin et al. (2008) and Hoang et al. (1997) are also shown as squared boxes.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.