| Issue |
A&A
Volume 654, October 2021
|
|
|---|---|---|
| Article Number | A34 | |
| Number of page(s) | 16 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202141252 | |
| Published online | 07 October 2021 | |
Chemical analysis of prestellar cores in Ophiuchus yields short timescales and rapid collapse
1
Departamento de Astronomía, Facultad Ciencias Físicas y Matemáticas, Universidad de Concepción Av. Esteban Iturra s/n Barrio Universitario,
Casilla 160,
Concepción,
Chile
e-mail: stefanobovino@udec.cl
2
Dipartimento di Fisica G. Occhialini”, Università degli Studi di Milano-Bicocca,
Piazza della Scienza 3,
20126
Milano,
Italy
3
INAF – Istituto di Radioastronomia – Italian node of the ALMA Regional Centre (ARC),
via Gobetti 101,
40129
Bologna,
Italy
4
Dipartimento di Fisica e Astronomia “Augusto Righi”, Universitá degli Studi di Bologna,
via Gobetti 93/2,
40129
Bologna,
Italy
5
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel, 69,
53121
Bonn,
Germany
Received:
5
May
2021
Accepted:
20
July
2021
Sun-like stars form from the contraction of cold and dense interstellar clouds. How the collapse proceeds and what the main physical processes are driving it, however, is still under debate and a final consensus on the timescale of the process has not been reached. If the contraction proceeds slowly, supported by strong magnetic fields and mediated by ambipolar diffusion, or is driven by fast collapse with gravity dominating the entire process is still an open question. One way to answer this question is to measure the age of prestellar cores through statistical methods based on observations or via reliable chemical chronometers, which should better reflect the physical conditions of the cores. Here we report Atacama Pathfinder EXperiment observations of ortho-H2D+ and para-D2H+ for six cores in the Ophiuchus complex, and we combined them with detailed three-dimensional magneto-hydrodynamical simulations including chemistry, providing a range of ages for the observed cores of up to 200 kyr. The outcome of our simulations and subsequent analysis provides a good matching with the observational results in terms of physical parameters (core masses and volume densities) and dynamical parameters such as the Mach number and the virial parameter. We show that models of fast collapse successfully reproduce the observed range of chemical abundance ratios since the timescales to reach the observed stages is comparable to the dynamical time of the cores (i.e. the free-fall time) and much shorter than the ambipolar diffusion time, measured from the electron fraction in the simulations. To confirm that this ratio can be used to distinguish between different star-formation scenarios, a larger (statistically relevant) sample of star-forming cores should be explored.
Key words: astrochemistry / methods: numerical / methods: observational / magnetohydrodynamics (MHD) / stars: formation
© ESO 2021
1 Introduction
Star formation is a longstanding problem in astrophysics (Bergin & Tafalla 2007), and despite the observational and theoretical progress made over the last decades, there are still some fundamental questions that remain open. One of these relates to the timescale to go from the prestellar stage to the formation of a protostellar object. The latter is affected by the interplay of the physical processes that drive star formation during the gravitational collapse of the gas within the prestellar cores. Strong magnetic fields and ambipolar diffusion (Shu et al. 1987; Mouschovias 1991) tend to hinder the collapse, which occurs on timescales longer than the typical dynamical time (i.e. the free-fall time), while in fast collapse theories the process is dominated by gravity and the results are timescales comparable to the free-fall time or a few free-fall times (Vázquez-Semadeni et al. 2005; Galván-Madrid et al. 2007; Hartmann et al. 2012). Similarly, turbulence (Mac Low & Klessen 2004), before being dissipated, slows down the collapse process (see also Bergin & Tafalla 2007).
Measuring timescales and assessing the age of prestellar cores is challenging. One way to do so is to employ statistical methods based on observations (Lee & Myers 1999). A viable alternative is to use tracers showing strong monotonic behaviour with time (Pagani et al. 2013; Brünken et al. 2014), so called chemical clocks, which better reflect the physical conditions of the cores. This is particularly true in star-forming regions as the star-formation process itself goes through strong changes in density and temperature, which in turn affect the chemical evolution of specific tracers that are sensitive to these physical quantities.
The ideal chemical clock to trace the star-formation process would be the ortho-to-para ratio of the most abundant molecule in these regions, that is to say molecular hydrogen which is expected to decrease over time during cloud contraction (Pagani et al. 2009), even if a decrease in this quantity should already be in place at thelarge scales of molecular cloud formation (see Lupi et al. 2021). The impossibility to access H2 rotational transitions at the low temperatures of dense cores (T < 20 K) requires one to employ a proxy, which manifests similar evolutionary features as H2. The specific conditions of temperature and density (n(H2) > 104 cm−3) make dense cores the ideal places to boost the deuterium enrichment of key molecules, the so-called deuterium fractionation process (Caselli 2002; Ceccarelli et al. 2014), which has been extensively employed asa chemical clock and it is known to be strongly affected by changes in the ortho-to-para H2 ratio. Previous works focussed on the ortho-to-para H2 D+ ratio (Brünken et al. 2014) and N2 D+/N2H+ ratio (Caselli 2002; Pagani et al. 2013). However, the former one suffers from the challenges of accessing the THz domain to observe para-H2D+, whereas the latter one does not necessarily trace the very cold and early stages (Pillai et al. 2012; Giannetti et al. 2019). Furthermore, N2 D+ is also subject to depletion (Pagani et al. 2007; Redaelli et al. 2019; Lin et al. 2020), making the estimates of timescales less accurate.
In addition, it is very difficult to generalise the effectiveness of the aforementioned clocks with a statistically relevant sample due to the high level of THz continuum needed to detect the para-H2D+ line in absorption. Sources in very early stages of evolution simply do not satisfy this requirement.
Vastel et al. (2004, 2012), Parise et al. (2011), and Pagani et al. (2013) have also explored the ratio between ortho-H2D+ and para-D2H+, finding values around unity. The main advantage, compared to the para-H2D+, lies on the fact that both tracers are observable from the ground in emission, without the necessity of a strong background source (Brünken et al. 2014). However, in these works the possibility of using this ratio as a chemical clock was not established convincingly. In particular, Pagani et al. (2013), based on low-dimensional chemical models, claimed that the non-monotonic behaviour of this ratio prevents one from distinguishing between fast and slow-collapse scenarios.
In this work, we revise this ratio by targeting six cores embedded in the well characterised L1688 and L1689 regions, which are two of the densest clouds of Ophiuchus, the first one being considered more active than the second (Nutter et al. 2006). At a distance of 140 parsecs (Ortiz-León et al. 2018), and with a dense population of cores and young stellar objects (Motte et al. 1998), the Ophiuchus molecular cloud complex represents one of the closest active star-forming regions to the Solar System and thus the ideal place to study the reliability of this ratio under different conditions.
The paper is organised as follows: we first present the observational data and the analysis of the spectra (Sect. 2); in Sect. 3 we report the numerical simulations employed to interpret the observations; in Sect. 4 we compare observations and simulations and provide an estimate for the core ages. Finally, we present a comprehensive discussion and the conclusions in Sects. 5 and 6, respectively.
Observational properties of the sources in Ophiuchus.
2 Observational data
In the following sections we report the details of the observational data and the fitting procedure.
2.1 APEX data
We have observed six cores within the Ophiuchus complex with the Atacama Pathfinder EXperiment (APEX) 12-m radio telescope (Güsten et al. 2006) in both ortho-H2D+ (J = 11,0 − 11,1) at 372.42134 GHz and para-D2H+ (J = 11,0 − 10,1) at 691.66044 GHz (Amano & Hirao 2005). The sources have been chosen based on the properties of cores with already available observations of the ortho-H2D+ and para-D2H+ (Parise et al. 2011; Vastel et al. 2004), that is with a column density of molecular hydrogen of N(H2) > 3 × 1022 cm−2 and temperatures below 14 K. A summary of the properties of the targeted cores are reported in Table 1.
Because of the very different line frequencies, the telescope resolution changes significantly, from ~ 18″ at ~ 372.42 GHz to ~ 9″ at 691.66 GHz. This would make the source size critical for correctly deriving the ratio of the two lines. In order to avoid this uncertainty, we have observed the cores with a single pointing centred on the maximum of the H2 column density and the minimum of the dust temperature in the case of ortho-H2D+ (11,0 − 11,1), and we covered the same area with a small on-the-fly map in the case of para-D2H+ (11,0 − 10,1), so that the final extracted spectra are directly comparable.
The observations of ortho-H2D+ were performed on 27–28 April 2019 and on 6–8 June 2019 with the PI instruments LAsMA (Güsten et al. 2008) and FLASH+ (Klein et al. 2014) under good weather conditions, with a precipitable water vapour (PWV) ~ 0.5 mm. The average system temperatures were in the range 539–899 K. We used a position-switch scheme, with carefully selected off-positions (RA2000 = 16h 32m 05.51s, Dec2000 = −24d 52m 33.07s for cores 1 and 2, and RA2000 = 16h 27m 46.355s, Dec2000 = −24d 31m 24.93s for the other sources), where the continuum emission has a local minimum in the Herschel maps. The observations were organised in on-off loops of 20 s of integration, with regular chopper-wheel calibrations. Pointing and focus were performed as needed using Jupiter, NGC 6073, IRAS 15194, and IRC+10216. The total telescope time was typically 45 min per core, with an on-time of 20 min. The corrected antenna temperature was transformed to a main beam temperature (Tmb) using a beam efficiency of ηmb = 0.73 and ηmb = 0.62 for the LAsMA and FLASH+ receivers, respectively. The final rms noise is in the range 30–50 mK at a velocity resolution of 0.2 km s−1.
The ground-state line of para-D2H+ was observed with the SEPIA (band 9) receiver (Hesper et al. 2005) on the following days: 27 April 2019, 23–24 May 2019, 02–03 June 2019, 07 July 2019, 28–29 July 2019, and 31 July 2019. The weather was exceptionally good, with PWV between 0.15 and 0.3 mm; the observations with sub-optimal PWV (≳0.5 mm) were discarded due to the high noise levels. The average system temperatures were in the range 1047–2164 K. As mentioned, we observed small on-the-fly maps (18′′ × 18′′) in order to cover the beam area of the telescope at 372 GHz. The maps were observed following a zigzag pattern, with a dump time of one second; calibration was repeated after every complete execution. Pointing and focus were regularly performed on Jupiter, W-Hya, NGC 6334I, Rx-Boo, and IRC+10216. We applied a beam efficiency of ηmb = 0.52 to convert the corrected antenna temperature to a main beam temperature. The final spectra for para-D2H+ have an rms noise in the range 20–70 mK at a velocity resolution of 0.3 km s−1.
 |
Fig. 1 Observed and modelled spectra of ortho-H2D+ (left) and para-D2H+ (right) for the six cores. We note that the temperature scale of the spectra is not the same in each panel. We have centred the spectra at the systemic velocity of ortho-H2D+ (vertical line) of each source. |
2.2 Data analysis and fitting procedure
The data were reduced using the CLASS program of the GILDAS software1. After removing the spectra with clear problems, a baseline of degree-1 was subtracted around the line, and the spectra were finally averaged, weighting them on the noise level. For the SEPIA (band 9) observations, all positions were averaged as well to extract the spectrum over the same area as for ortho-H2D+.
We detected the ground-state line of ortho-H2D+ in the entire sample (six prestellar cores) with a signal-to-noise ratio (S/N) above 5σ. We also observed the ground state transition of the para-D2H+, obtaining two weak detections (S/N ~ 3σ) and securing one detection (S∕N ~ 5σ). For the other three sources, we can only provide upper limits. The spectra for both tracers are reported in Fig. 1.
Once the spectra of each core were produced, we employed MCWEEDS to estimate the column densities of ortho-H2D+ and para-D2H+ (Giannetti et al. 2017). MCWEEDS allows one to fit the observed spectrum with a number of algorithms (from simple maximum a posteriori estimates to Markov chain Monte Carlo), in order to obtain a robust estimate of the uncertainties. At every iteration, a synthetic spectrum is generated, under the assumption of local thermodynamic equilibrium (LTE, well justified by the high-density of the cores2), taking into account line opacity effects, and it is then compared to the observed spectrum. Given that we only have two lines, performing a non-LTE analysis would not improve the quality of our inference because of the additional free parameters that would be needed for this model.
We have selected Markov chain Monte Carlo (MCMC) as the fitting method to correctly evaluate the uncertainties in column densities and propagate them numerically onto the ortho-H2D+/para-D2H+ ratio, and other derived quantities. We have used 100 000 total iterations, with a burn-in period of 10 000 iterations, adelay for the adaptive sampling of 5000 iterations, and a thinning factor of 20. The traces were inspected toensure convergence and independence of the samples. The following six parameters could be varied: column density of the species, excitation temperature, source size, line full-width at half-maximum, vLSR, and a calibration factor. In this case, we fixed the source size, assuming that it is extended compared to the beam; this means that the column densities that we obtain are beam-averaged. An extended emission region is supported by the results reported in previous works (Vastel et al. 2006; Pagani et al. 2009; Parise et al. 2011). As we have only two transitions, we cannot independently constrain the excitation temperature Tex. We thus approximated the excitation temperature with the dust temperature (Tex = Tdust, see Table 1), assuming that gas and dust are coupled at the high central densities of the selected sources. While the dust temperatures can be influenced by an incomplete removal of the emission from the warmer, outer layers of the cores, the values that we obtain are low and reasonably compatible with cold, prestellar cores (Caselli et al. 2008). The effect of the background and foreground is thus relatively small. We have inspected NH3 data reported in literature on the same regions (Friesen et al. 2009, 2017; Chitsazzadeh et al. 2014), and they are consistent, within the errors, with our Tdust, which confirms that our assumption is reasonable. In Sect. 4.3 we provide a comparison of the results obtained at different Tex to assess the error introduced by our assumption.
Our final free parameters are then the column density, the line full-width at half-maximum, and vLSR. The priors we used are as follows: a normal distribution for the logarithm of the column density and vLSR, with a σ of 1.5 orders of magnitude, and 2 km s−1. For the linewidth we used a truncated normal distribution, with σ = 1 km s−1, truncated at 0.3 km s−1 and 5 km s−1. Tests with different priors show that their exact form and parameters do not have a strong influence on the fitting results.
Having a robust estimate for the uncertainty on the derived parameters is crucial for low signal-to-noise ratio observations. Since we combined observations carried out in different moments and with different receivers, it was particularly important to account for calibration uncertainties, also considering that the column density is proportional to the integrated intensity of the line. For this we used a normally distributed random factor, with σ = 5% and truncated at ± 30%. The latter was turned into a multiplicative factor that we used to adjust the line intensity at each iteration, thus including it in the error budget.
In the case of a non-detection, the upper limits of the column densities were derived by taking the value corresponding to the upper limit of the 95% of the high probability density interval. The linewidth was fixed at the ortho-H2D+ value.
We report in Fig.1 the modelled spectra for the cores for both ortho-H2D+ and para-D2H+ (blue and red lines for detections and non-detections, respectively), while in Table 2 we summarise the results of our analysis together with the constrained physical quantities derived for the six cores (see Appendix A) and the relative errors obtained from our Bayesian analysis. The abundances are in line with previous studies (Parise et al. 2011), and the ortho-H2D+/para-D2H+ ratio falls in the range from 0.81 to 2.18. The six targeted cores show observed temperatures and densities typical of prestellar cores (Tdust ~ 10–13 K and 105 ≤ ncore ≤ 106 cm−3, Table 1), and the analysis of the spectral features suggests a dynamical scenario with the cores being gravitationally unstable (α ≤ 2 and M > MJ, see Appendix A for details on how these quantities were calculated). This indicates that the energy support is not sufficient to prevent collapse and that the cores are likely to fragment. With the Mach number being close to one, we note that the effective Jeans mass could increase by a factor of  at most in the presence of turbulence (Mac Low & Klessen 2004). Even considering the effect of magnetic fields, it would require a magnetic field of at least 600–700 μG for the cores to be in virial equilibrium (for details on how this is calculated see Redaelli et al. 2021). Such values in principle are not too far from the observed values of magnetic fields (Crutcher & Kemball 2019) even though there is a considerable spread, and it mightbe that the system is approximately virialised on the core scale. However, as we show below (Sect. 5) from the comparison with the dynamical models, an approximate virialisation on the core scale does by no means imply that the system itselfis long-lived, and indeed virialisation on the core scale should naturally be expected even in models of a rapid collapse.
at most in the presence of turbulence (Mac Low & Klessen 2004). Even considering the effect of magnetic fields, it would require a magnetic field of at least 600–700 μG for the cores to be in virial equilibrium (for details on how this is calculated see Redaelli et al. 2021). Such values in principle are not too far from the observed values of magnetic fields (Crutcher & Kemball 2019) even though there is a considerable spread, and it mightbe that the system is approximately virialised on the core scale. However, as we show below (Sect. 5) from the comparison with the dynamical models, an approximate virialisation on the core scale does by no means imply that the system itselfis long-lived, and indeed virialisation on the core scale should naturally be expected even in models of a rapid collapse.
Summary of derived properties of the observed cores.
3 Simulations
To explore the physics of the observed cores and provide quantitative information on their dynamical state and temporal evolution, we performed a priori three-dimensional magneto-hydrodynamic simulations of star-forming filaments with on-the-fly non-equilibrium chemistry. Gravitationally bound cores are in fact embedded in thermally supercritical filaments, as reported by studies based on high resolution observations (André et al. 2010; Molinari et al. 2010) and in line with the hierarchical paradigm of solar-type star formation as the result of fragmentation processes within dense filaments. We followed a rigorous approach by exploring different physical and chemical initial conditions, particularly focussing on the parameters that mostly affect the collapse of the filament and the formation of overdense regions. Different configurations of the magnetic fields can affect the fragmentation mode and the final outcome of the star-formation process (Seifried & Walch 2015), and parameters such as the value of the cosmic-ray ionisation rate and the initial ortho-to-para H2 ratio may drastically change the chemical evolution (Sipilä et al. 2015; Bovino et al. 2019). In the following sections, we report the details of our numerical setup and chemical model as well as the post-processing of our simulations, before comparing with observations.
Details of the performed simulations.
3.1 Numerical setup
The simulations presented in this work have been performed with the publicly available hydrodynamic code GIZMO (Hopkins 2015), which is a descendant of GADGET2 (Springel 2005). The code evolves the magneto-hydrodynamics equations for the gas including a constrained-gradient divergence-cleaning method (Hopkins & Raives 2016; Hopkins 2016), together with the gas self-gravity. For the purpose of this study, we equipped the code with an on-the-fly non-equilibrium chemical network, which was implemented via the public chemistry library KROME (Grassi et al. 2014), similarly to Bovino et al. (2019). In particular, in our simulations, we assumed an isothermal equation of state for the gas, with the temperature set to 10 K or 15 K. These temperatures are in line with kinetic temperatures obtained from NH3 for the same regions (Friesen et al. 2009, 2017). The initial conditions of our simulations consist of a collapsing filament, modelled as a cylinder with a typical observed (Arzoumanian et al. 2011) Plummer-like density profile ![$n(R) = n_0/[1+(R/R_{\textrm{flat}}){}^2]^{p/2}$](/articles/aa/full_html/2021/10/aa41252-21/aa41252-21-eq2.png) , where R is the cylindrical radius, n0 is the ridge volume density and is constant along the filament axis, Rflat is the characteristic radius of the flat inner part of the density profile, and p is the characteristic exponent. Following observed estimates (Arzoumanian et al. 2011), we set p = 2 and Rflat = 0.033 pc, which gives a mean filament width of 3 × Rflat ~ 0.1 pc. The setup follows previous works (Seifried & Walch 2015; Körtgen et al. 2018). To avoid any spurious effect at the edges of the filament along its axis, we embed the cylinder in an exponentially decaying background, with the decay scale length set to the filament length Lfil = 1.6 pc. The box is large Lbox = 2.4 pc. We initialised the filament in a turbulent state, assuming a Burgers-like power spectrum that grows as ∝ k10 up to λpeak = Lbox∕6 and then decays as ∝ k−2 (see also Körtgen et al. 2018). Finally, we assumed the box is permeated by a constant magnetic field B0 = 40 μG (Seifried & Walch 2015; Körtgen et al. 2018).
, where R is the cylindrical radius, n0 is the ridge volume density and is constant along the filament axis, Rflat is the characteristic radius of the flat inner part of the density profile, and p is the characteristic exponent. Following observed estimates (Arzoumanian et al. 2011), we set p = 2 and Rflat = 0.033 pc, which gives a mean filament width of 3 × Rflat ~ 0.1 pc. The setup follows previous works (Seifried & Walch 2015; Körtgen et al. 2018). To avoid any spurious effect at the edges of the filament along its axis, we embed the cylinder in an exponentially decaying background, with the decay scale length set to the filament length Lfil = 1.6 pc. The box is large Lbox = 2.4 pc. We initialised the filament in a turbulent state, assuming a Burgers-like power spectrum that grows as ∝ k10 up to λpeak = Lbox∕6 and then decays as ∝ k−2 (see also Körtgen et al. 2018). Finally, we assumed the box is permeated by a constant magnetic field B0 = 40 μG (Seifried & Walch 2015; Körtgen et al. 2018).
In order to explore the parameter space of physical and chemical conditions of the observed prestellar cores and filaments, we performed a total of five runs in which we varied different parameters. In detail, we considered a highly turbulent filament (F1), with Mach number 5 and a ridge density of 7.6 × 104 cm−3, in which we varied the average dust grain size ⟨a⟩ (0.0035 μm or 0.1 μm)3 and the initial H2 ortho-to-para ratio (0.1 or 0.001), and two more gravitationally bound cases (F2 and F3) that started from a lower density (n0 = 5 × 104 cm−3) and a lower temperature (Tdust = 10 K), in which we assumed the fiducial chemical parameters: an average grain size of ⟨a⟩ = 0.1 and an H2 ortho-to-para ratio of 0.1, and varied the magnetic field direction, that is parallel or perpendicular to the filament axis, respectively. The choice of the initial H2 ortho-to-para ratio was dictated by the few observations of this quantity: the conservative value of 0.1 lies in between typical values in diffuse clouds (Neufeld et al. 1998; Crabtree et al. 2011) and indirect estimates obtained in dense clouds (Troscompt et al. 2009). We also report a case with 0.001, as recently estimated for star-forming regions (Brünken et al. 2014).
The filaments are ‘collapsing filaments’ with a mass per unit length (M∕L) three times the critical one (Ostriker 1964; André et al. 2010) and a total mass of 80–120 M⊙. The mass and spatial resolution of our simulations are 10−4 M⊙ and ~20 AU, respectively, and optimal to resolve the core structure. The parameters of the realised simulations are reported in Table 3. Possible caveats about the choice of our initial conditions are discussed in Sect. 5.1.
3.2 Chemical model
The chemical network employed in this study includes 134 species, with a total of 4616 reactions, which were self-consistently evolved for each gas particle in the simulation at every step of the run (Bovino et al. 2019). We included N–C–O bearing species up to three atoms (e.g. N2 H+, HCO+, among many others), with spin isomers of the main species (ortho-, para-, and meta-) and isotopologues (all the deuterated species, e.g. N2 D+, DCO+, etc.). We built this network performing benchmarks towards published works (Sipilä et al. 2015; Kong et al. 2015) and including the latest updates (Hugo et al. 2009; Pagani et al. 2009)4. The freeze-out of heavy species such as CO and N2 (and the O and N atoms) was followed time-dependently (Bovino et al. 2019), together with the thermal and non-thermal desorption5. We considered dust grains to be silicates with a typical specific density, ρ0 = 3 g cm−3, and a dust-to-gas mass ratio of  as reported in previous works (Kong et al. 2015). The chemical species were initialised by following Bovino et al. (2019), who considered afully molecular stage, but we note that changing the initial chemical abundances has a very minor effect on the evolution (see for instance Kong et al. 2015). The cosmic-ray ionisation flux per hydrogen molecule has been fixed to ζ2 = 2.5 × 10−17 s−1, which are typical values in the dense regions of molecular clouds (e.g. van der Tak & van Dishoeck 2000; Padovani et al. 2018; Bovino et al. 2020). Larger values have been also reported (Ivlev et al. 2019) and would, in general, favour the formation of deuterated species. It is worth noting that this is one of the most uncertain parameters and its effect on deuteration has already been reported in several previous works (e.g. Kong et al. 2015; Körtgen et al. 2018; Bovino et al. 2019). In Körtgen et al. (2018), the authors needed a factor of 5 difference inthe cosmic-ray ionisation rate to see a relevant difference in the deuteration. Bovino et al. (2019) reported a difference in the timescale of about 1.4 to reach the same deuteration fraction when going from 2.5 × 10−17 to 1.3 × 10−17 s−1, while this becomes more relevant (up to a factor of 4 in the timescale) when employing a very high cosmic-ray ionisation rate (e.g. 2.5 × 10−16 s−1). Our choice is very conservative and guarantees a certain robustness in the final timescale estimates, which in the worst case can be considered as upper limits due to the low value we employed.
as reported in previous works (Kong et al. 2015). The chemical species were initialised by following Bovino et al. (2019), who considered afully molecular stage, but we note that changing the initial chemical abundances has a very minor effect on the evolution (see for instance Kong et al. 2015). The cosmic-ray ionisation flux per hydrogen molecule has been fixed to ζ2 = 2.5 × 10−17 s−1, which are typical values in the dense regions of molecular clouds (e.g. van der Tak & van Dishoeck 2000; Padovani et al. 2018; Bovino et al. 2020). Larger values have been also reported (Ivlev et al. 2019) and would, in general, favour the formation of deuterated species. It is worth noting that this is one of the most uncertain parameters and its effect on deuteration has already been reported in several previous works (e.g. Kong et al. 2015; Körtgen et al. 2018; Bovino et al. 2019). In Körtgen et al. (2018), the authors needed a factor of 5 difference inthe cosmic-ray ionisation rate to see a relevant difference in the deuteration. Bovino et al. (2019) reported a difference in the timescale of about 1.4 to reach the same deuteration fraction when going from 2.5 × 10−17 to 1.3 × 10−17 s−1, while this becomes more relevant (up to a factor of 4 in the timescale) when employing a very high cosmic-ray ionisation rate (e.g. 2.5 × 10−16 s−1). Our choice is very conservative and guarantees a certain robustness in the final timescale estimates, which in the worst case can be considered as upper limits due to the low value we employed.
 |
Fig. 2 From left: map of N(o-H2D+), N(p-D2H+), and the N(o-H2D+)/N(p-D2H+) ratio from the reference run F1_01. Each panel reports the result for different snapshots in time. Contour regions represent the H2 total columndensity above 1022 cm−2 (cyan). As a reference, we also report the APEX beam used in the observations (18′′), the spatial scale in parsec, and the age of the core (tcore). The maps have been convolved with the APEX beam of FWHM 18′′ and 9′′ for the ortho-H2D+ and the para-D2H+, respectively. The total H2 column density distribution is shown after convolution with a typical Herschel beam of 36′′. The ratio was calculated on a pixel-to-pixel basis. |
3.3 Overall evolution
We evolved the filaments up to roughly 300 kyr and focussed on the ortho-H2D+/para-D2H+ (ratio between column densities). An example of our simulation results is reported in Fig. 2, showing the reference case F1_01: a massive (120M⊙), highly turbulent filament ( ), with ⟨a⟩ = 0.1 μm, T = 15 K, and an initial H2 OPR of 0.1. The left panels show the time evolution of the ortho-H2D+ and para-D2H+ column densities after convolution with the APEX beam point spread functions of FWHM 18′′ and 9′′, respectively.In the following analysis, the evolution is shown as a function of the core time tcore, which represents the time passed since the formation of the core at tform, the latter being measured from the beginning of the simulation. The last important timescale in the analysis is the age of the core tage, corresponding to the time at which we compared our simulations with the observations. The latter was taken at the minimum o-H2D+/p-D2H+ ratio reached in the simulations, which in most cases corresponds to the sink formation time.
), with ⟨a⟩ = 0.1 μm, T = 15 K, and an initial H2 OPR of 0.1. The left panels show the time evolution of the ortho-H2D+ and para-D2H+ column densities after convolution with the APEX beam point spread functions of FWHM 18′′ and 9′′, respectively.In the following analysis, the evolution is shown as a function of the core time tcore, which represents the time passed since the formation of the core at tform, the latter being measured from the beginning of the simulation. The last important timescale in the analysis is the age of the core tage, corresponding to the time at which we compared our simulations with the observations. The latter was taken at the minimum o-H2D+/p-D2H+ ratio reached in the simulations, which in most cases corresponds to the sink formation time.
To compute the column densities, we selected gas particles within a cylinder of radius 0.1 pc, with the axis aligned to the filament, and we integrated their species’ local density along the line-of-sight, over the corresponding kernel size. In this way, if observations are strongly affected by line-of-sight contamination, our results consistently mimic this effect.
As is clear from the figure, once the cores form and during their early evolution, the ortho-H2D+ column density is very compact (e.g. tcore ~ 6 kyr), and it shows values around 1012 cm−2. The column density starts to increase quickly with time, covering the entire filament when reaching ~131 kyr. We know from observations (e.g. Pillai et al. 2012; Friesen et al. 2014) that the ortho-H2D+ emission is very extended. This is resembled by our simulations, which indeed show a rather extended ortho-H2D+. At later times, densities are high enough to start the conversion of ortho-H2D+ into other isotopologues. On the other hand, the para-D2H+ is much more compact and needs at least 81 kyr to reach values around 1011 –1012 cm−2 in the very central region of the cores (less than 0.05 pc). This is due to the fact that to form para-D2H+, a certain amount of H2 D+ should be in place. Over time, the amount of para-D2H+ increases and covers the entire core (at a scale of 0.1 pc), resulting in ortho-to-para ratios around or below unity, as can be clearly observed in the middle-right panel, where we show the ortho-H2D+/para-D2H+ ratio, overlaid with the total column density (cyan contours). The specific ratio decreases over time (from top to bottom panel), and reaches typical observed values (0.7–1.0) in roughly 166 kyr since the formation of the cores, providing clear evidence for short lifetimes of the observed cores. Low ratios are observed in regions as large as 0.05–0.08 pc, triggered by the para-D2H+ evolution.
In Fig. 3, we report the ortho-/para-H2 ratio with overlaid the ortho-H2D+/para-D2H+. The values of ortho-/para- H2, as expected, decrease very quickly once the cores are formed. At 6 kyr, the ratio is still close to the initial one (0.1), while it decreases quickly when the gas becomes denser, reaching values below 10−2 at about 166 kyr, with central regions peaking at 10−3. In the same plot, we can appreciate how the ortho-H2D+/para-D2H+ (dashed contour value of 5, solid contour value of 1) probes the ortho-/para-H2 very well, particularly on scales of 0.02 pc. This confirms that the ortho-H2D+/para-D2H+ ratio can be used as a proxy to determine the elusive ortho-/para-H2 ratio. Further analysis on this specific point will be reported in a forthcoming paper.
Finally, a zoom into core F1_01_1 (rightmost panel in Fig. 2) is reported in Fig. 4, where we show its time evolution up to the formation of the sink particle (tcore = 181 kyr). From this plot we can appreciate the highly dynamical evolution of the core. The central region of the core collapses very fast in the first 30 kyr of evolution, with the accretion of material being from filament scales. After this phase, it experiences a quasi-static evolution for at least 50–60 kyr. At about tcore = 106 kyr, the core starts to collapse with a continuous flow of material from the surroundings, until reaching the formation of a protostellar object (sink particle) around 181 kyr, where some rotation is also very visible. This example shows that the evolution of the cores is highly non-linear and explains why the formation of the cores within certain simulations is taking hundreds of kiloyears. The detailed analysis of the cores formed within the filaments is discussed in the next section.
 |
Fig. 3 o/p H2 from the reference run F1_01 for different snapshots in time. Contour regions represent the N(o-H2D+)/N(p-D2H+), where the dashed contour has a value of 5 and solid contour 1. As a reference, we also report the APEX beam used in the observations(18′′), the spatial scale in parsec, and the age of the core (tcore). The total H2 column density distribution is shown after convolution with a typical Herschel beam of 36′′. The ratio was calculated on a pixel-to-pixel basis. |
4 Comparison between simulations and observations
As we are mainly interested in the identification of the cores that formed within the filaments and specifically in the time evolution of the ortho-H2D+/para-D2H+, we report the detailed description of how this is performed and present a detailed comparison with the observational data in the following sections.
4.1 Core identification in the simulated filaments
In order to identify the prestellar cores in the simulated filaments, we first computed 2D column density maps of H2, N(H2), starting from the last snapshot in time and moving back to the beginning6. At each step, we estimated the average ⟨N(H2)⟩ in the filament map from a rectangular region of size Lfil × 0.2 pc centred on the filament (in order to remove the low-density background from the analysis), and we selected all the pixels showing an overdensity of N(H2)/⟨N(H2)⟩ > 10. Then, we applied a connected component analysis (Fiorio & Gustedt 1996) on the filtered pixels, labelling the identified regions, that represent our candidate cores. To avoid possible artefacts and unrealistic cores, we removed all regions with an axis ratio larger than 5 or smaller than 1/5, and those composed of less than 10 pixels. The remaining structures were then accepted as actual cores if they are connected to their descendant via a minimum separation criterion, that is the cores were discarded if their centres are separated by more than 2 × max{rprog, rdesc}, where rprog and rdesc are the progenitor and the descendant core effective sizes, respectively. If a core is the result of a merger, only the most massive progenitor is tracked back in time. Finally, for each core history, we estimated the average H2 column density, the gas number and electron densities, and the effective size. In addition, we also computed column density maps of ortho-H2D+ and para-D2H+, from which we measured the values convolved with the point spread function in the corresponding cores, in an observer-like fashion, by assuming a beam size of 18′′ for the first one, and 9′′ for the latter, and averaging over the ortho-H2D+ beam, according to the observations procedure. The H2 column density has been convolved with a typical Herschel beam of 36′′ to match the angular resolution of the observations. All the quantities reported in this paper have been beam-averaged.
The analysis of the entire population of cores found in our simulations is reported in Table 4. The synthetic cores (sixteen in total), which formed in the filaments, share similar physical properties with the observed ones, as is shown in Fig. 5, with masses between 0.5 and 1.3 M⊙, densities around 5.8 × 105–1.6 × 106 cm−3, and transonic Mach numbers up to 1.2. The virial parameters estimated on the core scale lie between 0.8–1.9, indicating cores which are subvirial and/or virialised. The cores need an average time between 45 and 300 kyr to form (tform in Table 4), depending on the configuration of the magnetic field and the turbulence level. In Fig. 5 and Table 4, we also report the fractional abundances of the two tracers. The comparison between the observed values and the synthetic ones shows a very good agreement, confirming that our simulations are accurate and provide a realistic representation of the observed regions.
By inspecting the dynamical state of the cores, we can retrieve information on the evolution over time of physical quantities such as the virial parameter. We note that all the cores in our simulations show evidence of fast collapse in time, which is not reflected in the estimated virial parameter at tage. This confirms that estimates of the virial parameter from observations may not actually allow one to distinguish between rapid and slow collapse since, on the core scale, subvirial or virialised cores would be expected in both scenarios; however, when considering larger scales including the envelope, one would expect a supervirialised configuration in case of rapid collapse, and it then becomes relevant on which scale the virial parameter is measured (see also Gómez et al. 2021). We also estimated the average magnetic field strength along the line-of-sight for the synthetic cores. These are of the order of 70–300 μG and fall in the range of values obtained from the observational estimates of Ophiuchus (Soam et al. 2018; Pattle et al. 2021). Overall, within the approximations we have done in our simulations, and taking into account the errors coming from observations, we can state that our synthetic cores represent the observed ones well by matching both physical and chemical constraints. However, we do not exclude that different dynamical situations can lead to similar results. In fact, a certain degree of degeneracy in the final comparison is unavoidable and large-scale simulations, which are not currently available, are the only viable tool to reduce the errors introduced by the choice of the initial conditions. In Sect. 5.1 we discuss different scenarios and what the effect of a slow collapse is on our results.
 |
Fig. 4 Zoom on the core F1_01_1 reported in Fig. 2 within the filament (core on the right, see also Table 4). The time evolution starts from tcore =16 kyr and goes up to the time at which a sink particle (i.e. a protostellar object) is formed, tcore =181 kyr. The dashed circle represents the area over which we average the core quantities reported in Table 4, which corresponds to 0.02 pc (Herschel-beam) centred in the column density peak. We note that these maps are not convolved. |
4.2 Cores time evolution and timescales
In Fig. 6, we show the time evolution of the ortho-H2D+-to-para-D2H+ ratio of each core up to the minimum reached, by setting the zero time at the first appearance of the core (tform). A downward trend is clearly visible, confirming that this ratio evolves with time and it is sensitive to changes in density during the collapse, which implies the conversion of H2 D+ into D2 H+ (Flower et al. 2004; Pagani et al. 2013). Even if not reported in the figure, some of the cores show an increasing trend after the minimum, likely due to the expected conversion of D2 H+ into D with time (Flower et al. 2004) and most of them end up in a protostar, computationally defined by a sink particle. In the same plot, we also report the observed values (right panel and grey shaded area), including the only existing data from previous observations, that is the 16293E (Vastel et al. 2004) and the HMM1 (Parise et al. 2011) prestellar cores. It is clear from the results that the observed values of the ortho-to-para ratio can be reached in a time no longer than 200 kyr after the formation of the cores for the set of initial conditions employed here. For the lower limits provided in the same figure, the time represents an upper limit to the age of the cores. The non-detection of para-D2H+ for three of the observed cores suggests that those sources are at a very early stage of the collapse, and H2 D+ did not have time to be converted into D2 H+ (Flower et al. 2004). Core 1 represents a scenario of relatively slow collapse, being that this core is the one with the lowest density and the largest virial parameter (see Tables 2 and 1). However, without additional constraints (observational and theoretical), it is very difficult to firmly distinguish between a slow collapse, an early stage of collapse, or a quasi-static temporary stage; furthermore, as we discussed, the virial parameter alone is not a good indication of the dynamical state of the cores.
with time (Flower et al. 2004) and most of them end up in a protostar, computationally defined by a sink particle. In the same plot, we also report the observed values (right panel and grey shaded area), including the only existing data from previous observations, that is the 16293E (Vastel et al. 2004) and the HMM1 (Parise et al. 2011) prestellar cores. It is clear from the results that the observed values of the ortho-to-para ratio can be reached in a time no longer than 200 kyr after the formation of the cores for the set of initial conditions employed here. For the lower limits provided in the same figure, the time represents an upper limit to the age of the cores. The non-detection of para-D2H+ for three of the observed cores suggests that those sources are at a very early stage of the collapse, and H2 D+ did not have time to be converted into D2 H+ (Flower et al. 2004). Core 1 represents a scenario of relatively slow collapse, being that this core is the one with the lowest density and the largest virial parameter (see Tables 2 and 1). However, without additional constraints (observational and theoretical), it is very difficult to firmly distinguish between a slow collapse, an early stage of collapse, or a quasi-static temporary stage; furthermore, as we discussed, the virial parameter alone is not a good indication of the dynamical state of the cores.
Properties of the synthetic cores calculated at tage, i.e. at the minimum o-H2D+/p-D2H+.
 |
Fig. 5 Physical properties of the simulated and observed cores. We report the core mass and volume density (left column), as well as the virial parameter and Mach number (centre), calculated from the formulae reported in Appendix A. In the right column, we also report the fractional abundances of the two tracers in logarithmic scale, x(o-D2H+) and x(o-H2D+). Observed cores are reported as circles, while the green shaded area represents the range of values obtained for the simulated cores identified in our filaments (properties reported in Table 4). |
4.3 Implications of observational uncertainties for the comparison with simulation
In the analysis of the observational data, a main assumption has been that Tex= Tdust, which may not strictly be the case. A choice for the excitation temperature Tex, however, is needed to fit the spectra and retrieve the column densities of the two deuterated species. To check the dependence on this parameter, we performed the same fitting procedure outlined in Sect. 2.2, by assuming Tex= 10 K, and we calculated the resulting ortho-to-para ratios. The change in the assumed Tex led to a change in those ratios by roughly 10–15%. We also tested an extreme case with Tex= 0.7 × Tdust following previous works (Caselli et al. 2008) and observations of N2 H+ of the same region (Friesen et al. 2010), which report Tex being slightly lower than those obtained from NH3, with a mean value over the entire Ophiuchus B2 region around 7 ± 2.8 K. The differences in this case correspond to 45% on the final ortho-to-para ratios. In Fig. 7 we report the comparison between the different assumptionsfor Tex (symbols) and the simulations (green shaded area). Overall, if we exclude some outliers with an extremely low ortho-to-para ratio (e.g. core 3 and core 6), the assumption for Tex does not affect our conclusions on the estimated ages. In the future, the results could be further refined employing a non-LTE analysis, which would however require the observation of an additional line to break degeneracies between free parameters.
 |
Fig. 6 Comparison of the N[o-H2D+]/N[p-D2H+] ratio between observations and simulations. The different curves in the left panel refer to the time evolution of the cores identified within the simulations with a different set of physical and chemical conditions (see Tables 3 and 4 for details). We note that some cores are the result of merging and dissolving processes, which produce the visible oscillations in the curves. The stars represent tage, i.e. the time at which the minimum o-H2D+/p-D2H+ ratio is reached for each core and the point where we performed the calculations of the properties reported in Table 4 and the comparison with the observed cores. The right panel shows the observed values: the ones labelled 1–6 represent our APEX data, 16293E (blue circle) refers to previous observations of the two studied isotopologues (Vastel et al. 2004), and HMM1-10K and HMM1-13K (green squares) are taken from observations in the L1688 cloud(Parise et al. 2011). The grey shaded area represents the range of observed values with secure detection, considering their uncertainties. |
 |
Fig. 7 N(o-H2D+)/N(p-D2H+) ratio for different Tex assumptions. We report the following three main cases: our reference case Tex = Tdust and two additional cases where we assumed lower temperatures, Tex = 10 K and Tex = 0.7 × Tdust. The values in the coloured boxes mark the lower limits we calculated for the cases where para-D2H+ was not detected. The green shaded area represents the range of values obtained from our simulations. |
5 Discussion
To put our results in the context of the star-formation process, we calculated the ratio between the core age and the dynamical time ( ), where
), where  is the core free-fall time calculated by employing the density of the core at the identification time ncore(tform) (see Table 4)7. Theories of the slow-collapse point towards long timescales and strong magnetic or turbulence support, with an initial condition for the cores close to a virial equilibrium where all the forces at play are balanced (Shu et al. 1987; Mouschovias 1991). Rapid collapse, on the contrary, is based on the idea that the star-formation process occurs on typical dynamical timescales (Vázquez-Semadeni et al. 2005; Hartmann et al. 2012) (in this case
is the core free-fall time calculated by employing the density of the core at the identification time ncore(tform) (see Table 4)7. Theories of the slow-collapse point towards long timescales and strong magnetic or turbulence support, with an initial condition for the cores close to a virial equilibrium where all the forces at play are balanced (Shu et al. 1987; Mouschovias 1991). Rapid collapse, on the contrary, is based on the idea that the star-formation process occurs on typical dynamical timescales (Vázquez-Semadeni et al. 2005; Hartmann et al. 2012) (in this case 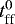 ). All our realisations support the rapid collapse scenario, as the time to reach observed ortho-to-para ratios is of the order of the free-fall time or a few free-fall times (values in between 0.5–5
). All our realisations support the rapid collapse scenario, as the time to reach observed ortho-to-para ratios is of the order of the free-fall time or a few free-fall times (values in between 0.5–5  ), and much shorter thanthe ambipolar diffusion time often invoked by slow-collapse theories (Mouschovias 1991). The analysis of the ambipolar diffusion time (
), and much shorter thanthe ambipolar diffusion time often invoked by slow-collapse theories (Mouschovias 1991). The analysis of the ambipolar diffusion time ( , with xe being the electron fraction, see Shu et al. 1987) in our simulated cores gives values of the order of 400 kyr up to 1 Myr (see Table 4), which is 4–5 times longer than the estimated cores lifetimes, confirming our conclusions. Our findings are supported by additional observations of the same regions (Pattle et al. 2015; Kerr et al. 2019), exploring energy balance and stability, including infall features reported in observed spectra of optically thick tracers (André et al. 2007; Chitsazzadeh et al. 2014; Punanova et al. 2016). These observational studies point towards highly unstable cores with, in some cases, blue-skewed features in the spectra as consequences of infall motions. In addition, estimates in line with our results have been provided from observational statistical methods (Enoch et al. 2008), which by assuming a protostellar stage of 0.54 Myr, obtained an average prestellar lifetime of roughly 500 kyr with an error of a factor of 2.
, with xe being the electron fraction, see Shu et al. 1987) in our simulated cores gives values of the order of 400 kyr up to 1 Myr (see Table 4), which is 4–5 times longer than the estimated cores lifetimes, confirming our conclusions. Our findings are supported by additional observations of the same regions (Pattle et al. 2015; Kerr et al. 2019), exploring energy balance and stability, including infall features reported in observed spectra of optically thick tracers (André et al. 2007; Chitsazzadeh et al. 2014; Punanova et al. 2016). These observational studies point towards highly unstable cores with, in some cases, blue-skewed features in the spectra as consequences of infall motions. In addition, estimates in line with our results have been provided from observational statistical methods (Enoch et al. 2008), which by assuming a protostellar stage of 0.54 Myr, obtained an average prestellar lifetime of roughly 500 kyr with an error of a factor of 2.
To check about possible effects on our sources from existing protostars, we reviewed the Spitzer results presented in previous works (Enoch et al. 2009; Dunham et al. 2015) and obtained the positions of 23 protostellar candidates over L1688 (18 sources) and L1689 (five sources). All young stellar objects are located at distances in between 0.02 and 0.12 pc from the cores reported in Table 1. Among the 18 objects identified, three have been classified as Class 0, I protostars, showing an IR index of αIR≥ 0.3 (Dunham et al. 2015), eight as flat-spectrum objects (−0.3 ≤ αIR < 0.3), and the remaining seven as Class II (−1.6 ≤ αIR < −0.3). Considering their luminosity and applying a simple Stefan-Boltzmann law, we can exclude that radiation feedback can have an effect on thestudied cores, consistent with numerical investigations of radiative feedback in low-mass star formation (Offner et al. 2009).
Two of the sources found in L1688 (J162728.4-242721 and J162730.1-242743) have been associated with an intense protostellar activity, identified to potentially be responsible for the single bright and extended gigantic outflow observed at the centre of Oph-B2 (Kamazaki et al. 2003; Nakamura et al. 2011). The outflow is extended up to 0.2 pc along the southeast-northwest direction (Kamazaki et al. 2019) and has been mapped with several 12CO, 13CO, and C18O low-J molecular transitions. Although encompassing a significant portion of Oph-B2, the outflow does not involve any of the four cores examined in this work. Core 6 appears to be closest to the blueshifted component of the outflow in the northwest direction, but the absence of any relevant broadening in both the observed o-H2D+ and p-D2H+ lines excludes any direct influence of the outflow at least in the region traced by the H isotopologues. In L1689, three Class 0, I and two Class II protostellar candidates are identified with distances between 0.03 and 0.11 pc around core 1, while no protostellar candidate was found close to core 2. L1689 is also known to be much less active than L1688 on average (Nutter et al. 2006). To our knowledge, there is no evidence for outflows in the immediate surroundings of both of the cores identified in L1689, consistent with the line profiles which indicate no signatures of outflows.
isotopologues. In L1689, three Class 0, I and two Class II protostellar candidates are identified with distances between 0.03 and 0.11 pc around core 1, while no protostellar candidate was found close to core 2. L1689 is also known to be much less active than L1688 on average (Nutter et al. 2006). To our knowledge, there is no evidence for outflows in the immediate surroundings of both of the cores identified in L1689, consistent with the line profiles which indicate no signatures of outflows.
In terms of chemical clocks, previous studies focussed on N2 D+/N2H+ (Pagani et al. 2013), which is known to have a different chemical evolution compared to the tracers we consider here and to trace mainly laterstages of the evolution (Bovino et al. 2019; Giannetti et al. 2019). They suggested lifetimes of 500–700 kyr. This is longer than the ages reported in this work, but still in line with our current results.
In addition, we checked the ratio of the ortho/para H2 D+ at the time just before a protostar would form8, and found values as low as 0.14. This is similar to the ratio of 0.07 ± 0.03 previously reported (Brünken et al. 2014), but it has been obtained in hundreds of thousands of years rather than millions of years. The previous measurements (Brünken et al. 2014) of course correspond to the envelope, not to the core, thereby providing an upper limit to the age of the protostar, which is nicely consistent with the observations provided here. We note that in a subsequent work (Harju et al. 2017), the long timescales previously proposed (Brünken et al. 2014) have been lowered to 0.5 Myr as a result of different assumptions and parameter choices in their model. This emphasises the need to produce self-consistent, fully dynamical simulations as pursued here in order to obtain the involved timescales from a physical model.
5.1 Caveats
Finally, it is important to notice that, even if our simulations require some assumptions as to the initial conditions, these still represent state-of-the art results due to the computational challenge of including complex chemistry in large-scale simulations. So far, chemical clocks have been explored in static and dynamical low-dimensional models, often tuned on observations and evolved on longer timescales, towards equilibrium configurations, without including non-linear effects induced by magnetic fields and turbulence. On the contrary, we started from conditions typical of observed filaments and allowed the cores to naturally form in a highly dynamical and complex environment. Some core candidates dissolve during the evolution, some others merge, and in general it takes 50–300 kyr to form the first cores. This means that starting from an already high density situation is not necessarily speeding up the formation of the cores and the chemistry associated to them, as non-linear effects induced by turbulence and magnetic fields act against the formation of overdensities (e.g. Vázquez-Semadeni et al. 2005).
It is also important to note that some of our cores experienced expansion phases before getting into rapid collapse that can be seen as quasi-static stages where the targeted ortho/para ratio is increasing rather than decreasing (see for example F1_0035_2 in Fig. 6, or the core evolution reported in Fig. 4). This points towards the need of an abrupt change in density to reproduce the observed ratios and then a rapid collapse scenario would be favoured. Even if we cannot exclude those situations of slow collapse that can lead to similar results, we have to consider that previous papers exploring sub-critical filaments (see e.g. Körtgen et al. 2018) did not find any fragmentation and no cores formed at all. In addition, none of the cores we formed in our simulations resemble virial conditions at their formation time. This could be the consequence of the idealised setup we are exploring and/or the result of the physics involved in the collapse process. To disentangle between these two scenarios, we would need to perform large-scale simulations following the formation of the filaments first and the subsequent fragmentation into small entities, within a highly dynamical environment where accretion processes towards the filaments, which can boost the fragmentation, are also taken into account. Such simulations are currently not available due to the high computational costs, and they represent a limitation to a comprehensive understanding of the star-formation process and the usefulness of chemical clocks in disentangling between the different existing star-formation scenarios.
5.2 The slow-collapse scenario
In order to assess how slow-collapse conditions would compare with our three-dimensional framework, in which these situations would have been hard to recreate, we ran a series of single-cell models exploring the speed of the collapse through a parameter βff similarly to what was done for instance in Kong et al. (2015). In the following, we only summarise the main results and report all the details in Appendix B. Our findings confirm that (i) models of slow collapse, for instance with timescales of 10 × tff, are never able to reproduce the physical and chemical properties of the observed cores, (ii) depending on the employed parameters, models with collapse timescales in between 1and 5 × tff are in line with the observed quantities independently of the parameters, and they agree with our more complex three-dimensional simulations well, within the explored parameter space, and (iii) the ortho-H2D+/para-D2H+ ratio seems to necessarily require fast collapses to reach the observed values, and this suggests its ability to distinguish between slow and fast collapse scenarios. In particular, slow collapse would favour lower ortho-to-para ratios (on much longer timescales) because of the long time available to pre-process the chemistry. The final values of the ratio are affected by the choice of the different physical parameters, such as the temperature and the cosmic-ray ionisation rate. Overall, the results from the qualitative single-cell models confirm the picture obtained from more complex simulations, and they seem to point towards a dynamical scenario driven by a rapid collapse. However, large-scale simulations are needed to completely break the degeneracy and further explore the reliability of this ratio as a chemical clock, together with a statistically relevant observational sample targeting the same tracers.
6 Conclusions
To conclude, we provide new observational results suggesting that the ortho-H2D+/para-D2H+ ratio might be a reliable chemical clock of star-forming regions. This represents a viable alternative to previously used clocks (Pagani et al. 2013; Brünken et al. 2014) due to the possibility of observing the para-D2H+ from the ground, compared to the difficulty to observe para-H2D+ in the THz domain. In addition, we have shown that this ratio is a good proxy for the elusive o/p H2 ratio, an aspect that we will explore in a forthcoming paper. Compared to previous works (e.g. Pagani et al. 2013), which ruled out this ratio as a chemical clock due to its non-monotonic behaviour, our findings show that this is mainly happening at late stages and is not affecting its effectiveness in tracing the collapse timescale. We have presented a detailed analysis with a comparison of state-of-the-art three-dimensional magneto-hydrodynamical simulations including a detailed chemical model. Our findings are very relevant to understand which physical processes affect the earliest stages of star formation and clarify results derived from more simplified models (Pagani et al. 2013; Brünken et al. 2014).
The comparison between observations and three-dimensional dynamical models provides an overall consistent picture between observations and simulations, where both the chemical abundance ratios as well as dynamical properties such as the virial parameter of the core can be explained with the framework of a rapid collapse. The short timescales we found are, in fact, much shorter than indicated from previous low-dimensional studies (Parise et al. 2011; Pagani et al. 2013; Brünken et al. 2014).
We aimed to obtain information on the physics of star formation by studying the chemistry of these regions, and the ages were obtained from cutting edge simulations properly compared with observations. From our analysis, we conclude that models of rapid collapse are more likely to represent the observed cores, resulting in a prestellar stage of a few hundreds of thousands of years. However, even if our qualitative single-cell models support our three-dimensional findings and seem to rule out the possibility that slow collapse could reproduce the observed features, a certain degree of degeneracy should be considered, particularly when taking into account the uncertainties introduced by the assumption of the excitation temperature in the observational analysis. To break this degeneracy, it is crucial to perform observations of this chemical clock on a statistical sample of low-mass cores to exploit the dynamical timescales of regions that could be in different environmental conditions. This will help to understand if rapid collapse is the only possible scenario or if star formation occurs in different modes, depending on the physical and chemical conditions of the clouds.
Acknowledgements
The computations and simulations were performed with resources provided by the Kultrun Astronomy Hybrid Cluster at Universidad de Concepción. This paper is based on data acquired with the Atacama Pathfinder EXperiment (APEX). APEX is a collaboration between the Max Planck Institute for Radioastronomy, the European Southern Observatory, and the Onsala Space Observatory. D.R.G.S. acknowledges support from Fondecyt Regular 1201280. A.L. acknowledges support from MIUR under the grant PRIN 2017-MB8AEZ.
Appendix A: Dynamical quantities
The mass and temperature were calculated from the dust continuum spectra, within a circular area of radius Reff, which represents the area of the extraction region. We employed the Herschel (Pilbratt et al. 2010) maps at 500, 350, and 250 μm from SPIRE (Griffin et al. 2010)and at 160 μm and 100 μm from PACS (Poglitsch et al. 2010) by evaluating the background contribution in two circular regions located in nearby local minima. The H2 total column density peak was calculated following a similar approach. The dust continuum spectra was fitted as a grey body with the dust opacity parameters from the ATLASGAL survey (Ossenkopf & Henning 1994; Schuller et al. 2009; König et al. 2017), while the best fit model was evaluated analogously to previous works (Sabatini et al. 2019). We note that the error on the final observed mass, H2 column density, and temperature is assumed to be around 20% (Pagani et al. 2015; Schisano et al. 2020).
The Jeans mass was computed as follows (Stahler & Palla 2004; Sadavoy et al. 2012):
 (A.1)
(A.1)
where the total number density was calculated from the core mass and the volume:  , with
, with  .
.
Dynamical quantities are good qualitative indicators of the gas motion. We calculated the virial parameter considering (MacLaren et al. 1988)
 (A.2)
(A.2)
where k2 = 210, and Δυobs is the full-width at half-maximum obtained from the spectra and Reff is reported in Table 1.
The Mach number, which provides the level of turbulence, is estimated as  , with the non-thermal velocity dispersion calculated as
, with the non-thermal velocity dispersion calculated as
 (A.3)
(A.3)
where  is the thermal velocity dispersion of the molecule, kb the Boltzmann constant, m = 6.692 × 10−24 the ortho-H2D+ mass in grams,
is the thermal velocity dispersion of the molecule, kb the Boltzmann constant, m = 6.692 × 10−24 the ortho-H2D+ mass in grams, 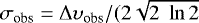 ),
),  the thermal sound speed for a particle with a mean molecular weight of μ = 2.33, and mH the hydrogen mass in grams. We note that, for the sake of consistency in the calculation of the virial parameter for the simulated cores, we added a thermal velocity dispersion component to the gas velocity dispersion obtained from the maps.
the thermal sound speed for a particle with a mean molecular weight of μ = 2.33, and mH the hydrogen mass in grams. We note that, for the sake of consistency in the calculation of the virial parameter for the simulated cores, we added a thermal velocity dispersion component to the gas velocity dispersion obtained from the maps.
Appendix B: Single-cell models
To follow the impact of the collapse speed on the final results, and particularly on the timescales to reach observed values, we employed a semi-analytical framework, where the evolution of the density was regulated by the following equation:
 (B.1)
(B.1)
with tff being the free-fall time calculated at the density ncore(t), and βff being an arbitrary parameter which determines the collapse speed. We assumed βff = [1, 2, 3, 5, 10], where the extreme cases represent the following: i) a collapse occurring on the free-fall timescale (βff = 1) and ii) a collapse on the ambipolar diffusion time (i.e. on a timescale of 10 × tff with βff = 10, see e.g. Vázquez-Semadeni et al. 2005). We have explored a large parameter space by changing the initial ortho-to-para H2 ratio (0.1 and 10−3), the initial collapse density (ncore = 103, 104, and 105 cm−3), the cosmic ray ionisation rate ζ2 (1.3 × 10−17 s−1, 2.5 × 10−17 s−1, and 5.0 × 10−17 s−1), and the temperature (T = 10 and 15 K). The initialisation of the chemical species is identical to the one used in the three-dimensional simulations. The main intent of these single-cell models is to mimic different dynamical environments, particularly in terms of collapse speed, and to see under which conditions we can reach the observed densities and oH2 D+/pD2H+ ratios. The list of performed runs is reported in Table B.1.
 |
Fig. B.1 Top: Time evolution of the ortho-H2D+/para-D2H+ ratio (top) and density (bottom) for a reference case with ncore = 104 cm−3, T = 10 K, CRIR = 2.5 × 10−17 s−1, and initial H2 OPR = 0.1, for different collapse speeds (βff = [1, 2, 3, 5, 10]). The green shaded area represents the range of observed values, only detections are considered in this specific case (see Table 2). Bottom: Evolution of the ortho-H2D+/para-D2H+ ratio with respect to the density for the same parameters. The red shaded area represents the range of densities for the observed cores. |
We assumed as a reference case the one with an initial density of ncore = 104 cm−3, a temperature of T = 10 K, ζ2 = 2.5 × 10−17 s−1, and an initial ortho-/para- H2 = 0.1. The results for this reference case are reported in Fig. B.1. We show the oH2 D+/pD2H+ ratio (OPR) and the density evolution over time for the different collapse cases. We can see how the collapse is delayed when we increase the βff parameter, going from a collapse occurring on the tff ~ 330 kyr (red lines), to one occurring on a scale of a few megayears (10 × tff), which should resemble the ambipolar diffusion time (black lines). Rapid collapse cases reach a low OPR in very short times, mainly driven by the changes in density, while the slow-collapse case evolves at roughly constant density for at least 1 Myr, allowing for a pre-processing of the chemistry, which leads to a low OPR even before the onset of the rapid contraction. Overall when the collapse kicks in, the OPR values are lower than in the fast collapse cases. This can also be seen by looking at the bottom panel of Fig. B.1, where we show the evolution of the OPR with density. All the cases reach an equilibrium OPR at densities similar to the observed ones (red shaded region). By comparing the obtained OPR with the observed ones (green shaded area), we can see that very slow collapses (i.e. 5-10 tff) lie at the lower limit of the observed values, while collapses occurring on the order of 2-3 × tff, representing fast collapses, are in line with observations.
Details of the performed single-cell models.
To have a broader overview of the effects of the collapse speed on the final OPR, we show the results of the large parameter study in Fig. B.2, in which the different sectors (enclosed within the black dashed lines and associated to the letters from A to K) correspond to the models in Table B.1, for which the five values of βff are reported counterclockwise. The orange ring in the polar-chart-like plot represents the observed values, and the blue colour in the stacked bars reflects the observed densities. A match between models and observations is in place when the blue portion of the stacked bar falls in the orange region. We can appreciate that the slow-collapse cases are always at the limit of the observed OPR values, or outside the range, because the long-time available to pre-process the chemistry allows one to reach lower OPR at the observed densities. This is particularly true for the case with 10 × tff which never enters the observed region defined by the orange ring and the blue frame of the bar. On average, the wide range of parameters explored points towards a good match for the cases with collapse times of 1-3 × tff, which is in agreement with our more complex three-dimensional simulations. There are a few cases where also 5 × tff is falling in the observed region when T = 10 K and the initial density is 105 cm−3, with a CRIR=2.5×10−17 s−1 and an initial H2 OPR of 0.1. Collapses on the free-fall timescale also give good results, but they show some discrepancies when the temperature is 10 K and the initial CRIR is 1.3 × 10−17 s−1. Even if this is a somewhat qualitative framework, it confirms that slow-collapse cases are not in line with observations and in general reach lower OPR at lower densities. The evolution of deuterated species is indeed driven both by time and density, leading to degeneracy, depending on if there is a long time to process the chemistry at almost constant density, or if there is an abrupt change in density in short time. Chemistry alone can lead to degeneracy in the results and in their interpretation. It is then fundamental when comparing it with the observations to also match the physical and dynamical quantities and not only the chemistry. Our 3D simulations (see Fig. 5), not only reproduce the chemical features but also the dynamical and physical properties of the cores, and this together with the results of the qualitative single-cell models points towards a rapid collapse scenario for the six cores observed in Ophiuchus. As a final note, the current comparison has been performed with our fiducial observational results (i.e. Tex = Tdust) and only considering the detections. If we widen the analysis by including the uncertainties induced by the Tex assumption and by also considering the lower limits, we would have a few cases where slow collapse would also match the observations. However, due to the large number of uncertainties, we can conclude that the majority of the single-cell models point towards fast rather than slow collapses.
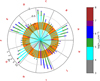 |
Fig. B.2 Polar-like chart summarising the results of our parameter study. Each slice represents a model (labelled with letters) with fixed initial conditions in terms of T, ζ2, initial density ncore, and initial H2 OPR (see Table B.1). Within the model slice, the different collapse speed cases defined by the parameter βff are represented by a stacked bar. The radial evolution of the bar reflects the oH2 D+/pD2H+ evolution and the bars are coloured by density (see associated colour bar). The orange ring was delimited by the observed oH2 D+/pD2H+ ratio and the blue region in the colour bar was set by the density of the observed cores (see also Table 1). This means that we have a match between the models and the observations when the blue frame of the bar falls into the orange region. |
References
- Amano, T., & Hirao, T. 2005, J. Mol. Spectro., 233, 7 [NASA ADS] [CrossRef] [Google Scholar]
- André, P., Belloche, A., Motte, F., & Peretto, N. 2007, A&A, 472, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, A102 [Google Scholar]
- Arzoumanian, D., André, P., Didelon, P., et al. 2011, A&A, 529, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Bovino, S., Ferrada-Chamorro, S., Lupi, A., et al. 2019, ApJ, 887, 224 [CrossRef] [Google Scholar]
- Bovino, S., Ferrada-Chamorro, S., Lupi, A., Schleicher, D. R. G., & Caselli, P. 2020, MNRAS, 495, L7 [CrossRef] [Google Scholar]
- Brünken, S., Sipilä, O., Chambers, E. T., et al. 2014, Nature, 516, 219 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Caselli, P. 2002, Planet. Space Sci., 50, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Vastel, C., Ceccarelli, C., et al. 2008, A&A, 492, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ceccarelli, C., Caselli, P., Bockelée-Morvan, D., et al. 2014, in Protostars and Planets VI, ed. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 859 [Google Scholar]
- Chitsazzadeh, S., Di Francesco, J., Schnee, S., et al. 2014, ApJ, 790, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Crabtree, K. N., Indriolo, N., Kreckel, H., Tom, B. A., & McCall, B. J. 2011, ApJ, 729, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R. M., & Kemball, A. J. 2019, Front. Astron. Space Sci., 6, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. M., Allen, L. E., Evans, Neal J., I., et al. 2015, ApJS, 220, 11 [Google Scholar]
- Enoch, M. L., Evans, Neal J., I., Sargent, A. I., et al. 2008, ApJ, 684, 1240 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M. L., Evans, Neal J., I., Sargent, A. I., & Glenn, J. 2009, ApJ, 692, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Fiorio, C., & Gustedt, J. 1996, Theor. Comput. Sci., 154, 165 [Google Scholar]
- Flower, D. R., Pineau des Forêts, G., & Walmsley, C. M. 2004, A&A, 427, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Friesen, R. K., Di Francesco, J., Shirley, Y. L., & Myers, P. C. 2009, ApJ, 697, 1457 [Google Scholar]
- Friesen, R. K., Di Francesco, J., Shimajiri, Y., & Takakuwa, S. 2010, ApJ, 708, 1002 [NASA ADS] [CrossRef] [Google Scholar]
- Friesen, R. K., Di Francesco, J., Bourke, T. L., et al. 2014, ApJ, 797, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Friesen, R. K., Pineda, J. E., co-PIs, et al. 2017, ApJ, 843, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Galván-Madrid, R., Vázquez-Semadeni, E., Kim, J., & Ballesteros-Paredes, J. 2007, ApJ, 670, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Giannetti, A., Leurini, S., Wyrowski, F., et al. 2017, A&A, 603, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giannetti, A., Bovino, S., Caselli, P., et al. 2019, A&A, 621, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gómez, G. C., Vázquez-Semadeni, E., & Palau, A. 2021, MNRAS, 502, 4963 [CrossRef] [Google Scholar]
- Grassi, T., Bovino, S., Schleicher, D. R. G., et al. 2014, MNRAS, 439, 2386 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güsten, R., Nyman, L. Å., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güsten, R., Baryshev, A., Bell, A., et al. 2008, in Millimeter and Submillimeter Detectors and Instrumentation for Astronomy IV, eds. W. D. Duncan, W. S. Holland, S. Withington, & J. Zmuidzinas, SPIE Conf. Ser. 7020, 702010 [Google Scholar]
- Harju, J., Sipilä, O., Brünken, S., et al. 2017, ApJ, 840, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Ballesteros-Paredes, J., & Heitsch, F. 2012, MNRAS, 420, 1457 [Google Scholar]
- Hesper, R., Jackson, B. D., Baryshev, A. M., et al. 2005, in Sixteenth International Symposium on Space Terahertz Technology, 110 [Google Scholar]
- Hopkins, P. F. 2015, MNRAS, 450, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F. 2016, MNRAS, 462, 576 [CrossRef] [Google Scholar]
- Hopkins, P. F., & Raives, M. J. 2016, MNRAS, 455, 51 [CrossRef] [Google Scholar]
- Hugo, E., Asvany, O., & Schlemmer, S. 2009, J. Chem. Phys., 130 [Google Scholar]
- Ivlev, A. V., Silsbee, K., Sipilä, O., & Caselli, P. 2019, ApJ, 884, 176 [Google Scholar]
- Kamazaki, T., Saito, M., Hirano, N., Umemoto, T., & Kawabe, R. 2003, ApJ, 584, 357 [Google Scholar]
- Kamazaki, T., Nakamura, F., Kawabe, R., et al. 2019, ApJ, 871, 86 [CrossRef] [Google Scholar]
- Kerr, R., Kirk, H., Di Francesco, J., et al. 2019, ApJ, 874, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, T., Ciechanowicz, M., Leinz, C., et al. 2014, IEEE Trans. Terahertz Sci. Technol., 4, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Kong, S., Caselli, P., Tan, J. C., Wakelam, V., & Sipilä, O. 2015, ApJ, 804, 98 [NASA ADS] [CrossRef] [Google Scholar]
- König, C., Urquhart, J. S., Csengeri, T., et al. 2017, A&A, 599, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Körtgen, B., Bovino, S., Schleicher, D. R. G., et al. 2018, MNRAS, 478, 95 [Google Scholar]
- Lee, C. W., & Myers, P. C. 1999, ApJS, 123, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, S.-J., Pagani, L., Lai, S.-P., Lefèvre, C., & Lique, F. 2020, A&A, 635, A188 [EDP Sciences] [Google Scholar]
- Lupi, A., Bovino, S., & Grassi, T., 2021, A&A, submitted [arXiv:2109.02655] [Google Scholar]
- Mac Low, M.-M., & Klessen, R. S. 2004, Rev. Mod. Phys., 76, 125 [NASA ADS] [CrossRef] [Google Scholar]
- MacLaren, I., Richardson, K. M., & Wolfendale, A. W. 1988, ApJ, 333, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, A&A, 518, A100 [Google Scholar]
- Motte, F., Andre, P., & Neri, R. 1998, A&A, 336, 150 [NASA ADS] [Google Scholar]
- Mouschovias, T. C. 1991, ApJ, 373, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, F., Kamada, Y., Kamazaki, T., et al. 2011, ApJ, 726, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Melnick, G. J., & Harwit, M. 1998, ApJ, 506, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Nutter, D., Ward-Thompson, D., & André, P. 2006, MNRAS, 368, 1833 [NASA ADS] [CrossRef] [Google Scholar]
- Offner, S. S. R., Klein, R. I., McKee, C. F., & Krumholz, M. R. 2009, ApJ, 703, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz-León, G. N., Loinard, L., Dzib, S. A., et al. 2018, ApJ, 869, L33 [Google Scholar]
- Ossenkopf, V.,& Henning, T. 1994, A&A, 291, 943 [Google Scholar]
- Ostriker, J. 1964, ApJ, 140, 1056 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Padovani, M., Ivlev, A. V., Galli, D., & Caselli, P. 2018, A&A, 614, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Bacmann, A., Cabrit, S., & Vastel, C. 2007, A&A, 467, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Vastel, C., Hugo, E., et al. 2009, A&A, 494, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Lesaffre, P., Jorfi, M., et al. 2013, A&A, 551, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Lefèvre, C., Juvela, M., Pelkonen, V. M., & Schuller, F. 2015, A&A, 574, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parise, B., Belloche, A., Du, F., Güsten, R., & Menten, K. M. 2011, A&A, 526, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pattle, K., Ward-Thompson, D., Kirk, J. M., et al. 2015, MNRAS, 450, 1094 [NASA ADS] [CrossRef] [Google Scholar]
- Pattle, K., Lai, S.-P., Di Francesco, J., et al. 2021, ApJ, 907, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Pillai, T., Caselli, P., Kauffmann, J., et al. 2012, ApJ, 751, 135 [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, A2 [Google Scholar]
- Punanova, A., Caselli, P., Pon, A., Belloche, A., & André, P. 2016, A&A, 587, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Redaelli, E., Bizzocchi, L., Caselli, P., et al. 2019, A&A, 629, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Redaelli, E., Bovino, S., Giannetti, A., et al. 2021, A&A, 650, A202 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sabatini, G., Giannetti, A., Bovino, S., et al. 2019, MNRAS, 490, 4489 [Google Scholar]
- Sadavoy, S. I., di Francesco, J., André, P., et al. 2012, A&A, 540, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schisano, E., Molinari, S., Elia, D., et al. 2020, MNRAS, 492, 5420 [Google Scholar]
- Schuller, F., Menten, K. M., Contreras, Y., et al. 2009, A&A, 504, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seifried, D., & Walch, S. 2015, MNRAS, 452, 2410 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H., Adams, F. C., & Lizano, S. 1987, ARA&A, 25, 23 [Google Scholar]
- Sipilä, O., Caselli, P., & Harju, J. 2015, A&A, 578, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sipilä, O., Harju, J., & Caselli, P. 2017, A&A, 607, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soam, A., Pattle, K., Ward-Thompson, D., et al. 2018, ApJ, 861, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [Google Scholar]
- Stahler, S. W., & Palla, F. 2004, The Formation of Stars (Wiley-VCH) [CrossRef] [Google Scholar]
- Troscompt, N., Faure, A., Maret, S., et al. 2009, A&A, 506, 1243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Tak, F. F. S., & van Dishoeck, E. F. 2000, A&A, 358, L79 [NASA ADS] [Google Scholar]
- Vastel, C., Phillips, T. G., & Yoshida, H. 2004, ApJ, 606, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Vastel, C., Caselli, P., Ceccarelli, C., et al. 2006, ApJ, 645, 1198 [NASA ADS] [CrossRef] [Google Scholar]
- Vastel, C., Caselli, P., Ceccarelli, C., et al. 2012, A&A, 547, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vázquez-Semadeni, E., Kim, J., Shadmehri, M., & Ballesteros-Paredes, J. 2005, ApJ, 618, 344 [NASA ADS] [CrossRef] [Google Scholar]
GILDAS is a software package developed by the Institute de Radio Astronomie Millimétrique (IRAM); see https://www.iram.fr/IRAMFR/GILDAS/
Processes such as freeze-out strongly depend on the grain size ( ). For this reason, we varied this quantity by taking the standard 0.1 μm average size and the one obtained from a proper distribution (Mathis et al. 1977) with a power-law index of 3.5 and amin = 10−7 and amax = 2.5 × 10−5 cm, which provides an average size of ⟨a⟩ = 0.035 μm.
). For this reason, we varied this quantity by taking the standard 0.1 μm average size and the one obtained from a proper distribution (Mathis et al. 1977) with a power-law index of 3.5 and amin = 10−7 and amax = 2.5 × 10−5 cm, which provides an average size of ⟨a⟩ = 0.035 μm.
We note that in Sipilä et al. (2017), some of the rates involving the H2 + H system were updated by considering not only the ground state of the molecules but also the rotational excited states. However, the changes can be considered negligible as they are within a few percent at the low temperatures (T < 15 K) of interest in this work.
system were updated by considering not only the ground state of the molecules but also the rotational excited states. However, the changes can be considered negligible as they are within a few percent at the low temperatures (T < 15 K) of interest in this work.
The ncore was calculated by following an observer-like approach, see also Appendix A, but we note that there are different approaches. We tried to calculate the core density as Σ∕L, with Σ being the surface density and L being the depth over which we integrated (i.e. a cylinder of 0.2 pc). This leads to densities on average smaller by a factor of 5–6, which provide free-fall times a factor of 2 longer and an overall shorter
 . These numbers are still in line with our main conclusions but we caution that the methodology could affect the results.
. These numbers are still in line with our main conclusions but we caution that the methodology could affect the results.
All Tables
Properties of the synthetic cores calculated at tage, i.e. at the minimum o-H2D+/p-D2H+.
All Figures
 |
Fig. 1 Observed and modelled spectra of ortho-H2D+ (left) and para-D2H+ (right) for the six cores. We note that the temperature scale of the spectra is not the same in each panel. We have centred the spectra at the systemic velocity of ortho-H2D+ (vertical line) of each source. |
| In the text | |
 |
Fig. 2 From left: map of N(o-H2D+), N(p-D2H+), and the N(o-H2D+)/N(p-D2H+) ratio from the reference run F1_01. Each panel reports the result for different snapshots in time. Contour regions represent the H2 total columndensity above 1022 cm−2 (cyan). As a reference, we also report the APEX beam used in the observations (18′′), the spatial scale in parsec, and the age of the core (tcore). The maps have been convolved with the APEX beam of FWHM 18′′ and 9′′ for the ortho-H2D+ and the para-D2H+, respectively. The total H2 column density distribution is shown after convolution with a typical Herschel beam of 36′′. The ratio was calculated on a pixel-to-pixel basis. |
| In the text | |
 |
Fig. 3 o/p H2 from the reference run F1_01 for different snapshots in time. Contour regions represent the N(o-H2D+)/N(p-D2H+), where the dashed contour has a value of 5 and solid contour 1. As a reference, we also report the APEX beam used in the observations(18′′), the spatial scale in parsec, and the age of the core (tcore). The total H2 column density distribution is shown after convolution with a typical Herschel beam of 36′′. The ratio was calculated on a pixel-to-pixel basis. |
| In the text | |
 |
Fig. 4 Zoom on the core F1_01_1 reported in Fig. 2 within the filament (core on the right, see also Table 4). The time evolution starts from tcore =16 kyr and goes up to the time at which a sink particle (i.e. a protostellar object) is formed, tcore =181 kyr. The dashed circle represents the area over which we average the core quantities reported in Table 4, which corresponds to 0.02 pc (Herschel-beam) centred in the column density peak. We note that these maps are not convolved. |
| In the text | |
 |
Fig. 5 Physical properties of the simulated and observed cores. We report the core mass and volume density (left column), as well as the virial parameter and Mach number (centre), calculated from the formulae reported in Appendix A. In the right column, we also report the fractional abundances of the two tracers in logarithmic scale, x(o-D2H+) and x(o-H2D+). Observed cores are reported as circles, while the green shaded area represents the range of values obtained for the simulated cores identified in our filaments (properties reported in Table 4). |
| In the text | |
 |
Fig. 6 Comparison of the N[o-H2D+]/N[p-D2H+] ratio between observations and simulations. The different curves in the left panel refer to the time evolution of the cores identified within the simulations with a different set of physical and chemical conditions (see Tables 3 and 4 for details). We note that some cores are the result of merging and dissolving processes, which produce the visible oscillations in the curves. The stars represent tage, i.e. the time at which the minimum o-H2D+/p-D2H+ ratio is reached for each core and the point where we performed the calculations of the properties reported in Table 4 and the comparison with the observed cores. The right panel shows the observed values: the ones labelled 1–6 represent our APEX data, 16293E (blue circle) refers to previous observations of the two studied isotopologues (Vastel et al. 2004), and HMM1-10K and HMM1-13K (green squares) are taken from observations in the L1688 cloud(Parise et al. 2011). The grey shaded area represents the range of observed values with secure detection, considering their uncertainties. |
| In the text | |
 |
Fig. 7 N(o-H2D+)/N(p-D2H+) ratio for different Tex assumptions. We report the following three main cases: our reference case Tex = Tdust and two additional cases where we assumed lower temperatures, Tex = 10 K and Tex = 0.7 × Tdust. The values in the coloured boxes mark the lower limits we calculated for the cases where para-D2H+ was not detected. The green shaded area represents the range of values obtained from our simulations. |
| In the text | |
 |
Fig. B.1 Top: Time evolution of the ortho-H2D+/para-D2H+ ratio (top) and density (bottom) for a reference case with ncore = 104 cm−3, T = 10 K, CRIR = 2.5 × 10−17 s−1, and initial H2 OPR = 0.1, for different collapse speeds (βff = [1, 2, 3, 5, 10]). The green shaded area represents the range of observed values, only detections are considered in this specific case (see Table 2). Bottom: Evolution of the ortho-H2D+/para-D2H+ ratio with respect to the density for the same parameters. The red shaded area represents the range of densities for the observed cores. |
| In the text | |
 |
Fig. B.2 Polar-like chart summarising the results of our parameter study. Each slice represents a model (labelled with letters) with fixed initial conditions in terms of T, ζ2, initial density ncore, and initial H2 OPR (see Table B.1). Within the model slice, the different collapse speed cases defined by the parameter βff are represented by a stacked bar. The radial evolution of the bar reflects the oH2 D+/pD2H+ evolution and the bars are coloured by density (see associated colour bar). The orange ring was delimited by the observed oH2 D+/pD2H+ ratio and the blue region in the colour bar was set by the density of the observed cores (see also Table 1). This means that we have a match between the models and the observations when the blue frame of the bar falls into the orange region. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


