| Issue |
A&A
Volume 653, September 2021
|
|
|---|---|---|
| Article Number | A107 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202140854 | |
| Published online | 15 September 2021 | |
Preparing for LSST data
Estimating the physical properties of z < 2.5 main-sequence galaxies
1
National Centre for Nuclear Research, ul. Pasteura 7, 02-093 Warszawa, Poland
e-mail: gabriele.riccio@ncbj.gov.pl
2
Aix Marseille Univ. CNRS, CNES, LAM, Marseille, France
3
SISSA, Via Bonomea 265, Trieste, Italy
4
Centro de Astronomía (CITEVA), Universidad de Antofagasta, Avenida Angamos 601, Antofagasta, Chile
5
Astronomical Observatory of the Jagiellonian University, ul. Orla 171, 30-244 Cracow, Poland
6
Astronomy Centre, Department of Physics and Astronomy, University of Sussex, Falmer, Brighton BN1 9QH, UK
7
Instituto de Astrofísica de Canarias, 38205 La Laguna, Tenerife, Spain
Received:
22
March
2021
Accepted:
18
June
2021
Aims. We study how the upcoming Legacy Survey of Space and Time (LSST) data from the Vera C. Rubin Observatory can be employed to constrain the physical properties of normal star-forming galaxies (main-sequence galaxies). Because the majority of the observed LSST objects will have no auxiliary data, we use simulated LSST data and existing real observations to test the reliability of estimates of the physical properties of galaxies, such as their star formation rate (SFR), stellar mass (Mstar), and dust luminosity (Ldust). We focus on normal star-forming galaxies because they form the majority of the galaxy population in the universe and are therefore more likely to be observed with the LSST.
Methods. We performed a simulation of LSST observations and uncertainties of 50 385 real galaxies within the redshift range 0 < z < 2.5. In order to achieve this goal, we used the unique multi-wavelength data from the Herschel Extragalactic Legacy Project (HELP) survey. Our analysis focused on two fields, ELAIS N1 and COSMOS. To obtain the physical properties of the galaxies, we fit their spectral energy distributions (SEDs) using the Code Investigating GALaxy Emission. We simulated the LSST data by convolving the SEDs fitted by employing the multi-wavelength observations. We compared the main galaxy physical properties, such as SFR, Mstar, and Ldust obtained from the fit of the observed multi-wavelength photometry of galaxies (from the UV to the far-IR) to those obtained from the simulated LSST optical measurements alone.
Results. We present the catalogue of simulated LSST observations for 23 291 main-sequence galaxies in the ELAIS N1 field and for 9093 galaxies in the COSMOS field. It is available in the HELP virtual observatory. The stellar masses estimated based on the LSST measurements agree with the full UV to far-IR SED estimates because they mainly depend on the UV and optical emission, which is well covered by LSST in the considered redshift range. Instead, we obtain a clear overestimate of the dust-related properties (SFR, Ldust, Mstar) estimated with the LSST alone. They are highly correlated with redshift. We investigate the cause of this overestimate and conclude that it is related to an overestimate of the dust attenuation in both UV and near-IR. We find that it is necessary to employ auxiliary rest-frame mid-IR observations, simulated UV observations, or the far-UV attenuation (AFUV)-Mstar relation to correct for the overestimate. We also deliver the correction formula log10(SFRLSST/SFRreal) = 0.26 ⋅ z2 − 0.94 ⋅ z + 0.87. It is based on the 32 384 MS galaxies detected with Herschel.
Key words: galaxies: fundamental parameters / galaxies: photometry / infrared: galaxies / galaxies: star formation / surveys
© ESO 2021
1. Introduction
In the past 20 years, the study of the multi-wavelength emission of galaxies from X-rays to radio was found to be necessary to properly analyse the physical properties of galaxies. Because the spectral energy distribution (SED) is the result of a complex interplay of several components, such as old and young stars, stellar remnants, the interstellar medium, dust, and supermassive black holes (Walcher et al. 2011; Conroy 2013), only the panchromatic view of galaxies can give the full information about their physical properties. For example, the emission from the hot interstellar medium, active galactic nuclei (AGN), or stellar remnants can be observed in the X-ray band (Fabbiano 2006), while the emission of the dust heated by interstellar radiation can be observed in the mid- and far-IR band (Silva et al. 1998; Noll et al. 2009; da Cunha et al. 2010; Hao et al. 2011; Calzetti et al. 2012; Schreiber et al. 2018; Leja et al. 2018). To fully comprehend the interactions between these parts, the simultaneous use of different spectral ranges is needed. As broad-band photometry is much less expensive than spectroscopy in terms of observation time, modelling the broad-band SED of galaxies has become one of the most commonly employed methods to evaluate and constrain the physical properties. In this way, properties such as the star formation rate (SFR) and stellar mass (Mstar), which are essential for a complete understanding of galaxy formation and evolution, can be evaluated.
However, modelling the SED can be an intricate problem because galaxies with very different properties can look similar over some wavelength range: that is, a young dusty galaxy can appear to be an old dust-free galaxy because they both look red in the optical. This is particularly the case when restricted wavelength ranges, instead of the full SED, are considered. The full SED is rarely available. This makes estimating the physical properties with only a limited wavelength range a great challenge for SED modelling.
In the literature (i.e. Kennicutt 1998; Le Floc’h et al. 2005; Schreiber et al. 2015; Whitaker et al. 2017) it has been shown that the ultraviolet (UV) to infrared (IR) SED contains important information about the star formation activity of galaxies. For example, some knowledge about newborn stars can be directly inferred from the UV band, making it a very efficient tracer of the SFR. The region in which these stars are created, however, is highly obscured by dust, which makes them very difficult to observe. Dust is composed of carbonaceous and silicate grains and absorbs part of the UV emission and re-emits it in the IR band. For example, Fig. 10 of Buat et al. (2019) shows that the total SFR of a galaxy is the sum of the SFR obtained from UV/optical measurements and the SFR estimated from IR data. Because the role played by dust is so important, it is fundamental for the SED fitting process to introduce attenuation laws that describe how dust obscures the light emitted by the stars.
The attenuation law developed by Calzetti et al. (1994) for nearby UV-bright starburst galaxies is by far the most commonly law used in literature. However, other laws such as those proposed by Charlot & Fall (2000) and Lo Faro et al. (2017) are widely employed in the SED fitting codes. Małek et al. (2018) used a combination of UV and IR observations to determine the best approach to fit SEDs of millions of galaxies from the Herschel Extragalactic Legacy Project (HELP) across a wide redshift range (0 < z < 6) to obtain homogeneous estimates of the main physical properties. They found that using three different attenuation laws, the estimate of stellar masses can change by a factor of 2 on average. Similar results were found in a sample of Ultra-Luminous IR Galaxies at z ∼ 2 for instance by Lo Faro et al. (2017), for galaxies obtained from the semi-analytic galaxy formation model GALFORM by Mitchell et al. (2013), and by Burgarella et al. (2013), who combined UV to IR measurements up to z = 3.6 to calculate the redshift evolution of the total SFR and dust attenuation. They found that the attenuation increases up to z = 1.2 and then decreases at higher redshift. The ratio of UV and far-IR (FIR) emission also serves as an indicator of the dust attenuation in galaxies (Buat et al. 2005; Takeuchi et al. 2005). All these factors require the combined usage of UV and IR observations to provide a better understanding of the star formation history (SFH), SFR, and dust attenuation properties of the galaxies. In order to perform the SED fitting of galaxies, different methods and codes were developed, such as STARLIGHT (Cid Fernandes et al. 2005), VESPA (Tojeiro et al. 2007), Hyperz (Bolzonella et al. 2000), Le Phare (Arnouts et al. 1999; Ilbert et al. 2006), PÉGASE.3 (Fioc & Rocca-Volmerange 2019), and COSMOS2020 (Weaver et al. 2021) together with Bayesian SED fitting codes such as GOSSIP (Franzetti et al. 2008), PROSPECTOR (Leja et al. 2017), Code Investigating GALaxy Emission (CIGALE; Noll et al. 2009; Boquien et al. 2019), and BayeSED (Han & Han 2014).
The main problem of the multi-wavelength fitting technique is the lack of high-quality IR observations, which is due to instrumental sensitivity and the lower resolution of wide IR cameras or extremely expensive sub-millimeter observations such as those with ALMA. In contrast, a very large and high-quality coverage of the optical part of the spectrum is usually available for wide-field surveys and narrow and deep-field imaging with several ground and space telescopes. With the upcoming Legacy Survey of Space and Time (LSST, Ivezić et al. 2019) from the Vera C. Rubin Observatory, we will obtain even higher-quality optical images in the ugrizy bands. The LSST survey will observe about 20 billion galaxies during ten years of observations. Most of these galaxies will not have any counterpart in the available IR catalogues. Moreover, IR astronomy often has blending issues, which makes a precise match of optical and IR sources even more difficult (Hurley et al. 2017; Pearson et al. 2018).
The LSST will be the largest (8.4 m of the primary mirror) wide-field ground telescope designed to obtain repeated images covering the sky that is visible from Cerro Pachón in Chile. The survey will observe about 30 000 deg2 of the southern sky, covering the wavelength range 320–1050 nm. At the end of the ten-year survey, it will reach a magnitude depth ∼27.5 in r band and similar in the other bands. Considering the depth of forthcoming observations, it is expected that the LSST will unveil a significant number of faint galaxies that have remained undetected in current wide-area surveys. These potentially large datasets will raise multifold questions, such as how we can use only LSST optical observations to obtain estimates of the main physical properties of galaxies, and how realistic and reliable they would be. We investigate these topics by performing a simulation of LSST observations of main-sequence (hereafter MS) galaxies that form a nearly linear relation (in log-log space) between their stellar mass and SFR (Noeske et al. 2007; Elbaz et al. 2010; Rodighiero et al. 2011; Speagle et al. 2014; Schreiber et al. 2015; Whitaker et al. 2015; Pearson et al. 2018). Main-sequence galaxies constitute the dominant population in deep fields such as COSMOS and ELAIS N1, which can reach very faint optical magnitudes (∼29–30 mag). The LSST is expected to expand the observed MS population of galaxies to other fields that are not currently covered by deep-field surveys. For this reason, we decided to focus on the MS galaxies.
The paper is organised as follows. In Sect. 2 we describe the data and the HELP project. In Sect. 3 we present the sample selection, outliers, and starburst, and the method we used for this work. In Sect. 4 we discuss the simulated LSST magnitude and errors. The same section, together with Sects. 5 and 6, presents the results. Our conclusions are presented in Sect. 7. Throughout this paper we use the WMAP7 cosmology (Komatsu et al. 2011): Ωm = 0.272, ΩΛ = 0.728, and H0 = 70.4 km s−1 Mpc−1.
2. Data
The HELP collaboration provides extremely valuable multi-wavelength data over the HerMES (Oliver et al. 2012) and the H-ATLAS survey fields (Eales et al. 2010) and other relevant Herschel fields. The total area of HELP is 1269.1 deg2 (Oliver et al., in prep, Shirley et al. 2019). Herschel was equipped with two imaging instruments, the Photodetector Array Camera and Spectrometer (PACS; Poglitsch et al. 2010), which observed the FIR at 100 and 160 μm, and the Spectral and Photometric Imaging Receiver (SPIRE; Griffin et al. 2010), which covered the 250, 350, and 500 μm wavelength ranges.
Surveys that combine a wide range of wavelengths have particular identification issues because the spatial resolution of the sources is different in different bands. To correct for this issue, HELP builds a master list catalogue of objects as complete as possible for each field and uses the near-IR (NIR) sources of this catalogue as prior information to deblend the Herschel maps. A detailed description can be found in Shirley et al. (2019). The tool developed to obtain the photometry of Herschel sources, XID+ (Hurley et al. 2017), is a probabilistic deblending algorithm that extracts source flux densities from photometry maps that show source confusion. It uses Bayesian inference to explore the posterior probability distribution and provide probability density functions (PDFs) for all prior sources, and thus flux and uncertainties can be estimates. A detailed description can be found in Hurley et al. (2017). The whole procedure is described in Notebook and stored in a GitHub repository1.
We use two HELP fields because many multi-wavelength data are available within their wide-field coverage: the European Large Area ISO Survey North 1, hereafter ELAIS N1 (Oliver et al. 2000), and the COSMOS field (Laigle et al. 2016). In addition to data from two PACS and three SPIRE maps, we used available sets of photometric data at shorter wavelengths for both fields (listed in Table 1 and described below in Sects. 2.1 and 2.2). Based on true galaxy observations from these fields, we evaluate the LSST-like observations we used for further analysis.
Filter for the ELAIS N1 and COSMOS fields.
2.1. ELAIS N1 field
According to the HELP strategy, all sources detected in any of the Spitzer IRAC bands were used as a prior for XID+ to obtain FIR fluxes. XID+ was run on the Spitzer MIPS 24 μm and Herschel PACS and SPIRE maps. The flux level at which the average posterior probability distribution of the source flux becomes Gaussian is 20 mJy for MIPS, 12.5 and 17.5 mJy for 100 μm and 160 μm PACS bands, respectively, and 4 mJy for all three (250, 350, and 500 μm) SPIRE bands (for more details, see Hurley et al. 2017; indicating that information from data dominates those of the prior). In the deblending procedure, the priors used to compute the fluxes satisfied two criteria: they must have an IRAC 1 band detection, and they must have been detected in either the optical or NIR wavelengths to eliminate artefacts. More information about the catalogue can be found in Małek et al. (2018), Shirley et al. (in prep.), and on the main webpage of the HELP project2.
In addition to the FIR bands, the catalogue is built on a position cross-match of all the public survey data available in the optical and mid-IR (MIR) range. This comprises observation from the Isaac Newton Telescope/Wide Field Camera (INT/WFC) survey (González-Solares et al. 2011), the Subaru Telescope/Hyper Suprime-Cam Strategic Program Catalogues (HSC-SSP; Aihara et al. 2018), the Panoramic Survey Telescope and Rapid Response System (Pan-STARRS; Chambers et al. 2016), the UK Infrared Telescope Deep Sky Survey – Deep Extragalactic Survey (UKIDSS-DXS) (Swinbank 2013; Lawrence et al. 2007), the Spitzer Extragalactic Representative Volume Survey (SERVS; Mauduit et al. 2012), and the Spitzer Wide InfraRed Extragalatic survey (SWIRE; Lonsdale et al. 2003; Stauffer et al. 2005). We show the list of filters for ELAIS N1 in Table 1. The whole matching procedure is described in Shirley et al. (2019).
2.2. COSMOS field
For the COSMOS field, the XID+ analysis was perfomed on Spitzer and Herschel maps for all the sources with fluxes greater than 1 μJy in any of the IRAC bands from the COSMOS2015 catalogue (Laigle et al. 2016). The fluxes obtained follow the criterion of goodness defined in XID+ and correspond to a Gaussian posterior distribution of the estimated flux.
Starting with this multi-wavelength catalogue, COSMOS2015 (Laigle et al. 2016), ancillary photometry was added with a position cross-match with other public survey, again containing optical and MIR observations. Other than the one already mentioned for ELAIS N1, this comprises the WIRCam Deep Survey (WIRDS, WIRcam bands J, H, Ks), the VLT Survey Telescope (VST; Arnaboldi et al. 1998), the Victor Blanco 4 m Telescope, the Visible and Infrared Survey Telescope for Astronomy (VISTA; Emerson et al. 2006; Dalton et al. 2006), and the UKIDSS-LAS (WFCAM bands J, H, K) catalogues. (The merging strategy is the same as for ELAIS N1 and is described in detail in Shirley et al. 2019). The list of filters used for COSMOS survey is shown in Table 1.
Detailed description of both fields (the area, mean depths in different filters, all raw files and ancillary data, and many others) can be found on the3 webpage.
2.3. Total sample
As part of the HELP database, both field catalogues include photometric redshifts generated using a template fitting method that is based on the Bayesian combination approach described in Duncan et al. (2018). The authors investigated the performance of three photometric redshift template sets as a function of redshift, radio luminosity, and infrared/X-ray properties over the NOAO Deep Wide Field Survey Bootes and COSMOS fields. The three template sets are (1) the default EZY reduced galaxy set (Brammer et al. 2008), (2) XMM COSMOS templates (Salvato et al. 2009), and (3) the atlas of Galaxy SEDs (Brown et al. 2014).
The total sample includes 39 329 objects for the ELAIS N1 survey and 14 864 for COSMOS, with FIR detections in at least two photometric bands with a signal-to-noise ratio (S/N) ≥ 3. This cut is performed to remove objects with unreliable photometry and thus improves the quality of the SED fitting process. We kept in mind that by employing the selection described above, we restricted our analysis to only a subsample of galaxies that LSST will observe, which are objects that are bright in the FIR. Then, as we show in the next section, we selected only the so-called MS galaxies observed in the spectral range from UV to FIR because these are the most commonly observed types of galaxy. The considered bands are u, g, r, i, z, N921, y, J, H, K, Spitzer IRAC 3.6, 4.5, 5.8, and 8.0 μm, Spitzer MIPS 24 μm, and five passbands from Herschel, two from PACS (100 and 160 μm), and three from SPIRE (250, 350 and 500 μm) across the ELAIS N1 and COSMOS fields.
3. Method: SED fitting, starbursts, and outlier detection
3.1. SED fitting with CIGALE
The SED fitting was performed with the Code Investigating GALaxy Emission4 (CIGALE). For a detailed description of the code, we refer to Boquien et al. (2019). We provide a brief summary here. CIGALE is a Bayesian SED fitting code that combines modelled stellar spectra with dust attenuation and emission. CIGALE preserves the energy balance considering the energy emitted by massive stars, which is partially absorbed by dust grains and then re-emitted in the MIR and FIR. The quality of the fit is expressed by the best χ2 (and a reduced best χ2 defined as 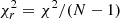 , with N the number of data points). The minimum value of
, with N the number of data points). The minimum value of 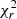 corresponds to the best model selected from the grid of all possible computed models from the input parameters. The physical properties and their uncertainties are estimated as the likelihood-weighted means and standard deviations.
corresponds to the best model selected from the grid of all possible computed models from the input parameters. The physical properties and their uncertainties are estimated as the likelihood-weighted means and standard deviations.
To obtain the starting MS sample of galaxies with the correct physical properties to compare them with those obtained with LSST alone, we ran CIGALE on the ELAIS N1 and COSMOS samples with the physical modules and parameters reported in Table 2. We did not use the AGN module (see Appendix B and Sect. 3.5). As shown in Małek et al. (2018), this set of parameters corresponds to the set that best fits a large sample of IR-detected galaxies in the 23 HELP fields for the redshift range 0 < z < 6. We used an SFH modelled as a delayed exponential function with an additional exponential burst to select and remove starburst galaxies from our sample in order to retain MS galaxies alone. We performed the SED fitting by employing the modified version of the Charlot & Fall (2000) attenuation law, which was employed in Małek et al. (2018) for a large sample of multi-wavelength HELP data. We used the Draine et al. (2014) dust emission module. A detailed description of each module can be found in Boquien et al. (2019) and Małek et al. (2018).
Input parameters for the code CIGALE.
To improve the quality of our selection, we selected only objects with redshift lower than 2.5 from the full sample. Our cut in redshift was not related with the LSST redshift range because the photometric redshifts for the LSST will be applied and calibrated over the range 0 < z < 4 for galaxies to r ∼ 27.5 (LSST Science Collaboration 2009). The z < 2.5 is related to the redshift distribution in the ELAIS N1 and COSMOS fields that were used in this analysis, and it also restricts us to high-quality data and so maximises the accuracy of the estimation of physical properties. Moreover, we removed all the objects recognized as possible stars by Gaia (flag Gaia > 0 in the database). In this way, we removed 2 921 objects (7.5% of the sample) from ELAIS N1 and 887 (6% of the sample) from the COSMOS catalogue. From now on, we refer to the remaining 36 408 and 13 977 galaxies from the ELAIS N1 and COSMOS fields as the real sample.
3.2. Selection of starburst galaxies
Galaxies can be classified according to their different properties: morphology, colour, environment, mass, etc. A property that is often used in the literature is the rate at which stars are forming out of gas, the SFR. This leads to a definition of three different types of galaxies: passive, normal/MS, and starburst (SB). The boundaries dividing these classifications are not precisely defined because different authors use different methods to distinguish starbursts from MS galaxies (i.e. Rodighiero et al. 2011; Speagle et al. 2014; Elbaz et al. 2018; Donevski et al. 2020). No universally accepted method exists. Nevertheless, there is agreement that the three groups differ in regard to their evolution and physical properties, such as SFH, dust and gas content, and others (Silverman et al. 2018; Elbaz et al. 2018).
Most galaxies observed with the LSST will be composed of active IR galaxies, but the majority of them are likely to be normal, MS–like, or passive galaxies. For example, the current estimate for the contribution of SB galaxies to the full star formation population is about 5% (Schreiber et al. 2016; Béthermin et al. 2017). However, this contribution increases when we isolate brighter IR galaxies (e.g., Miettinen et al. 2017).
To interpret possible bias for the physical parameter estimation, we have to ensure that the selection effects do not produce artificial trends in the analysis. To quantify the accuracy of the physical property estimates of LSST galaxies, we decided to focus on MS objects alone because we can select a large number of these galaxies from the HELP data to obtain a statistically important sample of real and simulated galaxies. The method we used to separate MS galaxies is described in detail in Rodighiero et al. (2011). We divided our sample into four redshift bins (Table 3) because the definition of starbursts changes with redshift. It was shown by Schreiber et al. (2015) that the average SFR of star-forming galaxies in the same mass ranges increases with redshift. In this work starbursts are defined according to their specific SFR distribution (SFR/Mstar, hereafter sSFR). Figure 1 shows that the sSFR follows a Gaussian distribution. We followed the same definition for starbursts as Rodighiero et al. (2011), that is, objects with sSFR that lie above 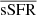 +3σ, where
+3σ, where 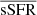 is the Gaussian mean of the sSFR distribution. The right panel in Fig. 1 shows the selected starbursts and the MS galaxies.
is the Gaussian mean of the sSFR distribution. The right panel in Fig. 1 shows the selected starbursts and the MS galaxies.
 |
Fig. 1. Left panel: example of the sSFR distribution of ELAIS N1 galaxies in the redshift range 1 < z < 1.5 obtained with the delayed SFH plus an additional burst. The orange line respresents the Gaussian fit, and the dashed black line corresponds to the division of starburst (SB galaxies are located on the right side of the line) and MS galaxies. The division is located 3σ away from the centre of the Gaussian. Right panel: MS distribution for the same redshift bin. Magenta circles represent SB galaxies selected from the sSFR distribution shown in the left panel. The dashed black line represents the Speagle et al. (2014) MS. |
Total number of galaxies and SB percentage for ELAIS and COSMOS fields in each redshift range.
To further test the reliability of the SB selection, we compared our distribution and the position of starbursts with the distribution found in Béthermin et al. (2017) (hereafter: B17), a catalogue of simulated galaxies. B17 was built on IR/sub-millimeter data, and it is one of only a few models that is able to simultaneously match the total IR number counts and the evolution of the sSFR. It simulates a 2 deg2 field including physical clustering from a dark matter simulation, and is thus perfectly suited for comparison purposes. Figure 2 shows the comparison of the SB distribution derived in this paper with the sample of simulated SBs from B17 (cyan distribution). The simulated SB sample extends to sSFR values that are lower than the sSFR range obtained from our analysis. The discrepancy arises because two different selection methods were used in our work and in B17. On the one hand, B17 randomly drew the SFR of each source using a continuous log-normal distribution (in agreement with the observational results, e.g., Rodighiero et al. 2011) and then used the Schreiber et al. (2015) definition of the MS to select the galaxies, with an additional offset correction for galaxies at z < 0.5. Specifically, B17 defined MS objects as those belonging to the distribution centred on 0.87 × SFRMS with 0.2 dex of width and SBs as those belonging to the distribution centred at 5.3 × SFRMS with 0.3 dex of width. On the other hand, our selection is based on the statistical analysis presented in Rodighiero et al. (2011), who used the sSFR distribution over a broad redshift range. This makes our selection more discrete, while the selection of B17 is continuous. Figure 2 shows that the purity of our selection is very high, but at the same time, it can be incomplete for less active galaxies.
 |
Fig. 2. sSFR distribution in four different redshift bins obtained with delayed SFH plus an additional burst. Open histograms are the galaxy distributions (MS+SB) derived in this work, the dashed black line is the division between SBs (right side of the line) and MS (left side of the line) in our sample, and the cyan full histograms represent the simulated SB sample from B17. The division is located at about 3σ from the Gaussian centre. The sample is the same as for Fig. 1, but the binning is different. |
We removed 763 SB galaxies from ELAIS N1 and 228 from COSMOS. Table 3 shows the fraction of SB galaxies in the ELAIS N1 and COSMOS field. Our findings for the ELAIS N1 field agree with the literature because it is expected that the fraction of SBs rises from 1% at low redshift to about 3% at higher redshift, and remains flat thereafter (i.e. Béthermin et al. 2012).
3.3. Selection of passive galaxies
The SFH with two or more stellar populations is suitable to fit active galaxies with moderate or high SFR. For this reason, we analysed the remaining objects without SBs employing the delayed SFH in the SED fitting, which is more suitable for normal MS galaxies (Ciesla et al. 2016). All parameters we used for the SED fitting are listed in Table 2. We again performed the SED fitting to obtain real physical properties of the sample of real MS galaxies. These values were then used to simulate the LSST observations (see Sect. 4.1).
To ensure the purity of the MS sample, we additionally removed possible passive galaxies. As for the starburst evaluation, many different methods were employed in the literature to select red passive galaxies, that is, an UVJ and NUVrK colour diagram analysis (Williams et al. 2009; Arnouts et al. 2013), a division based on sSFR (Vulcani et al. 2015; Salim et al. 2016, 2018), or unsupervised machine learning (Siudek et al. 2018). We decided to follow the method described by Salim et al. (2018) by removing all objects with log10(sSFR[yr−1]) < −11. In this way, we removed 340(1%) and 63(0.5%) galaxies from the ELAIS N1 and COSMOS field, respectively. The almost negligible number of passive galaxies in the HELP sample is related to our initial sample selection, which required at least two Herschel measurements with S/N > 3.
3.4. AGN contribution
Taking advantage of an IRAC detection for all galaxies included in our analysis, we used MIR detections to determine how numerous the AGN population in our sample is. We employed two different selection criteria based on MIR photometry (IRAC bands) analysis. They are explained in detail in Stern et al. (2005) and Donley et al. (2012). Figure B.1 shows the IRAC colour-colour selection using the methods of Donley et al. (2012) (upper panels) and Stern et al. (2005) (lower panels). Using both criteria, we find a negligible number of AGN in comparison to the final sample (1.56% and 5.16% for the criterion of Donley et al. 2012 and Stern et al. 2005, respectively; see Table 4 for detailed information for both fields). The redshift distribution of selected AGNs is shown in Fig. B.2. For consistency with the cuts made previously, we removed AGNs from our sample. We decided to use a conservative approach, and we removed all 2603 possible AGNs found with the method of Stern et al. (2005) because this selection includes all the AGNs that are detected with the approach of Donley et al. (2012).
Number of AGNs selected based on the MIR features for the ELAIS N1 and COSMOS fields.
3.5. Outlier selection
Because the number of galaxy free parameters is large and unknown, a simple 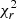 selection cannot reliably remove the majority of the outliers from our sample. Along with a
selection cannot reliably remove the majority of the outliers from our sample. Along with a 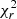 selection, we used an estimation of the physical properties Ldust and Mstar (see Appendix A) in order to eliminate possible outliers and to ensure a high quality of the SED fitting. A similar procedure was used by Małek et al. (2018) for the HELP ELAIS N1 field. Based on these criteria, we removed 2117 galaxies from ELAIS N1 and 640 from the COSMOS field. This is 5.81% and 4.75%, respectively.
selection, we used an estimation of the physical properties Ldust and Mstar (see Appendix A) in order to eliminate possible outliers and to ensure a high quality of the SED fitting. A similar procedure was used by Małek et al. (2018) for the HELP ELAIS N1 field. Based on these criteria, we removed 2117 galaxies from ELAIS N1 and 640 from the COSMOS field. This is 5.81% and 4.75%, respectively.
3.6. Final sample
To obtain the final sample of normal star-forming galaxies, we removed possible starbursts (Sect. 3.2), passive galaxies (Sect. 3.3), and possible AGNs (Sect. 3.4). We also performed additional cleaning using outlier selection (Sect. 3.5) to remove all galaxies with possibly incorrect photometry, or incorrect matches of UV-optical and FIR measurements. At the end of the process, 31 936 objects were left for ELAIS N1 (87% of the total sample) and 11 716 galaxies for COSMOS (84% of the total number). Furthermore, in order to validate the photometric redshift estimates used for these objects, we performed a comparison with spectroscopic redshift estimates, which are available for ∼5000 galaxies in the ELAIS N1 and COSMOS fields. Following the Duncan et al. (2018) definition of critical outliers (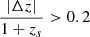 ), we find that the fraction of outliers in our sample is at a level of 4%, which agrees with what was found in previous works (Ilbert et al. 2009; Hildebrandt et al. 2010; Duncan et al. 2018). The final redshift distributions of both samples are shown in Fig. 3.
), we find that the fraction of outliers in our sample is at a level of 4%, which agrees with what was found in previous works (Ilbert et al. 2009; Hildebrandt et al. 2010; Duncan et al. 2018). The final redshift distributions of both samples are shown in Fig. 3.
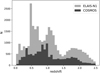 |
Fig. 3. Redshift distribution of ELAIS-N1 and COSMOS samples based on the approach of Duncan et al. (2018). |
4. Estimation of the LSST physical properties
In the following section we discuss the LSST data and uncertainties from simulations and the estimation of the physical properties of the galaxies obtained by performing the SED fitting of (i) the fiducial input parameters plus LSST data alone and (ii) the fiducial input parameters plus LSST data coupled with other observations.
4.1. Estimating LSST-simulated data and uncertainties
Simulating LSST data has been a popular topic in the past years because of the upcoming start of the survey (Ivezić et al. 2019). We derive an ‘LSST-like catalogue’ from the best fit of the observational data as described in Sect. 2. In this way, we are able to quantify the difference between estimating the physical properties based on the LSST measurements alone and the UV-to-FIR wavelength of the real, observed objects. Considering the depth reached with ten years of survey data, it is very likely that LSST will observe objects that are not visible with the current ground-based survey telescopes, and this work will be a starting point to learn how these objects should be treated with SED fitting methods.
We simulated the observed fluxes in the six LSST bands (ugrizy; the filter response curve is provided by the LSST developers team, Ivezić et al. 2019). To obtain LSST fluxes, we ran CIGALE by fitting the photometric measurements and providing the LSST filter response curves for the code. We used a CIGALE module (called fluxes) that is specifically designed to estimate the fluxes in the defined filters. We computed LSST fluxes from the best-fit model of each object. We included in our sample all the galaxies that will be detected in all bands at the depth of the ten-year survey: u < 26.1, g < 27.4, r < 27.5, i < 26.8, z < 26.1, y < 24.9. In this way we discard 8645 objects (23% of the total sample) from ELAIS N1 and 2623 (19% of the total sample) from COSMOS.
To incorporate an LSST-like observational uncertainty in our catalogue, we must take random phenomena into account that might occur during a real observation, such as a change in the sky seeing or the number of visits. The predicted magnitude errors that we converted into flux errors following the conversion provided in the LSST manual (Ivezić et al. 2019) depend on the galaxy magnitude, the sky seeing, and the total survey exposure time in a given filter. We used the LSST simulation software package CatSim5 to calculate magnitude errors. The error evaluation was based on Eq. (5) of Ivezić et al. (2019) and took variations in the photometry due to hardware and observational components (e.g., detector, darksky, and atmosphere) into account. The evaluated random error was then divided by the square root of the number of visits during the survey. The LSST manual provides mean values for all these components.
To mimic the real conditions, we added a value that was randomly chosen from a Gaussian distribution centred on the provided mean value to the average value of each component provided in the LSST manual, which had a standard deviation the 10% of the mean. In this process, we varied the number of visits and sky seeing. The assumed standard conditions for these components are 0.8 arcsec for the seeing and a uniform progression that assumes a total of 56, 80, 184, 184, 160, and 160 visits in filters ugrizy, respectively, in ten years, where each visit is 30 seconds of integration time.
At the end, to further mimic a possible divergence of the ‘real’ observed flux from the simulated value evaluated from the best-fit SED, we again added a value randomly chosen from a Gaussian distribution centred on 0 to the best-fit SED with the standard deviation of the flux error calculated before. Figure 4 shows the magnitude errors as a function of the simulated observed magnitude for our sample of galaxies. We only selected objects that would be observed in all six bands according to our simulation. As a result, we reached the LSST magnitude limit only for the u band. The final catalogue contains simulated LSST fluxes and uncertainties for 23 291 galaxies in the ELAIS N1 field and 9093 in the COSMOS field. The catalogues, together with the photometric redshifts and HELP IDs, are available at the HELP virtual observatory6.
 |
Fig. 4. Magnitude errors vs observed apparent magnitudes for simulated LSST observations from the ELAIS N1 sample. Simulations are cut to the maximum LSST limit. The choice to vary simulation parameters allows us to obtain different errors for similar magnitude values, as we would expect in the case of real observations. The brightest end we reached is 13 mag, but for clarity of the plot, we cut it at 21 mag. |
4.2. Fiducial parameters and LSST data alone
To estimate the main physical properties of the LSST sample, we ran CIGALE on simulated LSST observations and uncertainties employing the same modules and parameters as were used for the HELP MS sample (Table 2, with delayed SFH). Figure 5 shows two example SEDs of the same galaxy at redshift 0.92, obtained with the UV-FIR and LSST photometric-only data set, respectively. For this specific case, we found an agreement of estimated stellar masses (Mstar real = 6.05 × 1010 ± 5.62 × 109 M⊙, Mstar LSST = 5.59 × 1010 ± 1.80 × 1010 M⊙). Instead, the SFR calculated for the LSST-like photometric data alone is highly overestimated (by a factor of six) with respect to the real value obtained by employing the UV-FIR data set (SFRreal = 11.9 ± 2.16 M⊙ yr−1 and SFRLSST = 67.4 ± 45.9 M⊙ yr−1). Moreover, the residuals for the LSST are very small (but never null), as we can easly find a model that almost perfectly fits just six observations in the optical part. However, the IR part of the SED, and so the dust emission module, is completely unconstrained (we used the same dust emission module from Draine et al. 2014 as was used for the original HELP data with the same grid of parameters).
 |
Fig. 5. Comparison of SEDs evaluated for the same object at z ∼ 1 using the full UV-to-IR observations (upper panel) and the LSST optical bands alone (bottom panel). The blue square represents the observed fluxes, and red dots represent the fluxes predicted by the model. The magenta lines delimit the division between optical and IR bands, which is taken into account by CIGALE. The IR emission is not constrained for the LSST estimate. |
The relation of SFR and Mstar in the four redshift bins is shown in Fig. 6. In this figure, we compare the MS relation obtained for the LSST-like sample with the relation obtained from the full UV-FIR SED fitting. We show the MS from Speagle et al. (2014) as a reference. At low redshift, the LSST estimation fails to probe low-SFR objects, and this leads to a clear division between the respective MS relations, which overlap at higher redshifts, however. In Appendix D we discuss the scatter between our sample and the MS law. Figure 7 shows this overestimation as a function of redshift separately for ELAIS N1 and COSMOS (left upper panel). We also plot in the same figure the ratio of the LSST-derived stellar mass, Ldust, and Mstar and those from the full UV-IR SED fitting. We obtain an overestimation of the dust related properties (SFR, Ldust, and Mstar) but the values of Mstar are comparable. The overestimation of the SFR is strongly dependent on the redshift. The ratio of the stellar masses is evenly distributed around zero, leading to comparable results between the two runs because stellar masses mostly rely on optical data. This result holds for the ELAIS N1 and COSMOS fields and shows that there is no dependence on the field.
 |
Fig. 6. Main-sequence (SFR vs. Mstar) relation for the ELAIS N1 and COSMOS fields in four redshift bins. In blue we show the LSST-like sample, and in black the real sample. The solid black line represents the MS by Speagle et al. (2014), and the dashed lines mark the loci two times above and below the MS. This plot shows a clear SFR overestimate obtained using LSST bands alone, which tends to disappear at higher redshift ranges. |
These results can be explained when we consider how the physical properties are evaluated by the Bayesian method. This is basically done through a likelihood estimation. Each model in the grid of models built from the starting input parameters will have an associated likelihood taken as exp(−χ2/2) that is used as weight to estimate the physical parameters (the likelihood-weighted mean of the physical parameters attributed to each model) and the related uncertainty (see Sect. 4.3 of Boquien et al. 2019). Fitting just LSST optical observations results in high likelihood values even for templates that do not reflect the real physical properties of the modelled galaxy. Because the SFR is partly estimated from the UV emission of the massive young stars in star-forming regions and because this emission is attenuated by the dust and is re-emitted in the IR band, we find that the lack of information about the UV and MIR rest-frame wavelengths for the LSST sample causes CIGALE to overestimate the attenuation. Overestimated attenuation also results in an overestimation of the SFR.
The fluxes observed by the LSST in the optical at high redshift are in the UV rest-frame. Because the UV wavelengths trace young stellar populations, the estimates of the SFR from the SED fitting with CIGALE, significantly improves as a consequence. Figure 8 shows an example of an SED superimposed with LSST coverage at different redshifts. Even at z = 1, the LSST bands are almost entirely shifted to the rest-frame UV bands, which range between 0.01 and 0.38 μm. As a result, the dust attenuation is better probed because the LSST bands cover a larger portion of the UV rest-frame spectra, where dust attenuates more effectively, and a better constraint of the SFR is provided. As shown in Fig. 7, the differences in the estimated SFR become negligible for z ≳ 1.3.
 |
Fig. 7. Ratios of different physical properties obtained from fitting the simulated LSST data alone and from the UV-FIR SED (e.g., SFRratio = SFRLSST/SFRUV − FIR) as a function of redshift for the ELAIS N1 and COSMOS fields. The properties obtained from the UV-FIR SED fitting are considered as the true values. From the upper left panel we show clockwise the SFR, Mstar, Ldust, and Mstar comparisons. The dashed lines represent polynomial fits performed on the samples. The points are the median values in each redshift bin, with the median absolute deviation as errors. A ratio equal to zero corresponds to a perfect agreement between the estimates obtained based on the LSST-like sample and the real values. The distributions calculated for ELAIS N1 and COSMOS are comparable within the errors. |
 |
Fig. 8. LSST coverage of an example SED at different redshifts indicated in the panel. |
In order to obtain a useful function with which to correct for the overestimation of the SFR, we performed a polynomial fit on the SFR ratio distribution of ELAIS N1 and COSMOS combined,
where SFRratio stands for SFRLSST/SFRreal. However, this formula is highly dependent on the input parameters.
To determine whether the complex set of parameters used for the Draine et al. (2014) model is responsible for the overestimation of the SFR, we ran the whole analysis and adopted the Dale et al. (2014) model. Dust emission in this model is parametrised by a single parameter α defined as 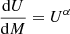 , where M is the dust mass heated by a radiation field at intensity U. We used the parameter α = 2 to better describe the stellar emission from MS galaxies. The module also allows adding an optional AGN component, which we set to 0 for this test. Comparing the LSST physical properties with the real one using the Dale et al. (2014) module, we obtain the same overestimation of the SFR and Ldust as was obtained with the Draine et al. (2014) dust emission. We were not able to compare dust mass because it is not an output parameter of the Dale et al. (2014) module. As we found no improvement by employing a simpler model, we decided to keep the results obtained with Draine et al. (2014) for homogeneity with the results published by HELP project (Małek et al. 2018; Shirley et al., in prep.).
, where M is the dust mass heated by a radiation field at intensity U. We used the parameter α = 2 to better describe the stellar emission from MS galaxies. The module also allows adding an optional AGN component, which we set to 0 for this test. Comparing the LSST physical properties with the real one using the Dale et al. (2014) module, we obtain the same overestimation of the SFR and Ldust as was obtained with the Draine et al. (2014) dust emission. We were not able to compare dust mass because it is not an output parameter of the Dale et al. (2014) module. As we found no improvement by employing a simpler model, we decided to keep the results obtained with Draine et al. (2014) for homogeneity with the results published by HELP project (Małek et al. 2018; Shirley et al., in prep.).
4.3. Fiducial parameters, LSST, and ancillary data
A different approach to correct for the overestimation consists of applying the SED procedure on the LSST data together with other available observations in different bands (e.g., MIR Spitzer bands, FIR Herschel Spire bands). Figure 9 shows the results for SFR ratios obtained by adding IRAC MIR and SPIRE FIR observations. We expect that by adding the rest-frame NIR part of the SED, the attenuation of the old stellar population will be better constrained, while the MID and FIR mainly constrain the dust emission from the star-forming regions and the missing SFR, which is hidden by dust. The upper left panel of Fig. 9 shows that when MIR observations alone are added, the overestimation of the SFR is fully corrected, regardless of the considered redshift range.
 |
Fig. 9. Upper left panel: SFR ratio, defined as in Fig. 7, estimated with LSST observations alone (red) and with LSST+IRAC observations (blue). The two samples disagree at low redshift, but the comparison improves at high redshift, highlighting the redshift dependence of the results. With the addition of MIR observations, the LSST-only estimates are consistent with the UV-IR estimates. Upper right panel: same comparison, but adding FIR SPIRE observations. In this case we did not fully remove the overestimation, which highlights that the problem lies in the lack of rest-frame MIR data. Lower left panel: same as in the other panels, but adding GALEX observations. We obtain a slight decrease in the overestimation. For this comparison we considered the ∼3000 objects that have a counterpart in the GALEX database. Lower right panel: Mstar ratio evaluated with LSST observations alone (red) and with LSST+SPIRE observations (blue). The results are consistent with the ‘real’ ratio with a very low scatter. |
The combined use of UV and LSST data might also be expected to correct for the overestimation of the SFR at low redshift. We tested this hypothesis by adding the UV observations from GALEX and performing the SED fitting. We performed a 1.5 arcsec cross-match with the HELP catalogue and identified ∼3000 galaxies with a GALEX counterpart. Figure 9 (bottom left panel) shows the comparison of the SFR estimation for LSST-like and the UV–FIR data set of these 3000 galaxies. We conclude from this plot that by adding GALEX observations, we obtain a slightly lower overestimation in general, which is still consistent with previous results, however, meaning that the observed UV fluxes are not enough to completely correct for the differences. Furthermore, for 0.5 < z < 1.5, we obtain a slight underestimation of the parameter. Nevertheless, we stress that this result can be biased by the low number of GALEX counterparts of the LSST-like catalogue and the low quality of GALEX observations for higher-redshift sources. To confirm this statement, we simulated GALEX near-UV (NUV) and far-UV (FUV) observations for the whole sample (we refer to it as GALEXtrue), again using the CIGALE module fluxes, and employed it together with the LSST to estimate the physical properties. We decided to cut objects with z > 1.5 because after this limit, both NUV and FUV GALEX bands probe emissions below the Lyman break. Figure C.1 shows the comparison of the SFR evaluated in this way and the SFR evaluated using LSST observations alone. We find a clear correction of the overestimation, highlighting the great effect that UV observations have on the SFR estimation. We confirm that the overestimation is partially due to the lack of the direct tracer of the young stellar population. Unfortunately, no new UV missions are planned in the near future, therefore we do not expect a UV coverage that large enough to be used in conjunction with the LSST in order to correctly estimate the physical parameters.
Figure 9 (bottom right panel) also shows the correction of Mstar estimates that we obtained by adding the SPIRE FIR observations. The good agreement of the LSST plus SPIRE and the real estimates arises because the FIR emission is a direct probe of the dust mass.
5. Testing different input parameters in CIGALE
As discussed in Sect. 3.1, the set of parameters we employed for the analysis presented so far corresponds to the best set to fit the large sample of objects in the area of ∼1300 deg2 of the HELP field. However, we also investigated how much the results obtained by fitting the LSST simulated data alone are dependent on the CIGALE input parameters. In particular, we tested possible variations of the derived galaxy physical quantities as a function of the input radiation field, PAH fraction, and dust attenuation law. To test how the variations in the dust attenuation laws change our results, we refitted the UV to IR photometry and rederived the LSST simulated data that were later refitted by adopting a different attenuation law.
5.1. Dust emission and mass
Dust continuum emission is only determined by the energy balance, and therefore it only depends on the amount of absorbed radiation. As a consequence, the total dust emission is not affected by the parameter Umin, but is only sensitive to the total absorbed radiation. In contrast, we find that Mstar is not constrained by using the LSST data alone, and its estimate is largely affected by the Umin parameter. When Umin is changed, the amount of radiation that irradiates the dust is modified, but the amount of dust emission is unaltered. As a consequence, higher input values of Umin are translated into lower Mstar and vice versa. High values of the Umin (Umin = 25) parameter yield an underestimation of Mstar. As a consequence, because the shape of dust emission is completely unconstrained using the LSST coverage alone, the Bayesian method cannot evaluate the Umin parameter and assigns an average value from all considered input parameters to all galaxies. This results in a strong dependence of dust mass estimates on the input parameters. When the dust emission is constrained using SPIRE observations, the Umin parameter is well evaluated by the Bayesian method, and so is the dust mass.
The use of different attenuation laws also changes the estimates of dust emission and mass because the radiation absorbed and the re-emitted by dust grains is modified. By using either the Calzetti et al. (2000) and Charlot & Fall (2000) attenuation laws, we obtain an overestimation of the dust luminosity over the entire redshift range. The trends of the dust luminosity ratios and the redshift are different, however. When we adopt Calzetti et al. (2000), we obtain a constant slight overestimation of the dust mass, centred around 0.3 dex throughout the whole redshift range, and when we use Charlot & Fall (2000), the dust mass is overestimated for local galaxies and underestimated for redshift greater than ∼1.
5.2. Dust attenuation laws and star formation history
We find that the SFR to is not affected by the PAH fraction or the input radiation field (Umin and α parameters) because the input quantities only shape dust emission. The SFR is instead affected by our choice of the attenuation law. When the Calzetti et al. (2000) modified attenuation law is employed, we obtain the results shown in Fig. 10. The results using the Calzetti et al. (2000) attenuation curve agree well with those obtained with the Charlot & Fall (2000) prescription at low redshift, but change in shape at higher z. The overestimation with the Calzetti et al. (2000) curve is more constant throughout the redshift range, but it decreases faster when the Charlot & Fall (2000) prescription is used.
 |
Fig. 10. SFR overestimation as a function of redshift for the Charlot & Fall (2000) (red) and Calzetti et al. (2000) (cyan) attenuation laws. |
Furthermore, we also examined the dependence of SFR estimates on the SFH module. Performing the entire process using a delayed plus additional burst SFH, we obtain an even higher overestimation when estimated using LSST observations alone, which again decreases at higher redshift.
We also inspected changes in the SFR difference when the best values were used instead of Bayesian values for the LSST-like sample. We find a consistency between the SFR from the LSST best fit and the one estimated from the UV-FIR best fit, finding log10(SFRLSST,best/SFRUV−FIR,best) very well distributed around zero with a scatter of 0.05 dex. This result shows a good agreement of the best templates of the two runs. It can be understood as follows: The fluxes for the LSST-like run were calculated based on the best template of the UV-FIR run. We confirm that the differences we found must be sought in the Bayesian analysis, which tends to overestimate the attenuation when it is employed on LSST data alone. Unfortunately, being estimated directly from the SED that best fits our data, the best-fit value has several drawbacks that make it unsuitable for this type of analysis. For example, it ignores the degeneracies that can be encountered because models with equally good fits can have very different properties. Moreover, the best fit in itself does not provide information about the uncertainties.
6. Application of the AFUV–Mstar relation to correct for the SFR overestimation
Previous results show major miscalculations of the SFR when LSST data alone are used. Due to the lack of information in the UV and MIR part of the spectrum, the SED fitting results in an overestimation of the attenuation, which leads to the general overestimation of the SFR. At the same time, as it is probed mainly from the optical emission of the galaxy, Mstar seems to be well estimated using LSST data alone. When we take into account that Mstar is the result of the previous star formation activity of the galaxy, which is responsible for producing the dust, it could be used as a promising tracer of the dust content.
Several works have recently explored possible relations of Mstar and dust attenuation (Xu et al. 2007; Martin et al. 2007; Buat et al. 2009; Bogdanoska & Burgarella 2020). Most of them suggest a possible linear relation between AFUV and log10(Mstar) over a wide mass range (9 ≤ log10(Mstar) ≤ 12). According to the literature, this relation is highly dependent on redshift.
Recently, Bogdanoska & Burgarella (2020, hereafter BB20), modelled a single parameter linear function, assuming a non-zero constant dust attenuation for low-mass galaxies (Eq. (6) in BB20). They used a sample of galaxies based on the selection criterion that requires IR excess7 (IRX) to be directly calculated from the IR-to-UV ratio or by SED fitting. This selection can introduce a bias in the local Universe and above redshift 2–3 due to the IR detection (at high redshift, only very dusty and massive galaxies are detected, while in the local universe, the IR-detected galaxies are rather rare). BB20 found that the AFUV–Mstar relation cannot be described with a simple linear function, and they concluded their work with a new relation between AFUV and Mstar as a function of redshift. In this section we try to use the AFUV–Mstar relation provided by BB20 to estimate the AFUV (we refer to it as AFUV BB20) of the LSST sample. The procedure is as follows: (1) from the LSST data we estimated the Mstar, (2) using Eqs. (5) and (6) from BB20, we calculated AFUV BB20, and finally, (3) we used AFUV BB20 as a prior of the new LSST CIGALE run.
Figure 11 shows the AFUV BB20 compared with the AFUV obtained from the full UV-FIR SED fitting as a function of Mstar. We find that the estimates AFUV BB20 are substantially lower than those obtained with the SED fitting process. The difference between AFUV BB20 and AFUV UV − FIR is shown in Fig. 12 (green line). The underestimation is accentuated for low-redshift objects. As expected, employing the AFUV BB20 as prior in the SED fitting process along with LSST observations results in an underestimation of the SFR, as shown in Fig. 13, where the ratios of the true SFR and the one derived by different methods are shown. We suspect that the reason for the substantial difference between the two estimates of AFUV can be traced back to the choice of the sample, as the sample used in BB20 is more general, while in our case, we focused on IR-bright galaxies to ensure the highest quality of the UV-FIR SED fitting process. It is clear from these results that we cannot directly empoly the relation of Bogdanoska & Burgarella (2020) to correct for the SFR overestimation for our sample.
 |
Fig. 11. AFUV as a function of stellar mass estimated from the UV-FIR SED fitting (blue density plot) compared with the AFUV estimated by employing Mstar from the relation of Bogdanoska & Burgarella (2020). |
We decided to incorporate the general idea presented in Bogdanoska & Burgarella (2020) and to use the AFUV–Mstar relation in order to correct the SFR for an LSST sample of data. We built a simplified relation that represented our sample of IR-bright main-sequence galaxies by following a procedure similar to that described by Bogdanoska & Burgarella (2020). For this purpose, we fit the AFUV estimated from the UV-FIR SED fitting as a function of the log10(Mstar). We used four redshift bins (0–0.5, 0.5–1.0, 1.0–1.5, and 1.5–2.5) to include the redshift dependence of the AFUV–Mstar relation. Linear, power-law, and exponential functions were tested to obtain the best fit, but we found a negligible difference between them. To be as consistent as possible with the results obtained in the previous works, we decided to use the linear function in the form
From the fitting process, we obtained a and b coefficients for each redshift bin. Table 5 shows all coefficients together with the uncertainties.
The blue line in Fig. 12 shows the difference between the AFUV − LSST calculated with our four linear relations and the one estimated from the UV-FIR SED fitting as a function of redshift. Our relation reproduces the far-UV attenuation (AFUV) derived from the fitting of the full SED better than the Bogdanoska & Burgarella (2020) relation. By employing the AFUV − LSST as a prior in the SED fitting along with LSST observations, we obtain the blue relation shown in Fig. 13. This figure shows that the SFR overestimation is fully corrected for when the AFUV − LSST prior is employed. This result also proves that knowing the AFUV–Mstar relation for a given sample of galaxies, it is possible to estimate SFR without the IR counterpart. This requires prior knowledge of the sample, which is often not available. We are aware that the relation constructed in this work may be applicable only to our sample, or at most to IR-bright normal star-forming galaxies, but further generalisation of our results is beyond the scope of this paper. However, considering the extreme usefulness of this relation for future surveys such as the LSST, we are planning to extend our analysis to a more general sample of galaxies in the next work.
 |
Fig. 12. Difference between AFUV estimated from AFUV–Mstar relations: Bogdanoska & Burgarella 2020 (green) and Eq. (2) with the coefficients reported in Table 5 (blue) and AFUV estimated from the UV-FIR SED fitting as a function of redshift. |
 |
Fig. 13. SFR ratio, defined as in Fig. 7, as a function of redshift. The result from the SED fitting employing LSST data alone is shown in red. Green and blue lines represent results from the SED fitting, adding as prior the AFUV from the relations of Bogdanoska & Burgarella (2020) and Eq. (2), respectively. |
7. Conclusions
We performed a reliability check of the physical properties estimation of MS galaxies by employing simulated LSST observations. For this purpose, we selected 50 135 and 15 754 objects from the ELAIS N1 and COSMOS fields, respectively, of the Herschel Extragalactic Legacy Project (HELP), in order to build the starting set of data to simulate observed LSST fluxes and to obtain reliable estimates of the physical properties of galaxies.
An important part of our analysis was the sample selection. We selected only galaxies from the so-called main sequence by removing all possible SBs from the sample using the same method as Rodighiero et al. (2011), and we removed passive galaxies using the method described in Salim et al. (2018). Furthermore, we also removed galaxies that contain AGN according to the selection of Stern et al. (2005). We also cleaned the sample from all non-typical galaxies by implementing additional quality criteria on physical properties following Małek et al. (2018): for our analysis we removed all galaxies for which Ldust and Mstar estimated from the full SED fitting (from UV to FIR) were different from those obtained from only the optical or only the infrared part of the spectrum. At the end of the sample selection, we selected 43 652 galaxies. This is 86% of the total sample.
We used this sample of MS galaxies as a prior to calculate the corresponding LSST fluxes in the ugrizy bands. We used the LSST simulation software package CatSim in order to simulate the uncertainties on the photometric measurements. We took the possible effects due to the hardware and observational components (e.g., detector, dark sky, and atmosphere) into account. We then estimated the main physical properties of galaxies by performing the SED fitting of the simulated LSST data by employing the same sets of modules and parameters as for the originally used HELP galaxies (Shirley et al. 2019, and in prep.).
We found that Mstar is well estimated by the LSST–like data set. At the same time, SFR, Ldust are overestimated using the LSST–like sample alone, while Mstar is completely unconstrained and dependent on the input parameters. The overestimation of the SFR is redshift dependent and clearly decreases with redshift. It disappears at about redshift ∼1. We found the relation that can correct the overestimation for the SFR parameter: log10(SFRratio) = 0.26 ⋅ z2 − 0.94 ⋅ z + 0.87.
We determined the photometric data that can be combined with the LSST data to remove the overestimation. In our analysis we used not simulated but real and sometimes uncompleted data to fully mimic the auxiliary data for the LSST because we do not expect to have better UV or FIR data soon. We found that the most efficient way to correct for the overestimation of the SFR is adding mid-IR observations (IRAC data), while Mstar is corrected for by adding the far-IR bands (SPIRE data). The addition of UV observations from GALEX does not correct the differences. Our findings suggest that the main problem of the pure LSST-like sample in the local Universe will be the inability to mimic the real attenuation for the old and young stellar populations.
By testing the input parameters of CIGALE, we found that the SFR overestimation is preserved using different attenuation laws that are commonly employed in the literature (e.g., Calzetti et al. 2000; Charlot & Fall 2000), but its trend as a function of the redshift changes. The estimate of Mstar is instead found to be dependent on both the input radiation field (Umin) and the attenuation law and is unconstrained if LSST data alone are employed for the SED fitting.
In Sect. 6 we showed that another efficient way to correct for the SFR is by exploiting a prior knowledge of AFUV, if this is available. We stress that the further analysis of the AFUV–Mstar relation can be useful for future surveys and help to properly estimate main physical parameters of galaxies without IR observations. As future work, we plan to extend this test to different SED fitting methods and HELP fields to confirm the systematics of our results.
Acknowledgments
We would like to thank William Pearson for his help in understanding our object’s behaviour in the SFR-Mstar diagram. G. R., K. M., A. N., M. H. and A. P. acknowledge support from the National Science Centre (UMO-2018/30/E/ST9/00082, UMO-2018/30/M/ST9/00757 and UMO-2020/38/E/ST9/00077). Authors are grateful for the support from Polish Ministry of Science and Higher Education through a grant DIR/WK/2018/12. We also thank the anonymous referee who has helped clarify and improve various aspects of this article.
References
- Aihara, H., Arimoto, N., Armstrong, R., et al. 2018, PASJ, 70, S4 [NASA ADS] [Google Scholar]
- Arnaboldi, M., Capaccioli, M., Mancini, D., et al. 1998, Messenger, 93, 30 [NASA ADS] [Google Scholar]
- Arnouts, S., Cristiani, S., Moscardini, L., et al. 1999, MNRAS, 310, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Arnouts, S., Le Floc’h, E., Chevallard, J., et al. 2013, A&A, 558, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Daddi, E., Magdis, G., et al. 2012, ApJ, 757, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Béthermin, M., Wu, H.-Y., Lagache, G., et al. 2017, A&A, 607, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bogdanoska, J., & Burgarella, D. 2020, MNRAS, 496, 5341 [NASA ADS] [CrossRef] [Google Scholar]
- Bolzonella, M., Miralles, J. M., & Pelló, R. 2000, A&A, 363, 476 [NASA ADS] [Google Scholar]
- Boquien, M., Burgarella, D., Roehlly, Y., et al. 2019, A&A, 622, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brammer, G. B., van Dokkum, P. G., & Coppi, P. 2008, ApJ, 686, 1503 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. J. I., Moustakas, J., Smith, J. D. T., et al. 2014, ApJS, 212, 18 [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Buat, V., Iglesias-Páramo, J., Seibert, M., et al. 2005, ApJ, 619, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Buat, V., Takeuchi, T. T., Burgarella, D., Giovannoli, E., & Murata, K. L. 2009, A&A, 507, 693 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buat, V., Ciesla, L., Boquien, M., Małek, K., & Burgarella, D. 2019, A&A, 632, A79 [CrossRef] [EDP Sciences] [Google Scholar]
- Burgarella, D., Buat, V., Gruppioni, C., et al. 2013, A&A, 554, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calzetti, D., Kinney, A. L., & Storchi-Bergmann, T. 1994, ApJ, 429, 582 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Liu, G., & Koda, J. 2012, ApJ, 752, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Chambers, K. C., Magnier, E. A., Metcalfe, N., et al. 2016, ArXiv e-prints [arXiv:1612.05560] [Google Scholar]
- Charlot, S., & Fall, S. M. 2000, ApJ, 539, 718 [Google Scholar]
- Cid Fernandes, R., Mateus, A., Sodré, L., Stasińska, G., & Gomes, J. M. 2005, MNRAS, 358, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Ciesla, L., Boselli, A., Elbaz, D., et al. 2016, A&A, 585, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Conroy, C. 2013, ARA&A, 51, 393 [NASA ADS] [CrossRef] [Google Scholar]
- da Cunha, E., Charmandaris, V., Díaz-Santos, T., et al. 2010, A&A, 523, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dale, D. A., Helou, G., Magdis, G. E., et al. 2014, ApJ, 784, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Dalton, G. B., Caldwell, M., Ward, A. K., et al. 2006, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, eds. I. S. McLean, M. Iye, et al., SPIE Conf. Ser., 6269, 62690X [Google Scholar]
- Donevski, D., Lapi, A., Małek, K., et al. 2020, A&A, 644, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donley, J. L., Koekemoer, A. M., Brusa, M., et al. 2012, ApJ, 748, 142 [Google Scholar]
- Draine, B. T., Aniano, G., Krause, O., et al. 2014, ApJ, 780, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, K. J., Brown, M. J. I., Williams, W. L., et al. 2018, MNRAS, 473, 2655 [NASA ADS] [CrossRef] [Google Scholar]
- Eales, S., Dunne, L., Clements, D., et al. 2010, PASP, 122, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Hwang, H. S., Magnelli, B., et al. 2010, A&A, 518, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elbaz, D., Leiton, R., Nagar, N., et al. 2018, A&A, 616, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Emerson, J., McPherson, A., & Sutherland, W. 2006, Messenger, 126, 41 [Google Scholar]
- Fabbiano, G. 2006, ARA&A, 44, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Fioc, M., & Rocca-Volmerange, B. 2019, A&A, 623, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Franzetti, P., Scodeggio, M., Garilli, B., Fumana, M., & Paioro, L. 2008, in Astronomical Data Analysis Software and Systems XVII, eds. R. W. Argyle, P. S. Bunclark, & J. R. Lewis, ASP Conf. Ser., 394, 642 [NASA ADS] [Google Scholar]
- González-Solares, E. A., Irwin, M., McMahon, R. G., et al. 2011, MNRAS, 416, 927 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [EDP Sciences] [Google Scholar]
- Han, Y., & Han, Z. 2014, ApJS, 215, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Hao, C.-N., Kennicutt, R. C., Johnson, B. D., et al. 2011, ApJ, 741, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrandt, H., Arnouts, S., Capak, P., et al. 2010, A&A, 523, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hurley, P. D., Oliver, S., Betancourt, M., et al. 2017, MNRAS, 464, 885 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Ž., Kahn, S. M., Tyson, J. A., et al. 2019, ApJ, 873, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Laigle, C., McCracken, H. J., Ilbert, O., et al. 2016, ApJS, 224, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Lawrence, A., Warren, S. J., Almaini, O., et al. 2007, MNRAS, 379, 1599 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Le Floc’h, E., Papovich, C., Dole, H., et al. 2005, ApJ, 632, 169 [Google Scholar]
- Leja, J., Johnson, B. D., Conroy, C., van Dokkum, P. G., & Byler, N. 2017, ApJ, 837, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Leja, J., Johnson, B. D., Conroy, C., & van Dokkum, P. 2018, ApJ, 854, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Lo Faro, B., Buat, V., Roehlly, Y., et al. 2017, MNRAS, 472, 1372 [NASA ADS] [CrossRef] [Google Scholar]
- Lonsdale, C. J., Smith, H. E., Rowan-Robinson, M., et al. 2003, PASP, 115, 897 [NASA ADS] [CrossRef] [Google Scholar]
- LSST Science Collaboration (Abell, P. A., et al.) 2009, ArXiv e-prints [arXiv:0912.0201] [Google Scholar]
- Małek, K., Buat, V., Roehlly, Y., et al. 2018, A&A, 620, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin, D. C., Small, T., Schiminovich, D., et al. 2007, ApJS, 173, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Mauduit, J. C., Lacy, M., Farrah, D., et al. 2012, PASP, 124, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Miettinen, O., Delvecchio, I., Smolčić, V., et al. 2017, A&A, 606, A17 [CrossRef] [EDP Sciences] [Google Scholar]
- Mitchell, P. D., Lacey, C. G., Baugh, C. M., & Cole, S. 2013, MNRAS, 435, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L43 [CrossRef] [Google Scholar]
- Noll, S., Burgarella, D., Giovannoli, E., et al. 2009, A&A, 507, 1793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oliver, S., Rowan-Robinson, M., Alexander, D. M., et al. 2000, MNRAS, 316, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Oliver, S. J., Bock, J., Altieri, B., et al. 2012, MNRAS, 424, 1614 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pearson, W. J., Wang, L., Hurley, P. D., et al. 2018, A&A, 615, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodighiero, G., Daddi, E., Baronchelli, I., et al. 2011, ApJ, 739, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Lee, J. C., Janowiecki, S., et al. 2016, ApJS, 227, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Boquien, M., & Lee, J. C. 2018, ApJ, 859, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Salvato, M., Hasinger, G., Ilbert, O., et al. 2009, ApJ, 690, 1250 [CrossRef] [Google Scholar]
- Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A&A, 575, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schreiber, C., Elbaz, D., Pannella, M., et al. 2016, A&A, 589, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schreiber, C., Elbaz, D., Pannella, M., et al. 2018, A&A, 609, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shirley, R., Roehlly, Y., Hurley, P. D., et al. 2019, MNRAS, 490, 634 [CrossRef] [Google Scholar]
- Silva, L., Granato, G. L., Bressan, A., & Danese, L. 1998, ApJ, 509, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Silverman, J. D., Rujopakarn, W., Daddi, E., et al. 2018, ApJ, 867, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Siudek, M., Małek, K., Pollo, A., et al. 2018, A&A, 617, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Speagle, J. S., Steinhardt, C. L., Capak, P. L., & Silverman, J. D. 2014, ApJS, 214, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Stauffer, J. R., Rebull, L. M., Backman, D. E., et al. 2005, Am. Astron. Soc. Meeting Abstr., 207, 63.11 [NASA ADS] [Google Scholar]
- Stern, D., Eisenhardt, P., Gorjian, V., et al. 2005, ApJ, 631, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Swinbank, A. M. 2013, in Thirty Years of Astronomical Discovery with UKIRT, 37 (Dordrecht: Springer Science+Business Media), 299 [CrossRef] [Google Scholar]
- Tacchella, S., Dekel, A., Carollo, C. M., et al. 2016, MNRAS, 457, 2790 [NASA ADS] [CrossRef] [Google Scholar]
- Takeuchi, T. T., Buat, V., & Burgarella, D. 2005, A&A, 440, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tojeiro, R., Heavens, A. F., Jimenez, R., & Panter, B. 2007, MNRAS, 381, 1252 [NASA ADS] [CrossRef] [Google Scholar]
- Vulcani, B., Poggianti, B. M., Fritz, J., et al. 2015, ApJ, 798, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Walcher, J., Groves, B., Budavári, T., & Dale, D. 2011, Ap&SS, 331, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Weaver, J. R., Kauffmann, O., Shuntov, M., et al. 2021, Am. Astron. Soc. Meeting Abstr., 53, 215.06 [NASA ADS] [Google Scholar]
- Whitaker, K. E., van Dokkum, P. G., Brammer, G., & Franx, M. 2012, ApJ, 754, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., Franx, M., Bezanson, R., et al. 2015, ApJ, 811, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., Pope, A., Cybulski, R., et al. 2017, ApJ, 850, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, R. J., Quadri, R. F., Franx, M., van Dokkum, P., & Labbé, I. 2009, ApJ, 691, 1879 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, C. K., Shupe, D., Buat, V., et al. 2007, ApJS, 173, 432 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Outlier selection
To implement additional quality criteria based on physical properties of the sample, we ran CIGALE two more times: (1) for optical data alone to estimate the stellar mass based on the optical measurements alone (from now, Mstar, OPT), and (2) for FIR data alone to calculate the dust luminosity (hereafter Ldust, IR). In Fig. A.1 we compare the physical properties obtained by employing this method with the properties from full-wavelength UV-FIR fits (Mstar, all and Ldust, all, respectively).
 |
Fig. A.1. Outlier selection. Comparison of Ldust, IR and Ldust, all (upper panel), and Mstar, OPT and Mstar, all (bottom panel). Ldust inconsistent objects are represented as magenta stars, and full blue stars correspond to the Mstar outliers. Grey circles represent objects with a consistent estimate of the Ldust and Mstar parameters. Inside each panel we present an example SED of the respective outliers represented with a black star. |
Based on this analysis, we eliminated galaxies that showed an Ldust and/or Mstar inconsistency with those estimated from the full SED fitting. Outliers were selected based on the distance from the 1:1 relation:
-
criterion 1: Ldust inconsistent (within the 2σ level) with the Ldust, IR
-
criterion 2: Mstar inconsistent (within the 3σ level) with the Mstar, OPT
As shown in Małek et al. (2018), the inconsistency between estimated Ldust values might be induced by energy balance issues of heavily dust-obscured galaxies or lensed objects. We also removed galaxies with an inconsistent Mstar estimation, mostly due to problems with optical and IR catalogues matching. Figure A.1 also shows two example SEDs for objects considered as outliers. Based on these criteria, we removed 1642 ELAIS N1 sources (4.5% of the total sample) and 460 COSMOS sources (3.2% of the total sample) with inconsistent estimates of Ldust. The Mstar inconsistency removed 475 (1.3% of the total sample) and 214 (1.5% of the total sample) galaxies for the ELAIS N1 and the COSMOS field, respectively.
Appendix B: AGN selection
The AGN selection in ELAIS N1 and COSMOS fields. We used two different selection criteria based on the MIR features (IRAC bands) analysis: Stern et al. (2005) and Donley et al. (2012). Figure B.1 shows the IRAC colour-colour selection using the methods of Donley et al. (2012) (upper panels) and Stern et al. (2005) (lower panels). The redshift distribution of selected AGNs is shown in Fig. B.2.
 |
Fig. B.1. IRAC colour-colour diagrams for the ELAIS N1 (left column) and COSMOS (right column) fields. The AGNs (magenta points) are selected following the criteria described in Donley et al. 2012 (upper row, black line) and Stern et al. 2005 (lower row, black line). |
 |
Fig. B.2. AGN redshift distribution for the full sample of ELAIS N1 +COSMOS fields. |
Appendix C: Simulating GALEX data
 |
Fig. C.1. SFR ratio, defined as in Fig. 7, estimated with LSST data alone (red) and LSST plus simulated GALEX observations (GALEXtrue, in blue). Differently from the result shown in Fig. 9, in this case we are able to correct the overestimation, underlining the effect that high-quality UV observations would have on the SFR estimate, when available for the entire sample. |
Appendix D: Scatter of the MS
Star-forming galaxies follow a relatively tight, almost linear relation between SFR and Mstar that is known as the MS. One of the most noticeable feature is that the MS relation at any given redshift shows a rather small scatter of σMS that can vary from ∼0.2 to ∼0.4 dex (Whitaker et al. 2012, Speagle et al. 2014, Pearson et al. 2018). Here we discuss the scatter of our sample from the MS, given that high scatter could lead to an incorrect estimate of the physical parameters. Figure D.1 shows the scatter of our objects from two reference main-sequence laws (Speagle et al. 2014; Whitaker et al. 2017), and we compare the results with the MS intrinsic scatter in the literature (Speagle et al. 2014; Pearson et al. 2018). The scatter found in our sample agrees with the scatter found previously in literature within the error bars. This is also valid for the lowest redshift bin where the scatter appears to be the largest. Therefore we are confident that these are MS objects and that the input parameters are adequate to provide us with reliable physical properties for the purposes of this analysis. The origin of this scatter can be traced back to different enhancement or decrement events of star formation that could occur during the galaxy lifetime. Large-scale gas inflow or outflow events can trigger gas compaction or depletion phenomena that can lead to an enhancement or decrement of the SFR of the galaxy (Tacchella et al. 2016).
 |
Fig. D.1. Intrinsic scatter of our objects around exemplar MS compared with the results found in previous works. Red and green points represent the scatter of our objects from the Speagle et al. (2014) and Whitaker et al. (2017) MS, respectively, blue points represent the results found in Pearson et al. (2018), and grey stars, triangles, and diamonds represent the results presented in Speagle et al. (2014). |
All Tables
Total number of galaxies and SB percentage for ELAIS and COSMOS fields in each redshift range.
Number of AGNs selected based on the MIR features for the ELAIS N1 and COSMOS fields.
All Figures
 |
Fig. 1. Left panel: example of the sSFR distribution of ELAIS N1 galaxies in the redshift range 1 < z < 1.5 obtained with the delayed SFH plus an additional burst. The orange line respresents the Gaussian fit, and the dashed black line corresponds to the division of starburst (SB galaxies are located on the right side of the line) and MS galaxies. The division is located 3σ away from the centre of the Gaussian. Right panel: MS distribution for the same redshift bin. Magenta circles represent SB galaxies selected from the sSFR distribution shown in the left panel. The dashed black line represents the Speagle et al. (2014) MS. |
| In the text | |
 |
Fig. 2. sSFR distribution in four different redshift bins obtained with delayed SFH plus an additional burst. Open histograms are the galaxy distributions (MS+SB) derived in this work, the dashed black line is the division between SBs (right side of the line) and MS (left side of the line) in our sample, and the cyan full histograms represent the simulated SB sample from B17. The division is located at about 3σ from the Gaussian centre. The sample is the same as for Fig. 1, but the binning is different. |
| In the text | |
 |
Fig. 3. Redshift distribution of ELAIS-N1 and COSMOS samples based on the approach of Duncan et al. (2018). |
| In the text | |
 |
Fig. 4. Magnitude errors vs observed apparent magnitudes for simulated LSST observations from the ELAIS N1 sample. Simulations are cut to the maximum LSST limit. The choice to vary simulation parameters allows us to obtain different errors for similar magnitude values, as we would expect in the case of real observations. The brightest end we reached is 13 mag, but for clarity of the plot, we cut it at 21 mag. |
| In the text | |
 |
Fig. 5. Comparison of SEDs evaluated for the same object at z ∼ 1 using the full UV-to-IR observations (upper panel) and the LSST optical bands alone (bottom panel). The blue square represents the observed fluxes, and red dots represent the fluxes predicted by the model. The magenta lines delimit the division between optical and IR bands, which is taken into account by CIGALE. The IR emission is not constrained for the LSST estimate. |
| In the text | |
 |
Fig. 6. Main-sequence (SFR vs. Mstar) relation for the ELAIS N1 and COSMOS fields in four redshift bins. In blue we show the LSST-like sample, and in black the real sample. The solid black line represents the MS by Speagle et al. (2014), and the dashed lines mark the loci two times above and below the MS. This plot shows a clear SFR overestimate obtained using LSST bands alone, which tends to disappear at higher redshift ranges. |
| In the text | |
 |
Fig. 7. Ratios of different physical properties obtained from fitting the simulated LSST data alone and from the UV-FIR SED (e.g., SFRratio = SFRLSST/SFRUV − FIR) as a function of redshift for the ELAIS N1 and COSMOS fields. The properties obtained from the UV-FIR SED fitting are considered as the true values. From the upper left panel we show clockwise the SFR, Mstar, Ldust, and Mstar comparisons. The dashed lines represent polynomial fits performed on the samples. The points are the median values in each redshift bin, with the median absolute deviation as errors. A ratio equal to zero corresponds to a perfect agreement between the estimates obtained based on the LSST-like sample and the real values. The distributions calculated for ELAIS N1 and COSMOS are comparable within the errors. |
| In the text | |
 |
Fig. 8. LSST coverage of an example SED at different redshifts indicated in the panel. |
| In the text | |
 |
Fig. 9. Upper left panel: SFR ratio, defined as in Fig. 7, estimated with LSST observations alone (red) and with LSST+IRAC observations (blue). The two samples disagree at low redshift, but the comparison improves at high redshift, highlighting the redshift dependence of the results. With the addition of MIR observations, the LSST-only estimates are consistent with the UV-IR estimates. Upper right panel: same comparison, but adding FIR SPIRE observations. In this case we did not fully remove the overestimation, which highlights that the problem lies in the lack of rest-frame MIR data. Lower left panel: same as in the other panels, but adding GALEX observations. We obtain a slight decrease in the overestimation. For this comparison we considered the ∼3000 objects that have a counterpart in the GALEX database. Lower right panel: Mstar ratio evaluated with LSST observations alone (red) and with LSST+SPIRE observations (blue). The results are consistent with the ‘real’ ratio with a very low scatter. |
| In the text | |
 |
Fig. 10. SFR overestimation as a function of redshift for the Charlot & Fall (2000) (red) and Calzetti et al. (2000) (cyan) attenuation laws. |
| In the text | |
 |
Fig. 11. AFUV as a function of stellar mass estimated from the UV-FIR SED fitting (blue density plot) compared with the AFUV estimated by employing Mstar from the relation of Bogdanoska & Burgarella (2020). |
| In the text | |
 |
Fig. 12. Difference between AFUV estimated from AFUV–Mstar relations: Bogdanoska & Burgarella 2020 (green) and Eq. (2) with the coefficients reported in Table 5 (blue) and AFUV estimated from the UV-FIR SED fitting as a function of redshift. |
| In the text | |
 |
Fig. 13. SFR ratio, defined as in Fig. 7, as a function of redshift. The result from the SED fitting employing LSST data alone is shown in red. Green and blue lines represent results from the SED fitting, adding as prior the AFUV from the relations of Bogdanoska & Burgarella (2020) and Eq. (2), respectively. |
| In the text | |
 |
Fig. A.1. Outlier selection. Comparison of Ldust, IR and Ldust, all (upper panel), and Mstar, OPT and Mstar, all (bottom panel). Ldust inconsistent objects are represented as magenta stars, and full blue stars correspond to the Mstar outliers. Grey circles represent objects with a consistent estimate of the Ldust and Mstar parameters. Inside each panel we present an example SED of the respective outliers represented with a black star. |
| In the text | |
 |
Fig. B.1. IRAC colour-colour diagrams for the ELAIS N1 (left column) and COSMOS (right column) fields. The AGNs (magenta points) are selected following the criteria described in Donley et al. 2012 (upper row, black line) and Stern et al. 2005 (lower row, black line). |
| In the text | |
 |
Fig. B.2. AGN redshift distribution for the full sample of ELAIS N1 +COSMOS fields. |
| In the text | |
 |
Fig. C.1. SFR ratio, defined as in Fig. 7, estimated with LSST data alone (red) and LSST plus simulated GALEX observations (GALEXtrue, in blue). Differently from the result shown in Fig. 9, in this case we are able to correct the overestimation, underlining the effect that high-quality UV observations would have on the SFR estimate, when available for the entire sample. |
| In the text | |
 |
Fig. D.1. Intrinsic scatter of our objects around exemplar MS compared with the results found in previous works. Red and green points represent the scatter of our objects from the Speagle et al. (2014) and Whitaker et al. (2017) MS, respectively, blue points represent the results found in Pearson et al. (2018), and grey stars, triangles, and diamonds represent the results presented in Speagle et al. (2014). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.