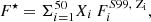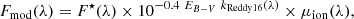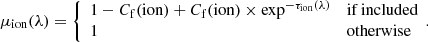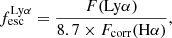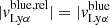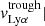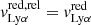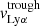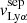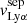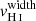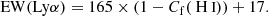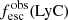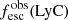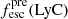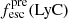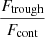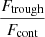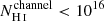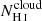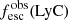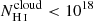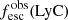| Issue |
A&A
Volume 639, July 2020
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 28 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202038096 | |
| Published online | 13 July 2020 | |
The origin of the escape of Lyman α and ionizing photons in Lyman continuum emitters
1
Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
e-mail: s.r.n.gazagnes@rug.nl
2
Observatoire de Genève, Université de Genève, 51 Ch. des Maillettes, 1290 Versoix, Switzerland
3
University of California-Santa Cruz, 1156 High Street, Santa Cruz, CA 95064, USA
4
CNRS, IRAP, 14 avenue E. Belin, 31400 Toulouse, France
5
Bogolyubov Institute for Theoretical Physics, National Academy of Sciences of Ukraine, 14-b Metrolohichna str., Kyiv 03143, Ukraine
Received:
5
April
2020
Accepted:
13
May
2020
Context. Identifying the physical mechanisms driving the escape of Lyman continuum (LyC) photons is crucial for the search of Lyman continuum emitter (LCE) candidates.
Aims. To understand the physical properties involved in the leakage of LyC photons, we investigate the connection between the H I covering fraction, H I velocity width, the Lyman α (Lyα) properties, and the escape of LyC photons in a sample of 22 star-forming galaxies, which includes 13 confirmed LCEs.
Methods. We fit the stellar continuum, dust attenuation, and absorption lines between 920 Å and 1300 Å to extract the H I covering fractions and dust attenuation. Additionally, we measure the H I velocity widths of the optically thick Lyman series and derive the Lyα equivalent widths (EW), escape fractions (fesc), peak velocities, and fluxes at the minimum of the observed Lyα profiles.
Results. Overall, we highlight strong observational correlations between the presence of low H I covering fractions and the observation of (1) low Lyα peak velocities; (2) more flux at the profile minimum; and (3) larger EW(Lyα), fesc(Lyα), and fescobs(LyC). Hence, low column density channels are crucial ISM ingredients for the leakage of Lyα and LyC photons. Additionally, galaxies with narrower H I absorption velocity widths have higher Lyα equivalent widths, larger Lyα escape fractions, and lower Lyα peak velocity separations. This may suggest that these galaxies have low H I column density. Finally, we find that dust also regulates the amount of Lyα and LyC radiation that actually escapes the ISM.
Conclusions. The ISM porosity is one of the origins of strong Lyα emission, enabling the escape of ionizing photons in low-z leakers. However, this is not sufficient to explain the largest fescobs(LyC), which indicates that the most extreme LCEs are likely to be density-bounded along all lines of sight to the observer. Overall, the neutral gas porosity provides a constraint for a lower limit to the escape fraction of LyC and Lyα photons, which offers a key estimator for assessing the leakage of ionizing photons.
Key words: dark ages, reionization, first stars / galaxies: ISM / ultraviolet: ISM / ISM: abundances / ISM: lines and bands / dust, extinction
© ESO 2020
1. Introduction
The Epoch of Reionization (EoR) is a key transition phase in the history of the Universe that is still largely unconstrained in observations. In the upcoming era of large telescopes, numerous galaxies within the EoR will be observable, however, determining the mechanisms responsible for the propagation of the ionizing radiation from the interstellar medium (ISM) to the intergalactic medium (IGM) is a crucial component of such future studies. Although the ionizing contribution of AGN during reionization is actively discussed (Fontanot et al. 2012, 2014; Robertson et al. 2015; Madau & Haardt 2015; Mitra et al. 2018; Dayal & Ferrara 2018; Dayal et al. 2020), many studies suggest that a population of low-mass star-forming galaxies with an average escape fraction of Lyman Continuum (LyC) photons of 10–20% probably dominates the contribution to the ionizing budget of the EoR (Ouchi et al. 2009; Robertson et al. 2013; Dressler et al. 2015; Finkelstein et al. 2019). However, the quest to find LyC leaking galaxies at high redshift (z > 6) is very challenging and direct observations of the ionizing flux at λ < 912 Å are complicated (or statistically unfeasible) due the attenuation of the IGM and the presence of interlopers along the line of sight.
These caveats have been overcome by searches for compact, low-mass, star-forming galaxies in the local universe, which can serve as analogs, and significant progress has been made over the past few years, with successful detections of LyC leakage at z < 0.5 (15 individual detections, Bergvall et al. 2006; Leitet et al. 2013; Borthakur et al. 2014; Leitherer et al. 2016; Izotov et al. 2016a,b, 2018a,b), and at z ∼ 2−3 (Vanzella et al. 2015; de Barros et al. 2016; Shapley et al. 2016; Bian et al. 2017; Steidel et al. 2018; Fletcher et al. 2019; Rivera-Thorsen et al. 2019). This recent breakthrough has provided an ideal laboratory for the exploration of the physical properties that favor the leakage of ionizing radiation in the LyC leakers.
Studies commonly refer to two major physical models in the aim of understanding how LyC photons escape galaxies (see e.g., Zackrisson et al. 2013). In a density-bounded ISM, the H I column density (NH I) surrounding the stellar populations is too low (< 1017.9 cm−2) to efficiently absorb all the ionizing photons passing through the neutral clouds and the fraction of LyC radiation that escapes the ISM is proportional to the residual NH I in the galaxy. Conversely, in a “picket-fence” or “ionization-bounded” system, the bulk of the stars is surrounded by an optically thick ISM, where the average NH I is high enough to efficiently absorb the LyC photons. In this model, ionizing photons escape through privileged paths through the ISM, referred to as holes or channels, which have no or little H I column densities. This scenario is mainly characterized by the porosity of the neutral gas, which is defined as the fraction of all sightlines to all of the ensemble of far-UV continua sources that are “covered” by H I gas with column densities above a certain value. One way to define this H I “covering fraction” (Cf(H I)) is by using a set of H I absorption lines in the far-UV that have a range of oscillator strengths and saturate above a certain column density (between ∼1015 and 1016 cm−2 for the range from Lyβ to Ly7). The range of oscillator strengths allows for simultaneous optical depth and covering fraction determination of the Lyman series lines. The H I covering fraction measured using this approach is always a lower limit to the true geometric covering fraction of the neutral gas, because of potential kinematic effects (Jones et al. 2013; Rivera-Thorsen et al. 2015; Vasei et al. 2016), or the presence of H I residuals (Kakiichi & Gronke 2019). Nevertheless, in this paper, we use this measure of Cf(H I) as a proxy of the overall neutral gas porosity and study how that porosity relates to the escape of Lyman α (Lyα) and LyC photons.
Investigating which model represents the ISM of Lyman continuum emitters (LCEs) is also crucial for finding indirect tracers of the leakage of ionizing photons. For this purpose, low-redshift observations continue to be the ideal approach. Indeed, far-UV spectroscopic observations are less likely to be contaminated by line-of-sight absorbers in the IGM, thus their LyC escape fraction can be measured directly from the flux at λ < 912 Å. Additionally, the study of their UV H I and metal lines constrain their neutral gas properties and identify the processes driving the LyC leakage. Reliable LyC probes have already been identified by studying the Lyα properties (see e.g., Verhamme et al. 2017; Izotov et al. 2018b, 2020).
Lyα also provides powerful insights on the distribution and kinematics of the neutral gas, and is closely related to the LyC properties. Indeed, the ionizing radiation arising from young massive stars creates H II regions surrounding the star-forming clusters, which produces Lyα radiation due to the recombination of hydrogen atoms. Lyα photons are resonantly scattered as they travel through the neutral gas, and the amount of scattering events, which is determined by the H I gas distribution and column density, strongly impacts the shape of the Lyα profile. Since Lyα and LyC photons interact with the same neutral gas, the underlying physical mechanisms driving their leakage are expected to be closely connected.
Nevertheless, this is not a trivial aspect because the Lyα transition is resonant. While LyC photons cannot escape from optically thick ISM, Lyα photons pass through dense neutral clouds by being scattered out of the velocity range covered by the neutral gas. The theoretical connection between Lyα and LyC was first investigated using radiative transfer models (Verhamme et al. 2015; Dijkstra et al. 2016). These studies highlighted that the Lyα spectral shape provides insights on the H I column density or the existence of holes in the neutral gas spatial distribution. The presence of paths entirely cleared of H I gas in the ISM should imprint a single Lyα peak emission at the systemic velocity, nevertheless, the presence of a double-peaked Lyα profile with a narrow peak separation in all the confirmed LCEs has suggested that they have density-bounded ISMs (Verhamme et al. 2017; Izotov et al. 2018b). However, a follow-up study revealed the presence of saturated Lyman series with non-unity covering fraction (Gazagnes et al. 2018). This outcome favors an ionization bounded model with holes in an optically thick interstellar medium, which appears, at first sight, to be incompatible with their double-peaked Lyα profile. Additionally, Steidel et al. (2018) reported a correlation between the EW(Lyα and the H I covering fraction in stacks of z ≈ 3 galaxies, while McKinney et al. (2019) found a significant trend connecting the escape fraction of Lyα photons and the Si II covering fraction in a sample of extreme Green Peas (GPs). Hence, the latest studies suggest that the ISM is likely to be a very complex environment and improved Lyα radiative transfer models are needed to constrain the origin of the connection between the Lyα spectral shape and the escape of LyC photons.
Promising insights were recently made by Lyα simulation studies showing that either a very clumpy distribution of neutral gas or low-density channels produced by turbulence could favor the leakage of LyC photons and create a double peak Lyα profile with low 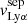 (Gronke et al. 2016, 2017; Kimm et al. 2019; Kakiichi & Gronke 2019). On the other hand, Jaskot et al. (2019) recently proposed that different Lyα markers probe different ISM properties; the peak separation could trace the presence of low-density gas, while the covering fraction relates to the gas porosity. Hence, further clarifications with regard to the physical properties of the neutral gas of known LCEs are crucial for testing the reliability of the Lyα-LyC correlations and to investigate the accuracy of indirect fesc(LyC)1 predictions that use the H I covering fraction (Chisholm et al. 2018).
(Gronke et al. 2016, 2017; Kimm et al. 2019; Kakiichi & Gronke 2019). On the other hand, Jaskot et al. (2019) recently proposed that different Lyα markers probe different ISM properties; the peak separation could trace the presence of low-density gas, while the covering fraction relates to the gas porosity. Hence, further clarifications with regard to the physical properties of the neutral gas of known LCEs are crucial for testing the reliability of the Lyα-LyC correlations and to investigate the accuracy of indirect fesc(LyC)1 predictions that use the H I covering fraction (Chisholm et al. 2018).
In this work, we investigate the connection between the ISM porosity (characterized by the H I covering fraction), the Lyα properties, and the LyC escape fraction in an unique sample of 22 star-forming galaxies, including 13 confirmed LCEs, which are characterized by neutral hydrogen Lyman series and Lyα observations. While we focus primarily on the presence of (dusty) low-density channels to explain the escape of LyC and Lyα photons, we also explore the impact of the width of saturated H I absorption lines on the spectral shape of the Lyα profile.
This paper is organized as follows: Sect. 2 describes the observational data. Section 3 defines the methods used to measure the neutral gas and Lyα properties of the galaxies in our sample. In Sect. 4, we compare and discuss the connection between the spatial distribution and kinematics of neutral gas on both the Lyα properties and the escape of LyC photons. In Sect. 5, we discuss how the porosity of the neutral gas triggers the LyC leakage and how it can be used to provide a lower limit to the total escape fraction of LyC photons in high-z galaxies. Finally, we summarize our main conclusions in Sect. 6.
2. Data
In this work, we investigate the relation between the neutral gas covering fraction, Lyα properties, and the escape of LyC photons in the sample of 22 star-forming galaxies, listed in Table 1. We selected these galaxies because they have publicly available rest-frame UV spectroscopy both for Lyα and for the rest of the Lyman series (i.e., between Lyman-β at 1025 Å and the Lyman limit at 912 Å). The latter can be observed with a spectral resolution R > 1500 for galaxies at z > 0.18 with the Cosmic Origins Spectrograph (COS) onboard the Hubble Space Telescope (HST; Green et al. 2012). The relation between the neutral gas properties and the escape of ionizing photons has already been explored for 16 of the 22 galaxies (Gazagnes et al. 2018; Chisholm et al. 2018). This includes 13 low redshift galaxies (z < 0.4), seven of which are confirmed LyC emitting galaxies; J0925+1409, J1503+3644, J1152+3400, J1333+6246, J1442−0209 from Izotov et al. (2016a, b), J0921+4509 from Borthakur et al. (2014) and Tol1247−232 from Leitherer et al. (2016). Four of them are Green Peas (GP) (Henry et al. 2015), two are Lyman break analogs (LBA) (Heckman et al. 2011, 2015) and the three remaining galaxies are gravitationally lensed galaxies at z ≈ 3 (SGAS J122651.3+215220, SGAS J152745.1+065219, and the Cosmic Eye, Stark et al. 2008; Koester et al. 2010) from the Magellan Evolution of Galaxies Spectroscopic and Ultraviolet Reference Atlas (MEGaSaURA; Rigby et al. 2018). Additionally, our sample includes six new galaxies that were not included in Gazagnes et al. (2018); specifically, the recently discovered low redshift (0.2 < z < 0.5) LyC emitting galaxies: J1154+2443, J1243+4646, J1256+4509, J1011+1947, J0901+2119, and J1248+4249 from Izotov et al. (2018a, b). Three of these six galaxies have extreme LyC escape fractions of 38, 46, and 72.6%.
Properties of galaxies with Lyman series observations.
Nineteen of the galaxies observed with HST/COS are at such redshift that at least the Lyβ line is observable with the COS G140L or G130M gratings. The resolving power (R) of the rest-frame UV spectra around the Lyman series is ≈1500 for all the confirmed leakers, except that of J0921+4509, which has a R ≈ 15 000 G130M spectra. The four GPs and the two LBAs have observations of one or several H I absorption lines with a spectral resolution of ≈15 000. Additionally, all the Lyα profiles were observed with the medium resolution grating G160M (R ≈ 16 000 at 1600 Å). The data for the 13 leakers were reduced using CALCOSv2.21 and a custom method for faint COS spectra (Worseck et al. 2016). The other COS/HST data were reduced with CALCOSv2.20.1 and the methods from Wakker et al. (2015). The three MEGaSaURA galaxies have been observed with the MagE spectrograph on the Magellan Telescopes (Marshall et al. 2008) and have moderate resolution spectroscopy (R ∼ 3000) both for their Lyman series and Lyα. They are the only galaxies in the MEGaSaURA sample with a signal-to-noise ratio (S/N) that is sufficient (> 2) to constrain their neutral gas properties with the Lyman series. In this paper, we use the following short names for the two sources: SGAS J122651.3+215220 = SGAS J1226 and SGAS J152745.1+065219 = SGAS J1527.
Table 1 summarizes the galaxy properties of the sample. The metallicities have been derived from the optical [O III] 4366 Å oxygen emission lines, using the direct Te method, in all the low redshift galaxies. The metallicity of the Cosmic Eye has been measured by Stark et al. (2008) using the R23 index, and an upper limit has been derived from the [N II]/Hα ratio for SGAS J1527 (12+log(O/H) < 8.5; Wuyts et al. 2012). The metallicity of SGAS J1226 has not been measured because these lines are not accessible from the ground. Several different measurements of the escape fraction of ionizing photons from Tol1247-232 are reported in the literature: 4.2 ± 1.2% in Leitherer et al. (2016), < 0.4% in Chisholm et al. (2017a) and 1.5 ± 0.5% in Puschnig et al. (2017). We used the value derived in Chisholm et al. (2017a) since the measurement method is consistent with the one used for the other leakers.
3. Method
Here we describe the methods used to study the ISM and Lyα properties of the 22 galaxies in our sample.
3.1. Neutral gas properties
To measure the H I velocity shift and covering fraction of the galaxies, we used the approach detailed in Gazagnes et al. (2018) and we recall the main steps in this section. We first correct the galaxy spectra for Milky Way extinction using the Cardelli et al. (1989) extinction law, R(V) = 3.1, and the galactic EB − V reported in the NASA Extragalactic Database (NED2). We then fit the stellar continuum as in Chisholm et al. (2019), including dust extinction, metal and H I absorption lines to consistently determine the UV attenuation in the galaxy, as well as the column densities and covering fractions of the individual ions. The stellar continuum model, F⋆, is a linear combination of 50 single-age fully theoretical stellar continuum models with 5 metallicities, 0.05, 0.2, 0.4, 1, and 2 Z⊙, with ages of 1, 2, 3, 4, 5, 8, 10, 15, 20, and 40 Myr, drawn from the STARBURST99 library (S99; Leitherer et al. 1999). This is numerically given as:
where Xi and 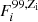 are, respectively, the linear coefficients and the STARBURST99 theoretical stellar continuum models for a given age and metallicity. The S99 spectra were computed with the WM-Basic spectral library (Leitherer et al. 2010), using a Kroupa initial mass function with a high and low mass exponent of 2.3 and 1.3, respectively, a high-mass cutoff of 100 M⊙, and the stellar evolution tracks with high mass-loss from Meynet et al. (1994). Additionally, the large amount of ionizing photons produced by young massive stars produces free-free, free-bound, and two-photon nebular continuum emission, and they can have a significant impact on the total continuum flux in young, low-metallicity stellar populations (Steidel et al. 2016; Byler et al. 2018). Following the procedure detailed in Chisholm et al. (2019), we created a nebular continuum for each single-age and metallicity stellar model using Cloudy v17.0 (Ferland et al. 2013, 2017), assuming similar gas-phase metallicity and stellar metallicity, a volume hydrogen density of 100 cm−3, and an ionization parameter log(U) = −2.5. The final output nebular continua were added to the stellar models and the final synthetic spectra have a spectral resolution R ≈ 2500, which is convolved to the resolution of the data. We used the far-UV dust attenuation curve from Reddy et al. (2016a) and an uniform dust screen model to account for the dust attenuation.
are, respectively, the linear coefficients and the STARBURST99 theoretical stellar continuum models for a given age and metallicity. The S99 spectra were computed with the WM-Basic spectral library (Leitherer et al. 2010), using a Kroupa initial mass function with a high and low mass exponent of 2.3 and 1.3, respectively, a high-mass cutoff of 100 M⊙, and the stellar evolution tracks with high mass-loss from Meynet et al. (1994). Additionally, the large amount of ionizing photons produced by young massive stars produces free-free, free-bound, and two-photon nebular continuum emission, and they can have a significant impact on the total continuum flux in young, low-metallicity stellar populations (Steidel et al. 2016; Byler et al. 2018). Following the procedure detailed in Chisholm et al. (2019), we created a nebular continuum for each single-age and metallicity stellar model using Cloudy v17.0 (Ferland et al. 2013, 2017), assuming similar gas-phase metallicity and stellar metallicity, a volume hydrogen density of 100 cm−3, and an ionization parameter log(U) = −2.5. The final output nebular continua were added to the stellar models and the final synthetic spectra have a spectral resolution R ≈ 2500, which is convolved to the resolution of the data. We used the far-UV dust attenuation curve from Reddy et al. (2016a) and an uniform dust screen model to account for the dust attenuation.
Absorption lines from different ions were included using Voigt profiles defined by four free parameters: the velocity shift (vshift), the Doppler parameter (b), the column density (N), and the covering fraction (Cf). The linear combination of stellar continuum models, interstellar absorption lines, and dust attenuation produces the final fitted spectrum.
As we are interested in the Lyman series, the spectral region that we fit is taken from 912 to 1050 Å. We include redder portions of the spectrum, up to 1300 Å, to further constrain the stellar model and dust attenuation. We aimed at including all the H I absorption lines that are observed to improve the constraints on the H I parameters. Nevertheless, in practice, the wavelength regime from 912 to 930 Å were excluded due to low S/N or geocoronal emission. Additionally, Lyβ is not systematically fit since it is located close to a strong O VI P Cygni profile, which synthetic stellar models sometimes fail to reproduce (see the fits in Appendix A), and it often decreases the fit quality when combined with bluer H I absorption lines. The O I absorption lines that directly blend with the Lyman series are always included and their parameters are mostly constrained by the O I 989 and 1039 Å lines. However, because of low S/N or low NO I, the latter are not always resolved, such that we cannot accurately recover the O I contribution in these galaxies. Finally, absorption lines from O VI, Si II, C II, C III or from the Milky Way are sometimes added, provided that they improve the fit around the Lyman series. For more details, see Gazagnes et al. (2018).
Assuming a foreground dust attenuation, the final fitted model, Fmod(λ), can be expressed as
where μion(λ) represents the fitted profiles of absorption lines given by:
Equation (2) assumes that all the photons escaping the ISM are affected by the same dust extinction. In practice, galaxies include several star-forming clumps, which might not be affected by the same dust attenuation. Thus, the recovered EB − V should be interpreted as the mean extinction in the galaxy.
The fitting method is based on an IDL routine that uses nonlinear least squares fitting, MPFIT (Markwardt et al. 2009), and returns the best fit parameters and their statistical errors for each free parameter fitted. In this work, we focus mainly on the fitted H I parameters: 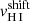 , NH I and Cf(H I). As discussed in Jones et al. (2013), Rivera-Thorsen et al. (2015) and Vasei et al. (2016), the interpretation of the measured Cf must be taken with caution. This is because the kinematics of the absorbing gas impacts the observed depth of the absorption lines. Indeed, two dense H I clouds with non-overlapping velocity distributions and each covering half of the galaxy will imprint H I absorption lines with Cf(H I) = 0.5. However, in this case, the total geometrical covering fraction is 1 because LyC photons are insensitive to kinematic effects (the H I absorbs ionizing photons at all wavelengths below the Lyman limit). Hence, Cf(H I) is always a lower limit to the covering fraction seen by the ionizing photons. Nevertheless, we showed in Gazagnes et al. (2018) that it seems to be a good proxy to the true geometric covering fraction of the optically thick H I clouds in the current sample.
, NH I and Cf(H I). As discussed in Jones et al. (2013), Rivera-Thorsen et al. (2015) and Vasei et al. (2016), the interpretation of the measured Cf must be taken with caution. This is because the kinematics of the absorbing gas impacts the observed depth of the absorption lines. Indeed, two dense H I clouds with non-overlapping velocity distributions and each covering half of the galaxy will imprint H I absorption lines with Cf(H I) = 0.5. However, in this case, the total geometrical covering fraction is 1 because LyC photons are insensitive to kinematic effects (the H I absorbs ionizing photons at all wavelengths below the Lyman limit). Hence, Cf(H I) is always a lower limit to the covering fraction seen by the ionizing photons. Nevertheless, we showed in Gazagnes et al. (2018) that it seems to be a good proxy to the true geometric covering fraction of the optically thick H I clouds in the current sample.
In Gazagnes et al. (2018), we used simulations to show that the NH I derived from the fits suffers from large uncertainties due to the degeneracy between the Doppler parameter b and the column density when the absorption lines are saturated. The typical resolution and S/N of the observations is too low to constrain NH I directly from the Lyman series. Consequently, we neither report nor use the NH I and b values derived using our fitting procedure. Alternatively, one can indirectly estimate NH I using an approach based on NO I and the metallicity, 12 + log(O/H). Nevertheless, O I is not detected in six galaxies, which might be due to low S/N, small NO I or low covering fraction. Conversely, we established in Gazagnes et al. (2018) that the H I covering fraction can be inferred with a reasonable accuracy from Voigt fitting methods given the spectral resolution and S/N of the galaxies observed in our sample. A systematic error, relative to the resolution and S/N of a given spectrum, needs to be included in the final error term because the statistical error returned by MPFIT does not account for it (see Sect. 2 and Table 3 in Gazagnes et al. 2018). The typical systematic error of the covering fraction derived from spectra with R = 1500 (typical resolution of the GL140 grating) and S/N ≈ 2 is 0.10. We note that this typical systematic error is only valid if the Lyman series lines are saturated. When the H I absorption lines are not saturated, the residual flux at the bottom of an absorption line is similarly impacted by the presence of low NH I and/or low Cf(H I), such that an accurate constraint on these parameters would require higher S/N and resolution.
Figure 1 shows the observed flux, the error on the flux, and the best fit obtained for the galaxy J1256+4509 using our fitting approach. It highlights the main regions masked during the fits, either due to geo-coronal emission, low S/N, Lyα emission, or ISM or Milky Way absorption lines that are not fit. We estimate an uncertainty on the fit using a Monte Carlo approach where the observed flux is modified by a Gaussian kernel centered on zero with standard deviation corresponding to the error on the flux. We performed 100 fit realizations and took the standard deviation as the error of the fit (represented by a blue shaded area in the figure). Figure 1 shows that this uncertainty is roughly on the order of the error of the observed flux in the highest S/N regions. Interestingly, the error is low around the Lyman series lines, suggesting that the latter are robustly constrained and little affected by fluctuations in the fitted stellar continuum. This point is further discussed in Sect. 3.2, where we emphasize the complexity of constraining the stellar continuum and dust extinction in galaxy spectra with low S/N. Section A presents the fits obtained for the five other leakers from Izotov et al. (2018a,b), the 16 remaining fits can be found in Gazagnes et al. (2018).
 |
Fig. 1. Best fit (blue solid line) obtained for the galaxy J1256+4509. The black and green solid lines show the observed flux and the error on the flux, respectively. Top panels: zooms on the individual Lyman series lines fitted. The gray shaded areas are the principal wavelength regions masked during the fit, due to geo-coronal emission, low S/N or Lyα emission. Additionally, in the top panels, we show the masks for ISM/Milky Way absorption lines that are not included during the fitting procedure. For display purposes, these masks do not appear in the main panel. The blue-shaded area represents the uncertainty on the fit, derived using a Monte-Carlo approach (see details in Sect. 3.1). |
When fitting the Lyman series using a Voigt profile, it is assumed that the lines follow a single Gaussian velocity distribution and this assumption might not be valid for absorption profiles arising from galactic outflows (Heckman et al. 2000; Pettini et al. 2002; Shapley et al. 2003; Weiner et al. 2009; Chisholm et al. 2017b). Consequently, we used the non-parametric approach described in Gazagnes et al. (2018) to measure the H I covering fraction from the residual flux of the Lyman series lines after removing the stellar continuum. This method does not presume a specific line profile or velocity distribution of the H I gas. However, this assumes that the H I absorption lines are saturated, that is, that NH I ≳ 1016 cm−2-pagination for the Lyman series lines that we fit (Lyβ to Ly6). In Gazagnes et al. (2018), we found evidence that the latter assumption is true for 13 galaxies which have NH I values > 1018.4 cm−2 using the observed NO I and the gas-phase metallicity. In the nine remaining galaxies, we did not find a reliable measurement of NO I (for J0925+1409 and the six new leakers included from Izotov et al. 2018a,b), or the galaxy metallicity has not been measured (SGAS J1226, SGAS J1527). Nevertheless, despite their different oscillator strengths, we observed a tendency for the observed Lyman series to have similar depths and shapes. This is illustrated in Fig. 2, where the Lyδ and Ly5 absorption lines are plotted in velocity space for J1256+4509. Similar depths and widths are robust indicators of saturated lines. No H I absorption lines are detected in J1243+4646, the highest LyC escape fraction (see Fig. A.4), which is likely due to either a very low H I neutral gas column density or covering fraction.
 |
Fig. 2. Lyδ (blue) and Ly5 (red) absorption lines in the galaxy J1256+4509. The flux has been normalized using the median of the observed spectra taken between 500 and 1000 km s−1 from the absorption lines. The two H I absorption lines have similar depth and width, which indicates that they are saturated. |
To measure the covering fraction from the residual flux, we used a Monte Carlo approach: the observed flux is first divided by the stellar continuum (fit as F⋆ in Eq. (1)) and modified by a Gaussian kernel centered on zero with standard deviation corresponding to the error array. Cf(H I) is derived from the median of 1 minus the residual flux in a velocity range that includes the deepest part of the absorption line. We repeated this procedure 1000 times and took the median and standard deviation of this distribution as the Cf value and uncertainty for each H I absorption line that is not polluted by Milky Way absorption lines or geocoronal emission. We additionally include the systematic errors in quadrature. We then obtain a final covering fraction by taking the error weighted mean of the i observed Lyman series transitions. Table B.1 lists the Cf derived from the residual flux of each Lyman series transition in each galaxy, the resulting Cf(H I) “Depth” and the measurement derived from the fitting method. The last column shows the final H I covering fraction, derived from the error weighted mean between the values obtained from the two different approaches. For J1243+4646, which has no detected Lyman series, we still measure the median residual flux in a velocity range chosen where the flux is minimal. We consider the final value as an upper limit. We do not report a Cf(H I) “Depth” for GP0303-0759 because its only H I absorption line observed is contaminated by a Milky Way absorption line.
We note that the galaxies in our sample have a different number of observed Lyman series lines. However, for galaxies with more than one observed H I absorption line, the individual Cf(H I) estimates using the depth of the absorption profiles are consistent at ±1σ with the value derived when all the lines are fitted simultaneously. Hence, we assume that the H I parameter values derived in galaxies with a single Lyman series line does not suffer from significant systematic effects. Additionally, Table B.1 shows that both approaches give comparable estimates and uncertainties, thus supporting the fact that both are robust techniques to measure the H I covering fraction from saturated Lyman series.
Finally, using the same methodology, we measured the velocity width of each H I absorption line, when it is not contaminated by foregrounds or Milky Way absorption, and has sufficient S/N so that the line profile is clearly observed. We estimate the velocity width as the velocity range where the absorption profile is at its maximum depth. The minimal and maximal velocities of this interval are chosen where the flux deviates by more than 20% from the residual flux measurements reported in Table B.1. The same Monte-Carlo approach is used to derive the resulting vwidth value and uncertainty for each absorption line, and we obtain the final 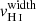 for each galaxy derived from the error weighted mean of the individual vwidth (last column of Table B.2).
for each galaxy derived from the error weighted mean of the individual vwidth (last column of Table B.2).
The final covering fraction values, as well as the velocity shift of the line 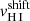 , the dust extinction EB − V obtained from the fitting method and average velocity width of the Lyman series are reported in Table 2. We note that in this work, the synthetic spectra used for the fitting are slightly different from that of Gazagnes et al. (2018), where the final spectra combined only ten single-age stellar populations of a single metallicity and did not include the nebular continuum. Therefore, we re-measured all the properties in all the galaxies in the sample. While the covering fractions and velocity shift measurements all remained consistent at ±1σ, we find some small variations in the dust extinction (0.01 to 0.06) for 8 galaxies (marked with * in Table 2). This is expected because the incorporation of nebular continuum and the combination of 5 different metallicities can change the final fitted stellar spectral shape and therefore impact the EB − V inferred (see Sect. 3.2). Overall, the variations are relatively small and do not impact the results obtained in Gazagnes et al. (2018) and Chisholm et al. (2018).
, the dust extinction EB − V obtained from the fitting method and average velocity width of the Lyman series are reported in Table 2. We note that in this work, the synthetic spectra used for the fitting are slightly different from that of Gazagnes et al. (2018), where the final spectra combined only ten single-age stellar populations of a single metallicity and did not include the nebular continuum. Therefore, we re-measured all the properties in all the galaxies in the sample. While the covering fractions and velocity shift measurements all remained consistent at ±1σ, we find some small variations in the dust extinction (0.01 to 0.06) for 8 galaxies (marked with * in Table 2). This is expected because the incorporation of nebular continuum and the combination of 5 different metallicities can change the final fitted stellar spectral shape and therefore impact the EB − V inferred (see Sect. 3.2). Overall, the variations are relatively small and do not impact the results obtained in Gazagnes et al. (2018) and Chisholm et al. (2018).
Dust extinction and H I properties derived from the Lyman series.
3.2. Constraining the dust extinction
Accurately fitting the dust attenuation in the ISM of the galaxies is important for placing constraints on its impact on the escaping radiation. Indeed, several dust models, or dust attenuation laws, might lead to various physical interpretations of the impact of dust on the Lyα or LyC radiations. Gazagnes et al. (2018) carefully discuss the effects of dust models with a uniform dust screen (all photons are homogeneously attenuated) or with dust free holes (dust only lies in optically thick neutral regions). It was shown that these models result in different values of Cf(H I) and EB − V, but lead to very similar estimates of the absolute escape fraction of LyC radiation.
Additionally, the choice of the dust extinction curve significant impacts the effect of dust obscuration on the wavelength region around and below the Lyman break. Typical dust attenuation curves (e.g., those of Calzetti et al. 2000, or the Small Magellanic Cloud (SMC) law) are unconstrained in the far-UV (λ < 1250 Å), while measuring the impact of dust at these wavelengths is crucial for investigating the escape of ionizing photons from dusty galaxies. In this work, we choose the dust extinction law derived in Reddy et al. (2016a). Our choice is motivated by the fact that the authors used a large sample of 933 far-UV observations of Lyman Break Galaxies at z ∼ 3, 121 of them having a deep spectroscopic coverage from 850 to 1300 Å, to robustly constrain the shape of the dust attenuation curve between 950 and 1500 Å. The authors report that the attenuation of LyC photons around 900 Å is ∼2 times lower than estimates derived from polynomial extrapolations of typical dust attenuation curves (Calzetti et al. 2000; Reddy et al. 2015). In Gazagnes et al. (2018), we investigated the effects of using different attenuation laws, such as the SMC attenuation law3, which is significantly steeper than the Reddy et al. (2016a) law, and showed that this had a relatively small impact on the derived values of the H I covering fractions. In this work, we reconsider the effects of different dust curves using the examples of J1154+2443 and J1256+4509, two of the three largest leakers in our sample, and we report in Table 3 the changes seen with respect to the stellar population age, the Cf(H I), as well as the dust extinction and attenuation at 912 Å and 1216 Å. We also report the value of the summed squared weighted residuals for the recovered parameter values, WSS, as returned by MPFIT, to demonstrate the differences in the quality of the fit in each case.
Investigating the impact of different dust extinction assumptions in J1154+2443 and J1256+4509.
The age of the stellar population and the H I covering fraction are insensitive to the dust attenuation law used. This is because the presence of specific stellar features in the spectra fix the stellar populations during the fit (Chisholm et al. 2019). However, we derive approximately an attenuation that is twice as low for the Lyα and LyC radiation in J1154+2445 when using the SMC law. Thus, the choice of the dust law can impact the fitted attenuation, while the differences in the summed, squared, weighted residuals are too small to choose a dust extinction curve that would significantly improve the final fit quality.
Additionally, we further investigated the fluctuations of the parameters inferred when EB − V is fixed to 0 and 0.2 for a given dust extinction law. These results are reported in Table 3 and the obtained fits are shown in Fig. 3. A ±0.2 difference in EB − V leads to small variations (within the flux error) in the shape of the fitted spectra while having a significant impact on the attenuation at 912 and 1216 Å, reducing the flux by 85% in the model with EB − V = 0.2 compared to that in the model with EB − V = 0. However, the differences in the residuals are insignificant for selection of EB − V. This is likely because there is a strong degeneracy between the stellar population age and the dust extinction needed to model the observed flux. Indeed, younger populations have a steeper continuum towards the far-UV wavelengths, and require a larger dust extinction to reproduce the observed flux compared to older star populations. This is consistent with the results in Table 3 since we obtained younger and older stellar populations when fixing EB − V to 0.2 and 0, respectively. The poorly constrained stellar population age can affect the reliability of 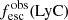 when the former is derived using the ratio of the observed flux at < 912 Å over the estimated intrinsic emission of ionizing photons.
when the former is derived using the ratio of the observed flux at < 912 Å over the estimated intrinsic emission of ionizing photons.
 |
Fig. 3. Top: observed flux in the galaxy J1256+4509 (black curve), error (green), fit obtained letting EB − V as a free parameter (orange), fits obtained when fixing EB − V to 0 and 0.2 (blue and red lines) respectively. Bottom: same for the galaxy J1154+2443. Both spectra have been normalized using the median flux between 1090 and 1100 Å. The wavelength regions with Lyα emission (between 1205 to 1225 Å) or low S/N (< 1) are masked during the fitting procedure (see Fig. 1). |
Robustly constraining the stellar populations requires the identification of specific markers of the presence of young or old star populations. Izotov et al. (2016a,b, 2018a,b) report that all leakers have large EW(Hβ) (> 200 Å), which should indicate young stellar populations (Stasińska & Leitherer 1996). However, in practice, exact age determinations from EW(Hβ) are complicated since it depends on the star formation history and the IMF of the stellar population. Additionally, the strength of the stellar features such as the O VI and N V P Cygni profiles at 1020–1040 Å and 1220–1240 Å, respectively, is related to the stellar population properties. However, the relatively low S/N of our observations make it challenging to constrain the age of the stellar population. Chisholm et al. (2019) recently emphasized that high S/N is required to properly constrain the stellar population of the galaxy, especially for accurately deriving the escape of ionizing photons from SED fitting. Therefore, robustly constraining the dust attenuation in our sample would require deeper observations.
Table 3 shows that the fitted Cf(H I) is rather insensitive to variations of stellar age or dust extinction. However, it still provides reliable covering fraction estimate for investigating its impact on the Lyα and LyC escape.
3.3. Lyα properties
Table 4 reports the Lyα properties for all galaxies in our sample. One galaxy has a Lyα absorption profile, two have Lyα seen both in absorption and emission with a single peak profile. The 19 remaining galaxies have Lyα seen in emission, 18 exhibiting a double peak profile and one having a triple peak profile (J1243+4646). Eighteen of the 22 galaxies have already had their Lyα profiles studied in the literature (Henry et al. 2015; Izotov et al. 2016a,b, 2018a,b; Verhamme et al. 2017; Puschnig et al. 2017; Orlitová et al. 2018). We re-measured the Lyα properties in all spectra to avoid inconsistencies due to different measurement methods. The Lyα escape fractions were re-calculated coherently using the equation:
Lyα properties.
where F(Lyα) is the observed Lyα flux, corrected for the Milky Way extinction, Fcorr(Hα) is the Hα flux corrected for both internal and Milky Way extinction, and 8.7 is the assumed ratio between the intrinsic Lyα and Hα flux assuming Case-B recombination with a temperature of 104 K and an electron density of ne = 350 cm−3. We note that Case-B recombination assumes that the gas in the ISM is optically thick to radiation above 13.6 eV, thus, it may not be valid for galaxies where a substantial amount of ionizing photons escape. In galaxies with an optically thin ISM (Case-A recombination), the effective recombination coefficient for the Balmer hydrogen lines can increase by a factor ∼1.5 (Osterbrock 1989). In Izotov et al. (2018a), the authors derived an intrinsic Lyα–Hα flux ratio of ≈11.2 in the galaxy J1154+2443 using CLOUDY models (Ferland et al. 2013, 2017). We investigated in Appendix B.3 the impact of using a different intrinsic F(Lyα)/F(Hα) ratio on the observed fesc(Lyα) trends derived in this work. Overall, we show that the new significance levels of these trends differ by at most −0.5σ, while all the correlations remain significant at least at the 2.5σ level. Thus we assume that fluctuations in the intrinsic Lyα Hα flux ratio should not substantially affect the results presented in this work.
For the low-redshift galaxies, we calculated fesc(Lyα) using the Lyα and Hα flux measurements, already corrected for internal and Milky Way extinction, reported in the reference papers. While some of the sources in our sample have Lyα emission outside the COS aperture (Henry et al. 2015), we did not apply aperture correction because the size of the extended Lyα emission varies from galaxy to galaxy. The final errors were derived by propagating the errors of the individual measurements. We derived an Lyα escape fraction of 61% for J1154+2443, which is inconsistent with the 98% reported in Izotov et al. (2018a). However, those authors corrected the Lyα flux with the galaxy internal extinction, which is incompatible with Eq. (4). For the three gravitationally lensed galaxies, we measured F(Lyα) using the Monte-Carlo approach described in the Sect. 3.1, accounting for the lensing magnification factor. The observed flux at Lyα in the Cosmic Eye is consistent with 0, hence we report 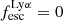 . For SGAS J1226 and SGAS J1527, we used the Hβ flux measurements reported in Wuyts et al. (2012) and assumed an intrinsic F(Hα)/F(Hβ) ratio of 2.85.
. For SGAS J1226 and SGAS J1527, we used the Hβ flux measurements reported in Wuyts et al. (2012) and assumed an intrinsic F(Hα)/F(Hβ) ratio of 2.85.
Table 4 reports the Lyα equivalent width, peak and trough velocities, and the normalized flux at the minimum of the profile. These different measurements are illustrated on the Lyα profile of the galaxy J1011+1947 in Fig. 4. All these properties have been measured using the Monte Carlo method to have consistent values and uncertainties for the entire sample. The Lyα equivalent widths were derived using the observed MW attenuation-corrected spectra, by integrating both the associated Lyα emission and absorption such that the integral limits are chosen, by eye, where the flux meets the stellar continuum. The reported EW(Lyα) values are respectively positive and negative for galaxies with a net emission or absorption Lyα profile. The flux above and below the continuum level are respectively The trough velocities 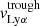 are taken as the values when the intensity of the Lyα flux reaches a local minimum. J0921+4509 and J1243+4509 have peculiar Lyα profiles. The former has two distinct troughs between the red and blue peaks (see Sect. 4.2), and both their velocities are reported in Table 4. The latter has two peaks bluer than the central trough (see Fig. 7 in Izotov et al. 2018b) and we only report the
are taken as the values when the intensity of the Lyα flux reaches a local minimum. J0921+4509 and J1243+4509 have peculiar Lyα profiles. The former has two distinct troughs between the red and blue peaks (see Sect. 4.2), and both their velocities are reported in Table 4. The latter has two peaks bluer than the central trough (see Fig. 7 in Izotov et al. 2018b) and we only report the 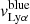 of the peak of maximal intensity. The peak separation,
of the peak of maximal intensity. The peak separation, 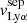 , is defined as
, is defined as 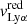 –
–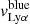 , and the error is derived from the quadratic sum of both uncertainties. Additionally, we measure the flux at the minimum of the Lyα profile as
, and the error is derived from the quadratic sum of both uncertainties. Additionally, we measure the flux at the minimum of the Lyα profile as 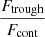 , where Ftrough is the minimum flux measured at the Lyα trough, and Fcont is the median value of the stellar continuum estimated between 1160 and 1270 Å, excluding all emission and absorption lines in that range. In this work, we assume that the spectral resolution has a negligible impact on the derived
, where Ftrough is the minimum flux measured at the Lyα trough, and Fcont is the median value of the stellar continuum estimated between 1160 and 1270 Å, excluding all emission and absorption lines in that range. In this work, we assume that the spectral resolution has a negligible impact on the derived 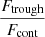 values, because the latter was measured in high-resolution Lyα spectra (R ≈ 16 000). However, the impact of low spectral resolution should be investigated to extend this analysis to samples with lower resolving power. Except for the Lyα escape fraction in J1154+2443, all the values presented in Table 4 are consistent at ±1σ with the previous measurements reported in the literature. Appendix C shows the Lyα profiles for all galaxies in our sample.
values, because the latter was measured in high-resolution Lyα spectra (R ≈ 16 000). However, the impact of low spectral resolution should be investigated to extend this analysis to samples with lower resolving power. Except for the Lyα escape fraction in J1154+2443, all the values presented in Table 4 are consistent at ±1σ with the previous measurements reported in the literature. Appendix C shows the Lyα profiles for all galaxies in our sample.
 |
Fig. 4. Lyα profile observed in the galaxy J1011+1947 with the characteristic measurements annotated. The observed flux has been smoothed by an arbitrary factor for display purposes, and normalized using the median of the flux between 1200 and 1210 Å. The gray shaded area represents the integrated region to compute the Lyα equivalent width. |
4. The ISM porosity enables the escape of Lyα and LyC photons
In this section, we examine the connection between the neutral gas properties, the Lyα properties, and the escape of LyC photons.
4.1. The scattering of Lyα photons in a porous ISM
The Lyα transition is a resonant line and each interaction between Lyα photons and hydrogen atoms shifts the photon’s frequency depending on the velocity of the H I gas. Therefore, the emergent Lyα profile provides insights on the neutral hydrogen spatial and velocity distribution. In this section, we investigate the connection between the H I covering fraction and the scattering of Lyα photons, depicted by the blue and red velocity shift of the double peak Lyα profiles. We chose to consider the Lyα emission velocity relative to the Lyα absorption trough velocity as 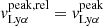 –
–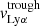 . Hence,
. Hence, 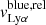 and
and 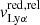 are derived by subtracting the Col. (5) from Cols. (6) and (7) in Table 4, respectively. This alternative approach provides insights about the velocity of the last scattering of the blue and red shifted Lyα photons relative to the velocity of the predominant absorption and also accounts for potential errors in the systemic redshifts (see the discussion in Orlitová et al. 2018). J0921+4509 is a peculiar case with two local minima at different velocities (−220 and 0 km s−1, see Fig. 9). We define its relative peak velocities with respect to the closest absorption troughs, such that
are derived by subtracting the Col. (5) from Cols. (6) and (7) in Table 4, respectively. This alternative approach provides insights about the velocity of the last scattering of the blue and red shifted Lyα photons relative to the velocity of the predominant absorption and also accounts for potential errors in the systemic redshifts (see the discussion in Orlitová et al. 2018). J0921+4509 is a peculiar case with two local minima at different velocities (−220 and 0 km s−1, see Fig. 9). We define its relative peak velocities with respect to the closest absorption troughs, such that 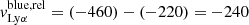 km s−1 and
km s−1 and 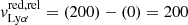 km s−1.
km s−1.
Figure 5 shows the relation between the 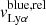 and
and 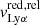 and the neutral gas covering fraction. We find a strong correlation between the blue and red relative velocities of the Lyα photons with respect to the H I gas covering fraction (3σ significance, p-value of 0.0026 and 0.0024 respectively). Additionally, in Fig. 6, we show the connection between the Lyα peak velocity separation and the H I covering fraction. We included the recent analysis of the neutral gas properties of 13 low-z GPs with HST-COS observations (GO-14080, PI Jaskot) studied in McKinney et al. (2019) and Jaskot et al. (2019). In the latter study, the authors measured the Cf(Si II) of these galaxies, from which we derived the corresponding Cf(H I) using the empirical relation Cf(Si II)-Cf(H I) found in Gazagnes et al. (2018). We report a correlation at the 3-σ level4 (p-value of 0.0018) between
and the neutral gas covering fraction. We find a strong correlation between the blue and red relative velocities of the Lyα photons with respect to the H I gas covering fraction (3σ significance, p-value of 0.0026 and 0.0024 respectively). Additionally, in Fig. 6, we show the connection between the Lyα peak velocity separation and the H I covering fraction. We included the recent analysis of the neutral gas properties of 13 low-z GPs with HST-COS observations (GO-14080, PI Jaskot) studied in McKinney et al. (2019) and Jaskot et al. (2019). In the latter study, the authors measured the Cf(Si II) of these galaxies, from which we derived the corresponding Cf(H I) using the empirical relation Cf(Si II)-Cf(H I) found in Gazagnes et al. (2018). We report a correlation at the 3-σ level4 (p-value of 0.0018) between 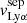 and 1-Cf(H I). The trends reported in Figs. 5 and 6 indicate that Lyα photons experience fewer scattering events in galaxies having low H I covering fraction. Interestingly, this somehow differs from Jaskot et al. (2019) and McKinney et al. (2019) who found a weak correlation between
and 1-Cf(H I). The trends reported in Figs. 5 and 6 indicate that Lyα photons experience fewer scattering events in galaxies having low H I covering fraction. Interestingly, this somehow differs from Jaskot et al. (2019) and McKinney et al. (2019) who found a weak correlation between 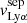 and Cf(Si II). This difference might be explained by the fact that Si II and H I may not trace exactly the same gas. The Si II and H I ionization potential are similar, but not identical. Hence, the Si II covering fraction is related to, but not equal to Cf(H I) (Reddy et al. 2016b; Gazagnes et al. 2018). Additionally, the Si II covering fractions measurements might be impacted by scattering and fluorescent emission in-filling (Prochaska et al. 2011; Scarlata & Panagia 2015, Mauerhofer et al., in prep).
and Cf(Si II). This difference might be explained by the fact that Si II and H I may not trace exactly the same gas. The Si II and H I ionization potential are similar, but not identical. Hence, the Si II covering fraction is related to, but not equal to Cf(H I) (Reddy et al. 2016b; Gazagnes et al. 2018). Additionally, the Si II covering fractions measurements might be impacted by scattering and fluorescent emission in-filling (Prochaska et al. 2011; Scarlata & Panagia 2015, Mauerhofer et al., in prep).
 |
Fig. 5. Left: relation between the relative Lyα blue peak velocity ( |
 |
Fig. 6. Relation between the Lyα peak velocity separation ( |
The scaling relation between 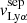 and Cf(H I) contrasts with the theoretical Lyα studies of Verhamme et al. (2015) and Dijkstra et al. (2016). The latter radiative transfer simulations showed that
and Cf(H I) contrasts with the theoretical Lyα studies of Verhamme et al. (2015) and Dijkstra et al. (2016). The latter radiative transfer simulations showed that 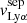 should scale with decreasing NH I in the ISM, but the presence of paths cleared of H I gas should imprint a single peak profile at the systemic velocity. Nevertheless, the latter analysis assumes that the escape channels are entirely cleared of gas. Other studies showed that the presence of a clumpy ISM (Gronke et al. 2016) or the presence of H I residuals in the channels (Kakiichi & Gronke 2019) could lead to a non-unity neutral gas covering fraction, while imprinting a double peak profile. Using the O I column densities and reported metallicities, we find that 13 of 22 galaxies in our sample have NH I larger than 1018 cm−2, while McKinney et al. (2019) found similar results in their sample using both O I and Si II. Hence, in these galaxies, the porosity of the ISM (low Cf(H I)) should be physically interpreted as the existence of channels with low column densities in an optically thick H I environment. To refer to this bi-modal distribution of H I, we introduce the notations
should scale with decreasing NH I in the ISM, but the presence of paths cleared of H I gas should imprint a single peak profile at the systemic velocity. Nevertheless, the latter analysis assumes that the escape channels are entirely cleared of gas. Other studies showed that the presence of a clumpy ISM (Gronke et al. 2016) or the presence of H I residuals in the channels (Kakiichi & Gronke 2019) could lead to a non-unity neutral gas covering fraction, while imprinting a double peak profile. Using the O I column densities and reported metallicities, we find that 13 of 22 galaxies in our sample have NH I larger than 1018 cm−2, while McKinney et al. (2019) found similar results in their sample using both O I and Si II. Hence, in these galaxies, the porosity of the ISM (low Cf(H I)) should be physically interpreted as the existence of channels with low column densities in an optically thick H I environment. To refer to this bi-modal distribution of H I, we introduce the notations  and
and 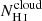 to denote the column densities within the channels and within the clouds, respectively. The scaling relation between
to denote the column densities within the channels and within the clouds, respectively. The scaling relation between 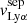 and Cf(H I) suggests that galaxies that have more of these channels also have lower
and Cf(H I) suggests that galaxies that have more of these channels also have lower  . Hence, the presence of low Cf(H I) could indirectly trace the abundance of H I in the lowest column density regions of the ISM.
. Hence, the presence of low Cf(H I) could indirectly trace the abundance of H I in the lowest column density regions of the ISM.
The tight connection between the velocity shift of the peaks of the Lyα emission and Cf(H I) additionally indicates that the porosity of the ISM impacts the shape of the Lyα profile. Indeed, in this work, we investigate the relative Lyα peak velocities which can be interpreted as the velocity shift of the escaping Lyα photons with respect to the velocity of the predominant H I absorption (similarly to Orlitová et al. 2018). In the literature, Lyα peak velocities are usually considered with respect to the systemic velocity. Interestingly, we do not find any correlation between the red peak velocity relative to the systemic velocity and the H I covering fraction and the significance level of the correlation between the blue peak velocity relative to the systemic velocity and Cf(H I) is lower (2σ). This suggests that the shift of both the blue and red-shifted Lyα photons relates to the properties of the main H I absorption, which traces the bulk of the H I gas along the line of sight (LOS). The velocity of the last scattering of Lyα photons is likely to be correlated with the velocity coverage of the thick H I gas, and with the presence of low-density channels in the ISM. This trend is somewhat surprising for the red Lyα emission. Indeed, the red peak of the Lyα profile corresponds to the back-scattered Lyα photons, which were first emitted in the direction opposite to the observer. In theory, they probe the properties of the gas in the back side of the galaxy ISM, and are expected to have a weaker connection to LOS-dependent properties, such as Cf(H I), than blue-shifted photons. Figure 5 shows that this is not the case. This could be because galaxies that have lower Cf(H I) also have lower H I column densities in the ISM, such that 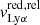 indirectly probes the average NH I of the neutral gas.
indirectly probes the average NH I of the neutral gas.
The strong correlation between the peak velocities and the presence of low column density channels could in principle be used to indirectly detect the leakage of Lyα and LyC photons through these sightlines. Kakiichi & Gronke (2019) suggested that, in an ionization-bounded ISM, the Lyα peak velocity separation could probe  . A similar idea was discussed in Jaskot et al. (2019) where the authors proposed
. A similar idea was discussed in Jaskot et al. (2019) where the authors proposed 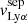 as a probe of the residual NH I along the paths of “least resistance” through which Lyα photons escape. These assumptions would explain the strong correlations between low peak velocity separations and
as a probe of the residual NH I along the paths of “least resistance” through which Lyα photons escape. These assumptions would explain the strong correlations between low peak velocity separations and 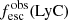 (Verhamme et al. 2017; Izotov et al. 2018b, 2020). Nevertheless, we further show in Sect. 4.2 that both low and high column densities of gas impact the Lyα peak separation, such that a single parameter does not fully determine fesc(LyC).
(Verhamme et al. 2017; Izotov et al. 2018b, 2020). Nevertheless, we further show in Sect. 4.2 that both low and high column densities of gas impact the Lyα peak separation, such that a single parameter does not fully determine fesc(LyC).
4.2. Narrower H I absorption lines lead to larger observed Lyα emission
Because the Lyα is a resonant transition, the Lyα photons are strongly impacted by the neutral gas kinematics. Rivera-Thorsen et al. (2015) outlined the role of the velocity coverage of the H I gas as an important factor governing the observed emission of Lyα photons. In Fig. 7, we compare the Lyα equivalent width (left panel) and the Lyα escape fraction (right panel) with the H I velocity width of the Lyman series in our sample. The latter is defined as the velocity interval where the H I absorption profile is at its maximum depth. We find strong anti-correlations both with EW(Lyα) (4σ, p-value of 0.000025) and with fesc(Lyα) (3σ, p-value of 0.0007) that confirm that the velocity width of the optically thick H I absorption significantly impacts the emission and escape of Lyα photons. These results suggest that fewer Lyα photons escape from galaxies with broad H I absorption lines because Lyα photons are more likely to encounter optically thick neutral gas and hence have a higher probability to be destroyed by dust grains. However, disentangling the physical origin of a large 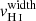 is not trivial. This can either result from large NH I, or from a broad velocity range of the absorbing gas. Both cases should similarly lower the escape and observed emission of Lyα photons because for Lyα photons to escape, it needs to be scattered to velocities where the gas is transparent. Nevertheless, this is different for LyC photons, since they are sensitive to the NH I in the ISM, but not to the kinematics of the H I gas.
is not trivial. This can either result from large NH I, or from a broad velocity range of the absorbing gas. Both cases should similarly lower the escape and observed emission of Lyα photons because for Lyα photons to escape, it needs to be scattered to velocities where the gas is transparent. Nevertheless, this is different for LyC photons, since they are sensitive to the NH I in the ISM, but not to the kinematics of the H I gas.
 |
Fig. 7. Lyα equivalent width (left) and escape fraction (right) versus the width of the H I maximal absorption. Galaxies with a lower velocity width of the Lyman series have higher EW(Lyα) and fesc(Lyα). |
Figure 8 provides additional insights about the origin and impact of broad H I absorption lines on the escape of Lyα and LyC photons. It shows the linear relation (at the 3σ significance, p-value of 0.0007) between the H I velocity width of the maximal absorption and the Lyα peak velocity separation. 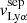 is linearly consistent at ±1σ with
is linearly consistent at ±1σ with 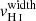 for 17 galaxies (∼80%) in our sample. Because
for 17 galaxies (∼80%) in our sample. Because 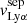 scales with NH I (Verhamme et al. 2015; Dijkstra et al. 2016), this trend could suggest that the observed width of the H I absorption lines indirectly probes the H I column densities in the dense regions (
scales with NH I (Verhamme et al. 2015; Dijkstra et al. 2016), this trend could suggest that the observed width of the H I absorption lines indirectly probes the H I column densities in the dense regions (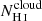 ) which are imprinted from the saturated Lyman series. Additionally, recent observational studies have highlighted the connection between low peak velocity separation and the escape of ionizing photons (Verhamme et al. 2017; Izotov et al. 2018b, 2020). Interestingly, we find that J1154+2443 and J1256+4509, the two largest leakers (38 and 46%) with Lyman series observations, have the lowest
) which are imprinted from the saturated Lyman series. Additionally, recent observational studies have highlighted the connection between low peak velocity separation and the escape of ionizing photons (Verhamme et al. 2017; Izotov et al. 2018b, 2020). Interestingly, we find that J1154+2443 and J1256+4509, the two largest leakers (38 and 46%) with Lyman series observations, have the lowest 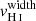 in our sample. Similarly, we do not detect H I in the largest
in our sample. Similarly, we do not detect H I in the largest 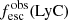 LCE (J1243+4646). Hence, in these galaxies, the thick neutral clouds in the ISM might have
LCE (J1243+4646). Hence, in these galaxies, the thick neutral clouds in the ISM might have 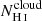 low enough to let a significant fraction of ionizing photons escape. We note that this hypothesis is not incompatible with the presence of saturated H I absorption lines because the range of Lyman series lines we study in this work (Lyβ to Ly6) saturates at NH I larger than ∼1016 cm−2. Additionally, we do not report any significant trend between
low enough to let a significant fraction of ionizing photons escape. We note that this hypothesis is not incompatible with the presence of saturated H I absorption lines because the range of Lyman series lines we study in this work (Lyβ to Ly6) saturates at NH I larger than ∼1016 cm−2. Additionally, we do not report any significant trend between 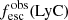 and
and 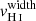 in the low LyC leakers (
in the low LyC leakers (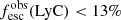 ). Hence, for these galaxies, the
). Hence, for these galaxies, the 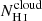 is likely too large and efficiently absorbs all the ionizing radiation that passes through the clouds. This is consistent with Gazagnes et al. (2018) where we estimated NH I larger than 1018 cm−2 using NO I for six of the ten low LyC leakers with observed O I absorption lines. Hence, this result could emphasize that the leakage of LyC photons in the largest leakers is a combination of ionization and density bounded mechanisms, highlighted by the presence of both low Cf(H I) and low
is likely too large and efficiently absorbs all the ionizing radiation that passes through the clouds. This is consistent with Gazagnes et al. (2018) where we estimated NH I larger than 1018 cm−2 using NO I for six of the ten low LyC leakers with observed O I absorption lines. Hence, this result could emphasize that the leakage of LyC photons in the largest leakers is a combination of ionization and density bounded mechanisms, highlighted by the presence of both low Cf(H I) and low 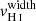 . However, this outcome should be taken with caution, because
. However, this outcome should be taken with caution, because 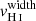 is highly degenerate with the velocity distribution of the H I gas. We discuss further this point in Sect. 4.5.
is highly degenerate with the velocity distribution of the H I gas. We discuss further this point in Sect. 4.5.
 |
Fig. 8. Lyα peak velocity separation versus the H I velocity width of maximal absorption. The color bar represents the H I covering fraction measurement of each galaxy. Overall, the Lyα peak velocity separation scales with the width of the maximal absorption of the H I gas, and galaxies with larger Cf(H I) have larger |
In Sect. 4.1, we showed the tight correlation between 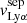 and the H I covering fraction. Figure 8 additionally shows the impact of low Cf(H I) on the relation between
and the H I covering fraction. Figure 8 additionally shows the impact of low Cf(H I) on the relation between 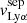 and
and 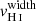 . Overall, galaxies with large Cf(H I) have
. Overall, galaxies with large Cf(H I) have 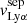 larger than
larger than 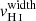 , such that the Lyα emission peaks at velocities beyond the H I absorption. This is illustrated in the left panel of Fig. 9, where we superpose the Lyα profile and the Lyβ line for the galaxy J0921+4509. As for J0921+4509, it has a relatively high covering fraction, (Cf(H I) ≈0.8), and the peaks of its Lyα emission are located on the edges of the optically thick H I absorption. On the other hand, Fig. 8 shows that galaxies with a lower Cf(H I) have
, such that the Lyα emission peaks at velocities beyond the H I absorption. This is illustrated in the left panel of Fig. 9, where we superpose the Lyα profile and the Lyβ line for the galaxy J0921+4509. As for J0921+4509, it has a relatively high covering fraction, (Cf(H I) ≈0.8), and the peaks of its Lyα emission are located on the edges of the optically thick H I absorption. On the other hand, Fig. 8 shows that galaxies with a lower Cf(H I) have 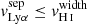 . This is because decreasing Cf(H I) increases the probability of Lyα photons to find an escape road through low-density channels and thus lowers the amount of scattering events for these photons (see Sect. 4.1). The right panel of Fig. 9 shows the superposition of Lyα and Lyβ for J1442-0209, which has a lower Cf(H I) (≈0.6). The blue peak falls directly on top of the optically thick part of the Lyβ absorption line, which implies that a dominant proportion of Lyα photons on the blue portion of the line escape at velocities where the neutral gas is optically thick. Thus, the presence of Lyα emission on the top of the H I absorption is evidence of the existence of low-density channels (low Cf(H I)) and strongly indicates whether Lyα photons are able to escape from the galaxy. This also supports a plausible origin for the role of the blue Lyα peak in identifying the LyC escape (Henry et al. 2015; Orlitová et al. 2018) because LyC photons should escape through the same low-density paths along the line of sight.
. This is because decreasing Cf(H I) increases the probability of Lyα photons to find an escape road through low-density channels and thus lowers the amount of scattering events for these photons (see Sect. 4.1). The right panel of Fig. 9 shows the superposition of Lyα and Lyβ for J1442-0209, which has a lower Cf(H I) (≈0.6). The blue peak falls directly on top of the optically thick part of the Lyβ absorption line, which implies that a dominant proportion of Lyα photons on the blue portion of the line escape at velocities where the neutral gas is optically thick. Thus, the presence of Lyα emission on the top of the H I absorption is evidence of the existence of low-density channels (low Cf(H I)) and strongly indicates whether Lyα photons are able to escape from the galaxy. This also supports a plausible origin for the role of the blue Lyα peak in identifying the LyC escape (Henry et al. 2015; Orlitová et al. 2018) because LyC photons should escape through the same low-density paths along the line of sight.
 |
Fig. 9. Left: Lyα emission line and Lyβ absorption line in J0921+4509 (Cf(H I) = 0.761). Right: Lyα emission line and Lyβ absorption line in J1442−0209 (Cf(H I) = 0.556). The Lyα spectra have been smoothed to half the resolution of the observations and scaled down with a power law for display purposes. The presence of Lyα emission on top of the optically thick H I absorption line suggests that Lyα photons can escape at lower velocities through low-density channels. Similar plots for all the galaxies in our sample are given in Appendix C. |
In Sect. 4.1, we described the tight correlation we found between 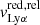 and Cf(H I), which indicates that the back-scattered emission is similarly affected by the presence of low-density channels. Nevertheless, Fig. 9 shows that the red emission peaks at velocities outside of the optically thick H I absorption. More generally, we found that this is the case for all galaxies in our sample (Appendix C shows the combinations of the Lyα and Lyman series profiles). In Sect. 4.1, we suggested that the relation between the velocity shift of the red peak of the Lyα profile and Cf(H I) could arise from the presence of both lower
and Cf(H I), which indicates that the back-scattered emission is similarly affected by the presence of low-density channels. Nevertheless, Fig. 9 shows that the red emission peaks at velocities outside of the optically thick H I absorption. More generally, we found that this is the case for all galaxies in our sample (Appendix C shows the combinations of the Lyα and Lyman series profiles). In Sect. 4.1, we suggested that the relation between the velocity shift of the red peak of the Lyα profile and Cf(H I) could arise from the presence of both lower  and lower
and lower 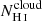 in the galaxies with the lowest neutral gas covering fraction. Hence, this may suggest that there exists a connection between low H I velocity width of maximal absorption (related to
in the galaxies with the lowest neutral gas covering fraction. Hence, this may suggest that there exists a connection between low H I velocity width of maximal absorption (related to 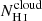 ) and low H I covering fraction (related to
) and low H I covering fraction (related to  ). We report a moderate 2-σ correlation between Cf(H I) and
). We report a moderate 2-σ correlation between Cf(H I) and 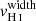 ; hence, we cannot significantly conclude that such relation exists.
; hence, we cannot significantly conclude that such relation exists.
Overall, the strong correlations between the peak velocity separation and the neutral gas covering fraction (Sect. 4.1), or the width of the saturated Lyman series, suggests that 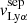 is sensitive both to the presence of low column density paths and to the properties of the dense H I regions in the ISM. As mentioned above, this might be because the blue peak is more sensitive to the existence of channels through which Lyα and LyC photons more easily escape, while the red peak probes the overall abundance of NH I in the ISM. Hence, both lower H I covering fraction and lower
is sensitive both to the presence of low column density paths and to the properties of the dense H I regions in the ISM. As mentioned above, this might be because the blue peak is more sensitive to the existence of channels through which Lyα and LyC photons more easily escape, while the red peak probes the overall abundance of NH I in the ISM. Hence, both lower H I covering fraction and lower 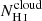 similarly impact the peak separation of the Lyα profile because the latter is sensitive to the “total” H I properties of the ISM of galaxies. While this outcome is somewhat surprising, it suggests that the peak velocity separation is a robust probe of the presence of low column density paths towards the observer and a key observable for investigating the escape of Lyα or LyC photons in low redshift LCE candidates (Verhamme et al. 2017; Izotov et al. 2018b, 2020). Nevertheless, these outcomes also suggest that measuring a low
similarly impact the peak separation of the Lyα profile because the latter is sensitive to the “total” H I properties of the ISM of galaxies. While this outcome is somewhat surprising, it suggests that the peak velocity separation is a robust probe of the presence of low column density paths towards the observer and a key observable for investigating the escape of Lyα or LyC photons in low redshift LCE candidates (Verhamme et al. 2017; Izotov et al. 2018b, 2020). Nevertheless, these outcomes also suggest that measuring a low 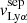 is not enough to disentangle the dominant leakage mechanisms because both the ISM porosity and the width of the saturated H I absorption lines impact the peak separation velocity. We discuss this point further in Sect. 5.1.
is not enough to disentangle the dominant leakage mechanisms because both the ISM porosity and the width of the saturated H I absorption lines impact the peak separation velocity. We discuss this point further in Sect. 5.1.
At higher redshift, where observing the Lyman series is highly unlikely because of the presence of line-of-sight neutral gas in the IGM, the ISM porosity can be traced with Cf(Si II), which probes the presence of low-density channels when the Lyman series is not observable (Gazagnes et al. 2018). Additionally, Chisholm et al. (2016) found tight correlations between the velocity widths of different ionic transitions and suggest that the velocity width of Si II is related to 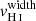 . The combination of both could be used to estimate the Lyα peak separation and probe the Lyα and LyC escape of photons at higher redshift. We discuss this further in Sect. 5.2.
. The combination of both could be used to estimate the Lyα peak separation and probe the Lyα and LyC escape of photons at higher redshift. We discuss this further in Sect. 5.2.
4.3. The Lyα equivalent width scales with low Cf(H I)
The EW(Lyα) and neutral gas properties of Lyman α emitters have been investigated in numerous studies (Rivera-Thorsen et al. 2015; Verhamme et al. 2017; Chisholm et al. 2017a; Steidel et al. 2018; Orlitová et al. 2018; Du et al. 2018; McKinney et al. 2019; Trainor et al. 2019; Jaskot et al. 2019; Runnholm et al. 2020). Figure 10 explores the connection between the EW(Lyα), the neutral gas coverage and the velocity width of the maximal absorption of the H I lines. Jaskot et al. (2019) found a positive correlation between the escape of Lyα photons and the Si II covering fraction in highly ionized GPs. Their sample, as well as J1243+4646, appear in grey in Fig. 10 as they do not have measured 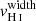 . We report a 2.5σ significance relation (p-value of 0.004), between EW(Lyα) and 1–Cf(H I). The trend is scattered and Fig. 10 shows that most galaxies with high EW(Lyα) have both low Cf(H I) and low
. We report a 2.5σ significance relation (p-value of 0.004), between EW(Lyα) and 1–Cf(H I). The trend is scattered and Fig. 10 shows that most galaxies with high EW(Lyα) have both low Cf(H I) and low 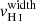 . This supports the picture where both the presence of channels with low
. This supports the picture where both the presence of channels with low  and narrower H I absorption lines increase the observed emission of Lyα photons. Nevertheless, the interpretation of the Lyα EW is not trivial because EW(Lyα) is also degenerate with varying galaxy properties, such as burst age, star formation history, or metallicity.
and narrower H I absorption lines increase the observed emission of Lyα photons. Nevertheless, the interpretation of the Lyα EW is not trivial because EW(Lyα) is also degenerate with varying galaxy properties, such as burst age, star formation history, or metallicity.
 |
Fig. 10. Lyα equivalent width versus the porosity of the neutral gas as given by 1–Cf(H I). The color bar represents the H I velocity interval where the Lyman series is at its maximum depth. Our sample is represented by triangles and circles for galaxies with unknown and known leakage respectively, and the sample from McKinney et al. (2019) and Jaskot et al. (2019) is shown with gray squares as they do not have H I velocity width measurements. The dashed line shows the empirical relation found in Steidel et al. (2018), while the dotted line is the fit to the data, excluding J1248+4259 (see Eq. (5)). This figure suggests that Lyα emission strongly scales with the covering fraction of the channels and with the width of the saturated H I absorption lines. |
We may note the peculiar case of the galaxy J1248+4259, with the largest EW(Lyα) in both samples (258 Å), but a relatively low 1–Cf(H I) (0.046). Surprisingly, J1248+4259 has one of the weakest O VI and N V P Cygni profiles in our sample (see Fig. A.4), which suggest the presence of an older population of stars, which is at first sight incompatible with the presence of large EW(Lyα) (Schaerer 2003). On the other hand, weak O VI and N V P Cygni profiles could be explained by a young stellar population, but without any formation of the most massive stars. We also report a low 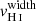 for J1248+4259, which could partly explain the large EW(Lyα) measured. Indeed, as seen in Sect. 4.2, low
for J1248+4259, which could partly explain the large EW(Lyα) measured. Indeed, as seen in Sect. 4.2, low 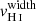 either trace a narrow H I velocity distribution or low NH I, both enhancing the observed emission of Lyα photons. However, the large EW(Lyα) in J1248+4259 is likely to result from a combination of several galaxy properties, such that disentangling its origin is not trivial. Consequently, we exclude J1248+4259 from the sample and derive the equation that linearly relates EW(Lyα) and 1–Cf(H I) as (4σ significance level, p-value < 0.00002):
either trace a narrow H I velocity distribution or low NH I, both enhancing the observed emission of Lyα photons. However, the large EW(Lyα) in J1248+4259 is likely to result from a combination of several galaxy properties, such that disentangling its origin is not trivial. Consequently, we exclude J1248+4259 from the sample and derive the equation that linearly relates EW(Lyα) and 1–Cf(H I) as (4σ significance level, p-value < 0.00002):
We include this relation in Fig. 10 (dotted line) and compare it with the one obtained by Steidel et al. (2018) (dashed line), where the authors investigated the connection between the neutral gas properties and the escape of Lyα and LyC photons in composite spectra of z ∼ 3 galaxies observed with the Low Resolution Imaging Spectrometer (LRIS; Oke et al. 1995; Steidel et al. 2004) on the Keck I telescope. Both linear relations have similar slopes, but the relation from Steidel et al. (2018) slightly underestimates the EW(Lyα) from our sample. One reason for this is that Steidel et al. (2018) sample is drawn from composite spectra with EW(Lyα) < 50 Å, while ∼60% of both our and the Jaskot et al. (2019), McKinney et al. (2019) samples have EW(Lyα) larger than 50 Å. Besides, the Lyα equivalent width is also known to relate to the aperture size of the instrument (Steidel et al. 2011; Hayes et al. 2014; Wisotzki et al. 2016), and therefore complicates direct comparison between samples observed with different instruments. Finally, the higher EW(Lyα) in our sample might be biased by different galaxy properties (i.e., stellar masses, velocity widths, etc) and because our sample was selected to be only galaxies with intense star formation and young stellar populations.
Although the physical interpretation of high EW(Lyα) is complex, the tight connection between EW(Lyα) and 1–Cf(H I) is consistent with the findings from Sects. 4.1 and 4.2 and confirms the strong impact of low neutral gas coverage on the observed emission of Lyα photons.
4.4. The escape of Lyα and LyC photons is larger in galaxies with lower Cf(H I) and EB–V
Investigating the connection between the H I column density, H I covering fraction, and the escape fraction of Lyα and LyC photons should allow us to understand the H I geometry that controls and regulates the leakage of these photons out of the ISM. Recently, we found saturated Lyman series with non-unity covering fraction in nine LCEs included in this work, highlighting the existence of both low and high column density paths in galaxies that leak ionizing photons (Gazagnes et al. 2018). Additionally, we found that six LCEs have NH I measurements supporting the presence of optically thick regions (> 1018 cm−2) in the ISM, which is incompatible with a density-bounded scenario. Several studies similarly highlighted the close connection between Cf(H I) and/or Cf(Si II) and the Lyα escape fraction and equivalent width (Rivera-Thorsen et al. 2015; Steidel et al. 2018; McKinney et al. 2019; Jaskot et al. 2019).
In Fig. 11, we analyze the dependence between the covering fraction and the observed escape fractions of Lyα and LyC photons. We find a 4σ correlation between 1–Cf(H I) and fesc(Lyα) (p-value < 0.00002) and a 3σ significance level for the trend that connects 1–Cf(H I) to 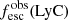 (p-value of 0.0005). Further, the left panel of Fig. 11 shows that most galaxies have a fesc(Lyα) lower than or equal to 1 − Cf(H I). For
(p-value of 0.0005). Further, the left panel of Fig. 11 shows that most galaxies have a fesc(Lyα) lower than or equal to 1 − Cf(H I). For 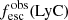 , the trend is slightly more scattered but it should be emphasized that 1–Cf(H I) always overestimates the observed escape fraction of ionizing photons. This observational result is consistent with theoretical studies which suggest that Cf(H I) is always an upper limit to the escape of ionizing photons (Kakiichi & Gronke 2019). Indeed, several reasons explain why the ionizing escape fraction should deviate from 1–Cf(H I): the presence of H I residuals in the channels, the necessity to account for the dust attenuation (Chisholm et al. 2018), or because the covering fraction measured is always a lower limit to the true geometrical neutral gas covering (see discussion in Rivera-Thorsen et al. 2015; Vasei et al. 2016; Gazagnes et al. 2018, Mauerhofer et al., in prep.). While these effects also impact the escape fraction of Lyα photons, Lyα photons have a higher chance to escape by being scattered and either shifted out of the velocity range of the optically thick neutral gas or re-emitted in the direction of a low column density sightline. Hence, the kinematics of the H I gas can affect the escape of Lyα photons, while it does not impact the escape of LyC photons. This could explain why the neutral gas coverage is more correlated with the escape of Lyα photons. Further LyC observations are needed to confirm this trend. Nonetheless, these results confirm that the common origin of the leakage of Lyα and LyC photons is the ISM porosity.
, the trend is slightly more scattered but it should be emphasized that 1–Cf(H I) always overestimates the observed escape fraction of ionizing photons. This observational result is consistent with theoretical studies which suggest that Cf(H I) is always an upper limit to the escape of ionizing photons (Kakiichi & Gronke 2019). Indeed, several reasons explain why the ionizing escape fraction should deviate from 1–Cf(H I): the presence of H I residuals in the channels, the necessity to account for the dust attenuation (Chisholm et al. 2018), or because the covering fraction measured is always a lower limit to the true geometrical neutral gas covering (see discussion in Rivera-Thorsen et al. 2015; Vasei et al. 2016; Gazagnes et al. 2018, Mauerhofer et al., in prep.). While these effects also impact the escape fraction of Lyα photons, Lyα photons have a higher chance to escape by being scattered and either shifted out of the velocity range of the optically thick neutral gas or re-emitted in the direction of a low column density sightline. Hence, the kinematics of the H I gas can affect the escape of Lyα photons, while it does not impact the escape of LyC photons. This could explain why the neutral gas coverage is more correlated with the escape of Lyα photons. Further LyC observations are needed to confirm this trend. Nonetheless, these results confirm that the common origin of the leakage of Lyα and LyC photons is the ISM porosity.
 |
Fig. 11. Observed fesc(Lyα) (left) and |
Additionally, we also investigated the impact of dust extinction on the escape fraction of Lyα and LyC photons. Several studies have shown that dust readily destroys Lyα photons (Neufeld 1991; Hayes et al. 2011; Verhamme et al. 2015, 2017; Du et al. 2018; Kimm et al. 2019; Jaskot et al. 2019), while Chisholm et al. (2018) showed that the dust attenuation is a crucial ingredient for the escape of ionizing photons. On the other hand, recent Lyα-LyC simulations from Kimm et al. (2019) found that the presence of dust grains should not significantly affect the leakage of LyC photons. Hence, the true impact of dust on the ionizing radiation is still poorly understood.
In Fig. 12, we compare the escape fractions of Lyα and LyC photons with the EB − V obtained from the stellar continuum UV fits. Both panels highlight that galaxies with large fesc(LyC) and fesc(Lyα) have lower dust extinction. Interestingly, the three largest LyC leakers have the lowest EB − V, suggesting that low amount of dust favors the escape of LyC photons. We superposed on the same figure the theoretical attenuation curve (dashed lines) given by 10−0.4A(λ), where A(λ) is derived using the dust extinction law from Reddy et al. (2016a) at λ = 1216 Å for Lyα photons and 912 Å for LyC photons. We find a 3σ significance level correlation between the dust attenuation and the escape fractions of LyC and Lyα photons (p-value of 0.0014 and 0.0011, respectively). Hence, this indicates that the presence of interstellar dust grains in the ISM has a significant impact the escape of both types of emission. However, these results need to be taken with caution.
 |
Fig. 12. Observed fesc(Lyα) (left) and |
Figure 12 shows that a few galaxies have their Lyα or LyC escape fractions above the dust attenuation curve. In theory, in galaxies having no H I and a screen layer of dust, the fraction of LyC and Lyα radiation escaping should be directly given by 10−0.4A(λ). Hence, no galaxies should have 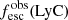 or fesc(Lyα) larger than the dust attenuation curve. Several reasons for this discrepancy are considered in Sect. 3.2, where we highlight the complex task of measuring EB − V and show that different dust extinction laws can lead in significant differences in the fitted attenuation at 1216 and 912 Å. Additionally, in this work, we use the Reddy et al. (2016a) dust attenuation curve, which is derived in the far-UV observations (λ = 950 − 1500 Å). Nevertheless, the physical impact of dust extinction on the ionizing flux (< 912 Å) is still unconstrained. Finally, the dust geometry model can also impact these results. A clumpy distribution of H I and dust could theoretically have a shielding effect such that Lyα photons have a lower probability to encounter dust (Neufeld 1991; Gronke et al. 2016), and enhance the observed emission of Lyα photons (Finkelstein et al. 2008). Scarlata et al. (2009) found that such clumpy distribution better reproduces the observed Lyα/Hα and Hα/Hβ ratio in 31 low-z Lyα emitters. Hence, several factors can lead to different estimations of the dust impact, and robustly constraining the latter requires deeper observations. Furthermore, both the
or fesc(Lyα) larger than the dust attenuation curve. Several reasons for this discrepancy are considered in Sect. 3.2, where we highlight the complex task of measuring EB − V and show that different dust extinction laws can lead in significant differences in the fitted attenuation at 1216 and 912 Å. Additionally, in this work, we use the Reddy et al. (2016a) dust attenuation curve, which is derived in the far-UV observations (λ = 950 − 1500 Å). Nevertheless, the physical impact of dust extinction on the ionizing flux (< 912 Å) is still unconstrained. Finally, the dust geometry model can also impact these results. A clumpy distribution of H I and dust could theoretically have a shielding effect such that Lyα photons have a lower probability to encounter dust (Neufeld 1991; Gronke et al. 2016), and enhance the observed emission of Lyα photons (Finkelstein et al. 2008). Scarlata et al. (2009) found that such clumpy distribution better reproduces the observed Lyα/Hα and Hα/Hβ ratio in 31 low-z Lyα emitters. Hence, several factors can lead to different estimations of the dust impact, and robustly constraining the latter requires deeper observations. Furthermore, both the 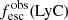 and fesc(Lyα) depend on accurately determining the intrinsic emission, which may be mis-estimated by our assumed models.
and fesc(Lyα) depend on accurately determining the intrinsic emission, which may be mis-estimated by our assumed models.
4.5. Predicting the LyC escape fraction from absorption line measurements
The outcomes of Figs. 11 and 12 favor an ionization-bounded scenario, where dusty channels with low NH I act as the dominant escape roads for Lyα and LyC photons and support the conclusions drawn in Gazagnes et al. (2018) and Chisholm et al. (2018). The latter work additionally proposed a novel approach to accurately recover the observed escape fractions based on the Cf(H I) and dust extinction. This indirect prediction method will be particularly useful at higher redshift where the flux at < 912 Å can not be directly observed. Indeed, the upcoming James Space Webb Telescope (JWST) will have a sufficient resolution to observe low-ionization interstellar (LIS) absorption lines and measure Cf(Si II), which can be then used to infer Cf(H I) (Gazagnes et al. 2018). The analysis done in Chisholm et al. (2018) included 9 LCEs5 with 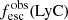 between 1 and 13%, and we test here its reliability using the six new leakers from Izotov et al. (2018a,b), three of them with large LyC escape fractions (≥38%).
between 1 and 13%, and we test here its reliability using the six new leakers from Izotov et al. (2018a,b), three of them with large LyC escape fractions (≥38%).
This is shown in Fig. 13, where we plot the predicted escape fraction of LyC photons (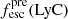 ), computed as (1−Cf(H I)) × 10−0.4A(λ = 912 Å) (see Chisholm et al. 2018), versus the observed escape fraction of LyC photons (
), computed as (1−Cf(H I)) × 10−0.4A(λ = 912 Å) (see Chisholm et al. 2018), versus the observed escape fraction of LyC photons (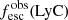 ), derived using the ratio of the observed flux at ∼900 Å over the modelled flux obtained from SED fitting for the 13 confirmed LCEs in our sample. The recovered LyC escape fractions accurately match at ±3σ with
), derived using the ratio of the observed flux at ∼900 Å over the modelled flux obtained from SED fitting for the 13 confirmed LCEs in our sample. The recovered LyC escape fractions accurately match at ±3σ with 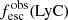 for 10 leakers, underestimates it for the two largest leakers, and overestimates it in Tol1247-232. For the latter, the bias is likely explained by a possible contamination from geocoronal emission, as discussed in Chisholm et al. (2017a); Chisholm et al. (2018). We mention in Sect. 2 that several studies using different measurement methods have reported LyC escape fractions varying from 0.004 to 0.042 for Tol1247-232 (Leitherer et al. 2016; Chisholm et al. 2017a; Puschnig et al. 2017), which gives an interval consistent with the predicted 4.8 ± 1.7%. For the two largest leakers, several factors can explain the inconsistency between
for 10 leakers, underestimates it for the two largest leakers, and overestimates it in Tol1247-232. For the latter, the bias is likely explained by a possible contamination from geocoronal emission, as discussed in Chisholm et al. (2017a); Chisholm et al. (2018). We mention in Sect. 2 that several studies using different measurement methods have reported LyC escape fractions varying from 0.004 to 0.042 for Tol1247-232 (Leitherer et al. 2016; Chisholm et al. 2017a; Puschnig et al. 2017), which gives an interval consistent with the predicted 4.8 ± 1.7%. For the two largest leakers, several factors can explain the inconsistency between 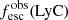 and
and 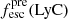 . The measurement of
. The measurement of 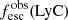 can suffer from poor constraints on the estimation of intrinsic emission of LyC photons (Chisholm et al. 2019), and different
can suffer from poor constraints on the estimation of intrinsic emission of LyC photons (Chisholm et al. 2019), and different 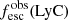 measurement approaches can lead to significant variations in some cases (for example J1011+1947 has
measurement approaches can lead to significant variations in some cases (for example J1011+1947 has 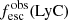 = 11.4 ± 1.8% when using an approach based on SED fitting, and
= 11.4 ± 1.8% when using an approach based on SED fitting, and 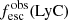 = 6.2 ± 0.7% when using the Hβ flux density; Izotov et al. 2018b). Similarly, reliable measurements of the dust attenuation are required to accurately estimate
= 6.2 ± 0.7% when using the Hβ flux density; Izotov et al. 2018b). Similarly, reliable measurements of the dust attenuation are required to accurately estimate 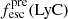 . We show in Sect. 3.2 that a 0.1 difference in EB − V varies by a factor of two in attenuation and, hence, in
. We show in Sect. 3.2 that a 0.1 difference in EB − V varies by a factor of two in attenuation and, hence, in 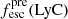 . Nevertheless, robustly constraining the stellar continuum and dust extinction is highly complicated in galaxies with low S/N spectra (see Sect. 3.2).
. Nevertheless, robustly constraining the stellar continuum and dust extinction is highly complicated in galaxies with low S/N spectra (see Sect. 3.2).
 |
Fig. 13. Predicted LyC escape fraction |
Additionally, we showed in Gazagnes et al. (2018), Chisholm et al. (2018) that the dust geometry should not impact the derived 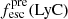 because only the combination of Cf(H I) and EB − V changes to match the observed data. We re-fitted J1154+2443 and J1256+4509 (
because only the combination of Cf(H I) and EB − V changes to match the observed data. We re-fitted J1154+2443 and J1256+4509 (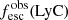 of 0.46 and 0.38, respectively) using a model where the dust lies only in the dense H I clouds to check if this is still the case in large leakers. We found
of 0.46 and 0.38, respectively) using a model where the dust lies only in the dense H I clouds to check if this is still the case in large leakers. We found 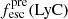 = 0.074 ± 0.048 and 0.242 ± 0.095 for J1154+2443 and J1256+4509 respectively, consistent with the predictions using the screen model (0.136 ± 0.054 and 0.240 ± 0.089) and assuming, hence, that a different dust model does not improve the fesc(LyC) estimation of galaxies with high
= 0.074 ± 0.048 and 0.242 ± 0.095 for J1154+2443 and J1256+4509 respectively, consistent with the predictions using the screen model (0.136 ± 0.054 and 0.240 ± 0.089) and assuming, hence, that a different dust model does not improve the fesc(LyC) estimation of galaxies with high 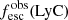 .
.
Finally, indirectly predicting the ionizing escape in very strong leakers might be more complicated because their escape fraction could be a combination of the ionization and density bounded models, as suggested in Kakiichi & Gronke (2019). The authors show that the leakage mechanisms in galaxies with a turbulent ISM dynamically evolve over time, such that the correlation between the leakage of LyC photons and the H I covering fraction becomes weaker as more and more channels with lower  form in the ISM. This is because these regions finally dominate the ISM to the point that the leakage is mostly regulated by the density-bounded scenario. While constraining the NH I requires a high S/N (Gazagnes et al. 2018), the shape of the Lyα profile can provide insights of the dominant escape mechanisms. Kakiichi & Gronke (2019) show that galaxies with a density-bounded ISM have a lower red peak asymmetry (Af) (defined by Eq. (33) in Kakiichi & Gronke 2019) than galaxies with an ionization bounded ISM. In particular, they find that the three largest leakers in our sample have a red peak asymmetry consistent with galaxies with a density bounded ISM. Additionally, we showed in Sect. 4.2 that two of these leakers had the lowest H I velocity width of the maximal H I absorption, while we do not observe H I absorption lines in the largest LCE. This supports the fact that galaxies with large
form in the ISM. This is because these regions finally dominate the ISM to the point that the leakage is mostly regulated by the density-bounded scenario. While constraining the NH I requires a high S/N (Gazagnes et al. 2018), the shape of the Lyα profile can provide insights of the dominant escape mechanisms. Kakiichi & Gronke (2019) show that galaxies with a density-bounded ISM have a lower red peak asymmetry (Af) (defined by Eq. (33) in Kakiichi & Gronke 2019) than galaxies with an ionization bounded ISM. In particular, they find that the three largest leakers in our sample have a red peak asymmetry consistent with galaxies with a density bounded ISM. Additionally, we showed in Sect. 4.2 that two of these leakers had the lowest H I velocity width of the maximal H I absorption, while we do not observe H I absorption lines in the largest LCE. This supports the fact that galaxies with large 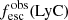 must also have lower H I column densities within the clouds that have the highest optical depth. In fact, Ramambason et al. (in prep.) find evidence from the optical emission lines pointing towards a density bounded ISM for these galaxies. This could explain why our approach based on Cf(H I) underestimates the LyC escape fraction in these extreme leakers. In any case, Fig. 13 shows that the UV absorption lines can be used to determine a reliable lower limit of the escape of LyC photons in LCEs candidates.
must also have lower H I column densities within the clouds that have the highest optical depth. In fact, Ramambason et al. (in prep.) find evidence from the optical emission lines pointing towards a density bounded ISM for these galaxies. This could explain why our approach based on Cf(H I) underestimates the LyC escape fraction in these extreme leakers. In any case, Fig. 13 shows that the UV absorption lines can be used to determine a reliable lower limit of the escape of LyC photons in LCEs candidates.
Overall, our results suggest that the H I porosity and dust attenuation play a crucial role in the escape of Lyα and LyC photons; also suggesting that fesc(LyC) predictions based on Cf(H I) and EB − V can provide a lower limit on the fesc(LyC) along the line of sight, despite the potentially complex leakage mechanisms in LCEs with high LyC escape fraction. This indirect approach might be valuable for high-redshift observations in order to compare the range of fesc(LyC) of galaxies during the Reionization era and, hence, investigate whether star-forming galaxies reionized the Universe. We discuss this point further in Sect. 5.2.
4.6. The flux at the Lyα profile minimum correlates with the LyC escape fraction
Finally, we find that the presence of Lyα emission at the profile trough is a valuable marker of peculiar neutral gas properties. Indeed, it suggests that a fraction of Lyα photons can escape unaffected where the optical depth of the H I gas should be maximal. In particular, a Lyα profile with a single peak at the systemic velocity should emerge from any patchy ISM with fully cleared holes (no H I residuals), because all the Lyα photons should find these holes after a negligible amount of scattering events (Verhamme et al. 2015; Dijkstra et al. 2016). None of the galaxies in our sample with Cf(H I) < 1 exhibit such Lyα spectral shape, including J1243+4646, which has no detected H I absorption (all Lyα profiles are shown in Appendix C). However, all LCEs have net flux at the Lyα trough, suggesting that some Lyα photons escaped without being scattered by the H I gas. This peculiarity has been observed in simulations in the presence of a very dense clumpy neutral gas distribution (Gronke et al. 2016, 2017), or when the H I column density is low enough such that Lyα photons escape with fewer scattering events (Kakiichi & Gronke 2019). In Sects. 4.1 and 4.2, we argued that Cf(H I) probes both the fraction of sightlines between the galaxy and the observer covered by low column density H I gas, such that Lyα and LyC photons passing through these escape roads have a lower probability to interact with the neutral gas. Hence, a larger 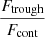 should correlate with the covering fraction of the low NH I channels (1–Cf(H I)) and with a larger escape fraction of ionizing photons.
should correlate with the covering fraction of the low NH I channels (1–Cf(H I)) and with a larger escape fraction of ionizing photons.
Figure 14 explores the connection between 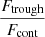 and 1–Cf(H I) in our sample and in the GP sample studied by McKinney et al. (2019) and Jaskot et al. (2019). The trend is slightly scattered, but the correlation is significant at the 3σ (p-value of 0.0014). Hence, the presence of more flux at the Lyα trough is related to a lower H I covering fraction. In a highly porous ISM, higher amounts of Lyα photons can escape at velocities where the H I optical depth is large because they find low column density sightlines (see Sect. 4.2). We note that, similarly to Orlitová et al. (2018) and Jaskot et al. (2019), we report a strong correlation (3.5σ) between the Lyα peak velocity separation and the strength of the flux at the Lyα profile minimum (not shown). Hence,
and 1–Cf(H I) in our sample and in the GP sample studied by McKinney et al. (2019) and Jaskot et al. (2019). The trend is slightly scattered, but the correlation is significant at the 3σ (p-value of 0.0014). Hence, the presence of more flux at the Lyα trough is related to a lower H I covering fraction. In a highly porous ISM, higher amounts of Lyα photons can escape at velocities where the H I optical depth is large because they find low column density sightlines (see Sect. 4.2). We note that, similarly to Orlitová et al. (2018) and Jaskot et al. (2019), we report a strong correlation (3.5σ) between the Lyα peak velocity separation and the strength of the flux at the Lyα profile minimum (not shown). Hence,  ,
, 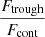 and Cf(H I) likely provide similar insights about the presence of channels with low
and Cf(H I) likely provide similar insights about the presence of channels with low  in the ISM.
in the ISM.
 |
Fig. 14. Normalized Lyα flux at the minimum of the Lyα profile |
Additionally, we investigate in Fig. 15 the connection between 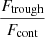 and the escape of LyC photons. This figure clearly highlights the finding that all LCEs have a net emission at the minimum profile, and larger
and the escape of LyC photons. This figure clearly highlights the finding that all LCEs have a net emission at the minimum profile, and larger 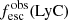 scales with larger
scales with larger 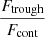 (at the 3.5σ level, p-value of 0.000022). Hence, similarly to
(at the 3.5σ level, p-value of 0.000022). Hence, similarly to 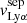 (Verhamme et al. 2017; Izotov et al. 2018b),
(Verhamme et al. 2017; Izotov et al. 2018b), 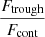 is likely to prove a reliable indicator of the presence of ISM properties that favor the leakage of ionizing photons. We derive the linear relation that relates fesc(LyC) to
is likely to prove a reliable indicator of the presence of ISM properties that favor the leakage of ionizing photons. We derive the linear relation that relates fesc(LyC) to 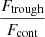 in our sample (with R ∼ 15 000 observations from COS):
in our sample (with R ∼ 15 000 observations from COS):
 |
Fig. 15. Observed escape fraction of LyC photons versus |
In Gazagnes et al. (2018), we posit that J0926+4427, J1429+0643, and GP1054+5238 are potential LCE candidates, and we estimate fesc(LyC) of ≈1% using their Cf(H I) and dust extinction measurements. Equation (6) suggests that follow-up observations could measure LyC escape fractions of < 1% in GP1054+5238 and J1429+0643 (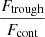 of 0.21 and 0.82, respectively) and 1.6% in J0926+4427 (
of 0.21 and 0.82, respectively) and 1.6% in J0926+4427 (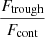 = 1.51). The largest measured flux at minimum of Lyα profile in the GPs sample analyzed by McKinney et al. (2019) and Jaskot et al. (2019) is J1608+3528 with
= 1.51). The largest measured flux at minimum of Lyα profile in the GPs sample analyzed by McKinney et al. (2019) and Jaskot et al. (2019) is J1608+3528 with 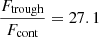 , which corresponds to a very large fesc(LyC) of ≈83% according to Eq. (6). Additionally, J1608+3528 also has a narrow peak velocity separation (214 ± 30 km s−1, McKinney et al. 2019), which strongly supports the presence of LyC leakage.
, which corresponds to a very large fesc(LyC) of ≈83% according to Eq. (6). Additionally, J1608+3528 also has a narrow peak velocity separation (214 ± 30 km s−1, McKinney et al. 2019), which strongly supports the presence of LyC leakage.
Overall, Eq. (6) suggests that galaxies with 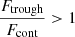 have fesc(LyC) > 1%. Nevertheless, the reliability of Eq. (6) should be taken with caution because this linear relation is largely constrained by the large fesc(LyC) LCEs, while the
have fesc(LyC) > 1%. Nevertheless, the reliability of Eq. (6) should be taken with caution because this linear relation is largely constrained by the large fesc(LyC) LCEs, while the 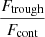 values of the low fesc(LyC) LCEs are largely scattered. Further observations with sufficiently high spectral resolution are needed to confirm its reliability.
values of the low fesc(LyC) LCEs are largely scattered. Further observations with sufficiently high spectral resolution are needed to confirm its reliability.
5. Discussion
5.1. The ISM porosity enables the escape of Lyα and LyC photons
The observations of partially covered, albeit saturated, Lyman series absorption lines suggest an inhomogeneous ISM with both high and low column density H I gas. In this work, we study the connection between the Lyα and the neutral gas properties and provide insights to improve the understanding of how this bi-modal distribution of H I gas (e.g., see Fig. 6 of Kakiichi & Gronke 2019) impacts the observed Lyα emission and LyC escape. Similarly to recent studies (Rivera-Thorsen et al. 2015; Steidel et al. 2018; McKinney et al. 2019) that highlight the connection between Lyα properties and the neutral gas covering fraction, we find that the observed emission and escape of Lyα photons of the 22 galaxies in our sample is closely connected to the fraction of sightlines between the galaxy and the observer covered by channels with low  (Sects. 4.3 and 4.4). Additionally, Sect. 4.4 shows the close connection between the escape of ionizing photons and 1–Cf(H I), confirming that LCEs all have a non-unity H I covering fraction (Gazagnes et al. 2018). These results emphasize that privileged escape roads exist for the Lyα and LyC radiation. More interestingly, we found in Sect. 4.1 that the Lyα peak separation strongly scales with the H I covering fraction. As we expect
(Sects. 4.3 and 4.4). Additionally, Sect. 4.4 shows the close connection between the escape of ionizing photons and 1–Cf(H I), confirming that LCEs all have a non-unity H I covering fraction (Gazagnes et al. 2018). These results emphasize that privileged escape roads exist for the Lyα and LyC radiation. More interestingly, we found in Sect. 4.1 that the Lyα peak separation strongly scales with the H I covering fraction. As we expect 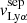 to scale with NH I (Verhamme et al. 2015; Dijkstra et al. 2016), this relation may suggest that a low Cf(H I) not only indicates the presence of low column density channels, but also lower
to scale with NH I (Verhamme et al. 2015; Dijkstra et al. 2016), this relation may suggest that a low Cf(H I) not only indicates the presence of low column density channels, but also lower  . This is similarly highlighted in Sect. 4.6, where we show that the Lyα flux at the minimum of the Lyα profile scales with Cf(H I). Hence, more Lyα photons escape unaffected by the H I gas when a larger fraction of low column density paths cut through the ISM.
. This is similarly highlighted in Sect. 4.6, where we show that the Lyα flux at the minimum of the Lyα profile scales with Cf(H I). Hence, more Lyα photons escape unaffected by the H I gas when a larger fraction of low column density paths cut through the ISM.
In Gazagnes et al. (2018), we constrained NH I in six low 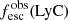 leakers and found that the dense neutral regions have column densities large enough (1018 cm−2) to absorb all of the ionizing radiation. McKinney et al. (2019) reported similar insights from a sample of highly ionized Green Peas, and further emphasized that the NH I derived from NO I is always a lower limit to other indirect approaches, where NH I is derived from
leakers and found that the dense neutral regions have column densities large enough (1018 cm−2) to absorb all of the ionizing radiation. McKinney et al. (2019) reported similar insights from a sample of highly ionized Green Peas, and further emphasized that the NH I derived from NO I is always a lower limit to other indirect approaches, where NH I is derived from 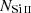 , or from the fit of the observed Lyα absorption profile. Hence, these results show that, in these LCEs, ionizing photons escape through optically thin channels or holes in an ISM, which is overall ionization bounded. Additionally, Sect. 4.5 highlighted that an indirect fesc(LyC) estimation method using Cf(H I) and the dust extinction (Chisholm et al. 2018) accurately recovers the observed escape fractions in the low fesc(LyC) LCEs.
, or from the fit of the observed Lyα absorption profile. Hence, these results show that, in these LCEs, ionizing photons escape through optically thin channels or holes in an ISM, which is overall ionization bounded. Additionally, Sect. 4.5 highlighted that an indirect fesc(LyC) estimation method using Cf(H I) and the dust extinction (Chisholm et al. 2018) accurately recovers the observed escape fractions in the low fesc(LyC) LCEs.
Nevertheless, the latter approach underestimates fesc(LyC) in LCEs with the largest 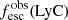 . This discrepancy could highlight that the escape mechanisms in these leakers cannot merely be explained by the presence of a low Cf(H I). In Sect. 4.2, we showed that the peak velocity separation is also tightly related to the velocity width of the maximal absorption of the saturated H I absorption lines. The connection between low
. This discrepancy could highlight that the escape mechanisms in these leakers cannot merely be explained by the presence of a low Cf(H I). In Sect. 4.2, we showed that the peak velocity separation is also tightly related to the velocity width of the maximal absorption of the saturated H I absorption lines. The connection between low 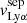 and low NH I (Verhamme et al. 2015; Dijkstra et al. 2016) could suggest that
and low NH I (Verhamme et al. 2015; Dijkstra et al. 2016) could suggest that 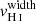 indirectly probes the presence of lower
indirectly probes the presence of lower 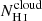 within the densest neutral clouds in the ISM, such that a fraction of LyC photons escape through these regions. Interestingly, two of the three largest leakers (with
within the densest neutral clouds in the ISM, such that a fraction of LyC photons escape through these regions. Interestingly, two of the three largest leakers (with 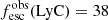 and 46 %) have the lowest
and 46 %) have the lowest 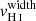 in our sample, and H I is not detected in the largest LCE. Hence, for the largest leakers, a LyC prediction method using the covering fraction likely underestimates the total escape fraction of ionizing photons because all the lines of sight to the observer are density-bounded.
in our sample, and H I is not detected in the largest LCE. Hence, for the largest leakers, a LyC prediction method using the covering fraction likely underestimates the total escape fraction of ionizing photons because all the lines of sight to the observer are density-bounded.
These outcomes are supported by the recent radiation-hydrodynamics simulations of galaxies with a turbulent ISM by Kakiichi & Gronke (2019). The authors showed that the early evolution of the turbulent gas kinematics generates channels with low  , forming a ionization-bounded ISM where the leakage of LyC photons is directly driven by the fraction of paths covered by photo-ionized channels. Additionally, the evolution of the turbulent gas forms new channels and modifies the densities within these channels, increasing the fraction of low column density paths in the ISM. As a consequence, the escape mechanisms of LyC photons progressively evolve from a ionization-bounded model (fesc(LyC) directly proportional to Cf(H I)) towards a density-bounded scenario (low NH I in all directions, with a weaker connection between fesc(LyC) and Cf(H I)). The authors show that markers of this trade-off can be found on the Lyα profile, for example, by using the red peak asymmetry (Af). Their simulations support the finding that the largest leakers from Izotov et al. (2018a,b) have Af consistent with a density-bounded scenario, while leakers with
, forming a ionization-bounded ISM where the leakage of LyC photons is directly driven by the fraction of paths covered by photo-ionized channels. Additionally, the evolution of the turbulent gas forms new channels and modifies the densities within these channels, increasing the fraction of low column density paths in the ISM. As a consequence, the escape mechanisms of LyC photons progressively evolve from a ionization-bounded model (fesc(LyC) directly proportional to Cf(H I)) towards a density-bounded scenario (low NH I in all directions, with a weaker connection between fesc(LyC) and Cf(H I)). The authors show that markers of this trade-off can be found on the Lyα profile, for example, by using the red peak asymmetry (Af). Their simulations support the finding that the largest leakers from Izotov et al. (2018a,b) have Af consistent with a density-bounded scenario, while leakers with 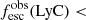 13% have Af consistent with an ionization-bounded model.
13% have Af consistent with an ionization-bounded model.
Overall, these results provide new valuable insights to understand the dominant escape mechanisms of LyC photons. In the low LyC leakers, the ISM porosity enables the leakage of LyC and Lyα photons, such that the ionising photons predominantly escape through low column density paths in the ISM, while the densest neutral clouds have 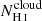 too large and efficiently absorb the LyC photons passing through them (panel a of Fig. 16). However, the dynamical evolution of the ISM could shift the escape mechanisms towards a density bounded model, where all sightlines are covered by NH I < 1017.9 cm−2 (fesc(LyC) ≈ 1%), enhancing the total escape fraction of LyC photons (panel b of Fig. 16). This outcome emphasizes the need to constrain the NH I in both the low- and high-density regions (
too large and efficiently absorb the LyC photons passing through them (panel a of Fig. 16). However, the dynamical evolution of the ISM could shift the escape mechanisms towards a density bounded model, where all sightlines are covered by NH I < 1017.9 cm−2 (fesc(LyC) ≈ 1%), enhancing the total escape fraction of LyC photons (panel b of Fig. 16). This outcome emphasizes the need to constrain the NH I in both the low- and high-density regions ( and
and 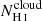 ) to obtain accurate LyC predictions. Figure 16 illustrates the two different ISM configurations for small and large
) to obtain accurate LyC predictions. Figure 16 illustrates the two different ISM configurations for small and large 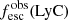 LCEs discussed in this section. Further low-redshift LyC observations ought to be capable of assessing this model.
LCEs discussed in this section. Further low-redshift LyC observations ought to be capable of assessing this model.
 |
Fig. 16. Illustration of the physical picture discussed in Sect. 5.1. Left: LyC photons escape through channels covered by |
5.2. Indirectly constraining fesc(LyC) at high-z
The upcoming era of telescopes such as JWST and Extremely Large Telescopes (ELTs; GMT, TMT, ELT) will probe galaxies within the Epoch of Reionization and provide valuable clues to understand how the Universe was reionized. However, preparing for future observations requires finding the right pre-selection markers to efficiently survey large samples of LyC candidates and indirectly constrain their fesc(LyC). To do this, low-redshift observations of the Lyman break in highly star-forming galaxies provides a unique laboratory of LCEs (Borthakur et al. 2014; Izotov et al. 2016b,a, 2018a,b; Wang et al. 2019) for the exploration of the connection between the Lyα, LyC and neutral gas properties. In this work, we highlight the finding that the neutral gas porosity comprises the plausible physical origin of the leakage of LyC and Lyα photons, but that density-bounded mechanisms could dominate in the largest leakers. Because the ISM porosity affects the shape of the Lyα emission, Lyα properties can provide valuable insights into the leakage of LyC photons. The scaling relations between 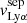 , NH I and Cf(H I) (Sect. 4.1) confirms that low peak-velocity separation is likely a reliable probe of LyC leakage (Verhamme et al. 2017; Izotov et al. 2018b, 2020). However, deriving an accurate estimate of fesc(LyC) from it might be complicated because the Lyα spectral shape is both sensitive to the covering fraction of low column density channels and to the width of the maximal absorption of the saturated Lyman series (Sect. 4.2). The positive correlation found between the red peak velocity and the H I covering fraction might also support the use of
, NH I and Cf(H I) (Sect. 4.1) confirms that low peak-velocity separation is likely a reliable probe of LyC leakage (Verhamme et al. 2017; Izotov et al. 2018b, 2020). However, deriving an accurate estimate of fesc(LyC) from it might be complicated because the Lyα spectral shape is both sensitive to the covering fraction of low column density channels and to the width of the maximal absorption of the saturated Lyman series (Sect. 4.2). The positive correlation found between the red peak velocity and the H I covering fraction might also support the use of 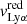 to probe the escape of LyC photons, but further theoretical simulations are required to understand its origin.
to probe the escape of LyC photons, but further theoretical simulations are required to understand its origin.
Additionally, we showed that EW(Lyα) or fesc(Lyα) scale with Cf(H I) (Sects. 4.3 and 4.4) and therefore could also indicate LyC leakage. Nevertheless, the EW(Lyα) is also tightly connected to the velocity width of the maximal absorption of the Lyman series (Figs. 7 and 10), and is degenerate with different galaxy properties, such as the star formation history or metallicity. Hence, galaxies with large EW(Lyα) may have moderate fesc(Lyα) and fesc(LyC) (Jaskot et al. 2019). On the other hand, Izotov et al. (2020) have derived an empirical relation between fesc(LyC) and fesc(Lyα). As both escape through channels with low NH I, it bolsters confidence in the presumption that such connection could be useful to indirectly derive fesc(LyC), despite the complex task of accurately measuring fesc(Lyα) due to scattering mechanisms and biases introduced from aperture corrections.
Finally, we show in Sect. 4.6 that the strength of the flux at the minimum of the Lyα profile, similarly to the peak velocity separation, is a robust tracer of the leakage of ionizing photons. Hence, our work supports the use of the Lyα properties to robustly pre-select LCEs candidate at low-redshift, and further constrain their fesc(LyC) using direct observations of the Lyman Break when possible.
However, probing the LyC escape with the Lyα properties at high redshift is more challenging. Wavelengths bluer than Lyα are highly contaminated by Lyα forest, such that Lyα diagnostics are less reliable (Schenker et al. 2014). Quantities such as 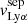 and
and 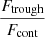 may not be accurately measured and different approaches must be found. At these high redshifts, the study of the LIS metal lines likely provide better constrains on the presence of favorable ISM properties for the LyC escape. LIS lines are often used as proxies to extract the neutral gas properties (Shapley et al. 2003; Jones et al. 2013; Alexandroff et al. 2015; Trainor et al. 2015; Reddy et al. 2016b; McKinney et al. 2019; Jaskot et al. 2019). Indeed, they are located at redder wavelengths and hence can be more easily observed at higher redshift. On the other hand, LIS metal lines also suffer some disadvantages, as they are potentially affected by scattering, fluorescent emission in-filling, and they often require high resolution observations to be fully resolved. Despite these caveats, they are currently one of the best LyC probes we have at high redshift. McKinney et al. (2019) and Jaskot et al. (2019) recently showed that LIS lines provide similar insights as Lyα properties.
may not be accurately measured and different approaches must be found. At these high redshifts, the study of the LIS metal lines likely provide better constrains on the presence of favorable ISM properties for the LyC escape. LIS lines are often used as proxies to extract the neutral gas properties (Shapley et al. 2003; Jones et al. 2013; Alexandroff et al. 2015; Trainor et al. 2015; Reddy et al. 2016b; McKinney et al. 2019; Jaskot et al. 2019). Indeed, they are located at redder wavelengths and hence can be more easily observed at higher redshift. On the other hand, LIS metal lines also suffer some disadvantages, as they are potentially affected by scattering, fluorescent emission in-filling, and they often require high resolution observations to be fully resolved. Despite these caveats, they are currently one of the best LyC probes we have at high redshift. McKinney et al. (2019) and Jaskot et al. (2019) recently showed that LIS lines provide similar insights as Lyα properties.
In Sect. 4.2, we highlighted the tight relation between the Lyα peak velocity separation and the velocity width of the saturated Lyman series. Chisholm et al. (2016) showed that different ionic transitions have similar velocity widths, thus, the Si II velocity width could provide an indirect estimation of 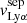 and indirectly probe the escape of ionizing photons. Similarly, in Gazagnes et al. (2018) and Chisholm et al. (2018), we show that Cf(Si II) can be used to empirically recover Cf(H I) and then combined to the dust attenuation at 912 Å to indirectly infer fesc(LyC).
and indirectly probe the escape of ionizing photons. Similarly, in Gazagnes et al. (2018) and Chisholm et al. (2018), we show that Cf(Si II) can be used to empirically recover Cf(H I) and then combined to the dust attenuation at 912 Å to indirectly infer fesc(LyC).
Section 4.5 shows that the latter approach is less accurate for galaxies with large observed escape fractions, likely due to the presence of more complex leakage mechanisms, such that the total fesc(LyC) along the line of sight cannot be inferred only using the neutral gas coverage (Kakiichi & Gronke 2019). Additionally, the strong trends found between the H I covering fraction and the escape of Lyα and LyC photons suggest that Cf(H I) is a good proxy of the true geometric covering fraction of the optically thick neutral gas clouds along the line of sight for the LCEs in our sample. As mentioned above, this might not be always the case because kinematic effects might bias the Cf measurements towards lower values. Despite these caveats, it remains a reliable approach to derive a lower limit to the true LyC escape fraction in compact star-forming galaxies where these effects might have less of an impact. Hence, it should provide valuable constraints on the expected impact of these galaxies during the Epoch of Reionization. Upcoming observations will allow us to confirm the robustness of the different pre-selection range and indirect estimation approaches discussed in this section.
6. Summary
We examined the neutral gas properties of a sample of 22 star-forming galaxies with existing Lyα and Lyman series observations. We fit the stellar continua, dust attenuations, H I covering fractions, H I velocity shifts and measured the Lyα properties, along with the H I velocity widths and depths of the Lyman series using a Monte Carlo approach. We investigated the relations between the neutral gas properties in galaxies with the escape and emission of Lyα photons and the observed LyC escape fractions. We summarize our results as follows:
-
Lyα photons are less scattered in galaxies with with a larger fraction of low density sightlines towards the observer (Sect. 4.1). Additionally, the scaling relation found between the Lyα peak velocities and the H I covering fractions (Cf(H I)) suggests that galaxies with lower neutral gas coverage also have lower H I column densities in the low-density channels (Fig. 6). Thus, low-z LCEs have small Lyα peak separations because photons find low column density escape roads out of the galaxy.
-
The velocity width of the H I gas, measured at the maximal depth of the H I absorption lines, has a significant impact on the Lyα emission, escape and velocity shift (Sect. 4.2). Galaxies with narrower H I absorption lines have higher EW(Lyα) and larger fesc(Lyα) (Fig 10). Additionally,
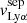 linearly scales with
linearly scales with 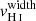 , and is lower in galaxies with lower H I covering fraction (Fig. 7). This highlights that the shape of the Lyα profile relates both to the presence of the low column density channels (low Cf(H I)) and to the properties of the denser neutral clouds imprinted from the saturated H I absorption lines (
, and is lower in galaxies with lower H I covering fraction (Fig. 7). This highlights that the shape of the Lyα profile relates both to the presence of the low column density channels (low Cf(H I)) and to the properties of the denser neutral clouds imprinted from the saturated H I absorption lines (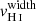 ). The presence of low
). The presence of low 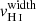 in the galaxies with the highest
in the galaxies with the highest 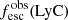 may suggest that they have less H I gas overall.
may suggest that they have less H I gas overall. -
Galaxies with lower covering fractions and/or dust attenuations have larger Lyα and LyC escape fractions (Figs. 11 and 12). The presence of a porous ISM (Cf(H I) < 1) is a necessary condition for observing a significant leakage of ionizing radiation (Fig. 13). At high redshift, the Cf(Si II) can be used to estimate Cf(H I) and provide valuable insights about the presence of LyC leakage. Additionally, using six recently observed LCEs, we find that the indirect approach to measure the line of sight fesc(LyC) proposed in Chisholm et al. (2018) accurately recovers their observed fesc(LyC) within ±3σ for nine leakers with
 %, and yields a lower limit on the total observed escape fractions in the LCEs with the largest LyC escape fractions. We suggest that recovering
%, and yields a lower limit on the total observed escape fractions in the LCEs with the largest LyC escape fractions. We suggest that recovering 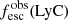 in these extreme leakers is more complex because their LyC leakage combines ionization and density bounded mechanisms (Fig. 16). Hence, an indirect prediction methods based only on Cf(H I) sets a lower limit to the true LyC escape fractions.
in these extreme leakers is more complex because their LyC leakage combines ionization and density bounded mechanisms (Fig. 16). Hence, an indirect prediction methods based only on Cf(H I) sets a lower limit to the true LyC escape fractions. -
Galaxies with lower Cf(H I) have a larger flux at the minimum of the Lyα profile (Fig. 14), and the Lyα profile minima scales strongly with the escape fraction of LyC photons (Fig. 15). Therefore, the presence of low-density paths in the ISM is presumably the common origin of low
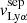 and high
and high 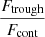 in the LCEs in our sample.
in the LCEs in our sample.
Our work emphasizes that the ISM porosity plays a major role in investigating the origin of the Lyα properties and the escape of LyC photons in LCEs, but additional escape mechanisms might be needed to explain the LyC escape fractions observed in the leakers with the largest LyC escape fractions (Fig. 16). Additionally, we show that the Lyα spectral shape, in particular through low 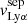 and high
and high 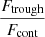 , probes ISM properties that favor the leakage of Lyα and LyC photons. At high redshift, the use of LIS lines is likely more appropriate to detect and constrain the ionizing escape fraction in Reionization era galaxies. Indeed, Si II can be used to infer Cf(H I) at high redshift (Gazagnes et al. 2018) and, hence, combined with EB − V to derive a lower limit of fesc(LyC) using the procedure from Chisholm et al. (2018). Recent additional approaches could further constrain the LyC escape fractions in currently confirmed LCEs (e.g., using Mg II; Chisholm et al., in prep.; Henry et al. 2018). Therefore, LIS diagnostics appear promising for future prospects at higher redshift for detecting LyC leaking candidates at high redshift (z > 6) with the upcoming era of new telescopes probing the Epoch of Reionization.
, probes ISM properties that favor the leakage of Lyα and LyC photons. At high redshift, the use of LIS lines is likely more appropriate to detect and constrain the ionizing escape fraction in Reionization era galaxies. Indeed, Si II can be used to infer Cf(H I) at high redshift (Gazagnes et al. 2018) and, hence, combined with EB − V to derive a lower limit of fesc(LyC) using the procedure from Chisholm et al. (2018). Recent additional approaches could further constrain the LyC escape fractions in currently confirmed LCEs (e.g., using Mg II; Chisholm et al., in prep.; Henry et al. 2018). Therefore, LIS diagnostics appear promising for future prospects at higher redshift for detecting LyC leaking candidates at high redshift (z > 6) with the upcoming era of new telescopes probing the Epoch of Reionization.
Values have been taken from the IDL routine from J. Xavier Prochaska: https://github.com/profxj/xidl/tree/master/Dust
In all this work, for galaxies only having upper limit on Cf(H I), we adopt the upper limit when deriving the significance level of the Cf(H I) correlations. In Appendix B.3, we investigate how the significance level of the reported trends changes for different assumptions, such as fixing Cf(H I) to the lower limit (0), or excluding one or several observations.
Tol0440-381 and Mrk54 (Leitherer et al. 2016), are not included in this work because they do not have Lyα observations.
Acknowledgments
The authors would like to thank the referee for the comments that helped improve the quality of this paper. The authors also thank Jed McKinney and Emil Rivera-Thorsen for the useful comments provided on a draft version of this paper. The position of SG was funded from a grant by the Center for Data Science and Systems Complexity (DSSC), University of Groningen. YI acknowledges support from the National Academy of Sciences of Ukraine by its priority project No. 0120U100935 “Fundamental properties of the matter in the relativistic collisions of nuclei and in the early Universe”. Support for this work was provided by NASA through the NASA Hubble Fellowship grant #51432 awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS5-26555.
References
- Alexandroff, R. M., Heckman, T. M., Borthakur, S., Overzier, R., & Leitherer, C. 2015, ApJ, 810, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Bergvall, N., Zackrisson, E., Andersson, B.-G., et al. 2006, A&A, 448, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bian, F., Fan, X., McGreer, I., Cai, Z., & Jiang, L. 2017, ApJ, 837, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Borthakur, S., Heckman, T. M., Leitherer, C., & Overzier, R. A. 2014, Science, 346, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Byler, N., Dalcanton, J. J., Conroy, C., et al. 2018, ApJ, 863, 14 [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, in Interstellar Dust, eds. L. J. Allamandola, & A. G. G. M. Tielens, IAU Symp., 135, 5 [Google Scholar]
- Chisholm, J., Tremonti, C. A., Leitherer, C., Chen, Y., & Wofford, A. 2016, MNRAS, 457, 3133 [NASA ADS] [CrossRef] [Google Scholar]
- Chisholm, J., Orlitová, I., Schaerer, D., et al. 2017a, A&A, 605, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chisholm, J., Tremonti, C. A., Leitherer, C., & Chen, Y. 2017b, MNRAS, 469, 4831 [NASA ADS] [CrossRef] [Google Scholar]
- Chisholm, J., Gazagnes, S., Schaerer, D., et al. 2018, A&A, 616, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chisholm, J., Rigby, J. R., Bayliss, M., et al. 2019, ApJ, 882, 182 [CrossRef] [Google Scholar]
- Dayal, P., & Ferrara, A. 2018, Phys. Rep., 780, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Dayal, P., Volonteri, M., Choudhury, T. R., et al. 2020, MNRAS, 495, 3065 [CrossRef] [Google Scholar]
- de Barros, S., Vanzella, E., Amorín, R., et al. 2016, A&A, 585, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dijkstra, M., Gronke, M., & Venkatesan, A. 2016, ApJ, 828, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., Henry, A., Martin, C. L., et al. 2015, ApJ, 806, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Du, X., Shapley, A. E., Reddy, N. A., et al. 2018, ApJ, 860, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Porter, R. L., van Hoof, P. A. M., et al. 2013, Rev. Mex. Astron. Astrofis., 49, 137 [Google Scholar]
- Ferland, G. J., Chatzikos, M., Guzmán, F., et al. 2017, Rev. Mex. Astron. Astrofis., 53, 385 [NASA ADS] [Google Scholar]
- Finkelstein, S. L., Rhoads, J. E., Malhotra, S., Grogin, N., & Wang, J. 2008, ApJ, 678, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Finkelstein, S. L., D’Aloisio, A., Paardekooper, J.-P., et al. 2019, ApJ, 879, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, T. J., Tang, M., Robertson, B. E., et al. 2019, ApJ, 878, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Fontanot, F., Cristiani, S., & Vanzella, E. 2012, MNRAS, 425, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Fontanot, F., Cristiani, S., Pfrommer, C., Cupani, G., & Vanzella, E. 2014, MNRAS, 438, 2097 [NASA ADS] [CrossRef] [Google Scholar]
- Gazagnes, S., Chisholm, J., Schaerer, D., et al. 2018, A&A, 616, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, J. C., Froning, C. S., Osterman, S., et al. 2012, ApJ, 744, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Gronke, M., Dijkstra, M., McCourt, M., & Oh, S. P. 2016, ApJ, 833, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Gronke, M., Dijkstra, M., McCourt, M., & Oh, S. P. 2017, A&A, 607, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayes, M., Schaerer, D., Östlin, G., et al. 2011, ApJ, 730, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, M., Östlin, G., Duval, F., et al. 2014, ApJ, 782, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., Lehnert, M. D., Strickland, D. K., & Armus, L. 2000, ApJS, 129, 493 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Heckman, T. M., Borthakur, S., Overzier, R., et al. 2011, ApJ, 730, 5 [Google Scholar]
- Heckman, T. M., Alexandroff, R. M., Borthakur, S., Overzier, R., & Leitherer, C. 2015, ApJ, 809, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, A., Scarlata, C., Martin, C. L., & Erb, D. 2015, ApJ, 809, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, A., Berg, D. A., Scarlata, C., Verhamme, A., & Erb, D. 2018, ApJ, 855, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Guseva, N. G., & Thuan, T. X. 2011, ApJ, 728, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Orlitová, I., Schaerer, D., et al. 2016a, Nature, 529, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Schaerer, D., Thuan, T. X., et al. 2016b, MNRAS, 461, 3683 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Schaerer, D., Worseck, G., et al. 2018a, MNRAS, 474, 4514 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Worseck, G., Schaerer, D., et al. 2018b, MNRAS, 478, 4851 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Schaerer, D., Worseck, G., et al. 2020, MNRAS, 491, 468 [CrossRef] [Google Scholar]
- Jaskot, A. E., Dowd, T., Oey, M. S., Scarlata, C., & McKinney, J. 2019, ApJ, 885, 96 [CrossRef] [Google Scholar]
- Jones, T. A., Ellis, R. S., Schenker, M. A., & Stark, D. P. 2013, ApJ, 779, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Kakiichi, K., & Gronke, M. 2019, ApJ, submitted [arXiv:1905.02480] [Google Scholar]
- Kimm, T., Blaizot, J., Garel, T., et al. 2019, MNRAS, 486, 2215 [NASA ADS] [CrossRef] [Google Scholar]
- Koester, B. P., Gladders, M. D., Hennawi, J. F., et al. 2010, ApJ, 723, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Leitet, E., Bergvall, N., Hayes, M., Linné, S., & Zackrisson, E. 2013, A&A, 553, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Ortiz Otálvaro, P. A., Bresolin, F., et al. 2010, ApJS, 189, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Hernandez, S., Lee, J. C., & Oey, M. S. 2016, ApJ, 823, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Haardt, F. 2015, ApJ, 813, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
- Marshall, J. L., Burles, S., Thompson, I. B., et al. 2008, Ground-based and Airborne Instrumentation for Astronomy II, Proc. SPIE, 7014, 701454 [CrossRef] [Google Scholar]
- McKinney, J. H., Jaskot, A. E., Oey, M. S., et al. 2019, ApJ, 874, 52 [CrossRef] [Google Scholar]
- Meynet, G., Maeder, A., Schaller, G., Schaerer, D., & Charbonnel, C. 1994, A&AS, 103, 97 [Google Scholar]
- Mitra, S., Choudhury, T. R., & Ferrara, A. 2018, MNRAS, 473, 1416 [CrossRef] [Google Scholar]
- Neufeld, D. A. 1991, ApJ, 370, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Oke, J. B., Cohen, J. G., Carr, M., et al. 1995, PASP, 107, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Orlitová, I., Verhamme, A., Henry, A., et al. 2018, A&A, 616, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osterbrock, D. E. 1989, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (University Science Books) [CrossRef] [Google Scholar]
- Ouchi, M., Mobasher, B., Shimasaku, K., et al. 2009, ApJ, 706, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., & Pagel, B. E. J. 2004, MNRAS, 348, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., Rix, S. A., Steidel, C. C., et al. 2002, ApJ, 569, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Prochaska, J. X., Kasen, D., & Rubin, K. 2011, ApJ, 734, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Puschnig, J., Hayes, M., Östlin, G., et al. 2017, MNRAS, 469, 3252 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Kriek, M., Shapley, A. E., et al. 2015, ApJ, 806, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Steidel, C. C., Pettini, M., & Bogosavljević, M. 2016a, ApJ, 828, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Steidel, C. C., Pettini, M., Bogosavljević, M., & Shapley, A. E. 2016b, ApJ, 828, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Rigby, J. R., Bayliss, M. B., Sharon, K., et al. 2018, AJ, 155, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Rivera-Thorsen, T. E., Hayes, M., Östlin, G., et al. 2015, ApJ, 805, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Rivera-Thorsen, T. E., Dahle, H., Chisholm, J., et al. 2019, Science, 366, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, B. E., Furlanetto, S. R., Schneider, E., et al. 2013, ApJ, 768, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, B. E., Ellis, R. S., Furlanetto, S. R., & Dunlop, J. S. 2015, ApJ, 802, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Runnholm, A., Hayes, M., Melinder, J., et al. 2020, ApJ, 892, 48 [CrossRef] [Google Scholar]
- Scarlata, C., & Panagia, N. 2015, ApJ, 801, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Scarlata, C., Colbert, J., Teplitz, H. I., et al. 2009, ApJ, 704, L98 [NASA ADS] [CrossRef] [Google Scholar]
- Schaerer, D. 2003, A&A, 397, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schenker, M. A., Ellis, R. S., Konidaris, N. P., & Stark, D. P. 2014, ApJ, 795, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Shapley, A. E., Steidel, C. C., Pettini, M., & Adelberger, K. L. 2003, ApJ, 588, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Shapley, A. E., Steidel, C. C., Strom, A. L., et al. 2016, ApJ, 826, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Swinbank, A. M., Ellis, R. S., et al. 2008, Nature, 455, 775 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stasińska, G., & Leitherer, C. 1996, ApJS, 107, 661 [Google Scholar]
- Steidel, C. C., Shapley, A. E., Pettini, M., et al. 2004, ApJ, 604, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Bogosavljević, M., Shapley, A. E., et al. 2011, ApJ, 736, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Strom, A. L., Pettini, M., et al. 2016, ApJ, 826, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Bogosavljević, M., Shapley, A. E., et al. 2018, ApJ, 869, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Trainor, R. F., Steidel, C. C., Strom, A. L., & Rudie, G. C. 2015, ApJ, 809, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Trainor, R. F., Strom, A. L., Steidel, C. C., et al. 2019, ApJ, 887, 85 [CrossRef] [Google Scholar]
- Vanzella, E., de Barros, S., Castellano, M., et al. 2015, A&A, 576, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasei, K., Siana, B., Shapley, A. E., et al. 2016, ApJ, 831, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Verhamme, A., Orlitová, I., Schaerer, D., & Hayes, M. 2015, A&A, 578, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verhamme, A., Orlitová, I., Schaerer, D., et al. 2017, A&A, 597, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakker, B. P., Hernandez, A. K., French, D. M., et al. 2015, ApJ, 814, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., Heckman, T. M., Leitherer, C., et al. 2019, ApJ, 885, 57 [CrossRef] [Google Scholar]
- Weiner, B. J., Coil, A. L., Prochaska, J. X., et al. 2009, ApJ, 692, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Wisotzki, L., Bacon, R., Blaizot, J., et al. 2016, A&A, 587, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Worseck, G., Prochaska, J. X., Hennawi, J. F., & McQuinn, M. 2016, ApJ, 825, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Wuyts, E., Rigby, J. R., Gladders, M. D., et al. 2012, ApJ, 745, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Zackrisson, E., Inoue, A. K., & Jensen, H. 2013, ApJ, 777, 39 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Fits
In Figs. A.1–A.5, we present fits for the galaxies J1154+2443, J0901+2119, J1011+1947, J1243+4646 and J1248+4259 from Izotov et al. (2018a,b) that have been included in this sample. The fit of J1256+4509 is shown in Fig. 1, while the fits for the 16 other galaxies can be found in Gazagnes et al. (2018). Each figure shows the full wavelength coverage; the observed flux is in black, the green line shows the error on the observed flux, and the resulting fit is in blue. The gray-shaded areas show the main regions that were masked during the fit because of geo-coronal emission, low S/N, or ISM or Milky Way absorption lines not included in the fit, or Lyα emission. In the top panels, we zoom in on individual Lyman series lines and denote the fitted Lyman series lines. We note that for display purposes, the masks on the ISM or Milky Way absorption lines are only shown when they appear in the top panels.
 |
Fig. A.1. Fit (in blue solid line) of the COS G140L spectrum of the galaxy J1154+2443 (Izotov et al. 2018a). The black line is the observed flux included in the routine either to fit the stellar continuum or the ISM absorption lines. Gray regions are masked out during the fit. The flux error array appears in green. The top panels present a zoom on the fitted Lyman series lines. |
 |
Fig. A.2. Same as Fig. A.1 but for the COS G140L spectrum of J0901+2119 (Izotov et al. 2018b). |
 |
Fig. A.3. Same as Fig. A.1 but for the COS G140L spectrum of J1011+1947 (Izotov et al. 2018b). |
 |
Fig. A.4. Same as Fig. A.1 but for the COS G140L spectrum of J1243+4646 (Izotov et al. 2018b). The best fit only includes the attenuated stellar continuum because the H I absorption lines were not found. |
 |
Fig. A.5. Same as Fig. A.1 but for the COS G140L spectrum of J1248+4259 (Izotov et al. 2018b). |
Appendix B: Tables
B.1. Lyman series covering fraction measurements
Table B.1 lists the different measurements of the H I covering fractions, from the fits and from the residual flux (see details in Sect. 3.1).
Measurement of H I covering fraction derived from the fits and from the residual flux of the individual Lyman series.
B.2. Lyman series velocity width measurements
Table B.2 lists the measurements of the H I velocity width for the Lyman series in each galaxy (see details in Sect. 3.1).
Measurement of H I velocity width of the individual Lyman series. See Sect. 3.1.
B.3. Significance levels of the trends reported in this work
In this section, we investigate the dependence of the significance levels of the trends reported in Sect. 4 on a few specific observations or on different assumptions of the intrinsic Lyα Hα flux ratio adopted to derive fesc(Lyα). Table B.3 lists the σ values quoted in the paper (Col. (2)) and the new significance levels when one observation is excluded, quoted as a jackknife test interval (Col. (3)), with the lowest significance and largest significance level obtained when one observation is removed from the sample. Col (3) shows that the lower bound is always larger than 2.5σ, except for three trends: 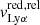 – Cf(H I),
– Cf(H I), 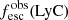 – Cf(H I) and
– Cf(H I) and 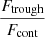 – Cf(H I). In the latter, the lowest σ value is only moderately significant (2σ) and is obtained when the largest fesc(LyC) galaxy, J1243+4646, is excluded from the sample. We note that two of these trends suffer some scatter (illustrated in Figs. 5 and 14), while the trend between
– Cf(H I). In the latter, the lowest σ value is only moderately significant (2σ) and is obtained when the largest fesc(LyC) galaxy, J1243+4646, is excluded from the sample. We note that two of these trends suffer some scatter (illustrated in Figs. 5 and 14), while the trend between 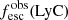 and Cf(H I) only has a limited number of irregularly-spaced points (Fig. 11). Future observations should confirm or rule out the existence of these trends.
and Cf(H I) only has a limited number of irregularly-spaced points (Fig. 11). Future observations should confirm or rule out the existence of these trends.
Impact of different assumptions on the reported significance level of observed trends.
In Col. (4), we compute the new significance levels when Cf(H I) is fixed to 0 for galaxies where we only measure an upper limit of the Cf(H I). Overall, the significance levels vary by ±0.5σ, except for the EW(Lyα) and fesc(Lyα) correlations which reach 1.5 and 5.0 σ, respectively. This is because the galaxies with an upper limit on Cf(H I) (1 in our sample, 3 in the sample included in McKinney et al. 2019) have similar fesc(Lyα), but varying EW(Lyα). Hence, fixing their Cf(H I) to the same value strengthens the correlation with the fesc(Lyα), but weakens the one with EW(Lyα). In Col. (5), we excluded the three z ∼ 3 MEGaSaURA galaxies to investigate the impact they have on the significance of the trends. All the trends, except for EW(Lyα) – Cf(H I), remain significant at least at the 2.5σ significance level.
Finally, we tested the impact of the Case-A/B assumptions on the trends that involve fesc(Lyα) in Cols. (6), (7), and (8). In the Case A recombination example (optically thin ISM), the intrinsic ratio of the Lyα and Hα flux can be 1.5 times higher (Osterbrock 1989, the effective recombination coefficient of the Balmer emission lines is ≈1.5 times higher than in the Case B assumption,) than in Case-B recombination (optically thick ISM, low-density case). For galaxies emitting ionizing photons, the Case-B assumption (adopted in this work) is not likely to be valid, hence, an optimal approach would consist of scaling down all fesc(Lyα) values from LCEs by 1.5. Nevertheless, this is not trivial because some galaxies in our sample, or in the sample from McKinney et al. (2019) and Jaskot et al. (2019), do not have observations at λ < 912 Å (unknown LyC leakage). Consequently, we chose to use a cut in the peak separation velocity of the Lyα profile to select galaxies with a Case-A ISM. The choice of 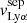 is motivated by the strong observational correlation found between
is motivated by the strong observational correlation found between 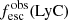 and
and  (Verhamme et al. 2017; Izotov et al. 2018b). Since low fesc(LyC) leakers might still be consistent with a Case-B recombination assumption, we selected three cuts in
(Verhamme et al. 2017; Izotov et al. 2018b). Since low fesc(LyC) leakers might still be consistent with a Case-B recombination assumption, we selected three cuts in  of 400, 300 and 200 km s−1, to successively select different sub-samples with larger fesc(LyC), and scaled-down their fesc(Lyα) by a factor 1.5. We found that the fesc(Lyα) trends are always significant at ≥2.5σ. Therefore, we conclude that variations in the intrinsic Lyα-Hα flux ratio should not affect the findings drawn in this work.
of 400, 300 and 200 km s−1, to successively select different sub-samples with larger fesc(LyC), and scaled-down their fesc(Lyα) by a factor 1.5. We found that the fesc(Lyα) trends are always significant at ≥2.5σ. Therefore, we conclude that variations in the intrinsic Lyα-Hα flux ratio should not affect the findings drawn in this work.
Appendix C: Plots of Lyα and H I absorption line profiles.
Figures C.1 and C.2 show the Lyα emission and Lyβ (or Lyγ when Lyβ is not observed) in the velocity space for the 22 galaxies in our sample.
 |
Fig. C.1. Lyα emission and the observed H I Lyman series line with the larger S/N in the velocity space for 15 of the 22 galaxies in our sample. The Lyα flux has been smoothed to the resolution of the Lyman series and scaled down by an arbitrary power law for display purpose. Gray-shaded regions show contamination from the geocoronal emission or Milky Way absorption lines next to the H I absorption line. |
All Tables
Investigating the impact of different dust extinction assumptions in J1154+2443 and J1256+4509.
Measurement of H I covering fraction derived from the fits and from the residual flux of the individual Lyman series.
Measurement of H I velocity width of the individual Lyman series. See Sect. 3.1.
Impact of different assumptions on the reported significance level of observed trends.
All Figures
 |
Fig. 1. Best fit (blue solid line) obtained for the galaxy J1256+4509. The black and green solid lines show the observed flux and the error on the flux, respectively. Top panels: zooms on the individual Lyman series lines fitted. The gray shaded areas are the principal wavelength regions masked during the fit, due to geo-coronal emission, low S/N or Lyα emission. Additionally, in the top panels, we show the masks for ISM/Milky Way absorption lines that are not included during the fitting procedure. For display purposes, these masks do not appear in the main panel. The blue-shaded area represents the uncertainty on the fit, derived using a Monte-Carlo approach (see details in Sect. 3.1). |
| In the text | |
 |
Fig. 2. Lyδ (blue) and Ly5 (red) absorption lines in the galaxy J1256+4509. The flux has been normalized using the median of the observed spectra taken between 500 and 1000 km s−1 from the absorption lines. The two H I absorption lines have similar depth and width, which indicates that they are saturated. |
| In the text | |
 |
Fig. 3. Top: observed flux in the galaxy J1256+4509 (black curve), error (green), fit obtained letting EB − V as a free parameter (orange), fits obtained when fixing EB − V to 0 and 0.2 (blue and red lines) respectively. Bottom: same for the galaxy J1154+2443. Both spectra have been normalized using the median flux between 1090 and 1100 Å. The wavelength regions with Lyα emission (between 1205 to 1225 Å) or low S/N (< 1) are masked during the fitting procedure (see Fig. 1). |
| In the text | |
 |
Fig. 4. Lyα profile observed in the galaxy J1011+1947 with the characteristic measurements annotated. The observed flux has been smoothed by an arbitrary factor for display purposes, and normalized using the median of the flux between 1200 and 1210 Å. The gray shaded area represents the integrated region to compute the Lyα equivalent width. |
| In the text | |
 |
Fig. 5. Left: relation between the relative Lyα blue peak velocity ( |
| In the text | |
 |
Fig. 6. Relation between the Lyα peak velocity separation ( |
| In the text | |
 |
Fig. 7. Lyα equivalent width (left) and escape fraction (right) versus the width of the H I maximal absorption. Galaxies with a lower velocity width of the Lyman series have higher EW(Lyα) and fesc(Lyα). |
| In the text | |
 |
Fig. 8. Lyα peak velocity separation versus the H I velocity width of maximal absorption. The color bar represents the H I covering fraction measurement of each galaxy. Overall, the Lyα peak velocity separation scales with the width of the maximal absorption of the H I gas, and galaxies with larger Cf(H I) have larger |
| In the text | |
 |
Fig. 9. Left: Lyα emission line and Lyβ absorption line in J0921+4509 (Cf(H I) = 0.761). Right: Lyα emission line and Lyβ absorption line in J1442−0209 (Cf(H I) = 0.556). The Lyα spectra have been smoothed to half the resolution of the observations and scaled down with a power law for display purposes. The presence of Lyα emission on top of the optically thick H I absorption line suggests that Lyα photons can escape at lower velocities through low-density channels. Similar plots for all the galaxies in our sample are given in Appendix C. |
| In the text | |
 |
Fig. 10. Lyα equivalent width versus the porosity of the neutral gas as given by 1–Cf(H I). The color bar represents the H I velocity interval where the Lyman series is at its maximum depth. Our sample is represented by triangles and circles for galaxies with unknown and known leakage respectively, and the sample from McKinney et al. (2019) and Jaskot et al. (2019) is shown with gray squares as they do not have H I velocity width measurements. The dashed line shows the empirical relation found in Steidel et al. (2018), while the dotted line is the fit to the data, excluding J1248+4259 (see Eq. (5)). This figure suggests that Lyα emission strongly scales with the covering fraction of the channels and with the width of the saturated H I absorption lines. |
| In the text | |
 |
Fig. 11. Observed fesc(Lyα) (left) and |
| In the text | |
 |
Fig. 12. Observed fesc(Lyα) (left) and |
| In the text | |
 |
Fig. 13. Predicted LyC escape fraction |
| In the text | |
 |
Fig. 14. Normalized Lyα flux at the minimum of the Lyα profile |
| In the text | |
 |
Fig. 15. Observed escape fraction of LyC photons versus |
| In the text | |
 |
Fig. 16. Illustration of the physical picture discussed in Sect. 5.1. Left: LyC photons escape through channels covered by |
| In the text | |
 |
Fig. A.1. Fit (in blue solid line) of the COS G140L spectrum of the galaxy J1154+2443 (Izotov et al. 2018a). The black line is the observed flux included in the routine either to fit the stellar continuum or the ISM absorption lines. Gray regions are masked out during the fit. The flux error array appears in green. The top panels present a zoom on the fitted Lyman series lines. |
| In the text | |
 |
Fig. A.2. Same as Fig. A.1 but for the COS G140L spectrum of J0901+2119 (Izotov et al. 2018b). |
| In the text | |
 |
Fig. A.3. Same as Fig. A.1 but for the COS G140L spectrum of J1011+1947 (Izotov et al. 2018b). |
| In the text | |
 |
Fig. A.4. Same as Fig. A.1 but for the COS G140L spectrum of J1243+4646 (Izotov et al. 2018b). The best fit only includes the attenuated stellar continuum because the H I absorption lines were not found. |
| In the text | |
 |
Fig. A.5. Same as Fig. A.1 but for the COS G140L spectrum of J1248+4259 (Izotov et al. 2018b). |
| In the text | |
 |
Fig. C.1. Lyα emission and the observed H I Lyman series line with the larger S/N in the velocity space for 15 of the 22 galaxies in our sample. The Lyα flux has been smoothed to the resolution of the Lyman series and scaled down by an arbitrary power law for display purpose. Gray-shaded regions show contamination from the geocoronal emission or Milky Way absorption lines next to the H I absorption line. |
| In the text | |
 |
Fig. C.2. Same as Fig. C.1 for the seven remaining galaxies. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.