| Issue |
A&A
Volume 639, July 2020
|
|
|---|---|---|
| Article Number | A34 | |
| Number of page(s) | 19 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202037905 | |
| Published online | 03 July 2020 | |
TESS unveils the phase curve of WASP-33b
Characterization of the planetary atmosphere and the pulsations from the star
1
Stellar Astrophysics Centre, Department of Physics and Astronomy, Aarhus University,
Ny Munkegade 120,
8000
Aarhus C,
Denmark
e-mail: cessen@phys.au.dk
2
Astronomical Observatory, Institute of Theoretical Physics and Astronomy, Vilnius University,
Sauletekio av. 3,
10257
Vilnius, Lithuania
3
Leibniz-Institut für Astrophysik Potsdam (AIP),
An der Sternwarte 16,
14482
Potsdam, Germany
4
DTU Space, National Space Institute, Technical University of Denmark,
Elektrovej 328,
2800
Kgs. Lyngby, Denmark
5
Department of Physics & Astronomy, Vanderbilt University,
6301 Stevenson Center Ln.,
Nashville,
TN
37235,
USA
6
Landessternwarte, Zentrum für Astronomie der Universität Heidelberg,
Königstuhl 12,
69117
Heidelberg, Germany
Received:
7
March
2020
Accepted:
22
April
2020
We present the detection and characterization of the full-orbit phase curve and secondary eclipse of the ultra-hot Jupiter WASP-33b at optical wavelengths, along with the pulsation spectrum of the host star. We analyzed data collected by the Transiting Exoplanet Survey Satellite (TESS) in sector 18. WASP-33b belongs to a very short list of highly irradiated exoplanets that were discovered from the ground and were later visited by TESS. The host star of WASP-33b is of δ Scuti-type and shows nonradial pulsations in the millimagnitude regime, with periods comparable to the period of the primary transit. These completely deform the photometric light curve, which hinders our interpretations. By carrying out a detailed determination of the pulsation spectrum of the host star, we find 29 pulsation frequencies with a signal-to-noise ratio higher than 4. After cleaning the light curve from the stellar pulsations, we confidently report a secondary eclipse depth of 305.8 ± 35.5 parts-per-million (ppm), along with an amplitude of the phase curve of 100.4 ± 13.1 ppm and a corresponding westward offset between the region of maximum brightness and the substellar point of 28.7 ± 7.1 degrees, making WASP-33b one of the few planets with such an offset found so far. Our derived Bond albedo, AB = 0.369 ± 0.050, and heat recirculation efficiency, ɛ = 0.189 ± 0.014, confirm again that he behavior of WASP-33b is similar to that of other hot Jupiters, despite the high irradiation received from its host star. By connecting the amplitude of the phase curve to the primary transit and depths of the secondary eclipse, we determine that the day- and nightside brightness temperatures of WASP-33b are 3014 ± 60 K and 1605 ± 45 K, respectively. From the detection of photometric variations due to gravitational interactions, we estimate a planet mass of MP = 2.81 ± 0.53 MJ. Based on analyzing the stellar pulsations in the frame of the planetary orbit, we find no signals of star-planet interactions.
Key words: planets and satellites: atmospheres / planets and satellites: fundamental parameters / stars: individual: WASP-33 / methods: observational
© ESO 2020
1 Introduction
The Transiting Exoplanet Survey Satellite (TESS, Ricker et al. 2015) has been scanning the southern and northern ecliptic hemispheres since August 2018 in the search for planets around bright stars. To date (April 2020), TESS has detected the dimming of light during transit of ~1800 TESS objects of interest (TOIs), about 45 of which have been confirmed as exoplanets1. Several TESS discoveries include the first Earth-sized planet (Dragomir et al. 2019), an eccentric massive Jupiter orbiting a subgiant star every 9.5 days (Rodriguez et al. 2019), and the first multiplanet systems (Kostov et al. 2019; Günther et al. 2019; Vanderburg et al. 2019).
In addition to the detection and characterization of new systems, TESS has also been contributing with the in-depth study of systems previously detected from the ground. Some TESS contributions are the detection of a decrease in the orbital period of WASP-4b (Bouma et al. 2019), and of particular interest to this work, the characterization of the phase curve and secondary eclipse depth of WASP-18b (Shporer et al. 2019), WASP-19b (Wong et al. 2020), WASP-121b (Bourrier et al. 2020; Daylan et al. 2019), WASP-100b (Jansen & Kipping 2020), and KELT-9b (Wong et al. 2019). The precision in the photometry of WASP-18b allowed Shporer et al. (2019) to unveil sinusoidal modulations across the orbital phase that were shaped by the atmospheric characteristics of the planet and by the gravitational interactions between the planet and host star. Data for WASP-19b revealed a strong atmospheric brightness modulation signal and no significant offset detected between the substellar point and the region of maximum brightness on the dayside of the planet, in full agreement with data for WASP-121b.
All these planets with full-orbit phase curves measured by TESS belong to the group of ultra-hot Jupiters. These planets receive such an extreme amount of stellar insolation that they exhibit dayside temperatures exceeding ~2200 K. Similar to hot Jupiters of more moderate temperatures, they are expected to be tidally locked because of their very close proximity to the host star. Another ultra-hot Jupiter observed by TESS is WASP-33b (Collier Cameron et al. 2010). With a dayside temperature close to 3200 K (Zhang et al. 2018), it belongs to the very top of a temperature ranking of highly irradiated super-hot exoplanets. The planet orbits a δ Scuti star of spectral type A that oscillates with pulsations commensurable to the transit duration and with amplitudes well within the millimagnitude regime (Smith et al. 2011; Herrero et al. 2011; von Essen et al. 2014). Relevant stellar and planetary parameters can be found in Tables 1 and 3. So far, the planet has been thoroughly investigated. Among others, observational data have revealed several secondary eclipse depths at different wavelengths (Smith et al. 2011; Deming et al. 2012; de Mooij et al. 2013; Haynes et al. 2015; von Essen et al. 2015), a detailed characterization of the pulsation spectrum of the host star with the goal of determining planetary parameters from pulsation-cleaned light curves (Herrero et al. 2011; von Essen et al. 2014), and the characterization of its atmospheric composition where aluminium oxide was unveiled for the first time (von Essen et al. 2019a). In addition to this detection, Yan et al. (2019) characterized its transmission spectrum around the individual lines of Ca II H&K in high resolution, finding the spectrum mostly ionized in its upper atmosphere, while Nugroho et al. (2017) found molecular TiO in the dayside spectra. Space-based Spitzer observations of the WASP-33 phase curves in the near-infrared (NIR) allowed Zhang et al. (2018) to estimate the planetary brightness temperature, albedo, and heat recirculation efficiency. The authorsfound that WASP-33b shares similarities with hot Jupiters, despite its unusually high irradiation level.
Phase-curve observations at TESS optical wavelengths allow measuring the combined reflected and thermally emitted planetary light as a function of longitude. Recent reviews of exoplanet phase curves were provided by Shporer (2017) and Parmentier & Crossfield (2018). For an ultra-hot Jupiter such as WASP-33b, we still expect the thermal light component to dominate, which is informative for the efficiency of the heat distribution from the insolated dayside to the nightside. This energy transport is expected to be less efficient for ultra-hot Jupiters than for hot Jupiters of more moderate temperature because radiative energy loss is stronger and the atmosphere is partially ionized, which prevents strong advective energy transport by a magnetic drag (e.g., Lothringer et al. 2018; Arcangeli et al. 2019). The optical phase curve of WASP-33b, presented in this work, sheds light on the energy recirculation by providing the related observing parameters of day-night temperature contrast and phase-curve offset for an extremely highly irradiated planet. Moreover, a comparison of the optical phase-curve results of this work and the NIR phase-curve results for the same planet as described by Zhang et al. (2018) will provide information about their wavelength dependence, and therefore about how similar the planet atmosphere is to that of a blackbody.
We describe in Sect. 2 the observations we used to characterize the secondary eclipse and the phase curve of WASP-33b in detail. In Sect. 3 we present our analysis of the third-light contamination (Sect. 3.1), our update on the transit parameters (Sect. 3.5), and our strategy of cleaning the light curves from transits to use them to determine the pulsation spectrum of the host star (Sect. 3.3). We introduce our models for interpreting the secondary eclipse and phase curve of WASP-33b in Sect. 4.3. In Sect. 5 we discuss the effect of the pulsations on the derived atmospheric parameters in detail (Sect. 4.7), derive relevant physical parameters in Sects. 5.1 and 5.2, place WASP-33b and our results in context in Sect. 5.3, and update the stellar and planetary parameters we presented in Sect. 3.6. We conclude in Sect. 6.
Effective temperature, metallicity, and surface gravity for WASP-33 and the stars included in the TESS aperture.
2 Observations
WASP-33 (TIC identifier 129979528) was observed by TESS in sector 18, more specifically, it was observed between November 3 and 26, 2019, during cycle 2. Camera 1 was used. The data have a cadence of 120 s and were analyzed and detrended by the Science Processing Operations Center (SPOC) pipeline, based on the NASA Kepler mission pipeline (Jenkins et al. 2016; Jenkins 2017). Time stamps are given in Barycentric Julian Dates (BJDTDB), and are therefore not converted into another time-reference frame.
The light curve of WASP-33 is shown in Fig. 1. The total time on target is of about 23 days, during which 16 primary transits were observed. The first ~800 data points were not considered in our analysis because they show some noise structure that is probably extrinsic to the star. An initial analysis was made on the simple aperture photometry (SAP) and presearch data conditioning (PDC) light curves (Smith et al. 2012; Stumpe et al. 2014), after which we decided to work on the SAP data using our own normalization strategy (see Sect. 3.4 for a motivation of our choice). To prepare the data for analysis, we first removed all flag points, both in time and in flux. Then, we binned the points each 8 h to minimize the normalization effect on the stellar pulsations, after which we interpolated a spline function. We used this to normalize the data and to remove outliers that were five times the standard deviation away. We removed about 100, and we analyzed in this work 14 000 points in total.
3 Analysis and model considerations
3.1 Third-light contamination
When photometric time series are analyzed including exoplanetary primary transits, special care has to be taken. In certain cases, light of another star than the planetary host is included inside the chosen photometric aperture, which dilutes the depth of the primary transits (see, e.g., Piskorz et al. 2015, Mugrauer 2019 and Belokurov et al. 2020 for a large systematic search of companions of nearby exoplanets). The TESS cameras have a pixel size of 21 × 21 arcsec. Under these circumstances, when a light curve is constructed by coadding the light of several pixels (see Fig. 2, top), it is very likely that the aperture will include light from other stars than that of the host (Fig. 2, bottom).
The first identified companion of WASP-33b, WASP-33B, lies at an angular separation of ~2 arcsec and is therefore included inside the TESS aperture. The substellar object was first reported by Moya et al. (2011) and then confirmed by Adams et al. (2013), Wöllert & Brandner (2015) and Ngo et al. (2016). Using years of follow-up observations, Ngo et al. (2016) carried out a combined analysis and determined that WASP-33 is a binary system candidate. Today, WASP-33 has been identified as a hierarchical triple star system (Mugrauer 2019) with a second companion, WASP-33C, that is ~49 arcsec away from the planet-host star. Owing to its orientation (southeast of WASP-33), WASP-33C is in principle not included inside the TESS aperture. However, because of the large point spread function of TESS, some light of WASP-33C might be included. Unfortunately, there is no way to quantify this except for comparing the derived transit depth to literature values and/or those expected from atmospheric models. A third star, located 23 arcsec northwest of WAP-33 (Gaia DR2 328636024020571008, Gaia Collaboration 2018, G = 14.6173 ± 0.0005), is included in the aperture. Even though the Science Processing Operations Center (SPOC) pipeline provides an estimate of the stellar crowding contamination, we thought it prudent to compare this with the estimate determined from our own analysis. Before the transit fitting, we therefore computed the third-light contribution of the WASP-33 companions within the TESS transmission response, that is, the contribution of WASP-33B and Gaia DR2 328636024020571008, and compared this to the value reported in the header of the WASP-33 fits file, specifically under the CROWDSAP keyword.
Because of the nature of the system, we can assume that WASP-33 and WASP-33B are at the same distance. We therefore reproduced their emission with PHOENIX synthetic spectra (Göttingen 2018) without the need of scaling the fluxes further to account for distances. Specifically, we used PHOENIX spectra with basic stellar parameters (Teff, [Fe/H]. log(g)) that match those of WASP-33 (Collier Cameron et al. 2010) and of the close-in companion (Ngo et al. 2016), as summarized in Table 1.
After convolving PHOENIX intensities with the TESS transmission response, we integrated the remaining fluxes and computed their ratio. In this way, we obtain a third-light contribution of WASP-33B of FW33B/FW33 = 0.018.
The case of Gaia DR2 328636024020571008 is slightly different because it is not bound to WASP-33 by gravity, therefore wecannot assume equal distances. Gaia Collaboration (2018) estimated its temperature to be ~5075 K, therefore we represented its emission using PHOENIX synthetic spectra for a main-sequence star of Teff = 5000 K. To compensate for the difference in distance, we computed the Gaia magnitude difference between WASP-33 (G = 8.0700 ± 0.0004) and this star, and we scaled PHOENIX flux ratios of WASP-33 and Gaia DR2 328636024020571008 integrated within the Gaia transmission response to meet the magnitude difference. Then, we used this factor to scale the spectra inside the TESS transmission response down. In this way, the third-light contribution of Gaia DR2 328636024020571008 was found to be FGaia/FW33 = 0.006. The total third-light contribution we used in our model is the addition of these two, and equal to ΔF = 0.024. In comparison, the value reported at CROWDSAP is 0.9789, equivalently 1 − 0.9789 = 0.0211, to be compared to our ΔF. Because these two values differ by only ~10%, we find the two values compatible, and we use our derived value to correct for third light throughout.
 |
Fig. 1 SAP normalized flux of WASP-33 observed by TESS shown as black circles, along with SAP raw data in blue. The pulsations of the star deform the continuum level. The 16 transits are indicated at the bottom with red lines. The gap in the middle is caused by data downlink dead time. |
3.2 Limb-darkening coefficients
We adopted a quadratic limb-darkening law,
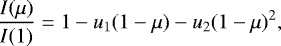 (1)
(1)
with corresponding linear (u1) and quadratic (u2) limb-darkening coefficients (LDCs). In the equation, I(1) is the specific intensity at the center of the stellar disk and μ = cos(γ), where γ is the angle between the line of sight and the emergent intensity. To compute our custom limb-darkening coefficients that meet the TESS transmission response, we used angle-dependent specific intensity spectra from PHOENIX (Göttingen 2018) with main stellar parameters corresponding to the effective temperature, Teff = 7400 K, surface gravity, log(g) = 4.5, and metallicity, [Fe/H] = 0.00. This matches the values of WASP-33 reported in Table 1 within the uncertainties. Following von Essen et al. (2017) and Claret & Bloemen (2011), we neglected the data points between μ = 0 and μ = 0.07 because the intensity drop given by PHOENIX models is too steep and might be unrealistic. After integrating the PHOENIX angle-dependent spectra convolved by the TESS response, we fit the derived intensities normalized by their maximum values with Eq. (1) using a Markov chain Monte Calro (MCMC) approach. The derived limb-darkening coefficients for WASP-33 are u1 = 0.246(6) and u2 = 0.252(6). Errors for the coefficients were derived from the posterior distributions of the MCMC chains after visually inspecting them for convergency. In order to assess the quality of our procedure, we fit the LDCs to TESS primary transit light curves. From their posterior distributions we obtained consistent results with their PHOENIX counterparts. Our derived LDCs agree well with those from Claret (2017) (u1 = 0.2446 and u2 = 0.2449). A word of caution has to be given here. Even though the precision of our fit lies in the fourth decimal, LDCs drag uncharacterized errors from the lack of precision of, for instance, stellar intensities. The precision of the fit therefore probably reflects the real precision at which we know any limb-darkening coefficient. Based on this assumption, we consider u1 and u2 as fixed in order to reduce the computational cost in this work.
 |
Fig. 2 Top: TPF of WASP-33 showing the chosen aperture mask. No stars can be visually resolved. Bottom: field of view of about 4 × 4 arcmin centered on WASP-33. The mask and pixels are schematized with white thick and thin lines, respectively. WASP-33C, the bright star south of WASP-33, is not included in the aperture. The field of view has been rotated to be aligned with the ecliptic system, and is oriented to coincide with the images given in the TESS summary report. |
3.3 Pulsation spectrum of the host star
The pulsation frequencies of the host star were determined using the code Period04 (Lenz & Breger 2005), after the primary transits were fit and removed. The complete procedure was carried out over the SAP and PDC light curves, from which we obtained consistent results. The software uses a fast Fourier transform to calculate the power spectrum and simultaneous least-squares fitting to derive the pulsation frequencies, their amplitudes, and phases. The pulsation frequencies were extracted one by one, starting with the one having the largest amplitude. We considered a peak to be statistically significant only if it was resolved, and if its corresponding signal-to-noise ratio (S/N) was higher than or equal to 4 (see, e.g., Breger et al. 1993 and von Essen et al. 2014). The S/N was calculated using the default setting, that is, a window of two cycles/day (cd−1) around each peak. We estimated the uncertainties using the MCMC tool of Period04. These are produced as described in Breger et al. (1999), are given at a 1σ level and are derived from 1000 MCMC iterations. The amplitude uncertainties depend only on the residuals and the number of data points in the time series, which explains why all the values are the same.
The power spectrum of WASP-33 is shown in Fig. 3, and the 29 extracted pulsation frequencies, with their associated amplitudes and phases, are given in Table 2. For completeness, we provide a comparison to the peaks found by von Essen et al. (2014).
Two frequencies identified by von Essen et al. (2014) were not reproduced in this analysis: 8.308 cd−1 (Puls7) and 10.825 cd−1 (Puls8). Both are located in a frequency range whose noise level in the TESS data is slightly higher, which is likely to be due to additional unresolved pulsation modes originating from the star. As a consequence, it is not clear whether these peaks now have a lower amplitude than before and are therefore buried in the noise, or whether the peaks identified before may have been the result of aliases. We note that δ Sct-type pulsations are known to show (sometimes strong) amplitude variability over time (see, e.g., Bowman & Kurtz 2018). In addition, the TESS bandpass is redder than the filters used in von Essen et al. (2014), which implies that the pulsation amplitudes are expected to be lower as well, also depending on the exact geometry of the mode. WASP-33 displays p-mode oscillations at high frequencies, which is characteristic for δ Scuti stars (see, e.g. Aerts et al. 2010 and Antoci et al. 2019). Owing to the 23 days of continuous monitoring provided by TESS data, we also detected statistically significant peaks at lower frequencies (F2 and F5 in Table 2). If these are independent pulsation modes, they would correspond to g-mode pulsations typical for γ Doradus stars (see, e.g. Aerts et al. 2010 and Li et al. 2020). Showing both g- and p-mode pulsations, WASP-33 would then fall into the γ Doradus-δ Scuti hybrid classification (Grigahcène et al. 2010; Balona & Dziembowski 2011; Uytterhoeven et al. 2011). However, with only two peaks detected at low frequencies, we prefer to wait for more data before classifying WASP-33 as such. von Essen et al. (2014) did not detect signals with frequencies lower than ~7 cd−1. In addition to the obvious gaps produced by the day-night cycle, the data were normalized on a nightly basis, which removed the long trends. Moreover, as a result of poor weather conditions, the observations could not be produced in consecutive nights, and on average had a duration of ~5 h. A longer time series than the one provided by TESS might resolve the pulsations at lower frequencies and thereby determine whether the star is purely a δ Scuti or a hybrid star.
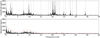 |
Fig. 3 Top panel: power spectrum of WASP-33. Pulsations are marked with dashed gray lines. Bottom panel: residuals after frequency extraction. The red line makes the S/N limit of 4. |
3.4 Noise treatment
Previous studies similar to this one, but based on other targets (see, e.g., Bourrier et al. 2020 and Wong et al. 2020), demonstrated that PDC data showed additional time-correlated residual features in the photometry that were absent from the SAP light curves. The authors typically carried out their own detrending strategy over SAP data and used these results as base for their analysis. In our case, the strong intrinsic variability of the star manifests itself as stellar pulsations, whose amplitudes are larger than the time-correlated features mentioned before. Because the pulsations hinder a proper analysis of the residual noise in our light curves, our approach in this work is slightly different. First, we recall that the criteria for considering a pulsation as detected are based on a very tight constraint of the amplitude S/N, AS/N > 4, which in turn is determined around a box of 2 cd−1, as detailed before. This constraint is significantly tighter than, for example, the use of the false-alarm probability in a periodogram to claim the detection of a pulsation frequency. The detected pulsations are therefore robust, despite the residual features of the PDC. Additionally, even though we have characterized the pulsation spectrum of the host star as has never been done before, there are residual pulsations in TESS photometry. To take the effect of the residual features in the PDC data into consideratio that we cannot clearly characterize, and the residual pulsation features left after accounting for our derived 29 pulsation frequencies in both SAP and PDC light curves, we computed in both cases the β factor, as specified by Carter & Winn (2009), and used the minimization of the β factor as a tool to determine which data set to use. To quantify to what extent TESS photometry is affected by systematic noise, we computed residuals for the PDC and SAP data by subtracting the primary transit light curves and the 29 pulsation frequencies. We then divided the residuals into M bins of equal duration, with N equal to the number of data points per bin. When the residuals are not affected by red noise, they probably follow the expectation of independent random numbers,
![\begin{equation*} \sigma_N = \sigma_1 N^{-1/2}[M/(M-1)]^{1/2}, \end{equation*}](/articles/aa/full_html/2020/07/aa37905-20/aa37905-20-eq2.png) (2)
(2)
where 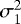 is the sample variance of the unbinned data and
is the sample variance of the unbinned data and 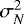 is the sample variance (or RMS) of the binned data, with the following expression:
is the sample variance (or RMS) of the binned data, with the following expression:
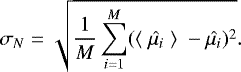 (3)
(3)
In the equation, 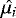 is the mean value of the residuals per bin, and
is the mean value of the residuals per bin, and 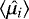 is the mean value of the means. In the presence of correlated noise, each σN differs by a factor of βN from their expectation. The β factor, usedto enlarge the individual photometric errors, is an average of all βN computed considering different timescales, Δt, that are judged to be most important. In our case, the nature of the noise and thus the relevant timescales differs drastically. To compute βN, we therefore considered Δt between 2 h (systematics due to residual pulsations) and 4 days (systematics due to PDM detrending), divided into steps of 1 h, corresponding to a total of 94 Δt. Figure 4 shows our resulting βN as a function of the frequency (1/Δt). In both cases, the highest βN values are at the lower end of the frequency range, where the TESS total time coverage does not allow us to resolve the pulsation frequencies from the high noise. βN increases drastically from SAP to PDC photometry by almost a factor of three. The corresponding β factors are computed from the average of the βN, with values βSAP = 3.545, and βPDC = 8.609. This work istherefore based on SAP data, where the individual error bars are increased by a factor of 3.545.
is the mean value of the means. In the presence of correlated noise, each σN differs by a factor of βN from their expectation. The β factor, usedto enlarge the individual photometric errors, is an average of all βN computed considering different timescales, Δt, that are judged to be most important. In our case, the nature of the noise and thus the relevant timescales differs drastically. To compute βN, we therefore considered Δt between 2 h (systematics due to residual pulsations) and 4 days (systematics due to PDM detrending), divided into steps of 1 h, corresponding to a total of 94 Δt. Figure 4 shows our resulting βN as a function of the frequency (1/Δt). In both cases, the highest βN values are at the lower end of the frequency range, where the TESS total time coverage does not allow us to resolve the pulsation frequencies from the high noise. βN increases drastically from SAP to PDC photometry by almost a factor of three. The corresponding β factors are computed from the average of the βN, with values βSAP = 3.545, and βPDC = 8.609. This work istherefore based on SAP data, where the individual error bars are increased by a factor of 3.545.
3.5 Primary transit parameters from TESS light curves
von Essen et al. (2014) derived the transit parameters with and without the intrinsic variability of the host star. After comparing the derived parameters, we found no significant differences in the two sets. The analysis of TESS data revealed no different results, which were derived in the following way. First, we analyzed TESS data including all the pulsation frequencies. We considered the data points around ±0.1 days centered on each mid-transit time, so that we had enough off-transit data to normalize each transit. For the normalization we used a second-order time-dependent polynomial that was simultaneously fit to the transit model (Mandel & Agol 2002). The degree of the polynomial was chosen from a prior analysis of the data, and as detrending functions, we tried a first-, second-, and third-degree time-dependent polynomial. After carrying out a simple least-squares fit between the primary transits and the detrending times the transit model, we computed the Bayesian information criterion (BIC) from the residuals, and analyzed which polynomial systematically minimized the BIC. The fitting parameters were the semimajor axis, a∕RS, the inclination in degrees, i, the orbital period, P, the planet-to-star radius ratio, RP/RS, and the mid-transit time of reference, T0. As specified before, we used a quadratic limb-darkening law. We considered the eccentricity fixed and equal to zero (Smith et al. 2011). Our joined model includes 3 × TN + 5 parameters, where TN = 16 corresponds to the total number of transits, 3 to the number of coefficients for the detrending polynomial, and 5 accounts for the primary transit parameters previously mentioned. The transit light curves, along with the derived best-fit transit model, are shown in Figs. A.1 and A.2. Subsequently, we analyzed TESS data after removing all the pulsation frequencies listed in Table 2, specifically, dividing away from the fluxes the summation of the 29 pulsation frequencies using the following equation:
![\begin{equation*} {\textrm{PM}(t) = \sum_{i=1}^{29}A_i \times \sin[2\pi(t\nu_i + \phi_i)]},\end{equation*}](/articles/aa/full_html/2020/07/aa37905-20/aa37905-20-eq8.png) (4)
(4)
where Ai, νi and ϕi are the amplitudes, frequencies, and phases listed in Table 2, respectively. The number of fitting parameters and the degree of the detrending function remained unchanged. All the primary transit light curves cleaned of the 29 pulsation frequencies, along with the best-fit transit model, are also shown in Figs. A.1 and A.2, vertically shifted down to allow for visual comparison. To derive the best-fit values for the model parameters and their corresponding uncertainties, we used an MCMC approach, which is implemented in the routines of PyAstronomy2 (Patil et al. 2010; Jones et al. 2001). We iterated 1 000 000 times, with a conservative burn-in of the first 20% samples. For all the parameters we considered uniform priors around ±50% of their corresponding starting values. These were taken from von Essen et al. (2014) for the primary transit model, as specified in the last column of Table 3. Starting values for each second-order time-dependent polynomial were derived from a simple least-squares minimization. We computed the median and standard deviation from the posterior distributions, and used these as our best-fit values and uncertainties, given at 1σ level. We confirmed the convergence of the chains by visually inspecting each one of them, and by dividing the chains into three subchains. In each case, we computed the usual statistics, and we considered that a chain converged when the derived parameters were consistent within their uncertainties.
The ephemerides following from 23 days of TESS data, derived from our transit fitting accounting for the stellar pulsations, are the following:
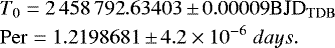
Our derived period agrees within 1σ with the period reported by Maciejewski et al. (2018). The semimajor axis and inclination agree at the same level with the corresponding values reported in von Essen et al. (2014). The only exception is the planet-to-star radius ratio. Even though this value does not agree with the value reported by von Essen et al. (2014), it perfectly agrees with the aluminum oxide model extrapolated to TESS wavelengths (see, e.g., von Essen et al. 2019a and Welbanks et al. 2019). This value also shows the accuracy on our treatment for third-light contribution. The phase-folded primary transit light curves are shown in Fig. 5. The asymmetry in the transit shape is caused by the improper treatment of the pulsation frequencies. For the further analysis, we solely consider the transit parameters listed in the third column of Table 3.
The posterior distributions and the corresponding correlations between parameters are presented in Fig. 6. In addition to the well-known correlation between a∕RS and i, and to a lesser extent, between P and T0, the remaining parameters are uncorrelated, with Pearson correlation values ranging between −0.05 and 0.04.
Pulsation frequencies of WASP-33 derived from TESS photometry.
 |
Fig. 4 Correlated noise in the TESS photometric products. βN as a functionof frequency (1/Δt) for the PDC(red circles) and SAP (black squares) data sets. |
 |
Fig. 5 Primary transit light curves without (left) and with (right) stellar pulsations. Black points correspond to TESS data, and the red continuous line shows the derived best-fit transit model. Corresponding residuals are shown below each transit. |
3.6 Updated stellar and planetary parameters
We redetermined the stellar and planetary radii and masses, taking advantage of the newly available parallax from Gaia DR2 together with the available photometry from all-sky broadband catalogs. We used the semi-empirical approach of measuring the stellar spectral energy distribution (SED) described by Stassun et al. (2017) and Stassun & Torres (2016).
We pulled the BTVT magnitudes from Tycho-2, the uvby magnitudes from Strömgren, uvby magnitudes from Paunzen (2015), the JHKS magnitudes from 2MASS, the W1–W4 magnitudes from WISE, and the GGBPGRP magnitudes from Gaia. Together, the available photometry spans the full stellar SED over the wavelength range 0.35–22 μm (see Fig. 7).
We performed a fit using Kurucz stellar atmosphere models, with the priors on effective temperature (Teff), surface gravity (logg), and metallicity ([Fe/H]) from the values reported in Table 1. The remaining free parameter is the extinction, AV, which we limit to the maximum for the line of sight from the dust maps of Schlegel et al. (1998). The resulting fit (Fig. 7) is very good, with a reduced χ2 of 2.7, and best-fit AV = 0.04 ± 0.04. Integrating the (unreddened) model SED gives the bolometric flux at Earth of Fbol = 1.455 ± 0.051 × 10−8 erg s−1 cm−2. The Fbol and Teff together with the Gaia DR2 parallax, adjusted by + 0.08 mas to account for the systematic offset reported by Stassun & Torres (2018), gives the stellar radius as R⋆ = 1.561 ± 0.052 R⊙. Estimating the stellar mass from the empirical relations of Torres et al. (2010) gives M⋆ = 1.59 ± 0.10 M⊙, which is consistent with that inferred from the spectroscopic log g together with the radius (1.77 ± 0.82 M⊙). Finally, the estimated mass together with the radius gives the mean stellar density ρ⋆ = 0.59 ± 0.07 g cm−3. With the updated value for the stellar radius and the planet-to-star radii ratio derived fitting TESS photometry, we report here the planetary radius in the TESS passband, RP = 1.627 ± 0.054 RJ.
Best-fit transit parameters obtained from TESS photometry (this work), compared to those determined by von Essen et al. (2014), accounting for pulsations.
 |
Fig. 6 Posterior distributions for the primary transit parameters. Gray to white contours indicate 1, 2, and 3σ intervals. The red points correspond to the best-fit values. The chains were shifted to the best-fit values of the parameters specified in Table 3 to allow for a better visual inspection of the uncertainties. |
3.7 Star–planet interaction
Compared to von Essen et al. (2014), the quality of TESS data allowed us to carry out a more thorough analysis of the pulsation spectrum of the host star. Because we now count almost four times more pulsation frequencies than before, we again investigated whether any of the observed pulsations were induced by planetary tides over the star.
To begin with, we do not find a nonradial mode around ~4 cd−1 as previously reported by Collier Cameron et al. (2010). In addition to this, tidally excited modes can be manifested by the commensurability between the orbital period of the planet and the pulsation frequencies (see, e.g. Hambleton et al. 2013). Similarly to von Essen et al. (2014), we used our best-fit orbital period to express the pulsation frequencies as cycles per orbital period (cP−1). These are given in the fifth column of Table 2. We found the closest commensurability to be 36.99669 cP−1, corresponding to the frequency 30.3283 ± 0.0088 cd−1. The difference to its closest integer number is equal to 0.00331. To assess whether this difference is significant enough to pinpoint this pulsation as being triggered by planetary tides, we carried out the same exercise as described in von Essen et al. (2014). Briefly, we randomly generated 29 frequencies between the lowest and highest detected frequencies that were in turn derived from a uniform distribution. Then, we converted these frequencies given in cd−1 to cP−1, and we selected the frequency closest to an integer number. We then computed the difference. We call this difference the “best match”. After 1 × 106 iterations, we computed the cumulative probability distribution for the minimum distance from an integer frequency ratio, dmin, as
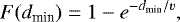 (5)
(5)
where v is obtained from fitting our Monte Carlo results with an exponential decay (see Fig. 8). The derived value is v = 0.0078 ± 0.0007. From this, we can determine that the probability of finding at least one of the ratios closer than 0.00331 c/per to an integer ratio, of 29 randomly produced pulsation frequencies, is 35%. This value is too high to confidentially claim that this particular pulsation is induced by the planet. It is therefore very unlikely that the system shows evidence of star-planet interactions.
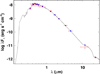 |
Fig. 7 SED of WASP-33. Red symbols represent the observed photometric measurements, where the horizontal bars represent the effective width of the passband. Blue symbols are the model fluxes from the best-fit Kurucz atmosphere model (black). |
 |
Fig. 8 Normalized histogram for the best-match frequencies generated from 106 iterations, compared to F(dmin), plotted as the continuous line. |
4 Joint model
4.1 Fitting strategy
Our model is the addition of five components that are explained in detail below and that were fit to the unbinned TESS photometry in simultaneous after the most prominent pulsations were removed (see Sect. 4.7). Equivalently to the primary transit-fitting approach, we used an MCMC to derive the best-fit values of our model. In this case, we iterated 10 000 times, with a burn-in of the first 2000 samples, after visually inspecting the chains for convergence. The best-fit values for the parameters, along with their corresponding 1σ uncertainties, were derived from the median and standard deviation of the posterior distributions, regardless the use of uniform or Gaussian priors.
To reduce the number of fitting parameters, when a given parameter was present in different model components, it was treated as equal by our MCMC algorithm. For each model component we detail the model parameters, differentiating those fit on their own and those treated as equal by our MCMC algorithm. In all cases, the variable t corresponds to the time provided by TESS. To ensure that our results are not affected by our choice of priors, and to investigate whether the planetary mass has any effect on our modeling, we carried out four different fits in parallel. Model 1 (M1) has uniform priors on all the parameters and considers the planetary mass as fixed. Model 2 (M2) has Gaussian priors on all the parameters and considers the planetary mass as fixed. Models 3 and 4 (M3 and M4) are similar to M1 and M2, with the difference that the planetary mass is considered as a fitting parameter. When we used uniform priors, we considered physically reasonable ranges that always fulfilled a conservative ±50% of each parameter, and when we used Gaussian priors, we either considered the best-fit values and uncertainties derived in this work and specified in the third column of Table 3 as starting values and errors, or we used those from the literature when not available from this work, for instance, the planetary mass. In both cases, to be conservative, the uncertainties were enlarged a factor of 3 when we used them as part of the Gaussian priors. At the end of this section we provide the four sets of results, and report as final values those corresponding to the smallest reduced chi-squared. Particularly, for the case of the ellipsoidal variation (Sect. 4.5) and the Doppler beaming (Sect. 4.6), we followed the prescription provided and fully described by Beatty et al. (2019), which we do not repeat here.
4.2 Primary transit model
We modeled the WASP-33b primary transit model (TM(t)) as specified before, using the model of Mandel & Agol (2002) and our custom linear and quadratic limb-darkening coefficients. The fitting parameters, that is, the semimajor axis, a∕RS, the inclination in degrees, i, the orbital period, P, the planet-to-star radius ratio, RP /RS, and the mid-transit time of reference, T0, are all parameters that affect the different model components, and are therefore always treated as equal. We recall that this joint model does not take into account a second-order time-dependent polynomial to normalize the light curves. Its use did not only account for the lack of the phase curve model around primary transit, but also for imperfections in the photometry (residual pulsations and other systematics present in the SAP photometry, as previously discussed). In consequence, the planet-to-star radius ratio will appear slightly enlarged to compensate for the lack of normalization. As starting values and standard deviation for the Gaussian priors, we used the values listed in the third column of Table 3. To be conservative, the uncertainties were enlarged by a factor of 3.
4.3 Secondary eclipse model
As secondary eclipse model we considered a scaled version of the transit model given by Mandel & Agol (2002), with the linear and quadratic limb-darkening coefficients set to zero. The contribution of the WASP-33 companion and the orbital eccentricity were considered in the same way as specified before. As described in von Essen et al. (2019b), the secondary eclipse model, SE(t), is given by
![\begin{equation*} \mathrm{SE(t)} = [\mathrm{TM(t)} - 1.] \times \mathrm{SF} + 1,\, \end{equation*}](/articles/aa/full_html/2020/07/aa37905-20/aa37905-20-eq11.png) (6)
(6)
where TM(t) corresponds to the primary transit model of Mandel & Agol (2002), and SF corresponds to the scaling factor that scales the transit to meet the secondary eclipse depth. From this factor, the secondary eclipse depth is computed as 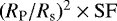 , and its error is computed from error propagation between the two. The fitting parameters are those from the transit model and the scaling factor.
, and its error is computed from error propagation between the two. The fitting parameters are those from the transit model and the scaling factor.
4.4 Phase curve model
As performed, for instance, by Cowan & Agol (2008) and Zhang et al. (2018) on the WASP-33 Spitzer photometry, we modeled the reflection of starlight and thermal emission from the dayside of the planet, here called planetary phase variability, PPV(t), as a series of first-order expansions in sines and cosines:
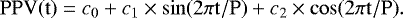 (7)
(7)
The fitting parameters are the offset, c0, the amplitudes of the sine and cosine, c1 and c2, respectively, and the orbital period, treated as equal. This linear combination of sines and cosines allows for a potential offset between the region of maximum brightness and the substellar point.
4.5 Ellipsoidal variation
Gravitational effects of a close-in exoplanet on its host create a distortion of the star that results in photometric variations with a minimum that occurs twice per orbit: during primary transit, and during secondary eclipse. This effect is called ellipsoidal variation, and it mainly depends on the properties of the stellar surface, the masses of planet and star, and their relative distances. The amplitude of the ellipsoidal variation of WASP-33, AEV, is given by
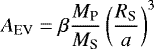 (8)
(8)
(Loeb & Gaudi 2003). Here, MP and MS correspond to the planetary and stellar masses, respectively, a∕RS is the semimajor axis scaled to the stellar radius, and β (Morris 1985) depends on the limb- and gravity-darkening coefficients. For WASP-33A and b, AEV = 27.4 ppm. The limb- and gravity-darkening coefficients were taken from Claret (2017), interpolated to the stellar parameters of WASP-33, and the mass of WASP-33b was taken from Lehmann et al. (2015) with MP = 2.1 ± 0.2 MJ. The remaining parameters were taken from this work. For this model component, the fitting parameters are those connected to TM(t), treated as equal, and the planetary mass.
4.6 Doppler beaming
The planet and star both orbit their common barycenter. While doing so, the star periodically moves toward and away from the observer. This creates a variation in the brightness of the host star that is in total synchronization with the frequency of the planet. The amplitude of the Doppler beaming is given by
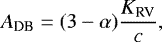 (9)
(9)
(Rybicki & Lightman 1979), where α is defined in Loeb & Gaudi (2003), KRV is the radial velocity amplitude of the planet, and c is the speed of light. For WASP-33, ADB = 2.7 ppm. As in the case of the ellipsoidal variation, the fitting parameters are those connected to TM(t) and the planetary mass, which is treated as equal to the mass from the ellipsoidal variation.
Figure 9 shows the thermal emission and reflected light, the ellipsoidal variation (EV), and the Doppler beaming (DB) for WASP-33b, to allow for a comparison of the amplitudes of the different effects. Even though the phase curve model is shown along the whole orbital phase, in our joint fit it is turned off during secondary eclipse because the planet is blocked by the star and therefore does not produce any signal. As previously mentioned, in Table 5 we provide four sets of results, with uniform and Gaussian priors, and with and without fitting for the planetary mass.
4.7 Pulsation effect on the derived secondary eclipse depth and phase curve amplitude
As reported in Sect. 3.3, 29 pulsations showed a significant signal above the noise and were accordingly detected as such. From Period04 we extracted the corresponding frequencies, amplitudes, and phases, which were used to clean the data from pulsations to recover the planetary signature. To do so, similarly to von Essen et al. (2014, 2015), we considered as pulsation model Eq. (4). The pulsation amplitudes listed at the top of the table are comparable to or even larger than the expected eclipse depth. Instead of considering them as noise, we carried out a thorough analysis of their effect over the planetary signature. As a counterpart, several high-frequency pulsations reported in this work have amplitudes smaller than 100 ppm, which means that they lie at the limit or even below the TESS point-to-point scatter. In consequence, these pulsations might be statistically irrelevant when they are included as part of our model budget, which was also analyzed.
Using Period04, we computed pulsation-corrected light curves (PCLCs) taking into account subgroups of pulsations, that is, the full set, and those with the 25, 20, 15, 10, 9, 8, 7, 6, 5, 4, 3, 2, and 1 highest amplitudes. The difference in step served as a way to carry out a more detailed investigation of the effect that the pulsation frequencies with the highest amplitudes have. We ended up with 14 PCLCs, each one of them with a different “pulsation noise” level. We prefer to use Period04 residuals because MCMC fits are time-consuming. The former has been shown to deliver robust results for pulsation frequency analysis.
To test whether the chosen number of pulsations affects the determination of the physical properties of WASP-33b, we repeated the same process for each of the 14 PCLCs. To speed the process up, we subtracted the primary transit model as evaluated with the parameters reported in Table 3, plus the EV and the DB that were evaluated considering the mass value given by Lehmann et al. (2015). Thus, we carried out an MCMC fit between the PCLCs and the phase curve and secondary eclipse models specified before. In each case we computed the best-fit parameters and their uncertainties, along with the standard deviation of the residuals (PCLCs minus best-fit SE(t) + PPV(t) model) and the BIC = χ2 + k ln(N). For the BIC, χ2 was computed in the usual way, between the PCLCs and the best-fit model. N corresponds to the total length of the photometry, and k is the number of fitting parameters. For k we considered the usual four parameters (SF, c0, c1, and c2), plus 3 × PN, where PN is the number of pulsations considered in each subgroup of PCLCs. The factor 3 accounts for each frequency, amplitude, and phase.
Figure 10 shows the evolution of the BIC, the standard deviation of the residuals, and some of the fitted parameters, specifically, SF, c1, and c2, which were computed after the primary transit, the ellipsoidal variation, and the DB were fit and removed in a previous step. This means that only the phase curve and the eclipse depth were isolated. These are given as a function of the number of pulsations taken into consideration in the pulsation model. The figure reveals two important aspects. First, a pulsation model that includes the frequencies with the three highest amplitudes favors the minimization of the BIC. However, there is a change by almost 50% in the scaling factor, when the first five frequencies are included. To investigate if this large difference is caused by an inadequate consideration of the pulsations of the host star, we proceeded as follows. We created 14 light curves using as time stamps those of TESS data, and as model, (SE(t) + PPV(t)) × PM(t). As frequencies, amplitudes and phases we used those shown in Table 2, considering them in the same way as the PCLCs were produced. As scaling factor we considered an arbitrary value of 0.03. For c1 and c2, we took 50 and −120 ppm, respectively. After the synthetic light curves were generated, we fit them back with the phase curve and secondary eclipse models. Theblack circles shown in the central panel of Fig. 10 reveal the retrieved scaling factors for each of the synthetic light curves. As expected, the recovered SFs follow the exact same behavior as those that were obtained from TESS photometry.The observed jump is therefore caused by an insufficient treatment of the pulsations of the host star. It does not come as a surprise that adding F5 into the pulsation modeling changes the parameters significantly because this pulsation frequency is close to 3 cP−1. From PN = 5 and onward, the derived SF is consistent within the errors. Among all these, PN = 5 corresponds to the smallest BIC value. In addition to this, the difference between the two lowest BIC values exceeds the required ΔBIC < −6 (Kass & Raftery 1995), which is strong evidence in favor of the pulsation model formed solely by the first five frequencies. The remaining pulsation frequencies have a negligible effect on the planetary features, and are therefore ignored for further analyses.
 |
Fig. 9 Photometric variability in ppm given by reflection and emission shown as the black continuous line, the EV as the red dotted line, and the DB as the blue dashed line, as derived in this work. Values are placed around zero to allow for visual comparison. |
 |
Fig. 10 Evolution of relevant parameters as a function of the number of pulsations considered to remove from the data. From top to bottom: the phase curve coefficients, c1 and c2, are shown as green points; the scaling factor and its injected counterpart are plotted as blue triangles and black circles, respectively,see text for details; and two statistics, the BIC as red circles and the standard deviation of the residual light curves as black squares, which was enlarged by a factor of 5 for better visualization. |
5 Discussion and results
5.1 Model parameters derived for WASP-33b
WASP-33b data, along with our best-fit joint model, are shown in Fig. 11. The most prominent first five pulsation frequencies were removed from the light curve. The last two panels are binned to Δϕ = 0.01 (equivalently, Δt ~ 17 min). At this cadence, the photometric precision is 159 ppm. Panels 2 and 3 show no visible difference. With this we emphasize that the amplitude of the EV and DB are significantly smaller than that of the thermal emission and reflected light (see Fig. 9). The best-fit values for the derived parameters of the four model approaches, along with their uncertainties computed in the usual way from their posterior distributions, are listed in Table 4.
We computed the amplitude of the phase curve as
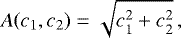 (10)
(10)
and we computed the eclipse depth as
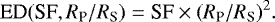 (11)
(11)
In both cases, the uncertainties were derived from error propagation of the involved parameters.
Table 4 shows general consistency of the results, not only when the different modeling approaches are compared, but also when the transit parameters between this and those listed in Table 3 are compared. An exception is the ratio of the planet-to-star radius. As mentioned before, this difference is caused by the lack of primary transit detrending in the joint model because adding an unphysical detrending would absorb the physics we wish to extract from the data. The photometry is so extensive and so strongly deformed by the pulsations of the host star that even the length of the off-transit data during the primary transit-fitting stage had to be carefully chosen to avoid an effect on the derived parameters. Thus, the transit parameters reported in this work are those listed in the third column of Table 3. In any case, either choosing the RP /RS derived in Sect. 3.5 or the one obtained here gives a fully consistent eclipse depth within its uncertainty. This means that this slight transit parameter difference does not affect our results for the phase curve and eclipse parameters. The model with the smallest BIC/ is M2, where the planetary mass is not a fitting parameter. However, the ΔBIC = − 5 compared to model M4 does not favor M2 significantly. To emphasize the additional benefit of an independent mass measurement for WASP-33b from the phase curve photometry, we discuss the results of M4 in the remainder of this paper. Nonetheless, it is worth to mention that the use of uniform and Gaussian priors on the mass of the planet returned different results. This is probably because TESS data, even though extremely rich, do not allow for a completely independent determination of the planetary mass without previous knowledge of it. Posterior probability distributions for the fitted parameters are shown in Fig. B.1 for M4 alone because all posteriors look alike.
is M2, where the planetary mass is not a fitting parameter. However, the ΔBIC = − 5 compared to model M4 does not favor M2 significantly. To emphasize the additional benefit of an independent mass measurement for WASP-33b from the phase curve photometry, we discuss the results of M4 in the remainder of this paper. Nonetheless, it is worth to mention that the use of uniform and Gaussian priors on the mass of the planet returned different results. This is probably because TESS data, even though extremely rich, do not allow for a completely independent determination of the planetary mass without previous knowledge of it. Posterior probability distributions for the fitted parameters are shown in Fig. B.1 for M4 alone because all posteriors look alike.
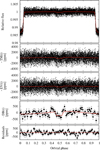 |
Fig. 11 From top to bottom: phase-folded light curve of WASP-33 presented as black points showing the primary transit around phases 0,1 and the residual pulsations of the host star; relative flux of WASP-33 in parts per million (ppm) after removing the primary TM (second panel), the EV (third panel), and the DB (fourth panel). Last two panels: data binned at ϕ = 0.01 with the secondary eclipse plus phase curve at the top, and residuals from the best-fit model at the bottom. Red lines always showthe different components of the best-fit model. |
5.2 Physical parameters derived from these observations
Following the prescription given by Cowan & Agol (2011), from our derived parameters we computed the Bond albedo,
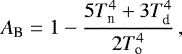 (12)
(12)
and the heat redistribution efficiency,
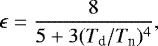 (13)
(13)
where Td and Tn correspond to the temperature of the dayside and the nightside, respectively. To compute the dayside temperature, we made use of the secondary eclipse depth divided by the primary transit depth because this is a direct measure of the ratio of the planetary dayside intensity to the stellar intensity, 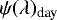 = ED/(RP/RS)2 = SF. Equivalently to this, to compute the nightside temperature, we used the difference between the secondary eclipse depth and the phase variation amplitude, combined with the offset between the region of maximum brightness and the substellar point,
= ED/(RP/RS)2 = SF. Equivalently to this, to compute the nightside temperature, we used the difference between the secondary eclipse depth and the phase variation amplitude, combined with the offset between the region of maximum brightness and the substellar point, 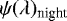 = ED - 2A × cos(ϕoff). We then computed the brightness temperature of the planet following the prescription given in Cowan & Agol (2011),
= ED - 2A × cos(ϕoff). We then computed the brightness temperature of the planet following the prescription given in Cowan & Agol (2011),
![\begin{equation*} T_{\textrm{b}}(\lambda) = \frac{hc}{\lambda k}\left[{\textrm{log}}\left(1 + \frac{\textrm{e}^{hc/\lambda k T*_b(\lambda)}-1}{\psi(\lambda)}\right)\right]^{-1} \,. \end{equation*}](/articles/aa/full_html/2020/07/aa37905-20/aa37905-20-eq23.png) (14)
(14)
Here, T *b(λ) is the stellar brightness temperature within the TESS passband, equal to 7337 K, and h, c, and k are the Planck constant, the speed of light, and the Boltzmann constant, respectively. Table 5 summarizes the values derived in this work, compared to those computed by Zhang et al. (2018). Results for all modeling approaches are provided to show that our analysis is reliable.
We obtained the uncertainties on these parameters using the posterior probability distributions for the values c1, c2, and SF. In detail, for each of the 8000 MCMC iterations, we computed the Bond albedo, recirculation efficiency, and day- and nightside brightness temperature. In this way, the values reported in Table 5 were obtained from their median and standard deviation. Our values are fully consistent with those reported by Zhang et al. (2018). Figure 12 shows our derived eclipse depth compared to literature measurements. Models 1 and 2 were taken from Deming et al. (2012) and correspond to a solar composition model with an inverted temperature in pink and a carbon-rich noninverted model in green, respectively. Model 3 was taken from Haynes et al. (2015) and reflects their best-fit inversion model with TiO. To determine the effective temperature of WASP-33b, we fit all the literature values to synthetic eclipse depths. These were created by integrating the flux ratio between a blackbody of different temperatures (the planet) and the PHOENIX intensities specified before (the star). From χ2 minimization we obtained Teff,W33 = 3105 ± 95 K. The error on the temperature was computed considering Δχ2 = 1.
When we fit model M4, the TESS phase curve also allowed for an independent mass measurement of WASP-33b by a fit for the photometric variations due to gravitational interactions between planet and host star. We derive a value of MP = 2.85 ± 0.51 MJ, which is consistent with the value of Lehmann et al. (2015) estimated by radial velocity measurements within 1.5 σ. A good agreement between photometric and radial velocity mass measurement was also achieved in the TESS full-orbit phase curve of WASP-18b (Shporer et al. 2019), for example. However, there are examples in the literature of discrepant mass values of these independentmethods that might be related to an insufficient knowledge of the host star. We refer to the extensive discussion of this problem in Shporer (2017).
Best-fit values and 1σ uncertainties for the parameters accompanying, among others, the Mandel & Agol (2002) model, a∕RS, i, RP /RS, P, and T0, the phase curve, c0, c1, and c2, and the scaling factor of the secondary eclipse model, SF.
Bond albedo, recirculation efficiency, and day- and nightside brightness temperatures for WASP-33b within the TESS passband derived from M1, M2, M3, and M4.
5.3 WASP-33b in context
Theoretical calculations predicted an energy transport by winds from the dayside to the nightside on hot Jupiters (Showman & Guillot 2002; Perez-Becker & Showman 2013). Early Spitzer phase curve observations provided observational indications in line with these predictions by measuring an eastward offset between the hottest measured longitude and the most strongly irradiated longitude at the substellar point (e.g., Knutson et al. 2007, 2012). With increasing number of available Spitzer data, a trend was revealed of a less pronounced phase offset and an increasing temperature day-night contrast with increasing stellar insolation of the planet. It was understood as a reduced efficiency of the heat transport for hotter planets, caused by the balance between advective and radiative cooling, and drag forces decelerating the advection (e.g., Komacek et al. 2017). Surprisingly, two more recent observations of the ultra-hot Jupiters WASP-103b and WASP-33b showed a comparably weakened temperature contrast between day and night sides (Kreidberg et al. 2018; Zhang et al. 2018). Bell & Cowan (2018) and Tan & Komacek (2019) explained this effect by taking into account the dissociation and recombination of hydrogen molecules, which plays a role only for the very hottest known exoplanets. Our derived values for day and night brightness temperature, and subsequently ɛ, agree very well with the results of Zhang et al. (2018) for WASP-33b, thus they strengthen the indication of a turn-around in day-night temperature contrast for the most insolated ultra-hot Jupiters. The TESS phase curve analysis of the hottest known gas giant, KELT-9b, by Wong et al. (2019) also confirm this result. Associated with the same phenomenon, Keating et al. (2019) described an increase of the nightside temperature with increasing stellar insolation, including the Zhang et al. (2018) temperature value of WASP-33b. Our result of this work is in line with this correlation.
The TESS light curve revealed a westward phase offset for WASP-33b, that is, the maximum in brightness occurred after the secondary eclipse. Westward phase offsets like this have been spotted in hot-Jupiter systems before. At NIR wavelengths, Spitzer 4.5 μm revealed an offset of 21 ± 4 degrees in CoRoT-2b, which in turn was not observed at 3.6 μm (Dang et al. 2018). To explain their observational evidences, the authors offered three possible scenarios: nonsynchronous rotation, magnetic effects, or eastern clouds. Even rarer results were revealed by Kepler photometry in HAT-P-7b because the observed phase offsets appeared to change in time (Armstrong et al. 2016). Assuming these changes were not caused by systematic noise over the data, Rogers (2017) explained them by magnetic interactions that might create phase offsets with periodic changes in position. For a hot Jupiter of more moderate temperature, Kepler-7b, the Kepler phase curves probe reflected light, therefore the measured westward offset might be caused by a cloudy western hemisphere (Demory et al. 2013). In addition to this work, another ultra-hot Jupiter showing a westward offset of ~14 degrees is WASP-12b (Bell et al. 2019). A recent collection of phase offset measurements are given in Keating et al. (2020), who focused only on Spitzer data at 3.6 and 4.5 μm. Their Fig. 7 reveals a wide spread, with a clear preference for eastward offsets. However, about six targets present westward offsets, and of this sample, two present both eastward and westward phase offsets. For WASP-33b, the effective temperature is above 3000 K. This means that the TESS wavelengths must be probing mostly thermal emission and to a lesser extent, reflected light. The observed westward offset might therefore be explained by the three hypotheses presented by Dang et al. (2018) for CoRoT-2b. However, in order to consolidate the observed eastward offset by Zhang et al. (2018) in Spitzer 4.5 and 3.6 μm with our detected westward offset in TESS light, time-variable clouds or magnetic fields would be the best explanations. All these mixed results might indicate that the atmospheric dynamics of hot and ultra-hot Jupiters are more complex than we thought.
We add an additional word of caution. In an earlier stage of our data analysis of this work, we carried out fits of the different model components in independent steps, rather than simultaneously, as presented here. The resulting phase offset we obtained was eastward and consistent with the offset detected by Zhang et al. (2018). In consequence, we might consider that phase offsets are prone to details in the analysis or systematics in the data. The reliable extraction of the phase offset from photometric data might be more challenging than we thought. Because the WASP-33 photometry is affected by intrinsic variability of the host star, we cannot reject a nonastrophysical origin of the westward phase offset.
The consistency in the measured dayside temperature between the optical phase curve analyzed in this work and the NIR phase curves of Zhang et al. (2018) indicate that the thermal emission of the WASP-33b dayside is similar to a blackbody, potentially caused by the continuum opacity of the hydrogen anion H− (Arcangeli et al. 2018; Kitzmann et al. 2018). However, the phase offset measured in this work of ϕoff = 28.7 ± 7.1 degrees deviates significantly from the negative (eastward) offset measured by Zhang et al. (2018) in the NIR. If considered as a real astrophysical phenomenon in the planetary atmosphere, a future 3D general circulation modeling (e.g., Kreidberg et al. 2018 and Arcangeli et al. 2019) might shed light on the underlying physical conditions.
Ultra-hot Jupiters such as WASP-33b are expected to be cloud-free on their daysides because the atmospheres are too hot for condensates to form, see Wakeford et al. (2017). The lack of clouds is expected to manifest itself as a low ability to reflect star light, thus a low value of geometric albedo. The amount of light reflected off the planet is included in the secondary eclipse depth, but it is merged with the light that is thermally emitted by the planet itself. To isolate and estimate thecomponent of reflected light, we followed the approach of Mallonn et al. (2019) and approximated the thermal emission by a blackbody radiation of a temperature estimated from previous NIR measurements. Pass et al. (2019) used Gaussian process regression to derive a blackbody temperature of 3108 K for WASP-33b based on the Hubble Space Telescope Wide Field Camera 3 (HST/WFC3) secondary eclipse depths of Haynes et al. (2015) and the Spitzer results of Zhang et al. (2018). The stellar effective temperature is 7430 K (Collier Cameron et al. 2010).
By Eq. (3) of Mallonn et al. (2019), we estimate a geometric albedo of − 0.04 ± 0.04, thus the 3 σ upper limit corresponds to 0.08. This low value of the geometric albedo is in line with the theoretical expectation of no reflection because the temperature on the dayside is too hot to form condensates. It also agrees with the generally rather low measured optical values of other hot Jupiters by the Kepler satellite (e.g., Esteves et al. 2015 and Angerhausen et al. 2015), and the ground-based z′ band upper limits derived by Mallonn et al. (2019). However, the low geometric albedo contrasts with the substantial value of the Bond albedo given in Table 5. Future secondary eclipse measurements near the wavelength of stellar peak emission at 400 nm might shed light on this issue. The null-detection of the geometric albedo proves that the TESS phase curve of WASP-33b is dominated by thermal emission compared to reflected light. The opposite has recently been found in the TESS phase curve of WASP-19b (Wong et al. 2020), showing a significantly nonzero albedo and dominating reflected light.
The approximation of the planetary thermal emission by a blackbody is valid for the derivation of an upper limit of the geometric albedo because more sophisticated emission modeling mostly points toward even higher thermal flux in the optical for ultra-hot Jupiters (Haynes et al. 2015; Mikal-Evans et al. 2019; Bourrier et al. 2020; Daylan et al. 2019). Higher thermal flux would translate into lower reflected light for a given value of the eclipse depth, therefore an upper limit of the reflected light component remains unaffected (Mallonn et al. 2019). We note that in the case of TiO absorption at optical wavelengths, suggested by Haynes et al. (2015) and Nugroho et al. (2017), the optical eclipse depth is predicted to be deeper than measured in this work, with a value of ~ 1000 ppm in the red part of the TESS bandpass (see Fig. 5 in Haynes et al. 2015). Hence, the TESS secondary eclipse depth seems to disfavor the best-fit model of Haynes et al. (2015) that includes TiO and a temperature inversion. However, because this indication is based on multiple individual publications of secondary eclipse depth in different wavelength regions, we suggest a homogeneous reanalysis of these data sets before drawing a clear conclusion, which is beyond scope of this work. Our suggestion is strengthened by our result in Sect. 4.7 that the eclipse depth is affected by the number of pulsations included in the modeling. All previous work on secondary eclipses has treated the pulsations in a different way, thus a homogeneous reanalysis appears useful.
 |
Fig. 12 Eclipse depth, in ppt, as a function of wavelength. The red triangle corresponds to the TESS value, reported in this work. Error bars are included in the size of the point. The gray area shows 1σ contour of the equilibrium temperature of WASP-33b. Literature measurements come from Smith et al. (2011) (triangle in yellow) Deming et al. (2012) (circles in violet), de Mooij et al. (2013) (empty circle in green) von Essen et al. (2015) (square in black), Haynes et al. (2015) (half-filled circles in blue), Zhang et al. (2018) (diamonds in yellow). Transmission responses are plotted as black continuous lines, with the exception of TESS, which is highlighted in red. Green and pink squares show Deming et al. (2012)’s models binned to their respective filters. |
6 Conclusion
We presented the first optical phase curve and secondary eclipse observations of WASP-33b, obtained from analyzing 23 days of TESS photometry. Based on the secondary eclipse depth, ED = 305.8 ± 35.5 ppm, the amplitude of the phase curve, A = 100.4 ± 13.1 ppm, and the offset between the region of maximum brightness and the substellar point of 28.7 ± 7.1 degrees, we used a simple model to derive the brightness temperatures, Tday = 3014 ± 60 K and Tnight = 1605 ± 45 K, Bond albedo AB = 0.369 ± 0.050, and recirculation efficiency, ɛ = 0.189 ± 0.014. While the low geometric albedo of below 0.08 (3 σ upper limit) is consistent with that of other hot Jupiters, the rather high recirculation efficiency is consistent with previous WASP-33b studies at NIR wavelengths and indicates the possibility of the dissociation and recombination of hydrogen molecules in the atmospheres of ultra-hot Jupiters. Additionally, the high photometric precision in the phase-folded TESS data allowed for a mass measurement by the photometric variations caused by gravitational interactions. This mass agrees well with the literature value obtained from radial velocity measurements. Because of the nature of the continuous TESS monitoring of WASP-33, we characterized the pulsation spectrum of the host star, finding 29 peaks with an AS/N higher than or equal to 4, instead of the 8 known so far. The newly unveiled low-frequency range of the star revealed two frequencies lower than 3 cd−1 that are consistent with gravity modes as observed in γ Doradus stars, making WASP-33 a γ Doradus-δ Scuti hybrid candidate. However, more data are required to confirm this candidacy. Paying special attention in the way the pulsation frequencies are considered while determining planetary parameters, we find that using the minimization of the BIC to quantify the amount of pulsation frequencies to be considered in our model alone does not provide correct planetary parameters. Special care has to be taken with pulsations with the highest amplitude. Future detailed asteroseismic analyses of WASP-33 will help to improve the stellar parameters and better understand possible star-planet interactions (or the lack thereof).
Acknowledgements
We thank the referee for an outstanding quick reply, given the times, and for contributing to significantly improve our work. C.vE. and G.T. acknowledge support from the European Social Fund (project No. 09.3.3-LMT-K-712-01-0103) under grant agreement with the Lithuanian Science Council (LMTLT). Funding for the Stellar Astrophysics Centre is provided by The Danish National Research Foundation (Grant agreement no.: DNRF106). This work was supported by a research grant (00028173) from VILLUM FONDEN.
Appendix A Primary transit photometry of WASP-33b
 |
Fig. A.1 Normalized flux as a function of orbital phase for the primary transits of WASP-33b observed by TESS. From top to bottom and left to right: time evolves. TESS observations are in black points, and the best-fit model in red continuous line. Individual error bars are not plotted to better visualize the effect of the pulsations over the photometry. |
Appendix B Posterior distributions
 |
Fig. B.1 Posterior distributions for the fitted parameters specified in Table 4, specifically for M4. |
References
- Adams, E. R., Dupree, A. K., Kulesa, C., & McCarthy, D. 2013, AJ, 146, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology (Berlin: Springer) [Google Scholar]
- Angelov, T. 1996, Bull. Astron. Belgrade, 154, 13 [Google Scholar]
- Angerhausen, D., DeLarme, E., & Morse, J. A. 2015, PASP, 127, 1113 [NASA ADS] [CrossRef] [Google Scholar]
- Antoci, V., Cunha, M. S., Bowman, D. M., et al. 2019, MNRAS, 490, 4040 [NASA ADS] [CrossRef] [Google Scholar]
- Arcangeli, J., Désert, J.-M., Line, M. R., et al. 2018, ApJ, 855, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Arcangeli, J., Désert, J.-M., Parmentier, V., et al. 2019, A&A, 625, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Armstrong, D. J., de Mooij, E., Barstow, J., et al. 2016, Nat. Astron., 1, 0004 [NASA ADS] [CrossRef] [Google Scholar]
- Balona, L. A., & Dziembowski, W. A. 2011, MNRAS, 417, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Beatty, T. G., Marley, M. S., Gaudi, B. S., et al. 2019, AJ, 158, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, T. J., & Cowan, N. B. 2018, ApJ, 857, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, T. J., Zhang, M., Cubillos, P. E., et al. 2019, MNRAS, 489, 1995 [CrossRef] [Google Scholar]
- Belokurov, V., Penoyre, Z., Oh, S., et al. 2020, MNRAS, 496, 1922 [CrossRef] [Google Scholar]
- Bouma, L. G., Winn, J. N., Baxter, C., et al. 2019, AJ, 157, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Bourrier, V., Kitzmann, D., Kuntzer, T., et al. 2020, A&A, 637, A36 [CrossRef] [EDP Sciences] [Google Scholar]
- Bowman, D. M., & Kurtz, D. W. 2018, MNRAS, 476, 3169 [NASA ADS] [CrossRef] [Google Scholar]
- Breger, M., Stich, J., Garrido, R., et al. 1993, A&A, 271, 482 [NASA ADS] [Google Scholar]
- Breger, M., Handler, G., Garrido, R., et al. 1999, A&A, 349, 225 [NASA ADS] [Google Scholar]
- Carter, J. A., & Winn, J. N. 2009, ApJ, 704, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 2017, A&A, 600, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collier Cameron, A., Guenther, E., Smalley, B., et al. 2010, MNRAS, 407, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, N. B., & Agol, E. 2008, ApJ, 678, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, N. B., & Agol, E. 2011, ApJ, 729, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Dang, L., Cowan, N. B., Schwartz, J. C., et al. 2018, Nat. Astron., 2, 220 [NASA ADS] [CrossRef] [Google Scholar]
- Daylan, T., Günther, M. N., Mikal-Evans, T., et al. 2019, ArXiv e-prints, [arXiv:1909.03000] [Google Scholar]
- de Mooij, E. J. W., Brogi, M., de Kok, R. J., et al. 2013, A&A, 550, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deming, D., Fraine, J. D., Sada, P. V., et al. 2012, ApJ, 754, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Demory, B.-O., de Wit, J., Lewis, N., et al. 2013, ApJ, 776, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Dragomir, D., Teske, J., Günther, M. N., et al. 2019, ApJ, 875, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Esteves, L. J., De Mooij, E. J. W., & Jayawardhana, R. 2015, ApJ, 804, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Göttingen, G.-A.-U. 2018, Göttingen Spectral Library by PHOENIX [Google Scholar]
- Grigahcène, A., Antoci, V., Balona, L., et al. 2010, ApJ, 713, L192 [NASA ADS] [CrossRef] [Google Scholar]
- Günther, M. N., Pozuelos, F. J., Dittmann, J. A., et al. 2019, Nat. Astron., 3, 1099 [CrossRef] [Google Scholar]
- Hambleton, K. M., Kurtz, D. W., Prša, A., et al. 2013, MNRAS, 434, 925 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Haynes, K., Mandell, A. M., Madhusudhan, N., Deming, D., & Knutson, H. 2015, ApJ, 806, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Herrero, E., Morales, J. C., Ribas, I., & Naves, R. 2011, A&A, 526, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jansen, T., & Kipping, D. 2020, MNRAS, 494, 4077 [CrossRef] [Google Scholar]
- Jenkins, J. M. 2017, Kepler Data Processing Handbook: KSCI-19081-002, Tech. rep. [Google Scholar]
- Jenkins, J. M., Twicken, J. D., McCauliff, S., et al. 2016, SPIE Conf. Ser., 9913, 99133E [Google Scholar]
- Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open source scientific tools for Python, http://www.scipy.org [Google Scholar]
- Kass, R. E., & Raftery, A. E. 1995, J. Am. Stat. Assoc., 90, 773 [CrossRef] [Google Scholar]
- Keating, D., Cowan, N. B., & Dang, L. 2019, Nat. Astron., 3, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Keating, D., Stevenson, K. B., Cowan, N. B., et al. 2020, AJ, 159, 225 [CrossRef] [Google Scholar]
- Kitzmann, D., Heng, K., Rimmer, P. B., et al. 2018, ApJ, 863, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H. A., Charbonneau, D., Allen, L. E., et al. 2007, Nature, 447, 183 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Knutson, H. A., Lewis, N., Fortney, J. J., et al. 2012, ApJ, 754, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Komacek, T. D., Showman, A. P., & Tan, X. 2017, ApJ, 835, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Kostov, V. B., Schlieder, J. E., Barclay, T., et al. 2019, AJ, 158, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Kreidberg, L., Line, M. R., Parmentier, V., et al. 2018, AJ, 156, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Lehmann, H., Guenther, E., Sebastian, D., et al. 2015, A&A, 578, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lenz, P., & Breger, M. 2005, Commun. Asteroseismol., 146, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Li, G., Van Reeth, T., Bedding, T. R., et al. 2020, MNRAS, 491, 3586 [NASA ADS] [CrossRef] [Google Scholar]
- Loeb, A., & Gaudi, B. S. 2003, ApJ, 588, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Lothringer, J. D., Barman, T., & Koskinen, T. 2018, ApJ, 866, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Maciejewski, G., Fernández, M., Aceituno, F., et al. 2018, Acta Astron., 68, 371 [NASA ADS] [Google Scholar]
- Mallonn, M., Köhler, J., Alexoudi, X., et al. 2019, A&A, 624, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Mikal-Evans, T., Sing, D. K., Goyal, J. M., et al. 2019, MNRAS, 488, 2222 [NASA ADS] [CrossRef] [Google Scholar]
- Morris, S. L. 1985, ApJ, 295, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Moya, A., Bouy, H., Marchis, F., Vicente, B., & Barrado, D. 2011, A&A, 535, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mugrauer, M. 2019, MNRAS, 490, 5088 [CrossRef] [Google Scholar]
- Ngo, H., Knutson, H. A., Hinkley, S., et al. 2016, ApJ, 827, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Nugroho, S. K., Kawahara, H., Masuda, K., et al. 2017, AJ, 154, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Parmentier, V., & Crossfield, I. J. M. 2018, Handbook of Exoplanets (Cham: Springer), 116 [Google Scholar]
- Pass, E. K., Cowan, N. B., Cubillos, P. E., & Sklar, J. G. 2019, MNRAS, 489, 941 [CrossRef] [Google Scholar]
- Patil, A., Huard, D., & Fonnesbeck, C. J. 2010, J. Stat. Softw., 35, 1 [CrossRef] [EDP Sciences] [Google Scholar]
- Paunzen, E. 2015, A&A, 580, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perez-Becker, D., & Showman, A. P. 2013, ApJ, 776, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Piskorz, D., Knutson, H. A., Ngo, H., et al. 2015, ApJ, 814, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, J. E., Quinn, S. N., Huang, C. X., et al. 2019, AJ, 157, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, T. M. 2017, Nat. Astron., 1, 0131 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1979, Astron. Q., 3, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A. P., & Guillot, T. 2002, A&A, 385, 166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shporer, A. 2017, PASP, 129, 072001 [NASA ADS] [CrossRef] [Google Scholar]
- Shporer, A., Wong, I., Huang, C. X., et al. 2019, AJ, 157, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, A. M. S., Anderson, D. R., Skillen, I., Collier Cameron, A., & Smalley, B. 2011, MNRAS, 416, 2096 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. C., Stumpe, M. C., Van Cleve, J. E., et al. 2012, PASP, 124, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Stassun, K. G., & Torres, G. 2016, AJ, 152, 180 [Google Scholar]
- Stassun, K. G., & Torres, G. 2018, ApJ, 862, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Stassun, K. G., Collins, K. A., & Gaudi, B. S. 2017, AJ, 153, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Stumpe, M. C., Smith, J. C., Catanzarite, J. H., et al. 2014, PASP, 126, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, X., & Komacek, T. D. 2019, ApJ, 886, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- Uytterhoeven, K., Moya, A., Grigahcène, A., et al. 2011, A&A, 534, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanderburg, A., Huang, C. X., Rodriguez, J. E., et al. 2019, ApJ, 881, L19 [CrossRef] [Google Scholar]
- von Essen, C., Czesla, S., Wolter, U., et al. 2014, A&A, 561, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Essen, C., Mallonn, M., Albrecht, S., et al. 2015, A&A, 584, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Essen, C., Cellone, S., Mallonn, M., et al. 2017, A&A, 603, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Essen, C., Mallonn, M., Welbanks, L., et al. 2019a, A&A, 622, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Essen, C., Stefansson, G., Mallonn, M., et al. 2019b, A&A, 628, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakeford, H. R., Visscher, C., Lewis, N. K., et al. 2017, MNRAS, 464, 4247 [NASA ADS] [CrossRef] [Google Scholar]
- Welbanks, L., Madhusudhan, N., Allard, N. F., et al. 2019, ApJ, 887, L20 [CrossRef] [Google Scholar]
- Wöllert, M., & Brandner, W. 2015, A&A, 579, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wong, I., Shporer, A., Morris, B. M., et al. 2019, AJ, submitted, [arXiv:1910.01607] [Google Scholar]
- Wong, I., Benneke, B., Shporer, A., et al. 2020, AJ, 159, 104 [CrossRef] [Google Scholar]
- Yan, F., Casasayas-Barris, N., Molaverdikhani, K., et al. 2019, A&A, 632, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, M., Knutson, H. A., Kataria, T., et al. 2018, AJ, 155, 83 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Effective temperature, metallicity, and surface gravity for WASP-33 and the stars included in the TESS aperture.
Best-fit transit parameters obtained from TESS photometry (this work), compared to those determined by von Essen et al. (2014), accounting for pulsations.
Best-fit values and 1σ uncertainties for the parameters accompanying, among others, the Mandel & Agol (2002) model, a∕RS, i, RP /RS, P, and T0, the phase curve, c0, c1, and c2, and the scaling factor of the secondary eclipse model, SF.
Bond albedo, recirculation efficiency, and day- and nightside brightness temperatures for WASP-33b within the TESS passband derived from M1, M2, M3, and M4.
All Figures
 |
Fig. 1 SAP normalized flux of WASP-33 observed by TESS shown as black circles, along with SAP raw data in blue. The pulsations of the star deform the continuum level. The 16 transits are indicated at the bottom with red lines. The gap in the middle is caused by data downlink dead time. |
| In the text | |
 |
Fig. 2 Top: TPF of WASP-33 showing the chosen aperture mask. No stars can be visually resolved. Bottom: field of view of about 4 × 4 arcmin centered on WASP-33. The mask and pixels are schematized with white thick and thin lines, respectively. WASP-33C, the bright star south of WASP-33, is not included in the aperture. The field of view has been rotated to be aligned with the ecliptic system, and is oriented to coincide with the images given in the TESS summary report. |
| In the text | |
 |
Fig. 3 Top panel: power spectrum of WASP-33. Pulsations are marked with dashed gray lines. Bottom panel: residuals after frequency extraction. The red line makes the S/N limit of 4. |
| In the text | |
 |
Fig. 4 Correlated noise in the TESS photometric products. βN as a functionof frequency (1/Δt) for the PDC(red circles) and SAP (black squares) data sets. |
| In the text | |
 |
Fig. 5 Primary transit light curves without (left) and with (right) stellar pulsations. Black points correspond to TESS data, and the red continuous line shows the derived best-fit transit model. Corresponding residuals are shown below each transit. |
| In the text | |
 |
Fig. 6 Posterior distributions for the primary transit parameters. Gray to white contours indicate 1, 2, and 3σ intervals. The red points correspond to the best-fit values. The chains were shifted to the best-fit values of the parameters specified in Table 3 to allow for a better visual inspection of the uncertainties. |
| In the text | |
 |
Fig. 7 SED of WASP-33. Red symbols represent the observed photometric measurements, where the horizontal bars represent the effective width of the passband. Blue symbols are the model fluxes from the best-fit Kurucz atmosphere model (black). |
| In the text | |
 |
Fig. 8 Normalized histogram for the best-match frequencies generated from 106 iterations, compared to F(dmin), plotted as the continuous line. |
| In the text | |
 |
Fig. 9 Photometric variability in ppm given by reflection and emission shown as the black continuous line, the EV as the red dotted line, and the DB as the blue dashed line, as derived in this work. Values are placed around zero to allow for visual comparison. |
| In the text | |
 |
Fig. 10 Evolution of relevant parameters as a function of the number of pulsations considered to remove from the data. From top to bottom: the phase curve coefficients, c1 and c2, are shown as green points; the scaling factor and its injected counterpart are plotted as blue triangles and black circles, respectively,see text for details; and two statistics, the BIC as red circles and the standard deviation of the residual light curves as black squares, which was enlarged by a factor of 5 for better visualization. |
| In the text | |
 |
Fig. 11 From top to bottom: phase-folded light curve of WASP-33 presented as black points showing the primary transit around phases 0,1 and the residual pulsations of the host star; relative flux of WASP-33 in parts per million (ppm) after removing the primary TM (second panel), the EV (third panel), and the DB (fourth panel). Last two panels: data binned at ϕ = 0.01 with the secondary eclipse plus phase curve at the top, and residuals from the best-fit model at the bottom. Red lines always showthe different components of the best-fit model. |
| In the text | |
 |
Fig. 12 Eclipse depth, in ppt, as a function of wavelength. The red triangle corresponds to the TESS value, reported in this work. Error bars are included in the size of the point. The gray area shows 1σ contour of the equilibrium temperature of WASP-33b. Literature measurements come from Smith et al. (2011) (triangle in yellow) Deming et al. (2012) (circles in violet), de Mooij et al. (2013) (empty circle in green) von Essen et al. (2015) (square in black), Haynes et al. (2015) (half-filled circles in blue), Zhang et al. (2018) (diamonds in yellow). Transmission responses are plotted as black continuous lines, with the exception of TESS, which is highlighted in red. Green and pink squares show Deming et al. (2012)’s models binned to their respective filters. |
| In the text | |
 |
Fig. A.1 Normalized flux as a function of orbital phase for the primary transits of WASP-33b observed by TESS. From top to bottom and left to right: time evolves. TESS observations are in black points, and the best-fit model in red continuous line. Individual error bars are not plotted to better visualize the effect of the pulsations over the photometry. |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1, but for the remaining 8 primary transits. |
| In the text | |
 |
Fig. B.1 Posterior distributions for the fitted parameters specified in Table 4, specifically for M4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


