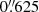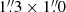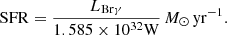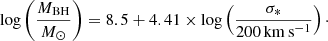| Issue |
A&A
Volume 638, June 2020
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 13 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201937092 | |
| Published online | 08 June 2020 | |
Near-infrared observations of the gas structure and kinematics in the circumnuclear region of NGC 1672⋆
1
I. Physikalisches Institut der Universität zu Köln, Zülpicher Str. 77, 50937 Köln, Germany
e-mail: fazeli@ph1.uni-koeln.de
2
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
3
LERMA, Observatoire de Paris, Collège de France, PSL Univ., CNRS, Sorbonne Univ., UPMC, 75014 Paris, France
Received:
10
November
2019
Accepted:
2
April
2020
We present our near-infrared, integral-field spectroscopy observations of the central 550 × 550 pc2 (10″ × 10″) of the local galaxy NGC 1672. Our aim is to investigate the morphology and kinematics of gas and stars to probe evidence for feeding and feedback phenomena. For this purpose the near-infrared wavelength regime and integral-field unit technique provide a vast amount of useful information. The narrow emission line ratios suggest that the galaxy hosts a low-luminosity active galactic nucleus. From the MBH − σ* relation, we find a black hole mass of a few 107 M⊙. The total reservoir of hot molecular and ionised gas is estimated, using flux of H2 and Brγ emission lines, to be 258 M⊙ and 2.3 × 106 M⊙ respectively. The most striking feature in the emission line flux maps is the star-forming ring at a radius of ∼3″. The stellar and gaseous kinematics both show a rotation pattern in a disc that is blue-shifted in the north-west and red-shifted in the south-east. However, unlike the stellar kinematics, gas kinematics show various complexities, such as higher amplitudes in the central region (within the star-forming ring). The molecular gas velocity-field map shows deviations from pure disc motion in the form of an S-shaped zero-velocity line. In particular the position angle of the zero-velocity line changes in the central arcsecond, resembling the decoupled nuclear disc or molecular torus found in CO(3–2). There is an offset of 0.″5 between the nuclear continuum barycentre and kinematic centre of molecular gas towards the north-west. The velocity field of Brγ emitting gas on the other hand, is highly red-shifted in the centre and offset from the continuum emission peak by about 1″. Investigating the spectra of this region we detect a doubled-horn Brγ emission line in the nucleus and north-west. This region is also luminous in radio 3 cm emission connecting the nucleus to the star-forming ring.
Key words: infrared: galaxies / galaxies: nuclei / galaxies: kinematics and dynamics / galaxies: active / galaxies: Seyfert / galaxies: individual: NGC 1672
© ESO 2020
1. Introduction
Active galactic nuclei (AGN) are not only amongst the most energetic phenomena in the Universe but it is also suggested that these sources play a key role in the evolution of their host galaxy. This co-evolution is observed through, for example the well-established MBH − σ relation (Gültekin et al. 2009). In addition, AGN feedback is one of the key requirements in cosmological simulations to manufacture the galaxy population observed today (e.g. Springel et al. 2005). This phenomenon is mostly associated with jets or fast outflows of ionised and atomic gas (e.g. Veilleux et al. 2005; Fiore et al. 2017) that can extend up to several kiloparsecs from the centre.
On the other hand, the feeding processes that fuel the AGN and star formation are revealed in the kinematics and morphology of the molecular gas in circumnuclear regions. In the case of nearby galaxies with low-luminosity AGN the gravitational torques by non-axisymmetric potentials funnel the gas to the inner kiloparsec (e.g. García-Burillo et al. 2005; García-Burillo & Combes 2012; Combes et al. 2013, 2014). Several hydrodynamic and observational studies show that in many galaxies the gas brought by the bar gets stalled in a nuclear ring at or near the inner Lindblad resonance (ILR). What happens to the gas from this point on is the subject of many recent studies. Subsequent dynamical instabilities such as bars-within-bars, warps or nuclear spirals, dynamical frictions, and viscosity are amongst the mechanisms suggested for funnelling the gas to within tens of parsecs of the SMBH (e.g. for hydrodynamic simulations and observational evidence; Martini et al. 2001; Hopkins & Quataert 2010; Smajić et al. 2014, 2015; Kim & Elmegreen 2017).
Integral-field unit (IFU) instruments alongside large radio interferometers have revolutionised the simultaneous study of the distribution and kinematics of both ionised and molecular gas at the same spatial scales. The near-infrared (NIR) wavelength region is particularly valuable, since it traces hot molecular and ionised gas and their excitation mechanisms, and reveals properties of the AGN, especially those properties with less extinction compared to the optical wavelength (Smajić et al. 2012). Therefore integral-field spectroscopy (IFS) in the NIR is ideal to study stellar populations and star formation in (dust-obscured) centres of galaxies.
This paper continues our previous work on a sample of nearby galaxies (NGC 1433, NGC 1566: Smajić et al. 2014, 2015, NGC 1808: Busch et al. 2017, NGC 1365: Fazeli et al. 2019, and NGC 1326: Fazeli et al., in prep.). We present NIR IFS of the galaxy NGC 1672, which is a barred spiral galaxy (SB(r)bc). The classification of the nucleus has been challenging since the centre appears to be obscured by dust. Brandt et al. (1996) in ROSAT observations of the galaxy reported a soft diffuse X-ray source. de Naray et al. (2000) suggested that there is a Seyfert 2 in the centre, obscured by a Compton thick nucleus with a column density of at least 1024 cm−2. Finally Jenkins et al. (2011) using the higher-resolution Chandra data, detected a hard X-ray nuclear source and conclude that the AGN is a low-luminosity Seyfert 2.
Jenkins et al. (2011) also studied the star-forming ring in NGC 1672 at a radius of r ≈ 5″ = 275 pc. Their observations show that the ring emits bright in the radio 3 cm data from the Australia Telescope Compact Array (ATCA), the Spitzer 8 μm band (tracing essentially the PAH dust), hard X-ray detected with Chandra, and Hα and continuum emission in the optical spectra. The CO(3–2) emission line observed by ALMA shows high concentrations in the ILR ring (Combes et al. 2019).
The galaxy has a strong 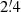 bar with a position angle (PA) of 92° and four spiral arms (Baumgart & Peterson 1986). The inclination of the galaxy is low (i = 34°; de Vaucouleurs et al. 1991), which makes it a good target for kinematical studies. However, as shown by previous studies, the kinematics at the centre of this galaxy seem to be very complex. Díaz et al. (1999), using the Multi-functional Integral Field Spectrograph (MIFiS) data studied the central 2 kpc, and Firpo et al. (2017), using the Gemini Multi-Object Spectrograph (GMOS) data studied the central
bar with a position angle (PA) of 92° and four spiral arms (Baumgart & Peterson 1986). The inclination of the galaxy is low (i = 34°; de Vaucouleurs et al. 1991), which makes it a good target for kinematical studies. However, as shown by previous studies, the kinematics at the centre of this galaxy seem to be very complex. Díaz et al. (1999), using the Multi-functional Integral Field Spectrograph (MIFiS) data studied the central 2 kpc, and Firpo et al. (2017), using the Gemini Multi-Object Spectrograph (GMOS) data studied the central 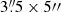 . Both studies analysed the kinematics of the NGC 1672 by fitting the Hα emission line profile. They both conclude that the nucleus is off centre with respect to the large-scale rotation disc. However, owing to the obscuration by dust and sensitivity of optical light to extinction, Firpo et al. (2017) suggested that NIR spectroscopy is needed to be certain. Díaz et al. (1999) also reported non-circular motions with an amplitude of 50−60 km s−1.
. Both studies analysed the kinematics of the NGC 1672 by fitting the Hα emission line profile. They both conclude that the nucleus is off centre with respect to the large-scale rotation disc. However, owing to the obscuration by dust and sensitivity of optical light to extinction, Firpo et al. (2017) suggested that NIR spectroscopy is needed to be certain. Díaz et al. (1999) also reported non-circular motions with an amplitude of 50−60 km s−1.
According to Combes et al. (2019, from ALMA data) the kinematics of the CO(3–2) emission line reveals a typical S-shaped velocity pattern related to non-circular motions. Additionally they report thin filaments joining towards a central concentration, which they conclude to be a torus of radius 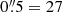 pc with decoupled kinematics from the large-scale disc.
pc with decoupled kinematics from the large-scale disc.
Figure 1 shows an optical image of NGC 1672. The field of view (FOV) of the Spectrograph for INtegral Field Observations in the Near Infrared (SINFONI) data, which is analysed in detail in this paper, is indicated in red.
 |
Fig. 1. Optical image of the spiral barred galaxy NGC 1672. The red box indicates the 10″ × 10″ (550 × 550 pc2) SINFONI data. Image courtesy: Carnegie-Irvine Galaxy Survey (Ho et al. 2011). |
Throughout this paper, we adopt a luminosity distance of DL = 11.4 Mpc which is the median value of the redshift-independent distances in NED (Steer et al. 2017). This corresponds to a scale of 55 pc arcsec−1.
This paper is structured as follows: Sect. 2 presents the observation and data reduction. Section 3 contains the explanation of our analysis methods, shows the results we find, and gives a discussion and comparison to the literature. Section 4 summarises the results and the conclusions we draw from this study.
2. Observations and data reduction
NGC 1672 was observed on October 7, 2014 with the IFS SINFONI mounted at the Unit Telescope 4 (UT4; Yepun) of the ESO Very Large Telescope in Chile (VLT; Eisenhauer et al. 2003; Bonnet et al. 2004).
The observations were taken in seeing-limited mode, the FOV of single exposures in this mode is 8″ × 8″ and the spatial sampling is 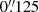 pixel−1. Using a jitter pattern with offsets ±1″ we minimised the effect of bad pixels and increased the FOV of the combined cube to 10″ × 10″, which corresponds to a linear scale of 550 pc. We used gratings in the H + K band with a spectral resolution of R ≈ 1500 and in the K band with a resolution of R ≈ 4000. We spent an integration time of 150 s per exposure. This leads to an overall on-source integration time of 1500 s (10 × 150 s) for the H + K-grating and 3000 s (20 × 150 s) for the K-band grating, as well as an additional 750 s in H +K-band and 1500 s in K band on-sky.
pixel−1. Using a jitter pattern with offsets ±1″ we minimised the effect of bad pixels and increased the FOV of the combined cube to 10″ × 10″, which corresponds to a linear scale of 550 pc. We used gratings in the H + K band with a spectral resolution of R ≈ 1500 and in the K band with a resolution of R ≈ 4000. We spent an integration time of 150 s per exposure. This leads to an overall on-source integration time of 1500 s (10 × 150 s) for the H + K-grating and 3000 s (20 × 150 s) for the K-band grating, as well as an additional 750 s in H +K-band and 1500 s in K band on-sky.
We used the ESO pipeline, up to single-exposure-cube reconstructions, for the data reduction. Initially some detector pattern features, which were imprinted in the SINFONI data, were corrected for (for more details see; Smajić et al. 2014) alignment, final coaddition, and telluric correction; our own PYTHON and IDL routines are used.
The G2V star HIP 039102 was observed in the H + K and K bands as two object-sky pairs for each band, with an integration time of 1 s. The spectrum of this star was used to correct for atmospheric telluric absorption and for flux calibration. Prior to using the spectrum we eliminated the intrinsic spectral features and black-body shape of the standard star. This procedure was done using a high-resolution solar spectrum (Maiolino et al. 1996), which was convolved with a Gaussian to match the resolution of SINFONI. A black-body function with temperature T = 5800 K was used for the spectral region between the two bands and at the spectral edges to extrapolate the solar spectrum.
The flux calibration was performed by extracting a spectrum from the telluric standard star (aperture size =3 × FWHMPSFHowell 2000). The full width at half maximum (FWHM) of the point spread function (PSF), measured by fitting a two-dimensional Gaussian to the telluric star, is 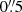 . The calibration for standard star counts was done at λ2.1 μm for both the H + K and K bands, to the flux taken from the 2MASS All-sky Point Source Catalogue (Skrutskie et al. 2006).
. The calibration for standard star counts was done at λ2.1 μm for both the H + K and K bands, to the flux taken from the 2MASS All-sky Point Source Catalogue (Skrutskie et al. 2006).
3. Results and discussion
The most prominent feature in the central 10″ of NGC 1672 is a nuclear ring that shows strong star-forming activity. Figure 2 (left) shows a composite image of the central region, where the FOV of SINFONI is overlaid in green. This image was obtained with the wide field channel (WFC) of the Advanced Camera for Surveys (ACS) instrument on-board the Hubble Space Telescope (HST) in broadband F814W, F555W and F435W filters1. The star-forming ring becomes apparent in the blue channel. The emission seems to be asymmetric, which can be the result of obscuration by dust lanes from the north towards the east side of the ring.
 |
Fig. 2. Left: HST/ACS composite image of the central region of NGC 1672 (red: F814W, green: F555W, blue: F435W). The green box indicates the FOV of our SINFONI observations. Right: K-band continuum extracted from the SINFONI data cube, by taking the median of the spectrum around λ ∼ 2.15 μm (extracted from the H + K data cube). The thicker black circle denotes the |
Figure 2 (right) shows a K-band continuum image that was extracted from the reduced SINFONI data cube.
In the spectra of the galaxy extracted from the data cube, we identified several hydrogen recombination lines (e.g. Paα, Brγ and Brδ) and ro-vibrational molecular hydrogen lines (H2(1–0)S(3) λ1.96 μm, H2(1–0)S(2) λ2.03 μm, H2(1–0)S(1) λ2.122 μm, H2(1–0)S(0) λ2.22 μm and H2(2–1)S(1) λ2.248 μm), as well as the forbidden iron line [Fe II]λ1.644 μm, He I, and many stellar absorption features. These lines are well-known tracers for physical conditions of different phases of the ISM. In the rest of this section we explain our analysis and results drawn from the SINFONI observations of the galaxy. In addition, we compare our results with the literature and discuss our findings.
3.1. Emission line fitting and flux distribution
To explore the distribution and kinematics of molecular and ionised (traced by hydrogen recombination lines here) gas in NGC 1672, we fit single Gaussian functions to the emission line profiles at each spatial pixel in the cube. To subtract the continuum baseline we fit a linear function to two spectral windows to the left and right of the emission line. For all line fits, we used the Levenberg-Marquardt algorithm as implemented in the Python library LMFIT (Markwardt 2009; Newville et al. 2014). Stated uncertainties correspond to the 1σ errors derived from the covariance matrix.
The forbidden iron-transition [Fe II] λ1.644 μm in the H band is slightly blended by the stellar absorption feature CO(7–4) λ1.641 μm. Therefore, before fitting the line we subtracted the stellar absorption features, using the PYTHON implementation of the penalized pixel-fitting method2 (Cappellari & Emsellem 2004; Cappellari 2017) with default parameters.
We used a set of synthetic model spectra from Lançon et al. (2007), which have assumed solar abundances, gravities of log(g/cm s−2) = [−1, − 0.5, 0, + 1], cover an effective temperature range of Teff = 2900−5900 K, and have masses of 1 M⊙ and 15 M⊙; red giants and supergiants which are representative of the intermediate-to-old stellar populations in the bulge. The model spectra were convolved with a Gaussian kernel to match the spectral resolution of our observation. To reach the necessary signal-to-noise ratio, prior to fitting the stellar absorption features, we spatially smoothed the SINFONI data cube with a three-pixel boxcar filter.
Maps of the emission line flux distributions of the lines that have the strongest emission, Brγ, H2λ2.122 μm, [Fe II] λ1.644 μm, and He I are shown in Fig. 3. The maps are clipped to have uncertainties in the emission line flux of less than 30%. In the maps we denote the position of the nucleus, that is where the continuum emission around 2.2 μm peaks, with an N.
 |
Fig. 3. Results of emission line fitting for the inner region of NGC 1672 using a single Gaussian component. From top left to bottom right: flux maps of Brγ λ2.166 μm, [Fe II] λ1.644 μm, H2λ2.12 μm, and He I emission lines. In all of the maps the flux units are 10−20 W m−2. All spatial pixels for which the uncertainty of the emission line fit is higher than 30% are clipped. These pixels are shown in white. North is up and east is to the left. |
In all the line flux maps we detect emission from hot spots in the ILR star-forming ring. Especially, the emission is asymmetric and stronger in south-east to west side and lower in the east and north-west side of the ring. At the centre the molecular gas shows extended emission. On the contrary, the emission of [Fe II] and Brγ have a very concentrated emission only in the nucleus region only (denoted by N).
We set several apertures with size 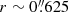 (5 pixels), at regions where the emission is stronger, to study their excitation mechanisms in more detail. The positions are tabulated in Table 1 and indicated in the flux maps in Fig. 3. The corresponding spectra are shown in Fig. 4. The stellar continuum emission was fitted, using PPXF as described above. The fitted continuum spectra are indicated in blue (Fig. 4).
(5 pixels), at regions where the emission is stronger, to study their excitation mechanisms in more detail. The positions are tabulated in Table 1 and indicated in the flux maps in Fig. 3. The corresponding spectra are shown in Fig. 4. The stellar continuum emission was fitted, using PPXF as described above. The fitted continuum spectra are indicated in blue (Fig. 4).
Coordinates, H- and K-band flux densities, H − K colour, and extinction calculated from the H − K colour for the apertures in the ILR ring and at the centre of NGC 1672.
 |
Fig. 4. Normalised spectra of the nuclear region and 11 apertures in the ILR ring and inside-the-ring regions. The positions at which the apertures are extracted are indicated in Fig. 3. Several emission and absorption lines are indicated with green vertical lines. The stellar continuum fit is shown in blue. |
3.2. Extinction correction
The extinction effect by dust is lower in the NIR compared to the optical, however not negligible. Extinction is often estimated by comparing the line ratios of two hydrogen recombination lines as predicted by models with those observed. It is then assumed that the deviation of the observed line ratio from the predicted line is solely caused by external extinction. However, this is only feasible when accurate line measurements are available throughout the FOV. We decided not to use the emission line ratios as Paα and Brδ lines both lie in a region where atmospheric effects produce significant noise contribution. Therefore we used the H − K colour map to estimate the extinction. A H − K colour map is shown in Fig. 5.
 |
Fig. 5. Colour map for H − K bands. North is up and east is to the left. |
In order to convert the H − K colour to visual extinction AV we used the following relation from Teixeira & Emerson (1999):
and employed the Calzetti et al. (2000) attenuation law for Galactic diffuse ISM (Rv = 3.12). This corresponds to a factor of k = 14.6.
The unreddened intrinsic colour of a typical quiescent galaxy is (H − K)0. We use (H − K)0 = 0.22 (Glass 1984). It is assumed that the stellar populations within the FOV, or to be accurate, their intrinsic H − K colours do not vary intrinsically but changes in the colour are caused by extinction only. Given that we see a star-forming ring with population ages of a few Myrs, this is probably not completely accurate. Stellar population models predict, depending on their set-up, a range from (H − K)0 = 0.1 to (H − K)0 = 0.4 mag for these populations (and references therein Grosbøl & Dottori 2012).
For typical colours of (H − K)≈0.55 in the ring, this leads to an AV range from ∼2.2 (high (H − K)0) to ∼6.5 (low (H − K)0), which means that in the case of higher (H − K)0 we tend to overestimate the flux by ∼20% and in the case of lower (H − K)0 we tend to underestimate the intrinsic flux by ∼20% when applying our correction.
Emission lines are also fitted in the apertures, following the stellar continuum subtraction (as described in Sect. 3.1). However, for the Brγ emission line in the nuclear aperture the stellar continuum fit produced an artificial effect, therefore we leave the stellar feature on the left side of this emission line as it is. The flux values, corrected for extinction (except for the nuclear aperture due to AGN contamination), for molecular gas are tabulated in Table 2, while the fluxes for ionised gas can be found in Table 3.
Molecular hydrogen emission lines in the apertures in the ILR ring, nucleus, and within-the-ring regions, and derived quantities for hot and cold molecular gas masses.
Emission line fluxes for the apertures and derived quantities ionised gas mass and star formation rate.
3.3. Gas excitation
In this section we assess the dominant mechanisms that excite the gas in different regions of the FOV. To do that, we use diagnostic line ratios. This means, we analyse the line ratios between lines that are excited by different excitation mechanisms to different amounts. In our investigation, we use the line ratio of the molecular hydrogen line H2λ2.12 μm, the forbidden iron line [Fe II] to the hydrogen recombination line Brγ, as well as between different species of H2 emission lines (Figs. 6 and 7). Line-ratio diagrams suggest certain thresholds and demarcations to separate between excitation mechanisms such as AGN photo-ionisation or UV ionisation by photons produced in, for example starburst regions. Since the lines [Fe II] and Brγ are located in two different bands (H and K-band) and have therefore a significant separation in wavelength, extinction can have a significant impact. We therefore use extinction-corrected line fluxes that are also in accordance with the literature.
 |
Fig. 6. Diagnostic diagram of the apertures in the central kiloparsec of NGC 1672. The locations of the apertures are indicated in the flux maps in Fig. 3. The flux ratios of the H2(1–0)S(1)λ2.122 μm/Brγ and [Fe II]λ1.644 μm/Brγ emission lines are used. The contours show the demarcation for young star formation, supernovae, and compact AGN; the solid lines denote upper limits for young star formation and AGN, both from Colina et al. (2015), derived using IFS data. The dashed lines denote upper limits for star formation and AGN activity (derived from slit-spectroscopy; Riffel et al. 2013b). An upper limit value for the [Fe II] flux was calculated for aperture 11. |
 |
Fig. 7. Diagnostic diagram of the apertures in the central kiloparsec of NGC 1672. The location of the apertures is indicated in the flux maps in Fig. 3. The flux ratios of the molecular hydrogen lines H2(2–1)S(1)λ2.248 μm/H2(1–0)S(1)λ2.122 μm and H2(1–0)S(2)λ2.034 μm/H2(1–0)S(0)λ2.223 μm are used (Mouri 1994; Rodríguez-Ardila et al. 2004, 2005). Models for thermal UV excitation (Sternberg & Dalgarno 1989), non-thermal excitation (Black & van Dishoeck 1987), X-ray heating (Draine & Woods 1990), and shock-heating (Brand et al. 1989) are indicated for comparison. |
The diagram in Fig. 6 uses the previous studies from Riffel et al. (2013a) and Colina et al. (2015) to set demarcation between young starburst, older supernova remnant, and AGN-dominated regions. The results show a clear deviation among ILR, central and nucleus apertures. The ILR apertures (1–9) mainly lie in young starburst-dominated regions. The nucleus and central apertures (10, 11) show more signs of AGN- and supernovae-dominated regions.
In Fig. 7 we display the H2(1–0)S(3)/H2(1–0)S(1) versus H2(2–1)S(1)/H2(1–0)S(1) line ratios. Molecular hydrogen can be excited by a variety of mechanisms as follows: thermal processes, in which shocks (Hollenbach & McKee 1989) collisionally excite the gas; X-ray (Maloney et al. 1996) radiation from, for example the AGN that heats up the gas; and non-thermal processes, i.e. UV fluorescence mechanisms, in which UV photons from for example OB stars or strong AGN continuum emission excite the H2 molecules (Black & van Dishoeck 1987). The diagram shows that in most of the apertures a combination of those excitation mechanisms is responsible for the gas excitation. However the line ratios of the nucleus imply a higher contribution of thermal and shock excitation mechanisms.
The significant contribution of non-thermal excitation that we see in the apertures in the ring is typical for star-forming regions (e.g. Rodríguez-Ardila et al. 2005; Busch et al. 2017; Fazeli et al. 2019). This underlines that the ring is dominated by star formation. The excitation of the nucleus is less clear. The observed line ratios could be caused by an (ageing) starburst but also by a (weak) AGN.
3.4. Molecular and ionised gas masses
We estimate the total hot molecular gas mass using the extinction-corrected H2 1–0S(1) emission line (Scoville et al. 1982; Wolniewicz et al. 1998).
In this equation DL = 11.4 Mpc is the luminosity distance of the galaxy and we assume that the gas is in local thermal equilibrium and has a typical vibrational temperature of Tvib = 2000 K (for better comparison with the literature where this value is most often chosen). It is important to mention that this assumption is not completely accurate and can lead to an overestimation of the hot molecular gas mass up to a factor of 2 (Busch et al. 2017). However for better comparison of our results with the literature values we follow this assumption.
We find a total hot molecular gas mass of 260 M⊙ in the 10″ × 10″ SINFONI FOV. This value only represents the hot surface of molecular gas clouds. To estimate the corresponding cold molecular gas mass we employ the conversion factor: MH2(cold)/MH2(hot) = (0.3−1.6) × 106 M⊙ from Mazzalay et al. (2013), which leads to (0.8−4.1) × 108 M⊙ cold molecular gas. The dispersion observed in the CO-to-H2 conversion factor is due to the variety of galaxy types that were used to measure this relation and the intrinsic regularities of the distribution of gas in these galaxies. The CO(3–2) flux integrated over a 10″ × 10″ aperture is SCO Δν = 465 Jy km s−1 (ALMA project ID 2015.1.00404.S, PI F. Combes). Using a Milky Way-like galaxy CO-to-H2 conversion factor (CO(3–2)/CO(1–0) ∼ 0.8 and αCO ∼ 4.36) this results in MH2(cold) = 0.9 × 108 M⊙ (F. Combes, priv. comm.), which is in good agreement with our estimated cold gas mass.
Furthermore, we estimate the mass of ionised gas using the extinction corrected flux of the Brγ emission line (assuming case B recombination, Osterbrock 1989) as follows:
We assume a temperature of T = 104 K and electron density of ne = 102 cm−2. We find the total ionised gas mass in the SINFONI FOV to be ≈2.3 × 106 M⊙.
We also report the estimated gas masses of the ionised and molecular (hot and cold) in the respective apertures. The results are listed in Tables 2 and 3.
Literature comparison. Using the Hα emission line flux of a 4″ diameter aperture drawn from the Siding Spring Southern Seyfert Spectroscopic Snapshot Survey (S7; for more details about data release; Thomas et al. 2017; Dopita et al. 2015) observed by the Wide Field Spectrograph (WiFeS) on ANU 2.3 m telescope at the Siding Spring Observatory, a flux value of 1.2 × 10−16 W m−2 is reported. We estimate an ionised gas mass of ≈4.5 × 105, which is consistent with our results (for a comparable aperture we get ≈2 × 105) for the ionised gas mass.
Typical gas masses in the central kiloparsec of nearby galaxies, found by the AGNIFS group (Riffel et al. 2016, and references therein) and our group are of the order of 10 < MH2 < 103 M⊙ (hot molecular gas) and 104 < MH II <107 M⊙ (ionised gas). Typical cold molecular gas masses, from CO observations, for nearby galaxies, are 108 < MH2 < 1010 M⊙ (Moser et al. 2012, and references therein). In that sense, NGC 1672 has very typical gas masses for nearby galaxies. The ratio of mass of ionised gas to hot molecular gas is MH II/MH2 ≈ 8900, which is at the upper end of ratios but still typical for nearby galaxies (Fazeli et al. 2019, case of NGC 1365 and references therein). Similar to NGC 1365, the high ratio could be caused by additional ionised gas excitation in the centre from a (weak) AGN (see Sect. 3.7 herein further discussion).
3.5. Stellar and gaseous kinematics
3.5.1. Stellar kinematics
In this section, we analyse the stellar kinematics that are traced by the CO absorption band heads at the red end of the K band; the CO(2–0) absorption band head at a rest-frame wavelength of 2.29 μm is most prominent.
We used the PPXF method (Cappellari & Emsellem 2004; Cappellari 2017) with default parameters to model the stellar continuum in a spectral window between 2.28 μm and 2.42 μm. As spectral templates, we use the Gemini library of late spectral templates (Winge et al. 2009). The 29 stars with spectral classes of F7 to M5 are selected to suit as stellar templates for velocity dispersion measurement studies in the NIR like this work. Convolution with a Gaussian function in the spectral axis was used to bring the templates to the same spectral resolution as the SINFONI spectra. In the spatial dimensions, we use a boxcar filter of three pixels in diameter to reach the necessary signal to noise of ≈50.
Stellar velocity dispersion. In Fig. 8, we show the map of the stellar velocity dispersion. In the centre, the velocity dispersion reaches values of 105−115 km s−1. This is consistent with the HyperLEDA value of 109.5 km s−1 (based on measurements of Garcia-Rissmann et al. 2005). Towards the edges of the FOV, the stellar velocity dispersion decreases significantly. Centrally peaked velocity dispersion profiles are often observed in classical bulges, while the profiles in pseudo-bulges are flatter (Fabricius et al. 2012). However, since the drop is most prominent at the location of the ring, star formation can also be an explanation for the lower velocity dispersions. Star formation regions are often observed to show a lower stellar velocity dispersion, which is explained by the stars still resembling the dynamics of the cold molecular gas from which they emerged (e.g. Riffel et al. 2011; Mazzalay et al. 2014; Busch et al. 2017). However, since the ring is located at the edge of our FOV and we cannot measure the stellar velocity dispersion outside of the ring towards larger radii, we cannot decide whether we see a drop due to the star-forming ring or just the transition between bulge and disc.
 |
Fig. 8. Stellar velocity dispersion. North is up and east is to the left. The black cross denotes the nucleus. |
Stellar line-of-sight velocity. The stellar line-of-sight velocity (LOSV) that we map in Fig. 9 (left) shows a very regular disc rotation with blueshifts in the north-west and redshifts in the south-east. The velocity amplitude within our FOV reaches about 100 km s−1.
 |
Fig. 9. Left: stellar velocity field map derived from fitting the spectral region around the CO(2–0) band head at ∼2.29 μm. Middle: model of the LOSV, assuming circular motions in a Plummer gravitational potential. Right: residuals after subtracting the model from the observed LOSV field. The systemic velocity derived in the model fit is subtracted from the maps. North is up and east is to the left. |
In order to quantify this finding, we fit a model to the observed LOSV field. We assume that the stars follow Keplerian orbits in the gravitational potential of the stellar bulge and that it can be described by a Plummer function. In this case, the radial velocity is given by
where G is the gravitational constant, R and Ψ are cylindrical coordinates, A is the scale length and M is the mass of the bulge, i is the inclination, and Ψ0 is the position angle of the line of nodes. The inclination was fixed to the inclination given in HyperLEDA (Makarov et al. 2014) of i = 29°. Further, we fixed the central position to the position of the peak of the K-band continuum emission. Our fit then results in a systemic velocity of vs = (1392 ± 1) km s−1 (after heliocentric correction) and a position angle of the line of- nodes of Ψ0 = (302.5 ± 0.9)°.
Figure 9 (middle panel) shows a map of the modelled LOSV. The residuals after subtracting the model from the observed LOSV, are shown in the right panel of Fig. 9. We do not see any systematic, only stochastic residuals with a rather low amplitude of ≲20 km s−1, which indicates a good match between observed velocity field and model.
3.5.2. Gas kinematics
The fit routine that we use in Sect. 3.1 to derive the emission line flux distributions also provides central positions and widths of the emission line fits, from which we derive the LOSV and velocity dispersion (σ). Velocity field maps of Brγ, [Fe II], and H2(1–0)S(1) are shown in Fig. 10. White pixels correspond to clipped areas, using the same criteria as for the emission line maps. The velocities are shown relative to the systemic velocity 1392 km s−1, derived from the stellar velocity model (Sect. 3.5.1).
 |
Fig. 10. Gas velocity fields, results of fitting Brγ, H2(1–0)S(1)λ2.122 μm, and [Fe II]λ1.644 μm emission lines. The black cross denotes the nucleus, where the continuum flux peaks. The circle in the H2 map indicates the central arcsec where Combes et al. (2019) found a molecular torus. All velocities are given relative to the systemic velocity of 1392 km s−1. North is up and east is to the left. |
Comparison of stellar and gas velocity maps. On first sight all the gas velocity field maps show signs of circular rotation, similar to the stellar velocity field, blue-shifted in the north-west and red-shifted in the south-east. However the gas velocities show higher amplitudes than stellar velocities. This could be because most of the kinetic energy of the stars go into random motion, contrary to the molecular gas that has lower velocity dispersion and therefore is more confined to the galaxy plane. Also unlike the stellar velocity field, which is fairly regular and can be fitted by a rotational model very well, leaving only stochastic residuals, the gas velocity fields show significant deviations from pure rotation. In particular, the twisted zero-velocity contours (Fig. 10), especially in molecular gas where the emission line has high signal-to-noise ratio in the centre (see Fig. 11, middle), are witnessing the presence of non-circular motions. A twisted zero-line velocity in (cold) molecular gas velocity fields has also been revealed by Combes et al. (2019, S-shaped zero-velocity in their Fig. 11) from their sub-millimetre CO(3–2) transition molecular gas velocity map.
 |
Fig. 11. From left to right: Brγ, H2(1–0)S(1)λ2.122 μm, and [Fe II] emission line fits detected in the nuclear aperture of radius |
Molecular and ionised gas. Zooming in to the central arcsecond of the H2(1–0)S(1) and [Fe II] velocity maps (denoted with a circle in Fig. 10, middle), we observe a shift in the PA of the zero-velocity line from ∼35° of the large scale rotation to ∼0°. This most probably reflects the circumnuclear disc observed by Combes et al. (2019) in CO(3–2). This structure which they call the molecular torus has a position angle of the zero-velocity line of 0° and an inclination of 64° and is therefore dynamically decoupled from the large-scale disc. However, since its size of 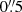 is of the order of our spatial resolution, we cannot resolve more details with our data.
is of the order of our spatial resolution, we cannot resolve more details with our data.
Position of the kinematical centre. Furthermore, the gas velocity gradients in the centre are very steep and the centre of the velocity field seems to be (about 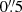 in H2 and 1″ in Brγ LOSV maps) shifted to north-west compared of the centre, where the K-band continuum and narrow emission lines peak. As mentioned in the introduction, Díaz et al. (1999) and Firpo et al. (2017) reported an offset of 60 pc (
in H2 and 1″ in Brγ LOSV maps) shifted to north-west compared of the centre, where the K-band continuum and narrow emission lines peak. As mentioned in the introduction, Díaz et al. (1999) and Firpo et al. (2017) reported an offset of 60 pc (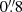 considering the distance they adopt), studying kinematics of Hα emission line.
considering the distance they adopt), studying kinematics of Hα emission line.
A gas kinematic centre offset from the nucleus has also been suggested for the Milky Way by Blitz (1994). In the Galactic scenario, this author proposed that the shallow gravitational potential towards the centre can result in the gas being less strongly bound to the nuclear stellar bulge region. In this shallow potential the gas can then slosh around the nuclear position. As a result the kinematic centre may be observed as being offset from the stellar and AGN centre. However, in NGC 1672 there is even a gap between the hot molecular and the ionised gas kinematics centre.
The presence of an outflow is another mechanism that might induce an offset in the kinematics centre of the gas. However, we rule out this scenario for NGC 1672 as we discuss in the following.
Double-component hydrogen recombination lines. Investigating the spectra of the galaxy in the centre we recognise that the Brγ and Paα emission line profiles at the nucleus and the regions north and north-west of the nucleus show a second component or double-horned profile. We display these emission line fits and the position of the apertures they were extracted from on the Brγ flux map in Fig. 12 (left).
 |
Fig. 12. Top left: flux map of the emission line Brγ λ2.16612 μm. Overlaid are the radio contours from Jenkins et al. (2011), which have an angular resolution of |
In the top panel of Fig. 12 we present the flux map of the emission line Hαλ6562.8 with a FOV of 38″ × 25″ and pixel size 1″. The data cube is drawn from the S7 (for more details about the data release, see Thomas et al. 2017; Dopita et al. 2015). We extract the spectra of the marked pixels in the Hα flux map (Fig. 12) and fit the profiles of the Hα emission lines. We detect a similar effect as in the Brγ emission line.
We observe that the blue-shifted part of the line, in the spectra in Fig. 12 (bottom left) denoted with blue lines, is strongest in aperture I1, which is in the north-west where the blue-shifted part of the large-scale rotational pattern is also located. The red-shifted part of the line, however, is stronger than the blue-shifted in aperture N; this is the only visible component in apertures I3 and I4, which are located in the south-east where the red-shifted part of the large-scale disc is located.
A jet or an outflow from the AGN, interacting with the galactic disc can result in a line split and radio emission. In NGC 1672 this seems not to be the case: we overlaid the contours of ATCA 3 cm radio data from Jenkins et al. (2011) on the Brγ flux map (Fig. 12). While the region with the prominent red-shifted second component of the Brγ gas emission coincides with the feature that connects the centre and the ring in the radio emission, Kakkad et al. (2018) ruled out the outflow scenario, since the [O III] emission line that they investigated in the S7 optical-blue spectra, has a width lower than 200 km s−1.
The simplest explanation for the complex kinematics in NGC 1672 is that the velocity field of the Brγ emitting gas is not sampling the circumnuclear disc and rather is strongly weighted by the emission from the ILR ring. The doubled-horn line shape is then produced by the emission from the very strong knots in the ring. The latter is not axi-symmetric and can therefore cause an asymmetric velocity field. This is in contrast to the stellar velocity field which is weighted neither by the ring nor the nuclear disc and is therefore symmetric. As mentioned before, the Brγ velocity field is off-centred towards the north-west with the centre falling into aperture I2. Furthermore, the velocity gradient in the centre is strong, which can produce a double-horned line profile as well.
3.6. ILR star-forming ring
NGC 1672 has a well-known ILR ring (first imaged by Evans et al. 1996) located at the turnover point of the large-scale bar. Jenkins et al. (2011, their Fig. 8) presented the ring in several wavelengths (from 0.3−10 keV X-ray to 3 cm radio images). The ring has a semi-major axis of ∼350 pc at a position angle of around 135°. It is clearly visible in our line maps, which are shown in Fig. 3 and trace the ionised regions (Brγ and He I), partially ionised regions ([Fe II]) and the hot molecular gas reservoir (H2(1–0)S(1)).
The emission line ratios log([Fe II]/Brγ) vs. log(H2(1−0) S(1) / Brγ) in the NIR diagnostic diagram (Fig. 6) indicate that excitation through young star formation dominates in the ring. Also the line ratios of molecular hydrogen emission lines (Fig. 7) indicate a significant contribution of non-thermal excitation, which is typical for young star formation (Sect. 3.3). Both of these indications confirm the star-forming nature of the ring.
Star formation rates. The luminosity of hydrogen recombination lines is proportional to the Lyman continuum and can therefore, in absence of an AGN, directly measure the instantaneous star formation rate. Using the luminosity of the Brγ emission line and the calibration from Panuzzo et al. (2003), we estimate the star formation rate (SFR) in the starburst regions:
The SFR of the apertures are listed in Table 3 and the values are in the range 0.01−0.05 M⊙ yr−1. We also estimate an upper limit for the SFR in the nuclear region of 0.04 M⊙ yr−1, however, the possible AGN contribution to production of the emission line has to be considered.
Star formation scenarios. Star formation scenarios in ILR rings are still under discussion. Böker et al. (2008) suggested to distinguish between the so-called pearls-on-a-string and popcorn models. In the first, star formation is triggered at the touch-points of ring and spirals where gas is compressed and the star-forming regions then age while travelling along the ring. In the latter model, star formation occurs stochastically within the ring.
We compared the emission line maps of He I which has a high ionisation potential of 24.6 eV and can therefore only be ionised by the most massive O and B stars which have short lifetimes of ≲5 Myr; Brγ, which has a lower ionisation potential of 13.6 eV; and [Fe II], which can trace supernovae that become frequent after ∼10 Myr when the most massive and short-lived stars explode in supernovae. In this comparision, we cannot see any gradient. Therefore, we conclude that there is no evidence for a sequence in star formation but the star formation is rather occurring stochastically along the ring.
3.7. Nature of the nuclear source
Classification of the nucleus in NGC 1672 has been complicated, partially because of the contamination of observations of the nucleus with the emission coming from strong star formation in the circumnuclear ring, which are mixed in observations with lower angular resolution. Therefore the nucleus was classified as a composite Seyfert 2/Starburst, where starburst dominates (e.g. Kewley et al. 2000; Storchi-Bergmann et al. 1995).
Similarly, in the X-ray wavelength, different classifications occurred owing to a lack of spatial resolution (Brandt et al. 1996; de Naray et al. 2000). However, Jenkins et al. (2011) using high-resolution Chandra data detected the nucleus in hard X-ray emission (Γ ∼ 1.5, L2−10 keV = 4 × 1038 erg s−1) for the first time. Therefore they concluded that there is a low-luminosity active galactic nucleus (LLAGN) at the centre of NGC 1672.
The spatial resolution of SINFONI also gives us the opportunity to study this region isolated from the circumnuclear starburst ring. The only ionised emission lines we detect in this region are Brγ and [Fe II]. However, as we show in Fig. 11, the spectra are very noisy and the emission lines have a low signal-to-noise ratio. For the spectra shown in this figure we did not subtract the stellar continuum. Several molecular hydrogen emission lines are observed at the nucleus and the amount of gas in the nuclear aperture (25 M⊙) is up to five times the star-forming knots in the star-forming ring. A cold molecular gas mass of 2.5 × 107 M⊙ is found in the central torus by Combes et al. (2019) using CO(3–2) emission. The emission line ratios in the diagnostic diagram Fig. 6 show a value at the border of AGN and starburst nature for the nucleus aperture of NGC 1672.
The ratio H2(1–0)S(1)/Brγ in the nuclear aperture is 1. This value is usually ≾0.6 in starburst galaxies, 0.6−6 in Seyferts, and >6 in low ionisation nuclear emission regions (LINER; e.g. Mazzalay et al. 2013). The ratio measured for NGC 1672 is consistent with low-luminosity AGNs (Seyfert2). We therefore conclude that our measurements support the classification of NGC 1672 as a weak AGN.
3.7.1. SMBH mass
We estimated the mass of the central supermassive black hole (SMBH) by fitting the stellar velocity dispersion in an aperture of 3″ radius at the centre. The aperture size was chosen to avoid the nuclear star-forming ring. As discussed in Sect. 3.5.1, the star-forming ring shows a lower stellar velocity dispersion which resembles the cold molecular gas of the underlying gas reservoir rather than that of the central spheroidal component.
Similar to Sect. 3.5.1, we applied the PPXF method with the same settings and measured a velocity dispersion value of σ = (106 ± 3) km s−1. We now employ the M − σ* relation from Kormendy & Ho (2013)
Using this relation and the fitted σ* value, we derive a black hole mass estimate of log(MBH/M⊙) = 7.3. Considering that the intrinsic scatter of the MBH − σ relation is higher than the measurements error, we refrain from stating formal errors on the BH mass estimates and the value reported in this work is an order of magnitude estimate.
This value is consistent with other black hole mass estimates in the literature: for example, Davis et al. (2014) derive log(MBH/M⊙) = (7.08 ± 0.90) for NGC 1672 using the relation between black hole mass and spiral arm pitch angle. The Sersic index of the central spheroidal component is n = (2.05 ± 0.17) according to Fisher & Drory (2010). Using the M − n relation of Graham & Driver (2007) we then derive an estimate log(MBH/M⊙) = 7.3, which is similar to our result. On the other hand, Combes et al. (2019) found a black hole mass of log(MBH/M⊙) = (7.7 ± 0.1) as a best-fit estimate from the CO molecular gas dynamics, which is significantly higher.
An issue to keep in mind in this context is that the central component of NGC 1672 seems to be of pseudo-bulge nature (Fisher & Drory 2010). There have been lively discussions on the nature of pseudo-bulges and whether they show correlations with properties of the central SMBH (e.g. Kormendy et al. 2011; Graham 2016). In that sense, the higher estimate from the gas dynamics would be more adequate in this case. Given the uncertainties, we only conclude that the mass of central SMBH is of the order of several 107 M⊙, which is a typical mass for SMBHs in nearby galaxies (e.g. Greene & Ho 2005; Busch et al. 2017; Humire et al. 2018; Slater et al. 2019; Fazeli et al. 2019).
4. Summary and conclusions
In this paper we have presented a comprehensive analysis of the NIR IFS data for the central 10″ × 10″ (550 × 550 pc2) of the Seyfert galaxy NGC 1672. The data was obtained with the instrument SINFONI at the VLT. The following summarises our most important results:
-
The most prominent feature detected in the emission line flux maps is the ILR star-forming ring. The ring is located at a radius of about 4″ ∼ 220 pc from the centre and contains patchy starburst regions. The emission is asymmetric and stronger in the south and east.
-
We find a hot molecular gas mass of ∼260 M⊙, using the H2 λ2.122 μm emission line flux and assuming a local thermal equilibrium with temperature T = 2000 K. This amount corresponds to (0.6−3) × 108 M⊙ of cold molecular gas mass.
-
We also estimate the ionised gas mass to ∼2.3 × 106 M⊙, using the flux of the hydrogen recombination emission line Brγ and assuming a temperature of T = 104 K and electron density of ne = 102 cm−2. The ionised gas is mostly concentrated in the star-forming ring.
-
The fits of stellar CO band head absorption lines are used to study the stellar kinematics. The LOSV map shows a rotating disc in the plane of the galaxy, which is blue-shifted in the north-west and red-shifted in the south-east of the FOV.
-
Gas kinematics show a similar rotation pattern to the stellar disc, blue-shifted in the north-west and red-shifted in the south-east. However, the comparison of the stellar and gas kinematics reveals that the gas has much higher velocity amplitudes north-west and south-east of the nucleus, within the ILR ring, which can partially be attributed to a significant fraction of the kinematic energy of the stars going into random motions. Furthermore, the gas kinematics reveal non-circular motions.
-
The position angle of the H2 molecular gas and [Fe II] emission changes from the large scale to the central arcsec, resembling the decoupled nuclear disc or molecular torus found in CO(3–2). Furthermore, a double-horn Brγ emission line profile is found at the nucleus and north-west of the centre, which spatially coincides with a filament in the 3 cm radio emission map, connecting the centre and the star-forming ring.
-
The diagnostics diagram, using the H2(1–0)S(1)λ2.122 μm/Brγ and [Fe II]λ1.644 μm/Brγ line ratios, suggests that the galaxy has a low-luminosity AGN. We estimated the black hole mass, based on black hole mass – host galaxy scaling relations, to be of the order of several 107 M⊙.
Retrieved from the Hubble Legacy Archive (http://hla.stsci.edu). Observations took place on August 1, 2005, proposal ID 10354, PI: L. Jenkins.
www-astro.physics.ox.ac.uk/~mxc/software/ PPXF version (V6.7.8).
Acknowledgments
The authors thank the anonymous referee for fruitful comments and suggestions. This research is carried out within the Collaborative Research Center 956, sub-project A2 (the studies of the conditions for star formation in nearby AGN and QSOs), funded by the Deutsche Forschungsgemeinschaft (DFG) – project ID 184018867. N. Fazeli is a member of the Bonn-Cologne Graduate School of Physics and Astronomy (BCGS). M. Yttergren is a member of the International Max Planck Research School for Astronomy & Astrophysics Bonn/Cologne.
References
- Baumgart, C. W., & Peterson, C. J. 1986, PASP, 98, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Black, J. H., & van Dishoeck, E. F. 1987, ApJ, 322, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Blitz, L. 1994, in Physics of the Gaseous and Stellar Disks of the Galaxy, ed. I. R. King, ASP Conf. Ser., 66, 1 [NASA ADS] [Google Scholar]
- Böker, T., Falcón-Barroso, J., Schinnerer, E., Knapen, J. H., & Ryder, S. 2008, AJ, 135, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnet, H., Abuter, R., Baker, A., et al. 2004, The Messenger, 117, 17 [NASA ADS] [Google Scholar]
- Brand, P. W. J. L., Toner, M. P., Geballe, T. R., et al. 1989, MNRAS, 236, 929 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, W. N., Halpern, J. P., & Iwasawa, K. 1996, MNRAS, 281, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Busch, G., Eckart, A., Valencia-S., M., et al. 2017, A&A, 598, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M. 2017, MNRAS, 466, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., & Emsellem, E. 2004, PASP, 116, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Colina, L., Piqueras López, J., Arribas, S., et al. 2015, A&A, 578, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Combes, F., García-Burillo, S., Casasola, V., et al. 2013, A&A, 558, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Combes, F., García-Burillo, S., Casasola, V., et al. 2014, A&A, 565, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Combes, F., García-Burillo, S., Audibert, A., et al. 2019, A&A, 623, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davis, B. L., Berrier, J. C., Johns, L., et al. 2014, ApJ, 789, 124 [NASA ADS] [CrossRef] [Google Scholar]
- de Naray, P. J., Brandt, W. N., Halpern, J. P., & Iwasawa, K. 2000, AJ, 119, 612 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, H. G., Jr., et al. 1991, Third Reference Catalogue of Bright Galaxies [Google Scholar]
- Díaz, R., Carranza, G., Dottori, H., & Goldes, G. 1999, ApJ, 512, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., Shastri, P., Davies, R., et al. 2015, ApJS, 217, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Woods, D. T. 1990, ApJ, 363, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenhauer, F., Abuter, R., Bickert, K., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, & A. F. M. Moorwood, SPIE Conf. Ser., 4841, 1548 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, I. N., Koratkar, A. P., Storchi-Bergmann, T., et al. 1996, ApJS, 105, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Fabricius, M. H., Saglia, R. P., Fisher, D. B., et al. 2012, ApJ, 754, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Fazeli, N., Busch, G., Valencia-S., M., et al. 2019, A&A, 622, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fiore, F., Feruglio, C., Shankar, F., et al. 2017, A&A, 601, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Firpo, V., Díaz, R., Dottori, H., et al. 2017, Bol. Asoc. Argent. Astron. Plata Argent., 59, 127 [NASA ADS] [Google Scholar]
- Fisher, D. B., & Drory, N. 2010, ApJ, 716, 942 [NASA ADS] [CrossRef] [Google Scholar]
- García-Burillo, S., & Combes, F. 2012, J. Phys. Conf. Ser., 372, 012050 [CrossRef] [Google Scholar]
- García-Burillo, S., Combes, F., Schinnerer, E., Boone, F., & Hunt, L. K. 2005, A&A, 441, 1011 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcia-Rissmann, A., Vega, L. R., Asari, N. V., et al. 2005, MNRAS, 359, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Glass, I. S. 1984, MNRAS, 211, 461 [NASA ADS] [Google Scholar]
- Graham, A. W. 2016, in Galactic Bulges, eds. E. Laurikainen, R. Peletier, & D. Gadotti, Astrophys. Space Sci. Lib., 418, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A. W., & Driver, S. P. 2007, ApJ, 655, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, J. E., & Ho, L. C. 2005, ApJ, 627, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Grosbøl, P., & Dottori, H. 2012, A&A, 542, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gültekin, K., Richstone, D. O., Gebhardt, K., et al. 2009, ApJ, 698, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, L. C., Li, Z.-Y., Barth, A. J., Seigar, M. S., & Peng, C. Y. 2011, ApJS, 197, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D., & McKee, C. F. 1989, ApJ, 342, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., & Quataert, E. 2010, MNRAS, 407, 1529 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, S. B. 2000, Handbook of CCD Astronomy (Cambridge: Cambridge University Press) [Google Scholar]
- Humire, P. K., Nagar, N. M., Finlez, C., et al. 2018, A&A, 614, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jenkins, L. P., Brandt, W. N., Colbert, E. J. M., et al. 2011, ApJ, 734, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Kakkad, D., Groves, B., Dopita, M., et al. 2018, A&A, 618, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kewley, L. J., Heisler, C. A., Dopita, M. A., et al. 2000, ApJ, 530, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, W.-T., & Elmegreen, B. G. 2017, ApJ, 841, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Ho, L. C. 2013, ARA&A, 51, 511 [Google Scholar]
- Kormendy, J., Bender, R., & Cornell, M. E. 2011, Nature, 469, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Lançon, A., Hauschildt, P. H., Ladjal, D., & Mouhcine, M. 2007, A&A, 468, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maiolino, R., Rieke, G. H., & Rieke, M. J. 1996, AJ, 111, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Makarov, D., Prugniel, P., Terekhova, N., Courtois, H., & Vauglin, I. 2014, A&A, 570, A13 [CrossRef] [EDP Sciences] [Google Scholar]
- Maloney, P. R., Hollenbach, D. J., & Tielens, A. G. G. M. 1996, ApJ, 466, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [NASA ADS] [Google Scholar]
- Martini, P., Pogge, R. W., Ravindranath, S., & An, J. H. 2001, ApJ, 562, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzalay, X., Saglia, R. P., Erwin, P., et al. 2013, MNRAS, 428, 2389 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzalay, X., Maciejewski, W., Erwin, P., et al. 2014, MNRAS, 438, 2036 [NASA ADS] [CrossRef] [Google Scholar]
- Moser, L., Zuther, J., Busch, G., Valencia-S., M., & Eckart, A. 2012, Proceedings of Nuclei of Seyfert Galaxies and QSOs – Central Engine & Conditions of Star Formation (Seyfert 2012), 6–8 November, 69 [Google Scholar]
- Mouri, H. 1994, ApJ, 427, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Newville, M., Stensitzki, T., Allen, D. B., & Ingargiola, A. 2014, https://doi.org/10.5281/zenodo.11813 [Google Scholar]
- Osterbrock, D. E. 1989, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (Mill Valley: University Science Books) [CrossRef] [Google Scholar]
- Panuzzo, P., Bressan, A., Granato, G. L., Silva, L., & Danese, L. 2003, A&A, 409, 99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riffel, R., Riffel, R. A., Ferrari, F., & Storchi-Bergmann, T. 2011, MNRAS, 416, 493 [NASA ADS] [Google Scholar]
- Riffel, R. A., Storchi-Bergmann, T., & Winge, C. 2013a, MNRAS, 430, 2249 [NASA ADS] [CrossRef] [Google Scholar]
- Riffel, R., Rodríguez-Ardila, A., Aleman, I., et al. 2013b, MNRAS, 430, 2002 [NASA ADS] [CrossRef] [Google Scholar]
- Riffel, R. A., Colina, L., Storchi-Bergmann, T., et al. 2016, MNRAS, 461, 4192 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-Ardila, A., Pastoriza, M. G., Viegas, S., Sigut, T. A. A., & Pradhan, A. K. 2004, A&A, 425, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodríguez-Ardila, A., Riffel, R., & Pastoriza, M. G. 2005, MNRAS, 364, 1041 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N. Z., Hall, D. N. B., Ridgway, S. T., & Kleinmann, S. G. 1982, ApJ, 253, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Slater, R., Nagar, N. M., Schnorr-Müller, A., et al. 2019, A&A, 621, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smajić, S., Fischer, S., Zuther, J., & Eckart, A. 2012, A&A, 544, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smajić, S., Moser, L., Eckart, A., et al. 2014, A&A, 567, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smajić, S., Moser, L., Eckart, A., et al. 2015, A&A, 583, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Springel, V., Di Matteo, T., & Hernquist, L. 2005, ApJ, 620, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Steer, I., Madore, B. F., Mazzarella, J. M., et al. 2017, AJ, 153, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Sternberg, A., & Dalgarno, A. 1989, ApJ, 338, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Storchi-Bergmann, T., Kinney, A. L., & Challis, P. 1995, ApJS, 98, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Teixeira, T. C., & Emerson, J. P. 1999, A&A, 351, 303 [NASA ADS] [Google Scholar]
- Thomas, A. D., Dopita, M. A., Shastri, P., et al. 2017, ApJS, 232, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Cecil, G., & Bland-Hawthorn, J. 2005, ARA&A, 43, 769 [Google Scholar]
- Winge, C., Riffel, R. A., & Storchi-Bergmann, T. 2009, ApJS, 185, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Wolniewicz, L., Simbotin, I., & Dalgarno, A. 1998, ApJS, 115, 293 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Coordinates, H- and K-band flux densities, H − K colour, and extinction calculated from the H − K colour for the apertures in the ILR ring and at the centre of NGC 1672.
Molecular hydrogen emission lines in the apertures in the ILR ring, nucleus, and within-the-ring regions, and derived quantities for hot and cold molecular gas masses.
Emission line fluxes for the apertures and derived quantities ionised gas mass and star formation rate.
All Figures
 |
Fig. 1. Optical image of the spiral barred galaxy NGC 1672. The red box indicates the 10″ × 10″ (550 × 550 pc2) SINFONI data. Image courtesy: Carnegie-Irvine Galaxy Survey (Ho et al. 2011). |
| In the text | |
 |
Fig. 2. Left: HST/ACS composite image of the central region of NGC 1672 (red: F814W, green: F555W, blue: F435W). The green box indicates the FOV of our SINFONI observations. Right: K-band continuum extracted from the SINFONI data cube, by taking the median of the spectrum around λ ∼ 2.15 μm (extracted from the H + K data cube). The thicker black circle denotes the |
| In the text | |
 |
Fig. 3. Results of emission line fitting for the inner region of NGC 1672 using a single Gaussian component. From top left to bottom right: flux maps of Brγ λ2.166 μm, [Fe II] λ1.644 μm, H2λ2.12 μm, and He I emission lines. In all of the maps the flux units are 10−20 W m−2. All spatial pixels for which the uncertainty of the emission line fit is higher than 30% are clipped. These pixels are shown in white. North is up and east is to the left. |
| In the text | |
 |
Fig. 4. Normalised spectra of the nuclear region and 11 apertures in the ILR ring and inside-the-ring regions. The positions at which the apertures are extracted are indicated in Fig. 3. Several emission and absorption lines are indicated with green vertical lines. The stellar continuum fit is shown in blue. |
| In the text | |
 |
Fig. 5. Colour map for H − K bands. North is up and east is to the left. |
| In the text | |
 |
Fig. 6. Diagnostic diagram of the apertures in the central kiloparsec of NGC 1672. The locations of the apertures are indicated in the flux maps in Fig. 3. The flux ratios of the H2(1–0)S(1)λ2.122 μm/Brγ and [Fe II]λ1.644 μm/Brγ emission lines are used. The contours show the demarcation for young star formation, supernovae, and compact AGN; the solid lines denote upper limits for young star formation and AGN, both from Colina et al. (2015), derived using IFS data. The dashed lines denote upper limits for star formation and AGN activity (derived from slit-spectroscopy; Riffel et al. 2013b). An upper limit value for the [Fe II] flux was calculated for aperture 11. |
| In the text | |
 |
Fig. 7. Diagnostic diagram of the apertures in the central kiloparsec of NGC 1672. The location of the apertures is indicated in the flux maps in Fig. 3. The flux ratios of the molecular hydrogen lines H2(2–1)S(1)λ2.248 μm/H2(1–0)S(1)λ2.122 μm and H2(1–0)S(2)λ2.034 μm/H2(1–0)S(0)λ2.223 μm are used (Mouri 1994; Rodríguez-Ardila et al. 2004, 2005). Models for thermal UV excitation (Sternberg & Dalgarno 1989), non-thermal excitation (Black & van Dishoeck 1987), X-ray heating (Draine & Woods 1990), and shock-heating (Brand et al. 1989) are indicated for comparison. |
| In the text | |
 |
Fig. 8. Stellar velocity dispersion. North is up and east is to the left. The black cross denotes the nucleus. |
| In the text | |
 |
Fig. 9. Left: stellar velocity field map derived from fitting the spectral region around the CO(2–0) band head at ∼2.29 μm. Middle: model of the LOSV, assuming circular motions in a Plummer gravitational potential. Right: residuals after subtracting the model from the observed LOSV field. The systemic velocity derived in the model fit is subtracted from the maps. North is up and east is to the left. |
| In the text | |
 |
Fig. 10. Gas velocity fields, results of fitting Brγ, H2(1–0)S(1)λ2.122 μm, and [Fe II]λ1.644 μm emission lines. The black cross denotes the nucleus, where the continuum flux peaks. The circle in the H2 map indicates the central arcsec where Combes et al. (2019) found a molecular torus. All velocities are given relative to the systemic velocity of 1392 km s−1. North is up and east is to the left. |
| In the text | |
 |
Fig. 11. From left to right: Brγ, H2(1–0)S(1)λ2.122 μm, and [Fe II] emission line fits detected in the nuclear aperture of radius |
| In the text | |
 |
Fig. 12. Top left: flux map of the emission line Brγ λ2.16612 μm. Overlaid are the radio contours from Jenkins et al. (2011), which have an angular resolution of |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



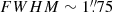
![$$ \begin{aligned} A_{ v} = k\,E(H-K) = k\,[(H-K)-(H-K)_0], \end{aligned} $$](/articles/aa/full_html/2020/06/aa37092-19/aa37092-19-eq9.gif)
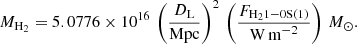
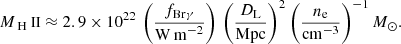
![$$ \begin{aligned} { v}_r = { v}_{\rm s} + \sqrt{\frac{R^2 G M}{(R^2 + A^2)^{3/2}}} \frac{\sin (i) \cos (\Psi - \Psi _0)}{\left[\cos ^2(\Psi - \Psi _0) + \frac{\sin ^2(\Psi - \Psi _0)}{\cos ^2(i)}\right]^{3/4}}, \end{aligned} $$](/articles/aa/full_html/2020/06/aa37092-19/aa37092-19-eq12.gif)