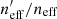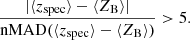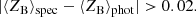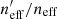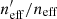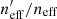| Issue |
A&A
Volume 637, May 2020
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 20 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201936782 | |
| Published online | 28 May 2020 | |
Photometric redshift calibration with self-organising maps
1
Ruhr-Universität Bochum, Astronomisches Institut, German Centre for Cosmological Lensing (GCCL), Universitätsstr. 150, 44801 Bochum, Germany
e-mail: awright@astro.rub.de
2
Institute for Astronomy, University of Edinburgh, Royal Observatory, Blackford Hill, Edinburgh, EH9 3HJ, UK
Received:
25
September
2019
Accepted:
17
March
2020
Accurate photometric redshift calibration is central to the robustness of all cosmology constraints from cosmic shear surveys. Analyses of the Kilo-Degree Survey (KiDS) re-weighted training samples from all overlapping spectroscopic surveys to provide a direct redshift calibration. Using self-organising maps we demonstrate that this spectroscopic compilation is sufficiently complete for KiDS, representing 99% of the effective 2D cosmic shear sample. We used the SOM to define a 100% represented “gold” cosmic shear sample, per tomographic bin. Using mock simulations of KiDS and the spectroscopic training set, we estimated the uncertainty on the SOM redshift calibration, and we find that photometric noise, sample variance, and spectroscopic selection effects (including redshift and magnitude incompleteness) induce a combined maximal scatter on the bias of the redshift distribution reconstruction (Δ⟨z⟩ = ⟨z⟩est − ⟨z⟩true) of σΔ⟨z⟩ ≤ 0.006 in all tomographic bins. Photometric noise and spectroscopic selection effects contribute equally to the observed scatter. We show that the SOM calibration is unbiased in the cases of noiseless photometry and perfectly representative spectroscopic datasets, as expected from theory. The inclusion of both photometric noise and spectroscopic selection effects in our mock data introduces a maximal bias of Δ⟨z⟩ = 0.013 ± 0.006, or Δ⟨z⟩ ≤ 0.025 at 97.% confidence, once quality flags have been applied to the SOM. The method presented here represents a significant improvement over the previously adopted direct redshift calibration implementation for KiDS, owing to its diagnostic and quality assurance capabilities. The implementation of this method in future cosmic shear studies will allow better diagnosis, examination, and mitigation of systematic biases in photometric redshift calibration.
Key words: techniques: photometric / cosmology: observations
© ESO 2020
1. Introduction
Comparisons between cosmological parameters from tomographic cosmic shear measurements (e.g. Hildebrandt et al. 2020; Troxel et al. 2018a; Hikage et al. 2019) and the cosmic microwave background (CMB; Planck Collaboration VI 2020) reveal some tension between the amount and clustering strength of (predominantly dark) matter. This is typically parameterised as 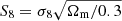 , where σ8 is related to the clustering amplitude of the dark matter power spectrum and Ωm describes the overall energy density of matter. Results from the recent Planck CMB measurements (Planck Collaboration VI 2020) suggest that the value of S8 observed at z ∼ 1100 is discrepant from that observed at low redshift by up to 3.2σ (see the combined analyses of cosmic shear surveys in Asgari et al. 2020).
, where σ8 is related to the clustering amplitude of the dark matter power spectrum and Ωm describes the overall energy density of matter. Results from the recent Planck CMB measurements (Planck Collaboration VI 2020) suggest that the value of S8 observed at z ∼ 1100 is discrepant from that observed at low redshift by up to 3.2σ (see the combined analyses of cosmic shear surveys in Asgari et al. 2020).
This result presents the tantalising possibility that the highly successful dark energy and cold dark matter paradigm (ΛCDM) does not perfectly describe the true nature of the Universe (see, e.g., Joudaki et al. 2017). However naturally such a claim requires significant evidence. Observations performed by different surveys within the tomographic cosmic shear community agree to better than 1σ (see, e.g., Hildebrandt et al. 2020; Joudaki et al. 2020), with the results from both the Dark Energy Survey (DES; Troxel et al. 2018a) collaboration and the HyperSuprime Camera (HSC; Hikage et al. 2019) surveys finding no significant tension with respect to Planck, compared to the mild 2.3σ tension reported by the Kilo Degree Survey (KiDS; Hildebrandt et al. 2020). This begs the question as to whether the reported CMB-cosmic shear tension is physical, or if it simply reflects systematic bias in the analysis methodologies of one or more of these weak-lensing surveys.
In an effort to explore the possible systematic biases within weak lensing analyses, members of both the DES and KiDS collaborations have performed their own re-analysis of data from one-another’s surveys. Troxel et al. (2018b) utilised the DES analysis method on KiDS data and find a revised value of S8 that is in closer agreement to the results found by the fiducial DES analysis (Troxel et al. 2018a). More recently, Joudaki et al. (2020) and Asgari et al. (2020) both performed a re-analysis of the DES data using the KiDS analysis methodology and found the converse to be true; DES data were in greater agreement with the fiducial results from KiDS (Hildebrandt et al. 2020).
This difference in result as a function of methodology suggests a fundamental difference, possibly from unrecognised systematic bias, in one or both of these analyses. Hildebrandt et al. (2020) explore the influence of various model and analytical choices on their cosmological constraints. In this analysis, they conclude that the only modification that can be made to their analysis method, which causes a decrease in the observed tension with the CMB results from Planck, is to utilise a different method of redshift calibration. Indeed, the approach to redshift calibration is the most fundamental difference between the methodologies of the DES, HSC, and KiDS collaborations, and therefore requires the most attention.
The role of redshift calibration in cosmic shear tomography is pivotal. This is because the signal measured is directly related to the strength of the gravitational distortion observed over redshift. If we estimate the true redshift distribution of all of our sources to be systematically lower than they are in reality, then we incorrectly attribute the observed gravitational distortions as originating from an overall denser, more highly clustered gravitational landscape than exists in reality. Hildebrandt et al. (2016) simulated the influence of redshift uncertainties on cosmic shear analyses found that their cosmological estimates were insensitive to redshift calibration biases of Δ⟨z⟩ ≤ 0.04. However, with increasing amounts of survey data and ever decreasing statistical uncertainties, biases at this level will be increasingly the dominant source of error in future analyses.
As a result of its importance, redshift calibration has been explored within (in particular) cosmic shear tomography for many years. Three different redshift calibration methods are most prevalent in the literature. These are estimation via: cross correlation (see, e.g., Schneider et al. 2006; Newman 2008; McQuinn & White 2013; Morrison et al. 2017); stacking of individual redshift probability distributions (Hildebrandt et al. 2012; Hoyle et al. 2018; Tanaka et al. 2018); and direct calibration incorporating spectroscopic redshift training samples, first presented by Lima et al. (2008), and implemented previously using k-nearest-neighbour methods (kNN; Hildebrandt et al. 2016, 2020) and unsupervised machine learning (Buchs et al. 2019).
In this work we develop and test a new implementation of direct redshift calibration, also utilising unsupervised machine learning methods. We use this new method to measure the spectroscopic representation of KV450 photometric (cosmic shear) sources, and subsequently explore, via a suite of simulations, how sample variance, photometric noise, and spectroscopic incompleteness influence photometric representation. We then use the simulations to estimate the influence of sample variance, photometric noise, and spectroscopic incompleteness on the redshift reconstruction bias present in the method.
The work presented in this paper is structured as follows. In Sect. 2 we describe the theory behind direct redshift calibration, and present the theory behind our implementation of the same. In Sects. 3 and 4 we describe the datasets and simulations utilised in this work. In Sect. 5 we present the main results of this work in four subsections. In Sect. 5.1 we estimate the representation of the KV450 photometric data using currently available spectroscopic compilations. In Sect. 5.2 we estimate the influence that systematic effects such as sample variance, photometric noise, and spectroscopic incompleteness have on these estimates of representation. In Sect. 5.3 we test the ability of our new implementation to calibrate redshift distributions, and explore the influence of a variety of systematic effects on these reconstructed redshift distributions. We further compare our new method to previous implementations of the direct calibration. In Sect. 5.4, we present an additional set of calibrated redshift distributions for the KiDS+VIKING-450 dataset, and propose an updated analysis methodology for the next iteration of KiDS cosmic shear analyses. In Sect. 6 we present a summary of our results, and our concluding remarks. This work also contains a number of technical (Appendices A–D) which are relevant to how we implement our new direct photometric redshift calibration.
2. Direct calibration with SOMs
The direct redshift calibration method was first proposed by Lima et al. (2008). The method involves matching two datasets, one with wide-field shear observations and one with deep spectroscopic observations, in high dimensional multiband magnitude space. In the original description, and in previous cosmic shear analyses within KiDS (Hildebrandt et al. 2017, 2020), this has been implemented using k-nearest-neighbour (kNN) methods. In this work, we present an updated direct calibration implementation using self-organising maps (Kohonen 1982). The formulae describing the reweighting method are therefore identical to those presented by Lima et al. (2008), Hildebrandt et al. (2017, 2020). Nonetheless, we reproduce them here for posterity. We also briefly describe the previous KiDS direct calibration implementation, and subsequently present our updated implementation utilising unsupervised machine learning methods.
In the recalibration method of Lima et al. (2008), the redshift distribution of an arbitrary set of photometric data, P, is estimated via a given a set of spectroscopic data, S. To do this one first associates the photometric and spectroscopic data in a way that maximises the spectroscopic redshift information. Typically this association involves matching the two sets using colours or magnitudes c, thereby creating m ≤ |S| associations1 between S and P. Each of the i ≤ m associations produces a (possibly improper) subset of S and P, which we define as 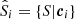 and
and 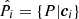 respectively.
respectively.
The goal of the redshift reconstruction procedure is to estimate the redshift distribution of the photometric data, p(z|P) using a weighted combination of spectroscopic associations:
where 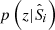 is the spectroscopic redshift distribution of the ith spectroscopic-to-photometric association, and wi is the reconstruction weight which maps the density of spectroscopic sources to the photometric data. In the case of unweighted photometric data, the weights required to reconstruct the photometric redshift distribution, p(z|P), from the spectroscopic set S is simply the ratio between the photometric and spectroscopic set cardinalities of each association
is the spectroscopic redshift distribution of the ith spectroscopic-to-photometric association, and wi is the reconstruction weight which maps the density of spectroscopic sources to the photometric data. In the case of unweighted photometric data, the weights required to reconstruct the photometric redshift distribution, p(z|P), from the spectroscopic set S is simply the ratio between the photometric and spectroscopic set cardinalities of each association 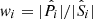 . When the photometric sample is weighted by some additional factor (such as a shear-measurement weight,
. When the photometric sample is weighted by some additional factor (such as a shear-measurement weight, 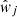 for j ∈ P), the weight formula changes to a simple sum over these weights per association;
for j ∈ P), the weight formula changes to a simple sum over these weights per association;
As discussed in Lima et al. (2008), this reconstruction will yield an unbiased estimate 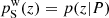 in the regime where
in the regime where 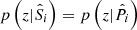 ; such as when the colour–redshift distributions of the spectroscopic and photometric subsets are exactly the same (including selection effects, photometric noise, Poisson noise, etc.). This is true for arbitrarily complex (e.g. broad) pi(z|P, ci). However in practice, due to spectroscopic selection effects for example, the redshift distribution of spectroscopic data are very different to those of photometrically defined data, p(z|S) ≠ p(z|P). Nonetheless, the recalibration remains valid provided that the colour–redshift relationship is unique: p(z|ci) → δ(z|ci). In this limit
; such as when the colour–redshift distributions of the spectroscopic and photometric subsets are exactly the same (including selection effects, photometric noise, Poisson noise, etc.). This is true for arbitrarily complex (e.g. broad) pi(z|P, ci). However in practice, due to spectroscopic selection effects for example, the redshift distribution of spectroscopic data are very different to those of photometrically defined data, p(z|S) ≠ p(z|P). Nonetheless, the recalibration remains valid provided that the colour–redshift relationship is unique: p(z|ci) → δ(z|ci). In this limit 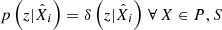 and so unbiased recovery is again possible even given p(z|S) ≠ p(z|P).
and so unbiased recovery is again possible even given p(z|S) ≠ p(z|P).
In Hildebrandt et al. (2020) a kNN method is used to estimate, for the ith spectroscopic galaxy, the nine-dimensional hyper-spherical volume, 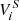 , that contains precisely
, that contains precisely 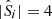 spectroscopic nearest-neighbours. The (shear-contribution weighted) number of photometric sources contained within the same volume,
spectroscopic nearest-neighbours. The (shear-contribution weighted) number of photometric sources contained within the same volume, 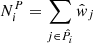 , is then also calculated, thereby allowing computation of the weights in Eq. (2). As stated earlier, in this work we perform a new association scheme utilising unsupervised machine learning.
, is then also calculated, thereby allowing computation of the weights in Eq. (2). As stated earlier, in this work we perform a new association scheme utilising unsupervised machine learning.
Self organising maps (SOMs; Kohonen 1982) are a form of unsupervised neural network which uses competitive learning of neurons to map a high dimensional manifold onto a low-dimensional grid. While SOMs were initially devised as a visualisation tool (Kohonen 1982), they have found a range of uses within the astronomical community over the last two decades (see, e.g., Naim et al. 1997; Davidzon et al. 2019). The most notable implementation has been in the Complete Calibration of the Colour-Redshift Relation (C3R2; Masters et al. 2017, 2019) project where the C3R2 team endeavour to utilise SOMs to identify unexplored parts of the n-dimensional colour–redshift plane (Masters et al. 2015), in an effort to subsequently observe spectra of such sources and thus, as the name suggests, completely calibrate the colour–redshift relation for future weak lensing surveys such as Euclid (Amendola et al. 2018; Laureijs et al. 2011).
The importance of the C3R2 analysis for our work here lies in the use of SOMs to create a high-fidelity discrimination of the colour–redshift relation. As the SOM allows for a sophisticated mapping of the complex n-dimensional colour-magnitude manifold, it can be used as the basis of association definitions 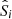 and
and 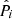 . Therefore, a SOM trained on the spectroscopic dataset S, and into which we subsequently map photometric data P, should generate a high fidelity weighting wi ∀ i ∈ [1, m], and therefore a high fidelity estimate of p(z|P).
. Therefore, a SOM trained on the spectroscopic dataset S, and into which we subsequently map photometric data P, should generate a high fidelity weighting wi ∀ i ∈ [1, m], and therefore a high fidelity estimate of p(z|P).
Recently Buchs et al. (2019) have presented an implementation of the direct redshift calibration method, utilising multiple SOMs, also for the purpose of calibrating cosmic shear studies. Their implementation is designed primarily for surveys observed in the manner of DES (that is, without comparable observations over both the wide-field and deep-spectroscopic survey fields). This type of survey design makes directly mapping the wide-field and deep spectroscopic surveys challenging, and as such Buchs et al. (2019) are required to estimate the mapping of the wide-field data onto the spectroscopy via a series of intermediate datasets. In their mock analysis, intermediate datasets are chosen to be noiseless and/or fully representative with zero redshift uncertainty. With these somewhat idealised conditions, Buchs et al. (2019) recover the underlying redshift distributions with maximal expected biases of σΔ⟨z⟩ ∼ 0.007 for DES-like wide-field observations and tomographic binning.
The results from C3R2 and Buchs et al. (2019) suggest that a new implementation of the traditional direct redshift calibration has merit. Naturally though, they do not guarantee that SOMs will return an unequivocally superior calibration method. The finite binning of the SOM manifold, for example, presents a limitation that is clearly not present when performing a kNN matching of every spectroscopic source individually. Such a binning creates discreteness in the final mapping, which could lead to a degradation of the final weighting. Conversely, the same continuity of the kNN method (which we just described as a positive) can also lead to pitfalls. For example, if the colour-magnitude space of the spectroscopic sample is not adequately representative of the photometric sample, then the kNN matching will be forced to extend to sources well beyond what we might consider the local region of the n-dimensional manifold. In the SOM implementation, such regions without spectroscopic representation are directly visible and so the misidentification of photometric sources can be kept to a minimum. These are but two examples of possible differences between the kNN and SOM direct calibration methods, and demonstrate why comprehensive testing of the two methods is necessary.
For all of the SOM analysis presented in this work, we utilise a branched version of the widely used and tested kohonen package (Wehrens & Kruisselbrink 2018; Wehrens & Buydens 2007) within R (R Core Team 2015). The original package version is available from the Comprehensive R Archive Network (CRAN). Our branched version of the CRAN package2 contains modifications for versatility and better plotting, and has been used for all SOM visualisations here. All of the scripts required to run the SOM direct calibration, and produce the figures here, are made public3.
3. Dataset
In this work we explore the performance of the SOM calibration method using a series of simulations, and then use the SOM to calibrate the KiDS+VIKING-450 dataset presented in Wright et al. (2019), Hildebrandt et al. (2020). Our simulations are built to resemble the KiDS+VIKING-450 dataset, which can be split into two fundamental sections: the photometric survey which contains shape measurements for cosmic shear, and the spectroscopic compilation which contains redshift estimates from spectroscopy.
3.1. Photometric survey
A comprehensive description of the combined full KiDS dataset is provided in Wright et al. (2019). The dataset comprises of KiDS optical imaging probing the 3000 to 9000 Ångstrom range in four bands (ugri). Imaging is taken with the OmegaCAM instrument, mounted at the Cassegrain focus of ESO’s VLT Survey Telescope (VST; de Jong et al. 2017) on Cerro Paranal, Chile. The imaging used here comprises of 454 distinct ∼1 deg2 pointings of the camera, which (after masking) covers 360.3 deg2 on-sky.
These optical data are then combined with the infrared imaging from the VISTA Kilo degree INfrared Galaxy (VIKING; Edge et al. 2013; Venemans et al. 2015) survey, probing the NIR wavelengths between 8000 and 24 000 Ångstroms. These data are taken using the Visible and InfraRed CAMera (VIRCAM) on ESO’s 4m VISTA telescope, also located on Cerro Paranal, Chile. The imaging is taken in five near-IR bands (ZYJHKs), using 16 individual HgCdTe detectors, each with a 0.2 × 0.2 square degree angular size, but which jointly span a ∼1.2 square degree field of view. These detectors are designed for dedicated near-IR observations, which allows for a vastly improved efficiency in even the bluest (Z) band compared to observations taken in a similar range using optical detectors.
The combined KiDS+VIKING dataset is extremely well matched in terms of depth and coverage. Photometry in every band is measured using the Gaussian Aperture and PSF (GAaP; Kuijken 2008; Kuijken et al. 2015) method, with additional methodological details described in Wright et al. (2019). Wright et al. (2019) also present statistics for the photometric detection of sources in the combined dataset, demonstrating that over 80% of KiDS+VIKING lensing sources have finite detections in all bands from g–Ks. The full KiDS+VIKING-450 dataset (after masking) comprises of 447 distinct ∼1 deg2 pointings of the camera, which (after masking) covers 341.3 deg2 on-sky (Wright et al. 2019).
3.2. Spectroscopic surveys
Spectroscopic data utilised for direct calibration in the KiDS survey originates from five distinct redshift surveys: zCOSMOS (the bright selection presented in Lilly et al. 2009, and a non-public deep compliment), the DEEP2 Redshift Survey (the colour-selected equatorial fields; Newman et al. 2013), VIMOS VLT Deep Survey (VVDS; Le Fèvre et al. 2013), GAMA G15-Deep (Kafle et al. 2018) and ESO-GOODS CDFS (Popesso et al. 2009; Balestra et al. 2010; Vanzella et al. 2008). These surveys were chosen for two reasons. Firstly, they each probe (at least partially) the colour-magnitude range of photometric sources utilised for KiDS cosmic shear. Secondly, they are selected because they all either overlap with the KiDS and VIKING photometry directly (G15-Deep, zCOSMOS4) or have dedicated KiDS- and VIKING-like observations (VVDS, CDFS, DEEP2).
Statistics for the various spectroscopic datasets are provided in Table 1. The full spectroscopic compilation is described in detail in Hildebrandt et al. (2020). The table shows the size of the individual spectroscopic datasets in area and number of spectra. We can see that the three largest of our spectroscopic datasets are zCOSMOS, DEEP2, and VVDS; combined they make up more than 85% of the spectroscopy used for our calibration. The table is complemented by Fig. 1, which shows the spectroscopic redshift distribution of the combined sample, coloured by the survey from which each source originated. The figure demonstrates the different selections that have been applied to the various spectroscopic datasets. zCOSMOS is a complicated combination of multiple spectroscopic campaigns, containing a bright low-redshift (z ∼ 0.35) population, a fainter middle-redshift (z ∼ 0.75) population, and finally a population of very high-redshift (z > 1.7) sources. Conversely, DEEP2 is a single population of colour-selected targets, which show a clear singular population between 0.7 ≲ z ≲ 1.5.
Spectroscopic redshift samples used for the direct redshift calibration in KiDS.
 |
Fig. 1. Spectroscopic redshift distribution of our combined spectroscopic calibration dataset. The figure shows the redshift distribution as a kernel density estimate (KDE), constructed using a rectangular δz = 0.1 kernel. The KDE is weighted such that lines are interpretable as the instantaneous counts per δz. The KDE is coloured by the fractional contribution from each of our five datasets to the total, which is shown by the black line. |
4. Simulations
In this section we describe the construction of our KiDS-like simulated datasets which we use to verify the performance of the SOM direct calibration methodology on a cosmological dataset such as KiDS. We therefore must construct a simulated dataset that mimics the complexity of KiDS and the spectroscopic compilation in terms of extraction depth, photometric depth, wavelength coverage, spectroscopic target selection, and shear estimation precision.
Our simulations are constructed from the MICE2 simulation which is presented in detail in Fosalba et al. (2015a,b), Crocce et al. (2015), Carretero et al. (2015), Hoffmann et al. (2015). MICE2 is based on an N-body dark matter simulation, which is used to derive an all-sky lensing mock catalogue between 0.1 ≤ z ≤ 1.4. The lensing catalogue contains source positions, morphological information, lensing convergence measurements, and model magnitudes in the ugriZYJHKs-bands. From these products, we are able to construct multiple realisations of high-fidelity KiDS-like mock photometric and spectroscopic catalogues. Given its construction, the MICE2 mocks present an excellent starting point for our analysis. Our simulations are constructed using the pipeline of van den Busch et al. (in prep.)5. We detail parts of the mock catalogue generation here, including a description of spectroscopic selections and sample definitions applied to the simulation.
Prior to selection of photometric and spectroscopic sources using MICE2, we apply the recommended evolution corrections to the model magnitudes:
and apply the required flux magnifications (Fosalba et al. 2015b) as determined by the lensing convergence, κ:
We then derive effective photometric apertures from the on-sky bulge and disc effective radii and the bulge fractions. The photometric aperture of each source, 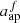 and
and 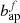 , is then approximated, per filter f, as a function of the effective radius of the two-component light-profile, Reff, the intrinsic two-component profile axis ratio bintr/aintr, and the filter f PSF FWHM
, is then approximated, per filter f, as a function of the effective radius of the two-component light-profile, Reff, the intrinsic two-component profile axis ratio bintr/aintr, and the filter f PSF FWHM 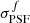 :
:
With these aperture parameters and the documented per-filter point-source magnitude limits (see Kuijken et al. 2019), we generate KiDS-like photometry for all sources in the MICE2 octant. We use the magnitude limits to calculate a true signal-to-noise (SN) for every source in every band of the simulated catalogue. These SN estimates incorporate realistic estimates of aperture noise, using the apertures calculated above, and all flux uncertainties encoded in the point source magnitude limits (shot noise, image noise, etc.). With these SN estimates, we calculate an “observed” flux for every source in each band, and compute a final uncertainty from these observed fluxes.
For the photometric sample definition, we first subset a section of the MICE2 octant into a KiDS sized patch of area 341.3 square degrees (i.e. the post-masking area of KV450). All simulated galaxies that lie within this footprint have KiDS-like photometric noise realisations, as described above. All sources are then matched in 9-band magnitude-space to the actual KiDS photometric data (via kNN within a maximum 1 mag Euclidean radius), and inherit the nearest-neighbour shear calibration weight6. Unmatched sources are assigned zero weight, as by definition they do not appear in the KiDS source sample. This latter step has the added benefit of implicitly encoding any unrecognised colour and magnitude dependant selection effects present in the KiDS data. The final simulated photometric source catalogue is then selected as being all sources with non-zero calibration weight.
We simulate our three primary spectroscopic datasets (zCOSMOS, DEEP2, and VVDS), using the evolution corrected photometry in the Johnson BVRI-bands, to simulate the selection of spectroscopic targets from deep imaging. We start by selecting all galaxies within distinct patches (i.e. not part of one-another nor the KV450 area), each of which is the same size as the spectroscopic survey being modelled (i.e. as shown in Table 1). Their various magnitude- and colour-based selection functions are applied, except typically with minor adjustments to better reproduce the observed redshift distributions of the surveys:
-
zCOSMOS: 15 < I < 22.5 (i.e. the bright selection only);
-
DEEP2: 18.5 < R < 24.0 and (B − R < 2.0(R − I) − 0.4 or R − I > 1.1 or B − R < 0.2); and
-
VVDS: 18.5 < I < 24.0.
After each of these selections is applied, we further trim each sample using documented (per-survey) spectroscopic failure or incompleteness functions (in both magnitude and redshift space, as described in Newman et al. 2013; Lilly et al. 2009; Le Fèvre et al. 2013). This process allows us to encode spectroscopic incompleteness, albeit imperfectly: we are unable to explicitly incorporate incompleteness as a function of colour in this implementation. Finally, if the number density of remaining spectra is higher than in the data, we perform a sparse sampling of each spectroscopic subset to reproduce the number of observed spectra (to within ∼3%).
As was shown in Table 1, our three main spectroscopic datasets correspond to 85% of the full spectroscopic dataset (although part of this is the zCOSMOS faint selection). We have opted not to include the G15DEEP, zCOSMOS-faint, and CDFS compilations in our simulations: G15Deep is small and relatively low-impact given our lensing sample (see Sect. 5.1), and both the CDFS and zCOSMOS-faint samples are complex combination of tens of individual survey datasets. These post-hoc combinations have naturally complex selection functions which are difficult to faithfully reconstruct in our simulations. Excluding these datasets from the simulated compilation ensures that we do not accidentally over-estimate the depth of our true spectroscopic data, and thus overestimate the performance of our redshift calibration methodology.
In cases where we test the effects of sample variance7, we perform the spectroscopic catalogue creation 100 times in 100 sets of completely independent fields (lines-of-sight); that is all 100 fields of all three surveys are independent of one-another. We also produce 100 realisations of the photometric noise in one realisation of the spectroscopic fields, to test the influence of photometric noise within the spec-z distributions.
Finally, we note that the limited redshift range of the MICE2 simulation places a limitation on the interpretability of the results with respect to redshift calibration for real cosmic shear surveys. However this limitation is somewhat common to the literature (see, e.g., Buchs et al. 2019; Alarcon et al. 2019), and will only be resolved with the construction of larger, deeper simulations of cosmic shear samples. To this end, simulations such as the Euclid Flagship8 and the Legacy Survey of Space and Time (LSST) DC2 (Korytov et al. 2019) represent an obvious testing-ground for this (and other) redshift calibration methods in the future.
5. Results
5.1. Suitability of current spectroscopy for direct photometric redshift calibration
In this section we explore the question of whether the currently available spectroscopic compilations, used primarily by the KiDS consortium, are of sufficient depth and diversity for use in direct photometric redshift calibration, so as to not cause significant biases in reconstructed redshift distributions. We explore this question of representation using the real KV450 photometric and spectroscopic datasets. We also measure the representation of KV450 photometric sources using the individual spectroscopic surveys, in an effort to quantify the influence that any one calibration dataset may have over the final calibrated redshift distribution estimates.
In order to estimate the representation of the KV450 photometric dataset, we first train a SOM using the full spectroscopic compilation. In our fiducial case, we train a 101 × 101 hexagonal-cell SOM with toroidal topology, using the combination of 36 colours and 1 mag; the r-band. Specific details regarding these construction and training parameters, and how they influence our results, can be found in Appendix A. We then propagate our full photometric and spectroscopic datasets into this trained SOM, producing like-for-like groupings between spectroscopic and photometric sources; specific details of this process are presented in Appendix B. Once we have constructed like-for-like groupings within the spectroscopic and photometric catalogue, we can then directly measure the number of photometric sources which are without a spectroscopic counterpart.
This direct measurement of representation is used to construct a sub-sample of the photometric catalogue which is represented by the spectroscopy. This sub-sample with guaranteed representation we define to be the “gold sample”.
A visual representation of the propagation of the spectroscopic data into our trained SOM is provided in Fig. 2. The figure shows our trained SOM coloured using a ternary scale, shown as the large triangle. It demonstrates the fractional contribution of each of our primary spectroscopic surveys to the individual SOM cells: blue for DEEP2, yellow for zCOSMOS, and pink for VVDS, with a continuum scale for intermediate mixtures of the three catalogues. We also show the cells which are filled by other spectroscopic datasets (but not any of the three primary sets) in white, and cells that have no spectroscopic data in black. The figure showcases a few interesting features of the KV450 spectroscopic compilation. Firstly, the complementarity of the three primary spectroscopic datasets is clear; cells are overwhelmingly either blue, yellow, or pink, rather than intermediate colours (green, purple, brown, grey). This is an indication that our spectroscopic datasets have little overlap in multidimensional colour-space.
 |
Fig. 2. Distribution of the three primary KV450 spectroscopic samples within the SOM. The figure on the left shows the SOM coloured by the fractional contribution of each of the three main spectroscopic samples from KV450. The ternary colour bar is shown on the right. The makeup of individual cells is annotated within the colour-bar as points. SOM cells that are filled entirely by sources from DEEP2, for example, are blue. Conversely cells that are filled by equal mixtures from all three samples are grey. Cells which contain spectroscopic data from other surveys (which are not shown) are coloured white. Cells which contain photometric galaxies but no spectroscopy from any survey are coloured black. The figure highlights the complementarity between the DEEP2 and zCOSMOS data, as well as the breadth of coverage of the VVDS data. |
We quantify the spectroscopic representation of KV450 photometric sources in Table 2. The table shows the coverage statistics of the SOM, for various splits of the spectroscopic compilation. Starting with the “Full Sample”, shown by all the non-black cells in Fig. 2, the table shows the overall size of the spectroscopic sample (“Training Size”; 25373 galaxies for the full sample), as well as the fraction of SOM cells that these sources occupy (fpix; 91.9% for the full sample)9. As can be seen in Fig. 2, ∼8% of SOM cells are unoccupied by spectra. However this is not indicative of the fraction of photometric sources which are missing spectra, as photometric counts vary strongly across the SOM. Furthermore, all photometric sources do not hold the same weight in cosmic shear estimates, owing to the shape measurement weighting described in Sect. 4. To correctly quantify the photometric representation, we choose a statistic that correctly accounts for the weights of the missed photometric sources. Heymans et al. (2012) define the effective number density of weighted photometric sources in cosmic shear studies, neff, as:
where wi is the lensing weight assigned to each photometric source (see Miller et al. 2007, for details), and A is the effective survey area. This statistic can be calculated for all of photometric sources (p), and the subset of photometric sources which reside within SOM groupings which contain spectroscopy (i.e. the gold sample; p′⊆p). We can then accurately compute fractional change in neff: 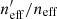 caused by the requirement of spectroscopic representation.
caused by the requirement of spectroscopic representation.
Table 2 shows the fractional changes in neff (as percentages) when going from the full to the gold sample for each combination of the spectroscopic data. We start by showing these values for the entire photometric catalogue (“All”), without tomographic binning. Looking first to the case of the full spectroscopic sample, we can see that while roughly 8% of our SOM cells contain no spectroscopy, these cells contain just 0.5% of the total lensing weight of the photometric catalogue. The cells lie in unimportant parts of the colour space (for the cosmic shear sample), and so contribute negligibly to the neff.
We also show the fractional change in neff for the five tomographic bins defined in Hildebrandt et al. (2020). The redshift limits of each of these bins are annotated in the table header. In these split statistics, both the spectroscopic and photometric dataset are selected such that they have photometric redshifts within the tomographic bin. This has the effect of decreasing the spectroscopic training size for each bin by a factor of roughly five10. As a result, the representation statistics also decrease. However this process is critical so as to not bias the resulting groupings (see Appendix D). In these tomographic bins, we see that the photometric data representation is between 83% (in the first and fourth tomographic bins) and as high as 94% in the fifth and highest redshift tomographic bin. This result is counterintuitive, as a naive expectation would suggest that poorer high-z spectroscopic success would translate to a dearth of representation at high photometric redshifts. However in practice volume effects and the choice of tomographic bins in KiDS means that the highest redshift bins contain the most spectra: Nspec = {2715, 3031, 4971, 6058, 6145} for the 5 tomographic bins, respectively. Furthermore, the increasing rate of spectroscopic failure is somewhat counter-balanced by the highly redshift and magnitude dependent shear-measurement efficiency, encoded by the shear measurement weight. Prior to consideration of the shape measurement weights, the highest tomographic bin has more than 10% misrepresentation. This indicates that spectroscopic failures and shape-measurement failures are correlated; sources for which it is difficult to measure shapes are also difficult to redshift. As a result, the highest tomographic bin is actually the best represented in KV450.
We further explore the makeup of our spectroscopic catalogue by splitting it into subsets. This is motivated by the possibility that one or more of the individual spectroscopic surveys within our compilation may be affected by unrecognised systematic effects. Recent re-observation and redshifting of VVDS high-confidence redshifts by the LEGA-C collaboration (Straatman et al. 2018), for example, suggests that the outlier rate for high-confidence redshifts may be higher than the expected ≲3% rate. Should future studies verify that any of our spectroscopic compilations have serious systematic effects present, then our Table 2 may be used to infer the impact that this may have over current and future KiDS analyses.
We look at the representation of each individual spectroscopic dataset (the “only” rows), and of the full compilation minus each individual dataset (the “without” rows). The representation statistics here are all calculated from the SOM trained on the full spectroscopic dataset; subsequent samples are simply propagated into the pre-trained SOM and the coverage statistics are then calculated.
Table 2 highlights that while the zCOSMOS dataset occupies the most individual SOM cells of any individual catalogue (fpix = 48.5%), it is the removal of the DEEP2 dataset which causes the greatest reduction in cell coverage compared to the full compilation (from 91.9% to 73.4%). This indicates that while zCOSMOS is the largest of the KV450 spectroscopic datasets, DEEP2 is the most unique; the sources within DEEP2 occupy the greatest fraction of systematically different SOM cells to those of any other survey.
Looking at the change to neff, the story changes slightly. We see that, when considering all photometric sources together without tomographic binning, it is VVDS which (despite being less than half the size of zCOSMOS) most effectively describes the lensing weighted KV450 photometric data (when each spectroscopic dataset is considered alone; 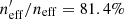 ). Per tomographic bin, however, the best-representation is split between our three main datasets: zCOSMOS best describes the two lowest tomographic bins (0.1 < z ≤ 0.5; 74.9% and 75.3%), VVDS best describes the middle bin (0.5 < z ≤ 0.7; 70.7%), and DEEP2 best describes the highest tomographic bins (0.7 < z ≤ 1.2; 68.8% and 89.5%). This result supports the hypothesis of Hildebrandt et al. (2020), who argued that the removal of DEEP2 from the spectroscopic compilation would preferentially affect the photometric representation of the higher tomographic bins, effectively pulling them to lower mean redshifts, and thus causing a bias in the estimated value of S8.
). Per tomographic bin, however, the best-representation is split between our three main datasets: zCOSMOS best describes the two lowest tomographic bins (0.1 < z ≤ 0.5; 74.9% and 75.3%), VVDS best describes the middle bin (0.5 < z ≤ 0.7; 70.7%), and DEEP2 best describes the highest tomographic bins (0.7 < z ≤ 1.2; 68.8% and 89.5%). This result supports the hypothesis of Hildebrandt et al. (2020), who argued that the removal of DEEP2 from the spectroscopic compilation would preferentially affect the photometric representation of the higher tomographic bins, effectively pulling them to lower mean redshifts, and thus causing a bias in the estimated value of S8.
Interestingly, the same trends are largely true for the compilations without each of these datasets. In the tomographically binned cases, all bins other than the 2nd are most heavily misrepresented when the most uniquely represented dataset is removed. In the 2nd bin, removal of VVDS (rather than zCOSMOS) causes the greatest decrease in neff. Overall, it is DEEP2 that is the most important dataset: while removal of all other datasets triggers a maximal reduction in neff of 7.1% (VVDS in bin 3), removal of DEEP2 sees a reduction of over 10% in both bins 4 and 5. This is more than twice the decrease seen when removing the next most important dataset in bin 4 (from 78.9% without zCOSMOS to 72.2% without DEEP2), and nearly 10 times smaller than the decrease seen when removing the next most important dataset in bin 5 (also zCOSMOS; from 92.6% to 80.8%). Overall, these statistics indicate that, for the calibration of the KiDS tomographic cosmic shear dataset, our three primary KV450 datasets are equal parts individually important and unique. As a result, for a coherent redshift offset in all tomographic bins to be seen, a conspiracy of unknown systematic biases in at least two major spectroscopic surveys would be needed.
5.2. Influence of sample variance, noise, and selection biases
Our second set of results regards the sensitivity of our photometric representation estimates to the presence of a number of systematic effects present in spectroscopic surveys: sample variance, photometric noise, and selection biases. To test the influence of these systematics we use our MICE2 simulations, for which we are able to generate many realisations of lines-of-sight (to analyse sample variance) and noise realisations (because we know the true fluxes).
Figure 3 shows the representation of the cosmic shear sample, 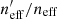 , for 100 realisations of different spectroscopic lines-of-sight within our MICE2 simulations (green with black outline). Each line-of-sight is unique, both per realisation and per spectroscopic survey (DEEP2, zCOSMOS, and VVDS), and so samples a unique part of the MICE2 octant. We use a single realisation of the photometric catalogue for these tests, to exclusively probe the impact of sample variance in the spectroscopic catalogues on our representation estimates. As the different lines-of-sight naturally contain independent galaxies, the width of our green histograms contain the influence of both sample variance and photometric noise. We therefore also show 100 realisations of a single set of spectroscopic lines-of-sight (orange), so as to demonstrate exclusively the influence of photometric noise. These histograms suggest that the joint effect of sample variance and photometric noise is to perturb our estimated
, for 100 realisations of different spectroscopic lines-of-sight within our MICE2 simulations (green with black outline). Each line-of-sight is unique, both per realisation and per spectroscopic survey (DEEP2, zCOSMOS, and VVDS), and so samples a unique part of the MICE2 octant. We use a single realisation of the photometric catalogue for these tests, to exclusively probe the impact of sample variance in the spectroscopic catalogues on our representation estimates. As the different lines-of-sight naturally contain independent galaxies, the width of our green histograms contain the influence of both sample variance and photometric noise. We therefore also show 100 realisations of a single set of spectroscopic lines-of-sight (orange), so as to demonstrate exclusively the influence of photometric noise. These histograms suggest that the joint effect of sample variance and photometric noise is to perturb our estimated 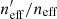 at the ∼1% level, and (more interestingly) that this scatter is overwhelmingly driven by photometric noise rather than sample variance; the width of the green histograms is equivalent to the width of the orange.
at the ∼1% level, and (more interestingly) that this scatter is overwhelmingly driven by photometric noise rather than sample variance; the width of the green histograms is equivalent to the width of the orange.
 |
Fig. 3. Change in the value of |
The figure also shows the observed representations for the KV450 dataset (vertical black dashed lines). These lines show that the simulation is a reasonable reflection of the representation seen in the data, being within ∼5% of the data representation in all bins. The simulations also show the same behaviour as the data with regard to the inclusion or exclusion of individual spectroscopic samples; we show the influence of removing DEEP2 (pink) causes a similar pathological reduction in representation, per tomographic bin, for the simulations as in the data (Sect. 5.1).
We demonstrate how the estimated value of 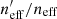 changes if we were able to use a perfectly representative spectroscopic compilation. To do this we construct a spectroscopic sample of the same size as our full spectroscopic compilation, but which is sparse sampled (100 times) from the photometric dataset itself. The results are shown in purple in Fig. 3. Surprisingly, the perfectly representative spectroscopic sample is typically only ∼5% better than that of our standard spectroscopic compilation. The exception here is again the third tomographic bin. This suggests that the decrease in KV450 representation is not driven predominantly by systematically missing spectra in the multidimensional colour space, but rather the dearth of spectra overall. Such a circumstance, however, is unlikely to be true (with this spectroscopic compilation) for stage-III cosmic-shear surveys like Euclid and LSST, which will extend to considerably higher redshifts than KiDS. These surveys will likely require additional dedicated programmes, such as C3R2, to compile samples of spectra capable of calibrating their highest redshift sources.
changes if we were able to use a perfectly representative spectroscopic compilation. To do this we construct a spectroscopic sample of the same size as our full spectroscopic compilation, but which is sparse sampled (100 times) from the photometric dataset itself. The results are shown in purple in Fig. 3. Surprisingly, the perfectly representative spectroscopic sample is typically only ∼5% better than that of our standard spectroscopic compilation. The exception here is again the third tomographic bin. This suggests that the decrease in KV450 representation is not driven predominantly by systematically missing spectra in the multidimensional colour space, but rather the dearth of spectra overall. Such a circumstance, however, is unlikely to be true (with this spectroscopic compilation) for stage-III cosmic-shear surveys like Euclid and LSST, which will extend to considerably higher redshifts than KiDS. These surveys will likely require additional dedicated programmes, such as C3R2, to compile samples of spectra capable of calibrating their highest redshift sources.
5.3. Accuracy of the SOM direct calibration
We now utilise our simulations to explore the bias and scatter in our photometric redshift calibration method by comparing the true and estimated redshift distributions from our mocks. In the following analyses we assume that all spectroscopy within our spectroscopic sample are recovered with 100% accuracy. For a discussion of the influence of catastrophic spectroscopic failures on our analysis, we direct the interested reader to Appendix E.
We estimate the tomographic redshift distributions for each of our 100 spectroscopic lines-of-sight, as described in Sect. 2, keeping the photometric dataset static. We explore the performance of our method with both noisy and noiseless photometry, and for both perfectly representative and systematically incomplete spectroscopic compilations. Measured redshift distribution biases for each of our simulations are given in Table 3.
Biases in the mean redshift estimation (Δ⟨z⟩ = ⟨z⟩est − ⟨z⟩true), per tomographic bin, for our various runs of the MICE2 simulations.
First we focus on the simulations run without photometric noise (“exact”). The results indicate that in all circumstances (i.e. with both perfect and biased spectroscopic compilations) the SOM direct photometric redshift calibration method is unbiased. All tomographic bins, in the case of complete and incomplete spectroscopy, show biases Δ⟨z⟩ = ⟨z⟩est − ⟨z⟩true ≤ 0.003. In the case of both perfectly representative spectra and noiseless photometry, all but the first tomographic bin shows both bias and scatter less than 0.001; these entries we simply mark with a null symbol (∅ ≡ < 10−3 ± < 10−3). Introducing incomplete spectroscopy causes the bias to increase very slightly, but nonetheless remains at a level that we would consider negligible for current weak lensing surveys.
Once we add photometric noise, we see that the results degrade. As a baseline for comparison, we include in Table 3 the biases measured using the kNN association using our noisy and systematically incomplete spectroscopic compilation. The kNN method returns a maximal biases of Δ⟨z⟩ = 0.047 ± 0.005, or Δ⟨z⟩ ≤ 0.057 at 97.5% confidence, in the first tomographic bin. The highest tomographic bin exhibits bias of Δ⟨z⟩ = −0.013 ± 0.004, or Δ⟨z⟩ ≥ −0.021 at 97.5% confidence. While the observed kNN biases are non-negligible, it is worth noting that they agree well with the estimated redshift uncertainties presented by Hildebrandt et al. (2020). They estimate the uncertainty on their kNN direct calibration via a spatial bootstrap analysis, and find biases of σΔ⟨z⟩ ∈ {0.039, 0.023, 0.026, 0.012, 0.011}. Furthermore, the biases estimated for the kNN method are incoherent (i.e. the sign of the bias changes for different tomographic bins) thereby limiting the impact that they would have on cosmological conclusions.
For our updated SOM implementation, we find that the method is still largely unbiased (Δ⟨z⟩ ≤ 0.006) in the case of perfectly representative spectroscopic data, as is expected from the theory of Lima et al. (2008). In the presence of biased spectroscopy, however, the biases increase to a value of Δ⟨z⟩ = 0.023 ± 0.006, or Δ⟨z⟩ ≤ 0.035 at 97.5% confidence, in the third tomographic bin. The magnitude of this bias remains unchanged when performing our redshift calibration with data detected in all photometric bands, indicating that our treatment of non-detections is not the cause of this bias. However we can leverage additional information, encoded by our new direct calibration, to improve these results and minimise systematic bias.
A primary strength of our direct calibration implementation is the ability to perform diagnostic and quality checks on the resulting calibration. We can then perform some simple quality control checks on the spectroscopic-to-photometric groupings as a means of minimising the bias introduced by photometric noise in our calibration. As a demonstration, we perform two sets of quality control checks on our simulations with noisy photometry and systematically incomplete spectroscopy. First, we flag and remove spectroscopic-to-photometric groupings which are catastrophic outliers in the distribution of photo-z vs. SOMz (i.e. the mean redshift of the SOM grouping):
This quality cut (“QC1”) effectively flags and removes regions of colour–colour space where template-fitting photo-z and machine learning photo-z catastrophically disagree. This simple quality control step removes {2.0, 0.3, 2.4, 0.6, 0.1}% of the photometric neff in each of the tomographic bins, and reduces the maximal bias to Δ⟨z⟩ = 0.013 ± 0.006, or Δ⟨z⟩ ≤ 0.025 at 97.5% confidence (see Table 3). We can then apply additional, stricter, layers of quality cuts (“QC2”) to further reduce the bias. This layer of quality control flags and removes regions of colour–colour space where the average photo-z of the spectroscopic and photometric sources disagree:
Such measures reduce the maximal bias to Δ⟨z⟩ = 0.009 ± 0.004 (now in the fourth tomographic bin), but at the cost of decreased photometric neff: Δneff = {15.9, 13.6, 23.3, 26.2, 21.1}%.
These quality controls steps are not designed to be final, but are merely a demonstration of the refinement which is possible using our updated direct calibration implementation. Determination of the best possible quality metrics should ideally be performed on simulations beyond those presented here, which extend to higher redshifts.
5.4. Gold-sample tomographic redshift distributions for KV450
Here we present the application of the SOM direct photometric redshift calibration method to the KV450 dataset, and derive tomographic redshift distributions for the KV450 gold-sample. Recall that the gold sample is the subset of the full photometric sample p which is represented by spectroscopic data, per tomographic bin, within our SOM (p′, such that p′⊆p). Importantly, for this gold selection we have also implemented the QC1 quality cuts described in Sect. 5.3. As the gold sample is not the same set of photometric galaxies as was used in previous KV450 cosmic shear analyses, we must note clearly that the gold-sample redshift distributions can not be directly applied to these previous analyses. A re-analysis of KV450 cosmic shear using various SOM-defined gold samples will be presented in a forthcoming paper.
Figure 4 shows the estimated gold-sample redshift distributions for KV450. Each panel shows one tomographic bin (the tomographic selection is shown by the grey shaded region), and contains two lines. The first is the unweighted N(z) distribution of the tomographically binned spectroscopic sample (“raw”; purple). The second is the weighted N(z) estimate of the photometric gold-sample (“w,g”; green). The panels are each annotated with the raw and weighted mean redshifts, ⟨z⟩, the difference between the two (Δ⟨z⟩), and the fractional loss of galaxies in the gold sample, of 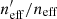 , for each bin (which were also shown in Table 2).
, for each bin (which were also shown in Table 2).
 |
Fig. 4. Our new KV450 redshift distribution estimates, for the gold sample; a reduced photometric sample of galaxies with 100% representation in the spectroscopic sample, and which satisfies the quality cuts QC1. The figure shows the reconstructed redshift distributions (green) alongside the purely tomographically binned spectroscopic data (purple). The figure is annotated with the mean redshift estimates for the purely tomographically binned sample (⟨z⟩raw) and the weighted gold sample (⟨z⟩w, g), the difference that our reweighting has had on the spectroscopic means (Δ⟨z⟩), and the fractional number of galaxies in the gold sample compared to the original KV450 cosmic shear sample |
The redshift distributions demonstrate that the weighting shifts the distribution means by between |Δz| = 0.05 and |Δz| = 0.13; significant shifts for the case of KV450-like cosmic shear studies. More importantly, we note that shifts are coherent, as the raw redshift distributions are consistently at higher redshift than their reweighted counterparts. This observation simply demonstrates the importance of the reweighting process for cosmic shear studies; a simple null test. In the first two tomographic bins the weighted PDF is less peaked than the raw, indicating that the reweighting is increasing the significance of sources in the wings of the distributions. In the highest four tomographic bins, however, the reverse is true; the gold selection and reweighting truncates the wings of the distributions.
6. Summary
We present an updated implementation of direct redshift calibration, utilising unsupervised machine learning methods. We verify, via a suite of simulations, the suitability of currently available spectroscopic datasets for direct calibration, and subsequently the fidelity of the direct calibration methodology as a whole. Testing using both data from the Kilo Degree Survey (KiDS) and simulated data from MICE2, we demonstrate via our SOMs that currently available spectroscopic compilations are sufficiently complete for use in KiDS, representing 99% of the effective 2D cosmic shear sample. The representations decrease slightly when performing tomographic binning, to ∼84% in the first four tomographic bins, and to 94% in the highest tomographic bin. Calibration of stage-III cosmic shear surveys with this archival spectroscopic dataset, however, would likely result in much lower levels of representation (particularly at high-redshift). We demonstrate using mock simulations of KiDS and the spectroscopic training set that these measured representation fractions are robust to the effects of photometric noise, sample variance, and spectroscopic incompleteness. We use this SOM-based selection to define a 100% represented “gold” cosmic shear sample, per tomographic bin. Using our mock simulations, we demonstrate that the mean redshift of the gold sample can be recovered by the SOM perfectly in the absence of photometric noise, agnostic to the effects of sample variance and spectroscopic incompleteness. Photometric noise does not introduce bias when analysing perfectly representative spectroscopic compilations. Under photometric noise and spectroscopic incompleteness, however, we find maximal biases of Δ⟨z⟩ = 0.023 ± 0.006, or Δ⟨z⟩ ≤ 0.035 at 97.5% confidence. The observed scatter in Δ⟨z⟩ in each tomographic bin, σΔ⟨z⟩ ≤ 0.006, is found to be driven equally by photometric noise and spectroscopic selection effects. With limited quality control (which induces a reduction in the effective source number density, Δneff, of ∼5%) these biases can be mitigated, to the maximal bias of: Δ⟨z⟩ = 0.013 ± 0.006, or Δ⟨z⟩ ≤ 0.025 at 97.5% confidence. With more restrictive quality control (Δneff ∼ 20%), the maximal bias can be reduced to Δ⟨z⟩ = 0.009 ± 0.004, or Δ⟨z⟩ ≤ 0.017 at 97.5% confidence. Finally, we apply our new SOM photometric redshift calibration to the KiDS+VIKING-450 data, deriving gold redshift distributions for use in future KV450 cosmological re-analyses.
The associations are defined with respect to the spectroscopic data, meaning that the maximal number of associations is equal to the cardinality of set S. In the kNN method of association m = |S| by definition, because the association is performed by searching independently around each element of the spectroscopic set s ∈ S. In the SOM implementation m is equal to the number of SOM clusters containing spectroscopic data (see Appendix B).
Available at https://github.com/AngusWright/kohonen.git
In the zCOSMOS field observations performed by VISTA have been undertaken extensively for the UltraVISTA survey (McCracken et al. 2012). UltraVISTA observations do not include data taken in the VISTA Z-band, and so we construct a VISTA-Z-like dataset from other deep z′ data in the field, taken with the MegaCAM instrument on the Canada-France-Hawaii-Telescope (CFHT; Bielby et al. 2012; Hudelot et al. 2012). Using this deep data we are able to construct a Z-band substitute that, for the photometric depth and redshift coverage probed by KiDS data, has similar colour properties for all galaxies at all redshifts to better than |z′−Z| < 0.1.
Publicly available at https://www.github.com/KiDS-WL/MICE2_mocks.git
Individual galaxy shear estimates in KiDS are made using the Lens fit algorithm (Miller et al. 2007), which produces an inverse variance weight per galaxy, which is highly magnitude dependant. Therefore matching simulated sources to KiDS galaxies in magnitude space is able to reproduce the shear-weight distribution of KiDS photometric galaxies well.
Sample variance here is used in the standard cosmological context, meaning the variance introduced in astronomical observations of finite area due to large scale structures along the line-of-sight. This is distinct from shot noise and cosmic variance, the latter of which relates to the variance induced by differing realisations of the observable Universe.
Acknowledgments
We thank the anonymous referee for their comments, which have improved the clarity and content of this paper. We acknowledge support from the European Research Council under grant numbers 770935 (AWH, HH, JvdB) and 647112 (CH). HH is also supported by Heisenberg grants (Hi1495/5-1) of the Deutsche Forschungsgemeinschaft. CH also acknowledges support from the Max Planck Society and the Alexander von Humboldt Foundation in the framework of the Max Planck-Humboldt Research Award endowed by the Federal Ministry of Education and Research. We thank C. Morrison for useful discussions. This work is based on observations made with ESO Telescopes at the La Silla Paranal Observatory under programme IDs 100.A-0613, 102.A-0047, 179.A-2004, 177.A-3016, 177.A-3017, 177.A-3018, 298.A-5015. The MICE simulations have been developed at the MareNostrum supercomputer (BSC-CNS) thanks to grants AECT-2006-2-0011 through AECT-2015-1-0013. Data products have been stored at the Port d’Informació Científica (PIC), and distributed through the CosmoHub webportal (cosmohub.pic.es).
References
- Alarcon, A., Sánchez, C., Bernstein, G. M., & Gaztañaga, E. 2019, MNRAS, submitted [arXiv:1910.07127] [Google Scholar]
- Amendola, L., Appleby, S., Avgoustidis, A., et al. 2018, Liv. Rev. Rel., 21, 2 [Google Scholar]
- Asgari, M., Tröster, T., Heymans, C., et al. 2020, A&A, 634, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balestra, I., Mainieri, V., Popesso, P., et al. 2010, A&A, 512, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bielby, R., Hudelot, P., McCracken, H. J., et al. 2012, A&A, 545, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buchs, R., Davis, C., Gruen, D., et al. 2019, MNRAS, 489, 820 [NASA ADS] [CrossRef] [Google Scholar]
- Carretero, J., Castander, F. J., Gaztañaga, E., Crocce, M., & Fosalba, P. 2015, MNRAS, 447, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Crocce, M., Castander, F. J., Gaztañaga, E., Fosalba, P., & Carretero, J. 2015, MNRAS, 453, 1513 [NASA ADS] [CrossRef] [Google Scholar]
- Davidzon, I., Laigle, C., Capak, P. L., et al. 2019, MNRAS, 489, 4817 [NASA ADS] [CrossRef] [Google Scholar]
- de Jong, J. T. A., Verdois Kleijn, G. A., Erben, T., et al. 2017, A&A, 604, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Edge, A., Sutherland, W., Kuijken, K., et al. 2013, The Messenger, 154, 32 [NASA ADS] [Google Scholar]
- Everitt, B. 1974, Cluster Analysis/[by] Brian Everitt (London: Heinemann Educational [for] the Social Science Research Council), VI, 122 [Google Scholar]
- Fosalba, P., Crocce, M., Gaztañaga, E., & Castander, F. J. 2015a, MNRAS, 448, 2987 [NASA ADS] [CrossRef] [Google Scholar]
- Fosalba, P., Gaztañaga, E., Castander, F. J., & Crocce, M. 2015b, MNRAS, 447, 1319 [NASA ADS] [CrossRef] [Google Scholar]
- Hartigan, J. A. 1975, Clustering Algorithms, 99th edn. (USA: John Wiley & Sons, Inc.) [Google Scholar]
- Heymans, C., Van Waerbeke, L., Miller, L., et al. 2012, MNRAS, 427, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Hikage, C., Oguri, M., Hamana, T., et al. 2019, PASJ, 71, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrandt, H., Erben, T., Kuijken, K., et al. 2012, MNRAS, 421, 2355 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrandt, H., Choi, A., Heymans, C., et al. 2016, MNRAS, 463, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrandt, H., Viola, M., Heymans, C., et al. 2017, MNRAS, 465, 1454 [Google Scholar]
- Hildebrandt, H., Köhlinger, F., van den Busch, J. L., et al. 2020, A&A, 633, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoffmann, K., Bel, J., Gaztañaga, E., et al. 2015, MNRAS, 447, 1724 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyle, B., Gruen, D., Bernstein, G. M., et al. 2018, MNRAS, 478, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Hudelot, P., Cuillandre, J. C., Withington, K., et al. 2012, VizieR Online Data Catalog: II/317 [Google Scholar]
- Joudaki, S., Mead, A., Blake, C., et al. 2017, MNRAS, 471, 1259 [NASA ADS] [CrossRef] [Google Scholar]
- Joudaki, S., Hildebrandt, H., Traykova, D., et al. 2020, A&A, in press, https://doi.org/10.1051/0004-6361/201936154 [Google Scholar]
- Kafle, P. R., Robotham, A. S. G., Driver, S. P., et al. 2018, MNRAS, 479, 3746 [NASA ADS] [CrossRef] [Google Scholar]
- Kohonen, T. 1982, Biol. Cybern., 43, 59 [Google Scholar]
- Korytov, D., Hearin, A., Kovacs, E., et al. 2019, ApJS, 245, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Kuijken, K. 2008, A&A, 482, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuijken, K., Heymans, C., Hildebrandt, H., et al. 2015, MNRAS, 454, 3500 [NASA ADS] [CrossRef] [Google Scholar]
- Kuijken, K., Heymans, C., Dvornik, A., et al. 2019, A&A, 625, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laigle, C., McCracken, H. J., Ilbert, O., et al. 2016, ApJS, 224, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Laigle, C., Davidzon, I., Ilbert, O., et al. 2019, MNRAS, 486, 5104 [NASA ADS] [CrossRef] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Le Fèvre, O., Cassata, P., Cucciati, O., et al. 2013, A&A, 559, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lilly, S. J., Le Brun, V., Maier, C., et al. 2009, ApJS, 184, 218 [Google Scholar]
- Lima, M., Cunha, C. E., Oyaizu, H., et al. 2008, MNRAS, 390, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Masters, D., Capak, P., Stern, D., et al. 2015, ApJ, 813, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Masters, D. C., Stern, D. K., Cohen, J. G., et al. 2017, ApJ, 841, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Masters, D. C., Stern, D. K., Cohen, J. G., et al. 2019, ApJ, 877, 81 [NASA ADS] [CrossRef] [Google Scholar]
- McCracken, H. J., Milvang-Jensen, B., Dunlop, J., et al. 2012, A&A, 544, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McQuinn, M., & White, M. 2013, MNRAS, 433, 2857 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, L., Kitching, T. D., Heymans, C., Heavens, A. F., & van Waerbeke, L. 2007, MNRAS, 382, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Morrison, C. B., Hildebrandt, H., Schmidt, S. J., et al. 2017, MNRAS, 467, 3576 [NASA ADS] [CrossRef] [Google Scholar]
- Naim, A., Ratnatunga, K. U., & Griffiths, R. E. 1997, ArXiv e-prints [arXiv:astro-ph/9704012] [Google Scholar]
- Newman, J. A. 2008, ApJ, 684, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, J. A., Cooper, M. C., Davis, M., et al. 2013, ApJS, 208, 5 [Google Scholar]
- Planck Collaboration VI. 2020, A&A, in press, https://doi.org/10.1051/0004-6361/201833910 [Google Scholar]
- Popesso, P., Dickinson, M., Nonino, M., et al. 2009, A&A, 494, 443 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- R Core Team 2015, R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria [Google Scholar]
- Schneider, M., Knox, L., Zhan, H., & Connolly, A. 2006, ApJ, 651, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Straatman, C. M. S., van der Wel, A., Bezanson, R., et al. 2018, ApJS, 239, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, M., Coupon, J., Hsieh, B.-C., et al. 2018, PASJ, 70, S9 [NASA ADS] [CrossRef] [Google Scholar]
- Troxel, M. A., MacCrann, N., Zuntz, J., et al. 2018a, Phys. Rev. D, 98, 043528 [NASA ADS] [CrossRef] [Google Scholar]
- Troxel, M. A., Krause, E., Chang, C., et al. 2018b, MNRAS, 479, 4998 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzella, E., Cristiani, S., Dickinson, M., et al. 2008, A&A, 478, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venemans, B. P., Verdoes Kleijn, G. A., Mwebaze, J., et al. 2015, MNRAS, 453, 2259 [NASA ADS] [CrossRef] [Google Scholar]
- Ward, J. H. J. 1963, J. Am. Stat. Assoc., 58, 236 [Google Scholar]
- Wehrens, R., & Buydens, L. M. C. 2007, J. Stat. Softw., 21, 1 [Google Scholar]
- Wehrens, R., & Kruisselbrink, J. 2018, J. Stat. Softw., 87, 1 [CrossRef] [Google Scholar]
- Wright, A. H., Hildebrandt, H., Kuijken, K., et al. 2019, A&A, 632, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: SOM implementation
In this appendix, we discuss the influence that the choice of SOM construction parameters and training data has on our estimates of the spectroscopic representation of our dataset, discussed in Sect. 5.1, using our MICE2 simulations.
A.1. SOM construction parameters
Here we detail the various SOM construction parameters that we must consider in order to generate a SOM for use in redshift calibration. There are undoubtedly more optional modifications that one can make to a SOM which are not discussed here, however we endeavour here to describe (albeit briefly) the parameters that are required for SOM generation. We quantify the impact of the choice of each of these parameters in terms of the SOM spectroscopic representation, which we quantify using the effective number density of the cosmic shear sample neff (Eq. (7)).
A.1.1. Dimensionality and topology
Two key choices related to SOM construction are those of the adopted dimensionality and topology. Dimensionality refers to jointly to the number and aspect ratio of individual cells that make up the final manifold which we then project onto 2D. Topology refers to the choices regarding how those cells are spread throughout the manifold.
When considering dimensionality, previous studies have varied in their choices as to the optimum dimension that can and/or should be used. Masters et al. (2015) implement a rectangular SOM with dimension 75 × 105 cells, arguing that the asymmetry in the SOM manifold gives preferential direction to the principal manifold component and thus improves convergence. Conversely, recent work by Davidzon et al. (2019) implements a square SOM with dimension 80 × 80 cells. They present a simple method for determining their optimum SOM dimension using, jointly: the fraction of cells with significant representation (i.e. many galaxies per cell) within the SOM, and the spread in the data about each weight vector relative to the source photometric uncertainties. They optimise their SOM configuration using these parameters and conclude that the 80 × 80 cell SOM is optimum for their application.
We also investigate both the symmetric and asymmetric SOM construction cases. Unlike Davidzon et al. (2019), however, we do not implement a range of SOMs with similar aspect ratio and different cell numbers. Instead, we use two dimensionalities (101 × 101 and 75 × 150), which we believe will exceed the maximum desirable fragmentation of the data (for our purposes). We then implement a hierarchical clustering of the SOM cells to produce n distinct groupings of the data. The importance of the cluster number n is discussed briefly below (Appendix A.1.2) and at length in Appendix B. We argue that this mode of analysis is preferential to using the SOM cells themselves to optimise the number of galaxies per group (as was done in Davidzon et al. 2019), as this separates the two somewhat different issues of optimising galaxy grouping and allowing the SOM due flexibility to accurately map the manifold.
Compounding the matter further, in addition to the raw number of cells in each SOM dimension, there are also questions regarding what cell shape and surface topology is best for the SOM. Cell shape becomes particularly relevant in dense areas of the manifold, where different cell shapes can cause data to be differently distributed in the final SOM (and thus impacting our grouping of like-with-like data). SOM topology, conversely, is most influenced in the sparser areas of the manifold. The choice of topology is typically either flat or toroidal; that is the edges of the SOM manifold are either free or reconnect to form a continuous surface, respectively.
Within our SOM implementation using the kohonen package (Wehrens & Kruisselbrink 2018; Wehrens & Buydens 2007), it is trivial to generate SOMs (and SuperSOMs, where multiple layers are used) with arbitrary dimensionality, using rectangular or hexagonal cells, and across a flat or toroidal manifold. We can therefore test the influence of these construction choices on our final SOMs.
A.1.2. Clustering
On top of performing the training of the SOM using a particular dimensionality and topology, one can then refine the grouping of the data within the SOM by using a hierarchical clustering on the final SOM optimisation tree. In this way, a high-resolution SOM grid can be adaptively lowered in its resolution after training, in an effort to test the influence of the overall clustering to the conclusions.
The choice of SOM clustering is particularly important to our SOM direct redshift calibration, as it dictates the number of discrete weights which are available to reweight the spectroscopic data. In addition, the coarseness (or fineness) of the SOM clustering will influence the width of the per-cluster N(z) distributions, possibly inducing biases if the clustering level is too small.
Due to its importance, we dedicate Appendix B to the exploration of SOM clustering, and its influence on our results. We find though, that the total number of clusters is irrelevant to our results beyond roughly 2000 (see Appendix B). For all tests in this work we use cluster numbers defined on the KV450 data, as described in Appendix B.
A.1.3. Training data
Finally, the training data itself is naturally of great importance to the fidelity of the SOM in terms of spectroscopic representation and redshift calibration. This includes the question of what information (from a given sample) is relevant to parse to the SOM for training. Given 9-band photometric data, the options are many-fold; as such we test a range of combinations of colours and magnitudes. Specifically, we test our training using each of the following combinations of colours and/or magnitudes: nine magnitudes only (0:9), eight colours only (8:0), eight colours and one magnitude (8:1), 37 colours and one magnitude (37:1), and 37 colours and nine magnitudes (37:9). Each of these options could provide more information to the SOM, allowing the calibration to improve, or it may add too-much redundancy to the dataset and dilute the maps ability to extract colour–redshift information.
In addition to which information to parse to the SOM during training, there is also an important question regarding which data to use for the training; what sample do we parse for training, and how does the sample’s cosmic variance, photometric noise, and object selection influence the results. To investigate the importance of the sample itself we can construct KV450-like spectroscopic samples, samples which are missing large and unique parts of the colour–redshift space, and/or perfectly representative spectroscopic compilations.
A.2. Parameter selection and uncertainties
Determination of the SOM parameters is, at least to some degree, arbitrary. That is, we may make some assumptions about the nature of the high-dimensional manifold and use this to influence our choices of dimension, topology, clustering, and training data; but due to our inability to visualise greater than 3-dimensional space, these assumptions will always be imperfect. Indeed, this is part of the reason SOMs were developed in the first instance.
We extend the methodology of Davidzon et al. (2019) to determine an optimal SOM construction, marginalising over arbitrarily chosen parameters in our SOM construction to produce an estimate of the method-induced uncertainty on our estimates of spectroscopic representation and redshift calibration accuracy. We perform a 2-stage process to (a) determine the SOM parameters that are most suitable for our analysis, and (b) quantify and incorporate the uncertainty on our analysis introduced by these somewhat arbitrary choices. To this end, we perform the SOM construction for our MICE2 simulations using the full grid of SOM options. We therefore test our construction using all combinations of differing dimensionality (75 × 150 or 101 × 101), topology (toroidal or non-toroidal), cell structure (hexagonal or rectangular), iteration steps (100 or 1000), training parameters (0:9, 37:1, or 37:9), and training data (KV450-like, noDEEP2, or perfectly sampled). We choose these options as we believe that they span the full gambit of possible options from the simplest (a square, non-toroidal SOM with rectangular cells, trained on 9-band photometry from a perfectly representative spectroscopic dataset) to the most complex (a rectangular, toroidal SOM with hexagonal cells, trained on 37 colours and 9 mag for a heavily biased spectroscopic sample). This creates a sample of 144 individual SOM setups, which we run for each of our 5 tomographic bins. Again, in order to maintain consistency between the different dimensionalities, we run these tests with the number of clusters set at 10 000. These options are all equally valid. It is therefore our hope that the resulting redshift distributions from each of these SOMs are largely consistent. Or, inverting the situation, we can use this grid of optional and arbitrary parameter choices to generate an estimate of the uncertainty imprinted on the final SOM calibration related to our choice of parameters; essentially exploring the uncertainty on the SOM N(z) when marginalising over the arbitrarily selected SOM construction parameters.
To quantify the influence of the SOM construction parameters, we use the measured representation of the spectral catalogue, quantified using the 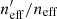 statistic from Sect. 5.1. This indicates the level to which the photometric data are represented by the spectroscopic catalogue.
statistic from Sect. 5.1. This indicates the level to which the photometric data are represented by the spectroscopic catalogue.
Figure A.1 shows the resulting values of 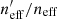 for our grid of SOM construction parameters, grouped into five individual (dominant) factors: the choice of input training parameters, and of training data.
for our grid of SOM construction parameters, grouped into five individual (dominant) factors: the choice of input training parameters, and of training data.
 |
Fig. A.1. Change in the effective number density of the MICE2 cosmic shear sample |
The choice of training parameters has a noticeable effect on the observed representation fractions, as the differing photometric information allow the SOM to learn more about the nature of SEDs. While one may naively expect the SOM to have equal success when provided with either 9 mag or 37 colours and 1 mag (i.e. all magnitude combinations), this is infact not the case. This can be seen in Fig. A.1 where, for example, the first tomographic bin representation (85% for the fiducial 37:1 training) has a considerably lower spectroscopic representation when trained on purely magnitude information alone (i.e. no colours; 76%). The interpretation of this is that, when providing the SOM with purely magnitude based training data, the SOM must learn itself that it is the magnitude combinations (i.e. the colours) which are important discriminants of the data. This learning appears to be facilitated better when the SOM is provided with all of the colours directly, especially in the lowest tomographic bins. The redundant information still has benefits in the training there. Interestingly, however, the addition of the raw magnitudes back into the training set with the full combination of colours has little effect (compare the 37:1 and 37:9 histograms in Fig. A.1); the information from the colours alone appears to saturate for KiDS-like data.
Finally, we look at the influence of the different training samples. While discussed at length in Sect. 5.1, we note here that the conclusions we make about the representation of individual spectroscopic subsets (such as zCOSMOS, DEEP2, and VVDS) are not impacted by the construction of our SOM. This can be seen by the noDEEP2 and perfect spectroscopic compilation histograms in Fig. A.1. They show that the construction only causes a ∼1% uncertainty on the overall representation statistics, regardless of the choice of training sample. Said differently, we conclude that the results presented in Sect. 5.1 are robust to the choices made in our SOM construction.
Appendix B: Influence of cluster number
With our SOM-based direct photometric redshift calibration method (Sect. 2), the weights which are applied to each spectroscopic galaxy are estimated using the groupings of self-similar photometric and spectroscopic data, as determined by the SOM. This creates a fundamental link between the number of groupings made and the flexibility of our method to reweight the spectroscopic data: increasing the number of groups allows for a more flexible weighting scheme. However there is also a counter-effect: with increased fragmentation of the datasets comes increased fractions of the photometric dataset which are no longer represented by the spectroscopy. These lost photometric sources decrease the signal-to-noise of cosmic shear, negatively impacting cosmic shear science. Therefore, a careful consideration of the interplay between the grouping of galaxies and redshift distribution estimation is crucial. In this appendix, we explore the interplay between the number of SOM groupings, the accuracy of the calibrated redshift distributions, and the number of sources which are represented by spectroscopy and therefore make it into our photometric “gold sample”.
First, we discuss the process of grouping galaxies within the SOM. In the simplest case, the grouping of galaxies can be determined by the SOM cells themselves. This necessitates adapting the number of SOM cells to the point where one is happy with the typical number of sources per group; such a process places a conflict between group number and SOM resolution.
SOM resolution is important in determining the ability of the SOM to map complex areas of the hyper-surface accurately. Therefore, instead of restricting the accuracy of the SOM surface mapping for the sake of increasing the number of galaxies per grouping, it would be optimal to generate the surface mapping using a high-dimensional grid and then group these SOM cells together post-facto, to produce the desired number of galaxies per grouping.
This is the process that we invoke here. To do this we utilise the native “hclust” function within R (R Core Team 2015). This function performs a hierarchical cluster analysis using a set of dissimilarities for the n objects being clustered. We opt to use a simple Euclidean distance matrix between SOM codebook vectors (i.e. the set of n vectors which jointly describe where a cell sits in n-dimensions) as our clustering basis. Initially, each object is assigned to its own cluster and then the algorithm proceeds iteratively, at each stage joining the two most similar clusters, and continuing until there is just a single cluster. At each stage distances between clusters are recomputed by the Lance-Williams dissimilarity update formula according to the particular clustering method being used. A number of different clustering methods are provided. We implement the complete linkage method of clustering, which finds similar clusters. This is preferable (for our purposes) compared to, for example, Ward’s minimum variance method (which aims at finding compact, spherical clusters in N dimensions; Ward 1963) or the single linkage method (which is closely related to the minimal spanning tree and adopts a “friends of friends” clustering strategy). Details of these algorithms and their implementation can be found in Everitt (1974), Hartigan (1975), and in the extensive R documentation. Using this clustering methodology, can group a SOM consisting of ∼10 000 cells into 3000 groupings, each with a different number of component cells (and therefore galaxies). We are thus able to generate arbitrary numbers of groupings without sacrificing SOM resolution.
Figure B.1 demonstrates the influence of the number of SOM hierarchical clusters on the resulting tomographic bin redshift means, the recovered photometric misrepresentation, and the redshift bin biases for the 100 line-of-sight realisations of our MICE2 simulated dataset. We compare the mean of the estimated tomographic redshift distribution with the final (most highly clustered) estimate, after the removal of sources that are classified as being unrepresented in the spectroscopic compilation (panel a). This allows us to explore how the mean estimates themselves are influenced by the choice of cluster number. Photometric misrepresentation is defined in using the same neff statistics as used in Sect. 5.1 (panel b). Finally the redshift distribution biases (panel c) are measured by comparing the estimated and mean true redshift distributions for each number of clusters. We show the bias of the individual redshift distribution estimates also after subtracting off the residual bias from the highest cluster number estimate (⟨z⟩max). Again, this allows us to remove the effects of noise and sample variance, which induce a maximal scatter and bias of σΔ⟨z⟩ ∼ 0.006 and |Δ⟨z⟩| ≤ 0.01 respectively (see Sect. 5.3).
 |
Fig. B.1. Influence of the number of SOM clusters on the resulting tomographic bin redshifts and the recovered photometric misrepresentation for the MICE2 simulation dataset. We show three statistics as a function of cluster number. Panel a: change in the tomographic mean estimate. Panel b: change in the representation of the spectroscopic catalogue. Panel c: change in the tomographic mean bias. The inset of panel a shows the distribution of PDFs estimated for the third tomographic bin with 10 000 and 2500 clusters. The black curve shows the distribution of the unweighted spec-z sample. Panel a demonstrates that, with increasing cluster number, our estimate of the tomographic redshift distribution mean changes significantly. Middle panel: demonstrates why: with more clusters there is more fragmentation of the photometric data and significant decreases in the spectroscopic representation, such that the “gold” sample decreases in size. However, crucially, panel c demonstrates that the loss of representation does not change the low level of bias in the recovered redshift distribution. |
Panel a of Fig. B.1 shows that the mean estimates appear quite sensitive to the choice of cluster number. The mean estimate for tomographic bin 1 varies by |⟨z⟩n − ⟨z⟩max|≈0.02 over the probed range of clusters. Simultaneously, as can be seen in panel b, the representation is also changing significantly. This is an indication of the loss of (typically high-redshift) sources that we experience when we overly fragment our SOM groupings. While this will considerably impact the cosmic shear signal for the final gold sample, it is important to recognise that these two effects, however, work in tandem to ensure that the final bias on each of the tomographic bin means remains negligible over essentially the entire range of cluster choices (panel c).
Overall, Fig. B.1 demonstrates that, beyond the regime where the clusters are large (and so the reweighting flexibility is small), the accuracy of the tomographic redshift calibration is essentially insensitive to the choice of the number of clusters. This is certainly not the case for the representation statistics, however, and therefore which we seek to maximise for our goal of cosmic shear science.
We typically observe a joint decrease in representation and bin average redshift with increasing cluster number. This indicates that the data being removed are preferentially at high-redshift, likely being expelled due to fluctuations in photometric noise; the spectroscopy scatter between SOM cells where the similarly-noisy photometric data reside.
This loss of high-redshift sources is relevant for both cosmic shear science and the representation statistics presented in Sects. 5.1 and 5.2. We can see from panel b of Fig. B.1 that, if we were to use only 10 clusters, we would infer that the spectroscopic catalogue was perfectly representative. However naturally this is a false interpretation, because hidden within this clustering are groups of cells with vastly different true N(z) distributions. Similarly, using the maximal cluster number will produce a very high fidelity gold sample, and a very accurate calibrated redshift distribution. However this distribution will be severely lacking in the highest-redshift sources; those which carry the most cosmic shear signal. We must therefore decide on the criteria to determine which number of clusters is adequate or necessary for the correct description of the data, without causing sources to be unnecessarily lost from our gold sample.
We can tie this decision back to our overall goal of photometric redshift calibration. Using the simulations, we can determine the point below which there are insufficient clusters to accurately recover the true redshift distribution, and use this as our cluster number for the simulations. Indeed, such an estimate would require only a simple threshold to be applied in panel c of Fig. B.1. However naturally such a determination cannot be made on the data (as the truth is not known) and the application of values estimated with the simulations to the data may risk bias: we know that the MICE2 simulations truncate abruptly at z = 1.4, whereas the Universe thankfully does not. Instead, we can define the clustering using a quantity that is measurable on both the simulations and the data: the change in the mean redshift (for a particular number of clusters n; ⟨z⟩n) compared to the maximally clustered data (i.e. where every cell is an individual cluster; ⟨z⟩max). This is the statistic shown in panel a of Fig. B.1, and now we also compute this statistic for the real KV450 data in Fig. B.2. Using this figure, we can apply a simple threshold and determine the acceptable number of clusters to use in our representation estimation. We opt to use a value of |⟨z⟩n − ⟨z⟩max| ≤ 0.01, and the resulting cluster numbers are shown using the dashed lines in the figure. Figure B.2 shows that the mean estimates do vary, and the strong function of representativeness as a function of cluster number is also evident in data, as with the simulations. Again, though, it is important to note that this value of |⟨z⟩n − ⟨z⟩max| ≤ 0.01 is not equivalent to a bias of |Δ⟨z⟩| ≤ 0.01, as was shown in Fig. B.1, as the “gold” sample for the maximally clustered case is very different from the optimal sample.
 |
Fig. B.2. Influence of the number of SOM clusters on the resulting tomographic bin redshifts and the recovered photometric misrepresentation for the full KV450 photometric and spectroscopic datasets. The figure is constructed in the same way as Fig. B.1. Here we additionally show the point at which the tomographic bin mean redshifts cross the |⟨z⟩n − ⟨z⟩max| ≤ 0.01 boundary (shown with grey shading). This criteria designates our per-tomographic-bin cluster-number choice for this work. |
We use Fig. B.2 to define the cluster number which we use for the entirety of this work, for both simulations and data, per tomographic bin. We determine the cluster number which satisfies |⟨z⟩n − ⟨z⟩max| ≤ 0.01, and annotate these points as dashed lines within the figure. We round these points to the nearest 100 clusters, and in this way define the number of clusters used to determine the representation statistics for the KV450 spectroscopic compilation, and determine which sources make up our photometric “gold sample”. The numbers for bins one to five are, respectively: nclust = 6200, 2700, 3500, 4400, 2200.
Appendix C: Spectroscopic versus photometric training
Previous works such as the C3R2 project aim to determine the sampling of spectroscopic data by constructing a SOM trained on the photometric data; essentially performing the reverse of our implemented method. The C3R2 project find a considerable number of cells (in Euclid-like data) which are lacking spectroscopic information. This raises the concern that our training on spectroscopic data may miss bubbles of n-dimensional colour space, and that photometric data in these bubbles would then be randomly scattered throughout our SOM, creating biases.
This is a fair concern, and is grounded in the idea that the SOM is unable to learn about parts of colour–colour space that are simply not present in the spectroscopic training data. Such an effect will be successfully mitigated in our methodology provided that the SOM is able to correctly partition sources from untrained parts of colour–colour space into specific cells; that the SOM has learned that there is a gap in its training set. We can test the robustness the influence of our choice of training in two ways. Firstly, we can simply perform our training using the photometric dataset, assess the quality of the resulting SOM, and estimate the robustness of our results to this alternative training. Secondly, we can perform our fiducial training on a spectroscopic compilation that we know is catastrophically under-representative in colour–redshift space, and determine the robustness of our results in this case.
C.1. Photometric training
We test how our method performs when training on the photometric dataset, rather than the spectroscopic. All other aspects of the process are the same (i.e. the bands used, SOM construction, cluster determination, etc.). We start by comparing the suitability of the photometrically trained SOM for use in our redshift distribution calibration method by exploring firstly the per-cluster N(z) distributions, and secondly the coverage statistics described in Sect. 5.1.
A primary assumption of our SOM photometric redshift calibration method is that the N(z) distributions assigned to each group within the spectroscopic catalogue be narrow; ideally delta-function like. We can estimate the typical spread of each cluster N(z) using the distribution of nMAD values for the spec-z within each cluster. In our spectroscopically trained SOM, the 75th percentile of the cluster N(z) width distribution (per tomographic bin) is Δzclust/(1 + zclust) ∈ {0.043, 0.048, 0.060, 0.048, 0.086} (we show the 75th percentile as the median nMAD is 0 for the first two tomographic bins). This indicates that the majority of cells (agnostic to the photometric representation therein) have typical spreads of Δzclust/(1 + zclust) ≲ 0.08 in all tomographic bins. Comparatively, the photometrically trained SOM has an average cluster N(z) width of Δzclust/(1 + zclust) ∈ {0.050, 0.040, 0.075, 0.055, 0.093}; 1−2% poorer than the spectroscopic training in all but the second bin. The same conclusion holds when weighting the clusters by their contribution to the tomographic effective number density (i.e. when weighting each cluster nMAD estimate by the photometric shear-measurement weights).
This demonstrates that, for the purposes of our redshift distribution calibration, the spectroscopic training yields groupings that more explicitly trace the colour–redshift relation than our photometric training. Examination of the photometric representation statistics gives an indication as to why this may be the case. We compute the representation statistic 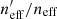 (shown in Table 2), but now for our SOM trained on the photometric data. The most dramatic change seen is in the fraction of cells which contain spectra (fpix). In our spectroscopically trained SOM this was fpix = 91.9%. For the photometrically trained SOM this value drops significantly, to fpix = 66.9%. However this is not accompanied by a corresponding catastrophic drop in the overall representation of the photometry:
(shown in Table 2), but now for our SOM trained on the photometric data. The most dramatic change seen is in the fraction of cells which contain spectra (fpix). In our spectroscopically trained SOM this was fpix = 91.9%. For the photometrically trained SOM this value drops significantly, to fpix = 66.9%. However this is not accompanied by a corresponding catastrophic drop in the overall representation of the photometry: 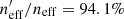 for our photometrically trained SOM. This indicates that considerable area (>20%) within our photometrically trained SOM is being allocated to photometric data which contribute just 6% of the shear measurement weight. As a result, the spectroscopic data are assigned to fewer SOM cells and therefore have greater per-cluster widths. Otherwise, the photometrically trained SOM demonstrates the same trends as seen in Table 2; DEEP2 remains the most unique and influential of our spectroscopic sub-samples, and different samples dominate the information contained in different tomographic bins. Finally, the representation of the photometric data is poorer in the first three tomographic bins when training on the photometric data,
for our photometrically trained SOM. This indicates that considerable area (>20%) within our photometrically trained SOM is being allocated to photometric data which contribute just 6% of the shear measurement weight. As a result, the spectroscopic data are assigned to fewer SOM cells and therefore have greater per-cluster widths. Otherwise, the photometrically trained SOM demonstrates the same trends as seen in Table 2; DEEP2 remains the most unique and influential of our spectroscopic sub-samples, and different samples dominate the information contained in different tomographic bins. Finally, the representation of the photometric data is poorer in the first three tomographic bins when training on the photometric data, 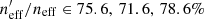 , with the second tomographic bin being the most heavily affected. In the highest two tomographic bins, however, the representation statistics remain unchanged under photometric training;
, with the second tomographic bin being the most heavily affected. In the highest two tomographic bins, however, the representation statistics remain unchanged under photometric training; 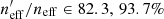 .
.
C.2. Catastrophically unrepresentative training
We can further test whether the SOM methodology is robust to the influence of such a catastrophic absence of data in the training sample. The simplest way to do this is to construct two trained SOMs: one based on the full spectroscopic compilation, and one based on the spectroscopic compilation without DEEP2 (our most influential dataset). We have already demonstrated that DEEP2 occupies a unique area of the colour-manifold (see Sect. 5.1), and so we know that the SOM trained without DEEP2 will be missing a large, unique, part of the colour–colour training set. We can then populate each of these SOMs with the full spectroscopic and photometric datasets and determine, firstly, how the photometric misrepresentation of the full photometric dataset differs between the two SOMs, and, secondly, how the DEEP2 data are distributed within the two different SOMs.
Figure C.1 shows our two trained SOMs, coloured by the counts of the spectroscopic and photometric datasets. The figure shows that the two SOMs distribute the photometric and spectroscopic data somewhat differently under the two trainings. Using the wedge of empty cells in the photometric SOMs for orientation11 (these are the bright-galaxy cells which exist in the spectroscopic compilation but not in the lensing sample), we can see that the no-DEEP2 training is dispersing the spectral and photometric data over a greater area within the SOM manifold. Put differently, the manifold cells have adapted to allocate fewer cells to the area of colour–colour space that houses DEEP2 and is missing from the training set. However, importantly, that space has still been mapped and allocated space within our SOM. This can be seen in Fig. C.2, which shows the same two SOMs now coloured by the occupation statistics of DEEP2, zCOSMOS, and CDFS (as in Fig. 2). The visual effect is clear; there are far fewer exclusively-DEEP2 (blue) cells in the no-DEEP2 trained SOM. Indeed, there is a ∼11% decrease in the total number of cells assigned to DEEP2: from 42.8% in the fiducial case to 31.8% in the no-DEEP2 training. This decrease in real estate, however, is not accompanied by a significant change in the estimated misrepresentation of the photometric data; a change of only 1% is seen.
 |
Fig. C.1. Distribution of spectroscopic (left column) and photometric (right column) data, within our SOMs trained on the full spectroscopic compilation (top row) and the without-DEEP2 compilation (bottom row). The photometric data have similar structures (the missing bright-magnitude wedge can be used as a reference in each of these panels). Despite the different distribution of spectral and photometric data in the two SOMs, the representation statistics remain essentially unchanged: in both cases ∼5% of the photometric data occupy cells not containing spectra. |
 |
Fig. C.2. Fractional occupation per SOM cell of each of the DEEP2, zCOSMOS, and VVDS samples. The upper row repeats the fiducial training shown in Fig. 2, which can be compared to the no-DEEP2 training in the lower row. DEEP2 is assigned far fewer cells in the SOM trained on the spectroscopic dataset excluding DEEP2 (∼11% fewer). |
So, the training without DEEP2 does cause a significant change in the SOM area allocated to the missing spectroscopic data. Crucially, however, the spectroscopic and photometric data which belong to DEEP2 are still correctly allocated to the same cells. The SOM has recognised that there is an area of colour–colour space missing, but naturally does not assign it the same weight in the final manifold mapping. Therefore, we conclude that, even in the case of catastrophically missing spectral data, we will not see extensive contamination of the redshift calibration by sources arbitrarily distributed within the SOM space.
Appendix D: N(z) biasing via sample selection
In the SOM photometric redshift calibration method we assume that redshift distributions per SOM cell or cluster are narrow, and therefore that each cell traces a single population of galaxies in colour–redshift space. When this assumption does not hold, the method can become sensitive to differences between population distributions in the photometric and spectroscopic samples. To combat this effect we implement tomographic binning of both the photometric and spectroscopic samples, in contrast to previous direct calibration implementations (see for example Hildebrandt et al. 2017, 2020). In this appendix, we demonstrate the importance of ensuring that photometric and spectroscopic samples have consistent redshift-dependent selection functions applied, and how the invocation of a SOM based direct redshift calibration without consistent selection functions can lead to considerable bias in the recovered redshift distributions.
We first consider a trained SOM which maps the full colour–redshift space of our MICE2 simulations. Figure D.1 shows the distribution of mean (simulated or true) redshifts within individual SOM cells (⟨z⟩phot, all; left panel). The cells map the colour–redshift distribution of the training sample, and we can see from the PDF of the ⟨z⟩phot, all values (shown within the colour-bar) that the number of cells with a particular mean redshift, closely traces the redshift distribution of the spectroscopic data (see Fig. 1 for comparison). cells in the SOM generally have a narrow spectroscopic redshift distribution (⟨σz⟩ = 0.08), however photometric noise and colour redshift degeneracies mean that cells can have low-significance wings in the redshift distribution. Such wings need not be a significant source of uncertainty or bias in redshift distribution calibration, provided that the spectroscopic and photometric data are similarly affected. The photometric and spectroscopic data must share the same noise properties over the manifold, which causes galaxies to scatter around the map in a consistent manner.
 |
Fig. D.1. Left: distribution of mean redshift as a function of SOM cell for the fiducial MICE2 simulation. Right: distribution of the difference in SOM cell mean redshifts for the full photometric sample compared to the first tomographic bin. The figure demonstrates that the N(z) of the high-z SOM cells in the lowest tomographic bin is systematically different to those cells in the full sample. This effect creates the bias observed in the SOM direct calibration. |
This requirement can, however, be easily violated. The right panel in Fig. D.1 shows the difference between SOM cell mean redshifts for the full photometric sample (⟨z⟩phot, all, as in the left panel) and the cell means of the same data after selecting only sources within the first tomographic bin (⟨z⟩phot, 1). Firstly we can see that the photometric galaxies in the first tomographic bin preferentially trace the low-redshift SOM cells; photometric redshift strongly correlates with SOM cell redshift. However due to the considerable size of the photometric catalogue, there are many nominally high-redshift cells which contain photometric galaxies that are exclusively at low-redshift, thus creating a considerable population of highly biased cells (⟨z⟩phot, all − ⟨z⟩phot, 1 > 0.1). It is clear from the figure that the high-z portion of sources in the first tomographic bin has a systematically biased per-cell N(z) compared to the overall sample. This in turn causes the reweighting to over-represent the high-z data in the log-z tomographic bins, leading to a bias in the estimated redshift distributions.
The conclusion is thus: tomographic binning imposes a strong redshift dependent selection on the photometric catalogue. This selection modifies the true N(z) per SOM cell for the photometric catalogue, thereby introducing a bias in the redshift calibration. Interestingly this effect cannot be mitigated by pre-selecting cells based on their spread in spectroscopic (or even simulated) redshifts. The asymmetric sampling of the N(z) affects all cells to some degree, and down-selecting cells based on their initial spread fails to remove the bias at any significant level. For this reason, in our analysis we apply tomographic binning to both the spectroscopic and photometric catalogues.
The observations here have a more fundamental impact, though, than simply that of dictating the method of implementing tomographic binning in our SOM. The result acts as a cautionary tale for all works utilising direct comparisons between SOM-based groupings of training and analysis data. It suggests that any form of systematic selection which differs between the training and analysis groupings used in SOM analysis has the ability to introduce complex biases. Should this bias be noise-dependent then the effect increases, as inter-cell scatter also varies between the two datasets.
Such an observation may be of importance to other SOM-based clustering studies, such as those of Davidzon et al. (2019) and Buchs et al. (2019). That is, should there exist even subtle noise and selection differences between the training and analysis datasets used in any SOM clustering study, it is possible that non-trivial biases in inference can be introduced.
Appendix E: Catastrophic spec-z failures
In Hildebrandt et al. (2020) the authors tested the impact of calibrating KiDS cosmic shear redshift distributions using the high-fidelity photometric redshift compilation of Lilly et al. (2009), finding that it caused a shift in their estimate of 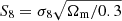 . It has been hypothesised that this observed shift could be due (at least in part) to the presence of catastrophically misidentified spectroscopic redshifts in the spectroscopic compilation used for direct photometric redshift calibration. One such form of catastrophic misidentification was reported recently in Laigle et al. (2019), where they explored outliers in the COSMOS15 (Laigle et al. 2016) photo-z vs. spec-z distribution and found ∼35% of outliers (which equates to roughly 1.3% of all sources) had evidence of contamination within the spectroscopic slit. The implication of this study being that ∼35% of outliers in the COSMOS15 photo-z vs. spec-z distribution are not failures of the photo-z, but rather are caused by failures in the spectroscopy. Should such a population of failed spectroscopic redshifts also be present in the spectroscopic compilation used for direct calibration, considerable increases in reconstruction bias could occur.
. It has been hypothesised that this observed shift could be due (at least in part) to the presence of catastrophically misidentified spectroscopic redshifts in the spectroscopic compilation used for direct photometric redshift calibration. One such form of catastrophic misidentification was reported recently in Laigle et al. (2019), where they explored outliers in the COSMOS15 (Laigle et al. 2016) photo-z vs. spec-z distribution and found ∼35% of outliers (which equates to roughly 1.3% of all sources) had evidence of contamination within the spectroscopic slit. The implication of this study being that ∼35% of outliers in the COSMOS15 photo-z vs. spec-z distribution are not failures of the photo-z, but rather are caused by failures in the spectroscopy. Should such a population of failed spectroscopic redshifts also be present in the spectroscopic compilation used for direct calibration, considerable increases in reconstruction bias could occur.
We therefore explore the effect of introducing catastrophic spec-z failures into the spectroscopic compilation. To simulate spectroscopic failures of the kind explored by Laigle et al. (2019), we make the conservative assumption that the observed fraction of catastrophic spectroscopic failures in the COSMOS15 observations of Laigle et al. (2019) apply equally to all samples within our spectroscopic dataset, even though this is known to be untrue. DEEP2, for example, is analysed such that any spectra which show features from multiple redshifts are always given low confidence (and are not included in the direct calibration compilation). Additionally, some spectra in DEEP2 are observed twice with different slit orientations, allowing estimation of the fraction of slit-orientation-induced catastrophic redshift failures. Their analysis indicates that repeated observations produce repeated reliable (nQ ≥ 3) redshifts 86% of the time, and that these discrepant 14% are dominated by technical failures or simply low signal-to-noise ratio (S/N) in one of the observations. Crucially, they find that pairs of high-confidence (expected 95% reliability; nQ = 3) and certain (expected 99.5% reliability; nQ = 4) sources have redshifts that differ by more than 500 km s−1 only 0.68% and 0.24% of the time, respectively (Newman et al. 2013). Therefore catastrophic failures of the form seen in Laigle et al. (2019) are, at minimum, greatly suppressed in DEEP2.
To simulate the effect of catastrophic misidentification of this type, we first identify the appropriate number of spectra to contaminate as a function of i-band magnitude. We do this by taking the observed photo-z vs. spec-z outlier rates, as a function of i-band magnitude, from Table 2 of Laigle et al. (2019): 1.7, 6.7, 10.2, 22.0% for the magnitude bins i ∈ (−∞, 23), [23, 24), [24, 25), [25, ∞). Again to be conservative, we have allowed the upper and lower magnitude bins to be open-ended; the brightest bin extends to all bright magnitudes and the faintest bin extends to all fainter magnitudes. The faint end choice, however, is of little consequence; there are very few spectroscopic sources in our simulation with i-band fluxes fainter than 24th magnitude.
We use the estimated outlier fractions and observed fraction of outlier spec-z failures to generate the relevant fraction of catastrophic mis-identifications in our MICE2 mock KiDS spectroscopic dataset. This equates to 0.6, 2.3, 3.6, 7.7% spec-z failures within each of the i-band magnitude bins. Weighting each of these bins by the number of spectra therein produces an expected catastrophic failure rate for our simulations of 1.07%. This is slightly lower than the same calculated on the real KV450 spectroscopic compilation (1.27%), due to the simulated spectroscopic data being slightly shallower than the full spectroscopic dataset. In order to account for this difference, we artificially inflate the rate of catastrophic failures across the full magnitude range by 25%, to 43.7% of observed outliers. This produces a simulated catastrophic outlier fraction of 1.33%, which we use for the following tests. We simulate the production of catastrophic failures in 3 ways.
1. We assume that the misidentified spec-z must come from a source with an observed i-band magnitude at least as bright as the source that it is replacing. This failure mode implies that the brightest of two sources within the slit will be the one for which a redshift is reported, and produces catastrophic failures that preferentially move to lower redshifts than the original source.
2. We allow the catastrophic redshift to be sampled arbitrarily from the distribution of all spectra. This mode of failure replicates the circumstance where the observed (secure) redshift distribution of a spectroscopic survey is determined exclusively by the true redshift distribution of the galaxies within the survey volume and the secure-redshift success function (dictated predominantly by the telescope and spectrograph design: wavelength range, resolution, spectrum S/N, etc.); that is, that there is no significant redshift-dependant spectroscopic pre-selection. If this is the case, catastrophic failure can only occur when the contaminating galaxy has a true redshift which lies within the secure-redshift success window. Therefore, catastrophic failure in this mode can be simply drawn from the observed distribution of galaxies with successful redshift estimates. This mode of failure will be increasingly unrealistic with increasingly heavy spectroscopic colour-preselection, however.
3. We allow catastrophic failures to be sampled uniformly in the simulation redshift range. For each of these three cases we generate such a contaminated sample 100 times, and calculate the resulting tomographic redshift distributions each time.
The results of our contaminations on each of the tomographic bins is shown in Table E.1. We find that the maximally induced bias is at the Δ⟨z⟩ < 0.005 level, and so is of little concern to our analysis12. This is true for all three forms of catastrophic failure in our MICE2 simulations. The maximal bias is also seen always in the highest tomographic bin, which is dominated by the DEEP2 dataset and therefore will have significantly better contamination properties than is assumed here. We therefore conclude that the catastrophic misidentification of spec-z, even for a greater fraction of spectra than is known to be possibly affected, cannot cause significant systematic biases in the estimated SOM redshift distributions for KiDS-like surveys.
Effect of catastrophic spec-z misidentification on the estimated SOM tomographic bin mean redshifts.
All Tables
Spectroscopic redshift samples used for the direct redshift calibration in KiDS.
Biases in the mean redshift estimation (Δ⟨z⟩ = ⟨z⟩est − ⟨z⟩true), per tomographic bin, for our various runs of the MICE2 simulations.
Effect of catastrophic spec-z misidentification on the estimated SOM tomographic bin mean redshifts.
All Figures
 |
Fig. 1. Spectroscopic redshift distribution of our combined spectroscopic calibration dataset. The figure shows the redshift distribution as a kernel density estimate (KDE), constructed using a rectangular δz = 0.1 kernel. The KDE is weighted such that lines are interpretable as the instantaneous counts per δz. The KDE is coloured by the fractional contribution from each of our five datasets to the total, which is shown by the black line. |
| In the text | |
 |
Fig. 2. Distribution of the three primary KV450 spectroscopic samples within the SOM. The figure on the left shows the SOM coloured by the fractional contribution of each of the three main spectroscopic samples from KV450. The ternary colour bar is shown on the right. The makeup of individual cells is annotated within the colour-bar as points. SOM cells that are filled entirely by sources from DEEP2, for example, are blue. Conversely cells that are filled by equal mixtures from all three samples are grey. Cells which contain spectroscopic data from other surveys (which are not shown) are coloured white. Cells which contain photometric galaxies but no spectroscopy from any survey are coloured black. The figure highlights the complementarity between the DEEP2 and zCOSMOS data, as well as the breadth of coverage of the VVDS data. |
| In the text | |
 |
Fig. 3. Change in the value of |
| In the text | |
 |
Fig. 4. Our new KV450 redshift distribution estimates, for the gold sample; a reduced photometric sample of galaxies with 100% representation in the spectroscopic sample, and which satisfies the quality cuts QC1. The figure shows the reconstructed redshift distributions (green) alongside the purely tomographically binned spectroscopic data (purple). The figure is annotated with the mean redshift estimates for the purely tomographically binned sample (⟨z⟩raw) and the weighted gold sample (⟨z⟩w, g), the difference that our reweighting has had on the spectroscopic means (Δ⟨z⟩), and the fractional number of galaxies in the gold sample compared to the original KV450 cosmic shear sample |
| In the text | |
 |
Fig. A.1. Change in the effective number density of the MICE2 cosmic shear sample |
| In the text | |
 |
Fig. B.1. Influence of the number of SOM clusters on the resulting tomographic bin redshifts and the recovered photometric misrepresentation for the MICE2 simulation dataset. We show three statistics as a function of cluster number. Panel a: change in the tomographic mean estimate. Panel b: change in the representation of the spectroscopic catalogue. Panel c: change in the tomographic mean bias. The inset of panel a shows the distribution of PDFs estimated for the third tomographic bin with 10 000 and 2500 clusters. The black curve shows the distribution of the unweighted spec-z sample. Panel a demonstrates that, with increasing cluster number, our estimate of the tomographic redshift distribution mean changes significantly. Middle panel: demonstrates why: with more clusters there is more fragmentation of the photometric data and significant decreases in the spectroscopic representation, such that the “gold” sample decreases in size. However, crucially, panel c demonstrates that the loss of representation does not change the low level of bias in the recovered redshift distribution. |
| In the text | |
 |
Fig. B.2. Influence of the number of SOM clusters on the resulting tomographic bin redshifts and the recovered photometric misrepresentation for the full KV450 photometric and spectroscopic datasets. The figure is constructed in the same way as Fig. B.1. Here we additionally show the point at which the tomographic bin mean redshifts cross the |⟨z⟩n − ⟨z⟩max| ≤ 0.01 boundary (shown with grey shading). This criteria designates our per-tomographic-bin cluster-number choice for this work. |
| In the text | |
 |
Fig. C.1. Distribution of spectroscopic (left column) and photometric (right column) data, within our SOMs trained on the full spectroscopic compilation (top row) and the without-DEEP2 compilation (bottom row). The photometric data have similar structures (the missing bright-magnitude wedge can be used as a reference in each of these panels). Despite the different distribution of spectral and photometric data in the two SOMs, the representation statistics remain essentially unchanged: in both cases ∼5% of the photometric data occupy cells not containing spectra. |
| In the text | |
 |
Fig. C.2. Fractional occupation per SOM cell of each of the DEEP2, zCOSMOS, and VVDS samples. The upper row repeats the fiducial training shown in Fig. 2, which can be compared to the no-DEEP2 training in the lower row. DEEP2 is assigned far fewer cells in the SOM trained on the spectroscopic dataset excluding DEEP2 (∼11% fewer). |
| In the text | |
 |
Fig. D.1. Left: distribution of mean redshift as a function of SOM cell for the fiducial MICE2 simulation. Right: distribution of the difference in SOM cell mean redshifts for the full photometric sample compared to the first tomographic bin. The figure demonstrates that the N(z) of the high-z SOM cells in the lowest tomographic bin is systematically different to those cells in the full sample. This effect creates the bias observed in the SOM direct calibration. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



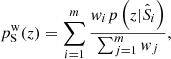
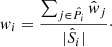
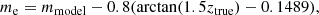
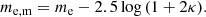
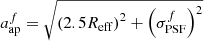
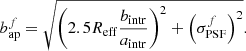
![$$ \begin{aligned} n_{\rm eff} = \frac{1}{A}\frac{\left[\Sigma _{i\in p} w_i\right]^2}{\left[\Sigma _{i\in p} w_i^2\right]}; \end{aligned} $$](/articles/aa/full_html/2020/05/aa36782-19/aa36782-19-eq24.gif)