EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 636 (April 2020) A&A, 636 (2020) A74 Full HTML
Open Access
Issue
A&A
Volume 636, April 2020
Article Number A74
Number of page(s) 16
Section Catalogs and data
DOI https://doi.org/10.1051/0004-6361/201936686
Published online 20 April 2020

© T. Trifonov et al. 2020

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Open Access funding provided by Max Planck Society.

1. Introduction

The High Accuracy Radial velocity Planet Searcher (HARPS, Pepe et al. 2002; Mayor et al. 2003) has been operated since 2003 at the 3.6 m telescope of the European Southern Observatory (ESO) in La Silla. It is the first fibre-fed high-resolution echelle spectrograph capable of measuring stellar radial velocity (RV) with a precision down to ∼1 m s−1. HARPS has discovered a plethora of exoplanets in the past 15 years. More notably, HARPS proved to be an effective hunter of small and some even potentially temperate exoplanet systems, for instance, around GJ 581 (Bonfils et al. 2005; Udry et al. 2007), GJ 536 (Suárez Mascareño et al. 2017), Proxima Centauri (Anglada-Escudé et al. 2016), and HD 10180 (Lovis et al. 2011). With its unprecedented precision, HARPS is the perhaps the most important Doppler validation instrument for the Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2015) in the southern hemisphere, which is uncovering hundreds of small rocky transiting exoplanet candidates around nearby stars. HARPS also offers a large publicly available spectral archive that has already allowed the post-detection Doppler validation of TESS candidates, for example, GJ 143, HD 23472 (Trifonov et al. 2019a), HD 15337 (Gandolfi et al. 2019; Dumusque et al. 2019), and GJ 357 (Luque et al. 2019).

The HARPS spectrograph is precise and stable on year-long timescales through active environmental control (mainly temperature and pressure) and the stability of its atomic standard calibration, typically a ThAr hollow cathode lamp, and since 2011 a Fabry–Perot etalon (Wildi et al. 2010). Although a laser frequency comb has been available since April 2015 (Lo Curto et al. 2012), it is not in routine operation yet because spectral coverage and fibre lifetime are limited.

Despite the stability of HARPS, its wavelength calibration, drift measurements, and cross-calibration are nontrivial procedures and are a potential bottleneck that limits the RV precision. The shortcomings in the pipeline, the instrument, or the observations may lead to systematic errors. An example is the so-called “CCD stitching” systematic, which was discovered with the laser frequency comb (Wilken et al. 2010) and is not handled by the current pipeline. It leads to a periodicity of ∼1 yr in the HARPS RVs that is correlated with the barycentric Earth radial velocity (Bauer et al. 2015; Dumusque et al. 2015; Coffinet et al. 2019). Another well-known systematic was introduced with the upgrade of the optical fibres in May 2015 (Lo Curto et al. 2015). This upgrade changed the instrumental profile and thus the RV offset between the pre- and post-upgrade RVs. This offset is not the same for all stars and might depend on the stellar spectral type.

In this work, we take advantage of the large set of HARPS publicly available wavelength-calibrated spectra accumulated over the years by many programs and groups with different observing strategies and goals. We analyzed the HARPS sample for common RV systematics in an attempt to deliver more precise Doppler measurements for the exoplanet community, and made these data available in a user-friendly catalog.

We rederived more than 212 000 RVs from publicly available stellar HARPS spectra with the SpEctrum Radial Velocity AnaLyser (SERVAL, Zechmeister et al. 2018) pipeline. We then searched for the presence of systematic effects by investigating the nightly zero-point RVs (NZPs) of HARPS: we have previously established this method for data collected with the CARMENES1 spectrograph (Trifonov et al. 2018) and for archival RVs collected with the HIRES2 (Tal-Or et al. 2019). Similar approaches have also been applied for the SOPHIE spectrograph (Courcol et al. 2015; Hobson et al. 2018). The systematics revealed in these works can often be traced back and attributed to known instrumental events such as detector changes or fibre coupling problems.

In Sect. 2 we introduce the publicly available HARPS data and the stellar sample we use in our analysis. In Sect. 3 we introduce our HARPS spectral reprocessing scheme with the SERVAL pipeline. In Sect. 4 we present our findings regarding the systematic RV variations of HARPS. In Sect. 5 we present the main results of our work, and Sect. 6 gives a brief summary and draws some conclusions.

2. HARPS data and the stellar sample

After they are made public, HARPS spectra can be queried and downloaded from the ESO archive using the generic query form3, which provides access to all phase 3 data reduced by the HARPS data-reduction software (DRS v3.5). The data products also contain detailed auxiliary information regarding the observation, such as target coordinates, Earth’s barycentric radial velocity, the signal-to-noise ratio (S/N) in each order, drift measure, etc. Furthermore, the DRS provides a precise RV measurement derived by the spectrum cross-correlation function (CCF) method using a weighted binary mask (Pepe et al. 2002), as well as the CCF full width at half-maximum (FWHM) and the bisector inverse slope span (BIS-span) measurements. The FWHM and BIS are often used as stellar activity indicators (e.g., Queloz et al. 2001).

We have developed a new pipeline that downloads, extracts, and reprocesses the large public HARPS archive in a consistent way, and creates easy user access to its scientific products such as high-precision Doppler measurements and activity indices (see Sect. 5.1). From the ESO-HARPS archive, we have downloaded a total of 264 058 publicly available reduced two-dimensional, multi-order spectra of more than 6100 objects that were observed with HARPS between 2003 and mid-2018. We have excluded from our analysis spectra that were not useful for high-precision stellar RV statistical analysis, such as solar spectra, asteroids, the Galilean moons, quasars, and supernova candidates, which have been obtained in different astrophysical contexts. Overall, we identified 5260 stellar targets in the HARPS sample. Additionally, we excluded stars with fewer than three usable spectra. Three spectra is the minimum requirement for creating a meaningful spectral template and thereafter precise RVs with SERVAL. Finally, we have selected a total of ∼3000 reliable targets of F, G, K, M and L spectral types to use for our subsequent NZP analysis.

Figure 1 shows a Hertzsprung–Russel (HR) diagram of the HARPS sample stars overplotted on the known stars within 100 pc, retrieved from the Gaia DR2 catalog (Gaia Collaboration 2016, 2018). During its operational time, HARPS observed mainly bright nearby main-sequence stars and late-type G and K giant stars. Other stellar objects, such as white dwarfs, very faint late-type M dwarfs, and brown dwarfs are less suitable for a 3.6 m class telescope and HARPS.

thumbnail Fig. 1.

Hertzsprung–Russel diagram of 212 728 stars within 100 pc observed by Gaia (gray dots). The red dots represent 5260 stars observed with HARPS, which we identified in the Gaia DR2 catalog.

Figure 2 describes the HARPS stellar sample in terms of distributions of the estimated stellar distances (Bailer-Jones et al. 2018), V magnitudes, and B − V colors. It is evident that the HARPS surveys conducted in the past 15 years mainly focused on nearby main-sequence stars of spectral types G0 V to M6 V, with a median B − V color of 0.722 mag, median apparent V magnitude of 8.4 mag, and with a median distance of ∼120 pc. The stars within 100 pc represent ∼67% of our HARPS sample. This collection of stars is representative of volume-limited, long-lasting HARPS surveys dedicated to solar-mass G dwarf stars (Pepe et al. 2004; Lo Curto et al. 2010, 2013; Moutou et al. 2011; Udry et al. 2019), low-mass M dwarfs (Bonfils et al. 2005, 2013; Mayor et al. 2009; Forveille et al. 2009; Anglada-Escudé et al. 2016; Astudillo-Defru et al. 2017; Ribas et al. 2018), and metal-poor stars (Santos et al. 2011; Faria et al. 2016; Mortier et al. 2016), which all target nearby stars. The remaining ∼28% of the HARPS sample (with distance > 120 pc) are typically bright main-sequence stars of spectral types A0 to F6, some fainter and more distant transiting-planet hosts observed by more recent RV follow-up campaigns of transiting-planet candidates from the HATSouth (Bakos et al. 2013; Brahm et al. 2016; Henning et al. 2018; Espinoza et al. 2019), WASP-south (Pollacco et al. 2006; Gillon et al. 2009; Nielsen et al. 2019), and the K2 extended mission (Howell et al. 2014; Grziwa et al. 2016; Johnson et al. 2018), or evolved sub-giant and giant branch stars of spectral types G8 IV − K4 III.

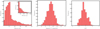thumbnail Fig. 2.

Properties of the HARPS sample of 5260 stars used in this work. The panels shows the distribution of the Gaia distances (left), of the apparent V magnitudes (middle), and of the B − V color (right).

Figure 3 shows some basic observational statistics from the employed HARPS sample. The left panel shows a histogram of the number of spectra per target, whereas the middle panel shows a histogram of the time baselines of the observed targets. The scatter plot in the rightmost panel shows the relation between the two quantities. It is evident from the figure that the majority of the targets observed in the sample have fewer than 50 spectra, with about 38% of the targets having fewer than 10 spectra. Some of the targets have a very short time baseline, shorter than two days, but nevertheless often have a sufficient number of spectra. These are likely the result of special observational campaigns such as transit spectroscopy or observations of the Rossiter–McLaughlin (RM; Rossiter 1924; McLaughlin 1924; Queloz et al. 2000) effect of known transiting planets, which require numerous consecutive observations within one or two nights. The observing time baselines of most of the stars are longer than three years, and those also tend to have many spectra. The majority of these are most likely known single- or multiple-planet hosts and “RV-standard” stars, which show a very low RV scatter, and thus have frequently been observed for instrument stability monitoring over the past 15 years of HARPS service. For example, the most frequently observed target with a total of 19 640 spectra that stood out in the top right corner in the right panel of Fig. 3 is our close neighbor α Cen B (Dumusque et al. 2012; Rajpaul et al. 2016). The second most observed star with a total of 11 666 spectra is the RV-standard τ Ceti (HD 10700), which according to Tuomi et al. (2013) has up to five super-Earth planets. The list of frequently observed stars is followed by another RV standard, ϵ Eri (HD 20794), with a total of 6775 spectra, which is also a potential multi-planet systems (Pepe et al. 2011; Feng et al. 2017), followed by δ Pav (GJ 780) with 6003 spectra, and many other long-term observed planetary systems (e.g., Udry et al. 2019).

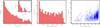thumbnail Fig. 3.

Observation statistics of the HARPS target sample of 5260 stars used in this work. The panels show the distribution of the number of spectra per target (left), the time baselines of the observed targets (middle), and a scatter plot of the time baseline against the number of spectra per target (right).

Figure 4 shows statistics of the exposure times and S/N at 550 nm of the public HARPS spectra. The left panel of Fig. 4 shows that in addition to the most commonly used exposure times of 300, 600, 900, 1200, and 1800 s, there is an abundance of exposures with fewer than 150 s. Again, these are likely spectra of the most heavily observed RV standard stars, which are very bright, hence the short exposures and large number of observations. The middle panel of Fig. 4 shows a histogram of the typical S/N at 550 nm calculated by the DRS pipeline. The distribution seems to be bimodal with a peak near S/N ∼ 50, and another broader peak near S/N ∼ 180. Overall, the stars in our HARPS sample are bright (see the middle panel in Fig. 2), and the exposure times were selected to achieve the high S/N needed for maximum RV precision. The right panel of Fig. 4 shows a scatter plot of the exposure times and the S/N. The red dashed lines mark the range of 10 <  S/N <  400 we adopted in our analysis to create the stellar template needed to derive precise RVs with SERVAL (see Sect. 3).

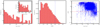thumbnail Fig. 4.

Observation statistics of the HARPS spectra used in this work (∼212 000 spectra). The panels show the distribution of the exposure times (left), the achieved S/N at 550 nm for the obtained spectra (middle), and a scatter plot of the exposure times vs. the S/N (right). The red dashed lines mark the range of S/N adopted in this work to create a template spectrum.

3. Deriving RVs and activity indicators with SERVAL

In addition to HARPS DRS RVs, we also derived precise RV measurements with SERVAL (Zechmeister et al. 2018) based on the same DRS spectrum extraction and the same wavelength solution. Instead of using a precalculated numeric mask, SERVAL creates a template spectrum with high S/N for each observed star by shifting and coadding all individual spectra of that star. The template is then used to derive the RVs from the same observed spectra by using a χ2-minimization approach. SERVAL is a data-driven approach that aims to exploit all the RV information in a self-consistent way. It post-processes the data, requires at least a few spectra, and provides differential RVs. In contrast, the DRS provides absolute RVs with an excellent precision in an online fashion and given a proper choice of a mask and an initial RV guess. Anglada-Escudé & Butler (2012) have demonstrated, however, that the coadding method can provide higher RV precision than the CCF method with a weighted binary mask employed in the standard HARPS DRS pipeline, in particular for stars with late spectral types. We compare the DRS and SERVAL RVs for a subset of the most quiet and heavily observed stars in our sample in Sect. 5.1.

A significant change in the HARPS instrumental profile accompanied the fibre upgrade in 2015 (Lo Curto et al. 2015), therefore we applied SERVAL separately to spectra obtained before and after the intervention. For each star that was observed both before and after the intervention, we accordingly created two templates with high S/N.

To create the template and conduct the NZP analysis, we used only spectra within the range 10 <  S/N <  400. Here we aim to coadd only high-quality spectra and avoid biases from noisy or saturated spectra. We derived RVs from observations within the range 3 <  S/N <  10 and 400 <  S/N <  500, but they were flagged as low-S/N and high-S/N observations, respectively, and must be taken with caution. Spectra with S/N <  3 and S/N >  500 were not considered for the SERVAL analysis.

The SERVAL pipeline also measures stellar activity indicators, which serve as important diagnostics of the planet-induced Doppler signal hypothesis. For the HARPS spectra SERVAL provides a measure of emission in the Hα, Na I D, and Na II D activity-related lines. To measure these activity indicators, SERVAL needs an estimate of the stellar absolute RV, which is requested from the fits header (here DRS-CCF) or as a fallback from SIMBAD. In addition, SERVAL measures the differential line width (dLW), quantifying variations in the spectral line widths, and the chromatic RV index (CRX) of the spectra, which provides information about the wavelength dependence of the RV from individual spectral orders as induced by spots, for example. All the spectral diagnostics obtained with SERVAL come with their uncertainties. For a more detailed description of the SERVAL activity indicators we refer to Zechmeister et al. (2018).

4. Systematic effects in HARPS RVs

4.1. Nightly zero-point variations

Because the calibrations for the HARPS observations are typically made at the beginning of each night, we focused our search for systematic effects by calculating the time series of NZP RVs. To calculate the NZPs we followed a procedure similar to the one described in Tal-Or et al. (2019), where a more detailed description of the algorithm can be found. In short, we calculated an NZP for each night in which at least three different RV-quiet stars (RV scatter < 10 m s−1) were observed by taking the weighted average of their RVs after subtracting its own weighted-average RV (stellar zero-point) from each star.

Unlike for HIRES data, where we had calculated only one NZP time series, for HARPS we calculated four different NZP time series: distinguishing between DRS-CCF and SERVAL RVs, and between RVs before the 2015 intervention (pre-RVs) and after the intervention (post-RVs). The latter separation was also made to prevent the stellar zero-point subtraction from influencing the NZP estimation. Because the intervention introduced discontinuous jumps in the stellar RV time series that depended on spectral type, the stellar zero-point of each star in a time series that contains both pre- and post-RVs heavily depends on the fraction of observations taken before or after the intervention (see also Sect. 4.3). Such inconsistent stellar zero-points would add scatter to the NZP time series, which would enhance the NZP uncertainties. In addition, we calculated the four NZP time series for each RV-quiet star individually after excluding the star itself from the NZP calculation process to avoid self biasing.

Figure 5 shows, separately for SERVAL and DRS RVs, the RVs that were used to calculate the NZPs, the derived individual NZPs, and the NZPs that were actually used to correct the originally derived RVs. The NZPs that were not used for RV correction are marked in red. These are either NZPs that were calculated with too few RV-quiet stars (nRV, n <  3) or NZPs with too large uncertainties (≳1 m s−1). The exact uncertainty threshold that we used to exclude an NZP from the correction stage slightly differs between the four different time series because it was taken as the scatter of the NZPs around a smoothed version of their time series, which was calculated with a moving weighted-average (21 d window) filter. To correct the originally derived RVs, we replaced the excluded NZPs with the filter value in these nights, and fixed their NZP uncertainties to the scatter mentioned above. In addition, about two dozen NZPs, significantly deviating from the filter, were adopted for the correction even if their uncertainties were above the threshold. Most of these outlier NZPs come from three week-long observing runs performed in 2013.

thumbnail Fig. 5.

HARPS NZPs based on SERVAL RVs (upper panel) and DRS RVs (lower panel). The stellar zero-point subtracted RVs (cyan dots) of all RV-quiet stars have been averaged in each night (NZPs, black points). NZPs calculated with too few RVs (nRV,n <  3, red boxes) or NZPs with too large uncertainties (≳1 m s−1, red circles) are excluded from correcting the stellar RVs. The RVs in these red-marked nights are corrected for using a smoothed version of the NZP curve, which was calculated with a moving weighted average (21 d window). For significantly deviating NZPs (magenta circles) we adopted their individual (unsmoothed) NZP value, regardless of their uncertainties. The green dots denote for each night the final NZP value that was used for the stellar RV correction. We note the broken x-axis at JD ∼2 457 169 (2015 May 26): because HARPS pre- and HARPS post-NZPs were calculated separately, which also included subtracting each star’s zero-point RV, both time series are centered around ∼0 m s−1 despite the jump in stellar absolute RVs (see Sect. 4.3). The RV axis was limited to ±10 m s−1 to highlight the small NZP variations.

This somewhat elaborate NZP correction strategy is tailored to the apparent characteristics of HARPS systematics. Similarly to Tal-Or et al. (2019), we searched for the typical timescale of HARPS NZP variations by varying the window size of the filter from 3 to 365 days and looking at the 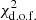and the p(Ftest)-value statistics of subtracting the filter from the NZPs. A moving weighted-average filter can be viewed as a nonparametric model of the data, with an effective number of parameters equal to the data time-span divided by the window size. To illustrate the search, Fig. 6 shows the results for HARPS pre-RVs. Unlike the case of the HIRES data, where both statistics indicated a similar typical timescale of one to two months (see Fig. 3, Tal-Or et al. 2019), for the HARPS NZPs the two statistics are not entirely consistent with each other. While the 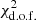statistic always preferred a smaller window, pointing toward a stochastic behavior of the NZPs, the p(Ftest)-value statistic showed a secondary minimum on a timescale of a few weeks, pointing toward a smooth NZP variation of the instrument. This behavior probably indicates two effects that drive HARPS NZP variations: a stochastic one, possibly related to calibration errors, and an additional effect related to more slowly varying instrumental drifts.

thumbnail Fig. 6.

Optimizing the window size of the smoothing filter for HARPS-pre RVs. Upper panel: p(Ftest)-value. Lower panel: . Both statistics were calculated for modeling the NZP time series with a moving weighted-average filter.

The NZP time series that were used to correct the originally derived RVs are given in a table available at the CDS. For each night since JD = 2 452 936 (2003 October 23), the table provides its NZP together with the uncertainty (δNZP), the number of RV-quiet stars used to calculate the NZP (nRV, n), and a flag specifying the type of the NZP. Table 1 summarizes the main characteristics of the four NZP sets. The upper panel shows the weighted rms (wrms), median NZP uncertainty (med(δNZP)), and the uncertainty threshold that was used to exclude an NZP from being used (max(δNZP)). The lower panel shows the number of nights with a certain flag. The five different flags are explained at the bottom of Table 1. The fact that the NZPs reveal a significant source of systematic RV scatter, in addition to the internal uncertainties, is expressed in the ratio wrms(NZP)/med(δNZP), which is in the range of 1.6–2.1 for the four RV sets.

Table 1.

Main characteristics of the four NZP sets.

4.2. Average intra-night drift

After correcting the RVs for NZP variations, as explained above, we checked the residual RVs for average intra-night drifts. A correlation between the RVs and the time relative to the local midnight tmid is a good indicator not only of actual nightly drifts of the spectrograph, but also of seasonal effects, such as correlations of the RVs with the BERV or the hour angle of observation.

Figures 7 and 8 show the four RV–tmid correlations: for pre- and post-SERVAL RVs, and pre- and post-DRS RVs. The correlation significance and slopes are given in the insets. While SERVAL RVs show no correlation in pre-RVs and slightly positive correlation in post-RVs, the DRS RVs show a weak but significant negative correlation in pre-RVs, corresponding to an average nightly drift of ≲ − 1 m s−1, and no correlation in post-RVs.

thumbnail Fig. 7.

Average nightly drift in HARPS-SERVAL RVs. Left: HARPS pre-RV. Right: HARPS post-RV. Only RV-quiet stars (RV scatter < 10 m s−1) were used for the line fits.

thumbnail Fig. 8.

Same as Fig. 7, but for HARPS-DRS derived RVs.

In many cases the DRS pipeline provides an estimate of the RV drift relative to the nightly calibration sequence, which is calculated using the light of a reference calibration source injected simultaneously with the star light through a second fibre. As part of deriving the RVs with SERVAL, we corrected the estimated Doppler shifts whenever the drift value was given. The same was done with DRS RVs. Nevertheless, the RV–tmid correlations in pre-DRS and post-SERVAL RVs remain.

We do not know the reason for these correlations, which can be further investigated on a deeper instrumental level. For instance, the correlation with other auxiliary information can be determined. For the purpose of this data-driven work, we simply corrected the RVs for the small correlations in all four RV sets. The final correction model for each RV therefore included both the NZP according to the night of observation and the average intra-night drift according to the tmid of observation. The model uncertainties were added in quadrature to the internal RV uncertainties.

4.3. 2015 instrumental RV jump

By the end of May 2015, the HARPS spectrograph underwent a major fibre link upgrade, during which the old circular fibres were replaced by octagonal ones, as described in Lo Curto et al. (2015). The authors reported that the main improvement was an increase in scrambling power by at least a factor of ten, and that therefore any decentring of the stellar light source on the fibre affects the measured RV by less than 0.5 m s−1. While this in general is expected to result in more stable RVs, the intervention resulted in a significant change of the instrumental profile. As reported, this introduced an RV offset between the pre- and post-upgrade epochs. Lo Curto et al. (2015) investigated this “jump” by comparing the pre- to post-upgrade RVs for more than 20 RV standard stars, and found RV offsets between −2.3 m s−1 and 20.0 m s−1. Their data also indicate that the offsets might be related to the spectral type of the targets. The reason for the jump is likely the missing optimization of the current DRS extraction pipeline. It might be better calibrated by a future DRS version, but in particular, asymmetry changes in the line spread function are challenging to model. A dependence on spectral type is expected because the systematics might vary across the detector, and the RV information also changes with spectral type across the detector.

We also investigated the magnitude of the jump with SERVAL. For this purpose, we again recomputed the HARPS RVs, but this time with a common stellar template, meaning that pre- and post-data were processed jointly and were not separated. Then we recomputed the NZPs for this entire data set as described in Sect. 4.1.

Following this procedure, we found that while the computed NZPs were stable for the pre-upgrade epoch, they showed a steady drift for the post-upgrade period. In order to estimate the RV offset, we therefore applied separate linear fits to the NZPs before and after the intervention break. Only valid NZPs that were computed from nights with sufficient RV data were used for the fits and consequently for the determination of the offset. This procedure, using the entire data set, yielded a jump of 8.19 ± 0.38 m s−1 between the last pre-upgrade night (JD = 2 457 163) and the first post-upgrade night (JD = 2 457 173)4.

In order to minimize systematics in the offset estimation that might be introduced by any drifts of the NZPs, in particular in combination with unequal distributions in the numbers of observations between the two epochs, we repeated the same procedure (NZP computation and jump determination) with a modified (reduced) data set. This “stripped” set was created by discarding for each star some of the earliest or latest RVs, so that the numbers of nights in which the stars were observed were equal for the two epochs. The NZPs estimated from these stripped data are illustrated in Fig. 9. The plot is clipped to a time span of four years around the instrumental intervention. The jump in the NZPs between nights before the upgrade and those after is evident and is also reflected in the bimodality of the NZP distribution. For the stripped data we found an RV offset of 7.93 ± 0.33 m s−1, which is consistent with the first approach. The reported errors are propagated from the linear fits, where the uncertainties of the regressions were estimated by bootstrapping, for which the data were resampled 1000 times. For comparison we repeated the entire analysis also with the DRS RVs. With offsets of 10.21 ± 0.43 m s−1 for the entire data set, and 9.35 ± 0.38 m s−1 for the stripped data set, they appear to show higher jumps than those determined from the SERVAL RVs.

thumbnail Fig. 9.

Estimated NZPs from the stripped data set of the SERVAL RVs, zoomed to four years around the fibre upgrade (vertical lines) together with the histogram of their distribution on the side. The corresponding linear fits are overplotted on the NZP data points.

We also investigated the dependence of the magnitude of the RV jump on spectral type. To do so, we grouped the stars by their spectral type, and repeated the analysis on each subsample. The results from all analyses are summarized in Table 2.

Table 2.

Radial velocity jumps between the pre- and post-upgrade epochs determined from RVs computed by both pipelines (SERVAL and DRS).

For the subsamples of later spectral types, the offset estimates from both methods (full data and stripped data) are similar and consistent within their uncertainties, while they deviate slightly for spectral type G. No jump values could be estimated for the stripped data sets of the F-type stars. This is due to the combination of a small number of stars and the reduced data set, which together lead to insufficient number of nights for which the NZPs could be estimated. However, they were determined for the full data sets. The dependence on spectral type is evident. The offsets are highest for early-type stars and appear to decrease for lower effective temperatures. For M dwarfs the sign of the jump is inverted. The apparent relationship is illustrated in Fig. 10, where all offset estimates from the SERVAL and DRS RVs are plotted. The shift between the SERVAL and the DRS results is visible and is highest for K stars. Still, the trend with spectral type is consistent in all different data sets. Our jump estimates from the DRS data are also consistent with those determined by Lo Curto et al. (2015).

thumbnail Fig. 10.

Radial velocity jump estimates from all data sets for different spectral types. The two RV pipelines SERVAL (blue circles) and DRS (orange squares) are color-coded. Offsets reported by Lo Curto et al. (2015) were grouped by spectral type and averaged for comparison (green diamonds). The dashed lines indicate stripped data sets, while the solid lines correspond to the full sets.

The resulting offsets should be treated with care because it is expected that the jumps vary from one source to another. However, the results presented here are still a valuable source of information. They can either be used for sanity checks when offsets between pre- and post-upgrade RV data are treated as free parameters in RV modeling, as is usually done in planet searches, or they can even serve as priors for the offset. Such priors can serve as useful constraints in particular for large amplitude signals.

5. Results

5.1. New HARPS RV database

Butler et al. (2017) published an example of a well-documented user-friendly high-precision RV database. Their database contains a large collection of precise Doppler measurements, derived from ∼65 000 spectra of ∼1700 stars, as well as stellar line activity-index measurements, obtained with the iodine cell method (Marcy & Butler 1992; Valenti et al. 1995; Butler et al. 1996) between 1996 and 2014 with the KECK-HIRES5 spectrograph (Vogt et al. 1994). The RVs published by Butler et al. (2017) were by far the most precise and extensive HIRES-RV archive available to the exoplanet community. These public HIRES RVs were the basis for a number of new exoplanet discoveries and orbital updates (e.g., Butler et al. 2017; Trifonov et al. 2018, 2019b; Kaminski et al. 2018; Tuomi et al. 2019), and form an important RV validation archive for the TESS candidates in the northern hemisphere. The large sample size of the HIRES RV archive has also allowed us to identify and correct the data for systematic variations by calculating NZP variations and an average intra-night drift (Tal-Or et al. 2019).

Following a similar route as Butler et al. (2017), we created HARPS-RVBANK, a public database based on the results presented in this work. HARPS-RVBANK is available at the CDS or at its official web page6 and provides the latest SERVAL and DRS data products for the HARPS targets. Table A.1 shows an excerpt of the database with some important columns. The HARPS-RVBANK provides original as well as NZP-corrected SERVAL and DRS RV measurements, their BJD epoch, activity index measurements, and uncertainties. From the DRS products, the user can find the CCFs FWHM, contrast, and the BIS-span measurements. From the SERVAL spectral analysis, we provide the chromatic index (CRX), the differential line width (dLW), and the Hα, Na I D, and Na II D activity-related line measurements. We note that the activity time series are also affected by the 2015 fibre upgrade (see Sect. 4.3), leading to a notable post-upgrade jump in the data. We recommend to treat the pre- and the post-upgrade activity time series as taken from two different instruments, before testing the data for the presence of periodic signals.

The new archive also provides all applied individual RV corrections to the data, such as barycentric Earth radial velocity (BERV), secular acceleration of the RV (SA; Kürster et al. 2003), Fabry–Perot (FP) drift, DRS and SERVAL NZP time series, and the final correction value of each RV, including the average intra-night drift. Additionally, we provide for each epoch auxiliary observational information such as exposure time, S/N of the spectra at 550 nm, quality flag, type of DRS binary mask used, principal investigator (PI), and ESO program-ID of the observation.

For user flexibility we also provide a GITHUB repository7 of the HARPS-RVBANK database, where the user can find the final products, useful tools, and instructions. There we also provide a MySQL, and a JavaScript Object Notation (JSON) versions of the HARPS-RVBANK database, which could be easily integrated as an object storage in modern programming languages such as Python, or used in web interfaces.

5.2. DRS versus SERVAL, and the effct of the NZP correction on RV-quiet stars

Figure 11 compares SERVAL and DRS-CCF as RV derivation tools. For the comparison, we focus on the most quiet stars (RV scatter < 5 m s−1) and compute the average (and median) ratio std(RV-SERVAL)/std(RV-DRS), where we use wrms as our std estimator. We find that for HARP pre-RV, SERVAL yields RVs with an average wrms improvement of ∼5% (∼4% median), while for HARPS post-RV, the average wrms improvement is ∼4% (∼2% median). This shows that for most stars SERVAL yields a slightly better RV precision, and it should in general be preferred over the nominal DRS RVs.

thumbnail Fig. 11.

Comparison of SERVAL and DRS-CCF as RV derivation tools. To estimate the std of the RVs of each star, we used wrms. Only stars with > 10 RVs and an observing time span of > 7 d are displayed (492 stars from HARPS pre-RV, and 128 stars from HARPS post-RV).

Figure 12 shows the effect of the NZP correction on the wrms of all RV-quiet stars (RV scatter < 10 m s−1). Comparing the effect of the correction between HARPS pre-RV and HARPS post-RV, we see that the average effect on HARPS pre-RV data is smaller than the average effect on HARPS post-RV data for SERVAL and DRS RVs both. In order to quantify the effect, we again consider the average (and median) wrms improvement due to the NZP correction. For both SERVAL and DRS RVs, the NZP correction yields only a marginal effect on HARPS pre-RV data (< 2%), while for HARPS post-RV data, the average reduction of wrms is ∼8% (∼6% median). This finding is consistent with the fact that for both RV-derivation pipelines, HARPS post-RV NZPs have larger scatter and smaller uncertainties than HARPS pre-RV NZPs (see Table 1), leading to a more significant correction of post-RVs with the calculated NZPs.

thumbnail Fig. 12.

Comparison of the std(RV) per star before and after correcting the RVs for NZP variations. Only stars with > 10 RVs and an observing time span of > 7 d are displayed. Left: SERVAL RVs (834 stars from HARPS pre-RV, and 213 stars from HARPS post-RV). Right: DRS RVs (711 stars from HARPS pre-RV, and 193 stars from HARPS post-RV).

Interestingly, in HARPS pre-RV there is a larger number of stars with a correction that significantly deviates from the mean. Specifically, in HARPS pre-RV there are ∼20 stars with a wrms improvement of ≳2 m s−1, while there are only four such stars in HARPS post-RV. This effect is probably related to the larger number of significantly outlying NZPs in HARPS pre-RV (see Table 1). For instance, there are two stars in HARPS pre-RV with a wrms reduction from > 5 m s−1 to < 2 m s−1: HD 145927 and HD 197818. HD 145927 has 10 of 37 of its RVs corrected by outlier NZPs of ∼ − 5 m s−1, and HD 197818 has one RV corrected by an outlier NZP of ∼ − 30 m s−1, which occurred on the night of JD = 2 456 246. In HARPS post-RV, three of the four stars with a wrms improvement of ≳2 m s−1 (HD 16417, HD 20781, and HD 197536) have at least one observation on the night of JD = 2 457 258, which has an outlier NZP of ∼ − 14 m s−1. The fourth star (GJ 506) has many exposures on the night of JD = 2 457 174, immediately after the fibre link upgrade.

Figure 13 shows the effect of the NZP correction on the median RV uncertainty per star (med(δRV)). Coadding the NZP uncertainties (δNZPs) to the original RV uncertainties enlarged the med(δRV) values. However, the estimated δNZPs rarely exceeded ∼1 m s−1. The new RV uncertainties probably represent the HARPS RV precision better and will require a smaller jitter term in modeling the RV time series with Keplerian orbits. Moreover, the nights with the largest number of bright RV-quiet stars, observed under good conditions, naturally give the smallest δNZPs. This in turn gives greater weight to the RVs from the nights in which we have a good estimate of the calibration errors.

thumbnail Fig. 13.

Effect of NZP error propagation on the median RV uncertainty per star (med(δR)). Left: SERVAL RVs. Right: DRS RVs. The solid lines demonstrate the effect of adding max(δNZP) as listed in Table 1.

Another demonstration of the importance of the NZP correction is shown in Fig. 14, which compares the RV wrms per star before and after the 2015 intervention. Without NZP correction, the HARPS fibre exchange actually worsened the wrms per star by ∼10% on average. However, after correcting for the NZPs, we find that it improves the wrms per star by ∼10% on average. Moreover, the pre- and post-wrms values are more correlated when we correct for the NZPs. This indicates that the fibre exchange indeed improved the instrument performance, but the wrms values of the most quiet stars were still dominated by instrumental systematic effects. The NZP correction enables the better precision that is achieved with the HARPS new fibres.

thumbnail Fig. 14.

Comparison of std(RV) per star before and after the 2015 intervention. Only stars with > 10 RVs and an observing time span of > 7 d are displayed. Left: SERVAL RVs (115 stars before NZP correction, and 120 stars after it). Right: DRS RVs (93 stars before NZP correction, and 99 stars after it).

Focusing again on the most quiet stars (RV scatter < 5 m s−1), Fig. 15 shows an end-to-end comparison between the RV performance of the nominal DRS-CCF (without NZP correction) and SERVAL with NZP correction. For HARPS pre-RV data, the average wrms improvement is ∼5% (∼4% median), which is dominated by a small number of stars with a relatively large wrms improvement. For HARPS post-RV data, the average wrms improvement is ∼15% (∼18% median), with only a few stars above the 1:1 line. The difference can be explained by the different NZP behaviors of HARPS pre- and HARPS post-RVs. We conclude that for HARPS spectra the NZP-corrected SERVAL RVs are in general more precise than the DRS RVs, and we regard them as the main product of this work.

thumbnail Fig. 15.

Combined effect of extracting HARPS RVs with SERVAL and correcting for the NZPs. Only stars with > 10 RVs and an observing time span of > 7 d are displayed (485 stars from HARPS pre-RV, and 126 stars from HARPS post-RV).

5.3. Practical example: Orbital update of the GJ 253 multi-planet system

We now make a direct comparison of the official HARPS-DRS RV data and our final product, the SERVAL NZP-corrected RV data, by testing their overall quality when modeling an actual planetary system discovered with HARPS. For this purpose we use the known multi-planet system GJ 253 (HD 51608), whose RVs are consistent with two Neptune-mass planets (Mayor et al. 2011; Udry et al. 2019). We have selected this system rather arbitrarily because in our HARPS archive we find many known planetary systems that might serve as better (or poorer) examples for testing our SERVAL-NZP data. The GJ 253 system, however, is appropriate in the context of the results presented in this work, because

  • the DRS data have no outliers (e.g., incorrect user RV-guess), meaning that we can compare a full data set with the SERVAL data;

  • data were taken both before (218 RVs) and after (9 RVs) the 2015 May fibre upgrade;

  • GJ 253 has a sufficient number of archival RV data for a proper statistical comparison;

  • the planetary signals are strong and unambiguous (i.e., likely real and not due to stellar activity);

  • the system is fairly complex (a two-planet system), but is still easy to analyze because no N-body modeling is required;

  • we can update the orbital solution of the system.

Figure 16 shows GLS periodogram analyses of the DRS and SERVAL RVs, and activity index time series of the HARPS spectra of GJ 253. Both data sets are clearly consistent with significant power at periods of 14.07 d and 96.11 d, which are the reported planetary periods of GJ 253 b and c. There is no evidence of significant GLS power in the activity indices from DRS and SERVAL that could be associated with the two RV signals. The only exception is the SERVAL NaD I activity indicator, which seems to show a marginally significant power near 14.04 d. This NaD I peak, however, is only the tenth strongest peak in the NaD I GLS power spectrum. A closer inspection of the RV and the NaD I time series showed that these two peaks are sufficiently distant (> 3σ) in frequency space, and they show no correlation. Therefore the strong RV signal and the marginally significant NaD I signal are likely not related.

thumbnail Fig. 16.

GLS power spectrum for the GJ 253 data, based on NZP-corrected SERVAL RVs, DRS RVs, and stellar activity indicators from DRS and SERVAL as labeled in the panels. The horizontal lines in the GLS periodograms show FAP levels of 10%, 1%, and 0.1%. Blue vertical lines indicate the orbital period of GJ 253 b and c. The magenta vertical line indicates the periodicity near 36 d, which is present in DRS FWHM, BIS-span, contrast, and the SERVAL dLW activity indicators that are likely related to the stellar rotational period.

For the fitting analysis of the GJ 253 system we used The Exo-Striker fitting toolbox8 (Trifonov 2019). To identify the planetary signals embedded in the data, we performed a blind search using The Exo-Striker Auto fit algorithm, which, as its name suggests, automatically inspects the RV data for periodic signals through a GLS periodogram search and performs prewhitening signal subtraction (Hatzes 2013). Finally, when no significant peaks are left in the RV data residual periodogram, The Exo-Striker performs a subsequent simultaneous best-fit optimization of the planetary semi-amplitude K, the orbital period P, eccentricity e, argument of periastron ω, and mean anomaly M at the first observational epoch. We consider the HARPS pre-RV and HARPS post-RV fibre upgrade data as obtained from separate instruments, and thus we optimized their RV offsets and RV velocity jitter (Baluev 2009) simultaneously with the planetary parameters. Using this approach, we were able to instantly identify the planetary signals published in the discovery paper by Mayor et al. (2011) in both the DRS data and the SERVAL NZP-corrected data. As a next step, The Exo-Striker employs a Markov chain Monte Carlo (MCMC, via the emcee sampler; Foreman-Mackey et al. 2013) sampling around the best fit, and we adopted the 1σ confidence level of the posterior distributions as parameters uncertainties.

Table 3 summarizes the best-fit parameters and MCMC-derived asymmetric uncertainties from our dual RV analysis, while Fig. 17 shows the best two-planet fits of the DRS and SERVAL NZP-corrected RV data sets. Both data sets lead to consistent best-fit planetary periods of Pb ∼ 14.07 days and Pc ∼ 95.9 d, which are in agreement with the period estimates by Mayor et al. (2011), who gives Pb = 14.070 ± 0.004 days and Pc = 95.42 ± 0.39 days. We derive lower and better constrained eccentricities than those provided in the discovery work of Mayor et al. (2011). 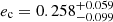The DRS data leads to and , SERVAL NZP-corrected data suggest 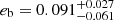and 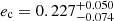, while Mayor et al. (2011) gives eb = 0.15 ± 0.06 and ec = 0.41 ± 0.18. We note that Mayor et al. (2011) have used only slightly more than half of the HARPS data we use in our analysis, and thus it is not surprising that our estimates are better constrained by the larger data set with its longer baseline.

thumbnail Fig. 17.

HARPS RVs of GJ 253 derived with DRS (left) and SERVAL (right panel) and modeled with a two-planet model. Blue data (218 RVs) are taken before the 2015 May fibre upgrade (pre), while red data (9 RVs) are after (post). Lower panels: RVs phase-folded to the Doppler signals of GJ 253 b and c.

Table 3.

Orbital parameters of the two-planet system GJ 253 derived from DRS and SERVAL-NZP data.

Udry et al. (2019) have recently published an orbital update of the GJ 253 system. They based their orbital solution and activity analyses only on HARPS spectra obtained before the fibre upgrade, but with a data reduction made using a new version of the HARPS-DRS pipeline. The MCMC-based best-fit solution given in Udry et al. (2019) is generally consistent with our best-fit estimates (see Table 10 in their paper).

To derive the planetary minimum masses and semi-major axes, we adopted the recent stellar mass estimates for GJ 253 by Soto & Jenkins (2018), who used HARPS spectra to infer stellar parameters and derived a stellar mass of M = 0.85 M⊙. The DRS data and the SERVAL-NZP-corrected data mutually agree on the RV semi-amplitudes of GJ 253 b and c, and thereafter on the derived minimum masses of mb sin i ∼ 0.04 Mjup and mc sin i ∼ 0.05 Mjup. Thus, our orbital update analysis is consistent with two warm Neptune-mass planets in orbit around GJ 253, as was reported by Mayor et al. (2009) and Udry et al. (2019).

The orbital dynamics of the GJ 253 system is beyond the scope of this work, but for the sake of completeness, we also examined the long-term orbital stability of the best-fit configurations achieved form the different data sets. For this purpose, we adopted the Wisdom-Holman (also known as MVS; Wisdom & Holman 1991) N-body integrator implemented in The Exo-Striker, which includes General Relativistic (GR) precession correction term. We find that given the small orbital separations and significant planetary eccentricities observed in the GJ 253 system, the GR precession effects on the orbital dynamics are significant, and thus the GR correction must be included in the long-term evolution of the system to ensure a realistic dynamical outcome. Overall, a crude stability analysis shows that the GJ 253 system is stable for at least 10 Myr, exhibiting an interesting apsidal alignment libration Δϖ = ϖb − ϖc ∼ 0° with a semi-amplitude of 60°, and significant oscillations of the planetary eccentricities in the range 0.02 <  eb <  0.17 and 0.21 <  ec <  0.23 with mean values of 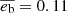, and 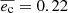, respectively. The timescale of the secular orbital oscilation is ≈37 000 yr.

In Fig. 16 it is evident that the SERVAL dLW, CRX, and Hα activity indicators suggest a periodicity near 36.5 d. It is particularly strong in the SERVAL dLW, where this periodicity has a significant power. A peak near this period is also detected in the DRS BIS-span and the DRS FWHM time series. A peak at a similar frequency was also detected by Udry et al. (2019) in their HARPS activity time series. We likely witness stellar spots that rotate with the rotational period of the star. Interestingly, the RV residuals in both DRS and SERVAL show a strong but insignificant GLS peak near 38.9 d. While this peak seems sufficiently distant from the ∼ 36.5-d period seen in the activity index time series, it is still possible that it could be related to the stellar rotation.

Finally, for the quality of the two fits, the DRS-CCF data yield Δlnℒ = 180.00 with respect to the null hypothesis (i.e., no planets), while the SERVAL-NZP has Δlnℒ = 185.99, which means that the SERVAL-NZP-corrected RV data add significant evidence in favor of the two planets. This also manifests itself in a lower weighted rms of the SERVAL-NZP residuals compared to DRS-CCF (see Table 3). Therefore, our orbital update on the GJ 253 system is based on the two-planet Keplerian modeling of the SERVAL NZP-corrected data.

This practical example of the GJ 253 system shows that our SERVAL data are indeed a better choice than the official DRS data. It is still possible that for other systems the DRS data would lead to better fits, but overall, given the sample statistics comparison given in Sect. 5.2 (see also Figs. 11 and 15), we are confident that the NZP-corrected SERVAL data should be preferred in most cases. In particular for stars of late spectral type such as K, M, and L, we expect SERVAL to outperform the DRS-CCF.

6. Summary and conclusions

We have presented an independent systematic analysis of the HARPS spectral archive. In particular, we recalculated Doppler velocity measurements of the publicly accessible spectra and performed a stellar line analysis, which is important for validating planetary induced Doppler signals. For this part of the analysis, we applied the SERVAL RV pipeline, with which we derived slightly more precise RV measurements than those derived by the official ESO-DRS pipeline. We find that for a subsample of stars with a very small RV scatter (< 5 m s−1), SERVAL RVs are more precise than DRS RVs by ∼5% on average.

We make all of our HARPS results publicly available as a service to the exoplanet community. We provide original uncorrected DRS and SERVAL pipeline data and self-corrected (for NZPs and average intra-night drifts) DRS and SERVAL RVs. All relevant results of our study are made public in the user-friendly database “HARPS-RVBANK”, which is available on the CDS, GITHUB, or as a stand-alone webpage where the user can browse for data. This makes our HARPS-RVBANK the first easy-to-access publicly available HARPS RV archive, which to our knowledge contains the most precise RV data products to date.

Another objective of our work was to study whether HARPS Doppler measurements suffer from systematic errors, which could bias the orbital parameter estimates of small planets, or worse, induce spurious planetary discoveries. We find that despite being, with no doubt, a state-of-the-art RV instrument, HARPS also suffers from small but significant systematic errors of the instrumental zero-point. Our NZP analysis reveals stochastic zero-point variations of ∼1 m s−1, smooth zero-point variations, with a magnitude of ∼1 m s−1 and a typical timescale of few weeks, and a few dozen nights whose NZPs significantly deviate from the general zero-point trend by few m s−1 (and up to 30 m s−1). In addition, we find small (≲1 m s−1) but significant intra-night drifts in DRS RVs before the 2015 intervention and in SERVAL RVs after it. The HARPS NZPs systematic errors are likely related to the instability of the daily wavelength calibration (Dumusque 2018). The next DRS version will likely have an improved wavelength calibration (Coffinet et al. 2019), which to a high degree might resolve these systematic errors. It would be interesting then to recompute the NZPs as a quality check of the new DRS wavelength calibration scheme.

Correcting HARPS RVs for the systematic model, we find additional improvement of the RV scatter, mainly for observations after the 2015 intervention. Considering the combined effect of deriving the RVs with SERVAL and correcting them for the small systematic errors, we find the average wrms improvement of pre-RVs to be ∼5%, and of post-RVs to be ∼15%. For a small number of stars, whose observations were most affected by the significantly deviating NZPs, we find a much more significant wrms improvement by a factor ≳2.

Investigating the RVs of a subsample of RV-quiet stars that were observed both before and after the 2015 HARPS optical fibre upgrade, we find a discontinuous jump in their absolute RVs that is independent of the RV derivation software (i.e., we find similar results with DRS and SERVAL). Similarly to Lo Curto et al. (2015), we find the jump to be strongly dependent on the spectral type of the target: from ∼14 m s−1 for late F-type stars to ∼ − 3 m s−1 for late-M dwarfs.

As a demonstration of the new data quality, we provide new orbital estimates of the GJ 253 multi-planet system based on our new HARPS-SERVAL NZP-corrected data, updating the planetary minimum masses and orbital elements. Similarly to Udry et al. (2019), we show that the GJ 253 b and c orbits are probably less eccentric than was previously estimated, when fewer RV data were available. This shows that it is important to update the orbital elements of known planetary systems when more data are accumulated because this might remove possible higher-eccentricity biases, for example. This is especially valid for multi-planet systems. In these systems the eccentricity is an important parameter that can determine their dynamical properties and might shed some light on their formation and evolution.

The HARPS-RVBANK is a valuable data source for planet search, reanalysis of known planetary systems, and validation of newly discovered transiting planets. For its better precision, we strongly recommend using the NZP-corrected SERVAL RVs, which are the main product of this work.

1

Calar Alto high-Resolution search for M dwarfs with Exoearths with Near-infrared and optical echelle Spectrographs (Quirrenbach et al. 2014).

2

HIgh REsolution Spectrograph (Vogt et al. 1994).

4

A few stars were observed with HARPS during this maintenance time, and consequently their DRS RVs appear in our database. However, we opted not to use these data for the precision analysis and avoided correcting them for NZPs.

5

Similarly to the ESO archive, publicly available spectra obtained with the HIRES can be found in the Keck Observatory Archive at https://koa.ipac.caltech.edu/cgi-bin/KOA/nph-KOAlogin, but to our knowledge, these data do not contain final-product RV measurements.

8

The Exo-Striker is freely available at https://github.com/3fon3fonov/exostriker

Acknowledgments

We thank the anonymous referee for thorough reading of the manuscript and thoughtful comments that helped to substantially improve this paper. We are deeply grateful to the HARPS team at Observatoire de Genève, Observatoire de Haute-Provence, Laboratoire d’Astrophysique de Marseille, Service d’Aéronomie du CNRS, Physikalisches Institut de Universität Bern, ESO La Silla, and ESO Garching, who built and maintained the HARPS instrument, and were generous enough to make the data public. Without their seminal work and consistent effort, this study could not have been performed. We are also extremely grateful to all the PIs and observers associated with the ESO programmes listed below. We respect their hard work, and we hope that they will benefit from our recomputed data. T. T. thanks to Thomas Henning and Martin Kürster for support during this study. L. T. and S. Z. acknowledge support from the Israel Science Foundation (grant no. 848/16). M. Z. is supported by the Deutsche Forschungsgemeinschaft under DFG RE 1664/12-1 and Research Unit FOR2544 “Blue Planets around Red Stars”, project no. RE 1664/14-1. T. T. acknowledges support by Bulgarian National Science Programme “Young Scientists and Postdoctoral Candidates 2019”. This work is based on observations collected at the European Organization for Astronomical Research in the Southern Hemisphere under ESO programmes: 0100.C-0097, 0100.C-0111, 0100.C-0414, 0100.C-0474, 0100.C-0487, 0100.C-0750, 0100.C-0808, 0100.C-0836, 0100.C-0847, 0100.C-0884, 0100.C-0888, 0100.D-0444, 0100.D-0717, 0101.C-0232, 0101.C-0274, 0101.C-0275, 0101.C-0379, 0101.C-0407, 0101.C-0516, 0101.C-0829, 0101.D-0717, 0102.C-0338, 0102.D-0717, 0103.C-0548, 0103.D-0717, 060.A-9036, 060.A-9700, 072.C-0096, 072.C-0388, 072.C-0488, 072.C-0513, 072.C-0636, 072.D-0286, 072.D-0419, 072.D-0707, 073.A-0041, 073.C-0733, 073.C-0784, 073.D-0038, 073.D-0136, 073.D-0527, 073.D-0578, 073.D-0590, 074.C-0012, 074.C-0037, 074.C-0102, 074.C-0364, 074.D-0131, 074.D-0380, 075.C-0140, 075.C-0202, 075.C-0234, 075.C-0332, 075.C-0689, 075.C-0710, 075.D-0194, 075.D-0600, 075.D-0614, 075.D-0760, 075.D-0800, 076.C-0010, 076.C-0073, 076.C-0155, 076.C-0279, 076.C-0429, 076.C-0878, 076.D-0103, 076.D-0130, 076.D-0158, 076.D-0207, 077.C-0012, 077.C-0080, 077.C-0101, 077.C-0295, 077.C-0364, 077.C-0530, 077.D-0085, 077.D-0498, 077.D-0633, 077.D-0720, 078.C-0037, 078.C-0044, 078.C-0133, 078.C-0209, 078.C-0233, 078.C-0403, 078.C-0751, 078.C-0833, 078.D-0067, 078.D-0071, 078.D-0245, 078.D-0299, 078.D-0492, 079.C-0046, 079.C-0127, 079.C-0170, 079.C-0329, 079.C-0463, 079.C-0488, 079.C-0657, 079.C-0681, 079.C-0828, 079.C-0927, 079.D-0009, 079.D-0075, 079.D-0118, 079.D-0160, 079.D-0462, 079.D-0466, 080.C-0032, 080.C-0071, 080.C-0664, 080.C-0712, 080.D-0047, 080.D-0086, 080.D-0151, 080.D-0318, 080.D-0347, 080.D-0408, 081.C-0034, 081.C-0119, 081.C-0148, 081.C-0211, 081.C-0388, 081.C-0774, 081.C-0779, 081.C-0802, 081.C-0842, 081.D-0008, 081.D-0065, 081.D-0109, 081.D-0531, 081.D-0610, 081.D-0870, 082.B-0610, 082.C-0040, 082.C-0212, 082.C-0308, 082.C-0312, 082.C-0315, 082.C-0333, 082.C-0357, 082.C-0390, 082.C-0412, 082.C-0427, 082.C-0608, 082.C-0718, 083.C-0186, 083.C-0413, 083.C-0794, 083.C-1001, 083.D-0668, 084.C-0185, 084.C-0228, 084.C-0229, 084.C-1039, 085.C-0019, 085.C-0063, 085.C-0318, 085.C-0393, 086.C-0145, 086.C-0230, 086.C-0284, 086.D-0240, 087.C-0012, 087.C-0368, 087.C-0649, 087.C-0831, 087.C-0990, 087.D-0511, 088.C-0011, 088.C-0323, 088.C-0353, 088.C-0513, 088.C-0662, 089.C-0006, 089.C-0050, 089.C-0151, 089.C-0415, 089.C-0497, 089.C-0732, 089.C-0739, 090.C-0395, 090.C-0421, 090.C-0540, 090.C-0849, 091.C-0034, 091.C-0184, 091.C-0271, 091.C-0438, 091.C-0456, 091.C-0471, 091.C-0844, 091.C-0853, 091.C-0866, 091.C-0936, 091.D-0469, 092.C-0282, 092.C-0454, 092.C-0579, 092.C-0721, 092.C-0832, 092.D-0261, 093.C-0062, 093.C-0409, 093.C-0417, 093.C-0474, 093.C-0919, 094.C-0090, 094.C-0297, 094.C-0428, 094.C-0797, 094.C-0894, 094.C-0901, 094.C-0946, 094.D-0056, 094.D-0596, 095.C-0040, 095.C-0105, 095.C-0367, 095.C-0551, 095.C-0718, 095.C-0799, 095.C-0947, 095.D-0026, 095.D-0717, 096.C-0053, 096.C-0082, 096.C-0183, 096.C-0210, 096.C-0331, 096.C-0417, 096.C-0460, 096.C-0499, 096.C-0657, 096.C-0708, 096.C-0762, 096.C-0876, 096.D-0402, 096.D-0717, 097.C-0021, 097.C-0090, 097.C-0390, 097.C-0434, 097.C-0561, 097.C-0571, 097.C-0864, 097.C-0948, 097.C-1025, 097.D-0156, 097.D-0717, 098.C-0269, 098.C-0292, 098.C-0304, 098.C-0366, 098-C-0518, 098.C-0518, 098.C-0739, 098.C-0820, 098.C-0860, 098.D-0717, 099.C-0093, 099.C-0138, 099.C-0205, 099.C-0303, 099.C-0304, 099.C-0374, 099.C-0458, 099.C-0491, 099.C-0798, 099.C-0880, 099.C-0898, 099.D-0717, 1101.C-0721, 180.C-0886, 183.C-0437, 183.C-0972, 183.D-0729, 184.C-0639, 184.C-0815, 185.D-0056, 188.C-0265, 188.C-0779, 190.C-0027, 191.C-0505, 191.C-0873, 192.C-0224, 192.C-0852, 196.C-0042, 196.C-1006, 198.C-0169, 198.C-0836, 198.C-0838, 281.D-5052, 281.D-5053, 282.C-5034, 282.C-5036, 282.D-5006, 283.C-5017, 283.C-5022, 288.C-5010, 292.C-5004, 295.C-5031, 495.L-0963, 60.A-9036, 60.A-9700, and 63.A-9036. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.

References

  1. Anglada-Escudé, G., & Butler, R. P. 2012, ApJS, 200, 15 [NASA ADS] [CrossRef] [Google Scholar]
  2. Anglada-Escudé, G., Amado, P. J., Barnes, J., et al. 2016, Nature, 536, 437 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  3. Astudillo-Defru, N., Forveille, T., Bonfils, X., et al. 2017, A&A, 602, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Mantelet, G., & Andrae, R. 2018, AJ, 156, 58 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bakos, G. Á., Csubry, Z., Penev, K., et al. 2013, PASP, 125, 154 [NASA ADS] [CrossRef] [Google Scholar]
  6. Baluev, R. V. 2009, MNRAS, 393, 969 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bauer, F. F., Zechmeister, M., & Reiners, A. 2015, A&A, 581, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Bonfils, X., Forveille, T., Delfosse, X., et al. 2005, A&A, 443, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Brahm, R., Jordán, A., Bakos, G. Á., et al. 2016, AJ, 151, 89 [NASA ADS] [CrossRef] [Google Scholar]
  11. Butler, R. P., Marcy, G. W., Williams, E., et al. 1996, PASP, 108, 500 [NASA ADS] [CrossRef] [Google Scholar]
  12. Butler, R. P., Vogt, S. S., Laughlin, G., et al. 2017, AJ, 153, 208 [NASA ADS] [CrossRef] [Google Scholar]
  13. Coffinet, A., Lovis, C., Dumusque, X., & Pepe, F. 2019, A&A, 629, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Courcol, B., Bouchy, F., Pepe, F., et al. 2015, A&A, 581, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Dumusque, X. 2018, A&A, 620, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Dumusque, X., Pepe, F., Lovis, C., et al. 2012, Nature, 491, 207 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  17. Dumusque, X., Pepe, F., Lovis, C., & Latham, D. W. 2015, ApJ, 808, 171 [NASA ADS] [CrossRef] [Google Scholar]
  18. Dumusque, X., Turner, O., Dorn, C., et al. 2019, A&A, 627, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Espinoza, N., Hartman, J. D., Bakos, G. Á., et al. 2019, AJ, 158, 63 [NASA ADS] [CrossRef] [Google Scholar]
  20. Faria, J. P., Santos, N. C., Figueira, P., et al. 2016, A&A, 589, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Feng, F., Tuomi, M., & Jones, H. R. A. 2017, A&A, 605, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
  23. Forveille, T., Bonfils, X., Delfosse, X., et al. 2009, A&A, 493, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Gandolfi, D., Fossati, L., Livingston, J. H., et al. 2019, ApJ, 876, L24 [Google Scholar]
  27. Gillon, M., Anderson, D. R., Triaud, A. H. M. J., et al. 2009, A&A, 501, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Grziwa, S., Gandolfi, D., Csizmadia, S., et al. 2016, AJ, 152, 132 [NASA ADS] [CrossRef] [Google Scholar]
  29. Hatzes, A. P. 2013, Astron. Nachr., 334, 616 [NASA ADS] [CrossRef] [Google Scholar]
  30. Henning, T., Mancini, L., Sarkis, P., et al. 2018, AJ, 155, 79 [NASA ADS] [CrossRef] [Google Scholar]
  31. Hobson, M. J., Díaz, R. F., Delfosse, X., et al. 2018, A&A, 618, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [NASA ADS] [CrossRef] [Google Scholar]
  33. Johnson, M. C., Dai, F., Justesen, A. B., et al. 2018, MNRAS, 481, 596 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kaminski, A., Trifonov, T., Caballero, J. A., et al. 2018, A&A, 618, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Kürster, M., Endl, M., Rouesnel, F., et al. 2003, A&A, 403, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Lo Curto, G., Mayor, M., Benz, W., et al. 2010, A&A, 512, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Lo Curto, G., Pasquini, L., Manescau, A., et al. 2012, The Messenger, 149, 2 [NASA ADS] [Google Scholar]
  38. Lo Curto, G., Mayor, M., Benz, W., et al. 2013, A&A, 551, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Lo Curto, G., Pepe, F., Avila, G., et al. 2015, The Messenger, 162, 9 [NASA ADS] [Google Scholar]
  40. Lovis, C., Ségransan, D., Mayor, M., et al. 2011, A&A, 528, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Luque, R., Pallé, E., Kossakowski, D., et al. 2019, A&A, 628, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Marcy, G. W., & Butler, R. P. 1992, PASP, 104, 270 [NASA ADS] [CrossRef] [Google Scholar]
  43. Mayor, M., Bonfils, X., Forveille, T., et al. 2009, A&A, 507, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
  45. Mayor, M., Marmier, M., Lovis, C., et al. 2011, ArXiv e-prints [arXiv:1109.2497] [Google Scholar]
  46. McLaughlin, D. B. 1924, ApJ, 60, 22 [NASA ADS] [CrossRef] [Google Scholar]
  47. Mortier, A., Faria, J. P., Santos, N. C., et al. 2016, A&A, 585, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Moutou, C., Mayor, M., Lo Curto, G., et al. 2011, A&A, 527, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Nielsen, L. D., Bouchy, F., Turner, O. D., et al. 2019, MNRAS, 489, 2478 [NASA ADS] [CrossRef] [Google Scholar]
  50. Pepe, F., Mayor, M., Rupprecht, G., et al. 2002, The Messenger, 110, 9 [NASA ADS] [Google Scholar]
  51. Pepe, F., Mayor, M., Queloz, D., et al. 2004, A&A, 423, 385 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Pepe, F., Lovis, C., Ségransan, D., et al. 2011, A&A, 534, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Pollacco, D. L., Skillen, I., Collier Cameron, A., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
  54. Queloz, D., Eggenberger, A., Mayor, M., et al. 2000, A&A, 359, L13 [NASA ADS] [Google Scholar]
  55. Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Quirrenbach, A., Amado, P. J., Caballero, J. A., et al. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, Proc. SPIE, 9147, 91471F [Google Scholar]
  57. Rajpaul, V., Aigrain, S., & Roberts, S. 2016, MNRAS, 456, L6 [NASA ADS] [CrossRef] [Google Scholar]
  58. Ribas, I., Tuomi, M., Reiners, A., et al. 2018, Nature, 563, 365 [NASA ADS] [CrossRef] [Google Scholar]
  59. Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [NASA ADS] [CrossRef] [Google Scholar]
  60. Rossiter, R. A. 1924, ApJ, 60, 15 [NASA ADS] [CrossRef] [Google Scholar]
  61. Santos, N. C., Mayor, M., Bonfils, X., et al. 2011, A&A, 526, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Soto, M. G., & Jenkins, J. S. 2018, A&A, 615, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Suárez Mascareño, A., González Hernández, J. I., Rebolo, R., et al. 2017, A&A, 597, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Tal-Or, L., Trifonov, T., Zucker, S., Mazeh, T., & Zechmeister, M. 2019, MNRAS, 484, L8 [NASA ADS] [CrossRef] [Google Scholar]
  65. Trifonov, T. 2019, Astrophysics Source Code Library [record ascl:1906.004] [Google Scholar]
  66. Trifonov, T., Kürster, M., Zechmeister, M., et al. 2018, A&A, 609, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Trifonov, T., Rybizki, J., & Kürster, M. 2019a, A&A, 622, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Trifonov, T., Stock, S., Henning, T., et al. 2019b, AJ, 157, 93 [NASA ADS] [CrossRef] [Google Scholar]
  69. Tuomi, M., Jones, H. R. A., Jenkins, J. S., et al. 2013, A&A, 551, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Tuomi, M., Jones, H. R. A., Anglada-Escudé, G., et al. 2019, AAS J., submitted [arXiv:1906.04644] [Google Scholar]
  71. Udry, S., Bonfils, X., Delfosse, X., et al. 2007, A&A, 469, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Udry, S., Dumusque, X., Lovis, C., et al. 2019, A&A, 622, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Valenti, J. A., Butler, R. P., & Marcy, G. W. 1995, PASP, 107, 966 [NASA ADS] [CrossRef] [Google Scholar]
  74. Vogt, S. S., Allen, S. L., Bigelow, B. C., et al. 1994, in Instrumentation in Astronomy VIII, eds. D. L. Crawford, & E. R. Craine, Proc. SPIE, 2198, 362 [NASA ADS] [CrossRef] [Google Scholar]
  75. Wildi, F., Pepe, F., Chazelas, B., Lo Curto, G., & Lovis, C. 2010, in Ground-based and Airborne Instrumentation for Astronomy III, SPIE Conf. Ser., 7735, 77354X [CrossRef] [Google Scholar]
  76. Wilken, T., Lovis, C., Manescau, A., et al. 2010, MNRAS, 405, L16 [NASA ADS] [CrossRef] [Google Scholar]
  77. Wisdom, J., & Holman, M. 1991, AJ, 102, 1528 [NASA ADS] [CrossRef] [Google Scholar]
  78. Zechmeister, M., Reiners, A., Amado, P. J., et al. 2018, A&A, 609, A12 [CrossRef] [Google Scholar]

Appendix A: Additional table

Table A.1.

RVs and auxiliary data for GJ 1.

All Tables

Table 1.

Main characteristics of the four NZP sets.

In the text
Table 2.

Radial velocity jumps between the pre- and post-upgrade epochs determined from RVs computed by both pipelines (SERVAL and DRS).

In the text
Table 3.

Orbital parameters of the two-planet system GJ 253 derived from DRS and SERVAL-NZP data.

In the text
Table A.1.

RVs and auxiliary data for GJ 1.

In the text

All Figures

thumbnail Fig. 1.

Hertzsprung–Russel diagram of 212 728 stars within 100 pc observed by Gaia (gray dots). The red dots represent 5260 stars observed with HARPS, which we identified in the Gaia DR2 catalog.
In the text
thumbnail Fig. 2.

Properties of the HARPS sample of 5260 stars used in this work. The panels shows the distribution of the Gaia distances (left), of the apparent V magnitudes (middle), and of the B − V color (right).
In the text
thumbnail Fig. 3.

Observation statistics of the HARPS target sample of 5260 stars used in this work. The panels show the distribution of the number of spectra per target (left), the time baselines of the observed targets (middle), and a scatter plot of the time baseline against the number of spectra per target (right).
In the text
thumbnail Fig. 4.

Observation statistics of the HARPS spectra used in this work (∼212 000 spectra). The panels show the distribution of the exposure times (left), the achieved S/N at 550 nm for the obtained spectra (middle), and a scatter plot of the exposure times vs. the S/N (right). The red dashed lines mark the range of S/N adopted in this work to create a template spectrum.
In the text
thumbnail Fig. 5.

HARPS NZPs based on SERVAL RVs (upper panel) and DRS RVs (lower panel). The stellar zero-point subtracted RVs (cyan dots) of all RV-quiet stars have been averaged in each night (NZPs, black points). NZPs calculated with too few RVs (nRV,n <  3, red boxes) or NZPs with too large uncertainties (≳1 m s−1, red circles) are excluded from correcting the stellar RVs. The RVs in these red-marked nights are corrected for using a smoothed version of the NZP curve, which was calculated with a moving weighted average (21 d window). For significantly deviating NZPs (magenta circles) we adopted their individual (unsmoothed) NZP value, regardless of their uncertainties. The green dots denote for each night the final NZP value that was used for the stellar RV correction. We note the broken x-axis at JD ∼2 457 169 (2015 May 26): because HARPS pre- and HARPS post-NZPs were calculated separately, which also included subtracting each star’s zero-point RV, both time series are centered around ∼0 m s−1 despite the jump in stellar absolute RVs (see Sect. 4.3). The RV axis was limited to ±10 m s−1 to highlight the small NZP variations.
In the text
thumbnail Fig. 6.

Optimizing the window size of the smoothing filter for HARPS-pre RVs. Upper panel: p(Ftest)-value. Lower panel: . Both statistics were calculated for modeling the NZP time series with a moving weighted-average filter.
In the text
thumbnail Fig. 7.

Average nightly drift in HARPS-SERVAL RVs. Left: HARPS pre-RV. Right: HARPS post-RV. Only RV-quiet stars (RV scatter < 10 m s−1) were used for the line fits.
In the text
thumbnail Fig. 8.

Same as Fig. 7, but for HARPS-DRS derived RVs.
In the text
thumbnail Fig. 9.

Estimated NZPs from the stripped data set of the SERVAL RVs, zoomed to four years around the fibre upgrade (vertical lines) together with the histogram of their distribution on the side. The corresponding linear fits are overplotted on the NZP data points.
In the text
thumbnail Fig. 10.

Radial velocity jump estimates from all data sets for different spectral types. The two RV pipelines SERVAL (blue circles) and DRS (orange squares) are color-coded. Offsets reported by Lo Curto et al. (2015) were grouped by spectral type and averaged for comparison (green diamonds). The dashed lines indicate stripped data sets, while the solid lines correspond to the full sets.
In the text
thumbnail Fig. 11.

Comparison of SERVAL and DRS-CCF as RV derivation tools. To estimate the std of the RVs of each star, we used wrms. Only stars with > 10 RVs and an observing time span of > 7 d are displayed (492 stars from HARPS pre-RV, and 128 stars from HARPS post-RV).
In the text
thumbnail Fig. 12.

Comparison of the std(RV) per star before and after correcting the RVs for NZP variations. Only stars with > 10 RVs and an observing time span of > 7 d are displayed. Left: SERVAL RVs (834 stars from HARPS pre-RV, and 213 stars from HARPS post-RV). Right: DRS RVs (711 stars from HARPS pre-RV, and 193 stars from HARPS post-RV).
In the text
thumbnail Fig. 13.

Effect of NZP error propagation on the median RV uncertainty per star (med(δR)). Left: SERVAL RVs. Right: DRS RVs. The solid lines demonstrate the effect of adding max(δNZP) as listed in Table 1.
In the text
thumbnail Fig. 14.

Comparison of std(RV) per star before and after the 2015 intervention. Only stars with > 10 RVs and an observing time span of > 7 d are displayed. Left: SERVAL RVs (115 stars before NZP correction, and 120 stars after it). Right: DRS RVs (93 stars before NZP correction, and 99 stars after it).
In the text
thumbnail Fig. 15.

Combined effect of extracting HARPS RVs with SERVAL and correcting for the NZPs. Only stars with > 10 RVs and an observing time span of > 7 d are displayed (485 stars from HARPS pre-RV, and 126 stars from HARPS post-RV).
In the text
thumbnail Fig. 16.

GLS power spectrum for the GJ 253 data, based on NZP-corrected SERVAL RVs, DRS RVs, and stellar activity indicators from DRS and SERVAL as labeled in the panels. The horizontal lines in the GLS periodograms show FAP levels of 10%, 1%, and 0.1%. Blue vertical lines indicate the orbital period of GJ 253 b and c. The magenta vertical line indicates the periodicity near 36 d, which is present in DRS FWHM, BIS-span, contrast, and the SERVAL dLW activity indicators that are likely related to the stellar rotational period.
In the text
thumbnail Fig. 17.

HARPS RVs of GJ 253 derived with DRS (left) and SERVAL (right panel) and modeled with a two-planet model. Blue data (218 RVs) are taken before the 2015 May fibre upgrade (pre), while red data (9 RVs) are after (post). Lower panels: RVs phase-folded to the Doppler signals of GJ 253 b and c.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.