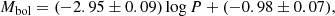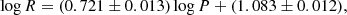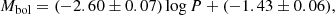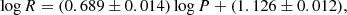| Issue |
A&A
Volume 635, March 2020
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 18 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201937060 | |
| Published online | 02 March 2020 | |
Analysing the spectral energy distributions of Galactic classical Cepheids⋆
Koninklijke Sterrenwacht van België, Ringlaan 3, 1180 Brussels, Belgium
e-mail: martin.groenewegen@oma.be
Received:
5
November
2019
Accepted:
11
January
2020
Spectral energy distributions (SEDs) were constructed for a sample of 477 classical Cepheids (CCs); including stars that have been classified in the literature as such but are probably not. The SEDs were fitted with a dust radiative transfer code. Four stars showed a large mid- or far-infrared excess and the fitting then included a dust component. These comprise the well-known case of RS Pup, and three stars that are (likely) Type-II Cepheids (T2Cs), AU Peg, QQ Per, and FQ Lac. The infrared excess in FQ Lac is reported for the first time in this work. The remainder of the sample was fitted with a stellar photosphere to derive the best-fitting luminosity and effective temperature. Distance and reddening were taken from the literature. The stars were plotted in a Hertzsprung-Russell diagram (HRD) and compared to evolutionary tracks for Cepheids and theoretical instability strips. For the large majority of stars, the position in the HRD is consistent with the instability strip for a CC or T2C. About 5% of the stars are outliers in the sense that they are much hotter or cooler than expected. A comparison to effective temperatures derived from spectroscopy suggests in some cases that the photometrically derived temperature is not correct and that this is likely linked to an incorrectly adopted reddening. Two three-dimensional reddening models have been used to derive alternative estimates of the reddening for the sample. There are significant systematic differences between the two estimates with a non-negligible scatter. In this work the presence of a small near-infrared (NIR) excess, as has been proposed in the literature for a few well-known Cepheids, is investigated. Firstly, this was done by using a sample of about a dozen stars for which a mid-infrared spectrum is available. This data is particularly constraining as the shape of the observed spectrum should match that of the photosphere and any dust spectrum, both dust continuum and any spectral features of, for example, silicates or aluminium oxide. This comparison provides constraints on the dust composition, in agreement with a previous work in the literature. Secondly, the SEDs of all stars were fitted with a dust model to see if a statistically significant better fit could be obtained. The results were compared to recent work. Eight new candidates for exhibiting a NIR excess are proposed, solely based on the photometric SEDs. Obtaining mid-infrared spectra would be needed to confirm this excess. Finally, period-bolometric luminosity and period-radius relations are presented for samples of over 370 fundamental-mode CCs.
Key words: stars: distances / stars: variables: Cepheids / parallaxes
Full Tables 1 and A.1 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/635/A33
© ESO 2020
1. Introduction
Classical Cepheids (CCs) are considered an important standard candle because they are bright and, thus, they comprise a link between the distance scale in the nearby universe and that further out via those galaxies that contain both Cepheids and SNIa (see Riess et al. 2019 for a determination of the Hubble constant to 1.9% precision, taking into account the new 1.1% precise distance to the Large Magellanic Cloud from Pietrzyński et al. 2019).
Therefore, it is not surprising that the Gaia 2nd data release (GDR2, Gaia Collaboration 2018) spurred a number of studies on the CCs listed in the GDR2 and on the period-luminosity (PL) relation. Riess et al. (2018a) analysed a sample of 50 CCs. They derived a parallax zeropoint offset of −0.046 ± 0.013 mas, compared to the −0.029 mas derived for quasars by Lindegren et al. (2018) and concluded that the need to independently determine the parallax zeropoint offset largely counters the higher accuracy of the parallaxes in determining an improved zeropoint of the PL-relation. Ripepi et al. (2019) re-classified all 2116 stars reported by Clementini et al. (2019) to be Cepheids in the Milky Way (MW). In total 1257 stars were classified as Cepheids (including 575 CCs pulsating in the fundamental mode (FU), 108 anomalous Cepheids (ACEP), and 336 Type-II Cepheids (T2C)). Period-Wesenheit relations in the Gaia bands were presented. Assuming a canonical distance modulus to the LMC of 18.50, a Gaia parallax zeropoint offset of ∼ − 0.07 to −0.1 mas was found. Groenewegen (2018) (hereafter G18) started from an initial sample of 452 Galactic CCs with accurate [Fe/H] abundances from spectroscopic analysis. Based on parallax data from DR2, supplemented with accurate non- parallax data when available, a final sample of about 200 FU mode Cepheids with good astrometric solutions was retained to derive PL and period-luminosity-metallicity (PLZ) relations. The influence of a parallax zeropoint offset on the derived PL(Z) relation is large and make that the current GDR2 results do not allow to improve on the existing calibration of the relation, or on the distance to the LMC (as also concluded by Riess et al. 2018a). The zeropoint, the slope of the period dependence, and the metallicity dependence of the PL(Z) relations are correlated with any assumed parallax zeropoint offset.
Based on a comparison for nine CCs with the best non- parallaxes (mostly from HST data) a parallax zeropoint offset of −0.049 ± 0.018 mas is derived, which is consistent with other values that appeared in the literature after the release of GDR2, from RGB stars using Kepler and APOGEE data (about −0.053 mas, Zinn et al. 2019), a sample of ∼150 eclipsing binaries (−0.082 ± 0.033 mas, Stassun & Torres 2018), a sample of 50 CCs (−0.046 ± 0.013 mas, Riess et al. 2018a), 140–300 RR Lyrae stars (∼ − 0.056 mas, Muraveva et al. 2018; −0.042 ± 0.013 mas, Layden et al. 2019), a sample of 34 stars with VLBI astrometry (−0.075 ± 0.029 mas, Xu et al. 2019), a sample of about seven million objects with a radial velocity (RV) in Gaia (∼ − 0.054 mas, Schönrich et al. 2019) a sample of ∼250 000 stars from APOGEE (−0.0523 ± 0.020 mas, Leung & Bovy 2019), a sample of ∼27 000 Red Clump stars selected from APOGEE (−0.048 ± 0.01 mas, Chan & Bovy 2019). These values are mostly all-sky averages, but when sufficient data is available it is clear that the parallax zeropoint offset depends on position on the sky, magnitude, and colour (Zinn et al. 2019; Khan et al. 2019; Leung & Bovy 2019; Chan & Bovy 2019).
The analysis by Ripepi et al. (2019) on the classification of CCs addresses one of the issues that also affected the analysis in G18. The classification as CCs was taken from the literature in that paper and the origin of this classification is sometimes hard to trace. In addition, some stars have alternative classifications reported in the literature. It is clear that the most accurate determination of PL- or period-radius (PR) relations would benefit from a “clean” sample.
To address this issue the spectral energy distributions (SEDs) of the sample in G18 are constructed in the present paper, and fitted with model atmospheres (and a dust component if needed). For a given distance and reddening this results in the absolute luminosity and (photometric) effective temperature. Placing the objects in the Hertzsprung-Russell diagram (HRD) and comparing the location to theoretical instability strips (ISs) and evolutionary tracks may show whether the derived stellar parameters are consistent with the variability classification as CCs. In addition, such a procedure may reveal stars whose SEDs are not well fitted by a stellar atmosphere, and that show the presence of infrared emission, such as observed and postulated in a number of well-known CCs (δ Cep, η Aql, X Sgr, T Mon, l Car, Y Oph, see Mérand et al. 2005, 2006, 2007, 2015; Kervella et al. 2006; Gallenne et al. 2013a; Breitfelder et al. 2016), or known to occur in some T2C (in particular RV Tau [RVT] variables, but recently also seen in lower-luminosity W Vir stars, see Kamath et al. 2016; Groenewegen & Jurkovic 2017a and references therein) that could be misclassified as CCs.
The paper is structured as follows. In Sect. 2 the sample of stars is briefly described. Section 3 describes the construction of the SEDs and the model fitting. Section 4 presents the results of the calculations in various subsection. A brief discussion and summary concludes the paper.
2. The sample
The sample studied here is the sample of 452 stars considered in G18 along with 25 additional stars, as described below. G18 compiled a list all CCs with individually determined accurate iron abundances from high-resolution spectroscopy. Some of the stars in the sample had alternative classifications in the literature or were even unlikely to be CCs but they are retained here for completeness. Since then, Luck (2018) published a list of abundances and parameters for 435 Cepheids, 20 of which were not in the G18 sample. In addition, Inno et al. (2019) (hereafter I19) recently determined the metallicity of five CCs in the inner disk of our Galaxy that are of interest. The sample considered in this paper is therefore 477 objects. The basic information for this sample is listed in Table 1. The pulsation type listed in Col. 2, the period (Col. 4) and the E(B − V values (Col. 5) are taken from G18 for the first 452 stars (based on compilations in the literature), Luck (2018) for the next 20 stars and I19 for the stars in the direction of the inner disk (with identifier ID 1–5 following the nomenclature in Inno et al.). In the case of the inner disk Cepheids the AKs values from col. 3 in Table 3 in I19 based on the Cardelli et al. (1989) reddening law were taken, converted to AV using AKs/AV = 0.114 and then converted to E(B − V) using a specific reddening of 3.1. The pulsation type listed in Col. 3 is from the independent classification by Ripepi et al. (2019). The adopted distance (d) is listed in Col. 6 based on the reference in Col. 7. When available this is based on parallax data, otherwise it is the distance quoted in the relevant papers, typically based on a PL-relation. In the case of a parallax, a parallax zero-point offset of −0.043 mas was adopted, following G18. The exact value of this offset, or the adopted distance in general, is not so crucial as it was in G18 or in other papers that aim to improve the PL-relation. The derived luminosities will scale with d2, and the derived effective temperatures are independent of the adopted distance. To give some feeling of the distance and the possible range in distances, Col. 9 reports the distance and error from Bailer-Jones et al. (2018) based on a Bayesian analysis taking into account a three-dimensional (3D) model of the Galaxy as prior and using a parallax zero-point offset of −0.029 mas.
Sample of stars (first entries only).
In general, the distances are in agreement within the margin of error. In only three cases do the adopted distance and the distance from Bailer-Jones et al. (2018) differ by more than 3σ and would this difference in distance lead to a difference in luminosity larger than a factor of three. They are EF Tau, RW Cam, TX Del, and V1359 Aql. Only EF Tau is classified as a CC, while the others are not.
3. Photometric data and SED fitting
The spectral energy distributions (SEDs) are constructed using photometry retrieved mostly, but not exclusively, via the VizieR web-interface1. Given the variability of the sources the aim is to use, as much as possible, magnitudes (and their error bars) at mean light. The optical data comes from GDR2 (G, Bp and Rp), Berdnikov (2008), Berdnikov et al. (2015), Mermilliod (1997), Droege et al. (2006), APASS (AAVSO Photometric All Sky Survey DR9, Henden et al. 2016), and data available throught the McMaster database2 initiated by Dr. Welch. Attention is given to include Walraven photometry from Walraven et al. (1964) and Pel (1976) as this provides a valuable source of photometric data in the blue part of the spectrum. Also GALEX data from Bianchi et al. (2017) is considered. In some case the individual epoch photometry is fitted with the code PERIOD04 (Lenz & Breger 2005) to obtain the mean magnitudes and error bar.
The near-infrared (NIR) photometry is more heterogeneous as it comes from a variety of sources, using different photometric systems and ranges from intensity-mean magnitudes from well sampled light curves to single-epoch photometry in some cases. Details are given in G18, but in brief, mean magnitudes are taken from Monson & Pierce (2011) (converted to the 2MASS system), SAAO-based photometry (mainly Laney & Stobie 1992, and Laney (priv. comm.) as quoted in Genovali et al. (2014), and Feast et al. 2008, and CIT-based photometry from Welch et al. (1984) and Barnes et al. (1997), converted to the 2MASS system. Additional single-epoch photometry is taken from McGonegal et al. (1983), Welch et al. (1984), Schechter et al. (1992), DENIS, 2MASS, 2MASS 6X, IRSF (Kato et al. 2007). Single-epoch NIR data is available from fourth data release of the VVV survey (Minniti et al. 2010)3 for ID 1,2, and 5.
At longer wavelengths generally no light-curve averaged mean magnitudes exist, but the photometric pulsation amplitudes decrease with increasing wavelength and so the effect of the variability on the derived luminosity will be less. An exception is Monson et al. (2012) who present intensity-averaged magnitudes in the Spitzer IRAC 3.6 and 4.5 μm bands for 37 Cepheids. Marengo et al. (2010) give single-epoch Spitzer data in all four IRAC bands and MIPS 24 and 70 μm for 29 Cepheids (only for nine stars in [70]). Additional single-epoch IRAC and MIPS photometry is available in the GLIMPSE (Spitzer Science 2009) and MIPSGAL (Gutermuth & Heyer 2015) catalogues. Single-epoch Akari data is available at 9 and 18 μm from Ishihara et al. (2010). Akari data at longer wavelengths (FIS, Kawada et al. 2007) is available for two objects (BQ Ser and V1344 Aql) but is unreliable. Averaged WISE data is available for the majority of objects (Cutri et bal. 2014). Finally, data from the IRAS Point Source Catalog (PSC, Beichmann 1985), the COBE-DIRBE PSC (Smith et al. 2004) and narrow-band filter data from Gallenne et al. (2012b) are added.
The smallest number of photometric data points over the different filters is nine (for two stars). On the other hand there are fifteen stars with 40 or more data points. The median number of data points is twenty-five.
Mid-infrared (MIR) spectra are available for more than a dozen stars. This is particularly useful data in the detection of infrared (IR) excess. Spitzer IRS spectra are retrieved using the CASSIS tool4 (Combined Atlas of Sources with Spitzer IRS spectra, Lebouteiller et al. 2011) for AY Cen, η Aql, S TrA, SU Cyg, V Cen, V1334 Cyg, ζ Gem, Polaris, δ Cep, l Car, and RS Pup. IRAS LRS spectra are retrieved for β Dor and V382 Car (as well as Polaris, l Car, and η Aql, but for which the higher quality IRS spectra is used) using the interface provided by Dr. Volk5. In addition, spectra are available for T Mon and X Sgr from the MIDI instrument (Gallenne et al. 2013a). All these objects are explicitly discussed in Sect. 4.8.
The SEDs are fitted with More of DUSTY (MoD, Groenewegen 2012)6 which uses a slightly updated and modified version of the DUSTY dust radiative transfer (RT) code (Ivezić et al. 1999) as a subroutine within a minimisation code.
Input to the model are the distance, reddening, a model atmosphere, and the absorption and scattering coefficients of any dust component. For a given set of observed photometric data and spectra (and visibility data, and 1D intensity profiles) the program determines the best fitting luminosity (L), dust optical depth (τ, at 0.55 μm), dust temperature at the inner radius (Tc), and slope of the density profile (ρ ∼ r−p) by minimising a χ2 based on every available photometric and spectroscopic datapoint and its error. Any of these parameters can also be fixed.
The model fluxes are reddened to be compared to the observations using the input value for E(B − V), a specific reddening of 3.1, and the reddening law from Cardelli et al. (1989) and O’Donnell (1994) from the UV to the NIR and with the MIR silicate extinction curve from the Local ISM model in Chiar & Tielens (2006). The comparison to the observed magnitudes is done by convolving the model SED with a large number of photometric filters with the appropriate zeropoints.
The SEDs are fitted under the assumption of being representative of a single star. Any unresolved binary will influence the photometry depending on the luminosity ratio and difference in spectral type and hence the resulting effective temperature and luminosity (see Sect. 4.6 for an estimate of the effect) MARCS model atmospheres are used as input (Gustafsson et al. 2008) with solar metallicity and a log g = 2. The model grid is available at 250 K intervals for the effective temperature range of interest, and adjacent model atmospheres are used to interpolate models at 125 K intervals, which reflects better the accuracy in Teff that can be achieved. Most stars have no dust and are best represented by a “naked” star. In those cases, the dust optical depth is fixed to a very small number (10−5, and Tc and p are also fixed to standard values of 1000 K and 2, respectively). For every model atmosphere (that is, Teff) a best-fitting luminosity (with its [internal] error, based on the covariance matrix) is derived with the corresponding reduced χ2 (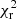 ) of the fit. The model with the lowest
) of the fit. The model with the lowest 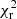 then gives the best-fitting effective temperature. Considering models within a certain range above this minimum
then gives the best-fitting effective temperature. Considering models within a certain range above this minimum 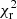 then gives the error in the effective temperature and luminosity. For the luminosity this error is added in quadrature to the internal error in luminosity.
then gives the error in the effective temperature and luminosity. For the luminosity this error is added in quadrature to the internal error in luminosity.
For some stars a better fit is achieved by adding a dust component. The Bayesian information criterion (BIC, see Schwarz 1978) is used to verify if the lower χ2 that is obviously obtained when adding additional parameters is, in fact, statistically significant.
In the next section the results of the various calculations are presented.
4. Results
4.1. Mid-IR and Far-IR excess
A visual inspection of the SEDs revealed four stars that evidently showed an IR excess. We note that this large excess is different from the excess of order a few percent that is claimed in a number of CCs (see introduction) and whose nature is explicitly investigated in Sect. 4.8.
One of the four is RS Pup and its excess in the far-IR is long known (Gehrz & Woolf 1970; McAlary & Welch 1986; Deasy & Butler 1986). The IRS spectrum that is used in the SED fitting is that of the emission close to the star and does not include the extended emission. In the SED fitting the part of the spectrum beyond 20 μm is excluded not no influence the fitting of the extended dust component.
The other three stars are AU Peg, FQ Lac, and QQ Per. The SEDs of these stars show an near- and mid-IR excess that is typical of that of RVT stars and also recently seen in a number of lower-luminosity W Vir stars in the Magellanic Clouds (Kamath et al. 2016; Groenewegen & Jurkovic 2017a). The adopted classification in G18 is CWB, CEP:?, CEP?, respectively, the classification in Ripepi et al. (2019) is BLHER, Fundamental mode CC, and WVIR, respectively (see Table 1). The fitting of the SED (also in the case of RS Pup) is performed as outlined in Groenewegen & Jurkovic (2017a) and includes a dust component (see Groenewegen & Jurkovic 2017a for details). The best-fit SEDs are shown in Fig. 1. It should be pointed out that the shape of the excess points to a a disc structure rather than an expanding outflow, so the use of a 1-D code is limited. For the purpose of the present paper we included a realistic dust component in order to get a more realistic estimate of the luminosity.
 |
Fig. 1. Best fit models of RS Pup, and the three (likely) T2Cs that show near- and mid-IR excess. Errorbars are plotted and are typically the size of the plot symbol. |
The dust temperature at the inner radius is found to be 46 K in the case of RS Pup, and 450–1050 K in the case of the T2Cs. For RS Pup this is close to the value of “around 40 K” derived in Deasy & Butler (1986) by a blackbody fit to the IRAS data. The IR excess in AU Peg was detected first by McAlary & Welch (1986) based on IRAS data. The SED of QQ Per was shown in Schmidt (2015) and identified as having a strong IR excess, but classified as a CC. The IR excess in FQ Lac seems to be reported for the first time in the present work it appears.
4.2. The standard case
In this subsection, the derived luminosities and effective temperatures are discussed in the standard case, that is fitting model atmospheres to the SEDs without circumstellar dust, except for the four stars just discussed. The results are listed in Col. 9 and 10 of Table 1. The HRD is shown in Fig. 2. To assist in the interpretation some ISs have been plotted. At log L ∼ 2 these are the blue and red edge of BL Her (T2C with period ≲ eight days) for a mass of 0.65 M⊙ (Di Criscienzo et al. 2007). Unfortunately, no ISs seem to be available in the literature for the brighter T2Cs, like the WVIR. The dashed (indicating Z = 0.008) and full lines (Z = 0.02) represent the blue and red edge for CCs from Bono et al. (2000). The near horizontal lines indicate the evolutionary tracks for Z = 0.014 and average initial rotation rate ωini = 0.5 from Anderson et al. (2016). The FO (red dot-dashed lines) and FU (green full lines) tracks are shifted by 0.01 dex in luminosity for clarity. Increasing in luminosity they are tracks for initial mass (number of the crossing through the IS): 3 (1), 4 (1), 5 (1), 5 (2), 5 (3), 7 (1), 7 (2), 7 (3), 9 (1), 9 (2), 9 (3), 12 (1).
 |
Fig. 2. Hertzsprung-Russell diagram. Stars located outside the bulk of objects have been labelled and are plotted with error bars. Blue and red lines indicate the blue and red edge of the IS. At log L ∼ 2 this is the IS for BLHER T2C; at brighter luminosities those for CCs. The near horizontal lines are stellar evolution tracks of CCs of different masses. See the main text for details. |
The bulk of stars located between log L ∼ 2.9 − 3.8 L⊙ would correspond to stars of initial mass ∼5 − 7 M⊙ most likely in their 2nd or 3rd crossing of the IS. The evolutionary time spent in the 1st crossing is an order of magnitude shorter and this explains qualitatively the lack of stars in the luminosity range covered by the 3 and 4 M⊙ tracks. The brightest stars in the sample would correspond to ∼12 M⊙ stars during their first crossing of the IS.
The location of the majority of stars in the HRS is consistent with the location of the IS of T2C and CCs. Error bars are plotted for some of the stars outside the bulk of objects, but they are typical for the entire sample. Based on this there are a few stars (notably DY Ser and ID 2) that are much hotter and about two dozen stars (∼5% of the sample) that are cooler than expected for a star located in the IS. In particular for three of the five stars in the sample in the direction of the inner disk the location in the HRD appears to be inconsistent with the IS. One obvious reason for this discrepancy is the degeneracy between interstellar reddening and the derived effective temperature. This is explicitly investigated in the next section, and more generally in Sect. 4.7.
4.3. The role of reddening for the Cepheids in the inner disk
In the standard case, the interstellar reddening is fixed from I19 and the SEDs are fitted to give the best fit effective temperature and luminosity (for the distance quoted in I19). The reddening is large and has a large formal error bar that is not explicitly considered in the fitting. An alternative is to fix the effective temperature to the value derived spectroscopically and then determine the best-fitting luminosity and value of AV. A third way is to fix Teff to a value that would put the star roughly in the middle of the IS and then fit for L and AV. The results of the calculations are reported in Table 2 and the HRD is shown in Fig. 3. For ID 2, 3, 5 the temperature determination is based on a single spectrum, for ID 1 and ID 4 the average of two determinations is used. As the temperature changes over the pulsation cycle this introduces additional uncertainty as in the case of ID 1 the two temperature determinations differed by 700 K. The impact of a change of effective temperature is large as shown in Fig. 3, and are strongly correlated with AV and L. When both the spectroscopic temperature or a temperature in the IS is chosen the resulting AV is larger than the value adopted in I19 for all five stars. This is an additional complication in deriving the parameters of these stars as the distances derived in I19 are based on infrared PL-relations that were dereddened using certain values of AK (and also depend on the reddening law).
 |
Fig. 3. Hertzsprung-Russell diagram, zoomed in on the region covered by the five object in the direction of the Galactic disk. The labelled points with the red vertical error bars indicate the standard case (Fig. 2). They are connected by green lines to the points with the green vertical error bars indicating the cases where the effective temperature is fixed to the value determined from spectroscopy, which in turn are connected by blue lines to the points with blue vertical error bars indicating the cases where the effective temperature is fixed to a value roughly in the middle of the IS. |
Classical Cepheids in the inner disk: variation in the parameters.
4.4. Angular diameters
Column 11 of Table 1 gives the predicted angular diameter with error, determined from luminosity, effective temperature, and distance.
As an aposteriori verification they are compared to observed angular diameters that are available for almost two dozen and that are listed in Col. 12. With the exception of the data in Gallenne et al. (2019), the values represent the mean angular diameter over the light curve. For 20 stars the predicted and observed angular diameters agree within the error bars given confidence to the fitting method and the derived parameters. Exceptions are T Vul and the overtone pulsator AH Vel.
4.5. Role of binarity
The standard case assumes that the SED is that of a single star, the CC. Many CCs are known to be in binaries, see, for example, the database of Szabados (2003)7, and the photometry extracted from the literature could be contaminated by an companion.
Three cases have been studied in detail on what the largest likely effect would be of a (probable) companion. Kervella et al. (2019a) looked for resolved common proper motion pairs among CCs and RR Lyrae using GDR2 data and found 27 resolved high-probability gravitationally-bound systems with CCs out of 456 stars examined. Their Table A.1 list the Gaia photometry of the CC and the bound candidates. Two stars are selected where this difference is smallest in the Bp band (∼3.3 mag), U Sgr and EV Sct. In the other 25 cases this difference is much larger, up to nine magnitudes. In fact the bound candidates are located at 25 and 72″ away from the CC, so in reality they do not contaminate the Cepheid, but one can make the experiment if companions of this type were in fact close physical companions.
The companion to U Sgr is thought to be of spectral type A0 (Kervella et al. 2019a) and a model atmosphere of a 10 000 K star is fitted to the Gaia Bp, G, and Rp photometry assuming the same distance and reddening as for U Sgr. The best fit resulted in a luminosity of L ∼ 110 L⊙. The predicted magnitudes of this star were then added to those of U Sgr, and the fit of the SED is repeated. The best-fitting luminosity is increased by 2%, while the best-fitting effective temperature remains unchanged indicating the effect is less than the grid interval of 125 K.
In the case of EV Sct, the spectral type of the companion is of spectral type B9 (Kervella et al. 2019a) and a model atmosphere of a 11 000 K star is fitted to Gaia Bp, G, and Rp and 2MASS JHK photometry. The best fit resulted in a luminosity of L ∼ 75 L⊙. The predicted magnitudes of this star are again added, and the fit of the SED of EV Sct is repeated. The results are very similar to those of U Sgr, the best-fitting effective temperature remains unchanged and the luminosity increases by 3%.
The third case is V1334 Cyg, a system with a close companion of spectral type B7 located at 8.5 mas (Gallenne et al. 2018) that does contaminate the photometry of the system. As this system has all orbital parameters, masses and distance determined with high precision from a combination of (optical) interferometry and spectroscopy (Gallenne et al. 2018) it also serves as an excellent system to test the methodology to search for companions from the difference between HIPPARCOS and Gaia proper motions (Kervella et al. 2019b). A model atmosphere of a 15 000 K star is fitted to a 2MASS H-band of 8.47 mag, which is based on the estimated flux-ratio of the Cepheid and the companion (ΔH = 3.70 ± 0.11) from NIR interferometry (Gallenne et al. 2018). The predicted magnitudes of this star are subtracted, and the fit of the SED of V1334 Cyg is repeated. In this (more uncertain) case the best fitting temperature shifts to the next point in the available grid (from 5875 to 5750 K) and the luminosity decreases by 7%.
In all three cases studied here there is some effect of a (potential) companion on the derived luminosity and effective temperature from the SED fitting. The effects are also systematic in nature. However, even for quite small contrast levels (3.3 − 3.7 mag between Cepheid and companion) the effects are (much) smaller than the random errors quoted on L and Teff. The effect of photometric contamination by a companion should have a small to negligible influence on the results in this paper.
4.6. A comparison of effective temperature and reddening values to the literature
The effective temperatures in the present work are derived by fitting model atmospheres to the SEDs (constructed to be representative of mean light), which are dereddened taking reddening values from the literature.
Effective temperature have been derived from spectroscopy for many stars in the sample. The case of the five Cepheids in the inner disk (Sect. 4.3) illustrated the sensitivity of the photometric temperature determination on the reddening. For both parameters it is interesting to compare the adopted reddenings and the derived effective temperatures to independently determined values.
In the case of the effective temperatures the results of Luck (2018) are used, which is by far the largest collection of uniformly reduced and analysed spectra for CCs, including multi-epoch data when available. Table 3 from that paper is used, and for the 432 stars in overlap with the present sample the following quantities are determined: number of epochs, and the minimum, maximum, average and median effective temperature. Inspecting the results for the Cepheids with the most multi-epoch data (also see Figs. 11–17 in Luck 2018) indicate that the highest effective temperatures are found in the phase range 0.9–0.1, and the lowest in the range 0.4–0.6. As the temperature from the SED fitting should be representative of mean light the number of epochs and the average temperature in the phase range 0.1–0.4 and 0.6–0.9 is also calculated. The same procedure is followed for ID 1–5 using the data in I19.
Infrared excess in CCs with mid-IR spectra.
In the upper panel of Fig. 4, the spectroscopic temperatures are compared to the photometric ones. If there are more than three determinations in the phase range representative of mean light the average over those values is taken (the thick solid circles), otherwise when there are two or more observations the average is taken (small open circles).
 |
Fig. 4. Comparison between the effective temperatures determined from the SED fitting, and in the literature. Stars outside the bulk of objects are identified and plotted with error bars. The one-to-one line is indicated. In the upper figure the temperatures are compared to the data in Luck (2018) (and I19 for ID 1–5). When there are three or more values available in the phase range representative of mean light the object is marked by a thick filled circle. Otherwise when there are two or more observations the average is taken (small open circles). Lower panel: difference between spectroscopic and photometric temperature. In the lower figure the effective temperatures from Trahin (2019) are compared to the present work. |
Some interesting features can be observed. The best determined spectroscopic temperatures correlate with the photometric determinations, but there is an offset of 200 ± 235 K (58 stars, excluding V898 Cep), and the panel with the residuals even suggests a trend, for which no explanation is apparent.
When the stars with two or more determinations are considered as well the scatter increases (as expected), but some very clear outliers also appear. All five stars that are significantly hotter than expected have exactly two measurements, and since the temperature changes over the pulsation cycle this could be a statistical effect.
Figure 5 shows the mean spectroscopic effective temperature versus period, and the difference between highest and lowest effective temperature over the pulsation cycle versus period and Teff. The data is from Luck (2018) and considers the 30 stars with seven or more determinations in the phase range typical of mean light. The top panel is quasi identical to that of Fig. 18 in Luck (2018). He used 52 stars (his criterion was five or more determinations in total) but did not distinguish between FU and FO pulsators. The two other panels show the range in effective temperature over the pulsation cycle as a function of temperature and period. Overtone pulsators show changes that are about a factor of three smaller than FU pulsators at the same period. The plot shows that changes of 1000 K over the pulsation cycle are quite common and possibly even higher at lower effective temperatures.
 |
Fig. 5. Using data from Luck (2018) the panels show the mean effective temperature, and the difference in Teff over the pulsation cycle against temperature and period for the 30 objects with seven or more datapoints in the phase range typical for mean light. Overtone pulsators are indicated by open circles. |
This indicates that the location of the five outliers can only partly be explained by the sampling of the two datapoints over the light curve. Another indication that the photometric temperature might be incorrect is that all these five stars (and to a lesser extent TU Cas and U TrA) are outliers in the HRD as well and that the spectroscopic temperature would put all these objects closer to the IS. Given the discussion in Sect. 4.3 one might reddening to play a role; this is investigated in the next section.
Another comparison of the effective temperatures is with the recent work of Trahin (2019), who applied the Spectro-Photo-Interferometry of Pulsating Stars (SPIPS) method (Mérand et al. 2015) to a sample of 74 CCs (and that all are in the present sample). In the SPIPS method light curves in different bands, radial velocity curves, spectroscopic temperature determinations, and angular diameter determinations are fitted to provide a consistent model fit to all data. What is interesting in the present context is that effective temperature (via ATLAS9 model atmospheres) and reddening are fitted simultaneously. The bottom panel in Fig. 4 shows the comparison between the effective temperatures found here and in Trahin (2019). The agreement is very good. The offset of 66 ± 230 K is not significant. The scatter suggests that the error bars in Trahin (2019) may be underestimated as the median error bar among the 74 stars is 52 K while it is 188 K in the temperature determinations derived in the present work.
Although different in detail, both SPIPS and the present work use grids of (different) model atmospheres to fit photometry. That the effective temperatures agree to within the errors with no significant offset is highly satisfactory.
4.7. Reddening
The discussion on the Cepheids in the direction of the inner disk and the discrepancy in some cases between spectroscopic and photometric temperature determinations suggests that reddening could play a role. Figure 6 compares the E(B − V) values determined in Trahin (2019) to the values adopted from the literature in the present work. The results are overall consistent with no significant outliers. A linear least-squares fit gives a slope not significantly different from unity: E(B − V)SPIPS = (1.02 ± 0.03) E(B − V)this work + (0.027 ± 0.012), with an rms of 0.051. This scatter is larger than might be expected based on the error bars in the two measurements. The median error bar in the reddening in these 74 stars is 0.02 mag in this work and 0.017 mag in Trahin (2019), suggesting that both errors are on average underestimated.
 |
Fig. 6. Comparison between the E(B − V) values in Trahin (2019) and the present work. The one-to-one line is indicated. The random and systematic error bars in Trahin (2019) have been added in quadrature. |
However, none of the two dozen outliers marked in Fig. 4 are in the sample of Trahin (2019) and therefor the role of reddening can not be excluded for these specific stars.
To investigate the matter further two recent 3D reddening models have been used to estimate the reddening in the direction of the stars in the sample.
The first is described in Lallement et al. (2018)8 (hereafter STILISM) and is based on Gaia, 2MASS and APOGEE-DR14 data. For a given galactic longitude, latitude and distance, the tool returns the value of E(B − V) and error, and the distance to which these values refer. If this distance is smaller than the input distance the returned value for the reddening is a lower limit. In these cases a simple estimate of the reddening at the distance of the Cepheid is made. A second reddening value is queried at a distance 0.75 times the maximum distance available in the grid in that direction. Based on this the first derivative (with error bar) is determined and the reddening at the distance of the target estimated. The error bar returned by STILISM is added in quadrature with the error due to a 1 degree change in l and b, and a 5% error in distance.
The second reddening model is that described in Green et al. (2019)9 and is based on Gaia DR2 data, 2MASS, and Pan-STARRS 1 data. Reddening values are provided out to “several” kpc for stars north of declination −30°, which means 340 stars in the sample. The output requested from the code are the 2.1, 50 and 97.9% probability values of the reddening. The two extremes are used to calculate the error in the reddening value. This error is added in quadrature to the error due to a 1 degree change in R.A. and Declination, and a 5% error in distance.
The adopted E(B − V) values from the literature, and those from Trahin (2019) and the two reddening models, are collected in Table A.1. The different sets are briefly compared and discussed in Appendix A. For some of the outliers in Figs. 2 and 4 the alternative reddening values are very different from the adopted ones, but not in all cases.
For two of the most prominent outliers in Fig. 2, DV Ser and V891 Per, the two 3D reddening models agree and give a E(B − V) value very different from the adopted ones. Redoing the fitting for an E(B − V) = 1.4 results in luminosities and effective temperatures that puts both stars inside the IS. However there are also outliers where the two reddening models and the adopted value agree (e.g. TU Cas, ASAS 1810-20), or where the two reddening models do not agree among them, but one of them agrees with the adopted reddening (e.g. BD Cas, IR Cep), or where the adopted value agrees with the single available value from a reddening model (e.g. V1210 Cen).
4.8. Dust and excess emission
Some stars in the sample have been proposed to show infrared excess which was suggested to be due to dust emission in a circumstellar envelope (CSE), see e.g. Mérand et al. (2005, 2006, 2007, 2015), Kervella et al. (2006), Barmby et al. (2011), Gallenne et al. (2012b, 2013a), Breitfelder et al. (2016).
In this section, the results are presented of a consistent model of the Cepheid surrounded by a (spherically symmetric) dust shell using MoD. An important ingredient to such a model is the dust opacity. Other parameters are the dust optical depth (τ), the inner radius of the CSE (or the dust temperature at Rinn), and the slope of the density law ∼r−p.
Gallenne et al. (2013a) also performed dust RT calculations to fit the SED and MIDI MIR spectra of T Mon and X Sgr. These two stars seem to be the only CCs for which quantitative RT calculations have been performed so far. They investigated combinations of several dust species and based on their results a similar approach was adopted and grains composed of metallic iron (optical constants from Henning et al. 1995), warm silicates (Ossenkopf & Henning 1994), and compact aluminium oxide (Begemann et al. 1997) are considered. A grain size of 0.1 μm is adopted and the absorption and scattering coefficients are calculated assuming a distribution of hollow spheres (Min et al. 2005).
The results of the calculations are shown in Fig. 7. The top panel shows the standard case, a model with no dust, and three models with dust composed of (top to bottom) 80, 94, and 100% iron and the remainder evenly split between silicates and aluminium oxide. One immediate notices that the MIDI spectrum of T Mon is not compatible with the rest of the SED. The SEDs for T Mon and X Sgr in the present paper have more datapoints (also in the 10–20 μm region) than considered in Gallenne et al. (2013a). However, also in Gallenne et al. (2013a) the spectrum lies well above their SED extrapolated from shorter wavelengths, and in fact, they caution that “the excess of T Mon ...might suffer from skybackground contamination”. This is indeed likely to be the case. Although one can fit the shape and flux level of the MIDI spectrum with featureless pure iron dust the fit to the photometric points excludes that the observed MIDI spectrum is associated to the star. As this discrepancy was noted early on in this study, the spectrum of T Mon was down-weighted when performing the standard fit without dust, not to influence the determination of effective temperature and luminosity.
 |
Fig. 7. Fits to the SED and mid-IR spectra of T Mon and X Sgr for different dust compositions. Top panel: standard model without dust component. Other three panels: models with dust composed of 80, 94, and 100% iron, respectively, with the remainder evenly split between silicates and aluminium oxide. The mid-IR spectrum is scaled to the model based on the average flux in the 10–10.5 μm region. |
The shape of the MIDI spectrum of X Sgr can be fit reasonably well with dust composed of 80 or 94% iron, similar to the results in Gallenne et al. (2013a). The temperature at the inner radius is found to be 1309 ± 40 K, corresponding to a size of 18 mas, and the dust optical depth at 0.55 μm to be (15 ± 1) 10−3 also in agreement with the values of, respectively, 1684 ± 225 K, (7.9 ± 2.1) 10−3, and (15.6 ± 2.9) mas in Gallenne et al. (2013a).
Based on these results the other CCs with MIR spectra are fitted with dust composed of 80, 90, 94, and 100% iron dust. The temperature at the inner radius and the slope of the density law were kept as free parameters, unless no convergence was achieved and p or Tinn, or both, were fixed. The results are collected in Table 3 and the best fits are shown in Fig. 8. The table first lists the luminosity and the statistics (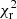 and BIC) for the model without dust and then the parameters for the best-fitting model with dust. In the case of V1334 Cyg a model was also run on the photometry corrected for the binary component (Sect. 4.6). The error bars on the luminosities are much smaller for the same star than those listed in Table 1. The reason is that the error in Table 1 includes the error in the effective temperature, while the error in Table 3 is that when the effective temperature is fixed to its best-fitting value. The errors on the luminosities are very small. The reason is the much larger number of available data points compared to the stars without spectral information. There are typical ∼380 datapoints contained in an IRS spectrum and ∼18 − 30 photometric datapoints. With a typical residual of 0.1 mag per data point one can estimate an error on the mean of order 0.5%. In three stars, no converging model or no significant improvement in the fit is obtained; in the other cases, a statistically better fit can be obtained by including a dust component.
and BIC) for the model without dust and then the parameters for the best-fitting model with dust. In the case of V1334 Cyg a model was also run on the photometry corrected for the binary component (Sect. 4.6). The error bars on the luminosities are much smaller for the same star than those listed in Table 1. The reason is that the error in Table 1 includes the error in the effective temperature, while the error in Table 3 is that when the effective temperature is fixed to its best-fitting value. The errors on the luminosities are very small. The reason is the much larger number of available data points compared to the stars without spectral information. There are typical ∼380 datapoints contained in an IRS spectrum and ∼18 − 30 photometric datapoints. With a typical residual of 0.1 mag per data point one can estimate an error on the mean of order 0.5%. In three stars, no converging model or no significant improvement in the fit is obtained; in the other cases, a statistically better fit can be obtained by including a dust component.
 |
Fig. 8. Fits to the SED and mid-IR spectra of the Cepheids which have an IRAS LRS or Spitzer IRS spectrum. The mid-IR spectrum is scaled to the model based on the average flux in the 10–10.5 μm region. |
One very interesting observation is that the best-fitting luminosity in the dust model is lower than in the standard case and that (in most cases) the V and K magnitudes in the model with dust are fainter than the model without dust. The excess compared to the photosphere is relatively small in the models with dust, 10 mmag at most in K. Its larger in the N-band, 10–40 mmag but smaller than the few percent claimed in the literature for both bands.
Within the assumptions of the adopted dust model one can relate the optical depth to a mass-loss rate. Assuming a dust-to-gas ratio of 1/200 and an expansion velocity of the CSE of 200 km s−1 (the escape velocity for a 5 M⊙ 45 R⊙ star) the mass-loss rates is about 3.6 ⋅ 10−9 M⊙ yr−1 in the case of AY Cen, and factors of 10–100 lower in the other stars.
Finally, the SEDs of all stars in the sample (except the three stars with a clear IR excess, FQ Lac, AU Peg, and QQ Per) are fitted with a dust model. As there are, in general, no spectra available to better constrain the fitting, the slope of the density law is fixed to 2.0 to reduce the number of free parameters, a value consistent with the results found for the objects with MIR spectra. Grains with 80% iron (and thus 10% silicate and 10% aluminium oxide grains) are assumed. Initial guesses for the optical depth are τ = 0.0002, 0.0007, 0.002, and Tinn = 1000, 1500 K are used based on the results in Table 3. The models are run over the grid of model atmospheres for each of the six initial guesses of the dust parameters, and the model with the lowest BIC is taken. It is compared to the BIC of the model without dust and the reduction in the BIC is compared to the change in BIC due to a 1σ change in effective temperature as a measure of the significance of the reduction in the BIC due to dust compared to other parameters.
For 331 stars in the sample, the models with dust do not converge or do not have a lower BIC. The results are displayed in Fig. 9. That figure also compares the results to the outcome of the SPIPS modelling from Trahin (2019). In that model an IR excess is parameterised using the functional form: IRex = 0 mag for λ < 1.2 μm and IRex = α ⋅ (λ − 1.2)0.4 mag for λ ≥ 1.2 μm, where α is one of the outputs of the SPIPS model, and the quantity plotted along the abscissa in Fig. 9. The value of α is effectively the excess in the K-band, while the excess in the N-band is about 2.5 times larger. Along the ordinate the ratio of the reduction in the BIC in the dust model divided by the reduction in BIC due to a 1σ change in effective temperature is used (hereafter SN). The stars in the sample that are not in Trahin (2019) are plotted at x = −0.06.
 |
Fig. 9. Measures of the IR excess from the present work, and a comparison to the measure of the IR excess from Trahin (2019) (see main text for details). |
There is a group of stars (ζ Gem, LS Pup, η Aql, SU Cyg) for which there is a good correspondence between the two works (α ≳ 0.05 mag, and SN ≳ 0.4). On the other hand, there are stars that have a large values for α for which the SEDs are well defined in the present work and for which there is no evidence for IR excess (in particular CS Vel).
It is remarked that a non-negligible number of stars in Trahin (2019) are quoted to have a negative IR excess, which is physically impossible. This is likely a testimony to the fact that it is very difficult to establish small levels of IR excess with confidence. It may point to uncertainties in other aspects of the SPIPS modelling, for example the value of the p-factor. It does suggest that the error bars quoted in Trahin (2019) for the IR excess are probably somewhat underestimated, and that the range −0.05 < α ≲ +0.05 mag is likely consistent with the absence of an IR excess. In this range our measure of the IR excess is also consistently small, SN ≲ 0.35.
Most of the stars that appear in Table 3 are also marked in Fig. 9 (V Cen, AY Cen, S TrA, V1334 Cyg, ζ Gem, SU Cyg, η Aql). Polaris is not analysed in Trahin (2019), but Mérand et al. (2006) quote α ∼ 0.016 mag also based on the SPIPS method. The value for SN is also small, and therefore the IR excess in α UMi is probably not significant. The second star is δ Cep with α = 0.06 mag. In this case the IR excess might be real. The value for SN is likely to be underestimated in this work because of the relatively large error bar on the effective temperature in this particular case.
The three stars in Table 3 for which no significant IR excess is found have been analysed by Trahin (2019): β Dor (α = 0.08), RS Pup (α = 0.04), and l Car (α = 0.04 mag). The case of β Dor is the most puzzling as the value of α appears significant. On the other hand only a relatively poor LRS spectrum is available which is less constraining than the IRS spectra. For the other two stars, the value of α is small and overall consistent with my finding of no excess. In earlier works on l Car by the same group Kervella et al. (2006) reported an IR excess similar to Trahin (2019), but Breitfelder et al. (2016) found no excess. Again, this points to the difficulty of establishing small levels of IR excess with confidence.
The analysis also revealed possible IR excess in stars that do not have an MIR spectrum available, namely LS Pup (confirmed by Trahin 2019 as well), and the stars with SN > 0.4, AD Cru, EX Cyg, XX Vel (the three most likely cases), and the more uncertain cases of V5567 Sgr, CR Cep, FN Vel, DF Lac, and HW Car. The Cepheid ID 2 is also marked in the figure. The analysis of the IR excess was done using the standard value of the interstellar reddening. If the analysis were repeated fixing the effective temperature to the spectroscopic one, or one consistent with the location of the IS (see Sect. 4.3), the excess would disappear. It indicates that a very wrong choice of the reddening could lead one to believe that there were an IR excess.
4.9. Period-luminosity and period-radius relations
The final topic to be discussed are the relations between period and bolometric luminosity and radius. In a first selection outliers in the HRD are excluded. As discussed, this could be due to a misclassification of the object, an incorrect distance (that is, luminosity), an incorrect reddening, or a combination of these effects. Improved distances (Gaia DR3), improved 3D reddening models, and improved light curve classification (possibly from end-of-mission Gaia light curves or light curves from other time-domain surveys) may in the future shed light on why exactly some stars are outliers in the present analysis.
Figure 10 shows the results. To be included in the fitting, objects are selected to have L < 50 000 L⊙, Teff < 7000 K, Teff > 4000 K, and (L < 350 L⊙ or log L > ( − 12.083 ⋅ log(Teff)+47.5)). The last relation is a line across the HRD that eliminates the stars that are much cooler than expected from the bulk of stars and the red-edge of the IS. The weighted linear least-squares fits are done using only FU mode pulsators (i.e. the period of overtone pulsators are not “fundamentalised” and included in the fit), and iterative 3σ clipping. The best fit relations are
 |
Fig. 10. Top panel: period-Mbol relation. Error bars in Mbol are not show as they are smaller than the symbol size. Some outlying stars are identified. The black line indicates the best fit to the fundamental mode Cepheids (excluding outliers). The blue line gives the PL relation for T2Cs in the MCs from Groenewegen & Jurkovic (2017b). Bottom panel: period-radius relation. Some outlying stars are identified. The black line indicates the best fit to the fundamental mode Cepheids (excluding outliers). The blue line gives the PR relation for T2Cs in the MCs from Groenewegen & Jurkovic (2017b). The green line is the theoretical PR relation from Anderson et al. (2016). |
using 380 stars and with an rms of 0.40 mag, and
using 372 stars and with an rms of 0.067 dex.
This empirical PR relation is based on the largest sample of Galactic Cepheids. It agrees largely with previous estimates (see the compilation in Table 4), although many PR-relations are based on the Baade-Wesselink method that depends on the adopted projection (p) factor that converts radial velocity to pulsational velocity. Theoretical PR relations tend to give slightly shallower slopes, but the maximum difference with the recent work of Anderson et al. (2016) (average rotation value, Z = 0.014, averaged over 2nd and 3rd crossing; the green line in Fig. 10) is only +13% at log P = 0.5, and −5% at log P = 1.8. These relations have been derived from the luminosities based on the adopted distance. Relations that also take into account an estimated error on the distance in the luminosities are given in Appendix B, but the effect is small.
Period-radius relations of the form log R = a log P + b.
What is noticeable is that a number of stars scatter around the PL and PR relation for T2Cs derived for the MCs (Groenewegen & Jurkovic 2017b). Some stars were already known to be T2C (SU Sct, AU Peg, BC Aql) but others have on occasion also been classified as CCs but are clearly T2C (e.g. QQ Per, HQ Car).
5. Discussion and summary
The spectral energy distributions representative of mean light of 477 Cepheids were constructed and modelled with stellar photospheres (and a dust component in some cases). Using distances and reddenings from the literature, this resulted in estimates of the bolometric luminosity and effective temperature at mean light, which ultimately allow for the derivation of the period-luminosity and period-radius relations based on a sample of more than 370 fundamental-mode classical Cepheids.
The average positions of the stars in the HRD are largely consistent with the theoretical ISs for CCs or T2Cs. About 5% of the stars in the sample are outliers in the sense that they are significantly cooler or hotter than expected. The likely cause in at least a fraction of the stars is the degeneracy between the fitting of the effective temperature and the adopted reddening. In cases when multiple effective temperature determinations from spectroscopy exist so that an accurate mean effective temperature can be determined this mean temperature is in better agreement with that expected from the IS. This suggests that the photometric Teff is biased by an incorrect reddening.
Two 3D reddening models (STILISM, Lallement et al. 2018, and from Green et al. 2019) have been used to compare the values to the adopted reddening values (see the appendix). There are systematic differences between these two models of order 15%. Compared to the adopted reddenings from the literature the Green et al. (2019) model shows a lower dispersion than the STILISM model, but it is limited to stars north of declination −30°. This uncertainty introduces an additional uncertainty in the derived parameters, in particular, luminosity and effective temperature. Some test calculations show that the uncertainty in the adoped E(B − V) in Table 1 could lead to changes in luminosity, but that these are smaller than the quoted error or smaller than 0.15L in 80% of the sample.
This paper, like G18, is written with the tremendous potential offered by Gaia in mind. Future data releases will provide information that will impact and improve on the results obtained here. Primarily improved parallaxes, taking into account binarity in the astrometrical solution. This impacts the Cepheids, but also the 3D reddening models that use Gaia parallaxes as input. Secondly, improved lightcurves that will allow an homogeneous an improved classification of variable stars and of their subtypes. Thirdly, astrophysical parameters derived from the Bp, Rp, and RVS spectra, in particular effective temperatures (but also metallicity or reddening).
One of the main topics addressed in this paper is the IR excess around CCs which is self-consistently modelled assuming a circumstellar dust shell. First the stars with MIR spectra are analysed (see Table 3) and then the entire sample. The results for the stars with a (likely) IR excess (SN > 0.4) are shown in Table 5. The first six stars (ζ Gem to V1334 Cyg also appear Table 3). The only difference in the fitting is that the slope of the density law is fixed p = 2 while previously is was also a free parameter (and the dust mixture is fixed to 80% iron). The other parameters do change noticeably, although formally mostly within the error bars. The results of having p fixed is that the dust optical depth and dust temperature at the inner radius are better constrained. A comparison of the results for the stars with spectra and those where the IR excess is only determined from photometry (LS Pup to HW Car) shows how important the spectra are in constraining the fit. The results on the dust parameters are much less constrained. Obtaining flux-calibrated MIR spectra for these ten stars would be valuable in confirming and better constraining the nature of the IR excess.
Although statistically significantly better fits can be obtained by including a circumstellar dust shell the question remains if this is a physically correct interpretation. The stars where Tinn is determined with a signal-to-noise better than three have values around 800 K (3 stars), and then ranging from 1000 to 2000 K (five stars). Condensation temperatures of corundum, forsterite and metallic iron are around 1670, 1350, and 1360 K, respectively, at a pressure typical of the Solar nebula (Lodders 2003). At lower pressures these temperatures are lower. The 50% condensation temperature of metallic iron condensing on pre-existing corundum grains is about 1250 K at 10−5 bar and about 970 K at 10−10 bar (Tachibana et al. 2011). Extrapolating the data in Fig. 5 in Grossman (1972) suggests condensation temperatures well below 1000 K for metallic iron as well as enstatite and forsterite at low pressures. So at least for some of the stars the high values of the temperature at the inner radius appear to be in conflict with the expected condensation temperature. In addition, interferometric observations have resolved the CSE around a few CCs (l Car, Kervella et al. 2006; Polaris, Mérand et al. 2006) that show the emission originates from 2 − 3R⋆, where temperatures are larger than the condensation temperatature (see the link between radius and dust temperature at the inner radius in Tables 3 and 5).
When this paper was ready for submission, a work by Hocdé et al. (2020) appeared also discussing the IR excess around CCs. They claim that the excess can not be explained by a hot or cold dust shell, and show that a thin shell of ionised gas is able to explain the observations. They investigated RS Pup, ζ Gem, η Aql, V Cen, SU Cyg and use the SPIPS method, paying special attention to the analysis of the Spitzer IRS spectra. They modelled the IR excess using DUSTY (Ivezić et al. 1999) and used two extreme dust models; pure silicates and pure iron dust. The silicate model is ruled out immediately because of the absence of the 9.7 μm feature, while the iron dust model is ruled out because the Tinn they find in their calculation (2238 K) to achieve a good fit is much larger than the condensation temperature. They then proceed to show that a thin shell of ionised gas can explain the IR excess around these five stars.
Unfortunately, Hocdé et al. (2020) did not try mixtures of dust species which might be key. Interestingly, although pure iron dust was also considered in the fitting of the twelve stars with MIR spectra, it never turned out to be the best fit, but rather the 80, 90, or 94% mixtures that were tried (Table 3). Nevertheless the condensation temperatures, condensation sequence and nucleation and dust growth under the low-density conditions expected in such a hypothetical CSE are a serious concern and the proposed thin shell of ionised gas by Hocdé et al. (2020) is an interesting and viable alternative to explain the IR excess.
https://stilism.obspm.fr/ (version 4.1).
https://argonaut.skymaps.info The “Bayestar19” dataset.
Acknowledgments
I would like to thank Dr. Jan Lub for stressing the importance of including Walraven photometry, Dr. Alexandre Gallenne for providing the mid-IR spectra of T Mon and X Sgr in electronic format, and Dr. Monika Jurkovic for interesting discussions during her visit to the ROB. This work has made use of data from the European Space Agency (ESA) mission Gaia (http://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, http://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This research is based on observations with AKARI, a JAXA project with the participation of ESA. This research has made use of the SIMBAD database and the VizieR catalogue access tool operated at CDS, Strasbourg, France.
References
- Acharova, I. A., Mishurov, Y. N., & Kovtyukh, V. V. 2012, MNRAS, 420, 1590 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, R. I., Saio, H., Ekström, S., Georgy, C., & Meynet, G. 2016, A&A, 591, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrievsky, S. M., Martin, R. P., Kovtyukh, V. V., Korotin, S. A., & Lépine, J. R. D. 2016, MNRAS, 461, 4256 [NASA ADS] [CrossRef] [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Mantelet, G., & Andrae, R. 2018, AJ, 156, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Barmby, P., Marengo, M., Evans, N. R., et al. 2011, AJ, 141, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, III., T. G., Fernley, J. A., Frueh, M. L., et al. 1997, PASP, 109, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Begemann, B., Dorschner, J., Henning, T., et al. 1997, ApJ, 476, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Beichmann, C. A. 1985, Infrared Astronomical Satellite (IRAS) catalogs andatlases, Explanatory supplement [Google Scholar]
- Benedict, G. F., McArthur, B. E., Feast, M. W., et al. 2007, AJ, 133, 1810 [NASA ADS] [CrossRef] [Google Scholar]
- Berdnikov, L. N. 2008, Vizier Online Data Catalog: II/285 [Google Scholar]
- Berdnikov, L. N., Kniazev, A. Y., Sefako, R., et al. 2015, Vizier Online Data Catalog: J/PAZh/41/27 [Google Scholar]
- Bianchi, L., Shiao, B., & Thilker, D. 2017, ApJS, 230, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Bono, G., Castellani, V., & Marconi, M. 2000, ApJ, 529, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Breitfelder, J., Mérand, A., Kervella, P., et al. 2016, A&A, 587, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, V. C., & Bovy, J. 2019, MNRAS, submitted [arXiv:1910.00398] [Google Scholar]
- Chiar, J. E., & Tielens, A. G. G. M. 2006, ApJ, 637, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Clementini, G., Ripepi, V., Molinaro, R., et al. 2019, A&A, 622, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cutri, R. M., et al. 2014, Vizier Online Data Catalog: II/328 [Google Scholar]
- Davis, J., Jacob, A. P., Robertson, J. G., et al. 2009, MNRAS, 394, 1620 [NASA ADS] [CrossRef] [Google Scholar]
- Deasy, H., & Butler, C. J. 1986, Nature, 320, 726 [NASA ADS] [CrossRef] [Google Scholar]
- Di Criscienzo, M., Caputo, F., Marconi, M., & Cassisi, S. 2007, A&A, 471, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Droege, T. F., Richmond, M. W., Sallman, M. P., & Creager, R. P. 2006, PASP, 118, 1666 [NASA ADS] [CrossRef] [Google Scholar]
- Feast, M. W., Laney, C. D., Kinman, T. D., van Leeuwen, F., & Whitelock, P. A. 2008, MNRAS, 386, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallenne, A., Kervella, P., Mérand, A., et al. 2012a, A&A, 541, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallenne, A., Kervella, P., & Mérand, A. 2012b, A&A, 538, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallenne, A., Mérand, A., Kervella, P., et al. 2013a, A&A, 558, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallenne, A., Monnier, J. D., Mérand, A., et al. 2013b, A&A, 552, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallenne, A., Kervella, P., Mérand, A., et al. 2017, A&A, 608, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallenne, A., Kervella, P., Evans, N. R., et al. 2018, ApJ, 867, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Gallenne, A., Kervella, P., Borgniet, S., et al. 2019, A&A, 622, A164 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gehrz, R. D., & Woolf, N. J. 1970, ApJ, 161, L213 [NASA ADS] [CrossRef] [Google Scholar]
- Genovali, K., Lemasle, B., Bono, G., et al. 2014, A&A, 566, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gieren, W. P., Fouqué, P., & Gómez, M. 1998, ApJ, 496, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Gieren, W. P., Moffett, T. J., & Barnes, T. G. I. 1999, ApJ, 512, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Green, G. M., Schlafly, E., Zucker, C., Speagle, J. S., & Finkbeiner, D. 2019, ApJ, 887, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Groenewegen, M. A. T. 2012, A&A, 543, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. A. T. 2013, A&A, 550, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. A. T. 2018, A&A, 619, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. A. T., & Jurkovic, M. I. 2017a, A&A, 603, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. A. T., & Jurkovic, M. I. 2017b, A&A, 604, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grossman, L. 1972, Geochim. Cosmochim. Acta, 36, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gutermuth, R. A., & Heyer, M. 2015, AJ, 149, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Henden, A. A., Templeton, M., Terrell, D., et al. 2016, Vizier Online Data Catalog: II/336 [Google Scholar]
- Henning, T., Begemann, B., Mutschke, H., & Dorschner, J. 1995, A&AS, 112, 143 [NASA ADS] [Google Scholar]
- Hocdé, V., Nardetto, N., Lagadec, E., et al. 2020, A&A, 633, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inno, L., Urbaneja, M. A., Matsunaga, N., et al. 2019, MNRAS, 482, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Ishihara, D., Onaka, T., Kataza, H., et al. 2010, A&A, 514, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivezić, Ž., Nenkova, M., & Elitzur, M. 1999, Astrophysics Source Code Library [record ascl:9911.001] [Google Scholar]
- Jacob, A. P. 2008, PhD Thesis, University of Sydney, Australia [Google Scholar]
- Kamath, D., Wood, P. R., Van Winckel, H., & Nie, J. D. 2016, A&A, 586, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kashuba, S. V., Andrievsky, S. M., Chekhonadskikh, F. A., et al. 2016, MNRAS, 461, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, D., Nagashima, C., Nagayama, T., et al. 2007, PASJ, 59, 615 [NASA ADS] [Google Scholar]
- Kawada, M., Baba, H., Barthel, P. D., et al. 2007, PASJ, 59, S389 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., Nardetto, N., Bersier, D., Mourard, D., & Coudé du Foresto, V. 2004a, A&A, 416, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Fouqué, P., Storm, J., et al. 2004b, ApJ, 604, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., Bersier, D., Mourard, D., et al. 2004c, A&A, 428, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Mérand, A., Perrin, G., & Coudé du Foresto, V. 2006, A&A, 448, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Trahin, B., Bond, H. E., et al. 2017, A&A, 600, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Gallenne, A., Evans, N. R., et al. 2019a, A&A, 623, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Gallenne, A., Remage Evans, N., et al. 2019b, A&A, 623, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khan, S., Miglio, A., Mosser, B., et al. 2019, 53rd ESLAB Symposium: The Gaia Universe, held 8-12 April, 2019 at ESTEC/ESA, Noordwijk, The Netherlands. Online at https://www.cosmos.esa.int/web/53rd-eslab-symposium, 13 [Google Scholar]
- Lallement, R., Capitanio, L., Ruiz-Dern, L., et al. 2018, A&A, 616, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laney, C. D., & Stobie, R. S. 1992, A&AS, 93, 93 [NASA ADS] [Google Scholar]
- Laney, C. D., & Stobie, R. S. 1995, MNRAS, 274, 337 [NASA ADS] [Google Scholar]
- Layden, A. C., Tiede, G. P., Chaboyer, B., Bunner, C., & Smitka, M. T. 2019, AJ, 158, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Lebouteiller, V., Barry, D. J., Spoon, H. W. W., et al. 2011, ApJS, 196, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Lenz, P., & Breger, M. 2005, Commun. Asteroseismology, 146, 53 [Google Scholar]
- Leung, H. W., & Bovy, J. 2019, MNRAS, 489, 2079 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E. 2014, AJ, 147, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E. 2018, AJ, 156, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Marengo, M., Evans, N. R., Barmby, P., et al. 2010, ApJ, 709, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, R. P., Andrievsky, S. M., Kovtyukh, V. V., et al. 2015, MNRAS, 449, 4071 [NASA ADS] [CrossRef] [Google Scholar]
- McAlary, C. W., & Welch, D. L. 1986, AJ, 91, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- McGonegal, R., McAlary, C. W., McLaren, R. A., & Madore, B. F. 1983, ApJ, 269, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Mel’nik, A. M., Rautiainen, P., Berdnikov, L. N., Dambis, A. K., & Rastorguev, A. S. 2015, Astron. Nachr., 336, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Mérand, A., Kervella, P., Coudé du Foresto, V., et al. 2005, A&A, 438, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mérand, A., Kervella, P., Coudé du Foresto, V., et al. 2006, A&A, 453, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mérand, A., Aufdenberg, J. P., Kervella, P., et al. 2007, ApJ, 664, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Mérand, A., Kervella, P., Breitfelder, J., et al. 2015, A&A, 584, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mermilliod, J. C. 1997, Vizier Online Data Catalog: II/168 [Google Scholar]
- Min, M., Hovenier, J. W., & de Koter, A. 2005, A&A, 432, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minniti, D., Lucas, P. W., Emerson, J. P., et al. 2010, New Astron., 15, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Molinaro, R., Ripepi, V., Marconi, M., et al. 2011, MNRAS, 413, 942 [NASA ADS] [CrossRef] [Google Scholar]
- Monson, A. J., & Pierce, M. J. 2011, ApJS, 193, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Monson, A. J., Freedman, W. L., Madore, B. F., et al. 2012, ApJ, 759, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Muraveva, T., Delgado, H. E., Clementini, G., Sarro, L. M., & Garofalo, A. 2018, MNRAS, 481, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- O’Donnell, J. E. 1994, ApJ, 422, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Pel, J. W. 1976, A&AS, 24, 413 [NASA ADS] [Google Scholar]
- Petroni, S., Bono, G., Marconi, M., & Stellingwerf, R. F. 2003, ApJ, 599, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrzyński, G., Graczyk, D., Gallenne, A., et al. 2019, Nature, 567, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Casertano, S., Anderson, J., MacKenty, J., & Filippenko, A. V. 2014, ApJ, 785, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., et al. 2018a, ApJ, 861, 126 [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., et al. 2018b, ApJ, 855, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., Macri, L. M., & Scolnic, D. 2019, ApJ, 876, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Ripepi, V., Molinaro, R., Musella, I., et al. 2019, A&A, 625, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schechter, P. L., Avruch, I. M., Caldwell, J. A. R., & Keane, M. J. 1992, AJ, 104, 1930 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, E. G. 2015, ApJ, 813, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., McMillan, P., & Eyer, L. 2019, MNRAS, 487, 3568 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, G. 1978, Ann. Stat., 6, 461 [Google Scholar]
- Smith, B. J., Price, S. D., & Baker, R. I. 2004, ApJS, 154, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer Science, C. 2009, Vizier Online Data Catalog: II/293 [Google Scholar]
- Stassun, K. G., & Torres, G. 2018, ApJ, 862, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Stevens, D. J., Stassun, K. G., & Gaudi, B. S. 2017, AJ, 154, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Szabados, L. 2003, Inf. Bull. Variable Stars, 5394, 1 [NASA ADS] [Google Scholar]
- Tachibana, S., Nagahara, H., Ozawa, K., et al. 2011, ApJ, 736, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Trahin, B. 2019, PhD Thesis, L’Université PSL, l’Observatoire de Paris, France [Google Scholar]
- Turner, D. G., & Burke, J. F. 2002, AJ, 124, 2931 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2008, Vizier Online Data Catalog: I/311 [Google Scholar]
- van Leeuwen, F., Feast, M. W., Whitelock, P. A., & Laney, C. D. 2007, MNRAS, 379, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Walraven, J. H., Tinbergen, J., & Walraven, T. 1964, Astron. Inst. Netherlands, 17, 520 [NASA ADS] [Google Scholar]
- Welch, D. L., Wieland, F., McAlary, C. W., et al. 1984, ApJS, 54, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, S., Zhang, B., Reid, M. J., Zheng, X., & Wang, G. 2019, ApJ, 875, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Zinn, J. C., Pinsonneault, M. H., Huber, D., & Stello, D. 2019, ApJ, 878, 136 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Different reddening values
As outlined in the main text, the choice of reddening in the fitting procedure can have an important impact on the results. This was shown for the CCs in the inner disk which have values of AV in the range 7–16. Other indications were stars where the spectroscopic effective temperatures differed significantly from the ones determined from the SED fitting and outliers in the HRD. Table A.1 collects the different reddening values, and Fig. A.1 shows the different values plotted against each other. Outliers are marked and plotted with error bars. In the top panel outliers witch large reddening from STILISM are likely due to an inappropriate extrapolation from the the reddening at the maximum distance available in the STLISM grid in that particular direction to the reddening at the distance of the Cepheid (see Sect. 4.7 for details).
 |
Fig. A.1. Different E(B − V) values plotted against each other. Outliers are marked and plotted with error bars. Top panel: some of the stars are connected by a blue line. The left point indicates the reddening at the maximum distance available in the STLISM grid in that particular direction. The right point indicates the reddening estimated at the distance of the Cepheid by a linear extrapolation (see Sect. 4.7 for details). The solid lines indicate the least-squares fir from Table A.2. |
Different reddening values (first entries only).
Linear bi-sector fits were made in all cases (excluding the marked outliers), as well as determining the median and median-absolute-deviation (MAD) of the ratio of the quantities (in the sense y-axis value/x-axis value). The fit results are collected in Table A.2. There are systematic differences between the three sets of reddenings (in the sense STILISM > adopted values > Green et al.) of order 5–15%.
Relations between different reddening values.
Appendix B: Additional fits and plots
Figure B.1 shows the period-luminosity and period-radius relations when the error in the distance is taken into account in the error estimate of the luminosity. The adopted error in the distance is listed in Col. 8 of Table 1. For the CCs in the inner disk they are based on I19, otherwise on the error estimates given in Bailer-Jones et al. (2018). If upper and lower error bars were given the geometric mean was taken. For stars were the GDR2 parallax clearly is in error (and thus also the value in Bailer-Jones et al. 2018) the value from G18 is taken (α UMi, l Car, δ Cep, S Mus). For stars not in GDR2 (and therefore not considered in G18) an error in distance was estimated from stars at very similar distances (RY Vel, V340 Nor, IY Cep).
The period-luminosity relation becomes
using 380 stars and with an rms of 0.42 mag. The difference with Eq. (1) at P = 10 d is 0.1 mag.
The period-radius relation becomes
using 375 stars and with an rms of 0.072 dex. The difference with Eq. (2) at P = 10 d is 0.011 dex (2.6%).
All Tables
All Figures
 |
Fig. 1. Best fit models of RS Pup, and the three (likely) T2Cs that show near- and mid-IR excess. Errorbars are plotted and are typically the size of the plot symbol. |
| In the text | |
 |
Fig. 2. Hertzsprung-Russell diagram. Stars located outside the bulk of objects have been labelled and are plotted with error bars. Blue and red lines indicate the blue and red edge of the IS. At log L ∼ 2 this is the IS for BLHER T2C; at brighter luminosities those for CCs. The near horizontal lines are stellar evolution tracks of CCs of different masses. See the main text for details. |
| In the text | |
 |
Fig. 3. Hertzsprung-Russell diagram, zoomed in on the region covered by the five object in the direction of the Galactic disk. The labelled points with the red vertical error bars indicate the standard case (Fig. 2). They are connected by green lines to the points with the green vertical error bars indicating the cases where the effective temperature is fixed to the value determined from spectroscopy, which in turn are connected by blue lines to the points with blue vertical error bars indicating the cases where the effective temperature is fixed to a value roughly in the middle of the IS. |
| In the text | |
 |
Fig. 4. Comparison between the effective temperatures determined from the SED fitting, and in the literature. Stars outside the bulk of objects are identified and plotted with error bars. The one-to-one line is indicated. In the upper figure the temperatures are compared to the data in Luck (2018) (and I19 for ID 1–5). When there are three or more values available in the phase range representative of mean light the object is marked by a thick filled circle. Otherwise when there are two or more observations the average is taken (small open circles). Lower panel: difference between spectroscopic and photometric temperature. In the lower figure the effective temperatures from Trahin (2019) are compared to the present work. |
| In the text | |
 |
Fig. 5. Using data from Luck (2018) the panels show the mean effective temperature, and the difference in Teff over the pulsation cycle against temperature and period for the 30 objects with seven or more datapoints in the phase range typical for mean light. Overtone pulsators are indicated by open circles. |
| In the text | |
 |
Fig. 6. Comparison between the E(B − V) values in Trahin (2019) and the present work. The one-to-one line is indicated. The random and systematic error bars in Trahin (2019) have been added in quadrature. |
| In the text | |
 |
Fig. 7. Fits to the SED and mid-IR spectra of T Mon and X Sgr for different dust compositions. Top panel: standard model without dust component. Other three panels: models with dust composed of 80, 94, and 100% iron, respectively, with the remainder evenly split between silicates and aluminium oxide. The mid-IR spectrum is scaled to the model based on the average flux in the 10–10.5 μm region. |
| In the text | |
 |
Fig. 8. Fits to the SED and mid-IR spectra of the Cepheids which have an IRAS LRS or Spitzer IRS spectrum. The mid-IR spectrum is scaled to the model based on the average flux in the 10–10.5 μm region. |
| In the text | |
 |
Fig. 9. Measures of the IR excess from the present work, and a comparison to the measure of the IR excess from Trahin (2019) (see main text for details). |
| In the text | |
 |
Fig. 10. Top panel: period-Mbol relation. Error bars in Mbol are not show as they are smaller than the symbol size. Some outlying stars are identified. The black line indicates the best fit to the fundamental mode Cepheids (excluding outliers). The blue line gives the PL relation for T2Cs in the MCs from Groenewegen & Jurkovic (2017b). Bottom panel: period-radius relation. Some outlying stars are identified. The black line indicates the best fit to the fundamental mode Cepheids (excluding outliers). The blue line gives the PR relation for T2Cs in the MCs from Groenewegen & Jurkovic (2017b). The green line is the theoretical PR relation from Anderson et al. (2016). |
| In the text | |
 |
Fig. A.1. Different E(B − V) values plotted against each other. Outliers are marked and plotted with error bars. Top panel: some of the stars are connected by a blue line. The left point indicates the reddening at the maximum distance available in the STLISM grid in that particular direction. The right point indicates the reddening estimated at the distance of the Cepheid by a linear extrapolation (see Sect. 4.7 for details). The solid lines indicate the least-squares fir from Table A.2. |
| In the text | |
 |
Fig. B.1. As Fig. 10, but error bars in Mbol are now plotted. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.