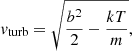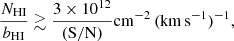| Issue |
A&A
Volume 634, February 2020
|
|
|---|---|---|
| Article Number | A106 | |
| Number of page(s) | 17 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201935846 | |
| Published online | 18 February 2020 | |
Hot WHIM counterparts of FUV O VI absorbers: Evidence in the line-of-sight towards quasar 3C 273
1
Department of Physics, University of Helsinki, PO Box 64, 00014 Helsinki, Finland
e-mail: jussi.ahoranta@helsinki.fi
2
Department of Physics, University of Alabama in Huntsville, Huntsville, AL, USA
3
Tartu Observatory, University of Tartu, Observatooriumi 1, 61602 Tõravere, Estonia
4
Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
5
NASA National Space Science and Technology Center, Huntsville, AL, USA
6
Leibniz-Institut für Astrophysik Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
7
Deparment of Physics & Astronomy, Regis University, Denver, CO 80221, USA
8
SRON Netherlands Institute for Space Research, Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
9
Finnish centre for Astronomy with ESO (FINCA), University of Turku, Quantum, Vesilinnantie 5, 20014 Turku, Finland
Received:
5
May
2019
Accepted:
7
December
2019
Aims. We explore the high spectral resolution X-ray data towards the quasar 3C 273 to search for signals of hot (∼106−7 K) X-ray-absorbing gas co-located with two established intergalactic far-ultraviolet (FUV) O VI absorbers.
Methods. We analyze the soft X-ray band grating data of all XMM-Newton and Chandra instruments to search for the hot phase absorption lines at the FUV predicted redshifts. The viability of potential line detections is examined by adopting the constraints of a physically justified absorption model. The WHIM hypothesis is investigated with a complementary 3D galaxy distribution analysis and by detailed comparison of the measurement results to the WHIM properties in the EAGLE cosmological, hydrodynamical simulation.
Results. At one of the examined FUV redshifts, z = 0.09017 ± 0.00003, we measured signals of two hot ion species, O VIII and Ne IX, with a 3.9σ combined significance level. While the absorption signal is only marginally detected in individual co-added spectra, considering the line features in all instruments collectively and assuming collisional equilibrium for absorbing gas, we were able to constrain the temperature (kT = 0.26 ± 0.03 keV) and the column density (NH × Z⊙/Z = 1.3−0.5+0.6 × 1019 cm−2) of the absorber. Thermal analysis indicates that FUV and X-ray absorption relate to different phases, with estimated temperatures, TFUV ≈ 3 × 105, and, TX − ray ≈ 3 × 106 K. These temperatures match the EAGLE predictions for WHIM at the FUV/X-ray measured Nion-ranges. We detected a large scale galactic filament crossing the sight-line at the redshift of the absorption, linking the absorption to this structure.
Conclusions. This study provides observational insights into co-existing warm and hot gas within a WHIM filament and estimates the ratio of the hot and warm phases. Because the hot phase is thermally distinct from the O VI gas, the estimated baryon content of the absorber is increased, conveying the promise of X-ray follow-up studies of FUV detected WHIM in refining the picture of the missing baryons.
Key words: X-rays: individuals: 3C 273 / intergalactic medium / large-scale structure of Universe
© ESO 2020
1. Introduction
The missing baryons problem (Persic & Salucci 1992) in the low-z universe is likely a manifestation of the limitations of current observational capabilities at the high-energy end of the electromagnetic spectrum. The majority of the non-detected baryons are expected to reside in the warm-hot intergalactic medium (WHIM), the shock-heated diffuse gas accumulated within the large scale structures of dark matter in the Universe (Cen & Ostriker 1999; Davé et al. 1999). Such concentrations of hot, highly-ionized gas are, in principle, observable in the far-ultraviolet (FUV) and X-ray bands. Whereas in the FUV band, measurements of broad Lyα and O VI absorption lines in the local (z < 1) universe have revealed the warm part (T ∼ 105 − 6 K) of the WHIM (e.g., Tripp et al. 2000), the number of X-ray observations of the hot WHIM phase remains limited. The low expected column densities (≲1016 cm−2) of the most prominent ions in the hot WHIM temperature range (∼106−7 K), such as O VII-VIII, Ne IX-X and N VII (e.g., Fang et al. 2002; Wijers et al. 2019), significantly limit the possibilities for studying the hot WHIM with observations using the present instrumentation.
Currently, the method with the most potential for the direct detection of the WHIM uses quasar or blazar emission as a backlight against which absorption signatures might be found. In the FUV band this approach has been successfully applied (e.g., Tripp et al. 2000; Sembach et al. 2001; Williger et al. 2010; Tilton et al. 2012; Shull et al. 2012; Danforth et al. 2016), in contrast to the X-ray band where the observational evidence is typically less solid and therefore subject to other interpretations (see, e.g., discussions in Rasmussen et al. 2007, Bonamente et al. 2017). Present high-energy resolution soft X-ray band instruments (the XMM-Newton RGS and Chandra LETG grating spectrometers) effective areas vary from a few to few tens of cm2 at the relevant energies, and consequently ∼-pagination Ms exposure times are typically required to attain sufficient photon statistics for possible WHIM line detections. In such observations, systematics such as instrument calibration uncertainties require special attention. In recent years, numerous studies of hot WHIM absorbers have been published, for example by Buote et al. (2009), Nicastro et al. (2010, 2018), Ren et al. (2014), Bonamente et al. (2016), and Kovacs et al. (2019), among others. However, the number and the significance of the possible hot WHIM detections has remained low, and the fundamental problem remains: about one third of the local baryons remain missing (e.g., Shull et al. 2012; Nicastro et al. 2017).
Future instruments, in particular, the Athena X-IFU (Barret et al. 2016; Kaastra et al. 2013), are targeted at increasing the prospects to measure weak signals from hot WHIM. With that regard, in this work we aim to improve the observational status of hot WHIM absorption under the hypothesis that the warm phase (T ∼ 105 K, well-detected in FUV) of the WHIM is spatially co-located with the hot (106−7 K) WHIM (see Nevalainen et al. 2019 for more discussion). Other authors have previously investigated such an approach. For instance, Yao et al. (2009) stacked the then available ACIS data of several AGN in order to detect possible hot counterparts to the FUV-detected O VI absorbers. Nevalainen et al. (2019) used all available Chandra ACIS and XMM-Newton RGS data to look for O VII and O VIII absorption at FUV-detected redshifts in the sight-line towards PKS2155-304. Neither study detected statistically-significant absorption, instead setting upper limits of 1014.5 − 15.5 cm−2 of the column densities of the two ions.
In this study, we investigate the sight-line towards the quasar 3C 273 (z ≈ 0.158, Schmidt 1963), also included in the Yao et al. (2009) sample. This sight-line was chosen because of the exceptionally good photon statistics available for high resolution X-ray spectroscopy. In addition, as we list in Table 1, FUV measurements have detected O VI and broad (> 40 km s−1) Lyman-alpha (BLA) absorption lines at several non-zero redshifts in this sight-line (e.g., Sembach et al. 2001; Williger et al. 2010; Tilton et al. 2012; Danforth et al. 2016). We utilize all the currently available ACIS and RGS data in our analysis (total exposure time > Ms) so that for a single AGN we reach a similar level of sensitivity as the stacked Yao et al. (2009) sample. This enables us to avoid possible problems with stacking data from different instruments, redshifts and targets, therefore improving constraints on potentially co-located warm and hot WHIM gas.
FUV absorbers towards the 3C 273.
Considering the presumed parameter space of the WHIM (i.e., nH, Z, T, etc.), it is not expected that photo-ionization by itself would produce high enough amounts of O VII or O VIII to be detectable with current X-ray instruments (e.g., Wijers et al. 2019). Since only collisional ionization seems capable of producing high enough ion column densities, in this study we adopt the assumption that collisional ionization equilibrium (CIE) describes the physical state of hot WHIM gas.
The search for the X-ray absorbing gas is conducted at the exact redshifts where significant detections of O VI absorption have been in obtained in the FUV. Although other authors have also used Ne VIII as a tracer of hot gas (e.g., Burchett et al. 2019; see also Wijers et al. 2019), the spectral data toward 3C 273 lack the necessary wavelength coverage for such an analysis, so we do not consider it in this analysis. After the initial search for the hot phase absorption lines at the O VI absorber redshifts, each tentative line detection is critically considered by: 1) confirming the signal is consistent between all the measuring instruments, 2) checking the spectral band at the location of potential line detections against possible spectral and co-adding artifacts, and 3) comparing the freely fitted line intensity ratios to the constraints set by the CIE model.
We complement the X-ray analysis with an optical study of the galactic filaments at the location of the absorbers, since large scale filaments are expected to harbor a major fraction of the local missing hot baryons. Finally, we compare our results to the WHIM observables predictions of the EAGLE (Schaye et al. 2015) cosmological, hydrodynamical simulations.
2. Observational X-ray data set
The absorption signatures of the hot WHIM filaments are expected to be close to or beyond the limits of detectability with the current high spectral resolution X-ray instruments. With this in mind, we analyzed all the long exposure (≳20 ks) 3C 273 observations (as available on Jan 2019) from the XMM-Newton RGS (first and second spectral orders), Chandra LETG (HRC and ACIS first-order), and Chandra MEG (ACIS first-order) instruments. The total RGS exposure times are ≈700 ks per instrument, which is substantially longer than that of the Chandra instruments (see Table 2).
Observational sample.
Due to the shorter observation times and smaller effective area of the Chandra instruments as compared to the RGS, the statistical weight of LETG and MEG data in the spectral modeling is much less than that of RGS data. We nevertheless found it beneficial to include the Chandra data into analysis, because due to the malfunctioning RGS2 CCD array #4, there are no RGS2 first-order data in the wavelength band between ≈20 − 24 Å. This band covers the redshifted wavelengths of the O VIII Lyα line for z ≈ 0.06 − 0.27 and O VII Heα for z ≲ 0.11 (which are the lines most likely to be detected), and because the second-order spectra of the RGS instruments have zero effective area at λ ≳ 19 Å, only LETG and MEG data can provide additional information to RGS1 first-order at these wavelengths. Also, since we are examining very weak spectral signatures, examining all the available data sets is useful for identifying false positives that could occur in individual data sets due to systematic effects such as calibration errors.
3. Data processing
3.1. XMM-Newton RGS
The RGS data were processed with the XMM-Newton SAS 16.0.0 software using the calibration file release XMM-CCF-REL-347. Both first- and second-order data were reduced with the rgsproc pipeline. We used somewhat more accurate processing options compared to the rgsproc defaults, in order to maximize the data quality for the examination of very weak spectral signals. Namely, we rejected the cool pixels from the data, and corrected for pixel-dependent energy offsets (rgsproc rgsenergy option withdiagoffset=yes). In addition, we decreased the aspect drift based frame grouping by a factor of two (i.e., driftbinsize=0.5″) and calculated the grating line spread functions using the full convolution space. It was confirmed that utilization of such more precise data processing options does improve the overall quality of the co-added spectra.
In addition, we created good time interval files by setting a threshold for the upper limit for the source flux, and filtered the data accordingly to remove the exposure time intervals contaminated by incidental Solar flares. We also employed the rgsproc binning algorithm to bin the data into 20 mÅ wavelength bins (i.e., twice the default bin width), a scheme that oversamples the instrument energy resolution by a factor of ≈3. The data was already rebinned during the spectral extraction phase because it provides numerically more stable results compared to rebinning the data later from the full resolution spectra, which was desirable since we aimed to use combined data sets to analyze signals close to the limits of detectability.
After reducing the RGS data sample as described above, we produced co-added spectra separately for each RGS instrument and spectral order using the rgscombine procedure. These co-added spectra were then converted into the SPEX1 format with the trafo (v. 1.03) software. The trafo was used to create separate spectra for each co-added dataset, and in addition, to prepare a combined spectral file in which each of these co-added spectra were included (including the Chandra spectra as described in the following section). Using this combined spectral file allows us to flexibly and correctly fit the data from the different instruments simultaneously with SPEX (Sects. 4.3 and 5). This approach maximizes the data contributing to the analysis.
3.2. Chandra instruments
3.2.1. LETG
The Chandra LETG ACIS and HRC data were processed with CIAO v. 4.10 using the CALDB 4.7.9 calibration files. The data reduction was conducted using the chandra_repro script with the default parameter settings, and afterwards, the spectra of each of the instruments were co-added separately using the combine_grating_spectra spectral stacking tool. Both positive and negative order dispersion data were co-added when producing the ACIS and HRC spectral files for the analysis.
The statistical errors in all of the processed Chandra LETG observations used the Gehrels approximation for Poisson confidence intervals (as defined in Gehrels 1986), which are not supported by the SPEX rebinning algorithm. Since the processed LETG data were over-sampled in the initial reduction, before converting the generated FITS data files into the SPEX format, we replaced the spectral data uncertainties with 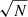 , where the N denotes the number of counts per spectral bin. The number N is in the range between 20 − 60 cts/bin (HRC) and 30 − 150 cts/bin (ACIS) in the studied wavelength band, meaning that the uncertainties are well approximated by
, where the N denotes the number of counts per spectral bin. The number N is in the range between 20 − 60 cts/bin (HRC) and 30 − 150 cts/bin (ACIS) in the studied wavelength band, meaning that the uncertainties are well approximated by  (as is shown, e.g., in Bonamente 2017).
(as is shown, e.g., in Bonamente 2017).
Rebinning of the data was conducted using the ftools grppha software tool with a binning factor of two, resulting in a 30 mÅ bin size, or 0.6 × Δλ channel width (we note that grppha rebinning is carried out by means of flagging, and is not a workaround for the rebinning issue mentioned above). Like with the RGS data, we then used trafo to create the separate co-added SPEX spectral files for each LETG instrument, and to add these spectra into the combined spectral file used in the simultaneous spectral modeling.
3.2.2. HETG
The HETG observations were reduced using the chandra_repro default processing, and the first-order data of the Chandra HETG Medium Energy Grating (MEG) arm were extracted. The data was co-added with the combine_grating_spectra tool and converted into the SPEX format with trafo. Like the data from the other instruments, we added this spectrum into the combined spectral file for the simultaneous analysis.
4. The analysis method
4.1. Data qualification
As described in Sect. 3, several steps were taken during data processing to minimize the risk of forming artificial absorption-like spectral features in the co-added spectra (especially in the case of the RGSs, which have the largest statistical weight in the sample). In addition, we applied two criteria throughout the analysis to further exclude sources of confusion. First, the closest CCD gap must be at least one HWHM away from the examined line centroid wavelength (only relevant to RGS since we co-added Chandra positive and negative orders), and second, no bad pixels or columns may be present in the immediate vicinity of examined lines (or more precisely, within the FWHM of the fitted line profile).
These criteria are important because small variations in telescope pointing (with respect to the dispersion direction) between different observations cause small shifts of the spectral wavelength scale at the detector plane. When such observations are co-added, the location of bad pixels and columns may vary in the detector wavelength space, which for a time-varying source such as 3C 273 can lead to an incorrectly defined effective area around the corresponding wavelength bins (more details of the issue can be found in Kaastra et al. 2011). As a result, spectral artifacts characteristically resembling those of absorption/emission lines may emerge in co-added spectra, or, if overlapping with an existing spectral feature, bias the measurements.
Manual inspection of RGS2 event files revealed bad pixels coinciding with the wavelength of the z = 0.09017 Ne IX Heα line in the RGS2 first-order data, and the data were therefore omitted from the analysis of this line. Other than that, no exclusion of data followed from these criteria for the line candidates examined in this study.
4.2. Redshift selection
To find the most likely locations of hot WHIM absorbers in the 3C 273 sight-line, we examined the FUV absorber data of the Tilton et al. (2012) FUSE+STIS survey (the sight-line has also recently been studied by Williger et al. 2010, Danforth & Shull 2008, Tripp et al. 2008 and Sembach et al. 2001), looking for the redshifts meeting our predetermined criteria. Namely, we were interested in the redshifts where: 1) at least two statistically significant metal absorption lines have been measured in the FUV, indicating a high concentration of metals in the absorber (we note that significant detections of two lines, such as those of the O VI doublet, makes it very likely that the FUV redshift is correctly determined), or 2) a broad Lyman alpha line with b > 70 km s−1 has been measured, indicating that the gas temperature may be high enough to produce significant lines in the soft X-ray band (as b = 70 km s−1 corresponds to a ≈3 × 105 K gas temperature assuming pure thermal line broadening).
Criterion 2 was adopted because it could reveal high temperature absorbers where the O VI ion fraction is too low to enable significant detection of O VI lines in the FUV, although the numerical value for the b-limit was chosen simply to exclude number of uninteresting (low temperature) Lyα absorbers from the X-ray analysis. We note, however, that without further information on the processes contributing to the Lyα line widths (turbulence, spectral line blending, etc), the thermal information content of the line width measurements is limited (e.g., Tepper-Garcia et al. 2012).
Two redshifts met the former criterion (0.09017, 0.12005, see Table 1). The O VI line profiles at these redshifts were checked against spectral characteristics typically associated with high velocity outflows (e.g., line profile asymmetries, velocity-dependent partial coverings, time variability, line widths), to exclude the possibility that the absorption lines are related to a high velocity outflow from 3C 273. No such indications were found for any of the examined FUV lines, implying the line detections most likely relate to intergalactic absorbers. These two FUV redshifts were adopted for the X-ray follow up study.
4.3. Modelling the 3C 273 emission and Galactic absorption
The X-ray spectra used in this analysis are combinations of multiple exposures from different epochs of a time-varying source. In such co-added spectra, the physical information carried by the continuum shape is largely averaged away. Indeed, we found that even when using limited wavelength bands, the complex shape of the quasar continuum was poorly fitted with power-law models. We therefore chose to model the emission continua of each dataset independently with a non-physical “spline” model, which is a model specifically designed for accurate modeling of X-ray continuum shapes in cases where the physics underlying the continuum shape is not sufficiently well known. Adopting a non-physical continuum model is also useful because it can compensate for possible wider band systematics in instrument effective area models, thus improving the accuracy of the examination of weak (and narrow) absorption features in the spectra, such as those expected for the hot WHIM absorbers.
In the analysis we used a “spline” model that consists of 17 uniformly spaced grid points between 13 and 29 Å, thus providing 1 Å intervals for the grid points; This scheme was found to enable accurate modeling of the continua, while the grid being sparse enough not to model any line features in the spectra. We allowed the “spline” y-parameters (i.e., the intensity) to vary throughout our analysis, so to ensure that the uncertainties in the continuum modeling were always properly propagated into the uncertainties of the model parameters of interest. The fitting band was fixed to 14 − 28 Å, which covers the most important transition lines of Ne IX, O VII-VIII, and N VII for both considered FUV redshifts.
We built a Galactic absorption model consisting of a component for the neutral disk and another one for the hot halo. For the neutral gas, we used the SPEX CIE absorption model called “hot” with the temperature fixed to 5 × 10−4 keV (SPEX “neutral plasma model”), and the hydrogen column to NH = 1.77 × 1020 cm−22. Although the used hydrogen column density value has a 16% systematic uncertainty (see Willingale et al. 2013), we found no benefit in letting it vary during the fits, because the “spline” model is able to compensate for the possible bias in NH. Instead, we found that when using the SPEX default for the line-broadening parameter (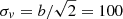 km s−1), the Solar abundances highly overestimate the O I lines of the component (blend at 23.5 Å), which is a possible indication of O I line saturation. We therefore measure the O I column density by letting the model oxygen abundance vary, while adopting the line-of-sight Doppler spread parameter b = 18.6 km s−1 for the line widths, which has been found to describe the low ionization state Galactic lines towards the 3C 273 elsewhere (Savage et al. 1993). We point out that even if the X-ray instruments are insensitive to line width information of narrow features (b < several hundred km s−1), the NOI will be correctly constrained by the equivalent width measurement over the doublet when the value of bOI is known. This fit yielded log
km s−1), the Solar abundances highly overestimate the O I lines of the component (blend at 23.5 Å), which is a possible indication of O I line saturation. We therefore measure the O I column density by letting the model oxygen abundance vary, while adopting the line-of-sight Doppler spread parameter b = 18.6 km s−1 for the line widths, which has been found to describe the low ionization state Galactic lines towards the 3C 273 elsewhere (Savage et al. 1993). We point out that even if the X-ray instruments are insensitive to line width information of narrow features (b < several hundred km s−1), the NOI will be correctly constrained by the equivalent width measurement over the doublet when the value of bOI is known. This fit yielded log (corresponding 0.8 times the Solar O abundance), a result in line with NOI at other lines of sight with similar NH (e.g., Cartledge et al. 2004). As far as we know, this is the most accurately constrained Galactic NOI measurement towards 3C 273.
(corresponding 0.8 times the Solar O abundance), a result in line with NOI at other lines of sight with similar NH (e.g., Cartledge et al. 2004). As far as we know, this is the most accurately constrained Galactic NOI measurement towards 3C 273.
To model the Galactic hot halo absorption (see e.g., Fang et al. 2003), we prepared another SPEX “hot” component where the free parameters were the electron temperature and NH, and the elemental abundances were fixed to Solar. Fits with a hot halo component alongside the neutral gas absorber yielded kT = 0.127 ± 0.007 keV and 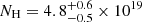 cm−2 (Table 3).
cm−2 (Table 3).
Foreground galactic absorption model.
The emission model with Galactic absorption, as described above, was used in all of the analysis described in the following sections. It is important to note that none of the freely varying parameters (as described above) were fixed at any point of the spectral analysis, to ensure proper error propagation in the calculation of the redshifted absorption component fit parameters. All the analyses were performed using SPEX version 3.03.00 with proto-Solar abundances of Lodders et al. (2009), which is the SPEX default, and the models were fitted using Cash Statistics (Cash 1979).
5. X-ray analysis and results
To verify the wavelength-scale accuracy of the co-added spectra, we first checked each of the spectra against linear shifts. This was done using the strongest spectral feature present in the 3C 273 X-ray spectrum, the Galactic O VII Heα line at λ = 21.602 Å. We fitted the data around this feature with a model combining a Gaussian absorption line with the “spline” continuum model, while letting the Gaussian line centroid wavelength and the line normalization parameter vary. We found that the centroid wavelengths of the Gaussian modeling were consistent with the rest wavelength of O VII Heα within the statistical uncertainties of ≲10 mÅ (see Table 4). This was true for each instrument, and indicates a redshift accuracy of σz ≈ 0.0005 (corresponding to velocity accuracy Δv ≈ 137 km s−1 at z = 0.09, and ≈132 km s−1 at z = 0.12). We will utilize this accuracy further when comparing the redshifts of the X-ray lines with those of the FUV lines (Sect. 5.1.1), and with those of the large scale filaments (Sect. 6.1).
X-ray line wavelengths.
Two different models were investigated in the spectral analysis. These were the emission model with Galactic absorption (Sect. 4.3) combined with: 1) a redshifted “slab” line absorption component (Model 1, Sect. 5.1), and 2) a redshifted gas absorption component in collisional ionization equilibrium with solar relative abundances, (Model 2, Sect. 5.2).
In addition to these models, we used a model combining Gaussian lines and the Galactic absorption model whenever determining absorption line centroid wavelengths in the spectra: This approach was used to avoid shifting of the “spline” emission component energy grid, which would take place if letting the model redshift to vary during the fits.
The initial search for redshifted absorption lines was conducted by fitting Model 1 independently to the co-added spectra of different instruments and spectral orders, and then by fitting the co-added spectra simultaneously with the same model. Considering all these measurement results together, we searched for inconsistencies between the results given by different instruments, and if such were found, the hypothesis of an astrophysical line origin was rejected.
Model 1 was also used in examining the effects of systematics on the measurement results of the putative redshifted lines. Namely, we re-fitted the RGS1 first-order data, which has the largest statistical weight in our sample, after adding a 2%-pagination Poissonian noise component to the data (corresponding to the systematic calibration uncertainty level of RGS first-order data, see de Vries et al. 2015). We found this noise component to have negligible effect on the fit parameters of interest, and therefore omitted its use in the further analysis.
After mapping the redshifted line candidates, the main analysis of this work was conducted using the simultaneous fitting method with Model 2, ensuring that all the information in each of the co-added spectra was taken into account in the analysis. The simultaneous fitting of data from different instruments and spectral orders was conducted with the appropriate SPEX tools3. Technically, in these fits, all the absorption components were coupled (i.e., both Galactic and redshifted components) between the models of the different co-added spectra, while the “spline” continuum emission models were uncoupled. With this method, the continua of all the separate datasets, observed at different epochs with different instruments, were fitted at a level which enabled the investigation of weak absorption components at high accuracy (we get C-statistics/d.o.f. < 1.07 in the used 14 − 28 Å fitting band).
5.1. The redshifted absorption line model (Model 1)
To search for X-ray absorption lines in the data, we added a redshifted SPEX “slab” component to the absorbed emission model described in Sect. 4.3. The “slab” component models the transmission of photons through an optically thin layer of gas, and enables measurement of column densities of different ion species while setting no constraints on the gas ionization balance. The “slab” component does, however, include the relative intensities of the spectrum of transition lines produced by the examined ion, thus providing more accurate results as compared to modeling the data with a single line profile. The SPEX “slab” absorption model fits the lines with the Voigt profile, in which the Gaussian component has an adjustable line broadening to account for the thermal and non-thermal velocity distributions of the absorbing gas. Because we did not have information on either of these components, and since the used instruments’ energy resolution is insufficient to model the line shapes, we fixed the “slab” line width parameter to the SPEX default value of 100 km s−1 at all times (corresponding T ∼ 107 K thermal broadening for oxygen lines).
The spectral analysis was conducted by fitting the ion column densities of the “slab” model’s O VII-VIII, Ne IX, Fe XVII, and N VII ions one by one, while fixing all the other “slab” ion columns to zero during each fit. Using this approach, we investigated both of the FUV guided redshifts (0.09017, 0.12005) by fixing the redshift to those values. We note that the major benefit of using the “slab” model to search for possible absorption lines is that it can be used to obtain the ion columns without any knowledge of the gas temperature. Therefore the analysis with the “slab” model set up useful limits for the examined ion column densities, whose credibility can be tested against the predictions of physically justified models, such as CIE.
5.1.1. Absorption line analysis results: z = 0.09017
We began the line analysis at the O VI absorber redshift z = 0.09017. Because the hot WHIM absorption lines are expected to have equivalent widths of only ≲10 mÅ (e.g., Oppenheimer et al. 2016; Wijers et al. 2019), the visual prominence of possible WHIM lines in the co-added spectra is expected to be weak. For this reason, any existing line features could easily be overlooked and interpreted as noise. However, if the absorption features do have an astrophysical origin, then one can improve their visual appearance by utilizing the procedure introduced in Kaastra et al. (2011). Following this method, the SAS program rgsfluxer was used to generate fluxed RGS1 and RGS2 spectra for each spectral order, which were then combined using the SPEX tool rgsfluxcombine to generate a single fluxed spectrum. We note that producing a fluxed spectrum also works as an independent sanity check, because the tool is less prone to produce stacking artifacts than rgscombine. We found that the resulting spectrum with increased photon statistics (at the wavelength bands where available) indeed shows a strengthened absorption feature at the wavelength ≈14.66 Å, which corresponds to the redshifted wavelength of the Ne IX Heα line at z = 0.09017 (Fig. 1).
 |
Fig. 1. Continuum normalized, co-added fluxed spectrum of RGS1 and RGS2 data at the wavelength around the putative redshift 0.09017 Ne IX Heα absorption line. The FUV predicted line centroid wavelength is shown with the orange line, while the dotted red curve shows the expected absorption signal based on the simultanous fitting of XMM-Newton and Chandra data with the redshifted slab model (Sect. 5.1.1). |
Quantitative analysis of Ne IX by simultaneous fitting of Model 1 to the co-added XMM-Newton and Chandra data yielded W = 2.7 ± 0.9 mÅ for the rest-frame equivalent width of the Ne IX Heα line, corresponding to an ion column density log for Ne IX. In Fig. 1 we plot this predicted absorption signal for the Ne IX Heα line on top of the fluxed spectrum for comparison. In addition, we found an absorption line feature at the wavelength corresponding the z = 0.09017 O VIII Lyα line, for which we measured a rest-frame W = 4.3 ± 1.6 mÅ corresponding log NOVIII(cm−2) = 15.5 ± 0.2. In case of O VIII Lyα, the application of the fluxed spectrum method was not useful, because the corresponding wavelength band is only observable in the RGS first-order spectrum and accordingly no improvement of photon statistics was available. We point out that the O VII Heα line, which is typically expected to be the strongest X-ray WHIM line, would blend with the (strong) Galactic O I line (
for Ne IX. In Fig. 1 we plot this predicted absorption signal for the Ne IX Heα line on top of the fluxed spectrum for comparison. In addition, we found an absorption line feature at the wavelength corresponding the z = 0.09017 O VIII Lyα line, for which we measured a rest-frame W = 4.3 ± 1.6 mÅ corresponding log NOVIII(cm−2) = 15.5 ± 0.2. In case of O VIII Lyα, the application of the fluxed spectrum method was not useful, because the corresponding wavelength band is only observable in the RGS first-order spectrum and accordingly no improvement of photon statistics was available. We point out that the O VII Heα line, which is typically expected to be the strongest X-ray WHIM line, would blend with the (strong) Galactic O I line ( Å,
Å, 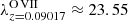 Å), thus preventing the analysis of this line. Accordingly, we are only able to report here the weak upper limits for O VII at z = 0.09017 based on the fits to the non-blended transition lines, including the O VII Heβ and others.
Å), thus preventing the analysis of this line. Accordingly, we are only able to report here the weak upper limits for O VII at z = 0.09017 based on the fits to the non-blended transition lines, including the O VII Heβ and others.
To double-check the measurement results obtained from simultaneous fitting with Model 1 (see the best-fit model on top of each of the individual co-added spectra in Figs. 3 and 4), we analyzed each of the co-added spectra separately with the same model. Similarly to the simultaneous modeling, the separate fits yielded ion column densities of the order of 1015 cm−2 for both ions (Ne IX, O VIII) in each co-added dataset, and no inconsistencies were found between different instruments. We present the complete line analysis results, including both the simultaneous and the individual fits to the co-added spectra, in the uppermost panels of Table 5.
 |
Fig. 2. Statistical probability of the Null hypothesis validity over the redshift range 0.005 − 0.158. The Null hypothesis is the emission model with Galactic absorption, which is compared to the WHIM hypothesis, i.e., a model including a redshifted hot (T = 106−7 K) CIE absorption component. The dashed black line marks the commonly adopted Null hypothesis rejection limit, p = 0.05. The FUV redshifts listed in Table 1 are shown together with the non-significant O VI doublet detections (from Table 4 in Tilton et al. 2012). The shaded color marks the confusion region of the redshifted absorption component with the Galactic hot halo. |
 |
Fig. 3. Normalized data (crosses) and the best-fit model (red line) of the z = 0.09017 Ne IX line (the FUV predicted line centroid wavelength is marked with a dashed line) for all the instruments and spectral orders employed. The normalization is done by dividing the spectra by the best-fit continuum model. The best-fit model was simultaneously fitted to RGS1 (first and second dispersion orders), RGS2 (second-order), LETG ACIS (first-order), MEG ACIS (first-order) and HRC data, while the RGS2 first-order data was omitted due to a bad column near the centroid wavelength of the line. The missing bins in RGS1 second-order were rejected by the reduction software due to bad response. The spectral data was rebinned for this illustration to improve the S/N-ratio. |
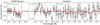 |
Fig. 4. As Fig. 3 but for O VIII. The grey bin near the border of the RGS1 CCD gap was not used in the minimization, but demonstrates a type of spectral artifact that can be produced when observations from different epochs and slightly different pointings with respect to the dispersion direction are co-added. |
Reshifted absorber at z = 0.09017.
The co-added spectra were also studied independently by adopting a model combining the absorbed emission model (Sect. 4.3) with Gaussian absorption lines, to confirm that the spectral features suspected as redshifted Ne IX and O VIII lines were indeed centered at the wavelengths predicted by the FUV redshift. The Gaussian line model was adopted for this analysis because of the technical limitations of “slab” modeling in this context, as mentioned in Sect. 5. In the fits we set the line parameters according to the results discussed above, and re-fitted the data while allowing the Gaussian line centroid wavelengths and line normalization parameters to vary. We found that within the error margins, the Gaussian lines yielded centroid wavelengths consistent with those predicted by the FUV redshift, and that this was true for both examined lines for each available instrument (see Table 4). Since the wavelength-scale of the X-ray data was found to be accurate to σz ≈ 0.0005, or ΔvX − ray ≈ 137 km s−1 (Sect. 5), and as the FUV redshifts are only expected to have a z uncertainty of ΔzFUV ∼ 3 × 10−5 (ΔvFUV ≈ 8 km s−1), the hypothesis of spatial co-location of the FUV and X-ray absorbers was found to be supported by all the observational data.
Finally, since it is possible that spectral co-addition produces small artifacts which can be erroneously interpreted as astrophysical lines, and because the two tentative X-ray lines only have equivalent widths of few mÅ, we chose to investigate this issue further. Here we used the RGS1 first-order data, which contains the majority of the statistical weight in the simultaneous fits and is co-added from 19 different observations. We refitted the RGS1 first-order data using the original, non-stacked spectra and applied the same method used in the simultaneous fits to the spectra of different instruments and spectral orders (i.e., coupled absorption - uncoupled emission). The results obtained for both absorption lines were practically identical to the fits to the co-added RGS1 data (Table 6), thus confirming that the examined spectral features are not co-adding artifacts.
Fits to stacked and non-stacked data.
To conclude the results of the line analysis, Model 1 yielded Nion ∼ 1015 cm−2 ion column densities for O VIII and Ne IX, which are in the range expected for hot WHIM absorbers. We found that all the instruments agree with these results, and that the features appear in the spectra at the wavelengths predicted by the FUV absorber redshift. The O VIII and Ne IX ion fractions peak at coinciding temperature ranges (i.e., T ≈ 106 − 6.5 K), and hence the two ions are likely indicators of a common gas phase for which the “slab” modeling yields a 3.9σ (quadratically summed) detection level. We therefore adopted the Ne IX and O VIII lines as hot WHIM line candidates at the O VI absorber redshift z = 0.09017. The obtained measurement results regarding these line candidates are next compared to the constraints from the physical WHIM absorption model (Model 2) in Sect. 5.2.
5.1.2. Absorption line analysis results: z = 0.12005
The “slab” analysis for the FUV redshift z = 0.12005 revealed no hot absorption line candidates at the predicted centroid wavelengths of any of the lines of interest (as listed in Sect. 5.1), making it uninteresting for the further spectral analysis. The X-ray non-detection is concordant with the earlier results of Tripp et al. (2008), where it was found that the O VI, HI Lyα line widths yield T < 104.7 K (3σ upper limit) for the FUV detected gas at the 3C 273 z = 0.12 absorber. These X-ray and FUV results may indicate that this absorber only has a warm component.
Furthermore, we note that the non-detection of hot phase ions at z = 0.12 means, for instance, that the 1σ limit on the O VI absorber associated NOVIII reduces from log NOVIII(cm−2) = 15.7 (as measured at z = 0.09) to 15.1 when both of the O VI absorber redshifts are considered simultaneously. This limit agrees well with the earlier results of Yao et al. (2009), where they measured a log NOVIII(cm−2) = 15.63 95 % upper limit on O VIII columns associated with the strong O VI WHIM absorbers. This upper limit comes from an analysis of zOVI blueshifted, stacked X-ray spectra from 6 different sight-lines (refer to Yao et al. 2009 for details). We note however, that while the zOVI based stacking of the X-ray data increases the spectral S/N -ratio, the sensitivity to measure the hot phase ion signals may be compromised in this method. This is because X-ray band detectable ion columns are produced in more limited WHIM parameter space region than FUV detectable O VI columns, and hence frequent non-detections of hot ion species are expected, which can effectively hide the X-ray signals in the zOVI shifted, stacked spectra. We will investigate the co-occurrence rate of detectable O VI and O VIII ion columns in the WHIM absorbers in more detail in Sect. 7.
5.2. Collisional ionization equilibrium modeling (Model 2)
The analysis with the “slab” absorption model (Sects. 5.1.1 and 5.1.2) yielded two absorption line candidates at the wavelengths matching those of Ne IX and O VIII lines at the FUV absorber redshift z = 0.09017 (Table 4). The ionization temperatures of Ne IX and O VIII are similar, and indicate log(T(K)) > 6 for the absorbing gas. Since at these temperatures photo-ionization is expected to be less important and collisional ionization equilibrium (CIE) is likely, we tested this hypothesis and modeled the data by adding a redshifted CIE absorption component with solar relative abundances to the emission model with Galactic absorption (hereafter CIE WHIM). The CIE WHIM modeling was performed using the simultaneous fitting of the co-added spectra, except that of the RGS2 first-order, which was omitted from the analysis due to the absence of reliable data at the wavelengths of either of the two putative absorption lines.
To ensure that the CIE WHIM model robustly detects the weak signals of interest, we utilized the model in a blind search test over the redshift range z = 0.005 − 0.1578. In this test, the lower z limit was chosen large enough to avoid considerable blending with the absorption lines of the hot Galactic halo, while the upper z limit corresponds to the nominal redshift of 3C 273. The redshift range was examined in steps so that each z-increment corresponded to a 60 mÅ wavelength shift of the Ne IX line centroid in the spectra. At each step the co-added spectra were fitted with the CIE WHIM model, and the fit C-statistics compared to that obtained without the redshifted component included (Null hypothesis). The improvement of the fit statistics due to the addition of the redshifted absorption component were converted into a Null hypothesis probability using a modified F-test (modified, since we used C-statistics instead of χ2 as a figure of merit). The results of this test are illustrated in Fig. 2. As might be expected based on the results of the “slab” analysis, we found that the lowest p-value is indeed obtained at z ≈ 0.09 (p ≈ 0.027), while at z ≈ 0.12 the Null hypothesis is valid. These findings support the applicability of the CIE WHIM modeling in the context of this study.
In addition to z = 0.09, the p-value falls below the often adopted Null hypothesis rejection limit, p = 0.05, at z ≈ 0.045 (p ≈ 0.035). This redshift does not fulfill our predetermined FUV z -criteria (Sect. 4.2), but we will make a few remarks on this minimum here. The best-fit CIE model is described by kT ≈ 0.10 keV (≈1.1 × 106 K) and NH ≈ 4.6 × 1018 cm−2, which together define a model producing one detectable absorption line in the examined spectral band (O VII Heα, EW ≈5 mÅ). Inspection of the spectra reveals that this model is minimized to a line-like feature present in the RGS1 first-order data at λ = 22.55 Å, while the other instruments’ data lack the sensitivity to confirm the existence of this feature. We note that the best-fit model does not predict any detectable signal in the FUV band (e.g., log NOVI(cm−2) < 13) and that there are no FUV detections at the corresponding redshift. In the absence of such supporting information, and since the best-fit CIE model is effectively a single line model, it remains uncertain whether the fit reveals CIE state O VII absorption at z ≈ 0.045, or some other (non-CIE) ionic line at a different redshift. Lacking additional observational evidence to support the physical origin of this feature, or to verify that the suspected redshift is correct, we will not consider the possible z ≈ 0.045 signal further in this work.
5.3. CIE absorber analysis results: z = 0.09017
The analysis results of the CIE WHIM modeling at the FUV redshift z = 0.09017 are listed in the bottom panel of Table 5. The CIE model yielded a gas temperature kT = 0.26 ± 0.03 keV (log T(K) = 6.48 ± 0.05) and hydrogen column density 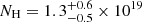 cm−2 (when Z = Z⊙), corresponding ion column densities log NNeIX (cm−2) = 14.9 ± 0.2 and log NOVIII (cm−2) = 15.4 ± 0.2. We note that no other lines with comparable equivalent widths were predicted in the fitting band, nor in the wavelength range accessible to any of the used instruments (i.e., λ ≈ 3 − 175 Å). We find that while the “slab” and CIE modeling yield matching ion columns for O VIII (log
cm−2 (when Z = Z⊙), corresponding ion column densities log NNeIX (cm−2) = 14.9 ± 0.2 and log NOVIII (cm−2) = 15.4 ± 0.2. We note that no other lines with comparable equivalent widths were predicted in the fitting band, nor in the wavelength range accessible to any of the used instruments (i.e., λ ≈ 3 − 175 Å). We find that while the “slab” and CIE modeling yield matching ion columns for O VIII (log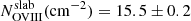 , log
, log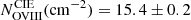 ), the CIE-predicted Ne IX column is lower than obtained with “slab” modeling (log
), the CIE-predicted Ne IX column is lower than obtained with “slab” modeling (log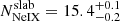 , log
, log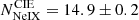 . Such discrepancy could be explained, for instance, by Ne IX excess within the particular integration path through the absorber, or as an indication of small deviations from the ionization equilibrium at the absorbing gas. We will consider this discrepancy further in Sect. 7.
. Such discrepancy could be explained, for instance, by Ne IX excess within the particular integration path through the absorber, or as an indication of small deviations from the ionization equilibrium at the absorbing gas. We will consider this discrepancy further in Sect. 7.
We also find that the CIE WHIM model predicted O VI column density, log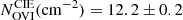 , is an order of a magnitude lower than indicated by the FUV data, log
, is an order of a magnitude lower than indicated by the FUV data, log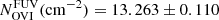 . The measured O VI absorption cannot therefore be explained by hot, collisionally ionized gas. The same conclusion can also be drawn from the FUV measured O VI line broadening (Table 1), which is smaller than thermal broadening at CIE WHIM model temperatures. We will examine these discrepancies in detail in Sects. 6.3 and 7.
. The measured O VI absorption cannot therefore be explained by hot, collisionally ionized gas. The same conclusion can also be drawn from the FUV measured O VI line broadening (Table 1), which is smaller than thermal broadening at CIE WHIM model temperatures. We will examine these discrepancies in detail in Sects. 6.3 and 7.
The temperature of the CIE WHIM model is remarkably tightly constrained. This can be understood through the constraints set by both the detections and non-detections of the most important absorption lines in the temperature range in question (see Fig. 5). Namely, the line equivalent width (W) ratio between the Fe XVII resonance line and O VIII Lyα is very sensitive to the temperature, and thus the non-detection of Fe XVII sets a strict upper limit on the temperature. At low temperature end, non-detections of O VII and N VII lines set constraints for the model temperature.
 |
Fig. 5. Origin of temperature constraints in CIE WHIM modeling. The figure illustrates CIE model temperature dependencies of various ionic line strengths relative to that of the O VIII Lyman α line. The dashed sections mark the regions where the Wion/WOVIII ratio is inconsistent with the 1σ limits of slab modeling. The ions shown in the figure produce the most important absorption lines in the spectra in the examined wavelength band of 14–28 Å and thus constrain the CIE temperature, marked with the shaded region. The data of the strongest available ionic lines were used to generate this figure. |
In Fig. 6, we show the best-fit CIE WHIM model prediction for the redshifted O VII Heα line, which could not be examined independently due to blending with the Galactic O I line but, nevertheless, contributes in constraining the free parameters of the CIE model. It is evident from this figure that within the obtained temperature constraints, the O VII Heα would not be strong enough for detection even without the incidental line blending.
 |
Fig. 6. Zoom-in on the continuum-normalized, RGS1 first-order co-added spectrum at the wavelength band of the Galactic O I (λ ≈ 23.51 Å) doublet, where the best-fit CIE WHIM model predicts an O VII Heα line (λ ≈ 23.55 Å). The different model components comprising the best-fit model (red line) are shown separately. The shaded area marks bins affected by instrumental absorption. |
6. Interpretation of the results
Here we discuss physical interpretations regarding to measurement results of X-ray and FUV absorption at z = 0.09, assuming that both FUV and X-ray detections are real. First, in Sect. 6.1, we consider the possibility that the absorbers are part of a WHIM filament crossing the sight-line at z ≈ 0.09. In Sect. 6.2, we speculate about an alternative interpretation that the absorption signals come from the Circumgalactic medium (CGM) of individual galaxies with small impact parameters to the sight-line. Then in Sect. 6.3, we discuss the thermal structure of the absorbing gas in view of the observational results.
6.1. Large scale galactic environment at z = 0.09
We studied the SDSS galaxy distribution in the 3C 273 sight-line around the FUV absorbers at z ≈ 0.09. 3C 273 is located in the main SDSS survey region. Our galaxy distribution analysis is based on the SDSS flux-limited (mr < 17.77) catalog. The catalogue and data preparation are described in Tempel et al. (2014a); Tempel et al. (2017).
We employed the Bisous model in order to detect possible galactic filaments, which are expected to harbour a large fraction of the local baryons in the form of the WHIM. The Bisous model is a marked object point process that is specifically designed to detect galactic filaments in spectroscopic galaxy distribution data, as described in Tempel et al. (2014b, 2016). The scale of the extracted filaments in the SDSS data is ∼1 Mpc, which corresponds to the scale of large-scale intergalactic medium filaments in simulations (based on visual inspection of simulated filaments in Kooistra et al. 2017, see also the discussion in Schaye 2001). Thus, if a filament axis passes the sight-line at a distance closer than 1 Mpc, we consider it to be crossing the sight-line.
We detected two filaments of ∼10 Mpc length at z ≈ 0.09 around the 3C 273 sight-line, as presented in Fig. 7 (see also the discussions in Williger et al. 2010). Filament F1 passes the 3C 273 sight line at a 3D distance smaller than 0.5 Mpc, that is, closer than the expected filament width. Thus we consider that 3C 273 sight line crosses the core of the filament F1 at a co-moving heliocentric distance of ≈378 Mpc. This crossing point is consistent with the FUV and X-ray line centroids, if their redshifts are entirely due to the Hubble expansion. Filament F2 (see Fig. 7) crosses the 3C 273 sight-line ∼10 Mpc away from the FUV centroid (closer to the observer), if the FUV absorber has no significant radial peculiar velocity component. Assuming alternatively that the FUV absorber is the filament F2, it should have a radial velocity of 800 km s−1. Infall with such a high velocity is unlikely, indicating that the FUV absorber is located close to the crossing point of filament F1 and the sight-line towards 3C 273 (see Fig. 7). Given the relatively large statistical uncertainties in the redshift of the X-ray absorber, and allowing an infall velocity of a few 100 km s−1 (i.e., a shift of a few Mpc in location), we cannot determine whether F1 or F2 is a more likely location for the X-ray absorber. However, the consistency of the FUV and X-ray centroid redshifts with each other and with the location of the major galactic filament F1 suggests that both absorbers are due to WHIM in F1.
 |
Fig. 7. Filament analysis for 3C 273 sight-line near z = 0.09. The figure shows the distribution of SDSS galaxies (points) in two orthogonal projections (upper and lower panels), each of which are 20 Mpc thick. Blue points represent galaxies in filaments and red points indicate additional galaxies in friends-of-friends groups. The detected filament axes F1 and F2, and the associated luminosity density profiles are denoted by yellow lines and grey curves, respectively. The crossing points of the filaments F1 and F2 and the sight-line to 3C 273 are denoted with labels “CP1” and “CP2”, respectively. The redshift of the O VI absorption is marked with the black vertical line, whereas the pink vertical line and area correspond to the X-ray measured O VIII line centroid and its 1σ measurement uncertainty, obtained in the Gaussian model fit to the O VIII Lyα feature (see Table 4) |
Using the galaxy distribution we also generated a three dimensional luminosity density (LD) field (for details, see Liivamagi et al. 2012; Tempel et al. 2014a). The LD profile along the sight-line (see Fig. 7) peaks at the crossing points of filaments F1 and F2. Assuming that the X-ray absorber is located at F1, and following the procedures described in Nevalainen et al. (2015), we converted the luminosity density profile along the sight-line in the radial range of 375–381 Mpc into a WHIM hydrogen column density estimate of NH, F1 ∼ 2 × 1019 cm−2. (Currently we cannot explicitly account for the possible selection effect induced uncertainties in the total error budget of NH, and consequently we only give the best estimate value here). The perpendicular orientation of F1 relative to the 3C 273 sight-line provides a minimal path length (∼1 Mpc) through the filament and thus gives a relatively low column density. Assuming a 1 Mpc path length and a constant density along the path yields a WHIM hydrogen number density of ∼6 × 10−6 cm−3, that is, a baryon overdensity of ∼20, a value consistent with the WHIM in simulations. We note that the estimate of the total hydrogen column density of F1 (∼2 × 1019 cm−2) is consistent with the value the X-ray data yielded for NH (Table 5), if the WHIM metallicity is ∼10−1 Solar (as we find that 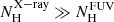 , see details in Sect. 6.3).
, see details in Sect. 6.3).
6.2. Absorption by circumgalactic medium at z = 0.09
We next considered the possibility that the haloes of galaxies close to the 3C 273 sight-line are the dominant source of the FUV and X-ray absorption we associated with the F1 filament above. The most likely object to provide sufficient ion columns is G1 (see Fig. 7), the nearest galaxy to the sight-line (bimpact ≈ 500 kpc) at a redshift close to F1. It is a spiral galaxy with Mr = −21.1, and hence photo-metrically similar to the Milky Way (Licquia et al. 2015). Using the IllustrisTNG simulations (Nelson et al. 2018a) for galaxies with halo mass log(Mhalo) = 12.0, that is, the same as for the Milky Way, for bimpact ≈ 500 kpc we obtained an average log NOVI(cm−2)≈12.2 with 1 σ halo-to-halo variation of ≈9.8 − 13.0 (D. Nelson, priv. comm.). Therefore the O VI column of the z = 0.09 absorber, log(NOVI) = 13.263 ± 0.110 (Tilton et al. 2012), seems consistent with absorption through the halo of G1. However, given that the halo-to-halo variation spans over three order of magnitudes, the consistency may be only coincidental and one cannot determine the origin of the absorption without further information on the absorber properties.
When it comes to the hot phase, we do not have similar simulation results available, and the relevant observational information is also very limited. As it stands, hot (∼106 K) coronae around spiral galaxies have only been directly measured for a few nearby massive spirals, and even in these cases the photon statistics have limited the detailed analysis to the centermost halo regions. For instance, Bogdan et al. (2013) reported hot haloes around the NGC 1961 and NGC 6753 spirals, in which ≈50 − 70 % of baryons were found to be missing from the volumes enclosed within Rvir. These results were later confirmed by Anderson et al. (2016) and Bogdan et al. (2017) with use of deeper data.
We note however, that there are indications that hot galactic haloes may extend very far out from the host galaxies (e.g., Wakker & Savage 2009; Tumlinson et al. 2011; Stocke et al. 2012; Johnson et al. 2015; Burchett et al. 2019), up to several hundred kpc distances in Milky Way-like galaxies (see e.g., Gupta et al. 2012; Fang et al. 2012). In the case of 3C 273, the sight-line has a ∼2.5Rvir impact parameter with respect to the galaxy G1. Hence, linking the X-ray absorption to the hot halo of G1 would require a substantial CGM, extending far beyond the virial radius. Unfortunately, the available X-ray instrumentation is not capable of providing the information required to determine the mass distribution of hot gas around spirals out to very large radii. (Note that current measurements of the missing baryon budget in spirals, such as those quoted above, are based on parametric profiles, extrapolated from a small fraction of Rvir around the central parts of the halo.) Therefore, while we cannot confirm or exclude the possibility that the 3C 273 hot gas absorption would mainly be associated with galaxy G1 (rather than with the filamentary WHIM gas residing in structure F1), this interpretation seems unlikely.
6.3. WHIM gas phases at z = 0.09
In this work, we have shown that X-ray grating data yields evidence of hot absorbing gas at z ≈ 0.09. Tilton et al. (2012), building on the work of Danforth & Shull (2008), Tripp et al. (2008), and Sembach et al. (2001) reported FUV detections of O VIλλ 1031.9, 1037.6 Å lines at the corresponding z at 5.0 and 2.8σ significance levels, indicating a log NOVI(cm−2) = 13.263 ± 0.110 column density for O VI. The CIE WHIM model presented in this work only predicts 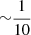 the O VI column density (Table 5) that the FUV data indicate, meaning that a one temperature CIE model is insufficient to explain all the observational results.
the O VI column density (Table 5) that the FUV data indicate, meaning that a one temperature CIE model is insufficient to explain all the observational results.
At present, observational information on the thermal structures of WHIM absorbers is absent, but, for example, the EAGLE (Schaye et al. 2015) simulations indicate that many high column density WHIM absorbers are multi-temperature (e.g., Oppenheimer et al. 2016; Wijers et al. 2019). For such absorbers, multiband analysis may often be required to yield information about the various temperature phases that may co-exist. This is also demonstrated by the CIE WHIM modeling results of this study; despite the fact that the hot phase predicts relatively high NOVI, its absorption imprint cannot be measured in the FUV because of the shallow line profile due to thermal line broadening.
In the absence of detailed knowledge of the z = 0.09 absorber’s local radiation field, we do not know the precise balance of ionization processes at work. However, if the ionizing radiation field can be predominantly characterized by the typical metagalactic ultraviolet background (UVB; e.g., Haardt & Madau 2012), it is unlikely that photoionization is the primary contributor to the observed O VI column densities, as photoionization calculations using a variety of UVB models fail to produce significant O VI column densities (e.g., Tepper-Garcia et al. 2011; Shull et al. 2015; Rahmati et al. 2016). Even in the circumgalactic medium of star-forming L* galaxies, photoionization is unlikely to drive the production of O VI unless the physical gas densities are extremely low (McQuinn & Werk 2018), or if there has been AGN activity within the last recombination time (Oppenheimer & Schaye 2013; Segers et al. 2017; Oppenheimer et al. 2018). The ionization of the observed O VI absorber is thus likely driven by collisional processes. Though the frequent association of O VI absorbers with photoionized gas (e.g., lower ionization states of C, N, and Si) suggests that at least some O VI absorbers arise in a non-equilibrium, multiphase gas, we limit our further discussion to the simplified case of collisional ionization equilibrium so that we can derive plausible temperatures for the observed gas.
Assuming the CIE conditions to be valid, the FUV observational results readily set constraints on the gas temperature of the warm absorber. Namely, combining the information of the upper limit on the C III ion column density (log NCIII(cm−2) < 12.590, Tilton et al. 2012) and the lower limit on NOVI, one gets the lower temperature limit if the relative elemental abundances are considered known (because of the C III, O VI ion fraction T-dependencies). On the other hand, assuming pure thermal line broadening for the O VI line broadening parameter (b = 22.2 ± 10.8 km s−1, Table 1) directly yields an upper temperature limit for absorbing gas.
However, we found that with the help of the X-ray data, these temperature limits can be constrained more accurately. In the two panels of Fig. 8 we present the results obtained with a two phase (warm-hot) CIE absorber model constructed around the relevant information obtained in the X-ray and FUV measurements. In the 2T model (the CIE WHIM model + additional SPEX “hot”-component for the warm absorber), the hot CIE absorption component was fixed to the best-fit values of the CIE WHIM (Table 5), while the total NOVI (=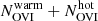 ) was fixed to the FUV measured value of log NOVI(cm−2) = 13.263. We then examined the goodness of fit as a function of warm CIE absorber temperature. We also conducted the same study by omitting the hot WHIM component from the model, to investigate the dependence of the results on the hot CIE component (1T, Fig. 8). We note that in both the 1 and 2T fits, the only free parameter was the warm WHIM temperature Twarm (in addition to the absorbed emission model, Sect. 4.3), as
) was fixed to the FUV measured value of log NOVI(cm−2) = 13.263. We then examined the goodness of fit as a function of warm CIE absorber temperature. We also conducted the same study by omitting the hot WHIM component from the model, to investigate the dependence of the results on the hot CIE component (1T, Fig. 8). We note that in both the 1 and 2T fits, the only free parameter was the warm WHIM temperature Twarm (in addition to the absorbed emission model, Sect. 4.3), as 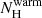 is defined by the CIE constraints from the fixed NOVI.
is defined by the CIE constraints from the fixed NOVI.
 |
Fig. 8. Thermal properties of the absorbing gas at z = 0.09017 assuming CIE. Left: temperature dependence of the two-phase absorption model fit statistics to the X-ray data (black solid curve) when NOVI is fixed to the FUV measured value. The shaded areas mark the forbidden regions based on the FUV measurements (the lower limit is yielded by the limits on NCIII and NOVI, whereas the upper limit is set by the O VI line broadening). The 1T curve shows the X-ray model fit statistics without the hot absorption component included, and is plotted for reference. Right: O VI (red), O VII (black) and O VIII (blue) ion fractions over the T -ranges of the warm and hot CIE components. The dotted lines mark the best-fit temperatures for both phases, while the white regions mark the 1σ uncertainty limits as yielded by X-ray data. The light gray shaded regions show the improvement which X-ray data provides to the Twarm determination as compared to the limits obtained with FUV data. |
We found that the 2T (and 1T) model yields a global minimum C-statistic in a temperature range matching the FUV derived T limits. More precisely, the 2T fit yielded 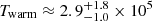 K (or kTwarm ≈ 0.025 keV) with
K (or kTwarm ≈ 0.025 keV) with 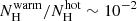 (see the left panel in Fig. 8). We note that this solution occurs because towards the lower temperatures, the ratio of NOVI to lower ionization states of oxygen quickly decreases, predicting rise of prominent O IV (blend at λ0 ≈ 22.7 Å) and O V (λ0 ≈ 22.37 Å) lines not present in the X-ray spectra (but observed, e.g., in Galactic halo, see Nevalainen et al. 2017). In contrast, when moving towards the higher temperatures, the
(see the left panel in Fig. 8). We note that this solution occurs because towards the lower temperatures, the ratio of NOVI to lower ionization states of oxygen quickly decreases, predicting rise of prominent O IV (blend at λ0 ≈ 22.7 Å) and O V (λ0 ≈ 22.37 Å) lines not present in the X-ray spectra (but observed, e.g., in Galactic halo, see Nevalainen et al. 2017). In contrast, when moving towards the higher temperatures, the 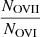 -ratio becomes inconsistent with the X-ray data. The attained 2T solution is in fact the only viable two-phase solution that can simultaneously fulfill both the FUV and X-ray constraints, which can also be understood through the visualization in the right panel of Fig. 8.
-ratio becomes inconsistent with the X-ray data. The attained 2T solution is in fact the only viable two-phase solution that can simultaneously fulfill both the FUV and X-ray constraints, which can also be understood through the visualization in the right panel of Fig. 8.
Considering the thermal analysis results and the redshift match between the hot and warm absorbers together implies that the FUV and X-ray absorbers are part of the same, multi-temperature structure of intergalactic gas. The redshift match does not necessarily signify strict spatial co-location of the detected gas phases, however, because different thermal phases can occupy spatially distinct physical environments within the same structure. Indeed, recent EAGLE simulations indicate that WHIM structures are often composed of a variety of thermodynamical environments characterized by wide range of densities, temperatures and pressures (e.g., Oppenheimer et al. 2016; Wijers et al. 2019). Such complexity limits our ability to further examine the absorber properties, by adopting the requirement of pressure equilibrium for different phases for instance, or by means of other similar constraints.
However, combining the information from the FUV and X-ray measurements does give weak constraints on the line-of-sight turbulent velocities vturb associated with the warm WHIM component. Namely, writing the definition of the line Doppler parameter b for vturb we have
where m is the mass of a given ion, of which we measure a rest-frame spectral linewidth b at gas temperature T. Thus, in the case in hand, the first term inside the square root can be determined by the FUV O VI measurements, whereas the second term can be obtained from the X-ray temperature constraints on the warm WHIM component. (We ignore any hot phase contribution to the FUV O VI line width, since we expect the hot phase to have only 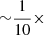 the O VI column and ∼10× the temperature). Using the obtained values gives us upper limit vturb ≲ 20 km s−1, or vturb/vthermal ≈ 0.5 ± 0.5. In order to obtain a lower limit for vturb, more accurate measurements of b would be required. We point out that this method could be applied to constrain vturb for any (collisionally ionized) warm O VI absorbers in lines-of-sight where high-resolution X-ray data with good photon statistics are available.
the O VI column and ∼10× the temperature). Using the obtained values gives us upper limit vturb ≲ 20 km s−1, or vturb/vthermal ≈ 0.5 ± 0.5. In order to obtain a lower limit for vturb, more accurate measurements of b would be required. We point out that this method could be applied to constrain vturb for any (collisionally ionized) warm O VI absorbers in lines-of-sight where high-resolution X-ray data with good photon statistics are available.
We will now consider the spectral properties of the BLA lines predicted by the two-phase model to check whether they contradict the non-detection of BLA lines at z = 0.09. Richter et al. (2006) found that the BLAs are detectable in STIS data if
where (S/N) denotes the signal-to-noise ratio per spectral resolution element at the location of the BLA. We examine the detectability of the predicted BLAs using the Williger et al. (2010) quoted sensitivity limit for STIS spectral data at the 3C 273 sight-line (log NHI/bHI ≈ 10.9 at z ≈ 0.09).
According to the best-fit 2T model, the two BLAs are characterized by 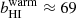 km s−1,
km s−1, 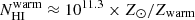 cm−2 and
cm−2 and 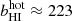 km s−1,
km s−1, 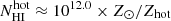 cm−2 (here we have neglected the non-thermal line broadening, which would effectively decrease the line detectability). The detection criterion in Eq. (2) may then be written as
cm−2 (here we have neglected the non-thermal line broadening, which would effectively decrease the line detectability). The detection criterion in Eq. (2) may then be written as 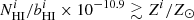 , which yields metallicity limits Zwarm ≈ 0.04 × Z⊙ and Zhot ≈ 0.06 × Z⊙, above which the lines are undetectable. Therefore neither of the phases produces detectable BLAs at the expected metallicity range of filamentary WHIM, Z = 0.1 − 0.4 × Z⊙ (Martizzi et al. 2019), and the non-detectability is also consistent with our weak limit on the hot phase metallicity, Zhot ∼ 10−1 (see Sect. 6.1).
, which yields metallicity limits Zwarm ≈ 0.04 × Z⊙ and Zhot ≈ 0.06 × Z⊙, above which the lines are undetectable. Therefore neither of the phases produces detectable BLAs at the expected metallicity range of filamentary WHIM, Z = 0.1 − 0.4 × Z⊙ (Martizzi et al. 2019), and the non-detectability is also consistent with our weak limit on the hot phase metallicity, Zhot ∼ 10−1 (see Sect. 6.1).
7. Comparison to simulations
In Sect. 6.1 we showed that the FUV and X-ray absorption at z ≈ 0.09 can originate from WHIM located in a large scale filamentary structure (of the Cosmic Web). Then, in Sect. 6.2 we found that the nearest detected galaxy to the absorber is unlikely to produce the measured absorption. However, it is still possible that at the location of the absorber there are galaxies fainter than the SDSS detection limit, which could produce the measured level of O VI. In this case, only the X-ray lines would originate from the intergalactic medium in the filament.
In order to gain more insight of the physics of the co-located FUV and X-ray absorbers, we investigated the EAGLE cosmological, hydrodynamical simulations (Schaye et al. 2015, Crain et al. 2015, McAlpine et al. 2016). Given the various possibilities for the environment of the z ≈ 0.09 absorbers, we did not attempt to separate the haloes and the filaments when extracting the simulated data for this study. In this section, we summarize the observable properties of spatially co-located hot (O VII, O VIII and Ne IX), and warm WHIM (O VI) absorbers in EAGLE, and compare these predictions to our measurements.
7.1. EAGLE simulation
The code for the EAGLE simulations is a modified version of GADGET3 (last described in Springel 2005). It uses a TREE-PM scheme to calculate gravitational forces. One of the modifications made to GADGET3 is the use of a different hydrodynamics solver: EAGLE uses a smoothed particle hydrodynamics (SPH) implementation known as ANARCHY (Schaye et al. 2015, Schaller et al. 2015). Cosmological parameters were taken from Planck Collaboration I (2014).
Gas cooling is implemented per element as described by Wiersma et al. (2009), using the abundances of 11 elements tracked in the simulation. Ionization equilibrium with collisional processes and photo-ionization by a Haardt & Madau (2001) UV and X-ray background is assumed. Since the particle mass of the simulations is ≈ 2 × 106 M⊙, we cannot resolve the formation of and feedback (stellar winds and supernovae) from individual stars, accretion disks, jets, etc. in AGN. Therefore, star formation and stellar and AGN feedback on the mass scales we can resolve are implemented using subgrid models. The feedback models have free parameters, which were chosen by calibrating them to reproduce the z = 0.1 galaxy stellar mass function, the relation between black hole mass and galaxy mass, and reasonable galaxy sizes. We use the 1003 Mpc3 simulation volume (L100N1504) at z = 0.1, which was run with the standard EAGLE subgrid parameters (the Reference model).
We compute column densities as in Wijers et al. (2019). In short, we assume the gas is in collisional and photo-ionisation equilibrium with the Haardt & Madau (2001) UV/X-ray background at z = 0.1. We then use the gas temperatures, densities, and oxygen mass fractions from the simulation to compute the number of ions in long, thin columns along the line of sight. The columns are thin enough that the column densities at the values we observe are converged. Their line of sight length was chosen to be 6.25 comoving Mpc, which corresponds to 404 km s−1 (rest-frame) in velocity space, ignoring peculiar velocities, or Δz = 0.0015. When comparing temperatures for the different ions, we measure ion-weighted temperatures in the same columns. We define counterpart column densities to be column densities measured in the same columns for different ions. Since we define our simulated absorbers by these fixed boxes, our column density and counterpart determinations from EAGLE are only an approximation of what an observer would measure in an EAGLE universe. The redshift range in these slices does roughly match the difference between the O VI and X-ray centroids, although the z uncertainty is large in the X-ray. While we did not impose any direct filament environment selection criteria on the EAGLE data, we note that concentrating on the densest hot WHIM, we are approximately focusing on locations close to the filament axes, as indicated by the cosmological simulations such as the EAGLE and IllustrisTNG (see Nelson et al. 2018b).
7.2. Results
In Fig. 9, we investigate what sort of X-ray counterparts we would expect to find for the O VI absorber at z = 0.09, based on its column density. In EAGLE, such an absorber can have a broad range of O VIII and Ne IX column densities, but the absorption in the two X-ray lines is strongly correlated. The measured X-ray column densities are large compared to the predictions, but not unreasonably so, especially considering the minimum detectable absorption and the non-detection of X-ray counterparts for the z = 0.12 O VI absorber. The CIE WHIM model column densities agree better with the EAGLE predictions than the “slab” column densities, but both are within 1 − 2 σ of the region where 90% of absorbers consistent with the observed O VI column densities lie in EAGLE, if the observed upper limit on O VII is ignored (left panel of Fig. 9). Including the “slab” model O VII upper limit means the O VIII/Ne IX absorption measured with the “slab” model agrees slightly less well with EAGLE (right panel of Fig. 9). However, given the ∼1015 cm−2 detection limit for O VIII and Ne IX, any of the most likely ∼90% of O VI, O VII upper limit counterparts would be undetectable with current instrumentation. Considering this selection effect, and the non-detection of a hot counterpart for the O VI absorber at z = 0.12 (characterized with similar NOVI to z = 0.09 absorber, Table 1), we find that the FUV and X-ray ion column density measurements are generally consistent with the EAGLE predictions.
 |
Fig. 9. Distribution of O VIII and Ne IX column densities in counterparts to O VI absorbers (grayscale and contours) according to the EAGLE simulation, compared to the measured column densities at z = 0.09 for the CIE and slab models. Left panel: counterparts to O VI absorbers with column densities of 1013.2–1013.4 cm−2, which is roughly the ±1σ range for the FUV absorber of Tilton et al. (2012). Right panel: subset of O VI counterparts with an O VII column density in agreement with the upper limit measured with the slab model. The contours enclose different fractions of the counterparts, as indicated in the legend, while the grayscale shows the fraction of all EAGLE absorbers satisfying the indicated constraints. Although most EAGLE O VI absorbers have weaker (and hence undetectable) associated Ne IX and O VIII absorption than observed at z = 0.09 (but consistent with the non-detection for the z = 0.12 O VI absorber), both the “slab” and CIE measuremets are consistent with EAGLE at the ≈1 − 2σ level. The O VII upper limit does not affect the distribution much. |
Then we ask the question of whether the EAGLE simulations support the 2-temperature solution we obtained with the X-ray and FUV spectroscopy for the absorber at z = 0.09. To answer this, we performed a test where we compared our 2T-fit temperatures Twarm and Thot (Sect. 6.3) with corresponding quantities obtained from the simulation: TOVI and TOVIII ion mass weighted temperatures. For the comparison, we had to choose a subsample of the simulations which represents the conditions of the z = 0.09 absorber. Since we were testing the temperatures, we obviously did not use the temperatures to select the subsample. Instead, we imposed the measured constraints on the absorber’s O VI (Tilton et al. 2012), O VII, O VIII and Ne IX (“slab” constraints) column densities as the selection criteria when extracting the simulation data.
We illustrate the result of this study in Fig. 10, where we examine the effect of different Nion constraints on EAGLE distribution one by one. Adding just the O VI constraint readily shows that O VIII and Ne IX often trace gas that is at different temperatures than the O VI-rich phase (top left panel). We find that adoption of the O VII upper limit does not strongly constrain the number of absorption systems in EAGLE (top right panel), whereas the opposite is true for O VIII and Ne IX, which strongly limit the temperature phase distribution of the absorption systems (bottom panels). Indeed, when all the Nion measurement constraints are applied, the necessity of 2T conditions emerges in EAGLE. This subsample behaves well in the TOVI-TOVIII plane, forming a regular, relatively narrow region. Notably, we find that absorption systems with column densities like those of the z = 0.09 absorber tend to have O VI and O VIII temperatures that agree well with the 2T CIE temperatures (bottom right panel). Thus, we find that the 2T CIE model is well supported by the simulations, which validates the use of CIE modeling adopted in this work.
 |
Fig. 10. Distribution of O VI-and O VIII-weighted temperatures in counterparts to O VI absorbers (grayscale and contours) according to the EAGLE simulation, compared to the best-fit temperatures at z = 0.09 for the 2-temperature CIE model (warm and hot phase, respectively). From left to right, top to bottom, we show how constraints on the column densities of different ions from the “slab” model affect the temperatures of O VI and O VIII absorbers in EAGLE. Column density ranges are shown in units of log10 cm−2 for the different ions. The O VI constraints are from Tilton et al. (2012). The contours enclose different fractions of the absorbers in each column density selection, as indicated in the legend, while the grayscale shows the fraction of all EAGLE absorbers satisfying the indicated constraints. The brown dashed line indicates where the temperatures are equal. Most absorbers are multiphase and the 2T CIE model is consistent with EAGLE. |
8. Discussion
In this work we search for the absorption imprints of hot WHIM at the redshifts of warm intergalactic (O VI) absorbers. We examine the X-ray data in a sight-line which provides one of the highest level photon statistics currently available, including observational data from 5 different high spectral-resolution X-ray instruments. Our analysis yielded a positive indication at one out of two examined O VI redshifts. However, given that we only analyzed two O VI absorbers, the uncertainty in the observational detection rate is large and one cannot draw a general conclusion from such small number statistics. Indeed, EAGLE predicts only an 11% chance of finding an O VIII counterpart as strong as we found (CIE model) to at least one of the two examined O VI absorbers, indicating that the observational detection rate was driven by luck.
Based on this study, we are able to make a few general remarks regarding FUV-guided searches for hot WHIM. First, two search criteria (as defined in Sect. 4.2) were initially set in order to filter out all but the most promising FUV absorber redshifts for the X-ray analysis. In hindsight it seems, however, that the BLA criterion might have only limited use for this. Namely, considering the inevitably large bHI associated with gas phases not producing a detectable O VI signal in the FUV yet still producing strong lines in X-ray, such BLA detections seem unlikely. This is because robust detections of broad HI lines require high NHI, in which cases the absorber metallicities should be low given the current upper limits on WHIM ionic columns, but still high enough to enable X-ray detection. Such special requirements for the environment likely mean the number of X-ray absorbers only traceable with BLAs is small.
Second, O VII is often expected to be the most prominent X-ray detectable ion species to accompany O VI absorbers, which is a justified assumption given the Oxygen ion fraction temperature dependencies. However, the evidence presented in this work demonstrates that O VI absorbers can also be used to reveal locations of hot X-ray absorbers whose O VII signal is below detectability, or in other words, when the circumstances are such that the two bands would effectively detect thermally distinct gas phases. As the combination of low O VI ion fractions and the broad line shapes of the hot WHIM phases significantly reduces the O VI FUV detectability, the FUV measured bOVI should not been interpreted as a direct proxy for the (maximum) temperature of the absorber. Rather, bOVI may often be merely a property of the most easily detectable gas phase within an otherwise thermally complex structure, as may also be inferred from the top panels of Fig. 10.
9. Conclusions
In this work we examined the O VI detection driven method to find missing baryons in the hot WHIM phase. We analyzed the available high-resolution spectral data of XMM-Newton RGS, Chandra LETG and MEG for the quasar 3C 273, which is one of the brightest quasars in X-ray. We searched for the hot WHIM absorption signatures at the two redshifts where O VI absorbers have been significantly detected in the FUV band. Our main results include:
-
At one of the FUV determined redshifts, z = 0.09017, spectral analysis with a line absorption model yields two X-ray line candidates whose centroid wavelengths match the Ne IX Heα (Wrest − frame = 2.7 ± 0.9 mÅ, confidence level 2.9σ) and O VIII Lyα (Wrest − frame = 4.3 ± 1.6 mÅ, 2.6σ) lines. These two ion species are prominent in the same temperature range (T ≈ 106 − 6.5 K), thus yielding 3.9σ combined (quadratically summed) confidence level for the hot phase lines.
-
Examining the spectral characteristics at the same redshift assuming collisional ionization equilibrium (CIE) for the absorber yields kT = 0.26 ± 0.03 keV and
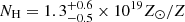 cm−2 for the absorbing medium. The column densities of O VIII and Ne IX predicted by this model (log NO VIII(cm−2) = 15.4 ± 0.2, log NNe IX (cm−2) = 14.9 ± 0.2) are in close agreement with those measured phenomenologically from the line flux (log NO VIII (cm−2) = 15.5 ± 0.2, log
cm−2 for the absorbing medium. The column densities of O VIII and Ne IX predicted by this model (log NO VIII(cm−2) = 15.4 ± 0.2, log NNe IX (cm−2) = 14.9 ± 0.2) are in close agreement with those measured phenomenologically from the line flux (log NO VIII (cm−2) = 15.5 ± 0.2, log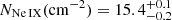 ), indicating the hot phase is well described by the CIE model.
), indicating the hot phase is well described by the CIE model. -
The thermal analysis implies a multi-temperature structure for the z ≈ 0.09 absorber, with dominant temperature components of Twarm ≈ 3 × 105 K and Thot ≈ 3 × 106 K, and hydrogen column density ratio
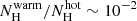 , when assuming CIE conditions and identical metallicities for both phases (Fig. 8). These results match the EAGLE hydrodynamical simulation temperature predictions for co-spatial WHIM absorbers characterized with ion column densities matching the FUV and X-ray measurements (lower right panel in Fig. 10).
, when assuming CIE conditions and identical metallicities for both phases (Fig. 8). These results match the EAGLE hydrodynamical simulation temperature predictions for co-spatial WHIM absorbers characterized with ion column densities matching the FUV and X-ray measurements (lower right panel in Fig. 10). -
SDSS galaxy distribution modeling detected a large scale filament of galaxies crossing the sight-line at the location matching the FUV and X-ray absorbing gas (Fig. 7). The total WHIM hydrogen column density at the 3C 273 sightline through the filament was estimated to be NH ∼ 2 × 1019 cm−2. Associating this value with the results of the X-ray analysis yields an absorber metallicity Z ∼ 10−1 × Z⊙, which is in the range expected for the WHIM. Combining our results hence supports the hypothesis that the X-ray and FUV absorption signals relate to a filamentary WHIM structure intersecting the 3C 273 sight-line at z ≈ 0.09.
-
We found no indications of X-ray absorbing gas at the other of the two examined O VI redshifts, z = 0.12005. Since this absorber is characterized by NOVI similar to the absorber at z = 0.09017, we have a nominal 50 % (1 of 2) detection-rate for X-ray absorbing counterparts to NOVI(cm−2)≈13.2 − 13.4 FUV absorbers at the examined sight-line. By comparison, EAGLE predicts 11% likelihood to find at least one log NOVIII(cm−2)≥15.4 counterpart per two randomly selected O VI absorbers in the coincident NOVI range. However, regarding future observations with X-ray instruments capable to detect log NOVIII(cm−2)≥15.0 signals, such as the Athena X-IFU, the same likelihood is already 29%. This reflects the potential in utilizing the information on O VI absorbers in finding missing baryons in hotter, X-ray absorbing phase.
Acknowledgments
JA and FA acknowledge the support received under X-IFU Athena project funding of University of Helsinki. ET was supported by ETAg grants IUT40-2, IUT26-2 and by EU through the ERDF CoE grant TK133 and MOBTP86. JA and FA would like to thank F. Nicastro for valuable discussions regarding to this work.
References
- Anderson, M. E., Churazov, E., & Bregman, J. N. 2016, MNRAS, 000, 449 [Google Scholar]
- Barret, D., Lam Trong, T., den Herder, J. W., et al. 2016, Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray, 9905, 99052F [Google Scholar]
- Bogdan, A., Forman, W. R., Vogelsberger, M., et al. 2013, ApJ, 772, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdan, A., Bourdin, H., Forman, W. R., et al. 2017, ApJ, 850, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Bonamente, M. 2017, Statistics and Analysis of Scientific Data, 2nd edn. (Springer, Graduate Texts in Physics) [CrossRef] [Google Scholar]
- Bonamente, M., Nevalainen, J., Tilton, E., et al. 2016, MNRAS, 457, 4236 [Google Scholar]
- Bonamente, M., Ahoranta, J., Tilton, E., Tempel, E., & Morandi, A. 2017, MNRAS, 469, 3984 [NASA ADS] [CrossRef] [Google Scholar]
- Buote, D. A., Zappacosta, L., Fang, T., et al. 2009, ApJ, 695, 1351 [NASA ADS] [CrossRef] [Google Scholar]
- Burchett, J. N., Tripp, T. M., Prochaska, J. X., et al. 2019, ApJ, 877, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Cartledge, I. B., Lauroesch, J. T., Meyer, D. M., & Sofia, U. J. 2004, ApJ, 613, 1037 [NASA ADS] [CrossRef] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Cen, R., & Ostriker, J. P. 1999, ApJ, 514, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Crain, R. A., Schaye, J., Bower, R. G., et al. 2015, MNRAS, 450, 1937 [NASA ADS] [CrossRef] [Google Scholar]
- Danforth, C. W., & Shull, J. M. 2008, ApJ, 679, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Danforth, C. W., Keeney, B. A., Tilton, E. M., et al. 2016, ApJ, 817, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Davé, R., Hernquist, L., Katz, N., & Weinberg, D. H. 1999, ApJ, 511, 521 [NASA ADS] [CrossRef] [Google Scholar]
- de Vries, C. P., den Herder, J. W., Gabriel, C., et al. 2015, A&A, 573, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fang, T., Bryan, G. L., & Canizares, C. R. 2002, ApJ, 564, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, T., Sembach, K. R., & Canizares, C. R. 2003, ApJ, 586, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, T., Bullock, J., & Boylan-Kolchin, M. 2012, ApJ, 762, 20 [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, A., Mathur, S., Krongold, Y., et al. 2012, ApJ, 756, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Madau, P. 2001, in Clusters of Galaxies and the High Redshift Universe Observed in X-rays, ed D. M. Neumann, & J. T. V. Tran [Google Scholar]
- Haardt, F., & Madau, P. 2012, ApJ, 746, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, S. D., Chen, H.-W., & Mulchaey, J. S. 2015, MNRAS, 449, 3263 [NASA ADS] [CrossRef] [Google Scholar]
- Kaastra, J. S., de Vries, C. P., Steenbrugge, K. C., et al. 2011, A&A, 534, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaastra, J., Finoguenov, A., Nicastro, F., et al. 2013, ArXiv e-prints [arXiv:1306.2324] [Google Scholar]
- Kooistra, R., Silva, M. B., & Zaroubi, S. 2017, MNRAS, 468, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Kovacs, O. E., Bogdan, A., Smith, R. K., Kraft, R. P., & Forman, W. R. 2019, ApJ, 872, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Licquia, T. C., Newman, J. A., & Brinchmann, J. 2015, ApJ, 809, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Liivamagi, L. J., Tempel, E., & Saar, E. 2012, A&A, 539, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lodders, K., Palme, H., & Gail, H.-P. 2009, Landolt-Börnstein - Group VI Astronomy and Astrophysics, 712 [Google Scholar]
- Martizzi, D., Vogelsberger, M., Artale, M. C., et al. 2019, MNRAS, 486, 3766 [Google Scholar]
- McAlpine, S., Helly, J. C., Schaller, M., et al. 2016, Astron. Comput., 15, 72 [NASA ADS] [CrossRef] [Google Scholar]
- McQuinn, M., & Werk, J. K. 2018, ApJ, 852, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, N., Kauffmann, G., Pillepich, A., et al. 2018a, MNRAS, 477, 450 [Google Scholar]
- Nelson, D., Pillepich, A., Nelson, D., et al. 2018b, MNRAS, 477, 1206 [NASA ADS] [CrossRef] [Google Scholar]
- Nevalainen, J., Tempel, E., Liivamagi, L. J., et al. 2015, A&A, 583, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nevalainen, J., Wakker, B., Kaastra, J., et al. 2017, A&A, 605, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nevalainen, J., Tempel, E., Ahoranta, J., et al. 2019, A&A, 621, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nicastro, F., Krongold, Y., Fields, D., et al. 2010, ApJ, 715, 854 [NASA ADS] [CrossRef] [Google Scholar]
- Nicastro, F., Krongold, Y., Mathur, S., & Elvis, M. 2017, Astron. Nachr., 338, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Nicastro, F., Kaastra, J., Krongold, Y., et al. 2018, Nature, 558, 406 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Oppenheimer, B. D., & Schaye, J. 2013, MNRAS, 434, 1063 [NASA ADS] [CrossRef] [Google Scholar]
- Oppenheimer, B. D., Crain, R. A., Schaye, J., et al. 2016, MNRAS, 460, 2157 [NASA ADS] [CrossRef] [Google Scholar]
- Oppenheimer, B. D., Segers, M. C., Schaye, J., Richings, A. J., & Crain, R. A. 2018, MNRAS, 474, 4740 [NASA ADS] [CrossRef] [Google Scholar]
- Persic, M., & Salucci, P. 1992, MNRAS, 258, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration I. 2014, A&A, 571, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rahmati, A., Schaye, J., Crain, R. A., et al. 2016, MNRAS, 459, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Rasmussen, A. P., Kahn, S. M., Parels, F., et al. 2007, ApJ, 656, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Ren, B., Fang, T., & Buote, D. A. 2014, ApJ, 782, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Richter, P., Savage, B. D., Sembach, K. R., & Tripp, T. M. 2006, A&A, 445, 827 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savage, B. D., Lu, L., Weymann, R. J., Morris, S. L., & Gilliland, R. L. 1993, ApJ, 404, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Schaller, M., Dalla Vecchia, C., Schaye, J., et al. 2015, MNRAS, 454, 2277 [NASA ADS] [CrossRef] [Google Scholar]
- Schaye, J. 2001, ApJ, 559, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Schaye, J., Crain, R. A., Bower, R. G., et al. 2015, MNRAS, 446, 521 [Google Scholar]
- Schmidt, M. 1963, Nature, 197, 1040 [NASA ADS] [CrossRef] [Google Scholar]
- Segers, M. C., Oppenheimer, B. D., Schaye, J., & Richings, A. J. 2017, MNRAS, 471, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Sembach, K. R., Howk, J. C., Savage, B. D., Shull, J. M., & Oegerle, W. R. 2001, ApJ, 561, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Shull, M. J., Smith, B. D., & Danforth, C. W. 2012, ApJ, 759, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Shull, M. J., Moloney, J., Danforth, C. W., & Tilton, E. M. 2015, ApJ, 811, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Stocke, J. S., Keeney, B. A., Danforth, C. W., et al. 2012, ApJ, 763, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Tempel, E., Tamm, A., Gramann, M., et al. 2014a, A&A, 566, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tempel, E., Stoica, R. S., Martinez, V. J., et al. 2014b, MNRAS, 438, 3465 [NASA ADS] [CrossRef] [Google Scholar]
- Tempel, E., Stoica, R. S., Kipper, R., & Saar, E. 2016, Astron. Comput., 16, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Tempel, E., Tuvikene, T., Kipper, R., & Libeskind, N. I. 2017, A&A, 602, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tepper-Garcia, T., Richter, P., Schaye, J., et al. 2011, MNRAS, 413, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Tepper-Garcia, T., Richter, P., Schaye, J., et al. 2012, MNRAS, 425, 1640 [NASA ADS] [CrossRef] [Google Scholar]
- Tilton, E., Danforth, C. W., Shull, M. J., & Ross, T. L. 2012, ApJ, 759, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Tripp, T. M., Savage, B. D., & Jenkins, E. B. 2000, ApJ, 534, L1 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tripp, T. M., Sembach, K. R., Bowen, D. V., et al. 2008, ApJS, 177, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Tumlinson, J., Thom, C., Werk, J. K., Prochaska, J. X., & Tripp, T. M. 2011, Science, 334, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Wakker, B. P., & Savage, B. D. 2009, ApJS, 182, 378 [NASA ADS] [CrossRef] [Google Scholar]
- Wiersma, R. P. C., Schaye, J., & Smith, B. D. 2009, MNRAS, 393, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Wijers, N., Schaye, J., Oppenheimer, B. D., Crain, R. A., & Nicastro, F. 2019, MNRAS, 488, 2947 [NASA ADS] [CrossRef] [Google Scholar]
- Williger, G. M., Carswell, R. F., Weymann, R. J., et al. 2010, MNRAS, 405, 1736 [NASA ADS] [CrossRef] [Google Scholar]
- Willingale, R., Starling, R. L. C., Beardmore, A. P., Tanvir, N. R., & O’Brien, P. T. 2013, MNRAS, 431, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Yao, Y., Tripp, T. M., Wang, Q. D., et al. 2009, ApJ, 697, 1784 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Continuum normalized, co-added fluxed spectrum of RGS1 and RGS2 data at the wavelength around the putative redshift 0.09017 Ne IX Heα absorption line. The FUV predicted line centroid wavelength is shown with the orange line, while the dotted red curve shows the expected absorption signal based on the simultanous fitting of XMM-Newton and Chandra data with the redshifted slab model (Sect. 5.1.1). |
| In the text | |
 |
Fig. 2. Statistical probability of the Null hypothesis validity over the redshift range 0.005 − 0.158. The Null hypothesis is the emission model with Galactic absorption, which is compared to the WHIM hypothesis, i.e., a model including a redshifted hot (T = 106−7 K) CIE absorption component. The dashed black line marks the commonly adopted Null hypothesis rejection limit, p = 0.05. The FUV redshifts listed in Table 1 are shown together with the non-significant O VI doublet detections (from Table 4 in Tilton et al. 2012). The shaded color marks the confusion region of the redshifted absorption component with the Galactic hot halo. |
| In the text | |
 |
Fig. 3. Normalized data (crosses) and the best-fit model (red line) of the z = 0.09017 Ne IX line (the FUV predicted line centroid wavelength is marked with a dashed line) for all the instruments and spectral orders employed. The normalization is done by dividing the spectra by the best-fit continuum model. The best-fit model was simultaneously fitted to RGS1 (first and second dispersion orders), RGS2 (second-order), LETG ACIS (first-order), MEG ACIS (first-order) and HRC data, while the RGS2 first-order data was omitted due to a bad column near the centroid wavelength of the line. The missing bins in RGS1 second-order were rejected by the reduction software due to bad response. The spectral data was rebinned for this illustration to improve the S/N-ratio. |
| In the text | |
 |
Fig. 4. As Fig. 3 but for O VIII. The grey bin near the border of the RGS1 CCD gap was not used in the minimization, but demonstrates a type of spectral artifact that can be produced when observations from different epochs and slightly different pointings with respect to the dispersion direction are co-added. |
| In the text | |
 |
Fig. 5. Origin of temperature constraints in CIE WHIM modeling. The figure illustrates CIE model temperature dependencies of various ionic line strengths relative to that of the O VIII Lyman α line. The dashed sections mark the regions where the Wion/WOVIII ratio is inconsistent with the 1σ limits of slab modeling. The ions shown in the figure produce the most important absorption lines in the spectra in the examined wavelength band of 14–28 Å and thus constrain the CIE temperature, marked with the shaded region. The data of the strongest available ionic lines were used to generate this figure. |
| In the text | |
 |
Fig. 6. Zoom-in on the continuum-normalized, RGS1 first-order co-added spectrum at the wavelength band of the Galactic O I (λ ≈ 23.51 Å) doublet, where the best-fit CIE WHIM model predicts an O VII Heα line (λ ≈ 23.55 Å). The different model components comprising the best-fit model (red line) are shown separately. The shaded area marks bins affected by instrumental absorption. |
| In the text | |
 |
Fig. 7. Filament analysis for 3C 273 sight-line near z = 0.09. The figure shows the distribution of SDSS galaxies (points) in two orthogonal projections (upper and lower panels), each of which are 20 Mpc thick. Blue points represent galaxies in filaments and red points indicate additional galaxies in friends-of-friends groups. The detected filament axes F1 and F2, and the associated luminosity density profiles are denoted by yellow lines and grey curves, respectively. The crossing points of the filaments F1 and F2 and the sight-line to 3C 273 are denoted with labels “CP1” and “CP2”, respectively. The redshift of the O VI absorption is marked with the black vertical line, whereas the pink vertical line and area correspond to the X-ray measured O VIII line centroid and its 1σ measurement uncertainty, obtained in the Gaussian model fit to the O VIII Lyα feature (see Table 4) |
| In the text | |
 |
Fig. 8. Thermal properties of the absorbing gas at z = 0.09017 assuming CIE. Left: temperature dependence of the two-phase absorption model fit statistics to the X-ray data (black solid curve) when NOVI is fixed to the FUV measured value. The shaded areas mark the forbidden regions based on the FUV measurements (the lower limit is yielded by the limits on NCIII and NOVI, whereas the upper limit is set by the O VI line broadening). The 1T curve shows the X-ray model fit statistics without the hot absorption component included, and is plotted for reference. Right: O VI (red), O VII (black) and O VIII (blue) ion fractions over the T -ranges of the warm and hot CIE components. The dotted lines mark the best-fit temperatures for both phases, while the white regions mark the 1σ uncertainty limits as yielded by X-ray data. The light gray shaded regions show the improvement which X-ray data provides to the Twarm determination as compared to the limits obtained with FUV data. |
| In the text | |
 |
Fig. 9. Distribution of O VIII and Ne IX column densities in counterparts to O VI absorbers (grayscale and contours) according to the EAGLE simulation, compared to the measured column densities at z = 0.09 for the CIE and slab models. Left panel: counterparts to O VI absorbers with column densities of 1013.2–1013.4 cm−2, which is roughly the ±1σ range for the FUV absorber of Tilton et al. (2012). Right panel: subset of O VI counterparts with an O VII column density in agreement with the upper limit measured with the slab model. The contours enclose different fractions of the counterparts, as indicated in the legend, while the grayscale shows the fraction of all EAGLE absorbers satisfying the indicated constraints. Although most EAGLE O VI absorbers have weaker (and hence undetectable) associated Ne IX and O VIII absorption than observed at z = 0.09 (but consistent with the non-detection for the z = 0.12 O VI absorber), both the “slab” and CIE measuremets are consistent with EAGLE at the ≈1 − 2σ level. The O VII upper limit does not affect the distribution much. |
| In the text | |
 |
Fig. 10. Distribution of O VI-and O VIII-weighted temperatures in counterparts to O VI absorbers (grayscale and contours) according to the EAGLE simulation, compared to the best-fit temperatures at z = 0.09 for the 2-temperature CIE model (warm and hot phase, respectively). From left to right, top to bottom, we show how constraints on the column densities of different ions from the “slab” model affect the temperatures of O VI and O VIII absorbers in EAGLE. Column density ranges are shown in units of log10 cm−2 for the different ions. The O VI constraints are from Tilton et al. (2012). The contours enclose different fractions of the absorbers in each column density selection, as indicated in the legend, while the grayscale shows the fraction of all EAGLE absorbers satisfying the indicated constraints. The brown dashed line indicates where the temperatures are equal. Most absorbers are multiphase and the 2T CIE model is consistent with EAGLE. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.