| Issue |
A&A
Volume 633, January 2020
|
|
|---|---|---|
| Article Number | A126 | |
| Number of page(s) | 16 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201936432 | |
| Published online | 22 January 2020 | |
The dynamically young outflow of the Class 0 protostar Cha-MMS1★
1
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
e-mail: labusch@mpifr-bonn.mpg.de
2
Argelander-Institut für Astronomie, Universität Bonn,
Auf dem Hügel 71,
53121
Bonn,
Germany
3
LERMA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Université,
UPMC Univ. Paris 06,
75014
Paris,
France
4
Université Grenoble Alpes, CNRS, IPAG,
38000
Grenoble,
France
5
AIM, CEA, CNRS, Université Paris-Saclay, Université Paris Diderot, Sorbonne Paris Cité,
91191
Gif-sur-Yvette,
France
6
Centre de Recherche Astrophysique de Lyon UMR5574, ENS de Lyon, Univ. Lyon1, CNRS, Université de Lyon,
69007
Lyon,
France
Received:
1
August
2019
Accepted:
18
November
2019
Context. On the basis of its low luminosity, its chemical composition, and the absence of a large-scale outflow, the dense core Cha-MMS1 located in the Chamaeleon I molecular cloud, was proposed a decade ago as a candidate for a first hydrostatic core (FHSC).
Aims. Our goal is to test this hypothesis by searching for a slow, compact outflow driven by Cha-MMS1 that would match the predictions of magnetohydrodynamic simulations for this short phase of star formation.
Methods. We used the Atacama Large Millimetre/submillimetre Array to map Cha-MMS1 at high angular resolution in CO 3–2 and 13CO 3–2 as well as in continuum emission.
Results. We report the detection of a bipolar outflow emanating from the central core, along a (projected) direction roughly parallel to the filament in which Cha-MMS1 is embedded and perpendicular to the large-scale magnetic field. The morphology of the outflow indicates that its axis lies close to the plane of the sky. We measure velocities corrected for inclination of more than 90 km s−1, which is clearly incompatible with the expected properties of an FHSC outflow. Several properties of the outflow are determined and compared to previous studies of Class 0 and Class I protostars. The outflow of Cha-MMS1 has a much smaller momentum force than the outflows of other Class 0 protostars. In addition, we find a dynamical age of 200–3000 yr indicating that Cha-MMS1 might be one of the youngest ever observed Class 0 protostars. While the existence of the outflow suggests the presence of a disk, no disk is detected in continuum emission and we derive an upper limit of 55 au to its radius.
Conclusions. We conclude that Cha-MMS1 has already gone through the FHSC phase and is a young Class 0 protostar, but it has not yet brought its outflow to full power.
Key words: stars: formation / stars: protostars / stars: jets / ISM: jets and outflows
The reduced datacubes are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/633/A126
© L. A. Busch et al. 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1 Introduction
Star formation undergoes several stages. In the early phase, an initial prestellar core collapses gravitationally and when thermal pressure is high enough, it forms a hydrostatic core in the center. This is called a Class 0 protostar. However, according to the early theoretical work of Larson (1969), there is an additional intermediate state whose central core is larger and less dense than the subsequent Class 0 protostar. This intermediate phase is referred to as the first hydrostatic core (FHSC) phase. This first core forms when thermal pressure balances the gravitational force and for a moment halts the collapse, with the gas being still molecular. As accretion continues, the central temperature continues to increase. At a temperature of 2000 K, H2 dissociates. This process consumes energy and eventually leads to a second fast collapse until pressure again balances the gravitational force and the second core or Class 0 protostar subsequently forms. Because the FHSC stage is expected to be short lived (~1000 yr for a strongly magnetized core, Commerçon et al. 2012), it is is rather challenging to detect, and only one of the candidates, Barnard 1b-N (Gerin et al. 2015), so far seems to fulfill the requirements predicted by magnetohydrodynamic (MHD) simulations. The results of these simulations depend on the level of rotation and the mass-to-magnetic-flux ratio, but they generally show that a FHSC is the driving source of a poorly collimated low-velocity outflow (~5 km s−1) (e.g., Hennebelle & Fromang 2008; Machida et al. 2008; Ciardi & Hennebelle 2010; Commerçon et al. 2010; Tomida et al. 2010; Machida 2014). This is different from Class 0 protostars, which after formation launch a highly collimated jet with velocities of >30 km s−1 (Banerjee & Pudritz 2006; Machida et al. 2008; Machida 2014). Because its velocity is low, the outflow remains very compact at the end of the FHSC stage (~1000 au for a speed of 5 km s−1 and a lifetime of 1000 yr). Simulations also predict internal luminosities of 0.1 L⊙ over most of the FHSC lifetime (Commerçon et al. 2012). Gerin et al. (2015) detected a slow compact outflow with which Barnard 1b-N was associated as the driving source. This detection, along with a dynamical age of ~1000 yr and a low internal luminosity, strongly suggests that Barnard 1b-N is an FHSC.
Another promising candidate has been proposed in the past. The dense core Cha-MMS1 is embedded in a filament within the Chamaeleon I molecular cloud (Belloche et al. 2011) at a distance of 192 pc (Dzib et al. 2018). After it hadbeen classified as a Class 0 protostar (Reipurth et al. 1996a; Lehtinen et al. 2001), Lehtinen et al. (2003) did not detect centimeter-wavelength continuum emission. This suggests that it is either in an earlier protostellar phase or still prestellar. Belloche et al. (2006) found high deuterium fractionation levels of HCO+ and N2 H+, which are typical for evolved prestellar or young protostellar cores (e.g., Crapsi et al. 2005; Emprechtinger et al. 2009). In addition, the detection of Cha-MMS1 at 24 μm by the Spitzer Space Telescope led Belloche et al. (2006) to infer that a compact hydrostatic core is already present. The comparison of the deuterium fractionation and IR flux of Cha-MMS1 to values of various known prestellar cores and Class 0 protostars led the authors to conclude that it might be an FHSC or an extremely young Class 0 protostar. Additionally, they failed to detect large-scale CO 3–2 outflows with the APEX telescope, suggesting that the source may not yet have entered the Class 0 phase. Tsitali et al. (2013) derived an internal luminosity for Cha-MMS1 that ranges from 0.08 to 0.18 L⊙ by comparison with FHSC predictions from radiation MHD simulations1. Furthermore, they found clear signatures of infall and rotation. Again, according to simulations, these are required ingredients for the launch of an outflow (Commerçon et al. 2012). The authors also reported wing emission in the central spectra of CS 2–1 and broadened blue and red peaks of CO 3–2, which are not reproduced by their infall model. These features may originate from a compact outflow consisting of denser high-velocity material close to the center of the core, but they might also be partly due to extended emission emanating from the nearby Class I protostar Ced 110 IRS 4 (Tsitali et al. 2013; Belloche et al. 2006). To determine whether Cha-MMS1 drives an outflow on small scales and thereby to clarify its current evolutionary stage, we performed observations at high angular resolution with the Atacama Large Millimetre/submillimetre Array (ALMA) and report the results in this paper. Section 2 describes the observational setup and the data reduction steps. The results are presented in Sect. 3 and discussed in Sect. 4. The conclusions are given in Sect. 5.
2 Observations and data reduction
2.1 Observations
We used ALMA to observe Cha-MMS1 in CO 3–2 and 13CO 3–2 emission. The field was centered at (α, δ)J2000 = (11h 06m33s.13, -77°23′35.′′1), which are the coordinates of the counterpart of Cha-MMS1 detected with the Multiband Imaging Photometer (MIPS) instrument on board the Spitzer satellite as reported by Belloche et al. (2011). The Band 7receiver was tuned to 345.8 GHz. The size of the primary beam of the 12 m antennas is 16.8′′ (half-power beam width, HPBW) at 345.8 GHz (Remijan et al. 2015). The observations were conducted in several sessions during Cycle 3 in two different configurations, with baselines up to 310 m for the first configuration and up to 700 m for the second (see Table 1). The shortest baselines of 15–17 m imply a maximum recoverable scale of about 7′′. The synthesized beam size at 345.8 GHz is ~ 1.0′′ × 0.8′′ for the first configuration and 0.6′′ × 0.3′′ for the second. The bandpass, amplitude, and phase calibrators are indicated in Table 1.
The data were recorded over four spectral windows, two broadband windows for the continuum emission covering the frequency ranges 331.6–333.6 GHz and 342.8–344.8 GHz with a spectral resolution of 15.6 MHz, and two narrowband windows covering 330.47–330.70 GHz and 345.66–345.90 GHz with a spectral resolution of 122.1 kHz (~0.11 km s−1) to target 13CO 3–2 and CO3–2, with rest frequencies of 330 587.9653 and 345 795.9899 MHz, respectively.
Setup of the ALMA observations.
2.2 Datareduction and imaging
The data were calibrated with the Common Astronomy Software Applications package (CASA) version 4.5.0 for the first configuration and version 4.5.3 for the second. We used the procedures provided by the Joint ALMA Observatory to apply the bandpass, amplitude, and phase calibrations. The splitting of the continuum and line emission was performed in the uv plane with the CASA task uvcontsub, with a polynomial fit of order 1. We used version 4.7.1 of CASA to image the calibrated data after merging the five datasets. The imaging was made with the CASA task clean with Briggs weighting, a robust parameter of 0.5, and a threshold of 13 mJy for CO 3–2, 17 mJy for 13 CO 3–2, and 0.15 mJy for the continuum. We produced cubes and images with 512 × 512 pixels, a pixel size of 0.07′′, and a channel width of 122.1 kHz. The imaged data have an rms of 3.6 and 4.7 mJy beam−1 per channel for CO 3–2 and 13CO 3–2, respectively, and 0.053 mJy beam−1 for the continuum emission. The synthesized beams (HPBW) are 0.58′′ × 0.37′′, 0.62′′ × 0.41′′, and 0.59′′ × 0.38′′, with position angles east of north of 47°, 48°, and 47°, respectively. In the course of data analysis in the subsequent sections, we used data cubes with different spectral resolutions. We used the smooth box command of the GILDAS/CLASS software which computes the average intensity of a number of channels.
3 Results
3.1 Continuum emission
The map of continuum emission averaged over both sidebands is shown in Fig. 1 in grayscale. The emission is centrally peaked. We performed an elliptical Gaussian fit in the uv plane in order to derive the peak position, size, and flux density of the compact emission. We used the task uv_fit of the GILDAS/MAPPING software2 for this purpose. The fit was performed on the visibilities of each sideband separately. We obtain an average peak position of 11h 06m33. s231 − 77°23′34.′′23 and an average emission size (full width at half-maximum, FWHM) of (0.61′′ ± 0.01′′) × (0.57′′ ± 0.02′′) with a position angle 50° ± 10°. At a distance of 192 pc, the geometrical mean of the angular sizes translates into a radius of ~55 au. The total flux density of the fitted Gaussian is 24.0 ± 0.1 mJy and 25.1 ± 0.1 mJy in the lower and upper sidebands, respectively. The cleaned map of the residual visibilities contains a weak (< 1 mJy beam−1), extended (~0.5′′) structure, a weak (> −1 mJy beam−1), negative residual ring, and an unresolved component at the peak position, with a peak flux density of ~2 mJy beam−1. The residual negative ring and unresolved component may both result from our assumption of a Gaussian shape to fit the envelope in the uv plane while it may actually have a power-law structure.
Following Appendix B.4 of Belloche et al. (2011), we assumed a dust mass opacity κ345 GHz = 0.02 cm2 g−1 of gas to convert the total flux density of the fitted Gaussian component into a gas mass. With a luminosity of ~0.2 L⊙, we expect a dust temperature on the order of 30 K at a radius of 55 au (Terebey et al. 1993; Motte & André 2001). With this dust mass opacity and temperature, we obtain a mass of 2.7 × 10−3 M⊙ provided the continuum emission is optically thin. The flux density of the Gaussian component derived above corresponds to about 1 K in temperature scale. This is much lower than the assumed dust temperature and thus confirms that the dust emission is still optically thin at the scales traced here with ALMA.
3.2 Detection of a fast outflow
Figure 2b shows the CO 3–2 spectrum toward the position of the continuum peak determined in Sect. 3.1 that is marked as a large yellow cross in Fig. 1a. It is located at (0.33′′, 0.87′′) from the phase center. The lines are broad, with strong wing emission that suggests outflow-like structures. Figure 1a shows CO 3–2 integrated intensity maps that reveal a bipolar outflow originating from the center of Cha-MMS1 with an axis approximately along the NE–SW direction. Figure 1b zooms in on the continuum and outflow emission to better display the structures close to the center. The inner integration limits we used in the integrated intensity maps in Figs. 1a and b are chosen such that the outflow emission remains clearly distinguishable from the emission of the surrounding envelope in the channel maps, with values of 3.4 and 5.5 km s−1 for the blue-and redshifted emission, respectively. The outer integration limits are determined by investigating the CO data cube containing spectra smoothed over eight channels (after imaging). The smoothed channel maps are shown in Fig. A.1. We searched for faint emission that can still be associated with the outflow. We find a minimum velocity of −6.1 km s−1 (blue) at (−1.2′′,−1.8′′) from the continuum peak and a maximum velocity of 21.8 km s−1 (red) at (0.5′′,0.4′′) from the continuum peak, which we set as the outer integration limits. This yields velocities of −10.6 km s−1 and 17.4 km s−1 with respect to the systemic velocity vsys = 4.43 km s−1 (Belloche et al. 2006) for the blue- and redshifted emission, respectively. In Figs. 2a and c we show additional CO 3–2 spectra toward positions of peak outflow intensities marked as small yellow crosses in Figs. 1a and b. The spectrum in Fig. 2a is located at (1.8′′,1.6′′) from the continuum peak position in the NE lobe. It shows lower peak intensities than the other two spectra, but reveals significant emission at high velocities. The spectrum in Fig. 2c is located at (−0.7′′,−1.1′′) from the continuum peak position in the SW lobe. It shows higher intensities than the other spectra and even broader wings.
Figures 3a and b show the position-velocity (PV) diagrams along the outflow axes indicated as green dashed arrows and labelled D1 and D2 in Fig. 1a. The morphology of the outflow and PV diagrams are similar to case 3 of Cabrit & Bertout (1990) where both lobes contain red- as well as blueshifted emission indicating that it is oriented almost in the plane of the sky. We give an estimate of the inclination in Sect. 3.4.
The PV diagrams reveal that the outflow emission covers a wide range of velocities, especially the redshifted emission along D1 and it shows bumps toward higher velocities that we label K1–K6. These bumps suggest the occurrence of episodic ejections. In Figs. 3c–h we show spectra taken along D1 and D2 indicated as green ticks on the x-axis in the PV diagrams. These spectra reveal multiple peaks that are characteristic of bullets resulting from an intermittent ejection process (see Bachiller 1996). We interpret the contour at ~8 km s−1 marked as F0 in Fig. 3a as tracing the slow-moving cavity at the interface with the ambient medium inside which the fast bullets propagate.
Assuming that the high velocities represent those of bullets rather than the bulk velocity of the outflow, we define maximum velocities such that the full length of each outflow component is still maintained using the channel maps in Fig. A.1. We use these values in Sect. 3.8.2. We find 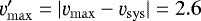 and 2.1 km s−1 for the blueshifted emission in the SW and NE lobes, respectively, and 4.7 and 11.5 km s−1 for the redshifted emission in the SW and NE lobes, respectively. However, as mentioned above (F0), the bulk velocity of the redshifted emission in the NE lobe may rather be
and 2.1 km s−1 for the blueshifted emission in the SW and NE lobes, respectively, and 4.7 and 11.5 km s−1 for the redshifted emission in the SW and NE lobes, respectively. However, as mentioned above (F0), the bulk velocity of the redshifted emission in the NE lobe may rather be 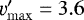 km s−1 with respectto the systemic velocity.
km s−1 with respectto the systemic velocity.
Furthermore, we measure projected spatial extents for each lobe that range from 4′′ to 13′′ where we did not include the separated emission labeled B1 in Fig. 1a. These values yield projected outflow lengths of 800–2500 au at a distance of 192 pc. The observed velocities and the length of each lobe are summarized in Table 2.
 |
Fig. 1 (a) CO 3–2 integrated intensities (blue and red contours) observed with ALMA toward Cha-MMS1. The continuum emission is shown in grayscale with black contours. The large yellow cross marks its peak position. The CO emission is integrated over the velocity ranges [−6.1, 3.4] km s−1 (blue) and [5.5, 21.8] km s−1 (red). The contours are − 2.5σ, 2.5σ, and 5σ, and then increase by a factor of two at each step with σ = 7.04 mJy beam−1 km s−1, 9.06 mJy beam−1 km s−1, and 0.05 mJy beam−1 for the blueshifted, redshifted, and the continuum emission, respectively. The HPBW is shown in the bottom left corner. The yellow crosses mark the positions of the spectra shown in Fig. 2. The green dashed arrows indicate the axes along which PV diagrams were taken for Figs. 3 and B.1. B1 and R1 indicate the less-collimated blue- and redshifted structures, respectively. (b) Same as a, but zoomed-in on the central region. The phase center is marked with a green cross in this panel. (c) CO 3–2 integrated intensities observed with APEX toward Cha-MMS1 (cross) (adapted from Belloche et al. 2006). The redshifted [6.6, 9.8] km s−1, blueshifted [−0.2, 1.0] km s−1, and less blueshifted [1.2, 2.4] km s−1 emission is plotted as solid red, solid blue, and dashed blue contours, respectively. The first contours and steps are 3σ, 6σ, and 3σ with σ = 0.13, 0.13, and 0.24 K km s−1, respectively, as in Belloche et al. (2006). The HPBW is shown in the bottom left corner. The star and square mark positions of NIR (Persi et al. 2001) and 3.5 cm sources (Lehtinen et al. 2003), respectively. (d) Same as c but for CO 3–2 integrated intensities at velocities close to vsys. The redshifted [5.5, 6.6] km s−1 emission is shown as dotted (3σ), dashed (6σ), and solid (9σ) contours with σ = 0.13 K km s−1. The blueshifted [2.4, 3.4] km s−1 emission is plotted as solid contours. The first contour and the steps are 6σ with σ = 0.13 K km s−1. The small box corresponds to the field of view shown in panel a. |
 |
Fig. 2 CO 3–2 spectra observed with ALMA toward Cha-MMS1 in brightness temperature scale and smoothed over five channels. The spectra are taken toward three positions marked with yellow crosses in Fig. 1: (a) in the NE lobe, (b) at the peak of the continuum emission, and (c) in the SW lobe. The red and blue dashed lines correspond to the integration intervals defined in Sect. 3.2 while the black dashed line indicates the systemic velocity of Cha-MMS1, vsys = 4.43 km s−1 (Belloche et al. 2006). |
 |
Fig. 3 (a and b) CO 3–2 PV diagrams along the outflow axes (a) D1 and (b) D2 shown as green dashed arrows in Fig. 1a. The origin of the position axes corresponds to the continuum peak. The intensity is smoothed over five channels. The contours are − 6σ, − 3σ, 3σ, 6σ, 12σ, 18σ, 24σ 48σ, 96σ, and 192σ with σ = 2.0 mJy beam−1. The red and blue dashed lines show the inner and outer integration limits. (c–h) CO 3–2 spectra in brightness temperaturescale taken along D1 and D2 at the positions marked as green ticks on the x-axis in the PV diagrams in panels a and b. K1–K6 denote the bumps corresponding to the bullets and F0 indicates the bulk flow. The intensity is smoothed over two channels. In all panels, the black dashed line indicates the systemic velocity of Cha-MMS1. |
Properties of each lobe of the outflow of Cha-MMS1 determined from CO 3–2 ALMA observations.
3.3 Morphology of the outflow
The maps in Figs. 1a and b further show that the NE and SW lobes possess different position angles. The axis of the NE lobe is at ~ 50° while the axis of the SW lobe is at approximately −150° which means that they are tilted by ~20° with respect to each other. Regarding the redshifted emission, the axis of the SW lobe reveals another conspicuous change of position angle to approximately −120° at (−1.9′′,−1.9′′) from the continuum peak position. The emission along this second axis in the SW lobe (labeled R1 in Fig. 1a) becomes increasingly less collimated with distance to the center. Farther in the SW, extended blueshifted emission (labeled B1 in Fig. 1a) appears at low velocities (see also Fig. A.1). Figure B.1 shows the PV diagram along R1 and B1, which is taken along the green dashed arrow labeled D3 in Fig. 1a. The arrow exactly covers the range of positions displayed in the PV diagram. In Sect. 4.4 we discuss these peculiarities in the morphology in more detail.
Figure 1c shows CO 3–2 integrated intensity maps obtained on larger scales with the single-dish APEX telescope reported by Belloche et al. (2006). They are dominated by an outflow driven by the nearby Class I protostar IRS 4. Additionally, we show in Fig. 1d, the APEX emission integrated over [5.5, 6.6] km s−1 and [2.4, 3.4] km s−1 to include the lowest velocities comprised in the ALMA integration ranges. This emission reveals large-scale structures that probably trace the ambient material in the filament, which is filtered out in the interferometric maps.
3.4 Inclination of the outflow
Based on the integrated intensity maps and the PV diagrams we already concluded that the outflow axis is almost perpendicular to the line of sight. The inclination i is in the range 90° −θ∕2 < i < 90° +θ∕2, where θ is the opening angle of the outflow. Using geometry, we determine θ = 22° ± 3° for the moreextended NE redshifted lobe which we adopt for both lobes. The inclination angle of Cha-MMS1 is therefore in the range 79° < i < 101°.
We used the minimum value of 79° to deproject the velocities. Considering the highest velocities reported in Sect. 3.2, we find maximum deprojected velocities of 55.2 km s−1 for the blueshifted emission and 91.0 km s−1 for the redshifted emission. If the true inclination is higher than 79°, the velocities will be even higher.
3.5 Optical depth
Both, CO 3–2 and 13CO 3–2 show strong self-absorption close to vsys, indicating high optical depths (see Figs. 2 and 4). To determine whether the CO emission remains optically thick in the wings of the spectral line, that is, in the outflow, we computed the ratio of CO to 13 CO emission. Figure 4 shows the spectra of CO and 13CO toward the continuum peak position with the ratio of the intensities overlaid as green square symbols. We plot the ratio only for values of 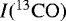 higher than 2.5σ. Unfortunately, the sensitivity of our 13CO data is not high enough to provide significant ratios far out in the wings. Therefore, we averaged the 13 CO wing emission over four channels and used the smoothed spectra down to 3σ. For channels with an intensity below this threshold, we used 3σ as an upper limit to
higher than 2.5σ. Unfortunately, the sensitivity of our 13CO data is not high enough to provide significant ratios far out in the wings. Therefore, we averaged the 13 CO wing emission over four channels and used the smoothed spectra down to 3σ. For channels with an intensity below this threshold, we used 3σ as an upper limit to 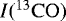 . We pursued thiscalculation until I(CO) ≈ 5σ. The resulting lower limits of the ratio are indicated with green arrows in Fig. 4. Based on the intensity ratio, the optical depth τ12 can be estimated using
. We pursued thiscalculation until I(CO) ≈ 5σ. The resulting lower limits of the ratio are indicated with green arrows in Fig. 4. Based on the intensity ratio, the optical depth τ12 can be estimated using
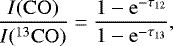 (1)
(1)
with τ13 = τ12∕X, where X is the local interstellar medium (ISM) 12 CO/13CO isotopic ratio equal to 77 (Wilson & Rood 1994). The opacity scale is displayed on the outer right axis of Fig. 4. Toward the continuum peak position, we find high optical depths τ12 ≳ 100 for the emission close to vsys, as expected. At the inner integration limit, the optical depth is still at ~15 for the blueshifted emission, and it decreases to 6 at ~2.8 km s−1. The optical depth of the redshifted emission remains higher than 30 up to at least ~6.2 km s−1. The lack of sensitivity of the 13CO observations prevents us from deriving the opacity below 2.8 km s−1 in the blue wing and above 6.2 km s−1 in the red wing. We therefore used for the following calculations the 13 CO and the 12CO emission (see Zhang et al. (2016) for a similar strategy applied to the HH 46/47 outflow). For each pixel in the outflow, the 13 CO emission was smoothed over four channels, corrected for optical depth where possible using Eq. (1), and integrated until the intensity reached a certain threshold. When the emission dropped below this threshold, we used the 12 CO emission, where we assumed two cases: an average optical depth of τ12 = 5, and optically thin emission.
 |
Fig. 4 CO 3–2 (solid black) and 13CO 3–2 (dotted black) spectra at the peak position of Cha-MMS1 in brightness temperature scale. Green squares show the ratio of CO to 13CO intensity, and green arrows indicate the lower limits of this ratio after smoothing over four channels. The scale is given on the first right axis. The optical depth scale is shown on the second right axis. The red and blue dashed lines mark the inner integration limits, and the black dashed line indicates the systemic velocity of Cha-MMS1. |
3.6 Outflow mass
We derived the outflow mass using integrated intensities that were first converted into column densities and subsequently into mass using the following equation:
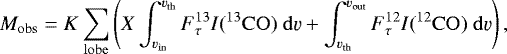 (2)
(2)
where the sum is over all pixels in the respective lobe (see below and Fig. A.1), 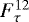 and
and 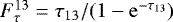 are correction factors for optical depth, and K = 5.07 × 10−10 M⊙ s K−1 km−1 is the conversion factor from intensity to mass. The calculation of K was adopted from van der Marel et al. (2013) (hereafter vdM13), where we assumed an excitation temperature of 30 K and a CO abundance of 8.3 × 10−5 relative to H2 (vdM13). As mentioned in Sect. 3.5, we accounted for the high optical depths at the inner velocity cutoffs using the 13 CO emission forthe mass calculation. Like for the inner integration limits for CO, we defined them for 13 CO by investigating the channel maps, which we show in Fig. A.2. We detect 13 CO outflow emission down to vin = 4.9 and 3.8 km s−1 for the red- and blueshifted emission, respectively. Starting from these velocities, we integrated the 13 CO emission as long as it was detected above 3.4σ and 3.8σ for the blue- and redshifted emission, respectively, and multiplied it by the isotopic ratio X = 77. The thresholds were chosen such that we certainly avoided the contribution of noise to the calculation. Because the 13 CO emission also shows high optical depths close to the systemic velocity, we applied the correction factor
are correction factors for optical depth, and K = 5.07 × 10−10 M⊙ s K−1 km−1 is the conversion factor from intensity to mass. The calculation of K was adopted from van der Marel et al. (2013) (hereafter vdM13), where we assumed an excitation temperature of 30 K and a CO abundance of 8.3 × 10−5 relative to H2 (vdM13). As mentioned in Sect. 3.5, we accounted for the high optical depths at the inner velocity cutoffs using the 13 CO emission forthe mass calculation. Like for the inner integration limits for CO, we defined them for 13 CO by investigating the channel maps, which we show in Fig. A.2. We detect 13 CO outflow emission down to vin = 4.9 and 3.8 km s−1 for the red- and blueshifted emission, respectively. Starting from these velocities, we integrated the 13 CO emission as long as it was detected above 3.4σ and 3.8σ for the blue- and redshifted emission, respectively, and multiplied it by the isotopic ratio X = 77. The thresholds were chosen such that we certainly avoided the contribution of noise to the calculation. Because the 13 CO emission also shows high optical depths close to the systemic velocity, we applied the correction factor 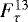 when the intensity ratio of the isotopologues dropped below 3.9, that is, when the correction became significant. In some channels the ratio dropped below 1 (see, e.g., Fig. 4 at ~6 km s−1). In these cases we did not apply any correction factor and assumed optically thin emission. When the 13 CO emission dropped below the intensity thresholds at vth, we used the CO emission and integrated to the outer integration limits vout defined in Sect. 3.2. Here, we applied the correction
when the intensity ratio of the isotopologues dropped below 3.9, that is, when the correction became significant. In some channels the ratio dropped below 1 (see, e.g., Fig. 4 at ~6 km s−1). In these cases we did not apply any correction factor and assumed optically thin emission. When the 13 CO emission dropped below the intensity thresholds at vth, we used the CO emission and integrated to the outer integration limits vout defined in Sect. 3.2. Here, we applied the correction 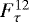 assuming the two cases of either optically thin (τ12 < < 1) or thick emission (τ12 = 5). The calculation was applied to every position in the respective lobe. We defined masks for the red- and blueshifted emission of the NE and SW lobes, respectively, based on the integrated intensity maps in Fig. 1a. The masks we used are shown in the first panel in Fig. A.1. The resulting observed outflow masses are summarized in Table 3 and lie in ranges of Mobs = (0.3−1.0) × 10−4 M⊙ and (1.0−1.7) × 10−4 M⊙ for the NE and SW lobes, respectively.
assuming the two cases of either optically thin (τ12 < < 1) or thick emission (τ12 = 5). The calculation was applied to every position in the respective lobe. We defined masks for the red- and blueshifted emission of the NE and SW lobes, respectively, based on the integrated intensity maps in Fig. 1a. The masks we used are shown in the first panel in Fig. A.1. The resulting observed outflow masses are summarized in Table 3 and lie in ranges of Mobs = (0.3−1.0) × 10−4 M⊙ and (1.0−1.7) × 10−4 M⊙ for the NE and SW lobes, respectively.
In order to derive the true mass, we applied two correction factors introduced by Downes & Cabrit (2007) (hereafter DC07). First, we accounted for material at low velocities that we might miss because its velocity is too close to the systemic velocity of Cha-MMS1.This correction factor depends on two parameters: the ratio of the jet to the ambient material density η, and inclination. At the scale where we detect the outflow of Cha-MMS1, we assumed the outflow to be less dense than the ambient material, with η = 0.1. The inclination estimate of Cha-MMS1is in between α = 0° and 30° with α =90 − i, therefore, we used an average value of 0.35−1 (see Col. 8 in Table 3 in DC07). The second correction factor 0.64−1 (Col. 2 of Table 1 in DC07) accounts for hidden atomic material. These corrections increase the outflow masses to Mcorr = (1.2−4.6) × 10−4 M⊙ and (4.4−7.5) × 10−4 M⊙ for the NE and SW lobes, respectively. The values are listed in Table 3.
Mass and momentum of the outflow.
3.7 Outflow momentum
Similarly to the calculation of the outflow mass, we also determined the momentum of the outflow by
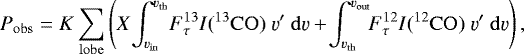 (3)
(3)
where before integrating, we multiplied the intensity of each channel by the corresponding velocity v′ = |v − vsys|. Depending again on optical depth of the CO emission, the observed momentum lies in the range of Pobs = (1.1−4.9) × 10−4 M⊙ km s−1 and (1.2−3.0) × 10−4 M⊙ km s−1 for the NE and SW lobes, respectively.
DC07 investigated the influence of an inclination correction on the momentum and concluded that for any inclination, a correction will overestimate the momentum, especially in our case, where the outflow is oriented almost in the plane of the sky. We therefore did not correct the momentum for inclination but only for missing material close to vsys by multiplying with 0.46−1 (Col. 10 of Table 3 in DC07), and for hidden atomic material by multiplying with 0.45−1 (Col. 3 of Table 1 in DC07). We again considered an inclination α between 0° and 30°, and the former correction denotes an average value. Then, the momenta increase to Pcorr = (5.1−23.9) × 10−4 M⊙ km s−1 and (5.8−14.2) × 10−4 M⊙ km s−1 for the NE and SW lobes, respectively. The values of observed and corrected momentum are listed in Table 3.
3.8 Age and momentum force of the outflow
Based on mass, momentum, and projected length of the outflow, we can estimate the dynamical age and determine the momentum force of the outflow. To do so, we used the perpendicular method of DC07 (M5 in vdM13), which, according tothe authors, provides the most accurate results compared to other methods they introduced because it has no strong dependence on inclination. Although the perpendicular method is believed to yield the best estimates on the dynamical age and the momentum force of the outflow, the more commonly used method is the vmax method (Cabrit & Bertout 1992, DC07, M1 in vdM13). We additionally report the results of this method for facilitate comparison to the results published in the past for outflows of other young protostars.
3.8.1 Perpendicular method
The methodconsiders most of the slow-moving material to be in transverse motion. We therefore used the maximum outflow radius Wlobe measured perpendicular to the jet axis as the characteristic length. We used the channel maps in Fig. A.1 at 5.7 and 4.0 km s−1 to measure the maximum radii of the lobes, and find ~330 and ~200 au for the NE and SW lobes, respectively. Furthermore, this method uses an intensity-weighted velocity 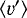 (Cabrit & Bertout 1992, DC07), which we determined using Eqs. (2) and (3) such that
(Cabrit & Bertout 1992, DC07), which we determined using Eqs. (2) and (3) such that
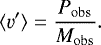 (4)
(4)
We find 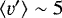 km s−1 for the NE lobe and
km s−1 for the NE lobe and 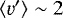 km s−1 for the SW lobe. The values of Wlobe and
km s−1 for the SW lobe. The values of Wlobe and 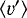 are listed in Table 4. Based on these values, we estimated the age of the outflow using the following equation from DC07:
are listed in Table 4. Based on these values, we estimated the age of the outflow using the following equation from DC07:
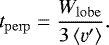 (5)
(5)
The results span a range of 100–300 yr depending on the lobe and optical depth. Again, we applied a correction factor to account for projection effects due to the inclination. Table 4 gives the corrected values for i = 90° and 60° using the correction factors listed in Col. 3 of Table 7 in DC07 (0.83−1 for α = 0° and 0.64−1 for α = 30°). This correction does not increase the age significantly. The maximum age is now 400 yr.
The observed momentum force was calculated with Fperp = Pobs∕tperp, which yields (0.8−4.6) × 10−6 M⊙ km s−1 yr−1 and (0.5−1.6) × 10−6 M⊙ km s−1 yr−1 for the NE and SW lobes, respectively, depending on the optical depth. We corrected again for hidden atomic material using 0.45−1 (Col. 3 in Table 1 in DC07) and for projection effects, 0.47−1 (α = 0°) and 0.89−1 (α = 30°) (Col. 5 in Table 7 in DC07). We obtained corrected values of the momentum force of Fcorr = (2.0−21.6) × 10−6 M⊙ km s−1 yr−1 and (1.2−7.9) × 10−6 M⊙ km s−1 yr−1 for the NE and SW lobes, respectively, which we show in Table 4.
Dynamical time and momentum of the outflow from the perpendicular method.
3.8.2 vmax method
The calculation of the dynamical time requires the maximum, observed velocities, and length of the lobes, which we list in Table 2. Although we determined the velocity for the red- and blueshifted emission in each lobe, we only used the higher value of the respective lobe because only one maximum velocity is allowed. These values are 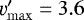 and 4.7 km s−1 for the NE and SW lobes, respectively. We determined the dynamical age by dividing the corresponding outflow length
and 4.7 km s−1 for the NE and SW lobes, respectively. We determined the dynamical age by dividing the corresponding outflow length 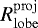 by
by 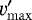 , which yields 3100 yr and 2500 yr for the NE and SW lobes, respectively. However, these values provide only upper limits because we did not correct for inclination. Based on the age, we computed the momentum force using
, which yields 3100 yr and 2500 yr for the NE and SW lobes, respectively. However, these values provide only upper limits because we did not correct for inclination. Based on the age, we computed the momentum force using 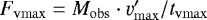 . We did not correct for hidden atomic material to avoid bias because this is generally not applied for other sources. Following the approach of vdM13, however, we applied a correction factor from Cabrit & Bertout (1992) that depends on inclination and takes material at low velocities into account. We took the correction factor for i = 70°, which is the highest inclination given. We thus only obtain a lower limit because the outflow seems to be more inclined as shown in Sect. 3.4. Cabrit & Bertout (1992) reported uncertainties on their correction factors, which we give as an uncertainty on our results. In this way, the momentum force is
. We did not correct for hidden atomic material to avoid bias because this is generally not applied for other sources. Following the approach of vdM13, however, we applied a correction factor from Cabrit & Bertout (1992) that depends on inclination and takes material at low velocities into account. We took the correction factor for i = 70°, which is the highest inclination given. We thus only obtain a lower limit because the outflow seems to be more inclined as shown in Sect. 3.4. Cabrit & Bertout (1992) reported uncertainties on their correction factors, which we give as an uncertainty on our results. In this way, the momentum force is 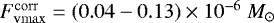 km s−1 yr−1 and (0.2 − 0.4) × 10−6 M⊙ km s−1 yr−1 for the NE and SW lobes, respectively, depending on optical depth (see Table 5).
km s−1 yr−1 and (0.2 − 0.4) × 10−6 M⊙ km s−1 yr−1 for the NE and SW lobes, respectively, depending on optical depth (see Table 5).
Outflow properties of B1b-N, B1b-S, GF 9–2, and Cha-MMS1 derived with the vmax method.
4 Discussion
4.1 Continuum emission
The elliptical Gaussian fit performed on the continuum emission map in the uv plane in Sect. 3.1 indicates a slight elongation of the emission along a direction close to the axis of the outflow, but this elongation may not be significant. Because the system is highly inclined and seen nearly edge-on, a circumstellar disk would manifest itself with a strong elongation perpendicular to the outflow axis. Therefore we conclude that the dust component of diameter ~110 au detected with ALMA must represent the inner parts of the collapsing envelope. After rescaling to the new distance of 192 pc, the mass of the envelope derived by Belloche et al. (2011) is 2.36 M⊙ in a (rescaled) radius of 4800 au. If the envelope has a spherical symmetry and the density profile is a power law, then the mass we obtain in a radius of ~55 au implies a power-law index of about − 1.5, which is reasonable for a collapsing envelope and strengthens our interpretation that the continuum source detected with ALMA corresponds to the inner parts of the envelope. If a disk is present, then it must have a radius significantly smaller than ~55 au. The unresolved residual component of 2 mJy/beam reported in Sect. 3.1 may correspond to such a disk, with a mass of ~2 × 10−4 M⊙ if the emission is optically thin, but this unresolved residual component, as well as the negative ring around it, may simply be due to our use, for simplicity, of a Gaussian function to fit the envelope emission. It may have a power-law structure in reality. The upper limit of 55 au to the disk radius is consistent with the small disks predicted by Hennebelle et al. (2016) for early circumstellar disks in collapsing magnetized cores, in which the disk size is self-regulated by magnetic braking and ambipolar diffusion.
4.2 Episodic ejections
Figures 3 and 5 show evidence for the presence of high velocity bullets in the outflow of Cha-MMS1,surrounded by slower-moving material that traces the interface region of the outflow cavity with the ambient medium. The bullets (K1–K6) are seen as compact blobs in Fig. 5, finger-like elongations in the PV diagrams shown in Figs. 3a and b, and peaks with wings extending to higher velocities in the spectra displayed in Figs. 3c–h. The presence of bullets has been reported in other protostellar outflows and suggests that the ejection phenomenon during the protostellar phase is intermittent in nature (see e.g., Bachiller 1996). The presence of bullets in Cha-MMS1’s outflow therefore suggests episodic ejections in this source. Plunkett et al. (2015) also inferred intermittency in the outflow of the Class 0 protostar SerpS-MM18 (which they called CARMA 7), and they derived a timescale of ejections of 80–540 yr (not corrected for inclination) based on their PV diagrams. In our case, the knots seem to be separated by ~2′′, which translates into a time between two knots of ~20 yr given a distance of 192 pc and assuming a velocity of ~90 km s−1. This is only the case if the knots remain at constant speed. However, in the PV diagrams in Fig. 3, we see that only the bump closest to the center K1 has this high velocity, K2–K4 move more slowly. Plunkett et al. (2015) reported a similar behavior of their outflow, which they attribute to an increasing entrainment of and hence momentum transfer to ambient material, leading to a slowing down of the outflow itself. Machida (2014) performed MHD simulations of protostellar outflows and reported on the occurrence of intermittent jets, but with more frequent ejections every 1–2 yr. They ascribed thetime-variability of the jet to episodic accretion processes, which Plunkett et al. (2015) also quoted as a reason.
 |
Fig. 5 Integrated intensity maps toward Cha-MMS1 (black cross) of the high-velocity redshifted CO 3–2 gas [15.0, 21.8] km s−1 shown with red contours and the low-velocity redshifted CO 3–2 gas [9.1, 11.6] km s−1 shown in grayscale and with black contours. The contour levels are − 3σ, 3σ, 6σ, 12σ, and 24σ with σ = 0.7 mJy beam−1 km s−1 and 1.1 mJybeam−1 km s−1 for the emissions at high velocities and low velocities, respectively. The green crosses K1–K6 mark the positions at which the spectra in Figs. 3c–h were taken. The HPBW is shown in the bottom left corner. The black cross marks the position of the continuum peak. |
 |
Fig. 6 Channel map of CO 3–2 emission (red) at 5.7 km s−1 from Fig. A.1 overlaid by 13CO intensity (black) integrated from 4.9 to 5.7 km s−1. The contour levels are −3σ, 3σ, 6σ, 12σ, 24σ, and 48σ with σ = 1.8 mJy beam−1 and σ = 2.5 mJy beam−1 for the CO and the 13CO intensity, respectively. The continuum peak is marked with the yellow cross. The HPBW is shown in the bottom left corner. |
4.3 Alignment with the filament
Belloche et al. (2011) showed a 870 μm continuum emission map of the Cha I region in which Cha-MMS1 is located. Remarkably, the outflow axis is parallel to the filament. Using a sample of 45 sources Anathpindika & Whitworth (2008) found that 72% of the protostellar outflows are within 45° of being orthogonal to the filaments in which the sources are embedded. However, based on a slightly larger sample (57 protostars in Perseus), Stephens et al. (2017) concluded that the distribution of outflow orientations is more consistent with a random orientation or a mix of parallel and orthogonal angles with respect to the filaments. Both studies attribute the orientation of the outflows to different core formation processes (see both papers and references therein). Because Stephens et al. (2017) observed a mix of orientations, they proposed that a combination of core formation mechanisms take place in the same cloud. We conclude from the results of these previous studies that the alignment of the Cha-MMS1 outflow with the filament in which the protostar is embedded is a common phenomenon in star-forming regions.
4.4 Spatial extent of the outflow
The integrated intensity maps in Fig. 1a have revealed poorly collimated redshifted emission (R1) at the tip of the SW lobe and extended blueshifted emission (B1) that is even separated from the lobe. The PV diagram in Fig. B.1 reveals that the redshifted emission of the kinked part of the SW lobe has a similar morphology as the redshifted emission in Fig. 3b, while the blueshifted emission seems to be a prolongation of the emission evident at 0–2′′, which presents another indication that B1 belongs to the outflow of Cha-MMS1. Regarding the channel maps in Fig. A.1, these structures become only prominent at low velocities, that is, close to the systemic velocity. The separated blueshifted structure may be part of an older ejection event that has slowed down and broadened with time. Alternatively, it may even present a remnant of the generally less collimated outflow that occurs during the FHSC phase. Another idea is that the blueshifted emission may be a bow shock driven by Cha-MMS1, given its orientation and structure. In any case, if the separated blueshifted emission is part of the Cha-MMS1 outflow, the dynamical age will increase to tvmax ≲ 7400 yr considering the larger spatial extent of ~3300 au and a maximum velocity at the tip of the outflow of 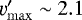 km s−1 (see Fig. A.1), which are again not corrected for inclination. In contrast, tperp will not change significantly because the intensity-weighted velocity and the radius of the lobe remain approximately the same.
km s−1 (see Fig. A.1), which are again not corrected for inclination. In contrast, tperp will not change significantly because the intensity-weighted velocity and the radius of the lobe remain approximately the same.
We cannot rule out that the outflow extends even beyond the field of view observed with ALMA. Frank et al. (2014) showed that the outflow length of the Class I protostar B5-IRS1 was found to be much more extended than initially thought after larger maps revealed outflowing emission at farther distances from the source (see their Fig. 9). However, no evidence was found for a NE-SW outflow emanating from Cha-MMS1 in the CO 3–2 single-dish maps of Belloche et al. (2006) and Hiramatsu et al. (2007).
4.5 Lobe misalignment and kink
In Fig. 1a, we showed that the axes of the NE and SW lobes have different position angles and that there is a kink within the SW lobe itself. We compare this result to simulations described by Ciardi & Hennebelle (2010) who investigated the influence on outflows of a misalignment of the rotation axis with respect to the magnetic field. The large-scale magnetic field traced by infrared polarimetry (McGregor et al. 1994) is roughly orthogonal to the filament in which Cha-MMS1 is embedded. The outflow of Cha-MMS1 is thus roughly perpendicular to this large-scale magnetic field. The result presented in Fig. 2c of Ciardi & Hennebelle (2010) closely resembles the case of the outflow of Cha-MMS1, where the NE lobe is stronger and more collimated than the SW lobe. In this simulation, the rotation axis and the magnetic field are misaligned by 70°, which results in an opening angle of the outflow of about 20°, similar to what we measure for Cha-MMS1. As a consequence of an increased misalignment, the outflow rate decreases and the protostar mass therefore grows more rapidly. Furthermore, as a result of precession, which is also induced by the misalignment, the NE and SW lobes may show different position angles. This is not clearly visible in Fig. 2c of Ciardi & Hennebelle (2010), however. The authors state, however, that kinks as well as fragmentation within the outflow lobes can be attributed to this precession.
These simulations may already explain the morphology of the Cha-MMS1 outflow, but there may also be another explanation for the observed change in position angle within the SW lobe itself. In a first scenario, the SW lobe may interact with the material traced by the extended continuum emission detected to the SW of Cha-MMS1 (see Fig. 1). If this material is dense enough, it could deflect the jet, which would result in a change of position angle. The deflection of a jet component was also proposed by Reipurth et al. (1996b) to explain the HH flow HH 110. Because the authors were unable to associate a protostellar source with it, they suggested that this HH object and a second nearby object, HH 270, belong to the same lobe of an outflow driven by the Class I protostar IRAS 05489+0256 (see their Figs. 3 and 4). When they made this connection, they had to explain a change in position angle and proposed the deflection of the jet by a dense cloud core. Raga et al. (2002) performed numerical simulations to test this scenario. They found that a jet with a speed of 300 km s−1 disperses the cloud with which it interacts in less than 1000 yr assuming a cloud-to-jet density of 100. To increase the timescale, they introduce precession of the jet to alternate the impact position and thus slow down the destruction of the cloud to a timescale of ~3000 yr. We calculated the density of the continuum where the SW lobe of the Cha-MMS1 outflow changes direction. When we assume a peak flux density of 4 × 10−4 Jy/0.47′′ beam, which translates into an H2 column density of ~5 × 1022 cm−2 assuming κ = 0.02 cm2 g−1 and an excitation temperature of 10 K, we obtain a mean particle density of ~107 cm−3, which should be sufficient to deflect the lobe. Both scenarios described by Raga et al. (2002) might be applicable to Cha-MMS1 because on the one hand, we cannot exclude precession of the outflow, and on the other hand, the Cha-MMS1 outflow may be younger than 1000 yr, which means that we would still be able to observe the deflection.
4.6 Surroundings of Cha-MMS1
Another possibility for the morphology of the SW lobe is that a second outflow is driven by a different source. Because we find no evidence for another protostar close by that might be responsible for a second outflow, we searched for candidates on larger scales. We investigated the Spitzer data reported by Luhman (2008) that include several young stellar objects (see his Fig. 8). The closest are IRS 2, IRS 4, and the Class I binary system IRS 6. IRS 6 is approximately located along the direction of the arrow D3 shown inFig. 1a. If one companion or both drive an outflow whose position angle coincides with that of the kinked SW outflow we observe, it may show the interaction region. However, no large-scale outflow emission is associated with IRS 6, therefore the only possibility may be an atomic outflow that becomes molecular when it interacts with the Cha-MMS1 outflow. However, this is unlikely given the location of IRS 6 in the filament in which Cha-MMS1 is also embedded.
We have shown the outflow emission associated with the Class 0 protostar IRS 4 in Fig. 1c. Ladd et al. (2011) discussed the interaction of this outflow with the Cha-MMS1 core. They suggested that the axis of the IRS 4 outflow is almost in the plane of the sky with a wide opening angle, which results in blue- and redshifted emission on either side of the central source. This is also evident in the maps of Hiramatsu et al. (2007), who showed similar maps as Belloche et al. (2006) and as in Fig. 1c, except that their field of view extended more to the North and revealed no clear bipolar structure around IRS 4. In order to link the IRS 4 outflow with the redshifted HH objects HH 49/50, which are located ~0.5 pc to the SW of IRS 4 (Ladd et al. 2011), they suggested that the lobe that passes Cha-MMS1 by interacts with it, where only the blueshifted part glances off and is deflected, but the redshifted part continues undisturbed. Consequently, the blueshifted outflow emission that initially moves southwestward turns SE (cf. dashed blue contours in Fig. 1c). In this way, the redshifted emission of the IRS 4 outflow may be connected to the redshifted Herbig Haro objects HH 49/50. Before, Bally et al. (2006) excluded IRS 4 as the driving source of these HH objects because of the discrepancy of blue- and redshifted emission of the IRS 4 outflow and HH 49/50. In turn, they assigned them to Cha-MMS1. Based on our detection of the outflow and given its position angles, we exclude that Cha-MMS1 is responsible for HH 49/50 but support Ladd et al. (2011), who attributed it to IRS 4.
Ladd et al. (2011) also debated the influence of the Class II protostar IRS 2 on the Cha-MMS1 dense core. It may not have a major impact on the Cha-MMS1 outflow, but Ladd et al. (2011) argued that a wind is pushed by IRS 2 toward Cha-MMS1, and thereby compresses and heats the gas. They also associated the Ced 110 reflection nebula with the Class II protostar. Although IRS 2 seems to illuminate the nebula, its u-shape suggests that it is created by another wind or jet that originates from a source farther NW. The axis along the assumed direction of motion of this jet or wind through the u-shaped nebula then passes south of IRS 2 and may reach the SW lobe of the Cha-MMS1 outflow, possibly causing the kink in the SW lobe if it is strong enough.
Bally et al. (2006) showed large-scale images of the Cha I region including all HH objects. In their Fig. 4, Cha-MMS1 is shown together with IRS 4, IRS 6, IRS 2, and several HH objects in their surroundings. Here, it is apparent that HH 49/50 does not coincide with the outflow of Cha-MMS1. In the background, the reflection nebula is evident as well. According to our suggestion of a more northeasterly located source driving a jet that is responsible for the u-shaped nebula, HH 48 may be a possible candidate. The small-scale structure shown by Wang & Henning (2006), however, makes HH 48 a less likely candidate due to its orientation.
Furthermore, we mention two other objects in this figure of Bally et al. (2006): HH 929 and HH 936. These two objects are located not far from the prolonged axes of the NE and SW lobes of the Cha-MMS1 outflow, respectively. This means that if the outflow of Cha-MMS1 is indeed spatially more extended than what we see based on our ALMA observations, these two objects might denote the end of a large outflow driven by Cha-MMS1. However, the axes of the NE and the kinked SW lobe miss the locations of the two HH objects by approximately 10°, respectively, which means that the outflow must have wandered to a greater extent.
4.7 Comparison to other Class 0 and Class I outflows
As there exist various methods of determining the momentum force, results for one source can vary by more than an order of magnitude (vdM13). It is therefore rather difficult to make reasonable comparisons between different sources using results published separately. Former studies (e.g. Cabrit & Bertout 1992; Bontemps et al. 1996; Hatchell et al. 2007, vdM13) worked out relations between bolometric luminosity Lbol, envelope mass Menv, and momentum force FCO, however, which show evolutionary trends from a Class 0 to a Class I protostar. It is widely believed that the outflow and luminosity are both generated by the same process, that is, accretion of matter originating from the surrounding envelope. These correlations make the three parameters indicators of the evolutionary stage of the protostar. Figure 7 shows recent results of vdM13, who combined data from various studies. Class 0 protostars are encircled. To make a meaningful comparison with the results of vdM13, we calculated the momentum force using the vmax method andapplied the correction factors from Cabrit & Bertout (1992) just as vdM13 in their paper (cf. Sect. 3.8.2). The results for Cha-MMS1 are shown in red. The envelope mass of Cha-MMS1 Menv = 2.36 M⊙ (Belloche et al. 2011, corrected for the new distance) is comparable to the masses of Class 0 protostars shown in Fig. 7a. Belloche et al. (2011) assumed an uncertainty on the mass of at least a factor of 2 which we use as an error bar. The momentum force of the Cha-MMS1 outflow, however, lies 1–2 orders of magnitude below the momentum forces of these Class 0 protostars, depending on optical depth. We used the values of Tsitali et al. (2013) for the bolometric luminosity. The authors worked out the internal luminosity of Cha-MMS1 at a distance of D = 150 pc and for an inclination of 45° < i < 60°. We corrected their values for the most recent distance of Cha-MMS1 and found Lint= 0.13−0.29 L⊙. However, it might well be higher considering the higher inclination of Cha-MMS1. From this range, we assumed an internal luminosity of Lint ≈ 0.2 L⊙. Cha-MMS1 thus is at the lower end of the Class 0 luminosity range shown in Fig. 7b, where we give the above luminosity range as the uncertainty. Due to its lower luminosity and its envelope mass, which is comparable to other Class 0 protostar, Cha-MMS1 lies in the upper left corner in the Menv–Lbol plot in Fig. 7c. The low luminosity may partly be explained by the high inclination when there is a disk of material that is oriented perpendicular to the jet axis and efficiently obscures the central core (Bontemps et al. 1996). The rather low values of the momentum force may arise because Cha-MMS1 is an extremely young Class 0 protostar and the outflow may not yet have been brought to full power (Smith 2000; Hatchell et al. 2007). In Sect. 3.8.2 we discussed that the values we found for the momentum force using the vmax method only present a lower limit because the inclination seems to be higher than 70°, for which we have corrected the results. We have found values, which are one to two orders of magnitudes lower than those found with the perpendicular method in Sect. 3.8.1. However, the results for the momentum force from the perpendicular method are still lower than the momentum forces of other Class 0 protostars. We discuss uncertainties on these calculations in Appendix C.
 |
Fig. 7 Correlation plots for (a) FCO and Menv, (b) FCO and Lbol, and (c) Menv and Lbol adapted from vdM13. Diamonds show their study, triangles the study of Cabrit & Bertout (1992) and filled circles that of Hogerheijde et al. (1996). The Class 0 protostars are encircled. The dashed lines indicate their best fit. The results for Cha-MMS1, GF 9–2 (Furuya et al. 2019), B1b-N, and B1b-S (Gerin et al. 2015) are shown in red, green, blue, and orange, respectively. The error bars on the total momentum force of the outflows represent the uncertainty on the inclination correction adapted from Cabrit & Bertout (1992). The error bars on the luminosity and the mass of Cha-MMS1 correspond to the range derived by Tsitali et al. (2013) and an uncertainty of a factor of 2 (Belloche et al. 2011), respectively. The results for Cha-MMS1 correspond to the optical depth case τ12 = 5. |
4.8 Evolutionary stage of Cha-MMS1
With ALMA we have been able to detect a bipolar outflow associated with Cha-MMS1 as the driving source with which we can finally draw a conclusion on the evolutionary stage of the young stellar object. Even without applying any inclination corrections, we detect outflow velocities up to ~17 km s−1, well above ~5 km s−1, which is clearly visible in the PV diagram in Fig. 3 and the channel maps in Fig. A.1. This is already inconsistent with FHSC outflow speeds predicted by numerical simulations (e.g., Commerçon et al. 2012; Machida et al. 2008) and implies that Cha-MMS1 has already left the FHSC phase and entered the Class 0 phase. When we correct for inclination, we determine maximum outflow velocities as high as at least 90 km s−1 for a likely conservative value of the inclination of 79°.
Commerçon et al. (2012) also showed that a first core can be detected at 24 and 70 μm if the source is inclined by less than 60° to the line of sight. However, if a source at the FHSC stage is inclined by more than 60°, it cannot be detected at these wavelengths over its whole lifetime because most of the radiation emanating from the first core is reprocessed by the surrounding envelope. We find that the outflow axis of Cha-MMS1 lies almost in the plane of the sky, implying that it should not be observable at 24 and 70 μm if it were in the FHSC stage. The fact that Belloche et al. (2006) detected Cha-MMS1 at these wavelengths supports the assumption that it is not an FHSC but in a more evolved state, that is, a Class 0 protostar.
In Sect. 1 we have introduced the dense cores B1b-N and B1b-S, the former of which seems to be an FHSC, while the latter is proposed to be already in a more evolved state (Gerin et al. 2015). The properties of the outflows are summarized in Table 5, where, based on the observed properties found by Gerin et al. (2015), we compute the momentum force in the same way as we did for Cha-MMS1 in Sect. 3.8.2, except that we use the correction factor from Cabrit & Bertout (1992) for i = 50° because the blue- and redshifted outflow emission of B1b-N and B1b-S are well separated. The momentum forces of B1b-N and B1b-N are larger than those found for Cha-MMS1. Their ranges of results are indicated in blue (B1b-N) and orange (B1b-S) in Fig. 7. The total observed outflow mass of Cha-MMS1 is lower by an order of magnitude than the outflow masses of B1b-N and B1b-S. Based on the vmax method, the dynamical age of the Cha-MMS1 outflow seems to be comparable to that of B1b-S while being slightly higher than that of B1b-N. The internal luminosity Lint= 0.2 L⊙ of Cha-MMS1 lies in between the luminosities of B1b-N and B1b-S (0.15 L⊙ and 0.31 L⊙), while the envelope mass is higher than that of B1b (0.36 M⊙) (Hirano & Liu 2014).
Another recent study by Furuya et al. (2019) reports on the detection of an outflow driven by the Class 0 protostar GF 9–2. Furuya et al. (2019) determined the outflow properties using a distance of 200 pc, but more recent results suggest a larger distance of 474 pc (Zucker et al. 2019, C. Zucker priv. comm.). We rescaled their results and show them in Table 5. After rescaling, the SW lobe of the GF 9–2 outflow shows the largest spatial extent in this sample. The dynamical age is only slightly higher than that of Cha-MMS1. Furuya et al. (2019) used two excitation temperatures to derive the outflow mass where we will compare to the values at T = 22.6 K. Although the mass of the NE lobe is significantly lower than that of the SW lobe, the total mass of the GF 9–2 outflow is roughly an order of magnitude higher than the mass of the Cha-MMS1 outflow. We determined the momentum force using the vmax method and applied the correction factor from Cabrit & Bertout (1992) for i = 70° to the results because Furuya et al. (2019) found an inclination of ~65° from spectral energy distribution modeling. The results for GF 9–2 are shown in green in Fig. 7. The momentum force of the GF 9–2 outflow is roughly an order of magnitude higher than the value obtained for the outflow of Cha-MMS1. However, they assumed only optically thin emission, and due to the ambiguous morphology of the outflow, it might also be inclined as highly as Cha-MMS1, which would in principle increase the momentum force. In Fig. 7 we use the internal luminosity and envelope mass adopted by Maury et al. (2019) from Wiesemeyer (1997) for a distance of 200 pc, ~0.3 L⊙ and ~0.5 M⊙, and rescaled them to the new distance (1.7 L⊙ and 2.8 M⊙).
All three sources show rather low values of momentum force compared to the other Class 0 protostars in Fig. 7. This may arise because the sources are extremely young Class 0 protostars (or an FHSC in the case of B1b-N) so that their outflows have not yet come to full power. Bontemps et al. (1996) suggested an outflow rate of ~10−6 M⊙ yr−1 for young Class 0 protostars. All sources introduced here show a lower rate of a few times 10−8 M⊙ yr−1 to a few times 10−7 M⊙ yr−1, which may support the hypothesis that their outflows are not yet fully developed.
Admittedly, the derived properties of the Cha-MMS1 outflow contradict the predictions of an FHSC, but they agree with those of a young Class 0 protostar. The comparison to other young Class 0 protostars and a promising FHSC candidate supports the classification of Cha-MMS1 as a young Class 0 protostar rather than an FHSC.
5 Conclusion
We observed Cha-MMS1 at high angular resolution in CO 3–2 and 13 CO 3–2 emission and in continuum emission at ~900 μm. The goal of the project was to search for a slow small-scale outflow to probe if Cha-MMS1 is at the stage of the first hydrostatic core. The ALMA observations reveal a bipolar outflow that is clearly associated with Cha-MMS1 as the driving source. Our main results are the following:
- 1.
The continuum emission detected at small scale originates from the inner parts of the Cha-MMS1 protostellar envelope. No direct evidence for a disk was found and we derived an upper limit to the disk radius of 55 au.
- 2.
The two lobes are oriented in the NE-SW direction, and both show blue- as well as redshifted emission. This indicates that the system is seen nearly edge-on. Because of its high inclination, Cha-MMS1 should not be visible at 24 μm if it were an FHSC according to MHD simulations, but it was detected by Spitzer at this wavelength.
- 3.
In the spectra, we observe maximum velocities of ~16.4 and ~10.6 km s−1 in the NE and SW lobes, respectively, which even without correction for inclination are already inconsistent with the low velocities (<5 km s−1) predicted by MHD simulations for FHSC outflows.
- 4.
We find an observed outflow mass of 3 × 10−4 M⊙, which is at least an order of magnitude lower than the outflow mass of other Class 0 protostars. However, when we corrected for hidden atomic material and material at low velocities, the mass increased by a factor ~4.5.
- 5.
We determined the dynamical age and momentum force of the outflow using two different methods. With the perpendicular method, we obtained ages of ~200 yr, while with the vmax method we derived an upper limit of ~3000 yr. We derived a total momentum force of (1.6 − 3) ×10−5 M⊙ km s−1 yr−1 using the perpendicular method, which is approximately two orders of magnitude higher than the value obtained with the vmax method which is ~ 5 × 10−7 M⊙ km s−1 yr−1.
- 6.
Compared to outflows of more evolved Class 0 protostars, the outflow of Cha-MMS1 has a much smaller momentum force. However, the result is similar to momentum forces of protostars with similar dynamical ages, such as GF 9–2 or B1b-S (and B1b-N), suggesting that these young Class 0 protostars have not yet brought their outflows to full power.
Based on these characteristics, we conclude that Cha-MMS1 is not an FHSC but has already entered the Class 0 protostar phase. Assuming that the outflow is not more extended than what we observe with ALMA, the outflow may be one of the youngest ever observed, with a dynamical age of 200–3000 yr.
Acknowledgements
We thank Anastasia Tsitali for her contribution during the initial stage of this project.
Appendix A: CO and 13CO channel maps
Figure A.1 shows the CO 3–2 channel maps smoothed over eight channels (0.88 km s−1) that cover a velocity range from 22.6 to − 7 km s−1. Figure A.2 shows the 13CO 3–2 channel maps that cover a velocity range from 2.6 to 6.2 km s−1.
 |
Fig. A.1 Velocity-channel maps of the CO 3–2 emission toward Cha-MMS1. The cross marks the peak continuum position. Each map is averaged over eight channels corresponding to ~ 0.88 km s−1 with the central velocity shown in km s−1 in the upper left corner. The contour steps are − 12σ, − 6σ, − 3σ, 3σ, 6σ, 12σ, 24σ, and 48σ with σ = 1.8 mJy beam−1. The light blue contours represent the negative levels. The primary beam (black circle) and the synthesized beam (red ellipse) are shown in the upper left panel. The red and blue contours represent the masks we used to calculate the outflow mass (see Sect. 3.6). The maps are not corrected for primary beam attenuation. The systemic velocity is vsys = 4.43 km s−1 (Belloche et al. 2006). |
 |
Fig. A.2 Velocity-channel maps of the 13CO 3–2 emission toward Cha-MMS1. The cross marks the peak continuum position. The central velocity is shown in km s−1 in the upper left corner. The contour steps are − 6σ, − 3σ, 3σ, 6σ, 12σ, 24σ, and 48σ with σ = 4.7 mJy beam−1. The light blue contours represent the negative levels. The primary beam (black circle) and the synthesized beam (red ellipse) are shown in the upper left panel. The maps are not corrected for primary beam attenuation. The systemic velocity is vsys = 4.43 km s−1 (Belloche et al. 2006). |
Appendix B: PV diagram of R1 and B1
 |
Fig. B.1 CO 3–2 PV diagram along the arrow labeled D3 shown as a green dashed arrow in Fig. 1a. The position axis originates from the start of the arrow in Fig. 1a. The intensity is smoothed over 5 channels. The contours are − 12σ, − 6σ, − 3σ, 3σ, 6σ, 12σ, 24σ, and 48σ with σ = 2.0 mJy beam−1. The red and blue dashed lines show the inner integration limits while the black dashed line indicates the systemic velocity of Cha-MMS1. |
Appendix C: Uncertainties
C.1 Inclination
The overlap between the red- and blueshifted emission suggests that the outflow of Cha-MMS1 has an axis close to the plane of the sky with an inclination i between 79° and 101°. However, it is also possible that the inclination is smaller than our results suggest. The channel maps in Figs. A.1 and A.2 indicate that the outflow becomes broader at velocities close to the systemic velocity. In Fig. 6 this indication is evident, too. Here, we overlay the CO emission of the channel at 5.7 km s−1 taken from the channel maps in Fig. A.1 and the 13 CO emission integrated in the range [4.9, 5.7] km s−1. This broadening would result in a larger opening angle and hence, increase the range of possible inclinations. This increase in opening angle with decreasing velocity has also been seen in early studies of other protostellar outflows (e.g., Bachiller et al. 1990). However, in the case of Cha-MMS1, this broadening is only seen after the kink noticed in the SW lobe, so it may result from the process which generates this kink and does not trace the intrinsic property oft the outflow as driven by Cha-MMS1.This is the reason why we did not take this broad width as the characteristic width of the outflow to estimate its inclination in Sect. 3.4.
C.2 Momentum force
We calculated the dynamical time and the momentum force of the outflow using two different methods where the results obtained from the perpendicular method are higher than those obtained from the vmax method by approximately an order of magnitude. Based on the discussion in DC07, we claim that the perpendicular method gives the more reliable estimates because the required parameters, which are the intensity-weighted velocity and the radius of the lobe, depend only minorly on inclination. On the contrary, the maximum outflow velocity and the length along the axis of the outflow as used in the vmax method strongly depend on inclination. To account for the inclination in the vmax method, we applied a correction from Cabrit & Bertout (1992) for i = 70° because this is the highest inclination for which they give the correction factor. Hence, we obtain only a lower limit for the momentum force. Further, in order to determine the maximum velocity for the vmax method, one needs to evaluate whether the highest velocities really trace the bulk of the outflow or bullets.
C.3 Opacity and outflow mass
Both methods consider the outflow mass that we derived from integrated intensities. The conversion factor K depends on the excitation temperature, for which we assumed 30 K. However, it would change by less than a factor of 2 for temperatures of 50 K or 20 K. Regardless of the method that is used, another uncertainty results from the optical depth. To account for the high optical depths at the inner velocity cutoffs, we used the 13 CO emission until a certain threshold and corrected for optical depth wherever possible3. We did not determine a correction for channels in which the intensity ratio of the isotopologues was lower than 1, which may underestimate the intensity in these channels. Beyond the 13 CO intensity threshold, we added the 12CO emission, where we consider two cases: optically thick (τ12 = 5) and thin (τ12 < < 1) CO emission. In this way, the results span a range in which the true mass and momentum force of the outflow should lie. The maximum recoverable scale of our observations is ~7′′. The outflow lobes are significantly narrower than this (~2–3′′), so that the outflow emission is not expected to be much affected by spatial filtering. 12 CO outflow emission close to the systemic velocity of the source is likely hidden behind optically thick larger-scale envelope emission filtered out by the interferometer, and thus cannot trace the outflow well, but our strategy to use 13 CO in the cases where 12CO is optically thick should reduce the effect of this on our estimates of the outflow mass and momentum force. Additionally, the mass and momentum force may still be underestimated when molecular dissociation is not considered (DC07). Only in the case of the perpendicular method did we allow for more undetected atomic gas by applying the correction factor introduced by DC07. We did not apply this correction to the results from the vmax method in order to make a more reliable comparison to other sources for which these factor was not applied either.
Furthermore, independently of the methods, we integrated intensities within fixed velocity intervals. Although we used the 13 CO emission to account for material closer to vsys and although we applied a correction factor to take into account missing material at velocities close to vsys, we may still have missed some material at low velocities. Figure 6 shows that the outflow emission becomes less collimated at low velocities. However, the choice of the outer velocity cutoffs does not introduce large uncertainties to the integrated intensities because most of the emission is found at lower velocities.
C.4 Outflow radius
In Fig. 6 we showed that the outflow is less collimated at low velocities, which results in a larger outflow radius Wlobe. We determined Wlobe at the lowest possible velocity showing the largest radii. If the true radius is even larger, however, the quantities computed from the perpendicular method of DC07, that is, dynamical age tperp and momentum force Fperp, increase and decrease, respectively.
C.5 Contamination from IRS 4
In the special case of Cha-MMS1, emission that originates from the nearby Class I protostar Ced 110 IRS 4 and its outflow might contaminate the emission of CO 3–2 (Belloche et al. 2006; Hiramatsu et al. 2007; Tsitali et al. 2013). We have shown the outflow emission of IRS 4 in Fig. 1c and the larger-scale emission at velocities close to vsys that probably traces ambient material of the filament in Fig. 1d. While the emission of the IRS 4 outflow may in principle contaminate our observations, most of the large-scale emission appears to be filtered by ALMA and the morphology of the emission detected close to Cha-MMS1 undoubtedly originates from Cha-MMS1 itself.
References
- Anathpindika, S., & Whitworth, A. P. 2008, A&A, 487, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bachiller, R. 1996, ARA&A, 34, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Bachiller, R., Cernicharo, J., Martin-Pintado, J., et al. 1990, A&A, 231, 174 [NASA ADS] [Google Scholar]
- Bally, J., Walawender, J., Luhman, K., et al. 2006, AAS Meeting Abstracts 207, 214.06 [Google Scholar]
- Banerjee, R., & Pudritz, R. E. 2006, ApJ, 641, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Belloche, A., Parise, B., van der Tak, F. F. S., et al. 2006, A&A, 454, L51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Schuller, F., Parise, B., et al. 2011, A&A, 527, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bontemps, S., Andre, P., Terebey, S., & Cabrit, S. 1996, A&A, 311, 858 [NASA ADS] [Google Scholar]
- Cabrit, S., & Bertout, C. 1990, ApJ, 348, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrit, S., & Bertout, C. 1992, A&A, 261, 274 [Google Scholar]
- Ciardi, A., & Hennebelle, P. 2010, MNRAS, 409, L39 [NASA ADS] [Google Scholar]
- Commerçon, B., Hennebelle, P., Audit, E., Chabrier, G., & Teyssier, R. 2010, A&A, 510, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Commerçon, B., Launhardt, R., Dullemond, C., & Henning, T. 2012, A&A, 545, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, C. M., et al. 2005, ApJ, 619, 379 [Google Scholar]
- Downes, T. P., & Cabrit, S. 2007, A&A, 471, 873 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dzib, S. A., Loinard, L., Ortiz-León, G. N., Rodríguez, L. F., & Galli, P. A. B. 2018, ApJ, 867, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Emprechtinger, M., Caselli, P., Volgenau, N. H., Stutzki, J., & Wiedner, M. C. 2009, A&A, 493, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frank, A., Ray, T. P., Cabrit, S., et al. 2014, Protostars and Planets VI (Tucson: University of Arizona Press), 451 [Google Scholar]
- Furuya, R. S., Kitamura, Y., & Shinnaga, H. 2006, ApJ, 653, 1369 [NASA ADS] [CrossRef] [Google Scholar]
- Furuya, R. S., Kitamura, Y., & Shinnaga, H. 2019, ApJ, 871, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Gerin, M., Pety, J., Fuente, A., et al. 2015, A&A, 577, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerin, M., Pety, J., Commerçon, B., et al. 2017, A&A, 606, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gueth, F., & Guilloteau, S. 1999, A&A, 343, 571 [NASA ADS] [Google Scholar]
- Hatchell, J., Fuller, G. A., & Richer, J. S. 2007, A&A, 472, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Fromang, S. 2008, A&A, 477, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., Commerçon, B., Chabrier, G., et al. 2016, ApJ, 830, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Hiramatsu, M., Hayakawa, T., Tatematsu, K., et al. 2007, ApJ, 664, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Hirano, N., & Liu, F.-c. 2014, ApJ, 789, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Hogerheijde, M. R., van Dishoeck, E. F., van Langevelde, H. J., & Blake, G. A. 1996, Disks and Outflows Around Young Stars (Heidelberg: Springer), 465, 504 [Google Scholar]
- Ladd, E. F., Wong, T., Bourke, T. L., et al. 2011, ApJ, 743, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1969, MNRAS, 145, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Lehtinen, K., Haikala, L. K., Mattila, K., & Lemke, D. 2001, A&A, 367, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lehtinen, K., Harju, J., Kontinen, S., & Higdon, J. L. 2003, A&A, 401, 1017 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luhman, K. L. 2008, Handbook of Star Forming Regions (California, USA: ASP), II, 169 [NASA ADS] [Google Scholar]
- Machida, M. N. 2014, ApJ, 796, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M. N., Inutsuka, S.-i., & Matsumoto, T. 2008, ApJ, 676, 1088 [NASA ADS] [CrossRef] [Google Scholar]
- Mattila, K., Liljeström, T., & Toriseva, M. 1989, Eur. S. Observ. Conf. Workshop Proc., 33, 153 [Google Scholar]
- Maury, A. J., André, P., Testi, L., et al. 2019, A&A, 621, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McGregor, P. J., Harrison, T. E., Hough, J. H., et al. 1994, MNRAS, 267, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., & André, P. 2001, A&A, 365, 440 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Persi, P., Marenzi, A. R., Gómez, M., & Olofsson, G. 2001, A&A, 376, 907 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pezzuto, S., Elia, D., Schisano, E., et al. 2012, A&A, 547, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plunkett, A. L., Arce, H. G., Mardones, D., et al. 2015, Nature, 527, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Raga, A. C., de Gouveia Dal Pino, E. M., Noriega-Crespo, A., et al. 2002, A&A, 392, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reipurth, B., Nyman, L.-A., & Chini, R. 1996a, A&A, 314, 258 [NASA ADS] [Google Scholar]
- Reipurth, B., Raga, A. C., & Heathcote, S. 1996b, A&A, 311, 989 [NASA ADS] [Google Scholar]
- Remijan, A., Adams, M., Akiyama, E., et al. 2015, ALMA Cycle 3 Technical Handbook Version 1 (Charlottesville, VA: NRAO) [Google Scholar]
- Smith, M. D. 2000, Irish Astron. J., 27, 25 [NASA ADS] [Google Scholar]
- Stephens, I. W., Dunham, M. M., Myers, P. C., et al. 2017, ApJ, 846, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Terebey, S., Chandler, C. J., & André, P. 1993, ApJ, 414, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Tomida, K., Tomisaka, K., Matsumoto, T., et al. 2010, ApJ, 714, L58 [NASA ADS] [CrossRef] [Google Scholar]
- Tsitali, A. E., Belloche, A., Commerçon, B., & Menten, K. M. 2013, A&A, 557, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Marel, N., Kristensen, L. E., Visser, R., et al. 2013, A&A, 556, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, H., & Henning, T. 2006, ApJ, 643, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Wiesemeyer, H. 1997, PhD Thesis, University of Bonn, Germany [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y., Arce, H. G., Mardones, D., et al. 2016, ApJ, 832, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Zucker, C., Speagle, J. S., Schlafly, E. F., et al. 2019, ApJ, 879, 125 [NASA ADS] [CrossRef] [Google Scholar]
Tsitali et al. (2013) assumed a distance of 150 pc and an inclination of Cha-MMS1 to the line of sight of 45° < i < 60°. With a distance of 192 pc, this range translates into 0.13–0.29 L⊙.
All Tables
Properties of each lobe of the outflow of Cha-MMS1 determined from CO 3–2 ALMA observations.
Outflow properties of B1b-N, B1b-S, GF 9–2, and Cha-MMS1 derived with the vmax method.
All Figures
 |
Fig. 1 (a) CO 3–2 integrated intensities (blue and red contours) observed with ALMA toward Cha-MMS1. The continuum emission is shown in grayscale with black contours. The large yellow cross marks its peak position. The CO emission is integrated over the velocity ranges [−6.1, 3.4] km s−1 (blue) and [5.5, 21.8] km s−1 (red). The contours are − 2.5σ, 2.5σ, and 5σ, and then increase by a factor of two at each step with σ = 7.04 mJy beam−1 km s−1, 9.06 mJy beam−1 km s−1, and 0.05 mJy beam−1 for the blueshifted, redshifted, and the continuum emission, respectively. The HPBW is shown in the bottom left corner. The yellow crosses mark the positions of the spectra shown in Fig. 2. The green dashed arrows indicate the axes along which PV diagrams were taken for Figs. 3 and B.1. B1 and R1 indicate the less-collimated blue- and redshifted structures, respectively. (b) Same as a, but zoomed-in on the central region. The phase center is marked with a green cross in this panel. (c) CO 3–2 integrated intensities observed with APEX toward Cha-MMS1 (cross) (adapted from Belloche et al. 2006). The redshifted [6.6, 9.8] km s−1, blueshifted [−0.2, 1.0] km s−1, and less blueshifted [1.2, 2.4] km s−1 emission is plotted as solid red, solid blue, and dashed blue contours, respectively. The first contours and steps are 3σ, 6σ, and 3σ with σ = 0.13, 0.13, and 0.24 K km s−1, respectively, as in Belloche et al. (2006). The HPBW is shown in the bottom left corner. The star and square mark positions of NIR (Persi et al. 2001) and 3.5 cm sources (Lehtinen et al. 2003), respectively. (d) Same as c but for CO 3–2 integrated intensities at velocities close to vsys. The redshifted [5.5, 6.6] km s−1 emission is shown as dotted (3σ), dashed (6σ), and solid (9σ) contours with σ = 0.13 K km s−1. The blueshifted [2.4, 3.4] km s−1 emission is plotted as solid contours. The first contour and the steps are 6σ with σ = 0.13 K km s−1. The small box corresponds to the field of view shown in panel a. |
| In the text | |
 |
Fig. 2 CO 3–2 spectra observed with ALMA toward Cha-MMS1 in brightness temperature scale and smoothed over five channels. The spectra are taken toward three positions marked with yellow crosses in Fig. 1: (a) in the NE lobe, (b) at the peak of the continuum emission, and (c) in the SW lobe. The red and blue dashed lines correspond to the integration intervals defined in Sect. 3.2 while the black dashed line indicates the systemic velocity of Cha-MMS1, vsys = 4.43 km s−1 (Belloche et al. 2006). |
| In the text | |
 |
Fig. 3 (a and b) CO 3–2 PV diagrams along the outflow axes (a) D1 and (b) D2 shown as green dashed arrows in Fig. 1a. The origin of the position axes corresponds to the continuum peak. The intensity is smoothed over five channels. The contours are − 6σ, − 3σ, 3σ, 6σ, 12σ, 18σ, 24σ 48σ, 96σ, and 192σ with σ = 2.0 mJy beam−1. The red and blue dashed lines show the inner and outer integration limits. (c–h) CO 3–2 spectra in brightness temperaturescale taken along D1 and D2 at the positions marked as green ticks on the x-axis in the PV diagrams in panels a and b. K1–K6 denote the bumps corresponding to the bullets and F0 indicates the bulk flow. The intensity is smoothed over two channels. In all panels, the black dashed line indicates the systemic velocity of Cha-MMS1. |
| In the text | |
 |
Fig. 4 CO 3–2 (solid black) and 13CO 3–2 (dotted black) spectra at the peak position of Cha-MMS1 in brightness temperature scale. Green squares show the ratio of CO to 13CO intensity, and green arrows indicate the lower limits of this ratio after smoothing over four channels. The scale is given on the first right axis. The optical depth scale is shown on the second right axis. The red and blue dashed lines mark the inner integration limits, and the black dashed line indicates the systemic velocity of Cha-MMS1. |
| In the text | |
 |
Fig. 5 Integrated intensity maps toward Cha-MMS1 (black cross) of the high-velocity redshifted CO 3–2 gas [15.0, 21.8] km s−1 shown with red contours and the low-velocity redshifted CO 3–2 gas [9.1, 11.6] km s−1 shown in grayscale and with black contours. The contour levels are − 3σ, 3σ, 6σ, 12σ, and 24σ with σ = 0.7 mJy beam−1 km s−1 and 1.1 mJybeam−1 km s−1 for the emissions at high velocities and low velocities, respectively. The green crosses K1–K6 mark the positions at which the spectra in Figs. 3c–h were taken. The HPBW is shown in the bottom left corner. The black cross marks the position of the continuum peak. |
| In the text | |
 |
Fig. 6 Channel map of CO 3–2 emission (red) at 5.7 km s−1 from Fig. A.1 overlaid by 13CO intensity (black) integrated from 4.9 to 5.7 km s−1. The contour levels are −3σ, 3σ, 6σ, 12σ, 24σ, and 48σ with σ = 1.8 mJy beam−1 and σ = 2.5 mJy beam−1 for the CO and the 13CO intensity, respectively. The continuum peak is marked with the yellow cross. The HPBW is shown in the bottom left corner. |
| In the text | |
 |
Fig. 7 Correlation plots for (a) FCO and Menv, (b) FCO and Lbol, and (c) Menv and Lbol adapted from vdM13. Diamonds show their study, triangles the study of Cabrit & Bertout (1992) and filled circles that of Hogerheijde et al. (1996). The Class 0 protostars are encircled. The dashed lines indicate their best fit. The results for Cha-MMS1, GF 9–2 (Furuya et al. 2019), B1b-N, and B1b-S (Gerin et al. 2015) are shown in red, green, blue, and orange, respectively. The error bars on the total momentum force of the outflows represent the uncertainty on the inclination correction adapted from Cabrit & Bertout (1992). The error bars on the luminosity and the mass of Cha-MMS1 correspond to the range derived by Tsitali et al. (2013) and an uncertainty of a factor of 2 (Belloche et al. 2011), respectively. The results for Cha-MMS1 correspond to the optical depth case τ12 = 5. |
| In the text | |
 |
Fig. A.1 Velocity-channel maps of the CO 3–2 emission toward Cha-MMS1. The cross marks the peak continuum position. Each map is averaged over eight channels corresponding to ~ 0.88 km s−1 with the central velocity shown in km s−1 in the upper left corner. The contour steps are − 12σ, − 6σ, − 3σ, 3σ, 6σ, 12σ, 24σ, and 48σ with σ = 1.8 mJy beam−1. The light blue contours represent the negative levels. The primary beam (black circle) and the synthesized beam (red ellipse) are shown in the upper left panel. The red and blue contours represent the masks we used to calculate the outflow mass (see Sect. 3.6). The maps are not corrected for primary beam attenuation. The systemic velocity is vsys = 4.43 km s−1 (Belloche et al. 2006). |
| In the text | |
 |
Fig. A.2 Velocity-channel maps of the 13CO 3–2 emission toward Cha-MMS1. The cross marks the peak continuum position. The central velocity is shown in km s−1 in the upper left corner. The contour steps are − 6σ, − 3σ, 3σ, 6σ, 12σ, 24σ, and 48σ with σ = 4.7 mJy beam−1. The light blue contours represent the negative levels. The primary beam (black circle) and the synthesized beam (red ellipse) are shown in the upper left panel. The maps are not corrected for primary beam attenuation. The systemic velocity is vsys = 4.43 km s−1 (Belloche et al. 2006). |
| In the text | |
 |
Fig. B.1 CO 3–2 PV diagram along the arrow labeled D3 shown as a green dashed arrow in Fig. 1a. The position axis originates from the start of the arrow in Fig. 1a. The intensity is smoothed over 5 channels. The contours are − 12σ, − 6σ, − 3σ, 3σ, 6σ, 12σ, 24σ, and 48σ with σ = 2.0 mJy beam−1. The red and blue dashed lines show the inner integration limits while the black dashed line indicates the systemic velocity of Cha-MMS1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


