| Issue |
A&A
Volume 632, December 2019
|
|
|---|---|---|
| Article Number | A82 | |
| Number of page(s) | 11 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201936838 | |
| Published online | 04 December 2019 | |
Improved detection of far-side solar active regions using deep learning
1
Instituto de Astrofísica de Canarias, 38205 C/ Vía Láctea, s/n, La Laguna, Tenerife, Spain
e-mail: tobias@iac.es
2
Departamento de Astrofísica, Universidad de La Laguna, 38205 La Laguna, Tenerife, Spain
Received:
3
October
2019
Accepted:
1
November
2019
Context. The analysis of waves on the visible side of the Sun allows the detection of active regions on the far side through local helioseismology techniques. Knowing the magnetism in the whole Sun, including the non-visible hemisphere, is fundamental for several space weather forecasting applications.
Aims. Seismic identification of far-side active regions is challenged by the reduced signal-to-noise ratio, and only large and strong active regions can be reliable detected. Here we develop a new method to improve the identification of active region signatures in far-side seismic maps.
Methods. We constructed a deep neural network that associates the far-side seismic maps obtained from helioseismic holography with the probability that active regions lie on the far side. The network was trained with pairs of helioseismic phase-shift maps and Helioseismic and Magnetic Imager (HMI) magnetograms acquired half a solar rotation later, which were used as a proxy for the presence of active regions on the far side. The method was validated using a set of artificial data, and it was also applied to actual solar observations during the period of minimum activity of solar cycle 24.
Results. Our approach shows a higher sensitivity to the presence of far-side active regions than standard methods that have been applied up to date. The neural network can significantly increase the number of detected far-side active regions, and will potentially improve the application of far-side seismology to space weather forecasting.
Key words: Sun: helioseismology / Sun: interior / Sun: activity / Sun: magnetic fields / methods: data analysis
© ESO 2019
1. Introduction
Helioseismology studies the solar interior by analyzing the oscillations that are observed at the surface. Its first applications were based on the interpretation of accurate measurements of the eigenfrequencies of the resonant oscillatory modes. This field has been labeled “global helioseismology”, and it has revealed the internal structure and rotation of the Sun (e.g., Christensen-Dalsgaard 2002). Since the late 1980s, a complementary set of techniques and theoretical methods, known as “local helioseismology”, have been developed in order to probe local regions of the solar interior or surface. Local helioseismology does not focus only on the resonant modes, but studies the full wave field instead. This approach allows measuring longitudinal variations and meridional flows, in contrast to global helioseismology. See Gizon & Birch (2005) for a review on local helioseismology.
One of the most remarkable applications of local helioseismology is the detection of active regions in the non-visible hemisphere of the Sun (on the far side). This was first achieved using the technique of helioseismic holography (Lindsey & Braun 2000; Braun & Lindsey 2001). Helioseismic holography was introduced by Lindsey & Braun (1990). A detailed description of the method can be found in Braun & Birch (2008). It uses the wavefield measured in a region of the solar surface (called “pupil”) to determine the wave field at a focus point that is located at the surface or at a certain depth. This inference is performed assuming that the observed wave field at the pupil (e.g., the line-of-sight Doppler velocity) is produced by waves converging toward the focus point or waves diverging from that point. Far-side helioseismic holography is a particular application of this method, where the pupil is located at the near-side hemisphere and the focus points are located at the surface in the far-side hemisphere (see Lindsey & Braun 2017, for a thorough discussion of this technique). The identification of active regions is founded on the fact that they introduce a phase shift between ingoing and outgoing waves (Braun et al. 1992). This phase shift (which can be characterized as a travel-time shift) is mainly due to the depression of the photosphere in magnetized regions, which causes the upcoming waves to reach the upper turning point a few seconds earlier in active regions than in quiet-Sun regions (Lindsey et al. 2010; Felipe et al. 2017). In this way, when an active region is located at the focus point, a negative phase shift (reduction in the travel time) is found. Far-side imaging has later been performed using time-distance helioseismology (Duvall & Kosovichev 2001; Zhao 2007; Ilonidis et al. 2009).
Far-side maps computed using helioseismic holography are routinely calculated twice a day using Doppler-velocity wave fields obtained in 24-h windows. They are archived and accessible through the internet. These maps are measured from GONG data1 and Helioseismic and Magnetic Imager (HMI) data2. The interest in the detection of active regions on the far side goes beyond the simple curiosity of measuring them before they rotate into the visible hemisphere. Knowing the magnetism in the whole Sun (including the non-visible hemisphere) is fundamental for several space weather forecasting applications. One of them is the forecasting of the UV and extreme-UV (EUV) irradiance on Earth because active regions have a strong impact on the irradiance at these wavelengths. Fontenla et al. (2009) showed that including the information of the helioseismic far-side maps significantly improves the Lyα irradiance forecasting. This method can be extended to forecast the entire far-UV (FUV) and EUV irradiance spectrum. Data-driven photospheric flux transport models including active regions on the far side also improve the solar wind forecast and the F10.7 index (solar radio flux at 10.7 cm) forecast (Arge et al. 2013) and allow successfully estimating the location and magnitude of large active regions before they are visible in the near side (Schrijver & De Rosa 2003). Models including far-side detection of active regions have also been used to explore the open flux problem, that is, the discrepancy between the magnetic flux in open field regions of the Sun and the flux measured in situ by spacecraft (Linker et al. 2017).
One of the main limitations of far-side helioseismology is the reduced signal-to-noise ratio. The signature of an active region detected on the far side has a signal-to-noise ratio of around 10, which means that only large and strong active regions can be reliably detected in far-side phase-shift maps (several hundred active regions per solar cycle, Lindsey & Braun 2017). The goal of this paper is to improve the identification of active region signatures in far-side phase-shift maps using a deep-learning approach. The paper is organized as follows: Sect. 2 describes the neural network, including the data employed for the training set, Sect. 3 shows the evaluation of the performance of our method using artificial data sets, Sect. 4 presents the results from the application of the network to actual solar data, and finally, in Sect. 5 we discuss the results and draw the conclusions.
2. Neural network approach
The recent success of machine learning is no doubt a consequence of our ability to train very deep neural networks (DNNs; see Goodfellow et al. 2016). DNNs can be seen as a very flexible and differentiable parametric mapping between an input space and an output space. These highly parameterized DNNs are then tuned by optimizing a loss function that measures the ability of the DNN to map the input space onto the output space over a predefined training set. The combination of loss function and specific architecture has to be chosen to solve the specific problem at hand.
Arguably the largest number of applications of DNNs has been in computer vision3. Problems belonging to the realm of machine vision can hardly be solved using classical methods, be they based on machine learning or on rule-based methods. Only now, with the application of very DNNs, have we been able to produce real advances. Applications in science, and specifically in astrophysics and solar physics, have leveraged the results of machine vision to solve problems that were difficult or impossible to deal with in the past with classical techniques. The literature is growing very fast, but as a summary, we find applications ranging from the classification of galactic morphologies (Huertas-Company et al. 2015) or the development of generative models to help constrain the deconvolution of images of galaxies (Schawinski et al. 2017) to the real-time multiframe blind deconvolution of solar images (Asensio Ramos et al. 2018) or the probabilistic inversion of flare spectra (Osborne et al. 2019). Our aim in this work is to apply convolutional neural networks to learn a very fast and robust mapping between consecutive maps of estimated seismic maps and the probability map of the presence of an active region on the far side.
2.1. Training set
We have designed a neural network that can identify the presence of active regions on the far side. As input, the network uses far-side phase-shift maps computed using helioseismic holography. As a proxy for the presence of active regions, we employed Helioseismic and Magnetic Imager (HMI) magnetograms measured on the near side (facing Earth). The details of the data are discussed in the following sections. The training set that we describe in this section was used to supervise the parameter tuning of the neural network with the aim of generalizing this to new data.
2.1.1. HMI magnetograms
The HMI magnetograms are one of the data products from the Solar Dynamics Observatory available through the Joint Science Operations Center (JSOC). In order to facilitate the comparison with the far-side seismic maps (next section), we are interested in magnetograms that are remapped onto a Carrington coordinate grid. We used data from the JSOC series hmi.Mldailysynframe_720s. This data series contains synoptic maps constructed of HMI magnetograms collected over a 27-day solar rotation, where the first 120° in longitude are replaced by data within 60° of the central meridian of the visible hemisphere observed approximately at one time. These maps are produced daily at 12 UT. We only employed the 120° in longitude including the magnetogram visible on the disk at one time. Magnetograms between 2010 June 1 (the first date available for the hmi.Mldailysynframe_720s data) and 2018 October 26 were extracted. Because one magnetogram is taken per day, this means a total of 3066 magnetograms. Figure 1 summarizes the data we employed for the training set. One of the original magnetograms in heliospheric coordinates is shown in the bottom left panel.
 |
Fig. 1. Example of one of the elements from the training set. Panels in the top row show 11 far-side seismic maps, each of them obtained from the analysis of 24 h of HMI Doppler data. The horizontal axis is the longitude (a total of 120°) and the vertical axis is the latitude (between −72° and 72°). The label above the panels indicates the number of days prior to the time t when the corresponding magnetogram was acquired (in this example, t is 2015 December 10 at 12:00 UT). Bottom row: magnetograms we used as a proxy for the presence of active regions. Left panel: original magnetogram in heliospheric coordinates, middle panel: magnetogram after active regions that emerged in the near side are removed and after a Gaussian smoothing was applied, and right panel: binary map in which a value of 1 indicates the presence of an active region in the locations whose magnetic flux in the smoothed magnetogram is above the selected threshold. Red contours in the bottom left panel delimit the regions where the binary map is 1. The neural network is trained by associating the 11 far-side seismic maps (top row) with the binary map. |
Because new active regions emerge and old regions decay, magnetograms obtained on the near side are an inaccurate characterization of the active regions on the far side half a rotation earlier or later. We have partially corrected this problem. The far-side maps are associated with the magnetogram that is obtained when the seismically probed region has fully rotated to the Earth side, that is, 13.5 days after the measurement of the far-side map. We removed the active regions that emerge on the near side because they were absent when the far-side seismic data were taken. In order to identify the emerging active regions, we have employed the Solar Region Summary (SRS) files4, where the NOAA registered active regions are listed. All the active regions that appear for the first time at a longitude greater than −60° (where 0 corresponds to the central meridian of the visible hemisphere and the minus sign indicates the eastern hemisphere) were masked in the magnetograms. The value of the magnetogram was set to zero in an area 15° wide in longitude and 12° wide in latitude, centered in the location of the active region reported in the SRS file of that date (after correcting for the longitude because we employed magnetograms retrieved at 12 UT and in the SRS files the location of the active regions are reported for 24 UT on the previous day). The active regions that emerge in the visible hemisphere too close to an active region that had appeared on the eastern limb due to the solar rotation were not masked. Of the 1652 active regions labeled by NOAA during the temporal period employed for the training set, 967 were masked because they emerged in the visible hemisphere.
The neural network is trained with binary maps, where the zeros correspond to quiet regions and the ones to active regions. This binary mask is built from the corrected magnetograms as follows. A Gaussian smoothing with a standard deviation of 3° was applied to the corrected magnetograms. This smoothing removed all small-scale activity in the map and facilitated the segmentation of active regions of importance in the magnetogram. Then, regions with a magnetic flux higher than 30 Mx cm2 were identified as active regions (and set to 1), and regions with lower magnetic flux were set to 0. The middle panel in the bottom row from Fig. 1 shows the magnetogram after the active regions that emerged in the visible solar hemisphere were removed and after Gaussian smoothing was applied. The active region visible in the original magnetogram (bottom left panel in Fig. 1) at a longitude −30° and a latitude −5° emerged on the near side and was therefore masked. The bottom right panel of Fig. 1 shows the binary map in which the location of the remaining active regions is indicated, those whose magnetic flux is above the selected threshold. Their positions match that of some regions with strong negative travel times in the seismic maps from about half a rotation earlier (case “t-13.0” in the top row of Fig. 1).
2.1.2. Far-side phase-shift maps
Phase-shift maps of the far-side region of the Sun are available through JSOC. They are computed from HMI Doppler data using temporal series of one or five days. The processing of series of five days is a novel approach since 2014, introduced to improve the signal-to-noise ratio of the phase-shift maps. They are provided in Carrington heliographic coordinates with a cadence of 12 h (maps are obtained at 0 and 12 UT). In this work, we focus on the far-side maps computed from 24 h of Doppler data. We employed far-side maps between 2010 May 18 and 2018 October 12. For each map, we selected a 120° region in longitude centered at the Carrington longitude of the central meridian of the visible hemisphere 13.5 days after the date of the far-side map. In this way, corrected magnetograms from which the new active regions are removed are associated with far-side maps that sample the same region in longitude. The training employed 11 consecutive far-side maps for each corrected magnetogram, which improved the seismic signal. These 11 consecutive far-side maps correspond to six days of data. The latitude span of the maps is between −72° and 72°. We chose a sampling of 1° in both latitude and longitude.
The JSOC also routinely reports the far-side active regions that are detected in the seismic analysis. A detection is claimed when the phase shift integrated over an area exceeds a certain threshold value. The area of integration is determined as a region where the phase shift is lower than −0.085 radian. The reports with the far-side active regions are published twice a day. We used these reports to evaluate the performance of the neural network in comparison with the traditional approach for detecting far-side active regions (see Sect. 4).
2.2. Neural network architecture
The neural network of choice in this work is a U-net (Ronneberger et al. 2015), a fully convolutional architecture that has been used extensively for dense segmentation of images and displayed in Fig. 2 (e.g., Hausen & Robertson 2019; Silburt et al. 2019, in astrophysics). The U-net is an encoder-decoder network, in which the input is successively reduced in size through contracting layers and is finally increased in size through expanding layers. This encoder-decoder architecture has three main advantages, all of them a consequence of the contracting and expanding layers. The first advantage is that the contracting layers reduce the size of the images at each step. This makes the network faster because convolutions have to be carried out over smaller images. The second advantage is that this contraction couples together pixels in the input image that were far apart, so that smaller kernels can be used in convolutional layers (we used 3 × 3 kernels) and the network is able to better exploit multiscale information. The final advantage is a consequence of the skip connections (gray arrows), which facilitates training by explicitly propagating multiscale information from the contracting layers to the expanding layers.
 |
Fig. 2. U-net architecture. The vertical extent of the blocks indicates the size of the image, and the numbers above each block shows the number of channels. |
As shown in Fig. 2, the specific U-net architecture we used in this work is a combination of several differentiable operations. The first operation, indicated with blue arrows, is the consecutive application of convolutions with 3 × 3 kernels, batch normalization (BN; Ioffe & Szegedy 2015), which normalizes the input so that its mean is close to zero and its variance close to unity (which is known to be an optimal range of values for neural networks to work best) and a rectified linear unit (ReLU) activation function, given by σ(x) = max(0, x) (Nair & Hinton 2010). This combination Conv+BN+ReLU was repeated twice as indicated in the legend of Fig. 2. Red arrows refer to max-pooling (e.g., Goodfellow et al. 2016), which reduces the resolution of the images by a factor 2 by computing the maximum of all non-overlapping 2 × 2 patches in the image. The expanding layers again increase the size of the images through bilinear interpolation (green arrows) followed by convolutional layers. Additionally, the layers in the encoding part transfer information to the decoding part through skip connections (gray arrows), which greatly improves the ability and stability of the network. Finally, because the output is a probability map, we forced it to be in the [0,1] range through a sigmoid activation function that was applied in the last layer after a final 1 × 1 convolution that we used to reduce the number of channels from 16 to 1.
The neural network was trained by minimizing the binary cross entropy between the output of the network per pixel (pi) and the binarized magnetograms (yi), summed over all pixels in the output magnetogram (N),
To optimize the previous loss function, we employed the Adam optimizer (Kingma & Ba 2014) with a constant learning rate of 3 × 10−4 during 300 epochs and a batch size of 30. The neural network makes use of the open-source packages numpy (van der Walt et al. 2011), matplotlib (Hunter 2007), astropy (Price-Whelan 2018), h5py (Koziol & Robinson 2018), scipy (Jones et al. 2001), and PyTorch (Paszke et al. 2017).
3. Artificial tests
We evaluated the performance of the neural network using artificial maps of far-side phase shifts. These artificial maps were constructed by adding a source (with a Gaussian shape) in the phase shift to far-side seismic maps that only contained noise. The procedure for building the artificial far-side maps is the following. First, we selected a set of observational far-side seismic maps that did not contain any signal from active regions. They must satisfy the following conditions: (1) They were measured around solar minimum, in order to minimize the chances of appearance of an active region. Maps between November 2017 and February 2019 were chosen. (2) No active region must be present in the visible eastern (western) limb in the 14 days after (prior to) the measurement of the seismic map. (3) The maximum magnitude of the phase shift must not exceed −8 s. A total of 111 noise maps that satisfy these conditions were selected.
Second, a temporal series was constructed by randomly selecting 11 maps from the whole set of noise maps. Because the original noise maps are located at different Carrington longitudes, they were displaced in longitude so that they resembled a continuous series with a map measured every 12 h. That is, the first noise map was placed at a certain longitude, and the successive maps were centered at a different longitude taking into account the solar rotation after half a day. The public far-side maps we employed are published every 12 h, and each of them is measured over a 24 h window. In this way, there is a 12-h overlap between two consecutive maps. In order to mimic this, each randomly selected noise map was averaged with the map we selected for the previous time step. We chose to use this method instead of just selecting 11 consecutive noise maps to avoid the signal from unnoticed active regions. With this approach, if an active region is present in the set of 111 noise maps, it will have a minor effect on the resulting noise series of 11 maps.
Third, a Gaussian phase-shift perturbation (representing the perturbation of an active region) was added to the noise maps of the temporal series. The Gaussian perturbation is characterized by its position in longitude and latitude, its amplitude (A), and its full width at half-maximum (FWHM). We also explored the temporal variations of the far-side signals. On the one hand, we evaluated the lifetime of the active region by including the Gaussian perturbation in a certain number of consecutive days from the 11 maps that compose each case. On the other hand, because far-side active regions that are detected helioseismically usually show obvious day-to-day variations (even some large active regions are not consistently visible in each image; they often disappear for one day and reappear again), we also studied the effect of the loss of signal for a certain time on the detection. Finally, a region of 120° in longitude centered at the middle position of the map (similar to the real far-side maps described in Sect. 2.1.2) was extracted for each time step.
Figure 3 shows an example of the 11 seismic maps constructed for a single artificial case. In this example, A = −9 s, FWHM = 15°, and the latitude is 15°. For the artificial cases we employed the same latitude and longitude coverage as we used for the training. In most of the maps the acoustic source is visible as a region with negative phase shift. As the time increases from panel a to panel k, it is displaced in longitude due to the solar rotation, approaching to the east limb. In some of the time steps the acoustic source is completely masked by the noise (e.g., panels h and i).
 |
Fig. 3. Artificial seismic maps for an acoustic source with A = −9 s, FWHM = 15°, and a latitude of 15°. Time increases from panel a to panel k, with a temporal step of 12 h. |
The top panel of Fig. 4 shows the five-day average of the artificial case discussed in the previous paragraph. It is obtained after averaging the data from panels b to j in Fig. 3, but keeping them in the Carrington coordinate system. In this system, the acoustic source is located at the same longitude for all time steps (in this example, at a Carrington longitude of −8°). The signature of the acoustic source stands out above the reduced noise obtained after the five-day average. The temporal duration of this average resembles the temporal span currently employed for the measurement of far-side seismic maps where the detection of active regions is reported. The retrieved noise of the averaged artificial seismic map is comparable to that of the actual observations. A detection of far-side active regions is claimed when a region is found with a seismic signature strength above a certain threshold. The strength S is computed as the integrated phase shift over an area where the phase shift exceeds 0.085 rad (≈4 s). With the area measured in millionths of a hemisphere (μHem), a far-side active region is reported when S > 400 μHem rad (see Liewer et al. 2017). The strength of the artificial acoustic source is indicated in the lower left corner in the top panel of Fig. 4, and the red contour delimits the region where the phase shift exceeds 0.085 rad. An active region with a seismic signature similar to that of the case represented in this artificial map would be detected by the current approach.
 |
Fig. 4. Top panel: five-day average of the phase shift for the artificial case illustrated in Fig. 3. The red contour delimits the region where the phase shift exceeds 0.085 rads. The strength of the acoustic source is shown in the bottom left corner. Bottom panel: probability map of the artificial active region illustrated in Fig. 3, as retrieved from the application of the neural network. The integrated probability Pi of the feature inside the blue circle is shown in the bottom left corner. In both panels the blue circle is centered at the location of the acoustic source, with a diameter of three times its FWHM. |
The bottom panel of Fig. 4 illustrates the probability map computed by the neural network after the maps shown in Fig. 3 are introduced as input. The blue circle in both panels indicates a region of three times the FWHM of the source around its central location. In this region lies a large patch with a high probability that an active region is present. We defined an integrated probability Pi, computed as the integral of the probability P in a continuous feature. The identification of the features is performed with the IDL routine rankdown.pro, part of the feature-tracking software YAFTA5. Even though this routine is optimized for application to magnetograms, it reliably groups and labels pixels that belong to the same feature. The Pi of the artificial seismic source is shown in the bottom left corner in the bottom panel of Fig. 4.
The neural network returns a probability map with values in the range [0,1]. An active region was then identified by examining these probability maps, instead of directly evaluating the travel times of the far-side seismic maps. The concept of “integrated probability” is equivalent to the “seismic strength” defined by the traditional method. Rather than simply search for continuous regions with strong negative travel times, an approach that is hindered by the usual strong noise of the seismic data, the neural network provides a cleaner picture of the locations where an active region is most probable. However, the probability maps usually exhibit some significant values in regions with negative travel time as a result of noise. See, for example, the small spot out of the blue circle in the bottom panel of Fig. 4. The Pi of this region is 12.
The value of Pi is given by the probability found in a continuous region and the area of that region. We analyzed a large set of 4048 artificial far-side maps where Pi ranged between 0 and ≈500 (see top panel of Fig. 5). The artificial cases we analyzed just evaluate the parameter space and include seismic signals whose size and strength are hardly found in the actual Sun. A strong detected far-side active region exhibit a Pi up to 350.
 |
Fig. 5. Analysis of 4048 artificial far-side maps. Panel a: integrated probability of the artificial acoustic source as a function of the seismic strength. The vertical black dotted line is the threshold for the identification of a far-side active region based on its seismic strength, and the horizontal black dashed line is the threshold for the detection of an active region using the neural network. The red solid line shows the integrated probability averaged in bins with a width of 50 in seismic strength. The red dotted lines illustrates the standard deviation of these averages. The rest of the panels shows the dependence of the success rate on the amplitude of the acoustic sources (panel b), their size (panel c), their latitude (panel d), their lifetime (panel e), and the number of seismic maps where the acoustic signal is lost (panel f). In panels b–f, the solid line with asterisks illustrates the success rate of the neural network, the dashed line with asterisks shows the success rate of the traditional method with a standard threshold of S = 400, and the dotted line with asterisks is the success rate of the traditional method with a threshold of S = 65. |
It is necessary to define an unequivocal criterion to decide whether a region with increased probability is claimed as an active region. We chose to define a threshold in the integrated probability as the minimum value for the detection of seismic sources, in the same way as the traditional method establishes a threshold in the seismic strength. The selection of the threshold was based on the evaluation of the artificial set of far-side maps for which we know the exact location of the seismic sources. A value of Pi = 100 proved to be a good compromise between the success in detecting the seismic sources and avoiding the claim of false positives. A false positive was identified when a feature with Pi > 100 was found out of a region of three times the FWHM of the Gaussian perturbation (i.e., out of the blue circle in the example from Fig. 4). With these criteria, 31 false positives were found in the 4048 artificial cases we explored. We note that when the network is applied to real data, false positives can be easily dealt with by discarding the cases where the detection does no appear consistently in successive dates at the same location.
We performed statistics on the performance of the neural network using the set of artificial far-side maps. Figure 5 illustrates the results of the analysis of 4048 artificial cases that differ in the position of the Gaussian perturbations, amplitude, size, lifetime, and number of days with the seismic signal lost. The top panel compares the integrated probability Pi of the sources as given by the network and their seismic strength S. There is a strong positive correlation, as shown by the Pi averaged in bins of 50 in seismic strength (red solid line). The standard deviations of those averaged (red dotted lines) do not show strong variations of the values of S, being slightly higher for lower S. The horizontal dashed line marks a value of Pi = 100, that is, the selected threshold for the detection of seismic sources. The vertical dotted line is the threshold that is currently applied for the detection of far-side active regions (S = 400). These lines divide the domain into four regions. The top right region corresponds to the acoustic sources that are detected by both approaches (32% of the cases). The top left part are the cases that are only detected by the neural network (43%), and the bottom right region are the sources that are detected only by the traditional approach (0%). Finally, the bottom left region includes weak acoustic sources that neither the neural network nor the traditional approach can identify (25%). The acoustic sources analyzed in this figure are just sampling a certain range in phase shift amplitude (−3 to −12 s), size (FWHM = 10−20°), and lifetime or number of days when the acoustic signal is lost (0.5 to more than 5.5 days). We made no effort to reproduce the distribution of seismic signals from active regions in actual observations.
Panels b–f in Fig. 5 compare the performance of the neural network (solid line with asterisks) and the traditional method (dashed line with asterisks) as a function of several parameters. They illustrate the success rate of the methods. For the neural network the success rate is defined as the ratio of the cases identified with Pi > 100 at the known location of the source to the total number of cases. The same definition is applied for the traditional approach, but using S > 400 as the criterion for a positive detection.
Figure 5b shows the success rate as a function of the amplitude of the sources, as given by a set of 1056 artificial cases. The FWHM of all the artificial cases included in the analysis is 15°, and the acoustic sources are present in the 11 consecutive maps that compose each case. The sources differ in their location (longitude and latitude) and A. The traditional approach can detect almost all the acoustic sources with an amplitude above 9 s. However, its success rate is reduced to 50% around A = −7 s, and sources with A below −5.5 s are not detected at all. The neural network exhibits a perfect success rate for all the sources with A stronger than −6.5 s. For A ≈ −5 s, the success rate is 50%, and even some cases with A = −3 s are detected (10% of the cases).
We also evaluated the performance of the neural network in identifying acoustic sources with different sizes. Another set of 1056 artificial cases was constructed, but in this analysis, all of them had the same amplitude A = −5 s and they differed in the FWHM and their location in longitude and latitude. The Gaussian signal was present in the 11 seismic maps we employed for each case. Figure 5c shows the success rate as a function of the size of the acoustic source. The performance of the neural network is again outstanding in comparison with the traditional approach. A FWHM of 14° is required to start detecting some sources with S > 400 in the classical approach, and a success rate of 20% is found for FWHM = 20°. The neural network reaches a higher success rate for acoustic sources with half this size, and delivers an almost total success for sources as small as FWHM = 16°.
Figure 5d illustrates the efficiency of the neural network as a function of the latitude of the sources. The remaining parameters of the set of cases included are the same. Their amplitude is A = −9 s and FWHM = 15°, and in some cases, the signal is absent in some of the individual maps. For these sources, the success rate of the network is around 80%, although it shows some dependence on the latitude. At the solar equator and for latitudes higher than ±20°, the performance of the network is slightly poorer. This is expected because the training set is constructed with actual solar data, and only a few active regions appear out of the activity belts. The network requires a stronger signal to confirm active regions at these latitudes where they barely emerge. The success rate of the neural network does not depend on the longitude of the active region (not shown in Fig. 5), as far as the seismic source is present in all the individual maps we employed for the inference.
In the last two panels, we explore the performance of the neural network when the signal is absent in some of the 11 maps that compose each case (six days of data with a cadence of 12 h). In both cases, the acoustic sources have the same properties (FWHM = 15° and A = −9 s). In Fig. 5e we show the efficiency of our model in detecting active regions whose lifetime is shorter than the six days of data we used as input for the network. The sources are introduced continuously in some of the 11 maps that compose each case, ranging from a lifetime of half a day (one map) to more than five and a half days (all maps). It shows that the neural network can detect almost all the active regions whose lifetime is at least three days, and it can even detect 15% of the active regions than only last one day and a half. The traditional method employs the Doppler data from five days, and the signal from these short-lived active regions is smeared out in these seismic maps. One of the main advantages of the network is the use of series of seismic maps that are computed over 24 h each, allowing us to keep the identity of signals with short lifetimes while enhancing their signature by incorporating multiple days. In Fig. 5f we explore the performance of the network when the seismic signal is lost in a certain number of nonsuccessive maps (as opposed to panel e, where the signal disappears for successive maps). The success rate falls below 50% when no acoustic signal is received for more than three days.
In the previous paragraphs we have discussed the comparison between the performance of the neural network using the selected threshold of Pi = 100 and the traditional approach using a threshold of S = 400, which is the value that is currently employed in standard analyses of far-side seismic maps. This evaluation is conditioned to the selection of the thresholds, and a lower threshold will obviously offer better performance (with an increased risk of false positives). The dotted lines with asterisks in Fig. 5b–f illustrate the success rate obtained from the traditional method but using a threshold of S = 65 (the seismic strength where the red line in Fig. 5a intersects the threshold selected for Pi), instead of the standard S = 400. A comparison of these lines with the neural network shows that the latter is still superior. The neural network exhibits a higher success rate when the seismic signal is absent in some of the dates (panels e and f) and for extended sources (FWHM > 12°) with low amplitude (panels b and c). Further analyses, based on the analysis of observational data, are required to determine the thresholds that optimize both approaches.
4. Application to solar data
We applied our model to actual far-side seismic maps measured between November 2018 and May 2019, out of the period that we employed for training the neural network. The predictions of the network were compared with the inferences of the traditional approach, and when available, with the EUV emission (171 Å passband) in the far-side hemisphere acquired by the STEREO-A spacecraft because magnetized regions exhibit increased brightness in the EUV. STEREO data have previously been employed to test the reliability of far-side seismic maps for detecting strong active regions (Liewer et al. 2014, 2017), and a deep-learning method has been developed to retrieve solar far-side magnetograms from these EUV data (Kim et al. 2019). During this time period, STEREO-A only partially covers the hemisphere that is not visible from the Earth. Table 1 shows a list of the detected far-side active regions. An active region is detected when a feature in the probability map exhibits Pi > 100 and it appears with significant Pi at the same Carrington longitude at least in one other prediction from the neighboring dates. A total of 11 active regions have been detected in that period. The three strongest were also identified by the traditional approach, and their counterpart in EUV emission is found in STEREO data. From the eight active regions that are exclusively detected by the network, the signature of five of them is also verified by STEREO data. The other three cases are detected beyond the field of view (FoV) of STEREO, and no signal is found when they rotate into the region observed by the spacecraft. They may have decayed before they were visible. The features that show Pi > 100 but do not appear in neighboring predictions are considered false positives. Five of them are found in the 353 cases explored (1.4%), which is similar to the percentage of false positives that are expected from the analysis of artificial data.
Summary of the far-side active regions detected in the period 2018 November–2019 May.
Table 1 illustrates several of the properties of the detected regions, including the given name, the date of their first detection, their NOAA designation on the visible side, and the number of days in which they are detected. For the latter, only detections above the thresholds (both for the neural network and the traditional method) are considered. In both approaches the identification can be extended by tracking the same location, even if the signature of the active region is below the threshold. Our results show that in the case of strong active regions (those that are detected by the traditional method), the neural network can identify them significantly earlier. Two of the cases were detected two days in advance, while the third case (NN-2019-004) was beyond the region that is covered by the network and it was identified only half day earlier. This is illustrated in Fig. 6, which shows the temporal evolution of the detection of the active region NN-2019-003. In addition, in all those cases the signal remains longer above the identification threshold for the neural network.
Our model can also detect a significant amount of active regions that are missed by the traditional approach. Figure 7 shows one of these cases (NN-2018-003). At the location of the active region, the seismic map exhibits a slightly negative phase shift. However, its strength is not enough to claim a detection because non-magnetized regions show a similar phase shift (e.g., latitude = 10° and Carrington longitude = 237° in the top left panel). We note that the use of a lower threshold S = 65 in the traditional method, as discussed in the previous section, would lead to a false positive. In contrast, our model unambiguously detects the active region at its correct location, as confirmed by EUV data from STEREO-A.
 |
Fig. 6. Detection of the far-side active region NN-2019-003 (FS-2019-001). Left column: far-side phase-shift maps obtained from 5 days of HMI Doppler velocity data. Bottom left corner of the panel: seismic strength of the strongest feature. Middle column: STEREO 171 Å data. Color contours indicate the active regions detected by the neural network (red) and by the traditional approach (blue). Right column: probability map, obtained as the output of the neural network. Bottom left corner of the panel: integrated probability of the strongest feature. Each row corresponds to a different time, indicated at the top part of the right panels. |
5. Discussion and conclusions
The measurement of the magnetic activity in the far-side hemisphere has multiple applications for solar physics, and specially for space weather forecasting. In the past years, NASA STEREO spacecraft have been monitoring the far side of the Sun, providing among other data, EUV images of this hemisphere. Recently, Kim et al. (2019) have developed a deep-learning method to retrieve solar far-side magnetograms from these EUV data. However, the STEREO spacecraft are currently returning to the Earth side of their orbit, and there are no guarantees that they will be operative ten years from now, when they will be back at the far side, because contact with STEREO-B is already lost. Thus, there are no prospects for using STEREO data to obtain far-side images in the future. In the next years, only the ESA mission Solar Orbiter (to be launched in 2020) will provide direct imaging of the far side, but only during some periods of its orbit. The importance of far-side magnetism for solar studies and space weather predictions means that in the future, telescopes should permanently observe the whole Sun. While we wait for this future to arrive, the only method capable of constantly monitoring the solar far side is helioseismology.
We here developed a new method for detecting far-side active regions in helioseismic data. We trained a neural network using pairs of far-side maps and HMI magnetograms obtained when the helioseismically probed region had rotated into the visible hemisphere6. Our results show that this method reduces the threshold of the required strength of the seismic signal to detect it. We are able to identify smaller active regions, which produce lower shifts in the phase, and also to detect active regions with shorter lifetimes or whose signature is lost in some of the far-side seismic maps. This allows a significant increment in the number of identified far-side active regions.
Previous works have shown the benefits of including the far-side magnetism as input in the forecast of several data of interest for space weather, such as the solar spectral irradiance and the solar wind (Fontenla et al. 2009; Arge et al. 2013). The identification of large active regions days before they rotate into the visible solar hemisphere is also relevant because these regions can generate sudden enhancements in the EUV irradiance at the Earth just after they appear at the eastern limb, and they are also a threat for solar flares.
The analysis of the seismic signatures of far-side active regions has some limitations regarding the inference of the far-side magnetism. The phase shifts produced by active regions and measured by helioseismology is mainly produced by the Wilson depression of the sunspots, which means that they are independent of the magnetic polarity. We might try to infer the magnetic flux, but not the sign of the polarity. It can only be guessed following the Hale law, which correctly predicts polarity in approximately 90% of the cases (Li & Ulrich 2012). However, inferring the magnetic flux is also a challenge. González Hernández et al. (2007) tried to calibrate the magnetic flux of far-side active regions as a function of their seismic signatures. They found a positive correlation (the higher the seismic signal, the higher the magnetic flux), but this correlation is quite poor, which inhibits a proper determination of the far-side magnetic flux based on the measured phase shift. We here avoided this limitation by focusing on determining the probability of the presence of an active region at a certain location of the far-side hemisphere, without associating it with the magnetic flux. Future efforts, exploiting the capabilities of neural networks, are expected to lead to a proper quantification of far-side magnetic flux based on the analysis of seismic data.
An obvious improvement on our approach is to completely overcome the use of seismic maps and work directly with Doppler maps. This approach might lead to the development of a data-driven far-side helioseismological method that might better exploit the information encoded in the Doppler maps. We anticipate that this would require an architecture that is able to deal with very long time series. The seismic maps we used were obtained with Doppler information with a cadence of 45 s, which means 1920 Doppler measurements per day. A possibility worth exploring is the use of recurrent neural networks with attention mechanisms, like those used in neural machine language translation (Bahdanau et al. 2014).
See, e.g., the curation on https://bit.ly/2ll0dQI
Available at ftp://ftp.swpc.noaa.gov/pub/warehouse
Publicly available at http://solarmuri.ssl.berkeley.edu/~welsch/public/software/YAFTA/
The neural network can be downloaded from the repository https://github.com/aasensio/farside
Acknowledgments
Financial support from the State Research Agency (AEI) of the Spanish Ministry of Science, Innovation and Universities (MCIU) and the European Regional Development Fund (FEDER) under grant with reference PGC2018-097611-A-I00 is gratefully acknowledged. This research has made use of NASA’s Astrophysics Data System Bibliographic Services. We acknowledge the community effort devoted to the development of the following open-source packages that were used in this work: numpy (numpy.org), matplotlib (matplotlib.org), astropy (astropy.org), h5py (h5py.org), scipy (scipy.org), and PyTorch (pytorch.org).
References
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Arge, C. N., Henney, C. J., Hernandez, I. G., et al. 2013, Sol. Wind, 13, 1539 [Google Scholar]
- Asensio Ramos, A., de la Cruz Rodríguez, J., & Pastor Yabar, A. 2018, A&A, 620, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bahdanau, D., Cho, K., & Bengio, Y. 2014, ArXiv e-prints [arXiv:1409.0473] [Google Scholar]
- Braun, D. C., & Birch, A. C. 2008, Sol. Phys., 251, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Braun, D. C., & Lindsey, C. 2001, ApJ, 560, L189 [NASA ADS] [CrossRef] [Google Scholar]
- Braun, D. C., Duvall, Jr., T. L., Labonte, B. J., et al. 1992, ApJ, 391, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J. 2002, Rev. Mod. Phys., 74, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Duvall, Jr., T. L., & Kosovichev, A. G. 2001, in Recent Insights into the Physics of the Sun and Heliosphere: Highlights from SOHO and Other Space Missions, eds. P.Brekke, B.Fleck, & J. B.Gurman, IAU Symp., 203, 159 [NASA ADS] [Google Scholar]
- Felipe, T., Braun, D. C., & Birch, A. C. 2017, A&A, 604, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontenla, J. M., Quémerais, E., González Hernández, I., Lindsey, C., & Haberreiter, M. 2009, AdSpR, 44, 457 [NASA ADS] [Google Scholar]
- Gizon, L., & Birch, A. C. 2005, Liv. Rev. Sol. Phys., 2, 6 [Google Scholar]
- González Hernández, I., Hill, F., & Lindsey, C. 2007, ApJ, 669, 1382 [NASA ADS] [CrossRef] [Google Scholar]
- Goodfellow, I., Bengio, Y., & Courville, A. 2016, Deep Learning (MIT Press), http://www.deeplearningbook.org [Google Scholar]
- Hausen, R., & Robertson, B. 2019, AASJ, submitted [arXiv:1906.11248] [Google Scholar]
- Huertas-Company, M., Gravet, R., Cabrera-Vives, G., et al. 2015, ApJS, 221, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ilonidis, S., Zhao, J., & Hartlep, T. 2009, Sol. Phys., 258, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Ioffe, S., & Szegedy, C. 2015, in Proceedings of the 32nd International Conference on Machine Learning (ICML-15), eds. D. Blei, & F. Bach, JMLR Workshop and Conference Proceedings, 448 [Google Scholar]
- Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open Source Scientific Tools for Python [Google Scholar]
- Kim, T., Park, E., Lee, H., et al. 2019, Nat. Astron., 3, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Kingma, D. P., & Ba, J. 2014, ArXiv e-prints [arXiv:1412.6980] [Google Scholar]
- Koziol, Q., & Robinson, D. 2018, HDF5, [Computer Software] https://doi.org/10.11578/dc.20180330.1 [Google Scholar]
- Li, J., & Ulrich, R. K. 2012, ApJ, 758, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Liewer, P. C., González Hernández, I., Hall, J. R., Lindsey, C., & Lin, X. 2014, Sol. Phys., 289, 3617 [Google Scholar]
- Liewer, P. C., Qiu, J., & Lindsey, C. 2017, Sol. Phys., 292, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Lindsey, C., & Braun, D. C. 1990, Sol. Phys., 126, 101 [Google Scholar]
- Lindsey, C., & Braun, D. C. 2000, Science, 287, 1799 [NASA ADS] [CrossRef] [Google Scholar]
- Lindsey, C., & Braun, D. 2017, Space Weather, 15, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Lindsey, C., Cally, P. S., & Rempel, M. 2010, ApJ, 719, 1144 [NASA ADS] [CrossRef] [Google Scholar]
- Linker, J. A., Caplan, R. M., Downs, C., et al. 2017, ApJ, 848, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Nair, V., & Hinton, G. E. 2010, in Proceedings of the 27thInternational Conference on Machine Learning (ICML-10), June 21–24, 2010, Haifa, Israel, 807 [Google Scholar]
- Osborne, C. M. J., Armstrong, J. A., & Fletcher, L. 2019, ApJ, 873, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Paszke, A., Gross, S., Chintala, S., et al. 2017, in NIPS Autodiff Workshop [Google Scholar]
- Ronneberger, O., Fischer, P., & Brox, T. 2015, ArXiv e-prints [arXiv:1505.04597] [Google Scholar]
- Schawinski, K., Zhang, C., Zhang, H., Fowler, L., & Santhanam, G. K. 2017, MNRAS, 467, L110 [NASA ADS] [Google Scholar]
- Schrijver, C. J., & De Rosa, M. L. 2003, Sol. Phys., 212, 165 [Google Scholar]
- Silburt, A., Ali-Dib, M., Zhu, C., et al. 2019, Icarus, 317, 27 [NASA ADS] [CrossRef] [Google Scholar]
- van der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
- Zhao, J. 2007, ApJ, 664, L139 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Summary of the far-side active regions detected in the period 2018 November–2019 May.
All Figures
 |
Fig. 1. Example of one of the elements from the training set. Panels in the top row show 11 far-side seismic maps, each of them obtained from the analysis of 24 h of HMI Doppler data. The horizontal axis is the longitude (a total of 120°) and the vertical axis is the latitude (between −72° and 72°). The label above the panels indicates the number of days prior to the time t when the corresponding magnetogram was acquired (in this example, t is 2015 December 10 at 12:00 UT). Bottom row: magnetograms we used as a proxy for the presence of active regions. Left panel: original magnetogram in heliospheric coordinates, middle panel: magnetogram after active regions that emerged in the near side are removed and after a Gaussian smoothing was applied, and right panel: binary map in which a value of 1 indicates the presence of an active region in the locations whose magnetic flux in the smoothed magnetogram is above the selected threshold. Red contours in the bottom left panel delimit the regions where the binary map is 1. The neural network is trained by associating the 11 far-side seismic maps (top row) with the binary map. |
| In the text | |
 |
Fig. 2. U-net architecture. The vertical extent of the blocks indicates the size of the image, and the numbers above each block shows the number of channels. |
| In the text | |
 |
Fig. 3. Artificial seismic maps for an acoustic source with A = −9 s, FWHM = 15°, and a latitude of 15°. Time increases from panel a to panel k, with a temporal step of 12 h. |
| In the text | |
 |
Fig. 4. Top panel: five-day average of the phase shift for the artificial case illustrated in Fig. 3. The red contour delimits the region where the phase shift exceeds 0.085 rads. The strength of the acoustic source is shown in the bottom left corner. Bottom panel: probability map of the artificial active region illustrated in Fig. 3, as retrieved from the application of the neural network. The integrated probability Pi of the feature inside the blue circle is shown in the bottom left corner. In both panels the blue circle is centered at the location of the acoustic source, with a diameter of three times its FWHM. |
| In the text | |
 |
Fig. 5. Analysis of 4048 artificial far-side maps. Panel a: integrated probability of the artificial acoustic source as a function of the seismic strength. The vertical black dotted line is the threshold for the identification of a far-side active region based on its seismic strength, and the horizontal black dashed line is the threshold for the detection of an active region using the neural network. The red solid line shows the integrated probability averaged in bins with a width of 50 in seismic strength. The red dotted lines illustrates the standard deviation of these averages. The rest of the panels shows the dependence of the success rate on the amplitude of the acoustic sources (panel b), their size (panel c), their latitude (panel d), their lifetime (panel e), and the number of seismic maps where the acoustic signal is lost (panel f). In panels b–f, the solid line with asterisks illustrates the success rate of the neural network, the dashed line with asterisks shows the success rate of the traditional method with a standard threshold of S = 400, and the dotted line with asterisks is the success rate of the traditional method with a threshold of S = 65. |
| In the text | |
 |
Fig. 6. Detection of the far-side active region NN-2019-003 (FS-2019-001). Left column: far-side phase-shift maps obtained from 5 days of HMI Doppler velocity data. Bottom left corner of the panel: seismic strength of the strongest feature. Middle column: STEREO 171 Å data. Color contours indicate the active regions detected by the neural network (red) and by the traditional approach (blue). Right column: probability map, obtained as the output of the neural network. Bottom left corner of the panel: integrated probability of the strongest feature. Each row corresponds to a different time, indicated at the top part of the right panels. |
| In the text | |
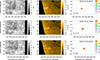 |
Fig. 7. Detection of the far-side active region NN-2018-003. Same description as Fig. 6. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.