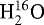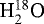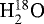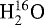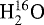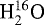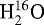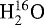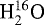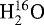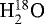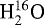EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 632 (December 2019) A&A, 632 (2019) A8 Full HTML
Open Access
Issue
A&A
Volume 632, December 2019
Article Number A8
Number of page(s) 18
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201935402
Published online 22 November 2019

© T. Putaud et al. 2019

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

Photon-dominated regions (PDRs) are surface layers of molecular clouds irradiated by a strong UV photon flux, such as those present in star-forming regions. Studies of the physical and chemical properties of molecules in such regions are of great interest for understanding the feedback of young stars on their surrounding medium.

The Orion Molecular Cloud 1 (OMC-1) contains two embedded star-forming regions: Orion BN/KL and Orion South, as well as a group of young massive stars known as the Trapezium Cluster. The Trapezium, and in particular the brightest O6 type star Θ1 Ori C, has irradiated the surrounding molecular cloud creating an Hii region, which is bordered by the Orion Bar on its southeastern side and by the Orion Ridge on its western side (Rodriguez-Franco et al. 1998). Close to Earth (414 pc; Menten et al. 2007) and with a nearly edge-on geometry (Hogerheijde et al. 1995; Jansen et al. 1995) explained by the blister model (see for example Wen & O’Dell 1995 and references therein), the Orion Bar is an excellent place to test PDR models (Tielens & Hollenbach 1985; Sternberg & Dalgarno 1989; Le Petit et al. 2006; Hollenbach et al. 2009; Andree-Labsch et al. 2017).

The Orion Bar has been observed extensively in multiple gas tracers (Fuente et al. 1996; Larsson et al. 2003; Leurini et al. 2006; van der Tak et al. 2012, 2013; Cuadrado et al. 2015, 2017; Nagy et al. 2017; Joblin et al. 2018). Previous studies have led to a UV flux of G0 = 1−4 × 104 in Habing units (Tielens & Hollenbach 1985; Marconi et al. 1998) impinging upon a molecular cloud with a mean H2 density of about 5 × 104 cm−3 (Wyrowski et al. 1997) and a kinetic temperature of 85 K (Hogerheijde et al. 1995). A model of the Orion Bar with a clumpy medium, based on high-density clumps (nH = 106−107 cm−3) embedded in an interclump medium (nH = 5 × 104−105 cm−3), was proposed to explain the following: the excitation of atomic lines, some excited CO lines, and warm H2 observations (Parmar et al. 1991; Tauber et al. 1994; van der Werf et al. 1996). The presence of high-density clumps was also suggested by observationsof H2CO, HCO+, and HCN (Hogerheijde et al. 1995; Young Owl et al. 2000; Lis & Schilke 2003). However, the clumpy model is challenged by the very high resolution observations provided by the Atacama Large Millimeter/submillimeter Array (ALMA) radiotelescope (Goicoechea et al. 2016, 2017), which show that, to the first order, the structure of the PDR is a compressed layer at high-pressure where a warm chemistry takes place, leading to the presence of molecules such as SH+ and high-J excited CO (Joblin et al. 2018). This structure is also observed in other PDRs, such as Trumpler 14 in the Carina nebula (Wu et al. 2018). High-density structures exist inside the PDR, as seen in OH (Goicoechea et al. 2011; Parikka et al. 2017) and H13CN maps (Lis & Schilke 2003), as well as in ALMA maps (Goicoechea et al. 2016). The high-pressure layer can be interpreted by the photo-evaporation effect as explained by Bron et al. (2018) with the PDR hydrodynamical code Hydra.

An important tracer for studying the physical and chemical evolution of the interstellar medium (ISM) is H2O. This molecule (like other hydrides) has two identical protons and exists in two nuclear configurations, called nuclear spin isomers, where the hydrogen nuclear spins are either parallel (ortho) or antiparallel (para). At the thermal equilibrium, the ortho-to-para ratio (OPR) of gas-phase water molecules is determined by the kinetic temperature of the gas. Some non-thermal equilibrium OPRs have been reported in different regions (Hogerheijde et al. 2011; Lis et al. 2013; Choi et al. 2014). In particular, Choi et al. (2014) derived a very low OPR of 0.1–0.5 in the Orion Bar, based on observations of two 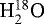emission lines. With such a low OPR, the so-called spin temperature does not exceed 10 K, which is much lower than the gas kinetic temperature in this region.

To explain the discrepancy between kinetic and spin temperatures, it was suggested that the spin temperature might reflect the temperature of the grains at the time the molecules formed. Indeed, a PDR model which considers oxygen grain chemistry has shown that the photodesorption of water molecules formed on grains could be an efficient pathway for gas-phase water production (Hollenbach et al. 2009). After desorption from grains, the non-thermal equilibrium OPR could have been preserved due to the very low pressure of the ISM (Cacciani et al. 2012). However, a recent laboratory study of water molecules photodesorbed from cold surfaces using a UV laser produced a gas-phase water with an OPR in agreement with the high thermal equilibrium value of three (Hama et al. 2016).

Further studies of the impact of grains on the abundance and quantum state of gas-phase molecules have yet to be carried out. However, the reanalysis of the observational data, using more sophisticated models, has sometimes modified the reported OPR of hydride molecules in the ISM. Better calibrated observational data and improved computational models have indeed shown that the low OPR value measured in TW Hydrae protoplanetary disk (Hogerheijde et al. 2011) is very model-dependent (Salinas et al. 2016). Furthermore, the observations are consistent, within the observational uncertainties, with the high-temperature equilibrium value.

We present a new analysis of the 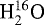and 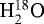lines observed toward the Orion Bar with Herschel/HIFI, which are reduced using the latest pipeline and with the latest calibration (Mueller et al. 2014). Careful corrections are applied to the spectra to account for the spatial offsets and beam coupling effects. The Meudon PDR code (Le Petit et al. 2006) is used to constrain the physical conditions inside the Orion Bar and derive the gas-phase water OPR. The impact of grain processes, such as water adsorption and thermal or photo-induced desorption, is also investigated.

2 Observations

Observations of the Orion Bar discussed here were carried out at the CO+ peak position (Stoerzer et al. 1995)(α2000 = 05h35m20.61s, δ2000 = −05°25′14.0′′) as part of the HEXOS1 (Bergin et al. 2010)guaranteed time key program (GTKP). The Heterodyne Instrument for the Far-Infrared (HIFI, de Graauw et al. 2010) aboard the Herschel Space Observatory (Pilbratt et al. 2010), operating with the wide-band spectrometer (WBS) as a backend, provided spectra at 1.1 MHz resolution for H and V orthogonal polarizations. The data were reduced with the Herschel Interactive Processing Environement (HIPE, Ott 2010) version 14.1.0. Within the whole HIFI’s frequency range (480–1250 GHz and 1410–1910 GHz), seven rotational emission lines of 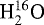and one of 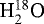were detected from March 2011 to October 2011, either in load chop, fast dual beam switch (DBS), or frequency switch observing mode. The upper limit of the ground state para 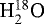line was also included in the analysis. Observations used in this article are listed in Table 1. Most of these lines were already presented in an extensive spectral survey carried out by Nagy et al. (2017).

In addition to the spectral scan observations, nine on-the-fly (OTF) HIFI maps using the WBS as a backend were also analyzed (see Table 1). Within the HEXOS GTKP (Bergin et al. 2010), Habart (2011) proposal, and calibration programs2, observationswere obtained from February 2010 to September 2012. The total field of view is roughly 50′′ × 100′′ (except for 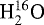110 − 101 and 212 − 101 where only a 100′′ perpendicular strip through the Bar was performed) with a position angle perpendicular to the Bar. The maps were regridded using the GILDAS3 software leading to a spatial resolution typically 5% lower than the Herschel telescope half-power beam width (HPBW). All water spectra and water maps are shown in Appendix A.

Further calibration corrections must be applied to the data. First, the antenna temperature on the 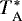scale, given by the pipeline, should be corrected by the ratio of the forward efficiency (ηl = 0.96, Roelfsema et al. 2012) and the main-beam efficiency (ηmb) to produce spectra on the main-beam brightness temperature scale Tmb (Mueller et al. 2014). 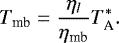(1)

This correction only considers the main detection lobe of the telescope. The latest values of ηmb and the HPBW, derived from Mars observations and complete optical model of the Herschel telescope (Mueller et al. 2014; Shipman et al. 2017), were used in the analysis. These numbers differ up to 20% from the previous estimates assuming a simplified Gaussian beam shape (Roelfsema et al. 2012). The exact values used for each H and V observations are listed in Table A.1.

Furthermore, owing to the variation in the HPBW with frequency, the beam coupling correction has to be carefully considered, as discussed below. To quantify this effect, three high angular resolution CO maps were convolved to the beam widths corresponding to the various water transitions. The beam coupling factor Ω is defined as the ratio between the convolved intensity at the targeted coordinates and the maximum intensity toward the Bar at high resolution. The CO 1−0 map is part of the CARMA-NRO Orion Survey (Kong et al. 2018) and was obtained by combining the CARMA4 interferometric data with NRO455 single-dish observations leading to a resolution of 9′′ over a 2° × 2° field of view. The 12CO 6− 5 and 13CO 6− 5 maps were obtained using the Caltech Submillimeter Observatory (CSO; Lis & Schilke 2003) at 11′′ resolution and cover respectively a 3′ × 4′ and 3′ × 2.5′ regions.

Table 1

Observations used for the analysis of water line emission in the Orion Bar.

3 Results

Integrated line intensities of the water spectra shown in Fig. 1 are given in Table 2. On average, the integration was performed from a local standard of rest velocity (VLSR) of 7.7 to 13.5 km s−1. Precise integration ranges for each line are listed in Table A.1. Linear baseline subtraction was carefully applied except for frequency switch observation mode where a fourth order polynomial baseline was used because of residual standing waves. The uncertainties of the integrated line intensities, in units of K km s−1, are computed as 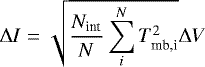(2)

where the summation runs over all the channels N outside the line integration velocity range, Nint is the number of channels inside the integration velocity range and ΔV is the width ofa velocity channel.

The average intensities of the H and V polarizations agree with the values previously reported (Nagy et al. 2017; Choi 2015), but are a factor of two higher than the intensities derived from SPIRE observations averaged along the Bar (Habart et al. 2010). The ortho 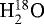line intensity is also very close to the one derived by Choi et al. (2014). However the para 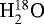line (a 4.7σ detection in Choi et al. 2014) is not clearly detected in our data set given the noise level in the spectrum.

3.1 Line profiles

Figure 1 shows the line profiles of the eight detected lines, and the spectrum in the para 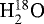111 −000 line region. Some of the lines have a profile inconsistent with a single Gaussian, in particular the 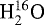ground state lines (111−000, 110 −101, and 212 −101) exhibit two velocity components around 9.5 and 11.5 km s−1. Previous studies of tracers arising close to the CO+ peak reported velocity components from the Orion Bar at 10.6 km s−1, as well as features from the Orion Ridge at 9 km s−1 (van der Tak et al. 2013; Goicoechea et al. 2015; Nagy et al. 2017; Cuadrado et al. 2017). Moreover lines between VLSR = 8 km s−1 and VLSR = 9 km s−1 were attributed to OMC-1 as suggested by IRAM 30 m telescope observations of small hydrocarbons (Cuadrado et al. 2015). Strips across the Bar have shown that CH+ peak velocity shifts from 9 km s−1 in front of the Bar to 11 km s−1 behind (Parikka et al. 2017).

In the case of water emission, the two-component line profiles are more likely explained by self-absorption in the low-energy lines, which are expected to be optically thicker than the excited lines (Choi 2015). Such an explanation is supported by the fact that excited lines exhibit a single component at an intermediate velocity, close to the expected velocity of the Bar (Nagy et al. 2017). The self-absorption dip also matches this velocity. Furthermore, a full width at half maximum (FWHM) of ~ 4.5 km s−1 is measured for the lines showing a self-absorption dip in good agreement with optically thick lines in the Orion Bar (Hogerheijde et al. 1995; Nagy et al. 2017) and ~ 2.5 km s−1 for the other ones which is close to the typical line width observed in this region (Choi et al. 2014; Cuadrado et al. 2015; Nagy et al. 2017). The FWHM line widths are reported in Table A.1.

Nevertheless, CO lines (Joblin et al. 2018) show a weak asymmetry at low velocities that could represent signal coming from the Orion Ridge or OMC-1. Assuming a peak velocity of 10.6 km s−1 and considering a symmetric line profile, velocity integration range is derived for each line from the half width measured at high velocity (see Table A.1). Even if a possible contamination of the line by surrounding features could still lead to an overestimate of the intensity, the resulting intensities are our best-estimates, because the optically thick character of the lines makes a fitting method unreliable.

Table 2

Observed intensities of water lines toward the Orion Bar and their correction for the beam coupling factor.

thumbnail Fig. 1

Averaged spectra of and lines toward the Orion Bar on the main-beam brightness temperature scale, not corrected for the beam coupling factor. The gray areas represent the velocity integration range. The blue dash-dotted line and red dashed line are the expected velocity components from Orion Ridge (9.0 km s−1) and Orion Bar (10.6 km s−1). lines were multiplied by a factor of 5.

3.2 Beam dilution

The observed water lines cover a wide range of frequencies, leading to a significant variation in the Herschel telescope beam width. Extreme beam sizes at the spectral scan coordinates are shown as white circles in the 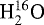202 −111 map in Fig. 2. In this map, corresponding to an intermediate frequency, the maximum HIFI beam size is larger than the spatial width of the Bar. Thus the coupling of the beam to the water-emitting region has to be considered when comparing the observed line intensities at different frequencies with model predictions. In addition, Fig. 2 clearly shows that water emission peaks deeper in the molecular cloud with respect to the CO+ peak position. Thus the observations were not centered on the water emission peak in the Orion Bar and only a fraction of the emission is included in the beam.

The offset effect can be easily taken into account using water maps by comparing the intensity at the targeted coordinates with the mean intensity along the Bar. This gives a rough estimate of the beam coupling factor of about 0.8. Nevertheless, applying this method does not consider the fact that the maximum intensity is already impacted by the size of the beam, in particular for low frequency transitions for which the HPBW of the Herschel telescope is the largest.

To retrieve the maximal intensity of each line in the Bar, the effect of the pointing offset and the beam width variations is investigated from high resolution maps. The intensity along the Bar at the full resolution is derived and compared to the intensity at the observed coordinates after convolution at the HPBW corresponding to the line frequency. Three CO maps were used to derive the beam coupling factor. These maps have a higher resolution than the most resolved water maps (9′′ for 12CO 1− 0, Kong et al. 2018 and 11′′ for 12CO 6− 5 and 13CO 6− 5, Lis & Schilke 2003) and are large enough to be convolved without edge effect. Moreover, they span different excitation conditions and different spatial extensions. Indeed, 12CO emission is slightly wider than the water one, whereas 13CO peaks slightly deeper into the cloud (4′′, see 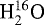111 −000 and 212 −101 maps in Fig. A.5). So averaging the beam coupling factors derived from each CO maps should give a good estimate of its value and its uncertainty (Table. 2). We note that the 4′′ offset between 13CO and water emission corresponds to a typical pointing error of the CSO telescope at this high frequency. Since only the spatial extension of the emission is considered in the estimation of the beam coupling factor, the 13CO map was shifted toward the ionization front by 4′′ to match the water emission, in order not to add artificial bias due to the position.

The beam coupling factors adopted for each observed transitions are given in Table A.1 together with our best-estimates for the intensity of each lines. The beam coupling factors are close to 0.8 whereas the values retrieved for high-J CO lines assuming a 2′′ filament for the Bar range from 0.07 to 0.23 (Joblin et al. 2018). Each H and V spectrum is corrected separately for beam coupling to account for a pointing offset between the two polarizations and the resulting spectra are then averaged with root mean square (rms) weighting: 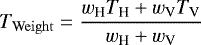(3)

where TH/V is the main-beam brightness temperature for H and V polarizations, corrected for the beam coupling factor, and wH/V the weight for each polarizations determined by 1∕σ2, with σ the rms noise measured outside the line window. The averaged spectra without beam coupling corrections are shown in Fig. 1 and the line intensities are listed in Table 2. The final uncertainties for the corrected intensities are computed as the quadratic sum of the spectral rms related to the signal-to-noise ratio (S/N), the absolute intensity calibration error (Teyssier et al. 2017), the main-beam coefficient uncertainty (Mueller et al. 2014), and the beam coupling factor uncertainty.

thumbnail Fig. 2

202 − 111 emission map at 988 GHz integrated from 7.7 to 13.5 km s−1. Contours represent the emission of 13CO 6− 5 at 95, 90, 75 and 50% of the maximum intensity, integrated from 2 to 17 km s−1, observed with the CSO at a resolution of 11′′. Black star marks the CO+ peak position, white circles show the HIFI HPBW at the extreme frequencies, black and magenta disks show the CSO and 988 GHz HIFI beam width (see Table 1). FUV field from the Trapezium cluster comes from the upper right corner.

4 Analysis

To model the water vapor emission in the Orion Bar, we use the Meudon PDR code6 (Le Petit et al. 2006) to fit the observed line intensities. The Meudon PDR code simulates a stationary plane-parallel slab of gas and dust and computes the radiative transfer along a line-of-siglht. At each position within the cloud, thermal and chemical balances are computed, as well as non-local thermodynamic equilibrium (non-LTE) level populations. Level populations and resulting line intensities are computed considering collisional and radiative processes, as well as chemical formation and destruction in various rotational levels. For radiative processes, the code takes into account non-local pumping bythe continuum (background and dust emission) and line emission, as explained in Gonzalez Garcia et al. (2008).

The incoming UV radiation field is based on the interstellar radiation field (ISRF; Mathis et al. 1983), scaled by a multiplicative factor G0. Mathis UV radiation field is about 1.3 factor as high as Habing one (Habing 1968) in the spectral range of 91.2–111 nm (Wu et al. 2018).

In the currently released version of the code (1.5.2), the formation of water molecules only includes gas-phase chemistry. The nuclear spin distribution of the water molecules formed follows the kinetic temperature at each point within the cloud with a non-thermal equilibrium rotational excitation.

4.1 Gas-phase chemistry model

Investigation of the input parameters of the Meudon PDR code such as the inclination angle, cloud depth, UV radiation field intensity, and density or thermal pressure (considering either isochoric or isobaric models) is performed by using the Interstellar Medium Database7 (ISMDB) to compare the observed line intensities with grids of model predictions (precomputed with the Meudon PDR code 1.5.2 and available online). Intensities given by the ISMDB (in cgs units) are compared with observations using the following conversion: 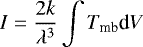(4)

with k the Boltzmann constant (erg K−1) and λ the wavelength (cm). Intensities in cgs units are given in Table 4.

As already shown using more than twenty lines emitted by nine species, the line emission at the edge of the Orion Bar is better explained by an isobaric model than by a constant density model (Joblin et al. 2018). This is understandable because a steep density and temperature gradient is expected to exist at the edge of a UV-illuminated molecular cloud (see Figs. 4 and 5). This agrees with other studies of the Orion Bar (Marconi et al. 1998; Allers et al. 2005), as well as in the northwest PDR in NGC 7023 (Joblin et al. 2018) and Carina PDR (Wu et al. 2018). A theoretical explanation, based on the photo-evaporation process, wasprovided by Bron et al. (2018). Consequently, an isobaric model is adopted.

To reproduce the nearly edge-on geometry of the Bar (Wen & O’Dell 1995; Hogerheijde et al. 1995; Jansen et al. 1995; Walmsley et al. 2000), the maximum viewing angle of 60° accepted by the code is adopted. This angle is defined as the angle between the normal to the ionization front and the line-of-sight, meaning that a viewing angle of 90° corresponds to an edge-on PDR. Using an isobaric model, the best-fit to our best-estimate intensities is obtained for a cloud depth corresponding to a visual extinction of , a UV field of G0 = 3.5 × 104−8 × 104 in Mathis units and a thermal pressure Pth = 6 × 107−2 × 108K cm−3. The 211−202 and 202 −111 line intensities require a UV field 40% lower (G0 = 3 × 104 in Mathis units) to match the observations, whereas the 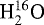212 −101 line requiresa higher pressure by a factor of five. It is worth noting that the intensity derived for this line is 20% higher than the one reported by Nagy et al. (2017) measured from a short integration-time observation8. 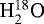lines are not used in the fitting procedure because the online ISMDB does not include 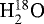predictions. Input parameters for the ISMDB model of the Meudon PDR code are listed in Table 3.

The best-fit parameters obtained for the observed 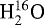intensities are close to those derived from high-J CO lines (Joblin et al. 2018) or small hydrocarbons and complex organic molecules (COM) emission (Cuadrado et al. 2015, 2017). Small deviations from the high-J CO line fit could be explained by the fact that water emits ~5′′ deeper in the cloud than CO (Parikka et al. 2017). However these deviations may also result from the data reduction method applied. Main-beam efficiencies reported by Roelfsema et al. (2012) were used by Joblin et al. (2018) along with a mean value between the antenna temperature and the main-beam brightness temperature to deal with a spatial emission in-between point-source and extended source (Ossenkopf et al. 2013). This method could lead to an underestimate of the main-beam brightness temperature by a factor close to 1.3. Moreover specific parameters of the code have been optimized for high-J CO fitting. In particular, the grain size distribution was adapted to model the extinction curve toward Θ1 Ori C (Fitzpatrick & Massa 1990; Marconi et al. 1998; Joblin et al. 2018), and a scaling factor was applied to correct the bias for the assumed geometry of the Bar, such as the beam coupling factor and the viewing angle, and get closer to an edge-on model.

The stand-alone version of the Meudon PDR code (1.5.2) was then used with the best-fit parameters derived from the water line observations to compute the intensities of water transitions and in particular those of 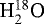. This is performed by extending the gas-phase 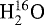chemistry to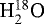, introducing the possible 18O fractionation reactions (Loison et al. 2019). The radiative excitation processes involving have been implemented from the HITRAN20169 database (Gordon et al. 2017). The 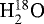de-excitation collisional rates are assumed to be identical to those of 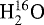. The upward collisional excitation rates of 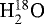are computed by introducing the appopriate energy defect for 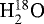and considering the different energy order involving highly-J excited rotational levels. Collisional rates for rotational excitation of 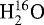by He are taken from Green et al. (1993) for which analytical temperature dependence was derived by Gonzalez Garcia et al. (2008). The collisional rates due to H2 are computed from these values by introducing the relative reduced mass factor. The computed intensities are given in Table 4 and compared with the corrected observed line intensities in Fig. 3.

The observed intensities are quite well reproduced by the Meudon PDR code with these parameters. Lines outside the observed uncertainty range are those mentioned above (212− 101, 202 −111, and 211 −202) and the 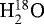ortho ground state line, which is clearly overestimated by the model. The value obtained for the 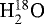111 −000 para line agrees with the upper limit observed.

In the Meudon PDR code, water vapor is produced with nuclear spin populations in agreement with the local kinetic temperature. The computed kinetic temperature varies from 2000 K close to the ionization front down to 30 K in the deepest part of the cloud (see Fig. 4). The OPR of water as a function of the depth into the cloud is shown in Fig. 4. To obtain the mean OPR of the water molecules along the line-of-sight, the OPR is averaged along the maximum density region of water vapor. Figure 5 shows that the density of gas-phase water peaks between AV = 5 and AV = 10. Thus the gas-phase water-emitting region is characterized by a temperature of (34.0 ± 0.5) K, implying an OPR of 2.7 ± 0.1. Computing the OPR with the ratio of ortho and para column densities of gas-phase water in the cloud up to AV = 15 leads to a value in good agreement within the uncertainty range. However this value is clearly higher than the value of 0.1–0.5 derived by Choi et al. (2014) from 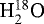observations.

The OPR uncertainty derived above only considers the predicted OPR variations through the cloud. To take into account the uncertainty due to discrepancies between the observations and the predicted intensities, models at the boundary UV field and thermal pressure regions giving a good fit lead to an OPR uncertainty of 0.1.

Table 3

Best-fit input parameters of the Meudon PDR code for the corrected intensities.

Table 4

Intensities of water lines toward the Orion Bar corrected for the beam coupling factor, in erg cm−2 s−1 sr−1, and predicted intensities from the Meudon PDR code using input parameters in Table 3 for the pure gas-phase chemsitry ISMDB model and the adsorption and desorption optimized model with H2 internal energy.

thumbnail Fig. 3

Comparison between observed intensities and the ones predicted by the pure gas-phase chemistry ISMDB model and the adsorption and desorption optimized model with H2 internal energy (Table 3). Bottom panel: relative difference between predictions and observations.

4.2 Adsorption and desorption model

We stress that gas-phase water population and spin distribution in the currently released version of the Meudon PDR code is only governed by gas-phase chemistry and thermal equilibrium. The presence of grains in the model only affects the thermal balance through photoelectric heating, while attenuating the UV flux (Le Petit et al. 2006) and catalysing the formation of H2 via surface chemistry (Le Petit et al. 2009; Le Bourlot et al. 2012). The need of surface chemistry was less important in previous studies, for which tracers that appear in a warmer medium (Fig. 6) were used (Cuadrado et al. 2015, 2017; Joblin et al. 2018). Up to AV = 3, Esplugues et al. (2016) have shown, with a PDR model considering adsorption and desorption processes and surface chemistry, that the gas-phase abundances of several species, such as H2 O, H2 CO, and CH3OH, are independentof the dust surface chemistry. Indeed, close to the ionization front, the high kinetic temperature of the gas and grains (see Fig. 7) is not suitable for long time residence of these molecules on grains (Hollenbach et al. 2009). However, for water molecules, surface chemistry could have an important role to play. Indeed the oxygen surface chemistry, introduced in the Hollenbach et al. (2009) PDR model, appears to dominate the gas-phase water production. Figures 4 and 5 show that the gas-phase water maximum density region from AV = 5–10 corresponds to a medium with a gas temperature below 40 K. In addition, the water vapor abundance remains relatively high for AV > 10, where a strong freeze-out of water molecules on grains is expected (Hollenbach et al. 2009; Esplugues et al. 2016). Thus the line emission of water molecules could be strongly modified by their interactions with cold grains.

The implementation of state-of-the-art surface chemistry processes in the Meudon PDR code is in progress. For this work, we have added adsorption and desorption processes of water. The adsorption is governed by a sticking coefficient proportionalto the inverse of the square root of the temperature for a kinetic temperature higher than 10 K and equals to 1 otherwise. Two desorption processes were considered. The thermal desorption is dependent on a binding energy of 5600 K (Garrod et al. 2009; Wakelam et al. 2017) and the photodesorption is related to a yield of 5 × 10−4 molecules per incident UV photon (Öberg et al. 2009).

Using our ISMDB best-fit parameters and adsorption and desorption processes, the overall water density was computed with the Meudon PDR code. Depletion of gas-phase water is clearly observed for AV > 5 when the adsorption process is included, in good agreement with Hollenbach et al. (2009). As expected, the depletion of water molecules decreases the computed intensity of water lines with an accentuated effect for the excited lines. The depletion is sufficiently significant that very high UV flux and thermal pressure are needed to match the observational data using regular parameters in the Meudon PDR code.

Gas-phase water is mainly formed by two processes (van Dishoeck et al. 2013 and references therein) represented by each water density maximum in Fig. 5. The first peak around AV = 1 is the result of the balance between water formation via OH and photodissociation.

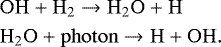
Then the gas-phase OH abundance decreases and the photodissociation reduces the gas-phase water density. From AV = 3 to AV = 5, the increase in water vapor abundance is caused by the recombination of H3 O+ with electrons, still softened by the photodissociation.

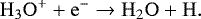
Adsorption and desorption processes compete with H3O+ recombination leading to an increase in the water ice abundance up to AV = 10 as represented in Fig. 7. Eventually, the electronic recombination is weakened and the gas-phase water abundance is reduced.

Without water surface chemistry, grains act as water trap which explains the discrepancy between observed and computed intensities. To reproduce the observed intensities, water should be formed or released from the grains more efficiently.

Close to the H/H2 transition, an activation energy of 3240 K has to be overcome to initiate the following reaction and increase the water precursor reservoir (van Dishoeck et al. 2013 and references therein).

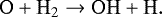
In the standard 1.5.2 version of the Meudon PDR code, energy for chemical reactions is only provided bythe kinetic energy of the reactants due to thermal motion. However, close to the H/H2 transition, H2 is highly ro-vibrationally excited (Hollenbach & Tielens 1997). This energy can be used to overcome the activation energy (Agúndez et al. 2010), as was already studied for the C+ + H2 reaction (Zanchet et al. 2013b; Herráez-Aguilar et al. 2014) and the S+ + H2 reaction (Zanchet et al. 2013a). To implement this effect in the model, the activation energy is thus taken as the difference between the activation energy and the ro-vibrational energy of H2. Reactions with vibrationally excited H2 were already included in the Meudon PDR code to reproduce the OH emission in the Orion Bar (Goicoechea et al. 2011). Considering this effect enhances the intensity predicted for the excited lines up to a factor of 2.5 due to the increase in the excited populations between AV = 6 and AV = 8.

Deeper into the cloud, where the gas is colder, gas-phase water is formed by the recombination of H3 O+ with electrons. This reaction is initiated by cosmic ray ionization producing 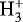and leading to H3O+ through ion-neutral reactions (Gerin et al. 2010). Moreover, in the cold region, where water is depleted by adsorption, desorption is mainly achieved by photodesorption triggered by the UV secondary photons induced by cosmic rays (Prasad & Tarafdar 1983). Following these two processes, the cosmic ray ionization rate should have a main impact on line intensities coming from the deepest part of the cloud. From our H column density (NH) estimate in the water region, a range of cosmic ray ionization rate can be estimated. For AV > 5, NH is higher than 1022 cm−2 and the cosmic ray ionization rate could be increased by a factor of ten in relation to the value used by Joblin et al. (2018), up to 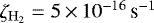per H2 (Padovani et al. 2018). This leads to an increase in the line intensities by a factor of the order of three, except for 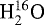211 −202 for which a factor of seven is obtained. Such an enhancement is mainly produced by the increase in the H3 O+ reservoir.

Finally, the water photodesorption yield used in the PDR Code could be tuned up. Recent study of Cruz-Diaz et al. (2018) reported photodesorption yield up to 2 × 10−3 molecule per photon at a temperature around 60 K, using a microwave discharged hydrogen flow lamp with a strong Ly-α emission component. Assuming this value increases the water line intensities by a factor of the order of two.

Considering the H2 internal energy, taking upper limit for the cosmic ray ionization rate and the water photodesorption yield, and using input parameters derived by Joblin et al. (2018) otherwise, the resulting intensities for adsorption and desorption model are in good agreement with the observed intensities (see Fig. 3 and Table 4). Input parameters of the adsorption and desorption optimized model are listed in Table 3. We note that the scaling factor used by Joblin et al. (2018) to correct bias for the assumed geometry of the Bar was not applied in this study.

With this model, the depletion of water by adsorption on grains is compensated in the maximum gas-phase water density region as seen in Fig. 5. Figure 7 shows that the water ice abundance reaches a plateau at a fractional abundance (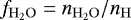) of 2 × 10−4 for AV > 10 leading to a decrease in the gas-phase water fractional abundance which peaks at 2 × 10−7 between AV = 7 and AV = 10. This gas-grains balance in relation to the depth agrees with what was predicted by Hollenbach et al. (2009) with oxygen surface chemistry. However, the fractional abundance derived from our best model is one order of magnitude higher than those reported in this former work for a UV field of G0 = 1 × 103 and a density of 1 × 104 cm−3. Water ice abundance increases from AV = 3 where the gas temperature is below 100 K and the grain temperature below 40 K. The grain temperature evolution with depth is consistent with dust observations (Arab et al. 2012).

Figure 6 shows the populations of gas-phase water rotational levels, which peaks between AV = 5 and AV = 10 without stratification. The averaged OPR in this region is equal to 2.8 ± 0.2 corresponding to a spin temperature of 36 ± 2 K (see Fig. 4) for a UV field of G0 = 3.1 × 104 in Mathis units and a thermal pressure Pth = 2.8 × 108 K cm−3. The spin temperature derived from this model agrees with the gas-phase kinetic temperature expected by Hollenbach et al. (2009) for G0 = 1 × 104 and nH = 1 × 105 cm−3.

thumbnail Fig. 4

Evolution of the water OPR (left axis) in agreement with the kinetic temperature (right axis) as a function of the visual extinction inside the molecular cloud for the pure gas-phase chemistry ISMDB model and the adsorption and desorption optimized model with H2 internal energy (Table 3).
thumbnail Fig. 5

Comparison of the spatial density of gas-phase water (left axis) and H density (right axis) as a function of the visual extinction inside the molecular cloud for the pure gas-phase chemistry ISMDB model and the adsorption and desorption optimized model with H2 internal energy (Table 3).
thumbnail Fig. 6

Evolution of the gas-phase rotational populations of (left axis), CO and 13CO (right axis) as a function of the visual extinction inside the molecular cloud for the adsorption and desorption optimized model with H2 internal energy (Table 3).
thumbnail Fig. 7

Evolution of the fractional abundance of gas and solid-phase (left axis) as a function of the visual extinction inside the molecular cloud for the adsorption and desorption optimized model with H2 internal energy (Table 3). Dashed lines show the gas-phase temperature and the smallest (SG ~ 3 nm) and biggest (BG ~ 300 nm) grain temperature (right axis).

5 Discussion

5.1 Self-absorption

The analysis of water line intensities with the Meudon PDR code brings a justification for the assumption made to derive the observed intensities. The presence of a central dip in line profiles is explained by the self-absorption by foreground gas (Choi 2015). In this scenario, the flux coming from layers deep inside the cloud is absorbed by the foreground layers when escaping the Bar.

The Meudon PDR code prediction of the line center opacities, defined as e−τ with τ the line center optical depth, are given in Fig. 8. This figure shows that the 110 −101, 111 −000, and 212 −101 transitions, which exhibit the deepest self-absorption, are by far optically thicker than the other lines. We have verified that the excitation temperature of the ground state water lines increases rapidly with AV near the location of the τ = 1 surface (AV ~ 1). The opacity is the highest at the line center and decreases going into the wings. An absorption dip at the central velocity is therefore expected. Thus line profiles predicted by the Meudon PDR code readily reproduce such a dip for the three most intense and broadest lines, while predicting single peak profiles for the other lines.

5.2 H218O intensities

This work has led to the first prediction of 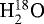line intensities by the Meudon PDR code. The comparison with observed intensities in Fig. 3 indicates that the computed intensities are overestimated. Furthermore, our estimated gas-phase column density for 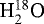ortho ground state line is two times higher than the one reported by Choi et al. (2014).

It appears that the gas-phase water 16O /18O isotopic ratio is lower than the typical value of 560 reported by Wilson & Rood (1994) for the local ISM and based on H2 CO surveys (Gardner & Whiteoak 1981). Moreover, the decreasing of the ratio is accentuated in the water emission region down to 350. This could be explained by the fact that only half of the 52 oxygen bearing molecules considered by the Meudon PDR code have their oxygen isomers taken into account. Thus a larger 18O reactants reservoir, in relation to 16O chemistry, is available to form 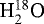. Considering the 16O /18O isotopic ratio of 560, and assuming that the intensity is impacted by the difference between the isotopic ratios in the main water emission region, it appears that the computed 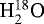line intensities are overestimated by a factor of 1.6. Applying this correction, the prediction of the 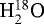ortho 110−101 intensity goes down to 6.3 × 10−8 erg cm−2 s−1 sr−1 in good agreement with the observed intensity. The para 111−110 intensity predicted by the model would thus be around 2.3 × 10−7 erg cm−2 s−1 sr−1. Removing this spurious effect requires experimental data for the rare isotope molecules.

thumbnail Fig. 8

Evolution of the line center opacity of and CO lines as a function of the visual extinction inside the molecular cloud for the adsorption and desorption optimized model with H2 internal energy (Table 3).

5.3 OPR

Water line intensities are well reproduced using the Meudon PDR code, considering either pure gas-phase chemistry model, or by adding adsorption and desorption of water from grains. In both cases, an OPR close to 2.8 is derived, whereas a previous estimate of the 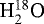OPR in the Orion Bar leads to a very low value between 0.1 and 0.5 (Choi et al. 2014). This low ratio was estimated from the column densities obtained with the RADEX low velocity gradient (LVG) code (van der Tak et al. 2007), assuming a single-slab geometry with a homogeneous density and temperature. As already discussed, the gas-phase 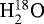column densities, derived from the Meudon PDR code using our adsorption and desorption optimized model, are probably overestimated due to the departure of the isotopic ratio from the typical local ISM value. Considering the ISM value of Wilson & Rood (1994), the gas-phase 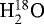column densities up to AV = 15 are ~8.2 × 109 cm−2 for the para 111 level and ~ 2.5 × 1010 cm−2 for the ortho 110 level. The para value is one order of magnitude lower than the one previously reported whereas the ortho value agrees with it (Choi et al. 2014). Using these two values, the 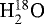OPR is estimated to be equal to 3.0.

Part of the discrepancy between the low OPR reported and our high thermal value derived could be assigned to the improvement of the data reduction pipeline. Indeed, with the latest HIPE version (14.1.0), the 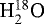para ground state line, which has a really low S/N, is barely detected and our upper limit for its intensity is roughly two times lower than the Choi et al. (2014) value10. It is worth noting that Nagy et al. (2017) have not reported the detection of this line, unlike the 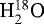ortho ground state transition.

However a rough estimate of the OPR in LTE, using the 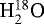ortho line intensity and the para upper limit still gives a low OPR of 0.7. Moreover, considering the two 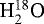intensities predicted by the Meudon PDR code, the OPR in LTE would be equal to 1.3. Thus the model used for the analysis hasa major impact on the results. RADEX LVG code (van der Tak et al. 2007), used to derive the 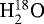OPR, assumes an isothermal homogeneous medium and solves the radiative transfer in non-LTE using radiative and collisional transition rates. Conversely, the Meudon PDR code derives the population considering chemistry, thermal balance and infrared pumping. With this more complete model and assuming an isobaric model, the kinetic temperature, and thus the density, is predicted tobe strongly dependent on the depth into the cloud as shown in Figs. 4 and 5. Alongside with an expanded dataset, the analysis of water lines intensity in the Orion Bar is consistent with the thermal equilibrium at 36 K.

To derive the water OPR, we computed an average over the main gas-phase water reservoir between AV = 5 and AV = 10. This assumption is justified by the spatial distribution of the water line emission in the Orion Bar. Indeed OH and H2 O emission seems to be decorrelated whereas OH emission matches high-J CO ones (Goicoechea et al. 2011; Parikka et al. 2017). As high-J CO lines arise from a layer between AV = 1 and AV = 3 (Joblin et al. 2018), the local water density maximum at AV = 1 − 2 should not significantly contribute to the observed water intensities.

This OPR agrees with OPRs at high thermal values from other tracers reported for the Orion Bar. Indeed an OPR of 2.8 ± 0.6 was derived for c − C3H2 (Cuadrado et al. 2015) and OPRs of the order of three were inferred for H2CO, H2 CS and H2 CCO (Hogerheijde et al. 1995; Cuadrado et al. 2017).

This work follows the trend of water OPR reanalysis initiated by better reduction pipeline for archival observations along with the development of more sophisticated models. Thus fewer very low OPRs are confirmed, as for example in the TW Hydrae protoplanetary disk, where the very low OPR reported by Hogerheijde et al. (2011) has been shown to be model-dependent and is consistent within the uncertainties with the high-temperature limit (Salinas et al. 2016).

5.4 Grain surface chemistry

The introduction of simple adsorption and desorption processes of water has emphasized the major role that grains could have for tracers of the deepest part of the cloud. To overcome the depletion produced by the adsorption of water molecules on grains, several parameters of the code had to be tuned up to their upper acceptable limits. However a careful study of other parameters could mitigate the extreme values adopted for the cosmic ray ionization rate and the water photodesorption yield.

First, considering the presence of X-ray photons in the Orion Nebula (Getman et al. 2005; Preibisch et al. 2005) could lead to a reduction of these parameters. The chemistry initiated by cosmic ray ionization, such as gas-phase water production via H3 O+, could also be activated by X-ray ionization (Gupta et al. 2010; Cuadrado et al. 2015). Furthermore, water X-ray photodesorption appears to be efficient and comparable to far-UV photodesorption (Dupuy et al. 2018).

On the other hand, the 60° limitation of the Meudon PDR code could lower the predicted intensity in relation to a more edge-on geometry. Indeed, previous studies have estimated the ionization front to be tilted from the line-of-sight by an angle between 3° and 20° (Wen & O’Dell 1995; Hogerheijde et al. 1995; Jansen et al. 1995; Walmsley et al. 2000) implying a nearly edge-on PDR. Joblin et al. (2018) have estimated that a scaling factor of 1.3 has to be applied to correct for the assumed geometries of the Bar from a model at a viewing angle of 60° and to fit high-J CO lines. A more edge-on PDR would be characterized by a scaling factor higher than 1.

Moreover, the grain size distribution adopted by Joblin et al. (2018) is optimized to reproduce the extinction curve toward Θ1 Ori C (Fitzpatrick & Massa 1990; Marconi et al. 1998). This distribution is kept constant through the cloud, whereas deeper in grains could be larger. Thus in the water-emitting region, the total surface of the grains for water molecules to stick onto would be reduced preventing gas-phase water density from dropping down dramatically.

Furthermore, adding only water adsorption and desorption processes on grains could introduce a bias on the chemistry balance and the radiative transfer computation. Indeed, if a full adsorption and desorption description is adopted, modifying the precursors reservoir by trapping them onto grains could change the chemical state of the cloud. This would also have an impact on the radiative transfer by limiting the UV shielding of the molecules that appear deeper into the cloud, and on the desorption processes that should be enhanced by the increase in the number of UV photons inside the cloud. Moreover, increasing the number of molecules on grains will emphasize the need of considering a full surface chemistry balance. Some PDR models have introduced surface chemistry calculations (Hollenbach et al. 2009; Esplugues et al. 2016) and raised the importance of surface chemistry to explain observed gas-phase abundances. In these models, the main ice water formation pathway begins with oxygen adsorption on grains followed by two reactions with hydrogen atoms. Hollenbach et al. (2009) have estimated that in the highest gas-phase water abundance region, 97% of gas or solid-phase water production is achieved by surface chemistry. However, owing to the high FUV field, the grain temperature is high enough to prevent O or OH to stick efficiently (Hollenbach et al. 2009; Melnick et al. 2012), as seen in Fig. 7. Thus the formation of water ice through this pathway should be reduced.

Implementing these processes in the Meudon PDR code is in progress. As already mentioned for isotopic computations, it is only achievable by gathering qualitative and quantitative processes from experimental data. For example adsorption and desorption considerations are mainly limited by the lack of photodesorption yield for astrophysical relevant molecules. In the past few years, several laboratory experiments have been conducted to describe photodesorption processes (Öberg et al. 2009; Muñoz Caro et al. 2016; Dupuy et al. 2017). Simulations of water surface chemistry have shown the importance of surface processes for the interstellar gas-phase (Cazaux et al. 2010). The development of experimental set-up to address surface chemistry (Hama & Watanabe 2013 and references therein) unveiled the various processes that could occur on interstellar grains and affect the physical and chemical state of interstellar objects.

Getting experimental data to deal with nuclear spin effects is crucial to simulate and understand nuclear spin population distributions. The nuclear spin conversion mechanism has been investigated to estimate the lifetime conservation of a potential thermal disequilibrium (Fillion et al. 2012; Cacciani et al. 2012; Turgeon et al. 2017), as well as the effect of adsorption and desorption on the OPR (Hama et al. 2016). Furthermore selective reaction or formation of water nuclear spin isomers could also be taken into account by the models (Kilaj et al. 2018). Considering these processes are the steps to examine the assumptions of water produced at the thermal equilibrium in the Meudon PDR code, used to fit the water observations of the Orion Bar.

6 Conclusions

An analysis of a set of seven 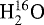lines and one 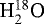line measured toward the Orion Bar with Herschel/HIFI is performed using the Meudon PDR code. The para 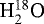ground state line is not unambiguously detected. Considering an isobaric model and assuming that gas-phase water is formed with an OPR in agreement with the local thermal equilibrium, an OPR of 2.7 ± 0.1 is derived.

Investigation of grain effects is made by adding adsorption and desorption processes of water on grains. After tuning the cosmic ray ionization rate and water photodesorption yield up to their upper acceptable limits, a good agreement with the observed intensity is obtained for an OPR of 2.8 ± 0.2. This OPR corresponds to a temperature of (36 ± 2) K, which is much higher than the spin temperature previously reported for 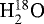in the Orion Bar and close to the high-temperature limit.

Acknowledgements

This work was supported by the Programme National de Physique et Chimie du Milieu Interstellaire (PCMI) of the CNRS/INSU, the INC/INP co-funded by the CEA and the CNES. Financial support from the LabEx MiChem, par of the French state funds managed by the ANR within the investissements d’avenir program under reference ANR-11-10EX-0004-02 is acknowledged. Fundings from the Ile-de-France region DIM ACAV + is acknowledged. Part of this research was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration.

Appendix A Observed lines and calibrations

Table A.1

Line intensities integrated with a linear baseline fit outside the line, except for 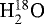110 − 101 where the frequency switch observing mode leads to optical standing waves that had to be corrected by a fouth order polynom.

thumbnail Fig. A.1

Line profile of for H (left panels) and V (right panels) polarization. The blue solid line is the spectrum corrected for HIFI calibration, the black solid line is the spectrum corrected for the beam coupling factor, the blue dash-dotted line and red dashed line represent Orion Bar and Orion Ridge velocity features and the gray area is the velocity integration range. See Tables 1 and A.1 for the definition of a and b labeled transitions.
thumbnail Fig. A.2

Line profile of for H (left panels) and V (right panels) polarization. The blue solid line is the spectrum corrected for HIFI calibration, the black solid line is the spectrum corrected for the beam coupling factor, the blue dash-dotted line and red dashed line lines represent Orion Bar and Orion Ridge velocity features and the gray area is the velocity integration range. See Tables 1 and A.1 for the definition of a and b labeled transitions.
thumbnail Fig. A.3

Line profile of for H (left panels) and V (right panels) polarization. The blue solid line is the spectrum corrected for HIFI calibration, the black solid line is the spectrum corrected for the beam coupling factor, the blue dash-dotted line and red dashed line represent Orion Bar and Orion Ridge velocity features and the gray area is the velocity integration range.
thumbnail Fig. A.4

Line profile of for H (left panels) and V (right panels) polarization. The blue solid line is the spectrum corrected for HIFI calibration, the black solid line is the spectrum corrected for the beam coupling factor, the blue dash-dotted line and red dashed line represent Orion Bar and Orion Ridge velocity features and the gray area is the velocity integration range.
thumbnail Fig. A.5

Water emission maps averaged for H and V polarizations. Integration ranges are given in Table A.1. Black solid contours represent the emission of 13CO 6− 5 at 95, 90, 75 and 50% of the maximum intensity integrated from 2 to 17 km s−1 observed with the CSO telescope and convolved at the averaged water line H and V beam width (Table A.1). Upward and downward triangles mark the targeted observations for H and V polarizations (blue ones are for the b labeled transitions, see Tables 1 and A.1). Black dashed circle is the HIFI HPBW at the water frequency centered on the CO+ peak.

References

  1. Agúndez, M., Goicoechea, J. R., Cernicharo, J., Faure, A., & Roueff, E. 2010, ApJ, 713, 662 [NASA ADS] [CrossRef] [Google Scholar]
  2. Allers, K. N., Jaffe, D. T., Lacy, J. H., Draine, B. T., & Richter, M. J. 2005, ApJ, 630, 368 [NASA ADS] [CrossRef] [Google Scholar]
  3. Andree-Labsch, S., Ossenkopf-Okada, V., & Röllig, M. 2017, A&A, 598, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Arab, H., Abergel, A., Habart, E., et al. 2012, A&A, 541, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bergin, E. A., Phillips, T. G., Comito, C., et al. 2010, A&A, 521, L20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Bron, E., Agúndez, M., Goicoechea, J. R., & Cernicharo, J. 2018, A&A, submitted [arXiv:1801.01547] [Google Scholar]
  7. Cacciani, P., Cosléou, J., & Khelkhal, M. 2012, Phys. Rev. A, 85, 012521 [NASA ADS] [CrossRef] [Google Scholar]
  8. Cazaux, S., Cobut, V., Marseille, M., Spaans, M., & Caselli, P. 2010, A&A, 522, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Choi, Y. 2015, PhD. Thesis, University of Groninge, Groningen [Google Scholar]
  10. Choi, Y., van der Tak, F. F. S., Bergin, E. A., & Plume, R. 2014, A&A, 572, L10 [Google Scholar]
  11. Cruz-Diaz, G. A., Martín-Doménech, R., Moreno, E., Muñoz Caro, G. M., & Chen, Y.-J. 2018, MNRAS, 474, 3080 [NASA ADS] [CrossRef] [Google Scholar]
  12. Cuadrado, S., Goicoechea, J. R., Pilleri, P., et al. 2015, A&A, 575, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Cuadrado, S., Goicoechea, J. R., Cernicharo, J., et al. 2017, A&A, 603, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. de Graauw, T., Helmich, F. P., Phillips, T. G., et al. 2010, A&A, 518, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Dupuy, R., Bertin, M., Féraud, G., et al. 2017, A&A, 603, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Dupuy, R., Bertin, M., Féraud, G., et al. 2018, Nat. Astron., 2, 796 [NASA ADS] [CrossRef] [Google Scholar]
  17. Esplugues, G. B., Cazaux, S., Meijerink, R., Spaans, M., & Caselli, P. 2016, A&A, 591, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Fillion, J.-H., Bertin, M., Lekic, A., et al. 2012, EAS Pub. Ser., 58, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Fitzpatrick, E. L., & Massa, D. 1990, ApJS, 72, 163 [NASA ADS] [CrossRef] [Google Scholar]
  20. Fuente, A., Rodriguez-Franco, A., & Martin-Pintado, J. 1996, A&A, 312, 599 [NASA ADS] [Google Scholar]
  21. Gardner, F. F., & Whiteoak, J. B. 1981, MNRAS, 194, 37P [NASA ADS] [Google Scholar]
  22. Garrod, R. T., Vasyunin, A. I., Semenov, D. A., Wiebe, D. S., & Henning, T. 2009, ApJ, 700, L43 [Google Scholar]
  23. Gerin, M., De Luca, M., Black, J., et al. 2010, A&A, 518, L110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Getman, K. V., Feigelson, E. D., Grosso, N., et al. 2005, ApJS, 160, 353 [NASA ADS] [CrossRef] [Google Scholar]
  25. Goicoechea, J. R., Joblin, C., Contursi, A., et al. 2011, A&A, 530, L16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Goicoechea, J. R., Teyssier, D., Etxaluze, M., et al. 2015, ApJ, 812, 75 [NASA ADS] [CrossRef] [Google Scholar]
  27. Goicoechea, J. R., Pety, J., Cuadrado, S., et al. 2016, Nature, 537, 207 [NASA ADS] [CrossRef] [Google Scholar]
  28. Goicoechea, J. R., Cuadrado, S., Pety, J., et al. 2017, A&A, 601, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Gonzalez Garcia, M., Le Bourlot, J., Le Petit, F., & Roueff, E. 2008, A&A, 485, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Gordon, I. E., Rothman, L. S., Hill, C., et al. 2017, J. Quant. Spectr. Rad. Transf., 203, 3 [Google Scholar]
  31. Green, S., Maluendes, S., & McLean, A. D. 1993, ApJS, 85, 181 [NASA ADS] [CrossRef] [Google Scholar]
  32. Gupta, H., Rimmer, P., Pearson, J. C., et al. 2010, A&A, 521, L47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Habart, E. 2011, OT2_ehabart_4: Unveiling the origin and excitation mechanisms of the warm CO, OH and CH+, Herschel Space Observatory Proposal, id.2039 [Google Scholar]
  34. Habart, E., Dartois, E., Abergel, A., et al. 2010, A&A, 518, L116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Habing, H. J. 1968, Bull. Astr. Inst. Netherlands, 19, 421 [Google Scholar]
  36. Hama, T., & Watanabe, N. 2013, Chem. Rev., 113, 8783 [CrossRef] [Google Scholar]
  37. Hama, T., Kouchi, A., & Watanabe, N. 2016, Science, 351, 65 [NASA ADS] [CrossRef] [Google Scholar]
  38. Herráez-Aguilar, D., Jambrina, P. G., Menéndez, M., et al. 2014, Phys. Chem. Chem. Phys., 16, 24800 [Google Scholar]
  39. Hogerheijde, M. R., Jansen, D. J., & van Dishoeck, E. F. 1995, A&A, 294, 792 [NASA ADS] [Google Scholar]
  40. Hogerheijde, M. R., Bergin, E. A., Brinch, C., et al. 2011, Science, 334, 338 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  41. Hollenbach, D. J., & Tielens, A. G. G. M. 1997, ARA&A, 35, 179 [NASA ADS] [CrossRef] [Google Scholar]
  42. Hollenbach, D. J., Kaufman, M. J., Bergin, E. A., & Melnick, G. J. 2009, ApJ, 690, 1497 [CrossRef] [Google Scholar]
  43. Jansen, D. J., Spaans, M., Hogerheijde, M. R., & van Dishoeck, E. F. 1995, A&A, 303, 541 [NASA ADS] [Google Scholar]
  44. Joblin, C., Bron, E., Pinto, C., et al. 2018, A&A, 615, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Kilaj, A., Gao, H., Rösch, D., et al. 2018, Nat. Commun., 9, 2096 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Kong, S., Arce, H. G., Feddersen, J. R., et al. 2018, ApJS, 236, 25 [NASA ADS] [CrossRef] [Google Scholar]
  47. Larsson, B., Liseau, R., Bergman, P., et al. 2003, A&A, 402, L69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Le Bourlot, J., Le Petit, F., Pinto, C., Roueff, E., & Roy, F. 2012, A&A, 541, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Le Petit, F., Nehmé, C., Le Bourlot, J., & Roueff, E. 2006, ApJS, 164, 506 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Le Petit, F., Barzel, B., Biham, O., Roueff, E., & Le Bourlot, J. 2009, A&A, 505, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Leurini, S., Rolffs, R., Thorwirth, S., et al. 2006, A&A, 454, L47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Lis, D. C., & Schilke, P. 2003, ApJ, 597, L145 [NASA ADS] [CrossRef] [Google Scholar]
  53. Lis, D. C., Bergin, E. A., Schilke, P., & van Dishoeck, E. F. 2013, J. Phys. Chem. A, 117, 9661 [CrossRef] [Google Scholar]
  54. Loison, J.-C., Wakelam, V., Gratier, P., et al. 2019, MNRAS, 485, 5777 [NASA ADS] [CrossRef] [Google Scholar]
  55. Marconi, A., Testi, L., Natta, A., & Walmsley, C. M. 1998, A&A, 330, 696 [NASA ADS] [Google Scholar]
  56. Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
  57. Melnick, G. J., Tolls, V., Goldsmith, P. F., et al. 2012, ApJ, 752, 26 [NASA ADS] [CrossRef] [Google Scholar]
  58. Menten, K. M., Reid, M. J., Forbrich, J., & Brunthaler, A. 2007, A&A, 474, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Muñoz Caro, G. M., Chen, Y.-J., Aparicio, S., et al. 2016, A&A, 589, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Mueller, M., Jellema, W., Olberg, M., Moreno, R., & Teyssier, D. 2014, The HIFI Beam: Release 1 - Release Note for Astronomers, Tech. Rep. HIFI-ICC-RP-2014-001, SRON Gronigen [Google Scholar]
  61. Nagy, Z., Choi, Y., Ossenkopf-Okada, V., et al. 2017, A&A, 599, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Öberg, K. I., Linnartz, H., Visser, R., & van Dishoeck, E. F. 2009, ApJ, 693, 1209 [NASA ADS] [CrossRef] [Google Scholar]
  63. Ossenkopf, V., Röllig, M., Neufeld, D. A., et al. 2013, A&A, 550, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Ott, S. 2010, in Astronomical Data Analysis Software and Systems XIX, eds. Y. Mizumoto, K.-I. Morita, & M. Ohishi, ASP Conf. Ser., 434, 139 [Google Scholar]
  65. Padovani, M., Galli, D., Ivlev, A. V., Caselli, P., & Ferrara, A. 2018, A&A, 619, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Parikka, A., Habart, E., Bernard-Salas, J., et al. 2017, A&A, 599, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Parmar, P. S., Lacy, J. H., & Achtermann, J. M. 1991, ApJ, 372, L25 [NASA ADS] [CrossRef] [Google Scholar]
  68. Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
  69. Prasad, S. S., & Tarafdar, S. P. 1983, ApJ, 267, 603 [NASA ADS] [CrossRef] [Google Scholar]
  70. Preibisch, T., McCaughrean, M. J., Grosso, N., et al. 2005, ApJS, 160, 582 [NASA ADS] [CrossRef] [Google Scholar]
  71. Rodriguez-Franco, A., Martin-Pintado, J., & Fuente, A. 1998, A&A, 329, 1097 [NASA ADS] [Google Scholar]
  72. Roelfsema, P. R., Helmich, F. P., Teyssier, D., et al. 2012, A&A, 537, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Salinas, V. N., Hogerheijde, M. R., Bergin, E. A., et al. 2016, A&A, 591, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Shipman, R. F., Beaulieu, S. F., Teyssier, D., et al. 2017, A&A, 608, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Sternberg, A., & Dalgarno, A. 1989, ApJ, 338, 197 [NASA ADS] [CrossRef] [Google Scholar]
  76. Stoerzer, H., Stutzki, J., & Sternberg, A. 1995, A&A, 296, L9 [NASA ADS] [Google Scholar]
  77. Tauber, J. A., Tielens, A. G. G. M., Meixner, M., & Goldsmith, P. F. 1994, ApJ, 422, 136 [NASA ADS] [CrossRef] [Google Scholar]
  78. Teyssier, D., Avruch, I., Beaulieu, S., et al. 2017, HIFI Handbook, HERSCHEL-HSC-DOC-2097 [Google Scholar]
  79. Tielens, A. G. G. M., & Hollenbach, D. 1985, ApJ, 291, 747 [NASA ADS] [CrossRef] [Google Scholar]
  80. Turgeon, P.-A., Vermette, J., Alexandrowicz, G., et al. 2017, J. Phys. Chem. A, 121, 1571 [NASA ADS] [CrossRef] [Google Scholar]
  81. van der Werf, P. P., Stutzki, J., Sternberg, A., & Krabbe, A. 1996, A&A, 313, 633 [NASA ADS] [Google Scholar]
  82. van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. van der Tak, F. F. S., Ossenkopf, V., Nagy, Z., et al. 2012, A&A, 537, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  84. van der Tak, F. F. S., Nagy, Z., Ossenkopf, V., et al. 2013, A&A, 560, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. van Dishoeck, E. F., Herbst, E., & Neufeld, D. A. 2013, Chem. Rev., 113, 9043 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  86. Wakelam, V., Loison, J.-C., Mereau, R., & Ruaud, M. 2017, Mol. Astrophys., 6, 22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Walmsley, C. M., Natta, A., Oliva, E., & Testi, L. 2000, A&A, 364, 301 [NASA ADS] [Google Scholar]
  88. Wen, Z., & O’Dell, C. R. 1995, ApJ, 438, 784 [NASA ADS] [CrossRef] [Google Scholar]
  89. Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
  90. Wu, R., Bron, E., Onaka, T., et al. 2018, A&A, 618, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Wyrowski, F., Schilke, P., Hofner, P., & Walmsley, C. M. 1997, ApJ, 487, L171 [NASA ADS] [CrossRef] [Google Scholar]
  92. Young Owl, R. C., Meixner, M. M., Wolfire, M., Tielens, A. G. G. M., & Tauber, J. 2000, ApJ, 540, 886 [NASA ADS] [CrossRef] [Google Scholar]
  93. Zanchet, A., Agúndez, M., Herrero, V. J., Aguado, A., & Roncero, O. 2013a, AJ, 146, 125 [NASA ADS] [CrossRef] [Google Scholar]
  94. Zanchet, A., Godard, B., Bulut, N., et al. 2013b, ApJ, 766, 80 [NASA ADS] [CrossRef] [Google Scholar]
1

Herschel observations of the EXtra-Ordinary Sources.

2

calibration_pvhifi_37 and calibration_pvhifi_85.

4

Combined Array for the Research in Millimeter Astronomy.

5

Nobeyama Radio Observatory 45 m telescope.

8

212−101-b, Obs. Id: 1342218426.

10

HIPE version 10.0 was used.

All Tables

Table 1

Observations used for the analysis of water line emission in the Orion Bar.

In the text
Table 2

Observed intensities of water lines toward the Orion Bar and their correction for the beam coupling factor.

In the text
Table 3

Best-fit input parameters of the Meudon PDR code for the corrected intensities.

In the text
Table 4

Intensities of water lines toward the Orion Bar corrected for the beam coupling factor, in erg cm−2 s−1 sr−1, and predicted intensities from the Meudon PDR code using input parameters in Table 3 for the pure gas-phase chemsitry ISMDB model and the adsorption and desorption optimized model with H2 internal energy.

In the text
Table A.1

Line intensities integrated with a linear baseline fit outside the line, except for 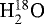110 − 101 where the frequency switch observing mode leads to optical standing waves that had to be corrected by a fouth order polynom.

In the text

All Figures

thumbnail Fig. 1

Averaged spectra of and lines toward the Orion Bar on the main-beam brightness temperature scale, not corrected for the beam coupling factor. The gray areas represent the velocity integration range. The blue dash-dotted line and red dashed line are the expected velocity components from Orion Ridge (9.0 km s−1) and Orion Bar (10.6 km s−1). lines were multiplied by a factor of 5.
In the text
thumbnail Fig. 2

202 − 111 emission map at 988 GHz integrated from 7.7 to 13.5 km s−1. Contours represent the emission of 13CO 6− 5 at 95, 90, 75 and 50% of the maximum intensity, integrated from 2 to 17 km s−1, observed with the CSO at a resolution of 11′′. Black star marks the CO+ peak position, white circles show the HIFI HPBW at the extreme frequencies, black and magenta disks show the CSO and 988 GHz HIFI beam width (see Table 1). FUV field from the Trapezium cluster comes from the upper right corner.
In the text
thumbnail Fig. 3

Comparison between observed intensities and the ones predicted by the pure gas-phase chemistry ISMDB model and the adsorption and desorption optimized model with H2 internal energy (Table 3). Bottom panel: relative difference between predictions and observations.
In the text
thumbnail Fig. 4

Evolution of the water OPR (left axis) in agreement with the kinetic temperature (right axis) as a function of the visual extinction inside the molecular cloud for the pure gas-phase chemistry ISMDB model and the adsorption and desorption optimized model with H2 internal energy (Table 3).
In the text
thumbnail Fig. 5

Comparison of the spatial density of gas-phase water (left axis) and H density (right axis) as a function of the visual extinction inside the molecular cloud for the pure gas-phase chemistry ISMDB model and the adsorption and desorption optimized model with H2 internal energy (Table 3).
In the text
thumbnail Fig. 6

Evolution of the gas-phase rotational populations of (left axis), CO and 13CO (right axis) as a function of the visual extinction inside the molecular cloud for the adsorption and desorption optimized model with H2 internal energy (Table 3).
In the text
thumbnail Fig. 7

Evolution of the fractional abundance of gas and solid-phase (left axis) as a function of the visual extinction inside the molecular cloud for the adsorption and desorption optimized model with H2 internal energy (Table 3). Dashed lines show the gas-phase temperature and the smallest (SG ~ 3 nm) and biggest (BG ~ 300 nm) grain temperature (right axis).
In the text
thumbnail Fig. 8

Evolution of the line center opacity of and CO lines as a function of the visual extinction inside the molecular cloud for the adsorption and desorption optimized model with H2 internal energy (Table 3).
In the text
thumbnail Fig. A.1

Line profile of for H (left panels) and V (right panels) polarization. The blue solid line is the spectrum corrected for HIFI calibration, the black solid line is the spectrum corrected for the beam coupling factor, the blue dash-dotted line and red dashed line represent Orion Bar and Orion Ridge velocity features and the gray area is the velocity integration range. See Tables 1 and A.1 for the definition of a and b labeled transitions.
In the text
thumbnail Fig. A.2

Line profile of for H (left panels) and V (right panels) polarization. The blue solid line is the spectrum corrected for HIFI calibration, the black solid line is the spectrum corrected for the beam coupling factor, the blue dash-dotted line and red dashed line lines represent Orion Bar and Orion Ridge velocity features and the gray area is the velocity integration range. See Tables 1 and A.1 for the definition of a and b labeled transitions.
In the text
thumbnail Fig. A.3

Line profile of for H (left panels) and V (right panels) polarization. The blue solid line is the spectrum corrected for HIFI calibration, the black solid line is the spectrum corrected for the beam coupling factor, the blue dash-dotted line and red dashed line represent Orion Bar and Orion Ridge velocity features and the gray area is the velocity integration range.
In the text
thumbnail Fig. A.4

Line profile of for H (left panels) and V (right panels) polarization. The blue solid line is the spectrum corrected for HIFI calibration, the black solid line is the spectrum corrected for the beam coupling factor, the blue dash-dotted line and red dashed line represent Orion Bar and Orion Ridge velocity features and the gray area is the velocity integration range.
In the text
thumbnail Fig. A.5

Water emission maps averaged for H and V polarizations. Integration ranges are given in Table A.1. Black solid contours represent the emission of 13CO 6− 5 at 95, 90, 75 and 50% of the maximum intensity integrated from 2 to 17 km s−1 observed with the CSO telescope and convolved at the averaged water line H and V beam width (Table A.1). Upward and downward triangles mark the targeted observations for H and V polarizations (blue ones are for the b labeled transitions, see Tables 1 and A.1). Black dashed circle is the HIFI HPBW at the water frequency centered on the CO+ peak.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.