EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 629 (September 2019) A&A, 629 (2019) A62 Full HTML
Highlight
Free Access
Issue
A&A
Volume 629, September 2019
Article Number A62
Number of page(s) 26
Section Galactic structure, stellar clusters and populations
DOI https://doi.org/10.1051/0004-6361/201935282
Published online 05 September 2019

© ESO 2019

1. Introduction

High-resolution spectroscopic surveys such as Gaia-ESO (Gilmore et al. 2012; Randich & Gilmore 2013), APOGEE (Holtzman et al. 2015), or GALAH (De Silva et al. 2015; Bland-Hawthorn et al. 2019) are providing us an extraordinary data set of radial velocities, stellar parameters, and elemental abundances for large samples of stars that belong to different Galactic components: from the thin and thick discs to the halo and bulge. This also includes many globular and open star clusters. Line-of-sight distances and proper motions obtained with the Gaia satellite (e.g. Bailer-Jones et al. 2018; Lindegren et al. 2018; Gaia Collaboration 2018), coupled with the information from spectroscopic surveys, are improving our knowledge of the spatial distribution of stellar populations by constraining their properties throughout our Galaxy (e.g. Monari et al. 2017; Randich et al. 2018; Li et al. 2018; Bland-Hawthorn et al. 2019), as well as by resolving multiple populations in young clusters (e.g. in Gamma Velorum and Chameleon I in Franciosini et al. 2018; Roccatagliata et al. 2018, respectively).

An important step forward to study how our Galaxy formed and evolved to its present-day structure is the determination of ages of individual stars to separate timescales of the formation within the different Galactic components. However, the ages of stars are elusive, and they cannot be directly measured. Measuring stellar ages is indeed one of the most difficult tasks of astrophysics (see e.g. Soderblom et al. 2014; Randich et al. 2018, and references therein).

The most commonly used technique to compute stellar ages is comparing quantities that are related to observations with the results of stellar evolution models. This comparison can be made on several planes, that is, using directly observed quantities such as magnitudes and colours, and with derived quantities such as surface gravities, log g, and effective temperatures, Teff. This method provides better results in regions of the planes where isochrones have a good separation, mainly close to the turn-off of the main sequence. On the other hand, isochrones of different ages almost overlap on the red giant branch and on the lower main sequence. Therefore, small uncertainties on Teff and log g or on magnitude and colour correspond to large uncertainties on the age. This method is more effective for stars that belong to clusters, for which we can observe several coeval member stars in different evolutionary stages. This places stronger constraints on the comparison with the isochrones. For instance, the combination of the Gaia-ESO survey and Gaia-DR1 data allowed a comparison of the observed sequences of open clusters with stellar evolutionary models and provided an accurate determination of their ages. It also paved the way to their exploitation as age calibrators to be adopted by other methods (Randich et al. 2018).

In addition to this classical procedure, several alternative methods can be used to estimate stellar ages. For instance, the review of Soderblom et al. (2014) presented several ways to estimate the ages of young stars, among them the lithium-depletion boundary, kinematics ages, pulsation and astroseismology, rotation, and activity. Moreover, in the past few years, several chemical indicators have been considered as possible age tracers. These include elemental abundance ratios dependent on the Galactic chemical evolution, such as [Y/Mg], [Ba/Fe] and [Y/Al] (e.g. Tucci Maia et al. 2016; Nissen et al. 2017; Feltzing et al. 2017; Slumstrup et al. 2017; Spina et al. 2018), and those related to stellar evolution, such as [C/N] (Salaris et al. 2015; Masseron & Gilmore 2015; Martig et al. 2016; Ness et al. 2016; Ho et al. 2017; Feuillet et al. 2018).

We here focus on the use of [C/N] measured in red giant stars as an age indicator. Carbon and nitrogen are processed through the CNO-cycle in previous evolutionary phases and taken towards the surface by the penetration of the convective stellar interior. The phase in which the convection reaches its maximum penetration is called the first dredge-up (FDU, hereafter). As a result of this convective mixing, the atmosphere shows a variation in the chemical composition, which in particular changes the abundance ratio [C/N]. Because the penetration of the convection in the inner regions, and therefore the abundances of C and N that is brought up to in the stellar surface, depends on the stellar mass and because the mass is related to the age, the [C/N] can be used to estimate stellar ages (e.g. Salaris et al. 2015; Lagarde et al. 2017).

The aim of this paper is to calibrate an empirical relation between the [C/N] ratio and stellar age using open clusters. Starting from the ages determined with isochrone fitting for the open clusters observed by Gaia-ESO and by APOGEE, we calibrate a relationship between cluster age and the [C/N] in their evolved stars by accurately selecting them among post-FDU stars and studying the occurrence of non-canonical mixing. In Sect. 2 we present our datasets and describe our pre-selection of the Gaia-ESO and APOGEE catalogues and the sample of open clusters that is observed in both surveys. In Sect. 3 we discuss the choice of the evolved stars that we used to compute [C/N], and in Sect. 4 we present the relationship between cluster ages and [C/N] abundances. In Sect. 5 we compare our relationship with theoretical predictions. The application of the relationship to the field stars of Gaia-ESO and APOGEE high-resolution samples is analysed in Sect. 6. Finally, in Sect. 7 we summarise and conclude.

2. Data samples

2.1. Gaia-ESO sample

The Gaia-ESO survey (Gilmore et al. 2012; Randich & Gilmore 2013, hereafter GES) is a high-resolution spectroscopic survey that observed about 105 stars whose spectra were collected with the Fiber Large Array Multi-Element Spectrograph (FLAMES) multi-fiber facility (Pasquini et al. 2002) at the Very Large Telescope (VLT). It has two different observing modes, using GIRAFFE, the medium-resolution spectrograph (R ∼ 20 000), and UVES, the high-resolution spectrograph (R ∼ 47 000).

The data were reduced as described in Sacco et al. (2014) and Gilmore et al. (in prep.) for UVES and GIRAFFE, respectively. The stellar atmospheric parameters of the stars considered here, UVES FGK stars, were determined as described in Smiljanic et al. (2014). The calibration and homogenisation of stellar parameters and abundances obtained by the different working groups were performed as described by Pancino et al. (2017) and Hourihane et al. (in prep.), respectively. All data used here are included in the fourth and fifth internal GES data releases (iDR4 and iDR5). Because the C and N abundances of the stars in common to both releases were not re-derived in iDR5, we adopted the C and N values presented in iDR4 for these stars. Hereafter we do not specify the GES release because we used iDR5, but for stars in common, we adopted the C and N abundances of iDR4, which are absent from iDR5. In particular, the method used to derive the abundances we discuss here is described in Tautvaišienė et al. (2015). Here, we briefly recall the main steps of the analysis. C and N abundances were derived from molecular lines of C2 (Brooke et al. 2013) and CN, respectively (Sneden et al. 2014). In the analysis of the optical stellar spectra, the 12C14N molecular bands in the spectral range 6470−6490 Å, the C2 Swan (1,0) band head at 5135 Å, the C2 Swan (0,1) band head at 5635.5 Å were used. The selected C2 bands do not suffer from non-local thermodynamical equilibrium (NLTE) deviations, and thus are better suited for abundance studies than [C I] lines. All molecular bands and atomic lines were analysed through spectral synthesis with the code BSYN (Tautvaišienė et al. 2015) and all synthetic spectra were calibrated to the solar spectrum of Kurucz (2005).

The selected clusters are shown in Table 1, where we summarise their basic properties from the literature: coordinates, Galactocentric distances (RGC), heights above the plane (z), mean radial velocity (RV) of cluster members, median metallicity [Fe/H], logarithmic ages, and the references for ages and distances.

Table 1.

Parameters of the open clusters in the GES sample.

We made a first quality check on the GES catalogue by excluding from our sample stars with highly uncertain stellar parameters (i.e. including only stars with Teff >  0, eTeff <  500, log g >  −0.5, and elog g <  0.5) and with a signal-to-noise ratio S/N <  20. We selected giant stars in open clusters and in the Galactic field. We performed a membership analysis of stars in clusters with a Bayesian approach that took into account GES and Gaia information. Membership probabilities were estimated from the RVs (from GES) and proper motion velocities (from Gaia) of stars observed with GIRAFFE. A maximum likelihood method was used to determine the probability of cluster membership by fitting two quasi-Gaussian distributions to the velocity data. The basic supposition was that the set of stars that we observed as potential cluster members is draw from two populations. One distribution defines cluster members, and a second much broader distribution represents the background population. These two populations show different velocity distributions: the velocities of the first are close to the average velocity of the cluster, and the second population shows a much wider range of velocities. The mean value and standard deviation of the background population were fixed for the final calculation of cluster membership. If substructure was evident in the velocity distributions, the cluster was simultaneously fitted with two independent populations and targets were assigned a membership probability for each population. Most clusters, especially the older ones, present a single population. More details on the membership estimation are reported in Jackson et al. (in prep.). For our analysis, we selected stars with a membership probability of at least 0.8, which means that the average probability is 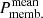P memb . mean $ P_{\mathrm{memb.}}^{\mathrm{mean}} $ for cluster members. This is listed in Table 4.

2.2. APOGEE sample

The Apache Point Observatory Galactic Evolution Experiment (APOGEE, Zasowski et al. 2013; Majewski et al. 2017) is a large-scale high-resolution spectroscopic survey with high S/N in the near-infrared (H band) that observed over 105 giant stars in the bulge, bar, discs, and halo of our Galaxy. The first set of observations of the APOGEE Survey was executed from September 2011 to July 2014 with a spectral resolution R ∼ 22 500 on the Sloan Foundation 2.5m Telescope of Apache Point Observatory (APO). The second instalment will continue the data acquisition at APO until June–August 2020. Other observations will be taken with the APOGEE-South spectrograph on the Irénée du Pont 2.5m Telescope of Las Campanas Observatory. We here use DR14 release1, which is the second data release of the fourth phase of the Sloan Digital Sky Survey (SDSS-IV York et al. 2000; Blanton et al. 2017). The APOGEE DR14 spectra were reduced with the pipeline ASPCAP (APOGEE Stellar Parameter and Chemical Abundances Pipeline, García Pérez et al. 2016). The DR14 release contains data for approximately 263 000 stars. In the same way as for the GES sample, we selected stars based on the quality of their measurements according to the following criteria: Teff >  0, eTeff <  500, log g >  −0.5, elog g <  0.5, and S/N >  20.

To identify the open clusters in the APOGEE catalogue, we started our search by defining a master list of known open clusters. We used the Kharchenko et al. (2013) catalogue, where coordinates and angular radii of clusters are listed. For most of the cluster in our list, a cluster membership has recently been published (Donor et al. 2018). For these clusters, we therefore selected the member stars of Donor et al. (2018), but for the four clusters that were not available, we computed the membership by adopting a similar approach as in Donor et al. (2018). We performed the membership selection by retaining all stars within a circle with a radius three times the reference radius and centred on the cluster coordinates. We selected as member stars those within ±2σ from the mean metallicity and RV. The open clusters we selected are listed in Table 2, where we give the following parameters: coordinates, Galactocentric distances RGC, heights from the Galactic plane z, mean RV, metallicities, and logarithmic ages.

Table 2.

Open clusters in the APOGEE sample.

The C and N abundances were computed within ASPCAP, which compares the observed spectra to a grid of synthetic spectra to determine stellar parameters. A χ2 minimisation determined the best-fit spectrum, and the corresponding stellar parameters were assigned to the observed star. The abundances of C and N were measured from molecular lines of CO and CN (García Pérez et al. 2016).

2.3. Age scale of open clusters

Star clusters offer a unique opportunity with respect to field stars because they have well-determined ages through isochrone fitting because so many members are observed throughout the cluster sequence. This makes them powerful tools for calibrating the relations between stellar ages and chemical properties of stars.

A large sample of clusters is observed in the GES and APOGEE surveys, which cover sizable ranges in ages, distances, and metallicities. The latest available GES data release, iDR5, contains 38 Galactic open clusters, and in 15 of them, red giant stars have been observed, while there are 23 clusters in APOGEE with red giant stars (see Tables 1 and 2).

We adopted cluster ages from the recent literature. Because a reliable and homogeneous age determination of star clusters is important for our project, we verified the literature ages against a common set of isochrones for consistency.

We compared the log g-Teff diagrams of member stars of GES and APOGEE clusters with the PISA isochrones (for details, see Dell’Omodarme et al. 2012; Tognelli et al. 2018). These correspond to the ages and metallicities in Tables 1 and 2.

For the open clusters in the GES sample, we also add stars that were observed with GIRAFFE, mainly in the main sequence, to better characterise the cluster sequence. The agreement between the literature ages and metallicities and the corresponding isochrones is remarkably good because most of them were recently redetermined by the Gaia-ESA consortium in a homogeneous way (see, e.g., Donati et al. 2014; Friel et al. 2014; Jacobson et al. 2016; Magrini et al. 2017; Overbeek et al. 2017; Tang et al. 2017; Randich et al. 2018). For the APOGEE sample, most of the clusters are in agreement with the PISA isochrones that were computed with the literature ages and metallicities. We only redetermined the age of FSR0494, for which the PISA isochrone for the age given by Kharchenko et al. (2013) was inconsistent with the present data. The new age is listed in Table 2. In the left panels of Fig. 3 in Sect. 3 and in Figs. A.1–A.3, we show the log g-Teff diagrams of member stars of each GES cluster with the corresponding PISA isochrones. The colour-magnitude diagrams of NGC 4815, NGC 6705 and Trumpler 20 are shown in Tautvaišienė et al. (2015). In Fig. 4 and in Figs. A.4–A.8 (left panels) we present the log g-Teff diagrams of APOGEE member stars and the PISA isochrones.

3. Selection criteria

To build up a relationship between the cluster [C/N] abundance ratios and their ages, it is necessary to select member stars in the red giant branch (RGB) whose carbon and nitrogen surface abundances have been modified by passing through the FDU event. Moreover, we excluded stars that have suffered extra-mixing effects.

3.1. Selection of red giant stars beyond the FDU

We derived a quantitative criterion to select among the member stars of our sample open clusters those that have passed the FDU. To identify the location in the log g-Teff diagram at which the FDU occurs for clusters of different ages and metallicities, in particularly the surface gravity log g, we used the same set of isochrones as we employed to determine the cluster ages. We considered isochrones in the age and metallicity ranges of our clusters, that is, with [Fe/H] from −0.4 to +0.4 dex and with ages from 0.1 to 10 Gyr. For these isochrones, we obtained the surface abundances of C and N.

The surface gravity that corresponds to the FDU was identified by selecting a proper value where the [C/N] starts to decrease monotonically. During the FDU, the surface [C/N] abundance progressively decreases as surface convection reaches increasingly deeper regions inside the star. We tried two different approaches: (1) the point where [C/N] starts to decrease monotonically, or (2) the point where the derivative d[C/N]/d log g is highest. We tested these two criteria on clusters with ages larger than 2 Gyr and found that the difference in the location of the FDU in the log g plane is quite negligible for our purposes (about 0.1 dex).

On the other hand, the second method (the point where d[C/N]/d log g is highest) is not suitable for clusters with ages below 500 Myr/1 Gyr. The reason is that for these ages, the extension of the convective envelope and consequently the surface [C/N] abundance changes slowly with log g. This causes a significant difference between the log g at FDU that is estimated using the two methods.

Figure 1 shows as an example the variation of [C/N] versus log g for isochrones of 200 Myr and 2 Gyr (for solar metallicity). For the 2 Gyr case the interval of log g where [C/N] decreases is Δ log g ≈ 0.3 − 0.4 dex, while for young clusters the interval is larger, about 0.6−0.7 dex. The maximum of the derivative d[C/N]/d log g corresponds to about the median point of the interval. Because the interval of log g during the giant branch in young clusters is large, the adoption of the maximum derivative underestimates log g at the FDU by about 0.3 dex with respect to the alternative criterion. For this reason, we decided to use the first approach, and accordingly identified the log g FDU as the point where [C/N] starts to decrease monotonically in all clusters we analysed.

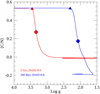thumbnail Fig. 1.

[C/N] vs. log g of 200 Myr (red line) and 2 Gyr (blue line) [Fe/H] = 0.0 dex PISA isochrones. The triangle represents the point where [C/N] starts to decrease monotonically, and the circle represents the point where the derivative d[C/N]/d log g is highest.

For each cluster in the GES and APOGEE samples, the values of log g that correspond to the FDU are shown in Table 3. To estimate the uncertainties in log g at which the FDU occurs, we considered the effect of the uncertainties on the age and metallicity on the position of the FDU in the age versus log g (FDU) plane, as shown in Fig. 2. At younger ages, the uncertainty on the location of the FDU is mainly due to the uncertainties on the age. For the youngest clusters with ages < 1 Gyr, the uncertainty in the determination of log g of the FDU can be very large because the log g range in which the FDU occurs is wide (∼1 dex in log g). Typical uncertainties of clusters with ages of about 1 Gyr range from 0.1 to 0.3 Gyr (see Tables 1 and 2), which implies an uncertainty in the determination of log g of the FDU of ∼0.05 dex. For the oldest clusters, the main variation in the FDU position is related to the uncertainty in metallicity: from 2 to 9 Gyr, a variation of [Fe/H] of ±0.15 dex (a typical 2 or 3σ uncertainty on cluster [Fe/H]) implies a change in the FDU log g from 0.05 to 0.1 dex, respectively. To select stars that have passed the FDU, we took the uncertainties on the estimation of the theoretical position of the FDU and on the derived spectroscopic gravities into account. These uncertainties were added to FDU log g in order to determine a lower limit in the selection of stars beyond the FDU.

Table 3.

Surface gravity, log g, at FDU for the open clusters in the GES and APOGEE samples.

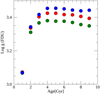thumbnail Fig. 2.

Theoretical log g at the FDU as a function of age and metallicity. Three different colours indicate three different metallicities: [Fe/H] = 0 (red), [Fe/H] = −0.15 (green), and [Fe/H] = +0.15 (blue).

3.2. C and N variations beyond the FDU: the effect of extra mixing

Selecting stars that have passed the FDU indeed defines a broad class of giant stars: lower RGB stars, that is, stars just after the subgiant phase, at the beginning of the RGB; stars in the red clump (RC), and stars in the upper RGB. After the FDU, a star evolves along the RGB where more mixing can occur, which further decreases the C/N ratio (see e.g. Gratton et al. 2000; Martell et al. 2008) through non-canonical mixing that might be driven by thermohaline mechanisms (Lagarde et al. 2012). These effects are mainly expected along the upper RGB, after the RGB bump phase, and they are stronger at low metallicity and for low-mass stars (see the lower panel of Fig. 1 of Masseron & Gilmore 2015; Shetrone et al. 2019). On the other hand, at solar metallicity and for massive stars, the effect is quite weak and almost negligible compared to the precision of measured C/N, unless other non-canonical extra-mixing processes have modified them in specific stars. Masseron et al. (2017) confirmed the universality of extra mixing in the upper part of the RGB for low-mass stars. They found an N depletion between the RGB tip and the red clump evolutionary phase, which is likely due to the mixing with the outer envelope during the He flash. This effect is particularly appreciable and strong at low metallicity, while at solar metallicity, RGB and RC stars present similar N abundances (Shetrone et al. 2019).

Observational evidence of extra-mixing processes that occur during the RGB bump phase has been the detection of a further depletion of Li abundance along the RGB in globular clusters (e.g. Lind et al. 2009; Mucciarelli et al. 2011). During the bump, the thermohaline convection is expected to be more efficient and to rapidly transport surface Li into the internal hotter regions, where it is destroyed. The same mechanism can modify C and N abundances.

Open clusters usually do not reach very low metallicities and thus are not expected to show strong extra mixing. Nevertheless, the GES data allow us to determine cluster by cluster whether this extra mixing occurs by considering the Li abundance, A(Li) = log(Li/H), and [C/N]. Then we can safely exclude the stars with strong extra mixing with lower [C/N], which would affect our age determination. In our sample, the lowest metallicities are those of Br 31 ([Fe/H] = −0.27 ± 0.06) and NGC 2243 ([Fe/H] = −0.38 ± 0.04) in the GES sample and of Trumpler 5 ([Fe/H] = −0.40 ± 0.01) and Teutsch 51 ([Fe/H] = −0.28 ± 0.03) in the APOGEE sample. As shown in Fig. 1 of Masseron & Gilmore (2015), [C/N] is expected to remain the same at solar metallicity from the lower RGB to RC, but is expected to be modified in the upper RGB, if at lower metallicity. Although from a theoretical point of view we do not expect strong extra-mixing effects in the metallicity range of open clusters, the Li abundance available in the GES sample can be used to determine correlations between Li, [C/N] abundances, and the evolutionary phase of member stars of the same clusters. We can thus identify possible extra-mixing processes in a metallicity range that has so far been poorly investigated in this respect.

In stars belonging to the same cluster, we expect to have a large dispersion of lithium abundance even before the RGB bump. This dispersion can be explained with several mechanisms: rotational mixing (Pinsonneault et al. 1992; Eggenberger et al. 2010), mass loss (Swenson & Faulkner 1992), diffusion (Michaud 1986), gravity waves (Montalbán & Schatzman 2000; Talon & Charbonnel 2005), and overshooting (Xiong & Deng 2009). For instance, stars with a range of rotation velocities might have depleted Li at different rate. Rotation velocity is indeed responsible for the transport of chemical species and a higher rotation allows a deeper dredge-up (e.g. Balachandran 1990; Lèbre et al. 2005), which modifies the Li content on the main sequence (e.g. the Li dip). However, the efficiency of this rotation-induced mixing can explain the spread of A(Li), but its effect is too weak to reproduce the drop of Li in some stars beyond the bump (see e.g. Mucciarelli et al. 2011). A non-canonical mixing is therefore necessary to explain Li depletion beyond the bump. Li depletion caused by thermohaline mixing is expected to be combined with a further decline of C and an enhancement of N, with a global decrease of [C/N] in lithium-depleted stars.

In Fig. 3 (we present all clusters in Figs. A.1–A.3) we show two examples of clusters in the GES survey. In these figures we present the log g-Teff diagrams (left panels), A(Li) versus [C/N] (central panels), and [C/N] abundance versus Teff (right panels) of giant stars that have passed the FDU. We consider a star to be Li-depleted if A(Li) < 0.4 dex or if its A(Li) is an upper limit. For most clusters, Li-depletion occurs in stars beyond the RGB bump (but not for all clusters, see e.g. M 67). In many cases, Li-depletion is associated with a variation of [C/N] with respect to the bulk of stars with A(Li) > 0.4 dex. In the rightmost panel, we also show [C/N] as a function of Teff. For our analysis, we conservatively removed stars with A(Li) < 0.4 dex to maintain a sample of giant stars with homogeneous conditions and similar [C/N] abundances (with the exception of the stars of M 67, for which we have only Li-depleted stars whose [C/N] is in good agreement with previous literature results; Bertelli Motta et al. (2017)). However, we recall that the final A(Li) during the giant phase is strongly related to the initial Li abundance during the main sequence: a main-sequence star with a strong rotational velocity might deplete its surface Li abundance more than a star that rotates at a lower rate. For stars with low A(Li) but normal [C/N] with respect to the bulk of stars of the cluster (see, e.g. Pismis 18, NGC 6067), the origin of the Li under-abundance might be related to their condition during the main sequence. We also considered the location of stars in the log g-Teff diagram and excluded stars beyond the RGB bump when their [C/N] differed by more than 1σ from the average [C/N] of the stars located before the bump.

thumbnail Fig. 3.

GES clusters NGC 2243 and Trumpler 23: log g-Teff diagrams with PISA isochrones 3.7, 4.0, 4.3, and 4.5 Gyr and 0.7, 0.8, 0.9, and 1.0 Gyr, respectively (left panels), and member stars beyond the FDU, A(Li) vs. [C/N] (central panel), and [C/N] abundance vs. Teff (right panel). Stars with A(Li) > 0.4 are shown with red circles, stars with A(Li) < 0.4 with blue circles, stars with upper limit measurements of A(Li) are indicated with empty circles, and main sequence, subgiant stars or stars without C and N are shown with grey circles. The green star represents the position of the RGB bump.

In Fig. 4 (in Figs. A.4–A.8 we present all clusters) we show the log g-Teff diagram (left panel) and [C/N] abundance versus Teff (right panels) in giant stars of the APOGEE sample of open clusters for two example clusters. For these clusters, we do not have information on Li abundance. We therefore used the information on the location on the log g-Teff diagram and the variation of [C/N] to exclude stars for our final sample: we excluded stars beyond the RGB bump, but only if their [C/N] differed by more than 1σ from the average [C/N] of the stars located before the bump (see Fig. A.9).

thumbnail Fig. 4.

APOGEE clusters NGC 6791 and NGC 6705: log g-Teff diagrams with PISA isochrones 7.3, 7.6, 7.9, and 8.2 Gyr for NGC 67091 and 0.1, 0.2, 0.3, and 0.4 Gyr for NGC 6705 (left panels) and [C/N] abundance vs. Teff (right panels). Symbols and colours are the same as in Fig. 3.

From stellar evolution theory, we would expect that stars that have evolved stars beyond the FDU to have lower [C/N] values if extra-mixing processes occur (see e.g. Lagarde et al. 2012). For some clusters we observe an opposite effect: at least one star that is more evolved along the isochrone has a higher [C/N] abundance (see e.g. NGC 6705 and NGC 6866) than the stars located at the clump. This unexpected result might be due to incorrect stellar parameters or abundances. These stars are not considered in the final average values. In addition, in many clusters (see e.g. NGC 2420, Trumpler 5, and NGC 6819) we removed several stars (blue circles) that are probably non-members based on their location, which quite far from the best-fit isochrone, and based on their discrepant [C/N]. They were not considered when we computed the final average value.

Globally, the effect of the extra mixing seems to be very limited in the metallicity range of open clusters: no clear and systematic correlation is found between the location of an RGB star in the log g-Teff diagram and the [C/N] value. For some clusters this effect is appreciable, for instance NGC 6791, in which many stars above the bump are observed which all have systematically lower [C/N] abundances, while in other clusters, for example, NGC 6819, the stars above the bump show similar [C/N] as the clump stars. In addition, where a Li abundance is available, the correlation of Li depletion with lower [C/N] values is weak, as expected as a consequence of an extra-mixing episode. Only for the oldest clusters do we observe a [C/N] decrease for stars with A(Li) < 0.4 dex caused by a more efficient dredge-up or thermohaline extra mixing (see e.g. Berkeley 31 and Berkeley 26). On the other hand, for younger clusters, A(Li) < 0.4 dex is often coupled with higher values of [C/N] with respect to stars with A(Li) > 0.4 dex (see e.g. NGC 6005, Rup 134, Pismis 18, and Trumpler 23). This can be related to the higher mass of their evolved stars in which thermohaline instability does not occur (Lagarde et al. 2019). Thus, the mechanisms of Li depletion can be uncorrelated to those that modify the C and N abundances. The latter can be related to rotation-induced mixing that has an effect on the internal chemical structure of main-sequence stars, observable during the RGB phase (see. e.g. Charbonnel & Lagarde 2010). The anti-correlation in young clusters between A(Li) and [C/N] in Li-depleted stars cannot easily be explained by the current models and deserves further investigation. It might be associated with the Li abundance in the main sequence and is inherited during the following evolutionary phases.

4. Age-[C/N] relationship using open clusters

In Table 4 we present the results of our analysis: the mean [C/N] abundance ratio of the member giant stars (with selection criteria described in the previous sections) and the number of stars for each cluster in the GES and APOGEE samples. The uncertainties in Table 4 are the formal errors on the weighted mean, and within brackets, we list the standard deviation σ. They take the uncertainties on C and N abundances into account. Using the solar values from Grevesse et al. (2007), we computed the average [C/N] ratio in each cluster in the GES sample. For APOGEE clusters the solar-scaled abundance ratios are already given in their database. Solar abundances in the APOGEE survey are adopted from Asplund et al. (2005), which is consistent, for most elements, with those in Grevesse et al. (2007), including C and N. For three clusters of the GES sample, Trumpler 20, NGC 6705, and NGC 4815, we used the literature [C/N] that is estimated only for post-FDU stars from Tautvaišienė et al. (2015) based on GES results (C and N abundances are not re-derived in the next data releases, therefore they are not present in GES iDR4 and iDR5, which we used here).

Table 4.

Mean post-FDU [C/N] of the open clusters in the GES and APOGEE samples.

Two clusters are in common between the two surveys, M 67 and NGC 6705. They can also be used to cross-calibrate the [C/N] abundances in the two surveys, together with a few other stars in common that mainly are benchmark stars.

In M 67, there are three stars in common between GES and APOGEE with [C/N] abundances. The average post-FDU abundance in M 67, using APOGEE DR14, is [C/N] = −0.57 ± 0.01, while the GES results give [C/N] = −0.37 ± 0.07. The C and N abundances of stars in M 67 along the evolutionary sequence have been studied in detail by Bertelli Motta et al. (2017) using APOGEE DR12. Their post-FDU stars have an average [C/N] = −0.46 ± 0.03, which is in good agreement with the expectation of theoretical models for stars with a mass and metallicity of the evolved stars of M 67 (Salaris et al. 2015), as shown in Fig. 9 of Salaris et al. (2015). The results for M 67 in APOGEE DR14 are slightly higher because of an offset in the [C/N] abundances from APOGEE DR12 to the latest APOGEE DR14 release. In Fig. 5 we compare [C/N] in three stars in common between APOGEE (DR12 and DR14) and GES. The [C/N] values of APOGEE DR14 are systematically lower than those in DR12. The values of GES and APOGEE DR12 are in better agreement (close to the one-to-one relationship). We note that Souto et al. (2019) have recently reanalysed 83 APOGEE DR14 spectra of stars in M 67. The analysis performed in this paper is more accurate than the standard analysis (Cunha & Hasselquist, priv. comm.). Five stars are in common between GES and the sample of Souto et al. (2019), two of them with C and N abundances. For these stars the agreement in [C/N] is within 0.01 dex. We therefore used the reanalysis of Souto et al. (2019) to compute the mean [C/N] of giant stars after the FDU in M 67, which is [C/N] = −0.50 ± 0.09. In the following analysis, we adopt for M 67 an average between the GES and the results of Souto et al. (2019). The three stars of M 67 in GES have A(Li) < 0.4 dex, but their [C/N] is consistent with the other stars in APOGEE and with the theoretical model of Salaris et al. (2015). For these reasons we include them in the analysis.

thumbnail Fig. 5.

Stars in common between GES and APOGEE (DR12 is shown by brown triangles and DR14 by cyan squares) in M 67. The continuous line is the one-to-one relation. The yellow star shows the theoretical location of the FDU in the models of Salaris et al. (2015) for the age and metallicity of M 67.

The other cluster in common between the two surveys is NGC 6705. In Fig. 6 we show the [C/N] abundances in stars in common between APOGEE (DR12 and DR14) and GES. As for M 67, the [C/N] values of APOGEE DR14 are systematically lower than those in DR12. On the other hand, for this cluster the values of DR14 are in much better agreement with the GES results.

thumbnail Fig. 6.

Stars in common between GES and APOGEE (DR12 is shown by brown triangles and DR14 by cyan squares) in NGC 6705. The continuous line is the one-to-one relation. The yellow star shows the theoretical location of the FDU in the models of Salaris et al. (2015) for the age and metallicity of NGC 6705.

In the following analysis, we adopt for NGC 6705 an average between the GES from Tautvaišienė et al. (2015) and the APOGEE DR14 results. To identify possible systematic offsets or trends, we made a global cross-match between APOGEE DR12 and DR14 and GES. In Fig. 7 we show the [C/N] abundances of stars in common between GES and the two APOGEE releases. We note a general better agreement of APOGEE DR14 with GES, while the [C/N] abundances in APOGEE DR12 are usually offset of ∼0.2 dex.

thumbnail Fig. 7.

Stars in common between GES and APOGEE (DR12 is shown by brown triangles and DR14 by cyan squares). The continuous line is the one-to-one relation. The red stars are the abundances in M 67 for APOGEE DR12 and the blue stars show APOGEE DR14.

In the plot of Fig. 7 we highlight the abundances of the three stars of M 67. These stars are indeed outliers in APOGEE DR14, with a negative offset with respect to GES. For the stars we used the improved analysis of Souto et al. (2019) as suggested by the APOGEE team (Cunha & Hasselquist, priv. comm.).

For the other stars, there are no systematic offsets and the agreement between the two sets of results is good within the errors. This allows us to securely combine the GES and APOGEE DR14 samples of clusters (with the exception of the results of M 67, for which we adopt the results of Souto et al. 2019).

In Fig. 8 we show the relationship between [C/N] in GES and APOGEE clusters and their logarithmic ages.

thumbnail Fig. 8.

Average [C/N] ratios of cluster member stars with log g cut as a function of log(Age[yr]) for the GES (orange circles) and the APOGEE (green circles) surveys. The yellow circles represent the GES literature results by Tautvaišienė et al. (2015). The red circles represent the mean value [C/N] for NGC 6705 and M 67. The straight line is the linear weighted least-squares fit of the data.

With the ages expressed in logarithmic form, the relationship is linear, with a Pearson coefficient R = 0.85, and it has the expression

log [ A g e ( y r ) ] = 10.54 ( ± 0.06 ) + 2.61 ( ± 0.10 ) [ C / N ] . $$ \begin{aligned} \log [\mathrm Age(yr)]=10.54(\pm 0.06)+2.61(\pm 0.10)\mathrm{[C/N]}. \end{aligned} $$(1)

This relationship has an important implication because if we know the evolutionary stage of a giant star and we can measure its [C/N] abundance ratio, we can infer its age. However, some caveats need to be explicitly discussed here: (i) the relationship in Eq. (1) is empirical and it is built using open clusters whose metallicity range is −0.4 < [Fe/H] < +0.4. Thus, its application outside this [Fe/H] range is not correct. (ii) At low metallicity, the effect of non-canonical extra mixing in post-FDU stars increases and thus the measured [C/N] loses its dependence on stellar mass (and thus age). (iii) Although the ages of giant stars are poorly constrained by isochrone fitting, and thus their age estimate through Eq. (1) is a step forwards, the uncertainties on [C/N] and ages are still high, as we discuss in the next paragraphs.

4.1. Error estimate

It is known that the measurements of stellar ages are usually affected by large uncertainties. However, accurate knowledge of stellar ages is a fundamental constraint for the scenarios of the formation and evolution of the different components of our Galaxy. Astroseismology data from CoRoT and Kepler have improved our knowledge of stellar ages, but they are limited to still small samples of stars. In this framework, chemical clocks such as [C/N], but also [Y/Mg] and [Y/Al] (Tucci Maia et al. 2016; Spina et al. 2016, 2018; Feltzing et al. 2017; Delgado Mena et al. 2019), might be important auxiliary tools because they can be obtained for large numbers of stars. However, it is important to have a clear idea of the uncertainties related to the use of abundance ratios to derive the age of a star.

From the GES results, the typical uncertainties on the C and N abundances are 0.05 dex and 0.065 dex, respectively, with typical uncertainties on the abundance ratio [C/N] of ∼0.10 dex. They affect the uncertainties on the logarithmic ages, giving a mean value of about ∼0.26 dex on the logarithm of the age. These uncertainties translate into ∼55−60% for the linear ages. For the APOGEE results, the typical uncertainties on the C and N abundances are ∼0.04 dex and ∼0.04 dex, respectively, with a typical uncertainty on the abundance ratio [C/N] of ∼0.06 dex. As for GES, this implies a mean uncertainty on the logarithm of the age of ∼0.17 dex and of ∼40−45% for the linear ages. Typical uncertainties are listed in Table 5.

Table 5.

Typical uncertainties on logarithmic and linear age in different ranges of logarithmic age.

However, another important part in the error budget is the uncertainty in the parameters of the fit of the linear relationship of Eq. (1). Combining both GES and APOGEE sample, we lower the uncertainties on the slope and on the intercept of the linear relationship. At the moment, the uncertainties on the parameters of the fit are of the order of ∼0.06 and ∼0.10 on the intercept and slope, respectively. We expect to have a more accurate fit of the relationship at GES completion, when about 70 open clusters will be available. At the moment, the age estimate with [C/N] abundance can be considered as an additional tool to give an independent estimate of the age of field stars, in particular for giant stars, for which it is not appropriate to determine the age through isochrone fitting because isochrones of different ages are only little different.

4.2. Comparison with previous results

A relationship between logarithmic age and [C/N] has been provided for the APOGEE catalogue: Martig et al. (2016) presented an empirical relationship between [C/N] and stellar masses (and thus stellar ages) based on the asteroseismic mass estimates from the APOKASC survey (a spectroscopic follow-up by APOGEE of stars with asteroseismology data from the Kepler Asteroseismic Science Consortium, Borucki et al. 2010). To compare this with our results, we cross-matched the APOKASC catalogue of Martig et al. (2016) with APOGEE DR14 and found the mean offset between the DR12 and DR14 abundances. We applied the offset to the DR12 APOKASC abundances to have them on the same scale as our clusters.

In Fig. 9 we plot the ages from Martig et al. (2016) and [C/N] measurements from DR12 (scaled to DR14), together with the results of our sample of the open clusters and the relation of Eq. (1). We note that the two samples have different slopes at older ages, where the effect of extra mixing might be higher. In the oldest regime (log(Age[yr]) > 9.5), the ages obtained by Martig et al. (2016) are ∼0.2 dex younger than ours at fixed [C/N]. Mackereth et al. (2017) showed that Martig et al. (2016) underestimated the ages in the older regime by up to a factor of 2 when compared with those based on asteroseismological masses. Therefore, our relationship provide ages that agree better with those of Mackereth et al. (2017).

thumbnail Fig. 9.

Comparison between the field stars in APOKASC with [C/N] vs. age computed by Martig et al. (2016) (red dots) and those obtained here using open clusters in the APOGEE and GES surveys (symbols and colour codes are the same as in Fig. 8).

For the youngest ages, at a given [C/N] our ages correspond to [C/N] values close to the APOGEE DR12 rescaled ages, although with a large dispersion. This is true in the region where the two samples overlap, even if the APOKASC sample does not populate the youngest-age regions, where many star clusters are located, reaching a lower limit of about log(Age[yr]) ∼ 8.8. The combination of ages from asteroseismology with those from isochrone fitting in young open clusters deserves to be investigated and to be fully exploited to obtain a calibration of the [C/N]-Age relation in a wider age range.

5. Comparison with theoretical models

Later phases of stellar evolution affect the abundances of C and N, and therefore the abundances of these elements do not trace the initial chemical composition of stars, but they are modified by stellar nucleosynthesis and by internal mixing. In this framework, it is of interest to compare our results with predictions of various theoretical models of stellar evolution, with the limits of such comparisons in mind, such as (i) imperfect correspondence between the stellar models that are used for the isochrones that were adopted to derive the ages of open clusters and those adopted to predict surface [C/N] abundances, (ii) possible offsets in [C/N] between models and observations, and (iii) comparison of different types of stars in model and observations.

We compared our results with models in two different ways: a classical comparison with a set of standard stellar evolution models that have been computed for different metallicities (Salaris et al. 2015), and a more innovative approach that combines a stellar population synthesis model of the Galaxy with a complete grid of stellar evolution models (Lagarde et al. 2017).

In Fig. 10 we compare the observed [C/N] at the FDU versus age with theoretical predictions of Salaris et al. (2015). We recall that in our observations we selected giant stars beyond the FDU, and avoided stars after the RGB bump with measurable effects of extra mixing in their [C/N] abundances and/or that were Li-depleted. The models of Salaris et al. (2015) are computed with the BaSTI stellar library (Pietrinferni et al. 2004, 2006), and they include the effect of the overshooting. The theoretical curves give the [C/N] abundance after the FDU at a given stellar age. They are provided for different metallicities in the age range 1−10 Gyr. We selected three curves that cover the metallicity range of our sample clusters.

thumbnail Fig. 10.

Comparison of [C/N] and age between the theoretical models by Salaris et al. (2015) and the open clusters in GES and APOGEE surveys. The models are computed for different metallicities. Their colour codes are shown in the legend. The clusters are divided into three metallicity bins: [Fe/H] ≤ −0.10 (light blue circles), −0.1 ≤ [Fe/H] ≤ +0.1 (pink circles), and [Fe/H] ≥ +0.1 (grey circles).

The data of open clusters follow the general trend of the models, which confirms the predicted increase in [C/N] with age. In the age range where both observations and models are available, we have colour-coded them in the same way to facilitate the association of the observations with the corresponding curves. Model curve and observations agree in general within the uncertainties, but no trend with metallicity can be seen for the observations.

In Fig. 11 we compare our data with the results of the model of Lagarde et al. (2017) for three ranges of metallicities. The models of Lagarde et al. (2012) have been applied to an improved stellar population model of the Galaxy by Lagarde et al. (2017), providing global, chemical, and seismic properties of the thin-disc stellar population. The authors estimated the effect of the thermohaline mixing in thin-disc giants, which produce measurable effects on the [C/N] ratios of stars of different metallicities. They derived mean relations between [C/N] and age, which can be used to estimate ages for thin-disc RC giants as a function of their [Fe/H]. Because the open clusters are a thin-disc population and we mainly selected low RGB and RC stars in them, we can compare our results with the models of Lagarde et al. (2017).

thumbnail Fig. 11.

Comparison between age and [C/N] of the thin-disc RC giant modelled by Lagarde et al. (2017) (continuous lines in light blue, pink, and grey) and the clusters in GES and APOGEE. The clusters and models are divided into three metallicity bins: [Fe/H] ≤ −0.10 (light blue circles), −0.1 ≤ [Fe/H] ≤ +0.1 (pink circles), and [Fe/H] ≥ +0.1 (grey circles).

The data are in qualitative agreement with the model curves of Lagarde et al. (2017), which predict lower [C/N] values for the oldest stars. On the other hand, the open cluster data are in better agreement with the model curves of Salaris et al. (2015), whose models show an increasing [C/N] abundance with age that better follows the observed trend in the oldest clusters. Both models are computed for ages > 1 Gyr and for different metallicities (in the plot we show the models computed for the metallicity range of our sample of clusters). In the data, at a given age, we do not distinguish between trends of clusters with different metallicities. However, in the metallicity range spanned by the data, model predictions would differ by only ∼0.1 dex considering the two metallicity extremes. This difference is comparable with typical [C/N] uncertainty.

6. Application to field stars

As mentioned by Masseron & Gilmore (2015), passing from [C/N] measurements to assign masses and ages is tempting, but at the same time, it is risky because of several unknown or underestimated effects such as the exact evolutionary stage of each of the observed stars, the metallicity dependence of C and N abundances after the FDU, and the effect of the extra mixing at different ages and metallicities (cf. Lagarde et al. 2017).

Keeping in mind these limits, we combined the sample of giant stars in the GES and APOGEE databases with C and N abundances aiming at identifying age trends in the disc populations. We selected giant stars have passed the FDU. To identify the maximum log g at which the FDU can appear, we considered our grid of isochrones (Pisa isochrones, Dell’Omodarme et al. 2012) at different ages and metallicities. For each of them we derived the value of log g that corresponds to the point where [C/N] starts to decrease monotonically, that is, log g (FDU). For most of the field stars, which are usually older than the cluster stars, the mean value of the surface gravity at the FDU is log g ∼3.4, with a slight dependence on metallicity (see Fig. 1). We also excluded stars above the RGB bump (considering the most conservative case of stars of 2−3 Gyr, the age of the bulk of the stars in our sample, for which the RGB bump is located at log g ∼2.4). Therefore, in the following analysis, we selected giant field stars with 2.4 < log g < 3.4. In addition, we used the line-of-sight distances derived by Bailer-Jones et al. (2018) with Gaia DR2. They used a distance prior that varies smoothly as a function of Galactic longitude and latitude according to a Galaxy model. We applied the relationship of Eq. (1) to giant field stars and took its limits of applicability into account: −0.4 < [Fe/H] < +0.4 and 0.1 Gyr < age < 10 Gyr, which is the range of metallicity and age of the clusters we studied here.

There are about 67 000 giant stars, of which ∼272 belong to GES, in the our combined sample for which we can estimate the age. Based on the distance obtained with Gaia, we can locate them in the Galaxy. With our determination of stellar ages, we can investigate the age trends in the thin- and thick-disc populations.

In Fig. 12 we show [α/Fe] (computed with Ca, Si, and Mg in both surveys) versus [Fe/H] for the APOGEE and GES sample, colour-coded by their [C/N] abundance ratio. The dichotomy between the α-enhanced thick-disc stars and the lower [α/Fe] thin-disc stars is also evident in terms of their [C/N]. As has been observed by Masseron & Gilmore (2015) in their analysis of the APOGEE catalogue for DR12, we can see a clear gradient in [C/N], with the thin-disc stars having a lower [C/N]. At a given metallicity, [C/N] increases for higher [α/Fe] (see also Hasselquist et al. 2019). The gradient in [C/N] can then be translated into a gradient in ages, as shown in Fig. 13. In this plot there are two approximations: (i) the relationship of Eq. (1) has been applied outside the range of metallicity −0.4 < [Fe/H] < +0.4 and also to thick-disc stars, with different [α/Fe] and thus different initial [C/Fe]; (ii) stars with derived age > 10 Gyr are shown in red. Their ages are estimated by applying the relationship outside its range of applicability, and for this reason, they do not represent a correct age estimate and we can just say they are old. There is a clear division in age between thin- and thick-disc stars: the youngest stars are present in the thin disc, and their ages become greater with increasing α-element content. The thick-disc stars are in general older than the thin-disc stars. Most of them have only lower limit estimate of their ages, with age ≳10 Gyr.

thumbnail Fig. 12.

[α/Fe] as a function of [Fe/H] for field stars in the APOGEE DR14 and GES samples. The stars are colour-coded by [C/N].

thumbnail Fig. 13.

[α/Fe] as a function of [Fe/H] for field stars in the APOGEE DR14 and GES samples. The stars are colour-coded by ages.

In Fig. 14 we present the histogram of the derived stellar ages in different bins of |z| and RGC, covering a radial region 3 < RGC < 15 kpc and a vertical region |z| <  2 kpc. We divided our sample into several radial and vertical regions, as was done by Hayden et al. (2015). In this plot and in the following Table 6 and Fig. 15, we apply the relationship of Eq. (1) in the metallicity range −0.4 < [Fe/H] < +0.4 and do not include lower limit measurements. In Table 6 we show the median ages and σ in each bin. The bins close to the plane contain the youngest stars, but they also have a non-negligible tail of old stars. The stars located in the bins at intermediate height are older, and even more so, stars located at 1 kpc < |z| < 2 kpc. This is also appreciable from Table 6, which shows a systematically increasing age for stars that are located above the Galactic plane. In the bins that characterise the thin disc 0 kpc < |z| < 0.5 kpc, the youngest population is located in the inner bins, and the ages slightly increase towards the outskirts.

thumbnail Fig. 14.

Histograms of the age for each bin in height on the plane |z| and Galactocentric distance RGC. Each panel corresponds to the respective panel in Fig. 15.

Table 6.

Median and σ of the age for each bin in height on the plane z and Galactocentric distance RGC.

In Fig. 15 we show the [α/Fe] versus [Fe/H] plane divided into same bins as in Fig. 14. For lower z, the thin-disc population is promiment. It is characterised by a low-[α/Fe]. Conversely, for higher z, the population of thick-disc stars starts to increase. It is more prominent in the inner regions.

thumbnail Fig. 15.

[α/Fe] as a function of [Fe/H] for field stars in the APOGEE sample. The stars are colour-coded by ages. The dashed line shows the separation between thin- and thick-disc populations. Each plot contains stars selected by means of Galactocentric radius RGC and height z, labelled in each figure.

The bottom panels of Fig. 15 show the thin-disc population closer to the plane. In the 3 kpc < RGC < 7 kpc ranges the population is dominated by thin-disc metal-rich stars, where the stars with the highest metallicity are the youngest stars. The histograms of the age distribution in each bin in |z| and RGC in Fig. 14 and the respective medians and σ in Table 6 show that the population in 3 kpc < RGC < 7 kpc at low z is mainly young. Therefore, the inner bin is dominated by young and metal-rich stars, with low [α/Fe]. In the outer regions 7 kpc < RGC < 11 kpc, the thin disc includes a wider range of [Fe/H], from −0.4 to 0.4. Following our age estimate, the younger stars are located in the lower envelope of the distribution, at low [α/Fe]. There is a consistent number of old stars with both super- and sub-solar metallicity. In the outer regions at 11 kpc < RGC < 15 kpc, the metal-rich stars start to disappear.

The central panels of Fig. 15 show the thin-disc population at intermediate height above the plane. In the innermost regions at 3 kpc < RGC < 7 kpc, the thin disc is poorly populated, unlike the region at 7 kpc < RGC < 11 kpc. This effect is due to the observational selection of the APOGEE survey, for which the observations are located in particular towards the outer regions at 7−11 kpc when compared with the inner regions at 3−7 kpc. The stars in these two panels do not reach the low [α/Fe] and the young ages of the corresponding panels at lower z. Their median ages are older than the medians at the same RGC, but lower z (see Table 6). The outer regions contain fewer metal-rich stars, and they are younger on average, as their medians show when compared with those in the inner regions at intermediate z (see Table 6).

The top panels of Fig. 15 show the thin-disc population at a great height above the plane. Stars are almost absent from the innermost regions because of the sample selection in the range of applicability of our relationship, based on which they would be older than 10 Gyr. From 7 to 11 kpc, there is a signature of thin-disc stars with a wide age range. Finally, in the outermost regions at 11−15 kpc only few young and intermediate-age thin disc stars are present.

7. Summary and conclusions

The databases of stellar spectra from high-resolution spectroscopic surveys such as GES and APOGEE provide extremely wide and accurate data sets of stellar parameters and abundances for large samples of stars in the different Galactic components. Some abundance ratios, for instance, [C/N], [Y/Mg], [Y/Al], and [Ba/Fe], have been recognised to be powerful chemical clocks, that is, they are strictly related to the stellar ages. In particular, the [C/N] abundance ratio is a good age indicator for stars in the RGB evolutionary phase after the FDU. Using open clusters in the GES and APOGEE Surveys, we calibrated the relationship between cluster age (from isochrone fitting of the whole cluster sequence) and [C/N] abundance ratio of stars that have passed the FDU. We selected RGB stars beyond the FDU to study the effects of extra-mixing processes in their [C/N] abundances. We compared the [C/N] measurements and ages of open clusters with the predictions of stellar evolutionary models by Salaris et al. (2015) and Lagarde et al. (2017) and found a good agreement. With the current accuracy of age and abundance measurements, however, we cannot confirm the variation in age-[C/N] relationship with metallicity in the [Fe/H] range that is traced by open clusters.

We used our relationship to derive the ages of field stars in a combined GES and APOGEE sample. In the plane [α/Fe] versus [Fe/H], a clear dichotomy between the [C/N] abundances in the thin and thick disc was evident, as has previously been observed by Masseron & Gilmore (2015), and consequently stellar ages. We extrapolated our relation to estimate the ages for thin-disc stars and derived lower limit ages for the thick-disc stars. As expected, we find that stars belonging to the thin disc are on average younger than the stars in the thick disc. The typical age of the thin-disc stars decreases in the inner part of the disc at low z and towards the outskirts. The former indicates that the metal-rich stars in the inner disc represent the later phases of the Galactic evolution, while the latter is expected from an inside-out formation of the disc.

These immediate applications of the relationships between ages and [C/N] probe the power of chemical clocks to improve our knowledge of stellar ages. The next step will be to estimate in a homogeneous way the age of the open clusters in the final data release of the GES survey to place them on a common stellar age scale. In addition, we plan to combine other chemical clocks, for instance, [Ba/Fe] or [Y/Mg], to give further constraints to the ages of stars in different evolutionary stages.

Acknowledgments

We are grateful to the referee for the comments and suggestions that improved our discussion. We thank the APOGEE team, in particular Katia Cunha, Sten Hasselquist, and Gail Zasowski for their suggestions and help in using and selecting the APOGEE results. Based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under programme ID 188.B-3002. These data products have been processed by the Cambridge Astronomy Survey Unit (CASU) at the Institute of Astronomy, University of Cambridge, and by the FLAMES/UVES reduction team at INAF/Osservatorio Astrofisico di Arcetri. These data have been obtained from the GES Survey Data Archive, prepared and hosted by the Wide Field Astronomy Unit, Institute for Astronomy, University of Edinburgh, which is funded by the UK Science and Technology Facilities Council (STFC). This work was partly supported by the European Union FP7 programme through ERC grant number 320360 and by the Leverhulme Trust through grant RPG-2012-541. We acknowledge the support from INAF and Ministero dell’ Istruzione, dell’ Università’ e della Ricerca (MIUR) in the form of the grant “Premiale VLT 2012”. The results presented here benefit from discussions held during the GES workshops and conferences supported by the ESF (European Science Foundation) through the GREAT Research Network Programme. T.B. was supported by the project grant? The New Milky Way? from the Knut and Alice Wallenberg Foundation. M. acknowledges support provided by the Spanish Ministry of Economy and Competitiveness (MINECO), under grant AYA-2017-88254-P. L.S. acknowledges financial support from the Australian Research Council (Discovery Project 170100521). F.J.E. acknowledges financial support from the ASTERICS project (ID:653477, H2020-EU.1.4.1.1. – Developing new world-class research infrastructures). U.H. acknowledges support from the Swedish National Space Agency (SNSA/Rymdstyrelsen).

References

  1. Alonso-Santiago, J., Negueruela, I., Marco, A., et al. 2017, MNRAS, 469, 1330 [NASA ADS] [CrossRef] [Google Scholar]
  2. Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes III, & F. N. Bash, ASP Conf. Ser., 336, 25 [NASA ADS] [Google Scholar]
  3. Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Mantelet, G., & Andrae, R. 2018, AJ, 156, 58 [NASA ADS] [CrossRef] [Google Scholar]
  4. Balachandran, S. 1990, ApJ, 354, 310 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bertelli Motta, C., Salaris, M., Pasquali, A., & Grebel, E. K. 2017, MNRAS, 466, 2161 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bland-Hawthorn, J., Sharma, S., Tepper-Garcia, T., et al. 2019, MNRAS, 486, 1167 [NASA ADS] [CrossRef] [Google Scholar]
  7. Blanton, M. R., Bershady, M. A., Abolfathi, B., et al. 2017, AJ, 154, 28 [NASA ADS] [CrossRef] [Google Scholar]
  8. Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  9. Bragaglia, A., & Tosi, M. 2006, AJ, 131, 1544 [NASA ADS] [CrossRef] [Google Scholar]
  10. Brooke, J. S. A., Bernath, P. F., Schmidt, T. W., & Bacskay, G. B. 2013, J. Quant. Spectr. Rad. Transf., 124, 11 [NASA ADS] [CrossRef] [Google Scholar]
  11. Cantat-Gaudin, T., Vallenari, A., Zaggia, S., et al. 2014, A&A, 569, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Carraro, G., Janes, K. A., Costa, E., & Méndez, R. A. 2006, MNRAS, 368, 1078 [NASA ADS] [CrossRef] [Google Scholar]
  13. Carrera, R. 2012, A&A, 544, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Charbonnel, C., & Lagarde, N. 2010, A&A, 522, A10 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
  15. Cignoni, M., Beccari, G., Bragaglia, A., & Tosi, M. 2011, MNRAS, 416, 1077 [NASA ADS] [CrossRef] [Google Scholar]
  16. Delgado Mena, E., Moya, A., Adibekyan, V., et al. 2019, A&A, 624, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Dell’Omodarme, M., Valle, G., Degl’Innocenti, S., & Prada Moroni, P. G. 2012, A&A, 540, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. De Silva, G. M., Freeman, K. C., Bland-Hawthorn, J., et al. 2015, MNRAS, 449, 2604 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  19. Dias, W. S., Alessi, B. S., Moitinho, A., & Lépine, J. R. D. 2002, A&A, 389, 871 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Donati, P., Cantat Gaudin, T., Bragaglia, A., et al. 2014, A&A, 561, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Donati, P., Cocozza, G., Bragaglia, A., et al. 2015, MNRAS, 446, 1411 [NASA ADS] [CrossRef] [Google Scholar]
  22. Donor, J., Frinchaboy, P. M., Cunha, K., et al. 2018, AJ, 156, 142 [NASA ADS] [CrossRef] [Google Scholar]
  23. Eggenberger, P., Meynet, G., Maeder, A., et al. 2010, A&A, 519, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Feltzing, S., Howes, L. M., McMillan, P. J., & Stonkutė, E. 2017, MNRAS, 465, L109 [NASA ADS] [CrossRef] [Google Scholar]
  25. Feuillet, D. K., Bovy, J., Holtzman, J., et al. 2018, MNRAS, 477, 2326 [NASA ADS] [CrossRef] [Google Scholar]
  26. Fornal, B., Tucker, D. L., Smith, J. A., et al. 2007, AJ, 133, 1409 [NASA ADS] [CrossRef] [Google Scholar]
  27. Franciosini, E., Sacco, G. G., Jeffries, R. D., et al. 2018, A&A, 616, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Frasca, A., Molenda-Żakowicz, J., De Cat, P., et al. 2016, A&A, 594, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Friel, E. D., Janes, K. A., Tavarez, M., et al. 2002, AJ, 124, 2693 [NASA ADS] [CrossRef] [Google Scholar]
  30. Friel, E. D., Jacobson, H. R., & Pilachowski, C. A. 2005, AJ, 129, 2725 [NASA ADS] [CrossRef] [Google Scholar]
  31. Friel, E. D., Donati, P., Bragaglia, A., et al. 2014, A&A, 563, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Gao, X.-H. 2014, Res. Astron. Astrophys., 14, 159 [NASA ADS] [CrossRef] [Google Scholar]
  34. García Pérez, A. E., Allende Prieto, C., Holtzman, J. A., et al. 2016, AJ, 151, 144 [NASA ADS] [CrossRef] [Google Scholar]
  35. Geller, A. M., Latham, D. W., & Mathieu, R. D. 2015, AJ, 150, 97 [NASA ADS] [CrossRef] [Google Scholar]
  36. Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
  37. Gratton, R. G., Sneden, C., Carretta, E., & Bragaglia, A. 2000, A&A, 354, 169 [NASA ADS] [Google Scholar]
  38. Grevesse, N., Asplund, M., & Sauval, A. J. 2007, Space Sci. Rev., 130, 105 [Google Scholar]
  39. Hasselquist, S., Holtzman, J. A., Shetrone, M., et al. 2019, ApJ, 871, 181 [NASA ADS] [CrossRef] [Google Scholar]
  40. Hayden, M. R., Bovy, J., Holtzman, J. A., et al. 2015, ApJ, 808, 132 [NASA ADS] [CrossRef] [Google Scholar]
  41. Ho, A. Y. Q., Rix, H.-W., Ness, M. K., et al. 2017, ApJ, 841, 40 [NASA ADS] [CrossRef] [Google Scholar]
  42. Holtzman, J. A., Shetrone, M., Johnson, J. A., et al. 2015, AJ, 150, 148 [NASA ADS] [CrossRef] [Google Scholar]
  43. Jacobson, H. R., Pilachowski, C. A., & Friel, E. D. 2011, AJ, 142, 59 [NASA ADS] [CrossRef] [Google Scholar]
  44. Jacobson, H. R., Friel, E. D., Jílková, L., et al. 2016, A&A, 591, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Janes, K., Barnes, S. A., Meibom, S., & Hoq, S. 2013, AJ, 145, 7 [NASA ADS] [CrossRef] [Google Scholar]
  46. Janes, K., Barnes, S. A., Meibom, S., & Hoq, S. 2014, AJ, 147, 139 [NASA ADS] [CrossRef] [Google Scholar]
  47. Kharchenko, N. V., Piskunov, A. E., Schilbach, E., Röser, S., & Scholz, R.-D. 2013, A&A, 558, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Kim, S. C., Kyeong, J., & Sung, E.-C. 2009, J. Korean Astron. Soc., 42, 135 [NASA ADS] [CrossRef] [Google Scholar]
  49. Kurucz, R. L. 2005, Mem. Soc. Astron. It. Suppl., 8, 14 [Google Scholar]
  50. Kyeong, J., Kim, S. C., Hiriart, D., & Sung, E.-C. 2008, J. Korean Astron. Soc., 41, 147 [NASA ADS] [CrossRef] [Google Scholar]
  51. Lagarde, N., Decressin, T., Charbonnel, C., et al. 2012, A&A, 543, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Lagarde, N., Robin, A. C., Reylé, C., & Nasello, G. 2017, A&A, 601, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Lagarde, N., Reylé, C., Robin, A. C., et al. 2019, A&A, 621, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Lèbre, A., Palacios, A., Jasniewicz, G., et al. 2005, in From Lithium to Uranium: Elemental Tracers of Early Cosmic Evolution, eds. V. Hill, P. Francois, & F. Primas, IAU Symp., 228, 399 [NASA ADS] [Google Scholar]
  55. Li, C., Zhao, G., Zhai, M., & Jia, Y. 2018, ApJ, 860, 53 [NASA ADS] [CrossRef] [Google Scholar]
  56. Lind, K., Primas, F., Charbonnel, C., Grundahl, F., & Asplund, M. 2009, A&A, 503, 545 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  57. Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Maciejewski, G., & Niedzielski, A. 2007, A&A, 467, 1065 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Maciejewski, G., Mihov, B., & Georgiev, T. 2009, Astron. Nachr., 330, 851 [NASA ADS] [CrossRef] [Google Scholar]
  60. Mackereth, J. T., Bovy, J., Schiavon, R. P., et al. 2017, MNRAS, 471, 3057 [NASA ADS] [CrossRef] [Google Scholar]
  61. Magrini, L., Randich, S., Donati, P., et al. 2015, A&A, 580, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Magrini, L., Randich, S., Kordopatis, G., et al. 2017, A&A, 603, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Magrini, L., Spina, L., Randich, S., et al. 2018, A&A, 617, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [NASA ADS] [CrossRef] [Google Scholar]
  65. Martell, S. L., Smith, G. H., & Briley, M. M. 2008, AJ, 136, 2522 [NASA ADS] [CrossRef] [Google Scholar]
  66. Martig, M., Fouesneau, M., Rix, H.-W., et al. 2016, MNRAS, 456, 3655 [NASA ADS] [CrossRef] [Google Scholar]
  67. Masseron, T., & Gilmore, G. 2015, MNRAS, 453, 1855 [NASA ADS] [CrossRef] [Google Scholar]
  68. Masseron, T., Lagarde, N., Miglio, A., Elsworth, Y., & Gilmore, G. 2017, MNRAS, 464, 3021 [NASA ADS] [CrossRef] [Google Scholar]
  69. Mermilliod, J.-C., Clariá, J. J., Andersen, J., Piatti, A. E., & Mayor, M. 2001, A&A, 375, 30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Mermilliod, J. C., Mayor, M., & Udry, S. 2008, A&A, 485, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Michaud, G. 1986, ApJ, 302, 650 [NASA ADS] [CrossRef] [Google Scholar]
  72. Molenda-Żakowicz, J., Brogaard, K., Niemczura, E., et al. 2014, MNRAS, 445, 2446 [NASA ADS] [CrossRef] [Google Scholar]
  73. Monari, G., Kawata, D., Hunt, J. A. S., & Famaey, B. 2017, MNRAS, 466, L113 [NASA ADS] [CrossRef] [Google Scholar]
  74. Montalbán, J., & Schatzman, E. 2000, A&A, 354, 943 [Google Scholar]
  75. Mucciarelli, A., Salaris, M., Lovisi, L., et al. 2011, MNRAS, 412, 81 [NASA ADS] [CrossRef] [Google Scholar]
  76. Ness, M., Hogg, D. W., Rix, H.-W., et al. 2016, ApJ, 823, 114 [NASA ADS] [CrossRef] [Google Scholar]
  77. Netopil, M., Paunzen, E., Heiter, U., & Soubiran, C. 2016, A&A, 585, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Nissen, P. E., Silva Aguirre, V., Christensen-Dalsgaard, J., et al. 2017, A&A, 608, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Overbeek, J. C., Friel, E. D., Donati, P., et al. 2017, A&A, 598, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Pancino, E., Carrera, R., Rossetti, E., & Gallart, C. 2010, A&A, 511, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Pancino, E., Lardo, C., Altavilla, G., et al. 2017, A&A, 598, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Park, H. S., & Lee, M. G. 1999, MNRAS, 304, 883 [NASA ADS] [CrossRef] [Google Scholar]
  83. Pasquini, L., Avila, G., Blecha, A., et al. 2002, The Messenger, 110, 1 [NASA ADS] [Google Scholar]
  84. Phelps, R. L., & Janes, K. A. 1996, AJ, 111, 1604 [NASA ADS] [CrossRef] [Google Scholar]
  85. Piatti, A. E., Clariá, J. J., Bica, E., Geisler, D., & Minniti, D. 1998, AJ, 116, 801 [NASA ADS] [CrossRef] [Google Scholar]
  86. Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
  87. Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2006, ApJ, 642, 797 [NASA ADS] [CrossRef] [Google Scholar]
  88. Pinsonneault, M. H., Deliyannis, C. P., & Demarque, P. 1992, ApJS, 78, 179 [NASA ADS] [CrossRef] [Google Scholar]
  89. Randich, S., Gilmore, G., & Gaia-ESO Consortium 2013, The Messenger, 154, 47 [NASA ADS] [Google Scholar]
  90. Randich, S., Tognelli, E., Jackson, R., et al. 2018, A&A, 612, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Roccatagliata, V., Sacco, G. G., Franciosini, E., & Randich, S. 2018, A&A, 617, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Sacco, G. G., Morbidelli, L., Franciosini, E., et al. 2014, A&A, 565, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Salaris, M., Weiss, A., & Percival, S. M. 2004, A&A, 414, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Salaris, M., Pietrinferni, A., Piersimoni, A. M., & Cassisi, S. 2015, A&A, 583, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  95. Schiappacasse-Ulloa, J., Tang, B., Fernández-Trincado, J. G., et al. 2018, AJ, 156, 94 [NASA ADS] [CrossRef] [Google Scholar]
  96. Shetrone, M., Tayar, J., Johnson, J. A., et al. 2019, ApJ, 872, 137 [NASA ADS] [CrossRef] [Google Scholar]
  97. Slumstrup, D., Grundahl, F., Brogaard, K., et al. 2017, A&A, 604, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Smiljanic, R., Korn, A. J., Bergemann, M., et al. 2014, A&A, 570, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Sneden, C., Lucatello, S., Ram, R. S., Brooke, J. S. A., & Bernath, P. 2014, ApJS, 214, 26 [Google Scholar]
  100. Soderblom, D. R., Hillenbrand, L. A., Jeffries, R. D., Mamajek, E. E., & Naylor, T. 2014, Protostars and Planets VI, 219 [Google Scholar]
  101. Souto, D., Allende Prieto, C., Cunha, K., et al. 2019, ApJ, 874, 97 [NASA ADS] [CrossRef] [Google Scholar]
  102. Spina, L., Meléndez, J., Karakas, A. I., et al. 2016, A&A, 593, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  103. Spina, L., Meléndez, J., Karakas, A. I., et al. 2018, MNRAS, 474, 2580 [NASA ADS] [Google Scholar]
  104. Subramaniam, A. 2003, Bull. Astron. Soc. India, 31, 49 [NASA ADS] [Google Scholar]
  105. Swenson, F. J., & Faulkner, J. 1992, ApJ, 395, 654 [NASA ADS] [CrossRef] [Google Scholar]
  106. Talon, S., & Charbonnel, C. 2005, A&A, 440, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  107. Tang, B., Geisler, D., Friel, E., et al. 2017, A&A, 601, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  108. Tautvaišienė, G., Drazdauskas, A., Mikolaitis, Š., et al. 2015, A&A, 573, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  109. Tofflemire, B. M., Gosnell, N. M., Mathieu, R. D., & Platais, I. 2014, AJ, 148, 61 [NASA ADS] [CrossRef] [Google Scholar]
  110. Tognelli, E., Prada Moroni, P. G., & Degl’Innocenti, S. 2018, MNRAS, 476, 27 [Google Scholar]
  111. Tucci Maia, M., Ramírez, I., Meléndez, J., et al. 2016, A&A, 590, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  112. Villanova, S., Carraro, G., Bresolin, F., & Patat, F. 2005, AJ, 130, 652 [NASA ADS] [CrossRef] [Google Scholar]
  113. Wu, T., Li, Y., & Hekker, S. 2014, ApJ, 786, 10 [NASA ADS] [CrossRef] [Google Scholar]
  114. Xiong, D. R., & Deng, L. 2009, MNRAS, 395, 2013 [NASA ADS] [CrossRef] [Google Scholar]
  115. York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [CrossRef] [Google Scholar]
  116. Zasowski, G., Johnson, J. A., Frinchaboy, P. M., et al. 2013, AJ, 146, 81 [NASA ADS] [CrossRef] [Google Scholar]
  117. Zhang, B., Chen, X.-Y., Liu, C., et al. 2015, Res. Astron. Astrophys., 15, 1197 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: log g-Teff diagrams

thumbnail Fig. A.1.

log g-Teff diagram with PISA isochrones (left panel) and member stars beyond the FDU, A(Li) vs. [C/N] (central panel), and [C/N] abundance vs. Teff (right panel) of the GES clusters. Symbols and colours are the same as in Fig. 3. The isochrones are 2.1, 2.3, 2.5, and 2.7 Gyr, 6.0, 6.5, 7.0, and 7.5 Gyr, 1.1, 1.4, 1.7, and 2.0 Gyr, and 0.7, 0.8, 0.9, and 1.0 Gyr, respectively.

thumbnail Fig. A.2.

log g-Teff diagram with PISA isochrones (left panel) and member stars beyond the FDU, A(Li) vs. [C/N] (central panel), and [C/N] abundance vs. Teff (right panel) of the GES clusters. Symbols and colours are the same as in Fig. 3. The isochrones are 3.7, 4.0, 4.3, and 4.5 Gyr, 0.7, 0.8, 0.9, and 1.0 Gyr, 0.8, 1.0, 1.2, and 1.4 Gyr, and 0.8, 1.0, 1.2, and 1.4 Gyr, respectively.

thumbnail Fig. A.3.

log g-Teff diagram with PISA isochrones (left panel) and member stars beyond the FDU, A(Li) vs. [C/N] (central panel), and [C/N] abundance vs. Teff (right panel) of the GES clusters. Symbols and colours are the same as in Fig. 3. The isochrones are 0.8, 1.0, 1.2, and 1.4 Gyr for the first two clusters, and 0.05, 0.1, 0.2, and 0.3 Gyr, and 0.1, 0.2, 0.3, 0.4 Gyr.

thumbnail Fig. A.4.

log g-Teff diagram with PISA isochrones (left panel) and [C/N] abundance vs. Teff (right panel) of the APOGEE clusters. Symbols and colours are the same as in Fig. 4. The isochrones are 8.8, 9.1, 9.4, and 9.7 Gyr, 0.1, 1.2, 1.4, and 1.7 Gyr, 3.2, 3.4, 3.6, and 3.8 Gyr, and 0.8, 0.9, 1.0, and 1.1 Gyr, respectively.

thumbnail Fig. A.5.

log g-Teff diagram with PISA isochrones (left panel) and [C/N] abundance vs. Teff (right panel) of the APOGEE clusters. Symbols and colours are the same as in Fig. 4. The isochrones are 0.4, 0.5, 0.6, and 0.7 Gyr, 0.6, 0.8, 1.0, and 1.2 Gyr, 1.0, 1.2, 1.4, and 1.7 Gyr, and 0.4, 0.5, 0.6, and 0.7 Gyr, respectively.

thumbnail Fig. A.6.

log g-Teff diagram with PISA isochrones (left panel) and [C/N] abundance vs. Teff (right panel) of the APOGEE clusters. Symbols and colours are the same as in Fig. 4. The isochrones are 4.6, 4.8, 5.0, and 5.2 Gyr, 0.7, 0.8, 0.9, and 1.0 Gyr, 1.0, 1.2, 1.4, and 1.7 Gyr, and 7.3, 7.6, 7.9, and 8.2 Gyr, respectively.

thumbnail Fig. A.7.

log g-Teff diagram with PISA isochrones (left panel) and [C/N] abundance vs. Teff (right panel) of the APOGEE clusters. Symbols and colours are the same as in Fig. 4. The isochrones are 1.7, 1.9, 2.1, and 2.3 Gyr, 2.6, 2.8, 3.0, and 3.2 Gyr, 0.7, 0.8, 0.9, and 1.0 Gyr, and 2.6, 2.8, 3.0, and 3.2 Gyr, respectively.

thumbnail Fig. A.8.

log g-Teff diagram with PISA isochrones (left panel) and [C/N] abundance vs. Teff (right panel) of the APOGEE clusters. Symbols and colours are the same as in Fig. 4. The isochrones are 0.8, 1.0, 1.2, and 1.4 Gyr, 1.7, 1.9, 2.1, and 2.3 Gyr, 0.7, 0.8, 0.9, and 1.0 Gyr, and 1.0, 1.2, 1.4, and 1.7 Gyr, respectively.

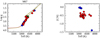thumbnail Fig. A.9.

log g-Teff diagram with PISA isochrones (left panel) and [C/N] abundance vs. Teff (right panel) of M 67 by Souto et al. (2019). Symbols and colours are the same as in Fig. 4. The isochrones are 3.8, 4.0, 4.2, and 4.4 Gyr.

All Tables

Table 1.

Parameters of the open clusters in the GES sample.

In the text
Table 2.

Open clusters in the APOGEE sample.

In the text
Table 3.

Surface gravity, log g, at FDU for the open clusters in the GES and APOGEE samples.

In the text
Table 4.

Mean post-FDU [C/N] of the open clusters in the GES and APOGEE samples.

In the text
Table 5.

Typical uncertainties on logarithmic and linear age in different ranges of logarithmic age.

In the text
Table 6.

Median and σ of the age for each bin in height on the plane z and Galactocentric distance RGC.

In the text

All Figures

thumbnail Fig. 1.

[C/N] vs. log g of 200 Myr (red line) and 2 Gyr (blue line) [Fe/H] = 0.0 dex PISA isochrones. The triangle represents the point where [C/N] starts to decrease monotonically, and the circle represents the point where the derivative d[C/N]/d log g is highest.
In the text
thumbnail Fig. 2.

Theoretical log g at the FDU as a function of age and metallicity. Three different colours indicate three different metallicities: [Fe/H] = 0 (red), [Fe/H] = −0.15 (green), and [Fe/H] = +0.15 (blue).
In the text
thumbnail Fig. 3.

GES clusters NGC 2243 and Trumpler 23: log g-Teff diagrams with PISA isochrones 3.7, 4.0, 4.3, and 4.5 Gyr and 0.7, 0.8, 0.9, and 1.0 Gyr, respectively (left panels), and member stars beyond the FDU, A(Li) vs. [C/N] (central panel), and [C/N] abundance vs. Teff (right panel). Stars with A(Li) > 0.4 are shown with red circles, stars with A(Li) < 0.4 with blue circles, stars with upper limit measurements of A(Li) are indicated with empty circles, and main sequence, subgiant stars or stars without C and N are shown with grey circles. The green star represents the position of the RGB bump.
In the text
thumbnail Fig. 4.

APOGEE clusters NGC 6791 and NGC 6705: log g-Teff diagrams with PISA isochrones 7.3, 7.6, 7.9, and 8.2 Gyr for NGC 67091 and 0.1, 0.2, 0.3, and 0.4 Gyr for NGC 6705 (left panels) and [C/N] abundance vs. Teff (right panels). Symbols and colours are the same as in Fig. 3.
In the text
thumbnail Fig. 5.

Stars in common between GES and APOGEE (DR12 is shown by brown triangles and DR14 by cyan squares) in M 67. The continuous line is the one-to-one relation. The yellow star shows the theoretical location of the FDU in the models of Salaris et al. (2015) for the age and metallicity of M 67.
In the text
thumbnail Fig. 6.

Stars in common between GES and APOGEE (DR12 is shown by brown triangles and DR14 by cyan squares) in NGC 6705. The continuous line is the one-to-one relation. The yellow star shows the theoretical location of the FDU in the models of Salaris et al. (2015) for the age and metallicity of NGC 6705.
In the text
thumbnail Fig. 7.

Stars in common between GES and APOGEE (DR12 is shown by brown triangles and DR14 by cyan squares). The continuous line is the one-to-one relation. The red stars are the abundances in M 67 for APOGEE DR12 and the blue stars show APOGEE DR14.
In the text
thumbnail Fig. 8.

Average [C/N] ratios of cluster member stars with log g cut as a function of log(Age[yr]) for the GES (orange circles) and the APOGEE (green circles) surveys. The yellow circles represent the GES literature results by Tautvaišienė et al. (2015). The red circles represent the mean value [C/N] for NGC 6705 and M 67. The straight line is the linear weighted least-squares fit of the data.
In the text
thumbnail Fig. 9.

Comparison between the field stars in APOKASC with [C/N] vs. age computed by Martig et al. (2016) (red dots) and those obtained here using open clusters in the APOGEE and GES surveys (symbols and colour codes are the same as in Fig. 8).
In the text
thumbnail Fig. 10.

Comparison of [C/N] and age between the theoretical models by Salaris et al. (2015) and the open clusters in GES and APOGEE surveys. The models are computed for different metallicities. Their colour codes are shown in the legend. The clusters are divided into three metallicity bins: [Fe/H] ≤ −0.10 (light blue circles), −0.1 ≤ [Fe/H] ≤ +0.1 (pink circles), and [Fe/H] ≥ +0.1 (grey circles).
In the text
thumbnail Fig. 11.

Comparison between age and [C/N] of the thin-disc RC giant modelled by Lagarde et al. (2017) (continuous lines in light blue, pink, and grey) and the clusters in GES and APOGEE. The clusters and models are divided into three metallicity bins: [Fe/H] ≤ −0.10 (light blue circles), −0.1 ≤ [Fe/H] ≤ +0.1 (pink circles), and [Fe/H] ≥ +0.1 (grey circles).
In the text
thumbnail Fig. 12.

[α/Fe] as a function of [Fe/H] for field stars in the APOGEE DR14 and GES samples. The stars are colour-coded by [C/N].
In the text
thumbnail Fig. 13.

[α/Fe] as a function of [Fe/H] for field stars in the APOGEE DR14 and GES samples. The stars are colour-coded by ages.
In the text
thumbnail Fig. 14.

Histograms of the age for each bin in height on the plane |z| and Galactocentric distance RGC. Each panel corresponds to the respective panel in Fig. 15.
In the text
thumbnail Fig. 15.

[α/Fe] as a function of [Fe/H] for field stars in the APOGEE sample. The stars are colour-coded by ages. The dashed line shows the separation between thin- and thick-disc populations. Each plot contains stars selected by means of Galactocentric radius RGC and height z, labelled in each figure.
In the text
thumbnail Fig. A.1.

log g-Teff diagram with PISA isochrones (left panel) and member stars beyond the FDU, A(Li) vs. [C/N] (central panel), and [C/N] abundance vs. Teff (right panel) of the GES clusters. Symbols and colours are the same as in Fig. 3. The isochrones are 2.1, 2.3, 2.5, and 2.7 Gyr, 6.0, 6.5, 7.0, and 7.5 Gyr, 1.1, 1.4, 1.7, and 2.0 Gyr, and 0.7, 0.8, 0.9, and 1.0 Gyr, respectively.
In the text
thumbnail Fig. A.2.

log g-Teff diagram with PISA isochrones (left panel) and member stars beyond the FDU, A(Li) vs. [C/N] (central panel), and [C/N] abundance vs. Teff (right panel) of the GES clusters. Symbols and colours are the same as in Fig. 3. The isochrones are 3.7, 4.0, 4.3, and 4.5 Gyr, 0.7, 0.8, 0.9, and 1.0 Gyr, 0.8, 1.0, 1.2, and 1.4 Gyr, and 0.8, 1.0, 1.2, and 1.4 Gyr, respectively.
In the text
thumbnail Fig. A.3.

log g-Teff diagram with PISA isochrones (left panel) and member stars beyond the FDU, A(Li) vs. [C/N] (central panel), and [C/N] abundance vs. Teff (right panel) of the GES clusters. Symbols and colours are the same as in Fig. 3. The isochrones are 0.8, 1.0, 1.2, and 1.4 Gyr for the first two clusters, and 0.05, 0.1, 0.2, and 0.3 Gyr, and 0.1, 0.2, 0.3, 0.4 Gyr.
In the text
thumbnail Fig. A.4.

log g-Teff diagram with PISA isochrones (left panel) and [C/N] abundance vs. Teff (right panel) of the APOGEE clusters. Symbols and colours are the same as in Fig. 4. The isochrones are 8.8, 9.1, 9.4, and 9.7 Gyr, 0.1, 1.2, 1.4, and 1.7 Gyr, 3.2, 3.4, 3.6, and 3.8 Gyr, and 0.8, 0.9, 1.0, and 1.1 Gyr, respectively.
In the text
thumbnail Fig. A.5.

log g-Teff diagram with PISA isochrones (left panel) and [C/N] abundance vs. Teff (right panel) of the APOGEE clusters. Symbols and colours are the same as in Fig. 4. The isochrones are 0.4, 0.5, 0.6, and 0.7 Gyr, 0.6, 0.8, 1.0, and 1.2 Gyr, 1.0, 1.2, 1.4, and 1.7 Gyr, and 0.4, 0.5, 0.6, and 0.7 Gyr, respectively.
In the text
thumbnail Fig. A.6.

log g-Teff diagram with PISA isochrones (left panel) and [C/N] abundance vs. Teff (right panel) of the APOGEE clusters. Symbols and colours are the same as in Fig. 4. The isochrones are 4.6, 4.8, 5.0, and 5.2 Gyr, 0.7, 0.8, 0.9, and 1.0 Gyr, 1.0, 1.2, 1.4, and 1.7 Gyr, and 7.3, 7.6, 7.9, and 8.2 Gyr, respectively.
In the text
thumbnail Fig. A.7.

log g-Teff diagram with PISA isochrones (left panel) and [C/N] abundance vs. Teff (right panel) of the APOGEE clusters. Symbols and colours are the same as in Fig. 4. The isochrones are 1.7, 1.9, 2.1, and 2.3 Gyr, 2.6, 2.8, 3.0, and 3.2 Gyr, 0.7, 0.8, 0.9, and 1.0 Gyr, and 2.6, 2.8, 3.0, and 3.2 Gyr, respectively.
In the text
thumbnail Fig. A.8.

log g-Teff diagram with PISA isochrones (left panel) and [C/N] abundance vs. Teff (right panel) of the APOGEE clusters. Symbols and colours are the same as in Fig. 4. The isochrones are 0.8, 1.0, 1.2, and 1.4 Gyr, 1.7, 1.9, 2.1, and 2.3 Gyr, 0.7, 0.8, 0.9, and 1.0 Gyr, and 1.0, 1.2, 1.4, and 1.7 Gyr, respectively.
In the text
thumbnail Fig. A.9.

log g-Teff diagram with PISA isochrones (left panel) and [C/N] abundance vs. Teff (right panel) of M 67 by Souto et al. (2019). Symbols and colours are the same as in Fig. 4. The isochrones are 3.8, 4.0, 4.2, and 4.4 Gyr.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.