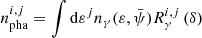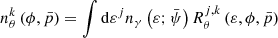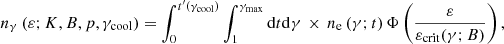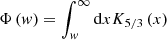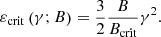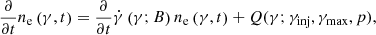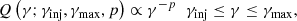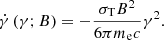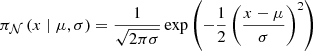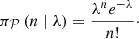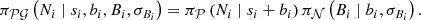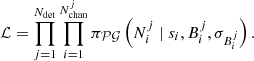| Issue |
A&A
Volume 627, July 2019
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201935056 | |
| Published online | 08 July 2019 | |
Time-resolved GRB polarization with POLAR and GBM
Simultaneous spectral and polarization analysis with synchrotron emission⋆
1
Max-Planck-Institut fur extraterrestrische Physik, Giessenbachstrasse 1, 85748 Garching, Germany
e-mail: jburgess@mpe.mpg.de; fberlato@mpe.mpg.de
2
Excellence Cluster Universe, Technische Universität München, Boltzmannstraße 2, 85748 Garching, Germany
3
University of Geneva (DPNC), quai Ernest-Ansermet 24, 1205 Geneva, Switzerland
e-mail: merlin.kole@unige.ch
4
Hansen Experimental Physics Lab, Stanford University, 452 Lomita Mall, Stanford, CA 94305-4085, USA
5
Astronomy Departement University of Geneva, Versoix, Switzerland
6
Key Laboratory of Particle Astrophysics, Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, PR China
7
University of Chinese Academy of Sciences, Beijing 100049, PR China
Received:
13
January
2019
Accepted:
18
April
2019
Context. Simultaneous γ-ray measurements of γ-ray burst spectra and polarization offer a unique way to determine the underlying emission mechanism(s) in these objects, as well as probing the particle acceleration mechanism(s) that lead to the observed γ-ray emission.
Aims. We examine the jointly observed data from POLAR and Fermi-GBM of GRB 170114A to determine its spectral and polarization properties, and seek to understand the emission processes that generate these observations. We aim to develop an extensible and statistically sound framework for these types of measurements applicable to other instruments.
Methods. We leveraged the existing 3ML analysis framework to develop a new analysis pipeline for simultaneously modeling the spectral and polarization data. We derived the proper Poisson likelihood for γ-ray polarization measurements in the presence of background. The developed framework is publicly available for similar measurements with other γ-ray polarimeters. The data are analyzed within a Bayesian probabilistic context and the spectral data from both instruments are simultaneously modeled with a physical, numerical synchrotron code.
Results. The spectral modeling of the data is consistent with a synchrotron photon model as has been found in a majority of similarly analyzed single-pulse gamma-ray bursts. The polarization results reveal a slight trend of growing polarization in time reaching values of ∼30% at the temporal peak of the emission. We also observed that the polarization angle evolves with time throughout the emission. These results suggest a synchrotron origin of the emission but further observations of many GRBs are required to verify these evolutionary trends. Furthermore, we encourage the development of time-resolved polarization models for the prompt emission of gamma-ray bursts as the current models are not predictive enough to enable a full modeling of our current data.
Key words: polarization / γ-ray burst: general / methods: data analysis / methods: statistical
Reduced data are only available at https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/MTDPTA
© J. M. Burgess et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1. Introduction
Polarization measurements from astrophysical objects are a key piece of information to decipher the physics and geometry of regions that emit the observed photons. The emission from γ-ray bursts (GRBs) has been notoriously difficult to understand due to the complexity of modeling their broadband, prompt γ-ray emission. Recent results have provided evidence that the prompt emission is the result of synchrotron radiation from electrons accelerated to ultra-high energies via magnetic reconnection (Burgess et al. 2014, 2018a; Zhang et al. 2016, 2018). Measurements of the optical polarization from a GRB’s prompt emission have similarly pointed to a synchrotron origin of the emission (Troja et al. 2017). However, spectral modeling of photospheric based emission has also provided adequate fits to a subset of GRBs (Ryde et al. 2010; Ahlgren et al. 2015; Vianello et al. 2018a). Measurements of polarization can break this degeneracy (Toma et al. 2009; Gill et al. 2018). Photospheric emission will typically produce unpolarized emission although a moderate polarization level is possible in special circumstances (Lundman et al. 2018) and predicts very specific changes of the polarization angle (Lundman et al. 2014). On the other hand, synchrotron emission naturally produces a range of polarized emission depending on the structure of the magnetic field and outflow geometry (Waxman 2003; Lyutikov et al. 2003; Granot 2003). Thus, being able to fit synchrotron emission to the observed spectrum while simultaneously detecting polarization provides a clear view of the true emission process.
Several reports of polarization measurements have been produced by a variety of instruments. An overview of which can be found in Covino (2016). Of these measurements, those by non-dedicated instruments like those reported by BATSE and RHESSI suffer from problems with instrumental effects or poorly understood systematics (McConnell 2017) making it impossible to draw conclusions based on these results. Additionally, several measurements were performed using data from two instruments onboard the INTEGRAL satellite, IBIS, and SPI. Several of the GRB polarization measurements performed by these instruments do not suffer from obvious errors in the analysis and allow us to constrain the polarization parameter space. However, for several of these measurements systematic uncertainties also make it difficult to draw conclusions (McGlynn et al. 2007). Furthermore as stated in for example Pearce et al. (2019), a lack of on-ground calibration of the instrument responses of both IBIS and SPI to polarized beams creates additional doubt on the validity of polarization results from these instruments within the community. This indicates the importance of performing polarization measurements with carefully calibrated and dedicated instrumentation. More recently, the AstroSAT collaboration has reported preliminary polarization analysis results of several GRBs (Chattopadhyay et al. 2017). The systematics and procedures related to obtaining these measurements is not immediately clear. The quoted error distributions contain unphysical regions of parameter space (polarization degrees greater than 100%) and are thus questionable. Past measurements of polarization by the first dedicated GRB polarimeter, GAP, provided hints of polarized emission (Yonetoku et al. 2011). The results presented there indicate an overall low polarization potentially resulting from an evolution of the polarization angle during the long multipulse GRB, something also reported in Götz et al. (2009) for GRB 041219A. Measurements by COSI provided an upper limit on the polarization degree (Lowell et al. 2017). The statistics of these measurements do not, however, allow constraints on the emission mechanisms. Furthermore, the techniques for all these measurements relied on background subtraction. As both the background and signal counts are Poisson distributed, subtraction is an invalid procedure that destroys statistical information, thus all reported significances are questionable.
The POLAR experiment (Produit et al. 2018) on board the Chinese space laboratory Tiangong-2 observed 55 GRBs and reported polarization measurements for five of these GRBs (Zhang et al. 2019). Time-integrated analysis of these GRBs resulted in strict upper limits on the polarization degrees. The most likely polarization degrees found in that analysis are non-zero but remain compatible with an unpolarized emission, leading to the conclusion that GRBs are at most moderately polarized. Using time-resolved analysis it was however found that the polarization of GRB 170114A was most compatible with a constant polarization degree of ∼28% with a varying polarization angle. Summing polarized fluxes with varying polarization degrees produces an unpolarized flux. The detection of an evolution in polarization angle within this single pulse GRB could explain the low polarization degrees found for all five GRBs. The results presented in Zhang et al. (2019) do not, however allow for a detailed time-resolved study of the remaining four GRBs, nor do they allow determination of the nature of the evolution of the polarization angle in GRB 170114A.
Coincidentally, several of the GRBs observed by POLAR were simultaneously observed by the Fermi-GBM. In this paper, we present a technically advanced modeling of the polarization and spectral data simultaneously with data from both instruments. This allows the incorporation of information contained in both data sets leading to improved sensitivity and an altogether more robust analysis. This work is organized as follows: The methodology and modeling is described in Sects. 2 and 3 and the results are interpreted in Sect. 4.
2. Data analysis and methodology
For the analysis herein, we have developed a new approach of simultaneously fitting both the spectral data from POLAR and GBM along with the POLAR scattering angle (SA) or polarization data (the subset of POLAR data usable for polarization analysis selected with cuts as defined in Li et al. 2018). This simultaneous fitting alleviates the need for approximate error propagation of the spectral fits into the polarization analysis. Using the abstract data modeling capabilities of 3ML1 (Vianello et al. 2015), a framework was developed to directly model all data simultaneously with a joint-likelihood in each dataset’s appropriate space. Below, we describe in detail each part of the methodology.
We focus on the analysis of GRB 170114A (Veres 2017) which is a single-pulse, bright GRB lasting approximately 10s which allows us to perform detailed time-resolved spectroscopy. The event occurred on January 14th 2017 with an initially estimated fluence between 10–1000 keV of ∼1.93 × 10−5 erg cm−2. The high peak flux of the GRB triggered an autonomous repoint request for the Fermi satellite, however, no LAT detection of photons occurred.
2.1. Location and temporal analysis
Spectral and polarization analysis for both GBM and POLAR rely on knowledge of the sky-position (δ) of the GRB in question. As they are both all-sky surveyors, GBM and POLAR lack the ability to image GRBs directly. However, using the BALROG technique (Burgess et al. 2018b), we can use the spectral information obtained in the GBM data to locate the GRB. Using a synchrotron photon model (see Sect. 3), we were able to locate the GRB to RA = 13.10 ± 0.5 deg, Dec. = −13.0 ± 0.6 deg. Using this location, spectral and polarization responses were generated for all data types. We note that a standard GBM position2 exists and, along with their uncertainties, was used for the polarization results presented in Zhang et al. (2019), however, the standard localization technique has known systematics and now possess arbitrarily inflated error distributions (Connaughton et al. 2015). We find the BALROG derived location much more precise than that of the standard location analysis (see Fig. 1), allowing us to reduce the systematic errors included in the polarization results presented in Zhang et al. (2019). Additionally, it has now been shown that the BALROG locations are systematically more accurate (Berlato et al. 2019).
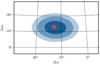 |
Fig. 1. BALROG location (red posterior samples) of GRB 170114A derived by fitting the peak of the emission for both the location and spectrum simultaneously. The blue contours display the 1,2, and 3 σ standard GBM catalog location as obtained from the Fermi Science Support Center (FSSC). |
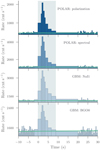 |
Fig. 2. Light curves of the POLAR polarization and spectral data (the difference is explained in Appendix A) as well as two GBM detector data. The green line is the fitted background model and the gray shaded regions show the time-intervals used for the analysis. The binning in the analysis region is derived via Bayesian blocks. |
The chief focus of this analysis is temporal variation in the polarization parameters. We computed the minimum variability timescale (MVT; see Vianello et al. 2018a, for details) on the POLAR SA light curve. The MVT infers the minimum timescale above the Poisson noise floor of which variability exists in the data. This yields an MVT of ∼0.3 s (Fig. 3). For completeness, the MVTs for both the GBM and POLAR spectral light curves were computed as well. Both analyses yield similar results. Therefore, we were able to analyze data on this timescale without the concern of summing over evolution of spectral (Burgess & Ryde 2015). However, the raw polarization data do not allow for us to check for variability in the polarization angle prior to fitting. Therefore, it is possible that the angle could change on a timescale smaller than our selected time-intervals. This could reduce the overall inferred polarization.
 |
Fig. 3. Minimum variability timescales for the polar polarization data (left) and the GBM spectral data (right). The black line indicates the background power spectrum determined via Monte Carlo calculations and the shaded regions indicates the uncertainty in the background. Notably, both data sets have nearly equivalent MVTs. |
With the MVT determined, we utilized the Bayesian blocks algorithm (Scargle et al. 2013) to objectively identify temporal bins for the analysis. The SA light curve was utilized to perform the analysis. The temporal bins created are on the order of the MVT. A total of nine bins were selected and used for spectral and polarization analysis (see Table 1).
Parameters with their 68% credible regions.
2.2. Spectral analysis
The standard γ-ray forward-folding approach to spectral fitting is adopted, in which we have sky location (δ) dependent responses for both the GBM and POLAR detectors (Rγ) and fold the proposed photon model (nγ) solution through these responses to produce detector count spectra (npha). Thus,
for the ith detector in the jth pulse-height amplitude (PHA) channel, ε is the latent photon energy and 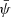 are a set of photon model parameters. Here, δ is the sky location of the GRB. Both POLAR and GBM have Poisson-distributed total observed counts, and their backgrounds determined via fitting polynomials in time to off-source regions of the light curves. Thus, Gaussian-distributed background counts are estimated by integrating these polynomial models over the source interval of interest. The uncertainty on these estimated counts is derived via standard Gaussian uncertainty propagation. This leads us to use a Poisson-Gaussian likelihood3 for each detector for the spectral fitting.
are a set of photon model parameters. Here, δ is the sky location of the GRB. Both POLAR and GBM have Poisson-distributed total observed counts, and their backgrounds determined via fitting polynomials in time to off-source regions of the light curves. Thus, Gaussian-distributed background counts are estimated by integrating these polynomial models over the source interval of interest. The uncertainty on these estimated counts is derived via standard Gaussian uncertainty propagation. This leads us to use a Poisson-Gaussian likelihood3 for each detector for the spectral fitting.
2.3. Polarization analysis
To enable performing joint fits of the spectra and the polarization a novel analysis technique was developed. Traditional polarization analysis techniques, such as those employed in Yonetoku et al. (2011), Chattopadhyay et al. (2017) as well as in Zhang et al. (2019), rely on fitting data to responses produced for a specific spectrum. This method does not allow joint fits of both the spectrum and polarization parameters, nor does it allow naturally including systematic uncertainties from the spectral fits into the systematic uncertainties of the polarization. Here, in order to model the polarization signal seen in the data, we invoked a forward-folding method similar in concept to our approach to spectral analysis. We simulated polarized signals as function of polarization angle, degree and energy to create a matrix of SA distributions (often called modulation curves within the field of polarimetry) which can be compared to the data via the likelihood in data space. For details on the creation of the matrix see Appendix A. Mathematically,
where nθ are counts in SA bin k, and Rθ is the simulated response of the corresponding scattering bin. In words, we convolved the photon spectrum over the jth photon energy bin with the polarization response to properly weight the number of counts observed in each SA bin. Figure 4 demonstrates how changes in polarization angle and degree appear in the POLAR data space. Hence, our need to simultaneously fit for the photon spectrum which allows for direct accounting of the uncertainties in the weighting.
 |
Fig. 4. Folded POLAR count space for two polarization angles and ten levels of polarization degree. The rates have been artificially scaled to between the different angles for visual clarity. The green lines for both angles represent the polarization degree |
POLAR observed SAs are measured as detector counts and thus Poisson distributed. The pollution of the source signal by background cannot be handled by background subtraction as has been done in previous work. Instead, a temporally off-source measurement of the background polarization is made in order to model the background contribution to the total measurement during the observation intervals. The background measurement is Poisson distributed in each of the k scattering bins. Due to the temporal stability of the background, as presented in Zhang et al. (2019), we fit a polynomial in time to each of the k scattering bins via an unbinned Poisson likelihood. This allowed us to reduce the uncertainty of the background by leveraging the temporal information. We were able to estimate the on-source background contribution (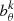 ) by integrating the polynomials over time and propagating the temporal fit errors. This implies that the polarization likelihood is also a Poisson-Gaussian likelihood just as with the spectral data. We verified that our approach allowed us to identify the latent polarization parameters via simulations in Appendix B. The count rates are corrected for the proper exposure by computing the total dead-time fraction associated with each interval. The method employed for dead-time calculation is equivalent to that of Zhang et al. (2019).
) by integrating the polynomials over time and propagating the temporal fit errors. This implies that the polarization likelihood is also a Poisson-Gaussian likelihood just as with the spectral data. We verified that our approach allowed us to identify the latent polarization parameters via simulations in Appendix B. The count rates are corrected for the proper exposure by computing the total dead-time fraction associated with each interval. The method employed for dead-time calculation is equivalent to that of Zhang et al. (2019).
The full joint likelihood of the data is thus a product over the spectral and polarization likelihoods which is detailed in Appendix C (see also Fig. 5). We re-emphasize that the spectral model and polarization model communicate with each other through the likelihood. This implies that the posterior density of the model is fully propagated to both datasets without any assumptions such as Gaussian error propagation. As is seen in the following sections, the resulting parameter distributions can be highly asymmetric.
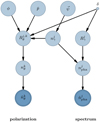 |
Fig. 5. Directed graph model describing the full likelihood of our approach. Model parameters are shown in light blue, and the data in dark blue. The graph shows how the latent parameters of the model are connected to each other and eventually the data. It is important to note that the latent photon model connects both sides of the model. The position (δ) is a fixed parameter. Here ψ represents the set of spectral parameters. |
In a perfect world where all instruments are cross-calibrated over the full energy range, the instruments’ various responses would predict similar observed fluxes for each measurement. However, we allowed for a normalization constant between GBM and POLAR to account for any unmodeled discrepancies between the instruments. Both POLAR’s polarization and spectral data are scaled by these constants which are unity when no correction is required4. This constant scale for the effective area by no means accounts for energy-dependent calibration issues.
In order to obtain the posterior parameter distributions, we used MULTINEST (Feroz et al. 2009; Buchner et al. 2014) to simulate the model’s posterior. MULTINEST utilizes nested sampling which is suitable for the multimodal distributions we observe, as well as for the non-linear model and high-dimension of our parameter space. For the polarization parameters, we used uninformative priors of appropriate scale. The effective area normalizations are given informative (truncated Gaussians) priors centered at unity with a 10% width. The priors for the spectral modeling are discussed in the Sect. 3. We ran MULTINEST with 1500 live points to achieve a high number of samples for posterior inference. Model comparison was not attempted and thus we did not use the marginal likelihood calculations5.
As stated, for both 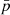 and ϕ, we used uninformative priors in each parameters’ domain. This is a valid choice for ϕ, but we note that an informative prior for the expected polarization from synchrotron emission could be used as an assumption. However, as discussed in Sect. 5, the theoretical predictions for GRB synchrotron models are not mature enough for us to assume such a prior at the current time. Nevertheless, in our work we tested Gaussian priors centered at moderate polarization and found that the data allowed for this assumption. Moreover, we found that our recovered ϕ was not affected by out choice of prior on
and ϕ, we used uninformative priors in each parameters’ domain. This is a valid choice for ϕ, but we note that an informative prior for the expected polarization from synchrotron emission could be used as an assumption. However, as discussed in Sect. 5, the theoretical predictions for GRB synchrotron models are not mature enough for us to assume such a prior at the current time. Nevertheless, in our work we tested Gaussian priors centered at moderate polarization and found that the data allowed for this assumption. Moreover, we found that our recovered ϕ was not affected by out choice of prior on 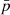 .
.
3. Synchrotron modeling
With the recent finding that synchrotron emission can explain the majority of single-pulse GRBs, we chose to model the time-resolved photon spectrum with a physical synchrotron model. Following Burgess et al. (2018a), we set
where K is the arbitrary normalization of the flux, B is the magnetic field strength in Gauss, p is the injection index of the electrons, γcool is the energy to which an electron will cool during a synchrotron cooling time,
and
Here, K5/3 is a Bessel function, Bcrit = 4.13 × 1013 G, and ne is determined by solving the cooling equation for electrons with the Chang and Cooper method (Chang & Cooper 1970). In mathematical expression,
where the injected electrons are defined by a power law of index p
where γinj and γmax are the minimum and maximum injected electron energies respectively and the synchrotron cooling is
For our numerical calculations we created a 300-point grid, logarithmically distributed in γ. The linear equations in the implicit scheme form a tridiagonal matrix which is solved numerically with standard methods. The method of Chang & Cooper (1970) is numerically stable and inexpensive as well as shown to conserve particle number in the absence of sources and sinks. Thus, we are able to solve for the synchrotron emission spectrum quickly during each iteration of the fit. The numeric code is implemented in C++ and interfaced with Python into astromodels (Vianello et al. 2018b).
The overall emission is characterized by five parameters: B, γinj, γcool, γmax, and p. However, a strong co-linearity exists between B and γinj as their combination sets the peak of the photon spectrum. Thus, both parameters serve as an energy scaling which forces the setting of one of the parameters. We chose to set γinj = 105 though the choice is arbitrary and does not affect our results. It is therefore important to note that all parameters are determined relatively, that is, the values of γcool and γmax are determined as ratios to γinj. Similarly, the value of B is only meaningful when determining the characteristic energies of γcool and γmax or hνcool and hνmax respectively. In other words, with our parameterization the spectra are scale free. The degeneracies can be eliminated by specifying temporal and radial properties of the GRB outflow which we have neglected in this analysis.
Ideally, we would fit for the full set of parameters in the model. However, the already high-dimensionality of the model does not allow us to fit for the cooling regime of the model simultaneously with the polarization due to computational time constraints. Therefore, we first fit the spectral data alone to determine the amount of cooling present in the data. All spectra were found in the slow-cooling regime (Sari et al. 1998; Beniamini & Piran 2013). Thus, we fixed the ratio of γcool to γinj during the full fits to the slow-cooling regime. Tests revealed that the cooling had no impact on the recovered polarization parameters. Additionally, the lack of high-energy data (via the Fermi-LAT) forces us to fix γmax such that the synchrotron cutoff is above the spectral window. We obtain three parameter fit for the spectrum: B, p and the arbitrary spectral normalization (K). B and K are given uninformative scale priors and p a weakly-informative, Gaussian prior centered around p = 3.5. The effective area constants applied to the POLAR response are given truncated Gaussian priors centered at unity with a width of 10% to reflect our prior belief that the instruments are well-calibrated to one another6.
4. Results
In the following two sections, we present the results from the combined polarization and spectral analysis separately. Corner plots of the important (non-nuisance) parameter marginal distributions are displayed in Appendix D.
4.1. Polarization
The POLAR polarization data are well described by our modeling of the POLAR instrument. The scattering angle data show good agreement between the data and the model as demonstrated in Fig. 6. In order to validate the model’s ability to generate the data, we performed posterior predictive checks (PPCs; Betancourt 2018) of the polarization data for all time intervals. For a subset of posterior samples chosen with appropriate posterior probability, latent polarization and spectral models were generated and subsequent data quantities where sampled from the likelihood. The model was able to sufficiently generate replicated data similar to the observed (see Fig. 7) in most cases. It is likely that minor deficiencies still exist in the instrumental responses.
 |
Fig. 6. Net SA data for each fitted time interval in our analysis. Superimposed are the posterior model predictions from the fits. The data have been rebinned for visual clarity. The SA presented here is measured within an arbitrary local coordinate system of POLAR. |
 |
Fig. 7. Posterior predictive checks for the total polarization count rate data. The dark to light blue shaded regions indicate the 50th, 60th, 70th, 80th, and 90th percentiles of the replicated data respectively of the replicated data. The observed data are displayed in red. The estimated background count rates are displayed in green. |
The polarization observed here is compatible with that presented in Zhang et al. (2019) where an unpolarized flux was excluded for this single pulse GRB with 99.7% confidence. The analysis presented here does, however, allow us to study the time evolution in significantly more detail. This is because, unlike in the study (Zhang et al. 2019), the polarization degree is not forced to be equal over all the studied time intervals but is instead left as a free parameter, while the number of studied time bins is increased from three to nine. Despite this significant increase in free parameters constraining measurements can still be performed. We observe no polarization at the beginning of the pulse and moderate (∼30%) polarization as time proceeds. Interestingly, we observe a large change in the polarization angle with time (see Fig. 8). Although the time intervals used in this study are different from those used in Zhang et al. (2019), it can be deduced that the polarization angles found here agree with those in Zhang et al. (2019). The end of the pulse has a relatively weak signal and thus poorly identified polarization parameters. The 68% credible regions are listed in Table 1. Clearly, the level of polarization during the peak of the emission is probabilistically equivalent to both moderate, low or even 0% polarization during several intervals whereas during the beginning of the emission the polarization is definitely low even though the ratio of background to total signal is high.
 |
Fig. 8. Posterior polarization results. The radial coordinate represents polarization degree and the angular coordinate the polarization angle. The polarization angle here is transformed to equatorial coordinates. The contours are for the 30th, 60th, and 90th percentiles of the credible regions. The plots are reflected about the periodic boundary of 180° for visual clarity. For the last three time intervals, we do not display contours and instead show the posterior samples as the parameters are poorly identified. The arrows that point from the last to the current position are meant as visual guides only. |
We stress that it is not appropriate to perform model comparison on nested model parameters, for example, comparing between zero polarization and greater than zero polarization. This includes the use of Bayes factors (Chattopadhyay et al. 2017) which are ill-defined for improper priors and for comparing between discrete values of a continuous parameter (Gelman et al. 2013). Polarization is not a detected quantity, but a parameter. Given that we have detected the GRB, it is important to quote the credible regions of the polarization parameter rather than perform model comparison between discrete values.
4.2. Spectra
POLAR and GBM observed data both agree in overall spectral shape and relative normalization of the observed flux. Moreover, the spectral results demonstrate that the synchrotron spectrum is a good, predictive description of the spectral data as displayed in Fig. 9. This is both a confirmation that past studies with synchrotron relying on GBM data alone are reliable, as well as the outstanding calibration between the GBM and POLAR.
 |
Fig. 9. Count spectra of POLAR and GBM from the joint spectral and polarization fits. The shaded regions indicate the 2σ credible regions of the fit. Data from a GBM NaI, BGO, and POLAR and displayed in green, black, and red respectively. |
As noted above, it is not possible to disentangle the intrinsic parameters of the synchrotron emission without further assumptions. Therefore, we only quote the injection energy in Table 1. The evolution of the spectrum is shown in Fig. 10. The temporal evolution of the νFν spectral peak follows a broken power law. We find values between approximately three and four for the electron power law injection spectral index. These values are steeper than those of the canonical index expected from shock acceleration (Kirk et al. 2000).
 |
Fig. 10. νFν spectra of the synchrotron fits scaled with increasing time. The width of the curves represents the 1σ credible regions of the model. |
It is possible that other physical spectral models also provide acceptable, predictive, fits to the data. However, these models – for example subphotospheric dissipation – have yet to demonstrate acceptable spectral fits on a large sample of GRBs. Moreover, the numerical schemes (Pe’er & Waxman 2005) required to compute the emission form these models are more complex than that of our synchrotron modeling, require far more computational time, and are not publicly available for replication. Photospheric models also require special geometrical setups to produce polarization. This makes them more predictive, and indeed a pertinent set of models to test.
5. Discussion
For the first time, the polarization and spectrum of GRB prompt γ-ray emission has been fitted simultaneously. Furthermore, the spectral data have been described with a physical synchrotron model consistent with the spectral data of two very distinct spectrometers. We argue that it is unlikely for the spectral and polarization data to conspire to point toward an optically thin synchrotron origin of the emission. However, the current predictive power of GRB prompt emission polarization theory is not developed enough for our measurements to definitively select synchrotron over other emission mechanisms. Therefore, we speculatively leverage previous spectral results that show that synchrotron emission is dominant mechanism in single-pulse GRBs.
Burgess et al. (2018a) argue that the observation of synchrotron emission in GRBs invalidates the standard fireball model (Eichler & Levinson 2000). Similar predictions were made before they were supported by data (e.g., Zhang & Pe’er 2009). These results allude to a magnetically dominated jet acceleration mechanism possibly resulting in comoving emission sites or mini-jets (Barniol Duran et al. 2016; Beniamini et al. 2018). These results were arrived at considering spectral analysis alone. The moderate polarization degree observed in this work requires a development in the prediction of the temporal polarization predictions of these models in order to fully interpret their meaning.
While our observations provide broad ranges for the observed polarization degree, the changing polarization angle is easily observed. Although an evolution of the polarization angle has been reported before for multipulse GRBs using data from both the GAP and IBIS instruments (Yonetoku et al. 2011; Götz et al. 2009), this intrapulse evolution has not been observed before. Figure 11 shows the way in which both the peak of the synchrotron spectrum and the polarization angle grossly track each other in time. Detailed model predictions for the evolution of the polarization angle during the GRB are not available. We are therefore not able to interpret the change in angle and encourage the community to develop detailed predictions which can be fitted to our data in the future. With more predictive models, appropriate informative priors can be adopted. Moreover, spectral parameters can be formulated in terms of polarization parameters making the models stricter and the data more useful. Thus, we are hopeful that models are developed in the near future.
 |
Fig. 11. Temporal evolution of hν + inj and the polarization angle which has been doubled for visual clarity. hνinj falls as the polarization angle increases in time. The red and yellow areas are illustrative guides for the evolution the parameters. No fits were performed. |
The combination of POLAR and GBM observations of GRBs enables energy-dependent polarization measurements and is a project currently under development. These measurements will allow us to decipher if polarization increases around the peak of the photon spectrum which would be a signature of synchrotron emission, or if the polarization is higher at low energies as predicted by Lundman et al. (2018). We encourage researchers to carry out further multimessenger studies and missions to answer these questions.
6. Software availability
The analysis software utilized in this study are primarily 3ML and astromodels. We have designed a generic, preliminary, polarization likelihood for similar X-ray polarization instruments both within 3ML7 and astromodels8. Additionally, the POLAR pipeline9 we have developed is fully designed to be easily modified for other instruments with polarimetric data. We note that these software distributions are preliminary, and we encourage the community to participate in their development.
Data obtained from https://heasarc.gsfc.nasa.gov/FTP/fermi/data/gbm/bursts/
Indeed, astrophysical models operate in the ℳ-open probabilistic setting and marginal likelihood is an ℳ-closed tool (Vehtari et al. 2018).
See https://heasarc.gsfc.nasa.gov/xanadu/xspec/manual/XSappendixStatistics.html or https://giacomov.github.io/Bias-in-profile-poisson-likelihood/ for detailed discussion.
Acknowledgments
JMB acknowledges support from the Alexander von Humboldt Foundation. MK acknowledges support by the Swiss National Science Foundation and the European Cooperation in Science and Technology. The authors are grateful to the Fermi-GBM team and HEASARC for public access to Fermi data products. We thank Damien Bégué, Dimitrios Giannois, Thomas Siegert and Ramandeep Gill for fruitful discussions.
References
- Ahlgren, B., Larsson, J., Nymark, T., Ryde, F., & Pe’er, A. 2015, MNRAS, 454, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Barniol Duran, R., Leng, M., & Giannios, D. 2016, MNRAS, 455, L6 [NASA ADS] [Google Scholar]
- Beniamini, P., & Piran, T. 2013, ApJ, 769, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Beniamini, P., Barniol Duran, R., & Giannios, D. 2018, MNRAS, 476, 1785 [NASA ADS] [CrossRef] [Google Scholar]
- Berlato, F., Greiner, J., & Burgess, J. M. 2019, ApJ, 873, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Betancourt, M. 2018, ArXiv e-prints [arXiv:1803.08393] [Google Scholar]
- Buchner, J., Georgakakis, A., Nandra, K., et al. 2014, A&A, 564, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burgess, J. M., & Ryde, F. 2015, MNRAS, 447, 3087 [NASA ADS] [CrossRef] [Google Scholar]
- Burgess, J. M., Preece, R. D., Connaughton, V., et al. 2014, ApJ, 784, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Burgess, J. M., Bégué, D., Bacelj, A., et al. 2018a, ArXiv e-prints [arXiv:1810.06965] [Google Scholar]
- Burgess, J. M., Yu, H.-F., Greiner, J., & Mortlock, D. J. 2018b, MNRAS, 476, 1427 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, J. S., & Cooper, G. 1970, J. Comput. Phys., 6, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Chattopadhyay, T., Vadawale, S. V., Aarthy, E., et al. 2017, ApJ, submitted [arXiv:1707.06595] [Google Scholar]
- Connaughton, V., Briggs, M. S., Goldstein, A., et al. 2015, ApJS, 216, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Covino, S. G. 2016, Astron. Astrophys. Trans., 29 [Google Scholar]
- Eichler, D., & Levinson, A. 2000, ApJ, 529, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., Hobson, M. P., & Bridges, M. 2009, MNRAS, 398, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Gelman, A., Carlin, J. B., Stern, H. S., & Rubin, D. B. 2013, Bayesian Data Analysis, 3rd edn. (Chapman and Hall/CRC) [Google Scholar]
- Gill, R., Granot, J., & Kumar, P. 2018, MNRAS, submitted [arXiv:1811.11555] [Google Scholar]
- Götz, D., Laurent, P., Lebrun, F., Daigne, F., & Bošnjak, Ž. 2009, ApJ, 695, L208 [NASA ADS] [CrossRef] [Google Scholar]
- Granot, J. 2003, ApJ, 596, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J. G., Guthmann, A. W., Gallant, Y. A., & Achterberg, A. 2000, ApJ, 542, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Kole, M., Li, Z., Produit, N., et al. 2017, Nucl. Instrum. Methods Phys. Res. A, 872, 28 [Google Scholar]
- Li, Z., Kole, M., Sun, J., et al. 2018, Nucl. Instrum. Methods Phys. Res. A, 900, 8 [Google Scholar]
- Lowell, A. W., Boggs, S. E., Chiu, C. L., et al. 2017, ApJ, 848, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Lundman, C., Pe’er, A., & Ryde, F. 2014, MNRAS, 440, 3292 [NASA ADS] [CrossRef] [Google Scholar]
- Lundman, C., Vurm, I., & Beloborodov, A. M. 2018, ApJ, 856, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Lyutikov, M., Pariev, V. I., & Blandford, R. D. 2003, ApJ, 597, 998 [NASA ADS] [CrossRef] [Google Scholar]
- McConnell, M. L. 2017, New Astron. Rev., 76, 1 [NASA ADS] [CrossRef] [Google Scholar]
- McGlynn, S., Clark, D. J., Dean, A. J., et al. 2007, A&A, 466, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pearce, M., Eliasson, L., Iyer, N. K., et al. 2019, Astropart. Phys., 104, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Pe’er, A., & Waxman, E. 2005, ApJ, 628, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Produit, N., Bao, T., Batsch, T., et al. 2018, Nuclear Instruments and Methodsin Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 877, 259 [NASA ADS] [Google Scholar]
- Quinn, J. L. 2012, A&A, 538, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ryde, F., Axelsson, M., Zhang, B. B., et al. 2010, ApJ, 709, L172 [NASA ADS] [CrossRef] [Google Scholar]
- Sari, R., Piran, T., & Narayan, R. 1998, ApJ, 497, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Scargle, J. D., Norris, J. P., Jackson, B., & Chiang, J. 2013, ApJ, 764, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Toma, K., Sakamoto, T., Zhang, B., et al. 2009, ApJ, 698, 1042 [NASA ADS] [CrossRef] [Google Scholar]
- Troja, E., Lipunov, V. M., Mundell, C. G., et al. 2017, Nature, 547, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Vaillancourt, J. E. 2006, PASP, 118, 1340 [Google Scholar]
- Vehtari, A., Simpson, D. P., Yao, Y., & Gelman, A. 2018, ArXiv e-prints [arXiv:1810.05374] [Google Scholar]
- Veres, P. 2017, GCN 20461 [Google Scholar]
- Vianello, G., Lauer, R. J., Younk, P., et al. 2015, ArXiv e-prints [arXiv:1507.08343] [Google Scholar]
- Vianello, G., Burgess, J. M., Henrike, F., et al. 2018a, Astromodels, DOI: 10.5281/zenodo.1297576 [Google Scholar]
- Vianello, G., Gill, R., Granot, J., et al. 2018b, ApJ, 864, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Waxman, E. 2003, Nature, 423, 388 [NASA ADS] [CrossRef] [Google Scholar]
- Yonetoku, D., Murakami, T., Gunji, S., et al. 2011, ApJ, 743, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, H.-F., Preece, R. D., Greiner, J., et al. 2016, A&A, 588, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, B., & Pe’er, A. 2009, ApJ, 700, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B.-B., Uhm, Z. L., Connaughton, V., Briggs, M. S., & Zhang, B. 2016, ApJ, 816, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B. B., Zhang, B., Castro-Tirado, A. J., et al. 2018, Nat. Astron., 2, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, S., Kole, M., Bao, T., et al. 2019, Nat. Astron., 3, 258 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: The POLAR polarization response
The POLAR instrument is described in full detail in Produit et al. (2018). The instrument design is such that issues found in previously reported polarization measurements are mitigated, for example fast electronics allows to record events within a 50 ns coincidence window, thereby removing chance coincidence induced events which can induce fake polarization. The POLAR response was modeled using the POLAR simulation software presented in Kole et al. (2017) which was previously used for the analysis presented in Zhang et al. (2019). The spectral and polarization response are produced using the same simulation set. Different event selections were applied to produce the spectral and polarization response; whereas all clean photon-like triggers, as defined in Li et al. (2018), were used for the spectral response, additional cuts are applied in the event selection for the polarization response. This causes the count rate to be higher in the spectral light curve than in the polarization light curve as seen in Fig. 2. The selection criteria for polarization events are equal to those previously used in Zhang et al. (2019). In this event selection only triggers containing at least two energy depositions in non-neighboring bars are selected.
Simulations were performed for a grid of polarization parameters with steps of three degrees in ϕ while for 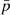 only 0 and 100% were simulated. All additional values of
only 0 and 100% were simulated. All additional values of 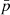 on the grid can be produced by combining these results. Such a grid in polarization space was produced for photon energies in the range of 30–850 keV in steps of 5 keV, thereby producing a 3D grid of the instrument response. The final result of each simulation is a binned modulation curve, with a total number of 360 bins, normalized to the effective area of POLAR for the specific photon energy. We note here that the effective area is found to be independent of the polarization, as could be naively expected. Therefore, the polarization sensitivity is proportional to the source counts, and thus highest in the ∼50–150 keV range.
on the grid can be produced by combining these results. Such a grid in polarization space was produced for photon energies in the range of 30–850 keV in steps of 5 keV, thereby producing a 3D grid of the instrument response. The final result of each simulation is a binned modulation curve, with a total number of 360 bins, normalized to the effective area of POLAR for the specific photon energy. We note here that the effective area is found to be independent of the polarization, as could be naively expected. Therefore, the polarization sensitivity is proportional to the source counts, and thus highest in the ∼50–150 keV range.
Uncertainties in the simulated response are taken into account by adding an additional uncertainty to each bin in addition to that coming from the statistical uncertainty. As presented in Li et al. (2018) the main uncertainty in the response stems from uncertainties of the gain calibration. The propagation of this uncertainty to the polarization response was studied here and is found to result in a typical relative uncertainty of 2% for each bin in the polarization response. All other uncertainties, such as those from other calibration parameters or uncertainties in the mass model of both POLAR and the surrounding materials, are found to be negligible, as previously presented in Li et al. (2018), Zhang et al. (2019). The systematic uncertainties in the polarization stemming from spectral uncertainties are naturally included by fitting for the spectrum and the polarization at the same time. Finally, unlike in the results presented in Zhang et al. (2019) the location induced uncertainty is negligible in this analysis due to the highly precise location acquired using the BALROG.
Appendix B: Polarization assessment
We wish to validate our analysis method via simulations to verify that under the assumption of the true model our inferences are identifiable. Therefore, we created simulations of both spectra and polarization for sets of 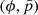 and an assumed power law spectrum and fit them with the same likelihood used for real data. To avoid pathologies that can be introduced with energy dispersion, we assumed an X-ray detector with an identity response and simulate a simple power law photon spectrum. Both the POLAR response and a simulated background are included as we are mainly concerned with validating our polarization inferences. The background simulations were performed by sampling events from real in-orbit data recorded by POLAR in a period both before and after the GRB 170114A. It should be noted here that the SA distribution of the POLAR background was found to be very stable (Zhang et al. 2019).
and an assumed power law spectrum and fit them with the same likelihood used for real data. To avoid pathologies that can be introduced with energy dispersion, we assumed an X-ray detector with an identity response and simulate a simple power law photon spectrum. Both the POLAR response and a simulated background are included as we are mainly concerned with validating our polarization inferences. The background simulations were performed by sampling events from real in-orbit data recorded by POLAR in a period both before and after the GRB 170114A. It should be noted here that the SA distribution of the POLAR background was found to be very stable (Zhang et al. 2019).
We simulated a nested grid of ϕ ∈ {0°,160°} in steps of 20° and 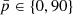 in steps of ten. We simulated at both low and high signal-to-noise ratio levels. The partial results from the high signal-to-noise ratio simulations are shown in Fig. B.1. Simulations at lower signal-to-noise ratios provide similar results but with broader parameter credible regions. From our simulations, we are satisfied that our construction of the likelihood provides valid inferences.
in steps of ten. We simulated at both low and high signal-to-noise ratio levels. The partial results from the high signal-to-noise ratio simulations are shown in Fig. B.1. Simulations at lower signal-to-noise ratios provide similar results but with broader parameter credible regions. From our simulations, we are satisfied that our construction of the likelihood provides valid inferences.
 |
Fig. B.1. Posterior samples from fits to simulated polarization and spectral data simulated with a high signal-to-noise ratio. The true simulated polarization degrees and lines are demonstrated with green lines and gray rays respectively. The posterior samples are colored from dark blue to light blue with increasing simulated polarization degree. Thus, we demonstrate that our posteriors encapsulate the simulated values directly without resorting to the statistical approximations of past works. |
In Fig. B.2 we display the posterior samples of the POLAR polarization and spectral normalization constants. The values obtained are not dissimilar from the values typically found between GBM detectors when those parameters are allowed to vary in the fits (Yu et al. 2016).
 |
Fig. B.2. Spectral and polarization normalization posteriors for the POLAR data. There is an evident ∼20 − 30% different in the relative flux between GBM and POLAR. |
Appendix C: The likelihood
Here we specify the full likelihood utilized in the analysis. We first defined basic distributions, that is, the Gaussian and Poisson distributions respectively:
The data from POLAR and GBM are inherently Poisson-distributed as they are counting experiments. The total count data in the ith detector channel (Ni) are a mixture of latent source (si) and background (bi) events. The transient nature of GRBs allowed us to naively separate the source observations into temporally on- and off-source regions. The background could then be modeled temporally in each detector channel as a polynomial resulting in estimate of the background counts (Bi) with and associated error (σBi). Thus our data for each detector channel (both PHA and SA channels) are the total counts Ni, Bi, and σBi. It is immediately obvious that we cannot simply subtract the background counts from the data as we (i) cannot know which counts are background and (ii) the background process has statistical properties. Thus, we must model the joint probability of the total and background process as
In our situation we did not have a spectral or polarization model for the background process. Thus, we adopt the common procedure of maximizing the probability with respect to bi a priori leading to the profile likelihood referred to as PGSTAT10.
Thus, with j datasets, that is, spectral or polarization detector’s data, the total likelihood for our observations is
Previous γ-ray polarization estimates have been achieved via background-subtracted data with the assumption of a Gaussian likelihood. This is improper and can lead to systematically biased results. There have also been attempts to transfer the statistical techniques used in optical polarimetry (Vaillancourt 2006; Quinn 2012) to γ-rays. These techniques are invalid for measurements that infer latent polarization via a secondary measurement such as the Compton scattering angle of a photon. Moreover, these techniques assume that none of the inherent difficulties of γ-ray photon measurement are present, namely, low counts and dispersion both in energy and scattering angle. We have dealt with this first issue via the proper Poisson-based likelihood. The second issue via our modeling of the responses of our instruments directly in the inference process.
Appendix D: Parameter corner plots
Here we present the parameter corner plots for the time intervals described in the analysis sections. See Figs. D.1–D.9 for these distributions. We have also plotted the posterior samples from the polarization analysis on a Cartesian grid for completeness in Fig. D.10.
 |
Fig. D.1. Parameter marginal distributions for time interval T: −0.2 − 1.4 s. |
 |
Fig. D.2. Parameter marginal distributions for time interval T: 1.4 − 1.8 s. |
 |
Fig. D.3. Parameter marginal distributions for time interval T: 1.8 − 2.4 s. |
 |
Fig. D.4. Parameter marginal distributions for time interval T: 2.4 − 3.0 s. |
 |
Fig. D.5. Parameter marginal distributions for time interval T: 3.0 − 3.6 s. |
 |
Fig. D.6. Parameter marginal distributions for time interval T: 3.6 − 4.8 s. |
 |
Fig. D.7. Parameter marginal distributions for time interval T: 4.8 − 6.6 s. |
 |
Fig. D.8. Parameter marginal distributions for time interval T: 6.6 − 8.9 s. |
 |
Fig. D.9. Parameter marginal distributions for time interval T: 8.9 − 20.0 s. |
 |
Fig. D.10. Posterior samples of the polarization quantities displayed in the common Cartesian projection. These samples correspond to those displayed in Fig. 8 but are shown here for readers used to quantities displayed in this fashion. |
All Tables
All Figures
 |
Fig. 1. BALROG location (red posterior samples) of GRB 170114A derived by fitting the peak of the emission for both the location and spectrum simultaneously. The blue contours display the 1,2, and 3 σ standard GBM catalog location as obtained from the Fermi Science Support Center (FSSC). |
| In the text | |
 |
Fig. 2. Light curves of the POLAR polarization and spectral data (the difference is explained in Appendix A) as well as two GBM detector data. The green line is the fitted background model and the gray shaded regions show the time-intervals used for the analysis. The binning in the analysis region is derived via Bayesian blocks. |
| In the text | |
 |
Fig. 3. Minimum variability timescales for the polar polarization data (left) and the GBM spectral data (right). The black line indicates the background power spectrum determined via Monte Carlo calculations and the shaded regions indicates the uncertainty in the background. Notably, both data sets have nearly equivalent MVTs. |
| In the text | |
 |
Fig. 4. Folded POLAR count space for two polarization angles and ten levels of polarization degree. The rates have been artificially scaled to between the different angles for visual clarity. The green lines for both angles represent the polarization degree |
| In the text | |
 |
Fig. 5. Directed graph model describing the full likelihood of our approach. Model parameters are shown in light blue, and the data in dark blue. The graph shows how the latent parameters of the model are connected to each other and eventually the data. It is important to note that the latent photon model connects both sides of the model. The position (δ) is a fixed parameter. Here ψ represents the set of spectral parameters. |
| In the text | |
 |
Fig. 6. Net SA data for each fitted time interval in our analysis. Superimposed are the posterior model predictions from the fits. The data have been rebinned for visual clarity. The SA presented here is measured within an arbitrary local coordinate system of POLAR. |
| In the text | |
 |
Fig. 7. Posterior predictive checks for the total polarization count rate data. The dark to light blue shaded regions indicate the 50th, 60th, 70th, 80th, and 90th percentiles of the replicated data respectively of the replicated data. The observed data are displayed in red. The estimated background count rates are displayed in green. |
| In the text | |
 |
Fig. 8. Posterior polarization results. The radial coordinate represents polarization degree and the angular coordinate the polarization angle. The polarization angle here is transformed to equatorial coordinates. The contours are for the 30th, 60th, and 90th percentiles of the credible regions. The plots are reflected about the periodic boundary of 180° for visual clarity. For the last three time intervals, we do not display contours and instead show the posterior samples as the parameters are poorly identified. The arrows that point from the last to the current position are meant as visual guides only. |
| In the text | |
 |
Fig. 9. Count spectra of POLAR and GBM from the joint spectral and polarization fits. The shaded regions indicate the 2σ credible regions of the fit. Data from a GBM NaI, BGO, and POLAR and displayed in green, black, and red respectively. |
| In the text | |
 |
Fig. 10. νFν spectra of the synchrotron fits scaled with increasing time. The width of the curves represents the 1σ credible regions of the model. |
| In the text | |
 |
Fig. 11. Temporal evolution of hν + inj and the polarization angle which has been doubled for visual clarity. hνinj falls as the polarization angle increases in time. The red and yellow areas are illustrative guides for the evolution the parameters. No fits were performed. |
| In the text | |
 |
Fig. B.1. Posterior samples from fits to simulated polarization and spectral data simulated with a high signal-to-noise ratio. The true simulated polarization degrees and lines are demonstrated with green lines and gray rays respectively. The posterior samples are colored from dark blue to light blue with increasing simulated polarization degree. Thus, we demonstrate that our posteriors encapsulate the simulated values directly without resorting to the statistical approximations of past works. |
| In the text | |
 |
Fig. B.2. Spectral and polarization normalization posteriors for the POLAR data. There is an evident ∼20 − 30% different in the relative flux between GBM and POLAR. |
| In the text | |
 |
Fig. D.1. Parameter marginal distributions for time interval T: −0.2 − 1.4 s. |
| In the text | |
 |
Fig. D.2. Parameter marginal distributions for time interval T: 1.4 − 1.8 s. |
| In the text | |
 |
Fig. D.3. Parameter marginal distributions for time interval T: 1.8 − 2.4 s. |
| In the text | |
 |
Fig. D.4. Parameter marginal distributions for time interval T: 2.4 − 3.0 s. |
| In the text | |
 |
Fig. D.5. Parameter marginal distributions for time interval T: 3.0 − 3.6 s. |
| In the text | |
 |
Fig. D.6. Parameter marginal distributions for time interval T: 3.6 − 4.8 s. |
| In the text | |
 |
Fig. D.7. Parameter marginal distributions for time interval T: 4.8 − 6.6 s. |
| In the text | |
 |
Fig. D.8. Parameter marginal distributions for time interval T: 6.6 − 8.9 s. |
| In the text | |
 |
Fig. D.9. Parameter marginal distributions for time interval T: 8.9 − 20.0 s. |
| In the text | |
 |
Fig. D.10. Posterior samples of the polarization quantities displayed in the common Cartesian projection. These samples correspond to those displayed in Fig. 8 but are shown here for readers used to quantities displayed in this fashion. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.