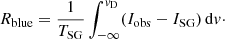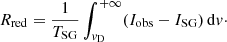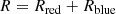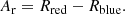| Issue |
A&A
Volume 626, June 2019
|
|
|---|---|---|
| Article Number | A98 | |
| Number of page(s) | 14 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201935165 | |
| Published online | 19 June 2019 | |
Plasma injection into a solar coronal loop⋆
1
CAS Key Laboratory of Solar Activity, National Astronomical Observatories, Chinese Academy of Sciences, 100101 Beijing, PR China
e-mail: lepingli@nao.cas.cn
2
Max Planck Institute for Solar System Research (MPS), 37077 Göttingen, Germany
3
University of Chinese Academy of Sciences, Beijing 100049, PR China
Received:
30
January
2019
Accepted:
18
May
2019
Context. The details of the spectral profiles of extreme UV emission lines from solar active regions contain key information for investigating the structure, dynamics, and energetics of the solar upper atmosphere.
Aims. We characterize the line profiles not only through the Doppler shift and intensity of the bulk part of the profile. More importantly, we investigate the excess emission and asymmetries in the line wings to study twisting motions and helicity.
Methods. We used a raster scan of the Interface Region Imaging Spectrograph (IRIS) in an active region. We concentrated on the Si IV line at 1394 Å, which forms just below 0.1 MK, and followed the plasma that moves in a cool loop from one footpoint to the other. We applied single-Gaussian fits to the line core, determined the excess emission in the red and blue wings, and derived the asymmetry of the red and blue wings.
Results. The blue wing excess at one footpoint shows injection of plasma into the loop that then flows to the other side. At the same footpoint, redshifts in the line core indicate that energy is deposited at around 0.1 MK. The enhanced pressure would then push the cool plasma down and inject some plasma into the loop. In the middle part of the loop, the spectral tilts of the line profiles indicate that the magnetic field has a helical structure, and the line wings are symmetrically enhanced. This is an indication that the loop is driven through the injection of helicity at the loop feet.
Conclusions. If the loop is driven to be helical, then the magnetic field can be expected to be in a turbulent state, as has been shown by existing magnetohydrodynamics models. The turbulent motions might explain the (symmetric) line wing enhancements that have also been seen in loops at coronal temperatures, but are not understood so far.
Key words: Sun: corona / Sun: transition region / Sun: UV radiation / line: profiles / techniques: spectroscopic
The movie associated to Fig. 7 is available at https://www.aanda.org
© ESO 2019
1. Introduction
The spectral profiles of the extreme-UV (EUV) emission lines from the Sun below ≈1600 Å contain essential information on the dynamic and thermal structure of the plasma in the solar upper atmosphere (e.g., Mariska 1992; Del Zanna & Mason 2018). It is quite common that optically thin emission lines in the EUV have non-Gaussian profiles with enhanced emission in the line wings, as first reported by Kjeldseth Moe & Nicolas (1977). These authors pointed out that a single-Gaussian can fit the core of the transition region lines, but cannot account for the enhanced line wings. Dere & Mason (1993) published a comprehensive summary of normal and exotic transition region line profiles and confirmed that the profiles of C IV and Si IV are in general not well described by a single Gaussian. The excess emission in the wings is commonly interpreted as being due to unresolved high-velocity flows. These flows might be caused by various processes, such as twisting motions (De Pontieu et al. 2014a), field-aligned flows (De Pontieu et al. 2009), reconnection outflows (Dere et al. 1989; Innes et al. 2015), or even more exotic effects (Peter 2010) such as non-Maxwellian velocity distribution functions.
When the transition region line profiles are not single Gaussians, they are in most cases well described either by a double- or a triple-Gaussian profile. In the quiet Sun, two-component profile fits typically have a narrow core and a broad second component that contributes up to 25% to the total intensity above the chromospheric network (Peter 2000). Peter (2001) proposed that the second component and the line core are formed in radically different physical regimes, namely small network loops and coronal funnels that are mixed along the line of sight. In active regions, Peter (2010) found that the spectra are mostly best fit by a narrow line core and a broad minor component. An association of the minor component with propagating disturbances was then reported by Tian et al. (2011a). However, these two-component profiles might also be three-component profiles, with narrow components accounting for the excess emission in the two wings (Wang et al. 2013). However, the spectral resolution is mostly not sufficient for distinguishing these two cases (Peter & Brković 2003). This three-component structure is only clear in cases like explosive events (e.g., Dere et al. 1989). More recent observations with the Interface Region Imaging Spectrograph (IRIS; De Pontieu et al. 2014b) at unprecedented spatial and spectral resolution showed even more complicated spectra, for instance, with chromospheric absorption lines in the continuum and in strong transition region lines (Peter et al. 2014), self-absorption in transition region lines (Yan et al. 2015), or complex bands of molecular lines in absorption and emission overlaid on the normal transition region spectra (Schmit et al. 2014). All these effects are best visible in UV bursts (Young et al. 2018).
Lines in the chromosphere, transition region, and corona ubiquitously show line profile asymmetries. Ding & Schleicher (1998) reported for chromospheric lines that the majority of Ca II K line profiles show a blue asymmetry. At loop footpoints, De Pontieu et al. (2009) quantified the red-blue asymmetry in the line profiles and identified faint but ubiquitous upflows from the chromosphere. In the network regions, spectral lines show significant asymmetry in the blue wing of the emission line profiles. The excess emission in the blue wing was also considered as a signature of the high-speed transition region and coronal upflows in the quiet Sun (McIntosh & De Pontieu 2009). Based on models and simulations, Martínez-Sykora et al. (2011) reported that the spectral asymmetry is sensitive to the velocity gradient with height (i.e., along the line of sight) in the transition region of coronal loops. In an active region, Brooks & Warren (2012) identified regions of asymmetric profiles, and found that the red-blue asymmetry is dependent on temperature. In some bright so-called moss areas of two active regions, Tripathi & Klimchuk (2013) measured the red-blue asymmetry in line profiles that formed over a wide range of temperatures, and derived emission measure distributions from the enhanced wing emission. They emphasized that the red-blue asymmetry and associated emission measures are small.
These non-Gaussians line profiles are also expected and found in hot active region structures. The nanoflare heating model predicts high-speed evaporative upflows (Antiochos & Krall 1979; Patsourakos & Klimchuk 2006; Li et al. 2015) that can be detected in the spectra. By generating synthetic line profiles based on one-dimensional hydrodynamic simulations, Patsourakos & Klimchuk (2006) predicted distinctive enhancements in the blue wing of the Fe XVII line profile. These characteristics have been found in line profiles near the footpoints of active region loops (Hara et al. 2008; Bryans et al. 2010). Hara et al. (2008) observed significant deviations in the blue wing from a single-Gaussian profile and suggested that unresolved high-speed upflows occur there. Tian et al. (2011b) reported that a faint excess emission at ∼100 km s−1 in the blue wing of coronal emission lines generally accompanies the enhancement of the moments of the line profile, which also supports the hypothesis that active regions have unresolved upflows. Peter (2010) pointed out that the excess emission in the line wing in active region loops is seen simultaneously in the blue and red wings near the loop apex. This is unlikely to be caused by a field-aligned flow, because in the observation described by Peter (2010), the line of sight seemed to be almost perpendicular to the loop. This raises the question whether the excess emission near loop footpoints in the blue wing of the profile can be solely explained as caused by upflows.
The EUV observations described above are based either on comparably large raster scans or on sit-and-stare observations. Both are acquired with slit spectrographs and cannot distinguish the spatial and temporal evolution. The raster maps provide only very limited time resolution (typically longer than some minutes). In the sit-and-stare mode the slit is at a fixed spatial position, so that the field of view of the spectroscopic information is limited to one dimension along the slit. Because loops are elementary components in the solar atmosphere that cover a certain range of sizes and timescales (e.g., Tian et al. 2009; Peter et al. 2013; Yan et al. 2013), it is important to understand their dynamic and thermal characteristics. For example, the spatial structure of the helicity in these loops can be investigated with spectroscopic maps (e.g., Li et al. 2014), but the question remains how these spatial structures in the spectroscopic data change in time.
We here investigate the temporal evolution of the spectroscopic features in a loop as they evolve in time. In the IRIS observations of the Si IV line we present here, the slit that scanned the raster map serendipitously and fortunately moved with just the right speed, so that it almost exactly followed a feature that was injected into the loop on one side and then propagated along the loop to the other footpoint. Because the apparent motion of the slit has the same velocity as the feature in the loop, we can follow the temporal evolution of the spectral features all along the loop.
2. Observations and data processing
The IRIS observatory provides simultaneous spectra and images of the upper solar atmosphere. IRIS scanned the active region we investigate here, NOAA AR 11850, several times during its emergence in September 2013. Hot explosions in the cool atmosphere of the Sun (Peter et al. 2014) and conversion from mutual helicity to self-helicity (Li et al. 2014) have previously been reported in this active region. We here use the raster map from 11:44 UT to 12:04 UT on 24 September 2014. The loop we investigate is located north of the active region (cf. Fig. 1). We use IRIS level 2 data1, which are already corrected for flat field, geometric distortion, and dark current.
 |
Fig. 1. Cool loop and context from the IRIS and SDO data. Panel a: snapshot of the IRIS slit-jaw images in the 1400 Å channel. Panels b–d: intensity (b), Doppler shift (c), and 1/e line width (d) maps of the Si IV (1394 Å) line. Panel e: HMI line-of-sight magnetogram. Panel f: snapshot from the AIA images at 171 Å. The dotted lines indicate the Si IV loop. The circles mark two footpoints of the loop, where E and W indicate the eastern and western feet. The blue vertical lines x3, x13, x23, x33, and x43 in (b) indicate five samples of the spatial positions of the spectra shown in Fig. 3. The field of view is 33.2″ × 10.0″ with the center at solar (X, Y) = (−251.9″, 56.4″). See Sects. 2 and 3.1. |
A large dense raster was acquired with 400 raster steps of 0.35″ each. The resulting field of view is about 140″ × 180″ centered at about 82″ north and 265″ east of disk center. The exposure time of the individual spectra was 2 s, the step cadence is 2.9 s, and the spatial scale along the slit is about 0.17″ per pixel. While all available wavelength bands have been recorded in the slit-jaw images, here we used only the 1400 Å channel. Taken together with the spectra, the 1400 Å images cover the corresponding field of view of the raster map, have a cadence of 12 s, and a spatial sampling of about 0.17″ per pixel. Using the fiducial marks on the slit, we aligned all the IRIS data. For the spectroscopic analysis, we concentrated on the transition region line of Si IV at 1394 Å, which is the stronger line of the Si IV doublet that is accessible to IRIS. Further details of the observations can be found in the Supplementary Material S1 of Peter et al. (2014).
The Doppler maps in the Si IV line require wavelength calibration. This is also provided with the level 2 data, but here we checked and reiterated the calibration. For this, the average spectrum of the quiet plage area surrounding the emerging active region was used. In particular, for the Si IV line at 1394 Å, we employed the nearby Ni II and Fe II lines that originate in the chromosphere and are expected to show small line shifts, smaller than 1 km s−1 (cf. Table 1). Considering also the uncertainties in the rest wavelengths, we expect the wavelength calibration to be limited to about 1 km s−1 (see Supplementary Material S1 of Peter et al. 2014), which is more than sufficient for the purpose of this study. In particular, the average Doppler shift of the Si IV line is about 6 km s−1 to the red, which is consistent with previous observations (e.g., Peter & Judge 1999).
Lines of interest.
To embed the IRIS observations into the context of the structure and evolution from the photosphere to the corona, we used data from the Solar Dynamics Observatory (SDO; Pesnell et al. 2012), namely of the Helioseismic and Magnetic Imager (HMI; Schou et al. 2012) and the Atmospheric Imaging Assembly (AIA; Lemen et al. 2012). The spatial and temporal sampling of the HMI line-of-sight magnetograms is 0.5″ per pixel and 45 s. For the AIA multiwavelength images, the respective values are 0.6″ per pixel and 12 s. We spatially scaled the SDO observations to match the IRIS slit-jaw images at 1400 Å and aligned them using several characteristic features, such as sunspots, network, and plage patterns. The exact spatial alignment is not crucial for our study because the SDO data are used mainly for context, and an accuracy of about 1″ is sufficient (and easily achievable).
3. Results
3.1. Overall properties of the emerging loop
We first investigate the general properties of the cool loop we see in the Si IV line. To show the context of the observation, we display the observed loop in its line profile parameters along with the underlying magnetic field and the coronal context in Fig. 1. The overall comparison of the snapshot of the 1400 Å slit-jaw image (Fig. 1a) and the raster map in the Si IV intensity from the spectra (Fig. 1b) shows that these are roughly similar. This demonstrates that in our observation in the loop, the 1400 Å channel is indeed dominated by the transition region Si IV line. However, some bright dots are visible in the 1400 Å channel that are not visible in the Si IV line intensity. These are most likely due to the chromospheric contribution to the 1400 Å channel.
The most prominent feature in the field of view in Fig. 1 is a cool loop that is visible in Si IV. This is stable at least during the 20 min when we built up the raster map. The central axes of the loop and its footpoints are highlighted in the figure (dotted line and red circles). We identified the loop and its footpoints visually based on the IRIS slit-jaw images in the 1400 Å channel. The corresponding HMI line-of-sight magnetogram (Fig. 1e) shows, as expected, that the loop connects two opposite-polarity plage-type features in the active region. South of the loop lies a highly dynamic region that hosts a UV burst that has been discussed by Peter et al. (2014, their bomb B4 in their Fig. 1). However, this UV burst is not connected to the loop we investigate here, at least in the sense that the temporal variability of the loop is not related to the UV burst. This is clearly visible in the movie provided with the study of Peter et al. (2014) (and is also visible in the animation we include with Fig. 7). Furthermore, the spectra in the UV burst are radically different from the loop (cf. Fig. S6 of Peter et al. 2014).
For a first characterization of the Si IV 1394 Å line profile, we performed a single-Gaussian fit with a constant background for the continuum. Because we concentrated on the line core, we applied the fit only within ±20 km s−1 from the peak of the line (and the continuum). To characterize the line core, we used the total intensity from the single-Gaussian fit, TSG = ∫ISG dv (ISG is the intensity profile of the fit), the Doppler shift, vD, and the Gaussian width, w1/e (half-width at 1/e of the peak intensity). Here we subtracted the instrumental width of about 26 mÅ (De Pontieu et al. 2014b), but not the thermal width. Because the thermal width of Si IV is small (smaller than 7 km s−1), the nonthermal broadening is very similar to the line width (within 1 km s−1). These line-core parameters are shown in Figs. 1b–d. The Si IV intensity shows the loop throughout the raster, that is., for at least 20 min, which is much longer than the ionization and recombination time of Si IV (cf. Peter et al. 2006, their Fig. 4). This indicates that the loop is stable and close to (or at least not too far from) ionization equilibrium. Therefore we can assume the loop to be a cool loop at a temperature close to the ionization equilibrium temperature of Si IV at about 80 000 K (cf. Peter et al. 2006, their Table 1 and Sect. 4.1). At least, there has to be a component of the loop (i.e., strand) that is relatively stable at this temperature.
The cool loop has a length of ≈15.8″ (≈12 Mm) and a width of ≈0.8″ (≈0.6 Mm). Here the width is measured as the full width at half-maximum after subtraction of the background. For the width estimate we used the spatial range between lines x23 and x43 in Fig. 1b, where the loop is most clearly defined with a background level of only about 20%. This width roughly corresponds to the width of loops found in several-MK hot coronal loops (Aschwanden & Boerner 2011) and is on the narrow side of the widths reported by Aschwanden & Peter (2017). In particular, it also roughly matches the loop width that was measured in the observations of the first Hi-C rocket flight (Cirtain et al. 2013) as seen in the 193 Å channel, which shows plasma at about 1.5 MK. In this channel, Peter et al. (2013) found that these coronal loops have a smooth cross-sectional intensity profile with little (or no) indication of substructures, which might be interpreted to mean that the loops are spatially resolved. IRIS and Hi-C have roughly the same spatial resolution (both about a factor of five better than AIA), therefore this result suggests that there might be a common intrinsic width of cool loops (at 0.1 MK) and hotter loops (at several MK) that deserves further investigation.
The large-scale dynamics in the cool loop are visualized by the Doppler map in Fig. 1c. This indicates that the eastern part (left) of the loop exhibits a blueshift, while the western part is redshifted. The red and blue pattern is consistent with the interpretation of a siphon flow along the cool loop (e.g., Bethge et al. 2012). The blueshift in the background surrounding the loop in-between the main polarities of the emerging active region might be interpreted as being due to flux emergence between the main polarities of the active region. Such general uplifts of the upper atmosphere as a whole in response to flux emergence are also seen in the simulation by Chen et al. (2014).
To show the internal dynamics within the loop, we display the line width in Fig. 1d (Gaussian 1/e width). While in quiet-Sun regions the (nonthermal) line width is about 20 km s−1, the line width at the location of the loop is significantly larger (by a factor of about 2). Because the thermal width of Si IV is only about 7 km s−1, the widths shown in Fig. 1d are basically the same as the nonthermal line widths. The nonthermal broadening is typically interpreted as being due to small-scale unresolved (bulk and wave) motions in response to small-scale heating events (e.g., Dere & Mason 1993; Chae et al. 1998; Peter 1999, 2001). Therefore (at least part of) the nonthermal broadening might be attributed to plasma heating along the loop. We emphasize that the width we find here applies to the line core only, and that the line wings contribute significantly to the total line intensity (sometimes up to 40%, see Sect. 3.5). To some small extent, the large line width of the single-Gaussian fits in the loop is therefore also due to the strong excess in the wings.
Interestingly, the loop in Si IV has a counterpart that is visible in the AIA channel at 171 Å (Fig. 1f). The 171 Å channel is in equilibrium dominated by emission from Fe IX that forms at about 0.8 MK, but it also receives some minor contribution from lines that form at lower temperatures around 0.25 MK (cf. Boerner et al. 2012). In principle, the emission detected in the 171 Å channel might be due to cool plasma. However, based on the greatly increased line width, which indicates strong heating in the cool loops (see Sect. 4.3), it is more probable that the loop in 171 Å is indeed due to hotter plasma of almost 1 MK (see Sect. 4.4). This means that this loop might be an example of plasma at transition region temperature (at about 0.1 MK) coexisting with coronal plasma at 1 MK in the same loop. This would indicate that some strands of the loop are still at 0.1 MK while others are already heated to coronal temperatures. Because the main emphasis of this study is on the non-Gaussian nature of the emission line profile in Si IV, we do not follow up this line of thought here.
3.2. Propagation of features along the loop
While overall the cool loop we study here was stable, numerous features can be seen that propagate along the loop, always in the same direction (east to west). To study this, we investigated the slit-jaw images in the IRIS channel at 1400 Å. This channel (in the loop) mainly shows the Si IV line (cf. Sect. 3.1). In particular, we followed the temporal evolution of the 1400 Å emission along the dotted line in Fig. 1a. The resulting space-time diagram is shown it in Fig. 2.
 |
Fig. 2. Proper motions along the loop. A space-time plot of a series of IRIS slit-jaw images in the 1400 Å channel along the dotted line EW as marked in Fig. 1. The dashed line and dash-dotted lines indicate proper motions along the loop. For comparison, the dotted line shows the sound speed near 80 000 K in the line formation region of Si IV. The respective mean velocity is denoted by the numbers in the plot. The black arrow marks the IRIS slit that scanned the loop. See Sect. 3.2. |
There are two prominent black linear features in Fig. 2, one starting at time 10 min, and the other at 11 min. The feature at 10 min with small spots (and marked by a small arrow) is the slit as it passes across the loop. The thicker black line is due to a bad spot on the detector (masked in black in the slit-jaw images). Projected onto the Sun, these artifacts move with an apparent speed of about 80 km s−1.
The actual bright patches that move along the loop in east-west direction are visible as inclined bright linear features, some of which are highlighted by the dotted lines. These features typically move with roughly constant speeds ranging from some 45 km s−1 to 60 km s−1. This is slightly higher than the sound speed in the Si IV source region of the emission of the cool loop (about 43 km s−1 at 80 000 K). This implies that here we see disturbances that propagate along the cool loop with about sound speed (e.g., waves or density enhancements). The individual bright features detected here have a spatial extent of some 2 Mm to 4 Mm. The strong brightening feature in the loop that appears around the time when the slit scans the loop (just above the dashed line starting at 8 min) propagates with a speed of more than 60 km s−1.
By coincidence, the apparent motion of the slit along the loop has a speed similar to (but slightly faster than) the solar structures that propagate within the loop. This is apparent when we follow the propagating brightening that moves along with the slit in Fig. 2. This fortunately enables us to follow the same structure as it moves and evolves along the loop. While the structure propagates along the loop (some two minutes), the difference between the apparent motion of the slit and the propagation of features along the loop translates into a difference in space of only about 2 Mm, which is smaller than the size of the brightening. Figure 2 also clearly shows that the slit (black dots starting at ≈10 min) are throughout well within the same bright feature that moves along the loop. We therefore assume in the following that the spectra taken while the slit scanned the loop do originate from the same feature that was injected at the eastern footpoint and then propagated westward along the loop.
Before this most prominent propagating feature appears (Fig. 2, at time 8 min), several smaller propagating brightenings started from the eastern footpoint. While it would be very interesting to study the spectra of these precursors as well, spectroscopic data are available only for the propagating feature that started around time 10 min.
3.3. Non-Gaussian line profiles in the loop: injection and wing enhancement
The Doppler shifts derived from the core of the Si IV profile indicate a smooth siphon flow from east to west (Sect. 3.1, Fig. 1c). In contrast, the emission in the wings of the Si IV line exhibits a complex evolution while the plasma evolves from the injection at the eastern footpoint and then propagates to the west along the loop.
As a first step to investigate the Si IV line profile along the loop, we display the corresponding parts of the detector images in Fig. 3. We used the following housekeeping for the spectra: the 45 raster positions from the eastern to the western footpoint along the solar-x direction are labeled x1…x45. As a reference, in the context figure (Fig. 1b) we indicate these positions for x3, x13, x23, x33, and x43 by blue vertical lines. The length of each of these lines is identical to the spatial coverage (along the slit) of the detector images in Fig. 3. The white marker in each of the spectra in Fig. 3 indicates the central axis of the loop, that is, the location of maximum brightness across the loop (which is the same as the dotted line in Fig. 1b).
 |
Fig. 3. Spectral detector images of Si IV (1394 Å) along the loop. The 45 raster steps from the eastern to the western footpoint in Fig. 1 are labeled x1 through x45. The locations of x3, x13, etc., and x43 are marked in Fig. 1b by five blue vertical lines. The white markers indicate the location of the central axis of the loop as displayed by the dotted line in Fig. 1b. The vertical dotted lines indicate zero Doppler shift. The red curves show the contours of the respective spectra at a level of 18% of its maximum. The blue lines connect two positions with the maximum enhancements in the blue and red wings. See Sects. 3.3 and 3.4. |
To highlight the asymmetry of the spectra, we also show contour lines of the spectral detector images in Fig. 3. Here we show contour levels of 18%, that is, at each spatial position we mark the wavelength (or Doppler shift) at which the intensity dropped to 18% of the peak intensity at that location. This choice of 18% is motivated by the residual of the Gaussian fits, which on average is 18% in the red and 21% in the blue wing. We simply took the smaller number. We also checked the contour levels at 15%, 20%, 25%, and 30%, but the results are qualitatively the same.
Near the eastern footpoint (x1) the detector images and the contours show a very clear signal of a one-sided excess emission in the blue wing, indicating the injection of plasma through an upflow into the loop (Fig. 3-x1). Away from the footpoint, from position x2 to x5, the clear single-sided excess in the blue wing ceases. No clear excess emission is seen in the red wing at these positions. This is also confirmed by the plots of the spectral profiles on the central axis of the loop in Fig. 4. From east to west, Fig. 4 shows the spectral profiles at the respective location of the peak intensity across the loop (i.e., at the location of the white markers in Fig. 3). Here the comparison to the single-Gaussian fits clearly reveals the line asymmetry, and at locations x1 to x5, it shows the clear single-sided enhancements in the blue wing. Starting with position x6, there is significant excess emission in both wings, with a peak around x11. Finally, toward the western footpoint (x45), the detector images in Fig. 3 and the line profiles in Fig. 4 both show a decrease of the excess emission in the wings. Near the western footpoint, the profiles are even close to single Gaussians.
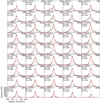 |
Fig. 4. Individual spectral profiles of Si IV (1394 Å) along the loop. Each profile was recorded in one spatial pixel on the central axis of the loop (i.e., maximum emission from the loop at the respective slot position; dotted line in Fig. 1b). These are the spectral profiles at the locations of the short horizontal white markers in the detector images from Fig. 3. The diamonds (with the bars) show the observed spectra and the red lines indicate single-Gaussian fits to the line core. To ensure that the single-Gaussian fits only represent the line core, the fit was performed only within ±20 km s−1 from the peak of the line. The parameters denoted by the numbers in the plots show the line centroid (vD) of the red fits, the total residual of the intensity (R), and the red-blue asymmetry (Ar). See Sects. 3.3 and 3.5. |
This simple check of the spectra already reveals the pattern of injection at one footpoint and enhanced emission in both wings through the most of the loop, before it becomes a more single-Gaussian profile at the other footpoint. Based on the discussion from Sect. 3.2, this implies that while a parcel of plasma flows from east to west, its spectroscopic properties change over time after the injection from non-Gaussian to close to single Gaussian. In the following we quantify this impression by first characterizing the spectral tilt in the detector images (Sect. 3.4) and then investigating the line asymmetries (Sect. 3.5).
Several options are available to quantify the non-single-Gaussian nature of the line profiles. For example, a kappa distribution might be fit to the spectra (e.g., Dudík et al. 2017). This could account for the enhanced emission in the line wing, but not for the asymmetries we see. We therefore did not consider this option. Another possibility would be to use double-Gaussian fits (e.g., Peter 2010). A second broad Gaussian component would then account for the excess emission in the line wing, and the relative shift of the core and the wing component would account for the line asymmetry. In this scenario, it is implicitly assumed that the loop has exactly one additional flow component that would account for the line wing excess. First, this would raise the question why a three-component fit might not be used (e.g., Wang et al. 2013). Second, and more importantly, if turbulence were to evolve in the loop (as discussed in Sect. 4.3), such a representation would be misleading. In that case, there would not be a distinct second flow component in the loop, but the excess emission in the line wing would be caused by the (continuous) distribution of the velocity within the turbulent medium. Yet another possibility to characterize the non-Gaussian profiles is to quantify the excess emission in the line wings (with respect to a single Gaussian) and the line profile asymmetry. This procedure does not use a priory assumption on the physical process that causes the non-Gaussian nature of the profile, and it allows a quantitative comparison to future models for the line profiles in loops. We therefore follow this last option in Sect. 3.5.
3.4. Quantifying the spectral tilt and helical flow
If a line profile gradually shifts its position (or centroid) with the spatial direction along the slit, the resulting detector image of the line profile will be tilted. This can be illustrated by the detector image at position x33 along the loop as shown in Fig. 3: With increasing position of solar Y along the slit (from about 56.0″ to 56.5″), the line shift seems to move gradually from the red to the blue. This change in line shift with position across the loop can indicate a rotational component of the flow in the loop. Here, at lower solar Y values, the plasma moves away from the observer, at higher solar Y, it moves toward the observer. Together with the flow along the loop, this would indicate a helical flow along the loop (e.g., Li et al. 2014).
To quantify the spectral tilt, we used the red contour lines (at the 18% level2) of the detector images in Fig. 3. We determined the maximum blueshifts Δvblue and redshifts Δvred (both numbers defined to be positive) of these contours with respect to the Doppler shift vD of the line core (cf. Sect. 3.1) at the respective location. The Doppler dispersion (i.e., width of the 18% contour level) is then given by the sum of these two, Δv = Δvred + Δvblue. By recording the position along the slit where the maximum redshift and blueshift occur, we can then determine the spatial offsets Δy between the maximum redshift and blueshift of the contours. This yields the spectral tilt, Δy/Δv. The spectral tilt is essentially a measure for the slope of the line that connects the location of maximum blueshift and redshift in each detector image (i.e., the blue lines in Fig. 3; e.g., see x33 for a good example). If there is no evident maximum red or blue wing contour (e.g., with x1 in Fig. 3), we assumed that Δy = 0. Of course, the values for the quantities Δvblue, Δvred, Δy, and Δy/Δv depend (slightly) on the choice of the contour level (here 18%). However, we used Δy/Δv mainly to investigate systematics of the spectral tilt and the actual values are therefore not important.
The Doppler dispersions (Δv, Δvred, Δvblue), the spatial offset (Δy), and the spectral tilt (Δy/Δv) are shown along the loop in Fig. 5. The Doppler dispersion peaks around 3″ to 4″ away from the eastern footpoint (just as the line asymmetry does; see Sect. 3.5). However, no clear trend can be seen in the spatial offset (as a very rough error estimate for Δy, we conservatively assume ±1 spatial pixel). The spectral tilt Δy/Δv does not show a clear trend either. However, one systematic is prominent: While there are not too many locations with a significant spectral tilt, the sign of the tilt is always the same. This implies that our results would be compatible with a systematic rotational component of the flow and thus consistent with a helical flow along the loop. This spectral tilt is caused almost solely by the excess emission in the line wings. The position of the line core (as characterized by the single-Gaussian fit) does not show a variation across the loop, that is, along the slit. This is evident by inspection of Fig. 1c, where no significant systematic change in the line shift is visible perpendicular to the dotted line that indicates the loop position.
 |
Fig. 5. Evolution of the spectral tilt of Si IV (1394 Å) along the loop. Panel a: Doppler dispersion separately for the blue wing (Δvblue), the red wing (Δvred), and a combination of both wings (Δv). Panel b: offset between the maximum enhancements in the blue and red wings along the slit (Δy). The errors are conservatively estimated to be ±1 spatial pixel. Panel c: spectral tilt (Δy/Δv). Because we follow a parcel of gas moving along the loop, the top axis shows the time to indicate the temporal evolution. See Sect. 3.4. |
Because the slit follows the flow along the loop, our finding does not necessarily imply a helical flow all along the loop all the time. We can only state that we see a systematic rotational component of the flow as it moves along the loop. We therefore include a time axis at the top of Fig. 5.
3.5. Quantifying the evolution of the plasma parcel that moves along the loop
To quantify the evolution of the plasma parcel that moves along the loop, we characterize the line core parameters and the asymmetry and excess emission in the wings of the Si IV profiles. This analysis uses the single-Gaussian fits of the line core (cf. Sect. 3.1), which provide the total intensity of the line core, TSG = ∫ISG dv, and its Doppler shift vD. We use ISG and Iobs to denote the profile of the single-Gaussian fit (of the core only) and the actually observed profile. Then the residual of the intensity in the blue wing can be defined as
Likewise, the residual in the red wing is
We can now define the total residual as
and the red-blue asymmetry as
The residuals provide the information on how strongly the observed profile deviates from the Gaussian fitting the core, for the blue and red wing separately and for the whole profile. These are relative measures, and we find that the excess emission in both the blue and the red wings can reach up to 40% of the total intensity of the Gaussian fit to the line core (e.g., in Fig. 6c at about 4″ from the eastern footpoint, we find Rblue ≈ 0.5, Rred ≈ 0.4). The total residual R reaches values of up to 0.8, which means that the excess emission in the wings can be almost as strong as the line core emission.
 |
Fig. 6. Evolution of the line profile characteristics of Si IV (1394 Å) along the loop. Panels a and b: total intensity (TSG) and Doppler shift (vD) of the single-Gaussian fits to the line core. Panel c: residuals of the intensity in the blue wing (Rblue), the red wing (Rred), and over the whole line (R) as defined in Eqs. (1)–(3). Panel d: red-blue asymmetry (Ar) as defined in Eq. (4). Because we follow a parcel of gas that moves along the loop, the top axis shows the time to indicate the temporal evolution. See Sect. 3.5. |
The technique of red-blue asymmetry as used here was introduced (in a different form) by De Pontieu et al. (2009). For their analysis, the authors used two (narrow) wavelength regions (or velocity offsets) that were symmetrically arranged with respect to the centroid of the profile (see also McIntosh & De Pontieu 2009; Tian et al. 2011b). In our study, we considered the whole wavelength range (formally from ±∞ to vD). Qualitatively, the results are the same as for a more restricted wavelength (or velocity) range. Most importantly, we did not only consider the red-blue asymmetry, Ar, as done before, but also the residual R. This is important for the following simple reason. Even if there is no asymmetry, Ar ≈ 0, there might be a significant deviation from a (single-) Gaussian profile as emphasized previously by Peter (2010). In our data set this is the case, for instance, around 5″ from the eastern footpoint (Figs. 6c and d): here the residuals in the red and blue wing are both about 0.3, and there is no asymmetry (cf. profile x13 in Fig. 4). Consequently, the red-blue asymmetry must not be studied alone, but the excess emission in the line wings also needs to be investigated. It is here characterized through R, Rred, and Rblue.
The variation in line profile parameters indicates not only a spatial variation, but mainly a temporal variation of a plasma parcel that moves along the loop (cf. Sect. 3.1). To illustrate this variation, we plot in Fig. 6 the (line core) intensity, TSG, the Doppler shift, vD, the residuals, R, and the line asymmetry, Ar, along the loop. The total intensity, TSG (Fig. 6a), peaks when the plasma parcel reaches the middle (apex) of the loop. During the injection and also when it reaches the opposite footpoint, the intensity is lower. When we examined the density-sensitive lines of O IV around 1400 Å, we found only a small change (smaller that 10%) in the ratios from the loop footpoint to the apex. This applies to both ratios, 1401/1400 and 1401/1404. We would therefore expect only a modest change in density from footpoint to apex that cannot account for the intensity increase. We argue instead that a small temperature change is responsible for the intensity variation (see Sect. 4.3). The line centroid of the line core profile, vD (Fig. 6b), shows a redshift in the immediate vicinity of the eastern footpoint (closer than 1.5″), which is also where the strongest excess emission in the blue wing is found (see below). In the major eastern part the shift is then toward the blue, and in the middle of the loop it turns to red. This is consistent with a continuous flow from east to west along the loop, where in the eastern half (“left” of the loop apex) we see the projected upflow and in the western half we see the downflow. These projected flow speeds near the footpoints are approximately 5 km s−1 (cf. Fig. 6b).
The enhancement in the blue wing, Rblue, is highest at the eastern footpoint, which is consistent with a plasma injection (Fig. 6c) because here the excess emission in the red wing is rather small. Inspection of the profiles (x1 to x3 in Fig. 4) indicates that this upflow reaches speeds of 50 km s−1 to 100 km s−1. Within 1″ to 1.5″ from the eastern footpoint, we therefore see a high-speed upflow into the loop, while the bulk part of the plasma imaged here by the Si IV line shows a net downflow (vD is about 5 km s−1 to the red). The high-speed injection is strong because its Rblue is up to 0.5, implying that the upflowing plasma emits 50% of the Si IV emission compared to the source region of the line core, which is associated with the slow downflow.
The excess emission in the red wing behaves quite differently from the emission in the blue wing. While the blue wing drops more or less continuously from the eastern to the western side of the loop (with some fluctuations), the excess in the red wing, Rred, first increases within the first 5″ from the eastern footpoint. When it reaches its maximum, the excess in the red wing roughly matches that in the blue wing, Rred ≈ Rblue. From there on to the western footpoint, the excess emission in the red and blue wings very roughly match and drop more or less monotonically (even though there is some fluctuation). This implies that at the western footpoint, the line profile is close to a (single) Gaussian. This quantitative result matches the visual impression of the line profiles in Fig. 4.
The evolution of the excess emission in the blue and red wing of course leaves its mark in the red-blue asymmetry of the profile, Ar (Fig. 6d). This asymmetry is very strong only close to the footpoint, while over most part of the loop (more than 4″ away from the eastern footpoint) the asymmetry is comparably small. Clearly, judging based on the red-blue asymmetry alone, no significant excess emission in both line wings would be recognized, with roughly the same magnitude that decreases while the gas parcel moves along the loop to the footpoint opposite to where it was injected.
While the above results have been derived only for the spine of the loop (i.e., the central axis of the loop, see dotted line in Fig. 1b), they are not particular to this thin on-axis part of the loop. To demonstrate this, in Appendix A we show the line profiles two IRIS pixels (or 0.33″) to the north and south of the central axis of the loop (Figs. A.1 and A.2), that is, at the edge of the loop. Likewise, we repeat plots with the variation in the various line profile parameters along the loop, once for the locations two pixels to the north and south (Fig. A.3) and for averaging the profiles in the north-south direction (Fig. A.4). This makes clear that the results we showed in this paper are robust and reliable, and do not depend on the exact spatial positions we chose within or across the loop.
4. Discussion
The IRIS slit scanned the Si IV loop with roughly the same speed as the plasma within the loop moved from east to west. This fortunate coincidence provides a good opportunity to follow the same gas parcel as it moves along the loop and to study its evolution.
4.1. Loop geometry
The cool loop seen here is (most probably) a rather flat loop. The proper motion along the loop from east to west is about 60 km s−1. The blueshift on the eastern and the redshift on the western side are about 5 km s−1. When we consider a simple geometry, the inclination angle of the flow, and thus the angle of the magnetic field channeling the flow, near its footpoints is only about 5°. When we consider that the footpoint distance of the loop is just below 16″ (or 12 Mm), the apex height of the loop should be below 1 Mm3. This means that this cool loop would be really flat. For comparison, the pressure scale height at the line formation temperature of Si IV (≈80 kK) is about 5 Mm. Therefore, the cool loop extends in height only over a small fraction of the scale height, and hence the density in the loop is not expected to change significantly (through gravitational stratification). For a constant mass flux we would therefore also expect a roughly constant (proper) motion along the flat loop, which is what we see (cf. dash-dotted lines in Fig. 2).
4.2. Heating and injection of plasma at the loop footpoint
Transiently brightening features at the eastern footpoint expand into the loop, and we then see the plasma moving along the loop (Sect. 3.2). Together with the clear excess emission in the blue wing (Sects. 3.3 and 3.5) at the eastern footpoint, this strongly supports the hypothesis that plasma is injected. Such injections at loop footpoints have been suggested before to supply mass to coronal structures (Xia et al. 2003; De Pontieu et al. 2009; Guo et al. 2010; He et al. 2010; Tian et al. 2011a) because this would naturally cause enhancements in the blue wing (De Pontieu et al. 2009; McIntosh & De Pontieu 2009; Tian et al. 2011b; Brooks & Warren 2012). Alternatively, the excess emission we see in the blue wing might also be due to high-speed evaporative upflows, as predicted in the nanoflare heating model (Patsourakos & Klimchuk 2006). However, those models would predict the upflows at very high temperatures (several MK; Li et al. 2015), while here we see the spectral signature in Si IV that shows plasma below 0.1 MK.
The spectral properties of the Si IV profile show an interesting feature that seems to contradict itself at first sight. As mentioned above, the excess emission in the blue wing as well as the proper motions indicate that plasma is injected into the loop. However, the core of the line profile shows a clear net redshift near the eastern footpoint. As expected from the general transition region redshifts, at this loop footpoint, C II at 1336 Å and O VI at 1401 Å also show a net redshift. The redshift of O IV is 2 km s−1 to 3 km s−1 higher than the redshift of the Si IV core. C II is not straightforward to interpret because of its self-absorption feature. The line core redshift and the strong line asymmetry to the blue side seem both to be restricted to the first 2″ from the footpoint (cf. Figs. 6b and d). This suggests that a fast up- and slow downflow coexist in the same resolution element of the observation.
This can be understood in the following scenario. If there is strong heating (with high energy input per particle) at around or just above the formation temperature of Si IV, for instance, at a few 0.1 MK, then at that location the pressure would be enhanced locally. This is consistent with the findings in 3D magnetohydrodynamics (MHD) models that predict a maximum of the energy input per particle at temperatures between 0.1 MK and 1 MK (Hansteen et al. 2010; Bingert & Peter 2011). In response, the bulk of the plasma below would be pushed down, causing a redshift of the line core. Because this pushes the plasma into the higher-density regions below, the speed would be rather limited. The enhanced pressure would then also accelerate some of the plasma upward, and because it moves into the thinner (hotter) parts, this upward acceleration would cause higher speeds, just as observed: the excess emission in the blue wing is found around 50 km s−1 or even more, while the core of the profile is shifted by only a few km s−1 (cf. x1 to x3 in Fig. 4). This is similar to the numerical models by Spadaro et al. (2006) and Hansteen et al. (2010). They see cool downward-moving plasma and upward-accelerated plasma that is heated (and seen then at higher temperatures), but accelerated by a much smaller degree (blueshifts of only a few km s−1). In our observation we see a coronal signature (i.e., heated plasma) in the loop as well, which is clearly visible in the 171 Å observations (see Fig. 1 and Sect. 4.4). However, there is also a cool loop at the same location, and the injected plasma (seen in the line wing) reaches much higher speeds of about 50 km s−1. In conclusion, this observation of the downward motion seen in the core of the line profile while at the same time there is an excess emission and strong asymmetry in the blue wing of the same Si IV line poses a challenge for current models.
4.3. Helical motion and turbulence along the loop
In our observations we find two spectral features that might be tightly connected: a spectral tilt (Sect. 3.4) and the (almost) symmetric excess emission in the line wings (Sect. 3.5) in the middle of the loop, that is, away from the loop footpoints. These two features might be related to the helical flow and to the turbulent state of the magnetic field in the loop.
Spectral tilts can be interpreted by a helical motion in the loop. The spatial offset of red and blue shifts on the two sides of the loop (cf. Fig. 3 and Sect. 3.3) indicates a rotational component of the flow. Together with the observed (proper) motion along the loop, this indicates a helical motion of the plasma. At the transition region temperatures where Si IV forms, the atmosphere should be in a low plasma-β stage (Peter et al. 2006; their Fig. 12a). Consequently, the flows should be parallel to the magnetic field, and the helical flow of the plasma indicates that the magnetic field in the loop is helical as well. Such helical (or twisting) motions have been seen before. For example, Li et al. (2014) interpreted the changes in the spectral tilt in time as being due to the change from mutual to self-helicity of two interacting loops, and De Pontieu et al. (2014a) found that twisting motions are ubiquitous.
These helical twisting motions might be related to the red-blue asymmetries. The asymmetry changes along the loop, that is, while we follow the ejected plasma packet (Figs. 6c and d). Therefore the twisting motions could show themselves as enhancements in the line wings. If this were the case, we would expect an oscillatory variation of the line asymmetry, that is, with the twisting moving back and forth, we would see the enhancements alternating between the red and blue wings. Instead, after the initial phase, we see only a small asymmetry, which mostly slightly leans to the blue wing (see Fig. 6). We therefore do not think that the line asymmetries are caused by helical twisting motions. Other possibilities for a (symmetric) enhancement of the line wings might be a change in velocity distribution of the ions due to ion heating by Alfvén waves or due to the motions that are directly associated with the different modes of MHD waves (Peter 2010; his Sects. 4.3 and 4.5.1).
A helical structure within the loop indicates that the loop might be driven through footpoint motions. The original idea of Parker (Parker 1972, 1988) was that irreversible horizontal motions in the photosphere braid the magnetic field and induce currents in the corona that will be dissipated in a transient fashion in the form of nanoflares. Numerous models have been constructed that use (simple helical) motions at the loop footpoints, and it has been investigated how these motions drive the heating and dynamics in the coronal part of a loop (e.g., Wilmot-Smith et al. 2011). Alternatively, some studies assumed a braided state of the loop as an initial condition (that would have been induced by, e.g., helical motions) and concentrated on the relaxation phase when the magnetic field reconnects and heats the plasma (e.g., Pontin et al. 2017). Models with sufficient resolution find that the magnetic field in the loop is in a turbulent state (e.g., Reid et al. 2018, their Fig. 5). If the magnetic field is in a turbulent state, the motions along the magnetic field will also be distributed in all directions (and not only along the major axis, i.e., the guide field, of the loop). We can consequently expect significant line broadening in this situation, which might be detected as a broadening of the line core and as a broad additional component in the emission line profiles, or in other words, as enhanced wings. In our observations we see the increased line width in the loop (cf. Fig. 1d) and also excess emission in both line wings (e.g., Fig. 4, x11 to x25).
If turbulence is present in the loop, it would also move with the plasma heating and consequently with an increase in the emission from the loop (Fig. 6a). The large line width in the loop (Fig. 1d) also supports the idea that the plasma is heated. When we consider the contribution function of Si IV, only a modest increase of the temperature from 60 000 K to below 80 000 K, for example, would be sufficient to explain an increase in intensity by a factor of two, consistent with Fig. 6a.
In general, helical motions in these 3D loop models will lead to a braided state that in turn results in a turbulent state of the magnetic field and conversion from magnetic to thermal (and kinetic) energy. Future numerical loop models will have to investigate if the turbulent state of the magnetic field will indeed result in a line broadening and wing enhancement, as we observe here. Only then we can clearly link the helical motions in the loop to the enhanced emission in the line wings.
4.4. Possible coronal component in the cool loop
If heating is present in the loop, (parts of) the plasma might also be heated to coronal temperatures. Our investigation so far concentrated on the spectral profiles of the Si IV line. In equilibrium, this line forms below 0.1 MK, and in the bright parts of an active region, it will dominate the slit-jaw images of IRIS in the 1400 Å band. We see the loop under investigation also in AIA data, for instance, in the 171 Å band (Fig. 1f). The loop is also visible in other AIA channels (e.g., 304 Å, 131 Å, and 193 Å), but we concentrate on the 171 Å band here.
That we see emission at 171 Å is not sufficient to argue that we indeed see hot coronal plasma here. The bulk of the 171 Å band is usually dominated by Fe IX that forms at coronal temperatures just below 1 MK. There is also a contribution from lower temperatures around 0.2 MK to 0.3 MK, however (e.g., Boerner et al. 2012). Because we see the loop in O IV 1401 Å forming at about 0.2 MK, it might be wondered whether the loop at 171 Å might be due to cool plasma at (a few) 0.1 MK and does not represent coronal emission at about 1 MK.
To test this, we compared the temporal evolution of the images in AIA 171 Å to the IRIS slit-jaw images at 1400 Å. If 171 Å were dominated by cool (a few 0.1 MK) plasma, then 171 Å and 1400 Å should show the same temporal evolution. In Fig. 7 we show snapshots in the two bands together with the evolution of the emission from the apex region of the loop. The movie that is attached to Fig. 7 displays the evolution in 171 Å and 1400 Å over the time in which the slit crosses the loop. There we see the apparent motion along the loop in 1400 Å that is captured in the space-time plot in Fig. 2. We also see a brightening near the loop apex in 171 Å, but because the spatial resolution of AIA is significantly lower than that of IRIS, apparent motions are more difficult to isolate on these scales. Still, we can study the temporal variation in the region around the apex of the flat loop, which we here approximate by a rectangle (Figs. 7a and b). We integrated the emission in 171 Å and 1400 Å in this rectangle and show the resulting light curves in Fig. 7c. There is a clear time lag between the two channels, with the 171 Å channel brightening about half a minute to one minute after the 1400 Å channel. This time lag shows that 171 Å in this loop cannot be dominated by cool plasma. The loop we see in 171 Å therefore probably originate from coronal plasma.
 |
Fig. 7. Temporal evolution of the loop intensity. Panels a and b: snapshots in the AIA 171 Å channel and the IRIS slit-jaw images at 1400 Å. The field of view is the same as in Fig. 1, but here we use a logarithmic scaling of the intensities. The apex region of the loop under investigation here is indicated by the boxes in panels a and b. Panel c: intensity integrated over the box in the two channels. The vertical blue line shows the time of the snapshots in panels a and b. The black vertical line in panel b is the spectrograph slit, the black feature at the bottom left edge of the box in panel b is an artifact on the detector. An animation showing the temporal evolution while the slit is passing the loop is available online. See Sect. 4.4. |
The time lag between the 1400 Å channel (0.1 MK) and the 171 Å band (1 MK) instead indicates that the plasma is heated. Thus we find further supporting evidence for heating in the loop, as discussed in Sect. 4.3.
5. Conclusions
Using the data of an emerging active region mapped by IRIS, we studied the evolution of plasma injected into a cool transition region loop by investigating the details of the Si IV (1394 Å) line profiles. In this low-lying loop, at some 12 Mm, it climbs probably less than 1 Mm, a steady flow from the eastern to the western side is established (Sect. 4.1).
At the eastern footpoint we see a clear high-speed injection of plasma into the loop, which is revealed by a strong excess of the emission in the blue wing of the Si IV line profile (Sect. 4.2). At the same time, the line core is redshifted at this same footpoint, which is indicative of a strong heating event at temperatures just slightly higher than those at which Si IV forms. This would cause a (local) pressure enhancement that would press the bulk of the plasma down, while some part is injected into the loop.
In the loop we find a signature for a helical flow, which implies that the magnetic field is also helical (Sect. 4.3). This could be a signature that the loop is driven by circular horizontal motions at its footpoint in the photosphere. This could lead not only to twisting motions, but also to a turbulent state of the magnetic field. The associated (small-scale unresolved) flows could then be responsible for the (almost) symmetric enhancement of both wings of the line profile in the middle section of the loop away from its footpoints (Sect. 4.3). Such profiles with symmetrically enhanced wings have been observed before (see Sect. 1 and, e.g., Peter 2010), but so far await a coherent interpretation. With new models of MHD turbulence in a loop, we might achieve a better understanding of the nature of these profiles.
Movies
Movie of Fig. 7 Access here
Data are available at http://iris.lmsal.com
The actual results do not depend on the exact choice of the level. See also Sect. 3.3 for a discussion on choosing the 18% level.
Acknowledgments
Sincere thanks are due to Davina Innes and Lijia Guo for discussions and comments on this study. HP is grateful for discussions on the turbulent state of the magnetic field with Lakshmi Pradeep Chitta and David Pontin. The authors thank the anonymous referee for helpful comments. IRIS is a NASA small explorer mission developed and operated by LMSAL with mission operations executed at NASA Ames Research center and major contributions to downlink communications funded by ESA and the Norwegian Space Centre. The AIA and HMI data used are provided courtesy of NASA/SDO and the AIA and HMI science teams. This work is supported by the National Foundations of China (11673034, 11533008, 11790304 and 11773039) and Key Programs of the Chinese Academy of Sciences (QYZDJ-SSW-SLH050).
References
- Antiochos, S. K., & Krall, K. R. 1979, ApJ, 229, 788 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., & Boerner, P. 2011, ApJ, 732, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., & Peter, H. 2017, ApJ, 840, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Bethge, C., Beck, C., Peter, H., & Lagg, A. 2012, A&A, 537, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bingert, S., & Peter, H. 2011, A&A, 330, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boerner, P., Edwards, C., Lemen, J., et al. 2012, Sol. Phys., 275, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Brooks, D., & Warren, H. 2012, ApJ, 760, L5 [CrossRef] [Google Scholar]
- Bryans, P., Young, P. R., & Doschek, G. A. 2010, ApJ, 715, 1012 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, J., Schühle, U., & Lemaire, P. 1998, ApJ, 505, 957 [CrossRef] [Google Scholar]
- Chen, F., Peter, H., Bingert, S., & Cheung, M. C. M. 2014, A&A, 564, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cirtain, J. W., Golub, L., Winebarger, A. L., et al. 2013, Nature, 493, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Del Zanna, G., & Mason, H. E. 2018, Sol. Phys., 15, 5 [Google Scholar]
- De Pontieu, B., McIntosh, S. W., Hansteen, V. H., & Schrijver, C. J. 2009, ApJ, 701, L1 [NASA ADS] [CrossRef] [Google Scholar]
- De Pontieu, B., Rouppe van der Voort, L., McIntosh, S. W., et al. 2014a, Science, 346, 1255732 [CrossRef] [Google Scholar]
- De Pontieu, B., Title, A. M., Lemen, J. R., et al. 2014b, Sol. Phys., 280, 417 [Google Scholar]
- Dere, K. P., & Mason, H. E. 1993, Sol. Phys., 144, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Dere, K. P., Bartoe, J.-D. F., & Brueckner, G. E. 1989, Sol. Phys., 123, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Ding, M. D., & Schleicher, H. 1998, A&A, 332, 767 [NASA ADS] [Google Scholar]
- Dudík, J., Polito, V., Dzifčáková, E., et al. 2017, ApJ, 842, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, L. J., Tian, H., & He, J. S. 2010, RAA, 10, 1307 [NASA ADS] [CrossRef] [Google Scholar]
- Hansteen, V. H., Hara, H., De Pontieu, B., & Carlsson, M. 2010, ApJ, 718, 1070 [Google Scholar]
- Hara, H., Watanabe, T., Harra, L. K., et al. 2008, ApJ, 678, L67 [NASA ADS] [CrossRef] [Google Scholar]
- He, J. S., Marsch, E., Tu, C. Y., et al. 2010, A&A, 516, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Innes, D. E. 2001, A&A, 378, 1067 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Innes, D. E., Guo, L.-J., Huang, Y.-M., & Bhattacharjee, A. 2015, ApJ, 813, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Kjeldseth Moe, O., & Nicolas, K. R. 1977, ApJ, 211, 579 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Li, L. P., Peter, H., Chen, F., & Zhang, J. 2014, A&A, 570, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, L. P., Peter, H., Chen, F., & Zhang, J. 2015, A&A, 583, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mariska, J. T. 1992, The Solar Transition Region (Cambridge: Cambridge University Press) [Google Scholar]
- Martínez-Sykora, J., De Pontieu, B., Hansteen, V., & McIntosh, S. 2011, ApJ, 732, 84 [NASA ADS] [CrossRef] [Google Scholar]
- McIntosh, S. W., & De Pontieu, B. 2009, ApJ, 707, 524 [NASA ADS] [CrossRef] [Google Scholar]
- Patsourakos, S., & Klimchuk, J. A. 2006, ApJ, 647, 1452 [NASA ADS] [CrossRef] [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1972, ApJ, 174, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1988, ApJ, 330, 474 [Google Scholar]
- Peter, H. 1999, ApJ, 516, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Peter, H. 2000, A&A, 360, 761 [NASA ADS] [Google Scholar]
- Peter, H. 2001, A&A, 374, 1108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peter, H. 2010, A&A, 521, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peter, H., & Brković, A. 2003, A&A, 403, 287 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peter, H., & Judge, P. G. 1999, ApJ, 522, 1148 [NASA ADS] [CrossRef] [Google Scholar]
- Peter, H., Gudiksen, B. V., & Nordlund, Å. 2006, ApJ, 638, 1086 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Peter, H., Bingert, S., Klimchuk, J. A., et al. 2013, A&A, 556, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peter, H., Tian, H., Curdt, W., et al. 2014, Science, 346, 1255726 [NASA ADS] [CrossRef] [Google Scholar]
- Pontin, D. I., Janvier, M., Tiwari, S. K., et al. 2017, ApJ, 837, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, J., Hood, A. W., Parnell, C. E., et al. 2018, A&A, 615, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandlin, G. D., Bartoe, J. D. F., Brueckner, G. E., et al. 1986, ApJS, 61, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Schmit, D. J., Innes, D., Ayres, T., et al. 2014, A&A, 569, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
- Spadaro, D., Lanza, A. F., Karpen, J. T., & Antiochos, S. K. 2006, ApJ, 642, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, H., Marsch, E., Curdt, W., & He, J. S. 2009, ApJ, 704, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, H., McIntosh, S., De Pontieu, B., et al. 2011a, ApJ, 738, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, H., McIntosh, S., & De Pontieu, B. 2011b, ApJ, 727, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Tripathi, D., & Klimchuk, J. A. 2013, ApJ, 779, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, X., McIntosh, S. W., Curdt, W., et al. 2013, A&A, 557, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilmot-Smith, A. L., Pontin, D. I., Yeates, A. R., & Hornig, G. 2011, A&A, 536, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xia, L. D., Marsch, E., & Curdt, W. 2003, A&A, 399, L5 [Google Scholar]
- Yan, X. L., Pan, G. M., Liu, J. H., et al. 2013, AJ, 145, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, L., Peter, H., He, J., et al. 2015, ApJ, 811, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Young, P. R., Tian, H., Peter, H., et al. 2018, Space Sci. Rev., 214, 120 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Profiles of Si IV along the loop in the center of the loop and at its edges
We concentrated on the central spine of the loop in the main text (i.e., the central axis of the loop, see the dotted line in Fig. 1b). Here we show that these results are not just valid on the thin on-axis part of the loop. We do this by checking the line profiles and profile parameters not just at the central loop axis, but also at spatial positions farther away. Because the loop runs roughly in the east-west direction, we here investigate the region up to two spatial IRIS pixels (0.33″ or 250 km) to the north and south of the loop center. The loop has a width of about 0.6 Mm (full width at half-maximum, see Sect. 3.1), so that these locations are still within the loop, but at its edge.
To examine the shape of the line profiles, we show the Si IV line two pixels below (south; Fig. A.1) and above (north; Fig. A.2) the spatial positions that we used in Fig. 4. In all other aspects, Figs. A.1 and A.2 are exactly the same as Fig. 4. The prominent enhanced emission in the blue wing near the eastern footpoint, the nearly single-Gaussian profiles near the western footpoint, and the evolution of the enhancements in both line wings along the loop are overall very similar at the edge of the loop and at its center. This proves that the discussion in Sect. 3.3 applies to the whole loop and not only to its central axis.
 |
Fig. A.1. Same as Fig. 4, but for the positions two spatial pixels below (south of) the pixels where the Si IV (1394 Å) spectra in Fig. 4 are taken. This essentially follows the southern edge of the loop. The central axis of the loop is shown in Fig. 1b. The diamonds (with the bars) show the observed spectra, and the red lines indicate single-Gaussian fits to the line core. The parameters denoted by the numbers in the plots show the line centroid (vD) of the red fits, the total residual of the intensity (R), and the red-blue asymmetry (Ar). |
 |
Fig. A.2. Same as Fig. A.1, but now for the positions two spatial pixels above (north of) the pixels where the Si IV (1394 Å) spectra in Fig. 4 are taken. |
Moreover, the loop-profile parameters as discussed in Sect. 3.5 and shown in Fig. 6 are taken at the central axis of the loop. To determine whether our results also apply to the whole part of the loop, we examined them north and south of the loop center (Fig. A.3) and considered averages across the loop (Fig. A.4). We first calculated the line profile parameters at two pixels below and above the loop, that is, for the profiles shown in Figs. A.1 and A.2. The results are shown in Fig. A.3 together with the parameters for the center of the loop as displayed in Fig. 6. The variation in line profile parameters along the loop is slightly different, but the quantitative variation is very similar overall. As a second test, we averaged the line profiles in the north-south direction centered around the central loop axis and calculated the parameters from these averaged profiles. We plot the results in Fig. A.4, again together with the results for the profiles along the central axis. The parameters of the averaged profiles match those at the central loop axis very well.
 |
Fig. A.3. Same as Fig. 6, but for the positions two spatial pixels below (south of) and above (north of) the pixels where the line profile parameters in Fig. 6 are taken. This essentially follows the southern and northern edges of the loop. The variation along the southern edge of the loop is denoted by asterisks, and the variation along the northern edge by crosses. The diamonds show the variation along the central loop axis (cf. dotted line in Fig. 1b) and are identical to the data shown in Fig. 6. |
 |
Fig. A.4. Similar to Fig. A.3, but for the parameters derived from profiles averaged in the north-south direction across the loop. Squares denote averages over five spatial pixels, and asterisks show the averages over three pixels. The diamonds show the variation along the central loop axis and are identical to the data shown in Fig. 6. |
This underlines that the results for the central axis of the loop are robust. The similarity of the line profiles and the good match of the variation in line profile parameters along the loop shows that in the framework of this study, we can consider this loop as a more or less monolithic structure.
All Tables
All Figures
 |
Fig. 1. Cool loop and context from the IRIS and SDO data. Panel a: snapshot of the IRIS slit-jaw images in the 1400 Å channel. Panels b–d: intensity (b), Doppler shift (c), and 1/e line width (d) maps of the Si IV (1394 Å) line. Panel e: HMI line-of-sight magnetogram. Panel f: snapshot from the AIA images at 171 Å. The dotted lines indicate the Si IV loop. The circles mark two footpoints of the loop, where E and W indicate the eastern and western feet. The blue vertical lines x3, x13, x23, x33, and x43 in (b) indicate five samples of the spatial positions of the spectra shown in Fig. 3. The field of view is 33.2″ × 10.0″ with the center at solar (X, Y) = (−251.9″, 56.4″). See Sects. 2 and 3.1. |
| In the text | |
 |
Fig. 2. Proper motions along the loop. A space-time plot of a series of IRIS slit-jaw images in the 1400 Å channel along the dotted line EW as marked in Fig. 1. The dashed line and dash-dotted lines indicate proper motions along the loop. For comparison, the dotted line shows the sound speed near 80 000 K in the line formation region of Si IV. The respective mean velocity is denoted by the numbers in the plot. The black arrow marks the IRIS slit that scanned the loop. See Sect. 3.2. |
| In the text | |
 |
Fig. 3. Spectral detector images of Si IV (1394 Å) along the loop. The 45 raster steps from the eastern to the western footpoint in Fig. 1 are labeled x1 through x45. The locations of x3, x13, etc., and x43 are marked in Fig. 1b by five blue vertical lines. The white markers indicate the location of the central axis of the loop as displayed by the dotted line in Fig. 1b. The vertical dotted lines indicate zero Doppler shift. The red curves show the contours of the respective spectra at a level of 18% of its maximum. The blue lines connect two positions with the maximum enhancements in the blue and red wings. See Sects. 3.3 and 3.4. |
| In the text | |
 |
Fig. 4. Individual spectral profiles of Si IV (1394 Å) along the loop. Each profile was recorded in one spatial pixel on the central axis of the loop (i.e., maximum emission from the loop at the respective slot position; dotted line in Fig. 1b). These are the spectral profiles at the locations of the short horizontal white markers in the detector images from Fig. 3. The diamonds (with the bars) show the observed spectra and the red lines indicate single-Gaussian fits to the line core. To ensure that the single-Gaussian fits only represent the line core, the fit was performed only within ±20 km s−1 from the peak of the line. The parameters denoted by the numbers in the plots show the line centroid (vD) of the red fits, the total residual of the intensity (R), and the red-blue asymmetry (Ar). See Sects. 3.3 and 3.5. |
| In the text | |
 |
Fig. 5. Evolution of the spectral tilt of Si IV (1394 Å) along the loop. Panel a: Doppler dispersion separately for the blue wing (Δvblue), the red wing (Δvred), and a combination of both wings (Δv). Panel b: offset between the maximum enhancements in the blue and red wings along the slit (Δy). The errors are conservatively estimated to be ±1 spatial pixel. Panel c: spectral tilt (Δy/Δv). Because we follow a parcel of gas moving along the loop, the top axis shows the time to indicate the temporal evolution. See Sect. 3.4. |
| In the text | |
 |
Fig. 6. Evolution of the line profile characteristics of Si IV (1394 Å) along the loop. Panels a and b: total intensity (TSG) and Doppler shift (vD) of the single-Gaussian fits to the line core. Panel c: residuals of the intensity in the blue wing (Rblue), the red wing (Rred), and over the whole line (R) as defined in Eqs. (1)–(3). Panel d: red-blue asymmetry (Ar) as defined in Eq. (4). Because we follow a parcel of gas that moves along the loop, the top axis shows the time to indicate the temporal evolution. See Sect. 3.5. |
| In the text | |
 |
Fig. 7. Temporal evolution of the loop intensity. Panels a and b: snapshots in the AIA 171 Å channel and the IRIS slit-jaw images at 1400 Å. The field of view is the same as in Fig. 1, but here we use a logarithmic scaling of the intensities. The apex region of the loop under investigation here is indicated by the boxes in panels a and b. Panel c: intensity integrated over the box in the two channels. The vertical blue line shows the time of the snapshots in panels a and b. The black vertical line in panel b is the spectrograph slit, the black feature at the bottom left edge of the box in panel b is an artifact on the detector. An animation showing the temporal evolution while the slit is passing the loop is available online. See Sect. 4.4. |
| In the text | |
 |
Fig. A.1. Same as Fig. 4, but for the positions two spatial pixels below (south of) the pixels where the Si IV (1394 Å) spectra in Fig. 4 are taken. This essentially follows the southern edge of the loop. The central axis of the loop is shown in Fig. 1b. The diamonds (with the bars) show the observed spectra, and the red lines indicate single-Gaussian fits to the line core. The parameters denoted by the numbers in the plots show the line centroid (vD) of the red fits, the total residual of the intensity (R), and the red-blue asymmetry (Ar). |
| In the text | |
 |
Fig. A.2. Same as Fig. A.1, but now for the positions two spatial pixels above (north of) the pixels where the Si IV (1394 Å) spectra in Fig. 4 are taken. |
| In the text | |
 |
Fig. A.3. Same as Fig. 6, but for the positions two spatial pixels below (south of) and above (north of) the pixels where the line profile parameters in Fig. 6 are taken. This essentially follows the southern and northern edges of the loop. The variation along the southern edge of the loop is denoted by asterisks, and the variation along the northern edge by crosses. The diamonds show the variation along the central loop axis (cf. dotted line in Fig. 1b) and are identical to the data shown in Fig. 6. |
| In the text | |
 |
Fig. A.4. Similar to Fig. A.3, but for the parameters derived from profiles averaged in the north-south direction across the loop. Squares denote averages over five spatial pixels, and asterisks show the averages over three pixels. The diamonds show the variation along the central loop axis and are identical to the data shown in Fig. 6. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.