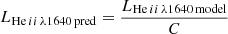| Issue |
A&A
Volume 624, April 2019
|
|
|---|---|---|
| Article Number | A89 | |
| Number of page(s) | 28 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201834565 | |
| Published online | 16 April 2019 | |
Exploring He II λ1640 emission line properties at z ∼2−4
1
Leiden Observatory, Leiden University, PO Box 9513 2300 RA Leiden, The Netherlands
e-mail: themiyananayakkara@gmail.com
2
Instituto de Astrofisica e Ciencias do Espaco, Universidade do Porto, CAUP, Rua das Estrelas, 4150-762 Porto, Portugal
3
ETH Zurich, Department of Physics, HIT J31.5, Wolfgang-Pauli-Strasse 27, 8093 Zurich, Switzerland
4
Univ. Lyon, Univ. Lyon1, ENS de Lyon, CNRS, Centre de Recherche Astrophysique de Lyon (CRAL), UMR 5574, 69230 Saint-Genis-Laval, France
5
Scuola Internazionale Superiore di Studi Avanzati (SISSA), Via Bonomea 265, 34136 Trieste, Italy
6
Institut für Astrophysik, Universität Göttingen, Friedrich-Hund Platz 1, 37077 Göttingen, Germany
7
Observatoire de Genève, Université de Genève, 51 Ch. des Maillettes, 1290 Versoix, Switzerland
Received:
2
November
2018
Accepted:
14
February
2019
Deep optical spectroscopic surveys of galaxies provide a unique opportunity to investigate rest-frame ultra-violet (UV) emission line properties of galaxies at z ∼ 2 − 4.5. Here we combine VLT/MUSE Guaranteed Time Observations of the Hubble Deep Field South, Ultra Deep Field, COSMOS, and several quasar fields with other publicly available data from VLT/VIMOS and VLT/FORS2 to construct a catalogue of He II λ1640 emitters at z ≳ 2. The deepest areas of our MUSE pointings reach a 3σ line flux limit of 3.1 × 10−19 erg s−1 cm−2. After discarding broad-line active galactic nuclei, we find 13 He II λ1640 detections from MUSE with a median MUV = −20.1 and 21 tentative He II λ1640 detections from other public surveys. Excluding Lyα, all except two galaxies in our sample show at least one other rest-UV emission line, with C III] λ1907, λ1909 being the most prominent. We use multi-wavelength data available in the Hubble legacy fields to derive basic galaxy properties of our sample through spectral energy distribution fitting techniques. Taking advantage of the high-quality spectra obtained by MUSE (∼10 − 30 h of exposure time per pointing), we use photo-ionisation models to study the rest-UV emission line diagnostics of the He II λ1640 emitters. Line ratios of our sample can be reproduced by moderately sub-solar photo-ionisation models, however, we find that including effects of binary stars lead to degeneracies in most free parameters. Even after considering extra ionising photons produced by extreme sub-solar metallicity binary stellar models, photo-ionisation models are unable to reproduce rest-frame He II λ1640 equivalent widths (∼0.2 − 10 Å), thus additional mechanisms are necessary in models to match the observed He II λ1640 properties.
Key words: galaxies: ISM / galaxies: star formation / galaxies: evolution / galaxies: high-redshift
© ESO 2019
1. Introduction
The transition of a chemically simple Universe to a complex and diverse structure was driven by the first generation of metal-free stars (Pop III stars) that were formed within the first few million years of the Big Bang. In the current cosmological evolution framework, Pop III stars formed as individual stars or within the first (proto-) galaxies produced high amounts of UV photons (UV ionising continuum), contributing to the re-ionisation of the Universe and thereby ending the cosmic “dark ages” (Tumlinson & Shull 2000; Tumlinson et al. 2001; Barkana & Loeb 2001; Bromm & Yoshida 2011; Wise et al. 2012, 2014). Additionally, these stars generated the first supernovae in the Universe, which drove the cosmic chemical evolution process by synthesising metals (elements heavier than He) and enriching the inter-galactic medium (IGM; e.g. Cooke et al. 2011).
The existence of Pop III stars is yet to be observationally confirmed, and numerous attempts are being made to explore the existence of such stars in the early Universe through current ground- and space-based telescopes. Narrow-band Lyα surveys (Hu et al. 2004; Tapken et al. 2006; Murayama et al. 2007; Ouchi et al. 2018) or Lyman-break techniques (Steidel et al. 2003; Bouwens et al. 2010; McLure et al. 2011; García-Vergara et al. 2017; Ono et al. 2018) observe galaxies at z ∼ 2 − 8 to make photometric pre-selections of high-z galaxies. These candidates are followed-up spectroscopically to obtain multiple emission lines to explore stellar population and interstellar medium (ISM) conditions to confirm or refute the existence of Pop III stars (e.g. Cassata et al. 2013; Sobral et al. 2015). With large samples of high-z galaxies, candidates for galaxies containing a significant population of Pop III stars can be selected due to the presence of strong Lyα and He II in the absence of other prominent emission lines. This can be interpreted as existence of pristine metal-poor stellar populations (Tumlinson et al. 2003; Raiter et al. 2010; Sobral et al. 2015).
The absence of metals in primordial gas might result in higher stellar masses for Pop III stars (Jeans 1902; Bromm & Larson 2004) leading to an extremely top-heavy initial mass function (IMF; e.g. Schaerer 2002). A stellar population with such an IMF will have relatively large numbers of very hot stars that produce He+ ionising photons with energies > 54.4 eV (λ < 228 Å). The resulting strong He II has been proposed as an indication of the presence of Pop III stars. This interpretation is challenging in the face of other processes that can produce He+ ionising photons, however. Additionally, the short life-time of ∼1 Myr of Pop III systems and resulting ISM/IGM pollution by pair-instability supernovae (Heger & Woosley 2002), uncertainties in photometric calibrations, presence of active galactic nuclei (AGN), pristine cold-mode gas accretion to galaxies, and limited understanding of high-redshift stellar populations and the ISM contribute further to the complexity of detecting and identifying Pop III host systems (Fardal et al. 2001; Yang et al. 2006; Sobral et al. 2015, 2018; Agarwal et al. 2016; Bowler et al. 2017; Matthee et al. 2017; Shibuya et al. 2018).
In order to make compelling constraints of stellar populations in the presence of strong He II emission and link with Pop III hosts, a comprehensive understanding of the He II emission mechanisms is required. The origin of He II emission, which is produced by cascading re-combination of He++, has been explored extensively, but the exact nature of physical mechanisms required to power the high-ionisation sources is still under debate (e.g. Shirazi & Brinchmann 2012; Senchyna et al. 2017). The shape of the He II profile has been attributed to different mechanisms that may contribute to the ionising photons.
Wolf–Rayet (W–R) stars are a long known source of He II λ1640 ionising photons in galaxies in the local Universe, which are hydrogen-stripped massive evolved stars with high surface temperatures and high mass-loss rates driven by strong and dense stellar winds (Allen et al. 1976). Broad He II features are expected to originate in the thick winds of W–R stars and are not recombination features. However, W–R stars are also extremely hot and produce photons with energies > 54 eV, allowing some nebular He II λ1640 emission. Therefore, in addition to nebular He II λ1640 emission (Ephoton > 54 eV), W–R stars and galaxies with W–R stars (WR galaxies, Osterbrock & Cohen 1982) show strong broad He II features (Ephoton > 28 eV) along with strong C or N emission lines with P-Cygni profiles (Crowther 2007). Traditional stellar population models only produce nebular He II when there is an abundance of W–R stars (Shirazi & Brinchmann 2012), and therefore are limited to high metallicity stellar populations. At lower metallicities, the abundance of W–R stars decreases and observed He II profiles become narrower (e.g. Senchyna et al. 2017). Systems with strong nebular He II emission in the absence of other W–R features require additional mechanisms that could produce high-energy photons at lower metallicities.
The lack of W–R features in strong He II emitters in local low-mass and metal-poor galaxies have led to multiple theories that could power the He II emission, and a new generation of stellar population and photo-ionisation models attempt to quantify the effects of such mechanisms (e.g. Gutkin et al. 2016; Eldridge et al. 2017). Increase in stellar rotation, quasi-homogeneous evolution (QHE), and production of stripped stars and X-ray binaries driven by binary interactions increase the surface temperatures of stars, resulting in a higher He+ ionising photon production efficiency (Garnett et al. 1991; Eldridge et al. 2008, 2017; Eldridge & Stanway 2012; Miralles-Caballero et al. 2016; Stanway et al. 2016; Casares et al. 2017; Götberg et al. 2017; Smith et al. 2018). In addition to stars, fast radiative shocks and pre-shock and compressed post-shock regions of slower radiative shocks have been suggested as possible mechanisms to produce He+ ionising photons (Allen et al. 2008; Izotov et al. 2012), but the abundance of such shocks as a function of metallicity is unclear. Post-asymptotic giant branch (AGB) stars become a dominant mechanism of ionising radiation at low star formation rates (SFRs), but whether the observed He II emission can be attributed to such stars, especially at lower metallicities (Shirazi & Brinchmann 2012; Senchyna et al. 2017) is questionable.
Ground- and space-based instruments have been used to observe rest-frame UV/optical features of local (e.g. Kehrig et al. 2015; Senchyna et al. 2017; Senchyna & Stark 2019) and high-redshift (e.g. Cassata et al. 2013; Steidel et al. 2016; Berg et al. 2018) galaxies to examine possible origins for He II. In order to determine the origin of He II and link it to mechanisms that could arise from Pop III stellar systems, observations should be made in young, low-metallicity, highly star-forming systems that can give rise to a diverse range of exotic phenomena capable of producing high-energy ionising photons. The Universe at z ∼ 2 − 4 was reaching the peak of the cosmic star-formation rate density (Madau & Dickinson 2014), where the systems were highly star-forming and evolving rapidly, giving rise to a diverse range of physical and chemical properties (e.g. Steidel et al. 2014, 2016; Sanders et al. 2015, 2016; Kacprzak et al. 2015, 2016; Wirth et al. 2015; Kewley et al. 2016; Strom et al. 2017; Nanayakkara et al. 2017). At z ∼ 2 − 4, the redshifted He II λ1640 along with other prominent rest-UV features can be observed through optical spectroscopy.
In order to accurately identify systems that harbour Pop III stellar populations, observational signatures that can indicate differences in stellar and ISM metallicity independent of other physical conditions of galaxies in the early Universe are required. To constrain stellar population and ISM properties, spectra with a high signal-to-noise (S/N) (≳20) of galaxies with multiple emission and absorption lines in rest-frame UV/optical regions are required. Previous studies that investigated rest-UV properties of galaxies have been limited to either a single galaxy (Erb et al. 2010; Vanzella et al. 2016; Patrício et al. 2016; Berg et al. 2018), low-resolution observations of individual systems (Cassata et al. 2013), or to a single stacked spectrum of ∼30 − 800 galaxies at moderate resolution (Shapley et al. 2003; Steidel et al. 2016; Nakajima et al. 2018; Rigby et al. 2018).
Surveys conducted using recently commissioned sensitive multiplex instruments in 8–10 m class telescopes are instrumental to obtain samples of galaxy spectra that show various physical and chemical compositions. Here, we use deep spectroscopic data obtained through the guaranteed time observations (GTO) of the Multi Unit Spectroscopic Explorer (MUSE) consortium to study properties of He II λ1640 emitters at z ∼ 2 − 4 in individual and stacked galaxies. We complement our study with deep photometric and spectroscopic data obtained by other public surveys.
The paper is arranged in the following way: in Sect. 2 we explain the sample selection, dust correction, and emission line fitting procedure of the sample. In Sect. 3 we perform spectrophotometric comparisons to our sample, and in Sect. 3.3 we compare emission line ratios of our sample with photo-ionisation models. We provide a brief discussion of the results of this study in Sect. 4 and outline our conclusions and future work in Sect. 5. Unless otherwise stated, we assume a Chabrier (2003) IMF and a cosmology with H0 = 70 km s−1 Mpc−1, ΩΛ = 0.7 and Ωm = 0.3. All magnitudes are expressed using the AB system (Oke & Gunn 1983).
2. Sample selection and characterisation
In this section, we describe the He II λ1640 sample selection procedure, dust corrections, and emission line fitting method used in this study. In general, we selected all galaxies with redshift detections, visually inspected the spectra to determine the spectra for presence of sky lines and residual calibration issues, and fit emission lines using a custom-built tool to obtain the systematic redshifts and line fluxes. We first briefly describe all deep MUSE GTO surveys explored and present a summary in Table 1.
Summary of MUSE GTO surveys explored.
2.1. He II λ1640 detections
MUSE (Bacon et al. 2010) is a second-generation panoramic integral field spectrograph on the Very Large Telescope (VLT) that is operational since 2014. The instrument covers a field of view (FoV) of 1′×1′ with a 0.2″ sampling in a medium spectral resolution of R ∼ 3000.
MUSE He II λ1640 detections are selected from three legacy fields, the Ultra Deep Field (UDF; Beckwith et al. 2006; Bacon et al. 2017), the Hubble Deep Field South (HUDF; Williams et al. 1996; Bacon et al. 2015), and the Cosmic Evolution Survey (COSMOS; Scoville et al. 2007) field along with the MUSE Extended quasar catalogue fields (Marino et al. 2018), all obtained as a part of the GTO awarded to the MUSE consortium. The MUSE spectra in our sample cover a nominal wavelength range of ∼4800–9300 Å, implying that He II λ1640 can be detected between z ∼ 1.93 − 4.67. Next we describe the sample selection from these fields.
2.1.1. MUSE Ultra Deep Field
The current MUSE UDF coverage includes two distinct observing depths observed in good seeing conditions with a full width at half-maximum (FWHM) of ∼0.6″ at 7750 Å. The 3 × 3 arcmin2 medium-deep field (henceforth referred to as the mosaic) has a depth of ∼10 h obtained with a position angle (PA) of −42°. A further 1′×1′ region with a PA of 0° was selected within the mosaic to be exposed for an additional ∼21 h. The final deep region, henceforth referred to as udf-10, comprises ∼31 h of exposure time.
The MUSE UDF catalogue used for this work includes 1574 galaxies with spectroscopic detections (Inami et al. 2017). We selected galaxies with secure spectroscopic redshifts (CONFID > 1) between z ∼ 1.93 − 4.67. With these selection cuts, we are left with 553 galaxies in the UDF, out of which 26 are flagged as merged1 (MERGED = 1). We visually inspected all 553 spectra and selected high-quality spectra to fit for He II λ1640 features using our custom-built line fitting tool (see Sect. 2.3).
Within UDF we identify nine unique galaxies with He II λ1640 emission. Two galaxies are classified as AGN (MUSE UDF AGN are flagged from the Luo et al. 2017, Chandra Deep Field South catalogue) and show strong broad He II λ1640 features, and four of the remaining galaxies show C III] in emission. One galaxy shows a broad He II λ1640 feature with a He II λ1640 FWHM of 1068 km s−1. We removed this galaxy from our sample because we are primarily interested in the narrow He II λ1640 component of galaxies and it is a clear outlier in terms of He II λ1640 FWHM compared to the rest of the sample (see Sect. 4.1.2).
2.1.2. MUSE Hubble Deep Field South
MUSE HDFS observations were obtained in 2014 during the commissioning of MUSE and all data products are publicly available (Bacon et al. 2015). However, we used an updated version of the MUSE data reduction pipeline (CubExtractor package; Borisova et al. 2016; Cantalupo et al., in prep.) with improved flat fielding and sky subtraction to generate a modified version of the MUSE data cube for our analysis.
The MUSE HDFS catalogue contains 139 secure spectroscopic redshifts (CONFID > 1) and 48 galaxies that fall within the spectral range for He II λ1640 detection with MUSE were investigated. Using a similar procedure to UDF, we identified three galaxies with He II λ1640 emission in the HDFS. Two galaxies have C III] spectral coverage and show prominent C III] emission. One galaxy shows C IV absorption, while another shows indications for C IV emission features.
2.1.3. MUSE groups catalogue
The MUSE groups GTO program targets galaxy groups (PI: T. Contini) identified by the zCOSMOS survey (Knobel et al. 2012). So far, 11 galaxy groups have been observed by the MUSE consortium with varying depths (Epinat et al. 2018). For our analysis we selected five fields with exposure times greater than 2 h: COSMOS-GR 114 (2.2 h), VVDS-GR 189 (2.25 h), COSMOS-GR 34 (5.25 h), COSMOS-GR 84 (5.25 h), and COSMOS-GR 30 (9.75 h). The seeing conditions of the fields vary between 0.5″ and 0.7″.
Without imposing a redshift quality cut, we selected galaxies that lie within the spectral range for He II λ1640 detection with MUSE. A total of 104 galaxy spectra were investigated to select one galaxy with He II λ1640 signatures from our fitting tool. The galaxy was selected from COSMOS-GR 30, the deepest pointing of the MUSE COSMOS group catalogue, and shows C III] and C IV in emission.
2.1.4. MUSE quasar fields
The MUSE extended quasar catalogue maps the cool gas distribution in the z ∼ 3 Universe by observing Lyα emission in the neighbourhood of high-redshift quasars at z > 3 (Marino et al. 2018). In total, the catalogue contains 22 fields with varying exposure times from 1–20 h.
For our analysis, we selected the three deepest quasar fields, J2321 (9.0 h), UM287 (9.0 h), and Q0422 (20.0 h). We selected all 49 galaxies with secure spectroscopic redshifts (CONFID> 1) within the spectral range for He II λ1640 detection with MUSE. Visual inspection of the selected galaxies showed no He II λ1640 features in the UM287 and J2321 fields. In Q0422 our fitting tool identified three galaxies with He II λ1640 features and one possible AGN with strong and broad He II λ1640, C III], C IV, and Lyα. We further analysed the C III], C IV, and He II λ1640 line ratios following the Feltre et al. (2016) diagnostics and found that line ratios are more likely to be powered by an AGN.
2.1.5. Other surveys explored
In addition to the MUSE GTO surveys, we also examined data from other public optical spectroscopic surveys to identify He II λ1640 line emitters. The Great Observatories Origins Deep Survey FOcal Reducer and low dispersion Spectrograph (GOODS FORS2; Vanzella et al. 2008), GOODS VIsible Multi-Object Spectrograph (GOODS VIMOS; Balestra et al. 2010), K20 (Cimatti et al. 2002), VANDELS (Grogin et al. 2011), VIMOS Public Extragalactic Redshift Survey (VIPERS; Garilli et al. 2014), VIMOS Ultra Deep Survey (VUDS; Le Fèvre et al. 2015), VIMOS very Large Telescope Deep Survey (VVDS; Le Fèvre et al. 2013), and zCOSMOS bright (Lilly et al. 2007) surveys are used for this purpose. All publicly available data have a lower spectral resolution than MUSE, and thus the spectra may suffer from blending between narrow and broad He II λ1640 components. However, these surveys provide a wealth of spectra to investigate the He II λ1640 and other UV nebular line properties of galaxies, and they are also suitable to be followed-up with higher resolution spectrographs. In Appendix A we provide a brief description of the examined surveys and provide a summary of the He II λ1640 detections in Table A.1.
2.2. Dust corrections
Dust corrections are crucial to obtain accurate estimates of rest-UV emission line features of galaxies. The total-to-selective extinction (k(λ)) of a galaxy depends crucially on the physical nature of the dust grains and is a strong function of wavelength. Galactic and extra-galactic studies show a non-linear systematic increase in k(λ) with decreasing wavelength (e.g. Cardelli et al. 1989; Calzetti et al. 1994; Reddy et al. 2015). UV dust extinction is further complicated by the presence of a high-UV absorption region at 2175 Å (UV absorption “bump” Mathis 1990; Buat et al. 2011), but its origin is not yet well understood (e.g. Calzetti 2001; Zagury 2017; Narayanan et al. 2018). For our analysis, we used the dust obscuration law parametrised by Calzetti et al. (2000), which is defined redwards of 1200 Å. In Sect. 4.1.1 we analyse how different dust laws affect our analysis.
The MUSE UDF, HDFS, and COSMOS groups fields contain multi-wavelength photometric coverage from Hubble legacy fields, which we used to match the MUSE observations (e.g. Inami et al. 2017). We used FAST (Kriek et al. 2009) to match synthetic stellar populations from Bruzual & Charlot (2003) models to the observed photometry using a χ2 fitting algorithm to derive best-fit stellar masses, ages, star formation timescales, and dust contents of galaxies. FAST does not include models of the nebular emission from the photo-ionised gas in addition to the continuum emission from stars. Even though the emission line contamination for stellar mass estimates have shown to be negligible for z ∼ 1 − 3 star-forming galaxies (Pacifici et al. 2015), the mass of galaxies in the presence of strong [O III]λ5007 EW, which are likely in strong He II λ1640 emitters, may be over-estimated.
Photometry used for SED fitting does not contain data redwards of the Hubble F160W filter, thus lacks near-infrared coverage to better constrain degeneracies between derived parameters (Conroy 2013). The MUSE quasar catalogues do not contain HST photometry, and therefore we used the rest-UV continuum slope (β) parametrised by a power law of the form:
where fλ is the observed flux at rest-frame wavelength λ, to obtain an estimate of the total dust extinction.
Following Meurer et al. (1999), we relate the UV slope β to the total extinction magnitude at 1600 Å (A(1600)) as
Meurer et al. (1999) demonstrated that the relationship in Eq. (2) is consistent with ionising stellar population model expectations in dust-free scenarios and with the Calzetti et al. (1994) extinction law within “reasonable” scatter (also see Reddy et al. 2018). Therefore, we expect our spectroscopically derived A(V) from β (A(V)β) to be consistent with photometrically derived FAST A(V) (A(V)SED) values within statistical uncertainty.
To validate our assumption, we used MUSE UDF data to investigate the relationship between A(V)β and A(V)SED. We used all galaxies in the MUSE UDF catalogue with a CONFID = 3 and z = 2.2 − 4.7 corresponding to galaxies with spectroscopic coverage between rest-frame 1500 − 1700 Å. Using these criteria, we selected a total of 59 galaxies from the UDF catalogue, of which we removed 23 galaxies that have weak continuum detections measured from the MUSE spectra (S/N ≲ 1 − 2) and 2 galaxies that have no stellar mass estimates from FAST. We divided the remaining 34 galaxies depending on their S/N level of the continuum into two bins by selecting galaxies with high (S/N ≳ 3) and low (S/N < 3) S/N.
For galaxies in these two bins, we masked out regions with rest-UV features as defined by Table 2 in Calzetti et al. (1994) and computed the inverse-variance weighted rest-UV power-law spectral slope between the wavelength range of 1300 − 1900 Å (1600 ± 300 Å) using the power-law function in the python LMFIT2 module. We then converted β into A(1600) using Eq. (2), and then used the Calzetti et al. (2000) dust-attenuation law to compute the A(V)β as follows:
where Rv(=4.05) is the total attenuation and k(1600)( = 9.97) is the star-burst reddening curve at 1600 Å.
Figure 1 shows the relationship between A(V)β and A(V)SED for the MUSE UDF galaxies. A(V)β shows good agreement with SED-derived extinction values. In general, lower stellar mass systems show low amounts of dust extinction. We conclude that the UV continuum slopes provide a reasonable estimate of the dust corrections required for galaxies (in comparison to estimates from SED fitting using FAST), which we used to calculate the dust extinction of galaxies in the MUSE quasar fields. All A(V)β < 0 was assigned an A(V)β = 0. A(V)SED values were used to correct for dust extinction in all other galaxies. Dust corrections for the observed spectra were performed as follows:
 |
Fig. 1. Comparison between A(V)β and A(V)SED. Galaxies from MUSE UDF with CONFID = 3 and z = 2.2 − 4.7 with continuum S/N ≳ 3 are shown here and are colour-coded by their mass. The one-to-one line is shown as a black dashed line. The solid black line shows the linear regression model fit to the data along with its 1σ uncertainty (computed using 1000 bootstrap resamples) shaded in grey. |
where f(λ)int and f(λ)obs are the intrinsic and observed flux at wavelength λ, A(V) is the attenuation by dust, and k(λ) is the star-burst reddening curve from Calzetti et al. (2000). Fifty percent of our galaxies have A(V) = 0, and for the other half, we assumed that the UV continuum shares the same attenuation as the emission lines. Since the UV continuum in these actively star-forming galaxies to a large extent originates from the stars responsible for the emission lines, this seems reasonable, but we will return to discuss this assumption in Sect. 4.1.1.
2.3. Emission line measurements
The line flux measurements of the MUSE surveys are performed using PLATEFIT (Tremonti et al. 2004; Brinchmann et al. 2008), which uses model galaxy templates from Bruzual & Charlot (2003) to fit the continuum of the observed spectra at a predefined redshift and compute the line fluxes of each expected emission line using a single Gaussian fit. The redshift of the galaxies was determined as described by Inami et al. (2017). We find the He II λ1640 profiles of our sample to be in general broader than the other observed rest-UV emission lines such as C III], which could be driven by multiple mechanisms that power He II λ1640 compared to other nebular lines explored in this analysis (see Sect. 4.2). To accurately quantify the He II λ1640 flux of our observed spectra, we used a custom-built fitting tool to perform the line fits and obtain the emission line fluxes and equivalent widths, allowing greater flexibility (±1.25 Å) in line centre and line widths.
Emission lines were fit allowing the line centre and line width to vary as free parameters. Except for He II λ1640, all other lines are fit such that line centre and line width were fixed to a common best-fit value using the python LMFIT routine, but because the He II λ1640 profiles are broader, we allowed greater flexibility in the fitting parameters for He II λ1640. In Sect. 4.1.2 we further discuss and quantify the effects of allowing greater freedom for fitting parameters for He II λ1640 than other lines.
The procedure we used to fit the lines and compute the equivalent-width (EW) is as follows:
1. We first manually inspected all spectra to identify galaxies with significant offsets between the Lyα redshift and the systemic redshift obtained via C III] and He II λ1640 emission lines. We modified the redshift of these galaxies to match the systemic redshift.
2. We excluded ±20× MUSE wavelength sampling (∼20 × 1.25 Å) around the rest-UV emission line regions of the spectra.
3. We defined a continuum by calculating a running median within a window of 300 pixels, excluding masked regions.
4. The emission line fluxes were calculated as follows:
4.1. Gaussian fits were performed on the continuum-subtracted spectra.
4.2. The flux of each emission line was computed by integrating the best-fit Gaussian within 5σ of the determined line centre and line width.
4.3. Line flux errors were computed by integrating the error spectrum within the same 5σΔλ Gaussian fit as was performed on the emission line.
5. The EW was calculated similarly using the same Gaussian parameters and the continuum level. For each emission line, if the continuum is lower than the 1σ error spectrum, the 1σ error level was considered as the continuum to derive a lower limit to the EW. The error in the measured EW was computed by bootstrap resampling the spectrum, where each pixel was resampled using a random number parametrised by a Gaussian function with mean at the flux value of the pixel in the observed spectrum and standard deviation by the corresponding value from the error spectrum.
Measured properties of the observed emission lines are presented in Tables 2–3. We divided the MUSE sample in two categories, depending on whether the galaxy showed broad AGN like features, and we excluded them from our analysis. Because the He+ ionisation potential is higher (54.4 eV) than the C+ ionisation potential (24.38 eV), it is plausible for galaxies to only show C III] nebular emission. However, the C++ ionisation potential is 47.89 eV, and the resulting C IV emission suffers from strong stellar wind absorption, thus only a handful of galaxy spectra show strong C IV nebular emission in the absence of AGN activity. Except for two galaxies, all show C III] in emission. One of the galaxies with no C III] in emission shows a prominent C IV emission feature, which suggests hard ionising fields. This implies a higher electron temperature and therefore more prominent higher energy collisionally excited lines than in sources with a softer radiation field. We note that in the deepest MUSE pointings (UDF10 and HDFS), out of 17 C III] emitters presented by Maseda et al. (2017), only one galaxy (HDFS 87) has a confident He II λ1640 detection.
Summary of the MUSE He II λ1640 sample.
EWs of the MUSE He II λ1640 sample used in this analysis.
3. MUSE He II λ 1640 sample analysis
3.1. Observed sample
In total, we have obtained 13 high-quality He II λ1640 emission line detections from the MUSE GTO surveys. In addition, three galaxies either show broad C IV and/or C III] emission or are flagged as AGN (Inami et al. 2017); we removed these from our sample. The spectra of our full He II λ1640 sample are shown in Fig. 2. As is evident, our sample spans a wide variety in spectral shape and emission line profiles. We defined S/N > 2.5 as a line flux detection, and three galaxies in our sample fall between S/N of 2.5 − 3.0. We additionally performed a false-detection test for these three galaxies by forcing our line fitting algorithm to fit a line iteratively at random bluewards of He II λ1640 between 1580 Å and 1620 Å. One hundred such iterations showed no false detections.
 |
Fig. 2. Spectra (blue) of the MUSE He II λ1640 detections with their respective noise spectrum (red). All spectra are shown at their rest-frame wavelength and are normalised at ∼1600 Å. The ID, field, and the spectroscopic redshift of each target is shown in the panels. The green vertical lines indicate selected rest-UV emission and absorption features. |
 |
Fig. 2. continued. The last three panels show the spectra dominated by AGN activity. |
In Fig. 3 we examine the He II λ1640 flux distribution of our sample as a function of redshift and continuum S/N. It is evident from the figure that MUSE achieves better flux limits of He II λ1640 than other surveys. We further show the absolute UV magnitude of the MUSE He II λ1640 detected and MUSE He II λ1640 coverage (set B, see Sect. 3.2) galaxies as a function of redshift. UV magnitudes were computed from rest-frame dust-corrected (following the Calzetti et al. 2000 attenuation curve) MUSE spectra using a box-car filter between 1500 ± 100 Å. We opted to use the MUSE spectra to compensate for limitations in rest-UV photometric coverage between our fields. Only galaxies with a UV magnitude detected above 1σ noise between 1500 ± 100 Å were selected for this analysis. The corresponding magnitude errors are computed using 100 bootstrap iterations of the spectra where the normalised median absolute deviation (σNMAD = 1.48 |xi − median(x)|) of the bootstrapped UV magnitudes are considered as the error. There is no statistically significant difference in absolute UV magnitude between MUSE He II λ1640 detected and He II λ1640 non-detected galaxies, and a simple two-sample Kennicut–Smith (K–S) test for the two samples gives a KS statistic of 0.40 and a p-value of 0.17, therefore we cannot reject the null hypothesis that the two independent samples are drawn from the same continuous distribution.
 |
Fig. 3. Top panel: He II λ1640 flux as a function of redshift. He II λ1640 detections from MUSE are shown as stars and are colour-coded depending on their median continuum flux at ∼1640 Å. He II λ1640 detections from other surveys within the plot range are shown by diamonds. The redshift-dependent MUSE wavelength coverage of a few prominent rest-UV features are shown at the top of the panel. Bottom panel: M1500 as a function of redshift for the MUSE He II λ1640 detected and He II λ1640 non-detected galaxies (set B, see Sect. 3.2). |
 |
Fig. 4. Similar to Fig. 2, but for the mass and redshift binned stacked spectra of the MUSE He II λ1640 detected sample. The corresponding bin parameters are shown in each panel. |
3.2. Spectral stacking
Driven by observational constraints, spectral stacking techniques are commonly used to obtain high S/N UV rest-frame spectra of high-redshift galaxies (e.g. Shapley et al. 2003; Steidel et al. 2016). While it provides strong constraints on the average properties of observed galaxies, stacking of galaxies without any prior information about them may not constrain the observed diversity of galaxies and could result in strong systematic biases. For our analysis, we divided our sample of He II λ1640 detected and non-detected galaxies into mass and redshift bins in order to mitigate any biases that may arise by having a wide range of galaxy masses and redshifts in a single stack.
We defined set A (N = 13) as the stack of all galaxies with He II λ1640 detections. Set B (N = 46) are all galaxies with no He II λ1640 detections in the individual spectra and contains all galaxies with CONFID=3 (secure redshift, determined by multiple features) redshift quality classification between 1.93 < z < 4.67, but the galaxies in set A were removed. Each bin was then divided into three mass and redshift bins. Because the MUSE quasar catalogue does not contain photometric information to constrain the stellar masses, galaxies in this field were not used for the mass stacks.
We first measured the systematic redshift of galaxies by excluding Lyα from the redshift fitting procedure. Then we resampled the rest-frame spectra onto a regular grid between 1400 and 2700 Å with a sampling of 0.367 Å, corresponding to the native resolution of MUSE at z = 2.5 in the rest-frame. The final stacked spectra were calculated by median stacking and fitted using the method described above with the errors determined using 1000 bootstrap repetitions. We quote uncertainties using σNMAD. We show our sample of stacked spectra in Figs. 4 (set A) and 5 (set B).
3.3. Comparison with Gutkin et al. (2016) photo-ionisation modelling
The nature of rest-frame UV emission lines that originate from the ISM is driven by the properties of stars that heat up the ISM and the physical and chemical conditions of the ISM itself. Therefore, by making simplifying assumptions about the stellar populations, the geometry of the ionisation regions, and the physics and chemistry of dust and ISM, the observed rest-UV emission line ratios can be used to infer average properties of the ISM and underlying stellar populations of the observed galaxies.
In this section we use photo-ionisation models by Gutkin et al. (2016) to infer the average ISM conditions of galaxies in our sample. The Gutkin et al. (2016) models are based on the new generation of Bruzual & Charlot (2003) stellar population models and uses the photo-ionisation model CLOUDY (c13.03, Ferland et al. 2013) to model emission lines of H II regions by self-consistently accounting for the influence of gas phase and interstellar abundances. The wide range of interstellar parameters spanned by these models makes them ideally suited for comparisons to the observed line ratios of our sample, for which we expect properties clearly different from the average population of local star-forming galaxies (e.g. Erb et al. 2010). We used the following emission lines for our analysis: He II λ1640, [C III]=([C III]λ1907+C III]λ1909), O III](=O III]λ1661+O III]λ1666), and Si III](=Si III]λ1883+Si III]λ1892). For each emission line ratio diagnostic, we selected a subsample of galaxies with S/N ≥ 3 for the emission lines considered in that specific diagnostic. A further analysis of the Gutkin et al. (2016) rest-UV emission line ratios discussed in our study is presented in Appendix B.
3.3.1. Individual detections
In order to probe the general ISM properties of our He II λ1640 detections and investigate whether we can constrain the dominant ionising source, in this section we explore the observed distribution of emission line ratios of the individual galaxies and make comparisons with the Gutkin et al. (2016) photo-ionisation models. In Fig. 6 we show three selected line ratio diagrams. Because of the wavelength coverage of MUSE and the detection thresholds of our observations, not all galaxies with He II λ1640 are detected with the full suite of rest-UV emission lines considered in the models. In each panel, we therefore selected all galaxies for which the considered emission lines would fall within the wavelength range of MUSE and divided them into two bins depending on their S/N, where S/N ≥ 2.5 were considered as MUSE detections, and galaxies that did not make the cut for at least one of the emission lines were considered as MUSE limits. The error level was constrained by the noise spectrum, and we considered the 3σ error level as the upper limit to the line flux for emission lines that failed the S/N cut. Because of the degeneracy between model parameters and observational constraints driven by weak line detections, quantitative predictions about specific ISM conditions of our sample cannot be inferred within the current scope of our work, and we therefore refrain from inferring best-fit model values on a per-galaxy basis.
 |
Fig. 6. Rest-frame UV emission line ratios of the MUSE He II λ1640 sample. Left panel: C III]/O III] vs. Si III]/C III] ratios. Individual galaxies with S/N > 2.5 for all four emission lines are shown as stars. Limits are shown as arrows. The tracks are from the Gutkin et al. (2016) models, which are powered by star-formation. Each set of tracks with the same colour show three C/O ratios, and the regions between the minimum and maximum C/O tracks are shaded by the same colour. From top to bottom, the ionisation parameter ncreases. Where available, line ratios from Patrício et al. (2016), Senchyna et al. (2017), and Berg et al. (2018) are shown for comparison. MUSE line ratios of the Lyman continuum emitting candidate from Naidu et al. (2017) are shown by the filled green star. Centre panel: similar to the left panel, but C III]/He II λ1640 vs. O III]/He II λ1640 emission line ratios, where detections are defined as galaxies with S/N > 2.5 for all three emission lines. Right panel: similar to the left panel, but O III]/He II λ1640 vs. C III]/Si III] emission line ratios, where detections are defined as galaxies with S/N > 2.5 for all four emission lines. |
In the C III]/O III] vs. Si III]/C III] line ratio diagram, all galaxies with MUSE line detections fall within reasonable limits of the Gutkin et al. (2016) models. With the existing data, we cannot place constraints on the metallicity, but most model tracks require an ionisation parameter (Us)≳ − 2. In MUSE data, the weakest emission line in this line ratio diagnostic is Si III], thus observed Si III]/C III] ratios of the MUSE limits should be considered as upper limits. Therefore, MUSE limits would prefer models with lower metallicity and lower ionisation parameters. Additionally, Fig. 6 shows that MUSE-detected emission line ratios agree well with emission line ratios obtained for the Berg et al. (2018) and Patrício et al. (2016) lensed galaxies at z ∼ 2 and z ∼ 3.5, respectively. The line ratios of most of the Berg et al. (2016)z ∼ 0 low-metallicity dwarf galaxies are also consistent with those measured in our MUSE sample
The C III]/He II λ1640 vs. O III]/He II λ1640 diagnostic diagram has been suggested as a rest-UV emission line diagnostic for the separation of AGN and stellar ionising sources (e.g. Feltre et al. 2016, however also see Xiao et al. 2018), and all our galaxies in the MUSE-detected sample occupy the region where the emission lines can be powered purely by star-formation processes. In this diagnostic diagram, MUSE galaxies occupy a region preferred by sub-solar metallicity tracks (∼1/5th to ∼1/100th) with low-ionisation parameters in conflict with the C III]/O III] vs. Si III]/C III] line ratio diagram. Higher metallicities can be accommodated, but would require C/O ratios lower than the typical C/O ratios (∼0.15 − 1.30) observed in high-z galaxies (Shapley et al. 2003; Erb et al. 2010; Steidel et al. 2016). This would require either a relatively low fraction of mass loss and ISM enrichment from massive stars for a given metallicity (Henry et al. 2000) or a longer time-delay in the production of carbon by lower-mass stars compared to oxygen (Chiappini et al. 2003, also see Akerman et al. 2004; Erb et al. 2010), which is primarily produced by massive stars. Here the MUSE limits are driven by a weak O III] emission line, and thus O III]/He II λ1640 limits should be considered as upper limits. The change of C III]/He II λ1640 vs. O III]/He II λ1640 line ratios as a function of Us is not linear (see Appendix B), and thus we cannot constrain the expected ISM conditions of the limits in this line ratio diagnostic. The high-z lensed galaxies from Berg et al. (2018) and Patrício et al. (2016) occupy a region similar to that of the MUSE detections. We also show the z ∼ 0 sample from Senchyna et al. (2017) which clearly requires higher-metallicity models to explain the emission line ratios. The low-metallicity z ∼ 0 dwarf galaxies from Berg et al. (2016) also on average prefer higher-metallicity models than the high-z samples.
Driven by the close proximity of the line wavelengths of O III]/He II λ1640 and C III]/Si III], we selected the O III]/He II λ1640 vs. C III]/Si III] line ratio diagram to measure the photo-ionisation properties of our sample relatively independently of dust attenuation. MUSE-detected galaxies in our sample favour models with solar to sub-solar (down to ∼1/200th) metallicities. However, at lower metallicity, the different stellar tracks cannot be distinguished from each other. At fixed metallicity, this line ratio diagnostic is ideal to constrain the C/O ratios of galaxies. As a result of multiple effects, the metallicity shows a complex relationship with semi- and forbidden emission line ratios. For example, Jaskot & Ravindranath (2016) showed that at lower metallicities where the C abundance is lower, the C III] flux is counter-intuitively enhanced because the harder ionising SED and higher gas temperature increase the C III] collisional excitation rate. Similar to the other line ratio diagrams, the Berg et al. (2018) and Patrício et al. (2016) lensed galaxies occupy a parameter space similar to that of our MUSE detections, but the Berg et al. (2016) sample shows higher O III]/He II λ1640 ratios than the high-z samples. MUSE limits within the plot range are driven by weak Si III] lines, and therefore the C III]/Si III] ratio should be considered as a lower limit.
Analysis of individual emission line ratios of the MUSE He II λ1640 sample in multiple line ratio diagnostics in general shows a good agreement with the line ratio space occupied by the Gutkin et al. (2016) models. As described above, we refrain from inferring best-fit model values on a per-galaxy basis due to modelling and observational constraints. Additionally, Lyman continuum leakage results in high-energy ionising photons to escape the dusty molecular clouds without being converted to lower-energy photons, as assumed by the photo-ionisation models. This results in additional complications for comparisons between observed line ratios with model predictions. We have one Lyman continuum leaking candidate (Naidu et al. 2017) in our sample, which we highlight in Fig. 6 (green star). The emission line ratios of this galaxy do not stand out relative to the rest of the sample, but given the estimated high escape fraction (fesc ∼ 60%), the parameters inferred from the Gutkin et al. (2016) models (which assume no escape) are expected to be biased. Because to first order, Lyman continuum escape implies reduced Balmer line fluxes, we would typically infer higher U and/or lower Z values than the intrinsic values.
3.3.2. Stacked sample
To improve the S/N in the weak lines, we now turn to the stacked spectra discussed in Sect. 3.3.1. As shown in Figs. 4 and 5, continuum-normalised He II λ1640 detected stacked spectra show a trend between He II λ1640 emission line strength and stellar mass, and the stacked sample of lowest mass galaxies shows the strongest He II λ1640 emission compared to the continuum level. Systems with higher stellar mass show broader He II λ1640 profiles, which might be linked to increased stellar contribution to the He II λ1640 emission. The stacks of He II λ1640 non-detected galaxies also show weak He II λ1640 emission, thus, it is possible that some galaxies show weak He II λ1640 emission that is below the MUSE detection limit for individual objects. There is no strong redshift evolution for the He II λ1640 detected sample, but high-redshift stacks of He II λ1640 undetected galaxies show weak narrow He II λ1640 features.
We show the emission line ratios of the He II λ1640 detected stacked sample in Fig. 7. In all three line ratio diagrams, the stacked galaxies with line detections occupy a region similar to that of the individual galaxies shown in Fig. 6. The low S/N of Si III] and O III] line fluxes of the stacked sample prevent us from placing strong constraints with emission line ratio diagnostics.
 |
Fig. 7. Rest-frame UV emission line ratios of the MUSE stacked galaxies compared with the Gutkin et al. (2016) models. Panels from left to right are similar to Fig. 6. Galaxies are stacked in mass and redshift bins, and the line width of the markers increases with mass and redshift. Limits resemble stacks with emission lines (considered in each panel) lower than the 3σ error limit. For such stacks, 3σ error is used as the respective line flux. Top panel: MUSE-stacked sample for stellar mass bins log10(M*/M⊙) < 9.5, 9.5 < log10(M*/M⊙) < 10.0, and log10(M*/M⊙) > 10.0. Bottom panel: MUSE-stacked sample for redshift bins z < 2.5, 2.5 < z < 3, and z > 3. |
The C III]/O III] vs. Si III]/C III] line ratios of the MUSE-stacked detections do not show any trend with either stellar mass or redshift. Driven by the weak O III] emission line, the C III]/He II λ1640 vs. O III]/He II λ1640 line ratios of the moderate-low mass bins show a preference for sub-solar models with low-ionisation parameter. As described above, higher-metallicity tracks with lower C/O ratios than are illustrated in the figure might also explain the emission line ratios of these bins. The higher-redshift stacks also show a similar preference. Low-mass and high-redshift systems have been shown to have a lower gas phase (e.g. Sanders et al. 2015; Kacprzak et al. 2015) and stellar metallicities (e.g. Steidel et al. 2016) than local galaxies, and thus such a trend is expected. The stacked galaxy sample shows no clear trend with either stellar mass or redshift in the O III]/He II λ1640 vs. C III]/Si III] line ratio distribution.
We performed a similar analysis on all galaxies for which we were unable to detect a narrow He II λ1640 emission line. Although individual galaxies do not show such features, when they are stacked, especially the lower mass and higher redshift stacks show narrow He II λ1640 emission. The C III]/O III]vs. Si III]/C III] emission line ratios of these galaxies show no trend with redshift either, but marginally prefer models with higher metallicities or C/O ratios than the He II λ1640 detected sample.
3.4. Comparison with BPASS Xiao et al. (2018) models
The Gutkin et al. (2016) photo-ionisation models are built on an updated version of the Bruzual & Charlot (2003) stellar population models (Charlot & Bruzual, in prep.), which consider stars up to 350 M⊙ in a range of metallicities. However, these models do not account for any effects of stellar rotation, nor for effects of stars interacting with each other, that is, binary stars. However, the Universe contains many binary stars. In the Galaxy, ∼50% of O stars have shown to be in binary systems (e.g. Langer 2012; Sana et al. 2012, 2013) and stellar population analysis of local massive star clusters in z ∼ 0 galaxies have shown the need to consider interactions between binary stars to accurately predict the observed photometry (Wofford et al. 2016). Additionally, modelling of rest-UV and optical spectra of galaxies at z ∼ 2 found that models that include binaries perform better than the single-star models considered (Steidel et al. 2016; Strom et al. 2017; Nanayakkara et al. 2017; Berg et al. 2018). In this section, we use photo-ionisation models by Xiao et al. (2018) to explore the effects of including binary star interactions in our rest-UV emission line/EW analysis of the He II λ1640 emitters.
3.4.1. Comparison of observed line ratios
Xiao et al. (2018) used BPASSv2 (Eldridge et al. 2017) stellar population models as the source for the ionising continuum to self-consistently predict the nebular continuum and emission line flux using the photo-ionisation code CLOUDY. These photo-ionisation models are generated as a function of time for a single stellar population with a constant SFH up to 100 Myr assuming a spherical ionisation bound gas nebula with uniform hydrogen density. The models assume no dust and consider the nebular gas metallicity to be same as that of the stellar metallicity. The Xiao et al. (2018) models were run on two distinct BPASSv2 stellar population implementations: models with and without binary star interactions. Here we only analyse the binary stellar populations. For a single star-burst, implementing the effects of binary evolution causes the ionising continuum to become harder for a prolonged period of time than for a non-interacting model with the same initial conditions. Binary interactions prolong the lifetime and/or rejuvenate the stars through gas accretion and rotational mixing that is enhanced by the angular momentum transfer, which results in efficient hydrogen burning within the stars (e.g. Stanway et al. 2016). Additionally, binary interactions effectively remove the outer layers of the massive red super-giants, resulting in a higher fraction of W–R stars and/or low-mass helium stars, especially at lower metallicities and at later times (> 5 Myr) in single-burst stellar populations. Including these effects in the ionising continuum causes the number of He+ ionising photons to increase (up to ∼3 orders of magnitude) at t > 10 Myr for higher metallicities and t ∼ 10 Myr for lower metallicity models. Therefore it is crucial to consider the effects of binaries to probe mechanisms of He II λ1640 production.
In Fig. 8 we show the distribution of the observed C III]/He II λ1640/ vs. O III]/He II λ1640 line ratios of the MUSE He II λ1640 sample with Xiao et al. (2018) models that include binary stellar populations. As discussed in Appendix B, at fixed ionisation parameter, the rest-UV emission line strengths of higher metallicity models have a strong dependence on hydrogen gas density, thus at log10(nH)≤1, super-solar metallicity models could also produce the observed line ratios, but only at extreme ionisation parameters (log10(U)≥ − 1.5). If sub-solar metallicity models (down to ∼1/200 Z⊙) are to produce the observed line ratios, the BPASS single stellar population model requires galaxies to harbour extremely young (< 10 Myr) stellar populations. One large uncertainty in the Xiao et al. (2018) models is that dust depletion and dust physics in the photo-ionisation modelling are neglected. When dust depletion is considered, it will lead to depletion of metals from the gas phase, which will further increase the parameter space of the models Charlot & Longhetti (2001); Brinchmann et al. (2013); Gutkin et al. (2016, also see the discussion in Sect. 4.1.1). When BPASS single stellar population models are considered, the observed line ratios can in general only be produced by solar metallicity models and are not shown in Fig. 8.
 |
Fig. 8. Rest-frame UV emission line ratios of the MUSE He II λ1640 sample compared with the model line ratios computed by Xiao et al. (2018) using BPASS binary stellar population models. Here we show the C III]/He II λ1640 vs. O III]/He II λ1640 line ratios for the MUSE He II λ1640 detected sample. Individual galaxies with S/N ≥ 2.5 for all three emission lines are shown as stars. Galaxies that fail the S/N cut are shown as arrows. The symbol size is proportional to the age from the onset of the star formation burst between t = 1 Myr (smallest) and t = 50 Myr. Models are computed with log10(nH)=1.0 with varying Us between −2.5 and −1.5. BPASS Z⊙ = 0.02. |
When binary stars are included, most parameters become degenerate with each other. Therefore, a variety of models ranging from Z⊙ to ∼1/200 Z⊙ is able to reproduce the observed line ratios largely independently from photo-ionisation properties (also see Fig. B2 of Xiao et al. 2018). However, the BPASS binary models rule out models with lower ionisation parameters (Us ≲ −2.5) at every metallicity considered. We therefore conclude that additional degeneracies introduced by including effects of binary star interactions prevent us from placing strong constraints on the ISM conditions of our He II λ1640 sample. Full spectral fitting analysis with higher S/N spectra of individual galaxies might allow stronger constraints on the binarity of the stellar populations, which in turn might enable a more detailed understanding of the stellar and ISM conditions of He II λ1640 emitters at high-z. However, this is beyond the scope of this paper. We further caution against a direct comparison of emission line ratios in the Gutkin et al. (2016) and Xiao et al. (2018) models because the differences in the underlying stellar population and photo-ionisation modelling assumptions are significant.
In Fig. 9 we examine the time evolution of C III]/He II λ1640 and O III]λ1666/He II λ1640 emission line ratios in the Xiao et al. (2018) models. Models with lower Us always show lower emission line ratios in both the C III]/He II λ1640 and O III]λ1666/He II λ1640 line ratios, with higher metallicity models in general showing a stronger dependence of Us. Lower metallicity models produce more He II λ1640 flux and therefore show lower line ratios than their higher metallicity models at earlier times. However, at later time, the enhanced production of W–R stars in higher metallicity systems decreases the emission line ratios. A mixture of QHE effects, ISM abundances, and W–R stars gives rise to the complex variations in the time evolution of the models (also see Fig. 12). Our observed emission line ratios can be produced by a variety of models relatively independently of the age within the first 100 Myr of the onset of the star burst.
 |
Fig. 9. Xiao et al. (2018) rest-UV emission line ratio evolution as a function of time. Here we show in the left panel C III]/He II λ1640 vs. time and in the right panel O III]λ1666/He II λ1640 vs. time for the BPASS binary models computed with a log10(nH)=1.0 and Us = −1.5 and Us = −3.5 (upper and lower limits of each shaded region, respectively) at different metallicities between 1 Z⊙ and 1/200th Z⊙. We only show a limited set of model metallicities for clarity. The black horizontal lines show the line ratios of the MUSE He II λ1640 sample. |
3.4.2. Comparison of observed EWs
Our analysis of emission line ratios demonstrates that the Xiao et al. (2018) models are able to reproduce the observed emission line ratios within the considered photo-ionisation parameter space. Next we use the Xiao et al. (2018) models to investigate if the observed He II λ1640 EWs of the MUSE sample might be reproduced by BPASS models.
We show the distribution of the C III] EW vs. He II λ1640 EW and O III]λ1666 EW vs. He II λ1640 EW of the MUSE sample in Fig. 10. The models are able to reproduce the C III] EWs at very early times of the star-burst at high Us and low metallicities. However, the models are unable to reproduce the He II λ1640 and O III]λ1666 EWs. This is in contrast to the ability of the Xiao et al. (2018) models to reproduce observed rest-UV emission line ratios within the photo-ionisation model parameter space. Therefore, it is evident that the relative strength of He II λ1640 compared to C III] and O III] is within the scope of model grids, but the He II λ1640 and O III] flux to their respective rest-UV continuum at ∼1640 Å and ∼1666 Å is not. Because the ionisation energy of C+ (∼24.38 eV) is relatively low compared to He+ and O+ (∼35.11 eV), it is likely that the lack of high-energy ionisation photons drives the low He II λ1640 and O III] EWs in the Xiao et al. (2018) models at fixed C/O.
 |
Fig. 10. EW comparison of the MUSE He II λ1640 sample using BPASS stellar population models. Left panel: [C III]λ1907+C III]λ1909 EW vs. He II λ1640 EW. Right panel: O III]λ1666 EW vs. He II λ1640 EW. Galaxies with S/N ≥ 2.5 are shown by stars, and others are shown as lower limits to the EW as triangles. We compare our observed EWs with model tracks from the Xiao et al. (2018) BPASS binary tracks. Models are computed for a log10(nH)=1.0 and Us = −1.5 at different metallicities between 2 Z⊙ and 1/200th Z⊙. The size of the symbols increases with time. EWs from the literature are also shown for comparison. |
In Sect. 3.5 we further discuss the ionisation photon production efficiency of the BPASS models. We also note that spectro-photometric modelling by Berg et al. (2018) was able to model the O III] doublet accurately, but was unable to reproduce the He II λ1640 emission. Therefore, additional constraints of the individual stellar populations along with additional far-UV ionising photons are required to accurately predict the additional source of ionisation photons. Steidel et al. (2016) argued that core-collapse supernovae dominating at high-z drives the ISM of z ∼ 2 galaxies to be O enriched with super-solar O/Fe (also see Matthee & Schaye 2018). Thus the stellar metallicity relevant to model the emission lines is lower than the gas-phase metallicity, which results in an ionising spectrum that is harder, resulting in a higher O III] flux.
3.5. Investigation of He+ ionising photon production
In this section we use the BPASS stellar population models to investigate their He+ ionising photon-production efficiencies and derive a simple calibration to investigate under which conditions the observed He II λ1640 luminosities might be reproduced by the models. In Fig. 11 we show the Lyman continuum spectra of the BPASS single and binary stellar models. Compared to single stellar populations, the effects of binary stellar evolution causes the Lyman continuum to increase substantially (× ≳ 2). The Lyman continuum flux is driven by the young O and B stars, and because of their high temperatures, an increase in flux of ∼400 − 600 Å is observed. At shorter wavelengths (λ ≲ 300 Å), the observed flux reduces rapidly, and between C++ and He+ ionisation limits, the flux therefore decreases by around one magnitude. However, we also note that our limited empirical constraints on far-UV spectroscopy of stars introduces additional uncertainties into stellar population modelling at this wavelength regime. Additionally, variations in the IMF also lead to an increase in Lyman continuum flux, which we discuss in Sect. 4.2.7.
 |
Fig. 11. Left panel: example BPASS v2.1 model spectra of a single-burst stellar population after 5 Myr from the star burst. The single (dashed) and binary (continuous) model predictions are shown for different IMFs (Γ = −1.0, −1.35, −1.70) with a high-mass IMF cutoff at 300 M⊙. The dashed black vertical lines mark λ = 228 Å, 353 Å, 508 Å, and 912 Å, below which He+, O++, C++, and H ionising photons are produced. Right panel: zoomed-in region λ < 275Å clearly showing the difference in flux around He+ ionising limits. |
In Fig. 12 we show the ionising photon production efficiency of BPASS models. For simplicity, we do not show the single stellar models in the figure, but we note that binary models show a higher amount of photon production than their single stellar model counterparts. Thus, binary stellar evolution plays a vital role in producing ionising photons for a prolonged time after a star burst. We additionally investigate the time-evolution of ξion for H and He+ in BPASS binary models. We define ξion for each element or ion as the Lyman continuum photon production efficiency above energies that could ionise the given element or ion, which is computed as
 |
Fig. 12. Top panels: BPASS stellar population predictions for the evolution of the number of ionisation photons produced by a single instantaneous star burst (106 M⊙) stellar population as a function of time. From left to right: H and He+ ionisation photons computed by integrating the spectra at λ = 228 Å and 912 Å, respectively. The models are computed at Z = 0.0001, 0.001, 0.002, 0.01, and 0.02 for binary models with different IMFs (Γ = −1.0, −1.35, and − 1.70) and IMF upper mass cutoffs (100 M⊙ and 300 M⊙). Bottom panels: similar to the top panels, but showing the evolution of ξion of H and He+ as a function of time. |
where N(X) is the ionising photon production rate of the considered element or ion (in 1 s−1) and LUV is the luminosity at 1500 Å (in erg s−1 Hz−1). Here we assume fesc = 0. Both N(X) as ξion are strongly sensitive to the metallicity, with lower metallicity models producing high values of N(X) and ξion. As discussed is Sect. 3.4 (also see Stanway et al. 2016; Eldridge et al. 2017; Xiao et al. 2018), the two main effects of binaries with regard to the production of ionising photons is to prolong the lifetime of massive O and B stars and enhance the production of W–R and helium stars even at lower metallicities.
We further developed a simple prescription to investigate the difference in He II λ1640 ionising photons between the observed data and the Xiao et al. (2018) model predictions.
We computed a normalisation constant (C) as
using the C III] luminosities of the models and observed data. We used the calibration constant to compute the predicted He II λ1640 luminosity from the models as
and obtained the approximate difference in He+ ionising photons between observations and models assuming that LHe II λ1640 ∝ Ni, He II λ1640. In Fig. 13 we show the fraction of observed He+ ionising photons compared to the predictions from the models. Only extreme sub-solar metallicities (∼1/200th) are able to accurately predict the observed He+ ionising photons. In Sect. 4.2.4 we discuss the mechanisms in binary models that drive the additional production of ionising photons in binary stellar models and the role of metallicity in these models.
 |
Fig. 13. Fraction of observed He+ ionising photons compared to the Xiao et al. (2018) model expectations as a function of observed He II λ1640 luminosity of the MUSE He II λ1640 sample. From left to right, we show the He+ model predictions computed for three metallicities, Z = 0.01, 0.001, and 0.0001 with log10(nH)=1.0 and Us = −1.5 for different times between 1 and 20 Myr from the onset of the star burst. The dashed horizontal line indicates y = 0, where there is no difference between observations and model predictions. |
4. Discussion
We have presented a population of He II λ1640 emitters from deep MUSE spectra obtained from a variety of spectroscopic surveys conducted by the MUSE consortium. By taking advantage of the other rest-UV emission lines with MUSE coverage, we have explored the stellar population/ISM properties of our sample.
4.1. Uncertainties affecting our analysis
4.1.1. Dust
Our limited understanding of interstellar dust at high redshift plays a role in our analysis of emission line properties in the rest-UV in many respects. Metal depletion and dust dissociation of galaxies play a role in the photo-ionisation models, with only a handful of models accounting for dust in chemical evolution models (e.g. Gutkin et al. 2016; Gioannini et al. 2017). Providing tight constraints for these parameters at high-z requires a thorough understanding of element abundances, which is currently limited at high-z through observational constraints. We further discuss uncertainties related to this in Appendix C.
In addition to the parameters related to photo-ionisation modelling, dust attenuation of the observed spectra introduces additional complexities when the observed emission lines are interpreted. If nebular emission has systematically higher attenuation, line flux values will change significantly (∼5%−80%), but line ratio diagnostics will be significantly less affected. We show this in Fig. 14, where we compare the observed emission line ratios with dust corrections applied using different attenuation laws and different extinction between stellar and ionised gas regions. Using the Calzetti et al. (2000) attenuation law for the continuum and the Cardelli et al. (1989) attenuation law for the nebular emission lines, we derived dust-corrected emission line flux ratios for our He II λ1640 sample considering (i) no difference in extinction between stellar and ionised gas regions, and (ii) that ionised gas regions are twice as extincted compared to stellar regions. Figure 14 shows that the changes in emission line ratios between (i) and (ii) are quite modest and are within the error limits of the line fluxes. We further showed the difference in dust-corrected emission line flux ratios between Cardelli et al. (1989); Calzetti et al. (2000), and Reddy et al. (2015); Reddy et al. (2016a). Regardless of the attenuation law, most galaxies lie within the line flux measurement errors. The significant outliers the in C III]/O III] vs. Si III]/C III] and C III]/He II λ1640 vs. O III]/He II λ1640 line ratios are primarily driven by the variations of the He II λ1640 fit performed on the spectra after dust corrections were applied using different attenuation laws.
 |
Fig. 14. Rest-frame UV emission line ratios of the MUSE He II λ1640 sample computed with different dust laws. The panels are similar to Fig. 6, but the Gutkin et al. (2016) models are removed for clarity. Only the galaxies with S/N ≥ 2.5 for emission line considered in each panel are shown in the figure. Observed emission line ratios are shown by stars. f = 1 and f = 2 resemble dust corrections that are applied considering no additional attenuation and twice the additional attenuation for ionised gas regions (computed using the Cardelli et al. 1989 attenuation law) compared to stars (computed using the Calzetti et al. 2000 attenuation law). We further show the distribution of the line ratios using the Cardelli et al. (1989), Calzetti et al. (2000), and Reddy et al. (2015, 2016a) attenuation laws. |
In this analysis we completely ignored the fact that the A(V) values of our are sample were obtained through either SED fitting or β, which are calibrated to a certain dust attenuation law and stellar population models. Therefore, a more accurate treatment of dust requires recalibrating attenuation laws with a variety of stellar population models (e.g. Reddy et al. 2018; Theios et al. 2018) and is beyond scope of this work. However, we showed that to first order for the rest-UV emission line ratios considered in our analysis, dust correction does not have a significant effect, and that only observed outliers are driven by variations introduced by wavelength-dependent broadening of emission lines.
4.1.2. S/N and line fitting
The low S/N of the observed spectra of our sample affects our analysis through (i) uncertainties associated with the continuum fitting process, and (ii) weak emission-line strengths compared to the continuum level. In our analysis, we completely ignored the uncertainties associated with the continuum fitting process. As shown in Fig. 2, the continuum levels of a majority of our galaxies are lower than 3σ of the noise level. Therefore, although visual identification of emission lines showed clear features, the line fluxes, which are measured by subtracting the continuum from the spectra may have larger uncertainties.
To quantify the low significance of the emission lines compared to the continuum level and uncertainties associated with the continuum fitting, we performed a bootstrap resampling analysis of the spectra. For each spectrum, we randomly resampled each pixel flux value with a Gaussian distribution around ±σ of the error level of that pixel. We then refit the continuum and measured the line fluxes and performed this iteratively 100 times. We considered the median value of the line flux distribution as the line flux and the standard deviation of the measured values as the associated error level of the line flux. Of the 13 galaxies identified with He II λ1640 detections, we find that although all He II λ1640 line fluxes are measured at > 2σ, 5 galaxies fail to make an S/N ≥ 2.5 cut for He II λ1640 emission and only 4 galaxies are detected with S/N ≥ 3. Therefore, we conclude that the low S/N of the data is a non-negligible uncertainty of our analysis, and we require deeper integrations to constrain the continuum of galaxies with greater significance.
Additionally, the method that we implemented to obtain the He II λ1640 fluxes may give rise to uncertainties associated with the emission line fitting algorithm. As we discussed in Sect. 2.3, we fit the He II λ1640 emission line width using a single-Gaussian parametric fit, which allows more freedom than the other emission lines. We opted for this approach in recognition of the fact that the He II λ1640 can originate from a multitude of processes (see Sect. 4.2). However, our photo-ionisation model comparisons assumed that the nature of He II λ1640 is purely nebular. Thus it is necessary to investigate how allowing more flexibility in the fit affects the He II λ1640 flux measured in the galaxy spectra (Brinchmann et al. 2008).
In Fig. 15 we show a comparison of He II λ1640 line flux measurements between different line fitting methods. We used the independently fit He II λ1640 single-Gaussian fit as the base line and compared with measurements obtained by (1) fitting He II λ1640 using a single Gaussian whose line centre and width were fixed with the other emission lines and (2) a double Gaussian profile whose one-component line centre and width were fixed with the other emission lines. For spectra with multiple emission line detections, after the He II λ1640 line centre and width were fixed with the other emission lines, there was a tendency for He II λ1640 flux to be underestimated by ∼20%±27% compared to the independently fit He II λ1640. Similarly, with a multi-Gaussian fit, the difference in flux for the nebular component is much greater with an observed underestimation of flux ∼36%±24%. In all cases, the He II λ1640 fit performed independently of the other emission lines better in obtaining a better fit to the observed emission line. Ambiguities associated with the line fitting are an inherent uncertainty in our analysis, and only high S/N emission line detections of weaker rest-UV nebular emission line features will grant stronger constraints on the nebular component of the He II λ1640 features.
 |
Fig. 15. Left panel: comparison of He II λ1640 line flux measurements obtained for different He II λ1640 line flux parametrisations. We compare the He II λ1640 line flux measurements of galaxies with an S/N > 3 obtained using an independently fit He II λ1640 single-Gaussian fit with measurements obtained by (1) fitting He II λ1640 using a single Gaussian whose line width was fixed with the other emission lines (diamonds) and (2) a double Gaussian profile whose one-component line width was fixed with the other emission lines (stars). For the double-Gaussian fit, we only consider the nebular component for comparison. Right panel: comparison of the FWHM of [C III]λ1907 with the FWHM of He II λ1640 fit independently of the other nebular emission lines. The solid line denotes x = y and the dashed line denotes x = 2y. |
When we consider the He II λ1640 line width to be independent of other nebular emission lines, the line width velocities of He II λ1640 and of the other nebular emission lines results to be systematically different. In Fig. 15 we compare the line FWHM of the Gaussian fits of the [C III]λ1907 and He II λ1640 emission lines. All our galaxies show that the He II λ1640 FWHM is higher than that of [C III]λ1907. Because [C III]λ1907 is purely driven by the nebular emission, the difference in line velocities suggests that He II λ1640 may also have a contribution from a different source. Because our data have a low S/N, we refrain from over-interpreting this result, but we discuss possible origins for a narrow star-driven He II λ1640 component in Sect. 4.2.3.
4.1.3. Stellar population models
The stellar population models used to infer ISM properties of our He II λ1640 sample contribute to the uncertainties in interpreting the observed emission line ratios. In Sect. 3.3 we show that the Gutkin et al. (2016) models, which do not account for the effects of stellar rotation or binary stars but treat element abundances and depletion onto dust grains self-consistently, show different emission line ratios than the Xiao et al. (2018) models, which incorporate effects of binary stellar evolution.
To obtain stronger constraints on the underlying stellar populations and the ISM, nebular emission lines should be jointly used with rest-UV/optical stellar and ISM (neutral plus ionised, e.g. Vidal-García et al. 2017) absorption lines for comparison with predictions from the stellar population models. Several advanced full spectral fitting algorithms for stellar population models have recently been developed to perform full spectro-photometric analyses of galaxies (e.g. Chevallard & Charlot 2016; Leja et al. 2017). In the local Universe, Senchyna et al. (2017) showed that at low metallicity, a full spectral fitting fails to accurately predict the observed He II λ1640 features using models that do not include stellar rotation or binaries.
At high redshift, most rest-UV studies suffer strong observational constraints as a result of the low S/N of the continua of galaxy spectra. To overcome the low S/N, studies have attempted spectral stacking techniques and gravitational lensing to obtain rest-UV spectra with high-S/N. Steidel et al. (2016) used STARBURST99 (Leitherer et al. 1999) and BPASSv2 models to obtain a best-fit spectral model for a stacked composite spectra at z ∼ 2. Their results demonstrated that the best-fit models showed considerable difference between STARBURST99 and BPASS for various spectral features. Stellar wind features, for example, lacked any metallicity dependence in the BPASS models. The analysis of Steidel et al. (2016) highlighted an important aspect with regard to He II λ1640: the observed He II λ1640 feature of the stacked spectrum was completely attributed to a stellar origin from BPASS, while STARBURST99 suggested a purely nebular feature arising from H II regions. However, Steidel et al. (2016) did not investigate if the Lyman continuum photons from the STARBURST99 best-fit SED were sufficient to produce the observed He II λ1640 feature. Using a gravitationally lensed galaxy at z ∼ 2, Berg et al. (2018) showed that all the observed emission lines except for He II λ1640 can be best fit by a BPASS stellar population model. We note that the Berg et al. (2018) galaxy has similar rest-UV emission line ratios as galaxies in our sample (e.g. see Fig. 6). The necessity for binary models to explain high-z observed spectral features (e.g. C III] EW) has also been demonstrated by Jaskot & Ravindranath (2016), but with the caveat that they were unable to reproduce the He II λ4686/Hβ ratios of z ∼ 0 galaxies.
Therefore, even the latest generation of Bruzual & Charlot (2003) or BPASS stellar population models is currently unable to accurately predict the observed He II λ1640 features. These complications in stellar population models make a cross-validation using a multitude of spectral diagnostics is imperative for strong conclusions about the ISM and stellar conditions of high-redshift galaxies. We discuss the effects of binaries on He II λ1640 emission in further detail in Sect. 4.2.4 and defer a full spectral fitting analysis of stacked spectra from MUSE to a future study.
4.2. Origin of He II λ1640
Many mechanisms are currently being used to describe the origin of the He II emission line (see Shirazi & Brinchmann 2012 and Senchyna et al. 2017 for a detailed discussion). Here we explore whether we can rule in favour or against of any of such mechanisms. However, we note that the lack of rest-frame optical coverage of our sample prevents strong conclusions about the origin of He II.
4.2.1. AGN
Fast-accreting supermassive black holes release high-energy photons to the surrounding environment (e.g. Kormendy & Richstone 1995; Magorrian et al. 1998), which contributes to strong rest-frame UV and optical nebular emission lines (Feltre et al. 2016). In our sample we identified three galaxies with possible strong AGN contribution based on X-ray detections and enhanced line widths. They all show broad C IV emission features that clearly distinguish them from stellar ionisation sources. We demonstrated in Fig. 6 that our He II λ1640 sample emission line ratios completely fall within the region powered by star-formation, and additionally, that the line ratios of our sample do not fall within the AGN segment of Feltre et al. (2016). However, we do not rule out effects of sub-dominant AGN, which may still contribute to the ionisation processes of our sample but to a lesser degree than stellar sources. Thus it is possible that at least some of the He II λ1640 emission of our sample is caused by AGN.
4.2.2. Radiative shocks
Radiative shocks in galaxies also contribute to ionising photons capable of producing He II λ1640 (e.g. Thuan & Izotov 2005; Allen et al. 2008; Jaskot & Ravindranath 2016) but are only expected to be dominant at higher metallicities (Shirazi & Brinchmann 2012). However, metallicity correlations are yet to be tested with a newer generation of stellar population models that include an advanced treatment of W–R stellar evolution (Charlot & Bruzual, in prep.), and binaries and stellar rotation (e.g. BPASS). Radiative shocks could also contribute to the spatial offsets between He II λ1640 emission and the continuum (Thuan & Izotov 2005)
In order to accurately distinguish whether shocks (or even AGN) play a dominant role in producing ionising photons, we require multiple emission line diagnostics or high S/N emission lines with broad components. Using emission line diagnostics alone to distinguish shocks and AGN from star formation activity requires caution at high redshift because of the significant differences in the ISM of high-redshift galaxies compared to local star-forming galaxies (e.g. Steidel et al. 2014; Kewley et al. 2016; Strom et al. 2017). Recent studies demonstrated that the capability to decompose narrow and broad components of observed emission lines is correlated with the S/N (Freeman et al. 2017). Thus, at lower S/Ns, the contribution to an emission line from star formation and shocks would become degenerate. If shocks are correlated with galactic outflows, the outflow mass per SFR will be higher at lower masses (Muratov et al. 2015) and thus if SFR ∝L (He II λ1640) (Schaerer 2003) it is plausible for the strongest He II λ1640 emitting low-mass galaxies to have a more shock contributed He II λ1640 emission. Because the He II λ1640 S/N of our sample is < 10, we are unable to perform a meaningful study on the individual He II λ1640 detections to distinguish between star formation and AGN and shocks, and we therefore refrain from fitting multiple Gaussian components to He II λ1640 to identify broader emission components. Additional rest-frame optical emission line diagnostics coupled with high S/N data from MUSE and the JWST will be crucial to distinguish the contribution of shocks to the emitted spectrum.
4.2.3. Wolf–Rayet stars
Strong winds driven by the powerful radiation pressure in the W–R stars result in characteristic broad emission lines, which means that star-forming galaxies with a significant population of W–R stars will show a composite of broad and narrow He II features (Crowther 2007). At low metallicities stellar winds will be weaker, which increases the relative efficiency of stellar rotation and mass transfer between binaries (Eldridge & Stanway 2009; Szécsi et al. 2015). Thus, W–R stars in metal-poor galaxies produce He+ ionising photons without broad W–R features that are characteristic of high-metallicity W–R stars (Schmutz et al. 1992; Crowther & Hadfield 2006; Gräfener & Vink 2015). The nebular He II components in z ∼ 0 galaxies show a very prominent transition to high He II λ4686/Hβ ratios as a function of metallicity, with low-metallicity systems requiring up to an order of magnitude higher He+ photons (Brinchmann et al. 2008; Shirazi & Brinchmann 2012; Senchyna et al. 2017). WC stars are formed in binary systems around more luminous O stars, but are hotter and bolometrically fainter than typical core-He burning W–R stars, which contribute to high-energy ionising photons while being “observationally invisible” (McClelland & Eldridge 2016). Additionally, very massive low-Z WNh stars (hydrogen-rich WN stars) produce narrow He II λ1640 emission features of ≳300 km s−1 with no other accompanying features (Gräfener & Vink 2015). In Fig. 15 we show that the He II λ1640 line widths of our sample are ∼200 − 400 km s−1, and thus it is plausible for a subset of our He II λ1640 emitters to be powered by stellar emission. Here, the He II λ1640 line width is a direct proxy for the velocities of the stellar winds, which are considerably weaker at low-Z, thus moderate- to high-resolution spectra with high S/N are required to accurately extract nebular and stellar components of the He II λ1640 emission (e.g. Senchyna et al. 2017). As we discuss in Sect. 4.1.2, we require high S/N data with multiple confident rest-UV emission line detections to accurately distinguish between different He II λ1640 mechanisms that produce comparable emission line features. We note that we removed one galaxy from our He II λ1640 sample (see Sect. 2.1.1) because of its broad He II λ1640 feature with a FWHM > 1000 km s−1, which can also be explained by WN type stars at ∼0.5 Z⊙ (Gräfener & Vink 2015). We can rule out that high-metallicity W–R stars with broader winds are a strong contributor to our He II λ1640 sample, but we cannot completely rule out the presence of low-metallicity WN-type stars, which may become more prominent at lower metallicities when effects of binaries are considered.
4.2.4. Effects of binary interactions
Effects of binaries have been shown to play a crucial role in increasing the ionising photon production in young stellar systems through multiple processes (Eldridge et al. 2017) and may contribute to alleviate the tension between models and data for He II emitters observed in low metallicity systems (Shirazi & Brinchmann 2012; Senchyna et al. 2017). In contrast to stellar population models that incorporate advanced treatments of stellar rotation (Leitherer et al. 2014), driven by large degeneracies between effects of stellar rotation and binaries, BPASSv2 stellar population models implement a simplified approach to consider effects of stellar rotation (Eldridge et al. 2017). Nonetheless, it is important to consider the effects of binaries and stellar rotation together because it has been shown that rapid rotation in stars may only arise through binary interactions (e.g. de Mink et al. 2013). At Z ≤ 0.004, BPASS models could generate up to > 0.1 dex more ionising photons from effects of QHE alone (see Fig. 6 of Stanway et al. 2016, also see Fig. 12 of this paper). A physically motivated gradual transition of QHE effects as a function of metallicity may provide further constraints to balance the production of He+ photons with observed W–R features.
Regarding the production of He II ionising photons, studies have shown that even BPASS models with effects of binaries do not produce sufficient He+ ionising photons to consistently model He II with other observed emission lines (Jaskot & Ravindranath 2016; Berg et al. 2018). In Fig. 12 we show that compared to the H ionising photons, the He+ ionising photon production rate is only mildly sensitive to the age of the stellar population within ∼20 Myr from the star burst. This is driven by the contribution of older W–R stars after the first few million years from the onset of the star burst. The effect of QHE can be clearly seen here, where the lower metallicity models produce significantly higher amounts of ionising photons than models with Z > 0.004. Therefore, in BPASS the contribution to He+ ionising photons is primarily driven by the additional production of W–R stars at lower masses and metallicities through binary interactions and is insufficient to match observed correlations. Compared to He+, the C++ ionising photon production rate is always higher (also see Fig. 11), and as we show in our analysis, BPASS models accurately predict observed C III] EWs but not higher energy O III] and He II λ1640 EWs. The lack of He+ ionising photons in BPASS could be driven by the white dwarf treatment where BPASS asymptotic giant branch (AGB) stellar models do not produce white dwarfs in the single-star mode, while in the binary mode, the stars do not evolve up to the AGB phase driven because of effects of binary interactions before the second dredge-up (Eldridge et al. 2017). A more advanced treatment of white dwarf production within BPASS and consideration of emission from white dwarf accretion discs (Woods & Gilfanov 2016) may contribute to an enhancement of He+ ionising photons within BPASS to account for the deficiency compared to observations.
4.2.5. X-ray binaries
X-ray binaries have been shown to produce hard ionising photons capable of ionising He+ (e.g. Garnett et al. 1991). A black hole or a neutron star or pulsar that is accreting material from their companion O/B star will undergo heating by the strong X-ray ionising photons that are produced during accretion. The strength of the X-binary binary is expected to be determined by the mass transfer rate of the secondary star, the magnetic field strength of the compact source, and by the X-ray luminosity, which contributes to the heating of the accretion disc (Casares et al. 2017). At fixed SFR, lower metallicity systems are found to have high X-ray luminosity, thus at lower metallicities, X-ray binaries may play a larger role in producing He+ ionising photons (Brorby et al. 2016; Schaerer et al. 2019). Low-redshift rest-UV studies have either not shown any strong evidence for X-ray point-source detections in strong He II emitters or show spatial offsets between He II λ1640 detections and the X-ray sources (Thuan & Izotov 2005; Kehrig et al. 2011, 2015; Shirazi & Brinchmann 2012; Senchyna et al. 2017). Additionally, X-rays will have an extremely shallow optical depth, and thus it is unclear to which extent the high-energy photons can influence the production of He+ ionising photons. However, X-ray photons would in principle degrade to lower-energy photons and ionise He+ over larger optical depths, which may be able to explain some of the spatial offsets. For our sample at z ∼ 3, which is limited by strong observational constraints of weak X-ray features at high redshift, we are unable to determine the role of X-ray binaries, if any, in producing He II λ1640.
4.2.6. Stripped stars
Recent studies have shown that low-mass stars in the presence of binary companions undergo stripping of (most but not all) their hydrogen envelope, exposing the very hot and compact helium core (Kippenhahn 1969; Podsiadlowski et al. 1992) capable of producing high-energy He+ photons (Götberg et al. 2017). In contrast to W–R stars, these stars are exclusively produced in binary systems and are produced by low-mass sub-dwarf O- and B-type stars. Götberg et al. (2017) found that every interacting binary produces a hot stripped star, which is powered by core helium burning up to ∼10% of its total lifetime. The amount to which stripped stars contribute to the ionisation of He+ is completely unconstrained, with variations of up to ∼6 orders of magnitude difference at higher metallicities (see Fig. 11 of Götberg et al. 2017). These variations, primarily driven by the uncertainties in the assumed mass-loss rate, are significantly reduced at extremely low metallicities (Z ≲ 0.0002), but are still in the order of ∼1 mag. However, because stripped stars are produced by low-mass stars that are favoured by the IMF and their prolonged lifetime in the helium-burning phase compared to their W–R counterparts could lead them to be a significant He+ photon-emitting mechanism in our He II λ1640 sample. Additionally, transparent stellar atmospheres coupled with the longer time-delay between star formation and stripped star production enables stripped stars to ionise far larger distances in the ISM/IGM (Götberg et al. 2017), which could result in the production of He II emission outside of central star-forming regions in galaxies.
4.2.7. IMF variations
Recent studies have demonstrated the possibility of systematic variations in the IMF in star-forming galaxies at low (Hoversten & Glazebrook 2008; Gunawardhana et al. 2011) and high (Nanayakkara et al. 2017) redshifts. If star-forming galaxies do contain systematically higher amounts of massive stars than what is expected by Salpeter (1955) like IMFs, the higher abundance of massive stars would lead to the production of additional ionising photons for a given SFR. In Fig. 12 we show the ionisation photon production efficiency for H and He+ in BPASS stellar population models for different IMFs. For clarity we removed effects of the upper mass IMF cutoff but we note that in both single and binary models it only has an influence between the first 1–3 Myr of the star-burst and then becomes negligible. This is driven by the relatively short lifetimes of 100–300 M⊙ stars. Changing the IMF slope shows a prominent effect even at later times from the onset of the star burst, with an up to ∼0.3 − 0.5 dex higher H ionising photon production rate predicted for binary models with the IMF slope change from Γ = −1.35 to Γ = −1.00. Additionally, at λ < 228 Å, binary stars play a vital role in producing higher amounts of ionising photons that could ionise He+. Thus, top-heavy IMFs could be one possible contributor to He II λ1640 emission in our sample (also see Kehrig et al. 2018). However, as we show in Fig. 12, the effect of IMF on ξion is negligible for He+ and thus may not contribute significantly to increase the He II λ1640 EW. Stacked galaxy analyses of z ∼ 2 rest-UV features by Steidel et al. (2016) have shown that IMF sensitive rest-UV features could be reproduced using BPASS binary models without invoking variations in the IMF and independently of the upper mass IMF cutoff (between 100 and 300 M⊙). However, their photo-ionisation models do not include dust depletion but include dust physics (e.g. photoelectric heating), which would boost the strength of the coolant lines and result in strong emission lines. In order to completely rule out that IMF variations are a contributing He+ emitting factor for our He II λ1640 sample, we require higher S/N rest-UV/optical spectra with IMF sensitive features.
5. Conclusions
We explored deep spectroscopic observations from the VLT/MUSE integral field spectrograph to compile a sample of strong He II λ1640 nebular emitters between 1.93 < z < 4.67. We have complemented our sample with other deep rest-UV spectroscopic surveys conducted around the same redshift as described in Sect. 2.1.5. Using custom-built emission line fitting codes, we obtained rest-UV emission line ratios to compare with expectations from photo-ionisation modelling. Our results are as summarised below.
-
The MUSE He II λ1640 sample comprises galaxies with multiple rest-UV emission line detections with a wide range in He II λ1640 EW (∼ an order of magnitude) and MUV (∼ − 19 to −23) (see Sect. 3.1: Fig. 3).
-
Using photo-ionisation modelling from Gutkin et al. (2016), we showed that the observed emission line ratios of our He II λ1640 sample can be reproduced primarily at sub-solar metallicities and high-ionisation parameters (see Sects. 3.3.1 and 3.3.2: Figs. 6 and 7).
-
We used BPASS binary stellar population models from Xiao et al. (2018) to show that BPASS binary models are also able to reproduce the observed line ratios in the C III/He II λ1640 vs. OHe III/He II λ1640 diagnostic. However, when effects of binaries were included, the models became degenerate (see Sect. 3.4: Fig. 8).
-
We showed that the dust attenuation law and assumption of dust sight-lines have only a negligible effect for our line-ratio analysis. However, photo-ionisation model assumptions of metal depletion and dust dissociation need stronger constraints at higher redshifts (see Sect. 4.1.1: Appendix C: Fig. 14).
-
We showed that BPASS models are able to reproduce the C III] EWs but not He II λ1640 and O III] EWs. This is possibly driven by the lack of ionisation photons blue-ward of 228 Å (and also by super-solar O/Fe abundance) (see Sect. 3.4.2: Figs. 10 and 11).
-
We showed that observed He II λ1640 luminosities could only be reproduced by BPASS models at ∼1/200th solar metallicity, which is in contrast with gas-phase metallicities inferred by rest-UV emission line diagnostics (see Sect. 3.5: Fig. 13).
-
We found the He II λ1640 line widths to be ∼200 − 400 km s−1 and showed the need for an emission line fitting algorithm that fits He II λ1640 independently of other emission lines to accurately constrain the shape of He II λ1640 and measure the line flux (see Sect. 4.1.2: Fig. 15).
-
We computed the ionising photon production efficiency and ξion for H and He+ ionising photons and found that binary stars and IMF have a significant effect (see Sect. 3.5: Fig. 12).
-
We explored possible mechanisms of He II λ1640 production (Sect. 4.2).
We ruled out high-metallicity W–R stars as a possible mechanism, but we were unable to place any constraints on the contribution by low-metallicity W–R stars (e.g. WNh stars).
We noted that binary stars can play a crucial role, but the current binary stellar evolution implementations still lack He II λ1640 ionising photons under the hypothesis that stars are the only ionising source.
Variations in the high-mass end IMF, with slopes steeper than the canonical Salpeter (1955) slope, could contribute to the missing He+ ionising photons.
We ruled out the contribution from strong AGN to the ionising photon flux for our He II λ1640 sample. However, we cannot rule out a sub-dominant contribution from weak- or low-luminosity AGN and/or shocks.
Future work should focus on a full spectral fitting analysis of individual rest-UV spectra of galaxies involving effects of binaries and varying IMF. More sophisticated binary stellar populations with realistic stellar atmosphere models including effects of low-Z very massive stars at Eddington limit are required to accurately determine the stellar and nebular production efficiencies of He II λ1640. Additionally, dust properties of galaxies at z > 2 requires stronger constraints for photo-ionisation modelling. Future sub-millimeter observations of galaxies will allow dust temperatures and geometries to be constrained, and linking with FIR emission lines would allow stronger constraints on the dust grain properties of galaxies in the early Universe. Links between gas metallicities and dust will be beneficial to understand the complicated processes the galaxies undergo in the epoch of the peak of the cosmic SFR density. The combined coverage of z = 2 − 4 galaxies by MUSE XDF survey3 and the JWST will provide an ideal sample with high S/N to study stellar and ISM conditions of galaxies, to determine the dominant mechanisms for the He II λ1640 emission at high redshift, and to constrain the role of pristine stellar-populations in the production of He II λ1640.
See Inami et al. (2017) for details.
Acknowledgments
The authors wish to thank the referee for constructive comments that improved the paper substantially. We thank the BPASS team for making the stellar population models available. We thank Elizabeth Stanway, Claus Leitherer, Daniel Schaerer, Jorick Vink, and Nell Byler for insightful discussions. We thank the Lorentz Centre and the scientific organizers of the Characterizing galaxies with spectroscopy with a view for JWST workshop held at the Lorentz Centre in 2017 October, which promoted useful discussions in the wider community. TN, JB, and RB acknowledges the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO) top grant TOP1.16.057. AF acknowledges support from the ERC via an Advanced Grant under grant agreement no. 339659-MUSICOS. JB acknowledges support by Fundação para a Ciência e a Tecnologia (FCT) through national funds (UID/FIS/04434/2013) and Investigador FCT contract IF/01654/2014/CP1215/CT0003, and by FEDER through COMPETE2020 (POCI-01-0145-FEDER-007672). JR acknowledges support from the ERC Starting grant 336736 (CALENDS). This research made use of astropy (http://www.astropy.org) a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018) and pandas (McKinney 2010). Figures were generated using matplotlib (Hunter 2007) and seaborn (https://seaborn.pydata.org). Facilities: VLT (MUSE).
References
- Agarwal, B., Johnson, J. L., Zackrisson, E., et al. 2016, MNRAS, 460, 4003 [NASA ADS] [CrossRef] [Google Scholar]
- Akerman, C. J., Carigi, L., Nissen, P. E., Pettini, M., & Asplund, M. 2004, A&A, 414, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen, D. A., Wright, A. E., & Goss, W. M. 1976, MNRAS, 177, 91 [NASA ADS] [Google Scholar]
- Allen, M. G., Groves, B. A., Dopita, M. A., Sutherland, R. S., & Kewley, L. J. 2008, ApJS, 178, 20 [Google Scholar]
- Amorín, R., Fontana, A., Pérez-Montero, E., et al. 2017, Nat. Astron., 1, 0052 [NASA ADS] [CrossRef] [Google Scholar]
- Asano, R. S., Takeuchi, T. T., Hirashita, H., & Nozawa, T. 2013, MNRAS, 432, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Bacon, R., Accardo, M., Adjali, L., et al. 2010, Proc. SPIE, 7735, 773508 [Google Scholar]
- Bacon, R., Brinchmann, J., Richard, J., et al. 2015, A&A, 575, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bacon, R., Conseil, S., Mary, D., et al. 2017, A&A, 608, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balestra, I., Mainieri, V., Popesso, P., et al. 2010, A&A, 512, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barkana, R., & Loeb, A. 2001, Phys. Rep., 349, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Beckwith, S. V. W., Stiavelli, M., Koekemoer, A. M., et al. 2006, AJ, 132, 1729 [NASA ADS] [CrossRef] [Google Scholar]
- Berg, D. A., Skillman, E. D., Henry, R. B. C., Erb, D. K., & Carigi, L. 2016, ApJ, 827, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Berg, D. A., Erb, D. K., Auger, M. W., Pettini, M., & Brammer, G. B. 2018, ApJ, 859, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Borisova, E., Cantalupo, S., Lilly, S. J., et al. 2016, ApJ, 831, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2010, ApJ, 709, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Aravena, M., Decarli, R., et al. 2016, ApJ, 833, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Bowler, R. A. A., McLure, R. J., Dunlop, J. S., et al. 2017, MNRAS, 469, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Kunth, D., & Durret, F. 2008, A&A, 485, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brinchmann, J., Charlot, S., Kauffmann, G., et al. 2013, MNRAS, 432, 2112 [NASA ADS] [CrossRef] [Google Scholar]
- Bromm, V., & Larson, R. B. 2004, ARA&A, 42, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bromm, V., & Yoshida, N. 2011, ARA&A, 49, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Brorby, M., Kaaret, P., Prestwich, A., & Mirabel, I. F. 2016, MNRAS, 457, 4081 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Buat, V., Giovannoli, E., Heinis, S., et al. 2011, A&A, 533, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calzetti, D. 2001, PASP, 113, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Kinney, A. L., & Storchi-Bergmann, T. 1994, ApJ, 429, 582 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cantalupo, S., Pezzulli, G., Lilly, S. J., et al. 2019, MNRAS, 483, 5188 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Casares, J., Jonker, P. G., & Israelian, G. 2017, X-Ray Binaries, 1499 [Google Scholar]
- Cassata, P., Le Fèvre, O., Charlot, S., et al. 2013, A&A, 556, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Charlot, S., & Longhetti, M. 2001, MNRAS, 323, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Chevallard, J., & Charlot, S. 2016, MNRAS, 462, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Romano, D., & Matteucci, F. 2003, MNRAS, 339, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Cimatti, A., Daddi, E., Mignoli, M., et al. 2002, A&A, 381, L68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Conroy, C. 2013, ARA&A, 51, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Cooke, R., Pettini, M., Steidel, C. C., Rudie, G. C., & Nissen, P. E. 2011, MNRAS, 417, 1534 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A. 2007, ARA&A, 45, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A., & Hadfield, L. J. 2006, A&A, 449, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cullen, F., McLure, R. J., Khochfar, S., et al. 2018, MNRAS, 476, 3218 [NASA ADS] [CrossRef] [Google Scholar]
- De Cia, A. 2018, A&A, 613, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Mink, S. E., Langer, N., Izzard, R. G., Sana, H., & de Koter, A. 2013, ApJ, 764, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Salpeter, E. E. 1979, ApJ, 231, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., Dale, D. A., Bendo, G., et al. 2007, ApJ, 663, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., & Stanway, E. R. 2009, MNRAS, 400, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., & Stanway, E. R. 2012, MNRAS, 419, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., Izzard, R. G., & Tout, C. A. 2008, MNRAS, 384, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., Stanway, E. R., Xiao, L., et al. 2017, PASA, 34, e058 [NASA ADS] [CrossRef] [Google Scholar]
- Epinat, B., Contini, T., Finley, H., et al. 2018, A&A, 609, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Erb, D. K., Pettini, M., Shapley, A. E., et al. 2010, ApJ, 719, 1168 [NASA ADS] [CrossRef] [Google Scholar]
- Erben, T., Hildebrandt, H., Miller, L., et al. 2013, MNRAS, 433, 2545 [NASA ADS] [CrossRef] [Google Scholar]
- Fardal, M. A., Katz, N., Gardner, J. P., et al. 2001, ApJ, 562, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Feltre, A., Charlot, S., & Gutkin, J. 2016, MNRAS, 456, 3354 [Google Scholar]
- Ferland, G. J., Porter, R. L., van Hoof, P. A. M., et al. 2013, Rev. Mex. Astron. Astrofis., 49, 137 [Google Scholar]
- Freeman, W. R., Siana, B., Kriek, M., et al. 2017, ArXiv e-prints [arXiv:1710.03230] [Google Scholar]
- García-Vergara, C., Hennawi, J. F., Barrientos, L. F., & Rix, H.-W. 2017, ApJ, 848, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Garilli, B., Guzzo, L., Scodeggio, M., et al. 2014, A&A, 562, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garnett, D. R., Kennicutt, Jr., R. C., Chu, Y.-H., & Skillman, E. D. 1991, ApJ, 373, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Gioannini, L., Matteucci, F., Vladilo, G., & Calura, F. 2017, MNRAS, 464, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Götberg, Y., de Mink, S. E., & Groh, J. H. 2017, A&A, 608, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gräfener, G., & Vink, J. S. 2015, A&A, 578, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grogin, N. A., Kocevski, D. D., Faber, S. M., et al. 2011, ApJS, 197, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Groves, B. A., Dopita, M. A., & Sutherland, R. S. 2004a, ApJS, 153, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Groves, B. A., Dopita, M. A., & Sutherland, R. S. 2004b, ApJS, 153, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Gunawardhana, M. L. P., Hopkins, A. M., Sharp, R. G., et al. 2011, MNRAS, 415, 1647 [NASA ADS] [CrossRef] [Google Scholar]
- Gutkin, J., Charlot, S., & Bruzual, G. 2016, MNRAS, 462, 1757 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., & Woosley, S. E. 2002, ApJ, 567, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, R. B. C., Edmunds, M. G., & Köppen, J. 2000, ApJ, 541, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Heymans, C., Van Waerbeke, L., Miller, L., et al. 2012, MNRAS, 427, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Hoversten, E. A., & Glazebrook, K. 2008, ApJ, 675, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, E. M., Cowie, L. L., Capak, P., et al. 2004, AJ, 127, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Inami, H., Bacon, R., Brinchmann, J., et al. 2017, A&A, 608, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Privon, G. 2012, MNRAS, 427, 1229 [NASA ADS] [CrossRef] [Google Scholar]
- Jaskot, A. E., & Ravindranath, S. 2016, ApJ, 833, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Jeans, J. H. 1902, Phil. Trans. R. Soc. London Ser. A, 199, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, E. B. 2009, ApJ, 700, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Kacprzak, G. G., Yuan, T., Nanayakkara, T., et al. 2015, ApJ, 802, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Kacprzak, G. G., van de Voort, F., Glazebrook, K., et al. 2016, ApJ, 826, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Kehrig, C., Oey, M. S., Crowther, P. A., et al. 2011, A&A, 526, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kehrig, C., Vílchez, J. M., Pérez-Montero, E., et al. 2015, ApJ, 801, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Kehrig, C., Vílchez, J. M., Guerrero, M. A., et al. 2018, MNRAS, 480, 1081 [NASA ADS] [Google Scholar]
- Kewley, L. J., Yuan, T., Nanayakkara, T., et al. 2016, ApJ, 819, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R. 1969, A&A, 3, 83 [NASA ADS] [Google Scholar]
- Knobel, C., Lilly, S. J., Iovino, A., et al. 2012, ApJ, 753, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Faber, S. M., Ferguson, H. C., et al. 2011, ApJS, 197, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Richstone, D. 1995, ARA&A, 33, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Kriek, M., van Dokkum, P. G., Labbé, I., et al. 2009, ApJ, 700, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G., Puget, J.-L., & Dole, H. 2005, ARA&A, 43, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N. 2012, ARA&A, 50, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Cassata, P., Cucciati, O., et al. 2013, A&A, 559, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Fèvre, O., Tasca, L. A. M., Cassata, P., et al. 2015, A&A, 576, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Ekström, S., Meynet, G., et al. 2014, ApJS, 212, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Leja, J., Johnson, B. D., Conroy, C., van Dokkum, P. G., & Byler, N. 2017, ApJ, 837, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Le Fèvre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Lo Faro, B., Buat, V., Roehlly, Y., et al. 2017, MNRAS, 472, 1372 [NASA ADS] [CrossRef] [Google Scholar]
- Luo, B., Brandt, W. N., Xue, Y. Q., et al. 2017, ApJS, 228, 2 [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [NASA ADS] [CrossRef] [Google Scholar]
- Marino, R. A., Cantalupo, S., Lilly, S. J., et al. 2018, ApJ, 859, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Maseda, M. V., Brinchmann, J., Franx, M., et al. 2017, A&A, 608, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, J. S. 1990, ARA&A, 28, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Matthee, J., & Schaye, J. 2018, MNRAS, 479, L34 [NASA ADS] [Google Scholar]
- Matthee, J., Sobral, D., Boone, F., et al. 2017, ApJ, 851, 145 [NASA ADS] [CrossRef] [Google Scholar]
- McClelland, L. A. S., & Eldridge, J. J. 2016, MNRAS, 459, 1505 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, W. 2010, in Proceedings of the 9th Python in Science Conference, eds. S. van der Walt, & J. Millman, 51 [Google Scholar]
- McLure, R. J., Dunlop, J. S., de Ravel, L., et al. 2011, MNRAS, 418, 2074 [NASA ADS] [CrossRef] [Google Scholar]
- McLure, R. J., Dunlop, J. S., Cullen, F., et al. 2018, MNRAS, 476, 3991 [NASA ADS] [CrossRef] [Google Scholar]
- Meurer, G. R., Heckman, T. M., & Calzetti, D. 1999, ApJ, 521, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Miralles-Caballero, D., Díaz, A. I., López-Sánchez, Á. R., et al. 2016, A&A, 592, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muratov, A. L., Kereš, D., Faucher-Giguère, C.-A., et al. 2015, MNRAS, 454, 2691 [NASA ADS] [CrossRef] [Google Scholar]
- Murayama, T., Taniguchi, Y., Scoville, N. Z., et al. 2007, ApJS, 172, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Naidu, R. P., Oesch, P. A., Reddy, N., et al. 2017, ApJ, 847, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Nakajima, K., Fletcher, T., Ellis, R. S., Robertson, B. E., & Iwata, I. 2018, MNRAS, 477, 2098 [NASA ADS] [CrossRef] [Google Scholar]
- Nanayakkara, T., Glazebrook, K., Kacprzak, G. G., et al. 2017, MNRAS, 468, 3071 [NASA ADS] [CrossRef] [Google Scholar]
- Narayanan, D., Conroy, C., Davé, R., Johnson, B. D., & Popping, G. 2018, ApJ, 869, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Nozawa, T., Asano, R. S., Hirashita, H., & Takeuchi, T. T. 2015, MNRAS, 447, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Ono, Y., Ouchi, M., Harikane, Y., et al. 2018, PASJ, 70, S10 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E., & Cohen, R. D. 1982, ApJ, 261, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Ouchi, M., Harikane, Y., Shibuya, T., et al. 2018, PASJ, 70, S13 [NASA ADS] [CrossRef] [Google Scholar]
- Pacifici, C., da Cunha, E., Charlot, S., et al. 2015, MNRAS, 447, 786 [NASA ADS] [CrossRef] [Google Scholar]
- Patrício, V., Richard, J., Verhamme, A., et al. 2016, MNRAS, 456, 4191 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Joss, P. C., & Hsu, J. J. L. 1992, ApJ, 391, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Raiter, A., Schaerer, D., & Fosbury, R. A. E. 2010, A&A, 523, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reddy, N. A., Kriek, M., Shapley, A. E., et al. 2015, ApJ, 806, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Steidel, C. C., Pettini, M., & Bogosavljević, M. 2016a, ApJ, 828, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Steidel, C. C., Pettini, M., Bogosavljević, M., & Shapley, A. E. 2016b, ApJ, 828, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Oesch, P. A., Bouwens, R. J., et al. 2018, ApJ, 853, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Rigby, J. R., Bayliss, M. B., Chisholm, J., et al. 2018, ApJ, 853, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Salmon, B., Papovich, C., Long, J., et al. 2016, ApJ, 827, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
- Sana, H., de Koter, A., de Mink, S. E., et al. 2013, A&A, 550, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanders, R. L., Shapley, A. E., Kriek, M., et al. 2015, ApJ, 799, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, R. L., Shapley, A. E., Kriek, M., et al. 2016, ApJ, 825, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, B. D., & Sembach, K. R. 1996, ApJ, 470, 893 [NASA ADS] [CrossRef] [Google Scholar]
- Schaerer, D. 2002, A&A, 382, 28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaerer, D. 2003, A&A, 397, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaerer, D., Fragos, T., & Izotov, Y. I. 2019, A&A, 622, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmutz, W., Leitherer, C., & Gruenwald, R. 1992, PASP, 104, 1164 [NASA ADS] [CrossRef] [Google Scholar]
- Scodeggio, M., Guzzo, L., Garilli, B., et al. 2018, A&A, 609, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N., Faisst, A., Capak, P., et al. 2015, ApJ, 800, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Senchyna, P., & Stark, D. P. 2019, MNRAS, 484, 1270 [NASA ADS] [CrossRef] [Google Scholar]
- Senchyna, P., Stark, D. P., Vidal-García, A., et al. 2017, MNRAS, 472, 2608 [NASA ADS] [CrossRef] [Google Scholar]
- Shapley, A. E., Steidel, C. C., Pettini, M., & Adelberger, K. L. 2003, ApJ, 588, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Shibuya, T., Ouchi, M., Harikane, Y., et al. 2018, PASJ, 70, S15 [NASA ADS] [CrossRef] [Google Scholar]
- Shields, J. C., & Kennicutt, Jr., R. C. 1995, ApJ, 454, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Shirazi, M., & Brinchmann, J. 2012, MNRAS, 421, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., Götberg, Y., & de Mink, S. E. 2018, MNRAS, 475, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Matthee, J., Darvish, B., et al. 2015, ApJ, 808, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Matthee, J., Brammer, G., et al. 2018, MNRAS, 2683, 1 [Google Scholar]
- Spitzer, L. 1978, Physical Processes in the Interstellar Medium (New York: Wiley-Interscience), 333 [Google Scholar]
- Stanway, E. R., Eldridge, J. J., & Becker, G. D. 2016, MNRAS, 456, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Adelberger, K. L., Shapley, A. E., et al. 2003, ApJ, 592, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Rudie, G. C., Strom, A. L., et al. 2014, ApJ, 795, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Strom, A. L., Pettini, M., et al. 2016, ApJ, 826, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Strom, A. L., Steidel, C. C., Rudie, G. C., et al. 2017, ApJ, 836, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Szécsi, D., Langer, N., Yoon, S.-C., et al. 2015, A&A, 581, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tapken, C., Appenzeller, I., Gabasch, A., et al. 2006, A&A, 455, 145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tasca, L. A. M., Le Fèvre, O., Ribeiro, B., et al. 2017, A&A, 600, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Theios, R. L., Steidel, C. C., Strom, A. L., et al. 2018, ApJ, submitted [arXiv:1805.00016] [Google Scholar]
- Thuan, T. X., & Izotov, Y. I. 2005, ApJS, 161, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Tumlinson, J., & Shull, J. M. 2000, ApJ, 528, L65 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tumlinson, J., Giroux, M. L., & Shull, J. M. 2001, ApJ, 550, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Tumlinson, J., Shull, J. M., & Venkatesan, A. 2003, ApJ, 584, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzella, E., Cristiani, S., Dickinson, M., et al. 2008, A&A, 478, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanzella, E., De Barros, S., Cupani, G., et al. 2016, ApJ, 821, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Vidal-García, A., Charlot, S., Bruzual, G., & Hubeny, I. 2017, MNRAS, 470, 3532 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkins, S. M., Coulton, W., Caruana, J., et al. 2013, MNRAS, 435, 2885 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, R. E., Blacker, B., Dickinson, M., et al. 1996, AJ, 112, 1335 [NASA ADS] [CrossRef] [Google Scholar]
- Wirth, G. D., Trump, J. R., Barro, G., et al. 2015, AJ, 150, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Wise, J. H., Turk, M. J., Norman, M. L., & Abel, T. 2012, ApJ, 745, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Wise, J. H., Demchenko, V. G., Halicek, M. T., et al. 2014, MNRAS, 442, 2560 [NASA ADS] [CrossRef] [Google Scholar]
- Wiseman, P., Schady, P., Bolmer, J., et al. 2017, A&A, 599, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wofford, A., Charlot, S., Bruzual, G., et al. 2016, MNRAS, 457, 4296 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, T. E., & Gilfanov, M. 2016, MNRAS, 455, 1770 [NASA ADS] [CrossRef] [Google Scholar]
- Xiao, L., Stanway, E. R., & Eldridge, J. J. 2018, MNRAS, 477, 904 [NASA ADS] [CrossRef] [Google Scholar]
- Yamasawa, D., Habe, A., Kozasa, T., et al. 2011, ApJ, 735, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, Y., Zabludoff, A. I., Davé, R., et al. 2006, ApJ, 640, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Zafar, T., Møller, P., Watson, D., et al. 2015, A&A, 584, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zagury, F. 2017, Astron. Nachr., 338, 807 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: He II λ1640 detections from other public surveys
We present a brief description of the public surveys we exploited to investigate He II λ1640 detections below. A summary is presented in Table A.1, accompanied by individual sources in Table A.2.
GOODS FORS2. The Great Observatories Origins Deep Survey (GOODS) FORS2 sample (Vanzella et al. 2008) comprises 1225 spectra of individual galaxies in the GOODS South field with a R = 660, which corresponds to 13 Å at 8600 Å. Out of 1166 galaxies in the GOODS FORS2 catalogue with a redshift quality flag A, B, or C, we selected 131 galaxies with spectroscopic redshifts between 2.65 < z < 5.71. However, as a result of variations in the slit-position in the masks, 33 galaxies fall outside the desired spectral coverage and were removed from the sample. From the remaining 98 galaxies, we removed galaxies that were contaminated with high continuum noise and broad-line AGN to select three galaxies with possible He II λ1640 detections through visual examination.
GOODS VIMOS. The VIMOS ESO/GOODS spectroscopic survey was designed to complement the GOODS FORS2 survey by increasing the optical completeness and sky coverage over the GOODS-South field (Balestra et al. 2010). The final catalogue4 comprises 4602 unique object spectra obtained with the VIMOS spectrograph with two resolution gratings: a low-resolution mode with a nominal R = 180 covering 3500 − 6900 Å, and a medium-resolution mode with R = 580 covering 4000 − 10 000 Å. Here, we combined galaxies observed in both modes to investigate He II λ1640 detections within the redshift range 1.13 < z < 5.10 and obtained 854 galaxies with with a redshift quality flag of A or B. We visually examined the spectra of the 854 galaxies and selected five spectra with tentative He II λ1640 detections.
VANDELS. The VANDELS survey (McLure et al. 2018) exploits multi-wavelength imaging and HST grism coverage in CANDELS UDS and CDFS footprints footprints (Grogin et al. 2011; Koekemoer et al. 2011) to investigate the properties of high-redshift galaxies through emission and absorption line spectroscopy using the VLT/VIMOS. The survey primarily targets bright (HAB < 27) star-forming galaxies between 2.5 < z < 5.5. The observations for the VANDELS survey have been carried out using the CG475 filter with the medium-resolution grism, and thus closely spaced lines are blended. VANDELS UDS catalogue contains 464 targets, out of which 292 have a zflg > 1 and fall within 1.9 ≲ z ≲ 5, the He II λ1640 wavelength coverage of the CG475 filter. We visually inspected the spectra of these 292 galaxies. Similarly, the CDFS catalogue contains 415 galaxies, out of which 285 galaxies were selected for visual inspection. After removing broad-line AGN, we selected 6 and 2 galaxies from the UDS and CDFS fields, respectively, with tentative He II λ1640 detections.
VIPERS. The VIMOS Public Extragalactic Redshift Survey (VIPERS; Garilli et al. 2014; Scodeggio et al. 2018) comprises 91 507 galaxies obtained with the VLT/VIMOS spectrograph using the R = 220 grism covering a wavelength range of 5500 − 9500 Å. Spectroscopic follow-up targets were selected from the CFHTLS survey (Heymans et al. 2012; Erben et al. 2013) covering a total FoV of ∼224 arcmin2. In the two VIPERS fields, we found 50 galaxies between 3.0 < z < 4.5 (the wavelength coverage for He II λ1640 detections in the VIMOS mode implemented by VIPERS) with a redshift quality flag of zflg-10 > 1. We visually inspected all spectra and found 8 galaxies with tentative He II λ1640 detections, but all of these galaxies show evidence of broad-line AGN.
VUDS. The VIMOS Ultra-Deep Survey (VUDS; Le Fèvre et al. 2015) obtained spectra of ∼10 000 galaxies up to IAB ∼ 27 using VLT/VIMOS. The Data Release 1 (Tasca et al. 2017) contains all data obtained in the CANDLES COSMOS and CDFS fields using the low-resolution grism and comprises 677 galaxy redshifts. VUDS observations were carried out to obtain the maximum wavelength coverage, and hence observations comprise ∼14 h per pointing per grism using the LRBLUE (3600 − 6700 Å) and LRRED (5500 − 9350 Å) grisms. This provides a total wavelength coverage between 3600 and 9350 Å. Therefore, VUDS obtained He II λ1640 coverage between 1.2 < z < 5.1 and comprises 132 and 122 galaxies each in COSMOS and CDFS fields with a redshift quality flag zflags > 1. We visually inspected all spectra and identified 3 galaxies with tentative He II λ1640 detections. We note that the full data set of VUDS contains additional He II λ1640 detections, as shown by Amorín et al. (2017).
zCOSMOS bright survey. zCOSMOS survey (Lilly et al. 2007) used the VLT/VIMOS over 600 h between 2005 and 2010 to obtain rest-frame UV and optical spectra of galaxies in the COSMOS field. The survey was designed in two parts: zCOSMOS-bright to obtain spectra of galaxies with IAB < 22.5 using the medium-resolution grism (R ∼ 600) with a spectral coverage between 5550 and 9650 Å, and zCOSMOS-deep to obtain preferentially high-redshift sources with a magnitude limit of BAB ∼ 25 using the low-resolution (R ∼ 200) blue grism covering a spectral range of 3600 − 6800 Å. The public zCOSMOS bright catalogue contains 20 689 galaxy spectra, out of which 48 fall within 2.4 < z < 4.8, the wavelength range to obtain He II λ1640 in the observed VIMOS configuration. We visually inspected all spectra and identified 13 galaxies with tentative He II λ1640 detections, but 11 galaxies we selected show either broad C III] or C IV emission lines, suggesting the presence of an AGN, thus the final sample presented contains 2 galaxies. The zCOSMOS deep survey would provide a better selection of higher-z targets, but the data are yet to be publicly released. Additionally, we explored the K20 survey (Cimatti et al. 2002) and did not find any convincing He II λ1640 emitters.
Catalogue of other He II λ1640 emitters.
Non-MUSE tentative He II λ1640 sample.
Appendix B: Analysis of the Gutkin et al. (2016) rest-UV emission line ratio models used in our analysis
The Gutkin et al. (2016) models are parametrised by the following six parameters: the interstellar metallicity (ZISM), the zero-age ionisation parameter at the Stromgren radius (Us), the dust-to-metal ratio (ξd), the carbon-to-oxygen abundance ratio (C/O), the hydrogen gas density (nH), and the upper mass cut-off of the IMF (mup). We used the following emission lines for our analysis: He II λ1640, [C III]=([C III]λ1907+C III]λ1909), O III](=O III]λ1661+O III]λ1666), and Si III](=Si III]λ1883+Si III]λ1892). For each emission line ratio diagnostic, we selected a sub-sample of galaxies with S/N ≥ 3 for the emission lines considered in that specific diagnostic.
 |
Fig. B.1. Similar to Fig. 6, but the emission line ratio diagnostic plots are zoomed out to demonstrate the dependence of emission line ratios on model parameters. |
In Fig. B.1 we show the model distribution in C III]/O III] vs. Si III]/C III], C III]/He II λ1640 vs. O III]/He II λ1640, and O III]/He II λ1640 vs. C III]/Si III] emission line ratio diagnostics. The line ratios of the model tracks from Gutkin et al. (2016) computed with nH = 100 cm−3, ξd = 0.5, mup = 300 M⊙ for (C/O)/(C/O)⊙ ratios of 0.14, 0.20, and 0.27, ZISM of 0.004, 0.008, 0.017, 0.02, 0.04, and log10(Us) between −1.0 and −4.0 in increments of 0.5 are shown in this figure. Here we briefly discuss the influence of the model parameters on the emission line ratios.
Increasing the C/O ratio results in an increase of the C abundance compared to other heavy elements, thus we observe an increase in the C III]/O III] ratio and a decrease in the Si III]/C III] ratio. When all other parameters are fixed, the tracks move towards the upper left as a function of C/O ratio in the C III]/O III] vs. Si III]/C III] line ratio diagram. Similarly, in the C III]/He II λ1640 vs. O III]/He II λ1640 line ratio diagram, the prominent rise in C III] results in higher C III]/He II λ1640, moving the tracks upwards, while tracks move leftwards in O III]/He II λ1640 vs. C III]/Si III] line ratio diagram. However, because C is a prominent coolant, it has been shown that C III] emission does not linearly correlate with the C/O ratio (e.g. Jaskot & Ravindranath 2016).
In the C III]/O III] vs. Si III]/C III] line ratio diagram, increasing nH while keeping the other parameters fixed moves the tracks towards the lower right, with the largest shift visible at higher metallicities and higher ionisation parameters (which increase from top to bottom). At higher nH, excited atoms will favour collisional de-excitation rather than radiative de-excitation. Therefore, increasing the nH will result in stronger collisional emission lines. However, the infrared fine structure transitions have a lower critical density than the UV/optical transitions, and thus at higher densities, cooling through UV/optical line transitions becomes prominent. At higher metallicities infrared transitions dominate the cooling process, therefore the shift in change is higher for rest-UV lines at higher metallicities. Similarly, the C III]/He II λ1640 vs. O III]/He II λ1640 and O III]/He II λ1640 vs. C III]/Si III] line ratio diagrams, which are relatively insensitive to changes in nH at lower metallicities, show some dependence at higher metallicities that is driven by the increase in strength of UV cooling lines that compensate for the lack of infrared transitions at higher nH.
At higher Us, H II regions become more compact and closer to the ionisation inner boundaries, favouring high-ionisation lines. Therefore, the O III] line becomes stronger than C III] and C III] becomes stronger by a lesser amount than Si III], resulting in a larger vertical shift and a slight horizontal shift to lower values with increasing Us when other parameters are fixed. Given the increase in UV line transitions and increase in high-ionisation line strength, at higher Us the change of line ratios is more prominent as a function of nH. With increasing Us, the models in C III]/He II λ1640 vs. O III]/He II λ1640 line ratio diagram show a curved shape where the tracks reach a maximum C III]/He II λ1640 and O III]/He II λ1640 value, after which all line fluxes reduce, with C III] showing the largest drop because of the lower ionisation potential of C++ (24.38 eV) compared to O++ (35.12 eV). In O III]/He II λ1640 vs. C III]/Si III] line ratio diagram, the higher metallicity models plateau towards higher Us.
When ξd is increased with other parameters fixed, the tracks are moved towards the left as a result of a balance between depletion of metals and electron temperature. An increase in ξd results in fewer coolants in the gas phase, thus the electron temperature and cooling through collisionally excited lines increases. However, in the Gutkin et al. (2016) models, the metals have relative differences in depletion (see Table 1 of Gutkin et al. 2016) and thus at higher metallicities the rise of electron temperature due to depletion of metal coolants is more prominent. In the C III]/O III] vs. Si III]/C III] line ratio diagram, given that Si has the highest amount of depletion compared to C and O, the Si III] intensity drops more prominently with the increase in ξd, resulting in the observed shift of the tracks to the right. Similarly, in the C III]/He II λ1640 vs. O III]/He II λ1640 line ratio diagram, C III] has the highest depletion, and the highest metallicity models show the lowest line ratios at high Us. At low ξd, high-metallicity models show a lower drop in line ratios at extreme Us driven by the rise in electron temperature that is caused by depletion of high-order metals. This is also seen in the O III]/He II λ1640 vs. C III]/Si III] line ratio diagram, where only higher metallicity models show evolution with ξd in the O III]/He II λ1640 ratio. Models at all metallicities show strong evolution in the C III]/Si III] ratio because the depletion factor of Si is about twice as high as that of C.
Appendix C: Effects of dust in the rest-UV
Here we provide a detailed discussion on the role of dust in photo-ionisation modelling and interpreting observed spectra. To the first order, dust grains primarily absorb UV light and re-emit the absorbed energy as IR emission (Spitzer 1978). The shorter wavelength light has a higher optical depth, thus the rest-UV regime probed in our study undergoes the highest amount of extinction, which means that accurate calibration and correction of dust attenuation is required to probe the underlying properties of the ISM of our galaxies. However, our understanding of dust at high redshift is limited, and variations in the dust-grain size distribution and variations in the spatial geometry of stars and dust have been shown to contribute significantly to the rest-UV dust attenuation properties (e.g. Reddy et al. 2015, 2016a).
Interstellar dust originates in natural condensation of stellar atmospheres and stellar winds and supernovae that release heavy elements produced by massive stars to the ISM (Lagache et al. 2005), and ∼30 − 50% of released metals condense into dust grains (Draine et al. 2007). Dust-grain models of local star-forming regions have been calibrated from abundances of the heavy elements, absorption, and scattering properties from rest-UV to rest-far-IR, IR emission properties, and polarisation of absorbed and emitted light from local star-forming regions. Results have shown that local regions primarily consist of a mixture of amorphous silicate and carbonaceous grains with a distribution in grain size (Draine 2003). Because of observational constraints in performing such a diverse analysis of emission line properties, our understanding of the dust-grain properties of high-redshift galaxies is limited and studies are yet to break the degeneracies between larger covering fraction of dust and differences in dust-grain size distributions (e.g. Reddy et al. 2015).
The uncertainties in dust grain models lead to three interdependent problems in our analysis. We describe them below.
Attenuation. Firstly, large dust grains lead to high scattering cross-sections, thus the dust composition results in complexities for dust absorption and scattering of rest-UV light. However, the shattering, grain growth, and coagulation of dust grains is a strong function of the SFH and IMF (Asano et al. 2013; Nozawa et al. 2015) and therefore requires strong constraints on cosmic galaxy evolution models to fully comprehend the physics of dust grains at high redshift. To first order, large dust grains that undergo efficient dissociation through strong UV radiation and supernova shocks and overabundance of silicate grains (Zafar et al. 2015) result in smaller grain sizes, primarily in the presence of young O and B stars. Smaller grains have lower scattering cross sections, which steepens the attenuation law in the rest-UV. Therefore, in the context of rest-UV emission lines, the uncertainty in the wavelength-dependent attenuation contributes to differences in the dust-corrected emission line ratios to the intrinsic emission line ratios. In Sect. 4.1.1 we discussed the implication of the dust law on the rest-UV emission line ratios.
Metal depletion. Secondly, our limited understanding of the depletion of metals onto dust grains adds complexity to photo-ionisation modelling. Dust grains, which consist of metals depleted from the gas phase, affect the UV radiation that is produced by the stars through absorption and scattering of incident radiation and influence the radiation pressure, photoelectric heating, and collisional cooling within the ISM (Shields & Kennicutt 1995; Groves et al. 2004a). Therefore, understanding the processes and rates that cause metals to deplete to dust is necessary to constrain the heating and cooling mechanisms of the ISM. Different elements deplete into dust at varying rates (Savage & Sembach 1996; Jenkins 2009), thus constraining relative abundances of refractory (elements that deplete rapidly to dust, e.g. Fe and Ni) to volatile elements (elements with lower depletion rates, e.g. Zn, P, and S) is necessary to probe fractions of metals that are locked within dust, but is observationally challenging. Dustier systems have been shown to have a significantly higher fraction of metals depleted onto dust grains, with a universal sequence observed at low and high-z systems (e.g. Brinchmann et al. 2013; Steidel et al. 2016; Wiseman et al. 2017; De Cia 2018) At high redshift, studies using gamma-ray burst damped Lyman-alpha absorbers have shown that the dust-to-metal ratios positively correlate with the ISM metallicity, but with significantly lower dust-metal ratios than in the Milky-Way (Wiseman et al. 2017). However, at high-z, intrinsic biases in selecting damped Lyman-alpha absorbers to probe dust properties and the confusion between circum-galactic dust absorption to ISM dust absorption introduce additional uncertainties. Because of these complications, photo-ionisation models make simplifying assumptions to compute heavy-element abundances and their depletion factors, such as the total mass of carbon depleted in dust that produces the carbonaceous grains, and most other heavy elements produce varieties of silicate grains (e.g. Groves et al. 2004a). However, the validity and consequences of such effects are yet to be explored.
Dust dissociation. Energetic events that occur within galaxies, such as star formation, provide high-energy photons that have been shown to destroy dust grains (e.g. Draine & Salpeter 1979; Yamasawa et al. 2011). When the collisional and photo-electrical charging rates balance in a dust grain, the full radiation pressure acting on the grain would rapidly accelerate the grain to its terminal velocity, thus increasing the probability of shattering through high-velocity grain–grain collisions. However, the equilibrium of charging rate and shattering cross-sections are a function of grain size and composition (Groves et al. 2004a), and the process leading to larger grains shattering to smaller ones until the sizes are small enough to dissociate through stochastic heating is yet to be incorporated into photo-ionisation models. The extent to which such processes would affect our analysis is unclear.
Quantifying the amount of metals depleted from the gas to the dust-phase and the dust dissociation is imperative to probe the influence of young stars on the ISM. The balance between these processes influences the gas-phase metallicity of the ISM. Metal coolants are important in regulating the temperature structure of the ISM. With the increase of the dust-to-metal ratio, the dust optical depth increases, which reduces the electron temperature through increased absorption of high-energy photons (Gutkin et al. 2016). Thus, the change in gas-to-dust ratio of galaxies results in multiple effects that influence the strength of the rest-UV emission line features, and accurate constraints of metal depletion and dust dissociation is important to explore the properties of the ISM through emission line ratios.
Only a handful of evolutionary models account for the role of dust in chemical evolution (e.g. Gioannini et al. 2017). In the Gutkin et al. (2016) photo-ionisation models considered in our analysis, the metal depletion uses the default CLOUDY values with updates from Groves et al. (2004b). In the three emission line ratios we explored in our analysis, C III]/O III] vs. Si III]/C III], C III]/He II λ1640 vs. O III]/He II λ1640, and O III]/He II λ1640 vs. C III]/Si III], the limited S/N of our sample and degeneracies between the variable parameters constrains our understanding of accurately interpreting rest-UV emission line diagnostics. Additionally, the dust attenuation law of high-z galaxies also plays a role in obtaining accurate intrinsic emission line ratios, especially for lines that are not far apart in wavelength space.
Several studies have explored the dust attenuation law of high-redshift star-forming galaxies (e.g. Wilkins et al. 2013; Reddy et al. 2015, 2016a,b, 2018; Scoville et al. 2015; Bouwens et al. 2016; Salmon et al. 2016; Lo Faro et al. 2017; Cullen et al. 2018) with some results favouring star-burst like attenuation curves similar to Calzetti et al. (2000) and others suggesting the need for flexible attenuation laws to constrain the dust of these systems. Dust attenuation from dust-to-metal ratios has been shown to introduce significant discrepancies compared to SED-derived attenuation estimates (Wiseman et al. 2017) thus has been shown not to be a good proxy to estimate dust attenuation.
Intrinsic galaxy spectra for our analysis were obtained using extinction values derived from FAST (except for the quasar field, where the UV slope A(V)β was used because we lack broad-band photometry, but we show in Fig. 1 that A(V)β shows good agreement with A(V)SED) assuming a Calzetti et al. (2000) dust attenuation law. If the physics of dust grains in the early Universe is quite different, variations in the total-to-selective dust extinction will introduce discrepancies from the z ∼ 0 calibrated attenuation laws. Additionally, variations with dust geometries have shown that nebular emission lines originating from the dense H II regions in the vicinity of young O,B stars have higher optical depths (Calzetti et al. 2000; Reddy et al. 2015; Theios et al. 2018), with z ∼ 0 star-forming galaxies showing about twice more attenuation for nebular emission lines than the continuum (Calzetti et al. 2000). However, in the context of our work, we have ruled out that effects of the considered dust law or dust sightlines (see Fig. 14) have significant effect on the analysis of our observed emission line ratios.
All Tables
All Figures
 |
Fig. 1. Comparison between A(V)β and A(V)SED. Galaxies from MUSE UDF with CONFID = 3 and z = 2.2 − 4.7 with continuum S/N ≳ 3 are shown here and are colour-coded by their mass. The one-to-one line is shown as a black dashed line. The solid black line shows the linear regression model fit to the data along with its 1σ uncertainty (computed using 1000 bootstrap resamples) shaded in grey. |
| In the text | |
 |
Fig. 2. Spectra (blue) of the MUSE He II λ1640 detections with their respective noise spectrum (red). All spectra are shown at their rest-frame wavelength and are normalised at ∼1600 Å. The ID, field, and the spectroscopic redshift of each target is shown in the panels. The green vertical lines indicate selected rest-UV emission and absorption features. |
| In the text | |
 |
Fig. 2. continued. The last three panels show the spectra dominated by AGN activity. |
| In the text | |
 |
Fig. 3. Top panel: He II λ1640 flux as a function of redshift. He II λ1640 detections from MUSE are shown as stars and are colour-coded depending on their median continuum flux at ∼1640 Å. He II λ1640 detections from other surveys within the plot range are shown by diamonds. The redshift-dependent MUSE wavelength coverage of a few prominent rest-UV features are shown at the top of the panel. Bottom panel: M1500 as a function of redshift for the MUSE He II λ1640 detected and He II λ1640 non-detected galaxies (set B, see Sect. 3.2). |
| In the text | |
 |
Fig. 4. Similar to Fig. 2, but for the mass and redshift binned stacked spectra of the MUSE He II λ1640 detected sample. The corresponding bin parameters are shown in each panel. |
| In the text | |
 |
Fig. 5. Similar to Fig. 4, but for the stacks of He II λ1640 undetected sample. |
| In the text | |
 |
Fig. 6. Rest-frame UV emission line ratios of the MUSE He II λ1640 sample. Left panel: C III]/O III] vs. Si III]/C III] ratios. Individual galaxies with S/N > 2.5 for all four emission lines are shown as stars. Limits are shown as arrows. The tracks are from the Gutkin et al. (2016) models, which are powered by star-formation. Each set of tracks with the same colour show three C/O ratios, and the regions between the minimum and maximum C/O tracks are shaded by the same colour. From top to bottom, the ionisation parameter ncreases. Where available, line ratios from Patrício et al. (2016), Senchyna et al. (2017), and Berg et al. (2018) are shown for comparison. MUSE line ratios of the Lyman continuum emitting candidate from Naidu et al. (2017) are shown by the filled green star. Centre panel: similar to the left panel, but C III]/He II λ1640 vs. O III]/He II λ1640 emission line ratios, where detections are defined as galaxies with S/N > 2.5 for all three emission lines. Right panel: similar to the left panel, but O III]/He II λ1640 vs. C III]/Si III] emission line ratios, where detections are defined as galaxies with S/N > 2.5 for all four emission lines. |
| In the text | |
 |
Fig. 7. Rest-frame UV emission line ratios of the MUSE stacked galaxies compared with the Gutkin et al. (2016) models. Panels from left to right are similar to Fig. 6. Galaxies are stacked in mass and redshift bins, and the line width of the markers increases with mass and redshift. Limits resemble stacks with emission lines (considered in each panel) lower than the 3σ error limit. For such stacks, 3σ error is used as the respective line flux. Top panel: MUSE-stacked sample for stellar mass bins log10(M*/M⊙) < 9.5, 9.5 < log10(M*/M⊙) < 10.0, and log10(M*/M⊙) > 10.0. Bottom panel: MUSE-stacked sample for redshift bins z < 2.5, 2.5 < z < 3, and z > 3. |
| In the text | |
 |
Fig. 8. Rest-frame UV emission line ratios of the MUSE He II λ1640 sample compared with the model line ratios computed by Xiao et al. (2018) using BPASS binary stellar population models. Here we show the C III]/He II λ1640 vs. O III]/He II λ1640 line ratios for the MUSE He II λ1640 detected sample. Individual galaxies with S/N ≥ 2.5 for all three emission lines are shown as stars. Galaxies that fail the S/N cut are shown as arrows. The symbol size is proportional to the age from the onset of the star formation burst between t = 1 Myr (smallest) and t = 50 Myr. Models are computed with log10(nH)=1.0 with varying Us between −2.5 and −1.5. BPASS Z⊙ = 0.02. |
| In the text | |
 |
Fig. 9. Xiao et al. (2018) rest-UV emission line ratio evolution as a function of time. Here we show in the left panel C III]/He II λ1640 vs. time and in the right panel O III]λ1666/He II λ1640 vs. time for the BPASS binary models computed with a log10(nH)=1.0 and Us = −1.5 and Us = −3.5 (upper and lower limits of each shaded region, respectively) at different metallicities between 1 Z⊙ and 1/200th Z⊙. We only show a limited set of model metallicities for clarity. The black horizontal lines show the line ratios of the MUSE He II λ1640 sample. |
| In the text | |
 |
Fig. 10. EW comparison of the MUSE He II λ1640 sample using BPASS stellar population models. Left panel: [C III]λ1907+C III]λ1909 EW vs. He II λ1640 EW. Right panel: O III]λ1666 EW vs. He II λ1640 EW. Galaxies with S/N ≥ 2.5 are shown by stars, and others are shown as lower limits to the EW as triangles. We compare our observed EWs with model tracks from the Xiao et al. (2018) BPASS binary tracks. Models are computed for a log10(nH)=1.0 and Us = −1.5 at different metallicities between 2 Z⊙ and 1/200th Z⊙. The size of the symbols increases with time. EWs from the literature are also shown for comparison. |
| In the text | |
 |
Fig. 11. Left panel: example BPASS v2.1 model spectra of a single-burst stellar population after 5 Myr from the star burst. The single (dashed) and binary (continuous) model predictions are shown for different IMFs (Γ = −1.0, −1.35, −1.70) with a high-mass IMF cutoff at 300 M⊙. The dashed black vertical lines mark λ = 228 Å, 353 Å, 508 Å, and 912 Å, below which He+, O++, C++, and H ionising photons are produced. Right panel: zoomed-in region λ < 275Å clearly showing the difference in flux around He+ ionising limits. |
| In the text | |
 |
Fig. 12. Top panels: BPASS stellar population predictions for the evolution of the number of ionisation photons produced by a single instantaneous star burst (106 M⊙) stellar population as a function of time. From left to right: H and He+ ionisation photons computed by integrating the spectra at λ = 228 Å and 912 Å, respectively. The models are computed at Z = 0.0001, 0.001, 0.002, 0.01, and 0.02 for binary models with different IMFs (Γ = −1.0, −1.35, and − 1.70) and IMF upper mass cutoffs (100 M⊙ and 300 M⊙). Bottom panels: similar to the top panels, but showing the evolution of ξion of H and He+ as a function of time. |
| In the text | |
 |
Fig. 13. Fraction of observed He+ ionising photons compared to the Xiao et al. (2018) model expectations as a function of observed He II λ1640 luminosity of the MUSE He II λ1640 sample. From left to right, we show the He+ model predictions computed for three metallicities, Z = 0.01, 0.001, and 0.0001 with log10(nH)=1.0 and Us = −1.5 for different times between 1 and 20 Myr from the onset of the star burst. The dashed horizontal line indicates y = 0, where there is no difference between observations and model predictions. |
| In the text | |
 |
Fig. 14. Rest-frame UV emission line ratios of the MUSE He II λ1640 sample computed with different dust laws. The panels are similar to Fig. 6, but the Gutkin et al. (2016) models are removed for clarity. Only the galaxies with S/N ≥ 2.5 for emission line considered in each panel are shown in the figure. Observed emission line ratios are shown by stars. f = 1 and f = 2 resemble dust corrections that are applied considering no additional attenuation and twice the additional attenuation for ionised gas regions (computed using the Cardelli et al. 1989 attenuation law) compared to stars (computed using the Calzetti et al. 2000 attenuation law). We further show the distribution of the line ratios using the Cardelli et al. (1989), Calzetti et al. (2000), and Reddy et al. (2015, 2016a) attenuation laws. |
| In the text | |
 |
Fig. 15. Left panel: comparison of He II λ1640 line flux measurements obtained for different He II λ1640 line flux parametrisations. We compare the He II λ1640 line flux measurements of galaxies with an S/N > 3 obtained using an independently fit He II λ1640 single-Gaussian fit with measurements obtained by (1) fitting He II λ1640 using a single Gaussian whose line width was fixed with the other emission lines (diamonds) and (2) a double Gaussian profile whose one-component line width was fixed with the other emission lines (stars). For the double-Gaussian fit, we only consider the nebular component for comparison. Right panel: comparison of the FWHM of [C III]λ1907 with the FWHM of He II λ1640 fit independently of the other nebular emission lines. The solid line denotes x = y and the dashed line denotes x = 2y. |
| In the text | |
 |
Fig. B.1. Similar to Fig. 6, but the emission line ratio diagnostic plots are zoomed out to demonstrate the dependence of emission line ratios on model parameters. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



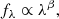
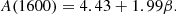
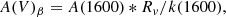
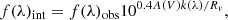
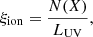
![$$ \begin{aligned} C=\frac{L_{\mathrm{C}\,iii ]\,\mathrm{model}}}{L_{\mathrm{C}\,iii ]\,\mathrm{data}}} \end{aligned} $$](/articles/aa/full_html/2019/04/aa34565-18/aa34565-18-eq6.gif)