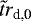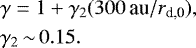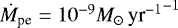© ESO 2019

1 Introduction

Earth-size planets are being discovered in habitable zones (HZs) in exoplanetary systems. These HZs are defined as a range of orbital radius, in which liquid water can exist on the planetary surface if H₂O exists there. However, as long as equilibrium temperature is concerned, H₂O ice grains condense only well beyond the HZs, because the gas pressure of protoplanetary disks is many orders of magnitude lower than that of planetary atmosphere and the condensation temperature is considerably lower than that at 1 atm. Hereafter, we simply call H₂O in a solid/liquid phase “water”. For the Earth, a volatile supply by the gas capture from the disk is ruled out because observed values of rare-Earth elements are too low in the Earth to be consistent with the disk gas capture (e.g., Brown 1949). Therefore, the water in the Earth would have been delivered from the outer regions of the disk during planet formation.

One possible water delivery mechanism to Earth is the inward scattering of water-bearing asteroids by Jupiter (e.g., Raymond et al. 2004). If this is a dominant mechanism of water delivery, the amount of delivered water is rather stochastic and depends on configurations of giant planets in the planetary systems. If water is not delivered, a rocky planet in a HZ may not be able to be an actual habitat. On the other hand, too much water creates a planet without continents, where the supply of nutrients may not be as effective as in the Earth. The oceans of the Earth comprise only 0.023% by weight and this amount enables oceans and continents to coexist. The mantle may preserve water in the transition zone with a comparable amount of ocean (e.g., Bercovici & Karato 2003; Hirschmann 2006; Fei et al. 2017), while the core could have H equivalent to 2% by weight of H₂ O of the Earth (Nomura et al. 2014). However, the original water fraction of the Earth would still be very small (~ 10⁻⁴−10⁻²), even with the possible water reservoir in the interior because neither stellar irradiation at ~ 1 au (Machida & Abe 2010) nor giant impacts (Genda & Abe 2005) can vaporize the majority of the water from the gravitational potential of Earth. We note that it is inferred that Mars may have subsurface water of 10⁻⁴ −10⁻³ of Mars mass (e.g., di Achille & Hynek 2010; Clifford et al. 2010; Kurokawa et al. 2014). From the high D/H ratio observed in the Venus atmosphere, early Venus may also have had oceans of the fraction 10⁻⁵ −10⁻³ and lost the H₂O vapor through runaway greenhouse effect (e.g., Donahue et al. 1982; Greenwood et al. 2018). The order of water fraction looks similar at least between the Earth and ancient Mars. Although the estimated total mass fraction of water in the Earth and Mars has relatively large uncertainty ranging from 10⁻⁴ to 10⁻², the range is stillmuch smaller than the dispersion predicted by the water-bearing asteroid collision model; this model ranges from 10⁻⁵ to 10⁻¹, depending on the formation timing, history of orbital migration/eccentricity evolution of gas giant planets, and the original surface density of planetesimals (e.g., Morbidelli et al. 2000; Lunine et al. 2003; Raymond et al. 2004; O’Brien et al. 2014; Matsumura et al. 2016). It is not clear if the similar orders of water fraction between the Earth and Mars is just a coincidence.

Sato et al. (2016) investigated water delivery by icy pebble accretion. Pebble accretion has been proposed as a new mode of planet accretion (e.g., Ormel & Klahr 2010; Lambrechts & Johansen 2012). Radiative transfer calculations for viscous accretion disk models show that the water snowline at ~ 170 K may migrate to inside 1 au with the grain opacity ≳mm size, when the disk accretion rate is Ṁ_g ≲ 10⁻⁸ M_⊙ yr⁻¹ (e.g., Garaud & Lin 2007; Min et al. 2011; Oka et al. 2011), which is a typical value of Ṁ_g of classical T Tauri stars (Hartmann et al. 1998). After the snowline inwardly passes a planetary orbit, icy pebbles can be accreted by the planet. In situ ice condensation near the planet orbit is unlikely because the disk gas there was once in the outer region before it migrated to the inner region and icy components have been already condensed to icy grains and subtracted in the outer region (Morbidelli et al. 2016; Sato et al. 2016). Sato et al. (2016) calculated the time evolution of icy pebble mass flux, the solid surface density in the disk, and the growth of a hypothetical planet at 1 au by icy pebble accretion with a 1D model. They found that pebble accretion is so efficient that the water fraction of the planet rapidly increases after the snowline passage. They assumed a static disk and artificially set the timings of snowline passage and removal of the disk that truncates pebble accretion. They found that the water mass fraction of the final planet is very sensitive to these timings and it is zero or more than 0.1 in many cases. The modest water mass fraction of 10⁻⁴ −10⁻² is possible only if the disk is compact (<100 au) and the snowline passage at 1 au later than 2–4 M yr after icy dust growth starts, which could be a narrow window of the parameters.

The sensitive dependence of the final water fraction requires that the snowline migration and the decay of the icy dust surface density must be consistently calculated in an evolving disk. We use the disk evolution model based on the self-similar solution for accretion disks with constant viscosity parameter α (Lynden-Bell & Pringle 1974)¹. The snowline migration, disk gas decay, and growth/drift of pebbles and the associated evolution of the icy dust surface density are simultaneously calculated by a 1D disk evolution model. The growth and drift of pebbles are tracked using the single-size approximation formulated by Ormel (2014) and Sato et al. (2016), which enables us to perform fast calculations and survey broad ranges of parameters. Using the numerical results, we also derive an analytical formula for the final water mass fraction of the planets determined by the disk model parameters.

In Sect. 2, we describe the calculation model that we used. In Sect. 3, the results of numerical simulation are shown. We derive the semi-analytical formula that successfully reproduces the numerical results in Sect. 4. In Sect. 5, using the analytical formula, we study the dependence of the planetary water fraction on the disk and pebble accretion parameters, and discuss the disk parameters to realize the water fraction of 10⁻⁴ −10⁻², which corresponds to the present Earth and ancient Mars. We show that the disk parameters are not in a narrow window and are rather realized in modest disks. Sections. 6 and 7 provide the discussion and summary.

2 Method

2.1 Gas disk model

In general, an accretion disk consists of an inner region in which the viscous heating is dominated and an outer region in which irradiation from the host star is dominated. According to Ida et al. (2016), we set the disk midplane temperature for the viscous-heating dominated region (T_vis) and the irradiation dominated region (T_irr) to be $$\begin{array}{l}{T}_{\text{vis}}\simeq 130{\left(\frac{\alpha }{{10}^{-2}}\right)}^{-1/5}{\left(\frac{M_{\ast }}{M_{\odot }}\right)}^{3/10}{\left(\frac{{\dot{M}}_{\text{g}}}{{10}^{-8}{M}_{\odot }{\text{yr}}^{-1}}\right)}^{2/5}{\left(\frac{r}{1\text{au}}\right)}^{-9/10}\text{K},\\ T_{\text{irr}}\simeq 130{\left(\frac{L_{\ast }}{L_{\odot }}\right)}^{2/7}{\left(\frac{M_{\ast }}{M_{\odot }}\right)}^{-1/7}{\left(\frac{r}{1\text{au}}\right)}^{-3/7}\text{K},\end{array}$$

where r is the distance from the host star, Ṁ_g is the disk gas accretion rate, which is almost independent of r except in outermost region, L_* and M_* are the luminosity and mass of the host star, respectively, and L_⊙ and M_⊙ are their values of the Sun. We adopt the alpha prescription for the disk gas turbulent viscosity (Shakura & Sunyaev 1973), 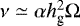$\nu \simeq \alpha h_{\text{g}}^2\Omega$, where h_g is the disk gas scale height, defined by h_g = c_s∕Ω, c_s and Ω are the sound velocity and Kepler frequency, respectively, and α (< 1) is a parameter that represents the strength of the turbulence. We use slightly lower T_irr than that in Ida et al. (2016), assuming lower opacity with millimeter-sized dust grains (Oka et al. 2011), because we consider relatively inner disk regions near the snowline and those pebbles which have grown in outer regions and drifted inward. If micron-sized grains are assumed, the same temperature is realized with about ten times smaller Ṁ_g.

One fundamental assumption behind Eq. (1) is that the rate of viscous heating per unit volume scales linearly with the gasdensity, and is therefore highest at the midplane. This assumption is questioned by magnetohydrodynamic (MHD) models of protoplanetary disks, which show that accretion heating dominantly takes place on the disk surface (Hirose & Turner 2011). Recently, Mori et al. (2019) investigated this issue using a series of MHD simulations including all nonideal MHD effects, finding that the midplane temperature derived from the simulations is generally lower than that from Eq. (1) because the heat generated near the disk surface can easily be lost through radiation. Mori et al. (2019) have also found that MHD disk winds, which are not included in our disk model, take away ≃ 30% of the magnetic energy that would be available for disk heating if the winds were absent. Although there are disk evolution models accounting for the mass and angular momentum loss due to MHD disk winds (e.g., Armitage et al. 2013; Suzuki et al. 2016; Bai et al. 2016; Hasegawa et al. 2017), none of these take into account the two effects mentioned above. For this reason, we opted to adopt the more classical viscous disk model in this study. We note that the viscous accretion model serves as a good approximation of real protoplanetary disks if some hydrodynamical instabilities drive turbulence near the midplane (see Lyra & Umurhan 2018; Klahr et al. 2018, for recent reviews on hydrodynamic instabilities of protoplanetary disks).

The gas disk aspect ratios corresponding to Eqs. (1) and (2) are $$\begin{array}{l}\frac{h_{\text{g},\text{vis}}}{r}\simeq 0.022{\left(\frac{\alpha }{{10}^{-2}}\text{}\right)}^{-1/10}\text{}{\left(\text{}\frac{M_{\ast }}{M_{\odot }}\text{}\right)}^{-7/20}\text{}{\left(\frac{{\dot{M}}_{\text{g}}}{{10}^{-8}{M}_{\odot }{\text{yr}}^{-1}}\right)}^{1/5}{\left(\text{}\frac{r}{1\text{au}}\right)}^{1/20},\\ \frac{h_{\text{g},\text{irr}}}{r}\simeq 0.022{\left(\frac{L_{\ast }}{L_{\odot }}\right)}^{1/7}{\left(\frac{M_{\ast }}{M_{\odot }}\right)}^{-4/7}{\left(\frac{r}{1\text{au}}\right)}^{2/7},\end{array}$$

where h_g,vis and h_g,irr are the gas scale height in the viscous-heating dominated and irradiation dominated regions, respectively. Hereafter, we perform simulations with L_* = L_⊙ and M_* = M_⊙, while we retain their dependences in the formulas. The disk region is viscous-heating dominated if T_vis > T_irr. Otherwise, the irradiation dominates. The transition radius between the viscous-heating and irradiation dominated regions is given by 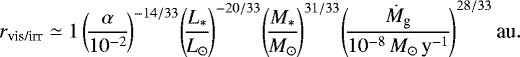$$r_{\text{vis/irr}}\simeq 1{\left(\text{}\frac{\alpha }{{10}^{-2}}\text{}\right)}^{-14/33}\text{}{\left(\text{}\frac{L_{\ast }}{L_{\odot }}\text{}\right)}^{-20/33}\text{}{\left(\text{}\frac{M_{\ast }}{M_{\odot }}\text{}\right)}^{31/33}\text{}{\left(\text{}\frac{{\dot{M}}_{\text{g}}}{{10}^{-8}{M}_{\odot }{\text{y}}^{-1}}\text{}\right)}^{28/33}\text{au}.$$(5)

Defining the snowline by the location at ~170 K, r_snow ≃max(r_snow,vis, r_snow,irr), where 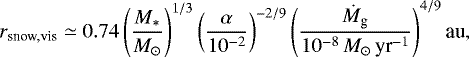$$r_{\text{snow},\text{vis}}\simeq 0.74{\left(\frac{M_{*}}{M_{\odot }}\right)}^{1/3}{\left(\frac{\alpha }{{10}^{-2}}\right)}^{-2/9}{\left(\frac{{\dot{M}}_{\text{g}}}{{10}^{-8}{M}_{\odot }{\text{yr}}^{-1}}\right)}^{4/9}\text{au},$$(6) $$r_{\text{snow},\text{irr}}\simeq 0.53{\left(\frac{L_{*}}{L_{\odot }}\right)}^{2/3}{\left(\frac{M_{*}}{M_{\odot }}\right)}^{-1/3}\text{au}.$$(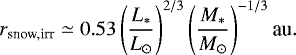7)

As Ṁ_g decreases with time, the snowline migrates inward in the viscous-heating dominated region until r_snow,vis becomes equal to r_snow,irr (Ṁ_g ≳ 5 × 10⁻⁹M_⊙ yr⁻¹ for α = 10⁻²). For calculating the evolution of the pebble flux, it may be enough to set up a static disk distribution as in Sato et al. (2016). However, to describe the snowline migration and disk gas depletion (which determines timings of start and termination of the icy pebble supply), we need an evolving gas disk model.

Specific orbital angular momentum is proportional to a square root of orbital radius r and most of disk mass exists in the outer irradiation dominated region. Angular momentum transfer in the entire disk that determines the snowline migration and the entire disk gas depletion is regulated by the evolution of the outer disk region. The region near the snowline is not a hot region where the viscous heating is significantly higher than the irradiation heating (Eqs. (5) and (6)). So, for our purpose, the entire disk evolution model can be approximated by a irradiation dominated disk. In the irradiation dominated disk, the viscosity ν ∝ αTr^3∕2 ∝ αr^15∕14 (Eq. (2)). Because it is similar to the disk with the viscosity ν ∝ r with a constant α, we adopted the self-similar solution with ν ∝ r by Lynden-Bell & Pringle (1974) for the dynamical evolution of the entire disk, while we took into account the snowline evolution regulated by time evolution of the viscous heating (Eq. (6)).

In the self-similar solution, well inside the initial characteristic disk size (r_d,0), beyond which the surface density decays exponentially, the disk accretion rate is given as a function of time by 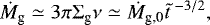$$\begin{array}{ll}{\dot{M}}_{\text{g}}\hfill & \simeq 3\pi {\Sigma }_{\text{g}}\nu \simeq {\dot{M}}_{\text{g},\text{0}}{\tilde{t}}^{-3/2},\hfill \end{array}$$(8)

where Σ_g is the disk gas surface density, ν is the effective viscosity at r, 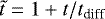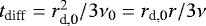$\tilde{t}=1+t/t_{\text{diff}}$, $t_{\text{diff}}=r_{\text{d},\text{0}}^2/3{\nu }_0=r_{\text{d},\text{0}}r/3\nu$ (where ν₀ is the viscosity at r_d,0), and Ṁ_g,0 is the initial disk accretion rate, respectively. Inversely, the time evolution of the surface gas density Σ_g is given by 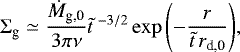$$\begin{array}{ll}{\Sigma }_{\text{g}}\hfill & \simeq \frac{{\dot{M}}_{\text{g},\text{0}}}{3\pi \nu }{\tilde{t}}^{-3/2}\exp \left(-\frac{r}{\tilde{t}{r}_{\text{d},\text{0}}}\right),\hfill \end{array}$$(9)

where we included the time-dependent exponential taper in the full form of the self-similar solution, because we need to evaluate the total disk mass. Because ν ∝ r, Σ_g ∝ 1∕r for r ≪ r_d,0.

We add the effect of the photoevaporation with the rate Ṁ_pe, although the standard self-similar solution does not have such a term (also see Sect. 3.1). We are concerned with the region near the snowline. We assume that r ≪ r_d,0 and the photoevaporation occurs mainly in the outer region with the constant rate of Ṁ_pe. Accordingly, we set $$\begin{array}{ll}{\dot{M}}_{\text{g}}\hfill & ={\dot{M}}_{\text{g},\text{0}}{\tilde{t}}^{-3/2}-{\dot{M}}_{\text{pe}},\hfill \\ {\Sigma }_{\text{g}}\hfill & \simeq \frac{{\dot{M}}_{\text{g},\text{0}}{\tilde{t}}^{-3/2}-{\dot{M}}_{\text{pe}}}{3\pi \nu }\exp \left(-\frac{r}{\tilde{t}{r}_{\text{d},\text{0}}}\right).\hfill \end{array}$$

Integrating Eq. (11), the disk mass at t is given by 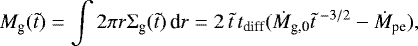$$M_{\text{g}}(\tilde{t})={\displaystyle \int 2}\pi r{\Sigma }_{\text{g}}(\tilde{t})\text{d}r=2\tilde{t}{t}_{\text{diff}}({\dot{M}}_{\text{g},\text{0}}{\tilde{t}}^{-3/2}-{\dot{M}}_{\text{pe}}),$$(12)

where we use r∕3ν = t_diff∕r_d,0. The above equations show that the disk accretion rate Ṁ_g and the disk gas surface density Σ_g quickly decay when Ṁ_g decreases to the level of Ṁ_pe. This photoevaporation effect avoids long-tail existence of disk gas significantly longer than a few M yr.

Here, we describe the disks with the parameters, t_diff, Ṁ_g,0, Ṁ_pe and r_d,0. The disk depletion timescale (t_dep) and the disk gas accretion rate onto the host star (Ṁ_g) are better constrained by observations than the other parameters, i.e., t_dep~10⁶−10⁷ yr and Ṁ_g~(10⁻⁹−10⁻⁷) M_⊙ yr⁻¹ for solar-type stars (e.g., Haisch et al. 2001; Hartmann et al. 1998, 2016; Williams & Cieza 2011). We focus on the systems around solar-type stars. We assume that angular momentum transfer by turbulent viscous diffusion is a major mechanism for disk depletion rather than photoevaporation. We identify t_dep as t_diff. We use Ṁ_g,0, which may be slightly higher than the observed averaged values of Ṁ_g because we want to set the snowline beyond the orbits of planetary embryos. We perform simulations with t_diff = 10⁶ and 3 × 10⁶ yr, Ṁ_g,0 = 3 × 10⁻⁸M_⊙ yr⁻¹, and 10⁻⁷M_⊙ yr⁻¹. Although r_d,0 is not observationally well constrained, Sato et al. (2016) showed that this parameter is most important for the time evolution of the pebble mass flux. For r_d,0, we use r_d,0 = 30, 100 and 300 au, which correspond to the range of the observationally inferred disk size (Williams & Cieza 2011). We adopt the photoevaporation rate Ṁ_pe = 10⁻⁹ and 10⁻⁸M_⊙ yr⁻¹.

The disk diffusion timescale is $$\begin{array}{ll}{t}_{\text{diff}}\hfill & \simeq \frac{r_{\text{d}.\text{0}}^2}{3{\nu }_0}=\frac{r_1{r}_{\text{d}.\text{0}}}{3{\nu }_1}=\frac{r_1^2}{3\alpha h_{\text{g},\text{1}}^2{\Omega }_{\text{K},\text{1}}}\frac{r_{\text{d}.\text{0}}}{r_1}\hfill \\ \hfill & =\frac{1}{6\pi \alpha }{\left(\frac{r_1}{h_{\text{g},\text{1}}}\right)}^2\frac{r_{\text{d}.\text{0}}}{r_1}\text{yr}\simeq {10}^2{\alpha }^{-1}\left(\frac{r_{\text{d}.\text{0}}}{1\text{au}}\right)\text{yr},\hfill \end{array}$$(13)

where subscript “1” expresses values at 1 au, ν_d.0 = ν(r_d.0) is viscous coefficient at the outer edge of the disk, and ν = ν₁ ⋅ (r∕r₁). From this equation, α is calculated as 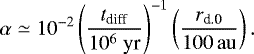$$\alpha \simeq {10}^{-2}{\left(\frac{t_{\text{diff}}}{{10}^6\text{yr}}\right)}^{-1}\left(\frac{r_{\text{d}.\text{0}}}{100\text{au}}\right).$$(14)

We note that the value of α that we use in our simulations depends on the choice of the parameters t_diff and r_d,0, but it is within a reasonable range, α = 10⁻³−3 × 10⁻². In our formulation for disks, we prefer the setting of the observable valuables, t_diff and r_d,0, within the observationally inferred ranges to a simple assumption of a constant α.

In Fig. 1, we show time evolution of the transition radius r_vis/irr, the snowline r_snow, the disk characteristic radius 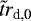$\tilde{t}{r}_{\text{d},\text{0}}$, and the pebble formation front r_pff, which are derived in Sect. 3.1 as Eq. (36), for six typical parameters of disk evolution. In general, r_pff in magenta lines evolves faster than 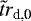$\tilde{t}{r}_{\text{d},\text{0}}$ in the green lines and the pebble flux quickly decays after r_pff exceeds 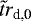$\tilde{t}{r}_{\text{d},\text{0}}$, as we discuss in Sect. 3.1. The snowline r_snow in the blue lines shrinks with time as long as it is in the viscous-heating region (inside of r_vis/irr in the red lines).

Fig. 1 Time evolution of the transition radius rvis/irr (Eq. (5); red lines), snowline rsnow = max(rsnow,vis, rsnow,irr) (Eqs. (6) and (7); blue lines), disk characteristic radius $\tilde{t}{r}_{\text{d},\text{0}}$ (green lines), and pebble formation front rpff (Eq. (36); magenta lines) for various disk evolution parameters. The parameters, rd,0 in units of auand Ṁg,0 in units of M⊙ yr−1 are labeled in the individual panels. The other parameters are the same for the four panels, i.e., Ṁpe =10−9 M⊙ yr−1 and tdiff = 106 yr.

2.2 Dust/pebble evolution model

We adopt the method with the single size approximation formulated by Ormel (2014) and Sato et al. (2016) to calculate the pebble mass flux. The size distribution of icy particles obtained by a full-size simulation is generally peaky at some size and the peak size depends on r. In the single size approximation, icy dust particles have a single size that depends on r, corresponding to the peak size.

We briefly summarize the dust evolution model (for more details, see Sato et al. 2016). We set the initial particle surface density as Σ_p = Z₀Σ_g. We adopt Z₀ = 0.01. The evolution of the dust/pebble surface density (Σ_p) and the peaked massof the particles (m_p) are calculated by the equation, $$\begin{array}{l}\frac{\partial {\Sigma }_{\text{p}}}{\partial t}+\frac{1}{r}\frac{\partial }{\partial r}(r{v}_{r,\text{d}}{\Sigma }_{\text{p}})=0,\\ \frac{\partial m_{\text{p}}}{\partial t}+v_{r,\text{d}}\frac{\partial m_{\text{p}}}{\partial r}=\frac{2\sqrt{\pi }{R}_{\text{p}}^2\Delta v_{\text{pp}}}{h_{\text{p}}}{\Sigma }_{\text{p}},\end{array}$$

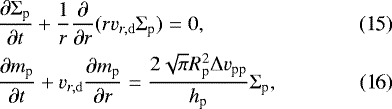
where 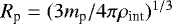$R_{\text{p}}={(3m_{\text{p}}/4\pi {\rho }_{\text{int}})}^{1/3}$ is the particle radius, ρ_int is the internal density of icy particles, v_r,d and Δv_pp are the radial and relative velocities of the particles at the midplane, respectively, and h_p is the scale height of the particles given by (e.g. Youdin & Lithwick 2007) 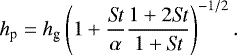$$h_{\text{p}}=h_{\text{g}}{\left(1+\frac{St}{\alpha }\frac{1+2St}{1+St}\right)}^{-1/2}.$$(17)

The Stokes number defined by St = t_sΩ is an important dimensionless number in pebble growth and radial drift, where t_s is the stopping time that represents the timescale of particles’s momentum relaxation due to gas drag, given by $$t_{\text{s}}=\{\begin{array}{ll}\frac{{\rho }_{\text{int}}{R}_{\text{p}}}{{\rho }_{\text{g}}{v}_{\text{th}}}\hfill & (R_{\text{p}}<\frac{9}{4}{\lambda }_{\text{mfp}};\text{Epstein}\text{regime})\hfill \\ \frac{4{\rho }_{\text{int}}{R}_{\text{p}}^2}{9{\rho }_{\text{g}}{v}_{\text{th}}{\lambda }_{\text{mfp}}}\hfill & (R_{\text{p}}>\frac{9}{4}{\lambda }_{\text{mfp}};\text{Stokes}\text{regime})\hfill \end{array}\text{}\text{}\text{},$$(18)

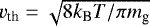where $v_{\text{th}}=\sqrt{8k_{\text{B}}T/\pi m_{\text{g}}}$ is the thermal velocity, λ_mfp is the mean free path of gas particles, and m_g is the gas molecule mass. The mean free path is expressed by λ_mfp = m_g∕(σ_molρ_g), where σ_mol = 2.0 × 10⁻¹⁵cm² is the molecular collision cross section.

Relative velocity of dust particles Δv_pp is given by 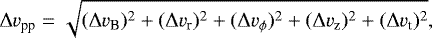$$\Delta v_{\text{pp}}=\sqrt{{(\Delta v_{\text{B}})}^2+{(\Delta v_{\text{r}})}^2+{(\Delta v_{\varphi })}^2+{(\Delta v_{\text{z}})}^2+{(\Delta v_{\text{t}})}^2},$$(19)

where Δv_B, Δv_r, Δv_ϕ, Δv_z, and Δv_t are the relative velocities induced by Brownian motion, radial drift, azimuthal drift, vertical settling, and turbulence, respectively (for detailed expressions, see Sato et al. 2016). We assume perfect sticking for Δv_pp < 30m s⁻¹; otherwise, we set the right-hand side of Eq. (16) to be zero.

The radial drift velocity of dust particles is 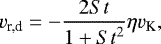$$v_{\text{r},\text{d}}=-\frac{2St}{1+S{t}^2}\eta v_{\text{K}},$$(20)

where v_K = rΩ_K is the Kepler velocity and η is a deviation of gas rotation velocity from Kepler velocity, which we set 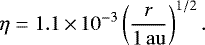$$\eta =1.1\times {10}^{-3}{\left(\frac{r}{1\text{au}}\right)}^{1/2}.$$(21)

If the effect of the disk gas accretion is taken into account, 2St in the numerator of Eq. (20) is replaced by (2St + α) (e.g., Ida et al. 2016). However, it is neglected here, because the numerical simulation shows St≳0.1 for migrating pebbles (Sect. 3.1). The radial drift timescale is 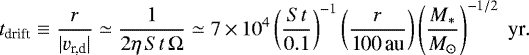$$t_{\text{drift}}\equiv \frac{r}{\left|v_{\text{r},\text{d}}\right|}\simeq \frac{1}{2\eta St\Omega }\simeq 7\times {10}^4{\left(\frac{St}{0.1}\right)}^{-1}\left(\frac{r}{\text{100}\text{au}}\right){\left(\frac{M_{\ast }}{M_{\odot }}\right)}^{-1/2}\text{yr}.$$(22)

The pebble mass flux through the disk is given by 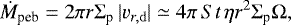$${\dot{M}}_{\text{peb}}=2\pi r{\Sigma }_{\text{p}}\left|v_{r,\text{d}}\right|\simeq 4\pi St\eta r^2{\Sigma }_{\text{p}}\Omega ,$$(23)

where Σ_p is the pebble surface density in the pebble migrating region and we assume St ² ≪ 1.

2.3 Pebble accretion onto planets

We use the same formulas as Sato et al. (2016) for the pebble accretion rate onto planets, assuming that the planets are already large enough for pebble accretion in the “settling regime” (e.g., Ormel & Klahr 2010; Guillot et al. 2014). Ormel & Klahr (2010) derived the cross section of pebble accretion as 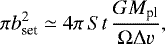$$\pi b_{\text{set}}^2\simeq 4\pi St\frac{G{M}_{\text{pl}}}{\Omega \Delta v},$$(24)

where M_pl is the planetary embryo mass and Δv is the relative velocity between the embryo and pebbles. The 3D pebble accretion rate Ṁ_pl onto the planetary embryo is given by 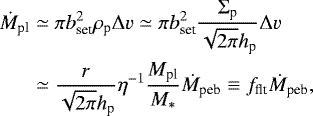$$\begin{array}{ll}{\dot{M}}_{\text{pl}}\hfill & \simeq \pi b_{\text{set}}^2{\rho }_{\text{p}}\Delta v\simeq \pi b_{\text{set}}^2\frac{{\Sigma }_{\text{p}}}{\sqrt{2\pi }{h}_{\text{p}}}\Delta v\hfill \\ \hfill & \simeq \frac{r}{\sqrt{2\pi }{h}_{\text{p}}}{\eta }^{-1}\frac{M_{\text{pl}}}{M_{\ast }}{\dot{M}}_{\text{peb}}\equiv f_{\text{flt}}{\dot{M}}_{\text{peb}},\hfill \end{array}$$(25)

where ρ_p is the spatial mass density of the pebbles and we used Eqs. (23) and (24). The parameter f_flt expresses the mass fraction of the accretion flow onto the planet in the pebble flux through the disk before the accretion, which is called a “filtering factor.” We note that f_flt does not directly depend on Δv, b_set, and St.

When b_set > h_p, the accretion is 2D and 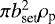$\pi b_{\text{set}}^2{\rho }_{\text{p}}$ in Eq. (25) is replaced by 2b_setΣ_p. Accordingly, a complete filtering factor is 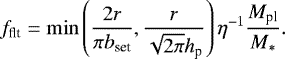$$f_{\text{flt}}=\min \left(\frac{2r}{\pi b_{\text{set}}},\frac{r}{\sqrt{2\pi }{h}_{\text{p}}}\right){\eta }^{-1}\frac{M_{\text{pl}}}{M_{\ast }}.$$(26)

While f_flt depends on b_set in 2D mode, it still does not depend directly on St and Δv. In our simulations, we set the planetary embryos with the masses and semimajor axes identical to Venus, Earth, and Mars (eccentricities are set to be zero). In these cases, the relative velocity is given by Δv = (3∕2)b_setΩ (“Hill regime”). Substituting this into Eq. (24), 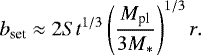$$b_{\text{set}}\approx 2S{t}^{1/3}{\left(\frac{M_{\text{pl}}}{3M_{\ast }}\right)}^{1/3}r.$$(27)

In the numerical simulations, we use a more general formula including “Bondi regime” and the cutoff parameter ($\exp [-{(St/2)}^{0.65}]$) for large St cases (Ormel & Kobayashi 2012). The dependence on Δv cancels in the accretion rate both in 2D and 3D cases and Ṁ_pl does not directly depend on b_set and St in the 3D case. For a small planet, the accretion is in 3D mode. The accretion becomes 2D mode when $$\begin{array}{ll}{M}_{\text{pl}}>M_{\text{2D3D}}\hfill & \simeq 3{\left(\frac{2}{\pi }\right)}^{3/2}S{t}^{-1}{\left(\frac{St}{\alpha }\right)}^{-3/2}{\left(\frac{h_{\text{g}}}{r}\right)}^3{M}_{*}\hfill \\ \hfill & \simeq 1.7{\left(\frac{M_{\ast }}{M_{\odot }}\right)}^{-5/7}{\left(\frac{St}{0.1}\right)}^{-5/2}{\left(\frac{\alpha }{{10}^{-2}}\right)}^{3/2}{\left(\frac{r}{1\text{au}}\right)}^{6/7}{M}_{\oplus }.\hfill \end{array}$$(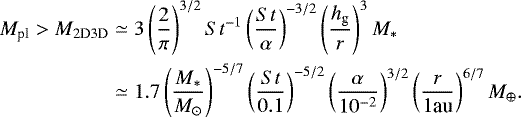28)

The filtering factor is given by $$f_{\text{flt}}\simeq \{\text{}\begin{array}{l}0.017{\left(\frac{M_{\ast }}{M_{\odot }}\right)}^{-1}{\left(\frac{\alpha }{{10}^{-2}}\right)}^{-1/2}{\left(\frac{h_{\text{g}}/r}{0.02}\right)}^{-1}{\left(\frac{St}{0.1}\right)}^{1/2}\left(\frac{M_{\text{pl}}}{0.1M_{\oplus }}\right){\left(\frac{r}{1\text{au}}\right)}^{-1/2}\hfill \\ [M_{\text{pl}}<M_{\text{2D3D}};\text{3D}]\hfill \\ 0.040{\left(\frac{M_{\ast }}{M_{\odot }}\right)}^{-2/3}{\left(\frac{St}{0.1}\right)}^{-1/3}{\left(\frac{M_{\text{pl}}}{0.1M_{\oplus }}\right)}^{2/3}{\left(\frac{r}{1\text{au}}\right)}^{-1/2}\hfill \\ [M_{\text{pl}}>M_{\text{2D3D}};\text{2D}],\hfill \end{array}$$(29)

where we used Eq. (21).

We take into account the decrease in dust surface density and pebble flux due to pebble accretion onto the planets. After the snowline passage, Eq. (15) is rewritten in the grid, where the planets exist, as 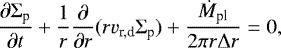$$\frac{\partial {\Sigma }_{\text{p}}}{\partial t}+\frac{1}{r}\frac{\partial }{\partial r}(r{v}_{\text{r},\text{d}}{\Sigma }_{\text{p}})+\frac{{\dot{M}}_{\text{pl}}}{2\pi r\Delta r}=0,$$(30)

where Δr is the radial grid size. After the icy pebble accretion onto the planet starts, the pebble mass flux decreases discontinuously at the planet orbits, according to the accretion onto the planets.

2.4 Simulation parameters

The parameters for our simulations are the initial disk characteristic size r_d,0, the diffusion timescale of the disk t_diff, the initial disk gas accretion rate Ṁ_g,0, and the photo-evaporation rate Ṁ_pe. As we explained in Sect. 2.1, the other disk parameters are calculated by these parameters. We perform simulations with

• (1)

  Ṁ_g,0 = 3 × 10⁻⁸, 10⁻⁷M_⊙ yr⁻¹,

• (2)

  Ṁ_pe = 10⁻⁹, 10⁻⁸M_⊙ yr⁻¹,

• (3)

  r_d,0 = 30, 100, 300 au,

• (4)

  t_diff = 10⁶, 3 × 10⁶ yr.

The initial total gas disk mass is given by Eq. (9) as 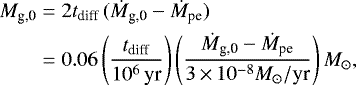$$\begin{array}{ll}{M}_{\text{g},\text{0}}\hfill & =2t_{\text{diff}}({\dot{M}}_{\text{g},\text{0}}-{\dot{M}}_{\text{pe}})\hfill \\ \hfill & =0.06\left(\frac{t_{\text{diff}}}{{10}^6\text{yr}}\right)\left(\frac{{\dot{M}}_{\text{g},\text{0}}-{\dot{M}}_{\text{pe}}}{3\times {10}^{-8}{M}_{\odot }/\text{yr}}\right)M_{\odot },\hfill \end{array}$$(31)

which ranges from 0.06 M_⊙ to 0.6 M_⊙ with the above parameters. Because we start with relatively large Ṁ_g,0, the initial disk mass is relatively large. As we show in Sect. 4, initially massive disks tend to produce dry planets, while small mass disks tend to produce water-rich planets.

The initial dust surface density distribution is simply given by 0.01 Σ_g,0. With the gas disk evolution, we simultaneously calculate the pebble growth from the dust disk and its migration. The dust disk is depleted by the formation and radial drift of pebbles.

We set Venus, Earth, and Mars analogs in circular orbits with the same masses and semimajor axes as the current Venus, Earth, and Mars in solar system. For the results presented in this work, we assume M_* = M_⊙ and L_* = L_⊙, while we retain the dependence on M_* and L_* in the equations. For other-mass stars, the dependence of Ṁ_g,0, Ṁ_pe, r_d,0, and t_diff on the stellar mass also have to be considered.

3 Numerical results

3.1 Icy grain/pebble evolution

We calculate the growth and radial drift of icy grains and pebbles following the method by Sato et al. (2016), which is described in Sect. 2.2. The evolution of icy particles (grains and pebbles) found by simulations of Sato et al. (2016) is summarized as follows:

• 1.

  The growth timescale of a particle with mass m_p is well approximated by the simple formula with Δv_pp ≃ Δv_t in the Epstein regime (also see Takeuchi & Lin 2005; Brauer et al. 2008) as 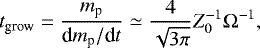$$t_{\text{grow}}=\frac{m_{\text{p}}}{\text{d}{m}_{\text{p}}/\text{d}t}\simeq \frac{4}{\sqrt{3\pi }}{Z}_0^{-1}{\Omega }^{-1},$$(32)

  where Z₀ is the initial particle-to-gas ratio in the disk. The timescale of growth from μm-sized grains to pebbles by several orders of magnitude in radius is 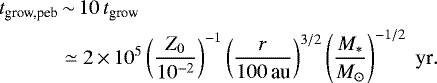$$\begin{array}{ll}{t}_{\text{grow},\text{peb}}\hfill & ~10t_{\text{grow}}\hfill \\ \hfill & \simeq 2\times {10}^5{\left(\frac{Z_0}{{10}^{-2}}\right)}^{-1}{\left(\frac{r}{100\text{au}}\right)}^{3/2}{\left(\frac{M_{\ast }}{M_{\odot }}\right)}^{-1/2}\text{yr}.\hfill \end{array}$$(33)

• 2.

  The drift timescale becomes shorter as m_p (equivalently, Stokes number St) increases (Eq. (22)), while the growth timescale is independent of m_p (Eq. (32)). When t_drift becomes smaller than t_grow, the particle drift effectively starts and Σ_p starts being sculpted. From Eqs. (22) and (32) with Z₀ replaced by the particle-to-gas ratio of drifting pebbles (Z), the equilibrium Stokes number of drifting pebbles is 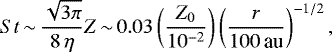$$St~\frac{\sqrt{3\pi }}{8\eta }Z~0.03\left(\frac{Z_0}{{10}^{-2}}\right){\left(\frac{r}{100\text{au}}\right)}^{-1/2},$$(34)

  where we used a typical value of the solid-to-gas ratio of migrating pebble, Z ~ 0.1 Z₀ (Ida et al. 2016). We adopt Z₀ as the initial particle-to-gas ratio and adopt Z₀ = 0.01 as a nominal value.

• 3.

  The sensitive r-dependence of t_grow,peb results in “an inside-out formation” of pebbles; formation is earlier in the inner region and the formation front migrates outward (also see Brauer et al. 2008; Okuzumi et al. 2012; Birnstiel et al. 2012; Lambrechts & Johansen 2014). After thepebble formation front reaches the characteristic disk radius (r_d,0), Σ_p rapidly decays uniformly in the disk because the supply from further outer regions to the region at r ~ r_d,0 is limited.

As we show below, the time (t_pff) at which the pebble formation front reaches the characteristic disk radius is a very important parameter. The timescale for the pebble formation front to reach the radius of r_d,0 is given with Eq. (33) by 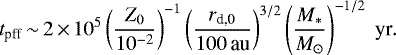$$t_{\text{pff}}~2\times {10}^5{\left(\frac{Z_0}{{10}^{-2}}\right)}^{-1}{\left(\frac{r_{\text{d},\text{0}}}{100\text{au}}\right)}^{3/2}{\left(\frac{M_{\ast }}{M_{\odot }}\right)}^{-1/2}\text{yr}.$$(35)

In other words, the pebble formation front radius is given as a function of time (t) by 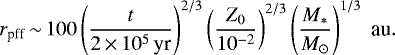$$r_{\text{pff}}~100{\left(\frac{t}{2\times {10}^5\text{yr}}\right)}^{2/3}{\left(\frac{Z_0}{{10}^{-2}}\right)}^{2/3}{\left(\frac{M_{\ast }}{M_{\odot }}\right)}^{1/3}\text{au}.$$(36)

The timescale t_pff is determined only by r_d,0 in the disk parameters. It is independent of the other disk parameters such as t_diff and Ṁ_g,0.

Once the formation front reaches r_d,0, the supply of solid materials from further outer regions is limited. Accordingly, the pebble formation and drift from there results in the decay of Σ_p near r_d,0. The solid surface density at r < r_d,0 also decays because it is contributed from drifting pebbles formed near the formation front. Thus, the decay rate of Σ_p for t > t_pff is regulated by the pebble growth near r_d,0, and is approximated as 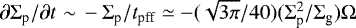$\partial {\Sigma }_{\text{p}}/\partial t~-{\Sigma }_{\text{p}}/t_{\text{pff}}\simeq -(\sqrt{3\pi }/40)({\Sigma }_{\text{p}}^2/{\Sigma }_{\text{g}})\Omega$. From this relation, Z = Σ_p∕Σ_g ∝ t⁻¹ at t > t_pff, which is approximated as 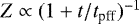$Z\propto {(1+t/t_{\text{pff}})}^{-1}$. However, the numerical results show a faster decrease due to the effect of finite r_d,0 (Sato et al. 2016). The numerically obtained time evolution of Z at r= r_d,0 with r_d,0 = 30, 100 and 300 au is shown in Fig. 2. For r_d,0 = 30, 100, and 300 au, t_pff ≃ 3.3 × 10⁴, 2.0 × 10⁵, and 1 × 10⁶ yr, respectively (Eq. (36)). We fit the numerical results as 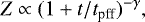$$\begin{array}{ll}Z\hfill & \propto {(1+t/t_{\text{pff}})}^{-\gamma },\hfill \end{array}$$(37)

where $$\begin{array}{l}\gamma =1+{\gamma }_2(300\text{au}/r_{\text{d},\text{0}}),\\ {\gamma }_2~\mathrm{0.15.}\end{array}$$(38)

Because t_pff ≳ t_diff and the effect of a finite r_d,0 is not important for r_d,0≳300 au (Eq. (36)), the r_d,0-dependence as a factor of (300 au∕r_d,0) is reasonable. Although the value of γ₂ may includean uncertainty due to the disk model and the single-size approximation, we show in Sect. 5 that the predicted function of the water fraction depends only weakly on γ₂.

We note that we assume that collisions between icy pebbles always result in sticking and the pebble size is determined by the drift limit. If the pebble growth is limited by bouncing collisions or collisional fragmentation, St is determined by the threshold velocity for bouncing or fragmentation, which is lower than the value in Eq. (34), and Eq. (36) depends on the threshold St. It is a widely accepted idea that pebbles made of H₂ O ice grains have a high sticking threshold velocity (Wada et al. 2009; Gundlach & Blum 2015), but this is not the case if the grains are mantled by poorly sticky CO₂ (Musiolik et al. 2016). Recent studies have found that this CO₂-induced fragmentation can have important implications for the growth of pebble-accreting protoplanets (Johansen et al. 2019)and for the observational appearance of protoplanetary disks (Okuzumi & Tazaki 2019). In a future work, we will study how the bouncing and fragmentation barriers affect the water delivery to rocky planets.

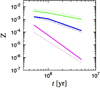Fig. 2 Time evolution of Z = Σp∕Σg obtained by the numerical simulation with Ṁg,0 = 10−7M⊙ yr−1, Ṁpe =10−9M⊙ yr−1, and tdiff = 106 yr. The magenta, blue, and green solid lines show Z obtained at rd,0 by the numerical results of with rd,0 = 30, 100 and 300 au. The dashed lines indicate gradients for individual cases given by Eqs. (37) and (38), where the absolute values of Z are arbitrary.

3.2 Water fraction

With the simulated pebble mass flux Ṁ_peb, we calculate the growth rate of a planet due to icy pebble accretion (Ṁ_pl). The filtering factor is defined by f_flt = Ṁ_pl∕Ṁ_peb. When the snowline passes each planetary orbit, we switch on the icy pebble accretion onto the planet. We assume that the 1:1 ratio of rocky to icy fraction of icy pebbles. We set the rocky planets with Venus, Earth, and Mars masses when the snowline passes 0.72, 1.0, and 1.52 au, respectively.

After the snowline passes a planetary orbit, icy pebble accretion starts. When the cumulative accreted mass by icy pebbles is ΔM_pl, the total ice mass in the planet is (1∕2)ΔM_pl. The water fraction of the planet at the mass M_pl is given by 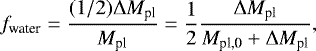$$f_{\text{water}}=\frac{(1/2)\Delta M_{\text{pl}}}{M_{\text{pl}}}=\frac{1}{2}\frac{\Delta M_{\text{pl}}}{M_{\text{pl},\text{0}}+\Delta M_{\text{pl}}},$$(39)

where M_pl,0 is the planetary mass at the snowline passage, M_pl = M_pl,0 + ΔM_pl. If ΔM_pl becomes much larger than M_pl,0, the water fraction saturates to f_water ≃ 1∕2.

We repeat the simulations with different disk parameters t_diff, Ṁ_g,0, r_d,0, and Ṁ_pe to investigate how the water fraction of the final planets depends on these parameters and which values of the parameters produce the water fraction consistent with the terrestrial planets in the solar system. As we show in Sect. 4, the water fraction of final planets is insensitive to M_pl,0.

Figure 3 shows the time evolution of water fraction for the models with t_diff = 10⁶ yr, Ṁ_g,0 = 10⁻⁷M_⊙ yr⁻¹, and Ṁ_pe = 10⁻⁹M_⊙ yr⁻¹. The left, middle, and right panels show the results of r_d,0 = 30, 100, and 300 au, respectively. We first explain general evolution pattern of the water fraction. In all cases, the water fraction rapidly increases once the snowline passes the planetary orbit and the icy pebble accretion starts. It is saturated to its asymptotic value, even sufficiently before completion of disk gas depletion. From Eqs. (6) and (14), 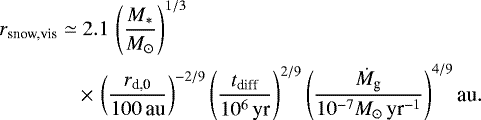$$\begin{array}{ll}{r}_{\text{snow},\text{vis}}\simeq \hfill & 2.1{\left(\frac{M_{*}}{M_{\odot }}\right)}^{1/3}\hfill \\ \hfill & \times {\left(\frac{r_{\text{d},\text{0}}}{100\text{au}}\right)}^{-2/9}{\left(\frac{t_{\text{diff}}}{{10}^6\text{yr}}\right)}^{2/9}{\left(\frac{{\dot{M}}_{\text{g}}}{{10}^{-7}{M}_{\odot }{\text{yr}}^{-1}}\right)}^{4/9}\text{au}.\hfill \end{array}$$(40)

At t = 0 with Ṁ_g,0 = 10⁻⁷M_⊙ yr⁻¹, the snowline is located outside the orbit of Mars. As shown in Fig. 1, the snowline migrates inward and passes through the planetary orbits one after another as the disk accretion rate Ṁ_g decreases with time as Eq. (10). The snowline passage always occurs in the order of Mars at 1.52 au, Earth at 1.0 au, and Venus at 0.72 au. Because the initial r_snow,vis is closer to the planetary orbits for larger r_d,0, the snowline passage is earlier for larger r_d,0, as shown in Fig. 3. The water fraction is saturated when Σ_p and Ṁ_peb significantly decay. The rapid decay starts at t ~ t_pff and Eq. (33) shows that t_pff is as short as approximately a few × 10⁵ yr for r_d,0 = 100 au. Even for r_d,0 = 300 au, the decay starts at t_pff ≃ 10⁶ yr before disk depletion. Therefore, the evolution of the water fraction evolution is mainly reduced by the consumption of icy dust grain reservoir rather than by the disk gas depletion.

Figure 3 shows a clear trend that the final water fraction is lower for smaller r_d,0. This trend is explained by a comparison between the snowline passage time t_snow and t_pff, as follows. The water fraction due to pebble accretion rapidly increases until Σ_p decays by more than an order of magnitude, which corresponds to, say, t > 10 t_pff (Eq. (37)). If t_snow > 10 t_pff, f_water can be ≪ 1. While t_pff is smaller for a smaller r_d,0 (Eq. (33)), t_snow is larger (Eq. (40)). The latter implies that the disk is warmer for a smaller r_d,0. The viscousheating increases as the blanketing effect by optical depth (∝ Σ_g) increases. In Fig. 3, Ṁ_g,0 and t_diff are fixed. Smaller r_d,0 means smaller α (Eq. (13)) and larger Σ_g (Eq. (9)), resulting in a warmer disk. Thereby, the final water fraction is lower for smaller r_d,0.

We examine the condition of t_snow∕t_pff > 10 or <10 in more detail. In the case of r_d,0 = 30 au, t_pff ≃ 4 × 10⁴ yr (Eq. (33)) and t_snow is identified by the timing at which f_water starts rapid increase, which is ≃1 × 10⁶, 2.5 × 10⁶, and 5 × 10⁶ yr for the Mars, Earth and Venus analogs, respectively (the left panel of Fig. 3). Because t_snow > 10 t_pff in this case, f_water ~ 10⁻² even for the outermost Mars analog. For the Earth and Venus analogs, f_water is further smaller. In the case of r_d,0 = 300 au, t_pff ≃ 1 × 10⁶ yr (Eq. (33)) and t_snow ≃ 1 × 10⁵, 1 × 10⁶ and 2 × 10⁶ yr for the Mars, Earth, and Venus analogs, respectively (right panel of Fig. 3). Because t_snow < 10 t_pff, f_water ~ 1∕2 for all of Mars, Earth, and Venus. In the middle panel of Fig. 3, r_d,0 = 100 au and t_pff ≃ 2 × 10⁵ yr (Eq. (33)). In this case, t_snow < 10 t_pff and f_water ≪ 1 for the Venus analog, while t_snow > 10 t_pff and f_water ~ 1∕2 for the Mars analog.

The condition of t_snow∕t_pff > 10 or < 10 also explains other results of the final water fraction of planets because this condition represents how much icy materials remain at the snowline passage. (In Sect. 5, we revisit this condition.) Figure 4 is the time evolution of water fraction of t_diff = 10⁶ yr (left panel) and t_diff = 3 × 10⁶ yr (right panel), respectively. The other disk parameters are the same. For both cases, 10 t_pff ≃ 2 × 10⁶ yr (Eq. (33)). The snowline is already inside Mars’ orbit from the beginning (t = 0) of the calculations, that is, t_snow = 0, which results in f_water ≃ 1∕2 for the Mars analog. The snowline passage time t_snow is smaller than10 t_pff only for the Venus analog in the case of t_diff = 10⁶yr (left panel), and for both the Earth and Venus analogs in the case of t_diff = 3 × 10⁶ yr (right panel). This explains the results in Fig. 4.

Figure 5 shows the results of Ṁ_g,0 = 3 × 10⁻⁸ M_⊙ yr⁻¹ (left) and 10⁻⁷ M_⊙ yr⁻¹ (right) with r_d,0 = 100 au, t_diff = 10⁶ yr, and Ṁ_pe = 10⁻⁹M_⊙ yr⁻¹. Again, 10 t_pff ≃ 2 × 10⁶ yr for both cases. Smaller Ṁ_g,0 with the fixed t_diff = 10⁶ yr⁻¹ means earlier passage of the snowline, resulting in a lower water fraction. Figure 6 shows the results of Ṁ_pe = 10⁻⁹M_⊙ yr⁻¹ (left) and Ṁ_pe = 3 × 10⁻⁹M_⊙ yr⁻¹ (middle) and Ṁ_pe = 10⁻⁸M_⊙ yr⁻¹. With larger Ṁ_pe, the outer disk region is truncated at shorter radius. The disk truncation reduces the reservoir of icy materials, resulting in a lower water fraction, for the planets (the Earth and Venus analogs) with t_snow ≳ 10 t_pff ≃ 2 × 10⁶ yr.

In Sect. 4, we derive a semi-analytical formula to predict the water fraction of planets after disk depletion. We show that the total mass (M_res) of the icy dust materials preserved in the disk determines the final water fraction because they eventually drift to the inner regions and pass the planetary orbits². Since our gas disk model is analytical, we can analytically evaluate t_snow. We already know the analytical expression of t_pff given by Eq. (36) is a good approximation. We also semi-analytically derive how the icy grain surface density evolves as Eq. (37). A synthesis of these results enables us to derive the semi-analytical formula for f_water.

Finally we point out that f_water is higher in the order of Mars, Earth, and Venus analogs according to the snowline passage timing, except for the fully saturated cases where f_water ~ 1∕2 for all the planets. We show that the final water fraction is insensitive to the embryo mass. The timing is the most important factor for f_water.

In the next section, we show that the derived semi-analytical expression of f_water reproduces the numerical results. Using the analytical expression, we clarify the dependence of the final water fraction on the disk parameters and pebble accretion parameters such as the initial planetary mass and Stokes number of accreting pebbles in Sect. 5. We also survey the disk parameter range that may reproduce f_water comparable to that of the terrestrial planets in our solar system.

Fig. 3 Time evolution of water fraction for the models with tdiff = 106 yr, Ṁg,0 = 10−7M⊙ yr−1, and Ṁpe = 10−9M⊙ yr−1. Left, center, and right panel: results of rd.0 = 30 100, and 300 au, respectively. The blue, red, and green lines represent the Earth, Mars and Venus analogs, respectively.

Fig. 4 Time evolution of water fraction for the models with rd.0 = 100 au, Ṁg,0 = 3 × 10−8M⊙ yr−1 and Ṁpe = 10−9M⊙ yr−1. Left and right panels: results of tdiff = 106 and 3 × 106yr, respectively.

4 Analytical formula for planetary water fraction

The planetary water fraction is calculated by estimating the cumulative mass of accreted icy pebbles ΔM_pl (Eq. (39)). We can simply estimate it as ΔM_pl ≃ f_flt(M_pl) × M_res, where M_res is the total icy dust mass preserved in outer disk regions at the snowline passage because the pebble flux integrated from the snowline passage time t_snow to infinity (effectively, to t_diff) must be similar to M_res.

Equation (39) is approximated to be $$\begin{array}{ll}{f}_{\text{water}}\hfill & \simeq \frac{1}{2}\frac{f_{\text{flt}}(M_{\text{pl}})}{M_{\text{pl},\text{0}}+f_{\text{flt}}(M_{\text{pl}})M_{\text{res}}}{M}_{\text{res}}\hfill \\ \hfill & \simeq \{\begin{array}{ll}\frac{1}{2}\frac{f_{\text{flt}}(M_{\text{pl},\text{0}})}{M_{\text{pl},\text{0}}}{M}_{\text{res}}\hfill & [\Delta M_{\text{pl}}\ll M_{\text{pl},\text{0}}]\hfill \\ \frac{1}{2}\hfill & [\Delta M_{\text{pl}}\gg M_{\text{pl},\text{0}}],\hfill \end{array}\hfill \end{array}$$(41)

where we use f_flt(M_pl) ≃ f_flt(M_pl,0) for ΔM_pl ≪ M_pl,0 in the upper line. For the range of the disk parameters we use in numerical simulations, the accretion is mostly in the 3D regime (Eq. (28)) and f_flt ∝ M_pl. In that case, Eq. (41) shows that f_water is independent of M_pl both in the cases of ΔM_pl < M_pl,0 and ΔM_pl > M_pl,0, while it depends on the disk parameters. Even if the transition to 2D accretion occurs at a smaller planet mass (which happens for smaller values of α), the mass dependence of f_water is still weak: it is proportional to 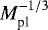$M_{\text{pl}}^{-1/3}$ for ΔM_pl < M_pl,0 and independentof M_pl otherwise. We can combine the two limits in Eq. (41) by a simple formula as

Fig. 5 Time evolution of water fraction for the models with rd.0 = 100 au, tdiff = 106 yr and Ṁpe = 10−9 M⊙ yr−1. Left and right panels: results of Ṁg,0 = 3 × 10−8 and 10−7M⊙ yr−1, respectively.

Fig. 6 Time evolution of water fraction for the models with rd.0 = 100 au, tdiff = 106 yr and Ṁini = 10−7M⊙ yr−1. Left, center, and right panels: results of Ṁpe = 10−9, 3 × 10−9, and 10−8M⊙ yr−1, respectively.

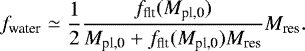$$f_{\text{water}}\simeq \frac{1}{2}\frac{f_{\text{flt}}(M_{\text{pl},\text{0}})}{M_{\text{pl},\text{0}}+f_{\text{flt}}(M_{\text{pl},\text{0}})M_{\text{res}}}{M}_{\text{res}}.$$(42)

In Fig. 7, f_water,sim obtained byour simulations is compared with Eq. (42) with the simulated M_res. This figure showsthat Eq. (42) reproduces the numerical results very well. Both the numerical results and Eq. (42) show f_water ∝ M_res for f_water ≪ 1∕2. The icy dust mass M_res depends sensitively on the disk parameters, Ṁ_g,0, Ṁ_pe, t_diff, and r_d,0. On the other hand, f_flt in 2D is independent of these disk parameters, while that in 3D depends only weakly (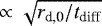$\propto \sqrt{r_{\text{d},\text{0}}/t_{\text{diff}}}$). In the case of ΔM_pl ≪ M_pl,0, f_water ≃ (f_flt∕M_pl,0)M_res. As we discussed, f_flt ∕M_pl,0 is almost constant, so that f_water should be almost proportional to M_res for ΔM_pl ≪ M_pl,0.

Because the analytical solution given by Eq. (42) reproduces the numerical results, we next derive an analytical formula for the icy dust mass M_res at the snowline passage as follows. From Eq. (6), the snowline passes the planet orbit at a_pl when 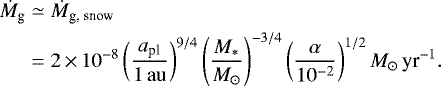$$\begin{array}{ll}{\dot{M}}_{\text{g}}\hfill & \simeq {\dot{M}}_{\text{g},\text{snow}}\hfill \\ \hfill & =2\times {10}^{-8}{\left(\frac{a_{\text{pl}}}{1\text{au}}\right)}^{9/4}{\left(\frac{M_{*}}{M_{\odot }}\right)}^{-3/4}{\left(\frac{\alpha }{{10}^{-2}}\right)}^{1/2}{M}_{\odot }{\text{yr}}^{-1}.\hfill \end{array}$$(43)

Using Eq. (14), 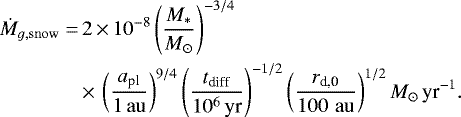$$\begin{array}{ll}{\dot{M}}_{g,\text{snow}}=\hfill & 2\times {10}^{-8}{\left(\frac{M_{*}}{M_{\odot }}\right)}^{-3/4}\hfill \\ \hfill & \times {\left(\frac{a_{\text{pl}}}{1\text{au}}\right)}^{9/4}{\left(\frac{t_{\text{diff}}}{{10}^6\text{yr}}\right)}^{-1/2}{\left(\frac{r_{\text{d},\text{0}}}{100\text{au}}\right)}^{1/2}{M}_{\odot }{\text{yr}}^{-1}.\hfill \end{array}$$(44)

From Eq. (10), the snowline passage time is $${\tilde{t}}_{\text{snow}}\simeq {\left(\frac{{\dot{M}}_{\text{g},\text{0}}}{{\dot{M}}_{g,\text{snow}}+{\dot{M}}_{\text{pe}}}\right)}^{2/3}\text{}\text{};t_{\text{snow}}\simeq \left[{\left(\frac{{\dot{M}}_{\text{g},\text{0}}}{{\dot{M}}_{g,\text{snow}}+{\dot{M}}_{\text{pe}}}\right)}^{2/3}\text{}\text{}-1\text{}\right]t_{\text{diff}}.$$(45)

From Eq. (12), the remaining gas disk mass at the snowline passage is given by 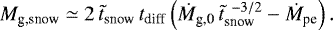$$M_{\text{g},\text{snow}}\simeq 2{\tilde{t}}_{\text{snow}}{t}_{\text{diff}}\left({\dot{M}}_{\text{g},\text{0}}{\tilde{t}}_{\text{snow}}^{-3/2}-{\dot{M}}_{\text{pe}}\right).$$(46)

Because M_res ~ Z M_g,snow, we obtain 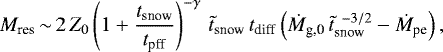$$M_{\text{res}}~2Z_0{\left(1+\frac{t_{\text{snow}}}{t_{\text{pff}}}\right)}^{-\gamma }{\tilde{t}}_{\text{snow}}{t}_{\text{diff}}\left({\dot{M}}_{\text{g},\text{0}}{\tilde{t}}_{\text{snow}}^{-3/2}-{\dot{M}}_{\text{pe}}\right),$$(47)

where we approximated Z as 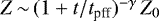$Z~{(1+t/t_{\text{pff}})}^{-\gamma }{Z}_0$ from Eq. (37), 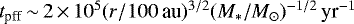$t_{\text{pff}}~2\times {10}^5{(r/100\text{au})}^{3/2}{(M_{*}/M_{\odot })}^{-1/2}{\text{yr}}^{-1}$ (Eq. (36)), and γ = 1 + 0.15(300 au∕r_d,0) (Eq. (38)). Substituting the filtering factor f_flt given by Eq. (29) with St = 0.1 and M_res estimated above into Eq. (42), we can analytically estimate the water fraction from the disk parameters, Ṁ_g,0, Ṁ_pe, t_diff, and r_d,0 as (Eqs. (29) and (39))

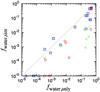Fig. 8 Comparison of the water fraction obtained by the numerical simulations (fwater,sim) with the analytical estimate (fwater,anly). The blue squares, red circles, and green cross represent the results for the Earth, Mars, and Venus analogs, respectively. If fwater,sim obtained by the numerical simulation is smaller than 10−5, we put fwater,sim = 10−5 because the numerical results would include a numerical uncertainty for such small values of fwater,sim.

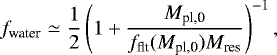$$f_{\text{water}}\simeq \frac{1}{2}{\left(1+\frac{M_{\text{pl},\text{0}}}{f_{\text{flt}}(M_{\text{pl},\text{0}})M_{\text{res}}}\right)}^{-1},$$(48)

where M_res is given by Eq. (47), f_flt = min(f_flt,3D, f_flt,2D), and $$\begin{array}{ll}{f}_{\text{flt},\text{3D}}\simeq \hfill & 0.017{\left(\frac{M_{\ast }}{M_{\odot }}\right)}^{-1}{\left(\frac{\alpha }{{10}^{-2}}\right)}^{-1/2}{\left(\frac{h_{\text{g}}/r}{0.02}\right)}^{-1}{\left(\frac{St}{0.1}\right)}^{1/2}\hfill \\ \hfill & \times \left(\frac{M_{\text{pl},\text{0}}}{0.1M_{\oplus }}\right){\left(\frac{r}{1\text{au}}\right)}^{-1/2},\hfill \\ f_{\text{flt},\text{2D}}\simeq \hfill & 0.040{\left(\frac{M_{\ast }}{M_{\odot }}\right)}^{-2/3}{\left(\frac{St}{0.1}\right)}^{-1/3}{\left(\frac{M_{\text{pl},\text{0}}}{0.1M_{\oplus }}\right)}^{2/3}{\left(\frac{r}{1\text{au}}\right)}^{-1/2}.\hfill \end{array}$$

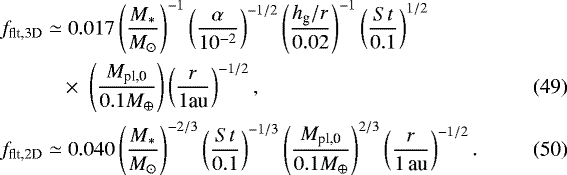
Except for the value of γ, which was fitted by the numerical results, the other derivations are analytical. We note that f_water ∝ M_res ∝ Z₀. Around metal-rich stars, f_water would be larger.

In Fig. 8, we compare the analytically estimated water fraction f_water,anly with the numerically simulated f_water,sim. In addition to the Earth analogs (M_pl,0 = 1M_⊕) at 1 au, we also plot the results for the Mars analogs (M_pl,0 = 0.11M_⊕) at 1.52 au and the Venus analogs (M_pl,0 = 0.82M_⊕) at 0.72 au. For the Earth and Mars analogs, f_water,anly reproduces f_water,sim within a factor of several, while the water fraction varies by several orders of magnitude, except for some runs for which the water fraction is overestimated by the analytical formula. The agreement both for the Earth and Mars analogs strongly suggests that the mass and semimajor axis dependences are also reproduced. In the case of Venus analogs, f_water,anly is larger by a factor of a few to a few tens than f_water,sim. When the Earth analog increases its mass by capture of pebbles, it captures a significant fraction of the pebble flux and the accretion of the Venus analogs that reside in inner region of the Earth analogs can be significantly decreased. This effect is included in the numerical simulation, while it is not taken into account in the analytical formula.

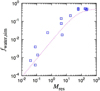Fig. 7 Water fraction fwater,sim and icy dust mass preserved in the outer disk at the snowline passage Mres obtained by our simulations. The blue squares show the simulation results for the Earth analogs with different values of Ṁg,0, Ṁpe, tdiff, and rd,0 (Sect. 2.4). The dotted curve represents the analytical solution given by Eq. (42).

5 Dependence of water fraction on disk parameters

Using the analytical formula, we investigate how the water fraction (f_water) is determined by the disk parameters. Figure 9 shows f_water for a planet at a_pl = 1.0 au as a function of the disk parameters, Ṁ_g,0 and r_d,0. The other parameters are Ṁ_pe = 10⁻⁹M_⊙ yr⁻¹ and t_diff = 3 × 10⁶ yr⁻¹. The panels a show the dependence on M_pl,0 for St = 0.1. The panels b show the dependence on St for M_pl,0 = 1M_⊕. The planetsformed with the parameters in the red region are very dry, f_water ≲ 10⁻⁴. Those in the green region have a modest amount of water, f_water ~ 0.1, and those in the blue region are icy planets, f_water ≃ 1∕2. The yellow and orange regions represent f_water ~ 10⁻⁴−10⁻², which corresponds to the water fraction of the current Earth and that estimated for ancient Mars.

We find that f_water is the most sensitive to Ṁ_g,0 and r_d,0. The common features in the contours in Fig. 9 are that (i) f_water is lower for smaller r_d,0 and larger Ṁ_g,0, and (ii) f_water ~ 10⁻⁴−10⁻² is realized at r_d,0 ~ 30−50 au and Ṁ_g,0 ≳ 10⁻⁸M_⊙ yr⁻¹. This is consistent with the conclusion by Sato et al. (2016) that such f_water can be realized for compact disks with sizes <100 au and late snowline passage (>2−4 M yr). We show that the disk parameters for f_water ~ 10⁻⁴−10⁻² is not in a very narrow window.

As we showed in Sect. 4, f_water is regulated by M_res and M_res is sensitive to Ṁ_g,0 and r_d,0, especially through the parameter t_snow∕t_pff (Eq. (47)). Because pebble accretion is fast to realize f_water ~ 10⁻⁴−10⁻², M_res has to have significantly decayed until t ~ t_snow. For small r_d,0, t_pff is small (Eq. (36)), while t_snow is large (Eq. (45)) due to small Ṁ_g,snow (Eq. (44)). For large Ṁ_g,0, t_snow is small (Eq. (44)) while t_pff is the same (Eq. (36)). As a result, Σ_p decays more quickly (Eq. (37)) for small r_d,0 and large Ṁ_g,0.

Figure 9 shows the dependences of f_water on the pebble accretion parameters: the initial planetary mass (M_pl,0) and the Stokes number (St) of pebbles that accrete onto the planet.

In the numerical simulations, the Stokes number of pebbles that accrete onto the planet is calculated by growth and radial drift of pebbles in an evolving disk. According to the simulations, the Stokes number of radially drifting particles is ~ 0.1 at early times (Eq. (34)), but decreases with time as the dust and gas disks evolve. As Eq. (37) shows, Σ_p decays more rapidly thanΣ_g for t > t_pff. Accordingly,Z decreases and the equilibrium Stokes number of migrating pebbles become smaller (Eq. (34); also see Sato et al. 2016). As we pointed out in Sect. 3.1, if a fragmentation/rebound barrier limits the icy pebble growth, St also becomes small. With this reasoning, we also showed plots with St = 0.01 and 0.001 inFig. 9.

Figure 9 shows that f_water is almost independent of M_pl,0 and St. The weak dependence on M_pl,0 is explained by the following arguments. The water fraction f_water is ~ (f_flt∕M_pl,0)M_res in the case of ΔM_pl ≪ M_pl,0. The dust mass M_res is independent of M_pl. As already explained in Sect. 4, the factor f_flt∕M_pl,0 is independent of M_pl,0 in 3D accretion and only weakly depends on M_pl,0 in 2D accretion (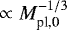$\propto M_{\text{pl},\text{0}}^{-1/3}$).

The weak dependence of f_water on Stokes number shown in Fig. 9 is the result of the assumption that M_res is independent of St; it depends on St only weakly (Eq. (29)) through f_flt. The parameter γ could be dependent on St because the sculpture rate of Σ_p at r = r_pff may depend on St. Figure 10 shows the dependence on γ₂, assuming that the functional form of γ = 1 + γ₂(300 au∕r_d,0) still holds. Because the sculpture rate may be lower for smaller values of St, we tested the cases of γ₂ = 0.05 and 0.1, in addition to the nominal case of γ₂ = 0.15. The result is insensitive to γ₂ for γ₂ ≳ 0.1, while the sculpture rate is lower and accordingly the f_water is relatively higher for γ₂ ~ 0.05. The detailed functional form of γ is left for future works.

Figure 11 shows the dependence on the other disk parameters, t_diff and Ṁ_pe. For larger t_diff, the evolution of the snowline is slower and the snowline passage is later (Eq. (45)). Before the passage, the icy dust disk has been more sculpted. As a result, M_res is smaller (Eq. (47)) because t_snow ∝ t_diff and γ ≥ 1. For smaller Ṁ_pe, the disk is hotter and the snowline passage is later (t_snow is larger), resulting in smaller M_res. If M_res is smaller, f_water is smaller. The water fraction corresponding to the current Earth is 10⁻⁴−10⁻² (the yellow and orange colored regions) are only slightly shifted to larger r_d,0 and lower Ṁ_g,0 for smaller t_diff and larger Ṁ_pe, because M_res is smaller for these parameters (Eq. (47)). We note that the parameter region with Ṁ_g,0 < Ṁ_pe is empty in the right panel of Fig. 11b because the disks do not exist under that condition.

In Fig. 12, the analytically estimated f_water is plotted for a_pl = 0.72, 1.00 and 1.52 au (the Venus, Earth, and Mars analogs, respectively). In the outer region, f_water is generally larger due to early snowline passage (smaller t_snow). In other words, Ṁ_g,snow is larger for larger a_pl. As mentioned in Sect. 4, the Venus analogs may have further lower f_water, if we take into account the decrease in the pebble flux due to accretion by the Earth analog. As shown in Eq. (7), the snowline cannot reach the region inside 0.53 au in our disk model. The planets there are completely dry. Although the dependence on the orbital radius exists, in the case of r_d,0 ~ 30−50 au and Ṁ_g,0 ≳ 2 × 10⁻⁸ M_⊙ yr⁻¹, f_water ~ 10⁻⁴−10⁻² for both the Earth and Mars analogs.

In Sect. 3, we pointed out that the simple condition of t_snow∕t_pff < 10 or > 10 discriminates between the water-rich case (f_water ~ 1∕2) and the water-poor case. The pebble formation timescale t_pff is given by Eq. (36) and the snowline passage time t_snow is given by Eq. (45). Both t_pff and t_snow are independent of M_pl and St, which is consistent with Fig. 9. The condition of t_snow = 10 t_pff is shown on the r_d,0 –Ṁ_g,0 plane in Fig. 13. We show the dependences on t_diff, Ṁ_pe, and a_pl. A comparison of this figure with Figs. 11 and 12 show that the simple condition approximately reproduces the more detailed evaluation except for r_d,0 > 100 au. As shown in Fig. 1, for r_d,0 > 100 au, the disk radius expands with the pebble formation front radius r_pff, so that the sculpture of icy dust reservoir is delayed, compared to the estimation of t_pff at r_d,0. The calculation of M_res does not have this problem.

As we have shown, f_water is the most sensitive to Ṁ_g,0 and r_d,0 and almost independentof the other parameters of disks and pebble accretion. A robust result would be that the water fraction inferred for the present Earth and ancient Mars, f_water ~ 10⁻⁴−10⁻², is realized at r_d,0 ~ 30−50 au and Ṁ_g,0 ≳ 2 × 10⁻⁸ M_⊙ yr⁻¹, which may correspond to median disks of classical T Tauri stars or slightly compact and massive disks.

Fig. 9 Analytical estimate of fwater at 1 au as a function of the initial disk radius (rd,0) and the initial disk accretion rate (Ṁg,0). Panels a: dependence on the planet mass (Mpl,0). Panels b: Stokes number (St) of pebbles. The other parameters are Ṁpe = 10−9M⊙ yr−1 and tdiff = 3 × 106 yr. In the panelsa, we use St = 0.1. In the panelsb, Mpl,0 = 1M⊕. The middle panels in a and b are identical. The color scales are log10fwater.

Fig. 10 Analytical estimate of fwater at 1 au as a function of the initial disk radius (rd,0) and the initial disk accretion rate (Ṁg,0), where γ2 = 0.05, 0.10, and 0.15. The other parameters are St = 0.1, Mpl,0 = 1M⊕, ${\dot{M}}_{\text{pe}}={10}^{-9}{M}_{\odot }{\text{yr}}^{-1}{}^{-1}$, and tdiff = 3 × 106 yr. The color scales are log10fwater.

Fig. 11 Analytical estimate of fwater at 1 au as a function of rd,0 and Ṁg,0. Panels a: The dependence on the disk diffusion timescale tdiff. Panels b: dependence on the photoevaporation rate (Ṁpe). The other parameters are St = 0.1 and Mpl,0 = 1M⊕. In the panels a, we used Ṁpe = 10−9M⊙ yr−1, and tdiff = 3 × 106 yr in the panels b. The middle panels of panels a and the right panel of panels b are identical. In the right panel of panel b, the region with Ṁg,0 < Ṁpe is empty because the disks do not exist under that condition. The color scales are log10 fwater.

Fig. 12 Analytical estimate of fwater as a functionof rd,0 and Ṁg,0, at 0.72, 1.00, and 1.52 au. The other parameters are St = 0.1, Mpl,0 = 1M⊕, Ṁpe =10−9M⊙ yr−1, and tdiff = 3 × 106 yr. The color scales are log10fwater.

6 Discussion

In this section, we comment on the effect of pebble isolation mass, which we did not include in our simulations. A planet with relatively large mass (M_pl) can make a dip in the gas disk along the planetary orbit to prevent the pebbles from passing the orbit. The threshold mass is called “pebble isolation mass” (M_peb,iso; Lambrechts et al. 2014; Bitsch et al. 2018; Ataiee et al. 2018). When the planetary mass reaches the isolation mass, pebble accretion onto the planet with M_pl > M_peb,iso and other planets inside the planetary orbit is truncated and the increases in their water fraction are stalled.

Bitsch et al. (2018) derived a detailed expression of the pebble isolation mass, $$M_{\text{peb},\text{iso}}\simeq 25{\left(\frac{h/r}{0.05}\right)}^3\left[0.34{\left(\frac{3}{{\log }_{10}(\alpha )}\right)}^4+0.66\right]M_{\oplus }.$$(51)

For example, M_peb,iso ≃ 4.1M_⊕ for t_diff = 3 × 10⁶ yr, Ṁ_g,0 = 10⁻⁸M_⊙ yr⁻¹, r_d,0 au, h∕r ≃ 0.0246 (at 1 au), and α ≃ 3 × 10⁻³. If M_pl,0 ≳several M_⊕, the effect of pebble isolation mass is not negligible. Figure 14 shows the water fraction for M_pl,0 = 3, 5, and 10 M_⊕. We stop pebble accretion when M_pl reaches M_peb,iso. Because α is smaller for smaller r_d,0 (Eq. (14)) and h∕r is lower for smaller Ṁ_g,0 and higher α (Eq. (3)), M_peb,iso is smaller for smaller r_d,0 and Ṁ_g,0. The dry regime (red-colored regime) in the left bottom part of the plots represent the cases of M_pl,0 > M_peb,iso. Because t_snow is small in the low Ṁ_g,0 regions, f_water rapidly increases because of a high pebble flux until M_pl increases to M_peb,iso. Thereby, the edge in f_water at M_pl,0 ≃ M_peb,iso is sharp.

For the same t_diff, Ṁ_g,0, and r_d,0 as the above, 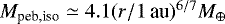$M_{\text{peb},\text{iso}}\simeq 4.1{(r/1\text{au})}^{6/7}{M}_{\oplus }$. The filtering rate for M_peb,iso is 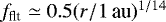$f_{\text{flt}}\simeq 0.5{(r/1\text{au})}^{1/14}$ in 2D case (Eq. (29)). If ice giants or cores of gas giants are formed, even before their mass exceeds M_peb,iso, the pebble flux is reduced by ~50% by individual ice giants.

If Jupiter’s core is formed in the outer region, it shuts down the pebble mass flux into the terrestrial planet region. Morbidelli et al. (2016) proposed that the pebble flux truncation by the formation of Jupiter accounts forthe dichotomy of our solar system – the total solid mass contained in Jupiter, Saturn, Uranus, and Neptune is about 50 times larger than the total mass of terrestrial planets. Jupiter’s core must be formed at M_res ≳ 10 M_⊕. From Eq. (47) with M_d,0 ~ 10⁻⁸ M_⊙ yr⁻¹ and t_diff ~ 3 × 10⁶ yr, 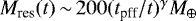$M_{\text{res}}(t)~200{(t_{\text{pff}}/t)}^{\gamma }{M}_{\oplus }$, which is 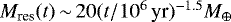$M_{\text{res}}(t)~20{(t/{10}^6\text{yr})}^{-1.5}{M}_{\oplus }$ for r_d,0 ~ 100 au. Hence, the Jupiter’s core formation time t_jup must be ≲ t_diff. If this is the case, the dichotomy of our solar system could be created. However, the water fraction of the terrestrial planets is a problem in this case, in addition to a problem of too fast type I migration of the core (Matsumura et al. 2017). Our results show that f_water rapidly increases after t = t_snow and becomes saturated before t ~ t_diff. If t_snow > t_jup, f_water = 0 for terrestrial planets. Otherwise, it is likely that f_water is already close to the saturated value because the increase of f_water is very rapid. It is difficult for giant planet formation to directly produce modestly low values of water mass fraction (~ 10⁻⁴−10⁻²) corresponding to the Earth and ancient Mars. The modestly low values are attained by disk parameters with t_snow ~ 10 t_pff as we showed.

We also point out that D/H ratio is expected to be radially uniform among the Earth, asteroids, and comets if water is delivered by icy pebbles that form in disk outer regions and drift all the way to the host star. However, observations show that in our solar system, D/H ratios of Oort cloud comets are clearly higher than the Earth (e.g., Marty 2012). One possibility to reconcile the discrepancy is the shutdown of the pebble flux by Jupiter formation (Kruijer et al. 2017). Because pebble formation front migrates outward, the isotope ratios of drifting pebbles before and after Jupiter formation, which are the building materials for terrestrial planets and those for comets, respectively, should be different. A more careful comparison should be necessary between planet formation model and cosmo-chemical data.

Fig. 13 Condition of tsnow = 10 tpff as a functionof rd,0 and Ṁg,0. Panels a: dependence on the disk diffusion timescale tdiff. Panels b: photoevaporation rate (Ṁpe). Panels c: planetary orbital radius (apl). The right regions from the curves represent water-rich regions (fwater ~ 1∕2). In the panelsa, we used Ṁpe = 10−9M⊙ yr−1 and apl= 1 au, tdiff = 3 × 106 yr and apl= 1 au in the panelsb, and Ṁpe = 10−9M⊙ yr−1 and tdiff = 3 × 106 yr in the panels c.

Fig. 14 Analytical estimate of fwater at 1 au as a function of the initial disk radius (rd,0) and the initial disk accretion rate (Ṁg,0), including the effect of the pebble isolation mass. The other parameters are Ṁpe =10−9M⊙ yr−1, tdiff = 3 × 106 yr, and St = 0.1. Pebble accretion is halted when Mpl reaches Mpeb,iso. The dry regime (red) in the left bottom part of the plots represents the cases of Mpl,0 > Mpeb,iso.

7 Summary

If water is not delivered to rocky planets in HZs, the planets cannot be actual habitats because H₂ O ice condenses in the disk regions well beyond the HZs. In the pebble accretion model, accretion of icy pebbles after the snowline passage may be a primary mechanism to deliver water to the rocky planets.

In this paper, we have investigated the water delivery to rocky planets by pebble accretion around solar-type stars through a 1D simulation of the growth of icy dust grains to pebbles and the pebble radial drift in an evolving disk. We assume that the planetary embryos did not migrate significantly and consist of pure rock, which means that accretion of ice starts when the snowline migrates inward and passes the planetary orbit due to disk evolution. Our previous paper, Sato et al. (2016), pointed out that the water fraction of the final planets are determined by the timings of the snowline passage through the planetary orbit (t = t_snow) and disk gas depletion because pebble accretion is fast and efficient. While Sato et al. (2016) used a simple static disk model, we used the evolving disk model due to viscous diffusion based on the self-similar solution with constant viscous α (Lynden-Bell & Pringle 1974) and simultaneously calculated pebble formation/drift/accretion and snowline migration with the disk model. Because the snowline migration is correlated with global disk diffusion in the evolving disk model, we found that for a water fraction of the final planets (f_water), the snowline passage time (t_snow) relative to the time (t_pff) at which pebble formation front reaches the disk outer edge is more important than that relative to the disk gas depletion timescale. Our simulation shows that the ice dust mass (M_res) preserved in the disk outer region at t = t_snow determines the water fraction of the final planets. The accreted ice mass to the planet is estimated by ~ (1∕2)f_fltM_res, where the filtering factor f_flt is the fraction of the pebble mass flux that is accreted onto the planet. Because M_res rapidly decreases after t ~ t_pff, t_snow∕t_pff > 10 or < 10 is crucial for final value of f_water. If t_snow∕t_pff > 10, M_res should have significantly decayed when icy pebble accretion starts at t = t_snow.

Using these numerical results, we derived an analytical formula for f_water by icy pebble accretion. In the formula, f_water is explicitly given as a function of the ratio t_snow∕t_pff and the disk parameters. The parameter t_snow∕t_pff is also determined by the disk parameters. As a result, f_water is predictedby the disk parameters, especially the initial disk mass accretion rate Ṁ_g,0 and initial disk size r_d,0. It is insensitive to pebble accretion parameters such as the planet mass and Stokes number of drifting pebbles.

We found that the expected water fraction of an Earth analog near 1 au has f_water ~ 10⁻⁴−10⁻², which may correspond to the value of the current Earth, in disks with an initial disk size of r_d,0 ~ 30–50 au and the initial disk mass accretion rate Ṁ_g,0 ~ (10⁻⁸−10⁻⁷)M_⊙ yr⁻¹. For Ṁ_g,0 ≳ 2 × 10⁻⁸M_⊙ yr⁻¹, both the Earth and Mars analogs have f_water ~ 10⁻⁴−10⁻², while f_water is generally larger for Mars than for Earth. Because these disks may be median or slightly compact/massive disks among classical T Tauri stars, our results suggest that rocky planets in HZs in exoplanatery systems around solar-type stars often have a water fraction similar to the Earth if pebble accretion is responsible for water delivery, while large diversity in the water fraction due to the variations of disk conditions may also exist.

Acknowledgements

We thank Michiel Lambrechts for detailed and helpful comments. This work was supported by JSPS KAKENHI 15H02065 and 16K17661 and by MEXT KAKENHI 18H05438.

References

All Figures

Fig. 1 Time evolution of the transition radius rvis/irr (Eq. (5); red lines), snowline rsnow = max(rsnow,vis, rsnow,irr) (Eqs. (6) and (7); blue lines), disk characteristic radius $\tilde{t}{r}_{\text{d},\text{0}}$ (green lines), and pebble formation front rpff (Eq. (36); magenta lines) for various disk evolution parameters. The parameters, rd,0 in units of auand Ṁg,0 in units of M⊙ yr−1 are labeled in the individual panels. The other parameters are the same for the four panels, i.e., Ṁpe =10−9 M⊙ yr−1 and tdiff = 106 yr.

In the text

	Fig. 2 Time evolution of Z = Σp∕Σg obtained by the numerical simulation with Ṁg,0 = 10−7M⊙ yr−1, Ṁpe =10−9M⊙ yr−1, and tdiff = 106 yr. The magenta, blue, and green solid lines show Z obtained at rd,0 by the numerical results of with rd,0 = 30, 100 and 300 au. The dashed lines indicate gradients for individual cases given by Eqs. (37) and (38), where the absolute values of Z are arbitrary.
In the text

	Fig. 3 Time evolution of water fraction for the models with tdiff = 106 yr, Ṁg,0 = 10−7M⊙ yr−1, and Ṁpe = 10−9M⊙ yr−1. Left, center, and right panel: results of rd.0 = 30 100, and 300 au, respectively. The blue, red, and green lines represent the Earth, Mars and Venus analogs, respectively.
In the text

	Fig. 4 Time evolution of water fraction for the models with rd.0 = 100 au, Ṁg,0 = 3 × 10−8M⊙ yr−1 and Ṁpe = 10−9M⊙ yr−1. Left and right panels: results of tdiff = 106 and 3 × 106yr, respectively.
In the text

	Fig. 5 Time evolution of water fraction for the models with rd.0 = 100 au, tdiff = 106 yr and Ṁpe = 10−9 M⊙ yr−1. Left and right panels: results of Ṁg,0 = 3 × 10−8 and 10−7M⊙ yr−1, respectively.
In the text

	Fig. 6 Time evolution of water fraction for the models with rd.0 = 100 au, tdiff = 106 yr and Ṁini = 10−7M⊙ yr−1. Left, center, and right panels: results of Ṁpe = 10−9, 3 × 10−9, and 10−8M⊙ yr−1, respectively.
In the text

	Fig. 7 Water fraction fwater,sim and icy dust mass preserved in the outer disk at the snowline passage Mres obtained by our simulations. The blue squares show the simulation results for the Earth analogs with different values of Ṁg,0, Ṁpe, tdiff, and rd,0 (Sect. 2.4). The dotted curve represents the analytical solution given by Eq. (42).
In the text