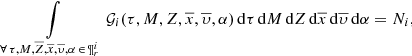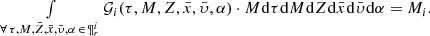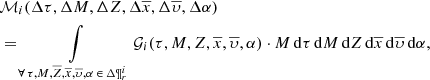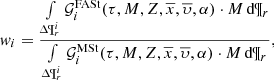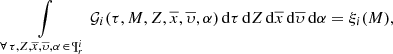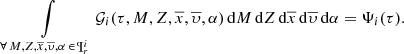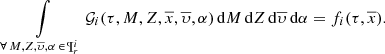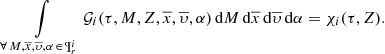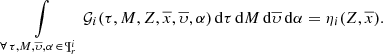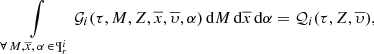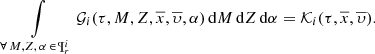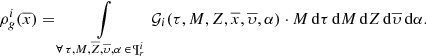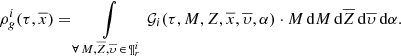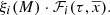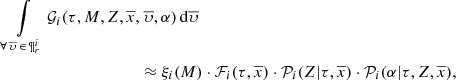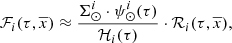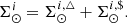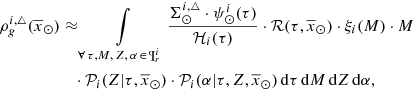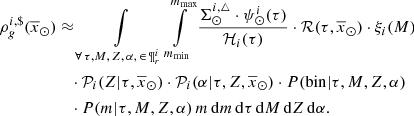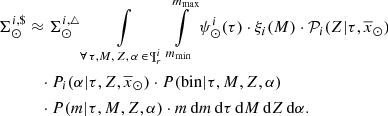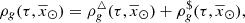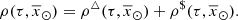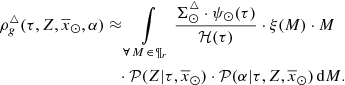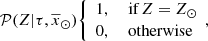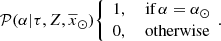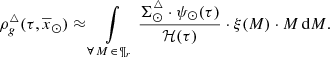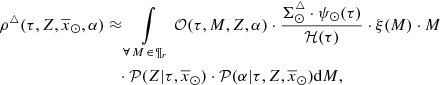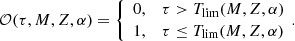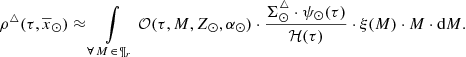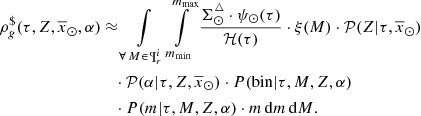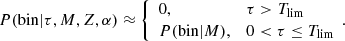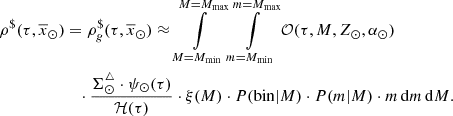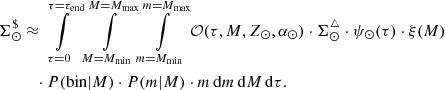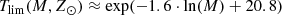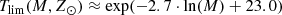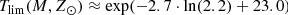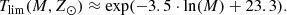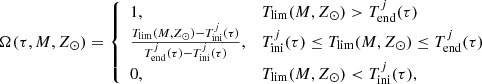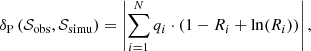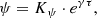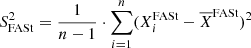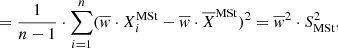| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | A79 | |
| Number of page(s) | 29 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201833501 | |
| Published online | 04 December 2018 | |
BGM FASt: Besançon Galaxy Model for big data
Simultaneous inference of the IMF, SFH, and density in the solar neighbourhood
1 Dept. Física Quàntica i Astrofísica, Institut de Ciències del Cosmos, Universitat de Barcelona (IEEC-UB), Martí Franquès 1, 08028 Barcelona, Spain
e-mail: rmor@fqa.ub.edu
2 Institut Utinam, CNRS UMR6213, Université de Bourgogne Franche-Comté, OSU THETA, Observatoire de Besançon, BP 1615, 25010 Besançon Cedex, France
Received:
25
May
2018
Accepted:
10
September
2018
Aims. We develop a new theoretical framework to generate Besançon Galaxy Model Fast Approximate Simulations (BGM FASt) to address fundamental questions of the Galactic structure and evolution performing multi-parameter inference. As a first application of our strategy we simultaneously infer the initial-mass function (IMF), the star formation history and the stellar mass density in the solar neighbourhood.
Methods. The BGM FASt strategy is based on a reweighing scheme, that uses a specific pre-sampled simulation, and on the assumption that the distribution function of the generated stars in the Galaxy can be described by an analytical expression. To evaluate the performance of our strategy we execute a set of validation tests. Finally, we use BGM FASt together with an approximate Bayesian computation algorithm to obtain the posterior probability distribution function of the inferred parameters, by automatically comparing synthetic versus Tycho-2 colour-magnitude diagrams.
Results. The validation tests show a very good agreement between equivalent simulations performed with BGM FASt and the standard BGM code, with BGM FASt being ∼104 times faster. From the analysis of the Tycho-2 data we obtain a thin-disc star formation history decreasing in time and a present rate of 1.2 ± 0.2 M ⊙ yr−1. The resulting total stellar volume mass density in the solar neighbourhood is 0.051−0.005+0.002 M⊙ pc−3 and the local dark matter density is 0.012 ± 0.001 M ⊙ pc−3. For the composite IMF, we obtain a slope of α2 = 2.1−0.3+0.1 in the mass range between 0.5 M⊙ and 1.53 M⊙. The results of the slope at the high-mass range are trustable up to 4 M⊙ and highly dependent on the choice of extinction map (obtaining α3 = 2.9−0.2+0.2 and α3 = 3.7−0.2+0.2, respectively, for two different extinction maps). Systematic uncertainties coming from model assumptions are not included.
Conclusions. The good performance of BGM FASt demonstrates that it is a very valuable tool to perform multi-parameter inference using Gaia data releases.
Key words: Galaxy: fundamental parameters / solar neighborhood / Galaxy: stellar content / stars: formation / methods: analytical / methods: statistical
© ESO 2018
1. Introduction
Recently, the astrophysics community has successfully carried out important ground-based and space missions generating very large data sets. Large sky surveys with photometric and astrometric data, such as Gaia data release 2 (Gaia Collaboration 2018), among others, represent a challenge for Galaxy modelling in terms of both the new types of data and the large amounts of data created. At the same time, new statistical techniques are having a significant effect on modern astronomy. The use of Bayesian statistics for the exploration of large parameter spaces, together with Monte Carlo Markov chains (MCMC) or approximate Bayesian computation (ABC), among others, are in rapid development.
Several attempts have been done to generate fast Milky Way simulations (e.g. Girardi et al. 2005; Jurić et al. 2008; Sharma et al. 2011 or Pasetto et al. 2016). It is demonstrated that the Galaxy models from Sharma et al. (2011) and Pasetto et al. (2016) can be used to explore large parameters spaces under machine-learning algorithms, MCMC, and ABC (e.g. Rybizki & Just 2015; Pasetto et al. 2016). The Galaxia code is able to work in two different modes: it can simulate the Milky Way from a Galaxy model based on Robin et al. (2003), or from N-body simulations. The fast performance of Galaxia relies on its sampling technique and its clever strategy adopted to avoid the simulation of unnecessary stars. The strategy of Pasetto et al. (2016) to perform fast simulations of the Milky Way is based on the use of distribution functions. It constructs colour-magnitude diagrams (CMDs) of single stellar populations from N-body simulations, with low computational cost (Pasetto et al. 2012).
The Besançon Galaxy Model (BGM; Robin et al. 2003) is also a stellar population synthesis model for the Milky Way. It is a very powerful and versatile tool for the statistical analysis of the structure and evolution of the Milky Way. Moreover, it is a valuable tool for the preparation and validation of catalogues for space- and ground-based observational instruments and surveys. Recently, BGM was used to study the kinematics of the local disc from the RAVE survey and the Gaia first data release (DR1; Robin et al. 2017), to evaluate the evolution of the Milky Way’s disc shape over time (Amôres et al. 2017), to constrain Galactic and stellar physics (Lagarde et al. 2017), to constrain the local initial-mass function (IMF) using Galactic Cepheids and Tycho-2 data (Mor et al. 2017), and to study microlensing events in the Galactic bulge (Awiphan et al. 2016). Furthermore, BGM has also been useful, together with other Milky Way models, to study the bulge bar (Simion et al. 2017) and for the validation of the Gaia DR1 (Arenou et al. 2017). Nowadays, a BGM standard (BGM Std) simulation (e.g. Czekaj et al. 2014) has a computational cost that is not adapted to exploring large parameter spaces using modern Bayesian iterative methods that require a very large number of simulations. To overcome this handicap we have developed a theoretical framework to generate very fast Milky Way approximate simulations based on BGM. This framework allows us to explore, among others, the parameter spaces of the IMF, the star formation history (SFH), and the density laws using ABC. The flexibility of the strategy presented here allows for the generation of fast approximate simulations for different Milky Way components, such as thin disc, thick disc, halo, and bulge. Our full strategy is codified to run on Apache Spark1 (Zaharia et al. 2012) and Apache Hadoop2, which are engines coming from business science suited to deal with large surveys. Thanks to its codification, BGM FASt is implemented in the big data infrastructure known as Gaia Data Analytics Framework (GDAF, e.g. Tapiador et al. 2017). As a first application of this complex strategy we use ABC algorithms, BGM, and Tycho-2 data to constrain the IMF, the local SFH, the local stellar mass density, and the thin-disc density laws.
In Sect. 2 we describe the BGM, and in Sect. 3 we present the framework to generate the BGM fast approximate simulations (BGM FASt). In Sect. 4 we describe the treatment of the local dynamical statistical equilibrium in the context of BGM FASt. In Sect. 5 we briefly describe the approximate Bayesian computation technique applied to explore the parameter space of the fundamental functions of the Milky Way. In Sect. 6 we present an evaluation of the BGM FASt performance in the solar neighbourhood. Results are presented in Sect. 7 while a discussion and conclusions are presented in Sects. 8 and 9.
2. The Besançon Galaxy Model
In the present paper we use the following versions of the Galactic components of BGM chosen from a compromise between recent and stable updates.
For the stellar halo component we use the model from Robin et al. (2014) and for the bulge-bar region we use the model described in Robin et al. (2012). For the thick disc component we use the model from the best fit obtained in Robin et al. (2014) which is a thick disc with two main star-formation episodes at 10 and 12 Gyr. For the thin disc component we use the model described in Czekaj et al. (2014) with the updates on the parameters introduced in Mor et al. (2017). The local dynamical statistical equilibrium of BGM is ensured by dynamical constraints based on Bienaymé et al. (1987). The last dynamics and kinematics updates from Bienaymé et al. (2015) and Robin et al. (2017) are not considered in the present paper and will be incorporated in the near future.
2.1. BGM star-generation strategy
The BGM has two main working modes to compute the generation of the stars in the Galaxy. The traditional approach relies on using a precomputed Hess diagram (Robin et al. 2003), while the more updated approach is able to generate the stars from a given set of fundamental functions (e.g. IMF, SFH, age-metallicity among others), making them evolve using a desired set of stellar evolutionary models (Czekaj et al. 2014). For each Galactic component we can choose whether we want to simulate it using the Hess diagram or the updated strategy. Alternatively, from the updated star-generation strategy we can build a Hess diagram from a given set of fundamental functions, and ingest it into BGM code afterwards to be used in a traditional way.
In this section we summarise the stellar generation strategy described in Czekaj et al. (2014), henceforth referred to as our standard strategy. Initially this strategy was developed for the thin-disc component but nowadays it can be used for other Galactic components.
In the BGM Std strategy, to generate stars born τ years ago for a given Galactic i-component (e.g. thin disc, thick disc, halo and bulge-bar), we start from a given total surface mass density at the position of the Sun 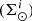 . We then use the SFH
. We then use the SFH 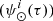 to distribute the surface mass density along τ as follows:
to distribute the surface mass density along τ as follows:
For simplicity, the current version neglects the radial migration. We setup the model so that the stars are born in the plane. We then redistribute them in the process of secular evolution by using the surface-to-volume mass density ratio at the position of the Sun 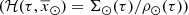 to compute the volume stellar mass density from
to compute the volume stellar mass density from 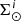 , as follows
, as follows
where we have expressed the position 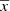 in Cartesian Galactic coordinates as (x, y, z). The volume mass density is distributed throughout the Galaxy as
in Cartesian Galactic coordinates as (x, y, z). The volume mass density is distributed throughout the Galaxy as
where ℛi(τ, x, y, z) are the density laws for the given i-component and ℛi(τ, x⊙, y⊙, z⊙)=1. We can then write ℋi(τ, x⊙, y⊙, z⊙) as the integral of the density law along the vertical direction at the position of the Sun:
Finally, from Eqs. (2)–(4), we can write the distribution of the volume mass density along position and age as follows
where for simplicity we call ℋi(τ) to ℋi(τ, x⊙, y⊙, z⊙). As explained in Czekaj et al. (2014), the IMF distributes this mass density in three mass ranges. The star generation process goes through all the volume elements in the Galaxy. First, in a given volume element, for a given age sub-population the age of the star is drawn uniformly within the age limits. Afterwards, the mass of the star is drawn from the IMF. Next, the metallicity is assigned depending on the age and position of the stars. In the most updated versions, the α-elements-to-iron abundance ([α/Fe]) is assigned to each star with a given probability (Lagarde et al. 2017). The evolutionary stage is then assigned to the star by interpolating the stellar evolutionary tracks. In a following step, the process assigns to the generated star a given probability to be the primary component of a stellar multiple system. This probability is assigned following the guidelines of Arenou (2011). Finally, if the star is flagged as a primary component of a stellar multiple system, the standard strategy generates a secondary star with a mass drawn from the probability distributions described in Arenou (2011).
For consideration in the following sections we define a BGM Std simulation to be one that works using the standard stellar generation strategy or a fixed Hess diagram built from the standard stellar generation strategy.
2.2. Standard thin disc component
The thin disc component is described in Czekaj et al. (2014). The stars are generated as described in Sect. 2.1. The thin disc population is divided in seven age sub-populations. Usually the chosen age intervals are those described in Bienaymé et al. (1987) but for the two youngest populations we use the age limits described in Mor et al. (2017). The density distribution of each sub-population of the thin disc is assumed to follow an Einasto density profile as described in Robin et al. (2012), except for the youngest sub-population which follows the expression described in Robin et al. (2003). These profiles are characterised by the eccentricities of the ellipsoid (i.e. the axis ratio), the radial scale length of the disc (hR), and the radial scale length of the disc hole (hRh). A velocity dispersion as a function of age is adopted and the dynamical statistical equilibrium is ensured by using the strategy described in Bienaymé et al. (1987). Stellar evolutionary tracks and model atmosphere, combined with an age-metallicity relation, allow us to go from masses, ages, and metallicities to the space of the observables. In this process a three-dimensional (3D) interstellar extinction map is adopted.
3. Framework for the Besançon Galaxy Model Fast Approximate Simulation
A BGM Std simulation has a computational cost of ∼432 h of CPU time for a simulation of 106 stars, excluding the use of iterative methods like ABC or MCMC to explore large parameter spaces. Hence, we have developed a new method, called BGM FASt, which is able to robustly simulate the Galaxy with a computational cost of ∼240 s of CPU time for a simulation of 106 stars. Thanks to the use of Apache Hadoop and Apache Spark environments (Zaharia et al. 2012) the computational cost should not scale with the number of stars as is the case in standard environments (Julbe, priv. comm.).
3.1. The BGM FASt concept
The BGM FASt is a population-synthesis simulation of the Milky Way, obtained from a clever modification of a BGM Std simulation. The BGM FASt development is based on the distribution function of the generated stars (𝒟i). The 𝒟i carries on the information about the generation of the stars in the i-component of the Galaxy (e.g. thin disc, thick disc, halo, bulge-bar) throughout the life of the given component up to the present day. This distribution function contains the chemo-dynamical information that is classically expressed by fundamental functions such as the IMF, the SFH, density distribution, the age-metallicity relation, and the radial metallicity gradient, among others. The 𝒟i is defined in a N dimensional space (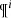 ) for each of the i-components of the Galaxy. This N dimensional space contains all the parameters that can be involved in a distribution function of the generated stars in the Galaxy. Let us introduce the parameter space as follows:
) for each of the i-components of the Galaxy. This N dimensional space contains all the parameters that can be involved in a distribution function of the generated stars in the Galaxy. Let us introduce the parameter space as follows:
where τ is the present age of the stellar object, M and Z are its initial mass and metallicity, and 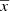 and
and 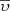 are position and velocity, respectively. p̄ accounts for other independent parameters that, for some specific purposes, would be interesting to have explicitly introduced in the distribution function. The α-elements-to-iron abundance ratio ([α/Fe]) is an example of one of the possible p̄ parameters and we treat this in the following section.
are position and velocity, respectively. p̄ accounts for other independent parameters that, for some specific purposes, would be interesting to have explicitly introduced in the distribution function. The α-elements-to-iron abundance ratio ([α/Fe]) is an example of one of the possible p̄ parameters and we treat this in the following section.
The strategy to generate a BGM FASt begins with the choice of a specific Mother Simulation with an imposed set of fundamental functions. We use Mother Simulation to refer to a BGM Std simulation used as a seed to generate a BGM FASt simulation. This Mother Simulation is used as a main constituent to generate one or several BGM FASt simulations with different assumptions for the fundamental functions. The idea behind the BGM FASt strategy is that the number of stars generated in a given interval of the parameter space (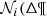 ) is proportional to the mass dedicated to generate stars for that given interval (
) is proportional to the mass dedicated to generate stars for that given interval (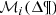 ):
):
where 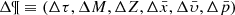 . Equation (7) is valid for both the Mother Simulation and the BGM FASt simulation. If
. Equation (7) is valid for both the Mother Simulation and the BGM FASt simulation. If 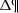 is small enough, we can write a proportion between the number of stars and the masses relating both the Mother Simulation and the BGM FASt simulation:
is small enough, we can write a proportion between the number of stars and the masses relating both the Mother Simulation and the BGM FASt simulation:
Then we can approximate the number of stars for a given interval for a BGM FASt simulation as follows:
Let us call weight to the mass ratio of Eq. (9):
where we compute the mass dedicated to generate stars, in a given interval, from the distribution function of the generated stars that we present in following sections.
In practice, we generate a BGM FASt simulation by applying a weight to each star of the Mother Simulation. This is done according to the parameters of the star, such as mass, age, position, and distance, among others. Thus, the resulting simulation is an approximation of the BGM Std simulation that would be obtained with the standard BGM star generation process.
We present the theoretical framework and the practical implementation for the generation of a BGM FASt as follows.
First, in Sect. 3.2, we describe the distribution function of the generated stars 𝒟i in the most generic context and its relation with the masses involved in Eq. (10). This allows us to introduce the classical fundamental functions, such as the IMF and the SFH, and functions describing more complex scenarios. In a following step we consider a set of assumptions and approximations to reach a 𝒟i function compatible with the 𝒟i implicitly involved in a BGM Std simulation.
Next, in Sect. 3.3, we discuss the treatment of stellar multiple systems as modelled in a BGM. We introduce the probability of obtaining a binary system at birth in our approximated 𝒟i. The obtained expressions are useful for both the process ensuring the local dynamical statistical equilibrium and the computation of the surface mass stellar density at the position of the Sun. Finally after describing a generalizable weight expression, in Sect. 3.4, we constrain it to the BGM context including stellar multiple systems.
3.2. The distribution function of the generated stars
3.2.1. Generic context and fundamental functions
In this section we describe the distribution function of the generated stars in its most generic context. Under the given definition of the parameter space (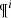 ) we can precisely define some of the parameters belonging to p̄. It is convenient for future purposes to write the distribution function
) we can precisely define some of the parameters belonging to p̄. It is convenient for future purposes to write the distribution function 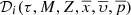 accounting explicitly for the ratio [α/Fe]. Subsequently, [α/Fe] is considered as one of the p̄ parameters and we can write
accounting explicitly for the ratio [α/Fe]. Subsequently, [α/Fe] is considered as one of the p̄ parameters and we can write ![$ {\mathcal{D}}_i(\tau, M, Z,\overline{x},\overline{\upsilon}, [\alpha/\mathrm{Fe}], \overline{p\prime}) $](/articles/aa/full_html/2018/12/aa33501-18/aa33501-18-eq29.gif) in the N dimensional space:
in the N dimensional space:
In our line of action, for the moment, we are interested in explicitly representing age, mass, metallicity, position, velocity, and the ratio [α/Fe] in the distribution function. Subsequently we marginalize ![$ {\mathcal{D}}_i(\tau, M, Z,\overline{x},\overline{\upsilon}, [\alpha/\mathrm{Fe}], \overline{p\prime}) $](/articles/aa/full_html/2018/12/aa33501-18/aa33501-18-eq31.gif) over the rest of the p̄′ parameters:
over the rest of the p̄′ parameters:
where 𝒢i is the distribution function of the generated stars for the i-component in the reduced space 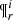 :
:
For simplicity let us henceforth refer to [α/Fe] using only α.
The 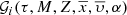 distribution function is such that the integral over all the parameters that belong to the parameter space is the total number of generated stars in the i-component of the Galaxy:
distribution function is such that the integral over all the parameters that belong to the parameter space is the total number of generated stars in the i-component of the Galaxy:
and if we multiply by the mass before the integration, we have the total mass of the generated stars for the i-component of the Galaxy:
The mass of Eq. (7) can then be expressed as the integral of the distribution function for a given interval in the parameter space 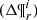 :
:
and we can write Eq. (10) as
where 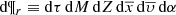 .
.
The true 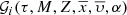 distribution function is unknown, but its marginalization over combinations of parameters results in deeply studied functions such as the IMF, the SFH, the age-metallicity relation, the radial metallicity gradient, and also functions carrying information about the density distribution of the Galaxy or dynamical and chemo-dynamical information. Let us exemplify mathematically how some of these fundamental functions can be treated related to the distribution function.
distribution function is unknown, but its marginalization over combinations of parameters results in deeply studied functions such as the IMF, the SFH, the age-metallicity relation, the radial metallicity gradient, and also functions carrying information about the density distribution of the Galaxy or dynamical and chemo-dynamical information. Let us exemplify mathematically how some of these fundamental functions can be treated related to the distribution function.
The marginalization over the parameters 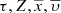 and α within the values that belong to the
and α within the values that belong to the 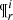 space can be written as:
space can be written as:
where ξi(M) is the composite IMF for each one of the i-components. Marginalizing now the 𝒢i over 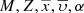 within the values that belong to the
within the values that belong to the 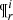 space we have the τ distribution of the generated stars that can be interpreted as the SFH of the whole i-component:
space we have the τ distribution of the generated stars that can be interpreted as the SFH of the whole i-component:
If we are interested in studying how the τ distribution depends on the position, we can then perform a marginalization over M, Z, 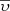 and α, obtaining
and α, obtaining
If in Eq. (20) we set 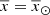 , the position of the Sun, then the resulting function can be interpreted as the SFH at the position of the Sun.
, the position of the Sun, then the resulting function can be interpreted as the SFH at the position of the Sun.
The functions involving metallicity, such as the age-metallicity relation or the radial metallicity gradient, could also be considered in BGM FASt. If we marginalize 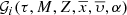 over mass, α, and phase-space we get the Z distribution of stars formed τ years ago:
over mass, α, and phase-space we get the Z distribution of stars formed τ years ago:
The radial metallicity gradient can be deduced from a more complex expression obtained marginalizing Gi over age, mass, velocity and α:
This latter expression is the position and metallicity distribution of the generated stars throughout the life of the i-component.
Finally, information about chemo-dynamics and kinematics can be introduced with the following two equations.
The spatial distribution of the volume mass density (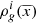 ) that has been dedicated to generating stars for the Galactic i-component throughout its life can be written as follows
) that has been dedicated to generating stars for the Galactic i-component throughout its life can be written as follows
In the following steps it is useful to have the equation of the mass density dedicated to generating stars born τ years ago in a position 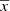 :
:
Until now, we have described the distribution function of the generated stars in the Galaxy in a generic context. We have emphasised that our strategy can be generalizable and any of the fundamental equations described above (Eqs. (18)–(24)) can be used if we are able to write an analytical expression for them.
3.2.2. The approximate solution
In this section we find an approximation to the distribution function of the generated stars compatible with BGM. At the same time this approximation aims to be extensible to other models of the Galaxy that use similar star-generation strategies. As the exploration of the velocity spaces is not included in the present paper, for simplicity we do not consider the kinematic part here. Our goal is therefore to find an approximate solution to the integral 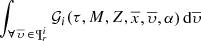 .
.
In this context the first assumption comes from a traditional strategy (e.g. Tinsley 1980), assuming that mass and age distributions are separated. Splitting the mass function from the function of τ and 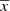 as follows
as follows
Moreover, the BGM assumes a metallicity distribution that depends on position and age. We can therefore introduce, in the equations, the probability that a star of a given age in a given position has a metallicity Z: 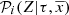 . Furthermore, BGM has recently included the possibility to use [α/Fe], a parameter which affects the stellar evolutionary tracks (Lagarde et al. 2017), assuming, from observational surveys, a certain probability that a given star has a given [α/Fe]. In general, for a given i-component, this probability depends on the age, the position, and the metallicity of the star and we denote it as
. Furthermore, BGM has recently included the possibility to use [α/Fe], a parameter which affects the stellar evolutionary tracks (Lagarde et al. 2017), assuming, from observational surveys, a certain probability that a given star has a given [α/Fe]. In general, for a given i-component, this probability depends on the age, the position, and the metallicity of the star and we denote it as 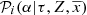 .
.
From Eq. (27), and the metallicity and [α/Fe] distributions, we can write:
where the assumptions and approximations behind the mathematical expression of the functions 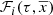 ,
, 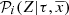 and
and 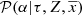 are imposed to be compatible with the BGM. Equation (28) assumes, from the statistical point of view, that the probability to generate a star with mass M and the probability to generate a star τ years ago in a given position are conditionally independent. This means that the IMF is assumed to be independent of time and position.
are imposed to be compatible with the BGM. Equation (28) assumes, from the statistical point of view, that the probability to generate a star with mass M and the probability to generate a star τ years ago in a given position are conditionally independent. This means that the IMF is assumed to be independent of time and position.
The standard star-generation strategy described in Sect. 2.1 guides us by using Eq. (5) to approximate the function 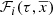 as follows
as follows
where 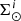 is the stellar surface mass density ( * /pc2) of the generated stars at the position of the Sun for the Galactic i-component, ℋi(τ) is the surface-to-volume-density ratio at the position of the Sun,
is the stellar surface mass density ( * /pc2) of the generated stars at the position of the Sun for the Galactic i-component, ℋi(τ) is the surface-to-volume-density ratio at the position of the Sun, 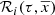 is the density distribution, and
is the density distribution, and 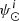 is the SFH in the solar neighbourhood.
is the SFH in the solar neighbourhood.
Taking into account the approximations implicitly or explicitly adopted in standard BGM we present a solid solution for the following integral
where the IMF is normalized as 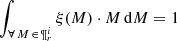 , the SFH in the solar neighbourhood is normalized as ∫∀ τ ∈ Πrψ⊙(τ) dτ = 1, and by definition
, the SFH in the solar neighbourhood is normalized as ∫∀ τ ∈ Πrψ⊙(τ) dτ = 1, and by definition 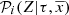 and
and 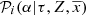 are normalized to 1.
are normalized to 1. 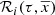 and ℋi(τ) are such that the integral over the whole parameter space of
and ℋi(τ) are such that the integral over the whole parameter space of 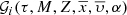 gives the total number of generated stars in the Galactic i-component.
gives the total number of generated stars in the Galactic i-component.
For simplicity, as BGM Std does, we assume an axi-symmetric structure with no radial migration. Additionally, we assume that for a given volume element, 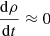 , where ρ is the stellar volume mass density. These assumptions allow us to use the density distributions (
, where ρ is the stellar volume mass density. These assumptions allow us to use the density distributions (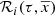 ) described in Robin et al. (2003) and Robin et al. (2014), derived to match the present density distribution of each Galactic i-component.
) described in Robin et al. (2003) and Robin et al. (2014), derived to match the present density distribution of each Galactic i-component.
3.3. Handling of the stellar multiple systems
The probability of obtaining a multiple system at birth in a star formation event is unknown, very complex, and can depend on many parameters, such as the metallicity, the mass of the molecular cloud, the turbulence, mass segregation, mass competition, and mass accretion rate (e.g. Bonnell et al. 2007; Kroupa et al. 2013). For these reasons, the BGM approach (e.g. Czekaj et al. 2014; Robin et al. 2012) is performed adopting an empirical law to match the observed present distribution function of multiple stellar systems (Arenou 2011). This approach assigns a certain probability to a generated star of being the primary component of a multiple system, depending on its mass and its luminosity class. Inside our framework this means a dependence on mass, age, and, through the stellar evolutionary models, Z and α. This probability is therefore P(bin|τ, M, Z, α).
Let us refer to the generated star susceptible to be flagged as either the single star or primary component of the binary system as the “primal star”. Once a primal star is decided as being a primary component of a multiple system, a secondary star is generated with a mass m. The mass m of the secondary is assigned following a probability distribution function (PDF) that depends mainly on the mass M and the luminosity class of the primary component, leading to P(m|τ, M, Z, α).
We introduce the stellar multiple systems in BGM FASt by simplifying their treatment under two assumptions: (1) The masses of primal stars (singles and primaries) are drawn from the IMF while the mass of the secondary follows the empirical laws described above, and (2) the age of the primary star follows the SFH, while the age of the secondary is assumed to be the same as the primary (i.e. both components were born together). With these two assumptions, the multiple stellar systems can be introduced in our analytical approach at low computational cost. We can compute first, at the position of the Sun, the surface mass density of secondary stars (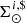 ) as a function of the surface mass density of the primal stars (
) as a function of the surface mass density of the primal stars (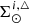 ) and afterwards compute
) and afterwards compute 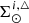 as a function of
as a function of 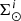 . We begin by expressing
. We begin by expressing 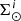 as
as
Subsequently, the stellar volume mass density of primary stars at the position of the sun for the i-component is given by
and the stellar volume mass density of secondary stars at the position of the sun for the i-component is given by
We also want to compute the surface mass density; then, if we leave out ℋi from the integrand of Eq. (33), we get the surface mass density of secondary stars at the position of the Sun:
Finally, 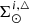 is computed from
is computed from 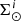 using Eqs. (31) and (34).
using Eqs. (31) and (34).
This result is very useful for both determining the weight function when considering multiple stellar systems as implemented in BGM (Sect. 3.4) and computing the local dynamical statistical equilibrium (Sect. 4). In Sect. 4 we also particularize the computation of 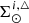 when specifically using the thin disc component as described in Czekaj et al. (2014).
when specifically using the thin disc component as described in Czekaj et al. (2014).
3.4. The weight
The strategy developed in previous sections allows us to give the analytical expression to compute the weights. These weights are able to transform the distribution of stars in the Mother Simulation, linked to a given set of Galactic fundamental functions, into the distribution of the stars linked to other Galactic fundamental functions adopted for a BGM FASt simulation. From (17) and (30) we obtain an expression for the weights applicable to Galaxy models that sample the stars from a distribution function of the form of Eq. (28), considering the assumptions discussed in Sect. 3:
In the BGM context, including multiple stellar systems and taking into account the scenario described in Sect. 3.3, the weight that we apply in practice to generate a BGM FASt simulation is the following
where we have substituted 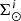 with
with 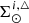 from Eq. (35).
from Eq. (35).
In our approach, the stellar evolutionary tracks are the same for both the Mother Simulation and the BGM FASt simulation. For simplicity, the probabilities 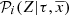 and
and 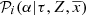 are imposed and we are not going to explore them; they are equal for both the Mother Simulation and the BGM FASt simulation and we can marginalize the numerator and denominator over Z and α to obtain the final expression for the weights:
are imposed and we are not going to explore them; they are equal for both the Mother Simulation and the BGM FASt simulation and we can marginalize the numerator and denominator over Z and α to obtain the final expression for the weights:
In practice, the weight in Eq. (37) is applied to each single star and each stellar system. This means that both the primary and the secondary components of the stellar system are weighted with the same value, according to the parameters of the primary component. We choose this way to apply the weights because in BGM Std the mass and age of the secondary star are drawn according to the mass and the age of the primary star. This choice ensures that the mass and age distributions of the primal stars in a BGM FASt simulation follow the pertinent IMF and SFH, and that the mass distribution of the secondary stars follows the empirical distributions described in Arenou (2011).
The choice of the intervals for the integrals must be discussed for each particular case. Generally they must be small enough to preserve Eqs. (8) and (9). For tests and cases presented in the present paper, the choice of the mass interval is set to be very small (0.025 M⊙). For a given star of age τ we set the limits of the integral to be the age limits of the age sub-populations to which the star belongs. Finally, as the BGM Std generation strategy assigns the density of its centre to the whole volume element, in BGM FASt we do not need to perform a volume element integral.
4. Local dynamical statistical equilibrium (LDSE)
By local dynamical statistical equilibrium we understand that, at the position of the Sun, the mass density distribution and the potential satisfy both the Poisson equation and the first-order moment of the collisionless Boltzmann equation for the vertical direction (Bienaymé et al. 1987). In this approach we consider axi-symmetry to solve both equations. To solve the first-order moment of the collisionless Boltzmann equation in the vertical direction, we also assume steady state, isothermal state, and decoupled radial and vertical motions. One possible methodology to ensure the LDSE is described in Czekaj et al. (2014) and summarised in Sect. 4.1. As it requires a computational time that is not affordable for the methodology presented in this paper, we develop here analytical (Sect. 4.2) and approximate (Sect. 4.4) methods that ensure LSDE, significantly reducing the computational cost.
4.1. Full LDSE
The iterative strategy described in Czekaj et al. (2014) performs, for a given set of Galactic fundamental functions, a local normalization and a sphere simulation around the Sun to compute at the position of the Sun: the surface mass density of the generated stars, Σ⊙, the volume mass density of the stars generated τ years ago, that is 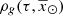 , and the volume mass density for stars generated τ years ago which are not stellar remnants at present, that is
, and the volume mass density for stars generated τ years ago which are not stellar remnants at present, that is 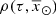 3. We define the stars which are not remnant at present as those with τ ≤ Tlim(M, Z, α), where Tlim(M, Z, α) is the maximum age that a star of a given mass, metallicity, and [α/Fe] reaches without becoming a remnant object. The stellar mass density at the position of the Sun is fitted with the stars that are not remnants at present and the white dwarfs’ density is added separately. The mass lost by the stars during their evolution and the interaction between components of a stellar multiple system are neglected. The total mass in stars, plus that of the interstellar medium, the dark matter, and the central mass, allows us to compute the radial force. At this stage, the dark matter density distribution and the central mass is adjusted such that the model rotation curve fits the observations, the fit is done using the least-squares method in velocity. Finally, the Poisson and the first-order moment of the collisionless Boltzmann equation in the vertical direction are iteratively solved. The whole strategy is iterated from the beginning until convergence is reached.
3. We define the stars which are not remnant at present as those with τ ≤ Tlim(M, Z, α), where Tlim(M, Z, α) is the maximum age that a star of a given mass, metallicity, and [α/Fe] reaches without becoming a remnant object. The stellar mass density at the position of the Sun is fitted with the stars that are not remnants at present and the white dwarfs’ density is added separately. The mass lost by the stars during their evolution and the interaction between components of a stellar multiple system are neglected. The total mass in stars, plus that of the interstellar medium, the dark matter, and the central mass, allows us to compute the radial force. At this stage, the dark matter density distribution and the central mass is adjusted such that the model rotation curve fits the observations, the fit is done using the least-squares method in velocity. Finally, the Poisson and the first-order moment of the collisionless Boltzmann equation in the vertical direction are iteratively solved. The whole strategy is iterated from the beginning until convergence is reached.
4.2. Analytical LDSE
In this analytical approach to ensure LDSE, we follow the process described in Sect. 4.1, but instead of using a simulation of a sphere around the Sun, we analytically derive the surface mass density of the generated stars (Σ⊙), the volume mass density of the stars generated τ years ago (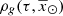 ), and the volume mass density for stars generated τ years ago which are not remnant at present (
), and the volume mass density for stars generated τ years ago which are not remnant at present (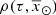 ). As this approach concerns only the thin-disc component, from now on we avoid the use of the index i.
). As this approach concerns only the thin-disc component, from now on we avoid the use of the index i.
Using Eq. (31) we can express Σ⊙ as the sum of the surface density for primal stars 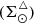 and the surface density for secondary stars
and the surface density for secondary stars 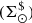 . In an equivalent way, the
. In an equivalent way, the 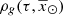 for the generated stars can be expressed as
for the generated stars can be expressed as
and the stellar volume mass density of the stars with τ ≤ Tlim(M, Z, α) can be expressed as
Now we want to derive the stellar volume mass density of the primal stars at the position of the Sun 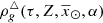 . Therefore, from equation (32) we obtain
. Therefore, from equation (32) we obtain
At this stage we assume that at the position of the Sun all the stars have solar metallicity Z = Z⊙ and for the moment BGM assumes that the α-elements-to-iron abundance for the thin disc is α = α⊙. The probabilities for Z and α then become
and
Combining Eqs. (40)–(42) we can approximate 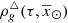 by
by
As mentioned above, the fit with the observational value of the volume stellar mass density at the position of the Sun is done with the stars with τ ≤ Tlim(M, Z, α). Therefore, as a next step, we need to derive an analytical expression for the density of non-remnant primal stars at the position of the Sun. This is given by
where the function 𝒪(τ, M, Z, α) discussed in Sect. 4.3 is defined as
As before, we assume all the stars at the position of the Sun have Z = Z⊙ and α = α⊙ (Eqs. (41) and (42)), thus
Up to now we have derived analytical expressions for the volume densities of the primal stars ((43) and (46)). To complete Eqs. (38) and (39) we need to derive the analytical expressions for the mass density of secondary components. Considering Eq. (33) we can write 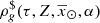 :
:
Next, to continue reducing computational time, we assume that the mass of the secondary is only dependent on the mass of the primary component P(m|τ, M, Z, α)≈P(m|M) and we consider this probability is uniform and given by
where Mmin is the minimum mass needed to generate a star. This expression states that the mass of the secondary star is always equal or less massive than the corresponding primary component.
We introduce a second approximation assuming that for a given generated primal star the probability of being the primary component of a multiple system is given by
This probability, as defined, is not null only for the non-remnant stars. Therefore, using Eq. (45), it can also be expressed as p(bin|τ, M, Z, α)=𝒪(τ, M, Z, α)⋅p(bin|M). In other words, this approach assumes that the probability of being a primary component of a binary system is null for those stars which are remnant at present. Introducing Eqs. (48) and (49) in (47), we have
The above assumptions imply that secondary stars are never remnants, thus 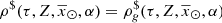 .
.
As done for primal stars, we assume that all the stars at the position of the Sun have solar metallicity Z = Z⊙ and α = α⊙. Therefore,
As done for primal stars, we leave out ℋ(τ) from (51) to reach the expression for 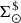 :
:
At this point we have on hand all the analytical expressions to compute the Σ⊙ that fits the observed stellar mass density at the position of the Sun (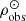 ) for the thin disc stars with τ ≤ Tlim(M, Z, α). To do so we use Eqs. (51) and (46) in (39) and set
) for the thin disc stars with τ ≤ Tlim(M, Z, α). To do so we use Eqs. (51) and (46) in (39) and set 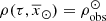 , with
, with 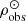 being the observed stellar mass volume density at the position of the Sun for stars which are not remnant at present. We then solve the resulting equation for
being the observed stellar mass volume density at the position of the Sun for stars which are not remnant at present. We then solve the resulting equation for 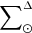 and compute Σ⊙ from (31) and (52).
and compute Σ⊙ from (31) and (52).
For the practical implementation of the analytical approach developed in this section we adopt Mmin = 0.09 M⊙ and Mmax = 120 M⊙, the mass range of the evolutionary models we are using at present (Chabrier & Baraffe 1997; Bertelli et al. 2008, 2009). For p(bin|M) in Eq. (49) we follow the expression for main sequence stars in Arenou (2011).
4.3. The non-remnant fraction (Ω)
The 𝒪 function (45) is directly related with the stellar evolutionary tracks considered through the expressions of Tlim(M, Z, α). We define Tlim(M, Z, α) as the maximum age for which a star of a given mass, metallicity, and α-elements-to-iron abundance is still not a stellar remnant. As discussed in the previous section, for the 𝒪 function we consider solar metallicity Z = Z⊙ and solar α = α⊙. We use, for the moment, the stellar evolutionary tracks Bertelli et al. (2008) and Chabrier & Baraffe (1997) considered in Czekaj et al. (2014) which do not consider the α-element abundance; therefore Tlim(M, Z, α)=Tlim(M, Z). From the mentioned stellar evolutionary tracks we derive Tlim(M, Z⊙) fitting three truncated logarithmic expressions to the two-dimensional (2D) grid of mass and age limit for Z = Z⊙. We end up with the following expressions
for M/M⊙ ≥ 7.
for 2.2 < M/M⊙ < 7.0,
for 2.0 < M/M⊙ < 2.2,
for M/M⊙ ≤ 2.2,
With these latter expressions we have everything we need for the execution of the analytical LDSE as described in Sect. 4.2. At this point, to take into account that the BGM Std strategy samples the age of the stars uniformly inside each age sub-population (see Sect. 2.2) we substitute the 𝒪 function by the Ω function in the equations of Sect. 4.2. The Ω(τ, M, Z⊙) function is defined as
where 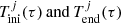 are respectively the low and high age boundaries for each of the seven age sub-populations of the thin disc (j = 1…7). We note that
are respectively the low and high age boundaries for each of the seven age sub-populations of the thin disc (j = 1…7). We note that 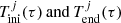 obviously depend on τ, because the age τ of the star establishes the j-sub-population to which the star belongs. We emphasise that the Ω function defined above gives the fraction of stars which are not remnant at present and is constant with τ inside the limits of each age sub-population. Furthermore, when defining 𝒪 and Ω functions we are neglecting both the entangled evolution of stars belonging to the multiple stellar systems and the mass lost by the star during its evolution. If in the future we want to implement the effect of the mass lost by the stars during its evolution, we can do this by introducing a new function, ℒ(τ, M, Z, α), into the equations, accounting for the fraction of mass that a given star has lost during its evolution up to the present time. If at some point we are interested in accounting for the entangled evolution of a stellar multiple system then we need to implement the desired evolutionary model of stellar systems directly in the BGM Std strategy, generate a Mother Simulation, and finally modify Tlim accordingly.
obviously depend on τ, because the age τ of the star establishes the j-sub-population to which the star belongs. We emphasise that the Ω function defined above gives the fraction of stars which are not remnant at present and is constant with τ inside the limits of each age sub-population. Furthermore, when defining 𝒪 and Ω functions we are neglecting both the entangled evolution of stars belonging to the multiple stellar systems and the mass lost by the star during its evolution. If in the future we want to implement the effect of the mass lost by the stars during its evolution, we can do this by introducing a new function, ℒ(τ, M, Z, α), into the equations, accounting for the fraction of mass that a given star has lost during its evolution up to the present time. If at some point we are interested in accounting for the entangled evolution of a stellar multiple system then we need to implement the desired evolutionary model of stellar systems directly in the BGM Std strategy, generate a Mother Simulation, and finally modify Tlim accordingly.
4.4. Approximate LDSE
In Sects. 4.2 and 4.3 we explained how, in the full process to ensure the LDSE (Sect. 4.1), we can substitute the entire simulation of a sphere around the Sun by crafted analytical expressions which are computationally undemanding. Here we complete the construction of an approximate LDSE strategy by complementing Sects. 4.2 and 4.3 with a final assumption to make the process even faster. As described in Sect. 4.1 in the full LDSE process, the central mass and the dark matter density distribution is adjusted such that the model rotation curve fits the observations. We can avoid the computational cost of this adjustment by assuming that the central mass density and the dark matter density distribution are invariant under variations of the Galactic fundamental functions4.
We now test the performance of the approximate LDSE to evaluate the assumptions that we made and to constrain its range of validity. In the following section we present a set of tests comparing the results obtained when applying the full LDSE process against the results of our approximate LDSE.
4.5. Validation of the approximate LDSE
We develop three tests to evaluate the goodness of our approximate method (Sects. 4.2–4.4). These tests quantify the differences, when using the approximate instead of full method, in some of the key parameters resulting from the LDSE process. All the tests are performed using the seven model variants described in Mor et al. (2017) that were built with different assumptions of the IMF, the SFH, and the density laws. In Table 1 we present their main parameters. These model variants cover the range of parameters that we want to explore in this paper well, and therefore they are a good set to perform the tests. The parameters for the thin disc density laws which are not listed in Table 1 are adopted to be the same as used in Mor et al. (2017), being the functional forms of the density laws listed in Robin et al. (2003). The rest of the model ingredients which are not specifically indicated in Table 1, for example the atmosphere models, the stellar evolutionary tracks, the age-metallicity relation, and the age-velocity dispersion, are adopted to be the same as in “Model B” listed in Table 5 of Czekaj et al. (2014).
Parameters for the SFH, the IMF and the density laws of the seven model variants adopted from Mor et al. (2017).
In the first test we show that our approximate method obtains a rotation curve compatible with the one resulting from the full method. For all model variants, we obtain differences of less than 2% in the rotational velocity between a galactocentric radius from 3 kpc to 14 kpc. Moreover these differences are much smaller than discrepancies between the observational values (e.g. Caldwell & Ostriker 1981 and Sofue 2015). In Fig. 1 we present the results for the two model variants where we found the highest discrepancies between the rotation curve obtained from both methods. The discrepancies along the curve from 3 kpc to 14 kpc are always smaller than 5 km s−1. Thus we consider that the approximated LDSE is valid within these galactocentric radii.
 |
Fig. 1. Two examples of the comparison between the rotation curve obtained with both the full process to ensure LDSE and the rotation curve obtained with the approximate LDSE. Top panel: results for the DAV variant from Mor et al. (2017). Bottom panel: results for the HRBV variant from Mor et al. (2017). The green triangles show the data points derived from the Caldwell & Ostriker (1981) rotation curve assuming R0 = 8000 pc and V0 = 230 km s−1 for the Sun. The magenta triangles show the data points of the rotation curve from Sofue (2015). For Sofue data, error bars are provided by the author, while we have estimated the errors of the data from Caldwell & Ostriker (1981) following the expressions and tables in their paper. |
The second test compares for each model variant the eccentricities of the Einasto density profiles which are fitted inside the process that ensures the LDSE. The Einasto eccentricities are computed for each one of the seven age sub-populations of the thin disc. In all cases we find differences smaller than 0.7%.
Our third test compares the local volume stellar mass density of all the thin-disc age sub-populations. For each model variant we check our capability to recover the density values of Table 1 of Mor et al. (2017). The discrepancies are within the error bars and are always smaller than 5%.
We want to point out that these tests are the first empirical demonstration that our strategy for the BGM FASt simulation is well founded. Whereas it is true that they validate the equations behind the weight function, they do not evaluate the capabilities of the weight function itself to generate a BGM FASt simulation. To do so we need to directly test distributions of observable parameters obtained with BGM FASt simulations. Tests on age and mass distribution are also needed to deeper validate the BGM FASt strategy. These tests are presented in Sect. 6 and Appendix A.1.
5. ABC to infer Galactic fundamental functions
5.1. The ABC method
For very complex models such as the BGM, to obtain the exact likelihood function is mathematically impossible or computationally prohibitive. In these cases the ABC algorithms allow us to compute an approximate posterior PDF of the explored parameters. In this paper we use a sequential Monte Carlo approximate Bayesian computation algorithm (SMC-ABC) because of its balance between high acceptance rate and independence of the outcomes. The algorithm that we use is further described in Jennings & Madigan (2017), and is available as a python package named astroABC. The SMC-ABC method is an improvement of basic ABC acceptance-rejection sampling (ARS-ABC) to optimise the acceptance rate. The basic ARS-ABC contains the theoretical bases of the SMC-ABC algorithm. This latter first generates a proposed set of parameters θ̄ from the prior PDF. Subsequently, the algorithm generates the simulated data using the proposed set of parameters in a given model, and finally the set of parameters is accepted as part of the posterior PDF if the simulated data (𝒟simu) are equal to the real data (𝒟); otherwise θ̄ is rejected and we start the process again. This algorithm is very restrictive because it is almost impossible to find a model with a given set of parameters that perfectly reproduces the data. Usually one uses the ARS-ABC, relaxing the condition 𝒟simu = 𝒟 and approximating the method as follows
-
(1)
Generate θ̄ from the prior PDF.
-
(2)
Simulate data 𝒟sim from the model ℳ with parameters θ̄
-
(3)
Calculate the distance δ(𝒟, 𝒟sim) between 𝒟 and 𝒟sim.
-
(4)
Accept θ̄ if δ is smaller than a given threshold (υ) δ ≤ υ; return to 1.
This approximate algorithm needs to adopt an adequate distance metric δ and a threshold υ. When υ → 0, the algorithm is sampling exactly from the posterior PDF. Very small values of υ diminish the acceptance rate of the algorithm, and therefore the choice of υ must be a compromise between computational cost and accuracy of the posterior PDF. We want to emphasise that ARS-ABC samplers generate independent outcomes; each iteration is independent from the previous.
Other ABC methods, like the so-called free likelihood MCMC samplers (MCMC-ABC), are also built to optimise the acceptance rate. The MCMC-ABC increases the acceptance rate by modifying MCMC sampling algorithms (such as Metropolis-Hastings) to be able to work without the need of the likelihood (Marjoram et al. 2003), but the price paid in this case is that the outcomes are dependent (Marjoram et al. 2003). In a different way, the SMC-ABC improves the acceptance rate with a double entangled optimisation. For each iteration, the algorithm uses kernels to assign a higher sampling probability to the sets of parameters with better results. The resulting new sampling probability is used in the next iteration. In other words, regions of the parameter space with better results are visited more frequently. The application of kernels in the limits of the prior PDF can sometimes produce a posterior PDF slightly wider than the limits stated by the prior PDF. The use of the kernels is complemented with an adaptive threshold υ, where the upper and lower limits have to be set. This allows to go from a more relaxed threshold in the first iterations down to a small threshold for the last ones, optimising the sampling of the posterior PDF in terms of computational time. We emphasise that for a given expression for the distance metric and a given υ, the outcomes are still independent in the SMC-ABC.
Now we need to choose the data in accordance with the parameters that we want to infer. Observations can only provide a small subset of all the potential data defining the Milky Way system. This limitation forces us to search for summary statistics, which are of a lower dimension and are incomplete. If the chosen summary statistics, 𝒮, are statistically sufficient for 𝒟 then the posterior PDF under the summary data P(θ|𝒮) is equivalent to the posterior PDF under the full data P(θ|𝒟). In practice it is very difficult, or impossible, to formally identify rigorous summary statistics sufficient for 𝒟. As suggested in Marjoram et al. (2003) we use a more heuristic approach for our specific problem. In the following section we propose summary statistics 𝒮 that capture information on the θ̄ essential parameters of the Milky Way. Once sufficient statistics are established, 𝒟 is replaced by 𝒮 in the algorithm as done in Marjoram et al. (2003). The theoretical basis for these algorithms can be found in Marin et al. (2011), Beaumont et al. (2009) and Sisson & Fan (2010), for example.
5.2. Bayesian inference in the solar neighbourhood
For the appropriate use of the ABC algorithm described above, we need to define, for each of the specific scientific goals that we want to achieve, our sufficient statistics 𝒮, a distance metric δ, and a threshold υ. For both the evaluation of the BGM FASt performance (Sect. 6) and the science demonstration cases (Sect. 7), we consider as our sufficient statistics 𝒮 the star counts in a binned four-dimensional space of position, apparent magnitude, and observed colour. This means that for the purposes of this paper we define our sufficient statistics as the number of stars in each bin of latitude, longitude, visual Tycho magnitude (VT), and Tycho-2 colour (B − V)T. Specifically, our 𝒮 is the colour-magnitude diagram split in three latitude ranges: (|b|< 10), (10 < |b|< 30), and (30 < |b|< 90). We choose the bin size of the colour-magnitude diagram to be large enough to allow for a robust statistical analysis to be performed, but small enough to avoid loosing information. As mentioned in the previous section, our choice of 𝒮 is based on our previous experience when comparing BGM with observational data. We know that the observed colour-magnitude diagrams in different regions of the sky offer very valuable information to constrain the IMF, the SFH, the local stellar mass density, and the density laws (e.g. Mor et al. 2017; Robin et al. 2014, 2012). In some of these papers these colour-magnitude diagrams have already been used as sufficient statistics combined with ABC algorithms (e.g. Robin et al. 2014). Furthermore, in Czekaj et al. (2014) it was demonstrated that the division of the sky into the three above-mentioned latitude ranges is very useful to analyse the Galactic fundamental functions by fitting BGM to Tycho-2 data. In our star counts analysis we always work inside the completeness limits of the observational catalogues and therefore our sufficient statistics when using Tycho-2 data are limited at VT = 11 where Tycho-2 is complete up to 99%.
Once our sufficient statistics are defined, we need to choose the distance metric to quantify differences between the observed and simulated data, δ(𝒮obs,𝒮simu). We use this to compare the simulated 𝒮simu and the observed 𝒮obs data. For this paper we use the following expression, which we call Poissonian distance:
where Ri is defined as the quotient Ri = fi/qi and qi and fi are the number of stars in the data and the model, respectively. Additionally, we penalise the cases where there are no stars observed in the bin but the model predicts stars to be present by replacing qi and fi in the formula with qi + 1 and fi + 1, respectively. The defined distance metric becomes zero when the simulation and the observations have the same number of stars in each bin. The smaller the value of the distance metric, the closer 𝒮simu is to 𝒮obs. From Kendall & Stuart (1973) and Bienaymé et al. (1987) we know this formula is a good choice for the comparison between observed and simulated colour-magnitude diagrams in terms of star counts. Furthermore, in Mor et al. (2017) we already introduced the idea that expression (58) can be understood as a distance metric.
Finally, we choose an upper limit and a lower limit for the threshold υ by experimenting with different values to have a good balance between computational cost and accuracy of the posterior PDF.
6. Evaluating BGM FASt at the solar neighbourhood
In this section we evaluate the behaviour of BGM FASt in the solar neighbourhood and we demonstrate that the performance of the BGM FASt strategy is independent of the Mother Simulation. In Sect. 6.1 we use both BGM FASt and BGM Std to simulate the solar neighbourhood. We then analyse the resulting samples limited in apparent magnitude by comparing colour distributions and CMDs. Additionally, we extend the comparison to mass and age distributions for a deeper analysis of the BGM FASt performance. We do these comparisons in the completeness regime of Tycho-2 catalogue, and therefore we use samples limited in Tycho visual apparent magnitude (VT) up to 11, where Tycho-2 is complete at 99%.
In Sect. 6.2 we present a test for the BGM FASt framework together with the ABC algorithm, consisting in exploring the parameter space of the SFH, demonstrating that we are able to correctly recover an imposed SFH in the solar neighbourhood.
6.1. BGM FASt versus BGM Std
To evaluate the performance of the BGM FASt we compare simulations generated with the same sets of fundamental functions obtained from both the BGM FASt and BGM Std strategy. We have selected five model variants from Mor et al. (2017): DAV, DBV, DCV, HRV and SV. All of them constitute a good framework to analyse the BGM FASt behaviour in the solar neighbourhood as they adequately cover the parameter space that we want to explore with BGM FASt in Sect. 7. For each model variant we perform the tests using both the Drimmel & Spergel (2001) and Marshall et al. (2006) extinction maps5. The main set of comparisons aims to evaluate the behaviour of BGM FASt when using as Mother Simulation the best fit variant from Mor et al. (2017) (the DAV variant) obtained using Galactic Cepheids and Tycho-2 data. The DAV variant is our choice for the Mother Simulation when exploring a six-dimensional (6D) parameter space in Sect. 7.2. In the tests we evaluate the effects of changing one or more parameters of the fundamental functions when generating BGM FASt simulations according to the model variants DBV, DCV, HRV and SV.
Additionally we repeat the comparisons but use the DCV variant (constant SFH) as the Mother Simulation. These additional tests help us to evaluate the BGM FASt performance in several aspects. First, they allow us to demonstrate whether or not the performance of the BGM FASt strategy is independent of the Mother Simulation. Second, we are able to analyse possible dependencies on the total number of stars of the Mother Simulation. Third, they allow us to study simultaneous changes of the IMF and the SFH. Finally, they provide us with more data, which can be used to better interpret the obtained results.
In Table 2 we summarise the parameters of the IMF, the SFH, and the density laws for the variants involved in the tests. The functional form for the SFH is assumed to be an exponential law, the IMF is assumed to be a three-times-truncated power law and the density profiles are assumed to be of Einasto shape. In the first column we show the parameters that we use for the Mother Simulation: the DAV and DCV. In the second column we show the parameters for the BGM FASt simulations. The same parameters are also used to perform BGM Std simulations. We mark in bold text the parameters that have been modified from the Mother Simulation to generate the BGM FASt simulation. In the third column (FASt vs. Std) we present a summary of the global results comparing BGM FASt with BGM Std simulations, δp is for the Poissonian distance from Eq. (58) and % refers to the discrepancies of the total number of stars between BGM FASt and BGM Std simulations, that is ((# Stars in BGM FASt – # Stars in BGM Std)/# Stars in BGM Std) 100. We note that for all cases except the SV variant the discrepancies in the total number of stars is smaller than 4%. When looking to the Poissonian distance metric we note that all the values are below 2000, except, again, for the SV variant. The Poissonian distance between BGM FASt and BGM Std simulations is one order of magnitude smaller than the difference between the best fit variant from Mor et al. (2017) and Tycho-2 data.
Summary of the results of the BGM FASt vs. BGM Std tests and the parameters for the SFH, the IMF, and the density laws of the model variants.
When comparing colour, age, and mass distributions between BGM FASt and BGM Std, for the cases of Table 2, we note that in general the differences in relative counts per bin are smaller than 5% (see Figs. A.1–A.3, for details). In some cases, such as when using the IMF (SV variant) from Salpeter (1955) or when changing the mass limits of the IMF (HRV variant), the difference in the youngest population of the thin disc and for the high mass range can reach about 10%. These differences are also reflected in the colour distributions. We demonstrate in Appendix B that these discrepancies (> 10%) come from the sampling noise involved in the BGM Std generation strategy. Occasionally, mostly for flat values of the IMF at high masses, the mass distribution of the youngest massive stars is influenced by the distribution of sampling noise in very low-mass reservoirs6. The sampling noise in very-low-mass reservoirs produces, on average, more stars than predicted by the imposed distribution function for the mass range between 1.53 M⊙ and 4 M⊙. From Appendix B, we deduce that we must use a Mother Simulation such that the combination of the imposed fundamental function minimises the effects of the noise in the very small mass reservoir; this is the case of the DAV variant, for example.
After the analysis presented in this section and also in Sect. 4.5 we conclude that BGM FASt is performing correctly in the solar neighbourhood.
6.2. Recovering an imposed SFH
To show that BGM FASt together with the ABC algorithm is capable of inferring a given parameter, we perform several tests trying to recover an imposed SFH of the thin disc. We assume the SFH to be a decreasing exponential function:
where Kψ is the normalization constant, γ is the inverse of the characteristic timescale (e.g. Snaith et al. 2015 7) and τ is the time. The coordinate origin of the τ space is at present (τ = 0) and the values are positive in the direction backwards in time, to the past, until the age of the thin disc (in this case we impose τ = 10 Gyr). We use one BGM Std simulation, with an imposed value of γ, playing the role of the observations, and we use one BGM Std simulation, with an imposed γ, as a Mother Simulation to generate BGM FASt simulations while mapping the parameter space.
We use Eq. (58) as a distance metric and the sufficient statistics 𝒮 described in Sect. 5.2. The threshold υ is set to be small enough to obtain statistically significant results. The simulations are covering the full sky with a limiting apparent magnitude of VT = 11 to mimic the completeness selection function of Tycho-2. Moreover we added the Tycho-2 photometric errors to the simulated observables (Czekaj et al. 2014; Mor et al. 2017). The first test consists in using a BGM Std simulation with γ = 0.12 Gyr−1 as the observational data and as the Mother Simulation. For the second test, we use a BGM Std simulation with γ = 0.12 Gyr−1 as observational data and another BGM Std simulation with γ = 0.00 Gyr−1 as the Mother Simulation. Our third test consists in using a BGM Std simulation with γ = 0.00 Gyr−1 as observational data and another BGM Std simulation with γ = 0.12 Gyr−1 as the Mother Simulation, that is, the inverse of the second test. We find that in the three tests presented here our strategy succeeded in recovering the imposed γ value with a narrow posterior PDF. The posterior probability distribution for the γ parameter resulting from the last test is plotted in Fig. 2. In green we show the prior PDF while in red we plot the posterior PDF. It is interesting to see how from a given prior PDF we end up with a posterior PDF of a very different shape. This is expected as according to the Bayesian statistics theory, the better the information coming from the data, the smaller the dependency of the posterior PDF on the prior PDF.
 |
Fig. 2. Probability distribution function for the inverse of the characteristic time scale (γ parameter) of the thin disc SFH, assuming a decreasing exponential shape. The right vertical blue dotted line indicates the γ value of the Mother Simulation used in the test. The left black dotted vertical line (γ = 0) indicates the value to be recovered by the test. In green we show the prior PDF assumed for the test (uniform distribution between −0.05 and 0.20). In red we show the resulting approximate posterior PDF P(γ|data). |
7. BGM FASt science demonstration cases
To show the capabilities and the strength of BGM FASt simulations, we present two science demonstration cases using Tycho-2 data. We want to prove that our BGM FASt strategy together with the ABC algorithm obtain consistent results by analysing data from the solar neighbourhood. The solar vicinity is a good region to start with, allowing comparisons with previous results. In both cases we use Tycho-2 data with VT < 11. We transform the photometry from Johnson to Tycho as done in Mor et al. (2017). Following Czekaj et al. (2014) we adopt a spacial resolution of 0.8 arcsec, according to the Tycho-2 catalogue, to decide if the binary stellar systems are resolved or unresolved. In addition, we add photometric errors to the simulations to mimic Tycho-2 data. In both cases, for the ABC, we use the sufficient statistics defined in Sect. 5.2 and the distance metric from Eq. (58). The lower limit of the threshold is chosen in each case to be large enough to ensure the existence of sets of parameters (θ̄) able to fulfil the condition δP < υ ( that is: ∃θ̄| δP(θ̄) < υ) and at the same time to be small enough to achieve an accurate posterior PDF.
7.1. Case A: The SFH in the solar neighbourhood
The goal of case A is twofold. On one hand, we evaluate 12 sets of parameters under variations of the thin disc SFH to analyse which one best fits the observational data, obtaining a posterior PDF for the SFH under the given prior. On the other hand, the obtained results allow us to decide which Mother Simulation and parameter space are the best to design case B (see Sect. 7.2).
For case A we work in a 2D space. The first dimension is the inverse of the characteristic time scale (γ) for a SFH modelled with an exponential law (see Eq. (59)). The second dimension is the projection of all the other parameters involved in the thin disc simulation, which we call the Variant dimension. For the γ parameter of the SFH we choose a uniform prior within γ = 0 (constant SFH) and γ = 1/3. We set these limits to be the minimum and maximum value of the inverse of the characteristic timescale compatible with the data in Snaith et al. (2015, their Fig. 5), when fitting a SFH with an exponential shape. To build the prior for the variant dimension we select six model variants (DAV, DM, DBV, HRV, HRVB and SV) whose details are shown in Table 1 and Sect. 4.5. These model variants, using two different extinction maps, one from Drimmel & Spergel (2001) and the other from Marshall et al. (2006), constitute 12 sets of parameters belonging to our second dimensional space. We then assign a prior probability of 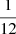 to each set. This is a very restrictive prior and limits our exploration to 12 slices of the full parameter space.
to each set. This is a very restrictive prior and limits our exploration to 12 slices of the full parameter space.
In Fig. 3 we present the projection to the γ space of the approximate posterior PDF. The obtained value for the γ parameter is 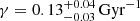 . In Fig. 4 we present the projection to the Variant space of the approximate PDF. We show here that the DAV variant with Drimmel extinction map is the most probable result. We also show that variants using the Drimmel extinction map are carrying more than 80% of the probability. Moreover, the variants using Salpeter IMF has almost null probability.
. In Fig. 4 we present the projection to the Variant space of the approximate PDF. We show here that the DAV variant with Drimmel extinction map is the most probable result. We also show that variants using the Drimmel extinction map are carrying more than 80% of the probability. Moreover, the variants using Salpeter IMF has almost null probability.
In Fig. 5 we present, for the accepted sets of parameters in the ABC algorithm, the Poissonian distance (δP) as a function of the γ parameter for the 12 model variants in the Variant space. The variant giving the best fit (smaller δp) is the DAV variant using the Drimmel extinction. Furthermore, we want to emphasise that this variant gives a better fit in a large range of γ values, that is, from γ ≈ 0.10 to γ ≈ 0.16. As discussed for Fig. 4, the four variants closest to the data (pink, cyan, green and red) use the Drimmel extinction map. We show using the horizontal solid line how three variants (HRVB, DM and DBV) with different combinations of parameters could result in the same Poissonian distance (δP) to Tycho-2 data. We note that within 1σ (black dotted vertical lines show the 0.16 and 0.84 quantiles) in Fig. 5, the DAV variant can have a δP that is compatible with the δP of HRVB, DM and DBV variants.
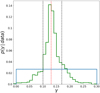 |
Fig. 3. P(γ|data) (in green) Approximate posterior PDF for the γ parameter resulting from case A, given the adopted prior (see text). The vertical red dotted line indicates the mode of the distribution γ = 0.13 with an uncertainty in the range indicated by the two black vertical lines corresponding to the quantiles 0.16 and 0.84, respectively ( |
 |
Fig. 4. P(Model|data): approximate posterior PDF for the variants (see Table 2) given the adopted prior (see text). We obtain these results when using as observational data the stars in Tycho-2 catalogue with visual apparent magnitude VT < 11. Variants whose names end with “-D” use the extinction maps from Drimmel & Spergel (2001) while names ending with “-M” use those from Marshall et al. (2006). With a dotted blue line we show the adopted prior PDF. |
 |
Fig. 5. This plot is built from the results of Case A shown in Figs. 6 and 7. Each point in the plot represents a set of parameters accepted by the ABC algorithm as part of the posterior PDF. For each accepted set we plot the Poissonian distance (δP) as a function of the inverse of the characteristic timescale (γ parameter) of an assumed decreasing exponential SFH. δP is computed using the expression of Eq. (58); the smaller the value of δP, the better its agreement with the data. Dotted horizontal line gives the δP value around the best fit (δP ≈ 16 000) and the solid horizontal line is to emphasise the degeneracy for three different sets of parameters of the model variants (see Table 2). The vertical dashed black lines denote the quantile 0.16 (left) and quantile 0.84 (right) for the distribution of Fig. 3. The vertical red dashed line is for the mode of the γ distribution in Fig. 3. We obtain these results when using as observational data the stars in the Tycho-2 catalogue with visual apparent magnitude VT < 11. Variant/extinction map combinations are as described in Fig. 4. |
By analysing the obtained approximate posterior PDF we can state that when modelling the SFH as a simple exponential law (allowing constant SFH when γ = 0) our results point to a decreasing SFH in the solar neighbourhood with 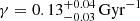 . However, we must keep in mind that in our parameter space the dimension of the SFH is continuously covered while the second dimension is discrete. Therefore, non-considered combinations of the full parameter space could lead to a better fit with Tycho-2 data (see case B).
. However, we must keep in mind that in our parameter space the dimension of the SFH is continuously covered while the second dimension is discrete. Therefore, non-considered combinations of the full parameter space could lead to a better fit with Tycho-2 data (see case B).
As mentioned above, the results obtained from case A guide us for the design of case B. We want to choose a Mother Simulation for case B as close to the observational data as possible. This choice minimises the effects of the approximations taken in BGM FASt and also the effects due to noise explained in Appendix B. From Fig. 4 it is clear that the Mother Simulation for case B should be the DAV variant.
Finally, to design the parameter space of case B we must try to include both the most important parameters as well as the ones that produce degeneracies in the results. From Figs. 4 and 5 it is clear that the IMF and the SFH produce important variations on the results. In Fig. 5 we note that the stellar volume mass density at the position of the Sun is causing degeneracy among three models differing by the IMF and the SFH. Therefore, the parameter space of case B should contemplate the IMF, the SFH, and the density laws.
7.2. Case B: Simultaneous inference of the SFH, the IMF, and the density laws
In this second science demonstration case we explore a 6D parameter space of the IMF, the SFH, and the density laws for the thin disc component. As in case A, the SFH is assumed to be an exponential law. Therefore, one of the dimensions is the inverse of the characteristic timescale γ. The IMF is assumed to be a Kroupa-like IMF; this is a three truncated power law with three slopes α1, α2, and α3 and two mass limits x1 and x2. For simplicity in this case we fix x1 = 0.5 M⊙ and x2 = 1.53 M⊙ which are the values used in the best-fit models from Czekaj et al. (2014). Finally, for the thin disc density laws we use as main parameters the scale length (hR) and the thin disc stellar volume mass density at the position of the Sun (ρ⊙). As the youngest sub-population is too young to be considered isothermal, the dynamical constraints are not applied on the population with age less than 0.10 Gyr and its hR is fixed to be the one assumed in Robin et al. (2003), that is hR = 5000 pc. We explore the scale-length value for the rest of the age sub-populations assuming that it is independent of the age.
The Mother Simulation that we use in this case B is the DAV variant (see Table 2). We use the 3D extinction map from Drimmel & Spergel (2001) and additionally an alternative 3D extinction map called Stilism. This new map was constructed using the method of Capitanio et al. (2017) but setting the Marshall et al. (2006) map as a prior at a distance of 1.5 kpc. The full process is explained in Lallement et al. (2018, their Sect. 5). This map is still at the testing stage. However, we find it interesting to include this preliminary version in our study because it is the most updated 3D extinction map built specially for the BGM.
To sum up, we explore a 6D space that includes γ, α1, α2, α3, hR and ρ⊙. For all of these parameters we consider a uniform prior PDF within the values of Table 3. In the Bayesian strategy for the parameter inference the assumption of the prior is of marginal importance if the data are good enough to constrain the explored parameters. Our choice for the low and high limits aims to cover the range of values reported in the literature for the explored parameters.
Lower and upper limits of the imposed initial uniform Prior PDF for each of the explored parameters.
In Figs. 6 and 7 we show the corner plot resulting from the 6D exploration using BGM FASt and the ABC algorithm, using the Drimmel and Stilism 3D extinction maps, respectively. The green histograms are the 1D marginal posterior PDFs obtained directly from the ABC algorithm. The blue solid lines are the posterior PDFs of the six explored parameters accounting explicitly for the differences between BGM FASt and BGM Std simulations. To build these PDFs we first assume that the computed Poissonian distance between simulations and observations has a Gaussian error, with σ equal to the mean Poisson distance8 (δP) between BGM FASt and BGM Std simulations (σ = 1445). Then, for each set of parameters accepted by the SMC-ABC algorithm, we transform their single distance δp to a Gaussian distribution centred on the pertinent δp and with σ = 1445. After this transformation we recompute the 1D distributions and finally, normalizing accordingly, we get the blue PDFs.
 |
Fig. 6. Corner plot with the projection of the approximate posterior PDF obtained from the exploration of the six parameters of the thin disc component, including the IMF, the SFH, and the density laws. The vertical solid red lines and the vertical green dashed lines indicate the mode and the median for each parameter, respectively. For α3, the median and the mode are superimposed. Green 2D contours and 1D distributions are for the distributions obtained directly from the ABC algorithm. The blue 1D posterior PDFs are built by accounting, in the posterior PDF, for the differences between BGM Std and BGM full simulations (see text). The vertical black dashed lines indicate the quantiles 0.16 and 0.84 of this distribution. On top of each 1D histogram the mode of the distribution and the interval of the 0.16 and 0.84 quantiles for the blue distributions are indicated. In black at the top right of each one of the 2D panels we show the Pearson’s correlation coefficient. The magenta cross indicates the parameters of the adopted Mother Simulation. γ is the inverse of the characteristic timescale when assuming an exponentially decreasing SFH. α1, α2 and α3 are the slopes of the IMF assumed to be a three-times truncated power law with the mass limits fixed at x1 = 0.5 M⊙ and x2 = 1.53 M⊙. ρ⊙ is the thin disc stellar volume mass density at the position of the Sun and hR is the radial scale length of the thin-disc density profile assumed to be an Einasto shape (see units in Table 1). We obtain these results assuming the Drimmel & Spergel (2001) extinction map and using as observational data the stars in Tycho-2 catalogue with visual apparent magnitude VT < 11. |
The results point towards a decreasing SFH with 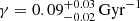 (using Drimmel) and
(using Drimmel) and 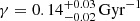 (using Stilism). We obtain almost the same value of the slope of the IMF at the low mass range of
(using Stilism). We obtain almost the same value of the slope of the IMF at the low mass range of 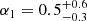 when using the Drimmel map and
when using the Drimmel map and 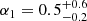 when using the Stilism map. The same occurs for the IMF slope in the mass range between 0.5 M⊙ and 1.53 M⊙ where we obtain values of
when using the Stilism map. The same occurs for the IMF slope in the mass range between 0.5 M⊙ and 1.53 M⊙ where we obtain values of 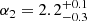 and
and 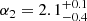 when using Drimmel and Stilism maps, respectively. For masses greater than 1.53 M⊙, we find a very steep IMF with a slope value of
when using Drimmel and Stilism maps, respectively. For masses greater than 1.53 M⊙, we find a very steep IMF with a slope value of 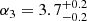 for the Drimmel map and a more common slope for Stilism (
for the Drimmel map and a more common slope for Stilism (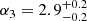 ). The value obtained for the thin disc stellar mass volume density at the position of the Sun is
). The value obtained for the thin disc stellar mass volume density at the position of the Sun is 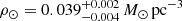 and
and 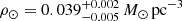 for Drimmel and Stilism, respectively. The radial scale length for the thin disc component has large uncertainty, being
for Drimmel and Stilism, respectively. The radial scale length for the thin disc component has large uncertainty, being 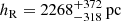 and
and 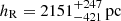 for Drimmel and Stilism, respectively.
for Drimmel and Stilism, respectively.
In both corner plots (Figs. 6 and 7) we can see in the 2D projection of the PDF the correlations (degeneracies) between the explored parameters. The γ parameter of the SFH is clearly correlated with the α2 and α3 slopes of the IMF. Steeper values of the SFH correspond to flatter slopes of the IMF. This effect is largely discussed in the literature (e.g. Haywood et al. 1997; Aumer & Binney 2009). Steeper values of the SFH lead to less young stars and hence less massive stars alive at present. Flatter IMFs are therefore needed to compensate for this effect and reproduce the observations. On the contrary, flatter values of the SFH produce more young stars and hence more massive stars alive at present. Steeper IMFs are therefore needed to compensate this effect and reproduce the observations. We also note the correlation between the density ρ⊙ and the second slope of the IMF (α2). A flatter slope corresponds to smaller density and a steeper slope to higher density. One possible explanation for this is based on two facts. First, about 60% of our sample belongs to the mass range of α2. Second, in general for fixed values of α1 and α3, the smaller the value of α2, the higher the amount of mass dedicated to generate stars in its mass range. As a consequence, flatter slopes need smaller values of ρ⊙ to fit the data. The last correlation that can be seen in the figure is between α1 and α2 because of the continuity at the IMF mass limit.
Using the most probable values shown in Figs. 6 and 7, we built two new model variants, the Most Probable (MP) variant for Drimmel and Stilism extinction maps, respectively. In Fig. 8, we present the apparent visual magnitude Tycho (VT) versus Tycho (B − V)T colour divided in three latitude ranges, |b|< 10, 10 < |b|< 30, and 30 < |b|< 90 and for the whole sky. The colour-map shows the Poissonian distance (δLr) between model and Tycho-2 data computed for each bin. This visualisation allows us to identify differences between model and data in the CMDs. The fifth column is for the MP model variant using the Drimmel extinction map versus Tycho-2. In the fourth column, for comparison, we show the DAV model variant versus Tycho-2, in order to show the improvement that the MP variant represents with respect to the best fit model obtained in Mor et al. (2017). The improvements are significant in the three latitude ranges, with a clear impact on the bluest half ((B − V)T < 1.0) of the diagrams while the reddest half ((B − V)T > 1.0) behaves almost equally for the DAV and MP variants.
 |
Fig. 8. Colour-magnitude diagram ( apparent visual magnitude Tycho (VT) vs. Tycho (B − V)T colour) divided into three latitude ranges: first row: |b|< 10, second row: 10 < |b|< 30 third row: 30 < |b|< 90 and for the whole sky (bottom row). The colour-map of the first, second, and third columns shows the logarithm of the star counts in each bin. First column: Tycho-2 data, second column: best-fit model variant from Mor et al. (2017) (DAV) obtained using Galactic classical Cepheid and Tycho-2 data, and third column: MP variant combination of the most probable value for six parameters explored in Sect. 7.2. The BGM simulations performed for this figure use the Drimmel extinction map. The colour map of the fourth and fifth rows represents the Poissonian distance computed for each bin. The total distance indicated in each plot is the Poissonian distance (δP) computed using Eq. 58. The smaller the value of δP, the better the agreement. fourth column: Poissonian distance between DAV and Tycho-2, and fifth column: Poissonian distance between MP and Tycho-2. Observational data and simulations are samples limited in visual apparent magnitude considering the stars with VT < 11. |
Previous works fitting the BGM thin disc component with observational data result in an excess of blue stars in the simulations at all latitudes (Czekaj et al. 2014; Mor et al. 2017). As can be seen in Fig. 8, the MP variant is improving the fit on the blue side, where young stars dominate, in all latitude ranges, even in the high latitudes where the impact of the assumption of a 3D extinction map is expected to be small.
In Fig. 9 we present the colour distribution of Tycho-2 data (green) and the MP variant (red) using the Drimmel extinction map. Our Bayesian approach allows for the first time to introduce error bars in this comparison that account for the 1σ level. The agreement of MP with Tycho-2 is very good in the blue peak while, as already reported in Czekaj et al. (2014) and Mor et al. (2017), the red peak is shifted by about 0.05 magnitudes to the right.
Finally, we ran a BGM Std simulation of the MP variants, using both Drimmel and Stilism extinction maps, and then we have compared this with our BGM FASt simulation confirming that the differences between them are within the 5% reported in Sects. 4 and 6 (see detailed tests in Appendix A.2). To perform these two BGM Std simulations we previously ran the full process to ensure the local dynamical statistical equilibrium (see Sect. 4). With the obtained results we have the local densities of the Milky Way components for the MP variant and the eccentricities of the Einasto density profiles (ϵ) for the age sub-populations of the thin disc. The results are shown in Table 4, the components tagged with an asterisk are imposed while the others are derived in our strategy. We obtain a total volume mass density in the solar neighbourhood of 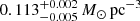 and a local dark matter density of 0.012 ± 0.001 M⊙ pc−3. For the total stellar volume mass density of the thin disc we obtain
and a local dark matter density of 0.012 ± 0.001 M⊙ pc−3. For the total stellar volume mass density of the thin disc we obtain 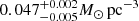 (see the Table 4 for details on the density of each thin disc age range). Finally, for the total stellar volume mass density in the solar neighbourhood we obtain
(see the Table 4 for details on the density of each thin disc age range). Finally, for the total stellar volume mass density in the solar neighbourhood we obtain 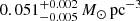 .
.
7.3. The local star-formation scene
In this section we discuss the results obtained in Sect. 7.2. The whole IMF that we have obtained for the thin disc component, when using the Stilism 3D extinction map, is, within 1σ level, compatible for all mass ranges with the Galactic-field IMF given in Kroupa et al. (2013), their Eq. (59)). For the very-low-mass range, our results (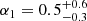 ) are compatible with a flat function and have large uncertainties. We have to take into account that the number of stars with M/M⊙ < 0.5 in our simulations is smaller than 0.02% of the total sample; this is about 100 stars with very low weight in the comparison of synthetic versus observed CMDs. The integral over the whole mass range from 0.09 M⊙ to 0.5 M⊙ is in this case more important than the slope itself. The value obtained for the second slope of the IMF, in the mass range from 0.5 M⊙ to 1.53 M⊙, is
) are compatible with a flat function and have large uncertainties. We have to take into account that the number of stars with M/M⊙ < 0.5 in our simulations is smaller than 0.02% of the total sample; this is about 100 stars with very low weight in the comparison of synthetic versus observed CMDs. The integral over the whole mass range from 0.09 M⊙ to 0.5 M⊙ is in this case more important than the slope itself. The value obtained for the second slope of the IMF, in the mass range from 0.5 M⊙ to 1.53 M⊙, is 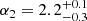 and it is very close to the value reported in Kroupa et al. (2008) (α2 = 2.2 ± 0.5) and not far from the Salpeter IMF (α = 2.35). We stress that about 60% of our simulated sample belongs to stars in this second mass range. For the high-mass range we found an IMF slope not compatible with Salpeter IMF (α = 2.35) at ∼3σ level. We obtain
and it is very close to the value reported in Kroupa et al. (2008) (α2 = 2.2 ± 0.5) and not far from the Salpeter IMF (α = 2.35). We stress that about 60% of our simulated sample belongs to stars in this second mass range. For the high-mass range we found an IMF slope not compatible with Salpeter IMF (α = 2.35) at ∼3σ level. We obtain 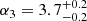 (with Drimmel 3D extinction map) and
(with Drimmel 3D extinction map) and 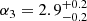 (with Stilism 3D extinction map). We want to emphasise that our slope of the IMF at high mass range is only valid up to 4 M⊙ as we estimate that in our samples just 1% of the stars have masses larger that 4 M⊙. As largely discussed in Mor et al. (2017), the IMF considered in BGM is a composite IMF (or Integrated Galactic IMF; IGIMF). Moreover, the Tycho-2 data are a mixture of stars in the field and clusters. The abundant low-mass clusters do not have massive stars while the rare massive clusters do. This leads to a steepening of the composite IMF (αfield > αcluster), which is a sum of all the IMFs in all the clusters that spawn the Galactic population (Kroupa & Weidner 2003; Kroupa et al. 2013). Additionally, the deduced shape of the IMF, when studying field stars, could be influenced by the dynamical ejection of OB stars from dynamically unstable cores of young clusters (Elmegreen & Scalo 2006). This may lead to IMFs that are steeper than those of Salpeter (1955) because, as dynamical work suggests, the less massive members of a core of massive clusters are preferentially ejected (Clarke & Pringle 1992; Pflamm-Altenburg & Kroupa 2006). In Kroupa & Weidner (2003), the authors point toward αfield ≳ 2.8, compatible with our results. Scalo (1986) obtain α = 2.7 for stars with M > 1M⊙ and in Kroupa et al. (2013) a slope of α = 2.7 ± 0.4 is reported for masses M ≳ 1M⊙, both within 1σ of our result obtained with Stilism 3D extinction map. Also compatible with our results is the work of Rybizki & Just (2015), that, from the population synthesis side, using Galaxia (Sharma et al. 2011), obtained a slope of α = 3.02 ± 0.06 at the high mass range. Some studies found steeper values, such as for example Miller & Scalo (1979) who reported a galactic field IMF of α ≈ 3.3, and later Massey (1998) who found very steep values of the IMF of OB stars in the field for the SMC and LMC, with values around α ≈ 4.5 (while they found values similar to those of Salpeter (1955) for stars in OB associations). We note here that the value of the slope depends on the specific range of masses upon which it is based. Finally, we note that, as reported in Kroupa & Weidner (2003), the mass function of the clusters themselves over the mass range of 10 M⊙–107 M⊙ can be represented with a power-law with slope β. Analysing the results presented in [see their Fig. 2]Kroupa2003 our results favour values of the slope of the clusters’ mass function of β ≥ 2.
(with Stilism 3D extinction map). We want to emphasise that our slope of the IMF at high mass range is only valid up to 4 M⊙ as we estimate that in our samples just 1% of the stars have masses larger that 4 M⊙. As largely discussed in Mor et al. (2017), the IMF considered in BGM is a composite IMF (or Integrated Galactic IMF; IGIMF). Moreover, the Tycho-2 data are a mixture of stars in the field and clusters. The abundant low-mass clusters do not have massive stars while the rare massive clusters do. This leads to a steepening of the composite IMF (αfield > αcluster), which is a sum of all the IMFs in all the clusters that spawn the Galactic population (Kroupa & Weidner 2003; Kroupa et al. 2013). Additionally, the deduced shape of the IMF, when studying field stars, could be influenced by the dynamical ejection of OB stars from dynamically unstable cores of young clusters (Elmegreen & Scalo 2006). This may lead to IMFs that are steeper than those of Salpeter (1955) because, as dynamical work suggests, the less massive members of a core of massive clusters are preferentially ejected (Clarke & Pringle 1992; Pflamm-Altenburg & Kroupa 2006). In Kroupa & Weidner (2003), the authors point toward αfield ≳ 2.8, compatible with our results. Scalo (1986) obtain α = 2.7 for stars with M > 1M⊙ and in Kroupa et al. (2013) a slope of α = 2.7 ± 0.4 is reported for masses M ≳ 1M⊙, both within 1σ of our result obtained with Stilism 3D extinction map. Also compatible with our results is the work of Rybizki & Just (2015), that, from the population synthesis side, using Galaxia (Sharma et al. 2011), obtained a slope of α = 3.02 ± 0.06 at the high mass range. Some studies found steeper values, such as for example Miller & Scalo (1979) who reported a galactic field IMF of α ≈ 3.3, and later Massey (1998) who found very steep values of the IMF of OB stars in the field for the SMC and LMC, with values around α ≈ 4.5 (while they found values similar to those of Salpeter (1955) for stars in OB associations). We note here that the value of the slope depends on the specific range of masses upon which it is based. Finally, we note that, as reported in Kroupa & Weidner (2003), the mass function of the clusters themselves over the mass range of 10 M⊙–107 M⊙ can be represented with a power-law with slope β. Analysing the results presented in [see their Fig. 2]Kroupa2003 our results favour values of the slope of the clusters’ mass function of β ≥ 2.
The posterior PDF that we obtain for the inverse of the characteristic timescale of the thin disc SFH assuming a simple exponential law is not compatible with flat values. When we adopt the extinction map from Drimmel & Spergel (2001) we obtain 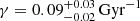 . This is compatible with the value obtained by Aumer & Binney (2009), see their Table 8: γ ≈ 0.09) when considering the SFH of the thin and thick discs separately. The value obtained when using the Stilism extinction map is
. This is compatible with the value obtained by Aumer & Binney (2009), see their Table 8: γ ≈ 0.09) when considering the SFH of the thin and thick discs separately. The value obtained when using the Stilism extinction map is 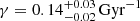 , that is, very close to the results obtained in our case A (
, that is, very close to the results obtained in our case A (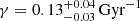 ), and falls in the high range of the values discussed in Aumer & Binney (2009). Although the γ values that we obtain depend on the assumption of the 3D extinction map, the value that we estimate for the present rate of star formation in the disc (averaged along the last 100 Myr) is very similar for both, being 1.2 ± 0.2 M⊙ yr−1. This is possible because the total surface mass density at the position of the Sun is found to be higher for the case of γ = 0.14. Our result is compatible with the values found by Robitaille & Whitney (2010) (0.68 − 1.45 M⊙ yr−1) derived from Spitzer young stellar objects. Additionally, Licquia & Newman (2015) obtain a value for the current Milky Way rate of star formation of 1.65±0.19 which accounts for both the disc and the bulge. Using chemical data, Snaith et al. (2015) found a higher value of the present rate of star formation, that is, approximately 2 M⊙ yr−1.
), and falls in the high range of the values discussed in Aumer & Binney (2009). Although the γ values that we obtain depend on the assumption of the 3D extinction map, the value that we estimate for the present rate of star formation in the disc (averaged along the last 100 Myr) is very similar for both, being 1.2 ± 0.2 M⊙ yr−1. This is possible because the total surface mass density at the position of the Sun is found to be higher for the case of γ = 0.14. Our result is compatible with the values found by Robitaille & Whitney (2010) (0.68 − 1.45 M⊙ yr−1) derived from Spitzer young stellar objects. Additionally, Licquia & Newman (2015) obtain a value for the current Milky Way rate of star formation of 1.65±0.19 which accounts for both the disc and the bulge. Using chemical data, Snaith et al. (2015) found a higher value of the present rate of star formation, that is, approximately 2 M⊙ yr−1.
We focus now on our findings for the density laws. For the radial scale length (hR) of the thin disc component we obtain a wide posterior PDF showing large uncertainties. Tycho-2 data up to a magnitude of VT = 11 cover heliocentric radii up to 1.5 − 2 kpc. Therefore the constraints that can be obtained on the radial scale length counting the stars over all the longitude ranges, as we do, are weak. Nonetheless the most probable value obtained when using the Stilism extinction map (hR = 2151 pc) is very close to the value obtained in Robin et al. (2012) (hR = 2170 pc). For the total stellar volume mass density at the position of the Sun (ρ⊙) we obtain a value of 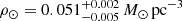 (see Table 4). Excluding white and brown dwarfs, we obtain a value of
(see Table 4). Excluding white and brown dwarfs, we obtain a value of 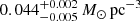 , compatible within 1σ with the results in Bovy (2017) where he found a value for the giants + main sequence stars in the solar neighbourhood of 0.040 ± 0.002 M⊙ pc−3, and within 2σ with McKee et al. (2015) who found a value of 0.036±0.005 M⊙ pc−3. The results from Reid et al. (2002) (0.034−0.037 M⊙ pc−3) and Flynn et al. (2006) (0.0334M⊙ pc−3) point towards lower values. We obtain a local dark matter volume density of
, compatible within 1σ with the results in Bovy (2017) where he found a value for the giants + main sequence stars in the solar neighbourhood of 0.040 ± 0.002 M⊙ pc−3, and within 2σ with McKee et al. (2015) who found a value of 0.036±0.005 M⊙ pc−3. The results from Reid et al. (2002) (0.034−0.037 M⊙ pc−3) and Flynn et al. (2006) (0.0334M⊙ pc−3) point towards lower values. We obtain a local dark matter volume density of 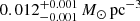 pc−3 when fitting the Galactic rotation curve in the process to ensure the LDSE. This value is compatible with Catena & Ullio (2010), Salucci et al. (2010), McMillan (2011) and Bovy & Tremaine (2012). Our value for the local total mass density (
pc−3 when fitting the Galactic rotation curve in the process to ensure the LDSE. This value is compatible with Catena & Ullio (2010), Salucci et al. (2010), McMillan (2011) and Bovy & Tremaine (2012). Our value for the local total mass density (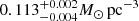 ) is compatible with the values of Korchagin et al. (2003) (0.1 − 0.11 M⊙ pc−3), Holmberg & Flynn (2000) (0.102 ± 0.1M⊙ pc−3), and van Leeuwen (2007) (0.112 ± 0.019M⊙ pc−3); all three were obtained with Hipparcos data.
) is compatible with the values of Korchagin et al. (2003) (0.1 − 0.11 M⊙ pc−3), Holmberg & Flynn (2000) (0.102 ± 0.1M⊙ pc−3), and van Leeuwen (2007) (0.112 ± 0.019M⊙ pc−3); all three were obtained with Hipparcos data.
We discuss below four points that could impact our parameter inference: (1) the fixed ingredients of BGM, (2) the Tycho-2 photometric error modelling, (3) the assumptions on the other Galactic components in the BGM (e.g. thick disc, halo, and bulge-bar) and (4) the choice of extinction map.
Local densities M⊙/pc3.
The assumptions for the fixed ingredients of the BGM, for example, atmosphere models, stellar evolutionary tracks, chemical distribution, or the mass limits of the IMF x1 and x2, could produce degeneracies between the fixed ingredients and the explored ingredients or biases introduced by the fixed ingredients. One example of these biases could be the shift of the red peak between simulations and Tycho-2 data observed in Fig. 9 that was already reported in Czekaj et al. (2014) and Mor et al. (2017). This shift could be caused by several of the fixed BGM ingredients, for example the atmosphere models, the stellar evolutionary tracks, the photometric transformation between Johnson and Tycho bands, or the treatment of unresolved stellar multiple systems. In practice, a shift in the red peak implies that there is no combination of the six explored parameters that is able to exactly reproduce the data, and therefore the obtained posterior PDFs are affected by this impossibility. We suspect that this is the reason why the improvements on the fit comparing the MP variant with the DAV variant are mostly concentrated in the blue half of the CMD (see Fig. 8).
 |
Fig. 9. Colour distribution of MP variant and Tycho-2 with a limit in magnitude of VT = 11. Our Bayesian approach allows us to compute the error bars (dotted blue) from the simulations computed using the parameters inside the 1σ level of the posterior PDFs shown in Fig. 6. |
The Tycho-2 photometric error modelling could be an additional source of uncertainty for the derivation of the SFH and IMF parameters. Assumptions on the other galactic components considered in the BGM could also influence the results. The amount of stars from the inner region of the Galaxy and the halo in the solar neighbourhood is known to be negligible. We estimate that less than 0.5% of the stars in our sample belong to the halo. The density of the bulge/bar stars is much smaller, even null. Therefore, our assumptions on the structure of the halo and the bulge/bar marginally affect our results. The case of the thick disc component is more complex. We assume the structure of the thick disc from Robin et al. (2014) with two star-formation episodes at 10 Gyr and 12 Gyr. With these assumptions we estimate that the amount of thick-disc stars in our sample is about 10%. This is small but not negligible. Most of these stars have ages of the order of 10 Gyr, and thus have a similar age to the older stars from the thin disc. The consideration of other age distributions for the thick disc would imply that the thin and thick discs overlap in different age ranges. Thus the results on the thin disc, as shown here, could be impacted by our (fixed) hypotheses on the thick-disc SFH. This question will be considered in the near future. Other structures, such as the spiral arms, are not considered in the model, and therefore irregularities in the spatial density distribution are smoothed in the BGM. The simulated CMDs that fit the Tycho-2 CMDs are thus resulting from a smoothed simulated solar neighbourhood, while the Tycho-2 CMDs can result from inhomogeneous structures, such as clusters, associations, and resonant structures. This is why we emphasise that the IMF that we are deriving is the composite IMF (or integrated galactic IMF) as we are not simulating the inhomogeneities of the star formation in the Galactic disc.
As we can see throughout this paper the choice of the extinction map is a critical ingredient for our parameter inference. An overestimation or underestimation of the extinction generally leads to an underestimation or overestimation of the star counts that could bias our results. An example of the effects of the choice of the extinction map is the different IMFs (at high masses) and SFHs that we are obtaining for Drimmel and Stilism extinction maps. On average, the absorption of the Stilism map is higher than that of the Drimmel map, producing slightly smaller star counts, especially in the blue. As a consequence, to fit the observations when using the Drimmel map we need a steeper slope of the IMF, at high masses, because in the Drimmel map the bluest stars are less absorbed than in the Stilism map. The differences in the absorption of both maps is also responsible for the slightly different SFHs. For the moment we do not have enough evidence to decide which map is more precise. In a future paper, external tests of the Stilism map will be provided to answer this question.
8. BGM FASt in the context of Galaxy modelling
We have presented the BGM Fast Approximate Simulations (BGM FASt) which is a strategy to generate Milky Way simulations at low computational cost. The computational time of a BGM FASt simulation represents only 0.02% of the equivalent simulation using the BGM Std strategy. We dedicate the following paragraphs to contextualising BGM FASt in the environment of the Galaxy models. We consider, for this contextualisation, the Galaxy models that could be fast enough to be used together with iterative processes like machine learning, ABC, or MCMC to study the structure and evolution of the Milky Way.
The Galaxy model from Pasetto et al. (2016) is also a population synthesis model to deal with large amounts of data from surveys of the Milky Way. It allows for very quick computation of CMDs from the distribution function in a given line of sight avoiding star-by-star sampling. This is a very valuable property to work with iterative inference processes such as ABC or genetic algorithms. However, when making comparisons with observational data other than that from CMDs (e.g. parallax or proper motions), star-by-star sampling (e.g. Fig. 15 in Pasetto et al. 2016) is required. Our strategy, on the other hand, starts with a Mother Simulation which is already sampled and therefore BGM FASt never needs to re-sample star-by-star. This allows for quick generation not only of CMDs but also distributions of other observables such as parallax or proper motions. Moreover, the CMDs built with BGM FASt have a rigorous treatment of the stellar multiple systems, where we consider if a stellar multiple system is merged or resolved according to the angular resolution of the observational catalogue to be compared with the simulations. This effect is not considered in the quick CMDs of Pasetto et al. (2016). These authors paid special attention to the kinematic constraints and dynamical consistency of the model. As in BGM FASt, the authors consider stationary state but they emphasise the non-isothermality of the disc and the formulation for the mixed terms of the Jeans equation obtained with consistency from the potential; their method ends up with a dynamical consistency stronger than the one adopted in BGM FASt where isothermal state is considered and radial and vertical motions are assumed to be decoupled. However, as described in Sect. 4, the process that ensures LDSE in BGM FASt runs at a very cheap computational cost. Without doubt the stronger point of the Galaxy model in Pasetto et al. (2016), in relation to BGM FASt, is the introduction of the spiral arms as a perturbation of the stellar distribution function. Although they have a perturbed disc, they still compute its dynamical constraints with the same Poisson solver as in Robin et al. (2003), which makes the assumption of an axi-symmetric potential to solve the Poisson equation. In the future we may consider a similar technique (to that used in Robin et al. 2012) for BGM FASt, such as the possibility of introducing spiral arms in BGM FASt using an axi-symmetric Mother Simulation.
TRILEGAL has been used as a prior for a Bayesian study but its computational cost is probably too expensive for parameter exploration using iterative algorithms. Initially it provided only photometry of any field of the Galaxy but no kinematic parameters such as proper motions or radial velocities. Nowadays, TRILEGAL incorporates a kinematic module. Dynamical consistency is not analysed in Girardi et al. (2005). Compared with TRILEGAL we consider BGM FASt to be more adapted to exploiting extremely large surveys.
Galfast (Jurić et al. 2008) takes advantage of the use of graphics processing units (GPUs) instead of central processing units (CPU), and due to the computational cost reported in Juric et al. (2010), it could be fast enough to be used, in some cases, together with Bayesian iterative techniques. However, as pointed out in Loebman et al. (2014) this galaxy model does not consider inputs such as SFH, age-metallicity relation, or the IMF. It is simply a sophisticated Monte Carlo generator designed to produce a snapshot of the current sky with the stellar content consistent with SDSS observations and where initially the luminosity function was taken from Kroupa et al. (1993). Therefore, nowadays Galfast is not ready to infer the IMF and SFH as BGM FASt is.
Galaxia code from Sharma et al. (2011) is, for the moment, fast enough to work with modern Bayesian techniques as seen in Rybizki & Just (2015). Galaxia can sample stars from an N-body simulation by splitting each N-body particle into several stellar populations of different ages and masses, imposing a given IMF and SFH. On the one hand, the possibility to sample stars from an N-body simulation is a clear advantage from the point of view of dynamical consistency, as the N-body evolves naturally from the interaction of the particles. On the other hand, if one samples an N-body model with Eq. (11) from Sharma et al. (2011), for a given N-body particle, the kinematic behaviours of the young and old stars are going to be exactly the same, thus not following the Jeans equation. Another approach using Galaxia was taken by Rybizki & Just (2015), where they apply the SFH to build the N-body simulation, each particle being representative of an age range. They subsequently use Galaxia to simply convert each particle to a single stellar population for a given IMF. They include the Jeans equation implicitly when calculating the local SFH for their volume complete sample (their Fig. 1). Recalculating the N-body input for different SFHs is computationally inexpensive but the use of Galaxia to explore the IMF is relatively slow. Here, BGM FASt is faster than Galaxia (Rybizki, J. private comm.). Alternatively, if one wants to study the SFH and the IMF simultaneously with Galaxia, one can use it in the analytical model mode based on the model by Robin et al. (2003). In Galaxia, the code can be edited to update the density distribution to the latest versions of the BGM (e.g. Robin et al. (2012); Robin et al. (2014); Czekaj et al. (2014)). In BGM FASt, it is also straightforward to work with the most updated version of the BGM Std simply by changing the Mother Simulation. For the moment, Galaxia is not incorporating a rigorous treatment for the resolution of the stellar multiple systems according to the angular resolution of the pertinent observational catalogue as we do in BGM FASt. Therefore, CMDs coming from Galaxia do not consider this effect. Galaxia in its analytical mode uses the same dynamical constraints as Bienaymé et al. (1987), as we do in BGM FASt. The sampling of the distribution function used in Galaxia is known to be very efficient. It incorporates, among others, a clever strategy that, given an imposed limiting apparent magnitude for the simulation, they computes the lowest stellar mass that can generate a visible star, and then they exclusively generate stars with masses above this limit. Their sampling strategy is one of the clues that makes Galaxia a tool fast enough to use it in an iterative processes.
In summary, several Galaxy models and codes have been built to explore the structure and evolution of the Milky Way. Their advantages and disadvantages depend on the specific scientific goals. They are certainly all extremely valuable tools for the study of the Galaxy but BGM FASt is especially suited to exploring more complex models with more free parameters, as is needed, for example, when working with Gaia data.
9. Conclusions
We have developed, tested, and applied a new framework to perform BGM Fast Approximate Simulations (BGM FASt). We have shown BGM FASt to be a powerful tool to study the Milky Way using modern computational Bayesian techniques. This strategy allows one to explore large parameter spaces using huge observational surveys (e.g. Gaia DR2). We have demonstrated the robustness of BGM FASt through several validation tests. In the context of dynamical consistency, we have shown that the results obtained using the approximate method to ensure LDSE, implemented in BGM FASt, are totally compatible with the results obtained with the full LDSE, implemented in BGM Std. We have rigorously compared colour-magnitude diagrams and distributions of mass, age, and colour obtained from both BGM FASt and BGM Std, demonstrating the superior performance of BGM FASt. Thanks to the structure of BGM FASt, any improvement on the Galaxy model used as the Mother Simulation is naturally incorporated.
As examples of application of BGM FASt, we have presented two science demonstration cases using solar neighbourhood data. Of special scientific interest is case B, where we have explored a 6D space of the thin disc component, including the SFH, the IMF, and the density laws, using Tycho-2 and assuming two 3D extinction maps, one from Drimmel & Spergel (2001) and another from Stilism (Lallement et al. 2018). We have seen that the values of the slopes of the IMF at the first and second mass ranges (α1 and α2), the values of the thin disc stellar mass density at the position of the Sun ( ρ⊙), and the values of the thin disc radial scale length (hR) are almost independent of our choice of 3D extinction map. The results obtained for the composite IMF (or IGIMF) for the low mass range (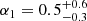 ) are compatible with a flat function and have large uncertainties. In the mass range between 0.5 M⊙ and 1.53M⊙ we obtain
) are compatible with a flat function and have large uncertainties. In the mass range between 0.5 M⊙ and 1.53M⊙ we obtain 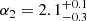 . The value for the total stellar mass density in the solar neighbourhood is
. The value for the total stellar mass density in the solar neighbourhood is 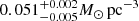 and the local dark matter density was found to be 0.012 ± 0.001 M⊙ pc−3. We obtain a total mass volume density in the solar neighbourhood of
and the local dark matter density was found to be 0.012 ± 0.001 M⊙ pc−3. We obtain a total mass volume density in the solar neighbourhood of 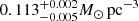 (see Table 4). The value of the radial scale length for the thin disc is obtained with very large uncertainties (e.g.
(see Table 4). The value of the radial scale length for the thin disc is obtained with very large uncertainties (e.g. 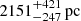 using Stilism). Our results show that the determination of the slope of the IMF at the high mass range (α3) and the inverse of the characteristic time scale of the SFH (γ) is degenerated with the choice of the 3D extinction map. We have obtained a very steep slope of
using Stilism). Our results show that the determination of the slope of the IMF at the high mass range (α3) and the inverse of the characteristic time scale of the SFH (γ) is degenerated with the choice of the 3D extinction map. We have obtained a very steep slope of 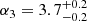 using the Drimmel extinction map and a more common slope
using the Drimmel extinction map and a more common slope 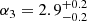 using the Stilism extinction map. However, both results discard a Salpeter (1955) slope at the ∼3σ level. Our result of the α3 at high mass ranges favour values of β greater than 2.0 for the mass function of the clusters (see Fig. 2 in Kroupa & Weidner (2003)). Finally, for the SFH we have obtained
using the Stilism extinction map. However, both results discard a Salpeter (1955) slope at the ∼3σ level. Our result of the α3 at high mass ranges favour values of β greater than 2.0 for the mass function of the clusters (see Fig. 2 in Kroupa & Weidner (2003)). Finally, for the SFH we have obtained 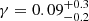 and
and 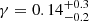 when using the maps of Drimmel and Stilism, respectively. Despite the differences in the shape of the two SFHs that we found, the present rate of star formation that we derived from them is almost identical, being 1.2 ± 0.2 M⊙ yr−1. With the obtained results we have notably improved the fit of the BGM with the solar neighbourhood stellar content. We conclude that the BGM with these new parameters will provide a better tool to simulate new Milky Way surveys.
when using the maps of Drimmel and Stilism, respectively. Despite the differences in the shape of the two SFHs that we found, the present rate of star formation that we derived from them is almost identical, being 1.2 ± 0.2 M⊙ yr−1. With the obtained results we have notably improved the fit of the BGM with the solar neighbourhood stellar content. We conclude that the BGM with these new parameters will provide a better tool to simulate new Milky Way surveys.
BGM FASt framework will also allow us, in the future, to constrain the kinematics, the age-metallicity, and chemo-dynamics, among others. Increasingly complex expressions for the IMF are also possible, such as for example ones including dependencies of the IMF with the metallicity, as done in Jerabkova et al. (2018). Time variation of the thin disc structure can also be introduced as in Amôres et al. (2017). Moreover, BGM FASt can also be used to constrain the SFH (and the age of the thin disc) considering a more flexible, non-parametric distribution. The structure of the BGM FASt code is built in order to work efficiently with the ABC algorithms but it can be used with other techniques, such as for example machine learning tools. Although BGM FASt is designed to work with a BGM simulation, as a Mother Simulation it can be used with simulations from other Galaxy models that can be described with Eq. (28) even assuming different functional forms of the fundamental functions. In this case, Eq. (35) should be used to compute the weights. The next step in this work will be the use of the Gaia data together with a non-parametric SFH in BGM FASt.
To conclude, we want to stress that BGM FASt also constitutes a large technical step in population synthesis galaxy modelling, as for the first time a simulation of the Milky Way is performed using the Apache Hadoop and Apache Spark environments (Zaharia et al. 2012). The appropriate big data platform and the efficient ABC algorithm that we use together with the BGM FASt allow us to address fundamental questions of the Milky Way structure and evolution using extremely large surveys.
We note that the equivalent nomenclature for 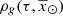 and
and 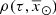 in Czekaj et al. (2014) is
in Czekaj et al. (2014) is 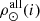 and
and 
In practice we impose that the central mass density and the dark matter density distribution take the values of the Default Model Variant in Mor et al. (2017).
The Marshall et al. (2006) extinction map covers the longitude ranges −100 < l < 100 and the latitude ranges |b|< 10. Therefore, when simulating with the Marshall map we use the Drimmel map for the rest of the sky.
As described in Czekaj et al. (2014) Eq. (1) in each age bin, the mass available to be spent on star production in a given volume element, is the mass reservoir.
We want to emphasise that we use different nomenclature from Snaith et al. (2015).
Acknowledgments
Substantial thanks go to J. Rybizki, the referee, for the constructive report which helped to improve the quality of the work. This work was supported by the MINECO (Spanish Ministry of Economy) – FEDER through grant ESP2014-55996-C2-1-R and MDM-2014-0369 of ICCUB (Unidad de Excelencia “María de Maeztu”), the French Agence Nationale de la Recherche under contract ANR-2010-BLAN-0508-01OTP and the European Community’s Seventh Framework Programme (FP7/2007-2013) under grant agreement GENIUS FP7 – 606740. We also acknowledge Dr. X. Luri and the team of engineers (GaiaUB-ICCUB) in charge of setting up and maintaining the big data platform (GDAF) at University of Barcelona. We also acknowledge E. Jennings for some clarifications about the python package astroABC.
References
- Amôres, E. B., Robin, A. C., & Reylé, C. 2017, A&A, 602, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arenou, F. 2011, in AIP Conf. Ser., eds. J. A. Docobo, V. S. Tamazian, & Y. Y. Balega, 1346, 107 [NASA ADS] [Google Scholar]
- Arenou, F., Luri, X., Babusiaux, C., et al. 2017, A&A, 599, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aumer, M., & Binney, J. J. 2009, MNRAS, 397, 1286 [NASA ADS] [CrossRef] [Google Scholar]
- Awiphan, S., Kerins, E., & Robin, A. C. 2016, MNRAS, 456, 1666 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beaumont, M. A., Cornuet, J.-M., Marin, J.-M., & Robert, C. P. 2009, Biometrika, 96, 983 [CrossRef] [Google Scholar]
- Bertelli, G., Girardi, L., Marigo, P., & Nasi, E. 2008, A&A, 484, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertelli, G., Nasi, E., Girardi, L., & Marigo, P. 2009, A&A, 508, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bienaymé, O., Robin, A. C., & Creze, M. 1987, A&A, 180, 94 [Google Scholar]
- Bienaymé, O., Robin, A. C., & Famaey, B. 2015, A&A, 581, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonnell, I. A., Larson, R. B., & Zinnecker, H. 2007, Protostars and Planets V, 149 [Google Scholar]
- Bovy, J. 2017, MNRAS, 470, 1360 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., & Tremaine, S. 2012, ApJ, 756, 89 [Google Scholar]
- Caldwell, J. A. R., & Ostriker, J. P. 1981, ApJ, 251, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Capitanio, L., Lallement, R., Vergely, J. L., Elyajouri, M., & Monreal-Ibero, A. 2017, A&A, 606, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Catena, R., & Ullio, P. 2010, J. Cosmol. Astropart. Phys., 8, 004 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., & Baraffe, I. 1997, A&A, 327, 1039 [NASA ADS] [Google Scholar]
- Clarke, C. J., & Pringle, J. E. 1992, MNRAS, 255, 423 [NASA ADS] [Google Scholar]
- Czekaj, M. A., Robin, A. C., Figueras, F., Luri, X., & Haywood, M. 2014, A&A, 564, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drimmel, R., & Spergel, D. N. 2001, ApJ, 556, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., & Scalo, J. 2006, ApJ, 636, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Flynn, C., Holmberg, J., Portinari, L., Fuchs, B., & Jahreiß, H. 2006, MNRAS, 372, 1149 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gaia Collaboration, (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girardi, L., Groenewegen, M. A. T., Hatziminaoglou, E., & da Costa, L. 2005, A&A, 436, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M., Robin, A. C., & Creze, M. 1997, A&A, 320, 428 [NASA ADS] [Google Scholar]
- Holmberg, J., & Flynn, C. 2000, MNRAS, 313, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Jennings, E., & Madigan, M. 2017, Astron. Comput., 19, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Jerabkova, T., Zonoozi, A. H., Kroupa, P., et al. 2018, A&A, 620, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juric, M., Cosic, K., Vinkovic, D., & Ivezic, Z. 2010, in Amer. Astron. Soc. Meet. Abstr., #215, BAAS, 42, 222 [Google Scholar]
- Jurić, M., Ivezić, Ž., Brooks, A., et al. 2008, ApJ, 673, 864 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kendall, M. G., & Stuart, A. 1973, The Advanced Theory of Statistics (London: Griffin), 2 [Google Scholar]
- Korchagin, V. I., Girard, T. M., Borkova, T. V., Dinescu, D. I., & van Altena, W. F. 2003, AJ, 126, 2896 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2008, in Pathways Through an Eclectic Universe, eds. J. H. Knapen, T. J. Mahoney, & A. Vazdekis, ASP Conf. Ser., 390, 3 [NASA ADS] [Google Scholar]
- Kroupa, P., & Weidner, C. 2003, ApJ, 598, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Weidner, C., Pflamm-Altenburg, J., et al. 2013, in The Stellar and Sub-Stellar Initial Mass Function of Simple and Composite Populations, eds. T. D. Oswalt, & G. Gilmore, 115 [Google Scholar]
- Lagarde, N., Robin, A. C., Reylé, C., & Nasello, G. 2017, A&A, 601, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lallement, R., Capitanio, L., Ruiz-Dern, L., et al. 2018, A&A, 616, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Licquia, T. C., & Newman, J. A. 2015, ApJ, 806, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Loebman, S. R., Ivezić, Ž., Quinn, T. R., et al. 2014, ApJ, 794, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Marin, J.-M., Pudlo, P., Robert, C. P., & Ryder, R. 2011, ArXiv e-prints [arXiv:1101.0955] [Google Scholar]
- Marjoram, P., Molitor, J., Plagnol, V., & Tavaré, S. 2003, Proc. Nat. Acad. Sci., 100, 15324 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, D. J., Robin, A. C., Reylé, C., Schultheis, M., & Picaud, S. 2006, A&A, 453, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massey, P. 1998, in The Stellar Initial Mass Function (38th Herstmonceux Conference), eds. G. Gilmore, & D. Howell, ASP Conf. Ser., 142, 17 [NASA ADS] [Google Scholar]
- McKee, C. F., Parravano, A., & Hollenbach, D. J. 2015, ApJ, 814, 13 [NASA ADS] [CrossRef] [Google Scholar]
- McMillan, P. J. 2011, MNRAS, 414, 2446 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, G. E., & Scalo, J. M. 1979, ApJS, 41, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Mor, R., Robin, A. C., Figueras, F., & Lemasle, B. 2017, A&A, 599, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pasetto, S., Chiosi, C., & Kawata, D. 2012, A&A, 545, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pasetto, S., Natale, G., Kawata, D., et al. 2016, MNRAS, 461, 2383 [NASA ADS] [CrossRef] [Google Scholar]
- Pflamm-Altenburg, J., & Kroupa, P. 2006, MNRAS, 373, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, I. N., Gizis, J. E., & Hawley, S. L. 2002, AJ, 124, 2721 [NASA ADS] [CrossRef] [Google Scholar]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robin, A. C., Marshall, D. J., Schultheis, M., & Reylé, C. 2012, A&A, 538, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robin, A. C., Reylé, C., Fliri, J., et al. 2014, A&A, 569, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robin, A. C., Bienaymé, O., Fernández-Trincado, J. G., & Reylé, C. 2017, A&A, 605, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robitaille, T. P., & Whitney, B. A. 2010, ApJ, 710, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Rybizki, J., & Just, A. 2015, MNRAS, 447, 3880 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Salucci, P., Nesti, F., Gentile, G., & Frigerio Martins, C. 2010, A&A, 523, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scalo, J. M. 1986, Fund. Cosmic Phys., 11, 1 [NASA ADS] [EDP Sciences] [Google Scholar]
- Sharma, S., Bland-Hawthorn, J., Johnston, K. V., & Binney, J. 2011, ApJ, 730, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Simion, I. T., Belokurov, V., Irwin, M., et al. 2017, MNRAS, 471, 4323 [NASA ADS] [CrossRef] [Google Scholar]
- Sisson, S., & Fan, Y. 2010, ArXiv e-prints [arXiv:1001.2058] [Google Scholar]
- Snaith, O., Haywood, M., Di Matteo, P., et al. 2015, A&A, 578, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sofue, Y. 2015, PASJ, 67, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Tapiador, D., Berihuete, A., Sarro, L. M., Julbe, F., & Huedo, E. 2017, Astron. Comput., 19, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Tinsley, B. M. 1980, Fund. Cosmic Phys., 5, 287 [Google Scholar]
- van Leeuwen, F., ed. 2007, in Hipparcos, the New Reduction of the Raw Data, Astrophysics and Space Science Library, 350 [Google Scholar]
- Zaharia, M., Chowdhury, M., Das, T., et al. 2012, in Presented as part of the 9th USENIX Symposium on Networked Systems Design and Implementation (NSDI 12) (San Jose (USENIX): CA), 15 [Google Scholar]
Appendix A: Testing BGM FASt vs. Std simulations
In this appendix we aim to present the detailed figures of the tests BGM FASt versus BGM Std reported in Sect. 6 when comparing the behaviour of colour, mass, and age distributions. Additionally we provide a comparison of colour, mass, and age distribution between the MP variant (using the combination of the six most probable of the explored parameters) simulated with BGM FASt and the MP variant (defined in Sect. 7.2) simulated using BGM Std.
A.1. Testing the BGM FASt performance
In Figs. A.1–A.3 we present the colour, age, and mass distributions of the tests BGM FASt versus BGM Std presented and discussed in Sect. 6. The age distribution is grouped by age-subpopulation (see Sect. 2.2). Comments on these data are presented in Sect. 6.1.
A.2. Testing the MP variant
To test if the obtained BGM FASt MP variant is equivalent to the BGM Std MP variant we have repeated the tests of Sects. 4.5 and 6.1 for this new variant. We have compared the eccentricities of the Einasto density profiles and the stellar volume mass density at the position of the Sun obtained from both the approximate local dynamical statistical equilibrium used in BGM FASt and the full LDSE used in the standard BGM. We find differences of the eccentricities of the Einasto density profiles always smaller than 1% while we find differences in the stellar volume densities at the position of the Sun smaller than 3%. Additionally we have checked that the difference in the local dark matter density is about 3.5% with negligible effects on the rotation curve as demonstrated in Sect. 4.5. These differences are inside the margins reported in Sect. 4.5.
In Fig. A.4 we present the colour, age, and mass distribution of the MP variant using the Drimmel & Spergel (2001) extinction map. The age distribution is grouped by age-subpopulation (see Sect. 2.2). From Sect. 6 we conclude that differences between BGM FASt and BGM Std are usually below 5%. Therefore, the error bars in the plots are set to be 5% of the star counts in the bin to visualise that the differences are smaller. We note that within the error bars both distributions match each other very well, demonstrating that BGM FASt provides a good approximation to the BGM standard for the best model variant fitting Tycho-2 data.
 |
Fig. A.1. Colour distribution,(B − V)T, for the BGM FASt vs. BGM Std tests presented in Table 2. All the plotted simulations use the Drimmel & Spergel (2001) extinction map. The dotted blue line is for the Mother Simulation (DAV variant for the first column and DCV variant for the second column). The thin green line and the thick red line signify BGM Std and BGM FASt simulations, respectively. |
 |
Fig. A.2. Age sub-population distribution for the BGM FASt vs. BGM Std tests presented in Table 2. All the plotted simulations use the Drimmel & Spergel (2001) extinction map. The blue dotted line is for the Mother Simulation (DAV variant for the first column and DCV variant for the second column). The thin green line and the thick red line signify BGM Std and BGM FASt simulations, respectively. The error bars are set to be 5% of the stars in the bin to visualise if the differences are below or above it. |
 |
Fig. A.3. Mass distribution for the BGM FASt vs. BGM Std tests presented in Table 2. All the plotted simulations use Drimmel & Spergel (2001) extinction map. The dotted blue line is for the Mother Simulation (DAV variant for the first column and DCV variant for the second column). The thin green line and the thick red line signify BGM Std and BGM FASt simulations, respectively. The error bars are set to be 5% of the stars in the bin to visualise if the differences are below or above it. |
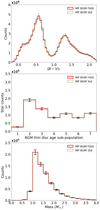 |
Fig. A.4. Top panel: (B − V)T distribution. Middle panel: star counts for each of the seven age sub-populations of the thin disc assumed in the BGM. Bottom panel: mass distribution. The simulations are done using the combination of the six most probable parameters (MP variant) with the Drimmel & Spergel (2001) extinction map; in red the simulation is done with BGM FASt while in black it is done with BGM Std. The error bars are set to be 5% of the stars in the bin to visualise that the differences between BGM FASt and BGM Std are below it. The simulations are samples limited in visual apparent magnitude VT < 11 and photometric errors are not considered. |
Appendix B: Evaluating the sampling noise in BGM
B.1. Sampling noise in BGM Standard
In this section we analyse the star-generation strategy of BGM Std to demonstrate that the discrepancies larger than 5% that we find occasionally when comparing BGM FASt and BGM Std (see Sect. 6 and Appendix A) can be explained by the sampling noise for very-low-mass reservoirs in BGM Std.
As described in Eq. (1) of Czekaj et al. (2014), for each thin-disc age sub-population the mass available to be spent on star production in a given volume element is quoted as the mass reservoir.
In Fig. B.1 we present, for the youngest sub-population of the thin disc component in BGM and for masses bigger than 1.53 M⊙, the relative differences in star counts per mass bin between the sampled stars and the stars predicted by the imposed distribution function 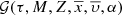 along 104 realisations. We expect that the Poisson distribution describes the distribution of the number of sampled stars of a given interval (e.g. mass or age) along the 104 realisations. The red boxes in the figure represent the relative differences between the sampled stars and the stars predicted by
along 104 realisations. We expect that the Poisson distribution describes the distribution of the number of sampled stars of a given interval (e.g. mass or age) along the 104 realisations. The red boxes in the figure represent the relative differences between the sampled stars and the stars predicted by 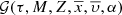 if the sampling distribution would follow exactly a Poisson distribution centred on the predicted theoretical value. The black boxes are the relative differences in star counts per mass bin between the stars generated by BGM Std and the stars predicted by the imposed
if the sampling distribution would follow exactly a Poisson distribution centred on the predicted theoretical value. The black boxes are the relative differences in star counts per mass bin between the stars generated by BGM Std and the stars predicted by the imposed 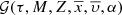 along 104 realisations. In the left panel we show the result for a mass reservoir of 104 M⊙ for a Salpeter IMF while in the middle and right panels we show the results for a mass reservoir of 150 M⊙ for a Salpeter IMF (middle) and Kroupa-like IMF (right). We note that for the mass reservoir of 104 M⊙ the BGM standard generation behaves as expected and approximately follows the Poisson distribution. We detect small discrepancies with the Poisson distribution that are caused by the fact that the mass in the mass reservoir runs out. It is important to notice that the mean value of the distribution coincides with the expected theoretical value, differing from each other by less than 0.01%. Regarding the middle panel (Salpeter IMF), we note that for the first three mass bins the noise is not Poissonian (red boxes are for Poisson distribution centred in the predicted value) and is clearly biased towards higher values, thus producing and oversampling the stars with masses 1.53 M⊙ < M < 4.5 M⊙; the grey shadow emphasises this bias towards higher values. In the right plot (Kroupa-like IMF) we note that the deviation from the Poisson noise is much smaller, marginally affecting the distribution.
along 104 realisations. In the left panel we show the result for a mass reservoir of 104 M⊙ for a Salpeter IMF while in the middle and right panels we show the results for a mass reservoir of 150 M⊙ for a Salpeter IMF (middle) and Kroupa-like IMF (right). We note that for the mass reservoir of 104 M⊙ the BGM standard generation behaves as expected and approximately follows the Poisson distribution. We detect small discrepancies with the Poisson distribution that are caused by the fact that the mass in the mass reservoir runs out. It is important to notice that the mean value of the distribution coincides with the expected theoretical value, differing from each other by less than 0.01%. Regarding the middle panel (Salpeter IMF), we note that for the first three mass bins the noise is not Poissonian (red boxes are for Poisson distribution centred in the predicted value) and is clearly biased towards higher values, thus producing and oversampling the stars with masses 1.53 M⊙ < M < 4.5 M⊙; the grey shadow emphasises this bias towards higher values. In the right plot (Kroupa-like IMF) we note that the deviation from the Poisson noise is much smaller, marginally affecting the distribution.
We can conclude that when the mass reservoir is large enough (M > 104 M⊙), we can consider as a first approximation that the probability of an occurrence of a star generation event is not affecting the probability of the occurrence of the following star generation event (necessary condition for a Poisson distribution). The results therefore approximately follow a Poisson distribution. When the mass reservoir is small (e.g. M < 500 M⊙) the approximation that the probability of the occurrence of two star generation events is conditionally independent is no longer valid and as a consequence the obtained distribution is slightly biased and does not follow the Poisson distribution.
We have performed the test for all populations and masses. We only find remarkable effects for the youngest population and for masses larger than M > 1.53 M⊙ when the slope of the IMF in the high mass range is flat. It is important to emphasise that we roughly estimate that only about 10% of the stars in the samples that we use in this paper (up to VT = 11) are generated in mass reservoirs small enough to be affected by the effects discussed in this appendix.
 |
Fig. B.1. Left panel: behaviour of the noise in BGM Std when the mass reservoir is large. This behaviour is obtained by reproducing a full star generation process of a mass reservoir of 104 M⊙ for the youngest age sub-population 104 times. The limits of the boxes show the position of the first and the third quartile. The limits of the bars show the position of −1.5 ⋅ IQR and +1.5 ⋅ IQR, where IQR is the interquartile range. Everything beyond the limits of the bar is considered an outlier. In black we show the relative differences in star counts between the expected number of stars in a given mass bin and the number of stars obtained with the standard BGM generation strategy. The red boxes show what these relative differences would be if the generation were to precisely follow a Poisson distribution centred in the expected value. The noise behaves approximately as a Poisson distribution, as expected. Middle and right panels: behaviour of the noise in BGM Std when the mass reservoir is small. This is obtained by by reproducing a full star generation process of a mass reservoir of 150 M⊙ for the youngest age sub-population 104 times. This small mass reservoir only appears occasionally. The middle panel is for very flat slopes of the IMF at high mass range (in this case α3 = 2.35). The right panel is for an IMF slope of α3 = 3.2 closer to the best slopes fitting the data. In black we show the relative differences in star counts between the expected number of stars in a given mass bin and the number of stars obtained with the standard BGM generation strategy. The red boxes show what these relative differences would be if the generation were to precisely follow a Poisson distribution centred in the expected value. The grey shadow emphasises the differences between the distribution obtained with BGM Std and the one that would follow exactly a Poisson distribution. We note that the effect is very small for the right panel. We show the results only for masses up to 5.5 M⊙ as about 99% of the stars in the simulated samples (limited at VT = 11) have masses smaller than 5.5 M⊙. |
The discrepancies bigger than 5% found in colour, mass, and age distributions (Figs. A.1–A.3) between BGM FASt and BGM Std simulations that we reported in Sect. 6 can be explained by the non-Poissonian sampling noise that we found in BGM Std for the youngest sub-populations at the high mass range when the mass reservoir is small. The comparisons in Sect. 4.5 of the densities in a sphere around the Sun are only minorly affected by this as BGM Std, when working in the sphere mode, has very large mass reservoirs to generate the stars at the position of the Sun. It is important to note that the non-Poissonian noise has a minor effect on the BGM simulations that better fit the thin disc at the solar neighbourhood. Work is in progress to further diminish the effects of the noise in the small mass reservoirs.
B.2. Weighting the sampling noise in BGM FASt
The BGM Std simulation that we use as a Mother Simulation is a random realisation of an imposed distribution function for the generated stars in the Galaxy (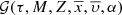 ). As a consequence when we weight the stars in BGM FASt strategy we also weight the noise. This implies, as we demonstrate in this appendix, that the noise in a BGM FASt simulation is approximately a factor
). As a consequence when we weight the stars in BGM FASt strategy we also weight the noise. This implies, as we demonstrate in this appendix, that the noise in a BGM FASt simulation is approximately a factor  of the noise in the Mother Simulation (where
of the noise in the Mother Simulation (where  is the mean weight applied to the Mother Simulation).
is the mean weight applied to the Mother Simulation).
 |
Fig. B.2. Distribution of weights applied to the Mother Simulation to obtain the MP variant when using the Drimmel & Spergel (2001) extinction map. The vertical dashed lines indicate the 0.16 and 0.84 quantiles. |
If we perform n realizations of a BGM Std simulation with an imposed 𝒢, the distribution of the number of stars Xi in a given interval of a given parameter, along the n realisations, can be approximated by a Poisson distribution. If the number of stars is large enough, the Poisson distribution can be approximated by a Gaussian distribution with μ = E[Xi] and σ2 = E[Xi], where E[Xi] is the expected number of stars in the interval given by the imposed distribution function of the generated stars in the Galaxy (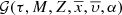 ). We discuss below which is, for n realisations of a BGM FASt simulation, the distribution of the number of stars Xi in a given interval of a given parameter. We start from a Mother Simulation with an imposed distribution function 𝒢MSt such as that in a given interval
). We discuss below which is, for n realisations of a BGM FASt simulation, the distribution of the number of stars Xi in a given interval of a given parameter. We start from a Mother Simulation with an imposed distribution function 𝒢MSt such as that in a given interval ![$ E\left[ {X_i^{{\rm{MSt}}}} \right] = {N_{\rm{MSt}}}\ $](/articles/aa/full_html/2018/12/aa33501-18/aa33501-18-eq214.gif) , where NMSt is the expected number of stars. Performing n realisations, we obtain, as discussed above, an approximately Gaussian distribution with
, where NMSt is the expected number of stars. Performing n realisations, we obtain, as discussed above, an approximately Gaussian distribution with ![$ {\mu _{{\rm{MSt}}}} = E\left[ {X_i^{{\rm{MSt}}}} \right] = {N_{{\rm{MSt}}}}\ $](/articles/aa/full_html/2018/12/aa33501-18/aa33501-18-eq215.gif) and
and ![$ \sigma _{_{{\rm{MSt}}}}^2 = E\left[ {X_i^{{\rm{MSt}}}} \right] = {N_{{\rm{MSt}}}}\ $](/articles/aa/full_html/2018/12/aa33501-18/aa33501-18-eq216.gif) . The sample mean, for a given interval, of the n realisations of the Mother Simulation is known to be an unbiased estimator for μ, and is computed as follows
. The sample mean, for a given interval, of the n realisations of the Mother Simulation is known to be an unbiased estimator for μ, and is computed as follows
The sample variance of the n realisations is known to be an unbiased estimator for σ2, and is computed as follows
Next, we build n realisations of a BGM FASt simulation with an imposed distribution function, 𝒢FASt, applying the pertinent weights wi to the stars of the n realisations of the Mother Simulation. We assume here that the mean weight applied to a given interval of a given parameter is approximately the same for the n realisations, that is 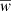 . The expected number of stars in the interval for the BGM FASt is therefore
. The expected number of stars in the interval for the BGM FASt is therefore ![$ E[X_i]=\overline{w} \cdot N_{\mathrm{MSt}} $](/articles/aa/full_html/2018/12/aa33501-18/aa33501-18-eq220.gif) . If the distribution were Poissonian we would expect, as discussed above, a Gaussian with
. If the distribution were Poissonian we would expect, as discussed above, a Gaussian with 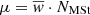 and
and 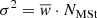 . As the n realisations of the BGM FASt are built from the n realisations of the Mother Simulation then we can write
. As the n realisations of the BGM FASt are built from the n realisations of the Mother Simulation then we can write 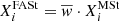 and the sample mean
and the sample mean 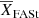 as follows
as follows
For n → ∞ we can write 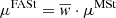 and that is exactly the expected value of stars in the given range for BGM FASt as mentioned above,
and that is exactly the expected value of stars in the given range for BGM FASt as mentioned above, ![$ E[X^{\mathrm{FASt}}_i]=\overline{w} \cdot N_{\mathrm{MSt}} $](/articles/aa/full_html/2018/12/aa33501-18/aa33501-18-eq227.gif) .
.
Now if we compute the sample variance:
for n → ∞ we can write 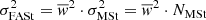 but we note that the variance for the Poisson distribution with
but we note that the variance for the Poisson distribution with ![$ E[X_i]=\overline{w} \cdot N_{\mathrm{MSt}} $](/articles/aa/full_html/2018/12/aa33501-18/aa33501-18-eq231.gif) would be
would be 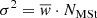 . As a consequence, the noise in BGM FASt simulation is a factor
. As a consequence, the noise in BGM FASt simulation is a factor 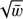 of the noise that a BGM Std simulation would have in its place. Therefore,
of the noise that a BGM Std simulation would have in its place. Therefore, 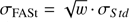 . This effect causes an increase or reduction of the variance proportional to the value of the weight. In the range of the parameter space that we are exploring, the mean values of the weights used go from about 0.8 to about 1.20. In Fig. B.2 we present the distribution of the weights needed to generate the MP variant. Its mean value is 1.023 while the quantiles 0.16 and 0.84 take the values 0.90 and 1.14, respectively. In this case the distribution of the weights is such that the effects discussed in this section are very small, as can be seen in Fig. A.4 when comparing the colour distribution of the MP variant simulated with BGM FASt and BGM Full. If for future studies we need weights much further away from 1 to explain the observational data, it will be necessary to introduce one or more intermediate steps to run BGM Std simulations closer to the data to perform the final parameter exploration.
. This effect causes an increase or reduction of the variance proportional to the value of the weight. In the range of the parameter space that we are exploring, the mean values of the weights used go from about 0.8 to about 1.20. In Fig. B.2 we present the distribution of the weights needed to generate the MP variant. Its mean value is 1.023 while the quantiles 0.16 and 0.84 take the values 0.90 and 1.14, respectively. In this case the distribution of the weights is such that the effects discussed in this section are very small, as can be seen in Fig. A.4 when comparing the colour distribution of the MP variant simulated with BGM FASt and BGM Full. If for future studies we need weights much further away from 1 to explain the observational data, it will be necessary to introduce one or more intermediate steps to run BGM Std simulations closer to the data to perform the final parameter exploration.
All Tables
Parameters for the SFH, the IMF and the density laws of the seven model variants adopted from Mor et al. (2017).
Summary of the results of the BGM FASt vs. BGM Std tests and the parameters for the SFH, the IMF, and the density laws of the model variants.
Lower and upper limits of the imposed initial uniform Prior PDF for each of the explored parameters.
All Figures
 |
Fig. 1. Two examples of the comparison between the rotation curve obtained with both the full process to ensure LDSE and the rotation curve obtained with the approximate LDSE. Top panel: results for the DAV variant from Mor et al. (2017). Bottom panel: results for the HRBV variant from Mor et al. (2017). The green triangles show the data points derived from the Caldwell & Ostriker (1981) rotation curve assuming R0 = 8000 pc and V0 = 230 km s−1 for the Sun. The magenta triangles show the data points of the rotation curve from Sofue (2015). For Sofue data, error bars are provided by the author, while we have estimated the errors of the data from Caldwell & Ostriker (1981) following the expressions and tables in their paper. |
| In the text | |
 |
Fig. 2. Probability distribution function for the inverse of the characteristic time scale (γ parameter) of the thin disc SFH, assuming a decreasing exponential shape. The right vertical blue dotted line indicates the γ value of the Mother Simulation used in the test. The left black dotted vertical line (γ = 0) indicates the value to be recovered by the test. In green we show the prior PDF assumed for the test (uniform distribution between −0.05 and 0.20). In red we show the resulting approximate posterior PDF P(γ|data). |
| In the text | |
 |
Fig. 3. P(γ|data) (in green) Approximate posterior PDF for the γ parameter resulting from case A, given the adopted prior (see text). The vertical red dotted line indicates the mode of the distribution γ = 0.13 with an uncertainty in the range indicated by the two black vertical lines corresponding to the quantiles 0.16 and 0.84, respectively ( |
| In the text | |
 |
Fig. 4. P(Model|data): approximate posterior PDF for the variants (see Table 2) given the adopted prior (see text). We obtain these results when using as observational data the stars in Tycho-2 catalogue with visual apparent magnitude VT < 11. Variants whose names end with “-D” use the extinction maps from Drimmel & Spergel (2001) while names ending with “-M” use those from Marshall et al. (2006). With a dotted blue line we show the adopted prior PDF. |
| In the text | |
 |
Fig. 5. This plot is built from the results of Case A shown in Figs. 6 and 7. Each point in the plot represents a set of parameters accepted by the ABC algorithm as part of the posterior PDF. For each accepted set we plot the Poissonian distance (δP) as a function of the inverse of the characteristic timescale (γ parameter) of an assumed decreasing exponential SFH. δP is computed using the expression of Eq. (58); the smaller the value of δP, the better its agreement with the data. Dotted horizontal line gives the δP value around the best fit (δP ≈ 16 000) and the solid horizontal line is to emphasise the degeneracy for three different sets of parameters of the model variants (see Table 2). The vertical dashed black lines denote the quantile 0.16 (left) and quantile 0.84 (right) for the distribution of Fig. 3. The vertical red dashed line is for the mode of the γ distribution in Fig. 3. We obtain these results when using as observational data the stars in the Tycho-2 catalogue with visual apparent magnitude VT < 11. Variant/extinction map combinations are as described in Fig. 4. |
| In the text | |
 |
Fig. 6. Corner plot with the projection of the approximate posterior PDF obtained from the exploration of the six parameters of the thin disc component, including the IMF, the SFH, and the density laws. The vertical solid red lines and the vertical green dashed lines indicate the mode and the median for each parameter, respectively. For α3, the median and the mode are superimposed. Green 2D contours and 1D distributions are for the distributions obtained directly from the ABC algorithm. The blue 1D posterior PDFs are built by accounting, in the posterior PDF, for the differences between BGM Std and BGM full simulations (see text). The vertical black dashed lines indicate the quantiles 0.16 and 0.84 of this distribution. On top of each 1D histogram the mode of the distribution and the interval of the 0.16 and 0.84 quantiles for the blue distributions are indicated. In black at the top right of each one of the 2D panels we show the Pearson’s correlation coefficient. The magenta cross indicates the parameters of the adopted Mother Simulation. γ is the inverse of the characteristic timescale when assuming an exponentially decreasing SFH. α1, α2 and α3 are the slopes of the IMF assumed to be a three-times truncated power law with the mass limits fixed at x1 = 0.5 M⊙ and x2 = 1.53 M⊙. ρ⊙ is the thin disc stellar volume mass density at the position of the Sun and hR is the radial scale length of the thin-disc density profile assumed to be an Einasto shape (see units in Table 1). We obtain these results assuming the Drimmel & Spergel (2001) extinction map and using as observational data the stars in Tycho-2 catalogue with visual apparent magnitude VT < 11. |
| In the text | |
 |
Fig. 7. As in Fig. 6 but using the Stilism extinction map. |
| In the text | |
 |
Fig. 8. Colour-magnitude diagram ( apparent visual magnitude Tycho (VT) vs. Tycho (B − V)T colour) divided into three latitude ranges: first row: |b|< 10, second row: 10 < |b|< 30 third row: 30 < |b|< 90 and for the whole sky (bottom row). The colour-map of the first, second, and third columns shows the logarithm of the star counts in each bin. First column: Tycho-2 data, second column: best-fit model variant from Mor et al. (2017) (DAV) obtained using Galactic classical Cepheid and Tycho-2 data, and third column: MP variant combination of the most probable value for six parameters explored in Sect. 7.2. The BGM simulations performed for this figure use the Drimmel extinction map. The colour map of the fourth and fifth rows represents the Poissonian distance computed for each bin. The total distance indicated in each plot is the Poissonian distance (δP) computed using Eq. 58. The smaller the value of δP, the better the agreement. fourth column: Poissonian distance between DAV and Tycho-2, and fifth column: Poissonian distance between MP and Tycho-2. Observational data and simulations are samples limited in visual apparent magnitude considering the stars with VT < 11. |
| In the text | |
 |
Fig. 9. Colour distribution of MP variant and Tycho-2 with a limit in magnitude of VT = 11. Our Bayesian approach allows us to compute the error bars (dotted blue) from the simulations computed using the parameters inside the 1σ level of the posterior PDFs shown in Fig. 6. |
| In the text | |
 |
Fig. A.1. Colour distribution,(B − V)T, for the BGM FASt vs. BGM Std tests presented in Table 2. All the plotted simulations use the Drimmel & Spergel (2001) extinction map. The dotted blue line is for the Mother Simulation (DAV variant for the first column and DCV variant for the second column). The thin green line and the thick red line signify BGM Std and BGM FASt simulations, respectively. |
| In the text | |
 |
Fig. A.2. Age sub-population distribution for the BGM FASt vs. BGM Std tests presented in Table 2. All the plotted simulations use the Drimmel & Spergel (2001) extinction map. The blue dotted line is for the Mother Simulation (DAV variant for the first column and DCV variant for the second column). The thin green line and the thick red line signify BGM Std and BGM FASt simulations, respectively. The error bars are set to be 5% of the stars in the bin to visualise if the differences are below or above it. |
| In the text | |
 |
Fig. A.3. Mass distribution for the BGM FASt vs. BGM Std tests presented in Table 2. All the plotted simulations use Drimmel & Spergel (2001) extinction map. The dotted blue line is for the Mother Simulation (DAV variant for the first column and DCV variant for the second column). The thin green line and the thick red line signify BGM Std and BGM FASt simulations, respectively. The error bars are set to be 5% of the stars in the bin to visualise if the differences are below or above it. |
| In the text | |
 |
Fig. A.4. Top panel: (B − V)T distribution. Middle panel: star counts for each of the seven age sub-populations of the thin disc assumed in the BGM. Bottom panel: mass distribution. The simulations are done using the combination of the six most probable parameters (MP variant) with the Drimmel & Spergel (2001) extinction map; in red the simulation is done with BGM FASt while in black it is done with BGM Std. The error bars are set to be 5% of the stars in the bin to visualise that the differences between BGM FASt and BGM Std are below it. The simulations are samples limited in visual apparent magnitude VT < 11 and photometric errors are not considered. |
| In the text | |
 |
Fig. B.1. Left panel: behaviour of the noise in BGM Std when the mass reservoir is large. This behaviour is obtained by reproducing a full star generation process of a mass reservoir of 104 M⊙ for the youngest age sub-population 104 times. The limits of the boxes show the position of the first and the third quartile. The limits of the bars show the position of −1.5 ⋅ IQR and +1.5 ⋅ IQR, where IQR is the interquartile range. Everything beyond the limits of the bar is considered an outlier. In black we show the relative differences in star counts between the expected number of stars in a given mass bin and the number of stars obtained with the standard BGM generation strategy. The red boxes show what these relative differences would be if the generation were to precisely follow a Poisson distribution centred in the expected value. The noise behaves approximately as a Poisson distribution, as expected. Middle and right panels: behaviour of the noise in BGM Std when the mass reservoir is small. This is obtained by by reproducing a full star generation process of a mass reservoir of 150 M⊙ for the youngest age sub-population 104 times. This small mass reservoir only appears occasionally. The middle panel is for very flat slopes of the IMF at high mass range (in this case α3 = 2.35). The right panel is for an IMF slope of α3 = 3.2 closer to the best slopes fitting the data. In black we show the relative differences in star counts between the expected number of stars in a given mass bin and the number of stars obtained with the standard BGM generation strategy. The red boxes show what these relative differences would be if the generation were to precisely follow a Poisson distribution centred in the expected value. The grey shadow emphasises the differences between the distribution obtained with BGM Std and the one that would follow exactly a Poisson distribution. We note that the effect is very small for the right panel. We show the results only for masses up to 5.5 M⊙ as about 99% of the stars in the simulated samples (limited at VT = 11) have masses smaller than 5.5 M⊙. |
| In the text | |
 |
Fig. B.2. Distribution of weights applied to the Mother Simulation to obtain the MP variant when using the Drimmel & Spergel (2001) extinction map. The vertical dashed lines indicate the 0.16 and 0.84 quantiles. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



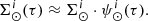
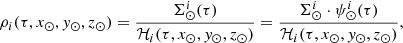
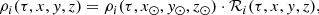
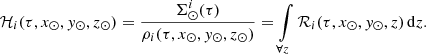
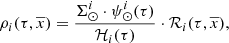
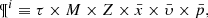
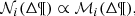
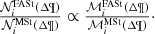
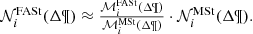
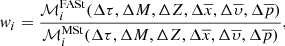
![$$ \begin{array}{*{20}{c}}{{{\rm{\P}}^i} \equiv \tau \times M \times Z \times \bar x \times \bar \upsilon \times \bar p = \tau \times M \times Z \times \bar x \times \bar \upsilon \times [\alpha /{\rm{Fe}}] \times \overline {{p^\prime }} .}\end{array} $$](/articles/aa/full_html/2018/12/aa33501-18/aa33501-18-eq30.gif)
![$$ \begin{array}{*{20}{c}}{{{\cal G}_i}(\tau ,M,Z,\bar x,\bar \upsilon ,[\alpha /{\rm{Fe}}]) = \mathop \int \limits_{\forall \overline {{p^\prime }} \in {{\rm{\P}}^i},} {{\cal D}_i}(\tau ,M,Z,\bar x,\bar \upsilon ,[\alpha /{\rm{Fe}}],\overline {{p^\prime }})\,{\rm{d}}\overline {{p^\prime }} ,}\end{array} $$](/articles/aa/full_html/2018/12/aa33501-18/aa33501-18-eq32.gif)
![$$ \begin{array}{*{20}{c}}{{\rm{\P}}_r^i \equiv \tau \times M \times Z \times \bar x \times \bar \upsilon \times [\alpha /{\rm{Fe}}].}\end{array} $$](/articles/aa/full_html/2018/12/aa33501-18/aa33501-18-eq34.gif)