| Issue |
A&A
Volume 617, September 2018
|
|
|---|---|---|
| Article Number | A136 | |
| Number of page(s) | 16 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201732157 | |
| Published online | 02 October 2018 | |
Reliable detection and characterization of low-frequency polarized sources in the LOFAR M51 field⋆
1
Department of Space, Earth and Environment, Chalmers University of Technology, Onsala Space Observatory, 439 92 Onsala, Sweden
e-mail: cathy.horellou@chalmers.se
2
Jodrell Bank Centre for Astrophysics, Alan Turing Building, School of Physics and Astronomy, The University of Manchester, Oxford Road, Manchester M13 9PL, UK
3
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
4
Astronomical Observatory, Jagiellonian University, ul. Orla 171, 30-244 Kraków, Poland
5
Department of Astrophysics/IMAPP, Radboud University, PO Box 9010, 6500 GL Nijmegen, The Netherlands
6
School of Mathematics and Statistics, Newcastle University, Newcastle upon Tyne NE1 7RU, UK
7
CSIRO Astronomy and Space Science, 26 Dick Perry Ave, Kensington, WA 6151, Australia
8
INAF – Osservatorio di Radioastronomia, Via P. Gobetti 101, 40129 Bologna, Italy
9
Kapteyn Astronomical Institute, University of Groningen, Postbus 800, 9700 AV Groningen, The Netherlands
Received:
23
October
2017
Accepted:
12
June
2018
Context. The new generation of broad-band radio continuum surveys will provide large data sets with polarization information. New algorithms need to be developed to extract reliable catalogs of linearly polarized sources that can be used to characterize those sources and produce a dense rotation measure (RM) grid to probe magneto-ionized structures along the line of sight via Faraday rotation.
Aims. The aim of the paper is to develop a computationally efficient and rigorously defined source-finding algorithm for linearly polarized sources.
Methods. We used a calibrated data set from the LOw Frequency ARray (LOFAR) at 150 MHz centered on the nearby galaxy M 51 to search for polarized background sources. With a new imaging software, we re-imaged the field at a resolution of 18″ × 15″ and cataloged a total of about 3000 continuum sources within 2.5° of the center of M 51. We made small Stokes Q and U images centered on each source brighter than 100 mJy in total intensity (201 sources) and used RM synthesis to create corresponding Faraday cubes that were analyzed individually. For each source, the noise distribution function was determined from a subset of the measurements at high Faraday depths where no polarization is expected; the peaks in polarized intensity in the Faraday spectrum were identified and the p-value of each source was calculated. Finally, the false discovery rate method was applied to the list of p-values to produce a list of polarized sources and quantify the reliability of the detections. We also analyzed sources fainter than 100 mJy but that were reported as polarized in the literature at at least another radio frequency.
Results. Of the 201 sources that were searched for polarization, six polarized sources were detected confidently (with a false discovery rate of 5%). This corresponds to a number density of one polarized source per 3.3 square degrees, or 0.3 source per square degree. Increasing the false discovery rate to 50% yields 19 sources. A majority of the sources have a morphology that is indicative of them being double-lobed radio galaxies, and the ones with literature redshift measurements have 0.5 < z < 1.0.
Conclusions. We find that this method is effective in identifying polarized sources, and is well suited for LOFAR observations. In the future, we intend to develop it further and apply it to larger data sets such as the LOFAR Two-meter Survey of the whole northern sky, LOTSS, and the ongoing deep LOFAR observations of the GOODS-North field.
Key words: polarization / radio continuum: galaxies / galaxies: magnetic fields / galaxies: individual: M51 / methods: data analysis / techniques: polarimetric
The FITS file of the LOFAR 150 MHz image shown in Fig. 1, the catalog of 201 radio sources, and 19 Faraday cubes are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/vizbin/qcat?J/A+A/617/A136
© ESO 2018
1. Introduction
One of the science drivers of the future Square Kilometre Array (SKA) is to produce a dense grid of polarized radio sources that could be used as background lights to probe magnetized media along their lines of sight in structures of various scales (e.g. Beck & Gaensler 2004; Gaensler et al. 2015; Johnston-Hollitt et al. 2015; Vacca et al. 2016). The key effect is Faraday rotation, a birefrigence effect that causes the polarization angle of the linearly polarized wave emitted by a source to rotate as it propagates through a magneto-ionized medium:
where χ is the polarization angle measured at the wavelength of observation, λ, χ0 is the polarization angle of the emitted wave, and RM is the rotation measure. In the simple case when Faraday rotation occurs in a non-emitting foreground medium, the value of RM is equal to that of the Faraday depth of the source, ϕ(L), where L is the entire pathlength to the source and ϕ(r) is a physical quantity which is proportional to the integral along the line of sight, ℓ, of the density of thermal electrons, ne, times the magnetic field component parallel to the line of sight, B∥:
Rotation measures of polarized radio sources have been used to obtain information on magnetic fields in our own galaxy (e.g. Brown & Taylor 2001; Brown et al. 2007), in nearby galaxies (e.g. Han et al. 1998; Gaensler et al. 2005; Kaczmarek et al. 2017), in clusters of galaxies (e.g. Bonafede et al. 2010), and to probe high-redshift absorbers (e.g. Bernet et al. 2013; Farnes et al. 2014). A high number density of background polarized sources is an obvious requirement for such studies (e.g. Stepanov et al. 2008). Observations of a nine-square-degree field centered on the Andromeda galaxy led to the detection of 33 polarized sources at 350 MHz; fractional polarizations and RM’s could be determined for those sources, but a larger catalog would be required to constrain the magnetic field pattern in M31 (Gießübel et al. 2013). The largest RM catalog available so far is based on the NVSS (NRAO VLA Sky Survey, Condon et al. 1998) that covers the entire sky north of −40° declination at 1.4 GHz; it contains about 40 000 sources, one polarized source per square degree (Taylor et al. 2009). A significant unknown is the number density of polarized sources at low flux densities (sub-mJy; Rudnick & Owen 2014) and at low frequencies, where depolarization effects are more significant (e.g. Farnsworth et al. 2011). Much work is ongoing to produce larger catalogs of polarized sources and characterize their properties (e.g. Van Eck et al. 2018).
Following the formalism of Burn (1966), the observed complex polarization  can be expressed as the integral over all Faraday depths of the complex Faraday dispersion function1 ℱ(ϕ), modulated by the Faraday rotation:
can be expressed as the integral over all Faraday depths of the complex Faraday dispersion function1 ℱ(ϕ), modulated by the Faraday rotation:
Equation (3) is a Fourier-transform type relationship that can, in principle, be inverted to obtain ℱ(ϕ):
In practice, ℱ(ϕ) has to be reconstructed from a finite number of measurements at discrete frequencies. The RM synthesis method proposed by Brentjens & de Bruyn (2005) can be implemented efficiently and is commonly used to analyze polarization data, sometimes in combination with direct q(λ2) and u(λ2) fitting (e.g. Mao et al. 2015), where q and u are the Q and U Stokes parameters normalised to the total intensity I at wavelength λ. While RM synthesis is well suited for single (and strong) Faraday depth components, it has difficulty recovering multiple and complex components (e.g. O’Sullivan et al. 2012; Anderson et al. 2015; Schnitzeler 2018) and it has been shown that the uncertainties on the derived RM are not accurate for sources with non-zero spectral indices (Schnitzeler & Lee 2017, 2018). Efficient and reliable source-finding algorithms need to be developed in order to analyze the large amount of data that upcoming radio surveys will deliver. Several packages are available to identify radio continuum sources in total intensity (see Hancock et al. 2012, for a review). For several reasons, those algorithms may not provide correct results when applied to polarization data. One of these reasons is the non-Gaussian nature of the noise in polarized intensity, P: the noise in P follows a Rician distribution in the case of Gaussian noise in Stokes Q and U (with zero mean and same variance). Methods have been developed to correct for the bias introduced by the non-Gaussianity in P (e.g. Wardle & Kronberg 1974; Müller et al. 2017). However, the noise in Q and U may be non-Gaussian, which causes a significant increase in the false detection rates when detection thresholds based on predefined signal-to-noise ratios (S/Ns) are used (George et al. 2012).
Another difficulty is the instrumental polarization that manifests itself as a leakage from Stokes I into Stokes Q and U and contaminates the measurements in the entire frequency band, and in both on-source and off-source regions of the Q and U images. This means that Q- and U-based detection methods (such as the analytic method by Hales et al. 2012) are not directly applicable to LOFAR data and the analysis must be done in Faraday space where the instrumental polarization effects are concentrated to a region near Faraday depth ϕ = 0.
Recently, Farnes et al. (2018) proposed a computationally efficient source-finding algorithm that makes use of so-called Faraday moments (moments of the Q, U, and P distributions: mean, standard deviation, skewness and excess kurtosis). The approach is easy to understand intuitively as a high polarization would produce a high mean in Q and/or U, and a high RM a high standard deviation in Q and U. However, the method provides a source list that, although complete, contains a large number of false detections due to instrumental polarization and needs to be followed up with RM synthesis to eliminate the unreliable sources.
Since the amount of Faraday rotation is proportional to λ2, it is of particular interest to observe at long wavelengths (low frequencies) and over a very broad frequency range to obtain more precise rotation measures. The LOw Frequency ARray (LOFAR; van Haarlem et al. 2013) operates in two frequency ranges: 30–80 MHz with the Low-Band Antennas (LBA) and 120–240 MHz with the HBA. For this work, low-frequency HBA data (up to about 180 MHz) were used as they offer greater and more uniform sensitivity as a function of frequency. Additionally, the process of data calibration is facilitated due to both the higher sensitivity and the fact that ionospheric effects are less severe in the higher band. LOFAR is equipped with receivers and correlators that allow observations across a large instantaneous bandwidth with a great number of frequency channels. This new instrumentation results in a significant boost in sensitivity. In addition, the large field of view of LOFAR makes it an efficient survey instrument (e.g. Heald et al. 2015; Shimwell et al. 2017).
Polarization work with LOFAR has been very challenging so far because of ionospheric Faraday rotation (Sotomayor-Beltran et al. 2013), instrumental polarization, uncertainty in the primary beam model, and the generally strong Faraday depolarization at low frequencies (e.g. Sokoloff et al. 1998, 1999). Calibration and imaging at high resolution (≤1′) is hard at low frequencies, and so beam depolarization can often be a limitation. Despite these difficulties, polarization studies are now becoming possible as the nature of the data and the characteristics of the instrument become better understood. This is also important for investigations of the epoch of reionization (EoR), since polarization leakage may mimic an EoR signal (Asad et al. 2016).
Diffuse Galactic foreground polarization has been detected by LOFAR in deep fields (the ELAIS N1 field, Jelić et al. 2014; the 3C 196 field, Jelić et al. 2015), and in the Galactic foreground of the nearby galaxy IC 342 (Van Eck et al. 2017). The MurchisonWidefield Array (MWA) also detects diffuse Galactic polarization with better sensitivity to the largest scale emission (Lenc et al. 2016), but relatively few extragalactic sources so far in polarization (Bernardi et al. 2013; Lenc et al. 2017). LOFAR provides higher angular resolution and sensitivity and thereby the potential to probe the fainter source population. Polarization was detected in the lobe of a radio galaxy (Orrù et al. 2015). No diffuse polarization was found toward the nearby spiral galaxy M51, but six background polarized sources were detected in the M51 field (Mulcahy et al. 2014). Farnes et al. (2018) applied their Faraday moments method to the LOFAR data of theM51 field. Recently, Van Eck et al. (2018) developed a pipeline to search for polarization in regions of the sky covered by the LOFAR Two-Meter Sky Survey (LOTSS; Shimwell et al. 2017). This work resulted in a catalog of 92 polarized sources at 150MHz in an area of 570 square degrees, corresponding to a density of one source per 6.2 square degrees. The data were imaged at low angular resolution (40) and were strongly affected by polarized foregrounds, so it is likely that the detection rate of polarized sources would increase at higher angular resolution.
In this study, we used the calibrated LOFAR measurement sets of the M 51 field published by Mulcahy et al. (2014) to carry out a systematic search for polarized sources in the field. We re-imaged the field with an up-to-date LOFAR imager and developed a new algorithm to extract a catalog of polarized sources and quantify the rate of false detections. The method is entirely empirical and no assumption is made on the nature of the noise.
The paper is organized as follows. The main characteristics of the data set are given in Sect. 2. The analysis of the continuum data is presented in Sect. 3 and that of the polarization in Sect. 4. The results are presented in Sect. 5. In Sect. 6, the sources that are most confidently detected in polarization are discussed individually and the LOFAR measurements are compared to other available radio polarization measurements. The method used to identify the polarized sources is compared to the more standard methods based on a fixed S/N. Depolarization effects and the insensitivity of the observations to Faraday-thick structures are discussed. Finally, we conclude in Sect. 7.
2. The LOFAR data
The M 51 field was observed in 2013 for eight hours using the LOFAR HBA2. During the observation, the field was never below 40° elevation. This is important as simulations have shown that LOFAR’s sensitivity to polarization is significantly reduced at low elevations (T. Carozzi, priv. comm.). There were eight frequency blocks, each approximately 6 MHz wide, spread evenly between 115 MHz and 175 MHz. In total there were 1952 frequency channels with a channel width of 24.4 kHz. 3C 295 was used for flux and initial phase calibration. We estimate a 10% calibration error in the total intensity flux. Due to the difficulty in calibrating polarization with LOFAR, we cannot estimate the calibration error in polarized intensity confidently. More details about the observation and calibration are available in Mulcahy et al. (2014).
3. Analysis of the continuum data
3.1. Imaging
The field was imaged in total intensity using WSCLEAN 2.23 (Offringa et al. 2014). We imaged a square of 6.25° × 6.25° centered on M 51, with a 18″ × 15″ elliptical beam and a pixel size of 5″. We used Briggs weighting (Briggs 1995) with a robustness parameter of 0. The image was cleaned down to 3σ, after which a mask was applied with WSCLEAN’s auto-masking option and the image was cleaned to the 0.3σ-level, as recommended in the WSCLEAN documentation. All frequency channels were imaged individually and those strongly affected by radio frequency interference were discarded, including the whole last block. This left 1694 channels with a maximum frequency of 168 MHz.
Figure 1 is an image of the field obtained after differential beam correction. The data that we used had already been corrected for the response of the LOFAR primary beam, calculated at the phase center (Mulcahy et al. 2014); we applied the differential beam correction in WSCLEAN4 based on the so-called Hamaker model5 (for more information, see e.g. Sect. 2.2.2 of Asad et al. 2015, and references therein).
 |
Fig. 1. LOFAR 150 MHz image of the field centered on nearby galaxy M 51. The size of the synthesized beam is 18″ × 15″. Roughly 3000 radio continuum sources were detected in this image within 2.5° of the center of M 51 (dotted-dashed black circle). We searched for polarization in all sources brighter than 100 mJy (201 sources; small blue squares). The locations of the sources that were found to be polarized in this work and or in other studies are also indicated. The entire field is included in the 1.4 GHz polarization catalog of Taylor et al. (2009). The regions examined in other studies are shown as the dotted black square (LOFAR 150 MHz, Mulcahy et al. 2014), dashed green circle (GMRT 610 MHz, Farnes et al. 2013, approximate), dashed magenta square (WSRT 1.4 and 1.6 GHz, Heald et al. 2009), dashed red square (VLA 1–2 GHz, Mao et al. 2015). The FITS file of the LOFAR total intensity image of the field are available at the CDS. |
The primary beam correction and phase errors cause the noise to vary across the image. Across the inner region of 2.5° radius the RMS noise in the full-bandwidth Stokes I image varies from 200 μJy beam−1 to 800 μJy beam−1, depending on distance from the phase center and proximity to bright sources.
We also produced full-bandwidth Q and U images using the same parameters as for the I image (but without cleaning, due to the low S/N). The noise in the Q and U images is not as affected by nearby sources; it varies mostly with distance from the phase center within the primary beam. It varied from 100 μJy beam−1 at the center to 200 μJy beam−1 at a distance of 2.5° from the center of M 51.
The characteristics of the full-bandwidth I image are given in Table 1. The table also lists the number of sources detected in the field, as discussed in the following Section.
3.2. Source identification
To identify the continuum sources in the field we used the Python Blob Detector and Source Finder, pyBDSF6. We used a 250″ box to calculate the RMS map7, while the other parameters were kept at the default values. This resulted in the detection of 3032 sources within 2.5° of the center of M 51, though a number of them (∼10–20) were visually determined to be false detections from phase errors around strong sources.
Figure 2 shows the corresponding number counts. The vertical dashed line indicates the 100 mJy flux density threshold used in the polarization search. The choice of this threshold is justified in Sect. 4.1.
 |
Fig. 2. Number counts of continuum sources detected within 2.5° of the center of M 51. The vertical line shows the 100 mJy flux density threshold used in the polarization search. The inset shows the distribution for sources brighter than 1 Jy. |
 |
Fig. 3. Comparison of the flux densities measured in the LOFAR image and in the first alternative data release of the TGSS survey (Intema et al. 2017). The diagonal (solid line) is the 1:1 line. The red markers represent the six continuum sources in which polarization was most securely detected. The dashed line at 102 mJy indicates the flux density threshold used in the polarization search. |
This LOFAR catalog was cross-matched with the first alternative data release of the Tata Institute of Fundamental Research (TIFR) Giant Metrewave Radio Telescope (GMRT) Sky Survey (TGSS, hereafter TGSS ADR1; Intema et al. 2017) in the same region. All but three of the 324 TGSS ADR1 sources were found in our LOFAR catalog. All three undetected TGSS ADR1 sources were located near sidelobes of bright sources in the LOFAR image.
Figure 3 shows a comparison between the LOFAR flux density measurements and those in TGSS ADR1. The LOFAR flux densities are higher by 20% on average, and this effect decreases with increasing flux density. This difference is too large to be only due to calibration error. An explanation might be that the higher sensitivity of LOFAR allows observation of diffuse emission that is not detected in the TGSS ADR1. Another explanation is that there is an increasing degree of incompleteness at low flux densities (because intrinsically faint sources are only seen at the center of the LOFAR image, whereas the bright sources are recovered at all radii). The faint end of the scatter in low-flux-density bins is truncated and we are left with a positive bias relative to TGSS which is mosaiced and has roughly uniform sensitivity across the survey area.
Characteristics of the imaging and field.
4. Analysis of the polarization data
A flowchart outlining the method is shown in Fig. 4.
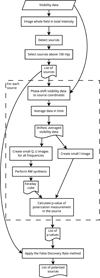 |
Fig. 4. Process used in this paper to obtain a list of polarized sources from visibility data (see Sects. 3 and 4). |
4.1. The sample
We searched for polarization in all sources of the LOFAR 150 MHz image with a flux density greater than 100 mJy and located within 2.5° of the center of M 51 (201 sources, eight of which are not in the TGSS ADR1 catalog). The catalog is published at the CDS.
The 100 mJy flux density threshold was set on the basis of the noise level in the images, σI < 0.8 mJy beam−1 across the entire field of view (FOV), so that all sources brighter than 100 mJy would be detected at an S/N greater than 100. A polarized source with a fractional polarization of 1% would be detectable at an S/N > 5, since σQ,U < 0.2 mJy beam−1 over the FOV. Lower fractional polarizations would be detectable in brigher sources.
We also examined six sources below this threshold that had been detected in polarization at other radio frequencies. These sources were imaged in Faraday space and were analyzed, but not included in the false discovery rate (FDR) analysis described in Sect. 4.5.3.
The locations of all examined sources are indicated in Fig. 1. The sources brighter than 100 mJy are distributed rather uniformly across the field. The six weaker sources are located in the central region, in the areas that were mapped in deep observations at higher frequencies by Farnes et al. (2013), Heald et al. (2009), or Mao et al. (2015).
4.2. Creating Faraday cubes
We imaged each source using the procedure described below.
First, we phase-shifted the (u,v) data to the source location and averaged them in time to 140 s, using DPPP8.
Then we used WSCLEAN to create small images (4.3′ × 4.3′) of all four Stokes parameters centered on the source for all frequencies. The small image size made the high time averaging possible; the smearing that occurs when averaging in time is smaller near the phase center. Only baselines shorter than 18 000 λ were included to give all channel maps the same angular resolution. The potential intensity loss due to time smearing given the parameters here (4.3′ image, 15″ beam, 140 s) is <1% (Bridle & Schwab 1999). The channel maps were not cleaned because of the low S/N in the individual Q, U images. Briggs’ weighting (Briggs 1995) was used, with a robustness parameter of 0. The WSCLEAN differential primary beam correction9 was applied. We also imaged the source in total intensity (combining all frequency channels). For this image, cleaning was performed in the same way as for the image of the whole field, as described in Sect. 3.1.
Finally, we performed RM synthesis on the Q and U images using pyrmsynth10. Faraday cubes were created between ±500 rad m−2 and cleaned to reduce the sidelobes in Faraday space down to 3σF (where σF is the standard deviation of the Faraday spectrum |F(ϕ)| at a given pixel in RA, Dec) with the RM-CLEAN algorithm (Heald et al. 2009). The rotation measure spread function (RMSF) is shown in Fig. 5. values of |ϕ|, we used slightly smaller Faraday cubes for the analysis:
The limits of RM synthesis given the frequency coverage of the data set can be calculated from Eqs. (61)–(63) in Brentjens & de Bruyn (2005):
where δϕ is the resolution in Faraday depth (strictly speaking the full-width half maximum of the RMSF), Δϕmax is the largest scale in Faraday depth to which the data are sensitive, and |ϕmax| is the largest Faraday depth in absolute value that can be detected. Since Δϕmax is barely larger than the resolution in Faraday depth, polarization will only appear as unresolved peaks in Faraday space.
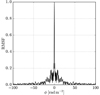 |
Fig. 5. Absolute value of the rotation measure spread function (RMSF) corresponding to the frequency coverage of the LOFAR data used in this work. The full-width half maximum of the RMSF is δϕ ≈ 0.96 rad m−2. |
4.3. Faraday voxels, Faraday cells, and local maxima
A Faraday voxel is a 3D pixel in the Faraday volume. Each voxel has a size of 2″ × 2″ × 0.2 rad m−2.
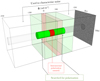 |
Fig. 6. Illustration of the different regions used in the analysis of a Faraday cube. The green cylinders represent the region searched for polarization (at Faraday depth |ϕ| < 100 rad m−2 and outside the central region that is contaminated by instrumental effects). The outer regions (100 rad m−2 < |ϕ| < 450 rad m−2) were used to characterize the noise. The images have a size of 3′ × 3′. |
A Faraday cube can be regarded as a number of independent resolution elements, which we will call Faraday cells. The spatial component of each Faraday cell has the size of the synthesized beam and the third dimension is the resolution element in Faraday space: 18″ × 15″ × 0.96 rad m−2.
Note that the Faraday cells are not rectangular parallelepipeds, but 3D Gaussians. Each imaged Faraday cube contained roughly 170 000 such independent cells. In the analysis, individual cells are not used; the relevant quantity is the number of cells in a Faraday volume, as it is the number of independent measurements.
Because the voxels in a Faraday volume are correlated due to oversampling, the analysis was performed on local maxima that were identified by examining the values of |F| in adjacent voxels11. We assume that each local maximum corresponds to one cell. The density of peaks at or above a given F was obtained by dividing the number of identified local maxima by the number of cells in the considered Faraday volume.
4.4. Regions in the Faraday cubes
Figure 6 is an illustration of the different regions used in the analysis. Those regions are listed below, and the criteria used to define their boundaries are explained.
The on-source and off-source regions.
The regions of high |ϕ|, both on- and off-source, where no polarization is expected. Those regions are used to characterize the noise.
The on-source region of low |ϕ| where polarization is searched for, excluding the region of instrumental polarization close to ϕ = 0.
The region of instrumental polarization close to ϕ = 0.
To define a region that may contain polarization from the source, all pixels in (RA, Dec) with an intensity greater than a certain threshold, Ithresh, were selected12. Typically, Ithresh was of the order of 10 mJy beam−1. Each source was inspected visually and the threshold was increased if artifacts (for instance due to phase errors) were seen. This was done for 28 sources.
In the Faraday depth dimension, we constrained our search to |ϕ| < 100 rad m−2. The range around ϕ = 0 rad m−2 required special attention because of the contamination by instrumental polarization. We always excluded |ϕ| ≤ 1.5 rad m−2 to exclude the instrumental peak itself. Additionally, instrumental polarization from the brightest sources creates artifacts at larger |ϕ| in the whole field. Therefore the standard deviation in each ϕ-slice was measured (only including off-source pixels), creating a spectrum of the noise as a function of Faraday depth. The average and standard deviation of this Faraday spectrum at |ϕ| > 20 rad m−2 were calculated, and we excluded the continuous range around ϕ= 0 rad m−2 where the values were greater than five times the standard deviation above the average.
4.5. Statistical analysis
The key issue is to characterize the noise properties of the data in order to quantify the likelihood that a peak in polarized intensity observed in the Faraday cube is real. In the following subsections we define the different regions of interest, characterize the noise properties, and calculate the p-values of all the radio sources in our sample. The p-value (also sometimes called “probability to exceed”) is the probability of obtaining a value at least as high as the measured one in the absence of signal (that is, if the data contained only noise). The lower the p-value the higher the likelihood that the detection is real. In Sect. 4.5.3 we describe how the FDR method (Benjamini & Hochberg 1995; Miller et al. 2001) can be applied to quantify in a rigorous manner the fraction of false detections in a sample, based on the distribution of the p-values of the sources.
4.5.1. The null hypothesis: noise characterization
We examined the distribution of local maxima at large Faraday depths (100 rad m−2 < |ϕ| < 450 rad m−2), where it is assumed that no polarization is present.
Figure 7 shows the distribution of local maxima in the Faraday cube of one of the sources in which polarization was found. On-source, the distribution of local maxima at |ϕ| < 100 rad m−2 shows an excess of high polarization values. Off-source, no difference can be seen between the distributions at high and low Faraday depths.
 |
Fig. 7. Histograms of local maxima in different regions of the Faraday cube around the polarized source J132626+473741. The histograms have been normalized to facilitate comparisons. The instrumental polarization range, as defined in Sect. 4.5.1, has been excluded from the data. The distribution of local maxima on-source and at Faraday depths |ϕ| < 100 rad m−2 shows a clear excess at larger F. |
 |
Fig. 8. Characterization of the noise in the Faraday volumes of the two polarized sources, J132626+473741 (in blue, also presented in Fig. 7) and 4C+47.38 (in green). The measurements were extracted in the range of Faraday depths 100 rad m−2 ≤ |ϕ | ≤ 450 rad m−2 where no polarized signal is expected. Upper panel: histograms of local maxima. The histograms were not normalized since the two regions contain the same number of voxels. The shaded areas correspond to flux values in the top 5% of the distribution. The noise in the Faraday cube of 4C+47.38 is higher than for the other source (the histogram is broader) because the source lies at a greater distance from the center of the field. Lower panel: complementary cumulative distribution function (CCDF) for the same sources as in the first panel. The dots show the actual CCDF and the solid line is the Gaussian fit used to model the distribution at high F (calculated at CCDF(F) ≤ 10−2, as indicated by the dashed line). The horizontal solid line at CCDF = 0.05 corresponds to the lower limit of the shaded distributions in the upper panel. |
Figure 8 shows the complementary cumulative distribution (CCDF) of peaks that corresponds to the distribution of local maxima shown in Fig. 7. Since we are interested in detecting polarized sources, which means identifying high values of F that have a low probability of being due to noise, we need to quantify the distribution of the noise at high values of F in regions where no polarized signal is expected. At high F, the CCDF of peaks can be well represented by a Gaussian. Therefore, we fit a Gaussian to the points at CCDF(F) ≤ 10−2 and use the fit as our CCDF at high values of F. The best-fit function is shown as a red dashed line in Fig. 8.
4.5.2. Calculating the p-value of a source
To calculate the p-value of a source, we searched for the highest peak (local maximum), Fmax, in the on-source region defined above. pcell(Fmax), is the probability of observing a peak at least as high as Fmax in a given cell devoid of polarization. The p-value for the source, psource is the probability of finding such a peak in any cell. This probability is given by
where Ncell is the number of cells in the examined region.
4.5.3. The false discovery rate method
Having calculated the p-value for each source, we used the FDR method (Benjamini & Hochberg 1995; Miller et al. 2001) to obtain a list of detected sources.
The FDR method allows one to select a number α in advance, and obtain a list of detections where the expected fraction of false detections is α. The method works as follows:
The p-values are sorted in ascending order, and each is given an index j. Then the largest index is found for which
where N is the total number of measurements. All measurements with p-values smaller than pj are counted as detections. This can be understood intuitively by observing that pjN is the expected number of measurements with p-values below pj, under the null hypothesis (i.e. false detections). j is the actual number of measurements with such p-values. The proof is available in Benjamini & Hochberg (1995).
In our case, the total number of measurements is the number of examined radio continuum sources, N = 201. An illustration for two values of α, 5% and 50%, is shown in Fig. 9. The green dots falling below the line that corresponds to α = 0.05 correspond to the sources with a false discovery rate of 5%. The results of the analysis are presented in the following Section.
 |
Fig. 9. Application of the FDR method to the 201 identified continuum sources around M 51 with two values of the false discovery rate, α (5% and 50%). Each dot shows the p-value of a source, pj. The sources have been sorted by increasing p-value. The FDR method finds the (last) intersection of this distribution and a line with the slope |
Most significant detections of polarization.
Sources with multiple Faraday depth measurements.
5. Results
In Fig. 9 we show the distribution of the examined sources sorted by increasing p-value. The inset shows more clearly the dots that fall below the lines that correspond to two values of the false discovery rate, α = 0.05 and α = 0.5. In Table 2 we list the properties of those sources.
Setting α = 0.05 yields six polarized sources. The area covered is 19.6 deg2. All of these sources were sufficiently polarized that the primary beam would not prevent detection anywhere within this region, and so the resulting detection rate is 1 source per 3.3 square degrees, or 0.3 source per square degree. These six sources are described individually in Sect. 6.
Setting α = 0.5 gives 19 sources. Since half of the sources are expected to be false detections, this means than 9–10 sources are expected to be real. The list include the 6 most securely detected sources. The probability of having only six polarized sources in a sample of at least 19 sources with α = 0.5 is only 8%. This indicates that a few more sources (3–4) can be expected to be polarized. This brings the number density of polarized sources to about 0.5 per square degree.
All the sources discussed above were part of the flux-density-limited sample (S150 MHz > 100 mJy). We also imaged six sources fainter than 100 mJy that have been detected in polarization in another radio frequency band. Of these, only one was detected (J132930+470612, with a p-value of 0.038). This p-value is low enough for the source to be included in α = 0.5 sample, but not in the top list with α = 0.05. To preserve the uniformity of the sample, this source is not included in Table 2, but it appears in Table 3 where detections in different data sets are presented.
The Faraday cubes of the 19 sources in the sample with a false discovery rate of 50% are available at the CDS.
6. Discussion
We start by comparing our measurements with those of Mulcahy et al. (2014) that were based on the same data set. In Sect. 6.2 we discuss the most securely detected sources (those with a FDR of 5%) individually; we look at their morphology in the Faint Images of the Radio Sky at Twenty Centimeters (FIRST; Becker et al. 1995) that have a higher angular resolution (5″) than the LOFAR images and search for optical counterparts and redshift estimates. Polarization measurements at other frequencies provide additional independent information that may help determine which ones of the sources in our second list (with an FDR of 50%) are real. In Sect. 6.3 we examine those measurements in more detail. In Sect. 6.4 we compare the advantages of using p-values and the FDR method relative to using pre-defined S/Ns. Many sources previously found to be polarized at higher frequencies (Farnes et al. 2013; Mao et al. 2015; Taylor et al. 2009; Heald et al. 2009) are not detected at 150 MHz by LOFAR. This is to be expected, as depolarization is expected to be stronger at low frequencies (e.g. Burn 1966). In Sect. 6.5 we discuss the insensitivity of LOFAR to Faraday-thick sources.
6.1. Comparison with Mulcahy et al. (2014)
Using the same LOFAR measurement set, Mulcahy et al. (2014) had idenfied six polarized sources in the field using a pre-defined S/N threshold. A comparison of our two lists can be summarized as follows:
There are four sources in common; they are the strongest detections and the measured Faraday depths are in very good agreement (see Tables 2 and 3).
Our fifth source (B3 1330+451) is outside the area searched by Mulcahy et al. (2014).
Our sixth source (J133613+490037) was not detected by Mulcahy et al. (2014) but was detected at 1.4 GHz by (Taylor et al. 2009; see Sect. 6.2).
The fifth source detected by (Mulcahy et al. 2014; J133258+454201) appears in our longer list of 19 sources with α = 0.5 (B3 1330+459); the measured Faraday depths differ slightly between our two measurements (−4.4 ± 0.1 rad m−2 versus −5.2 ± 0.1 rad m−2 for Mulcahy et al. 2014).
Mulcahy et al. (2014)’s sixth source (J133128+454002) is their most weakly polarized source. It did not make it into our list of sources with an estimated 50% false discovery rate.
6.2. Sources detected with a 5% false discovery rate
Let us examine more closely our most securely detected sources, i.e. the subsample with a false discovery rate of 5%. In the left column of Fig. 2 we show images of the sources observed at higher angular resolution (5″) at 1.4 GHz by the VLA FIRST (Faint Images of the Radio Sky at Twenty Centimeters) Survey (Becker et al. 1995). The LOFAR 150 MHz total-intensity images are shown in the middle column, and in the right column we show the Faraday spectra extracted from regions in which polarized emission was detected in the LOFAR data.
Source 1 (J133920+464115) has a complex radio morphology. We find two regions of strong polarization in the northern part, peaking at 20.4 ± 0.1 rad m−2 and 20.6 ± 0.1 rad m−2, in agreement with what was found by Mulcahy et al. (2014). Like Mulcahy et al. (2014), who discussed the source as a radio galaxy as a core and a single lobe, we do not detect polarization from the bright “core” at the center of the image. However, from the morphology of the high-resolution FIRST image it is not certain that the fainter features to the north are related to the “core”. There is no clear counterpart in SDSS, which suggests that the source(s) are distant or highly obscured.
Source 2 (4C+47.38; B3 1339+472) is a double-lobed radio galaxy (only partially resolved with LOFAR) and the brightest source in the sample. Between the lobes there is a quasar with redshift z = 0.502 ± 0.003 (Vigotti et al. 1997). Klein et al. (2003) derived an RM of 46.4 ± 2.7 rad m−2 from polarization measurements at 1.4, 2.7, 4.8 and 10.5 GHz, which is about twice as high as the Faraday depth that we measure in the LOFAR 150 MHz data. They also derived a spectral index of −1.01 between 408 MHz and 10.6 GHz.
Source 3 (J132626+473741) consists of three parts. The middle component is not visible in this observation, but can be seen in the FIRST image. A counterpart to the middle component was observed by the SDSS, with a redshift of z = 0.68240 ± 0.000351 (Hewett & Wild 2010).
Source 4 (J133707+485801) is partly resolved as a double source in FIRST, but not by LOFAR. SDSS has an optical counterpart with a photometric redshift z = 0.975 (Richards et al. 2009).
Source 5 (B3 1330+451) was not observed by Mulcahy et al. (2014), as it was outside their imaged field. It is only partially resolved by LOFAR. It is resolved into four sources by FIRST. The polarization detected by LOFAR is associated with the SW part.
Source 6 (J133613+490037) shows two distinct peaks in the northwest part, both at 9.2 ± 0.1 rad m−2. Both parts of the source were detected in polarization at 1.4 GHz, with the southeast at an RM of 10.7 ± 16.5 rad m−2 and the northwest at 11.1 ± 10.6 rad m−2 (Taylor et al. 2009). It was not detected in polarization by Mulcahy et al. (2014).
The six detected sources appear to be at least partially resolved by FIRST, and have a morphology consistent with that of double-lobed radio galaxies (Fig. 10).
6.3. Sources detected at other radio frequencies
Table 3 lists the Faraday depths of the sources in the field that have been measured in at least two of the following studies:
This work;
Mulcahy et al. (2014): same calibrated LOFAR data as in this work, but analyzed differently;
Farnes et al. (2013): 610 MHz GMRT observation of a fraction of the field; the polarization fraction was calculated for sources within a radial distance ≤35.6′ from the center and should be considered as upper limits for the sources beyond a radial distance of 22.2′ from the center; the full resolution of the data was ∼5″ and the analysis of the polarization was done on images at a resolution of 24″;
Taylor et al. (2009)’s RM catalog is based on the NVSS survey (Condon et al. 1998) at 1.4 GHz with a resolution of 45″. It covers the whole sky north of −40° and has an average density of about one RM value per square degree.
Heald et al. (2009): 1.4 and 1.6 GHz WSRT observations of the central part of the field (34′ × 34′) at a resolution of >15″.
Mao et al. (2015): 1–2 GHz JVLA observations of the central part of the field (40′ × 40′) at a resolution of 13.2″ × 8.7″. We noted typographical errors in one of the tables 13.
The fields of view of those observations are marked on Fig. 1. Most of the sources that are listed in our Table 2 are outside the fields of view of the targeted observations at higher frequencies. The RM catalog of Taylor et al. (2009) covers the entire field, and we compare it with our detections in Sect. 6.3.1.
Mao et al. (2015) used a number of depolarization models to fit to their polarization measurements in the 1–2 GHz band. In total, they modeled six sources (their Table 2; since some of the sources had multiple components, a total of 10 components was modeled). Only one of their listed sources is detected in our study (our Source 7a; Mao et al. 2015’s source J1330+4703b). This source is particularly interesting because it was also detected at 610 MHz by Farnes et al. (2013) and lies behind the prominent H I tail of M 51. We discuss this source in Sect. 6.3.3.
 |
Fig. 10. The six sources detected in polarization in the LOFAR 150 MHz data with a 5% false discovery rate. Left and middle column: 3′ × 3′ VLA FIRST 1.4 GHz images (5″ resolution; Becker et al. 1995) and LOFAR 150 MHz images. The synthesized beams of the images are displayed in the bottom left corners. Right column: LOFAR Faraday spectra at the most highly polarized location. The contours correspond to the FWHM of the peak in polarized intensity; they were omitted when their shape was significantly affected by noise. The red and green colors are used to show Faraday spectra at two nearby locations in the same source. The grey shading around ϕ = 0 shows the region of instrumental polarization that was excluded from the analysis (Sect. 4.4). |
6.3.1. Comparison with the Taylor et al. (2009) RM catalog
Of our six securely detected sources, four have an RM listed in Taylor et al. (2009)’s catalog. We note that Source 3 was detected in polarization in the NVSS catalog (3.08 ± 0.69 mJy), but below the 8σ threshold to be included in the Taylor et al. (2009) RM catalog. Source 5 was not clearly detected in the NVSS, with a polarized flux density of 0.83 ± 0.51 mJy. Of the two additional sources detected by Mulcahy et al. (2014), one has an RM entry in Taylor et al. (2009)’s catalog; the other one, which coincides with our Source 14, has a polarized flux of only 0.81 ± 0.40 mJy in NVSS, so well below Taylor et al. (2009)’s selection threshold. Of the 13 others that are included in our sample with a 50% false discovery rate, only one source (our Source 8) figures in Taylor et al. (2009)’s RM catalog.
This shows that detection of polarization at 1.4 GHz in the NVSS catalog or inclusion in Taylor et al. (2009)’s RM catalog does not imply that the source may be detected in polarization in these 150 MHz LOFAR data. For the sources in common, there is no general agreement between the Faraday depths measured at 150 MHz and those measured by Taylor et al. (2009) at 1.4 GHz. This might be due to resolution, sensitivity, and/or Faraday depolarization effects.
6.3.2. Galactic RM foreground
M 51 is located at a high Galactic latitude (b = +68.5°) where the rotation measure due to the Milky Way is expected to be low. From the five polarized sources in the field of their WSRT observations Heald et al. (2009) estimated a foreground RM of 12 ± 2 rad m−2. Mao et al. (2015) derived a median RM of 13 rad m−2 with a standard error of 1 rad m−2 from their JVLA 1–2 GHz measurements, excluding the sources located on sightlines with a neutral hydrogen column density larger than 1020 cm−2 in the H I map of Rots et al. (1990). For our entire field (RM 51 < 2.5°), the mean RM of sources in the Taylor et al. (2009) catalog is 12.0 ± 14.8 rad m−2. The mean and standard deviation of RM values of the six polarized sources that are securely detected in the LOFAR data is 13.1 ± 7.6 rad m−2. All those values are in agreement and provide an estimate of the Milky Way RM foreground in the direction of our observations.
6.3.3. Source 7: a radio source behind M 51′s H I tail
 |
Fig. 11. Top row: same subfigures as in Fig. 2, for Source 7. The grey shading around ϕ = 0 shows the region of instrumental polarization that was excluded from the analysis (Sect. 4.4). Second row, left panel: (1′ × 1′) FIRST 1.4 GHz image of our Source 7 in grey scale and in contours (1 and 3 mJy beam−1). The red cross indicates the location of the optical counterpart to the radio core. The color scale ranges from −0.3 to 3 mJy beam−1 and the angular resolution is 5″, as indicated by the grey circle in the bottom left corner. Second row, right panel: H I integrated intensity (moment 0) image of M 51 from THINGS. The red square has a size of 1′ × 1′ and indicates the location of Source 7, the radio galaxy displayed in the previous panel. The grey scale is in Jy beam−1 M s−1. Third row, left panel: zoom of the previous image: (1′ × 1′) H I high-resolution (5.8″ × 5.5″) moment 0 image in grey scale. The yellow contours are the same radio contours of the FIRST image shown in the top left panel. Third row, right panel: measurements of the fractional polarization in the northern radio lobe of Source 7 (white circles) and the southern lobe (black squares). The dashed lines show the depolarization models that best fit the high-frequency data (JVLA 1–2 GHz, Mao et al. 2015) and the solid lines depolarization models that match the averaged 1–2 GHz measurements and the GMRT 610 MHz of Farnes et al. (2013). The LOFAR measurements are not used to constrain the models. |
Source 7 lies at an angular distance of 12′ from the center of M 51 (or 26.5 kpc, assuming a distance to M 51 of 7.6 Mpc, Ciardullo et al. 2002). This source source is of special interest because of its detection in polarization at several frequencies and its location behind the prominent tidal tail of neutral hydrogen discovered by Rots et al. (1990) and imaged more recently by The H I Nearby Galaxy Survey, THINGS (Walter et al. 2008). In the top right panel of Fig. 11 we show the THINGS H I integrated intensity image; the right square indicates the location of Source 7. No diffuse radio continuum emission of M 51 is detected in the area of the H I tail (e.g. Horellou et al. 1992; Fletcher et al. 2011; Mulcahy et al. 2014), as expected in the absence of cosmic-ray electrons outside the main star-forming disk of the galaxy. The tidal tail may, however, contain thermal electrons and magnetic fields that could cause Faraday rotation and/or depolarization from a background polarized source.
In Fig. 11 (top left panel) we show the image from the FIRST 1.4 GHz survey centered at the location of the radio source. The source has the morphological appearance of a double-lobed radio galaxy. Three sources are listed in the FIRST catalog:
the rather faint core (with an integrated flux density of about 4 mJy; FIRST J133045.1+470316);
a northern component (S1.4 M GHz ≃ 9 mJy; FIRST J133045.3+ 470324);
and a brighter southern component (S1.4 M GHz ≃ 11.8 mJy; FIRST J133045.0+470309) that is slightly more extended than the FIRST beam.
The combined flux of those three components is in excellent agreement with the NVSS flux measurement of 24.8 ± 1.2 mJy (Condon et al. 1998), indicating that no extended emission is lost. There is an optical counterpart to the radio core, SDSS J133045.13+470317.2, marked by a red cross on Fig. 11, with a photometric redshift of z = 0.816 ± 0.0432 (there is, however, a note in SDSS that the object’s photometry may be unreliable). In the standard λCDM cosmology14, this gives a scale of 7.56 kpc arcsec−1. The distance between the northern and the southern radio components is 15″ (∼113 kpc), with the northern component at a projected distance of about 60 kpc from the core and the southern one at about 56 kpc, on the plane of the sky. Those rather large distances suggest that both radio lobes are located outside the main halo of the host galaxy.
Mao et al. (2015) detected polarization in the 1–2 GHz band from both radio lobes, the southern one being more polarized (7.6 ± 0.4%) than the northern one (4.6 ± 0.3%). Their best-fit model to the northern source is that of a simple uniform rotating Faraday screen, with a Faraday depth of 10 ± 2 rad m−2 and a constant fractional polarization of 4.6%. This model overestimates the fractional polarization at 610 MHz, that was measured to be 2.74 ± 0.24% (Farnes et al. 201315). The Faraday depth at 610 MHz is −15.97 ± 0.03 rad m−2 (Farnes et al. 2013), which is different from the value measured at 1–2 GHz.
For the southern source, Mao et al. (2015)’s best-fit model is a depolarizing Faraday screen (external Faraday dispersion, with σRM = 8.4 rad m−2). In this case, the model underestimates the polarization at 610 MHz, measured to be 1.98 ± 0.02% (Farnes et al. 2013). The Faraday depths are also different at the two frequencies: 17.2 ± 0.8 rad m−2 at 1–2 GHz and −3.24 ± 0.03 rad m−2 at 610 MHz.
What about the LOFAR measurements? The source has two components named 7a and 7b in our Table 3. Our algorithm identifies a polarized signal in the overall region of the northern lobe in the LOFAR image (the radio source is barely resolved in LOFAR and the detection is slightly offset from the peak in total intensity, see first row of Fig. 11). Source 7a is not included in our top list of most securely detected sources but appears in the second list of sources detected in polarization with a false discovery rate of 50%. The measured Faraday depth is very large in absolute value (close to −100 rad m−2). The Faraday spectra is the area of the radio source contains a number of other peaks of similar strength at lower Faraday depths (in absolute value). For those reasons, we do not regard the measured level of polarized emission (0.48 ± 0.08 mJy) as a robust measurement of polarization from the northern lobe. The algorithm does not find any polarization towards the southern lobe.
To calculate the degree of polarization of each lobe at 150 MHz, we assume that the core has a constant a flux density of 5 mJy (in agreement with the observations at higher frequencies), and estimate the flux density of each lobe by assuming that the lobes have the same flux density ratio as at 1.4 GHz. The total flux density is  mJy. This gives about 49 mJy for the northern lobe and 65 mJy for the southern one, and a fractional polarization of 1% for the northern lobe, and an upper limit of 0.15% for the southern lobe, adopting a limit on the polarized emission of 0.1 mJy.
mJy. This gives about 49 mJy for the northern lobe and 65 mJy for the southern one, and a fractional polarization of 1% for the northern lobe, and an upper limit of 0.15% for the southern lobe, adopting a limit on the polarized emission of 0.1 mJy.
From the measurements at 1–2 GHz by Mao et al. (2015) and at 610 MHz by Farnes et al. (2013), we can use a simple depolarization model of an external Faraday screen to calculate the Faraday dispersion. For the northern lobe, we obtain σRM = 2.2 ± 0.2 rad m−2, and for the southern lobe σRM = 3.6 ± 0.2 rad m−2. In the last panel of Fig. 11 we show the measurements, the depolarization models of Mao et al. (2015) (dashed lines), and the depolarization models by external Faraday dispersion derived from the averaged 1–2 GHz and the 610 MHz measurements (solid lines). The 1–2 GHz measurements gave a significantly larger Faraday dispersion for the southern lobe and therefore a stronger depolarization at longer wavelengths. Given the uncertainty of the LOFAR detection towards the northern lobe, we refrain from using this measurement to constrain the nature of the depolarization. However, if the LOFAR detection towards the northern lobe is real, then the fractional polarization would decrease less steeply with wavelength than in the Burn (1966) model. It woud be more compatible with the model for external Faraday dispersion discussed by Tribble (1991) that decreases as the inverse of σRM λ2 at long wavelengths, as found in other low-frequency observations of polarized sources (e.g. Gießübel et al. 2013).
The high-resolution (∼5″) H I image of the region shows some substructure, with an H I peak in M 51 south of the radio core of the background source (bottom left panel of Fig. 11). There is little neutral hydrogen, however, at the location of the radio lobes. We also examined the corresponding first and second moment images (velocity field and velocity dispersion) from THINGS and did not find any clear evidence of regular or turbulent velocity flows in that region that may have helped interpret the measurement (the very large Faraday depth in absolute value seen by LOFAR and the stronger Faraday dispersion towards the southern lobe).
In the future, more sensitive broad-band polarization measurements and H I observations with higher surface brightness sensitivity may make it possible to investigate in more details the magneto-ionic medium in the outer regions of galaxies via Faraday tomography of background sources. The VLASS16, MeerKAT’s MIGHTEEpol and MHONGOOSE surveys (Jarvis et al. 2016; de Blok et al. 2016) Blok+ and ASKAP’s WALLABY17 and POSSUM18 surveys will give just these improvements.
6.4. p-values versus S/Ns
A natural question is whether the method presented here has clear advantages over the traditional “sigma clipping” method based on selecting sources above of a pre-selected S/N, where the noise is usually taken as the standard deviation of a distribution of measurements that are expected to be free from signal.
The two approaches have several steps in common. In particular, the regions expected to be signal-free have to be defined. In the case of Gaussian statistics, the two methods are strictly equivalent. For a Gaussian distribution of noise, the significance of a given peak in the data cube can be uniquely quantified by its S/N or its p-value. A non-Gaussian noise distribution cannot, in general, be uniquely described by its standard deviation. In that case, looking at the p-values might be more relevant as it gives the probability of having a peak of a certain strength given the underlying noise distribution. The stronger the source the lower the probability of having a similar one in the noise distribution, and therefore the actual noise distribution has to be modeled, based on the weaker data points, and extrapolated to high values, as we did in Sect. 4.5.1.
The noise distribution of the polarized intensity in the Faraday cubes is clearly non Gaussian. Nevertheless, we calculated the standard deviation and the S/N for the investigated radio continuum sources. We found that the six securely detected sources all have an S/N > 10. For the others, there is a clear anticorrelation between the S/N and p-values, as expected, but the relation has a large scatter.
When choosing selection criteria for larger surveys one must always balance the power of the survey against the possibility of false detections. Erring on the side of inclusion and assigning a p-value to each source in the resulting catalog gives users the ability to modify this balance to suit their own needs. The fraction of false detections is an intuitive parameter to use for this purpose.
6.5. Insensitivity to Faraday-thick sources?
The LOFAR data set used in this study has a very small maximum scale in Faraday depth (Δϕmax ∼ 1 rad m−2). This means that the measurements are partly insensitive to Faraday-thick sources. The Faraday spectra, in effect, pass through a high-pass filter. At these low frequencies, this effect is so large that we do not observe the total polarized emission, but instead steep gradients in emission with respect to Faraday depth. Differences in the maximum Faraday range that can be detected by different instruments might explain the non-detection of some of the sources that were detected at other wavelengths. For instance, the 1–2 GHz VLA observations of Mao et al. (2015) have a poorer resolution in Faraday space (the FWHM of their RMSF is 90 rad m−2), but they are more sensitive to extended structure in Faraday space (with a 50% sensitivity to Faraday extents of 118 rad m−2). The different Faraday depths observed at different wavelengths may be an indication that many sources are Faraday complex.
Faraday-thick emission with internal structure on scales of 1 rad m−2 or less would show up as several smaller peaks. While any given peak might be too small to be detected confidently, the on-source Faraday spectra would still be busier than the surroundings. “Busy spectra” can be due to turbulent magnetic fields, as shown in the model by Beck et al. (2012; see their Fig. 3, and what LOFAR can detect, their Figs. 8 and 9). Our method might be extended to deal with multiple Faraday peaks. One could, for example, calculate a p-value using the few highest peaks. A positive correlation between the noise of adjacent cells may, however, cause false positives.
7. Summary and conclusion
We have developed a new method to identify polarized sources in radio continuum data. We calculate the p-values of sources in Faraday cubes and use the FDR method to construct a list of polarized sources, of which a preselected fraction are expected to be false detections. We applied this method to the LOFAR observations of the M 51 field and confidently identified six sources, giving a number density of 1 polarized source per 3.3 square degrees at 150 MHz, or 0.3 source per square degree. The number density increases to 0.5 per square degree taking into account the larger sample of 19 sources with a FDR of 50%.
All six most secure detections are associated with radio sources that have multiple radio components and/or diffuse continuumm emission. Their morphology is consistent with that of double-lobed radio galaxies and in some cases the polarization comes from the outer lobes. Correlation of our Table 3 (19 sources) with the catalog of double-lobed radio sources identified in the FIRST survey by van Velzen et al. (2015) gave 10 matches (50%); cross-correlation of the whole catalog of 201 sources gave 83 matches (41%). This indicates that a significant fraction of the sources that are polarized at low frequencies are classical radio galaxies, possibly of FR II type (Fanaroff & Riley 1974). This is also found in the polarization study by Van Eck et al. (2018) of part of the LOFAR Two-meter Sky Survey (Shimwell et al. 2017) that resulted in a catalog of 92 polarized sources. Low-frequency observations of polarization and Faraday rotation bring valuable information to constrain the properties of radio galaxies and their surroundings (e.g. O’Sullivan et al. 2018).
Our search was done on data from one LOFAR field image at a resolution of 18″ × 15″, while Van Eck et al. (2018) surveyed a much larger area at lower angular resolution (∼4′). The M 51 field is included in the data set used by Van Eck et al. (2018), and only one polarized source was found (the brightest one in our sample).
Our pipeline is well suited to LOFAR data but could be applied to other radio polarization measurements (e.g. MeerKAT, POSSUM, SKA-low and SKA-mid). Imaging individual sources at higher resolution and analyzing the corresponding RM cubes is computationally more efficient than dealing with very large cubes; it makes it possible to identify a larger number of polarized sources and quantify the rate of false detections.
In the future, we intend to apply the method to more polarization data sets, in particular fields from the LOFAR Two-meter Sky Survey of the entire northern hemisphere, LOTSS, and the deep ongoing LOFAR observations of the GOODS-North field19.
Future improvements will include the identification of several peaks in the Faraday spectra (not only the strongest one), since a number of sources seem to have a complex Faraday spectrum. Depolarization may affect different Faraday components differently and might be the reason why the Faraday depths that are measured at low radio frequencies sometimes differ from the ones measured at higher frequencies.
In this paper we call the Faraday dispersion function the complex-valued function denoted ℱ and obtained from Eq. (4) where the integration is continuous and goes from −∞ to +∞; we denote F the reconstructed ℱ obtained from applying RM synthesis to a discrete set of measurements at defined frequencies and call it a Faraday spectrum.
Formerly pyBDSM (Mohan & Rafferty 2015). http://www.astron.nl/citt/pybdsf
Formerly NDPPP, part of the standard LOFAR imaging pipeline (e.g. Heald et al. 2010).
The first column of Table 3 of Mao et al. (2015) lists properties of polarized sources that are common to their study and to that of Farnes et al. (2013). The sources seem to be sorted in increasing values of RA, as in Farnes et al. (2013), but their names were extracted from Mao et al. (2015)’s Table 2 where they had been listed in a different order. The correct order in the first column of Table 3 of Mao et al. (2015) should be: J1329+4658c; J1330+4710; J1330+4703a; J1330+4703b; J1331+4713a; J1331+4713b.
The sources’ two components are listed as #9 and #10 in Farnes et al. (2013)’s Table 1, where Source #10 is the northern component, that corresponds to J1330+4703b of Mao et al. (2015).
Acknowledgments
LOFAR, the Low Frequency Array designed and constructed by ASTRON, has facilities in several countries, that are owned by various parties (each with their own funding sources), and that are collectively operated by the International LOFAR Telescope (ILT) foundation under a joint scientific policy. This work made use of THINGS, “the H I Nearby Galaxies Survey” (Walter et al. 2008). This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This research has made use of the VizieR catalogue access tool, CDS, Strasbourg, France. The original description of the VizieR service was published in Ochsenbein et al. (2000). We have also made use of the table analysis software topcat (Taylor 2005). This research made use of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration 2013). This research also made use of the Matplotlib plotting library (Hunter 2007). We thank Aritra Basu for useful comments on the manuscript. We thank Steven Black Design for producing Fig. 6. D.D.M. gratefully acknowledges support from ERCStG 307215 (LODESTONE). C.H. and A.F. gratefully acknowledge support from the Gothenburg Centre for Advanced Studies, GoCAS. AF also thanks STFC and the Leverhulme Trust for support. We thank the referee for pointing out interesting references and for other useful comments.
References
- Anderson, C. S., Gaensler, B. M., Feain, I. J., & Franzen, T. M. O. 2015, ApJ, 815, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Asad, K. M. B., Koopmans, L. V. E., Jeli´c, V., et al. 2015, MNRAS, 451, 3709 [NASA ADS] [CrossRef] [Google Scholar]
- Asad, K. M. B., Koopmans, L. V. E., Jeli´c, V., et al. 2016, MNRAS, 462, 4482 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, R., & Gaensler, B. M. 2004, New Ast., 48, 1289 [Google Scholar]
- Beck, R., Frick, P., Stepanov, R., & Sokoloff, D. 2012, A&A, 543, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Becker, R. H., White, R. L., & Helfand, D. J. 1995, ApJ, 450, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Benjamini, Y., & Hochberg, Y. 1995, J. R. Stat. Soc. Ser. B, 57, 289 [Google Scholar]
- Bernardi, G., Greenhill, L. J., Mitchell, D. A., et al. 2013, ApJ, 771, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Bernet, M. L., Miniati, F., & Lilly, S. J. 2013, ApJ, 772, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Bonafede, A., Feretti, L., Murgia, M., et al. 2010, A&A, 513, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brentjens, M. A., & de Bruyn, A. G. 2005, A&A, 441, 1217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bridle, A. H., & Schwab, F. R. 1999, in Synthesis Imaging in Radio Astronomy II, eds. Taylor, G. B. Carilli C. L., & Perley R. A., ASP Conf. Ser., 180, 371 [NASA ADS] [Google Scholar]
- Briggs, D. S. 1995, in BAAS, 27, 1444 [Google Scholar]
- Brown, J. C., & Taylor, A. R. 2001, ApJ, 563, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., Haverkorn, M., Gaensler, B. M., et al. 2007, ApJ, 663, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Burn, B. J. 1966, MNRAS, 133, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R., Feldmeier, J. J., Jacoby, G. H., et al. 2002, ApJ, 577, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- de Blok, W. J. G., Adams, E. A. K., Amram, P., et al. 2016, Proc. MeerKAT Science: On the Pathway to the SKA (MeerKAT2016), https://pos.sissa.it/cgi-bin/reader/conf.cgi?confid=277, 7 [Google Scholar]
- Fanaroff, B. L., & Riley, J. M. 1974, MNRAS, 167, 31P [Google Scholar]
- Farnes, J. S., Green, D. A., & Kantharia, N. G. 2013, Conf. Proc. Magnetic Fields in the Universe IV, submitted [arXiv:1309.4646] [Google Scholar]
- Farnes, J. S., O’Sullivan, S. P., Corrigan, M. E., & Gaensler, B. M. 2014, ApJ, 795, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Farnes, J. S., Heald, G., Junklewitz, H., et al. 2018, MNRAS, 474, 3280 [NASA ADS] [CrossRef] [Google Scholar]
- Farnsworth, D., Rudnick, L., & Brown, S. 2011, AJ, 141, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, A., Beck, R., Shukurov, A., Berkhuijsen, E. M., & Horellou, C. 2011, MNRAS, 412, 2396 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gaensler, B. M., Haverkorn, M., Staveley-Smith, L., et al. 2005, Science, 307, 1610 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gaensler, B., Agudo, I., Akahori, T., et al. 2015, Advancing Astrophysics with the Square Kilometre Array (AASKA14), 103 [CrossRef] [Google Scholar]
- George, S. J., Stil, J. M., & Keller, B. W. 2012, PASA, 29, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Gießübel, R., Heald, G., Beck, R., & Arshakian, T. G. 2013, A&A, 559, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hales, C. A., Gaensler, B. M., Norris, R. P., & Middelberg, E. 2012, MNRAS, 424, 2160 [NASA ADS] [CrossRef] [Google Scholar]
- Han, J. L., Beck, R., & Berkhuijsen, E. M. 1998, A&A, 335, 1117 [NASA ADS] [Google Scholar]
- Hancock, P. J., Murphy, T., Gaensler, B. M., Hopkins, A., & Curran, J. R. 2012, MNRAS, 422, 1812 [NASA ADS] [CrossRef] [Google Scholar]
- Heald, G., Braun, R., & Edmonds, R. 2009, A&A, 503, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heald, G., McKean, J., Pizzo, R., et al. 2010, Proc. ISKAF2010 Science Meeting, PoS(ISKAF2010)057, accepted [arXiv:1008.4693] [Google Scholar]
- Heald, G. H., Pizzo, R. F., Orrú, E., et al. 2015, A&A, 582, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hewett, P. C., & Wild, V. 2010, MNRAS, 405, 2302 [NASA ADS] [Google Scholar]
- Horellou, C., Beck, R., Berkhuijsen, E. M., Krause, M., & Klein, U. 1992, A&A, 265, 417 [NASA ADS] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
- Intema, H. T., Jagannathan, P., Mooley, K. P., & Frail, D. A. 2017, A&A, 598, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jarvis, M. J., Taylor, A. R., Agudo, I., et al. 2016, Proc. MeerKAT Science: On the Pathway to the SKA, https://pos.sissa.it/cgi-bin/reader/conf.cgi?confid=277, 6 [Google Scholar]
- Jeli´c, V., de Bruyn, A. G., Mevius, M., et al. 2014, A&A, 568, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeli´c, V., de Bruyn, A. G., Pandey, V. N., et al. 2015, A&A, 583, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnston-Hollitt, M., Govoni, F., Beck, R., et al. 2015, Advancing Astrophysics with the Square Kilometre Array (AASKA14), 92 [CrossRef] [Google Scholar]
- Kaczmarek, J. F., Purcell, C. R., Gaensler, B. M., McClure-Griffths, N. M., & Stevens, J. 2017, MNRAS, 467, 1776 [NASA ADS] [Google Scholar]
- Klein, U., Mack, K.-H., Gregorini, L., & Vigotti, M. 2003, A&A, 406, 579 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lenc, E., Gaensler, B. M., Sun, X. H., et al. 2016, ApJ, 830, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Lenc, E., Anderson, C. S., Barry, N., et al. 2017, PASA, 34, e040 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, S. A., Zweibel, E., Fletcher, A., Ott, J., & Tabatabaei, F. 2015, ApJ, 800, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, C. J., Genovese, C., Nichol, R. C., et al. 2001, AJ, 122, 3492 [NASA ADS] [CrossRef] [Google Scholar]
- Mohan, N., & Rafferty, D. 2015, Astrophysics Source Code Library [record ascl:1502.007] [Google Scholar]
- Mulcahy, D. D., Horneffer, A., Beck, R., et al. 2014, A&A, 568, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, P., Beck, R., & Krause, M. 2017, A&A, 600, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ochsenbein, F., Bauer, P., & Marcout, J. 2000, A&AS, 143, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Offringa, A. R., McKinley, B., Hurley-Walker, N., et al. 2014, MNRAS, 444, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Orrù, E., van Velzen, S., Pizzo, R. F., et al. 2015, A&A, 584, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Sullivan, S. P., Brown, S., Robishaw, T., et al. 2012, MNRAS, 421, 3300 [NASA ADS] [CrossRef] [Google Scholar]
- O’Sullivan, S. P., Lenc, E., Anderson, C. S., Gaensler, B. M., & Murphy, T. 2018, MNRAS, 475, 4263 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Myers, A. D., Gray, A. G., et al. 2009, ApJS, 180, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Rots, A. H., Bosma, A., van der Hulst, J. M., Athanassoula, E., & Crane, P. C. 1990, AJ, 100, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Rudnick, L., & Owen, F. N. 2014, ApJ, 785, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Schnitzeler, D. H. F. M. 2018, MNRAS, 474, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Schnitzeler, D. H. F. M., & Lee, K. J. 2017, MNRAS, 466, 378 [NASA ADS] [CrossRef] [Google Scholar]
- Schnitzeler, D. H. F. M., & Lee, K. J. 2018, MNRAS, 473, 3732 [NASA ADS] [CrossRef] [Google Scholar]
- Shimwell, T. W., Röttgering, H. J. A., Best, P. N., et al. 2017, A&A, 598, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sokoloff, D. D., Bykov, A. A., Shukurov, A., et al. 1998, MNRAS, 299, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Sokoloff, D. D., Bykov, A. A., Shukurov, A., et al. 1999, MNRAS, 303, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Sotomayor-Beltran, C., Sobey, C., Hessels, J. W. T., et al. 2013, A&A, 552, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stepanov, R., Arshakian, T. G., Beck, R., Frick, P., & Krause, M. 2008, A&A, 480, 45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, M. B. 2005, in Astronomical Data Analysis Software and Systems XIV, eds. Shopbell, P. Britton M., & Ebert R., ASP Conf. Ser., 347, 29 [Google Scholar]
- Taylor, A. R., Stil, J. M., & Sunstrum, C. 2009, ApJ, 702, 1230 [NASA ADS] [CrossRef] [Google Scholar]
- Tribble, P. C. 1991, MNRAS, 250, 726 [NASA ADS] [CrossRef] [Google Scholar]
- Vacca, V., Oppermann, N., Enßlin, T., et al. 2016, A&A, 591, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Eck, C. L., Haverkorn, M., Alves, M. I. R., et al. 2017, A&A, 597, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Eck, C. L., Haverkorn, M., Alves, M. I. R., et al. 2018, A&A, 613, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Velzen, S., Falcke, H., & Körding, E. 2015, MNRAS, 446, 2985 [Google Scholar]
- Vigotti, M., Vettolani, G., Merighi, R., Lahulla, J. F., & Pedani, M. 1997, A&AS, 123, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walter, F., Brinks, E., de Blok, W. J. G., et al. 2008, AJ, 136, 2563 [NASA ADS] [CrossRef] [Google Scholar]
- Wardle, J. F. C., & Kronberg, P. P. 1974, ApJ, 194, 249 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. LOFAR 150 MHz image of the field centered on nearby galaxy M 51. The size of the synthesized beam is 18″ × 15″. Roughly 3000 radio continuum sources were detected in this image within 2.5° of the center of M 51 (dotted-dashed black circle). We searched for polarization in all sources brighter than 100 mJy (201 sources; small blue squares). The locations of the sources that were found to be polarized in this work and or in other studies are also indicated. The entire field is included in the 1.4 GHz polarization catalog of Taylor et al. (2009). The regions examined in other studies are shown as the dotted black square (LOFAR 150 MHz, Mulcahy et al. 2014), dashed green circle (GMRT 610 MHz, Farnes et al. 2013, approximate), dashed magenta square (WSRT 1.4 and 1.6 GHz, Heald et al. 2009), dashed red square (VLA 1–2 GHz, Mao et al. 2015). The FITS file of the LOFAR total intensity image of the field are available at the CDS. |
| In the text | |
 |
Fig. 2. Number counts of continuum sources detected within 2.5° of the center of M 51. The vertical line shows the 100 mJy flux density threshold used in the polarization search. The inset shows the distribution for sources brighter than 1 Jy. |
| In the text | |
 |
Fig. 3. Comparison of the flux densities measured in the LOFAR image and in the first alternative data release of the TGSS survey (Intema et al. 2017). The diagonal (solid line) is the 1:1 line. The red markers represent the six continuum sources in which polarization was most securely detected. The dashed line at 102 mJy indicates the flux density threshold used in the polarization search. |
| In the text | |
 |
Fig. 4. Process used in this paper to obtain a list of polarized sources from visibility data (see Sects. 3 and 4). |
| In the text | |
 |
Fig. 5. Absolute value of the rotation measure spread function (RMSF) corresponding to the frequency coverage of the LOFAR data used in this work. The full-width half maximum of the RMSF is δϕ ≈ 0.96 rad m−2. |
| In the text | |
 |
Fig. 6. Illustration of the different regions used in the analysis of a Faraday cube. The green cylinders represent the region searched for polarization (at Faraday depth |ϕ| < 100 rad m−2 and outside the central region that is contaminated by instrumental effects). The outer regions (100 rad m−2 < |ϕ| < 450 rad m−2) were used to characterize the noise. The images have a size of 3′ × 3′. |
| In the text | |
 |
Fig. 7. Histograms of local maxima in different regions of the Faraday cube around the polarized source J132626+473741. The histograms have been normalized to facilitate comparisons. The instrumental polarization range, as defined in Sect. 4.5.1, has been excluded from the data. The distribution of local maxima on-source and at Faraday depths |ϕ| < 100 rad m−2 shows a clear excess at larger F. |
| In the text | |
 |
Fig. 8. Characterization of the noise in the Faraday volumes of the two polarized sources, J132626+473741 (in blue, also presented in Fig. 7) and 4C+47.38 (in green). The measurements were extracted in the range of Faraday depths 100 rad m−2 ≤ |ϕ | ≤ 450 rad m−2 where no polarized signal is expected. Upper panel: histograms of local maxima. The histograms were not normalized since the two regions contain the same number of voxels. The shaded areas correspond to flux values in the top 5% of the distribution. The noise in the Faraday cube of 4C+47.38 is higher than for the other source (the histogram is broader) because the source lies at a greater distance from the center of the field. Lower panel: complementary cumulative distribution function (CCDF) for the same sources as in the first panel. The dots show the actual CCDF and the solid line is the Gaussian fit used to model the distribution at high F (calculated at CCDF(F) ≤ 10−2, as indicated by the dashed line). The horizontal solid line at CCDF = 0.05 corresponds to the lower limit of the shaded distributions in the upper panel. |
| In the text | |
 |
Fig. 9. Application of the FDR method to the 201 identified continuum sources around M 51 with two values of the false discovery rate, α (5% and 50%). Each dot shows the p-value of a source, pj. The sources have been sorted by increasing p-value. The FDR method finds the (last) intersection of this distribution and a line with the slope |
| In the text | |
 |
Fig. 10. The six sources detected in polarization in the LOFAR 150 MHz data with a 5% false discovery rate. Left and middle column: 3′ × 3′ VLA FIRST 1.4 GHz images (5″ resolution; Becker et al. 1995) and LOFAR 150 MHz images. The synthesized beams of the images are displayed in the bottom left corners. Right column: LOFAR Faraday spectra at the most highly polarized location. The contours correspond to the FWHM of the peak in polarized intensity; they were omitted when their shape was significantly affected by noise. The red and green colors are used to show Faraday spectra at two nearby locations in the same source. The grey shading around ϕ = 0 shows the region of instrumental polarization that was excluded from the analysis (Sect. 4.4). |
| In the text | |
 |
Fig. 11. Top row: same subfigures as in Fig. 2, for Source 7. The grey shading around ϕ = 0 shows the region of instrumental polarization that was excluded from the analysis (Sect. 4.4). Second row, left panel: (1′ × 1′) FIRST 1.4 GHz image of our Source 7 in grey scale and in contours (1 and 3 mJy beam−1). The red cross indicates the location of the optical counterpart to the radio core. The color scale ranges from −0.3 to 3 mJy beam−1 and the angular resolution is 5″, as indicated by the grey circle in the bottom left corner. Second row, right panel: H I integrated intensity (moment 0) image of M 51 from THINGS. The red square has a size of 1′ × 1′ and indicates the location of Source 7, the radio galaxy displayed in the previous panel. The grey scale is in Jy beam−1 M s−1. Third row, left panel: zoom of the previous image: (1′ × 1′) H I high-resolution (5.8″ × 5.5″) moment 0 image in grey scale. The yellow contours are the same radio contours of the FIRST image shown in the top left panel. Third row, right panel: measurements of the fractional polarization in the northern radio lobe of Source 7 (white circles) and the southern lobe (black squares). The dashed lines show the depolarization models that best fit the high-frequency data (JVLA 1–2 GHz, Mao et al. 2015) and the solid lines depolarization models that match the averaged 1–2 GHz measurements and the GMRT 610 MHz of Farnes et al. (2013). The LOFAR measurements are not used to constrain the models. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.











![$$\begin{equation}p_\mathrm{source}=1-[1-p_\mathrm{cell}(F_\mathrm{max}) ] ^{N_{\rm cell}},\end{equation}$$](/articles/aa/full_html/2018/09/aa32157-17/aa32157-17-eq10.gif)

