EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 614 (June 2018) A&A, 614 (2018) A85 Full HTML
Free Access
Issue
A&A
Volume 614, June 2018
Article Number A85
Number of page(s) 22
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201732302
Published online 19 June 2018

© ESO 2018

1 Introduction

The formation of galaxies supported mostly by velocity dispersion is currently thought to encompass different physical processes. The monolithic collapse model (Eggen et al. 1962) is in disagreement with compelling globular cluster observations. The scenario proposed by Searle & Zinn (1978) agrees partially with a hierarchical clustering scenario in the context of the current cosmological paradigm. Within this scenario, massive early-type galaxies (ETGs) are often assumed to be the results of massive and dry mergers (Toomre 1977; Hernquist 1993; Kauffmann 1996). While this mechanism is efficient at producing classical ellipticals, detailed photometric and spectroscopic observations report a more complex situation (Gerhard et al. 1999; Rix et al. 1999). Massive ellipticals are reported to be slow rotators, supported by velocity dispersion, while low- and intermediate-mass ETGs tend to be fast rotators and show power-law surface brightness profiles (Emsellem et al. 2007). This has been confirmed by results from ATLAS3D (Cappellari et al. 2011) where ETGs supported by rotation are seven times more frequent (Emsellem et al. 2011). The presence of discs in elliptical galaxies varies from embedded to more intermediate-scale systems (Graham et al. 2016). As ETGs tend to populate high-density regions, the interaction of galaxies with their environments is a key process which might prevent the growth of extended discs via ram pressure stripping (Gunn & Gott 1972) or “strangulation” (Larson et al. 1980), contributing to the quenching of the star formation (SF) activity. In low-density environments these effects are not expected to be efficient, and galaxies may thus follow different evolutionary paths.

As described in Kormendy (2016), there are different formation scenarios to explain the observed differences among ETGs. Dry mergers are efficient at forming dispersion-dominated galaxies. Naab (2013) stress that this scenario may be incomplete and that observations require a two-phase assembly: dissipative processes with in situ SF at high redshifts and the accretion of stars formed in other galaxies. Minor mergers with mass ratios of ~ 1:5 may lead to the formation of fast rotator ETGs (Oser et al. 2012; Gabor & Davé 2012; Lackner et al. 2012). Both major and minor mergers have also been proposed as possible quenching mechanisms in cosmological simulations (e.g. Hopkins et al. 2008). Another possible scenario is secular evolution, driven by internal dynamical instabilities or by interactions/mergers. These mechanisms lead to gas inflows and the formation of pseudobulges due to angular momentum redistribution. This process requires that a disc be previously in place (e.g. Tissera et al. 2001; Pedrosa & Tissera 2015). Indeed, several works have shown that bulges and ellipticals (spheroids in general) could have formed in several phases by mergers and secular processes in such a way that they are currently composed by multiple stellar populations (e.g. Zavala et al. 2012; Tissera 2012; Perez et al. 2013; Avila-Reese et al. 2014, and references therein). These studies find that the fraction of ex situ and in situ stars in ETGs correlates with mass: the most massive ETGs are dominated by ex situ stars from major mergers, intermediate-mass ETGs have similar fractions of ex situ and in situ stars, and less massive ETGs are dominated by in situ stars.

While the ETGs are mostly red and quiescent, there is also a fraction of blue, star-forming ETGs that host some young stellar populations. The blue, star-forming fraction increases for smaller galaxies and decreases for denser environments (e.g. Schawinski et al. 2009, 2014; Kannappan et al. 2009; Thomas et al. 2010; McIntosh et al. 2014; Vulcani et al. 2015; Lacerna et al. 2016). Kaviraj et al. (2007) studied the UV colours of ~2100 galaxies from the Sloan Digital Sky Survey (SDSS) at very low redshift and found that at least ~30% are consistent with recent SF. They found that many ETGs at z < 0.11 have 1–3% of their stellar mass younger than 1 Gyr. The origin of these younger stellar populations is still under debate. Physical mechanisms such as galaxy interactions or secular evolution could be an explanation if there is remnant gas in the galaxies. Recently, Lacerna et al. (2016) have discussed the main photometric, SF, and structural properties of elliptical galaxies from a complete SDSS subsample of isolated galaxies (the UNAM-KIAS Catalog; Hernández-Toledo et al. 2010) and compared them to those of cluster ellipticals. They find that the fraction of blue, star-forming, isolated ellipticals is only slightly higher than that found in clusters (see also Schawinski et al. 2009, 2014; Kannappan et al. 2009; Thomas et al. 2010; McIntosh et al. 2014). The fractions increase at lower masses, but they are never as high as predicted in Λ -cold dark matter (Λ -CDM)-based semi-analytical models (Kauffmann 1996; Niemi et al. 2010).

On the other hand, ETGs follow clear scaling relations. The Faber–Jackson relation (FJR; Faber & Jackson 1976) relates structural (photometric) and kinematic properties so that the luminosity increases with increasing velocity dispersion, L  ∝   σ4. However, the exponent may depend on the galaxy type and luminosity band (Kormendy & Bender 2013). The most notable relation followed by ETGs is the called the fundamental plane (FP; Faber et al. 1987; Dressler et al. 1987; Djorgovski & Davis 1987), which links the effective radius Reff , the stellar velocity dispersion σe, and the average surface brightness Σe. An unsolved issue regarding this observed relation is a tilt from the predictions of the virial theorem (Cappellari et al. 2013a). It may be related to a systematic variation in the stellar population or initial mass function (IMF; Prugniel & Simien 1996; Forbes et al. 1998) or the non-homology in the surface brightness distribution (e.g. Prugniel & Simien 1997; Graham & Colless 1997; Bertin et al. 2002; Trujillo et al. 2004) or the variation in the amount of dark matter (e.g. Renzini & Ciotti 1993; Ciotti et al. 1996; Borriello et al. 2003), among others. However, the FP is in agreement with the virial predictions if dynamical mass is used instead (Cappellari 2016). Recent studies also find that ETGs with a gaseous disc follow the Tully–Fisher relation (TFR; Tully & Fisher 1977). den Heijer et al. (2015) measured HI rotation velocities for a subsample of ETGs from the ATLAS3D sample and determined the TFR using magnitudes in the K band and stellar masses.

In this paper we analyse the main structural-dynamical relations and the stellar population properties of spheroid-dominated galaxies (SDGs) in a Λ-CDM based cosmological simulation (Pedrosa & Tissera 2015). These SDGs can be related to low- and intermediate-mass ETGs in the field. Furthermore, we compare the properties of our simulated SDGs with those of isolated ETGs (including lenticular galaxies) from the UNAM-KIAS Catalog. We also compare the global and radial stellar mass growth histories calculated from the archaeological analysis of the stellar populations with the corresponding histories inferred for ETGs from the MaNGA/SDSS-IV survey (Bundy et al. 2015) by means of the fossil record method (Ibarra-Medel et al. 2016). Our aim is to explore whether the simulated SDGs within the context of the Λ-CDM scenario are consistent with the observed field ETGs.

The results for SDGs discussed in this paper are complementary to those reported by Pedrosa & Tissera (2015), and Tissera et al. (2016a,b) regarding disc-dominated galaxies (DDGs). Simulated galaxies are identified from the same simulation and by following similar criteria. In the mentioned papers, the authors report that the simulated disc galaxies follow the size-stellar mass relation, the TFR, and that the chemical gradients are in agreement with observations. It is then relevant to analyse whether the simulated galaxies with a dominating velocity-dispersion component also satisfy observational constraints. Our findings will also be important in order to study the effects of environment on the preprocessing of physical properties as galaxies move to higher density regions. New observations are starting to provide information on dispersion-dominated galaxies in low-density environments (Ashley et al. 2017) which will be available for comparison in the near future.

This paper is organised as follows. We present our numerical simulations in Sect. 2. In Sect. 3 we characterise simulated galaxies, and mention how the morphological decomposition was made and describe the surface brightness profile of the selected ETGs. Our results are presented in Sects. 4 and 5 for the main scaling relations and colour and specific SF rate (sSFR), respectively, and in Sect. 6 we analyse stellar mass growth histories. In all cases, we compare our results with observations. Finally, a summary of our results is presented in Sect. 7. Table A.1 lists most of the acronyms and definitions used in this paper.

2 Numerical simulations

In this work we use the cosmological simulation S230D from the Fenix set analysed first by Pedrosa & Tissera (2015), which is consistent with a Λ-CDM Universe with Ωm = 0.3, Ω Λ = 0.7, Ω b =0.04, and H0 = 100 h km s-1 Mpc-1 with h = 0.7, and a normalisation of the power spectrum of σ8 = 0.9. The size of the simulated box is 14 Mpc per side. The initial condition has 2 × 2303 total particles with a mass resolution of 5.9  × 106 h−1 M⊙ and 9.1 ×105 h−1 M⊙ for the dark matter particle and initial gas particle, respectively. The maximum gravitational softening is 0.5 h−1 kpc.

The initial conditions were chosen to describe a typical region of the Universe where no massive group is present (the largest halos have virial masses smaller than ~1013 M⊙). To check the effects that the small simulated volume might have on the growth of the structure, De Rossi et al. (2013) compared the halo mass growth histories of galaxies in a simulation similar to the one used here with those estimated by Fakhouri et al. (2010) for the halos from the Millennium Simulation. This comparison showed that the growth of the simulated halos is accurately described in these simulations in the mass range of interest.

The simulation was run using GADGET-3, an updated version of GADGET-2 (Springel & Hernquist 2003; Springel 2005), optimised for massive parallel simulations of highly inhomogeneous systems. It includes treatments for metal-dependent radiative cooling, stochastic SF, and chemical and energetic supernova (SN) feedback (Scannapieco et al. 2005, 2006). The SN feedback model is capable of triggering galactic mass-loaded winds without introducing mass-scale parameters. As a consequence, galactic winds naturally adapt to the potential wells of galaxies where SF takes place. It also includes a multiphase model for the ISM that allows the coexistence of the hot diffuse phase and the cold dense gas phase (Scannapieco et al. 2006, 2008). Stars form in dense and cold gas clouds. Some of them end their lives as SNe, injecting energy and chemical elements into the ISM assuming a Salpeter IMF (Salpeter 1955). Each SN event releases 7  ×   1050 erg, which are distributed equally between the cold and hot phases surrounding the stellar progenitor. Our simulation does not include the effects of feedback from active galactic nuclei (AGNs). Previous results show that AGN feedback is expected to play an important role in the evolution of massive galaxies formed in halos with masses larger than ~1012 M⊙ (see e.g. Somerville & Davé 2015; Rosas-Guevara et al. 2016). Most of our galaxies formed in halos less massive than 1012 M⊙.

The adopted code uses the chemical evolution model developed by Mosconi et al. (2001) and adapted to GADGET-3 by Scannapieco et al. (2005). This model considers the enrichment by SNeII and SNeIa adopting the yield prescriptions of Woosley & Weaver (1995) and Iwamoto et al. (1999), respectively. A detailed description of this SN feedback model is given extensively by Scannapieco et al. (2008). It is important to stress that the SN feedback scheme does not include parameters that depend on the global properties of the given galaxy (e.g. total mass, size). Pedrosa & Tissera (2015) analysed the angular momentum content of the disc and spheroid components of galaxies in the S230D using a higher gas density threshold for SF and a lower energy per SN event than in previous experiments of this project (e.g. De Rossi et al. 2013; Pedrosa et al. 2014). They found that this combination of SF and feedback parameters produces systems that can better reproduce observational trends such as the size-mass relation and the angular momentum content (Pedrosa & Tissera 2015), the metallicity gradients of the disc components (Tissera et al. 2016a, 2017), and the chemical abundances of the circumgalactic medium (Machado et al. 2018).

The synthesised chemical elements are distributed between the cold and hot phase (80% and 20%, respectively). These values were tuned in order to provide a better description of metallicity gradients of the stellar populations and the gas-phase medium in the disc components of the galaxies (Tissera et al. 2016a,b) and the circumgalactic medium (Machado et al. 2018).

The lifetimes for SNeIa are randomly selected within the range [0.1, 1] Gyr. This model is found to nicely reproduce mean chemical trends (Jiménez et al. 2015).

3 Characterisation of simulated galaxies

We use the galaxy catalogue constructed by Pedrosa & Tissera (2015) where a friends-of-friends algorithm is applied to identify the virialised structures at z = 0 and then the SUBFIND code (Springel et al. 2001) to select 317 galaxies. For our analysis, only galaxies resolved with more than 10 000 baryonic particles within the Ropt 1 are considered. This minimum number of baryonic particles yields a subsample of 39 galaxies, with stellar masses in the range [0.27–11.6] × 1010 M⊙. The stellar masses are measured within the Ropt.

To assess the global environment inhabited by simulated galaxies, for each central galaxy we identify its neighbours within a distance of 1.5 times the virial radius and with a minimum stellar mass of ~ 4 × 108 M⊙. We find that the maximum ratio between stellar mass of the neighbours and that of the central galaxy is ~0.2. Hence, the simulated central galaxies have no close massive companions, and are consequently classified as field galaxies. Satellite galaxies will not be studied in this paper because they are expected to follow different evolutionary paths than central galaxies. In any case, there are only three satellite galaxies with more than 10 000 baryonic particles.

3.1 Morphological decomposition

We classify galaxy morphology by resorting to a dynamical decomposition, applying the method and criteria described by Tissera et al. (2012). We calculate ϵ = Jz∕Jz,max(E) for each particle, where Jz is the angular momentum component in the direction of the total angular momentum and Jz,max(E) is the maximun Jz over all particles at a given binding energy (E). We adopt the criterion that those particles with ϵ > 0.5 are associated with the disc component and the rest of them with the spheroid component. In order to discriminate between the bulge (hereafter also called the spheroid) and the stellar halo, we consider the particle binding energy so that the most bounded particles are taken to belong to the spheroid.

To classify the simulated galaxies according to morphology, the bulge-to-total stellar mass ratios (B/T) are estimated using the stellar masses of the bulge (central spheroid) and disc, defined as mentioned above. We adopt a threshold of B∕T = 0.5 to separate between spheroid-dominated (SDG) and disc-dominated (DDG) galaxies. In Fig. 1 we show a histogram of the B∕T ratios of the subsample. Those with B∕T > 0.5 (i.e. the SDGs) are analysed here. Central galaxies with B∕T < 0.5 have been studied in previous papers (Pedrosa & Tissera 2015, Tissera et al. 2016a,b). From Fig. 1 we can appreciate that all of the SGDs have a disc component, and hence that there are no pure ellipticals in this sample. This is a very important aspect to bear in mind for the comparison with observations, as discussed in Sect. 5.

After applying the morphological selection, the final sample of SDGs contains 18 objects, with stellar masses in the range [0.27 − 6.33] × 1010 M⊙, i.e. all of them are sub-Milky Way mass galaxies. The total stellar mass of the simulated galaxies is obtained by adding the stellar masses of the spheroid and disc components within Ropt. We also estimate the stellar half-mass radius, Rhm, as the radius that encloses 50% of the total stellar mass. Table 1 summarises the properties of the 18 analysed central spheroid-dominated galaxies. Although our sample is small, we carry out a detailed analysis of the dynamical and astrophysical properties which contribute to understanding the complex history of formation of these galaxies and to set constraints on the subgrid physics. This is of utmost importance, since the interpretation of the observations relies on the comparison with numerical models.

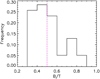thumbnail Fig. 1

Distribution of the dynamical B/T ratios for the 39 well-resolved simulated galaxies. Only those with B∕T > 0.5 (red dashed line) are classified as SDGs.

3.2 Spheroid and disc surface mass densities

For the discand spheroid components, the projected stellar-mass surface density distributions are computed. As we have dynamically separated spheroid and disc components, it is straightforward to fit a Sersic profile (Sersic 1968) to the projected surface distributions, obtaining the central surface brightness I0 , the scale radius Rb, and the Sersic index n: 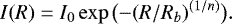I(R)=I0exp(−(R/Rb)(1/n)).\begin{equation*} I(R)=I_{0}\exp{\big({-(R/R_{b})^{(1/n)}}\big)}.\end{equation*}(1)

For our analysis the projected stellar-mass surface density is considered a proxy of the luminosity surface brightness (equivalent to adopting a mass-to-light ratio M∕L = 1, which is close to observations for optical-infrared bands). When n = 1, the Eq. (1) recovers the exponential profile that is fitted to the stellar-mass surface density of the disc components, obtaining in this way the scale length Rd (Table 1).

For the spheroid component, the surface density profiles are fitted within the radial range defined by the gravitational softening and the radius that encloses 90% of the total spheroid mass. In the case of the disc component, the fit is performed within the latter and Ropt.

In Appendix B, Fig. B.1 shows the synthetic images of the 18 SDGs, the distributions of ϵ, and the projected surface density for the spheroid and disc components, and the corresponding best-fitted profiles. We also include the projected density profiles of those particles supported by rotation but coexisting with the spheroid. As can be seen, these particles determine a variety of surface density profiles: some SDGs have discs which continue exponentially to the central part (e.g. SDG 897), while others get flatter (e.g. SDG 925) or change the profiles to merge with that of the spheroid components (e.g. SDG 790). As mentioned before, with different degrees of importance, all the SDGs have a disc components. In this figure we also include the observability radius2. As can be seen in all cases, the disc components are below the observability threshold. This is also seen in the right panels of Fig. B.1, where the horizontal dotted lines indicate the stellar surface density of the given galaxy corresponding to the observability radius. Most of the external discs of the simulated galaxies would not be observed in the SDSS galaxy images. In particular, as can be seen from Fig. B.1, SDG 288 also has spiral arms. According to the morphological classification of Sandage (1961), this galaxy might not be an ETG. However, according to the dynamical B/T ratio (0.74 in this case), the disc components represents a small fraction of the total stellar mass (i.e. the disc is a tenuous extended rotating system).

As mentioned above, the inner discs that coexist with the spheroids have stellar-mass surface density profiles that behave differently. Some of them follow the exponential profiles of the discs determining a unique exponential profile, while others break off either to follow the spheroid profiles or to set a new flatter trend. We detect that 3 out of the 18 analysed SDGs have discs with stellar-mass surface density profiles following those of the spheroid components. These spheroids have n ~ 2–3.

In order to quantify the relative importance of the inner discs with respect to the spheroid components (i.e. defined by the dispersion-dominated stars), we calculate the stellar mass fraction, Frot , of stars with ϵ > 0.5 and with binding energies low enough to be classified as part of the spheroid component. This fraction is a measure of the rotating component embedded in the spheroid region. As can be seen from Fig. 2, a clear correlation between Frot and B/T is found with a Spearman correlation coefficient of − 0.77 (p = 0.0002). Figure 2 shows that those systems which overall are more dominated by the spheroid component have a smaller contribution of an inner rotating disc. We note that the dispersion is significant, particularly for those SDGs with B∕T ~ 0.5–0.6, where Frot can vary between ~0.2 and ~0.5, reflecting very different dynamical assembly histories.

The significant variations in the morphologies and the spheroid (bulge)–disc coexistence are the result of the different formation histories. In the following sections, we study these features and to what extent they are able to reproduce observed properties of SDGs.

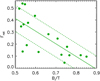thumbnail Fig. 2

Stellar-mass fractions of the discs that coexist with the spheroidal components as a function of the fraction B/T. A linear regression fit is included (green solid line) along with its 1σ dispersion (green dashed lines).

3.3 Spheroid Sersic index versus B∕T

As shown in Fig. 3, a correlation is detected between the dynamical B∕T ratio and the Sersic index. The Spearman correlation coefficient obtained is 0.63 (p = 0.01), implying that the trend is statistically significant, albeit with a large dispersion. A linear regression yields a slope of 5.72± 1.89 and an intercept of − 1.99 ± 1.13. The errors are calculated by a bootstrap method. The simulated B/T ratios are in a range of values associated with elliptical and lenticular (S0) galaxies. In particular, ~50% could be classified as S0 galaxies. Hereafter, we refer to them as spheroidal-dominated systems for the sake of simplicity and because the spheroidal component is always the more massive one. On the other hand, we note that if the stellar mass of the disc coexisting with the spheroid (Frot, see Fig. 2) is assigned to the spheroid (as probably done in the photometric bulge/disc decompositions), then the B/T ratios of the simulated galaxies is larger than shown in Figs. 1 and 2.

It has also been claimed that the structural Sersic index, n, is able to distinguish between classical bulges and pseudo-bulges, being n ~ 2 the value that separates these two types (e.g. Tonini et al. 2016; Fisher & Drory 2008; Combes 2009). Not only does this parameter change for the classical and pseudo-bulges, but also many other galaxy properties such as colour, sSFR, rotational support, and kinematics (see Kormendy 2016, for a recent review). From Fig. 3, we can see that half of our SDGs have n ≤2. These changes and the presence of a disc component inside the spheroids (see above) suggest that the simulated spheroids (bulges) are composite stellar systems formed by the action of different formation channels such as mergers, interactions, or local instabilities (De Lucia et al. 2010; Zavala et al. 2012; Perez et al. 2013, see also Tissera et al. 2017). The extended discs could grow because our SDGs inhabit low-density environments. In higher density regions, these discs would be prevented from growing or surviving by a higher impact of ram pressure stripping or strangulation.

Table 1

Main properties of simulated SDGs.

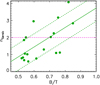thumbnail Fig. 3

Spheroid Sersic index obtained for the simulated SDGs as a function of their dynamical B/T mass ratios. The green solid and dashed lines represent the best linear regression fit and the 1σ dispersion. The magenta dashed line denotes n = 2, which is often assumed to be the limit between classical and pseudo-bulges.

4 Scaling relations

In this section, we analyse the size-mass relation, the FJR, the FP, and the TFR determined for the simulated SDGs. It is important to analyse these relations since none of them has been used to set the parameters of the subgrid physics modelling, and the degree of agreement (or disagreement) thus provides important clues for improving the models. In all figures in this section, simulated galaxies are distinguished according to the B/T ratio. However, the global relations are calculated over the whole sample in order to have a better statistical estimation.

Since our simulated galaxies are dynamically dominated by the velocity dispersion components, we resort to the samples of observed ETGs from the ATLAS3D Project (Cappellari et al. 2011, 2013a) and ETGs with HI disc components identified from the ATLAS3D survey by den Heijer et al. (2015). The presence of these discs allows rotation velocities to be measured accurately. We compile a clean ATLAS3D sample by excluding those galaxies that belong to the Virgo cluster since our SDGs are field systems. The clean ATLAS3D sample is compared with simulated trends when appropiate.

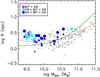thumbnail Fig. 4

Mass-size relation estimated for the simulated SDGs (Rhm, big circles, and Reff, small circles, both coloured according to the dynamical B/T ratios), ETGs from the clean ATLAS3D sample (black crosses), and the observed relations reported by Mosleh et al. (2013; green solid line) and Bernardi et al. (2014; red dashed line) for ETGs.

4.1 Size-mass relation

One of the fundamental scaling relations is the size-mass relation (e.g. Mosleh et al. 2013; Bernardi et al. 2014). To check that our SDGs satisfy this observed relation, we first use the Rhm , which in simulations is straightforward to measure (see above). Observationally, this radius is commonly estimated from an infrared surface brightness profile down to a given aperture (in the infrared the mass-to-light ratio is close to 1) or by fitting a given law to the profile and extrapolating this law to calculate the total galaxy light. Applying a similar procedure, we then define the effective radius Reff. To better compare these data with observations, we use the Sersic profiles fitted to the total surface density obtained by combining the disc and spheroid components within Ropt. Then, Reff is calculated by applying the well-known relation (e.g. Sáiz et al. 2001) 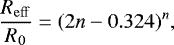ReffR0=(2n−0.324)n,\begin{equation*} \frac{R_{\mathrm{eff}}}{R_{0}}=(2n-0.324)^n,\end{equation*}(2)

which links scale lengths and the Sersic index; R0 is the scale length of the Sersic profile fitted as mentioned above.

To compare the simulations with observations, we use the results reported by Mosleh et al. (2013) and Bernardi et al. (2014) for ETGs. Mosleh et al. (2013) have adopted the functional form to relate stellar mass (MStar) and size for spiral galaxies given by Shen et al. (2003) 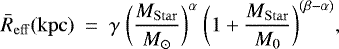R¯eff(kpc) = γ (MStarM⊙)α (1+MStarM0)(β−α),\begin{equation*} \bar{R}_{\mathrm{eff}}(\mathrm{kpc}) \ = \ \gamma \ \bigg( \frac{M_{\mathrm{Star}}}{M_{\odot}} \bigg)^{\alpha} \ \bigg(1&#x002B;\frac{M_{\mathrm{Star}}}{M_{0}} \bigg)^{(\beta - \alpha)},\end{equation*}(3)

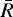where R¯$\bar{R}$ is the median of the log-normal distribution of Reff (in kpc) in stellar mass bins. Mosleh et al. (2013) study a sample selected from the Max-Planck-Institute for Astrophysics (MPA)–Johns Hopkins University (JHU) SDSS (Kauffmann et al. 2003; Salim et al. 2007). The fitted parameters (α, β, γ, M0) vary with morphology, colour, or sSFR. We take those corresponding to ETGs (Table 1 in Mosleh et al. 2013).

Bernardi et al. (2014) also find that the size-mass relation depends on morphology using the SDSS DR7. They calculate Reff from different fits to the surface brightness profiles finding 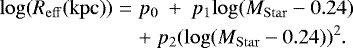log(Reff(kpc))=p0 + p1log(MStar−0.24)+ p2(log(MStar−0.24))2. \begin{eqnarray*} \mathrm{log}(R_{\mathrm{eff}} {\mathrm{(kpc)}}) & =& p_0 \ &#x002B; \ p_1 \mathrm{log}( M_{\mathrm{Star}}-0.24) \nonumber\\ && &#x002B; \ p_2 (\mathrm{log}(M_{\mathrm{Star}}-0.24))^2.\end{eqnarray*}(4)

From Bernardi et al. (2014) we take the case of a single-Sersic profile fit for ETGs (their Table 4). A correction from Chabrier (Chabrier 2003) IMF to Salpeter (Salpeter 1955) is applied.

Finally, we also compare the simulated trends with the ETGs from the clean ATLAS3D sample. Thestellar masses are calculated from the luminosities given in Table 1 in Cappellari et al. (2013a), using the mass-to-light ratios from Table 1 in Cappellari et al. (2013b) for a Salpeter IMF.

In Fig. 4, we show the comparison between the simulated SDGs and the above-described observational estimates. As can be seen the simulated SDGs have Reff in reasonably good agreement with observations, whereas the Rhm are slightly larger (~ 0.2 dex), especially at lower masses. It is possible that these characteristic radii of our simulated SDGs are indeed slightly larger than those of observed ETGs, due to the presence of extended discs in all of the simulated galaxies.

Hence, overall the simulated mass-size relations of the ETGs are in good agreement with observations. We note that Pedrosa & Tissera (2015) reported that the sizes of the DDGs are also in reasonable agreement with observations. These findings suggest that the adopted SN feedback model is able to reproduce the mass-size relations of both types of galaxies without resorting to any fine-tuning.

thumbnail Fig. 5

Faber–Jackson relation for the simulated SDGs (filled circles, coloured according to the dynamical B/T ratios) estimated by using σ0 (left panel) or σe (right panel). For comparison, the corresponding relations obtained from the clean ATLAS3D sample are included (see Sect. 4). The linear regression to the simulated data (green solid lines) and observational data (black dashed lines) are depicted for comparison.

4.2 Faber–Jackson relation

The FJR (Faber & Jackson 1976) relates the luminosity and the central velocity dispersion so that 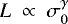L ∝ σ0γ$ L\ \propto \ \sigma_{0}^{\gamma}$, where γ is a constant. We use the dynamical masses instead of luminosities. For the simulated SDGs, the central velocity dispersion (σ0) is calculated within 1.5 h−1 kpc (corresponding to three gravitational softening radii) and the dynamical masses at Rhm. For galaxies in the clean ATLAS3D sample, the dynamical masses are estimated by following Cappellari et al. (2013a): MJAM ≈ 2 × M1∕2, where M1∕2 is the total mass within a sphere enclosing half of the galaxy light. To make the conversion to mass, the mass-to-light ratios provided by Cappellari et al. (2013a) are adopted. We also explore whether the same relation holds when the central velocity dispersion is replaced by the velocity dispersion calculated within Reff (σe).

Figure 5 shows both the observational and the simulated FJRs obtained by using σ0 (left panel) or σe (right panel). The linear regression for the simulated SDGs yields 0.40 ± 0.05 for both slopes. The errors are calculated via a bootstrap method. Similar linear regression fits to relations defined by the clean ATLAS3D galaxies yield 0.36 ± 0.01 and 0.33 ± 0.01 respectively.Hence, the simulated SDGs follow a FJR in agreement with observations within one standard deviation. No clear dependence is found on the dynamical B/T ratio as can be seen from this figure. We note, however, that our galaxy sample is too small to be able to see a robust trend on this point.

4.3 Fundamental plane

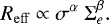
The FP (Dressler et al. 1987; Djorgovski & Davis 1987; Faber et al. 1987) relates the size (Reff) with the surface density (Σe) and velocity dispersion (σ): Reff∝σα Σeβ.\begin{equation*} R_{\mathrm{eff}} \propto \sigma^{\alpha} \ \mathrm{\Sigma}_{e}^{\beta}.\end{equation*}

The surface brightness given by the data available in Table 1 in Cappellari et al. (2013a) is transformed into mass surface densities by adopting M∕L = 1 (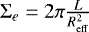Σe=2πLReff2$ \mathrm{\Sigma}_{e}= 2 \pi\frac{L}{R_{\mathrm{eff}}^2} $). Similarly to the FJR, the FP is estimated for σe and σ0.

In Fig. 6 we compare the simulated FP obtained using our clean ATLAS3D sample. For this sample, using σe for the fit, α = 0.92 and β =−0.69 (left panel) for the observed data. When fitting using σ0, α =0.87, and β =−0.66 (right panel). The black line corresponds to the one-to-one relation (y = x). As can be seen, the simulated FP (green lines) is within one standard deviation of the observed relation.

As is well-known, ETGs tend to show a tilt in the FP with respect to the value derived assuming virialisation (Binney & Tremaine 1987). Its origin is still under debate and there are a variety of possible causes such as a variable or non-homologous IMF (Prugniel & Simien 1996; Forbes et al. 1998), dependence on dark matter halo features caused by the non-linear assembly of the structure, among others. However, the FP obtained by using dynamical masses is consistent with the predictions from the virial theorem (Cappellari 2016).

thumbnail Fig. 6

Fundamental plane for the simulated SDGs calculated with the parameters estimated for our clean ATLAS3D sample. The black line denotes the one-to-one relation and the green line shows the best fit to our simulated SDGs (solid circles, coloured according to the dynamical B/T ratios). The rms is 0.19 and 0.18 for the least squares regression (dashed green lines) when considering velocity dispersion within Reff and central velocity dispersion, respectively, and the corresponding regression for the one-to-one relation (rms = 0.19 for both cases) is shown by dotted black lines.

4.4 Tully–Fisher relation

Although ETGs are dominated by a velocity dispersion component, a rotating disc is also frequently detected through cold or ionised gas observations. Emsellem et al. (2011) report most of the ETGs in the ATLAS3D sample as fast rotators. In particular, den Heijer et al. (2015) study the TFR for 16 ETGs from the ATLAS3D survey using an extended HI-component which determines a disc component. In this work, the rotation velocity is measured at very large radius (on average, within R∕Reff = 7.3). We comparethis sample with the simulated TFR. For consistency with our previous comparison, a galaxy that belongs to the Virgo cluster has been excluded.

We determine the stellar and baryonic TFRs for our simulated SDGs and fit a relation of the form log (Mi) = a (log(W) − 2.6) + b, where i represents the stellar or the baryonic mass and W is twice the rotational velocity V calculated at twice Ropt. The stellar and baryonic masses are determined within Ropt. The estimation of stellar masses for the sample of den Heijer et al. (2015, Table 1) is done in the same way as in Sect. 4.1 by using r-band mass-to-light ratios, i.e. their star formation history (SFH) case. The baryonic masses are calculated as the sum of stellar mass and HI mass multiplied by a factor of 1.4 to take into account helium and metals (den Heijer et al. 2015).

In Fig. 7 (left panel) we show the stellar TFR. In this case, the linear regression yields a = 3.81 ± 0.20 and b = 10.70 ± 0.04 for the simulated SDGs. This is steeper than that reported by den Heijer et al. (2015) (a = 2.40 ± 0.50 and 10.72 ± 0.06), but within the scatter and uncertainties involved in the stellar mass determination of the observations and in agreement with the TFR for spiral galaxies. For disc galaxies, it is known that the slope of stellar TFR is steeper than that of the baryonic TFR, and the scatter of the former is smaller than that of the latter (e.g. Avila-Reese et al. 2008). These trends are followed by our simulated SDGs. Our simulated stellar TFR is also in agreement with results from the cosmological EAGLE simulation (Ferrero et al. 2017).

Similarly, Fig. 7 (right panel) shows the baryonic TFR for the simulated SDGs and that reported in den Heijer et al. (2015). The best fitting parameters for the simulated relation are a = 2.95 ± 0.31 and b = 10.81 ± 0.08, which are in agreement with the observed values within the estimated errors. In particular, the unconstrained observed TFR (i.e. when they calculate the parameters without fixing any of them), where the baryonic mass is calculated with SFH, yields a slope of a = 2.51 ± 0.42 and zero-point of b = 10.71 ± 0.05.

For comparison, in Fig. 7 we include the subsample of simulated DDGs with more than 10000 baryonic particles (black filled circles). Both the SDGs and DDGs follow roughly similar stellar and baryonic TFRs, although disc-dominated galaxies seem to determine a slightly flatter relation in the former case. This might be caused by the action of the SN feedback which is more efficient for lower stellar mass galaxies in the velocity range where most of the SDGs are (De Rossi et al. 2010).

Overall, the main structural and dynamical relations of our simulated SDGs are in reasonably good agreement with those reported for observed ETGs. This is an encouraging result, considering that none of these relations has been fine tuned to be reproduced as mentioned before.

4.5 Darkmatter fraction as a function of stellar mass

A key prediction of the Λ-CDM scenario is that galaxies are embedded in dark matter halos. However, it is not yet clear what the fraction of dark matter within ETGs is. Thanks to integral field spectroscopy studies, like those performed in the ATLAS3D survey, estimations of Fdm = Mdm∕Mdyn are now possible for ETGs (Cappellari et al. 2013b).

In Fig. 8, the Fdm measured for our SDGs at Rhm and Reff are plotted. Since Fdm increases with the radius, the values of Fdm are higher for Rhm than for Reff. For both definitions of Fdm the smaller the galaxy, the larger the dark matter fraction. This trend is in agreement with the dynamical inference for the ATLAS3D survey (Cappellari et al. 2013a), as shown in Fig. 8 (for the observed values we have used the stellar masses calculated in Sect. 4.1). The agreement with the observational inferences is reasonable. However, none of the simulated SDGs has values of Fdm(< Reff) smaller than 0.15, while many of the ATLAS3D ETGs have these values. These are galaxies dominated by baryons and should be very compact in the centre, with high surface densities. The presence of discs in all of our SDGs make them likely less compact.

thumbnail Fig. 7

Stellar (left panel) and baryonic (right panel) TFRs for the simulated SDGs (filled circles coloured according to the dynamical B/T ratio) and DDGs (black solid circles), and the observed values reported by den Heijer et al. (2015) for ETGs with extended disc components (black crosses). The linear regression for simulated SDGs (green lines) are shown; the rms dispersions are also shown (dashed lines).
thumbnail Fig. 8

Dark matter fraction, Fdm = Mdm∕Mdyn, within Rhm (big solid circles) and Reff (small solid circles), both coloured according to the dynamical B/T ratios as a function of stellar mass for the simulated SDGs. The crosses are dynamical estimates for the ATLAS3D ETGs (Cappellari et al. 2013a,b).

5 Galaxy colours and specific star formation activity

In this section, we focus on the analysis of the SF activity and the galaxy colours of the simulated SDGs. Integrated magnitudes and colours are computed from the resulting fully integrated spectral energy distribution (SED) of each galaxy, based on its age, mass, and metallicity (for more details see Appendix B). We compare our data with the sample of ETGs (elliptical and lenticular) from the UNAM-KIAS Catalog of Isolated Galaxies (Hernández-Toledo et al. 2010) selected from DR5 SDSS under strict isolation criteria. Lacerna et al. (2016) have studied in detail a subsample of pure elliptical galaxies from the UNAM-KIAS Catalog (see more details therein).

In Fig. 9 (left panel) the g − i colours are plotted against MStar. As can be seen, the simulated SDGs occupy a range of stellar masses shifted to lower masses with respect to the bulk of the observations, but in the mass interval where they overlap the simulated galaxies are clearly bluer than the observed ones. The black line separates blue and red galaxies according to a relation presented in Lacerna et al. (2014), g−i=0.16 [log(MStar)−10.56]+1.05,\begin{equation*}g-i= 0.16 \ [\mathrm{log}(M_{\mathrm{Star}})-10.56]&#x002B;1.05 , \end{equation*}(5)

where MStar is in units of M⊙, and the masses were corrected to a Salpeter IMF (Salpeter 1955). All the simulated SDGs lie on the blue side of the g − i versus MStar relation, while most of the observed isolated pure ETGs are in the red sequence. In particular, only 20% of these observed galaxies in the same mass range (approximately [109.4, 1010.8] M⊙) are blue. The blue colours of simulated SDGs are consistent with a more important contribution of young stellar populations.

To investigate the SF activity of the simulated galaxies and the relation with the colour distributions, we calculated the SFR by using stars younger than 1 Gyr. This SFR is not an “instantaneous” measure of the activity, but we choose it because it is less affected by numerical noise than measures using lower ages given that most of the SDGs have low values of SFR at z = 0.

In Fig. 9 (right panel), we plot sSFR (= SFR/MStar), as a function of MStar. The black line separates passive and star-forming galaxies according to Lacerna et al. (2014), log(sSFR)=−0.65 [log(MStar)−10.56]−10.94,\begin{equation*}\mathrm{log}(\mathrm{sSFR})=-0.65 \ [\mathrm{log}(M_{\mathrm{Star}})-10.56]-10.94 , \end{equation*}(6)

where MStar is in units of M⊙ and sSFR in units of yr−1 (corrected for Salpeter IMF). There are 6 out of 18 SDGs (~33%) in the star-forming region, while the rest are below the demarcation line and follow the same trend. With respect to the isolated ETGs from the observations (Hernández-Toledo et al. 2010), our simulated SDGs are about ~0.5–1 dex more active.The six star-forming SDGs are highlighted with a blue open square in this figure and in the following ones. As can be seen in both panels of Fig. 9, the fraction of simulated blue star-forming SDGs is higher than the observed fraction for isolated ETGs (33% vs. 14% in the same mass range).

thumbnail Fig. 9

Colours and sSFRs as a function of the MStar (left and right panels, respectively) for the simulated SDGs (filled circles coloured according to the dynamical B∕T ratios). Observational results for isolated ETGs (black asterisks; Hernández-Toledo et al. 2010) are included. In the left panel, blue and red galaxies are separated by the black line reported by Lacerna et al. (2014), while in the right panel the black line depicts the limit between star-forming and passive galaxies (Lacerna et al. 2014). Galaxies that are blue and star-forming at the same time are marked with black open squares.
thumbnail Fig. 10

Properties of the spheroid (red circles) and disc (blue circles) components: g–i (top panel) and sSFR (bottom panel) as a function of MStar. For comparison, we include the same observations as in Fig. 9 (black asterisks). We depict blue star-forming galactic objects as black open squares, and the limiting lines reported by Lacerna et al. (2014) between red and blue galaxies in the bottom panel, and between star-forming and non-star-forming galaxies in the top panel.

5.1 Properties of spheroids and discs

Because each simulated SDG has been decomposed dynamically into a spheroid and a disc component, similar estimations of colours and sSFRs as presented above can be performed for each of these components. In particular, we explore whether the colours and sSFR of the spheroids would agree more closely with observations.

In Fig. 10 we show the sSFR and g–i colour as a function of the stellar mass for the disc and spheroid components. The differences between the two components are evident. The disc components of the simulated SDGs are nearly all blue according to Lacerna et al. (2014) and with high sSFR (there are only two red discs and both of them are passive), whereas the spheroid components show redder colours and much lower sSFR values, as we expected. We find ~39% of the spheroids are red and ~94% are quiescent. In the mass range in common with the observations, [109.4, 1010.8] M⊙, ~50% of the spheroids are red and all are quiescent (except only one which is just above the limit). Therefore, comparing these fractions with those of observed isolated ETGs in the mentioned mass range, we find that the SF activity of the spheroids are in rough agreement. However the colours of the simulated spheroids are still bluer than observations (~80%).

As expected, the disc components form stars more actively than the spheroids. This can be quantified by estimating the fraction of young stars.In Fig. 11 we show the distribution of the fraction of stars younger than 3 Gyr as a function of g − i for the spheroid and disc components. It is clear that most spheroids have no recent SF, while the discs show the opposite, i.e. that most of them have experienced more recent active episodes, except a single disc which does not have stars younger than 3 Gyr (not shown in Fig. 11). A similar trend is found when a 2 Gyr threshold is adopted instead. In Table 2 the fractions of young stars using different age thresholds are given. The colours of the spheroids are not as red as expected and this is due to the presence of an intermediate-age stellar population of about 3–4 Gyr old that, although small, it is enough to make colours bluish.

We can also estimate the average ages of the stars in the spheroid and disc components of the simulated SDGs. Figure 12 shows these distributions. As expected, the disc components are younger (horizontal lines correspond to each group average age) than the spheroids: ~6.7 Gyr compared to ~8.5 Gyr. There is no clear dependence of the mean ages on the stellar mass in agreement with the results reported by Lacerna et al. (2016).

Our findings show that the simulation produces field SDGs which are globally bluer and more star-forming than observed isolated ETGs, mainly due to the persistence of a disc component in all of them. We note, however, that even for the spheroid components the simulations show a trend where an excess of blue systems is formed, with a significant fraction of intermediate-age stellar populations. Some extra mechanisms for avoiding further disc growth and/or efficiently quenching SF seem to be necessary. For our most massive simulated galaxies, the inclusion of AGN feedback could work in this direction. Simulations of massive galaxies with AGN feedback have shown that the SF rate is reduced whilst this feedback is active (e.g. Khalatyan et al. 2008; Grand et al. 2017). As a result, the galaxies end with a lower fraction of intermediate-age stars that are redder than when AGN feedback is not included. Dubois et al. (2013) have shown that in the absence of AGN feedback, a large number of stars accumulate in the central galaxies to form overly massive, blue, compact, and rotation-dominated galaxies; instead, when AGN feedback is included, these blue massive LTGs turn into red ETGs. However, Newton & Kay (2013) and Park et al. (2017) have explicitly shown that the reduction in SF is significant only for merging galaxies (which is common for massive halos), mainly because the AGN feedback heats the gas and prevents the formation of a new disc, eliminating the possibility of a SF burst that would otherwise happen. For Milky Way-sized galaxies without mergers or with minor mergers, the effect of AGN feedback is minor for the SFH. All analysed galaxies are sub-Milky Way systems, so the effects of AGN feedback is expected to be minor.

Table 2

Fraction of young stars in the spheroid and disc components.

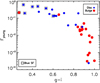thumbnail Fig. 11

Fraction of stars younger than 3 Gyr as a function of the g–i for the spheroid (large red circles) and disc (small blue circles) components. We also depict blue star-forming galaxies with open black squares.
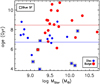thumbnail Fig. 12

Average mass-weighted ages of the stellar populations in the spheroid (large red circles) and disc (small blue circles) components of the SDGs. The horizontal lines represent the average ages of all spheroids (red) and discs (blue).
thumbnail Fig. 13

Normalised MGHs estimated in three radial intervals of our 18 SDGs, in order of descending stellar masses (from left to right and from top to bottom). In each panel, the nSersic parameter and the dynamical B/T ratio are also included.
thumbnail Fig. 14

Average global and radial normalised MGH for our simulations (top) and MaNGA ETGs at z < 0.037 (bottom). We make the division between low (left panels) and high (right panels) stellar mass, adopting log (MStar) = 9.9 as a threshold. Radial bins of [0–0.5], [0.5–1.0], and [1.0–1.5] Rhm are represented by solid, dashed, and dotted lines, respectively.

6 Stellar mass growth histories

In this section, we analyse the global and radial “archaeological” mass growth histories (MGHs) of the simulated SDGs. This study provides clues to the galaxy assembly in a cosmological framework and allows a direct comparison with observational findings obtained from integral field spectroscopy. Ibarra-Medel et al. (2016) have analysed galaxies over a wide mass range from the first data release of the Mapping Near Galaxies at APO (MaNGA; Bundy et al. 2015; Albareti et al. 2017) survey from SDSS-IV (Blanton et al. 2017). These authors confirm that the global MGHs significantly depend on stellar mass: the more massive the system, the earlier their stars formed on average (downsizing). They have also found that the way galaxies radially grow their stellar masses depends significantly on galaxy morphology, sSFR, or colour. Regarding ETGs, Ibarra-Medel et al. (2016) have found that for a given mass they assemble earlier than late-type galaxies, but also follow a clear downsizing trend. The radial MGHs of ETGs are more homogeneous than those of late-type galaxies (LTGs). On average, the radial MGHs tend to follow a weak inside-out behaviour, but individually there are many cases where the outer regions can be younger than the innermost ones, suggesting either an outside-in assembly at some epochs or processes of global stellar migration from inside to outside. Paths involving inside-out or outside-in scenarios have been reported (e.g. Sánchez-Blázquez et al. 2007). Currently, the formation of spheroidal systems is expected to be a complex process as different mechanisms can contribute, such as gas collapse and infall, mergers, and internal dynamical processes (for recent reviews, see e.g. Brooks & Christensen 2016; Kormendy 2016).

Ibarra-Medel et al. (2016) analysed 454 galaxies at z < 0.037. The global MGHs and those in radial bins were normalised to their corresponding final masses at z = 0.037 (look-back time of ~0.5 Gyr); fixing the same final epoch for all galaxies is necessary for calculating the mean MGHs. They explore the dominant direction of mass growth as a function of mass or morphology.

We perform a similar archaeological analysis of our SDGs to that of Ibarra-Medel et al. (2016). The age distribution of the stellar particles at z = 0 is used to construct the MGHs. In Fig. 13 the normalised MGHs in three radial bins for the analysed galaxies are plotted. The radial bins are defined at [0–0.5], [0.5–1.0], and [1.0–1.5] Rhm. The panels are in order of decreasing total stellar masses (from left to right and from top to bottom).

As can be seen in Fig. 13, most of systems experience periods of fast growth in the cumulative mass distributions associated with mergers and starbursts. The rates of growth are quite different among the SDGs, with weak dependence on mass. In general, our SDGs show an inside-out formation mode although there is a large variety of behaviours when looked at in detail. Some systems exhibit a combination of modes in their radial MGHs (e.g. SDG 735, SDG 885, SDG 925), while a few galaxies show a clear outside-in mode (e.g. SDG 904).

In Fig. 14 we plot the average global and radial MGHs of the simulated SDGs (upper panels) and the MaNGA ETGs (E/S0; lower panels) in two mass ranges. In this case, the MGHs are normalised and start at a look-back time of 0.5 Gyr (see above). The average radial MGHs of the more massive SDGs attain 70% of their masses at look-back times ≈ 8, 7, and 6 Gyr for the inner, intermediate, middle and outer radial bins, respectively, while for the less massive SDGs this happens at 6.2, 6.4, and 6.1 Gyr, respectively. The radial MGHs show an average trend of inside-out growth mode, though very moderate. For the massive SDGs, the outer MGHs (dotted line) are shifted to later times with respect to the inner MGHs. For the less massive SDGs, this happens only at late times.

The global average MGHs (insets in Fig. 14) of the simulated SDGs are shifted to later times with respect to those inferred from observations, in particular at the earliest epochs. As discussed in Ibarra-Medel et al. (2016), the fossil record determinations for the oldest ages are very uncertain (see horizontal error bars in the lower panels) and likely bias the stellar population ages to even older values. Both observations and simulations show evidence of mass downsizing, but for the latter the trend is weaker. Regarding the radial MGHs, the simulated galaxies show evidence of a more pronounced inside-out growth mode than observations.

In summary, the simulated SDGs tend to form their stellar populations slightly later and with an inside-out radial growth mode slightly more pronounced than the inferences obtained from the fossil record method applied to MaNGA ETGs. This is in line with the fact that our SDGs are on average bluer and more star-forming than observed isolated ETGs (see previous section). We also note that all the simulated SDGs present a disc component. The SDGs with log (MStar) ≲ 10 are gas-rich galaxies with a mean gas fraction of 34% within the optical radius. More massive galaxies show gas fractions around 18%. These gas fractions are more typical of LTGs (e.g. Calette et al. 2018). The larger gas fractions can account for a more active SF activity. In a previous work, De Rossi et al. (2013) find that the SN feedback adopted in this simulation is able to regulate the SF activity in galaxies with rotational velocity smaller than ~100 km s−1 so that these systems reach an equilibrium point where the SN feedback produced by a mild SFR is enough to keep the gas turbulent and warm and at the same time allows the SF to be fed smoothly. Observational constraints on the gas fraction andthe SFH of ETGs galaxies in this stellar mass range would be important to further improve the SN feedback models.

7 Conclusions

We have analysed the properties of simulated galaxies dominated by the spheroid components in a Λ -CDM Universe with the aim to investigate to what extent these systems are consistent with the observations. In previous works, the dynamical and chemical properties of disc-dominated galaxies have been studied in great detail, finding very good agreement with observations (Pedrosa & Tissera 2015; Tissera et al. 2016a,b, 2017). Since the evolutionary paths of spheroid-dominated galaxies are expected to be different, it is of relevance to assess to what extent the same models and simulations reproduce the two kinds of systems.

After identifying the velocity dispersion-dominated spheroid and the rotation-dominated disc by means of a dynamical criterion, we classify our simulated (field) galaxies as SDGs as those with B∕T > 0.5. We notice that all our SDGs actually have an extended disc component, although all of them are found to be below the SDSS observability limit, and that an inner disc component coexists with a spheroid. It is important to keep in mind these particularities when explaining the differences between observed galaxies and our simulations. The main results from our analysis are as follows:

  • (i)

    The values of the spheroid Sersic index increases on average with the dynamical B/T, in agreement with observational results (e.g. Fisher & Drory 2008).

  • (ii)

    The sizes of the simulated SDGs as a function of MStar are consistent with observational determinations. We measure both Rhm directly from the simulation and Reff from the Sersic fits to the whole galaxy. While the former radii are slightly larger (~0.2 dex) than the observational estimates, specially at low masses, the latter agree with them.

  • (iii)

    The dynamical relations of our SDGs are in reasonable agreement with observational results for ETGs. The FJR defined as the correlation between σ (central or at Rhm) and the dynamical mass at Rhm has a slope of ~0.4, in good agreement with the ATLAS3D ETGs (Cappellari et al. 2013a). SDGs also exhibit a tilt in the FP consistent with these observations. The stellar and baryonic TFRs calculated from the disc components are consistent with the corresponding relations determined for a small subsample of ATLAS3D ETGs, those that present an extended HI disc (den Heijer et al. 2015). Interestingly enough, the TFRs of the SDGs are similar to the TFRs of the DDGs.

  • (iv)

    The Fdm measured at Reff increases for smaller SDGs, a trend also seen in the observational inferences from the ATLAS3D ETGs (Cappellari et al. 2013a,b). The simulated values of Fdm and their dependence on mass are consistent with the observational inferences, but none of the simulated SDGs attains values below 0.15.

  • (v)

    Our SDGs are significantly bluer and with higher values of sSFR than the observed isolated ETGs in the same mass range. This is partially due to the persistence of extended discs in the simulations, which tend to have young stellar populations. Part of the disc coexists with the spheroidal component. Only a few discs (5/18) have fractions of young stars (<3 Gyr) smaller than 5%, while this fraction is smaller than 5% for most of the spheroids (16/18). The average mass-weighted stellar ages of the spheroids is ~8.5 Gyr, while for discs the average is ~6.7 Gyr, though the scatter is quite large. The colours and sSFR values of the spheroid components are then closer to those observed for isolated ETGs.

  • (vi)

    The archaeological radial MGHs of our SDGs are on average dominated by a moderate inside-out growth mode, though some galaxies present periods of outside-in and inside-out modes, and two are dominated by the outside-in growth mode. Compared to the fossil record inferences applied to the observed MaNGA ETGs, the simulated SDGs form on average their stellar populations later and with an inside-out radial growth mode which is slightly more prominent. Larger stellar-mass galaxies are predicted to assemble on average at earlier times than the less massive ones (downsizing), but the differences are smaller than for observations.

We conclude that cosmological simulations in the context of the Λ -CDM hierarchical scenario are able to produce isolated galaxies dominated by spheroids with structural and dynamical properties in good agreement with observations. This is encouraging since the subgrid parameters have not been fine-tuned to reproduce any of them. However, all our simulated field SDGs have a disc component that extends to much further away than the spheroid and with stellar populations younger than the spheroid. As a result, our SDGs are bluer and with higher sSFR values than the observed isolated ETGs of similar masses. Even by not taking into account the disc components, our SDGs are on average slightly bluer than the observed ETGs. We have shown that the extended discs in our simulations likely would not be detectable in observational surveys like SDSS; however, they might be detected by the LSST survey.

The above-mentioned tension with the observations could be alleviated by introducing mechanisms able to avoid disc growth after major mergers and/or to quench SF efficiently. Our simulations do not include the effect of feedback by AGNs. AGN feedback could prevent the formation of gaseous discs after major mergers, and consequently could eliminate the possibility of post starbursts. However, the presence of luminous AGNs in galaxies of low- and intermediate-masses such as the ones studied here, is not expected to be common. It is more feasible that our results point out the necessity of more efficient feedback driven by both type-II and type-Ia SNe (see also Conroy et al. 2015 for an alternative heating source). It is also important to consider new observational results regarding ETGs where discs and younger stellar populations are being identified (e.g. McIntosh et al. 2014; Schawinski et al. 2014).

There are still many open problems in the study of spheroid-dominated galactic objects. It is therefore important to continue to investigate, and to compare simulations with new observational results. Fortunately, a number of advances have been made in recent years. We expect to shed light on these issues through our research.

Acknowledgements

We acknowledge Dr. Héctor Hernández-Toledo for making available in electronic form the UNAM-KIAS Catalog of Isolated Galaxies. This work was partially supported by PICT 2011-0959 and PIP 2012-0396 (Mincyt, Argentina) and the Southern Astrophysics Network (SAN; Conicyt Chile). PBT acknowledges partial support from Nucleo UNAB 2015 of Universidad Andres Bello and Fondecyt 1150334 (Conicyt). The Fenix simulation was run at the Barcelona Supercomputing Centre.

Appendix A Acronyms and definitions

Table A.1

List of acronyms and definitions used in this paper.

Appendix B Synthetic images of spheroid-dominated galaxies

We generated synthetic images of the SDGs using the radiative transfer code SKIRT (Baes et al. 2005). The images are generated using the stellar population synthesis models of Bruzual & Charlot (2003) to assign a SED to each star particle in a

given galaxy, based on their age, mass, and metallicity. Then SKIRT calculates the propagations of photons towards a simulated imaging instrument using a Monte Carlo technique. The photons considered are emitted with wavelengths between 0.1 and 100 μm in a logarithmic grid with 100 points. No gas or dust is considered in the computations. The simulated imaging instrument corresponds to a 256 × 256 pixel camera placed 10 Mpc away from the galaxy and with a spectral sensitivity equal to the SDSS u, g, r, i, and z broadband filters. Integrated magnitudes and colours are computed from the resulting fully integrated SED of the galaxy. Similar techniques have been used to compute mock images and colours in the Illustris simulation (e.g. Torrey et al. 2015; Bignone et al. 2017).

The left panels of Fig. B.1 show synthetic images of the 18 SDGs. We include synthetic colour-composite images combining SDSS g, r, and i mock images which show a variety of systems from the morphological point of view. By construction, all galaxies have B∕T > 0.5; hence, even if the disc components are clearly in place, the dispersion-dominated component is more massive. The distributions of ϵ parameters (middle panels) and the projected surface density for the spheroid and disc components (right panels) are also shown in Fig. B.1.

To determine the observability of our galactic discs, we assume that the synthetic galaxies are at z ~ 0.05 and process the images to have the same pixel scale and similar PSF as SDSS. The limit radii, where the integrated surface brightness is less than 23 mag arcsec−2 in the r band, is estimated. This is the surface brightness limit for the main galaxy sample target selection in SDSS using the mean surface brightness within the Petrosian half-light radius (Strauss et al. 2002). The circles in the left panel of Fig. B.1 show the limit radii. Therefore, we can appreciate that most of the disc components are below the SDSS observability.

thumbnail Fig. B.1

Left panels: synthetic images of 18 SDGs obtained with the SKIRT code (Baes et al. 2005) with a box side of 30 kpc. The red circles show the limit radii for SDSS observability (see Appendix B for details). Middle panels: distributions of the ϵ parameter for star particles within the optical radius. Right panels: projected stellar-mass surface profiles for the spheroids (red diamonds) and the disc components (blue diamonds). Part of the disc components coexist spatially with the spheroid component (magenta diamonds). The best fit Sersic profile for the spheroid component (red solid lines) and the exponential profiles for the discs (blue dashed lines) are also included. We indicate with a red, black, and blue arrow the RSersic, Rhm , and Rd (see Table A.1). We also include the total surface brightness at the limit radius where the galaxy could be detected with the SDSS (black dotted line). The relations are shown out to Ropt. The rows show galaxies in order of descending stellar mass. The galaxy ID is indicated above each middle and right panel.

References

  1. Albareti, F. D., et al. (SDSS Collaboration) 2017, ApJS, 233, 25 [NASA ADS] [CrossRef] [Google Scholar]
  2. Ashley, T. L., Marcum, P. M., & Fanelli, M. N. 2017, AAS Meeting Abstracts, 230, 214.07 [Google Scholar]
  3. Avila-Reese, V., Zavala, J., Firmani, C., & Hernández-Toledo, H. M. 2008, AJ, 136, 1340 [NASA ADS] [CrossRef] [Google Scholar]
  4. Avila-Reese, V., Zavala, J., & Lacerna, I. 2014, MNRAS, 441, 417 [NASA ADS] [CrossRef] [Google Scholar]
  5. Baes, M., Dejonghe, H., & Davies, J. I. 2005, in The Spectral Energy Distributions of Gas-Rich Galaxies: Confronting Models with Data, eds. C. C. Popescu, R. J., Tuffs, AIP Conf. Proc., 761, 27. [Google Scholar]
  6. Bernardi, M., Meert, A., Vikram, V., et al. 2014, MNRAS, 443, 874 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bertin, G., Ciotti, L., & Del Principe M. 2002, A&A, 386, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Bignone, L. A., Tissera, P. B., Sillero, E., et al. 2017, MNRAS, 465, 1106 [NASA ADS] [CrossRef] [Google Scholar]
  9. Binney, J., & Tremaine, S. 1987, Galactic Dynamics (Princeton: Princeton University Press) [Google Scholar]
  10. Blanton, M. R., Bershady, M. A., Abolfathi, B., et al. 2017, AJ, 154, 28 [NASA ADS] [CrossRef] [Google Scholar]
  11. Borriello, A., Salucci, P., & Danese, L. 2003, MNRAS, 341, 1109 [NASA ADS] [CrossRef] [Google Scholar]
  12. Brooks, A., & Christensen, C. 2016, Galactic Bulges, 418, 317 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
  14. Bundy, K., Bershady, M. A., Law, D. R., et al. 2015, ApJ, 798, 7 [NASA ADS] [CrossRef] [Google Scholar]
  15. Calette, A. R., Avila-Reese, V., Rodríguez-Puebla, A., et al. 2018, Rev. Mex. Astron. Astrofis, submitted [arXiv:1803.07692] [Google Scholar]
  16. Cappellari, M. 2016, ARA&A, 54, 597 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cappellari, M., Emsellem, E., Krajnović, D., et al. 2011, MNRAS, 413, 813 [NASA ADS] [CrossRef] [Google Scholar]
  18. Cappellari, M., Scott, N., Alatalo, K., et al. 2013a, MNRAS, 432, 1709 [CrossRef] [Google Scholar]
  19. Cappellari, M., McDermid, R. M., Alatalo, K., et al. 2013b, MNRAS, 432, 1862 [NASA ADS] [CrossRef] [Google Scholar]
  20. Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
  21. Ciotti, L., Lanzoni, B., & Renzini, A. 1996, MNRAS, 282, 1 [NASA ADS] [CrossRef] [Google Scholar]
  22. Combes, F. 2009, in Galaxy Evolution: Emerging Insights and Future Challenges, eds. S., Jogee, I., Marinova, L., Hao, & G. A. Blanc, ASP Conf. Ser., 419 31 [NASA ADS] [Google Scholar]
  23. Conroy, C., van Dokkum, P. G., & Kravtsov, A. 2015, ApJ, 803, 77 [NASA ADS] [CrossRef] [Google Scholar]
  24. De Lucia, G., Boylan-Kolchin, M., Benson, A. J., Fontanot, F., & Monaco, P. 2010, MNRAS, 406, 1533 [NASA ADS] [Google Scholar]
  25. den Heijer, M., Oosterloo, T. A., Serra, P., et al. 2015, A&A, 581, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. De Rossi, M. E., Tissera, P. B., & Pedrosa, S. E. 2010, A&A, 519, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. De Rossi, M. E., Avila-Reese, V., Tissera, P. B., González-Samaniego, A., & Pedrosa, S. E. 2013, MNRAS, 435, 2736 [NASA ADS] [CrossRef] [Google Scholar]
  28. Djorgovski, S., & Davis, M. 1987, ApJ, 313, 59 [NASA ADS] [CrossRef] [Google Scholar]
  29. Dressler, A., Lynden-Bell, D., Burstein, D., et al. 1987, ApJ, 313, 42 [NASA ADS] [CrossRef] [Google Scholar]
  30. Dubois, Y., Gavazzi, R., Peirani, S., & Silk, J. 2013, MNRAS, 433, 3297 [NASA ADS] [CrossRef] [Google Scholar]
  31. Eggen, O. J., Lynden-Bell, D., & Sandage, A. R. 1962, ApJ, 136, 748 [NASA ADS] [CrossRef] [Google Scholar]
  32. Emsellem, E., Cappellari, M., Krajnović, D., et al. 2007, MNRAS, 379, 401 [NASA ADS] [CrossRef] [Google Scholar]
  33. Emsellem, E., Cappellari, M., Krajnović, D., et al. 2011, MNRAS, 414, 888 [NASA ADS] [CrossRef] [Google Scholar]
  34. Faber, S., & Jackson, R. 1976, ApJ, 204, 668 [NASA ADS] [CrossRef] [Google Scholar]
  35. Faber, S. M., Dressler, A., Davies, R. L., et al. 1987, in Nearly Normal Galaxies: From the Planck Time to the Present (New York: Springer-Verlag), 175 [Google Scholar]
  36. Fakhouri, O., Ma, C.-P., & Boylan-Kolchin, M. 2010, MNRAS, 406, 2267 [NASA ADS] [CrossRef] [Google Scholar]
  37. Ferrero, I., Navarro, J. F., Abadi, M. G., et al. 2017, MNRAS, 464, 4736 [NASA ADS] [CrossRef] [Google Scholar]
  38. Fisher, D. B., & Drory, N. 2008, AJ, 136, 773 [NASA ADS] [CrossRef] [Google Scholar]
  39. Forbes, D. A., Ponman, T. J., & Brown, R. J. N. 1998, ApJ, 508, L43 [NASA ADS] [CrossRef] [Google Scholar]
  40. Gabor, J. M., & Davé, R. 2012, MNRAS, 427, 1816 [NASA ADS] [CrossRef] [Google Scholar]
  41. Gerhard, O. E., Jeske, G., Saglia, R. P., & Bender, R. 1999, in Galaxy Interactions at Low and High Redshift, eds. J. E., Barnes, & D. B., Sanders, IAU Symp., 186, 189 [NASA ADS] [Google Scholar]
  42. Graham, A., & Colless, M. 1997, MNRAS, 287, 221 [NASA ADS] [CrossRef] [Google Scholar]
  43. Graham, A. W., Ciambur, B. C., & Savorgnan, G. A. D. 2016, ApJ, 831, 132 [NASA ADS] [CrossRef] [Google Scholar]
  44. Grand, R. J. J., Gómez, F. A., Marinacci, F., et al. 2017, MNRAS, 467, 179 [NASA ADS] [Google Scholar]
  45. Gunn, J. E., & Gott III, J. R. 1972, ApJ, 176, 1 [NASA ADS] [CrossRef] [Google Scholar]
  46. Hernández-Toledo, H. M., Vázquez-Mata, J. A., Martínez-Vázquez, L. A., Choi, Y.-Y., & Park, C. 2010, AJ, 139, 2525 [NASA ADS] [CrossRef] [Google Scholar]
  47. Hernquist, L. 1993, ApJ, 409, 548 [NASA ADS] [CrossRef] [Google Scholar]
  48. Hopkins, P. F., Hernquist, L., Cox, T. J., & Kereš D. 2008, ApJS, 175, 356 [NASA ADS] [CrossRef] [Google Scholar]
  49. Ibarra-Medel, H. J., Sánchez, S. F., Avila-Reese, V., & Hernández-Toledo, H. M. 2016, MNRAS, 463, 2799 [NASA ADS] [CrossRef] [Google Scholar]
  50. Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  51. Jiménez, N., Tissera, P. B., & Matteucci, F. 2015, ApJ, 810, 137 [NASA ADS] [CrossRef] [Google Scholar]
  52. Kannappan, S. J., Guie, J. M., & Baker, A. J. 2009, AJ, 138, 579 [NASA ADS] [CrossRef] [Google Scholar]
  53. Kauffmann, G. 1996, MNRAS, 281, 487 [NASA ADS] [CrossRef] [Google Scholar]
  54. Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003, MNRAS, 341, 54 [Google Scholar]
  55. Kaviraj, S., Schawinski, K., Devriendt, J. E. G., et al. 2007, ApJS, 173, 619 [NASA ADS] [CrossRef] [Google Scholar]
  56. Khalatyan, A., Cattaneo, A., Schramm, M., et al. 2008, MNRAS, 387, 13 [NASA ADS] [CrossRef] [Google Scholar]
  57. Kormendy, J. 2016, Galactic Bulges, 418, 431 [NASA ADS] [CrossRef] [Google Scholar]
  58. Kormendy, J., & Bender, R. 2013, ApJ, 769, L5 [NASA ADS] [CrossRef] [Google Scholar]
  59. Lacerna, I., Rodríguez-Puebla, A., Avila-Reese, V., & Hernández-Toledo, H. M. 2014, ApJ, 788, 29 [NASA ADS] [CrossRef] [Google Scholar]
  60. Lacerna, I., Hernández-Toledo, H. M., Avila-Reese, V., Abonza-Sane, J., & del Olmo A. 2016, A&A, 588, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Lackner, C. N., Cen, R., Ostriker, J. P., & Joung, M. R. 2012, MNRAS, 425, 641 [NASA ADS] [CrossRef] [Google Scholar]
  62. Larson, R. B., Tinsley, B. M., & Caldwell, C. N. 1980, ApJ, 237, 692 [NASA ADS] [CrossRef] [Google Scholar]
  63. Machado, R. E. G., Tissera, P. B., Lima Neto, G. B., & Sodré, L. 2018, A&A, 609, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. McIntosh, D. H., Wagner, C., Cooper, A., et al. 2014, MNRAS, 442, 533 [NASA ADS] [CrossRef] [Google Scholar]
  65. Mosconi, M. B., Tissera, P. B., Lambas, D. G., & Cora, S. A. 2001, MNRAS, 325, 34 [NASA ADS] [CrossRef] [Google Scholar]
  66. Mosleh, M., Williams, R. J., & Franx, M. 2013, ApJ, 777, 117 [NASA ADS] [CrossRef] [Google Scholar]
  67. Naab, T. 2013, in The Intriguing Life of Massive Galaxies, IAU Symp., 295, 340 [NASA ADS] [Google Scholar]
  68. Newton, R. D. A., & Kay, S. T. 2013, MNRAS, 434, 3606 [NASA ADS] [CrossRef] [Google Scholar]
  69. Niemi, S.-M., Heinämäki, P., Nurmi, P., & Saar, E. 2010, MNRAS, 405, 477 [NASA ADS] [Google Scholar]
  70. Oser, L., Naab, T., Ostriker, J. P., & Johansson, P. H. 2012, ApJ, 744, 63 [NASA ADS] [CrossRef] [Google Scholar]
  71. Park, J., Smith, R., & Yi, S. K. 2017, ApJ, 845, 128 [NASA ADS] [CrossRef] [Google Scholar]
  72. Pedrosa, S. E., & Tissera, P. B. 2015, A&A, 584, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Pedrosa, S. E., Tissera, P. B., & De Rossi M. E. 2014, A&A, 567, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Perez, J., Valenzuela, O., Tissera, P. B., & Michel-Dansac, L. 2013, MNRAS, 436, 259 [NASA ADS] [CrossRef] [Google Scholar]
  75. Prugniel, P., & Simien, F. 1996, A&A, 309, 749 [NASA ADS] [Google Scholar]
  76. Prugniel, P., & Simien, F. 1997, A&A, 321, 111 [NASA ADS] [Google Scholar]
  77. Renzini, A., & Ciotti, L. 1993, ApJ, 416, L49 [NASA ADS] [CrossRef] [Google Scholar]
  78. Rix, H.-W., Carollo, C. M., & Freeman, K. 1999, ApJ, 513, L25 [NASA ADS] [CrossRef] [Google Scholar]
  79. Rosas-Guevara, Y., Bower, R. G., Schaye, J., et al. 2016, MNRAS, 462, 190 [NASA ADS] [CrossRef] [Google Scholar]
  80. Sáiz, A., Domínguez-Tenreiro, R., Tissera, P. B., & Courteau, S. 2001, MNRAS, 325, 119 [NASA ADS] [CrossRef] [Google Scholar]
  81. Salim, S., Rich, R. M., Charlot, S., et al. 2007, ApJS, 173, 267 [NASA ADS] [CrossRef] [Google Scholar]
  82. Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
  83. Sánchez-Blázquez, P., Forbes, D. A., Strader, J., Brodie, J., & Proctor, R. 2007, MNRAS, 377, 759 [NASA ADS] [CrossRef] [Google Scholar]
  84. Sandage, A. 1961, The Hubble Atlas of Galaxies (Washington: Carnegie Institution) [Google Scholar]
  85. Scannapieco, C., Tissera, P. B., White, S. D. M., & Springel, V. 2005, MNRAS, 364, 552 [NASA ADS] [CrossRef] [Google Scholar]
  86. Scannapieco, C., Tissera, P. B., White, S. D. M., & Springel, V. 2006, MNRAS, 371, 1125 [NASA ADS] [CrossRef] [Google Scholar]
  87. Scannapieco, C., Tissera, P. B., White, S. D. M., & Springel, V. 2008, MNRAS, 389, 1137 [NASA ADS] [CrossRef] [Google Scholar]
  88. Schawinski, K., Lintott, C., Thomas, D., et al. 2009, MNRAS, 396, 818 [NASA ADS] [CrossRef] [Google Scholar]
  89. Schawinski, K., Urry, C. M., Simmons, B. D., et al. 2014, MNRAS, 440, 889 [NASA ADS] [CrossRef] [Google Scholar]
  90. Searle, L., & Zinn, R. 1978, ApJ, 225, 357 [NASA ADS] [CrossRef] [Google Scholar]
  91. Sersic, J. L. 1968, Atlas de Galaxias Australes (Córdoba: Observatorio Astronómico) [Google Scholar]
  92. Shen, S., Mo, H. J., White, S. D. M., et al. 2003, MNRAS, 343, 978 [NASA ADS] [CrossRef] [Google Scholar]
  93. Somerville, R. S., & Davé, R. 2015, ARA&A, 53, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
  95. Springel, V., & Hernquist, L. 2003, MNRAS, 339, 289 [Google Scholar]
  96. Springel, V., Yoshida, N., & White, S. D. M. 2001, New Astron., 6, 79 [Google Scholar]
  97. Strauss, M. A., Weinberg, D. H., Lupton, R. H., et al. 2002, AJ, 124, 1810 [NASA ADS] [CrossRef] [Google Scholar]
  98. Thomas, D., Maraston, C., Schawinski, K., Sarzi, M., & Silk, J. 2010, MNRAS, 404, 1775 [NASA ADS] [Google Scholar]
  99. Tissera, P. B. 2000, ApJ, 534, 636 [NASA ADS] [CrossRef] [Google Scholar]
  100. Tissera, P. B. 2012, Boletín de la Asociación Argentina de Astronomía, 55, 233 [Google Scholar]
  101. Tissera, P. B., Domínguez-Tenreiro, R., Sáiz, A., & Goldschmidt, P. 2001, Ap&SS, 276, 1087 [NASA ADS] [CrossRef] [Google Scholar]
  102. Tissera, P. B., White, S. D. M., & Scannapieco, C. 2012, MNRAS, 420, 255 [NASA ADS] [CrossRef] [Google Scholar]
  103. Tissera, P. B., Machado, R. E. G., Sanchez-Blazquez, P., et al. 2016a, A&A, 592, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  104. Tissera, P. B., Pedrosa, S. E., Sillero, E., & Vilchez, J. M. 2016b, MNRAS, 456, 2982 [NASA ADS] [CrossRef] [Google Scholar]
  105. Tissera, P. B., Machado, R. E. G., Vilchez, J. M., et al. 2017, A&A, 604, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  106. Tonini, C., Mutch, S. J., Croton, D. J., & Wyithe, J. S. B. 2016, MNRAS, 459, 4109 [NASA ADS] [CrossRef] [Google Scholar]
  107. Toomre, A. 1977, in Evolution of Galaxies and Stellar Populations, eds. B. M., Tinsley, & R. B., Larson (New Haven: Yale University Observatory), 401 [Google Scholar]
  108. Torrey, P., Snyder, G. F., Vogelsberger, M., et al. 2015, MNRAS, 447, 2753 [NASA ADS] [CrossRef] [Google Scholar]
  109. Trujillo, I., Burkert, A., & Bell, E. F. 2004, ApJ, 600, L39 [NASA ADS] [CrossRef] [Google Scholar]
  110. Tully, R. B., & Fisher, J. R. 1977, A&A, 54, 661 [NASA ADS] [Google Scholar]
  111. Vulcani, B., Poggianti, B. M., Fritz, J., et al. 2015, ApJ, 798, 52 [NASA ADS] [CrossRef] [Google Scholar]
  112. Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
  113. Zavala, J., Avila-Reese, V., Firmani, C., & Boylan-Kolchin, M. 2012, MNRAS, 427, 1503 [NASA ADS] [CrossRef] [Google Scholar]
1

The optical radius, Ropt, is defined as the radius that encloses ~80% of the baryonic mass (gas and stars) of the galaxy (Tissera 2000).

2

From the post-processed galaxies we find the radius where the cumulative surface brightness in the r band attains a value of 23 mag arcsec−2. This is roughly the detection limit for the SDSS galaxies, see Appendix B.

All Tables

Table 1

Main properties of simulated SDGs.

In the text
Table 2

Fraction of young stars in the spheroid and disc components.

In the text
Table A.1

List of acronyms and definitions used in this paper.

In the text

All Figures

thumbnail Fig. 1

Distribution of the dynamical B/T ratios for the 39 well-resolved simulated galaxies. Only those with B∕T > 0.5 (red dashed line) are classified as SDGs.
In the text
thumbnail Fig. 2

Stellar-mass fractions of the discs that coexist with the spheroidal components as a function of the fraction B/T. A linear regression fit is included (green solid line) along with its 1σ dispersion (green dashed lines).
In the text
thumbnail Fig. 3

Spheroid Sersic index obtained for the simulated SDGs as a function of their dynamical B/T mass ratios. The green solid and dashed lines represent the best linear regression fit and the 1σ dispersion. The magenta dashed line denotes n = 2, which is often assumed to be the limit between classical and pseudo-bulges.
In the text
thumbnail Fig. 4

Mass-size relation estimated for the simulated SDGs (Rhm, big circles, and Reff, small circles, both coloured according to the dynamical B/T ratios), ETGs from the clean ATLAS3D sample (black crosses), and the observed relations reported by Mosleh et al. (2013; green solid line) and Bernardi et al. (2014; red dashed line) for ETGs.
In the text
thumbnail Fig. 5

Faber–Jackson relation for the simulated SDGs (filled circles, coloured according to the dynamical B/T ratios) estimated by using σ0 (left panel) or σe (right panel). For comparison, the corresponding relations obtained from the clean ATLAS3D sample are included (see Sect. 4). The linear regression to the simulated data (green solid lines) and observational data (black dashed lines) are depicted for comparison.
In the text
thumbnail Fig. 6

Fundamental plane for the simulated SDGs calculated with the parameters estimated for our clean ATLAS3D sample. The black line denotes the one-to-one relation and the green line shows the best fit to our simulated SDGs (solid circles, coloured according to the dynamical B/T ratios). The rms is 0.19 and 0.18 for the least squares regression (dashed green lines) when considering velocity dispersion within Reff and central velocity dispersion, respectively, and the corresponding regression for the one-to-one relation (rms = 0.19 for both cases) is shown by dotted black lines.
In the text
thumbnail Fig. 7

Stellar (left panel) and baryonic (right panel) TFRs for the simulated SDGs (filled circles coloured according to the dynamical B/T ratio) and DDGs (black solid circles), and the observed values reported by den Heijer et al. (2015) for ETGs with extended disc components (black crosses). The linear regression for simulated SDGs (green lines) are shown; the rms dispersions are also shown (dashed lines).
In the text
thumbnail Fig. 8

Dark matter fraction, Fdm = Mdm∕Mdyn, within Rhm (big solid circles) and Reff (small solid circles), both coloured according to the dynamical B/T ratios as a function of stellar mass for the simulated SDGs. The crosses are dynamical estimates for the ATLAS3D ETGs (Cappellari et al. 2013a,b).
In the text
thumbnail Fig. 9

Colours and sSFRs as a function of the MStar (left and right panels, respectively) for the simulated SDGs (filled circles coloured according to the dynamical B∕T ratios). Observational results for isolated ETGs (black asterisks; Hernández-Toledo et al. 2010) are included. In the left panel, blue and red galaxies are separated by the black line reported by Lacerna et al. (2014), while in the right panel the black line depicts the limit between star-forming and passive galaxies (Lacerna et al. 2014). Galaxies that are blue and star-forming at the same time are marked with black open squares.
In the text
thumbnail Fig. 10

Properties of the spheroid (red circles) and disc (blue circles) components: g–i (top panel) and sSFR (bottom panel) as a function of MStar. For comparison, we include the same observations as in Fig. 9 (black asterisks). We depict blue star-forming galactic objects as black open squares, and the limiting lines reported by Lacerna et al. (2014) between red and blue galaxies in the bottom panel, and between star-forming and non-star-forming galaxies in the top panel.
In the text
thumbnail Fig. 11

Fraction of stars younger than 3 Gyr as a function of the g–i for the spheroid (large red circles) and disc (small blue circles) components. We also depict blue star-forming galaxies with open black squares.
In the text
thumbnail Fig. 12

Average mass-weighted ages of the stellar populations in the spheroid (large red circles) and disc (small blue circles) components of the SDGs. The horizontal lines represent the average ages of all spheroids (red) and discs (blue).
In the text
thumbnail Fig. 13

Normalised MGHs estimated in three radial intervals of our 18 SDGs, in order of descending stellar masses (from left to right and from top to bottom). In each panel, the nSersic parameter and the dynamical B/T ratio are also included.
In the text
thumbnail Fig. 14

Average global and radial normalised MGH for our simulations (top) and MaNGA ETGs at z < 0.037 (bottom). We make the division between low (left panels) and high (right panels) stellar mass, adopting log (MStar) = 9.9 as a threshold. Radial bins of [0–0.5], [0.5–1.0], and [1.0–1.5] Rhm are represented by solid, dashed, and dotted lines, respectively.
In the text
thumbnail Fig. B.1

Left panels: synthetic images of 18 SDGs obtained with the SKIRT code (Baes et al. 2005) with a box side of 30 kpc. The red circles show the limit radii for SDSS observability (see Appendix B for details). Middle panels: distributions of the ϵ parameter for star particles within the optical radius. Right panels: projected stellar-mass surface profiles for the spheroids (red diamonds) and the disc components (blue diamonds). Part of the disc components coexist spatially with the spheroid component (magenta diamonds). The best fit Sersic profile for the spheroid component (red solid lines) and the exponential profiles for the discs (blue dashed lines) are also included. We indicate with a red, black, and blue arrow the RSersic, Rhm , and Rd (see Table A.1). We also include the total surface brightness at the limit radius where the galaxy could be detected with the SDSS (black dotted line). The relations are shown out to Ropt. The rows show galaxies in order of descending stellar mass. The galaxy ID is indicated above each middle and right panel.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.