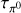| Issue |
A&A
Volume 612, April 2018
H.E.S.S. phase-I observations of the plane of the Milky Way
|
|
|---|---|---|
| Article Number | A3 | |
| Number of page(s) | 18 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201732125 | |
| Published online | 09 April 2018 | |
Population study of Galactic supernova remnants at very high γ-ray energies with H.E.S.S.
1
Centre for Space Research, North-West University,
Potchefstroom 2520, South Africa
2
Universität Hamburg, Institut für Experimentalphysik,
Luruper Chaussee 149,
22761
Hamburg, Germany
3
Max-Planck-Institut für Kernphysik,
PO Box 103980,
69029
Heidelberg, Germany
4
Dublin Institute for Advanced Studies,
31 Fitzwilliam Place,
Dublin 2, Ireland
5
National Academy of Sciences of the Republic of Armenia,
Marshall Baghramian Avenue,
24, 0019
Yerevan, Republic of Armenia
6
Yerevan Physics Institute,
2 Alikhanian Brothers St.,
375036
Yerevan, Armenia
7
Institut für Physik, Humboldt-Universität zu Berlin,
Newtonstr. 15,
12489
Berlin, Germany
8
University of Namibia, Department of Physics,
Private Bag 13301,
Windhoek, Namibia
9
GRAPPA, Anton Pannekoek Institute for Astronomy, University of Amsterdam,
Science Park 904, 1098 XH
Amsterdam, The Netherlands
10
Department of Physics and Electrical Engineering, Linnaeus University,
351 95
Växjö, Sweden
11
Institut für Theoretische Physik, Lehrstuhl IV: Weltraum und Astrophysik, Ruhr-Universität Bochum,
44780
Bochum, Germany
12
GRAPPA, Anton Pannekoek Institute for Astronomy and Institute of High-Energy Physics, University of Amsterdam,
Science Park 904,
1098 XH Amsterdam, The Netherlands
13
Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität Innsbruck, 6020,
Innsbruck, Austria
14
School of Physical Sciences, University of Adelaide,
Adelaide 5005, Australia
15
LUTH, Observatoire de Paris, PSL Research University, CNRS, Université Paris Diderot,
5 Place Jules Janssen,
92190
Meudon, France
16
Sorbonne Universités, UPMC Université Paris 06, Université Paris Diderot, Sorbonne Paris Cité, CNRS, Laboratoire de Physique Nucléaire et de Hautes Energies (LPNHE),
4 place Jussieu,
75252,
Paris Cedex 5, France
17
Laboratoire Univers et Particules de Montpellier, Université Montpellier, CNRS/IN2P3,
CC 72, Place Eugène Bataillon, 34095
Montpellier Cedex 5, France
18
IRFU, CEA, Université Paris-Saclay,
91191
Gif-sur-Yvette, France
19
Astronomical Observatory, The University of Warsaw,
Al. Ujazdowskie 4,
00-478
Warsaw, Poland
20
Aix Marseille Université, CNRS/IN2P3, CPPM,
Marseille, France
21
Instytut Fizyki Ja̧drowej PAN,
ul. Radzikowskiego 152,
31-342
Kraków, Poland
22
Funded by EU FP7 Marie Curie, grant agreement No. PIEF-GA-2012-332350
23
School of Physics, University of the Witwatersrand,
1 Jan Smuts Avenue, Braamfontein,
Johannesburg
2050, South Africa
24
Laboratoire d’Annecy-le-Vieux de Physique des Particules, Université Savoie Mont-Blanc, CNRS/IN2P3,
74941
Annecy-le-Vieux, France
25
Landessternwarte, Universität Heidelberg,
Königstuhl,
69117
Heidelberg, Germany
26
Université Bordeaux, CNRS/IN2P3, Centre d’Études Nucléaires de Bordeaux Gradignan,
33175
Gradignan, France
27
Oskar Klein Centre, Department of Physics, Stockholm University, Albanova University Center,
10691
Stockholm, Sweden
28
Wallenberg Academy Fellow
29
Institut für Astronomie und Astrophysik, Universität Tübingen,
Sand 1,
72076
Tübingen, Germany
30
Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS/IN2P3,
91128
Palaiseau, France
31
APC, AstroParticule et Cosmologie, Université Paris Diderot, CNRS/IN2P3, CEA/Irfu, Observatoire de Paris, Sorbonne Paris Cité,
10, rue Alice Domon et Léonie Duquet,
75205
Paris Cedex 13, France
32
Univ. Grenoble Alpes, CNRS, IPAG,
38000
Grenoble, France
33
Department of Physics and Astronomy, The University of Leicester,
University Road,
Leicester
LE1 7RH, UK
34
Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences,
ul. Bartycka 18,
00-716
Warsaw, Poland
35
Institut für Physik und Astronomie, Universität Potsdam,
Karl-Liebknecht-Strasse 24/25,
14476
Potsdam, Germany
36
Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen Centre for Astroparticle Physics,
Erwin-Rommel-Str. 1,
91058
Erlangen, Germany
37
DESY,
15738
Zeuthen, Germany
38
Obserwatorium Astronomiczne, Uniwersytet Jagielloński,
ul. Orla 171, 30-244
Kraków, Poland
39
Centre for Astronomy, Faculty of Physics, Astronomy and Informatics, Nicolaus Copernicus University,
Grudziadzka 5,
87-100
Torun, Poland
40
Department of Physics, University of the Free State,
PO Box 339,
Bloemfontein 9300, South Africa
41
Heisenberg Fellow (DFG),
ITA Universität Heidelberg, Germany
42
Department of Physics, Rikkyo University,
3-34-1 Nishi-Ikebukuro,
Toshima-ku, Tokyo 171-8501,
Japan
43
Japan Aerpspace Exploration Agency (JAXA), Institute of Space and Astronautical Science (ISAS),
3-1-1 Yoshinodai, Chuo-ku, Sagamihara,
Kanagawa
229-8510, Japan
44
Department of Physics & Astronomy, University of Manitoba,
Winnipeg
MB R3T 2N2, Canada
45
Now at The School of Physics, The University of New South Wales,
Sydney,
2052, Australia
46
Now at Instituto de Física de São Carlos, Universidade de São Paulo, Av. Trabalhador São-carlense,
400 - CEP 13566-590,
São Carlos,
SP, Brazil
47
Now at Kavli Institute for Particle Astrophysics and Cosmology, Department of Physics and SLAC National Accelerator Laboratory, Stanford University,
Stanford,
CA
94305, USA
★ Corresponding authors: H.E.S.S. Collaboration,
e-mail: contact.hess@hess-experiment.eu
Received:
18
October
2017
Accepted:
8
February
2018
Shell-type supernova remnants (SNRs) are considered prime candidates for the acceleration of Galactic cosmic rays (CRs) up to the knee of the CR spectrum at E ≈ 3 × 1015 eV. Our Milky Way galaxy hosts more than 350 SNRs discovered at radio wavelengths and at high energies, of which 220 fall into the H.E.S.S. Galactic Plane Survey (HGPS) region. Of those, only 50 SNRs are coincident with a H.E.S.S source and in 8 cases the very high-energy (VHE) emission is firmly identified as an SNR. The H.E.S.S. GPS provides us with a legacy for SNR population study in VHE γ-rays and we use this rich data set to extract VHE flux upper limits from all undetected SNRs. Overall, the derived flux upper limits are not in contradiction with the canonical CR paradigm. Assuming this paradigm holds true, we can constrain typical ambient density values around shell-type SNRs to n ≤ 7 cm−3 and electron-to-proton energy fractions above 10 TeV to ϵep ≤ 5 × 10−3. Furthermore, comparisons of VHE with radio luminosities in non-interacting SNRs reveal a behaviour that is in agreement with the theory of magnetic field amplification at shell-type SNRs.
Key words: gamma rays: general / ISM: supernova remnants
© ESO 2018
1 Introduction
Supernova remnants (SNRs) are considered the most promising candidates for the origin of Galactic cosmic rays (CRs), a long-standing open problem in astroparticle physics. These objects are also a very prominent source class in high-energy astrophysics, emitting non-thermal radiation in the form of radio waves, X-rays, and γ-rays. According to diffusive shock acceleration (DSA) theory, with magnetic field amplification (see e.g. Malkov & Drury 2001) hadronic CR particles such as protons and heavier nuclei can be accelerated up to PeV energies (the “knee” in the CR spectrum) at the expanding SNR shock front or shell. When these relativistic particles collide with other nuclei, for example in the nearby interstellar medium (ISM), they emit γ-rays in the very high-energy (VHE; 0.1≲Eγ≲100 TeV) band. Thus, observations with Cherenkov telescopes, sensitive to VHE γ-rays, provide a promising avenue to investigate not only the astrophysics of energetic SNRs themselves but also their putative connection to the origin of Galactic CRs (see e.g. Drury et al. 1994). In particular, certain aspects of DSA theory, such as the efficiency of particle acceleration mechanisms, can be constrained through such observations.
The High Energy Stereoscopic System (H.E.S.S.) is an array of five imaging atmospheric Cherenkov telescopes (IACTs) situated in Namibia. The telescope array has a field of view of approximately 5° and can detect γ-rays above an energy threshold of ~ 50 GeV. This array has an energy resolution of ~ 15% and a angular resolution of ~ 0.1°1 (Aharonian et al. 2006). The H.E.S.S. Galactic Plane Survey (HGPS; H.E.S.S. Collaboration 2018b) programme has led to the detection of 78 sources of VHE γ-rays, of which 8 have been firmly identified as emission from SNRs, typically by resolving shell-like morphologies matching those observed at lower energies. These are RX J1713.7−3946 (H.E.S.S. Collaboration 2018b), RX J0852.0−4622 (H.E.S.S. Collaboration 2018c), HESS J1731−347 (Abramowski et al. 2011), RCW 86 (H.E.S.S. Collaboration 2018d), W28 (Aharonian et al. 2008b), G349.7+0.2 (Abramowski et al. 2015), W49B (H.E.S.S. Collaboration 2018b), and HESS J1534−571 (H.E.S.S. Collaboration 2018b). One SNR outside of the HGPS region has also been firmly identified, SN 1006 (Acero et al. 2010), bringing the tally to 9. In addition, H.E.S.S. has detected emission from 8 composite SNRs. For these latter types, it is currently difficult to determine whether the γ-rays originate in the interior pulsar wind nebula (PWN), the surrounding shell, or a combination of these two. In addition to the firm identifications, 16 additional HGPS sources have also been associated with SNRs based on spatial coincidence, see H.E.S.S. Collaboration (2018b).
Using a ~10-year HGPS data set collected between 2004 and 2013, we investigate the sample of known radio and X-ray SNRs that so far have not been detected by IACTs. To that end, we select a subset of SNRs devoid of any unrelated VHE emission (the VHE-dark sample, Sect. 2) and derive flux upper limits (Sect. 4), which we use to test the standard paradigm of the SNRs as the origin of Galactic CRs. Assuming hadronic emission, we calculate a constraint on the fraction of the SNR explosion energy that is converted to CR protons in Sect. 5.3. We also apply a simple parametric estimate of the inverse-Compton (IC) emission to our results in order to probe the relevant parameter space in a mixed scenario where both leptonic and hadronic channels contribute to the source emission. Based on our formalism, we furthermore present expectations on the portion of this parameter space that will be accessible to the future Cherenkov Telescope Array (CTA; Actis et al. 2011) observatory. Finally, in Sect. 5.4, we compare the derived flux upper limits to the radio flux densities that have been observed for the investigated source sample and put these into context of the IACT detections.
2 Candidate source selection and data sample
We obtained the sample of source candidates from the SNRcat catalogue2 (Ferrand & Safi-Harb 2012), which provides an up-to-date catalogue of SNRs detected from radio to VHE. The catalogue comprises SNRs of different morphological types: shell-type, composite, and filled-centre. In the context of this work, we treated only the shell-type and composite SNRs, as filled-centre SNRs correspond to pulsar wind nebulae, which are discussed in H.E.S.S. Collaboration (2018b). Also, we ignored sources of uncertain morphology (type “?” in SNRcat).
For our study we used the HGPS data set, which consists of ~ 2700 h of observations and features a sensitivity of better than ~1.5% of the Crab flux in the innermost Galactic regions.
Of the more than 300 shell-type and composite SNRs listed in SNRcat, 220 fall within the HGPS region (Galactic longitude from 65° to 250°, latitude from −3.5° to 3.5°). However, as this region is populated by almost 80 sources detected by H.E.S.S. (see H.E.S.S. Collaboration 2018b) signal contamination of the analysis regions of the investigated SNRs is an important consideration. Any unrelated VHE emission in the analysis regions weaken the derived flux upper limits and complicate physical interpretation.
In orderto obtain a sample of SNRs that does not suffer from this problem, we selected a VHE-dark sample from SNRcat consisting of sources that fall outside of regions of VHE emission. We note that by focussing on SNRs that are not detected at VHE we are biasing ourselves towards low VHE-flux objects. Assessing the impact of this bias and a possible correction would require population modelling and go beyond the main scope of this paper, which is to derive H.E.S.S. flux upper limits for VHE-undetected SNRs. The selection method is as follows: We used the HGPS significance map (see H.E.S.S. Collaboration 2018b) in an iterative way to identify VHE-bright regions around HGPS catalogue sources in the Galactic plane. More precisely, we chose the significance map with a 0.2° correlation radius, since this radius roughly corresponds to the maximum of the source radius distribution for shell-type and composite SNRs listed in SNRcat. As starting points for this iteration, we used all bins3 of the significance map that both fall into the 80% signal containment radii of the HGPS sources (“R80” in the HGPS catalogue) and have significance values ≥4σ. We then saved their respective neighbouring bins with significances ≥4σ and used these as starting points for the next iteration step. The iteration stops when there are no neighbouring bins with significances ≥4σ around the starting points of a given step. This procedure results in sets of bins that define contiguous and VHE-bright regions, in the following referred to as de-selection regions. By construction, these regions overlap with the circular HGPS source regions, but are in most cases asymmetric in shape (see Fig. 1). Such regions are similar to the pre-defined HGPS exclusion regions (H.E.S.S. Collaboration 2018b) but smaller in extent to allow for a less conservative compromise between SNR sample size and signal leakage.
We tested the analysis region (see below) of any candidate object from SNRcat for overlap with one of the de-selection regions. If there was at least one bin in the analysis region belonging to such a region, we discarded the respective object from the VHE-dark SNR sample. In Fig. 1, we illustrate the method. This procedure results in a sample of 108 SNRs with H.E.S.S. observations, of which 83 are of shell-type and 25 are of composite morphology. The latter group includes eight sources with thermal and 15 sources with plerionic characteristics, and two objects that feature both characteristics.
 |
Fig. 1 Illustration of the source selection scheme on the γ-ray excess image from a given region. The known H.E.S.S. sources HESS J1857+026 and HESS J1858+020 with their 80% flux containment radii are shown with a dashed circle. The de-selection region resulting from the algorithm explained inSect. 2 is shown with a solid curve. Because of the overlap with the de-selection region, the SNR G35.6 −0.4 is discarded whereas SNR G36.6 −0.7 is selected. |
3 Analysis
In this study, we selected only data of high quality using the criteria described in Aharonian et al. (2006) and the quality cut on atmospheric transparency conditions developed by Hahn et al. (2014). The observation live time of the analysed regions, corrected by the H.E.S.S. γ-ray acceptance, spans a range from ~10 min to ~80 h with a median value of 14.5 h. The majority of data ( ~80%) have been recorded at average zenith angles smaller than 40°. Table A.1 lists the analysed source sample and the corrected observation live time, the averaged zenith angle for the observations of each source, and the closest H.E.S.S. source.
We analysed the data using the multivariate analysis method described in Ohm et al. (2009) with the same analysis configuration used in H.E.S.S. Collaboration (2018b), TMVA Hard Cuts. For the background estimation, the Reflected Background method (Berge et al. 2007), was applied. This method is largely insensitive to acceptance gradients in the cameras and therefore ideally suited for spectral analysis. A cross-check was performed using the Model++ Faint Cuts analysis (de Naurois & Rolland 2009) and yielding compatible results.
The analysis region for every source is given by its position provided in SNRcat as well as the quoted radii therein and is defined to be circular. If an SNR is reported with an elliptical shape, we used the semi-major axis. A margin of 0.1° is added to this radius, which conservatively takes the H.E.S.S. point spread function into account. Figure A.1 shows the analysis regions for our source sample.
For each source, we used all events above the safe energy threshold in the analysis. The safe energy is defined as the energy above which the energy bias is less than 10% (Aharonian et al. 2006).
We notethat the diffuse emission measured in Abramowski et al. (2014a) was not taken into account in this analysis. This would resultin conservative upper limits, especially for sources close to the Galactic plane. An attempt to quantify the effect of this component is described in Sect. 5 using the maps and large-scale emission model from H.E.S.S. Collaboration (2018b).
4 Results
In Table A.1 we list the significance and upper-limit results for the individual sources. We calculate the significance using the method proposed by Li & Ma (1983). To obtain the upper limits on the excess counts above the safe energy, we use the profile likelihood method as described in Rolke et al. (2005) and assumed a confidence level of 99%. We then express this result as an upper limit on the integrated flux in the (1, 10) TeV interval assuming a power-law source of index 2.3. Such a value is typical for Galactic sources detected in the VHE range (H.E.S.S. Collaboration 2018b).
Figure 2 shows the distribution of upper limits for the VHE-dark source sample. The total distribution is peaked at the typical H.E.S.S. sensitivity in the HGPS region of ~2% of the Crab nebula flux. The median and variance values of the distribution of logarithmic flux upper limits are M(log10 (Ful∕(cm−2 s−1)) = −12.4 and S2 (log10 (Ful∕(cm−2 s−1)) = 0.14, respectively.
The significance distribution features median and variance values of M(σ) = 1.1 and S2 (σ) = 2.4, respectively. From Table A.1, one can notice that the γ-ray excess from the plerionic composite SNR G34.7 −0.4 (W44) shows a significance of 6.2σ. However, we are prevented from claiming a detection because this object is a rather large SNR embedded in a region of high diffuse emission that is not claimed as a source in the HGPS catalogue (see H.E.S.S. Collaboration 2018b) and because the signal is below the detection criteria of the independent cross-check analysis.
We show the significance distribution in the left panel of Fig. 3 together with a normal Gaussian, corresponding to the expectation in the absence of any source signal. There is no significant difference in the shape of the significance distribution with respect to the source type, as can be seen in the cumulative distributions shown in the right panel of Fig. 3. All pair-wise comparisons of the various significance distributions with two-sided Kolmogorov–Smirnov tests result in p-values larger than 0.42. Therefore we see no indication that the various samples stem from incompatible underlying distributions. In particular, we find no indication that the possible additional presence of a PWN in plerionic composites on average results in higher significance values in the VHE range.
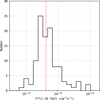 |
Fig. 2 Distribution of flux upper limits (99% confidence level) of all investigated SNRs. The red line indicates the median value of ~ 2% of the Crab nebula flux. |
 |
Fig. 3 Left: significance distribution of the VHE-dark sample of SNRs (black, blue, red, and green) and the corresponding median value (grey solid). The grey dashed curve indicates a normal Gaussian. Right: cumulative significance distribution of all sources(black), those of shell-type (blue), and composite (red and green) morphology. The grey dashed line represents a cumulative normal Gaussian. |
5 Discussion
5.1 Significance offset
As shown in Fig. 3, the median value of the measured significance distribution is offset from the normal Gaussian distribution, which constitutes the expectation for pure noise (null hypothesis), and a Gaussian fit to the distribution results in best-fit values for mean and standard deviation of 1.01 and 1.51, respectively. A Kolmogorov–Smirnov test of the measured significance distribution against the null hypothesis rejects the latter with a p-value of p = 8 × 10−15. The origin of this collective excess in positive significance values may arise from several contributions:
-
Low-level signal leakage into the analysis regions from known VHE γ-ray sources cannot be completely dismissed.
-
Imperfect background modelling can also lead to spurious excess emission, especially in background-dominated observations such as those made by H.E.S.S. The background reconstruction, however has been thoroughly studied in several publications (e.g. Berge et al. 2007 and Abramowski et al. 2012), typically resulting in small systematic uncertainties far below the excess observed here.
-
Galactic diffuse emission (Abramowski et al. 2014a) in the VHE range might cause the positive offset in thesignificance distribution. While the nature of this emission remains under discussion, it is believed that it consists both of a diffuse component of propagating CRs interacting with their environment and a population of unresolved sources (possibly including SNRs), which emit VHE γ-rays and a priori are unrelated to the individual SNRs investigated in this study.
-
The significance distribution offset might be the result of a cumulation of localised emission from the investigated SNR shells, which individually fall below the HGPS sensitivity.
The four components are hard to disentangle, and it is possible that we impose flux limits on a sum of these contributions. However, contribution(1) seems negligible, since no correlation between excess significance and angular distance to the nearest HGPS source is apparent, as shown in Fig. 4.
The diffuse emission described in (3) extends out well beyond many regions of strong source emission and thus also the de-selection regions. As a result, this emission may be present in the investigated analysis regions. In Fig. 5, we show the cumulative significance distribution of the investigated SNR sample (compare to the right panel of Fig. 3) together with the analogous distribution that results if the diffuse emission contribution is accounted for in the significance calculation. To obtain the latter, we applied the parametric model of the diffuse emission component presented in H.E.S.S. Collaboration (2018b) to the data. It should be mentioned that for this calculation the significance values were derived directly from the HGPS maps. A Kolmogorov–Smirnov test of the distribution corrected in this way (red line in Fig. 5) against a normal (noise-) distribution (grey) results in a p-value of p = 1.8 × 10−2, roughly corresponding to a significance value of ~2.1σ, which suggests that the parametric diffuse emission model can account for a large portion, but not all of the significance offset.
In orderto investigate contribution (4), we performed an analysis of randomised SNR analysis regions. That is, if the observed significance offset was indeed due to localised, faint emission from SNRs, we would expect this effect to be absent in a sample of randomised test regions. We determined the random positions by adding a uniform variate l ∈ [−5 , 5)° to the Galacticlongitude value of each real SNR. We left the Galactic latitude value unchanged so as not to introduce a bias regarding component (3), which shows a Galactic latitude dependence; see H.E.S.S. Collaboration (2018b). Also, we added a variate number s ∈ [−0.05 , 0.05)° to the radius of the test region, with a lower ceiling of the resulting radius of 0.1°. Once the random test region is generated, we subjected it to our source selection method (see Sect. 2), and additionally tested whether it overlaps with a previously generated region, in which case we rejected it. If the random test region was rejected, a new test region was generated in the same manner and tested again until it passed selection. We created and analysed 28 randomised samples of the real set of SNRs, and each sample yields a set of 108 significance values. From these 28 sets, we calculated the average cumulated and normalised significance distribution.We then used this distribution as the cumulative density function in a Kolmogorov–Smirnov test against the significance distribution of the real SNR sample (blue line in Fig. 5). This results in a p-value of p = 5 × 10−3, approximately corresponding to a significance of σ ~ 2.6, which does not allow us to claim the detection of a cumulated SNR signal.
Our results indicate that the observed shift in the significance distribution might be the result of the sum of components (3) and (4), although a deeper understanding of the large-scale VHE emission along the Galactic plane as well as improved analysis methods and observation exposure are required to provide definitive answers. Future studies with CTA should be able to shed light on thisquestion.
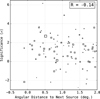 |
Fig. 4 Source significance values of the VHE-dark source sample vs. the angular distance to the nearest detected H.E.S.S. source. The angular distance between the edges of our test regions to that of detected H.E.S.S. sources is shown; the marker size is proportional to the integrated flux above 1 TeV of the latter. The source region positions and sizes are taken from the HGPS, where they are defined as the centroids and 80% containment radii of symmetric and two-dimensional Gaussian fits to the integrated flux map, respectively (see H.E.S.S. Collaboration 2018b for more details). Negative distance values are possible for asymmetric sources where the Gaussian fit does not describe the source morphology well, see e.g. SNR G36.6 −0.7 in Fig. 1. |
 |
Fig. 5 Cumulated significance distribution of the SNR sample (black) and analogous distribution corrected for the Galactic diffuse emission component (dash-dotted red). The cumulated density function from the analysis of randomised test regions is shown in dotted blue. The grey dashed curve represents a cumulated normal Gaussian distribution. |
5.2 Fermi-LAT comparison
The Fermi-LAT (Large Area Telescope) collaboration has recently performed a systematic survey in the 1–100 GeV energy band towards known Galactic SNRs (Acero et al. 2016). Among the 102 source candidates, 30 are classified as likely GeV SNRs, and an additional 14 “marginally classified” candidates could be associated with the SNRs.
We compared the H.E.S.S. upper limits for all the GeV SNR candidates in our VHE-dark SNR sample with their extrapolated 1–10 TeV fluxes from the Fermi-LAT measurements. We note that the coordinates and radii of our analysis regions (see Sect. 3) differ from those found with Fermi-LAT. The H.E.S.S. upper limits are only constraining for two sources, namely G6.1+0.5 and G310.8 −0.4; and hence, these upper limits point towards a spectral steepening in or before the VHE domain. However, these two sources are neither safely nor marginally classified GeV SNR candidates; the emission from G6.1+0.5 is flagged as doubtful and the GeV extent of G6.1+0.5 and G310.8 −0.4 (0.64° and ~ 1°, respectively) are much larger than their radio SNR size (0.1°–0.15° and 0.1°, respectively). The γ-ray spectra of these two sources are shown in Fig. 6.
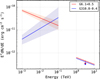 |
Fig. 6 Gamma-ray spectral energy distributions of G6.1+0.5 and G310.8 −0.4. The Fermi-LAT spectra are derived from the spectral parameters reported in the first Fermi-LAT SNR catalogue. Statistical errors are indicated by the shaded bands. |
5.3 Constraints on the accelerated particles in SNRs
By comparing to model expectations, the derived integral flux upper limits may be used to estimate upper limits on the energy content in high-energy particles. In the following, we limit our considerations to inelastic proton-proton collisions and the subsequent π0 -decay and inverse-Compton (IC) emission since these processes are believed to be the most relevant γ-ray emission mechanism in SNRs for the VHE regime.
If the corresponding π0 production timescale due to inelastic proton-proton scattering, 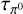 , and electroncooling time, tIC, are known4 and a distance estimate for a source is given, the presented flux upper limits can be used to place upper limits on the total energy in electrons and protons at the time of emission. In the following, we assume that γ-rays with energies larger than 1 TeV mainly probe particles with energies above 10 TeV in both the IC and π0 -decay emission channels.
, and electroncooling time, tIC, are known4 and a distance estimate for a source is given, the presented flux upper limits can be used to place upper limits on the total energy in electrons and protons at the time of emission. In the following, we assume that γ-rays with energies larger than 1 TeV mainly probe particles with energies above 10 TeV in both the IC and π0 -decay emission channels.
We used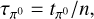 , where n is the number density of ambient gas nuclei in units of 1 cm−3 and
, where n is the number density of ambient gas nuclei in units of 1 cm−3 and 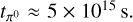 . Unlike in the hadronic case, the IC cooling time depends strongly on the electron energy and the energy densities of the ambient radiation fields. We adopted a conservative value of the cooling time by assuming the cosmic microwave background (CMB) as the only ambient photon field and using the value for 10 TeV electrons scattering in the Thomson regime5 . This results in a cooling time of
. Unlike in the hadronic case, the IC cooling time depends strongly on the electron energy and the energy densities of the ambient radiation fields. We adopted a conservative value of the cooling time by assuming the cosmic microwave background (CMB) as the only ambient photon field and using the value for 10 TeV electrons scattering in the Thomson regime5 . This results in a cooling time of 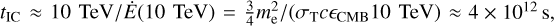 , where me is the electron rest mass, σT is the Thomson cross section, c is the speed of light, and ϵCMB is the energy density of the CMB.
, where me is the electron rest mass, σT is the Thomson cross section, c is the speed of light, and ϵCMB is the energy density of the CMB.
Using these values it is possible to convert the upper limits on the integrated energy flux above 1 TeV into upper limits on the total energy in protons and electrons above 10 TeV at the time of emission. In general, for power-law spectra with Γ≠ 2 upper limits on the energy flux, 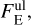 , between energies E1 and E2 are connected to the corresponding integral flux upper limits, Ful, between E1 and E2 via
, between energies E1 and E2 are connected to the corresponding integral flux upper limits, Ful, between E1 and E2 via
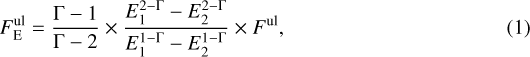
where in our case E1 = 1 TeV, E2 = 10 TeV, and Γ = 2.3.
Upper limits on the total energy content in electrons can be derived as
![$ W_{\mathrm{e}}^{\mathrm{ul}}[{>}10\,\mathrm{TeV}] \approx F_{\mathrm{E}}^{\mathrm{ul}}[{>}1\,\mathrm{TeV}] \times t_{\mathrm{IC}}\times 4\pi d^2. $](/articles/aa/full_html/2018/04/aa32125-17/aa32125-17-eq7.png)
The comparable procedure in the case of protons yields
![$W_{\mathrm{p}}^{\mathrm{ul}}[{>}10\,\mathrm{TeV}] \approx F_{\mathrm{E}}^{\mathrm{ul}}[{>}1\,\mathrm{TeV}] \times \tau_{\pi^0} \times 4\pi d^2 ,$](/articles/aa/full_html/2018/04/aa32125-17/aa32125-17-eq8.png)
or more explicitly, if n is unknown,
![$ (W_{\mathrm{p}}[{>}10\,\mathrm{TeV}]\times n)^{\mathrm{ul}} \approx F_{\mathrm{E}}^{\mathrm{ul}}[{>}1\,\mathrm{TeV}] \times t_{\pi^0} \times 4\pi d^2,$](/articles/aa/full_html/2018/04/aa32125-17/aa32125-17-eq9.png)
implying that Wp[>10 TeV] and n are degenerate in this case, such that with this method upper limits on the proton energy content can only be placed if the corresponding values of the target gas densities are available.
These limits are conservative estimations. The exact proportionality coefficients cx, defined by W = cx × FE × tx × 4πd2 for π0 -decay are ![$c_{\pi^0}=[0.7,0.7,0.95,0.81]$](/articles/aa/full_html/2018/04/aa32125-17/aa32125-17-eq10.png) , using the recent parametrisation of the total inelastic p-p cross section for Geant4, Pythia8, SIBYLL2.1, and QGSJET-I from Kafexhiu et al. (2014), respectively. For the IC mechanism we obtained cIC-CMB = 0.73 applying the full Klein–Nishina cross section and taking the shape of the electron spectrum into account.
, using the recent parametrisation of the total inelastic p-p cross section for Geant4, Pythia8, SIBYLL2.1, and QGSJET-I from Kafexhiu et al. (2014), respectively. For the IC mechanism we obtained cIC-CMB = 0.73 applying the full Klein–Nishina cross section and taking the shape of the electron spectrum into account.
In Table A.1 we list the individual values for 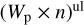 and
and 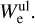 . The top panel in Fig. 7 shows our limits of
. The top panel in Fig. 7 shows our limits of 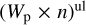 versus the estimated source distance, where we also show the corresponding estimates for the VHE-detected sample of isolated shell-type SNRs (see Table A.3 for references). Using the published flux values in case of VHE detections or our calculated flux upper limits for the undetected sources, we calculate the values according to Eq. (3) using the distance estimates listed in Table A.2. We see that the H.E.S.S. upper limits are most constraining for relatively close sources. Assuming a hypothetical average ambient density around SNRs of n ~ 1 cm −3 and an intrinsic proton power-law spectrum resulting from classical first-order Fermi acceleration with index Γ = 2, a handful of sources within a few kpc distance constrain the CR paradigm. This paradigm identifies SNRs as the sources of Galactic CR assuming that 10% of the blast energy of 1051 erg goes into the acceleration of CR up to PeV energies. However, ambient density values vary strongly from object to object, and in the bottom panel of Fig. 7 we use the literature estimates listed in Table A.2 to derive values for Wp. The reported density values in this table are in some cases derived from fits to X-ray spectra rather than direct measurements (e.g. from CO or HI observations). These values are characterised by the density inside the X-ray emitting bubble (i.e. the inter-clump density), which might not be the relevant quantity for hadronic high-energy processes. Multi-TeV protons suffer less from energy losses than electrons of similar energy and are therefore able to propagate further and consequently probe a different environment than X-ray emitting electrons of similar energy. For instance, recent work suggests a correlation between TeV γ-rays brightness and cold HI gas density, for example in the cases of HESS J1731 −347 (Fukuda et al. 2014) and RX J1713.7 −3946 (Fukui et al. 2012, Sano et al. 2015). This correlation points to γ-ray production at dense clumps with number densities well above 10 cm−3 rather than the rarefied inter-clump medium. Therefore, we treat ambient density values that have been derived from X-ray spectra as lower limits,which results in conservative upper limits on the proton energy content. In the cases in which studies reveal a correlation between γ-ray emission and gas clumps, we calculate the proton energy content for the two scenarios assuming either the low inter-clump medium density or the high value inside the clumps, which are both listed in Table A.2.
versus the estimated source distance, where we also show the corresponding estimates for the VHE-detected sample of isolated shell-type SNRs (see Table A.3 for references). Using the published flux values in case of VHE detections or our calculated flux upper limits for the undetected sources, we calculate the values according to Eq. (3) using the distance estimates listed in Table A.2. We see that the H.E.S.S. upper limits are most constraining for relatively close sources. Assuming a hypothetical average ambient density around SNRs of n ~ 1 cm −3 and an intrinsic proton power-law spectrum resulting from classical first-order Fermi acceleration with index Γ = 2, a handful of sources within a few kpc distance constrain the CR paradigm. This paradigm identifies SNRs as the sources of Galactic CR assuming that 10% of the blast energy of 1051 erg goes into the acceleration of CR up to PeV energies. However, ambient density values vary strongly from object to object, and in the bottom panel of Fig. 7 we use the literature estimates listed in Table A.2 to derive values for Wp. The reported density values in this table are in some cases derived from fits to X-ray spectra rather than direct measurements (e.g. from CO or HI observations). These values are characterised by the density inside the X-ray emitting bubble (i.e. the inter-clump density), which might not be the relevant quantity for hadronic high-energy processes. Multi-TeV protons suffer less from energy losses than electrons of similar energy and are therefore able to propagate further and consequently probe a different environment than X-ray emitting electrons of similar energy. For instance, recent work suggests a correlation between TeV γ-rays brightness and cold HI gas density, for example in the cases of HESS J1731 −347 (Fukuda et al. 2014) and RX J1713.7 −3946 (Fukui et al. 2012, Sano et al. 2015). This correlation points to γ-ray production at dense clumps with number densities well above 10 cm−3 rather than the rarefied inter-clump medium. Therefore, we treat ambient density values that have been derived from X-ray spectra as lower limits,which results in conservative upper limits on the proton energy content. In the cases in which studies reveal a correlation between γ-ray emission and gas clumps, we calculate the proton energy content for the two scenarios assuming either the low inter-clump medium density or the high value inside the clumps, which are both listed in Table A.2.
As can be seen, five of our limits are constraining the canonical expectation in this case: G290.1 −0.8 (source 9 in plot), G296.1 −0.5 (10) as well as G53.6 −2.2 (5), G306.3 −0.9 (14), and G350.1 −0.3 (20), if its distance is at the lower end of the uncertainty interval. The limits become less stringent if the proton spectra are softer. However, even if a typical Galactic particle spectral index of Γ = 2.3 is assumed, inferred from the large number of HGPS sources, two sources still constrain the theoretical expectation: that is G306.3 −0.9 (14), if the source is situated at the very low end of the distance error interval, and G290.1 −0.8 (9). However, the latter is a thermal composite SNR (as is also G53.6 −2.2), estimated tobe of an evolved age (>10 kyr) and thus unlikely to be a place of efficient particle acceleration to PeV energies as assumed in the canonical picture (see e.g. Ptuskin & Zirakashvili 2005). Therefore we consider this limit as not constraining. Also, the well-studied sources Cassiopeia A, Kepler’s SNR, and Tycho lie below the canonical estimate if Γ = 2. However, the latter two sources require larger indices in order to model their VHE emission (see Acciari et al. 2011 and Ahnen et al. 2017), and thus in these cases the comparison to the canonical value is of limited validity.
In another form of presentation, Fig. 8 shows the upper limits on Wp [> 10 TeV] for all objects that have been investigated, assuming a canonical ISM value of n = 1 cm −3 as ambient density and a typical source distance of d = 5 kpc, where this information is not available. It also shows the corresponding values for the VHE-detected SNRs.
The sample shows very high limits, which by far exceed the canonical expectation. This indicates that in these cases the sensitivity for the direction of the corresponding sources is not sufficient to provide constraining flux upper limits.
In those cases where clump interaction has been observed we see excessive values for Wp, especially RX J0852.0 −4622, RX J1713.7 −3946 and HESS J1731 −347 if the rarefied inter-clump density values are assumed. Adopting a high density inside the clumps leads to very low values of Wp that lie below the canonical expectation. Most notably, the derived value for RX J1713.7 −3946 is about 1.5 orders of magnitudes below the canonical expectation for Γ = 2.3. This value seems very low as in a hadronic emission scenario a high value for the cut-off in the proton spectrum of ~90 TeV is required to model the H.E.S.S. spectrum (see H.E.S.S. Collaboration 2018a).
Perhaps the inclusion of γ-ray emission from electrons via the IC mechanism may be a solution to this problem. Combining both the hadronic and leptonic estimations and introducing the electron to proton energy fraction above 10 TeV, ϵep, we can write
![$ W_{\mathrm{p}}^{\mathrm{ul}}[{>}10\,\mathrm{TeV}] = \frac{F_{\mathrm{E}}^{\mathrm{ul}}[{>}1\,\mathrm{TeV}]\times 4\pi d^2}{n/t_{\pi^0} + \epsilon_{\mathrm{ep}}/t_{\mathrm{IC}}}. $](/articles/aa/full_html/2018/04/aa32125-17/aa32125-17-eq14.png)
In the following we want to determine the portion of the {n, ϵep } parameter space that is excluded by the flux upper limits, assuming that the accelerated proton distributions in SNRs meet the canonical expectation mentioned in the earlier paragraphs and follow a power-law distribution with a spectral index of Γ = 2.3.
Our upper limits are constraining a parameter set in the {n, ϵep }-plane if ![$W_\mathrm{p}^\mathrm{ul}[{>}10\,\mathrm{TeV}]~<~W_\mathrm{p}^\mathrm{th}[{>}10\,\mathrm{TeV}]$](/articles/aa/full_html/2018/04/aa32125-17/aa32125-17-eq15.png) , where
, where ![$W_\mathrm{p}^\mathrm{th}[{>}10\,\mathrm{TeV}]$](/articles/aa/full_html/2018/04/aa32125-17/aa32125-17-eq16.png) is the theoretically expected value from the canonical assumption. Each individual upper limit then results in a curve in this parameter space above which the corresponding source would have been detected by H.E.S.S. and is therefore excluding the corresponding portion of the parameter space for this object. The set of curves is shown in Fig. 9. This figure also shows the distribution of constraints on ϵep and n in the asymptotic leptonic- and hadronic-dominated scenario limits as one-dimensional histograms. The logarithmic medians of those distributions are log(ϵep) and log(n∕1 cm−3) are −2.28 and 0.83, respectively. The variance in both cases is 0.26.
is the theoretically expected value from the canonical assumption. Each individual upper limit then results in a curve in this parameter space above which the corresponding source would have been detected by H.E.S.S. and is therefore excluding the corresponding portion of the parameter space for this object. The set of curves is shown in Fig. 9. This figure also shows the distribution of constraints on ϵep and n in the asymptotic leptonic- and hadronic-dominated scenario limits as one-dimensional histograms. The logarithmic medians of those distributions are log(ϵep) and log(n∕1 cm−3) are −2.28 and 0.83, respectively. The variance in both cases is 0.26.
In the canonical picture of particle acceleration in SNRs, these values constrain hadronic-dominated emission scenarios to ambient density values n≲7 cm −3 and leptonic-dominated emission scenarios to ϵep≲0.5%. The most stringent upper limit yields n≲0.6 cm−3 and ϵep ≲0.05%.
For comparison, we also show in Fig. 9 the {n, ϵep }-ntuples for the VHE-detected shell-type SNRs. We derive these values from the models in the publications listed in Table A.3. For a valid comparison with the constraints in the {n, ϵep } parameter space, we scale the parameters values by a factor f = Wp,i∕(1050 erg), where Wp,i is the total energy in CR protons that has been derived for the sources i in the literature because in most cases the latter deviates from the canonical 1050 erg. In some publications the authors discuss both hadronic- and leptonic-dominated scenarios, in which case we show the respective points in the parameter space for both cases. The majority of the detected sources fall into the part of the parameter space that would allow for the detection by the HGPS. However, its sensitivity would not allow for the detection of the two VHE-faintest SNRs: Tycho’s SNR, detected by the VERITAS collaboration (Acciari et al. 2011), and SN 1006. These sources required pointed observations to reach the exposure necessary for detection.
It should be stressed that the theoretical interpretation of the presented analysis results is rather simple and does not take into accountthe full complexity of the SNRs (which is beyond the scope of this paper). Also, many distance and density estimates used in this study suffer from large uncertainties with factors of a few; see Table A.2.
That said, if the assumptions made in our considerations are roughly plausible for the average young to middle-agedSNR, the next generation observatory, CTA, holds great potential for SNR science. An improvement in instrument sensitivity by an order of magnitude, as planned with CTA, will allow it to probe a considerably increased fraction of the parameter space, corresponding to the portion of the parameter space above the blue dotted line in Fig. 9. If our theoretical expectations are sound, we can expect CTA to test the SNR paradigm for ambient densities in the typical ISM range independent of the primary emission mechanism. If the γ-ray emission is dominated by the leptonic channel, even SNRs in rarefied environments such as the interior of bubbles blown by the main-sequence winds of the SNR progenitor stars should be detectable with CTA.
 |
Fig. 7 Upper limits and measurements on the product of proton energy content above 10 TeV and ambient density (top) and proton energy content above 10 TeV (bottom) vs. source distance. We assume the ambient density and distance estimates from the publications listed in Table A.2 and also show the corresponding values for VHE-detected shell-type SNRs. For the latter, we use the flux normalisations as reported in the publications listed in Table A.3. In several sources a gas clump correlation of γ-ray emission was observed. In these cases, filled points indicate the result if the low density values in the rarefied inter-clumpmedium are used in the calculation, while open points show the result if the high density values inside the clumps are assumed. We also show the canonical expectation, assuming an acceleration efficiency of Θ = 10%, a SN blast energy of ESN = 1051 erg, and a power- law spectrum with spectral index of Γ = 2 (expected from standard first order Fermi acceleration) and Γ = 2.3 (corresponding to the average spectral index of HGPS sources) up to Emax = 1 PeV, assuming n = 1 cm−3 in the top panel. Furthermore, we show in the top panel the sensitivity of the HGPS (assuming a mean value of ~1.5% Crab) and the projected sensitivity of CTA (assuming a ten times higher sensitivity). Red points represent old sources (>10 kyr) that are not expected to accelerate protons to PeV energies, grey limits in the top panel indicate SNRs that are likely to interact with molecular clouds (see Table A.1). Values for Kepler’s SNR (source 2), G1.9+0.3 (1) and G330.2+1.0 (41 top, 19 bottom) are derived from the limits in Aharonian et al. (2008a) and Abramowski et al. (2014b). |
 |
Fig. 8 Sample of upper limits on the proton energy content above 10 TeV (triangles). Values are derived using the centre of the distance uncertainty interval. Blue triangles indicate SNRs that are likely to interact with molecular clouds (see Table A.1). Points are shown for the VHE-detected sample of SNRs, where the error arising from the distance uncertainty is indicated. In several sources a gas clump correlation of γ-ray emission was observed. In these cases, filled points indicate the result if the low density values in the rarefied inter-clump medium are used in the calculation, while open points show the result if the high density values inside the clumps are assumed. |
 |
Fig. 9 Constraints on the ϵep and n parameter space as imposed by the flux upper limits (grey bands, each limit constitutes one band). For each constraint a source-intrinsic power-law spectrum with index Γ = 2.3 was assumed. Solid and dotted red lines represent the constraints corresponding to the median and lowest value of the flux upper limit distribution, respectively. The blue line indicates the boundary above which CTA might be able to probe the parameter space, assuming a ten times higher sensitivity than H.E.S.S. and taking the lowest flux upper limit as a reference. Additionally, values of ϵep and n for VHE-detected shell-type SNRs are shown, extracted from the publications in Table A.3. For better comparison, these values are rescaled to the canonical total CR energy in SNRs of 1050 erg. The dashed and dotted black lines indicate how the median of the distribution shifts if one limits the maximum proton energy to 100 TeV and 20 TeV, respectively. The histograms show the parameter limit distributions in the extreme hadronic- and leptonic-dominated scenarios. |
5.4 Luminosity evolution of SNRs in the radio and VHE bands
The average sensitivity of the HGPS is at the level of ~2% of the Crab nebula VHE flux. There are sky regions of deeper exposure and thus lower values around prominent sources such as the Galactic centre. Because of the limited sensitivity, we can expect selection effects in the sample of detected SNRs roughly following the relations LVHE∕4πd2 > S and LVHE ∕4πd > S for point-like and extended sources, respectively. In this work, S is the H.E.S.S. point-like source sensitivity in a given field of view, d is the distance to the source, and LVHE is the source luminosity between 1 TeV and 10 TeV. By including the sample of flux upper limits on radio SNRs in our considerations, we can achieve a more complete and less biased view on the VHE emission properties of this source class.Also, we want to make use of the large amount of radio information on SNRs and compare the VHE γ-ray fluxes to those observed at radio wavelengths.
To that end, we consider LVHE and used the radio flux density values at 1 GHz, as provided in the Green SNR catalogue (Green 2014), to calculate the corresponding luminosity LRadio . We furthermore formally assume a uniform bandwidth of 1 GHz to convert from radio flux density to radio flux. The spectral assumptions used in the derivation of the VHE γ-ray luminosities of the VHE-detected shell-type SNRs are listed in Table A.3, along with the radio flux densities and age estimates from the SNRcat and Green catalogues. Finally, we remove SNRs from the sample for which interaction with molecular clouds is established or probable because in this study we want to investigate the physical processes at isolated SNR shocks. The information about whether a cloud interaction is occurring is also provided by SNRcat. However, such information is not available for all SNRs and thus it is possible that interacting SNRs are still present in the resulting source sample.
In the following, we investigate the data for linear correlations of both the VHE-luminosity (y = log (LVHE)) and the ratio of VHE-to-radio luminosities (y = log(LVHE∕LRadio)) with source age (x = log(Age∕1 kyr)). The fit results can be found in Table 1.
In the top panel panel of Fig. 10 we show the VHE luminosities of shell-type and thermal-composite SNRs as a function of source age. A linear fit in estimated source age to the data points of those SNRs detected in both the radio and the VHE bands (black points) shows no sign of correlation (with a p-values of p = 0.1 testing the null-hypothesis of a non-correlation). Also the inclusion of upper limits6 that fall into the same age interval as the detected SNRs (<5.1 kyr) does not change this situation. In this figure, to be conservative, we assumed the largest distances compatible with uncertainties.
There is a large scatter in the data points that partially stems from substantial uncertainties in the distance estimates. One way to address this problem is to look at the ratio (LVHE ∕Lradio), as it eliminates this uncertainty by construction. Indeed, the resulting values of the VHE detections show considerably less scatter in the ordinate values around the best-fit linear regression, as can be seen in the bottom panel of Fig. 10, where we show (LVHE∕Lradio) versus source age. We find evidence for correlation for the sample of shell-type SNRs that have been detected in both the radio and VHE bands (black) with a p-value of p = 2.3 × 10−3. Adding the corresponding upper limit values for SNRs that fall into the same age window as the VHE detections, i.e. with ages <5.1 kyr, weakens the correlation with age (p = 2.7 × 10−2). An inclusion of the upper limit values for the older SNRs in the age fit results in a high probability of a non-correlation (p = 0.9). While it is expected that the spread in (LVHE∕Lradio) increases with source age as the diverse environment around SNRs becomes more and more important for the SNR evolution, the sample of upper limit values from evolved (≳104 yr) SNRs lies consistently below the extrapolated correlation by some orders of magnitude. It should be stressed that the correlations found might be different for interacting SNRs, since we excluded these systems from our test sample.
From our limited data set we find that the increase of VHE luminosity with source age is smaller than that of (LVHE ∕Lradio), which implies that in the first several thousand years of SNR evolution the radio-synchrotron emission decreases more rapidly than the VHE emission increases. Therefore, although we prefer to look at the ratio (LVHE ∕Lradio) instead of the individual radio and VHE luminosities to eliminate the large distance uncertainties, we note that the observed correlation is mainly driven by the strong decrease in Lradio with time rather than the relatively constant behaviour of LVHE. A time decrease of SNR luminosities at lower energies has been directly observed in Cas A for non-thermal X-ray and radio emission (see Dent et al. 1974; Vinyaikin 2014; Patnaude et al. 2011 and Sato et al. 2017).
At higher ages, there are no more VHE detections of shell-type or thermal composite SNRs, while synchrotron emission at radio energies continues. The latter finding agrees with the theoretical expectation that effective particle acceleration to multi-TeV energies occurs mainly in young SNRs but not in more evolved systems. The observed behaviour of the younger sources can be interpreted by invoking the notion of magnetic field amplification at SNR shocks. In this theory, the amplified B-field is fuelled by a fraction of the shock-generated CR pressure (see e.g. Bell 2004 and Völk et al. 2005), and is therefore expected to decrease as the shock slows down with increasing source age, which in turn would lead to a decreased overall synchrotron luminosity.
Fit results from correlation testing.
 |
Fig. 10 Correlations of VHE luminosity between 1 TeV and 10 TeV of LVHE (top) and (LVHE∕Lradio) (bottom) with source age, where Lradio is the luminosity at 1 GHz. Points: detected shell-type SNRs in the VHE regime. Arrows: upper limits. Red: shell-type SNRs. Blue: thermal composite SNRs. Values for Kepler’s SNR, G1.9+0.3 and G330.2+1.0 from Aharonian et al. (2008a) and Abramowski et al. (2014b). Grey lines and uncertainty bands: Best-fit correlations taking only the detected SNRs into account. Red lines and uncertainty bands: Best-fit correlations when including also those upper limits into the fit where SNRs fall into the age interval defined by the sample of VHE-detections (<5.1 kyr, upper age limit of RX J0852.0 −4622). |
6 Conclusions
In this work we investigated a sample of 108 Galactic SNRs, comprised of sources that have been detected in lower energy bands, for VHE γ-ray emission using the H.E.S.S. Phase I data coming from the HGPS programme (H.E.S.S. Collaboration 2018b). For the first time, upper limits on the integrated γ-ray flux between 1 and 10 TeV are provided for such a large set of Galactic SNRs. We note that the presented upper limits may be useful for continuing studies, such as in Cristofari et al. (2013), where VHE data were compared to a SNR population synthesis model to investigate the CR standard paradigm.
We paid special attention to the selection of these sources to minimise a possible signal leakage from unrelated H.E.S.S. detections (see H.E.S.S. Collaboration 2018b) into the analysis regions. We found a positive offset of the significance distribution corresponding to a median value of 1σ. To at least a large degree, the origin of this offset can be attributed to the diffuse Galactic TeV emission detected by H.E.S.S. We applied generic models of the two VHE γ-ray emission processes believed to be dominant in SNRs to the data, i.e. the π0 -decay in a hadronic and IC emission in a leptonic emission scenario to place constraints on the acceleration efficiency in SNRs and the energy content in electrons and protons above 10 TeV. Assuming typical parameters of the ambient gas density and the SN blast energy, the resulting values do not contradict the standard expecation that ~10% of the SN blast energyis converted to CR in SNRs. We also investigated the opposite problem assuming that this canonical paradigm is valid and put constraints on the parameter space spanned by the ambient gas density around the shock and electron-to-proton energy fraction.
Overall,the derived flux upper limits are not in contradiction with the canonical CR paradigm. Assuming this paradigm holds true, we can constrain typical ambient density values around shell-type SNRs to n ≤ 7 cm −3 and electron-to-proton energy fractions above 10 TeV to ϵep ≤ 5 × 10−3.
Finally, we compared the presented flux upper limits to the flux measurements of the seven non-interacting shell-type SNRs detected both in the radio and VHE range. We found evidence of correlation between the ratio of VHE γ-ray luminosity to radio luminosity, (LVHE∕Lradio), and source age. This correlation can be explained by invoking the theory of magnetic field amplification at SNR shocks, which accounts for the rapid decrease in radio luminosity by predicting a declining magnetic field strength as the shock slows down with increasing source age.
Further development in the SNR population from the observational point of view should be achieved with the next generation instrument: the CTA observatory. In this work we have also estimated the performance of this future observatory to probe the ambient gas density and the SN blast energy parameter space. The results suggest that this instrument will be an important leap forward in the investigation of the Galactic SNRs and will likely be able to confirm or invalidate the CR paradigm.
Acknowledgements
The support of the Namibian authorities and of the University of Namibia in facilitating the construction and operation of H.E.S.S. is gratefully acknowledged, as is the support by the German Ministry for Education and Research (BMBF), the Max Planck Society, the German Research Foundation (DFG), the Alexander von Humboldt Foundation, the Deutsche Forschungsgemeinschaft, the French Ministry for Research, the CNRS-IN2P3 and the Astroparticle Interdisciplinary Programme of the CNRS, the U.K. Science and Technology Facilities Council (STFC), the IPNP of the Charles University, the Czech Science Foundation, the Polish National Science Centre, the South African Department of Science and Technology and National Research Foundation, the University of Namibia, the National Commission on Research, Science & Technology of Namibia (NCRST), the Innsbruck University, the Austrian Science Fund (FWF), andthe Austrian Federal Ministry for Science, Research and Economy, the University of Adelaide and the Australian Research Council, the Japan Society for the Promotion of Science, and the University of Amsterdam. We appreciate the excellent work of the technical support staff in Berlin, Durham, Hamburg, Heidelberg, Palaiseau, Paris, Saclay, and in Namibia in the construction and operation of the equipment. This work benefited from services provided by the H.E.S.S. Virtual Organisation, supported by the national resource providers of the EGI Federation.
Appendix A Additional material
Results overview.
Literature estimates on source ages, distances, and ambient densities.
Spectral parameters of the shell-type SNRs detected in both the radio and VHE bands.
 |
Fig. A.1 HGPS sensitivity map (for a correlation radius of 0.2°) overlaid with the analysis regions of our source sample (grey) and the de-selection regions (black); see also Sect. 2. |
References
- Abramowski, A., Acero, F., Aharonian, F., et al. 2011, A&A, 531, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abramowski, A., Acero, F., Aharonian, F., et al. 2012, ApJ, 757, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowski, A., Aharonian, F., Ait Benkhali, F., et al. 2014a, Phys. Rev. D, 90, 122007 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowski, A., Aharonian, F., Benkhali, F. A., et al. 2014b, MNRAS, 441, 790 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowski, A., Aharonian, F., Ait Benkhali, F., et al. 2015, A&A, 574, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Acciari, V. A., Aliu, E., Arlen, T., et al. 2011, ApJ, 730, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Acero, F., Ballet, J., Decourchelle, A., et al. 2009, A&A, 505, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Acero, F., Aharonian, F., Akhperjanian, A. G., et al. 2010, A&A, 516, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Acero, F., Ackermann, M., Ajello, M., et al. 2016, ApJS, 224, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Actis, M., Agnetta, G., Aharonian, F., et al. 2011, Exp. Astron., 32, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006, A&A, 457, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Barres de Almeida, U., et al. 2008a, A&A, 488, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2008b, A&A, 481, 401 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Ahnen, M. L., Ansoldi, S., Antonelli, L. A., et al. 2017, MNRAS, 472, 2956 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, G. E., Chow, K., DeLaney, T., et al. 2015, ApJ, 798, 82 [Google Scholar]
- Auchettl, K., Slane, P., Castro, D., Foster, A. R., & Smith, R. K. 2015, ApJ, 810, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 2004, MNRAS, 353, 550 [Google Scholar]
- Berge, D., Funk, S., & Hinton, J. 2007, A&A, 466, 1219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Broersen, S., & Vink, J. 2015, MNRAS, 446, 3885 [NASA ADS] [CrossRef] [Google Scholar]
- Broersen, S., Chiotellis, A., Vink, J., & Bamba, A. 2014, MNRAS, 441, 3040 [NASA ADS] [CrossRef] [Google Scholar]
- Busser, J.-U., Egger, R., & Aschenbach, B. 1996, A&A, 310, L1 [NASA ADS] [Google Scholar]
- Carlton, A. K., Borkowski, K. J., Reynolds, S. P., et al. 2011, ApJ, 737, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Cassam-Chenaï, G., Decourchelle, A., Ballet, J., et al. 2004, A&A, 427, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castro, D., Slane, P. O., Gaensler, B. M., Hughes, J. P., & Patnaude, D. J. 2011, ApJ, 734, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y., Seward, F. D., Sun, M., & Li, J.-t. 2008, ApJ, 676, 1040 [NASA ADS] [CrossRef] [Google Scholar]
- Cristofari, P., Gabici, S., Casanova, S., Terrier, R., & Parizot, E. 2013, MNRAS, 434, 2748 [NASA ADS] [CrossRef] [Google Scholar]
- de Naurois, M., & Rolland, L. 2009, Astropart. Phys., 32, 231 [NASA ADS] [CrossRef] [Google Scholar]
- DeLaney, T., & Rudnick, L. 2003, ApJ, 589, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Dent, W. A., Aller, H. D., & Olsen, E. T. 1974, ApJ, 188, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Drury, L. O., Aharonian, F. A., & Voelk, H. J. 1994, A&A, 287, 959 [NASA ADS] [Google Scholar]
- Ferrand, G., & Safi-Harb, S. 2012, Adv. Space Res., 49, 1313 [NASA ADS] [CrossRef] [Google Scholar]
- Fukuda, T., Yoshiike, S., Sano, H., et al. 2014, ApJ, 788, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Fukui, Y., Sano, H., Sato, J., et al. 2012, ApJ, 746, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Green, D. A. 2014, Bull. Astron. Soc. India, 42, 47 [NASA ADS] [Google Scholar]
- Hahn, J., de los Reyes, R., Bernlöhr, K., et al. 2014, Astropart. Phys., 54, 25 [NASA ADS] [CrossRef] [Google Scholar]
- H.E.S.S. Collaboration (Abdalla, H., Abramowski, A., et al.) 2018a, A&A, 612, A6 (H.E.S.S. SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- H.E.S.S. Collaboration (Abdalla, H., Abramowski, A., et al.) 2018b, A&A, 612, A1 (H.E.S.S. SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- H.E.S.S. Collaboration (Abdalla, H., Abramowski, A., et al.) 2018c, A&A, 612, A7 (H.E.S.S. SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- H.E.S.S. Collaboration (Abramowski, A., Aharonian, F., et al.) 2018d, A&A, 612, A4 (H.E.S.S. SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huang, R. H. H., Wu, J. H. K., Hui, C. Y., et al. 2014, ApJ, 785, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Hui, C. Y., & Becker, W. 2009, A&A, 494, 1005 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hui, C. Y., Seo, K. A., Huang, R. H. H., et al. 2012, ApJ, 750, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Hwang, U., & Laming, J. M. 2003, ApJ, 597, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Kafexhiu, E., Aharonian, F., Taylor, A. M., & Vila, G. S. 2014, Phys. Rev. D, 90, 123014 [NASA ADS] [CrossRef] [Google Scholar]
- Lavalley, M., Isobe, T., & Feigelson, E. 1992, ASP Conf. Ser., 25, 245 [NASA ADS] [Google Scholar]
- Lee, J.-J., Park, S., Hughes, J. P., & Slane, P. O. 2014, ApJ, 789, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Li, T.-P., & Ma, Y.-Q. 1983, ApJ, 272, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Long, K. S., Blair, W. P., Matsui, Y., & White, R. L. 1991, ApJ, 373, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Lovchinsky, I., Slane, P., Gaensler, B. M., et al. 2011, ApJ, 731, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Malkov, M. A., & Drury, L. O. 2001, Rep. Prog. Phys., 64, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Minami, S., Ota, N., Yamauchi, S., & Koyama, K. 2013, PASJ, 65, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Moriguchi, Y., Yamaguchi, N., Onishi, T., Mizuno, A., & Fukui, Y. 2001, PASJ, 53, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Ohm, S., van Eldik, C., & Egberts, K. 2009, Astropart. Phys., 31, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Pannuti, T. G., Rho, J., Heinke, C. O., & Moffitt, W. P. 2014, AJ, 147, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Park, N., & VERITAS Collaboration 2015, Proc. 34th Int. Cosmic Ray Conf. (ICRC2015), 769 [Google Scholar]
- Park, S., Kargaltsev, O., Pavlov, G. G., et al. 2009, ApJ, 695, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Patnaude, D. J., Vink, J., Laming, J. M., & Fesen, R. A. 2011, ApJ, 729, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Prinz, T., & Becker, W. 2012, A&A, 544, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prinz, T., & Becker, W. 2013, A&A, 550, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ptuskin, V. S., & Zirakashvili, V. N. 2005, A&A, 429, 755 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Rakowski, C. E., Hughes, J. P., & Slane, P. 2001, ApJ, 548, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Rakowski, C. E., Badenes, C., Gaensler, B. M., et al. 2006, ApJ, 646, 982 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, S. P., Borkowski, K. J., Hwang, U., et al. 2006, ApJ, 652, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, S. P., Borkowski, K. J., Green, D. A., et al. 2008, ApJ, 680, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, M. T., Loi, S. T., Murphy, T., et al. 2013, ApJ, 766, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Rolke, W. A., López, A. M., & Conrad, J. 2005, Nucl. Instr. Meth. Phys. Res. A, 551, 493 [CrossRef] [Google Scholar]
- Sánchez-Ayaso, E., Combi, J. A., Albacete Colombo, J. F., et al. 2012, Ap&SS, 337, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Ayaso, E., Combi, J. A., Bocchino, F., et al. 2013, A&A, 552, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sano, H., Fukuda, T., Yoshiike, S., et al. 2015, ApJ, 799, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, T., Maeda, Y., Bamba, A., et al. 2017, ApJ, 836, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Slane, P., Lee, S.-H., Ellison, D. C., et al. 2014, ApJ, 783, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, W. W., Haverkorn, M., & Zhang, H. Y. 2007, MNRAS, 378, 1283 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. 2008, ApJ, 689, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Vinyaikin, E. N. 2014, Astron. Rep., 58, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Völk, H. J., Berezhko, E. G., Ksenofontov, L. T., & Rowell, G. P. 2002, A&A, 396, 649 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Völk, H. J., Berezhko, E. G., & Ksenofontov, L. T. 2005, A&A, 433, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winkler, P. F., Williams, B. J., Reynolds, S. P., et al. 2014, ApJ, 781, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshita, K., Miyata, E., & Tsunemi, H. 2000, PASJ, 52, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Zoglauer, A., Reynolds, S. P., An, H., et al. 2015, ApJ, 798, 98 [NASA ADS] [CrossRef] [Google Scholar]
The mean point spread function 68% containment radius is 0.08°, see H.E.S.S. Collaboration (2018b).
http://www.physics.umanitoba.ca/snr/SNRcat/ Version used here as of 12.14.2015.
Correlation testing including upper limits was performed using the Cox hazard model and the EM algorithm regression provided by the asurv package (Lavalley et al. 1992), which is available at http://ascl.net/1406.001
All Tables
Spectral parameters of the shell-type SNRs detected in both the radio and VHE bands.
All Figures
 |
Fig. 1 Illustration of the source selection scheme on the γ-ray excess image from a given region. The known H.E.S.S. sources HESS J1857+026 and HESS J1858+020 with their 80% flux containment radii are shown with a dashed circle. The de-selection region resulting from the algorithm explained inSect. 2 is shown with a solid curve. Because of the overlap with the de-selection region, the SNR G35.6 −0.4 is discarded whereas SNR G36.6 −0.7 is selected. |
| In the text | |
 |
Fig. 2 Distribution of flux upper limits (99% confidence level) of all investigated SNRs. The red line indicates the median value of ~ 2% of the Crab nebula flux. |
| In the text | |
 |
Fig. 3 Left: significance distribution of the VHE-dark sample of SNRs (black, blue, red, and green) and the corresponding median value (grey solid). The grey dashed curve indicates a normal Gaussian. Right: cumulative significance distribution of all sources(black), those of shell-type (blue), and composite (red and green) morphology. The grey dashed line represents a cumulative normal Gaussian. |
| In the text | |
 |
Fig. 4 Source significance values of the VHE-dark source sample vs. the angular distance to the nearest detected H.E.S.S. source. The angular distance between the edges of our test regions to that of detected H.E.S.S. sources is shown; the marker size is proportional to the integrated flux above 1 TeV of the latter. The source region positions and sizes are taken from the HGPS, where they are defined as the centroids and 80% containment radii of symmetric and two-dimensional Gaussian fits to the integrated flux map, respectively (see H.E.S.S. Collaboration 2018b for more details). Negative distance values are possible for asymmetric sources where the Gaussian fit does not describe the source morphology well, see e.g. SNR G36.6 −0.7 in Fig. 1. |
| In the text | |
 |
Fig. 5 Cumulated significance distribution of the SNR sample (black) and analogous distribution corrected for the Galactic diffuse emission component (dash-dotted red). The cumulated density function from the analysis of randomised test regions is shown in dotted blue. The grey dashed curve represents a cumulated normal Gaussian distribution. |
| In the text | |
 |
Fig. 6 Gamma-ray spectral energy distributions of G6.1+0.5 and G310.8 −0.4. The Fermi-LAT spectra are derived from the spectral parameters reported in the first Fermi-LAT SNR catalogue. Statistical errors are indicated by the shaded bands. |
| In the text | |
 |
Fig. 7 Upper limits and measurements on the product of proton energy content above 10 TeV and ambient density (top) and proton energy content above 10 TeV (bottom) vs. source distance. We assume the ambient density and distance estimates from the publications listed in Table A.2 and also show the corresponding values for VHE-detected shell-type SNRs. For the latter, we use the flux normalisations as reported in the publications listed in Table A.3. In several sources a gas clump correlation of γ-ray emission was observed. In these cases, filled points indicate the result if the low density values in the rarefied inter-clumpmedium are used in the calculation, while open points show the result if the high density values inside the clumps are assumed. We also show the canonical expectation, assuming an acceleration efficiency of Θ = 10%, a SN blast energy of ESN = 1051 erg, and a power- law spectrum with spectral index of Γ = 2 (expected from standard first order Fermi acceleration) and Γ = 2.3 (corresponding to the average spectral index of HGPS sources) up to Emax = 1 PeV, assuming n = 1 cm−3 in the top panel. Furthermore, we show in the top panel the sensitivity of the HGPS (assuming a mean value of ~1.5% Crab) and the projected sensitivity of CTA (assuming a ten times higher sensitivity). Red points represent old sources (>10 kyr) that are not expected to accelerate protons to PeV energies, grey limits in the top panel indicate SNRs that are likely to interact with molecular clouds (see Table A.1). Values for Kepler’s SNR (source 2), G1.9+0.3 (1) and G330.2+1.0 (41 top, 19 bottom) are derived from the limits in Aharonian et al. (2008a) and Abramowski et al. (2014b). |
| In the text | |
 |
Fig. 8 Sample of upper limits on the proton energy content above 10 TeV (triangles). Values are derived using the centre of the distance uncertainty interval. Blue triangles indicate SNRs that are likely to interact with molecular clouds (see Table A.1). Points are shown for the VHE-detected sample of SNRs, where the error arising from the distance uncertainty is indicated. In several sources a gas clump correlation of γ-ray emission was observed. In these cases, filled points indicate the result if the low density values in the rarefied inter-clump medium are used in the calculation, while open points show the result if the high density values inside the clumps are assumed. |
| In the text | |
 |
Fig. 9 Constraints on the ϵep and n parameter space as imposed by the flux upper limits (grey bands, each limit constitutes one band). For each constraint a source-intrinsic power-law spectrum with index Γ = 2.3 was assumed. Solid and dotted red lines represent the constraints corresponding to the median and lowest value of the flux upper limit distribution, respectively. The blue line indicates the boundary above which CTA might be able to probe the parameter space, assuming a ten times higher sensitivity than H.E.S.S. and taking the lowest flux upper limit as a reference. Additionally, values of ϵep and n for VHE-detected shell-type SNRs are shown, extracted from the publications in Table A.3. For better comparison, these values are rescaled to the canonical total CR energy in SNRs of 1050 erg. The dashed and dotted black lines indicate how the median of the distribution shifts if one limits the maximum proton energy to 100 TeV and 20 TeV, respectively. The histograms show the parameter limit distributions in the extreme hadronic- and leptonic-dominated scenarios. |
| In the text | |
 |
Fig. 10 Correlations of VHE luminosity between 1 TeV and 10 TeV of LVHE (top) and (LVHE∕Lradio) (bottom) with source age, where Lradio is the luminosity at 1 GHz. Points: detected shell-type SNRs in the VHE regime. Arrows: upper limits. Red: shell-type SNRs. Blue: thermal composite SNRs. Values for Kepler’s SNR, G1.9+0.3 and G330.2+1.0 from Aharonian et al. (2008a) and Abramowski et al. (2014b). Grey lines and uncertainty bands: Best-fit correlations taking only the detected SNRs into account. Red lines and uncertainty bands: Best-fit correlations when including also those upper limits into the fit where SNRs fall into the age interval defined by the sample of VHE-detections (<5.1 kyr, upper age limit of RX J0852.0 −4622). |
| In the text | |
 |
Fig. A.1 HGPS sensitivity map (for a correlation radius of 0.2°) overlaid with the analysis regions of our source sample (grey) and the de-selection regions (black); see also Sect. 2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.