| Issue |
A&A
Volume 612, April 2018
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 14 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201731810 | |
| Published online | 17 April 2018 | |
Unveiling the chemistry of interstellar CH
Spectroscopy of the 2 THz N = 2 ← 1 ground state line★
1
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn, Germany
e-mail: hwiese@mpifr.de
2
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Str 77,
50937
Köln, Germany
Received:
22
August
2017
Context. The methylidyne radical CH is commonly used as a proxy for molecular hydrogen in the cold, neutral phase of the interstellar medium. The optical spectroscopy of CH is limited by interstellar extinction, whereas far-infrared observations provide an integral view through the Galaxy. While the HF ground state absorption, another H2 proxy in diffuse gas, frequently suffers from saturation, CH remains transparent both in spiral-arm crossings and high-mass star forming regions, turning this light hydride into a universal surrogate for H2. However, in slow shocks and in regions dissipating turbulence its abundance is expected to be enhanced by an endothermic production path, and the idea of a “canonical” CH abundance needs to be addressed.
Aim. The N = 2 ← 1 ground state transition of CH at λ149 μm has become accessible to high-resolution spectroscopy thanks to the German Receiver for Astronomy at Terahertz Frequencies (GREAT) aboard the Stratospheric Observatory for Infrared Astronomy (SOFIA). Its unsaturated absorption and the absence of emission from the star forming regions makes it an ideal candidate for the determination of column densities with a minimum of assumptions. Here we present an analysis of four sightlines towards distant Galactic star forming regions, whose hot cores emit a strong far-infrared dust continuum serving as background signal. Moreover, if combined with the sub-millimeter line of CH at λ560 μm , environments forming massive stars can be analyzed. For this we present a case study on the “proto-Trapezium” cluster W3 IRS5.
Methods. While we confirm the global correlation between the column densities of HF and those of CH, both in arm and interarm regions, clear signposts of an over-abundance of CH are observed towards lower densities. However, a significant correlation between the column densities of CH and HF remains. A characterization of the hot cores in the W3 IRS5 proto-cluster and its envelope demonstrates that the sub-millimeter/far-infrared lines of CH reliably trace not only diffuse but also dense, molecular gas.
Results. In diffuse gas, at lower densities a quiescent ion-neutral chemistry alone cannot account for the observed abundance of CH. Unlike the production of HF, for CH+ and CH, vortices forming in turbulent, diffuse gas may be the setting for an enhanced production path. However, CH remains a valuable tracer for molecular gas in environments reaching from diffuse clouds to sites of high-mass star formation.
Key words: ISM: abundances / ISM: clouds / ISM: lines and bands / ISM: molecules / ISM: structure
The reduced spectra (Fig. 2) are only and Table 2 is also available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/612/A37
© ESO 2018
1 Introduction
The methylidyne radical, CH, was the first molecule observed in space (Dunham 1937) and identified by Swings & Rosenfeld (1937). Most CH originates in the diffuse gas of the cold, neutral matter (CNM) via the slow radiative association of C+ with H2 forming CH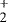 , which converts to CH via dissociative recombination CH
, which converts to CH via dissociative recombination CH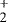 (e−,H)CH (e.g., Gerin et al. 2016). Owing to the former reaction, one expects the CH abundance to scale with that of H2 , making CH a proxy for molecular hydrogen. Other reaction channels are the dissociative recombination of CH
(e−,H)CH (e.g., Gerin et al. 2016). Owing to the former reaction, one expects the CH abundance to scale with that of H2 , making CH a proxy for molecular hydrogen. Other reaction channels are the dissociative recombination of CH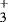 , and the photodissociation of CH2 . The usefulness of CH as a surrogate for H2 is confirmed by Sheffer et al. (2008), who observed the CH A − X(0 − 0) band at 430 nm. They derive CH column densities that range from ~1011 to ~1013 cm-2. The reference column densities of H2 were derived from UV spectra of the Lyman B − X bands. However, UV and optical studies are restricted to distances of up to ~7 kpc, with the vast majority being much smaller (e.g., Sheffer et al. 2008), owing to Galactic extinction in the UV, and to the requirement of bright background stars in the optical. Pan et al. (2005) found that there are two populations of CH bearing clouds, one being associated with CN, the other one with CH+ . The abundance of CH+ and subsequently CH may indeed be enhanced by the molecular hydrogen abstraction reaction C+ (H2,H)CH+. This reaction is endothermic by 0.398 ± 0.003 eV or about 4620 K (Hierl et al. 1997, while earlier measurements yielded ~4300 K, Gerlich et al. 1987). The supply activating this reaction is thought to be provided by the dissipation of turbulence and by ion-neutral drift (Godard et al. 2009) or by slow, non-dissociative shocks permeating the CNM (Gerin et al. 2016, further references therein). Indeed, Godard et al. (2014) demonstrated that at nH = 50 cm−3, 80% to 90% of the CH column density and all of the CH+ arise from bursts of dissipation, while the remaining fraction is associated with gas in the ambient medium or relaxing towards it. Only at gas densities in excess of typically 100 cm−3 does the abundance of CH become nearly constant (Sheffer et al. 2008; Levrier et al. 2012). As a matter of fact, at nH = 300 cm−3, about 70% of the CH originates in ambient conditions (Godard et al. 2009).
, and the photodissociation of CH2 . The usefulness of CH as a surrogate for H2 is confirmed by Sheffer et al. (2008), who observed the CH A − X(0 − 0) band at 430 nm. They derive CH column densities that range from ~1011 to ~1013 cm-2. The reference column densities of H2 were derived from UV spectra of the Lyman B − X bands. However, UV and optical studies are restricted to distances of up to ~7 kpc, with the vast majority being much smaller (e.g., Sheffer et al. 2008), owing to Galactic extinction in the UV, and to the requirement of bright background stars in the optical. Pan et al. (2005) found that there are two populations of CH bearing clouds, one being associated with CN, the other one with CH+ . The abundance of CH+ and subsequently CH may indeed be enhanced by the molecular hydrogen abstraction reaction C+ (H2,H)CH+. This reaction is endothermic by 0.398 ± 0.003 eV or about 4620 K (Hierl et al. 1997, while earlier measurements yielded ~4300 K, Gerlich et al. 1987). The supply activating this reaction is thought to be provided by the dissipation of turbulence and by ion-neutral drift (Godard et al. 2009) or by slow, non-dissociative shocks permeating the CNM (Gerin et al. 2016, further references therein). Indeed, Godard et al. (2014) demonstrated that at nH = 50 cm−3, 80% to 90% of the CH column density and all of the CH+ arise from bursts of dissipation, while the remaining fraction is associated with gas in the ambient medium or relaxing towards it. Only at gas densities in excess of typically 100 cm−3 does the abundance of CH become nearly constant (Sheffer et al. 2008; Levrier et al. 2012). As a matter of fact, at nH = 300 cm−3, about 70% of the CH originates in ambient conditions (Godard et al. 2009).
These results notwithstanding, CH is commonly used as a proxy for H2 . It shares this virtue with HF, which was first detected in the ISM by Neufeld et al. (1997). Because HF is the only neutral light hydride that exothermically forms in a triatomic reaction with H2 (Neufeld et al. 2005; Zhu et al. 2002), it is considered the more pristine H2 tracer. However, unlike for CH, its ground-state absorption often saturates, not only towards the dense molecular gas associated with star-forming regions. The same holds for the ground-state absorption of OH at 2.5 THz which can be considered a secondary H2 tracer (e.g., Wiesemeyer et al. 2016). This leaves CH as an important proxy at high column densities. In the more diffuse gas, below AV = 1, all three species are more reliable H2 tracers than CO, which suffers from insufficient self-shielding (Gerin et al. 2016, further references therein).
These findings leave their fingerprint in the measured abundances and their mutual correlations. Thanks to the operation of spaceborne and airborne far-infrared instrumentation with adequate spectral resolution (HIFI and GREAT2 aboard the Herschel Space Observatory3 and SOFIA, respectively),
such studies can now be conducted Galaxy-wide, unlike UV and optical observations. The spectroscopy of ground-state lines of the aforementioned light hydrides, observed in absorption along sightlines towards the hot, far-infrared bright dust associated with sites of high-mass star formation (for many of which distances have been determined from maser parallaxes, e.g., Reid et al. 2014), provides a clear-cut setting to determine the column density profiles of spiral-arm crossings with a minimum of assumptions: as an indication, only ~100 ppm of the total population in diffuse clouds resides in excited states (for details we refer to Appendix D, in particular Table D.1). Historically, besides the aforementioned UV/optical studies, CH column densities were determined using the radio transitions between the hyperfine-split ground-state levels (e.g., Liszt & Lucas 2002). Although the involved level populations are affected by non-LTE level occupations, the error in the derived column densities remains moderate if the transition is optically thin and inverted, and if the uncertain excitation temperature is expected to obey the condition |Tex|≫ Tbg (where Tbg is the temperature of the continuum background against which the radio spectrum is observed, and assuming that beam filling factors are sufficiently well known to ensure that this condition holds). The non-LTE effect is briefly discussed in Appendix D.
The installation of the upGREAT array and its extended tuning range (Risacher et al. 2016) made the transition of CH molecules from the N = 1, J = 1∕2 ground state into the N = 2, J = 3∕2 state accessible to observations (the energy level diagram of CH is shown in Fig. 1). This transition comprises two triplets of hyperfine structure lines with wavelengths near 149 μm, two of which were first detected with very low spectral resolution with the Kuiper Airborne Observatory (Stacey et al. 1987). With adequate spectral resolution to distinguish the features originating in different spiral arms, this line lends itself particularly well to absorption studies of diffuse and translucent clouds because it remains in absorption even in the background source. The rotational λ560 μm transition between the N = 1, J = 3∕2 → 1∕2 shares its lower level with the ground-state transition studied here, and was detected with HIFI at high spectral resolution (Gerin et al. 2010). Because the λ560 μm line of CH is easier to excite than its counterpart at λ149 μm (cf. Fig. 1), in the environment of the background source it appears in emission, which, by virtue of its hyperfine splitting (cf. Table 1), blends with the sight-line features from spiral arms and interarm gas, rendering the analysis more difficult. In a similar context, the detection of the A − X(0, 0) band of CH near 4304 Å in the environment of Herschel 36, the O-star primarily illuminating the hourglass nebula M8, reveals that its lower level, the excited 2Π, J = 3∕2 fine structure state 25.6 K above ground, is significantly populated (Oka et al. 2013).
The aim of this work is therefore to establish the λ149 μm line as a tool allowing us to obtain CH (and ultimately H 2 ) column densities from first principles, with a minimum of a priori knowledge required. We will compare CH column density profiles with those of HF (Sonnentrucker et al. 2015, further references therein) and OH (Wiesemeyer et al. 2016), so as to assess the usefulness of CH as a tracer for molecular gas in diffuse clouds. We extend our analysis to the envelopes around regions forming high-mass stars, where, despite the high densities, the CH absorptions at λ149 μm and λ560 μm do not saturate. When analyzed together with the emission in the λ560 μm line, CH remains a suitable H 2 tracer in such environments.
 |
Fig. 1 Lowest rotational energy levels of the CH radical. The sub-millimeter/far-infrared transitionsdiscussed here, at 533/537 GHz (i.e., λ560 μm ) and 2007/2010 GHz (λ149 μm ) are indicated by the dashed arrows. Hyperfine splitting is not to scale. |
Hyperfine splitting of the N = 2 ← 1, J = 3∕2 ← 1∕2 transitions.
2 Observations and data analysis
The observations were performed on several SOFIA flights in the observatory’s cycle 4 (F298 and F301 on 2016 May 18 and 24, respectively, F346 on 2016 November 8, and F369 on 2017 February 3). The aircraft altitudes were 41.7–42.6 kft. The configuration of GREAT was single-pixel channel L1 and upGreat’s arrays LFA-H and -V (seven pixels each). The frequency of the N = 2 ← 1, J = 3∕2 ← 1∕2 transition ofCH at 2006.762 GHz (Table 1) was tuned to the upper sideband, so as to avoid a prominent telluric ozone feature appearing in the image band of a lower sideband tuning. Typical single-sideband receiver temperatures were 1650–1750 K, while the signal-band opacity varied from 0.2 to 0.3. The spectra were taken in chop-nod mode, with a chop amplitude of 80″ and a frequency of 2.5 Hz. The CH absorption spectrum appears in the central pixel of the LFA-H array, while its remaining six pixels, covering a hexagonal arrangement with 33″ spacing (Risacher et al. 2016, this corresponds to 2.3 times the beam width (full width at half maximum, FWHM) at the observing frequency) were used to better define the atmospherictotal power emission off the source. After down-conversion to an intermediate-frequency bandpass of 4 GHz, the raw data were analyzed with XFFTS spectrometers providing 283 kHz resolution, covering the bandpass with 214 channels (Klein et al. 2012). The spectra were calibrated with the KALIBRATE program (Guan et al. 2012), which is part of the KOSMA package also used to execute the observations. The underlying forward and main-beam efficiencies are 0.97 and 0.68, respectively. Further processing with the CLASS software4 included spectral smoothing to 0.36 km s−1 -wide velocity bins, which is a good compromise between sensitivity and resolving power for narrow absorption features, and a correction for spectral baselines by removing polynomials of up to third order. The continuum level, determined by means of a dedicated double-sideband calibration, was added back to the spectra in order to ensure a correct line-to-continuum ratio.
In contrast to techniques applied for optical/UV spectroscopy, the analysis of rotational ground state lines arising in diffuse clouds needs no excitation or extinction corrections. At their typical temperatures of 15–100 K, one can safely assume that the CH radical is almost entirely in its 2Π1∕2 ground state (cf. Appendix D), and spontaneous de-excitation can be neglected. The opacity for a velocity component i and a hyperfine component j therefore reads
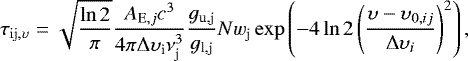 (1)
(1)
where AE,j is the Einstein coefficient and Δυi the half-power width of the Gaussian profile of the velocity component centered at υ0,ij. The degeneracies of the upper and lower level of hyperfine components j involved in the transition are denoted gu,j and gl,j, respectively. N is the total column density of CH in the ground state, and the factor wj = gl,j exp(−El,j∕(kT))∕Q(T) describes the fractional population in the hyperfine-split level j, at an energy El,j above ground and for an excitation temperature T, with partition function Q(T).
In the following analysis, we fit ensembles of Gaussian velocity components to the opacity spectra obtained from the observations, that is, each component follows the ansatz given by Eq. (1). The numerical implementation of this method is described in Wiesemeyer et al. (2016). In view of the saturated absorption in portions of the absorption spectra of OH and HF, we emphasize that such an approach implies two features: entirely saturated velocity components do not arise in the analysis, because they can evidently not constrain the minimization of the merit function. On the other hand, components of which only a minor portion is affected by saturated absorption still constrain the column density across the full velocity interval (but only for the cloud entity that they represent). The propagation of the baseline noise and of the uncertainty in the line-to-continuum ratio into the determination of column densities is discussed in Appendix A. A note on the treatment of asymmetric error distributions is given in Appendix B.
3 Results
3.1 Maincharacteristics of the observed sightlines
The spectra of the λ149 μm transition ofCH are shown in Fig. 2, along with the deduced velocity distributions of the column density (typically 1013 cm−2). Before we proceed to their quantitative analysis, we briefly summarize the main characteristics of the observed sightlines.
The mini-starburst template W49 N, forming a young massive cluster (Galván-Madrid et al. 2013), is located in the Perseus spiral arm, at 11.1 kpc distance (Zhang et al. 2013). The sightline grazes the Sagittarius spiral arm, which displays absorption at velocities from 30 to 70 km s−1 , in two groups corresponding to the near and far side. The velocity interval from − 10 to + 30km s−1 represents the Perseus spiral arm. Being close to zero velocity, these absorption components may also contain gas from the local arm, a conjecture corroborated by the sightline to W51 e1/e2 discussed below. Thanks to the ~80 km s−1 wide velocity range and its length, this sightline provides a good basis for abundance studies with solid statistics (e.g., Monje et al. 2011 for the HF 1–0 line, and Gerin et al. 2010 for the λ560 μm CH doublet), while it avoids the complexity of the central molecular zone of the Galaxy. We therefore used this sightline to confirm that the calibration of the line-to-continuum ratios in the upGREAT and HIFI spectra is consistent (Appendix C).
The second target, W51 e1/e2 (which is part of the W51 A region), is a similar protocluster, though less massive than W49 N (e.g., Ginsburg et al. 2017). At a similar Galactic longitude, its distance of 5.4 kpc (Sato et al. 2010) locates this complex in the near-side crossing of the Sagittarius spiral arm, where the CH column is distributed across a ~30 km s−1 -wide velocity range, separated from the gas in the 0–20 km s−1 interval by a 25 km s−1 -wide gap void of CH. The CH column across these low velocities must arise from gas located closer to, or located in, the solar neighborhood. It cannot arise from the Perseus arm as in the case of W49 N, given the shorter distance to W51 e1/e2. The presence of CH in this velocity component is not surprising, since it was known to be traced by other molecules or molecular ions like CH+ (Falgarone et al. 2010a), OH+ and OH (Wiesemeyer et al. 2016), and HF and H2 O (Sonnentrucker et al. 2015). The component consists of partially molecular, diffuse gas, since it is also present in the atomic tracers HI (Winkel et al. 2017), CII (Gerin et al. 2012, 2015) and OI (R. Güsten, 2017, priv. comm.).
The W3 complex is located in the second quadrant of the Galaxy in the Perseus arm. It consists of a classical HII region/radio continuum source associated with a prominent far infrared source. Its most prominent, high-mass star forming sub-regions are W3(OH) and W3 Main (for an overview see e.g., Megeath et al. 2008); in projection they are ~10 pc apart. The archetypical ultracompact HII region W3(OH) (e.g., Qin et al. 2016) is located at a distance of 2 kpc (Xu et al. 2006; Hachisuka et al. 2006). W3 Main contains several luminous infrared sources, out of which W3 IRS5, harboring a massive protocluster (Wang et al. 2013), is the IR-brightest. Far-infrared continuum emission from both sources has been imaged with FORCAST and SOFIA (Salgado et al. 2012; Hirsch et al. 2012). The velocity distribution of CH towards W3(OH) shows two major components, of which one is attributed to the target itself and its envelope, and the other one to the local spiral arm. Towards W3 IRS5, this latter component is much less prominent. The sightlines to both targets contain a component close to − 20km s−1 , which is attributed to the near side of the Perseus arm (e.g., Vallée 2008).
 |
Fig. 2 CH λ149 μm spectra (left panel, the reference frequency for the velocity scale givenby the second HFC) and deduced column density profiles (right panel) for (from top to bottom): W49 N, W51 e2, W3(OH), W3 IRS5. The blue markers in the W3(OH) spectrum show the hyperfine splitting and weights). The median column densities are indicated by the red lines. The dark-gray-shadowed profiles indicate the (−σ− , +σ+) limits, that is, 84.13% confidence, assuming a 5% error in the continuum level. |
3.2 Quantitative analysis
In the following analysis we use the HF ground-state absorption as reference for the available H2 reservoir, which we will correlate with the column densities of CH. As already stated in the introduction, the exothermic direct association of F with H2 (Neufeld et al. 2005; Zhu et al. 2002) lends HF its virtue as primary H2 tracer. Here we use archival HF data from the Herschel guaranteed time key program PRISMAS5 (P.I. Maryvonne Gerin). The analysis (Fig. 3) yields N(HF)∕N(CH) ratios of 0.30 ± 0.01, 0.34 ± 0.02, 0.26 ± 0.02 and 0.13 ± 0.04 towards W49 N, W51 e2, W3(OH) and W3 IRS5, respectively. The corresponding correlation coefficients are 0.87, 0.85, 0.94 and 0.98.
For the evaluation of false-alarm probabilities various statistical tests exist (i.e., for the likelihood that a chance coincidence mimics a correlation between the column densities of HF and CH). If we interpreted Pearson’s p value as false-alarm probability against our null hypothesis (the column densities of CH and HF being uncorrelated), our results would be significant at the 1% level. However, the usefulness of p value testing has been questioned by a controversy which became known as the “p value fallacy” (Sellke et al. 2001). We therefore provide an independent test: the non-zero column densities of CH are randomly permuted among the available velocity intervals (of 1 km s−1 width each),using a modified Fisher-Yates algorithm. We then count the number of false alarms (i.e., correlations detected with a p threshold of 0.05) out of a total of 1000 Monte Carlo tests. This yields false-alarm probabilities of 4.0, 4.2, 6.0 and 7.9%, respectively. If these probabilities were p values, the correlations towards W3(OH) and W3 IRS5 would merely be considered “quasi-significant”. However, given that our test is more critical, it seems fair to say that all four sightlines support the conjecture that HF and CH form out of a common H2 reservoir. Assuming that the average physical conditions on these sightlines are comparable, one can also stack the data (Fig. 4). This yields a highly significant p value ( ≪0.01%), while the Monte Carlo analysis detects a false alarm in 4.4% of the sample, which renders the correlation significant. We performed a dedicated regression analysis, accounting for the individual errors in N(HF) and N(CH) using the merit function
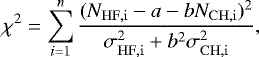 (2)
(2)
(Press et al. 1992, their equation (15.3.2)) where n is the number of spectral channels, and σCH,i and σHF,i are the root mean square (r.m.s.) errors in the individual spectral channels, as given by the distributions resulting from the Bayesian estimate. The analysis reveals that the scatter in the data is not due to sensitivity limitations or uncertainties in the line-to-continuum ratio (see Appendices A and B), but rather due to the chemical diversity on the sightlines. The consequences of this finding will be discussed in the following section.
The abundance of HF was determined by Indriolo et al. (2013) using the 2.5 μmro-vibrational transition. Sonnentrucker et al. (2015) compared the distribution of HF with that of H2O on twelve sightlines (further references can be found in these studies); their models predict HF abundances (with respect to H2) of X(HF) ~ 0.9 × 10−8 in the low-density regime (at AV = 0.9) to X(HF) = 3.3 × 10−8 at AV ~ 4 (for further references to determinations of X(HF) see Wiesemeyer et al. 2016). With these values, our mean HF/CH of 0.3 translates to X(CH) = 0.3–1.1 × 10−7. For comparison, the “canonical” CH-H2 relationship, derived from optical and UV spectroscopy, is 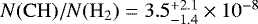 (Sheffer et al. 2008). In both studies the uncertainties reflect the chemical diversity along the sightlines, not the measurement errors. The analysis of Indriolo et al. (2013) and Sonnentrucker et al. (2015) suggests a mean abundance ratio of N(HF)∕N(CH) = 0.4. Some of our data, at N(CH) ≳ 0.1 × 1013 cm-2, agree with this relation (blue lines in Fig. 3). However, on the sightlines to W49 N and W51 e2, the correlation widens for N(HF) ≲ 0.1 × 1013 cm-2. We suggest that this is due to a distinctly different chemistry, leading to an over-abundance of CH. We emphasize that the assumption of an overly low excitation temperature for the velocity intervals coinciding with the star-forming regions in the background is not the reason for this bimodal distribution: first, using a higher, more realistic excitation towards the hot cores (cf. Sect. 4.2) would simply move the data points upwards along the bisecting line without considerably changing the apparent bimodality. In the spectrum of W49 N, this bimodality is most striking for the data points with N(CH) ~ 0.1 × 1013 cm-2, derived from sightline velocities below υlsr < −1.0km s−1 . The negative velocities towards W49 N are known to partially originate from expanding gas driven by an energetic outflow, evidence supported not only by the wide line-wings seen in HCN (Liu et al. 2015), but also by the OH 2Π1∕2, J = 3∕2 → 1∕2 emission (Menten et al., in prep.) and whose blue wing coincides with less prominent p-H2O emission (Sonnentrucker et al. 2015). Notwithstanding, it is plausible that we also see unrelated (e.g., local) diffuse foreground gas at the negative velocities: first, if the absorption there was contaminated by the blue-shifted line wing related to the outflow-driven expanding gas, we would expect to also see its red-shifted counterpart (traced by the prominent emission from the excited OH line). This is obviously not the case; at + 28km s−1 , between the Perseus and Sagittarius spiral arms, the CH column density drops to almost zero. Second, towards W51 e2 we also find three data points that exhibit a statistically significant over-abundance and that do not belong to the gas envelope in which W51 e2 is embedded. As already mentioned, they are rather located in the diffuse gas of the Sagittarius spiral arm where the assumption of a complete ground-state population is realistic, or at least inconsequential.
(Sheffer et al. 2008). In both studies the uncertainties reflect the chemical diversity along the sightlines, not the measurement errors. The analysis of Indriolo et al. (2013) and Sonnentrucker et al. (2015) suggests a mean abundance ratio of N(HF)∕N(CH) = 0.4. Some of our data, at N(CH) ≳ 0.1 × 1013 cm-2, agree with this relation (blue lines in Fig. 3). However, on the sightlines to W49 N and W51 e2, the correlation widens for N(HF) ≲ 0.1 × 1013 cm-2. We suggest that this is due to a distinctly different chemistry, leading to an over-abundance of CH. We emphasize that the assumption of an overly low excitation temperature for the velocity intervals coinciding with the star-forming regions in the background is not the reason for this bimodal distribution: first, using a higher, more realistic excitation towards the hot cores (cf. Sect. 4.2) would simply move the data points upwards along the bisecting line without considerably changing the apparent bimodality. In the spectrum of W49 N, this bimodality is most striking for the data points with N(CH) ~ 0.1 × 1013 cm-2, derived from sightline velocities below υlsr < −1.0km s−1 . The negative velocities towards W49 N are known to partially originate from expanding gas driven by an energetic outflow, evidence supported not only by the wide line-wings seen in HCN (Liu et al. 2015), but also by the OH 2Π1∕2, J = 3∕2 → 1∕2 emission (Menten et al., in prep.) and whose blue wing coincides with less prominent p-H2O emission (Sonnentrucker et al. 2015). Notwithstanding, it is plausible that we also see unrelated (e.g., local) diffuse foreground gas at the negative velocities: first, if the absorption there was contaminated by the blue-shifted line wing related to the outflow-driven expanding gas, we would expect to also see its red-shifted counterpart (traced by the prominent emission from the excited OH line). This is obviously not the case; at + 28km s−1 , between the Perseus and Sagittarius spiral arms, the CH column density drops to almost zero. Second, towards W51 e2 we also find three data points that exhibit a statistically significant over-abundance and that do not belong to the gas envelope in which W51 e2 is embedded. As already mentioned, they are rather located in the diffuse gas of the Sagittarius spiral arm where the assumption of a complete ground-state population is realistic, or at least inconsequential.
4 Discussion
4.1 Chemistry of CH in diffuse gas
The most compelling explanation for the overabundance of CH with respect to its canonical value is the endothermic hydrogen abstraction reaction forming CH+ from C+ , followed by the exothermic hydrogen abstraction reactions leading to CH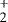 and CH
and CH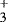 , from where dissociative recombinations lead to the formation of CH and CH2 , respectively. The mystery around the ubiquity of CH+, identified in the CNM by means of absorption spectroscopy in optical lines (1Π →1Σ transitions, Douglas & Herzberg 1941) and in the far-infrared (1Σ, J = 1 → 0 transition, Naylor et al. 2010; Falgarone et al. 2010a) was long ago discussed in the literature (e.g., Black et al. 1975; Black & Dalgarno 1977). CH+ is also found to be highly abundant in the Orion bar (Naylor et al. 2010; Parikka et al. 2017), a prototypical PDR, and in dense, strongly UV-illuminated gas in regions forming high-mass stars (Naylor et al. 2010; Falgarone et al. 2010b). It is worth noting that vibrationally excited H2 makes the reaction C+ (H2,H)CH+ exothermic (Hierl et al. 1997; Zanchet et al. 2013), and that the vibrational excitation of H2 may be chemically pumped thanks to its formation on carbonaceous dust grains (Gough et al. 1996). However, while this reaction channel plays a significant role in photo-dissociation regions (Agúndez et al. 2010; Faure et al. 2017), it cannot account for the large CH+ abundance in diffuse and translucent clouds (Agúndez et al. 2010). For these media, one mechanism suggested to overcome the endothermicity of 4620 K is shock chemistry (Pineau des Forets et al. 1986; Draine 1978). Another mechanism proposed for the high abundance of CH+ throughout the CNM and compact HII regions (Naylor et al. 2010) is the dissipation of turbulence (Godard et al. 2009). In this scenario, the synthesis of CH+ and, subsequently, CH is more efficient for lower gas densities, where more and larger vortices form in the turbulent, diffuse gas, with an increased lifetime. On the other hand, the majority of the HF column density builds up in ambient diffuse gas not exposed to dissipating turbulent cells or slow shocks (Godard et al. 2014). A closer look at the correlation between the abundances of HF and CH (Fig. 3) reveals a substantial fraction of material at N(CH) ≲ 1013 cm−2 that would not be expected solely from the corresponding HF abundance. This conclusion is corroborated by the analysis of the stacked data shown in Fig. 4. On the other hand, the resulting regression coefficient a does not significantly deviate from zero. Based on this data it therefore seems fair to conclude that CH and HF always coexist, but with abundance ratios varying within the limits that become apparent in Figs. 3 and 4. This variation is also a caveat against an overinterpretation of the stacking analysis.
, from where dissociative recombinations lead to the formation of CH and CH2 , respectively. The mystery around the ubiquity of CH+, identified in the CNM by means of absorption spectroscopy in optical lines (1Π →1Σ transitions, Douglas & Herzberg 1941) and in the far-infrared (1Σ, J = 1 → 0 transition, Naylor et al. 2010; Falgarone et al. 2010a) was long ago discussed in the literature (e.g., Black et al. 1975; Black & Dalgarno 1977). CH+ is also found to be highly abundant in the Orion bar (Naylor et al. 2010; Parikka et al. 2017), a prototypical PDR, and in dense, strongly UV-illuminated gas in regions forming high-mass stars (Naylor et al. 2010; Falgarone et al. 2010b). It is worth noting that vibrationally excited H2 makes the reaction C+ (H2,H)CH+ exothermic (Hierl et al. 1997; Zanchet et al. 2013), and that the vibrational excitation of H2 may be chemically pumped thanks to its formation on carbonaceous dust grains (Gough et al. 1996). However, while this reaction channel plays a significant role in photo-dissociation regions (Agúndez et al. 2010; Faure et al. 2017), it cannot account for the large CH+ abundance in diffuse and translucent clouds (Agúndez et al. 2010). For these media, one mechanism suggested to overcome the endothermicity of 4620 K is shock chemistry (Pineau des Forets et al. 1986; Draine 1978). Another mechanism proposed for the high abundance of CH+ throughout the CNM and compact HII regions (Naylor et al. 2010) is the dissipation of turbulence (Godard et al. 2009). In this scenario, the synthesis of CH+ and, subsequently, CH is more efficient for lower gas densities, where more and larger vortices form in the turbulent, diffuse gas, with an increased lifetime. On the other hand, the majority of the HF column density builds up in ambient diffuse gas not exposed to dissipating turbulent cells or slow shocks (Godard et al. 2014). A closer look at the correlation between the abundances of HF and CH (Fig. 3) reveals a substantial fraction of material at N(CH) ≲ 1013 cm−2 that would not be expected solely from the corresponding HF abundance. This conclusion is corroborated by the analysis of the stacked data shown in Fig. 4. On the other hand, the resulting regression coefficient a does not significantly deviate from zero. Based on this data it therefore seems fair to conclude that CH and HF always coexist, but with abundance ratios varying within the limits that become apparent in Figs. 3 and 4. This variation is also a caveat against an overinterpretation of the stacking analysis.
Correlating the CH overabundance, defined as 0.4N(CH)∕N(HF), with NH_2, or, for lack of it, with N(HF) as substitute, indeed yields a fall-off of the CH overabundance with increasing column density – as expected if one associates larger column densities with larger volume densities, rather than with sightline crowding. The thus defined overabundance is shown in Fig. 6, against 1.65× 1011 cm−2 and 3.3 × 1011 cm−2-wide HF column density intervals (for W49 N and W51 e2, respectively). We limit the analysis to column densities below the threshold where the bimodality becomes apparent. The width of the intervals is chosen so as to obtain a statistically meaningful result, as confirmed by the error bars derived from the variance of the overabundance within each interval. We selected only data points with at least 3 σ determinations of both CH and HF column densities, which excludes theportions of the HF spectrum affected by saturated absorption. The overabundances observed towards W49 N and W51 e2 leveloff from values of 3–4 to the canonical value of ~1 when the H2 column density increases by a factor of ~5. Interestingly, Godard et al. (2009), exploring the parameter space for the dissipation of turbulence, find similar ratios for a model with AV = 0.4 (after correcting for the varying molecular hydrogen content), while at AV = 0.1 the CH abundance varies only mildly. On the other hand, a single sightline contains diffuse cloud entities of markedly different characteristics, ranging from vortices embedded in a turbulent medium, with varying molecular content, to the precursors of molecular clouds. It seems fair to say that this statement holds throughout the whole Galaxy, not only in its central molecular zone, where these contrasting characteristics are much more pronounced (e.g., Ginsburg et al. 2016). Moreover, these manifestations of diffuse, cold gas may blend with each other even within a given spiral arm. Therefore, more spiral-arm crossings need to be investigated, including so far unexplored sightlines, because only solid statistical evidence can corroborate the theoretical work in a meaningful way.
Previous studies remain inconclusive regarding an over-abundance of CH. The dual-slope relationship between the column densities of CO and CH, with a break close to N(CH) ~ 1013 cm−2, is attributedto increasing self-shielding of CO above the break point (Sheffer et al. 2008), and has nothing to do with a variation of the abundance of CH.
The crossings of Galactic spiral arms are traced as clearly in CH as they are in HF (Table 2) and OH (Wiesemeyer et al. 2016). For instance, the contrast between the far-side crossing of the Sagittarius spiral arm and the adjacent interarm region in front of the Perseus arm is ~10 in CH and HF, but only ~2 in molecularhydrogen fraction. This can be easily explained by the fact that W49 N is located at a galactocentric distance of 7.6 kpc, where atomic gas is more abundant relative to molecular gas than on sightlines towards the inner Galaxy. A similar contrast has been found in OH, which can be considered a secondary molecular hydrogen tracer (Gerin et al. 2016); Mookerjea (2016) indeed find no correlation of the N(OH)∕N(CH) abundance ratio with the molecular hydrogen fraction, suggesting that both molecules trace H2 equally well, whatever proportion of the total hydrogen budget applies, and that the observed scatter in this abundance ratio is rather due to other factors, for example, a varying cosmic ray ionization rate. With our data we can confirm this conjecture: Fig. 5 shows the correlation between the column densities of OH and CH towards W49 N (excluding velocity components where the entire OH absorption profile saturates). The correlation has a coefficient (r-value) of 0.67 (falling below the r-value for the CH-HF correlations), a p-value of 1% and is significant (the Monte Carlo analysis detects a false alarm probability of 2.7%). The weighted linear regression predicts an OH/CH abundance ratio
of 2.37 ± 0.15, which, for the Sheffer et al. (2008) relationship N(CH)∕N(H2) = 3.5 × 10−8, converts to N(OH)∕N(H2) = 8.3 × 10−8, reasonably close to both predicted and measured OH abundances (Albertsson et al. 2014; Wiesemeyer et al. 2016, respectively). Except for one outlier, the scatter in the OH/HF abundance ratio is not larger than the scatter in the CH/HF. As a consequence, the over-abundance of CH at low column densities should also appear when, instead of HF, OH is used as H2 tracer. This is indeed suggested by the distribution shown in Fig. 7 (totally absorbed velocity components are not considered in this analysis, as in the case of HF).However, owing to the larger errors, the evidence is less compelling. As a reminder, we recall that even within a narrow velocity interval all correlated quantities are averages of diffuse and translucent cloud entities along the sightline, exposed to varying conditions. As a matterof fact, the abundances of CH, OH, and H2 O are particularly sensitive to the cosmic ray ionization rate (Godard et al. 2014). One may also speculate that the correlation between CH and OH is less pronounced than that between CH and HF because at low densities (nH ≲30 cm−3) OH has a production channel in the relaxation stage following a burst of turbulent dissipation, as shown by Godard et al. (2014): while the OH abundance falls below that of CH immediatelyafter the burst, the OH/CH exceeds unity during the subsequent relaxation stage, on a timescale that depends on the dissipated energy per unit length. It is interesting to note that Liszt & Lucas (2002) determine (across a limited N(H2) range) a ratio of N(OH)∕N(CH) = 3.0 ± 0.9, in good agreement with our value derived from the W49 N sightline (in their study, the uncertain microwave-derived CH column densities were augmented by optical measurements). Even more remarkable is their significant correlation between the microwave CH and OH emission-line areas; the data from the sightline to ζ Oph seem to suggest a bimodal distribution of CH at low OH column densities. From a compilation of four sightlines and two dark clouds they conclude that when the main gas-phase carrier of carbon is CO rather than C+ , the CH abundance declines markedly, in contrast to that of OH. This may be another indication of a bimodal or dual-slope relationship between N(CH) and N(H2).
We conclude this section with a remarkable detail observed on the sightlines to W3(OH) and W3 IRS5. Although the illuminating hot cores are separated by only 16.′ 6 (9.7 pc), the column density profiles are quite different, even in the local arm where only the sightline to W3(OH) sees a narrow, ~1 km s−1 -wide feature (unlike the sightline to W49 N, there is no risk of confusion with other spiral arms close to zero velocity). Assuming a length of at most 500 pc for the path through the local arm (Lallement et al. 2014), this converts to an upper limit of 2.4 pc for the diffuse cloud size. A similar upper limit was estimated by Winkel et al. (2017) for the sightline to SgrB2 M/N. Interestingly, Liszt & Gerin (2016) determine a clumping scale of 5.5 pc for the gas on the sightline to W 31C. It seems fair to say that these estimates refer to the largest scales in diffuse gas entities, with presumably considerable sub-structure.
 |
Fig. 3 Correlation between HF and CH column densities towards W49 N, W51 e2, W3 IRS5 and W3(OH) (clockwise from top left). Column densities are for 1 km s −1 wide velocity intervals (Fig. 2). Ordinate offsets and slopes from the weighted regression (parameters a and b in Eq. (2)) are given in the lower-right corners. The red lines show the corresponding fits, the blue lines a ratio of HF/CH = 0.4 (Shefferet al. 2008; Sonnentrucker et al. 2015). Double-logarithmic scales illustrate the bimodal distribution at low column densities towards W49 N and W51 e2. Black markers indicate the absorption around, or close to, the location of the continuum source (W49 N: υlsr < 27km s−1 ; W51 e2: υlsr > 30km s−1 ; W3(OH), W3 IRS5: υlsr < −30km s−1 ). Green markers indicate: for W49 N, 27 km s-1 < υlsr < 47 km s-1, for W51 e2, υlsr < 30km s−1 , and for W3(OH), W3 IRS5 − 30 km s-1 < υlsr < −15 km s-1. Remaining velocities are shown in cyan. |
 |
Fig. 4 As in Fig. 3, but for all data. A legend for the colors is given in the upper-left corner. The gray-shaded area covers all data points within the 3σ limits of theweighted linear regression. |
 |
Fig. 5 Correlation between OH and CH column densities towards W49 N. The blue line is for a N(OH )∕N(H2) of 10−7 . The red line shows the weighted linear regression, the resulting OH/CH abundance ratio is given in the lower-right corner. Velocity bins for the column densities and color-codes are as in Fig. 3. |
 |
Fig. 6 Over-abundance of CH, defined as 0.4N(CH)∕N(HF) vs. N(HF). Column densities are derived from 1 km s −1 -wide velocity intervals in the spectral distribution of Nv (cf. Fig. 2). Only column densities with at least a 3σ detection are used. Error-bars are deduced from the variances of the abundances within each histogram bin. |
Synopsis of velocity-integrated column densities of CH, HF, and OH on the sightline to W49 N.
 |
Fig. 7 As in Fig. 6, but using OH as H2 proxy instead of HF. The ordinate shows the ratio between H2 column densities derived from CH and those derived from OH (assuming an OH ∕H2 abundance of 10−7). |
 |
Fig. 8 CH emission and absorption towards W3 IRS5. Top panel: λ560 μm line (HIFI/PRISMAS). Bottom panel: λ149 μm (upGREAT). The red lines indicate the commonfit to both spectra (in the χ2 sense). The hyperfine splitting is indicated by blue markers, scaling with the corresponding weight for a complete ground-state level population. The strongest hyperfine component of the λ560 μm line is centered close to the systemic velocity. For details see text. |
 |
Fig. 9 Breakup of CH components observed around W3 IRS5. Red: d N∕d υ for the two hot core components (scaled down by a factor of 50). Cyan: same for the three common-envelope components. Blue: cold foreground components. The gray histogram shows the P Cygni profile of the HF ground-state transition (J = 1 → 0, archival HIFI data, PRISMAS key science project). For details see text and Table 3. |
4.2 CH as molecular gas tracer in environments forming high-mass stars
The following section demonstrates the usefulness of the CH ground state transitions in the high-density environments associated with sites of high-mass star formation. Because of the saturated absorption in HF and OH towards the background sources, only the optically thin line wings of these tracers are usable as tools for measuring the H2 column density in the star-forming environment, provided that they do not blend with unrelated foreground gas. As already mentioned, the far-infrared lines of CH do not suffer from this drawback, and the combined analysis of the λ149 μm and λ560 μm lines allows one to further constrain the physical conditions characterizing the emission region. For OH, such an approach was demonstrated by Csengeri et al. (2012). In the following we try to extract a maximum of quantities directly from the sub-millimeter/far-infrared spectroscopy of CH, with an indispensable minimum of assumptions. For the far-infrared transition, only one lambda doublet component is available. Because the spectroscopic properties of both components are not very different (Table 1), this does not result in a major lack of information; fitting both components merely represents an additional consistency check for the derived column density of CH. Among the targets presented above, we select W3 IRS5. Its location at a distance of 2.0 kpc in the second quadrant of the Galaxy in the Perseus arm avoids the confusion arising in the λ560 μm line owing to its large hyperfine splitting and leading to a blend of emission and absorption components originating from different locations on the sightline.
W3 IRS5 is a bright infrared source discovered by Wynn-Williams et al. (1972) and harbors a cluster of hyper-compact HII regions (e.g., Wilson et al. 2003; van der Tak & Menten 2005) powered by five proto-OB stars (Megeath et al. 2005), which lend the object the designation of a “Trapezium in its making” by the latter authors. The dust continuum emission of its components SMM1 to SMM5 was analyzed by Wang et al. (2013); they derive column densities of N(H2) = 1.0 − 4.4 × 1023 cm−2, assuming a dust temperature of 150 K and source diameters of ~1″ (confirmed by a visibility analysis of their Submillimeter Array (SMA) data, see also Wilson et al. 2003).
Our model consists of an ensemble of hot cores (labeled hc in the following), corresponding to SMM1 to SMM5, a common envelope (ce) associated with the entire W3 IRS5 complex, and a foreground screen (fg) representing the Perseus spiral arm and gasin the solar neighborhood. The objective function of the model is given by
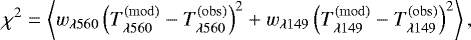 (3)
(3)
with (omitting the indices λ149, λ560)
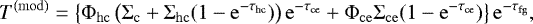 (4)
(4)
where T(mod) and T(obs) represent the modeled and observed brightness temperature of either line, respectively. The average is to be taken across the spectral bandpass of the full line profiles; wλ560 and wλ149 are weight factors accounting for the individual signal-to-noise ratio in each transition. Φhc and Φce are the beam-filling factors of the hot core and common envelope, respectively (assuming that the hot dust continuum and the hot-core emission fill the same beam fractions). The source functions Σ c for the continuum emission, and Σhc and Σce for the hot core and common envelope line emission, respectively, are expressed as Rayleigh-Jeans temperatures. We note that in Eq. (4) the source functions are expressed as unique, equivalent excitation temperatures, related to the actual source function profile along the sightline, Σ (z), by
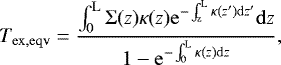 (5)
(5)
where L is the length of the sightline through the source. We emphasize that a unique emissivity is not required for Eq. (4) to be valid, that is, the opacity coefficient κ of a given component does not need to be constant. While the width and center velocities of the Gaussian decomposition of the dN∕dυ profile are well constrained by the λ149 μm absorption spectrum, the degeneracy between the filling factors and excitation temperatures can only be lifted by the dependence of the optical depths on the excitation. As shown in Fig. C.1, the λ560 μm line is more sensitive to the excitation than the line at λ149 μm. For a least-square fit to both CH lines, we apply the Metropolis algorithm (Metropolis et al. 1953, see also Press et al. 1992 for an extension to continuous minimization). A straightforward implementation of the algorithm yields a satisfactory fit, although the convergence is slow. When the convergence became quasi-linear, it was possible to accelerate it by minimization of residua (Auer 1987).
The result is shown in Fig. 8, and the best-fit parameters are listed in Table 3. The normalized χ2 of our fit falls below 1%, a result which could only be achieved by assigning three components to the warm, common envelope (likewise, various H2 O lines observed with HIFI were easier to fit with a double component model, Chavarría et al. 2010). These components appear in absorption against two highly excited emission components (presumably co-spatial with the hot core dust), otherwise inemission. The prominent self-absorption at − 40km s−1 , in the strongest hyperfine-component of the λ560 μm line, coincides with the radial velocity of the H2 O masers at − 40.7 ± 1.3km s−1 (Imai et al. 2000, their group A outflow). Rather than treating the beam-filling factors in Eq. (4) as additional free parameters in a high-dimensional parameter space, we fix them by means of ancillary continuum data: identifying the aforementioned compact, ~1″-wide dust sourcesin the SMA continuum image (Wang et al. 2013) with our hot emission components, the filling factor for the 39. ′′ 5 -wide HIFI beam (FWHM) amounts to Φhc = 0.003. For the moderately warm common envelope, the SMA data are less reliable for an estimate of Φce , not least due to the lack of short spatial frequencies in the continuum visibilities. We follow Chavarría et al. (2010) and use a λ800 μm single-dish continuum map (Oldham et al. 1994), allowing us to estimate a beam-deconvolved size of ≃15″, which converts to a beam filling of Φce = 0.15. Finally, two cold foreground components were needed for a satisfactory fit. Given their velocities, they are probably related to the outer layers of the common envelope. The narrower component (at − 39.5km s−1 ) coincides with a common envelope component of comparable width. This suggests that both components belong to the same structure, characterized by a negative excitation gradient. Replacing these two components by a single one increases the normalized χ2 by 6% and yields an unsatisfactory fit in the (−50, −40)km s−1 velocity interval, regardless of whether this component is located in the common envelope or the cold foreground gas. As a matter of fact, we note that around 50 km s−1 the fit to the λ560 μm line is still imperfect, even with the nine components ultimately retained. Two further components at υlsr = 0.5 and − 21km s−1 are unrelated to W3 IRS5 and can be identified with local gas and with the near-side boundary of the Perseus spiral arm, respectively. Thus, rather than freely fitting these two components, we kept their parameters fixed, adopting the values from the analysis described in Sect. 4.1.
Evidently, only a dedicated non-LTE simulation can explain the fitted excitation temperatures as a function of the physical conditions encountered in the hot core and common envelope components. While this is beyond the scope of this paper, we conclude this discussion with a comparison with the P Cygni-type profile seen in the HF J =1 → 0 line and other light hydrides (Benz et al. 2010). Figure 9 shows the column density profiles for the various components against the HF spectrum. While the dominant contribution to the total column density originates from the two hot core components, the prominent, saturated absorption feature seen in HF is due to the same low-excitation material in the common envelope and foreground that is also traced by the absorption seen in the CH lines. Our component separation clearly demonstrates that the bulk of this absorption occurs at velocities that are blue-shifted with respect to the emission components. The driving agent for the expansion of the common envelope is most likely a system of multiple outflows (Rodón et al. 2008). Another hint that in such an environment CH remains a reliable tracer for molecular hydrogen is provided by the comparison of the derived column densities with corresponding estimates using the λ850 μm dust emission (Wang et al. 2013): the H2 column densities in the two emission components amount to 2.3 and 1.8 × 1023 cm-2 (for N(CH)∕N(H2) = 3.5 × 10−8), which agree within a factor 2 with those derived from the emission from the two dominant dust-continuum components (sources SMM1 and SMM2 in Wang et al. 2013). However, this good agreement may be a chance coincidence: we have no proof that the best-fit solution summarized in Table 3 is unique. The same holds for the rough dust-mass estimates (which, instead of a full continuum radiative transfer, assume an ad-hoc dust temperature of 150 K).
Best-fit parameters of the model for CH emission/absorption towards W3 IRS5.
5 Conclusions
We close this work with a summary of its main results:
- 1.
For diffuse and translucent interstellar clouds, we confirm a prominent, but not very tight correlation between the column densities of CH and HF. While a ratio of N(CH)∕N(HF) ≃ 0.4 represents rather a boundary to the observed relationship, a bimodal distribution of CH (with respect to HF) was found below N(CH) ≲ 1013 cm-2 (i.e., N(H2) ≃ 3 × 1020 cm−2 or AV ≲ 0.3). We identify the lower branch of this distribution with the action of the endothermic reaction pathway, forming CH+ thanks to the molecular hydrogen abstraction reaction C+ (H2,H)CH+. The subsequent, fast hydrogen abstraction reaction forms
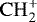 ,which is a prerequisite to form
CH via dissociative recombination:
,which is a prerequisite to form
CH via dissociative recombination:
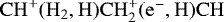 .
Because the alternative pathway (forming
CH
.
Because the alternative pathway (forming
CH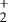 by a slow radiative association of
C+
with H2)
is less efficient, the former pathway efficiently
boosts the CH abundance. Our finding that this
over-abundance of CH appears in the lower-density
regime strongly suggests that the agent to overcome
the activation barrier of 4640 K is dissipation
of turbulence. Using OH instead of HF as a
H2
proxy yields the same conclusion (albeit at
lower significance). By the same token we
determine an OH/CH abundance ratio of
2.37 ± 0.15.
by a slow radiative association of
C+
with H2)
is less efficient, the former pathway efficiently
boosts the CH abundance. Our finding that this
over-abundance of CH appears in the lower-density
regime strongly suggests that the agent to overcome
the activation barrier of 4640 K is dissipation
of turbulence. Using OH instead of HF as a
H2
proxy yields the same conclusion (albeit at
lower significance). By the same token we
determine an OH/CH abundance ratio of
2.37 ± 0.15. - 2.
In the envelopes surrounding cores forming high-mass stars, the combined analysis of the λ149 μm and λ560 μm ground state transitions of CH allows to separate emission features from absorbing layers in the second transition, and therefore to better constrain both the column density and excitation of CH in such environments. Follow-up studies will include a better determination of the beam-filling factors for the far-infrared/sub-millimeter observations, by means of radio interferometry of the 3 GHz transitions between the hyperfine components in the ground state. While these lines, fraught with non-LTE effects such as population inversion, will be difficult to interpret without reliable collision coefficients at hand, radiative transfer models for the far-infrared/sub-millimeter lines would be the next step in the analysis, for which this work may provide suitable boundary conditions.
Acknowledgements
Based in part on observations made with the NASA/DLR Stratospheric Observatory for Infrared Astronomy. SOFIA Science Mission Operations are conducted jointly by the Universities Space Research Association, Inc., under NASA contract NAS2-97001, and the Deutsches SOFIA Institut under DLR contract 50 OK 0901. We gratefully acknowledge the support by the observatory staff. An anonymous referee provided valuable comments which improved the paper.
Appendix A Error estimates for double-sideband receiving systems
The determination of column densities from absorption spectra is straightforward. This holds also for the case of hyperfine-split spectra where the total column densities can be derived either by least-square fitting of a correspondingly weighted target function, or by direct deconvolution (Gerin et al. 2010; Jacob et al., in prep.). Nevertheless, a candid discussion of measurement errors is essential. This statement holds in particular for a double-sideband receiving system, where the calibration of the continuum level is fraught with uncertainties arisi ng from, for example, the atmospheric transmission or the signal-to-image band gain ratio. The measurement equation reads
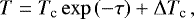 (A.1)
(A.1)
where ΔTc is an unknown contribution from the image band. While the variance of Tc can be guessed from the unnormalized χ2 of a least-square fit, ΔTc is a priori unknown, which is why the target function is assumed to read
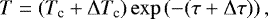 (A.2)
(A.2)
where Δτ is the error resulting from the wrong attribution of Δ Tc to the signal band. Introducing r = ΔTc∕Tc, one finds from the above equations
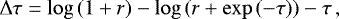 (A.3)
(A.3)
which is converted into a column density error thanks to Eq. (1). The Bayesian error estimates throughout this paper are based on Monte Carlo simulations assuming Gaussian distributions of Tc (with σ2 = χ2) and ΔTc. From a closer inspection of the atmospheric transmission in the signal and image band of the λ149 μm line, and assuming typical calibration errors, we use a Gaussian distribution of ΔTc with σr = 0.05Tc. The assessment of the resulting asymmetric errors will be discussed in the next section.
Our assumption of a 5% uncertainty (r.m.s.) in the continuum level is motivated by aspects related to hardware performance, and to the origin and transmission of the intrinsic continuum emission. As for the hardware, hot electron bolometer mixers (e.g., Pütz et al. 2012) are characterized by signal-to-image band gain ratios close to unity. Kester et al. (2017) provide a comprehensive study, showing that for HIFI bands 6 and 7, using the same technology as upGreat, the uncertainty in the gain ratio falls below 4%. At this accuracy, there is no evidence for a departure from the theoretically expected 1:1 gain ratio. Even a significant departure would not necessarily entail a corresponding calibration error as long as the spectral index of the continuum emission remains sufficiently small. The rest frequency of the far-infrared ground-state transition of CH falls below the power-law part and the maximum of the spectral energy distribution of ~150 K hot dust. For dust opacity indices of 1.0 (expected for a predominant population of large dust grains) and 2.0, the relative difference in the continuum emission in the signal and image band amounts to 0.5 and 0.7%, respectively, for the applied sideband separations of 3.4 and 3.6 GHz (for W49 N/W51 e2, and W3 OH/W3 IRS5, respectively). The coupling efficiencies of the upGreat pixels are monochromatic across the frequency range framed by the sidebands. Under the observing conditions described in Sect. 2, the relative difference in the atmospheric signal and image band transmissions amounts to at most 1%. Quadratically adding the quoted errors yields a 4.2% uncertainty, falling short of the therefore conservative, retained 5% level. For the HF J = 1 → 0 line, which was observed in HIFI band 5, a similar error estimate applies, despite the different technology (SIS mixers, see, however, Kester et al. 2017). The overall calibration uncertainty, assumed to amount to ~10%, is irrelevant here because we need only the line-to-continuum ratio.
Appendix B Assessment of asymmetric errors
Column densities directly derived from substantial optical depths, which in turn are determined from the line-to-continuum ratio in absorption spectra, are fraught with asymmetric errors. The accuracy of the line-to-continuum ratio (hereafter referred to as r) is limited by radiometric, Gaussian baseline noise, and, sometimes, the uncertainty of the continuum level. This leads to uncertainties in the fitted line-to-continuum ratio, of which the non-linear transformation to column densities lead to asymmetric errors. The analysis applied in this work follows Barlow (2003): in his model (1) the errors in the derived quantity are estimated by straight lines leaving from the central value, with slopes of σ+ and σ− when the normal distribution of r is transformed to a unit Gaussian. With the given opacity mean τμ = ⟨τ⟩, its variance 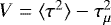 and the unnormalized skewness,
and the unnormalized skewness, 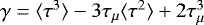 , at hand, this leads to a system of three coupled, nonlinear equations for the median τm and the asymmetric errors στ,+ and στ,−, namely,
, at hand, this leads to a system of three coupled, nonlinear equations for the median τm and the asymmetric errors στ,+ and στ,−, namely,
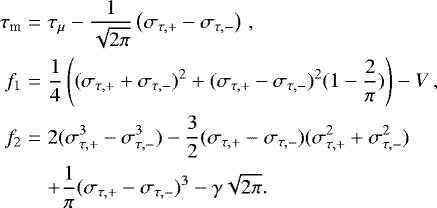 (B.1)
(B.1)
Model (2) of Barlow (2003) considers a parabolic fit through the three points (i.e., the central value and ± σ), rather than the piecewise defined straight lines of model (1). The above system of equations for στ,± and τm then reads
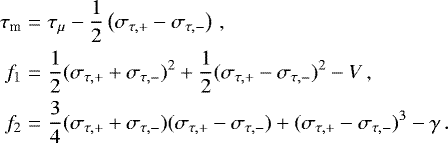 (B.2)
(B.2)
The solution of Eq. (B.1) or (B.2) is determined (iteratively or graphically) by the crossings of the f1(στ,+, στ,−) = 0 and the f2(στ,+, στ,−) = 0 contours. The resulting (στ,+, στ,−) pair is subsequently used to determine τm from the first equation of the set B.1 or B.2 (for model (1) and model (2), respectively).
A demonstration of this approach is shown in Fig. B.1, for a two-component opacity profile (a saturated absorption of τ0 = 8, and an unsaturated yet substantial one of τ0 = 2, located in the wing of the stronger absorption). We note that in both cases the median value determined with the above models is within 1σ limits from the original values, with the stronger deviation for the saturated case. We also note that the line center opacity in the saturated component could be determined thanks to the curvature of the line profile in its unsaturated line wing opposite to the wing that contains the unsaturated component. As expected, the asymmetry parameter α =(στ,+ − στ,−)∕2 is larger for the saturated absorption component. One can also see that the difference between both models is almost unnoticeable and irrelevant. Without loss of generality, the error analysis applied in this paper relies on model (1).
 |
Fig. B.1 Demonstration of Bayesian error estimation according to Barlow (2003). Top panel: test profile. The signal-to-noise ratio of the continuum is 20. Center and bottom panels: histograms of the optical depth distribution, for the saturated absorption (center panel) and the narrower, unsaturated component (bottom panel). The dimidated Gaussians from models (1) and (2) are shown in red and blue, respectively, along with the asymmetric errors (arrows) and the asymmetry parameters α. |
Appendix C Comparison of column densities derived from the λ560 μm and λ149 μm transitions
A comparison of CH column densities derived from the λ149 μm and the λ560 μm lines may be instructive here. The weighted linear regression is shown in Fig. C.1. Assuming a 5% error in the continuum level, the column densities derived from the λ149 μm line are systematically (−0.40 ± 0.05) × 1013 cm−2 below those derived from the λ560 μm line, with a slope of (0.93 ± 0.03) × 1013 cm−2 (λ149 μm vs. λ560 μm ). It seems fair to say that the explanation for this discrepancy is either one of the following: (1) as stated in the introduction, the determination of column densities derived from the λ560 μm spectra needs to make an ad-hoc assumption about the emission profile. Due to the mix of emission and absorption around the hot core, the emission component is difficult to define, but subsequently needed to disentangle the sightline absorption from the emission component (which folds into the absorption by the spiral arms owing to the relatively large hyperfine splitting). (2) Any inconsistency in the calibration of the continuum level (e.g., of the contribution from the image band), with respect to that of the spectral line, will lead to a corresponding error in the opacity determination (cf. the discussion in Appendix A). The common assumption that all CH molecules in the diffuse gas are in the ground state is unlikely to be invalid here, as shown in Table D.1. Without a deeper analysis, it will therefore be difficult to identify the origin of the discrepancy, and it seems both suggestions made above are at work.
 |
Fig. C.1 Comparison of column densities derived from the λ149 μm and λ560 μm lines, assuming a 5% error in the continuum level (top panel) and a 10% error (center panel). The gray-shaded area covers all data points within the 1σ limits of the weighted linear regression (derived slopes in the bottom right corners). The column densities refer to 3 km s−1 wide velocity intervals in the spectral distribution of Nv (cf. Fig. 2). Only velocities above 30 km s−1 were considered. The dotted blue line indicates the bisector for identical column densities derived from both lines. Bottom panel: normalized statistical weights to convert the total column densities to opacities. |
Appendix D Non-LTE effects in the hyper-fine split CH ground state
Here we provide a short demonstration of NLTE effects in the ground state level populations of CH under conditions typical for diffuse clouds. Table D.1 lists the departure coefficients for two models, one corresponding to a diffuse cloud with low molecular content, the other one to a translucent cloud with a substantial fraction of molecules; the calculations have been performed with the MOLPOP-CEP code (Elitzur & Asensio Ramos 2006), assuming a simple slab model. All rotational CH levels up to Eu = 1120 K were considered. This implies radiative pumping, externally by the interstellar radiation field (ISRF), as given by Mathis et al. (1983) and Draine (1978), and by the cosmic microwave background, and internally by dust heated by the ISRF (resulting dust temperatures are from Voshchinnikov et al. 1999). The quantities defining the clouds are from Snow & McCall (2006). The escape probability is from Capriotti (1965). Alternatively, the exact CEP solution was used, the relative differences in the level populations amount to at most 1–3%. For both techniques we assume astatic cloud with a turbulent Doppler width of 2 km s−1 (3.3 km s−1 FWHM). This choice is at the lower end of the linewidth-size relation for diffuse gas on spatial scales from 10 to 100 pc (Falgarone et al. 2009) and close to the median width resulting from fits to OH 2 Π3∕2, J = 5∕2 → 3∕2 absorption line systems, observed on nine sightlines through the first and fourth quadrant of the Galaxy (Wiesemeyer et al. 2016). Collision rates are from Marinakis et al. (2015, scaled from collisions with He to those with H and H2 ). The departure from LTE is model-dependent and varies within an order of magnitude.
Conditions in diffuse cloud models and coefficients for departure from LTE of the population in the CH N = 1, J = 1∕2 HFS.
References
- Agúndez, M., Goicoechea, J. R., Cernicharo, J., Faure, A., & Roueff, E. 2010, ApJ, 713, 662 [NASA ADS] [CrossRef] [Google Scholar]
- Albertsson, T., Indriolo, N., Kreckel, H., et al. 2014, ApJ, 787, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Auer, L. H. 1987, Acceleration of Convergence, in Numerical Radiative Transfer, ed. W. Kalkofen (Cambridge: Cambridge University Press), 101 [Google Scholar]
- Barlow, R. 2003, ArXiv e-prints [arXiv:physics/0306138] [Google Scholar]
- Benz, A. O., Bruderer, S., van Dishoeck, E. F., et al. 2010, A&A, 521, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Black, J. H., & Dalgarno, A. 1977, ApJS, 34, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Black, J. H., Dalgarno, A., & Oppenheimer, M. 1975, ApJ, 199, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Capriotti, E. R., 1965, ApJ, 142, 1101 [NASA ADS] [CrossRef] [Google Scholar]
- Chavarría, L., Herpin, F., Jacq, T., et al. 2010, A&A, 521, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Csengeri, T., Menten, K. M., Wyrowski, F., et al. 2012, A&A, 542, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Douglas, A. E., & Herzberg, G. 1941, ApJ, 94, 381 [Google Scholar]
- Draine, B. T. 1978, ApJS, 36, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham,, T. Jr. 1937, PASP, 49, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Elitzur, M., & Asensio Ramos, A. 2006, MNRAS, 365, 779 [Google Scholar]
- Falgarone, E., Pety, J., & Hily-Blant, P. 2009, A&A, 507, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falgarone, E., Godard, B., Cernicharo, J., et al. 2010a, A&A, 521, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falgarone, E., Ossenkopf, V., Gerin, M., et al. 2010b, A&A, 518, L118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faure, A., Halvick, P., Stoecklin, T., et al. 2017, MNRAS, 469, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Galván-Madrid, R., Liu, H. B., Zhang, Z.-Y., et al. 2013, ApJ, 779, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Gerin, M., de Luca, M., Goicoechea, J. R., et al. 2010, A&A, 521, L16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerin, M., Levrier, F., Falgarone, E., et al. 2012, Phil. Trans. R. Soc. London, Ser. A, 370, 5174 [NASA ADS] [CrossRef] [Google Scholar]
- Gerin, M., Ruaud, M., Goicoechea, J. R., et al. 2015, A&A, 573, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerin, M., Neufeld, D. A., & Goicoechea, J. R. 2016, ARA&A, 54, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Gerlich, D., Disch, R., & Scherbarth, S. 1987, J. Chem. Phys., 87, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Ginsburg, A., Henkel, C., Ao, Y., et al. 2016, A&A, 586, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ginsburg, A., Goddi, C., Kruijssen, J. M. D., et al. 2017, ApJ, 842, 92 [Google Scholar]
- Godard, B., Falgarone, E., & Pineau Des Forêts, G. 2009, A&A, 495, 847 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Godard, B., Falgarone, E., & Pineau Des Forêts, G. 2014, A&A, 570, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gough, S., Schermann, C., Pichou, F., et al. 1996, A&A, 305, 687 [NASA ADS] [Google Scholar]
- Guan, X., Stutzki, J., Graf, U. U., et al. 2012, A&A, 542, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hachisuka, K., Brunthaler, A., Menten, K. M., et al. 2006, ApJ, 645, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Hierl, P. M., Morris, R. A., & Viggiano, A. A. 1997, J. Chem. Phys., 106, 10145 [NASA ADS] [CrossRef] [Google Scholar]
- Hirsch, L., Adams, J. D., Herter, T. L., et al. 2012, ApJ, 757, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Imai, H., Kameya, O., Sasao, T., et al. 2000, ApJ, 538, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Indriolo, N., Neufeld, D. A., Seifahrt, A., & Richter, M. J. 2013, ApJ, 764, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Kester, D., Higgins, R., & Teyssier, D. 2017, A&A, 599, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klein, B., Hochgürtel, S., Krämer, I., et al. 2012, A&A, 542, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lallement, R., Vergely, J.-L., & Puspitarini, L. 2014, Mem. Soc. Astron. It., 85, 339 [NASA ADS] [Google Scholar]
- Levrier, F., Le Petit, F., Hennebelle, P., et al. 2012, A&A, 544, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liszt, H., & Lucas, R. 2002, A&A, 391, 693 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liszt, H. S., & Gerin, M. 2016, A&A, 585, A80 [Google Scholar]
- Liu, T., Kim, K.-T., Wu, Y., et al. 2015, ApJ, 810, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Marinakis, S., Dean, I. L., Kłos, J., & Lique, F. 2015, Phys. Chem. Chem. Phys., 17, 21583 [CrossRef] [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
- Megeath, S. T., Wilson, T. L., & Corbin, M. R. 2005, ApJ, 622, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Megeath, S. T., Townsley, L. K., Oey, M. S., & Tieftrunk, A. R. 2008, in Handbook of Star Forming Regions, I: The Northern Sky, ed. B. Reipurth (ASP Monograph Publications), 4, 264 [NASA ADS] [Google Scholar]
- Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., & Teller, E. 1953, J. Chem. Phys., 21, 1087 [NASA ADS] [CrossRef] [Google Scholar]
- Monje, R. R., Emprechtinger, M., Phillips, T. G., et al. 2011, ApJ, 734, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Mookerjea, B., 2016, MNRAS, 459, 2822 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Zmuidzinas, J., Schilke, P., & Phillips, T. G. 1997, ApJ, 488, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Wolfire, M. G., & Schilke, P. 2005, ApJ, 628, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Naylor, D. A., Dartois, E., Habart, E., et al. 2010, A&A, 518, L117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oka, T., Welty, D. E., Johnson, S., et al. 2013, ApJ, 773, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Oldham, P. G., Griffin, M. J., Richardson, K. J., & Sandell, G. 1994, A&A, 284, 559 [NASA ADS] [Google Scholar]
- Pan, K., Federman, S. R., Sheffer, Y., & Andersson, B.-G. 2005, ApJ, 633, 986 [NASA ADS] [CrossRef] [Google Scholar]
- Parikka, A., Habart, E., Bernard-Salas, J., et al. 2017, A&A, 599, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spectr. Rad. Transf., 60, 883 [NASA ADS] [CrossRef] [Google Scholar]
- des Pineau, G., Flower, D. R., Hartquist, T. W., & Dalgarno, A. 1986, MNRAS, 220, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in C. The Art of Scientific Computing (Cambridge: Cambridge University Press) [Google Scholar]
- Pütz, P., Honingh, C. E., Jacobs, K., et al. 2012, A&A, 542, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Qin, S.-L., Schilke, P., Wu, J., et al. 2016, MNRAS, 456, 2681 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2014, ApJ, 783, 130 [Google Scholar]
- Risacher, C., Güsten, R., Stutzki, J., et al. 2016, A&A, 595, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodón, J. A., Beuther, H., Megeath, S. T., & van der Tak, F. F. S. 2008, A&A,490, 213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salgado, F., Berné, O., Adams, J. D., et al. 2012, ApJ, 749, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, M., Reid, M. J., Brunthaler, A., & Menten, K. M. 2010, ApJ, 720, 1055 [NASA ADS] [CrossRef] [Google Scholar]
- Sellke, T., Bayarri, M. J., & Berger, J. O. 2001, Am. Stat., 55, 62 [CrossRef] [Google Scholar]
- Sheffer, Y., Rogers, M., Federman, S. R., et al. 2008, ApJ, 687, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, T. P., & McCall, B. J. 2006, ARA&A, 44, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Sonnentrucker, P., Wolfire, M., Neufeld, D. A., et al. 2015, ApJ, 806, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Stacey, G. J., Lugten, J. B., & Genzel, R. 1987, ApJ, 313, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Swings, P., & Rosenfeld, L. 1937, ApJ, 86, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Vallée, J. P. 2008, AJ, 135, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tak, F. F. S., & Menten, K. M. 2005, A&A, 437, 947 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voshchinnikov, N. V., Semenov, D. A., & Henning, T. 1999, A&A, 349, L25 [NASA ADS] [Google Scholar]
- Wang, K.-S., Bourke, T. L., Hogerheijde, M. R., et al. 2013, A&A, 558, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiesemeyer, H., Güsten, R., Heyminck, S., et al. 2016, A&A, 585, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, T. L., Boboltz, D. A., Gaume, R. A., & Megeath, S. T. 2003, ApJ, 597, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Winkel, B., Wiesemeyer, H., Menten, K. M., et al. 2017, A&A, 600, A2 [Google Scholar]
- Wynn-Williams, C. G., Becklin, E. E., & Neugebauer, G. 1972, MNRAS, 160, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Y., Reid, M. J., Zheng, X. W., & Menten, K. M. 2006, Science, 311, 54 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zanchet, A., Godard, B., Bulut, N., et al. 2013, ApJ, 766, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B., Reid, M. J., Menten, K. M., et al. 2013, ApJ, 775, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, C., Krems, R., Dalgarno, A., & Balakrishnan, N. 2002, ApJ, 577, 795 [NASA ADS] [CrossRef] [Google Scholar]
Development led by IRAM, http://www.iram.fr/IRAMFR/GILDAS/
All Tables
Synopsis of velocity-integrated column densities of CH, HF, and OH on the sightline to W49 N.
Conditions in diffuse cloud models and coefficients for departure from LTE of the population in the CH N = 1, J = 1∕2 HFS.
All Figures
 |
Fig. 1 Lowest rotational energy levels of the CH radical. The sub-millimeter/far-infrared transitionsdiscussed here, at 533/537 GHz (i.e., λ560 μm ) and 2007/2010 GHz (λ149 μm ) are indicated by the dashed arrows. Hyperfine splitting is not to scale. |
| In the text | |
 |
Fig. 2 CH λ149 μm spectra (left panel, the reference frequency for the velocity scale givenby the second HFC) and deduced column density profiles (right panel) for (from top to bottom): W49 N, W51 e2, W3(OH), W3 IRS5. The blue markers in the W3(OH) spectrum show the hyperfine splitting and weights). The median column densities are indicated by the red lines. The dark-gray-shadowed profiles indicate the (−σ− , +σ+) limits, that is, 84.13% confidence, assuming a 5% error in the continuum level. |
| In the text | |
 |
Fig. 3 Correlation between HF and CH column densities towards W49 N, W51 e2, W3 IRS5 and W3(OH) (clockwise from top left). Column densities are for 1 km s −1 wide velocity intervals (Fig. 2). Ordinate offsets and slopes from the weighted regression (parameters a and b in Eq. (2)) are given in the lower-right corners. The red lines show the corresponding fits, the blue lines a ratio of HF/CH = 0.4 (Shefferet al. 2008; Sonnentrucker et al. 2015). Double-logarithmic scales illustrate the bimodal distribution at low column densities towards W49 N and W51 e2. Black markers indicate the absorption around, or close to, the location of the continuum source (W49 N: υlsr < 27km s−1 ; W51 e2: υlsr > 30km s−1 ; W3(OH), W3 IRS5: υlsr < −30km s−1 ). Green markers indicate: for W49 N, 27 km s-1 < υlsr < 47 km s-1, for W51 e2, υlsr < 30km s−1 , and for W3(OH), W3 IRS5 − 30 km s-1 < υlsr < −15 km s-1. Remaining velocities are shown in cyan. |
| In the text | |
 |
Fig. 4 As in Fig. 3, but for all data. A legend for the colors is given in the upper-left corner. The gray-shaded area covers all data points within the 3σ limits of theweighted linear regression. |
| In the text | |
 |
Fig. 5 Correlation between OH and CH column densities towards W49 N. The blue line is for a N(OH )∕N(H2) of 10−7 . The red line shows the weighted linear regression, the resulting OH/CH abundance ratio is given in the lower-right corner. Velocity bins for the column densities and color-codes are as in Fig. 3. |
| In the text | |
 |
Fig. 6 Over-abundance of CH, defined as 0.4N(CH)∕N(HF) vs. N(HF). Column densities are derived from 1 km s −1 -wide velocity intervals in the spectral distribution of Nv (cf. Fig. 2). Only column densities with at least a 3σ detection are used. Error-bars are deduced from the variances of the abundances within each histogram bin. |
| In the text | |
 |
Fig. 7 As in Fig. 6, but using OH as H2 proxy instead of HF. The ordinate shows the ratio between H2 column densities derived from CH and those derived from OH (assuming an OH ∕H2 abundance of 10−7). |
| In the text | |
 |
Fig. 8 CH emission and absorption towards W3 IRS5. Top panel: λ560 μm line (HIFI/PRISMAS). Bottom panel: λ149 μm (upGREAT). The red lines indicate the commonfit to both spectra (in the χ2 sense). The hyperfine splitting is indicated by blue markers, scaling with the corresponding weight for a complete ground-state level population. The strongest hyperfine component of the λ560 μm line is centered close to the systemic velocity. For details see text. |
| In the text | |
 |
Fig. 9 Breakup of CH components observed around W3 IRS5. Red: d N∕d υ for the two hot core components (scaled down by a factor of 50). Cyan: same for the three common-envelope components. Blue: cold foreground components. The gray histogram shows the P Cygni profile of the HF ground-state transition (J = 1 → 0, archival HIFI data, PRISMAS key science project). For details see text and Table 3. |
| In the text | |
 |
Fig. B.1 Demonstration of Bayesian error estimation according to Barlow (2003). Top panel: test profile. The signal-to-noise ratio of the continuum is 20. Center and bottom panels: histograms of the optical depth distribution, for the saturated absorption (center panel) and the narrower, unsaturated component (bottom panel). The dimidated Gaussians from models (1) and (2) are shown in red and blue, respectively, along with the asymmetric errors (arrows) and the asymmetry parameters α. |
| In the text | |
 |
Fig. C.1 Comparison of column densities derived from the λ149 μm and λ560 μm lines, assuming a 5% error in the continuum level (top panel) and a 10% error (center panel). The gray-shaded area covers all data points within the 1σ limits of the weighted linear regression (derived slopes in the bottom right corners). The column densities refer to 3 km s−1 wide velocity intervals in the spectral distribution of Nv (cf. Fig. 2). Only velocities above 30 km s−1 were considered. The dotted blue line indicates the bisector for identical column densities derived from both lines. Bottom panel: normalized statistical weights to convert the total column densities to opacities. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


