| Issue |
A&A
Volume 601, May 2017
|
|
|---|---|---|
| Article Number | A104 | |
| Number of page(s) | 17 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201630339 | |
| Published online | 11 May 2017 | |
The effect of ISM absorption on stellar activity measurements and its relevance for exoplanet studies
1 Space Research Institute, Austrian Academy of Sciences, Schmiedlstrasse 6, 8042 Graz, Austria
e-mail: luca.fossati@oeaw.ac.at
2 School of Physical Sciences, The Open University, Walton Hall, Milton Keynes MK7 6AA, UK
3 Laboratory for Atmospheric and Space Physics, University of Colorado, 600 UCB, Boulder, CO 80309, USA
4 Department of Economics and Business – University of Catania, Corso Italia, 55, 95100 Catania, Italy
5 Departamento de Astronomia, Universidad de Chile, Camino el Observatorio 1515, Las Condes, Santiago, Casilla 36-D, Chile
6 Lunar and Planetary Laboratory, University of Arizona, 1629 East University Boulevard, Tucson, AZ 85721-0092, USA
7 INAF–Osservatorio Astrofisico di Catania, via S. Sofia, 78, 95123 Catania, Italy
8 Wesleyan University Astronomy Department, Van Vleck Observatory, 96 Foss Hill Drive, Middletown, CT 06459, USA
9 Institute for Physics/IGAM, NAWI Graz, Karl-Franzens-Universität, Universitätsplatz 5/II, 8010 Graz, Austria
Received: 23 December 2016
Accepted: 7 February 2017
Past ultraviolet and optical observations of stars hosting close-in Jupiter-mass planets have shown that some of these stars present an anomalously low chromospheric activity, significantly below the basal level. For the hot Jupiter planet host WASP-13, observations have shown that the apparent lack of activity is possibly caused by absorption from the intervening interstellar medium (ISM). Inspired by this result, we study the effect of ISM absorption on activity measurements (S and log R 'HK indices) for main-sequence late-type stars. To this end, we employ synthetic stellar photospheric spectra combined with varying amounts of chromospheric emission and ISM absorption. We present the effect of ISM absorption on activity measurements by varying several instrumental (spectral resolution), stellar (projected rotational velocity, effective temperature, and chromospheric emission flux), and ISM parameters (relative velocity between stellar and ISM Ca ii lines, broadening b-parameter, and Ca ii column density). We find that for relative velocities between the stellar and ISM lines smaller than 30–40 km s-1 and for ISM Ca ii column densities log NCaII ⪆ 12, the ISM absorption has a significant influence on activity measurements. Direct measurements and three dimensional maps of the Galactic ISM absorption indicate that an ISM Ca ii column density of log NCaII = 12 is typically reached by a distance of about 100 pc along most sight lines. In particular, for a Sun-like star lying at a distance greater than 100 pc, we expect a depression (bias) in the log R 'HK value larger than 0.05–0.1 dex, about the same size as the typical measurement and calibration uncertainties on this parameter. This work shows that the bias introduced by ISM absorption must always be considered when measuring activity for stars lying beyond 100 pc. We also consider the effect of multiple ISM absorption components. We discuss the relevance of this result for exoplanet studies and revise the latest results on stellar activity versus planet surface gravity correlation. We finally describe methods with which it would be possible to account for ISM absorption in activity measurements and provide a code to roughly estimate the magnitude of the bias. Correcting for the ISM absorption bias may allow one to identify the origin of the anomaly in the activity measured for some planet-hosting stars.
Key words: stars: activity / stars: chromospheres / stars: late-type / ISM: general / planets and satellites: general
© ESO, 2017
1. Introduction
Since the discovery of the first hot Jupiter (Jupiter-mass planets orbiting at less than 0.1 AU from the host star), these planets were predicted to be affected by atmospheric escape (Mayor & Queloz 1995). The detection of a 15% dip in the Lyα transit light curve of HD 209458b confirmed it (Vidal-Madjar et al. 2003). Escape processes, the upper atmosphere of planets, and star-planet interactions can be best studied observationally at ultraviolet (UV) wavelengths (at longer wavelengths the optical depth of the escaping material is low). So far, thorough UV observations have been published for three hot Jupiters (HD 209458b, HD 189733b, and WASP-12b; e.g. Vidal-Madjar et al. 2004; Linsky et al. 2010; Fossati et al. 2010a; Lecavelier des Etangs et al. 2012; Haswell et al. 2012), a warm-Neptune (GJ 436b; e.g. Kulow et al. 2014; Ehrenreich et al. 2015), and two super-Earths (55 Cnc e and HD 97658b; Ehrenreich et al. 2012; Bourrier et al. 2016). The detection of the upper atmosphere of the hot Jupiter HD 189733b has also been reported at optical wavelengths (Jensen et al. 2012; Cauley et al. 2016), though see Barnes et al. (2016) for a cautionary note when interpreting transmission spectroscopy of lines which have a chromospheric emission component. These discoveries aided the development of sophisticated models of the upper atmosphere of close-in planets capable of treating various escape regimes (e.g. Lammer et al. 2003; Yelle 2004; Lecavelier des Etangs et al. 2004; García Muñoz 2007; Murray-Clay et al. 2009; Koskinen et al. 2014; Salz et al. 2015, 2016; Erkaev et al. 2016; Owen & Wu 2016).
The hot Jupiter WASP-12b orbits a late F-type star (Fossati et al. 2010b) and is one of the hottest (Teq ≈ 2200 K), most inflated known hot Jupiters, with an extremely short period (about 1 day; Hebb et al. 2009). The near-UV transit observations, conducted with the Cosmic Origins Spectrograph (COS) on board the Hubble Space Telescope (HST), led to the detection of dips almost three times deeper than in the optical, revealing the presence of an escaping atmosphere (Fossati et al. 2010a; Haswell et al. 2012). The observations led to the detection in the planetary upper atmosphere of Mg ii (Fossati et al. 2010a) and Fe ii (Haswell et al. 2012), the heaviest species yet detected in an exoplanet transit, and of a variable and early-ingress (Fossati et al. 2010a; Haswell et al. 2012; Nichols et al. 2015), which stimulated a number of theoretical works (e.g. Lai et al. 2010; Vidotto et al. 2010; Llama et al. 2011; Bisikalo et al. 2013; Alexander et al. 2016).
The observations also revealed an anomaly in the stellar spectrum: a broad depression in place of the normally bright emission cores in the Mg ii h&k resonance lines (Haswell et al. 2012). The anomaly is always present, regardless of the planet’s orbital phase. Haswell et al. (2012) analysed whether the anomalous line cores could be due to (i) intrinsically low stellar activity, or (ii) extrinsic absorption from either the interstellar medium (ISM) or from material within the WASP-12 system itself, presumably lost by the planet.
The comparison of optical spectra of WASP-12 with that of other distant and inactive stars revealed that WASP-12’s Ca ii H&K line cores also show broad depressions similar to the Mg ii h&k line profiles (Fossati et al. 2013). Measurements of the ISM absorption along the WASP-12 sight line showed that the ISM absorption is insufficient to produce these anomalies. Extrinsic absorption by material local to the WASP-12 system is therefore the most likely cause of the line core anomalies: gas escaping from the heavily irradiated planet (Haswell et al. 2012) and/or from evaporating rocky Trojan satellites (Kislyakova et al. 2016) could form a diffuse nebula enshrouding the entire system. Indirect observational and theoretical support to this scenario comes from the interpretation of the correlation between planetary surface gravity and stellar activity index  (Hartman 2010; Figueira et al. 2014; Lanza 2014; Fossati et al. 2015a) and from 3D hydrodynamic simulations (e.g. Carroll-Nellenback et al. 2016).
(Hartman 2010; Figueira et al. 2014; Lanza 2014; Fossati et al. 2015a) and from 3D hydrodynamic simulations (e.g. Carroll-Nellenback et al. 2016).
For WASP-12, Knutson et al. (2010) measured a  value of −5.5, which is well below the basal level of main-sequence solar-type stars of −5.1 (Wright 2004). This anomalously low
value of −5.5, which is well below the basal level of main-sequence solar-type stars of −5.1 (Wright 2004). This anomalously low  value is the direct consequence of the line core absorption, so similar activity index deficiencies might signal the presence of translucent circumstellar gas surrounding other stars hosting evaporating planets. Following this idea, Fossati et al. (2013) and Staab et al. (2017) identified about 20 other systems with an anomalously low activity index. Some of them are known hot Jupiter hosts, while others are candidates for dedicated follow-up studies to search for planets with escaping atmospheres.
value is the direct consequence of the line core absorption, so similar activity index deficiencies might signal the presence of translucent circumstellar gas surrounding other stars hosting evaporating planets. Following this idea, Fossati et al. (2013) and Staab et al. (2017) identified about 20 other systems with an anomalously low activity index. Some of them are known hot Jupiter hosts, while others are candidates for dedicated follow-up studies to search for planets with escaping atmospheres.
The hot Jupiter planet host WASP-13 (Skillen et al. 2009) is one of the stars identified by Fossati et al. (2013) as presenting an anomalously low  value. On the basis of COS far-UV spectra of WASP-13, Fossati et al. (2015b) showed that, despite the anomalously low
value. On the basis of COS far-UV spectra of WASP-13, Fossati et al. (2015b) showed that, despite the anomalously low  value, the strength of the far-UV chromospheric emission lines is that of a typical middle-aged solar-type star, pointing toward the presence of significant extrinsic absorption. The further analysis of a high-resolution optical spectrum covering the Ca ii H&K resonance lines indicates that for WASP-13 the ISM absorption, as opposed to absorption in the immediate circumstellar environment, is the likely origin of the anomaly.
value, the strength of the far-UV chromospheric emission lines is that of a typical middle-aged solar-type star, pointing toward the presence of significant extrinsic absorption. The further analysis of a high-resolution optical spectrum covering the Ca ii H&K resonance lines indicates that for WASP-13 the ISM absorption, as opposed to absorption in the immediate circumstellar environment, is the likely origin of the anomaly.
The vast majority of stars known to host a transiting planet lie rather far away from the solar system, in particular beyond 100–300 pc, where the Ca ii ISM column density is about 1012 cm-2 or larger (see Sect. 6; we note that for stars in the Kepler field, K i ISM column densities have been derived by Johnson et al. 2015). For most of these stars, ISM absorption is likely to affect the shape of the emission core of the Ca ii H&K resonance lines, hence affecting the measurement of the  value. In particular, ISM absorption introduces a bias that leads to a
value. In particular, ISM absorption introduces a bias that leads to a  value that is systematically smaller compared to the unbiased one. We note that this bias does not affect the majority of the stars currently known to host planets detected by radial velocity due to their proximity to Earth.
value that is systematically smaller compared to the unbiased one. We note that this bias does not affect the majority of the stars currently known to host planets detected by radial velocity due to their proximity to Earth.
In this work, we explore the effects of ISM absorption on measurements of the Ca ii H&K line core emission. Activity measurements, and the  value in particular, are currently used in the stellar and extra-solar planet (exoplanet) fields. Stellar activity measurements are of crucial importance for the study of late-type stars and, for distant objects, ISM absorption would lead to an underestimate of the activity and the amplitude of the activity cycle (see Sect. 6). In the exoplanet field, stellar activity measurements are used to constrain, for example, the amplitude of the intrinsic radial velocity jitter for planet searches (Haywood et al. 2016) and to study star-planet interactions (e.g. Canto Martins et al. 2011; Miller et al. 2015). It is therefore extremely important to be aware of the possible presence and magnitude of the bias introduced by ISM absorption in activity measurements.
value in particular, are currently used in the stellar and extra-solar planet (exoplanet) fields. Stellar activity measurements are of crucial importance for the study of late-type stars and, for distant objects, ISM absorption would lead to an underestimate of the activity and the amplitude of the activity cycle (see Sect. 6). In the exoplanet field, stellar activity measurements are used to constrain, for example, the amplitude of the intrinsic radial velocity jitter for planet searches (Haywood et al. 2016) and to study star-planet interactions (e.g. Canto Martins et al. 2011; Miller et al. 2015). It is therefore extremely important to be aware of the possible presence and magnitude of the bias introduced by ISM absorption in activity measurements.
This paper is organised as follows. Section 2 describes the tools employed to carry out the analysis, while in Sect. 3 we examine the effects of varying spectral resolution, normalisation, and background subtraction on activity measurements. In Sects. 4 and 5 we explore the effect of ISM absorption on activity measurements first for a Sun-like star and then extend it to other stellar types. In Sect. 6 we discuss the results and present the conclusions in Sect. 7.
2. Input parameters and activity measurements
This work is based on synthetic photospheric stellar spectra calculated in local thermodynamical equilibrium (LTE) employing the LLmodels stellar atmosphere code (Shulyak et al. 2004). We computed models for the Sun (i.e. effective temperature Teff of 5777 K, surface gravity log g of 4.438, microturbulence velocity of 0.875 km s-1, and abundances from Asplund et al. 2009) and for stars with Teff ranging between 4000 and 6500 K, in steps of 100 K, log g fixed at a value of 4.4, to simulate main-sequence late-type stars, a microturbulence velocity of 1.0 km s-1, and solar abundances. The synthetic fluxes were calculated with a sampling of 0.005 Å bin width in the region covered by the Ca ii H&K lines. The full-width-half-maximum of the chromospheric emission lines is about 0.15 Å, while that of the photospheric Ca ii H&K lines is several Angstroms. In Sects. 3 and 4, we present in detail the results obtained when considering the synthetic spectrum of the Sun, while in Sect. 5 we extend the main results to the other simulated stars. Throughout, we do not include any rotational and macroturbulent broadening in the stellar spectra unless explicitly stated.
Since LLmodels computes only photospheric fluxes, we artificially added the chromospheric emission in the core of the Ca ii H&K lines using Gaussian profiles broadened to match the line width of the solar emission line profiles (e.g. Fossati et al. 2015b). We control the line core emission strength through a parameter E (in units of erg cm-2 s-1), which is the disk-integrated Ca ii emission flux at 1 AU and we distribute the emission between the H and K lines according to their relative strengths (i.e. following their log gf values). The parameter E is the same provided by the empirical relations of Linsky et al. (2013). For reference, the average solar S-index is 0.176 (Mamajek & Hillenbrand 2008) corresponding to an E value of 25.53 erg cm-2 s-1, which is very close to the value of 24.67 ± 0.42 erg cm-2 s-1 obtained by Oranje (1983) from spectroscopic observations of the Sun as a star between 1979 and 1981. At solar maximum and minimum the S values are respectively 0.226 and 0.146, which correspond to E values of 41.9 and 15.7 erg cm-2 s-1.
The  parameter gives a measure of the emission present in the core of the Ca ii H&K lines, independent of the stellar effective temperature. The
parameter gives a measure of the emission present in the core of the Ca ii H&K lines, independent of the stellar effective temperature. The  value is derived from a calibration of the S-index (S) (Noyes et al. 1984; Mittag et al. 2013) that is calculated as
value is derived from a calibration of the S-index (S) (Noyes et al. 1984; Mittag et al. 2013) that is calculated as 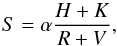 (1)where α is an historical (dimensionless) conversion factor (Hall et al. 2007), H and K are fluxes within triangular bandpasses covering the Ca ii H&K line cores, and R and V are fluxes within continuum windows on either side of the Ca ii lines, as shown for example in Fig. 1 of Jenkins et al. (2006). The centres and widths (in Å) of the H, K, R, and V bands are 3968.470, 3933.664, 4001.07, 3901.07 Å and 1.09, 1.09, 10.0, 10.0 Å, respectively. To compute the S index, we calculate the mean flux in each bandpass instead of using integrated fluxes. This reduces edge effects from finite sampling at the boundaries of the four bands and it leads to α ≈ 1 (Lovis et al. 2011). The fact that the real line core emission observed for the Sun is double peaked, while we simulate the emission with a single Gaussian profile, has a small effect on the measurement of the S values because the H and K bandpasses are broader than the emission features. We tested this by looking at the difference in the S value for a Sun-line star where the line core emission was simulated with a single- or double-peaked Gaussian, obtaining Ssingle−Sdouble = 0.0015. We remark that the true chromospheric emission lines are best reproduced by partial frequency redistribution non-LTE line profiles that lead to small departures from the assumed LTE photospheric profile plus Gaussian emission and should not significantly affect the results of this work. This is confirmed by the agreement we obtain for the solar chromospheric flux measured from the S index and that given by Oranje (1983). We, however, come back to this point in Sect. 4.1.
(1)where α is an historical (dimensionless) conversion factor (Hall et al. 2007), H and K are fluxes within triangular bandpasses covering the Ca ii H&K line cores, and R and V are fluxes within continuum windows on either side of the Ca ii lines, as shown for example in Fig. 1 of Jenkins et al. (2006). The centres and widths (in Å) of the H, K, R, and V bands are 3968.470, 3933.664, 4001.07, 3901.07 Å and 1.09, 1.09, 10.0, 10.0 Å, respectively. To compute the S index, we calculate the mean flux in each bandpass instead of using integrated fluxes. This reduces edge effects from finite sampling at the boundaries of the four bands and it leads to α ≈ 1 (Lovis et al. 2011). The fact that the real line core emission observed for the Sun is double peaked, while we simulate the emission with a single Gaussian profile, has a small effect on the measurement of the S values because the H and K bandpasses are broader than the emission features. We tested this by looking at the difference in the S value for a Sun-line star where the line core emission was simulated with a single- or double-peaked Gaussian, obtaining Ssingle−Sdouble = 0.0015. We remark that the true chromospheric emission lines are best reproduced by partial frequency redistribution non-LTE line profiles that lead to small departures from the assumed LTE photospheric profile plus Gaussian emission and should not significantly affect the results of this work. This is confirmed by the agreement we obtain for the solar chromospheric flux measured from the S index and that given by Oranje (1983). We, however, come back to this point in Sect. 4.1.
By following the method described by Middelkoop (1982) and Rutten (1984), or in Sect. 3.3 of Mittag et al. (2013), we concluded that our calculated S index is not in the Mount Wilson system (SMW). We therefore derived the conversion factor β between S and SMW using the relation (Eq. (2) of Mittag et al. 2013) 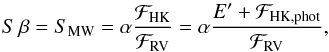 (2)where ℱHK is the total stellar surface flux (i.e. photospheric plus chromospheric not weighted by the triangular bandpasses) in the core of the H and K lines, ℱRV is the stellar photospheric flux in the R and V continuum bands, E′ is the chromospheric stellar surface flux (i.e.
(2)where ℱHK is the total stellar surface flux (i.e. photospheric plus chromospheric not weighted by the triangular bandpasses) in the core of the H and K lines, ℱRV is the stellar photospheric flux in the R and V continuum bands, E′ is the chromospheric stellar surface flux (i.e. 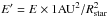 ), and ℱHK,phot is the photospheric stellar surface flux in the core of the H and K lines. Following Mittag et al. (2013), ℱRV and ℱHK,phot are a function of the B−V colour as follows
), and ℱHK,phot is the photospheric stellar surface flux in the core of the H and K lines. Following Mittag et al. (2013), ℱRV and ℱHK,phot are a function of the B−V colour as follows 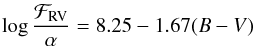 (3)and
(3)and 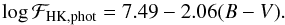 (4)The expressions given in Eqs. (3) and (4) are valid for main-sequence stars with 0.44 ≤ B−V ≤ 1.28 (i.e. 4000 ≲ Teff ≲ 6300 K). For cooler stars, B−V is no longer a good measure of Teff. Since β depends on B−V (hence Teff) and E, we mapped the value of β in the parameter space considered in this work (Fig. 1) and used it to convert our results into the Mount Wilson system. The B−V values have been derived from the Teff values interpolating Table B1 of Gray (2005).
(4)The expressions given in Eqs. (3) and (4) are valid for main-sequence stars with 0.44 ≤ B−V ≤ 1.28 (i.e. 4000 ≲ Teff ≲ 6300 K). For cooler stars, B−V is no longer a good measure of Teff. Since β depends on B−V (hence Teff) and E, we mapped the value of β in the parameter space considered in this work (Fig. 1) and used it to convert our results into the Mount Wilson system. The B−V values have been derived from the Teff values interpolating Table B1 of Gray (2005).
 |
Fig. 1 Conversion factor β between S and SMW as a function of Teff and E. The values along the line of each contour quantify β. |
Since the parameter E is not of common use for activity measurements, we give in Eq. (5) the linear relationship between E and SMW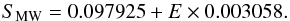 (5)For several of the tests presented below, we use the SMW value corresponding to a chromospheric emission of E = 100 erg cm-2 s-1 and no ISM absorption. Following Eq. (5), this emission value corresponds to SMW = 0.404.
(5)For several of the tests presented below, we use the SMW value corresponding to a chromospheric emission of E = 100 erg cm-2 s-1 and no ISM absorption. Following Eq. (5), this emission value corresponds to SMW = 0.404.
To illustrate the interplay between the photospheric and chromospheric fluxes and the ISM absorption component, we present in Fig. 2 two examples of how the line core emission and ISM absorption modify the initial photospheric spectrum. We also show here comparisons to the observed spectra of EK Dra (a very active nearby Sun-like star) and HD 29587 (a hyper-velocity halo Sun-like star), obtained with HIRES at KECK observatory, and the corresponding synthetic spectra obtained by adding to the photospheric spectrum a line core emission of E ≈ 112 and 15 erg cm-2 s-1, respectively. We chose these stars because they lack ISM absorption lines close to the Ca ii H&K line cores. The E values are those that lead to the same SMW values measured from the two spectra.
 |
Fig. 2 Top left: LLmodels photospheric spectrum of the Sun in the region of the Ca ii K line core (black solid line) modified by adding a line core emission of 112 erg cm-2 s-1 (red solid and dashed lines). This composite spectrum has then been modified by two ISM absorption features, located at the line centre, calculated with Ca ii column densities of 1012 and 1016 cm-2 (blue and green dashed and solid lines). Bottom left: comparison between a high resolution HIRES spectrum of the young Sun-like star EK Dra and the corresponding synthetic spectrum obtained by adding a line core emission of E = 112 erg cm-2 s-1 to the photospheric spectrum. The two spectra return the same SMW value of 0.440. The synthetic spectrum accounts also for the instrumental spectral resolution and the stellar projected rotational velocity (≈15 km s-1). Right: same as the left panels, but for the hyper-velocity halo Sun-like star HD 29587. In this case, the emission flux is 15 erg cm-2 s-1, corresponding to a SMW value of 0.144. The synthetic spectrum does not match the line profile in detail, possibly due to non-LTE effects, but it reproduces the empirical S value. In the top panels, the red solid lines are visible just in the very core of the line, as it is otherwise covered by the blue solid line. |
Despite the possibility to directly convert the SMW values into  values, in this work we consider mostly the SMW values, which are the actual measured quantities, while the
values, in this work we consider mostly the SMW values, which are the actual measured quantities, while the  values are derived through calibrations. Nevertheless, to give an idea of how a variation in the SMW value maps into
values are derived through calibrations. Nevertheless, to give an idea of how a variation in the SMW value maps into  , we show in Fig. 3 the relation between differences in the SMW and
, we show in Fig. 3 the relation between differences in the SMW and  values for three different cases: a Sun-like star with a chromospheric emission of 20 and 100 erg cm-2 s-1, and a star with Teff = 5000 K with a chromospheric emission of 20 erg cm-2 s-1. We chose these three cases to highlight the effects of changing E and stellar spectral type.
values for three different cases: a Sun-like star with a chromospheric emission of 20 and 100 erg cm-2 s-1, and a star with Teff = 5000 K with a chromospheric emission of 20 erg cm-2 s-1. We chose these three cases to highlight the effects of changing E and stellar spectral type.
For completeness, we describe here how we converted the SMW values into  . For this operation, we followed the procedure described by Noyes et al. (1984) and converted the Teff values into B−V colours interpolating from Table B1 of Gray (2005). The range of validity of this conversion is the same as that of Eqs. (3) and (4). For the Sun, we adopted a B−V colour of 0.642 mag (Cayrel de Strobel 1996). In practice, we converted the SMW values into
. For this operation, we followed the procedure described by Noyes et al. (1984) and converted the Teff values into B−V colours interpolating from Table B1 of Gray (2005). The range of validity of this conversion is the same as that of Eqs. (3) and (4). For the Sun, we adopted a B−V colour of 0.642 mag (Cayrel de Strobel 1996). In practice, we converted the SMW values into  as follows. We first derived the RHK parameter as (Noyes et al. 1984)
as follows. We first derived the RHK parameter as (Noyes et al. 1984) 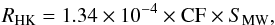 (6)where, for main-sequence stars, CF is (Rutten 1984)
(6)where, for main-sequence stars, CF is (Rutten 1984) 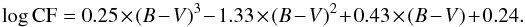 (7)Following Noyes et al. (1984), for main-sequence stars the photospheric flux contribution in the core of the Ca ii lines is
(7)Following Noyes et al. (1984), for main-sequence stars the photospheric flux contribution in the core of the Ca ii lines is 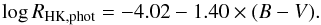 (8)We note that this expression has been revised by Mittag et al. (2013) using the PHOENIX stellar atmosphere code as
(8)We note that this expression has been revised by Mittag et al. (2013) using the PHOENIX stellar atmosphere code as 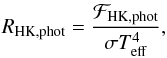 (9)where for main-sequence stars ℱHK,phot is that given in Eq. (4). Finally, the
(9)where for main-sequence stars ℱHK,phot is that given in Eq. (4). Finally, the  value is obtained from
value is obtained from 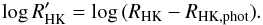 (10)Figure 7 of Staab et al. (2017) shows the observed distribution of
(10)Figure 7 of Staab et al. (2017) shows the observed distribution of  values, as a function of effective temperature, for main-sequence stars.
values, as a function of effective temperature, for main-sequence stars.
 |
Fig. 3 Relation between differences in the SMW and |
3. Effects of spectral resolution, background subtraction, and normalisation on the S index of a Sun-like star
As shown in Sect. 6, the stars for which the effect of ISM absorption on activity measurements is relevant lie relatively far away from Earth (i.e. beyond 100 pc). Because of the large distances, these stars are typically faint and it is difficult to obtain high quality spectra, particularly in the region of the Ca ii lines. For this reason, the spectral background subtraction may not always be optimal. Therefore, we analyse here the effects of an under- or over-subtraction of the background on activity measurements. We also take advantage of the freedom given by synthetic spectra to analyse the effects on the SMW value of varying spectral resolution and normalisation.
To study the impact of spectral resolution, we added an emission E = 100 erg cm-2 s-1 to the synthetic photospheric spectrum of the Sun and convolved it with Gaussians to reach resolving powers ranging from 500 to 100 000 in steps of 100. Figure 4 shows how SMW varies as a function of spectral resolution and compares it to typical photon-noise uncertainties obtained from measurements of SMW conducted on real spectra (signal-to-noise ratio of the spectra of about 50; e.g. Jenkins et al. 2008). The measurement of the S-index is not affected by the instrumental resolving power down to values of about 20 000. In the case of real stars and observed spectra, the spectral resolution has actually a small effect on activity measurements. This is because the calibration onto the Mount Wilson system, carried out using calibration stars, corrects for most of the distortions possibly caused by a low resolution (Jenkins et al. 2011).
 |
Fig. 4 Deviation of the SMW value from that at R = 100 000 as a function of spectral resolution. The dotted lines indicate typical photon noise uncertainties on SMW (i.e. 0.002). |
A more important effect for measurements of the S index from real stellar spectra is that of a non-optimal removal of the background during spectral reduction (e.g. residual instrumental scattered light, non-optimal removal of the detector dark level). This is particularly important in the case of low signal-to-noise spectra for which the background subtraction is difficult and has a large impact on the extracted spectrum. Figure 5 shows the effect of a non-optimal background subtraction on the measurement of the S value, assuming five different chromospheric emission levels. We implemented non-optimal background subtraction in the synthetic spectra using the following formula ![\begin{equation} \label{eq:BS} Syn_{{\rm BS}}=1-[{\rm BS}\times(1-Syn)]/100, \end{equation}](/articles/aa/full_html/2017/05/aa30339-16/aa30339-16-eq51.png) (11)where SynBS is the modified synthetic spectrum, BS is the amount of non-optimal background subtraction (in %), and Syn is the initial (i.e. unmodified) synthetic spectrum. As expected, an over-subtraction of the background (BS values greater than 100%) decreases the flux in the Ca ii H&K line cores, compared to that of the R and V bands, leading to a decrease of the S value. The opposite occurs with an under-subtraction of the background, or equivalently the presence of residual scattered light. Figure 5 shows that the impact of background subtraction on the S value depends also on the emission level.
(11)where SynBS is the modified synthetic spectrum, BS is the amount of non-optimal background subtraction (in %), and Syn is the initial (i.e. unmodified) synthetic spectrum. As expected, an over-subtraction of the background (BS values greater than 100%) decreases the flux in the Ca ii H&K line cores, compared to that of the R and V bands, leading to a decrease of the S value. The opposite occurs with an under-subtraction of the background, or equivalently the presence of residual scattered light. Figure 5 shows that the impact of background subtraction on the S value depends also on the emission level.
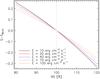 |
Fig. 5 Deviation of the S value from that derived with perfect background subtraction as a function of the deviation from a perfect background subtraction, considering five different chromospheric emission levels. |
We also checked the sensitivity of the S index to the normalisation procedure, hence considering un-normalised spectra, as is the case for most measurements in the literature. We multiplied or divided a spectrum to which we added a chromospheric emission of E = 100 erg cm-2 s-1 by polynomials of 1st, 2nd, and 3rd degree, also varying their coefficients, always obtaining an S value within 0.002 of the reference. This agrees with, for example, Gray et al. (2003).
4. Effects of ISM absorption on the S index: break the case of a Sun-like star
We present here the effects of ISM absorption on SMW, varying both the ISM radial velocity (RV)1 and the Ca ii column density (log NCaII), and considering the synthetic fluxes calculated for a Sun-like star. We modelled the ISM absorption using Voigt profiles whose strength is controlled by the Ca ii column density and a broadening b-parameter of 2.0 km s-1. We adopted this value following the results of Redfield & Linsky (2002), Redfield & Linsky (2004), and Wyman & Redfield (2013) who measured Ca ii ISM absorption lines for stars within 100 pc obtaining average b-parameters below 2.5 km s-1. As a further confirmation, Welty et al. (1996), for stars lying between 100 pc and 1 kpc, measured broadening b-parameters ranging predominantly between 0.5 and 2.5 km s-1. However, in Sect. 4.4 we explore the effects of varying the b-parameter. Throughout, we consider the effect of just one ISM absorption component, but discuss, however, the case of multiple ISM components in Sect. 4.5.
4.1. Variable ISM radial velocity and fixed column density
We first looked at the effect of varying the radial velocity of the ISM absorption line keeping E and log NCaII fixed at 100 erg cm-2 s-1 and 12, respectively. We varied RV from −120.0 to +120 km s-1, in steps of 0.5 km s-1, recalculating SMW at each position of the ISM absorption line. When compared to the case of observed spectra, the RV is the difference between the stellar and ISM radial velocities.
Figure 6 shows how SMW varies as a function of the ISM radial velocity. The general shape of the variation drawn in Fig. 6 is driven by the fact that the effect of the absorption on SMW depends on the relative strengths between the stellar flux (photospheric plus chromospheric) and the ISM absorption itself. In particular, the ISM has a larger impact on SMW when the absorption line is located in a region where the stellar fluxes are higher and where the triangular core bandpasses peak.
At large velocities, the ISM absorption line lies outside of the band used to measure the S index, which is why there is no variation beyond ±86 km s-1. Within these limits, the ISM absorption significantly reduces the S value with the maximum obtained at RV = 0 km s-1. However, the curve shown in Fig. 6 should in reality be slightly asymmetric with a double-peaked minimum because of the real shape of the chromospheric emission (see for example the bottom-right panel of Fig. 2), while we approximate the chromospheric emission with a single Gaussian (this consideration holds also for the contour plots shown in the next sections). Deviations from the Gaussian profile are, however, expected to be small. The bump located at a radial velocity of about +60 km s-1 is caused by the presence of a strong photospheric absorption line just redwards of the core of the Ca ii H line.
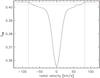 |
Fig. 6 Variation of SMW as a function of radial velocity of the ISM absorption line. The dashed red line shows the SE = 100 value and the horizontal dotted blue line indicates the typical photon noise uncertainty, while the vertical dotted black lines represent the boundaries of the H and K passbands used to calculate the S value, converted to velocity space. |
4.2. Variable ISM column density and fixed radial velocity
To explore the effect of the amount of ISM absorption on SMW, we fixed E equal to 20, 100, or 500 erg cm-2 s-1 and the radial velocity of the ISM absorption line equal to 0.0 km s-1, varying the ISM column density log NCaII from 9.0 to 19.02, in steps of 0.2, recalculating SMW at each step. The result is shown in Fig. 7. As expected, the value of SMW decreases with increasing column density. Already at log NCaII ≈ 10.5 the deviation becomes significant compared to typical photon noise uncertainties. The bias on SMW caused by ISM absorption increases with increasing chromospheric emission.
With increasing ISM column density, SMW decreases because the ISM line absorbs the chromospheric emission. The bend present at log NCaII ≈ 14.0–15.0 is caused by the saturation of both (H and K) ISM absorption lines. For larger values of log NCaII, SMW decreases monotonically with increasing log NCaII until the emission (photospheric and chromospheric) in both line cores is completely absorbed. Figure 7 also shows that the effect of the ISM absorption on SMW increases with increasing line core emission.
 |
Fig. 7 Variation of SMW as a function of log NCaII. Each line has been obtained considering different values of the emission E, as indicated in the legend. The dashed line shows the value of SE = 100, while the dotted line indicates typical photon noise uncertainties. For comparison purposes, the blue and red lines have been rescaled in order to match the black line at log NCaII = 0. |
4.3. Saturation
Line saturation plays an important role in shaping the effect of ISM absorption on activity measurements. Figure 8 shows the absorption (in %) caused by various amounts of Ca ii ISM column density (one absorption line) on a chromospheric emission of E = 100 erg cm-2 s-1, assuming four different values of the broadening b-parameter. The absorption increases linearly up to a column density of log NCaII ≈ 11.5–12, where the absorption saturates and depends strongly on the broadening b-parameter, up to log NCaII ≈ 15–16. With increasing column density, the absorption increases as the square root of log NCaII. At log NCaII ≈ 17, the chromospheric emission is completely absorbed.
 |
Fig. 8 Absorption (in %) caused by one ISM line as a function of Ca ii column density assuming four different values of the broadening b-parameter. The chromospheric emission is E = 100 erg cm-2 s-1. The y-axis is in log scale. |
4.4. Variable ISM column density and radial velocity
In the remainder of the paper, we consider ISM Ca ii column densities ranging between 109 and 1014 cm-2, which is roughly the range expected for stars closer than 500–600 pc (see Sect. 6). Figure A.1 shows the differences between the reference S value SE = 100 (i.e. without ISM absorption) and the SMW values obtained by changing the spectral resolution (100 000, 65 000, 45 000, 20 000, 10 000, and 5000) and the ISM parameters (RV and log NCaII), keeping E fixed at 100 erg cm-2 s-1. This plot indicates that the spectral resolution does not dramatically affect the results, allowing us to fix the spectral resolution to 100 000 and hence to concentrate on the other parameters. However, unless the chromospheric emission is particularly strong and/or the ISM column density is particularly high, below a resolution of about 10 000, it becomes difficult to visually identify the presence of an ISM absorption line, even with a spectrum of very high quality.
In Fig. A.2, we explore the effect of varying stellar projected rotational velocity (υsini) and determine that it has a small impact on the differences between SE = 100 and SMW compared to other effects. We therefore maintain the assumption of no rotation.
In Fig. 9, we show instead the effect of varying the ISM broadening (b-parameter), radial velocity, and column density, keeping E fixed at 100 erg cm-2 s-1. As one may expect, by increasing the broadening of the ISM absorption line, the bias on SMW increases as well. In particular, by doubling the b-parameter, the systematic decrease of SMW increases by about a factor of two.
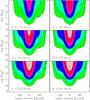 |
Fig. 9 Difference between SE = 100 and SMW obtained by varying the ISM broadening (b-parameter), radial velocity (RV), and column density (log NCaII), keeping E fixed at 100 erg cm-2 s-1. The values along the lines of each contour (0.001, 0.004, 0.01, 0.03, 0.06, 0.11) quantify the SE = 100 − SMW difference. |
The left panel of Fig. 10 shows the differences between the unbiased S, calculated for different values of the chromospheric emission E, and SMW obtained by varying the ISM radial velocity and column density (the b-parameter is fixed at 2 km s-1). The left panel of Fig. 10 shows that the effect of the ISM absorption on SMW increases with increasing line core emission. This is most evident at RV close to 0 km s-1 and at large log NCaII values, where the differences between the five panels are caused by the fact that a smaller ISM absorption is necessary to absorb a weaker emission.
 |
Fig. 10 Left: differences between the reference S value calculated without ISM absorption, and SMW obtained by varying the ISM parameters for five different values of E. The adopted spectral resolution is 100 000. The values along the line of each contour (0.001, 0.005, 0.01, 0.02, 0.04, 0.08) quantify the difference. The results shown in the third and fifth panels can be directly converted into differences in |
4.5. Multiple ISM components
We tested the effect of the presence of two (or more) ISM absorption lines on SMW. We did this by considering one absorption line calculated for a value of the Ca ii column density that does not saturate the line (i.e. log NCaII < 12.0) and by adding further absorption lines with log NCaII varying between 9 and 19. If the lines are at the same radial velocity and are not saturated, their contribution is additive and there is no difference from the case of a single line. Differences are present if the absorption lines do not have the same radial velocity. In this case, the effect of the ISM absorption on SMW depends not only on the strength of the absorption lines, but also on their position with respect to the core of the Ca ii H&K lines. If one of the ISM absorption lines is saturated, the contribution of the two lines is not additive and the bias completely depends then on the position of the ISM lines with respect to each other and of the photospheric lines. Indeed, the saturated component may hide the non-saturated ones.
Figure 11 shows two examples of the difference occurring when considering the presence of one or two ISM absorption components, in the case of saturated (bottom panel) and non-saturated (top panel) lines, as a function of velocity separation of the absorption features from the line centre. The plot indicates for example that in the case of saturated features at the line centre, the presence of multiple components leads to about the same bias as that given by one saturated component.
 |
Fig. 11 Top: difference between the reference S value SE = 100 calculated without ISM absorption, and SMW obtained considering two non-saturated (log NCaII = 11.5) ISM absorption components as a function of velocity separation (Δvr in km s-1) of each ISM feature from the line centre. With increasing Δvr, the two features move in opposite directions. The black dashed line shows the case of a single ISM absorption component moving redwards of the line centre. The short dashed vertical lines are colour-coded by the absorption features shown in the insert and indicate their position relative to the line centre. The insert shows the photospheric plus chromospheric flux (the photospheric spectrum is shown by a dashed line) in black and, as an example, absorption components lying at a velocity separation of 0.0 (red), ±10.0 (blue), ±30.0 (green), and ±50.0 (orange) km s-1 from the line centre. Bottom: as the top panel, but considering saturated (log NCaII = 14.0) ISM absorption lines. |
The increase in the number of free parameters does not allow us to show exhaustive plots for the results of this analysis. Multiple components are common: even for the closest sight lines (<100 pc) the average is 1.7 components per sight line (e.g. Redfield & Linsky 2004). For distant stars we are therefore very likely to encounter the case of multiple ISM absorption lines at different velocities. It is not possible to define averages in terms of number and radial velocity of the ISM components, particularly beyond 100 pc (e.g. Wyman & Redfield 2013). In most cases, our work can therefore provide only an upper limit (i.e. we assume the presence of one ISM component at the line core) of the effect of ISM absorption. Dedicated simulations, based on the measured radial velocity and strength of the different absorption components, need to be done for a more reliable assessment of the bias on the S index for a particular star.
5. Effects of ISM absorption on the S index as a function of stellar effective temperature
With decreasing stellar effective temperature, the photospheric flux in the region of the Ca ii H&K lines decreases. This implies that, with decreasing temperature and at equal chromospheric emission E, the S value increases because the emission becomes more prominent compared to that of the nearby continuum (for active late-type stars the S index can be larger than unity). The effect of ISM absorption on SMW is therefore also dependent on the stellar effective temperature.
The right panel of Fig. 10 shows the differences between the unbiased S, calculated for different values of the chromospheric emission E, and SMW obtained by varying the ISM parameters for the coolest (Teff = 4000 K) star for which we calculated synthetic fluxes. A comparison between the two panels of Fig. 10 indicates that the stronger the emission, relative to the nearby stellar continuum, the stronger can be the effect of ISM absorption on the derived SMW.
When comparing the left and right panels of Fig. 10, it is important to keep in mind that stars with the same values of E, but different effective temperatures, have also different surface chromospheric emissions per cm-2. This is because E is the disk-integrated flux at a distance of 1 AU and stars with different temperatures have different radii. As an example, at equal E, there is a difference of a factor of about 4.5 in the surface chromospheric emission per cm-2 between the two stars considered in Fig. 10.
6. Discussion
6.1. How relevant is the effect of ISM absorption on activity measurements?
To answer this question, we must first estimate the actual Ca ii column density at different distances and sight lines. The top panel of Fig. 12 shows measurements of log NCaII collected by Welsh et al. (2010) for a large number of stars at different distances and sight lines. This plot indicates that on average, for galactic stars more distant that 100–200 pc, one may expect log NCaII values of the order of 11.5–12. This conclusion is confirmed, for example, by Wyman & Redfield (2013) who derived Ca ii column densities from a sample of early-type stars along the direction of the past solar trajectory, obtaining log NCaII > 11 (about 12 on average) for each star lying beyond 120 pc.
 |
Fig. 12 Top: measurements of log NCaII as a function of stellar distance collected by Welsh et al. (2010). Red pluses indicate upper limits. Bottom: log NCaII–E(B−V) correlations obtained by converting first E(B−V) into log NHI, using the relation given by Savage & Mathis (1979, SM79; black), Diplas & Savage (1994, DS94; red), Güver & Özel (2009, GO09; blue), Predehl & Schmitt (1995, PS95; purple), and Gudennavar et al. (2012, G12; yellow), and then log NHI into log NCaII, using either the log NHI–log NCaII relation given by Wakker & Mathis (2000, WM00; solid lines) or by using the Ca ii ISM ionisation fraction measured by Frisch & Slavin (2003, FS03) and assuming a solar Ca abundance (Asplund et al. 2009, A09; dashed lines). The “X” in the legend stands for any of SM79, DS94, GO09, PS95, or G12. The vertical dotted lines indicate the average distance at which a given E(B−V) value can be expected following the ISM extinction maps of Amôres & Lépine (2005). This figure justifies the upper boundary of log NCaII = 14 used for the analysis carried out in Sects. 4 and 5. |
As described in Sect. 6.3, it is practical to have an analytical relation between the ISM Ca ii column density and the interstellar reddening E(B−V). To this end, we first derived the ISM H i column density from E(B−V) using the relations given by Savage & Mathis (1979), Diplas & Savage (1994), Güver & Özel (2009), Predehl & Schmitt (1995), and Gudennavar et al. (2012). We then converted log NHI into the Ca ii column density using either the log NHI–log NCaII relation given by Wakker & Mathis (2000) or by using the Ca ii ISM ionisation fraction measured by Frisch & Slavin (2003) and assuming a solar Ca abundance (Asplund et al. 2009). The log NCaII–E(B−V) relationships obtained in these ways are shown in the bottom panel of Fig. 12. We finally used the ISM extinction maps of Amôres & Lépine (2005) to extract the average (across the sky) E(B−V) value as a function of distance and marked it in the bottom panel of Fig. 12, up to 500 pc.
The bottom panel of Fig. 12 displays a large difference, increasing with E(B−V)/distance, between the two sets of lines. This difference is caused by the fact that the work of Frisch & Slavin (2003) focuses on the local ISM (LISM), within about 100 pc of the Sun, while the work of Wakker & Mathis (2000) is based on measurements of objects, mostly at high galactic latitudes, outside the LISM. This difference affects two properties of Ca in the ISM: the abundance and the ionisation fraction. On the one hand, the adopted solar Ca abundance is most likely too high for the average ISM as the Ca abundance is expected to be 60%–70% subsolar, at least within 200 pc (Frisch & Slavin 2003), and much lower beyond the LISM. In fact, Wakker & Mathis (2000)’s measurements indicate a decreasing Ca ii abundance with increasing distance. On the other hand, Frisch et al. (2011) showed that in the LISM 98.4% of the Ca is doubly ionised (i.e. Ca iii), while only 1.55% is singly ionised (i.e. Ca ii). Beyond the LISM, it is instead the opposite, with Ca ii being the dominant species.
The set of solid lines in the bottom panel of Fig. 12 best matches the observations displayed in the top panel, which is why we consider this set of curves to be more reliable. In addition, the stars for which the activity measurements are most affected by the ISM absorption lie beyond the LISM (see below). We must, however, remember that Fig. 12 gives only a rough indication of the possible Ca ii column density at a given E(B−V)/distance. For example, because of the higher Ca ii abundance along the galactic plane (Gray & Scannapieco 2016), one may find there stars presenting log NCaII values ranging between 14.1 and 15.1 for E(B−V) values from 0.02 to 0.2 mag. This warning is to indicate that it is always better to measure the ISM towards the line of sight of the star of interest and to consider the results shown in Fig. 12 when nothing better is available.
For a Sun-like star, assuming no radial velocity displacement between the star and the ISM absorption, the left panel of Fig. 10 shows that a Ca ii ISM column density of log NCaII = 12 would lead to an underestimation of SMW ranging between about 0.005 and 0.04, depending on the stellar chromospheric emission. Figure 3 shows that this would correspond to an underestimation of the  value of about 0.05–0.1 dex. We thus conclude that for a Sun-like star beyond 100 pc, the presence of ISM absorption typically leads to an underestimate of the measured
value of about 0.05–0.1 dex. We thus conclude that for a Sun-like star beyond 100 pc, the presence of ISM absorption typically leads to an underestimate of the measured  values by roughly 0.05–0.1 dex. The bias caused by the ISM absorption may be even larger for cooler stars.
values by roughly 0.05–0.1 dex. The bias caused by the ISM absorption may be even larger for cooler stars.
To find out whether such a bias is really relevant or not, we need to compare it to the typical uncertainties obtained when measuring SMW and  . Typical photon noise uncertainties in the measurements of SMW are of the order of 0.002 and are usually negligible compared to other uncertainties connected to the various calibrations necessary to derive the
. Typical photon noise uncertainties in the measurements of SMW are of the order of 0.002 and are usually negligible compared to other uncertainties connected to the various calibrations necessary to derive the  value. For example, the typical uncertainty considered when transforming the measured S values into the Mount Wilson system (SMW) is of the order of about 0.015 in
value. For example, the typical uncertainty considered when transforming the measured S values into the Mount Wilson system (SMW) is of the order of about 0.015 in  (Gray et al. 2003; Jenkins et al. 2006; Mittag et al. 2013).
(Gray et al. 2003; Jenkins et al. 2006; Mittag et al. 2013).
These considerations indicate that the magnitude of the bias introduced by the ISM absorption for stars beyond 100 pc is likely to be comparable, or even larger, than the uncertainties related to the measurement of the SMW and  values. This conclusion is strengthened by the fact that the maximum root mean square (RMS) scatter of
values. This conclusion is strengthened by the fact that the maximum root mean square (RMS) scatter of  measurements for a large number of active and inactive stars is of the order of 0.08 (Gomes da Silva et al. 2014), which is comparable to the bias introduced by the ISM absorption for stars beyond 100 pc.
measurements for a large number of active and inactive stars is of the order of 0.08 (Gomes da Silva et al. 2014), which is comparable to the bias introduced by the ISM absorption for stars beyond 100 pc.
6.2. Relevance for exoplanet studies
Classical stellar activity studies concentrate mostly on bright nearby stars, for which the bias due to the ISM absorption is small compared to the other uncertainties. However, the discovery of exoplanets has led to an increasing interest in measuring the activity of more distant stars. Figure 13 shows that the majority of known transiting planets lie beyond 100–300 pc. This is caused by the fact that it is difficult to detect from the ground transiting planets orbiting nearby (hence generally bright) stars and that the Kepler satellite, which discovered the majority of the known transiting planets, concentrated on rather faint and distant stars. We can therefore conclude that the effect of ISM absorption on activity measurements will be relevant for most of the stars currently known to host transiting planets. The most important planets are those transiting bright, nearby stars. For these, detailed follow-up is possible and for these we can get a measurement of the stellar activity which is not likely to be significantly biased by ISM absorption.
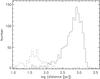 |
Fig. 13 Number of transiting (solid line) and non-transiting (dashed line) planets as a function of logarithm of the distance to the solar system, in pc. The distance ranges between about 10 pc and 3.2 kpc. The total number of planets is 2167 (1527 transiting and 640 non-transiting). Data downloaded from Han et al. (2014) in January 20173. |
Activity measurements are used to guide the detection of planets through radial velocity. In particular, the S index is used to track stellar magnetic cycles, which are then connected to peaks in the periodograms obtained from the radial velocity measurements. On the one hand, within time-scales of tens of years, the ISM absorption can be considered to be stable (e.g. Boissé et al. 2013), hence it does not introduce spurious variability that may interfere with planet detections. On the other hand, ISM absorption dims the stellar activity signal, up to the point where it may mask the Ca ii line core variability, leading to a mis- or non-detection of periodicities connected to stellar rotation and activity cycles, though they may be clearly present in the periodograms obtained from analysing the radial velocity measurements. This would possibly cause misinterpretations of the periodograms, affecting in turn planet detections. However, the careful analysis of the bisectors of the cross-correlation function can usually pin down spurious radial velocity signals related to stellar rotation and activity.
On the other hand, if the ISM absorption is not strong enough to completely mask the detection of stellar magnetic cycles, the ISM absorption has no impact on the derivation of the radial velocity jitter from the activity measurements, at least if one adopts a linear correlation between the radial velocity variation induced by stellar activity and the S index. This is because the slope of the correlation is not modified when subtracting a constant offset from the true S index. The situation would be different if a non-linear correlation is adopted. In this case the subtracted offset matters and the effect could become important for distant stars.
ISM absorption may also affect the relation between stellar activity and planet surface gravity (Hartman 2010; Figueira et al. 2014; Lanza 2014; Fossati et al. 2015a). Fossati et al. (2015a) analysed this relation concluding that it has a bimodal nature. For their analysis, Fossati et al. (2015a) selected planetary systems with stellar magnitude V ≤ 13 mag and expected colour excess E(B−V) ≤ 0.06 mag. This was derived from the maps of Amôres & Lépine (2005), with the aim of reducing the systematic effects of ISM absorption on the  measurements.
measurements.
Nevertheless, on average more distant stars are more affected by ISM absorption and are also apparently fainter. So planets with large radii are detected in transit around them, while small transiting planets would be undetected for these stars. In addition, on average planets with larger radii have lower gravities, hence one may statistically expect to have a lower  associated to a star hosting a planet with a lower gravity, in line with the observed correlation. To test this hypothesis we first took the systems considered by Fossati et al. (2015a) and looked for a correlation between planet surface gravity and distance to the system. We obtained a Spearman-rank correlation coefficient of 0.035, with a probability of chance occurrence (i.e. no correlation) of 0.843, and a Pearson correlation coefficient of 0.085, indicating that no correlation is found between these parameters. This means that the bias introduced by ISM absorption on the
associated to a star hosting a planet with a lower gravity, in line with the observed correlation. To test this hypothesis we first took the systems considered by Fossati et al. (2015a) and looked for a correlation between planet surface gravity and distance to the system. We obtained a Spearman-rank correlation coefficient of 0.035, with a probability of chance occurrence (i.e. no correlation) of 0.843, and a Pearson correlation coefficient of 0.085, indicating that no correlation is found between these parameters. This means that the bias introduced by ISM absorption on the  measurements should have no effect on the observed stellar activity versus planet surface gravity correlation.
measurements should have no effect on the observed stellar activity versus planet surface gravity correlation.
To strengthen this conclusion, we converted the E(B−V) derived for each star considered by Fossati et al. (2015a, see their Sect. 2) into log NCaII using the H i column density vs. E(B−V) relation by Diplas & Savage (1994) and the log NHI vs. log NCaII relation given by Wakker & Mathis (2000). We then used the tools described in Sect. 2 and the available stellar parameters (Fossati et al. 2015a) to estimate for each star the maximum correction in the  value caused by ISM absorption (see Sect. 6.3 for more information). The corrections we applied to the
value caused by ISM absorption (see Sect. 6.3 for more information). The corrections we applied to the  values are listed in Table 1. We finally applied the derived corrections and repeated the statistical analysis thoroughly described in Sect. 3 of Fossati et al. (2015a), using the cluster-weighted model (CWM) proposed in Ingrassia et al. (2014). In particular, a statistical model based on t-student components has been considered. The results of the analysis are shown in Fig. 14. We still find that the stellar activity versus planet surface gravity correlation has a bimodal nature, with the modulus of the slope being directly proportional to the intercept, as predicted by the model of Lanza (2014). We conclude therefore that ISM absorption does not significantly affect the stellar activity versus planet surface gravity correlation and hence it does not modify the main results of Fossati et al. (2015a).
values are listed in Table 1. We finally applied the derived corrections and repeated the statistical analysis thoroughly described in Sect. 3 of Fossati et al. (2015a), using the cluster-weighted model (CWM) proposed in Ingrassia et al. (2014). In particular, a statistical model based on t-student components has been considered. The results of the analysis are shown in Fig. 14. We still find that the stellar activity versus planet surface gravity correlation has a bimodal nature, with the modulus of the slope being directly proportional to the intercept, as predicted by the model of Lanza (2014). We conclude therefore that ISM absorption does not significantly affect the stellar activity versus planet surface gravity correlation and hence it does not modify the main results of Fossati et al. (2015a).
 |
Fig. 14 Chromospheric emission index |
Corrections to the  values due to ISM absorption for the systems considered in the work of Fossati et al. (2015a).
values due to ISM absorption for the systems considered in the work of Fossati et al. (2015a).
6.3. Correcting activity measurements for the ISM absorption bias
As demonstrated by the analyses and results presented in Sects. 4 and 5, correcting activity measurements for the ISM absorption is not trivial and it depends on a large number of factors, some of them very difficult, if not impossible, to estimate precisely. For example, to reliably derive the corrections, one would actually need to know a priori the unbiased stellar chromospheric emission and the ISM parameters (broadening, column density, and radial velocity). The ISM parameters could be obtained for example from extinction maps, such as those of Amôres & Lépine (2005), though this may present rather large uncertainties. This approach may be useful for statistical analyses of large samples. For inactive stars, one could also use the Na i D lines to identify the ISM Na i column density and radial velocity. The Na i column density could then be converted into a Ca ii column density using relations, such as those given by Vallerga et al. (1993), Welty et al. (1996), Welsh et al. (2002), Welsh & Sallmen (2003), Welsh et al. (2005), Welsh et al. (2009), or Wyman & Redfield (2013). However, the relation between Na i and Ca ii is usually inaccurate beyond the LISM (i.e. ≈100 pc), where Na i and Ca ii become the dominant ionisation states. The optimal way to measure the ISM parameters would certainly be to directly measure the ISM absorption from a high resolution spectrum of early-type stars lying in the field of view of the target star, if this is a possibility (see e.g. Fossati et al. 2013, 2014). In this case, however, one could directly correct the spectrum of the target star before measuring the activity.
Inferring the unbiased (i.e. ISM-free) chromospheric emission is problematic for stars located beyond the Local Bubble. Ideally, one could use other activity indicators, possibly not affected by the ISM absorption, such as emission lines of highly ionised elements (e.g. Si iv) present in the far ultraviolet spectral region. The strength of these lines could then be converted into a Ca ii emission flux using, for example, the scaling relations of Linsky et al. (2013, 2014). Fossati et al. (2015b) followed this procedure for the analysis of the WASP-13 system. The major problem with this approach is that it is currently not possible to detect the far ultraviolet spectrum of main-sequence solar-like stars unless they are bright and lie not too far away from us ( 200–250 pc). This renders the procedure impractical for most of the known transiting planets. This may change though in the next 20–25 yr with the next generation of space telescopes with ultraviolet capabilities, such as LUVOIR, for which the larger aperture and higher efficiency of the instruments (France et al. 2016) would enable the detection of the far ultraviolet spectra of more distant stars.
200–250 pc). This renders the procedure impractical for most of the known transiting planets. This may change though in the next 20–25 yr with the next generation of space telescopes with ultraviolet capabilities, such as LUVOIR, for which the larger aperture and higher efficiency of the instruments (France et al. 2016) would enable the detection of the far ultraviolet spectra of more distant stars.
Despite the difficulty and possible unreliability of inferring corrections to the activity parameters, we compiled a code that allows the user to roughly estimate the correction in terms of SMW and  because of ISM absorption. This is the code we adopted to correct the
because of ISM absorption. This is the code we adopted to correct the  values for the stars analysed by Fossati et al. (2015a, Sect. 6.2). The code is available in both IDL and Python, and can be downloaded4. The code asks the user to insert (either at terminal or through an input file) the stellar B−V colour or Teff, the measured SMW or
values for the stars analysed by Fossati et al. (2015a, Sect. 6.2). The code is available in both IDL and Python, and can be downloaded4. The code asks the user to insert (either at terminal or through an input file) the stellar B−V colour or Teff, the measured SMW or  values, the colour excess E(B−V) or the ISM log NCaII, and the radial velocity of the ISM absorption feature with respect to the star. The code assumes the presence of one ISM absorption line and uses the library of photospheric fluxes described in Sect. 2. The code derives the chromospheric emission flux using the SMW and/or
values, the colour excess E(B−V) or the ISM log NCaII, and the radial velocity of the ISM absorption feature with respect to the star. The code assumes the presence of one ISM absorption line and uses the library of photospheric fluxes described in Sect. 2. The code derives the chromospheric emission flux using the SMW and/or  values provided by the user (if the
values provided by the user (if the  lies below the basal level of −5.1, the code automatically sets
lies below the basal level of −5.1, the code automatically sets  = −5.1, which is the minimum possible value without extrinsic absorption). Finally, the code allows the user to choose between two ways of converting the colour excess E(B−V) into log NCaII following the procedures described in the first paragraph of Sect. 6.1 and adopting the H i column density versus E(B−V) relation by Diplas & Savage (1994). The code assumes infinite spectral resolution, no line broadening from rotation and/or macroturbulence, and a broadening b-parameter for the ISM absorption line of 2 km s-1. This last parameter can be modified inside the code. When using the results of this code, the user should be aware of the assumptions and caveats described herein.
= −5.1, which is the minimum possible value without extrinsic absorption). Finally, the code allows the user to choose between two ways of converting the colour excess E(B−V) into log NCaII following the procedures described in the first paragraph of Sect. 6.1 and adopting the H i column density versus E(B−V) relation by Diplas & Savage (1994). The code assumes infinite spectral resolution, no line broadening from rotation and/or macroturbulence, and a broadening b-parameter for the ISM absorption line of 2 km s-1. This last parameter can be modified inside the code. When using the results of this code, the user should be aware of the assumptions and caveats described herein.
7. Conclusion
Optical and ultraviolet observations have revealed that some stars hosting transiting planets, usually hot Jupiters, present an anomalously low activity, well below the basal level of main-sequence late-type stars of  = −5.1. Fossati et al. (2015b) concluded that this anomaly may be caused by ISM absorption. Inspired by this result, we study in detail the effect of ISM absorption on activity measurements, concentrating particularly on the S and
= −5.1. Fossati et al. (2015b) concluded that this anomaly may be caused by ISM absorption. Inspired by this result, we study in detail the effect of ISM absorption on activity measurements, concentrating particularly on the S and  indices. To this end, we model the wavelength region covered by the Ca ii H&K lines employing photospheric synthetic spectra of stars in the 4000–6400 K temperature range, to which we add varying amounts of chromospheric emission, simulated as a single Gaussian, and ISM absorption, simulated as a single Voigt profile.
indices. To this end, we model the wavelength region covered by the Ca ii H&K lines employing photospheric synthetic spectra of stars in the 4000–6400 K temperature range, to which we add varying amounts of chromospheric emission, simulated as a single Gaussian, and ISM absorption, simulated as a single Voigt profile.
We first considered a Sun-like star with a total chromospheric emission at 1 AU of 100 erg cm-2 s-1, fixed the spectral resolution at 100 000, assumed a non-rotating star, fixed the Ca ii ISM column density at log NCaII = 12, and varied the relative velocity between the stellar and ISM spectral features. We found that the bias caused by ISM absorption is significant for relative radial velocities below 30–40 km s-1, in modulus. The bias becomes progressively less important for higher velocities, up to about ±86 km s-1 where the ISM absorption line starts falling outside of the band used to measure the S index. We then fixed the relative velocity to 0 km s-1 and varied the Ca ii column density, keeping all other parameters fixed. We found that the bias exceeds photon noise uncertainties on the S value for Ca ii logarithmic column densities greater than 10.5. We found also that the bias increases with increasing chromospheric emission.
We explored the effect of varying: relative velocity and Ca ii column density, spectral resolution, stellar projected rotation velocity, ISM broadening b-parameter, and chromospheric emission, one at a time. We found that varying the spectral resolution, stellar projected rotation velocity, and b-parameter produces similar, and relatively small, changes on the bias caused by ISM absorption. We conclude that the amount of chromospheric emission plays the greatest role. We found that the bias caused by ISM absorption increases with decreasing stellar effective temperature.
We found for relative radial velocities smaller than 30 km s-1, in modulus, that the bias that ISM absorption causes on the SMW and  indices exceeds typical photon noise and calibration uncertainties for ISM column densities greater than log NCaII ≈ 12. Such a column density can be expected for stars beyond 100 pc. For both active and inactive late-type stars beyond 100 pc, the bias in activity measurements caused by ISM absorption can be important. The bias increases with increasing activity.
indices exceeds typical photon noise and calibration uncertainties for ISM column densities greater than log NCaII ≈ 12. Such a column density can be expected for stars beyond 100 pc. For both active and inactive late-type stars beyond 100 pc, the bias in activity measurements caused by ISM absorption can be important. The bias increases with increasing activity.
We considered just one ISM absorption line, while observations clearly indicate the presence of multiple ISM clouds, even within very short distances (i.e. <100 pc). It is not possible to take this additional level of complication into account in a systematic way. We show that differences from the case of a single line occur when the ISM absorption components do not have the same radial velocity and if one (or more) of the absorption lines is saturated.
Since the ISM absorption differs according to the position of a star in the sky and its effects on activity measurements depend on the number and radial velocity of the ISM components, and not just on the stellar distance, it is not possible to quantify the bias introduced by ISM absorption as a function of distance, expecting that it would be valid across the whole sky. However, our results clearly show that ISM absorption does significantly affect activity measurements. Hence activity studies should either impose a reasonable distance cut-off on their samples (e.g. ≈100 pc) or statistically account for how ISM absorption may affect the results.
ISM absorption should be taken into account by either directly measuring the ISM Ca ii column density (as done by Fossati et al. 2013, for WASP-12) or by inferring the Ca ii column density from the extinction (e.g. from fitting of the spectral energy distribution or extinction maps) and calibrations published in the literature. There are many assumptions implicit in the latter method, so it is much more uncertain than the former, though it allows one to infer a rough correction for any star.
We provide a routine to roughly account for ISM absorption when measuring the SMW and  indices using the latter method. We employ this code to show that the bias caused by ISM absorption does not affect the latest interpretation and results of the stellar activity versus planet surface gravity correlation presented by Fossati et al. (2015a).
indices using the latter method. We employ this code to show that the bias caused by ISM absorption does not affect the latest interpretation and results of the stellar activity versus planet surface gravity correlation presented by Fossati et al. (2015a).
Our results could be used to identify whether the anomalously low activity level of certain planet-hosting stars is caused by ISM absorption or by the presence of a translucent circumstellar cloud or torus, as suggested by Haswell et al. (2012). In the latter case, the  value corrected for the ISM absorption would still lie well below the basal level.
value corrected for the ISM absorption would still lie well below the basal level.
Acknowledgments
S.E.M. acknowledges financial support from the FEMTECH programme financed by the Austrian Forschungsförderungs-gesellschaft (FFG). D.S. is supported by an STFC studentship. J.S.J. acknowledges funding by Fondecyt through grant 1161218, partial support from CATA-Basal (PB06, Conicyt). C.H. is supported by STFC under grant ST/L000776/1. The authors thank the anonymous referee for the valuable comments. This research has made use of the Exoplanet Orbit Database and the Exoplanet Data Explorer at exoplanets.org.
References
- Alexander, R. D., Wynn, G. A., Mohammed, H., Nichols, J. D., & Ercolano, B. 2016, MNRAS, 456, 2766 [NASA ADS] [CrossRef] [Google Scholar]
- Amôres, E. B., & Lépine, J. R. D. 2005, AJ, 130, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. R., Haswell, C. A., Staab, D., & Anglada-Escudé, G. 2016, MNRAS, 462, 1012 [Google Scholar]
- Bisikalo, D., Kaygorodov, P., Ionov, D., et al. 2013, ApJ, 764, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Boissé, P., Federman, S. R., Pineau des Forêts, G., & Ritchey, A. M. 2013, A&A, 559, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourrier, V., Ehrenreich, D., King, G., et al. 2016, A&A, 597, A26 [Google Scholar]
- Canto Martins, B. L., Das Chagas, M. L., Alves, S., et al. 2011, A&A, 530, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carroll-Nellenback, J., Frank, A., Liu, B., et al. 2017, MNRAS, 466, 2458 [NASA ADS] [CrossRef] [Google Scholar]
- Cauley, P. W., Redfield, S., Jensen, A. G., & Barman, T. 2016, AJ, 152, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Cayrel de Strobel, G. 1996, A&ARv, 7, 243 [CrossRef] [Google Scholar]
- Diplas, A., & Savage, B. D. 1994, ApJ, 427, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Ehrenreich, D., Bourrier, V., Bonfils, X., et al. 2012, A&A, 547, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ehrenreich, D., Bourrier, V., Wheatley, P. J., et al. 2015, Nature, 522, 459 [Google Scholar]
- Erkaev, N. V., Lammer, H., Odert, P., et al. 2016, MNRAS, 460, 1300 [NASA ADS] [CrossRef] [Google Scholar]
- Figueira, P., Oshagh, M., Adibekyan, V. Z., & Santos, N. C. 2014, A&A, 572, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fossati, L., Haswell, C. A., Froning, C. S., et al. 2010a, ApJ, 714, L222 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, L., Bagnulo, S., Elmasli, A., et al. 2010b, ApJ, 720, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, L., Ayres, T. R., Haswell, C. A., et al. 2013, ApJ, 766, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, L., Ayres, T. R., Haswell, C. A., et al. 2014, Ap&SS, 354, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, L., Ingrassia, S., & Lanza, A. F. 2015a, ApJ, 812, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, L., France, K., Koskinen, T., et al. 2015b, ApJ, 815, 118 [NASA ADS] [CrossRef] [Google Scholar]
- France, K., Fleming, B., & Hoadley, K. 2016, Proc. SPIE, 9905, 990506 [CrossRef] [Google Scholar]
- Frisch, P. C., & Slavin, J. D. 2003, ApJ, 594, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, P. C., Redfield, S., & Slavin, J. D. 2011, ARA&A, 49, 237 [NASA ADS] [CrossRef] [Google Scholar]
- García Muñoz, A. 2007, Planet. Space Sci., 55, 1426 [NASA ADS] [CrossRef] [Google Scholar]
- Gomes da Silva, J., Santos, N. C., Boisse, I., Dumusque, X., & Lovis, C. 2014, A&A, 566, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gray, D. F. 2005, The Observation and Analysis of Stellar Photospheres, 3rd edn., eds. D. F. Gray (Cambridge: Cambridge University Press) [Google Scholar]
- Gray, R. O., Corbally, C. J., Garrison, R. F., McFadden, M. T., & Robinson, P. E. 2003, AJ, 126, 2048 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, W. J., & Scannapieco, E. 2016, ApJ, 818, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Gudennavar, S. B., Bubbly, S. G., Preethi, K., & Murthy, J. 2012, ApJS, 199, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Güver, T., & Özel, F. 2009, MNRAS, 400, 2050 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, J. C., Lockwood, G. W., & Skiff, B. A. 2007, AJ, 133, 862 [NASA ADS] [CrossRef] [Google Scholar]
- Han, E., Wang, S. X., Wright, J. T., et al. 2014, PASP, 126, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D. 2010, ApJ, 717, L138 [NASA ADS] [CrossRef] [Google Scholar]
- Haswell, C. A., Fossati, L., Ayres, T., et al. 2012, ApJ, 760, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, R. D., Collier Cameron, A., Unruh, Y. C., et al. 2016, MNRAS, 457, 3637 [NASA ADS] [CrossRef] [Google Scholar]
- Hebb, L., Collier-Cameron, A., Loeillet, B., et al. 2009, ApJ, 693, 1920 [NASA ADS] [CrossRef] [Google Scholar]
- Ingrassia, S., Minotti, S. C., Punzo, A. 2014, Computational Statistics & Data Analysis, 71, 159 [CrossRef] [Google Scholar]
- Jenkins, J. S., Jones, H. R. A., Tinney, C. G., et al. 2006, MNRAS, 372, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J. S., Jones, H. R. A., Pavlenko, Y., et al. 2008, A&A, 485, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jenkins, J. S., Murgas, F., Rojo, P., et al. 2011, A&A, 531, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jensen, A. G., Redfield, S., Endl, M., et al. 2012, ApJ, 751, 86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnson, M. C., Redfield, S., & Jensen, A. G. 2015, ApJ, 807, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Kislyakova, K. G., Pilat-Lohinger, E., Funk, B., et al. 2016, MNRAS, 461, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H. A., Howard, A. W., & Isaacson, H. 2010, ApJ, 720, 1569 [NASA ADS] [CrossRef] [Google Scholar]
- Koskinen, T. T., Lavvas, P., Harris, M. J., & Yelle, R. V. 2014, Philos. Trans. Roy. Soc. London Ser. A, 372, 20130089 [Google Scholar]
- Kulow, J. R., France, K., Linsky, J., & Loyd, R. O. P. 2014, ApJ, 786, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Lai, D., Helling, C., & van den Heuvel, E. P. J. 2010, ApJ, 721, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Lammer, H., Selsis, F., Ribas, I., et al. 2003, ApJ, 598, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Lanza, A. F. 2014, A&A, 572, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lecavelier des Etangs, A., Vidal-Madjar, A., McConnell, J. C., & Hébrard, G. 2004, A&A, 418, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lecavelier des Etangs, A., Bourrier, V., Wheatley, P. J., et al. 2012, A&A, 543, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Linsky, J. L., Yang, H., France, K., et al. 2010, ApJ, 717, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Linsky, J. L., France, K., & Ayres, T. 2013, ApJ, 766, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Linsky, J. L., Fontenla, J., & France, K. 2014, ApJ, 780, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Llama, J., Wood, K., Jardine, M., et al. 2011, MNRAS, 416, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Lovis, C., Dumusque, X., Santos, N. C., et al. 2011, unpublished [arXiv:1107.5325] [Google Scholar]
- Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Middelkoop, F. 1982, A&A, 107, 31 [NASA ADS] [Google Scholar]
- Miller, B. P., Gallo, E., Wright, J. T., & Pearson, E. G. 2015, ApJ, 799, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Mittag, M., Schmitt, J. H. M. M., & Schröder, K.-P. 2013, A&A, 549, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murray-Clay, R. A., Chiang, E. I., & Murray, N. 2009, ApJ, 693, 23 [Google Scholar]
- Nichols, J. D., Wynn, G. A., Goad, M., et al. 2015, ApJ, 803, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Noyes, R. W., Weiss, N. O., & Vaughan, A. H. 1984, ApJ, 287, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Oranje, B. J. 1983, A&A, 122, 88 [NASA ADS] [Google Scholar]
- Owen, J. E., & Wu, Y. 2016, ApJ, 817, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Predehl, P., & Schmitt, J. H. M. M. 1995, A&A, 293, 889 [NASA ADS] [Google Scholar]
- Redfield, S., & Linsky, J. L. 2002, ApJS, 139, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Redfield, S., & Linsky, J. L. 2004, ApJ, 613, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- Rutten, R. G. M. 1984, A&A, 130, 353 [NASA ADS] [Google Scholar]
- Salz, M., Banerjee, R., Mignone, A., et al. 2015, A&A, 576, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salz, M., Czesla, S., Schneider, P. C., & Schmitt, J. H. M. M. 2016, A&A, 586, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savage, B. D., & Mathis, J. S. 1979, ARA&A, 17, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Shulyak, D., Tsymbal, V., Ryabchikova, T., Stütz, C., & Weiss, W. W. 2004, A&A, 428, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skillen, I., Pollacco, D., Collier Cameron, A., et al. 2009, A&A, 502, 391 [Google Scholar]
- Staab, D., Haswell, C. A., Smith, G., et al. 2017, MNRAS, 466, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Vallerga, J. V., Vedder, P. W., Craig, N., & Welsh, B. Y. 1993, ApJ, 411, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Vidal-Madjar, A., Lecavelier des Etangs, A., Désert, J.-M., et al. 2003, Nature, 422, 143 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Vidal-Madjar, A., Désert, J.-M., Lecavelier des Etangs, A., et al. 2004, ApJ, 604, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Vidotto, A. A., Jardine, M., & Helling, C. 2010, ApJ, 722, L168 [NASA ADS] [CrossRef] [Google Scholar]
- Wakker, B. P., & Mathis, J. S. 2000, ApJ, 544, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Welsh, B. Y., & Sallmen, S. 2003, A&A, 408, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Welsh, B. Y., Rachford, B. L., & Tumlinson, J. 2002, A&A, 381, 566 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Welsh, B. Y., Sallmen, S., & Jelinsky, S. 2005, A&A, 440, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Welsh, B. Y., Wheatley, J., & Lallement, R. 2009, PASP, 121, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Welsh, B. Y., Lallement, R., Vergely, J.-L., & Raimond, S. 2010, A&A, 510, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Welty, D. E., Morton, D. C., & Hobbs, L. M. 1996, ApJS, 106, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, J. T. 2004, AJ, 128, 1273 [NASA ADS] [CrossRef] [Google Scholar]
- Wyman, K., & Redfield, S. 2013, ApJ, 773, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Yelle, R. V. 2004, Icarus, 170, 167 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Effect of spectral resolution and stellar rotation on the S values calculated including ISM absorption
 |
Fig. A.1 Difference between SE = 100 and the S values obtained by varying the spectral resolution and the ISM parameters (RV and log NCaII), keeping E fixed at 100 erg cm-2 s-1. The values along the lines of each contour (0.001, 0.004, 0.01, 0.02, 0.04, 0.08) quantify the SE = 100−S difference. The adopted spectral resolution is written in the bottom-right corner of each panel. |
All Tables
Corrections to the  values due to ISM absorption for the systems considered in the work of Fossati et al. (2015a).
values due to ISM absorption for the systems considered in the work of Fossati et al. (2015a).
All Figures
 |
Fig. 1 Conversion factor β between S and SMW as a function of Teff and E. The values along the line of each contour quantify β. |
| In the text | |
 |
Fig. 2 Top left: LLmodels photospheric spectrum of the Sun in the region of the Ca ii K line core (black solid line) modified by adding a line core emission of 112 erg cm-2 s-1 (red solid and dashed lines). This composite spectrum has then been modified by two ISM absorption features, located at the line centre, calculated with Ca ii column densities of 1012 and 1016 cm-2 (blue and green dashed and solid lines). Bottom left: comparison between a high resolution HIRES spectrum of the young Sun-like star EK Dra and the corresponding synthetic spectrum obtained by adding a line core emission of E = 112 erg cm-2 s-1 to the photospheric spectrum. The two spectra return the same SMW value of 0.440. The synthetic spectrum accounts also for the instrumental spectral resolution and the stellar projected rotational velocity (≈15 km s-1). Right: same as the left panels, but for the hyper-velocity halo Sun-like star HD 29587. In this case, the emission flux is 15 erg cm-2 s-1, corresponding to a SMW value of 0.144. The synthetic spectrum does not match the line profile in detail, possibly due to non-LTE effects, but it reproduces the empirical S value. In the top panels, the red solid lines are visible just in the very core of the line, as it is otherwise covered by the blue solid line. |
| In the text | |
 |
Fig. 3 Relation between differences in the SMW and |
| In the text | |
 |
Fig. 4 Deviation of the SMW value from that at R = 100 000 as a function of spectral resolution. The dotted lines indicate typical photon noise uncertainties on SMW (i.e. 0.002). |
| In the text | |
 |
Fig. 5 Deviation of the S value from that derived with perfect background subtraction as a function of the deviation from a perfect background subtraction, considering five different chromospheric emission levels. |
| In the text | |
 |
Fig. 6 Variation of SMW as a function of radial velocity of the ISM absorption line. The dashed red line shows the SE = 100 value and the horizontal dotted blue line indicates the typical photon noise uncertainty, while the vertical dotted black lines represent the boundaries of the H and K passbands used to calculate the S value, converted to velocity space. |
| In the text | |
 |
Fig. 7 Variation of SMW as a function of log NCaII. Each line has been obtained considering different values of the emission E, as indicated in the legend. The dashed line shows the value of SE = 100, while the dotted line indicates typical photon noise uncertainties. For comparison purposes, the blue and red lines have been rescaled in order to match the black line at log NCaII = 0. |
| In the text | |
 |
Fig. 8 Absorption (in %) caused by one ISM line as a function of Ca ii column density assuming four different values of the broadening b-parameter. The chromospheric emission is E = 100 erg cm-2 s-1. The y-axis is in log scale. |
| In the text | |
 |
Fig. 9 Difference between SE = 100 and SMW obtained by varying the ISM broadening (b-parameter), radial velocity (RV), and column density (log NCaII), keeping E fixed at 100 erg cm-2 s-1. The values along the lines of each contour (0.001, 0.004, 0.01, 0.03, 0.06, 0.11) quantify the SE = 100 − SMW difference. |
| In the text | |
 |
Fig. 10 Left: differences between the reference S value calculated without ISM absorption, and SMW obtained by varying the ISM parameters for five different values of E. The adopted spectral resolution is 100 000. The values along the line of each contour (0.001, 0.005, 0.01, 0.02, 0.04, 0.08) quantify the difference. The results shown in the third and fifth panels can be directly converted into differences in |
| In the text | |
 |
Fig. 11 Top: difference between the reference S value SE = 100 calculated without ISM absorption, and SMW obtained considering two non-saturated (log NCaII = 11.5) ISM absorption components as a function of velocity separation (Δvr in km s-1) of each ISM feature from the line centre. With increasing Δvr, the two features move in opposite directions. The black dashed line shows the case of a single ISM absorption component moving redwards of the line centre. The short dashed vertical lines are colour-coded by the absorption features shown in the insert and indicate their position relative to the line centre. The insert shows the photospheric plus chromospheric flux (the photospheric spectrum is shown by a dashed line) in black and, as an example, absorption components lying at a velocity separation of 0.0 (red), ±10.0 (blue), ±30.0 (green), and ±50.0 (orange) km s-1 from the line centre. Bottom: as the top panel, but considering saturated (log NCaII = 14.0) ISM absorption lines. |
| In the text | |
 |
Fig. 12 Top: measurements of log NCaII as a function of stellar distance collected by Welsh et al. (2010). Red pluses indicate upper limits. Bottom: log NCaII–E(B−V) correlations obtained by converting first E(B−V) into log NHI, using the relation given by Savage & Mathis (1979, SM79; black), Diplas & Savage (1994, DS94; red), Güver & Özel (2009, GO09; blue), Predehl & Schmitt (1995, PS95; purple), and Gudennavar et al. (2012, G12; yellow), and then log NHI into log NCaII, using either the log NHI–log NCaII relation given by Wakker & Mathis (2000, WM00; solid lines) or by using the Ca ii ISM ionisation fraction measured by Frisch & Slavin (2003, FS03) and assuming a solar Ca abundance (Asplund et al. 2009, A09; dashed lines). The “X” in the legend stands for any of SM79, DS94, GO09, PS95, or G12. The vertical dotted lines indicate the average distance at which a given E(B−V) value can be expected following the ISM extinction maps of Amôres & Lépine (2005). This figure justifies the upper boundary of log NCaII = 14 used for the analysis carried out in Sects. 4 and 5. |
| In the text | |
 |
Fig. 13 Number of transiting (solid line) and non-transiting (dashed line) planets as a function of logarithm of the distance to the solar system, in pc. The distance ranges between about 10 pc and 3.2 kpc. The total number of planets is 2167 (1527 transiting and 640 non-transiting). Data downloaded from Han et al. (2014) in January 20173. |
| In the text | |
 |
Fig. 14 Chromospheric emission index |
| In the text | |
 |
Fig. A.1 Difference between SE = 100 and the S values obtained by varying the spectral resolution and the ISM parameters (RV and log NCaII), keeping E fixed at 100 erg cm-2 s-1. The values along the lines of each contour (0.001, 0.004, 0.01, 0.02, 0.04, 0.08) quantify the SE = 100−S difference. The adopted spectral resolution is written in the bottom-right corner of each panel. |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1, but varying stellar υsini. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.