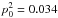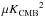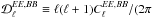| Issue |
A&A
Volume 601, May 2017
|
|
|---|---|---|
| Article Number | A71 | |
| Number of page(s) | 18 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201629829 | |
| Published online | 04 May 2017 | |
Modelling and simulation of large-scale polarized dust emission over the southern Galactic cap using the GASS Hi data
1 California Institute of Technology, Pasadena, California, USA
e-mail: tghosh@caltech.edu
2 Institut d’Astrophysique Spatiale, CNRS (UMR 8617) Université Paris-Sud 11, Bâtiment 121, Orsay, France
3 CITA, University of Toronto, 60 St. George St., Toronto, ON M5S 3H8, Canada
4 Laboratoire AIM, IRFU/Service d’Astrophysique – CEA/DSM – CNRS – Université Paris Diderot, Bât. 709, CEA-Saclay, 91191 Gif-sur-Yvette Cedex, France
5 Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, California, USA
6 Tartu Observatory, 61602 Tõravere, Tartumaa, Estonia
7 Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
Received: 2 October 2016
Accepted: 24 January 2017
The Planck survey has quantified polarized Galactic foregrounds and established that they are a main limiting factor in the quest for the cosmic microwave background B-mode signal induced by primordial gravitational waves during cosmic inflation. Accurate separation of the Galactic foregrounds therefore binds this quest to our understanding of the magnetized interstellar medium. The two most relevant empirical results from analysis of Planck data are line of sight depolarization arising from fluctuations of the Galactic magnetic field orientation and alignment of filamentary dust structures with the magnetic field at high Galactic latitude. Furthermore, Planck and H I emission data in combination indicate that most of the filamentary dust structures are in the cold neutral medium. The goal of this paper is to test whether these salient observational results, taken together, can account fully for the statistical properties of the dust polarization over a selected low column density region comprising 34% of the southern Galactic cap (b ≤ −30°). To do this, we construct a dust model that incorporates H I column density maps as tracers of the dust intensity structures and a phenomenological description of the Galactic magnetic field. By adjusting the parameters of the dust model, we were able to reproduce the Planck dust observations at 353GHz in the selected region. Realistic simulations of the polarized dust emission enabled by such a dust model are useful for testing the accuracy of component separation methods, studying non-Gaussianity, and constraining the amount of decorrelation with frequency.
Key words: dust, extinction / ISM: magnetic fields / ISM: structure / polarization / Galaxy: general / submillimeter: ISM
© ESO, 2017
1. Introduction
An intense focus in current observational cosmology is detection of the cosmic microwave background (CMB) B-mode signal induced by primordial gravitational waves during the inflation era (Starobinsky 1979; Fabbri & Pollock 1983; Abbott & Wise 1984). The BICEP2 experiment1 puts an upper bound on the amplitude of the CMB B-mode signal, parameterized by a tensor-to-scalar ratio (r) at a level of r< 0.09 (95% confidence level BICEP2 and Keck Array Collaboration et al. 2016). Therefore, the major challenge for a BICEP2-like experiment with limited frequency coverage is to detect such an incredibly faint CMB B-mode signal in the presence of foreground Galactic contamination (Betoule et al. 2009). The dominant polarized foreground above 100GHz come from thermal emission by aligned aspherical dust grains (Planck Collaboration Int. XXII 2015; Planck Collaboration X 2016). Unlike the CMB, the polarized dust emission is distributed non-uniformly on the sky with varying column density over which are summed contributions from multiple components with different dust composition, size, and shape and with different magnetic field orientation (see reviews by Prunet & Lazarian 1999; Lazarian 2008). Acknowledging these complexities, the goal of this paper is to model the principal effects, namely multiple components with different magnetic field orientations, to produce realistic simulated maps of the polarized dust emission.
Our knowledge and understanding of the dust polarization has improved significantly in the submillimetre and microwave range through exploitation of data from the Planck satellite2 (Planck Collaboration I 2016; Planck Collaboration X 2016; Planck Collaboration Int. XIX 2015), which provides important empirical constraints on the models. The Planck satellite has mapped the polarized sky at seven frequencies between 30 and 353GHz (Planck Collaboration I 2016). The Planck maps are available in HEALPix3 format (Górski et al. 2005) with resolution parameter labelled with the Nside value. The general statistical properties of the dust polarization in terms of angular power spectrum at intermediate and high Galactic latitudes from 100 to 353GHz are quantified in Planck Collaboration Int. XXX (2016).
Two unexpected results from the Planck observations were an asymmetry in the amplitudes of the angular power spectra of the dust E- and B-modes (EE and BB spectra, respectively) and a positive temperature E-mode (TE) correlation at 353GHz. Explanation of these important features was explored by Planck Collaboration Int. XXXVIII (2016) through a statistical study of the filamentary structures in the Planck Stokesmaps and Caldwell et al. (2017) discussed them in the context of magnetohydrodynamic interstellar turbulence. They are a central focus of the modelling in this paper.
The Planck 353GHz polarization maps (Planck Collaboration Int.XIX 2015) have the best signal-to-noise ratio and enable study of the link between the structure of the Galactic magnetic field (GMF) and dust polarization properties. A large scatter of the dust polarization fraction (p) for total column density NH< 1022 cm-2 at low and intermediate Galactic latitudes is reported in Planck Collaboration Int. XIX (2015). Based on numerical simulations of anisotropic magnetohydrodynamic turbulence in the diffuse interstellar medium (ISM), it has been concluded that the large scatter of p in the range 2 × 1021 cm-2<NH< 2 × 1022 cm-2 comes mostly from fluctuations in the GMF orientation along the line of sight (LOS) rather than from changes in grain shape or the efficiency of the grain alignment (Planck Collaboration Int. XX 2015). To account for the observed scatter of p in the high latitude southern Galactic sky (b ≤ −60°), a finite number of polarization layers was introduced (Planck Collaboration Int. XLIV 2016). The orientation of large-scale GMF with respect to the plane of the sky (POS) also plays a crucial role in explaining the scatter of p (Planck Collaboration Int. XX 2015).
The Planck polarization data reveal a tight relationship between the orientation of the dust intensity structures and the magnetic field projected on the plane of the sky (BPOS, Planck Collaboration Int. XXXII 2016; Planck Collaboration Int.XXXV 2016; Planck Collaboration Int.XXXVIII 2016). In particular, the dust intensity structures are preferentially aligned with BPOS in the diffuse ISM (Planck Collaboration Int. XXXII 2016). Similar alignment is also reported between the Galactic Arecibo L-Band Feed Array (GALFA, Peek et al. 2011) HI filaments and BPOS derived either from starlight polarization (Clark et al. 2014) or Planck polarization data (Clark et al. 2015). Furthermore, a detailed all-sky study of the HI filaments, combining the Galactic All Sky Survey (GASS, McClure-Griffiths et al. 2009) and the Effelsberg Bonn HI Survey (EBHIS, Winkel et al. 2016), shows that most of the filaments occur in the cold neutral medium (CNM, Kalberla et al. 2016). The HI emission in the CNM phase has a line profile with 1σ velocity dispersion 3kms-1 (FWHM 7kms-1) in the solar neighbourhood (Heiles & Troland 2003) and filamentary structure on the sky, which might result from projection effects of gas organized primarily in sheets (Heiles & Troland 2005; Kalberla et al. 2016). Alignment of CNM structures with BPOS from Planck has been reported towards the north ecliptic pole, among the targeted fields of the Green Bank Telescope HI Intermediate Galactic Latitude Survey (GHIGLS, Martin et al. 2015). Such alignment can be induced by shear strain of gas turbulent velocities stretching matter and the magnetic field in the same direction (Hennebelle 2013; Inoue & Inutsuka 2016).
Alignment between the CNM structures and BPOS was not included in the pre-Planck dust models, for example Planck Sky Model (PSM, Delabrouille et al. 2013) and FGPol (O’Dea et al. 2012). The most recent version of post-Planck PSM uses a filtered version of the Planck 353GHz polarization data as the dust templates (Planck Collaboration XII 2016). Therefore, in low signal-to-noise regions the PSM dust templates are not reliable representations of the true dust polarized sky. In Planck Collaboration Int. XXXVIII (2016) it was shown that preferential alignment of the dust filaments with BPOS could account for both the E-B asymmetry in the amplitudes of the dust 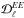 and
and 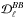 angular power spectra4 over the multipole range 40 <ℓ< 600 and the amplitude ratio
angular power spectra4 over the multipole range 40 <ℓ< 600 and the amplitude ratio 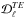 /
/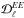 , as measured by Planck Collaboration Int. XXX (2016). Clark et al. (2015) showed that the alignment of the BPOS with the HI structures can explain the observed E-B asymmetry.
, as measured by Planck Collaboration Int. XXX (2016). Clark et al. (2015) showed that the alignment of the BPOS with the HI structures can explain the observed E-B asymmetry.
Recently, Vansyngel et al. (2017) have extended the approach introduced in Planck Collaboration Int. XLIV (2016) using a parametric model to account for the observed dust power spectra at intermediate and high Galactic latitudes. Our work in this paper is complementary, incorporating additional astrophysical data and insight and focusing on the cleanest sky area for CMB B-mode studies from the southern hemisphere.
In more detail, the goal of this paper is to test whether preferential alignment of the CNM structures with BPOS together with fluctuations in the GMF orientation along the LOS can account fully for a number of observed statistical properties of the dust polarization over the southern low column density sky. These statistical properties include the scatter of the polarization fraction p, the dispersion of the polarization angle ψ around the large-scale GMF, and the observed dust power spectra 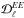 ,
, 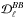 , and
, and 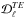 at 353GHz. In doing so we extend the analysis of Planck Collaboration Int. XXXVIII (2016) and Planck Collaboration Int. XLIV (2016) to sky areas in which the filaments have very little contrast with respect to the diffuse background emission. Within the southern Galactic cap (defined here to be b ≤ −30°), in which dust and gas are well correlated (Boulanger et al. 1996; Planck Collaboration XI 2014) and the GASS HI emission is a good tracer of the dust intensity structures (Planck Collaboration Int. XVII 2014),we focus our study on the low column density portion. We choose to model the dust polarization sky at 1° resolution, which corresponds to retaining multipoles ℓ ≤ 160 where the Galactic dust dominates over the CMB B-mode signal. Also, most of the ground-based CMB experiments are focusing at a degree scale for the detection of the recombination bump of the CMB B-mode signal. Our dust polarization model should be a useful product for the CMB community. It covers 34% of the southern Galactic cap, a 3500 deg2 region containing the cleanest sky accessible to ongoing ground and balloon-based CMB experiments: ABS (Essinger-Hileman et al. 2010), Advanced ACTPol (Henderson et al. 2016), BICEP/ Keck (Ogburn et al. 2012), CLASS (Essinger-Hileman et al. 2014), EBEX (Reichborn-Kjennerud et al. 2010), Polarbear (Kermish et al. 2012), Simons array (Suzuki et al. 2016), SPIDER (Crill et al. 2008), and SPT3G (Benson et al. 2014).
at 353GHz. In doing so we extend the analysis of Planck Collaboration Int. XXXVIII (2016) and Planck Collaboration Int. XLIV (2016) to sky areas in which the filaments have very little contrast with respect to the diffuse background emission. Within the southern Galactic cap (defined here to be b ≤ −30°), in which dust and gas are well correlated (Boulanger et al. 1996; Planck Collaboration XI 2014) and the GASS HI emission is a good tracer of the dust intensity structures (Planck Collaboration Int. XVII 2014),we focus our study on the low column density portion. We choose to model the dust polarization sky at 1° resolution, which corresponds to retaining multipoles ℓ ≤ 160 where the Galactic dust dominates over the CMB B-mode signal. Also, most of the ground-based CMB experiments are focusing at a degree scale for the detection of the recombination bump of the CMB B-mode signal. Our dust polarization model should be a useful product for the CMB community. It covers 34% of the southern Galactic cap, a 3500 deg2 region containing the cleanest sky accessible to ongoing ground and balloon-based CMB experiments: ABS (Essinger-Hileman et al. 2010), Advanced ACTPol (Henderson et al. 2016), BICEP/ Keck (Ogburn et al. 2012), CLASS (Essinger-Hileman et al. 2014), EBEX (Reichborn-Kjennerud et al. 2010), Polarbear (Kermish et al. 2012), Simons array (Suzuki et al. 2016), SPIDER (Crill et al. 2008), and SPT3G (Benson et al. 2014).
This paper is organized as follows. Section2 introduces the Planck observations and GASS H I data used in our analysis, along with a selected sky region within the southern Galactic cap, called SGC34. In Sect.3, we summarize the observational dust polarization properties in SGC34 as seen by Planck. A model to simulate dust polarization using the GASS HI data and a phenomenological description of the GMF is detailed in Sect.4. The procedure to simulate the polarized dust sky towards the southern Galactic cap and the choice of the dust model parameters are discussed in Sect.5. Section5.4 presents the main results where we statistically compare the dust model with the observed Planck data. In Sect.6, we make some predictions using our dust model. We end with an astrophysical perspective in Sect.7 and a short discussion and summary of our results in Sect.8.
2. Data sets used and region selection
2.1. Planck 353GHz data
In this paper we used the publicly available5 maps from the Planck 2015 polarization data release (PR2), specifically at 353GHz (Planck Collaboration I 2016)6. The data processing and calibration of the Planck High Frequency Instrument (HFI) maps are described in Planck Collaboration VIII (2016). We used multiple Planck 353GHz polarization data sets: the two yearly surveys, Year 1 (Y1) and Year 2 (Y2), the two half-mission maps, HM1 and HM2, and the two detector-set maps, DS1 and DS2, to exploit the statistical independence of the noise between them and to test for any systematic effects7. The 353GHz polarization maps are corrected for zodiacal light emission at the map-making level (Planck Collaboration VIII 2016). These data sets are described in full detail in Planck Collaboration VIII (2016).
All of the 353GHz data sets used in this study have an angular resolution of FWHM 4.′82 and are projected on a HEALPix grid with a resolution parameter Nside=2048 (1.′875pixels). We corrected for the main systematic effect, that is leakage from intensity to polarization, using the global template fit, as described in Planck Collaboration VIII (2016), which accounts for the monopole, calibration, and bandpass mismatches. To increase the signal-to-noise ratio of the Planck polarization measurements over SGC34, we smoothed the Planck polarization maps to 1° resolution using a Gaussian approximation to the Planck beam and reprojected to a HEALPix grid with Nside=128(30′pixels). We did not attempt to correct for the CMB polarization anisotropies at 1° resolution because they are negligibly small compared to the dust polarization at 353GHz.
The dust intensity at 353GHz, D353, is calculated from the latest publicly available Planck thermal dust emission model (Planck Collaboration Int. XLVIII 2016), which is a modified blackbody (MBB) fit to maps at ν ≥ 353GHz from which the cosmic infrared background anisotropies (CIBA) have been removed using the generalized linear internal combination (GNILC) method and zero-level offsets (e.g. the CIB monopole) have been removed by correlation with H I maps at high Galactic latitude. By construction, this dust intensity map is corrected for zodiacal light emission, CMB anisotropies, and resolved point sources as well as the CIBA and the CIB monopole. As a result of the GNILC method and the MBB fitting, the noise in the D353 map is lower than in the StokesI frequency map at 353GHz. We also smoothed the D353 map to the common resolution of 1°, taking into account the effective beam resolution of the map.
2.2. GASS Hi data
We use the GASS H I survey8 (McClure-Griffiths et al. 2009; Kalberla et al. 2010; Kalberla & Haud 2015) which mapped the southern sky (declination δ< 1°) with the Parkes telescope at an angular resolution of FWHM 14.′4. The rms uncertainties of the brightness temperatures per channel are at a level of 57mK at δv = 1kms-1. The GASS survey is the most sensitive and highest angular resolution survey of H I emission over the southern sky. The third data release version has improved performance by the removal of residual instrumental problems along with stray radiation and radio-frequency interference, which can be major sources of error in H I column density maps (Kalberla & Haud 2015). The GASS HI data are projected on a HEALPix grid with Nside=1024 (3.′75pixels).
For this optically thin gas, the brightness temperature spectra Tb of the GASS H I data are decomposed into multiple Gaussian components (Haud & Kalberla 2007; Haud 2013) as ![\begin{equation} T_{\rm b}= \sum_i T_0^i ~ \exp\left[-\frac{1}{2} \left(\frac{v_{\rm LSR}-v_{\rm c}^i}{\sigma^i} \right)^2 \right] , \end{equation}](/articles/aa/full_html/2017/05/aa29829-16/aa29829-16-eq36.png) (1)where the sum is over all Gaussian components for a LOS, vLSR is the velocity of the gas relative to the local standard of rest (LSR), and
(1)where the sum is over all Gaussian components for a LOS, vLSR is the velocity of the gas relative to the local standard of rest (LSR), and 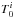 ,
, 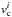 , and σi are the peak brightness temperature (inK), central velocity, and 1σ velocity dispersion of the ith Gaussian component, respectively. Although the Gaussian decomposition does not provide a unique solution, it is correct empirically. Haud (2013) used the GASS survey at Nside=1024 and decomposed the observed 6655155 HI profiles into 60349584Gaussians. In this study, we use an updated (but unpublished) Gaussian decomposition of the latest version of the GASS HI survey (third data release). The intermediate and high velocity gas over the southern Galactic cap has negligible dust emission (see discussion in Planck Collaboration Int. XVII 2014) and in any case lines of sight with uncorrelated dust and H I emissions are removed in our masking process (Sect.2.3).
, and σi are the peak brightness temperature (inK), central velocity, and 1σ velocity dispersion of the ith Gaussian component, respectively. Although the Gaussian decomposition does not provide a unique solution, it is correct empirically. Haud (2013) used the GASS survey at Nside=1024 and decomposed the observed 6655155 HI profiles into 60349584Gaussians. In this study, we use an updated (but unpublished) Gaussian decomposition of the latest version of the GASS HI survey (third data release). The intermediate and high velocity gas over the southern Galactic cap has negligible dust emission (see discussion in Planck Collaboration Int. XVII 2014) and in any case lines of sight with uncorrelated dust and H I emissions are removed in our masking process (Sect.2.3).
Broadly speaking, the Gaussian H I components represent the three conventional phases of the ISM. In order of increasing velocity dispersion these are: (1) a cold dense phase, the CNM, with a temperature in the range ~40−200K; (2) a thermally unstable neutral medium (UNM), with a temperature in the range ~200−5000K; and (3) a warm diffuse phase, the warm neutral medium (WNM), with a temperature in the range ~5000−8000K. Based on sensitive high-resolution Arecibo observations, Heiles & Troland (2003) found that a significant fraction of the H I emission is in the UNM phase at high Galactic latitude. Numerical simulations of the ISM suggest that the magnetic field and dynamical processes like turbulence could drive H I from the stable WNM and CNM phases into the UNM phase (Audit & Hennebelle 2005; Hennebelle & Iffrig 2014; Saury et al. 2014).
The total H I column density along the LOS, NHi, in units of 1018 cm-2, is obtained by integrating the brightness temperature over velocity. We can separate the total NHi into the three different phases of the ISM based on the velocity dispersion of the fitted Gaussian. Thus ![\begin{eqnarray} \NHI & = & 1.82\times \int T_{\rm b} ~ {\rm d}v_{\rm LSR} \nonumber \\ &=& 1.82 \times \int \sum_i T_0^i ~ \exp\left[-\frac{1}{2} \left(\frac{v_{\rm LSR}-v_{\rm c}^i}{\sigma^i} \right)^2 \right] {\rm d}v_{\rm LSR} \nonumber \\ & =& 1.82 \times \sqrt{2\pi} \sum \left ( T_0^i ~ \sigma^i ~ w_{\rm c} + T_0^i ~ \sigma^i ~ w_{\rm u} + T_0^i ~ \sigma^i ~ w_{\rm w} \right) \nonumber \\ & \equiv& \NHI^{\rm c} + \NHI^{\rm u} + \NHI^{\rm w}, \label{eq:3.1.1} \end{eqnarray}](/articles/aa/full_html/2017/05/aa29829-16/aa29829-16-eq48.png) (2)where wc, wu, and ww are the weighting factors to select the CNM, UNM, and WNM components, respectively, and
(2)where wc, wu, and ww are the weighting factors to select the CNM, UNM, and WNM components, respectively, and 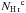 ,
, 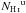 , and
, and 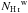 are the CNM, UNM, and WNM column densities, respectively. The weighting factors are defined as
are the CNM, UNM, and WNM column densities, respectively. The weighting factors are defined as ![\begin{eqnarray} &&w_{\rm c}=\left\{\begin{array}{ll} 1 & \sigma < \sigma_{\rm c} \\ \frac{1}{2}\left[1 + \cos\left( \frac{\pi}{g} \frac{\sigma -\sigma_{\rm c}}{\sigma_{\rm c}}\right)\right] & \sigma_{\rm c} \le \sigma \le \sigma_{\rm c} (1+g)\\ 0 & \sigma > \sigma_{\rm c} (1+g) \end{array}\right. \nonumber \\ &&w_{\rm w}=\left\{ \begin{array}{ll} 0 & \sigma < \sigma_{\rm u} \\ \frac{1}{2}\left[1 - \cos\left( \frac{\pi}{g} \frac{\sigma -\sigma_{\rm u}}{ \sigma_{\rm u}}\right)\right] & \sigma_{\rm u} \le \sigma < \sigma_{\rm u} (1+g)\\ 1 & \sigma \ge \sigma_{\rm u} (1+g) \\ \end{array}\right. \\ &&w_{\rm u} = 1 - w_{\rm c} - w_{\rm w} . \nonumber \end{eqnarray}](/articles/aa/full_html/2017/05/aa29829-16/aa29829-16-eq55.png) (3)We use overlapping weighting factors to avoid abrupt changes in the assignment of the emission from a given H I phase to another, adopting g = 0.2. There is a partial correlation between two neighbouring H I components. To select local velocity gas, we included only Gaussian components with
(3)We use overlapping weighting factors to avoid abrupt changes in the assignment of the emission from a given H I phase to another, adopting g = 0.2. There is a partial correlation between two neighbouring H I components. To select local velocity gas, we included only Gaussian components with 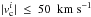 .
.
For our analysis we also smoothed these NHi maps to the common resolution of 1°, taking into account the effective beam resolution of the map. Figure1 shows the separation of the total NHi into the three Gaussian-based H I phases, CNM, UNM, and WNM. The weights were calculated with σc = 7.5 km s-1 and σu = 10 km s-1 as adopted in Sect.5.2. The total NHi map obtained by summing these component phases is very close to the Low velocity cloud (LVC) map in Fig.1 of Planck Collaboration Int. XVII (2014) obtained by integrating over the velocity range defined by Galactic rotation, with dispersion only 0.012 × 1020cm-2 in the difference or 0.8% in the fractional difference over the selected region SGC34 defined below.
 |
Fig. 1 NHi maps of the three Gaussian-based HI phases: CNM (top left), UNM (top right), and WNM (bottom left) over the portion of the southern Galactic cap (b ≤ −30°) covered by the GASS HI survey, at 1° resolution. Coloured region corresponds to the selected region SGC34 (bottom right). Orthographic projection in Galactic coordinates: latitudes and longitudes marked by lines and circles respectively. |
To build our CNM map we use an upper limit to the velocity dispersion (σc = 7.5 km s-1) larger than the conventional line width of cold H I gas (Wolfire et al. 2003; Heiles & Troland 2005; Kalberla et al. 2016). The line width can be characterised by a Doppler temperature TD. Because the line width includes a contribution from turbulence, TD is an upper limit to the gas kinetic temperature. In Kalberla et al. (2016), the median Doppler temperature of CNM gas is about TD = 220K, corresponding to a velocity dispersion of about σc = 1.3kms-1, while the largest value of TD = 1100K corresponds to σc = 3.0kms-1. The value of σc = 7.5kms-1 in our model follows from the model fit to the Planck polarization data (the observed E−B asymmetry and the 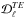 /
/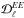 ratio over SGC34, see Sect.5.2). Thus our CNM component (
ratio over SGC34, see Sect.5.2). Thus our CNM component (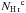 ) includes some UNM gas. To investigate the impact of this on our modelling, we divided our CNM component map into two parts corresponding to components with velocity dispersions above and below σc = 3.0 km s-1. We then repeated our data fitting with these two separate maps replacing our single CNM component map and found no significant difference in the model results.
) includes some UNM gas. To investigate the impact of this on our modelling, we divided our CNM component map into two parts corresponding to components with velocity dispersions above and below σc = 3.0 km s-1. We then repeated our data fitting with these two separate maps replacing our single CNM component map and found no significant difference in the model results.
2.3. Selection of the region SGC34
For our analysis we select a low dust column density region of the sky within the southern Galactic cap. As a first cut, we retain only the sky pixels that have NHi below a threshold value, NH i ≤ 2.7 × 1020 cm-2. Molecular gas is known from UV observations to be negligible at this threshold NHi value (Gillmon et al. 2006). We adopt a second mask, from Planck Collaboration Int. XVII (2014), to avoid sky pixels that fall off the main trend of gas-dust correlation between the GASS H I column density and Planck HFI intensity maps, in particular applying a threshold of 0.21MJysr-1 (3σ cut, see Fig.4 of Planck Collaboration Int. XVII 2014) on the absolute value of the residual emission at 857GHz after subtraction of the dust emission associated with HI gas. We smooth the second mask to Gaussian 1° FWHM resolution and downgrade to Nside=128 HEALPix resolution. Within this sky area, we also mask out a 10° radius patch centred around 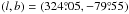 to avoid H I emission from the Magellanic stream, whose mean radial velocity for this specific sky patch is within the Galactic range of velocities (Nidever et al. 2010).
to avoid H I emission from the Magellanic stream, whose mean radial velocity for this specific sky patch is within the Galactic range of velocities (Nidever et al. 2010).
After masking, we are left with a 3500 deg2 region comprising 34% of the southern Galactic cap, referred to hereafter as SGC34. This is presented in Fig.1. The mean NHi over SGC34 is ⟨ NHi ⟩ = 1.58 × 1020cm-2. For the adopted values of σc and σu, the mean column densities of the three ISM phases (Fig.1) are 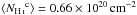 ,
, 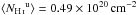 , and
, and 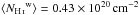 . SGC34 has a mean dust intensity of ⟨ D353 ⟩ = 54 kJysr-1. Correlating the total NHi map with the D353 map, we find an emissivity (slope) 32 kJysr-1(1020 cm-2)-1 at 353GHz (Sect.5.2) and an offset of just 3kJysr-1, which we use below as a 1σ uncertainty on the zero-level of the Galactic dust emission.
. SGC34 has a mean dust intensity of ⟨ D353 ⟩ = 54 kJysr-1. Correlating the total NHi map with the D353 map, we find an emissivity (slope) 32 kJysr-1(1020 cm-2)-1 at 353GHz (Sect.5.2) and an offset of just 3kJysr-1, which we use below as a 1σ uncertainty on the zero-level of the Galactic dust emission.
For computations of the angular power spectrum, we apodized the selection mask by convolving it with a 2° FWHM Gaussian. The effective sky coverage of SGC34 as defined by the mean sky coverage of the apodized mask is 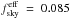 (8.5%), meaning that the smoothing extends the sky region slightly but conserves the effective sky area.
(8.5%), meaning that the smoothing extends the sky region slightly but conserves the effective sky area.
2.4. Power spectrum estimator
We use the publicly available Xpol code (Tristram et al. 2005) to compute the binned angular power spectra over a given mask. A top-hat binning in intervals of 20 ℓ over the range 40 <ℓ< 160 is applied throughout this analysis. The upper cutoff ℓmax = 160 is set by 1° smoothed maps used throughout this paper. The lower cutoff ℓmin = 40 is chosen to avoid low ℓ systematic effects present in the publicly available Planck polarization data (Planck Collaboration Int. XLVI 2016). The Xpol code corrects for the incomplete sky coverage, leakage from E- to B-mode polarization, beam smoothing, and pixel window function. Other codes such as PolSpice (Chon et al. 2004) and Xpure (Grain et al. 2009) also compute angular power spectra from incomplete sky coverage. We prefer Xpol over other codes because it directly computes the analytical error bars of the power spectrum without involving any Monte-Carlo simulations. The final results of this paper do not depend on the Xpol code, as the same mean power spectra are returned by other power spectrum estimators.
3. Planck dust polarization observations over the selected region SGC34
In this section we derive the statistical properties of the Planck dust polarization over SGC34. These statistical properties include normalized histograms from pixel space data, specifically of p2 and of ψ with respect to the local polarization angle of the large-scale GMF, and the polarized dust power spectra in the harmonic domain.
Dust polarization fraction p statistics at 353GHz and the best-fit mean direction of the large-scale GMF over SGC34 using multiple subsets of the Planck data.
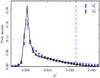 |
Fig. 2 Normalized histograms of p2 over SGC34 at 353GHz. Planck data, |
3.1. Polarization fraction
The naive estimator of p, defined as 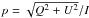 , is a biased quantity. The bias in p becomes dominant in the low signal-to-noise regime (Simmons & Stewart 1985). Montier et al. (2015) review the different algorithms to debias the p estimate. To avoid the debiasing problem, we choose to work with the unbiased quantity
, is a biased quantity. The bias in p becomes dominant in the low signal-to-noise regime (Simmons & Stewart 1985). Montier et al. (2015) review the different algorithms to debias the p estimate. To avoid the debiasing problem, we choose to work with the unbiased quantity 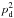 derived from a combination of independent subsets of the Planck data at 353GHz (see Eq.(12) of Planck Collaboration Int. XLIV 2016):
derived from a combination of independent subsets of the Planck data at 353GHz (see Eq.(12) of Planck Collaboration Int. XLIV 2016): 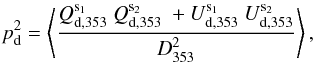 (4)where the subscript “d” refers to the observed polarized dust emission from the Planck 353GHz data (as distinct from “m” for the model below).
(4)where the subscript “d” refers to the observed polarized dust emission from the Planck 353GHz data (as distinct from “m” for the model below).
Normalized histograms of 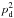 are computed over SGC34 from the cross-products of the three subsets of the Planck data where (s1,s2)={(HM1, HM2), (Y1,Y2), (DS1, DS2)}. Figure2 presents the mean of these three normalized histograms (blue inverted-triangles). The two main sources of uncertainty that bias the normalized histogram of
are computed over SGC34 from the cross-products of the three subsets of the Planck data where (s1,s2)={(HM1, HM2), (Y1,Y2), (DS1, DS2)}. Figure2 presents the mean of these three normalized histograms (blue inverted-triangles). The two main sources of uncertainty that bias the normalized histogram of 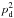 are data systematics and the uncertainty of the zero-level of the Galactic dust emission. The former is computed per histogram bin using the standard deviation of
are data systematics and the uncertainty of the zero-level of the Galactic dust emission. The former is computed per histogram bin using the standard deviation of 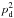 from the three subsets of the Planck data. The latter is propagated by changing the dust intensity D353 by ±3kJysr-1. The total 1σ error bar per histogram bin is the quadrature sum of these two uncertainties.
from the three subsets of the Planck data. The latter is propagated by changing the dust intensity D353 by ±3kJysr-1. The total 1σ error bar per histogram bin is the quadrature sum of these two uncertainties.
The mean, median, and maximum values of the dust polarization fraction for the three subsets of the Planck data are presented in Table1. The maximum value of pd at 1° resolution is consistent with the ones reported in Planck Collaboration Int.XLIV (2016) over the high latitude southern Galactic cap and the Planck Collaboration Int. XIX (2015) value at low and intermediate Galactic latitudes. We define a sky fraction f(pd> 25%) where the observed dust polarization fraction is larger than a given value of 25% or 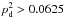 . In SGC34 this fraction is about 1%. The small scatter between the results from the three different subsets shows that the Planck measurements are robust against any systematic effects.
. In SGC34 this fraction is about 1%. The small scatter between the results from the three different subsets shows that the Planck measurements are robust against any systematic effects.
The negative values of 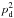 computed from Eq.(4) arise from instrumental noise present in the three subsets of the Planck data. The width of the
computed from Eq.(4) arise from instrumental noise present in the three subsets of the Planck data. The width of the 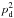 normalized histogram is narrower than the width reported by Planck Collaboration Int. XLIV (2016) over the high latitude southern Galactic cap. We were able to reproduce the broader distribution of
normalized histogram is narrower than the width reported by Planck Collaboration Int. XLIV (2016) over the high latitude southern Galactic cap. We were able to reproduce the broader distribution of 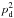 by adopting the same analysis region as in Planck Collaboration Int. XLIV (2016), showing the sensitivity to the choice of sky region.
by adopting the same analysis region as in Planck Collaboration Int. XLIV (2016), showing the sensitivity to the choice of sky region.
3.2. Polarization angle
We use multiple subsets of the Planck polarization data at 353GHz to compute the normalized Stokesparameters 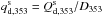 and
and  , where s = {DS1, DS2, HM1, HM2, Y1, Y2}. Using these data over SGC34, we fit the mean direction of the large-scale GMF, as defined by two coordinates l0 and b0, using model A of Planck Collaboration Int.XLIV (2016). The best-fit values of l0 and b0 for each of the six independent subsets of the Planck data are quoted in Table1. The mean values of l0 and b0 and their dispersions from the independent subsets are
, where s = {DS1, DS2, HM1, HM2, Y1, Y2}. Using these data over SGC34, we fit the mean direction of the large-scale GMF, as defined by two coordinates l0 and b0, using model A of Planck Collaboration Int.XLIV (2016). The best-fit values of l0 and b0 for each of the six independent subsets of the Planck data are quoted in Table1. The mean values of l0 and b0 and their dispersions from the independent subsets are 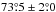 and
and 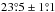 , respectively. Our error bars are smaller than those (5°) reported by Planck Collaboration Int. XLIV (2016) because the latter include the difference between fit values obtained with and without applying the bandpass mismatch (BPM) correction described in Sect. A.3 of Planck Collaboration VIII (2016). The mean values of l0 and b0 reported by Planck Collaboration Int. XLIV (2016) were derived using maps with no correction applied. The difference of
, respectively. Our error bars are smaller than those (5°) reported by Planck Collaboration Int. XLIV (2016) because the latter include the difference between fit values obtained with and without applying the bandpass mismatch (BPM) correction described in Sect. A.3 of Planck Collaboration VIII (2016). The mean values of l0 and b0 reported by Planck Collaboration Int. XLIV (2016) were derived using maps with no correction applied. The difference of 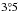 relative to our mean value of l0 arises primarily from the BPM correction used in our analysis.
relative to our mean value of l0 arises primarily from the BPM correction used in our analysis.
 |
Fig. 3 Similar to Fig.2, but for normalized histograms of ψR, the polarization angle relative to the local polarization angle of the large-scale GMF. The vertical dashed line corresponds to a model in which the turbulence is absent (Bturb = 0 so that ψR = 0°). |
The best-fit values of l0 and b0 are used to derive a map of a mean-field polarization angle  (see Planck Collaboration Int. XLIV 2016, for the Q and U patterns associated with the mean field). We then rotate each sky pixel with respect to the new reference angle
(see Planck Collaboration Int. XLIV 2016, for the Q and U patterns associated with the mean field). We then rotate each sky pixel with respect to the new reference angle  , using the relation
, using the relation ![\begin{eqnarray} \left[\! \!\begin{array}{c} Q_{\rm d, 353}^{\rm R} (\hat{\vec{n}}) \\[1mm] U_{\rm d, 353}^{\rm R} (\hat{\vec{n}}) \end{array}\! \!\right]& =&\left(\! \!\begin{array}{ccc} \cos{2 \psi_0} (\hat{\vec{n}}) && - \sin{2 \psi_0} (\hat{\vec{n}}) \\[1mm] \sin{2 \psi_0} (\hat{\vec{n}}) && \cos{2 \psi_0} (\hat{\vec{n}}) \end{array}\! \!\right) \nonumber \\ &&\quad\times\left[\! \!\begin{array}{c} Q_{\rm d, 353}^{\rm s}(\hat{\vec{n}}) \\[1mm] U_{\rm d, 353}^{\rm s} (\hat{\vec{n}}) \end{array}\! \!\right] , \end{eqnarray}](/articles/aa/full_html/2017/05/aa29829-16/aa29829-16-eq122.png) (5)where
(5)where  and
and 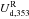 are the new rotated Stokesparameters. The “butterfly patterns” caused by the large-scale GMF towards the southern Galactic cap (Planck Collaboration Int. XLIV 2016) are now removed from the dust polarization maps. Non-zero values of the polarization angle,
are the new rotated Stokesparameters. The “butterfly patterns” caused by the large-scale GMF towards the southern Galactic cap (Planck Collaboration Int. XLIV 2016) are now removed from the dust polarization maps. Non-zero values of the polarization angle, 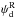 , derived from the
, derived from the  and
and 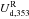 maps via
maps via 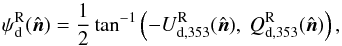 (6)result from the dispersion of BPOS around the mean direction of the large-scale GMF. The minus sign in
(6)result from the dispersion of BPOS around the mean direction of the large-scale GMF. The minus sign in 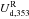 is necessary to produce angles in the IAU convention from HEALPix format Stokesmaps in the “COSMO” convention as used for the Planck data.
is necessary to produce angles in the IAU convention from HEALPix format Stokesmaps in the “COSMO” convention as used for the Planck data.
The mean normalized histogram of 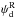 is computed from the multiple subsets of the Planck data and is presented in Fig.3 (blue inverted-triangles). The 1σ error bars on
is computed from the multiple subsets of the Planck data and is presented in Fig.3 (blue inverted-triangles). The 1σ error bars on 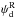 are derived from the standard deviation of the six independent measurements of the Planck data, as listed in Table1. We fit a Gaussian to the normalized histogram of
are derived from the standard deviation of the six independent measurements of the Planck data, as listed in Table1. We fit a Gaussian to the normalized histogram of 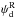 and find a 1σ dispersion of
and find a 1σ dispersion of 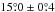 over SGC34. Our 1σ dispersion value of
over SGC34. Our 1σ dispersion value of 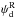 is slightly higher than the one found over the high latitude southern Galactic cap (Planck Collaboration Int. XLIV 2016). This result is not unexpected because SGC34 extends up to b ≤ −30° and adopting a mean direction of the large-scale GMF is only an approximation.
is slightly higher than the one found over the high latitude southern Galactic cap (Planck Collaboration Int. XLIV 2016). This result is not unexpected because SGC34 extends up to b ≤ −30° and adopting a mean direction of the large-scale GMF is only an approximation.
 |
Fig. 4 Left column: Planck 353GHz |
Fitted 353GHz dust power spectra of the Planck data and of the dust model over SGC34, for which the mean dust intensity ⟨ D353 ⟩ is 54 ± 3kJysr-1.
3.3. Polarized dust power spectra
We extend the analysis by Planck Collaboration Int. XXX (2016) of the region LR24 (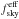 =0.24 or 24% of the total sky) to the smaller lower column density selected area SGC34 within it (
=0.24 or 24% of the total sky) to the smaller lower column density selected area SGC34 within it (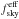 =0.085). We compute the polarized dust power spectra
=0.085). We compute the polarized dust power spectra 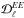 ,
, 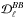 , and
, and 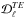 by cross-correlating the subsets of the Planck data at 353GHz in the multipole range 40 <ℓ< 160 over SGC34. We use the same D353 map for all subsets of the Planck data. The binning of the measured power spectra in six multipole bins matches that used in Planck Collaboration Int. XXX (2016). We take the mean power spectra computed from the cross-spectra of DetSets (DS1×DS2), HalfMissions (HM1×HM2), and Years (Y1 × Y2). The mean dust
by cross-correlating the subsets of the Planck data at 353GHz in the multipole range 40 <ℓ< 160 over SGC34. We use the same D353 map for all subsets of the Planck data. The binning of the measured power spectra in six multipole bins matches that used in Planck Collaboration Int. XXX (2016). We take the mean power spectra computed from the cross-spectra of DetSets (DS1×DS2), HalfMissions (HM1×HM2), and Years (Y1 × Y2). The mean dust 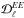 is corrected for the CMB contribution using the Planck best-fit ΛCDM model at the power spectrum level, while the mean
is corrected for the CMB contribution using the Planck best-fit ΛCDM model at the power spectrum level, while the mean 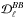 and
and 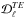 are kept unaltered. Figure4 shows that the contribution of the CMB BB spectra (for r = 0.15 with lensing contribution) is negligibly small as compared to the mean dust spectra
are kept unaltered. Figure4 shows that the contribution of the CMB BB spectra (for r = 0.15 with lensing contribution) is negligibly small as compared to the mean dust spectra 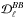 over SGC34. The mean
over SGC34. The mean 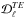 is unbiased because we use D353 as a dust-only StokesI map. However, the unsubtracted CMB E-modes bias the 1σ error of the dust
is unbiased because we use D353 as a dust-only StokesI map. However, the unsubtracted CMB E-modes bias the 1σ error of the dust 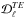 power spectrum by a factor
power spectrum by a factor ![\hbox{$\sqrt{[\dltt (\text{dust}) \times \dlee (\text{CMB})]/\nu_{\ell}}$}](/articles/aa/full_html/2017/05/aa29829-16/aa29829-16-eq165.png) , where νℓ is associated with the effective number of degrees of freedom (Tristram et al. 2005).
, where νℓ is associated with the effective number of degrees of freedom (Tristram et al. 2005).
The mean dust power spectra 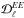 ,
, 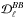 , and
, and 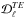 of the Planck 353GHz data are presented in the left column of Fig.4. The 1σ statistical uncertainties from noise (solid error bar in the left column of Fig.4) are computed from the analytical approximation implemented in Xpol. The 1σ systematic uncertainties are computed using the standard deviation of the dust polarization power spectra from the three subsets of the Planck data (as listed in Table1). The total 1σ error bar per ℓ bin (dashed error bar in the left column of Fig.4) is the quadrature sum of the two. The measured Planck 353GHz polarized dust power spectra
of the Planck 353GHz data are presented in the left column of Fig.4. The 1σ statistical uncertainties from noise (solid error bar in the left column of Fig.4) are computed from the analytical approximation implemented in Xpol. The 1σ systematic uncertainties are computed using the standard deviation of the dust polarization power spectra from the three subsets of the Planck data (as listed in Table1). The total 1σ error bar per ℓ bin (dashed error bar in the left column of Fig.4) is the quadrature sum of the two. The measured Planck 353GHz polarized dust power spectra 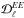 ,
, 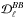 , and
, and 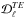 are well described by power laws in multipole space, consistent with the one measured at intermediate and high Galactic latitudes (Planck Collaboration Int. XXX 2016). Similar to the analysis in Planck Collaboration Int. XXX (2016), we fit the power spectra with the power-law model,
are well described by power laws in multipole space, consistent with the one measured at intermediate and high Galactic latitudes (Planck Collaboration Int. XXX 2016). Similar to the analysis in Planck Collaboration Int. XXX (2016), we fit the power spectra with the power-law model, 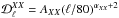 , where AXX is the best-fit amplitude at ℓ = 80, αXX is the best-fit slope, and XX = { EE,BB,TE }. We restrict the fit to six band-powers in the range 40 <ℓ< 160 so that we can compare the Planck data directly with the low-resolution dust model derived using the GASS H I data. The exponents αXX of the unconstrained fits are quoted in the top row of Table2. Next, we perform the fit with a fixed exponent −2.3 for the appropriate αXX. The resulting power laws are shown in the left column of Fig.4 and the values of χ2 (with number of degrees of freedom, Nd.o.f. = 6) and the best-fit values of AXX are presented in Table2.
, where AXX is the best-fit amplitude at ℓ = 80, αXX is the best-fit slope, and XX = { EE,BB,TE }. We restrict the fit to six band-powers in the range 40 <ℓ< 160 so that we can compare the Planck data directly with the low-resolution dust model derived using the GASS H I data. The exponents αXX of the unconstrained fits are quoted in the top row of Table2. Next, we perform the fit with a fixed exponent −2.3 for the appropriate αXX. The resulting power laws are shown in the left column of Fig.4 and the values of χ2 (with number of degrees of freedom, Nd.o.f. = 6) and the best-fit values of AXX are presented in Table2.
The ratio of the dust B- and E-mode power amplitudes, roughly equal to a half (Table2), is maintained from LR24 to SGC34. The measured amplitude ABB = 8.85 μKCMB2 at ℓ = 80 is about ~35% lower than the value expected from the empirical power-law ABB ∝ ⟨ D353 ⟩ 1.9 (Planck Collaboration Int. XXX 2016) applied to SGC34. For future work, it will be important to understand the amplitude and variations of the dust B-mode signal in these low column density regions.
We find a significant positive TE correlation, 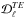 , over SGC34; the amplitude ATE normalized at ℓ = 80 hasmore than 4σ significance when the multipoles between 40 and 160 are combined in this way. Similarly, a positive TE correlation was reported over LR24 (see Fig.B.1 of Planck Collaboration Int. XXX 2016). The non-zero positive TE correlation is a direct consequence of the correlation between the dust intensity structures and the orientation of the magnetic field. Planck Collaboration Int. XXXVIII (2016) report that oriented stacking of the dust E-map over T peaks of interstellar filaments identified in the dust intensity map picks up a positive TE correlation (see their Fig.10).
, over SGC34; the amplitude ATE normalized at ℓ = 80 hasmore than 4σ significance when the multipoles between 40 and 160 are combined in this way. Similarly, a positive TE correlation was reported over LR24 (see Fig.B.1 of Planck Collaboration Int. XXX 2016). The non-zero positive TE correlation is a direct consequence of the correlation between the dust intensity structures and the orientation of the magnetic field. Planck Collaboration Int. XXXVIII (2016) report that oriented stacking of the dust E-map over T peaks of interstellar filaments identified in the dust intensity map picks up a positive TE correlation (see their Fig.10).
For comparison in Fig.4 we show the Planck 2015 best-fit ΛCDM CMB 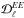 ,
, 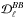 (primordial tensor-to-scalar ratio r = 0.15 plus lensing contribution), and
(primordial tensor-to-scalar ratio r = 0.15 plus lensing contribution), and 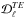 expectation curves (Planck Collaboration XIII 2016). Then assuming that the dust spectral energy distribution (SED) follows a MBB spectrum with a mean dust spectral index 1.59 ± 0.02 and a mean dust temperature of 19.6K (Planck Collaboration Int. XXII 2015), we extrapolate the best-fit dust power spectra from 353GHz to 150GHz (scaling factor s150/353 = 0.04082) in order to show the level of the dust polarization signal (red dashed lines in Fig.4) relative to the CMB signal over SGC34.
expectation curves (Planck Collaboration XIII 2016). Then assuming that the dust spectral energy distribution (SED) follows a MBB spectrum with a mean dust spectral index 1.59 ± 0.02 and a mean dust temperature of 19.6K (Planck Collaboration Int. XXII 2015), we extrapolate the best-fit dust power spectra from 353GHz to 150GHz (scaling factor s150/353 = 0.04082) in order to show the level of the dust polarization signal (red dashed lines in Fig.4) relative to the CMB signal over SGC34.
4. Model framework
In this section we extend the formalism developed in Planck Collaboration Int. XLIV (2016) to simulate the dust polarization over SGC34 using a phenomenological description of the magnetic field and the GASS H I emission data. We introduce two main ingredients in the dust model: (1) fluctuations in the GMF orientation along the LOS and (2) alignment of the CNM structures with BPOS. Based on the filament study by Planck Collaboration Int. XXXVIII (2016), we anticipate that alignment of the CNM structures with BPOS will account for the positive dust TE correlation and the 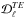 /
/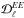 ratio over SGC34.
ratio over SGC34.
4.1. Formalism
We use the general framework introduced by Planck Collaboration Int.XX (2015) to model the dust Stokesparameters, I, Q, and U, for optically thin regions at a frequencyν: ![\begin{eqnarray} &&I_{\rm m, \nu} (\hat{\vec{n}}) = \int \left [1- p_0 \left ( \cos^2 \gamma^i(\hat{\vec{n}}) - \frac{2}{3} \right ) \right ] S_{\nu}^i (\hat{\vec{n}}) \ {\rm d}\tau_{\nu} \nonumber \\ &&Q_{\rm m, \nu} (\hat{\vec{n}}) = \int p_0 \cos^2 \gamma^i(\hat{\vec{n}}) \cos 2\psi^i(\hat{\vec{n}}) S_{\nu}^i (\hat{\vec{n}}) \ {\rm d}\tau_{\nu} \label{eq:4.1}\\ &&U_{\rm m, \nu} (\hat{\vec{n}}) = - \int p_0 \cos^2 \gamma^i(\hat{\vec{n}}) \sin 2\psi^i(\hat{\vec{n}}) S_{\nu}^i (\hat{\vec{n}}) \ {\rm d}\tau_{\nu} , \nonumber \end{eqnarray}](/articles/aa/full_html/2017/05/aa29829-16/aa29829-16-eq184.png) (7)where (see Appendix B of Planck Collaboration Int. XX 2015, for details)
(7)where (see Appendix B of Planck Collaboration Int. XX 2015, for details) 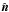 is the direction vector, Sν is the source function given by the relation Sν = ndBν(T)Cavg, τν is the optical depth, p0 = pdustR is the product of the “intrinsic dust polarization fraction” (pdust) and the Rayleigh reduction factor (R, related to the alignment of dust grains with respect to the GMF), ψ is the polarization angle measured from Galactic North, and γ is the angle between the local magnetic field and the POS. Again, like in Sect.3.2, the minus sign in Um,ν is necessary to work from the angle map ψ given in the IAU convention to produce HEALPix format Stokesmaps in the COSMO convention. We start with the same dust Stokesparameters equations as in the Vansyngel et al. (2017) parametric dust model.
is the direction vector, Sν is the source function given by the relation Sν = ndBν(T)Cavg, τν is the optical depth, p0 = pdustR is the product of the “intrinsic dust polarization fraction” (pdust) and the Rayleigh reduction factor (R, related to the alignment of dust grains with respect to the GMF), ψ is the polarization angle measured from Galactic North, and γ is the angle between the local magnetic field and the POS. Again, like in Sect.3.2, the minus sign in Um,ν is necessary to work from the angle map ψ given in the IAU convention to produce HEALPix format Stokesmaps in the COSMO convention. We start with the same dust Stokesparameters equations as in the Vansyngel et al. (2017) parametric dust model.
Following the approach in Planck Collaboration Int. XLIV (2016), we replace the integration along the LOS over SGC34 by the sum over a finite number of layers with different polarization properties. These layers are a phenomenological means of accounting for the effects of fluctuations in the GMF orientation along the LOS, the first main ingredient of the dust model. We interpret these layers along the LOS as three distinct phases of the ISM. The Gaussian decomposition of total NHi into the CNM, UNM, and WNM components based on their line-widths (or velocity dispersion) is described in detail in Sect.2.2.
We can replace the integral of the source function over each layer directly with the product of the column density maps of the three H I components and their mean dust emissivities. Within these astrophysical approximations, we can modify Eq.(7)to be ![\begin{eqnarray} I_{\rm m, \nu} (\hat{\vec{n}}) &=& ~\sum_{i=1}^{3} \left [1- p_0 \left ( \cos^2 \gamma^i(\hat{\vec{n}}) - \frac{2}{3} \right ) \right ] \langle \epsilon_{\nu}^i \rangle \NHIi (\hat{\vec{n}}) \nonumber \\ Q_{\rm m, \nu}(\hat{\vec{n}}) &=& ~ \sum_{i=1}^{3} p_0 \cos^2 \gamma^i(\hat{\vec{n}}) \cos 2\psi^i(\hat{\vec{n}}) \langle \epsilon_{\nu}^i \rangle \NHIi (\hat{\vec{n}}) \label{eq:4.2} \\ U_{\rm m, \nu}(\hat{\vec{n}}) &=& - \sum_{i=1}^{3} p_0 \cos^2 \gamma^i(\hat{\vec{n}}) \sin 2\psi^i(\hat{\vec{n}}) \langle \epsilon_{\nu}^i \rangle \NHIi (\hat{\vec{n}}),\nonumber \end{eqnarray}](/articles/aa/full_html/2017/05/aa29829-16/aa29829-16-eq194.png) (8)where
(8)where  is the mean dust emissivity for each of the three H Icomponents.
is the mean dust emissivity for each of the three H Icomponents.
In general, the emissivity is a function not only of frequency, but also of sky position 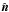 and different H I phases. However, in SGC34 the overall emissivity D353/NHi is quite uniform (see Sect.5.2) and from a simultaneous fit of the D353 map to all three component NHi maps we find little evidence, for our decomposition, that the emissivities of the individual components are different than the overall mean.
and different H I phases. However, in SGC34 the overall emissivity D353/NHi is quite uniform (see Sect.5.2) and from a simultaneous fit of the D353 map to all three component NHi maps we find little evidence, for our decomposition, that the emissivities of the individual components are different than the overall mean.
Similarly, the effective degree of alignment p0 = pdustR could be a function of frequency and different for different H I components. Equation(8)also tells us that the product p0 is degenerate with ⟨ ϵν ⟩ for the dust StokesQm,ν and Um,ν parameters. Such effects could make the source functions in the layers even more different from one another.
In this paper we explore how models based on simplifying assumptions, namely a constant p0 and a frequency dependent⟨ ϵν ⟩ common to the three H I components, might despite the reduced flexibility nevertheless provide a good description of the data.
This use of the GASS NHi data can be contrasted to the approach of Planck Collaboration Int. XLIV (2016) and Vansyngel et al. (2017), where the source functions are assumed to be the same in each layer. Furthermore, Planck Collaboration Int. XLIV (2016) choose to ignore the correction term involving p0 in the integrand for 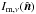 .
.
This phenomenological dust model based on the GASS H I data is not unique. It is based on several astrophysical assumptions as noted in this section. Within the same general framework, we could contemplate replacing the H I emission with three-dimensional (3D) extinction maps, though no reliable maps are currently available over the SGC34 region (Green et al. 2015). Furthermore, the HI emission traces the temperature or density structure of the diffuse ISM, whereas the dust extinction traces only the dust column density. Thus, using the HI emission to model the dust polarization is an interesting approach even if we had reliable 3D extinction maps toward the southern Galactic cap.
4.2. Structure of the Galactic magnetic field
The Galactic magnetic field, B, is expressed as a vector sum of a mean large-scale (ordered, Bord) and a turbulent (random, Bturb) component (Jaffe et al. 2010) 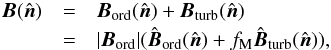 (9)where fM is the standard deviation of the relative amplitude of the turbulent component | Bturb | with respect to the mean large-scale | Bord |. The butterfly patterns seen in the orthographic projections of the Planck polarization maps, Qd,353 and Ud,353, centred at (l,b) = (0°,−90°) are well fitted by a mean direction of the large-scale GMF over the southern Galactic cap (Planck Collaboration Int. XLIV 2016). We assume that the mean direction of the large-scale GMF is still a good approximation to fit the butterfly patterns seen in the Planck StokesQd,353 and Ud,353 maps over SGC34 (Fig.1). The unit vector
(9)where fM is the standard deviation of the relative amplitude of the turbulent component | Bturb | with respect to the mean large-scale | Bord |. The butterfly patterns seen in the orthographic projections of the Planck polarization maps, Qd,353 and Ud,353, centred at (l,b) = (0°,−90°) are well fitted by a mean direction of the large-scale GMF over the southern Galactic cap (Planck Collaboration Int. XLIV 2016). We assume that the mean direction of the large-scale GMF is still a good approximation to fit the butterfly patterns seen in the Planck StokesQd,353 and Ud,353 maps over SGC34 (Fig.1). The unit vector 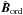 is defined as
is defined as 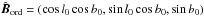 .
.
We model Bturb with a Gaussian realization on the sky with an underlying power spectrum, Cℓ ∝ ℓαM, for ℓ ≥ 2 (Planck Collaboration Int. XLIV 2016). The correlated patterns of Bturb over the sky are needed to account for the correlated patterns of dust p and ψ seen in Planck 353GHz data (Planck Collaboration Int. XIX 2015). Following Fauvet et al. (2012), we only consider isotropic turbulence in our analysis. We produce a spatial distribution of Bturb in the x, y, and z direction from the above power spectrum on the celestial sphere of HEALPix resolution Nside. We add Bturb to Bord with a relative strength fM as given in Eq.(9).
4.3. Alignment of the CNM structures with the magnetic field
We use the algebra given in Sect.4.1 of Planck Collaboration Int.XLIV (2016) to compute cos2γi for the three H I components. For the UNM and WNM components, we assume that there is no TE correlation and the angles ψu and ψw are computed directly from the total B again using the algebra by Planck Collaboration Int. XLIV (2016). For the CNM we follow a quite different approach to compute ψc.
We introduce a positive TE correlation for the CNM component through the polarization angle ψc. The alignment between the CNM structures and BPOS is introduced to test whether it fully accounts for the observed E-B power asymmetry or not. To do that, we assume that the masked 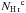 map is a pure E-mode map and define spin-2 maps QT and UT as
map is a pure E-mode map and define spin-2 maps QT and UT as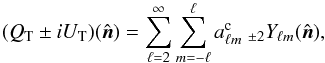 (10)where
(10)where 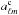 are the harmonic coefficients of the masked
are the harmonic coefficients of the masked 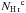 map. In the flat-sky limit,
map. In the flat-sky limit, 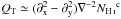 and
and 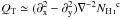 , where ∇-2 is the inverse Laplacian operator (Bowyer et al. 2011). We compute the angle ψc using the relation, ψc = (1/2)tan-1(−UT,QT) (see Planck Collaboration XVI 2016, for details). The polarization angle ψc is the same as the angle between the major axis defined by a local quadrature expansion of the
, where ∇-2 is the inverse Laplacian operator (Bowyer et al. 2011). We compute the angle ψc using the relation, ψc = (1/2)tan-1(−UT,QT) (see Planck Collaboration XVI 2016, for details). The polarization angle ψc is the same as the angle between the major axis defined by a local quadrature expansion of the 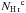 map and the horizontal axis. This idea of aligning perfectly the CNM structures with BPOS is motivated from the H I studies by Clark et al. (2015), Martin et al. (2015), and Kalberla et al. (2016), and Planck dust polarization studies by Planck Collaboration Int. XXXII (2016) and Planck Collaboration Int. XXXVIII (2016). This is the second main ingredient of the dust model.
map and the horizontal axis. This idea of aligning perfectly the CNM structures with BPOS is motivated from the H I studies by Clark et al. (2015), Martin et al. (2015), and Kalberla et al. (2016), and Planck dust polarization studies by Planck Collaboration Int. XXXII (2016) and Planck Collaboration Int. XXXVIII (2016). This is the second main ingredient of the dust model.
4.4. Model parameters
The dust model has the following parameters: ⟨ ϵν ⟩, the mean dust emissivity per H I component at frequency ν; p0, the normalization factor to match the observed dust polarization fraction over the southern Galactic cap; l0 and b0, describing the mean direction of Bord in the region of the southern Galactic cap; fM, the relative strength of Bturb with respect to Bord for the different components; αM, the spectral index of Bturb power spectrum for the different components; and σc and σu to separate the total NHi into the CNM, UNM, and WNM components (phases).
We treat the three H I components with different density structures and magnetic field orientations as three independent layers. Because we include alignment of the CNM structures with BPOS, we treat the CNM polarization layer separately from the WNM and UNM polarization layers. The value of 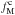 for the CNM component is different than the common
for the CNM component is different than the common 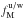 for the UNM and WNM components. For the same reason, the spectral index of the turbulent power spectrum
for the UNM and WNM components. For the same reason, the spectral index of the turbulent power spectrum 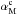 for the CNM component could be different than the common
for the CNM component could be different than the common 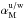 for the UNM and WNM components, but we take them to be the same, simplifying the model and reducing the parameter space in our analysis. We also use the same values of ⟨ ϵν ⟩ and p0 for each layer. This gives a total of nine parameters.
for the UNM and WNM components, but we take them to be the same, simplifying the model and reducing the parameter space in our analysis. We also use the same values of ⟨ ϵν ⟩ and p0 for each layer. This gives a total of nine parameters.
In this analysis, we do not optimize the nine parameters of the dust model explicitly. Instead, we determine five parameters based on various astrophysical constraints and optimize only⟨ ϵν ⟩, p0, 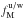 , and σc simultaneously (Sect.5.2). Our main goal is to test quantitatively whether the fluctuations in the GMF orientation along the LOS plus the preferential alignment of the CNM structures with BPOS can account simultaneously for both the observed dust polarization power spectra and the normalized histograms of p2 and ψR over SGC34.
, and σc simultaneously (Sect.5.2). Our main goal is to test quantitatively whether the fluctuations in the GMF orientation along the LOS plus the preferential alignment of the CNM structures with BPOS can account simultaneously for both the observed dust polarization power spectra and the normalized histograms of p2 and ψR over SGC34.
We review here the relationship between the nine dust model parameters and the various dust observables.
-
The emissivity ⟨ ϵν ⟩ simply converts the observed NHi (1020cm-2) to the Planck intensity units (in μKCMB) (Planck Collaboration Int. XVII 2014). This parameter is optimized in Sect.5.2, subject to a strong prior obtained by correlating the map D353 with the NHi map.
-
The parameter p0 is constrained by the observed distribution of
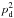 at 353GHz and the amplitude of the dust polarization power spectra
at 353GHz and the amplitude of the dust polarization power spectra 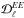 ,
, 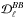 , and
, and 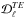 . It is optimized using the latter in Sect.5.2.
. It is optimized using the latter in Sect.5.2. -
The two model parameters l0 and b0 determine the orientation of the butterfly patterns seen in the orthographic projections of the Planck polarization maps, Qd,353 and Ud,353 (Planck Collaboration Int. XLIV 2016). They are found by fitting these data (Sect.3.2).
-
The parameter fM for each polarization layer is related to the dispersion of
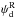 and
and 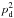 (the higher the strength of the turbulent field with respect to the ordered field, the higher the dispersion of
(the higher the strength of the turbulent field with respect to the ordered field, the higher the dispersion of 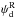 and
and 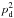 ) and to the amplitude of the dust polarization power spectra. Our prescription for the alignment of CNM structure and BPOS subject to statistical constraints from polarization data determines
) and to the amplitude of the dust polarization power spectra. Our prescription for the alignment of CNM structure and BPOS subject to statistical constraints from polarization data determines 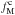 (Sect.5.1);
(Sect.5.1); 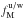 is optimized using the dust polarization band powers in Sect.5.2.
is optimized using the dust polarization band powers in Sect.5.2. -
The parameter
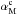 is constrained by the alignment of the CNM structures with BPOS (Sect.5.1).
is constrained by the alignment of the CNM structures with BPOS (Sect.5.1). -
The parameter σc controls the fraction of the H I in the CNM and hence sets the amount of E-B power asymmetry and the
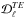 /
/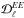 ratio through the alignment of the CNM structures with BPOS. It is optimized in Sect.5.2. Our dust model is insensitive to the precise value of the parameter σu, which is used to separate the UNM and WNM into distinct layers.
ratio through the alignment of the CNM structures with BPOS. It is optimized in Sect.5.2. Our dust model is insensitive to the precise value of the parameter σu, which is used to separate the UNM and WNM into distinct layers.
To break the degeneracy between different dust model parameters and obtain a consistent and robust model, we need to make use of dust polarization observables in pixel space as well as in harmonic space.
5. Dust sky simulations
We simulate the dust intensity and polarization maps at only a single Planck frequency 353GHz. It would be straightforward to extrapolate the dust model to other microwave frequencies using a MBB spectrum of the dust emission (Planck Collaboration Int.XVII 2014; Planck Collaboration Int.XXI 2015; Planck Collaboration Int. XXX 2016) or replacing the value of ⟨ ϵν ⟩ from Planck Collaboration Int. XVII (2014). However, such a simple-minded approach would not generate any decorrelation of the dust polarization pattern between different frequencies, as reported in Planck Collaboration Int. L (2017).
 |
Fig. 5 Mean power spectra of cos2γ (top panel) and cos2ψ (bottom panel) over SGC34 for a set of αM and fM parameters in the multipole range 40 <ℓ< 160. The 1σ error bars are computed from the standard deviations of the 100Monte-Carlo realizations of the dust model. The alignment of the CNM structures with BPOS (see Sect.5.1 for details) constrains the value of |
5.1. Constraining the turbulent GMF for the CNM component
As discussed in Sect.4.3, we adopted an alternative approach to compute the polarization angle ψc for the CNM component. At first sight, it might look physically inconsistent and therefore a main source of bias. However, we now show that the original and alternative approaches lead to statistically similar results and so can be compared in order to constrain the parameters of Bturb, that is 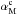 and
and 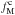 , for the CNM component.
, for the CNM component.
To do this we first adopt the original approach from Planck Collaboration Int. XLIV (2016; and used for the UNM and CNM components). We generate Gaussian realizations of Bturb for a set of (αM,fM) values. We assume a fixed mean direction of Bord as 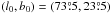 (Table1) and add to it Bturb to derive a total B. We use the algebra given in Sect.4.1 of Planck Collaboration Int. XLIV (2016) to compute the two quantities cos2γ and cos2ψ for different values of αM and fM. Because the polarization angles γ and ψ are circular quantities, we choose to work with quantities like cos2γ and cos2ψ as they appear in the StokesQ and U parameters (Eq.(8)). We then apply the Xpol routine to compute the angular power spectra of these two quantities for each sky realization over SGC34. The mean power spectra of cos2γ and cos2ψ are computed by averaging 100Monte-Carlo realizations and are presented in Fig.5. The power spectra of the two polarization angles are well described by power-laws in multipole space,
(Table1) and add to it Bturb to derive a total B. We use the algebra given in Sect.4.1 of Planck Collaboration Int. XLIV (2016) to compute the two quantities cos2γ and cos2ψ for different values of αM and fM. Because the polarization angles γ and ψ are circular quantities, we choose to work with quantities like cos2γ and cos2ψ as they appear in the StokesQ and U parameters (Eq.(8)). We then apply the Xpol routine to compute the angular power spectra of these two quantities for each sky realization over SGC34. The mean power spectra of cos2γ and cos2ψ are computed by averaging 100Monte-Carlo realizations and are presented in Fig.5. The power spectra of the two polarization angles are well described by power-laws in multipole space, 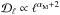 , where αM is the same as the spectral index of Bturb power spectrum. The amplitudes and slopes of these two quantities are related systematically to the values of αM and fM. The higher the fM value, the higher is the amplitude of the power spectra in Fig.5. The best-fit slope of the power spectrum over the multipole range 40 < ℓ < 160 is the same as the spectral index of the Bturb power spectrum for relevant fM values.
, where αM is the same as the spectral index of Bturb power spectrum. The amplitudes and slopes of these two quantities are related systematically to the values of αM and fM. The higher the fM value, the higher is the amplitude of the power spectra in Fig.5. The best-fit slope of the power spectrum over the multipole range 40 < ℓ < 160 is the same as the spectral index of the Bturb power spectrum for relevant fM values.
For each Monte Carlo realization we also calculated ψc for the CNM component by the alternative approach and from that computed the power spectra of cos2ψ for the CNM component over SGC34. By comparing these results to the spectra from the first Planck Collaboration Int. XLIV (2016) approach, as in Fig.5 (bottom panel), we can constrain the values of 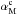 and
and 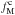 . The typical values of
. The typical values of 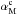 and
and 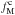 are −2.4 and 0.4, respectively. One needs a Monte-Carlo approach to put realistic error bars on the
are −2.4 and 0.4, respectively. One needs a Monte-Carlo approach to put realistic error bars on the 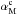 and
and 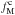 parameters, which is beyond the scope of this paper. However, we do note that the value of
parameters, which is beyond the scope of this paper. However, we do note that the value of 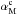 is close to the exponent of the angular power spectrum of the
is close to the exponent of the angular power spectrum of the 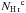 map computed over SGC34, reflecting the correlation between the structure of the intensity map and the orientation of the field.
map computed over SGC34, reflecting the correlation between the structure of the intensity map and the orientation of the field.
We stress that the values of 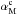 and
and 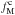 derived from Fig.5 are valid only over SGC34. If we increase the sky fraction to b ≤ −30° covered by the GASS H I survey, we get the same
derived from Fig.5 are valid only over SGC34. If we increase the sky fraction to b ≤ −30° covered by the GASS H I survey, we get the same 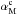 value, but a slightly higher
value, but a slightly higher 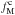 value (
value (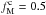 ). This suggests that the relative strength of Bturb with respect to Bord might vary across the sky.
). This suggests that the relative strength of Bturb with respect to Bord might vary across the sky.
5.2. Values of model parameters
Here we describe how the nine model parameters were found.
We found the mean direction of Bord to be 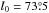 and
and 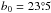 from a simple model fit of normalized Stokesparameters for polarization over SGC34 (Sect.3.2, Table1).
from a simple model fit of normalized Stokesparameters for polarization over SGC34 (Sect.3.2, Table1).
As described in Sect.5.1, using 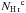 as a tracer of the dust polarization angle gives the constraints
as a tracer of the dust polarization angle gives the constraints 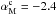 and
and 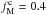 . The spectral index
. The spectral index 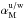 of Bturb for the UNM and WNM components is assumed to be same as the
of Bturb for the UNM and WNM components is assumed to be same as the 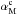 value of the CNM component, for simplicity.
value of the CNM component, for simplicity.
Only four model parameters, ⟨ ϵ353 ⟩, p0, 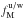 , and σc, are adjusted by evaluating the goodness of fit through a χ2-test, specifically
, and σc, are adjusted by evaluating the goodness of fit through a χ2-test, specifically ![\begin{equation} \chi_{XX}^2 = \sum_{\ell_{\rm min}}^{\ell_{\rm max}} \left[ \frac{\dlxx - \mlxx (\langle \epsilon_{353} \rangle, p_0, f_{\rm M}^{\rm u/w}, \sigma_{\rm c})}{\sigma_{\ell}^{XX}} \right]^2 \end{equation}](/articles/aa/full_html/2017/05/aa29829-16/aa29829-16-eq253.png) (11)and
(11)and ![\begin{equation} \chi^2 = \sum_i^{N_{\rm pix}} \left[ \Dmodel\ - s I_{\rm m, 353} (\langle \epsilon_{353} \rangle, p_0, f_{\rm M}^{\rm u/w}, \sigma_{\rm c}) - o \right]^2 , \end{equation}](/articles/aa/full_html/2017/05/aa29829-16/aa29829-16-eq254.png) (12)where XX = { EE,BB,TE },
(12)where XX = { EE,BB,TE }, 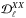 , and
, and 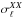 are the mean observed dust polarization band powers and standard deviation at 353GHz, respectively,
are the mean observed dust polarization band powers and standard deviation at 353GHz, respectively, 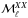 is the model dust polarization power spectrum over SGC34, Npix is the total number of pixels in SGC34, s and o are the slope and the offset of the “T-T” correlation between the D353 and Im,353 maps. We evaluated
is the model dust polarization power spectrum over SGC34, Npix is the total number of pixels in SGC34, s and o are the slope and the offset of the “T-T” correlation between the D353 and Im,353 maps. We evaluated 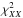 using the six band powers in the range 40 <ℓ < 160. For χ2 minimization, we put a flat prior on the mean dust emissivity, ⟨ ϵ353 ⟩ = (111 ± 22) μKCMB(1020 cm-2)-1 at 353GHz, as obtained by correlating NHi with D353 map over SGC34. Based on the observed distribution of the polarization fraction (Sect.3.1), we put a flat prior on p0 = (18 ± 4)%. To match the observed dust amplitude at 353GHz, the value of s should be close to 1 and is kept so by adjusting ⟨ ϵ353 ⟩ during the iterative solution of the two equations.
using the six band powers in the range 40 <ℓ < 160. For χ2 minimization, we put a flat prior on the mean dust emissivity, ⟨ ϵ353 ⟩ = (111 ± 22) μKCMB(1020 cm-2)-1 at 353GHz, as obtained by correlating NHi with D353 map over SGC34. Based on the observed distribution of the polarization fraction (Sect.3.1), we put a flat prior on p0 = (18 ± 4)%. To match the observed dust amplitude at 353GHz, the value of s should be close to 1 and is kept so by adjusting ⟨ ϵ353 ⟩ during the iterative solution of the two equations.
The typical mean values of ⟨ ϵ353 ⟩, p0, 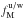 , and σc that we obtained are 121.8 μKCMB(1020 cm-2)-1, 18.5%, 0.1, and 7.5kms-1, respectively, with
, and σc that we obtained are 121.8 μKCMB(1020 cm-2)-1, 18.5%, 0.1, and 7.5kms-1, respectively, with 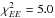 ,
, 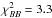 , and
, and 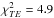 for six degrees of freedom (or band-powers). The precise optimization is not important and is beyond the scope of this paper.
for six degrees of freedom (or band-powers). The precise optimization is not important and is beyond the scope of this paper.
The model is not particularly sensitive to the value of the final parameter, σu, but it is important to have significant column density in each of UNM and WNM so as to have contributions from three layers; we chose σu = 10kms-1, for which the average column densities of the phases over SGC34 are rather similar (Sect.2.3).
Our value of ⟨ ϵ353 ⟩ differs slightly from the mean value ⟨ ϵ353 ⟩ quoted in Table2 of Planck Collaboration Int. XVII (2014), where the Planck intensity maps are correlated with HI LVC emission over many patches within Galactic latitude b< −25°. A difference in the mean dust emissivity is not unexpected because our study is focussed on the low column density region (NH i ≤ 2.7 × 1020 cm-2) within the Planck Collaboration Int. XVII (2014) sky region (NH i ≤ 6 × 1020 cm-2).
 |
Fig. 6 Correlation of the Planck 353GHz dust intensity map and the dust model StokesI map. The dashed line is the best-fit relation. |
Figure6 shows the correlation between the data D353 and the model Im,353 over SGC34. The parameters of the best fit line are s = 1.0 (iteratively by construction) and o = −6.6 μKCMB. We compute a residual map Δ ≡ D353−Im,353 over SGC34. The dispersion of the residual emission with respect to the total D353 emission is σΔ/σD353 = 0.36. This means that the residual emission accounts for only 13% (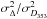 ) of the total dust power at 353 GHz. We calculate the Pearson correlation coefficients over SGC34 between the residual map and the three H I templates, namely the CNM, UNM, and WNM, finding −0.09, −0.17, and 0.13, respectively. The residual might originate in pixel-dependent variations of ϵ353 or possibly from diffuse ionized gas that is not spatially correlated with the total NHi map. Planck Collaboration Int. XVII (2014) explored these two possibilities (see their Appendix D) and were able to reproduce the observed value of σΔ/ ⟨ D353 ⟩ at 353GHz. We do not use the residual emission in our analysis because our main goal is to reproduce the mean dust polarization properties over the SGC34 region. For future work, the pixel-dependent variation of ϵ353, like in the Planck Collaboration Int. XVII (2014) analysis, could be included so that one could compare the refined dust model with the observed dust polarization data for a specific sky patch (e.g. the BICEP2 field).
) of the total dust power at 353 GHz. We calculate the Pearson correlation coefficients over SGC34 between the residual map and the three H I templates, namely the CNM, UNM, and WNM, finding −0.09, −0.17, and 0.13, respectively. The residual might originate in pixel-dependent variations of ϵ353 or possibly from diffuse ionized gas that is not spatially correlated with the total NHi map. Planck Collaboration Int. XVII (2014) explored these two possibilities (see their Appendix D) and were able to reproduce the observed value of σΔ/ ⟨ D353 ⟩ at 353GHz. We do not use the residual emission in our analysis because our main goal is to reproduce the mean dust polarization properties over the SGC34 region. For future work, the pixel-dependent variation of ϵ353, like in the Planck Collaboration Int. XVII (2014) analysis, could be included so that one could compare the refined dust model with the observed dust polarization data for a specific sky patch (e.g. the BICEP2 field).
5.3. Monte-Carlo simulations
Using the general framework described in Sect.4, we simulate a set of 100 polarized dust sky realizations at 353GHz using a set of model parameters, as discussed in Sect.4.4. Because the model of the turbulent GMF is statistical, we can simulate multiple dust sky realizations for a given set of parameters. The simulated dust intensity and polarization maps are smoothed to an angular resolution of FWHM 1° and projected on a HEALPix grid of Nside=128. These dust simulations are valid only in the low column density regions.
To compare the dust model with the Planck observations, we add realistic noise simulations called full focal plane 8 or “FFP8” (Planck Collaboration XII 2016). These noise simulations include the realistic noise correlation between pair of detectors for a given bolometer. For a given dust realization, we produce two independent samples of dust StokesQ and U noisy model maps as 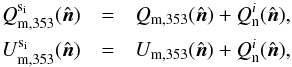 (13)where i = 1,2 are two independent samples, and
(13)where i = 1,2 are two independent samples, and 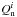 and
and 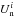 are the statistical noise of the subsets of the Planck polarization maps (as listed in Table1).
are the statistical noise of the subsets of the Planck polarization maps (as listed in Table1).
 |
Fig. 7 Best-fit power law dust model TT power spectra at 353GHz (black dashed line) and extrapolated dust power spectra at 150GHz (red dashed line) as computed over SGC34. For comparison, we also show the Planck 2015 best-fit ΛCDM expectation curves of the CMB signal. |
5.4. Comparison of the dust model with Planck observations
In this section we compare the statistical properties of the dust polarization from the dust model with the Planck 353GHz observations over the selected region SGC34.
We showed in Fig.6 that the model Stokes provides a good fit to the D353 map in amplitude. Here we show that this is the case for the shape of the
provides a good fit to the D353 map in amplitude. Here we show that this is the case for the shape of the  power spectrum too. We compute the model dust TT power spectrum,
power spectrum too. We compute the model dust TT power spectrum, 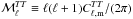 , over SGC34 in the range 40 <ℓ< 600. The dust
, over SGC34 in the range 40 <ℓ< 600. The dust  power spectrum is well represented with a power-law model,
power spectrum is well represented with a power-law model, 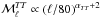 , with a best-fit slope αTT = −2.59 ± 0.02, as shown in Fig.7. Our derived best-fit value of αTT is consistent with that measured in Planck Collaboration XVI (2014) and Planck Collaboration XIII (2016) at high Galactic latitude. For comparison, we also show the TT power spectrum of the CMB signal for the Planck 2015 best-fit ΛCDM model (Planck Collaboration XIII 2016). The best-fit dust
, with a best-fit slope αTT = −2.59 ± 0.02, as shown in Fig.7. Our derived best-fit value of αTT is consistent with that measured in Planck Collaboration XVI (2014) and Planck Collaboration XIII (2016) at high Galactic latitude. For comparison, we also show the TT power spectrum of the CMB signal for the Planck 2015 best-fit ΛCDM model (Planck Collaboration XIII 2016). The best-fit dust  power spectrum extrapolated from 353GHz to 150GHz, scaling as in Fig.4 and shown here as a dashed red line, reveals that over SGC34 the amplitude of the dust emission at 150GHz is less than 1% compared to the amplitude of the CMB signal.
power spectrum extrapolated from 353GHz to 150GHz, scaling as in Fig.4 and shown here as a dashed red line, reveals that over SGC34 the amplitude of the dust emission at 150GHz is less than 1% compared to the amplitude of the CMB signal.
Next we show that the dust model is able to reproduce the observed distribution on 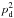 and dispersion of
and dispersion of  over SGC34 shown in Figs.2 and 3. We note that these statistics were not used to optimize the four model parameters in Sect.5.2, and so this serves as an important quality check for the model. We compute the square of the polarization fraction,
over SGC34 shown in Figs.2 and 3. We note that these statistics were not used to optimize the four model parameters in Sect.5.2, and so this serves as an important quality check for the model. We compute the square of the polarization fraction, 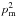 , for the dust model
, for the dust model 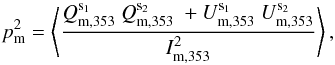 (14)where the index “m” again refers to the dust model. We use the two independent samples to exploit the statistical independence of the noise between them. The mean normalized histogram of
(14)where the index “m” again refers to the dust model. We use the two independent samples to exploit the statistical independence of the noise between them. The mean normalized histogram of  and the associated 1σ error bars are computed over SGC34 using 100 Monte-Carlo simulations. Returning to Fig.2, we compare the normalized histogram of
and the associated 1σ error bars are computed over SGC34 using 100 Monte-Carlo simulations. Returning to Fig.2, we compare the normalized histogram of  (black circles) with the normalized histogram of
(black circles) with the normalized histogram of  (blue inverted-triangles). The Planck instrumental noise (FFP8 noise) added in the dust model accounts nicely for the observed negative values of
(blue inverted-triangles). The Planck instrumental noise (FFP8 noise) added in the dust model accounts nicely for the observed negative values of 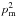 and also contributes the extension of the
and also contributes the extension of the 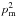 distribution beyond the input value of
distribution beyond the input value of 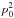 . The value of p0 found in this paper is close to the value of 19% deduced at 1° resolution over intermediate and low Galactic latitudes (Planck Collaboration Int. XIX 2015).
. The value of p0 found in this paper is close to the value of 19% deduced at 1° resolution over intermediate and low Galactic latitudes (Planck Collaboration Int. XIX 2015).
We also compute the dispersion of the polarization angle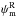 for the dust model. We follow the same procedure as discussed in Sect.3.3 and compute the angle
for the dust model. We follow the same procedure as discussed in Sect.3.3 and compute the angle 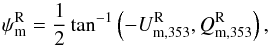 (15)where
(15)where 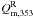 and
and 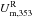 are rotated Stokesparameters with respect to the local direction of the large-scale GMF. We make the normalized histogram of
are rotated Stokesparameters with respect to the local direction of the large-scale GMF. We make the normalized histogram of 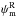 over SGC34. The mean normalized histogram and associated 1σ error bars of
over SGC34. The mean normalized histogram and associated 1σ error bars of 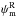 for the dust model are computed from 100 Monte-Carlo simulations. Returning to Fig.3, we compare the dispersion of
for the dust model are computed from 100 Monte-Carlo simulations. Returning to Fig.3, we compare the dispersion of 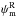 (black points) with the dispersion of
(black points) with the dispersion of  (blue points). The 1σ dispersion of
(blue points). The 1σ dispersion of 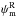 derived from the mean of 100 dust model realizations is
derived from the mean of 100 dust model realizations is 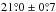 , slightly larger than for the Planck data (
, slightly larger than for the Planck data (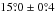 , Sect.3.2). This could come from the simple modelling assumptions used in our analysis. In particular, the histograms of
, Sect.3.2). This could come from the simple modelling assumptions used in our analysis. In particular, the histograms of 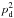 and
and 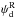 depend on the dust modelling at low multipoles (ℓ< 40), which are not constrained by our data fitting. Varying some of the model parameters such as
depend on the dust modelling at low multipoles (ℓ< 40), which are not constrained by our data fitting. Varying some of the model parameters such as 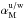 , different R for different ISM phases, or introducing a low-ℓ cutoff in the spectral index of the Bturb (Cho & Lazarian 2002, 2010) might provide a better fit of these histograms to the Planck data. Due to the limited sky coverage over SGC34 and residual systematics in the publicly available Planck PR2 data at low multipoles (Planck Collaboration Int. XLVI 2016), we are unable to test some of these possibilities within our modelling framework.
, different R for different ISM phases, or introducing a low-ℓ cutoff in the spectral index of the Bturb (Cho & Lazarian 2002, 2010) might provide a better fit of these histograms to the Planck data. Due to the limited sky coverage over SGC34 and residual systematics in the publicly available Planck PR2 data at low multipoles (Planck Collaboration Int. XLVI 2016), we are unable to test some of these possibilities within our modelling framework.
Finally, we compute power spectra of the dust model over SGC34 using the cross-spectra of two independent samples as described in Sects.3.3 and 5.3. Mean dust polarization power spectra of the noisy dust model, 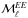 ,
, 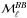 , and
, and 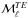 , over the multipole range 40 < ℓ < 160 are calculated from 100Monte-Carlo simulations and presented in the right column of Fig.4. The associated 1σ error bar per ℓ bin is also derived from the Monte-Carlo simulations. All of the dust polarization power spectra are well represented by a power law in ℓ. We fit the model spectra with a power-law model over the multipole range 40 < ℓ < 160. The best-fit values of the exponents and then of the amplitudes with exponent −2.3 are quoted in Table2. Because of the χ2 optimization of the four model parameters (Sect.5.2), these power spectra agree well with the observed power spectra over SGC34.
, over the multipole range 40 < ℓ < 160 are calculated from 100Monte-Carlo simulations and presented in the right column of Fig.4. The associated 1σ error bar per ℓ bin is also derived from the Monte-Carlo simulations. All of the dust polarization power spectra are well represented by a power law in ℓ. We fit the model spectra with a power-law model over the multipole range 40 < ℓ < 160. The best-fit values of the exponents and then of the amplitudes with exponent −2.3 are quoted in Table2. Because of the χ2 optimization of the four model parameters (Sect.5.2), these power spectra agree well with the observed power spectra over SGC34.
 |
Fig. 8 Left column: orthographic projections of the Planck 353GHz D353 (StokesI) map (top row) and the square of the polarization intensity P2 (bottom row), at 1° resolution over the southern Galactic cap covered by the GASS H I survey, with the selected region SGC34 outlined by a black contour. The same coordinate system is used as in Fig.1. Right column: similar to left panels, but for a realization of the 353GHz dust model. Judged visually, the dust model is able to reproduce roughly the observed dust polarization sky over SGC34, and indeed over the entire field shown. |
6. Predictions from the dust model
The simulated dust emission maps with FFP8 noise approximate the Planck 353GHz data well over SGC34. In this section we use noiseless dust simulations to make a few predictions concerning the foreground dust B-mode that are important for the search for the CMB B-mode signal. These predictions include the TB and EB correlation for the dust emission and the statistical variance of the dust B-modes at the power spectrum level.
But first we compare the spatial distribution of StokesI and the polarization intensity (P2) of the noiseless dust model with the Planck 353GHz data over the southern Galactic cap. The comparison between one realization of the dust model and the Planck data is presented in Fig.8. The dust simulation is derived completely from the GASS HI data and a phenomenological description of the large-scale and turbulent components of the GMF with parameters optimized over SGC34, a subregion of the SGC. We find a good match between the data and the dust model over SGC34, outlined by the black contour. Outside of SGC34, the brightest emission features appear stronger in the Planck 353GHz data because the HI-based dust model does not account for dust emission associated with H2 gas and with H I gas that is too cold to result in significant net emission.
6.1. Dust TB and EB correlation
The TB and EB cross-spectra vanish for the CMB signal in the standard ΛCDM model (Zaldarriaga & Seljak 1997). Here we test whether the corresponding dust model TB and EB cross-spectra vanish or not in the low column density region SGC34. To do this we simulate 100 Monte-Carlo realizations of noiseless dust skies and compute the cross-spectra for each realization.
The mean model dust 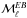 spectrum over the multipole range 40 < ℓ < 160 is presented in Fig.9. Similar to Abitbol et al. (2016), we fit the EB power spectrum with a power-law model,
spectrum over the multipole range 40 < ℓ < 160 is presented in Fig.9. Similar to Abitbol et al. (2016), we fit the EB power spectrum with a power-law model, 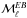 = AEB(ℓ/ 80)αEB + 2 with a fixed slope αEB = −2.3 and extrapolate it to 150GHz using the scaling factor s150/353. Our dust model predicts AEB = 0.31 ± 0.13 μKCMB2 (2.4σ level) at 353GHz. The best-fit value of AEB at ℓ = 80translates into an EB amplitude of
= AEB(ℓ/ 80)αEB + 2 with a fixed slope αEB = −2.3 and extrapolate it to 150GHz using the scaling factor s150/353. Our dust model predicts AEB = 0.31 ± 0.13 μKCMB2 (2.4σ level) at 353GHz. The best-fit value of AEB at ℓ = 80translates into an EB amplitude of 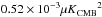 at 150GHz, consistent with the results presented in TableA1 of Abitbol et al. (2016) over the BICEP2 patch (1.3% of the cleanest sky region). Because our dust simulations are noiseless, we can determine the amplitude of the EB spectrum with relatively small error bars. This non-zero dust EB spectrum towards the SGC34 region can produce a spurious B-mode signal, if not taken into account in the self-calibrated telescope polarization angle (Abitbol et al. 2016). Comparing our result with Abitbol et al. (2016) indicates that the amplitude of spurious B-mode signal is negligible at ν ≤ 150GHz, but becomes important at dust frequency channels ν > 217GHz.
at 150GHz, consistent with the results presented in TableA1 of Abitbol et al. (2016) over the BICEP2 patch (1.3% of the cleanest sky region). Because our dust simulations are noiseless, we can determine the amplitude of the EB spectrum with relatively small error bars. This non-zero dust EB spectrum towards the SGC34 region can produce a spurious B-mode signal, if not taken into account in the self-calibrated telescope polarization angle (Abitbol et al. 2016). Comparing our result with Abitbol et al. (2016) indicates that the amplitude of spurious B-mode signal is negligible at ν ≤ 150GHz, but becomes important at dust frequency channels ν > 217GHz.
 |
Fig. 9 Predicted dust model power spectra |
On the other hand, the mean model dust 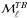 spectrum is mostly negative, but consistent with zero within the 3σ error bar for each multipole bin except for ℓ = 110. The amplitude
spectrum is mostly negative, but consistent with zero within the 3σ error bar for each multipole bin except for ℓ = 110. The amplitude 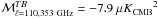 (or
(or 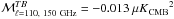 is consistent with the Abitbol et al. (2016) value over the BICEP2 patch (1.3% of the cleanest sky region). The origin of the negative
is consistent with the Abitbol et al. (2016) value over the BICEP2 patch (1.3% of the cleanest sky region). The origin of the negative 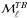 at ℓ = 110 is currently unknown. However, the significance of the negative
at ℓ = 110 is currently unknown. However, the significance of the negative 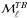 amplitude goes down with the choice of binning Δℓ> 30. It would be interesting to check our predicted model dust
amplitude goes down with the choice of binning Δℓ> 30. It would be interesting to check our predicted model dust 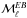 and
and 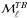 spectra with the upcoming BICEP2 dust power spectra at 220 GHz.
spectra with the upcoming BICEP2 dust power spectra at 220 GHz.
 |
Fig. 10 Comparison of the cosmic variance of the dust model |
6.2. Statistical variance of the dust model
In the analysis in BICEP2/Keck Array and Planck Collaborations (2015), Gaussian random realizations of the dust sky are simulated with a spatial power law ℳℓ ∝ ℓ-0.42 at 353GHz (and scaled to other microwave frequencies using a MBB spectrum with βd = 1.59 and Td = 19.6K). In contrast to that Gaussian dust model, our dust model produces non-Gaussianity because it is based on the GASS H I data. Here we test to what degree the statistical variance of the new dust simulations is compatible with the pure Gaussian model approximation.
For this test we proceed as in Sect.5.4 by estimating the mean dust 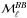 power spectrum at 353GHz over the multipole range 40 < ℓ < 160 and the 1σ standard deviations from 100, in this case noiseless, dust sky realizations over SGC34. These dust model results are shown in Fig.10 as black points, with a power-law fit as the dashed line. Then we assume the hypothesis of Gaussian and statistical isotropy and simulate 100 Gaussian dust sky realizations. The 1σ error range for the BB power from these Gaussian dust realizations is shown as the shaded region in Fig.10.
power spectrum at 353GHz over the multipole range 40 < ℓ < 160 and the 1σ standard deviations from 100, in this case noiseless, dust sky realizations over SGC34. These dust model results are shown in Fig.10 as black points, with a power-law fit as the dashed line. Then we assume the hypothesis of Gaussian and statistical isotropy and simulate 100 Gaussian dust sky realizations. The 1σ error range for the BB power from these Gaussian dust realizations is shown as the shaded region in Fig.10.
Comparing these results, our dust simulation band powers shown by the black symbols have less statistical variance at low multipoles ℓ < 80 compared to the variance from the Gaussian sky simulations. This reflects the fact that the model is not constrained exclusively by the dust polarization power spectra. In our dust model, the mean GMF orientation is fixed and the polarization angle of the CNM layer is determined by the GASS H I data. However, at high multipoles ℓ > 80, the effect of Bturb starts dominating over Bord, leading to a statistical variance that is comparable to or higher than that from the Gaussian sky simulations.
In summary, our dust model predicts smaller statistical variance at multipoles ℓ < 80 compared to the Gaussian dust approximation. Such an effect in the variance is not seen in the Vansyngel et al. (2017) dust model over the same multipole range for the LR regions defined in Planck Collaboration Int.XXX (2016). This is because the amplitudes of the dust polarization power in the Vansyngel et al. (2017) analysis are dominated by the brightest sky areas within these larger regions, whereas by its selection criteria the SGC34 region is more homogeneous.
7. Astrophysical interpretation
In this section we present an astrophysical interpretation of our dust modelling results.
In our analysis the alignment of the CNM structures with BPOS sets the spectral index of the Bturb power spectrum, 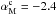 . The Vansyngel et al. (2017) parametric dust model reports αM = −2.5 for each polarization layer using the CIB-corrected 353 GHz GNILC dust map (Planck Collaboration Int. XLVIII 2016). These two complementary analyses show that the spectral index of the Bturb power spectrum is very close to the slope of the polarized dust power spectra (
. The Vansyngel et al. (2017) parametric dust model reports αM = −2.5 for each polarization layer using the CIB-corrected 353 GHz GNILC dust map (Planck Collaboration Int. XLVIII 2016). These two complementary analyses show that the spectral index of the Bturb power spectrum is very close to the slope of the polarized dust power spectra (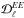 ,
,  , and
, and  ).
).
 |
Fig. 11 Summary of the observed spectral indices of the power spectrum as a function of length scales (in pc), from dust polarization (solid), synchrotron emission (dashed), synchrotron polarization (dashed-dot), and rotation measures (dotted). See Sect.7 for a detailed description. |
Our value of the spectral index αM is significantly higher (the spectrum is less steep) than the value of −11/3 from the Kolmogorov spectrum. In Fig.11, we compare our result with the spectral indices obtained in earlier studies using starlight polarization (Fosalba et al. 2002), synchrotron emission (Iacobelli et al. 2013; Remazeilles et al. 2015), synchrotron polarization (Haverkorn et al. 2003; Planck Collaboration X 2016), and rotation measures (Oppermann et al. 2012). For each data set we convert the ℓ range to physical sizes. We used a scale-height of 1kpc for the warm ionized medium and the synchrotron emission. For the study of SGC34 here, the maximum distance of the dust emitting layer is Lmax = 100−200pc, a range between estimates of the typical distance to the local bubble (Lallement et al. 2014) and of the dust emission scale height (Drimmel & Spergel 2001). All of the values are larger than the spectral index of the Kolmogorov spectrum. In several papers this is explained by introducing an outer scale of turbulence close to the measured physical sizes. However, the current data do not show a consistent systematic trend of spectra steepening towards smaller sizes. Such a trend might be difficult to see combining different tracers of the magnetic field. For dust polarization, we fit the Planck observations over the multipole range 40 < ℓ < 160, which corresponds to physical scales of 2−15pc on the sky. At larger scales, the spectral index from starlight dust polarization (interstellar polarization) is flatter. If this interpretation is correct, then we expect to see further flattening of the Bturb power spectrum at low multipoles (see Fig.20 of Planck Collaboration Int. XLVI 2016). Such flattening, which we neglected in this analysis, could possibly account for the slight differences in the histograms of p2 and ψR between the Planck data and the dust model (Figs.2 and3).
With our modelling assumption of the same dust alignment parameter (R; see Sect.4.1) for each HI component, we find that the value of  is significantly larger than the value of
is significantly larger than the value of  . The size of
. The size of 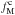 follows from the statistics of the H I CNM map because we assume that BPOS is aligned with CNM structures (Sect.5.1). From
follows from the statistics of the H I CNM map because we assume that BPOS is aligned with CNM structures (Sect.5.1). From 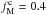 , the value of
, the value of 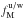 (0.1) is set by the amplitudes of the observed polarization power spectra (Sect.5.2). Through a consistency check we find that the dispersion of
(0.1) is set by the amplitudes of the observed polarization power spectra (Sect.5.2). Through a consistency check we find that the dispersion of 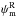 depends on the
depends on the 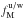 value. If we increase the size of
value. If we increase the size of 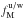 , the dispersion of
, the dispersion of 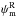 becomes larger than the observed dispersion of
becomes larger than the observed dispersion of 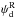 . Thus our modelling indicates that the CNM component is more turbulent than the UNM/WNM components. This is the first time that this behaviour has been observed in the Planck polarization data. Kalberla et al. (2016) and Heiles & Troland (2003) have shown that the CNM has the largest sonic Mach number. If both the sound and Alfvén speed change by a same factor (≃10) between the CNM and WNM, we also expect a higher Alfvénic Mach number for the CNM than the WNM component (Hennebelle & Passot 2006). This would fit with the larger fM value in the CNM.
. Thus our modelling indicates that the CNM component is more turbulent than the UNM/WNM components. This is the first time that this behaviour has been observed in the Planck polarization data. Kalberla et al. (2016) and Heiles & Troland (2003) have shown that the CNM has the largest sonic Mach number. If both the sound and Alfvén speed change by a same factor (≃10) between the CNM and WNM, we also expect a higher Alfvénic Mach number for the CNM than the WNM component (Hennebelle & Passot 2006). This would fit with the larger fM value in the CNM.
Alternatively, the lower value of fM for the WNMcomponent could result from our modelling that reduces the LOS integration to a small number of discrete layers. Planck Collaboration Int. XLIV (2016) argued that the number of layers (Nlayers) is related to the multiphase structure of the ISM and to the correlation length of the GMF. For the CNM, dust polarization traces the GMF at discrete locations along the LOS. For the WNM, dust polarization samples the variations of the GMF orientation along the LOS. For that ISMphase, Nlayers is coming from the correlation length of the GMF that depends on the spectral index of the Bturb power spectrum. For a typical value of αM = −2.4, the value of Nlayers is 6 (Planck Collaboration Int. XLIV 2016). If that reasoning applies, our value of 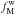 is effectively a factor
is effectively a factor 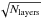 smaller than the true value. The same argument might hold for the UNM component too.
smaller than the true value. The same argument might hold for the UNM component too.
Various alignment mechanisms, such as paramagnetic, mechanical, and radiative torques, have been proposed to explain the efficiency of the alignment of dust grains with respect to the magnetic field (see Lazarian 2003; Andersson et al. 2015, for a review). Draine & Weingartner (1996, 1997) argued that the radiative torques mechanism is the dominant process in the diffuse ISM. We have assumed that the degree of grain alignment and the dust polarization properties are the same in all ISM phases, but they might differ. We investigated this possibility explicitly in our model by keeping fixed pdust and 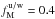 and varying the alignment parameter in the cold phase(Rc) and warm phase (Rw). If we lower Rw compared to Rc, the dispersion of
and varying the alignment parameter in the cold phase(Rc) and warm phase (Rw). If we lower Rw compared to Rc, the dispersion of 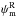 becomes broader than the best-fit model presented in this paper. While a lower value Rc compared to Rw provides a better fit to the dispersion of
becomes broader than the best-fit model presented in this paper. While a lower value Rc compared to Rw provides a better fit to the dispersion of 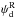 , such a model does not reproduce the E−B asymmetry in the power spectrum amplitudes. In summary, within our modelling framework with three H I layers, changes in the (relative) degree of alignment cannot account for the lower value of
, such a model does not reproduce the E−B asymmetry in the power spectrum amplitudes. In summary, within our modelling framework with three H I layers, changes in the (relative) degree of alignment cannot account for the lower value of 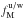 .
.
Our values of 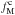 and
and 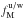 are lower than the one reported by Planck Collaboration Int. XLIV (2016) and Vansyngel et al. (2017). This difference follows from the model assumptions. We account for the multiphase structure of the ISM and find
are lower than the one reported by Planck Collaboration Int. XLIV (2016) and Vansyngel et al. (2017). This difference follows from the model assumptions. We account for the multiphase structure of the ISM and find 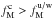 , while Planck Collaboration Int. XLIV (2016) and Vansyngel et al. (2017) keep the same dust total intensity map and fM value for all of the polarization layers. As discussed in Planck Collaboration Int. XLIV (2016), the best fit values of fM and p0 increase with Nlayers. In our model, the turbulence is most important in the CNM layer and our value of
, while Planck Collaboration Int. XLIV (2016) and Vansyngel et al. (2017) keep the same dust total intensity map and fM value for all of the polarization layers. As discussed in Planck Collaboration Int. XLIV (2016), the best fit values of fM and p0 increase with Nlayers. In our model, the turbulence is most important in the CNM layer and our value of 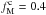 is in agreement with the best fit value in Planck Collaboration Int. XLIV (2016) for their one layer model. We also note that our
is in agreement with the best fit value in Planck Collaboration Int. XLIV (2016) for their one layer model. We also note that our 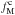 value applies to the SGC34 region, which by definition is a low column density region (NH i ≤ 2.7 × 1020 cm-2). Our data analysis suggests that the
value applies to the SGC34 region, which by definition is a low column density region (NH i ≤ 2.7 × 1020 cm-2). Our data analysis suggests that the 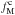 value might be higher for the whole SGC region. In our model, we put the mean large-scale GMF in both the UNM and WNM components, thus affecting both ψu and ψw. This feature of the model can be investigated with numerical simulations. Using a simulation of supernova-driven turbulence in the multiphase ISM, Evirgen et al. (2017) suggest that the mean field might reside preferentially in the WNM.
value might be higher for the whole SGC region. In our model, we put the mean large-scale GMF in both the UNM and WNM components, thus affecting both ψu and ψw. This feature of the model can be investigated with numerical simulations. Using a simulation of supernova-driven turbulence in the multiphase ISM, Evirgen et al. (2017) suggest that the mean field might reside preferentially in the WNM.
8. Discussion and summary
We have constructed a phenomenological dust model based on the publicly available GASS H I data and an astrophysically motivated description of the large-scale and turbulent Galactic magnetic field. The two main ingredients of the model are: (1)fluctuations in the GMF orientation along the LOS and (2)a perfect alignment of the CNM structures and BPOS. We model the resulting LOS depolarization by replacing the integration along the LOS by the sum of three distinct components that represent distinct phases of the diffuse neutral atomic ISM. By adjusting a set of nine model parameters suitably, we are able to reproduce the observed statistical properties of the dust polarization in a selected region of low column density (NH i ≤ 2.7 × 1020 cm-2) that comprises 34% of the southern Galactic cap (SGC34). This dust model is valid only over SGC34.
Unlike PSM dust templates, this dust model is not noise-limited in low column density regions and can be used to predict the average dust polarization at any sky position over the selected region SGC34 at any frequency. This new dust model should be useful for simulating realistic polarized dust skies, testing the accuracy of component separation methods, and studying non-Gaussianity.
Recently, Tassis & Pavlidou (2015) and Poh & Dodelson (2016) showed that multiple dust components along the LOS with different temperatures (in general SEDs) and polarization angles lead to frequency decorrelation in both amplitude and polarization direction. Our dust modelling framework allows us to introduce frequency decorrelation of the dust polarization readily by adopting different dust SEDs for the three H I components and then extrapolating the dust model to other microwave frequencies. With the current Planck sensitivity the current constraint on the dust frequency decorrelation is only marginal at high Galactic latitude (Planck Collaboration Int. L 2017). Although we could use the dust model to explore the frequency decorrelation of the polarized dust emission, this is beyond the scope of this paper.
The main results of the paper are summarized below.
-
The observed distributions of p2 and ψ over SGC34 can be accounted for by a model with three ISM components: CNM, WNM, and UNM. Each ISM phase has different density structures and different orientations of the turbulent component of the GMF.
-
The slopes of
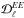 ,
, 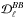 , and
, and 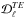 angular power spectra over the multipole range 40 < ℓ < 160 are represented well with the same power-law exponent, which is close to the spectral index of the turbulent magnetic field, αM = −2.4.
angular power spectra over the multipole range 40 < ℓ < 160 are represented well with the same power-law exponent, which is close to the spectral index of the turbulent magnetic field, αM = −2.4. -
The positive
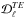 correlation and E-B power asymmetry over SGC34 can be accounted for by the alignment of the CNM structures with BPOS.
correlation and E-B power asymmetry over SGC34 can be accounted for by the alignment of the CNM structures with BPOS. -
The E-B power asymmetry for small sky patches depends on the fraction of the total dust emission in the CNM, UNM, and WNM phases. We expect to find the ratio
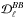 /
/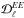 close to 1 where the UNM/WNM structures dominate over the CNM structures.
close to 1 where the UNM/WNM structures dominate over the CNM structures.
Planck (http://www.esa.int/Planck) is a project of the European Space Agency (ESA) with instruments provided by two scientific consortia funded by ESA member states and led by Principal Investigators from France and Italy, telescope reflectors provided through a collaboration between ESA and a scientific consortium led and funded by Denmark, and additional contributions from NASA (USA).
The noise is partially correlated between the two half-ring maps (Planck Collaboration VI 2014) and so those maps are not used in our analysis.
Acknowledgments
The research leading to these results has received funding from the European Research Council grant MISTIC (ERC-267934). Part of the research described in this paper was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration. U.H. acknowledges the support by the Estonian Research Council grant IUT26-2, and by the European Regional Development Fund (TK133). The Parkes Radio Telescope is part of the Australia Telescope, which is funded by the Commonwealth of Australia for operation as a National Facility managed by CSIRO. Some of the results in this paper have been derived using the HEALPix package. Finally, we acknowledge the use of Planck data available from Planck Legacy Archive (http://www.cosmos.esa.int/web/planck/pla).
References
- Abbott, L.F., & Wise, M.B. 1984, Nucl. Phys. B, 244, 541 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Abitbol, M.H., Hill, J.C., & Johnson, B.R. 2016, MNRAS, 457, 1796 [NASA ADS] [CrossRef] [Google Scholar]
- Andersson, B.-G., Lazarian, A., & Vaillancourt, J.E. 2015, ARA&A, 53, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Audit, E., & Hennebelle, P. 2005, A&A, 433, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benson, B.A., Ade, P.A.R., Ahmed, Z., et al. 2014, in Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VII, Proc.SPIE, 9153, 91531P [Google Scholar]
- Betoule, M., Pierpaoli, E., Delabrouille, J., Le Jeune, M., & Cardoso, J.-F. 2009, A&A, 503, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- BICEP2/Keck Array and Planck Collaborations 2015, Phys. Rev. Lett., 114, 101301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- BICEP2 and Keck Array Collaboration, Ade, P.A.R., Ahmed, Z., et al. 2016, Phys. Rev. Lett., 116, 031302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Boulanger, F., Abergel, A., Bernard, J.-P., et al. 1996, A&A, 312, 256 [NASA ADS] [Google Scholar]
- Bowyer, J., Jaffe, A.H., & Novikov, D.I. 2011, MasQU: Finite Differences on Masked Irregular StokesQ, U Grids, Astrophysics Source Code Library [Google Scholar]
- Caldwell, R.R., Hirata, C., & Kamionkowski, M. 2017, ApJ, 839, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Cho, J., & Lazarian, A. 2002, ApJ, 575, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Cho, J., & Lazarian, A. 2010, ApJ, 720, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Chon, G., Challinor, A., Prunet, S., Hivon, E., & Szapudi, I. 2004, MNRAS, 350, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, S.E., Peek, J.E.G., & Putman, M.E. 2014, ApJ, 789, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, S.E., Hill, J.C., Peek, J.E.G., Putman, M.E., & Babler, B.L. 2015, Phys. Rev. Lett., 115, 241302 [NASA ADS] [CrossRef] [Google Scholar]
- Crill, B.P., Ade, P.A.R., Battistelli, E.S., et al. 2008, in Space Telescopes and Instrumentation 2008: Optical, Infrared, and Millimeter, Proc.SPIE, 7010, 70102 [Google Scholar]
- Delabrouille, J., Betoule, M., Melin, J.-B., et al. 2013, A&A, 553, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B.T., & Weingartner, J.C. 1996, ApJ, 470, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B.T., & Weingartner, J.C. 1997, ApJ, 480, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Drimmel, R., & Spergel, D.N. 2001, ApJ, 556, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Essinger-Hileman, T., Appel, J.W., Beall, J.A., et al. 2010, ArXiv e-prints [arXiv:1008.3915] [Google Scholar]
- Essinger-Hileman, T., Ali, A., Amiri, M., et al. 2014, in Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VII, Proc.SPIE, 9153, 91531 [Google Scholar]
- Evirgen, C.C., Gent, F.A., Shukurov, A., Fletcher, A., & Bushby, P. 2017, MNRAS, 464, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Fabbri, R., & Pollock, M.D. 1983, Phys. Lett. B, 125, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Fauvet, L., Macías-Pérez, J.F., Jaffe, T.R., et al. 2012, A&A, 540, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fosalba, P., Lazarian, A., Prunet, S., & Tauber, J.A. 2002, ApJ, 564, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Gillmon, K., Shull, J.M., Tumlinson, J., & Danforth, C. 2006, ApJ, 636, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K.M., Hivon, E., Banday, A.J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Grain, J., Tristram, M., & Stompor, R. 2009, Phys.Rev.D, 79, 123515 [NASA ADS] [CrossRef] [Google Scholar]
- Green, G.M., Schlafly, E.F., Finkbeiner, D.P., et al. 2015, ApJ, 810, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Haud, U. 2013, A&A, 552, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haud, U., & Kalberla, P.M.W. 2007, A&A, 466, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haverkorn, M., Katgert, P., & de Bruyn, A.G. 2003, A&A, 403, 1045 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiles, C., & Troland, T.H. 2003, ApJ, 586, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C., & Troland, T.H. 2005, ApJ, 624, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Henderson, S.W., Allison, R., Austermann, J., et al. 2016, J. Low Temperature Phys., 184, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P. 2013, A&A, 556, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Iffrig, O. 2014, A&A, 570, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Passot, T. 2006, A&A, 448, 1083 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iacobelli, M., Haverkorn, M., Orrú, E., et al. 2013, A&A, 558, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inoue, T., & Inutsuka, S.-I. 2016, ApJ, 833, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Jaffe, T.R., Leahy, J.P., Banday, A.J., et al. 2010, MNRAS, 401, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P.M.W., & Haud, U. 2015, A&A, 578, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P.M.W., McClure-Griffiths, N.M., Pisano, D.J., et al. 2010, A&A, 521, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P.M.W., Kerp, J., Haud, U., et al. 2016, ApJ, 821, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Kermish, Z.D., Ade, P., Anthony, A., et al. 2012, in Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VI, Proc. SPIE, 8452, 84521 [Google Scholar]
- Lallement, R., Vergely, J.-L., Valette, B., et al. 2014, A&A, 561, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lazarian, A. 2003, J.Quant.Spec.Radiat.Transf., 79, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Lazarian, A. 2008, ArXiv e-prints [arXiv:astro-ph/0811.1020] [Google Scholar]
- Martin, P.G., Blagrave, K.P.M., Lockman, F.J., et al. 2015, ApJ, 809, 153 [NASA ADS] [CrossRef] [Google Scholar]
- McClure-Griffiths, N.M., Pisano, D.J., Calabretta, M.R., et al. 2009, ApJS, 181, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Montier, L., Plaszczynski, S., Levrier, F., et al. 2015, A&A, 574, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nidever, D.L., Majewski, S.R., Butler Burton, W., & Nigra, L. 2010, ApJ, 723, 1618 [NASA ADS] [CrossRef] [Google Scholar]
- O’Dea, D.T., Clark, C.N., Contaldi, C.R., & MacTavish, C.J. 2012, MNRAS, 419, 1795 [NASA ADS] [CrossRef] [Google Scholar]
- Ogburn, R.W., Ade, P.A.R., Aikin, R.W., et al. 2012, in Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VI, Proc.SPIE, 8452, 84521 [Google Scholar]
- Oppermann, N., Junklewitz, H., Robbers, G., et al. 2012, A&A, 542, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peek, J.E.G., Heiles, C., Douglas, K.A., et al. 2011, ApJS, 194, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration VI. 2014, A&A, 571, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2014, A&A, 571, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2016, A&A, 594, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VIII. 2016, A&A, 594, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration X. 2016, A&A, 594, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XII. 2016, A&A, 594, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVI. 2016, A&A, 594, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XVII. 2014, A&A, 566, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XIX. 2015, A&A, 576, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XX. 2015, A&A, 576, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXII. 2015, A&A, 576, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXX. 2016, A&A, 586, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXXII. 2016, A&A, 586, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXXV. 2016, A&A, 586, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXXVIII. 2016, A&A, 586, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XLIV. 2016, A&A, 596, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XLVI. 2016, A&A, 596, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XLVIII. 2016, A&A, 596, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. L. 2017, A&A, 599, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poh, J., & Dodelson, S. 2016, ArXiv e-prints [arXiv:1606.08922] [Google Scholar]
- Prunet, S., & Lazarian, A. 1999, in Microwave Foregrounds, eds. A.de Oliveira-Costa, & M.Tegmark, ASP Conf. Ser., 181, 113 [Google Scholar]
- Reichborn-Kjennerud, B., Aboobaker, A.M., Ade, P., et al. 2010, in Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy V, Proc.SPIE, 7741, 77411 [Google Scholar]
- Remazeilles, M., Dickinson, C., Banday, A.J., Bigot-Sazy, M.-A., & Ghosh, T. 2015, MNRAS, 451, 4311 [NASA ADS] [CrossRef] [Google Scholar]
- Saury, E., Miville-Deschênes, M.-A., Hennebelle, P., Audit, E., & Schmidt, W. 2014, A&A, 567, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simmons, J.F.L., & Stewart, B.G. 1985, A&A, 142, 100 [Google Scholar]
- Starobinsky, A.A. 1979, Pisma v Zhurnal Eksperimentalnoi i Teoreticheskoi Fiziki, 30, 719 [NASA ADS] [Google Scholar]
- Suzuki, A., Ade, P., Akiba, Y., et al. 2016, J. Low Temperature Phys., 184, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Tassis, K., & Pavlidou, V. 2015, MNRAS, 451, L90 [NASA ADS] [CrossRef] [Google Scholar]
- Tristram, M., Macías-Pérez, J.F., Renault, C., & Santos, D. 2005, MNRAS, 358, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Vansyngel, F., Boulanger, F., Ghosh, T., et al. 2017, A&A, in press, DOI:10.1051/0004-6361/201629992 [Google Scholar]
- Winkel, B., Kerp, J., Flöer, L., et al. 2016, A&A, 585, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolfire, M.G., McKee, C.F., Hollenbach, D., & Tielens, A.G.G.M. 2003, ApJ, 587, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Zaldarriaga, M., & Seljak, U. 1997, Phys.Rev.D, 55, 1830 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Dust polarization fraction p statistics at 353GHz and the best-fit mean direction of the large-scale GMF over SGC34 using multiple subsets of the Planck data.
Fitted 353GHz dust power spectra of the Planck data and of the dust model over SGC34, for which the mean dust intensity ⟨ D353 ⟩ is 54 ± 3kJysr-1.
All Figures
 |
Fig. 1 NHi maps of the three Gaussian-based HI phases: CNM (top left), UNM (top right), and WNM (bottom left) over the portion of the southern Galactic cap (b ≤ −30°) covered by the GASS HI survey, at 1° resolution. Coloured region corresponds to the selected region SGC34 (bottom right). Orthographic projection in Galactic coordinates: latitudes and longitudes marked by lines and circles respectively. |
| In the text | |
 |
Fig. 2 Normalized histograms of p2 over SGC34 at 353GHz. Planck data, |
| In the text | |
 |
Fig. 3 Similar to Fig.2, but for normalized histograms of ψR, the polarization angle relative to the local polarization angle of the large-scale GMF. The vertical dashed line corresponds to a model in which the turbulence is absent (Bturb = 0 so that ψR = 0°). |
| In the text | |
 |
Fig. 4 Left column: Planck 353GHz |
| In the text | |
 |
Fig. 5 Mean power spectra of cos2γ (top panel) and cos2ψ (bottom panel) over SGC34 for a set of αM and fM parameters in the multipole range 40 <ℓ< 160. The 1σ error bars are computed from the standard deviations of the 100Monte-Carlo realizations of the dust model. The alignment of the CNM structures with BPOS (see Sect.5.1 for details) constrains the value of |
| In the text | |
 |
Fig. 6 Correlation of the Planck 353GHz dust intensity map and the dust model StokesI map. The dashed line is the best-fit relation. |
| In the text | |
 |
Fig. 7 Best-fit power law dust model TT power spectra at 353GHz (black dashed line) and extrapolated dust power spectra at 150GHz (red dashed line) as computed over SGC34. For comparison, we also show the Planck 2015 best-fit ΛCDM expectation curves of the CMB signal. |
| In the text | |
 |
Fig. 8 Left column: orthographic projections of the Planck 353GHz D353 (StokesI) map (top row) and the square of the polarization intensity P2 (bottom row), at 1° resolution over the southern Galactic cap covered by the GASS H I survey, with the selected region SGC34 outlined by a black contour. The same coordinate system is used as in Fig.1. Right column: similar to left panels, but for a realization of the 353GHz dust model. Judged visually, the dust model is able to reproduce roughly the observed dust polarization sky over SGC34, and indeed over the entire field shown. |
| In the text | |
 |
Fig. 9 Predicted dust model power spectra |
| In the text | |
 |
Fig. 10 Comparison of the cosmic variance of the dust model |
| In the text | |
 |
Fig. 11 Summary of the observed spectral indices of the power spectrum as a function of length scales (in pc), from dust polarization (solid), synchrotron emission (dashed), synchrotron polarization (dashed-dot), and rotation measures (dotted). See Sect.7 for a detailed description. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.