| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A11 | |
| Number of page(s) | 13 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201527925 | |
| Published online | 28 April 2016 | |
Investigating magnetic activity in very stable stellar magnetic fields
Long-term photometric and spectroscopic study of the fully convective M4 dwarf V374 Pegasi ⋆
1
Konkoly Observatory, MTA CSFK, Konkoly Thege M. út 15-17,
1121
Budapest,
Hungary
e-mail:
vidakris@konkoly.hu
2
University of Graz, Institute of Physics, Department for
Geophysics, Astrophysics and Meteorology, NAWI Graz, Universitätsplatz
5, 8010
Graz,
Austria
3
Space Research Institute, Austrain Academy of
Sciences, Schmiedlstrasse
6, 8042
Graz,
Austria
4
Finnish Centre for Astronomy with ESO, University of
Turku, Väisäläntie
20, 21500
Piikkiö,
Finland
5
Dark Cosmology Centre, Niels Bohr Institute, Copenhagen
University, Juliane Maries Vej
30, 2100
Copenhagen Ø,
Denmark
6 University of Victoria and Guest Observer, Dominion
Astrophysical Observatory, Victoria, BC V9E2E7, Canada
7
ELTE Gothard Astrophysical Observatory,
Szent Imre herceg út 112,
9704
Szombathely,
Hungary
Received: 8 December 2015
Accepted: 2 March 2016
The ultrafast-rotating (Prot ≈ 0.44 d) fully convective single M4 dwarf V374 Peg is a well-known laboratory for studying intense stellar activity in a stable magnetic topology. As an observable proxy for the stellar magnetic field, we study the stability of the light curve, hence the spot configuration. We also measure the occurrence rate of flares and coronal mass ejections (CMEs). We have analysed spectroscopic observations, BV(RI)C photometry covering 5 yrs, and additional RC photometry that expands the temporal base over 16 yr. The light curve suggests an almost rigid-body rotation and a spot configuration that is stable over about 16 yrs, confirming the previous indications of a very stable magnetic field. We observed small changes on a nightly timescale and frequent flaring, including a possible sympathetic flare. The strongest flares seem to be more concentrated around the phase where the light curve indicates a smaller active region. Spectral data suggest a complex CME with falling-back and re-ejected material with a maximal projected velocity of ~675 km s-1. We observed a CME rate that is much lower than expected from extrapolations of the solar flare-CME relation to active stars.
Key words: stars: activity / stars: flare / stars: individual: V374 Peg / stars: late-type / stars: low-mass / starspots
Tables of the photometry are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/590/A11
© ESO, 2016
1. Introduction
V374 Peg is an M4 dwarf (Reid et al. 1995) that first raised interest when Greimel & Robb (1998) detected frequent strong flares on the star. Batyrshinova & Ibragimov (2001) later observed several flares, including a superflare event, having 11m amplitude in the U filter. Montes et al. (2001) found that V374 Peg is part of the Castor kinematic group, so it has an age of approximately 200 Myr. This young age is also supported by Vidotto et al. (2011), who found evidence of a strong coronal wind.
Its high activity level and relative brightness (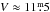 ) make V374 Pega popular astrophysical laboratory for studying stellar magnetic fields in young, fully convective stars. Donati et al. (2006) studied the magnetic field of V374 Peg using Zeeman–Doppler imaging on data covering three non-consecutive rotations. They found that the star was rotating as a solid body and that it has a dipole-like axisymmetric magnetic field. This result challenged theoretical dynamo models, which predicted either rigid-body rotation with non-axisymmetric magnetic field (e.g. Küker & Rüdiger 1999) or axisymmetric fields, but with differential rotation (e.g. Dobler et al. 2006). A recent study by Yadav et al. (2015) proposes a dynamo model that can explain solid-body rotation with dipole-like field and predicted long-term stable magnetic configuration. Based on observations from three epochs spanning more than a year, Morin et al. (2008a) detected a very weak differential rotation and concluded that the magnetic field of V374 Peg is stable on this timescale.
) make V374 Pega popular astrophysical laboratory for studying stellar magnetic fields in young, fully convective stars. Donati et al. (2006) studied the magnetic field of V374 Peg using Zeeman–Doppler imaging on data covering three non-consecutive rotations. They found that the star was rotating as a solid body and that it has a dipole-like axisymmetric magnetic field. This result challenged theoretical dynamo models, which predicted either rigid-body rotation with non-axisymmetric magnetic field (e.g. Küker & Rüdiger 1999) or axisymmetric fields, but with differential rotation (e.g. Dobler et al. 2006). A recent study by Yadav et al. (2015) proposes a dynamo model that can explain solid-body rotation with dipole-like field and predicted long-term stable magnetic configuration. Based on observations from three epochs spanning more than a year, Morin et al. (2008a) detected a very weak differential rotation and concluded that the magnetic field of V374 Peg is stable on this timescale.
In this paper we present analysis of photometric and spectroscopic data spanning more than half a decade.
2. Observations
 |
Fig. 1 BV(RI)C photometry of V374 Peg from the Piszkéstető observations. Ranges marked in the ΔB light curve were used for flare statistics (see Sect. 4.1). Arrows over the ΔI light curve point at the dates of the spectroscopic observations during this time. |
Photometric observations in BV(RI)C passbands were carried out using the 1-m RCC telescope of Konkoly Observatory at Piszkéstető Mountain Station equipped with a Princeton Instruments 1300 × 1300 CCD. The observations cover 71 nights in total between 2008 July 31 and 2013 July 28 (HJDs 2 454 679–2 456 502). Data reduction was done using standard IRAF1 procedures. Differential aperture photometry was done using the DAOPHOT package. The resulting BV(RI)C light curves are shown in Fig. 1. All ΔV data of this dataset are plotted together against the rotational phase (see Sect. 3.3) in Fig. 2. We used GSC 02215-01602 as comparison star for our light curves.
Additional CCD photometric data in Cousins R filter were obtained from the automated 0.5-m telescope of the Climenhaga Observatory of the University of Victoria from 1998 and 2000, which were partly published in Greimel & Robb (1998).
The spectroscopic observations in 2012/2013 were carried out by the 1-m RCC telescope, using the eShel spectrograph of the Gothard Astronomical Observatory, Szombathely, Hungary, in the spectral range 4200–8700 Å with a resolution of R ≈ 11 000 (Csák et al. 2014). The wavelength calibration was done using a ThAr lamp. These data were reduced using standard IRAF procedures.
Additional spectra were downloaded from the public database of the Canada–France–Hawaii Telescope (CFHT)2. The spectra were obtained between 2005 and 2009 by ESPaDOnS (Donati 2003) with a spectral resolution of R ≈ 65 000 covering the range between 3700–10 400 Å. The spectroscopic observations are summarised in Table 1.
3. Analysis
3.1. Mass
 |
Fig. 2 ΔV light curve of V374 Peg at the top and the marked parts phased at the bottom. Continuous line shows a model fit with two spots (see Sect. 3.4). The plot does not show most of the flares. |
Summary of spectroscopic observations.
Using the empirical absolute magnitude-mass calibration for very low mass stars (M< 0.6M⊙) of Delfosse et al. (2000), we can get an empirical mass value following Morin et al. (2008a). According to the Two Micron All Sky Survey (2MASS), the magnitude of V374 Peg in J, H, and K passbands are 7.635, 7.035, and 6.777 mag (Cutri et al. 2003), which translate to the absolute magnitudes of 7.887, 7.287, and 7.029, respectively, using the parallax of 112.33 mas from the Hipparcos survey (van Leeuwen 2007), if we neglect interstellar absorption (as the distance of the object is only 8.9 pc). These magnitudes yield mass values of 0.282, 0.285, and 0.281 M⊙ for the three passbands, respectively.
Using the magnitude-mass and magnitude-radius calibrations for M dwarfs of Mann et al. (2015) based on the K magnitudes, we get a somewhat different result than previously: 0.338 M⊙ for the mass and 0.335 R⊙ for the radius, in good agreement with Morin et al. (2008b). We can conclude that from these different methods, the mass of V374 Peg is 0.30 ± 0.03M⊙(the error estimated using the standard deviation of the different mass values).
3.2. Spectral energy distribution: is there an IR excess?
 |
Fig. 3 Spectral energy distribution of V374 Peg from the ultraviolet to mid-infrared using NextGen model atmospheres (see text for more details). Errors bars are smaller than the symbols used for the plot. |
Scaltriti et al. (1993) studied active RS CVn systems and found infrared excess in 5 of 12 cases, which the authors interpreted as evidence of an absorbing shell, which is a result of strong stellar wind. Such excess was (unsuccessfully) sought in active single stars as well (Pandey et al. 2005), but was found in many fast-rotating evolved stars (Rodrigues da Silva et al. 2015). The latter authors also considered the dust to be the result of planetary collisions.
If we neglect interstellar reddening, we can easily determine the intrinsic infrared colours of V374 Peg: (J − K)0 = 0.858 and (H − K)0 = 0.258 using the 2MASS magnitudes (Cutri et al. 2003). Comparing these values to the intrinsic colours of a main-sequence M4 star (J − K = 0.839, H − K = 0.282) based on the work of Pecaut & Mamajek (2013), we find a difference of 0.02 and −0.02 mag, which is around the typical error of 0.03 mag of the 2MASS observations.
The suggestion of Scaltriti et al. (1993) that stellar winds caused by a high level of activity can induce infrared excess, was further tested by plotting the spectral energy distribution (SED) (see Fig. 3). We used the VOspec tool3 that is capable of obtaining both multi-wavelength photometric observations and theoretical spectra. We downloaded ultraviolet observations from the GALEX survey (Bianchi et al. 2011) and infrared observations from the 2MASS (Cutri et al. 2003), WISE (Cutri & et al. 2014) and AKARI (Ishihara et al. 2010) surveys. We also plotted our BV(RI)C observations from the Piszkéstető RCC telescope. To describe the photosphere, we used the NextGen (Hauschildt et al. 1999) model with the astrophysical parameters of V374 Peg. All the points fit the model photosphere, but only the measurements in the ultraviolet regime show a very strong excess consistent with the high chromospheric activity level. Thus we conclude that V374 Peg does not have a significant colour excess in the infrared bands, and does not possess a hot dust shell.
3.3. Fourier analysis
 |
Fig. 4 Fourier spectrum of the ΔR light curve (top), the spectrum pre-whitened with the rotation frequency (middle), the inset showing a zoom-in to the rotation area, and the spectral window (bottom). |
Fourier analysis of the photometric ΔRC data was performed using MUFRAN4 (Kolláth 1990) – a code that can do discrete Fourier transformation of data and pre-whiten light curves with the detected frequencies – since this filter has the longest time base of 16 yrs (1998–2013), because the observations at the Climenhaga Observatory (Greimel & Robb 1998) were done using only this filter. First, due to the different comparison stars used at the two observatories, the 1998 and 2000 datasets were shifted to the mean RC of the Konkoly dataset, and then small-amplitude long-term trends were removed from the data. No systematic long-term change resembling a spot cycle or part of it was found. The final Fourier spectrum and the spectral window are shown in Fig. 4. The peak corresponding to stellar rotation is at 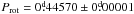 , which is quite close to the finding of 0.445679 days in Vida et al. (2011). We found the same result, Prot = 0.44570 days using the SLLK method (string-length method with Lafler-Kinman statistics, see Clarke 2002). In this paper we used the following ephemeris:
, which is quite close to the finding of 0.445679 days in Vida et al. (2011). We found the same result, Prot = 0.44570 days using the SLLK method (string-length method with Lafler-Kinman statistics, see Clarke 2002). In this paper we used the following ephemeris: 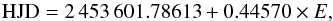 (1)where HJD0 = 2 453 601.78613 is taken from Vida et al. (2011), and E is the cycle count. After pre-whitening the Fourier spectrum with the signal of the rotation period, a very small peak (with
(1)where HJD0 = 2 453 601.78613 is taken from Vida et al. (2011), and E is the cycle count. After pre-whitening the Fourier spectrum with the signal of the rotation period, a very small peak (with 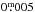 amplitude) corresponding to P = 0.445518 days in the Fourier spectrum is seen. If we accept this as a signal that also stems from the rotation, this would yield a differential rotation shear of | α | = | ΔP/P | ≳ 0.0004, which is very close to a rigid-body rotation, in agreement with the findings of Vida et al. (2013), of Morin et al. (2008a) (α = 0.0004), and of Donati et al. (2006) (α = 0.0014). On GJ 1243, another M4 star with a fast rotation of 0.59 days, Davenport et al. (2015) found a similar differential rotation (| α | = 0.0011) to our estimate on V374 Peg.
amplitude) corresponding to P = 0.445518 days in the Fourier spectrum is seen. If we accept this as a signal that also stems from the rotation, this would yield a differential rotation shear of | α | = | ΔP/P | ≳ 0.0004, which is very close to a rigid-body rotation, in agreement with the findings of Vida et al. (2013), of Morin et al. (2008a) (α = 0.0004), and of Donati et al. (2006) (α = 0.0014). On GJ 1243, another M4 star with a fast rotation of 0.59 days, Davenport et al. (2015) found a similar differential rotation (| α | = 0.0011) to our estimate on V374 Peg.
3.4. Light curve modelling
Light curve modelling was done using the code SpotModeL (Ribárik et al. 2003) that applies an analytic approach and uses at most three circular starspots of homogeneous temperature to fit the photometric data. Limb-darkening coefficients were adopted from Claret et al. (2012). From the colour indices, we can estimate the spot temperatures, and we got about 3250 K for B − V and V − IC indices (3267 ± 5 K and 3244 ± 8 K, respectively, with formal errors), supposing an unspotted temperature of 3400 K corresponding to the dM4 spectral type. Thus, from the photometric spot temperature model, we concluded that the spots are ~150 K cooler than the unspotted surface.
During the almost five years of observations, the light curve was very stable (see Fig. 2). It can be described reasonably well by a two-spot model. From the ΔV light curve, we can estimate the spot parameters λ1 = 143 ± 2°, β1 = 67 ± 3°, γ1 = 42 ± 3° and λ2 = 342 ± 2°, β2 = 71 ± 4°, γ2 = 36 ± 4°, where λ, β, and γ mean the spot longitude, latitude, and radius, respectively. According to this model, the cool spots cover approximately 43% of the stellar surface. This solution is of course not unique, and the parameters are not independent. Spot latitude is the most uncertain, since photometric observations hold only very little information about the latitude of the spots, and the (formal) errors do not indicate the uncertainty of the inclination.
4. Results
4.1. Photometric flares
To study flares on the star, we applied time series spot models to remove the contribution of cool spots (see also Vida et al. 2009). This was performed by SpotModeL by modelling the four-colour light curves that were cleaned from flares, in a time window of 100 days, and by shifting this window by 30-day steps, thus reaching a better-fitting analytic solution to the observations. This analytic solution was then subtracted from the original observations, leaving only the flares and small scatter/variations on the level of a few hundredths of a magnitude.
All ΔB observations are plotted in Fig. 5 where the highest amplitude flares are truncated, showing the spotted light curve better. We can see in the top panel that flares occur in every phase of the rotational modulation. This could mean there are many different flaring regions even near the pole so the flares are seen regardless of rotational phase. Such a polar spot would only cause very small variations in the light curve, so other (non-polar) active regions must still be present.
Since the time resolution of the data is not too high (around 3 min on average), small amplitude and short flares could be represented only by one to two deviating data points. The two histograms in the bottom panel of Fig. 5 show the distribution of such deviating points over 2σ (left) and 3σ (right) above the folded light curve. A certain increase in such events is seen between phases 0.3–0.7, which suggests a more active centre of flaring on the stellar surface.
 |
Fig. 5 Phased ΔB light curves as used for flare statistics (top) and number of light curve points above 2σ/3σ after removing the effect of spottedness (bottom). The top plot does not show the whole magnitude range of flares to better visualise the spotted light curve. |
To determine the flare frequency, we used the method of Ishida et al. (1991), who defined the mean occurrence rate of flares as 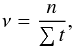 (2)n being the number of observed flares, and ∑ t (h) the monitoring time. We selected flare events using the unspotted ΔB light curve (see Sect. 3.4) by visual inspection, selecting flares that were brighter than 0.05 mag. To detect possible variations in the flaring activity, the ΔB light curve was divided into five blocks (see top panel of Fig. 1). The flare frequencies at the different blocks of the observations are summarised in Table 2. A histogram of flares with different brightness is shown in Fig. 6. The occurrence rate seems to be around 0.2–0.3 h-1, which is relatively stable during the observations. However, flares with peak brightness higher than
(2)n being the number of observed flares, and ∑ t (h) the monitoring time. We selected flare events using the unspotted ΔB light curve (see Sect. 3.4) by visual inspection, selecting flares that were brighter than 0.05 mag. To detect possible variations in the flaring activity, the ΔB light curve was divided into five blocks (see top panel of Fig. 1). The flare frequencies at the different blocks of the observations are summarised in Table 2. A histogram of flares with different brightness is shown in Fig. 6. The occurrence rate seems to be around 0.2–0.3 h-1, which is relatively stable during the observations. However, flares with peak brightness higher than 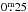 were only found in the second and fourth blocks. In Fig. 6 we also show the cumulative flare frequency distribution (log number of flares that have larger amplitude than log B, see e.g. Lacy et al. 1976; Hawley et al. 2014) as a function of the flare amplitudes in B passband.
were only found in the second and fourth blocks. In Fig. 6 we also show the cumulative flare frequency distribution (log number of flares that have larger amplitude than log B, see e.g. Lacy et al. 1976; Hawley et al. 2014) as a function of the flare amplitudes in B passband.
 |
Fig. 6 Top plots: numbers of flares are shown to their peak B brightness. Bottom plot: cumulative number of flares per day vs. flare amplitudes. |
Summary of flare statistics from the ΔB light curve.
4.2. Flare energies
We selected a few well-observed flare events that were detected in at least two colours. There were deviating points also caused by flares in the RC and IC passbands, but these detections were too weak for modelling. We estimate flare energies in different colours following the method in Kővári et al. (2007). Derived values are listed in Table 3. Flare energy estimations are carried out as follows. First, to derive the relative flare energy for a given event, the  expression is integrated over the flare duration, where
expression is integrated over the flare duration, where 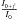 is the ratio of the flaring and the quiescent intensities at the selected photometric band. This quantity, defined by Eq. (2) in Gershberg (1972), is often mentioned in the literature as equivalent duration. The total integrated flare energy is then obtained by multiplying the relative flare energy by the basal (i.e. quiescent) stellar flux (see Kővári et al. 2007 for a more detailed description). Flare energy values are only estimated for those events, which are covered sufficiently by multicolour observations.
is the ratio of the flaring and the quiescent intensities at the selected photometric band. This quantity, defined by Eq. (2) in Gershberg (1972), is often mentioned in the literature as equivalent duration. The total integrated flare energy is then obtained by multiplying the relative flare energy by the basal (i.e. quiescent) stellar flux (see Kővári et al. 2007 for a more detailed description). Flare energy values are only estimated for those events, which are covered sufficiently by multicolour observations.
Studies dedicated to photometric monitoring of dMe stars, such as EV Lac and AD Leo (Leto et al. 1997; Dal & Evren 2012), detected several flares in the B band with energies up to 1033 erg, which fits the determined flare energies of V374 Peg very well. Moreover, the most energetic solar flares show total energies up to 1033 erg (Schrijver et al. 2012; Kretzschmar et al. 2010). As one can see from Table 3, there are flare energies determined from B-band photometry, which show similar values, underlining the violent and energetic nature of dMe star flares.
The energy ratio emitted in the different colours are about the same for the first event of a triple outburst at HJD 2 454 715.394 and for the single events at HJDs 2 455 059.362 and 2 455 087.276, being 1.37, 1.41, 1.41 for EB/EV, respectively. However, in the case of the triple event at 2454715 (see Fig. 9 for a detailed light curve), the energy ratio EB/EV is decreasing during the three consecutive outbursts (separated by about 1.4 and 0.5 h) as 1.37, 1.28, and 1.10. The emitted energy decreases more slowly in the V than in the B passband. This result strongly suggests that the three consecutive eruptions are related. Such events are called sympathetic flares, and they were observed many times on the Sun, where the origin of the flares on the solar surface is seen well. One such interesting example is the 2010 August 1 event on the Sun where three prominence eruptions were observed in the same active region consecutively with about 6 and 12 h difference. The details of this event and its theoretical modelling is found in Török et al. (2011; see also Attrill et al.2007; and cf. Kővári et al.2007). Briefly, these flare events originate in successive flux rope eruptions triggered by nearby eruptions in the appropriate magnetic field structure of the solar corona.
The structure of the magnetic fields of M-dwarf stars, on a much smaller surface are – to the best of our knowledge – simpler than that of the Sun. Concerning stellar sympathetic flares, similar repetitive events to the triple flare of V374 Peg were observed on UV Cet by Panagi & Andrews (1995). The authors explained the phenomenon by supposing strong dipolar magnetic field on the star, where propagation of MHD waves between the poles through the corona and chromosphere triggers the eruptions at the opposite poles. Such scenario is not unlikely on V374 Peg either. According to the Zeeman-Doppler imaging results of Donati et al. (2006) and Morin et al. (2008a) V374 Peg do have a strong dipolar magnetic field, which, similar to UV Cet, may help trigger sympathetic eruptions.
 |
Fig. 7 Phased dynamic Hα spectra from 2005, 2006, 2009 (CFHT observations, top row), 2012, and 2013 (RCC observations, bottom row). Triangles mark the rotational phases of the individual spectra, and a dotted line shows the 0 km s-1 velocity shift. |
Measured flare parameters from different passbands.
4.3. Variations in the Hα region
We obtained spectroscopic observations covering eight years from 2005 August to 2013 August. The last three spectroscopic observing runs – one with the CFHT, the last two with the 1-m RCC telescope – have photometric support from the same observing season (cf. Fig. 1). As an example, the Hα regions from the RCC observations are plotted in Fig. B.1.
To study the behaviour of the Hα line, we plotted its region as dynamic spectra in Fig. 7. In these plots the horizontal and vertical axes represent the wavelength/velocity shift and the phase, respectively. The colour coding corresponds to the intensity of the Hα region; i.e., colours darken with line strength. Triangles on the left-hand side of the plots show the phases of the observations. The plot regions at missing phases were interpolated to the closest measurements using spline interpolation. Colour coding is set individually for each plot so the typical variations can be seen well.
 |
Fig. 8 Dynamic Hα spectra of V374 Peg from 2005, showing strong flare events. First two plots: same data with different wavelength scales. This way the CME signature – the blue wing enhancement – can be also seen (their start indicated with arrows in the second plot). |
The equivalent width of the Hα line was measured for each spectrum using the splot task of IRAF. The variations in the equivalent width with phase was plotted along with a phased light curve (after pre-whitening with long-term trends) for comparison in Fig. 10 (cf. Fig. 10 of Morin et al. 2008a for a similar analysis of the 2005 observations).
The Hα line of V374 Peg is constantly in strong emission. Obvious rotational modulation can only be seen in the 2009 CFHT spectra, and in other cases, the phased data are mainly influenced by the flares. (This can also be a result of the low resolution.) The most powerful Hα flares were observed in 2005. Here, the increase in the Hα emission reappears after the consecutive rotations around both phases 0.2 and 0.9 with a small phase shift (see also Fig. 10). A possible explanation for this could be long-lived loop systems in the chromosphere that generate flares and coronal mass ejections (CMEs).
On HJD 2 453 603 (see dynamic spectra in Fig. 8, H, He lines in Fig. 11 and intensity curves for the Balmer lines in Fig. 13), one can see three distinct blue wing enhancements with different durations and projected velocities, spanning more than three hours. The detailed chronology of these events is described in Appendix A.
Interestingly, the overall level of the Hα line is quite low at the time of the first, double-peaked (or triple) spectrum (see the spectrum plotted in blue in Fig. 11). This could be similar to the pre-flare “dips” observed by Leitzinger et al. (2014) in the young open cluster Blanco-1, although this feature – if real – is only seen in one spectrum and only in the Hα region. Unfortunately, these events are very short (from a few seconds to a few minutes, see Leitzinger et al. 2014, and references therein) and rather weak, so that the five-minute sampling in our spectra is not optimal for detecting these events.
To measure the flux of the enhancement we selected wavelength windows that vary from 6547.0–6561.1 Å (722–78 km s-1) to 6555.0–6561.1 Å (357–78 km s-1) from which we subtracted the continuum flux measured in the same windows. The continuum flux level was adopted from the M4V star GJ699 taken from Cincunegui & Mauas (2004). Since the blue-wing enhancement occurred during a flare on V374 Peg, it is difficult to disentangle the contribution from the flare and the CME. We expect that the contamination of the blue wing of Hα from the flare occurs at low velocities close to Hα line centre. Using fixed windows, we underestimate the total flux caused by the ejection. The estimation of the CME mass depends on the measured flux. However, with the method we used for the estimation of the CME mass (see next paragraph) we are able to determine a lower limit to the CME mass only.
From the Hα blue wing flux enhancement, one can estimate the mass of the CME. We use 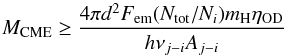 (3)adopted from Houdebine et al. (1990). Equation (3) is comprised of the distance of the star d, the flux of the emission feature Fem, the total number of hydrogen atoms Ntot, the number of hydrogen atoms in an excited state i, Ni, the opacity damping factor ηOD, the mass of a hydrogen atom mH, the Einstein coefficient for transition Aj − i, frequency ν, and Planck’s constant h. Since we have no estimation for the ratio Ntot/N3 (corresponding to Hα), we follow the method from Leitzinger et al. (2014). First they used the Balmer decrement (BD) to scale the measured Hα flux to Hγ, i.e. Fem,γ = Fem,α/BD, with BD = 3 valid for solar and stellar flares (Butler et al. 1988). Then the parameters of the Hγ line can be used in Eq. (3), including the value Ntot/N5 ~ 2 × 109 given by Houdebine et al. (1990), which is valid for temperatures of about 20 000 K and densities of 1010 − 1012 cm-3 and which was derived from NLTE radiative transfer modelling. Furthermore, we adopt ηOD = 2 to account for optical thickness of the lower Balmer lines (Houdebine et al. 1990).
(3)adopted from Houdebine et al. (1990). Equation (3) is comprised of the distance of the star d, the flux of the emission feature Fem, the total number of hydrogen atoms Ntot, the number of hydrogen atoms in an excited state i, Ni, the opacity damping factor ηOD, the mass of a hydrogen atom mH, the Einstein coefficient for transition Aj − i, frequency ν, and Planck’s constant h. Since we have no estimation for the ratio Ntot/N3 (corresponding to Hα), we follow the method from Leitzinger et al. (2014). First they used the Balmer decrement (BD) to scale the measured Hα flux to Hγ, i.e. Fem,γ = Fem,α/BD, with BD = 3 valid for solar and stellar flares (Butler et al. 1988). Then the parameters of the Hγ line can be used in Eq. (3), including the value Ntot/N5 ~ 2 × 109 given by Houdebine et al. (1990), which is valid for temperatures of about 20 000 K and densities of 1010 − 1012 cm-3 and which was derived from NLTE radiative transfer modelling. Furthermore, we adopt ηOD = 2 to account for optical thickness of the lower Balmer lines (Houdebine et al. 1990).
 |
Fig. 9 ΔB and ΔV light curve of the complex flare event from HJD 2 454 715. |
 |
Fig. 10 Top plot: folded and averaged ΔR light curve of V374 Peg, including the observations from 1998 and 2000, after removing long-term trends. Bottom plots: change in Hα equivalent width with rotational phase, colours brightening with time. |
According to the estimation of the CME mass described above, we find a minimum CME mass in the order of 1016 g. This value is comparable to the most massive solar CME masses reaching 1017 g (see e.g. Vourlidas et al. 2010).
To estimate the expected number of CMEs above 1016 g mass, we make use of the method applied in Leitzinger et al. (2014). This method uses flare rates predicted by the scaling of flare rate with stellar X-ray luminosity from Audard et al. (2000) together with a CME mass-flare energy relation from the Sun (Drake et al. 2013) to estimate stellar CME rates from stellar X-ray luminosities. Adopting log LX ≈ 28.4 erg s-1 for V374 Peg (Hünsch et al. 1999), we infer 15–60 CMEs per day with a mass >1016 g for a range of flare power law indices α of 1.8–2.3 (Leitzinger et al. 2014, their Fig. 5). These numbers are larger than what has been observed in this study (1 event in 10 h), but the detectability of stellar CMEs is affected by projection effects (random directions of ejection, not always leading to sufficiently blue-shifted signals). Moreover, the extrapolation of flare-CME relations known from the Sun to young active stars is still debated (Drake et al. 2013). In Sect. 5.3 we discuss these results with respect to the stellar CMEs detected thus far, which are sparse.
In the case of the HJD 2 453 605 flare event, no significant velocity shifts can be seen that could indicate CMEs.
 |
Fig. 11 Individual Hα, Hβ, Hγ, and He i spectra from the beginning of the 2 453 603 flare event. Grey lines show pre-flare spectra, coloured lines show the brightening part of the flare. The spectra were corrected for the radial velocity of V374 Peg with the value of Vγ = −3 km s-1 (Montes et al. 2001). |
 |
Fig. 12 Dynamic Hβ, Hγ, and He i spectra of V374 Peg from HJD 2 453 603, showing strong flare events. Arrows indicate the start of the blue wing enhancements(see text). |
5. Discussion
5.1. Connection between the photosphere and chromosphere
The connection between the chromospheric and photospheric activity on the Sun has been known for a long time. This connection was also observed on other active stars, such as in the case of the dM1-2 type EY Dra (Korhonen et al. 2010), the fully convective K7-type T Tauri star TWA 6 (Skelly et al. 2008), and other BY Dra type stars (Pandey et al. 2005). To study the behaviour of the chromosphere, the Hα region is the most widely used proxy for M dwarfs. In the case of a Sun-like connection between the photosphere and chromosphere, we would expect anticorrelation between the light curve and the Hα equivalent width, meaning that the chromospheric activity would increase in those phases, where we see the dark spots in the light curve. The case is not necessarily that obvious, since bright photospheric structures on the Sun, as well as prominence-like features, are seen better off-limb rather than when projected against the stellar disc (Hall & Ramsey 1992). In Fig. 10 the Hα equivalent widths from different epochs are plotted along with the phased ΔR light curve. This dataset has the longest time span of 16 yrs and shows a stable light curve all the time, before and after the spectroscopic observations were taken. Unfortunately, the spectroscopic results from the RCC telescope (in 2012 and 2013) are quite inconclusive, because the size of the telescope did not allow using short exposures, thus the shorter-term variations caused by possible flares cannot be temporally resolved. In the case of the CFHT data (between 2005 and 2009), an obvious anticorrelation can be seen in 2009 September. Without any indication of flares, only a rotational modulation was apparent. Interestingly, this is the part of the photometric observation, where frequent strong flare activity was observed. There are photometric observations three weeks before and one week after these spectra were obtained. No global trends are seen for the 2005 and 2006 spectra, just variations caused by flares, especially in 2005. Here, the increase in the Hα activity seems to be concentrated around phases 0.2 and 0.8–1.0, the latter being the part where the light curve shows the faintest state.
 |
Fig. 13 Light curves for the HJD 2 453 603 event for Hα, Hβ, Hγ, and Hδ. The flare, which can be seen easily, is pronounced in Hβ, Hγ, and Hδ, and much weaker in Hα. The starting times of the BWE are indicated with arrows. |
 |
Fig. 14 Phased ΔB light curves as used for flare statistics. Colours brighten with HJD. The second and fourth plots do not show the strongest flares. |
In Fig. 14 folded ΔB light curves are plotted in those epochs that were used for flare statistics (see Sect. 4.1). The global shape of the light curve, i.e. the large-scale spot configuration, does not change in this time significantly. Flares can be seen in all cases at every phase, however the strongest flares seem to be more concentrated around phase 0.3–0.7 (see also Fig. 5).
5.2. Photometric variability
We found that the light curve, thus the overall surface structures are stable for at least 16 yrs on V374 Peg (cf. Fig. 10, top panel). This agrees with the finding of Morin et al. (2008a) that the magnetic configuration did not change on a yearly timescale. The star furthermore seems to rotate as a rigid body or has a very weak differential rotation, as we found from the Fourier analysis (see Sect. 3.3), in agreement with the results of Donati et al. (2006) based on Zeeman-Doppler images. According to the theoretical model of Küker & Rüdiger (2011), we would expect α ≈ 0.008 for a star of 0.3 M⊙ and Prot = 0.5 d. Our findings are in good agreement with the recent theoretical dynamo model for fully convective stars of Yadav et al. (2015), which suggests that these stars have stable magnetic fields, very small differential rotation, polar spots, and active regions distributed throughout the stellar phase (implying flare distribution independent of rotation phase).
However, besides this stable spot configuration, the light curve is not constant at all: small changes can be seen continuously on a nightly timescale (see Fig. 14). These variations are mainly seen between phases 0.3–0.6. These minute intensity variations could be caused by newly born and decaying small spots in the same active nest, similarly to the emerging flux ropes in active nests on our Sun.
5.3. CMEs
The CME/flare detected on V374 Peg in the CFHT data on HJD 2 453 603 represents a unique event compared to the ones from literature. First of all the length of the observations (more than 10 h of continuous monitoring) enables comparison of variability before and after the event. Stellar CMEs are sporadically observed phenomena, and their detection so far presented in literature happened by chance, except the event presented by Guenther & Emerson (1997), who performed a dedicated search for stellar activity through spectrophotometry in Hα. In the literature, only single events that the authors have assigned to stellar CMEs can be found. Houdebine et al. (1990) detected the fastest CME on a late-type main-sequence star AD Leo in the optical, which showed a maximum projected velocity of ~5800 km s-1. Other events in the optical domain were presented by Gunn et al. (1994) on the dMe star AT Mic, Guenther & Emerson (1997) on a dM0 weak-line T-Tauri star, and Fuhrmeister & Schmitt (2004) on an old dM star. Stellar CME events in the UV/FUV were presented by Bond et al. (2001) on the pre-cataclysmic binary V471 Tau, and Leitzinger et al. (2011) again on AD Leo. Interestingly, all detected CMEs with the method of Doppler-shifted emission in optical spectra have so far been detected on dMe stars.
In the case of V374 Peg, we detected three distinct blue-wing enhancements that occurred during a flare (cf. the discussion on sympathetic flares in Sect. 4.2), after a quiet period of at least three hours (see Figs. 8, 1113). The chronology of the three events is that at t0, BWE1 arises simultaneously with an Hα flare. Nearly two hours later, BWE2 begins to rise, and finally 50 min later the fastest event, BWE3 starts. We calculated an escape velocity for V374 Peg of ve ≈ 580 km s-1 using 0.30 M⊙ and 0.34 R⊙ (see Sect. 3.1). The projected maximum velocity of BWE3 (675 km s-1) is above the escape velocity, which means that during this event, mass was ejected from the star. The two precursor events (BWE1, BWE2) show maximum velocities below ve (each ~−350 km s-1) and therefore cannot be distinctively assigned to mass ejected from the star. If we assume that all three events belong to the same active nest, then BWE1 and BWE2 could also be failed eruptions. On the Sun, events have been reported (Zhou et al. 2006) where prominences failed to erupt, while the remaining filament has reformed, since then ejected, and observed as a CME. The observed red-wing enhancements after the CME event could be a result of material falling back on the stellar surface, as seen on the Sun.
If we assume that the event is connected with the photospheric active regions, as seen for instance on the Sun, but also other stars (see e.g. Korhonen et al. 2010), we can estimate the real velocity of the CMEs. According to the spot models, both active nests are located around 70° latitude (although this is the most uncertain spot parameter), this means that the CME happened roughly along the line of sight, assuming an inclination of 70° (see Donati et al. 2006). This suggests that the projected velocity could be close to the true velocity of the ejection. An uncertainty of ~10° in the inclination or the spot latitude would cause only a difference of 1–2% in the maximal speed of the ejecta.
The three events span a time range of about three hours, which corresponds to about 30% of the stellar rotation period. If, as assumed above, the signatures are connected to the same active nest, then the rotation of the nest has a significant influence on the projected velocity of the events. BWE1 started at phase 0.72, while the centre of the large spotted region is at λ ≈ 340°, i.e. the 0.94 phase. If this eruption happened in the middle of this nest, we would thus only observe ~19% of the actual velocity (neglecting the effect of the latitude). For BWE2 and BWE3 this value is 95% and 98%, respectively. The large size of the active region (γ ≈ 42° radius), however, causes a rather large uncertainty in these estimated values.
Although V374 Peg has a rotation period of <0.5 days, its Hα profile is not rotationally broadened enough (vsini = 36.5 km s-1, see Morin et al. 2008b) to detect absorption features as signatures of co-rotating clouds (Collier Cameron & Robinson 1989), which are commonly interpreted as stellar analogues of solar prominences.
The ejected mass at BWE3 that we deduced to be in the range of ~1016g fits the mass of massive solar CMEs. However, the method of determining the mass of stellar CMEs used in this paper is probably accurate only within an order of magnitude. Non-local thermal equilibrium (NLTE) modelling is necessary to self consistently calculate the radiative transfer from which a more accurate mass may be determined.
The theoretical CME rate that we deduced based on the method presented in Leitzinger et al. (2014) relies on the solar CME mass-flare energy relation (Aarnio et al. 2012) and the empirically determined flare power law from Audard et al. (2000). Depending on the flare index α, the obtained CME rate is 15–60 CMEs (M>Mc, Mc = 1016 g) per day. However, only a fraction of this number can be observed owing to projection effects when assuming that CMEs can be ejected anywhere from the star.
The stellar parameter on which the theoretical CME rate depends is the stellar X-ray luminosity as indicator for activity. V374 Peg has a log Lx of 28.4 erg s-1 (Hünsch et al. 1999), which is roughly one order of magnitude higher than for the Sun during activity cycle maximum (Peres et al. 2000). The observed CME rate of the Sun, considering a whole cycle (Robbrecht et al. 2009), lies between 0.5 and 8 CMEs per day on average, which is lower than the theoretical CME rate of V374 Peg, as expected (although it is possible that the reason for this discrepancy is that we simply cannot observe most of the stellar CMEs). One has to keep in mind that the solar-stellar analogy might work for solar-like stars, so the extrapolation of solar knowledge to dM stars has to be done very carefully. The question of whether young stars also exhibit more massive CMEs than the Sun is still open.
However, the extrapolation of solar CME parameter distributions is the only possibility at the moment to gain knowledge on CME frequency on stars others than the Sun, since no observationally determined CME parameter distributions of late-type main-sequence stars exist.
6. Summary
Using long-term photometric and spectroscopic observations we studied V374 Peg, an active, fully convective cool dwarf. In this paper, we refined the stellar parameters, which are summarised in Table 4. From our analysis the following conclusions can be drawn:
Parameters of V374 Peg.
-
The light curve is stable over about 16 yrs, which confirms the previous indications of a very stable magnetic field.
-
Besides the stable spot configuration, small changes can be seen on a nightly timescale, possibly caused by newly born and decaying small spots in the same active nest.
-
According to Fourier analysis, there is only one significant peak in the power spectrum that corresponds to the stellar rotation and an additional small amplitude signal close to it.
-
The Fourier spectrum suggests very weak differential rotation (almost solid-body), and we found indications of a shear parameter of α = 0.0004.
-
There is no sign of activity cycles in the light curve.
-
Frequent flaring was observed. The occurrence rate of weak flare seems to be similar in every season on average, but the frequency of strong flares varies on weekly-monthly timescales within a year.
-
Flares were observed at every rotation phase, the strongest flares seem to be more concentrated around phase 0.3–0.7, i.e. where the light curve indicates a smaller active region (or an activity nest on the southern hemisphere that can be only partly seen).
-
In the light curve, a complex flare was detected with repeated eruptions. The similar B/V energy ratios suggest a sympathetic flare event.
-
In the spectroscopic data, a complex eruption including a CME was detected with falling-back and re-ejected material, with a maximal projected velocity of ~675 km s-1.
-
We estimated that the mass of the ejecta is higher than 1016 g, which is comparable to the strongest solar CME masses.
-
The observed CME rate is much lower than expected from extrapolation of the solar flare-CME relation to active stars, which could indicate that the solar-stellar analogy could not be applied to the cool dMe stars directly.
-
The spectral energy distribution does not suggest hot dust around the star that could be a result of high activity and strong stellar wind.
Available at http://www.cadc-ccda.hia-iha.nrc-cnrc.gc.ca/en/cfht/
Available at http://www.sciops.esa.int/index.php?project=SAT&page=vospec
Acknowledgments
The authors would like to thank A. Moór for the helpful discussions and the anonymous referee for the helpful comments that improved the paper significantly. The authors acknowledge support from the Hungarian Research Grants OTKA K-109276, OTKA K-113117, the Lendület-2009 and Lendület-2012 Programme (LP2012-31) of the Hungarian Academy of Sciences, and the ESA PECS Contract No. 4000110889/14/NL/NDe. This research used the facilities of the Canadian Astronomy Data Centre operated by the National Research Council of Canada with the support of the Canadian Space Agency.
M.L. and P.O. acknowledge support from the FWF project P22950-N16.
This research used observations obtained at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council of Canada, the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientique of France, and the University of Hawaii.
The Two Micron All Sky Survey (2MASS) is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation, USA. (http://www.ipac.caltech.edu/2mass/)
This publication makes use of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration.
References
- Aarnio, A. N., Matt, S. P., & Stassun, K. G. 2012, ApJ, 760, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Attrill, G. D. R., Harra, L. K., van Driel-Gesztelyi, L., & Démoulin, P. 2007, ApJ, 656, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Audard, M., Güdel, M., Drake, J. J., & Kashyap, V. L. 2000, ApJ, 541, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Batyrshinova, V. M., & Ibragimov, M. A. 2001, Astron. Lett., 27, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, L., Herald, J., Efremova, B., et al. 2011, Ap&SS, 335, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Bond, H. E., Mullan, D. J., O’Brien, M. S., & Sion, E. M. 2001, ApJ, 560, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Cincunegui, C., & Mauas, P. J. D. 2004, A&A, 414, 699 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., Hauschildt, P. H., & Witte, S. 2012, A&A, 546, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clarke, D. 2002, A&A, 386, 763 [Google Scholar]
- Collier Cameron, A., & Robinson, R. D. 1989, MNRAS, 236, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Csák, B., Kovács, J., Szabó, G. M., et al. 2014, Contributions of the Astronomical Observatory Skalnate Pleso, 43, 183 [NASA ADS] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
- Cutri, R. M., & et al. 2014, VizieR Online Data Catalog: II/328 [Google Scholar]
- Dal, H. A., & Evren, S. 2012, New Astron., 17, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Davenport, J. R. A., Hebb, L., & Hawley, S. L. 2015, ApJ, 806, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Delfosse, X., Forveille, T., Ségransan, D., et al. 2000, A&A, 364, 217 [NASA ADS] [Google Scholar]
- Dobler, W., Stix, M., & Brandenburg, A. 2006, ApJ, 638, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F. 2003, in Solar Polarization, eds. J. Trujillo-Bueno, & J. Sanchez Almeida, ASP Conf. Ser., 307, 41 [Google Scholar]
- Donati, J. F., Forveille, T., Collier Cameron, A., et al. 2006, Science, 311, 633 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Drake, J. J., Cohen, O., Yashiro, S., & Gopalswamy, N. 2013, ApJ, 764, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmeister, B., & Schmitt, J. H. M. M. 2004, A&A, 420, 1079 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gershberg, R. E. 1972, Ap&SS, 19, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Greimel, R., & Robb, R. M. 1998, Information Bulletin on Variable Stars, 4652, 1 [Google Scholar]
- Guenther, E. W., & Emerson, J. P. 1997, A&A, 321, 803 [NASA ADS] [Google Scholar]
- Gunn, A. G., Doyle, J. G., Mathioudakis, M., Houdebine, E. R., & Avgoloupis, S. 1994, A&A, 285, 489 [NASA ADS] [Google Scholar]
- Hackman, T., Jetsu, L., & Tuominen, I. 2001, A&A, 374, 171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hall, J. C., & Ramsey, L. W. 1992, AJ, 104, 1942 [NASA ADS] [CrossRef] [Google Scholar]
- Hauschildt, P. H., Allard, F., & Baron, E. 1999, ApJ, 512, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, S. L., Davenport, J. R. A., Kowalski, A. F., et al. 2014, ApJ, 797, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Houdebine, E. R., Foing, B. H., & Rodono, M. 1990, A&A, 238, 249 [NASA ADS] [Google Scholar]
- Hünsch, M., Schmitt, J. H. M. M., Sterzik, M. F., & Voges, W. 1999, A&AS, 135, 319 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ishida, K., Ichimura, K., Shimizu, Y., & Mahasenaputra. 1991, Ap&SS, 182, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Ishihara, D., Onaka, T., Kataza, H., et al. 2010, A&A, 514, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kővári, Zs., Vilardell, F., Ribas, I., et al. 2007, Astron. Nachr., 328, 904 [NASA ADS] [CrossRef] [Google Scholar]
- Kolláth, Z. 1990, Konkoly Observatory Occasional Technical Notes, 1, 1 [Google Scholar]
- Korhonen, H., Vida, K., Husarik, M., Mahajan, S., & Oláh, K. 2010, Astron. Nachr., 331, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Kretzschmar, M., de Wit, T. D., Schmutz, W., et al. 2010, Nat. Phys., 6, 690 [NASA ADS] [CrossRef] [Google Scholar]
- Küker, M., & Rüdiger, G. 1999, A&A, 346, 922 [NASA ADS] [Google Scholar]
- Küker, M., & Rüdiger, G. 2011, Astron. Nachr., 332, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Kurucz, R. I. 1993, ATLAS-9, CD-ROM 13 [Google Scholar]
- Lacy, C. H., Moffett, T. J., & Evans, D. S. 1976, ApJS, 30, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Leitzinger, M., Odert, P., Ribas, I., et al. 2011, A&A, 536, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leitzinger, M., Odert, P., Greimel, R., et al. 2014, MNRAS, 443, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Leto, G., Pagano, I., Buemi, C. S., & Rodono, M. 1997, A&A, 327, 1114 [NASA ADS] [Google Scholar]
- Mann, A. W., Feiden, G. A., Gaidos, E., Boyajian, T., & von Braun, K. 2015, ApJ, 804, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Montes, D., López-Santiago, J., Gálvez, M. C., et al. 2001, MNRAS, 328, 45 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Morin, J., Donati, J. F., Forveille, T., et al. 2008a, MNRAS, 384, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Morin, J., Donati, J.-F., Petit, P., et al. 2008b, MNRAS, 390, 567 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Panagi, P. M., & Andrews, A. D. 1995, MNRAS, 277, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Pandey, J. C., Singh, K. P., Drake, S. A., & Sagar, R. 2005, AJ, 130, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Peres, G., Orlando, S., Reale, F., Rosner, R., & Hudson, H. 2000, ApJ, 528, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Piskunov, N. E., Tuominen, I., & Vilhu, O. 1990, A&A, 230, 363 [NASA ADS] [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
- Reid, I. N., Hawley, S. L., & Gizis, J. E. 1995, AJ, 110, 1838 [NASA ADS] [CrossRef] [Google Scholar]
- Ribárik, G., Oláh, K., & Strassmeier, K. G. 2003, Astron. Nachr., 324, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, J. B., Wehlau, W. H., & Khokhlova, V. L. 1989, A&A, 208, 179 [NASA ADS] [Google Scholar]
- Robbrecht, E., Berghmans, D., & Van der Linden, R. A. M. 2009, ApJ, 691, 1222 [NASA ADS] [CrossRef] [Google Scholar]
- Rodrigues da Silva, R., Canto Martins, B. L., & De Medeiros, J. R. 2015, ApJ, 801, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Scaltriti, F., Busso, M., Ferrari-Toniolo, M., et al. 1993, MNRAS, 264, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., Beer, J., Baltensperger, U., et al. 2012, J. Geophys. Res. (Space Phys.), 117, 8103 [NASA ADS] [CrossRef] [Google Scholar]
- Skelly, M. B., Unruh, Y. C., Collier Cameron, A., et al. 2008, MNRAS, 385, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Török, T., Panasenco, O., Titov, V. S., et al. 2011, ApJ, 739, L63 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vida, K., Oláh, K., Kővári, Z., et al. 2009, A&A, 504, 1021 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vida, K., Oláh, K., & Kővári, Zs. 2011, The Physics of Sun and Star Spots, 273, 460 [NASA ADS] [Google Scholar]
- Vida, K., Kriskovics, L., & Oláh, K. 2013, Astron. Nachr., 334, 972 [Google Scholar]
- Vidotto, A. A., Jardine, M., Opher, M., Donati, J. F., & Gombosi, T. I. 2011, MNRAS, 412, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Vourlidas, A., Howard, R. A., Esfandiari, E., et al. 2010, ApJ, 722, 1522 [NASA ADS] [CrossRef] [Google Scholar]
- Yadav, R. K., Christensen, U. R., Morin, J., et al. 2015, ApJ, 813, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, G. P., Wang, J. X., Zhang, J., et al. 2006, ApJ, 651, 1238 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Detailed description of the complex CME event on HJD 2 453 603
On HJD 2 453 603 a complex CME event was observed in the spectra (see dynamic spectra in Fig. 8, H, He lines in Fig. 11, and intensity curves for the Balmer lines in Fig. 13). The chronology is as follows: blue wing enhancement ?1 (BWE1) starts at HJD 2 453 603.89 (t1), lasts for nearly 30 min. and reaches a maximum projected velocity of ~−350 km s-1. Also the red wing of Hα is increased but is not as significant as the Hα blue wing. At the same time the Hα profile starts to rise and marks the beginning of an impulsive flare phase. We detect a double-peaked Hα line, with maxima at −45 km s-1 and 15 km s-1, and also an additional narrower peak at −65 km s-1 (see also Fig. 11). At the same time the Hβ and Hγ lines rise dramatically and show a symmetrically broadened line profile, in contrast to the blue asymmetric broadened Hα profile (BWE1). Moreover, the He i line strength at 5876 Å also dramatically increases during the impulsive flare phase (see Figs. 11 and 12). In the next spectrum about 15 min later, the narrow peak cannot be seen any more, and the double peaked feature is also less prominent. In the next spectrum, about five minutes later the double peak almost disappears, and the continuum levels is also lowered. During the next one-and-a-half hours, the Hα peak stays high, whereas the wings are not broadened anymore.
Then at HJD 2 453 603.966 (t2), the blue wing of Hα starts to rise again (BWE2), although the peak is still increased. The blue-wing asymmetry lasts for 50 min and shows a maximum projected velocity of −350 km s-1 again. The red wing of Hα increases much more slowly. Also the blue wings of Hβ and Hγ increase and show projected velocities of −275 km s-1.
Although the blue wing of Hα did not reach its quiescent form, the Hα blue wing starts to rapidly increase (BWE3)at HJD 2 453 604.001 (t3) and forms a broad enhancement present for ~45 min, showing a maximum projected velocity of −675 km s-1. And also the Hβ and Hγ show similar blue wing enhancement with maximum projected velocities of −620 km s-1. After this turbulent events Hα, Hβ, and Hγ show red wing enhancements lasting for nearly two hours.
Appendix B: Attempts on Doppler imaging
We have tried to derive Doppler images from the CFHT spectra downloaded from the CFHT Science Archive with two codes: TempMap (Rice et al. 1989) and INVERS7PD (Piskunov et al. 1990; Hackman et al. 2001). In both cases, three consecutivespectra were averaged in order to increase S/N. The resulting smearing were always lower than the surface resolution of our reconstructions, i.e., 5°. Astrophysical parameters were adopted from Donati et al. (2006) and Morin et al. (2008a). With TempMap, Kurucz atmospheric models (Kurucz 1993) were used, while the INVERS7PD attempts were carried out with the MARCS models. Atomic parameters were obtained from the VALD database (Piskunov et al. 1995; Kupka et al. 1999).
 |
Fig. B.1 Hα profiles from the 1-m RCC telescope (2012/2013) (colour saturation increasing with time). |
The inversions were attempted on both Ca i 6439 and Fe i 6430. Other mapping lines in the region have not been used owing to insufficient line strength or heavy blending with molecular bands. Ultimately, both inversion attempts proved unsuccessful. We suspect that the causes are the following:
-
Both the Kurucz and the MARCS models are insufficient in the domain of M dwarfs.
-
It is possible that the extremely strong chromospheric activity leads to the otherwise photospheric lines (mostly in case of the Ca i 6439) being burdened with emission cores.
-
The region containing the lines used during the inversion is heavily affected by molecular bands.
Thus, synthesizing adequate model spectra and fitting them to the observed data proved virtually impossible. We conclude, however, that an inversion attempt on TiO bands might be possible with data of higher S/N.
All Tables
All Figures
 |
Fig. 1 BV(RI)C photometry of V374 Peg from the Piszkéstető observations. Ranges marked in the ΔB light curve were used for flare statistics (see Sect. 4.1). Arrows over the ΔI light curve point at the dates of the spectroscopic observations during this time. |
| In the text | |
 |
Fig. 2 ΔV light curve of V374 Peg at the top and the marked parts phased at the bottom. Continuous line shows a model fit with two spots (see Sect. 3.4). The plot does not show most of the flares. |
| In the text | |
 |
Fig. 3 Spectral energy distribution of V374 Peg from the ultraviolet to mid-infrared using NextGen model atmospheres (see text for more details). Errors bars are smaller than the symbols used for the plot. |
| In the text | |
 |
Fig. 4 Fourier spectrum of the ΔR light curve (top), the spectrum pre-whitened with the rotation frequency (middle), the inset showing a zoom-in to the rotation area, and the spectral window (bottom). |
| In the text | |
 |
Fig. 5 Phased ΔB light curves as used for flare statistics (top) and number of light curve points above 2σ/3σ after removing the effect of spottedness (bottom). The top plot does not show the whole magnitude range of flares to better visualise the spotted light curve. |
| In the text | |
 |
Fig. 6 Top plots: numbers of flares are shown to their peak B brightness. Bottom plot: cumulative number of flares per day vs. flare amplitudes. |
| In the text | |
 |
Fig. 7 Phased dynamic Hα spectra from 2005, 2006, 2009 (CFHT observations, top row), 2012, and 2013 (RCC observations, bottom row). Triangles mark the rotational phases of the individual spectra, and a dotted line shows the 0 km s-1 velocity shift. |
| In the text | |
 |
Fig. 8 Dynamic Hα spectra of V374 Peg from 2005, showing strong flare events. First two plots: same data with different wavelength scales. This way the CME signature – the blue wing enhancement – can be also seen (their start indicated with arrows in the second plot). |
| In the text | |
 |
Fig. 9 ΔB and ΔV light curve of the complex flare event from HJD 2 454 715. |
| In the text | |
 |
Fig. 10 Top plot: folded and averaged ΔR light curve of V374 Peg, including the observations from 1998 and 2000, after removing long-term trends. Bottom plots: change in Hα equivalent width with rotational phase, colours brightening with time. |
| In the text | |
 |
Fig. 11 Individual Hα, Hβ, Hγ, and He i spectra from the beginning of the 2 453 603 flare event. Grey lines show pre-flare spectra, coloured lines show the brightening part of the flare. The spectra were corrected for the radial velocity of V374 Peg with the value of Vγ = −3 km s-1 (Montes et al. 2001). |
| In the text | |
 |
Fig. 12 Dynamic Hβ, Hγ, and He i spectra of V374 Peg from HJD 2 453 603, showing strong flare events. Arrows indicate the start of the blue wing enhancements(see text). |
| In the text | |
 |
Fig. 13 Light curves for the HJD 2 453 603 event for Hα, Hβ, Hγ, and Hδ. The flare, which can be seen easily, is pronounced in Hβ, Hγ, and Hδ, and much weaker in Hα. The starting times of the BWE are indicated with arrows. |
| In the text | |
 |
Fig. 14 Phased ΔB light curves as used for flare statistics. Colours brighten with HJD. The second and fourth plots do not show the strongest flares. |
| In the text | |
 |
Fig. B.1 Hα profiles from the 1-m RCC telescope (2012/2013) (colour saturation increasing with time). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


