| Issue |
A&A
Volume 589, May 2016
|
|
|---|---|---|
| Article Number | A77 | |
| Number of page(s) | 16 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201526706 | |
| Published online | 15 April 2016 | |
Characterization of a dense aperture array for radio astronomy
1 Station de radioastronomie de Nançay, Observatoire de Paris, CNRS, 75014 Paris, France
e-mail: steve.torchinsky@obspm.fr
2 Onsala Space Observatory, Chalmers University of Technology, 41258 Gothenburg, Sweden
3 Astrophysics, University of Oxford, Denys Wilkinson Building, Keble Road, Oxford OX1 3RH, UK
4 Department of Physics and Electronics, Rhodes University, PO Box 94, 6140 Grahamstown, South Africa
5 Department of Physics & Astronomy, University of the Western Cape, 7535 Cape Town, South Africa
6 SKA South Africa, 7405 Cape Town, South Africa
Received: 9 June 2015
Accepted: 16 February 2016
EMBRACE@Nançay is a prototype instrument consisting of an array of 4608 densely packed antenna elements creating a fully sampled, unblocked aperture. This technology is proposed for the Square Kilometre Array and has the potential of providing an extremely large field of view making it the ideal survey instrument. We describe the system, calibration procedures, and results from the prototype.
Key words: instrumentation: interferometers / telescopes
© ESO, 2016
1. Introduction
The Square Kilometre Array (SKA; Dewdney et al. 2009) will be the largest radio astronomy facility ever built with more than ten times the equivalent collecting area of currently available facilities. The SKA will primarily be a survey instrument with exquisite sensitivity and an extensive field of view, providing an unprecedented mapping speed. This capability will enormously advance our understanding of fundamental physics including gravitation, the formation of the first stars, and the origin of magnetic fields, and it will give us a new look at the variability of the Universe with a survey of transient phenomena.
A revolution in radio-receiving technology is underway with the development of densely packed phased arrays. This technology can provide an exceptionally large field of view, while at the same time sampling the sky with high angular resolution. The Nançay radio observatory is a major partner in the development of dense phased arrays for radio astronomy, working closely with The Netherlands Institute for Radio Astronomy (ASTRON). The joint project is called EMBRACE (Electronic MultiBeam Radio Astronomy Concept). Two EMBRACE prototypes have been built. One at Westerbork in The Netherlands (called EMBRACE@Westerbork) and one at Nançay (EMBRACE@Nançay, see Fig. 1). The EMBRACE prototypes are recognized as “Pathfinders” for the SKA project. Conclusions from the EMBRACE testing will directly feed into the SKA and will have a decisive impact on whether dense array technology is used for the SKA.
 |
Fig. 1 EMBRACE@Nançay is composed of 4608 Vivaldi antenna elements separated from each other by 12.5 cm, making it a dense array for frequencies above 1200 MHz. EMBRACE@Nançay measures 8.42 m × 8.42 m for a total area of 70.8 m2. |
The date for selecting technology for the SKA is 2018. If dense arrays are not selected for the SKA, then the SKA will have a much reduced mapping speed compared to what has come to be expected by the astronomical community. It is therefore crucial that work on EMBRACE succeeds in showing the viability of dense arrays for radio astronomy.
The two EMBRACE stations began with an initial period of engineering testing on the partially complete arrays (Olofsson et al. 2009; Wijnholds et al. 2009). EMBRACE@Nançay has been fully operational since 2011 and now performs regularly scheduled astronomical observations, such as pulsar observations and extragalactic spectral line observing (Torchinsky et al. 2013, 2015). EMBRACE system characteristics, such as beam main lobe and system temperature, are behaving as expected. EMBRACE has long-term stability, and after four years of operation it continues to prove itself as a robust and reliable system capable of sophisticated radio astronomy observations.
 |
Fig. 2 EMBRACE@Nançay system architecture consists of a four level hierarchy of analogue beamforming starting with 4608 Vivaldi antenna elements leading finally to 16 inputs to each of two digital backends. |
Components in the beamforming hierarchy.
2. EMBRACE system description
EMBRACE@Nançay is a phased-array of 4608 densely packed antenna elements (64 tiles of 72 elements each). For mechanical and electromagnetic performance reasons, EMBRACE@Nançay has, in fact, 9216 antenna elements, but only one polarization (4608 elements) has fully populated signal chains. The orientation of the linear polarized elements at Nançay is with the electric field sensitivity in the north-south direction. The tuning range for EMBRACE was originally designed to be from 500 MHz to 1500 MHz, however, the extremely powerful digital television transmitter in UHF channel 66 at 834 MHz created problems of saturation and intermodulation of the analogue components, especially the beamformer chip. As a result, high-pass filters were added to the system to restrict the tuning range to frequencies above 900 MHz. For more details on EMBRACE architecture, see Kant et al. (2009, 2011)
2.1. Hierarchical analogue beam forming
EMBRACE@Nançay uses a hierarchy of four levels of analogue beamforming leading to 16 inputs to the LOFAR backend system used for digital beamforming (van Haarlem et al. 2013). An overview of the hierarchy is shown in the frontend architecture diagram (Fig. 2) and Table 1 gives a summary of the total number of components at each stage of analogue beamforming.
The first level of beamforming is done for four Vivaldi elements within the integrated circuit “beamformer chip” developed at Nançay (Bosse et al. 2010). This chip applies the phase shifts necessary to four antenna elements to achieve pointing in the desired direction. The phase shift required for each Vivaldi element is calculated from the array geometry of a tileset (4 tiles) for a given pointing direction. In this way, the subsequent stages of analogue summing are done by simple combining. No further phase shifts are applied.
The beamformer chip forms two independent beams for each set of four antenna elements. The beamformer chip splits the analogue signal from the antennas into two signals and then applies different sets of phase shift parameters to each signal. The beamformer chip therefore has four inputs for four Vivaldi antennas, and two independent outputs. The independent outputs is what makes it possible for EMBRACE to have two independent fields of view, often referred to as RF Beams, which are named Beam-A and Beam-B.
The output of 3 beamformer chips is summed together on a “hexboard” and 6 hexboards make a tile. The EMBRACE array at Nançay has a further analogue summing stage with 4 tiles making a tileset. This final stage is done on the Control and Down Conversion (CDC) card in the shielded container which is connected to the tiles via 25 m long coaxial cables.
2.2. Control and down conversion
The CDC cards are responsible for three important tasks (Bianchi 2009; Monari et al. 2009): 1) Frequency mixing the radio frequency (RF) for conversion to a 100 MHz bandwidth centred at 150 MHz; 2) 48 Volt Power distribution to the tiles; 3) Distribution of command and housekeeping data communication to the tiles. The RF, 48 Volt power supply, and ethernet protocol monitoring and control communication are all multiplexed on the coaxial cables connecting the tiles to the CDC cards (Berenz 2009).
The frequency down-conversion is done by heterodyne mixing in two steps. A first local oscillator (LO) is mixed with the RF signal of interest which is between 500 MHz and 1500 MHz. This LO is tuned within the range of 1500 MHz to 2500 MHz such that the upper side band frequency is precisely 3000 MHz. The resulting signal is in turn mixed with a second LO which is fixed at 2850 MHz resulting in the intermediate frequency (IF) centred at 150 MHz.
There are 3 signal generators used to supply the LO signal to the mixers in the CDC cards. The LO at 2850 MHz is split by a 3 dB power splitter to supply the Beam-A and the Beam-B system. This signal is in turn divided by a cascade of 3 dB power splitters to be distributed amongst the 16 CDC cards. Similarly, the tunable LO is split amongst 16 CDC cards. There is a separate signal generator providing the tunable LO for the Beam-A and the Beam-B electronics (16 CDC cards for each).
The fact that the LO is distributed amongst the CDC cards is a potential source of an undesirable artefact in the final signal. The distributed LO signals could radiate directly into the CDC cards, or possibly mixing products could have a component which is correlated between all the outputs of the CDC card leading to a correlator offset in the beamformed data of the whole array. This is discussed further in Sect. 4.
2.3. Digital processing
The output of the tilesets is fed into a LOFAR-type digital receiver unit (RCU) and remote station processing (RSP) system for digital beamforming (Picard et al. 2009). The RSP performs the digital beamforming of the entire array, producing pencil beams which are usually called digital beams. These digital beams can have pointings within the RF-beam produced by the individual inputs to the RCU. For EMBRACE@Nançay, the inputs to each RCU is the signal from a tileset with a beam width of approximately 8.5° (see Fig. 4 and Sect. 6).
Digital beamforming as described above is done in order to reduce the volume of data produced by the system. The alternative method of producing the antenna cross correlations has the advantage of providing a spatially fully sampled image of the entire field of view every data dump (5.12 μs). This however produces an enormous volume of data which cannot be managed by the acquisition system. As a result, the phased-array technique is used in the digital beamforming to produce multiple beams on the sky, not necessarily covering the entire field of view.
EMBRACE is a single polarization instrument but the LOFAR RSP system has the capacity to produce two outputs per digital beam which correspond to the two orthogonal linear polarizations in LOFAR. These are called the X and Y beams. For EMBRACE, X and Y are two, possibly different, pointing directions within the field of view (the RF beam). This means that for each digital beam, there are two directions, and there can be any number of digital beams as long as the total bandwidth remains within the limit of RSP processing capacity (36 MHz for each RF beam for EMBRACE@Nançay). The dual pointing per digital beam is discussed further in Sect. 9.2.
Fast data acquisition from the RSP boards is done by the backend called the Advanced Radio Transient Event Monitor and Identification System (ARTEMIS) developed at Oxford University (Karastergiou et al. 2015; Serylak et al. 2013; Armour et al. 2012). ARTEMIS is a combined software/ hardware solution for both targeted observations and real-time searches for millisecond radio transients which uses graphical processing unit (GPU) technology to remove interstellar dispersion and detect millisecond radio bursts from astronomical sources in real-time. The pulsar observations with EMBRACE@Nançay are targeted at known pulsars applying known Dispersion Measure and timing parameters, and for this reason the GPU are not used on the EMBRACE@Nançay ARTEMIS backend.
The ARTEMIS hardware is also used for recording raw data packets from the RSP boards containing the digitized beam formed wavefront data. This is used for the high spectral resolution observation of the extra galactic source M33 (see Sect. 9.2)
2.4. Statistics data
In addition to the high rate beamformed data produced by the RSP system, there are also slower cadence data produced at a rate of once per second: the crosslet statistics, the beamlet statistics, and the sub-band statistics.
The LOFAR RCU system digitizes and channelizes the 100 MHz wide RF bandpass into 512 so-called sub-bands, each of 195.3125 kHz bandwidth. The cross correlations of all tilesets are calculated once per second and are called crosslet statistics. The default mode of operation for LOFAR is to calculate the crosslet statistics for each sub-band in succession such that it takes 512 s to cycle through the full RF band.
Another possibility is to request a given sub-band, and the crosslet statistics are calculated each second for the same sub-band. This is the mode of operation used most often at EMBRACE@Nançay. The sub-band statistics is simply the sub-band total powers of the 100 MHz bandpass for each tileset. The beamlet statistics are the beamformed total powers for the full array (16 inputs for EMBRACE@Nançay) dumped at 1 s intervals, and are identical to the fast data integrated over 1 s.
2.5. EMBRACE monitoring and control software
The Monitoring and Control software for EMBRACE was developed at Nançay. An extensive Python package library on the Station Control Unit (SCU) computer gives scripting functionality for users to easily setup and run observations depending on various parameters such as, for example, the type of the target, pointing, frequency selection, etc. Integrated statistics data are acquired from the Local Control Unit (LCU) and saved into FITS files including header information with essential meta data including pointing information, timestamp, frequencies, etc. Raw data (beamlets) are captured from LCU Ethernet 1 Gbps outputs and saved into binary files (Renaud et al. 2011).
3. Calibration
3.1. First stage phase calibration
EMBRACE@Nançay has a hierarchy of four analogue beam forming stages. The first three are done on the tile boards, while the last one is done on the CDC card in the shielded container. The cables running from individual tiles to the CDC cards are 25 m in length, and there are phase perturbations between the various connectors and length of cable leading from each tile. This is calibrated out using an algorithm implemented in the Local Control Unit.
The phase correction between tiles in a tileset is measured by successively maximizing the output power from pairs of tiles. Initially, the required phase shift for each of the 72 antennas in the tile is calculated from purely geometrical considerations (i.e. antenna position and desired pointing direction). This results in a value between 0 and 360°, different for each antenna. Afterwards, an additional phase shift is added to all the antennas in the tile in order to compensate the imperfections in the components and cables. Finally, the phase shift to be applied to each antenna is quantized to 45° steps.
This procedure is done in 24 phase steps, each time incrementing the additional phase shift to be added to all the antennas in the tile by 15°. The step size of 15°, followed by quantization to 45° required by the beamformer chips, results in a slightly improved configuration for the tile. For example, if the phase shift required by geometry for a given antenna is 7°, and an additional phase shift of 15° is added, the result will be 22°, which is quantized to 0°. A nearby neighbour might require a phase shift of 8°, and an additional shift of 15° would result in a quantized step of 45°. In this way, the quantization as the final step after application of a global phase shift of 15° allows for different configurations of phase shifts amongst the 72 antennas.
The phase shift which gives the maximum result is then converted to a value from 1 to 8 corresponding to the 8 phase steps available in each beamformer chip. This process is repeated for each of three pairs of tiles in a tileset, with one tile acting as a reference in each case (Tile 0). At each iteration, two tiles are set in “no output” mode while the other two make observations at each of 24 phase shift settings (see example in Fig. 3). The calibration scheme is done in parallel for each of the 16 tilesets which make up the Nançay EMBRACE station.
Since the analogue beam steering is based on signal phase shifts and not true time delays, the corrections found are only strictly valid for the centre frequency. This does introduce an error in the off-centre sub-bands but it is small since the bandpass is narrow compared to the RF frequency, and it is mostly compensated in the digital phase calibration which is the next step in the observation.
A strong source is necessary for this calibration procedure because the source must be detectable by individual tiles, each with just over 1 m2 of collecting area. For EMBRACE, the Sun is often used as a calibration source, as well as GPS satellites. In particular, the GPS BIIF series of satellites which use the L5 carrier centred at 1176.45 MHz are good calibration sources. Only the sub-bands that receive significant power will be usefully calibrated, but the commonly used GPS L5 carrier is broad enough to calibrate at least 61 sub-bands (~12 MHz, one full “lane”).
Once the necessary phase offsets for each tile have been measured, they are stored in memory and used for the subsequent observation. The phase offsets are also written to disk and can be used in future observations without going through the calibration procedure described here. The use of calibration tables is the default mode of operation and has been used successfully without updating the tables over periods of many months (see for example the pulsar observations described in Sect. 9.3).
The measured phase offsets are different for different pairs of tiles, and have values within the full range of 0 to 360° which corresponds to apparent path length errors of up to half a wavelength (−λ/ 2 < Δpathlength<λ/ 2). For example, at 970 MHz, the path length error for some pairs of tiles is as much as ~15 cm.
 |
Fig. 3 An example output of the RF calibration scheme for one tileset as described in the text. The response of tile pairs for each of the 24 phase steps applied to the second tile in the pair is shown within the three groups of vertical dashed lines. The response is clustered in groups of three corresponding to the constraint of the phase shift step size, however within each group of three there is some variation. |
 |
Fig. 4 Drift scan signals of the GPS BIIF-1 L5 carrier 2013-01-10 at 80° elevation in the north. Each line corresponds to a tile set and their half-widths, combined with the spacecraft’s drift rate, can be converted to a HPBW beam size of ~ 8.5° which is close to what is suggested by the standard formula 1.2 × λ/D where D is the tileset side of 2.1 m. The drift peaks are aligned as a result of applying the necessary phase shifts to each tile. |
Figure 4 shows a drift scan of satellite GPS BIIF-1 and each line is the output from a different tileset. As can be seen, each tileset is phased-up correctly, and they all show the satellite peak at the expected time. Gain equalization has not been applied, but may be implemented in the future (see Sect. 3.3). The data here are from the Sub-band Statistics. For more details on this observation, see Sect. 6.
3.2. Second stage phase calibration
The RSP digital electronics of EMBRACE described in Sect. 2.3 produce high speed beamformed data by combining the complex waveform voltages of each tileset and multiplying by a complex steering vector which gives the beamformed output in a desired pointing direction. The goal of the phase calibration is to determine the modification to the complex weights required to compensate for any instrumental offsets.
In order to describe the procedure for determining the phase calibrated pointing, matrix operations are used including the matrix dot product (denoted by the central dot) and element-wise multiplication of matrix elements, also called the Hadamard product, denoted by⊙. Complex conjugate of a matrix is denoted by a superscript asterisk and the transpose with a superscript T.
The RSP system produces the high cadence beamformed voltages by forming the dot product of a complex steering row-vector w with the complex voltage column-vector T received per tileset: 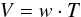 (1)The steering vector depends on the array geometry given by the tileset positions, and on the desired pointing in the sky given by the direction cosines (see for example Thompson et al. 2004). The steering vector must be modified further to take instrumental offsets into account.
(1)The steering vector depends on the array geometry given by the tileset positions, and on the desired pointing in the sky given by the direction cosines (see for example Thompson et al. 2004). The steering vector must be modified further to take instrumental offsets into account.
The calibration procedure makes use of the fact that beamforming in a given direction can be done equivalently by combining the steering vector with the cross-correlation matrix X which is the correlations between tilesets, and this produces the beamformed power P, 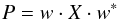 (2)and we maximize P while pointing at a calibration point source.
(2)and we maximize P while pointing at a calibration point source.
The cross correlation between tilesets is calculated each second as described above in Sect. 2.4. This is not fast enough to produce the high speed beamformed data at 5.12 μs intervals, but the cross correlation data can be used to estimate phase errors between each tileset, per sub-band. Each second, the RSP returns a matrix with the cross correlations between tilesets at a given frequency sub-band.
If the tilesets are pointing at a strong point source, then it is possible to calculate an additional phase correction matrix which, when multiplied element wise by the measured correlation matrix X, results in the expected point source at the centre of the field of view. For an ideal instrument, this phase correction matrix would be simply the identity matrix. In a real system, there are various disturbances to the phase along the signal chain which varies from tileset to tileset (cables, filters, amplifiers, mixers, analogue-to-digital converters, etc.). These phase differences must be measured using a strong source in the sky, and calibrated for future observations.
We look for a phase correction matrix Wcal such that the element-wise product 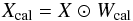 (3)results in the matrix Xcal which is the corrected correlation matrix fixed according to a theoretical model of centred point source. This means that the Xcal elements are all real. Wcal may be further decomposed into a steering matrix Wgeom giving the phase required to steer the beam in a given direction given the array geometry, and a correction matrix Wcor including the corrections of all other sources of phases errors. We then have
(3)results in the matrix Xcal which is the corrected correlation matrix fixed according to a theoretical model of centred point source. This means that the Xcal elements are all real. Wcal may be further decomposed into a steering matrix Wgeom giving the phase required to steer the beam in a given direction given the array geometry, and a correction matrix Wcor including the corrections of all other sources of phases errors. We then have 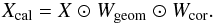 (4)The phase relations between elements at a given i,j is thus
(4)The phase relations between elements at a given i,j is thus 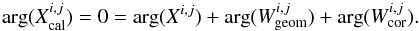 (5)Wcor can then be computed by a simple element wise division:
(5)Wcor can then be computed by a simple element wise division: 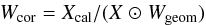 (6)which corresponds to the phase relation for given i,j indices:
(6)which corresponds to the phase relation for given i,j indices: 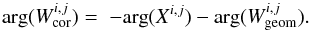 (7)A complete phase correction matrix Wcal can then be created with magnitude unity and with the phases required to correct the measured cross correlation matrix, including the steering step and the phase correction to be applied:
(7)A complete phase correction matrix Wcal can then be created with magnitude unity and with the phases required to correct the measured cross correlation matrix, including the steering step and the phase correction to be applied: 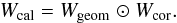 (8)In order to use the calibrated steering matrix for the high cadence beamforming, it is necessary to convert it back to a steering vector. This is done according to the relation
(8)In order to use the calibrated steering matrix for the high cadence beamforming, it is necessary to convert it back to a steering vector. This is done according to the relation 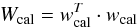 (9)and wcal can be extracted using the method of Singular Value Decomposition (see for example Noble & Daniel 1977). It is this calibrated steering vector which is used by the RSP system to calculate the EMBRACE beamformed data at 5.12 μs intervals using Eq. (1).
(9)and wcal can be extracted using the method of Singular Value Decomposition (see for example Noble & Daniel 1977). It is this calibrated steering vector which is used by the RSP system to calculate the EMBRACE beamformed data at 5.12 μs intervals using Eq. (1).
As with the calibration of the tilesets described above in Sect. 3.1, these calibration parameters are saved to disk and can be used for future observations without the necessity of making a calibration measurement before each observation run. The calibration table measured once has been valid for many months, as discussed further in Sect. 9.3.
3.3. Redundancy gain calibration
A further digital calibration method based on the redundancy method (Liu et al. 2010) is used in post processing. This method is particularly well suited to EMBRACE given the inherent level of baseline redundancy. EMBRACE@Nançay is made of 16 tilesets placed on a regular 4 × 4 grid and therefore one point in the UV space is measured by several different baselines sharing a common length and orientation.
The problem becomes one of solving an ill-conditioned set of equations in which there are more equations than there are parameters to be determined. 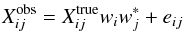 (10)where
(10)where 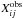 and
and 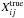 are respectively the observed and true cross correlations corresponding to baseline ij; wi is the complex gain of tileset i; and eij is the noise affecting baseline ij. One solves this system for all
are respectively the observed and true cross correlations corresponding to baseline ij; wi is the complex gain of tileset i; and eij is the noise affecting baseline ij. One solves this system for all 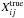 and wi, with baseline redundancy giving a redundant structure to
and wi, with baseline redundancy giving a redundant structure to 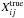 (several baseline outputs modeled by the same true cross correlation). As shown in e.g. Liu et al. (2010) and Noorishad et al. (2012), there exist several ways of implementing a redundancy calibration method which solves Eq. (10). We implemented a non-linear method based on a classical steepest gradient algorithm (see e.g. Marthi et al. 2014).
(several baseline outputs modeled by the same true cross correlation). As shown in e.g. Liu et al. (2010) and Noorishad et al. (2012), there exist several ways of implementing a redundancy calibration method which solves Eq. (10). We implemented a non-linear method based on a classical steepest gradient algorithm (see e.g. Marthi et al. 2014).
In addition to phase calibration, the redundancy method allows for an estimation and correction of gain amplitude disparity between tilesets, which is the main reason for its implementation. This equalization of tileset gains allows for optimization of beam shape features like symmetry, resolution and stability over time (see Sect. 6.2). It can also be used to clean the data from unwanted instrumental effects by comparison with an ideal square aperture model. Note however that this method is not intended to optimize the signal-to-noise which may require a different weighting of tilesets based on individual signal-to-noise ratios and side lobe levels.
The redundancy calibration is robust since it relies only on the similarity of the individual elements. The calibration quality depends only on the signal-to-noise. The point-like or extended nature of the source does not affect the result. It nevertheless requires the position of the source as an input for an absolute phase calibration, since the resolution of Eq. (10) is invariant with respect to a global shift of the sky (absolute calibration of gain amplitude will not be dealt with here). This can be done by adding dedicated constraints to the solver, for example with the implementation of a phase correction gradient minimization across the array, or the inclusion of a model of the observed source. (Liu et al. 2010; Noorishad et al. 2012).
The only limitations are thus expected at low signal over noise, or when individual elements have significantly different behaviour from each other. The latter cause may come from intrinsic inhomogeneities in the numerous system electronic components on the array itself, the mass production employing industrial techniques with good reproducibility should nevertheless strongly mitigate this risk. It may also arise from environmental effects, e.g. temperature inhomogeneities in the electronic components over the array. The self-heating of dissipating electronics seems however to ensure a rather stable and homogeneous temperature over the electronic boards that form the array. Finally mutual coupling between antennas could also be a source of disparity among the elements. Nothing so far indicates that such coupling is of importance on EMBRACE@Nançay, but the dense aspect of the array calls for caution on that point. An application of redundancy calibration on a relatively dense array can be found in Noorishad et al. (2012) where data from a LOFAR HBA station are analyzed near the critical wavelength λc defined by the minimum distance dc between individual antennas. While those HBA arrays have been designed as “semi sparse” across their entire frequency band (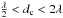 ), EMBRACE has access to both semi-sparse regime (F> 1200 MHz) and truely dense regime (F< 1200 MHz). The possible mutual coupling effects will be investigated with further development of the system model (see Sect. 6.2), if needed a refinement of the model in Eq. (10) could be implemented to take mutual coupling into account.
), EMBRACE has access to both semi-sparse regime (F> 1200 MHz) and truely dense regime (F< 1200 MHz). The possible mutual coupling effects will be investigated with further development of the system model (see Sect. 6.2), if needed a refinement of the model in Eq. (10) could be implemented to take mutual coupling into account.
4. Correlator offset
4.1. Description of the problem
Long duration tracking observations of weaker sources revealed an apparent power variation as a function of pointing direction that was highly repeatable between observations. After some analysis of this problem it was realized that the cross-correlation matrix data product contained time-invariant complex offsets that are much larger than white noise component when observing empty sky. As it turns out the “direction dependence” is only an artefact of applying a varying set of complex weights (while steering the beam to track a source) to a fixed non-changing pattern of complex numbers. That description of the problem was observationally confirmed by noting that the wobbly trace was present and exactly the same whether we tracked a real source or just empty sky, as long as we followed the same trajectory in the local sky. For strong sources, such as the Sun or satellite carriers, this additive contribution is completely negligible and does not become an issue, but by pure coincidence the amplitude of the variation is comparable to the continuum power of Cassiopeia A and Cygnus A (the two strongest extra-solar radio sources at low frequencies). This can be seen clearly in Fig. 5. It shows power versus time from a Cyg A tracking, and also tracking an empty position with the same declination but different RA. The average power difference in these two signals corresponds to the Cyg A continuum level (the real astronomical signal) but as is also evident, the magnitude of the variation in the signals is about of the same strength as the average power difference.
 |
Fig. 5 Power as a function of time while tracking Cassiopeia A, and tracking an empty sky position with the same declination. Note that the solid black line is the only on-source signal. Each tracking produces two curves due to the dual digital beams used as illustrated in Fig. 6. |
4.2. Strategies for correcting the correlator offset
An obvious quick method to get rid of the variation is to subtract the (solid) blue and red signals shown if Fig. 5 and in order to have that possibility, we routinely employ the scheme outlined in Fig. 6. The LOFAR-type backend is always outputting two digital beams (see Sect. 2.3) and we use one of them to track the source, and the other to observe an off position that follows the same trajectory on the sky. Both beams are placed symmetrically within the tileset FoV so that the gains within the two beams are the same.
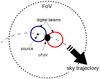 |
Fig. 6 Source tracking strategy. Two digital beams are placed symmetrically within the FoV (tileset beam) following the same sky trajectory but with a time delay. One of them is centred on the source, the other is used as an off-position. |
Such a measure is more similar to mitigating the symptom rather than curing the cause of the problem. Cross correlations are easily corrected by subtracting (per sub-band) a reference cross correlation slice measured towards empty sky and this can be done in post-processing. We subtract all slices in the dataset in question with the same reference slice that may have been measured weeks or months earlier while tracking a different part of the sky. With corrected cross correlations we can then create our own digital beams in any direction within the FoV by applying the required complex weights. This method cures the problem to a large extent as is demonstrated in Fig. 7.
 |
Fig. 7 Correlator offset seen in sky images. The correlator offset problem discussed in the text is also manifested by blob-like features when imaging the tileset FoV. Here the left and right upper panels show FoV images of Cygnus A, and towards an empty sky position, based on uncorrected cross correlations. The bottom panels show the same data but with images created from cross correlations corrected by subtracting a reference matrix of complex constants (the same reference was used for both images). In the left bottom panel, Cygnus A is now clearly seen and at its expected position (offset from centre due to the scheme outlined in Fig. 6). |
But there are severe limitations to this approach: the maximum cadence for cross correlations is one matrix per second and then only for one and the same sub-band. For N sub-bands, the cadence is decreased further to one matrix every N seconds for each sub-band.
The high cadence data stream is unfortunately not straight forward to cure. It consists of beamformed complex voltages every 5.12 μs which is the vector product of a row weight vector and a column tileset voltage vector (see Sect. 3.2 Eq. (1)). The complex offsets seen in the cross correlations (conjugate products of tileset pair voltages) must in turn be caused by complex offsets in the individual tileset signals themselves. We then have 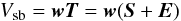 (11)where V is the beamformed voltage for a given sub-band sb, w is the steering vector, T are the complex voltages received per tileset, S is the true uncorrupted sky signal from each tileset, and E is an error vector with complex constants. It is not possible to correct the complex voltages in post processing because they are the product of beamforming which is done in real time. We do not have access to the individual tileset voltages for post processing. It may be possible to determine the error vector E by using the 1 s cadence cross correlation data, but in order to use this, the backend must calculate a subtraction before applying the complex steering vector, and this is not possible within the current processing power of the LOFAR-RSP system.
(11)where V is the beamformed voltage for a given sub-band sb, w is the steering vector, T are the complex voltages received per tileset, S is the true uncorrupted sky signal from each tileset, and E is an error vector with complex constants. It is not possible to correct the complex voltages in post processing because they are the product of beamforming which is done in real time. We do not have access to the individual tileset voltages for post processing. It may be possible to determine the error vector E by using the 1 s cadence cross correlation data, but in order to use this, the backend must calculate a subtraction before applying the complex steering vector, and this is not possible within the current processing power of the LOFAR-RSP system.
One can note that having a constant amplitude and phase value added to the tileset signal for a given sub-band, that is changing in between tilesets, is equivalent to injecting a tone into the system at the particular frequency that is picked up differently per tileset (modified amplitude and phase). This “tone” – that appears to be always present as soon as the instrument is turned on, and which is independent of the current analogue direction (beamformer chip settings) – might be described as a waveform since the values for neighbouring sub-bands follow one another logically.It may also be of great importance to note that LOFAR data, which are produced by a virtually identical backend and deliver the same data products, do not at all suffer from this effect. This suggests an origin in the analogue side of the instrument which is of radically different design compared to LOFAR, one example being that EMBRACE has an additional IF stage and subsequent downmixing is using a common LO source for all CDC cards (see Sect. 2.2).
4.3. Investigation of the correlator offset
We have previously noted that the fixed error pattern in the baseline correlations is stable enough to allow subtracting it out using a template correlation matrix observed weeks or months earlier. Furthermore, the template can be observed when the frontends are internally phased up to an arbitrary direction on the sky. The correction usually improves the beamformed continuum time stability down to a level where the remaining variation is comparable to what is seen while staring at a fixed point.
During an observation, an artificial ondulation in the beamformed power trace is created by applying varying complex steering gains to static tileset signals that are erroneuously correlated (see Fig. 5). In fact, there is no true temporal instability as one is first led to believe. Whereas the backend does not allow access to individual tileset signals in the digital domain, we continue to employ the 1-s integration correlation matrices to analyse the problem. Primarily we aim to understand the origin and behaviour of the problem that we refer to as “correlator offsets”.
In order to quantify the variability of the correlator offsets, we have selected one sub-band in a 3-day data set where correlations for all baseline pairs were sampled every second. The frontends were fixed to the same analogue beam steering through the observation. The observation was configured to let Cas A drift through the beam once per sidereal day thus regularly verifying that the system was operating normally. We chose portions of ten minutes every day, separated by exactly 24 h, well away from the Cas A drift signal and obvious transients, to study the daily fluctuations of correlator offsets and compare them to the thermal noise as measured during each 600 s sequence (Fig. 8). We find that the thermal 1-sigma scatter is 20–100 times weaker than the magnitude of the complex offsets. The large range is due to the varying offset magnitudes; the thermal scatter is rather constant over all baseline pairs. The magnitudes of the average daily change of the offsets were found to be comparable to the thermal scatter, meaning that the thermal scatter is 15–100 times smaller than the offset magnitude.
 |
Fig. 8 A plot of the complex plane showing the correlator offsets while observing empty sky. The offset is much larger than the thermal scatter of the points during 10 min observations. The red lines are simply to mark the separation from the plot origin. |
To study the long-term stability of the offsets, we make use of the quasi-continuous pulsar tracking observations at 970 MHz that have been conducted with EMBRACE@Nançay since 2013. The pulsar signal is effectively negligible in the baseline correlations and we pick one correlation matrix per observation from ~400 observations spread out over 20 months. Two different sub-bands were used and we first discuss the batch which used the same sub-band continously for seven months. During this time we find that the complex correlator offsets varied somewhat – up to 3–4 times the thermal scatter – mostly in the radial direction, indicating a fluctuation in input powers but not a change in relative phases between tileset signals. In occasional observations all correlations with one particular tileset were rotated exactly 90° indicating a corresponding jump in phase for this tileset. At other observations exhibiting this effect, it may have been another tileset that was affected. Lastly, after ~40 days into the sequence (186 days in total) the LO powers were permanently modified as part of a test and here we see a jump in the positions of the offsets, again mostly in the radial direction.
In order to definitively confirm that the erroneous correlated signals are not in any way related to the RF signals from the tiles themselves, we disconnected the tiles for one tileset and instead replaced the cables with termination loads directly at the inputs of the associated CDC card (see Fig. 9). It turns out that this did not affect the correlator offsets significantly, all correlations with that tileset remained in the same place in the complex plane even though the autocorrelation power level for that tileset clearly changed (as it should since no effort was made to perfectly simulate the normal tile output power levels).
 |
Fig. 9 Correlator offset without frontend. When one tileset is replaced by a 50 Ohm load, the correlator offset remains, showing that the correlator offset is not due to the frontend system (antennas, amplifiers, beamformer chips, etc.). |
On the other hand, turning off the LO amplifiers for all LO signals led to the backend outputting correlations that were two magnitudes smaller, and now spread symmetrically around the origin. Thus we conclude that the offsets are not produced by a malfunctioning backend, but rather with the LOs or their mixing scheme or the CDC card electronics.
Comparisons were made with the second RF beam, “Beam B”. It is configured the same way as Beam A except that 20 dB attenuators, normally located just before the RCU inputs, were removed. We see that fundamentally the problem exists in Beam B as well, but here the scatter in angles around the real axis is larger (ca +–90°), and crucially the magnitudes are almost exactly 100 times stronger. The latter should provide another piece of evidence that the undesired correlated signals are created before the RCUs (and the location of the attenuators). The Beam B offset magnitudes, when normalized by the Cas A signal strength, are still about two times larger than for Beam A but this is probably unrelated to the removal of the attenuators.
The EMBRACE instrument has features in common with a LOFAR station. Their backends are virtually identical allowing convenient comparisons of data products. The LOFAR data normally show no or little sign of correlator offset problems. By selecting correlations from 16 tiles (LOFAR HBA) and plotting them in the complex plane (Fig. 10), we can see that for LOFAR, at least 100 out of 120 unique baseline correlations are concentrated symmetrically around the origin (within a 1–2 thermal spreads when observing for 20 min). The 10–20 outlier clusters (on the order of 10 thermal spreads from the origin) are all pairs who are direct neighbours or two tiles/antennae away, possibly indicating that the offset is due to crosstalk between array elements. Overall we conclude that the LOFAR correlations behaves fundamentally different than for EMBRACE and more in line with what one should expect from an ideal interferometer, namely that the expectation value of correlations between array elements is zero when not observing a source.
 |
Fig. 10 Correlator offset for the High Band Antenna array of the LOFAR station at Nançay. Note that the plot scale is 3 orders of magnitude smaller than the corresponding EMBRACE plot. The outliers are all neighbour antennas indicating the offset is due to cross talk between those antennas. |
4.4. Local oscillator distribution as a potential source of correlator offset
The correlator offset described above is seen as a constant offset in the cross-correlations between the tilesets of EMBRACE. It behaves as a constant signal which is common in all the tilesets and is correlated by the EMBRACE backend. One can see this by producing a skymap image in the usual manner while assuming the array is pointing at zenith. Figure 11a is an image of “empty sky” from a drift scan of the Sun after the source has left the field of view. There are no detectable sources in the field. The result is clearly an image of a point source, but with a much lower intensity level compared to an image of the Sun (Fig. 11b).
 |
Fig. 11 Sky images without and with a source in the field. Using the cross-correlation statistics data, interferometric images can be made at a given sub-band. a) A phantom point source can be seen in images produced from data pointing at “empty sky” and assuming zenith pointing. b) The image of the Sun has peak more than an order of magnitude larger than the phantom point source. |
The point source of Fig. 11a can be seen at any time in the data as long as there is no strong source in the field of view. It is always the same, as already noted above, and is independent of the instrument pointing parameters. In order to create this stable, “phantom” point source, there must be a signal common to all the tilesets analogous to a source in the sky impinging a signal on all the tilesets, but the signal must be internal to the instrument and independent of pointing parameters.
The frequency downconversion stage described in Sect. 2.2 uses signal generators and power splitters to provide the Local Oscillator (LO) signal to all the CDC cards. This LO distribution is an obvious candidate for the source of the phantom point source (i.e. the correlator offset). Although care has been taken to avoid having LO or mixing products within the RF band, it appears that the LO or mixing products are nevertheless modulating signals on the CDC card, possibly by radiating onto the CDC card.
5. Astronomical measurement of the embrace geometry
The 72 Vivaldi antennas within a tile are laid out in rows rotated 45° from the tile side so that the main diagonal has 12 elements separated by 12.5 cm. Then the 64 tiles in the array are placed side by side in a right-angle rhombus pattern with respect to the North-South meridian. Distances within tiles and tilesets are easily measured down to the necessary accuracy (fractions of a wavelength), and it turns out that the nominal values can be used, e.g. neighbouring tileset distances along a row can be assumed to be 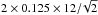 metres apart. Thus it is easy to construct the 4 × 4 matrix of relative positions needed for the complex weight calculation in the beam forming procedure, however, such properties as overall tilt and rotation must also be known down to fractions of a degree to avoid problems with pointing offsets when tracking sources (compare with a minimum synthesized beam size of ~1.1°).
metres apart. Thus it is easy to construct the 4 × 4 matrix of relative positions needed for the complex weight calculation in the beam forming procedure, however, such properties as overall tilt and rotation must also be known down to fractions of a degree to avoid problems with pointing offsets when tracking sources (compare with a minimum synthesized beam size of ~1.1°).
The rotation was initially known within a few degrees which is sufficient for shorter observations because the digital phase calibration (see Sect. 2.3) will correct the error as long as the pointing direction does not change much compared to the position of the calibration source during the time of phase calibration.
In 2012, two independent efforts were made to more accurately measure the rotation, both mechanically and by using a celestial source. In the latter case we made use of the low cadence tileset cross correlations produced in the backend every second and dumped into FITS files by the control software. The Sun was tracked starting approximately mid-day (19 July 2012) from south to west thus spanning almost a quarter of the local sky. An image was made within the tilesets’ FoV every 10 min and by retroactively assuming different instrument rotations when computing the complex weights for the phase calibration and actual data imaging, we could iteratively converge towards the best number that kept the Sun’s maximum intensity pixel at the expected position throughout the measurement. The number arrived at with this method was ΔΘ = −3.7°. Incidentally this exercise was also an important step in verifying that all sign and ordering conventions were consistent between the various coordinate frames and cross correlation data files.
 |
Fig. 12 Drift scan of Cas A at 1171.4 MHz in a bandwidth of ~1 MHz. The top image shows the full time span of the drift scan with a baseline fit. The bottom plot is a zoom to the main lobe with the baseline fit removed. The measured FWHM is 1.476deg which is very close to the expected value of 1.466deg. |
The direct estimate of the physical rotation of the instrument was done by measuring positions of corner antennas in three dimensions with respect to a reference point at the observatory site. The resulting offset angles along the north-south and east-west lines were found to be ΔΘ = −3.673° and ΔΘ = −3.714°, respectively. It should be noted that although these physical measurements were done about one month prior to the on-sky experiment described above, the result was not yet known to the observer during the data analysis. The on-sky result thus turned out to be an excellent blind verification of the geometric parameters of the instrument.
The tilt angle was found to be small, ca 0.06°, mostly about the north-south axis, estimated from a one centimetre height difference of two reference points separated by nine metres along the east-west direction.
Those results have been confirmed by another method based on a model point spread function fit on a point source skymap (see Sect. 6.2). This is a sampled rectangle aperture model, with physical rotation and tilt of the array as 2 of the free parameters to be optimized. The best fit performed on several observations gives a consistent result of ΔΘ = −3.714° ± 0.0005 for the rotation angle, and a tilt angle ranging from 10-4 to a few 10-3 deg.
6. Beam pattern
6.1. Beam pattern measurements
At the single tile level, the main beam was first seen to agree with expectations for a one metre square phased up array when bore sight drift scans of GPS L2 carriers were conducted in October/November 2009. This result is described in detail in Olofsson et al. (2009).
The fundamental properties of the tileset beams and the full array beam were quickly established after the installation of the hardware was finished and phase calibration schemes were implemented during the summer months of 2011.
Figure 12 shows an example of a drift scan of Cassiopeia A pointing at its maximum elevation point. The east-west HPBW was computed by converting the time axis to an angular scale and performing a Gaussian fit to the normalized baseline subtracted signal.
Figure 4 shows the time signals from a satellite carrier drift scan for all individual 16 tile sets that constitute the array members in the final digital beam forming. The slight dispersion of the times of maximum signal is caused by the 45° quantization of the phase settings that are used to create (or “steer”) the analogue tile beams, and to measure the global phase offsets between tiles in a tile set (see Sect. 3.1).
Sidelobe levels (along the east-west direction) can be seen in the logarithmic intensity scale solar drift scan in Fig. 13. The first secondary lobes can be seen to be ≳15 dB down from the main lobe which is within design goals.
 |
Fig. 13 Drift scan of the Sun across the stationary digital beam pointing reaches its maximum at the expected time. The sidelobe levels are below the 15 dB design criterion. |
The 2D sidelobe pattern at the smallest spatial scales could conveniently be studied once algorithms were in place to read and analyse the raw cross correlations data product. Figure 14 shows a narrow band instantaneous radio image of a point source (GPS satellite) in linear and logarithmic units. This can be compared with the simulated pattern (see Sect. 6.2). Note that the sky projection used (collapsing the azimuth/elevation sky position onto a flat plane by taking the cosine of the elevation) falsely leads to a beam shape that is independent of elevation, whereas on the sky the beam gets elongated in the up-down dimension at low elevations due to the shortening projected baselines (zero at the horizon). The pattern is repeated along the NW–SE and NE–SW axes due to the symmetry of the tileset grid and the resulting ambiguity that arises when phase-shifting exactly one whole wavelength on the shortest baselines (2.1 m) to create the image pixels.
 |
Fig. 14 Snapshot image of the GPS BIIF-1 satellite on 2012-09-05 at 1175 MHz. The angular range covered approximately corresponds to two times the tileset FoV. Note that for the full up instrument beam layout, the pattern shown is tapered by the larger scale tileset main beam which is outlined in Fig. 4. |
6.2. Beam pattern simulation
When pointing towards an unresolved source, the cross correlation statistics data (once per second, per sub-band) gives access to a full 2D measurement of the point spread function (PSF) of the instrument.
We fit a sampled rectangle aperture model to the cross correlation data with array length dimensions a and b, rotation and tilt angles of the array respectively rot and tilt, field of view width fov, and power offset P0 as free parameters, following the theoretical square aperture: ![\begin{eqnarray} {\rm PSF} (\theta,\phi)=(1-P0)\left[{\rm sinc}^{2}\left(\frac{k\theta a}{2\pi}\right)\, {\rm sinc}^{2} \left(\frac{k\phi b}{2\pi}\right)\right]+P0 \label{eq:PSF} \end{eqnarray}](/articles/aa/full_html/2016/05/aa26706-15/aa26706-15-eq68.png) (12)where θ and φ are angles with respect to the centre of the field of view, and taken along two great circles on sky that have been rotated by an angle rot and tilted by an angle tilt with respect to the celestial meridian.
(12)where θ and φ are angles with respect to the centre of the field of view, and taken along two great circles on sky that have been rotated by an angle rot and tilted by an angle tilt with respect to the celestial meridian.
When periodized, this model may be seen as an ideal case where the array would behave exactly as a sampled square aperture with independent and identical receivers on its whole surface. It is thus taking limitations such as diffraction-limited resolution, overall beam shape, or PSF aliasing into account, but neglects other possible influences like gain variations across the array or mutual coupling. As already discussed in Sect. 3.3, those latter effects could nevertheless explain some fine effects, and the gain variations are corrected by the redundancy method.
 |
Fig. 15 Contour plot (dB scale, 0 at maximum amplitude) of the interferometric imaging in one sub-band and after a phase-only calibration (top panel), and a full redundancy-based calibration (bottom panel), for a GPS satellite observation with EMBRACE@Nançay. Observed data are shown as dashed contours, while the best-fit rectangle aperture model is shown as continuous ones. The periodization of the main pattern is due to sampling of the UV plane, here the equivalent of 3 fields of view is shown. |
Figure 15 shows both observed PSF and a best-fit as contour plots of an interferometric image in one sub-band, during the observation of a GPS satellite. Two cases are presented: one with phase-only calibration, and one where the complex gains of each tileset has been corrected by redundancy-based calibration on the same source. The root mean square residual amplitude between redundancy calibrated data and best-fit model is less than 0.3%, and about twice as large in the phase-only calibration case.
One may note the periodization of an underlying PSF pattern corresponding to a perfectly sampled UV plane. Since our sampling is here limited to tilesets, and given the total size of the array, this periodization leads to an aliasing effect that tends to increase the Side Lobe Level (SLL). Our model takes it into account by periodizing the expression given in Eq. (12), with an angular period corresponding to the field of view 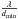 , where λ is the observed wavelength and dmin is the minimum separation between two tilesets. As a result, the observed SLL is bigger than the expected one for a fully sampled rectangular aperture (–13.2 dB of expected attenuation for the first side lobe (Johnson et al. 1993), –11.9 dB when summing the first and second side lobes), as seen in Fig. 16.
, where λ is the observed wavelength and dmin is the minimum separation between two tilesets. As a result, the observed SLL is bigger than the expected one for a fully sampled rectangular aperture (–13.2 dB of expected attenuation for the first side lobe (Johnson et al. 1993), –11.9 dB when summing the first and second side lobes), as seen in Fig. 16.
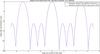 |
Fig. 16 1D Diagonal of 2D interferometric PSF (dB scale, 0 at maximum amplitude), for both GPS observation and best-fit model. |
This limitation is expected, given the relative small size of EMBRACE@Nançay. We may extrapolate our model for a larger array, with higher spatial resolution and thus less of these aliasing effects. Figure 17 shows the modeled PSF for an EMBRACE-type station with 50 times longer sides (2500 times bigger area). The remaining aliasing contribution to the first side lobe level is of the order of 0.4 dB.
After redundancy calibration, the observed Full Width Half Maximum (FWHM) is smaller than theoretically expected, reflecting the over-estimated best-fit length and width. By comparison, the phase calibrated data (no gain amplitude correction between tilesets) shows an asymmetric rectangular aperture model, with one side length as expected and another one under estimated, reflecting the degraded spatial resolution in this direction along the side. The behaviour of tileset amplitude gain corrections given by the redundancy method shows this can be interpreted in terms of an apodization effect. For these observations, the tileset gains repartition over the array is indeed close to a bilinear function, with a gradient aligned with one side of the square array. Before gain amplitude correction, the array thus behaves with a smaller effective area, and a degraded angular resolution in one direction. This kind of regular pattern in gain correction over the array’s tilesets is sometimes encountered, but it may vary from observation to observation. The origin is not yet fully understood, but the redundancy calibration can correct for the gain variation. Starting from a corrected array, one can then choose a tileset apodization scheme (complex weights) that will suit the desired trade-off between SLL and FWHM.
On the other hand, the best-fit SLL on fully calibrated data is also bigger than the expected one for a realistically sampled square aperture by about 0.1 dB (see Figs. 15 and 16). This residual may be interpreted in terms of mutual coupling, and a simple toy model allows an estimate of the strength of these couplings between closest elements on the order of a few percent at most. That interpretation will be further investigated. If the coupling origin is confirmed, a more precise quantification at different frequencies and line of sight as well as the possibility for correcting it will be tested Censier et al. (in prep.).
 |
Fig. 17 1D Diagonal of 2D interferometric PSF (dB scale, 0 at maximum amplitude), for an EMBRACE-like array with 50 times larger side length (about 400 m side length), following the square aperture model best-fit parameters. |
7. Multibeaming
Figure 18 shows a drift scan of the Sun using the multibeam capability of EMBRACE@Nançay. Six beams were pointed on the sky along the trajectory of the Sun, including three partially overlapping beams. The result shows the Sun entering and exiting each beam and the off-pointed beams are approximately 3 dB down from the peak, as expected.
 |
Fig. 18 This drift scan of the Sun used 6 beams of EMBRACE@Nançay pointing along the trajectory of the Sun across the sky (inset top right). |
8. Noise performance and efficiencies
8.1. Sensitivity/efficiency
The system noise cannot be directly determined without filling the whole beam pattern with two known noise sources (such as cold sky and a hot load that covers the entire array) which is not practical for an instrument such as EMBRACE, however, the ratio of noise and efficiency can be determined while observing small sources with known flux densities or known brightness temperature distributions.
For instance, the expected main beam brightness temperature from the Sun is 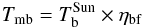 (13)where ηbf is the beam filling factor for a disk-shaped source of size θS and a Gaussian HPBW main lobe θB:
(13)where ηbf is the beam filling factor for a disk-shaped source of size θS and a Gaussian HPBW main lobe θB: 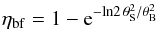 (14)Given a linear receiver in the Rayleigh-Jeans regime and a switched measurement with total power values (or spectra) “on” and “off”, the antenna temperature should be
(14)Given a linear receiver in the Rayleigh-Jeans regime and a switched measurement with total power values (or spectra) “on” and “off”, the antenna temperature should be 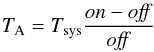 (15)if we neglect the CMB and atmospheric contributions which are small in this context. By using the relation TA = ηmbTmb we can now put everything together to find a simple expression for the ratio of system temperature and main beam efficiency:
(15)if we neglect the CMB and atmospheric contributions which are small in this context. By using the relation TA = ηmbTmb we can now put everything together to find a simple expression for the ratio of system temperature and main beam efficiency: 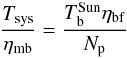 (16)where Np is shorthand for the normalized raw power (on-off)/off.
(16)where Np is shorthand for the normalized raw power (on-off)/off.
Unfortunately, the Sun is highly variable at decimeter wavelengths and longer where the chromosphere and later the corona is starting to dominate over the photosphere. There are no telescopes that monitor the Sun in the low L-band range on a daily basis and we are forced to use interpolations for “Quiet Sun” brightness temperatures and accept that the result may be uncertain by up to ~50%.
For small sources with relatively well known flux densities, one can more directly arrive at another performance measure, namely the ratio of system noise and aperture efficiency. The latter is simply the effective collecting (Aeff) area over the physical area (Aphys), which can be measured by comparing observed power from a source with its intrinsically available power over the instrument as given by the flux density multiplied by the bandwidth.The resulting expression is 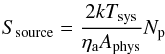 (17)where Tsys/ηa is the sought quantity. Often the entire fraction in Eq. (17) is used instead:
(17)where Tsys/ηa is the sought quantity. Often the entire fraction in Eq. (17) is used instead:
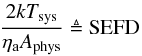 where SEFD refers to “System Equivalent Flux Density”.
where SEFD refers to “System Equivalent Flux Density”.
An additional complication in the case of a dense aperture array is that the cross sectional area goes down for elevations progressively away from zenith and this can be viewed either as a decrease in physical area, or as a decrease in ηa. Theoretically, if each Vivaldi element was truly isotropic and the array perfectly dense, the received power should decrease proportionally to the projected area, i.e., as sin(el.) × Aphys. In reality it does not follow such a curve and it is of interest to try to characterize its elevation dependence. Since the beam pattern is not circular symmetric, the preferred manner to do this would be to track a source along fixed azimuths from zenith to low elevation. No sources follow such sky trajectories1 and we will have to draw tentative conclusions based on results interleaved between our stronger sources (Sun, GPS, Cas A, Cyg A).
Lastly, it can also be of interest to compare the performance between the different hierarchical stages in the interferometer. Here, we restrict ourselves to compare the area efficiency of a single tileset to that of the whole array.
As can be seen, there is a difference of approximately a factor of two and we could attribute this to an additional “array efficiency” as defined in Thompson et al. (2004). Using that formalism, the ηa used previously for the full array would then be replaced with ηaηarray where ηa now is the tileset value.
8.2. Elevation limit due to the forest
 |
Fig. 19 Received intensity as a function of elevation for CasA and CygA at three frequencies. The vertical red lines indicate 45° elevation which is the nominal scan angle limitation for EMBRACE. The effect of the treeline is also visible at elevations below 45°. |
Figure 19 shows the normalized intensity for a number of observations as a function of elevation at three frequencies, using either of the two RF beams. The trends at high elevations seem mostly linear and we have tried to extrapolate these trends in order to phenomenologically estimate the value at zenith (noted at the right edge of the plots).
As comparisons to the actual measured values, we have drawn two lines. The upper dashed line is the trend the received power would follow at lower elevations if the instrument was a perfectly flat, fully sampled, infinitely thin, isotropic 2d array (i.e., having a geometric cross section fall-off as the cosine of elevation). The lower dashed line is simply a 1st order polynomial that goes through the estimated peak value, and the origin (i.e., assuming zero power at zero elevation).
When analysing the Cygnus A measurements, we consistently noted that results appear more erratic below a certain elevation when the source is setting. We have previously mostly only observed at low elevations in the south and a theory was advanced that obstruction from local vegetation could create the observed effects. An inspection of the treeline around the instrument confirmed that trees in the north west block the view up to elevations of circa 45°, whereas the view to the north east – where the source is rising – is clear down to much lower elevations.
8.3. Stability
It is already clear that the stability is such that we can successfully subtract data to get rid of systemic patterns (see Sects. 4 and 9.2). We have also tried to estimate the Allan variance although we cannot shield the instrument from the outside world. Preferably one would like to expose the instrument to a constant signal source such as a hot load. The results achieved, where we clearly still have some variability due to external sources, should thus be considered a conservative limit to the true Allan variance.
 |
Fig. 20 Allan variance as a function of time. This observation was performed as a three-day drift scan of Cas A pointing at ~ 79° elevation due south. The signals from the daily Cas A passages have been removed. In the lower panels also a few strong signals have been removed that occurred on a solar day basis (those could be due to any kind of human activity such as a transmitter that is scheduled to turn on or increase its power for a short while every day, or artificially induced changes to the instrument environment such as variations in the AC power grid). |
In Fig. 20, we show the Allan variance for a constant pointing stretching over three days where the total power was sampled every second. Values for six different beamlets are shown from a bandpass of 61 beamlets (beamlet = sub-band here since all beamlets were pointing in the same direction). The lower panel shows the same type of analysis but for the difference signal of two digital beams. This could be considered a measure of what is sometimes referred to as the “spectroscopic” Allan variance which normally shows better stability than the raw total power signal. To further improve the lower limit to the best-case Allan variance time we also removed a small number of relatively narrow strong features from the time signal. These signals occured with a period of exactly one solar day and must hence be of terrestrial origin and as can be seen they had an effect on the Allan variance down to time scales <10 s. The lower panel demonstrates with some confidence that the Allan time of the system (where drift noise starts to dominate over thermal noise) is better than 30 s.
9. Astronomical sources
9.1. Cassiopeia A
Cas A is one of our two good candidates for absolute efficiency estimations due to its constant flux (on short time-scales) and being a point source for EMBRACE. A detailed flux model over frequency and time for Cas A (which is an expanding supernova remnant that fades over time in the radio) has not been presented since Baars et al. (1977) who assembled observations during the 1950’s, 60’s, and 70’s and calculated fading rates over a large set of frequencies and extrapolated an equivalent flux density spectrum for the epoch 1980. The 1980 values are still sometimes used today and they severely overestimate the current flux density of Cas A. On the other hand, if one uses the fading rates of Baars et al. (1977), valid some 50 yr ago, to extrapolate from 1980 to a much later time, one significantly under estimates the flux because there is ample proof that the fading rates have decreased.
In our observations of Cas A and Cyg A in 2012, we noted that Cas A seemed to be ~10% stronger than Cyg A at 1176 MHz. This assumes that the system and ambient noises were constant between the measurements which may not be true but we find it unlikely that it varied by more than 10%. According to the flux model by Baars et al. (1977), the flux for epoch 2012.6 at this frequency should be lower than that of Cyg A. Since no large span absolute flux spectrum of Cas A has been measured in recent years, our approach to this conflict is to still use the 1980 model spectrum from Baars et al. (1977), but extrapolate using the few more recent estimates for fading rates that can be found in the literature, notably at 927 MHz (Vinyajkin & Razin 2004) and 1405 MHz (Reichart & Stephens 2000), and made linear interpolations to find fading rates for the frequencies observed with EMBRACE@Nançay. Although it does not perfectly fit with our observed SCasA/SCygA, it does agree better than either using the Baars model propagated to the 2010’s or than directly using the 1980 spectrum ignoring any fading during the last 30 yr.
It should be noted that, according to Reichart & Stephens (2000), fading rate decrease is only seen at lower frequencies (the transition being anywhere between λ ≈ 4–10 cm). Furthermore, according to them, the fading rate of 0.6–0.7% per year previously seen at 7.8 GHz and above, now appears to apply to all frequencies down to a few 10ths of MHz.
9.2. Spectral line observation of Messier 33
With a relatively modest collecting area, strong distinct spectral signatures are restricted to artificial sources such as satellite carriers, and the Milky Way HI line at 1420.4 MHz. The latter is distributed throughout the entire sky and mostly lacks clear unique features on spatial scales of the array beam. An example of an early EMBRACE HI observation – at a time when tilesets could not yet be phased up to form an array beam – was to point all tileset beams to a certain longitude in the galactic plane and verify that the resulting spectra had the Doppler components expected in that slot of the plane compared to published surveys.
The Triangulum galaxy (M 33) is the most distant object that can be observed with the naked eye in the optical (under very good conditions). It is an ideal source to observe with EMBRACE due to its size (about 1° diameter, i.e., slightly smaller than the synthesized beam) and its radial velocity (vLSR ≈ −200 km s-1).
For atomic hydrogen 21 cm observations (the strongest astronomical spectral line within the EMBRACE bandpass by orders of magnitude), the latter fact is very fortuitous; the line-of-sight orientation of the M 33 disk leads to a relatively narrow line profile (FWZI ~ 200 km s) that is clearly separated from the much stronger local Milky Way foreground which lie at at an LSR velocity near zero in the direction of M 33. Most other nearby spiral galaxies overlap with the galactic foreground and are weaker due to larger distances. The nearby M 31 (Andromeda) overlaps marginally with local gas but is much larger and closer to edge-on orientation and would be more suitable for one-dimensional mapping observations with EMBRACE.
During the summer of 2013, M 33 was observed both at the coarse sub-band spectral resolution (1 sub-band = 195 kHz = 41.2 km s-1) as a prepatory test, and then at high resolution by capturing the stream of UDP packets for half an hour (160 Gbyte in total) and channelizing each sub-band 16-fold. The two digital beams that are always present in the backend output (referred to as the X and Y directions due to its LOFAR heritage) were employed to create FoV symmetric on- and off-beams in a manner described in Fig. 6. A spectrum was subsequently created in the simplest way possible; by coaveraging all data for each position separately before off-position subtraction and normalization, and then multiplying by a constant factor so that our result matches a template spectrum we retrieved from the LAB survey (Kalberla et al. 2005)2 convolved to the EMBRACE array beam size.
 |
Fig. 21 Top left: raw averaged spectra (blue = on, red = off). Note that the horizontal axis has increasing frequency to the right. The galactic foreground is visible in both positions around channel 470. Mid right: coarsely calibrated spectrum with four offset sub-bands corrected by adjusting their level to that of neighbouring sub-bands. Also shown in green is a second order baseline fit. Bottom left: baseline subtracted spectrum where obvious spikes have been interpolated out. A comparison with the LAB survey spectrum is shown in golden/yellow. The detailed line shape agreement is excellent apart from a portion that is obviously asscociated with an unstable sub-band. Note that the galactic foreground has mostly been subtracted out in the EMBRACE spectrum with only a negative residual remaining. |
The result and several steps in the process are illustrated in Fig. 21. This approach yields overall rather benign baseline shapes indicating that much weaker signals can probably be detected. The sub-band “staircasing” and spikes/perturbations may be caused by external or internal RFI. The first portion of Fig. 21 clearly shows that raw channelized spectra are not dominated by thermal noise but rather a static square wave pattern originating in the polyphase filter stage earlier in the chain (an identical effect is seen in channelized single station LOFAR spectra). The (on-off)/off operation appears to remove this pattern extremely effectively.
9.3. Pulsar PSR B0329+54
Figure 22 demonstrates over 9 h of tracking the pulsar PSR B0329+54. Its pulsed signal is clearly detected after several minutes, and the array continues tracking, measuring continuously the pulsar, except where RFI has been filtered at 21 500 s. The array was configured with a bandwidth of 12 MHz (62 beamlets) centred at 1176.45 MHz. The array was phased-up using the GPS BIIF-2 satellite, and the phase parameters were applied for the observation of PSR B0329+54. The high data rate output from the RSP boards is read by a data acquisition system running the Oxford ARTEMIS pulsar processing software (Serylak et al. 2013).
 |
Fig. 22 PSR B0329+54. The pulsar is detected after several minutes as shown in this dynamic plot folded at the pulsar period of 715 msec. The figure was plotted using PSRCHIVE software (Hotan et al. 2004; van Straten et al. 2012). |
9.4. Daily observations
In November 2013, EMBRACE@Nançay began a long term campaign of observation of pulsar B0329+54. EMBRACE@Nançay has been running autonomously and performing the pulsar observation every day centred at two frequencies: 970 MHz and 1176 MHz (Nov. 2013 to Aug. 2014) and 970 MHz and 1420 MHz (Aug. 2014 to present). Since August 2014, EMBRACE@Nançay has been using saved calibration tables which greatly simplified the observation planning. There is no need to plan for a calibration run before each observation. In August 2015, drift scans of Cas A and Cyg A were added to the daily observational programme. EMBRACE@Nançay is ow operating in the manner of a facility instrument, doing pre-planned observations, and running a long term observational campaign.
10. Summary and future work
The technology of dense aperture array uses a large number of antenna elements at half wavelength spacings to fully sample the aperture. EMBRACE@Nançay is the first fully operational demonstrator of this technology which is large enough to make interesting radio astronomical detections.
One of the main concerns with the dense aperture array technology is the high system complexity which could complicate operations and some have expressed doubt that operating such a complicated instrument might not be feasible for a facility observatory but EMBRACE@Nançay has clearly shown that dense aperture array technology is perfectly viable for radio astronomy. We have demonstrated its capability as a radio astronomy instrument, including astronomical observations of pulsars and spectroscopic observations of galaxies. We have also demonstrated its multibeam capability.
While the system setup is complex, once implemented, EMBRACE@Nançay behaves with remarkable stability. System issues, such as the correlator offset, are characterized and corrections applied to the data are valid in the very long term and need not be remeasured frequently. EMBRACE@Nançay has been in operation for four years with little or no change in its performance. In particular, calibration tables used for phase calibration continue to be valid over at least a period of 6 months.
The dense aperture array technology has the advantage of relatively low cost fabrication being composed of large numbers of small components which can be easily shipped and assembled on site. After an initial period of commissioning, the system will operate with reliability and with predictable and stable performance.
An important disadvantage of the dense aperture array technology is its relatively large power requirement. The large number of analogue electronic components associated with the signal chain of each antenna element, together with the digital processing requirements for beamforming and/or aperture synthesis, makes a system which is rather power hungry. A number of solutions are being studied to reduce the overall power consumption (bij de Vaate et al. 2014), including the use of high speed digital samplers which will eliminate the frequency down-coversion stage and not only reduce overall power consumption but will also solve the problem of correlator offset due to a distributed Local Oscillator signal.
Dense aperture array technology is a viable solution for the SKA, offering the benefit of an enormous field of view together with great flexibility for system setups, including multibeaming with multiple and independent observation modes. The SKA built using dense aperture array technology will be the most rapid astronomical survey machine.
Acknowledgments
EMBRACE was supported by the European Community Framework Programme 6, Square Kilometre Array Design Studies (SKADS), contract No. 011938. We are grateful to ASTRON for initiating and developing the EMBRACE architecture. M.S. acknowledges the financial assistance of the South African SKA Project (SKA SA). A.O.H.O., A.K., and M.S., were supported for multiple working visits to Nançay by grants from the Scientific Council of the Paris Observatory.
References
- Armour, W., Karastergiou, A., Giles, M., et al. 2012, Astronomical Data Analysis Software and Systems XXI, 461, 33 [NASA ADS] [Google Scholar]
- Baars, J. W. M., Genzel, R., Pauliny-Toth, I. I. K., & Witzel, A. 1977, A&A, 61, 99 [NASA ADS] [Google Scholar]
- Berenz, T. 2009, Proc. Wide Field Science and Technology for the SKA, Limelette, Belgium, eds. S. A. Torchinsky et al., 039 [Google Scholar]
- Bianchi, G., Morawietz, J., Mariotti, S., et al. 2009, Proc. Wide Field Science and Technology for the SKA, Limelette, Belgium, eds. S. A. Torchinsky et al., 041 [Google Scholar]
- bij de Vaate, J. G., Torchinsky, S.A., Faulkner A. J., et al. 2014, SKA Mid Frequency Aperture Arrays: Technology for the Ultimate Survey Machine, in Proc. URSI General Assembly Beijing, China, 16–23 August [Google Scholar]
- Bosse, S., Barth, S., Torchinsky, S .A., & Da Silva, B. 2010, Proc. European Microwave Integrated Circuits Conference (EuMIC 2010), 27–28 September 2010, Paris, France, 106 [Google Scholar]
- Braun, R., & van Cappellen, W. 2006, Aperture Arrays for the SKA: Dense or Sparse? SKA Memo 87 [arXiv:astro-ph/0611160] [Google Scholar]
- Dewdney, P. E., Hall, P. J., Schilizzi, R. T., & Lazio, T. J. W. 2009, Proc. IEEE, 97, 1482 [NASA ADS] [CrossRef] [Google Scholar]
- Hotan, A. W., van Straten, W., & Manchester, R. N. 2004, PASA, 21, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, R. C. 1993, Antenna Engineering Handbook, 3rd edn. (McGraw-Hill) [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kant, G. W., van der Wal, E., Ruiter, M., & Benthem, P. 2009, Proc. Wide Field Science and Technology for the SKA, Limelette, Belgium, eds. S. A. Torchinsky et al., 037 [Google Scholar]
- Kant, G. W., Patel, P. D., Wijnholds, S. J., Ruiter, M., & van der Wal, E. 2011, IEEE Trans. Antennas Propagation 59, 1990 [Google Scholar]
- Karastergiou, A., Chennamangalam, J., Armour, W., et al. 2015, MNRAS, 452, 1254 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, A., Tegmark, M., Morrison, S., Lutomirski, A., & Zaldarriaga, M. 2010, MNRAS, 408, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Marthi, V. R., & Chengalur, J. 2014, MNRAS, 437, 524 [NASA ADS] [CrossRef] [Google Scholar]
- Monari, J., Perini, F., Mariotti, S., et al. 2009, Proc. Wide Field Science and Technology for the SKA, Limelette, Belgium, eds. S. A. Torchinsky et al., 040 [Google Scholar]
- Noble, B., & Daniel, J. W. 1977, Applied Linear Algebra, Prentice-Hall (Englewood Cliffs, NJ) [Google Scholar]
- Noorishad, P., Wijnholds, S. J., van Ardenne, A., & van der Hulst, J. M. 2012, A&A, 545, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olofsson, A. O. H. Torchinsky, S.A., Chemin, L., et al. 2009, Proc. Wide Field Science and Technology for the SKA, Limelette, Belgium, eds. S. A. Torchinsky et al., 042 [Google Scholar]
- Picard, P., Renaud, P., Taffoureau, C., et al. 2009, Proc. Wide Field Science and Technology for the SKA, Limelette, Belgium, eds. S. A. Torchinsky et al., 038 [Google Scholar]
- Renaud, P., Taffoureau, C., Picard, P., et al. 2011, Monitoring and Control of EMBRACE, a 4608 Elements Phased Array for Radio Astronomy, Proc. Astron. Data Analysis Software Systems, Paris, 6–10 November [Google Scholar]
- Reichart, D. E., & Stephens, A. W. 2000, ApJ, 537, 904 [NASA ADS] [CrossRef] [Google Scholar]
- Serylak, M., Karastergiou, A., Williams, C., et al. 2013, IAU Symp., 291, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Singh, H., Sneha, H. L., & Jha, R. M. 2013, Mutual Coupling in Phased Arrays: A Review, Int. J. Antennas and Propagation, ID 348123 [Google Scholar]
- Thompson, A. R., Moran, J. M., Swenson, G. W. Jr. 2004, Interferometry and Synthesis in Radio Astronomy, 2nd edn. (Wiley-VCH) [Google Scholar]
- Torchinsky, S. A., Olofsson, A. O. H., Karastergiou, A., et al. 2013, SF2A-2013: Proc. Annual meeting of the French Society of Astronomy and Astrophysics, 439 [Google Scholar]
- Torchinsky, S. A., Olofsson, A. O. H., Censier, B., et al. 2015, J. Instr., 10, C07002 [Google Scholar]
- van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Straten, W., Demorest, P., & Oslowski, S. 2012, Astron. Res. Technol., 9, 237 [NASA ADS] [Google Scholar]
- Vinyajkin, E. N., & Razin, V. A. 2004, ArXiv e-prints [arXiv:astro-ph/0412593] [Google Scholar]
- Wijnholds, S. J., Kant, G. W., van der Wal, E., et al. 2009, Proc. Wide Field Science and Technology for the SKA, Limelette, Belgium, eds. S. A. Torchinsky et al., 043 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 EMBRACE@Nançay is composed of 4608 Vivaldi antenna elements separated from each other by 12.5 cm, making it a dense array for frequencies above 1200 MHz. EMBRACE@Nançay measures 8.42 m × 8.42 m for a total area of 70.8 m2. |
| In the text | |
 |
Fig. 2 EMBRACE@Nançay system architecture consists of a four level hierarchy of analogue beamforming starting with 4608 Vivaldi antenna elements leading finally to 16 inputs to each of two digital backends. |
| In the text | |
 |
Fig. 3 An example output of the RF calibration scheme for one tileset as described in the text. The response of tile pairs for each of the 24 phase steps applied to the second tile in the pair is shown within the three groups of vertical dashed lines. The response is clustered in groups of three corresponding to the constraint of the phase shift step size, however within each group of three there is some variation. |
| In the text | |
 |
Fig. 4 Drift scan signals of the GPS BIIF-1 L5 carrier 2013-01-10 at 80° elevation in the north. Each line corresponds to a tile set and their half-widths, combined with the spacecraft’s drift rate, can be converted to a HPBW beam size of ~ 8.5° which is close to what is suggested by the standard formula 1.2 × λ/D where D is the tileset side of 2.1 m. The drift peaks are aligned as a result of applying the necessary phase shifts to each tile. |
| In the text | |
 |
Fig. 5 Power as a function of time while tracking Cassiopeia A, and tracking an empty sky position with the same declination. Note that the solid black line is the only on-source signal. Each tracking produces two curves due to the dual digital beams used as illustrated in Fig. 6. |
| In the text | |
 |
Fig. 6 Source tracking strategy. Two digital beams are placed symmetrically within the FoV (tileset beam) following the same sky trajectory but with a time delay. One of them is centred on the source, the other is used as an off-position. |
| In the text | |
 |
Fig. 7 Correlator offset seen in sky images. The correlator offset problem discussed in the text is also manifested by blob-like features when imaging the tileset FoV. Here the left and right upper panels show FoV images of Cygnus A, and towards an empty sky position, based on uncorrected cross correlations. The bottom panels show the same data but with images created from cross correlations corrected by subtracting a reference matrix of complex constants (the same reference was used for both images). In the left bottom panel, Cygnus A is now clearly seen and at its expected position (offset from centre due to the scheme outlined in Fig. 6). |
| In the text | |
 |
Fig. 8 A plot of the complex plane showing the correlator offsets while observing empty sky. The offset is much larger than the thermal scatter of the points during 10 min observations. The red lines are simply to mark the separation from the plot origin. |
| In the text | |
 |
Fig. 9 Correlator offset without frontend. When one tileset is replaced by a 50 Ohm load, the correlator offset remains, showing that the correlator offset is not due to the frontend system (antennas, amplifiers, beamformer chips, etc.). |
| In the text | |
 |
Fig. 10 Correlator offset for the High Band Antenna array of the LOFAR station at Nançay. Note that the plot scale is 3 orders of magnitude smaller than the corresponding EMBRACE plot. The outliers are all neighbour antennas indicating the offset is due to cross talk between those antennas. |
| In the text | |
 |
Fig. 11 Sky images without and with a source in the field. Using the cross-correlation statistics data, interferometric images can be made at a given sub-band. a) A phantom point source can be seen in images produced from data pointing at “empty sky” and assuming zenith pointing. b) The image of the Sun has peak more than an order of magnitude larger than the phantom point source. |
| In the text | |
 |
Fig. 12 Drift scan of Cas A at 1171.4 MHz in a bandwidth of ~1 MHz. The top image shows the full time span of the drift scan with a baseline fit. The bottom plot is a zoom to the main lobe with the baseline fit removed. The measured FWHM is 1.476deg which is very close to the expected value of 1.466deg. |
| In the text | |
 |
Fig. 13 Drift scan of the Sun across the stationary digital beam pointing reaches its maximum at the expected time. The sidelobe levels are below the 15 dB design criterion. |
| In the text | |
 |
Fig. 14 Snapshot image of the GPS BIIF-1 satellite on 2012-09-05 at 1175 MHz. The angular range covered approximately corresponds to two times the tileset FoV. Note that for the full up instrument beam layout, the pattern shown is tapered by the larger scale tileset main beam which is outlined in Fig. 4. |
| In the text | |
 |
Fig. 15 Contour plot (dB scale, 0 at maximum amplitude) of the interferometric imaging in one sub-band and after a phase-only calibration (top panel), and a full redundancy-based calibration (bottom panel), for a GPS satellite observation with EMBRACE@Nançay. Observed data are shown as dashed contours, while the best-fit rectangle aperture model is shown as continuous ones. The periodization of the main pattern is due to sampling of the UV plane, here the equivalent of 3 fields of view is shown. |
| In the text | |
 |
Fig. 16 1D Diagonal of 2D interferometric PSF (dB scale, 0 at maximum amplitude), for both GPS observation and best-fit model. |
| In the text | |
 |
Fig. 17 1D Diagonal of 2D interferometric PSF (dB scale, 0 at maximum amplitude), for an EMBRACE-like array with 50 times larger side length (about 400 m side length), following the square aperture model best-fit parameters. |
| In the text | |
 |
Fig. 18 This drift scan of the Sun used 6 beams of EMBRACE@Nançay pointing along the trajectory of the Sun across the sky (inset top right). |
| In the text | |
 |
Fig. 19 Received intensity as a function of elevation for CasA and CygA at three frequencies. The vertical red lines indicate 45° elevation which is the nominal scan angle limitation for EMBRACE. The effect of the treeline is also visible at elevations below 45°. |
| In the text | |
 |
Fig. 20 Allan variance as a function of time. This observation was performed as a three-day drift scan of Cas A pointing at ~ 79° elevation due south. The signals from the daily Cas A passages have been removed. In the lower panels also a few strong signals have been removed that occurred on a solar day basis (those could be due to any kind of human activity such as a transmitter that is scheduled to turn on or increase its power for a short while every day, or artificially induced changes to the instrument environment such as variations in the AC power grid). |
| In the text | |
 |
Fig. 21 Top left: raw averaged spectra (blue = on, red = off). Note that the horizontal axis has increasing frequency to the right. The galactic foreground is visible in both positions around channel 470. Mid right: coarsely calibrated spectrum with four offset sub-bands corrected by adjusting their level to that of neighbouring sub-bands. Also shown in green is a second order baseline fit. Bottom left: baseline subtracted spectrum where obvious spikes have been interpolated out. A comparison with the LAB survey spectrum is shown in golden/yellow. The detailed line shape agreement is excellent apart from a portion that is obviously asscociated with an unstable sub-band. Note that the galactic foreground has mostly been subtracted out in the EMBRACE spectrum with only a negative residual remaining. |
| In the text | |
 |
Fig. 22 PSR B0329+54. The pulsar is detected after several minutes as shown in this dynamic plot folded at the pulsar period of 715 msec. The figure was plotted using PSRCHIVE software (Hotan et al. 2004; van Straten et al. 2012). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


