| Issue |
A&A
Volume 588, April 2016
|
|
|---|---|---|
| Article Number | A78 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201527436 | |
| Published online | 22 March 2016 | |
AGN host galaxy mass function in COSMOS
Is AGN feedback responsible for the mass-quenching of galaxies?
1 INAF–Osservatorio Astronomico di Roma, via Frascati 33, 00040 Monteporzio Catone, Italy
e-mail: angela.bongiorno@oa-roma.inaf.it (OAR)
2 Kavli Institute for the Physics and Mathematics of the Universe, Todai Institutes for Advanced Study, the University of Tokyo, 277-8583 Kashiwa, Japan (Kavli IPMU, WPI)
3 Max-Planck-Institut fuer Extraterrestrische Physik (MPE), Postfach 1312, 85741 Garching, Germany
4 INAF–Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
5 Aix-Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de Marseille) UMR 7326, 13388 Marseille, France
6 Dipartimento di Matematica e Fisica, Università Roma Tre, via della Vasca Navale 84, 00146 Roma, Italy
7 Cavendish Laboratory, University of Cambridge, 19 J. J. Thomson Ave., Cambridge CB3 0HE, UK
8 European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching bei Muenchen, Germany
9 Dipartimento di Fisica e Astronomia, Università di Bologna, viale Berti Pichat 6/2, 40127 Bologna, Italy
10 California Institute of Technology, MC 249-17, 1200 East California Boulevard, Pasadena, CA 91125, USA
Received: 23 September 2015
Accepted: 5 January 2016
We investigate the role of supermassive black holes in the global context of galaxy evolution by measuring the host galaxy stellar mass function (HGMF) and the specific accretion rate, that is, λSAR, the distribution function (SARDF), up to z ~ 2.5 with ~1000 X-ray selected AGN from XMM-COSMOS. Using a maximum likelihood approach, we jointly fit the stellar mass function and specific accretion rate distribution function, with the X-ray luminosity function as an additional constraint. Our best-fit model characterizes the SARDF as a double power-law with mass-dependent but redshift-independent break, whose low λSAR slope flattens with increasing redshift while the normalization increases. This implies that for a given stellar mass, higher λSAR objects have a peak in their space density at earlier epoch than the lower λSAR objects, following and mimicking the well-known AGN cosmic downsizing as observed in the AGN luminosity function. The mass function of active galaxies is described by a Schechter function with an almost constant M∗⋆ and a low-mass slope α that flattens with redshift. Compared to the stellar mass function, we find that the HGMF has a similar shape and that up to log (M⋆/M⊙) ~ 11.5, the ratio of AGN host galaxies to star-forming galaxies is basically constant (~10%). Finally, the comparison of the AGN HGMF for different luminosity and specific accretion rate subclasses with a previously published phenomenological model prediction for the “transient” population, which are galaxies in the process of being mass-quenched, reveals that low-luminosity AGN do not appear to be able to contribute significantly to the quenching and that at least at high masses, that is, M⋆ > 1010.7 M⊙, feedback from luminous AGN (log Lbol ≳ 46 [erg/s]) may be responsible for the quenching of star formation in the host galaxy.
Key words: galaxies: active / galaxies: high-redshift / galaxies: evolution
© ESO, 2016
1. Introduction
Supermassive black hole (SMBH) growth, nuclear activity, and galaxy evolution have been found to be closely related. In the past 15 years, the discovery of tight correlations between galaxies and their central nuclei properties (see Kormendy & Ho 2013, and references therein) as well as similar evolutionary trends between the growth histories of SMBHs and galaxies (e.g., Boyle & Terlevich 1998; Marconi et al. 2004) have established a new paradigm that shows active galactic nuclei (AGN) to be the key in the process of galaxy formation and evolution. Several theoretical models (e.g., Somerville et al. 2001; Granato et al. 2004; Monaco & Fontanot 2005; Springel et al. 2005; Croton et al. 2006; Hopkins et al. 2006; Schawinski et al. 2006; Cen & Chisari 2011) have been developed to explain this co-evolution and find the mechanism responsible for the simultaneous fuelling of the central BH and the formation of new stars in the host galaxy and the quasi-simultaneous shut-off of these two processes. While the physical scales of interest (a few pc) cannot be directly resolved in these models and in current numerical simulations (e.g., Sijacki et al. 2015), the models usually propose the presence of an energetic AGN-driven feedback, which is a strong wind originating from the AGN that deposits the energy released by the accretion process within the host galaxy (Faucher-Giguère & Quataert 2012). This mechanism is able to link black hole growth and star formation and the shut-off of these two processes in a self-regulated manner. However, it is still unclear and observationally not proven whether AGN-driven feedback processes do indeed have an effect on the global properties of the galaxy population, in particular in suppressing the star formation (SF) in their host galaxy heating and/or pushing away the gas that forms stars.
Star formation quenching by some mechanism is also required to prevent the overgrowth of massive galaxies that are hosted in the most massive dark-matter haloes (e.g., Read & Trentham 2005). This “mass quenching” mechanism, regardless of its physical origin, would suppress the growth of massive galaxies and explain the steep decline of the galaxy mass function above a given characteristic mass. While supernova feedback is not energetic enough in this mass regime, a central AGN would be an efficient mechanism.
To investigate whether AGN could play this role, detailed studies on single objects have been performed to search for signatures of AGN feedback. Massive outflows on several kpc scales have been observed in a few cases (Cano-Díaz et al. 2012; Feruglio et al. 2010; Cresci et al. 2015a; Feruglio et al. 2015), but up to now the evidence that such outflows are indeed responsible for suppressing star formation in the region of the outflow is circumstantial (Cano-Díaz et al. 2012; Cresci et al. 2015a,b). Further progress can be made through statistical studies of the properties of active galaxies (e.g., SFR) compared to normal galaxies. However, results have often been contradictory: some authors found that AGN mainly lie above or on the main sequence (MS) of galaxies (Santini et al. 2012; Mullaney et al. 2012), while others (Bongiorno et al. 2012; Mullaney et al. 2015) found the SFR of AGN hosts to be lower than the average MS galaxies, as expected from the models that include AGN feedback. Bundy et al. (2008) compared the star formation quenching rate with the rate at which AGN activity is triggered in galaxies and showed that these two quantities agree over a range of masses. They interpreted this as a physical link between these two phenomena, which does not directly imply a causal link, however.
Regardless of AGN feedback, an essential pre-requisite for understanding the role of black hole activity in galaxy evolution is to have a accurate and unbiased census of the AGN population and its relation to the properties of their host galaxies. The former is basically provided by the AGN luminosity function, which is now well established over a wide range of redshift and luminosity (Ueda et al. 2014; Buchner et al. 2015; Aird et al. 2015; Miyaji et al. 2015; Silverman et al. 2008). Deep X-ray surveys established a trend of AGN downsizing, which means that the most luminous AGN have the peak in their space density at earlier times than lower luminosity AGN (Ueda et al. 2003; Hasinger et al. 2005), which is also seen in optical surveys (Bongiorno et al. 2007; Croom et al. 2009). This trend is similar to the downsizing in the galaxy population (Cowie et al. 1996), where the most massive galaxies build their mass at earlier times than lower mass galaxies.
Linking black hole growth to their host galaxies requires studying their stellar mass function and/or the active fraction or duty cycle of AGN occurrence in galaxies of a given stellar mass (e.g., Bundy et al. 2008; Xue et al. 2010; Georgakakis et al. 2011; Aird et al. 2012; Bongiorno et al. 2012; Lusso et al. 2012). Most of these studies define AGN activity above a certain X-ray luminosity threshold and found the fraction of AGN at given LX to increase with stellar mass. However, this may lead to a biased view, since AGN at different masses cover different ranges of Eddington ratios for a given luminosity range, and AGN have been found to show a wide distribution of Eddington ratios (e.g., Kauffmann & Heckman 2009; Schulze & Wisotzki 2010). Aird et al. (2012) showed that the intrinsic distribution of specific accretion rates at z< 1 follows a power law whose shape does not evolve with redshift, independent of stellar mass. This result has been confirmed and extended out to z< 2.5 by Bongiorno et al. (2012).
We here build upon these previous studies of AGN hosts by establishing the bivariate distribution function of stellar mass and specific accretion rate for a hard X-ray selected AGN sample over the redshift range 0.3 <z< 2.5. We use the derived AGN host galaxy stellar mass function to test the hypothesis of AGN feedback as driver of star formation quenching. In particular, we test whether the AGN population can be associated with and/or be responsible for mass quenching using the model prediction from Peng et al. (2010) for the mass function of the transient population (these are galaxies in the process of being mass-quenched).
The paper is organized as follows: in Sect. 2 we present the X-ray selected sample. Section 3 presents the method used to derive the specific accretion rate distribution function and the AGN host galaxy mass function (Sects. 3.2 and 3.3) and their results (Sect. 3.4). In Sect. 4 we address the question of the link between AGN and star formation quenching by comparing the AGN host galaxy mass function, computed for different subsamples, with the model prediction for quenching galaxies by Peng et al. (2010).
Throughout this paper, a standard cosmology (Ωm = 0.3, Ωλ = 0.7 and H0 = 70 km s-1 Mpc-1) has been assumed. The stellar masses are given in units of solar masses for a Chabrier IMF (Chabrier 2003).
2. Sample
The AGN sample considered here was extracted from the XMM-COSMOS point-like source catalog (Hasinger et al. 2007; Cappelluti et al. 2009), whose optical identifications and multiwavelength properties were presented by Brusa et al. (2010). The catalog contains ~1800 X-ray sources detected above flux limits of ~5 × 10-16, ~3 × 10-15 and ~7 × 10-15 erg cm-2 s-1 in the [0.5−2] keV, [2−10] keV and [5−10] keV bands, respectively.
Our analysis is based on objects that have been detected in the hard [2−10] keV band. The restriction to a hard X-ray selected sample was chosen since the soft band can be affected by obscuration that can lead to a redshift-dependent incompleteness (flux-limited surveys pick up more obscured objects at higher redshift, see, e.g., Gilli et al. 2010). However, this band may still suffer from incompleteness that is due to heavily obscured and Compton-thick (CT, log (NH) > 24 [cm-2]) AGN, whose detection probability is strongly reduced because the intrinsic emission can be significantly suppressed by repeated Compton scattering and photoelectric absorption.
Out of the full ~1800 sources, we identified a final sample of 927 hard X-ray selected AGN in the redshift range 0.3 <z< 2.5. All hard X-ray sources have accurate photometric redshifts (Salvato et al. 2011), while about half (581 of 927) have secure spectroscopic redshifts.
2.1. X-ray luminosities, host galaxy stellar masses, and specific accretion rates
Rest-frame, intrinsic X-ray [2−10] keV luminosities for the final sample were derived from the observed hard X-ray flux. Following La Franca et al. (2005), we converted the observed [2−10] keV fluxes to the intrinsic [2−10] keV luminosities for each AGN with a given measured NH by applying a K-correction computed by assuming an intrinsic X-ray spectrum with a photon index Γ = 1.8, an exponential cut-off at E = 200 keV and, a photoelectric absorption corresponding to the observed NH column density. The [2−10] keV luminosity is given by![\begin{equation} L_{[2-10]~\rm keV}^{\rm rf} = F_{[2-10]~\rm keV} 4 \pi D_{\rm L}^2 K(z,N_{\rm H}) , \end{equation}](/articles/aa/full_html/2016/04/aa27436-15/aa27436-15-eq26.png) (1)where DL is the luminosity distance and K(z,NH) is the term that accounts for the K-correction and absorption correction. The absorbing column density NH for our sample was derived as in Merloni et al. (2014). For the brightest sources (above 200 pn counts in the 0.5−10 keV band of XMM-Netwton) NH was obtained from the full spectral analysis of Mainieri et al. (2011), which is available for 195 of 927 of the AGN. For the remaining sources, NH was estimated in a statistical fashion by assessing the value of the observed spectral slope from the hardness ratio and assessing the value of the intrinsic spectral slope drawn from a normal distribution with mean and dispersion of Γint = 1.8 ± 0.2. While this estimate shows a significant scatter, there are no apparent systematic biases, as demonstrated in Merloni et al. (2014). Therefore these estimates can be robustly used for the statistical studies performed in this paper.
(1)where DL is the luminosity distance and K(z,NH) is the term that accounts for the K-correction and absorption correction. The absorbing column density NH for our sample was derived as in Merloni et al. (2014). For the brightest sources (above 200 pn counts in the 0.5−10 keV band of XMM-Netwton) NH was obtained from the full spectral analysis of Mainieri et al. (2011), which is available for 195 of 927 of the AGN. For the remaining sources, NH was estimated in a statistical fashion by assessing the value of the observed spectral slope from the hardness ratio and assessing the value of the intrinsic spectral slope drawn from a normal distribution with mean and dispersion of Γint = 1.8 ± 0.2. While this estimate shows a significant scatter, there are no apparent systematic biases, as demonstrated in Merloni et al. (2014). Therefore these estimates can be robustly used for the statistical studies performed in this paper.
 |
Fig. 1 Bivariate distribution for the analyzed hard X-ray selected sample in the M⋆−λSAR plane color-coded according to the redshift bins. The horizontal and vertical dashed lines correspond to the lower limit cuts applied in M⋆ and λSAR. |
Host galaxy stellar masses have been derived in Bongiorno et al. (2012) using a two-component (AGN and galaxy) SED-fitting technique. We refer to this paper for a detailed description of the method.
Following Aird et al. (2012) and Bongiorno et al. (2012), we define the specific accretion rate λSAR≡ LX/M⋆ (see also Brusa et al. 2009; Georgakakis et al. 2014) as a directly measurable quantity that can be regarded as a proxy for the black hole growth rate relative to the stellar mass of the host galaxy, ṀBH/M⋆, after taking into account the (luminosity-dependent) bolometric correction (e.g., Marconi et al. 2004; Lusso et al. 2012) and a radiative efficiency factor. It is also related to the Eddington ratio of the SMBH, λEdd = Lbol/MBH, by applying the bolometric correction factor and the scaling relationship between black hole mass and host stellar mass. Assuming as an approximation a mean bolometric correction kbol = 25 (Marconi et al. 2004; Lusso et al. 2012) and a constant mass ratio of the stellar host to the black hole of 500 (Marconi & Hunt 2003; Häring & Rix 2004), log λSAR = 34 [erg/s /M⊙] approximately corresponds to the Eddington limit, while log λSAR = 32 [erg/s /M⊙] would give 1% of the Eddington limit. The bivariate distribution M⋆ −λSAR for the analyzed sample is shown in Fig. 1, where different colors correspond to different redshift ranges as labeled.
To determine the mass function, we furthermore restricted our sample in stellar mass M⋆ and specific accretion rate λSAR by applying the following cuts: M⋆> 109.5 M⊙ and λSAR> 1032 erg/s /M⊙. The latter criterion is motivated by the requirement of having a clear cut in λSAR above which we define the AGN as active (see below). The chosen minimum λSAR value corresponds to the lowest observed value in our intermediate-redshift bin and furthermore corresponds approximately to 1% of the Eddington limit, which we chose in the following as our lowest threshold to define an active black hole, consistent with studies of type 1 AGN (Schulze et al. 2015). After applying these limits, our sample is reduced to 877 AGN with 0.3 <z< 2.5.
3. AGN host galaxy mass function and specific accretion rate distribution function
To derive the AGN host galaxy mass function (HGMF) and the specific accretion rate distribution function (SARDF), we have to account for various selection effects in our flux-limited AGN sample. This requires a careful assessment of the incompleteness function.
Completeness in LX does not directly ensure completeness in M⋆. As previously reported, AGN show a wide range of Eddington ratios (Kauffmann & Heckman 2009; Schulze & Wisotzki 2010), and thus also a wide range of LX/M⋆ (λSAR), with a distribution falling below the corresponding Eddington limit approximately following a power-law distribution (Aird et al. 2012; Bongiorno et al. 2012).
A luminosity-complete AGN sample will be biased toward high-mass BHs and high galaxy mass. This means that because an AGN with a low Eddington ratio will be included in the sample only if its MBH is high enough to be above the given luminosity (LX) limit, a bias toward high-mass black holes induces a bias toward high-mass galaxies because of the relation between MBH−M⋆. This effect has to be carefully taken into account when building a galaxy-mass-complete sample starting from an X-ray flux-limited AGN sample.
3.1. Incompleteness function
Our corrections for incompleteness account for three effects: (1) the X-ray sensitivity function; (2) the absorption correction f(NH | LX,z); and (3) the stellar mass completeness down to our threshold in units of specific accretion rate log λSAR = 32 [erg/s /M⊙].
The first selection effect to consider is the position-dependent X-ray flux limit based on the sensitivity map computed by Cappelluti et al. (2009). The absorption correction accounts for the sources that were missed in the sample because of their high column density NH. For this correction we used the NH distribution as a function of z and LX that was published by Ueda et al. (2014) based on several X-ray AGN surveys (see their Eqs. (5) and (6)). We integrated over the NH distribution between 20 < log NH< 24, i.e., we did not include Compton-thick AGN in our HGMF determination. The fraction of CT AGN is still uncertain and the NH distribution above log NH = 24 is poorly known (Ueda et al. 2014; Buchner et al. 2015; Aird et al. 2015). The contribution of CT AGN to the AGN space density is expected to lie between ~10−40% (Gilli et al. 2007; Treister et al. 2009; Vignali et al. 2014; Buchner et al. 2015; Lansbury et al. 2015). These two corrections applied to the flux-limited sample result in a luminosity-complete sample.
As described above, the sample is also significantly incomplete because a broad range of M⋆ can be associated with a given luminosity LX. To account for this effect in the HGMF, we need to include an additional term to the incompleteness function based on the distribution of λSAR. Using this distribution function, we corrected for incompleteness down to a fixed threshold in λSAR, which we set at log λSAR = 32 [erg/s /M⊙]. The HGMF is therefore defined as the mass function of all AGN above this λSAR threshold. The most rigorous and self-consistent approach to do this is by determining the HGMF and the SARDF simultaneously, for instance, with the maximum likelihood method described in the next section.
 |
Fig. 2 Bivariate distribution function Ψ(M⋆,λSAR,z), for our best-fitting parametric model, derived through the maximum likelihood method, in three redshifts bins. The orange contours indicate lines of constant space density (from 10-10 to 10-3 Mpc-3), separated by a factor of 10 each. |
3.2. Maximum likelihood method
We here present the method of determining the SARDF and the HGMF simultaneously as a bivariate distribution function of stellar mass and specific accretion rate, Ψ(M⋆,λSAR,z), where Ψ(M⋆,λSAR,z)dlog M⋆dlog λSAR gives the space density of AGN with stellar mass host galaxies between log M⋆ and log M⋆ + dlog M⋆ and a specific accretion rate between log λSAR and log λSAR + dlog λSAR at the redshift z. The HGMF, SARDF, and the X-ray AGN LF (XLF) can be derived as different marginalizations over this bivariate distribution function. We used the maximum likelihood method developed by Schulze & Wisotzki (2010) and extended by Schulze et al. (2015) to compute Ψ(M⋆,λSAR,z). While these works focused on the joint determination of the active black hole mass function and the Eddington ratio distribution function (using type 1 AGN), the method was implemented here for the joint determination of the HGMF and SARDF.
The technique minimizes the likelihood function S = −2 ∑ lnpi, where the probability distribution pi for each object is given by 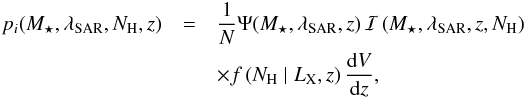 (2)where Ψ(M⋆,λSAR,z) is the bivariate distribution function of stellar mass and specific accretion rate that we wish to derive,
(2)where Ψ(M⋆,λSAR,z) is the bivariate distribution function of stellar mass and specific accretion rate that we wish to derive, 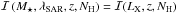 is the X-ray selection function given by the sensitivity map in the 2−10 keV band, and f(NH | LX,z) is the absorption distribution function, taken from Ueda et al. (2014). We used the NH estimates presented in Sect. 2.1 to compute LX (and therefore λSAR) and f(NH | LX,z) for our sample. The factor N corresponds to the total number of objects in the sample predicted by the model, and it is given by integrating over M⋆, λSAR NH, and z,
is the X-ray selection function given by the sensitivity map in the 2−10 keV band, and f(NH | LX,z) is the absorption distribution function, taken from Ueda et al. (2014). We used the NH estimates presented in Sect. 2.1 to compute LX (and therefore λSAR) and f(NH | LX,z) for our sample. The factor N corresponds to the total number of objects in the sample predicted by the model, and it is given by integrating over M⋆, λSAR NH, and z, 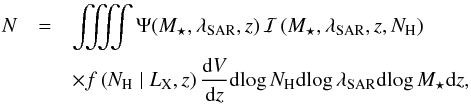 (3)where we integrated over the NH distribution between 20 < log NH< 24, while our integration ranges in M⋆, λSAR and z are 9.5 < log M⋆< ∞, 32 < log λSAR< ∞ and 0.3 <z< 2.5, as discussed in Sect. 2.1.
(3)where we integrated over the NH distribution between 20 < log NH< 24, while our integration ranges in M⋆, λSAR and z are 9.5 < log M⋆< ∞, 32 < log λSAR< ∞ and 0.3 <z< 2.5, as discussed in Sect. 2.1.
Our sample also contains 12 AGN without M⋆ measurements because of poor-quality photometry. However, we accounted for these sources using their luminosity and redshift information integrated over the entire mass range,  (4)Our XMM-COSMOS based sample covers only a limited dynamical range in LX, narrower than the full range over which the XLF is currently determined. This might lead to degenerate solutions for the bivariate distribution function, some of which may be inconsistent with the XLF. Ideally, we would like to construct the HGMF and SARDF including deeper and larger area surveys, but this is beyond the scope of the present work. To reduce this effect, we included the XLF as additional observational data. In this way, we ensured consistency with the XLF observations over its full observationally determined luminosity range. In particular, we used the binned XLF from Miyaji et al. (2015) and computed the χ2 value for the comparison with the XLF implied by the HGMF and SARDF. We then added this likelihood to that of the XMM-COSMOS sample. The study by Miyaji et al. (2015) used the same NH distribution as Ueda et al. (2014) to determine the XLF as we employed here. Over our range in redshift and luminosity, the XLF by Miyaji et al. (2015) is consistent with other recent studies (Ueda et al. 2014; Buchner et al. 2015; Aird et al. 2015), thus our results are robust against the specific choice of XLF.
(4)Our XMM-COSMOS based sample covers only a limited dynamical range in LX, narrower than the full range over which the XLF is currently determined. This might lead to degenerate solutions for the bivariate distribution function, some of which may be inconsistent with the XLF. Ideally, we would like to construct the HGMF and SARDF including deeper and larger area surveys, but this is beyond the scope of the present work. To reduce this effect, we included the XLF as additional observational data. In this way, we ensured consistency with the XLF observations over its full observationally determined luminosity range. In particular, we used the binned XLF from Miyaji et al. (2015) and computed the χ2 value for the comparison with the XLF implied by the HGMF and SARDF. We then added this likelihood to that of the XMM-COSMOS sample. The study by Miyaji et al. (2015) used the same NH distribution as Ueda et al. (2014) to determine the XLF as we employed here. Over our range in redshift and luminosity, the XLF by Miyaji et al. (2015) is consistent with other recent studies (Ueda et al. 2014; Buchner et al. 2015; Aird et al. 2015), thus our results are robust against the specific choice of XLF.
We caution that the faint end of the XLF is not directly constrained by our sample: the XLF will also include AGN below our threshold in M⋆ and λSAR, which are not accounted for in our bivariate distribution function fit. This may lead to an overestimate of the space density at log LX< 43 [erg/s].
The total likelihood to minimize is given by 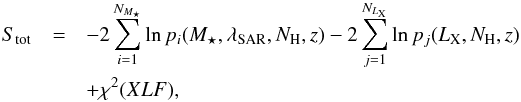 (5)where NM⋆ is the number of AGN with M⋆ measurements in our sample and NLX is the number of AGN with only LX known. The absolute normalization of the bivariate distribution function is then determined by scaling to the total observed number of objects in the sample.
(5)where NM⋆ is the number of AGN with M⋆ measurements in our sample and NLX is the number of AGN with only LX known. The absolute normalization of the bivariate distribution function is then determined by scaling to the total observed number of objects in the sample.
Following Aird et al. (2012) and Bongiorno et al. (2012), we first assumed that the bivariate distribution function Ψ(M⋆,λSAR,z) is separable, meaning that the specific accretion rate distribution is mass independent and vice versa. Under this assumption, the bivariate distribution function is given by 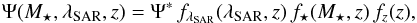 (6)where Ψ∗ is the normalization of the bivariate distribution function, fλSAR(λSAR,z) is the SAR term, f⋆(M⋆,z) is the M⋆-term and fz(z) is a redshift evolution term.
(6)where Ψ∗ is the normalization of the bivariate distribution function, fλSAR(λSAR,z) is the SAR term, f⋆(M⋆,z) is the M⋆-term and fz(z) is a redshift evolution term.
However, for the SAR term, we also tested a mass-dependent model and found this model to provide a better description of our data (see Appendix A for more details). The bivariate distribution function is therefore written as 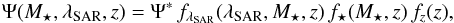 (7)where fλSAR(λSAR,M⋆,z) now also contains a dependence on the mass. We used this more general parametrization as our default model. We point out that the SAR term fλSAR and the M⋆ term f⋆ are not equal to the SARDF and HGMF.
(7)where fλSAR(λSAR,M⋆,z) now also contains a dependence on the mass. We used this more general parametrization as our default model. We point out that the SAR term fλSAR and the M⋆ term f⋆ are not equal to the SARDF and HGMF.
The HGMF and the SARDF are calculated by integrating Ψ(M⋆,λSAR,z) over λSAR and over M⋆, respectively. To be specific, 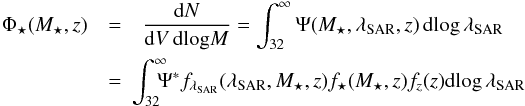 (8)and
(8)and 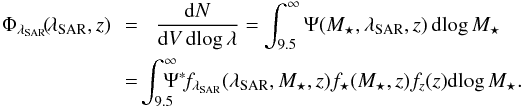 (9)In case of separable SAR- and M⋆-terms, as in Eq. (6), the SARDF (HGMF) has the same shape as fλSAR (f⋆) and only the absolute normalization is determined by the marginalization. However, in the more general case of Eq. (7), this is not necessarily the case, which is why the HGMF and SARDF then cannot be explicitly expressed as analytic functions.
(9)In case of separable SAR- and M⋆-terms, as in Eq. (6), the SARDF (HGMF) has the same shape as fλSAR (f⋆) and only the absolute normalization is determined by the marginalization. However, in the more general case of Eq. (7), this is not necessarily the case, which is why the HGMF and SARDF then cannot be explicitly expressed as analytic functions.
We here considered the following parametric models for the individual terms: the M⋆ term is modeled using a Schechter function: 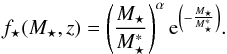 (10)While a model with a low-mass slope α evolving with redshift was included, we found that the best-fit parameters are indeed consistent with no z-evolution in α.
(10)While a model with a low-mass slope α evolving with redshift was included, we found that the best-fit parameters are indeed consistent with no z-evolution in α.
The SAR term is instead described by a double power-law:  (11)where the low λSAR slope γ1(z) = γ1,0 + kγ(z−z0), with z0 set at 1.1, and the break
(11)where the low λSAR slope γ1(z) = γ1,0 + kγ(z−z0), with z0 set at 1.1, and the break 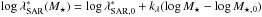 with log M⋆,0 = 11.
with log M⋆,0 = 11.
The assumption of a double power-law for fλSAR, allows recovering the double power-law shape of the XLF with a Schechter function HGMF, as demonstrated by Aird et al. (2013). We fixed the break value to ![\hbox{$\log\lambda^*_{\rm SAR,0}=33.8\, [{\rm erg/s}/M_{\odot}]$}](/articles/aa/full_html/2016/04/aa27436-15/aa27436-15-eq114.png) to limit the number of free parameters. This value is close to the implied Eddington limit, consistent with the approach in the study of Aird et al. (2013), and with the tentative evidence for such a break first reported in Bongiorno et al. (2012).
to limit the number of free parameters. This value is close to the implied Eddington limit, consistent with the approach in the study of Aird et al. (2013), and with the tentative evidence for such a break first reported in Bongiorno et al. (2012).
Finally, we parameterized the redshift evolution of the normalization of the space density as 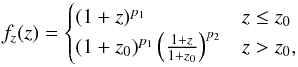 (12)where we fixed z0 = 1.1, motivated by the break redshift used in the LDDE model in the XLF from Miyaji et al. (2015) and approximately corresponding to the central redshift in our sample.
(12)where we fixed z0 = 1.1, motivated by the break redshift used in the LDDE model in the XLF from Miyaji et al. (2015) and approximately corresponding to the central redshift in our sample.
The best-fit bivariate distribution function Ψ(M⋆,λSAR,z) is shown in Fig. 2, the best-fitting parameters and their errors are given in Table 1. We computed the uncertainties of each parameter using a Markov chain Monte Carlo (MCMC) sampling of the likelihood function space, using emcee (Foreman-Mackey et al. 2013), a Python implementation of an affine invariant MCMC ensemble sampler as presented by Goodman et al. (2010). We used uniform priors for our free parameters and initialized the MCMC “walkers” around the best-fit maximum likelihood solution. The quoted uncertainties represent the 16 and 84 percentile of the parameter distribution, marginalized over all other parameters except for Ψ∗. The latter is not determined by the maximum likelihood fit, and their error is given by 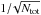 .
.
As mentioned above, our best-fit HGMF and SARDF given by Eqs. (8) and (9) cannot be expressed as simple analytic functions because M⋆ and λSAR are too entangled in the SARDF term. For a better quantitative representation of the redshift evolution of HGMF and SARDF and for illustrative purposes, we provide an analytic approximation of the two distribution functions, evaluated at the center of our three redshift bins. For this, we performed a least-squares fit to the HGMF (computed via Eq. (8)) at each redshift with a standard Schechter function with normalization 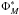 , break
, break 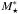 , and low-mass slope α, and the SARDF (computed via Eq. (9)) with a double power-law with normalization
, and low-mass slope α, and the SARDF (computed via Eq. (9)) with a double power-law with normalization 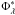 , break
, break 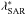 , and slopes γ1, γ2. We provide the best-fit parameters in Tables 2 and 3.
, and slopes γ1, γ2. We provide the best-fit parameters in Tables 2 and 3.
Best-fit model parameters for the AGN host galaxy mass Schechter function, computed in our three redshift bins.
Best-fit model parameters of the AGN specific accretion rate double power-law function, computed in our three redshift bins.
 |
Fig. 3 Upper panels: total AGN HGMF with the associated errors in three redshift bins derived through the maximum likelihood (black line and gray shaded area) and the Vmax (data points) methods. In each bin the lowest z fit is reported for reference with a dashed line. The red and blue lines are the total and the star-forming galaxy stellar mass functions with the associated errors (shown in magenta and cyan shaded areas) from Ilbert et al. (2013). Lower panels: ratio of AGN host galaxies to the total (red line) and the star-forming (blue line) galaxy population as a function of stellar mass in the same redshift bins. |
 |
Fig. 4 Upper panels: the SAR term split into three redshift bins and described as a double power-law with a mass dependent λSAR∗ as in Eq. (11). Lower panels: SARDF derived through the maximum likelihood method by integrating the bivariate distribution function over M⋆ (Eq. (8)). The shaded area includes the errors on the parameters. |
3.3. Vmax method
An additional consistency check can be obtained by computing the AGN host galaxy mass function using the Vmax method. The Vmax for each individual object is given by 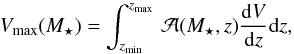 (13)where
(13)where 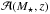 is the effective area as a function of M⋆ and z given by the total survey area Ω times the incompleteness function. We emphasize here that the Vmax(M⋆) values used are not identical to the Vmax(LX) values that would be used to computate the AGN luminosity function. This is because, as discussed above, we also have to account in the incompleteness function for the SARDF in addition to the sensitivity function and the absorption correction. The incompleteness function thus includes three terms and can be written as
is the effective area as a function of M⋆ and z given by the total survey area Ω times the incompleteness function. We emphasize here that the Vmax(M⋆) values used are not identical to the Vmax(LX) values that would be used to computate the AGN luminosity function. This is because, as discussed above, we also have to account in the incompleteness function for the SARDF in addition to the sensitivity function and the absorption correction. The incompleteness function thus includes three terms and can be written as 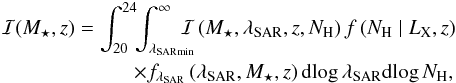 (14)where
(14)where 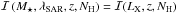 is the X-ray selection function given by the sensitivity map in the [2−10] keV band, f(NH | LX,z) is the absorption distribution function from Ueda et al. (2014), and
is the X-ray selection function given by the sensitivity map in the [2−10] keV band, f(NH | LX,z) is the absorption distribution function from Ueda et al. (2014), and 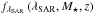 is the SARDF term in ΨλSAR(M⋆,λSAR,z). The latter term is required for the mass-dependent incompleteness function
is the SARDF term in ΨλSAR(M⋆,λSAR,z). The latter term is required for the mass-dependent incompleteness function 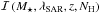 in addition to the terms needed to compute the luminosity-dependent incompleteness function ℐ(LX,z).
in addition to the terms needed to compute the luminosity-dependent incompleteness function ℐ(LX,z).
While the Vmax method has the advantage of providing a non-parametric estimate of the AGN host galaxy mass function, it has the disadvantages that it requires a specific assumption for the SARDF term and, furthermore, it does not include the additional constraints from the AGN XLF, which, as a result of the limited luminosity range probed by our sample, makes the results less robust in particular at the low-mass end, where we only probe a limited range in λSAR. In contrast, the maximum likelihood provides a parametric estimate of the mass function and determines the HGMF and SARDF simultaneously and self-consistently. Therefore we only used the Vmax method as a consistency check. For the function fλSAR(λSAR,M⋆,z) we assumed the best-fit M⋆-dependent SAR-term determined above (Eq. (11)), normalized within log λSAR> 32 [erg/s /M⊙], which again defines our lower integration limit.
The AGN host galaxy mass function is thus computed in three redshift bins as 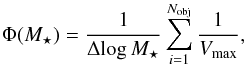 (15)and the binned values are shown in Fig. 3 together with the maximum likelihood result. The error bars are determined by bootstrapping of the sample with their Vmax(M⋆) values.
(15)and the binned values are shown in Fig. 3 together with the maximum likelihood result. The error bars are determined by bootstrapping of the sample with their Vmax(M⋆) values.
As shown in the figure, we find a good overall agreement between the Vmax binned AGN HGMF and the AGN HGMF based on the maximum likelihood method. This confirms the adopted parametric model in the maximum likelihood approach and verifies the robustness of our results.
3.4. Results
In the upper panles of Fig. 4 we show the SAR term fλλSAR (Eq. (11)), described by a double power-law with mass-dependent, but redshift-independent break 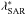 . The SARDF, shown in the lower panels of the same figure, is obtained by integrating the bivariate distribution function (including the above function) over M⋆. The SARDF can be described by a double power-law whose low λSAR characteristic slope flattens from −1.35 to −0.54 from the lowest to the highest redshift bin. Conversely, the overall normalization
. The SARDF, shown in the lower panels of the same figure, is obtained by integrating the bivariate distribution function (including the above function) over M⋆. The SARDF can be described by a double power-law whose low λSAR characteristic slope flattens from −1.35 to −0.54 from the lowest to the highest redshift bin. Conversely, the overall normalization 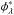 increases for increasing redshift (see Table 3). The increasing normalization with redshift was noted in Aird et al. (2012) and Bongiorno et al. (2012). In these works, the specific accretion rate distribution was parametrized with a single power-law over the full redshift range, but Bongiorno et al. (2012) noted the presence of a break above log λSAR> 34 [erg/s/M⊙]. Furthermore, Aird et al. (2013) argued for a break in the specific accretion rate distribution to be consistent with the XLF.
increases for increasing redshift (see Table 3). The increasing normalization with redshift was noted in Aird et al. (2012) and Bongiorno et al. (2012). In these works, the specific accretion rate distribution was parametrized with a single power-law over the full redshift range, but Bongiorno et al. (2012) noted the presence of a break above log λSAR> 34 [erg/s/M⊙]. Furthermore, Aird et al. (2013) argued for a break in the specific accretion rate distribution to be consistent with the XLF.
While these previous studies did not report a change in the shape of the specific accretion rate distribution with redshift, we find a SARDF clearly flattening toward higher redshift. It is important to note that compared to the aforementioned works, there are some differences. First, here we determined the SARDF, that is, the absolute space density as a function of λSAR, while the previous studies present pAGN(λSAR | M⋆), which is the AGN fraction in the galaxy population. Furthermore, we accounted for obscuration by integration over the NH distribution, which generally steepens our low λSAR slope.
 |
Fig. 5 Left panel: redshift evolution of the SARDF space density for different λSAR. Magenta: log(λSAR)= 32 [erg/s /M⊙] (~1% Edd); green: log(λSAR)= 32.5 [erg/s /M⊙] (~3% Edd); yellow: log(λSAR)= 33 [erg/s /M⊙] (~10% Edd); red: log(λSAR)= 33.5 [erg/s /M⊙] (~30% Edd); blue: log(λSAR)= 34.0 [erg/s /M⊙] (~Edd); and black: log(λSAR)= 34.5 [erg/s /M⊙] (>Edd). Central panel: redshift evolution of the HGMF space density for different M⋆. Right panel: redshift evolution of the XLF space density for different LX by Miyaji et al. (2015). |
Aird et al. (2012) refers to 0.2 <z< 1.0 and thus it did not cover a sufficiently broad redshift range to constrain this shape evolution. The sample used in Bongiorno et al. (2012) is instead similar and largely overlaps the one used in this study. A more accurate analysis of the sample used in Bongiorno et al. (2012) could indeed reveal the redshift dependence of the specific accretion rate, which was not included in the parametric model presented in Bongiorno et al. (2012) because of the simpler single power-law parametrization. Finally, we modeled the bivariate distribution function of λSAR and M⋆ and not only the SARDF and included additional information on the XLF. We discuss the effect of the latter in more detail in the Appendix.
The best-fit HGMF (black line in Fig. 3) is well described by a Schechter function with constant 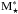 and a low-mass slope α flattening with redshift (i.e., α = −0.41 in the first redshift bin, −0.24 in the second, and −0.03 in the third; see Eq. (2)). We compared the AGN HGMF with the total galaxy stellar mass function (red curve and shaded magenta region) and the star-forming galaxy mass function (blue curve and shaded cyan region) by Ilbert et al. (2013). We note that at log (M⋆/M⊙) > 11.5, the HGMF but also the total and SF galaxy mass functions are only poorly constrained by the data (see Fig. 1) because of the limited volume sampled in both cases. This region is indicated by the dashed lines in Fig. 3. Furthermore, in the highest z-bin the galaxy mass function of Ilbert et al. (2013) shows an upturn at low masses, captured in their double Schechter function model, which is not captured in our more restricted single Schechter function model for the HGMF. Our data do not allow constraining such an upturn for our AGN sample, which would require a larger sample and probably a deeper flux limit for the galaxies including lower luminosity AGN.
and a low-mass slope α flattening with redshift (i.e., α = −0.41 in the first redshift bin, −0.24 in the second, and −0.03 in the third; see Eq. (2)). We compared the AGN HGMF with the total galaxy stellar mass function (red curve and shaded magenta region) and the star-forming galaxy mass function (blue curve and shaded cyan region) by Ilbert et al. (2013). We note that at log (M⋆/M⊙) > 11.5, the HGMF but also the total and SF galaxy mass functions are only poorly constrained by the data (see Fig. 1) because of the limited volume sampled in both cases. This region is indicated by the dashed lines in Fig. 3. Furthermore, in the highest z-bin the galaxy mass function of Ilbert et al. (2013) shows an upturn at low masses, captured in their double Schechter function model, which is not captured in our more restricted single Schechter function model for the HGMF. Our data do not allow constraining such an upturn for our AGN sample, which would require a larger sample and probably a deeper flux limit for the galaxies including lower luminosity AGN.
The ratio of AGN HGMF over total galaxy mass function is shown by the red line and the shaded magenta area in the lower panels of Fig. 3. This ratio indicates the active fraction or duty cycle of AGN activity in the galaxy population, if we consider AGN with log λSAR> 32 (~1% of the Eddington limit), which corresponds to the definition of an AGN assumed in this paper.
We find a redshift evolution in the mass dependence of the active fraction. At M⋆ = 1010 M⊙, the active fraction is approximately constant at ~ 10%, while at M⋆ = 1011.5 M⊙ it increases over our three redshift bins from ~3% to ~8% to ~20%. This trend qualitatively agrees with the results for the SMBH mass dependence of the active fraction of the black hole mass function presented in Schulze et al. (2015). This might be related to the redshift evolution of the gas reservoir available to fuel the AGN, since in high-redshift galaxies a greater amount of gas can be responsible for triggering AGN activity (Tacconi et al. 2010).
The ratio of AGN HGMF to the star-forming mass function (shown by the blue line in the lower panels of Fig. 3) traces the average relation between star-forming and AGN activity as a function of stellar mass. It extends the well-known average agreement between star formation rate density and black hole accretion density (e.g., Marconi et al. 2004) to its stellar mass dependence. Overall, we find a weaker redshift evolution in the shape of this ratio than for the active fraction, where the ratio stays almost constant over 1010<M⋆< 1011 M⊙, the mass range tracing the bulk of the population, in all three redshift bins. At the high-mass end for z> 0.8 the AGN/SF galaxy ratio and for z> 1.5 also the active fraction appear to increase with stellar mass. Future studies are required to confirm or disprove the reality of this trend.
 |
Fig. 6 Total AGN HGMF in three redshift bins derived through the maximum likelihood (black line) and compared with the AGN HGMF for different AGN subsamples in (upper panels) luminosities. log(LX) < 43 [erg/s] (magenta); log(LX) > 43 [erg/s] (cyan), log(LX) > 43.5 [erg/s] (green), log(LX) > 44 [erg/s] (red), and log(LX) > 44.5 [erg/s] (blue); and (lower panels) specific accretion rates λSAR, i.e., log λSAR> 32.5 [erg/s/M⊙] (magenta); log λSAR>33 [erg/s/M⊙] (cyan), log λSAR> 33.5 [erg/s/M⊙] (green), and log λSAR> 34 [erg/s/M⊙] (red). |
The redshift evolution of the SARDF and HGMF allows a more detailed look at the AGN downsizing behavior, i.e., the luminosity-dependent evolution, seen in the XLF out to z ~ 2.5. They probe the more physically meaningful quantities stellar mass and specific accretion rate distribution, and by inference relate to black hole mass and Eddington ratio. In Fig. 5 we show the global trend of the redshift evolution of the space density in bins of λSAR (left panel), M⋆ (central panel) and LX (right panel). The LX dependence, based on the XLF from Miyaji et al. (2015) shows the well-known AGN downsizing behavior (e.g., Ueda et al. 2003; Hasinger et al. 2005; La Franca et al. 2005; Bongiorno et al. 2007; Silverman et al. 2008). For the λSAR dependence, we see that higher λSAR objects (log λSAR> 33.5 [erg/s /M⊙]) peak in their space density at an earlier cosmic epoch than the lower λSAR objects (log λSAR< 33.5 [erg/s /M⊙]), which means that they also show a clear downsizing trend. The M⋆ dependence, based on the HGMF, also indicates a downsizing trend, with AGN in lower stellar mass galaxies showing a steeper decline in their space density toward high redshift than higher stellar mass galaxies, but less pronounced than what is seen in the SARDF. This suggests that the downsizing in the AGN luminosity function is due to the combination of a (weak) mass-dependent evolution of the HGMF and the stronger evolution of the SARDF.
In the upper panels of Fig. 6 we show the AGN HGMF for different luminosity subclasses: log (LX) < 43 [erg/s] (magenta), log (LX) > 43 [erg/s] (cyan), log (LX) > 43.5 [erg/s] (green), log (LX) > 44 [erg/s] (red), and log (LX) > 44.5 [erg/s] (blue). As expected, the high-mass end is dominated by luminous AGN (log LX> 43 [erg/s]), while the low-mass bins are mainly populated by low-luminosity objects (log LX< 43 [erg/s]) whose contribution above log (M⋆/M⊙) ~ 11 is negligible. Our definition threshold of log LX/M⋆> 32 directly excludes any AGN with log LX< 43 [erg/s] above M⋆> 1011 M⊙. This also implies that when applying an AGN definition by a luminosity threshold, as is usually done, an active fraction increasing with mass is usually found, consistent with previous work (e.g., Bundy et al. 2008; Xue et al. 2010; Aird et al. 2012; Silverman et al. 2009).
In the lower panels, we instead show the total AGN HGMF in λSAR bins: log λSAR> 32.5 [erg/s /M⊙] (magenta), log λSAR> 33 [erg/s /M⊙] (cyan), log λSAR> 33.5 [erg/s /M⊙] (green), and log λSAR> 34 [erg/s /M⊙] (red). Overall, the mass distributions of AGN of different specific accretion rate have a similar shape, only mildly affected by the M⋆ dependence in our SARDF model.
4. Mass function of galaxies in the process of being mass-quenched
According to the model described in Peng et al. (2010), the quenching process, that is, the process that leads to the transition from star-forming to passive galaxies, independent of its physical origin, can be described by two different modes: mass and environment quenching, whose differential effects on the fraction of passive or red galaxies are separable.
Peng et al. (2010) speculated that the environment quenching occurs in satellite galaxies, while the mass quenching could reflect a feedback mechanism related to star-formation or AGN. In a subsequent paper, Peng et al. (2012) confirmed the expectation on the environment quenching as due to satellite galaxies from studying the mass function of central and satellite galaxies. Here we wish to test whether the mass quenching process can be linked to AGN feedback.
The strength of the approach of Peng et al. (2010) is that this phenomenological model is based on simple observational inputs, which allows successfully reproducing many of the features of the galaxy population. Moreover, the model is able to clearly predict the mass function of the galaxies in the process of being mass-quenched and the inter-relationships between the Schechter parameters for star-forming and passive galaxies.
 |
Fig. 7 Predicted MF of transient galaxies as derived starting from a single Schechter function based on the data from Ilbert et al. (2013, green line), using the Peng recipe (Peng et al. 2010) for τ = 5 × 107 yr (blue solid line), τ = 1 × 107 yr and τ = 1 × 108 yr (blue dashed lines). We compare them with the total AGN HGMF (black line) and with the HGMF computed with different luminosity cuts. In particular in the first redshift bin, cuts of log LX> 43.8 [erg/s] (red solid line) and log LX> 44.2 and log LX> 43.5 [erg/s] for the lower and upper boundary, respectively, have been applied; while in the second and third redshift bins, these cuts are log LX> 44 (brown solid line) and log LX> 44.5 [erg/s] and log LX> 43.5 [erg/s] for the lower and upper boundaries. |
The mass function of the transient population can be described by a single Schechter function with parameters (see Eq. (28) of Peng et al. 2010) 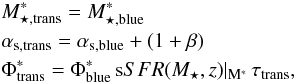 (16)where
(16)where 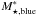 , αs,blue, and
, αs,blue, and 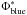 are the parameters of the Schechter function that describes the star-forming galaxy mass function, and β is the exponent in the power-law relation that links the specific star formation rate (sSFR) and the stellar mass (see Eq. (17)). Here we used the data for star-forming galaxies from Ilbert et al. (2013) and forced the fit with a single Schechter function. This parametric choice is required to use the model fits provided by Peng et al. (2010) with a single Schechter function as starting MF. This introduces some uncertainties especially with respect to the slope of the high-mass end, which is the most difficult part of the stellar MF to be constrained, as we point out below. The value τtrans is the period of time that the transient signature is visible and is not constrained by the model of Peng et al. (2010). Here, we assumed that the transient phase corresponds to the active feedback or blow-out phase, which is the gas-depletion timescale associated with the outflow. Current observations suggest this timescale to be on the order of 1−10 × 107 yr (Maiolino et al. 2007; Feruglio et al. 2010; Cicone et al. 2014). Finally, sSFR(M⋆,z) is the evolving specific star formation rate. Here we consider the recent measurement of the sSFR from Lilly et al. (2013, Eq. (2)),
are the parameters of the Schechter function that describes the star-forming galaxy mass function, and β is the exponent in the power-law relation that links the specific star formation rate (sSFR) and the stellar mass (see Eq. (17)). Here we used the data for star-forming galaxies from Ilbert et al. (2013) and forced the fit with a single Schechter function. This parametric choice is required to use the model fits provided by Peng et al. (2010) with a single Schechter function as starting MF. This introduces some uncertainties especially with respect to the slope of the high-mass end, which is the most difficult part of the stellar MF to be constrained, as we point out below. The value τtrans is the period of time that the transient signature is visible and is not constrained by the model of Peng et al. (2010). Here, we assumed that the transient phase corresponds to the active feedback or blow-out phase, which is the gas-depletion timescale associated with the outflow. Current observations suggest this timescale to be on the order of 1−10 × 107 yr (Maiolino et al. 2007; Feruglio et al. 2010; Cicone et al. 2014). Finally, sSFR(M⋆,z) is the evolving specific star formation rate. Here we consider the recent measurement of the sSFR from Lilly et al. (2013, Eq. (2)), 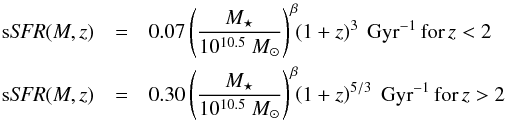 (17)with β ~ −0.1.
(17)with β ~ −0.1.
Starting from the star-forming galaxy mass function (green line in Fig. 7), we then derived with the above equations the predicted mass function of the “transient” (i.e. in the process of being mass-quenched) population. Given the uncertainties on the value of τtrans, we show in Fig. 7 the predictions for a range of τtrans = 1−10 × 107; the blue solid line is for τ = 5 × 107 while the blue dashed lines correspond to 1 × 107 yr and 1 × 108yr (lower and upper boundary, respectively).
To test whether AGN can be responsible for the mass-quenching of galaxies, we chose to restrict our analysis to the most luminous objects. Theory indeed predicts that the capability of AGN outflows of perturbing the ISM depends on AGN luminosity as 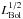 (Menci et al. 2008) and that galaxy-scale outflows are energy-driven, meaning that their mechanical energy is proportional to the AGN luminosity (Zubovas & King 2012). This scenario is supported by observations that find that the momentum rate of kpc-scale outflows (Sturm et al. 2011; Cicone et al. 2014; Feruglio et al. 2015) is ≥10−20 LBol/c. This means that the more luminous the AGN, the more powerful the outflows that are produced. Accordingly, the AGN-driven feedback mechanism should become increasingly more efficient in halting the star-formation in the host galaxy for higher AGN luminosities.
(Menci et al. 2008) and that galaxy-scale outflows are energy-driven, meaning that their mechanical energy is proportional to the AGN luminosity (Zubovas & King 2012). This scenario is supported by observations that find that the momentum rate of kpc-scale outflows (Sturm et al. 2011; Cicone et al. 2014; Feruglio et al. 2015) is ≥10−20 LBol/c. This means that the more luminous the AGN, the more powerful the outflows that are produced. Accordingly, the AGN-driven feedback mechanism should become increasingly more efficient in halting the star-formation in the host galaxy for higher AGN luminosities.
In Fig. 7 we compare the prediction for the mass function of mass quenching transient objects with the HGMF of the total population, that is, log λSAR> 32, and of different subsamples. We tested the agreement using subsamples by also applying different cuts on either LX or λSAR, as shown in Fig. 6. To keep the comparsion simple, we did not consider more complicated cuts or a luminosity-dependent transition timescale, for instance, which could improve the agreement between the two mass functions. We found that the class of objects that best reproduces the expected mass function in terms of shape and normalization are 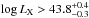 [erg/s] (red solid line and yellow shaded area) at 0.3 <z< 0.8, and log LX> 44 ± 0.5 [erg/s] at 0.8 <z< 2.5. Reducing the threshold in LX leads to a space density in the HGMF higher than expected for the transient objects at the low-mass end. Conversely, specific accretion-rate-based subsamples do not seem to reproduce the expected mass function particularly well. This is because within the model of Peng et al. (2010), the fractional density of the transition population strongly decreases at low masses for a constant τtrans: only very few low-mass galaxies experience quenching at any redshift. On the other hand, the poluation of AGN above any given λSAR threshold increases toward low stellar masses (see the bottom panel of Fig. 6): rapidly growing objects with a high Eddington ratio can be found in galaxies of any mass, at all redshifts. Thus, any model that invokes a fixed threshold in λSAR to explain the quenching population (see, e.g., Zubovas & King 2012) would predict a too high fraction of low-mass galaxies in the transition phase, in strong contrast with the finding of Peng et al. (2010).
[erg/s] (red solid line and yellow shaded area) at 0.3 <z< 0.8, and log LX> 44 ± 0.5 [erg/s] at 0.8 <z< 2.5. Reducing the threshold in LX leads to a space density in the HGMF higher than expected for the transient objects at the low-mass end. Conversely, specific accretion-rate-based subsamples do not seem to reproduce the expected mass function particularly well. This is because within the model of Peng et al. (2010), the fractional density of the transition population strongly decreases at low masses for a constant τtrans: only very few low-mass galaxies experience quenching at any redshift. On the other hand, the poluation of AGN above any given λSAR threshold increases toward low stellar masses (see the bottom panel of Fig. 6): rapidly growing objects with a high Eddington ratio can be found in galaxies of any mass, at all redshifts. Thus, any model that invokes a fixed threshold in λSAR to explain the quenching population (see, e.g., Zubovas & King 2012) would predict a too high fraction of low-mass galaxies in the transition phase, in strong contrast with the finding of Peng et al. (2010).
We note that the disagreement between the Peng model prediction and the AGN HGMF present at the high mass end of the third redshift bin arises because we used a single Schechter function to fit the star-forming galaxy mass function to apply the recipe from Peng et al. (2010), which, as pointed out by Ilbert et al. (2013), is not a good fit of the data, especially at the high mass end. The fit with a double Schechter function (as performed in Ilbert et al. (2013) and shown in Fig. 3) would indeed be steeper, thus reducing the number of predicted high-mass objects and the discrepancy with the AGN HGMF.
Overall, we find the space density of luminous AGN (log LX> 43.5−44.5 [erg/s]) at stellar masses M⋆> 1010.7 M⊙ to be consistent with the space density of galaxies in the star formation quenching phase. This non-trivial result is consistent with the notion that feedback from luminous AGN can be associated with the mass-quenching of galaxies. At lower masses the difference in space density between the luminous AGN mass function and the quenching mass function leaves room for a contribution from another mechanism. Lower luminosity AGN might contribute here, if their AGN feedback mechanism would operate on a different transition timescale τtrans. Furthermore, Peng et al. (2015) recently suggested that strangulation (a mechanism for which the supply of cold gas is halted) is the primary mechanism responsible for quenching star-formation in local galaxies with a stellar mass lower than 1011 M⊙. Our results are complementary to this work, proposing AGN-driven outflows as a plausible mechanism for halting star formation at higher redshift and for more massive galaxies, although a causal connection is not substantiated.
5. Summary and conclusions
We have studied the host galaxy stellar mass function of a sample of ~1000 AGN detected in the XMM-COSMOS field in the 2−10 keV band at 0.3 <z< 2.5. We derived the SARDF and the HGMF simultaneously as a bivariate distribution function of stellar mass and specific accretion rate λSAR≡ LX/M⋆, using the maximum likelihood method developed by Schulze & Wisotzki (2010) and extended by Schulze et al. (2015).
Our results can be summarized as follows:
-
(i)
The SARDF is best described by a double power-law with a mass-dependent but redshift-independent break
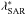 and a low λSAR characteristic slope that flattens from −1.35 to −0.54 with increasing redshift. The overall normalization
and a low λSAR characteristic slope that flattens from −1.35 to −0.54 with increasing redshift. The overall normalization 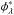 , in contrast, increases for increasing redshift.
, in contrast, increases for increasing redshift. -
(ii)
The AGN HGMF is described by a Schechter function with constant
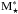 and a low-mass slope α flattening with redshift from α = −0.41 at z = 0.55 to α = −0.03 at z = 2.0. We derived the active fraction of AGN activity by comparison with the stellar mass function by Ilbert et al. (2013), and we found a redshift evolution in its mass dependence at the high-mass end, where the fraction of AGN in massive galaxies increases from ~3% at z ~ 0.55 to ~20% at z ~ 2.
and a low-mass slope α flattening with redshift from α = −0.41 at z = 0.55 to α = −0.03 at z = 2.0. We derived the active fraction of AGN activity by comparison with the stellar mass function by Ilbert et al. (2013), and we found a redshift evolution in its mass dependence at the high-mass end, where the fraction of AGN in massive galaxies increases from ~3% at z ~ 0.55 to ~20% at z ~ 2. -
(iii)
The redshift evolution of the SARDF and AGN HGMF allows us to gain a deeper understanding of the physical drivers of the AGN downsizing behavior, which is seen in the XLF out to z ~ 2.5. We find that that the downsizing in the AGN luminosity function is due to the combination of a (weak) mass-dependent evolution of the HGMF and the stronger evolution of the SARDF. In particular, we see that higher λSAR objects have a peak in their space density at earlier epoch than the lower λSAR AGN.
-
(iv)
We compared the mass function of the population in the process of being mass-quenched, predicted by the phenomenological model by Peng et al. (2010), with the HGMF computed for different subsamples obtained with different luminosity and λSAR-cuts. We find at the high masses (i.e., M⋆> 1010.7 M⊙) that the population that agrees with the model prediction is that of luminous AGN with log LX> 43.5−44.5 [erg/s] (i.e., log Lbol ≳ 46 [erg/s]). Their number density and stellar mass distribution are consistent with those of the transition galaxy population, a crucial, and non-trivial, result of our analysis. While this agreement does not establish a causal connection between star formation quenching and AGN activity, it suggests AGN feedback by powerful outflows from luminous AGN as a plausible mechanism for the mass-quenching of star forming galaxies. This scenario would agree and be complementary to the recent findings by Peng et al. (2015), who suggested strangulation as the primary quenching mechanism at lower masses (i.e., M⋆< 1011 M⊙).
Acknowledgments
We thank the referee for the careful reading and helpful suggestions that helped to improve the manuscript. This work is based on the COSMOS program. The HST COSMOS Treasury program was supported through NASA grant HST-GO-09822. This work is mainly based on observations obtained with XMM-Newton, an ESA Science Mission with instruments and contributions directly funded by ESA Member States and the USA (NASA), and with the European Southern Observatory under Large Program 175.A-0839, Chile. A.B. and E.P. acknowledge financial support from INAF under the contract PRIN-INAF-2012. A.S. acknowledges support by JSPS KAKENHI Grant Number 26800098. MCMC corner plots make use of triangle.py (Foreman-Mackey et al. 2013).
References
- Aird, J., Coil, A. L., Moustakas, J., et al. 2012, ApJ, 746, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Aird, J., Coil, A. L., Moustakas, J., et al. 2013, ApJ, 775, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Aird, J., Coil, A. L., Georgakakis, A., et al. 2015, MNRAS, 451, 1892 [NASA ADS] [CrossRef] [Google Scholar]
- Akaike, H. 1974, IEEE Transactions on Automatic Control, 19, 716 [Google Scholar]
- Bongiorno, A., Zamorani, G., Gavignaud, I., et al. 2007, A&A, 472, 443 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bongiorno, A., Merloni, A., Brusa, M., et al. 2012, MNRAS, 427, 3103 [NASA ADS] [CrossRef] [Google Scholar]
- Boyle, B. J., & Terlevich, R. J. 1998, MNRAS, 293, L49 [CrossRef] [Google Scholar]
- Brusa, M., Fiore, F., Santini, P., et al. 2009, A&A, 507, 1277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brusa, M., Civano, F., Comastri, A., et al. 2010, ApJ, 716, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Buchner, J., Georgakakis, A., Nandra, K., et al. 2015, ApJ, 802, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Georgakakis, A., Nandra, K., et al. 2008, ApJ, 681, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Cano-Díaz, M., Maiolino, R., Marconi, A., et al. 2012, A&A, 537, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cappelluti, N., Brusa, M., Hasinger, G., et al. 2009, A&A, 497, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cen, R., & Chisari, N. E. 2011, ApJ, 731, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Cicone, C., Maiolino, R., Sturm, E., et al. 2014, A&A, 562, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cowie, L. L., Songaila, A., Hu, E. M., & Cohen, J. G. 1996, AJ, 112, 839 [Google Scholar]
- Cresci, G., Mainieri, V., Brusa, M., et al. 2015a, ApJ, 799, 82 [Google Scholar]
- Cresci, G., Marconi, A., Zibetti, S., et al. 2015b, A&A, 582, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Croom, S. M., Richards, G. T., Shanks, T., et al. 2009, MNRAS, 1439 [Google Scholar]
- Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Faucher-Giguère, C.-A., & Quataert, E. 2012, MNRAS, 425, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Feruglio, C., Maiolino, R., Piconcelli, E., et al. 2010, A&A, 518, L155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feruglio, C., Fiore, F., Carniani, S., et al. 2015, A&A, 583, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Georgakakis, A., Coil, A. L., Willmer, C. N. A., et al. 2011, MNRAS, 418, 2590 [NASA ADS] [CrossRef] [Google Scholar]
- Georgakakis, A., Pérez-González, P. G., Fanidakis, N., et al. 2014, MNRAS, 440, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Gilli, R., Comastri, A., & Hasinger, G. 2007, A&A, 463, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilli, R., Vignali, C., Mignoli, M., et al. 2010, A&A, 519, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goodman, J., & Weare, J. 2010, Commun. Appl. Math. Comput. Sci., 5, 65 [Google Scholar]
- Granato, G. L., De Zotti, G., Silva, L., Bressan, A., & Danese, L. 2004, ApJ, 600, 580 [Google Scholar]
- Häring, N., & Rix, H. 2004, ApJ, 604, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Hasinger, G., Miyaji, T., & Schmidt, M. 2005, A&A, 441, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hasinger, G., Cappelluti, N., Brunner, H., et al. 2007, ApJS, 172, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., et al. 2006, ApJS, 163, 1 [Google Scholar]
- Ilbert, O., McCracken, H. J., Le Fèvre, O., et al. 2013, A&A, 556, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kauffmann, G., & Heckman, T. M. 2009, MNRAS, 397, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Ho, L. C. 2013, ARA&A, 51, 511 [Google Scholar]
- La Franca, F., Fiore, F., Comastri, A., et al. 2005, ApJ, 635, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Lansbury, G. B., Gandhi, P., Alexander, D. M., et al. 2015, ApJ, 809, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Carollo, C. M., Pipino, A., Renzini, A., & Peng, Y. 2013, ApJ, 772, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Lusso, E., Comastri, A., Simmons, B. D., et al. 2012, MNRAS, 425, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Mainieri, V., Bongiorno, A., Merloni, A., et al. 2011, A&A, 535, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maiolino, R., Neri, R., Beelen, A., et al. 2007, A&A, 472, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marconi, A., & Hunt, L. K. 2003, ApJ, 589, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., Risaliti, G., Gilli, R., et al. 2004, MNRAS, 351, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Menci, N., Fiore, F., Puccetti, S., & Cavaliere, A. 2008, ApJ, 686, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A., Bongiorno, A., Brusa, M., et al. 2014, MNRAS, 437, 3550 [NASA ADS] [CrossRef] [Google Scholar]
- Miyaji, T., Hasinger, G., Salvato, M., et al. 2015, ApJ, 804, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Monaco, P., & Fontanot, F. 2005, MNRAS, 359, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Mullaney, J. R., Pannella, M., Daddi, E., et al. 2012, MNRAS, 419, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Mullaney, J. R., Alexander, D. M., Aird, J., et al. 2015, MNRAS, 453, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y.-J., Lilly, S. J., Kovač, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y.-J., Lilly, S. J., Renzini, A., & Carollo, M. 2012, ApJ, 757, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y., Maiolino, R., & Cochrane, R. 2015, Nature, 521, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Read, J. I., & Trentham, N. 2005, Roy. Soc. London Philosophical Trans. Ser. A, 363, 2693 [Google Scholar]
- Salvato, M., Ilbert, O., Hasinger, G., et al. 2011, ApJ, 742, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Santini, P., Rosario, D. J., Shao, L., et al. 2012, A&A, 540, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schawinski, K., Khochfar, S., Kaviraj, S., et al. 2006, Nature, 442, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Schulze, A., & Wisotzki, L. 2010, A&A, 516, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schulze, A., Bongiorno, A., Gavignaud, I., et al. 2015, MNRAS, 447, 2085 [NASA ADS] [CrossRef] [Google Scholar]
- Sijacki, D., Vogelsberger, M., Genel, S., et al. 2015, MNRAS, 452, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Silverman, J. D., Green, P. J., Barkhouse, W. A., et al. 2008, ApJ, 679, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Silverman, J. D., Lamareille, F., Maier, C., et al. 2009, ApJ, 696, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Somerville, R. S., Primack, J. R., & Faber, S. M. 2001, MNRAS, 320, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Di Matteo, T., & Hernquist, L. 2005, ApJ, 620, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Sturm, E., González-Alfonso, E., Veilleux, S., et al. 2011, ApJ, 733, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., Neri, R., et al. 2010, Nature, 463, 781 [Google Scholar]
- Treister, E., Urry, C. M., & Virani, S. 2009, ApJ, 696, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Ueda, Y., Akiyama, M., Ohta, K., & Miyaji, T. 2003, ApJ, 598, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Ueda, Y., Akiyama, M., Hasinger, G., Miyaji, T., & Watson, M. G. 2014, ApJ, 786, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Vignali, C., Mignoli, M., Gilli, R., et al. 2014, A&A, 571, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xue, Y. Q., Brandt, W. N., Luo, B., et al. 2010, ApJ, 720, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Zubovas, K., & King, A. 2012, ApJ, 745, L34 [Google Scholar]
Appendix A: Model comparison
As mentioned in Sect. 3.2, we derived uncertainties through an MCMC computation of the posterior distribution function (PDF). In Fig. A.1 we show the 1D marginalized PDF for the free parameters of our model and the 2D marginalized PDF for parameter pairs. The latter shows the covariance between these pairs. We find covariance between several parameters, for instance, between the break 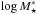 and the slope α of the M⋆ term f⋆, or between several of the redshift evolution parameters (p1, p2, kγ).
and the slope α of the M⋆ term f⋆, or between several of the redshift evolution parameters (p1, p2, kγ).
 |
Fig. A.1 Posterior probability distribution for the free parameters of our best-fit model. The histograms at the top show the marginalized probability distribution function for each free parameter, while the contour plots show the marginalized 2D probability distribution function for each pair of parameters, to illustrate their covariances. |
In addition to the default parametric model we presented above, we explored parametric models for the HGMF and SARDF. We here discuss the results of this exercise and provide a justification for our chosen parameterization. To compare the relative quality of our respective parametric model given our data set, we used the Akaike information criterion (AICc; Akaike 1974). It is given by AICc = S + 2K + 2K(N/ (N−K−1)), where S is the likelihood as defined above, K is the number of parameters in the model, and N is the size of the sample. While the AICc penalizes against overfitting, it is known to be less penalizing than the Bayesian information criterion (BIC), for example. Nevertheless, the difference in AIC between the models tested below is in general significant enough to draw firm conclusions.
 |
Fig. A.2 Comparison of the bivariate distribution in the M⋆−λSAR plane between the observations (symbols) and the prediction from the best-fit model (black contours) in the three redshift bins as labeled. The upper panels show the comparison for our default model A), the middle panels show the prediction from the best-fit M⋆-independent SARDF model B), and the lower panels show the best-fit solution if no XLF data are included in the likelihood function (“no XLF”). Open symbols indicate upper limits in M⋆. |
 |
Fig. A.3 Comparison of the X-ray luminosity function (XLF) predicted by the bivariate distribution Ψ(M⋆,λSAR,z) with direct observations. The blue solid line shows the XLF derived from our default model (A), the red dashed line is for the best-fit M⋆-independent SARDF model (B), and the green solid line is for the best fit without the XLF into the likelihood function (no XLF). The black circles show the binned XLF for our XMM-COSMOS sample using the Vmax method, indicating the luminosity range covered by XMM-COSMOS. The shaded cyan and yellow areas show the XLF by Miyaji et al. (2015) and Ueda et al. (2014), respectively, where the shaded area includes the variation of the XLF over the redshift range of the bin and the uncertainty of the XLF determination. |
Best-fit model parameters for the bivariate distribution function of stellar mass and SAR for other models, which have been tested but were not considered further.
Comparison between different parametric models and our default model through their difference in AICc and their corresponding relative likelihood.
Our default model (hereafter model A) allows for a mass dependence on the SARDF, while previous studies assumed a λSAR distribution, independent of mass (e.g., Aird et al. 2012; Bongiorno et al. 2012). We first started our analysis with a model without such a mass-dependent term, kλ = 0 (hereafter model B). Our best-fit model B provides an almost equivalent fit to the XLF as our default model A (see red dashed line in Fig. A.3) and fits well over most of the M⋆−λSAR plane, as shown in the middle panels of Fig. A.2. We provide the best-fit parameters in Table A.1. However, it is unable to recover the observed number of objects at low masses and high-λSAR (upper left corner). In the upper panels of Fig. A.2 we show the M⋆−λSAR plane for our
default model A. This mass-dependent SARDF model is able to match the observations in this region as well (since the SARDF has a higher break at low mass). The AICc ratio between the two models prefers our model A with a relative likelihood of 10-68, providing strong evidence that this model better describes our data set.
An important constraint on this mass dependence in the SARDF is set by the inclusion of the XLF information in our likelihood function, since our sample does not cover a very wide dynamical range in luminosity. If we neglect the XLF and only use the data from our XMM-COSMOS sample, such a mass dependence is not strongly required and the flattening in the SARDF is likewise weaker, while still present. We give the best-fit solution without XLF data as model “no XLF” in Table A.1. It also matches the XMM-COSMOS sample in the M⋆−λSAR plane well (see lower panels in Fig. A.2). However, this is achieved by proposing a high space density of objects with low M⋆ and low λSAR, below the luminosity limit of the XMM-COSMOS sample. Such a high space density of low-luminosity AGN violates observations of the XLF from deeper surveys (Miyaji et al. 2015; Aird et al. 2015) and is thus deemed not physical. This is demonstrated in Fig. A.3, where we show the XLF predicted by our bivariate distribution function models. The “no XLF” model (shown by the green solid line) is consistent with our default model (blue line) and the XLF at z< 0.8, where XMM-COSMOS still probes a relatively wide luminosity range. At higher redshift it clearly overpredicts the XLF. This motivates the additional inclusion of the XLF information in
this work, to find a solution to our data set that is consistent with XLF measurements beyond the luminosity range directly covered and thus constrained by our sample. On the other hand, the XLF alone is degenerate between M⋆ and λSARand thus does not constrain the SARDF and HGMF, as demonstrated by the identical XLF for models A and B. When combining the XMM-COSMOS data with the XLF, the discussed mass and redshift dependencies are required by the data. However, the mass dependence of the SARDF is mainly driven by the number of the few low-mass and high- λSAR objects. Future studies, incorporating both deeper surveys (e.g., CDFS, CDFN) and shallower, larger area surveys (e.g., XMM-XXL, Stripe 82X), will be essential to settle this question.
In addition, we also tested a model where we allowed for redshift evolution in the slope of the M⋆ term α(z) = α0 + kα(z−z0), with z0 fixed to 1.1 (hereafter model C). However, we found the best-fit redshift evolution parameter to be consistent with zero kα = −0.017 ± 0.043, thus the inclusion of this additional parameter is not statistically justified. This is also confirmed by the AICc ratio between the two models. Similarly, we found that the addition of another parameter that allows for redshift evolution in the break of the M⋆ term, 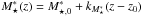 , is not statistically justified (see Table A.2).
, is not statistically justified (see Table A.2).
We also performed the same test of goodness to justify the redshift dependence on the slope of the SAR term kγ and found this term to be statistically justified. We provide the relative AICc values and the corresponding relative likelihood for different models, compared to our default model (A), in Table A.2.
All Tables
Best-fit model parameters for the AGN host galaxy mass Schechter function, computed in our three redshift bins.
Best-fit model parameters of the AGN specific accretion rate double power-law function, computed in our three redshift bins.
Best-fit model parameters for the bivariate distribution function of stellar mass and SAR for other models, which have been tested but were not considered further.
Comparison between different parametric models and our default model through their difference in AICc and their corresponding relative likelihood.
All Figures
 |
Fig. 1 Bivariate distribution for the analyzed hard X-ray selected sample in the M⋆−λSAR plane color-coded according to the redshift bins. The horizontal and vertical dashed lines correspond to the lower limit cuts applied in M⋆ and λSAR. |
| In the text | |
 |
Fig. 2 Bivariate distribution function Ψ(M⋆,λSAR,z), for our best-fitting parametric model, derived through the maximum likelihood method, in three redshifts bins. The orange contours indicate lines of constant space density (from 10-10 to 10-3 Mpc-3), separated by a factor of 10 each. |
| In the text | |
 |
Fig. 3 Upper panels: total AGN HGMF with the associated errors in three redshift bins derived through the maximum likelihood (black line and gray shaded area) and the Vmax (data points) methods. In each bin the lowest z fit is reported for reference with a dashed line. The red and blue lines are the total and the star-forming galaxy stellar mass functions with the associated errors (shown in magenta and cyan shaded areas) from Ilbert et al. (2013). Lower panels: ratio of AGN host galaxies to the total (red line) and the star-forming (blue line) galaxy population as a function of stellar mass in the same redshift bins. |
| In the text | |
 |
Fig. 4 Upper panels: the SAR term split into three redshift bins and described as a double power-law with a mass dependent λSAR∗ as in Eq. (11). Lower panels: SARDF derived through the maximum likelihood method by integrating the bivariate distribution function over M⋆ (Eq. (8)). The shaded area includes the errors on the parameters. |
| In the text | |
 |
Fig. 5 Left panel: redshift evolution of the SARDF space density for different λSAR. Magenta: log(λSAR)= 32 [erg/s /M⊙] (~1% Edd); green: log(λSAR)= 32.5 [erg/s /M⊙] (~3% Edd); yellow: log(λSAR)= 33 [erg/s /M⊙] (~10% Edd); red: log(λSAR)= 33.5 [erg/s /M⊙] (~30% Edd); blue: log(λSAR)= 34.0 [erg/s /M⊙] (~Edd); and black: log(λSAR)= 34.5 [erg/s /M⊙] (>Edd). Central panel: redshift evolution of the HGMF space density for different M⋆. Right panel: redshift evolution of the XLF space density for different LX by Miyaji et al. (2015). |
| In the text | |
 |
Fig. 6 Total AGN HGMF in three redshift bins derived through the maximum likelihood (black line) and compared with the AGN HGMF for different AGN subsamples in (upper panels) luminosities. log(LX) < 43 [erg/s] (magenta); log(LX) > 43 [erg/s] (cyan), log(LX) > 43.5 [erg/s] (green), log(LX) > 44 [erg/s] (red), and log(LX) > 44.5 [erg/s] (blue); and (lower panels) specific accretion rates λSAR, i.e., log λSAR> 32.5 [erg/s/M⊙] (magenta); log λSAR>33 [erg/s/M⊙] (cyan), log λSAR> 33.5 [erg/s/M⊙] (green), and log λSAR> 34 [erg/s/M⊙] (red). |
| In the text | |
 |
Fig. 7 Predicted MF of transient galaxies as derived starting from a single Schechter function based on the data from Ilbert et al. (2013, green line), using the Peng recipe (Peng et al. 2010) for τ = 5 × 107 yr (blue solid line), τ = 1 × 107 yr and τ = 1 × 108 yr (blue dashed lines). We compare them with the total AGN HGMF (black line) and with the HGMF computed with different luminosity cuts. In particular in the first redshift bin, cuts of log LX> 43.8 [erg/s] (red solid line) and log LX> 44.2 and log LX> 43.5 [erg/s] for the lower and upper boundary, respectively, have been applied; while in the second and third redshift bins, these cuts are log LX> 44 (brown solid line) and log LX> 44.5 [erg/s] and log LX> 43.5 [erg/s] for the lower and upper boundaries. |
| In the text | |
 |
Fig. A.1 Posterior probability distribution for the free parameters of our best-fit model. The histograms at the top show the marginalized probability distribution function for each free parameter, while the contour plots show the marginalized 2D probability distribution function for each pair of parameters, to illustrate their covariances. |
| In the text | |
 |
Fig. A.2 Comparison of the bivariate distribution in the M⋆−λSAR plane between the observations (symbols) and the prediction from the best-fit model (black contours) in the three redshift bins as labeled. The upper panels show the comparison for our default model A), the middle panels show the prediction from the best-fit M⋆-independent SARDF model B), and the lower panels show the best-fit solution if no XLF data are included in the likelihood function (“no XLF”). Open symbols indicate upper limits in M⋆. |
| In the text | |
 |
Fig. A.3 Comparison of the X-ray luminosity function (XLF) predicted by the bivariate distribution Ψ(M⋆,λSAR,z) with direct observations. The blue solid line shows the XLF derived from our default model (A), the red dashed line is for the best-fit M⋆-independent SARDF model (B), and the green solid line is for the best fit without the XLF into the likelihood function (no XLF). The black circles show the binned XLF for our XMM-COSMOS sample using the Vmax method, indicating the luminosity range covered by XMM-COSMOS. The shaded cyan and yellow areas show the XLF by Miyaji et al. (2015) and Ueda et al. (2014), respectively, where the shaded area includes the variation of the XLF over the redshift range of the bin and the uncertainty of the XLF determination. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


