| Issue |
A&A
Volume 586, February 2016
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201527361 | |
| Published online | 27 January 2016 | |
On the growth of pebble-accreting planetesimals
Astronomical Institute Anton Pannekoek, University of Amsterdam, Science Park 904, PO box 94249, Amsterdam, The Netherlands
e-mail: r.g.visser@uva.nl; c.w.ormel@uva.nl
Received: 14 September 2015
Accepted: 10 November 2015
Context. Pebble accretion is a newly discovered mechanism to quickly grow the cores of planets. In pebble accretion, gravity and gas drag conspire to yield large collisional cross sections for small particles in protoplanetary disks. However, before pebble accretion commences, aerodynamic deflection may act to prevent planetesimals from becoming large, because particles tend to follow gas streamlines.
Aims. We derive the planetesimal radius where pebble accretion is initiated and determine the growth timescales of planetesimals by sweep-up of small particles.
Methods. The equation of motion for a pebble, including gas drag and gravitational interactions, was integrated in three dimensions at distances of 1, 3, and 10 AU from the star. We obtained the collision efficiency factor as the ratio of the numerically obtained collisional cross section to the planetesimal surface area, from which we obtained the growth timescales. Integrations were conducted in the potential flow limit (steady, inviscid) and in the Stokes flow regime (steady, viscid).
Results. Only particles of stopping time ts ≪ tX where tX ≈ 103 s experience aerodynamic deflection. Even in this case, the planetesimal’s gravity always ensures positive collision factors. The planetesimal radius where growth proceeds slowest is ≈ 100 km (less for colder disks) corresponding to interactions shifting from the geometric to the Safronov focusing regime. For particles ts ≫ tX pebble accretion only commences after this phase and is characterized by a steep drop in growth timescales. At 1 AU, growth timescales are shorter than the disk lifetime for pebbles larger than 0.03 cm. The planetesimal radius RPA where pebble accretion commences increases with disk orbital radius. At distances beyond ~ 10 AU, sweep-up growth times are always longer than 10 Myr, while in the inner disk (≲3 AU) the viability of the sweep-up scenario is determined by the outcome of pebble-planetesimal collisions in the geometric regime. We present analytical fits for the collision efficiency factors and the minimum planetesimal radius RPA required for pebble accretion.
Key words: planets and satellites: formation / methods: numerical / protoplanetary disks / minor planets, asteroids: general / hydrodynamics
© ESO, 2016
1. Introduction
Pebble accretion (PA) is an accretion mechanism involving both gravitational and dissipative (gas drag) forces. Thus, PA covers interactions between a large body (planetesimal or planet) and small particles in the presence of gas. During their accretion, pebbles settle in the gravitational field of the large body, just like the buildup of sediments in seas or rivers1. This is in contrast to gas-free encounters, which rely on hitting the surface of the large body. As first demonstrated by Ormel & Klahr (2010), PA rates can be much higher than the corresponding gas-free limit, since cross sections can become as large as the Hill sphere (Lambrechts & Johansen 2012). If there is a massive pebble reservoir, this virtually eradicates the timescale problem that (giant) planet formation faces in the classical scenario of planetesimal accretion. PA is especially attractive because protoplanetary disks are inferred to harbor large amounts of pebble-sized particles, as suggested by radio observations (Andrews et al. 2009; Ricci et al. 2010; Testi et al. 2014). Furthermore, a strong concentration of these particles will trigger streaming instabilities, which leads to gravitationally bound objects that can produce planetesimals (Youdin & Goodman 2005; Johansen et al. 2009) – the seeds required for the PA mechanism.
Recent works have advanced the PA theory and applied the concept to planet formation in the solar system and exoplanetary systems (Bitsch et al. 2015). Compared to planetesimals, pebbles are quite mobile and drift toward the central star (Weidenschilling 1977a). Therefore, PA is not an isolated problem, but requires global solutions for the pebble density in the disk as a function of time (Lambrechts & Johansen 2014; Birnstiel et al. 2012; Krijt et al. 2016). How PA proceeds also depends on the size distribution of large bodies (planetesimal, protoplanets); and it is essential for reproducing the solar system architecture that only the largest bodies in the distribution profit from PA (Kretke & Levison 2014; Levison et al. 2015). PA ceases when planets become massive enough to alter the gas structure of the protoplanetary disk – the pebble isolation mass – which, applied to the solar system, is consistent with the heavy element contents of the giant planets (Lambrechts et al. 2014). In the inner solar system, PA has been invoked to explain the small size of Mars (Morbidelli et al. 2015) and it has been applied to explain the asteroid size distribution (Johansen et al. 2015b).
Under certain conditions, PA results in high accretion rates. But that does not necessarily imply that PA is efficient, as particles may drift past the (proto)planet before they can be accreted (Ormel & Kobayashi 2012; Chambers 2014; Guillot et al. 2014; Sato et al. 2015). In particular, Guillot et al. (2014) calculated the probability of a collision for a particle traversing a planetesimal belt. This resulted in complex dependencies on the model parameters, but this filtering by planetesimals was generally seen to be most efficient for large planetesimals (protoplanets, operating in the settling regime) or for small planetesimals (which profit from a high ratio of surface area to mass) and for weak turbulence levels (which confines particles to the midplane). On the other hand, intermediate-sized planetesimals collect solids only inefficiently. In addition, Guillot et al. (2014) highlighted the importance of hydrodynamic flow effects, where small particles are so tightly coupled that they follow the streamlines of the gas, avoiding accretion by planetesimals (Michael & Norey 1969; Whipple 1972; Slinn 1976; Sekiya & Takeda 2003; Sellentin et al. 2013). Physically, aerodynamic deflection occurs when the particle stopping time ts (which equals the particle momentum divided by the gas drag force) becomes shorter than the time it takes to cross the large body; that is, when the Stokes number2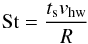 (1)becomes lower than unity, where R is the planetesimal radius and vhw the headwind velocity of the gas that the planetesimal faces and with which the tightly coupled particles approach it.
(1)becomes lower than unity, where R is the planetesimal radius and vhw the headwind velocity of the gas that the planetesimal faces and with which the tightly coupled particles approach it.
Guillot et al. (2014) conjectured that this aerodynamic deflection suppresses accretion of small particles by planetesimals. However, planetesimals do exert a gravitational force on the pebbles, which may mitigate the effect. By numerically integrating the pebble equation of motion, it is the goal of this work to quantify how severe the suppression becomes. We further calculate the mass-doubling timescales for planetesimals embedded in a sea of pebbles, identify the planetesimal size where growth experiences its key bottleneck, and the size where PA commences (these two sizes do not necessarily coincide).
We carry out integrations for both Stokes (high viscosity or Reynolds number Re ≪ 1) flow and inviscid (potential) flow. A caveat is that only steady flow patterns are considered, whereas planetesimals in the protoplanetary disk typically have Reynolds number ≫1, implying that the flow structure is turbulent. However, by carrying out integrations for both the Re ≪ 1 and the inviscid limits, we anticipate to bracket the uncertainty in the results to some extent.
We show that by virtue of gravitational settling, planetesimal accretion rates are always higher than zero, even for the smallest grains (although in that case the collisional cross section will be much smaller than the geometrical cross section). These results agree with the Stokes flow integrations by Johansen et al. (2015b). Physically motivated expressions are presented that fit our numerical results, which are valid as long as Keplerian shear effects are unimportant (i.e., small planetesimals or small particles). In particular, we derive a critical stopping time of ≈103 s, above which particles avoid aerodynamic deflection.
The plan of the paper is as follows. In Sect. 2 we discuss the model setup and assumptions, including the adopted disk model and the dynamics of gas and pebbles, followed by the numerical methods. In Sect. 3 we present the collisional efficiency factors and growth timescales as a function of planetesimal size, pebble size, and location in the disk. In Sect. 4 we present analytical fitting expressions to our numerical data. In Sect. 5 we discuss some implications of our results, and we list our key conclusions in Sect. 6.
2. Model setup and assumptions
2.1. Disk model
The temperature and density profiles for the protoplanetary disk follow from the minimum mass solar nebula (MMSN; Weidenschilling 1977b; Hayashi et al. 1985), 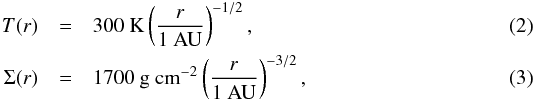 with r the distance from the star. If we assume hydrostatic equilibrium and an isothermal temperature profile in the vertical direction, the density profile is a Gaussian:
with r the distance from the star. If we assume hydrostatic equilibrium and an isothermal temperature profile in the vertical direction, the density profile is a Gaussian:![\begin{equation} \rho_{\rm g}(r,z) =\frac{\Sigma (r) }{H\sqrt{2\pi}} \exp\left[{-\frac{1}{2}\left ( \frac{z}{H} \right )^2}\right], \label{eq:density} \end{equation}](/articles/aa/full_html/2016/02/aa27361-15/aa27361-15-eq21.png) (4)with z the vertical distance and the scale height H = cs/ Ω0, Ω0 the local Keplerian frequency and
(4)with z the vertical distance and the scale height H = cs/ Ω0, Ω0 the local Keplerian frequency and 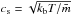 , the isothermal sound speed, kb Boltzmann’s constant, and
, the isothermal sound speed, kb Boltzmann’s constant, and 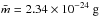 the mean molecular weight. Since the gas in the disk is partially pressure supported, it rotates at speeds slightly below the Kepler speed (vk). The planetesimal thus faces a headwind of magnitude (Nakagawa et al. 1986)
the mean molecular weight. Since the gas in the disk is partially pressure supported, it rotates at speeds slightly below the Kepler speed (vk). The planetesimal thus faces a headwind of magnitude (Nakagawa et al. 1986) 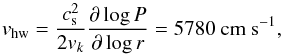 (5)with P(r) the pressure of the gas. For power-law profiles of T and Σ the headwind velocity is independent of disk orbital radius r. In Eq. (5) that the MMSN profile has been adopted for convenience; more realistic disk models give rise to different profiles than Eqs. (2) and (3). For example, the hydrodynamical simulations of Bitsch et al. (2015), which include radiative transport, result in a headwind velocity that is lower than Eq. (5). In Sect. 3.3 we briefly consider alternative disk profiles. We note, however, that the dimensionless fit formulas that we present in Sect. 4 cover every disk profile.
(5)with P(r) the pressure of the gas. For power-law profiles of T and Σ the headwind velocity is independent of disk orbital radius r. In Eq. (5) that the MMSN profile has been adopted for convenience; more realistic disk models give rise to different profiles than Eqs. (2) and (3). For example, the hydrodynamical simulations of Bitsch et al. (2015), which include radiative transport, result in a headwind velocity that is lower than Eq. (5). In Sect. 3.3 we briefly consider alternative disk profiles. We note, however, that the dimensionless fit formulas that we present in Sect. 4 cover every disk profile.
2.2. The pebble equation of motion
To integrate pebble streamlines we chose a local frame comoving with the planetesimal. The planetesimal was assumed to be massive and to move on a circular Keplerian orbit. The equation of motion in three dimensions is given by (Ormel & Klahr 2010) 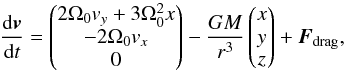 (6)where v is the velocity, G Newton’s gravitational constant, M the mass of the planetesimal, (x,y,z) the coordinates of the pebble in the local frame, and Fdrag the drag force. The first terms of Eq. (6) consist of the Coriolis acceleration and tidal accelerations, respectively, while the second term describes the planetesimal gravity. We note that the stellar acceleration term in the z-direction
(6)where v is the velocity, G Newton’s gravitational constant, M the mass of the planetesimal, (x,y,z) the coordinates of the pebble in the local frame, and Fdrag the drag force. The first terms of Eq. (6) consist of the Coriolis acceleration and tidal accelerations, respectively, while the second term describes the planetesimal gravity. We note that the stellar acceleration term in the z-direction 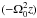 has been omitted because this would otherwise render vertical impact parameters infinite for a laminar gas flow adopted here.
has been omitted because this would otherwise render vertical impact parameters infinite for a laminar gas flow adopted here.
 |
Fig. 1 Velocity vectors and gas streamlines around a sphere (planetesimal) for potential flow (left half; Eq. (7)) and Stokes flow (right half; Eq. (8)) as seen in the frame of the sphere. |
We used two steady prescriptions for the gas flow in the vicinity of the planetesimals (see Fig. 1): inviscid potential flow and (highly viscid) Stokes flow. The velocity ofpotential flow past a sphere reads, in spherical coordinates (Batchelor 1967) 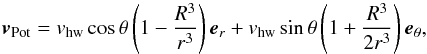 (7)with θ the angle between the direction of the unperturbed flow (here: −ey) and a point x in the local frame and R is the planetesimal radius. Similarly, the Stokes flow solution reads (Batchelor 1967)
(7)with θ the angle between the direction of the unperturbed flow (here: −ey) and a point x in the local frame and R is the planetesimal radius. Similarly, the Stokes flow solution reads (Batchelor 1967) 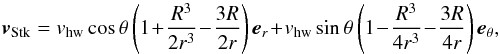 (8)see Fig. 1. Compared to Stokes flow, the potential solution does not contain ∝ 1 /r terms. Stokes flow therefore modifies the unperturbed flow even at large distances from the planetesimal, which is a consequence of viscosity. In addition, in Stokes flow the gas velocity is identically 0 at r = R, whereas in potential flow vr = 0, but vθ ≠ 0 (see Fig. 1).
(8)see Fig. 1. Compared to Stokes flow, the potential solution does not contain ∝ 1 /r terms. Stokes flow therefore modifies the unperturbed flow even at large distances from the planetesimal, which is a consequence of viscosity. In addition, in Stokes flow the gas velocity is identically 0 at r = R, whereas in potential flow vr = 0, but vθ ≠ 0 (see Fig. 1).
To these solutions, we added the shear-corrected gas velocity, rendering the combined flow velocity of the gas to become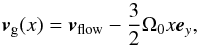 (9)with vflow either the Stokes or the potential flow solution. Strictly, the addition in Eq. (9) is not self-consistent: it would, for example, violate the irrotational assumption used in deriving Eq. (7). However, as the scales on which Eqs. (7) and (8) and the Keplerian shear apply are very different (RΩ0 ≪ vhw), we expect the error to be negligible and irrelevant to the results of this work.
(9)with vflow either the Stokes or the potential flow solution. Strictly, the addition in Eq. (9) is not self-consistent: it would, for example, violate the irrotational assumption used in deriving Eq. (7). However, as the scales on which Eqs. (7) and (8) and the Keplerian shear apply are very different (RΩ0 ≪ vhw), we expect the error to be negligible and irrelevant to the results of this work.
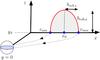 |
Fig. 2 Sketch of the procedure we used to obtain the collisional cross section. In the comoving frame, the planetesimal resides at the origin (y = 0) and pebbles start at a distance yS far enough to be unperturbed by the gravity of the planetesimal. Integrations are first carried out in the x-direction, and the impact parameter bcoll,x is determined from the first and last trajectory that hits the planetesimal (xmin and xmax). Starting at the average of these two coordinates x0, the integrations are extended to the z-direction to obtain the vertical impact parameter bcoll,z. |
The gas drag force Fdrag felt by the particles reads 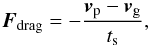 (10)where vp is the velocity of the particle, vg the gas velocity, and ts the stopping time for a spherical particle with radius s (Whipple 1972; Weidenschilling 1977a):
(10)where vp is the velocity of the particle, vg the gas velocity, and ts the stopping time for a spherical particle with radius s (Whipple 1972; Weidenschilling 1977a): ![\begin{equation} t_{\rm s} = \left\{\begin{matrix} \displaystyle \frac{\rho_{\bullet\mathrm{s}} s}{\rho_{\mathrm{g}} c_{\mathrm{s}}} & \textrm{Epstein regime: } \quad s<\frac{9}{4}l_{\mathrm{mfp}} \\[5mm] \displaystyle \frac{2 \rho_{\bullet\mathrm{s}}s^{2}}{9 \eta} & \textrm{Stokes regime:} \quad s \geq \frac{9}{4}l_{\mathrm{mfp}},\\ \end{matrix}\right. \label{eq:tstop} \end{equation}](/articles/aa/full_html/2016/02/aa27361-15/aa27361-15-eq64.png) (11)with \begin{lxirformule}$l_{\mathrm{mfp}}$\end{lxirformule} the mean free path of the gas molecules, ρ•,s the internal particle density taken to be 1 g cm-3 and η the dynamic viscosity. As our largest particle sizes are 30 cm, these are the relevant stopping time regimes.
(11)with \begin{lxirformule}$l_{\mathrm{mfp}}$\end{lxirformule} the mean free path of the gas molecules, ρ•,s the internal particle density taken to be 1 g cm-3 and η the dynamic viscosity. As our largest particle sizes are 30 cm, these are the relevant stopping time regimes.
Overview of the parameter space and the corresponding numerical results at given orbital distance r.
 |
Fig. 3 Collision factor fcoll as a function of planetesimal radius R for a constant internal density ρ• = 1 g cm-3. Crosses indicate numerical data, while solid lines are fits. The color scale ranges from dark to light blue for increasing particle radius. a) Results obtained with the (inviscid) potential solution (Eq. (7)) at 1 AU orbital distance from the star. For a small planetesimal size, the collision factor is approximately geometrical (fcoll ≈ 1). However, for small pebble sizes, aerodynamic deflection results in a significant drop of fcoll (see Table 1 for the minimum collision efficiency, fcoll,min). b) Results with the (highly viscid) Stokes flow solution (Eq. (8)). Settling occurs at smaller sizes due to the increase in encounter time. c) Results at 3 AU orbital distance show a shallow barrier only for the lowest particle size. d) At 10 AU a barrier is no longer present because of the reduced gas density. |
 |
Fig. 4 Growth timescale tgrowth as function of planetesimal radius R for a constant internal density ρ• = 1 g cm-3. Crosses indicate numerical data, while the solid lines are fits. The color scale extends from dark blue to light blue, transitioning from lowest particle radius to highest particle radius. a) tgrowth obtained with the potential flow solution at 1 AU orbital distance and a pebble density of ρp = ρg/ 100, showing maxima at Rgr,max ~ 100 km. b) tgrowth with the Stokes flow solution at 1 AU orbital distance and a pebble density of ρp = ρg/ 100 , showing early settling and flattening out of the curves. c) tgrowth with the potential flow solution at 3 AU orbital distance and a pebble density of ρp = ρg/ 100. d) tgrowth with the potential flow solution at 10 AU orbital distance and a pebble density of ρp = ρg/ 100 (top, blue) and a pebble density of ρp = ρg (bottom, red). |
2.3. Numerical integrations
We numerically integrated the particle streamlines with the Runge-Kutta-Fehlberg variable step method (RKF45). This integration method uses variable steps and compares a fourth-order solution with a fifth-order solution to determine the next step size (Fehlberg 1969; Eshagh 2005; Ormel & Klahr 2010). We used a relative error tolerance of 10-8, small enough to ensure convergence. The goal of the integrations is to determine the collisional cross-sections of pebbles of a radius s hitting a planetesimal of radius R. This is achieved by integrating the pebble equation of motion, Eq. (6), starting at a position (xS,yS) from the planetesimal, see Fig. 2. At this point, the initial velocities read: 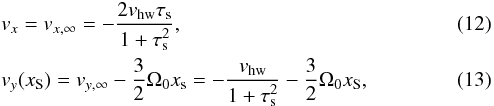 with vx,∞,vy,∞ the (unperturbed) radial and azimuthal drift velocities of the pebble (Weidenschilling 1977a),
with vx,∞,vy,∞ the (unperturbed) radial and azimuthal drift velocities of the pebble (Weidenschilling 1977a), 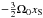 the correction for Keplerian shear, and τs = Ω0ts the dimensionless stopping time. The initial starting line y = yS was chosen to be far enough from the planetesimal to ensure that the gravitational force at the starting location is much smaller than the gas drag force. Specifically, we adopted
the correction for Keplerian shear, and τs = Ω0ts the dimensionless stopping time. The initial starting line y = yS was chosen to be far enough from the planetesimal to ensure that the gravitational force at the starting location is much smaller than the gas drag force. Specifically, we adopted 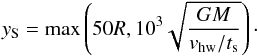 (14)Starting in the midplane (z = 0), we first varied xS and determined whether the integration results in a hit or a miss. Thus, we searched for the positions { xmin, xmax } separating hits from misses. The condition for a hit is given by
(14)Starting in the midplane (z = 0), we first varied xS and determined whether the integration results in a hit or a miss. Thus, we searched for the positions { xmin, xmax } separating hits from misses. The condition for a hit is given by 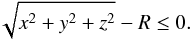 (15)We then determined the impact parameter as bcoll,x = (xmax−xmin)/2. By focusing our search around x = xmin,xmax we ensured that the error in bcoll,x is at most 1%. Next, we integrated in the z-direction starting at the midpoint (x0 = (xmax + xmin)/2,yS,z = 0) to determine the impact parameter in the vertical direction bcoll,z (see Fig. 2). We assumed that the impact geometry is ellipsoidal and that the impact area (at y = yS) is A = πbcoll,xbcoll,z. The corresponding pebble flux is
(15)We then determined the impact parameter as bcoll,x = (xmax−xmin)/2. By focusing our search around x = xmin,xmax we ensured that the error in bcoll,x is at most 1%. Next, we integrated in the z-direction starting at the midpoint (x0 = (xmax + xmin)/2,yS,z = 0) to determine the impact parameter in the vertical direction bcoll,z (see Fig. 2). We assumed that the impact geometry is ellipsoidal and that the impact area (at y = yS) is A = πbcoll,xbcoll,z. The corresponding pebble flux is 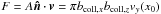 , with
, with 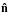 the unit vector perpendicular to A. Multiplied by ρp, the spatial density of pebbles in the midplane, this gives a total accretion rate Ṁ. As in the geometric limit the flux is πR2vhw, the collisional efficiency is therefore
the unit vector perpendicular to A. Multiplied by ρp, the spatial density of pebbles in the midplane, this gives a total accretion rate Ṁ. As in the geometric limit the flux is πR2vhw, the collisional efficiency is therefore 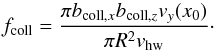 (16)In terms of fcoll, the accretion rate is
(16)In terms of fcoll, the accretion rate is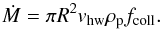 (17)
(17)
3. Results
Results for fcoll are obtained as function of particle radius s, planetesimal radius R, disk orbital radius (1, 3, and 10 AU) and flow pattern (Stokes or potential). We adopted internal densities of ρ• = 1 g cm-3 for both planetesimals and pebbles. Results of the integrations are given in Table 1 and in Figs. 3 and 4.
3.1. Collision efficiencies
For small planetesimals, the collisional cross section equals the geometric cross section, fcoll ≈ 1. However, the Stokes number (Eq. (1)) decreases for increasing planetesimal sizes. When it reaches unity, aerodynamic deflection can become important as the particle will adjust to the flow on a timescale (ts) that is shorter than the crossing time R/ Δv. Furthermore, for small particles, (below 0.1 cm) the two-body gravitational force is weak. Consequently, the collision factor becomes (much) smaller than unity. This is consistent with the non-gravitational hydrodynamical simulations by Sekiya & Takeda (2003); under these conditions, particles hardly hit the planetesimal. For our smallest size of 10-2 cm, collisional deflection factors reach a minimum of 10-3 for the potential case and slightly higher for the Stokes case. In addition, the minimum in Stokes flow occurs at smaller planetesimals. On the other hand, Figs. 3a and b show that fcoll never reaches zero. The minimum value for the collision factor, fcoll,min, is listed in Table 1.
This difference between the two flow patterns can be explained as follows. In both cases the radial velocity is zero at the surface of the planetesimal. However, whereas the angular component is zero in the viscous case (zero slip boundary), it is of the order of the headwind velocity for potential flow. For the potential case this explains the deep barrier that is seen in Fig. 3a: particles feel a centrifugal force (of the order of 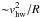 ) that competes with the gravitational attraction. On the other hand, for Stokes flow the almost vanishing azimuthal velocities means that the crossing times become significantly longer than R/vhw, which has two consequences: (i) aerodynamic deflection becomes effective at higher Stokes number (smaller planetesimal size for fixed ts); and (ii) gravity has more time to act, promoting accretion by settling. As a result, the minimum of the collisional efficiencies for Stokes flow occurs at a smaller planetesimal radius.
) that competes with the gravitational attraction. On the other hand, for Stokes flow the almost vanishing azimuthal velocities means that the crossing times become significantly longer than R/vhw, which has two consequences: (i) aerodynamic deflection becomes effective at higher Stokes number (smaller planetesimal size for fixed ts); and (ii) gravity has more time to act, promoting accretion by settling. As a result, the minimum of the collisional efficiencies for Stokes flow occurs at a smaller planetesimal radius.
In Table 1 two modes can be identified. (i) For pebbles smaller than 0.1 cm hydro effects operate to slow down particles within the time pebbles encounter the planetesimal. The collision factor steadily decreases, with fcoll,min possibly ≪1 due to aerodynamic deflection, before settling interactions reverse the decline. (ii) Larger pebbles (s> 0.1 cm at 0.1 AU) never experience aerodynamic deflection. Instead, we see a gradual increase of fcoll, characteristic of the smooth transition to Safronov gravitational focusing. Collision factors then increase with planetesimal size. Eventually, gravity becomes strong enough to trap pebbles in the Hill sphere, initiating the onset of pebble accretion, which expresses itself as a steep upturn in fcoll.
As was explained above, the onset of pebble accretion also depends on disk radius. The integrations at 3 AU and 10 AU with the potential flow solution are shown in Figs. 3c and d. In Fig. 3c only the smallest particle shows a barrier (see Table 1). For larger particle radii, the collision efficiency factors start in the geometric regime, smoothly make the transition to the Safronov regime, and then enter the settling regime. Since stopping times increase with disk radius and with particle radius, the onset of pebble accretion occurs at larger planetesimal radius, explaining the prolonged duration of ballistic encounters.
 |
Fig. 5 Growth timescale tgrowth for a pebble of radius s = 30 cm as function of planetesimal radius R at 3 AU. The black dashed curve shows the default model (as in Fig. 4). The other curves consecutively give the effects of a colder disk resulting in a headwind of vhw = 28 cm s-1 (blue dashed line) and a threefold increase in gas density (green curve) with a −0.5 power-law index for the surface density (Eq. (3)). The crosses represent numerical results and the solid (and dashed) lines represent fits. |
3.2. Growth timescale for sweep-up
Equation (17) defines the timescale for the planetesimal to e-fold its mass: 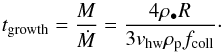 (18)The growth timescales for the same parameter space as our results for fcoll are shown in Fig. 4 and listed in Table 1. The density of pebbles is taken ρp = ρg/ 100, the typical solid-to-gas ratio. In Fig. 4d, however, we also consider the case of equal pebble and gas density. Figures 4a and b show growth timescales using the potential and Stokes flow solutions at 1 AU orbital distance. The time needed for the planetesimal to increase its mass by a factor e increases for small planetesimal size R up to a maximum Rgr,max. In the potential case, this maximum is centered around Rgr,max ~ 100 km (see Table 1). For the simulations with the Stokes flow pattern, the maximum shifts to smaller pebble sizes.
(18)The growth timescales for the same parameter space as our results for fcoll are shown in Fig. 4 and listed in Table 1. The density of pebbles is taken ρp = ρg/ 100, the typical solid-to-gas ratio. In Fig. 4d, however, we also consider the case of equal pebble and gas density. Figures 4a and b show growth timescales using the potential and Stokes flow solutions at 1 AU orbital distance. The time needed for the planetesimal to increase its mass by a factor e increases for small planetesimal size R up to a maximum Rgr,max. In the potential case, this maximum is centered around Rgr,max ~ 100 km (see Table 1). For the simulations with the Stokes flow pattern, the maximum shifts to smaller pebble sizes.
The features presented in Fig. 4 reflect those of Fig. 3. In the geometrical regime, growth timescales increase since the dependency of planetesimal mass on radius is cubic and the dependency on the impact parameter is quadratic. For pebble sizes ≲ 0.1cm, the increase in growth time is especially dramatic due to the aerodynamic deflection discussed in Sect. 3.1. Pebbles ≳10 cm never experience aerodynamic deflection, but instead enter the Safronov regime (as was discussed in Sect. 3.1). Although Safronov focusing causes a decrease in growth timescale with planetesimal radius (runaway growth), growth timescales remain long. Nevertheless, growth inevitably transitions to the pebble accretion regime, which commences with a steep drop in tgrowth.
At 3 and 10 AU orbital distances aerodynamic deflection is absent, except for pebbles smaller than 0.01 cm at 3 AU. For larger pebbles, the growth time initially decreases slowly (Safronov), but is followed by a sharp transition to pebble accretion (Figs. 4c and d). Because gas densities decrease with disk radius (Eq. (4)), tgrowth increases for most pebble radii. We see that in many cases peak growth timescales are much longer than the expected lifetimes of 6−10 Myr of gas-rich protoplanetary disks around low-to-intermediate-mass stars (Yasui et al. 2014; Pfalzner et al. 2014; Ribas et al. 2015). Planet formation by pebble sweep-up starting from small planetesimals would therefore be too slow. However, particle settling to the mid-plane of the disk (Youdin & Lithwick 2007; Andrews et al. 2009) will increase pebble densities. In Fig. 4d we included the case that ρg = ρp, which reduces the timescales a hundred fold. Nevertheless, at 10 AU, the resulting peak growth timescales of 107 yr are still rather long.
3.3. Varying the disk model
Until now we have adopted the disk profile as given by Eqs. (2) and (3). In reality, however, there is no clear physical reason why a protoplanetary disk should be characterized by these MMSN-like profiles. We therefore considered the effect of changing the temperature and density. In Fig. 5 we show the growth timescale of a 30 cm particle at 3 AU for a disk with a temperature of 90 K (green solid curve), which is half that of the standard model (black dashed curve). Such colder disk conditions may follow from more efficient cooling (Bitsch et al. 2015). The key consequence of the temperature drop is that it reduces the headwind of the disk (Eq. (5)) by a factor 2. The reduced headwind increases the interaction timescale, providing more time for gravity to act. Thus, settling interactions now occur at a small planetesimal size (200 km instead of 450 km) and the peak growth times also shift to smaller planetesimal sizes (≃50 km) because Safronov focusing also profits from a lower vhw. On the other hand, geometric encounters, which scale ∝ vhw, are less effective, explaining the increase of the growth timescale at small R. Consequently, the peak growth timescale hardly changes; the growth time bottleneck remains but shift to smaller sizes.
The green line in Fig. 5 corresponds to the case of a more massive disk than in the default model. Here, we adopted a −0.5 exponent in the surface density expression of Eq. (3), which results in an increase of the gas density by a factor 3. The pebble density ρp was kept the same as in the default model, however. Because of the shallower density profile, the headwind velocity drops slightly (to 40 m s-1), but the main effect of the enhanced gas density is that the 30 cm size particles have become aerodynamically smaller (lower ts). Increasing the pebble density by a factor of three, such that ρg/ρp is back at 100 (not shown), causes the growth timescale to drop by a factor of three.
4. Analysis: the onset of pebble accretion
4.1. Fitting expressions for ballistic and settling interactions
Pebble accretion occurs when particles settle to the planetesimal at terminal velocities vsettl = fgts, with fg = GM/b2 the gravitational acceleration and b the impact parameter. The equation that determines the impact parameter bset of these settling encounters is the cubic 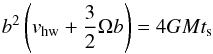 (19)(Ormel & Klahr 2010). This equation follows from equating the settling timescale b/vsettl with the encounter timescale, b/ Δv where Δv, the approach velocity, is the term in braces in Eq. (19). The numerical factor 4 follows from the strongly coupled limit (ts → 0), which allows closed-form solutions (Ormel & Klahr 2010). Since we consider only the onset of pebble accretion, the shear term,
(19)(Ormel & Klahr 2010). This equation follows from equating the settling timescale b/vsettl with the encounter timescale, b/ Δv where Δv, the approach velocity, is the term in braces in Eq. (19). The numerical factor 4 follows from the strongly coupled limit (ts → 0), which allows closed-form solutions (Ormel & Klahr 2010). Since we consider only the onset of pebble accretion, the shear term, 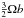 , can be ignored; then,
, can be ignored; then, 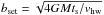 .
.
 |
Fig. 6 Contour plot of fcoll (Eq. (21)) forpotential flow as a function of Safronov number (x-axis) and dimensionless stopping time τX = ts/tX (y-axis). The former is a proxy for the planetesimal size, whereas τX is a measure of the particle aerodynamical size. The dashed curve gives the transition between ballistic and settling interactions. The dotted lines Θ = 1 and St = 1 separate the geometric regime (where fcoll ≈ 1) from the Safronov (where Θ > 1) and aerodynamic deflection (A.D., where St < 1) regimes. At small Stokes number, aerodynamic deflection suppresses accretion because these particles couple too well to the gas for ballistic interactions to be effective. Particles of τX ≲ 1 experience aerodynamic deflection before entering the settling regime, while τX ≳ 1 particles experience Safronov focusing before entering the pebble accretion regime. (⋆: the conversion of τX,Θ to physical parameters has been conducted for the default parameters at 1 AU.) |
At long stopping times interactions are too fast for settling because the interaction timescale ~ b/ Δv becomes shorter than the stopping time and particles never reach terminal velocities during the encounter. Consequently, Eq. (19) becomes invalid and pebble accretion inefficient for stopping times beyond a critical stopping time: 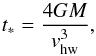 (20)implying that pebble accretion cross sections are largest for particles of stopping time ts ~ t∗ (Lambrechts & Johansen 2012).
(20)implying that pebble accretion cross sections are largest for particles of stopping time ts ~ t∗ (Lambrechts & Johansen 2012).
For stopping times longer than t∗ particles experience the well-known (Safronov) gravitational focusing 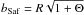 , where Θ = (vesc/vhw)2 is the Safronov number (Safronov 1972) with
, where Θ = (vesc/vhw)2 is the Safronov number (Safronov 1972) with 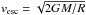 the surface escape velocity of the body. We refer to these encounters as “ballistic”3 because the encounter that grazes the object determines the impact parameter. This is in contrast to the settling mode, where bset is independent of the physical size R – the defining characteristic of pebble accretion. When encounters become too long, gas drag acts to diminish the efficacy of ballistic interactions: projectiles follow gas streamlines. Specifically, gas drag prevents small particles from colliding with the target when the stopping time is much shorter than R/vhw, or St ≪ 1. Such particles never ballistically collide with a planetesimal.
the surface escape velocity of the body. We refer to these encounters as “ballistic”3 because the encounter that grazes the object determines the impact parameter. This is in contrast to the settling mode, where bset is independent of the physical size R – the defining characteristic of pebble accretion. When encounters become too long, gas drag acts to diminish the efficacy of ballistic interactions: projectiles follow gas streamlines. Specifically, gas drag prevents small particles from colliding with the target when the stopping time is much shorter than R/vhw, or St ≪ 1. Such particles never ballistically collide with a planetesimal.
In conclusion, hydrodynamical effects suppress ballistic encounters below St ~ 1, whereas for larger Stokes numbers (stopping times) settling encounters vanish. We can describe both behaviors with a fitting function of the form ![\begin{equation} f_\mathrm{coll} = f_\mathrm{coll,0} \exp \left[a\left(\frac{\mathrm{St}}{\mathrm{St}_\ast}\right)^b \right] \label{eq:fcoll-fit} , \end{equation}](/articles/aa/full_html/2016/02/aa27361-15/aa27361-15-eq230.png) (21)where fcoll,0 is the uncorrected collision efficiency, and a and b are fit parameters that depend on the adopted flow pattern. The critical Stokes number St∗ is fixed at 1 for ballistic encounters and 2Θ (corresponding to t∗ in Eq. (20)) for settling interactions in potential flow. For Stokes flow we adopted a different prescription for St∗. The parameters are listed in Table 2.
(21)where fcoll,0 is the uncorrected collision efficiency, and a and b are fit parameters that depend on the adopted flow pattern. The critical Stokes number St∗ is fixed at 1 for ballistic encounters and 2Θ (corresponding to t∗ in Eq. (20)) for settling interactions in potential flow. For Stokes flow we adopted a different prescription for St∗. The parameters are listed in Table 2.
These fits were kept relatively simple and do not cover all situations. For example, in the zero-gravity limit (Θ = 0) fcoll does not become identically 0 below a critical Stokes number (Slinn 1976). Generally, fcoll in the ballistic regime depends on the Reynolds number of the flow. For turbulent flows, furthermore, the suppression of fflow at low St is much diminished (Homann et al. 2015, see Sect. 5.2). In the settling regime, fcoll is consistent with earlier results (Ormel & Klahr 2010; Ormel & Kobayashi 2012) barring three-body effects4.
Contours of fcoll for potential flow are plotted in Fig. 6 as function of Safronov number Θ and 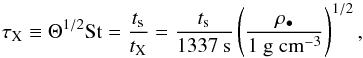 (22)where
(22)where 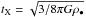 depends only on the planetesimal internal density. When ρ• is constant, τX can therefore be identified with the pebble aerodynamical properties (in contrast to St, which is a mix of planetesimal and pebble properties), allowing us to convert the dimensionless axes of Fig. 6 to physical parameters. At high Stokes number (large τX) and small Θ, ballistic encounters operate in the geometric regime (top left). With decreasing τX (smaller particle sizes) interactions suffer aerodynamic deflection as the Stokes number decreases. Collision efficiency factors then rapidly decrease, until the point where fcoll becomes determined by settling encounters (dashed curve). Nevertheless, for τX ≲ 1 settling accretion rates are always modest even for Θ ≫ 1 (bottom right corner). On the other hand, for τX ≳ 1 particles, the journey to pebble accretion involves the Safronov regime. This already ensures that fcoll increases above unity, but fcoll is especially boosted by pebble accretion after the dashed curve has been crossed (top right).
depends only on the planetesimal internal density. When ρ• is constant, τX can therefore be identified with the pebble aerodynamical properties (in contrast to St, which is a mix of planetesimal and pebble properties), allowing us to convert the dimensionless axes of Fig. 6 to physical parameters. At high Stokes number (large τX) and small Θ, ballistic encounters operate in the geometric regime (top left). With decreasing τX (smaller particle sizes) interactions suffer aerodynamic deflection as the Stokes number decreases. Collision efficiency factors then rapidly decrease, until the point where fcoll becomes determined by settling encounters (dashed curve). Nevertheless, for τX ≲ 1 settling accretion rates are always modest even for Θ ≫ 1 (bottom right corner). On the other hand, for τX ≳ 1 particles, the journey to pebble accretion involves the Safronov regime. This already ensures that fcoll increases above unity, but fcoll is especially boosted by pebble accretion after the dashed curve has been crossed (top right).
The fits of Table 2 provide a good match to the data, see Fig. 3. We note that St∗ in the Stokes flow fit in the settling regime becomes ≫1 for small planetesimals (Θ ≪ 1). This extends the power-law solution of the settling regime and results in “flat” growth timescales (see Fig. 4b). The physical reason behind this change is that for low-impact parameters (b ≪ R) encounter times are much longer than the bset,0/vhw that is assumed in the derivation of t∗ (Eq. (20)) because the transverse velocity (vθ) approaches zero (see Fig. 1). In fact, in Stokes flow the interaction time increases with decreasing cross section: tenc ~ R/δv ~ R2/bvhw, where δv is the transverse velocity at a distance δr from the sphere and δr ~ b (cf. Johansen et al. 2015b). Continuing this order-of-magnitude analysis, the collision factor is still given by 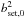 , but the critical Stokes number (where ts = tenc) is now St∗ ~ Θ-1. This explains the expression for St∗ adopted in Table 2.
, but the critical Stokes number (where ts = tenc) is now St∗ ~ Θ-1. This explains the expression for St∗ adopted in Table 2.
In the potential case a similar analysis results in St∗ ≃ 1 + 2Θ, but we found that the offset made little difference. More importantly, the fit expressions for potential flow fail at very small impact parameters (see Fig. 3a). The reason is that centrifugal forces due to the flow curvature overwhelm gravitational forces, that is, particles are propelled away from the planetesimals, unless they collide head-on. This results in another reduction of the collision efficiency compared to the fit in Fig. 3a.
4.2. Critical stopping time for accretion
From Fig. 6 it is clear that the value of τX is a key factor in the growth of planetesimals. In Fig. 6, particles of the same stopping time move from left to right in Fig. 6 as the planetesimal size increases. Starting from this point (Θ ≪ 1 and fcoll = 1) and increasing the planetesimal size (Θ), two growth modes can be identified:
-
1.
τX ≪ 1 particles become affected by aerodynamic deflection (St ≲ 1) before gravitational focusing starts (Θ > 1). With increasing planetesimal size (decreasing Stokes number), collision factors become significantly suppressed, fcoll ≪ 1, stalling the growth of the planetesimal. At some point, settling interactions will take over from ballistic encounters, after which fcoll increases with Θ in the settling regime. The settling regime accretion rates for τX ≪ 1 particles are nevertheless modest: fcoll ∝ M ( neutral growth).
-
2.
τX ≫ 1 particles experience gravitational focusing (Θ > 1) first and are never affected by aerodynamic deflection. Initially, fcoll increases due to (classical) Safronov gravitational focusing, fcoll ≃ Θ, but when ts ~ t∗ at a Safronov number of
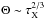 , collision efficiencies exponentially increase as interactions transition to the settling regime. Collisional focusing factors jump from ~
, collision efficiencies exponentially increase as interactions transition to the settling regime. Collisional focusing factors jump from ~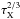 to ~
to ~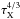 over a relatively short range in Θ5. For longer stopping times, the jump in fcoll associated with entering the pebble accretion regime is therefore more dramatic – but occurs at a higher planetesimal mass.
over a relatively short range in Θ5. For longer stopping times, the jump in fcoll associated with entering the pebble accretion regime is therefore more dramatic – but occurs at a higher planetesimal mass.
5. Discussion
5.1. Viability of the incremental growth of small planetesimals
In our calculations of the growth timescale we assumed perfect sticking of pebbles with planetesimals. However, dust collisional experiments often give a plethora of collisional outcomes, ranging from sticking, bouncing, erosion and catastrophic destruction (Blum & Wurm 2008; Güttler et al. 2010). This raises the question whether the reported growth timescales are realistic. Windmark et al. (2012) concluded that the (positive) mass transfer at small projectile sizes transitions to (negative) erosion if the projectile size becomes larger than ~ 0.1 mm, and Krijt et al. (2015) argued that erosion of large, fluffy planetesimals replenishes disks with a fresh reservoir in small grains.
 |
Fig. 7 Scatter plot of planetesimal radius R vs. particle radius s for potential flow at 1 AU from the star. The scatter plot shows the result of streamline integrations of the same parameter space as in Fig. 3a, assuming particles bounce off the surface. After 10 bounces, particles are considered accreted. The red crosses represent a sticking fraction of fstick< 0.1, the gray dots of 0.1 <fstick ≤ 0.9 and the green crosses fstick> 0.9. |
To assess the dependence of the collisional physics on the growth rates, we considered a simulation where particles bounce off the surface of the planetesimal. We adopted the same parameters as in Fig. 3a (1 AU, potential flow) and, following Johansen et al. (2015b), adopted a coefficient of restitution of 50% for a single bounce. Particles were considered accreted after they had bounced ten times with the planetesimal. Clearly, the accretion cross section including bouncing will not exceed the previously determined collisional cross section. Let this ratio be called fstick. Hence, fstick = 0 implies that all particles bounce off (to become re-entrained in the gas flow), whereas fstick = 1 means that all colliding particles return to the planetesimal (because of its gravity). The results of these bouncing simulations are presented in Fig. 7, where symbols indicate the value of fstick. The parameter space where the sticking fraction is low (red crosses: fstick ≤ 0.1) approximately correspond to the geometrical regime. On the other hand, in the Safronov regime (Θ > 1), corresponding to a planetesimal size of 100 km, accretion becomes more effective, while in the settling regime fstick = 1 is guaranteed. At small particle radii (s = 0.01 cm and s = 0.03 cm), the sticking fraction again increases because the few particles that accrete in this aerodynamic deflection regime do so by virtue of settling. All these findings are (qualitatively) consistent with Johansen et al. (2015b), who considered a Stokes flow.
These results therefore show that planetesimals below 100 km cannot grow merely by gravitational effects. However, the laboratory collision experiments that most resemble our case – small projectiles that are being fired onto a solid wall – present a more positive view. Teiser & Wurm (2009) studied collisions between centimeter dust projectiles and a steel plate with velocities ranging from 30 to 47 m s-1. This experiment shows that the accretion efficiency is positive (30%). Furthermore, Meisner et al. (2013) studied the continuous impact of submillimeter (0.1–1 mm) dust particles onto larger objects. The results are consistent with the findings of Teiser & Wurm (2009) and show that planetesimals indeed gain net mass with an accretion efficiency of 30% on average. Therefore, collision physics is not necessarily an impediment for the sweep-up growth scenario in the ballistic regime.
But are these loosely bound pebbles not simply blown off the surface of the planetesimals as the latter moves through the nebular gas? On Earth, lift forces arise because of variations in flow velocities and pressure near the ground. On Earth, as well on Mars, lifting of small grains is the first step toward saltation – a process that shapes desert landscapes and causes dust storms. Modeling these effects, Shao & Lu (2000) presented an empirical but physically motivated expression for the velocity required to initiate saltation (also known as the fluid threshold; Bagnold 1936): 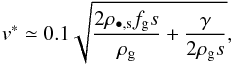 (23)where v∗ is the threshold velocity for lifting (which must be compared to the headwind velocity vhw), fg is the gravitational acceleration and γ ~ 0.1 g s-2 an empirical constant that represents the strength of the interparticle forces. The same forces operate on a rubble pile planetesimal moving through the nebular gas at velocities vhw. Therefore, when the magnitude of the lift force exceeds that of the gravity and interparticle forces, pebbles may be lifted from the planetesimal. Equation (23) suggests that small particles as well as large pebbles will remain bound because of sticking and high inertia, respectively. Nevertheless, for the relatively high densities in the inner disk v∗ may become lower than the planetesimal headwind velocity for small planetesimals6.
(23)where v∗ is the threshold velocity for lifting (which must be compared to the headwind velocity vhw), fg is the gravitational acceleration and γ ~ 0.1 g s-2 an empirical constant that represents the strength of the interparticle forces. The same forces operate on a rubble pile planetesimal moving through the nebular gas at velocities vhw. Therefore, when the magnitude of the lift force exceeds that of the gravity and interparticle forces, pebbles may be lifted from the planetesimal. Equation (23) suggests that small particles as well as large pebbles will remain bound because of sticking and high inertia, respectively. Nevertheless, for the relatively high densities in the inner disk v∗ may become lower than the planetesimal headwind velocity for small planetesimals6.
5.2. Importance of the flow near the planetesimal
In this work we have demonstrated that sweep-up growth timescales increase for particles below a critical stopping time of tX ≈ 103 s. In this case, St ≪ 1 before Safronov focusing becomes important (Fig. 6). Under these conditions, we showed that there is some difference in collision efficiency factors between the potential and Stokes flow solutions. Which of the two adopted solutions is more realistic?
Without access to hydrodynamical simulations, we can only be descriptive. However, as the planetesimal Reynolds number is ≫1, it may be argued that the potential flow solution – as unphysical as it is – is perhaps more applicable than the Stokes flow solution, which unrealistically alters the flow pattern at distances beyond several planetesimal radii (see our Fig. 1 and Beard & Grover 1974). On the other hand, at very small impact parameters (fcoll ≪ 1) velocities close to the planetesimal surface must vanish, which renders the Stokes solution more appropriate. Continuing this reasoning, we may define a distance δr from the surface of the planetesimal where the molecular diffusion timescale (δr)2/ν equals the inertial transport time vhw/R. We then obtain 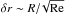 (essentially the width of the boundary layer) to be the distance from the planetesimal beyond which the gas flow is better described by potential flow.
(essentially the width of the boundary layer) to be the distance from the planetesimal beyond which the gas flow is better described by potential flow.
Another situation arises when the medium itself is turbulent. The gas in the protoplanetary disk, for one, is believed to be mildly turbulent due to hydrodynamic or magneto-hydrodynamical instabilities (Balbus & Hawley 1991). Recently, Homann et al. (2015) numerically determined the collision efficiencies as a function of Stokes number and turbulent intensity, finding a much shallower exponential decline (i.e., a fit parameter a (see Table 2) much closer to zero). This means that the ballistic regime in Fig. 6 becomes gains in importance: the dashed line separating the geometric and aerodynamic deflection regimes shifts down.
At ~3 AU particles of stopping time ts ≪ tX correspond to μm-grains. Since these particles are accreted at fcoll ≪ 1 efficiencies, meteorites can only accrete trace amounts of them. While this is sufficient to explain the few presolar grains that are found in meteorites (Clayton & Nittler 2004), it is clear that accretion of micron-size grains will not significantly contribute to the total mass. Therefore, the bulk of the matrix material found in chondrites must have been brought in through larger, aerodynamically more weakly coupled particles – for example, as dust-rimmed chondrules or aggregates of dust-rimmed chondrules (Cuzzi 2004; Ormel et al. 2008; Johansen et al. 2015a).
Finally, while we proposed aframework applicable to calculate accretion rates on planetesimals, it would be highly desirable to further refine our results by hydrodynamical simulations, which includes inertial particles that feel the gravity of the planetesimal7.
5.3. Onset of pebble accretion
Especially in the outer disk peak growth timescales can easily become longer than the disk lifetime. This means that the fast pebble accretion regime is not accessible by incremental growth processes – a situation exacerbated when pebbles are drifting very quickly inward and may be lost from the disk before the disk itself disappears. Therefore, a more attractive scenario for the growth of planets is to start from a planetesimal seed massive enough for interactions to fall in the pebble accretion regime. Such large planetesimals may be produced by gravitational instabilities involving pebble-size particles (for instance streaming instabilities; Johansen et al. 2007, 2009, 2012), be scattered from the inner disk, or be the collisional product of a population of small planetesimals. However, this threshold for the onset of pebble accretion RPA shifts to progressively larger sizes for increasing disk orbital radii and increasing particle stopping times (Table 2).
We can obtain RPA by equating fcoll in the Safronov and settling regime. However, this is a transcendental equation in R. To still obtain an (approximate) closed-form expression, we assume that the transition occurs near the point where t∗ ≈ ts, yielding R ≈ vhwtX(ts/ 2tX)1/3. Modifying this expression slightly to be in line with our numerical results, we obtain that the onset of pebble accretion occurs at a planetesimal radius 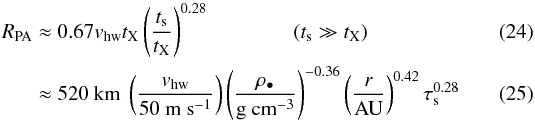 where the latter expression is valid for particles of τs = tsΩ < 1. Equation (24) agrees well with our numerical results.
where the latter expression is valid for particles of τs = tsΩ < 1. Equation (24) agrees well with our numerical results.
6. Conclusions
We identified the onset of pebble accretion by finding the collision factor for 1–103 km planetesimals at 1, 3, and 10 AU orbital distance for pebble sizes in the range of 0.01–30 cm. To investigate the influence of the flow pattern in the vicinity of the planetesimal, we conducted numerical integrations for both potential and Stokes flow. From our numerical integrations and analytical fits we calculated a growth timescale on which the planetesimal mass e-folds by sweep-up of pebbles, investigating thereby the conditions under which small planetesimals can grow large enough for pebble accretion to become important. We conclude the following from our study:
-
1.
Gravitational interactions between pebbles and planetesimalsensure that the collisional efficiency factors never become zero,even for the smallest particles.
-
2.
Peak growth timescales for planetesimal sweep-up of pebble-sized particles occur at ~100 km, corresponding roughly to the point where the headwind velocity equals the surface escape velocity of the planetesimal. This transition size therefore decreases when the disk headwind is lower, for instance, for a colder disk. For very small particles (very small stopping times) peak growth timescales are longer because of aerodynamic deflection.
-
3.
ForStokes flow, where the gas velocities vanish at the planetesimal surface, encounter times increase for smaller pebbles, increasing the likelihood to be captured by gravitational settling. In contrast, pebbles are centrifugally ejected in potential flow, strengthening the aerodynamic barrier.
-
4.
A critical particle stopping time of tX ≈ 103 s (see Eq. (22)) distinguishes between the slow pebble accretion regime, where particles suffer from aerodynamic deflection, and the fast pebble accretion regime, where growth proceeds by ballistic encounters (Safronov focusing), before transitioning to the settling regime (pebble accretion).
-
5.
The onset of pebble accretion occurs when the planetesimal radius equals RPA (Eq. (24)). This is followed by an abrupt increase in the collision rate. Pebble accretion starts at larger planetesimal sizes at increasing distance from the star.
-
6.
At ~1 AU orbital distances, growth timescales are shorter than the disk lifetime of 10 Myr for any planetesimal size, provided pebble sizes are > 0.1 cm. For small planetesimals (below 100 km) growth primarily depends on the collisional outcome (sticking, bouncing, or fragmentation) of the pebble-planetesimal collision.
-
7.
In the outer disk the maximum growth timescale exceed 10 Myr. Therefore, planetary seeds must have formed from planetesimals large enough to gravitationally attract pebble-sized particles: R ≫ 100 km (Safronov focusing) or the even faster pebble accretion, whence R>RPA.
For this reason, Ormel & Klahr (2010) referred to these interactions as “settling” and the corresponding parameter space where they occur as the “settling regime”. We use this phrasing as a synonym with “pebble accretion”, coined by Lambrechts & Johansen (2012).
Since the parameter space is enormous, gas drag-mediated accretion can be (sub-)categorized into several regimes. Originally, Ormel & Klahr (2010) identified “settling”, “hyperbolic” (=ballistic), and three-body (more massive particles that experience little gas drag) encounters. Lambrechts & Johansen (2012) divided the settling regime into Hill accretion (for massive bodies) and a Bondi regime (used here). Guillot et al. (2014) subdivided the ballistic regime into “geometric” (where fcoll ≈ 1), “Safronov” (fcoll> 1), and “hydro”, where fcoll ≪ 1 due to aerodynamic deflection.
The scalings follow by evaluating fcoll in the ballistic and settling regime for St = St∗, which occurs at Θ = (τX/ 2)2/3. In reality, particles enter the settling regime at even lower Θ as a result of the exponential tail, and the jump is even larger (see Eq. (24)).
Care must be taken to extrapolate Eq. (23), which has been tailored for terrestrial conditions, towards the much rarefied nebular gas. Equation (23) must at least be modified in two points. First, it assumes a quadratic dependence on velocity of the gas drag law (as on Earth). Second, we can expect that small particles in the Epstein regime experience much reduced lift forces.
Acknowledgments
The authors would like to thank Sebastiaan Krijt, Carsten Dominik, Tristan Guillot, Ralph Wijers, Lucia Klarmann for useful discussions and the referee, Anders Johansen, for an insightful report. C.W.O. is supported by the Netherlands Organization for Scientific Research (NWO).
References
- Andrews, S. M., Wilner, D. J., Hughes, A. M., Qi, C., & Dullemond, C. P. 2009, ApJ, 700, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Bagnold, R. A. 1936, Proc. R. Soc. Lond. A, 157, 594 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Batchelor, G. K. 1967, An introduction to fluid dynamics (Cambridge University Press) [Google Scholar]
- Beard, K. V., & Grover, S. N. 1974, J. Atmos. Sci., 31, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Lambrechts, M., & Johansen, A. 2015, A&A, 582, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blum, J., & Wurm, G. 2008, ARA&A, 46, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chambers, J. E. 2014, Icarus, 233, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Clayton, D. D., & Nittler, L. R. 2004, ARA&A, 42, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Cuzzi, J. N. 2004, Icarus, 168, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Eshagh, M. 2005, J. Earth Space Phys., 31, 1 [Google Scholar]
- Fehlberg, E. 1969, Nasa Technical Report, NASA TR R-315 [Google Scholar]
- Guillot, T., Ida, S., & Ormel, C. W. 2014, A&A, 572, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güttler, C., Blum, J., Zsom, A., Ormel, C. W., & Dullemond, C. P. 2010, A&A, 513, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayashi, C., Nakazawa, K., & Nakagawa, Y. 1985, in Protostars and Planets II, eds. D. C. Black, & M. S. Matthews (Tuscon: Univ. of Arizona Press), 1100 [Google Scholar]
- Homann, H., Guillot, T., Bec, J., et al. 2015, A&A, submitted [Google Scholar]
- Johansen, A., Oishi, J. S., Low, M., et al. 2007, Nature, 448, 1022 [Google Scholar]
- Johansen, A., Youdin, A., & Mac Low, M. 2009, ApJ, 704, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Youdin, A. N., & Lithwick, Y. 2012, A&A, 537, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johansen, A., Jacquet, E., Cuzzi, J. N., Morbidelli, A., & Gounelle, M. 2015a, ArXiv e-prints [arXiv:1505.02941] [Google Scholar]
- Johansen, A., Mac Low, M.-M., Lacerda, P., & Bizzarro, M. 2015b, Sci. Adv., 1, 15109 [Google Scholar]
- Kretke, K. A., & Levison, H. F. 2014, AJ, 148, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Krijt, S., Ormel, C. W., Dominik, C., & Tielens, A. G. G. M. 2015, A&A, 574, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krijt, S., Ormel, C. W., Dominik, C., & Tielens, A. G. G. M. 2016, A&A, 586, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2012, A&A, 544, A32 [Google Scholar]
- Lambrechts, M., & Johansen, A. 2014, A&A, 572, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., Johansen, A., & Morbidelli, A. 2014, A&A, 572, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levison, H. F., Kretke, K. A., & Duncan, M. J. 2015, Nature, 524, 322 [CrossRef] [Google Scholar]
- Meisner, T., Wurm, G., Teiser, J., & Schywek, M. 2013, A&A, 559, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michael, D. H., & Norey, P. W. 1969, J. Fluid Mech., 37, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., Lambrechts, M., Jacobson, S., & Bitsch, B. 2015, Icarus, 258, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Nakagawa, Y., Sekiya, M., & Hayashi, C. 1986, Icarus, 67, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., & Klahr, H. H. 2010, A&A, 520, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ormel, C. W., & Kobayashi, H. 2012, ApJ, 747, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., Cuzzi, J. N., & Tielens, A. G. G. M. 2008, ApJ, 679, 1588 [NASA ADS] [CrossRef] [Google Scholar]
- Pfalzner, S., Steinhausen, M., & Menten, K. 2014, ApJ, 793, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Ribas, Á., Bouy, H., & Merín, B. 2015, A&A, 576, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricci, L., Testi, L., Natta, A., & Brooks, K. J. 2010, A&A, 521, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Safronov, V. S. 1972, Evolution of the protoplanetary cloud and formation of the earth and planets (Keter Publishing House) [Google Scholar]
- Sato, T., Okuzumi, S., & Ida, S. 2015, A&A, submitted [arXiv:1512.02414] [Google Scholar]
- Sekiya, M., & Takeda, H. 2003, Earth, Planets, and Space, 55, 263 [Google Scholar]
- Sellentin, E., Ramsey, J. P., Windmark, F., & Dullemond, C. P. 2013, A&A, 560, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shao, Y., & Lu, H. 2000, J. Geophys. Res., 105, 22437 [Google Scholar]
- Slinn, W. G. N. 1976, Geophys. Res. Lett., 3, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Teiser, J., & Wurm, G. 2009, MNRAS, 393, 1584 [NASA ADS] [CrossRef] [Google Scholar]
- Testi, L., Birnstiel, T., Ricci, L., et al. 2014, Protostars and Planets VI, 339 [Google Scholar]
- Weidenschilling, S. J. 1977a, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J. 1977b, Ap&SS, 51, 153 [Google Scholar]
- Whipple, F. L. 1972, in Proc. Symp., From Plasma to Planet, ed. A. Elvius, 211 [Google Scholar]
- Windmark, F., Birnstiel, T., Güttler, C., et al. 2012, A&A, 540, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yasui, C., Kobayashi, N., Tokunaga, A. T., & Saito, M. 2014, MNRAS, 442, 2543 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., & Goodman, J. 2005, ApJ, 620, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., & Lithwick, Y. 2007, Icarus, 192, 588 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Overview of the parameter space and the corresponding numerical results at given orbital distance r.
All Figures
 |
Fig. 1 Velocity vectors and gas streamlines around a sphere (planetesimal) for potential flow (left half; Eq. (7)) and Stokes flow (right half; Eq. (8)) as seen in the frame of the sphere. |
| In the text | |
 |
Fig. 2 Sketch of the procedure we used to obtain the collisional cross section. In the comoving frame, the planetesimal resides at the origin (y = 0) and pebbles start at a distance yS far enough to be unperturbed by the gravity of the planetesimal. Integrations are first carried out in the x-direction, and the impact parameter bcoll,x is determined from the first and last trajectory that hits the planetesimal (xmin and xmax). Starting at the average of these two coordinates x0, the integrations are extended to the z-direction to obtain the vertical impact parameter bcoll,z. |
| In the text | |
 |
Fig. 3 Collision factor fcoll as a function of planetesimal radius R for a constant internal density ρ• = 1 g cm-3. Crosses indicate numerical data, while solid lines are fits. The color scale ranges from dark to light blue for increasing particle radius. a) Results obtained with the (inviscid) potential solution (Eq. (7)) at 1 AU orbital distance from the star. For a small planetesimal size, the collision factor is approximately geometrical (fcoll ≈ 1). However, for small pebble sizes, aerodynamic deflection results in a significant drop of fcoll (see Table 1 for the minimum collision efficiency, fcoll,min). b) Results with the (highly viscid) Stokes flow solution (Eq. (8)). Settling occurs at smaller sizes due to the increase in encounter time. c) Results at 3 AU orbital distance show a shallow barrier only for the lowest particle size. d) At 10 AU a barrier is no longer present because of the reduced gas density. |
| In the text | |
 |
Fig. 4 Growth timescale tgrowth as function of planetesimal radius R for a constant internal density ρ• = 1 g cm-3. Crosses indicate numerical data, while the solid lines are fits. The color scale extends from dark blue to light blue, transitioning from lowest particle radius to highest particle radius. a) tgrowth obtained with the potential flow solution at 1 AU orbital distance and a pebble density of ρp = ρg/ 100, showing maxima at Rgr,max ~ 100 km. b) tgrowth with the Stokes flow solution at 1 AU orbital distance and a pebble density of ρp = ρg/ 100 , showing early settling and flattening out of the curves. c) tgrowth with the potential flow solution at 3 AU orbital distance and a pebble density of ρp = ρg/ 100. d) tgrowth with the potential flow solution at 10 AU orbital distance and a pebble density of ρp = ρg/ 100 (top, blue) and a pebble density of ρp = ρg (bottom, red). |
| In the text | |
 |
Fig. 5 Growth timescale tgrowth for a pebble of radius s = 30 cm as function of planetesimal radius R at 3 AU. The black dashed curve shows the default model (as in Fig. 4). The other curves consecutively give the effects of a colder disk resulting in a headwind of vhw = 28 cm s-1 (blue dashed line) and a threefold increase in gas density (green curve) with a −0.5 power-law index for the surface density (Eq. (3)). The crosses represent numerical results and the solid (and dashed) lines represent fits. |
| In the text | |
 |
Fig. 6 Contour plot of fcoll (Eq. (21)) forpotential flow as a function of Safronov number (x-axis) and dimensionless stopping time τX = ts/tX (y-axis). The former is a proxy for the planetesimal size, whereas τX is a measure of the particle aerodynamical size. The dashed curve gives the transition between ballistic and settling interactions. The dotted lines Θ = 1 and St = 1 separate the geometric regime (where fcoll ≈ 1) from the Safronov (where Θ > 1) and aerodynamic deflection (A.D., where St < 1) regimes. At small Stokes number, aerodynamic deflection suppresses accretion because these particles couple too well to the gas for ballistic interactions to be effective. Particles of τX ≲ 1 experience aerodynamic deflection before entering the settling regime, while τX ≳ 1 particles experience Safronov focusing before entering the pebble accretion regime. (⋆: the conversion of τX,Θ to physical parameters has been conducted for the default parameters at 1 AU.) |
| In the text | |
 |
Fig. 7 Scatter plot of planetesimal radius R vs. particle radius s for potential flow at 1 AU from the star. The scatter plot shows the result of streamline integrations of the same parameter space as in Fig. 3a, assuming particles bounce off the surface. After 10 bounces, particles are considered accreted. The red crosses represent a sticking fraction of fstick< 0.1, the gray dots of 0.1 <fstick ≤ 0.9 and the green crosses fstick> 0.9. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


