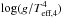| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 15 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201526035 | |
| Published online | 28 August 2015 | |
The flux-weighted gravity-luminosity relationship of blue supergiant stars as a constraint for stellar evolution
1 Geneva Observatory, University of Geneva, Maillettes 51, 1290 Sauverny, Switzerland
e-mail: georges.meynet@unige.ch
2 Institute for Astronomy, University of Hawaii, 2680 Woodlawn Drive, Honolulu, HI 96822, USA
3 University Observatory Munich, Scheinerstr. 1, 81679 Munich, Germany
4 Astrophysics, Lennard-Jones Laboratories, EPSAM, Keele University, Staffordshire ST5 5BG, UK
Received: 6 March 2015
Accepted: 3 May 2015
Context. The flux-weighted gravity-luminosity relationship (FGLR) of blue supergiant stars (BSG) links their absolute magnitude to the spectroscopically determined flux-weighted gravity 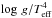 . BSG are the brightest stars in the universe at visual light and the application of the FGLR has become a powerful tool for determining extragalactic distances.
. BSG are the brightest stars in the universe at visual light and the application of the FGLR has become a powerful tool for determining extragalactic distances.
Aims. Observationally, the FGLR is a tight relationship with only small scatter. It is, therefore, ideal for using as a constraint for stellar evolution models. The goal of this work is to investigate whether stellar evolution can reproduce the observed FGLR and to develop an improved foundation for the FGLR as an extragalactic distance indicator.
Methods. We used different grids of stellar models for initial masses between 9 and 40 M⊙ and for metallicities between Z = 0.002 and 0.014, with and without rotation, which were computed with various mass loss rates during the red supergiant phase. For each of these models, we discuss the details of post-main sequence evolution and construct theoretical FGLRs by means of population synthesis models that we then compare with the observed FGLR.
Results. In general, the stellar evolution model FGLRs agree reasonably well with the observed one. There are, however, differences between the models, in particular with regard to the shape and width (scatter) in the flux-weighted gravity-luminosity plane. The best agreement is obtained with models that include the effects of rotation and assume that the large majority, if not all, of the observed BSG evolve toward the red supergiant phase and that only a few are evolving back from this stage. The effects of metallicity on the shape and scatter of the FGLR are small.
Conclusions. The shape, scatter, and metallicity dependence of the observed FGLR are explained well by stellar evolution models. This provides a solid theoretical foundation for using this relationship as a robust extragalactic distance indicator.
Key words: supergiants / stars: rotation / galaxies: distances and redshifts
© ESO, 2015
1. Introduction
Blue supergiants (BSG) are massive stars in the mass range between 10 to 40 M⊙ in the short-lived evolutionary phase when they cross the Hertzsprung-Russel diagram (HRD) between the hydrogen main sequence (MS) and the red supergiant (RSG) stage (see Fig. 1). BSGs may also evolve from a RSG stage as a result of very strong mass loss. With effective temperatures in a range between 20 000 K and 8000 K, the maximum of the energy distribution of these extremely luminous objects shifts toward visible wavelengths, which makes them the brightest stars in the universe at visual light. With absolute visual magnitudes MV ≅ −9.5 mag, a single BSG can be as bright as a globular cluster or a dwarf galaxy. Because of their brightness, they are ideal objects for studying the chemical composition of the young stellar population in galaxies far beyond the local group and for determining extragalactic distances using the tools of quantitative stellar spectral analysis (see, for instance, Kudritzki et al. 2014, and references therein). At the same time, BSGs are also extremely useful for constraining models of stellar evolution either through investigation of their chemical surface composition, revealing the presence of rotationally or convectively induced mixing (see, e.g., Gies & Lambert 1992; Hunter et al. 2008b,a; Przybilla et al. 2010; Urbaneja et al. 2011; Firnstein & Przybilla 2012; McEvoy et al. 2015; Maeder et al. 2014), through the number ratios of BSG, RSG, and MS stars (Dohm-Palmer & Skillman 2002; Eggenberger et al. 2002), or through study of their pulsational properties (Saio et al. 2013).
 |
Fig. 1 Evolutionary tracks in the Herstzsprung-Russel diagram calculated for solar metallicity Z = 0.014 for initial masses 9, 12, 15, 20, 25, 32, and 40 M⊙. The continuous lines show the track until the red supergiant phase. After the red supergiant stage, either dashed or dotted lines are used. The BSG phase is highlighted in red for the evolution toward the RSG phase (Group 1, see text) and in blue (dashed) for the evolution back after the RSG stage (Group 2). The models are from Ekström et al. (2012). Left panel: models without the effects of stellar rotation. Right panel: models including rotation (see text). |
Guided by the theory of stellar evolution, which predicts that BSG cross the HRD at approximately constant luminosity and constant mass, Kudritzki et al. (2003; see also Kudritzki et al. 2008b) have detected a tight relationship between absolute bolometric magnitude Mbol and the spectroscopically determined flux-weighted gravity 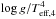 , the flux-weighted gravity – luminosity relationship (FGLR) (g is the gravity and Teff,4, the effective temperature in units of 104 K). The application of the FGLR using low-resolution optical spectra of individual BSGs in galaxies has strong potential as a precision distance indicator for the extragalactic distance scale. The spectroscopic determination of stellar temperature, gravity, and metallicity, combined with multi-color photometry, allows for the accurate determination of reddening, reddening law, and extinction of each individual BSG, thus avoiding the extinction and metallicity induced uncertainties encountered with Cepheid stars. The dereddened apparent magnitude in conjunction with the absolute magnitude obtained from the FGLR and with the spectroscopically determined flux-weighted gravity
, the flux-weighted gravity – luminosity relationship (FGLR) (g is the gravity and Teff,4, the effective temperature in units of 104 K). The application of the FGLR using low-resolution optical spectra of individual BSGs in galaxies has strong potential as a precision distance indicator for the extragalactic distance scale. The spectroscopic determination of stellar temperature, gravity, and metallicity, combined with multi-color photometry, allows for the accurate determination of reddening, reddening law, and extinction of each individual BSG, thus avoiding the extinction and metallicity induced uncertainties encountered with Cepheid stars. The dereddened apparent magnitude in conjunction with the absolute magnitude obtained from the FGLR and with the spectroscopically determined flux-weighted gravity 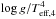 can then be used to determine accurate distances. In recent years, this new method has been successfully applied to galaxies out to a distance of 7 Mpc (Urbaneja et al. 2008; U et al. 2009; Kudritzki et al. 2012, 2013, 2014; Hosek et al. 2014).
can then be used to determine accurate distances. In recent years, this new method has been successfully applied to galaxies out to a distance of 7 Mpc (Urbaneja et al. 2008; U et al. 2009; Kudritzki et al. 2012, 2013, 2014; Hosek et al. 2014).
Besides the potential as distance indicator, the observed FGLR of BSG can also be used to constrain the stellar evolution models. This is purpose of the work presented in this paper. Using stellar evolutionary tracks we mainly address three questions:
-
1)
The population of blue supergiants is made from stars that starttheir evolution with different initial rotational velocities. Thisleads to the question of how important the effects of rotation are forthe post-main sequence evolution.
-
2)
How does stellar metallicity affect the post-main sequence evolution and the FGLR?
-
3)
As indicated in Fig. 1, BSG can be in two different evolutionary phases, evolving toward the RSG or back to hotter temperatures from the RSG stage. That some core collapse supernovae have a yellow or even a blue progenitor (e.g., see Table 6 in Meynet et al. 2015) indicates that the latter phase does indeed occur in nature and is not just a theoretical artifact. Moreover, some pulsation properties of blue supergiants are accounted for much better if the objects are in a post RSG stage (Saio et al. 2013). This leads to the immediate question about the fraction of post-RSG objects among the BSG stars and the reliability of post-RSG evolutionary tracks.
The stellar models used to investigate these questions are briefly presented in Sect. 2. Section 3 describes the stellar evolution background for the existence of the FGLR. Section 4 compares theoretical FGLRs with the empirical one. We demonstrate that indeed some stellar evolution models can be ruled out as representative of the bulk population. Section 5 shows the results of population synthesis models that provide an alternative way to compare predictions of the theory with the observed FGLR. Section 6 contains the main conclusions and discusses some aspects of future works.
2. The stellar models
The stellar evolution models used for this investigation are from the solar metallicity grid of Ekström et al. (2012), the grid of Georgy et al. (2013a) for the metallicity Z = 0.002, and from an unpublished grid of stellar models for the metallicity Z = 0.006 (Eggenberger et al., in prep.). Moreover, we use the models with an enhanced mass loss rate model during the RSG phase recently published by Meynet et al. (2015).
 |
Fig. 2 Left panel: evolutionary tracks at solar metallicity without rotation in the (log M/M⊙, log L/L⊙)-plane. M is the actual mass of the star during the evolution. The dashed lines are mass-luminosity relations with α = 3 and b = 0.72316, 1.17955, 1.54727, and 2.03346 (bottom-up). The lower vertical or nearly vertical (magenta) part of the track corresponds to the main-sequence phase, while the red and blue parts show the Groups 1 and 2 phases before and after the RSG stage. Right panel: flux-weighted gravity-luminosity relations obtained from Eq. (0) and the mass-luminosity relations labeled G1, G2a, and G2b in the left panel. The points represent observations of individual BSG. The black squares are the values for NGC 300 given by Kudritzki et al. (2008b). The full triangles are for supergiants in other galaxies studied by Kudritzki et al. (2008a). Full circles and crosses are BSGs in M 33 (U et al. 2009) and M 81 (Kudritzki et al. 2012), respectively. The empty stars and empty squares show the data for the metal-poor Local Group galaxies WLM (Urbaneja et al. 2008) and NGC 3109 by (Hosek et al. 2014). The empty triangles and the full pentagons correspond to BSG in NGC 3621 (Kudritzki et al. 2014) and in NGC 4258 (Kudritzki et al. 2013), respectively. The dotted magenta line represents the FGLR calibration obtained by Kudritzki et al. (2008b). |
The models are computed using the Schwarzschild criteria for convection with core overshooting. The core extension due to overshooting is taken as equal to 10% of the pressure scale height estimated at the Schwarzschild core boundary. Non-adiabatic convection is considered in the outer convective zone with a mixing length scale equal to 1.6 times the local pressure scale height. In rotating models, the shear turbulence coefficient is taken from Maeder (1997), while the horizontal turbulence and the effective diffusion coefficients are those from Zahn (1992). Initial velocities on the zero age main sequence (ZAMS) have been taken equal to 40% the critical velocity. Typically for the models at Z = 0.014, this corresponds to initial equatorial velocities between 248 and 314 km s-1 for initial masses between 9 M⊙ and 40 M⊙.
The mass-loss prescription for the hot part of the evolutionary tracks is that of de Jager et al. (1988) for the initial masses 9 M⊙ and 15 M⊙ and for log (Teff/ K) > 3.7. For log (Teff/ K) < 3.7, we use a fit to the data by Sylvester et al. (1998) and van Loon et al. (1999) as suggested by Crowther (2001). Above 15 M⊙, the prescription given by Vink et al. (2001) is used on the MS phase as long as log (Teff/ K) > 3.9, and the recipe from de Jager et al. (1988) is used for the non-RSG phase. For log (Teff/ K) < 3.7, the prescription is the same as for lower initial mass stars. The effects of rotation on the mass-loss rates are accounted for as in Maeder & Meynet (2000). These effects are quite negligible for the rotation rates considered in this work.
As explained in Ekström et al. (2012), for massive stars (>15 M⊙) in the RSG phase, some parts of the most external layers of the stellar envelope might exceed the Eddington luminosity of the star: LEdd = 4πcGM/κ (with κ the opacity). This is due to the opacity peak produced by the variation in the ionization level of hydrogen beneath the surface of the star. We account for this phenomenon by increasing the mass-loss rate of the star (computed as described above) by a factor of 3. Once the supra-Eddington layers disappear later during the evolution, we come back to the usual mass-loss rate.
For the enhanced mass-loss rate models, we just multiply our standard mass-loss rates by a factor 10 or 25 during the whole period when the stars are in the RSG phase. (We consider a star to be a RSG when its effective temperature (Teff), as estimated by the Geneva code, is log Teff(/K) < 3.7.) When the enhanced mass loss rates are used, we do not account for the effect of the supra-Eddington layers as described in Ekström et al. (2012). This means that the enhancement of the mass-loss rates with respect to those used in Ekström et al. (2012) are actually a little less than a factor 10 and 25 (see Meynet et al. 2015, for a more detailed discussion).
3. Some theoretical considerations about the flux-weighted gravity-luminosity relation
As shown in Kudritzki et al. (2008b), assuming a mass-luminosity relation of the type log L/L⊙ = αlog M/M⊙ + b, and the definition of Mbol, Mbol = −2.5log L/L⊙ + 4.75, one obtains the FGLR as a linear relationship between Mbol and log g/Teff,4, ![\begin{align} {M}_\text{bol}=\,&2.5 \frac{\alpha}{\alpha-1}\left[\log\frac{g}{T_\text{eff,4}^4}-16\right]\notag\\ &-2.5\frac{\alpha}{\alpha-1}\left[\log(4\pi \sigma G)+\log\frac{M_\odot}{L_\odot}\right]\notag\\ &+2.5\frac{b}{\alpha-1}+4.75.\label{eqone} \end{align}](/articles/aa/full_html/2015/09/aa26035-15/aa26035-15-eq52.png) (0)The symbols have their usual meaning. We see that the slope of the mass-luminosity relation α affects the slope of the FGLR. When α decreases, the FGLR slope increases. At the same time, Mbol decreases (i.e., it becomes more negative). We also see that Mbol increases with b.
(0)The symbols have their usual meaning. We see that the slope of the mass-luminosity relation α affects the slope of the FGLR. When α decreases, the FGLR slope increases. At the same time, Mbol decreases (i.e., it becomes more negative). We also see that Mbol increases with b.
Do the BSGs follow a well-defined mass-luminosity relation? To investigate this point, we constructed Fig. 2. In the lefthand panel, the non-rotating solar metallicity evolutionary tracks are shown in a luminosity-mass diagram. The evolutionary tracks start vertically from the bottom but then evolve toward the left with decreasing mass due to mass loss. The vertical phase at the very beginning coincides with the main-sequence phase, where the mass loss rates are very modest. After the main-sequence phase, the extension to the left is a consequence of mass loss, while the luminosity keeps a nearly constant value. The evolutionary stage of BSGs defined here as post MS stars with effective temperatures in the range between log Teff = 3.9 and 4.4 is indicated as heavy red sections, when the BSG are on their first crossing toward the RSG phase (Group 1 BSG), and in blue, when they come back after the red supergiant phase (group 2 BSG). We exclude late-phase stellar evolution models with extremely high helium surface abundance (corresponding to a hydrogen surface mass fraction Xsurf lower than 0.3) from the BSG group 2. Such high helium abundances are not found by the quantitative spectral analyses of normal BSGs (Firnstein & Przybilla 2012) and may belong to objects with Wolf-Rayet-star or luminous-blue-variable spectral characteristics.
We also overplot some mass-luminosity relations with constant and parallel slopes. This is an approximation made for simplicity. In reality the mass luminosity relation flattens at the high-mass end, an effect caused by the increasing importance of radiation pressure in the stellar interior (see, e.g., Maeder 2009; Yusof et al. 2013). However, to demonstrate the most important effects, the simple approximation of constant slope is sufficient.
Relation Z represents the ZAMS evolutionary stages. Relation G1 connects the Group-1 BSG. We note, however, that the blue-loop core He-burning phase of the 9 M⊙ track produces Group-2 BSG with very similar mass and luminosity. This comes from the fact that mass loss is not important for this relatively low mass. The relations G2a and G2b represent the two phases at higher mass of the Group-2 BSGs (see Fig. 1).
In the next step, we use the different mass-luminosity relations connecting the various groups of BSGs to construct flux-weighted gravity-luminosity relations. We obtain the three lines plotted in the right-hand panel of Fig. 2. The sample of observed BSGs used to obtain the empirical flux-weighted gravity-luminosity relation is also shown (see the caption for the references of these observations).
We see that assuming the luminosity scaling with the third power of the mass provides a good fit of the average slope of the empirical relation. We also see that the empirical relation deduced by Kudritzki et al. (2008b) has a slope very close to the simple theoretical relations. In addition, we note that the flux-weighted gravity-luminosity relations of Group-2 BSGs are shifted downward. The shift of G2b amounts to almost one bolometric magnitude. This shift is not so much due to a decrease in luminosity (see the left panel of Fig. 2), but to a decrease in 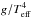 (rightward shift in the right panel of Fig. 2). This can be understood in the following way:
(rightward shift in the right panel of Fig. 2). This can be understood in the following way: 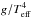 is proportional to M/L, and while L remains more or less constant between the evolutionary phases of Groups 1 and 2, the mass is decreased due to strong mass-loss during the RSG stage, where stars may lose between 25–40% of their initial mass (see, e.g., Fig. 3 in Meynet et al. 2015).
is proportional to M/L, and while L remains more or less constant between the evolutionary phases of Groups 1 and 2, the mass is decreased due to strong mass-loss during the RSG stage, where stars may lose between 25–40% of their initial mass (see, e.g., Fig. 3 in Meynet et al. 2015).
From this brief discussion, we can summarize the following main points: there is a one-to-one connection between mass-luminosity relations and flux-weighted gravity-luminosity relations. The Group-1 and Group-2 BSGs follow different mass-luminosity relations, hence different flux-weighted gravity-luminosity relations. Group 1 appears to form the upper envelope of the observed points in the Mbol versus 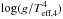 plane, while Group 2 covers the averaged positions of the observed points, as well as their lower envelope.
plane, while Group 2 covers the averaged positions of the observed points, as well as their lower envelope.
At first sight, one could conclude from these first comparisons that the observed scatter is compatible with the existence of Group-1 and Group-2 BSGs as predicted by the models. However, as we see below, this is not correct. Actually, this simple comparison suffers from many weaknesses: First, while we have plotted the relations G2a and G2b over the whole flux-weighted gravity range, the models predict the corresponding Group-2 stars only for the highest masses and luminosities. Second, we need to consider the time scales during the evolutionary phases corresponding to Group-1 and the various Group-2 phases in order to assess how, according to the models, the BSGs should be distributed along the different relations. Third, the scatter of the observed FGLR is, of course, not only affected by the presence of various types of blue supergiants but also by the observational uncertainties in the determination of bolometric magnitude and flux-weighted gravity. To disentangle these effects for a more precise comparison, we need to construct the flux-weighted gravity-luminosity relations resulting from the computed tracks (and not from a linear fit as in this section), including the information of the relative time scales spent in the various groups of BSGs. This is the topic of the next sections.
4. Comparisons with observations
In the following we discuss a sequence of evolutionary models in the (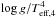 , Mbol)-plane of the FGLR and compare with the observed distribution of BSG. The plots show only post-main sequence evolution and again highlight the Groups 1 and 2 phases as before. We start with models at solar metallicity that assume standard rates of mass loss. We then consider the effects of enhancing mass loss in the RSG phase and finish this section by investigating the effects of reduced metallicity.
, Mbol)-plane of the FGLR and compare with the observed distribution of BSG. The plots show only post-main sequence evolution and again highlight the Groups 1 and 2 phases as before. We start with models at solar metallicity that assume standard rates of mass loss. We then consider the effects of enhancing mass loss in the RSG phase and finish this section by investigating the effects of reduced metallicity.
4.1. Models for solar metallicity with standard mass loss rates
 |
Fig. 3 Post-main sequence evolutionary tracks labeled by the original mass on the ZAMS in the ( |
Figure 3 shows Z = 0.014 models calculated with standard mass-loss rates (see Sect. 2). We begin with a discussion of non-rotating models. The first important fact we note is that the heavy red Group-1 phases of each track are not reduced to a single point as it would be if mass and luminosity were strictly constant. However, the Group-1 segments corresponding to each track are very short and more or less parallel to each other. In consequence, the hatched area that connects these segments forms a narrow sequence, which represents the BSG Group 1 FGLR for these models. At higher mass or luminosity, the slope of this FGLR sequence becomes steeper. As already noted in the previous section, this is because the slope of the mass-luminosity flattens when the initial mass increases. We also see that the sequence constitutes an upper envelope of the observed points in the upper luminosity range. This was already mentioned in Kudritzki et al. (2008b). Taken at face value, this could indicate that Group 1 does not constitute the bulk of the BSG population at high luminosity. This would be in line with the evolutionary time scales in the high-mass range, indicating, for instance, for the 32 M⊙ model that only about 14% of the BSGs are Group-1 BSGs, while 47% and 39% would be in the two Group-2 regions. Thus, in this luminosity range, Group-2 BSGs could indeed reproduce the shape of the observed FGLR including its width at the high-luminosity end. For lower luminosities, however, the models appear to be in slight disagreement with the observations, because of the absence of Group-2 BSG and because the Group-1 sequence is at bolometric magnitudes that are too high.
The situation changes with the models that include the effects of rotation. First, the Group-1 sequence shifts to the right toward slightly lower flux-weighted gravities. This is the effect of the rotational mixing of helium and heavier elements, which decreases the stellar mass-luminosity ratio (see, e.g., the review by Maeder & Meynet 2012, and references therein). The effect becomes more efficient at higher stellar mass, which leads to a significantly shallower slope of the Group-1 FGLR sequence in better agreement with the observations. Second, the Group-2 BSG extends toward lower stellar masses. This results from stronger mass losses during the RSG phase, which comes from the rotating models having higher luminosities. The higher luminosity and the reduced mass due to stronger mass loss also causes a shift to the right for the Group-2 objects.
As in the case of the non-rotating models, the evolutionary time scales indicate that most of the BSGs are expected to be Group-2 BSG. This does not seem to agree with the observations. However, we have to add a few cautious remarks at this point: The observed sample should result from stars with different initial velocities, and therefore, it may be that most observed stars begin their evolution with rotation less than 40% of the critical velocity on the ZAMS. Second, the observed BSGs displayed in Fig. 3 have different initial metallicities. In fact, slightly more than half of the observed stars (about 53%) actually have a metallicity lower than half solar. As we see later, while the influence of metallicity on the Group-1 BSGs in the Mbol versus 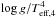 plane is very weak, the impact on Group 2 is, in contrast, quite important. Third, the mass-loss rates during the RSG stages are still very poorly known. Lower mass loss rates during the RSG stage would shift the blue regions in Fig. 3 to the left, making the positions of these stars more compatible with the observed scatter. At the same time, this also reduces the evolutionary time in the Group-2 phase, since with lower mass-loss rates, the stars spend more time in the RSG stage and after that evolve faster back to hotter temperatures.
plane is very weak, the impact on Group 2 is, in contrast, quite important. Third, the mass-loss rates during the RSG stages are still very poorly known. Lower mass loss rates during the RSG stage would shift the blue regions in Fig. 3 to the left, making the positions of these stars more compatible with the observed scatter. At the same time, this also reduces the evolutionary time in the Group-2 phase, since with lower mass-loss rates, the stars spend more time in the RSG stage and after that evolve faster back to hotter temperatures.
To summarize the discussion of solar metallicity evolution models with standard mass-loss rates we note:
-
Group 1 BSGs form a well-defined FGLRsequence with a width that is much smaller than the one observed.Models with rotation agree better with the observations.
-
The predicted location of Group-2 BSG is in marginal agreement with the observations only for non-rotating tracks. For tracks with rotation, mass loss in the RSG phase plays an important role and high mass-loss rates seem to lead to a disagreement with the observations.
The second point is investigated further in the next section for the case of higher mass-loss rates.
4.2. Models at solar metallicity with RSG enhanced mass-loss rates
 |
Fig. 4 Upper left panel: same as Fig. 3 for models without rotation but with RSG mass-loss rate enhanced by a factor 10 and for Z = 0.014. Upper right panel: same as the upper left panel but for models with rotation. Lower left panel: models without rotation but with RSG mass-loss rate enhanced by a factor 25. Lower right panel: same as the lower left panel but for models with rotation. |
 |
Fig. 5 Upper left panel: same as Fig. 3 for models without rotation and with standard RSG mass loss rates, but for a metallicity Z = 0.006. Upper right panel: same as left panel but for models with rotation. Lower left panel: same as Fig. 3 for models without rotation and standard RSG mass loss rates and for Z = 0.002. Lower right panel: same as lower left panel but for models with rotation. |
Recently, Georgy (2012) and Meynet et al. (2015) have presented tracks with RSG mass-loss enhanced by a factor 10 and 25. The rationale for computing such models is the observational fact that some core collapse supernovae have a yellow or even sometimes a blue progenitor in the luminosity range where RSG stars are found. A famous example is the progenitor of SN 1987A (see, e.g., Walborn et al. 1989). A way to explain the colors of these progenitors is through RSG-enhanced mass-loss rate models. The mass loss rate enhancement can be due to the presence of a close companion that will trigger the removal of part of the RSG envelope (see, e.g., Podsiadlowski et al. 1990) or to some other physical mechanisms, such as pulsations (see, e.g., Yoon & Cantiello 2010) that may occur in single stars. The enhancement factors in the range from 10 to 25 produce mass-loss rates that are compatible with some spectroscopically estimated mass-loss rates of RSGs. While these measurements may not be representative for the whole RSG phase, they were used as a guideline for exploring the consequences of strongly enhanced mass loss.
It is thus tempting to investigate the effects of strongly enhanced RSG mass loss on the FGLR. The results are shown in Fig. 4. As expected already after the discussion in the previous section, the areas corresponding to Group 2 are shifted to the right in the FGLR plane, and lifetimes during this phase are increased. (Of course, the areas linked to Group 1 BSG remains the same as before in Fig. 3.) We can indeed safely conclude that the majority of BSG forming the observed FGLR cannot be the result of such an evolutionary scenario.
While this makes the strongly enhanced mass loss unlikely to be the rule in RSG evolution, the question arises whether this is still a valid scenario for explaining the core collapse supernovae (CCSNe) progenitors with a yellow or a blue supergiant. We think of three possible solutions: The first is that the frequency of yellow and blue progenitors for CCSNe is very low (at least at solar metallicity). At the moment, the statistics of the distribution of the known progenitors among red, yellow, and blue supergiants is still poorly constrained, and this possibility cannot be ruled out. Another possibility is that the yellow and blue CCSNe progenitors explode in a very short phase immediately after the RSG phase. It seems that the progenitor of the supernova 1987A, which was a RSG 20 000 years before exploding as a BSG (see, e.g., the discussion in Morris & Podsiadlowski 2007), could be an example for such a case. Finally, a third possibility is a scenario in which less mass is lost during the RSG phase, but still the star evolves back to the blue making BSGs with a moderate decrease in the M/L ratio, which is still compatible with the small scatter of the flux-weighted gravity-luminosity relation. We come back to that discussion in the conclusions of this paper.
4.3. Models for SMC and LMC metallicities
Flux-weighted gravity-luminosity relations for metallicities lower than solar, obtained from models with and without rotation, are shown in Fig. 5. We see that the Group 1 BSG, in the case of the non-rotating stellar models for both Z = 0.006 and 0.002, again define a narrow FGLR sequence although slightly wider than the one obtained in the solar metallicity case. This comes from the fact that in these lower metallicity models, a larger portion of core He-burning occurs during the BSG Group-1 phase (see, for instance, the discussion in Maeder & Meynet 2001). This means that the crossing of the HR diagram on the way to the RSG takes a longer time and that the the lifetime as a Group-1 BSG is much longer. As a result, the stars have more time to lose mass, and with the M/L ratio decreasing, the Group-1 FGLR becomes wider.
Mass loss by stellar winds is not the only player in this game. Rotational mixing is also a key factor. For instance, it has been shown by Meynet et al. (2013) that depending on the sets of diffusive coefficients used for describing mixing, very different situations can appear. In all the cases except one, rotation tends to favor a blue location for a significant part of the core He-burning. Only in one case does rotation favor a rapid crossing of the Hertzsprung gap and a core He-burning phase that occurs mostly during the RSG phase and later stages. The present models have been computed with one of the prescriptions favoring a blue location. This produces a wider Group-1 FGLR. It also produces a bump around the 25 M⊙ model at Z = 0.006. At Z = 0.002, this bump shifts to higher initial masses. This behavior can be explained by two facts: first, all other ingredients being kept the same, rotational mixing, which favors a blue location, is more efficient in high-mass stars (hence the bump in the high-mass range). On the other hand, mass loss by stellar winds increases with the mass and the metallicity. At Z = 0.006, above about 30 M⊙, stellar winds overcome the effects of the rotational mixing (for the initial rotation considered here) and reduce the time spent as a Group-1 BSG , and thus the bump disappears. At Z = 0.002, the mass-loss rates are smaller, so the bump shifts to higher initial masses.
 |
Fig. 6 Distributions of observed blue supergiants in the Mbol versus |
As can be seen from Fig. 5, this broadening of the Group-1 sequence is compatible with the observed scatter of the flux-weighted gravity-luminosity relation for both metallicities, 0.006 and 0.002.
Concerning the group 2 BSG, we only have a very modest shift to the right for the positions of these stars in the Mbol versus 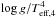 plane. This comes from the fact that, owing to the effect discussed just above (long duration in the Group-1 BSG stage), the stars enter at a late stage of the core He-burning phase into the RSG phase, so that little time is left for them to lose large amounts of mass. Despite this, the most massive models can still evolve back to the blue but with M/L ratios that are barely lower than for Group 1. This is very different from the solar metallicity case and in better agreement with the observations.
plane. This comes from the fact that, owing to the effect discussed just above (long duration in the Group-1 BSG stage), the stars enter at a late stage of the core He-burning phase into the RSG phase, so that little time is left for them to lose large amounts of mass. Despite this, the most massive models can still evolve back to the blue but with M/L ratios that are barely lower than for Group 1. This is very different from the solar metallicity case and in better agreement with the observations.
If we compare the Group 1 sequences for the Z = 0.014, 0.006, and 0.002 models with or without rotation, we see that they produce very well defined and very similar sequences with very small scatter. Therefore, one of the main conclusions of this section is that the flux-weighted gravity-luminosity relation built with the Group-1 BSGs does not depend much on metallicity.
Using the observed BSGs FGLR sequence, we can check this point, at least with regard to the observed scatter of the relationship. The empirical sequence is made of stars with metallicities that are quite diverse, between one tenth of the solar metallicity and above the solar metallicity. If we plot those stars having a metallicity above half solar and below half solar in separate figures, we obtain the two distributions shown in Fig. 6. We see that the solar metallicity objects do not show a larger scatter than the ones at low metallicity. This indicates that the solar metallicity models produce Group-2 BSGs that are too dispersed especially with the rotating models. As already indicated above, this may be due to mass-loss rates adopted during the RSG stage that are too high (even for the standard mass-loss rate).
4.4. Stellar evolution models from other groups
It is important to check whether the conclusions obtained so far are independent of the specific properties of the stellar evolution models used. To this extent we compare the FGLR obtained from the models of Ekström et al. (2012) with the FGLRs constructed from two sets of independent models, published by Chieffi & Limongi (2013) and Brott et al. (2011). This comparison is carried out in Fig. 7.
There are many differences between the three sets of models. We mention here the most significant ones. Brott’s code uses the Ledoux criterion for convection and includes semi-convection, while the other two use Schwarzschild. The models differ by the amount of overshooting considered. In Ekström et al. (2012), the overshooting parameter was chosen equal to 0.1 Hp, while in Chieffi & Limongi (2013), it was chosen equal to 0.2 Hp and, in Brott et al. (2011), equal to 0.335 Hp. In addition, there is a difference in the adopted initial metallicity on the ZAMS. Ekström et al. (2012) and Chieffi & Limongi (2013) have an initial metallicity mass fraction of 0.014, whereas the models by Brott et al. (2011) start with 0.0088. The details of the differences of the models including rotation are discussed further below. The models by Brott et al. (2011) allow comparisons only for the Group-1 BSG, since the computations of the stellar models were stopped at the beginning of the core He-burning phase.
Despite these significant differences, the three grids of non-rotating stellar models predict very similar positions in the (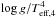 , Mbol)-plane as can be seen in the upper lefthand panel of Fig. 7. The scatter for the Group-1 BSGs between the models is well below the observed one.
, Mbol)-plane as can be seen in the upper lefthand panel of Fig. 7. The scatter for the Group-1 BSGs between the models is well below the observed one.
The Group-2 BSGs for the non-rotating models of Chieffi & Limongi (2013) exist for the 25, 30, and 40 M⊙ models. These BSGs are at much lower values of 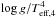 than the Group-1 BSGs. The time spent in Group 2 corresponds to 61% of the total BSG lifetime for the 25 M⊙ model and to 90% for the 30 M⊙ and 40 M⊙ stellar models. This is in a remarkable qualitative agreement with the models by Ekström et al. (2012)1.
than the Group-1 BSGs. The time spent in Group 2 corresponds to 61% of the total BSG lifetime for the 25 M⊙ model and to 90% for the 30 M⊙ and 40 M⊙ stellar models. This is in a remarkable qualitative agreement with the models by Ekström et al. (2012)1.
 |
Fig. 7 Left panel: comparisons between the positions of blue supergiants obtained in various grids of stellar models in the ( |
Comparisons between rotating stellar models are carried out in the lower lefthand panel of Fig. 7. We note that the initial rotation velocities considered by the different authors are different. In Ekström et al. (2012), the initial velocities span the range between 248 and 314 km s-1 for the initial masses between 9 and 40 M⊙ (see their Table 2). The models by Chieffi & Limongi (2013) have initial velocities on the ZAMS equal to 300 km s-1. The models by Brott et al. (2011), shown in Fig. 7, have initial velocities between 216 and 226 km s-1. The physics of rotation is not the same in these three grids. The models by Brott et al. (2011) use a very efficient transport for the angular momentum driven by a dynamo activity in radiative layers, following the theoretical approach by Spruit (2002). These models rotate nearly like solid bodies during the main-sequence phase. The models by Ekström et al. (2012) and Chieffi & Limongi (2013), on the other hand, consider transport by shear turbulence and meridional currents following the theory proposed by Zahn (1992). These models present differential rotation as a function of radius during the whole evolution.
Again, despite these very significant differences, the models predict very similar positions for the Group-1 BSGs (see the lower panel of Fig. 7). This is quite remarkable and underlines the robustness of the theoretical relation with respect to changes in the stellar models. What is even more remarkable is the good agreement also for the predictions concerning the Group-2 stars. Thus we can conclude that regardless of the grid we used, very similar conclusions would have been obtained.
We can investigate whether exploring a wider range of initial velocities could increase the scatter predicted by the stellar models. For this purpose, we use the models by Brott et al. (2011), which have considered a wide range of initial velocities over the range of initial masses that is of interest here. In the righthand panel of Fig. 7, we show superposed to the observed BSGs, the lines connecting models at similar stages of their evolution having different initial velocities. All Group-1 BSGs with initial velocities between 0 and 431 km s-1 are predicted to be found between the lines labeled by 0 and 431 km s-1. We see that the region is narrow and has a much narrower width than the observed scatter. Most of the stars will likely begin their evolution inside this very wide range of initial velocities. Only when considering initially very fast rotators, with velocities between about 431 and 542 km s-1 would the scatter cover a significant part of the observed scatter. However, the frequency of these very fast rotators is likely very low and their successor will not contribute significantly to the observed sample of BSGs. We conclude that using a wider range of initial velocities would hardly change the conclusions obtained previously based on non-rotating and moderately fast-rotating models.
One might wonder whether for the fast-rotating models, we should not account for the scatter produced in the luminosity, effective temperature, and gravity due to the darkening of the equatorial regions and the brightening of poles, the so-called von Zeipel effect (von Zeipel 1924). However, even starting with a high initial surface velocity on the ZAMS, in the BSG-phase, the star will have a surface velocity well below the critical value, and thus the corrections to that effect will be small.
As a final test, we also compared the 15 M⊙ models by Brott et al. (2011) with the 15 M⊙ stellar model computed by Georgy et al. (2013b), which treats rotation in a similar way to Ekström et al. (2012). Differences to the Brott et al. (2011) models in overshooting parameter and metallicity have a slight effect, but the scatters due to changes in the initial rotation remain similar.
In summary, we conclude that differences in the physics of the stellar evolution models used do not affect the conclusions obtained from the comparison with the observations.
5. Population synthesis models
In this last section, we use a different tool to compare stellar evolution models with the observations. Up to this point we have directly transformed stellar tracks into the FGLR-plane and then compared their locations with the observed BSG distribution, while simultaneously considering stellar lifetimes in the Groups 1 and 2 BSG evolutionary phases.
Now we improve this comparison by computing virtual stellar populations as they would appear from continuous star formation during the past 70 million years, assuming the initial stellar masses are distributed according to an initial mass function (IMF). For our sample of observed BSG, the hypothesis of a constant star formation rate during the past 70 million years appears to be reasonable. We also note that we do not intend to compare the relative predicted number of stars at low, middle, and high luminosities, because the observed sample is heavily biased by selection effects with regard to luminosity (see below). Instead, our intention is to compare whether the predicted location in the FGLR-plane described by isocontours of high probability at each luminosity agrees with the location of the observed sample.
Such population synthesis models have the qualities (and defects) of the stellar tracks; however, they add two features that otherwise are difficult to assess: 1) they provide quantitative information about the expected number distribution of BSG in the FGLR-plane; and 2) the population synthesis technique easily allows the effects of observational errors to be included. Both together will allow us to investigate much better whether models agree with the observations or not. We now investigate the cases of Z = 0.014 (solar metallicity) and Z = 0.002 (SMC metallicity), with and without rotation, when assuming standard mass-loss rates in the RSG phase.
 |
Fig. 8 Population synthesis of blue supergiants in the FGLR-plane compared with the observations. The color-coded areas indicate the expected relative numbers of BSG. Triangles pointed up are “high-metallicity” (more than half solar) observed blue supergiants, and triangles down are “low metallicity” (less than half solar) ones. The triangles corresponding to the metallicity of the plot are larger. In the present plot, for example, the triangles up are bigger. Left upper panel: non-rotating models at Z = 0.014 calculated with standard mass-loss rates. Right upper panel: same as the upper left panel but for models that include stellar rotation. Lower left panel: same as the upper left panel but including the effects of observational uncertainties. Lower right panel: same as the upper right panel but including the effects of observational uncertainties. |
For this purpose, we use the population synthesis tool SYCLIST (Georgy et al. 2014a). Assuming a Salpeter IMF with exponent 2.35 in a mass range from 5 to 120 M⊙, we divide the main sequence into 10 000 mass intervals and follow the entire evolution for each of these masses as a function of time using a grid of 5000 time steps. The FGLR plane displayed in the subsequent population synthesis plots is divided into 200 × 200 pixels of 0.0325 mag in ΔMbol and 0.01 dex in Δlog g/Teff,4. At each time step, the fraction of the 10 000 evolutionary tracks with different initial masses falling into one of these pixels is noted, providing the probability distribution function in the FGLR-plane at each time step by taking the original probability on the main-sequence into account for such tracks to occur. Adding up the probabilities of the 5000 time steps, we then obtain the distribution function in the FGLR plane for continuous star formation, which for convenience is normalized to a total number of 1000 stars. Random observational uncertainties are accounted for by spreading the probability value of each pixel by a bi-Gaussian distribution with standard deviations of 0.15 mag in absolute magnitude and 0.075 dex in flux-weighted gravity, respectively. These values represent average uncertainties of the observed BSG sample (see references given in the caption of Fig. 2). In this procedure, we assume that a star is a BSG if it fulfills the following criteria: 1) it has left the main sequence stage of core hydrogen burning; 2) its log Teff is between 3.9 and 4.4; and 3) it is not an extremely helium-enriched Wolf-Rayet-like star: i.e., its surface hydrogen mass fraction Xsurf is above 0.3 (same criterion as in Georgy et al. 2009).
Figure 8 summarizes the calculation at solar metallicity. The upper panels show the population synthesis results without accounting for observational uncertainties to provide the information coming solely from the evolutionary tracks, whereas the lower panels include the observational errors and allow for a more realistic comparison. We start the discussion with the non-rotating models in the upper lefthand panel. The shape of the blue supergiant region is now more complex than in Fig. 3, because of the much finer discretization in stellar mass. Nevertheless, the overall shape, of course, follows the one obtained in Fig. 3. The peaks of high densities correspond to stages that are favored either because the mass is low (IMF effect) or because their duration is long enough, or both. (Typically this is the case for the yellow region in-between log g/Teff,4 = 1.9 and 1.5.) At this point, it is important to note that the distribution of the observed BSG along the FGLR as a function of bolometric magnitude is heavily biased by a selection that tends to create a flat distribution in the higher magnitude range for the purpose of distance determinations. This explains why there are only a few observed BSG in the magnitude range between −4 to −6, which has the highest probability. These objects would simply require too much spectroscopic observing time.
For both cases, evolution models with and without rotation, the sequence of BSGs divides into different channels at higher luminosity corresponding to Groups 1 and 2 in our previous discussion. (In our population synthesis model, we define a Group-2 BSG as a star that had an effective temperature log Teff< 3.8 at some point in its past history.) The Group-2 channels, which are shifted to lower gravities at a given Mbol, are favored in terms of the expected number of stars as a consequence of the predicted stellar lifetimes. We also see that the Group-1 BSG sequence for the rotating models is shifted slightly to the right with respect to the non-rotating ones. As already explained above, this comes from the fact that models with rotation are overluminous for a given initial mass with respect to non-rotating models as a result of rotational mixing. That implies a decrease in the M/L ratio and a shift to the right.
By including the effects of observational errors, the probability of finding BSG in each pixel of the FGLR-plane is spread out over a larger surface. This is shown in the lower panels of Fig. 8. At first glance, the agreement between the observed and predicted distributions is reasonable. However, with more careful inspection we identify interesting features common to tracks with rotation and without, but also significant differences. First, a small valley exists between the red region in the lower lefthand corner and the diagonal extending upward toward the center of the figure. This small valley corresponds to the positions of 12 M⊙ models. These models evolve very rapidly to the red after the MS phase, spending little time of their core He-burning lifetime in the blue. They also do not come back from the blue and, thus, spend only a modest amount of time as BSG. For higher initial masses, a larger portion of the core He-burning phase happens at high effective temperatures, and thus, the lifetime during the BSG Group-1 phase increases. The presence of this valley is most likely dependent on physical ingredients of the models, such as the metallicity, the mass loss rates, and the internal mixing. The present set of observational data does not allow this prediction to be tested. A more complete spectroscopic survey at lower bolometric magnitudes would be needed for this purpose. However, the observed distribution can be used to test other features predicted by the models. For instance, the diagonal probability ridge line in the magnitude range −6.5 mag ≤ Mbol ≤ −9.5 should coincide with the location of the observed sequence. Obviously, this is not the case for the non-rotating tracks that predict magnitudes that are too bright for 1.9 ≥ log g/Teff,4 ≥ 1.3 and magnitudes that are too faint at lower flux-weighted gravities. Figure 9, in which we make the ad-hoc assumption that the Group-2 BSG does not exist, demonstrates that the orange high-probability area of the models at log g/Teff,4 ≥ 1.3 corresponds to Group-1 BSG, whereas the orange area at lower gravity is created by Group 2.
 |
Fig. 9 Same as lower panel of Fig. 8 but assuming that there is no Group-2 BSG (see text). Left panel: tracks without rotation. Right panel: tracks with rotation. |
The situation is different for evolutionary models with rotation. Figures 8 and 9 reveal that the Group-1 BSG predicted location in the FGLR-plane agrees much better with the observations. On the other hand, the prediction for the Group-2 BSG is in clear disagreement with the observations. We conclude that, at solar metallicity, models with rotation are in reasonable agreement with the observations provided there is a mechanism that suppresses the significant decrease in flux-weighted gravity for high-mass Group 2 BSG or suppresses the evolution back from the RSG stage, hence the existence of Group 2 at all.
 |
Fig. 10 Same as lower panel of Fig. 8 but for a metallicity of Z = 0.002. Left panel: tracks without rotation. Right panel: tracks including rotation. |
 |
Fig. 11 Predicted density plots of evolutionary masses compared with observed BSG spectroscopic masses. Upper left panel: tracks without rotation at Z = 0.014. Upper right panel: tracks with rotation at Z = 0.014. Lower left panel: tracks with rotation at Z = 0.014 without Group 2 BSG. Lower right panel: tracks with rotation at Z = 0.002. |
Figure 10 shows the population synthesis calculations for reduced stellar metallicity Z = 0.002, corresponding, for instance, to the SMC. As already discussed in Sect. 4.3, at this low metallicity the stellar evolution tracks spend most of their time in the Group-1 BSG phase, and Group 2 becomes unimportant. In consequence, we see only a Group-1 sequence that is predicted by the theory. For evolutionary models without rotation, this sequence is very similar to the solar metallicity Z = 0.014 Group-1 sequence and, thus, also disagrees with the observed FGLR sequence. On the other hand, as for models with solar metallicity, the sequence produced by the models that include the effects of rotation is in good agreement with the observations.
The main result of the above discussion is that models accounting for rotation do a better job reproducing the observed FGLR relation, provided most of the observed BSG belong to Group 1. Interestingly, we can check this conclusion independently by comparing predicted evolutionary masses with observed spectroscopic masses. First, we can test whether rotating models indeed reproduce the spectroscopic masses better and, second, whether population synthesis without Group 2 BSG leads to better agreement at Z = 0.014. These comparisons are shown in Fig. 11, where a typical error of 10 M⊙ has been assumed.
In the range 1.9 ≥ log g/Teff,4 ≥ 1.3, the models that include the effects of rotation indeed produce a probability ridge line, which agrees closely with observations, whereas models without rotation predict masses that are too high. For log g/Teff,4< 1.3, however, both sets of models seem to fail when predicted masses are too low. As demonstrated by the lower lefthand panel of the figure, this is due to the Group-2 BSGs.
The lower righthand panel of Fig. 11 displays the population synthesis with low-metallicity models at Z = 0.002, which include rotation. In this case, Group-2 BSGs were not removed, since for reasons already explained above, the evolution models predict only a small number of Group-2 BSG with masses not much lower than for Group 1. Most important is that the high-density probability ridge line is again in good agreement with the observations. The comparison of predicted stellar evolution masses with observed spectroscopic masses thus corroborates the conclusions obtained from the comparison of observed and model FGLRs.
Finally, we note the presence of three high-mass stars among the observed BSGs at log g/Teff,4 ≈ 1.25, which do not seem to agree with the trend predicted by the models and which also appear to be somewhat separated from the other BSGs that were observed. In the FGLR-plane, these three points are also slightly above the bulk of the other observed points. It is tempting to explain this discrepancy by unresolved binarity or multiplicity. However, while this can never be ruled out completely, it would require two objects of very similar effective temperature and gravity and roughly equal luminosity to produce a spectrum of one single BSG. Given the short evolutionary lifetime of BSGs, we regard this as unlikely. We also note that the objects are in a domain where the probability for their existence is not completely unlikely. Thus, their existence could just be a chance effect of small numbers.
Using the models by Brott et al. (2011) and Georgy et al. (2013b), we tested whether assuming a range in initial rotational velocities could affect the comparison between stellar and evolutionary masses. We concluded that the observed scatter cannot be explained by considering a range in initial rotational velocities, and we obtained a confirmation that rotation tends to improve the agreement between evolutionary and spectroscopic masses.
6. Conclusions
Summarizing the results from the previous sections we conclude that
-
The observed FGLR sequence of BSG stars is reproduced best bystellar evolution models that include the effects of rotation andrepresent the evolutionary phase when theBSG evolve toward the RSG stage(Group 1).
-
The Group-1 stellar model FGLR sequence is not affected by variations in metallicity. This provides strong support for the FGLR as a tool for determining extragalactic distances.
-
Models without rotation generate a Group-1 FGLR sequence that is too bright when compared with the observations.
-
At solar metallicity, stellar models also predict the existence of Group-2 BSGs that represent the evolutionary stage returning from the RSG stage with flux-weighted gravities distinct from Group 1 and in much larger numbers. The difference in flux-weighted gravity of Group 2 is caused by mass loss in the RSG stage. The observations do not support that there is a Group 2 or a difference with respect to Group 1 in flux-weighted gravity.
While the overall good representation of the observed FGLR by the stellar models can be regarded as a success of stellar evolution theory, the disagreement with regard to Group 2 at solar metallicity poses a problem, which leads to three possibilities for the post main-sequence evolution scenarios of solar metallicity stars with initial masses between 12 and 40 M⊙:
-
Possibility 1: stars cross the Hertzsprung-Russel diagram andend their evolution as RSG. In that case, no Group-2 BSGs arepredicted.
-
Possibility 2: stars cross the Hertzsprung-Russel diagram, go through a RSG phase, start to evolve back to the blue, but explode as core collapse supernova either prior to the Group-2 phase or soon after entering it. In that case, Group-2 BSGs have such short lifetimes that the probability of observing them is very low.
-
Possibility 3: stars evolve back to the blue after a RSG phase but without losing too large amounts of mass during the RSG phase. The physics responsible for the blueward evolution after the RSG phase is the development of a relatively massive helium core that drives the star back to the helium-burning sequence, which for pure helium stars is at effective temperatures hotter than the hydrogen-burning sequence. According to Giannone (1967), the minimum mass fraction of the helium core to evolve back should be 60–70% of the total mass. Such a high fraction can be obtained through strong mass loss but also through mixing processes. In this scenario, strong mixing processes would drive the star back with M/L ratios that are not very different from Group 1.
The three possibilities are not exclusive in the sense that they may all occur either in different initial mass regimes or for the same initial mass, but may present an additional difference caused, for instance, by rotation and/or the presence of a companion star. What does appear to be excluded or to be an infrequent scenario is the one in which the stars evolve into the RSG stage, lose large amounts of mass, and then spend a significant part of the core He-burning lifetime as Group 2 BSG.
The three possibilities above predict different outcomes that could be tested by observations. If the first possibility is the most frequent one, then the number of stars ending their lifetimes as a blue or yellow supergiant should be very rare. On the other hand, if possibility two is the most frequent, then many supernovae should explode inside material very recently released by the last strong mass-loss episode. This may lead to narrow absorption lines superimposed on the supernova spectra and caused by the low velocity stellar wind surrounding the star. Possibility 3 should produce a significant amount of Group-2 BSGs. While the stellar gravities of these objects would be comparable to Group 1, the chemical composition will probably be very different because of the strong effects of mixing during the RSG stage.
While tests of Possibilities 1 and 2 require either extended surveys for the progenitors of core collapse supernovae or high resolution, high signal-to-noise spectroscopy of such supernovae, an investigation of Possibility 3 by distinguishing Group 1 and 2 BSGs appears to be more straightforward. The surface composition of Group-2 BSGs should present stronger signs of CNO processing than Group 1. A comprehensive project that studies the surface composition of solar metallicity BSG by means of high-resolution, high signal-to-noise spectroscopy could provide a way to distinguish between the pre- and post RSG blue supergiants. However, the mixing induced by rotation during the main sequence phase can blur the picture somewhat, since depending on the initial rotation rate, significant changes in the surface abundances can already be obtained at the end of the main-sequence phase. Thus, surface abundances can result from either strong mixing during the main sequence or from a much less efficient mixing during the main-sequence phase and a dredge-up effect during a RSG stage. Moreover, close binary evolution may also deeply modify the surface composition of BSGs. The questions is complicated by the possibility that mergers make the star appear as single. It is however the hope that further studies will find relations between surface rotation, surface abundances, and pulsation properties that will be specific signatures of the single, respectively close binary, scenarios. We also note that the abundances obtained at the surface of post red supergiant are sensitive to the way convection is computed. Different results are obtained when the Schwarzschild or the Ledoux criterion for convection is used (Georgy et al. 2014b). Still, accurate spectroscopy will very likely reveal whether the third scenario is likely or not.
Another approach to observationally investigating the three possible scenarios is a detailed and comprehensive study of BSG photometry. Saio et al. (2013) predict that Group-2 BSGs have very different pulsational properties compared to Group 1. It would, therefore, be possible to determine the fraction of Groups 1 and 2 BSGs observationally by a careful analysis of their variability.
Independent of the problem of how to explain the apparent absence of Group 2 objects in the observed FGLR sequence of BSGs, our investigation provides an improved foundation for using the FGLR-method for determining extragalactic distances. A major remaining uncertainty of the application of this method so far has been the potential metallicity dependence of this relationship, although the spectroscopic work by Urbaneja et al. (2008) and Hosek et al. (2014) indicate that metallicity effects should be small. The population synthesis results obtained in this study based on the most recent stellar evolution models support this conclusion, thereby establishing the FGLR-method as a robust and accurate way to determine distances to galaxies. A needed follow-up of the present work will be to study the impact of close binary evolution on the small scatter of the FWGL relation.
The two grids of models do not use the same mass-loss rates during the RSG phase, see the references in Ekström et al. (2012) and Chieffi & Limongi (2013).
Acknowledgments
This work was supported by the Swiss National Science Foundation (project number 200020-146401) to GM, by the National Science Foundation under grants AST-1008798 and AST-1108906 to RPK, and by the European Research Council under the European Union Seventh Framework Program (FP/2007-2013)/ERC Grant Agreement n. 306901. G.M. gratefully acknowledges the hospitality of the Institute for Astronomy, University of Hawaii, where part of this work was carried out.
References
- Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chieffi, A., & Limongi, M. 2013, ApJ, 764, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A. 2001, in The Influence of Binaries on Stellar Population Studies, ed. D. Vanbeveren, Astrophys. Space Sci. Lib., 264, 215 [Google Scholar]
- de Jager, C., Nieuwenhuijzen, H., & van der Hucht, K. A. 1988, A&AS, 72, 259 [NASA ADS] [Google Scholar]
- Dohm-Palmer, R. C., & Skillman, E. D. 2002, AJ, 123, 1433 [NASA ADS] [CrossRef] [Google Scholar]
- Eggenberger, P., Meynet, G., & Maeder, A. 2002, A&A, 386, 576 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Firnstein, M., & Przybilla, N. 2012, A&A, 543, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgy, C. 2012, A&A, 538, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgy, C., Meynet, G., Walder, R., Folini, D., & Maeder, A. 2009, A&A, 502, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgy, C., Ekström, S., Eggenberger, P., et al. 2013a, A&A, 558, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgy, C., Ekström, S., Granada, A., et al. 2013b, A&A, 553, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgy, C., Granada, A., Ekström, S., et al. 2014a, A&A, 566, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgy, C., Saio, H., & Meynet, G. 2014b, MNRAS, 439, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Giannone, P. 1967, Z. Astrophys., 65, 226 [NASA ADS] [Google Scholar]
- Gies, D. R., & Lambert, D. L. 1992, ApJ, 387, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Hosek, Jr., M. W., Kudritzki, R.-P., Bresolin, F., et al. 2014, ApJ, 785, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, I., Brott, I., Lennon, D. J., et al. 2008a, ApJ, 676, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, I., Lennon, D. J., Dufton, P. L., et al. 2008b, A&A, 479, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kudritzki, R. P., Bresolin, F., & Przybilla, N. 2003, ApJ, 582, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R. P., Urbaneja, M. A., Bresolin, F., & Przybilla, N. 2008a, Phys. Scr. T, 133, 014039 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R.-P., Urbaneja, M. A., Bresolin, F., et al. 2008b, ApJ, 681, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R.-P., Urbaneja, M. A., Gazak, Z., et al. 2012, ApJ, 747, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R.-P., Urbaneja, M. A., Gazak, Z., et al. 2013, ApJ, 779, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R.-P., Urbaneja, M. A., Bresolin, F., Hosek, Jr., M. W., & Przybilla, N. 2014, ApJ, 788, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 1997, A&A, 321, 134 [NASA ADS] [Google Scholar]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars (Heidelberg: Springer, Berlin) [Google Scholar]
- Maeder, A., & Meynet, G. 2000, A&A, 361, 159 [NASA ADS] [Google Scholar]
- Maeder, A., & Meynet, G. 2001, A&A, 373, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maeder, A., & Meynet, G. 2012, Rev. Mod. Phys., 84, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., Przybilla, N., Fernanda Nieva, M., et al. 2014, A&A, 565, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McEvoy, C. M., Dufton, P. L., Evans, C. J., et al. 2015, A&A, 575, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., Ekstrom, S., Maeder, A., et al. 2013, in Lect. Not. Phys. 865 (Berlin: Springer Verlag), eds. M. Goupil, K. Belkacem, C. Neiner, F. Lignières, & J. J. Green, 3 [Google Scholar]
- Meynet, G., Chomienne, V., Ekström, S., et al. 2015, A&A, 575, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morris, T., & Podsiadlowski, P. 2007, Science, 315, 1103 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Joss, P. C., & Rappaport, S. 1990, A&A, 227, L9 [NASA ADS] [Google Scholar]
- Przybilla, N., Firnstein, M., Nieva, M. F., Meynet, G., & Maeder, A. 2010, A&A, 517, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saio, H., Georgy, C., & Meynet, G. 2013, MNRAS, 433, 1246 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sylvester, R. J., Skinner, C. J., & Barlow, M. J. 1998, MNRAS, 301, 1083 [NASA ADS] [CrossRef] [Google Scholar]
- U, V., Urbaneja, M. A., Kudritzki, R.-P., et al. 2009, ApJ, 704, 1120 [NASA ADS] [CrossRef] [Google Scholar]
- Urbaneja, M. A., Kudritzki, R.-P., Bresolin, F., et al. 2008, ApJ, 684, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Urbaneja, M. A., Herrero, A., Lennon, D. J., Corral, L. J., & Meynet, G. 2011, ApJ, 735, 39 [NASA ADS] [CrossRef] [Google Scholar]
- van Loon, J. T., Groenewegen, M. A. T., de Koter, A., et al. 1999, A&A, 351, 559 [NASA ADS] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R., Prevot, M. L., Prevot, L., et al. 1989, A&A, 219, 229 [NASA ADS] [Google Scholar]
- Yoon, S.-C., & Cantiello, M. 2010, ApJ, 717, L62 [NASA ADS] [CrossRef] [Google Scholar]
- Yusof, N., Hirschi, R., Meynet, G., et al. 2013, MNRAS, 433, 1114 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1 Evolutionary tracks in the Herstzsprung-Russel diagram calculated for solar metallicity Z = 0.014 for initial masses 9, 12, 15, 20, 25, 32, and 40 M⊙. The continuous lines show the track until the red supergiant phase. After the red supergiant stage, either dashed or dotted lines are used. The BSG phase is highlighted in red for the evolution toward the RSG phase (Group 1, see text) and in blue (dashed) for the evolution back after the RSG stage (Group 2). The models are from Ekström et al. (2012). Left panel: models without the effects of stellar rotation. Right panel: models including rotation (see text). |
| In the text | |
 |
Fig. 2 Left panel: evolutionary tracks at solar metallicity without rotation in the (log M/M⊙, log L/L⊙)-plane. M is the actual mass of the star during the evolution. The dashed lines are mass-luminosity relations with α = 3 and b = 0.72316, 1.17955, 1.54727, and 2.03346 (bottom-up). The lower vertical or nearly vertical (magenta) part of the track corresponds to the main-sequence phase, while the red and blue parts show the Groups 1 and 2 phases before and after the RSG stage. Right panel: flux-weighted gravity-luminosity relations obtained from Eq. (0) and the mass-luminosity relations labeled G1, G2a, and G2b in the left panel. The points represent observations of individual BSG. The black squares are the values for NGC 300 given by Kudritzki et al. (2008b). The full triangles are for supergiants in other galaxies studied by Kudritzki et al. (2008a). Full circles and crosses are BSGs in M 33 (U et al. 2009) and M 81 (Kudritzki et al. 2012), respectively. The empty stars and empty squares show the data for the metal-poor Local Group galaxies WLM (Urbaneja et al. 2008) and NGC 3109 by (Hosek et al. 2014). The empty triangles and the full pentagons correspond to BSG in NGC 3621 (Kudritzki et al. 2014) and in NGC 4258 (Kudritzki et al. 2013), respectively. The dotted magenta line represents the FGLR calibration obtained by Kudritzki et al. (2008b). |
| In the text | |
 |
Fig. 3 Post-main sequence evolutionary tracks labeled by the original mass on the ZAMS in the ( |
| In the text | |
 |
Fig. 4 Upper left panel: same as Fig. 3 for models without rotation but with RSG mass-loss rate enhanced by a factor 10 and for Z = 0.014. Upper right panel: same as the upper left panel but for models with rotation. Lower left panel: models without rotation but with RSG mass-loss rate enhanced by a factor 25. Lower right panel: same as the lower left panel but for models with rotation. |
| In the text | |
 |
Fig. 5 Upper left panel: same as Fig. 3 for models without rotation and with standard RSG mass loss rates, but for a metallicity Z = 0.006. Upper right panel: same as left panel but for models with rotation. Lower left panel: same as Fig. 3 for models without rotation and standard RSG mass loss rates and for Z = 0.002. Lower right panel: same as lower left panel but for models with rotation. |
| In the text | |
 |
Fig. 6 Distributions of observed blue supergiants in the Mbol versus |
| In the text | |
 |
Fig. 7 Left panel: comparisons between the positions of blue supergiants obtained in various grids of stellar models in the ( |
| In the text | |
 |
Fig. 8 Population synthesis of blue supergiants in the FGLR-plane compared with the observations. The color-coded areas indicate the expected relative numbers of BSG. Triangles pointed up are “high-metallicity” (more than half solar) observed blue supergiants, and triangles down are “low metallicity” (less than half solar) ones. The triangles corresponding to the metallicity of the plot are larger. In the present plot, for example, the triangles up are bigger. Left upper panel: non-rotating models at Z = 0.014 calculated with standard mass-loss rates. Right upper panel: same as the upper left panel but for models that include stellar rotation. Lower left panel: same as the upper left panel but including the effects of observational uncertainties. Lower right panel: same as the upper right panel but including the effects of observational uncertainties. |
| In the text | |
 |
Fig. 9 Same as lower panel of Fig. 8 but assuming that there is no Group-2 BSG (see text). Left panel: tracks without rotation. Right panel: tracks with rotation. |
| In the text | |
 |
Fig. 10 Same as lower panel of Fig. 8 but for a metallicity of Z = 0.002. Left panel: tracks without rotation. Right panel: tracks including rotation. |
| In the text | |
 |
Fig. 11 Predicted density plots of evolutionary masses compared with observed BSG spectroscopic masses. Upper left panel: tracks without rotation at Z = 0.014. Upper right panel: tracks with rotation at Z = 0.014. Lower left panel: tracks with rotation at Z = 0.014 without Group 2 BSG. Lower right panel: tracks with rotation at Z = 0.002. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.