EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 580 (August 2015) A&A, 580 (2015) A119 Full HTML
Free Access
Issue
A&A
Volume 580, August 2015
Article Number A119
Number of page(s) 18
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/201526228
Published online 14 August 2015

© ESO, 2015

1. Introduction

In cosmological structure formation, tiny matter perturbations grow through supersonic accretion of smooth and cold (T ≤ 104 K) matter. In the process, matter is shock heated, thereby converting the infall kinetic energy into thermal energy (Sunyaev & Zeldovich 1972). Cosmological simulations have been used to measure the distribution of Mach numbers in cosmic shocks using a variety of methods. It has been found that weak (M ~ 2–4) merger shocks inside galaxy clusters are responsible for most of the conversion of the kinetic energy into gas heating, while stronger external accretion shocks (M ~ 10−103) are localised in the peripheral regions of large-scale structures (e.g. Ryu et al. 2003; Pfrommer et al. 2006; Skillman et al. 2008; Vazza et al. 2009, 2011; Araya-Melo et al. 2012; Schaal & Springel 2015). All mass in the warm-hot intergalactic medium (WHIM) with temperatures in the range ~105–107 K has been processed by accretion shocks. Up to ≈90 percent of the total baryon and dark matter mass in the Universe is expected to reside in this gas phase (Cen & Ostriker 1999; Davé et al. 2001), which is extremely difficult to observe at most wavelengths. Indeed, only a few tentative detections of the WHIM associated with cosmic filaments have been claimed in X-ray (e.g. Finoguenov et al. 2003; Werner et al. 2008; Nicastro et al. 2010, 2013) or at microwaves using the Sunyaev-Zeldovich effect (Planck Collaboration Int. VII 2013). A few possible detections of shocks emitting in radio have also been reported (Bagchi et al. 2002; Kronberg et al. 2007; Giovannini et al. 2010; Farnsworth et al. 2013). It has been pointed out that the accretion shocks around cosmological filaments may be detected with radio telescopes provided these shocks are efficient enough in accelerating electrons to relativistic energies (Keshet et al. 2004; Brown 2011; Araya-Melo et al. 2012; Vazza et al. 2015b; Giovannini et al. 2015). A few authors have studied the emission from electrons that are accelerated at the intersections of galaxy clusters and cosmic filaments (e.g. Keshet et al. 2004; Battaglia et al. 2009; Skillman et al. 2011), but the detections were mostly related to intermittent mergers of galaxy clusters, not to stationary accretion shocks. Bagchi et al. (2002) used the numerical method of Miniati et al. (2001) to simulate a scenario in which a filament shock causes the observed radio emission in the cluster ZwCl 2341.1+0000. To explain the observed radio emission, ~2 percent of the shock ram energy has to go into relativistic electrons and a magnetic energy of ~1.5 μG is required, probably indicating that the emission is related to more standard merger shocks (van Weeren et al. 2009; Giovannini et al. 2010).

thumbnail Fig. 1

3D rendering of the projected temperature (purple for T ≤ 105 K and red for T ≥ 105 K) and magnetic field intensity (yellow for B ≥ 10 nG and orange for B < 10 nG) for our simulated (50 Mpc)3 volume at z = 0, simulated with 24003 cells and DM particles.

More recently, Araya-Melo et al. (2012) studied the emission from primary electrons accelerated at cosmological shock waves and concluded that filaments must host fewer radio objects than galaxy clusters, with an average of a few radio objects brighter than 1032 erg/(s Hz) at 1.4 GHz within (500 Mpc/h)3, and that most of this emission probably comes from the intersections with surrounding galaxy clusters. They predicted a flux density of radio emission from filaments of the order of 0.12 μJy at redshift z ~ 0.15 and at a frequency of 150 MHz.

We recently found that the detection of the largest filaments of the cosmic web might be within reach of the Square Kilometer Array if the magnetic field there reaches ~10–100 nG (Vazza et al. 2015b). While these first results were based on the simple assumption of a fixed magnetic field for a representative filament of our sample, in this work we use magnetohydrodynamic (MHD) simulations with ENZO (Bryan et al. 2014) and study a much larger volume.

2. Methods

2.1. Numerical simulations with ENZO

ENZO is a highly parallel code for cosmological simulations that uses a particle-mesh N-body method (PM) to follow the dynamics of the DM and offers a variety of MHD-hydro solvers to compute the evolution of cosmic gas.

Here we mostly analyse simulations obtained with ENZO-MHD as described in Vazza et al. (2014a), which belong to a large project run on Piz Daint (Lugano, Switzerland) for a CHRONOS1 proposal. This version of ENZO is based on the Dedner formulation of MHD equations (Dedner et al. 2002), which uses hyperbolic divergence cleaning to keep the ∇·B as small as possible during the computation. The MHD solver adopted here uses a piecewise linear method reconstruction (PLM), where fluxes at cell interfaces are calculated using the local Lax-Friedrichs Riemann solver (LLF Kurganov & Tadmor 2000). Time integration is performed using a total variation diminishing (TVD) second-order Runge-Kutta (RK) scheme (Shu & Osher 1988). The PLM+MHD solver used in the simulations presented here (as well as the non-MHD version of the PPM hydro solver) was ported to Nvidia’s CUDA framework, allowing ENZO to take advantage of modern graphics hardware (Wang et al. 2010; Bryan et al. 2014). In simulations using a single-level mesh, the GPUs provide a factor of ~4 in speed-up over CPU-only runs. Our run with the highest spatial resolution is a (50 Mpc)3 volume simulated using 24003 cells and 24003 DM particles (resolution 20.8 kpc), which, as far as we know, is the largest MHD cosmological simulation to date (Vazza et al. 2014a). This run used ~4.5 million core hours running on 512 nodes (2048 cores in total) on Piz Daint in Lugano. Figure 1 shows the projected (mass-weighted) temperature and magnetic field strength at z = 0 for our best-resolved run (24003). The intricate network shows the outer shell of accretion shocks where kinetic energy is thermalised. In the inner regions, in the centres of halos, and along the spine of filaments, the magnetic field is amplified. A list of the simulations analysed for this work is given in Table 1. To extend our results to a larger volume and include the role of secondary electrons injected by cosmic-ray (CR) protons, we analysed a set of simulations that include CRs (details in the appendix and in Vazza et al. 2014b).

Table 1

List of the simulations run for this project.

2.2. Cosmological model

We assumed a WMAP 7-year cosmology (Komatsu et al. 2011) with Ω0 = 1.0, ΩB = 0.0455, ΩDM = 0.2265, ΩΛ = 0.728, Hubble parameter h = 0.702, a normalisation for the primordial density power spectrum σ8 = 0.81, and a spectral index of ns = 0.961 for the primordial spectrum of initial matter fluctuations. All runs started at zin ≥ 50, the exact value of which varies with resolution.

2.3. Non-thermal processes

To model the synchrotron emission, we have to know the energy spectrum of relativistic electrons and the magnetic field at each point in space and time. Both are largely unknown, especially at the low-density regime of cosmic filaments. In our analysis, we tried to constrain the possible range by varying model parameters.

2.3.1. Magnetic fields

The degree of magnetisation in the low-density cosmic web is largely uncertain. The predictions from cosmological simulations lie in the range of ~ 10-4–0.1 μG for filaments, depending on numerical resolution of the cosmological simulation and on the assumed seeding scenario (e.g. Dolag et al. 1999; Brüggen et al. 2005; Sigl et al. 2003; Ryu et al. 2008; Xu et al. 2009; Donnert et al. 2009; Marinacci et al. 2015). Since the growth of primordial magnetic fields in filaments is dominated by compressive motions and small-scale shocks (Ryu et al. 2008; Vazza et al. 2014a), the dynamical memory of the system might persist over long cosmological times and the observed magnetisation level closely connects to the seeding process(es). This is different from galaxy clusters where most of the magnetic energy is extracted from the kinetic energy, thereby quickly erasing previous dynamical information. In our latest MHD runs we investigated the growth of magnetic fields starting from B0 = 10-10 G (comoving), seeded at high redshift (e.g. Widrow et al. 2012; Ryu et al. 2012, and references therein). However, the magnetic field measured even in our most massive clusters hardly reaches ~0.01–0.05μG, while in filaments the magnetic field are never larger than a few nG. In clusters, these values are ~10–100 times lower than the typical magnetic field inferred using the Faraday rotation effect (e.g. Murgia et al. 2004; Bonafede et al. 2010, 2013). Therefore, something appears to be missing in our numerical modelling of magnetic fields. On the one hand, we might have a large enough dynamical range to simulate a small-scale dynamo only within galaxy clusters (e.g. Schekochihin et al. 2004; Schleicher et al. 2013). In filaments, however, the dominance of compressive forcing makes dynamo amplification inefficient. Even in high-resolution adaptive-mesh refinement runs we did not measure any strong field growth beyond that caused by mere compression and magnetic flux conservation. On the other hand, additional seeding from astrophysical sources (star-forming regions, galaxies, and galaxy clusters) can magnetise large scales, even if with unknown efficiency and duty cycles (e.g. Kronberg et al. 1999; Donnert et al. 2009; Xu et al. 2009; Schober et al. 2013; Beck et al. 2013). Fast-growing plasma instabilities, such as firehose and mirror instabilities in large β plasmas (where β is the ratio between the thermal and the magnetic energy), might be able to amplify magnetic fields up to values we observe in clusters (Schekochihin et al. 2005; Kunz et al. 2011; Mogavero & Schekochihin 2014), or at least provide additional seeding for the dynamo. Indications of substantial magnetisation along the filamentary region in the SW sector of the Coma cluster have been reported in Bonafede et al. (2013). Finally, it has also been suggested that cosmic-ray particles accelerated at strong shocks can substantially amplify upstream magnetic fields (Drury & Downes 2012; Brüggen 2013).

In summary, there is no firm conclusion about the strength of magnetic fields outside galaxy clusters, neither from observations nor from theory. Future radio observations will be crucial to assess this, and our goal here is to provide quantitative predictions for different magnetic field models, starting from extreme cases. Hence, in post-processing we renormalised the magnetic field using two separate recipes: a high-amplification model (HA) and a low-amplification model (LA). In both cases, the normalisation depends on the local gas overdensity, n/ncr, where n is the gas density and 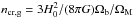ncr,g=3H02/(8πG)Ωb/ΩM\hbox{$n_{\rm cr,g}=3 H^2_{\rm 0}/(8 \pi G) \Omega_{\rm b}/\Omega_{\rm M}$} is the critical density rescaled for the gas fraction. In the HA case, we modelled the efficient magnetisation of all large-scale structures and increased the magnetic field for n/ncr> 2. In the LA case, we limited the renormalisation to densities higher than the gas density at the virial radius of resolved halos in the simulation, n/ncr> 50. In both cases, the strength of all components of the magnetic field in each cell was renormalised to β = 100, where β is the ratio between the thermal and the magnetic energy. On the scale of clusters and filaments, the HA model typically yields a ~10 times stronger magnetic field than what is predicted by our MHD runs, up to several ~μG. The projected maps of magnetic fields and the (B,n/ncr) phase diagrams for these two models are given in Fig. 2. In the density range of filaments (n ~ 5−30ncr) the prediction of the two models differ significantly: B ~ 0.001 μG in the LA model (equivalent to our original MHD run for n ≤ 50ncr) and B ~ 0.05 μG in the HA model. For B ≤ 3.2 μG and flat electron spectra the synchrotron emission scales as Pν ∝ B2 (Eq. (1) below) and, hence, this difference can have a strong effect on the detectability of filaments in radio. Cells in the regime n ~ 10−100 ncr are more relevant for giant filaments and the outskirts of galaxy clusters, and the magnetic field varies from 0.001–0.01 μG (MHD model) to 0.1–1 μG (HA and LA). As we show below, the detectability of filaments in radio will crucially depend on the level of magnetisation at their typical overdensity, and therefore radio observations may have the potential of probing the mechanisms for magnetic field amplification in these regions.

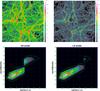thumbnail Fig. 2

Top panel: mass-weighted magnetic field maps for the HA and LA model, for the same volume as in Fig. 1. The colour bar is in units of log 10( [μG]). Bottom panel: phase diagrams on the (B,n/ncr) plane for the same models. We additionally draw isocontours increased tenfold in the number of cells contributing to the pixels in the phase diagrams, starting from 100 cells.

thumbnail Fig. 3

ξ(M,T) function we used to compute the acceleration of CR-electrons at shocks, based on Hoeft & Brüggen (2007).

2.3.2. Acceleration of relativistic particles at shocks

A plethora of mechanisms can contribute to the acceleration of electrons, for instance, direct injection from galactic winds and AGN, acceleration by cosmological shock waves, continuous injection by hadronic collisions, and turbulent reacceleration. Simulations suggest that a vast majority of relativistic electrons in the WHIM are produced by cosmological shock waves (e.g. Ryu et al. 2003; Pfrommer et al. 2006; Araya-Melo et al. 2012), even though electron acceleration in high-β plasmas is poorly understood (e.g. Guo et al. 2014). The theory of diffusive shock acceleration (DSA) offers a theoretical framework to estimate the fraction of the kinetic energy that shocks dissipate into the acceleration of cosmic rays, and it links the slope of the produced momentum distribution to the shock Mach number (e.g. Kang & Ryu 2013, and references therein). However, the microphysical details are largely unknown, and the efficiency of this process, especially at the weak shocks (M ≤ 5) in clusters, is not understood (e.g. Vazza & Brüggen 2014; Vazza et al. 2015a, and discussion therein). To predict the synchrotron emission from accelerated electrons, we used the formalism by Hoeft & Brüggen (2007) that assumes an exponential cutoff in the energy distribution of electrons, determined by the balance of the acceleration rate from DSA and of the (synchrotron and inverse-Compton) cooling rate. In the downstream region, DSA is assumed to generate supra-thermal electrons that follow a power law in energy. The total emission in the downstream region is computed by summing the contributions from all electrons accelerated at the shock.

The monochromatic radio power at frequency ν, Pν, depends on the shock surface area, S, the downstream electron density, nd, the electron acceleration efficiency, ξ(M,T)2 , the downstream electron temperature, Td, the spectral index of the radio emission, s = δ/ 2, the magnetic field to the cosmic microwave background (CMB) energy density, BCMB and the magnetic field in each cell, B: 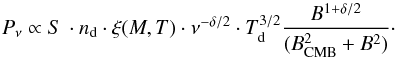Pν∝S ·nd·ξ(M,T)·ν−δ/2·Td3/2B1+δ/2(BCMB2+B2)·\begin{equation} P_{\nu}\propto S\, \cdot n_{\rm d} \cdot \xi(M,T) \cdot \nu^{-\delta/2} \cdot T_{\rm d}^{3/2} \frac{B^{1+\delta/2}}{(B_{\rm CMB}^2+B^2)} \cdot \label{eq:hb} \end{equation}(1)Relic relativistic electrons resulting from previous shocks are expected to accumulate around γ ~ 102 (Brunetti et al. 2001) and can be re-accelerated by subsequent shocks at much higher efficiency. The net effect of freshly injected and re-accelerated particles can be modelled using the formalism by Kang & Ryu (2013), where the global effect of re-acceleration can be incorporated into the acceleration efficiency of CRs to correct the ξ(M,T) function of the HB07 model. It has been estimated in Pinzke et al. (2013) that for weak enough shocks in the ICM (M ≤ 3), re-accelerated electrons dominate over directly injected electrons. For the sake of simplicity, we assumed here that everywhere in the simulated volume the overall acceleration efficiency of CRs for M ≤ 3 is affected by the re-acceleration of previously injected electrons. In this case, the acceleration efficiency is ~10-5−10-6 for M = 3 (depending on the temperature) and ~ 4−8 × 10-4 for M = 10. Figure 3 gives the shape of the ξ(M,T) function for different temperatures and shows the role of shock re-acceleration for M ≤ 10 shocks. Given the very strong dependence on Mach number of the acceleration efficiency at weak shocks, re-accelerated particles can boost the net acceleration by one order of magnitude.

Shock waves were identified in post-processing using the same procedure as in Vazza et al. (2009), which is based on the analysis of velocity jumps of cells that are preliminary tagged based on the local 3D divergence. When there were multiple shocked cells along the shock propagation axis, we performed additional cleaning to select only the cell yielding the highest Mach number. To mask out some small differences in the reionization background, in post-processing we imposed a temperature floor of Tre = 5 × 103 K everywhere (Vazza et al. 2009). The upstream/downstream shock parameters were then used in Eq. (1) to compute the synchrotron emission as a function of frequency and build full-sky emission maps of our simulated volumes. The procedure was run in parallel for the two magnetic field models of Sect. 2.3.1 to produce a full catalogue of mock radio observations.

Figure 4 shows the emission-weighted projected map of the mean radio spectral index along the line of sight for our highest resolution box and assuming the HA model for the magnetic field. The accretion shocks have flat radio spectra, s ~ 1−1.5, while weaker shocks within clusters or filaments have steeper spectra, s ≈ 1.5−3, as in the case of typical radio relics (e.g. Hoeft & Brüggen 2007).

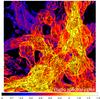thumbnail Fig. 4

Emission-weighted projected mean radio spectral index for a subregion with side 27 Mpc (and depth 50 Mpc) through our highest resolution volume, assuming the HA model for the magnetic field. The additional contours show the projected gas pressure for the same volume.

Table 2

Fiducial parameters for our simulated radio observations.

2.3.3. Mock radio observations

In Vazza et al. (2015b) we explored the possibilities of future surveys and deep pointings with the SKA to detect the radio emission from filaments in targeted observations. In general, predicting the emission from specific filaments is difficult, and the spatial distribution of gas in filaments in the surroundings of galaxy clusters is not known either. In this work, we instead explored the potential of current and future radio surveys to detect the diffuse radio emission from the cosmic web in a statistical way and without a priori knowledge of the best fields to target. Table 2 gives the full set of specifications used to produce a mock observation of a simulated field, according to a procedure similar to Vazza et al. (2015b):

  • 1.

    We compute the radio emission at different redshifts producedduring the simulation, in their comoving frame, and compute thetotal emission map by summing the contribution of all cells alongthe line of sight.

  • 2.

    We convert the emitted power in the physical frame, assuming an observer at different redshift, that is, we include the effect of the luminosity distance of the emitting frame and the effect of cosmological dimming.

  • 3.

    We transform the images in the Fourier space using fast Fourier transformation (FFT). We remove the frequencies smaller than the minimum antenna baseline of each specific radio configuration from the Fourier plane, mimicking the loss of signal from scales larger than the minimum instrumental baseline. This is particularly relevant for the large-scale diffuse emission we investigate here.

  • 4.

    The images are converted back into real space after baseline removal. Then the emission is convolved for the beam using a 2D Gaussian filter.

  • 5.

    Only the pixels whose emission is I(x,y,z) ≥ 3σ are considered as detected by the specific observation. Depending on the array configuration, σ is either the confusion limit (e.g. the contribution of unresolved background of continuum radio sources below the beam size) or the thermal noise of the instrument. The equivalent noise per beam is computed as 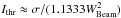Ithr≈σ/(1.1333WBeam2)\hbox{$I_{\rm thr} \approx \sigma/(1.1333 W^2_{\rm Beam})$}, where WBeam is the beam size.

In all cases, we implicitly assumed a perfect removal of the Milky Way foreground (e.g. Bonaldi & Brown 2015, for the case of SKA observations) and of all resolved point-like radio sources, as well as an ideal calibration and deconvolution of the radio data. We post-processed our simulated boxes under many different observing configurations, exploring the capabilities of existing and future surveys in radio. The past and current surveys are a) VLSS Redux survey at 74 MHz with the VLA (Lane et al. 2012); b) NVSS survey at 1400 MHz with the VLA (Condon et al. 1998); c) the WENSS survey at 330 MHz with Westerbork (Rengelink et al. 1997); d) the TGSS survey at 150 MHz with GMRT (Bagchi et al. 2011); and e) the SUMSS survey at 840 MHz with Molonglo (Bock et al. 1999). For the future surveys it is more difficult to quote specific numbers. In some cases we therefore explored a few possible configurations that include their specifications. In detail, we studied four surveys: a) the Large Area surveys with LOFAR HBA (120 MHz) and LBA (40 MHz) (Röttgering et al. 2011). The beam of LOFAR is formed digitally and the final resolution or sensitivity that each survey will be able to reach is not yet fixed. For this reason, we studied two cases, based on Cassano et al. (2015); b) the SKA1-LOW (120 MHz) and SKA1-MID (1000 MHz) surveys. In this latter case, we also explored two possible SKA1-MID configurations, as in Prandoni & Seymour (2015); c) the Broad Band Survey with MWA at 150 MHz, as in Tingay et al. (2013); d) and finally, the EMU survey with ASKAP at 1400 MHz (Norris et al. 2013).

All used parameters are given in Table 2. The last column lists the detection level in surface brightness for each survey. For SKA1-LOW, this is computed considering confusion noise. We also list the field of view of each instrument, but this never entered our calculations since we considered full-sky surveys or very large surveys obtained by adding many pointings.

A public repository of radio maps for the full volumes studied in this work is available at3.

thumbnail Fig. 5

Radio distribution function for the clusters in our three simulated volumes at 1.4 GHz, using the LA model. No observational effects are considered in this case.

thumbnail Fig. 6

Radio distribution function for the clusters in our (100 Mpc)3 volume, normalised to Gpc3, for all investigated emission models. The additional grey lines show the range of the best fit to the distribution of radio relics based on the NVSS, computed by Nuza et al. (2012).

3. Results

3.1. Comparison with radio-relic emission in the NVSS

First, we checked our emission model against the available constraints from the NVSS using relics in galaxy clusters. The model by Hoeft & Brüggen (2007) has been derived to model radio relics, and in our case it fits the distribution of relic emission in clusters rather well. We computed the radio emission within R200 (≈ 0.7 Rvir) of all identified clusters in the three simulated volumes at z = 0.05 and compared the observed statistics of radio-relic emission for the same reference magnetic field model (here the LA model), first excluding observational effects to better focus on the effects of resolution and volume in our runs. The result is shown in Fig. 5, where we renormalised the measured statistics to the same volume of (1 Gpc)3. Two clear trends stand out. First, the distribution functions of the different volumes have the same shape, with a normalisation different by a factor of ~10 in the number of objects when the high resolution and low resolution are compared. This follows from the fact that the internal dynamics (leading to merger shocks) of clusters is better resolved at higher resolution (Vazza et al. 2011), producing more radio-emitting objects. Second, the increase in the simulated volume enables the formation of more massive clusters, enabling more powerful major mergers. For this reason, our largest volume has a tail of high radio power ~10 times more powerful. These trends are in line with what is already known in the literature and are based on shock statistics (e.g. Ryu et al. 2003; Pfrommer et al. 2006; Vazza et al. 2009, 2011) and on simulated radio relics (Skillman et al. 2011). A simulation that combines the exquisite uniform resolution of our 24003 run with the large volume of the (200 Mpc)3 is presently unfeasible. In the following, we explore the simulations we have presented here to extract as much information as possible about cosmic filaments in radio emission. We note, however, that weak merger shocks leading to relics are more subject to resolution effects in grid methods than strong accretion shocks and that a resolution of ~200 kpc is already sufficient to capture the bulk of the energy dissipation in large-scale shocks (e.g. Ryu et al. 2003; Vazza et al. 2009, 2011). All runs presented in this work have a spatial resolution better than this, and the estimated radio power of our filaments is therefore a more robust statistics.

Second, to better compare with the observed distribution of radio relics, we computed the radio distribution function for each magnetic field model in our intermediate (100 Mpc)3 volume at z = 0.05 and compared it with the relic distribution function based on the NVSS that was derived by Nuza et al. (2012). This is so far the best guess for the abundance of radio relics in the local Universe, obtained by extrapolating the distribution function of radio relics in simulations, with adjustable parameters calibrated using all radio relics in the NVSS and with X-ray scaling relations. Now we also introduce the observational effect discussed in Sect. 2.3.3 and mimic the sensitivity of the NVSS survey. The result is shown in Fig. 6. As expected, the baseline MHD model cannot reproduce the distribution of bright radio relics owing to its very low magnetic fields in clusters. The other models instead show a reasonable agreement with the statistics derived from NVSS, with significant gaps only at high radio power (≥1026 W/Hz) due to the lack of massive objects. They also have very low radio power (Pradio ≤ 1023 W/Hz) due to the combined effect of limited spatial resolution to properly resolve the internal structure of the smallest clusters in the box and of the loss of low-surface brightness objects when the observational cuts are introduced. The differences between magnetic field models with post-processing amplification are very small because their differences only come into effect beyond the virial radii of clusters.

Even if the DSA model for the weak shocks responsible for relics is still under debate, it is reassuring that our models do not overestimate the counts of radio relics in the NVSS. We assume that the extrapolation of these models to the stronger accretion shocks around filaments and the typical condition of the WHIM is valid.

3.2. Which level of magnetisation can be detected?

We start by focusing on the minimum magnetic field strength that can enable a detection of the cosmic web at any redshift. Figure 7 gives the total radio emission found with the HA and LA model for our most resolved run (503 Mpc3) with a resolution of 20.8 kpc), with additional contours of gas pressure to trace the distribution of baryons. In both models the strongest emission patterns trace merger shocks inside clusters, producing structures similar to giant radio relics. The flux densities from these relics reach ~0.01–0.1 Jy/arcsec2 in the HA model and ~ 10-5−10-4 Jy/arcsec2 in the LA model. The differences are similar at the accretion shocks around clusters and filaments: the flux densities typically reach ~10-8 Jy/arcsec2 in the HA model and ~10-11 Jy/arcsec2 in the LA model. No significant differences are found at the scale of filaments when the re-acceleration of electrons at shocks is neglected (not shown), which means that filaments only produce radio emission where M ≥ 10.

thumbnail Fig. 7

Radio emission from a subregion with side 27 Mpc (and depth 50 Mpc) through our highest resolution volume for the HA and LA magnetic field models (units of log 10[Jy/arcsec2] assuming a luminosity distance of 200 Mpc). The white contours show the projected gas pressure.

Next we computed how much of these emission patterns can be detected by real radio telescopes, and we started with one of the most promising cases explored here, the Large Survey with LOFAR-HBA (first configuration in Table 2, assuming a noise per beam of 0.25 mJy and a resolution beam of 25′′) at 120 MHz (Fig. 8). The region covers a projected area of (50 Mpc)2 with ~(205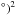)2◦\hbox{$^{\circ})^2$} at z = 0.05 and ~(5.3°)2 at z = 0.5, while for comparison the field of view of a single LOFAR-HBA pointing is (100°)2. The comparison between the high and low amplification model shows that most bright regions inside of halos (considering projected spheres of radius 1.5 Rvir at all epochs) are identified in both cases (blue regions in the figure), the detectable regions outside of halos strongly depend on the amplification model. In the HA model the LOFAR-HBA survey should detect several bright emission spots within a volume z ≤ 0.5, in most cases related to outer accretion regions surrounding galaxy clusters. The best chances of detecting ~Mpc-sized shocked regions of the WHIM in filaments are for z ~ 0.1, which is a good compromise between a good coverage of the necessary short baselines and a too strong effect of the cosmological dimming in surface brightness. Only sparse and more compact knots of bright enough emission are detectable in the LA model, with a poor reconstruction of the underlying WHIM distribution. At z = 0.5 (and also up to z = 1, limited to a very few bright spots) only a magnetic field as high as in our HA model will allow some detection of gas that is not associated with the virial region of clusters. Basically no detection will be possible in the LA case.

3.3. Performances of radio surveys

Next we investigated in depth the chances of detecting the cosmic web by existing and future surveys. First, we assessed the role played by spatial resolution by comparing the maps of four low-frequency surveys, which are the most promising for a detection of the cosmic web in a high-amplification scenario (see also discussion below). Figure 9 shows a region of 5° × 7° for the highest resolution volume of (50 Mpc)3, observed by LOFAR-HBA at two resolutions, SKA1-LOW and MWA. The spatial resolutions here span from 10′′ (SKA1-LOW) to 120′′ (MWA). Each survey should be able to detect a few bright emission regions from the WHIM. However, only with a sufficiently high resolution is it possible to guess the morphology and spatial orientation of these features, which are otherwise difficult to distinguished from the possible signal of relic-like emission from distant clusters that are not yet detected in the X-rays (e.g. Macario et al. 2014). Furthermore, achieving the highest possible resolution is important for removing point sources and thereby for reducing the confusion noise, which is expected to limit the sensitivity of SKA1-LOW (e.g. Prandoni & Seymour 2015).

thumbnail Fig. 8

Mock observation of the (50 Mpc)3 volume using the configuration of LOFAR-HBA (Large Survey1, see Table 2) for increasing redshift (z = 0.05, z = 0.1 and z = 0.5) for the HA (left) and LA (right) magnetic field models. The blue and red regions show the emission that is detectable for each model and redshift, divided into emission coming from ≤1.5 rvir (blue) of each identified halo, or generated outside and therefore most likely related to filaments (red). The additional contours show the projected gas pressure. The units of the axes are given in cell units (Δx = 20.8 kpc).

Second, we studied the performances of all surveys in Table 2 using a more realistic setup, where we integrated a long rectangular volume covering 14° × 14° in the sky and sampling all cosmic volume from z = 0.02 to z = 0.5 (corresponding to a comoving radial distance of ≈1.892 Gpc). To do so, we stacked many simulated volumes along the line of sight, starting with a few replicas of the (100 Mpc)3 box to give a better angular resolution at low redshift, and then by stacking several replicas of the (200 Mpc)3 volume to cover the whole projected volume up to z = 0.5. We first computed the radio emission in the comoving frame of each box at the appropriate redshift and then “moved” each map away from the observer by applying the cosmological corrections for the surface brightness and the luminosity distance of each redshift. We also decreased the pixel size of each box as a function of distance using a cubic interpolation on the input map. Possible artefacts due to the periodicity of structures along the line of sight were minimised by shifting each box with a random offset in both directions. We note that the first simulated volume along the line of sight is large enough that the change of redshift across the volume cannot be neglected. Therefore, we furthermore subdivided it into four slabs (starting at z ≈ 0.023, 0.029, 0.035 and 0.044) and accordingly computed the cosmological corrections for each of them independently.

thumbnail Fig. 9

Role of resolution in different radio surveys at low frequency. The colours show the detectable emission by different surveys at low frequency for the HA model (units of log 10 [Jy/arcsec2]), considering a field of view of 5° × 7°. The emission in each map has been convolved with the corresponding resolution beam. The white contours show the projected gas pressure.

Figure 10 shows the effect of adding more volume along a projected field of view, where we show the proxy of X-ray emission (∝n2T1/2) and the radio emission for a subset of the full map created above, assuming the HA model and for a Large Survey with LOFAR-LBA. Despite the evident appearance of many additional clusters in the field, the detectable radio emission does not change much when our integration region changes from z = 0.03 to z = 0.5 because of the strong cosmological dimming for z ≤ 0.1. A few brighter spots, correlated with higher redshift merging clusters, appear in the full-volume image, but most of the cosmic web remains below the detectability threshold for LOFAR-LBA (large survey with a resolution of 25′′).

To give a more quantitative view of which portion of the cosmic web can actually be detected by different surveys and for different magnetic field models, we give in Fig. 11 the result for the full integrated volume. We show the total emission from all shocked cells or from the WHIM only after excision of the projected virial volume of each identified cluster or group. In the HA model, the power in the WHIM is ~1% of the radio power emitted by clusters, while this is ~0.1% in the LA model. Most of the emission in the projected volume comes from clusters, and all surveys appear to be able to detect most of it (within a factor ~2), with the least detection coming from the highest frequency surveys. On average, we measure a diffuse radio flux density of ~0.1 Jy/deg2 (100 MHz/ν) from all shocks in our simulated volume (very similar numbers for the two magnetic field models), while the contribution from the WHIM is ~ 5 × 10-3−10-2 Jy/deg2 (100 MHz/ν) in the HA case and ~ 10-3−5 × 10-3 Jy/deg2 (100 MHz/ν) in the LA model.

The differences in the performance between surveys become more apparent if we only consider the residual WHIM emission. The most satisfactory reconstruction of the WHIM is obtained with LOFAR (HBA Large 1 and LBA Large surveys), SUMSS, WENSS, SKAl-LOW, SKA1-MID, and MWA-SUR, where the fraction of the recovered flux is 1/50–1/100 of the total WHIM emission. A larger gap between the total and the detectable emission from the WHIM is measured for the LA case.

thumbnail Fig. 10

Emission from our simulated light cone at z = 0.03, z = 0.05 and z = 0.5, obtained by stacking replicas of our (100 Mpc)3 and (200 Mpc)3 simulated volumes. The top panels show the total X-ray emission proxy (∝ n2T1/2) and the lower panels show the radio emission for LOFAR-LBA (units of log 10 [Jy/arcsec2]) for a projected area of 3.5° × 3.5°, assuming the high-amplification model (HA). The white contours of the X-ray emission proxy are drawn in the lower panels to allow a better comparison of structures.

thumbnail Fig. 11

Performance of different radio surveys observing a region of 14° × 14°. We simulated the whole radio-emitting volume from z = 0.02 to z = 0.5 and present for both models the radio emission from the ICM+WHIM (blue) or from the WHIM only (red), distinguishing the total emission (large squares) and the one detected by each survey configuration (small diamonds). All emissions have been rescaled by (110 MHz /ν [MHz]) for better comparison of surveys at different frequencies.

3.4. Filaments connecting clusters

Even before the completion of future deep radio surveys, it will be possible to detect the radio emitting WHIM with long exposures targeting galaxy clusters at low frequency. Close pairs of interacting clusters are particularly interesting for this (e.g. Planck Collaboration Int. VII 2013; Farnsworth et al. 2013). Although these objects are much smaller than the ~10–20 Mpc filaments that can be detected in our simulations, they can give us a first hint of the active mixing between the ICM and the WHIM. First DM-only simulations showed that most of simulated clusters are found to be surrounded by filaments with typical lengths ≤20 Mpc/h and with a weak mass-dependence: clusters with M ~ 1014M⊙ are on average surrounded by about two to three filaments, while this increases to about four to five for M ~ 1015M⊙ objects (e.g. Colberg et al. 2005). Our recent analysis of the gas properties of the filaments in large cosmological simulations showed that up to ~103 filaments can be identified in (100 Mpc)3 at z = 0, with a decreasing power-law distribution of lengths from one Mpc up to several tens of Mpc (Gheller et al., 2015). Deep imaging of the region between close pairs of galaxy clusters is potentially an efficient way to search for cosmic filaments, even if in such close configurations it might be difficult to separate the emission from cluster accretion shocks and filaments shocks.

In a first exploratory study, we extracted the position of halos with ≥5 × 1013M⊙ in our most resolved box and extracted various quantities along the line joining the centres of close clusters. A more complete survey of the cluster-to-filament connections (involving the cross-correlation of cluster and filament catalogues) will be the subject of future work. Here we show some representative cases where some emission from the WHIM can be detected. Figure 12 shows the projected maps of magnetic fields (with isodensity contours) and of radio emission at 120 MHz (observed with the LOFAR-HBA Large Survey 1) for two pairs of interacting clusters in the (50 Mpc)3 box. The distances between the centres of the gas halos are ~4.5 and 6 Mpc, and the connecting bridges are ~1 Mpc thick. The magnetic field along the two filaments is ~0.05–0.1 G in the HA model and ~0.001 μG in the LA model (except that in a few dense substructures within the filament), as shown by Figs. 13 and 14. The interaction region of both pairs hosts significant radio emission, associated with several shocks within the filaments and around the gas substructures internal to it. For a high level of magnetisation a few bright emission regions ~100–200 kpc long can be detected in both cases, while most of the weaker shocks close to the spine of the bridges will remain below the sensitivity of LOFAR. Basically no detection from these bridges will be possible in a low-magnetisation scenario, while the relic-like emission inside the main halos remains similar. The presence of radio galaxies can add radio-emitting plasma on these bridges, especially if such close pairs are found in a rich cosmic environment.

3.5. Alternative scenarios

We plan to investigate the role played by galaxies and active galactic nuclei in the seeding of large-scale magnetic fields with direct more complex numerical simulations in future work. Here we briefly discuss a few possible variations of the magnetic field models studied above, which we can easily test with existing runs. A possibility suggested in the literature is that cosmic rays accelerated by strong shocks can induce turbulence in the shocks upstream and trigger substantial magnetic field amplification (Drury & Downes 2012; Brüggen 2013). We tested this scenario (labelled HSA) by computing the kinetic energy flux that is expected to be dissipated into CRs based on our shock finder and on the acceleration efficiency by Kang & Ryu (2013). This was converted into a magnetic field for each cell by integrating for the cell size and the time step of the simulation: 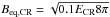Beq,CR=0.1ECR8π\hbox{$B_{\rm eq,CR}=\sqrt{0.1 E_{\rm CR} 8 \pi}$}, that is, we assumed that a 10% of the energy of accelerated CR amplifies the magnetic field. The field obtained in this way was added to the field in the previous HA model. Figure 15 shows the radio emission obtained in this scenario: the observed morphologies and power are very similar to the HA case, with the exception of the accretion shocks, where the magnetic field can be amplified by a factor ~10 and the emission can be increased up to ~10–100 at accretion shocks around clusters and filaments. However, this extra amplification is often found at densities too low to contribute significantly to the observable radio emission. Figure 16 shows the outcome of the HSA model on the emitted and detected radio emission for the same long projected volume analysed in the previous sections. The total emission in the box, largely dominated by clusters, is the same when the HA and HSA model are compared, and the total emission from the WHIM also remains basically the same. However, this mechanism remains speculation for the moment, given the largely unknown acceleration efficiency of CR-protons by cosmological shocks, and the complex details related to the diffusion coefficient of particles in the upstream (see discussions in Drury & Downes 2012; Brüggen 2013).

Second, we tested the case in which the radio-emitting electrons are only those that are freshly accelerated by shocks and there is no contribution from re-accelerated electrons at low Mach number (Sect. 2.3.2). Figure 16 shows that neglecting shock re-acceleration decreases the total emission by a factor ~2 by reducing the relic emission in clusters (as described in Sect. 3.1). The WHIM emission is also reduced by a similar factor.

In summary, additional amplification by cosmic-ray-driven turbulence or pre-existing electrons will probably only affect our estimates by a very small factor, ≤2 in the total and detectable emission.

Finally, we note that the total emitted power from the WHIM essentially scales linearly with the saturated value of ξ(M,T) for strong shocks (Eq. (1)). In this work, this is ξ ~ 0.7−0.9 × 10-4, of the same order as what is usually assumed to explain the observed spectra of supernova remnants (Edmon et al. 2011; Ferrand et al. 2014). Given that the predicted radio spectra of most shocks in the WHIM is flat Pν ∝ ν-1, Eq. (1) predicts that for a magnetic field lower than 3.2 μG and at low redshift, different combinations of ξ·B2 will yield the same emission level. Considering the level of predicted emission from the WHIM in our runs (Sect. 3.3), we can therefore reformulate our model prediction in the following way: 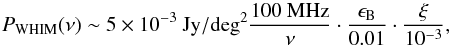PWHIM(ν)~5×10-3Jy/deg2100MHzν·ϵB0.01·ξ10-3,\begin{equation} P_{\rm WHIM}(\nu) \sim 5 \times 10^{-3}~\rm {Jy/deg^2}\frac{100~MHz}{\nu} \cdot \frac{\epsilon_{\rm B}}{0.01} \cdot \frac{\xi}{10^{-3}} , \label{eq1} \end{equation}(2)where ϵB is the magnetisation level of the WHIM we assumed in the HA model, that is, 1% of the thermal gas energy. This can also be roughly translated into a prescription for the mean magnetic field of the WHIM, assuming a mean density of n/ncr ≈ 10: 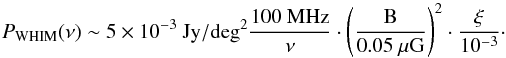PWHIM(ν)~5×10-3Jy/deg2100MHzν·(B0.05μG)2·ξ10-3·\begin{equation} P_{\rm WHIM}(\nu) \sim 5 \times 10^{-3}~\rm {Jy/deg^2}\frac{\rm 100~MHz}{\nu}\cdot \left(\frac{B}{0.05~\mu {\rm G}}\right)^2 \cdot \frac{\xi}{10^{-3}} \cdot \label{eq2} \end{equation}(3)Thus, the level of radio emission we predict for the WHIM can be rescaled for the simple cases of a different constant magnetisation level of the WHIM (e.g. assuming a different cosmological seed magnetic field) or of a revised acceleration efficiency for electrons (e.g. revised acceleration efficiency from supernovae).

thumbnail Fig. 12

Maps of intracluster filaments in the (50 Mpc)3 volume at z = 0.05. The left panels show the projected mass-weighted magnetic field (HA model, units of log 10 [μG]), and the white contours give the projected gas density. The right panels show the intrinsic radio emission in the same model ([Jy/arcsec2]).

thumbnail Fig. 13

Profiles along the white line in the first panel of Fig. 12, showing the trend of mean gas density along the line of sight, the magnetic field (each colour represents a different model, with blue =LA and green =HA), intrinsic radio emission (same colour coding) and detectable radio emission assuming the sensitivity of LOFAR HBA Large Survey at 120 MHz (resolution of 25′′).

thumbnail Fig. 14

Same as Fig. 13, but for the second cluster association in the figure.

thumbnail Fig. 15

Similar to Fig. 7, but using the HSA model (high amplification and CR-driven dynamo).

thumbnail Fig. 16

Comparison of the emitted and detected radio emission for the same region of 14° × 14° as in Fig. 11, using SKA1-LOW. Each column shows the outcome of different models for the magnetic fields (HA, LA, and HSA) also without the contribution from re-accelerated electrons.

4. Conclusions

We studied the detectability of the cosmic web using existing and future radio surveys. We simulated the acceleration of electrons by cosmological shock waves (Hoeft & Brüggen 2007) and applied it to large cosmological volumes produced using the MHD version of ENZO (Vazza et al. 2014a). In post-processing we modified the magnetic field as a function of density such as to reproduce the magnetic filed levels observed in galaxy clusters. We increased the magnetic field according to high-amplification (HA) or low-amplification (LA) models, which both push the magnetic field in clusters close to the observed values (a few ~μG), but differ in filaments: in the HA model the magnetic field in a filament is set to 1% of the thermal gas energy of cells, while in the LA it remains the one from the MHD simulation, that is, ≤nG. We produced mock radio observation with the specific parameters of real surveys (including the lack of short baseline, of the spatial resolution and sensitivity of each instrument) and quantified the chance of detecting the WHIM in large projected volumes (up to z = 0.5).

Our main results can be summarised as follows:

  • Only the high-amplification scenario allows detecting thehighest WHIM radio emission, limited to the brightest emissionspots in filaments and accretion shocks. The high magnetisationmight come from unresolved small-scale dynamo (orfast-growing instabilities in a high plasma β) and/or from seeding mechanisms not yet included in our MHD runs (e.g. outflows from galaxies, AGN), which push the magnetic field up to ~1% of the thermal energy of the WHIM as in clusters (Sect. 3.2).

  • Low-frequency (≤300 MHz) observations are best suited to detect the large-scale diffuse emission produced by cosmological shocks, at the scale of cluster accretion shocks or in filaments. These shocks are usually several ~Mpc wide, are characterised by a flat emission spectrum (Pν ∝ ν− 1 ÷ −1.5), and emit at the level of ~μJy/arcsec2 at low redshift in a high-amplification model (Sect. 3.3).

  • Most of the detectable radio emission is caused by structures at z ≤ 0.1 because of cosmological dimming. Especially at high frequencies, the detection of structures of the cosmic web that are too close (z ≤ 0.02) is made difficult by the lack of short baselines.

  • Of all investigated surveys, the highest fraction of detected flux from the WHIM phase is obtained by LOFAR (HBA-Large survey and LBA-Large), SKA1-LOW, and the MWA Broadband survey. In all these cases ~10-2 of the WHIM emission can be detected, mostly associated with shocks internal to filaments, both driven by the accretion of smooth gas in rich environment or driven by supersonic motions internal to filaments.

  • The highest resolution accessible to LOFAR (≤25′′) and SKA1-LOW (~10′′) should enable a much better identification of the morphology of the underlying filamentary environment compared to MWA and to exclude the contamination from cluster shocks and active galaxies. High resolution will also be important to reduce the confusion noise (e.g. in the SKA1-LOW).

  • In a low-amplification scenario the detection chance of these surveys will be reduced by ~10 and only a very limited number of bright spots (mostly associated with dense substructures within filaments) will be detectable, offering a poor tracing of the WHIM distribution.

  • We estimate a background of unresolved radio emission from the WHIM in the range ~ 10-3−10-2 Jy/deg2 (100 MHz/ν), depending on the amplification model (Eqs. (2) and (3)).

  • Clusters interacting on short distances (~4–6 Mpc) can be connected by magnetised bridges, hosting internal shocks that can be observed if the magnetisation level is ~1% of the thermal gas (Sect. 3.4).

  • Our modelling does not yet cover the effect of magnetised outflows from galaxies and active galactic nuclei in a proper way. We investigated a few alternative scenarios for the amplification of magnetic field and for the acceleration of particles at strong shocks, finding only minor differences with respect to the main results of our baseline model (Sect. 3.5).

  • Radio emission from secondary electrons injected by hadronic collisions is negligible in the WHIM (see the appendix).

An important caveat in our analysis is that we assumed that DSA can operate at all density and magnetisation levels in our simulated volume, which may not be true for very low levels of magnetic fields. Recent results from particle-in-cell simulations (PIC) pointed out that the topology of the upstream magnetic field is more important for the onset of DSA at non-relativistic shock than its initial value. In particular, if the upstream magnetic field is aligned with the shock normal (i.e. parallel shocks), the rapid development of the Weibel instability might amplify the magnetic field and enable the formation of a shock precursor leading to DSA (Caprioli 2012; Caprioli & Spitkovsky 2014; Guo et al. 2014). For this reason, the presence of shock-accelerated electrons in the WHIM is a realistic possibility.

An important aspect of this scenario is that both a detection and a non-detection of the cosmic web in radio within the next decade will be helpful to place constraints on the magnetic field in the WHIM, given that to a first approximation the radio emission from the WHIM is expected to scale as Pν ∝ ξB2 (Eqs. (2) and (3)). The lack of detection in radio from large observed volume will limit the magnetic energy in the WHIM to values much below ~1% of the thermal gas energy in these environments. In this case, the effect of cosmic magnetic fields on the propagation of UHECRs is predicted to be negligible (Sigl et al. 2003; Dolag et al. 2005), and so is the effect of magnetic fields in producing axion-like particle oscillations (Horns et al. 2012).

On the other hand, in the case of systematic detection of emission patches connected to the WHIM, the analysis of their morphology and large-scale distribution will be important to distinguish competing scenarios. For example, the detection of coherent magnetic fields on ≫Mpc scales will favour a distributed amplification process as an obliquitous small-scale dynamo. Our models show that if the growth of the cosmic web is linked to the thermal gas energy of the WHIM, the cosmic web should be maximally emitting in radio at moderately low redshift (z ≤ 0.1). Any unambiguous detection of radio emission from much higher redshift will further distinguish between seeding models and favour a strong magnetisation activity of large-scale structures by high-z star-forming galaxies.

In addition to continuum radio emission, other complementary techniques should be able to probe the existence of the cosmic web, using different effects: polarised radio emission (e.g. Govoni et al. 2015), Faraday rotation (e.g. Akahori et al. 2014; Bonafede et al. 2015; Taylor et al. 2015), neutral hydrogen emission (e.g. Popping et al. 2015), absorption and emission features of highly ionised elements in the WHIM (e.g. Barcons et al. 2012), and fast radio bursts (Zheng et al. 2014; Dolag et al. 2015). Considering the extreme difficulty of obtaining the expected weak signal from the cosmic web, the use of statistical and stacking techniques will increase the chances of success (e.g. Vacca et al. 2015; Stil & Keller 2015).

Online material

Appendix A: Contribution from secondary electrons

We briefly report here on the contribution from secondary electrons injected by hadronic proton-proton collision (Blasi & Colafrancesco 1999; Dolag & Enßlin 2000) to the total radio emission. The injection rate of secondary electrons is computed from the pool of CR-protons simulated at run-time by our ENZO cosmological simulation using PPM and a two-fluid model for modelling cosmic rays, as in Vazza et al. (2014b). For this we used the formalism by Dolag & Enßlin (2000), assuming a constant energy spectrum of α = 1.1 (N(E) ∝ E− α) for cosmic-ray protons. The final budget of cosmic rays in the simulation follows from the assumed acceleration efficiency at shocks, which we took from Kang & Ryu (2013) and renormalised downwards by a factor 10 to be consistent with the upper limits from the Fermi satellite (Ackermann et al. 2014). Here we used the result from a (300 Mpc)3 volume simulated with 20483 cells and DM-particles. This run did not use MHD, and therefore we assumed the magnetic field entirely in post-processing. Similar to the main article, we computed the gas energy in all cells and computed the magnetic field in a HA and LA model.

Figure A.1 shows the outcome of these two acceleration mechanisms for the HA model: the contribution from secondary electrons to the diffuse cosmic web is negligible everywhere, that is, it is only a few percent of the primary contribution. The emission increases in the centre of the clusters owing to the increase of the gas density and only forms rather low-power radio halos (e.g. Dolag & Enßlin 2000). Outside the central cluster regions, however, this signal usually is much weaker than the primary emission from strong accretion shocks. The distribution function of pixels in the maps (Fig. A.2) shows that the primary contribution by far dominates the high end of the emission tail in both magnetic field models. However, the secondary contribution becomes dominant in the low-brightness end of the emission distribution in an LA scenario because of the decrease

in primary emission from the WHIM outside of halos and because the secondary emission is nearly unaltered in the LA scenario since it mostly comes from well within the halos. The confusion caused by the secondary emission from galaxy clusters will probably become stronger at high redshift, where massive bright clusters can dominate the low-power background emission compared to the filaments in the LA scenario. Overall, we conclude that regardless of the assumed amplification model, the brightest emission from the cosmic web is expected to originate from primary electrons accelerated by cosmic shocks, and that the signal from secondary particles can only be relevant at very low surface brightness values and at high redshift in a low magnetisation scenario of the WHIM.

thumbnail Fig. A.1

Distribution of radio emission from the HA and the LA model in a cosmological run with CR-protons and including the effect of “secondary” radio emission from electrons injected by hadronic collision.

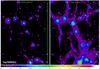thumbnail Fig. A.2

Total radio emission from primary electrons injected by shocks (right) and from secondary electrons injected by hadronic collisions (left) in a subvolume of our 20483 simulation with CR-physics (Vazza et al. 2014b). The colour bar gives the emission in units of [log 10 W/Hz].

2

We note that, in agreement with most of the literature on the DSA of electrons, we include in our definition of the electron acceleration efficiency the dependence on M in Eq. (1), i.e. ξ(M,T) = ξe,0Ψ(M), where ξe,0 = 10-3 and Ψ(M,T) is given in Eq. (31) of HB07.

Acknowledgments

Computations described in this work were performed using the ENZO code (http://enzo-project.org), which is the product of a collaborative effort of scientists at many universities and national laboratories. We gratefully acknowledge the ENZO development group for providing extremely helpful and well-maintained online documentation and tutorials. We acknowledge the usage of computing time at CSCS, for the allotted CHRONOS project in 2014, and the precious support by CSCS-ETH in Lugano (http://www.cscs.ch). We also acknowledge PRACE for awarding us access to CURIE-Genci based in France at Bruyeres-le-Chatel in 2013. The support of the TGC Hotline from the Centre CEA-DAM Ile de France to the technical work is gratefully acknowledged. F.V. and M.B. acknowledge the usage of computational resources on the JUROPA cluster at the at the Juelich Supercomputing Centre (JSC), under project nos. 5018, 5984, 5056 and 7006. F.V. and M.B. acknowledge support from the grant FOR1254 from the Deutsche Forschungsgemeinschaft. We thankfully acknowledge R. Pizzo and H. Röttgering of fruitful scientific discussion, and I. Prandoni for carefully reading the manuscript. We acknowledge the use of the online Cosmology Calculator by Wright (2006).

References

  1. Ackermann, M., Ajello, M., Albert, A., et al. 2014, ApJ, 787, 18 [NASA ADS] [CrossRef] [Google Scholar]
  2. Akahori, T., Gaensler, B. M., & Ryu, D. 2014, ApJ, 790, 123 [NASA ADS] [CrossRef] [Google Scholar]
  3. Araya-Melo, P. A., Aragón-Calvo, M. A., Brüggen, M., & Hoeft, M. 2012, MNRAS, 423, 2325 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bagchi, J., Enßlin, T. A., Miniati, F., et al. 2002, New A, 7, 249 [Google Scholar]
  5. Bagchi, J., Sirothia, S. K., Werner, N., et al. 2011, ApJ, 736, L8 [NASA ADS] [CrossRef] [Google Scholar]
  6. Barcons, X., Barret, D., Decourchelle, A., et al. 2012, ArXiv e-prints [arXiv:1207.2745] [Google Scholar]
  7. Battaglia, N., Pfrommer, C., Sievers, J. L., Bond, J. R., & Enßlin, T. A. 2009, MNRAS, 393, 1073 [NASA ADS] [CrossRef] [Google Scholar]
  8. Beck, A. M., Hanasz, M., Lesch, H., Remus, R.-S., & Stasyszyn, F. A. 2013, MNRAS, 429, L60 [NASA ADS] [CrossRef] [Google Scholar]
  9. Blasi, P., & Colafrancesco, S. 1999, Astropart. Phys., 122, 169 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bock, D. C.-J., Large, M. I., & Sadler, E. M. 1999, AJ, 117, 1578 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bonafede, A., Feretti, L., Murgia, M., et al. 2010, A&A, 513, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Bonafede, A., Vazza, F., Brüggen, M., et al. 2013, MNRAS, 433, 3208 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bonafede, A., Vazza, F., Brüggen, M., et al. 2015, in Proc. Advancing Astrophysics Square Kilometre Array (AASKA14), 95 [Google Scholar]
  14. Bonaldi, A., & Brown, M. L. 2015, MNRAS, 447, 1973 [NASA ADS] [CrossRef] [Google Scholar]
  15. Brown, S. D. 2011, J. Astrophys. Astron., 32, 577 [NASA ADS] [CrossRef] [Google Scholar]
  16. Brüggen, M. 2013, MNRAS, 436, 294 [NASA ADS] [CrossRef] [Google Scholar]
  17. Brüggen, M., Ruszkowski, M., Simionescu, A., Hoeft, M., & Dalla Vecchia, C. 2005, ApJ, 631, L21 [NASA ADS] [CrossRef] [Google Scholar]
  18. Brunetti, G., Setti, G., Feretti, L., & Giovannini, G. 2001, MNRAS, 320, 365 [NASA ADS] [CrossRef] [Google Scholar]
  19. Bryan, G. L., Norman, M. L., O’Shea, B. W., et al. 2014, ApJS, 211, 19 [NASA ADS] [CrossRef] [Google Scholar]
  20. Caprioli, D. 2012, J. Cosmol. Astropart. Phys., 7, 38 [Google Scholar]
  21. Caprioli, D., & Spitkovsky, A. 2014, ApJ, 783, 91 [NASA ADS] [CrossRef] [Google Scholar]
  22. Cassano, R., Bernardi, G., Brunetti, G., et al. 2015, in Proc. Advancing Astrophysics Square Kilometre Array (AASKA14), 73 [Google Scholar]
  23. Cen, R., & Ostriker, J. P. 1999, ApJ, 514, 1 [NASA ADS] [CrossRef] [Google Scholar]
  24. Colberg, J. M., Krughoff, K. S., & Connolly, A. J. 2005, MNRAS, 359, 272 [NASA ADS] [CrossRef] [Google Scholar]
  25. Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
  26. Davé, R., Cen, R., Ostriker, J. P., et al. 2001, ApJ, 552, 473 [NASA ADS] [CrossRef] [Google Scholar]
  27. Dedner, A., Kemm, F., Kröner, D., et al. 2002, J. Comput. Phys., 175, 645 [Google Scholar]
  28. Dolag, K., & Enßlin, T. A. 2000, A&A, 362, 151 [NASA ADS] [Google Scholar]
  29. Dolag, K., Bartelmann, M., & Lesch, H. 1999, A&A, 348, 351 [NASA ADS] [Google Scholar]
  30. Dolag, K., Grasso, D., Springel, V., & Tkachev, I. 2005, J. Cosmol. Astropart Phys., 1, 9 [Google Scholar]
  31. Dolag, K., Gaensler, B. M., Beck, A. M., & Beck, M. C. 2015, MNRAS, 451, 4277 [NASA ADS] [CrossRef] [Google Scholar]
  32. Donnert, J., Dolag, K., Lesch, H., & Müller, E. 2009, MNRAS, 392, 1008 [NASA ADS] [CrossRef] [Google Scholar]
  33. Drury, L. O., & Downes, T. P. 2012, MNRAS, 427, 2308 [NASA ADS] [CrossRef] [Google Scholar]
  34. Edmon, P. P., Kang, H., Jones, T. W., & Ma, R. 2011, MNRAS, 414, 3521 [NASA ADS] [CrossRef] [Google Scholar]
  35. Farnsworth, D., Rudnick, L., Brown, S., & Brunetti, G. 2013, ApJ, 779, 189 [NASA ADS] [CrossRef] [Google Scholar]
  36. Ferrand, G., Decourchelle, A., & Safi-Harb, S. 2014, ApJ, 789, 49 [NASA ADS] [CrossRef] [Google Scholar]
  37. Finoguenov, A., Briel, U. G., & Henry, J. P. 2003, A&A, 410, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Gheller, C., Vazza, F., Favre, J., & Brüggen, M. 2015, MNRAS, submitted [arXiv:1507.05806] [Google Scholar]
  39. Giovannini, G., Bonafede, A., Feretti, L., Govoni, F., & Murgia, M. 2010, A&A, 511, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Giovannini, G., Bonafede, A., Brown, S., et al. 2015, in Proc. Advancing Astrophysics Square Kilometre Array (AASKA14), 104 [Google Scholar]
  41. Govoni, F., Murgia, M., Xu, H., et al. 2015, in Proc. Advancing Astrophysics Square Kilometre Array (AASKA14), 105 [Google Scholar]
  42. Guo, X., Sironi, L., & Narayan, R. 2014, ApJ, 797, 47 [NASA ADS] [CrossRef] [Google Scholar]
  43. Hoeft, M., & Brüggen, M. 2007, MNRAS, 375, 77 [NASA ADS] [CrossRef] [Google Scholar]
  44. Horns, D., Maccione, L., Meyer, M., et al. 2012, Phys. Rev. D, 86, 075024 [NASA ADS] [CrossRef] [Google Scholar]
  45. Kang, H., & Ryu, D. 2013, ApJ, 764, 95 [NASA ADS] [CrossRef] [Google Scholar]
  46. Keshet, U., Waxman, E., & Loeb, A. 2004, ApJ, 617, 281 [NASA ADS] [CrossRef] [Google Scholar]
  47. Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
  48. Kronberg, P. P., Lesch, H., & Hopp, U. 1999, ApJ, 511, 56 [NASA ADS] [CrossRef] [Google Scholar]
  49. Kronberg, P. P., Kothes, R., Salter, C. J., & Perillat, P. 2007, ApJ, 659, 267 [NASA ADS] [CrossRef] [Google Scholar]
  50. Kunz, M. W., Schekochihin, A. A., Cowley, S. C., Binney, J. J., & Sanders, J. S. 2011, MNRAS, 410, 2446 [NASA ADS] [CrossRef] [Google Scholar]
  51. Kurganov, A., & Tadmor, E. 2000, J. Comput. Phys., 160, 241 [Google Scholar]
  52. Lane, W. M., Cotton, W. D., Helmboldt, J. F., & Kassim, N. E. 2012, Radio Science, 47, RS0K04 [Google Scholar]
  53. Macario, G., Intema, H. T., Ferrari, C., et al. 2014, A&A, 565, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Marinacci, F., Vogelsberger, M., Mocz, P., & Pakmor, R. 2015, MNRAS, submitted [arXiv:1506.00005] [Google Scholar]
  55. Miniati, F., Jones, T. W., Kang, H., & Ryu, D. 2001, ApJ, 562, 233 [NASA ADS] [CrossRef] [Google Scholar]
  56. Mogavero, F., & Schekochihin, A. A. 2014, MNRAS, 440, 3226 [NASA ADS] [CrossRef] [Google Scholar]
  57. Murgia, M., Govoni, F., Feretti, L., et al. 2004, A&A, 424, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Nicastro, F., Krongold, Y., Fields, D., et al. 2010, ApJ, 715, 854 [NASA ADS] [CrossRef] [Google Scholar]
  59. Nicastro, F., Elvis, M., Krongold, Y., et al. 2013, ApJ, 769, 90 [NASA ADS] [CrossRef] [Google Scholar]
  60. Norris, R. P., Afonso, J., Bacon, D., et al. 2013, PASA, 30, 20 [Google Scholar]
  61. Nuza, S. E., Hoeft, M., van Weeren, R. J., Gottlöber, S., & Yepes, G. 2012, MNRAS, 420, 2006 [NASA ADS] [CrossRef] [Google Scholar]
  62. Pfrommer, C., Springel, V., Enßlin, T. A., & Jubelgas, M. 2006, MNRAS, 367, 113 [NASA ADS] [CrossRef] [Google Scholar]
  63. Pinzke, A., Oh, S. P., & Pfrommer, C. 2013, MNRAS, 435, 1061 [NASA ADS] [CrossRef] [Google Scholar]
  64. Planck Collaboration, Int. VII. 2013, A&A, 550, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Popping, A., Meyer, M., Staveley-Smith, L., et al. 2015, in Proc. Advancing Astrophysics Square Kilometre Array (AASKA14), 132 [Google Scholar]
  66. Prandoni, I., & Seymour, N. 2015, in Proc. Advancing Astrophysics Square Kilometre Array (AASKA14), 67 [Google Scholar]
  67. Rengelink, R. B., Tang, Y., de Bruyn, A. G., et al. 1997, A&AS, 124, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Röttgering, H., Afonso, J., Barthel, P., et al. 2011, J. Astrophys. Astron., 32, 557 [Google Scholar]
  69. Ryu, D., Kang, H., Hallman, E., & Jones, T. W. 2003, ApJ, 593, 599 [NASA ADS] [CrossRef] [Google Scholar]
  70. Ryu, D., Kang, H., Cho, J., & Das, S. 2008, Science, 320, 909 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  71. Ryu, D., Schleicher, D. R. G., Treumann, R. A., Tsagas, C. G., & Widrow, L. M. 2012, Space Sci. Rev., 166, 1 [NASA ADS] [CrossRef] [Google Scholar]
  72. Schaal, K., & Springel, V. 2015, MNRAS, 446, 3992 [NASA ADS] [CrossRef] [Google Scholar]
  73. Schekochihin, A. A., Cowley, S. C., Taylor, S. F., Maron, J. L., & McWilliams, J. C. 2004, ApJ, 612, 276 [NASA ADS] [CrossRef] [Google Scholar]
  74. Schekochihin, A. A., Cowley, S. C., Kulsrud, R. M., Hammett, G. W., & Sharma, P. 2005, ApJ, 629, 139 [NASA ADS] [CrossRef] [Google Scholar]
  75. Schleicher, D. R. G., Schober, J., Federrath, C., Bovino, S., & Schmidt, W. 2013, New J. Phys., 15, 023017 [NASA ADS] [CrossRef] [Google Scholar]
  76. Schober, J., Schleicher, D. R. G., & Klessen, R. S. 2013, A&A, 560, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Shu, C.-W., & Osher, S. 1988, J. Comp. Phys., 77, 439 [Google Scholar]
  78. Sigl, G., Miniati, F., & Ensslin, T. A. 2003, Phys. Rev. D, 68, 043002 [NASA ADS] [CrossRef] [Google Scholar]
  79. Skillman, S. W., O’Shea, B. W., Hallman, E. J., Burns, J. O., & Norman, M. L. 2008, ApJ, 689, 1063 [NASA ADS] [CrossRef] [Google Scholar]
  80. Skillman, S. W., Hallman, E. J., O’Shea, B. W., et al. 2011, ApJ, 735, 96 [NASA ADS] [CrossRef] [Google Scholar]
  81. Stil, J., & Keller, B. 2015, in Proc. Advancing Astrophysics Square Kilometre Array (AASKA14), 112 [Google Scholar]
  82. Sunyaev, R. A., & Zeldovich, Y. B. 1972, A&A, 20, 189 [NASA ADS] [Google Scholar]
  83. Taylor, R., Agudo, I., Akahori, T., et al. 2015, in Proc. Advancing Astrophysics Square Kilometre Array (AASKA14), 113 [Google Scholar]
  84. Tingay, S. J., Goeke, R., Bowman, J. D., et al. 2013, PASA, 30, 7 [Google Scholar]
  85. Vacca, V., Oppermann, N., Ensslin, T. A., et al. 2015, in Proc. Advancing Astrophysics Square Kilometre Array (AASKA14), 114 [Google Scholar]
  86. van Weeren, R. J., Röttgering, H. J. A., Bagchi, J., et al. 2009, A&A, 506, 1083 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Vazza, F., & Brüggen, M. 2014, MNRAS, 437, 2291 [NASA ADS] [CrossRef] [Google Scholar]
  88. Vazza, F., Brunetti, G., & Gheller, C. 2009, MNRAS, 395, 1333 [NASA ADS] [CrossRef] [Google Scholar]
  89. Vazza, F., Dolag, K., Ryu, D., et al. 2011, MNRAS, 418, 960 [NASA ADS] [CrossRef] [Google Scholar]
  90. Vazza, F., Brüggen, M., Gheller, C., & Wang, P. 2014a, MNRAS, 445, 3706 [NASA ADS] [CrossRef] [Google Scholar]
  91. Vazza, F., Gheller, C., & Brüggen, M. 2014b, MNRAS, 439, 2662 [NASA ADS] [CrossRef] [Google Scholar]
  92. Vazza, F., Eckert, D., Brueggen, M., & Huber, B. 2015a, MNRAS, 451, 2198 [NASA ADS] [CrossRef] [Google Scholar]
  93. Vazza, F., Ferrari, C., Bonafede, A., et al. 2015b, in Proc. Advancing Astrophysics Square Kilometre Array (AASKA14), 97 [Google Scholar]
  94. Wang, P., Abel, T., & Kaehler, R. 2010, New A, 15, 581 [Google Scholar]
  95. Werner, N., Finoguenov, A., Kaastra, J. S., et al. 2008, A&A, 482, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Widrow, L. M., Ryu, D., Schleicher, D. R. G., et al. 2012, Space Sci. Rev., 166, 37 [NASA ADS] [CrossRef] [Google Scholar]
  97. Wright, E. L. 2006, PASP, 118, 1711 [NASA ADS] [CrossRef] [Google Scholar]
  98. Xu, H., Li, H., Collins, D. C., Li, S., & Norman, M. L. 2009, ApJ, 698, L14 [NASA ADS] [CrossRef] [Google Scholar]
  99. Zheng, Z., Ofek, E. O., Kulkarni, S. R., Neill, J. D., & Juric, M. 2014, ApJ, 797, 71 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

List of the simulations run for this project.

In the text
Table 2

Fiducial parameters for our simulated radio observations.

In the text

All Figures

thumbnail Fig. 1

3D rendering of the projected temperature (purple for T ≤ 105 K and red for T ≥ 105 K) and magnetic field intensity (yellow for B ≥ 10 nG and orange for B < 10 nG) for our simulated (50 Mpc)3 volume at z = 0, simulated with 24003 cells and DM particles.
In the text
thumbnail Fig. 2

Top panel: mass-weighted magnetic field maps for the HA and LA model, for the same volume as in Fig. 1. The colour bar is in units of log 10( [μG]). Bottom panel: phase diagrams on the (B,n/ncr) plane for the same models. We additionally draw isocontours increased tenfold in the number of cells contributing to the pixels in the phase diagrams, starting from 100 cells.
In the text
thumbnail Fig. 3

ξ(M,T) function we used to compute the acceleration of CR-electrons at shocks, based on Hoeft & Brüggen (2007).
In the text
thumbnail Fig. 4

Emission-weighted projected mean radio spectral index for a subregion with side 27 Mpc (and depth 50 Mpc) through our highest resolution volume, assuming the HA model for the magnetic field. The additional contours show the projected gas pressure for the same volume.
In the text
thumbnail Fig. 5

Radio distribution function for the clusters in our three simulated volumes at 1.4 GHz, using the LA model. No observational effects are considered in this case.

In the text
thumbnail Fig. 6

Radio distribution function for the clusters in our (100 Mpc)3 volume, normalised to Gpc3, for all investigated emission models. The additional grey lines show the range of the best fit to the distribution of radio relics based on the NVSS, computed by Nuza et al. (2012).
In the text
thumbnail Fig. 7

Radio emission from a subregion with side 27 Mpc (and depth 50 Mpc) through our highest resolution volume for the HA and LA magnetic field models (units of log 10[Jy/arcsec2] assuming a luminosity distance of 200 Mpc). The white contours show the projected gas pressure.
In the text
thumbnail Fig. 8

Mock observation of the (50 Mpc)3 volume using the configuration of LOFAR-HBA (Large Survey1, see Table 2) for increasing redshift (z = 0.05, z = 0.1 and z = 0.5) for the HA (left) and LA (right) magnetic field models. The blue and red regions show the emission that is detectable for each model and redshift, divided into emission coming from ≤1.5 rvir (blue) of each identified halo, or generated outside and therefore most likely related to filaments (red). The additional contours show the projected gas pressure. The units of the axes are given in cell units (Δx = 20.8 kpc).
In the text
thumbnail Fig. 9

Role of resolution in different radio surveys at low frequency. The colours show the detectable emission by different surveys at low frequency for the HA model (units of log 10 [Jy/arcsec2]), considering a field of view of 5° × 7°. The emission in each map has been convolved with the corresponding resolution beam. The white contours show the projected gas pressure.
In the text
thumbnail Fig. 10

Emission from our simulated light cone at z = 0.03, z = 0.05 and z = 0.5, obtained by stacking replicas of our (100 Mpc)3 and (200 Mpc)3 simulated volumes. The top panels show the total X-ray emission proxy (∝ n2T1/2) and the lower panels show the radio emission for LOFAR-LBA (units of log 10 [Jy/arcsec2]) for a projected area of 3.5° × 3.5°, assuming the high-amplification model (HA). The white contours of the X-ray emission proxy are drawn in the lower panels to allow a better comparison of structures.
In the text
thumbnail Fig. 11

Performance of different radio surveys observing a region of 14° × 14°. We simulated the whole radio-emitting volume from z = 0.02 to z = 0.5 and present for both models the radio emission from the ICM+WHIM (blue) or from the WHIM only (red), distinguishing the total emission (large squares) and the one detected by each survey configuration (small diamonds). All emissions have been rescaled by (110 MHz /ν [MHz]) for better comparison of surveys at different frequencies.
In the text
thumbnail Fig. 12

Maps of intracluster filaments in the (50 Mpc)3 volume at z = 0.05. The left panels show the projected mass-weighted magnetic field (HA model, units of log 10 [μG]), and the white contours give the projected gas density. The right panels show the intrinsic radio emission in the same model ([Jy/arcsec2]).
In the text
thumbnail Fig. 13

Profiles along the white line in the first panel of Fig. 12, showing the trend of mean gas density along the line of sight, the magnetic field (each colour represents a different model, with blue =LA and green =HA), intrinsic radio emission (same colour coding) and detectable radio emission assuming the sensitivity of LOFAR HBA Large Survey at 120 MHz (resolution of 25′′).
In the text
thumbnail Fig. 14

Same as Fig. 13, but for the second cluster association in the figure.
In the text
thumbnail Fig. 15

Similar to Fig. 7, but using the HSA model (high amplification and CR-driven dynamo).
In the text
thumbnail Fig. 16

Comparison of the emitted and detected radio emission for the same region of 14° × 14° as in Fig. 11, using SKA1-LOW. Each column shows the outcome of different models for the magnetic fields (HA, LA, and HSA) also without the contribution from re-accelerated electrons.
In the text
thumbnail Fig. A.1

Distribution of radio emission from the HA and the LA model in a cosmological run with CR-protons and including the effect of “secondary” radio emission from electrons injected by hadronic collision.
In the text
thumbnail Fig. A.2

Total radio emission from primary electrons injected by shocks (right) and from secondary electrons injected by hadronic collisions (left) in a subvolume of our 20483 simulation with CR-physics (Vazza et al. 2014b). The colour bar gives the emission in units of [log 10 W/Hz].
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.