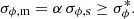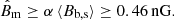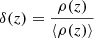| Issue |
A&A
Volume 679, November 2023
|
|
|---|---|---|
| Article Number | A107 | |
| Number of page(s) | 12 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202346303 | |
| Published online | 29 November 2023 | |
Constraints on the magnetic field in the intercluster bridge A399–A401
1
INAF – IASF Milano, via A. Corti 12, 20133 Milano, Italy
e-mail: marco.balboni@inaf.it
2
DiSAT, Università degli Studi dell’Insubria, via Valleggio 11, 22100 Como, Italy
3
DIFA – Università di Bologna, via Gobetti 93/2, 40129 Bologna, Italy
4
INAF – IRA, Via Gobetti 101, 40129 Bologna, Italy
5
Department of Physics and Electronics, Rhodes University, PO Box 94, Makhanda 6140, South Africa
6
South African Radio Astronomy Observatory (SARAO), Black River Park, 2 Fir Street, Observatory, Cape Town 7925, South Africa
7
Hamburger Sternwarte, Gojenbergsweg 112, 21029 Hamburg, Germany
8
Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
9
ASTRON, the Netherlands Institute for Radio Astronomy, Postbus 2, 7990 AA Dwingeloo, The Netherlands
10
INAF – Osservatorio Astronomico di Cagliari, via della Scienza 5, 09047 Selargius (CA), Italy
Received:
2
March
2023
Accepted:
13
September
2023
Galaxy cluster mergers are natural consequences of structure formation in the Universe. Such events involve the dissipation of a large amount of energy (∼1063 erg) during the process. Part of this energy can be channelled in particle acceleration and magnetic field amplification, enhancing non-thermal emission of the intra- and intercluster environment. Recently, low-frequency observations led to the detection of a bridge of diffuse synchrotron emission connecting two merging galaxy clusters, Abell 399 and Abell 401. This result provides clear observational evidence of relativistic particles and magnetic fields in between clusters. In this work, we used LOw Frequency ARray (LOFAR) observations at 144 MHz to study the polarised emission in the A399–A401 bridge region for the first time. No polarised emission was detected from the bridge region. Assuming a model where polarisation is generated by multiple shocks, depolarisation can be due to Faraday dispersion in the foreground medium with respect to the shocks. We constrained its Faraday dispersion to be greater than 0.10 rad m−2 at 95% confidence level, which corresponds to an average magnetic field in the bridge region of greater than 0.46 nG (or 0.41 nG if we include regions of the Faraday spectrum that are contaminated by Galactic emission). This result is largely consistent with the predictions from numerical simulations for megaparsec regions where the gas density is about 300 times higher than the mean gas density.
Key words: magnetic fields / galaxies: clusters: general / radiation mechanisms: non-thermal / polarization / techniques: interferometric
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Galaxy clusters are the most massive gravitationally bound structures in the Universe. They are the natural outcome of the hierarchical process of structure formation, where clusters grow through merger events and the accretion of small substructures. This accretion process occurs inside the so-called cosmic web, which is made of elongated filaments of matter (galaxies, dark matter, and magnetised gas called warm hot intergalactic medium, WHIM) located between clusters and through which matter flows and collapses onto such objects.
In recent decades, non-thermal, diffuse radio emission has been widely observed in galaxy clusters, implying particle reacceleration on clusters scales (e.g. van Weeren et al. 2019, for a recent observational review). Merger events could provide the energy necessary for particle reacceleration (e.g. Brunetti & Jones 2014, for a theoretical review). The most striking examples of these processes in clusters are giant radio halos and relics, which have been widely used to study the intracluster medium (ICM) in the inner regions of clusters. The new generation of radio telescopes have been key to revealing that the diffuse radio emission from clusters is more extended than previously reported (e.g. Rajpurohit et al. 2021a,b; Botteon et al. 2022; Cuciti et al. 2022), showing its presence even outside the cluster regions in the form of bridges (e.g. Govoni et al. 2019; Botteon et al. 2020; Venturi et al. 2022).
The origin of the observed (∼μG) magnetic fields that accelerate particles within clusters and beyond remains largely uncertain. A commonly accepted hypothesis is that these fields result from the amplification of much weaker pre-existing seeds via shock or compression and/or turbulence or dynamo mechanisms during merger events and structure formation. Therefore, magnetic fields will emerge with different intensities at different physical scales as the result of turbulent motions (see Donnert et al. 2018; Vazza et al. 2021, for reviews on magnetic field amplification at cluster scales). The origin of seed fields can either be primordial – that is, generated in the early Universe prior to recombination – or produced locally at later epochs of the Universe in early stars and/or (proto)galaxies before being injected into the interstellar and intergalactic medium (e.g. Widrow et al. 2012; Subramanian 2016, for reviews). Another source of magnetic field seeds can be the feedback events following gas cooling and the formation of primary structures, such as stellar populations or black holes. These astrophysical sources can inject magnetic fields inside circumgalactic medium and cosmic voids at z ≤ 10 in an inside-out scenario from galaxies to larger scales (e.g. Vazza et al. 2021). A possible way to discriminate between models might be to estimate the magnetic field strength in rarefied environments, such as filaments, sheets, and voids. Simulations indeed show that magnetic field profiles resulting from different models tend to diverge beyond the periphery of galaxy clusters because of the model-dependent efficiency in producing large-scale magnetic field (Vazza et al. 2017). Despite the difficulty in observing such faint filamentary emission outside clusters at radio wavelengths, previous works constrained the magnetic field strength (up to a few tens of nG) on scales larger than typical cluster sizes (≳Mpc; Neronov & Vovk 2010; Pshirkov et al. 2016; Brown et al. 2017; Vernstrom et al. 2017; Paoletti & Finelli 2019; Natwariya 2021). Different observational approaches have been identified in order to study large-scale magnetic fields. One promising example is the Faraday rotation technique (e.g. Govoni & Feretti 2004), which estimates the line of sight magnetic field. Exploiting this effect, Vernstrom et al. (2019) studied the emission from extragalactic sources and placed an upper limit on the cosmic magnetic field strength at 40 nG. Similarly, O’Sullivan et al. (2020) used an analogous technique to study prospective or real pairs of sources, obtaining upper limits on the comoving cosmological magnetic field (B0) of B0 ≤ 4 nG on megaparsec scales. Carretti et al. (2022) recently used ∼144 MHz observations of several filaments to study the Faraday rotation properties of low-density regions and their evolution with redshift, deriving an average magnetic field of Bf = 32 ± 3 nG in filaments. In a follow-up work, Carretti et al. (2023) compared LOFAR observations with magnetohydrodynamical (MHD) cosmological simulations and found that the magnetic field in cosmic web filaments at z = 0 is in the 8 − 26 nG range for a typical filament gas overdensity1 of δg = 10. Vernstrom et al. (2021) used pairs of luminous red galaxies as a tracer of cluster pairs. Using a stacking technique, these latter authors estimated the intensity of the magnetic field on 1 − 15 Mpc scales to be in the 30 − 60 nG range. This result implies that primordial magnetic field seeds should be more than a factor of approximately 6 stronger than the simulated ones using only shock acceleration (see also Hodgson et al. 2022). With a different approach (injection), Locatelli et al. (2021) combined upper limits on the radio emission from two intercluster filaments and numerical simulations of the magnetic cosmic web in order to constrain the intergalactic magnetic field in the 0.2 − 0.6 μG range on 10 Mpc scales. Even more recently, Vernstrom et al. (2023) used stacking to derive information on polarised emission and magnetic field in the peripheries of clusters and intercluster filaments. These authors found a diffuse polarised emission with a ∼20% polarised fraction, which can be attributed to a Fermi-type reacceleration process as a consequence of large-scale accretion, and implies an ordered magnetic field.
Recent low-frequency (∼140 MHz) observations with LOFAR led to the detection of diffuse synchrotron emission (a radio bridge) connecting the two merging galaxy clusters, Abell 399 and Abell 401 (Govoni et al. 2019), providing observational evidence of relativistic particles and magnetic fields in the intercluster region. The origin of the non-thermal emission is still uncertain, although it could be caused by multiple weak shocks present in the bridge region that reaccelerate a pre-existing population of mildly relativistic particles (Govoni et al. 2019). Alternatively, turbulent reacceleration in the early phases of the merging event could amplify magnetic fields and reaccelerate particles (Brunetti & Vazza 2020). In this work, we used new LOFAR observations to study the polarised emission of the A399–A401 radio bridge, and provide constraints on the magnetic field in the bridge. The paper is organised as follows: in Sect. 2, we describe the target, its properties, and past studies; in Sect. 3, we present the observations, data reduction, and imaging process used in this work; in Sect. 4, we constrain the Faraday dispersion of the depolarisation mechanism that we use to constrain the average intensity of the magnetic field in Sect. 5. We provide conclusions in Sect. 6. Following Nunhokee et al. (2023), we used the Planck cosmology throughout our work (Planck Collaboration VI 2020), where 1″ = 1.345 kpc at the cluster pair distance.
2. The A399–A401 pair
A399 and A401 are two massive galaxy clusters separated by a projected distance of ∼3 Mpc, both hosting a radio halo (Murgia et al. 2010) that is likely powered by matter accretion. Radio, optical, and X-ray observations support the scenario where the system is in the initial phase of a merger and the two clusters have not yet started to interact (e.g. Fujita et al. 1996; Sakelliou & Ponman 2004; Murgia et al. 2010; Govoni et al. 2019). X-ray observations reveal the presence of hot gas (∼7 − 8 keV) not only inside the central parts of the two objects but also in the connecting intercluster region (6.5 keV), which shows enhanced X-ray emission (Akamatsu et al. 2017). Moreover, observations of the Sunyaev-Zeldovich (SZ; Sunyaev & Zeldovich 1969) effect confirmed the presence of a connecting bridge between the two clusters (Planck Collaboration Int. VIII 2013; Bonjean et al. 2018; Hincks et al. 2022). Information about the system is summarised in Table 1.
Summary of the main characteristics of the A399–A401 pair.
Govoni et al. (2019) studied the A399–A401 cluster pair, detecting both diffuse and compact radio emission. These authors also discovered radio emission connecting the two radio halos, providing evidence of relativistic electrons and magnetic fields on megaparsec scales in the intercluster environment. Nunhokee et al. (2023) used observations at 346 MHz – where they did not detect the bridge – in order to constrain the average bridge spectral index to be α > 1.5 at 95% confidence level. Even more recently, de Jong et al. (2022) and Radiconi et al. (2022) investigated the thermal and non-thermal intercluster emission of the pair. Radiconi et al. (2022) did not find any correlation between radio and X-ray emission. Instead, with deeper observations and an improved calibration method, de Jong et al. (2022) found a positive trend between the thermal and non-thermal emission in the bridge. Although the spectral index constraints disfavour the scenario where particles are accelerated by weak shocks, no stringent conclusions about the emission model or constraints on the magnetic field in the bridge region have been obtained so far.
3. Observations and data analysis
Observations used in this work are part of the LOFAR Two-meter Sky Survey (LoTSS; Shimwell et al. 2017, 2019, 2022), a deep, 120 − 168 MHz survey of the Northern sky with a ∼100 μJy beam−1 sensitivity at ∼6″ resolution. The A399–A401 pair was observed within a single LoTSS pointing for 8 h, divided into two sets of 4 h each due to its low declination (δ ∼ 13°; see Table 2). Each 4 h set was followed by 10 minutes of calibrator observations, using 3C196. As we are performing polarisation studies, the direct combination of both observations would likely introduce depolarisation if not properly corrected for the likely different polarisation angle. For this reason, we only used one of the two tracks, n. L576817.
Description of the available observations.
We used the visibilities calibrated by the PREFACTOR3 pipeline (de Gasperin et al. 2019) and by the direction-independent calibration in the LoTSS-DR2 pipeline (Shimwell et al. 2022). The polarisation calibration process applied to our data is the standard LOFAR calibration adopted by the Magnetism Key Science Project (MKSP). For further details on the LoTSS polarised products, the readers may consult Shimwell et al. (2022) and O’Sullivan et al. (2023), or past works such as Vernstrom et al. (2018), O’Sullivan et al. (2020, 2023), Pomakov et al. (2022).
During the calibration process, the integrated polarisation over the field of view is assumed to be negligible. While this is usually a valid assumption at low frequencies, it does not consistently hold in our field because of the presence of a strong polarised source. We nevertheless retained the standard assumption, with the caveat that it may lead to a bias in the polarisation properties of strong, compact sources. As we clarify below, this has no impact on our analysis, as we are interested in the polarised emission of the bridge. The total frequency coverage (120 − 168 MHz) is subdivided into 480 channels, each of them ∼97 kHz in width. Such high-frequency sampling allows us to use the rotation measure (RM; Brentjens & de Bruyn 2005) synthesis technique, which minimises bandwidth depolarisation in reconstructing the polarised emission (Brentjens & de Bruyn 2005).
3.1. Imaging
LoTSS pointings have a field of view of 3° −4° (full width at half maximum), depending on the wavelength. The area covered by the bridge is ∼ 0.05 deg2, and therefore in order to speed up the subsequent steps, we select the data corresponding to the bridge region with a procedure called ‘extraction’ (see van Weeren et al. 2021). From the visibilities, we subtract the model components corresponding to sources outside the bridge as far out as 6 deg2. Therefore, our final dataset contains the emission from the region close to the A399–A401 pair. After the subtraction, we compute the primary beam correction towards the target coordinates and apply it directly to the visibilities. We then proceed to image both total intensity and polarised emission. Calibrated visibilities are imaged using WSCLEAN V2.10.0, which allows us to perform multi-scale and multi-frequency deconvolution (Offringa et al. 2014; Offringa & Smirnov 2017). Initially, we make images at 6″ and 20″ angular resolution: as no evidence of bridge emission is visible at 20″ resolution, we further reduce the resolution down to 107″, where we obtain a clear detection of the bridge (Fig. 1). Following Govoni et al. (2019), we extract the radial surface brightness profile as made by Govoni et al. (2019) after subtracting sources embedded in the bridge region and masking out the sources not related to the radio ridge (white areas in Fig. 2, detected using PYBDSFMohan & Rafferty 2015 when considering all the emission above 5 × RMS, and by visually inspecting the results to check whether or not there is residual unmasked emission clearly associated with compact source).
 |
Fig. 1. Image of the A399–A401 pair at 144 MHz. The 107″ × 107″ restoring beam is shown in white in the bottom left corner. Black contours are drawn at 4, 20, 40, 80, 160, and 320 × RMS, where the RMS is 620 μJy beam−1. |
 |
Fig. 2. Bridge emission profile after masking of unrelated sources. Upper panel: compact source-subtracted image (see Sect. 4 and Fig. 6) with non-bridge sources masked out (white ellipses). A white line grid is used to measure the bridge brightness profile. The grid is tilted by 25° and has the same reference point (centre) as Govoni et al. (2019). The lines are separated by 144 kpc (one beam width) and their length is 3 Mpc. Lower panel: surface brightness profile extracted by measuring the average surface brightness in each slice. |
We report an average surface brightness of ⟨I⟩143 MHz = 4.29 ± 0.06 mJy beam−1 and a S143 MHz = 429 ± 6 mJy flux density for the bridge (considering 100 beams in the selected region). Compared with Govoni et al. (2019), our flux density and surface brightness measurements are ≈20% lower. This difference may be due to the different calibration procedures and/or differences between the two observations, although it does not affect the remainder of our analysis.
The shortest baseline, uvmin, of our observations is ∼35 m (or ∼18λ), implying that the largest angular size structure detectable is ∼3.5°. This is much larger than the projected distance between the two clusters (∼0.62°), and therefore we do not expect diffuse emission to be filtered out. We finally generate total intensity and polarisation images at 6″, 20″, and 107″ respectively.
3.2. Polarisation and rotation measure synthesis recap
Synchrotron polarised radiation can be generally described in terms of Stokes I, Q, U, and V parameters, which can be used to represent the orientation and intensity of the incoming electric field. We define the complex linear polarisation P as:
where Ψ is the observed polarisation angle (e.g. O’Sullivan et al. 2012). The degree of linear (V = 0) polarisation p is
and the polarisation angle Ψ is
When a linearly polarised wave propagates through a magnetised plasma extending over a path length L, the intrinsic polarisation angle Ψ0 is rotated by an angle ΔΨ. This effect is called Faraday rotation and can be described by introducing the Faraday depth ϕ (Burn 1966; Brentjens & de Bruyn 2005):
where ne is the electron number density in cm−3, B the magnetic field in μG, and dl is the infinitesimal path length in parsecs. In the case where the polarised radiation is emitted by a background source and the rotation is only due to a foreground magneto-ionic medium, the source is said to be ‘Faraday thin’ and the variation in the polarisation angle ΨO can be written as:
In this work, we adopt this technique for our analysis.
In the simplest case, where only Faraday rotation occurs, the complex polarisation P can be written as
where p0 is the intrinsic degree of polarisation of the synchrotron emission and ϕ describes the Faraday rotation caused by the foreground magneto-ionic medium. The RM synthesis technique takes advantage of the similarity between Eq. (6) and a Fourier transform relationship by introducing the Faraday dispersion function (FDF) F(ϕ), or Faraday spectrum:
where
and therefore we can measure or recover the amount of polarised emission of a source once its radiation has been derotated to a given Faraday depth. Brentjens & de Bruyn (2005) also introduce the rotation measure transfer function (RMTF), which is the Fourier transform of the wavelength sampling function (W(λ2)). In particular, a few specifications of an observation define some of the characteristics of the measured Faraday spectrum: the λ2 coverage (Δλ2) defines the resolution in Faraday space (δϕ), and the wavelength resolution of the observation (δλ2) sets the maximum observable Faraday depth (ϕmax). Also, the largest scale in ϕ space to which the observation is sensitive depends on the shortest wavelength 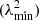 :
:
In our observations, the shortest wavelength is ∼1.79 m – which corresponds to a ∼1.76 rad m−2 max-scale2 – the resolution is δϕ ≃ 1.17 rad m−2, and the maximum observable Faraday depth is ||ϕmax|| ≃ 170 rad m−2.
We compute the Faraday spectrum cube from the 107″ resolution polarisation images (RMSQ,U ∼ 0.18 mJy beam−1) using a publicly available RM synthesis code (Purcell et al. 2020)3 and considering the average of the amplitude of the polarised emission over the bridge region (Fig. 3).
 |
Fig. 3. Faraday depth amplitude averaged over all the lines of sight within the bridge region at 107″ resolution. Two peaks can be seen, which are due to the Galactic foreground medium and the instrumental leakage, respectively. |
Most of the Faraday depth cube shows no emission, with the exception of diffuse emission that spans a large area of the field of view and peaks at ϕ ∼ 7.5 rad m−2 (Fig. 4). This emission is largely uncorrelated with the total intensity emission and appears at relatively small Faraday depths, which are typical characteristics of the Galactic emission at low frequencies (e.g. Bernardi et al. 2013; Van Eck et al. 2019; Erceg et al. 2022). We note that this Galactic foreground partially extends over the bridge region, although most of its emission appears outside of it. Figure 3 shows the FDF amplitude averaged over the bridge region, which is defined as the 4σ contour total intensity emission (Fig. 1). The Galactic foreground peak is clearly visible, together with a fainter, second peak at ϕ = ϕinstr ≈ 2.1 rad m−2 which is likely due to instrumental leakage that is not corrected by our calibration procedure. Such instrumental features are not uncommon in LOFAR observations and can appear up to ±3 rad m−2 (e.g. O’Sullivan et al. 2019). No polarised emission from the bridge region is visible in the Faraday spectrum at any depth above the noise. We use this lack of detection in the following sections to constrain the bridge emission mechanism and magnetic field.
 |
Fig. 4. Slice of the FDF cube at ϕ ∼ 7.5 rad m−2 showing the Galactic polarised emission detected in the field. Total intensity is overlaid with contours at 4, 20, 40, and 80 × RMS taken from Fig. 1. |
4. Polarisation analysis
The absence of polarised emission from the bridge can be used to place constraints on its magnetic field and, in turn, its origin.
4.1. Simulation expectations
First, we test whether our observations are consistent with the prediction from the shock model proposed by Govoni et al. (2019) to explain the origin of the bridge. These authors suggested that such intercluster radio emission may be the result of gas (re)energisation and magnetic field amplification from several weak shocks (M ∼ 2 − 3) originated in the initial merger phase. In the adopted simulation of this system, a large distribution of weak shock waves – occupying a large volume filling factor (∼1%) and an even larger surface filling factor (≥30%) when seen in projection – forms as an effect of the supersonic turbulence developed in this region. These shocks may or may not emit synchrotron radiation, depending on the distribution of the relativistic electrons in the region. In particular, Govoni et al. (2019) found that a pre-existing, mildly relativistic population of electrons could be reaccelerated by shocks and generate radio emission over the bridge extension that, in turn, ought to be polarised to some extent (we refer the readers to Govoni et al. 2019, for further details about the emission model).
A model of polarised emission from the bridge P(x, y, ν), where (x, y) are sky directions and ν is the frequency, can be generated if the total intensity I(x, y), the polarisation fraction p(x, y), and the polarisation angle Ψ(x, y) are known (Eq. (1)). We derive a total intensity template I(x, y) from our total intensity observations. We first subtract bright sources located within or just around the bridge area (Fig. 5). We then generate low-resolution residual images where we eventually masked out all the pixels outside the bridge area defined by the 5σ contours (Fig. 6).
 |
Fig. 5. Zoom onto the bridge field. Highlighted are the sources subtracted in order to retrieve the bridge emission model. Contours are drawn at 5 × RMS, where RMS ∼ 350 μJy beam−1. The image has a 20″ resolution. |
 |
Fig. 6. Image of the A399–A401 pair at 144 MHz once the sources within and around the bridge are subtracted (Fig. 5). The region chosen to obtain the bridge emission model is highlighted in yellow. The 107″ × 107″ restoring beam is shown in white in the bottom left corner. The RMS of the image is ∼650 μJy beam−1, with contours at 4, 10, 40, and 80 × RMS. |
Here, we compare our results with a cosmological simulation of a merging galaxy cluster. This simulation has been run with the ENZO-code and is part of a larger suite of cosmological simulations that have been extensively studied in Vazza et al. (2018) and Domínguez-Fernández et al. (2019). Here, we analyse the cluster E5A, and for details on the simulation, we refer to the cited publications. The cluster E5A is undergoing an active merger, and throughout its formation, it hosts a bridge region similar to the one in the A399–A401 system. It is therefore an ideal candidate for comparison. We can detect the shock waves in the simulation using a velocity-based shock finder (Vazza et al. 2009). Following the approach of Wittor et al. (2019b), we compute the polarised and unpolarised radio emission associated with electrons undergoing diffusive shock acceleration (DSA) in the bridge region. Eventually, we find a polarisation fraction close to the 70% theoretical limit across the whole simulation volume (see also Vazza et al. 2018; Wittor et al. 2019b, for details of the simulation). However, after convolving the Q and U simulated data cube to the resolution of our images, we obtain an average polarisation fraction of ∼30%. Therefore, we assume a constant p = 30% across the bridge area (we also consider the limiting case of an intrinsic polarisation of 10%).
Finally, for simplicity, we assume Ψ(x, y) = 0 and a constant Faraday depth ϕ across the bridge, which is the case where polarised emission is Faraday thin. In order to avoid any confusion with Galactic emission, we consider a constant ϕ ≫ ϕgal = 7.5 rad m−2, specifically ϕ = 20 rad m−2, across the bridge. Under these assumptions, complex polarised emission P can be generated following Eq. (6):
In practice, we want to simulate Stokes Q and U parameters as they are what we observe. We generate Q and U model images of the bridge following Eq. (13):
then Fourier transform and add (‘inject’) them to our visibility data after point sources have been subtracted (similar to the procedure in Venturi et al. 2008; Bonafede et al. 2017; Locatelli et al. 2021; Nunhokee et al. 2023). Visibilities are then imaged following the same procedure as for the real data, but this time averaging in frequency over 100 channels in order to reduce computing time. This choice reduces ϕmax to be ∼35 rad m−2, which is still adequate for our simulations.
Results of the injections are shown in the first panels of Figs. 7 and 8. The Faraday spectrum in Fig. 8 is different from that shown in Fig. 3 as we sum the amplitudes of the Faraday spectra over the bridge region:
 |
Fig. 7. Slices of the Faraday spectrum cube at ϕ = 20 rad m−2 as a function of Faraday dispersion σϕ, obtained from the injection of the bridge polarised emission model in the data; see text for details. It is evident that the bridge polarised emission decreases as the Faraday dispersion increases until it completely disappears when σϕ = 0.18 rad m−2. The top left panel is the case where no depolarisation occurs, but only the rotation of the injected signal. |
 |
Fig. 8. Examples of FDFs of the bridge region as a function of Faraday dispersion σϕ after injection of the depolarisation model into the data; see text for details. The peak at 20 rad m−2 decreases until it completely disappears below the nose for the σϕ = 0.18 rad m−2 model. |
where x indicates the pixel coordinates and the sum runs over the total number of pixels N of the bridge. Hereafter, we refer to this quantity as the FDF.
Figure 8 shows that the injected signal is detected in our data with a signal-to-noise ratio (S/N)≈100, and if present in our data it would have been clearly detected. Therefore, the absence of any polarised signal indicates that the emission generated in the weak shock scenario must be depolarised. Given the large scale of the emission, this is not surprising; however, under some assumptions, it allows us to put constraints on the magnetic field.
4.2. Constraints on the depolarisation mechanism
Depolarisation refers to a process that reduces the intrinsic degree of polarisation of a source. Two typical cases of depolarisation are beam and bandwidth depolarisation. The first occurs when the polarisation angle changes significantly on scales smaller than the beam size. In this case, Stokes Q and U parameters change their sign and their integral over the beam area is smaller than in the case where the polarisation angle is uniformly distributed.
Bandwidth depolarisation occurs when the polarisation angle changes significantly over the observing band; which is the case for sources with high RM. In this case, similarly to the beam polarisation effect, the polarised intensity integrated over the bandwidth is smaller than the case where no rotation occurs.
The two aforementioned mechanisms are of instrumental origin, but depolarisation can have a physical origin and can provide information about the physics of the source itself. A depolarisation effect that is of interest in our case occurs in the presence of a turbulent magnetic field in front of an emitting source, when spatial magnetic field fluctuations can be considered Gaussian. If the typical scale of turbulence of the magnetic field is smaller than the resolution element of the observation, the complex polarisation P then becomes (e.g. Sokoloff et al. 1998; O’Sullivan et al. 2012):
where σϕ is the Faraday dispersion, which quantifies spatial fluctuations of the Faraday depth due to the magnetic field variations. We note that the polarisation amplitude is reduced by a factor 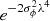 with respect to Eq. (13), which is strongly wavelength dependent. This case is referred to as depolarisation due to external Faraday dispersion (e.g. Tribble 1991). We consider external Faraday dispersion as a depolarisation mechanism in our case. In particular, we retain the assumption that the polarised emission is Faraday thin, that is, the shock width is much smaller than the bridge. In addition, our observations are not sensitive to Faraday-thick structures, and therefore we dismiss the case of internal Faraday depolarisation. In this framework, the magnetic field fluctuations in front of the shocks are responsible for the depolarisation. Our observations can therefore place a lower limit on σϕ; that is, the minimum magnetic field fluctuation in the foreground screen necessary to completely depolarise the bridge signal.
with respect to Eq. (13), which is strongly wavelength dependent. This case is referred to as depolarisation due to external Faraday dispersion (e.g. Tribble 1991). We consider external Faraday dispersion as a depolarisation mechanism in our case. In particular, we retain the assumption that the polarised emission is Faraday thin, that is, the shock width is much smaller than the bridge. In addition, our observations are not sensitive to Faraday-thick structures, and therefore we dismiss the case of internal Faraday depolarisation. In this framework, the magnetic field fluctuations in front of the shocks are responsible for the depolarisation. Our observations can therefore place a lower limit on σϕ; that is, the minimum magnetic field fluctuation in the foreground screen necessary to completely depolarise the bridge signal.
We follow the same procedure as that described earlier to generate Stokes Q and U parameters, with the only difference being that we added the depolarisation term to Eq. (13), that is,
where in this case, ϕ(x, y) is a realisation drawn from a Gaussian distribution with a mean of 20 rad m−2 and a standard deviation of σϕ. Performing the injection steps described above, we obtain a Faraday spectrum cube for each value of σϕ taken in the 0 − 0.24 rad m−2 range, with steps of 0.03 rad m−2. The results for a few selected σϕ values are shown in Figs. 7 and 8. The σϕ = 0 rad m−2 case has been discussed previously and shows that the polarised emission from a weak shock model should be visible in our data in case of Faraday rotation without depolarisation. As σϕ increases, the polarised emission quickly decreases, until it completely disappears when σϕ = 0.18 rad m−2. This is also evident in the FDF profile, which becomes consistent with noise in the σϕ = 0.18 rad m−2 case. These results imply that a minimum value of σϕ = σ* < 0.18 rad m−2 must therefore exist below which the signal is not sufficiently depolarised and should be visible in our observations. In order to estimate such a lower limit on σϕ, we follow a procedure similar to that used by Nunhokee et al. (2023) and calculate the cumulative distribution function of the following ratio:
where 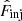 and
and 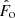 are the injected and observed FDF, respectively, and ϕ1 = 15 rad m−2 and ϕ1 = 25 rad m−2. In other words, the ratio Pexc is the excess of the injected polarised emission with respect to the data as a function of σϕ– calculated in a region centred on the average injected Faraday depth ϕ = 20 rad m−2.
are the injected and observed FDF, respectively, and ϕ1 = 15 rad m−2 and ϕ1 = 25 rad m−2. In other words, the ratio Pexc is the excess of the injected polarised emission with respect to the data as a function of σϕ– calculated in a region centred on the average injected Faraday depth ϕ = 20 rad m−2.
We note that
which means Pexc is a monotonically decreasing function of σϕ. We find a probability F(Pexc < 0.95) for 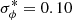 rad m−2 (Fig. 9); in other words, if the σϕ is smaller than 0.10 rad m−2, polarised emission should be detected in our data with a 95% confidence level (or greater). As there is no detection, our observations set a limit on the Faraday dispersion of σϕ > 0.10 rad m−2 at 95% confidence level. In the following section, we turn this lower limit into a lower limit on the magnetic field in the bridge.
rad m−2 (Fig. 9); in other words, if the σϕ is smaller than 0.10 rad m−2, polarised emission should be detected in our data with a 95% confidence level (or greater). As there is no detection, our observations set a limit on the Faraday dispersion of σϕ > 0.10 rad m−2 at 95% confidence level. In the following section, we turn this lower limit into a lower limit on the magnetic field in the bridge.
 |
Fig. 9. Normalised cumulative distribution F(Pexc) as a function of σϕ, with the polarised emission from the bridge injected at ϕ = 20 rad m−2. The red line indicates the threshold value of σϕ at which the cumulative distribution function is 95%. |
5. Constraints on the bridge magnetic field
The lower limit on the Faraday dispersion σϕ can be translated into a limit on the magnetic field using the relation between Faraday depth and magnetic field (Eq. (4)). The standard deviation σϕ of the spatial distribution of the Faraday depth ϕ is defined as:
where x indicates the line of sight (or spatial coordinate) and ⟨⟩ is the average ensemble. By using the definition of Faraday depth (Eq. (4)), Eq. (21) becomes:
where L becomes, in our case, the line-of-sight depth of the bridge. Equation (22) shows that the standard deviation of the Faraday depth is a function of the (density-weighted) fluctuations of the magnetic field, and therefore a lower limit on the standard deviation of the Faraday depth imposes a lower limit on the spatial fluctuations of the magnetic field. In order to derive such a lower limit we make a few simplifying assumptions. Firstly, we do not consider the electron density as a free parameter, but assume it from the cluster simulation (Domínguez-Fernández et al. 2019; Wittor et al. 2019a). We also assume the magnetic field from the cluster simulation but we allow it to be scaled by an overall, spatially independent factor α. A theoretical Faraday dispersion σϕ, m can therefore be computed from the simulation:
where the subscript s indicates all quantities derived from the cluster simulation and α is the free parameter constrained by the observational lower limit on σϕ, that is,
The standard deviation of the Faraday depth from the cluster simulation is computed by identifying a region similar to the observed bridge. Here, we consider the electron density cube of the Wittor et al. (2019a) simulation (shown by white contours in Fig. 2 in their work). We then select the intercluster region so that it has a physical dimension equal to the one defined through observations (the final region is highlighted in red in Fig. 10). We compute the Faraday depth for each pixel of the selected region by integrating the density-weighted magnetic field and then we smooth the Faraday depth map at the same resolution as the observed bridge, that is 107″, corresponding to a 144 kpc physical size (Fig. 11). We derive the simulated Faraday dispersion σϕ,s from the map and substitute it into Eq. (24) in order to obtain α ≥ 7.2 × 10−3 (where as σϕ,m we use the observational limit derived in Sect. 4.2). In other words, the simulated Faraday dispersion is already higher than the observed lower limit, which is consistent with the injection results from Sect. 4.
 |
Fig. 10. Central slice of the cube density from simulations. Moving towards the density cube, the average density of the medium initially increases, indicating the presence of the cluster pair, then starts to decrease until reaching zero in the last slice, showing the ending regions of the cluster pair. We therefore selected the central slice of the cube as the best indicator of the density distribution. The density contours are at 1, 1.24, 2.61, 10.3, and 53.5 × 10−28 g cm−3. The region selected as the bridge region in the simulation is highlighted in red. Every pixel is ∼16 kpc long. |
 |
Fig. 11. Faraday-depth map obtained using the cluster simulation (Wittor et al. 2019a; see text for details). The contours are from the density field in Fig. 10, and the selected bridge region is highlighted in red. Every pixel is ∼16 kpc in length. |
The lower limit on the model parameter α can be turned into a lower limit on the average magnetic field in the bridge region, indeed assuming that α is a scaling factor of the magnetic field in the cluster simulations (Eq. (23)). In order to find the average magnetic field along the bridge extension, we first compute the total magnetic field intensity in each pixel from the simulated cube. We then derive the density-weighted average magnetic field intensity for each layer of the cube and, eventually, average these values across all layers, obtaining a mean magnetic field intensity of ⟨Bb, s⟩ = 0.064 μG for the bridge region. The distribution of the magnetic field intensity along the selected bridge region in the simulation cube is shown in Fig. 12. This procedure allows us to set a lower limit on the mean magnetic field in the bridge region 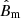 :
:
 |
Fig. 12. Distribution of the density-weighted average magnetic field intensity of each layer of the simulation cube. The average value of all the layers is indicated by the orange line. |
We also derive the magnetic field limit by considering a lower limit polarised fraction of 10%. This turns into a lower limit of σϕ > 0.09 and a consequent magnetic field limit of Bb, s ≥ 0.41 nG.
5.1. Instrumental and Galactic peak injection
Above, we inject the bridge at ϕ = 20 rad m−2, away from the instrumental and Galactic Faraday depth peaks. In this section, we relax this assumption in order to derive upper limits on the Faraday dispersion and bridge magnetic field in the presence of Galactic and instrumental ‘contamination’.
We follow the same injection procedure as that described in Sects. 4.2 and 5, simulating Stokes Q and U visibilities from the cluster simulations, only this time at ϕ = 7.5 rad m−2, which is the Faraday depth where the maximum of the Galactic emission appears. By applying the same procedure as in the previous sections, we are assuming no significant contribution from the bridge to the real Faraday spectrum (Fig. 3) and that the polarised emission is due only to the Galactic foreground. As shown in Fig. 4, the galaxy polarised emission is clearly prevalent in the field. Furthermore, from this image, it is evident that when we increase the region within which the Faraday spectrum is being extracted, the Galactic polarised peak becomes even more dominant than in Fig. 3. In conclusion, we cannot completely rule out a minimal contribution from bridge polarised emission, but it is reasonable to assume that such emission is negligible with respect to the strong Galactic one.
As in the previous analysis, we constructed a cumulative probability function for depolarisation models that samples the 0 ≤ σϕ ≤ 0.24 rad m−2 range (as in Sect. 4.2) and set an upper limit to the Faraday dispersion σϕ ≥ 0.09 rad m−2 at 95% confidence level.
We repeat the same procedure for the instrumental case, where we injected the simulated polarised signal at ϕ = 2.1 rad m−2, the Faraday depth at which the instrumental leakage appears. In this case, we set an upper limit σϕ ≥ 0.10 rad m−2 at 95% confidence level.
Both limits are somewhat lower than the case where the signal was injected in the featureless part of the Faraday spectrum, as qualitatively expected. If we take the lowest of the two limits, we derive a slightly lower limit on the mean magnetic field of the bridge, 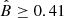 nG.
nG.
5.2. Comparison with equipartition results
It is useful to compare our upper limits to the standard estimate that can be obtained via the standard equipartition assumption, that is, of a minimum energy of the relativistic plasma. The equipartition magnetic field Beq can be derived following Govoni & Feretti (2004, Eqs. (25) and (26)), and assuming a spectral index α = 1.4, a bridge size of 1 Mpc, and a filling factor of unity. We obtained Beq = 0.24 μG, which is well above our lower limit. We also note that, considering the thin shock scenario, the filling factor is likely to be smaller than one, leading to a higher equipartition magnetic field, which is still consistent with our limit. Finally, it is also worth noting that the equipartition magnetic field is approximately three times larger than values found in intercluster regions (Hoang et al. 2023).
6. Discussion and conclusions
In this paper, we present a radio polarisation study of the merging cluster pair Abell 399–Abell 401. Govoni et al. (2019) studied this system through LOFAR observations at 144 MHz, and found the first evidence of a radio bridge connecting the two clusters. The authors suggested a shock-driven emission model, where multiple weak shocks originated by the motion of the clusters during the merging event reaccelerate a pre-existing population of electrons, triggering the radio emission. Considering the proposed scenario, numerical simulations suggested that the emission can be ∼70% polarised (Wittor et al. 2019a). However, at the resolution of our observations, the observed polarised emission is expected to be lower, at ∼30%. We imaged LOFAR observations of the bridge region at 144 MHz at angular resolutions of 6″, 20″, and 107″. Total intensity images at 6″ and 20″ show only emission from compact sources, whereas the bridge emission is clearly evident in images with 107″ angular resolution, essentially confirming results from Govoni et al. (2019) and more recently from de Jong et al. (2022). In order to search for polarised emission from the bridge, we performed an RM synthesis analysis on the 107″ resolution images. We did not reveal any significant polarised emission from the bridge, but only from Galactic foreground and instrumental leakage. We therefore used our observations to set an upper limit on the bridge polarised emission.
We assumed the model used by Govoni et al. (2019) to justify the bridge emission and the simulation of Wittor et al. (2019a) to compute the expected polarised fraction. Accounting also for the beam geometric depolarisation, we found that the polarised emission expected from the simulation should have been easily detectable in our observations, suggesting the presence of a depolarisation mechanism. Under the assumption that the shock width is negligible with respect to the bridge extension, depolarisation is due to the remaining portion of the bridge that acts as an external Faraday screen. We derived a lower limit on the dispersion of the external Faraday screen of σϕ ≥ 0.10 rad m−2 (≥0.09 rad m−2, if the bridge polarised emission falls near the FDF Galactic peak), which in turn becomes a lower limit on the mean magnetic field of the bridge 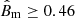 nG (≥0.41 nG). We stress that this lower limit is valid for the bridge medium that acts as an external Faraday screen. This is not a limit on the radio-emitting regions (shock regions). However, for such emitting regions, we would expect: (i) a higher (0.2–0.4 μG) magnetic field strength, which if taken into account would only increase the average B value; and (ii) shock emitting regions, which in our approximation are small regions, and so our lower limit is still representative of the majority of the intercluster medium. Therefore, in the framework of an external Faraday screen originated by the bridge, we are, again, in a conservative condition.
nG (≥0.41 nG). We stress that this lower limit is valid for the bridge medium that acts as an external Faraday screen. This is not a limit on the radio-emitting regions (shock regions). However, for such emitting regions, we would expect: (i) a higher (0.2–0.4 μG) magnetic field strength, which if taken into account would only increase the average B value; and (ii) shock emitting regions, which in our approximation are small regions, and so our lower limit is still representative of the majority of the intercluster medium. Therefore, in the framework of an external Faraday screen originated by the bridge, we are, again, in a conservative condition.
Assuming a bridge mean density4 of ∼3.4 × 10−4 cm−3 (Fujita et al. 2008), the corresponding overdensity is δ ∼ 300. Figure 13 shows predictions for the magnetic field intensity as a function of the gas overdensity (Vazza et al. 2021). Almost all models predict a magnetic field intensity of greater than ∼1 nG at an overdensity of ∼300, which is largely consistent with our constraints.
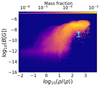 |
Fig. 13. Phase diagram of the statistical distribution of the magnetic field strength as a function of gas overdensity (|B|−ρ/⟨ρ⟩) from simulations (Vazza et al. 2021). The cyan and the white arrows are the 0.41 and 0.46 nG lower limits on the magnetic field from this work. |
The max-scale set by our data would prevent us from detecting Faraday-thick sources. However, this is not an issue because we assume a Faraday-thin bridge emission (Sect. 4.2).
We notice that the recent study of Hincks et al. (2022) on the A399–A401 cluster pair through the SZ effect, reported a much lower density estimate for the bridge region ((0.88 ± 0.24)×10−4 cm−3). Such a low density value is the result of a larger estimate of the bridge length, which, following the authors, is observed at a small angle with respect to the line of sight. Despite our technique could, in principle, be applied also to such a scenario, we could not include it in our study because the used simulation refers to an epoch at which the merging clusters are separated by ∼3.5 Mpc.
Acknowledgments
We thank the referee Steve Spangler for the valuable comments and suggestions on our work. LOFAR (van Haarlem et al. 2013) is the Low Frequency Array designed and constructed by ASTRON. It has observing, data processing, and data storage facilities in several countries, which are owned by various parties (each with their own funding sources), and thatare collectively operated by the ILT foundation under a joint scientific policy. The ILT resources have benefited from the following recent major funding sources: CNRS-INSU, Observatoire de Paris and Université d’Orléans, France; BMBF, MIWF-NRW, MPG, Germany; Science Foundation Ireland (SFI), Department of Business, Enterprise and Innovation (DBEI), Ireland; NWO, The Netherlands; The Science and Technology Facilities Council, UK; Ministry of Science and Higher Education, Poland; The Istituto Nazionale di Astrofisica (INAF), Italy. This research made use of the Dutch national e-infrastructure with support of the SURF Cooperative (e-infra 180169) and the LOFAR e-infra group. The Jülich LOFAR Long Term Archive and the German LOFAR network are both coordinated and operated by the Jülich Supercomputing Centre (JSC), and computing resources on the supercomputer JUWELS at JSC were provided by the Gauss Centre for Supercomputing e.V. (grant CHTB00) through the John von Neumann Institute for Computing (NIC). This research made use of the University of Hertfordshirehigh-performance computing facility and the LOFAR-UK computing facility located at the University of Hertfordshire and supported by STFC [ST/P000096/1], and of the Italian LOFAR-IT computing infrastructure supported and operated by INAF, and by the Physics Department of Turin university (under anagreement with Consorzio Interuniversitario per la Fisica Spaziale) at the C3S Supercomputing Centre, Italy. Annalisa Bonafede acknowledges support from the ERC-Stg DRANOEL n.714245 and from the MIUR grant FARE “SMS”. D.W. is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 441694982. The authors gratefully acknowledge the Gauss Centre for Supercomputing e.V. (https://www.gauss-centre.eu) for supporting this project by providing computing time through the John von Neumann Institute for Computing (NIC) on the GCS Supercomputer JUWELS at Jülich Supercomputing Centre (JSC), under project no. hhh44. F.V. acknowledges financial support from the Horizon 2020 program under the ERC Starting Grant MAGCOW, no. 714196. Our simulations were run on the Piz Daint supercomputer at CSCS-ETH (Lugano), on the JUWELS cluster at Juelich Superc omputing Centre (JSC), under projects “radgalicm” and on the Marconi100 clusters at CINECA (Bologna), under project INA21. A. Botteon acknowledges support from the ERC-StG DRANOEL n. 714245. R.J.v.W. acknowledges support from the VIDI research programme with project number 639.042.729, which is financed by the Netherlands Organisation for Scientific Research (NWO). V.V. acknowledges support from INAF mainstream project “Galaxy Clusters Science with LOFAR” 1.05.01.86.05. Data used in this work are available upon reasonable request to the authors.
References
- Akamatsu, H., Fujita, Y., Akahori, T., et al. 2017, A&A, 606, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernardi, G., Greenhill, L. J., Mitchell, D. A., et al. 2013, ApJ, 771, 105 [Google Scholar]
- Bonafede, A., Cassano, R., Brüggen, M., et al. 2017, MNRAS, 470, 3465 [Google Scholar]
- Bonjean, V., Aghanim, N., Salomé, P., Douspis, M., & Beelen, A. 2018, A&A, 609, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Botteon, A., van Weeren, R. J., Brunetti, G., et al. 2020, MNRAS, 499, L11 [Google Scholar]
- Botteon, A., van Weeren, R. J., Brunetti, G., et al. 2022, Sci. Adv., 8, eabq7623 [NASA ADS] [CrossRef] [Google Scholar]
- Brentjens, M. A., & de Bruyn, A. G. 2005, A&A, 441, 1217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, S., Vernstrom, T., Carretti, E., et al. 2017, MNRAS, 468, 4246 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, G., & Jones, T. W. 2014, Int. J. Mod. Phys. D, 23, 1430007 [Google Scholar]
- Brunetti, G., & Vazza, F. 2020, Phys. Rev. Lett., 124, 051101 [Google Scholar]
- Burn, B. J. 1966, MNRAS, 133, 67 [Google Scholar]
- Carretti, E., Vacca, V., O’Sullivan, S. P., et al. 2022, MNRAS, 512, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Carretti, E., O’Sullivan, S. P., Vacca, V., et al. 2023, MNRAS, 518, 2273 [Google Scholar]
- Cuciti, V., de Gasperin, F., Brüggen, M., et al. 2022, Nature, 609, 911 [NASA ADS] [CrossRef] [Google Scholar]
- de Gasperin, F., Dijkema, T. J., Drabent, A., et al. 2019, A&A, 622, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Jong, J. M. G. H. J., van Weeren, R. J., Botteon, A., et al. 2022, A&A, 668, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domínguez-Fernández, P., Vazza, F., Brüggen, M., & Brunetti, G. 2019, MNRAS, 486, 623 [Google Scholar]
- Donnert, J., Vazza, F., Brüggen, M., & ZuHone, J. 2018, Space Sci. Rev., 214, 122 [Google Scholar]
- Erceg, A., Jelić, V., Haverkorn, M., et al. 2022, A&A, 663, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fujita, Y., Koyama, K., Tsuru, T., & Matsumoto, H. 1996, PASJ, 48, 191 [NASA ADS] [Google Scholar]
- Fujita, Y., Tawa, N., Hayashida, K., et al. 2008, PASJ, 60, S343 [Google Scholar]
- Govoni, F., & Feretti, L. 2004, Int. Mod. Phys. D, 13, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Govoni, F., Orrù, E., Bonafede, A., et al. 2019, Science, 364, 981 [Google Scholar]
- Hincks, A. D., Radiconi, F., Romero, C., et al. 2022, MNRAS, 510, 3335 [NASA ADS] [CrossRef] [Google Scholar]
- Hoang, D. N., Brüggen, M., Zhang, X., et al. 2023, MNRAS, 523, 6320 [CrossRef] [Google Scholar]
- Hodgson, T., Vazza, F., Johnston-Hollitt, M., & McKinley, B. 2022, PASA, 39, e033 [NASA ADS] [CrossRef] [Google Scholar]
- Locatelli, N., Vazza, F., Bonafede, A., et al. 2021, A&A, 652, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mohan, N., & Rafferty, D. 2015, Astrophysics Source Code Library [record ascl:1502.007] [Google Scholar]
- Murgia, M., Govoni, F., Feretti, L., & Giovannini, G. 2010, A&A, 509, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Natwariya, P. K. 2021, Eur. Phys. J. C, 81, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Neronov, A., & Vovk, I. 2010, Science, 328, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Nunhokee, C. D., Bernardi, G., Manti, S., et al. 2023, MNRAS, 522, 4421 [CrossRef] [Google Scholar]
- Offringa, A. R., & Smirnov, O. 2017, MNRAS, 471, 301 [Google Scholar]
- Offringa, A. R., McKinley, B., Hurley-Walker, N., et al. 2014, MNRAS, 444, 606 [Google Scholar]
- O’Sullivan, S. P., Brown, S., Robishaw, T., et al. 2012, MNRAS, 421, 3300 [CrossRef] [Google Scholar]
- O’Sullivan, S. P., Machalski, J., Van Eck, C. L., et al. 2019, A&A, 622, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Sullivan, S. P., Brüggen, M., Vazza, F., et al. 2020, MNRAS, 495, 2607 [Google Scholar]
- O’Sullivan, S. P., Shimwell, T. W., Hardcastle, M. J., et al. 2023, MNRAS, 519, 5723 [CrossRef] [Google Scholar]
- Paoletti, D., & Finelli, F. 2019, JCAP, 2019, 028 [CrossRef] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. VIII. 2013, A&A, 550, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pomakov, V. P., O’Sullivan, S. P., Brüggen, M., et al. 2022, MNRAS, 515, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Pshirkov, M. S., Tinyakov, P. G., & Urban, F. R. 2016, Phys. Rev. Lett., 116, 191302a [NASA ADS] [CrossRef] [Google Scholar]
- Purcell, C. R., Van Eck, C. L., West, J., Sun, X. H., & Gaensler, B. M. 2020, Astrophysics Source Code Library [record ascl:2005.003] [Google Scholar]
- Radiconi, F., Vacca, V., Battistelli, E., et al. 2022, MNRAS, 517, 5232 [NASA ADS] [CrossRef] [Google Scholar]
- Rajpurohit, K., Brunetti, G., Bonafede, A., et al. 2021a, A&A, 646, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rajpurohit, K., Vazza, F., van Weeren, R. J., et al. 2021b, A&A, 654, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sakelliou, I., & Ponman, T. J. 2004, MNRAS, 351, 1439 [NASA ADS] [CrossRef] [Google Scholar]
- Shimwell, T. W., Röttgering, H. J. A., Best, P. N., et al. 2017, A&A, 598, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shimwell, T. W., Tasse, C., Hardcastle, M. J., et al. 2019, A&A, 622, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shimwell, T. W., Hardcastle, M. J., Tasse, C., et al. 2022, A&A, 659, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sokoloff, D. D., Bykov, A. A., Shukurov, A., et al. 1998, MNRAS, 299, 189 [Google Scholar]
- Subramanian, K. 2016, Rep. Prog. Phys., 79, 076901 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1969, Nature, 223, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Tribble, P. C. 1991, MNRAS, 250, 726 [NASA ADS] [CrossRef] [Google Scholar]
- Van Eck, C. L., Haverkorn, M., Alves, M. I. R., et al. 2019, A&A, 623, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Weeren, R. J., de Gasperin, F., Akamatsu, H., et al. 2019, Space Sci. Rev., 215, 16 [Google Scholar]
- van Weeren, R. J., Shimwell, T. W., Botteon, A., et al. 2021, A&A, 651, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazza, F., Brunetti, G., & Gheller, C. 2009, MNRAS, 395, 1333 [CrossRef] [Google Scholar]
- Vazza, F., Brüggen, M., Gheller, C., et al. 2017, CQG, 34, 234001 [NASA ADS] [CrossRef] [Google Scholar]
- Vazza, F., Brunetti, G., Brüggen, M., & Bonafede, A. 2018, MNRAS, 474, 1672 [NASA ADS] [CrossRef] [Google Scholar]
- Vazza, F., Locatelli, N., Rajpurohit, K., et al. 2021, Galaxies, 9, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Venturi, T., Giacintucci, S., Dallacasa, D., et al. 2008, A&A, 484, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venturi, T., Giacintucci, S., Merluzzi, P., et al. 2022, A&A, 660, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vernstrom, T., Gaensler, B. M., Brown, S., Lenc, E., & Norris, R. P. 2017, MNRAS, 467, 4914 [NASA ADS] [CrossRef] [Google Scholar]
- Vernstrom, T., Gaensler, B. M., Vacca, V., et al. 2018, MNRAS, 475, 1736 [NASA ADS] [CrossRef] [Google Scholar]
- Vernstrom, T., Gaensler, B. M., Rudnick, L., & Andernach, H. 2019, ApJ, 878, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Vernstrom, T., Heald, G., Vazza, F., et al. 2021, MNRAS, 505, 4178 [NASA ADS] [CrossRef] [Google Scholar]
- Vernstrom, T., West, J., Vazza, F., et al. 2023, Sci. Adv., 9, eade7233 [NASA ADS] [CrossRef] [Google Scholar]
- Widrow, L. M., Ryu, D., Schleicher, D. R. G., et al. 2012, Space. Sci. Rev., 166, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Wittor, D., Hoeft, M., Vazza, F., Brüggen, M., & Domínguez-Fernández, P. 2019a, MNRAS, 490, 3987 [Google Scholar]
- Wittor, D., Domínguez-Fernández, P., Vazza, F., & Brüggen, M. 2019b, ArXiv e-prints [arXiv:1909.10792] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Image of the A399–A401 pair at 144 MHz. The 107″ × 107″ restoring beam is shown in white in the bottom left corner. Black contours are drawn at 4, 20, 40, 80, 160, and 320 × RMS, where the RMS is 620 μJy beam−1. |
| In the text | |
 |
Fig. 2. Bridge emission profile after masking of unrelated sources. Upper panel: compact source-subtracted image (see Sect. 4 and Fig. 6) with non-bridge sources masked out (white ellipses). A white line grid is used to measure the bridge brightness profile. The grid is tilted by 25° and has the same reference point (centre) as Govoni et al. (2019). The lines are separated by 144 kpc (one beam width) and their length is 3 Mpc. Lower panel: surface brightness profile extracted by measuring the average surface brightness in each slice. |
| In the text | |
 |
Fig. 3. Faraday depth amplitude averaged over all the lines of sight within the bridge region at 107″ resolution. Two peaks can be seen, which are due to the Galactic foreground medium and the instrumental leakage, respectively. |
| In the text | |
 |
Fig. 4. Slice of the FDF cube at ϕ ∼ 7.5 rad m−2 showing the Galactic polarised emission detected in the field. Total intensity is overlaid with contours at 4, 20, 40, and 80 × RMS taken from Fig. 1. |
| In the text | |
 |
Fig. 5. Zoom onto the bridge field. Highlighted are the sources subtracted in order to retrieve the bridge emission model. Contours are drawn at 5 × RMS, where RMS ∼ 350 μJy beam−1. The image has a 20″ resolution. |
| In the text | |
 |
Fig. 6. Image of the A399–A401 pair at 144 MHz once the sources within and around the bridge are subtracted (Fig. 5). The region chosen to obtain the bridge emission model is highlighted in yellow. The 107″ × 107″ restoring beam is shown in white in the bottom left corner. The RMS of the image is ∼650 μJy beam−1, with contours at 4, 10, 40, and 80 × RMS. |
| In the text | |
 |
Fig. 7. Slices of the Faraday spectrum cube at ϕ = 20 rad m−2 as a function of Faraday dispersion σϕ, obtained from the injection of the bridge polarised emission model in the data; see text for details. It is evident that the bridge polarised emission decreases as the Faraday dispersion increases until it completely disappears when σϕ = 0.18 rad m−2. The top left panel is the case where no depolarisation occurs, but only the rotation of the injected signal. |
| In the text | |
 |
Fig. 8. Examples of FDFs of the bridge region as a function of Faraday dispersion σϕ after injection of the depolarisation model into the data; see text for details. The peak at 20 rad m−2 decreases until it completely disappears below the nose for the σϕ = 0.18 rad m−2 model. |
| In the text | |
 |
Fig. 9. Normalised cumulative distribution F(Pexc) as a function of σϕ, with the polarised emission from the bridge injected at ϕ = 20 rad m−2. The red line indicates the threshold value of σϕ at which the cumulative distribution function is 95%. |
| In the text | |
 |
Fig. 10. Central slice of the cube density from simulations. Moving towards the density cube, the average density of the medium initially increases, indicating the presence of the cluster pair, then starts to decrease until reaching zero in the last slice, showing the ending regions of the cluster pair. We therefore selected the central slice of the cube as the best indicator of the density distribution. The density contours are at 1, 1.24, 2.61, 10.3, and 53.5 × 10−28 g cm−3. The region selected as the bridge region in the simulation is highlighted in red. Every pixel is ∼16 kpc long. |
| In the text | |
 |
Fig. 11. Faraday-depth map obtained using the cluster simulation (Wittor et al. 2019a; see text for details). The contours are from the density field in Fig. 10, and the selected bridge region is highlighted in red. Every pixel is ∼16 kpc in length. |
| In the text | |
 |
Fig. 12. Distribution of the density-weighted average magnetic field intensity of each layer of the simulation cube. The average value of all the layers is indicated by the orange line. |
| In the text | |
 |
Fig. 13. Phase diagram of the statistical distribution of the magnetic field strength as a function of gas overdensity (|B|−ρ/⟨ρ⟩) from simulations (Vazza et al. 2021). The cyan and the white arrows are the 0.41 and 0.46 nG lower limits on the magnetic field from this work. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



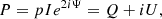
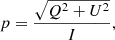
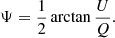
![$$ \begin{aligned} \phi \simeq 0.81 \int _{\rm {source}}^\mathrm{{telescope}} n_{\rm e} \, \boldsymbol{B} \cdot \mathrm{d}\boldsymbol{l} \left[ \frac{\text{rad}}{\text{ m}^2} \right], \end{aligned} $$](/articles/aa/full_html/2023/11/aa46303-23/aa46303-23-eq4.gif)
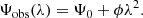
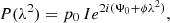
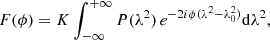
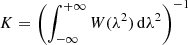
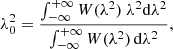
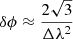
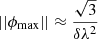
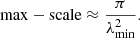
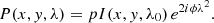
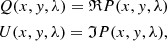
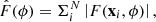
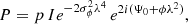
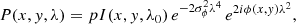
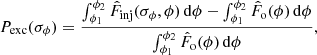
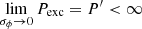
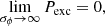
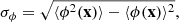
![$$ \begin{aligned} \sigma _\phi = 0.81 \left[\left\langle \left( \int _L n_{\rm e}(\mathbf{x}) \, \boldsymbol{B}(\mathbf{x}) \cdot \mathrm{d} \mathbf{l} \right)^2 \right\rangle - \left( \left\langle \int _L n_{\rm e}(\mathbf{x}) \, \boldsymbol{B}(\mathbf{x}) \cdot \mathrm{d} \mathbf{l} \right\rangle \right)^2 \right] ^{1/2} ,\end{aligned} $$](/articles/aa/full_html/2023/11/aa46303-23/aa46303-23-eq27.gif)
![$$ \begin{aligned}&\sigma _{\phi ,\mathrm m} = 0.81 \left[ \left\langle \left( \int _L n_{\rm e,s}(\mathbf{x}) \, \alpha \boldsymbol{B}_{\rm s} (\mathbf{x}) \cdot \mathrm{d} \mathbf{l} \right)^2 \right\rangle - \right. \nonumber \\&\qquad \quad \left. \left( \left\langle \int _L n_{\rm e,s} (\mathbf{x}) \, \alpha \boldsymbol{B}_{\rm s} (\mathbf{x}) \cdot \mathrm{d} \mathbf{l} \right\rangle \right)^2 \right]^{1/2} \nonumber \\&\qquad = \alpha \left( 0.81 \left[\left\langle \left( \int _L n_{\rm e,s}(\mathbf{x}) \, \alpha \boldsymbol{B}_{\rm s} (\mathbf{x}) \cdot \mathrm{d} \mathbf{l} \right)^2 \right\rangle - \right. \right. \nonumber \\&\qquad \quad \left. \left. \left( \left\langle \int _L n_{\rm e,s} (\mathbf{x}) \, \alpha \boldsymbol{B}_{\rm s} (\mathbf{x}) \cdot \mathrm{d} \mathbf{l} \right\rangle \right)^2 \right]^{1/2} \right) \nonumber \\&\qquad = \alpha \, \sigma _{\rm \phi ,s}, \end{aligned} $$](/articles/aa/full_html/2023/11/aa46303-23/aa46303-23-eq28.gif)